- Преподавателю
- Математика
- Методы решения показательных уравнений
Методы решения показательных уравнений
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | Филатова А.В. |
| Дата | 15.10.2015 |
| Формат | doc |
| Изображения | Есть |
Содержание
-
Методы решения показательных уравнений
-
Примеры решения заданий ЕГЭ
Задания на решение показательных уравнений могут
встретиться в любой группе заданий ЕГЭ. В заданиях группы В обычно предлагается непосредственно решить простейшие показательные уравнения или воспользоваться решением показательного уравнения для исследования некоторой функции. В третьей группе можно встретить более сложные показательные уравнения, решение которых обычно является одним из этапов выполнения задания.
Теоретические сведения
Свойства степени положительного числа
Если а >0, b>0, r, s- Действительные числа, то:
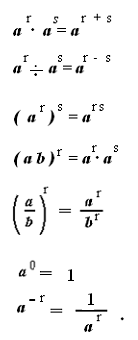
Методы решения показательных уравнений
При решении показательных уравнений необходимо помнить, что решение любого показательного уравнения сводится к решению "простейших" показательных уравнений, то есть уравнений вида:
1. af(x)=ag(x) или 2. af(x)=b.
Очевидно, что уравнение типа 2 сводится к уравнению типа 1 с помощью основного логарифмического тождества:
2! af(x)=  .
.
Уравнение (1) равносильно уравнению f(x)=g(x) при а > 0, а ¹ 1.
Этот переход называется потенцированием.
Способы решения показательных уравнений
1 тип: приведение к одному основанию левой и правой частей, применяя свойства степеней:
а)  .
.
Проверка:  ;
;  ;
;  =
= ;
;
б)  .
.
Решение:  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
(х+5)(х-3)=(х+25)(х-7); х2+5х-3х-15=х2+25х-7х-175; 16х=160; х=10.
Проверка: х=10.  ;
; 
 ;
;  ;
;
 ;
;  =
= - верно.
- верно.
Ответ: х=10;
в)  .
.
Решение:  ;
;  ;
;  ;
;  ;
;  ; x=1.
; x=1.
Проверка:  ;
;  ;
;  =
= - верно.
- верно.
Ответ: х=1;
г)  .
.
Решение:  ; ½3х-4½=4х-4,
; ½3х-4½=4х-4,
для х ³![]() имеем ½3х-4½=3х-4 и тогда уравнение запишем в виде
имеем ½3х-4½=3х-4 и тогда уравнение запишем в виде
3х-4=4х-4; -х=0; х=0; для х < имеем ½3х-4½=4-3х и уравнение запишем в виде 4-3х=4х-4; -7х=-8; х=
имеем ½3х-4½=4-3х и уравнение запишем в виде 4-3х=4х-4; -7х=-8; х= .
.
Проверка: х=0.  ;
;  ;
;  - не верно.
- не верно.
х= .
.  ;
;  ;
; 
 - верно.
- верно.
Ответ: х= .
.
2 тип - уравнения вида P(ax)=0, где P(y) - многочлен 2 или 3 степени, или уравнения, сводящиеся к ним. Такие уравнения решаются методом подстановки: ax=y, решаем уравнение P(y)=0, находим его корни yi и потом решаем простейшее уравнение ax= yi.
Пример: а)  .
.
Решение:  .
.
Обозначаем:  = y; 3y2-10y+3=0; D=25-9=16; y1=3; y2=
= y; 3y2-10y+3=0; D=25-9=16; y1=3; y2= .
.
Получаем: 1.  =3;
=3;  ;
;  ; х1=2.
; х1=2.
2. ![]() =
= ;
;  ;
;  ; х2=-2.
; х2=-2.
Проверка: 1.  ; 3×9-10×3+3=0 - верно.
; 3×9-10×3+3=0 - верно.
2.  ;
;  ;
;  - верно.
- верно.
Ответ: х=2; х=-2;
б)  .
.
Решение:  . Пусть 4х=y, y2+12y-64=0,
. Пусть 4х=y, y2+12y-64=0,
y1,2=-6± =-6±10,
=-6±10,
y1=4; y2=-16 (п.к.), т.к. 4х> 0, 4х=4 Þ х=1.
Проверка:  ; 16+3×16-64=0; 16+48-64=0 - верно.
; 16+3×16-64=0; 16+48-64=0 - верно.
Ответ: х=1;
в)  .
.
Решение:  ,
,  .
.
Пусть ![]() ,
,  ,
, ,
,
 ,
,
 ;
;  ;
;  ;
;  ;
;  ;
;  ; x=20.
; x=20.
Проверка: x=20.  ,
,  - верно.
- верно.
Ответ: х=20.
г)  .
.
Решение:  . Пусть
. Пусть  ; тогда уравнение запишем в виде
; тогда уравнение запишем в виде  ; y1,2=2
; y1,2=2 ; y1=3 и y2=1;
; y1=3 и y2=1;  или
или  ; x2-1=1;
; x2-1=1;
x2-1=0; x= ; x=±1.
; x=±1.
Проверка: x= ;
;  ; 9-12+3=0 - верно;
; 9-12+3=0 - верно;
х=±1;  ; 1-4+3=0 - верно.
; 1-4+3=0 - верно.
Ответ: x= ; х=±1.
; х=±1.
3 тип - метод вынесения общего множителя за скобки:
а)  .
.
Решение:  ;
;  ;
;  ;
;
 ;
;  ;
;  ; х=0.
; х=0.
Проверка:  ;
;  ; 0,992=0,992 - верно.
; 0,992=0,992 - верно.
Ответ: х=0;
б)  .
.
Решение:  ;
;  ;
;
 ;
;  ; х=0.
; х=0.
Проверка:  ; 49-1+2-2=48; 48=48 - верно.
; 49-1+2-2=48; 48=48 - верно.
Ответ: х=0;
в)  .
.
Решение:  ;
;  ;
;
 ;
;  ;
;  ;
;  ; х=2.
; х=2.
Проверка:  ;
;  ; 2-8+3=-3;
; 2-8+3=-3;
-3=-3 - верно.
Ответ: х=2.
4 тип - уравнения вида  решаются путем деления членов на
решаются путем деления членов на  или
или  .
.
а)  .
.
Решение: Делим на  .
.
 ;
;  .
.
Положим  , тогда имеем
, тогда имеем  ;
;  . Решаем это уравнение и получаем y1=1, y2=
. Решаем это уравнение и получаем y1=1, y2= . следовательно:
. следовательно:  ;
;  .
.
Проверка: х=0;  ; 3+2=5 - верно;
; 3+2=5 - верно;
х= ;
;  ; 12+18=30 - верно.
; 12+18=30 - верно.
Ответ: х=0; х= .
.
б)  .
.
Решение:  ;
;  . Разделим обе части данного уравнения на
. Разделим обе части данного уравнения на  .
.  ;
;  . Пусть
. Пусть  , тогда уравнение примет вид:
, тогда уравнение примет вид:  ;
;  ,
,  ;
;  ;
;  ;
;
 ;
;  .
.
Проверка:  ;
;  . Делим на
. Делим на ![]() .
.
 ;
;  ;
;  ;
;
6=6 - верно;
 ;
;  . Делим на
. Делим на ![]() ;
;
 ;
;  ; 6=6 - верно.
; 6=6 - верно.
Ответ:  ;
;  .
.
Решение типовых заданий
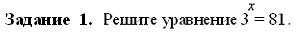
Решение. 1-й способ. Представим правую и левую части уравнения в виде
степени с основанием 3 и от равенства степеней с одинаковым основанием

2-й способ. Это простейшее показательное уравнение, значит
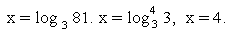

Задание 2. Решите уравнение 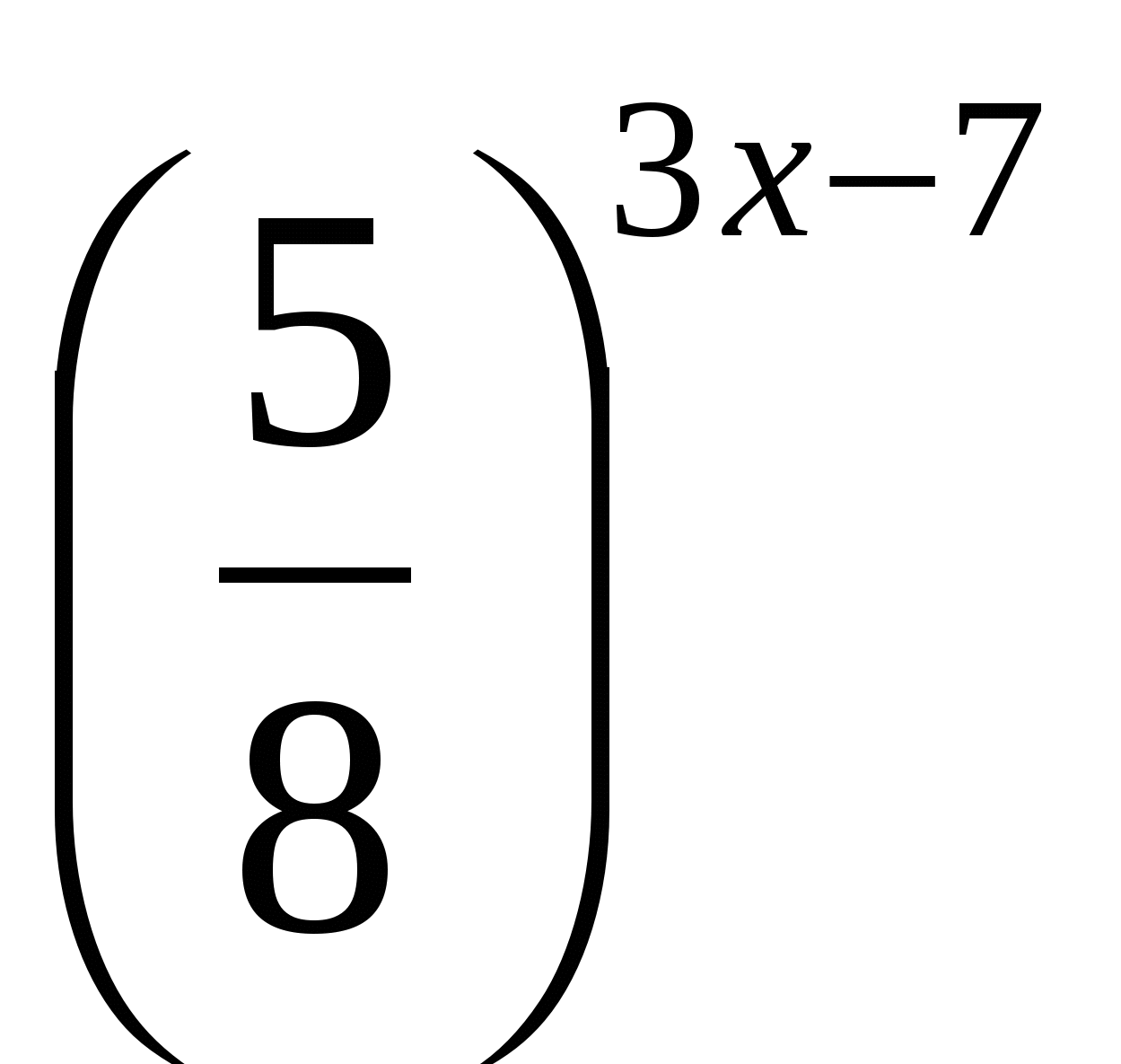 =
= 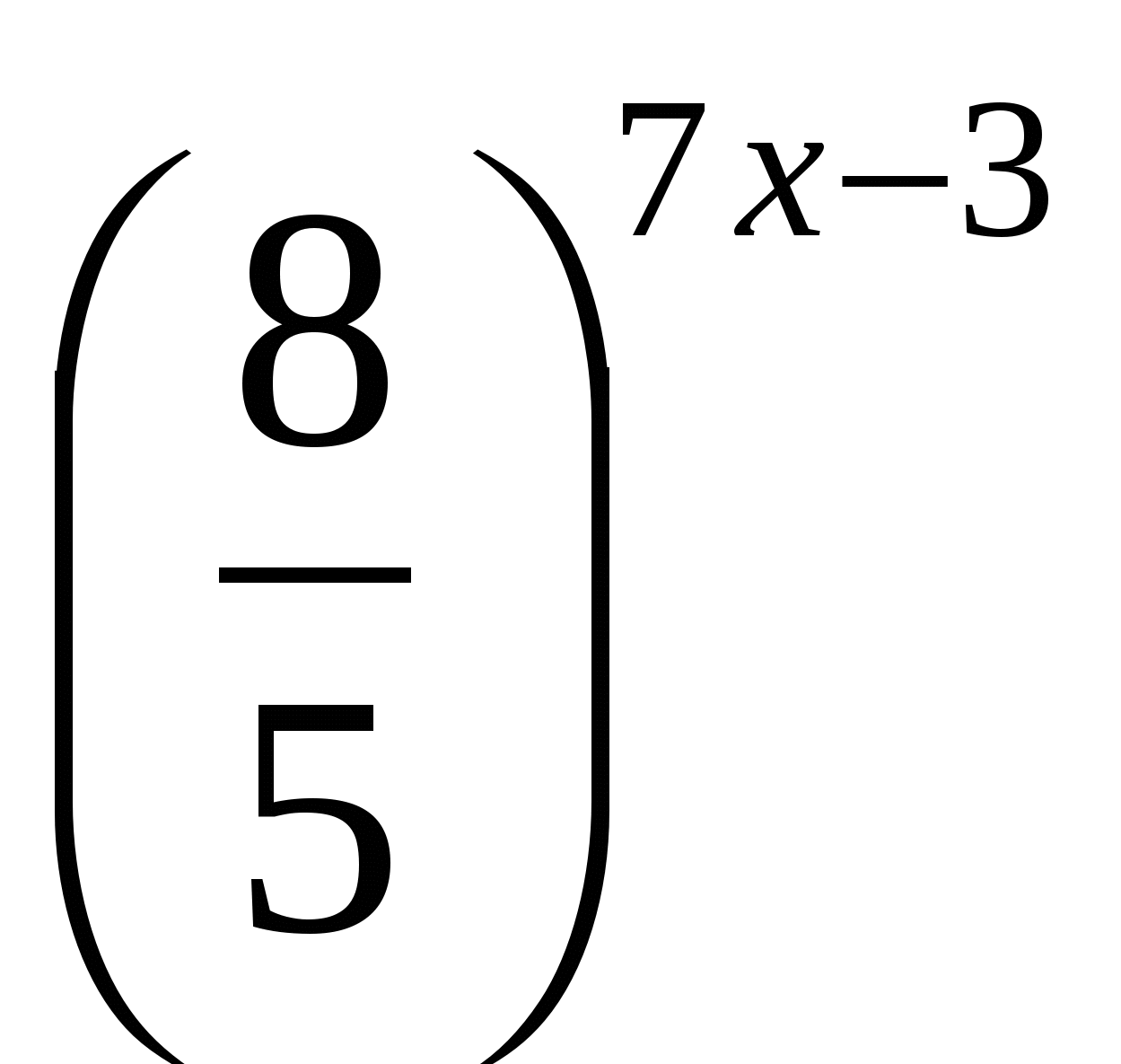
Решение. Преобразуем правую часть уравнения с помощью свойства (7).
Получим 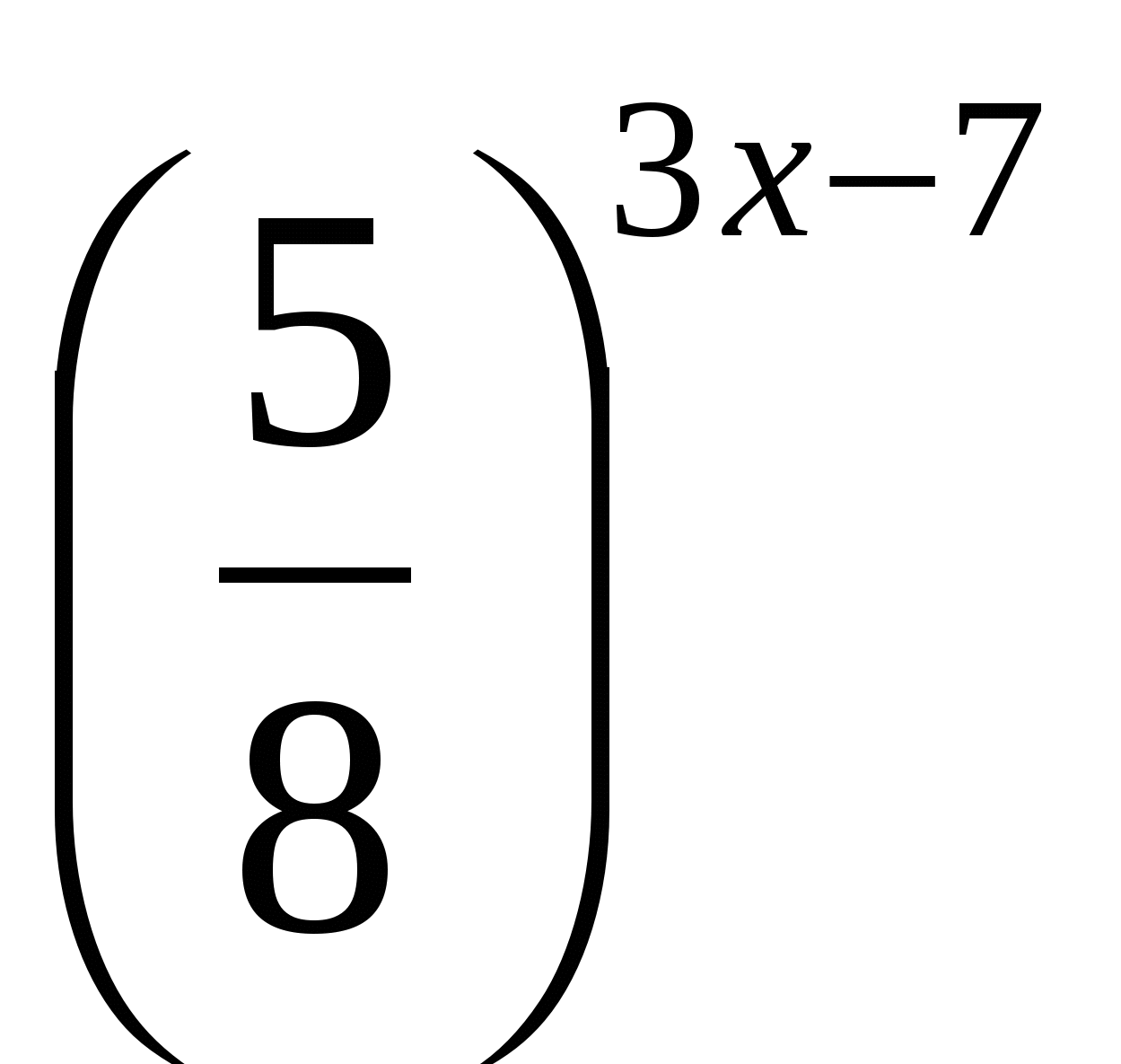 =
= 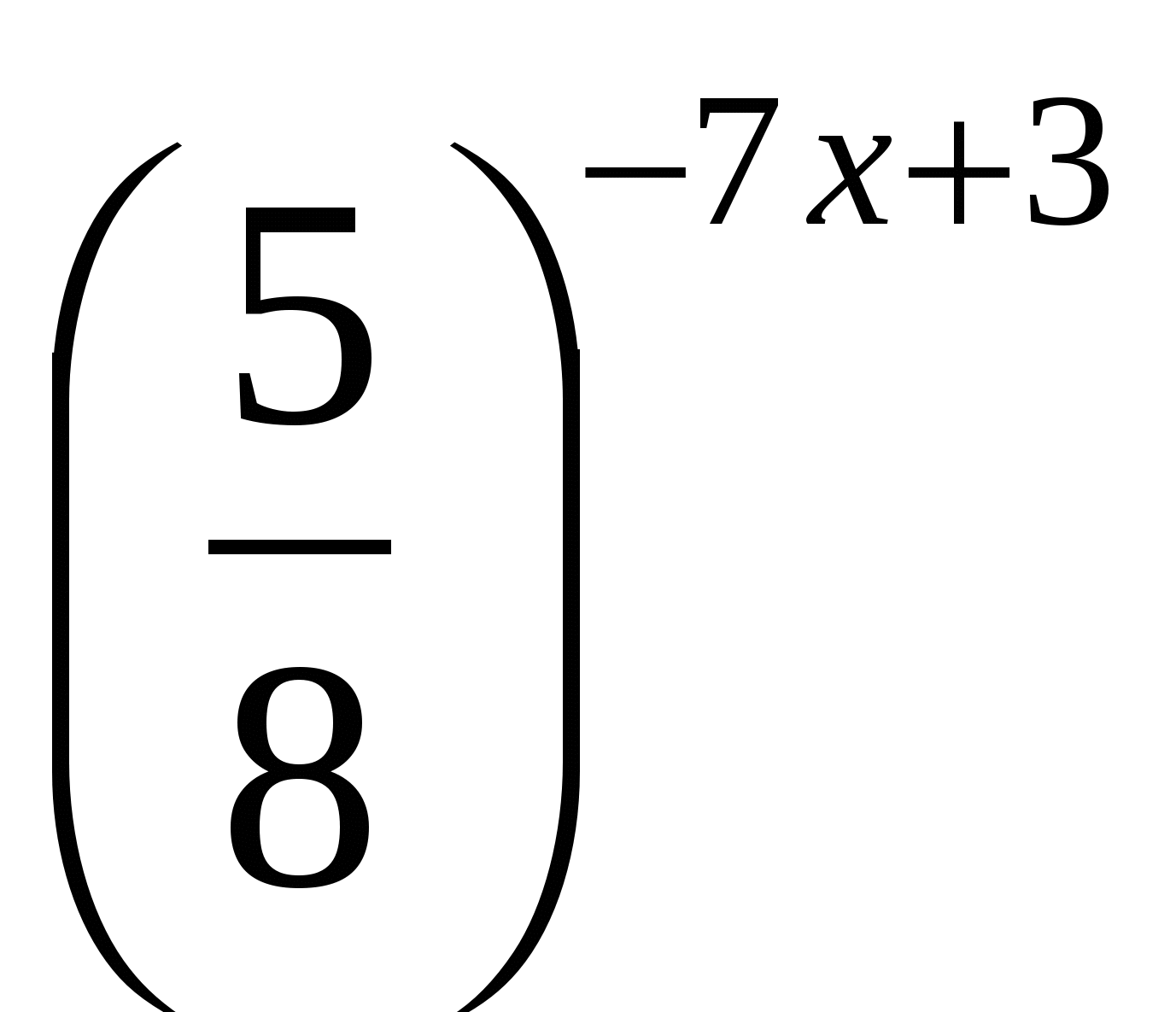 . Применяя теорему 1, получим уравнение, равносильное данному: 3x - 7 = -7x + 3, 10x = 10, x = 1.
. Применяя теорему 1, получим уравнение, равносильное данному: 3x - 7 = -7x + 3, 10x = 10, x = 1.
Ответ: 1.
Задание 3. Решите уравнение 0,04 ∙ 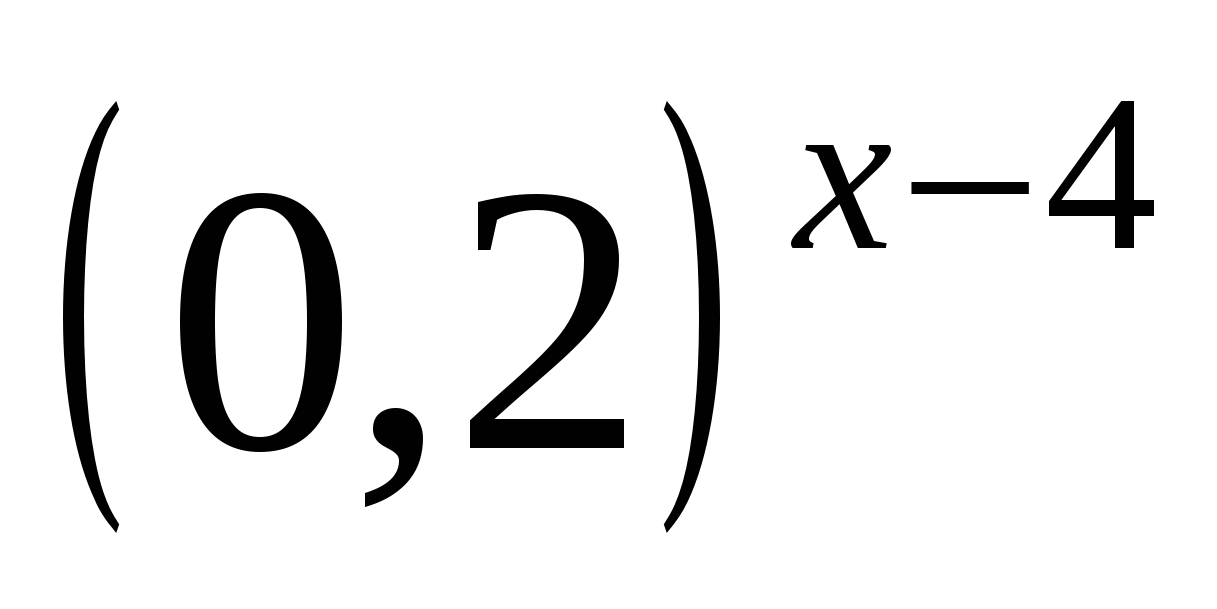 =
= 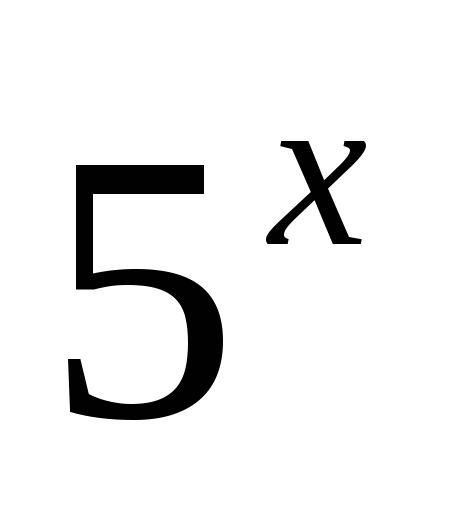 .
.
Решение. Преобразуем уравнение к виду 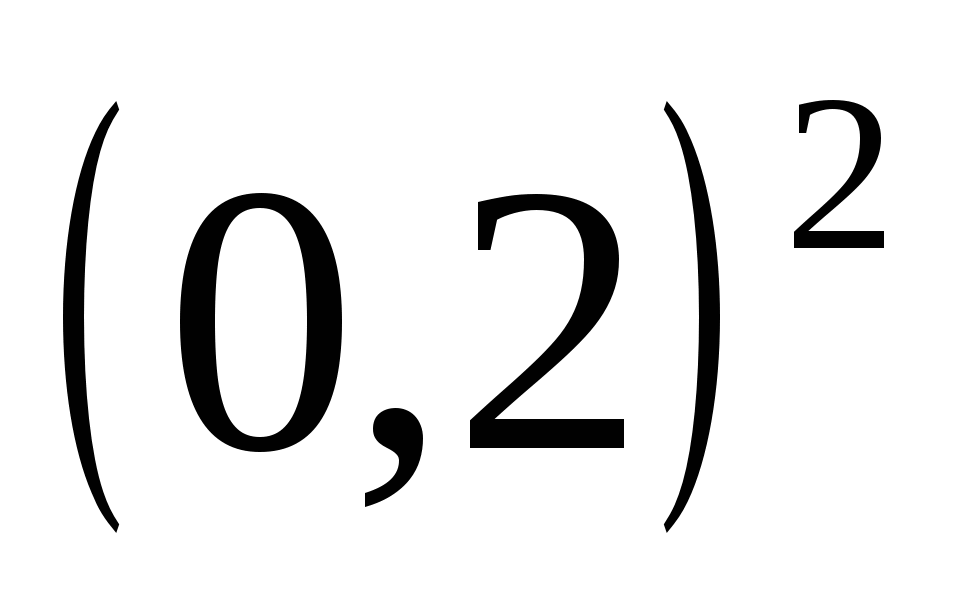 ∙
∙ 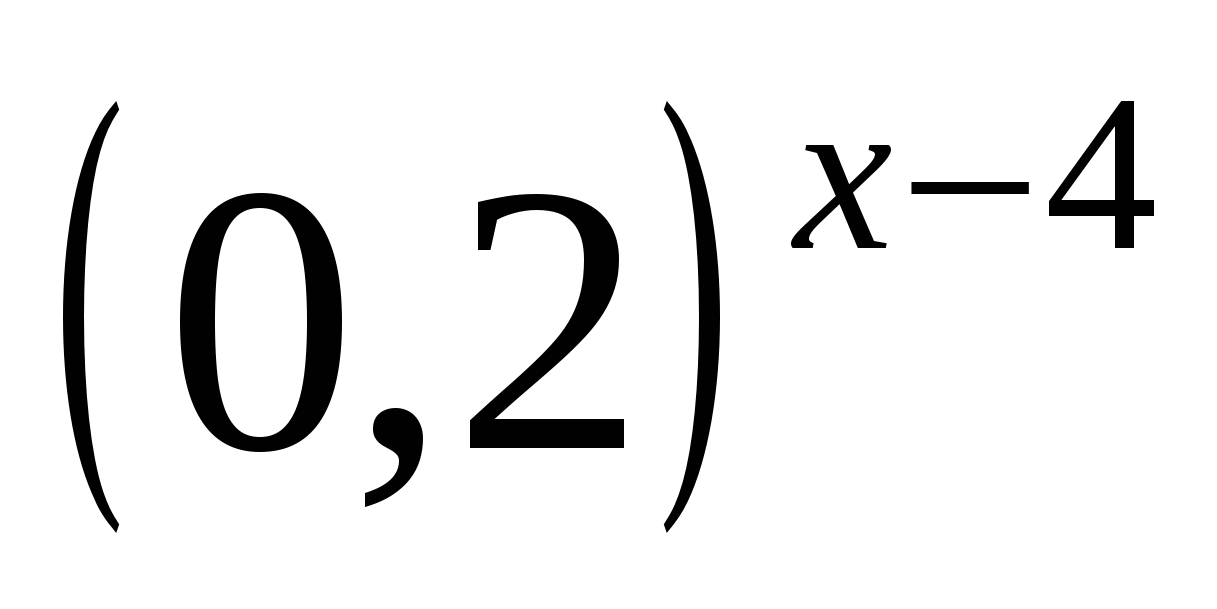 =
= 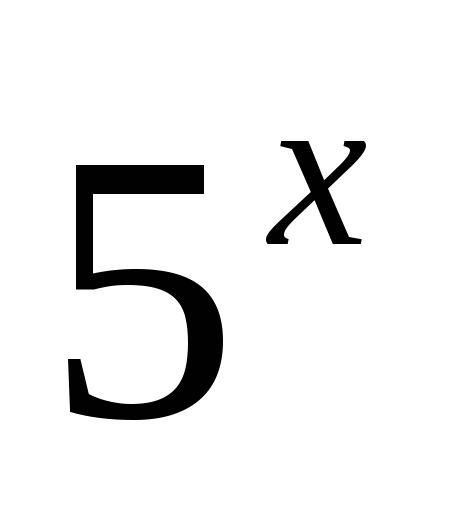 .
.
Применяя свойства (1) и (7) степени с одинаковым основанием, получаем
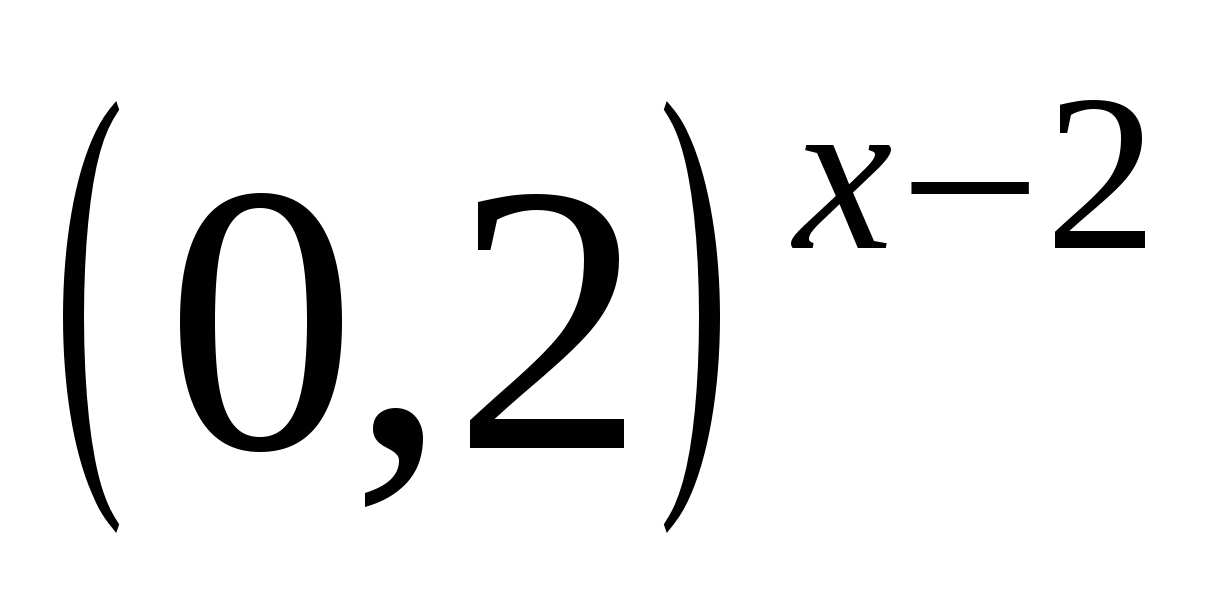 =
= 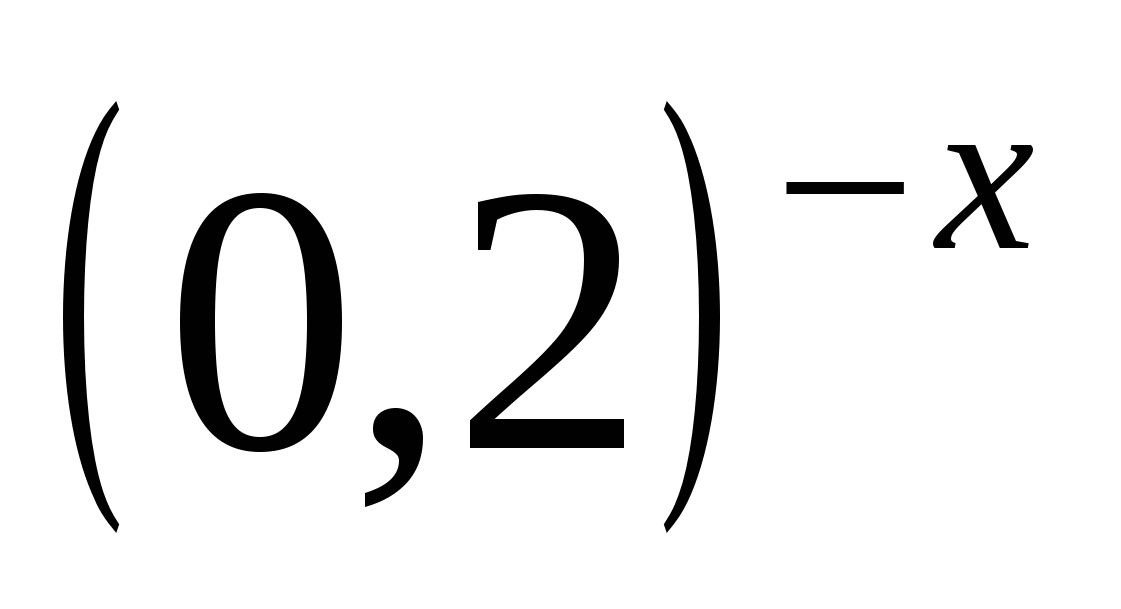 . Из равенства степеней с одинаковыми основаниями следует равенство показателей степеней: x - 2 = -x , 2x = 2, x = 1.
. Из равенства степеней с одинаковыми основаниями следует равенство показателей степеней: x - 2 = -x , 2x = 2, x = 1.
Ответ: 1.
Если в показательном уравнении несколько показательных выражений
с одинаковым основанием, то выражения можно преобразовать с помощью
свойств степени (1) и (2): 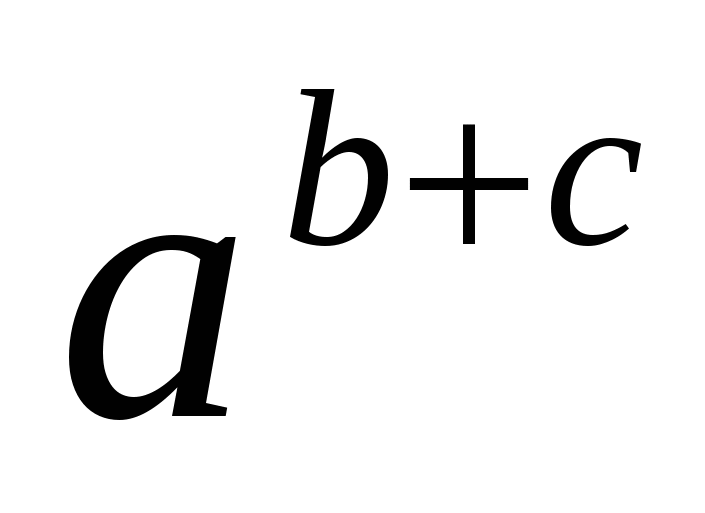 =
= 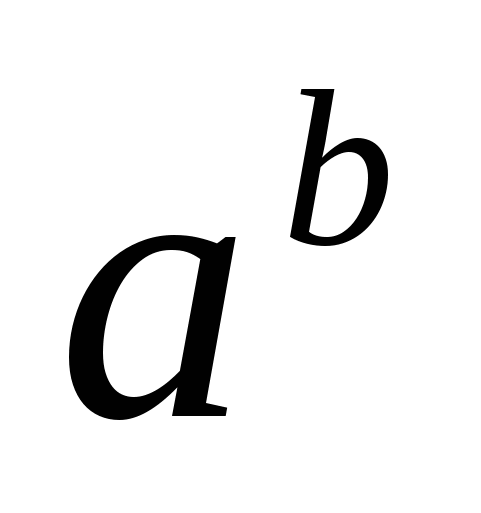 ∙
∙ 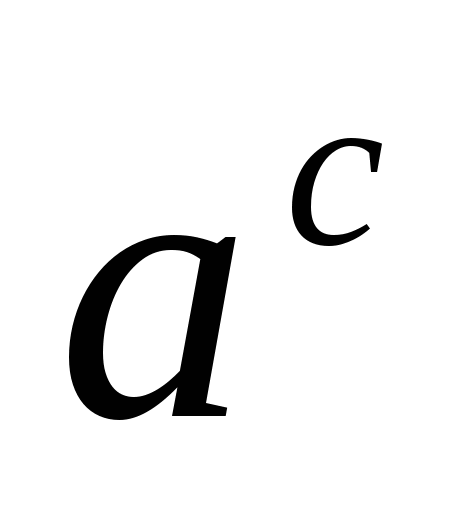 и
и 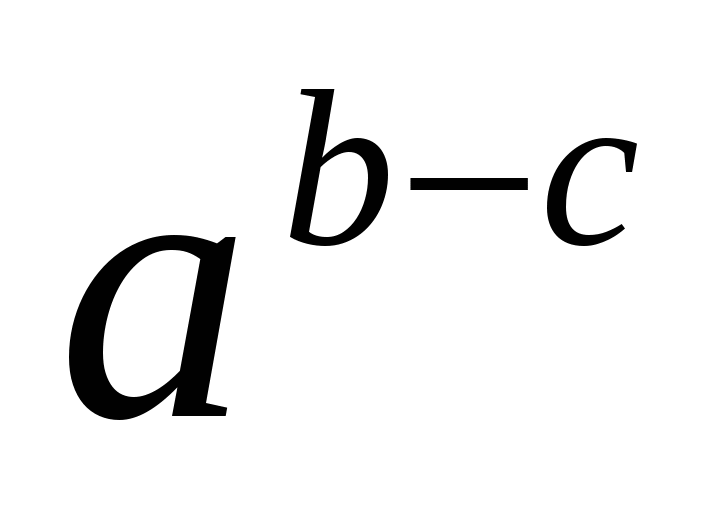 =
= 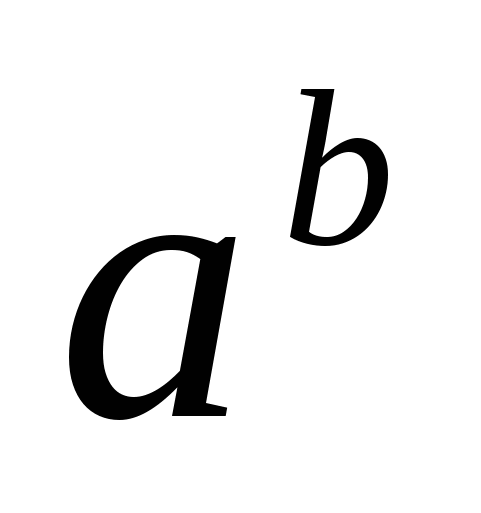 :
: 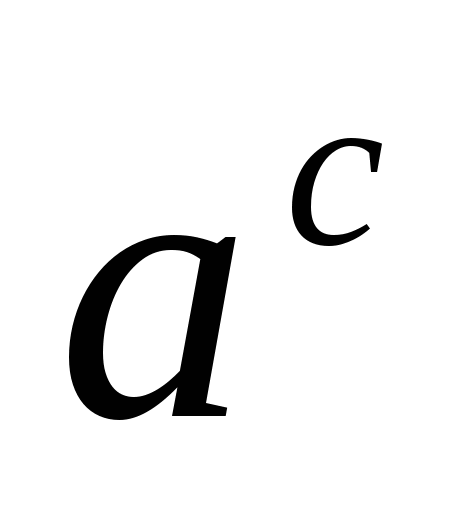 ( a > 0). После таких
( a > 0). После таких
преобразований уравнение обычно решается методом введения новой переменной или разложением на множители.
Задание 4. Решите уравнение 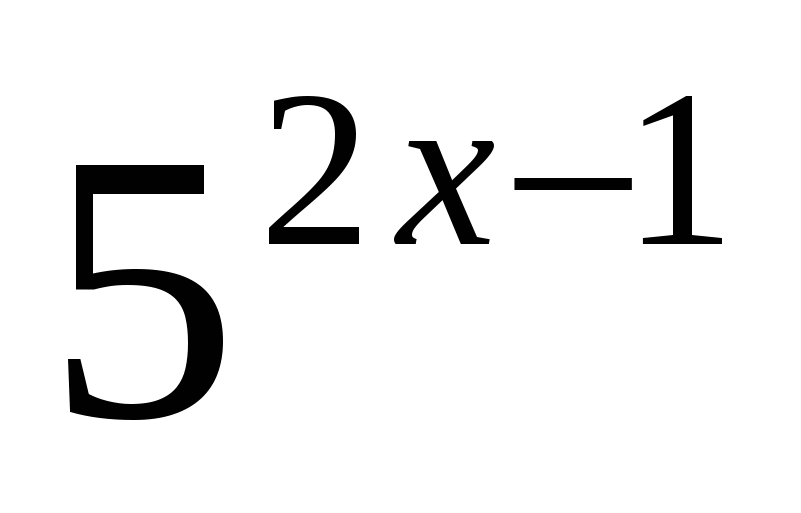 +
+ 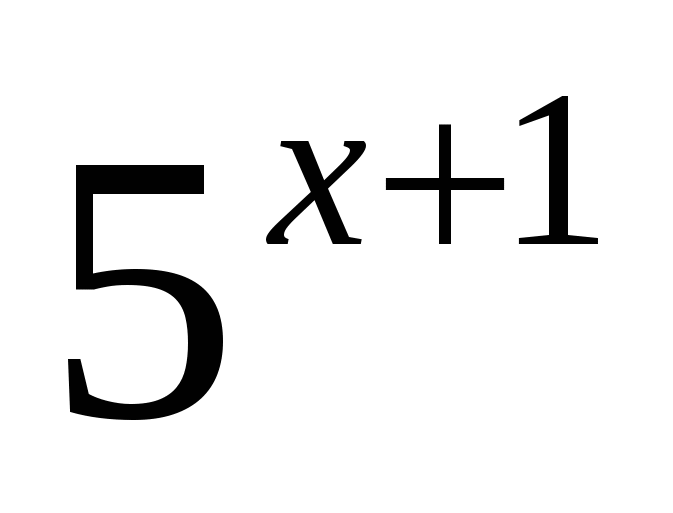 = 250.
= 250.
Решение. Преобразуем левую часть уравнения с помощью свойств степени (1) и (2):
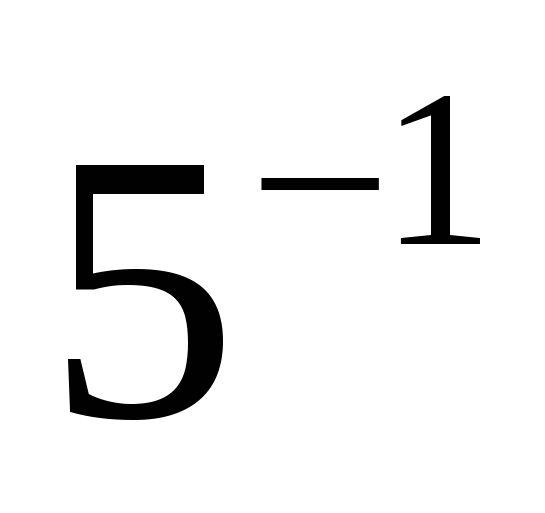 ∙
∙ 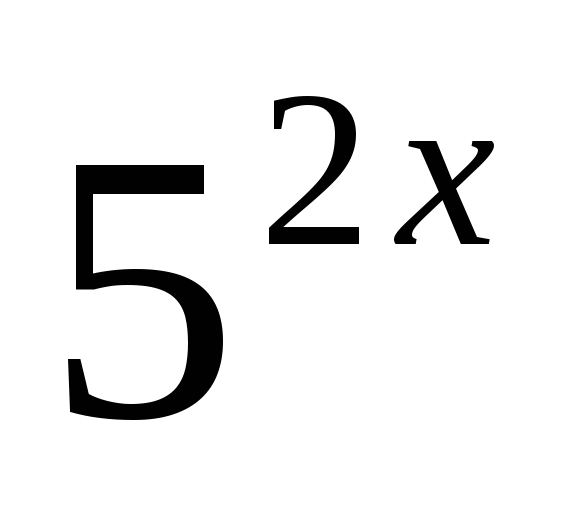 + 5 ∙
+ 5 ∙ 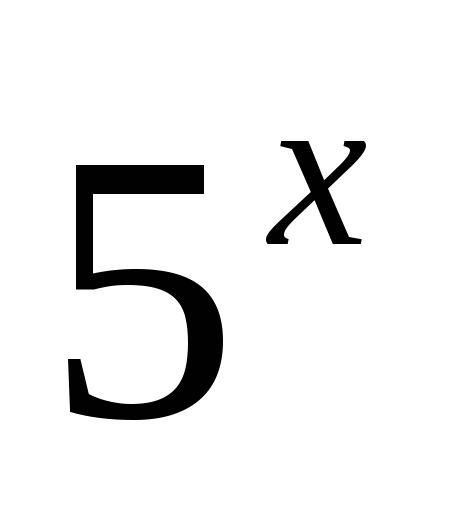 = 250,
= 250,
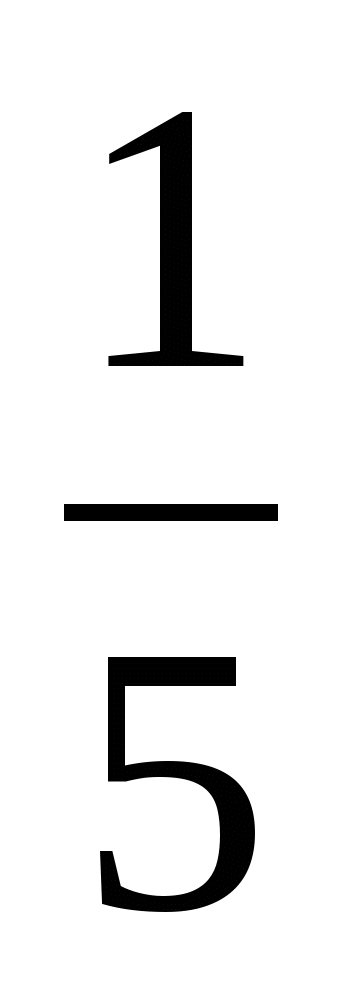 ∙
∙ 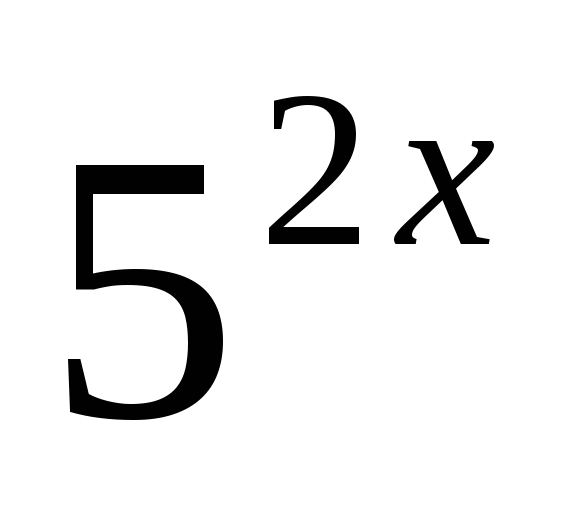 + 5 ∙
+ 5 ∙ 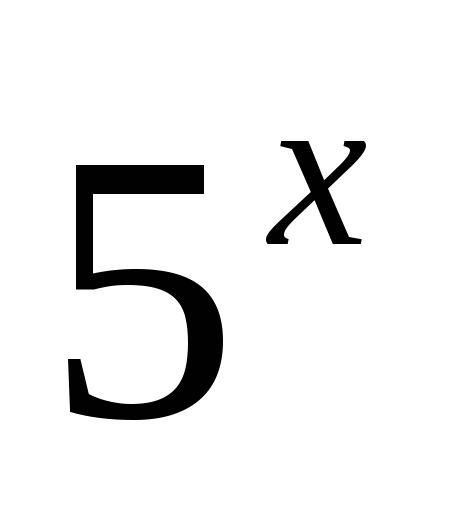 = 250,
= 250,
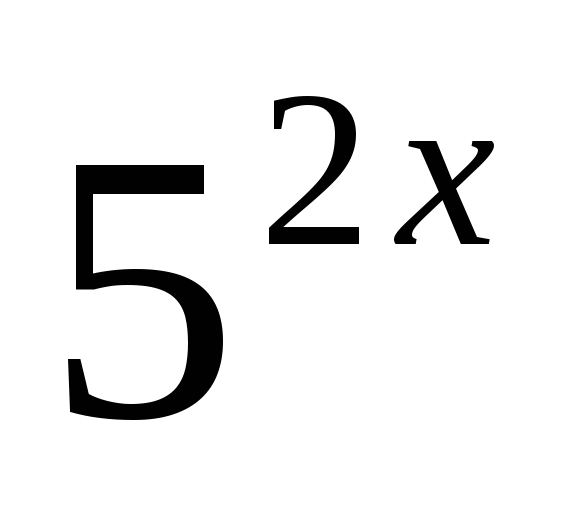 + 25 ∙
+ 25 ∙ 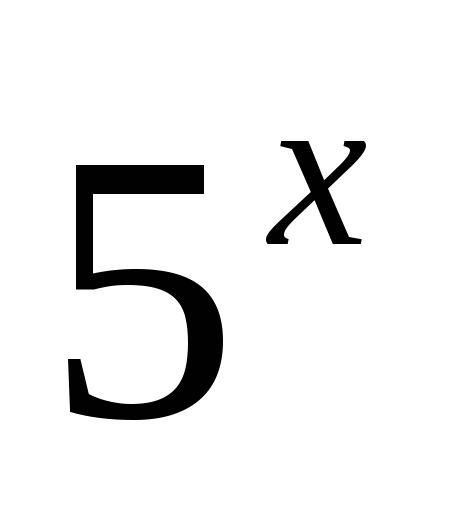 - 1250 = 0.
- 1250 = 0.
Введем замену ![]() = a , a > 0. Уравнение принимает вид
= a , a > 0. Уравнение принимает вид 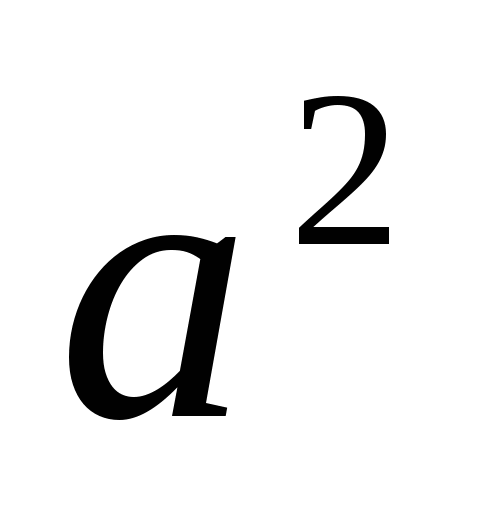 + 25a -
+ 25a -
- 1250 = 0. Решая уравнение, находим его корни: a = 25 или a = -50.
Учитывая условие a > 0, отбросим a = -50. Переходя к прежней переменной x, остается решить уравнение 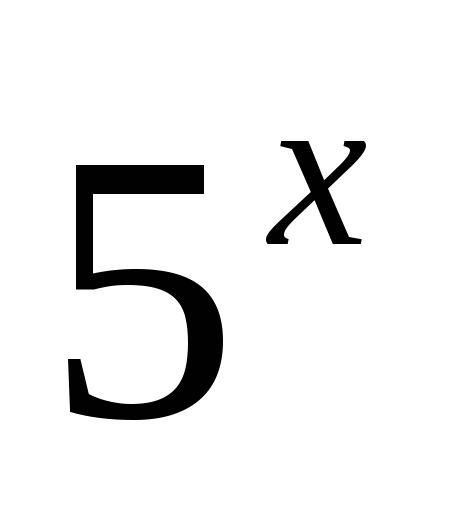 = 25. Оно имеет корень x=2.
= 25. Оно имеет корень x=2.
Ответ: 2.
Задание 5. Решите уравнение 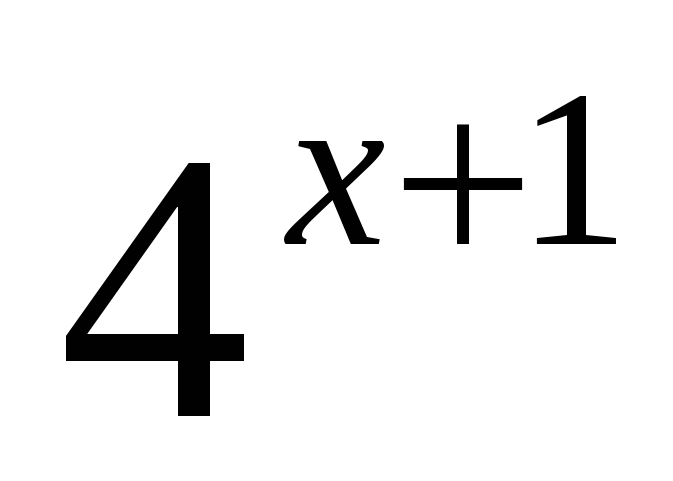 −2 ∙
−2 ∙ 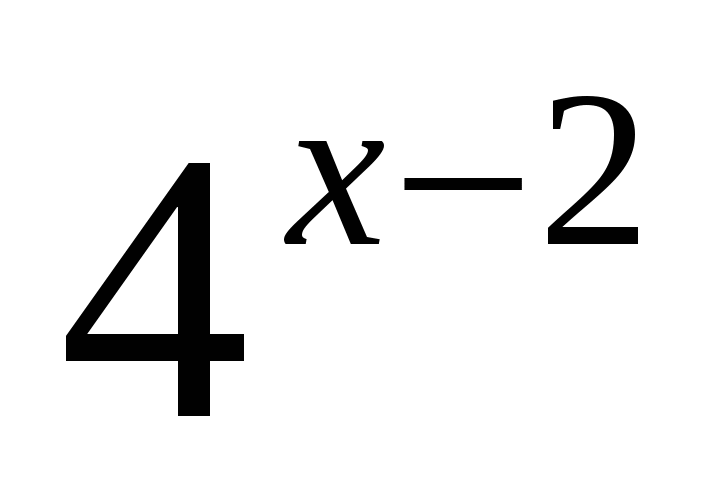 = 124.
= 124.
Решение. Преобразуем левую часть уравнения с помощью свойств (1), (2) и вынесем за скобки степень с наименьшим показателем 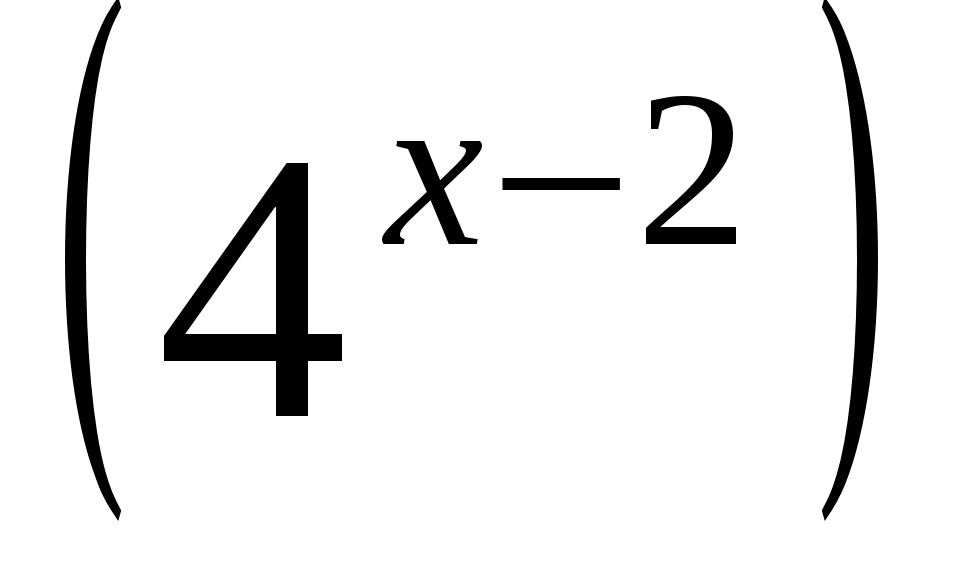 :
:
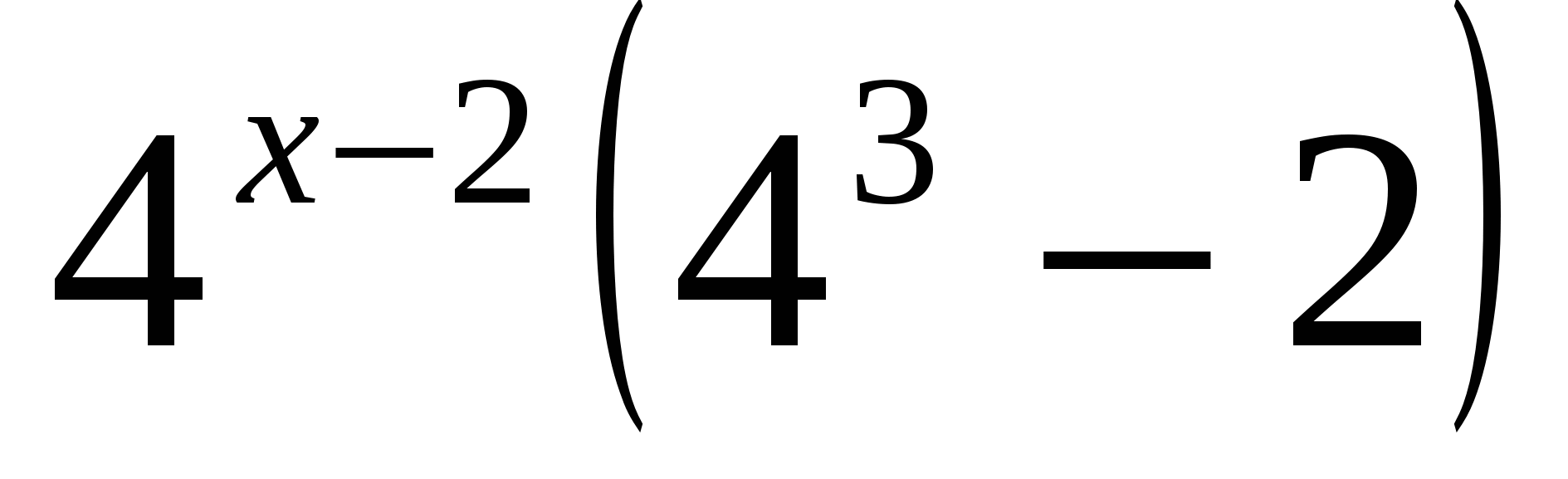 = 124,
= 124,
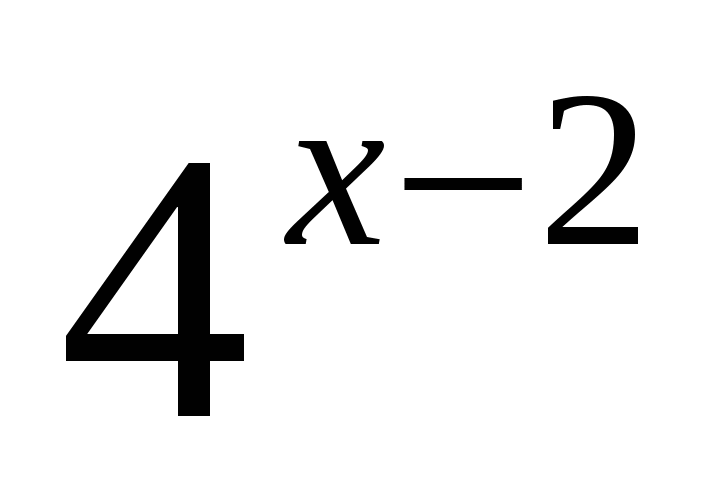 ∙ 62 = 124,
∙ 62 = 124,
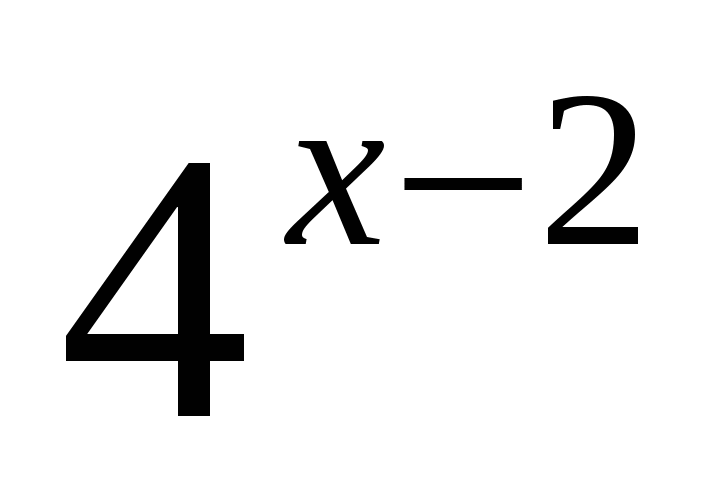 = 2,
= 2,
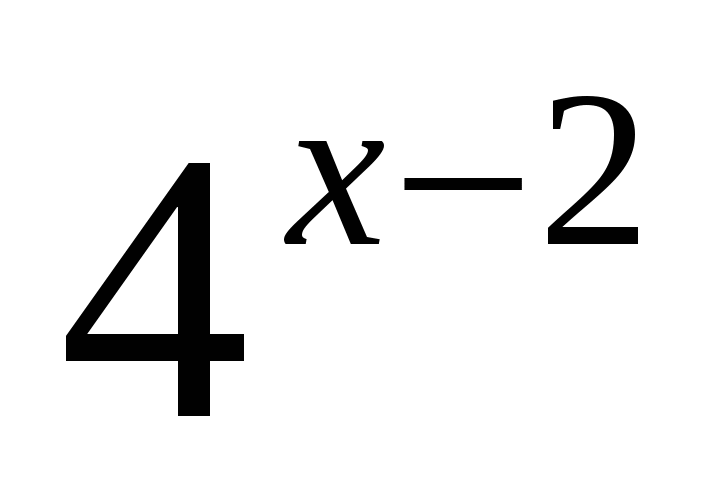 =
= 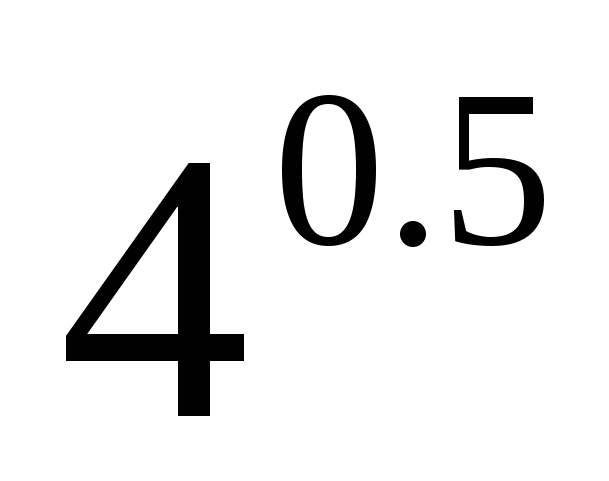 ,
,
x−2 = 0,5,
x=2,5.
Ответ: 2,5.
Рассмотрим уравнения (неравенства), идея решения которых состоит в делении обеих частей уравнения на некоторое показательное выражение.
Такая операция не приводит к потере корней (решений), потому что показательные выражения больше нуля ( см. область значений функции y=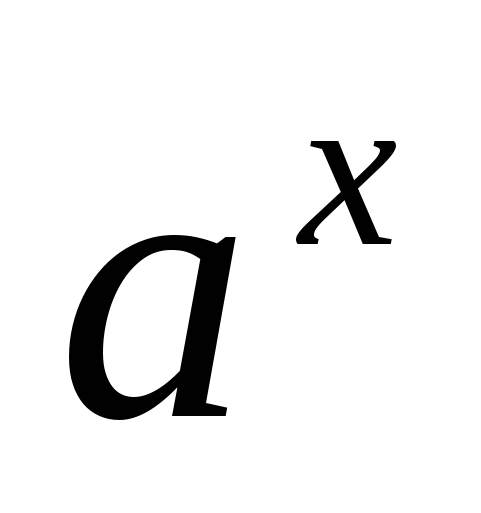 ).
).
Задание 6. Решите уравнение 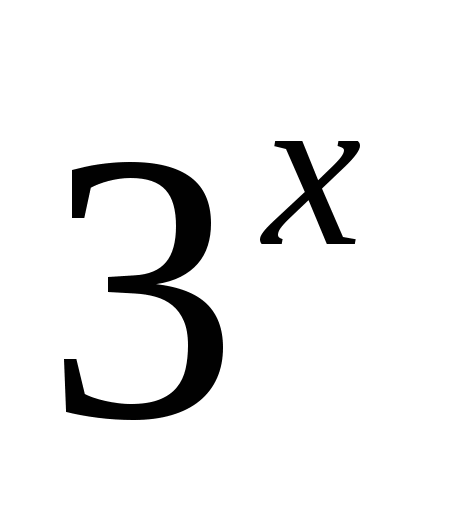 +
+ 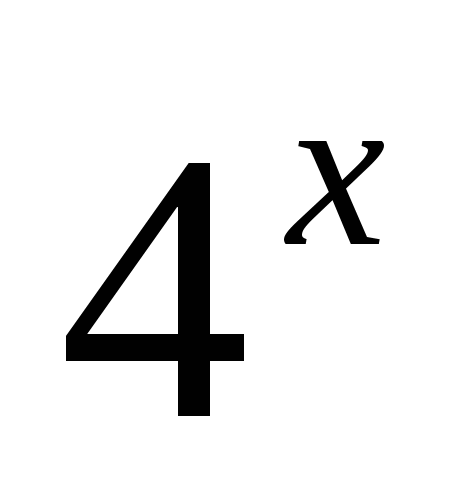 =
= 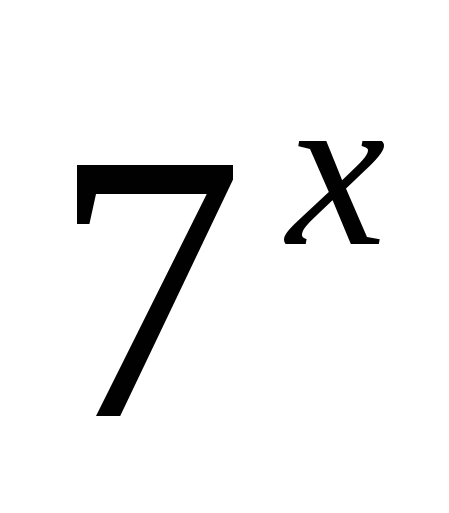 .
.
Решение. Подбором устанавливаем, что корнем уравнения является x=1. Докажем, что других корней нет. Так как 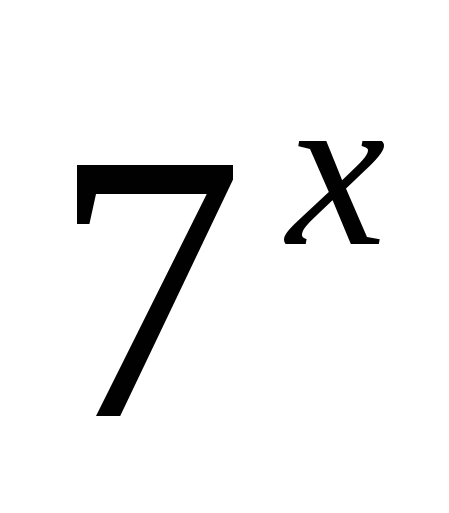 > 0, разделим обе части уравнения на выражение
> 0, разделим обе части уравнения на выражение ![]() .
.
Получим уравнение 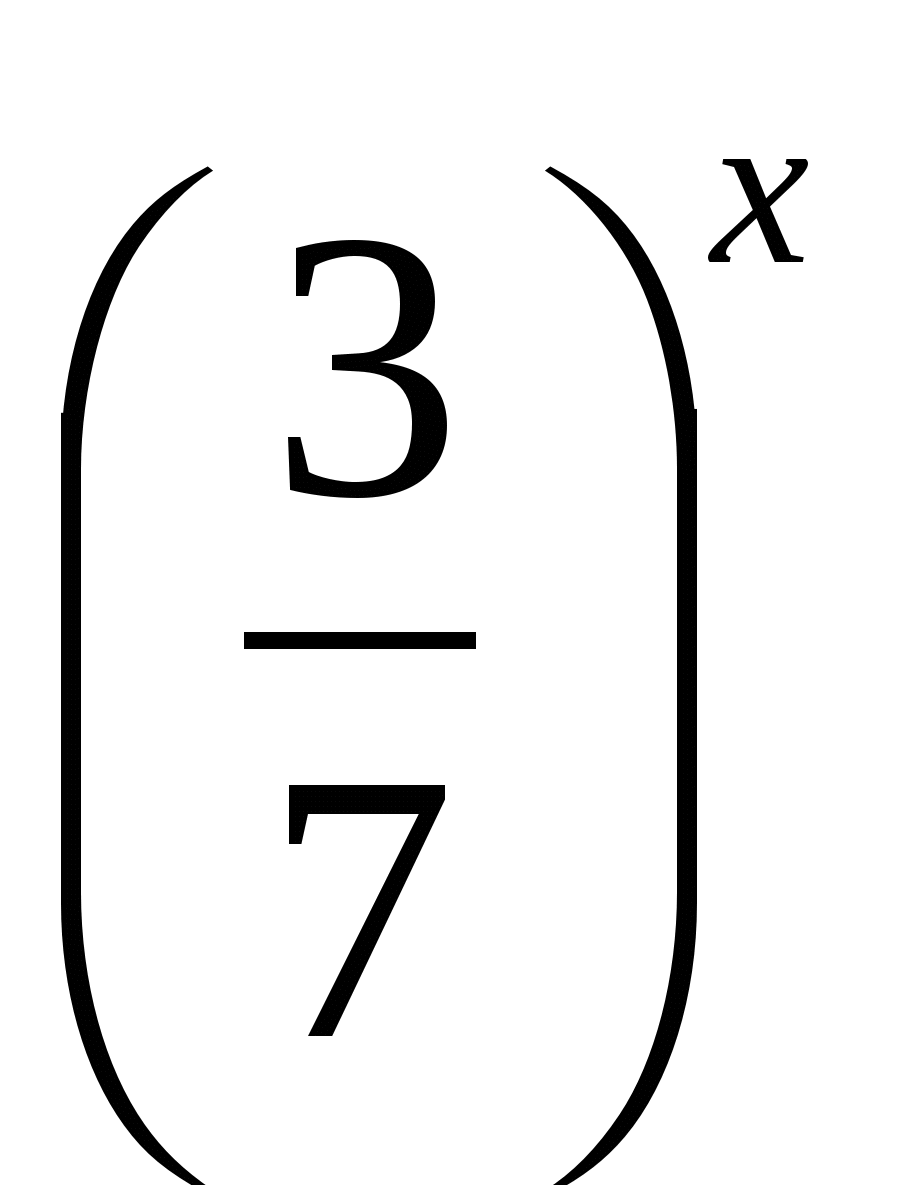 +
+ 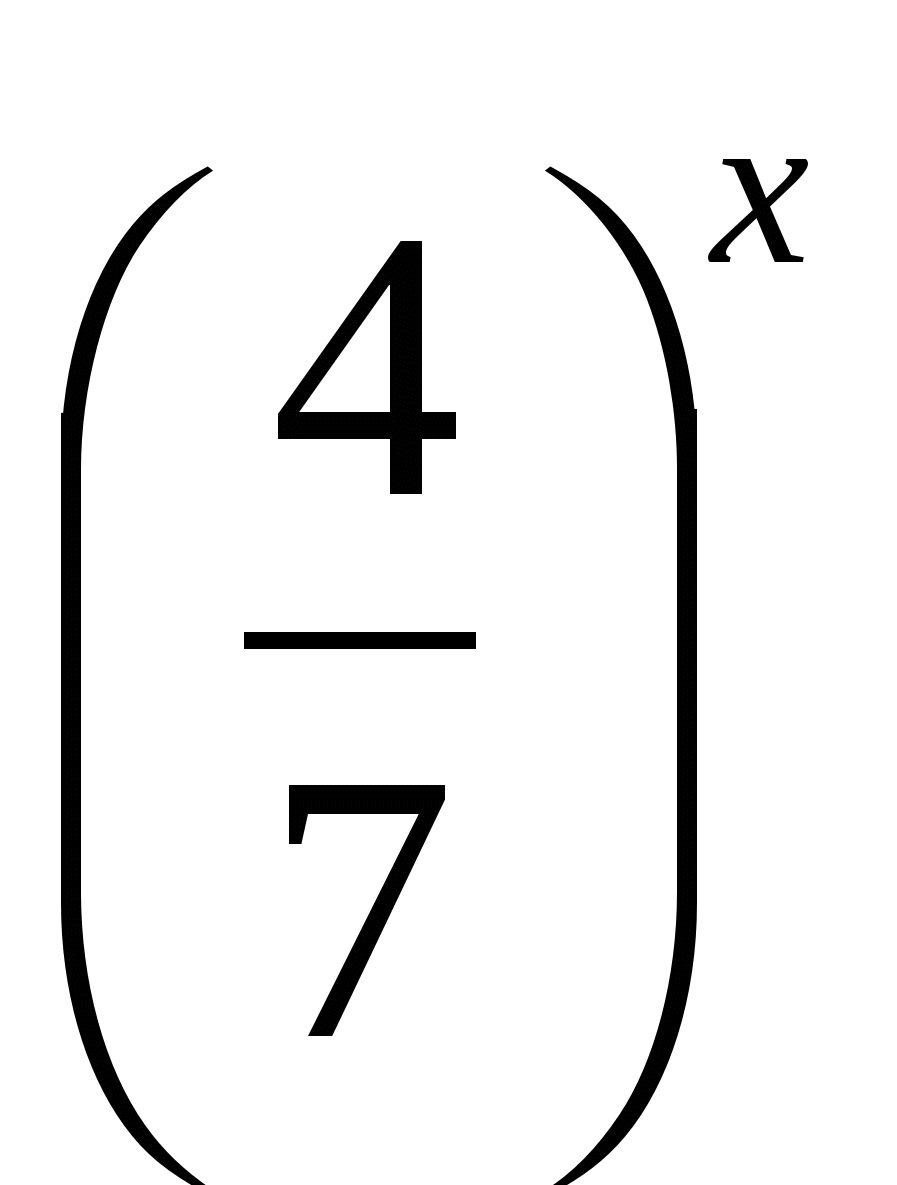 = 1.
= 1.
В левой части уравнения − сумма монотонных функций − монотонная функция ( убывающая ), поэтому любое свое значение эта функция принимает только один раз, в том числе и значение, равное 1. Значит, уравнение имеет единственный корень, который уже найден.
Ответ: 1.
Замечание. Уравнение 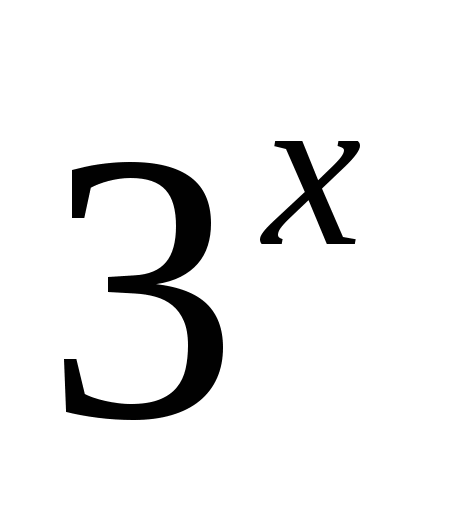 +
+ 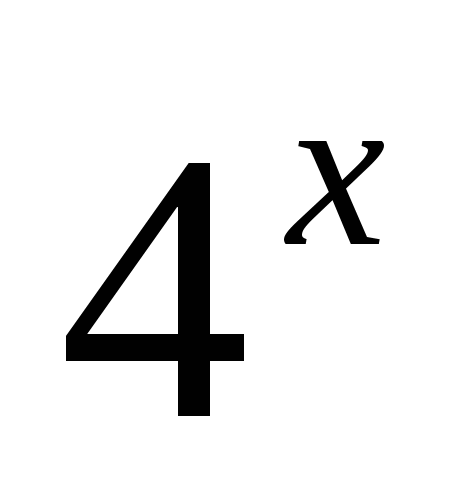 =
= 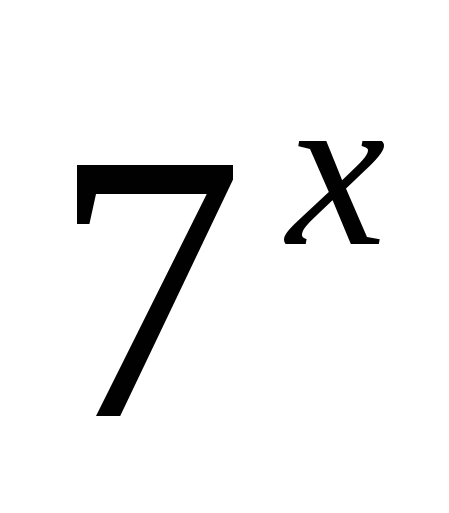 также решается функционально-графическим методом, но без деления: в левой части − возрастающая функция, которая принимает значение 7 только в одной точке x = 1.
также решается функционально-графическим методом, но без деления: в левой части − возрастающая функция, которая принимает значение 7 только в одной точке x = 1.
Используем прием деления на показательное выражение при решении однородных показательных уравнений ( неравенств ).
Если при замене показательных выражений, входящих в показательное уравнение, новыми переменными, получается однородное уравнение, то этот тип показательных уравнений называют однородными показательными уравнениями. Например, если в уравнении 3 ∙ 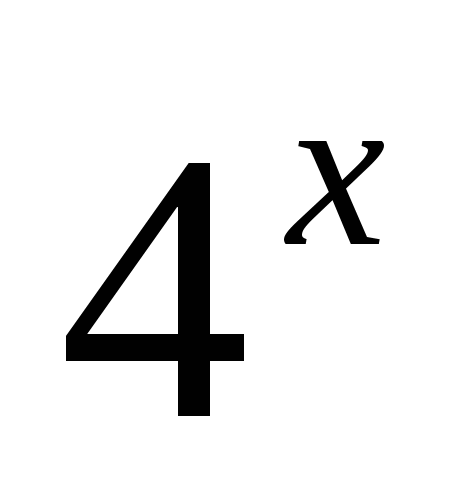 −
−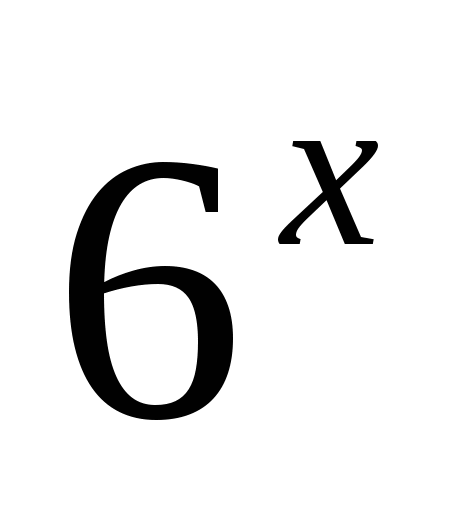 −2∙
−2∙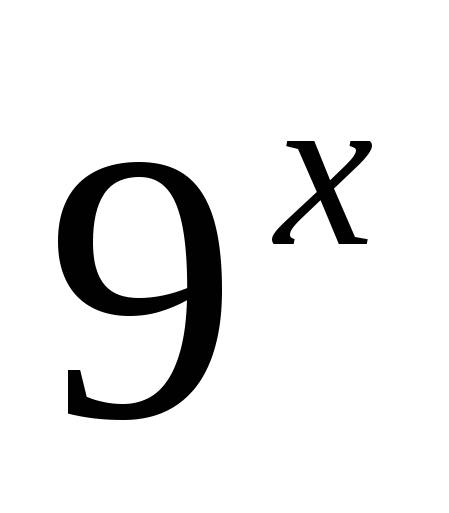 = 0 заменить
= 0 заменить 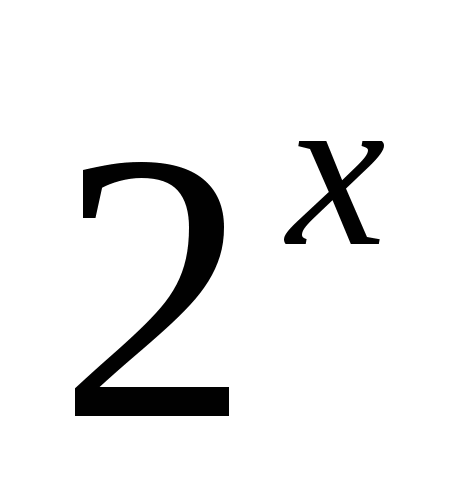 новой переменной a , а
новой переменной a , а 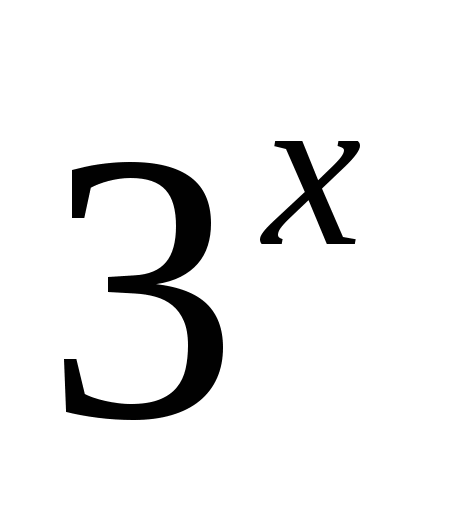 − новой переменной b, то получим однородное уравнение второй степени
− новой переменной b, то получим однородное уравнение второй степени 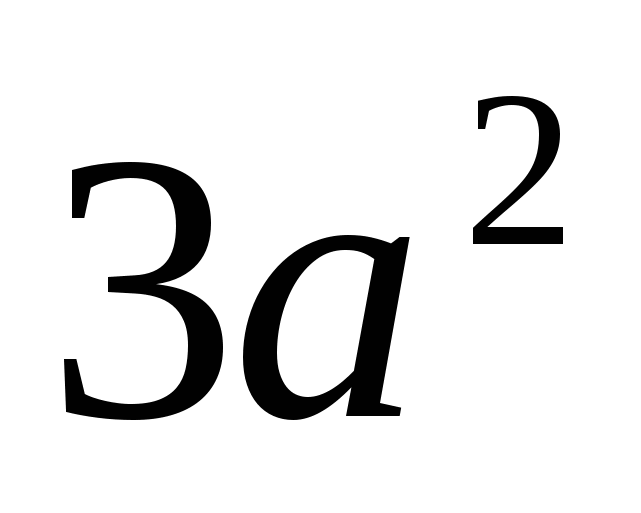 −
− 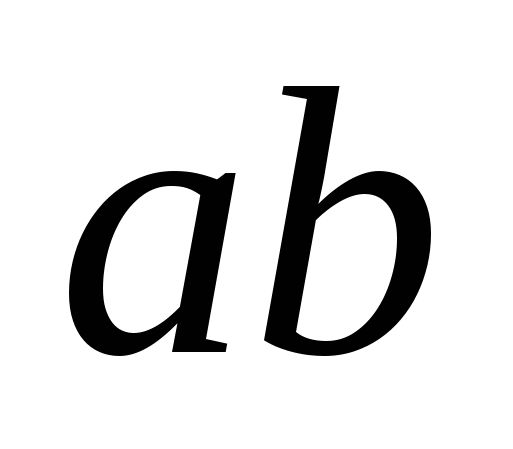 −
−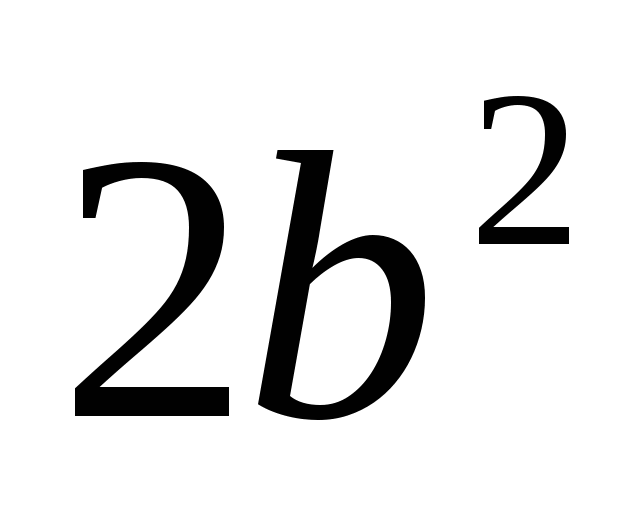 = 0 ( сумма показателей степеней каждого члена равна двум ).
= 0 ( сумма показателей степеней каждого члена равна двум ).
Однородное показательное уравнение решаются путем деления обеих частей уравнения на входящее в уравнение показательное выражение с наибольшим основанием и сведением данного уравнения к квадратному  ( можно делить и на любое показательное выражение, входящее в уравнение ).
( можно делить и на любое показательное выражение, входящее в уравнение ).
Задание 8. Решите уравнение 2 ∙ 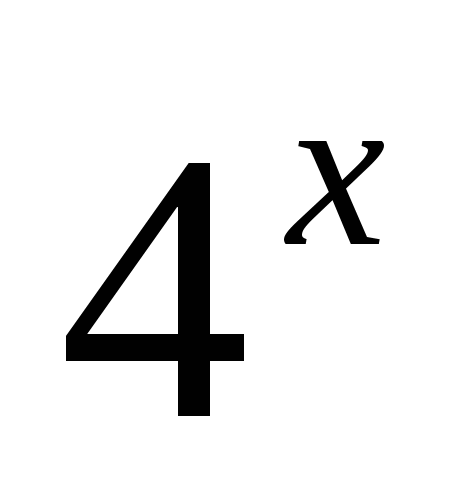 − 3 ∙
− 3 ∙ 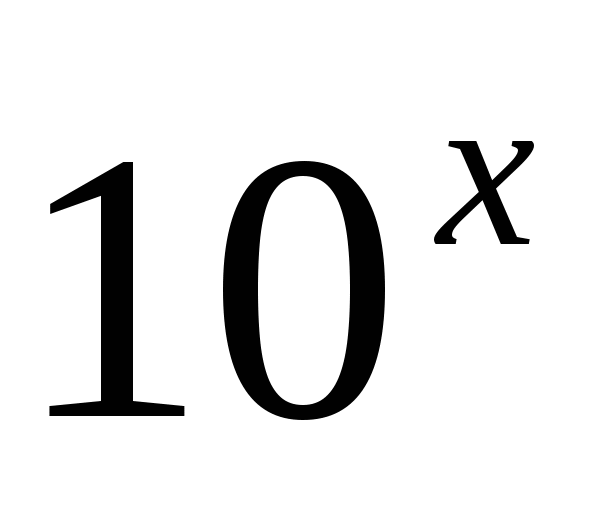 = 5 ∙
= 5 ∙ 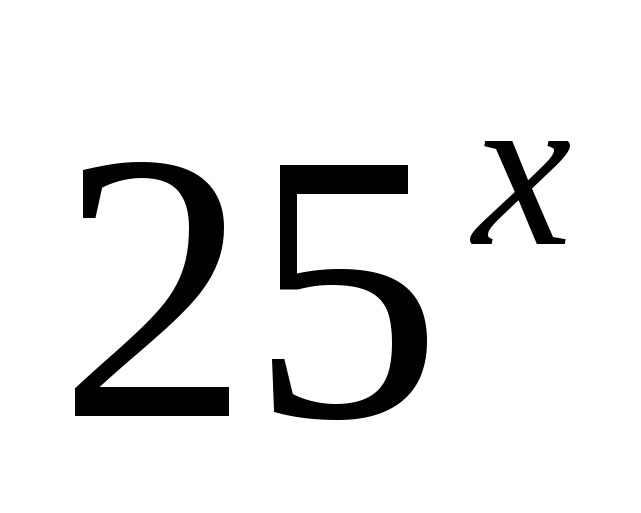 .
.
Решение. Данное уравнение является однородным ( почему?). Разделим  обе части уравнения на выражение
обе части уравнения на выражение 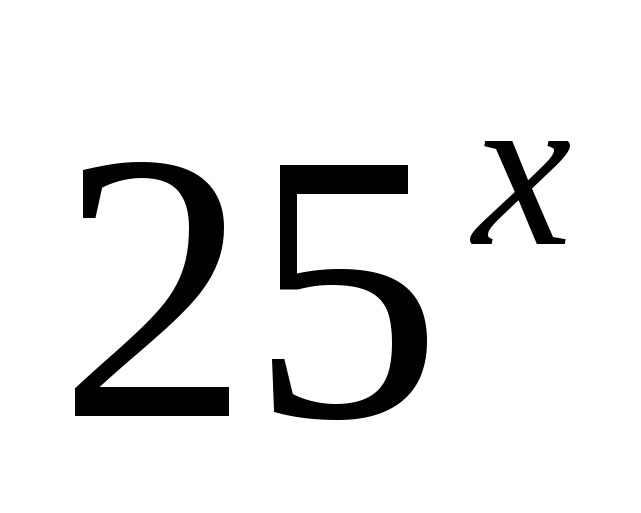 , большее нуля для любых x.
, большее нуля для любых x.
2∙ 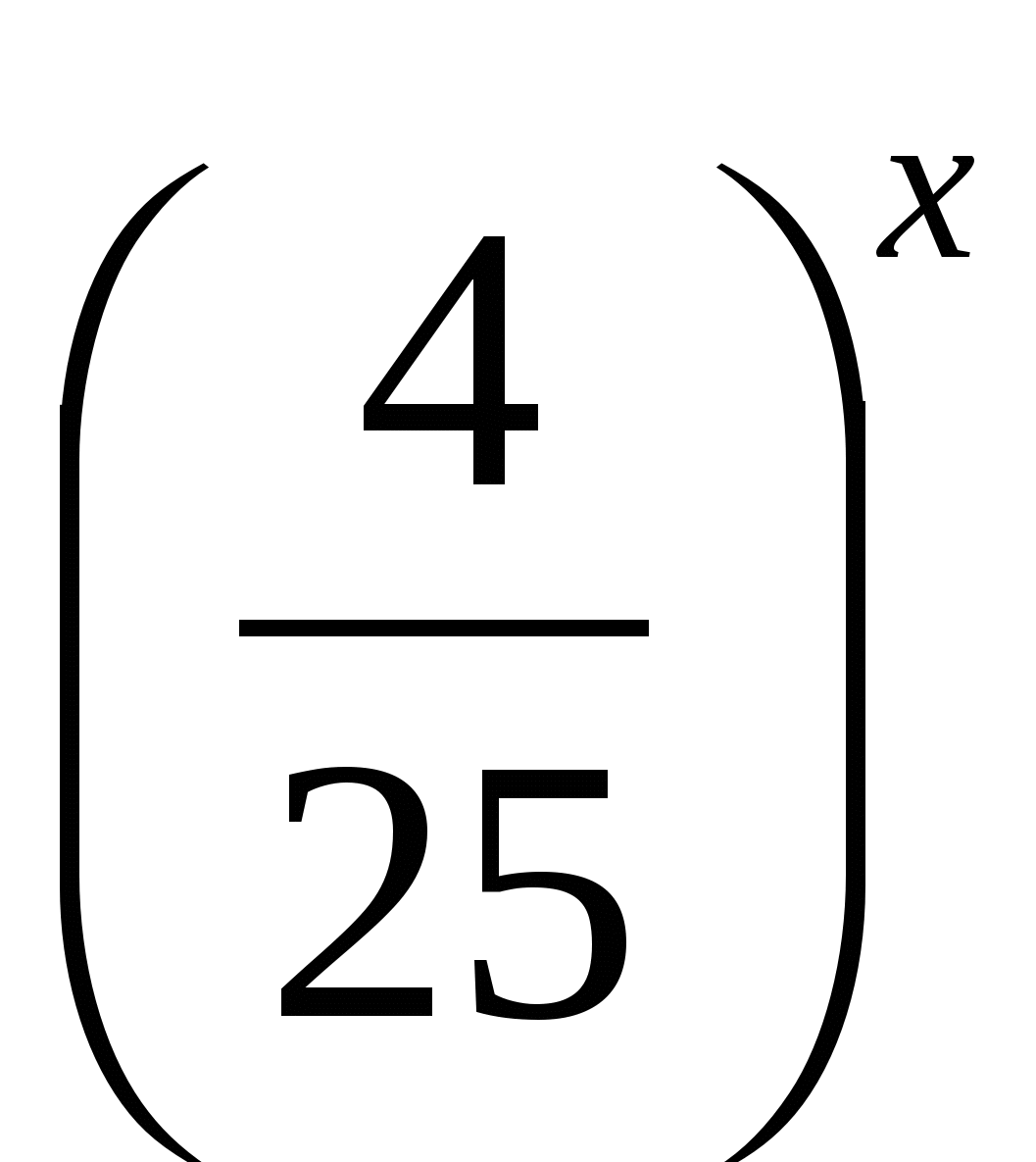 − 3∙
− 3∙ 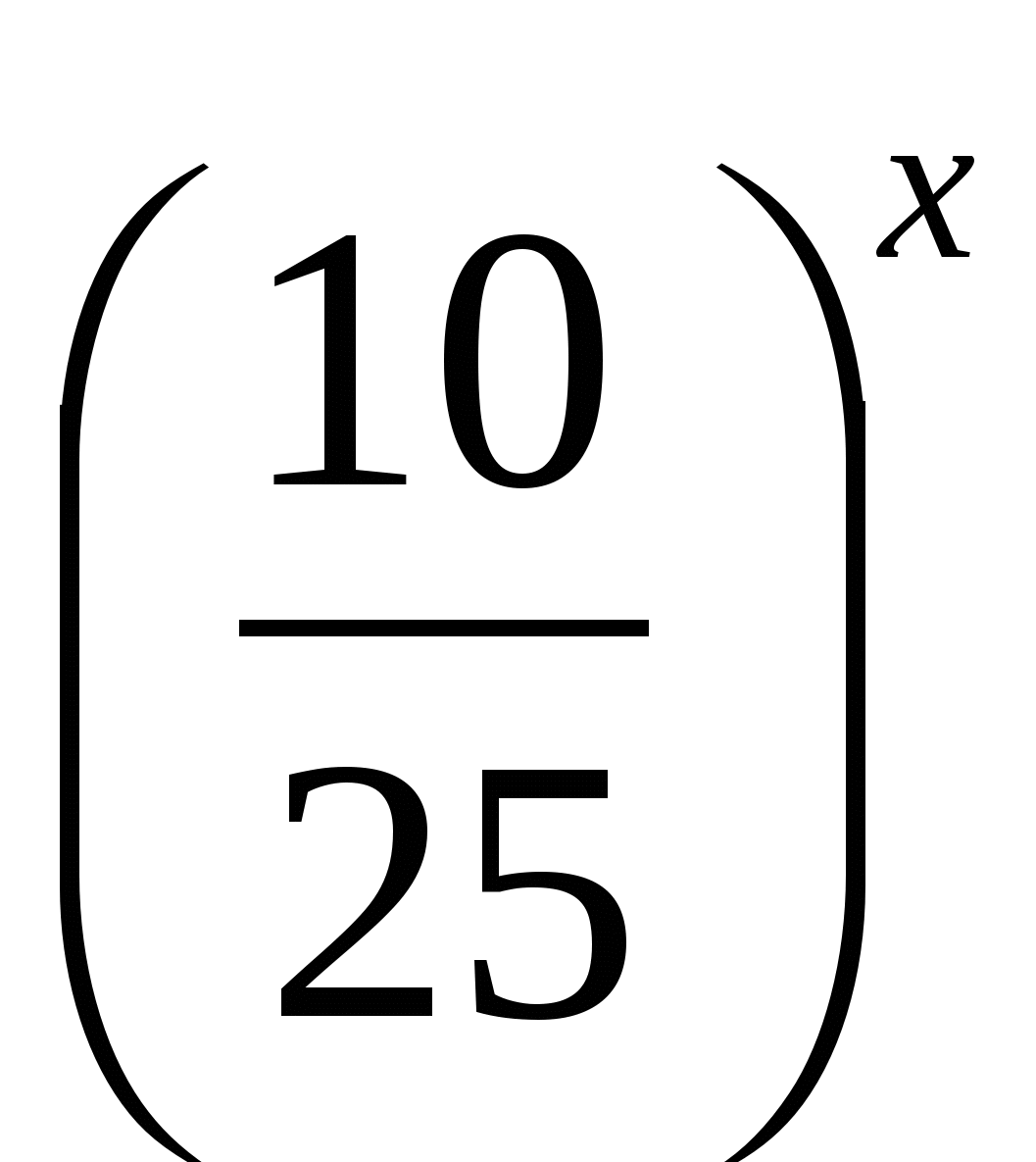 = 5, 2∙
= 5, 2∙ 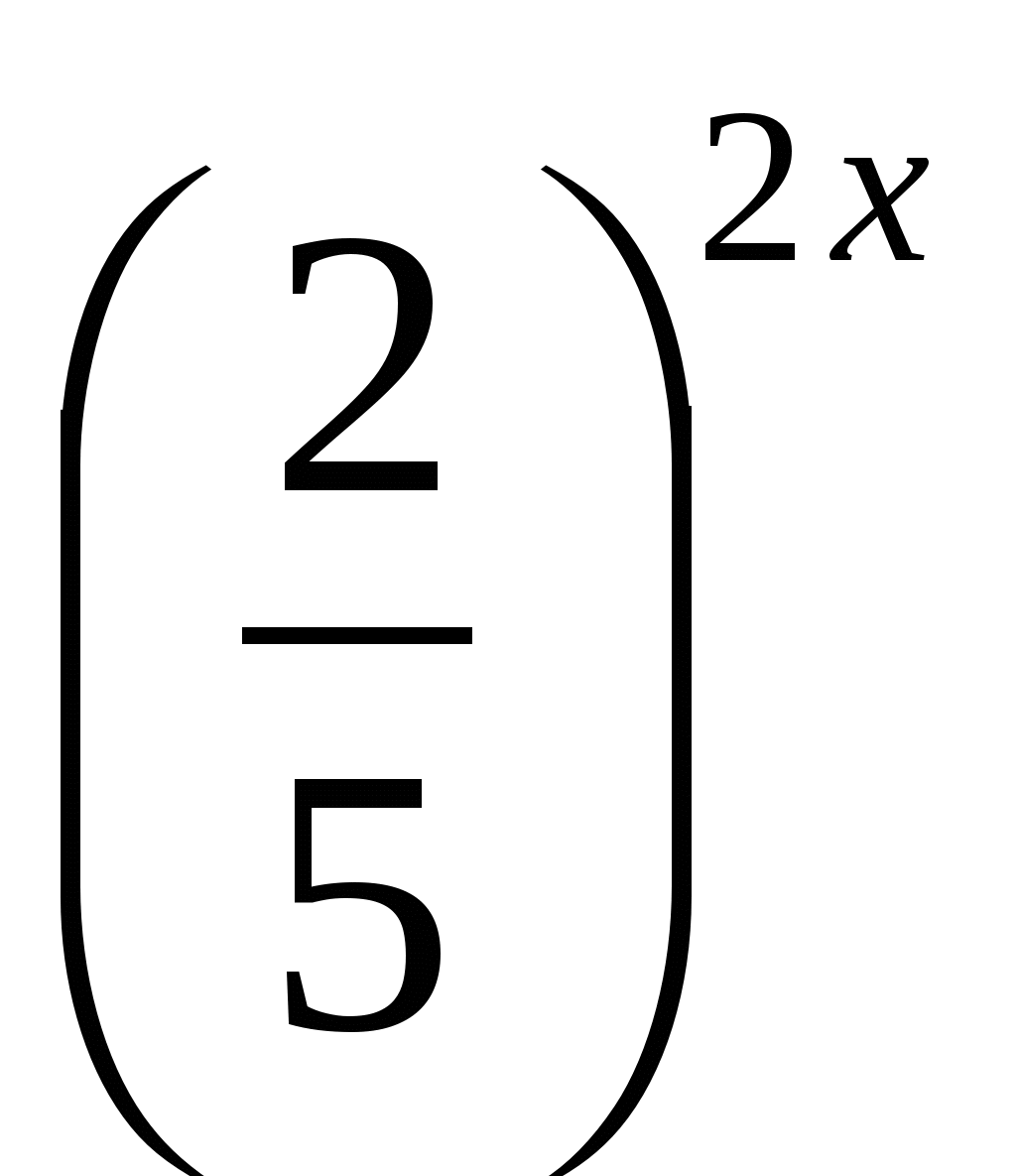 − 3∙
− 3∙ 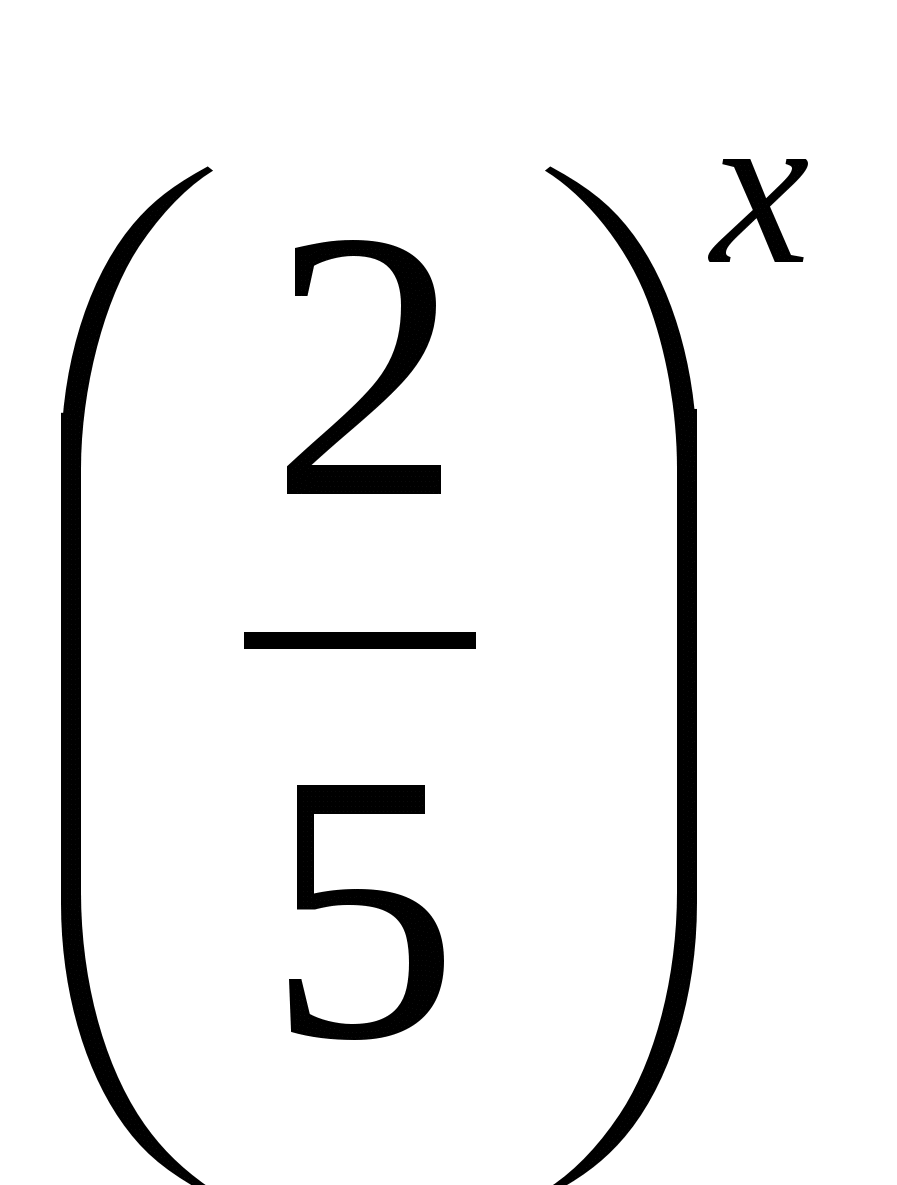 = 5.
= 5.
Введем новую переменную t = 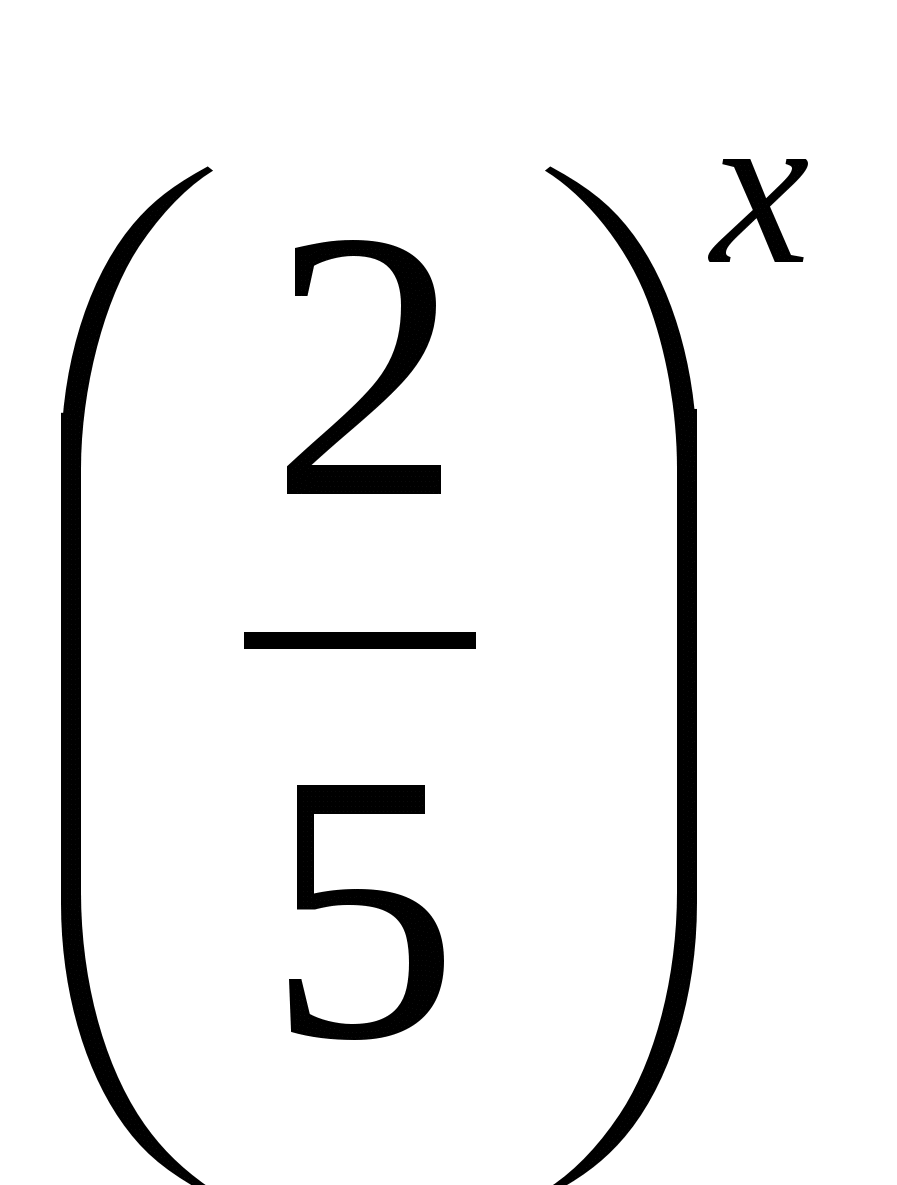 , t > 0.
, t > 0.
Уравнение 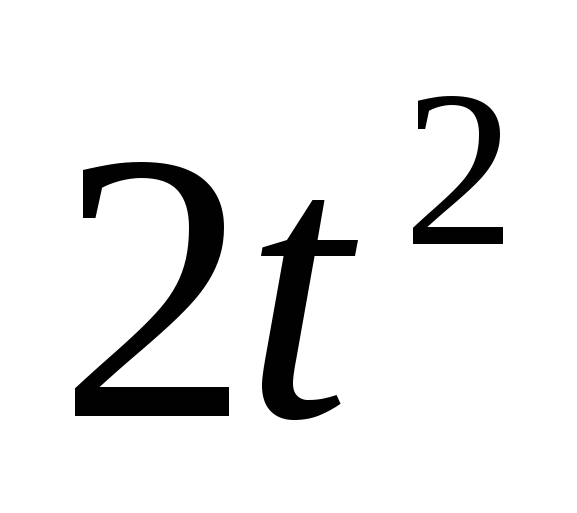 − 3t − 5 = 0 имеет два корня
− 3t − 5 = 0 имеет два корня 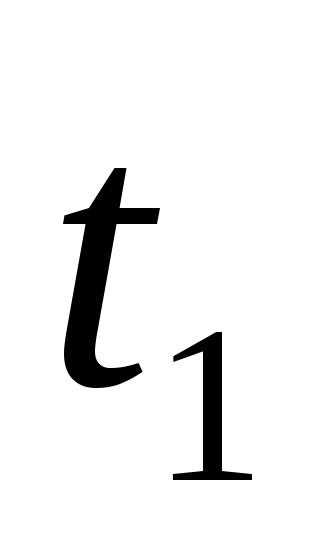 = -1 и
= -1 и 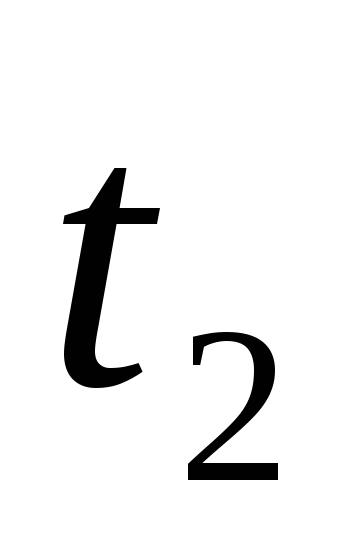 =
= 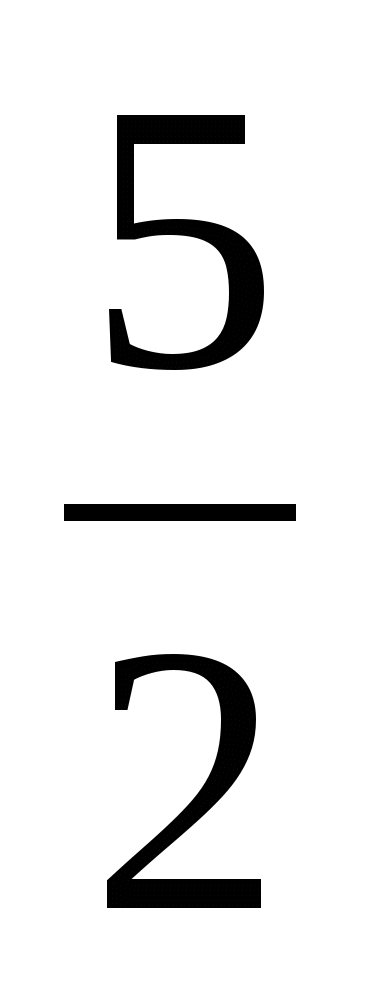 . С учетом условия t > 0 отбрасываем
. С учетом условия t > 0 отбрасываем 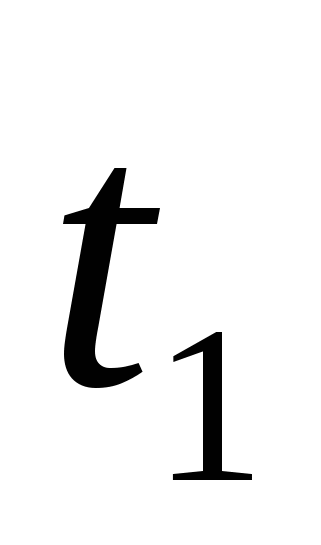 = − 1. Остается решить уравнение
= − 1. Остается решить уравнение ![]() =
= 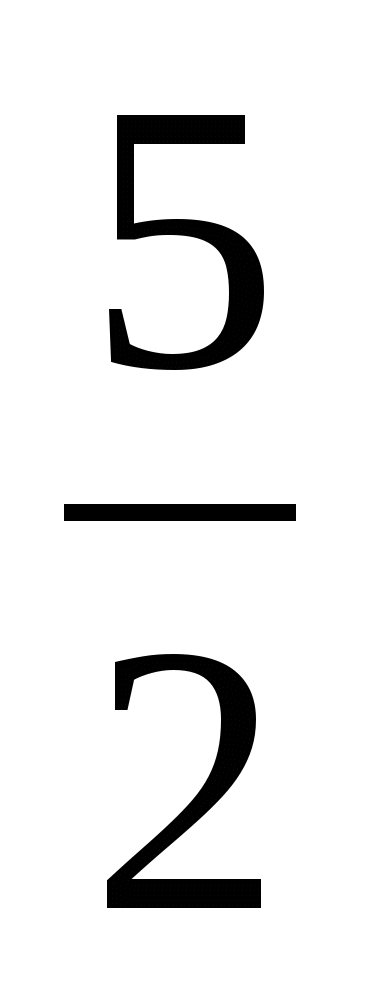 , x = −1.
, x = −1.
Ответ: − 1.
Рассмотрим более сложные задания.
Задание 9. Решите уравнение (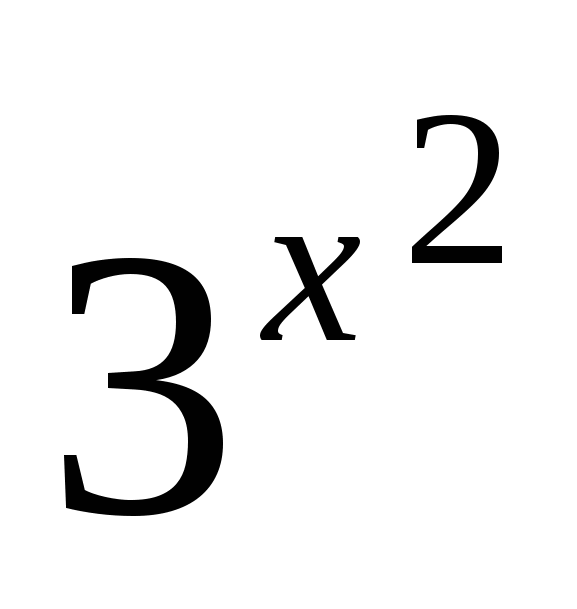 − 81) ∙
− 81) ∙ 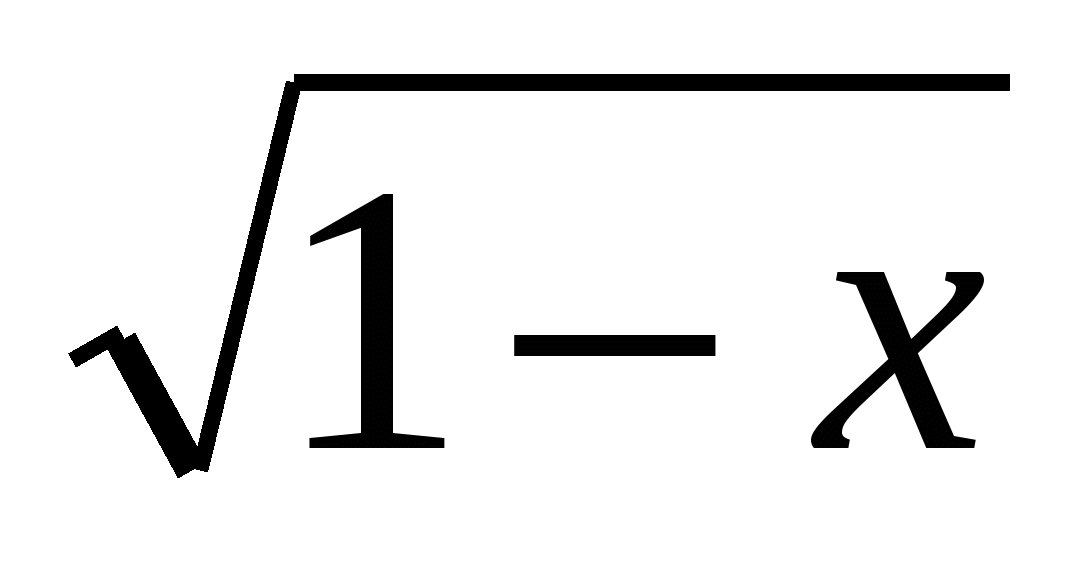 = 0.
= 0.
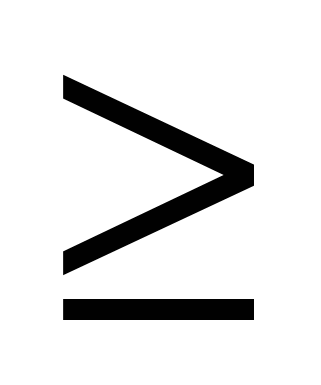
Решение. 1-й способ. В основе решения уравнения лежит условие равенства произведения двух выражений нулю: произведение двух выражений равно нулю, если хотя бы один из множителей равен нулю, а второй при этом не теряет смысл.
1) 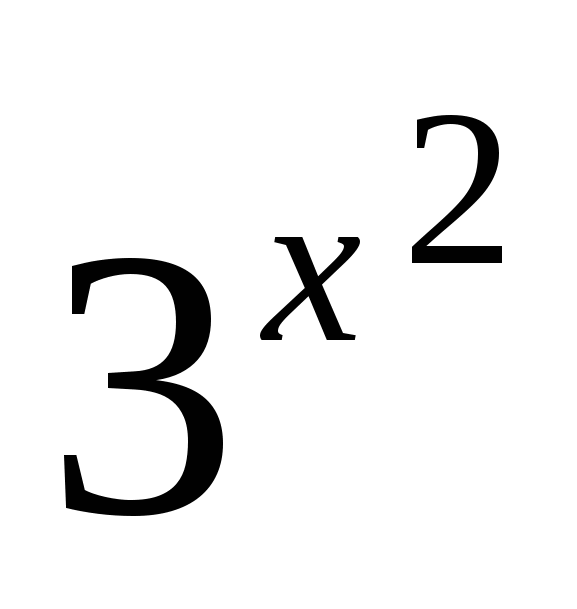 − 81 = 0,
− 81 = 0, 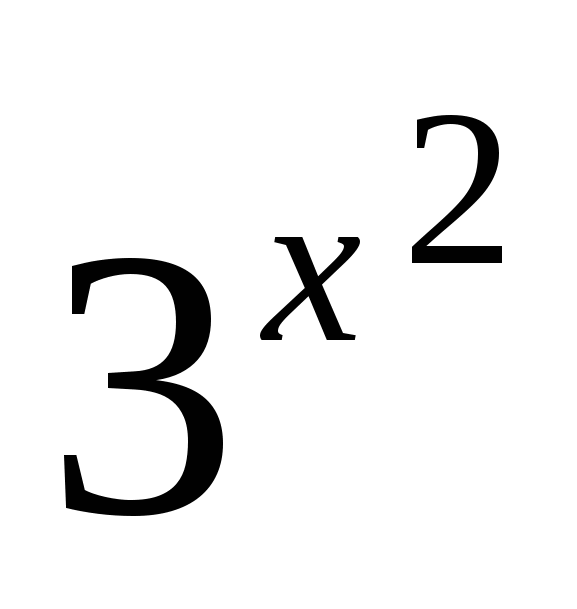 =
= 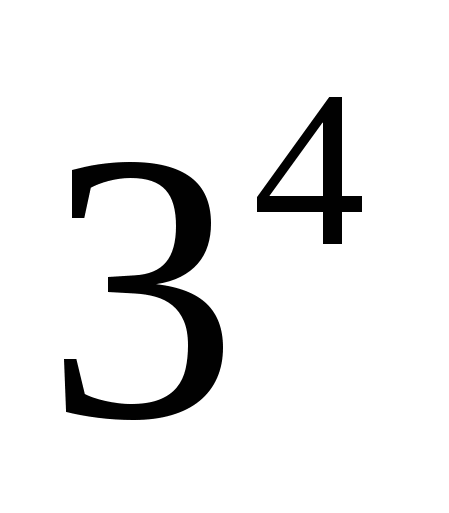 ,
, 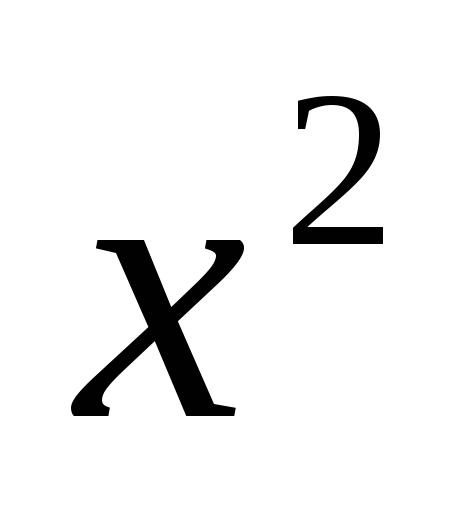 = 4, x = 2 или x = − 2. При x =2 подкоренное выражение отрицательно, значит, число 2 не является корнем уравнения.
= 4, x = 2 или x = − 2. При x =2 подкоренное выражение отрицательно, значит, число 2 не является корнем уравнения.
2) 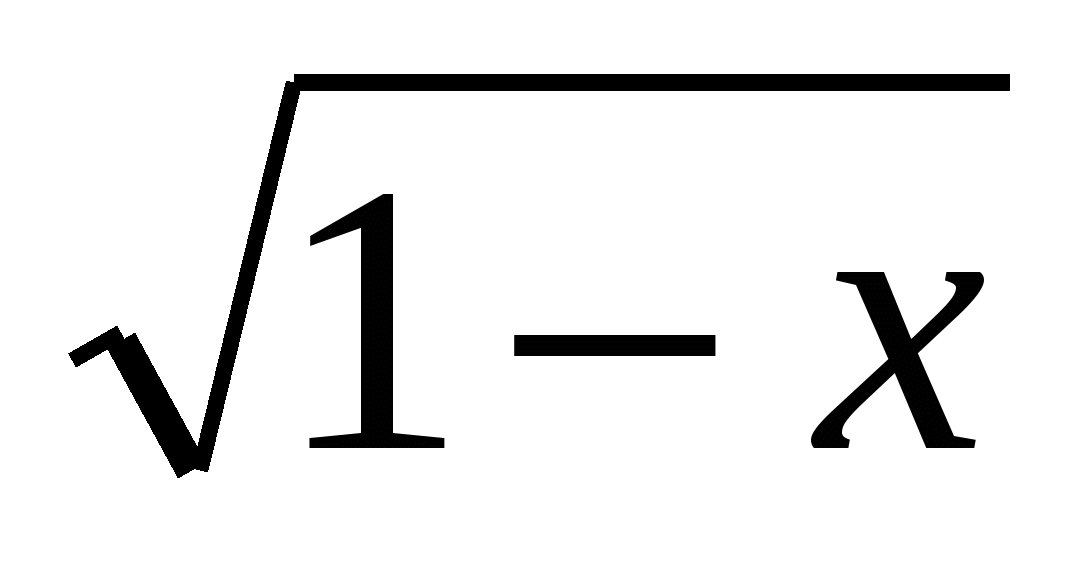 = 0 при x=1. Это число является корнем данного уравнения, так
= 0 при x=1. Это число является корнем данного уравнения, так
как выражение ![]() − 81 имеет смысл при любом x.
− 81 имеет смысл при любом x.
Ответ: 1, -2.
2-й способ. Если решать уравнение с помощью равносильности, то решение
основано на применении следующего утверждения:
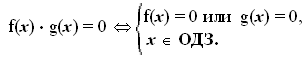
Уравнение равносильно системе:
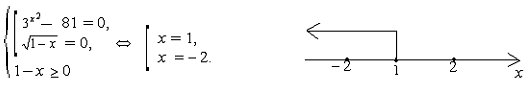
Задание 10. Решите систему уравнений
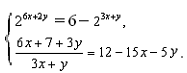
Решение. Преобразуем первое уравнение системы, получим 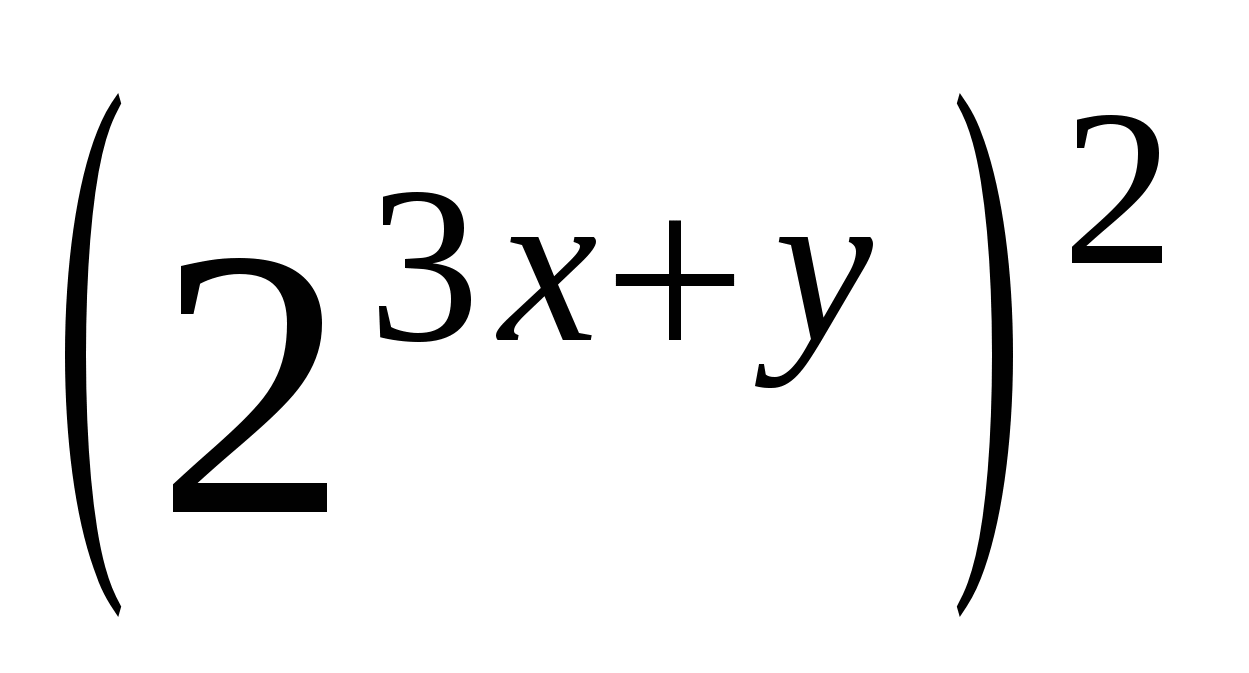 +
+ 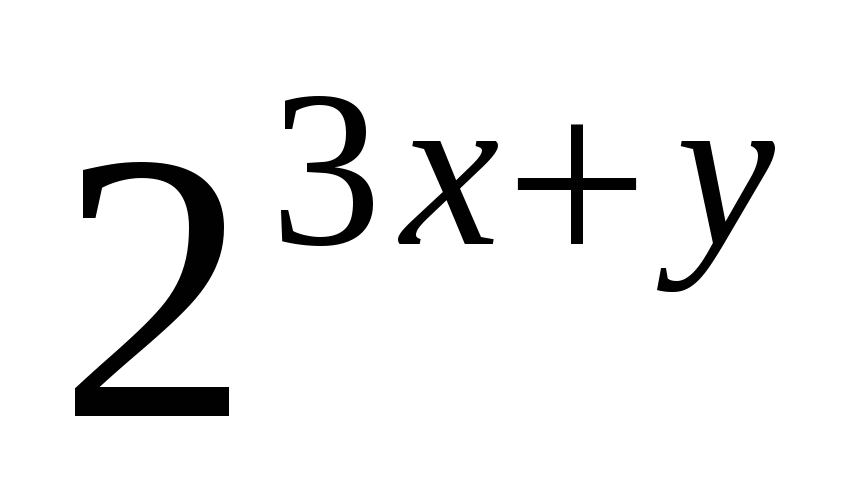 − 6 = 0. Введем новую переменную
− 6 = 0. Введем новую переменную 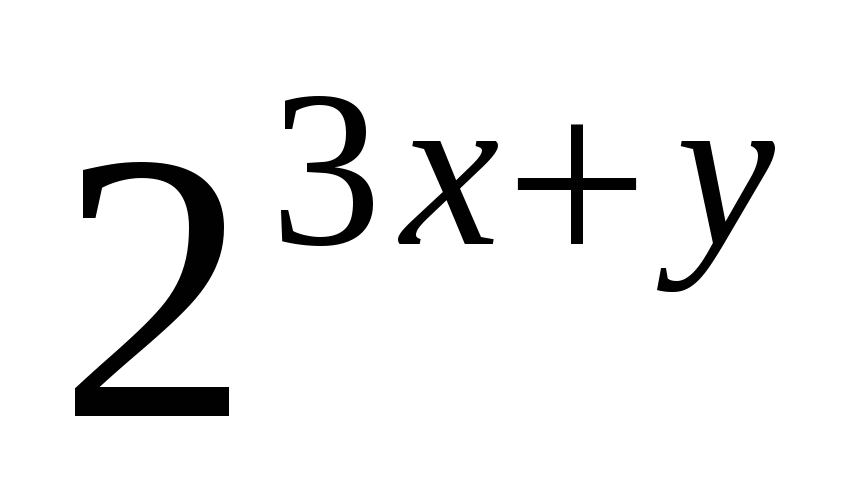 = t, t < 0.
= t, t < 0.
Решениями уравнения 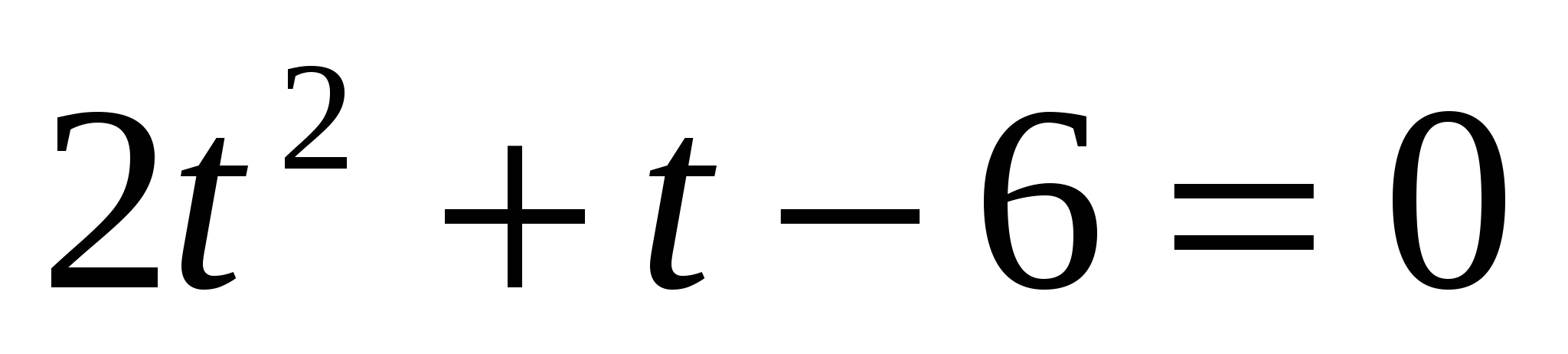 являются числа t = 2 или t = −3. С учетом ограничения, накладываемого на t, оставляем только значение
являются числа t = 2 или t = −3. С учетом ограничения, накладываемого на t, оставляем только значение
t = 2.
Возвращаясь к неизвестным x и y, получим 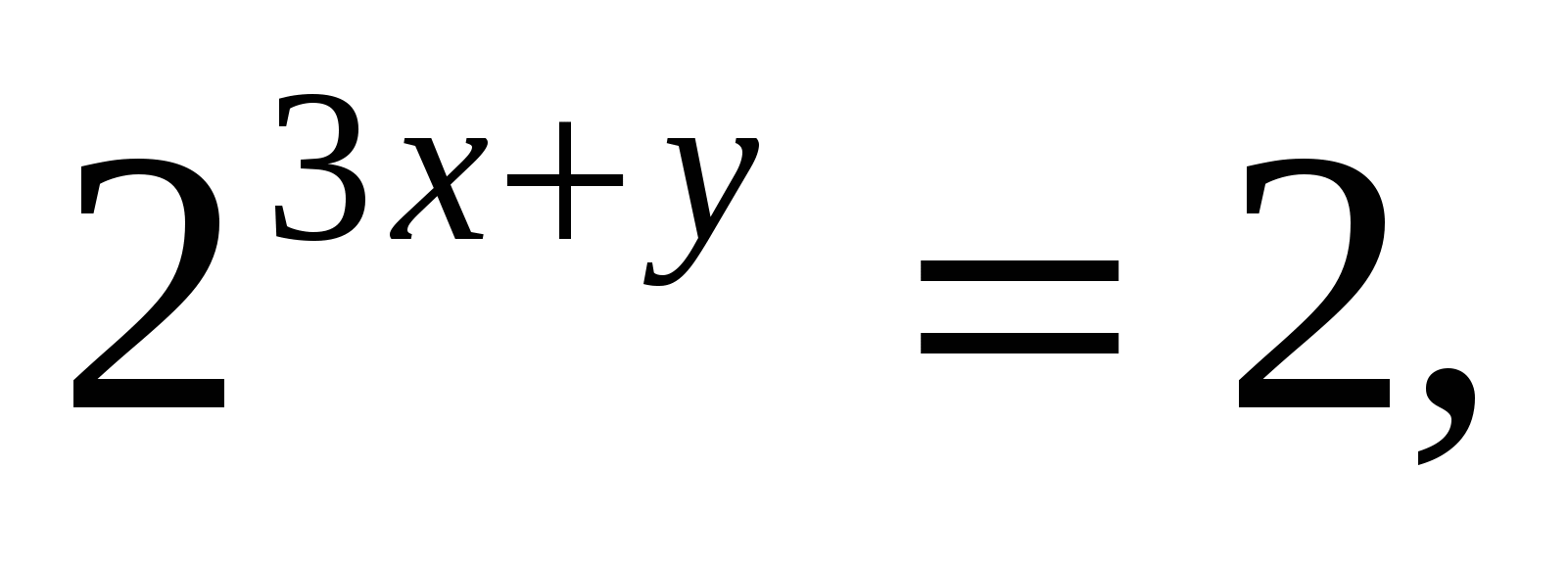
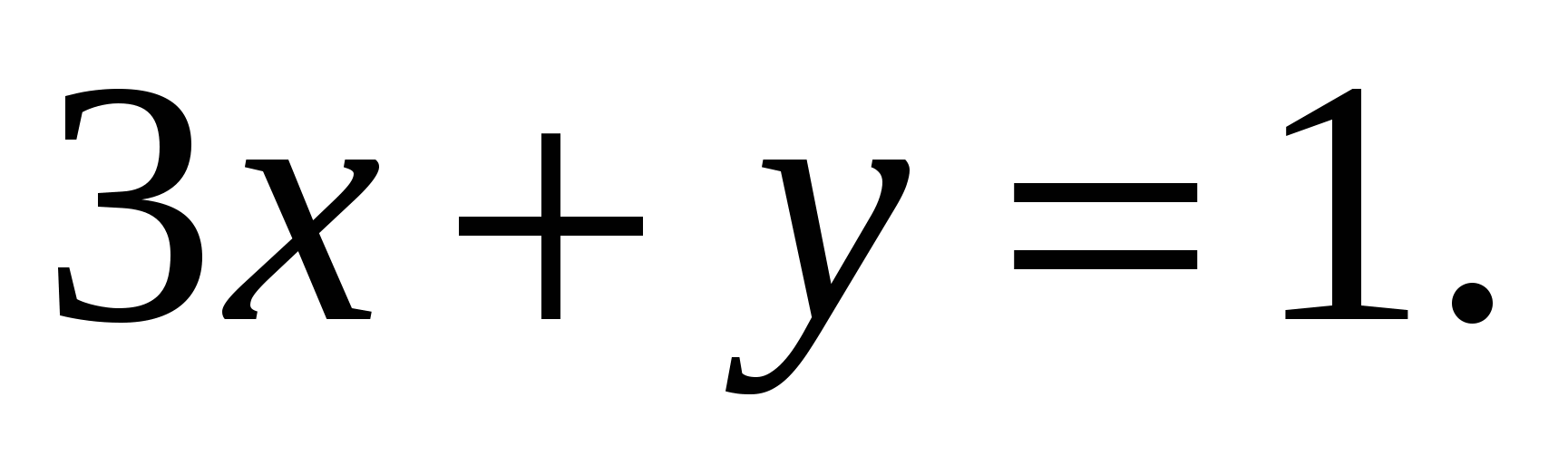
Преобразуем второе уравнение системы к виду:
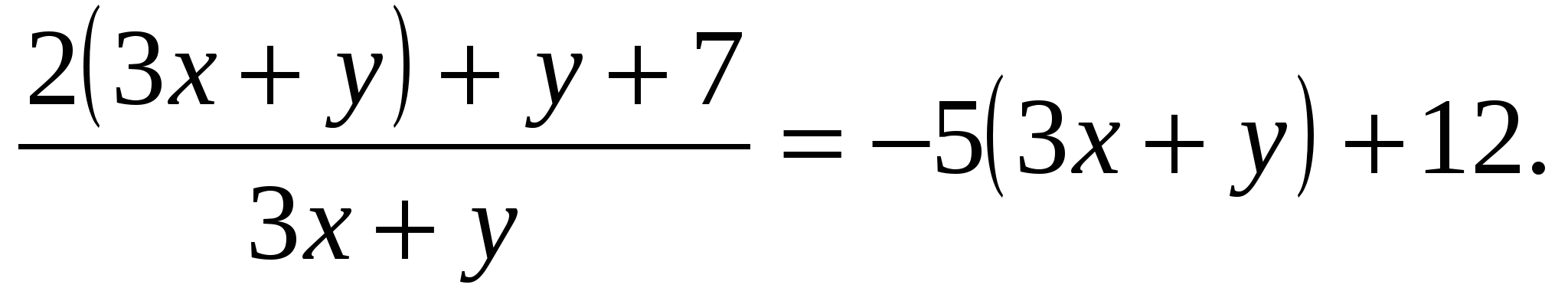
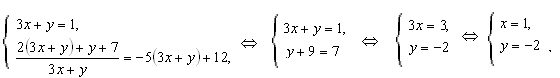
Ответ: (1; − 2).
Задание 11. При каких значениях m уравнение 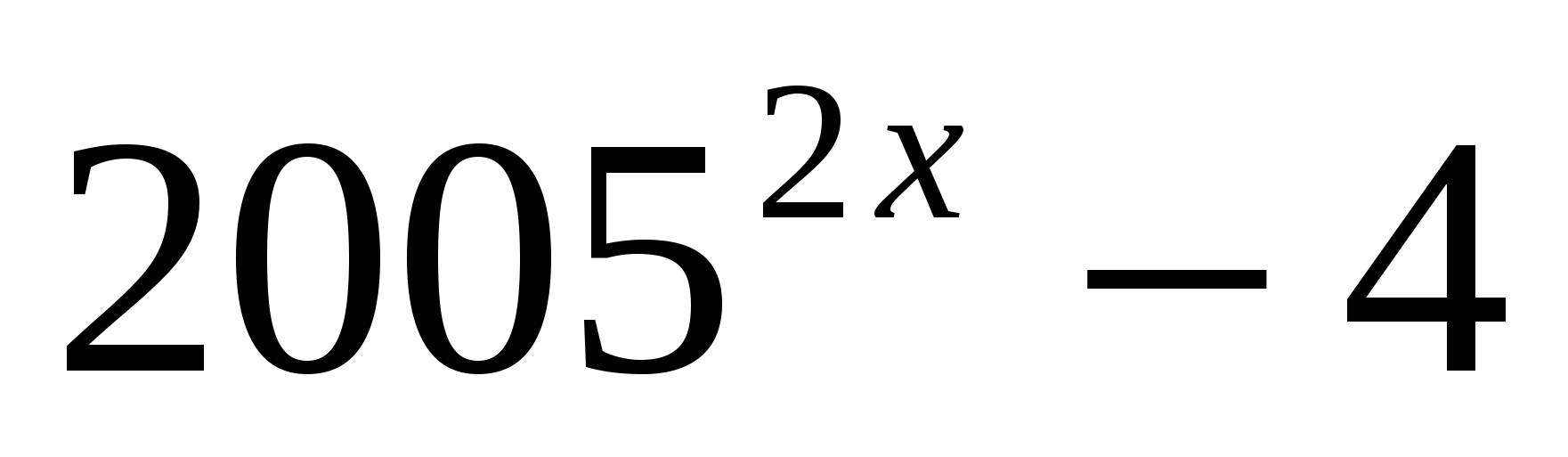 ∙
∙ 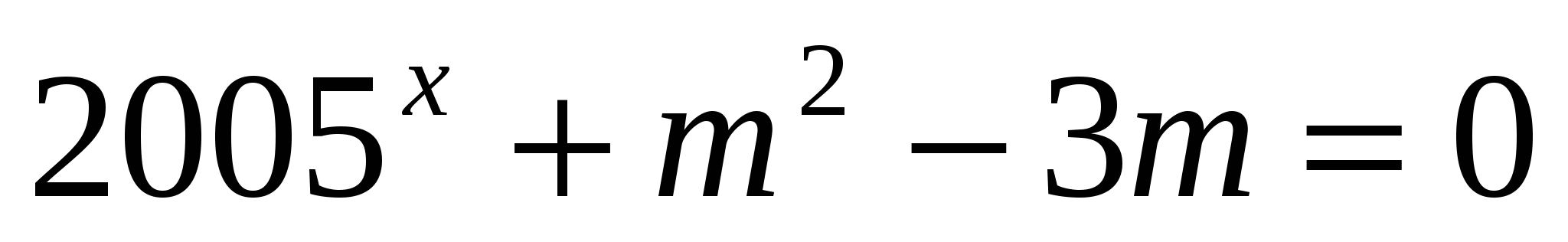
имеет единственный корень?
Решение. Введем новую переменную 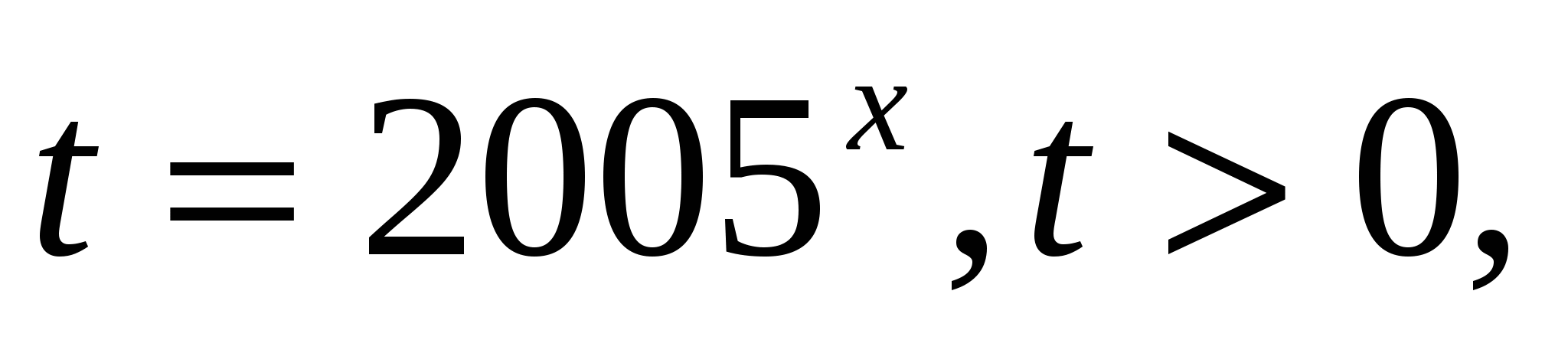 тогда уравнение примет вид:
тогда уравнение примет вид: 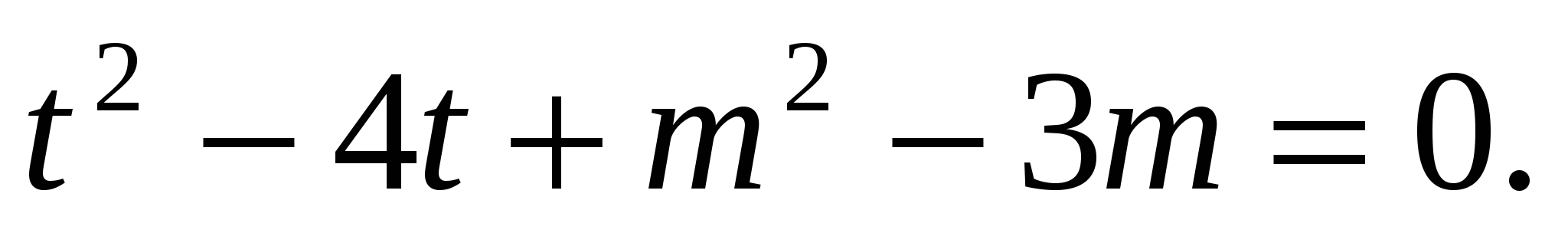 Это квадратное уравнение при t > 0 имеет единственный корень в двух случаях:
Это квадратное уравнение при t > 0 имеет единственный корень в двух случаях:
1) если его дискриминант D = 0 и корень квадратного уравнения положительный;
2) если дискриминант D > 0 и только один корень квадратного уравнения положительный. В этом случае квадратное уравнение имеет два корня, но показательное уравнение имеет единственный корень.
Рассмотрим первый случай. Найдем дискриминант:
D = 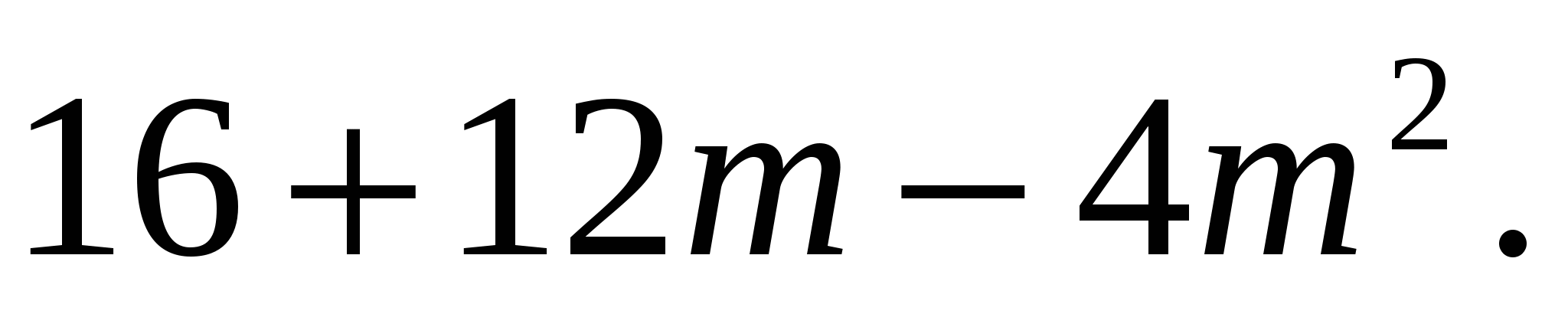
Решим квадратное уравнение 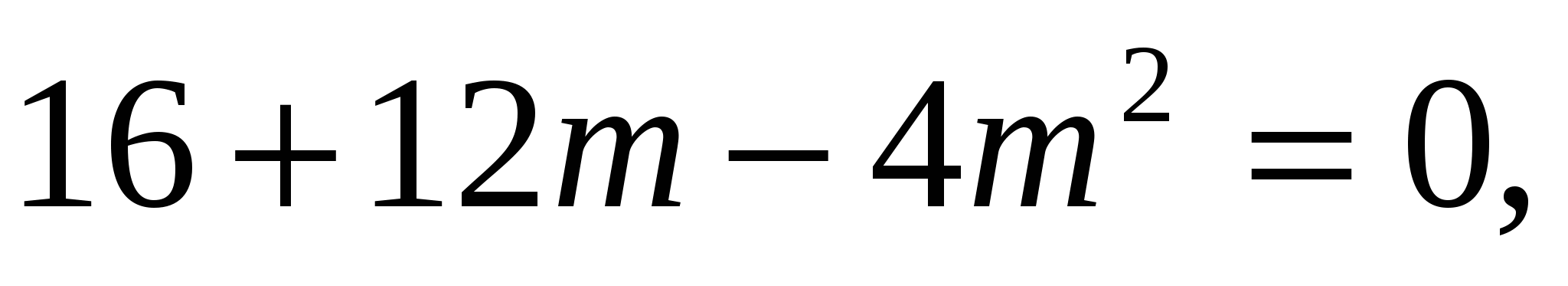 получим, что m = 4 или
получим, что m = 4 или
m = − 1. При каких значениях параметра m квадратное уравнение имеет единственный корень t = 2 > 0, следовательно, первоначальное показательное уравнение также будет иметь единственный корень.
Рассматривая второй случай, решим квадратное неравенство
( D > 0 ) : 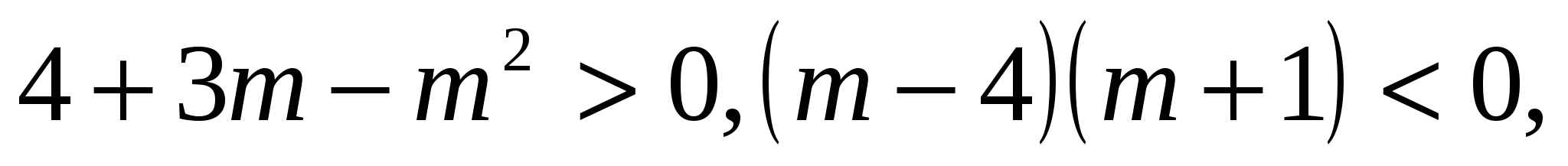
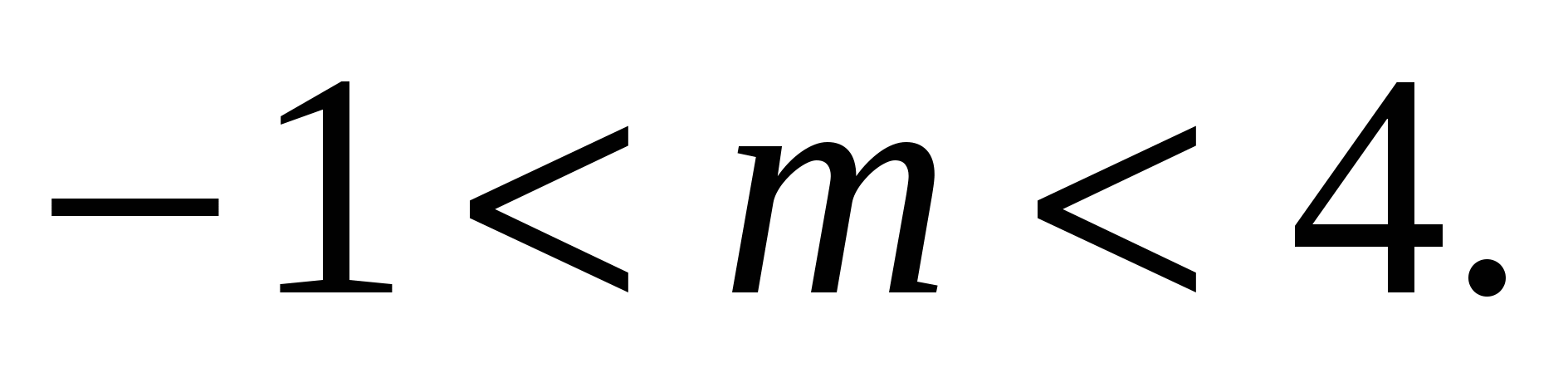
Для того чтобы один корень квадратного уравнения был положительным (при условии существования двух корней), второй должен быть отрицательным или равным нулю. Рассмотрим отдельно каждый из случаев.
Если корни имеют разные знаки, значит, их произведение отрицательно, поэтому, применяя теорему Виета, получим 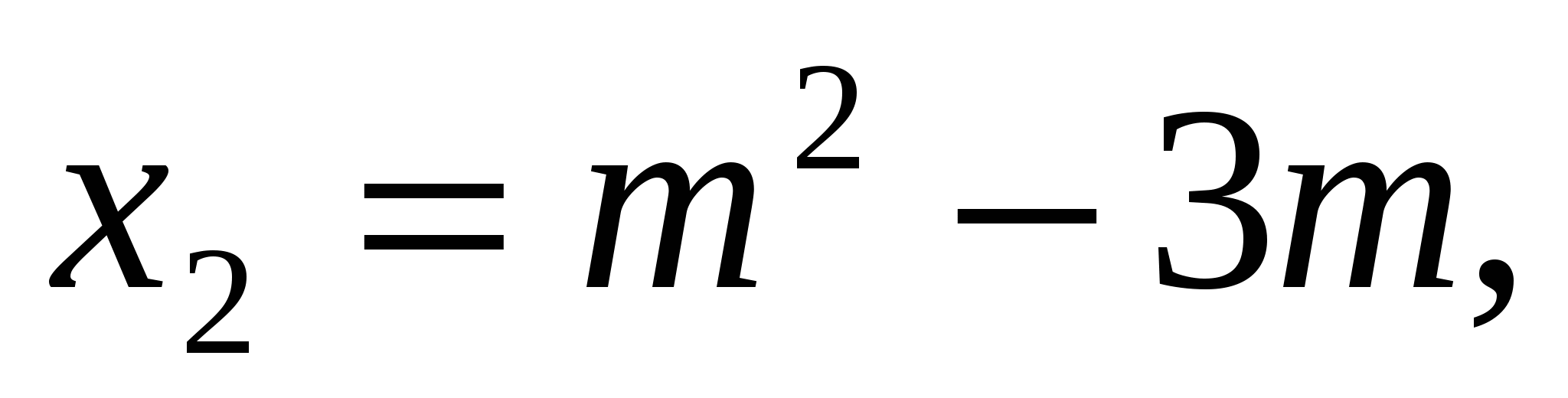
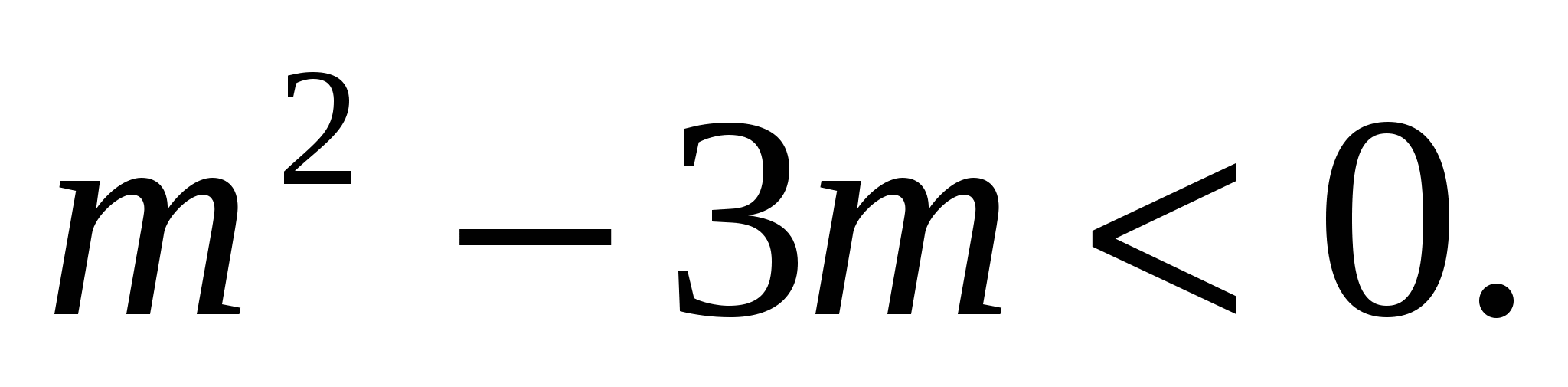 Решая последнее неравенство, получим 0 < m < 3.
Решая последнее неравенство, получим 0 < m < 3.
Если один из корней равен нулю, то, подставив его в квадратное уравнение, получим, что второй может быть найден из условия 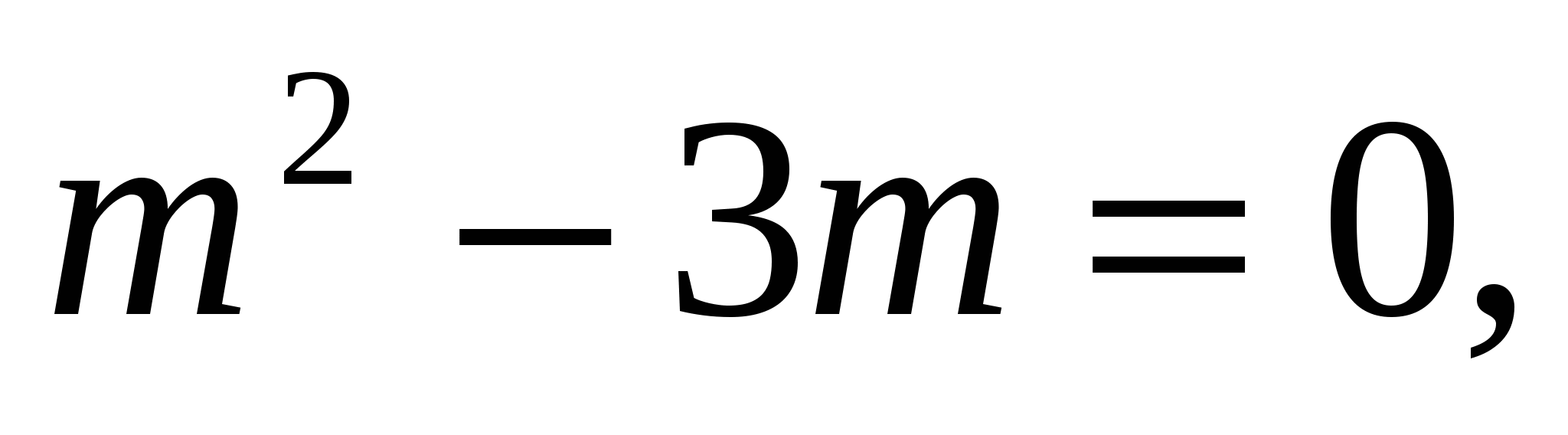
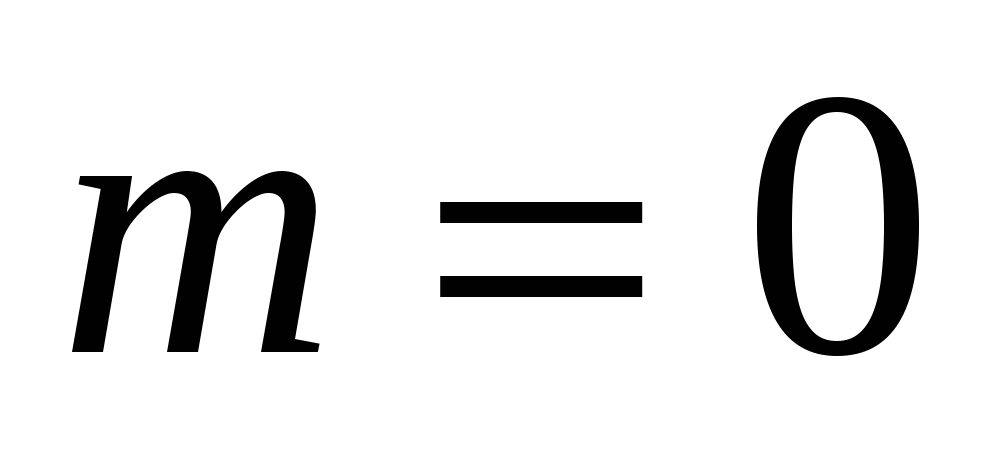 или
или 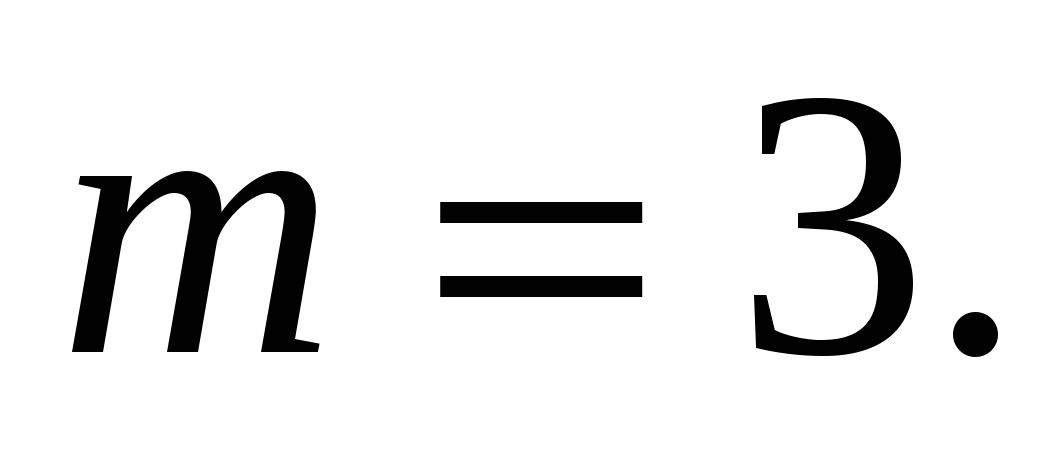
Объединяя все возможные значения параметра m, получим, что данное показательное уравнение имеет единственный корень при 
Ответ: [0; 3] ![]() {-1; 4}.
{-1; 4}.
Задание 12.
Решите неравенство 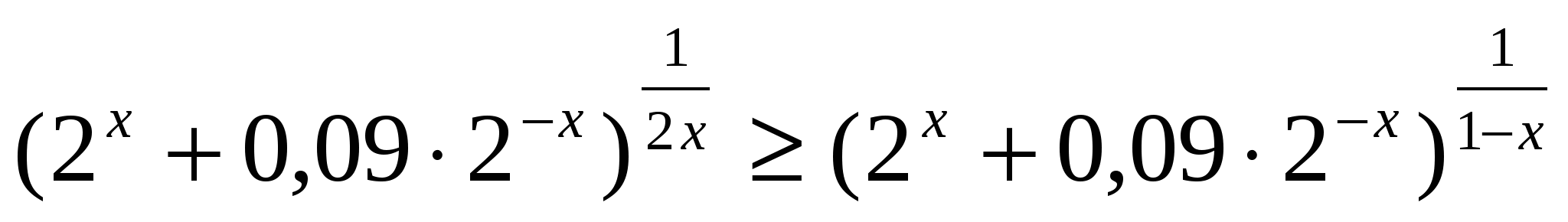 .
.
Решение. По правилу 2:
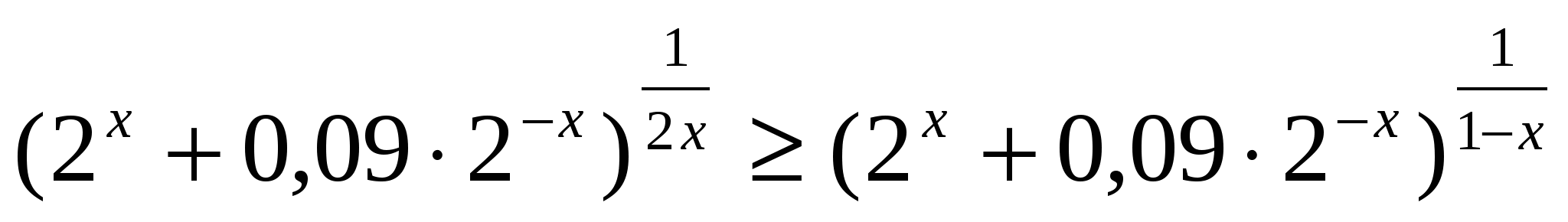
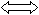
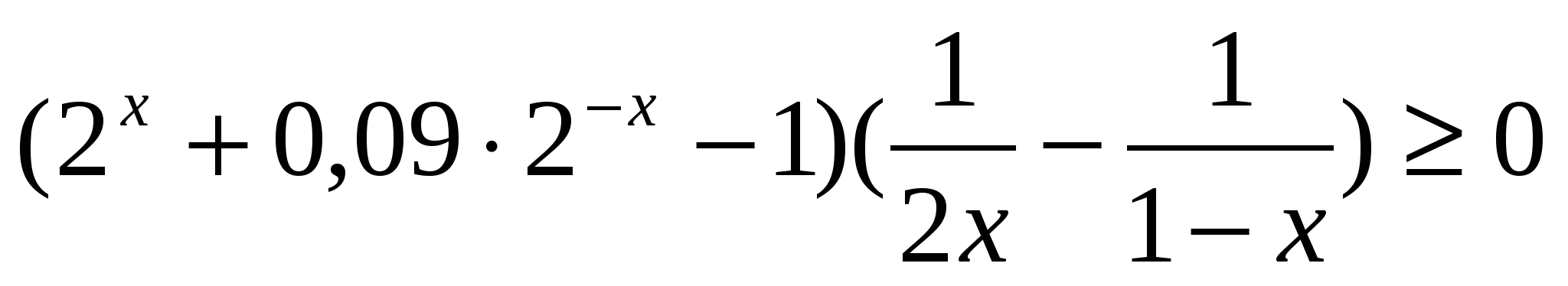
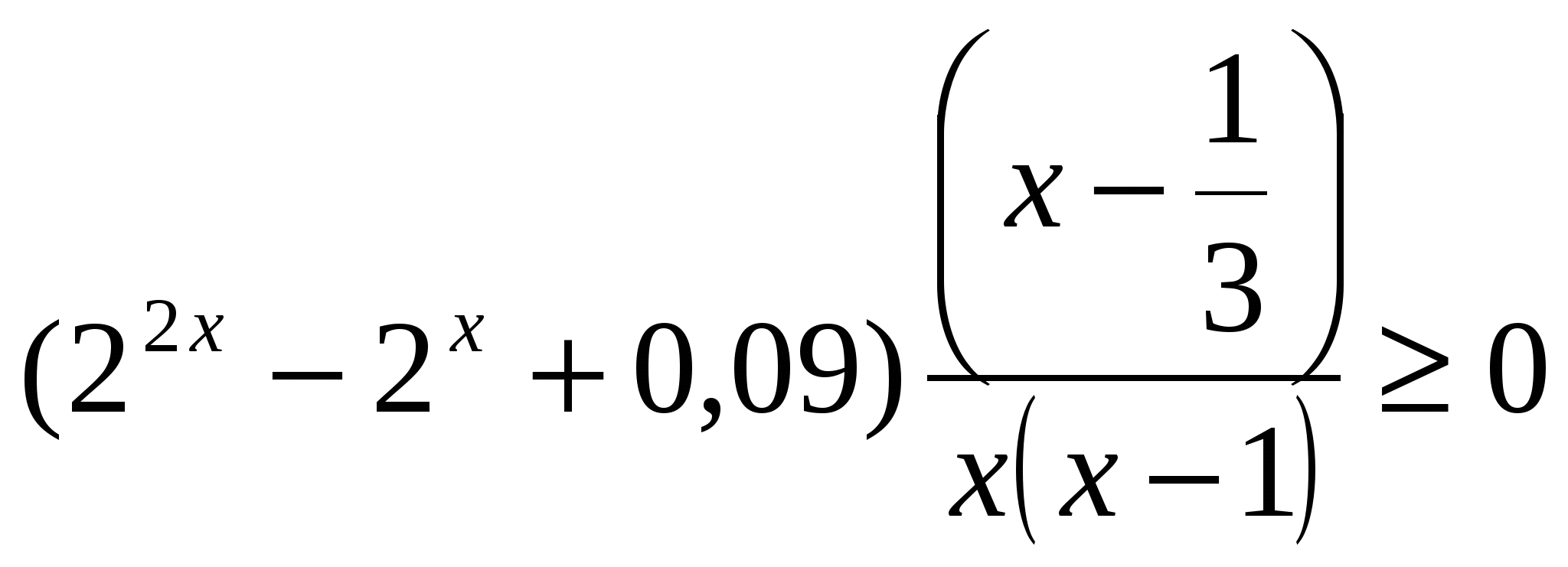
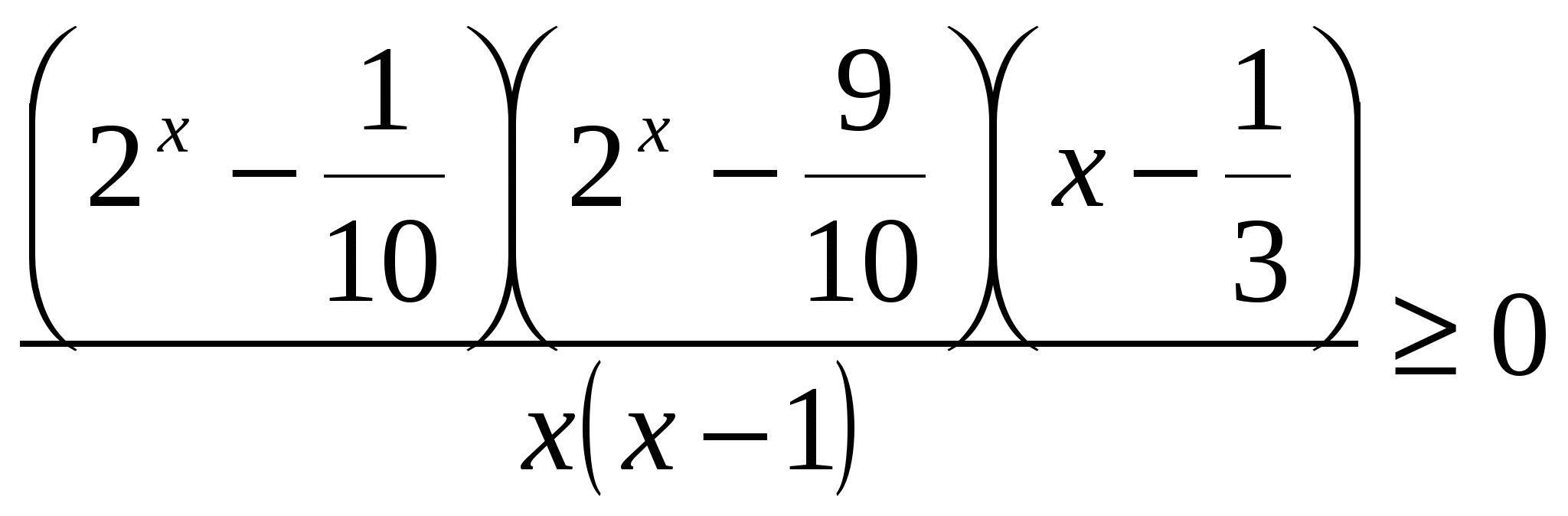
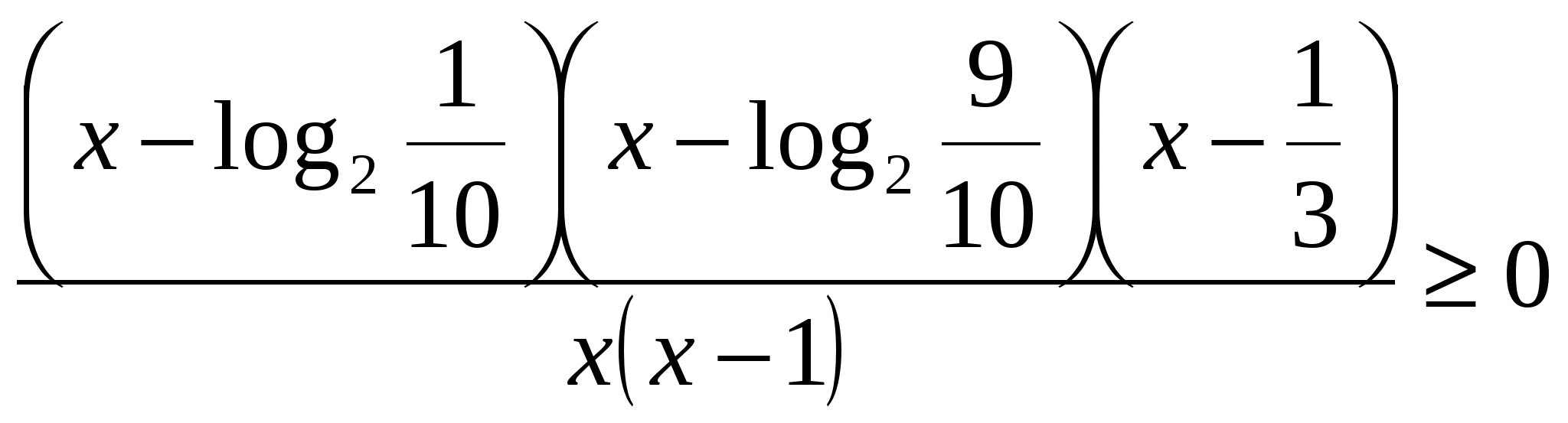 .
.
Ответ: 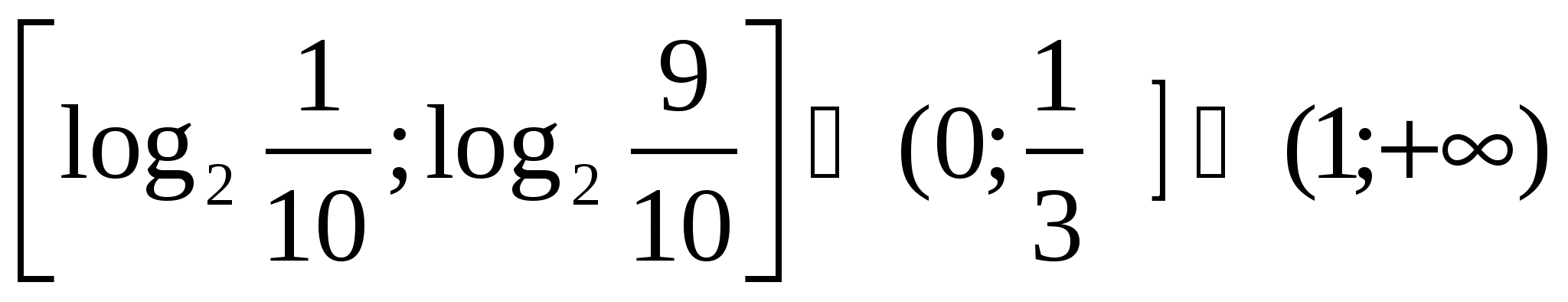
Используемая литература
-
А.Г. Мордкович. Алгебра - 10-11: Часть I учебник. / М. Мнемозина, 2009.
-
А.Г. Мордкович и др. Алгебра -10-11: Часть II задачник. / М. Мнемозина, 2009.
-
Алгебра. 10-11 класс. Методическое пособие для учителя. Мордкович А.Г. М.: 2008.
-
Алгебра. 10-11 класс. Самостоятельные работы. Александрова Л.А. 9-е изд., М. :2008.
-
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2013г.
-
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
-
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2015г.
-
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2014г.
-
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2015г.
-
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2016г.
-
Журнал математика в школе. М.: 2013
-
Учебно-методическое пособие для подготовки к ЕГЭ по математике «Решение показательных уравнений». С.С.Самарова.М.:2014.
-
Математика для учителей и учащихся. Показательные уравнения и неравенства.В.И.Тишин.М.:2013
-
fipi.ru/
-
alexlarin.net/


