- Преподавателю
- Математика
- Лекция на тему: Тригонометрическая форма комплексного числа
Лекция на тему: Тригонометрическая форма комплексного числа
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Оверченко Г.Л. |
| Дата | 26.11.2015 |
| Формат | docx |
| Изображения | Есть |
Лекция
Тригонометрическая форма комплексного числа
План
1.Геометрическое изображение комплексных чисел.
2.Тригонометрическая запись комплексных чисел.
3.Действия над комплексными числами в тригонометрической форме.
Геометрическое изображение комплексных чисел.
а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).
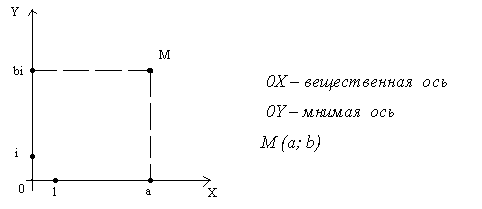
Рисунок 1
б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).
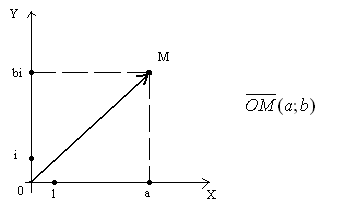
Рисунок 2
Пример 7. Постройте точки, изображающие комплексные числа: 1; - i; - 1 + i; 2 - 3i (рис.3).
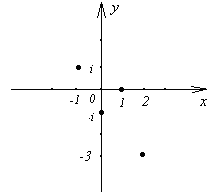
Рисунок 3
Тригонометрическая запись комплексных чисел.
Комплексное число z = a + bi можно задать с помощью радиус - вектора 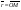 с координатами (a; b) (рис.4).
с координатами (a; b) (рис.4).
Рисунок 4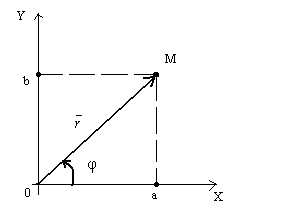
Определение. Длина вектора 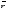 , изображающего комплексное число z, называется модулем этого числа и обозначается
, изображающего комплексное число z, называется модулем этого числа и обозначается 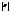 или r.
или r.
Для любого комплексного числа z его модуль r = | z | определяется однозначно по формуле 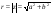 .
.
Определение. Величина угла между положительным направлением действительной оси и вектором 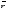 , изображающим комплексное число, называется аргументом этого комплексного числа и обозначается Аrg z или φ.
, изображающим комплексное число, называется аргументом этого комплексного числа и обозначается Аrg z или φ.
Аргумент комплексного числа z = 0 не определен. Аргумент комплексного числа z ≠ 0 - величина многозначная и определяется с точностью до слагаемого 2πк (к = 0; - 1; 1; - 2; 2; …): Arg z = arg z + 2πк, где arg z - главное значение аргумента, заключенное в промежутке (-π; π], то есть -π < arg z ≤ π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0; 2π)).
a = r · cos φ, b = r · sin φ.
Следовательно, комплексное число z = a + bi можно записать в виде: z = r · cos φ + i r · sin φ или z = r · (cos φ + i sin φ).
Такая запись комплексного числа называется тригонометрической формой комплексного числа.
Пример 8. Представить в тригонометрической форме комплексное число 1- i.
a = 1, b = -1.
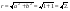
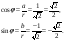
φ = 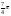 .
.
1 - i = 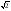 (cos
(cos 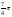 + i sin
+ i sin 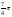 ).
).
Действия над комплексными числами в тригонометрической форме.
1) Умножение.
Пусть два числа заданы и в алгебраической и в тригонометрической формах: z1 = a1 + b1i = r1 (cos φ1 + i sin φ1),
z2 = a2 + b2i = r2 (cos φ2 + i sin φ2).
На основании исходного определения правила умножения и формулы косинуса и синуса суммы получаем:
z1· z2 = r1 · r2 (cos (φ1 + φ2) + i sin (φ1 + φ2)); r1 · r2>0.
Умножение комплексных чисел в тригонометрической форме обладает следующими свойствами:
1º. Коммутативность: z1z2 = z2z1
2º. Ассоциативность: (z1z2) z3 = z1 (z2 z3).
Пример 9. Найти произведение комплексных чисел
z1 = 2cos 50º + 2 i sin 50º, z2 = cos 40º + i sin 40º.
Решение. Тригонометрические формы этих чисел имеют вид:
z1 = 2 · (cos 50º + i sin 50º), z2 = 1· (cos 40º + i sin 40º). Тогда
z1 · z2 = 1· 2 · (cos (50º + 40º) + i sin (50º + 40º)) = 2(cos 90º + i sin 90º) = = 2(0 + i) = 2i.
2) Деление комплексных чисел в тригонометрической форме.
Деление в поле комплексных чисел на числа, отличные от нуля, всегда выполнимо. Если числа z1 и z2 заданы в тригонометрической форме z1 = r1 (cos φ1 + i sin φ1), z2 = r2 (cos φ2 + i sin φ2), причем z1 ≠ 0, то комплексное число 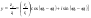 является частным чисел z1 и z2 (то есть z1y = z2).
является частным чисел z1 и z2 (то есть z1y = z2).
Пример 10. Найти частное комплексных чисел z1 = 2cos50º + 2i sin50º, z2 = cos40º + i sin40º.
Решение. Тригонометрические формы этих чисел имеют вид:
z1 = 2 · (cos50º + i sin50º), z2 = 1· (cos40º + i sin40º).
Тогда 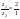 (cos (50º - 40º) + i sin (50º - 40º)) = 2(cos10º + i sin10º).
(cos (50º - 40º) + i sin (50º - 40º)) = 2(cos10º + i sin10º).
3) Возведение в степень.
Определение. n - ой степенью комплексного числа z называется комплексное число, получающееся в результате умножения числа z самого на себя n раз.
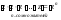
Число z называется основанием степени, а натуральное число n - показателем степени.
Возвести комплексное число в n - ую степень можно по формуле: z n = (r n) [cos (nφ) + i sin (nφ)].
Эту формулу при r =1 часто называют формулой Муавра:
(cos φ + i sin φ) n = cos (nφ) + i sin (nφ), n N.
Пример 11. Вычислите (1 + i)100.
Запишем комплексное число 1 + i в тригонометрической форме.
a = 1, b = 1.
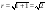 .
.
cos φ = 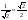 , sin φ =
, sin φ = 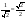 , φ =
, φ = 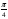 .
.
(1+i)100 = [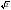 (cos
(cos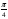 + i sin
+ i sin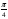 )]100= (
)]100= (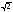 )100 (cos
)100 (cos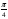 ·100 + i sin
·100 + i sin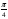 ·100) = = 250(cos 25π + i sin 25π) = 250(cos π + i sin π) = - 250.
·100) = = 250(cos 25π + i sin 25π) = 250(cos π + i sin π) = - 250.
4) Извлечение квадратного корня из комплексного числа.
При извлечении квадратного корня из комплексного числа a + bi имеем два случая:
если b > о, то 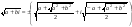 ;
;
если b < о, то 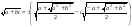 .
.
Так как из комплексного числа всегда можно извлечь квадратный корень, то любое квадратное уравнение всегда будет иметь решения во множестве комплексных чисел. Решения квадратного уравнения ах2 + bх + с = 0 можно найти по известной формуле:
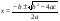 .
.
Пример 12. Вычислите 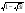 .
.
Так как b < о, то воспользуемся формулой
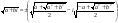
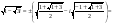
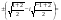
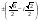 .
.
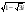 =
= 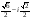 ,
,
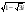 =
= 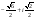 .
.
Упражнения
1.Записать в тригонометрической форме число 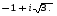
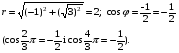
Т.к.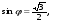 то
то 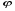 нужно взять равным
нужно взять равным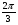 .Значит,
.Значит,
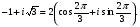
2. Записать в тригонометрической форме число - 1 - і.
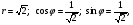
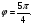 Тогда
Тогда
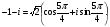
3. Записать в тригонометрической форме число 1.Имеем 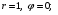
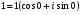 , или
, или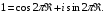
4.Выполнить действия
1)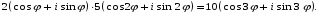
5. Представить следующие комплексные числа в тригонометрическом виде:
1) 1, 1, i, i;
2) z = 3 3i;
3) 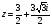 .
.
6. Даны числа
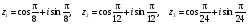 .
.
Вычислить: 1) 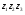 ; 2)
; 2) 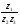 ; 3)
; 3) 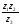 ; 4)
; 4) 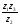 .
.
Вопросы для самопроверки:
1.Дать определение модуля комплексного числа. Каков его геометрический смысл?
2. Комплексное число умножили на 2. изменился модуль этого числа?
3. Почему равны модули чисел: i; -i; 1; 1; 0?
4. Что такое аргумент комплексного числа?
5. Как определить главное значение аргумента числа z = a + bi?
6. Могут ли аргументом комплексного числа быть одновременно углы а и -а?
7. Найти геометрическое место точек плоскости, изображают комплексные числа с одинаковыми модулями.
8.Как размещаются на плоскости точки, изображающие комплексные числа с одинаковыми аргументами?
9. Как представить комплексное число вида а + bi в тригонометрической форме? Как найти модуль и аргумент этого числа?
10. Как перейти от тригонометрической формы комплексного числа в алгебраической?
11. Вывести правила умножения и деления комплексных чисел, записанных в тригонометрической форме.
12. По какому правилу выполняют действие возведения в степень комплексных чисел, записанных в тригонометрической форме?


