- Преподавателю
- Математика
- По математике на тему Формула Пика
По математике на тему Формула Пика
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Мягкова М.Г. |
| Дата | 17.08.2015 |
| Формат | doc |
| Изображения | Есть |
Формула Пика
Содержание
1. Введение
2. Формула Пика. Доказательство I.
Доказательство II.
Доказательство Ш.
3. Задачи.
4. Формула площади многоугольника через координаты вершин.
5. Задачи.
6. Литература
Формула Пика.
1. Введение.
В истории черпаем мы мудрость,
в поэзии - остроумие,
в математике - проницательность.
Ф. Бэкон
Сюжет будет разворачиваться на обычном листке клетчатой бумаги.
Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток - узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдём его площадь.
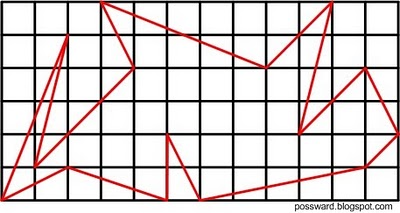
Искать её можно по - разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить.
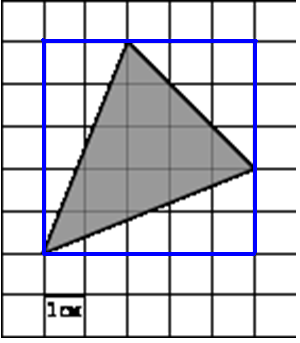
Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.
Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причудливо? Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.
2. Формула Пика.
Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + 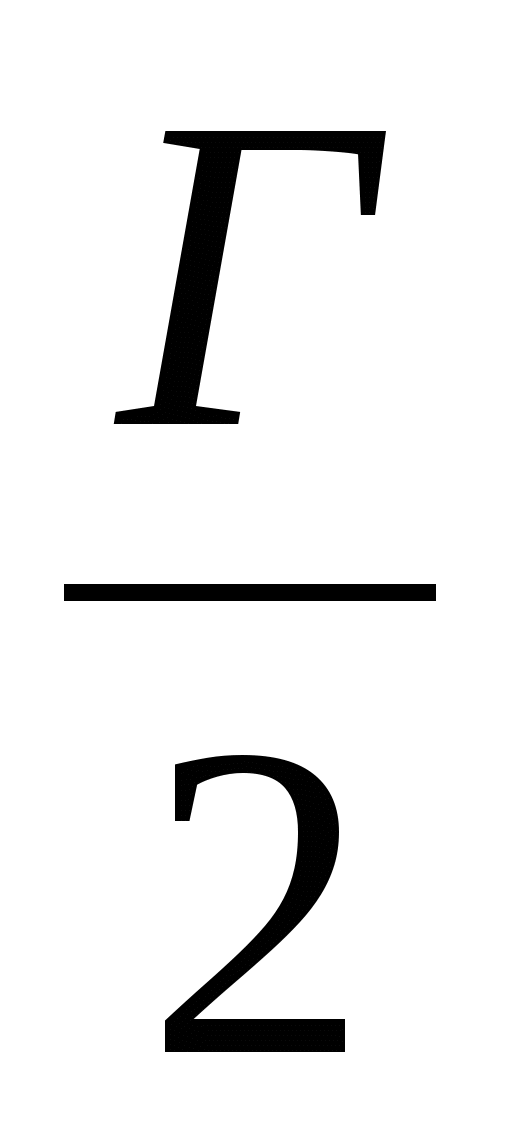 - 1 (формула Пика).
- 1 (формула Пика).
Доказательство I.
Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.
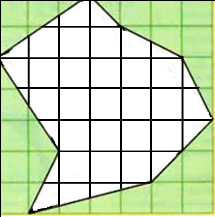
Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.
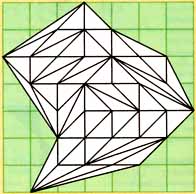
Обозначим:
n - число сторон многоугольника,
m - количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,
В - число узлов внутри многоугольника,
Г - число узлов на сторонах, включая вершины.
Площади всех этих треугольников одинаковы и равны 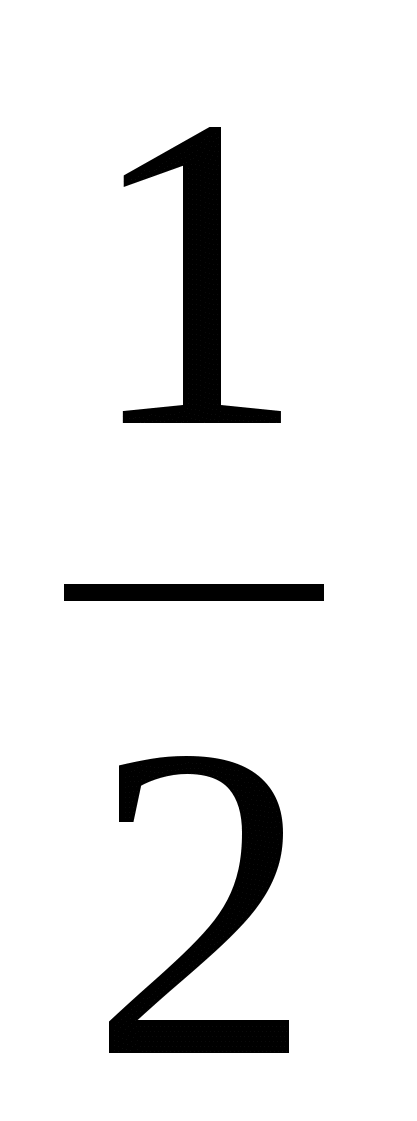 .
.
Следовательно, площадь многоугольника равна 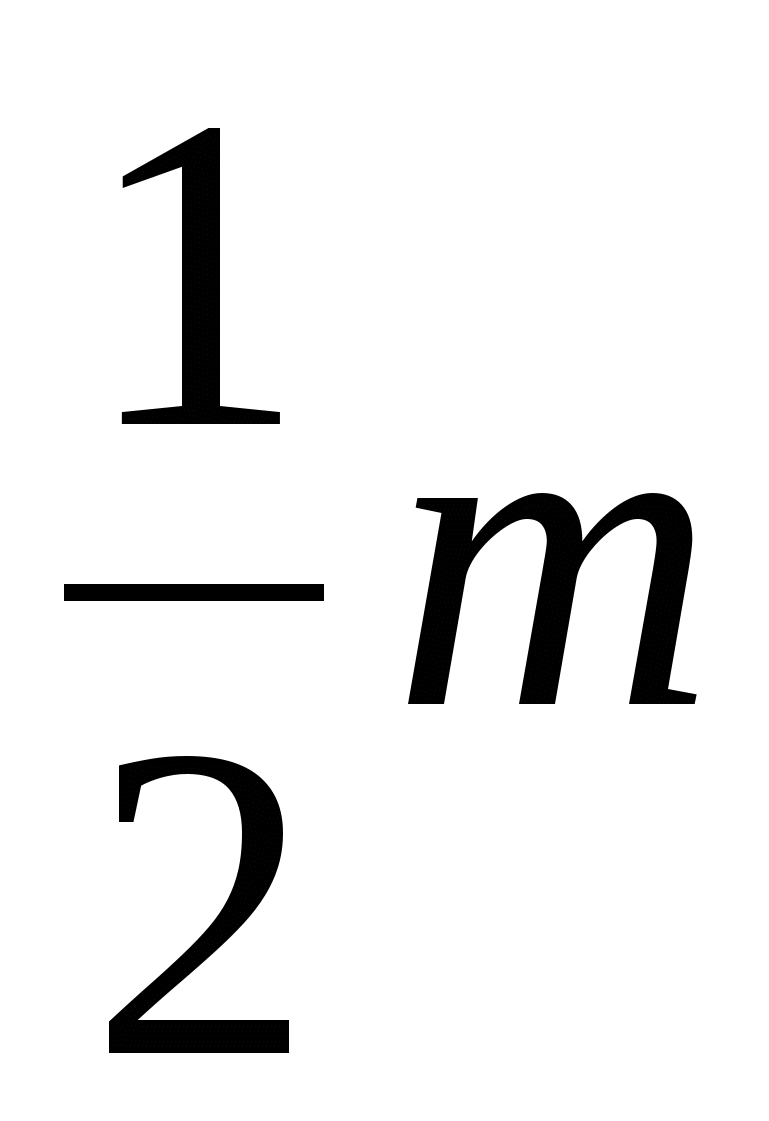 .
.
Общая сумма углов всех треугольников равна 1800m.
Теперь найдём эту сумму другим способом.
Сумма углов с вершиной в любом внутреннем узле составляет 3600.
Тогда сумма углов с вершинами во всех внутренних узлах равна 3600 В.
Общая сумма углов при узлах на сторонах, но не в вершинах равна 1800 (Г - n).
Сумма углов при вершинах многоугольника равна 1800 (n - 2) .
Общая сумма углов всех треугольников равна 3600 В + 1800 (Г - n) + 1800 (n - 2).
Таким образом, 1800 m = 3600 В + 1800 (Г - n) + 1800 (n - 2),
1800 m = 3600 В + 1800 Г - 1800 n + 1800n - 1800 ·2,
1800 m = 3600 В + 1800 Г- 3600 ,
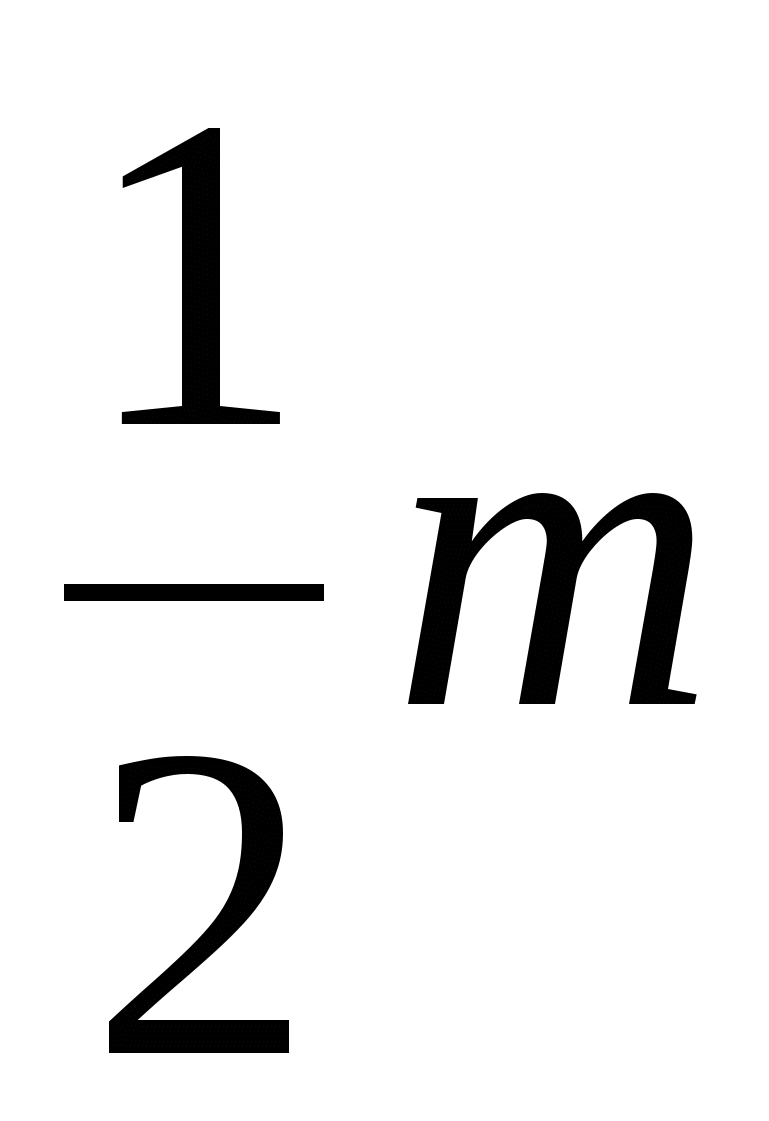 = В +
= В + 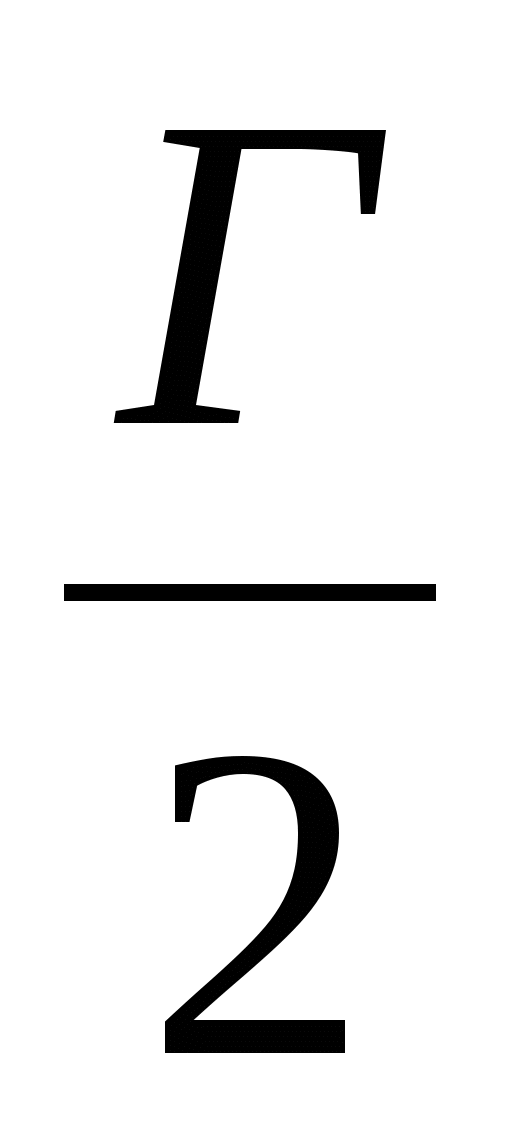 - 1 ,
- 1 ,
откуда получаем выражение для площади S многоугольника:
S = В + 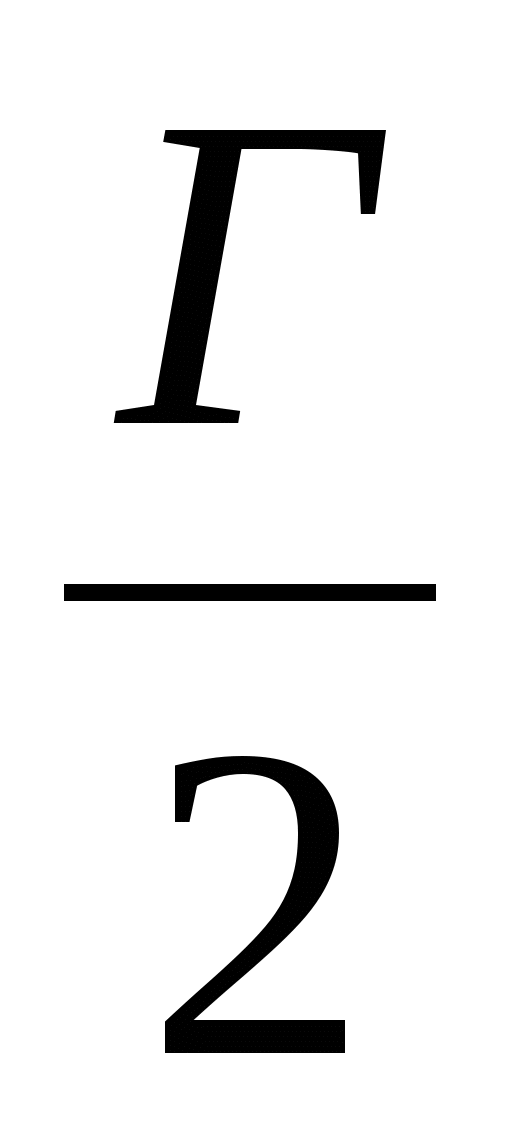 - 1 ,
- 1 ,
известное как формула Пика.
На рисунке: В = 24, Г = 9, следовательно, S = 24 + 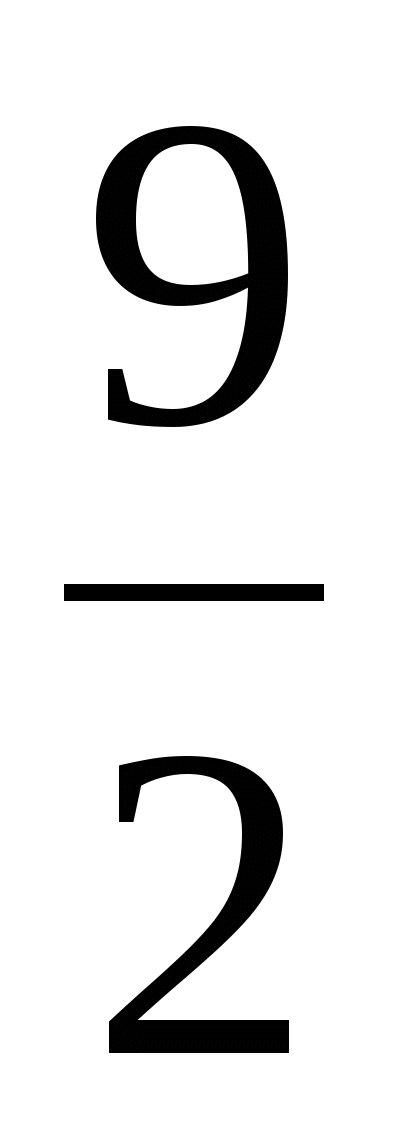 - 1 = 27,5.
- 1 = 27,5.
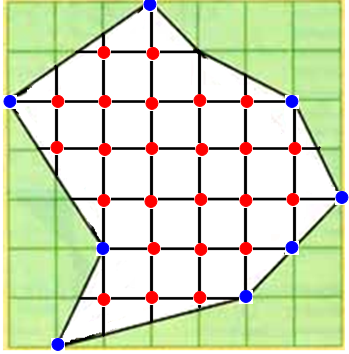
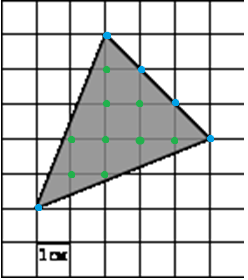
Найдём площадь первого многоугольника по формуле Пика:
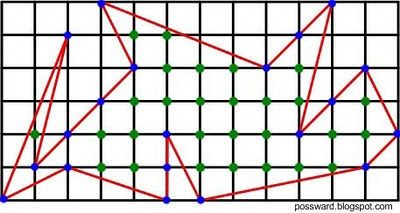
В = 28 (зеленые точки);
Г = 20 (синие точки).
Получаем, S = ![]() = 37 кв.ед.
= 37 кв.ед.
Доказательство II.
Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) = 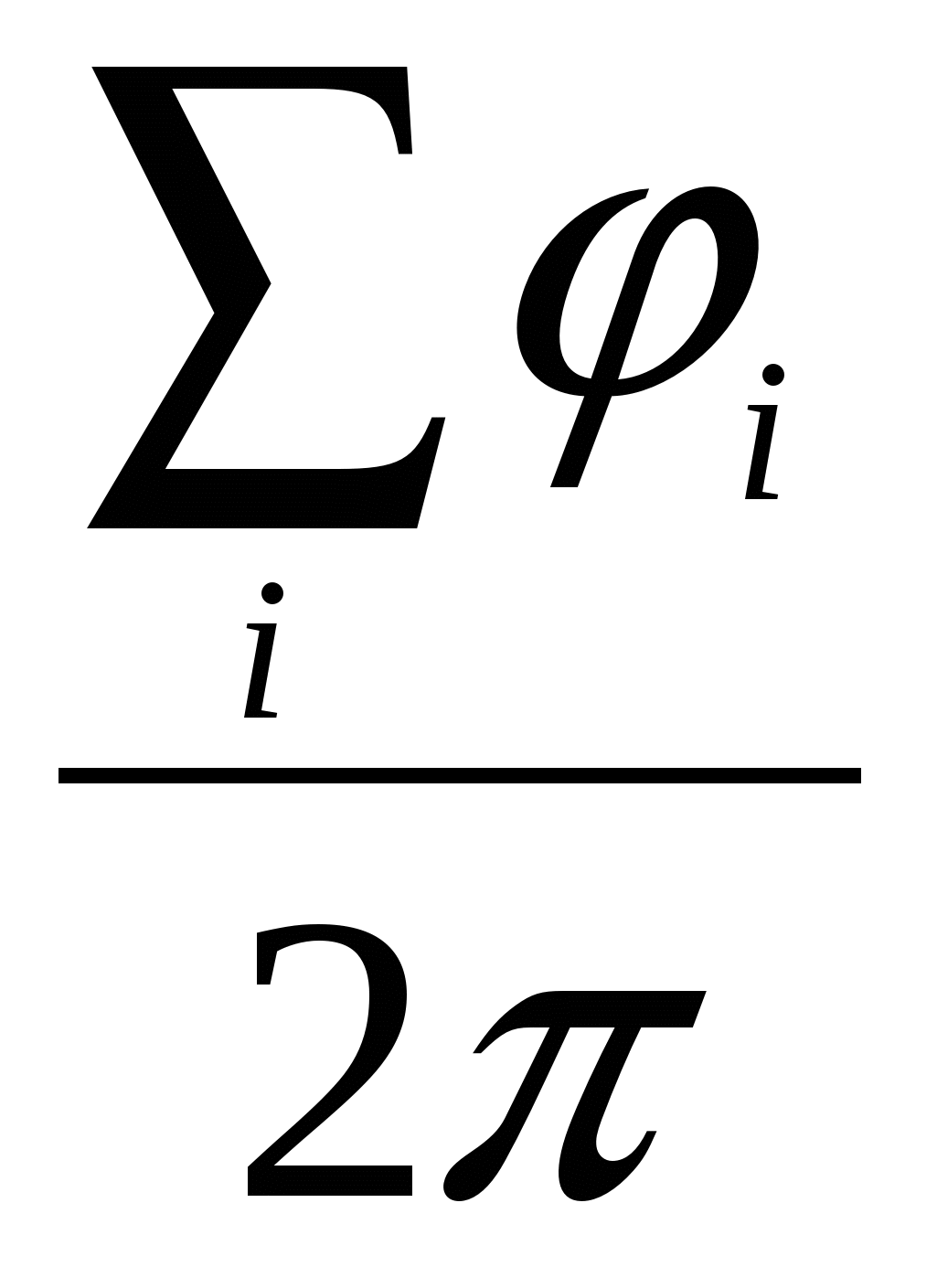 , где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол
, где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол  определяется следующим образом:
определяется следующим образом:  =
= 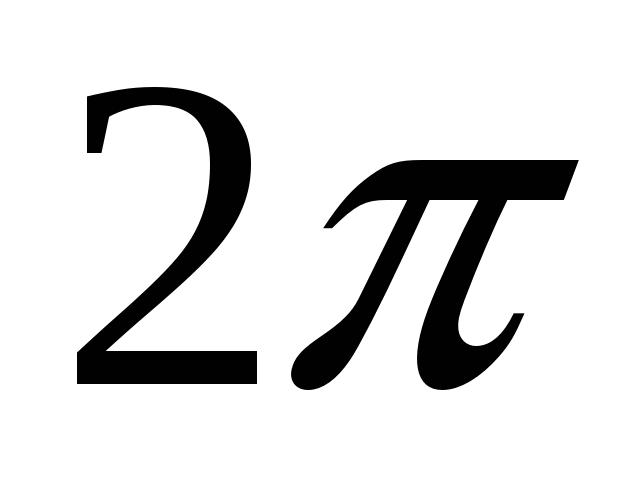 для внутренней точки многоугольника,
для внутренней точки многоугольника, ![]() =
=  для граничной точки, отличной от вершины, и
для граничной точки, отличной от вершины, и  - угол при вершине, если данный узел - вершина. Легко видеть, что f (M) =
- угол при вершине, если данный узел - вершина. Легко видеть, что f (M) = 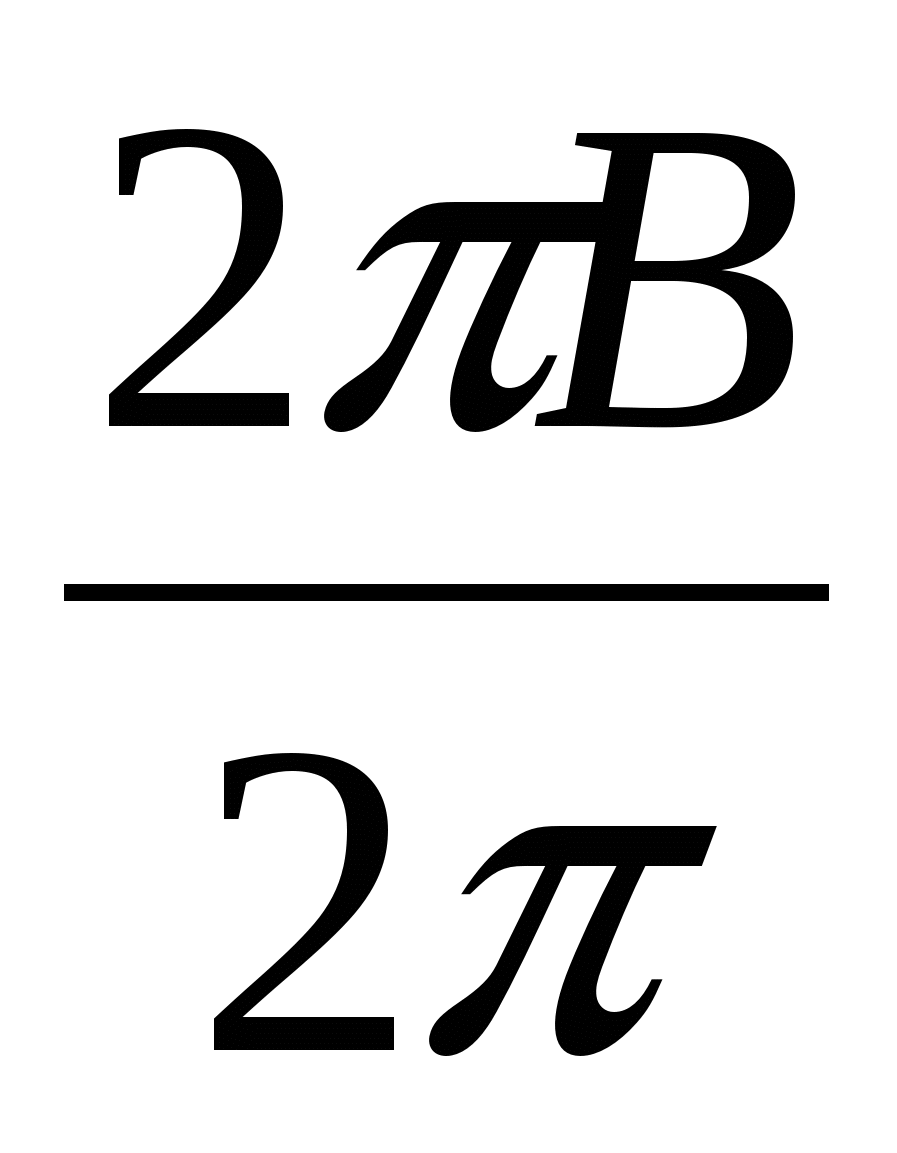 +
+ 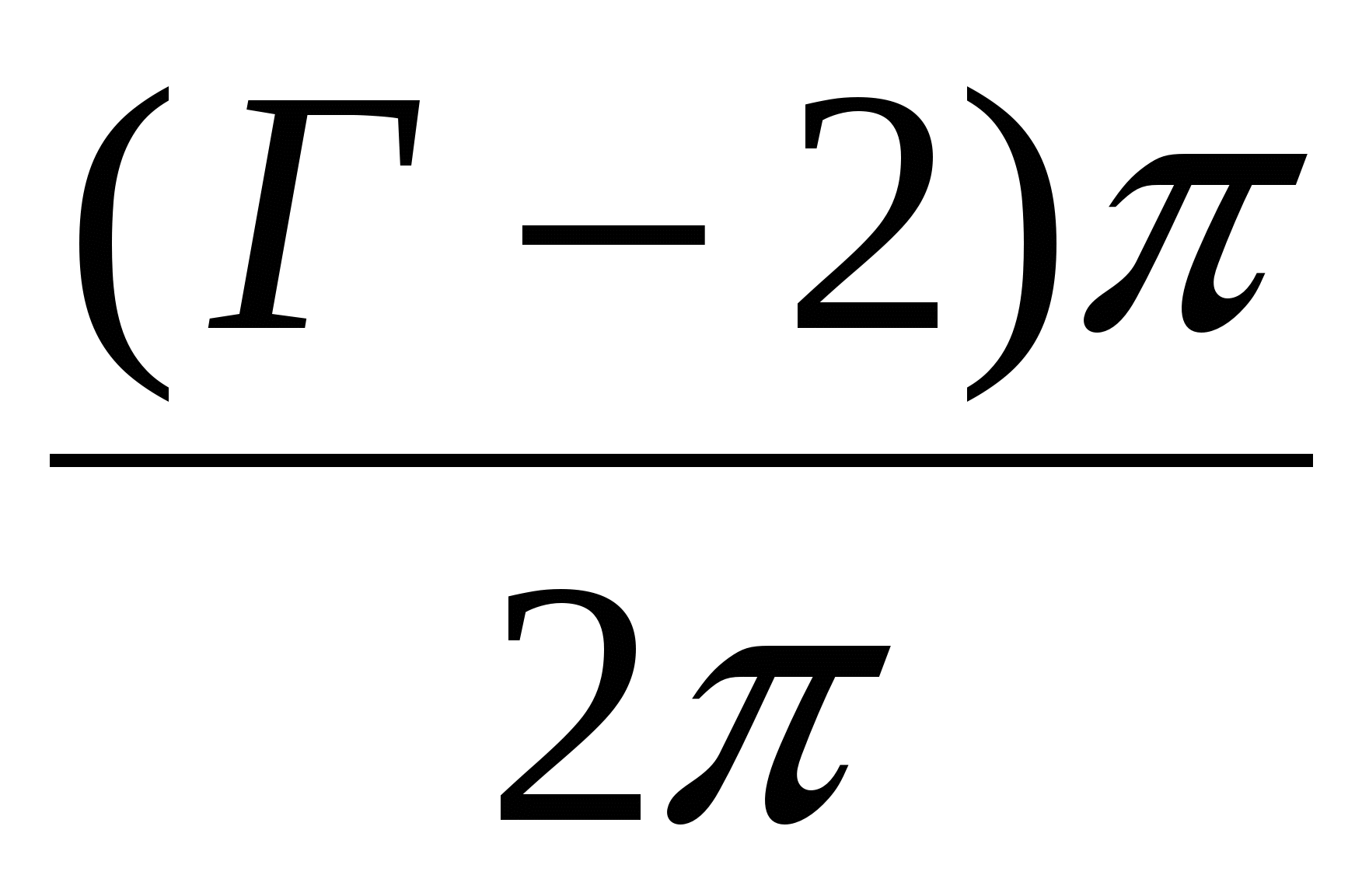 = В +
= В + 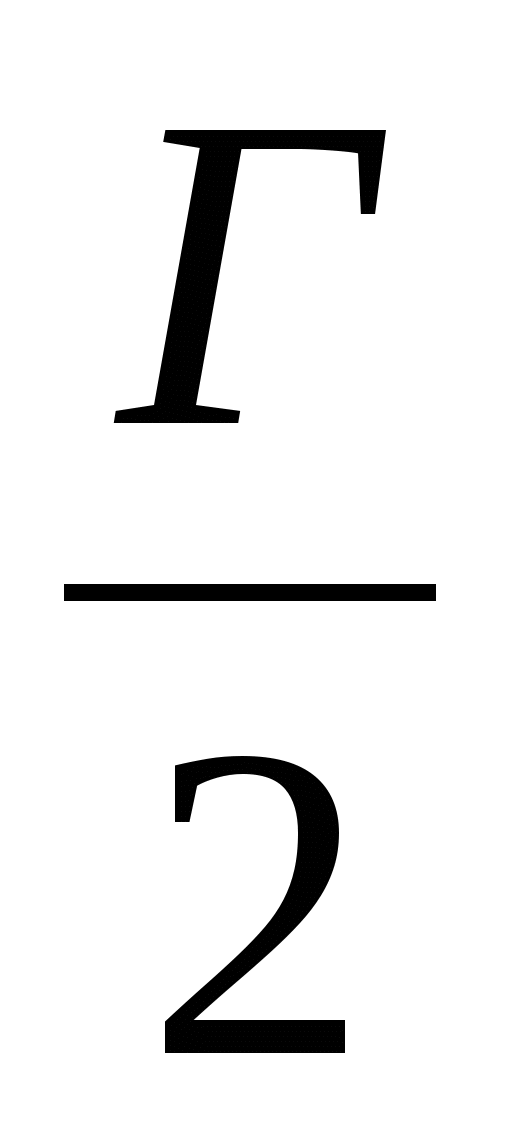 - 1. Остаётся проверить, что число f (M) равно площади многоугольника M.
- 1. Остаётся проверить, что число f (M) равно площади многоугольника M.
Пусть многоугольник M разрезан на многоугольники M1 и M2 с вершинами в узлах решетки. Тогда f (M) = f (M1) + f (M2), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M1 и M2, то она верна и для третьего.
Если M - прямоугольник со сторонами p и q, направленными по линиям решетки, то
f (M) = (p - 1)(q - 1) + 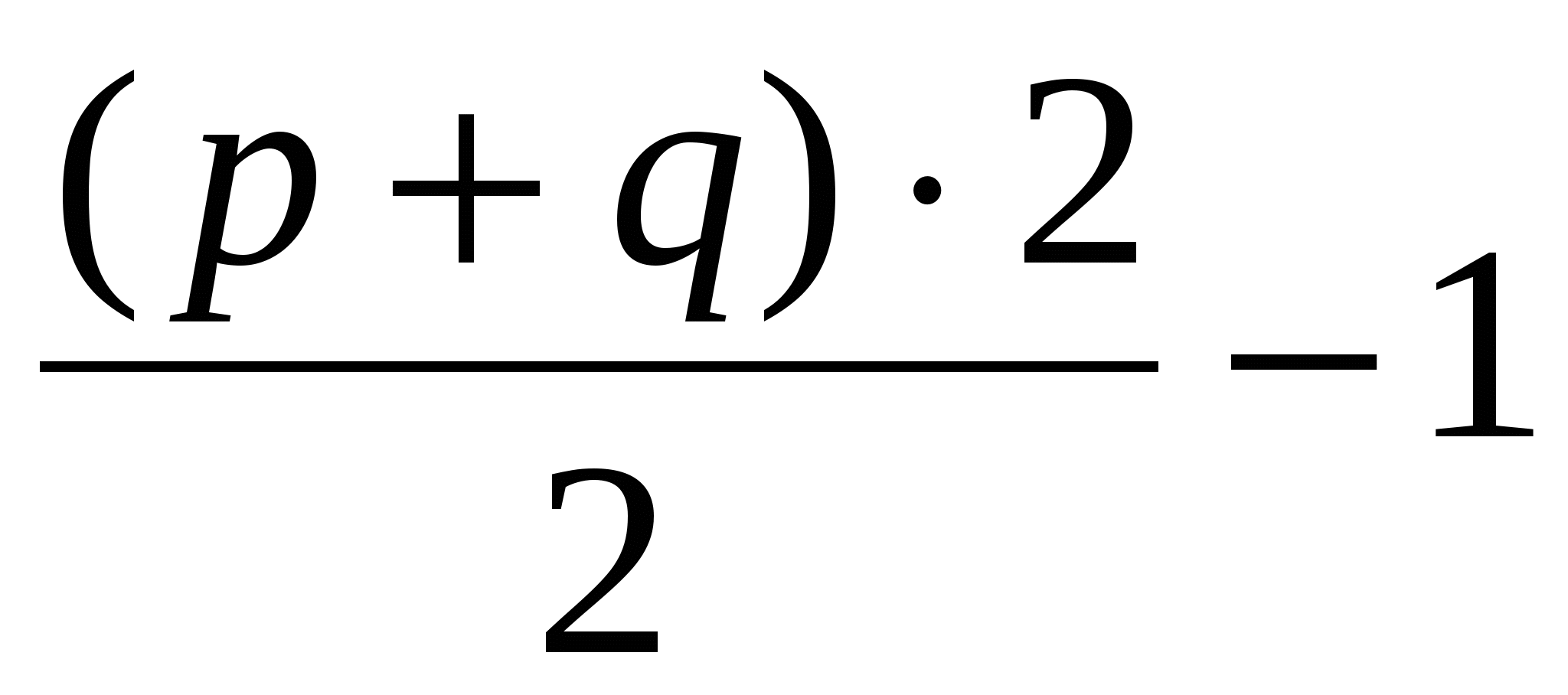 = pq.
= pq.
В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M1 и M2 и воспользовавшись тем, что f (M) = f (M1) + f (M2) и f (M1) = f (M2), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.
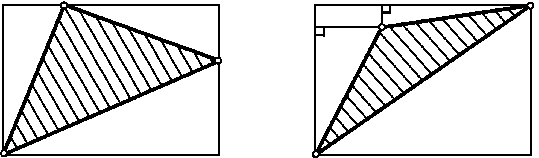
Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.
Доказательство Ш.
Связь между площадью фигуры и количеством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.
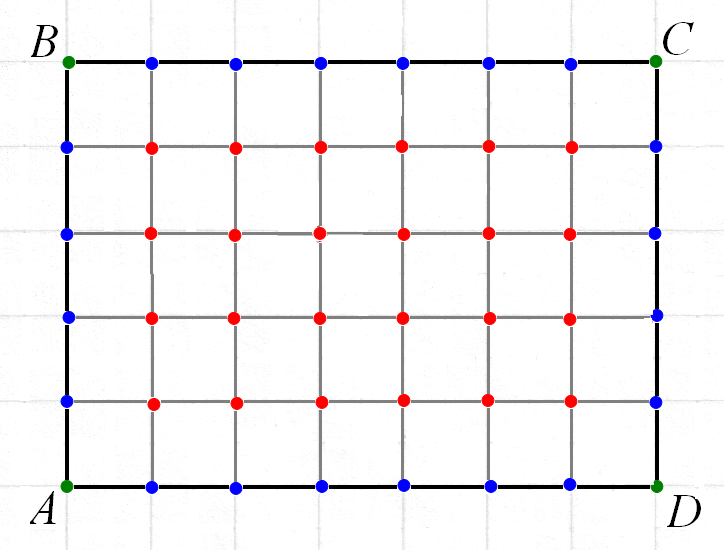
Пусть ABCD - прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки.
Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г - количество узлов на его границе. Сместим сетку на пол клетки вправо и полклетки вниз.
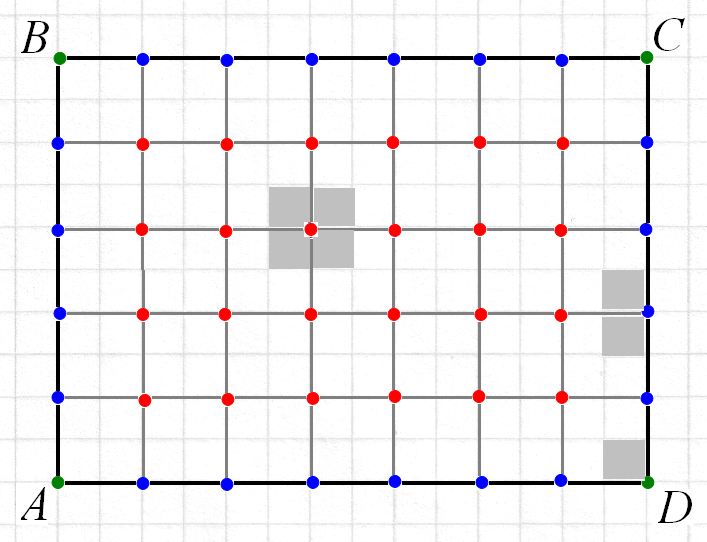
Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г - 4 граничных неугловых узла - половину клетки, а каждая из угловых точек - четверть клетки. Поэтому площадь прямоугольника S равна
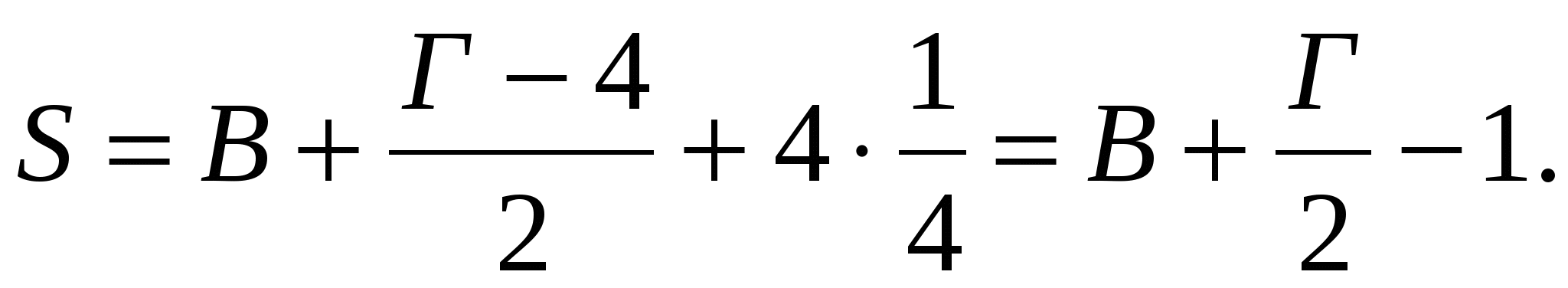
Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу 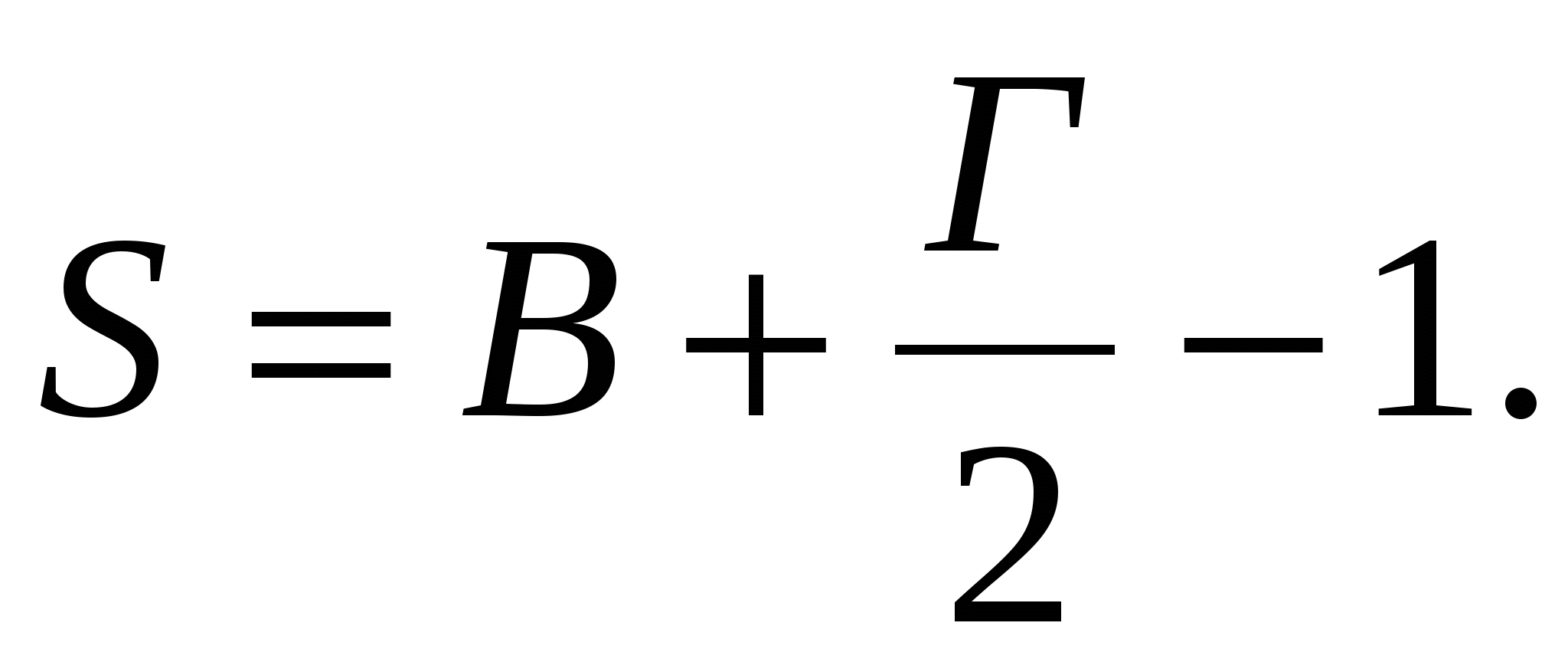
Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.
Обозначим через Sм площадь многоугольника М с вершинами в узлах, а через Пм - величину 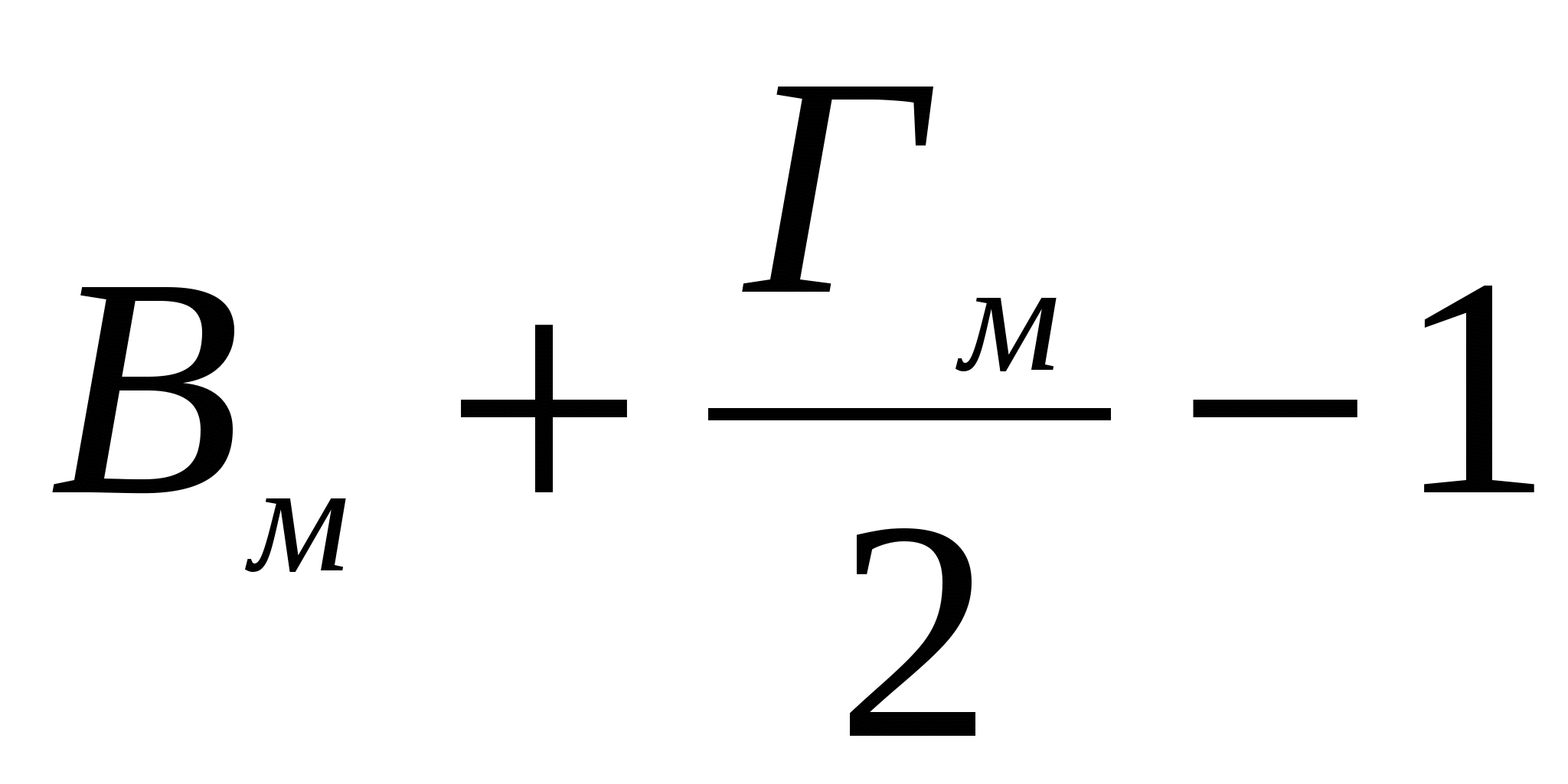 , где Вм - число узлов внутри М, а Гм - число узлов на границе. Тогда формулу Пика можно записать в виде
, где Вм - число узлов внутри М, а Гм - число узлов на границе. Тогда формулу Пика можно записать в виде 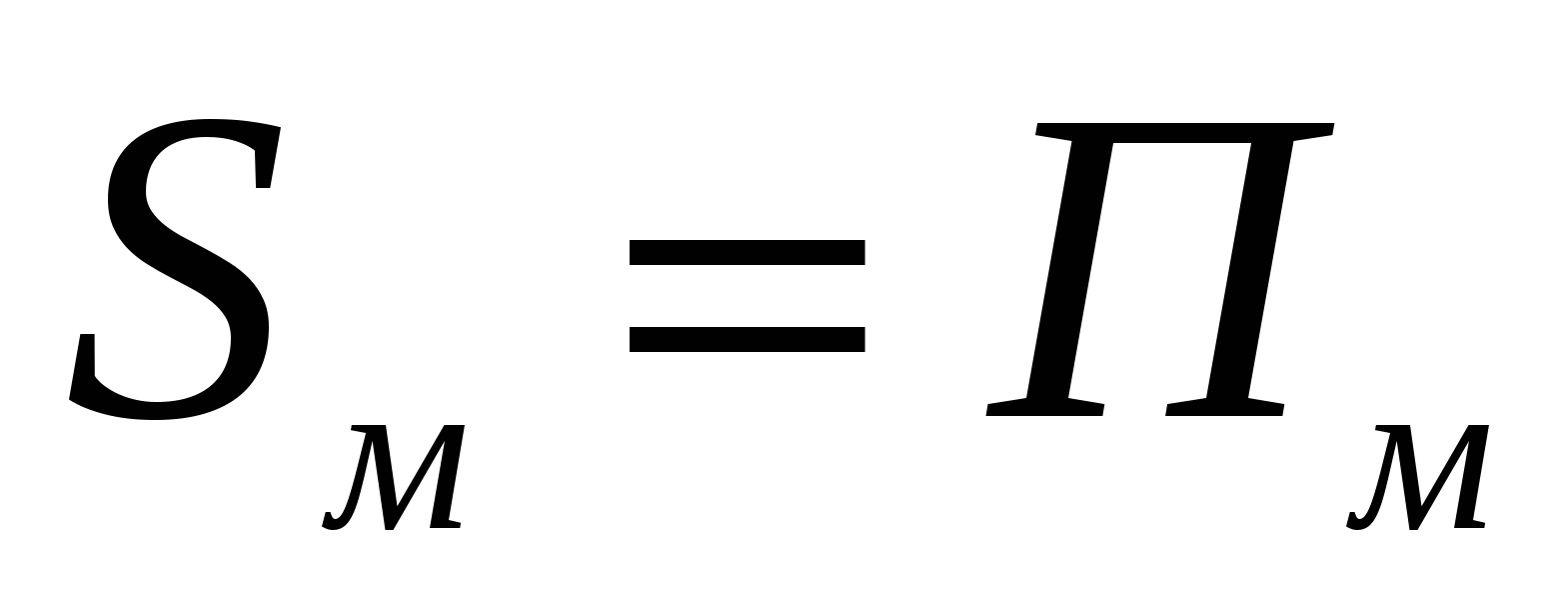 .
.
Доказательство формулы разобьем на несколько шагов.
Шаг 1.
Если многоугольник М с вершинами в узлах сетки разрезан на 2 многоугольника М1 и М2, также имеющих вершины только в узлах сетки, то 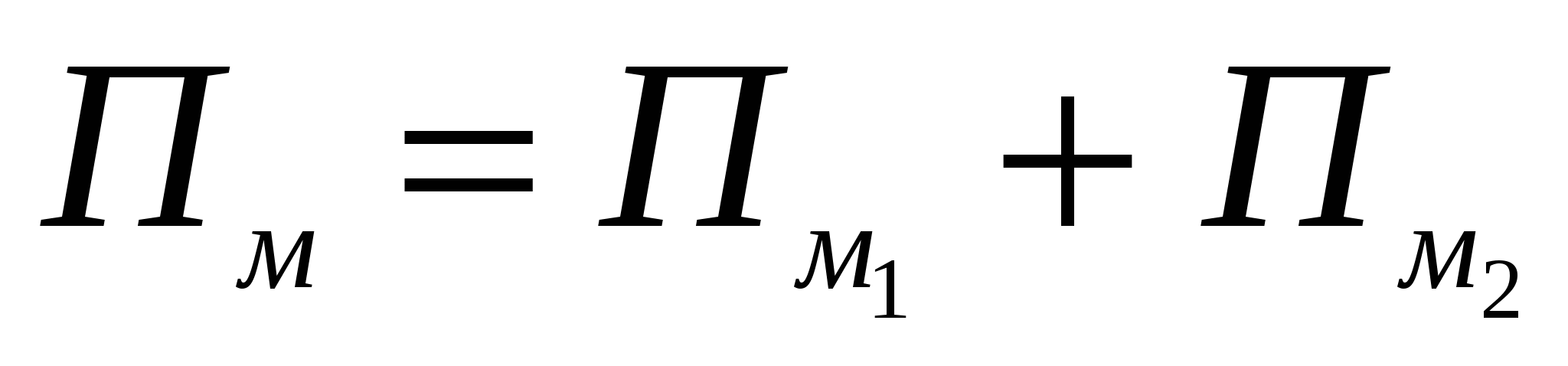 . Пусть многоугольник М разрезан на многоугольники М1 и М2 с вершинами в узлах отрезком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.
. Пусть многоугольник М разрезан на многоугольники М1 и М2 с вершинами в узлах отрезком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.
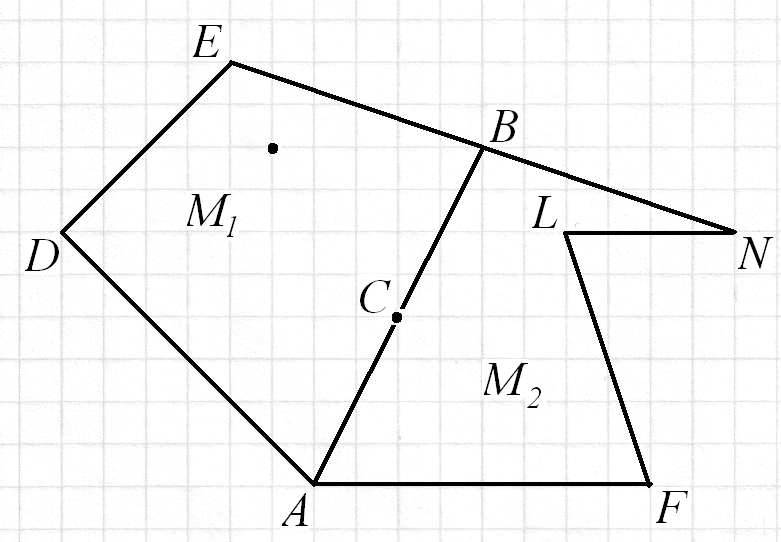
Если такой узел лежит между А и В (например, С), то для многоугольника М он внутренний, а для многоугольников М1 и М2 - граничный. Поэтому его вклад в Пм равен 1, а в каждое из выражений 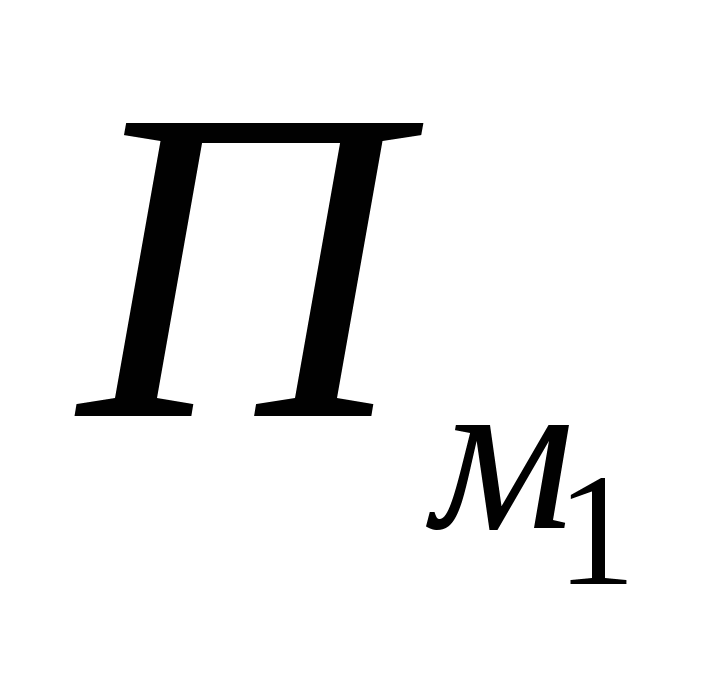 и
и 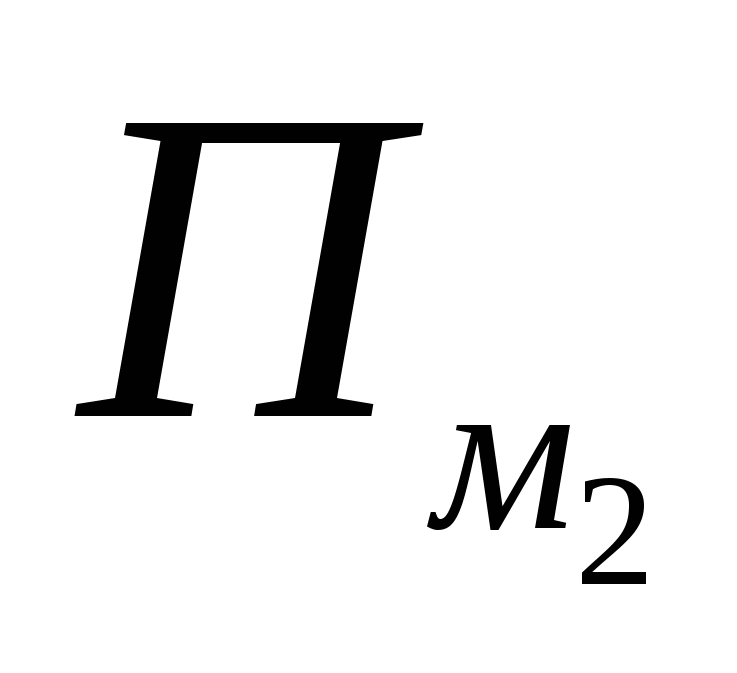 - по 0,5, то есть вклады такого узла в Пм и
- по 0,5, то есть вклады такого узла в Пм и 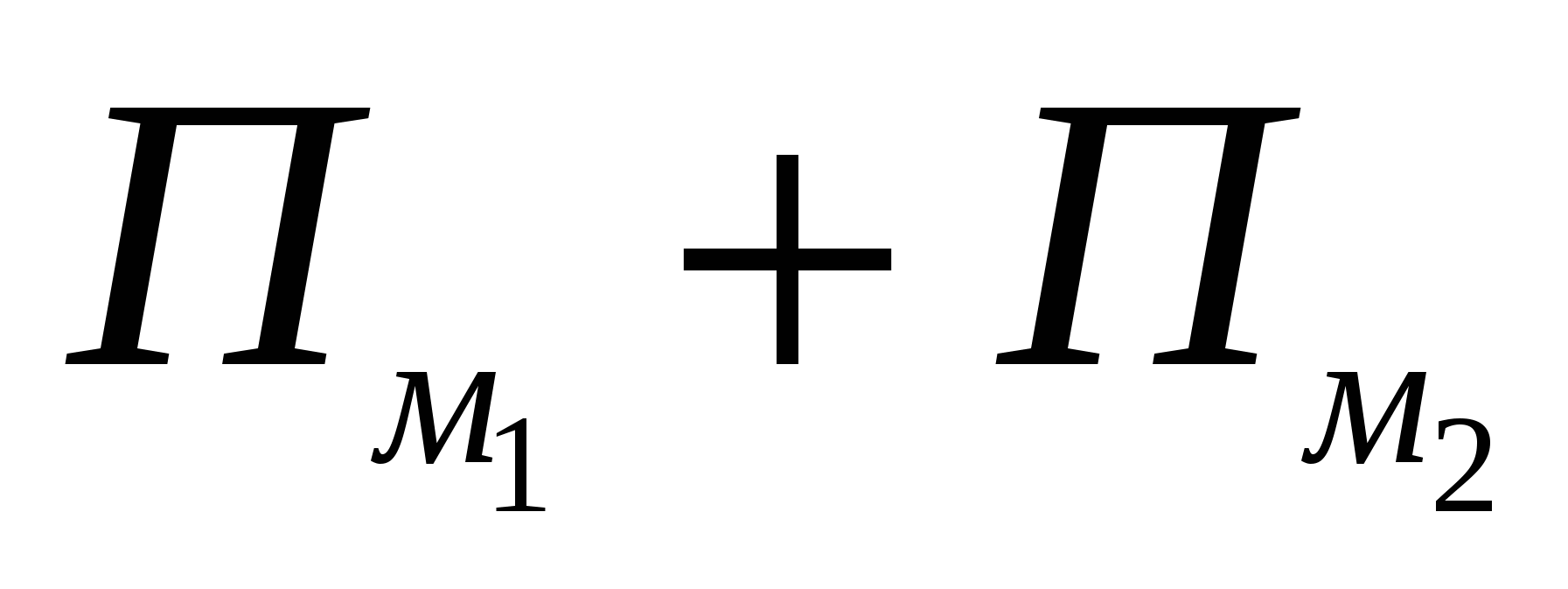 равны.
равны.
Рассмотрим узлы А и В. Они граничные как для М, так и для М1 , М2.
Поэтому вклад каждого из этих узлов в Пм равен 0,5 а в 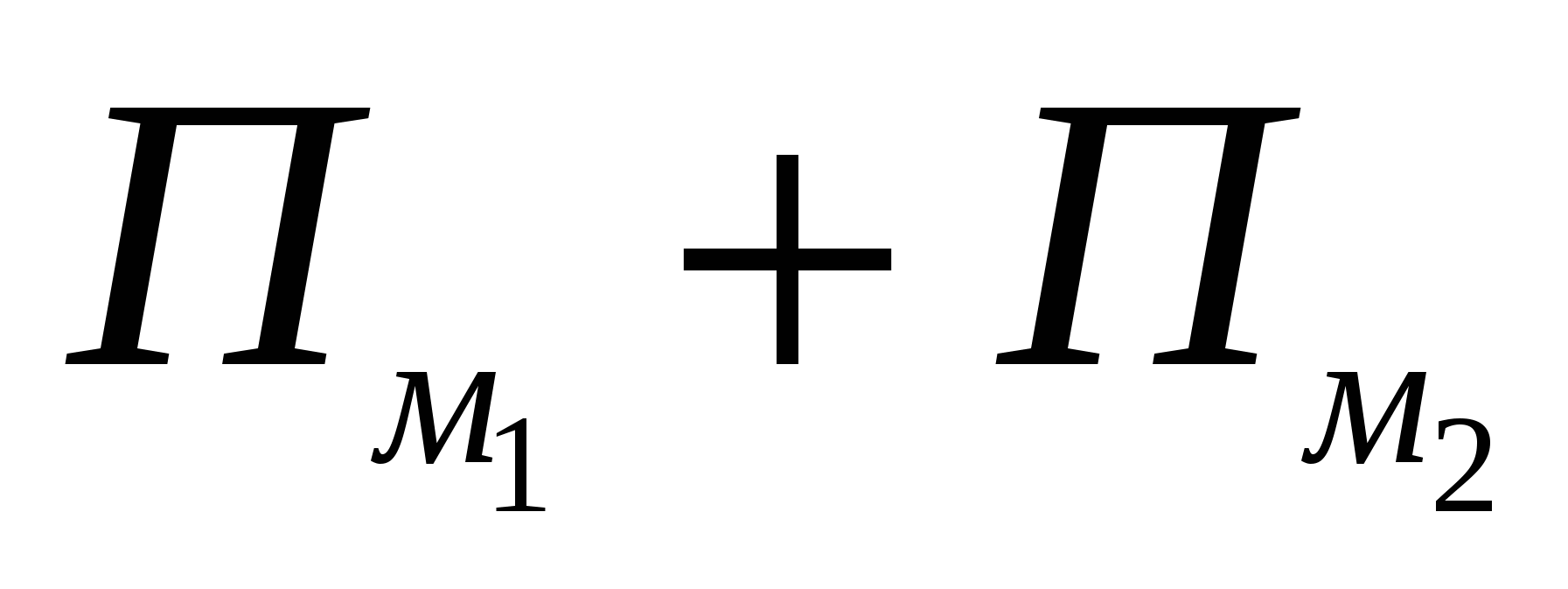 - единице. Значит, суммарный вклад узлов А и В в Пм равен 1, что на 1 меньше, чем их вклад в
- единице. Значит, суммарный вклад узлов А и В в Пм равен 1, что на 1 меньше, чем их вклад в 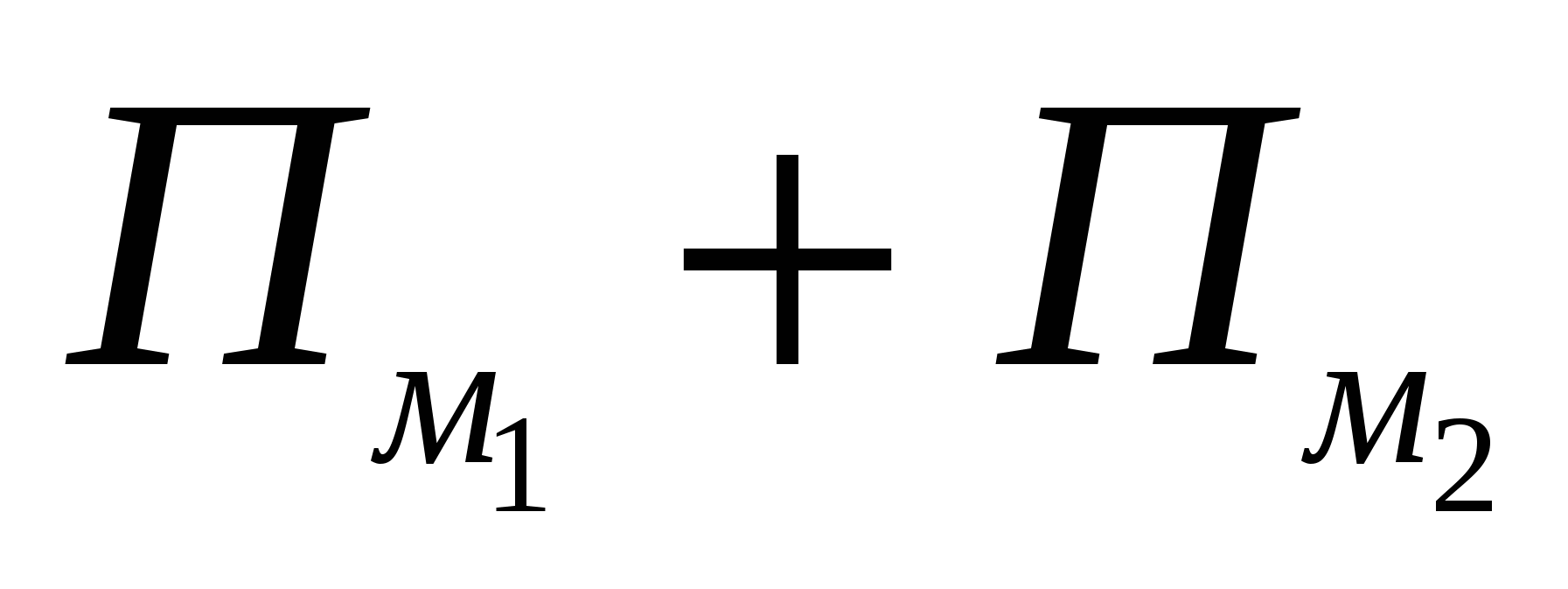 . Но
. Но 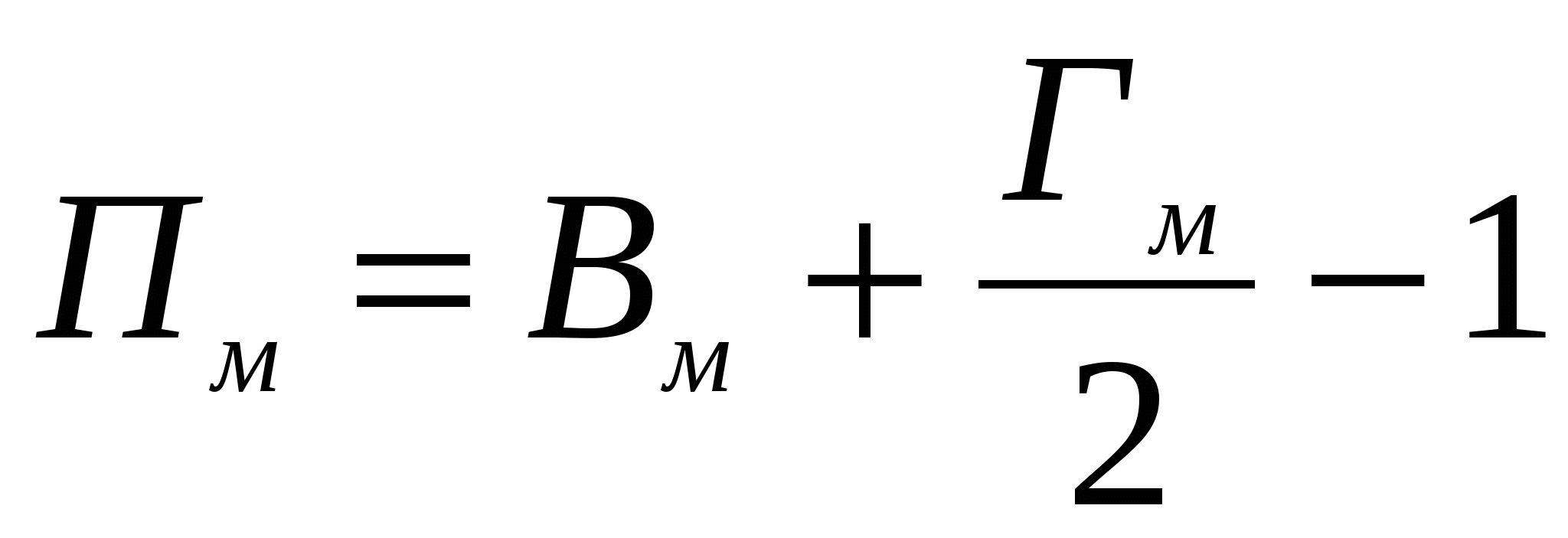 , а
, а 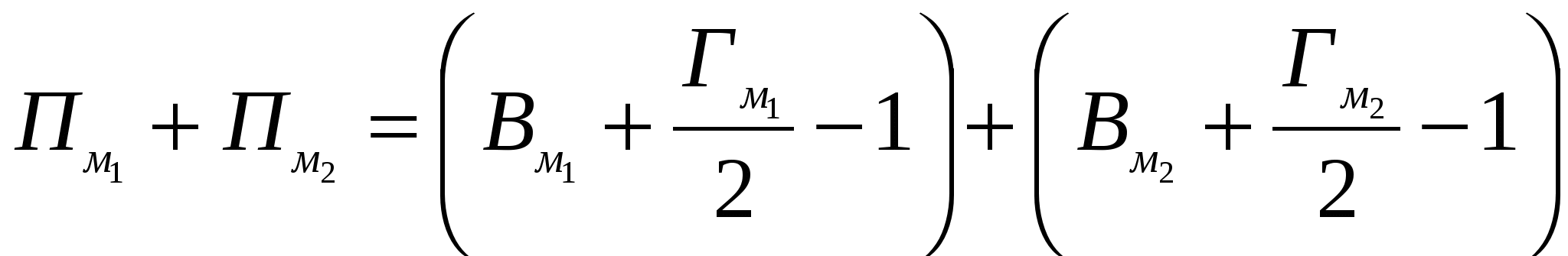 .
.
Из общего «вклада» всех узлов Пм вычитается 1, а из 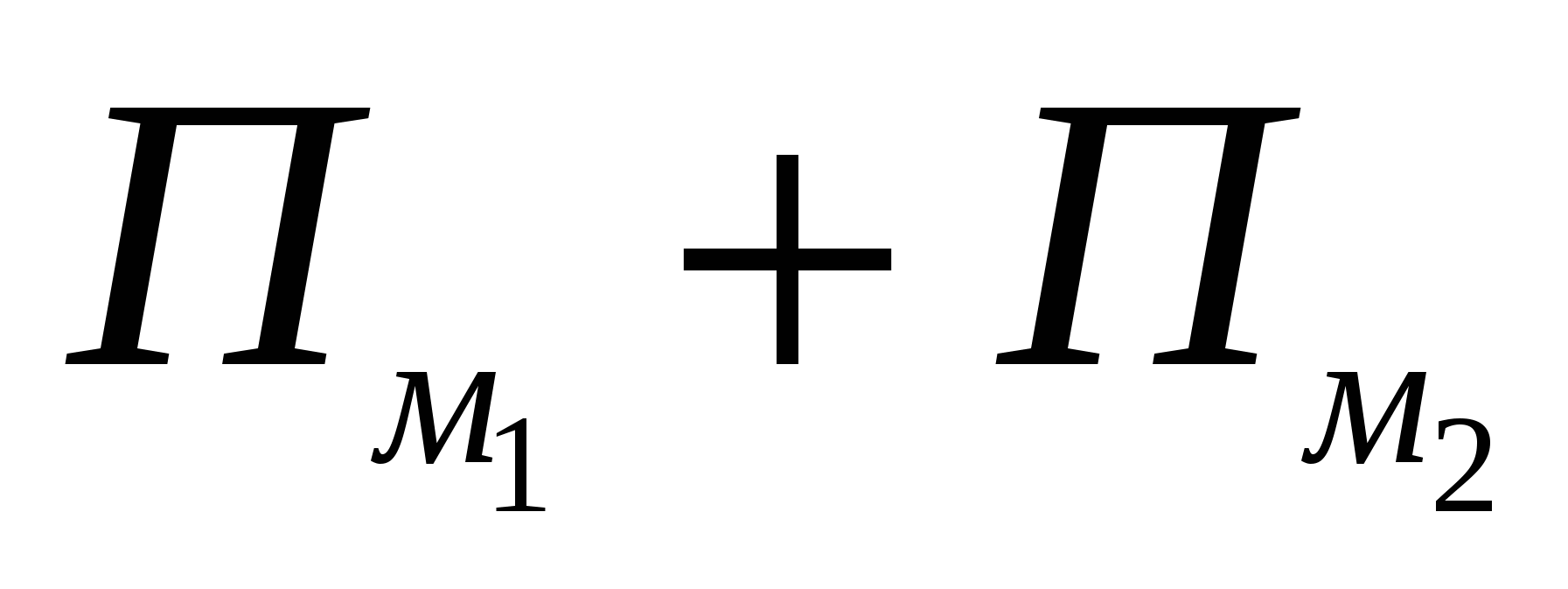 вычитается 2, и это компенсирует разницу вкладов узлов А и В.
вычитается 2, и это компенсирует разницу вкладов узлов А и В.
Итак, 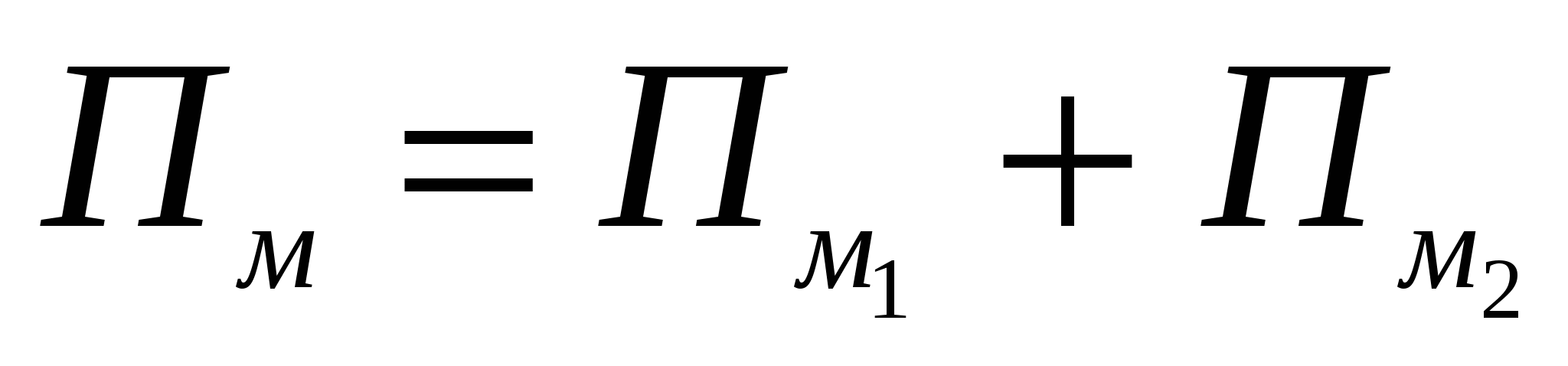 .
.
Шаг 2.
Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М1 и М2 (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М1, М2, то она верна и для третьего многоугольника.
Пусть, например, она верна для М1 и М2 , то есть 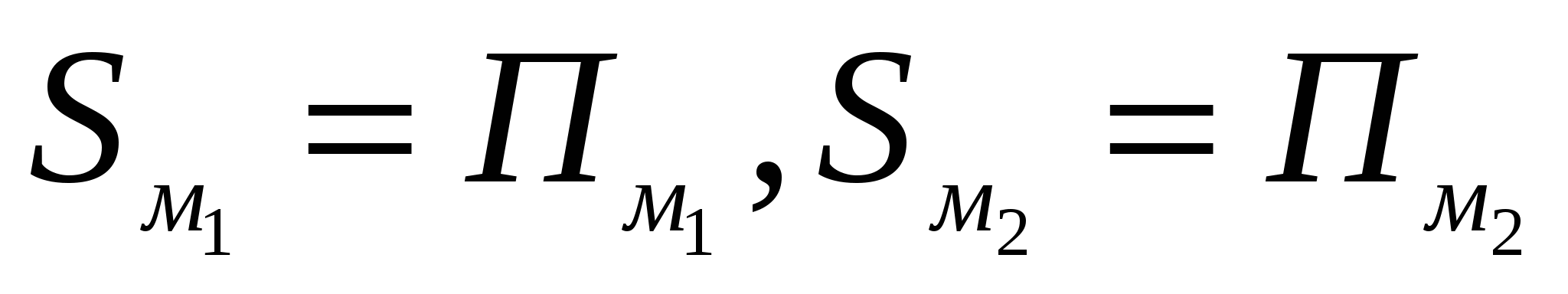 . Тогда (по первому шагу)
. Тогда (по первому шагу) 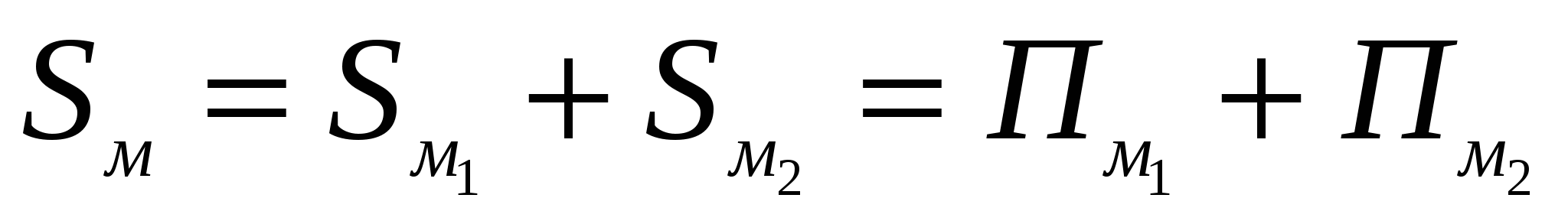 , но (по первому шагу) последнее выражение равно Пм, а равенство
, но (по первому шагу) последнее выражение равно Пм, а равенство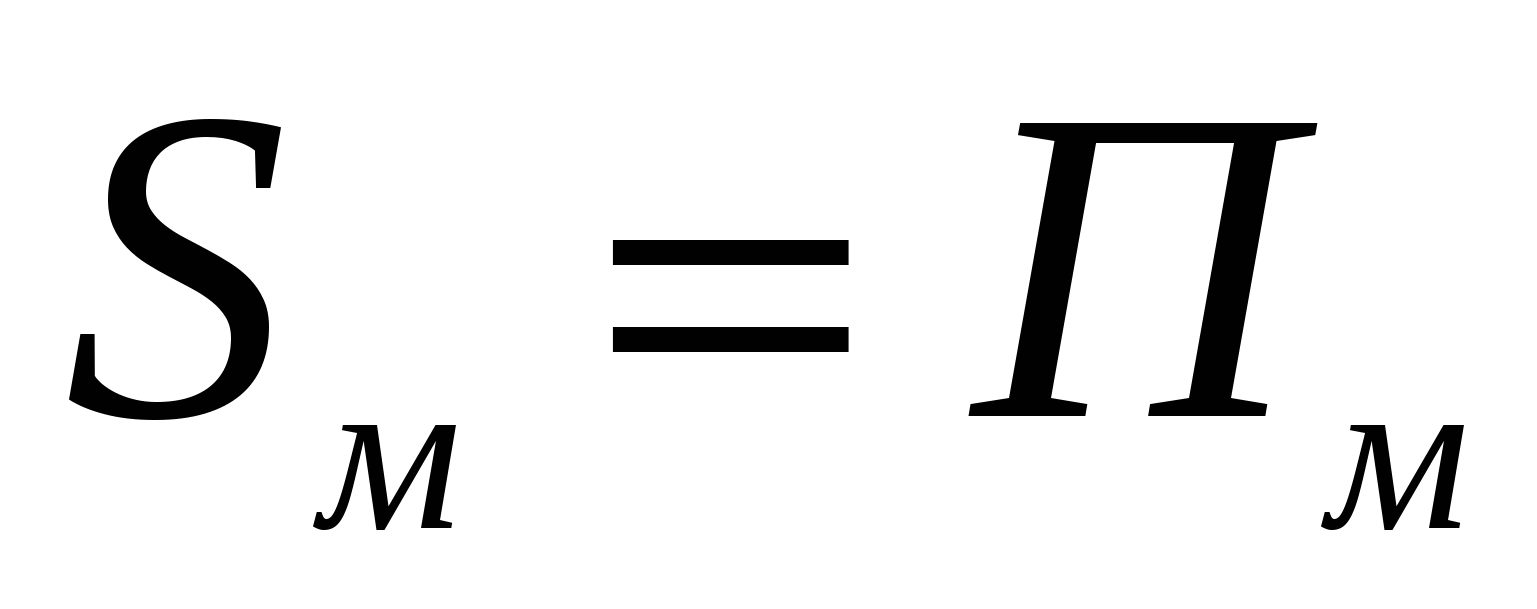 и есть формула Пика.
и есть формула Пика.
Шаг 3.
Докажем формулу Пика для прямоугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.
Треугольник АВС достроим до прямоугольника ABCD .
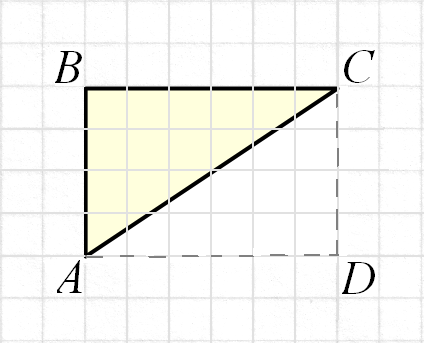
Для прямоугольников формула Пика верна: SABCD = ПABCD. Согласно первому шагу ПABCD = ПABC + ПACD , ПABC = ПACD , так что ПABCD = 2ПABC . Но SABCD = 2 SABC . Поэтому SABC = ПABC.
Шаг 4.
Формула Пика верна для произвольного треугольника с вершинами в узлах сетки.
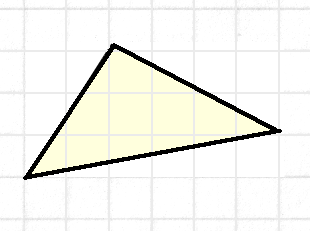
Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямоугольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.
Мы доказали, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
3. Задачи.
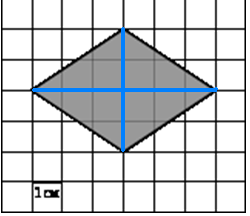
Найдите площади фигур:
1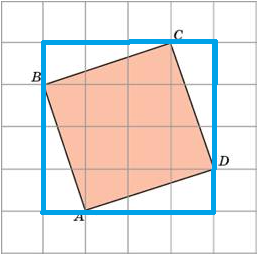
.
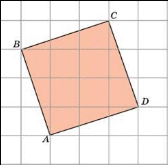
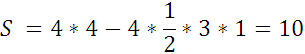
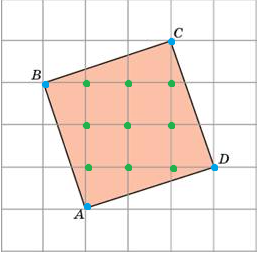
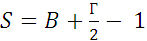
B = 9
Г = 4
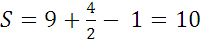
2.
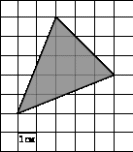
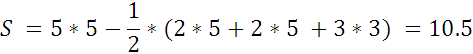
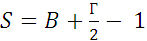
B = 9
Г = 5
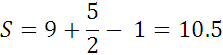
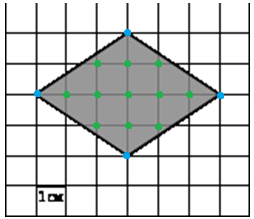
3.
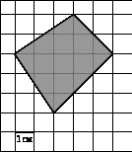
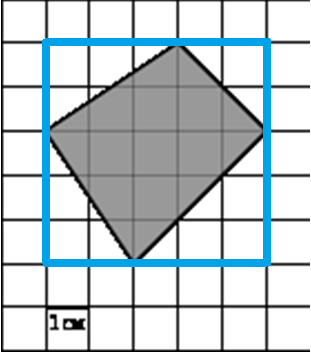
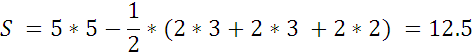
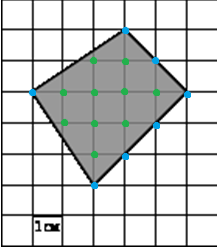
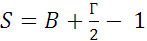
B = 10
Г = 7
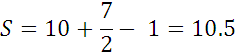
4.
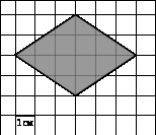
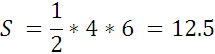
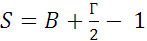
B = 11
Г = 4
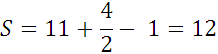
4. Формула площади многоугольника через координаты вершин.
В общем случае приходится довольствоваться формулой, выражающей площадь через координаты (х1; у1), (х2; у2), …, (хп; уп) последовательных вершин п-угольника:
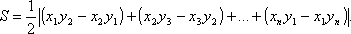 (1)
(1)
Отличительной особенностью данной формулы является то, что площадь здесь выражается не через характеристики самого п-угольника (стороны, углы), а через координаты его вершин. Последние же зависят от расположения п-угольника относительно осей координат. А потому данную формулу считают не вполне «геометричной». Однако она достаточно удобна в практических задачах.
5. Задачи.
Найдите площади фигур:
1.
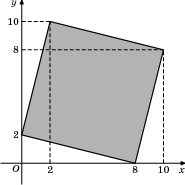
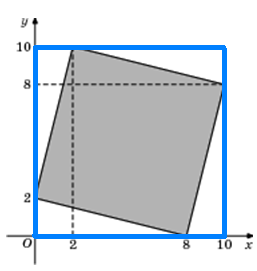
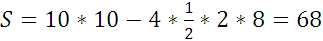
По формуле (1):

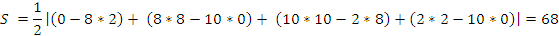
2.
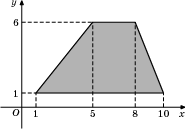
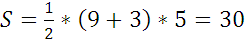
По формуле (1):
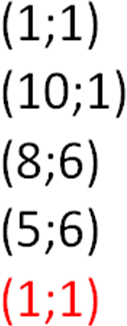
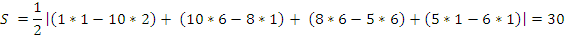
3.
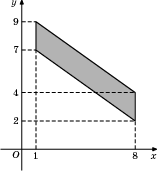
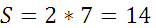
По формуле (1):
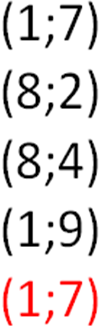
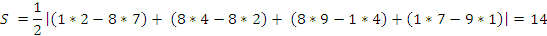
4.
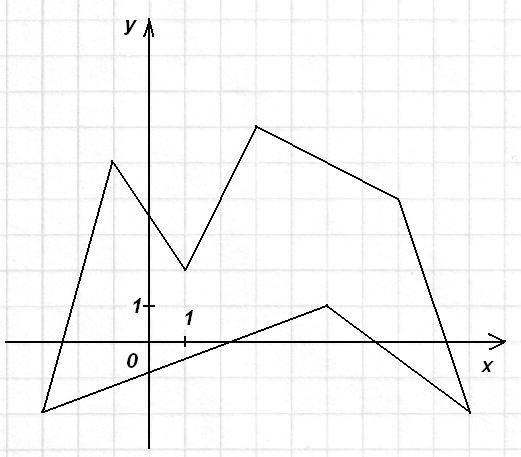
По формуле (1):
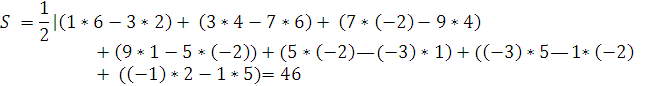
6. Литература.
1. Вокруг формулы Пика / Н. Б. Васильев // Квант. - 1974. - №12. - С. 39-43.
2. Многоугольники на клетчатой бумаге / В. Гальперин, В. Калинников // Квант. - 1978. - № 6. - С. 38-41.
3. Решетки и правильные многоугольники / А. А. Егоров // Квант. - 1974. - № 12. - С. 26-33.
4. А. Г. Кушниренко. Целые точки в многоугольниках и многогранниках // Квант. - 1977. - № 4. - С. 13-20.
5. В. В. Прасолов. Задачи по планиметрии. - М.: МЦНМО, 2001.
6. В.В. Вавилов, А.В. Устинов. Многоугольники на решетках. - М.: МЦНМО, 2006.
7. В.В. Вавилов, А.В. Устинов. Две знаменитые формулы. Журнал «Квант». - 2008. - № 2.
8. Газета Математика -2009. - № 23.
9. Открытый банк задач ЕГЭ по математике.


