Добавить в избранное

Решение стереометрических задач методом координат

Существует два способа решения стереометрических задач:  - классический, требующий отличного пространственного воображения, отличного знания аксиом и теорем геометрии,логики, умения строить чертеж,умения свести объемную задачу к последовательности планиметрических задач; - применене векторов и метода координат, требующий знания конкретных формул, умения действовать по алгоритму и отличных вычислительных навыков. В данной разработке дан  ответ на вопрос "Что нужно знать, уметь и понимать для успе...
Раздел Математика
Класс -
Тип Конспекты
Автор
Дата
Формат doc
Изображения Есть
For-Teacher.ru - все для учителя
Поделитесь с коллегами:

Существует два способа решения задач по стереометрии:

  • классический, требует отличного пространственного воображения, отличного знания аксиом и теорем геометрии, логики, умения строить чертеж, свести объемную задачу к последовательности планиметрических задач;

  • применение векторов и метода координат, требует знания конкретных формул, умения действовать по алгоритму и отличные вычислительные навыки.

Одним из рациональных способов решения стереометрических задач иногда является применение векторов и метода координат, хотя в условиях никаких координат и векторов нет. Что нужно знать, уметь и понимать для успешного применения этого метода?

Знать:

1. Если заданы точки А(х1,у1,z1) и В(x2; y2; z2)

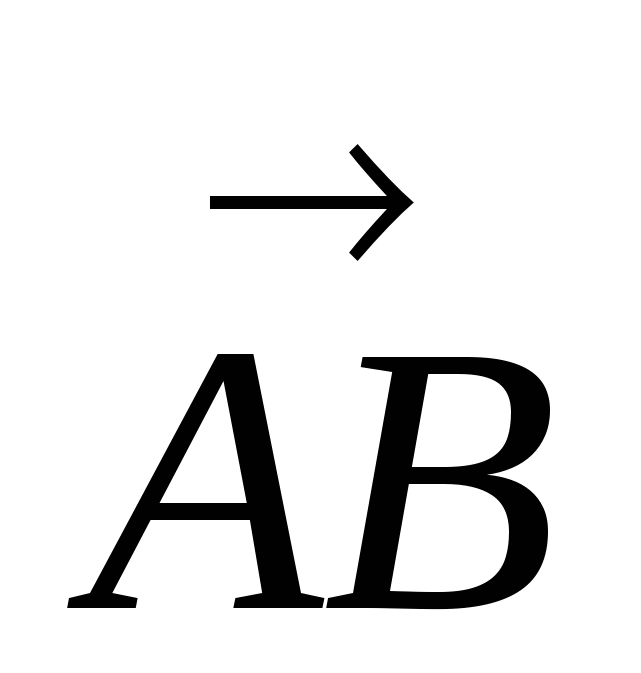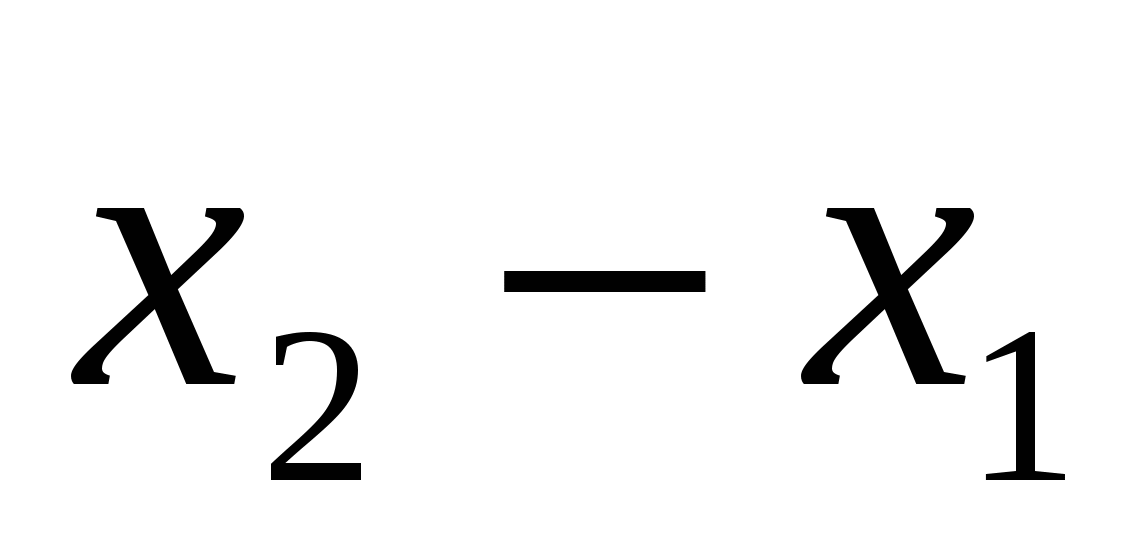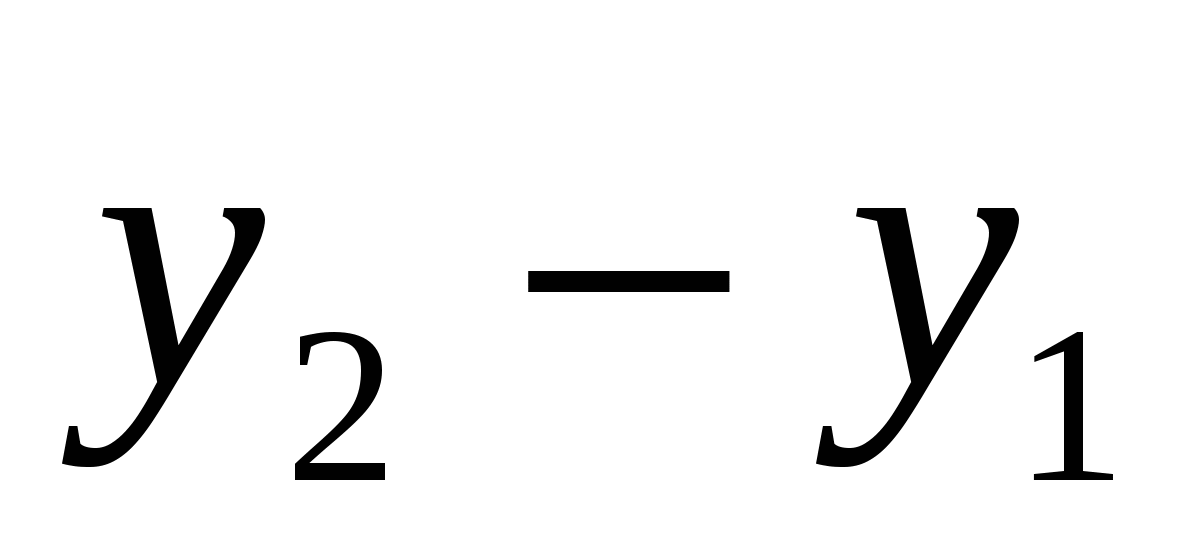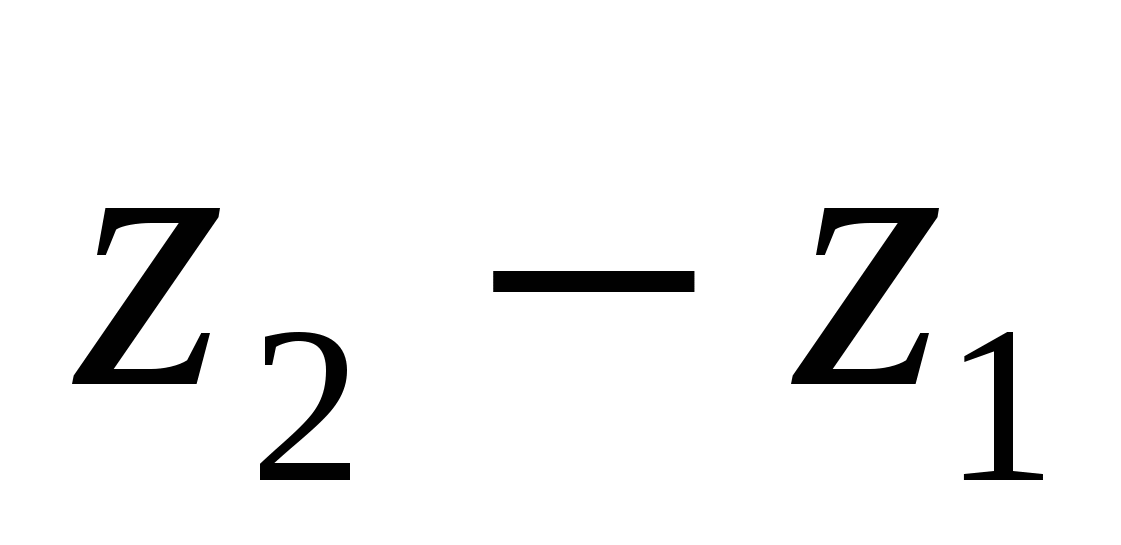Координаты вектора Решение стереометрических задач методом координат(Решение стереометрических задач методом координат;Решение стереометрических задач методом координат;Решение стереометрических задач методом координат)

Расстояние между этими точками или длина вектора:

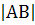Решение стереометрических задач методом координат=

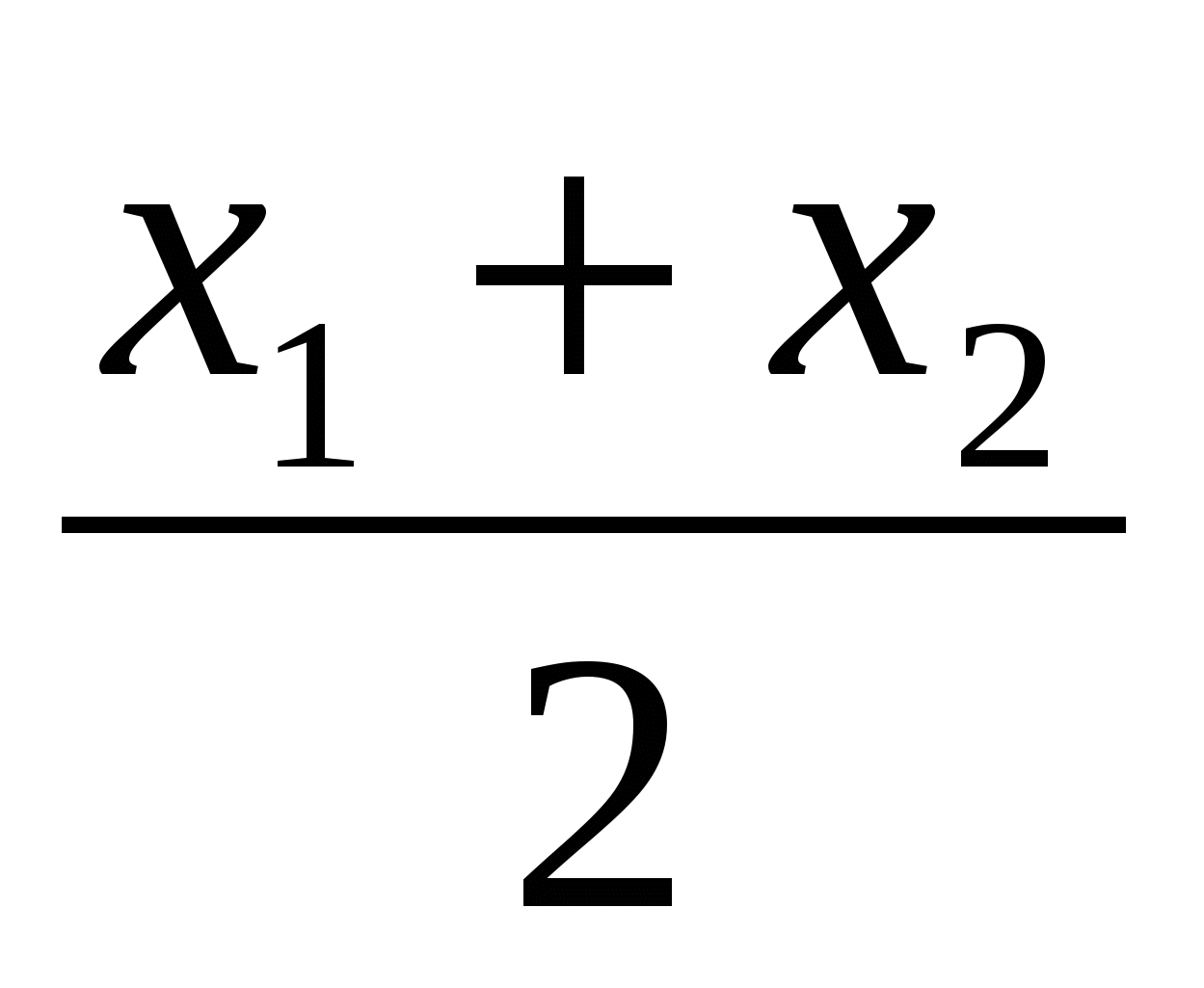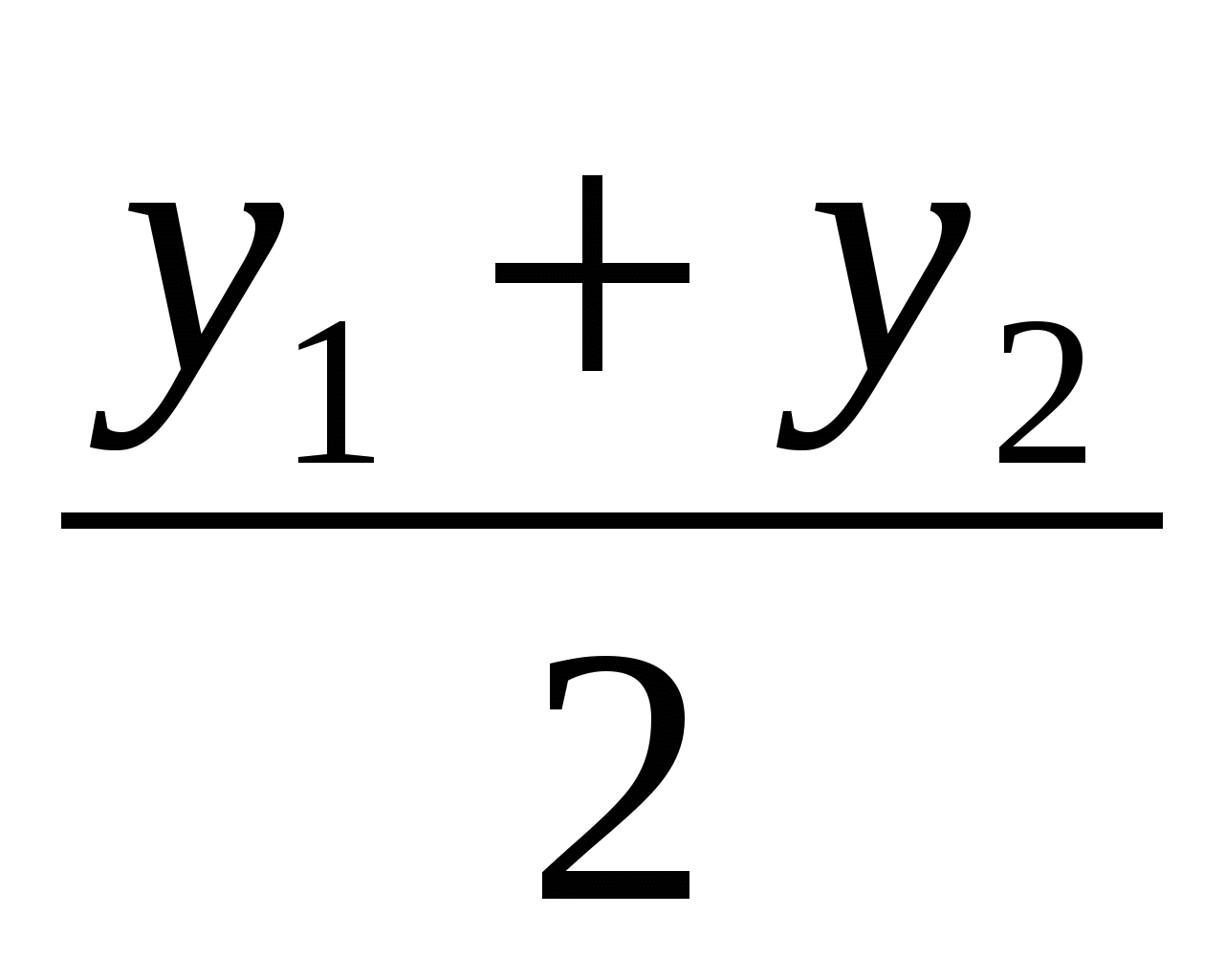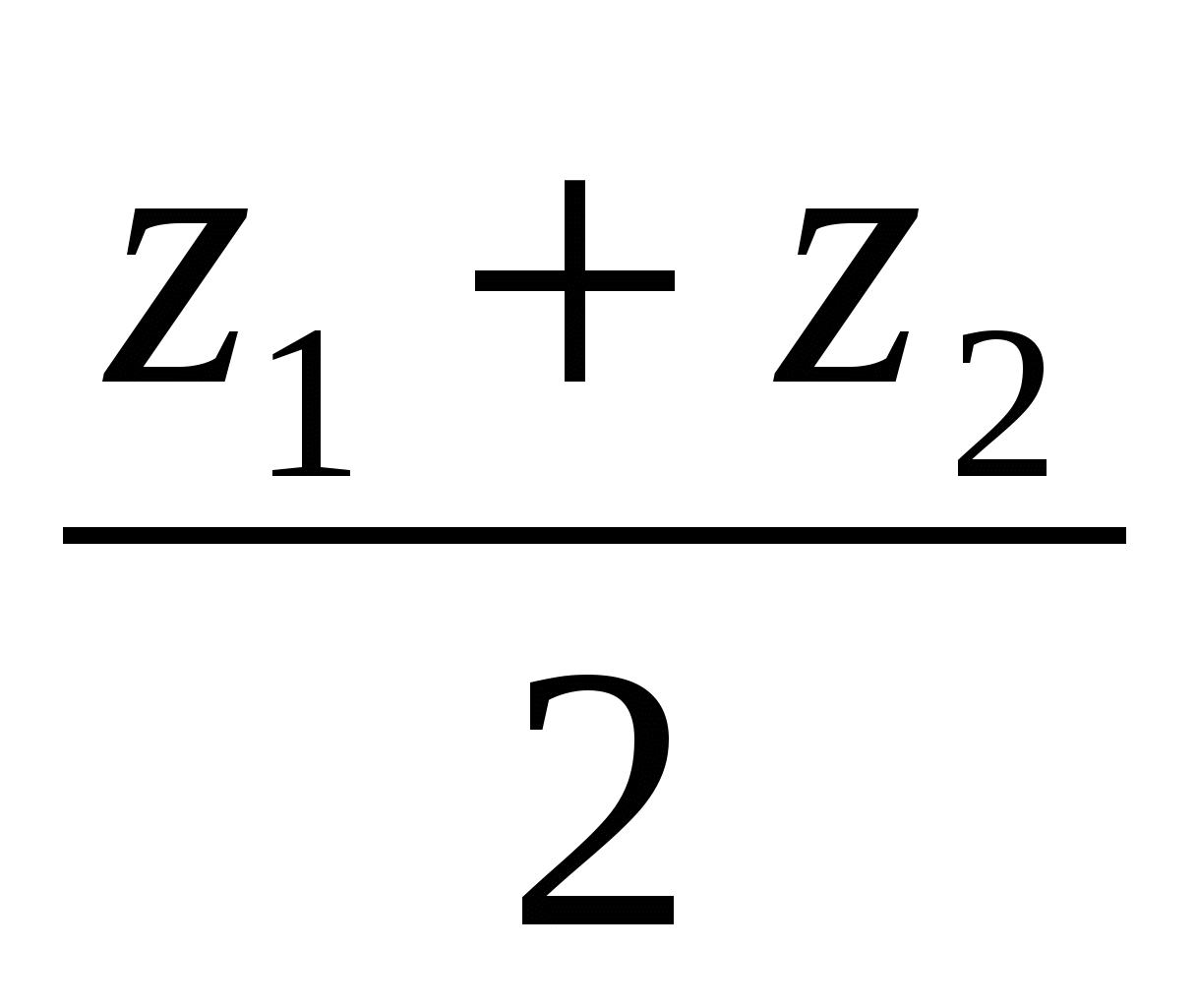Координаты точки С - середины отрезка АВ: С(Решение стереометрических задач методом координат; Решение стереометрических задач методом координат; Решение стереометрических задач методом координат)

  1. Формула - косинус угла φ между векторами 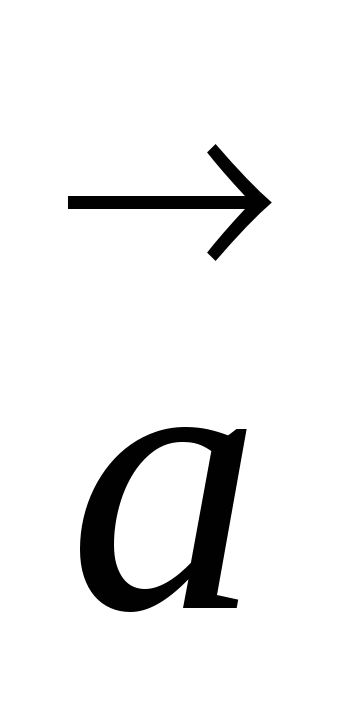Решение стереометрических задач методом координат(x1; y1; z1), 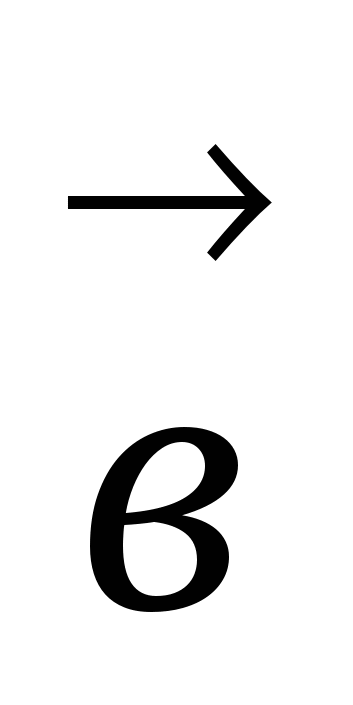Решение стереометрических задач методом координат(x2; y2; z2):

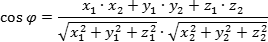
Решение стереометрических задач методом координат

  1. Уравнение плоскости в трехмерном пространстве:

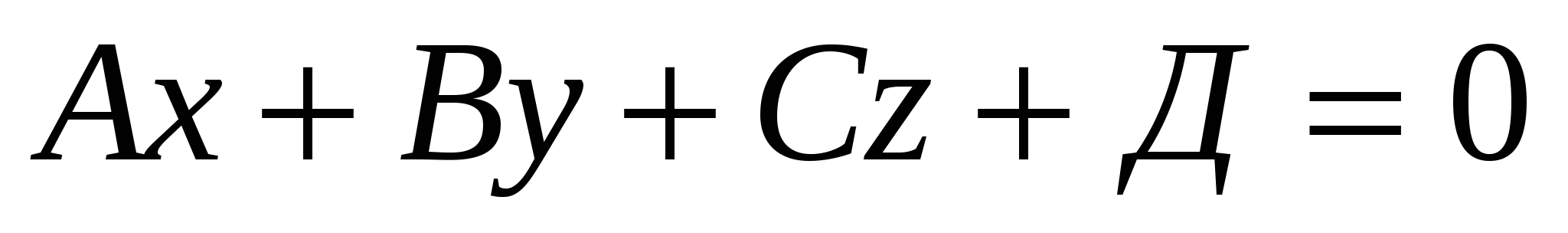Решение стереометрических задач методом координат, где A, B, C и D - действительные числа.

Вектор, перпендикулярный к плоскости 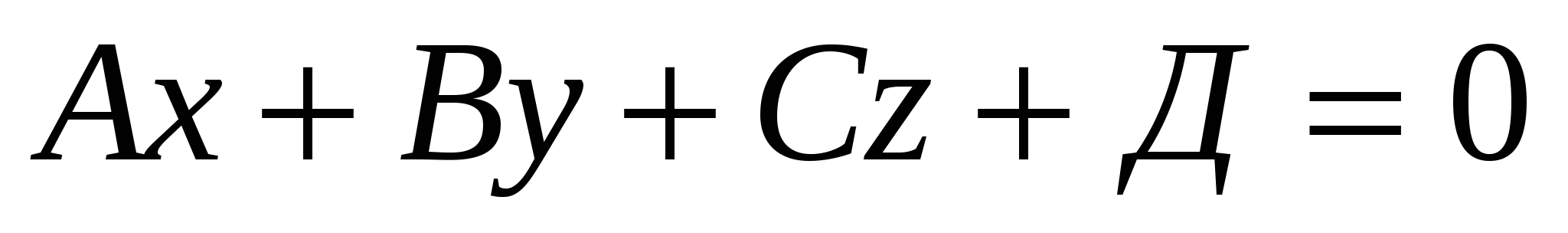Решение стереометрических задач методом координат, имеет координаты 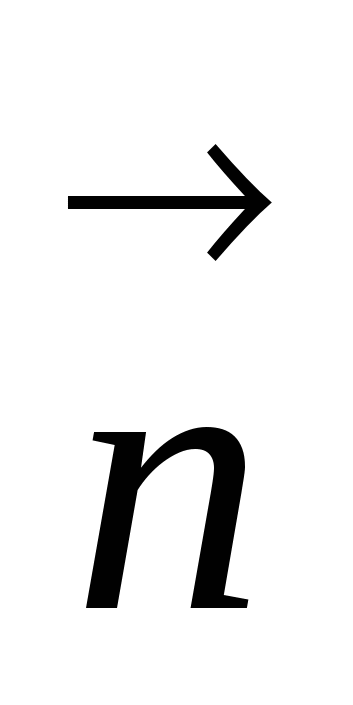Решение стереометрических задач методом координат(A; B; C) - нормаль к плоскости.

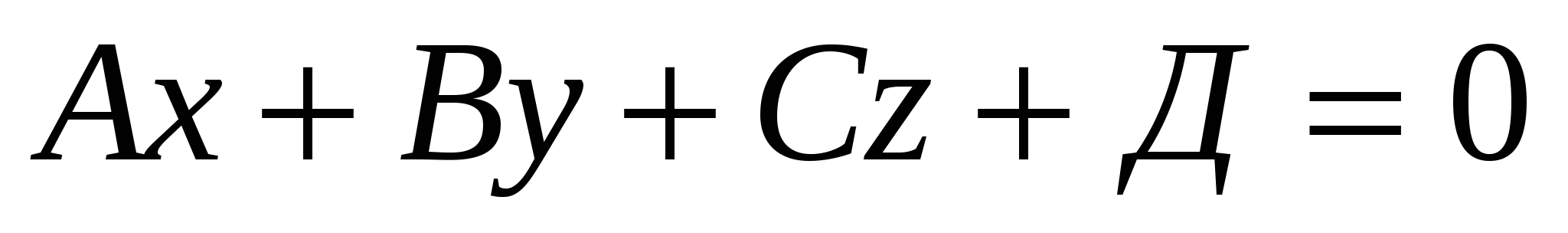
  1. Расстояние от точки М(х0, у0, z0) до плоскости Решение стереометрических задач методом координат

ρ=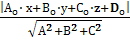Решение стереометрических задач методом координат.Решение стереометрических задач методом координат


  1. Угол между плоскостями равен углу между нормалями к этим плоскостям:

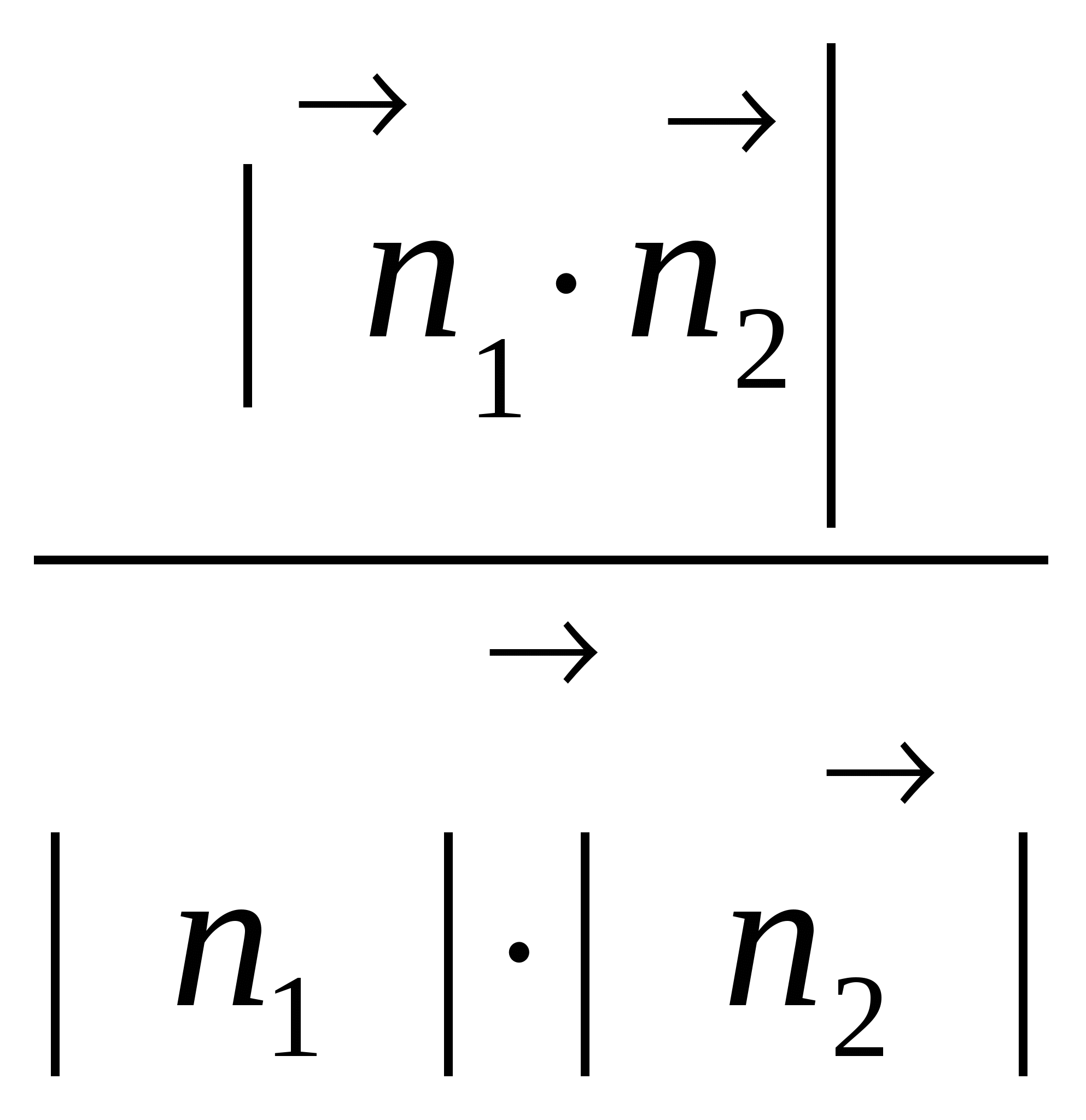
cosРешение стереометрических задач методом координат= Решение стереометрических задач методом координат

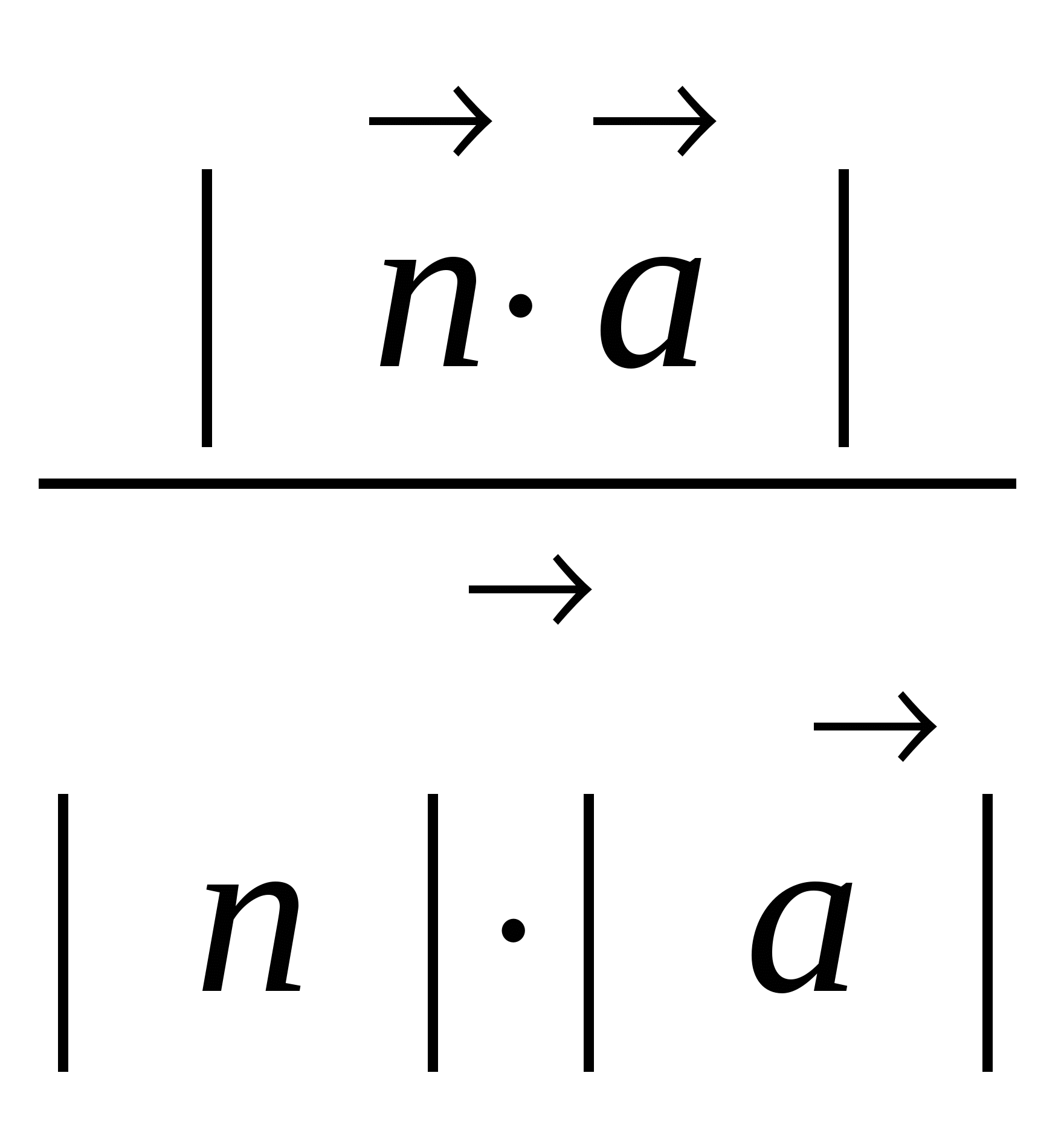
  1. Синус угла между прямой и плоскостью: sin Решение стереометрических задач методом координат= Решение стереометрических задач методом координат

Уметь:

  • вводить систему координат;

  • определять координаты точек;

  • определять координаты вектора;

  • записывать уравнение плоскости;

Задачи типа С2 делятся на два основных вида: на нахождение расстояний и на нахождение углов.



Понимать

Нахождение расстояния

между прямыми

длина общего перпендикуляра - расстояние от произвольной точки одной из них до плоскости, проходящей через вторую параллельно первой

от точки до прямой

длина перпендикуляра, проведенного из точки к прямой

от точки до плоскости

длина перпендикуляра, проведенного из точки к плоскости, вычисляется по формуле

Нахождение угла

между прямыми

это угол между соответствующими векторами.

между прямой и плоскостью

это угол между прямой и нормалью к плоскости

между плоскостями

это угол между нормалями к этим плоскостям

Рассмотрим применение метода в решениях задач из сборника «Самое полное издание типовых вариантов заданий ЕГЭ: 2012» под редакцией А.Л. Семенова, И.В. Ященко.

Пример 1 (8 вариант сборника)

В правильной треугольной призме АВСА1В1С1, все ребра которой равны 1, найдите расстояние между прямыми АА1 и ВС1.

Р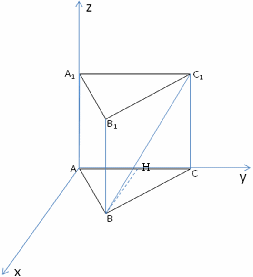Решение стереометрических задач методом координатешение: Введем систему координат: начало координат а точке А, ось х направляем по ребру АС, z - по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC, она будет параллельна ВН, высоте основания АВС.



З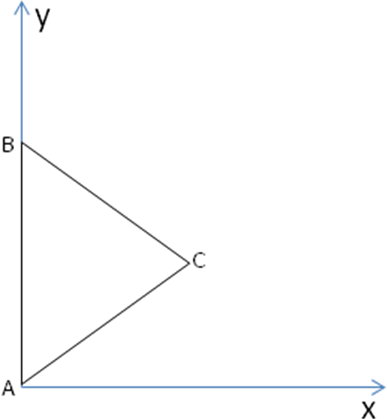Решение стереометрических задач методом координатдесь требуются некоторые пояснения. Дело в том, что ось y не совпадает с ребром AВ, т.к. треугольник ABC - равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:



Расстояние между прямыми АА1 и ВС1найдем, как расстояние от точки А до параллельной АА1 плоскости ВСС1.

Найдем координаты точек А(0;0;0), В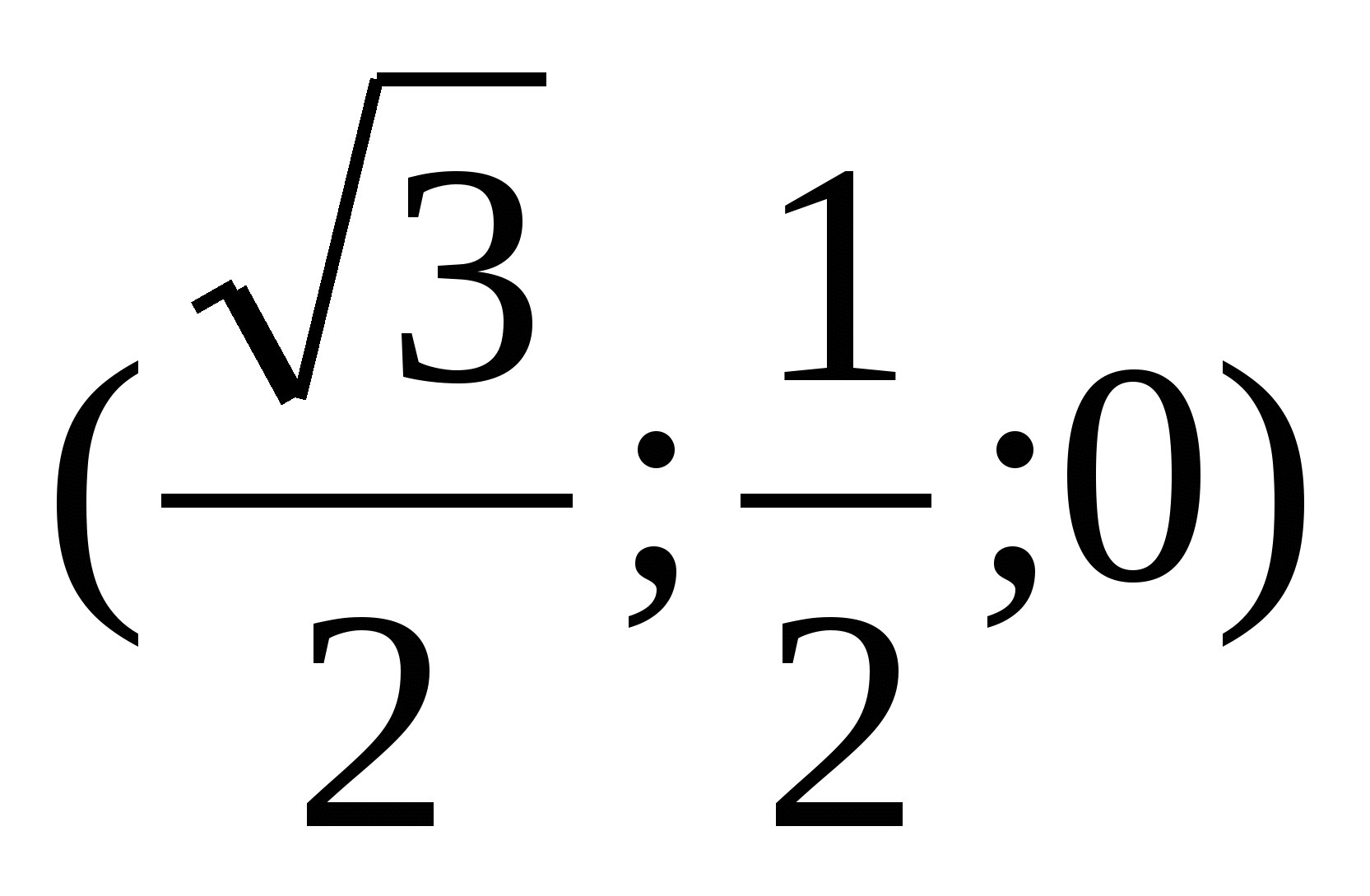Решение стереометрических задач методом координат, С(0;1;0), С1(0;1;1).

Общий вид уравнения плоскости 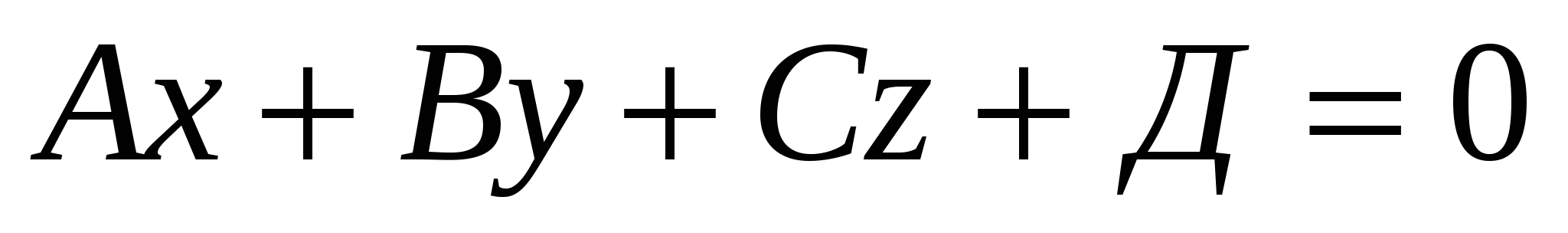Решение стереометрических задач методом координат. Напишем уравнение плоскости, проходящей через точки В, С, С1.

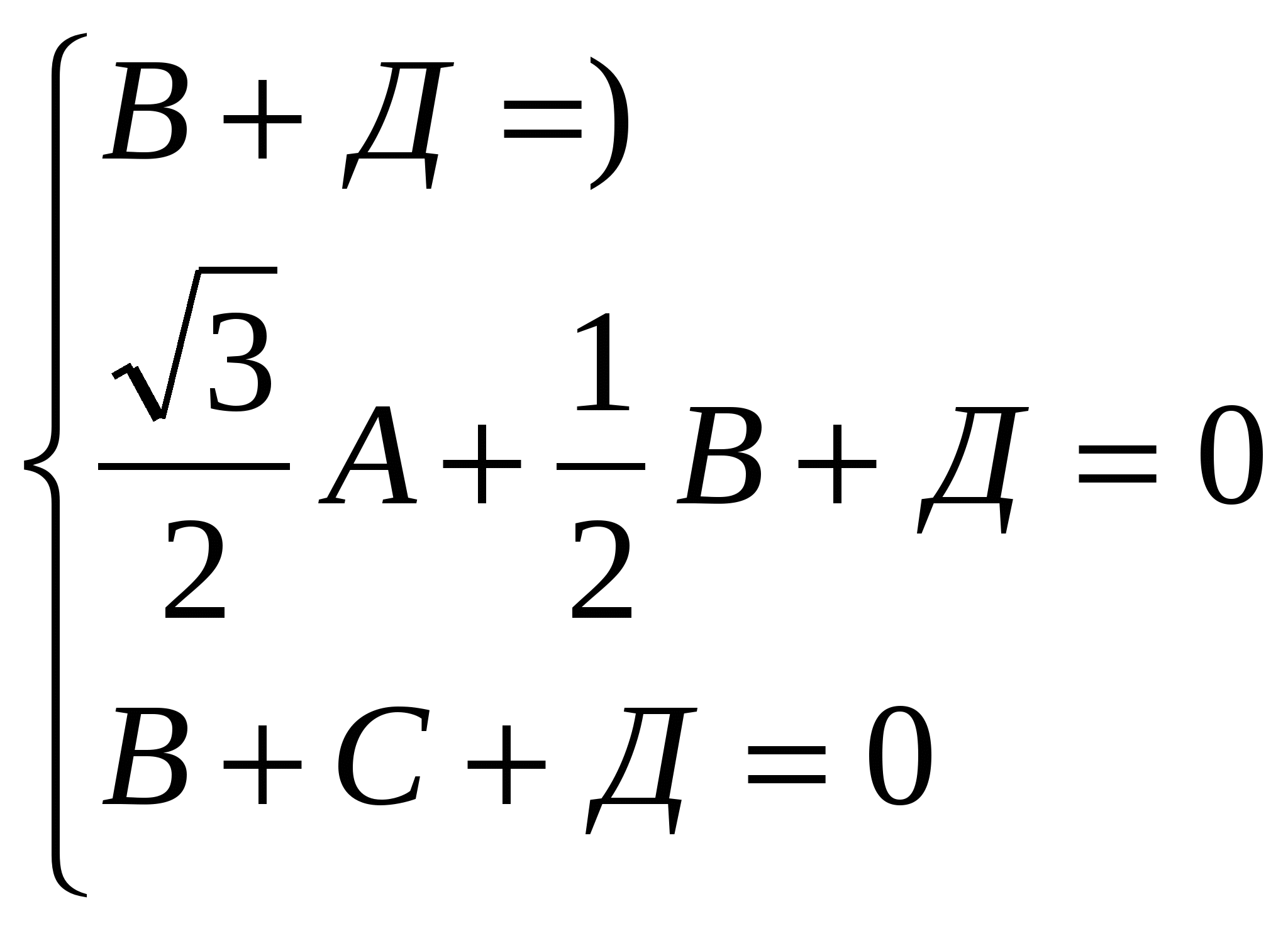
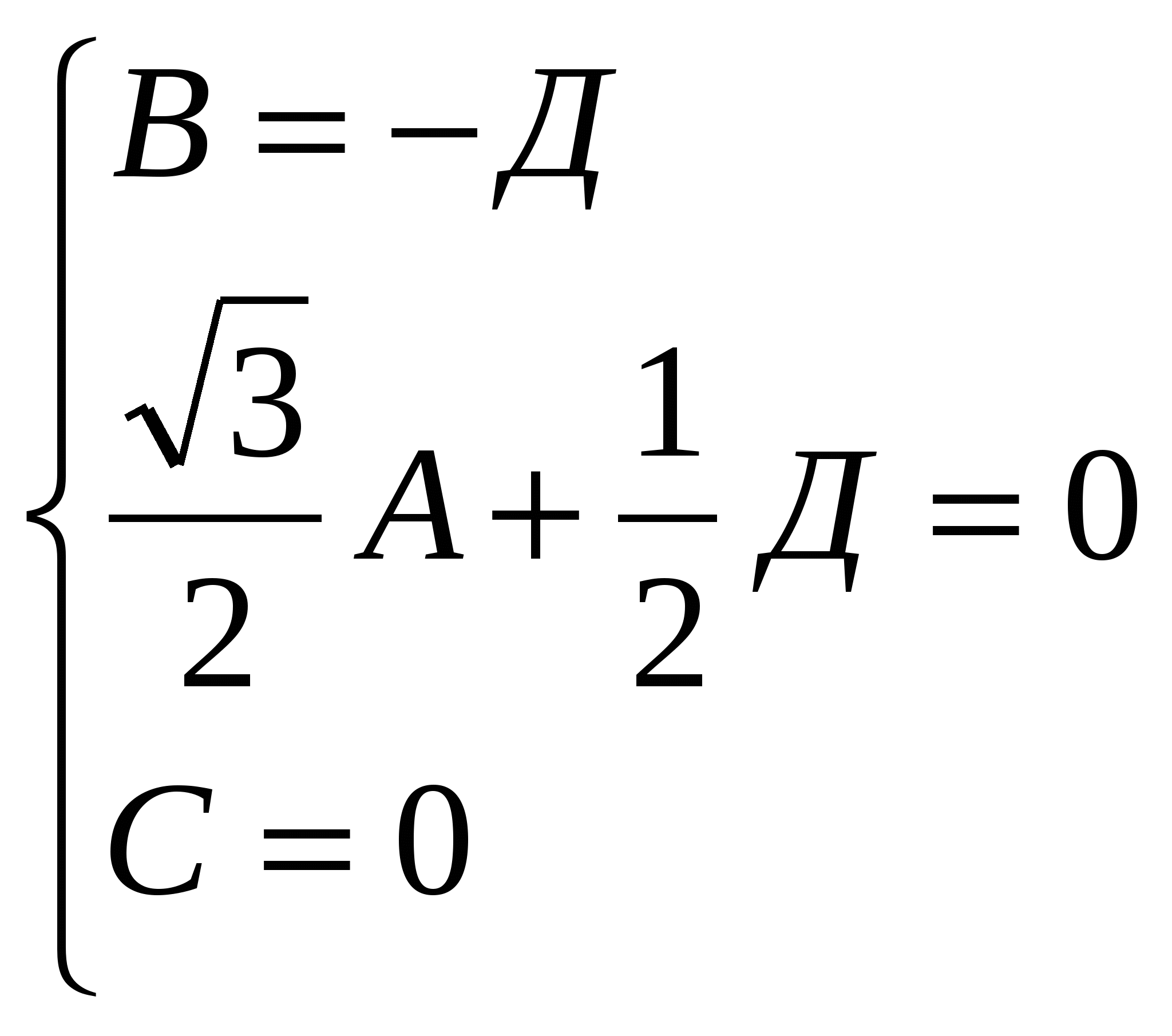
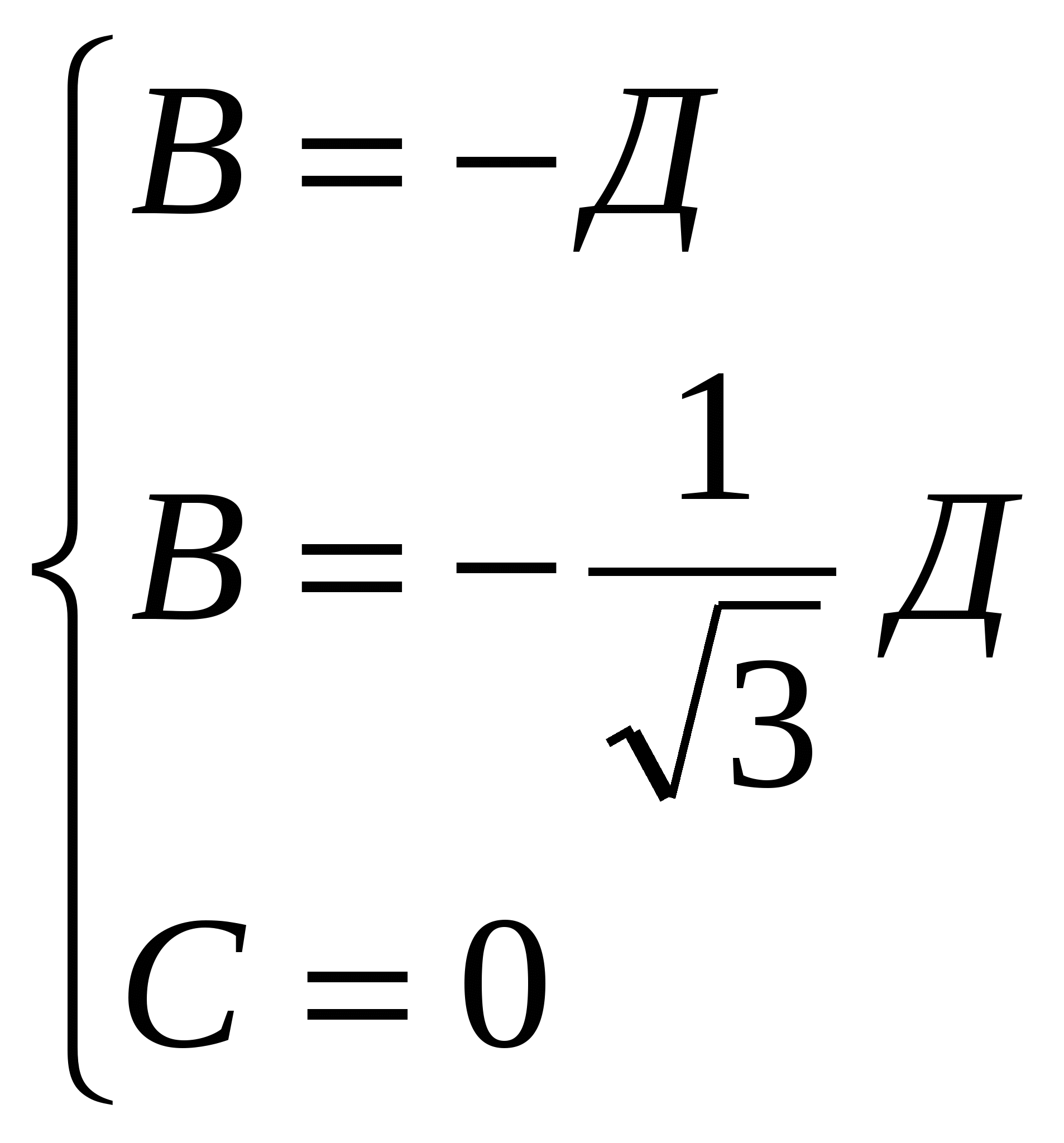
Решение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координат

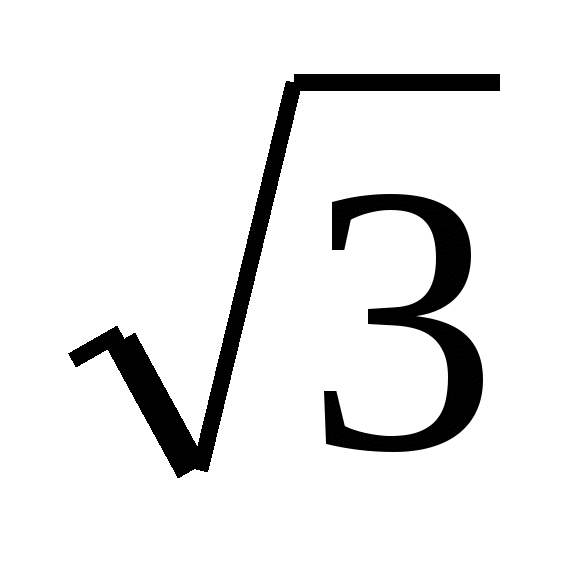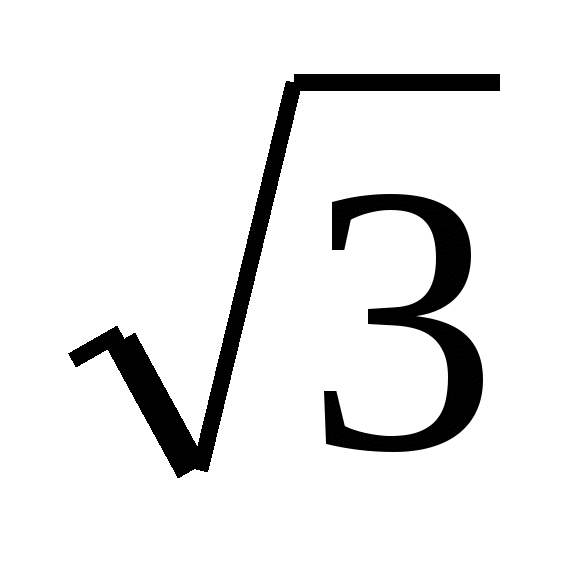Уравнение плоскости ВСС1 : х+Решение стереометрических задач методом координату - Решение стереометрических задач методом координат=0

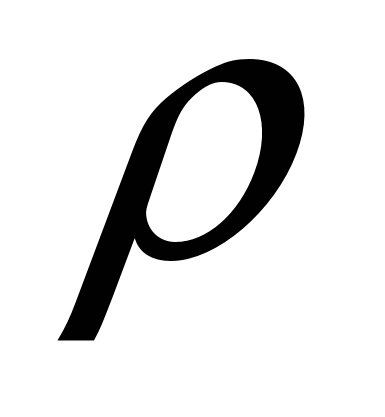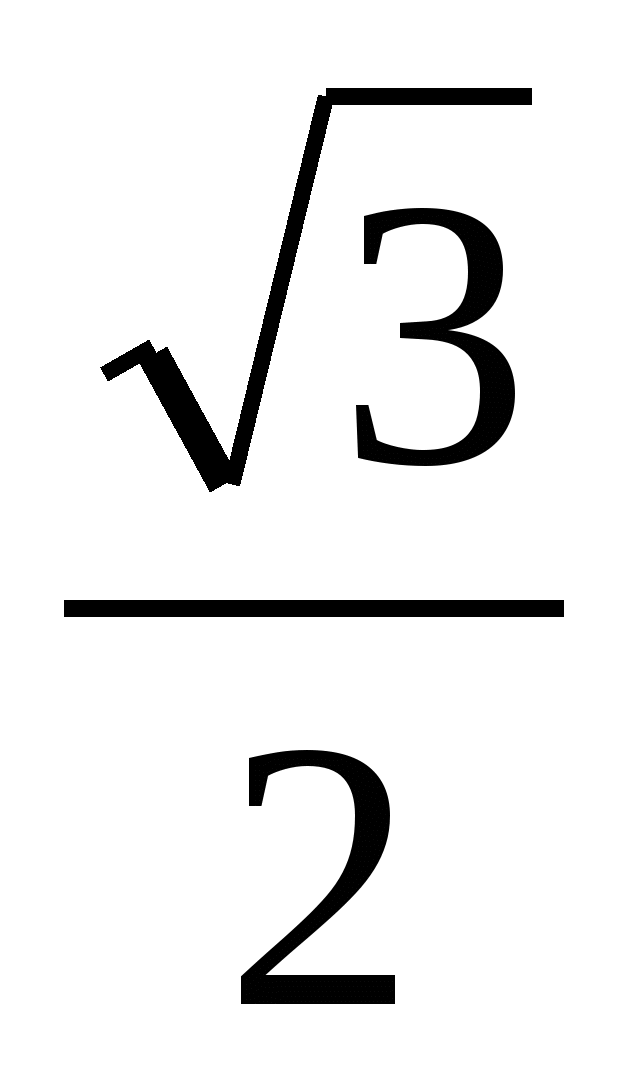По формуле расстояние от точки А до данной плоскости равно Решение стереометрических задач методом координат = Решение стереометрических задач методом координат.

Ответ: 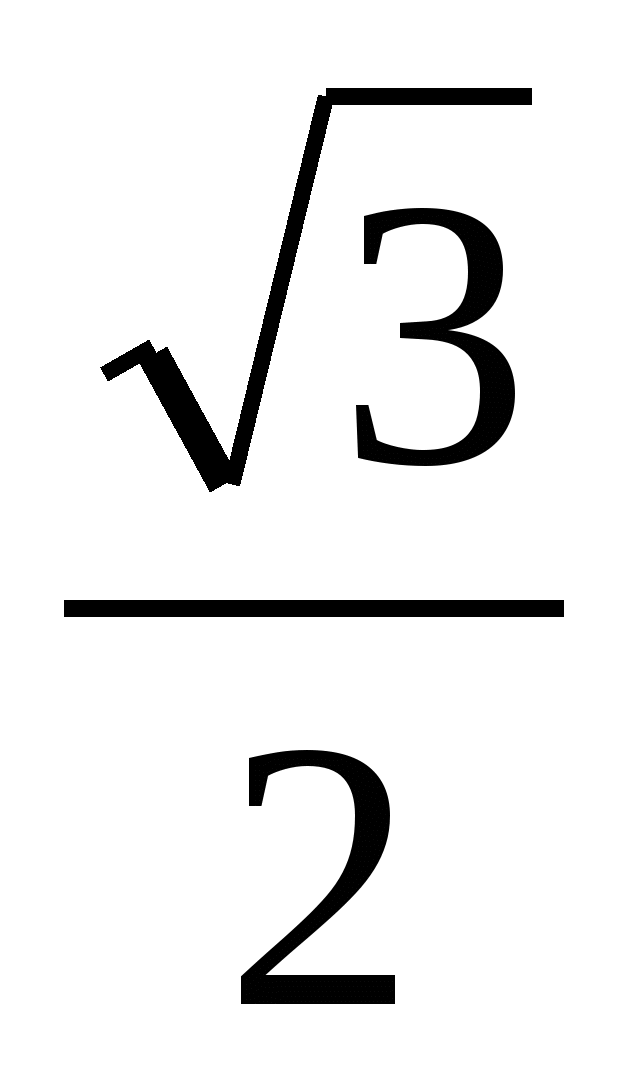Решение стереометрических задач методом координат.

Пример 2.

В единичном кубе АВСДА1 В1 С1 Д1 найдите расстояние от точки Д1 до прямой РQ, где Р и Q - середины соответственно ребер А1В1 и ВС.

Р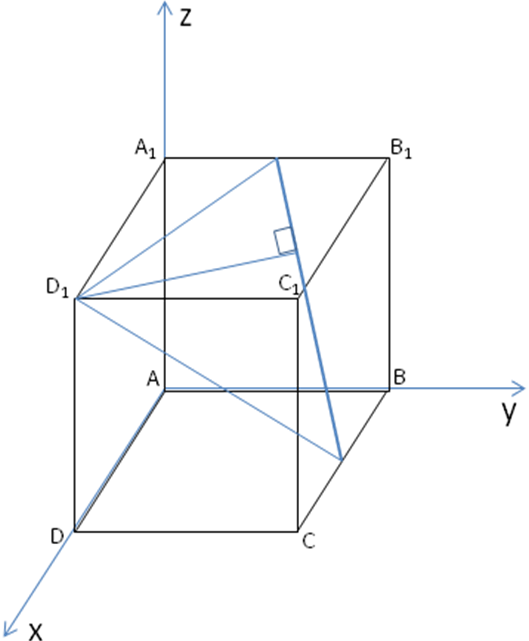Решение стереометрических задач методом координатешение: Если в задаче дан куб - значит повезло. Он отлично вписывается в прямоугольную систему координат.

Найдем координаты точек Р(0;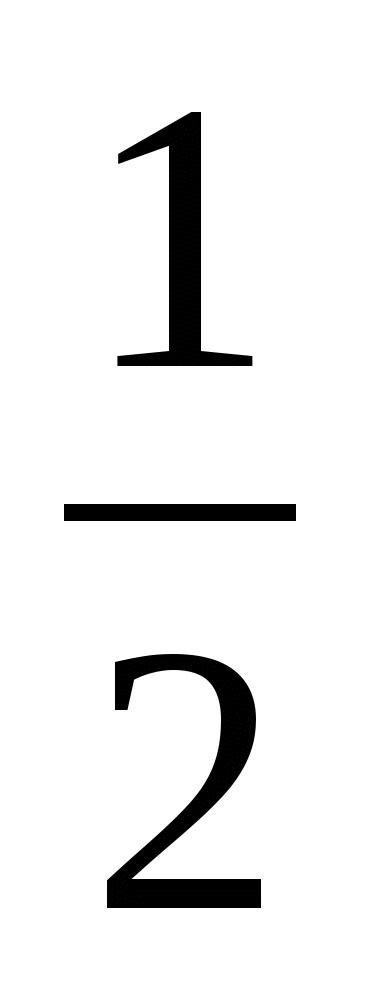Решение стереометрических задач методом координат;1), Q(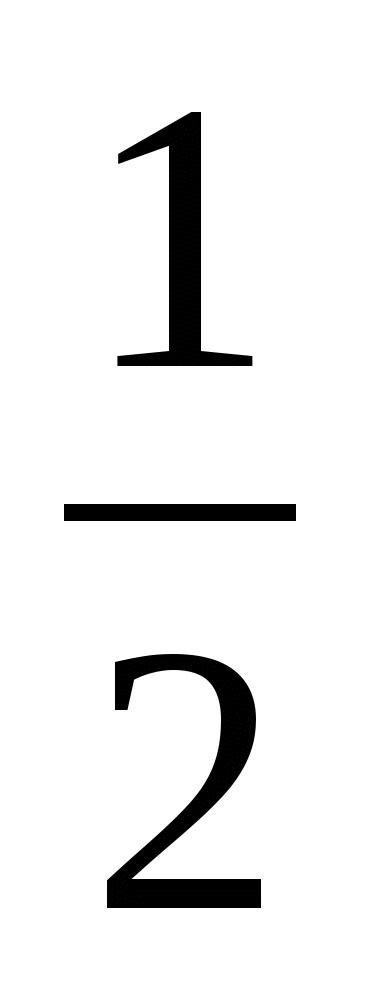Решение стереометрических задач методом координат;1;0), Д1(1;0;1).

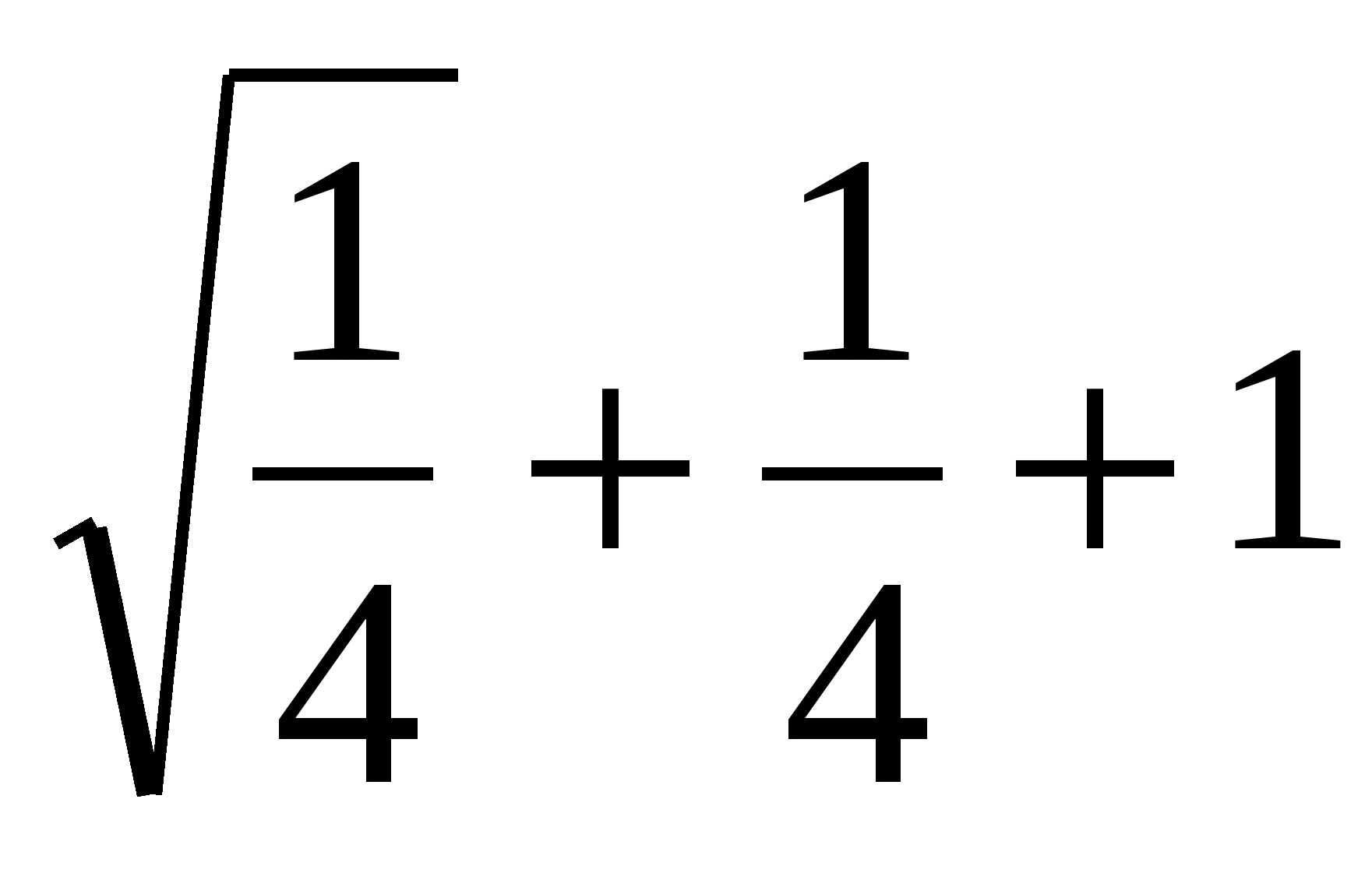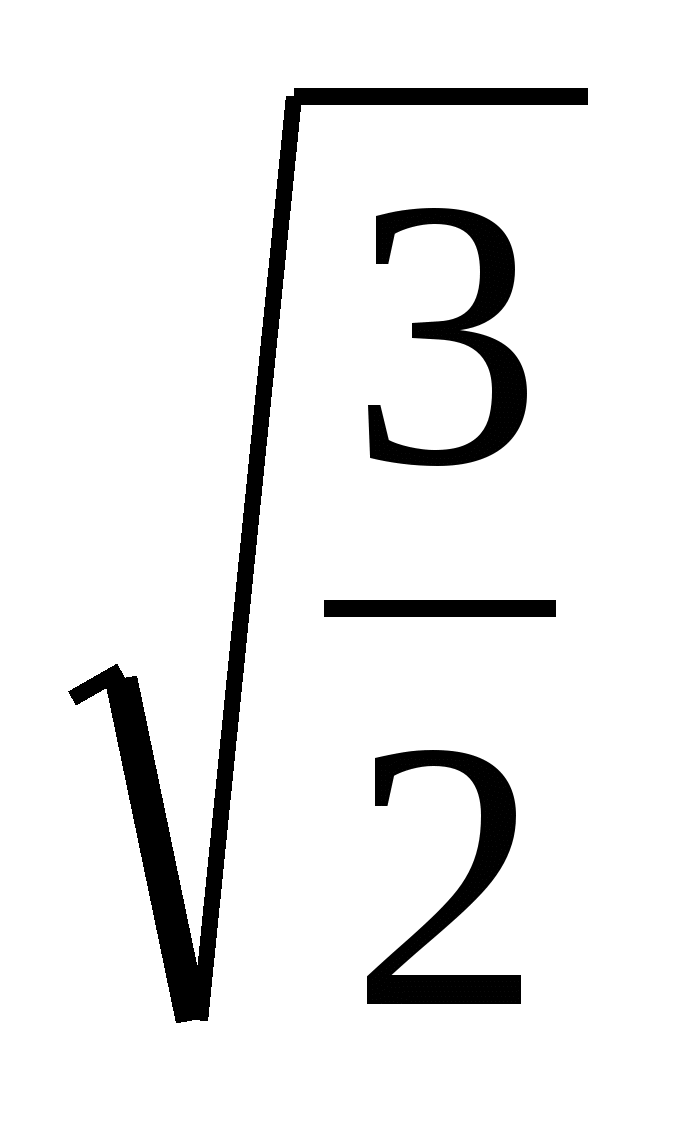Тогда РQ = Решение стереометрических задач методом координат = Решение стереометрических задач методом координат,

Д1Q= 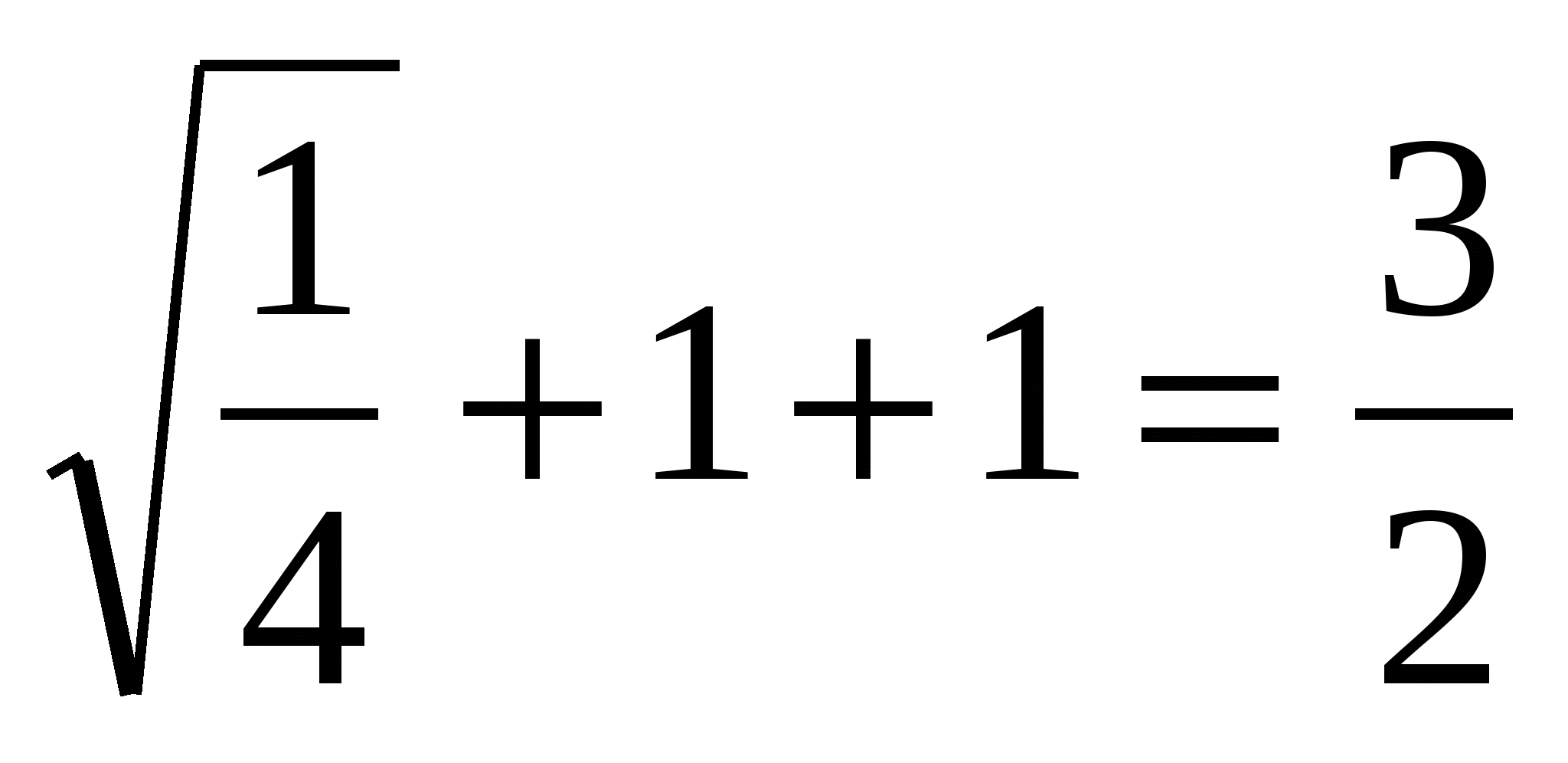Решение стереометрических задач методом координат,

Д1Р = 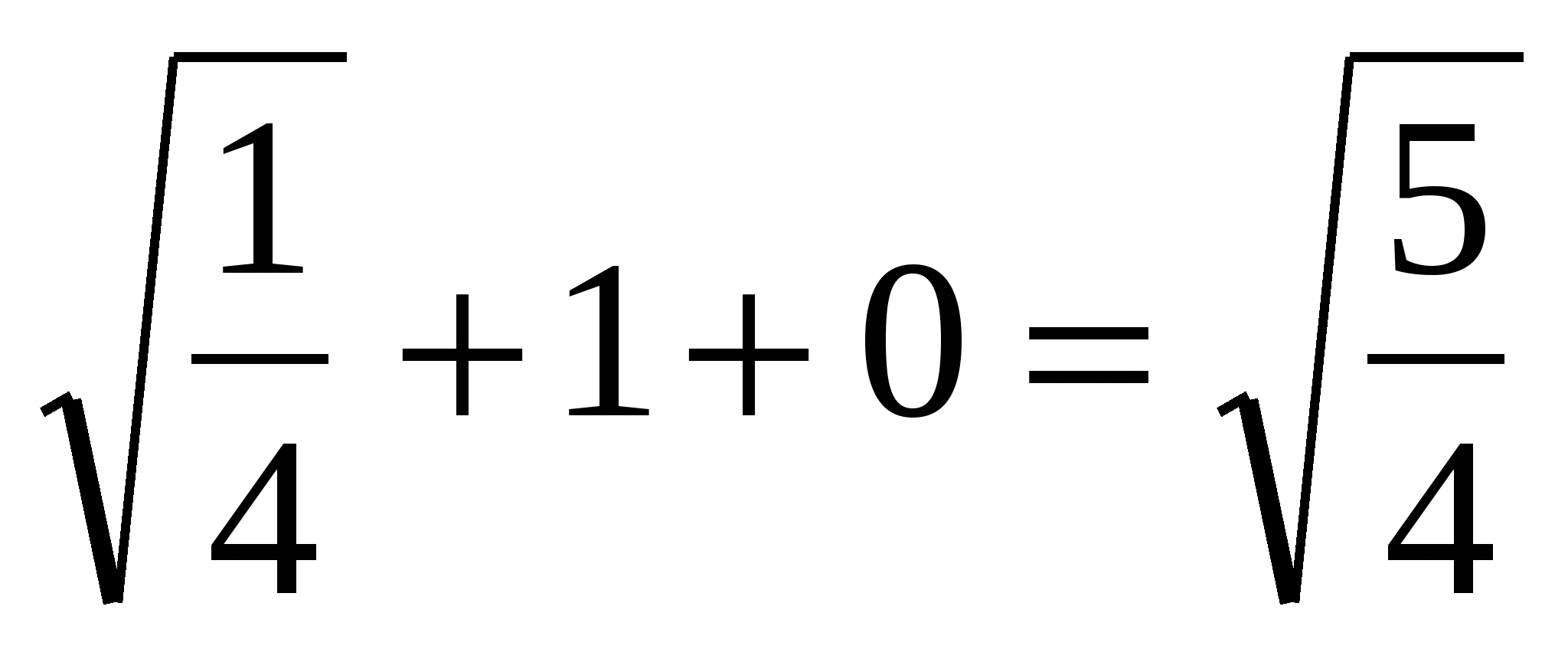Решение стереометрических задач методом координат.

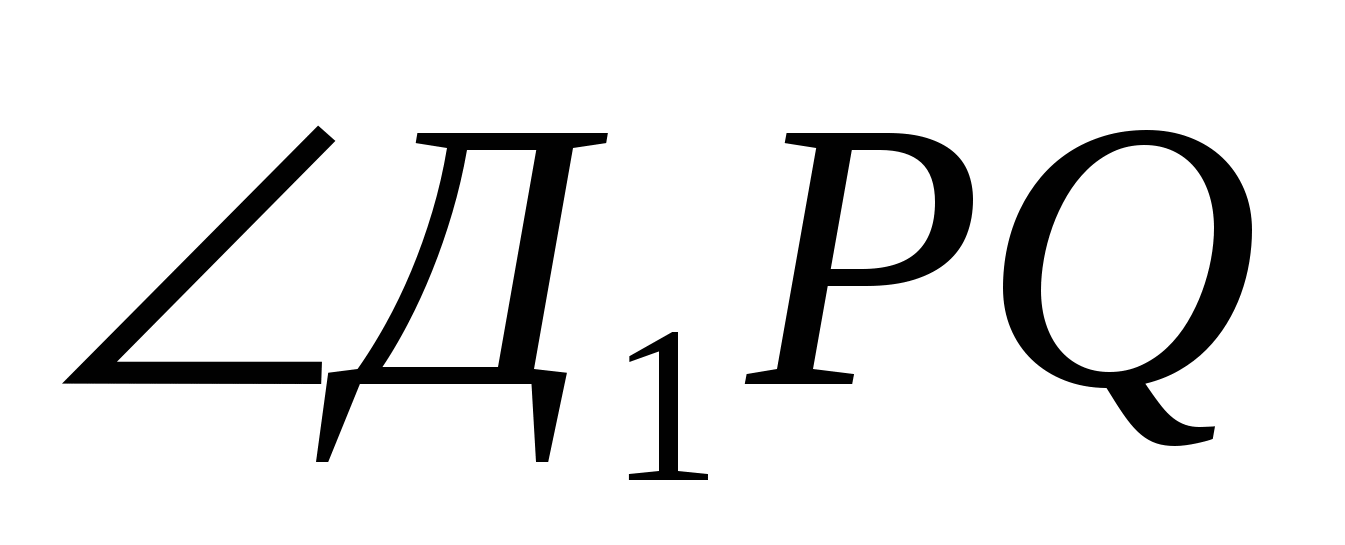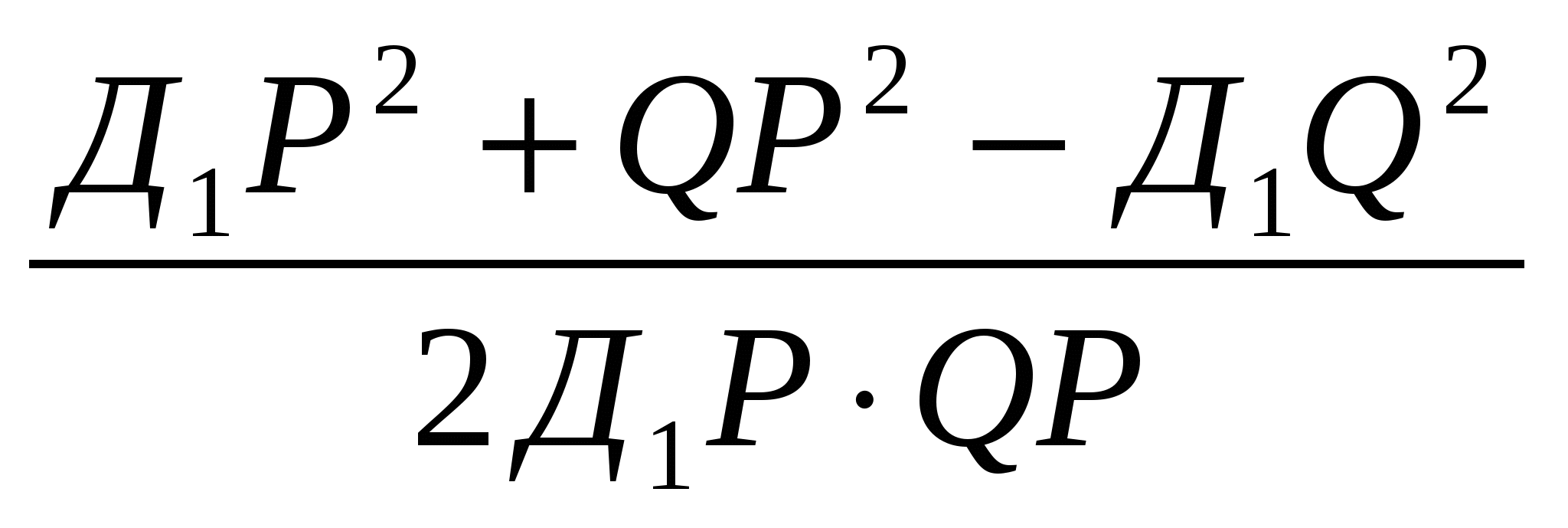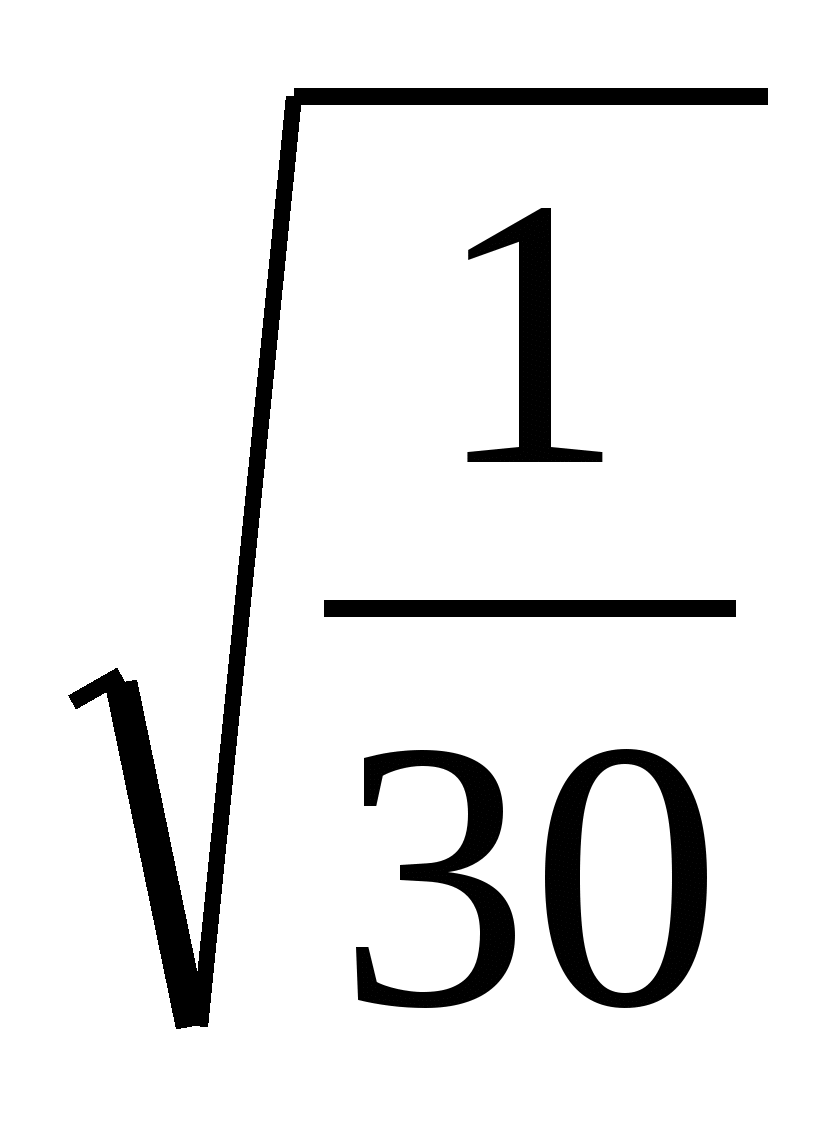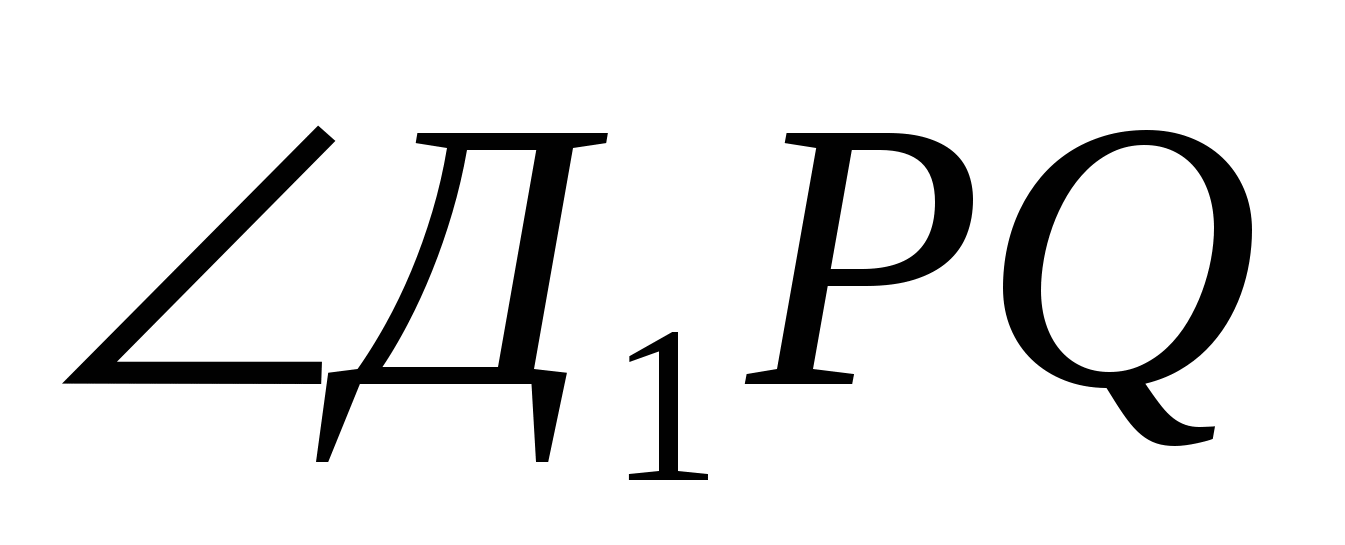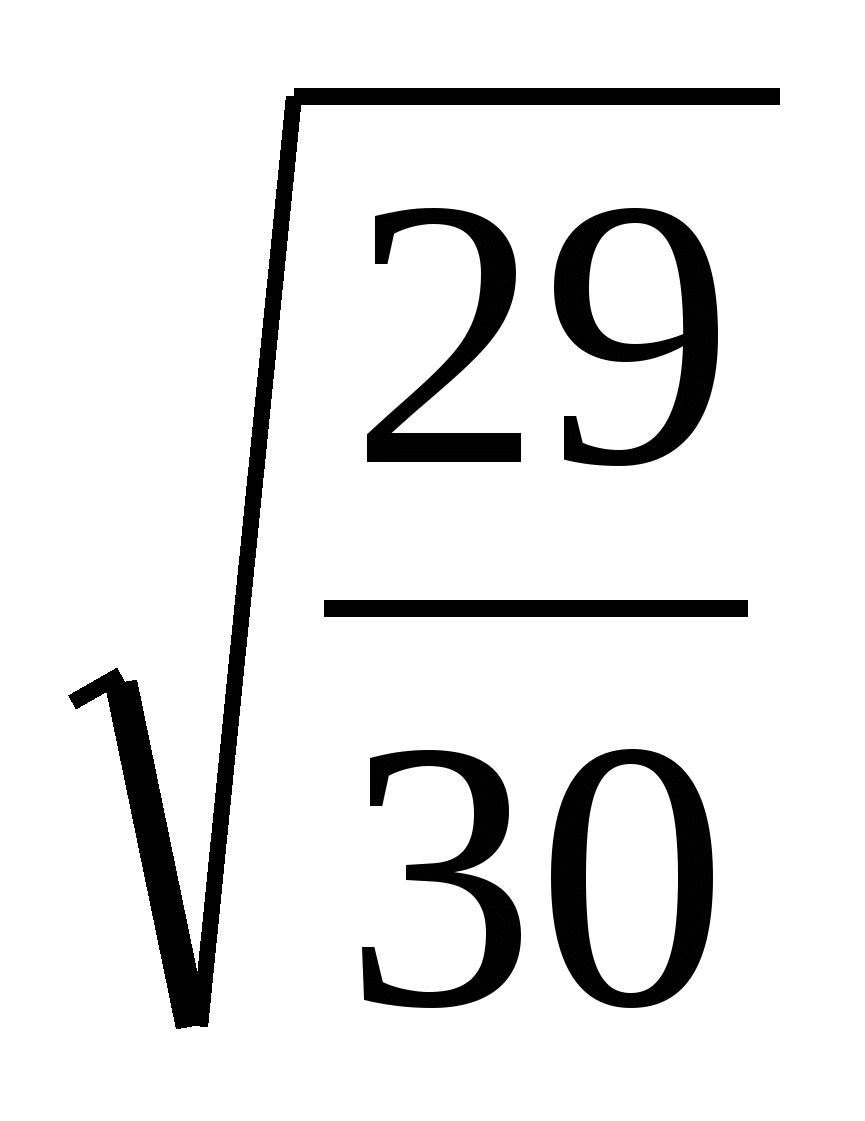Из треугольника Д1РQ, найдем cosРешение стереометрических задач методом координат= Решение стереометрических задач методом координат = Решение стереометрических задач методом координат, по тригонометрическому тождеству sinРешение стереометрических задач методом координат= Решение стереометрических задач методом координат.

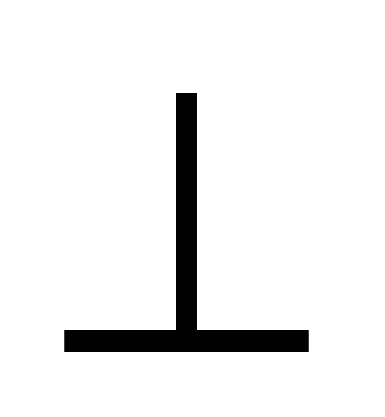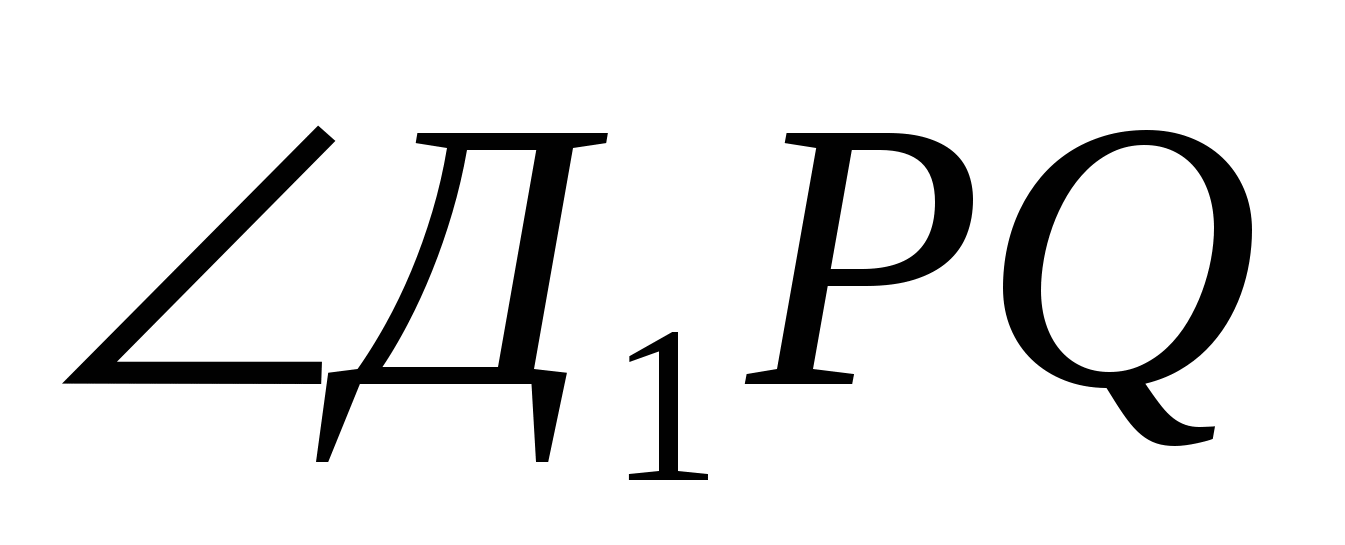Пусть Д1N Решение стереометрических задач методом координатРQ, где NРешение стереометрических задач методом координатРQ. Тогда Д1N=Д1Р sinРешение стереометрических задач методом координат.

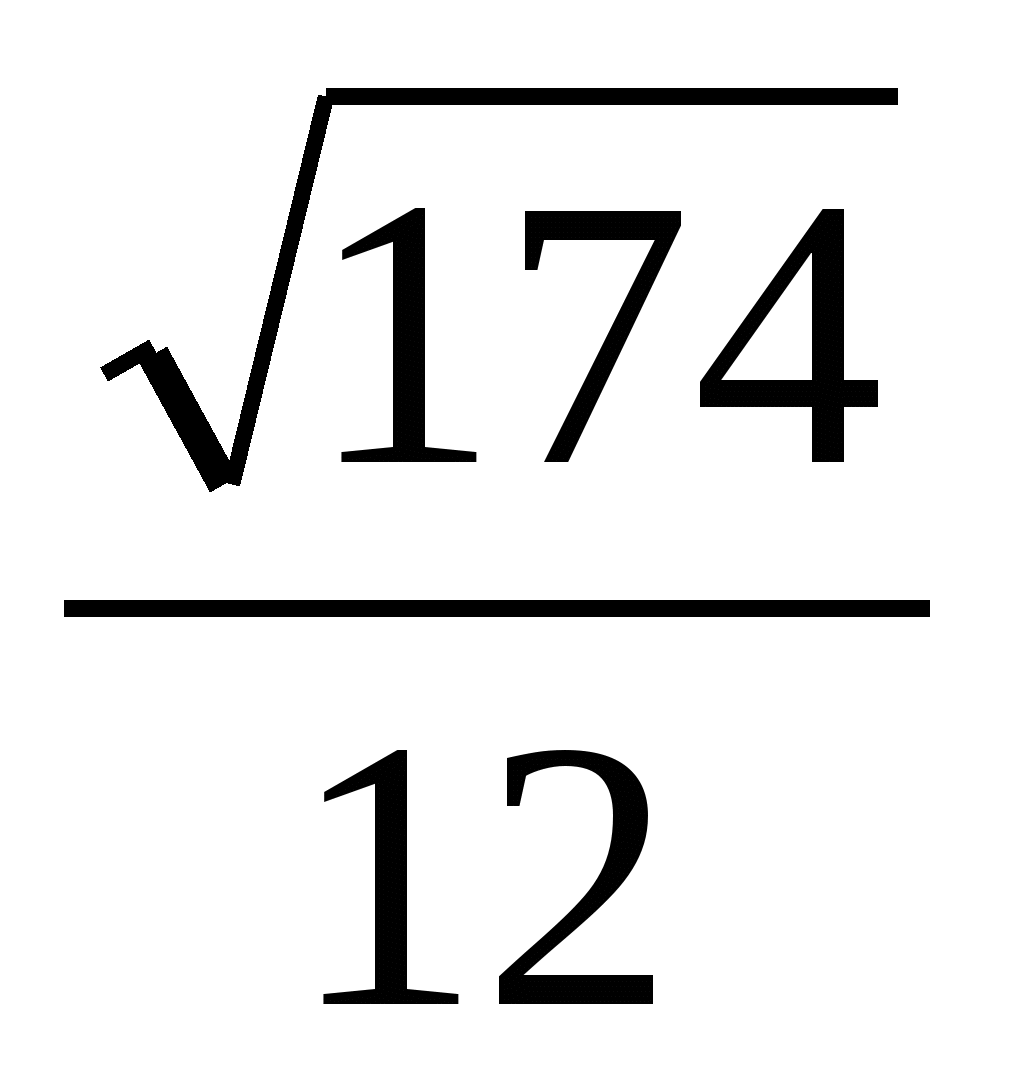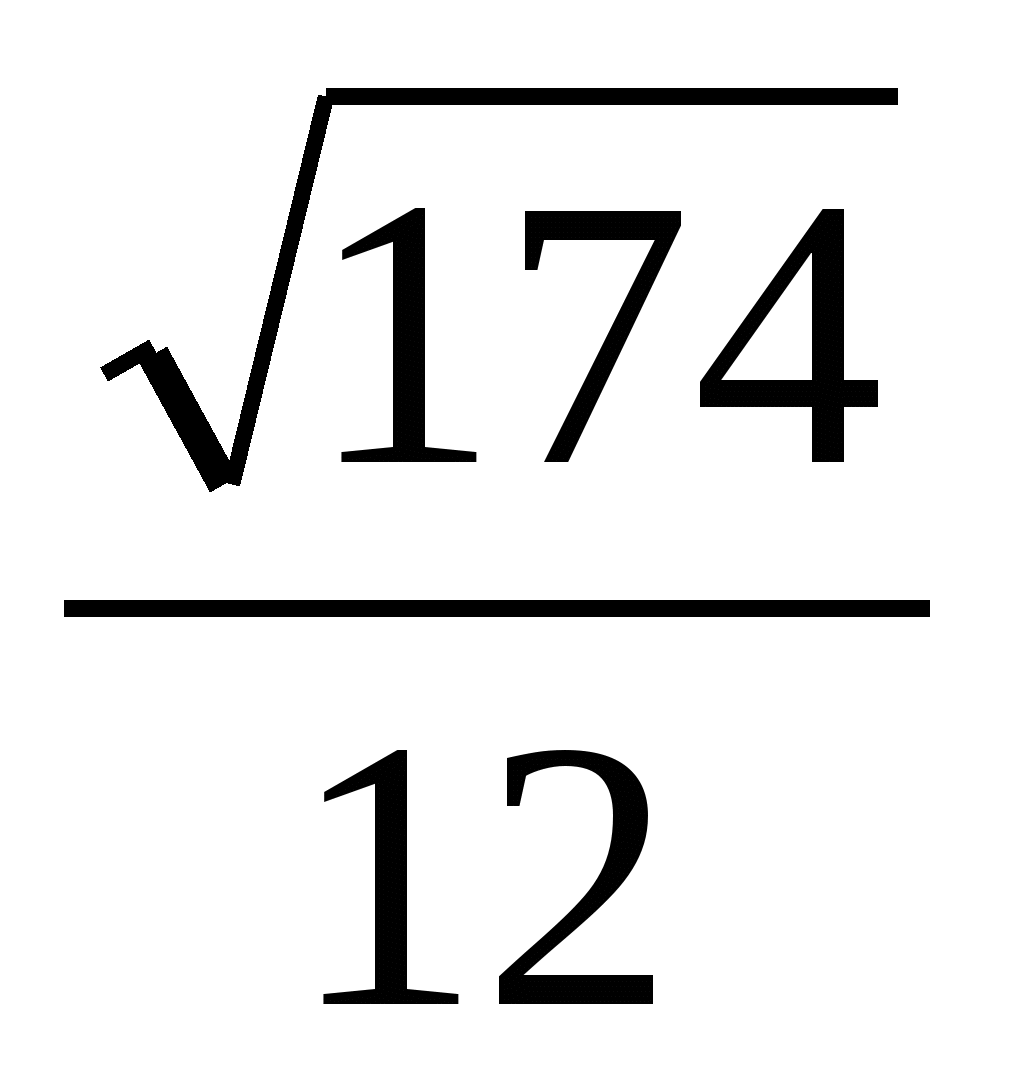Д1N=Решение стереометрических задач методом координат=Решение стереометрических задач методом координат.

Ответ: Решение стереометрических задач методом координат.

Пример 3. (6 вариант сборника)

В правильной четырехугольной пирамиде SАВСД, все ребра которой 1. найдите расстояние от середины ребра ВС до плоскости SСД.

Р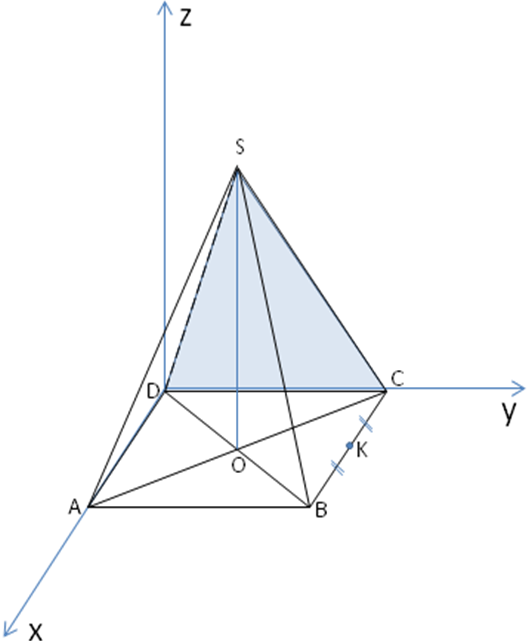Решение стереометрических задач методом координатешение: Введем систему координат: начало в точке Д, ось x направим вдоль ДA, ось y - вдоль DС, а ось z - вверх, перпендикулярно плоскости OXY.

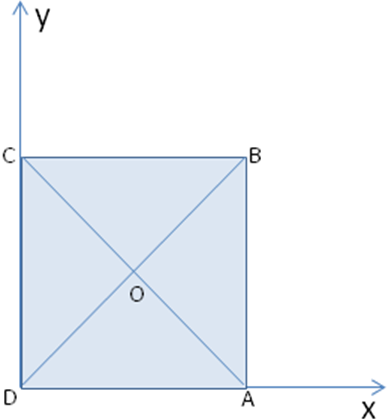
Решение стереометрических задач методом координат



Найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны.

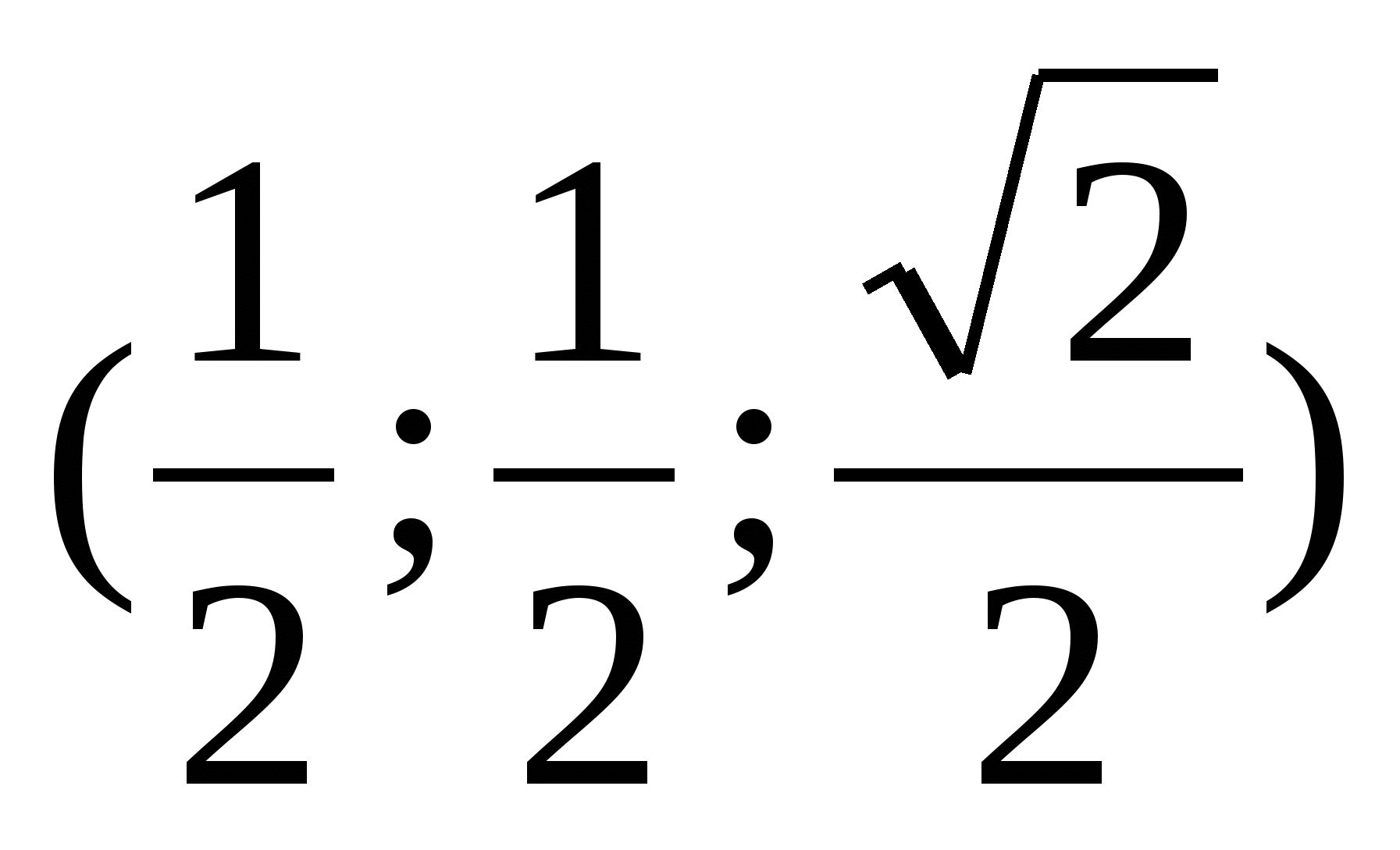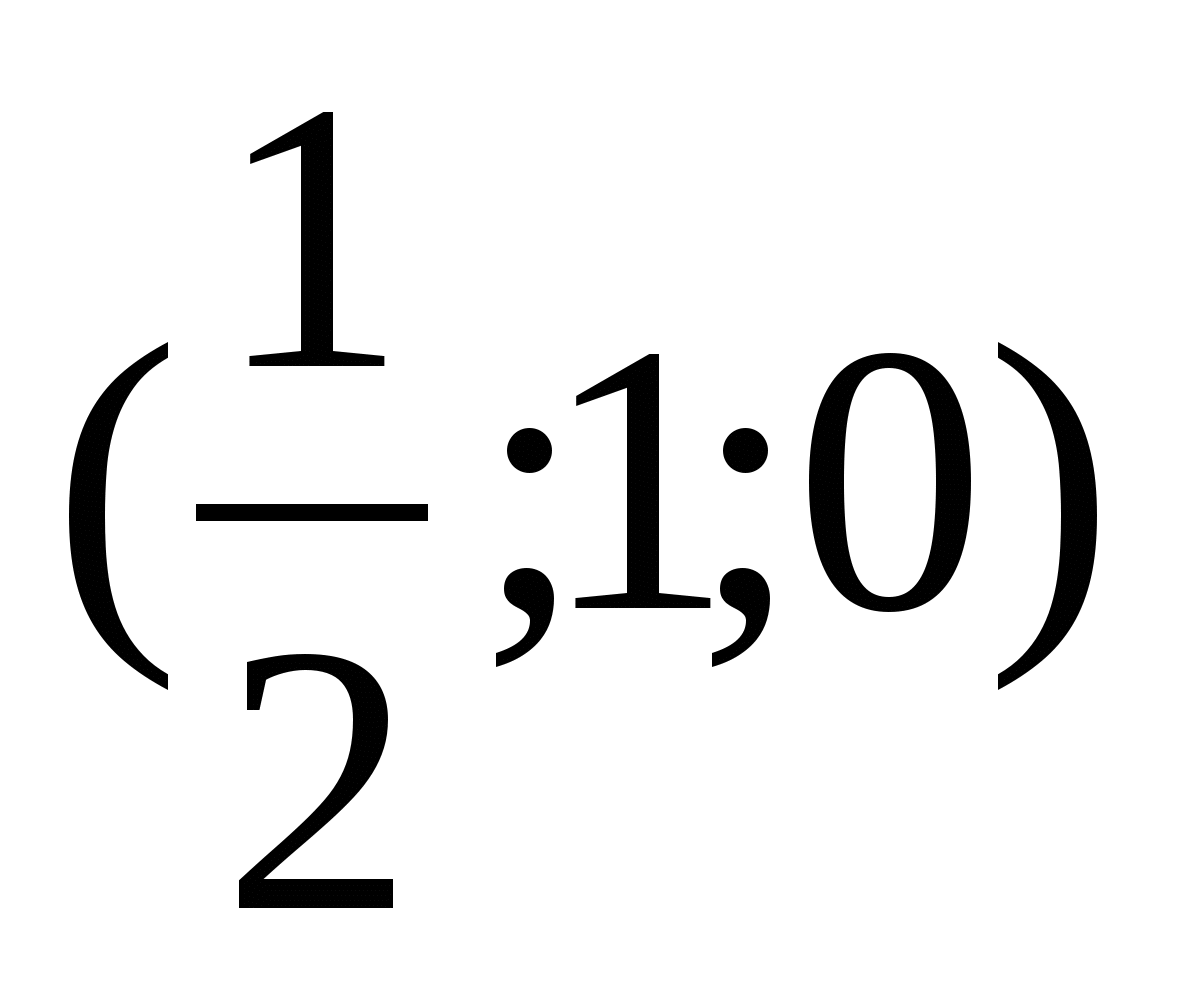Проблемы возникают с точкой S. Поскольку SО - высота пирамиды, точки S и О отличаются лишь координатой z. Длина отрезка SО - это и есть координата z для точки S. Координаты точек :Д(0;0;0), С(0;1;0), SРешение стереометрических задач методом координат, КРешение стереометрических задач методом координат.

Напишем уравнение плоскости 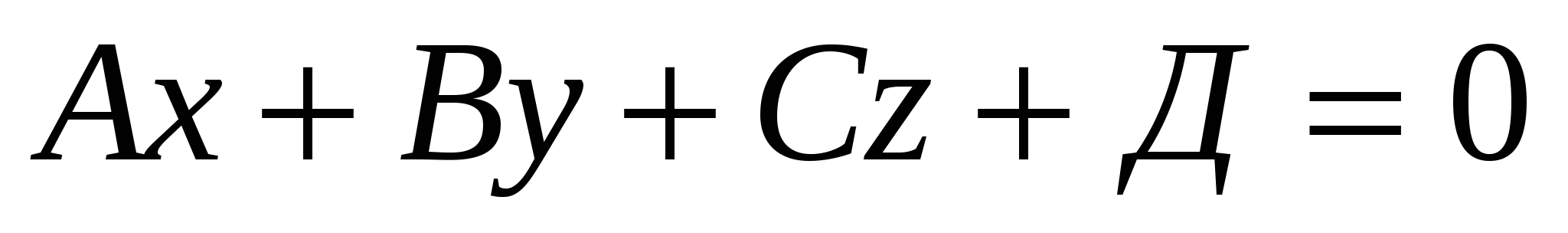Решение стереометрических задач методом координат, проходящей через точки Д, С, S.

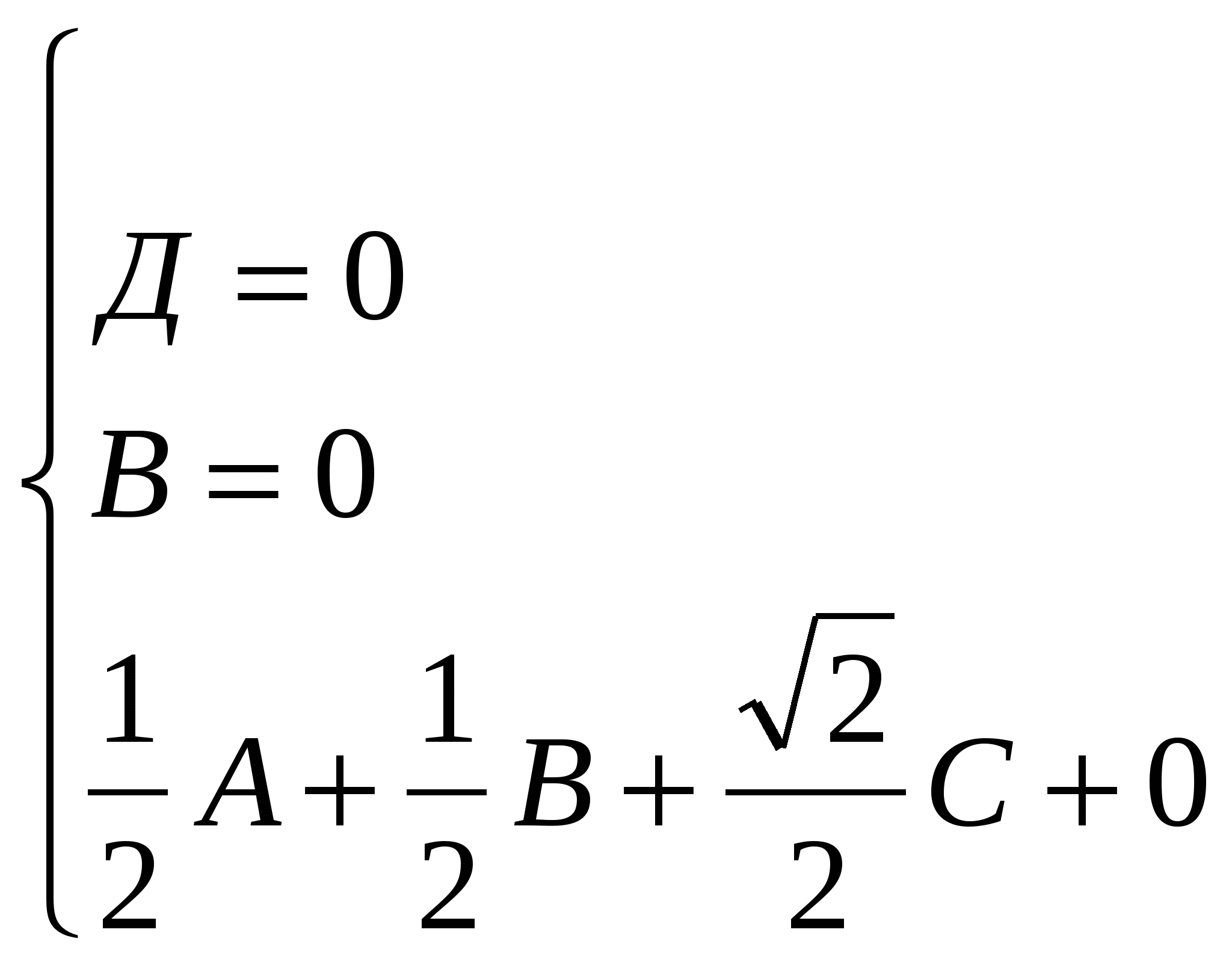
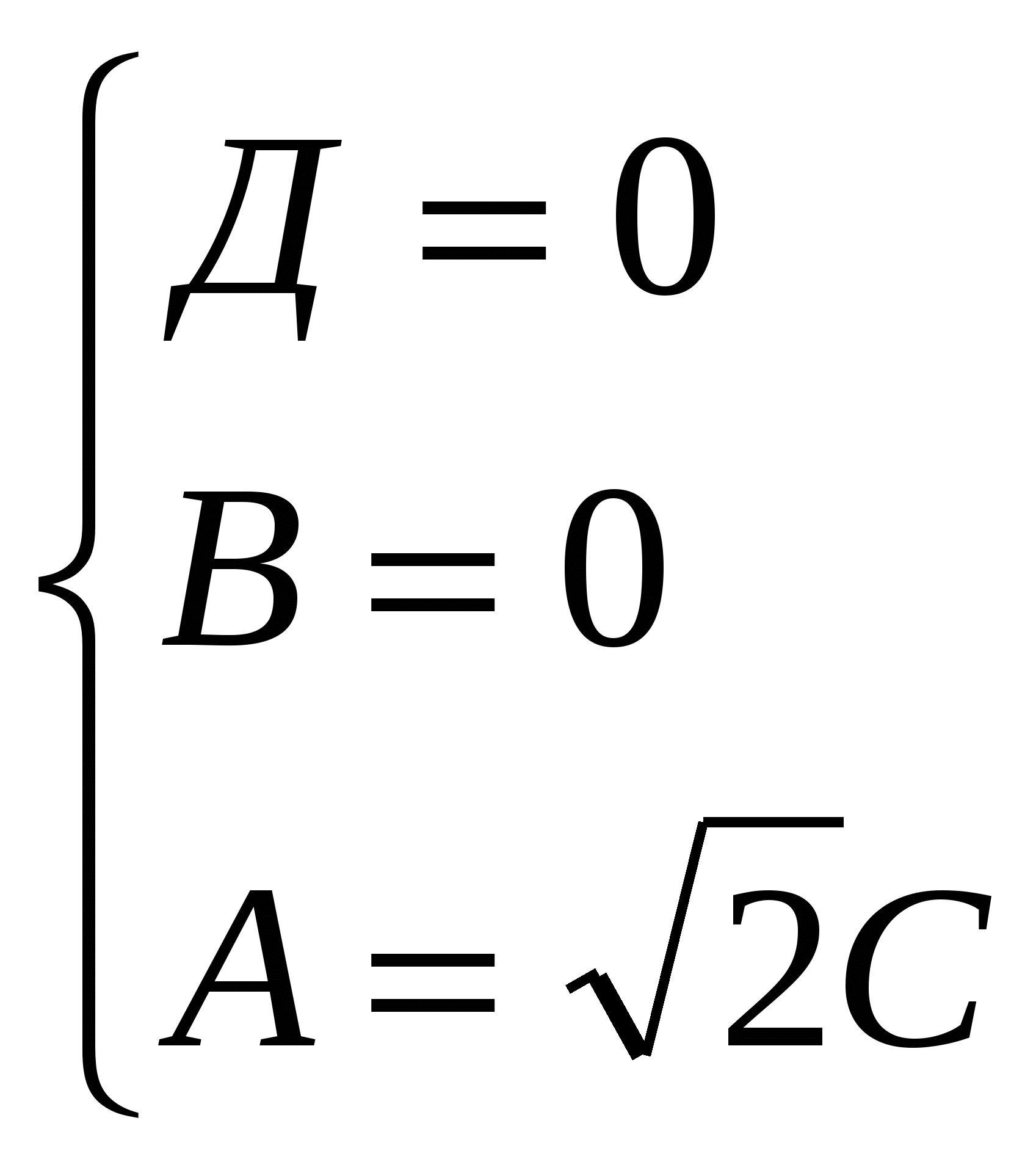
Решение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координат

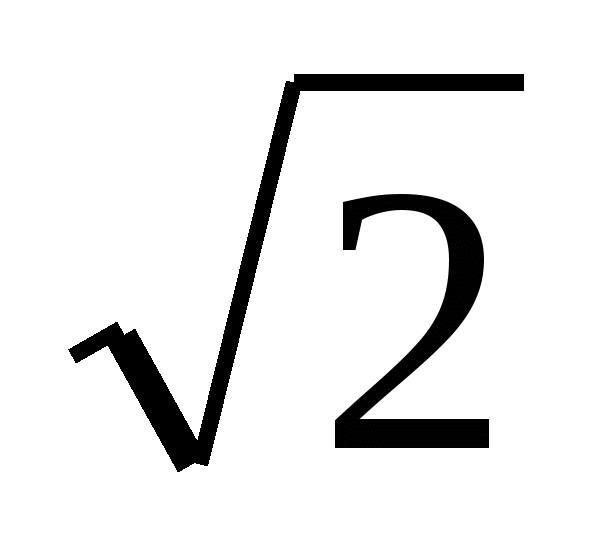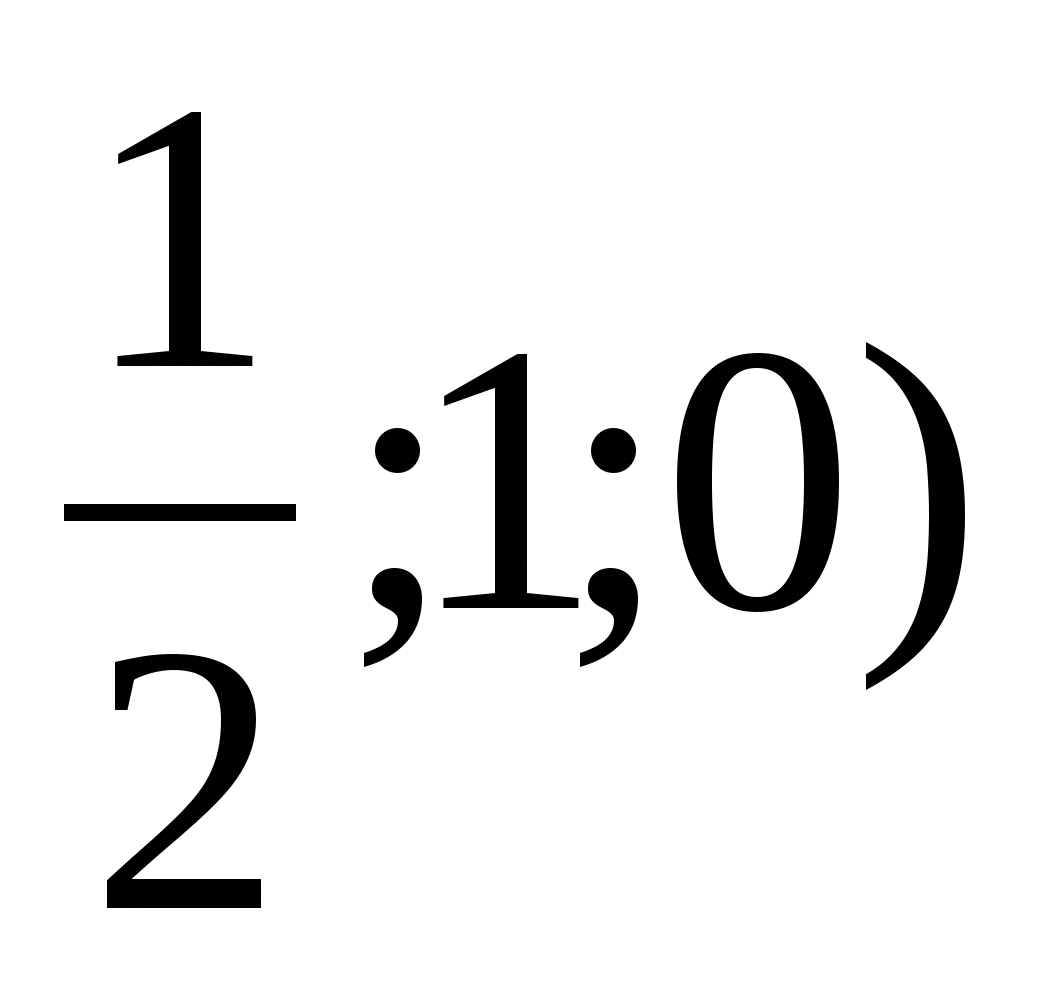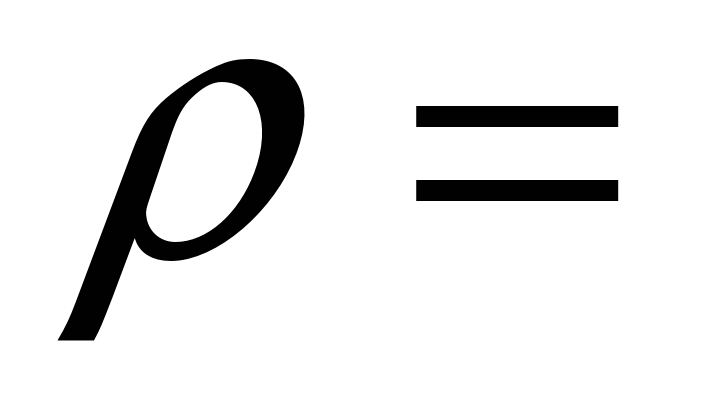
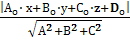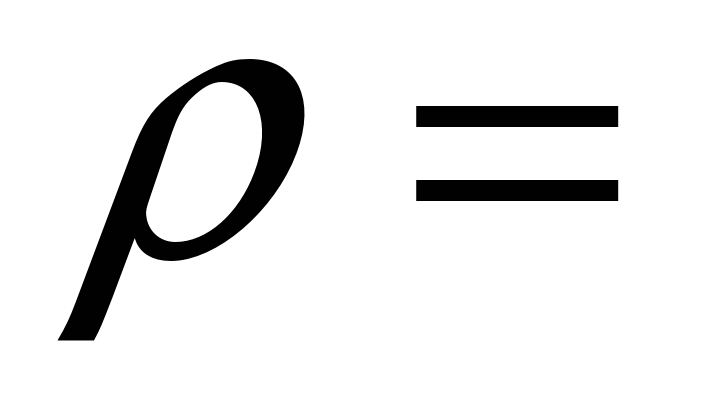
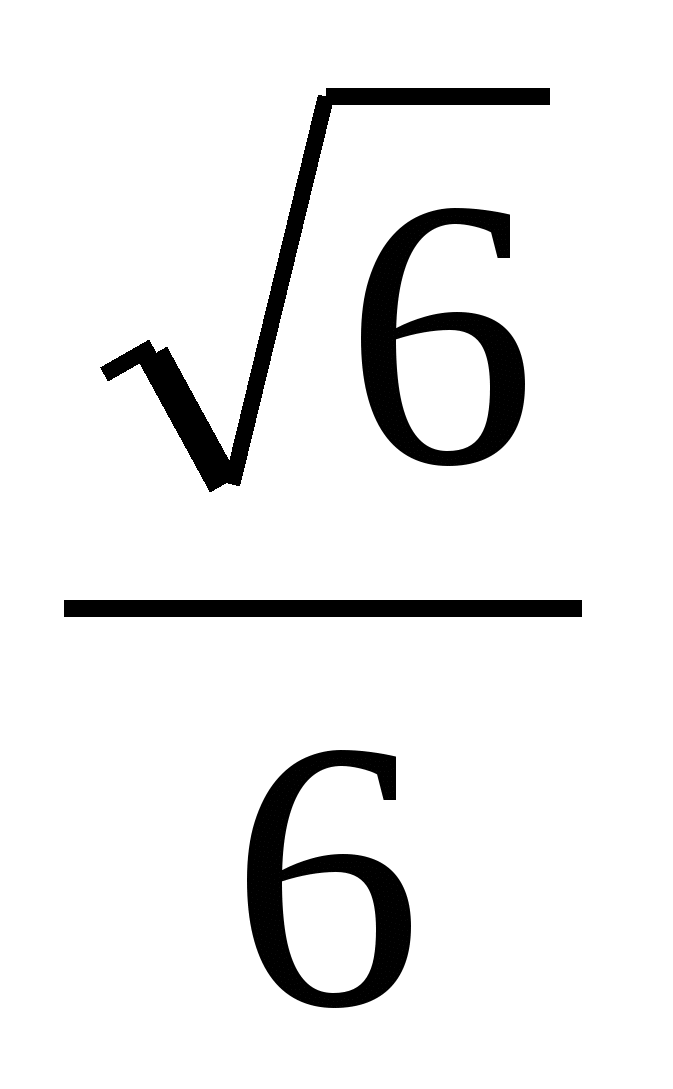Получим уравнение плоскости SСД: Решение стереометрических задач методом координатх+ z =0 и найдем расстояние от точки К(Решение стереометрических задач методом координат до данной плоскости по формуле Решение стереометрических задач методом координатРешение стереометрических задач методом координат.

Решение стереометрических задач методом координатРешение стереометрических задач методом координат.

Ответ: 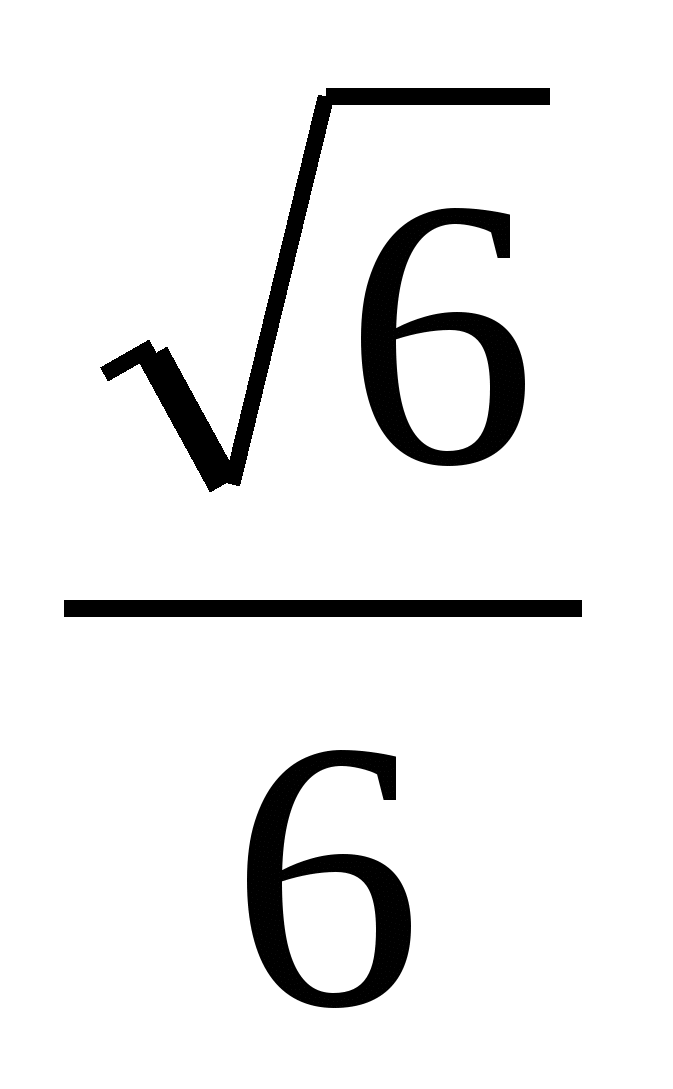Решение стереометрических задач методом координат.

Пример 4 (10 вариант сборника)

В правильной шестиугольной призме АВСДЕFА1В1С1Д1Е1F1, все ребра которой равны 1, найдите угол между прямыми АВ1 и ВЕ1.

Р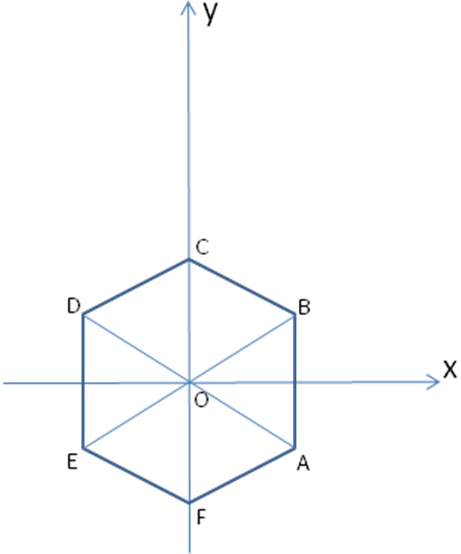Решение стереометрических задач методом координатешение: Введем систему координат. Начало координат - точку O - поместим в центр симметрии шестиугольника ABCDEF. Ось х - через середины отрезков AB и DE, ось у пойдет вдоль FC, ось z проведем перпендикулярно плоскости OXY.

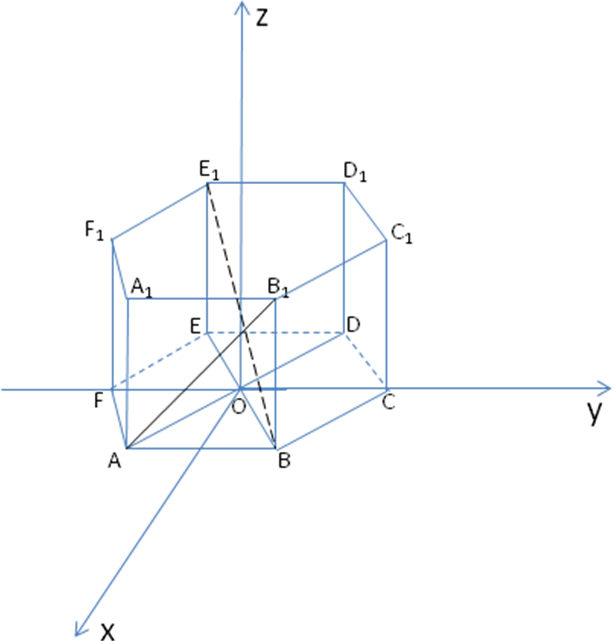
Решение стереометрических задач методом координат



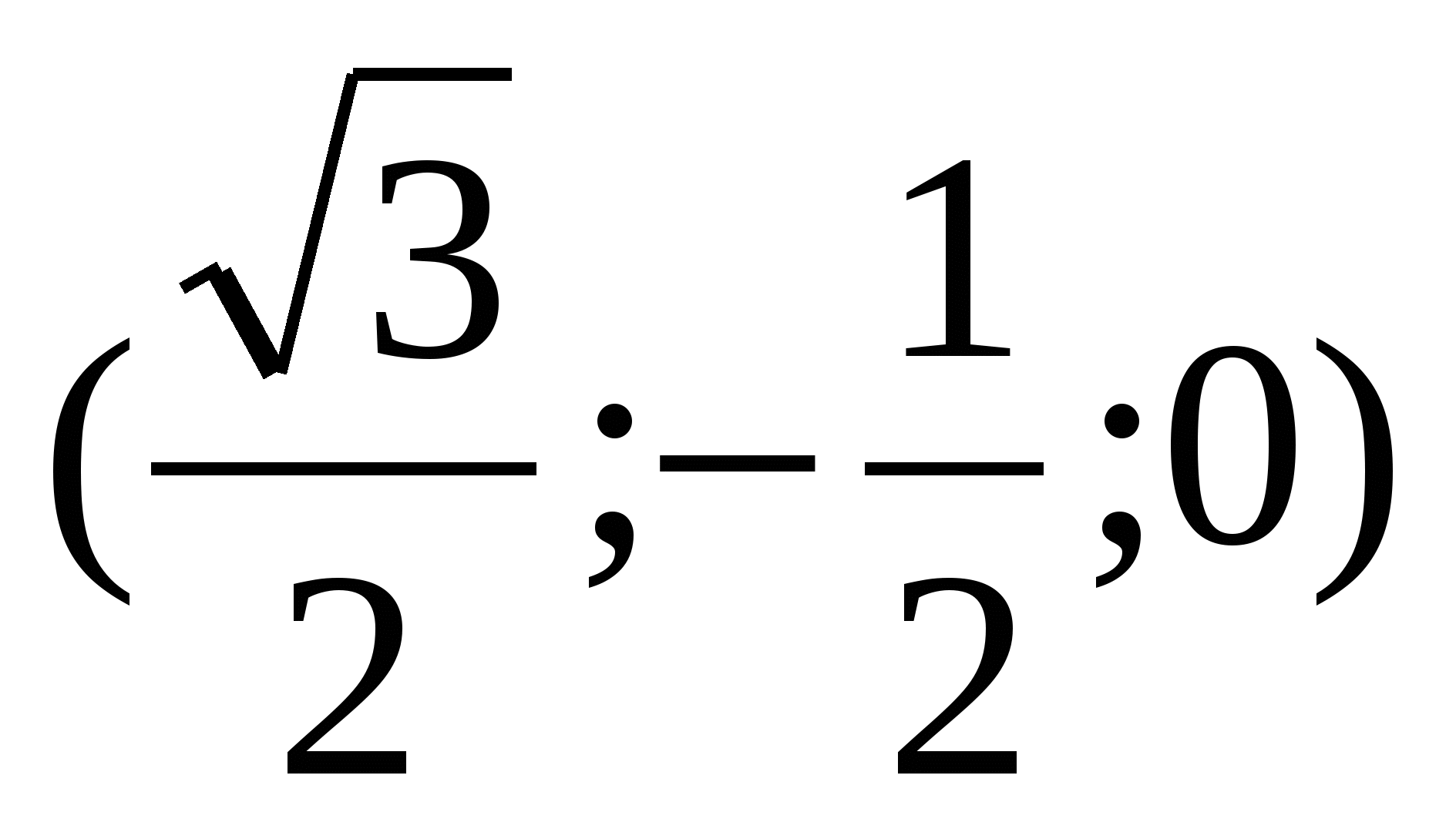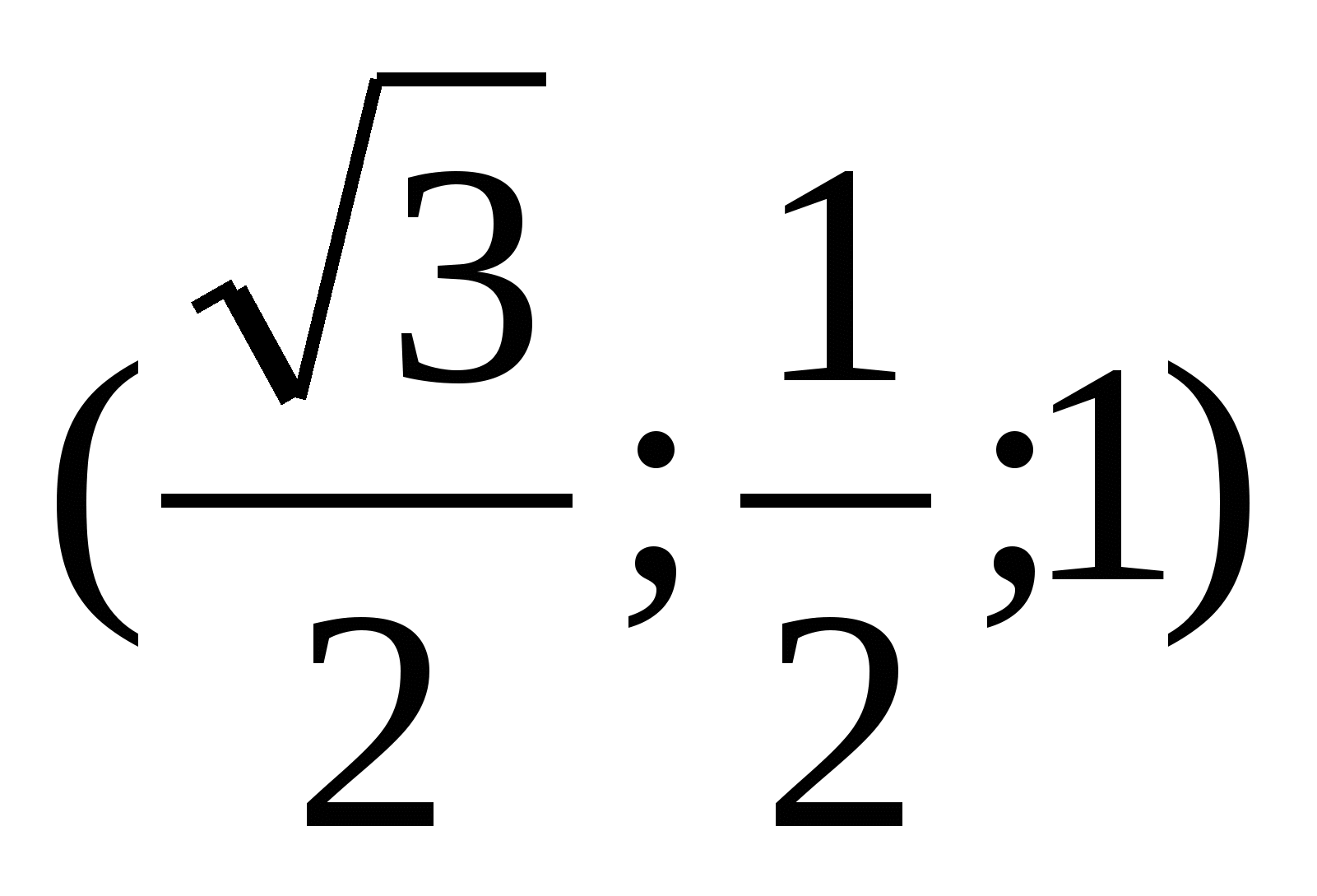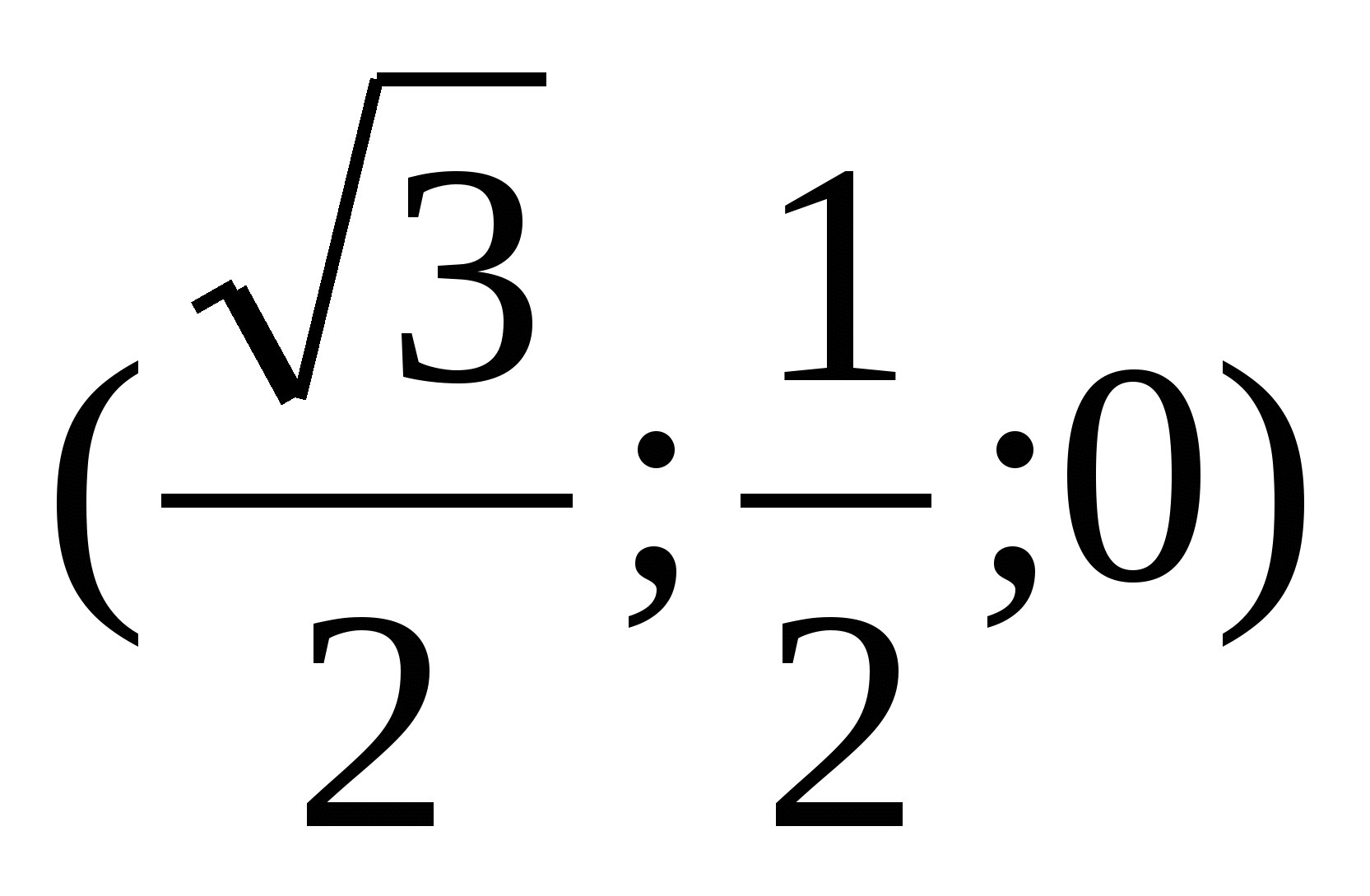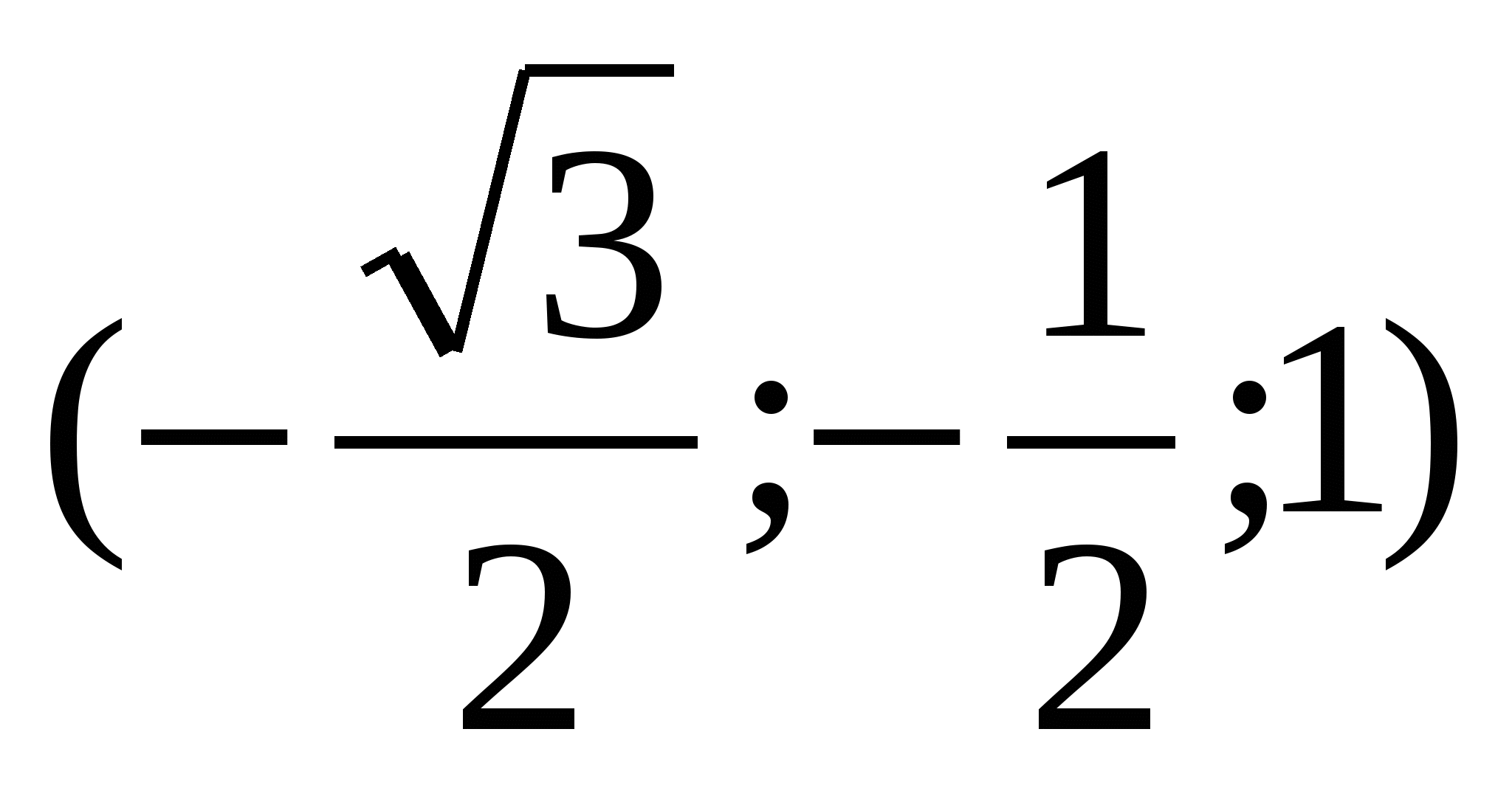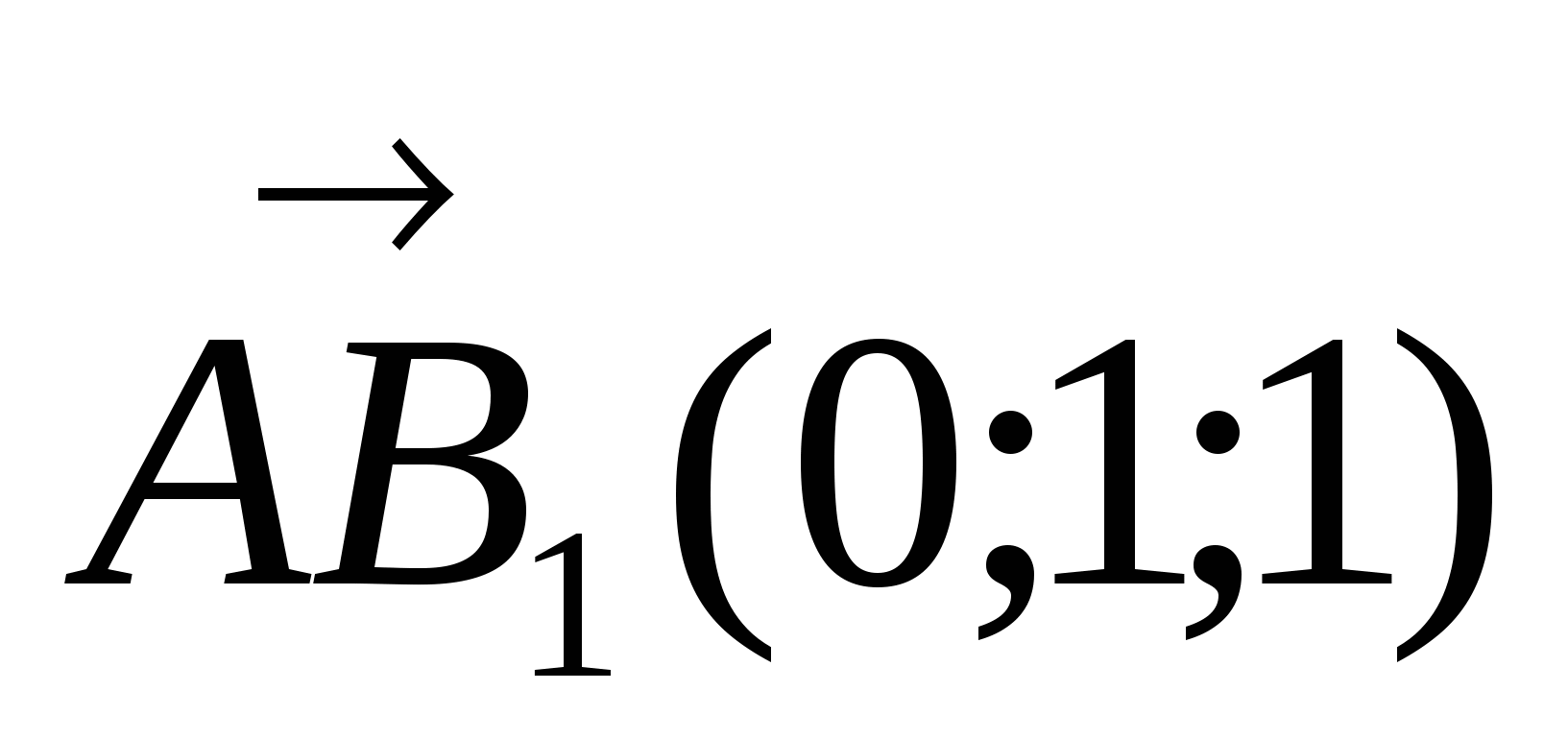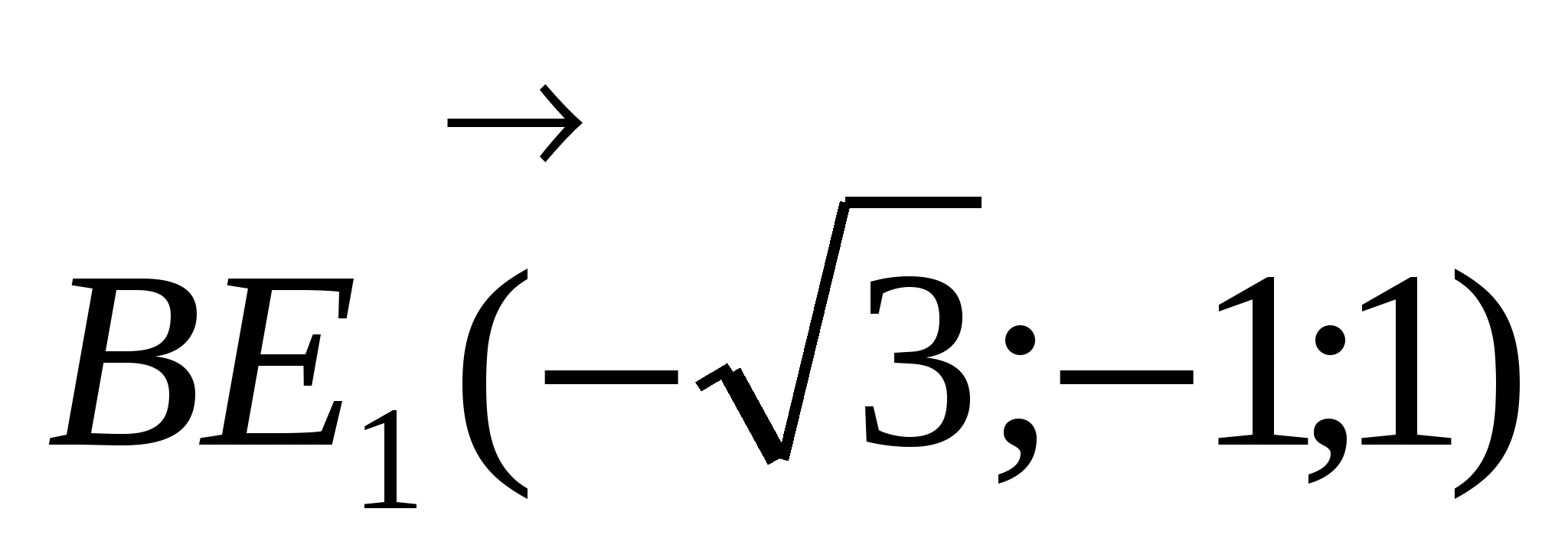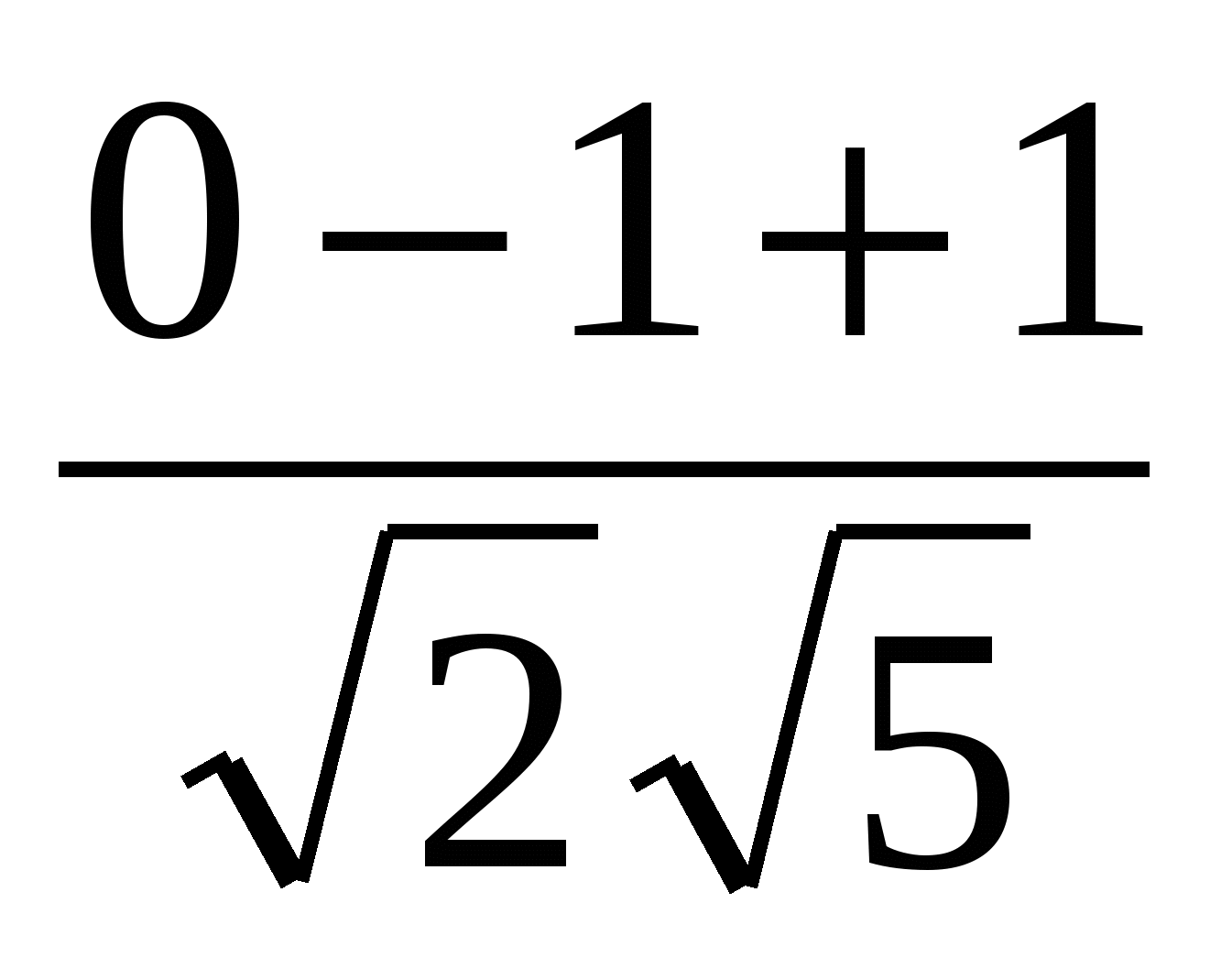Найдем координаты точек: АРешение стереометрических задач методом координат, В1Решение стереометрических задач методом координат, ВРешение стереометрических задач методом координат, Е1Решение стереометрических задач методом координат. Угол между прямыми найдем как угол между соответствующими векторами Решение стереометрических задач методом координат и Решение стереометрических задач методом координат.

cosРешение стереометрических задач методом координат= Решение стереометрических задач методом координат=0 , отсюда Решение стереометрических задач методом координат=900.

Ответ: 900.

Пример 5 (3 вариант сборника)

В правильной треугольной пирамиде SАВС с основанием АВС известны ребра: АВ=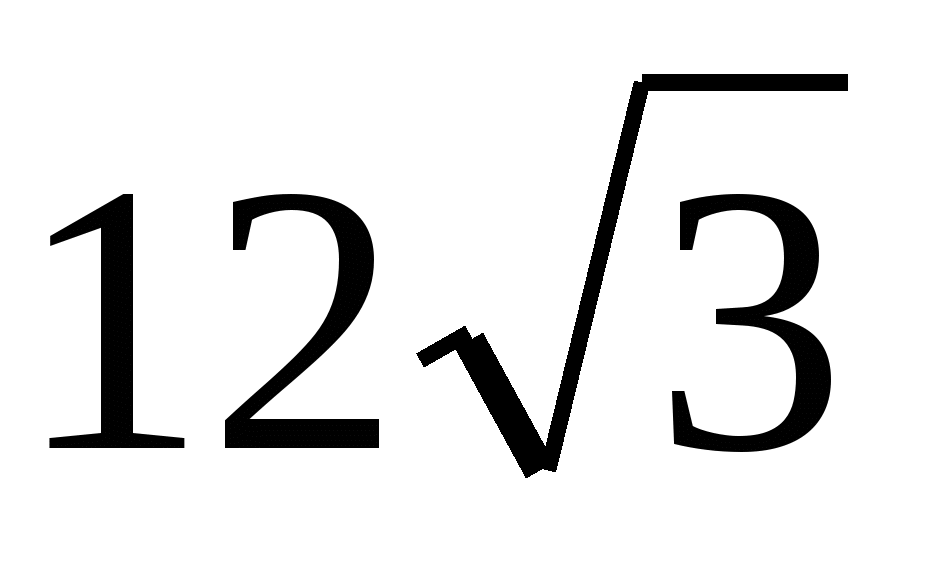Решение стереометрических задач методом координат,SС=13. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер АS и ВС.

Решение: Введем систему координат: начало координат а точке А, ось х направляем по ребру АС, z - по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC, она будет параллельна ВН, высоте основания АВС.

С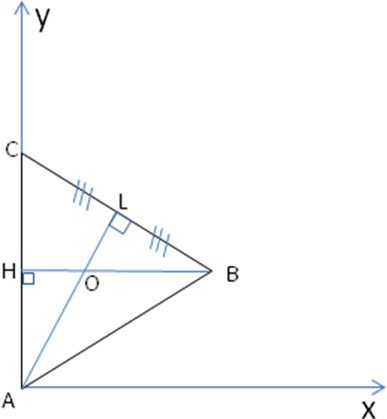Решение стереометрических задач методом координатделаем некоторые вычисления. АL=18, SО= 5.

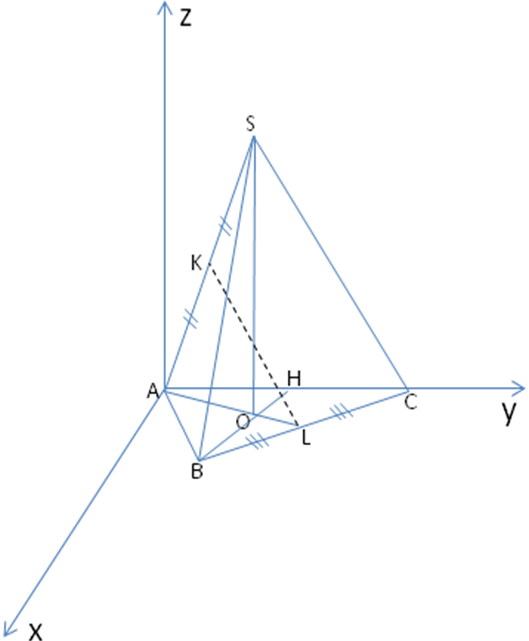
Решение стереометрических задач методом координат



Координаты точек L(9;9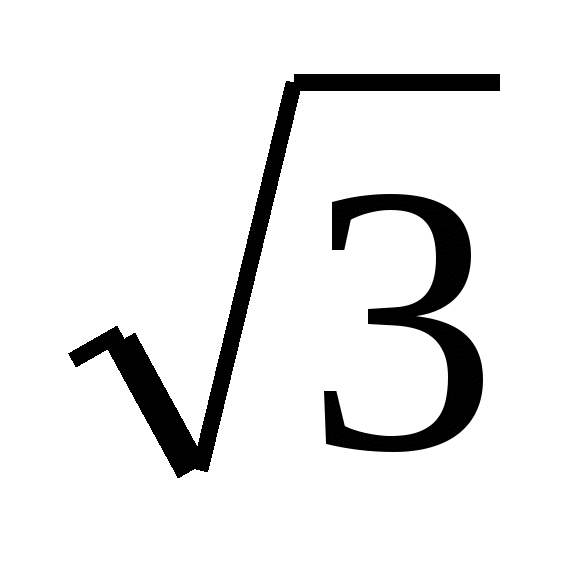Решение стереометрических задач методом координат;0), К(3;3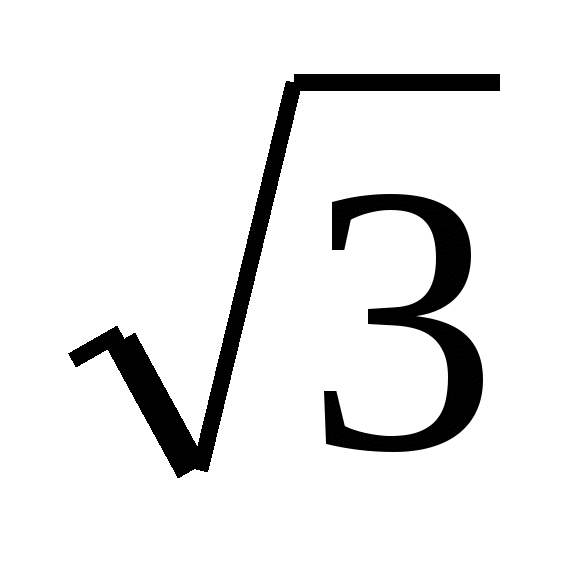Решение стереометрических задач методом координат;2,5), тогда вектор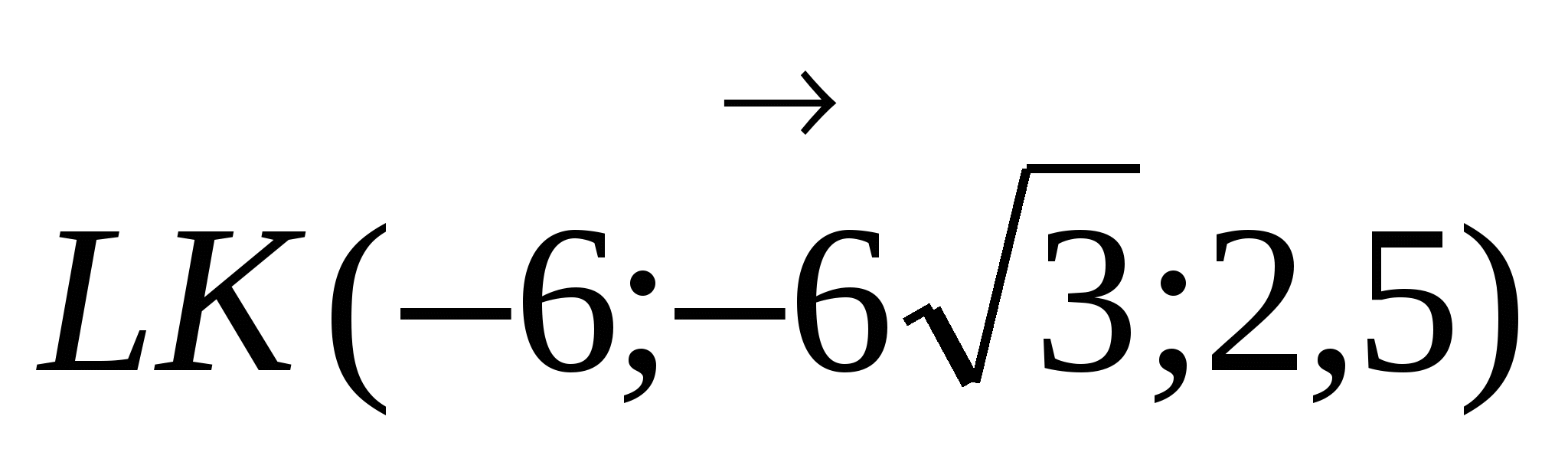 Решение стереометрических задач методом координат

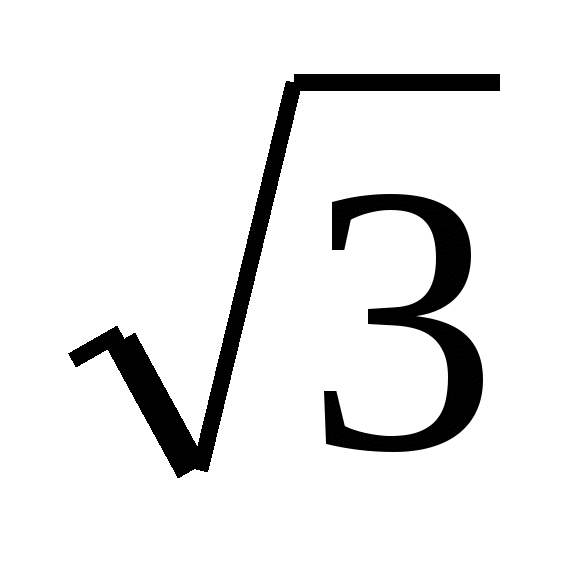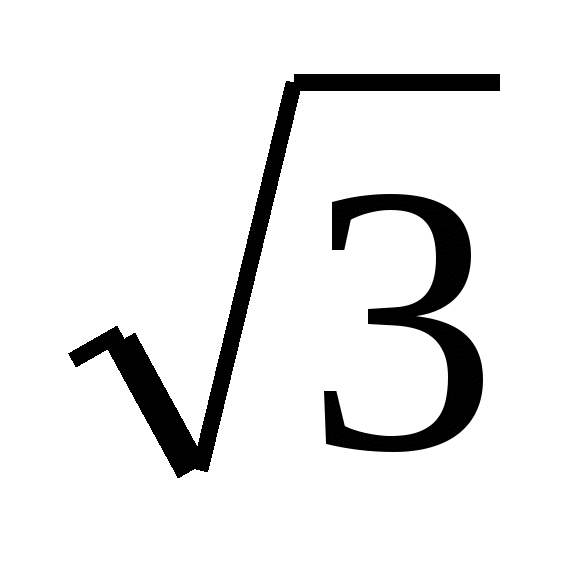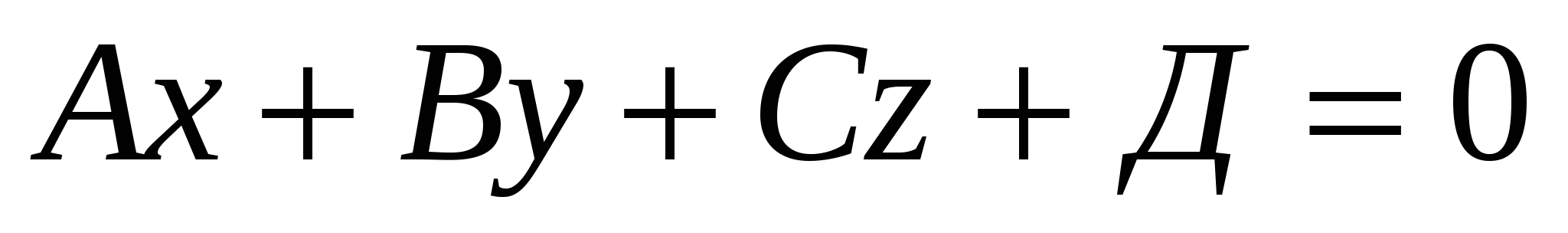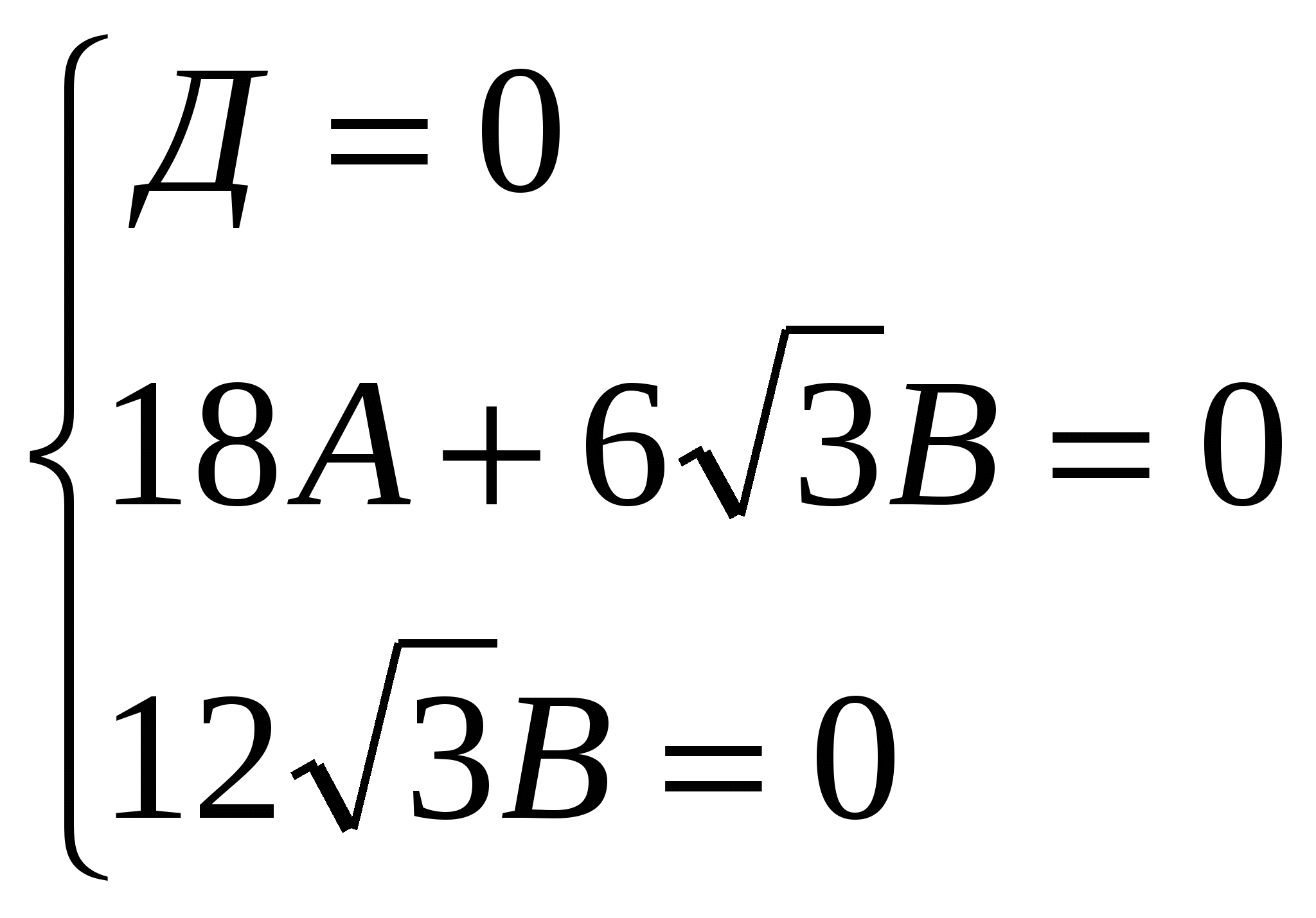
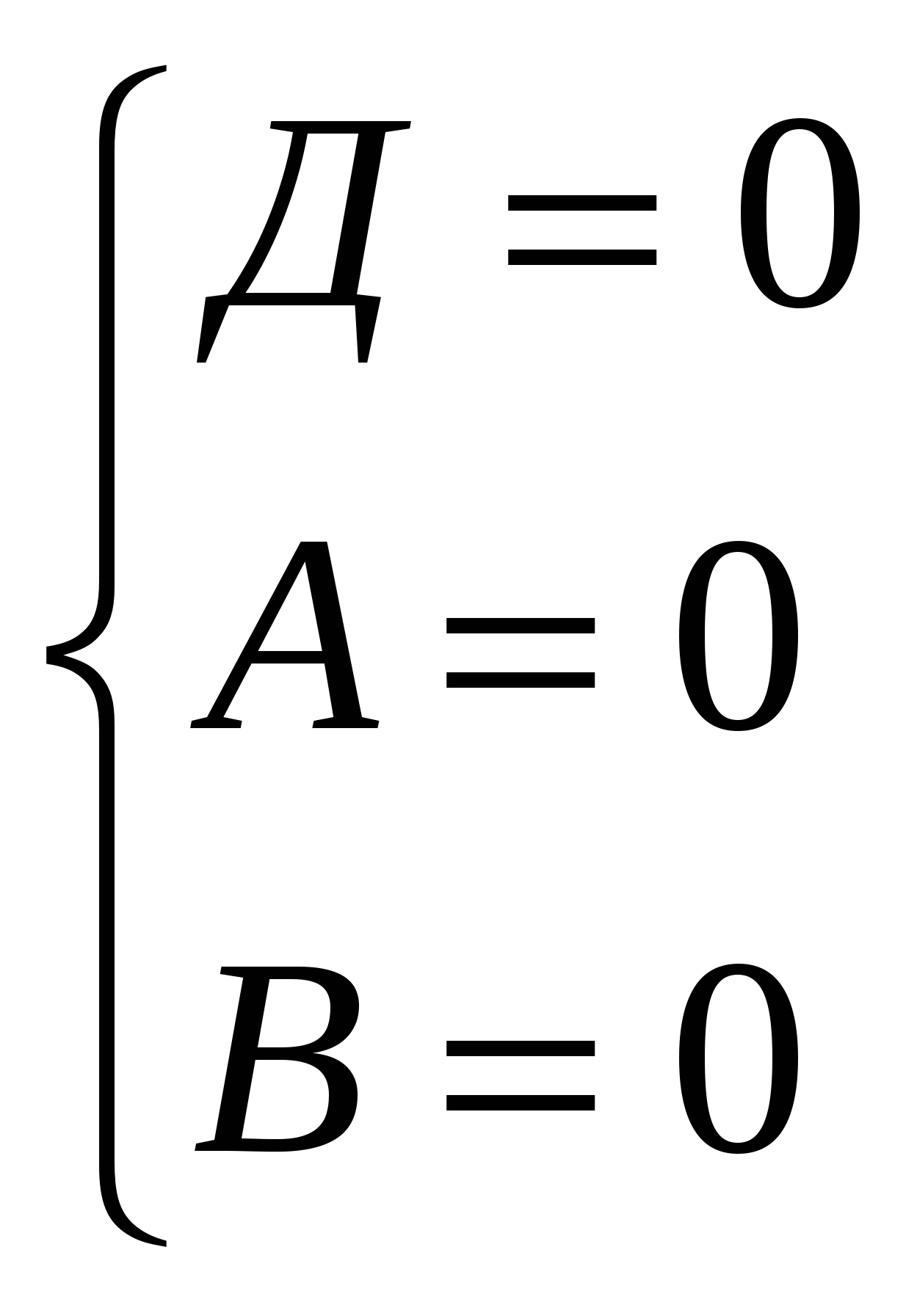Найдем ординаты точек, задающих плоскость: А(0;0;0), В (18; 6Решение стереометрических задач методом координат;0 ), С(0;12Решение стереометрических задач методом координат;0) и напишем уравнение плоскости Решение стереометрических задач методом координат.

Решение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координат.

Уравнение плоскости z=0, нормаль к плоскости имеет координаты 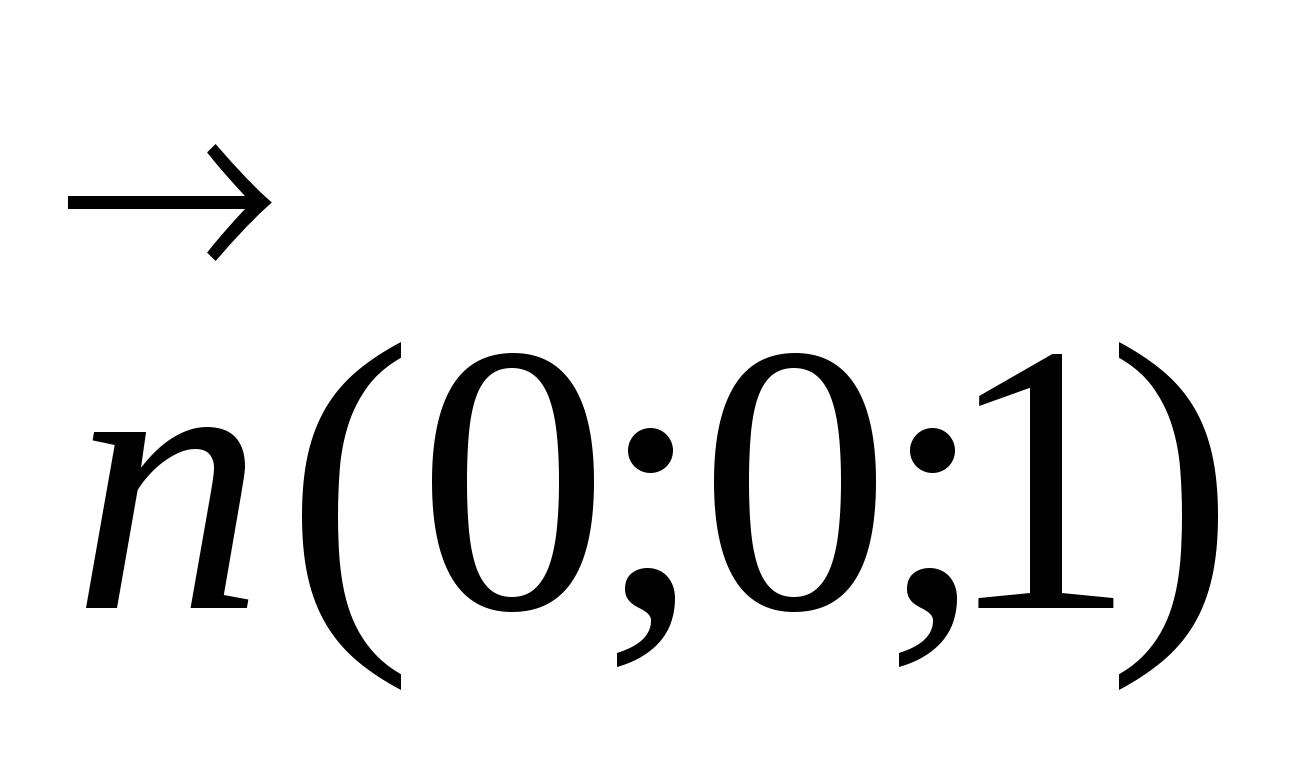Решение стереометрических задач методом координат.

Угол между прямой и плоскостью - это угол между вектором, лежащим на заданной прямой и нормалью к плоскости.

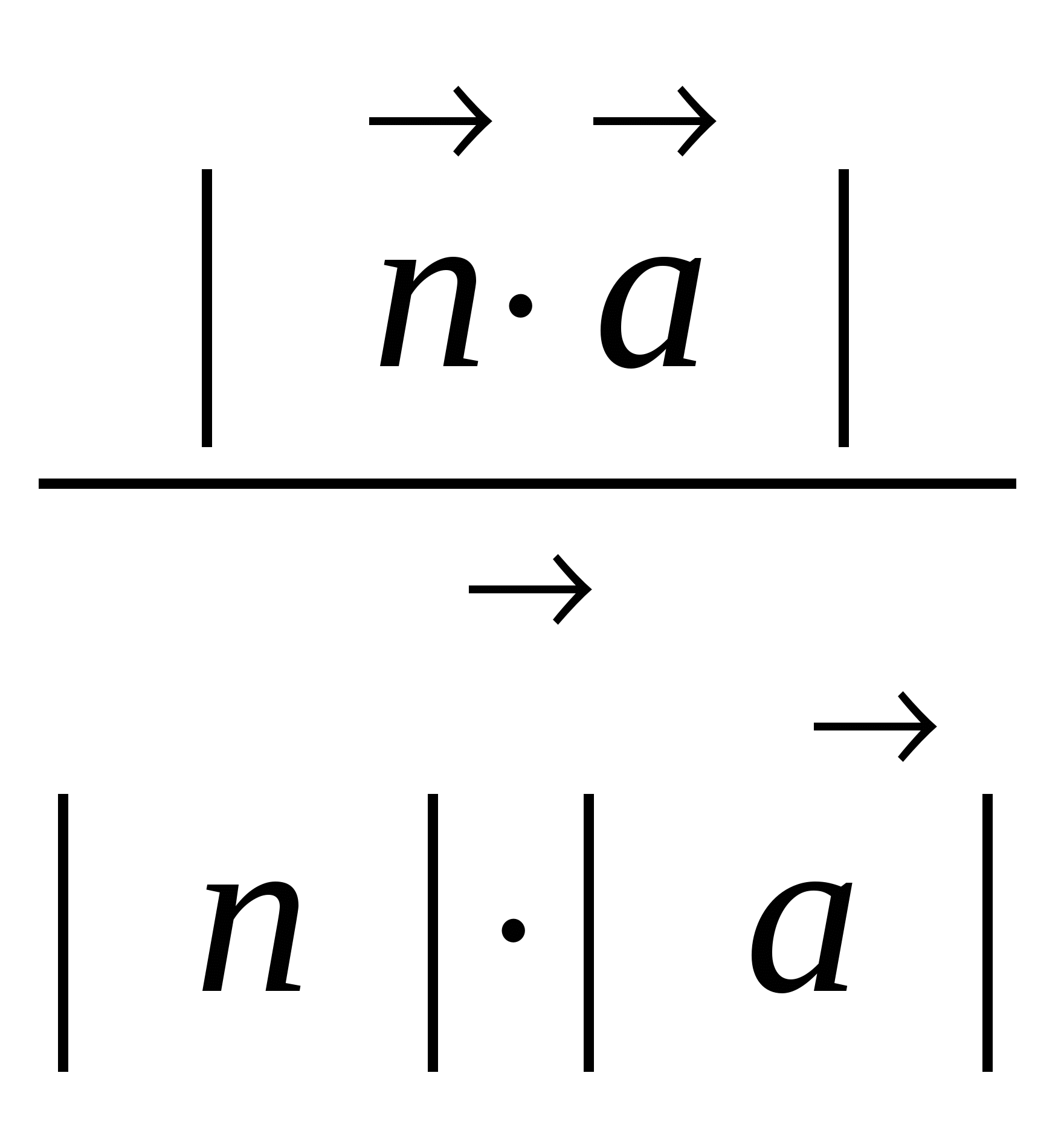
sin Решение стереометрических задач методом координат= Решение стереометрических задач методом координат

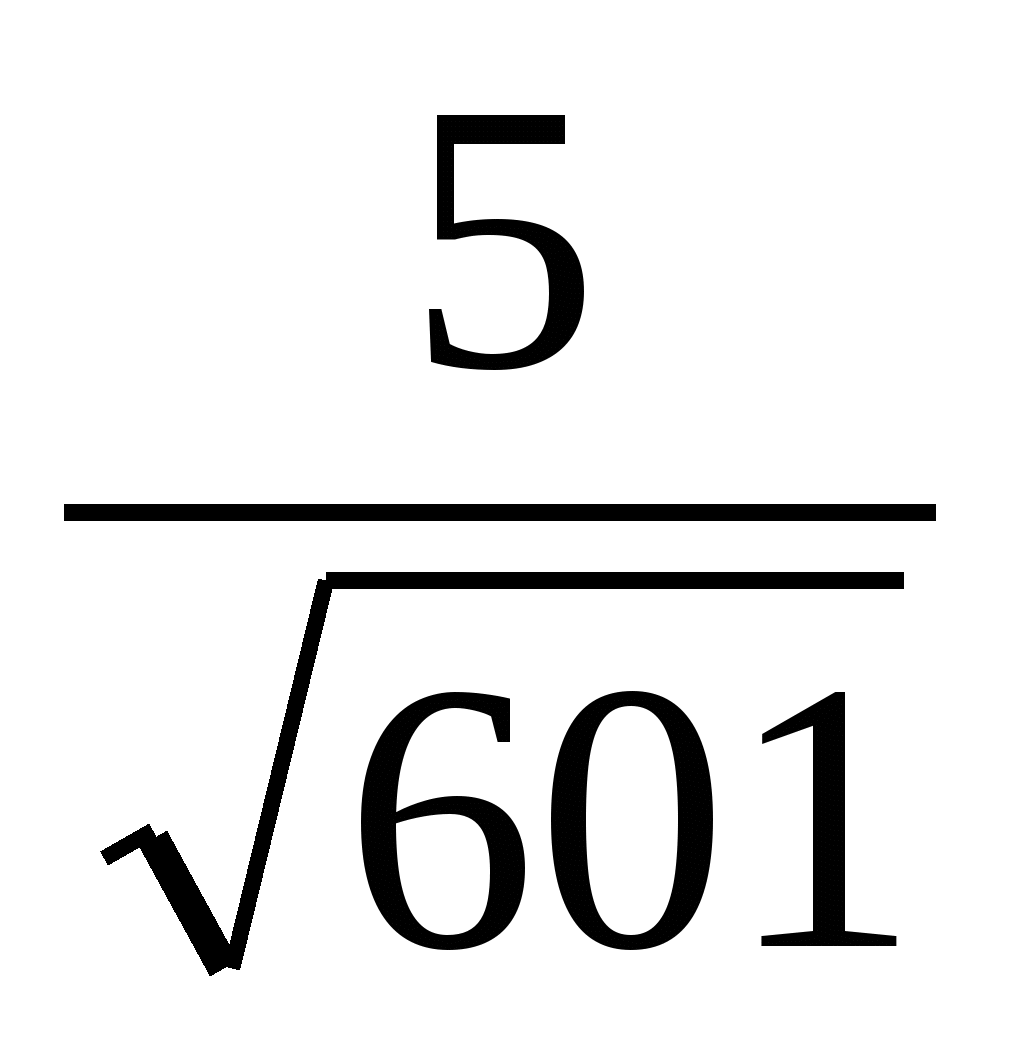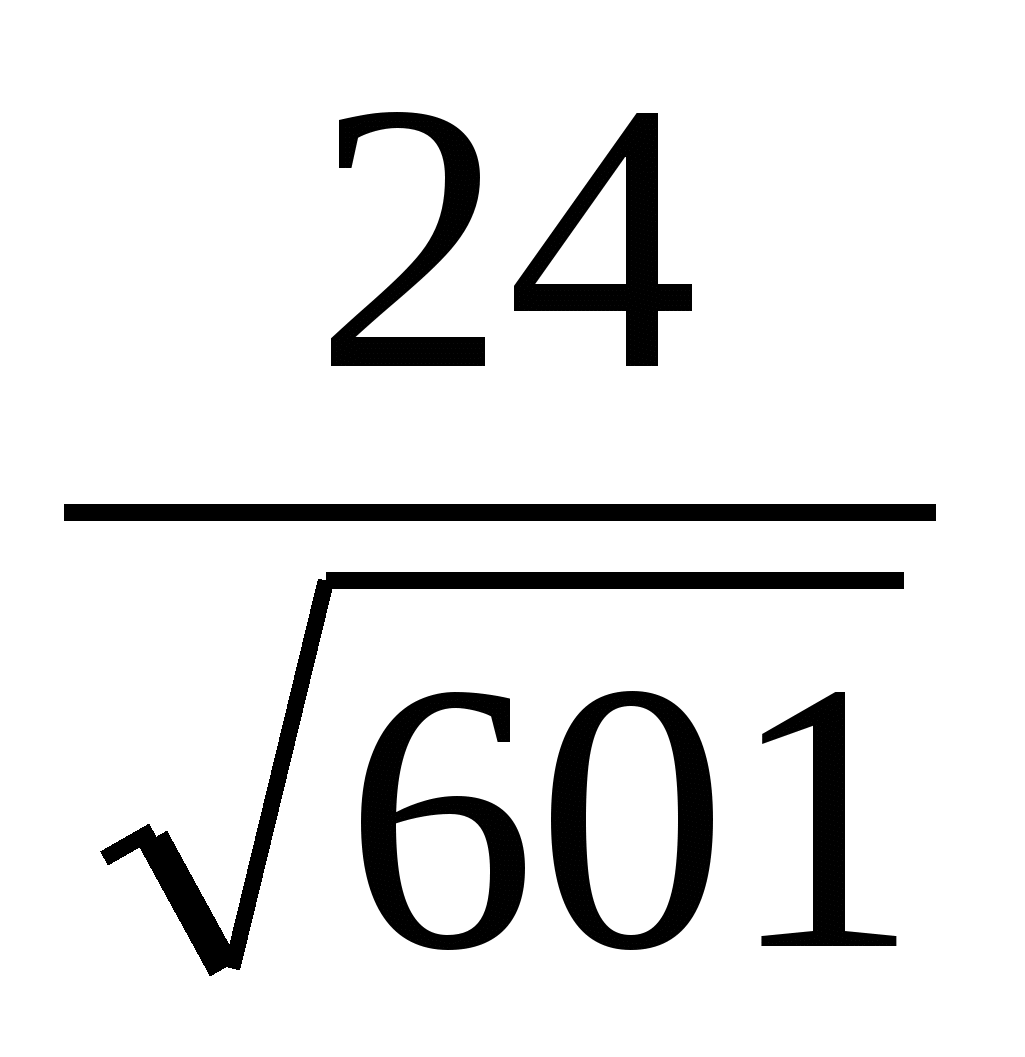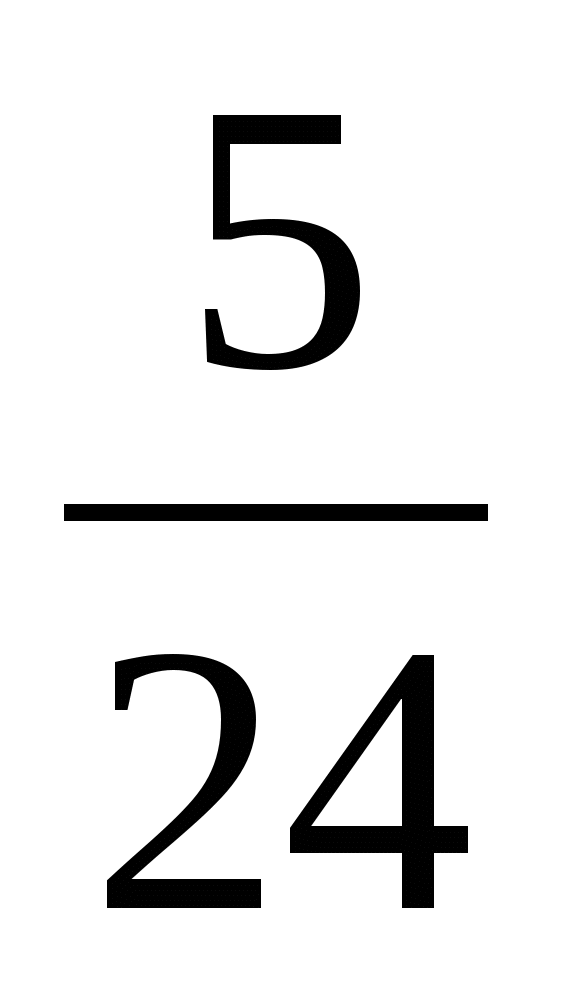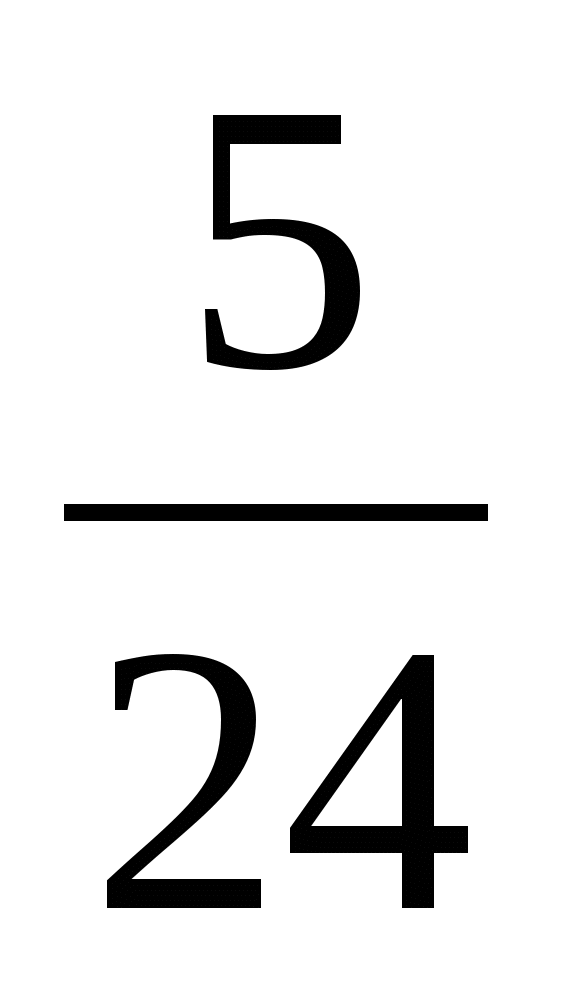Получим sin Решение стереометрических задач методом координат= Решение стереометрических задач методом координат, cosРешение стереометрических задач методом координат= Решение стереометрических задач методом координат, отсюда tgРешение стереометрических задач методом координат= Решение стереометрических задач методом координат.

Ответ: Решение стереометрических задач методом координат= arctgРешение стереометрических задач методом координат.

Пример 6 (4 вариант сборника)

В прямоугольном параллелепипеде АВСДА1 В1 С1 Д1 известны ребра: АВ=35, АД=12, СС1= 21. Найдите угол между плоскостями АВС и А1ДВ.

Р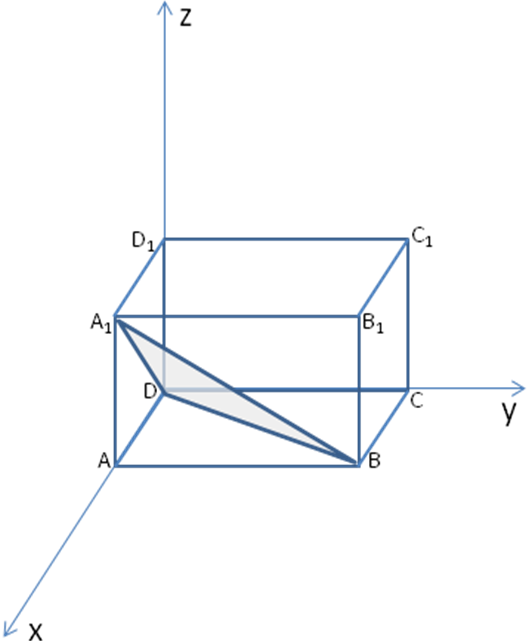Решение стереометрических задач методом координатешение: Прямоугольный параллелепипед, как и квадрат, отлично вписывается в прямоугольную систему координат. Введем координатную плоскость и найдем координаты точек, задающих плоскости АВС и А1ДВ.



Д(0;0;0), А(12;0;0), В(12; 35;0), А1(12;0;21). Напишем уравнения плоскостей АВС.

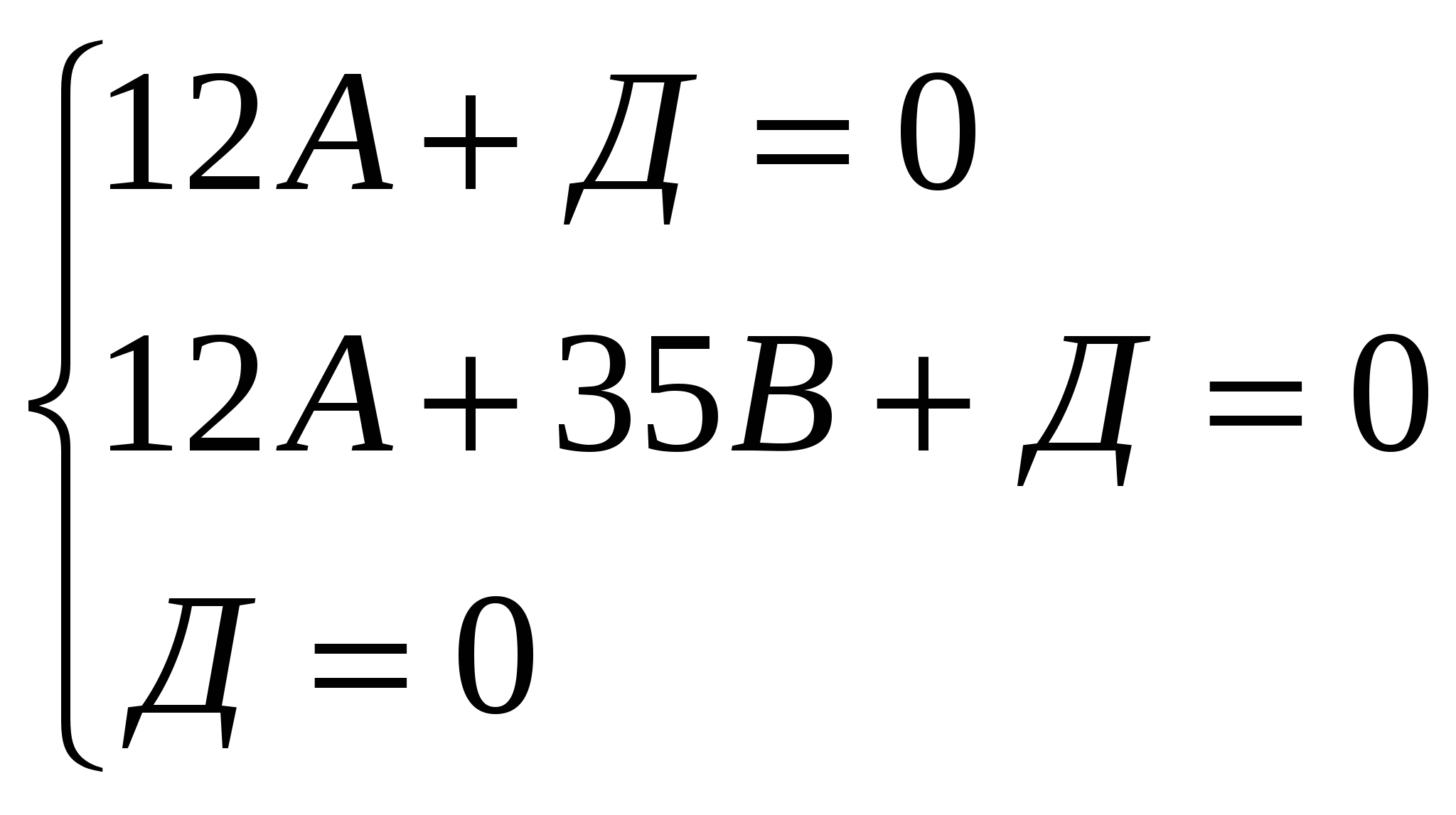
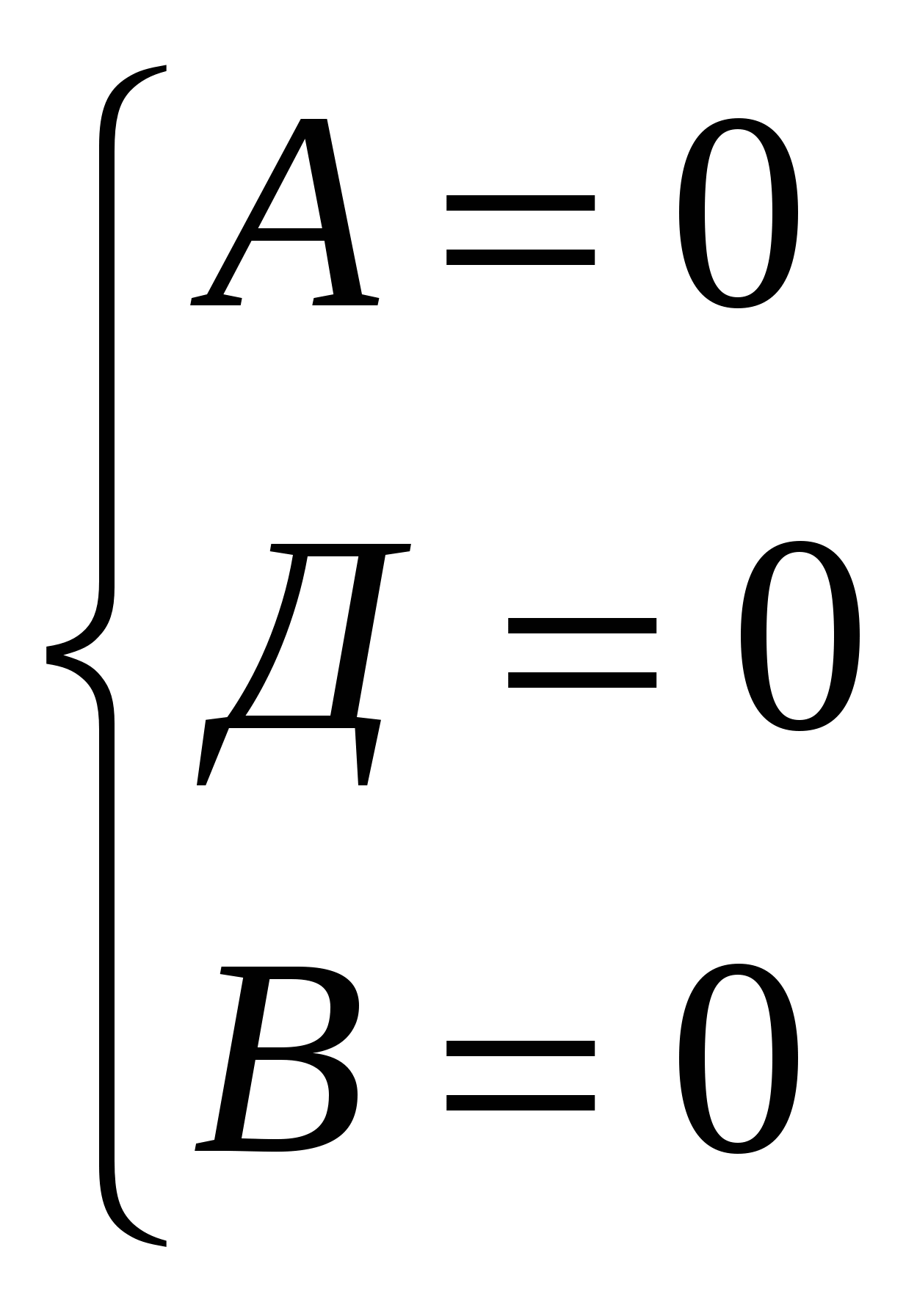
Решение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координат

Уравнение плоскости АВС z=0, нормаль к плоскости имеет координаты 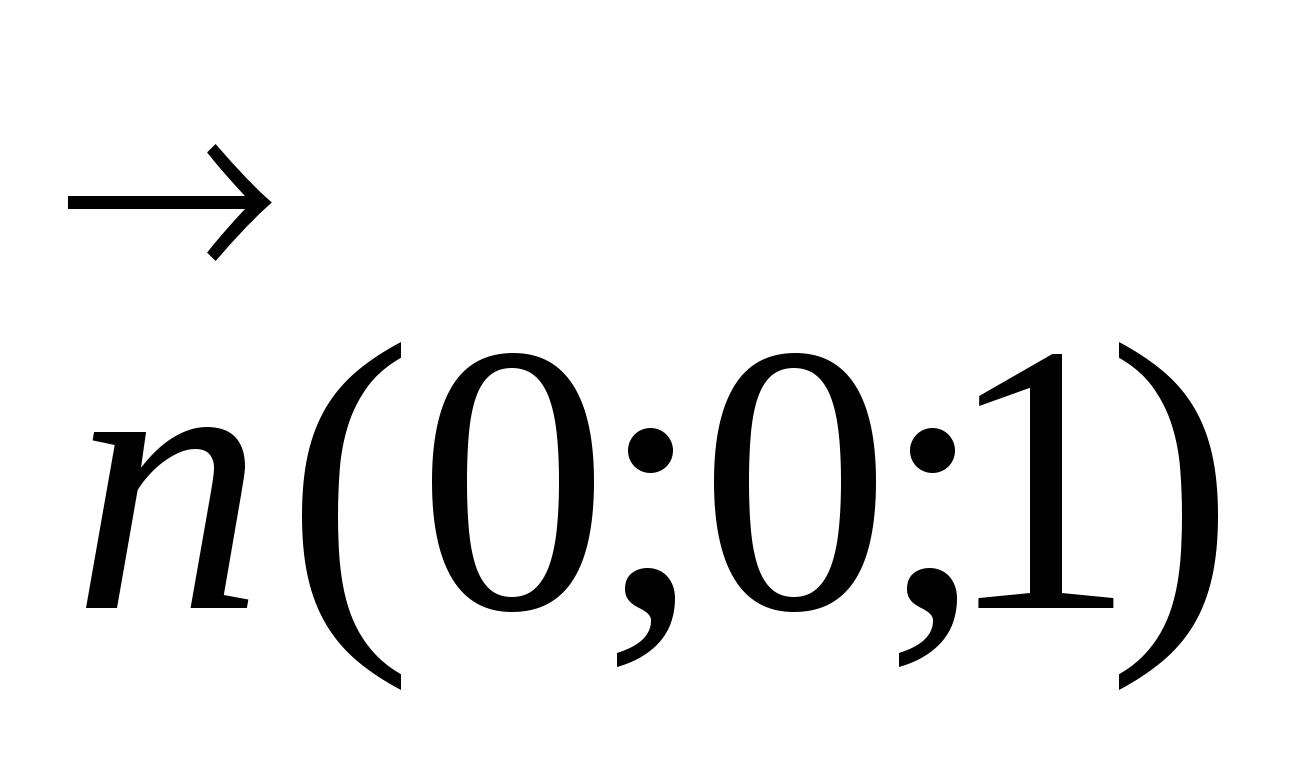Решение стереометрических задач методом координат.

Напишем уравнение плоскости ВДА1.

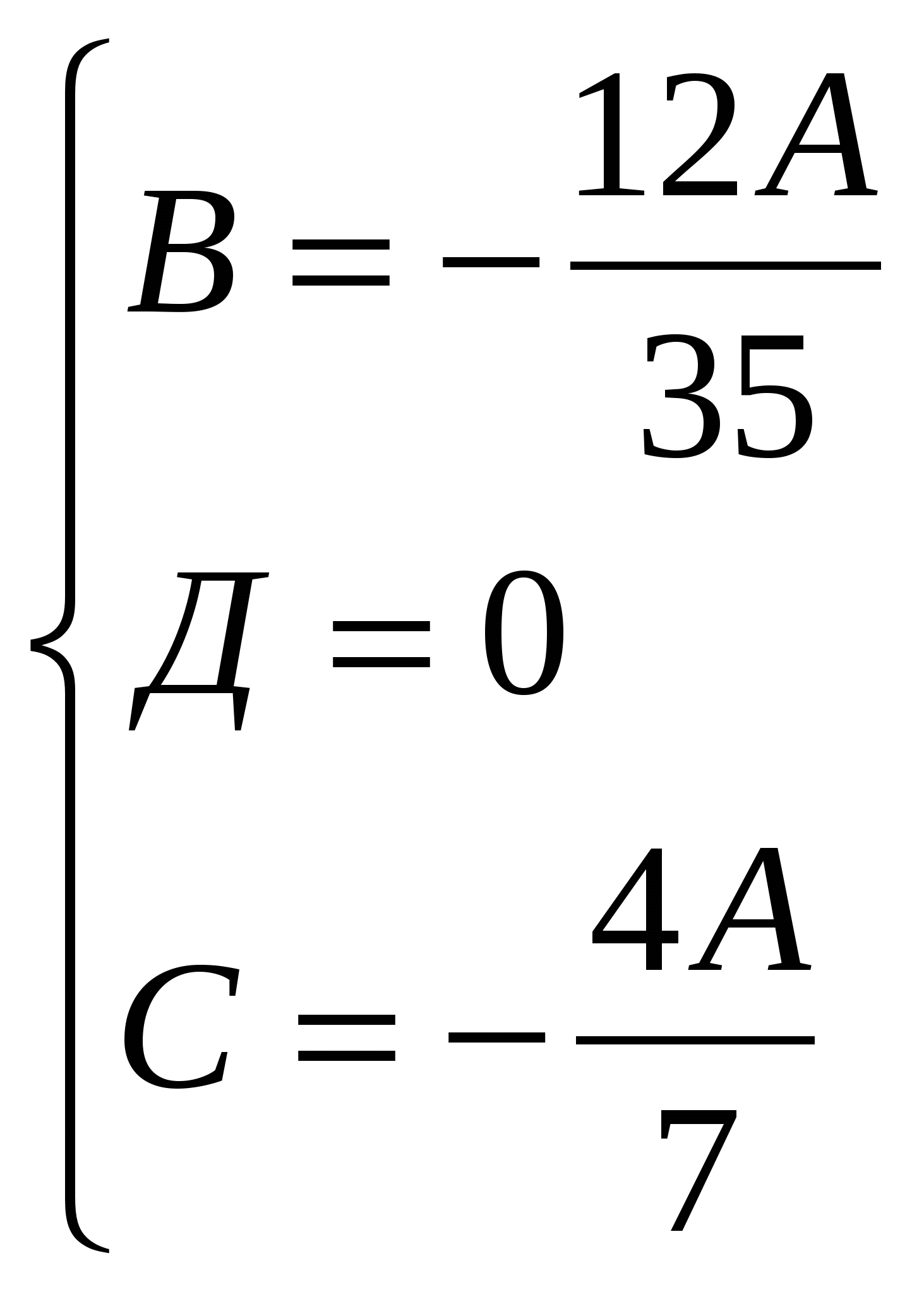
Решение стереометрических задач методом координатРешение стереометрических задач методом координатРешение стереометрических задач методом координат

Уравнение плоскости 35х-12у-20z=0, нормаль к плоскости имеет координаты 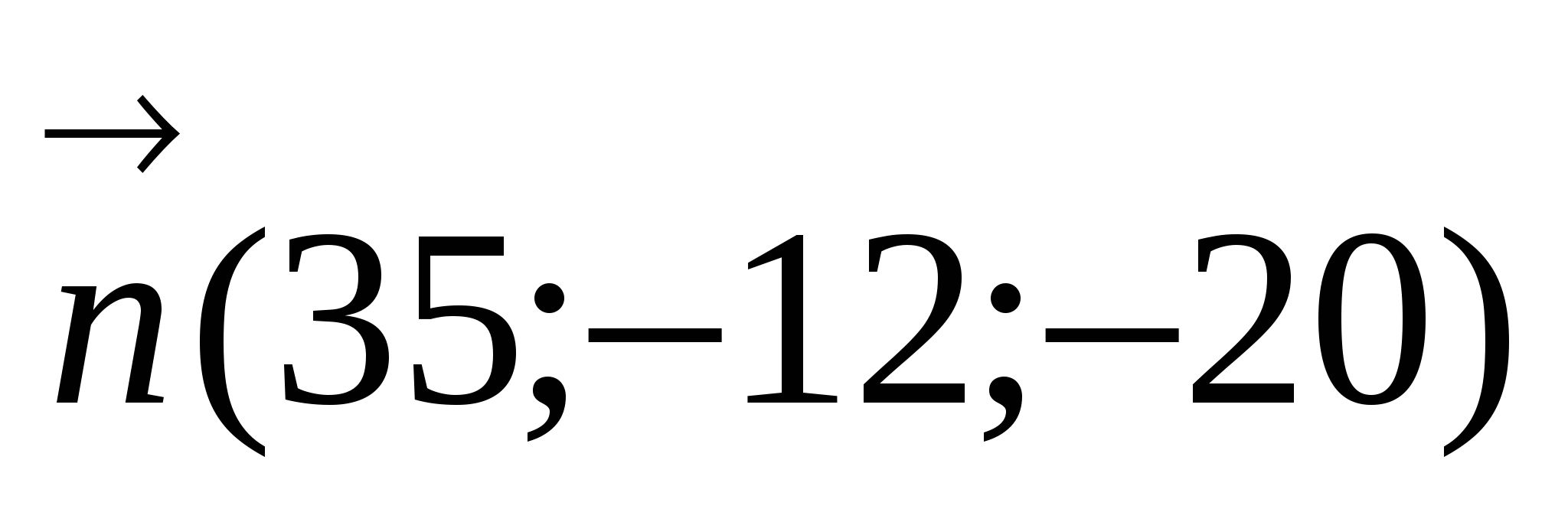Решение стереометрических задач методом координат.

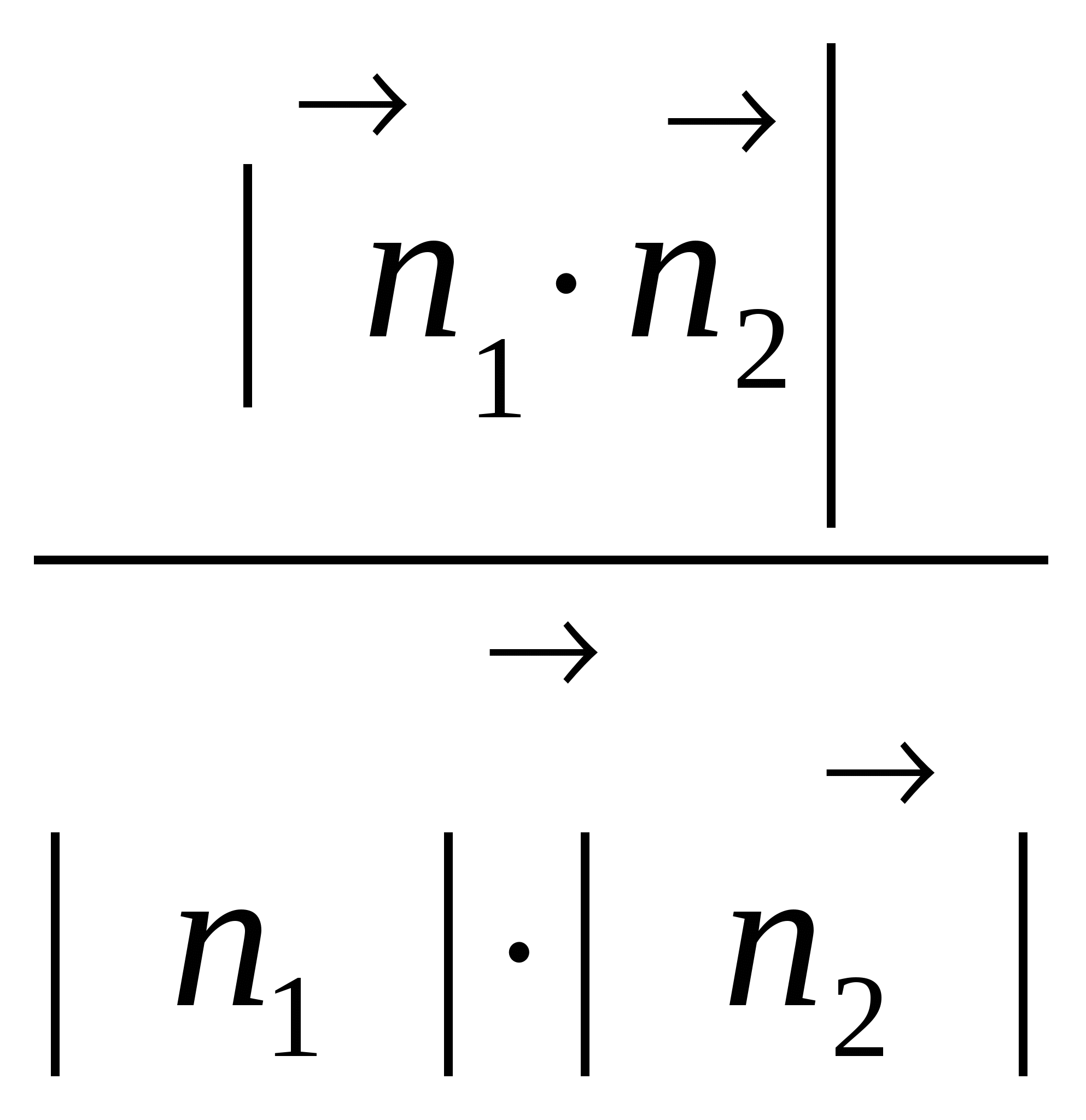Угол между плоскостями найдем по формуле cosРешение стереометрических задач методом координат= Решение стереометрических задач методом координат.

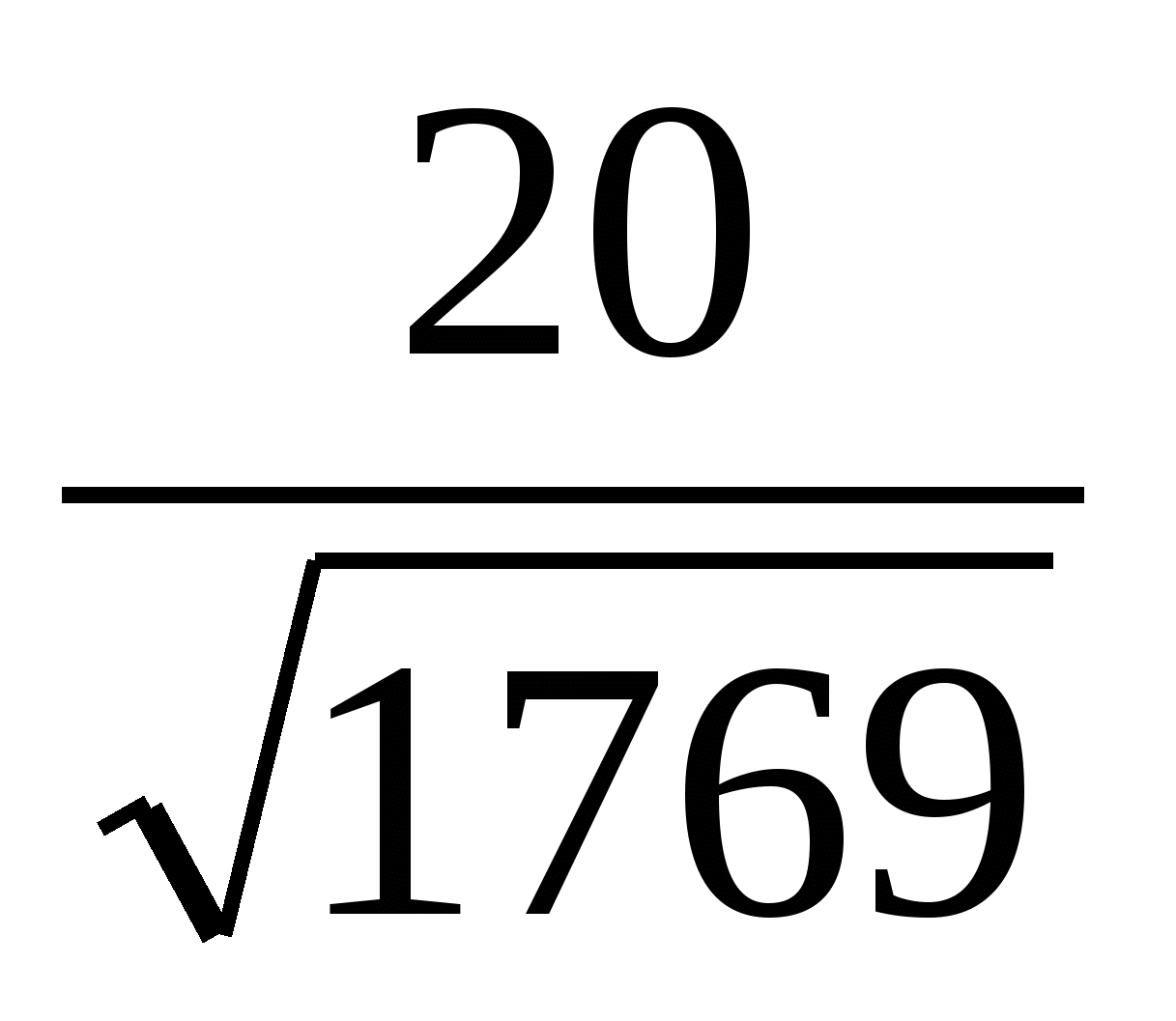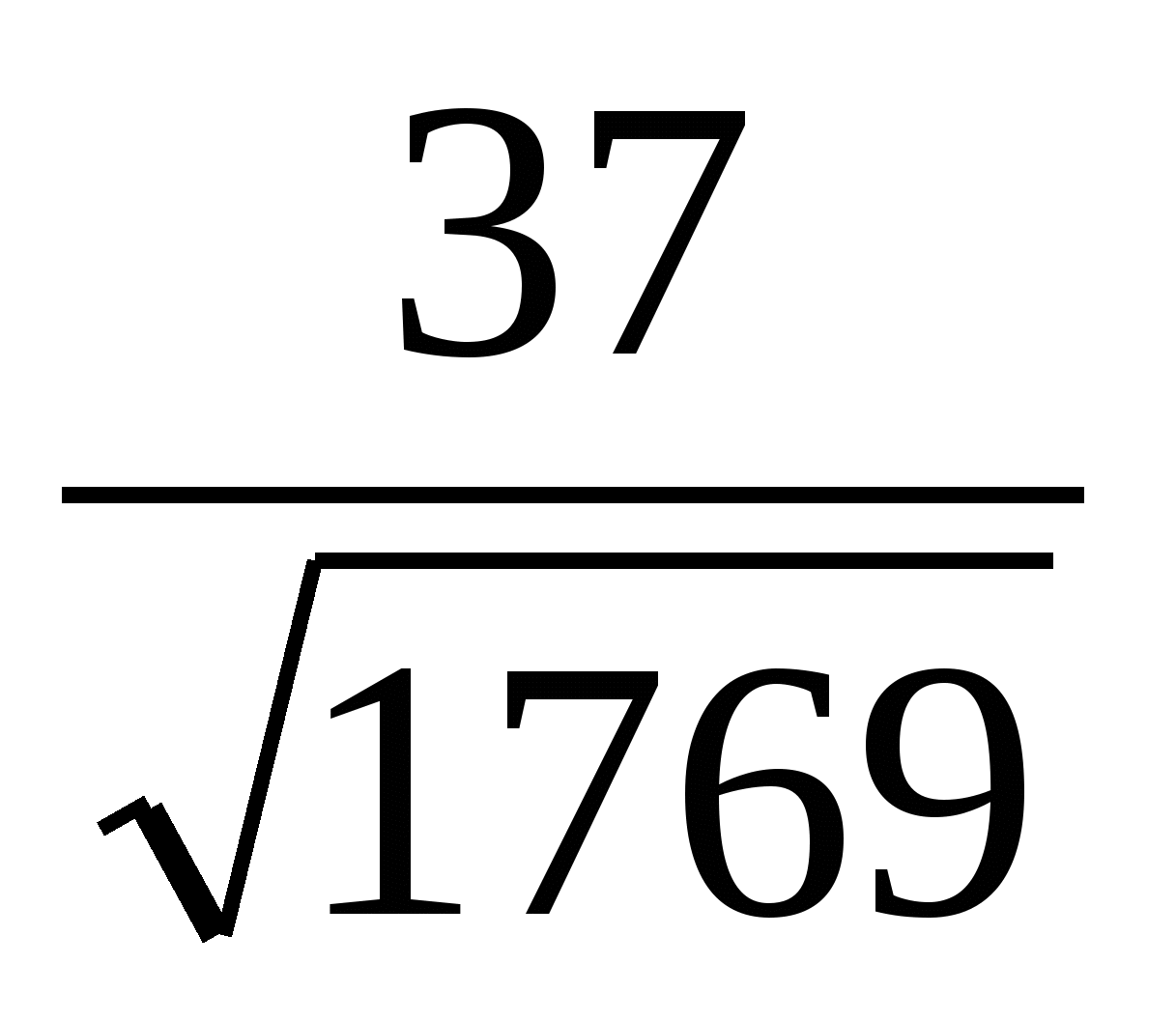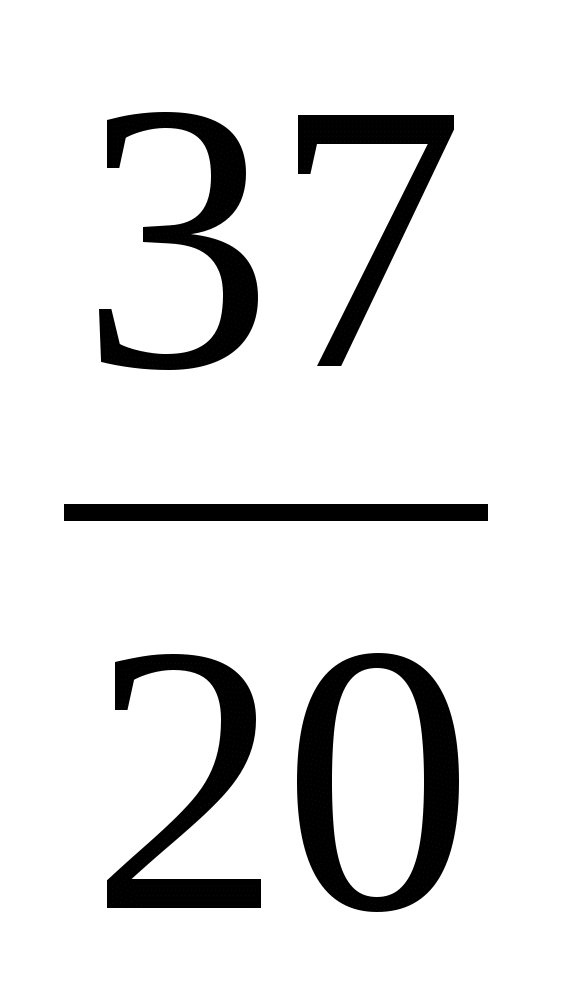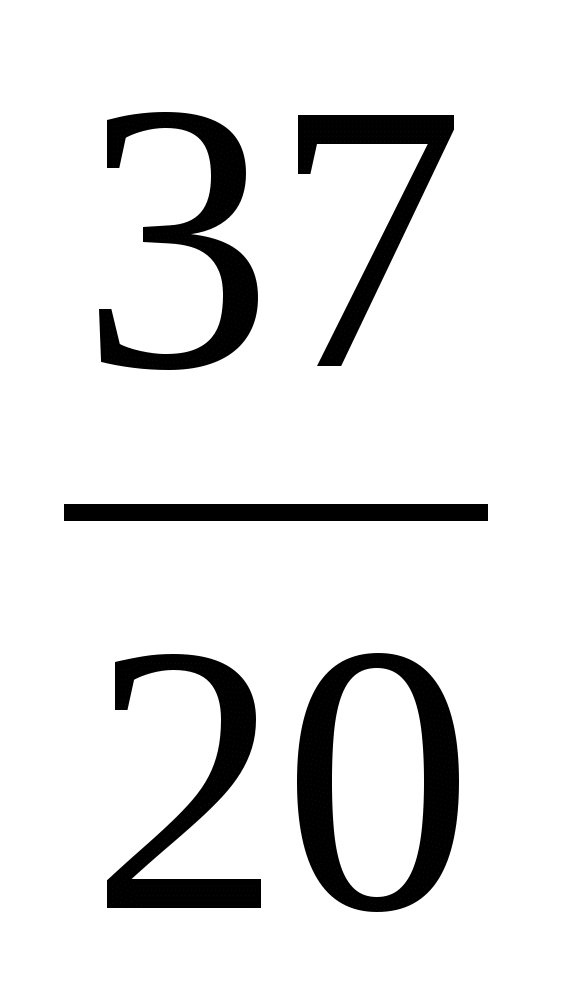Получим cosРешение стереометрических задач методом координат= Решение стереометрических задач методом координат, sin Решение стереометрических задач методом координат=Решение стереометрических задач методом координат, тогда tgРешение стереометрических задач методом координат=Решение стереометрических задач методом координат.

Ответ: Решение стереометрических задач методом координат= arctgРешение стереометрических задач методом координат.

Задачи для самостоятельного решения.


  1. В правильной трехгранной призме ABCA1 B1 C1, все ребра которой равны 1, отмечены точки D и E - середины ребер A1 B1 и B1 C1 соответственно. Найдите угол между прямыми AD и BE. ( Ответ: arccos 0,7)

  2. В правильной шестиугольной призме АВСДЕFА1В1С1Д1Е1F1, все ребра которой равны 1, найдите косинус угла между прямыми АВ1 и ВС1.

(ответ: 0,75)

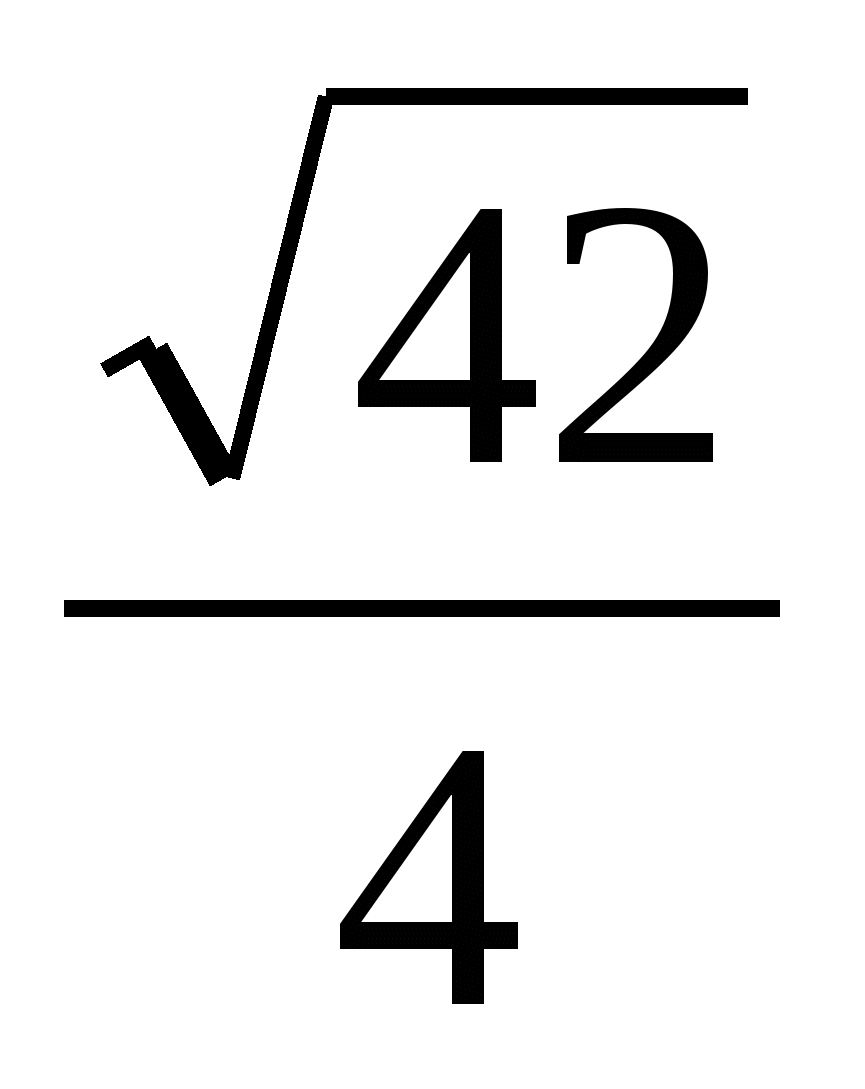  1. В правильной шестиугольной пирамиде SАВСДЕF, сторона основания равна 1, а боковые ребра равны 2. Найдите расстояние от точки F до прямой ВG, где G - середина ребра SС. (ответ: Решение стереометрических задач методом координат).

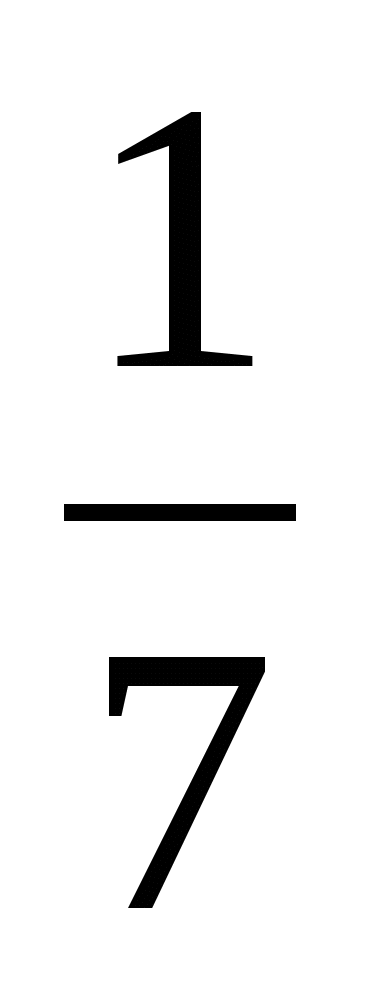  2. В правильной треугольной призме АВСА1 В1 С1 все ребра которой равны 1, найдите косинус угла между плоскостями АВС1 и ВА1С1. (ответ Решение стереометрических задач методом координат)

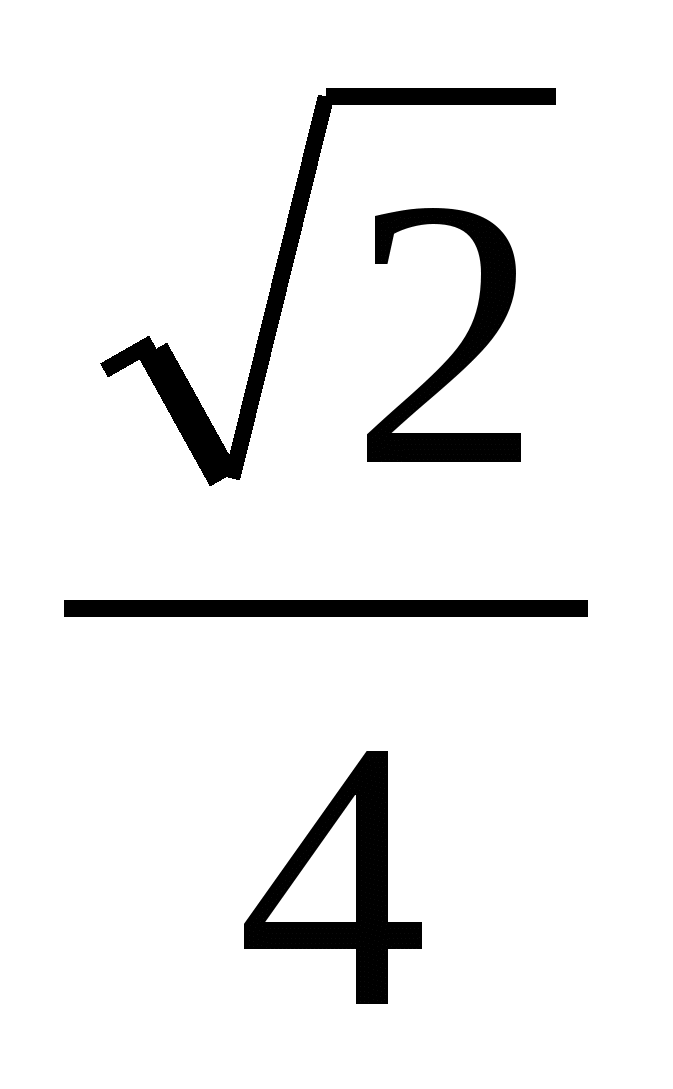  3. В правильной шестиугольной призме АВСДЕFА1В1С1Д1 Е1 F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости ВFЕ1. (ответРешение стереометрических задач методом координат)

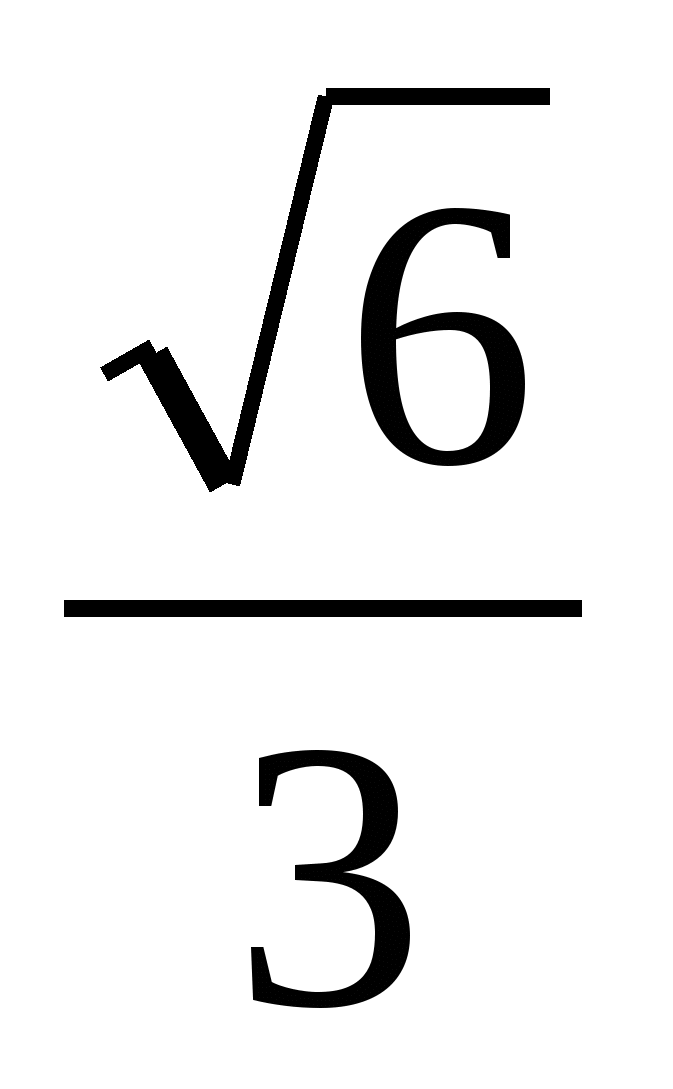  4. В правильно четырехугольной пирамиде SАВСД все ребра раны 1. Найти расстояние между прямыми SА и ВС. ( ответ Решение стереометрических задач методом координат)

загрузить
Пользовательское соглашениеО проектеОбратная связьАрхивные статьи
© 2010-2022