- Преподавателю
- Математика
- Разработка занятия по теме «Уравнение касательной к графику функции»
Разработка занятия по теме «Уравнение касательной к графику функции»
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Марина Н.Ш. |
| Дата | 03.05.2014 |
| Формат | rar |
| Изображения | Есть |
Приложение 2
Выполнение упражнений
Первый тип заданий
1. Найти уравнение касательной к графику функции f(x) в точке с абсциссой х0.(Выбрать правильный ответ из предложенных)
1. f(x)=-x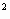 -4x+2, х0=-1.
-4x+2, х0=-1.
1) y=-2x-3;
2) y=2x-1;
3) y=-2x+3;
4) y=2x+3.
2. f(x)=-x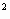 +6x+8, х0=-2.
+6x+8, х0=-2.
1) y=2x-6;
2 )y=10x+12;
3) y=4x+8;
4) y=-10x+8.
3. f(x)=x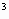 +5x+5, х0=-1.
+5x+5, х0=-1.
1) y=7x+8;
2) y=8x+7;
3) y=9x+8;
4) y=8x+6.
4. f(x)=2cosx, х0=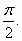
1) y=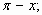
2) y=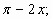
3) y=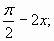
4) y=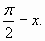
5. f(x)=tgx, х0=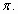
1) y=x
2) y=x+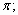
3) y=x-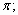
4) y=x-1.
6. f(x)=1-sin2x, х0=0.
1) y=1-2x;
2) y=2x;
3) y = -2x;
4) y=2x+1.
7. f(x)=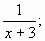 х0=-2.
х0=-2.
1) y = -x+1;
2) y = x+1;
3) y = -x-1;
4) y = -x-2.
Ответы к упражнениям
Задание
1
2
3
4
5
6
7
Номер ответа
3
2
2
2
3
1
3
Второй тип заданий
Задача1 В каких точках касательные к кривой у=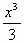 - х
- х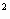 - х+1 параллельны прямой y=2x-1?
- х+1 параллельны прямой y=2x-1?
Решение. Так как касательные параллельны прямой у=2х-1 то их угловые коэффициенты совпадают. Т. е. угловой коэффициент касательной в этой точке есть к = 2 .
Находим у' = х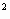 -2х-1; к= у'(х
-2х-1; к= у'(х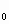 )= х
)= х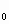
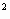 -2х
-2х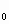 -1=2.
-1=2.
Решив уравнение х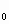
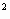 -2х
-2х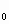 -1=2; х
-1=2; х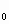
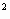 -2х
-2х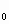 -3=0, получим (х
-3=0, получим (х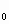 )
)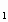 =3, (х
=3, (х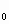 )
)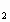 =-1, откуда (у
=-1, откуда (у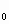 )
)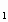 = -2, (у
= -2, (у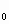 )
)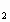 =
= 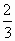 . Итак, искомыми точками касания являются А(3;-2) и В(-1;
. Итак, искомыми точками касания являются А(3;-2) и В(-1;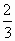 )
)
Ответ: (3;-2) и (-1;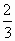 ).
).
Задача 2. Найти абсциссу точки, в которой касательная к графику функции f(x) = 2x-lnx, параллельна прямой у = х.
Решение. Пусть х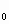 - абсцисса точки касания. Угловой коэффициент касательной в этой точке есть к=1. Находим f '(x)=2-
- абсцисса точки касания. Угловой коэффициент касательной в этой точке есть к=1. Находим f '(x)=2-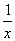 . К= f ' (х
. К= f ' (х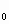 )=2-
)=2-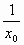 =1.
=1.
Решив уравнение 2-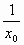 =1, получим х
=1, получим х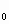 =1.
=1.
Упражнения
1. Найти абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой у(х).
1. f(x)= х+е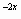 , у(х)= -х.
, у(х)= -х.
1) -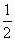 ; 2) 0; 3)
; 2) 0; 3) 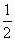 ; 4) 1.
; 4) 1.
2. f(x)=х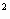 -5х, у(х)= -х.
-5х, у(х)= -х.
1) -2; 2) 3; 3) -3; 4) 2.
3. f(x)=2lnх-x, у(х)= 0.
1) -2; 2) 0; 3) 2; 4) 1.
4. f(x)=-х-е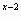 , у(х)= 4-2х.
, у(х)= 4-2х.
1) 3; 2) 2; 3) 0; 4) -2.
Ответы к упражнениям
Задание
1
2
3
4
Номер ответа
2
4
2
2
2


