- Преподавателю
- Математика
- Исследовательская работа Арифметика фигур
Исследовательская работа Арифметика фигур
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Макурова И.В. |
| Дата | 05.01.2016 |
| Формат | doc |
| Изображения | Есть |
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
по теме:
«АРИФМЕТИКА ФИГУР»
Введение
В повседневной жизни мы очень часто используем арифметику чисел, составляющую основу математики. Данная работа содержит результаты исследований за два года; в ней рассмотрены различные варианты выполнения арифметических операций над точками и фигурами. Свойства фигур в этих арифметиках рассмотрены по одним и тем же параметрам для удобства их сравнительного анализа.
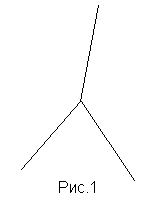
В первой части представлена арифметика трех лучей. Как видно из названия, универсумом является пространство, составленное из трех лучей.
Во второй части рассмотрена мультипликативная арифметика, в которой под произведением точек А и В подразумевается отрезок АВ.
Все теоремы и свойства, рассмотренные в работе, доказаны самостоятельно.
Содержание
1.3.Умножение фигур 7
1. Арифметика трех лучей
-
Основы арифметики
В прошлом году я рассматривала так называемую мультипликативную арифметику, где произведением точек являлся соединяющий их отрезок. Универсумом в ней являлась плоскость, и я рассматривала только фигуры, являющиеся ее подмножествами. В арифметике трех лучей универсумом являются три луча, выходящие из одной точки (рис.1). Все последующие операции будут рассматриваться только для фигур, являющихся подмножествами этого трехлучевого пространства.
-
Понятие умножения. Свойства умножения точек
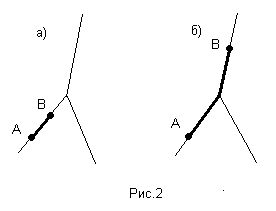
Под произведением двух точек А и В будем подразумевать отрезок, соединяющий эти точки (рис.2). Отрезок с концами А и В в трехлучевой арифметике - это кратчайшая ломаная, соединяющая точки А и В.
Существуют два принципиально различных варианта расположения двух точек в трехлучевом пространстве, но произведение этих точек для любых точек А и В определяется единственным образом. На рисунке 2а рассмотрен вариант , при котором точки А и В расположены на одном луче, а на рисунке 2б - на разных.
Такое умножение точек обладает следующими свойствами:
А) Коммуникативность
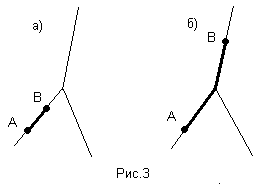
АВ=ВА
Свойство доказано графически, перебором всех принципиально различных вариантов расположения точек (рис.3) На рисунке 3а рассмотрен случай, когда обе точки лежат на одном луче, а на рисунке 3б - когда они лежат на разных лучах. Таким образом, рассмотрены все принципиально различные варианты расположения точек А и В (случаи аналогичных ситуаций, когда точки А и В просто лежат на других лучах, можно не рассматривать, т.к. они абсолютно идентичны при повороте универсума).
При графическом доказательстве дальнейших свойств метод и ход доказательства аналогичен, поэтому подробное описание каждого случая опускается.
Б) Ассоциативность
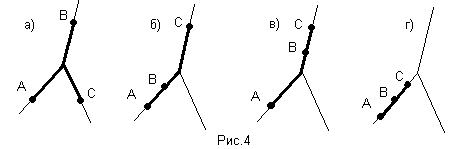
(АВ)С=А(ВС)
Доказательством этого свойства является перебор всех принципиально различных вариантов расположений точек А, В и С, с проверкой выполнения данного свойства (рис.4), как и в случае с коммутативностью.
В) Дистрибутивность относительно сложения
Под суммой двух точек будем подразумевать их объединение.
А(В+С)=АВ+АС. Доказательство графическое (рис.5).
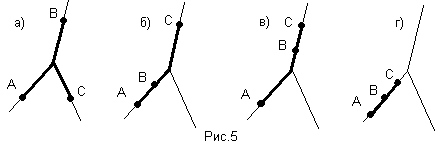
Г) Идемпотентность
АА=А. Произведением точки А самой на себя является кратчайшая ломаная, соединяющая точку А с самой точкой А. Этой кратчайшей ломаной является сама точка А.
-
Умножение фигур
Под произведением фигур 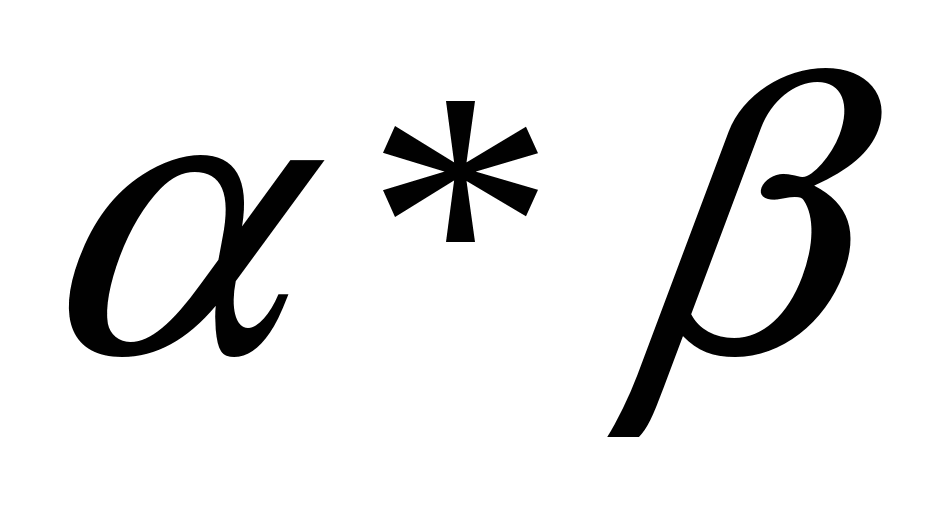 будем подразумевать объединение произведений всех точек фигуры
будем подразумевать объединение произведений всех точек фигуры  на каждую точку фигуры
на каждую точку фигуры 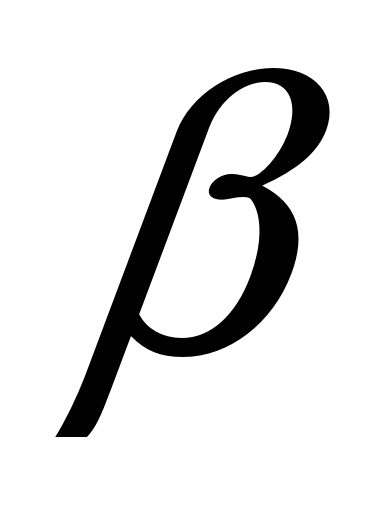 .
.
Такое умножение обладает следующими свойствами:
А) Коммуникативность
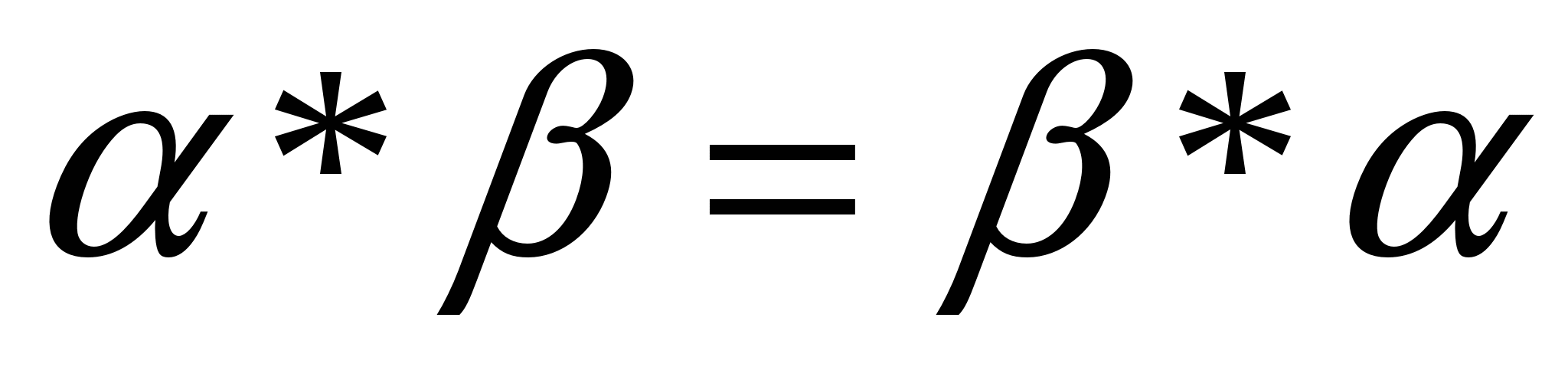
Теорема (о коммутативности умножения фигур)
Произведение двух фигур коммутативно.
Доказательство
По определению умножения фигур мы должны умножить все точки фигуры  на каждую точку фигуры
на каждую точку фигуры 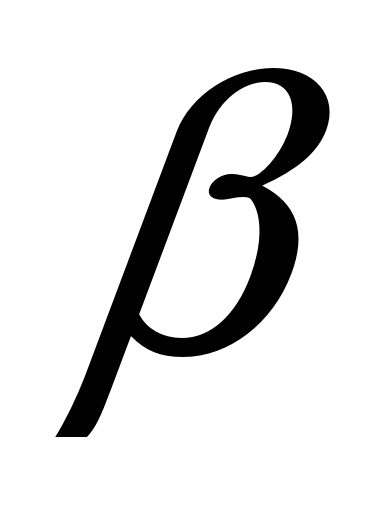 . Таким образом, мы можем представить произведение
. Таким образом, мы можем представить произведение 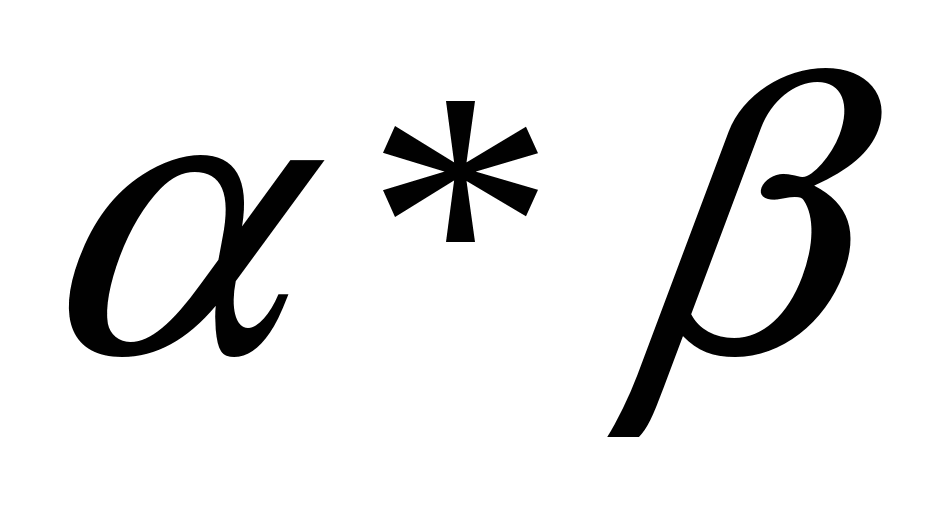 как объединение произведений точек фигур
как объединение произведений точек фигур  и
и 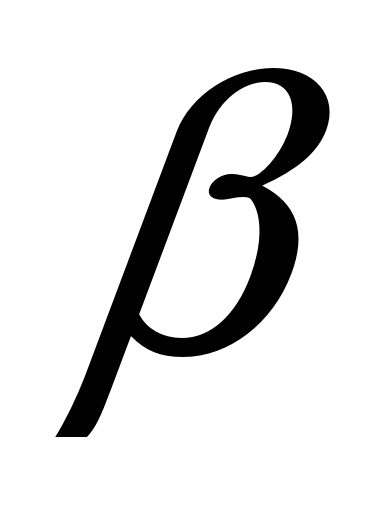 . Умножение точек коммутативно, поэтому можно во всех таких произведениях можно переставить точки исходных фигур.
. Умножение точек коммутативно, поэтому можно во всех таких произведениях можно переставить точки исходных фигур.
Теорема доказана.
Для доказательства дальнейших свойств нам потребуется определить понятия ограниченных и неограниченных фигур.
Ограниченная на луче фигура в трехлучевой арифметике - это такая фигура, для которой можно определить расстояния от центра универсума до наиболее удаленной точки на этом луче.
Неограниченная на луче фигура в трехлучевой арифметике - это фигура, для которой нельзя определить расстояние от центра универсума до точки, наиболее удаленной от него на этом луче.
Фигура может быть ограниченной на одном луче и неограниченной на другом.
Б) Ассоциативность
Теорема (об ассоциативности умножения фигур)
Произведение трех фигур ассоциативно.
Доказательство
Пусть  ,
,  и
и 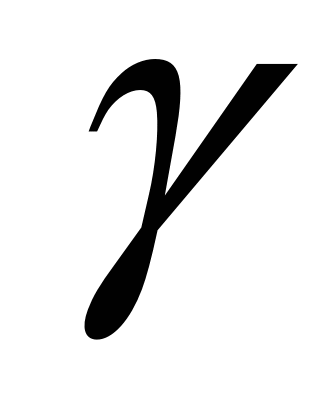 - это исходные фигуры. Требуется доказать, что
- это исходные фигуры. Требуется доказать, что 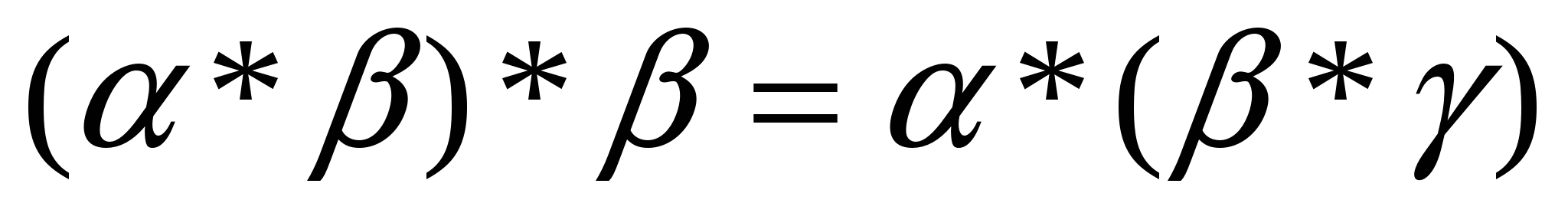 . Разобьем доказательство на три случая - когда точки объединения фигур лежат на одном, двух и трех луча универсума, а каждый из этих случаев - на подслучаи, когда это объединение является ограниченной и неограниченной фигурой на различных лучах.
. Разобьем доказательство на три случая - когда точки объединения фигур лежат на одном, двух и трех луча универсума, а каждый из этих случаев - на подслучаи, когда это объединение является ограниченной и неограниченной фигурой на различных лучах.
1 случай: объединение лежит на одном луче.
1 подслучай: объединение ограничено на этом луче. Определим наиболее и наименее удаленные от центра универсума точки. Независимо от порядка умножения результатом будет являться отрезок, соединяющий эти точки.
2 подслучай: объединение неограниченно на этом луче. Определим наименее удаленную от центра универсума точку. Независимо от порядка умножения результатом будет являться луч с началом в наименее удаленной от центра универсума точке объединения, продолжение которого проходит через воображаемую бесконечно удаленную от центра универсума точку.
2 случай: объединение лежит на двух лучах.
1 подслучай: объединение ограниченно на обоих лучах. Определим наиболее удаленные от центра универсума точки объединения. Независимо от порядка умножения результатом будет отрезок, соединяющий эти точки.
2 подслучай: объединение ограниченно на одном луче и неограниченно на другом. Определим наиболее удаленную от центра универсума точку объединения на луче, на котором объединение ограниченно. Независимо от порядка умножения результатом будет объединение отрезка, соединяющего центр универсума и наиболее удаленную точку, и луча, на котором объединение фигур неограниченно.
3 подслучай: объединение неограниченно на обоих лучах. Независимо от порядка умножения результатом будет объединение лучей, на которых объединение фигур неограниченно.
3 случай: объединение фигур лежит на трех лучах.
1 подслучай: объединение ограниченно на всех трех лучах. Определим наиболее удаленные от центра универсума точки на каждом из лучей. Независимо от порядка умножения результатом будет объединение отрезков, соединяющих центр универсума с наиболее удаленными точками на каждом луче.
2 подслучай: объединение ограниченно на двух лучах и неограниченно на третьем. Определим наиболее удаленные от центра универсума точки на лучах, на которых объединение фигур ограниченно. Независимо от порядка умножения результатом будет объединение отрезка, соединяющего эти точки, и луча, на котором юбъединение исходных фигур неограниченно.
3 подслучай: объединение ограниченно на одном луче и неограниченно на двух других. Определим наиболее удаленную от центра универсума точку на луче, на котором объединение фигур ограниченно. Независимо от порядка умножения результатом будет объединение отрезка, соединяющего эту точку с центром универсума. и лучей, на которых объединение фигур неограниченно.
4 подслучай: объединение неограниченно на всех трех лучах. Независимо от порядка умножения результатом будет весь универсум.
Теорема доказана
Соответственно, доказано и свойство.
В) Дистрибутивность относительно сложения
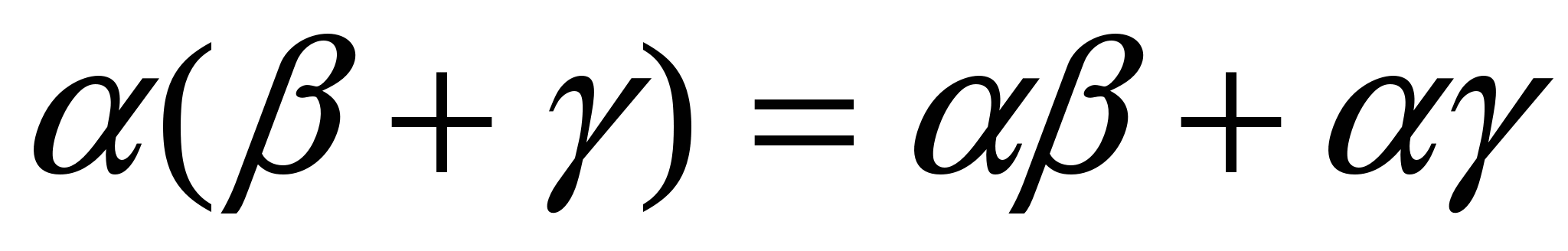 . Это очевидно, т.к для того, чтобы умножить одну фигуру на другую, нужно перемножить все их точки, а в роли второй фигуры сейчас выступает объединение фигур.
. Это очевидно, т.к для того, чтобы умножить одну фигуру на другую, нужно перемножить все их точки, а в роли второй фигуры сейчас выступает объединение фигур.
Более того, можно заметить, что действует следующее свойство:
Г) Псевдокоммутативность
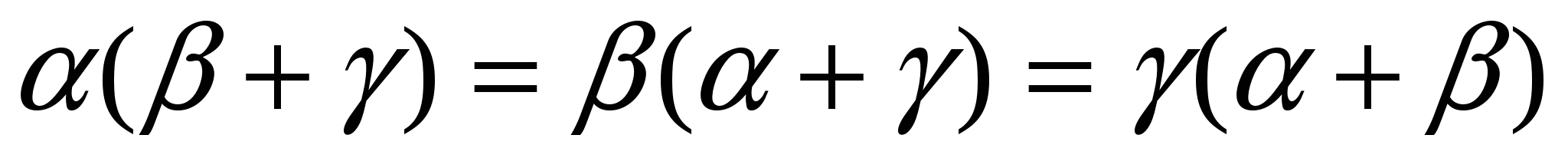
Разобьем доказательство на три случая - когда точки объединения фигур лежат на одном, двух и трех луча универсума, а каждый из этих случаев - на подслучаи, когда это объединение является ограниченной и неограниченной фигурой на различных лучах.
1 случай: объединение лежит на одном луче.
1 подслучай: объединение ограничено на этом луче. Определим наиболее и наименее удаленные от центра универсума точки. Независимо от способа умножения результатом будет являться отрезок, соединяющий эти точки.
2 подслучай: объединение неограниченно на этом луче. Определим наименее удаленную от центра универсума точку. Независимо от способа умножения результатом будет являться луч с началом в наименее удаленной от центра универсума точке объединения, продолжение которого проходит через воображаемую бесконечно удаленную от центра универсума точку.
2 случай: объединение лежит на двух лучах.
1 подслучай: объединение ограниченно на обоих лучах. Определим наиболее удаленные от центра универсума точки объединения. Независимо от способа умножения результатом будет отрезок, соединяющий эти точки.
2 подслучай: объединение ограниченно на одном луче и неограниченно на другом. Определим наиболее удаленную от центра универсума точку объединения на луче, на котором объединение ограниченно. Независимо от способа умножения результатом будет объединение отрезка, соединяющего центр универсума и наиболее удаленную точку, и луча, на котором объединение фигур неограниченно.
3 подслучай: объединение неограниченно на обоих лучах. Независимо от способа умножения результатом будет объединение лучей, на которых объединение фигур неограниченно.
3 случай: объединение фигур лежит на трех лучах.
1 подслучай: объединение ограниченно на всех трех лучах. Определим наиболее удаленные от центра универсума точки на каждом из лучей. Независимо от способа умножения результатом будет объединение отрезков, соединяющих центр универсума с наиболее удаленными точками на каждом луче.
2 подслучай: объединение ограниченно на двух лучах и неограниченно на третьем. Определим наиболее удаленные от центра универсума точки на лучах, на которых объединение фигур ограниченно. Независимо от способа умножения результатом будет объединение отрезка, соединяющего эти точки, и луча, на котором юбъединение исходных фигур неограниченно.
3 подслучай: объединение ограниченно на одном луче и неограниченно на двух других. Определим наиболее удаленную от центра универсума точку на луче, на котором объединение фигур ограниченно. Независимо от способа умножения результатом будет объединение отрезка, соединяющего эту точку с центром универсума. и лучей, на которых объединение фигур неограниченно.
4 подслучай: объединение неограниченно на всех трех лучах. Независимо от способа умножения результатом будет весь универсум.
Свойство доказано.
Д) Идемпотентность
В трехлучевом пространстве она действительна только для выпуклых фигур, определение которых совпадает со связными, т.к:
Выпуклая фигура - это такая фигура, любые две точки которой можно соединить отрезком, целиком принадлежащим исходной фигуре.
Связная фигура - это такая фигура, у которой любые две точки можно соединить ломаной, лежащей целиком в этой фигуре.
Изначально мы зафиксировали, что определения отрезка и ломаной в трехлучевой арифметике совпадают, значит, совпадают и определения связных и выпуклых фигур.
Что же касается идемпотентности выпуклых фигур, то это свойство очевидно - любые две точки связной фигуры  уже можно соединить лежащим внутри нее отрезком, поэтому
уже можно соединить лежащим внутри нее отрезком, поэтому 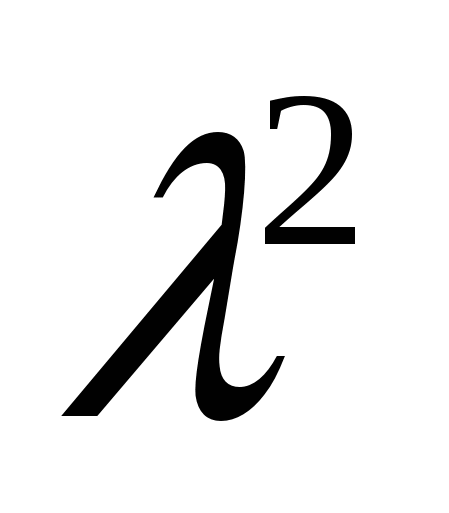 уже не будет содержать какой-то новой точки.
уже не будет содержать какой-то новой точки.
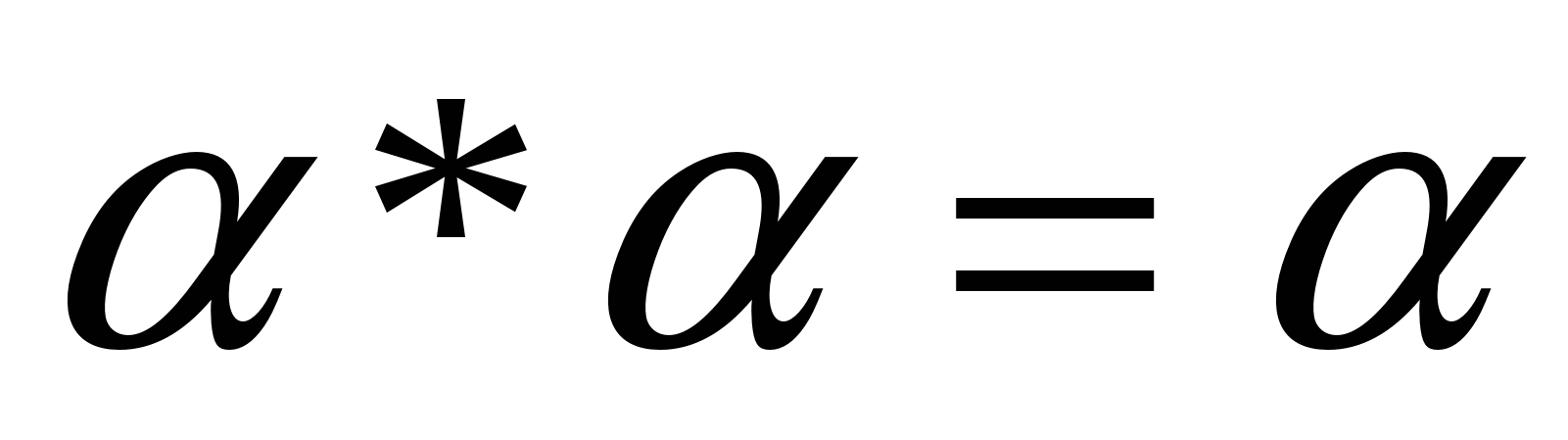 , где
, где  - выпуклая (связная) фигура.
- выпуклая (связная) фигура.
В случае, если фигура  - невыпуклая, свойство не действует. Примером является случай, когда фигура
- невыпуклая, свойство не действует. Примером является случай, когда фигура  состоит из двух точек, не совпадающих друг с другом. Результатом умножения будет являться отрезок, соединяющий эти точки; он не совпадет с исходной фигурой.
состоит из двух точек, не совпадающих друг с другом. Результатом умножения будет являться отрезок, соединяющий эти точки; он не совпадет с исходной фигурой.
Интересно рассмотреть аналог выпуклой оболочки фигуры из моей прошлой работы.
Выпуклая оболочка фигуры - это наименьшая степень, при возведении в которую фигура становится выпуклой.
Теорема (о выпуклой оболочке фигур в трехлучевом пространстве)
Выпуклой оболочкой любой фигуры в трехлучевом пространстве будет ее вторая степень.
Доказательство
Пусть точки А и В принадлежат несвязной фигуре  , причем не все точки отрезка АВ принадлежат этой фигуре. Умножим фигуру
, причем не все точки отрезка АВ принадлежат этой фигуре. Умножим фигуру  саму на себя; по определению умножения мы перемножим точки А и В, тогда отрезок АВ будет являться подмножеством
саму на себя; по определению умножения мы перемножим точки А и В, тогда отрезок АВ будет являться подмножеством ![]() , то есть
, то есть 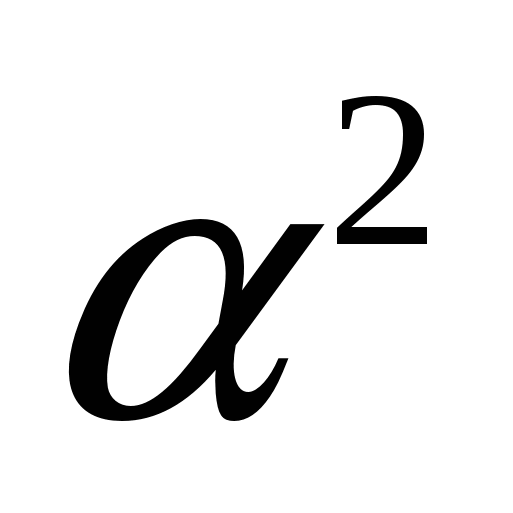 - всегда выпуклая фигура, а вторая степень - это выпуклая оболочка фигуры
- всегда выпуклая фигура, а вторая степень - это выпуклая оболочка фигуры  .
.
Теорема доказана
-
Понятие деления. Свойства деления
В обычной, числовой арифметике деление является обратной умножению операцией, в трехлучевой же арифметике результатом деления А на В будет являться такая фигура  , результат умножения которой на В будет всегда содержать точку А. Так как нам нужен определяющийся единственным образом результат, то вы можете видеть различные варианты частного А/В, в зависимости от расположения точек А и В.(рис.6) На рисунке 6а точки А и В лежат на одном луче, причем точка А более удалена от центра универсума, чем точка В; на рисунке 6б точки А и В лежат на разных лучах; на рисунке 6в точки А и В лежат на одном луче, но точка В более удалена от центра универсума, чем точка А.
, результат умножения которой на В будет всегда содержать точку А. Так как нам нужен определяющийся единственным образом результат, то вы можете видеть различные варианты частного А/В, в зависимости от расположения точек А и В.(рис.6) На рисунке 6а точки А и В лежат на одном луче, причем точка А более удалена от центра универсума, чем точка В; на рисунке 6б точки А и В лежат на разных лучах; на рисунке 6в точки А и В лежат на одном луче, но точка В более удалена от центра универсума, чем точка А.
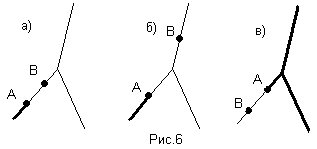
Такое деление точек обладает несколькими свойствами:
А) (А/В)/С=А/(ВС). Свойство доказано графически (рис.7)
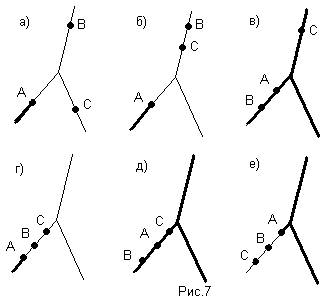
Б) (А+В)/С=(А/С)+(В/С). Свойство доказано графически (рис.8).
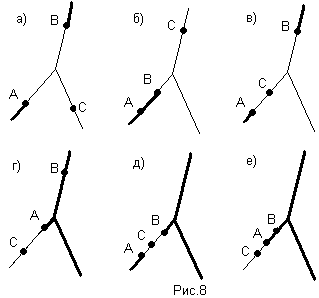
Следующие три свойства не существуют для арифметики чисел:
В) А/(В+С)=(А/В)+(А/С). (рис.9)
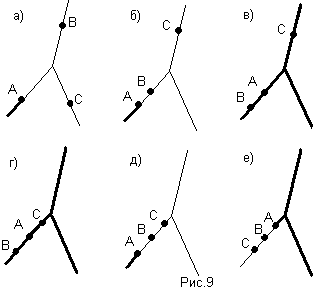
Г) (АВ)/С=(А/С)(В/С). (рис.10)
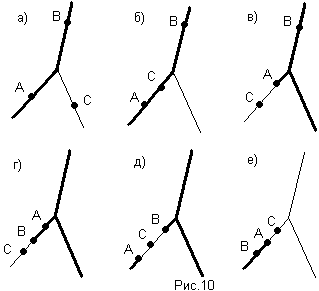
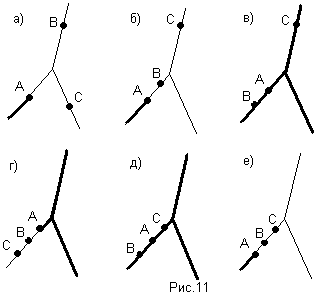
Д) А/(ВС)=(А/В)(А/С). (рис.11)
Аналогично определению деления точек следует определение деления фигур - для того, чтобы получить частное  , нужно поделить все точки фигуры
, нужно поделить все точки фигуры  на все точки фигуры
на все точки фигуры  .
.
-
Деление фигур самих на себя
В прошлом году особое внимание в делении фигур самих на себя привлекли два крайних случая результата - когда 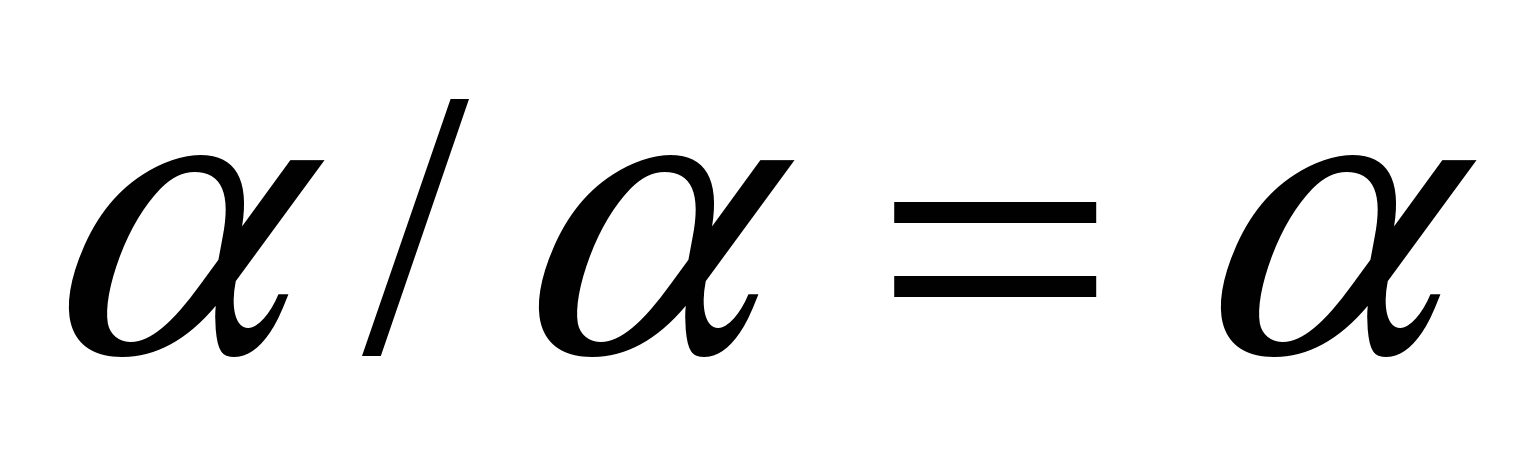 и когда
и когда 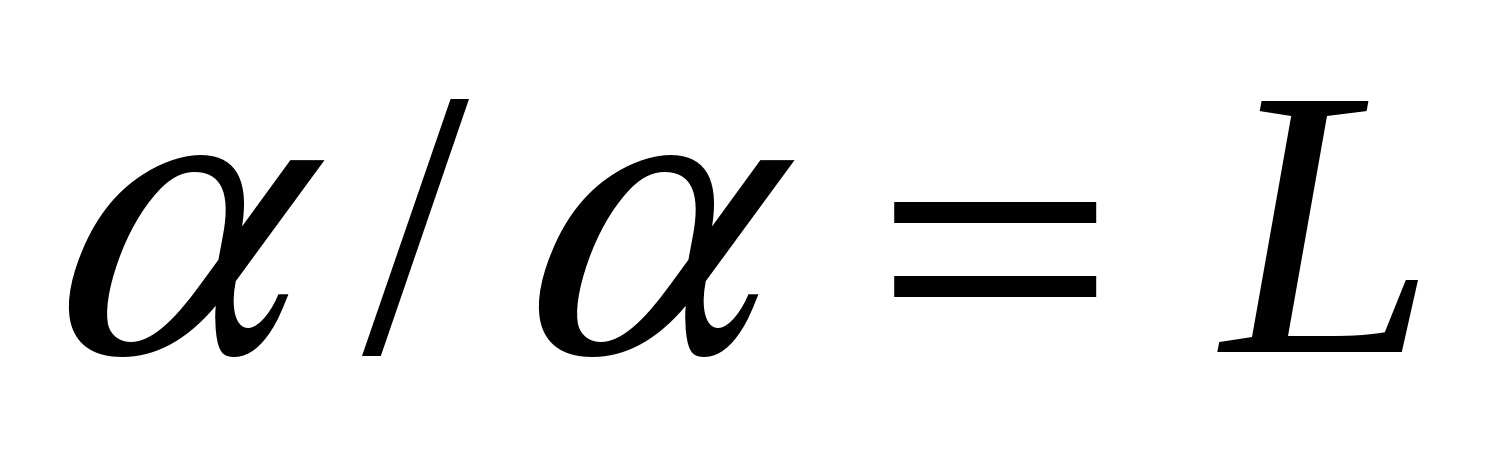 .
.
Рассмотрим первый случай.
Теорема(о линейных фигурах)
Линейными фигурами в трехлучевом пространстве являются точка и весь универсум.
Доказательство.
То, что эти фигуры являются линейными, очевидно - результат деления точки самой на себя - это луч с началом в этой точке и с продолжением в ней же, т.е. сама точка. При делении универсума самого на себя мы не можем получить что-то, выходящее за его пределы - но, так как результат деления фигуры саму на себя содержит эту фигуру, мы получим в результате деления сам универсум.
В случае с остальными фигурами поделим их на связные и несвязные. При делении связной фигуры самой на себя (исключая случай одной точки) мы получим весь универсум, а не исходную фигуру. При делении несвязной фигуры самой на себя мы получим либо универсум (если в ней есть связное подмножество), или же какую-то другую несвязную фигуру.
Линейные фигуры исчерпываются точкой и универсумом.
Теорема доказана.
Относительно случая, где частным является универсум, действует следующая теорема:
Теорема (о частном, совпадающем с универсумом).
Результат деления фигуры самой на себя совпадает с универсумом, если фигура содержит связное подмножество.
Доказательство.
Рассмотрим фигуру  , содержащую связный элемент. Из этого элемента можно выделить отрезок. При делении
, содержащую связный элемент. Из этого элемента можно выделить отрезок. При делении 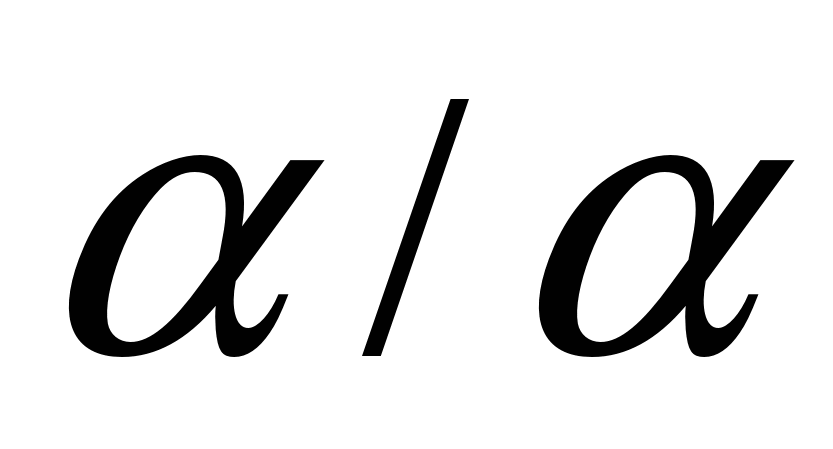 мы поделим этот отрезок сам на себя, а так как результатом деления отрезка самого на себя является универсум, то и результатом деления
мы поделим этот отрезок сам на себя, а так как результатом деления отрезка самого на себя является универсум, то и результатом деления 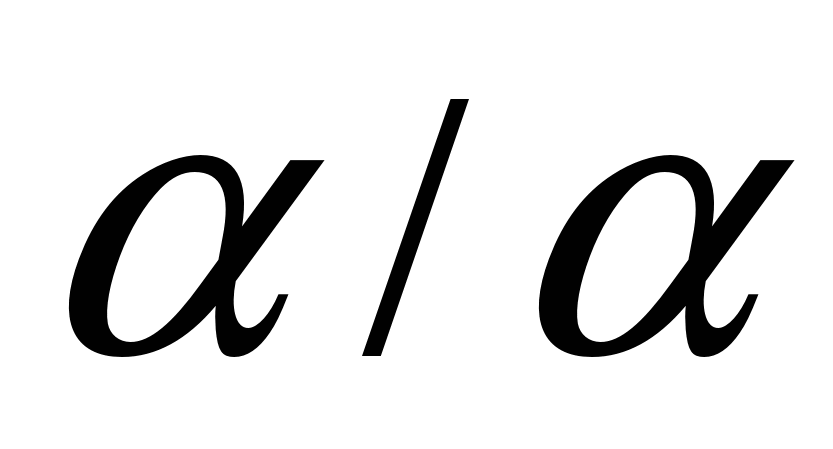 будет универсум.
будет универсум.
Теорема доказана.
-
Мультипликативная арифметика фигур
-
Умножение точек и фигур на плоскости
-
Свойства умножения
-
-
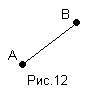
Отрезок с концами А и В часто обозначается символом АВ (рис.12). Эта запись подсказывает неожиданную терминологию: отрезок АВ назовем произведением точек А и В.
Аналогично, произведением фигур  и
и  мы назовем объединения всех возможных произведений точек фигуры
мы назовем объединения всех возможных произведений точек фигуры  на точки фигуры
на точки фигуры  . Умножение точек обладает следующими свойствами:
. Умножение точек обладает следующими свойствами:
а) Умножение точек коммутативно
АВ=ВА.
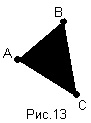
б) Умножение точек ассоциативно
(АВ)С=А(ВС) Это свойство проиллюстрировано на рисунке 13.
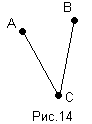
в) Умножение точек дистрибутивно относительно их сложения.
(А+В)С=АС+ВС. Под сложением точек А и В мы подразумеваем объединение точек А и В. Это свойство проиллюстрировано на рисунке 14.
г) Умножение фигур идемпотентно, т.е АА - отрезок со слившимися концами, т.е. сама точка А.
Первые три свойства переносятся и на произвольные фигуры:
А) Умножение фигур коммутативно (рис.15), очевидно из определения.
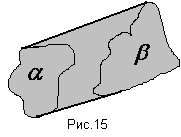
Б) умножение фигур ассоциативно
(АВ)С=А(ВС)
В)Умножение фигур дистрибутивно относительно их сложения. А(В+С)=АВ+АС. Под понятием сложения подразумевается объединение отрезков.
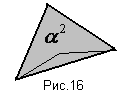
Г) Несмотря на то, что идемпотентность умножения фигур места не имеет, верно следующее свойство: произведение любой фигуры самой на себя содержит эту фигуру как подмножество, т.е. 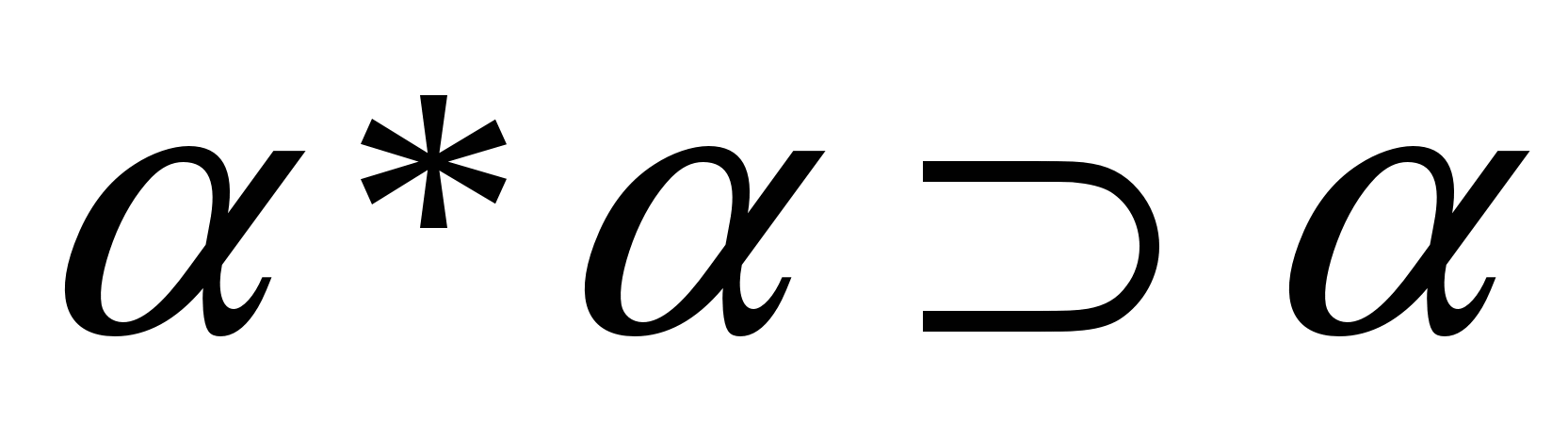 (рис.16)
(рис.16)
Некоторыми замечательными свойствами обладает особая категория фигур - выпуклые фигуры. В данной статье выпуклая фигура определяется как фигура, любые две точки которой можно соединить отрезком, все точки которого принадлежат данной фигуре.
Теорема (об умножении выпуклых фигур). Произведение двух выпуклых фигур выпукло. (Выпуклая фигура - это такая фигура, любые две точки которой можно соединить отрезком, который целиком принадлежит этой фигуре).
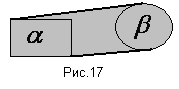
Доказательство (от противного). Возьмем две произвольные выпуклые фигуры  и
и 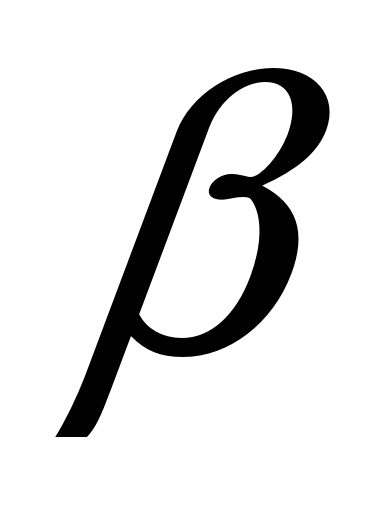 (Рис.17). Предположим, что их произведение не выпукло, тогда имеются хотя бы две точки
(Рис.17). Предположим, что их произведение не выпукло, тогда имеются хотя бы две точки 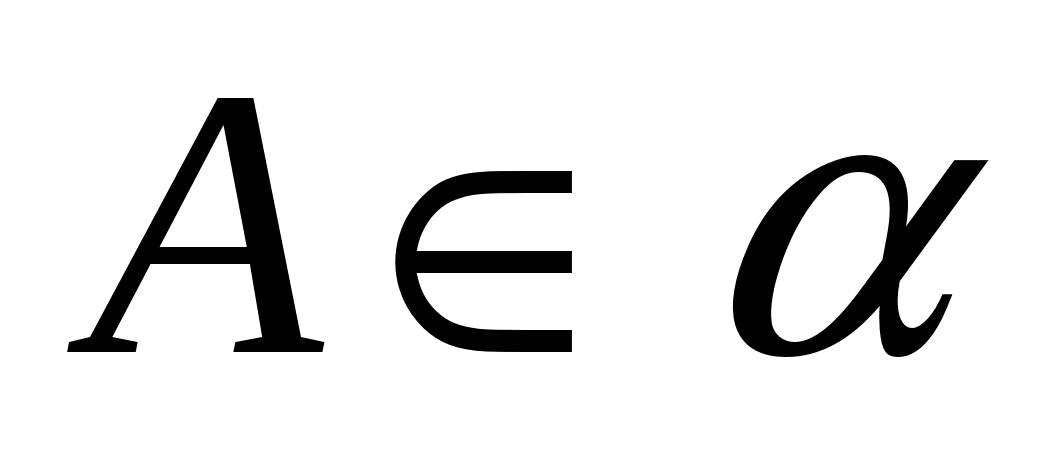 ,
,  , которые мы не можем соединить отрезком, принадлежащим данной фигуре. Но по определению произведения фигур
, которые мы не можем соединить отрезком, принадлежащим данной фигуре. Но по определению произведения фигур 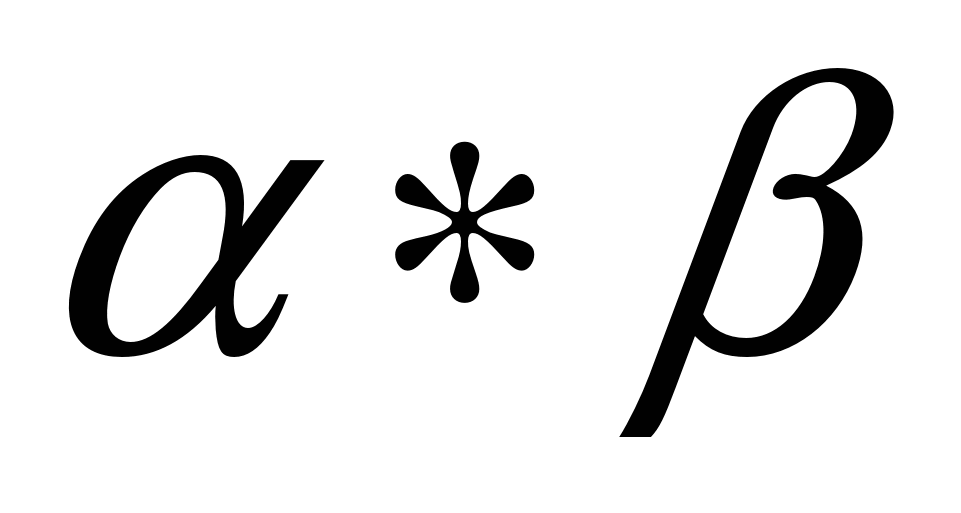 - это объединение всех отрезков, соединяющих всевозможные точки фигур
- это объединение всех отрезков, соединяющих всевозможные точки фигур  и
и 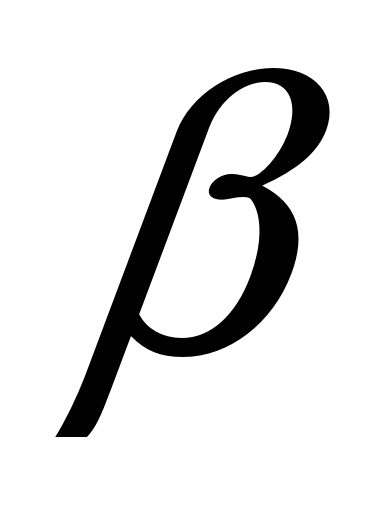 , т.е. любые две точки соединены отрезком внутри произведения. Значит, получили противоречие, следовательно, наше предположение не верно, значит, произведение двух выпуклых фигур - выпукло. Теорема доказана.
, т.е. любые две точки соединены отрезком внутри произведения. Значит, получили противоречие, следовательно, наше предположение не верно, значит, произведение двух выпуклых фигур - выпукло. Теорема доказана.
-
Задачи
В данном пункте приведены примеры умножения различных фигур.
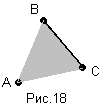
На рисунке 18 показано умножение точки на отрезок.
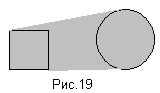
На рисунке 19 - результат умножения квадрата на круг.
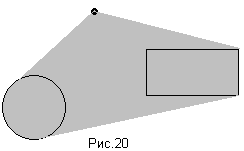
На рисунке 20 вы можете увидеть результат умножения точки на круг на прямоугольник.
Натуральная степень фигур.
В арифметике и в алгебре особую роль играют те числа, квадрат которых равен им самим. Ясно, что этим свойством обладают лишь два числа: 1 и 0.
В мультипликативной геометрии этим свойством обладают выпуклые фигуры. Фигура - это произвольное множество точек плоскости. Выпуклая оболочка фигуры - это наименьшая степень, при возведении в которую мы получаем выпуклую фигуру.
Теорема (о выпуклой оболочке плоских фигур). Выпуклой оболочкой любой фигуры на плоскости будет ее третья степень.
Доказательство. Пусть точки А и В принадлежат фигуре 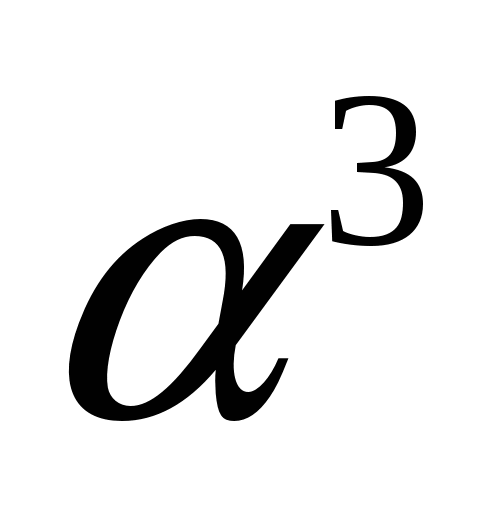 . Для доказательства теоремы нам достаточно доказать, что отрезок АВ будет подмножеством этой фигуры. Пусть точки А и В принадлежат отрезку PN, причем Р принадлежит фигуре
. Для доказательства теоремы нам достаточно доказать, что отрезок АВ будет подмножеством этой фигуры. Пусть точки А и В принадлежат отрезку PN, причем Р принадлежит фигуре  , а точка N - фигуре
, а точка N - фигуре ![]() . Т.к. произведение любой фигуры саму на себя содержит эту фигуру, то точки Р и N принадлежат фигуре
. Т.к. произведение любой фигуры саму на себя содержит эту фигуру, то точки Р и N принадлежат фигуре 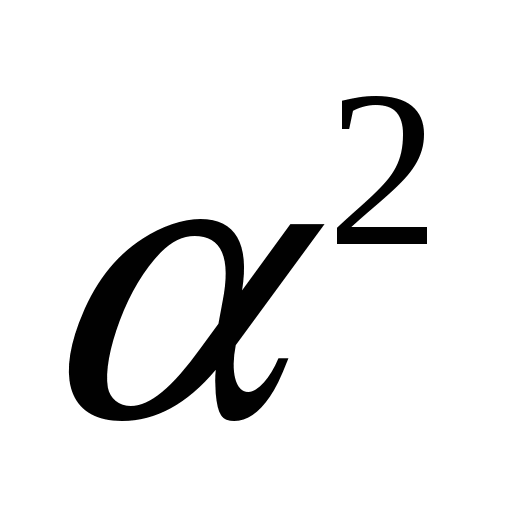 . При умножении
. При умножении 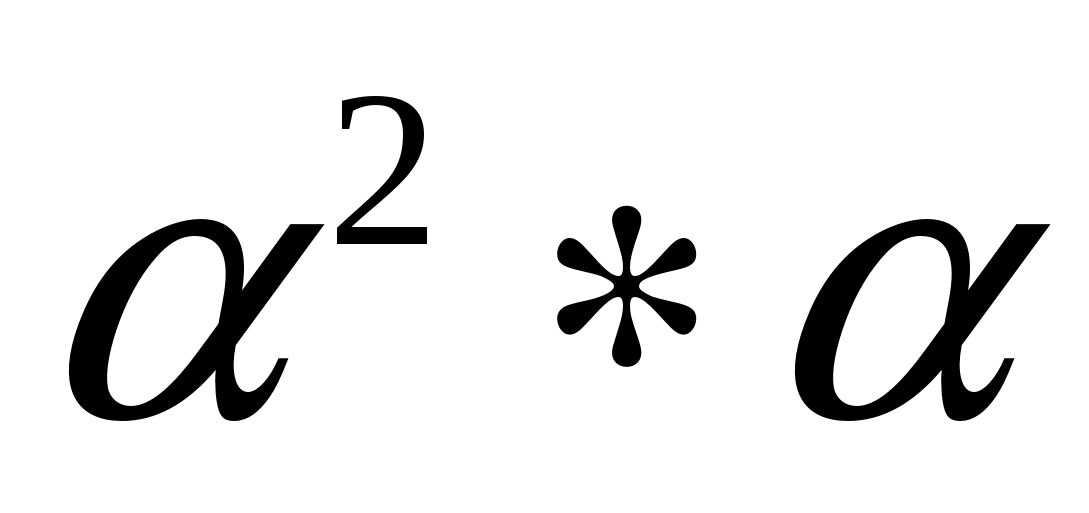 мы умножаем точки Р и N (по определению умножения фигур), значит, все точки отрезка PN принадлежат фигуре
мы умножаем точки Р и N (по определению умножения фигур), значит, все точки отрезка PN принадлежат фигуре 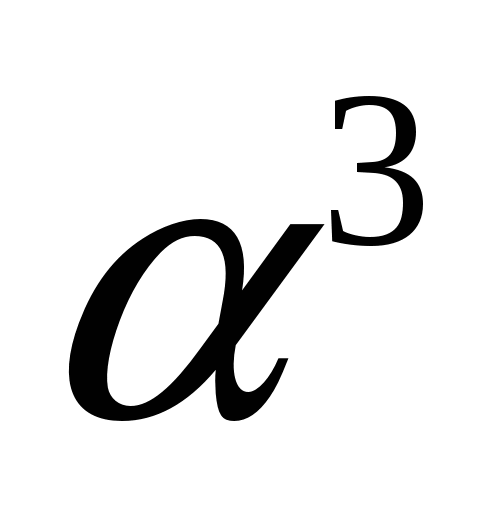 , следовательно, и отрезок АВ принадлежит этой фигуре. Теорема доказана.
, следовательно, и отрезок АВ принадлежит этой фигуре. Теорема доказана.
-
Деление фигур на плоскости
-
Определение и свойства деления фигур.
-
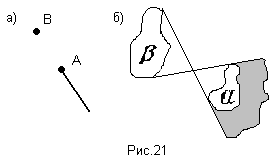
Частное А/В двух точек - это луч с началом А, продолжение которого проходит через В. (или тень, отбрасываемая "колышком" А, освещенным "фонариком" В. (рис.21а).
Аналогично , частное 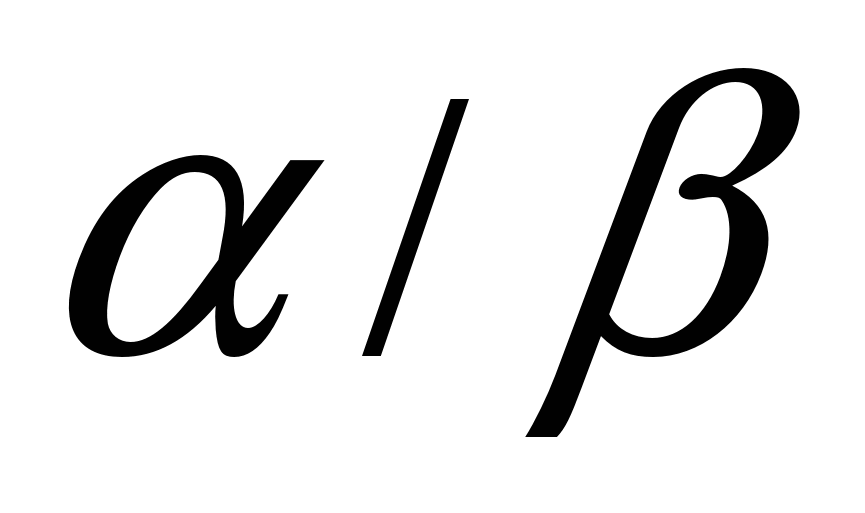 двух фигур - это объединение всех лучей А/В, где А принадлежит
двух фигур - это объединение всех лучей А/В, где А принадлежит  , а В принадлежит
, а В принадлежит  . (рис.21б)
. (рис.21б)
Свойства деления точек А, В и С:
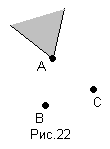
А) (А/В)/С=А/(ВС) (рис.22)
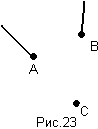
Б) (А+В)/С=(А/С)+(В/С) (рис.23)
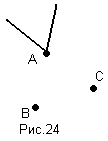
В) А/(В+С)=(А/В)+(А/С) (рис.24)
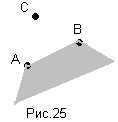
Г) (АВ)/С=(А/С)(В/С) (рис.25)
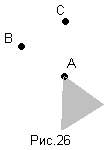
Д) А/(ВС)=(А/В)(А/С) (рис.26).
-
Теоремы о частном
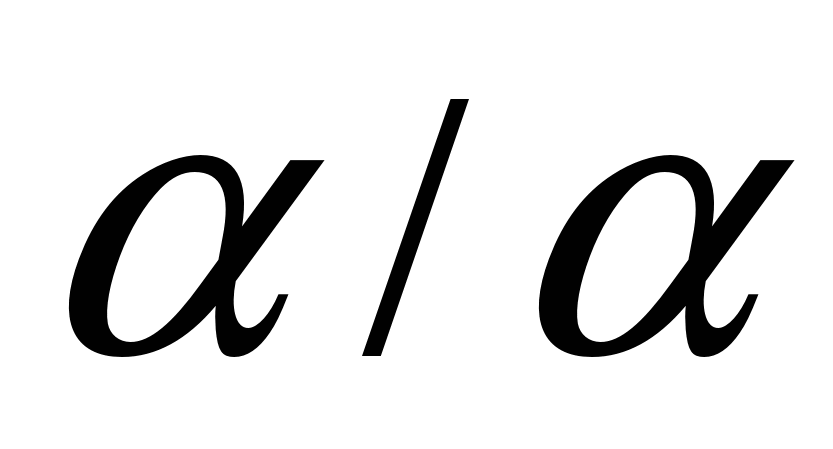
Для доказательства теорем нам понадобится лемма, доказательство которой очевидно.
Лемма (о делении фигур самих на себя). Результат деления любой фигуры саму на себя содержит эту фигуру.
Далее рассмотрены крайние случаи: когда 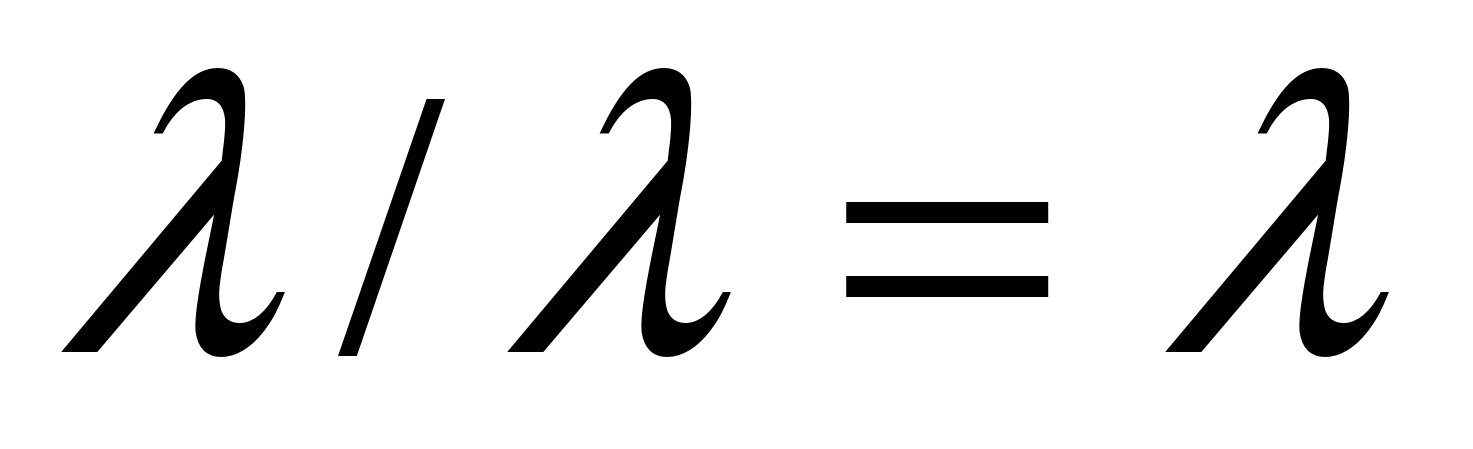 (в этом случае фигуру называют линейной) и когда
(в этом случае фигуру называют линейной) и когда 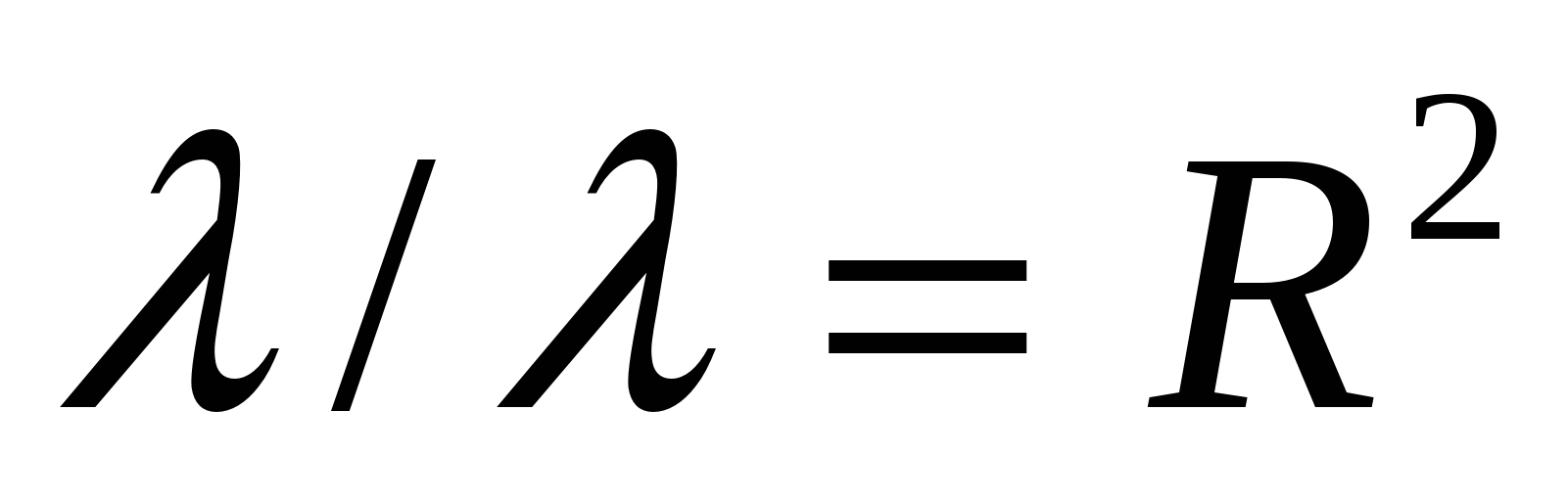 .
.
Теорема (о линейных фигурах). Все линейные фигуры плоскости исчерпываются точками, прямыми и всей плоскостью.
Доказательство. Если фигура 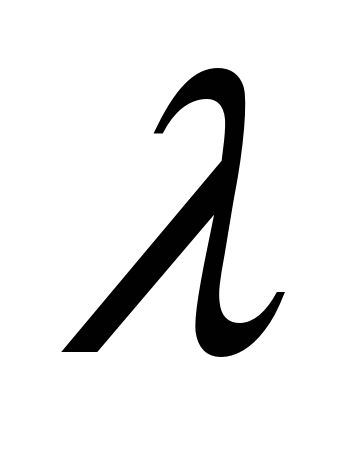 содержит более одной точки, то результат деления
содержит более одной точки, то результат деления ![]() будет содержать как минимум два луча. Лучи - фигуры неограниченные, а значит, линейные фигуры - это фигуры неограниченные (за исключением случая точки - при делении точки А самой на себя мы получаем "слившийся" с точкой А луч).
будет содержать как минимум два луча. Лучи - фигуры неограниченные, а значит, линейные фигуры - это фигуры неограниченные (за исключением случая точки - при делении точки А самой на себя мы получаем "слившийся" с точкой А луч).
Возьмем две точки А и В. При делении этих точек самих на себя мы получаем лучи с началами в этих точках, лежащие на прямой АВ. В одномерном пространстве возможны два варианта, соответствующих этим условиям: прямая и луч.
При делении луча самого на себя мы получаем прямую, а при делении прямой самой на себя - эта же прямая. В нульмерном пространстве вариант один: точка, а результат деления точки самой на себя является, как уже упомянуто выше, лучом, слившимся с этой точкой, т.е., этой точкой, и точка является линейной фигурой.
Рассмотрим двухмерное пространство. В нем тоже возможны варианты неограниченных множеств: части плоскости, ограниченные прямой, лучами, кривыми… В любой части плоскости всегда найдутся три точки, не лежащие на одной прямой. При делении трех точек самих на себя мы получим 6 лучей, являющихся продолжениями отрезков сторон треугольника, образованного этими точками. Всегда найдется при этом луч, выходящий за пределы рассмотренной части плоскости. Таким образом, вся плоскость также является линейной фигурой.
Таким образом, все линейные фигуры плоскости исчерпываются точками, прямыми и всей плоскостью. Теорема доказана.
Теорема (о делении фигур с ненулевой площадью самих на себя). Результатом деления любой фигуры с ненулевой площадью самой на себя всегда является вся плоскость.
Доказательство. Возьмем некоторую фигуру 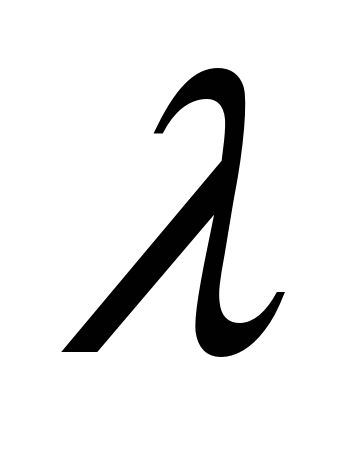 с ненулевой площадью. Для доказательства теоремы нам достаточно доказать, что результат деления
с ненулевой площадью. Для доказательства теоремы нам достаточно доказать, что результат деления 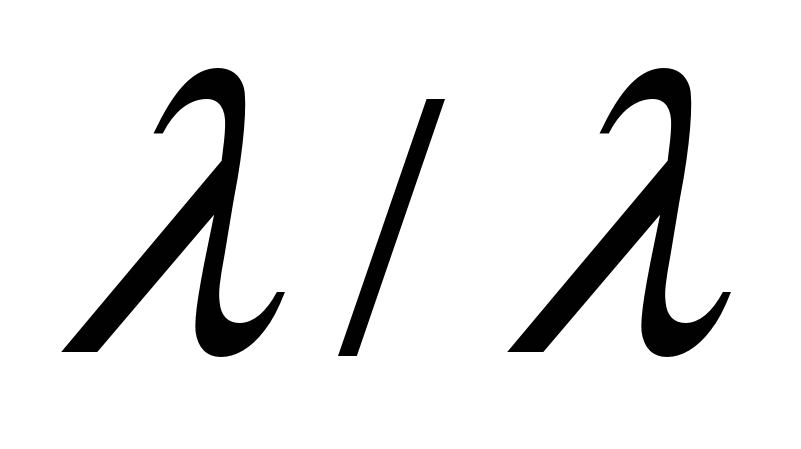 содержит любую точку А, не принадлежащую фигуре
содержит любую точку А, не принадлежащую фигуре ![]() . В любую фигуру с ненулевой площадью можно вписать окружность, с центром в некоторой точке О. Как известно, через любые две точки можно провести прямую, и притом только одну. Проведем прямую ОА. Эта прямая обязательно пересечет окружность в некоторой точке С. Т.к. окружность является подмножеством фигуры
. В любую фигуру с ненулевой площадью можно вписать окружность, с центром в некоторой точке О. Как известно, через любые две точки можно провести прямую, и притом только одну. Проведем прямую ОА. Эта прямая обязательно пересечет окружность в некоторой точке С. Т.к. окружность является подмножеством фигуры 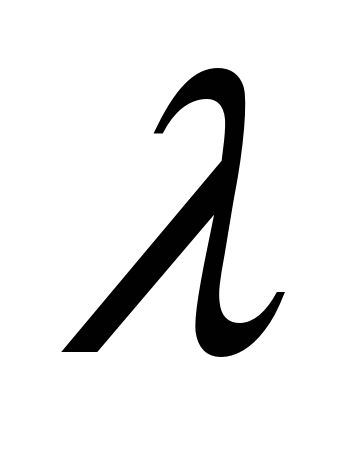 , то при делении
, то при делении 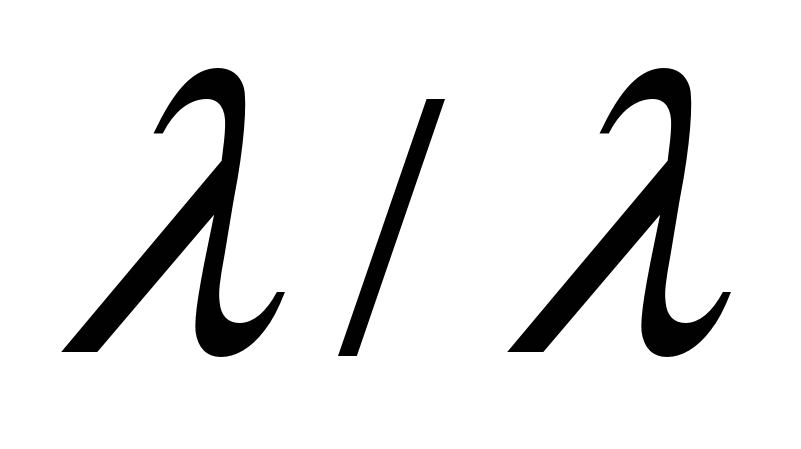 мы обязательно поделим точку С на точку О (по определению деления фигур), а так как точка С принадлежит прямой ОА, то результат деления С/О будет содержать точку А, а значит, и результат деления
мы обязательно поделим точку С на точку О (по определению деления фигур), а так как точка С принадлежит прямой ОА, то результат деления С/О будет содержать точку А, а значит, и результат деления 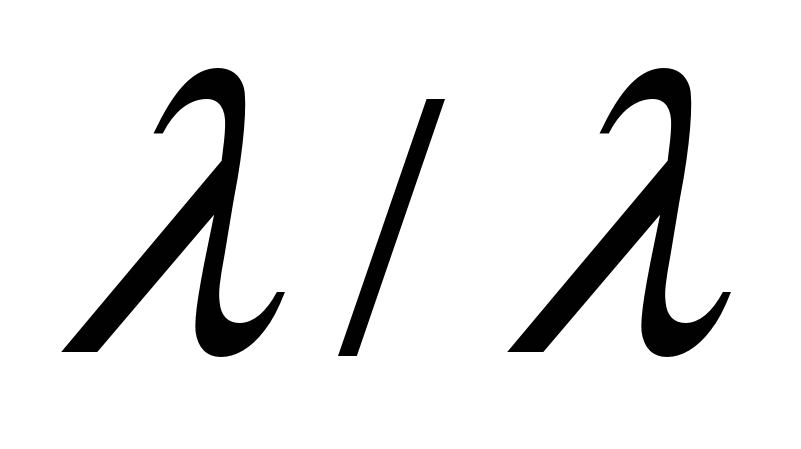 будет содержать эту точку. Вся плоскость состоит из бесконечного количества таких точек А, и для каждой из них будет действовать выше доказанное. Теорема доказана.
будет содержать эту точку. Вся плоскость состоит из бесконечного количества таких точек А, и для каждой из них будет действовать выше доказанное. Теорема доказана.
Список литературы
-
Рыжик В. Давайте складывать точки // Квант. - № 1 - 1976
-
Яглом И. Соединим две точки отрезком // Квант. - № 4 - 1981
-
"Арифметика фигур" /Статья "Векторы и их применение в геометрии". Энциклопедия элементарной математики, т.IV.
-
Геометрия 7 - 9: Учебник для общеобразовательных учреждений./ Л. С. Анастасян, Б. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. - 13-е издание - М.; Просвещение, 2003.


