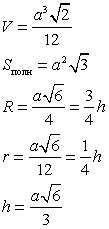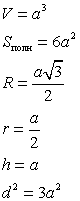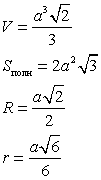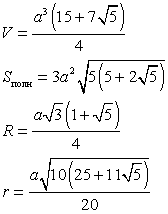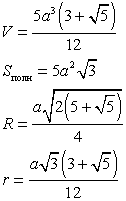- Преподавателю
- Математика
- Методическая разработка по стереометрии для учащихся 10-11 классов
Методическая разработка по стереометрии для учащихся 10-11 классов
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | Белоусова Е.Н. |
| Дата | 17.03.2014 |
| Формат | doc |
| Изображения | Есть |
МКОУ "СОШ №7"
Методическая разработка
по стереометрии
для учащихся 10 класса
(Рекомендуемый учебник: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г., Геометрия 10-11. Учебник для 10-11 классов средней школы. М., 1994 и последующие годы издательства)
Белоусова Е.Н., учитель математики
2014г, Нальчик
«Основные понятия и аксиомы стереометрии.
Параллельность прямых и плоскостей»
Стереометрия - это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» - объемный, пространственный и «μετρεο» - измерять.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.

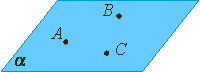
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д.
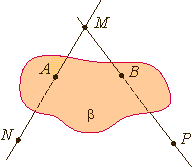
Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
Аксиомы стереометрии и их следствия
Аксиома 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
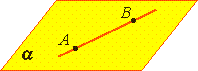
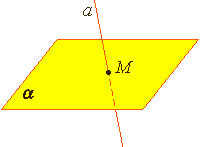
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3.
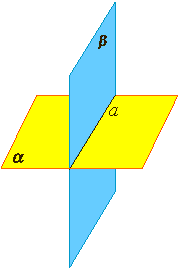
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
Некоторые следствия из аксиом
Теорема 1.
Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
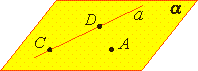
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
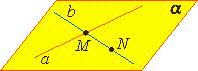
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
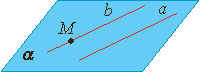
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
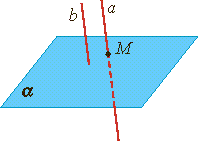
Теорема о трех прямых в пространстве.
Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).
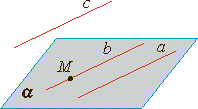
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Теорема.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
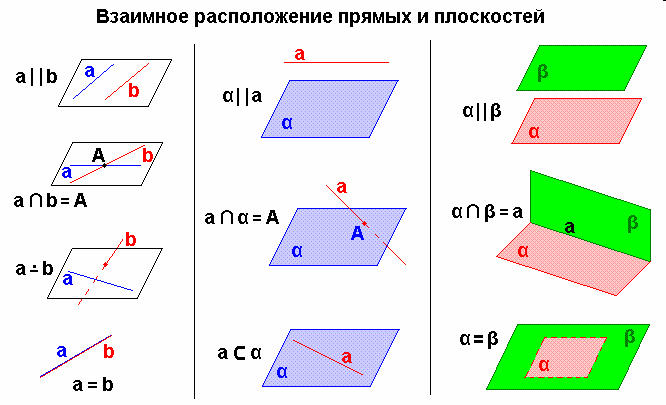
Взаимное расположение прямых в пространстве
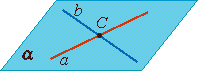
Пересекающиеся прямые:
лежат в одной плоскости, имеют одну общую точку.
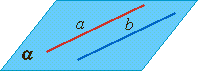
Параллельные прямые:
лежат в одной плоскости, не имеют общих точек (не пересекаются)
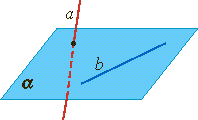
Скрещивающиеся прямые:
не лежат в одной плоскости, не имеют общих точек (не пересекаются)
Параллельность плоскостей
Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β.
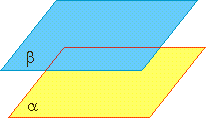
Признак параллельности двух плоскостей
Теорема.
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны.
Если а∥а1 и b∥b1, то α∥β.
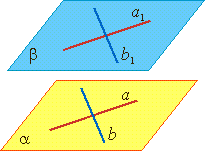
Свойства параллельных плоскостей
Если α∥β и они пересекаются с γ, то а∥b.
Е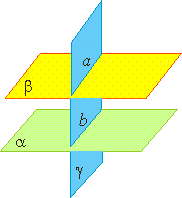 сли две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
сли две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
О трезки параллельных прямых, заключенные между параллельными плоскостями, равны.
трезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Перпендикулярность прямых и плоскостей
Определение
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
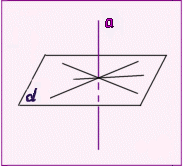
Теорема (ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ).
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Теорема. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Теорема. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Перпендикуляр и наклонная
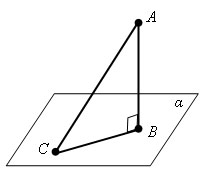
Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной.
Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
AB - перпендикуляр к плоскости α.
AC - наклонная, CB - проекция.
С - основание наклонной, B - основание перпендикуляра.
Теорема о трех перпендикулярах
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.
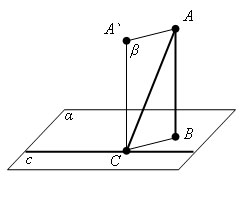
Обратная теорема о трех перпендикулярах
Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Перпендикулярные плоскости
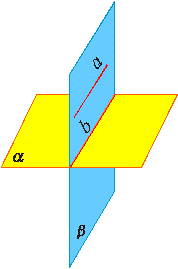
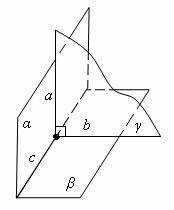
Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
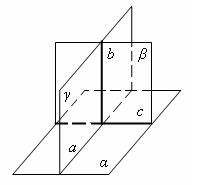
Плоскость α перпендикулярна плоскости β. Они пересекаются по прямой с. Плоскость γ перпендикулярна с и пересекает плоскости α и β по прямым a и b соответственно.
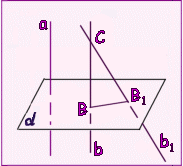
Признак перпендикулярности плоскостей
Теорема. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Расстояние между скрещивающимися прямыми
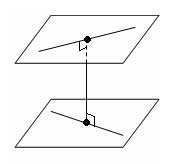
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые.
Расстояние между скрещивающимися прямыми. Свойства
Теорема. Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.

Двугранный угол
Двугранным углом называется фигура, образованная двумя плоскостями с общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая их прямая - ребром двухгранного угла.
Плоскость, перпендикулярная ребру двухгранного угла, пересекает его грани по двум полупрямым.
Угол, образованный этими полупрямыми, называется линейным углом двухгранного угла.


Многогранники
Обозначения:
V - объем;
Sполн - площадь полной поверхности;
Sбок - площадь боковой поверхности;
Sо - площадь основания;
Pо - периметр основания;
Pо - периметр перпендикулярного сечения;
l - длина ребра;
h - высота.
Формула Эйлера: N − L + F = 2 ; N - число вершин, L - число ребер, F - число граней выпуклого многогранника.
Призма - многогранник, две грани которого - равные многоугольники, расположенные в параллельных плоскостях, а остальные - параллелограммы.
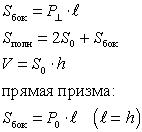
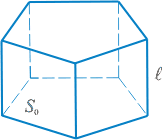
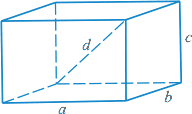
Параллелепипед - призма, основание которой - параллелограмм.
Параллелепипед имеет шесть граней и все они - параллелограммы.
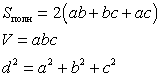
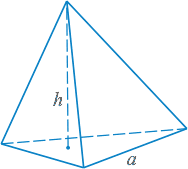
Пирамида - многогранник, у которого одна грань n-угольник - основание пирамиды, а остальные боковые грани - треугольники с общей вершиной - вершиной пирамиды.
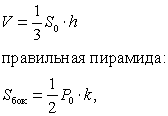
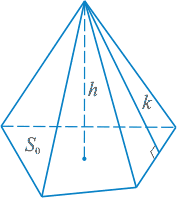
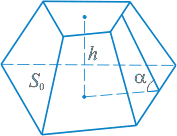
Если в пирамиде провести сечение параллельное основанию, то тело, ограниченное этим сечением, основанием, и заключенной между ними боковой поверхностью пирамиды, называется усеченной пирамидой.
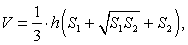
где S1 и S2 - площади оснований
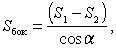 где α - двугранный угол при ребре нижнего основания.
где α - двугранный угол при ребре нижнего основания.
| Правильные многогранники | |
| Многогранник называется правильным, если все его грани - равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней. Все ребра правильного многогранника - равные отрезки, все плоские углы правильного многогранника также равны. Существует пять различных правильных многогранников (выпуклых): правильный четырехгранник (правильный тетраэдр), правильный шестигранник (куб), правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (правильный додекаэдр), правильный двадцатигранник (правильный икосаэдр).
| Обозначения: а - длина ребра; V - объем; Sбок - площадь боковой поверхности; Sполн - площадь полной поверхности; R - радиус описанной сферы; r - радиус вписанной сферы; h - высота. |
| Тетраэдр - четыре грани - равносторонние равные треугольники. Тетраэдр имеет четыре вершины и шесть ребер
|
|
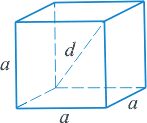
| Куб - шесть граней - равные квадраты. Куб имеет восемь вершин и двенадцать ребер.
|
|
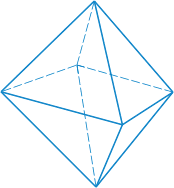
| Октаэдр - восемь граней - равносторонние равные треугольники. Октаэдр имеет шесть вершин и двенадцать ребер
|
|
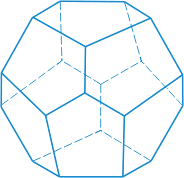
| Додекаэдр - двенадцать граней - правильные равные пятиугольники. Додекаэдр имеет двадцать вершин и тридцать ребер.
|
|
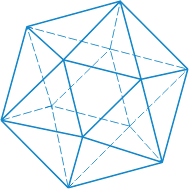
| Икосаэдр - двадцать граней - равносторонние равные треугольники. Икосаэдр имеет двенадцать вершин и тридцать ребер.
|
|
7