- Преподавателю
- Математика
- Методическое пособие для студенов Решение логарифмических уравнений
Методическое пособие для студенов Решение логарифмических уравнений
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Сыровая И.С. |
| Дата | 27.08.2015 |
| Формат | doc |
| Изображения | Есть |

Авторская педагогическая разработка
Методическое пособие
для студентов по дисциплине «Математика»
Тема: «Решение логарифмических уравнений»
Иркутск, 2015
Пояснительная записка.
Методическое пособие «Логарифмические уравнения» выполнено для использования его студентами техникума при самостоятельных занятиях по данной теме в разделе «Показательная, логарифмическая и степенная функции» с целью углубления знаний по этой теме и отработки практических навыков решения логарифмических уравнений.
В главе I данного пособия приведены определения логарифма и свойства логарифмов, которые необходимо знать при решении логарифмических уравнений.
В главе II дано определение логарифмического уравнения и приведены примеры логарифмических уравнений.
В главе III рассмотрены 5 основных методов решения логарифмических уравнений и приведены примеры, демонстрирующие применение этих методов.
I. Вопросы для повторения:
-
что называется логарифмом?
-
как записывается основное логарифмическое тождество?
-
log ab - какие ограничения накладываются на а?
-
чему равен log a a ?
-
чему равен log a (x1*x2)?
-
чему равен log a (x1/x2)?
-
чему равен log a am ?
-
если а>1 и х1 > х2, то какой знак нужно поставить между
log a x1 и log a x2 ?
Если вы смогли ответить на все эти вопросы, то можете сразу переходить к главе II. Если же на какие-либо вопросы вы не смогли дать ответ, стоит почитать всю эту главу.
-
Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число b, (а>0, a ≠ 1, b>0)
log ab = х
Например, log 2 8 = 3, так как 23 = 8
log 3 1/27 = -3, так как 3 -3 = 1/27
2. Основное логарифмическое тождество имеет вид:
а lоgb = b
-
log a a = 1
-
log a (x1*x2) = log a x1 + log a x2
-
log a (x1/x2) = log a x1 - log a x2
-
log aam = m log aa
-
Если а>1 и х1 > х2, то log ax1 > log ax2
II. Определение. Уравнение, в котором переменная находится под знаком логарифма, называется логарифмическим.
Например: 2 log 2 x - 7 = 0, log x 4 = 2, 2 lg x - 1 = 0.
Простейшим логарифмическим уравнением является уравнение вида: log ax = b, где a >0 и a ≠ 1.
Его решением является x = ab, x > 0.
Если логарифмическое уравнение имеет вид: log af(x) = b, то есть под знаком логарифма находится некоторая функция f(x), то его решение сводится к решению уравнения f(x) = ab (по определению логарифма). При этом уравнение имеет множество допустимых значений x, задаваемых неравенством f(x) > 0.
После того, как логарифмическое уравнение решено, то есть найдены корни уравнения, необходимо произвести проверку всех полученных корней.
Иногда сначала находят множество допустимых значений x.
III. Основные способы решения логарифмических уравнений:
-
применение определения логарифма;
-
применение свойств логарифмов;
-
предварительная замена числа его логарифмом;
-
введение вспомогательной переменной;

-
почленное логарифмирование.
-
Применение определения логарифма.
Данный метод применяется в том случае, когда в одной части логарифмического уравнения имеется логарифм, а в другой - число.
log x-1 (x2 - 7x + 41) = 2
По определению логарифма log ax = b ═► ab= х
Получим: (x -1)2 = x2 - 7x + 41
x2 - 2x + 1 = x2 - 7x + 41
x2 - 2x + 1 - x2 + 7x - 41 = 0
5х = 40 ═► х = 8
Проверка: подставив в уравнение значение x = 8, получим:
log 8-1 (64 -56 + 41) = 2 ═► log 7 49 = 2
72 = 49 - верно.
Ответ: х = 8
-
Применение свойств логарифмов.
Данный метод применяется в том случае, когда в уравнении имеется сумма или разность логарифмов по одному и тому же основанию.
4 lg 2 + 2 lg (x - 3) = lg 3 + lg (7x + 1) + lg (x - 6)
Пользуясь свойствами логарифмов, преобразуем:
lg 24 + lg (x - 3)2 = lg (3(7x + 1)(x - 6))
lg (24 (x -3)2) = lg ((21x + 3)(x - 6))
Так как логарифмы по одному и тому же основанию равны, то равны и выражения, стоящие под знаками этих логарифмов:
24 (x - 3)2 = (21x + 3) (x - 6)
16 (x2 - 6х + 9) = 21x2 + 3x - 126x - 18
16x2 - 96х + 144 = 21x2- 123x - 18
16x2 - 96х + 144 - 21x2 + 123x +18 = 0
- 5x2 + 27x + 162 =0
5x2 - 27x - 162 =0
Решив полученное квадратное уравнение, получим:
x1 = -3.6 и x2 = 9
Проверка показывает, что значение x = -3.6 не удовлетворяет данному уравнению.
Ответ: x = 9.
3. Предварительная замена числа его логарифмом.
Данный метод применяется в том случае, когда в уравнение наряду с логарифмами входит число.
lg (2x+ x - 5) = x(1 - lg 5)
Заменив 1 его эквивалентом lg 10, получим:
lg (2x + x - 5) = x( lg 10 - lg 5)
Пользуясь свойствами логарифмов, преобразуем:
lg (2x + x - 5) = x lg 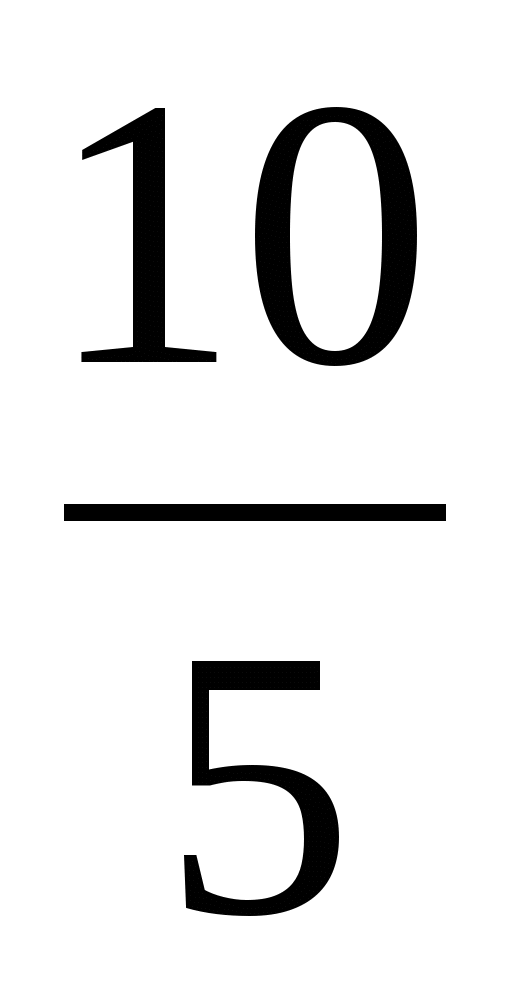
lg (2x + x - 5) = x lg 2
lg (2x + x - 5) = lg 2x
2x + x - 5 = 2x
2x + x - 5 - 2x = 0
x - 5 = 0
x = 5
Проверка показывает, что полученный корень удовлетворяет уравнению.
Ответ: x = 5.
-
Введение новой переменной.
Данный метод применяется в том случае, когда в уравнение входят логарифмы во второй и в первой степени. Введение новой переменной позволяет свести логарифмическое уравнение к квадратному.
lg 2x + lg x - 2 = 0
Обозначим lg x = y, получим уравнение:
y2 + y - 2 =0
y1 = -2 и y2 = 1
Возвращаясь к старой переменной, получим:
lg x = y1 ═► lg x = -2 ═► x = 10-2 ═► x = 0.01
lg x = y2 ═► lg x = 1 ═► x = 10
Проверка показывает, что оба корня удовлетворяют уравнению.
Ответ: x1 = 0.01, x2 = 10.
5. Почленное логарифмирование.
Данный метод применяется в том случае, когда в уравнении логарифм находится в показателе степени.
x lgx= 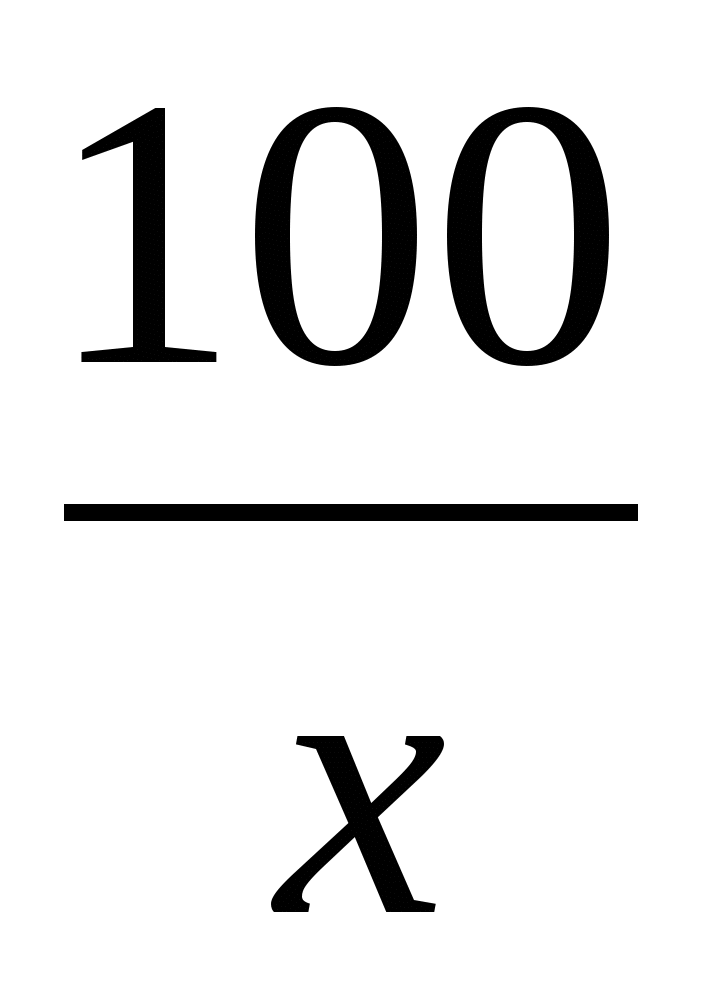
Воспользуемся свойством логарифма степени, получим:
lg x lg x = lg 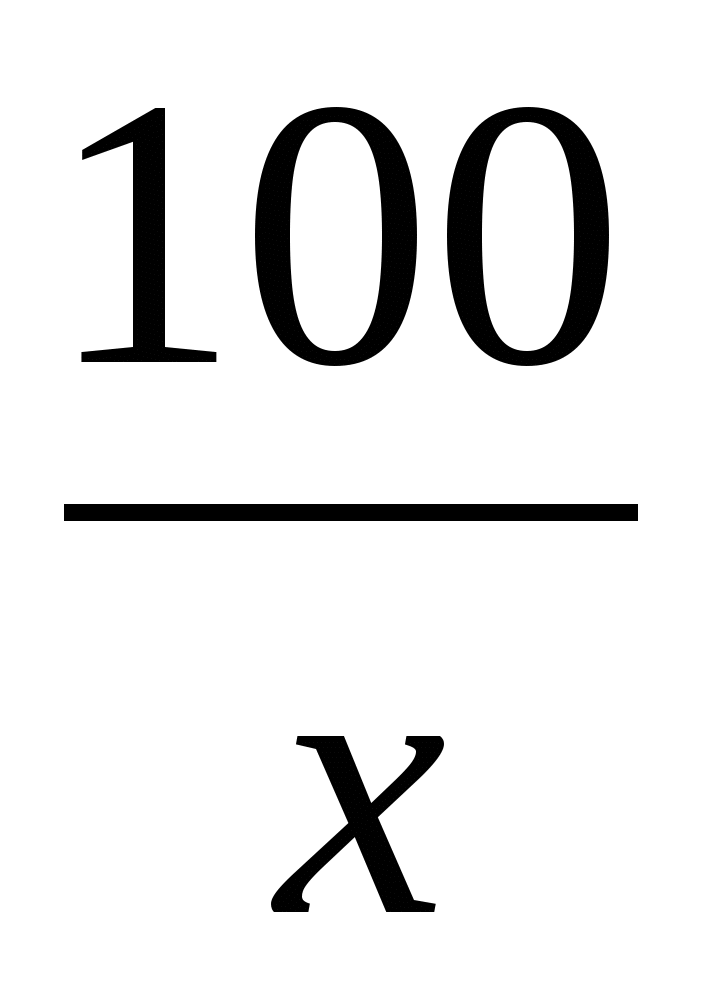
lg x lg x = lg 100 - lg x
lg 2 x = 2 - lg x
lg 2 x + lg x - 2 = 0
Получили квадратное уравнение, подобное тому, что мы решали в п.3.
Обозначим lg x = y, получим уравнение:
y2 + y - 2 =0
y1 = -2 и y2 = 1
Возвращаясь к старой переменной, получим:
lg x = y1 ═► lg x = -2 ═► x = 10-2 ═► x = 0.01
lg x = y2 ═► lg x = 1 ═► x = 10
Проверка показывает, что оба корня удовлетворяют уравнению.
Ответ: x1 = 0.01, x2 = 10.
6. Примеры:
-
log 5 x = log 5 (6 - x2)
-
log x +1 (2x2 +1) = 2
-
log x - 6 (x2 - 5) = log x - 6 (2x + 19)
-
lg2 x = 3 - 2 lg x
-
log2 3 x - log 3 x = 2
Ответы:
1) 2; 2) 2; 3) корней нет; 4) 1; 10; 5) 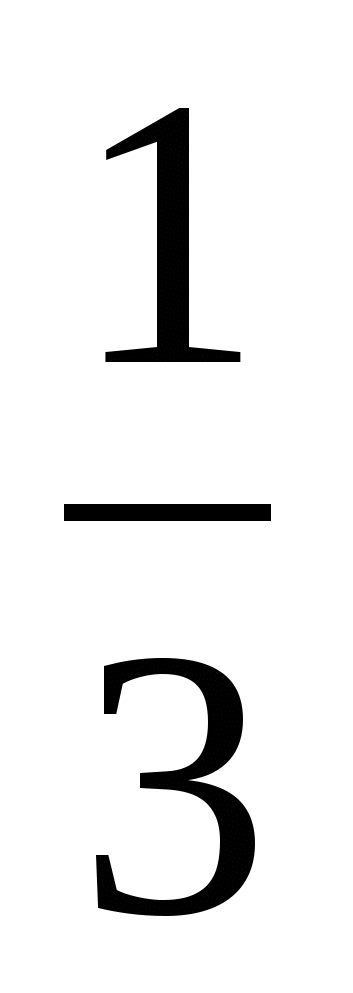 ; 9.
; 9.
Литература:
1. Лисичкин В.Т., Соловейчик И.Л. Математика в задачах с решениями: Учебное пособие. 3-е изд., стер. - СПб,: Издательство "Лань", 2011. - 464 с.
2. Алгебра и начала анализа 10-11классы: учеб. для общеобразоват. учреждений: базовый уровень/[Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др.]-16-е изд., перераб.-М.: Просвещение, 2010.-464с.
Дополнительные источники:
3. Богомолов Н.В. Практические занятия по математике: Учебное пособие для техникумов.- 3-е изд.- М.: Высшая школа, 1990.-495с.


