- Преподавателю
- Математика
- Проект Методы решения тригонометрических уравнений!
Проект Методы решения тригонометрических уравнений!
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Остапенко Т.И. |
| Дата | 17.05.2015 |
| Формат | doc |
| Изображения | Есть |
Областное государственное автономное
образовательное учреждение
дополнительного профессионального образования
«Белгородский институт развития образования»
Методы решения тригонометрических уравнений
(проектное задание)
Выполнила:
Остапенко Татьяна Ивановна,
учитель математики и физики
МБОУ «Бехтеевская СОШ
Корочанского района
Белгородскойобласти
Руководитель курса:
Вертелецкая О.В.,
старший преподаватель
кафедры естественно-
математического образования
Белгород
СОДЕРЖАНИЕ
стр.
Введение…………………………………………………………………….3
Теоретическая часть……………………………………………………....4-6
Практическая часть………………………………………………………7-18
Заключение………………………………………………………………19-20
Библиография……………………………………………………………....21
Приложение
Введение
Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Еще древнегреческие математики, используя элементы тригонометрии для решения прямоугольных треугольников, фактически составляли и решали простейшие тригонометрические уравнения. Исторически учение о решении тригонометрических уравнений формировалось с развитием теории тригонометрических функций, а также черпало из алгебры общие методы их решения.
Цель работы: изучить методы решения тригонометрических уравнений, исследовать применение их к решению уравнений повышенной сложности и задач различного содержания.
Теоретическая часть
Уравнение, содержащее неизвестную величину под знаком тригонометрической функции, называется тригонометрическим.
Часть тригонометрических уравнений непосредственно решается сведением их к простейшему виду, иногда - с предварительным разложением левой части уравнения на множители, когда правая часть равна нулю. В некоторых случаях удается произвести замену неизвестных таким образом, что тригонометрическое уравнение преобразуется в «удобное» для решения алгебраическое уравнение.
Простейшие тригонометрические уравнения - это уравнения вида
sin x = a, cos x= a, tq x = a, ctq x = a
Каждое из таких уравнений решается по формулам, которые следует знать.
sinx = a, x = (-1)karcsin a + πk, kЄZ,
arcsin a - угол, содержащийся в промежутке от - π/2 до π/2, синус которого равен a.
cosx= a, x=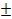 arccos a +2πk, kЄZ,
arccos a +2πk, kЄZ,
arccos a - угол, содержащийся в промежутке от 0 до π, косинус которого равен a.
tq x = a, x = arctq a + πk, kЄZ,
arctg a - угол, содержащийся в промежутке от - π/2 до π/2, тангенс которого равен a.
ctq x = a, x = arcctq a + πk, kЄZ,
arcctg a - угол, содержащийся в промежутке от 0 до π, котангенс которого равен a.
Поскольку каждому значению тригонометрической функции соответствует неограниченное множество углов, то тригонометрическое уравнение, если не сделано каких-либо оговорок, имеет бесчисленное множество решений.
Особо используются частные случаи элементарных тригонометрических уравнений, когда тригонометрические функции равны -1, 0, 1, в которых решение записывается без применения общих формул.
Частные случаи
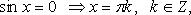
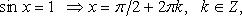
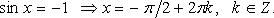
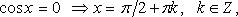
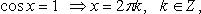
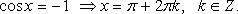
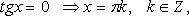
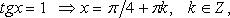
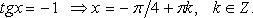
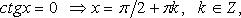
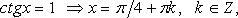
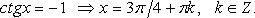
При решении тригонометрических уравнений важную роль играет период тригонометрических функций.
Рекомендации по решению тригонометрических уравнений
-
Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.
-
Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.
-
Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.
-
Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.
-
Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.
-
Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.
-
Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента:
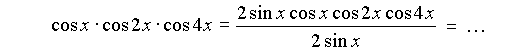
-
Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:
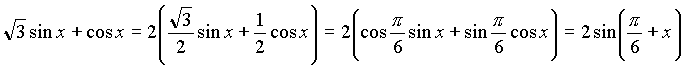
Практическая часть
Методы решения тригонометрических уравнений.
При решении тригонометрических уравнений все задачи сводятся к тому, чтобы привести к такому виду, чтобы слева стояла элементарная тригонометрическая функция, а справа - число. После того, как это будет достигнуто, следует найти значение аргумента функции, используя одну из основных формул выражения аргумента через обратные тригонометрические функции.
-
Алгебраические уравнения относительно одной из тригонометрических функций.
Необходимо произвести замену неизвестных таким образом, чтобы тригонометрическое уравнение преобразовалось в «удобное» для решения алгебраическое уравнение.
Примеры
1)Решить уравнение 2sin2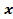 + 3sin
+ 3sin![]() -2 = 0.
-2 = 0.
Это уравнение является квадратным относительно sin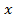 .
.
Его корни: sin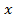 =
=  , sin
, sin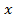 =-2. Второе из полученных простейших уравнений не имеет решений, так как Isin
=-2. Второе из полученных простейших уравнений не имеет решений, так как Isin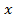 l
l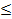 1, решения первого можно записать так:
1, решения первого можно записать так:
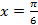 +2k
+2k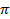 ,
,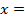 π
π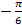 + 2k
+ 2k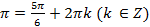
Если в уравнении встречаются разные тригонометрические функции, то надо заменить их все на какую-нибудь одну, используя тригонометрические тождества.
2) Решить уравнение 2sin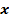 + cos
+ cos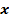 = 2.
= 2.
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используем формулы, выражающие синус и косинус через тангенс половинного угла:
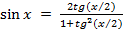 и
и 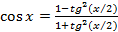 .
.
Делая замену, получаем уравнение относительно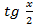 :
: 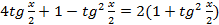 .
.
Квадратное уравнение 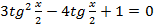 имеет корни
имеет корни 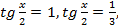 откуда
откуда
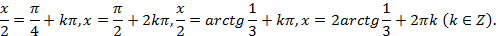
Это же уравнение можно решить другим способом, вводя вспомогательный угол:
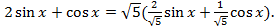
Пусть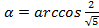 . Тогда можно продолжить преобразование:
. Тогда можно продолжить преобразование: 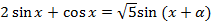 . Получаем простейшее уравнение
. Получаем простейшее уравнение 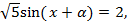 т. е.
т. е. 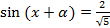 , откуда
, откуда 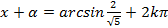 , или
, или 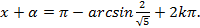
Ответ получился в другом виде, однако можно проверить, что решения на самом деле совпадают.
-
Понижение порядка уравнения.
Формулы удвоения 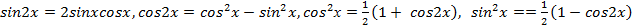 позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
Примеры
1)Решить уравнение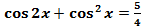 .
.
Можно заменить cos2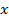 на 2cos2
на 2cos2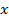 -1 и получить квадратное уравнение относительно cos
-1 и получить квадратное уравнение относительно cos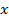 , но проще заменить
, но проще заменить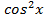 на
на 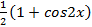 и получить линейное уравнение относительно
и получить линейное уравнение относительно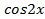 .
.
2) Решить уравнение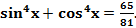
Подставляя вместо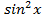 ,
, 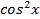 их выражения через
их выражения через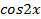 , получаем:
, получаем:
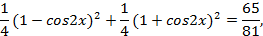
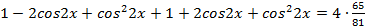 ,
,
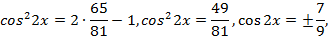
2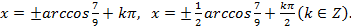
-
Использование тригонометрических формул сложения и следствий из них.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы сложения.
Примеры
1) Решить уравнение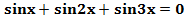 .
.
Сложим два крайних слагаемых: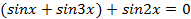 , откуда
, откуда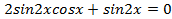 ,
,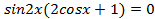 . Тогда
. Тогда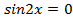 ,
, 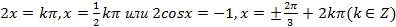 .
.
2) Решить уравнение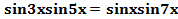 .
.
Преобразуем произведение синусов в сумму: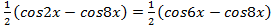 ,
,
откуда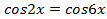 . Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать
. Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать 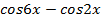 в произведение. Удобнее воспользоваться условием равенства косинусов двух углов
в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 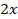 и
и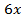 :
: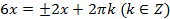 .
.
Получаем два уравнения: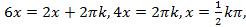
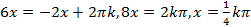 .
.
Здесь решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче: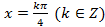 .
.
-
Однородные уравнения.
Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решить, выполнив деление на старшую степень синуса (или косинуса).
Так как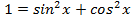 , то постоянные слагаемые можно считать членами второй степени.
, то постоянные слагаемые можно считать членами второй степени.
Пример: 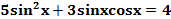 .
.
Заменяя 4 на 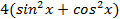 ,получаем:
,получаем: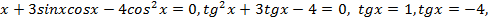
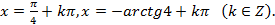
-
Переход к половинному углу
Рассмотрим этот метод на примере:
Пример 6. Решить уравнение: 3 sin x - 5 cos x = 7.
Решение.
6 sin ( x / 2 ) · cos ( x / 2 ) - 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) - 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tg ² ( x / 2 ) - 3 tg ( x / 2 ) + 6 = 0 ,
-
Введение вспомогательного угла
Рассмотрим уравнение вида:
a sin x + b cos x = c,
где a, b, c - коэффициенты; x - неизвестное.
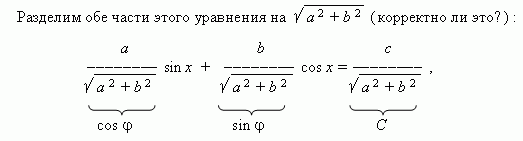
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos 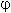 и sin
и sin ![]() ( здесь
( здесь ![]() - так называемый вспомогательный угол ), и наше уравнение принимает вид:
- так называемый вспомогательный угол ), и наше уравнение принимает вид:
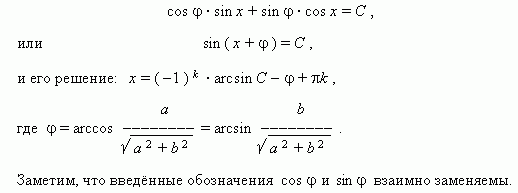
Пример. Решить уравнение: 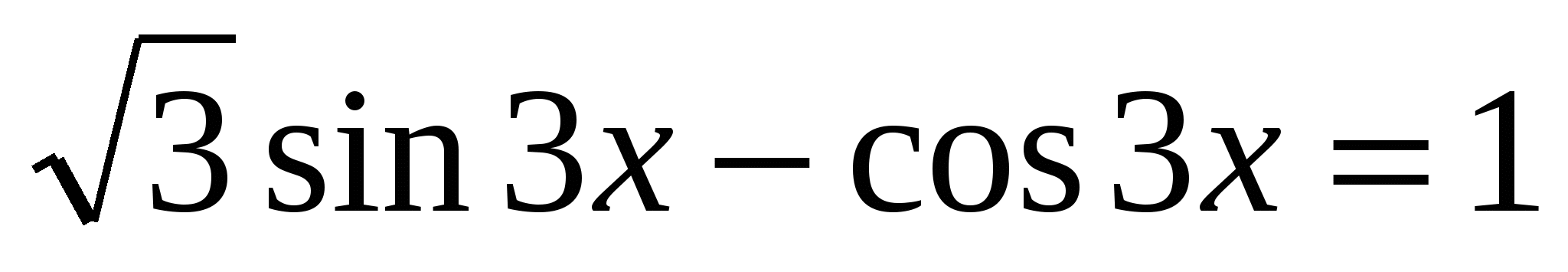
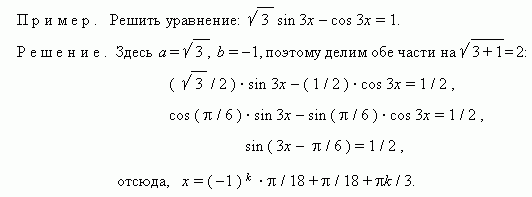
Приемы решения тригонометрических уравнений, требующих искусственных преобразований.
-
Умножение обеих частей уравнения на одну и ту же тригонометрическую функцию.
Пример. Решите уравнение 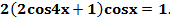
Решение. Раскроем скобки и преобразуем произведение
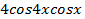 в сумму:
в сумму: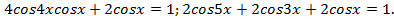
Умножим обе части уравнения на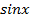 . Заметим, что
. Заметим, что 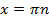 ,
, 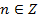 не является решением данного уравнения.
не является решением данного уравнения. 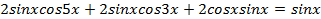 . Преобразуем левую часть уравнения:
. Преобразуем левую часть уравнения:
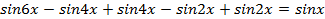 ;
; 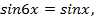 или
или 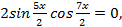 тогда
тогда
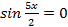 или
или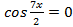 , т.е.
, т.е. 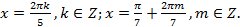
Исключим из найденных серий корни вида 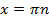 ,
, 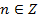 :
:
а)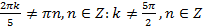 . Ясно, что
. Ясно, что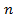 - четное число, т.е.
- четное число, т.е. 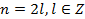 , а потому
, а потому 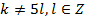 .
.
б)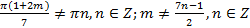 .Tax как
.Tax как 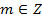 , то
, то 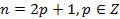 ,но тогда
,но тогда 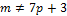 ,
,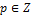 .
.
Ответ: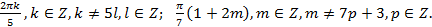
-
Прибавление к обеим частям уравнения одного и того же числа, одной и той же тригонометрической функции.
Пример. Решите уравнение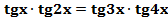 .
.
Решение. Область определения уравнения задается неравенствами:
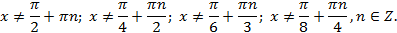
При6авим к обеим частям уравнения по единице. 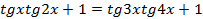 ;
;
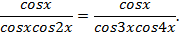
Разделим обе части уравнения на 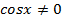 и после преобразований получим.
и после преобразований получим.
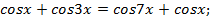
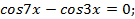
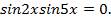
Тогда 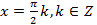 или
или 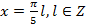 .
.
Из первой серии корней области определения принадлежит только 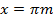 ,
,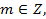 но это серия корней содержится в серии
но это серия корней содержится в серии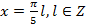 . Нетрудно убедиться, что
. Нетрудно убедиться, что 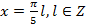 входит в область определения. Например:
входит в область определения. Например: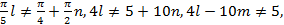 что верно, поскольку левая часть - число четное, а правая - нечетное.
что верно, поскольку левая часть - число четное, а правая - нечетное.
Ответ: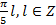 .
.
-
Тождественные преобразования одной из частей уравнения.
Пример. Решите уравнение 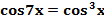 .
.
Решение. Преобразуем левую часть уравнения:
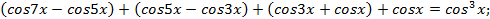
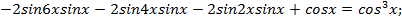
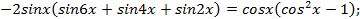
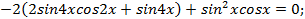
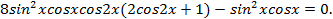
Откуда 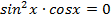 , тогда
, тогда 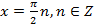 или
или 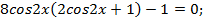
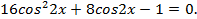
Легко видеть, что 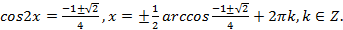
Ответ: 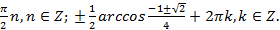
-
Использование свойств пропорции.
Необходимо помнить, что применение равенств
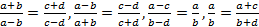 и т. д. приводит к изменению области определения уравнения. Так, у пропорции
и т. д. приводит к изменению области определения уравнения. Так, у пропорции![]() существует ограничение:
существует ограничение: 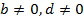 , а у пропорции
, а у пропорции 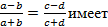 место другое ограничение:
место другое ограничение: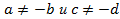 .
.
Пример. Решите уравнение 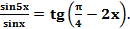
Решение. Применяя формулу тангенса разности, получим уравнение: 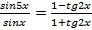 . Используем свойство пропорции:
. Используем свойство пропорции: 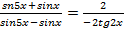 ;
; 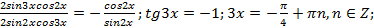
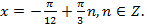 Область определения исходного уравнения:
Область определения исходного уравнения: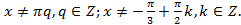
В ходе решения произошло сужение области определения, добавились новые, ограничения: 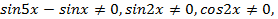 откуда
откуда 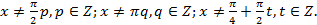
Проверим, удовлетворяют ли исходному уравнению значения
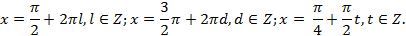
а) 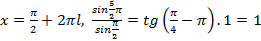 -верное равенство,
-верное равенство,
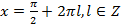 - решение исходного уравнения.
- решение исходного уравнения.
б) 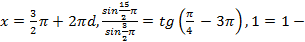 верное равенство.
верное равенство.
в)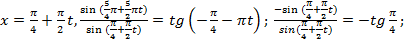 -1
-1 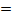 -1 - верное равенство, Ответ:
-1 - верное равенство, Ответ: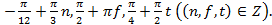
-
Решение тригонометрических уравнений методом экстремальных значений.
При решении некоторых тригонометрических уравнений бывает удобно использовать ограниченность функций, 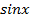 и
и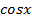 . Покажем это на конкретных примерах.
. Покажем это на конкретных примерах.
Пример 1. Решите уравнение 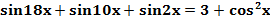 .
.
Решение. Так как 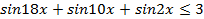 , то
, то 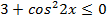 ,
,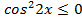 , откуда
, откуда 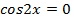 и возможные корни данного уравнения
и возможные корни данного уравнения 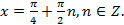 Подставив эти значения в левую часть уравнения, получим
Подставив эти значения в левую часть уравнения, получим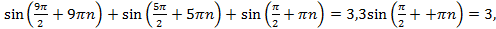 а последнее равенство возможно только при
а последнее равенство возможно только при 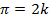 .
.
Следовательно, 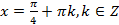 - решение данного уравнения.
- решение данного уравнения.
Ответ: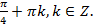
Пример 2. Решите уравнение 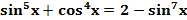 .
.
Решение. Легко видеть, что 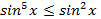 и
и 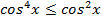 . Следовательно,
. Следовательно, 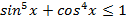 , но тогда
, но тогда 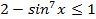 ,
, 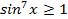 , откуда
, откуда 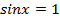 ,
, 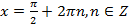 - возможные корни данного
- возможные корни данного
уравнения. Подстановка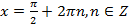 в данное уравнение показывает, что эти числа действительно являются его корнями.
в данное уравнение показывает, что эти числа действительно являются его корнями.
Ответ: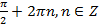 .
.
-
Уравнения, содержащие модуль функции и корень четной степени
Пример 1.
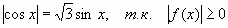

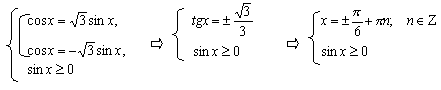
При отборе корней нет надобности решать неравенство, достаточно вынести корни на тригонометрический круг и выбрать нужные.
Ответ: 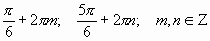
Пример 2.
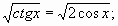
Решение: Учитывая ОДЗ функций, получим:
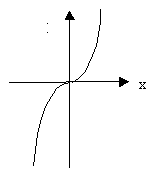
Ответ: 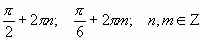
Уравнения повышенной сложности
-
( Сканави М.И.8.022)
2sin3 x +2sin2x cos x - sin x cos2x - cos3x = 0 | : cos3x ≠ 0;
т.к. уравнение однородное тригонометрическое 3-ей степени
2tg3x + 2tg2x - tgx - 1 = 0;
Разложим левую часть на множители, сгруппировав члены, получим
(tg x + 1)(2tg2x - 1) = 0;
 tgx = -1 х= -
tgx = -1 х= -  +
+ 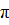 n , n ͼ Z
n , n ͼ Z
tgx= ![]()
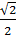 ; х=
; х= 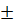 arctg
arctg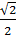 +
+ 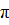 k, k ͼ Z.
k, k ͼ Z.
Ответ: -  +
+ 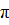 n , n ͼ Z ;
n , n ͼ Z ;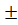 arctg
arctg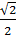 +
+ 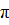 k, k ͼ Z.
k, k ͼ Z.
-
( Сканави М.И.8.081)
6sin2x + sin x cos x - cos2x = 2;
4sin2x + sin x cos x - 3 cos2x = 0; | : cos2x ≠ 0;
т. к. уравнение однородное тригонометрическое 2-ой степени
4tg2x + tg x - 3 = 0;
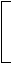 tgx = -1, х= -
tgx = -1, х= -  +
+ 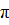 n , n ͼ Z
n , n ͼ Z
tgx= ![]() ; х= arctg
; х= arctg  +
+ 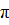 k, k ͼ Z.
k, k ͼ Z.
Ответ: -  +
+ 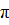 n , n ͼ Z;
n , n ͼ Z;
arctg ![]() +
+ 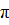 k, k ͼ Z.
k, k ͼ Z.
-
( Сканави М.И. 8.076)
sin x - sin 2x + sin 5x + sin 8x = 0;
сгруппировав первое с третьим, второе с четвертым слагаемые левой части и применив формулы суммы и разности синусов, получим
2sin 3x cos 2x + 2sin 3x cos 5x = 0;
вынесем в левой части общий множитель за скобки и применим формулу суммы косинусов
2sin 3x ∙ 2 cos 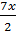 cos
cos 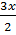 = 0;
= 0;
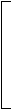
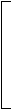 sin 3x = 0, x =
sin 3x = 0, x =  , n ͼ Z
, n ͼ Z
cos ![]() = 0, x =
= 0, x =  +
+ 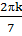 , k ͼ Z
, k ͼ Z
cos ![]() = 0; x =
= 0; x =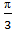 +
+ 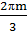 , m ͼ Z.
, m ͼ Z.
П роизведем отбор корней, воспользовавшись тригонометрической окружностью
роизведем отбор корней, воспользовавшись тригонометрической окружностью
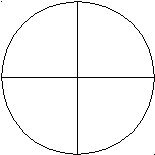
Ответ: ![]() , n ͼ Z;
, n ͼ Z;

 +
+ 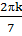 , k ͼ Z \ { 7m+3| m ͼ Z }.
, k ͼ Z \ { 7m+3| m ͼ Z }.
-
( Сканави М.И. 8.076)
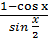 = 2;
= 2;
воспользуемся формулой косинуса двойного угла
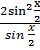 = 2;
= 2;
s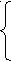 in
in  = 1,
= 1,
sin  ≠ 0;
≠ 0;
sin  = 1;
= 1;
х=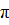 + 4
+ 4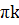 , k ͼ Z.
, k ͼ Z.
Ответ:![]() + 4
+ 4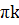 , k ͼ Z.
, k ͼ Z.
-
(Сканави М.И. 8.120)
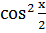 +
+ 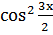 -
- 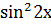 -
- 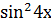 =0
=0
;понизим степень, воспользовавшись формулами косинуса двойного угла
1 +cos x +1 + cos 3x -1 +cos 4x -1 +cos 8x =0;
сгруппируем слагаемые и воспользуемся формулой суммы косинусов
2cos 2x cos x + 2cos 2x cos 6x =0;
2cos 2x 2cos 3,5x cos 2,5x=0;
произведение всюду определенных множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю

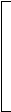 cos 2x=0 2x=
cos 2x=0 2x= +
+ 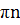 , n ͼ Z
, n ͼ Z
cos 3,5x=0 3,5x= +
+ 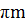 , m ͼ Z
, m ͼ Z
cos 2,5x=0; 2,5x= +
+ 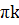 , k ͼ Z;
, k ͼ Z;
x =
= +
+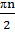 , n ͼ Z
, n ͼ Z
x= +
+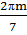 , m ͼ Z
, m ͼ Z
x= +
+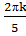 , k ͼ Z .
, k ͼ Z .
Ответ:![]() +
+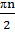 , n ͼ Z;
, n ͼ Z;
 +
+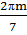 , m ͼ Z;
, m ͼ Z;
 +
+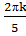 , k ͼ Z .
, k ͼ Z .
Заключение.
Изучение тригонометрических уравнений позволяет учащимся овладеть конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, развития умственных способностей, умение извлекать учебную информацию на основе сопоставительного анализа графиков, самостоятельно выполнять различные творческие работы.
В данной работе рассмотрены основные методы решения тригонометрических уравнений, причем, как специфические, характерные только для тригонометрических уравнений, так и общие функциональные методы решения уравнений, применительно к тригонометрическим уравнениям.
Для успешного решения уравнений необходимо знать формулы корней простейших тригонометрических уравнений, значение тригонометрических функций для основных углов и значение обратных тригонометрических функций, универсальные правила решения уравнений. Рассмотрено решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Указано, что при решении тригонометрических уравнений широко используются тождества, выражающие соотношение между тригонометрическими функциями одного и разных аргументов.
Приведенные методы не исчерпывают все многообразие способов решений тригонометрических уравнений. Однако рассмотренные типы уравнений встречаются наиболее часто и важно уметь распознавать в данном уравнении тот или иной тип.
Результаты данной работы могут быть использованы в качестве учебного материала при подготовке творческих работ, при составлении факультативных курсов для школьников, так же работа может применяться при подготовке учащихся к Единому государственному экзамену, вступительным экзаменам.
Библиография
-
Алексеев А. Тригонометрические подстановки. // Квант. - 1995. - №2. -с. 40 - 42.
-
Выгодский М. Я. «Справочник по элементарной математике». М., «Наука», 1982 г.
-
Г. И. Глейзер История математики в школе. - М.: «Просвещение» 1983г.
-
Карасев В.А., Лёвшина Г.Д. «12 уроков по тригонометрии» - М.: Илекса, 2013.- 200 с.:ил.
-
Крамор В.С. Тригонометрические функции. - М.: Просвещение, 1979.
-
Сост. Гряда Н. Н. и др. Обобщающее повторение в системе подготовки к ЕГЭ по теме «Тригонометрические уравнения», Армавир, 2005г.
-
Цукарь А.Я. Упражнения практического характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.
-
Шаталов В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии. - М.: Новая школа, 1993.


