- Преподавателю
- Математика
- Методы решения алгебраических уравнений высших степеней
Методы решения алгебраических уравнений высших степеней
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Хабибуллина А.Я. |
| Дата | 05.03.2014 |
| Формат | doc |
| Изображения | Есть |
Методы решения алгебраических уравнений высших степеней.
Хабибуллина Альфия Якубовна,
учитель математики высшей категории МБОУ СОШ №177
города Казани, Заслуженный учитель Республики Татарстан,
кандидат педагогических наук.
Определение 1. Алгебраическим уравнением степени n называется уравнение вида Pn(x)=0, где Pn(x) - многочлен степени n, т.е. Pn(x)= a0xn+a1xn-1+…+an-1x+an a0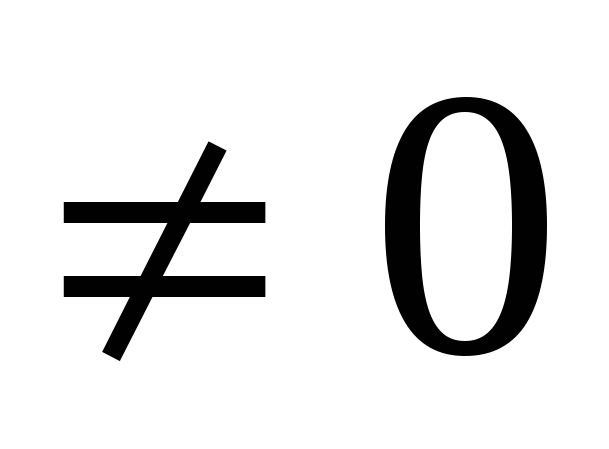 .
.
Определение 2. Корень уравнения - числовое значение переменной х, которое при подстановке в данное уравнение дает верное равенство.
Определение 3. Решить уравнение означает найти все его корни или доказать, что их нет.
I. Метод разложения многочлена на множители с последующим дроблением.
Уравнение можно разложить на множители и решить методом дробления, то есть, разбивая на совокупность уравнений меньших степеней.
Замечание: вообще, при решении уравнения методом дробления не следует забывать, что произведение равно нулю тогда, и только тогда, когда хотя бы один из множителей равен нулю, а другие при этом сохраняют смысл.
Пути разложения многочлена на множители:
1. Вынесение общего множителя за скобки.
2. Квадратный трехчлен можно разложить на множители с помощью формулы ах2+вх+с=а(х-х1)(х-х2), где а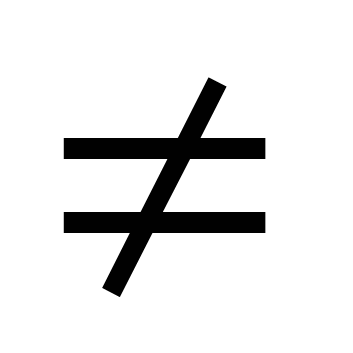 0, х1 и х2 - корни квадратного трехчлена.
0, х1 и х2 - корни квадратного трехчлена.
3. Использование формул сокращенного умножения :
аn - вn = (а - в)(аn-1 + Сn-2аn-2 в + Сn-3аn-3 в + …+ С1а вn-2 +вn-1), n N.
N.
Выделение полного квадрата. Многочлен можно разложить на множители с помощью формулы разности квадратов, предварительно выделив полный квадрат суммы или разности выражений.
4. Группировка (в сочетании с вынесением общего множителя за скобки).
5. Использование следствия теоремы Безу.
1)если уравнение а0хn + a1xn-1 +…+ an-1x + an = 0 , a0![]() 0 c целыми коэффициентами имеет рациональный корень х0 =
0 c целыми коэффициентами имеет рациональный корень х0 =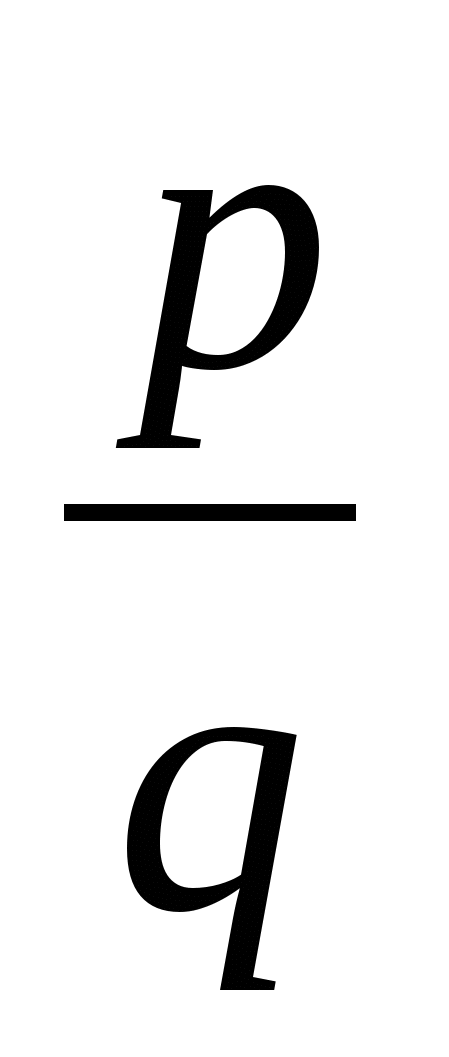 (где
(где 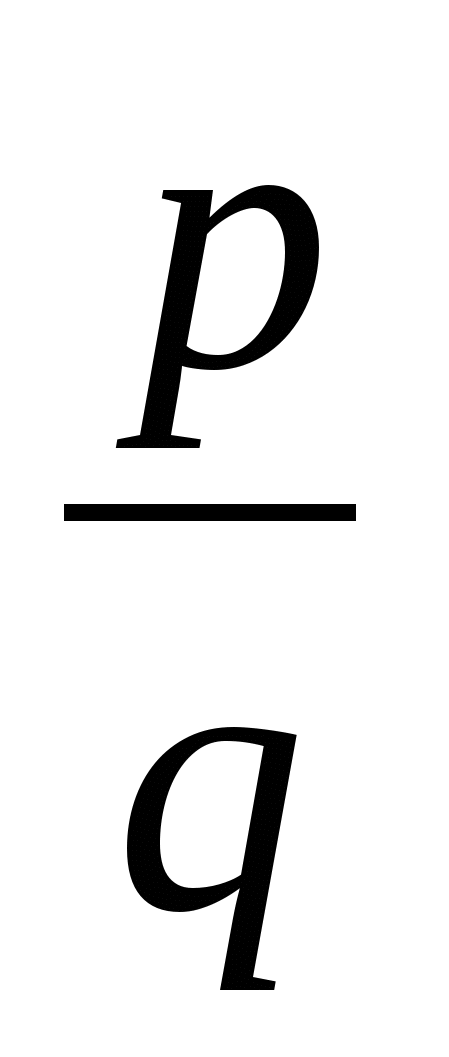 - несократимая дробь, p
- несократимая дробь, p q
q ), то p -делитель свободного члена an ,а q - делитель старшего коэффициента a0.
), то p -делитель свободного члена an ,а q - делитель старшего коэффициента a0.
2)если х = х0 - корень уравнения Рn(х) = 0, то Рn(х) = 0 равносильно уравнению
(х - х0)Рn-1(х)=0, где Рn-1(х) - многочлен, который можно найти при делении
Рn(х) на (х - х0) "уголком" или методом неопределенных коэффициентов.
II. Метод введения новой переменной (Подстановка)
Рассмотрим уравнение f(x)=g(x). Оно равносильно уравнению f(x)-g(х) = 0. Обозначим разность f(x)-g(х) = h(р (x)), причем 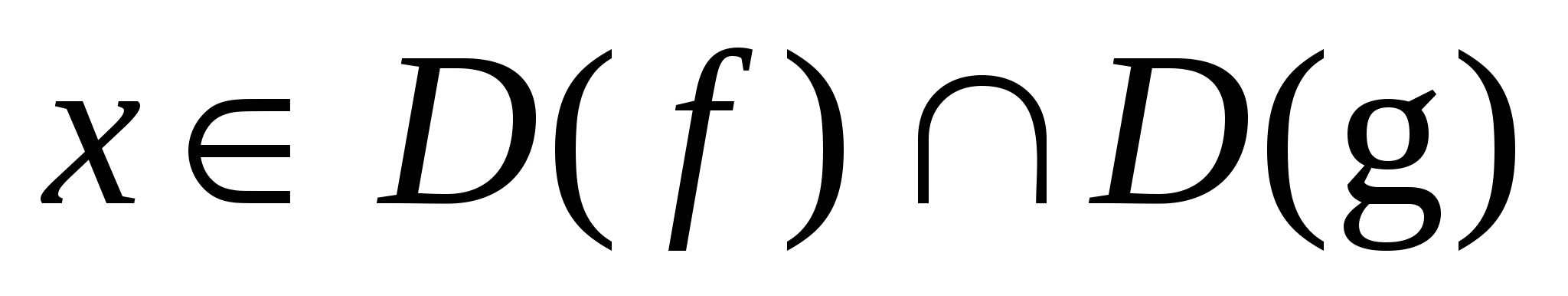 . Введем замену t=р (x) (функция t= р(x) называется подстановка). Тогда получим уравнение h(р (x)) =0 или h(t)=0 , решив последнее уравнение, находим t1, t2, … Вернувшись в подстановку р(x)=t1, р(x)=t2 ,…, находим значения переменной х.
. Введем замену t=р (x) (функция t= р(x) называется подстановка). Тогда получим уравнение h(р (x)) =0 или h(t)=0 , решив последнее уравнение, находим t1, t2, … Вернувшись в подстановку р(x)=t1, р(x)=t2 ,…, находим значения переменной х.
III Метод строгой монотонности.
Теорема. Если у= f(x) строго монотонна на P, то уравнение f(x)=а (а - const) имеет на множестве Р не более одного корня. (Функция строго монотонная: либо только убывающая, либо только возрастающая)
Замечание. Можно использовать модификацию этого метода. Рассмотрим уравнение f(x)=g(x). Если функция у= f(x) монотонно убывает на P, а функция у= g(x) монотонно убывает на Р (или наоборот), то уравнение f(x)=g(x) имеет на множестве Р не более одного корня.
IV . Метод сравнения множества значений обеих частей уравнения (метод оценки)
Теорема Если для любого x из множества P выполняются неравенства f(x)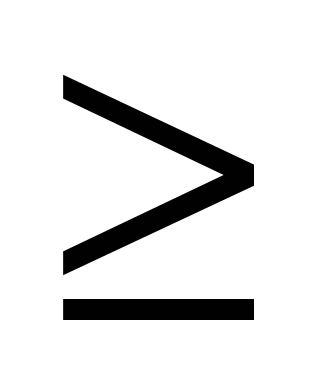 а, и g(x)
а, и g(x)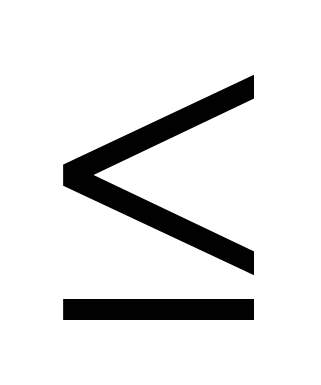 а, то уравнение f(x)=g(x) на множестве Р равносильно системе
а, то уравнение f(x)=g(x) на множестве Р равносильно системе 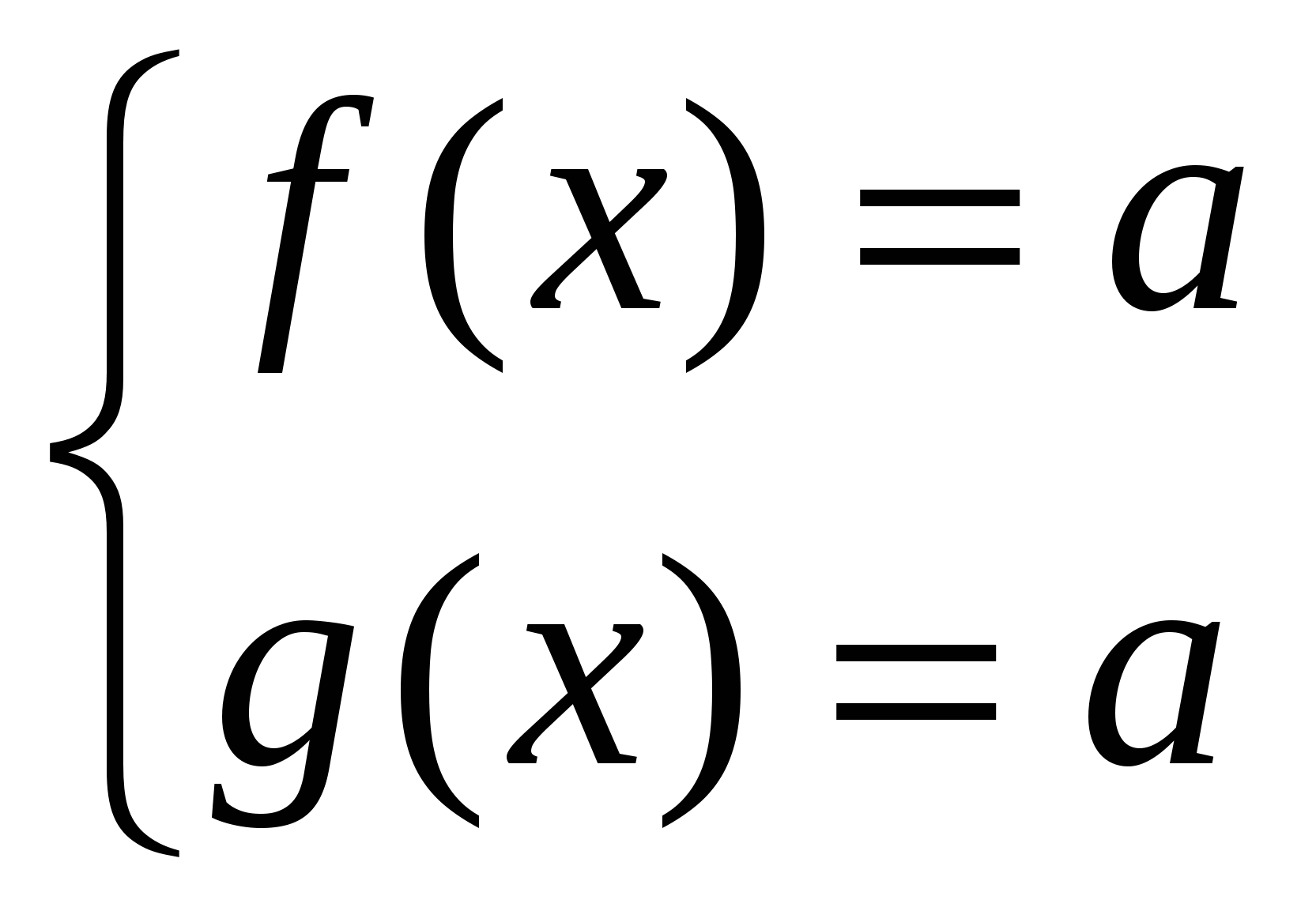 .
.
Следствие: Если на множестве Р 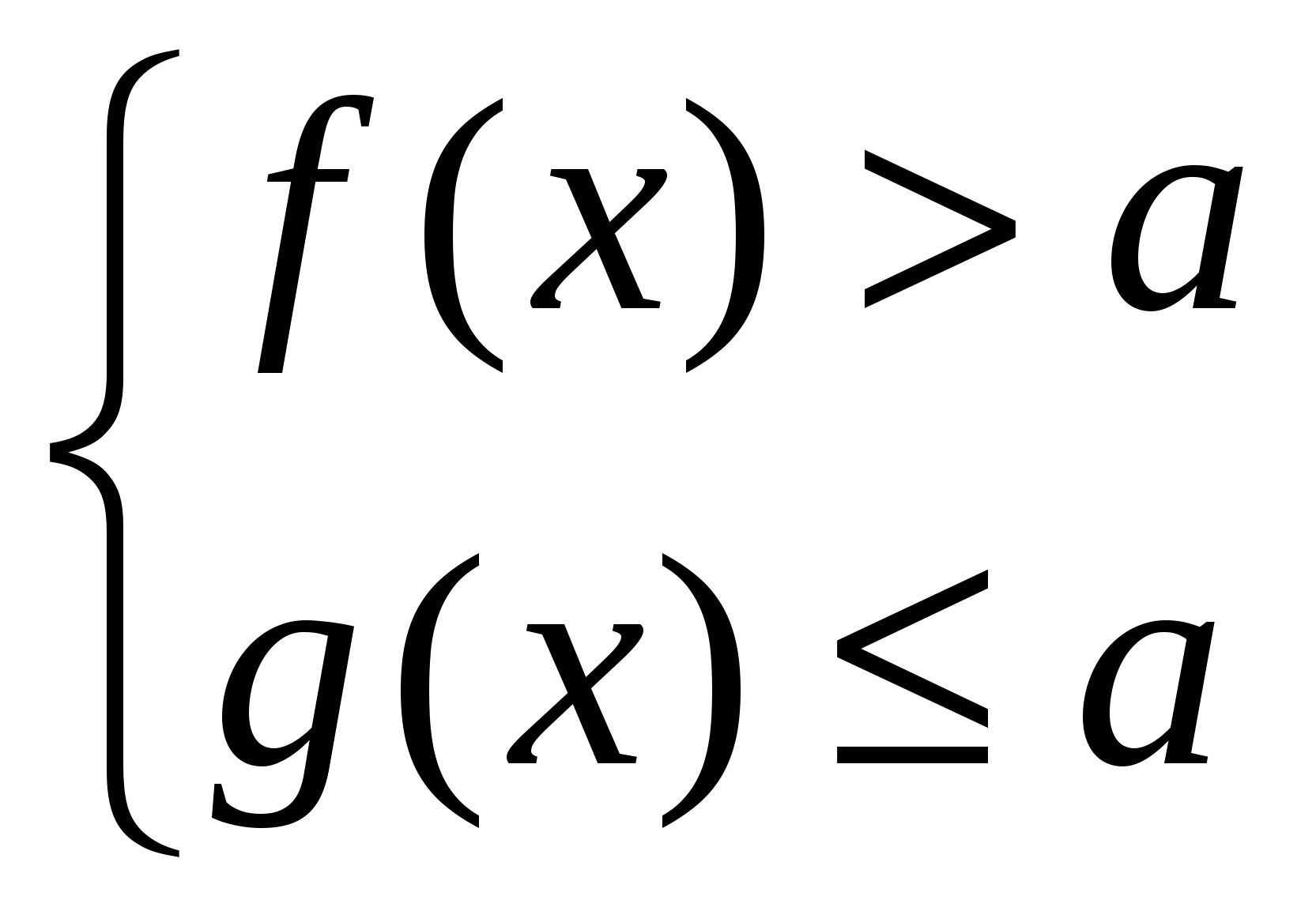 или
или 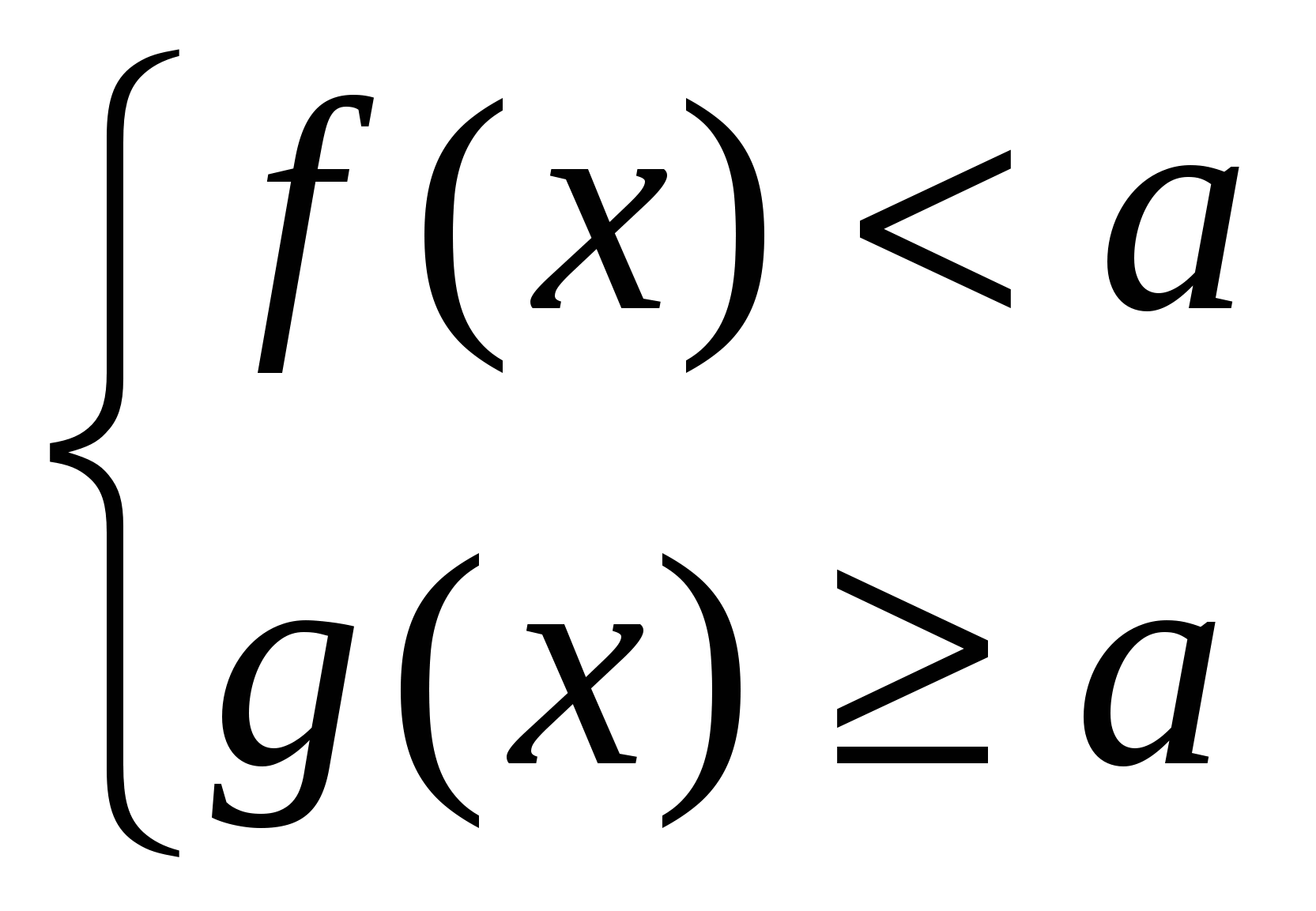 , то уравнение f(x)=g(x) не имеет корней.
, то уравнение f(x)=g(x) не имеет корней.
Этот метод достаточно эффективен при решении трансцендентных уравнений
V . Метод перебора делителей крайних коэффициентов
Рассмотрим уравнение a0xn+a1xn-1+…+an-1x+an = 0
Теорема. Если x0 = 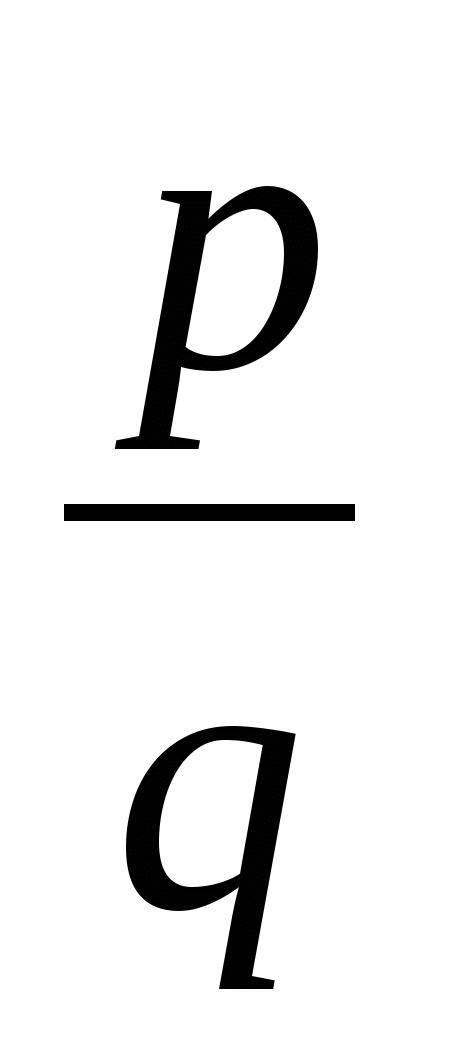 - корень алгебраического уравнения степени n, аi - целые коэффициенты, то p - делитель свободного члена аn, а q - делитель старшего коэффициента a0 . При а0=1 x0=p (делитель свободного члена).
- корень алгебраического уравнения степени n, аi - целые коэффициенты, то p - делитель свободного члена аn, а q - делитель старшего коэффициента a0 . При а0=1 x0=p (делитель свободного члена).
Следствие теоремы Безу: Если х0 - корень алгебраического уравнения, то Pn(x) делится на (x-x0) без остатка, т.е Pn(x)=(x-x0)Qn-1(x).
VI Метод неопределенных коэффициентов.
Он базируется на следующих утверждениях:
два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях х.
любой многочлен третьей степени разлагается в произведение двух множителей: линейного и квадратного.
любой многочлен четвертой степени разлагается в произведение двух многочленов
второй степени.
VII. Схема Горнера.
С помощью таблицы коэффициентов по алгоритму Горнера подбором находятся корни уравнения среди делителей свободного члена.
VIII . Метод производных.
Теорема. Если 2 многочлена P(x) и Q(x) имеют тождественно равные производные, то существует такая С- const, что P(x)=Q(x)+С для  x
x R.
R.
Tеорема. Если ![]() (x) и
(x) и 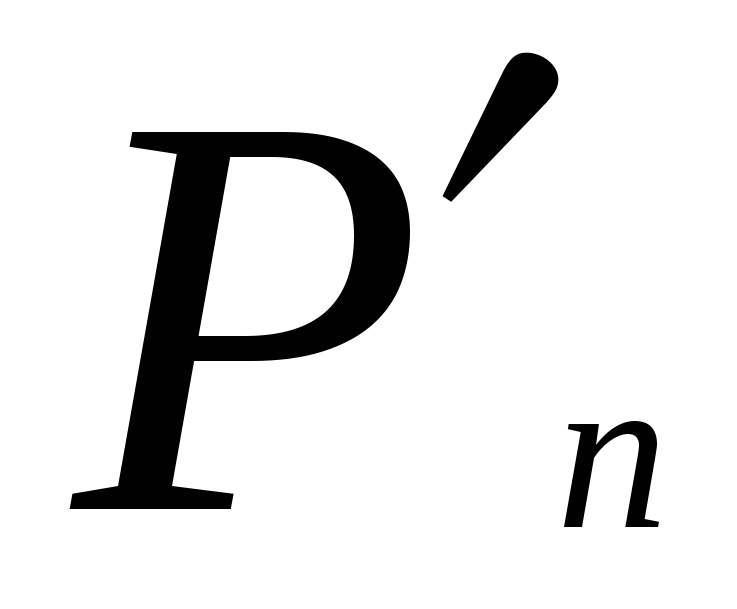 (x) делятся на
(x) делятся на 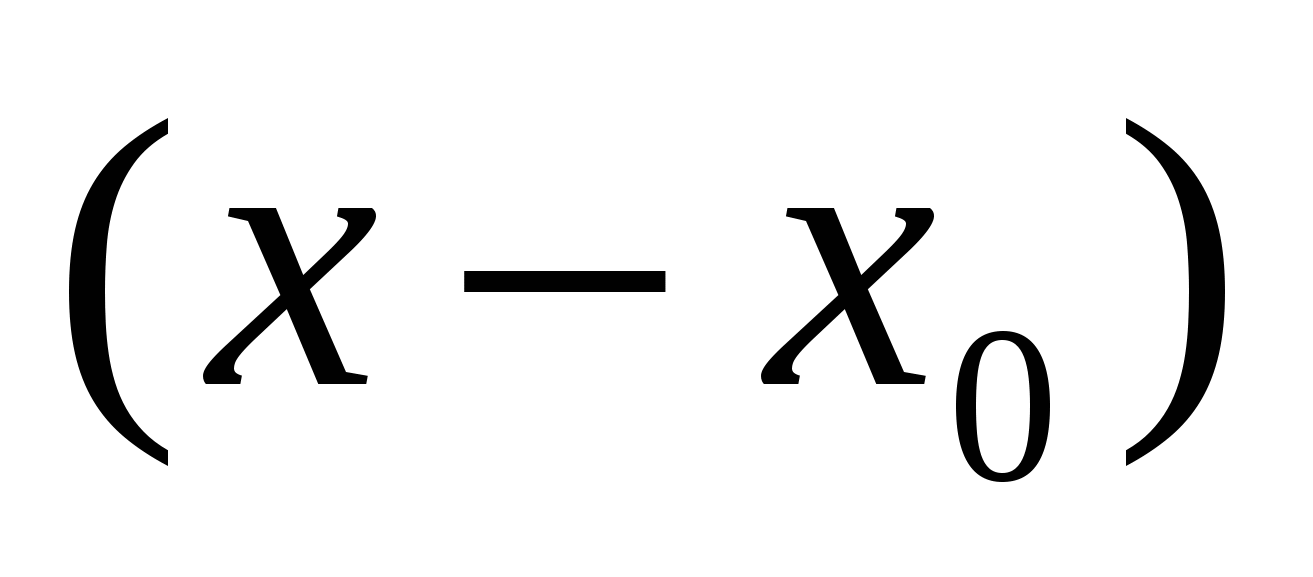 , то
, то 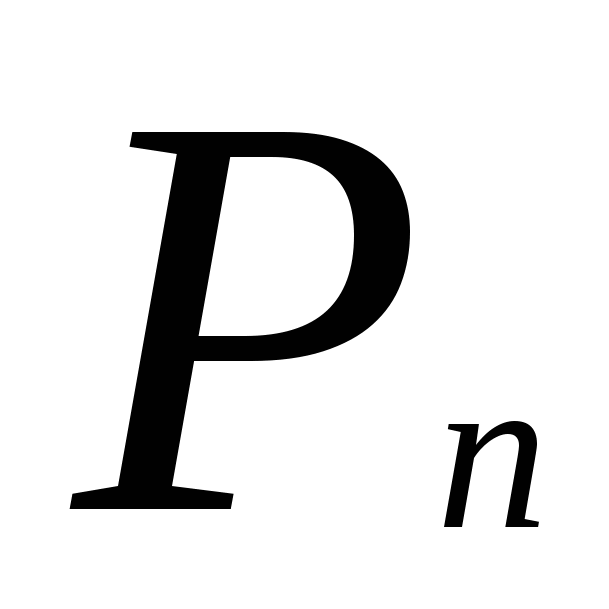 (x) делится на
(x) делится на 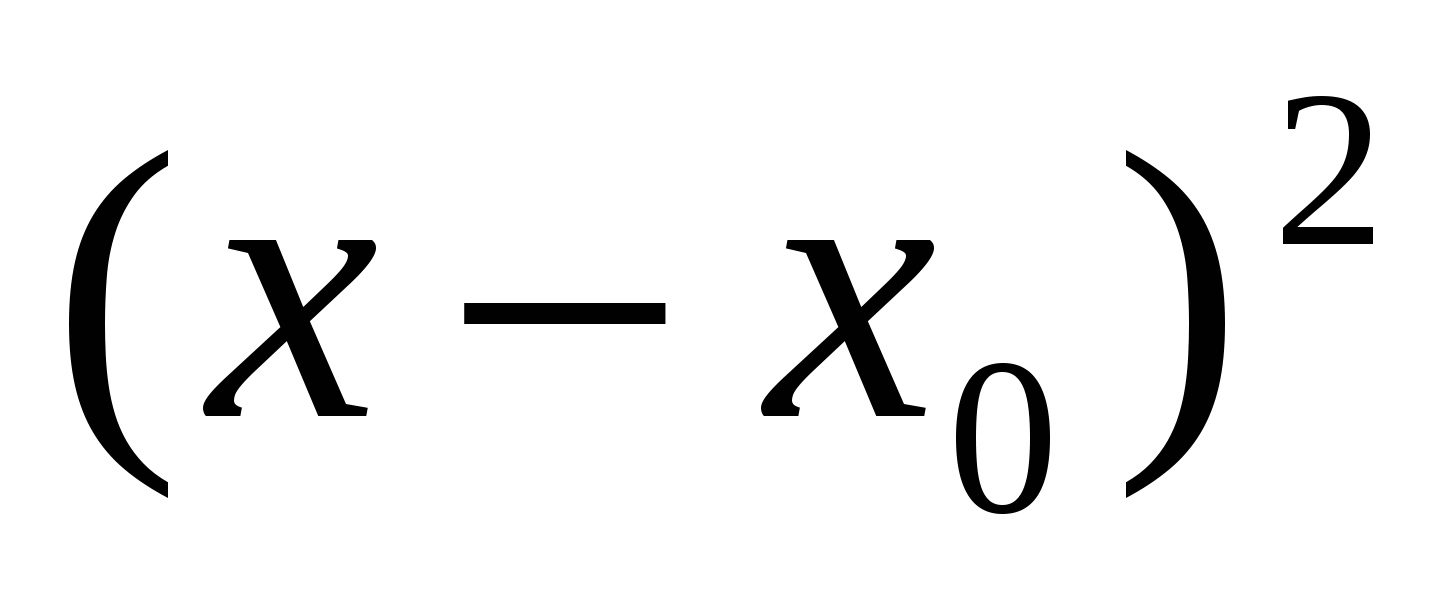 .
.
Следствие: Если 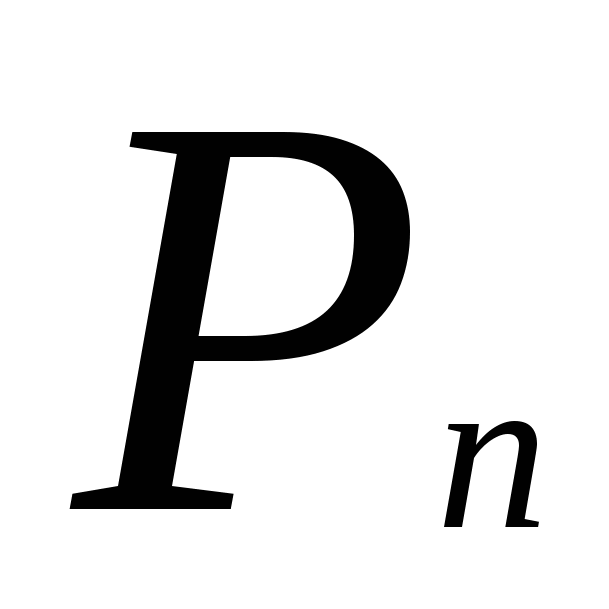 (x) и
(x) и 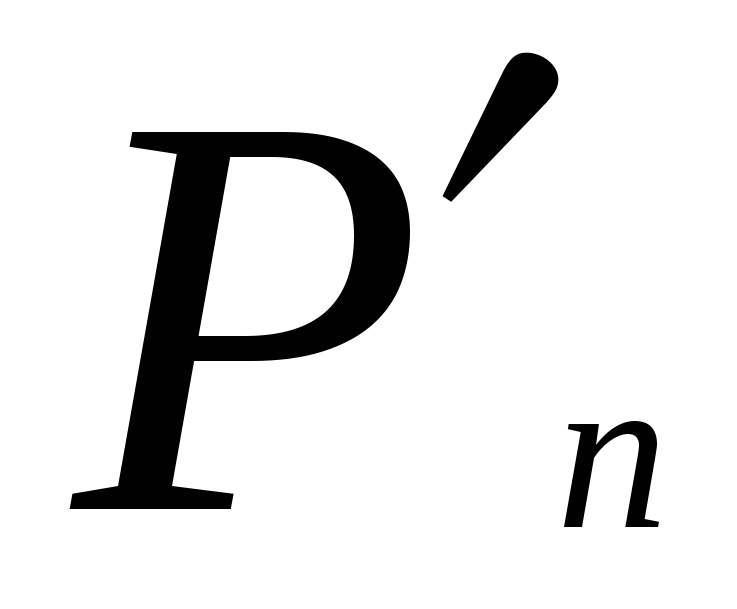 (x) делятся на многочлен R(x) , то
(x) делятся на многочлен R(x) , то 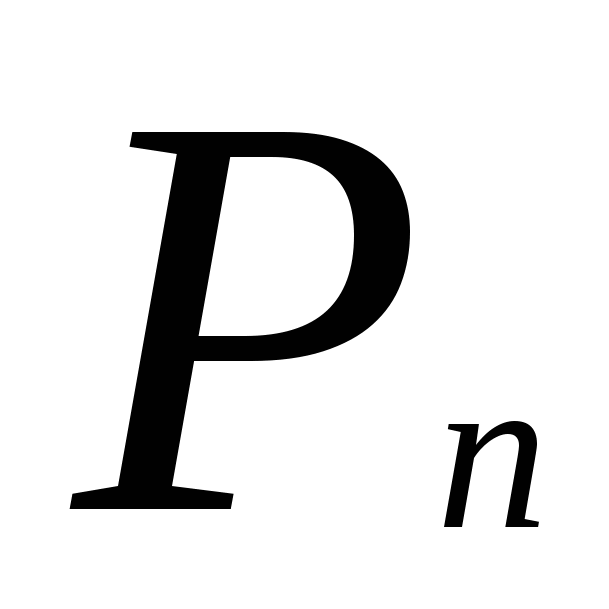 (x) делится на
(x) делится на 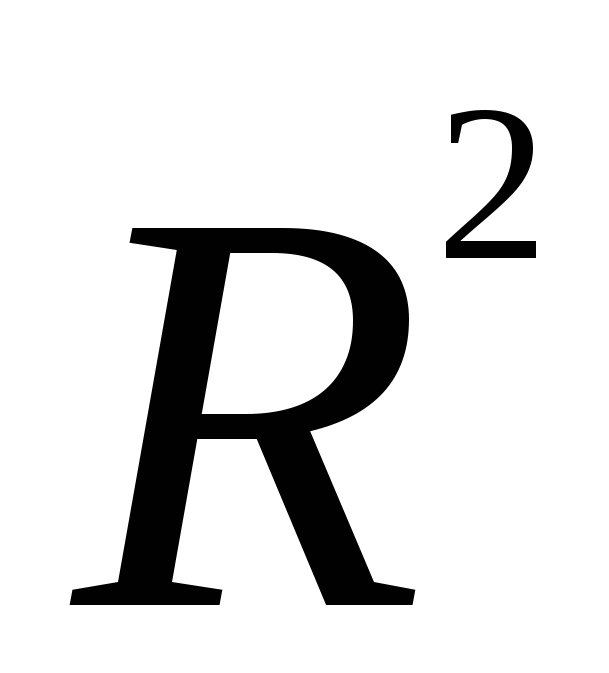 (x), а наибольший общий делитель многочленов
(x), а наибольший общий делитель многочленов 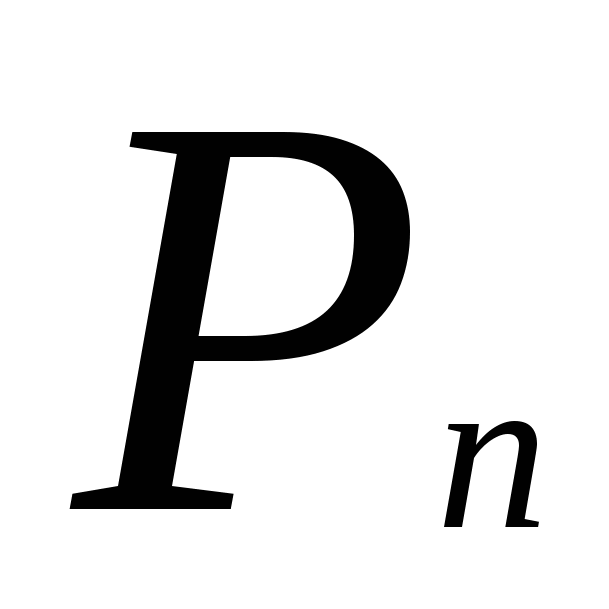 (x) и
(x) и 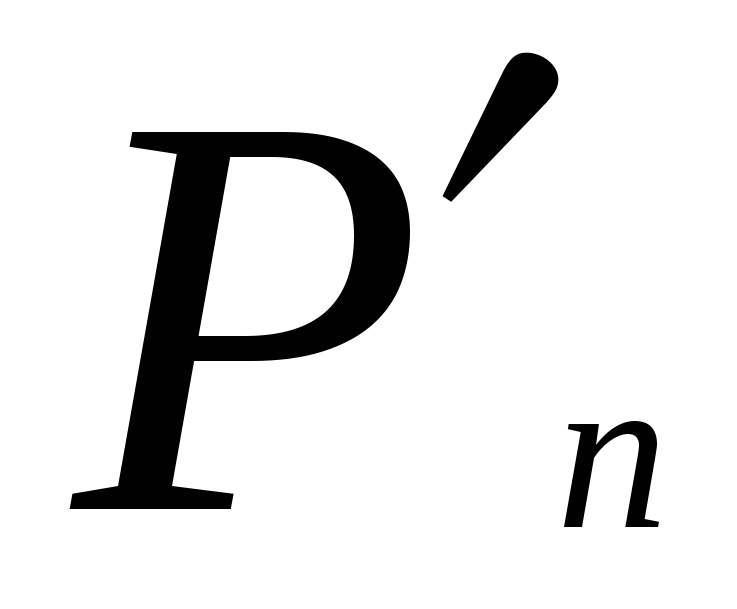 (x)
(x) имеет корни, являющиеся лишь корнями многочлена
имеет корни, являющиеся лишь корнями многочлена 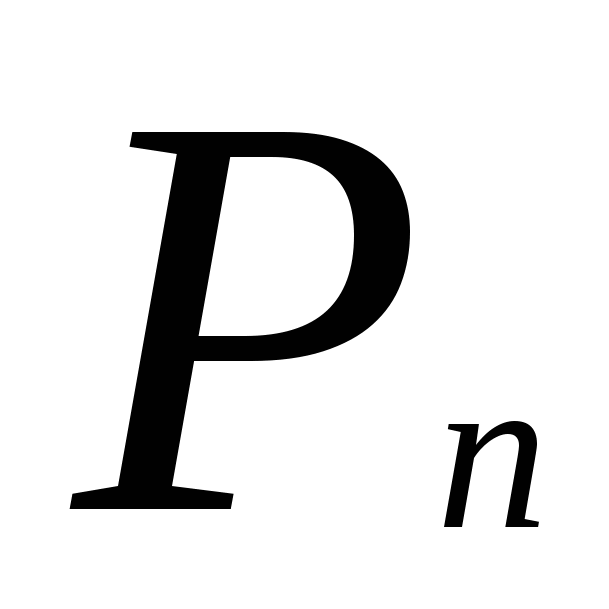 (x) кратностью не менее 2.
(x) кратностью не менее 2.
IX. Симметрические, возвратные уравнения.
Определение. Уравнение a0xn+a1xn-1+…+an-1x+an = 0 называется симметрическим, если 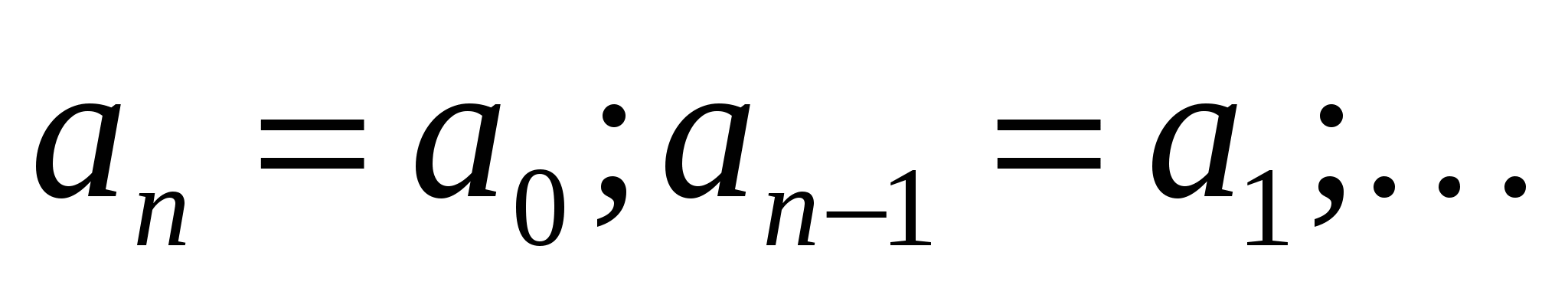
1. Рассмотрим случай, когда n-четное, n =2k. Если 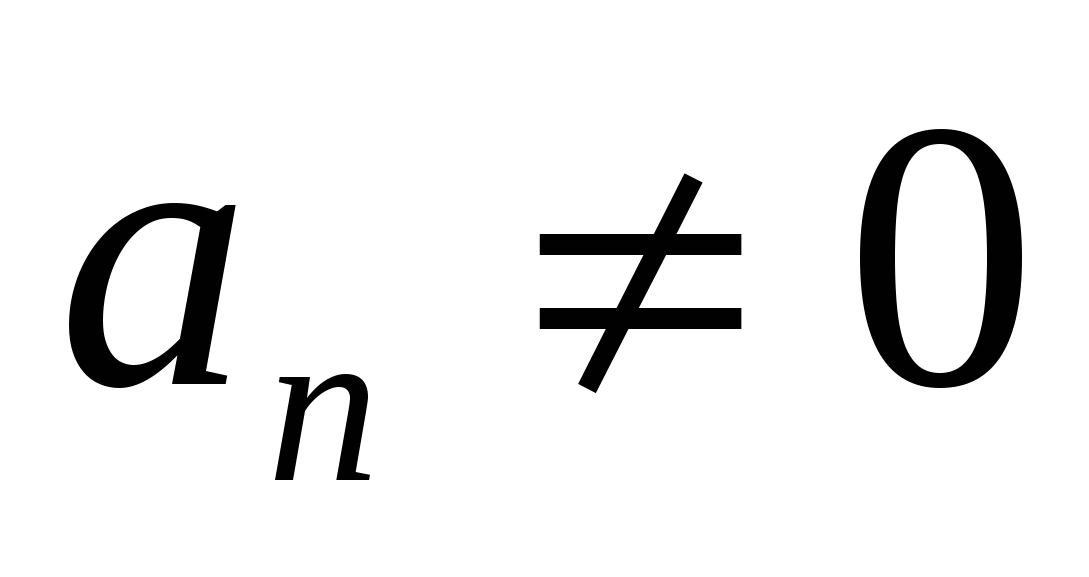 , тогда x = 0 не является корнем уравнения, что дает право разделить уравнение на
, тогда x = 0 не является корнем уравнения, что дает право разделить уравнение на 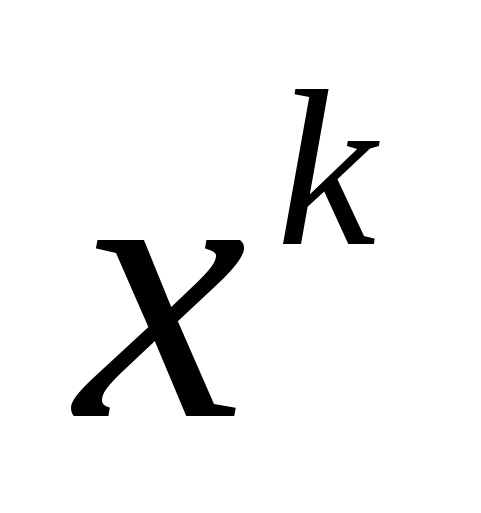
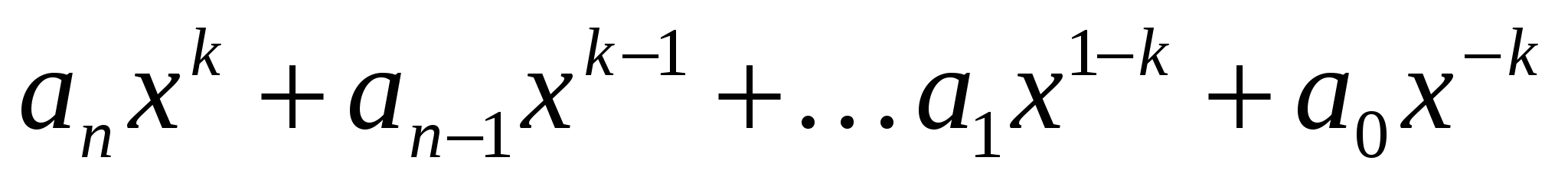 =0
=0 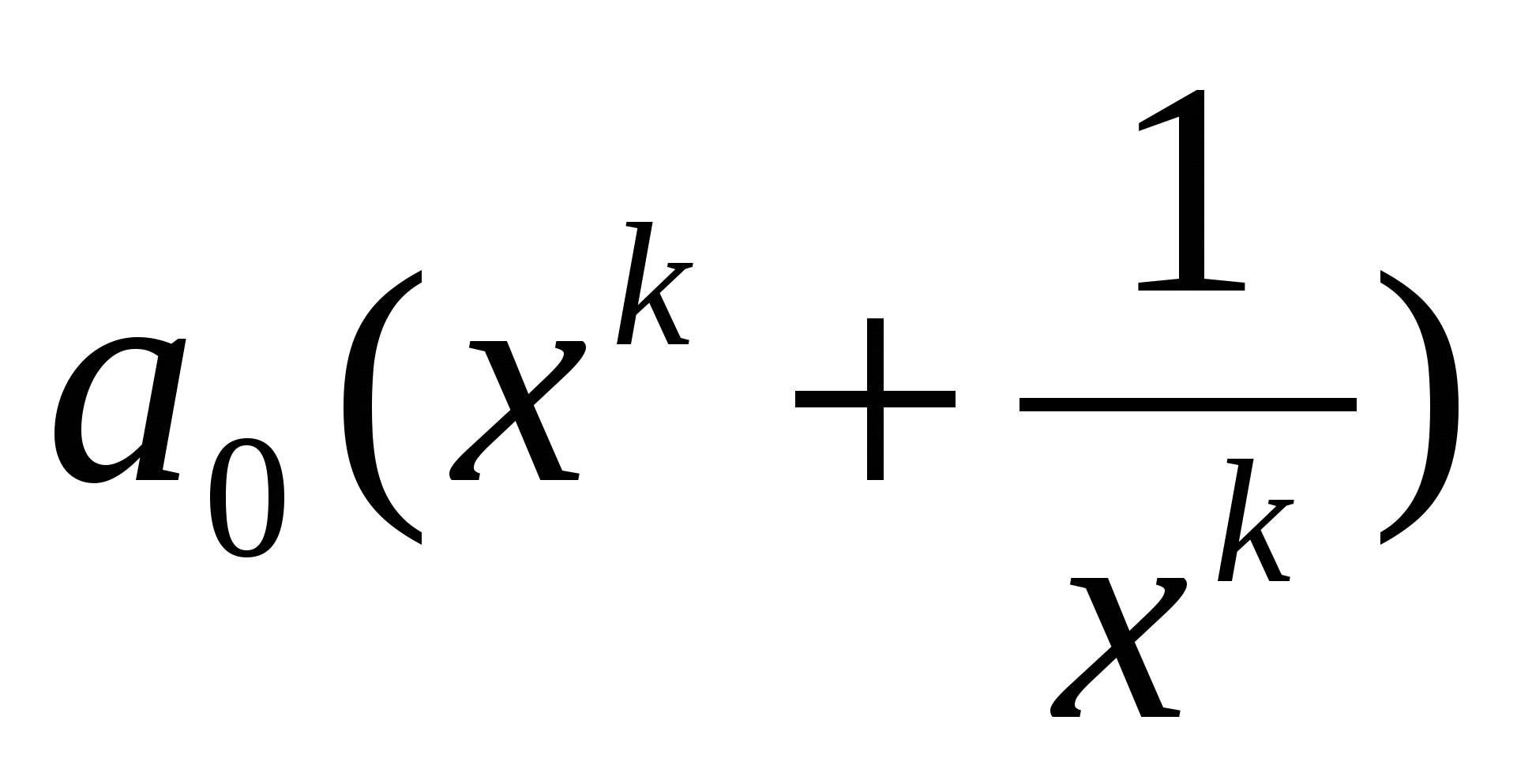 +
+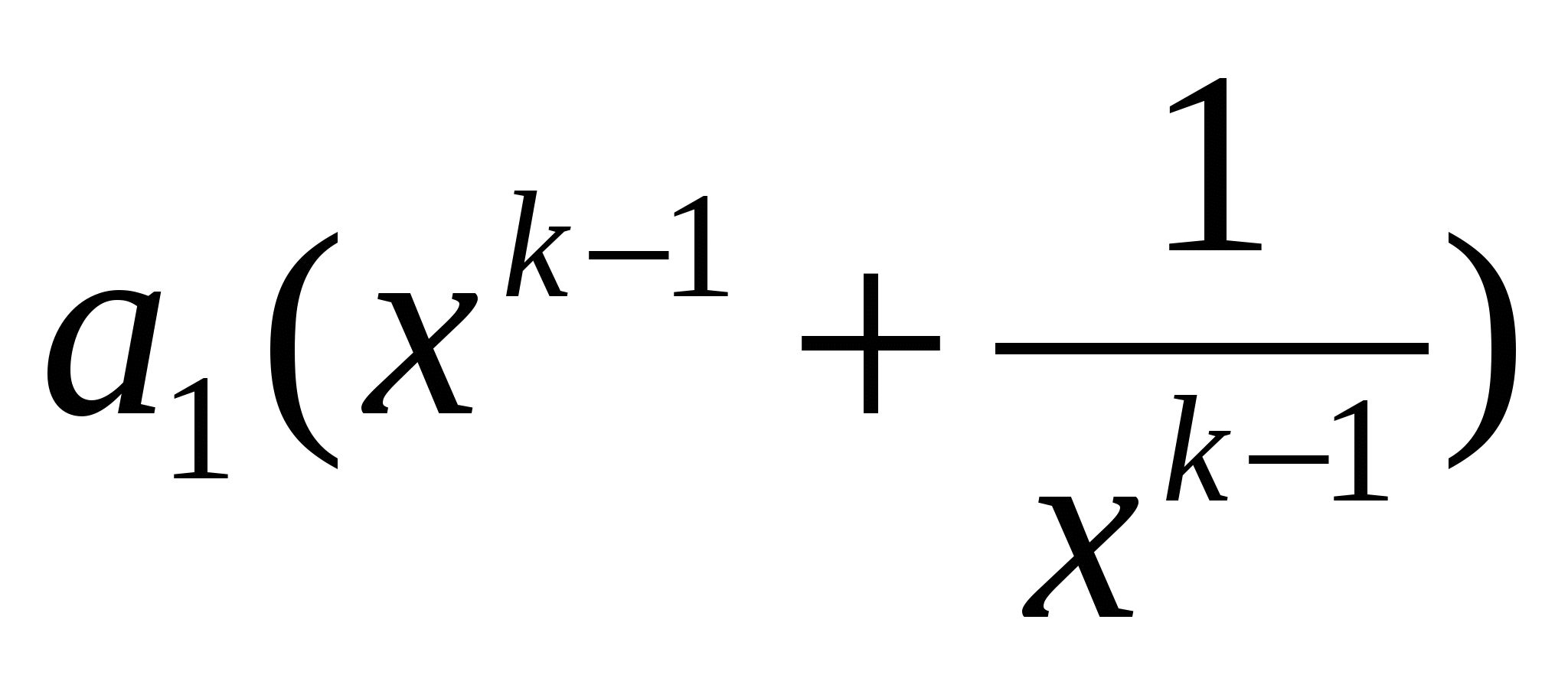 +
+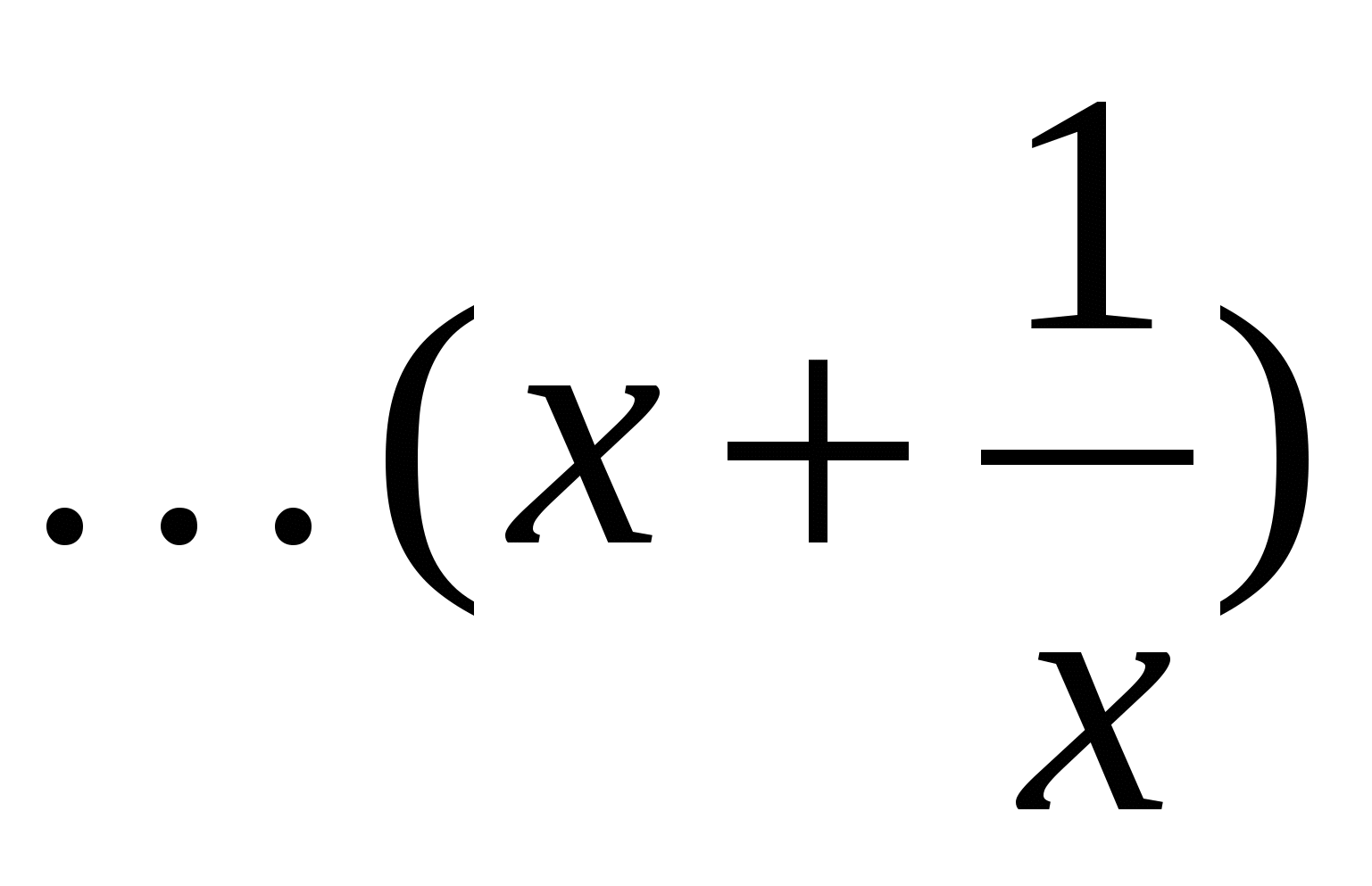 +
+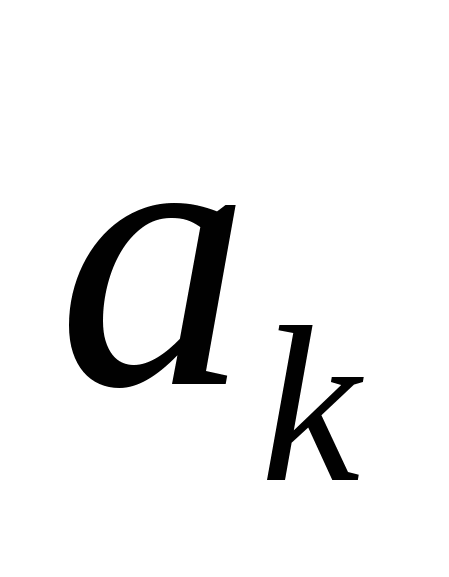 =0 Введем замену t=
=0 Введем замену t=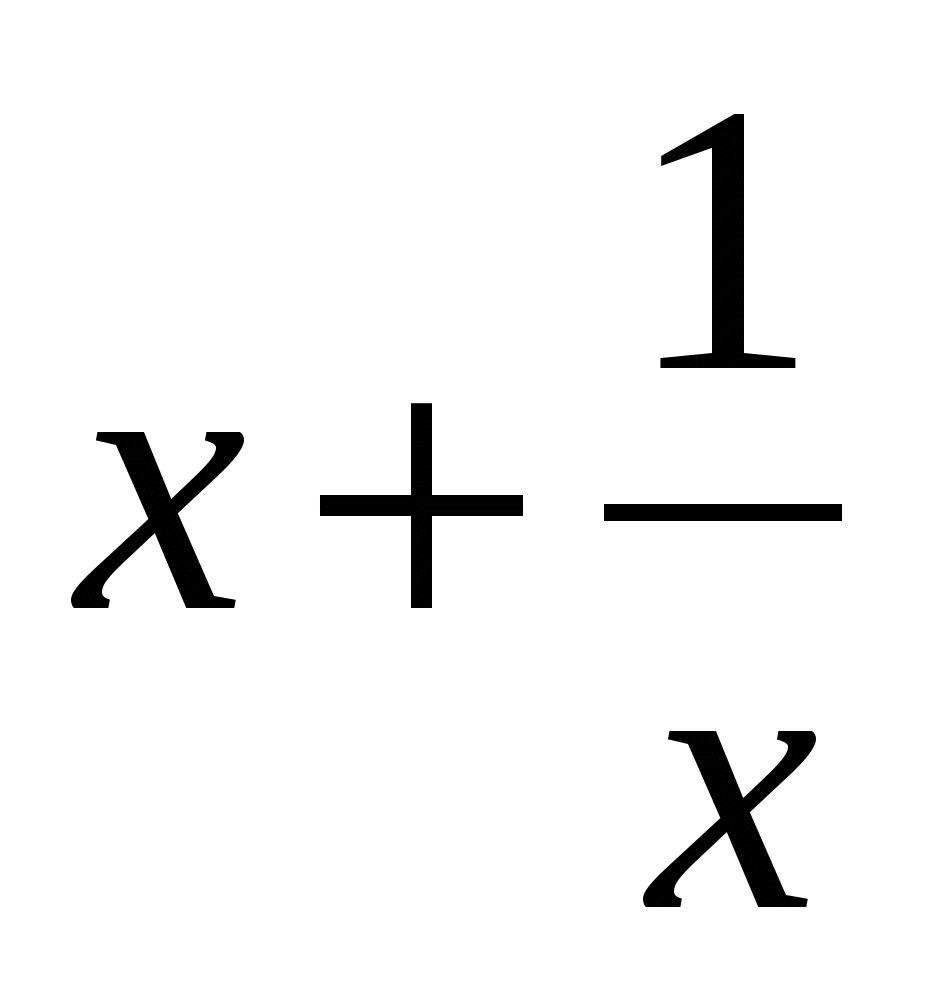 и, учитывая лемму, решим квадратное уравнение относительно переменной t. Обратная подстановка даст решение относительно переменной х.
и, учитывая лемму, решим квадратное уравнение относительно переменной t. Обратная подстановка даст решение относительно переменной х.
2. Рассмотрим случай, когда n-нечетное, n=2k+1. Тогда 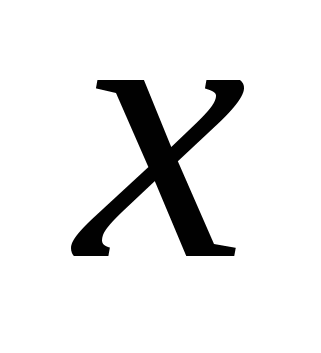 = -1 является корнем уравнения. Разделим уравнение на
= -1 является корнем уравнения. Разделим уравнение на 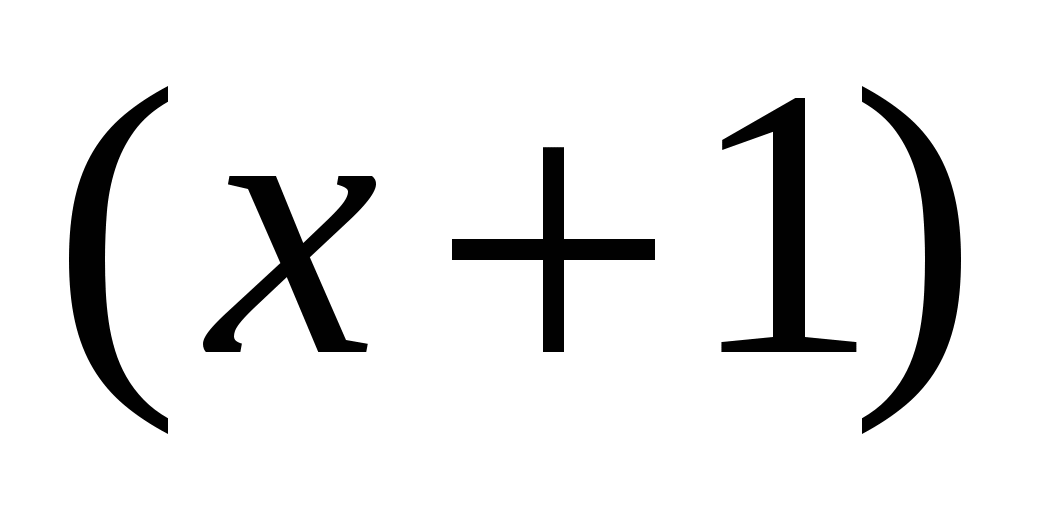 и получаем случай 1.
и получаем случай 1.
Определение. Возвратное уравнение 4 порядка - уравнение вида 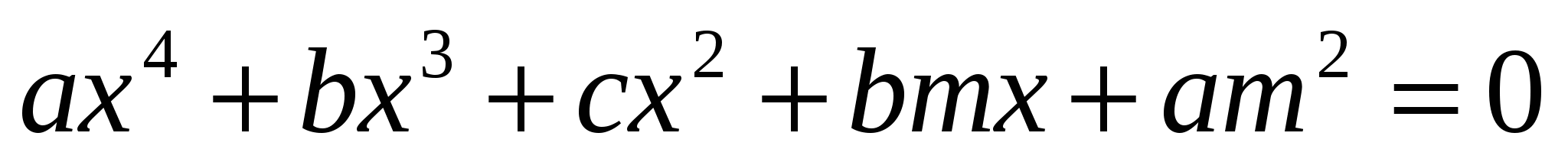
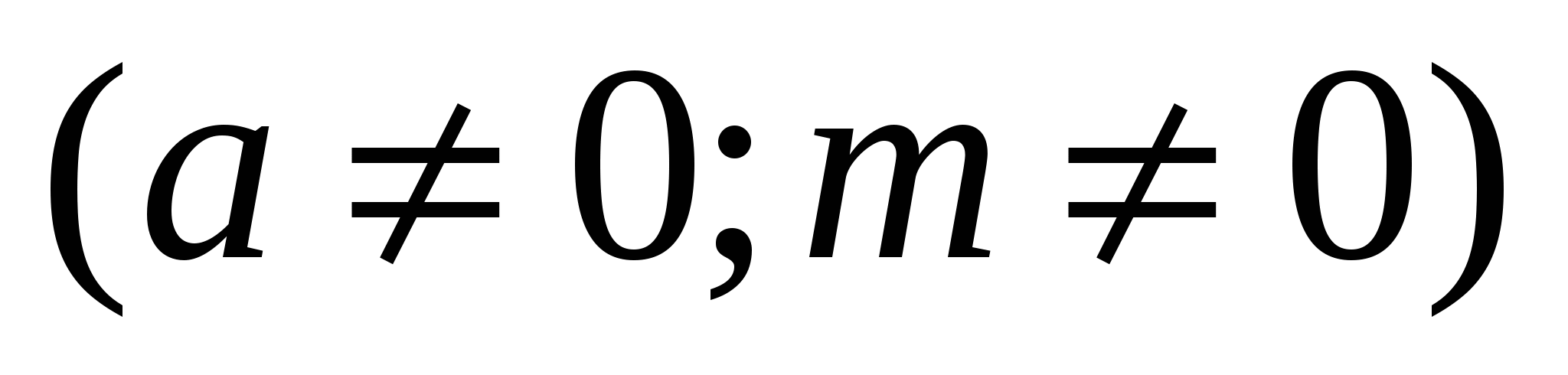
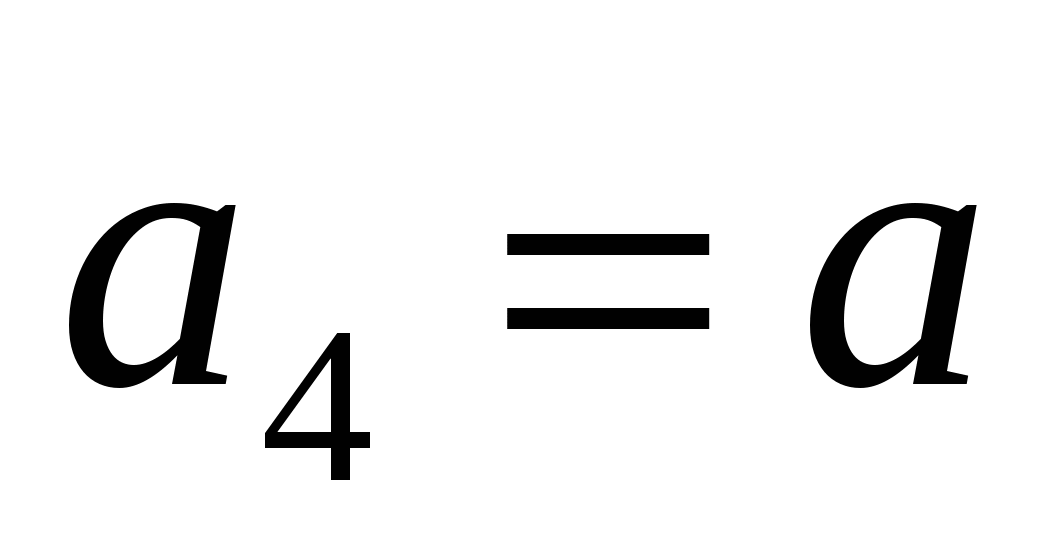
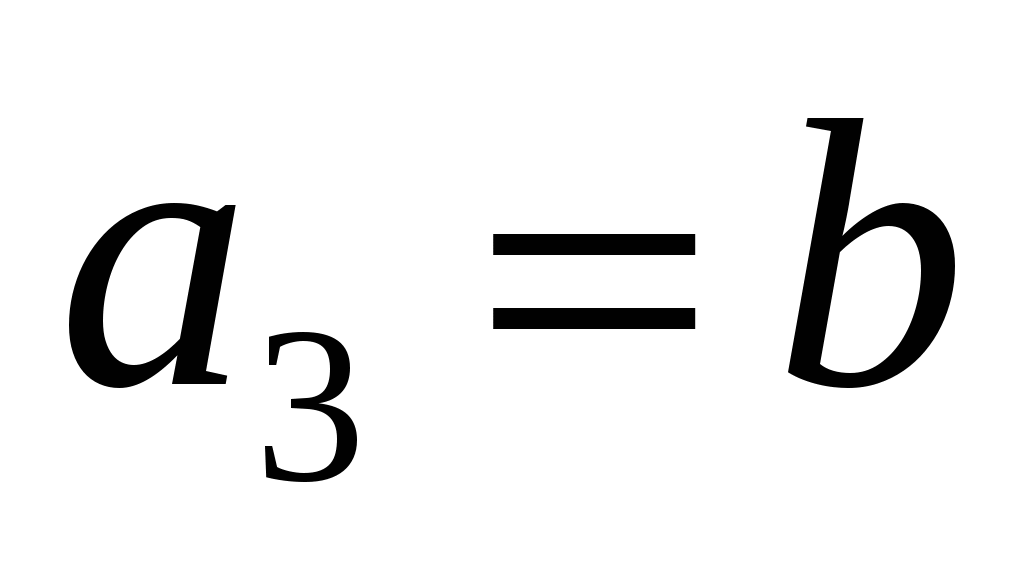
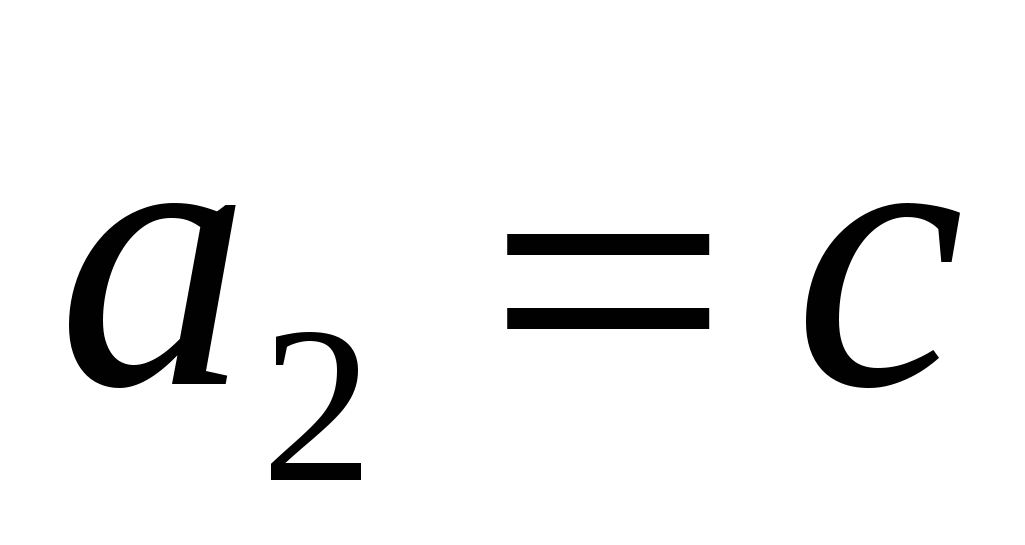
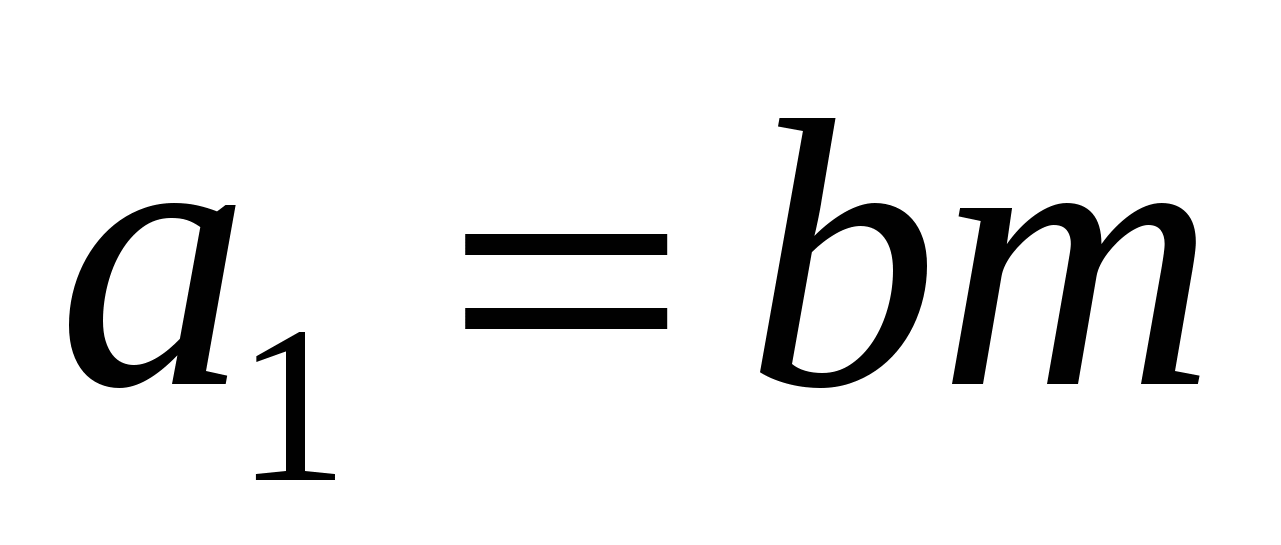
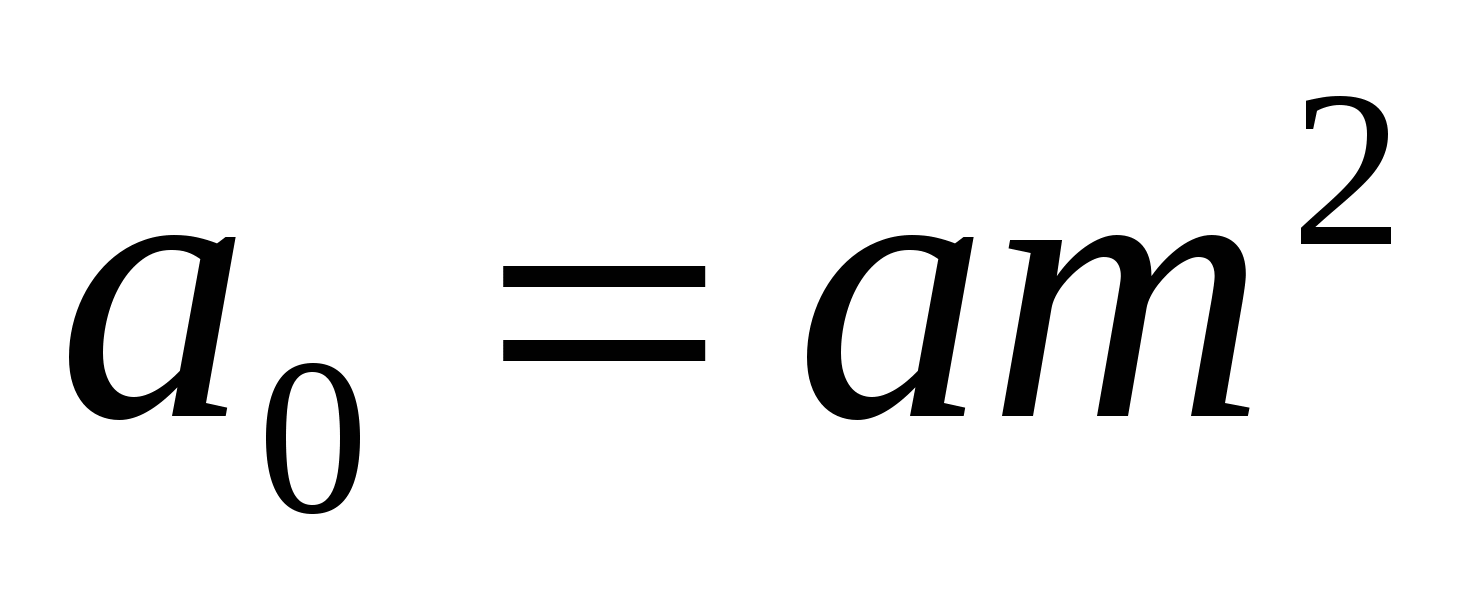 , заметим
, заметим 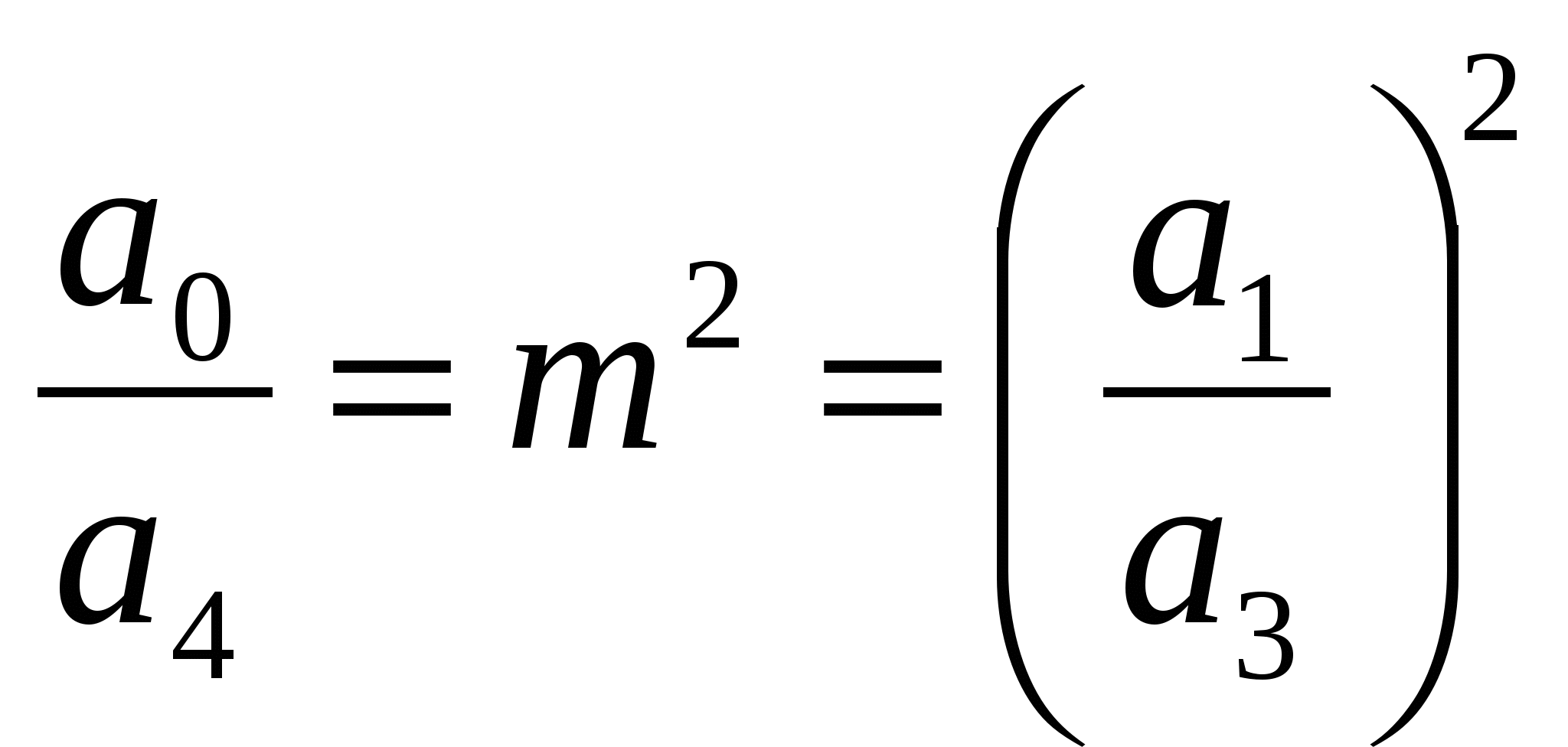 , тогда
, тогда
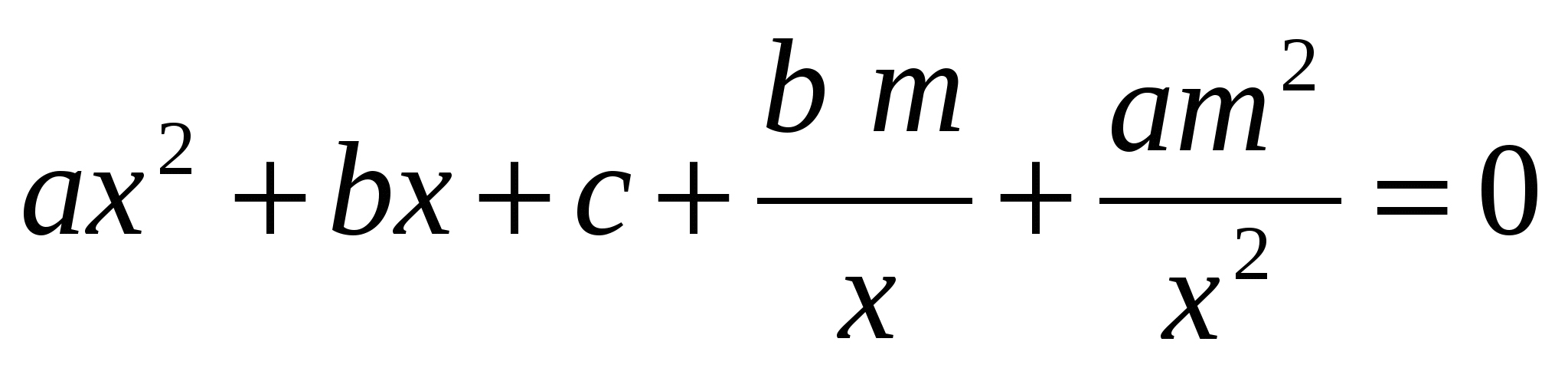 ,
, 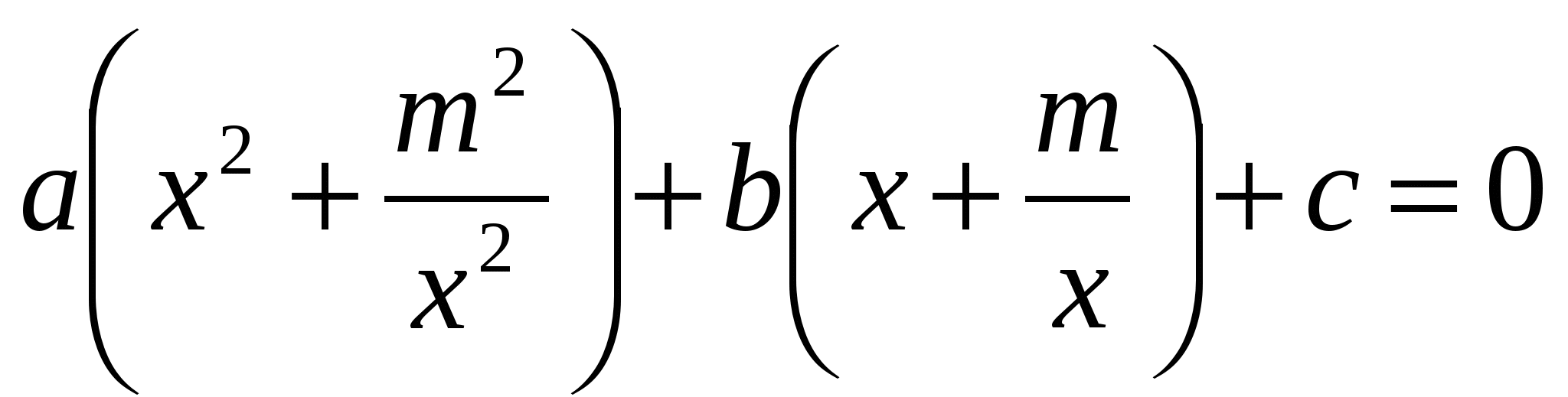 . Используем подстановку
. Используем подстановку 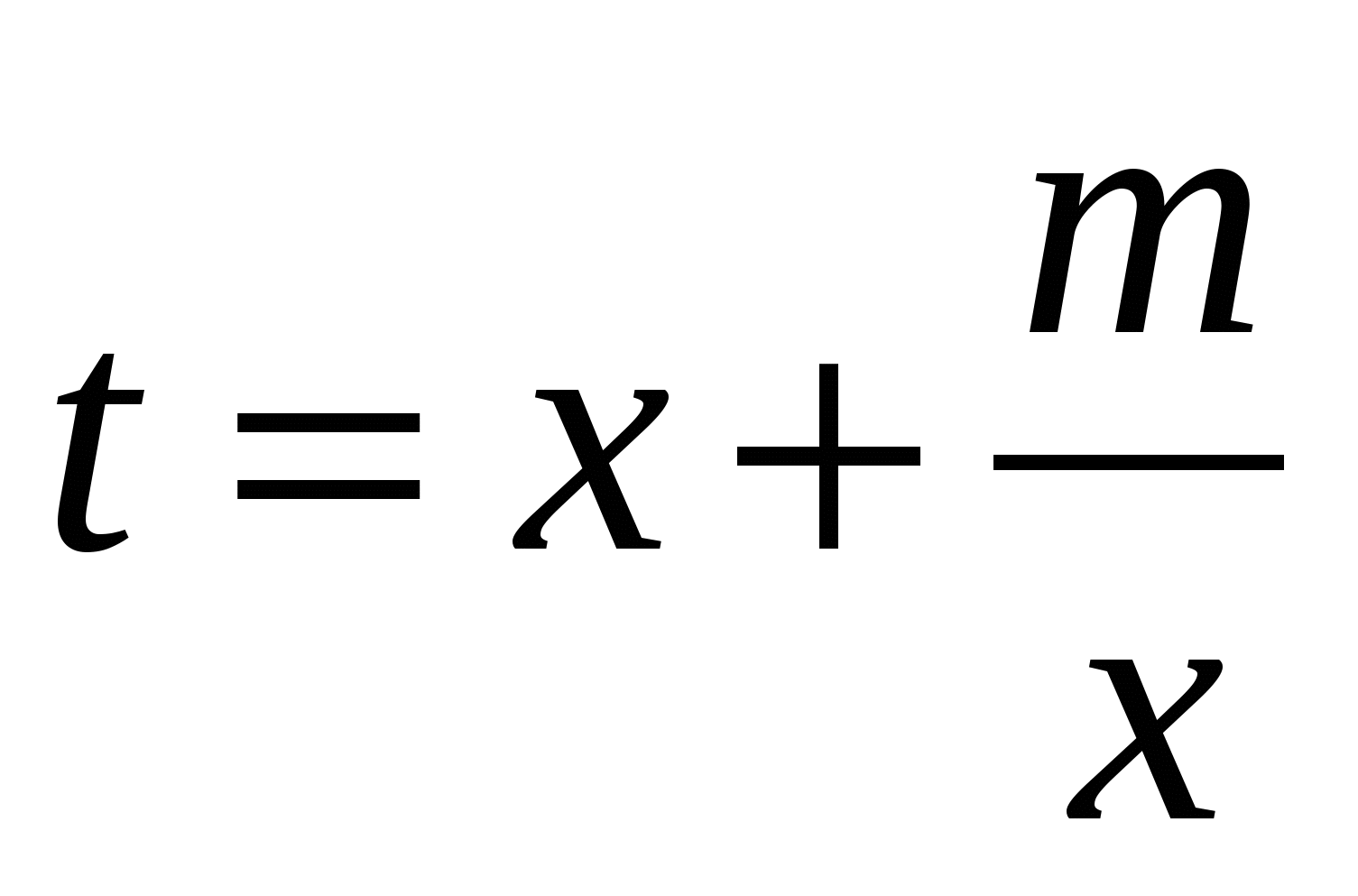 и решим уравнение
и решим уравнение 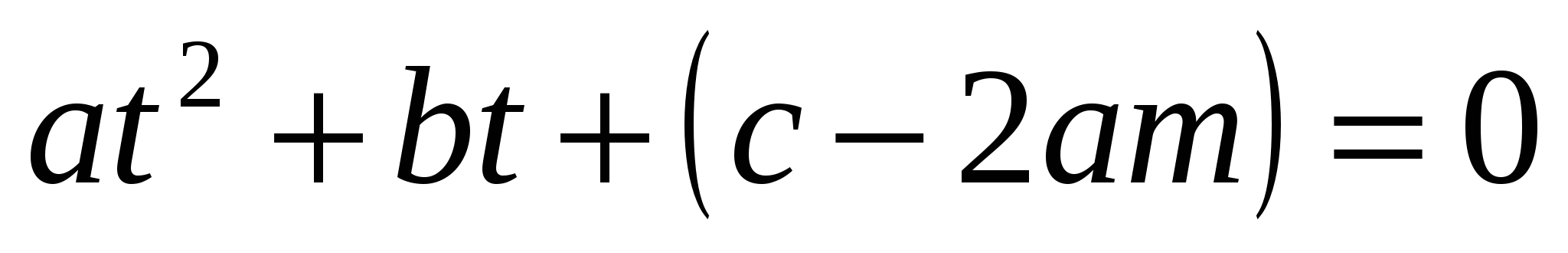 . Обратная подстановка позволяет найти значения х. Заметим, что при m=-1 уравнение называется кососимметрическим, тогда подстановка
. Обратная подстановка позволяет найти значения х. Заметим, что при m=-1 уравнение называется кососимметрическим, тогда подстановка 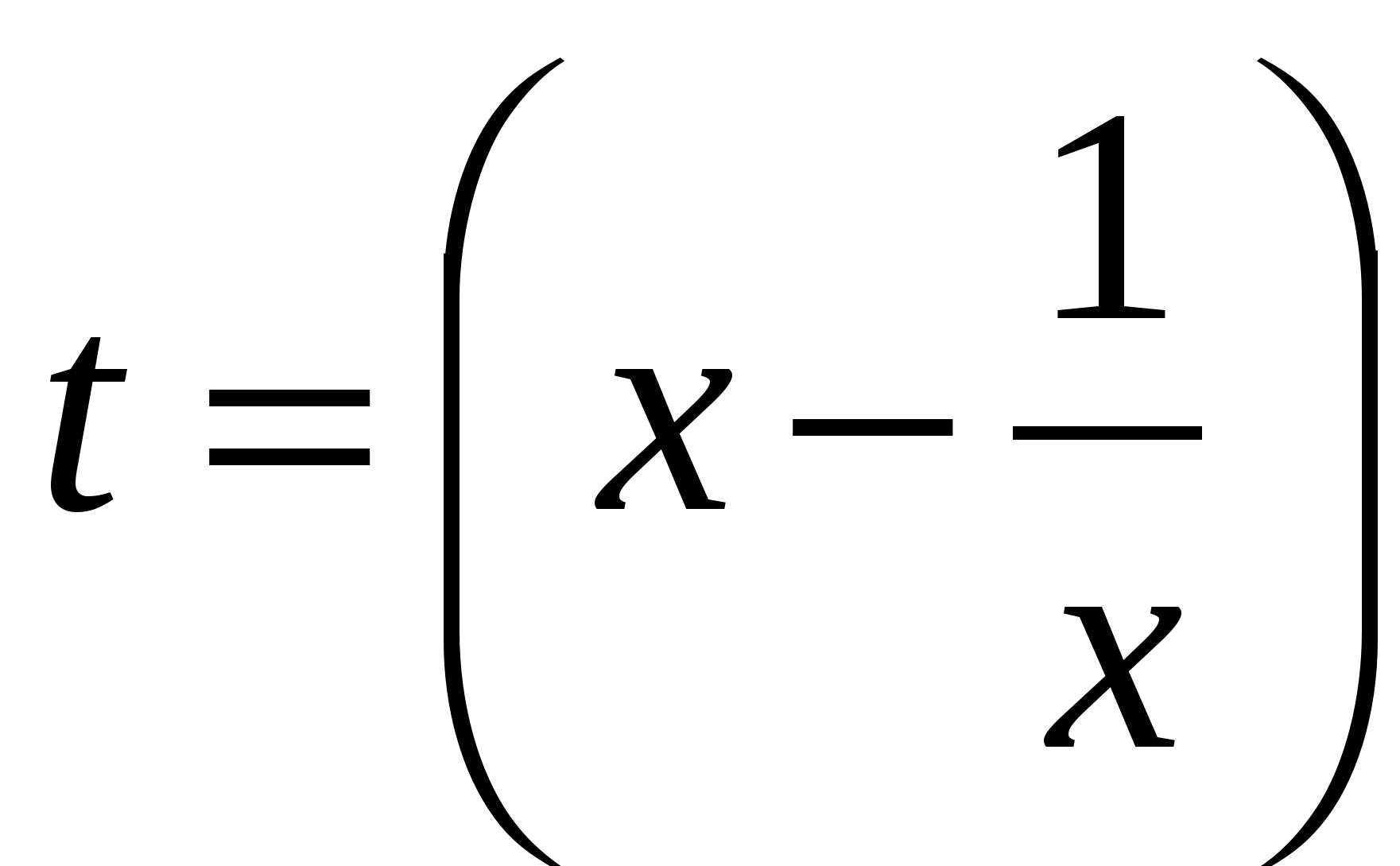 .
.
Теорема. Если ![]() - корень симметрического уравнения (возвратного), то
- корень симметрического уравнения (возвратного), то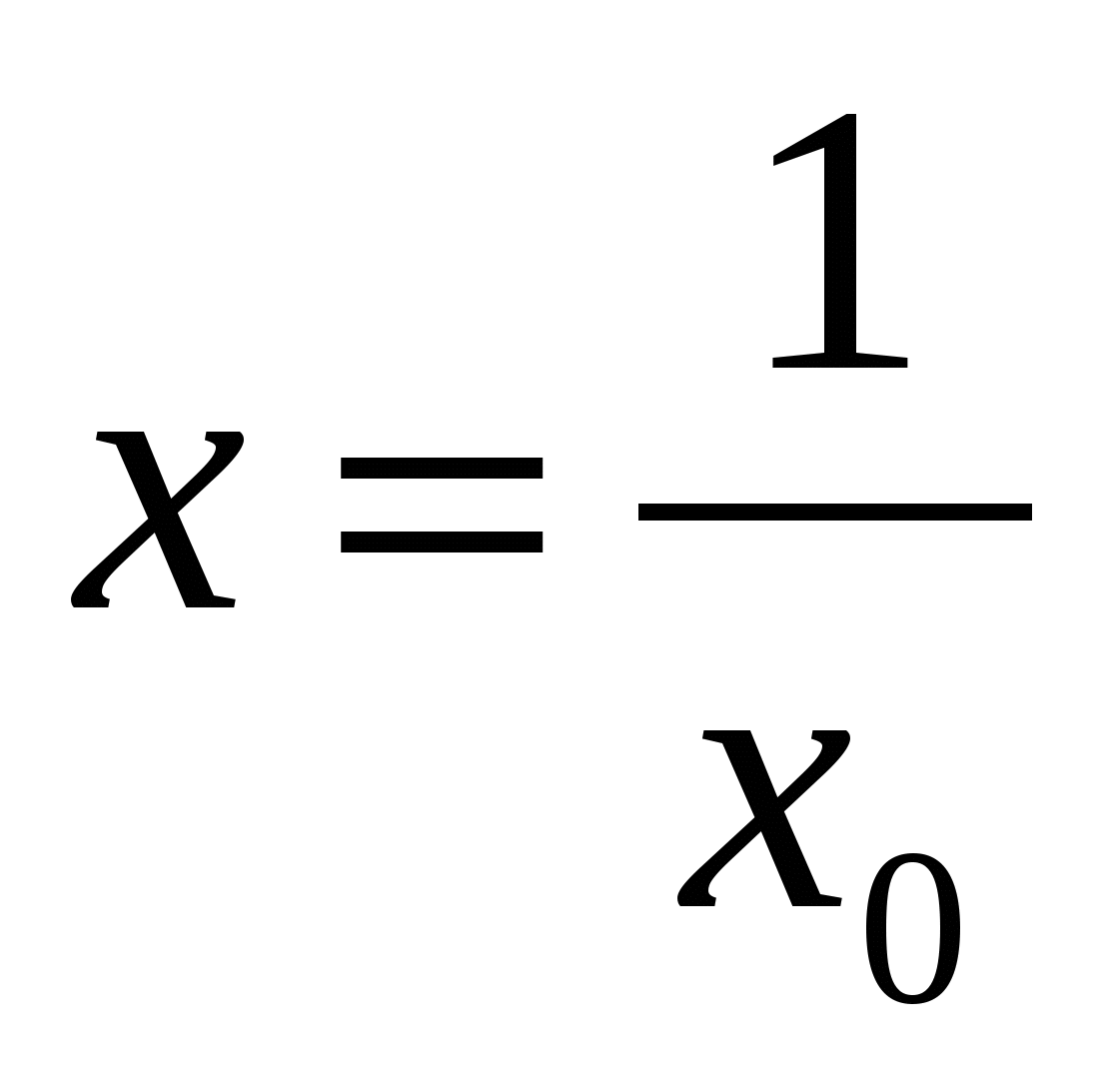 - тоже корень.
- тоже корень.
X. Однородные алгебраические уравнения.
Если Pn(x),Qm(x) - алгебраические многочлены, то уравнение вида aPn(x)+bQm(x)=0 - однородное уравнение I порядка, а aPn2(x)+bPn(x)Qm(x)+cQm2(x)=0 - однородное ур-е II порядка
Однородные алгебраические уравнения решаются делением на один из многочленов в степени, совпадающей с порядком уравнения, предварительно проверив, что многочлен отличен от нуля. При этом, происходит переход от двух данных функций к третьей.
XI. Функционально - графический метод.
Преобразуем алгебраическое уравнение Pn(x)=0 (где Pn(x)- многочлен степени n) в уравнение вида f(x)=g(x). Зададим функции у=f(x), у=g(x); опишем их свойства и построим графики в одной системе координат. Абсциссы точек пересечения будут являться корнями уравнения. Проверка выполняется подстановкой в исходное уравнение.
4


