- Преподавателю
- Математика
- Урок по алгебре на тему Комплексные числа
Урок по алгебре на тему Комплексные числа
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Конспекты |
| Автор | Оханцева И.В. |
| Дата | 12.04.2015 |
| Формат | docx |
| Изображения | Есть |
7
 "Комплексные числа: от прошлого к настоящему"
"Комплексные числа: от прошлого к настоящему"
обобщающий урок в 10 классе
Алгебра и начала анализа
Оханцева Ирина Владимировна, учитель математики
Цели урока
1. Систематизировать теоретический материал по теме.
2. Повторить перевод чисел из алгебраической в тригонометрическую форму записи комплексных чисел и обратно, действия с комплексными числами в алгебраической, тригонометрической форме.
3. Рассмотреть вопросы по теме «Функция комплексной переменной» в межпредметной связи с темой «Преобразования на плоскости».
4.Развивать: способности анализировать, обобщать, планировать, контролировать свою деятельность (взаимо- и самоконтроль).
5. Формировать коммуникативные навыки, оперировать математической терминологией.
План проведения урока
I. Организационный момент
Учащиеся записывают тему урока «Комплексные числа». Слайд 1.
Учитель: Итак, тема урока «Комплексные числа». О чем идет речь. Что это?
Определение: Комплексным числом называют сумму действительного числа и чисто мнимого числа.
Учитель:
Сформулируем основные задачи этого урока.
Что вы предлагаете повторить по теме?
Какие вопросы вас интересуют? Что, по вашему мнению, требует углубления?
Какие виды контроля считаете наиболее рациональными на этом уроке?
После обсуждения учащиеся знакомятся с предполагаемым планом.
Слайд 2
Учитель: Вы согласны, что эти этапы необходимы? Замечания, предложения.
Предлагаю вам повторить и обобщить основные вопросы темы «Комплексные числа», используя ленту времени.
II. Историческая справка
Впервые в истории комплексные числа появились в XVI веке в связи с решением уравнений. Несмотря на то, что с комплексными числами оперировать ничуть не сложнее, чем с действительными, но до начала XIX века комплексные числа рассматривались как очень сложные, почти мистические объекты.
Учитель: Как зародилось понятие комплексного числа, и кто из ученых работал в этой области математики? Давайте вспомним.
Слайд 4.
1545 год. Итальянский математик Джероламо Кардано (1501-1576), решая задачу о представлении числа 10 в виде суммы двух слагаемых так, чтобы произведение этих слагаемых равнялось 40, встретился с ситуацией, что система не имеет действительных решений. Величины, квадрат которых равен отрицательному числу Кардано назвал «софически отрицательными», считал, что они лишены всякого реального содержания. Писал: «Для осуществления таких действий нужна была бы новая арифметика, которая была бы настолько же утонченной, насколько бесполезной».
1572 год (через 27 лет). Р. Бомбелли - итальянский алгебраист ввёл правила арифметических действий с комплексными числами в алгебраической форме. Какие именно? Слайд 5.
II. Вычислительный практикум
Учитель: Проверим, как вы умеете применять формулы. В какой форме удобнее выполнять задание (алгебраической или тригонометрической)? Запишите только номер задания и ответ.
Слайд 6.

Выполните самопроверку.
Слайд 7
Учитель. Вспомним, что же отличает систему комплексных чисел, от других известных уже вам систем? Чем она универсальна?
Какие минимальные требования должны выполняться?
Не смотря на то, что система комплексных чисел построена, эти числа серьезно не воспринимались. Математики XVI в. и следующих поколений вплоть до начала XIX века относились к комплексным числам с явным недоверием и предубеждением.
Они считали эти числа «мнимыми» (Р. Декарт, французский математик и философ в 1637г. дал название «мнимые числа».), «несуществующими», вымышленными», «возникшими от избыточного мудрствования» (Д. Кардано)… Лейбниц называл эти числа «изящным и чудесным убежищем божественного духа», а √-1 считал символом потустороннего мира (и даже завещал начертать его на своей могиле). Слайд 9.
1748 г Эйлер - русский математик, швейцарец по происхождению, ввёл символ i, нашел формулу, носящую теперь его имя.
Слайд 10
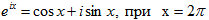 из формулы получается таинственное равенство единения арифметики, алгебры, геометрии и анализа.
из формулы получается таинственное равенство единения арифметики, алгебры, геометрии и анализа.
После того как в XIX в появилось наглядное геометрическое изображение комплексных чисел с помощью точек плоскости и векторов на плоскости (К. Гаусс в 1831 г, датчанин Вессель в 1799 г, француз Арган в 1806 г), стало возможным сводить к комплексным числам и уравнениям для них многие задачи естествознания, особенно гидро- и аэродинамики, электротехники, теории упругости и прочности, а также геодезии и картографии.
Комплексный-лат. составной, сложный. Термин введён Гауссом.
i - первая буква французского слова imaginaire, мнимый.
Инверсия, inversio - лат. переворачивание, перестановка
Сдайд 12.
С этого времени существование «мнимых», или комплексных чисел стало общепризнанным фактом и они получили такое же реальное содержание, как и числа действительные.
Софья Ковалевская (1850 - 1891) решила, используя теорию функции комплексного переменного, задачу о вращении твердого тела вокруг неподвижной точки.
Русский ученый в области механики, основоположник современной гидродинамики Николай Егорович Жуковский (1847-1921), вывел формулу для определения подъемной силы крыла, которая теперь носит его имя.
Учитель. Вспомним основные определения, связанные с комплексными числами.Слайд 13.

Слайд 14. Предложив геометрическую интерпретацию комплексных чисел, представив их в тригонометрической форме, были получены и основные формулы для выполнения действий с ними.
Учитель: Работаем с тригонометрической формой комплексного числа. Как изображается комплексное число?
Слайд 15. Изобразите комплексное число на плоскости z=-2+2i
Запишите данное число в тригонометрической форме.
Выполняется проверка, вызывается ученик со своим решением.
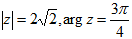
Проанализируйте, как изображение комплексного числа помогает при решении задачи?
Какие варианты ответов? Кто не согласен с ответом? Какие дополнения, уточнения?
Слайд 17.

Для тех, кто затрудняется, предлагается следующий слайд.
Слайд 18
1 способ
Если z=x+iy, то получаем уравнение 3x+3yi-x+yi=-4+8i, x+2yi=-2+4i,
Используем условие равенства комплексных чисел, получаем, что х=-2, у=2.
При возведении в квадрат, получаем число -8i, которое возводим в куб.
Ответ: 512i
2 способ
Представленное в тригонометрической форме число возвести по формуле Муавра в 6-ю степень.
Учитель: Выполните практическую работу в тетради (с обоснованием построения).
Слайд 17
«Этап 3.1.Геометрическое место точек»
Изобразите на плоскости ГМТ, удовлетворяющих условиям:
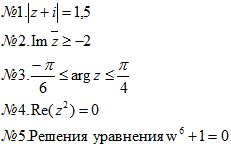
Учитель оказывает индивидуальную помощь.
Фронтальное обсуждение результатов практической работы. (Учитель может заранее приготовить варианты построений, но без нумерации. Ребята выбирают правильные решения.) Итак, проверьте правильность выполненных построений.
Слайд 20
Выход на новый материал
К настоящему времени изучение комплексных чисел развилось в важнейший раздел современной математики - теорию функций комплексного переменного (ТФКП), элементов которой мы с вами сейчас слегка коснемся. Слайд 21.

Учитель: Какие виды геометрических преобразований использовали при решении задач?
Выводы учащихся: выполняли преобразования - параллельный перенос; гомотетия; поворот.
Встретился и новый вид - преобразование инверсия, что в переводе с латинского, переворачивание, перестановка.


Контрольный элемент
Слайд 24.

Слайд 25. Ответы.
IV. Итог урока
Учитель: Удалось ли реализовать задачи данного урока? Что узнали нового? Что не совсем получилось?
На основании геометрической интерпретации применение комплексных чисел эффективно в тех областях, где приходится оперировать с величинами, которые можно представить в виде точки на плоскости или плоского вектора. Поэтому теория функции комплексного переменного нашла широкое употребление для решения вопросов теоретической физики, гидродинамики, электротехники, кораблестроения, картографии.
Те из вас, кто продолжит свое образование в технических вузах, смогут глубже ознакомиться с теорией функции комплексного переменного и её приложениями в различных областях науки и техники.
Но у меня к Вам остался еще один вопрос: мы представили комплексные числа точками на плоскости, а что если придумать еще более интересные числа, представив их точками пространства? Назвать их cупер комплексными или еще как-нибудь?
Здесь снова введем систему координат и запишем точки в виде набора уже трех координат (x; y; z). Эти так называемые триплеты тоже складываются покоординатно: (x; y; z) + (x'; y'; z') = (x + x'; y + y'; z + z').
Триплеты можно будет считать числами, если научиться их умножать, обладая, вместе со свойствами сложения, обычными способами умножения этих операций.
В 1833 г. умножением триплетов занимался ирландский математик У. Р. Гамильтон (1805 - 1865). О нем мы расскажем особо.
Уильям Роуан Гамильтон был человеком многосторонне развитым. В четырнадцать лет владел девятью языками, в 1824 г. опубликовал в трудах Королевской Ирландской Академии работу, посвященную геометрической оптике, в 1828 г. получил звание королевского астронома Ирландии. К 1833 г. Гамильтон занимал пост директора обсерватории в Денсинке и был известен работами по оптике и аналитической механики. Он предсказал эффект двойной конической рефракции в двуосных кристаллах.
В течение долгих десяти лет Гамильтон безуспешно пытался придумать правило умножения триплетов. Но несмотря на неудачи, Гамильтон пытался решить поставленную перед собой задачу. Но эта задача не могла быть решена (объяснение следует ниже).
Но труд не пропал даром. В 1843 г. Гамильтон вдруг решил, что для
определения умножения нужно рассматривать не триплеты (тройки чисел), а четверки, или кватернионы. Вот история их создания.
Случай на Брогемском мосту
В одном из писем к своему сыну Гамильтон писал: "Это был 16-й день
октября, который случился в понедельник, в день заседания Совета Королевской Ирландской Академии, где я должен был председательствовать. Я направлялся туда с твоей матерью вдоль Королевского канала; и, хотя она говорила мне какие-то отдельные фразы, я их почти не воспринимал, так как в моем сознании подспудно что-то творилось. Неожиданно как будто бы замкнулся электрический контур; блеснула искра, предвещающая многие длительные годы определенно направленной мысли и труда, моего - если доведется, или труда других, если мне будет даровано достаточно сознательной жизни, чтобы сообщить о своем открытии. Я оказался не в состоянии удержаться от желания высечь ножом на мягком камне Брогемского моста фундаментальную формулу о символах i, j, k, содержащую решение проблемы, но, конечно, эта запись с тех пор стерлась.
Однако более прочное упоминание осталось в Книге записей Совета Академии за этот день, где засвидетельствовано, что я попросил и получил разрешение на доклад о кватернионах на первом заседании сессии, который и был прочитан соответственно в Понедельник 13-го следующего месяца - ноября".
Спасибо за урок.


