- Преподавателю
- Математика
- Проект «Функции вокруг нас»
Проект «Функции вокруг нас»
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Соболева И.И. |
| Дата | 27.02.2014 |
| Формат | doc |
| Изображения | Есть |
23
Алгебра и начала анализа, 11 класс
Проектно-исследовательская технология
Составитель - Соболева Инна Ивановна, учитель математики МКОУ «Хохольский лицей».
Тема: Функции вокруг нас
Цель урока: 1. Актуализировать личностный смысл учащихся к изучению темы, помочь учащимся осознать социальную, практическую и личностную значимость учебного материала.
2. Создать содержательные и организационные условия для развития у школьников умений анализировать познавательный объект.
3. Обеспечить развитие у школьников умения ставить цель и планировать свою деятельность.
4. Обеспечить развитие у учащихся умения объективировать деятельность, т.е. переводить с языка непосредственных впечатлений и представлений на язык общих положений, схем и т.д.
Вид урока: урок-исследование.
Тип урока: учебное занятие по комплексному применению знаний и способов деятельности.
Оборудование:
-
Учебники.
-
Презентация.
-
Музыкальный инструмент.
Эпиграф: Во все царит гармонии закон,
И в мире все суть ритм, аккорд и тон.
Дж. Драйден
Ход урока:
1. Вступительное слово учителя.
Вы знаете, однажды русский математик Е.И. Игнатьев как-то проезжая через уездный город узнал, что в нем есть своего рода чудо-математик. Он решал «всякую» предложенную ему задачу чрезвычайно быстро, почти не думая, при помощи всего-навсего обыкновенной шахматной доски. Удивительно? «Простой и необразованный белорус решает все задачи с помощью шахматной доски, не прибегая при этом к выкладкам и вычислениям. Арифметика или алгебра без вычислений!..» - записал в свой дневник Е.И. Игнатьев.
Секрет его был прост: он представил, что шахматная доска - это та же бумага в клетку, удобная для построения графиков и решал предложенные задачи при помощи построения графиков.
Итак, тема сегодняшнего урока «Функции вокруг нас».
Большинство математических понятий прошли долгий путь развития. Сложный путь прошло и понятие функции. Исследованием этого вопроса занималась группа историков. Им слово.
Группа историков.
1 ученик. Понятие функции уходит корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше долетит стрела; чем дольше горит костер, тем теплее будет в пещере.
С развитием скотоводства, земледелия, ремесел и обмена увеличилось количество известных людям зависимостей между величинами. Идея зависимости некоторых величин восходит, по-видимому, к древнегреческой науке. Там величины имели геометрическую природу.
2 ученик. Сам термин «функция» возник лишь в 1664 г. в работах немецкого ученого Лейбница. Но Лейбниц все-таки оставался в сфере геометрических представлений. Только ученик Лейбница Бернулли в 1718 г. дал определение функции, свободное от геометрических образов: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных».
3 ученик. Гениальный ученик Бернулли петербургский академик Леонард Эйлер определяет функцию так: «Величины, зависящие от других так, что с изменением вторых меняются и первые, принято называть их функциями».
Таким образом, знание законов природы дало человеку возможность объяснять и предсказывать ее разнообразнейшие явления. «Математическими портретами» закономерностей природы и служит функция.
1 ученик. Может возникнуть вопрос: почему мы обозначаем функцию символом, и когда он появился. Этот символ изобрел в 1733 г. французский математик Клеро. А появился этот символ, когда формировался общий подход к понятию функции, когда потребовалось обозначение «функции вообще».
Учитель: Давайте вспомним понятие функции, ее основные свойства. Ученики вашего класса проводили урок в 7 классе по теме «Функция». Им слово.
Секция математиков.
1 ученик. Понятие функции вводится в школьном курсе математики в 7 классе. Давайте перенесемся с вами в 7 класс и вспомним, что такое функция.
Представьте себе, что перед вами не школьная доска, а аэропорт, а это не лужи, а множества Х - пассажиры, У - места в самолете. Пусть пассажиры рассаживаются так: мама (т) занимает кресло № 1, ребенок (r) - кресло № 2, папа (p) - кресло № 3, дядя (d) - № 4, тетя (t) - № 6 (рис. 1).
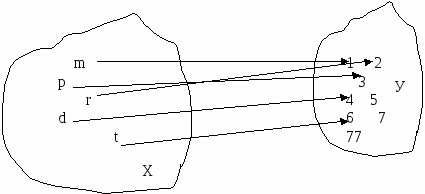
Рис. 1
Неважно, что часть кресел осталась незанятой. Главное то, что каждому пассажиру (каждому элементу х Х) досталось одно место (поставлен в соответствие единственный элемент у
Х) досталось одно место (поставлен в соответствие единственный элемент у  У).
У).
О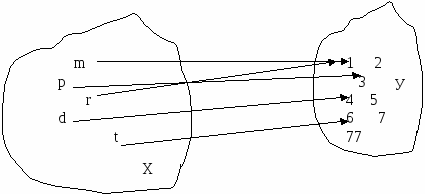 бстоятельства изменились, и маму просят взять на руки ребенка. Получается такая картина (рис. 2).
бстоятельства изменились, и маму просят взять на руки ребенка. Получается такая картина (рис. 2).
Рис. 2
Все равно, это функция, так как выполнено условие: каждому элементу множества Х поставлен в соответствие единственный элемент множества У.
В этом самолете летит очень «крутой» дядя, который хочет в одно кресло сесть, а на другое положить ноги. Такое соответствие функцией не является.
(Затем математик демонстрирует картинки, по которым следует определить, является ли изображенная зависимость функцией.)
2 ученик. Перейдем к более серьезному этапу урока. Давайте вспомним определение функции и ее свойства.
Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число у.
Обозначение: у = f(х), где х - независимая переменная (аргумент функции), у - зависимая переменная (функция),
Множество значений х называется областью определения функции (обычно обозначается D).
М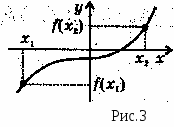 ножество значений у называется областью значений функции (обычно обозначается Е).
ножество значений у называется областью значений функции (обычно обозначается Е).
Графиком функции называется множество точек плоскости с координатами(x,f(x)) (рис. 3).
СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ
• Аналитический способ: функция задается с помощью математической формулы.
Примеры: у == х2, у = ln x
• Табличный способ: функция задается с помощью таблицы.
Пример.
х
1
2
8
4
5
У
2
4
6
8
10
• Описательный способ: функция задается словесным описанием.
П ример: функция Дирихле f(х) = 1 для рациональных х
ример: функция Дирихле f(х) = 1 для рациональных х
0 для иррациональных х
• Графический способ: функция задаётся с помощью графика.
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ
Ф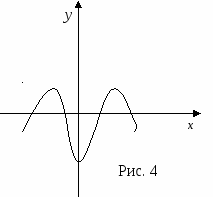 ункция называется четной, если:
ункция называется четной, если:
-
область определения функции симметрична относительно нуля,
-
для любого х из области определения f(-x) = f(x).
График четной функции симметричен относительно оси у (рис. 4).
Функция называется нечетной, если:
-
область определения функции симметрична относительно нуля.
-
для любого х из области определения f(-x) = - f(x).
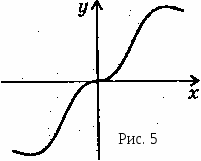
Г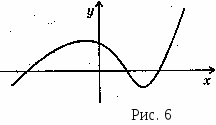 рафик нечетной функции симметричен относительно начала координат (рис. 5).
рафик нечетной функции симметричен относительно начала координат (рис. 5).
Многие функции не являются ни четными,
ни нечетными.
Пример графика функции, не являющейся ни четной,
ни нечетной (рис.6).
Примеры четных функций: у = х2n, п Z, у = cos х.
Z, у = cos х.
Примеры нечетных функций: у = х2n +1, п ![]() Z, у = sin х
Z, у = sin х
Примеры функций, не являющихся ни четными, ни нечетными:
у = ex, y= ln х, у = х - 2, у = (х + 1)2.
ПЕРИОДИЧНОСТЬ
Функция (х) называется периодической с периодом Т > 0, если для любого х из области определения значения x + T и x - T также принадлежат области определения и
f(х + Т) = f(x - T) = f(x) .
П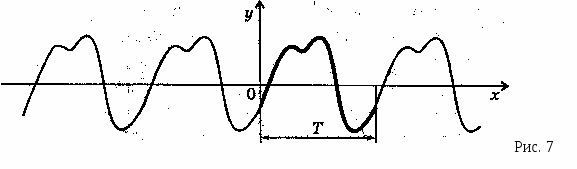 ри этом любое число вида Tn, где n
ри этом любое число вида Tn, где n![]() N, также является периодом этой функции.
N, также является периодом этой функции.
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов (рис. 7). Чтобы построить график периодической функции, строят фрагмент графика на любом отрезке длиной Т (например [0; Т]), затем производят последовательные параллельные переносы фрагмента графика на Т, 2Т, ЗТ и т.д. вдоль оси х (вправо и влево).
НУЛИ ФУНКЦИИ
Нулем функции у = f (х) называется такое значение аргумента х0, при котором функция обращается в нуль: f(xo)= 0.
В нуле функции ее график имеет общую точку с осью X (рис. 8).
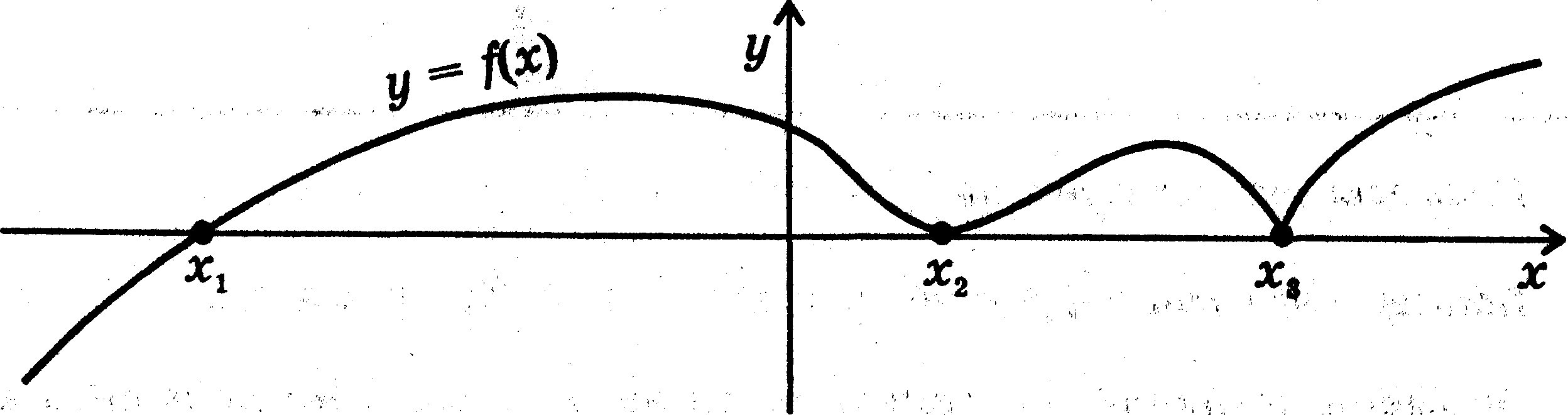
Рис. 8
х1, х2, х3 - нули функции у = f(x)
МОНОТОННОСТЬ (ВОЗРАСТАНИЕ, УБЫВАНИЕ)
Ф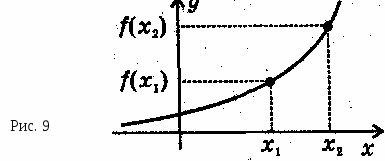 ункция у = f (х) называется возрастающей на интервале (а; b), если для любых х1 и х2 из этого интервала таких, что x1 < х2, справедливо неравенство f(x1) < f(x2) (рис. 9).
ункция у = f (х) называется возрастающей на интервале (а; b), если для любых х1 и х2 из этого интервала таких, что x1 < х2, справедливо неравенство f(x1) < f(x2) (рис. 9).
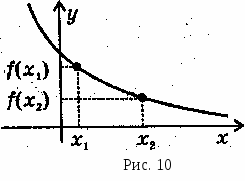
Функция у = f (х) называется убывающей
на интервале (а; b), если для любых х1 и х2
из этого интервала таких, что x1 < х2,
справедливо неравенство f(x1) < f(x2) (рис. 10)
ЭКСТРЕМУМЫ (МАКСИМУМЫ И МИНИМУМЫ)
В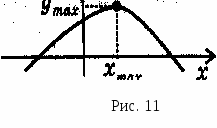 нутренняя точка хmax области определений называется точкой максимума, если для всех х из некоторой окрестности этой точки справедливо неравенство:
нутренняя точка хmax области определений называется точкой максимума, если для всех х из некоторой окрестности этой точки справедливо неравенство:
f(x) < f(хmax).
Значения уmax = f(хmax) называется максимумом этой функции.
хmax - точка максимума
уmax - максимум (рис. 11).
Внутренняя точка хmin области определений называется точкой минимума, если для всех х из некоторой окрестности этой точки справедливо неравенство:
f(x) > f(хmin).
З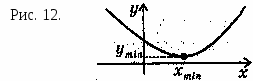 начения уmin = f(хmin) называется
начения уmin = f(хmin) называется
минимумом этой функции.
хmin - точка минимума, уmin - минимум (рис. 12)
АСИМПТОТЫ
Если график функции у == f(x) имеет бесконечную ветвь (ветви), у графика могут быть асимптоты.
Асимптотой графика называется прямая, к которой неограниченно приближается точка графика при удалении этой точки по бесконечной ветви.

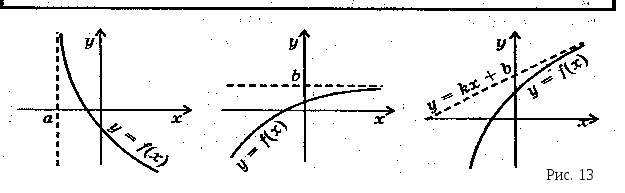

Прямая х = а является вертикальной асимптотой, если хотя бы один из пределов lim f(х) (предел справа) или lim f(x) (предел слева) равен бесконечности.
Прямая у =b является горизонтальной асимптотой. если существуют конечные пределы
lim f(x) = b или lim f(x) = b.
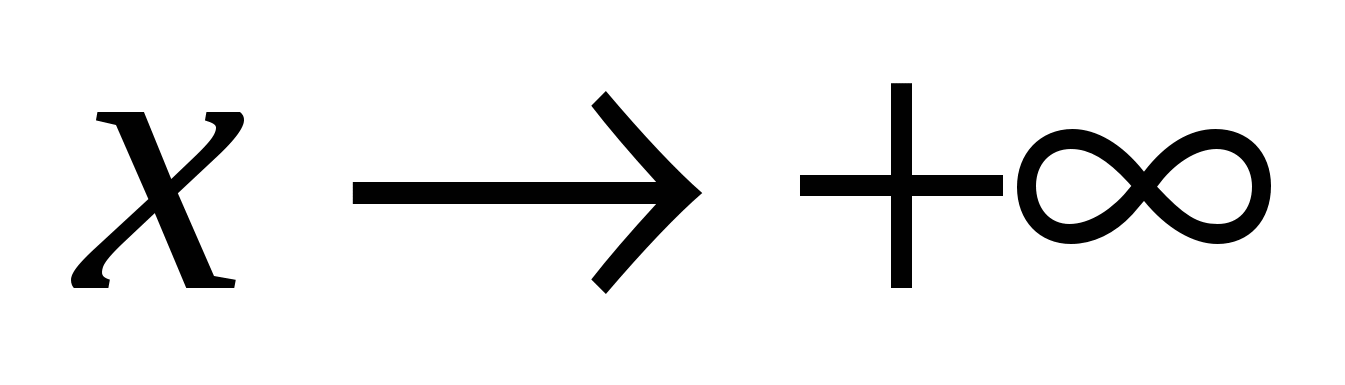
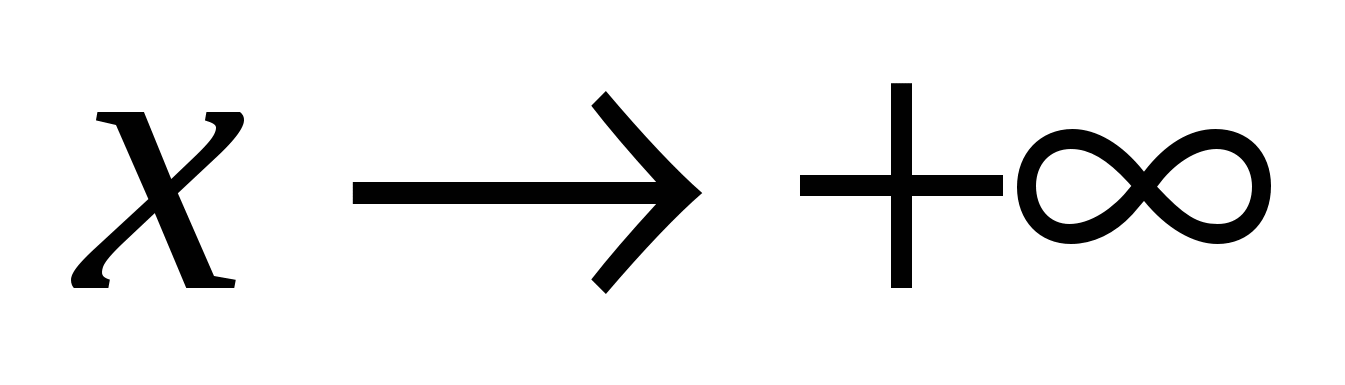
Прямая у = kx + b является наклонной асимптотой, если существуют конечные пределы k = lim 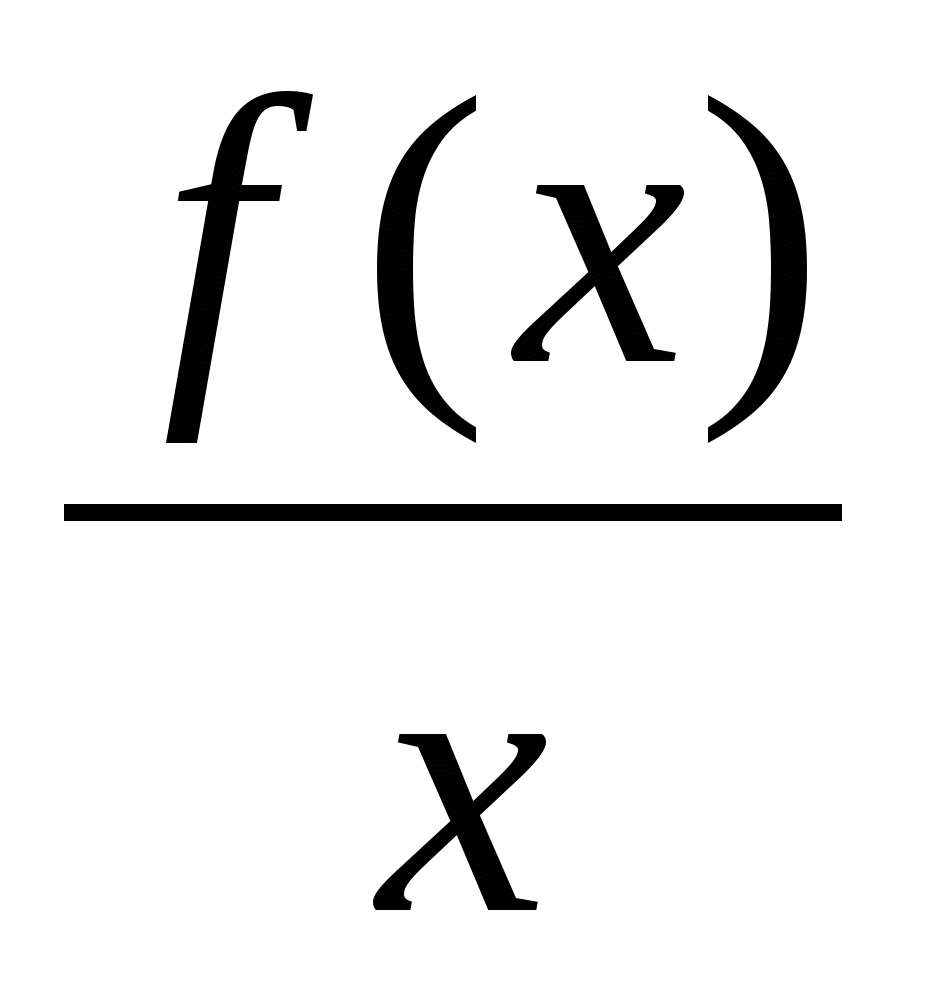 , b = lim(f(x) - kx)
, b = lim(f(x) - kx)
либо при 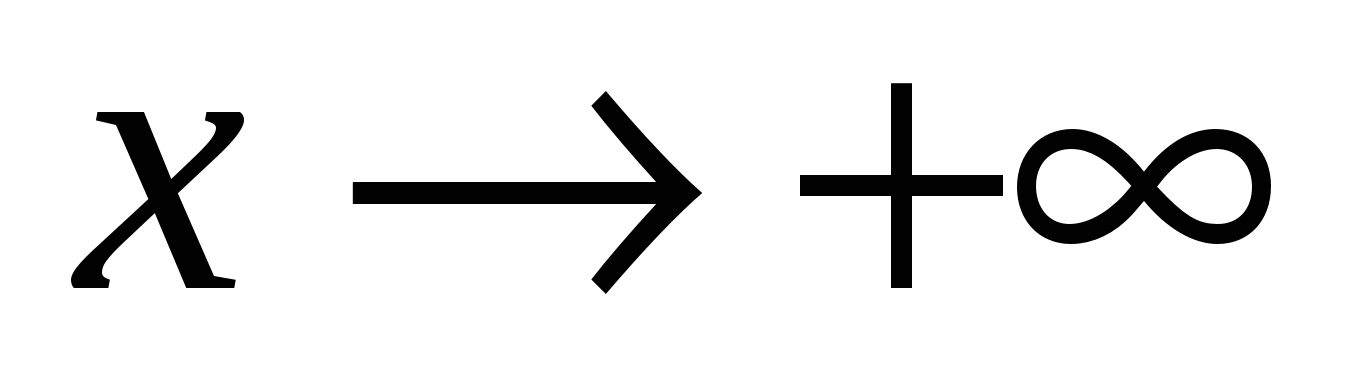 , либо при
, либо при 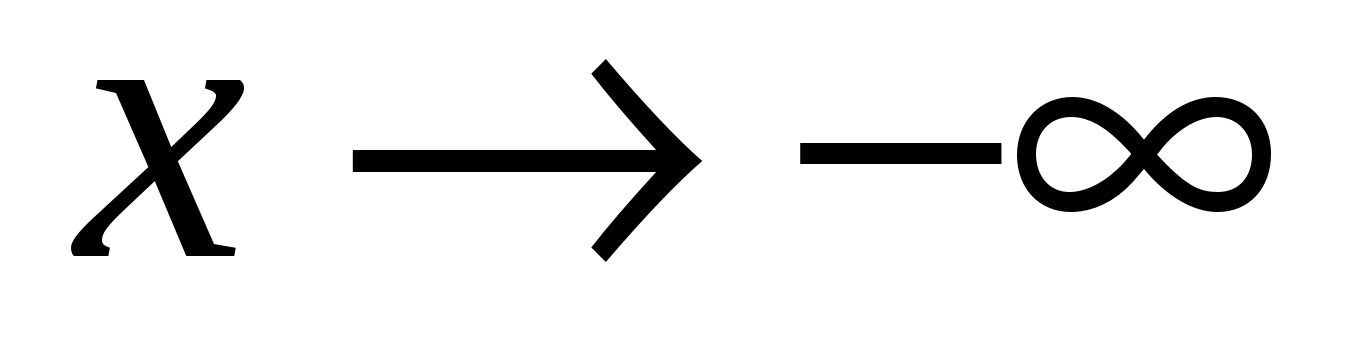
ОБРАТНЫЕ ФУНКЦИИ
Понятие обратной функции применимо к функциям, обладающим следующим свойством: каждому значению у из области значений функции соответствует единственное значение х из области определения этой функции.
Функция g называется обратной для функции f, если каждому у из области значений функции f функция g ставит в соответствие такое х из области определения функции f, что у = f(х). Таким образом, если у = f(х), то х = g(у).
Функции f и g являются взаимно обратными.
Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
Графики взаимно обратных функций симметричны друг другу относительно прямой у = х .
НАХОЖДЕНИЕ ФОРМУЛЫ ДЛЯ ФУНКЦИИ, ОБРАТНОЙ ДАННОЙ
Пользуясь формулой у = f(x), следует выразить х через у, а в полученной формуле х = g(у) заменить х на у, а у на х
Учитель: Секция математиков сформулировала современное определение функции и её свойства. Цель нашего урока не только обобщить знания о функциях и их свойствах, но и рассмотреть некоторые природные и общественные явления как функции, исследовать их и наглядно проиллюстрировать характерные их свойства. Это задание вы получили ранее и сегодняшний урок мы построим как отчет о вашей работе.
Секция математиков.
3 ученик. Функции, как правило, описываются словами. Словесное описание - один из способов задания функции, и притом не лучший.
Можно задавать функцию табличным способом. Выписать в ряд или в столбик несколько значений аргумента, а ниже или рядом поместить соответствующие значения функции.
За примером табличного задания функции мы обратимся к «Энциклопедии домашнего хозяйства».
Сечение жилы (мм2)
0,75
1
1,5
2,5
Допустимый ток (А)
13
15
20
27
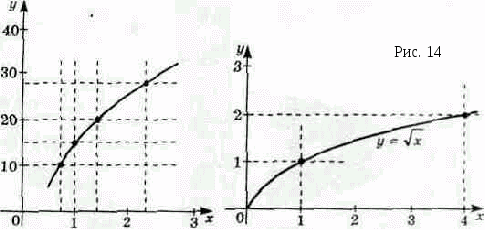
Перед нами таблица, в которой указаны длительно допустимые токи для проводов в зависимости от площади сечения. По данным таблицы можно построить график. Это графический способ задания функции. Он делает информацию о функции зримой и наглядной. Выразительная «картинка» вмиг расскажет о характерных особенностях и поведении функции.
Дело в том, что провода разогреваются, когда по ним течет ток. Нагрев прямо пропорционален квадрату тока и обратно пропорционален площади сечения провода. Увеличив ток в цепи в 2 раза, мы должны в 4 раза увеличить сечение проводов во избежание их перегрева.
Так мы приходим к формальному заданию интересующей нас функции - ток изменяется пропорционально корню квадратному из площади сечения проводов 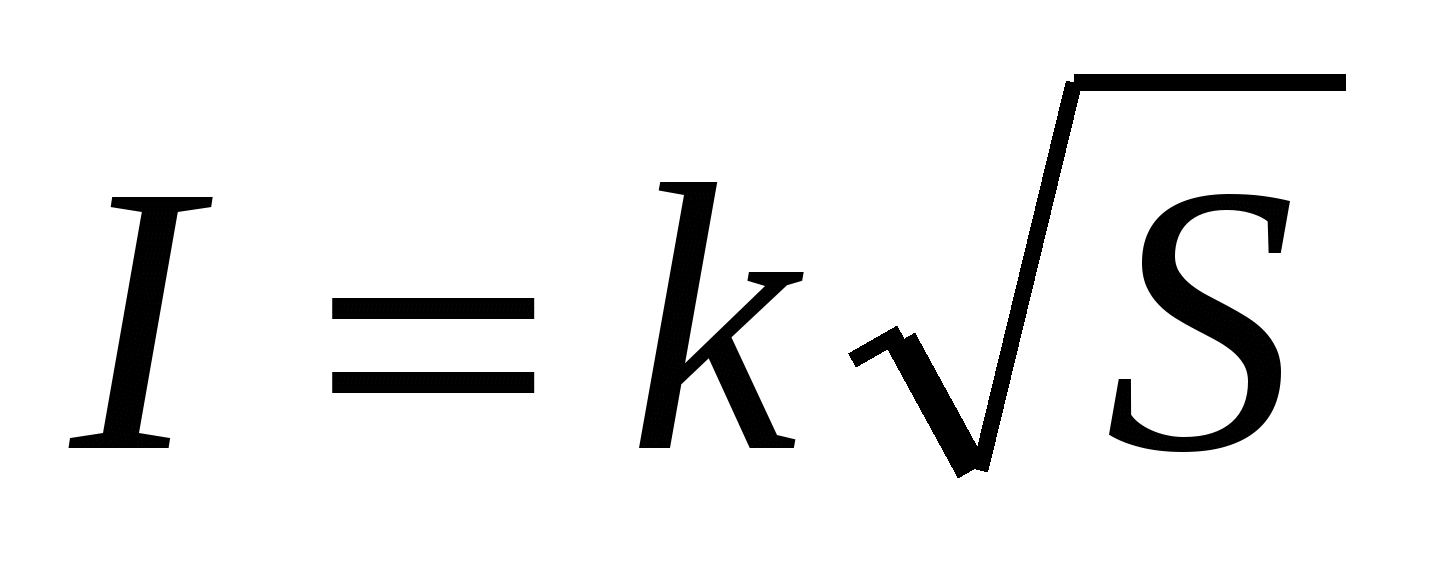
Вместо таблицы в «Энциклопедии домашнего хозяйства» можно было поместить лишь эту короткую формулу: она, как легко убедиться, соответствует табличным данным, а незначительные расхождения можно устранить ценою некоторого ее усложнения. Но!.. Домашний мастер вряд ли примет такую замену. Это и понятно, так как таблица дает готовые рекомендации на все случаи житейской практики, а формула еще требует вычислений. Это нагляднее на графике (рис. 14).
А как поступит математик? Конечно, он предпочтет формулы. В формальном представлении функции легче поддаются исследованию математическими методами.
Учитель: Если рассматривать функцию как зависимость между величинами, то нельзя ли установить функциональную зависимость в живой природе? Посмотрим, к каким выводам пришла группа биологов.
Секция биологов:
1 ученик. Обратившись к законам животного мира, мы задумались, почему не бывает животных какой угодно величины? Почему, например, нет слонов в три раза большего роста, чем существующие, но тех же пропорций?
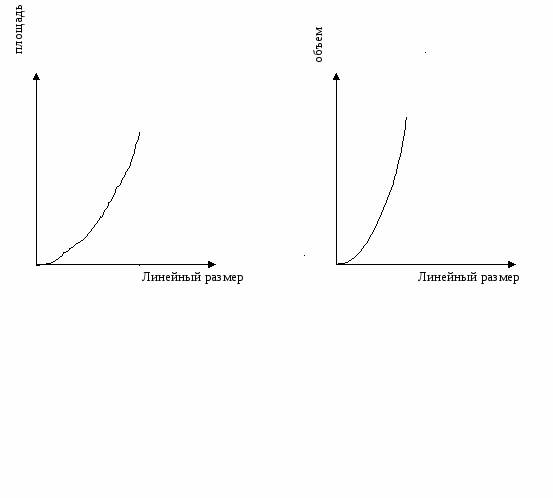
2 ученик. Ответ таков: стань слон в три раза больше, вес его увеличился бы в 27 раз, как куб размера, а площадь сечения костей и, следовательно, их прочность - только в 9 раз, как квадрат размера. Прочности костей не хватило бы выдержать непомерно увеличившийся вес. Такой слон был бы раздавлен собственной тяжестью.
3 ученик. Рассуждение вполне строгое и убедительное.
Эту строгость и убедительность ему придало знание двух функциональных зависимостей. Первая - устанавливает соответствие между размерами подобных тел и их объемами: объем изменяется как куб размера. Вторая - связывает размеры подобных фигур и их площади: площадь изменяется как квадрат размера. Говоря на языке математики, линейный размер играет роль независимой переменной или аргумента, а объем и площадь являются зависимыми переменными или функциями.
4 ученик. Леонард Фибоначчи, живший в XIII, написал «Книгу об абаке», которая несколько веков была основным хранителем сведений по арифметике и алгебре. Сейчас его имя все чаще встречается, прежде всего в связи с замечательной числовой последовательностью, которая получается так. Сначала идут две единицы, затем каждый последующий член получается как сумма двух предыдущих: 1; 1; 2; 3; 5; 8; 13; 21; ….
Если присмотреться к живой природе, то заметим, что эти числа часто встречаются в различных спиральных формах, которыми богат мир растений. Черенки листьев примыкают к стеблю по спирали, которая проходит между двумя соседними листьями: 1/3 часть полного оборота у орешника, 2/5 - у дуба, 3/8 - у тополя и груши, 5/13 - у ивы. Чешуйки на еловой шишке, ячейки на ананасе и семена подсолнечника расположены спиралями, причем количество спиралей каждого направления, как правило, числа Фибоначчи.
Учитель: Чтобы наглядно проиллюстрировать характерные свойства функций, обратимся к пословицам. Ведь пословицы - это тоже отражение устойчивых закономерностей, выверенных многовековым опытом народа.
Исследованием пословиц с математической точки зрения занималась секция литературоведов.
Секция литературоведов:
1 ученик. «Пересев хуже недосева», - издавна говорили земледельцы. Обратившись к агроному фермерского хозяйства Смольякову Г.А., выяснили: урожайность возрастает при увеличении плотности высева лишь до некоторой поры, а далее снижается, так как при чрезмерной густоте ростки начинают «глушить» друг друга, что подтверждает и вековой опыт ведения земледелия. Изобразим это в виде графика (рис. 15). Урожай максимален, когда поле засеяно в меру. Максимум - это наибольшее значение функции по сравнению с ее значениями во всех соседних точках. Это как бы «вершина горы», с которой все дороги ведут вниз, куда ни шагни.
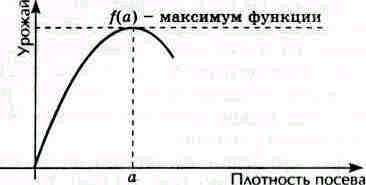
Рис. 15
(точка максимума)
«Чем дальше в лес, тем больше дров», - гласит пословица. Изобразим графиком, как нарастает количество дров по мере продвижения в глубь леса - от опушки (S), где давным-давно все собрано, до чащобы, куда еще не ступала нога заготовителя.
Горизонтальная черта - это лесная дорога. По вертикали будем откладывать (допустим, в кубометрах) количество топлива на данном километре дороги (рис. 16).
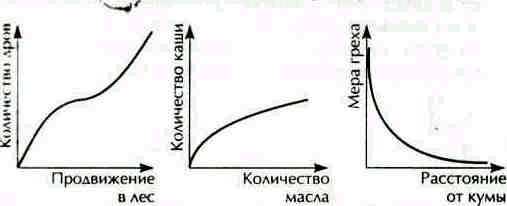
Рис.16 Рис.17 Рис.18
Сходное свойство иллюстрирует и пословица «Каши маслом не испортишь!». Количество каши можно рассматривать как функцию количества масла в ней (рис. 17). Согласно пословице, качество каши не понижается с добавкой масла. Подобного рода функции называются монотонно не убывающими.
Следующая пословица: «Дальше от кумы - меньше греха». Функция, которая показывает, как изменяется мера греха по мере удаления от кумы, - монотонно убывающая функция (рис. 18).
«Выше меры конь не скачет». Если изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой» (рис. 19).
Рис. 19
«Не круто начиная, круто кончай». Эта пословица может быть включена в правила научной организации труда. Тем более что за ней так и видится графическое выражение, к чему так склонны теоретики научной организации труда (рис. 20). Повелительное звучание пословицы явно рассчитано на борьбу с противоположной, весьма распространенной манерой работы. На нее тоже есть своя пословица: «Горяч на почине, да скоро остыл» (рис. 21). Обе функции, представленные на графиках, зависимы от времени, возрастающие. Но, как свидетельствуют кривые, «расти» можно по-разному.

Рис.21 Рис. 20
Группа актеров:
Сценка: (выходят два ученика и ведут между собой диалог, затем к ним присоединяется третий и т.д., для того, чтобы показать периодичность функции)
- Рассказать тебе сказку про белого бычка?
- Расскажи.
- Ты расскажи, я расскажу. Рассказать тебе сказку про белого бычка?
- Ну, так давай же! и т. д.
Если изобразить на графике эту сказку, мы получим периодическую функцию. Еще одним наглядным примером периодической функции является рассказка: «У попа была собака, он ее любил. Она съела кусок мяса - он ее убил. И в землю закопал, и надпись написал: «У попа была собака...» и т. д.
Учитель: Надеюсь, вы поняли, что группа актеров попыталась показать нам в игровой форме одно из свойств функции. Какое?
Что же такое периодичность?
Ученик из группы актеров. Периодичностью в обычной речи называют чуть ли не всякую повторяемость. Однако повторяемость может быть более или менее строгой, достаточно сравнить между собой приведенные тексты.
Учитель: Кто может ответить на вопрос «Почему летом теплее, чем зимой?»
Группа астрономов.
1 ученик. Иногда говорят: потому, что Земля, двигаясь по своей орбите, зимой находится от Солнца дальше, чем летом. Но это неверно! Орбита Земли - это почти окружность, в центре которой находится Солнце. Все дело в наклоне земной оси по отношению к плоскости земной орбиты.
Поток энергии, идущий от Солнца, одинаков во все времена года. Но в зависимости от наклона солнечный лучей, она по-разному распределяется по земной поверхности. Чем меньше угол, который образуют лучи с поверхностью, тем меньше их приходится на тот же участок.
Именно эту зависимость применяют (быть может, не думая об этом) курортники» загорающие под солнцем юга, когда они поворачивают свои топчаны так, чтобы солнечные лучи как можно менее отклонялись от перпендикуляра к плоскости топчана.
Давайте проследим по рисунку за эволюцией прямоугольного треугольника (рис. 22,а-в). Гипотенуза, на которую падают солнечные лучи, всюду одна и та же. Катет, через который проходят падающие лучи, меняется по длине, уменьшаясь вместе с углом, который образуют с гипотенузой падающие на нее лучи. Очевидно, доля солнечной энергии, приходящаяся на некоторый участок, равна отношению указанного катета к гипотенузе. Число, определенное таким образом, называется синусом этого угла.
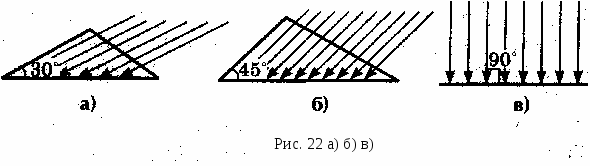
Как меняется доля солнечной энергии в зависимости от угла падения, удобно судить, если все прямоугольные треугольники собрать «в одну связку», где их катеты расположены параллельно друг другу, а гипотенуза стала радиусом некоторой окружности. Вновь мы встретились с периодической функцией.
2 ученик. Задумывался кто-нибудь над вопросом, сколько звезд на небе? Одним из первых, кто попытался точно ответить на этот вопрос, был древнегреческий астроном Гиппарх. При его жизни в созвездии Скорпиона вспыхнула новая звезда. Гиппарх был потрясен: звезды смертны. Гиппарх составил свой звездный каталог. Он насчитал около тысячу звезд и разбил их по видимому блеску на шесть групп. Самые яркие Гиппарх назвал звездами первой величины, заметно менее яркие - второй, еще столь же (величина постоянная) менее яркие - третьей и т. д. до звезд, едва видимых невооруженным глазом, которым была присвоена шестая величина.
В наше время существуют чувствительные приборы для световых измерений, - это дает возможность точно определить блеск звезд.
П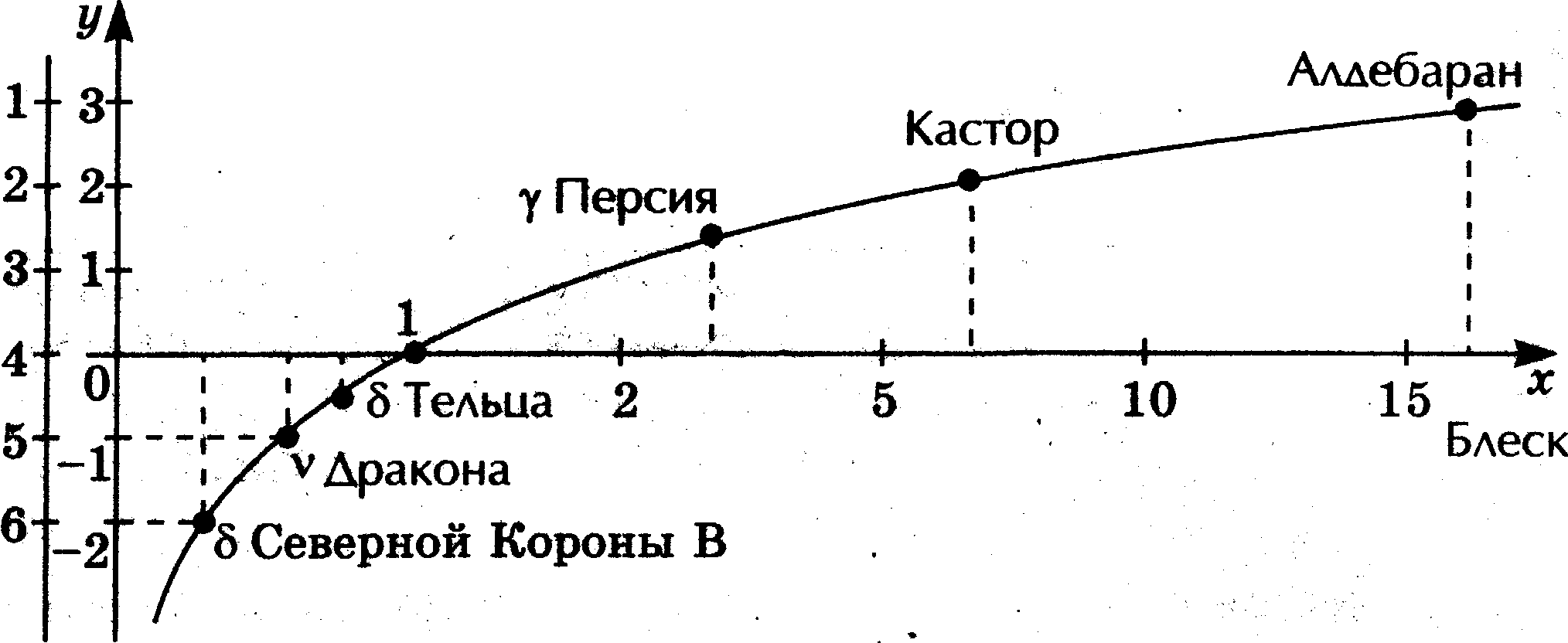 окажем на графике (рис. 23), насколько соответствует данным этих измерений распределение звезд по видимому блеску, произведенному на глаз. От каждой из шести групп, на которые распределял звезды Гиппарх, возьмем по одному типичному представителю.
окажем на графике (рис. 23), насколько соответствует данным этих измерений распределение звезд по видимому блеску, произведенному на глаз. От каждой из шести групп, на которые распределял звезды Гиппарх, возьмем по одному типичному представителю.
Рис. 23
По вертикальной оси будем откладывать блеск звезд (в единицах Гиппарха), по горизонтальной - показания приборов. Сразу же бросается в глаза, что объективные (прибор) и субъективные (глаз) характеристики блеска не пропорциональны друг другу. С каждым шагом по шкале звездных величин прибор регистрирует возрастание блеска не на одну и ту же величину, а примерно в 2,5 раза.
Выраженная графиком функциональная зависимость заключается в том, что положительным числам ставятся в соответствие их логарифмы. Значит это логарифмическая функция (рис. 24).
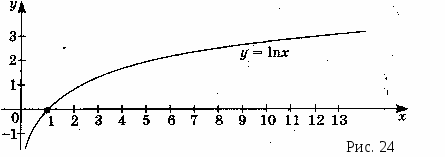
Учитель: Вся богатейшая семья механизмов, окружающих современного человека, начиналась когда-то с семи простых машин. Древние люди знали рычаг, блок, клин, ворот, винт, наклонную плоскость и зубчатые колеса. Эти механизмы умножали силу человека. Слово членам секции физиков.
Секция физиков.
1 ученик.
Конечно, все функциональные зависимости, изучаемые в физике, мы не сможем изложить, поэтому мы выбрали, на наш взгляд, наиболее яркие. «Во сколько раз выиграешь в силе, во столько же раз проиграешь в расстоянии». Так гласит золотое правило механики.
График - наглядный пример знаменитого правила (рис. 25). 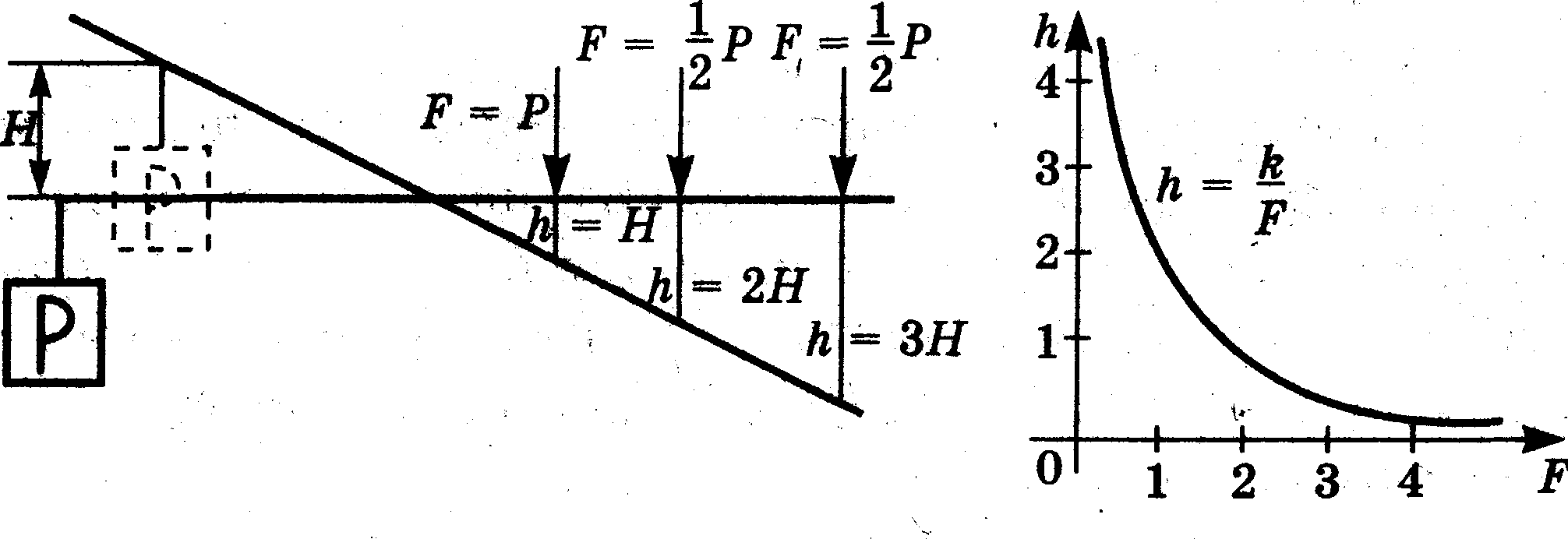 Рис. 25
Рис. 25
По горизонтальной оси отложена сила, с которой, например, нужно давить на плечо рычага, чтобы поднять заданный груз на высоту Н; по вертикали - расстояние, которое пройдет при этом точка приложения силы. Линия, выражающая функциональную зависимость, называется гиперболой (обратная пропорциональность).
2 ученик. Закон обратной пропорциональности «глядит на нас» со шкалы радиоприемника. Вы крутите ручку настройки, и стрелка движется вдоль шкалы, на которой два ряда чисел: метры и мегагерцы, длина волн и их частота. Длина волн растет - частота падает. Давайте присмотримся: при любом сдвиге стрелки во сколько раз увеличилась длина волны, во столько раз упала частота.
3 ученик. «Бросая в воду камешки, смотри на круги ими образованные, иначе такое бросание будет пустой забавою». Последуем совету Козьмы Пруткова и обратимся к рисунку. Вот что мы увидим, если остановим мгновение и рассечем пополам водную толщу.
 Рис. 26
Рис. 26
Такие явления природы описаны функциями Бесселя. Это колебания жидкости в топливном баке взлетающей ракеты, поведение плазменного шнура в магнитном поле, распространение тепла вокруг теплопроводящего стержня в ядерном реакторе - в любом из этих случаев найдется применение функциям Бесселя.
Учитель: Ребята! Если я вас спрошу, какого цвета миллион или как звучит в музыкальном исполнении таблица умножения, то это вам покажется по крайней мере странным.
Слово предоставляется секции искусствоведов.
Секция искусствоведов.
1 ученик. Оказывается можно установить зависимость между множеством всех натуральных чисел и цветом спектра. Мы знаем шутливую присказку, по которой запоминают цвета радуги: « Каждый охотник желает знать, где сидит фазан». Установим соответствие: числу 1 поставим в соответствие красный цвет и далее. Начиная с числа 8, все повторяется. А как определить, какого цвета число 29?
(Ответ: Надо найти остаток от деления 29 на 7. Это будет 1. Значит, 29 - красного цвета.)
2 ученик. Есть какая-то доля мистики в том, что красному цвету соответствует большая энергия и бодрость. Миллионером без этих качеств не станешь. Имея перед глазами таблицу 3, каждый из вас может определить, какого цвета ваш день рождения и что это означает.
3 ученик. (Выходит к музыкальному инструменту, играет гамму). Можно установить функциональную зависимость между натуральными числами и нотами. Я думаю, вы догадались, что 1 соответствует нота «до», 2 - «ре» и т.д.
4 ученик. Оказывается, можно установить зависимость между множеством натуральных чисел, цветом спектра и нотами. Обратимся к таблице умножения. Если ее раскрасить в соответствии с указанной зависимостью, то получим такую картину. Но самое интересное, что ее можно сыграть на музыкальном инструменте. Обратите внимание на таблицу умножения на 7. Она вся раскрашена в фиолетовый цвет. Это связано с тем, что эти числа делятся на 7 без остатка, а значит, «они фиолетовые» и им соответствует нота «си». А теперь послушайте, как звучит таблица на 2, а на 3…
ученик. Оказывается, можно установить зависимость между множеством натуральных чисел, цветом спектра и нотами. Обратимся к таблице умножения. Если ее раскрасить в соответствии с указанной зависимостью, то получим такую картину. Но самое интересное, что ее можно сыграть на музыкальном инструменте. Обратите внимание на таблицу умножения на 7. Она вся раскрашена в фиолетовый цвет. Это связано с тем, что эти числа делятся на 7 без остатка, а значит, «они фиолетовые» и им соответствует нота «си». А теперь послушайте, как звучит таблица на 2, а на 3…
Математика и музыка связаны между собой. Я согласна с высказыванием математика Г. Лейбница: « Музыка - это радость души, которая вычисляет, сама того не замечая».
Ученик: В одной из записей Льва Николаевича Толстого есть замечание, что у людей с возрастом время бежит быстрее. Действительно, многие это замечают. Лев Николаевич дал только качественную характеристику явления. Я набралась смелости и решила восполнить этот «недосмотр» Л.Н. Толстого, выведя формулу зависимости субъективного восприятия от объективной скорости бега времени. Вот эта формула: 
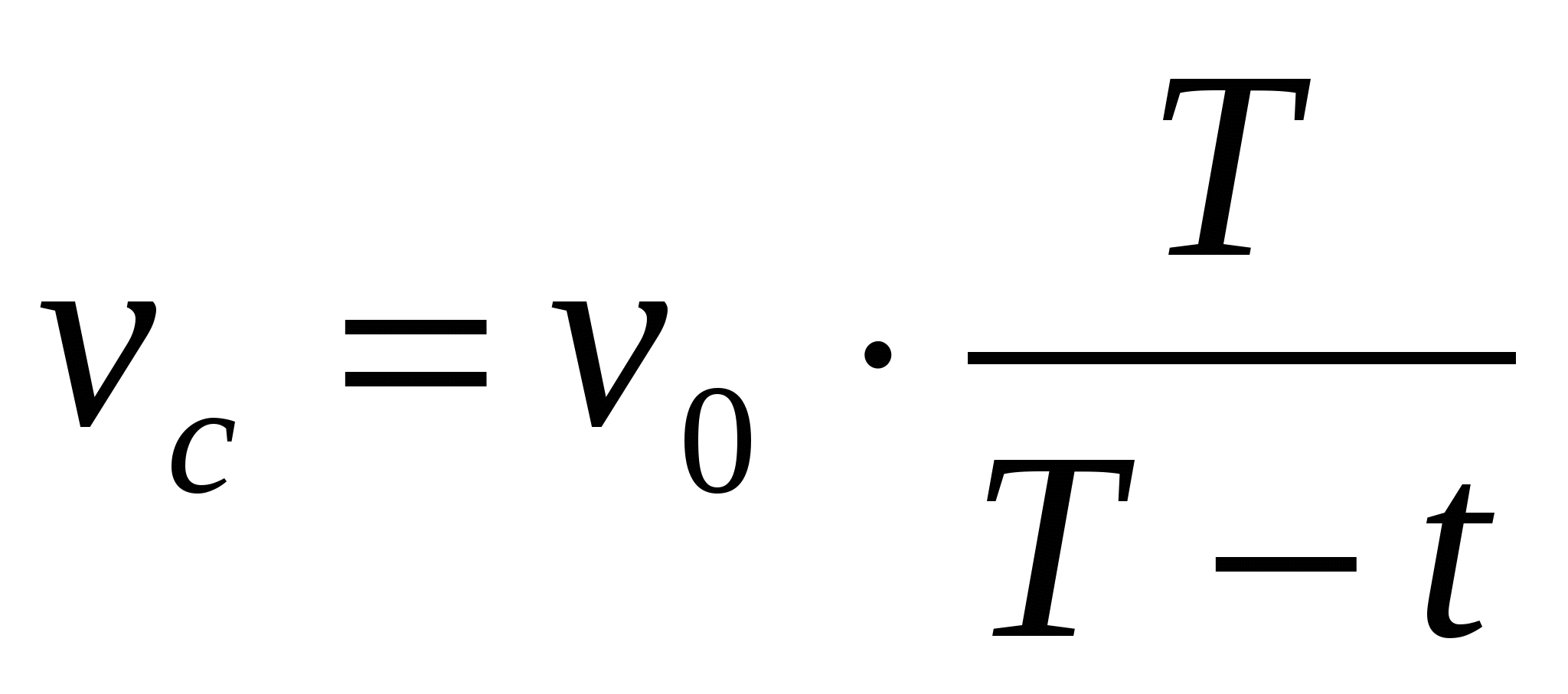 ,
,
где v c- субъективная скорость бега времени,
v o- объективная скорость бега времени,
Т - время жизни, «отпущенное» человеку,
t - время, которое прожил человек.
Ясно, что в момент рождения t = 0 и vс = vо, а со временем t увеличивается, следовательно, дробь растет и vс возрастает. Представим на графике.
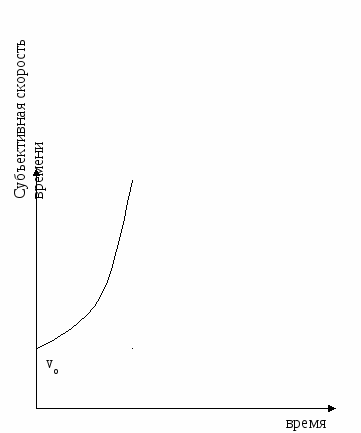

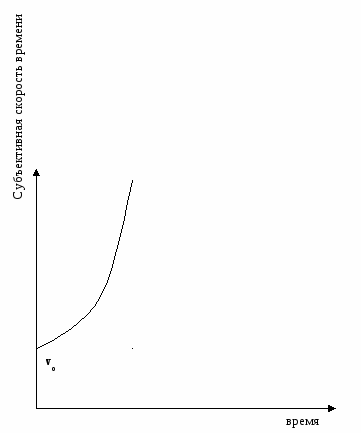
Рис. 27
Учитель: Итак, как показали наши исследования, современная математика знает множество функций, и у каждой свой «неповторимый облик», как неповторим облик каждого из миллиардов людей, живущих на Земле. Мы же познакомились только с некоторыми из функций.
Хочется закончить наш урок словами В.И. Гончарова: «Но кривая линия - геометрический эквивалент функции - гораздо больше говорит воображению, чем формула, и гораздо более легко обозрима, чем таблица числовых значений».


