- Преподавателю
- Математика
- Методическая разработка Теория и практика по теме Комплексные числа
Методическая разработка Теория и практика по теме Комплексные числа
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Пушкина Т.П. |
| Дата | 12.12.2015 |
| Формат | rar |
| Изображения | Есть |
16
Раздел III
ОСНОВЫ ТЕОРИИ КОМПЛЕКСНЫХ ЧИСЕЛ
Глава 8. Комплексные числа
Тема 8.1. Комплексные числа
1. Определение комплексных чисел в алгебраической форме
Одним из основных понятий математики является понятие числа. Это понятие прошло длительный путь развития, обогащаясь новым содержанием. Исторически первыми возникли в практике и были введены в науку натуральные числа, которые являются инструментом для счета количества отдельных предметов, например количества пальцев на руке. Они образуют бесконечное множество, которое принято обозначать буквой N.
Затем возникла необходимость во введении долей единицы и количества этих долей (например, для измерения длин отрезков), т. е. было введено так называемое дробное число.
Далее те же потребности измерения привели к необходимости введения отрицательных чисел (например, если за начало отсчета берется уровень моря, то для отметки положения горы берется положительное число - высота горы, а для отметки положения глубины моря - отрицательное число). Целые отрицательные числа вместе с натуральными числами и числом 0 образуют множество целых чисел, обозначаемое буквой Z
Множество, состоящее из всевозможных положительных и отрицательных целых и дробных чисел и числа Q, называется множеством рациональных чисел и обозначается буквой Q.
Очевидно, что N 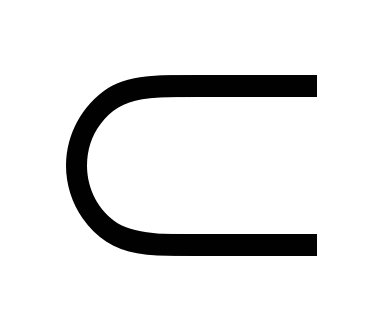 Z
Z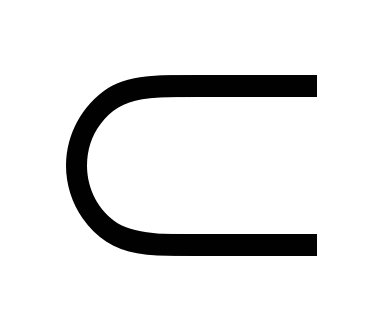 Q.
Q.
Потребности практики, а также внутренние требования самой математики, ее логического развития, показали недостаточность множества рациональных чисел для решения различных задач. Например, дано уравнение х2 = 2,
или х = 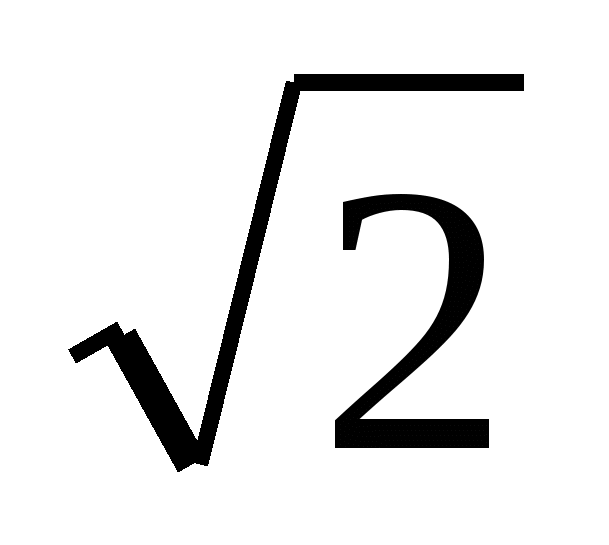 . Но не существует такого рационального числа, квадрат которого равен 2. Такие числа получили незнание иррациональных чисел.
. Но не существует такого рационального числа, квадрат которого равен 2. Такие числа получили незнание иррациональных чисел.
Поэтому появилась необходимость создать новое расширенное множество чисел, в котором для каждой точки числовой оси находилось бы числовое значение и в котором решалось бы любое уравнение вида хп = а.
Такое множество получило название вещественных(действительных ) чисел и обозначается буквой R, причем Q![]() R.
R.
Развитие науки и практики показало недостаточность введенного множества вещественных чисел.
Например, даже такое простейшее квадратное уравнение, как х2 + 1 = 0, не имеет решения в множестве действительных чисел, так как не существует такого действительного числа а, что а2 + 1 = 0. Это показывает необходимость дальнейшего расширения понятия числа. Кроме того, такие науки, как электротехника и различные разделы физики, рассматривают величины сложной природы, которые не могут быть охвачены понятием вещественных чисел.
В связи с этим возникла потребность нового расширения понятия числа.
Итальянские математики XVI в. Дж. Кардано и Р. Бомбелли, решая квадратные уравнения вида х2 + а2 = 0, ввели в рассмотрение символ 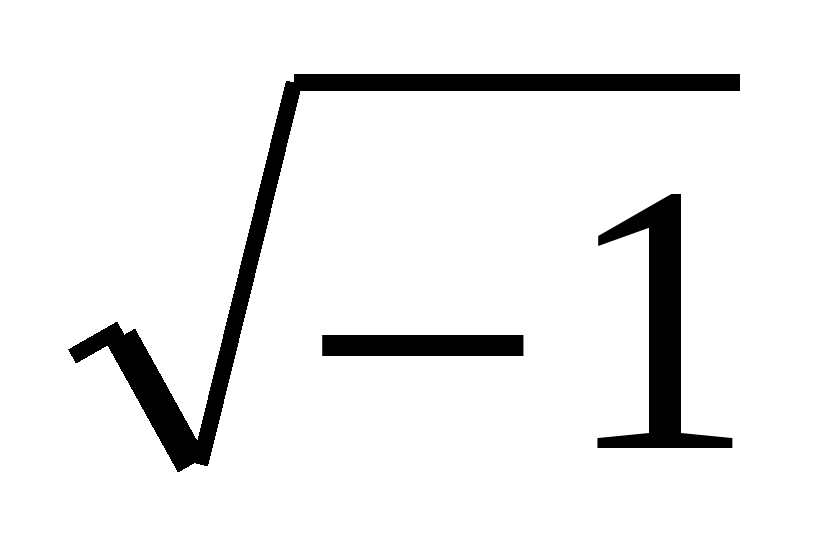 , который в XVIII в. петербургский математик Л. Эйлер(1708-1783) обозначил через i. Формальное решение уравнения х2 + а2 = 0 при использовании этого символа сводится к тому, что
, который в XVIII в. петербургский математик Л. Эйлер(1708-1783) обозначил через i. Формальное решение уравнения х2 + а2 = 0 при использовании этого символа сводится к тому, что 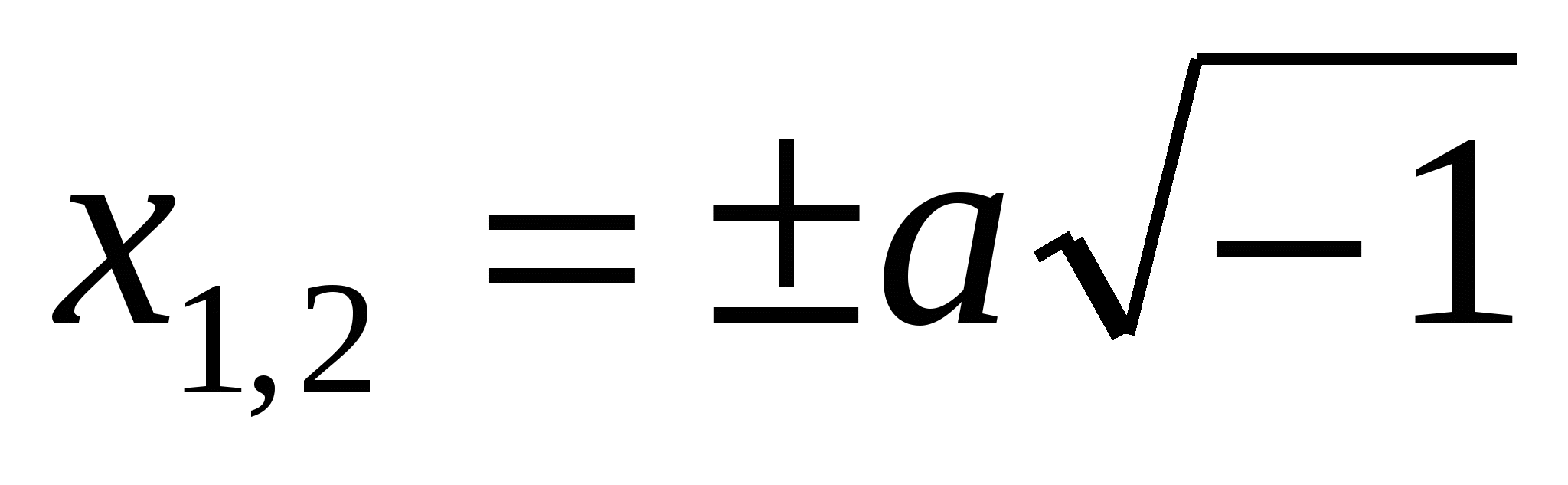 или, используя обозначение Эйлера,
или, используя обозначение Эйлера, 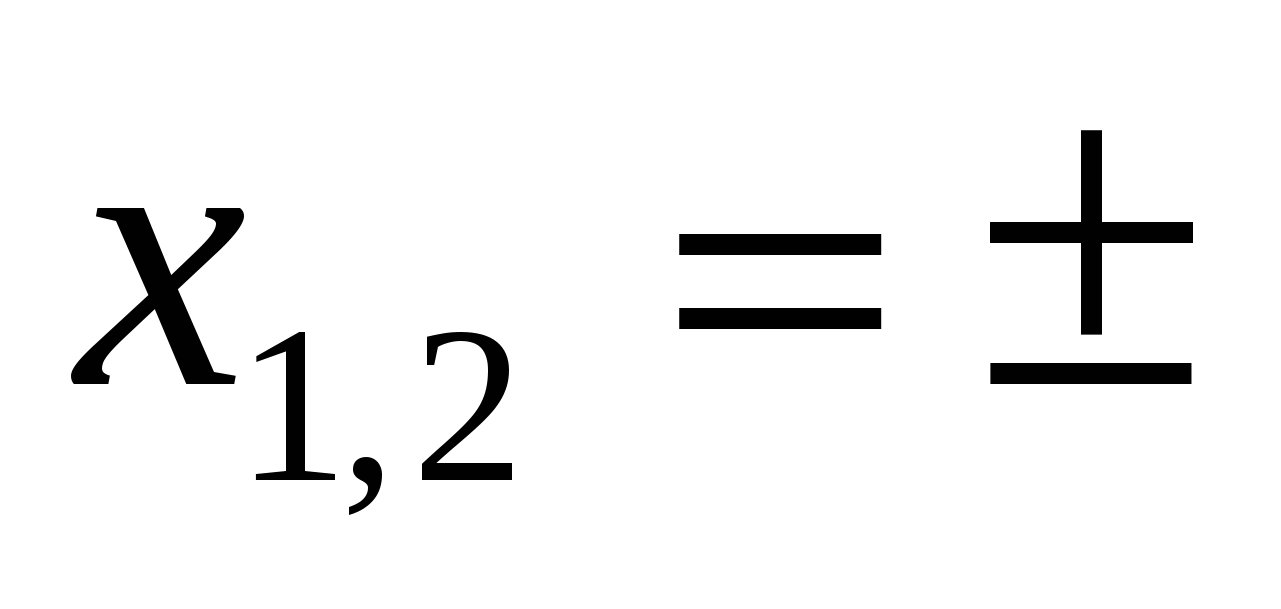 ai.
ai.
Таким образом, возникает необходимость в расширении множества действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида х2 + а2 = 0имели решения.
Ниже мы изложим краткую теорию такого расширения.
Определение 1. Комплексным числом z называется выражение вида а+bi, a и b-действительные числа, а символ i удовлетворяет условию i = - 1
Число а называется действительной частью комплексного числа, bi - мнимой частью, i- мнимой единицей.
Множество комплексных чисел обозначается буквой С.
Заметим, что множество R действительных чисел содержится в множестве комплексных чисел С: R 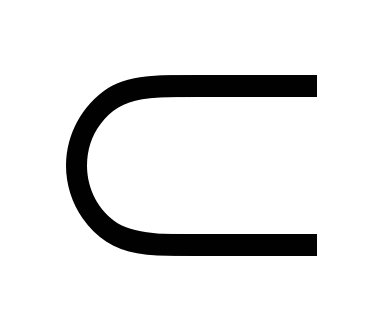 C . В самом деле, всякое действительное число а можно рассматривать как комплексное число вида а+0i.
C . В самом деле, всякое действительное число а можно рассматривать как комплексное число вида а+0i.
Комплексные числа вида biназываются чисто мнимыми. Они получаются из комплексных чисел z1 = а + biпри а = 0.
Определение 2. Два комплексных числа z1 = а + bi и z2 = с + di называются равными, если, соответственно, равны их действительные части и коэффициенты при мнимой единице, т. е. если а = с, b= d.
Комплексное число z = 0 + 0i называется нулем и обозначается через 0. Оно совпадает с числом нуль множества действительных чисел. Таким образом, z = а + bi = 0 тогда и только тогда, когда а = 0 и b= 0, или, что то же самое, когда а2+ b2= 0.
Определение 3. Комплексные числа а + bi и а - bi называются комплексно-сопряженными.
Число, комплексно-сопряженное числу z, обозначается через ![]() . Так, если z = а + bi, то
. Так, если z = а + bi, то  = а - bi, если же z = а − bi, то
= а - bi, если же z = а − bi, то  = а + bi. Понятие сопряженности взаимное. Например, для комплексного числа z = = -2 + 4i комплексно-сопряженным является комплексное число
= а + bi. Понятие сопряженности взаимное. Например, для комплексного числа z = = -2 + 4i комплексно-сопряженным является комплексное число  = - 2 - 4i; точно также для комплексного числа -2 - 4i комплексно-сопряженным является число -2 + 4i .
= - 2 - 4i; точно также для комплексного числа -2 - 4i комплексно-сопряженным является число -2 + 4i .
2. Геометрическая интерпретация комплексных чисел
Комплексное число z = а + bi геометрически можно представить точкой координатной плоскости Оху с координатами а, b (рис. 1).
Определение 4. Плоскость, служащая для изображения множества комплексных чисел, называется комплексной плоскостью. Так как любое комплексное число единственным образом определяется его действительной и мнимой частями, то каждому комплексному числу в комплексной плоскости соответствует единственная точка на плоскости. Очевидно, что справедливо и обратное утверждение: каждой точке (х; у) плоскости Оху соответствует единственное комплексное число z = х + yi.
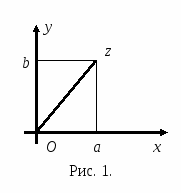
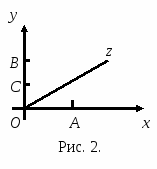
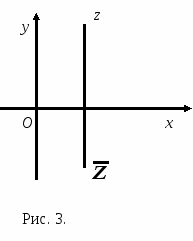
Таким образом, между множеством комплексных чисел и множеством точек плоскости существует взаимно-однозначное соответствие. При этом соответствии всякому действительному числу z = а + 0i соответствует точка А(а; 0) оси абсцисс, а всякому чисто мнимому числу z = 0 + bi - точка В(0; b) оси ординат. Числу z = i соответствует точка С(0; 1) (рис. 2). Если каждой точке М комплексной плоскости поставить в соответствие радиус-вектор ОМ этой точки, между множеством комплексных чисел множеством радиус-векторов можно также установить взаимно-однозначное соответствие. Ось Ох будем называть действительной осью, а ось Оу- мнимой.
Из определения комплексно-сопряженных чисел следует, что числа z и  на комплексной плоскости расположены симметрично относительно действительной оси (рис. 3).
на комплексной плоскости расположены симметрично относительно действительной оси (рис. 3).
Ранее мы отметили, что квадратное уравнение ax2+ bx + c = 0, для которого дискриминант D = b2 - 4ас < 0, в множестве R (действительных чисел) не имеет решения, так как корень из отрицательного числа в этом множестве не имеет действительного значения. Однако в множестве С (комплексных чисел) такое уравнение имеет два комплексно-сопряженных решения. В самом деле, пусть дано квадратное уравнение
ах2 + bx + c = 0.
причем D < 0.
Решения этого уравнения
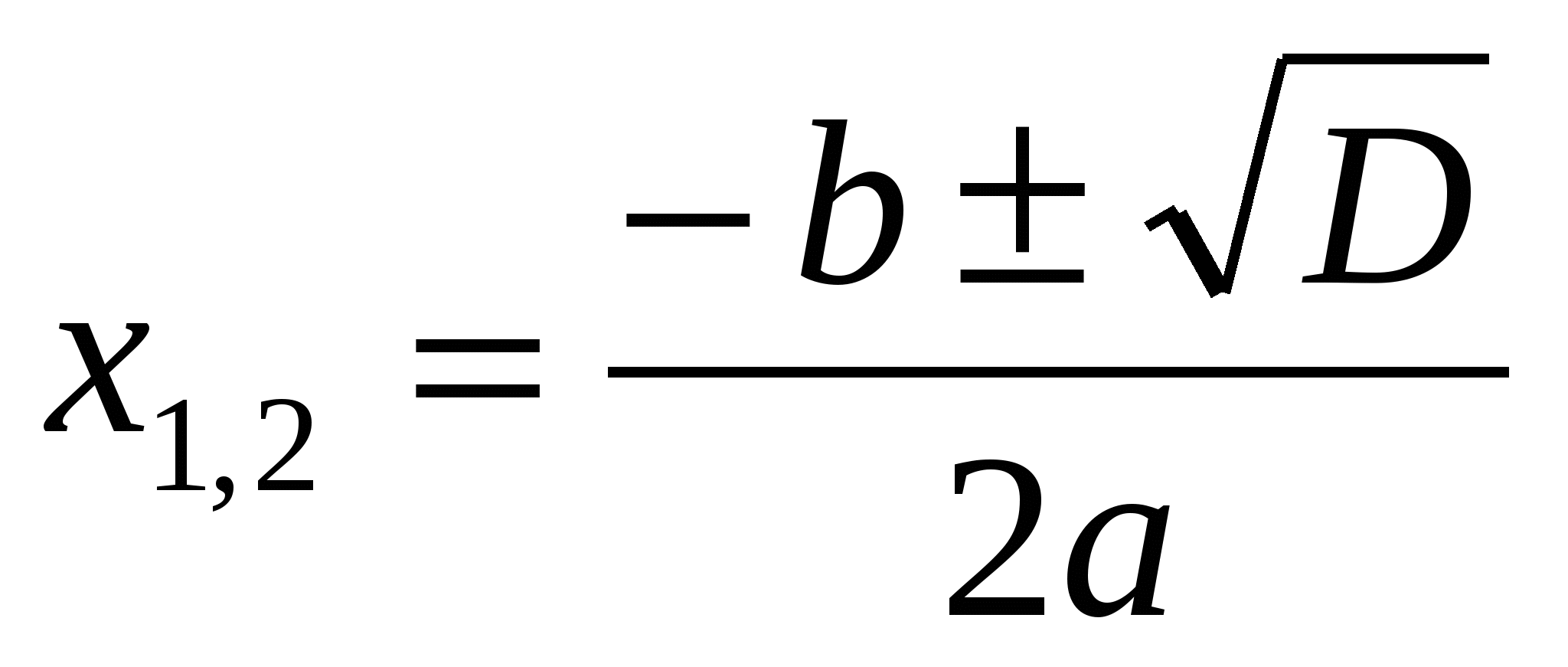 ,
,
представим в виде
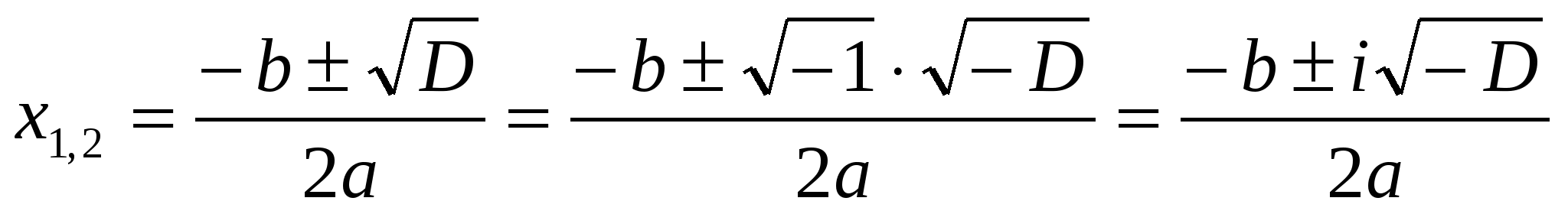 ,
,
где уже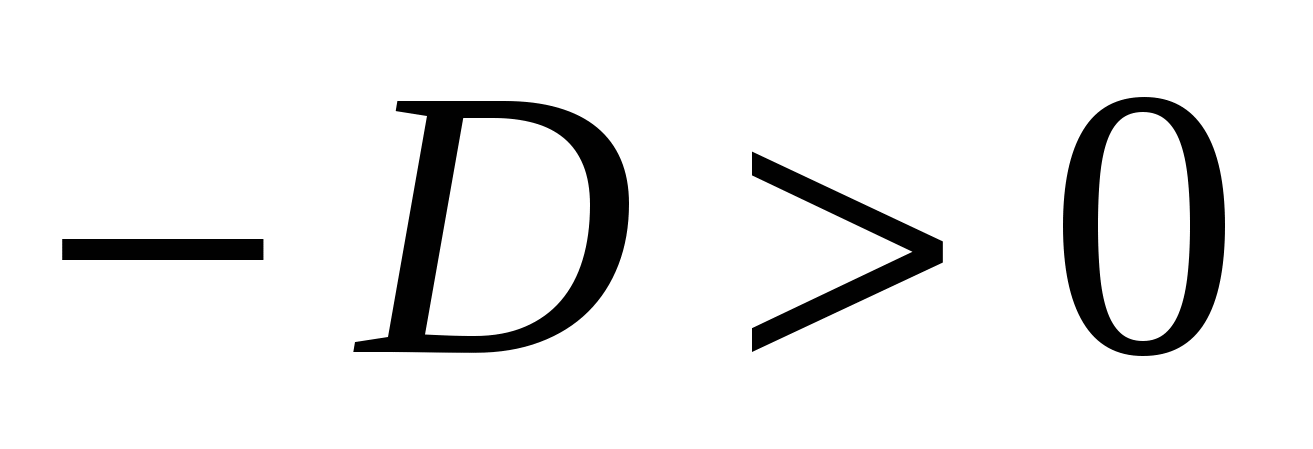 , а потому
, а потому 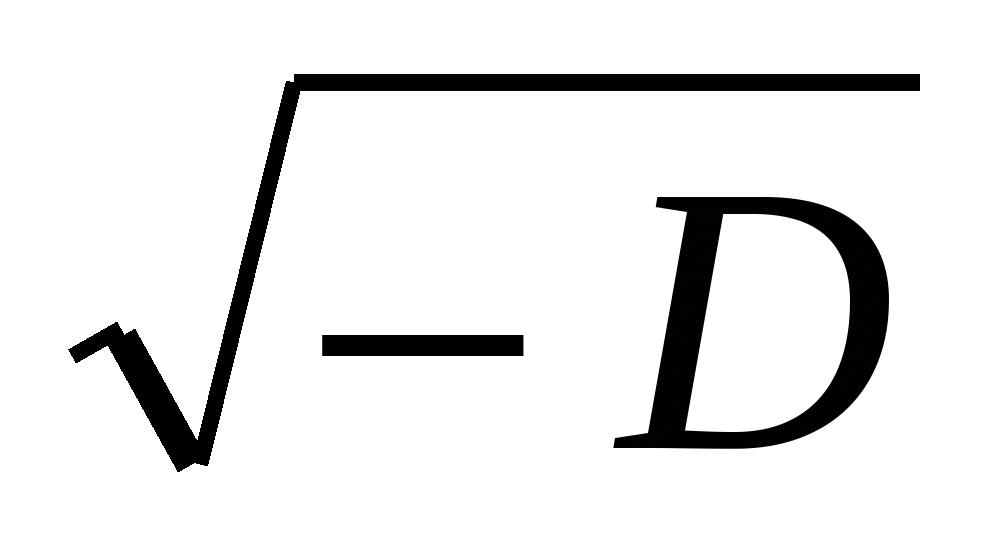 есть некоторое действительное число.
есть некоторое действительное число.
Следовательно, решениями квадратного уравнения будут два комплексно-сопряженных числа
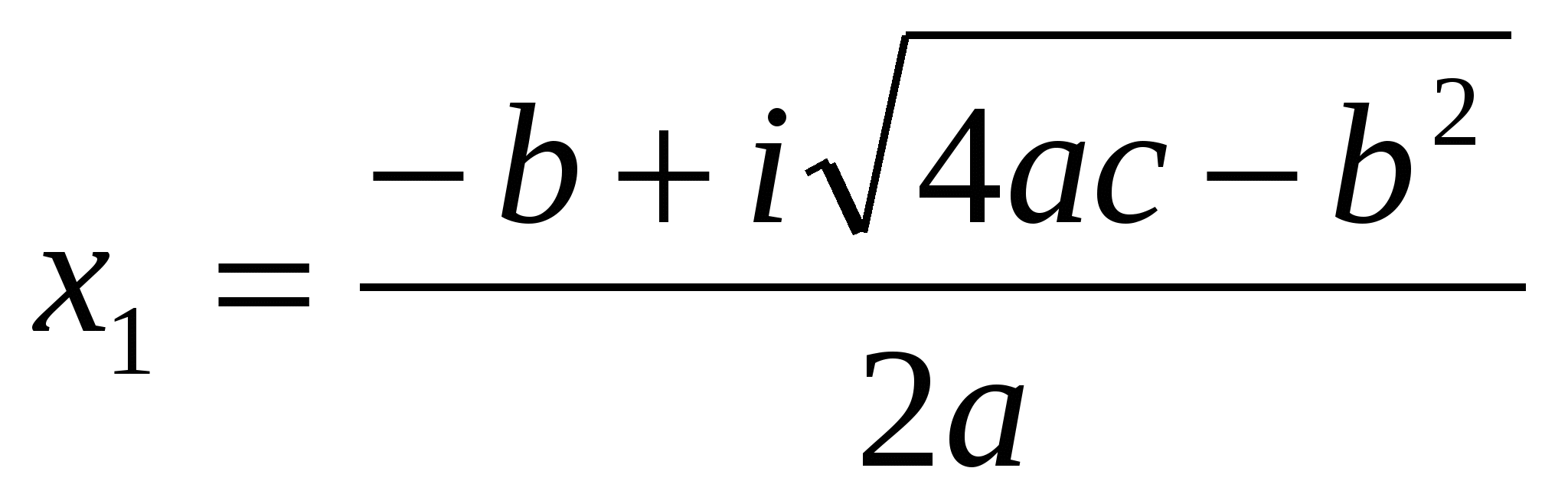 ,
, 
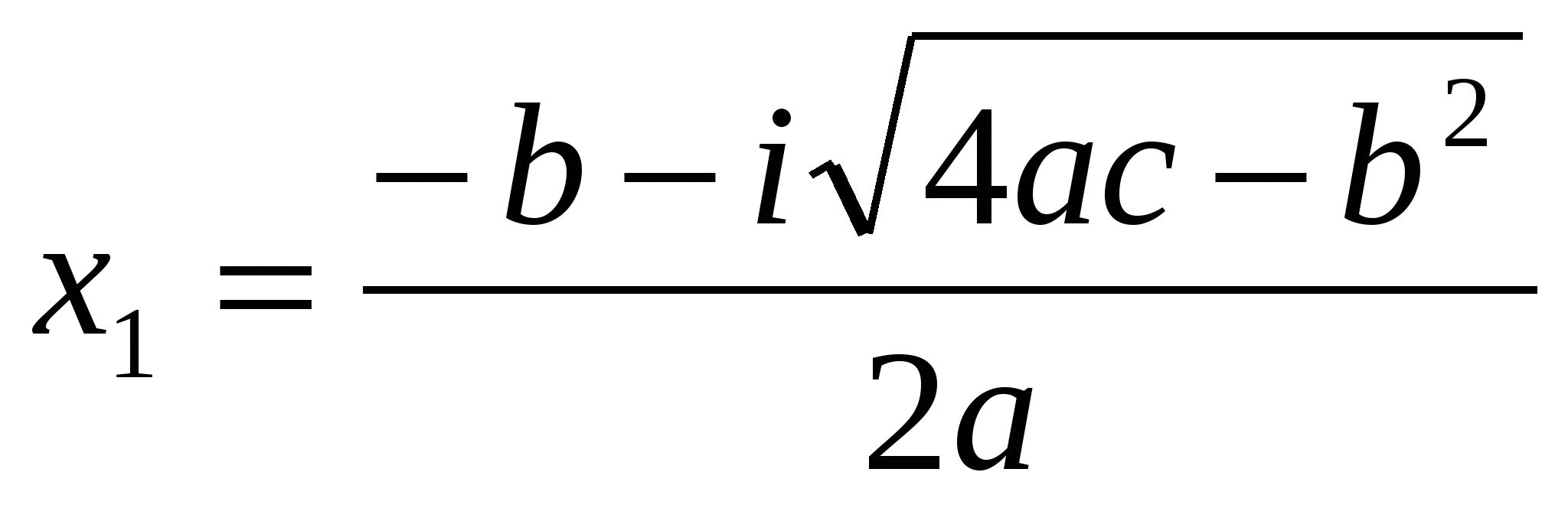 .
.
Пример 1. Решить квадратное уравнение 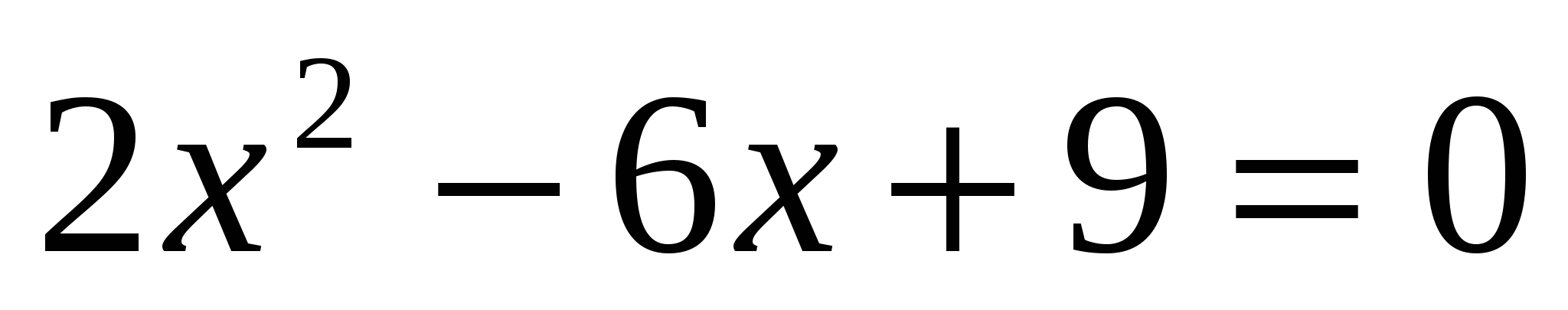 .
.
Решение. Находим:
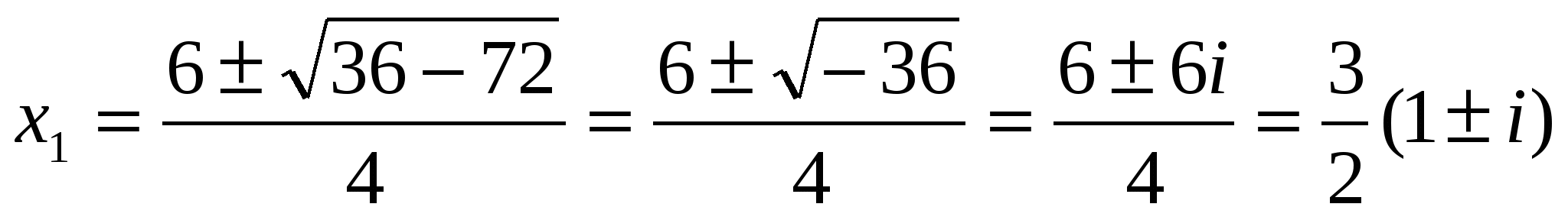 .
.
Таким образом, решениями данного квадратного уравнения будут два комплексно-сопряженных числа
![]() и
и 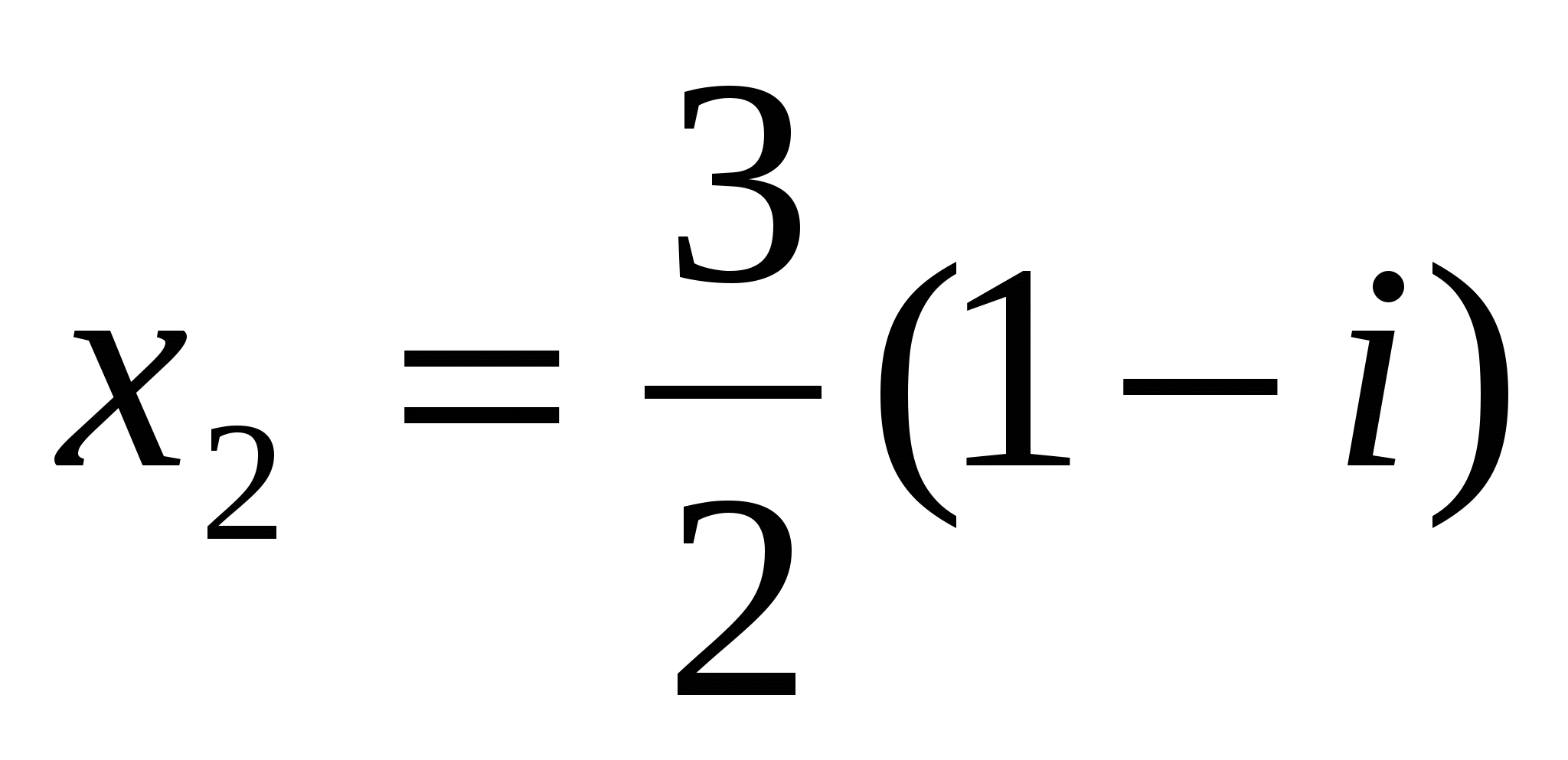 .
.
Итак, в множестве комплексных чисел любое квадратное уравнение имеет решение.
3. Действия над комплексными числами
Действия над комплексными числами определяются таким образом, чтобы для частного случая действительных чисел эти операции совпадали с известными операциями над ними.
Сумма z комплексных чисел 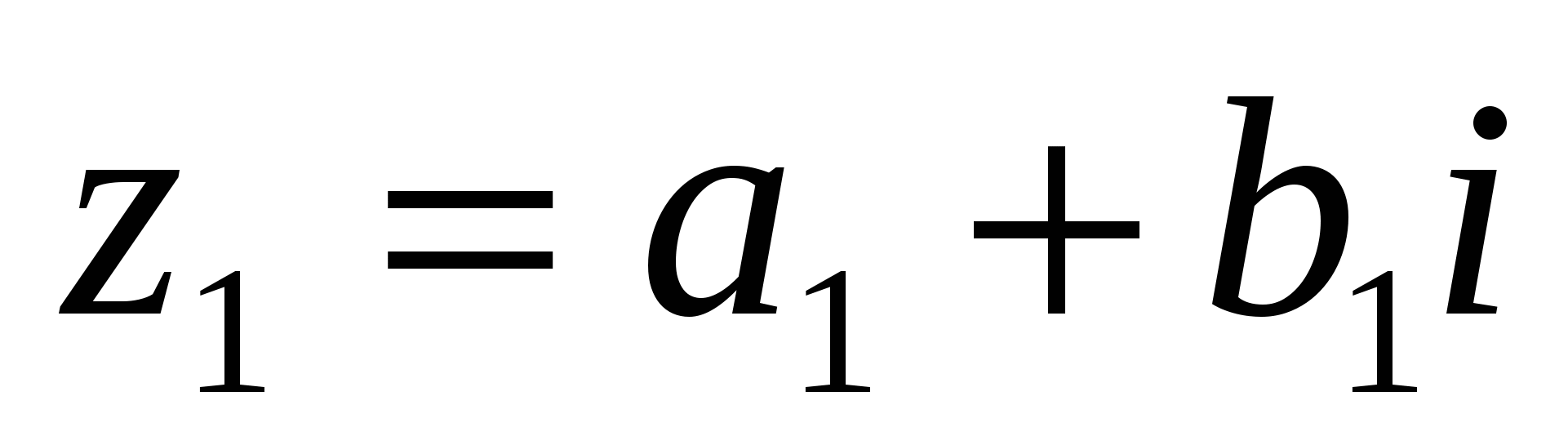 и
и 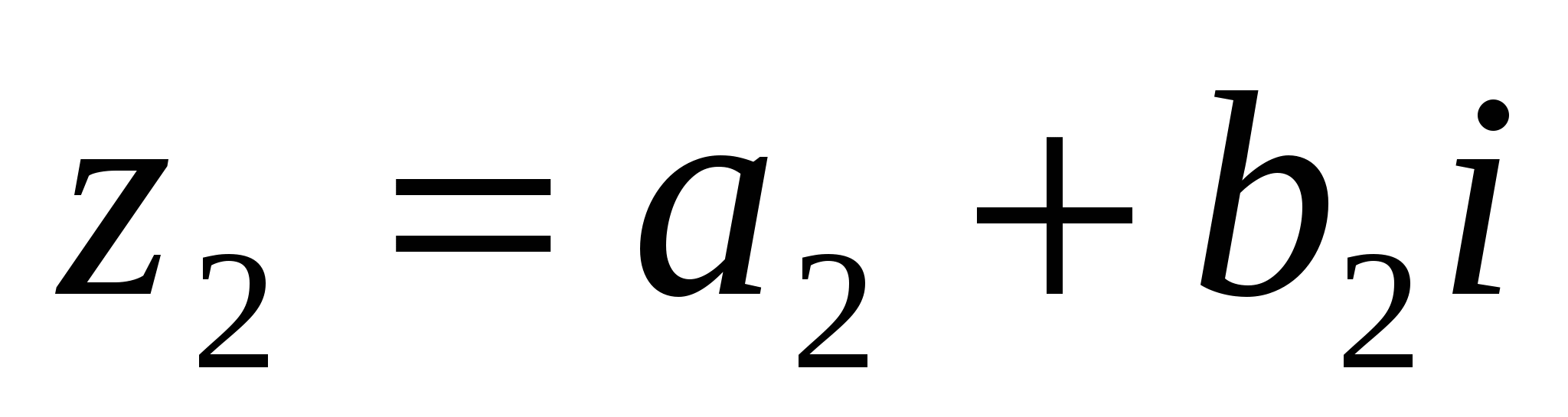 определяется как комплексное число
определяется как комплексное число 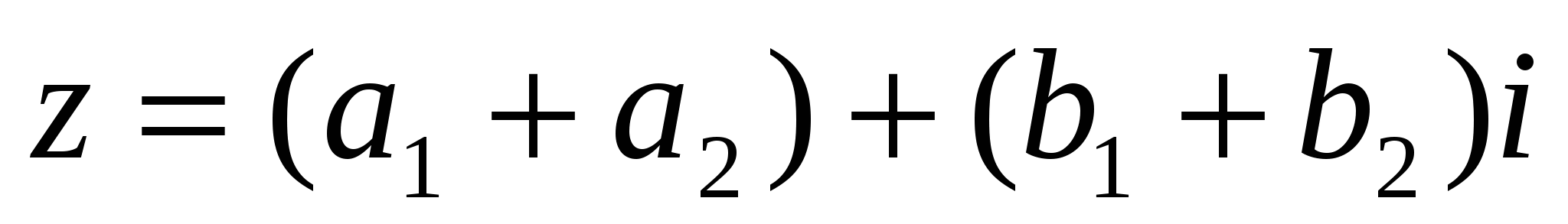 . Его обозначают
. Его обозначают 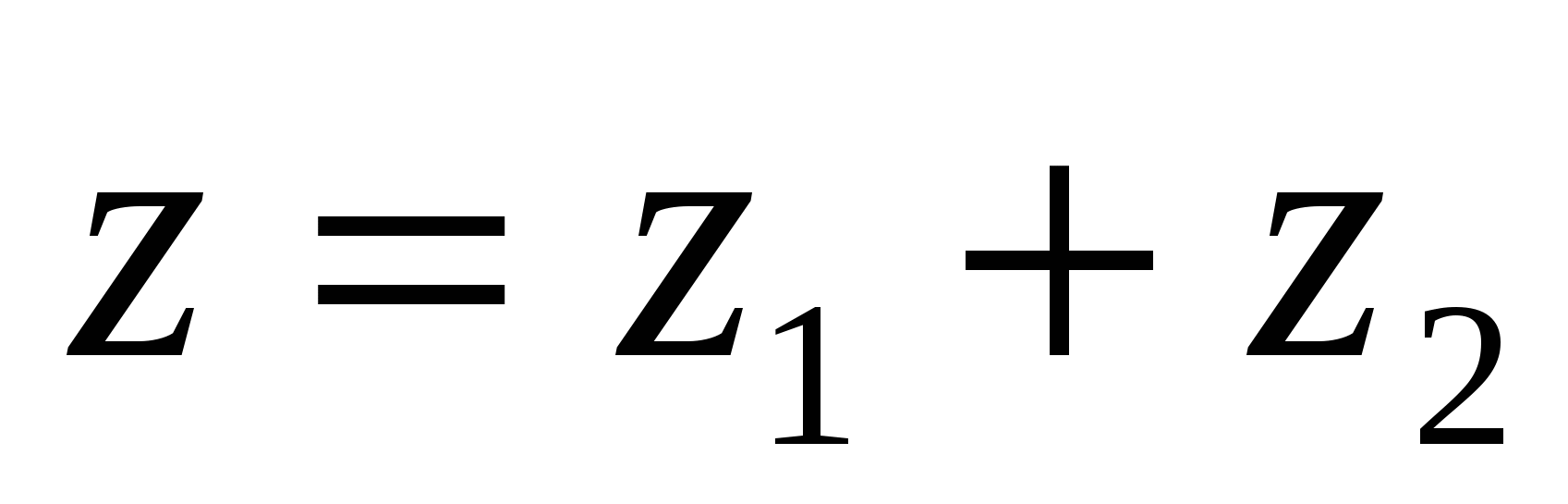 .
.
Таким образом,
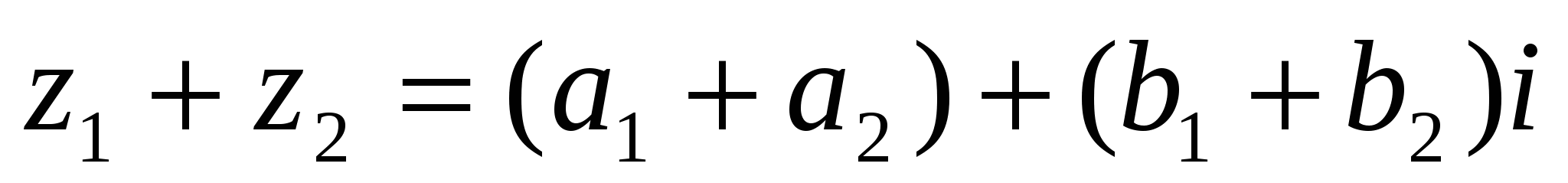 (1)
(1)
В частности, если 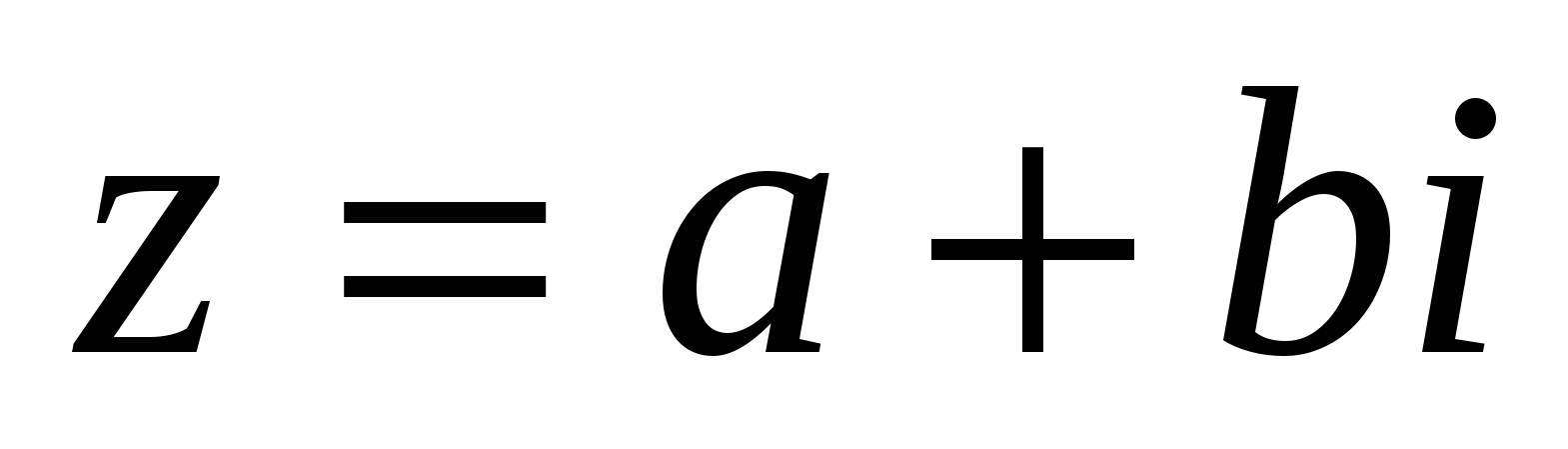 , то ,
, то , 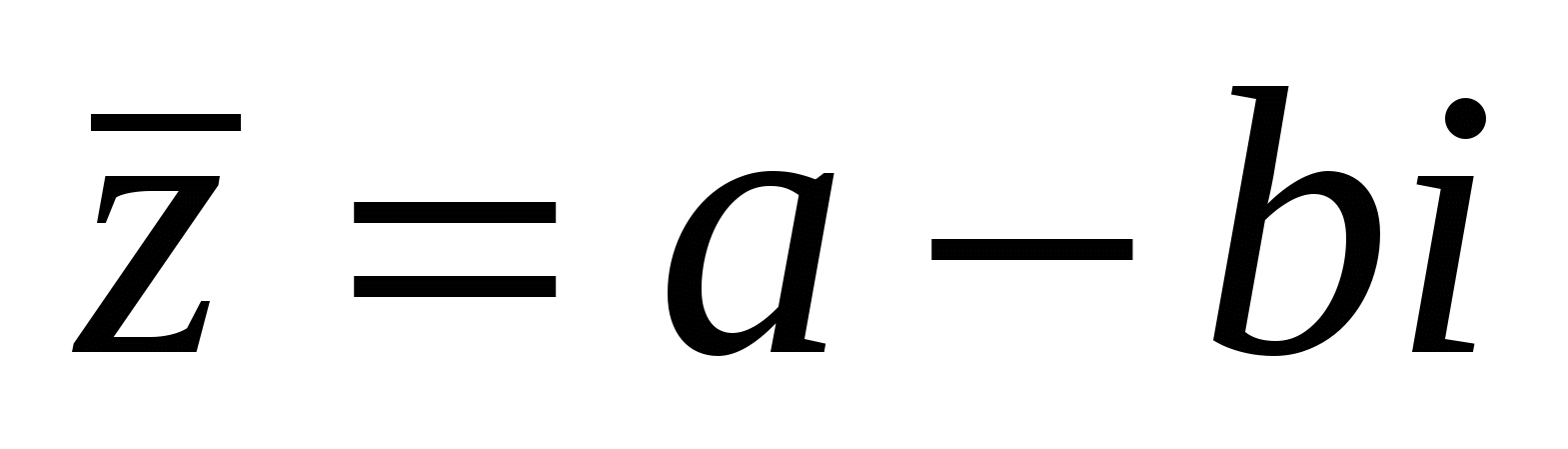 поэтому
поэтому 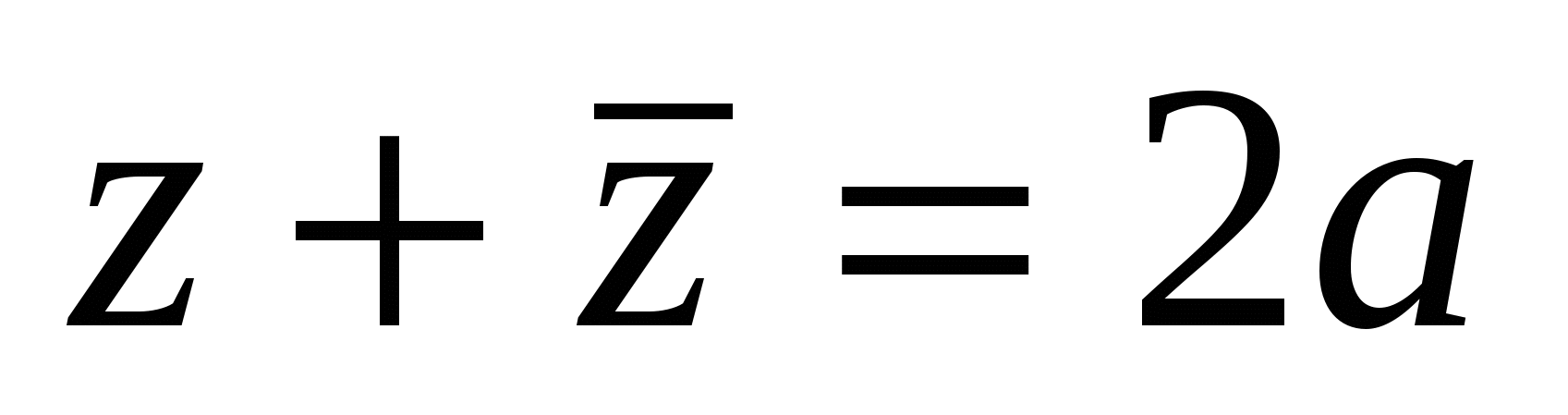 , следовательно, сумма комплексно-сопряженных чисел есть число действительное. Операцию сложения легко распространить и на сумму любого конечного числа комплексных чисел. Так, если
, следовательно, сумма комплексно-сопряженных чисел есть число действительное. Операцию сложения легко распространить и на сумму любого конечного числа комплексных чисел. Так, если
![]() ,
, 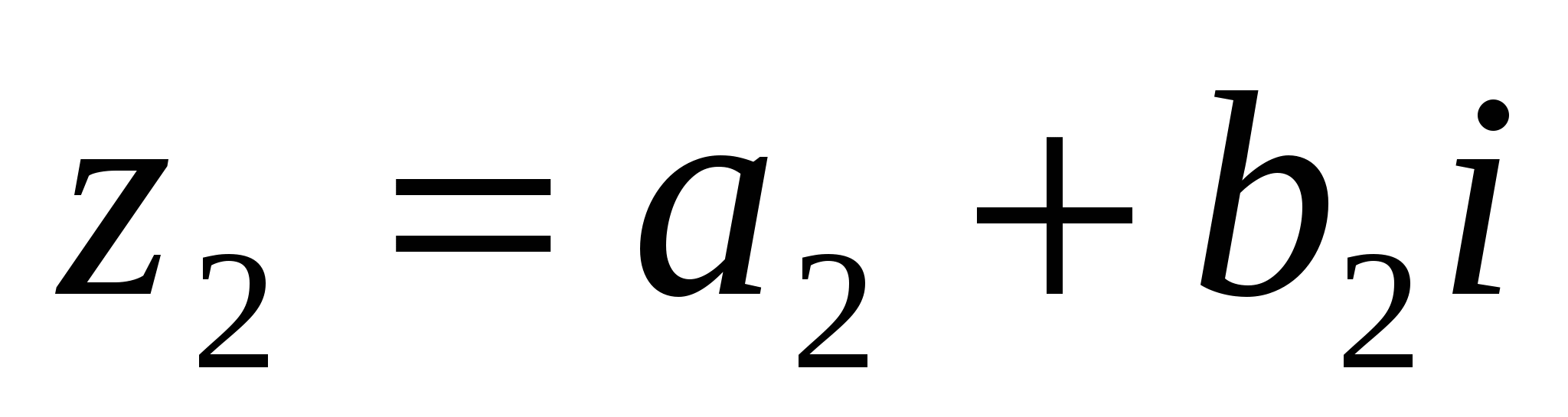 , …,
, …, 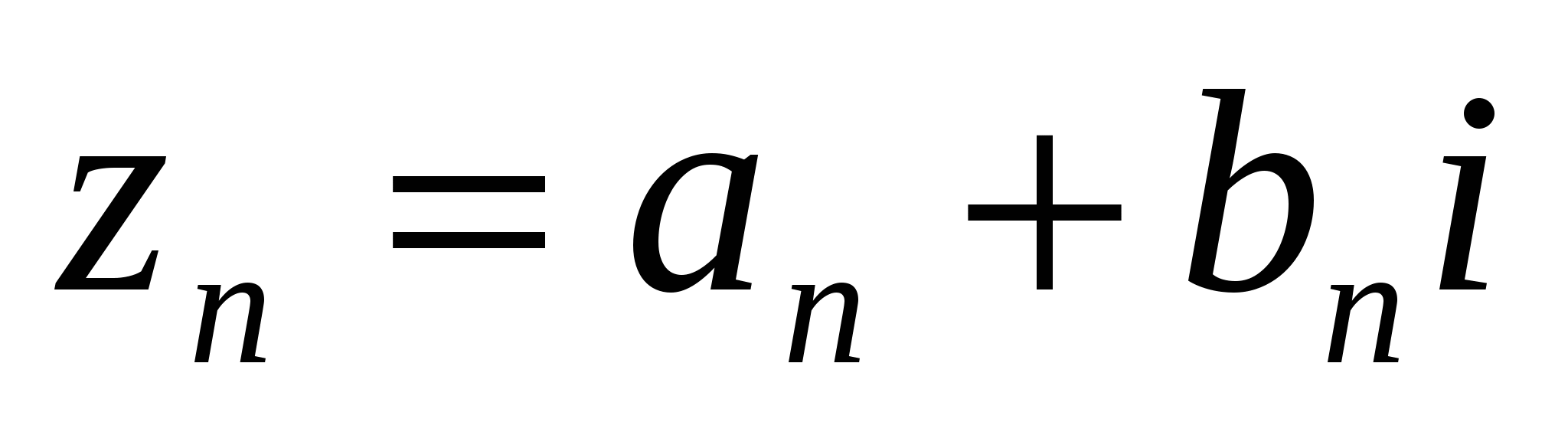
то
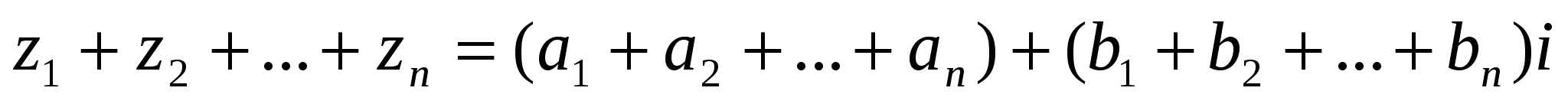 . (2)
. (2)
Пример 2. Найти комплексное число z из равенства 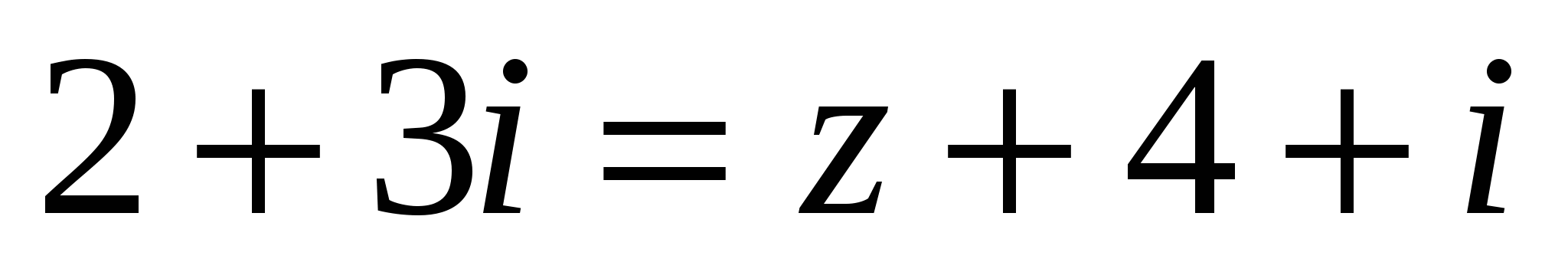 .
.
Решение. Пусть ![]() . Тогда
. Тогда 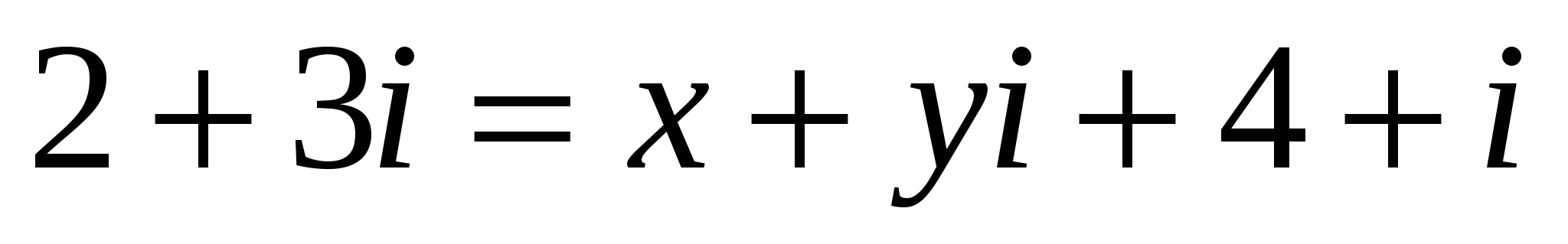
или
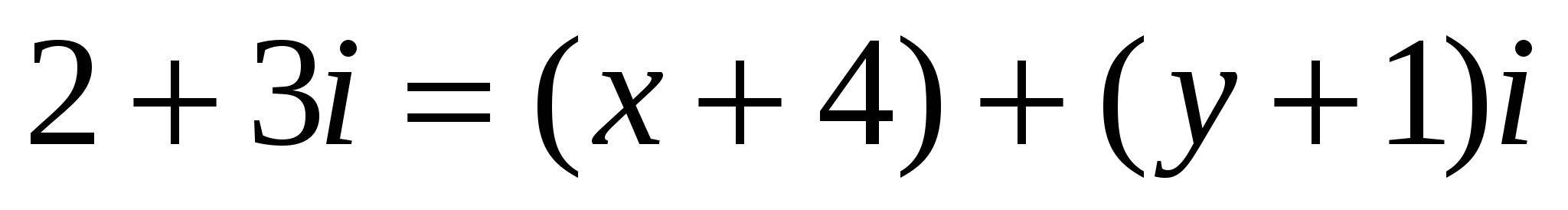 .
.
Два комплексных числа равны тогда и только тогда, когда соответственно равны их действительные и мнимые части. Следовательно,
х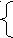 + 4 = 2;
+ 4 = 2;
у+ 1 =3.
Решив эту систему, находим х = - 2; у = 2. Таким образом, 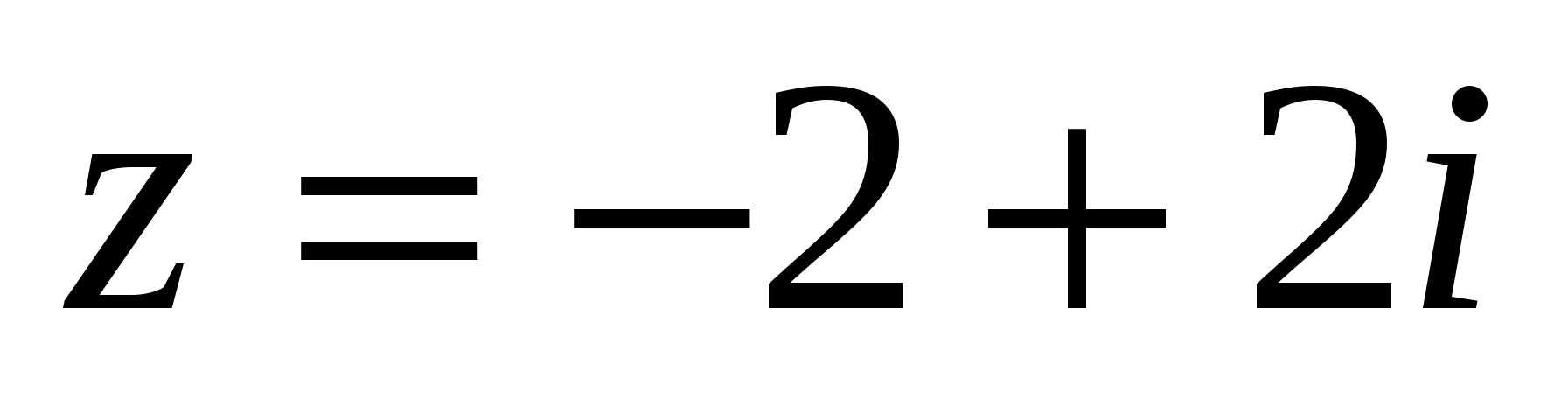 .
.
Вычитание двух комплексных чисел определяется как операция обратная сложению. Комплексное число 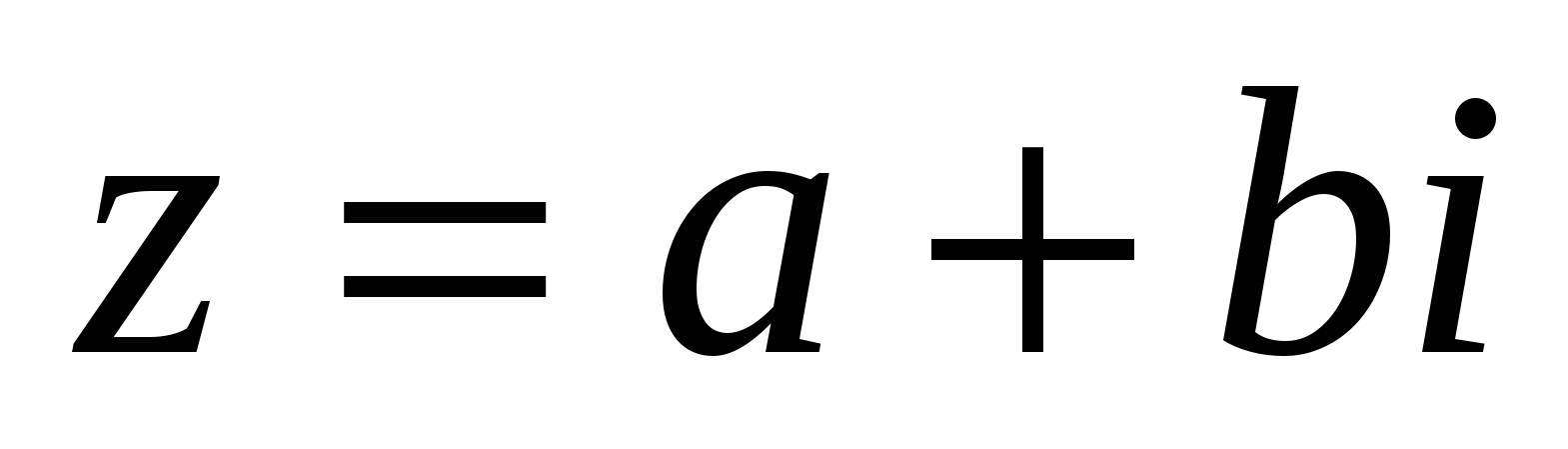 называется разностью комплексных чисел
называется разностью комплексных чисел 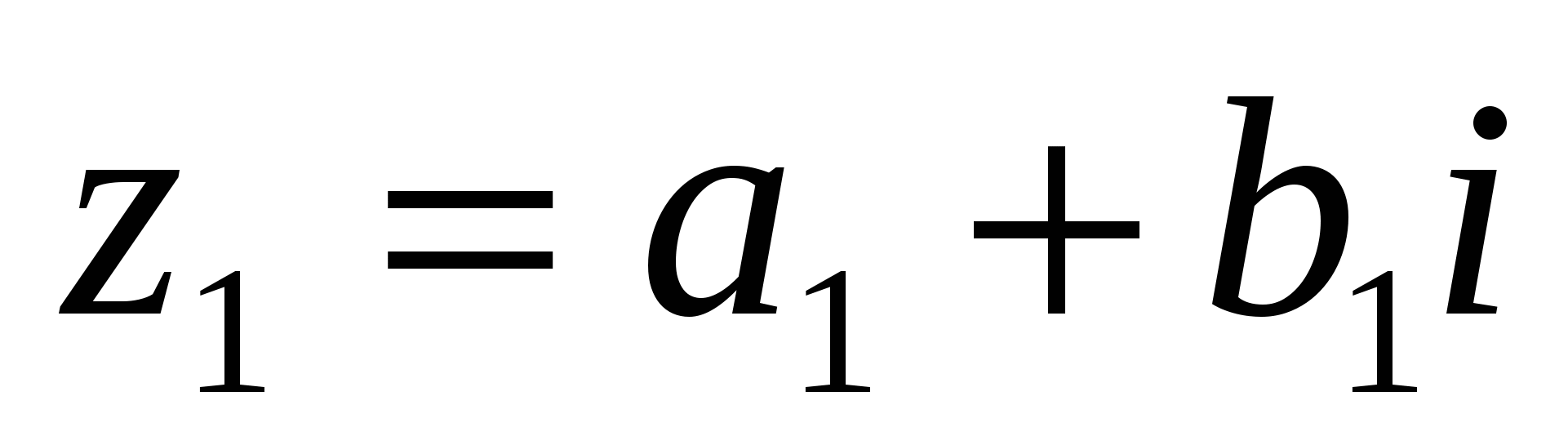 и
и 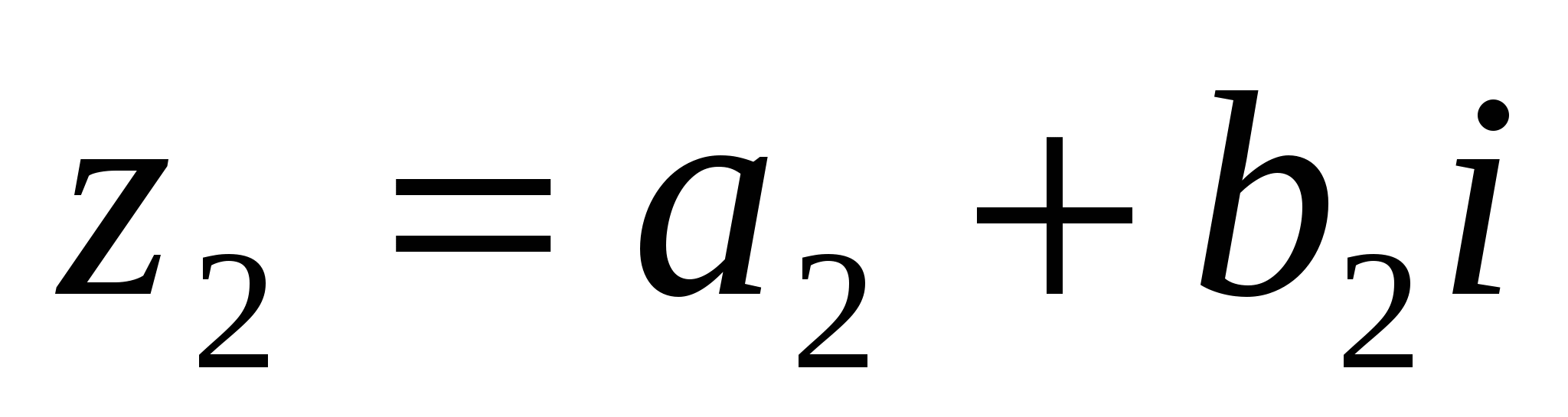 , если
, если 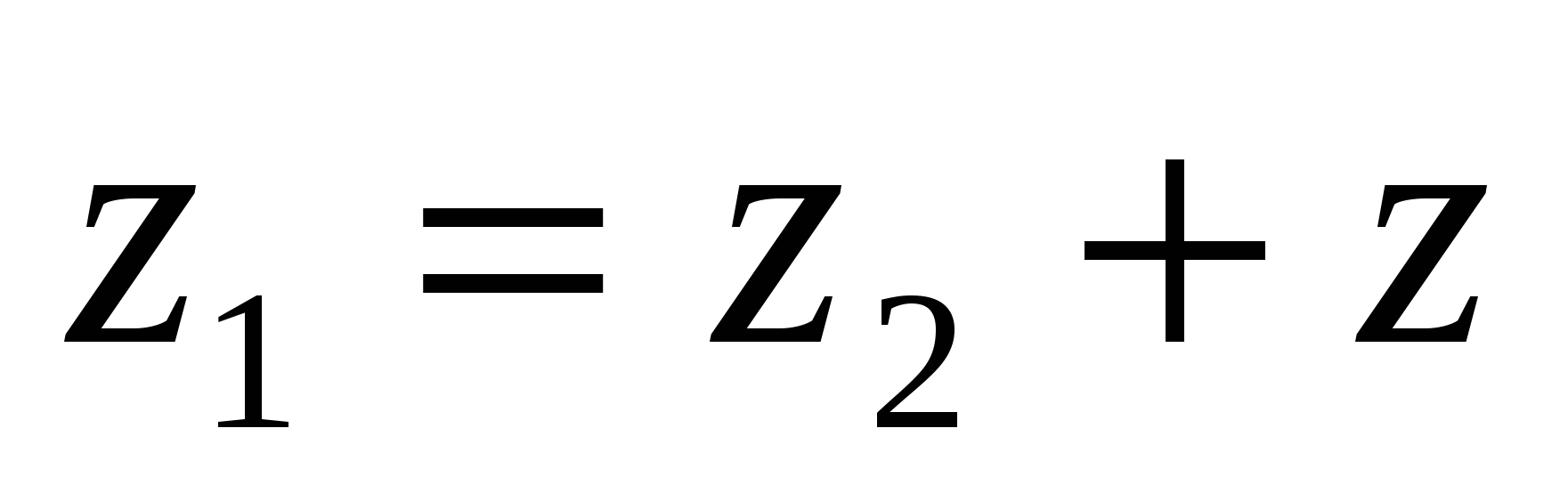 .
.
Разность комплексных чисел z1 и z2, обозначается z1- z2-
Из определения следует, что
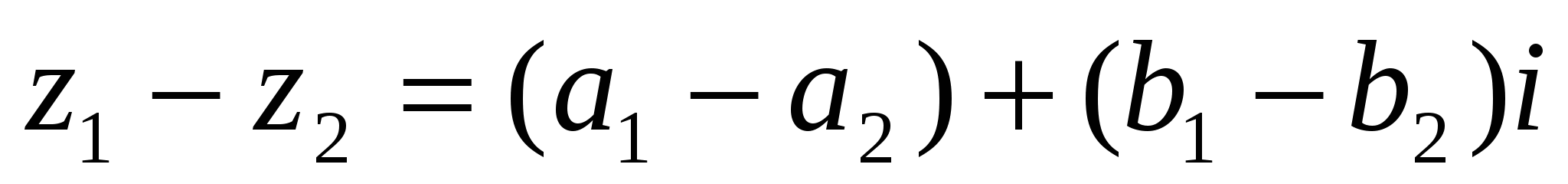 (3)
(3)
В частности,
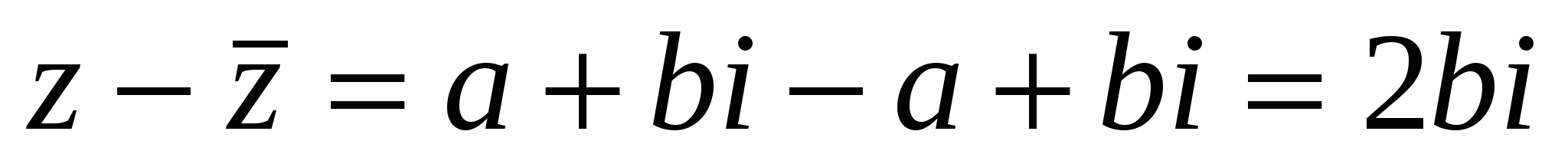 .
.
Умножение двух комплексных чисел 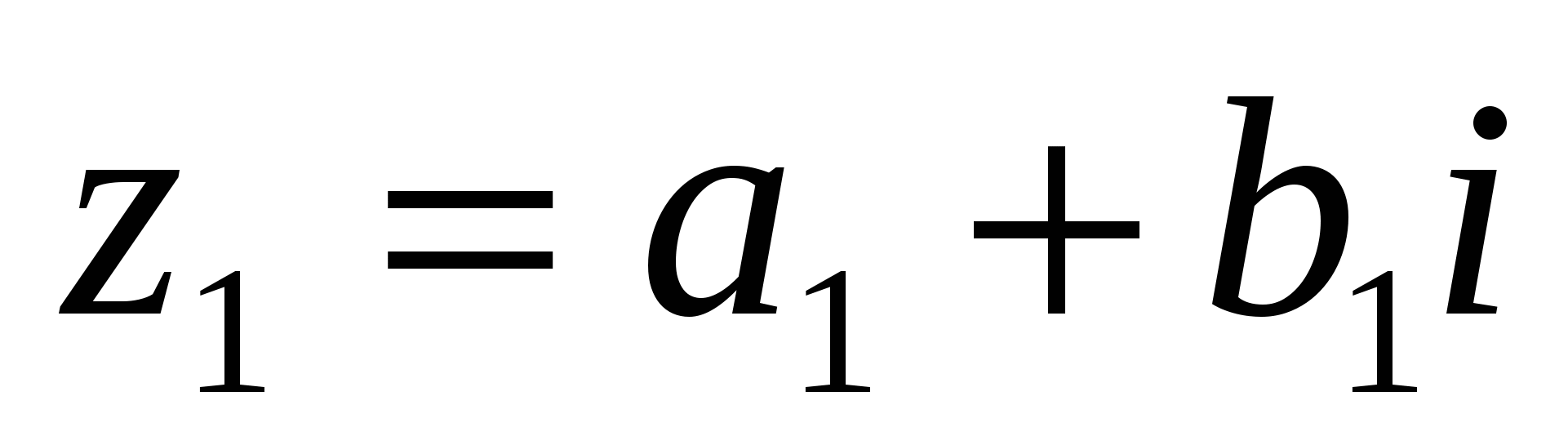 и
и 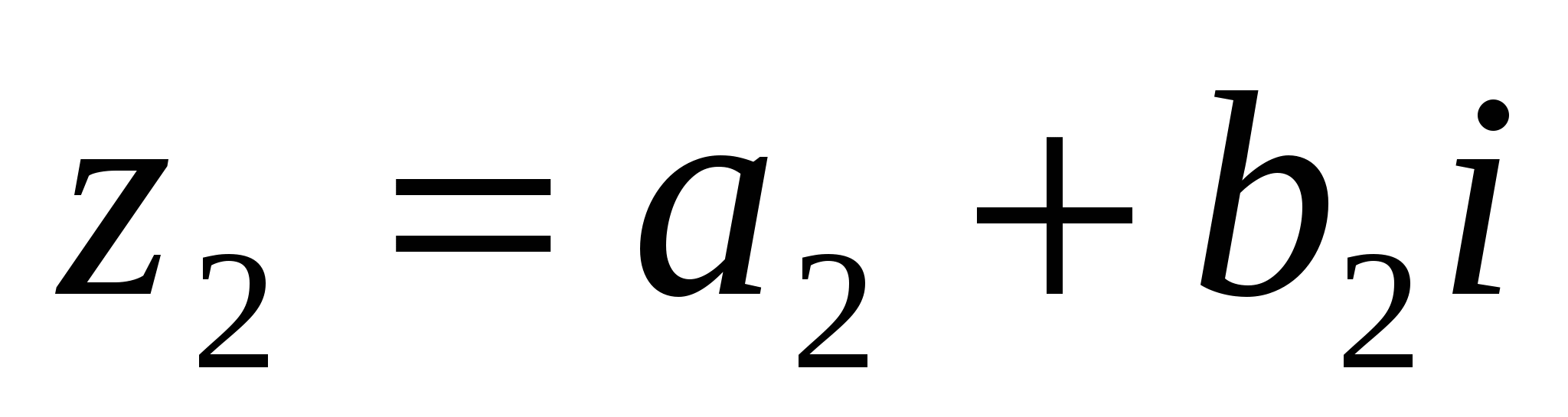 определяется следующим образом:
определяется следующим образом:
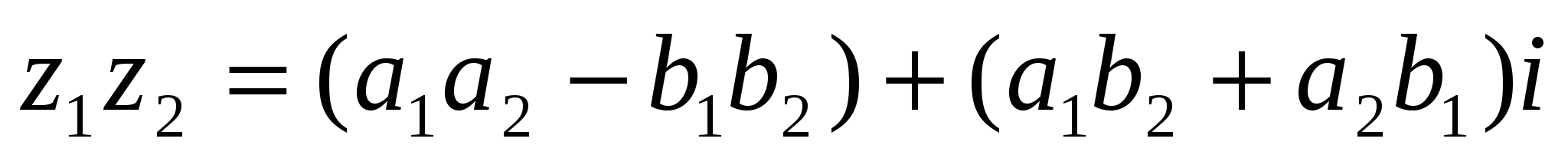 . (4)
. (4)
Отсюда следует, что два комплексных числа z1 = а + b и z2 = с - di можно умножать по правилу умножения многочленов при условии, что i2 = −1.В самом деле,
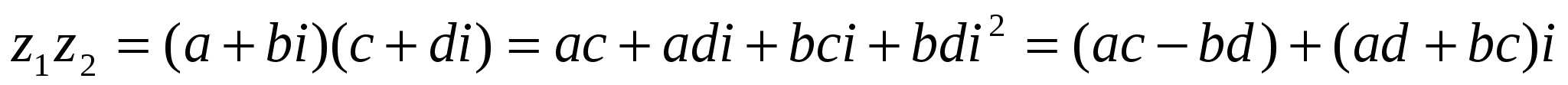
(сравните результат с определением (1)). В частности, если 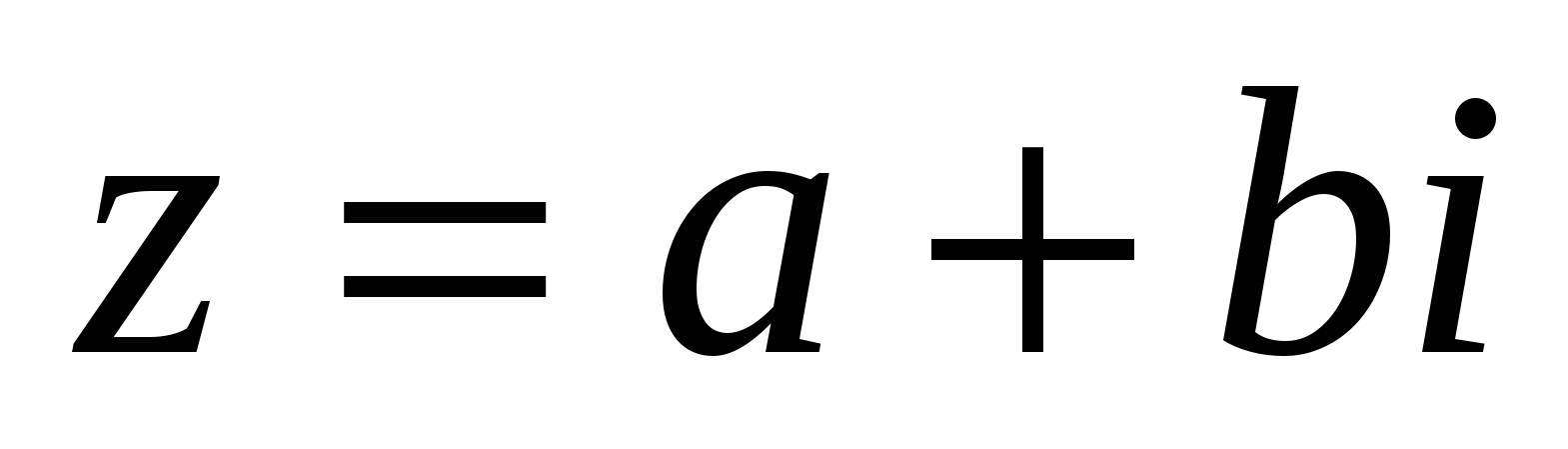 то
то 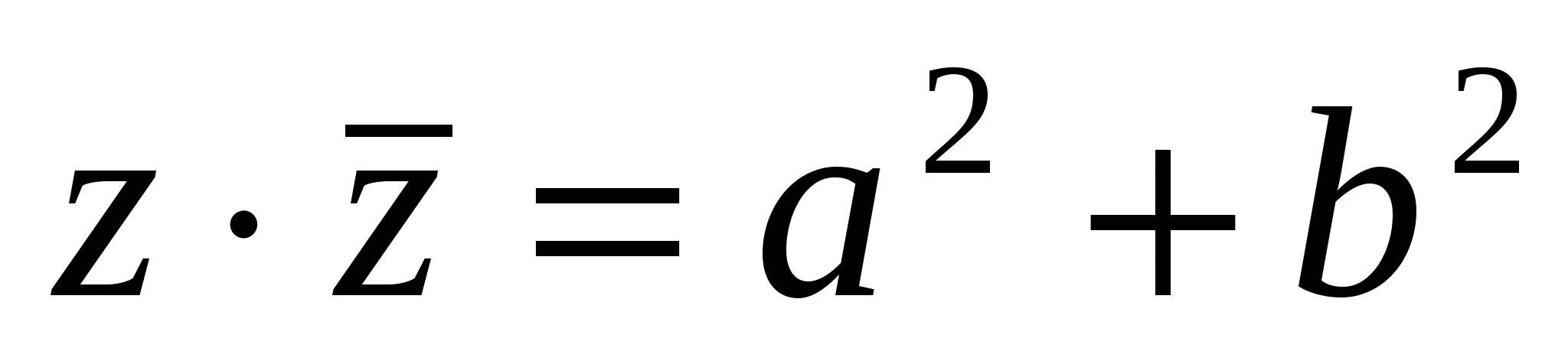 .
.
Пример 3. Найти произведение комплексных чисел 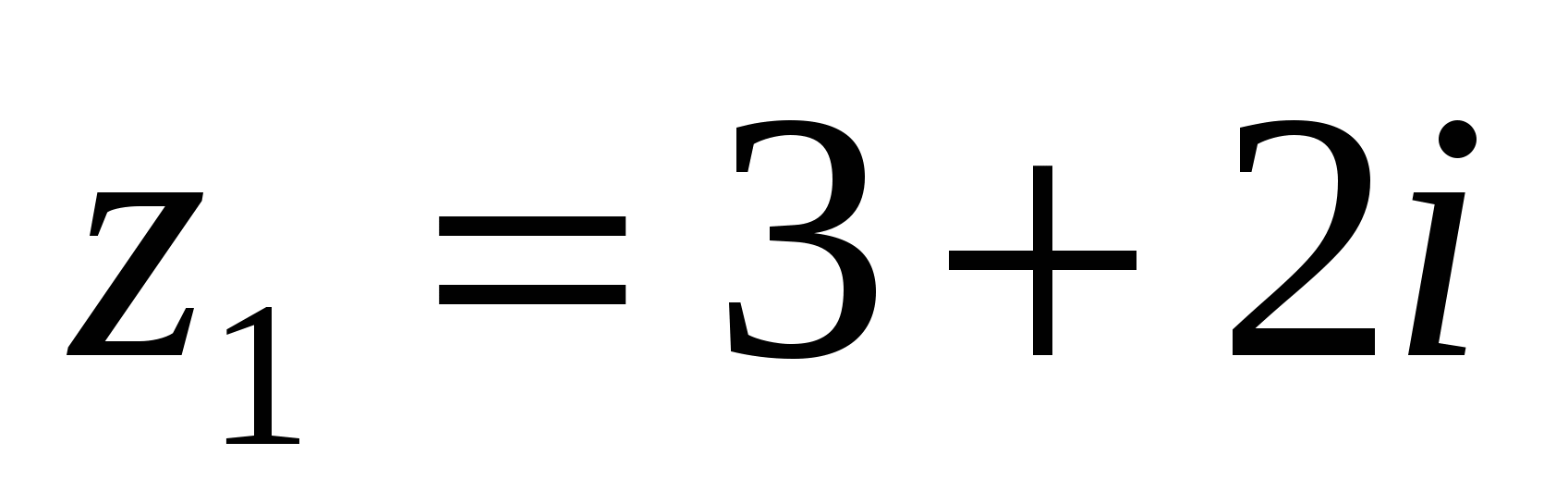 и
и 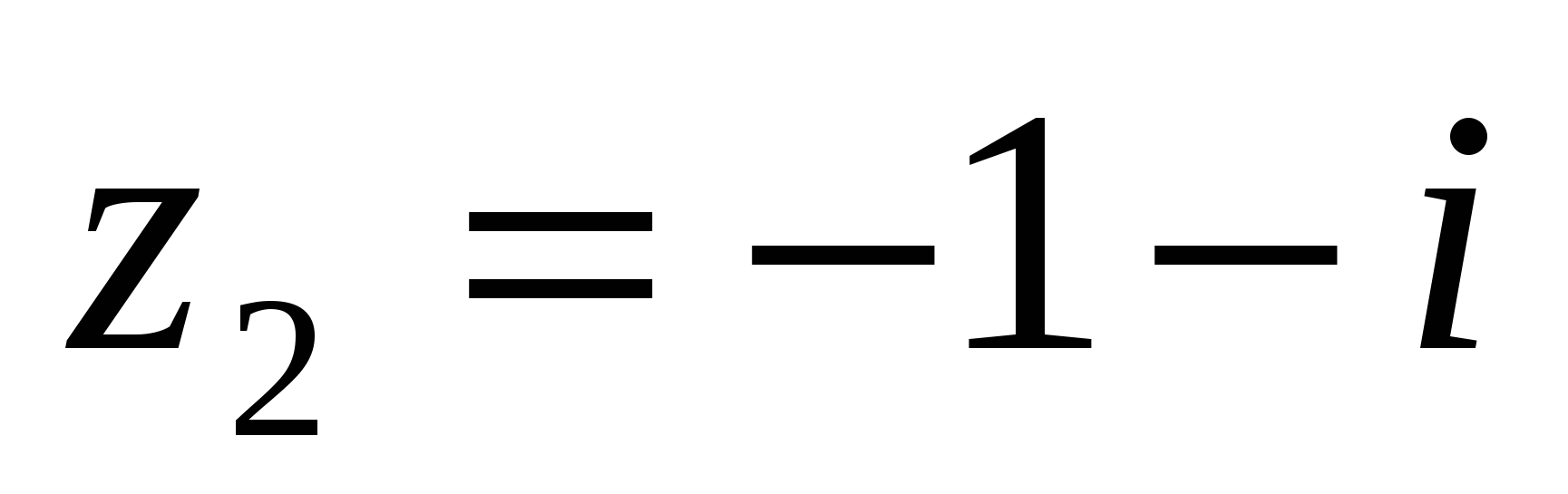
Решение. Очевидно, что 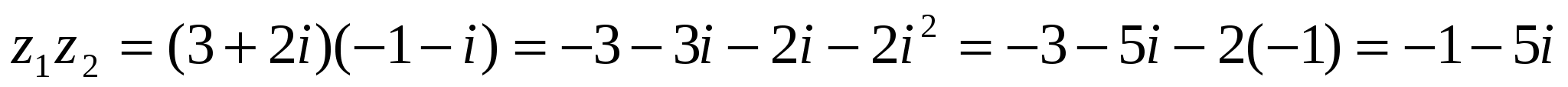
Деление вводится как действие, обратное умножению. Частным от деления комплексного числа 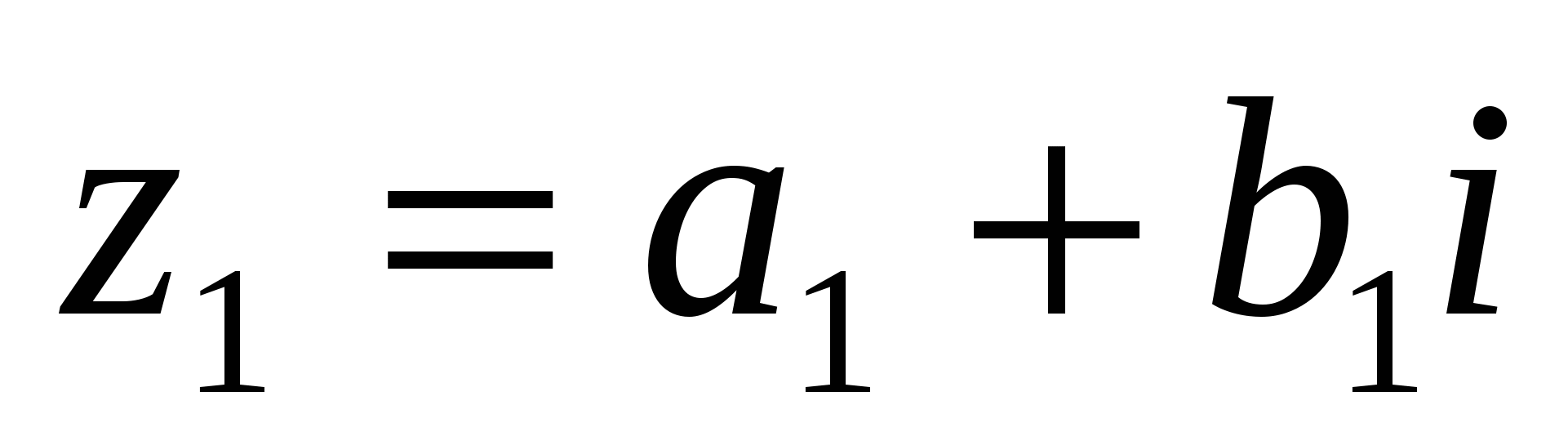 на число
на число ![]() называется комплексное число
называется комплексное число 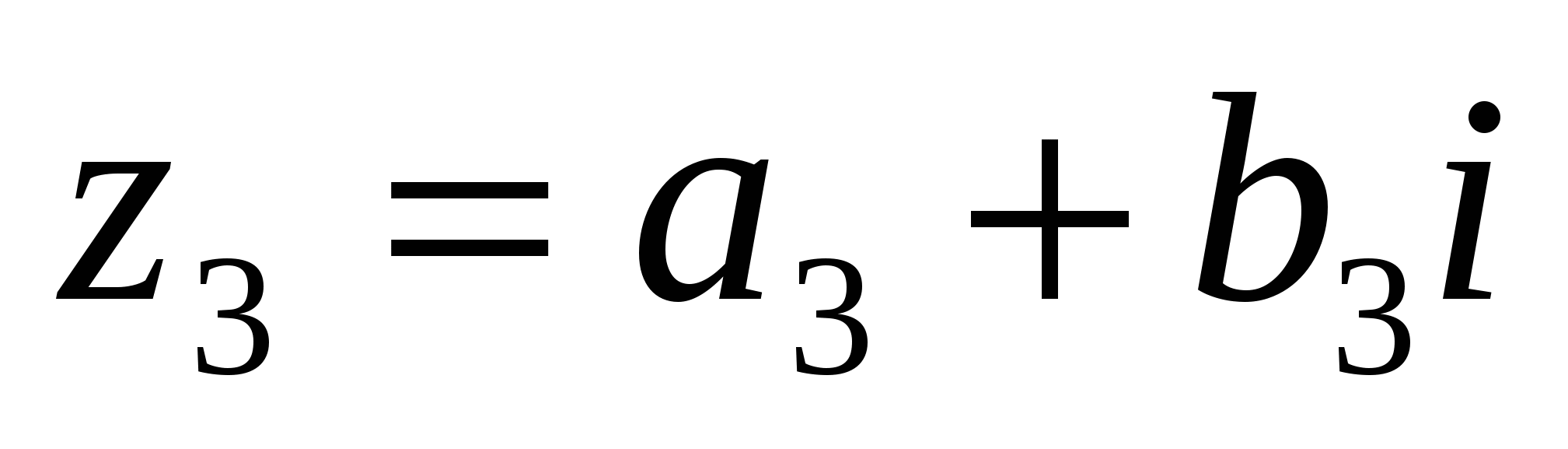 такое, что
такое, что ![]() , т. е.
, т. е.
а1+ b1 i = (a3+ b3 i)∙(a2+b2 i).
Отсюда на основании равенства (4.4) получаем:
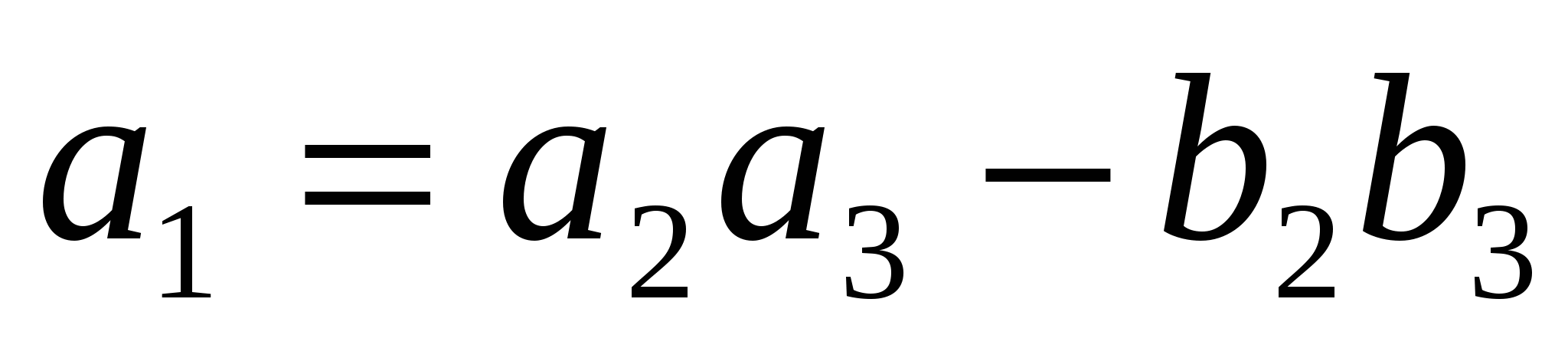 ;
; 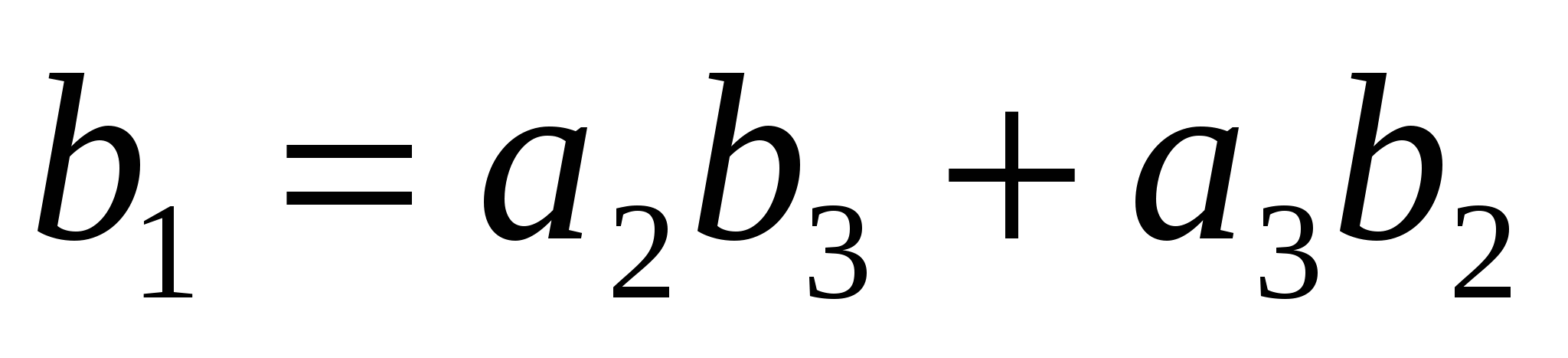 . (5)
. (5)
Решая систему уравнений (5) относительно а3 и b3 находим:
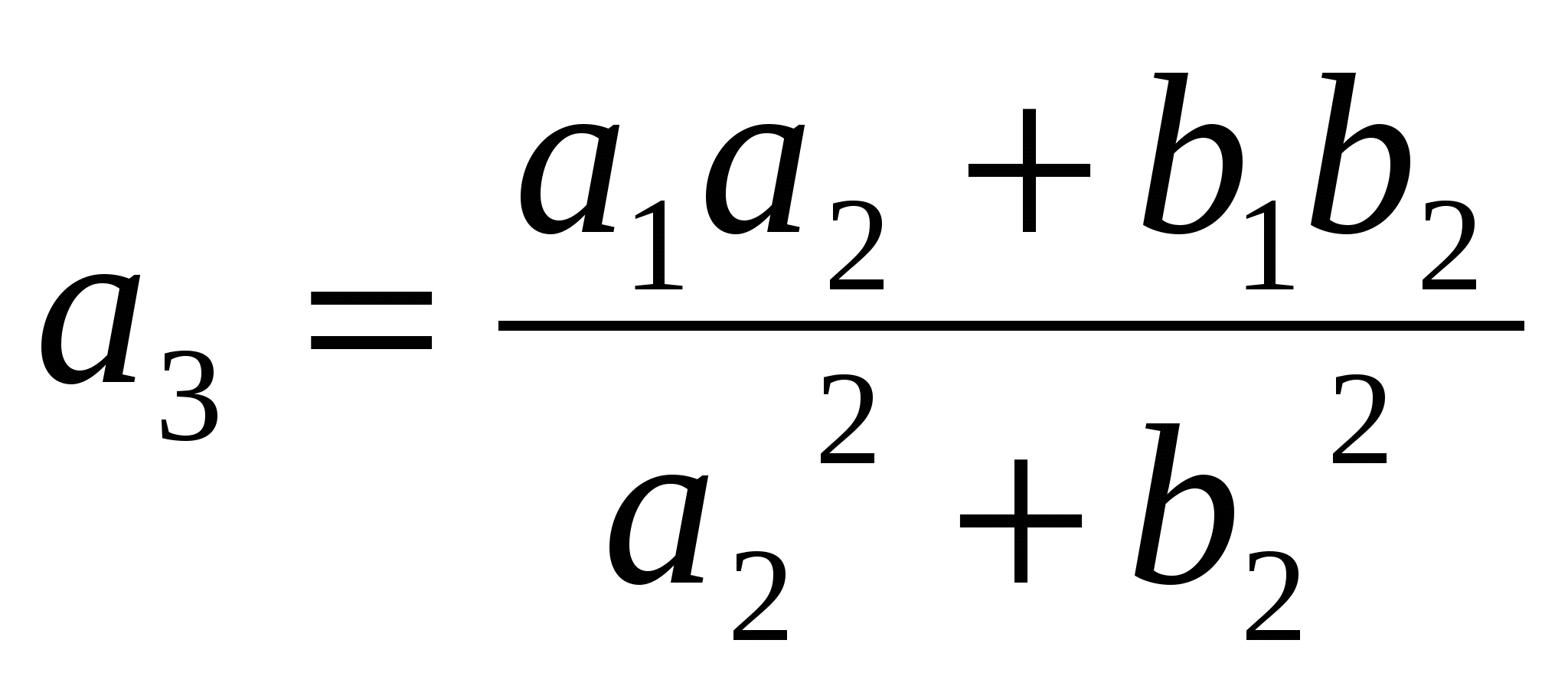 ,
, 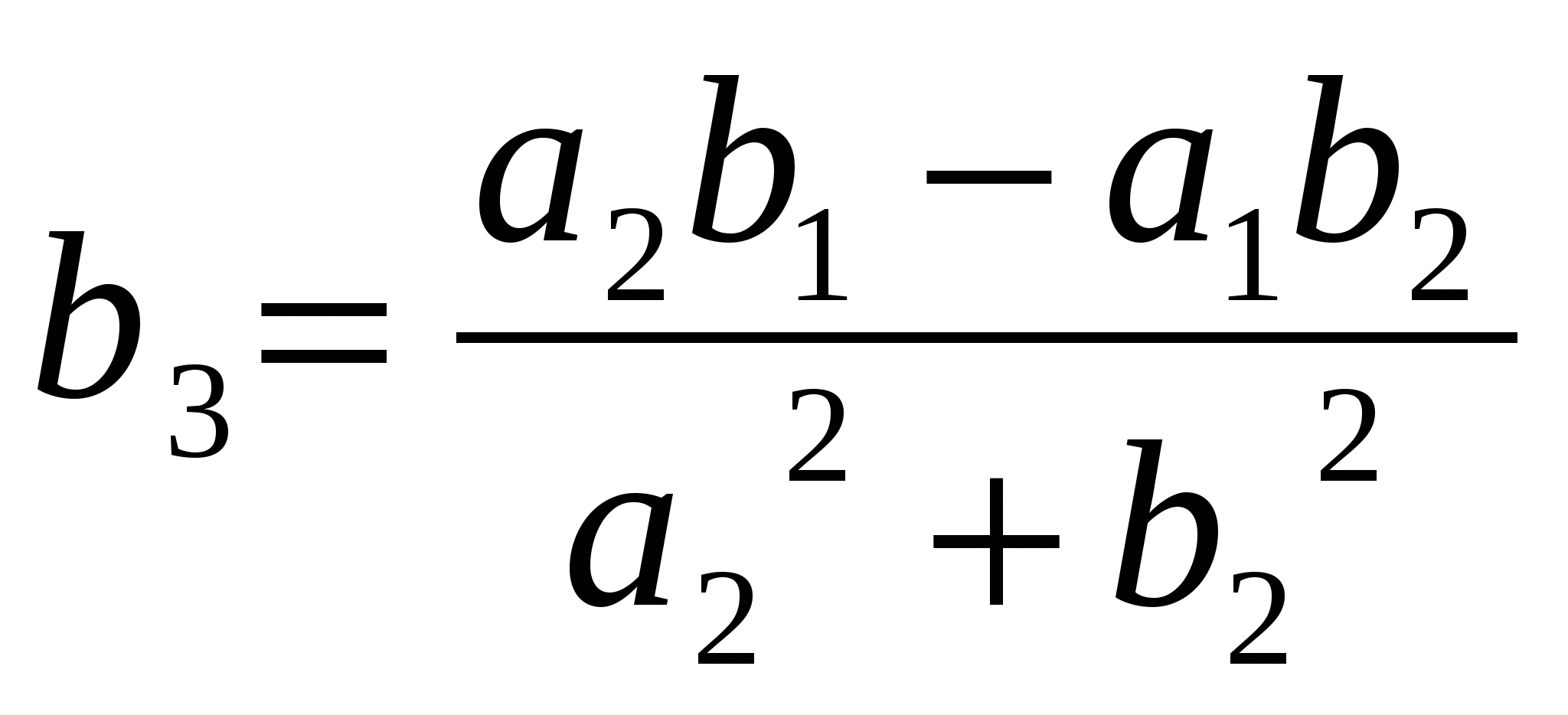 ,
,
причем,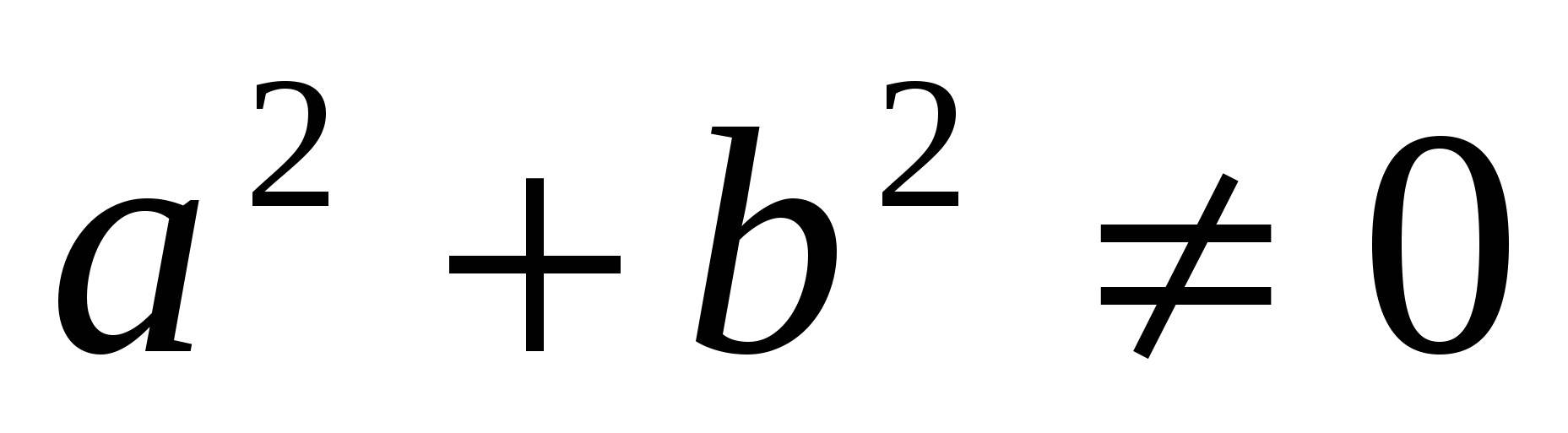 , так как по условию
, так как по условию 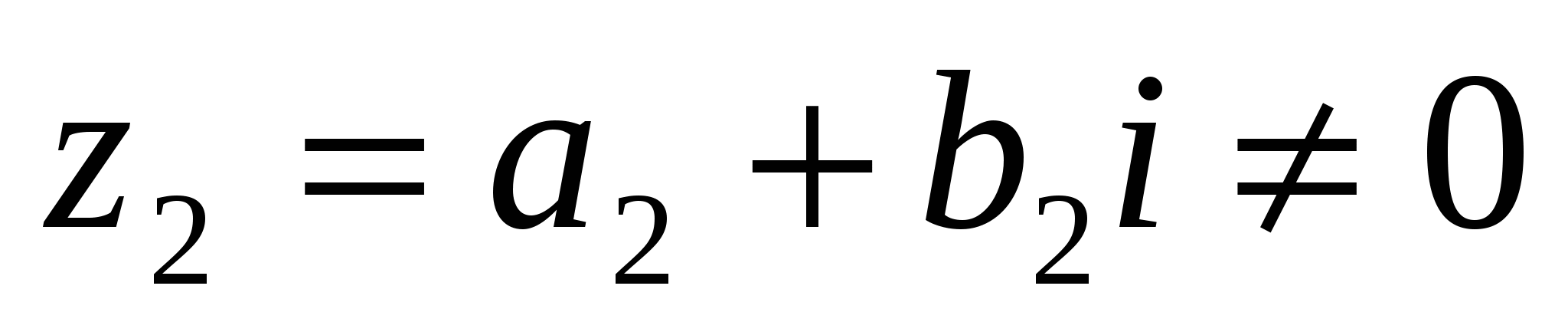 . Таким образом
. Таким образом
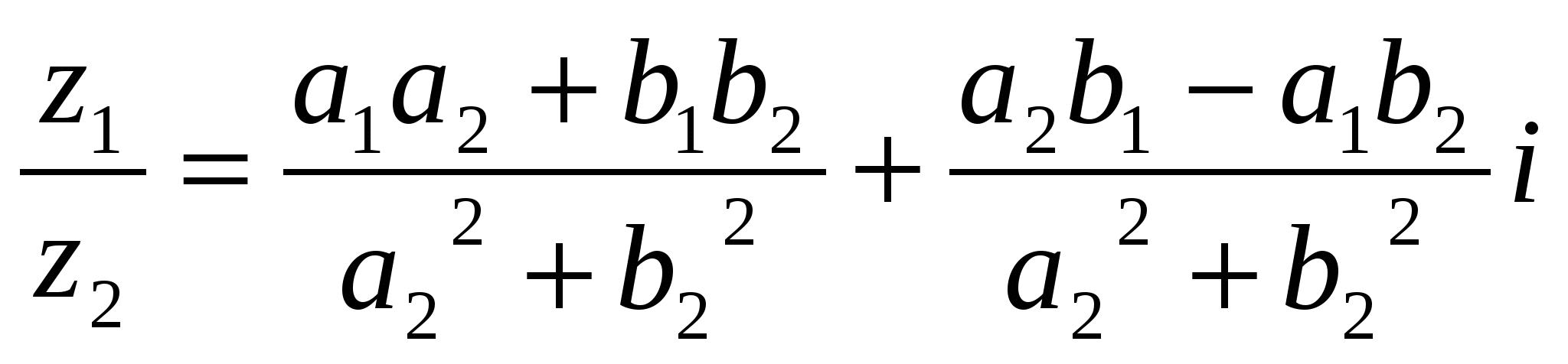 . (6)
. (6)
Равенство (6) можно получить путем умножения числителя и знаменателя дроби 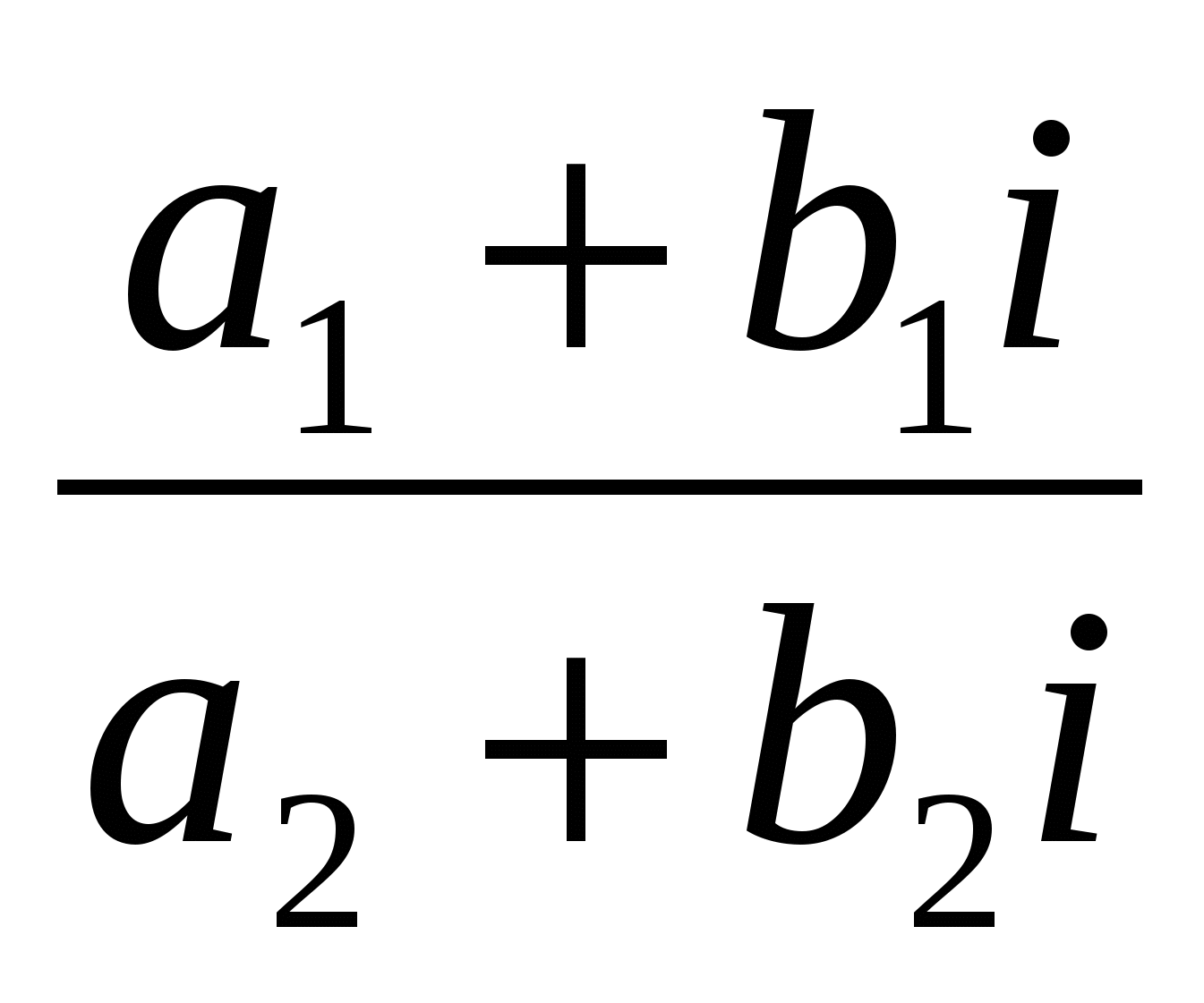 на число, комплексно-сопряженное знаменателю.
на число, комплексно-сопряженное знаменателю.
Пример 3. Найти частное от деления комплексного числа 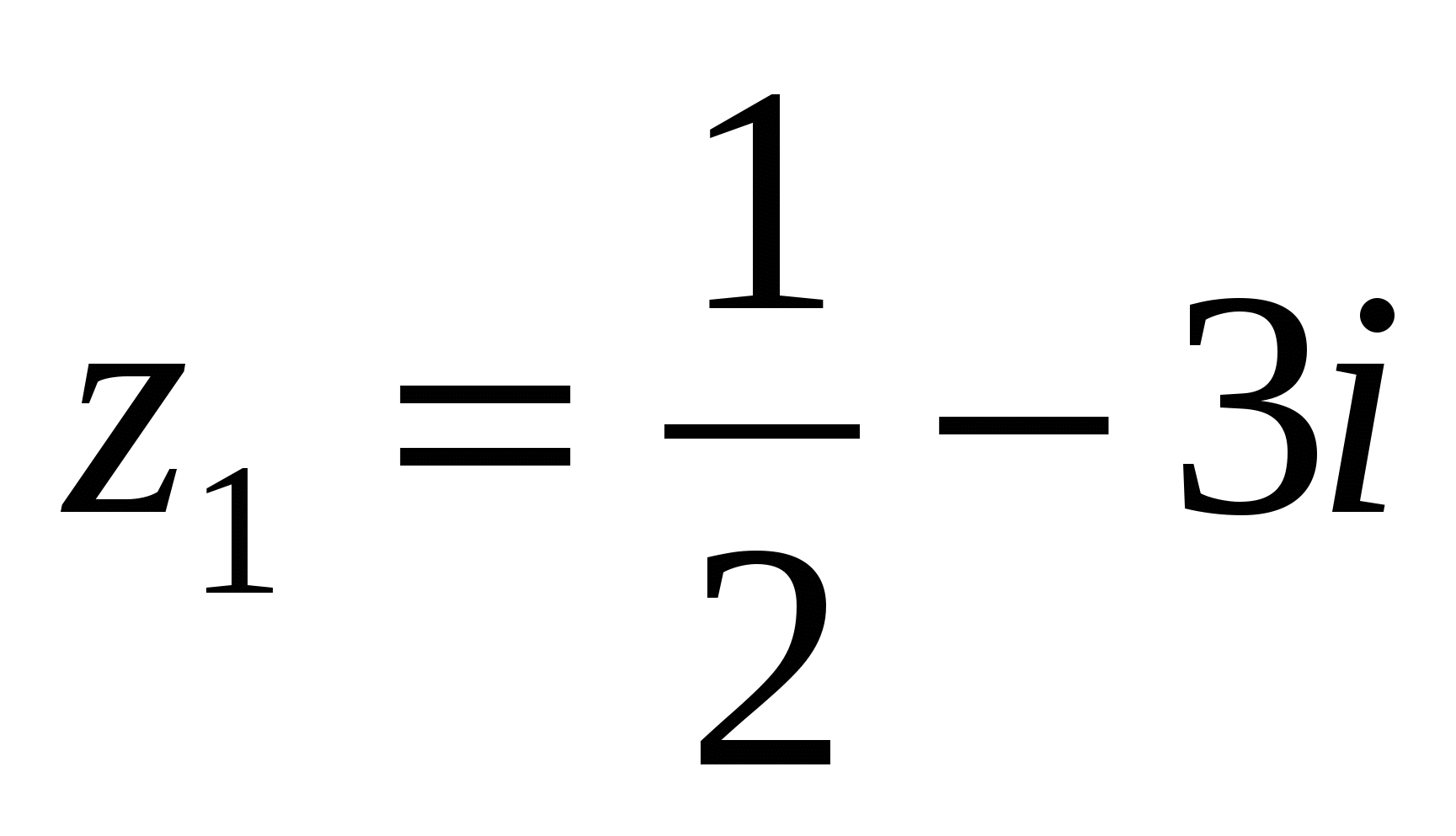 на число
на число 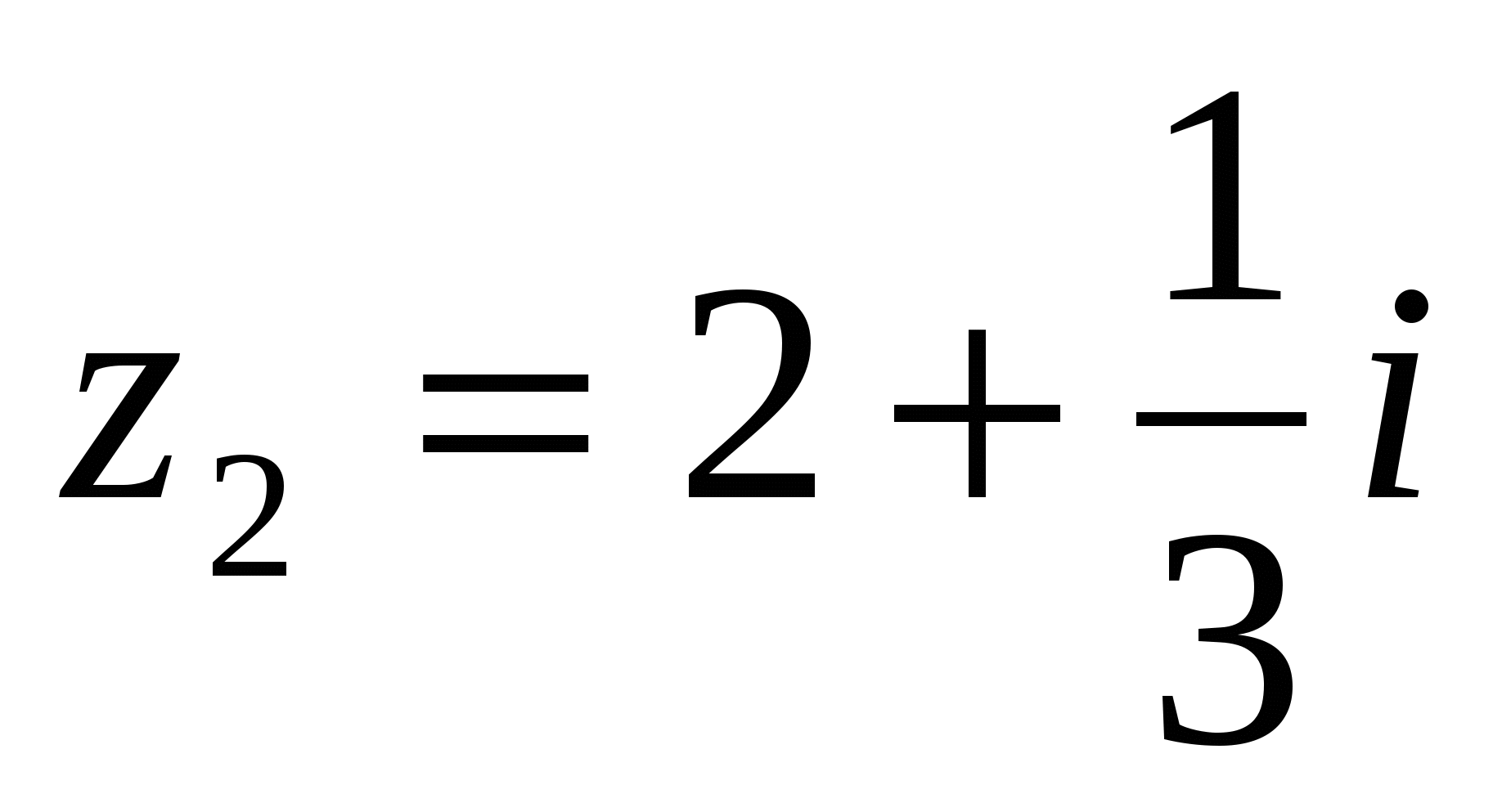 .
.
Решение. Очевидно, что
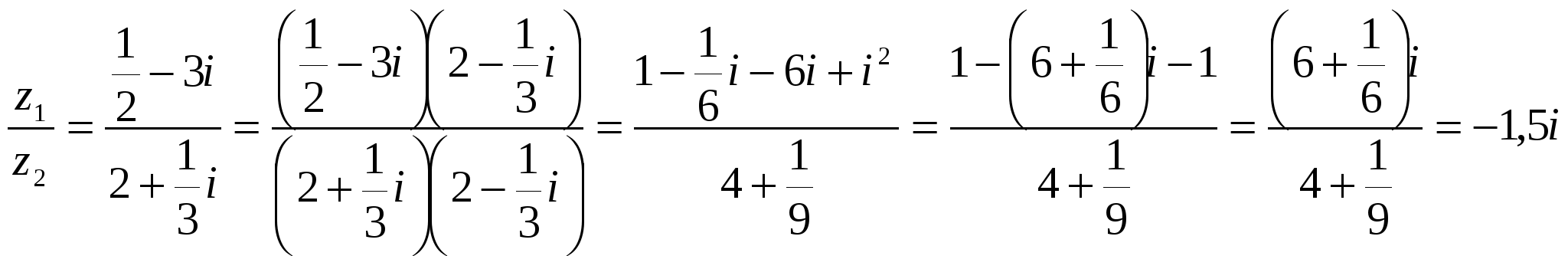 .
.
Возведение комплексного числа 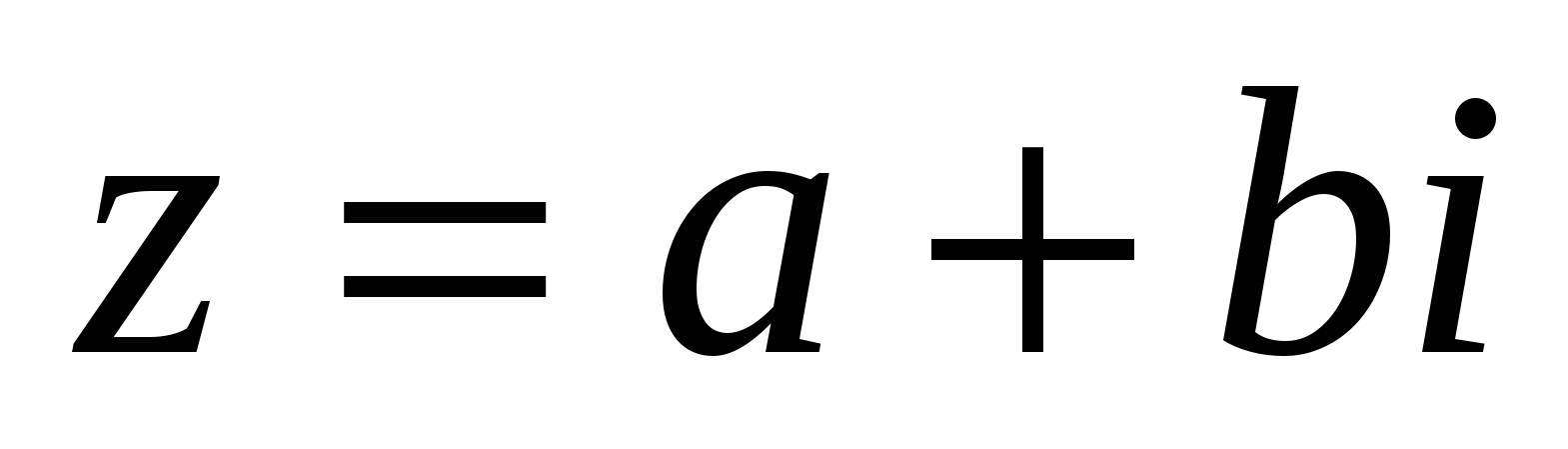 в степень п (п
в степень п (п N) рассматривается как частный случай умножения комплексных чисел:
N) рассматривается как частный случай умножения комплексных чисел:
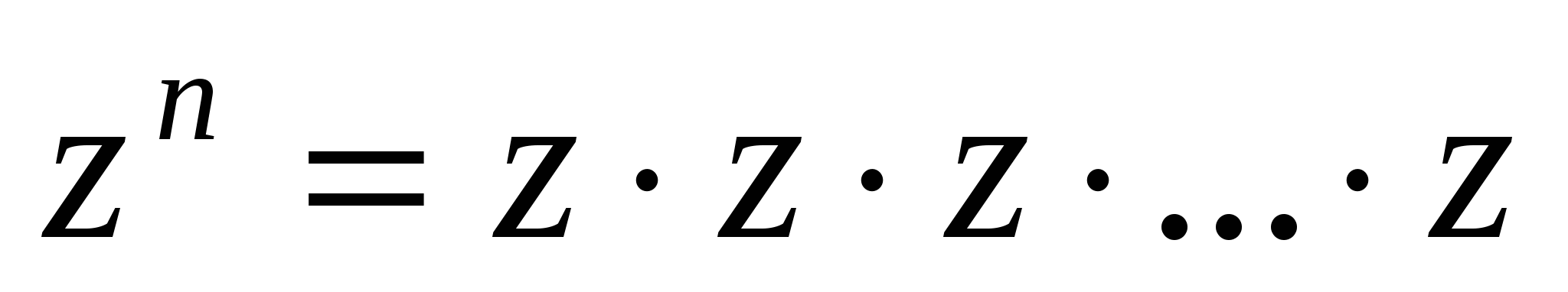 (п раз) (7)
(п раз) (7)
Найдем натуральные степени мнимой единицы i. На основании равенства (4) получаем:
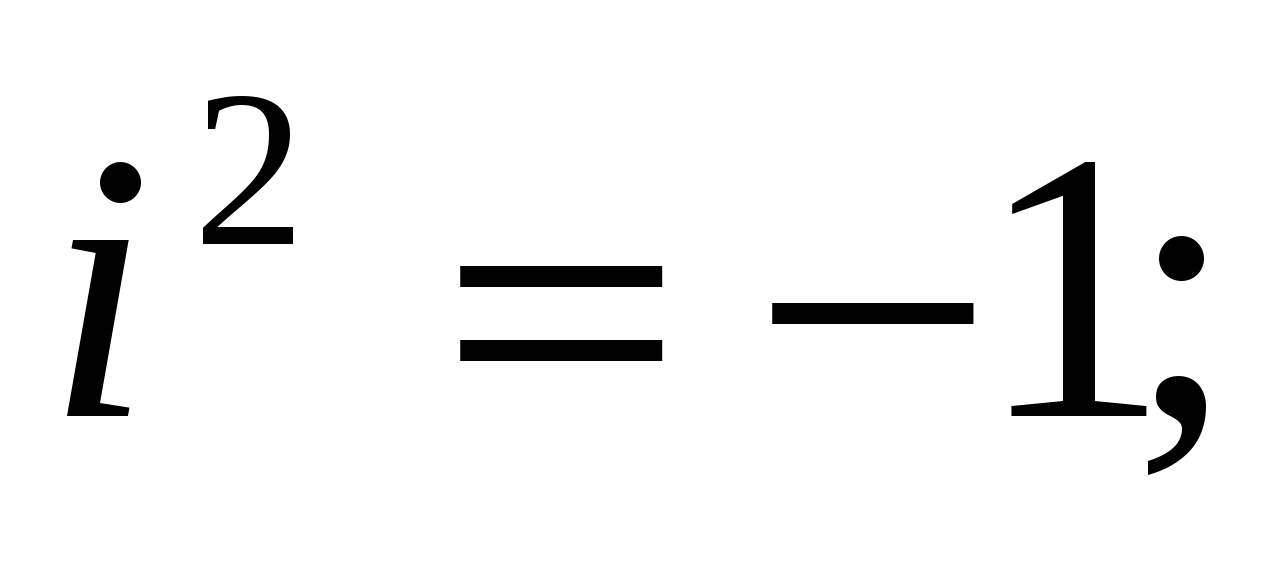

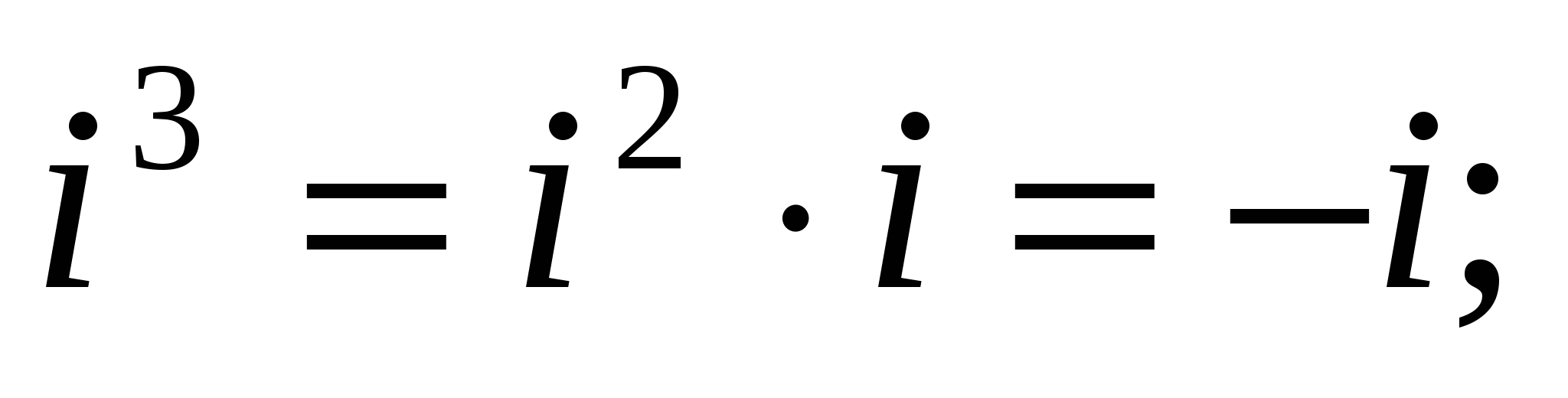
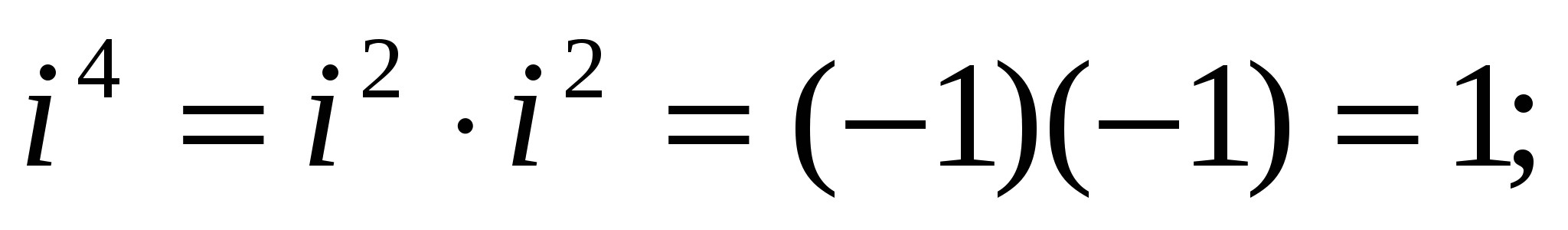
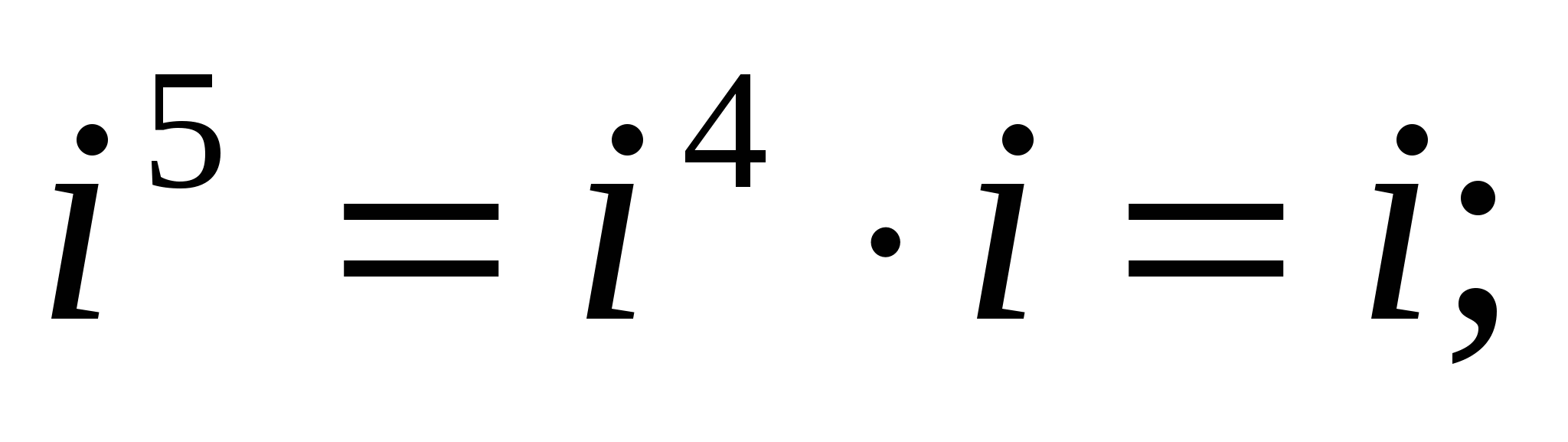
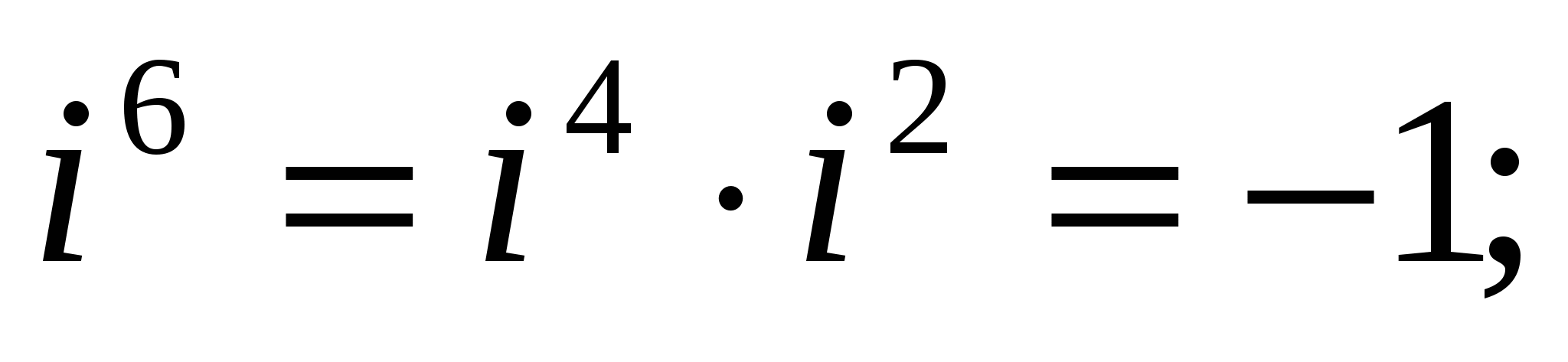
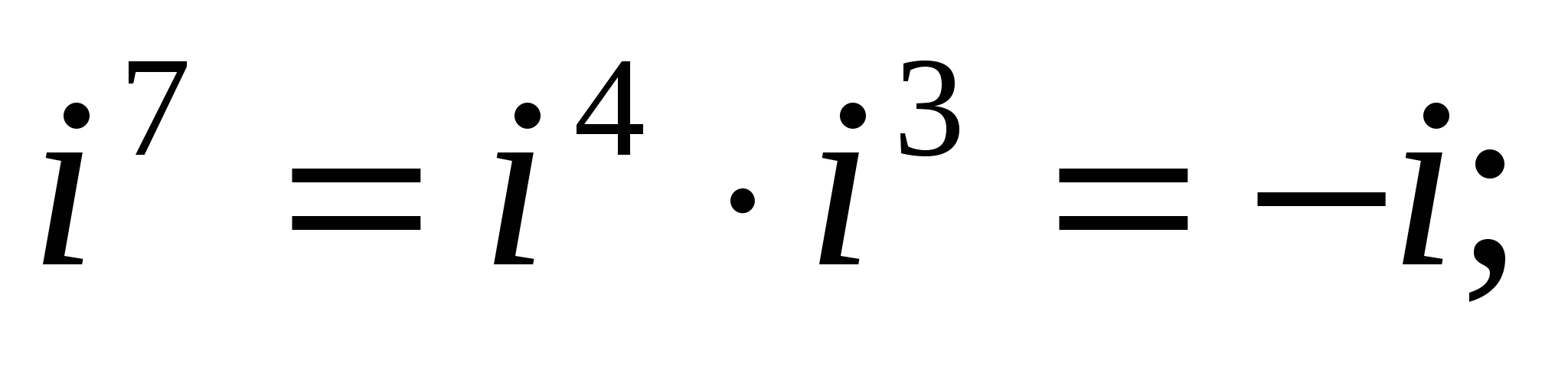
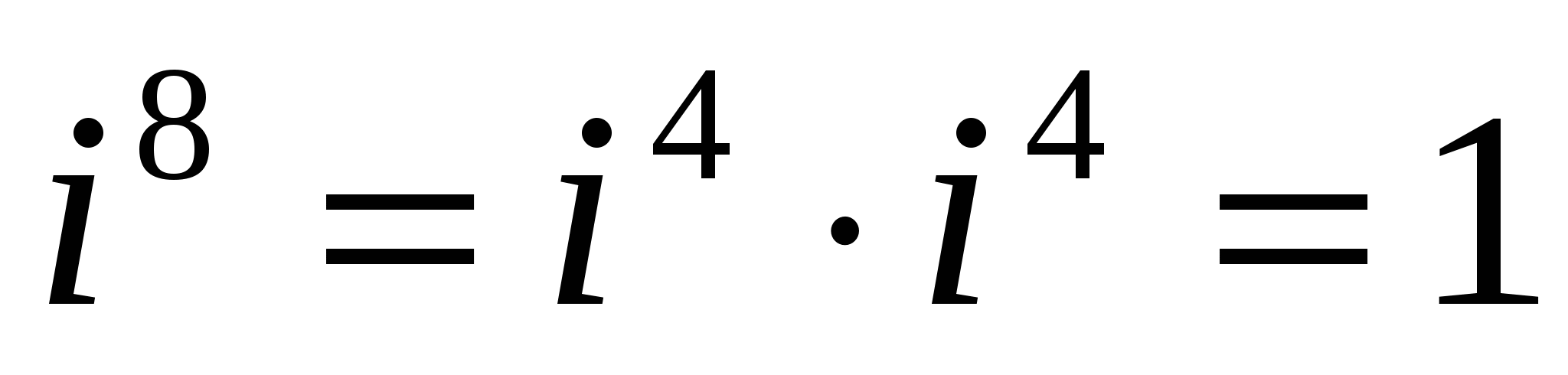 ,
,
и вообще
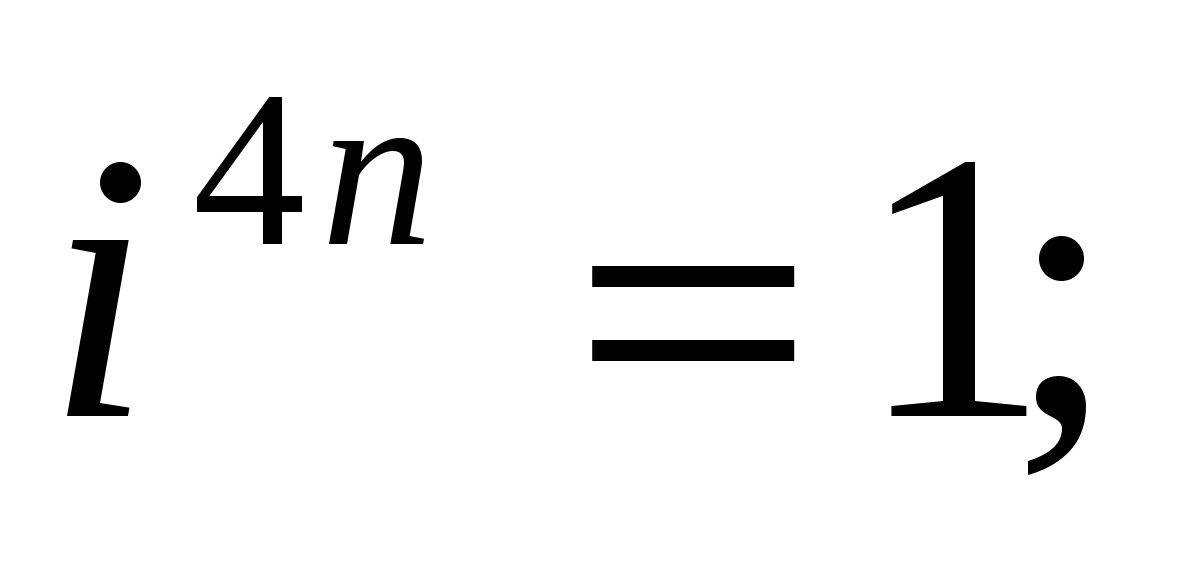
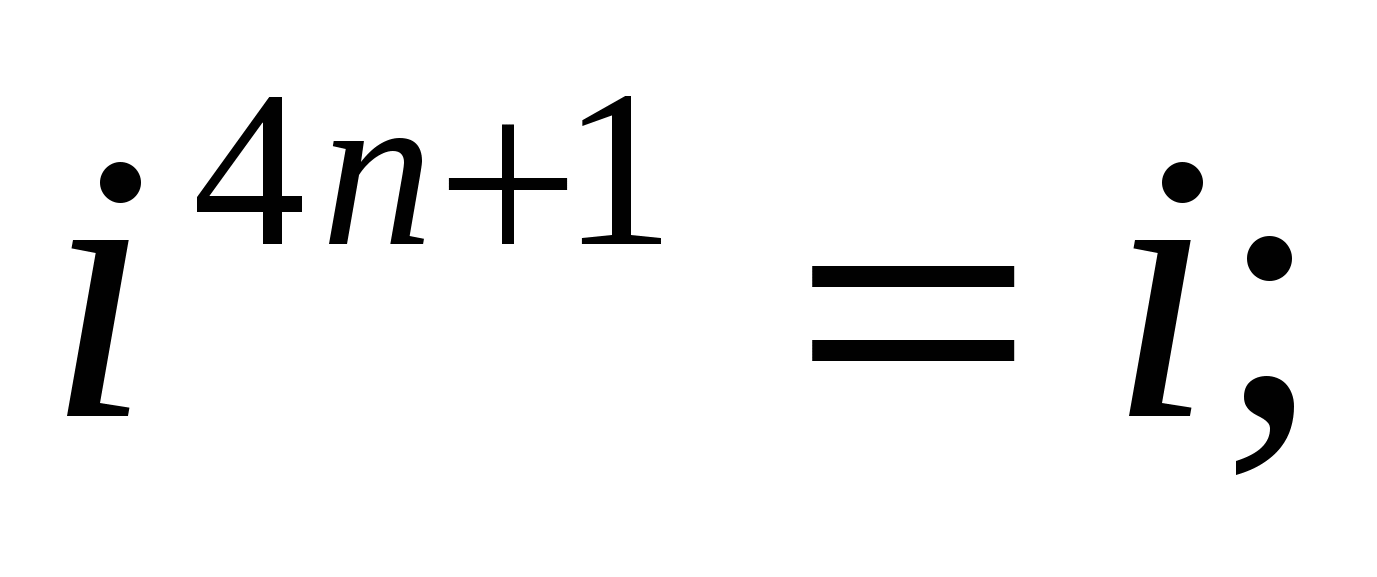
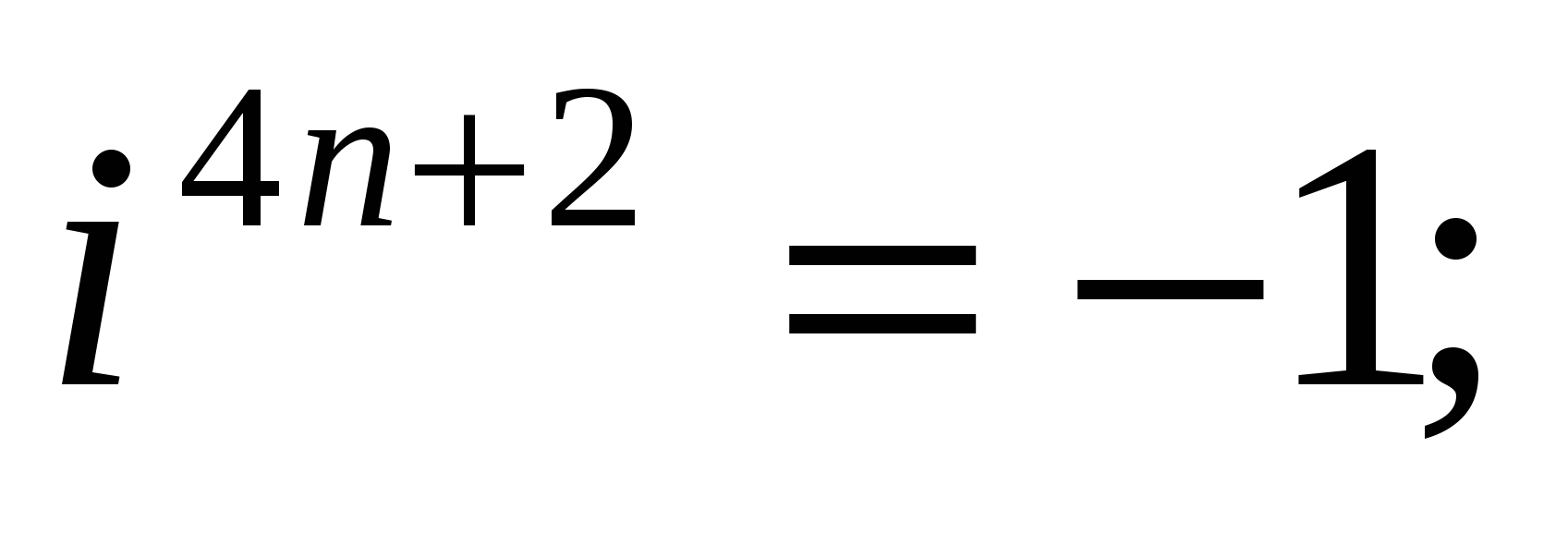
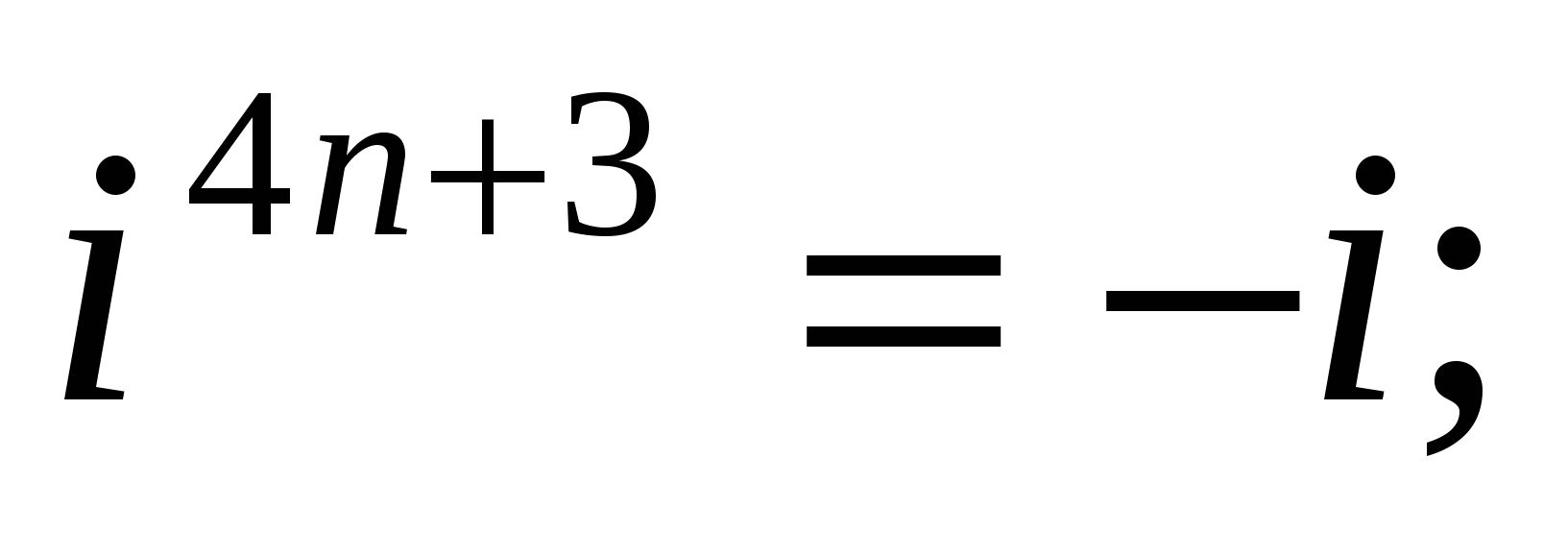
где п - любое натуральное число.
Пример 4. Найти 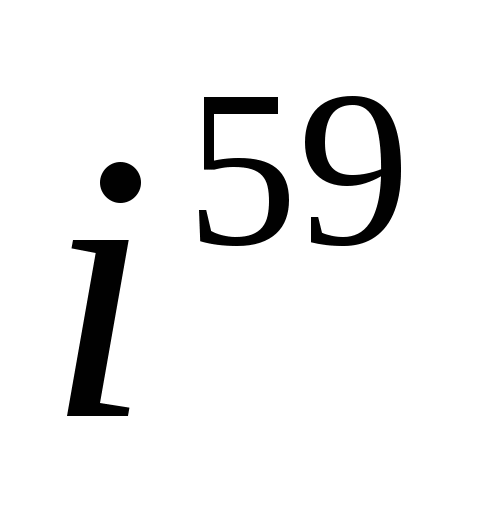 .
.
Решение. При делении числа 59 на 4 имеем: 59 = 14 • 4 + 3, поэтому
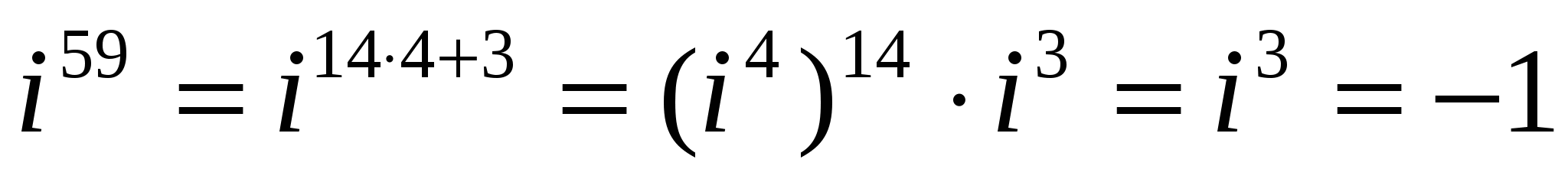 .
.
Предоставляем проверить самостоятельно, что для комплексно-сопряженных чисел выполняются следующие равенства:
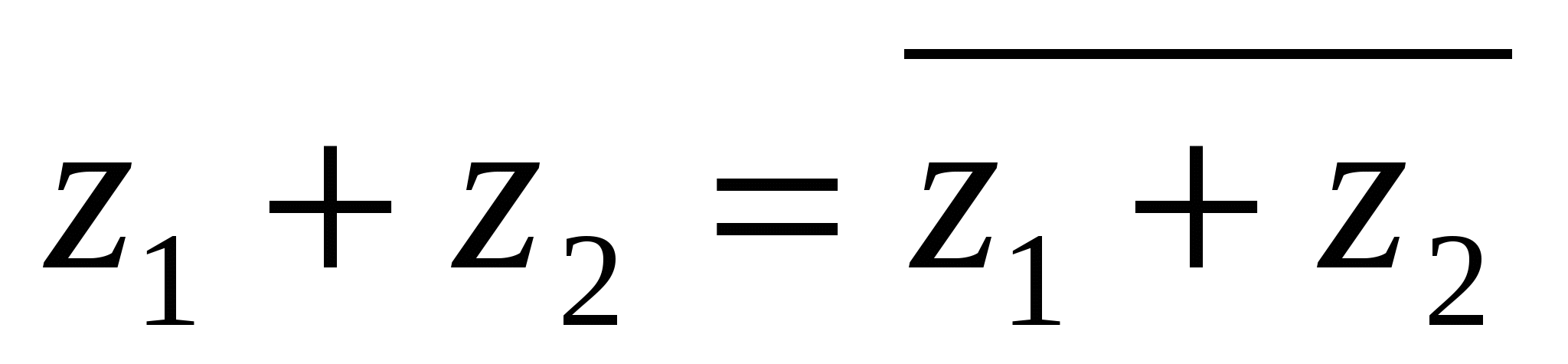 ;
; 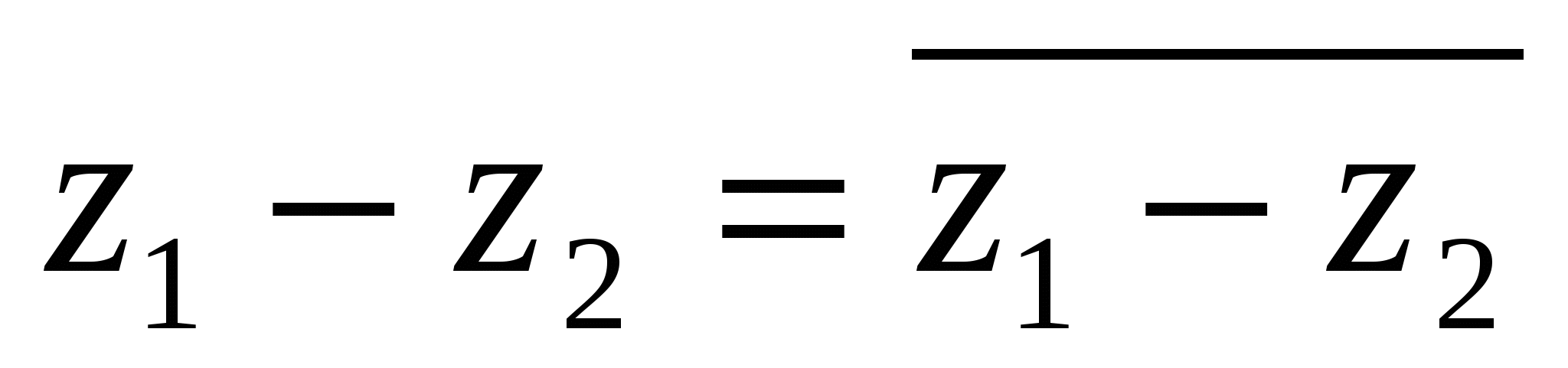 ;
; 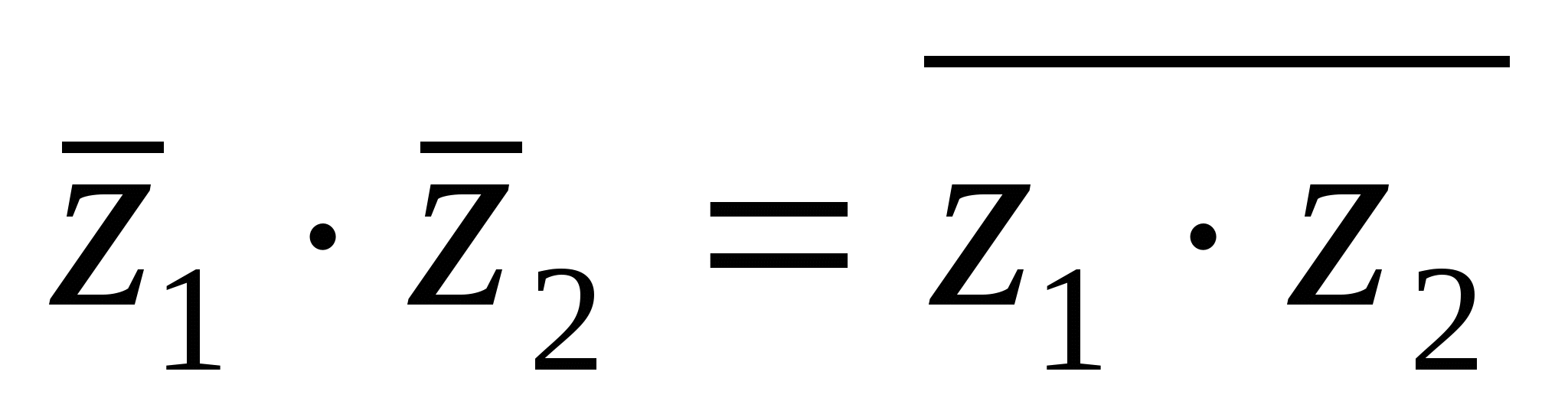 ;
; 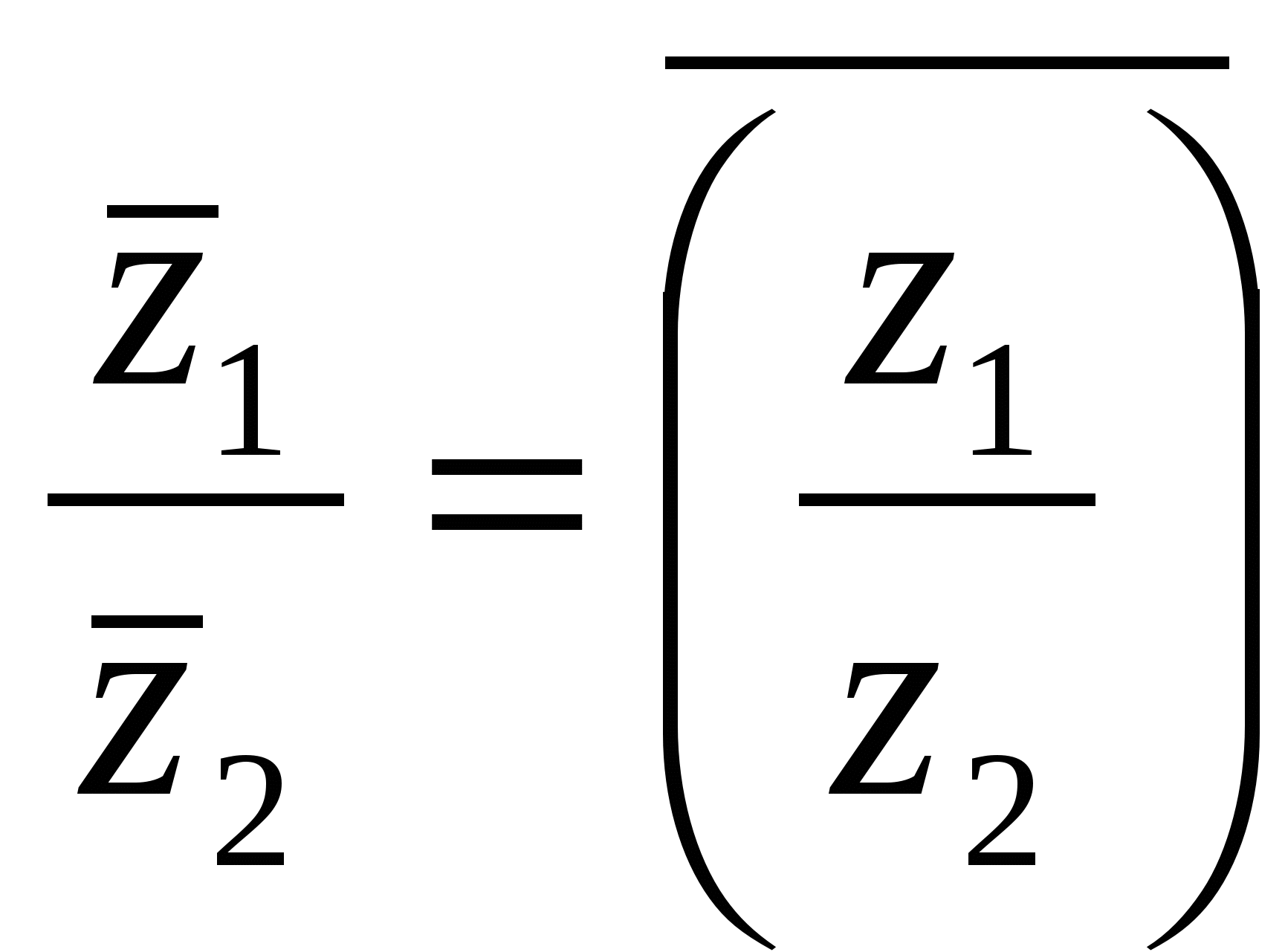 . (8)
. (8)
3.1. Решение алгебраических уравнений
Многочлены и алгебраические уравнения. Многочленом (полиномом или целой рациональной функцией) п-й степени называется функция вида
pn (z) = аn zn + аn-1zп-1 +…+a1z+ao (9)
где z C, аo, а1, .. . ,аn- коэффициенты (вообще говоря, комплексные), причем ап ≠ 0, n
C, аo, а1, .. . ,аn- коэффициенты (вообще говоря, комплексные), причем ап ≠ 0, n N- Уравнение
N- Уравнение
аn zn + аn-1zп-1 +…+a1z+ao = 0, аn ≠ 0, (10)
называется алгебраическим уравнением п-й степени. Число zo для которого рn(zо)=0, называется корнем многочлена (9) или уравнения (10).
Теорема Гаусса (основная теорема алгебры). Всякий многочлен ненулевой степени имеет по крайней мере один корень (вообще говоря, комплексный).
Число zo является корнем многочлена рп (z) в том и только в том случае, когда рп (z) делится без остатка на бином z-zo, т. е.
pп(z) = (z-zо)·qn-1(z),
где qn-1(z) - многочлен (n −1)-й степени. Если pn(z) делится без остатка на (z-zo)k, k ≥1, но не делится на (z-zo)k +1, то zo называется корнем кратности k многочлена рn(z); при этом
pп(z) = (z-zo)k qn-k (z),
где qn-k (z) ≠ 0.
Теорема Гаусса может быть уточнена следующим образом: многочлен п-й степени имеет ровно п корней, если каждый корень считать столько раз, какова его кратность.
Если коэффициенты многочлена (9)-действительные числа и zo= xo + iyo - его комплексный корень, то сопряженное число 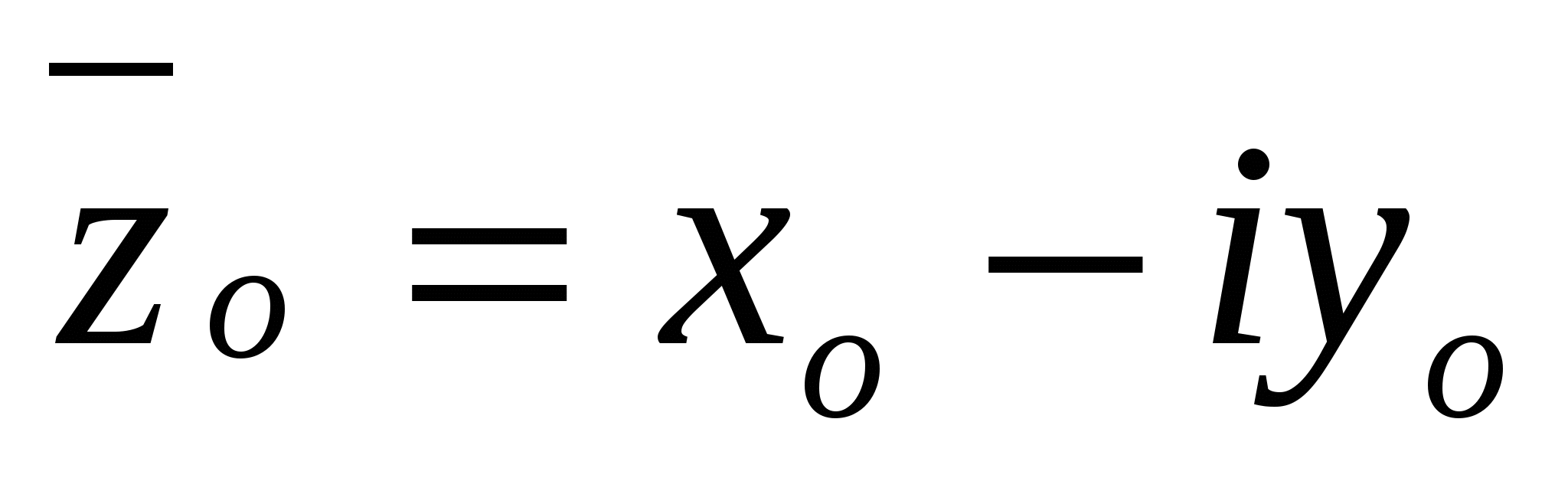 - также корень этого многочлена, причем корни z0 и
- также корень этого многочлена, причем корни z0 и 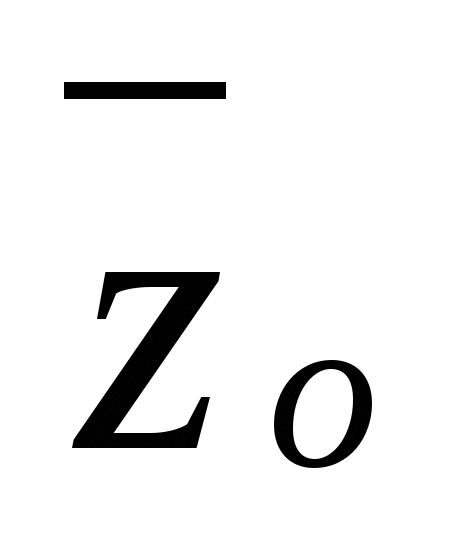 имеют одинаковую кратность.
имеют одинаковую кратность.
Пусть многочлен рn(z) имеет корни z1, z2, z3,..., zт (т ≤ п) кpатностей соответственно k1, k2, …km (k1+ k2+ …+km = п) Тогда
его можно разложить на линейные множители, т. е. справедливо тождество
pп(z) = an(z-z1)k1(z-z2)k2…(z-zm)km
Если при этом коэффициенты многочлена-действительные числа, то, объединяя скобки, соответствующие комплексно сопряженным корням, можно разложить этот многочлен в произведение линейных и квадратичных множителей* с действительными коэффициентами.
Пример 5. Найти корни многочлена z6 + 2z3 + 1 и разложить его на множители.
Решение. Так как z6 + 2z3 + 1 = (z3 + 1)2, то корнями этого многочлена являются корни 3-й степени из −1:
z1 = -1;
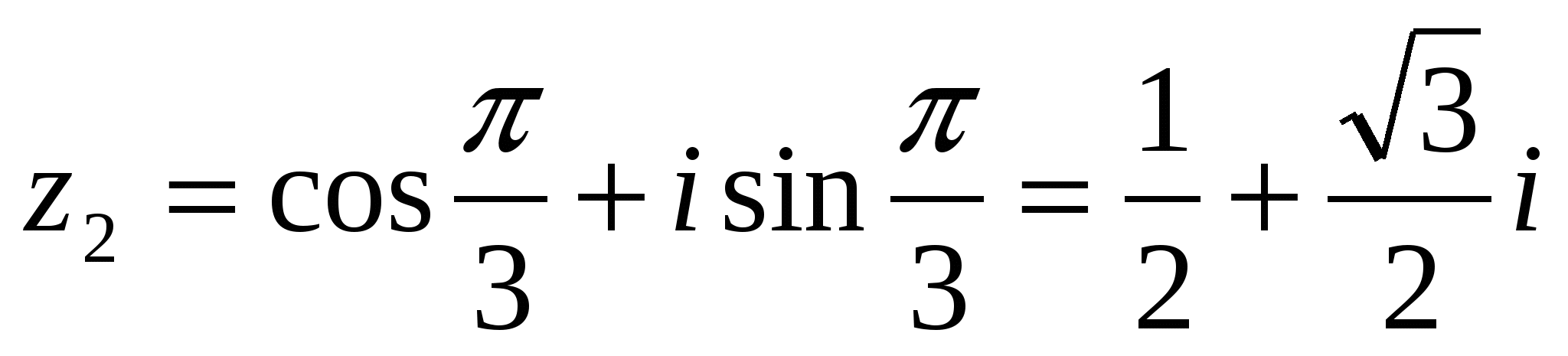 ;
;
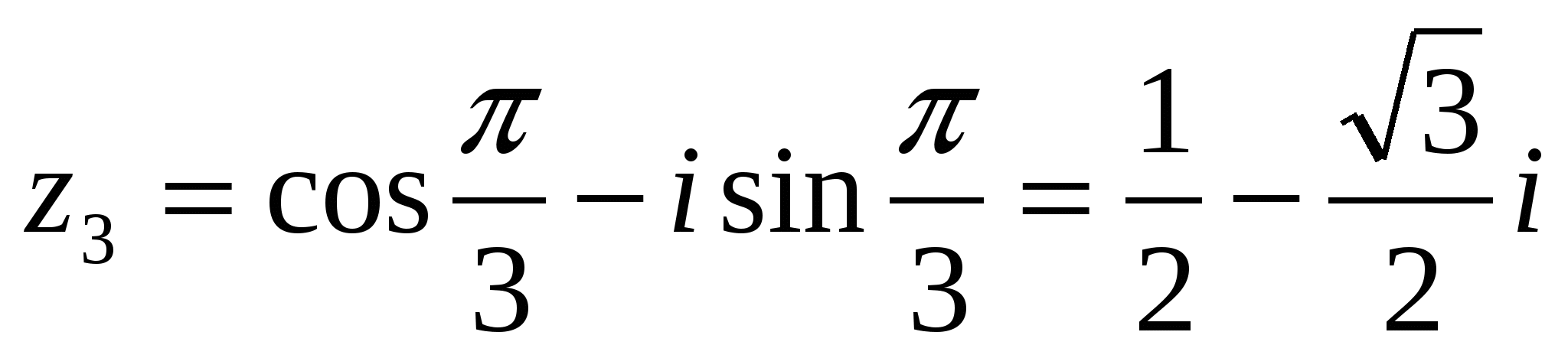
При этом каждый корень имеет кратность k= 2. Разложение этого многочлена на линейные множители имеет вид
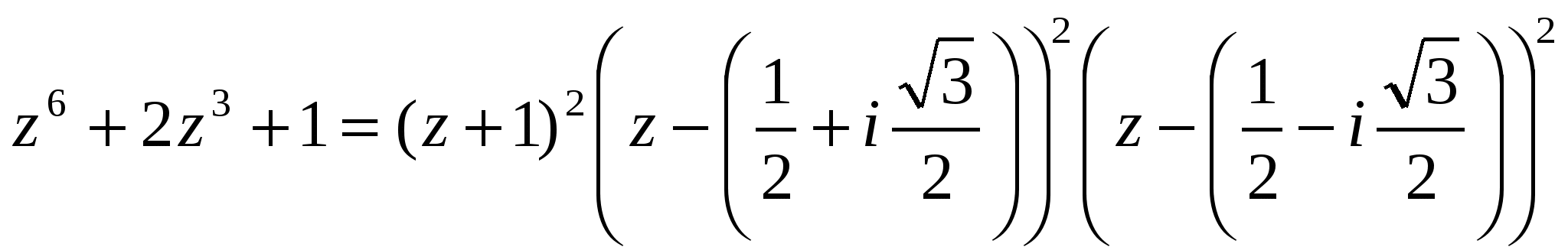
Объединяя последние две скобки в один сомножитель, получим разложение на множители с действительными коэффициентами
z6 + 2z3 + 1 = (z +1)2(z2 − z + 1)2.
Пример 5. Решить квадратные уравнения:
1) z2 + 2z + 5 = 0; 2) 4z2 -2z + 1= 0; 3) z2+ (5−2i) z + 5(1 − i) = 0; 4) (z + 1)4 +16 = 0;
5) z4+18z2 + 81=0.
Решение.
1) z2 + 2z + 5 = 0; D = 4 − 4∙ 5 = 4 - 20 = -16; 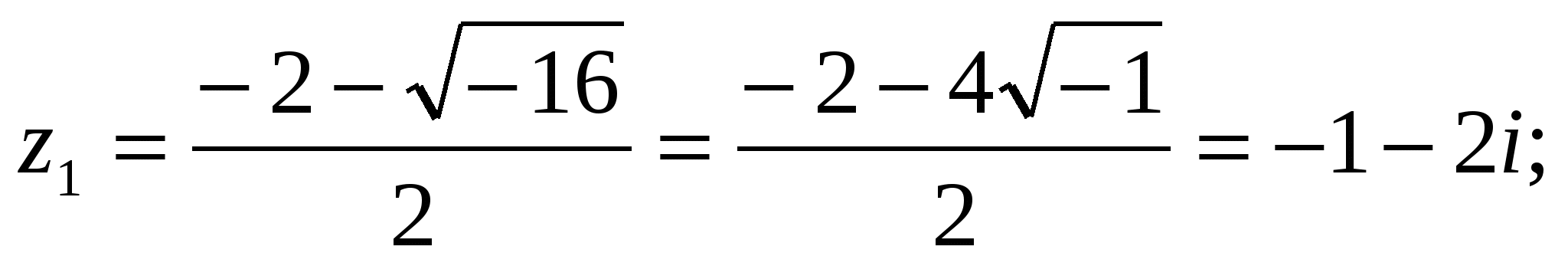 z2 = −1 + 2i .
z2 = −1 + 2i .
2) 4z2 − 2z + 1= 0; D = 4 − 4∙ 4∙ 1 = 4 - 16 = -12; 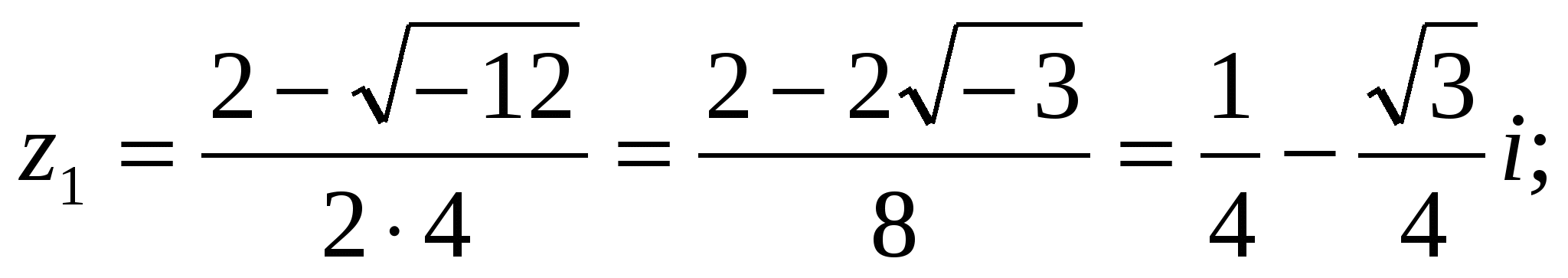
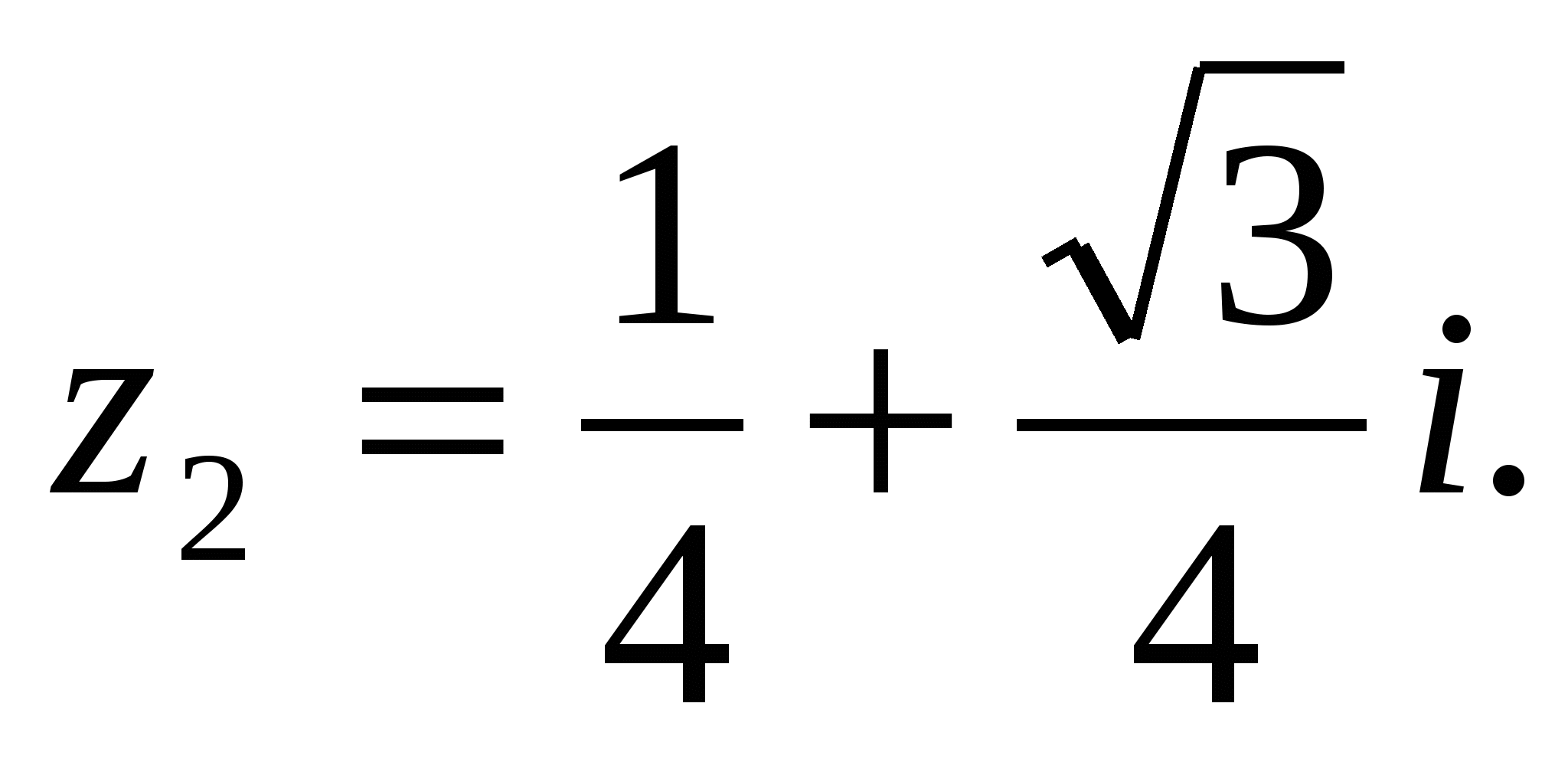
3) z2+ (5−2i) z + 5(1 − i) = 0; D = (5−2i)2 − 4∙5(1 − i) = 25 −20i +4i2 −20 +20i = 1;
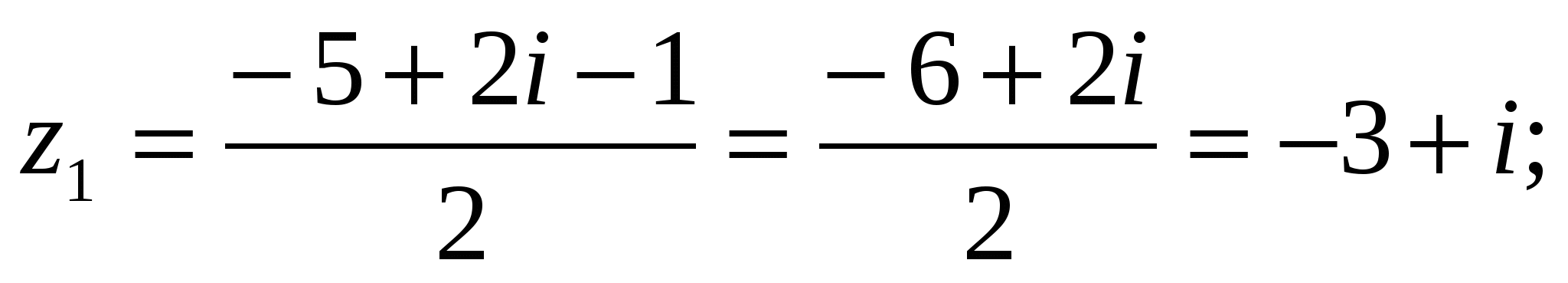
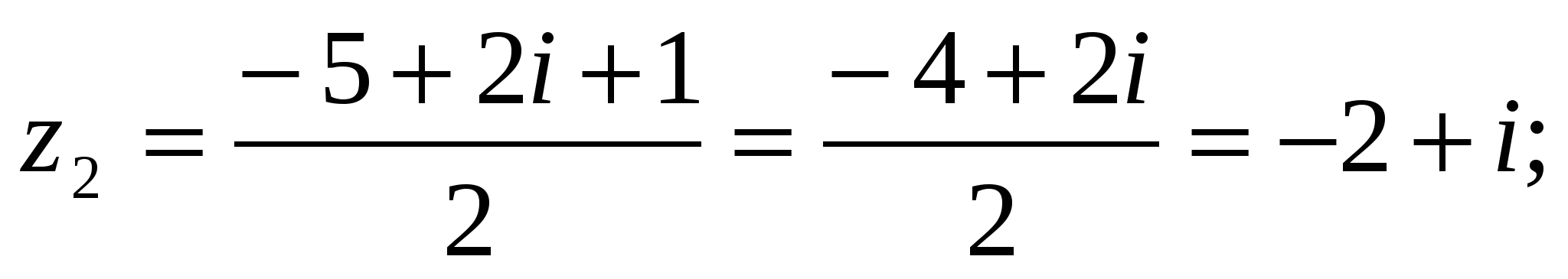 .
.
4) (z + 1)4 +16 = 0; (z + 1)4 = −16; (z + 1)2 = ± 4i; z + 1 = ± 2![]() = ± 2
= ± 2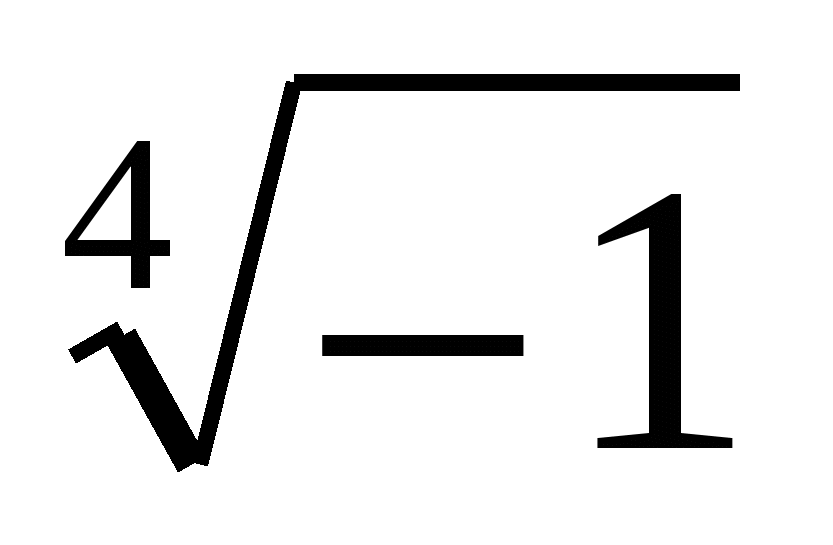 ;
;
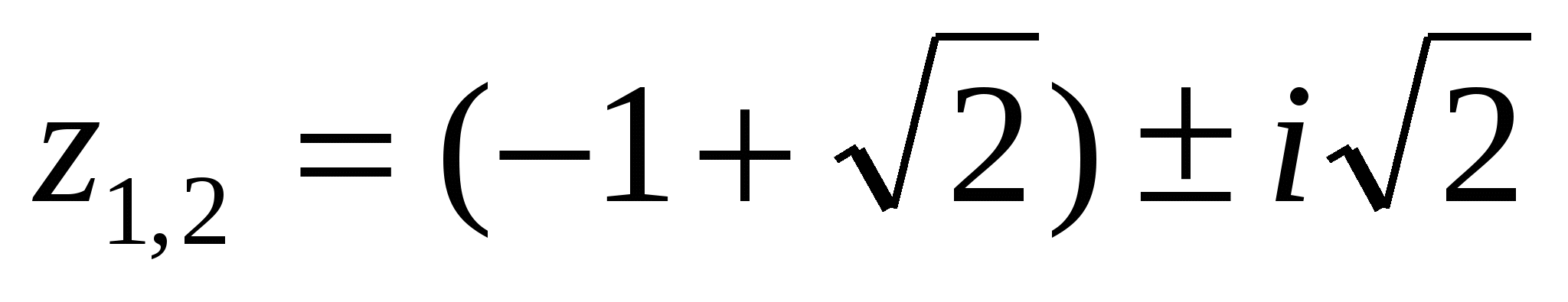 ;
; 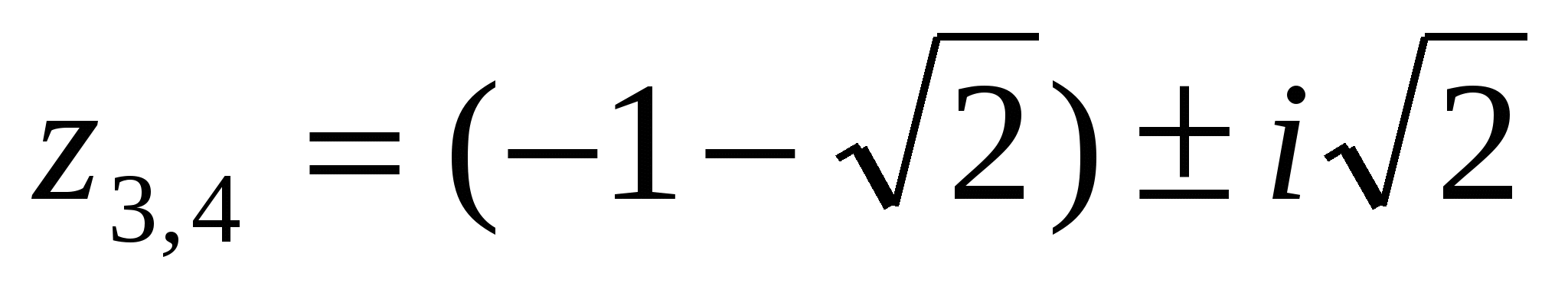 .
.
-
z4+18z2 + 81=0;
Обозначим t = z2 , тогда имеем
t2 +18t + 81=0; D = 182 - 4 ∙1∙81 = 324-324 = 0; два одинаковых корня t1,2= -9
t = z2; z2 = -9; z1,2= z3,4= ± 3i.
Ответ. 1) −1 ± 2i; 2) 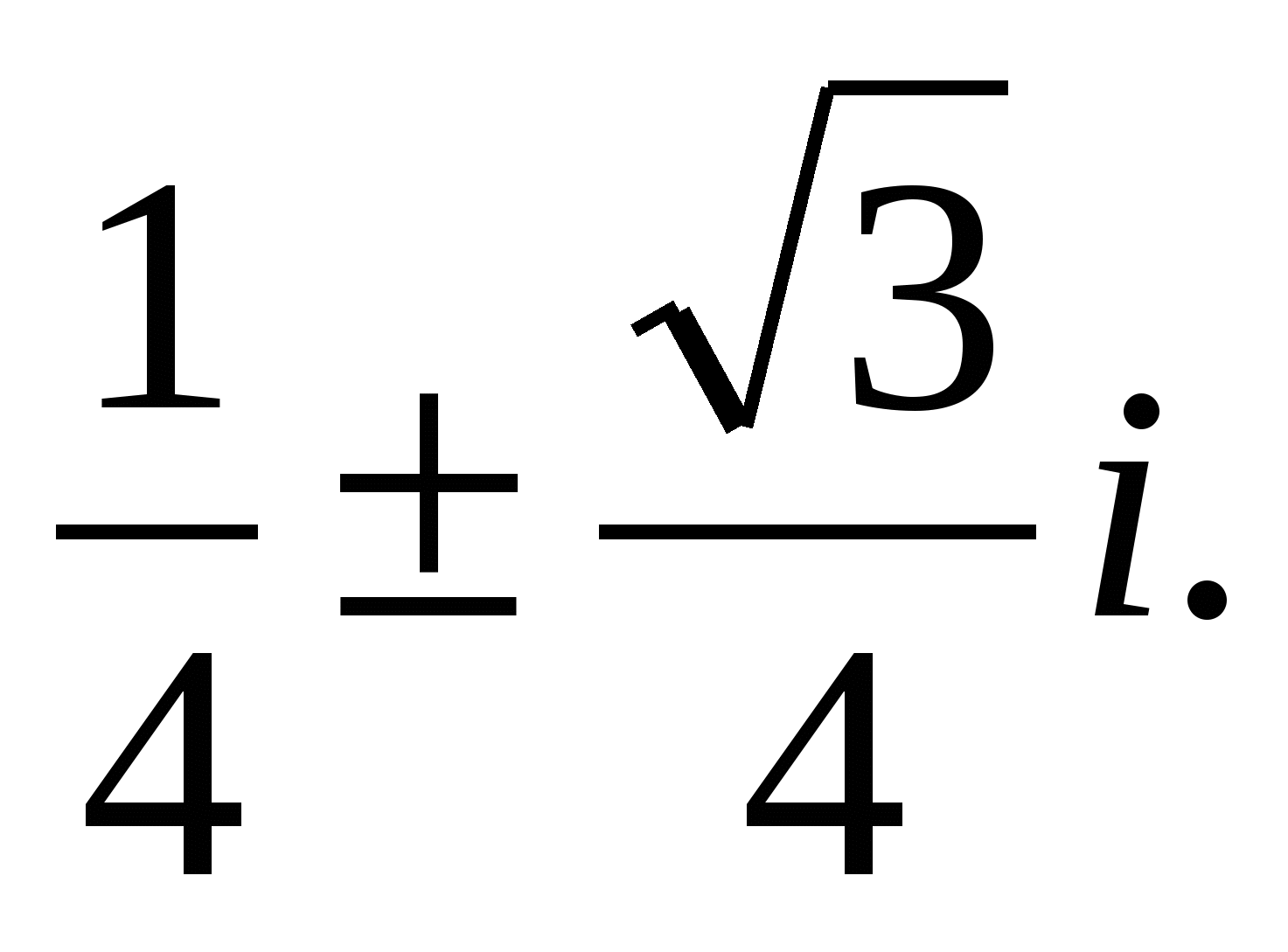 3) 3 ± i; 4)
3) 3 ± i; 4) ![]() ;
; 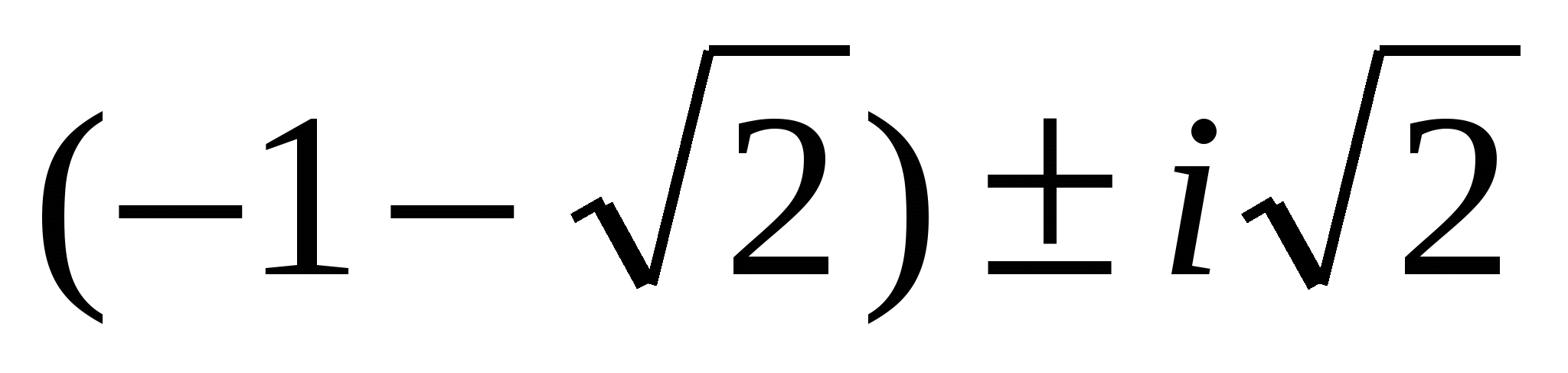 ; 5) ± 3i.
; 5) ± 3i.
4. Полярные координаты точки на плоскости
Возьмем на плоскости произвольную точку О и некоторую ось Or проходящую через эту точку. Ось может быть задана, например, единичным вектором ОЕ (рис. 4).
Произвольную точку М плоскости, не совпадающую с точкой С можно задать двумя числами: r - длиной отрезка ОМ и φ - углом, который образует отрезок ОМ с осью ОР в положительном направлении
Числа r и φ называются полярными координатами точки М. При этом r называется полярным радиусом точки М, а φ- ее полярным углом. Совокупность точки О и оси ОР образует систему координат на плоскости, которая называется полярной системой. Точка О называется полюсом, а ось ОР- полярной осью.
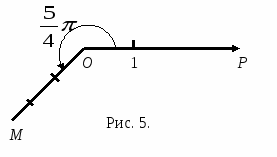
Так же, как и для декартовых координат точки, полярные координаты точки будем заключать в круглые скобки. Так, точка М, заданная на рис. 5, имеет полярные координаты 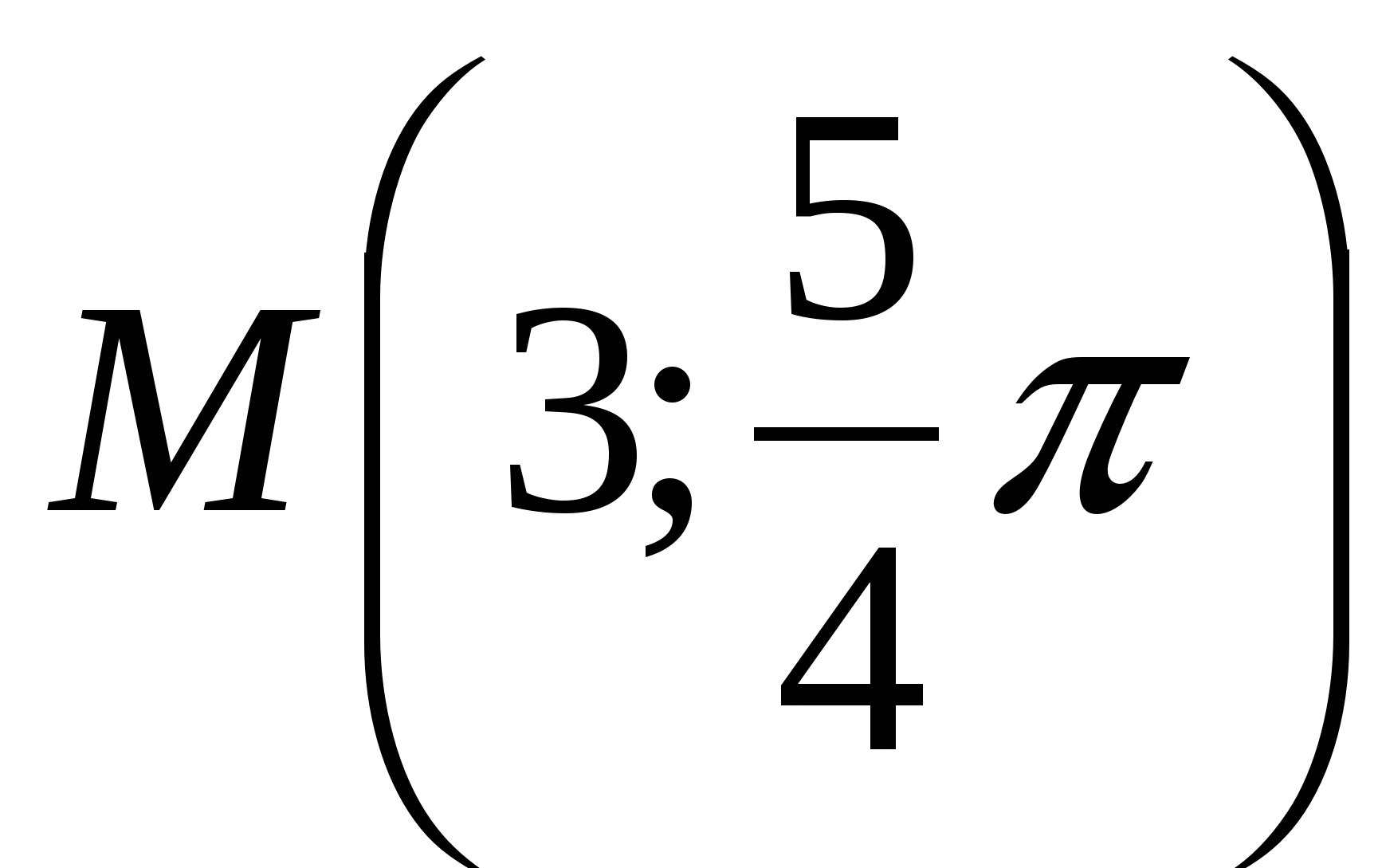 .
.
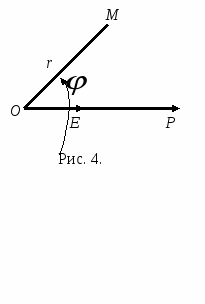
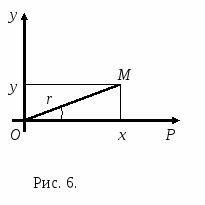
Точка О характеризуется условием r = 0.Полярный угол φ для этой точки не определен.
Будем считать, что полярные координаты точек плоскости изменяются в следующих пределах: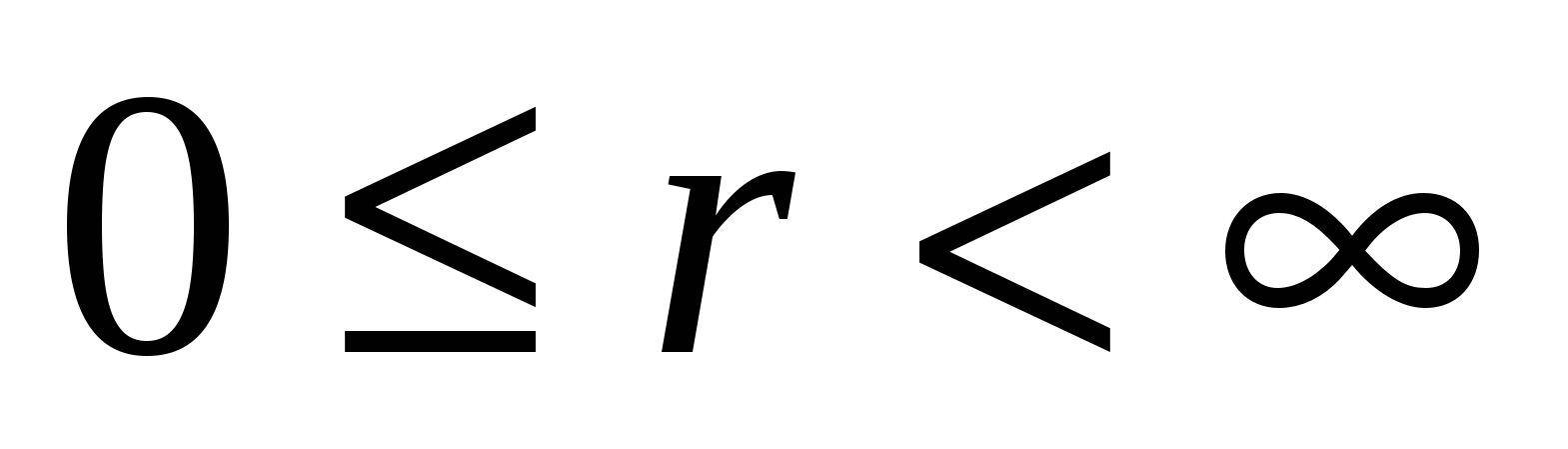 ;
;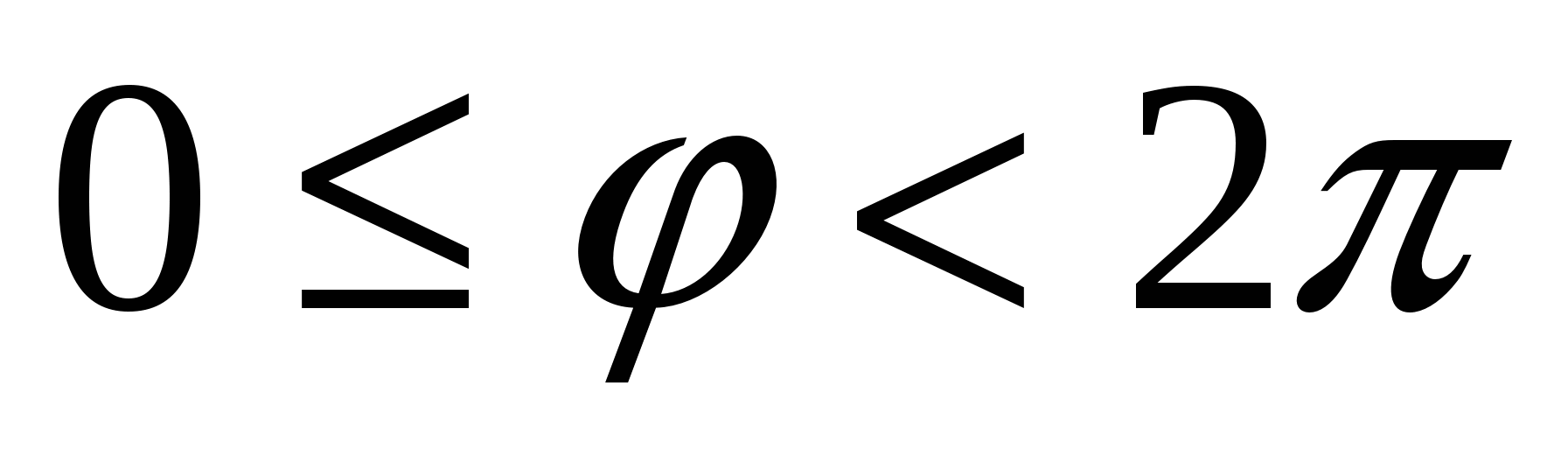 .
.
Для построения точки по полярным координатам необходимо построить луч с началом в точке О, на котором лежит искомая точка, и на этом луче от полюса отложить отрезок, длина которого равна полярному радиусу.
Пусть на плоскости выбраны одновременно полярные и прямоугольные системы координат таким образом, что полюс совпадает с началом декартовых координат, а полярная ось - с положительным направлением оси абсцисс (рис. 6). Если произвольная точка М в полярной системе имеет координатами числа r и φ , а в прямоугольной х, у, то очевидно
![]() ;
; 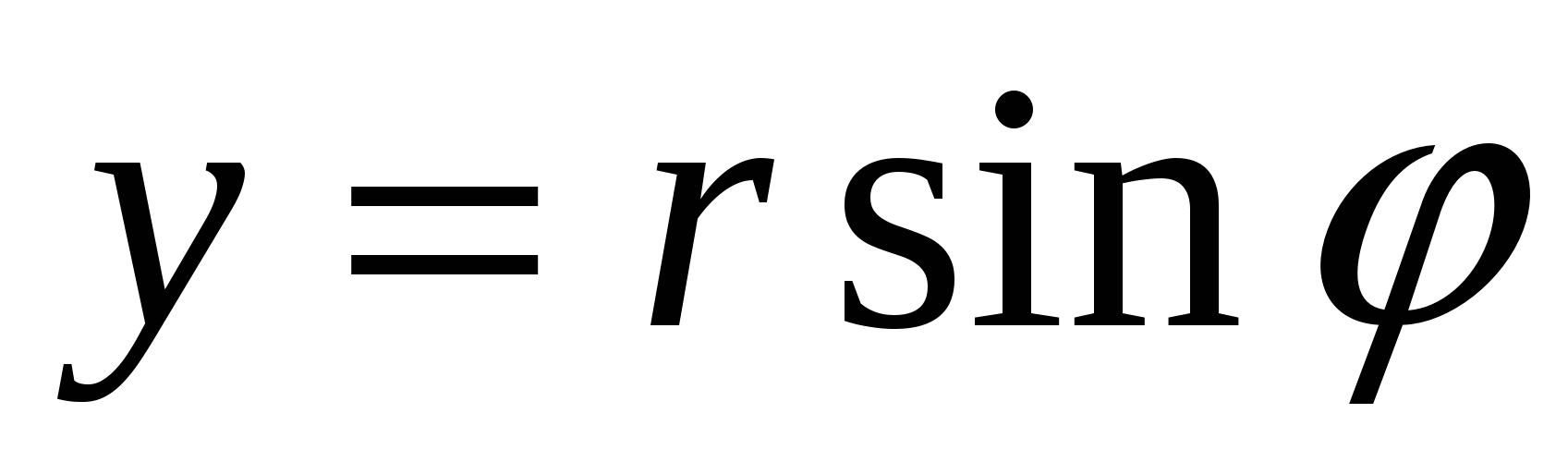 (11)
(11)
![]() ;
; 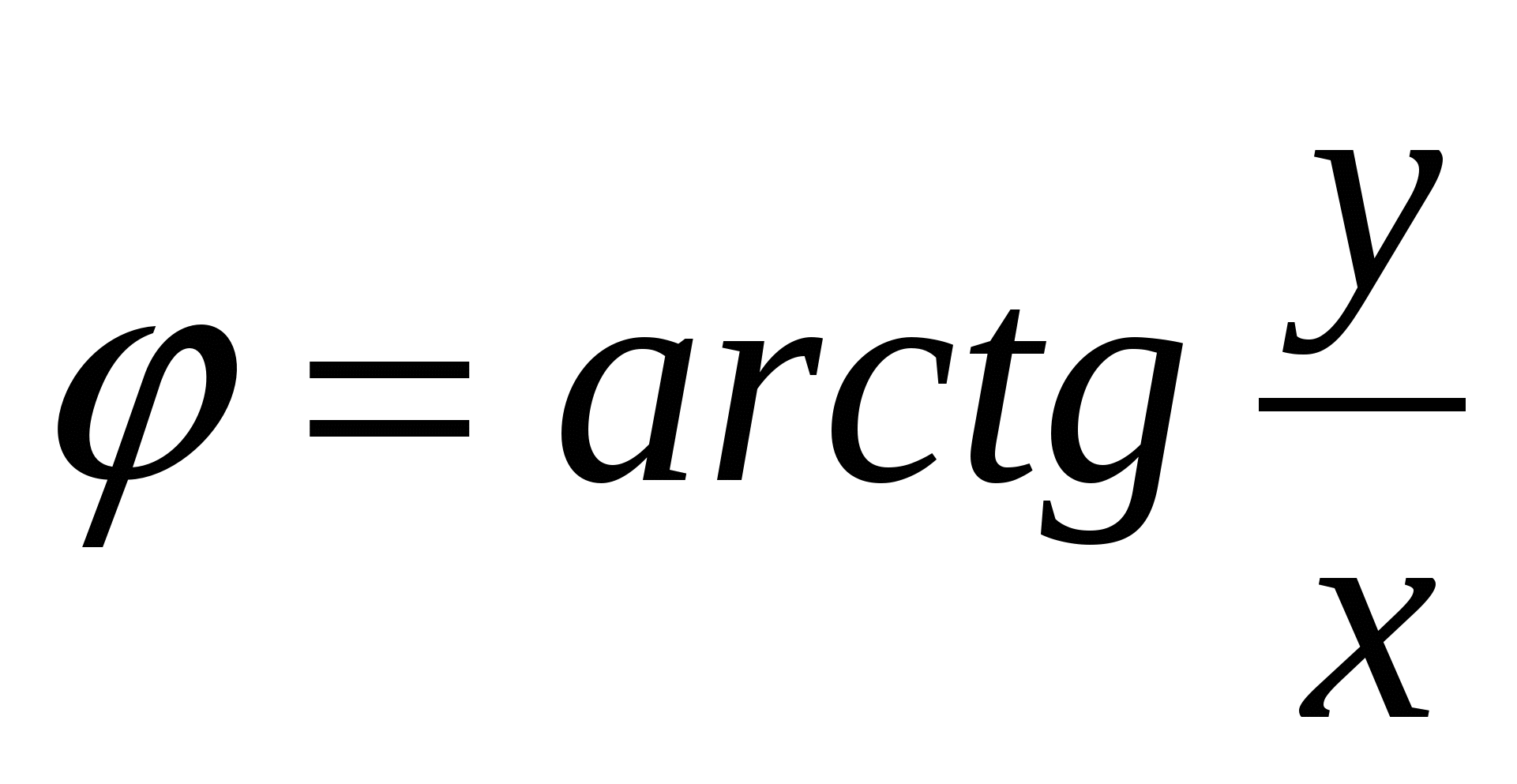 , (12)
, (12)
Таким образом, полярные и прямоугольные координаты одной и той же точки плоскости при указанном выборе систем координат связаны соотношениями (11) и (12). При этом из соотношения (11) по заданным полярным координатам r и φ определяются прямоугольные координаты, а из соотношений (12) по заданным прямоугольным координатам хи у определяются полярные координаты. Необходимо учесть, что из второй формулы (12) угол ср определяется не однозначно. Поэтому, вместо этого соотношения лучше воспользоваться соотношениями 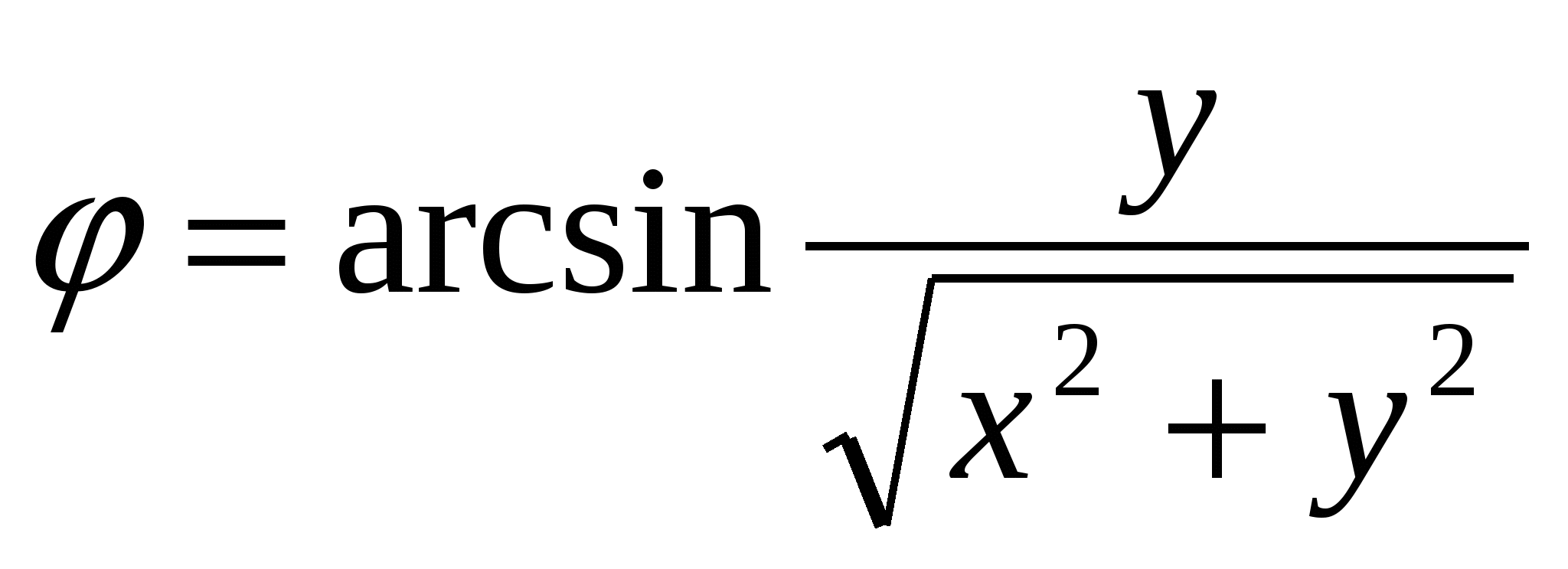 ;
; 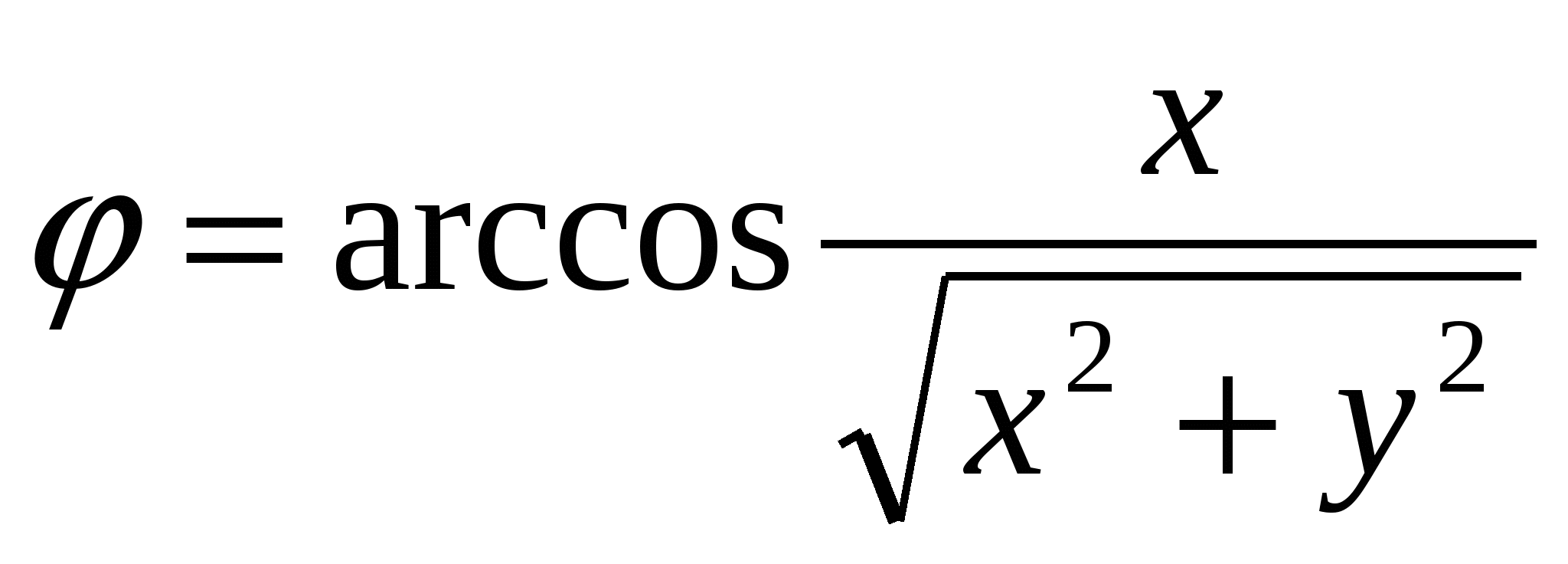 .
.
Пример. Даны полярная и прямоугольная системы координат (рис. 7). Найти: а) полярные координаты точки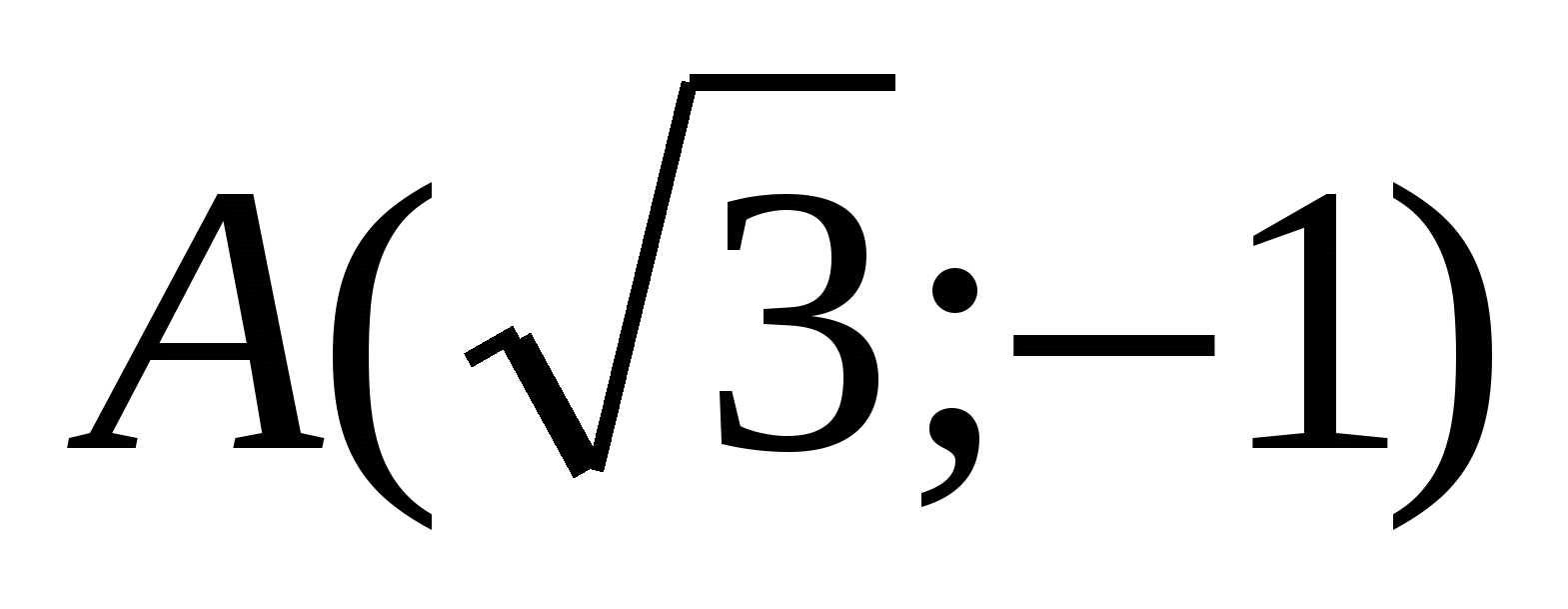 ; б) прямоугольные координаты точки
; б) прямоугольные координаты точки 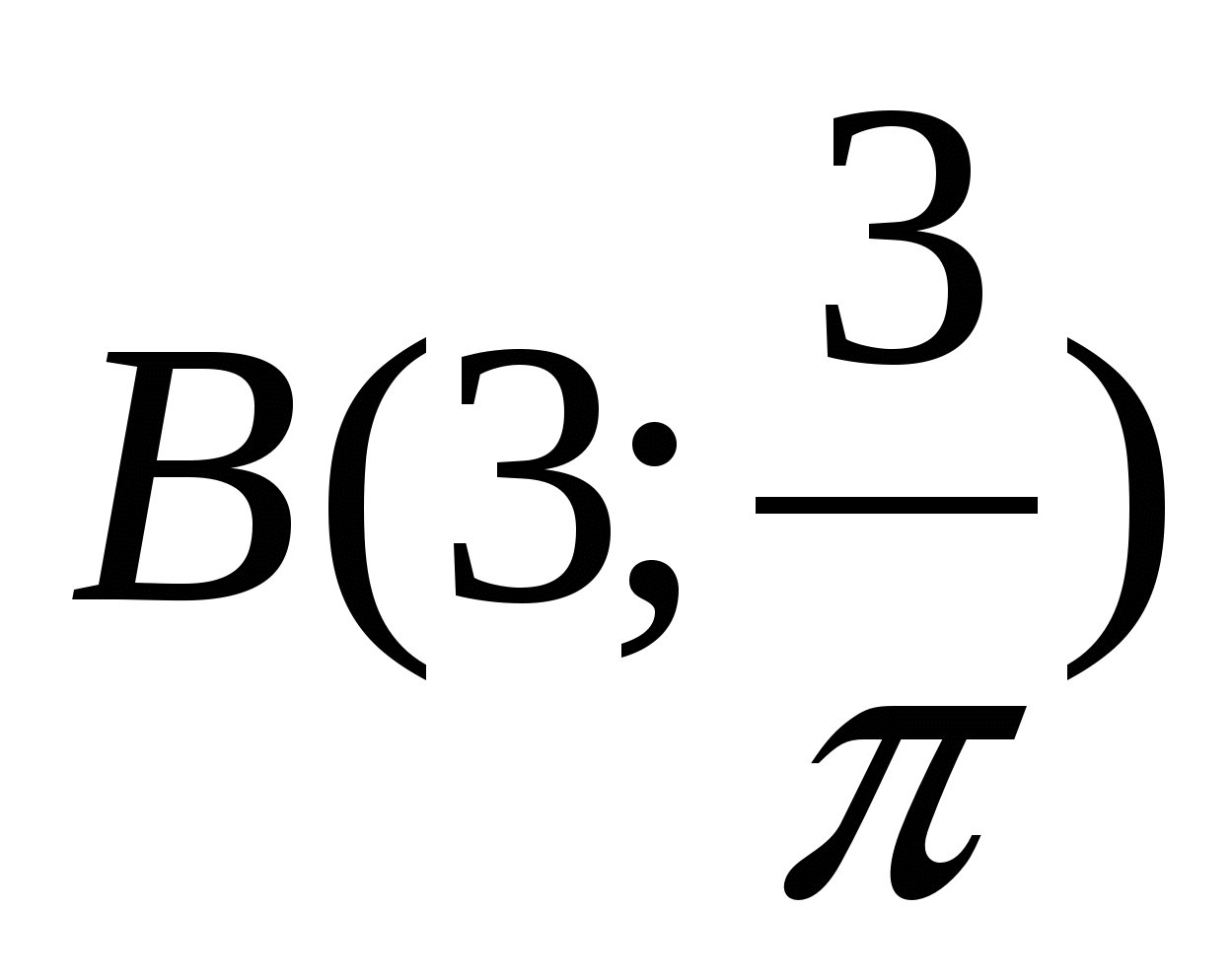 .
.
Решение, а) Пользуясь соотношениями (12), получим
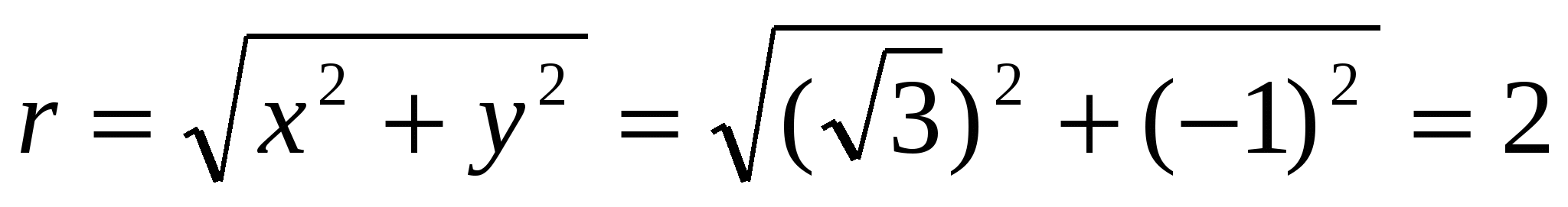 ;
;
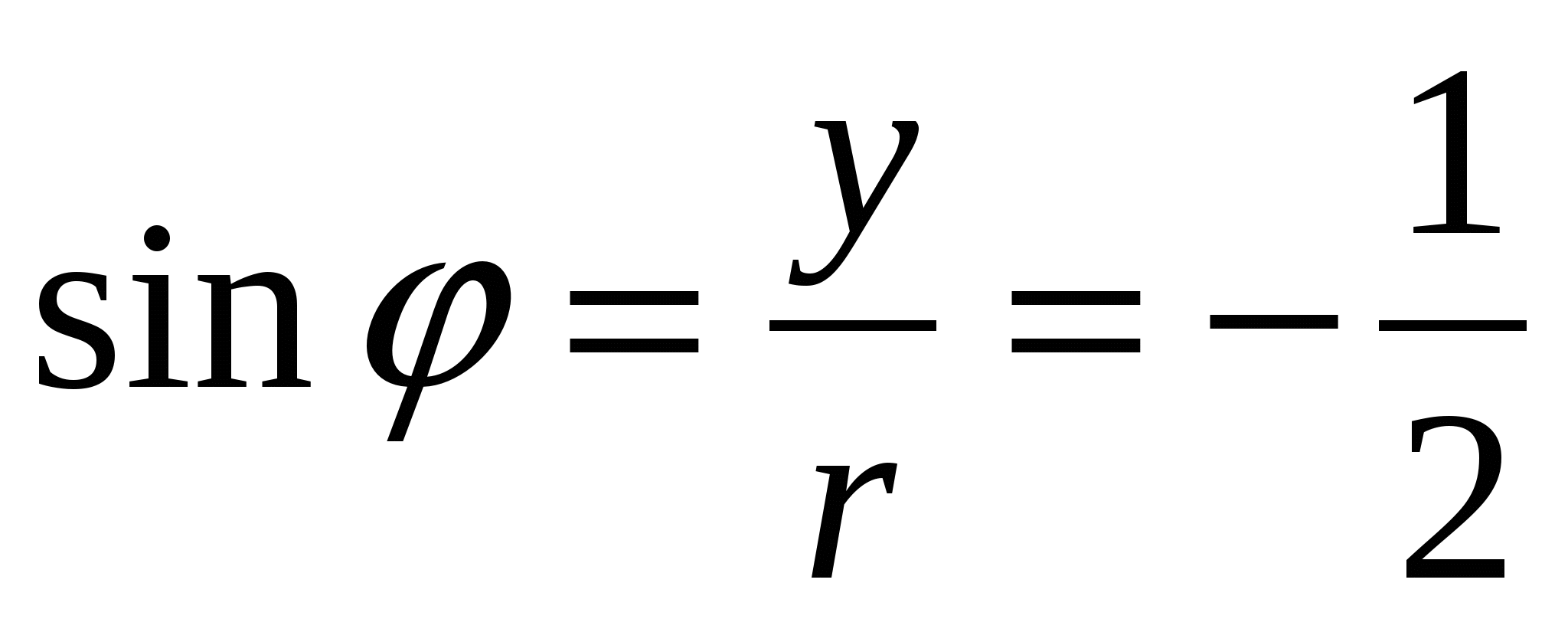 ;
; 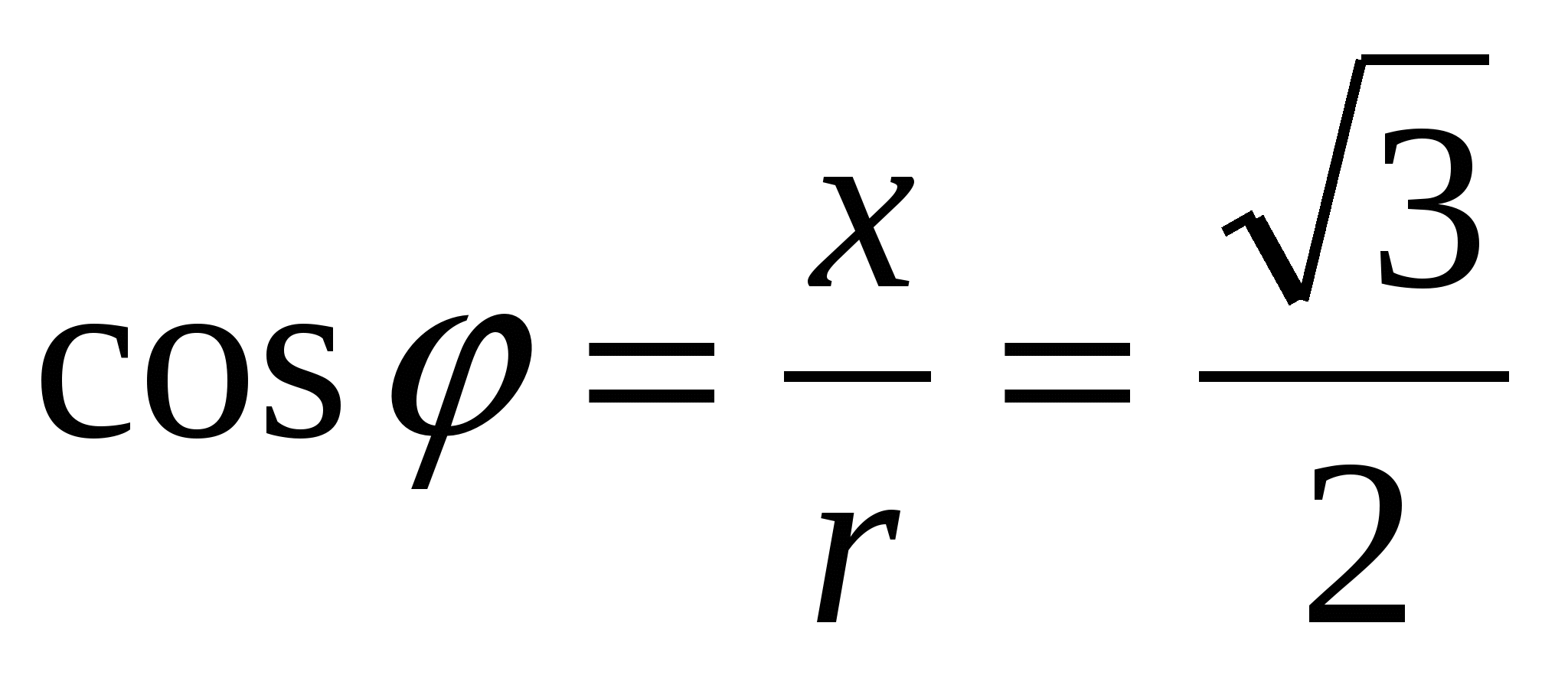 .
.
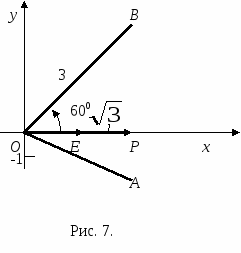
Из этих соотношений следует, что точка расположена в четвертой четверти, поэтому 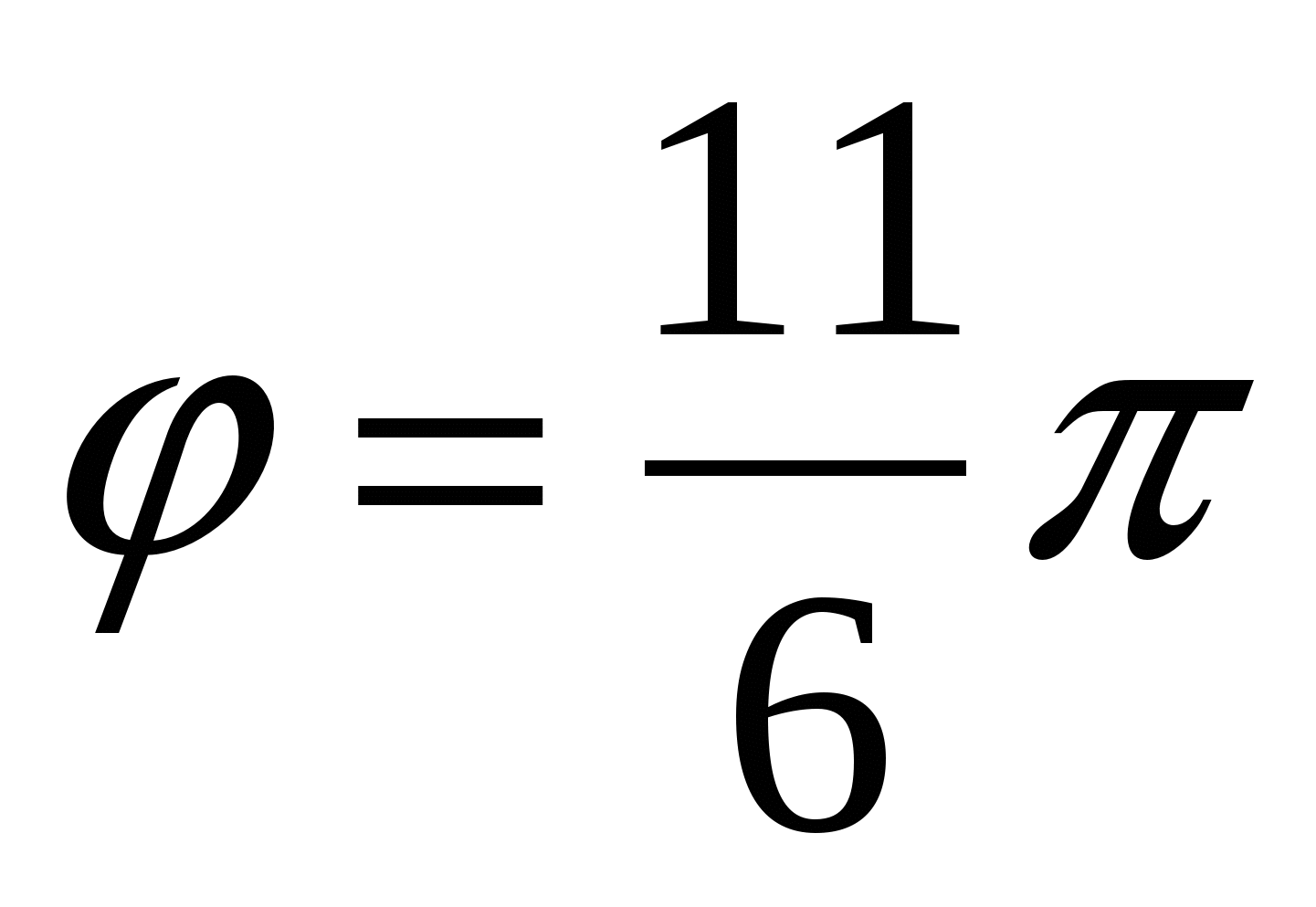 ;
;
б) пользуясь соотношениями (11), получим 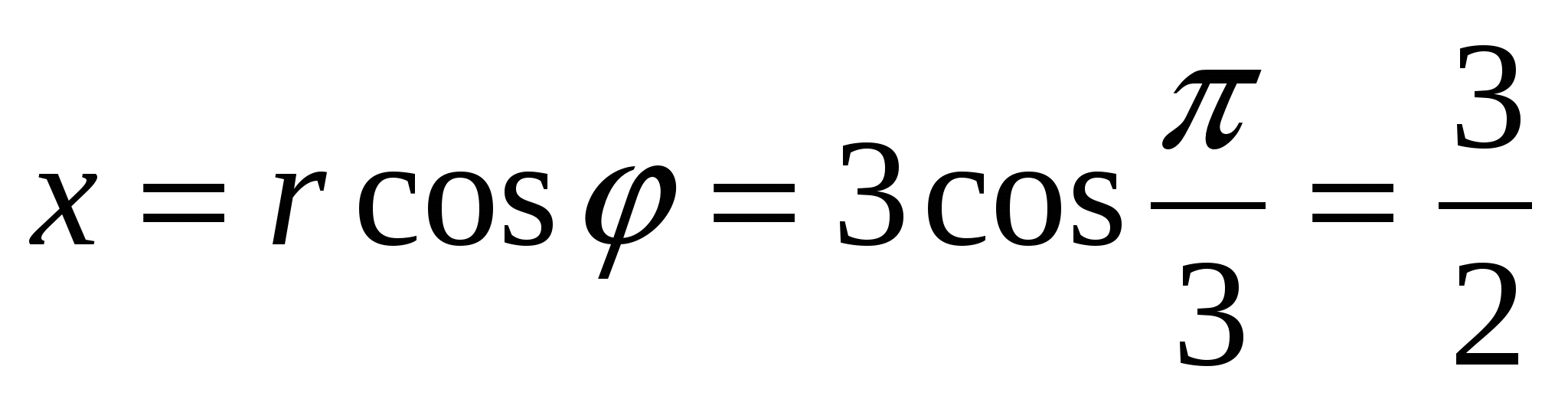 ;
; 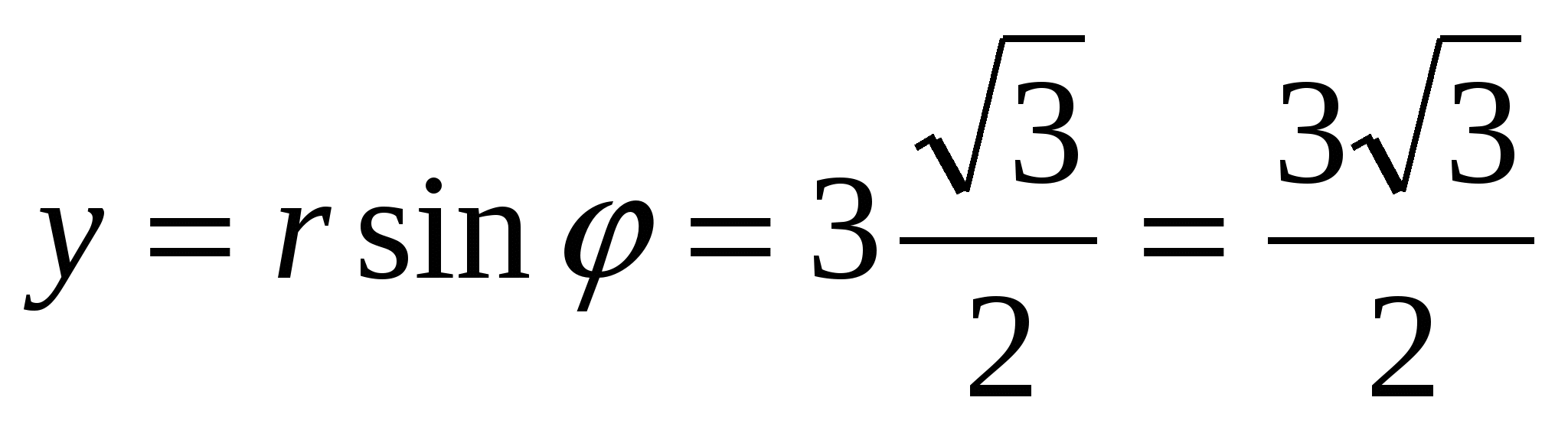 . Следовательно,
. Следовательно,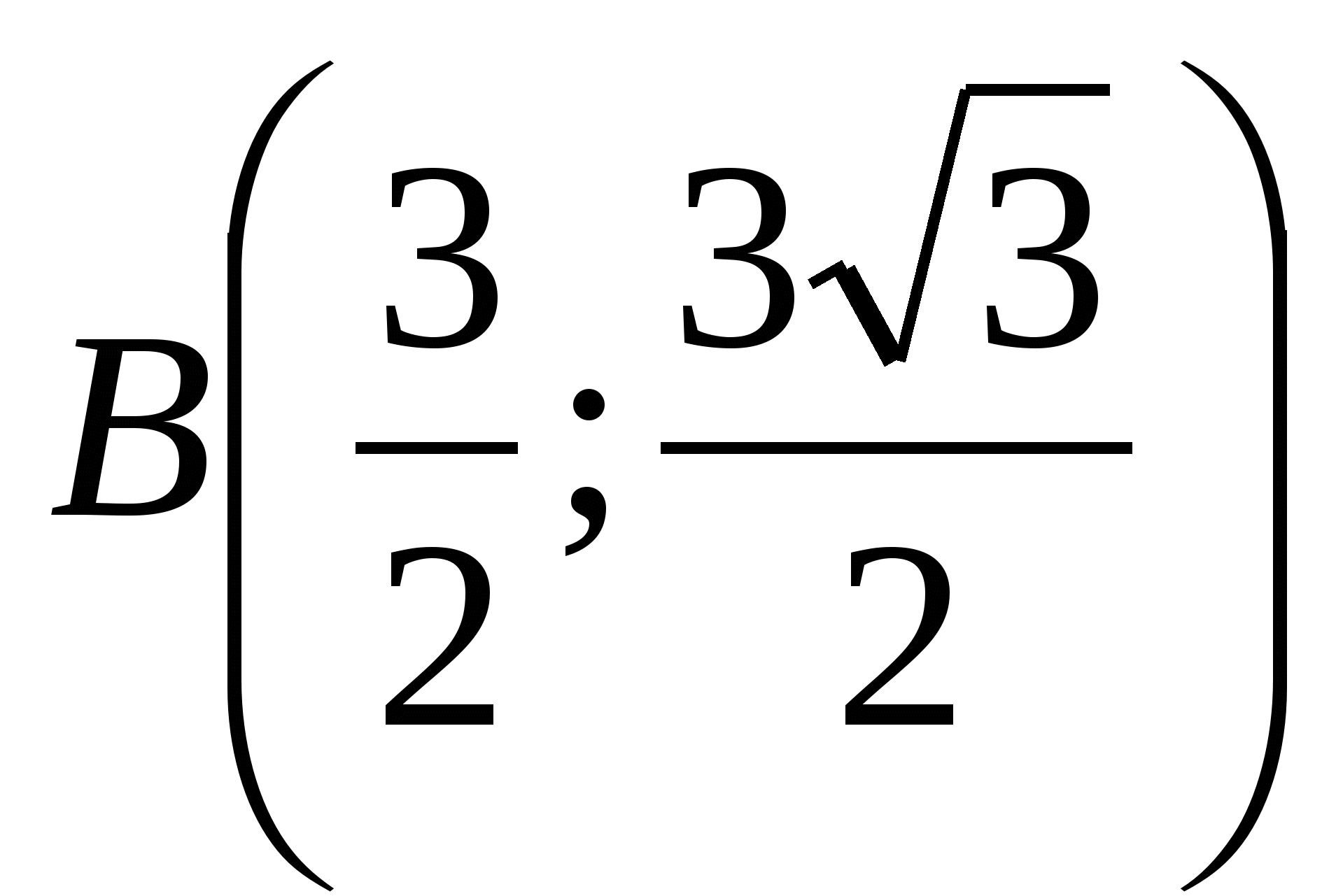 .
.
5. Тригонометрическая форма комплексного числа
Выберем на комплексной плоскости вместе с прямоугольной и полярную систему координат таким образом, как это изображено на рис. 6 Так как произвольное комплексное число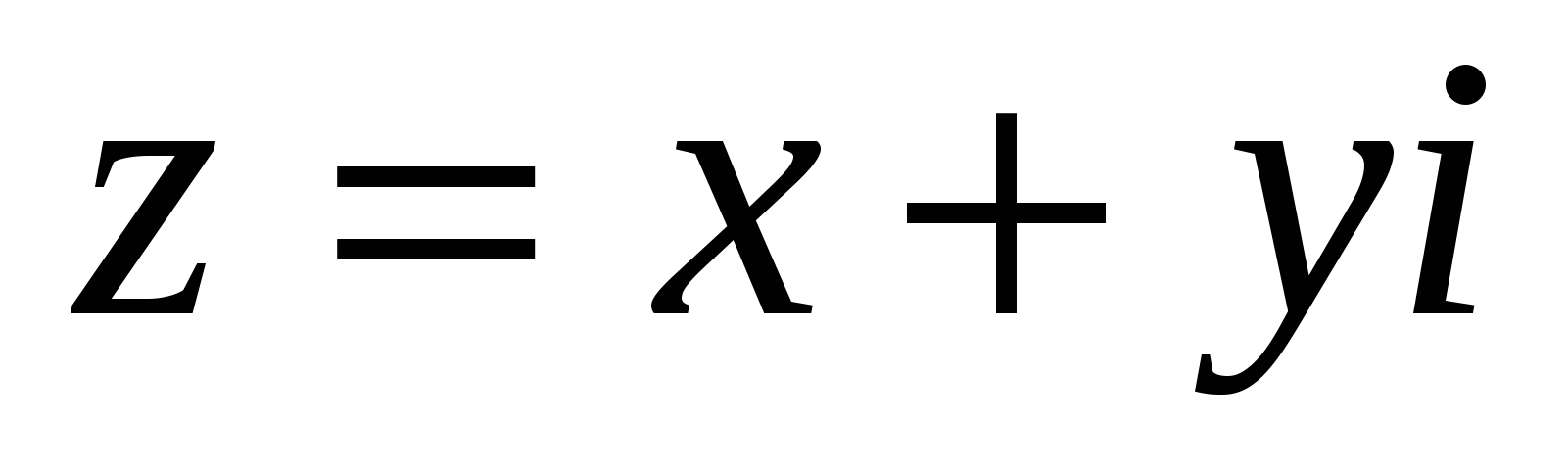 изображается точкой, то числа х и у являются ее прямоугольными координатами. Пусть
изображается точкой, то числа х и у являются ее прямоугольными координатами. Пусть  и
и - полярные координаты точки М(х;у). Полярный радиус
- полярные координаты точки М(х;у). Полярный радиус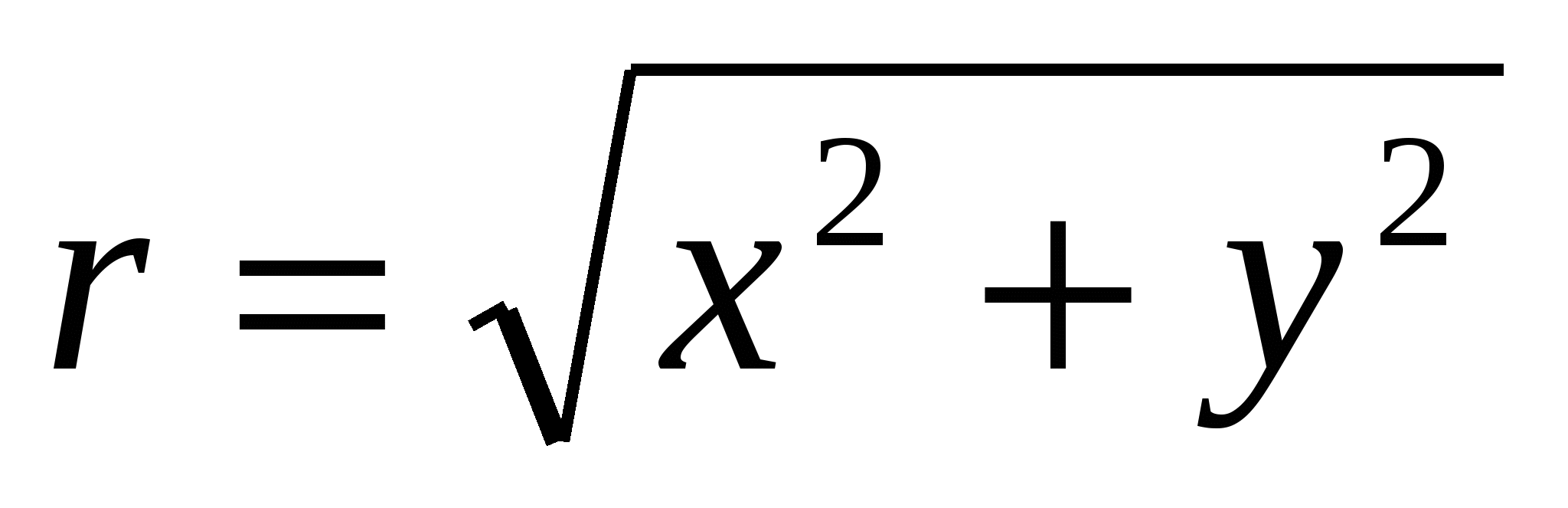 называется модулем, или абсолютной величиной комплексного числа z и обозначается
называется модулем, или абсолютной величиной комплексного числа z и обозначается ![]() , а полярный угол ф называется аргументом комплексного числа и обозначается arg
, а полярный угол ф называется аргументом комплексного числа и обозначается arg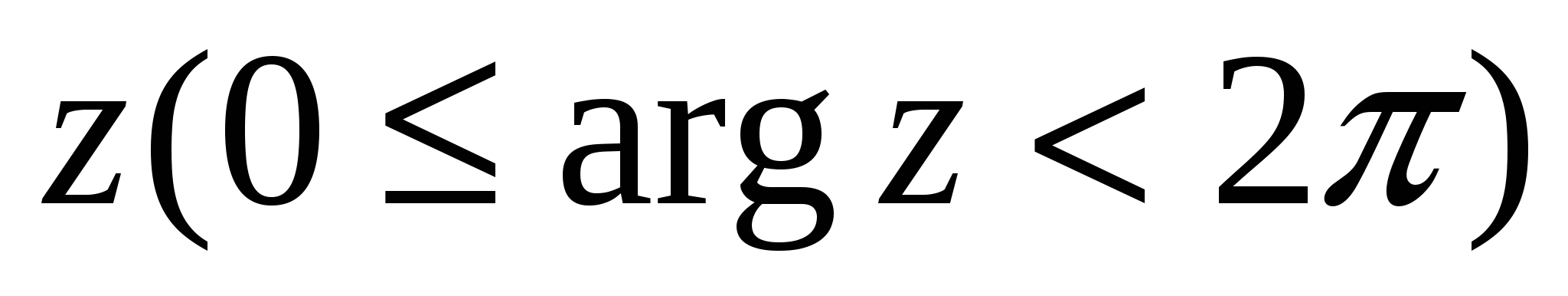 . Так как
. Так как
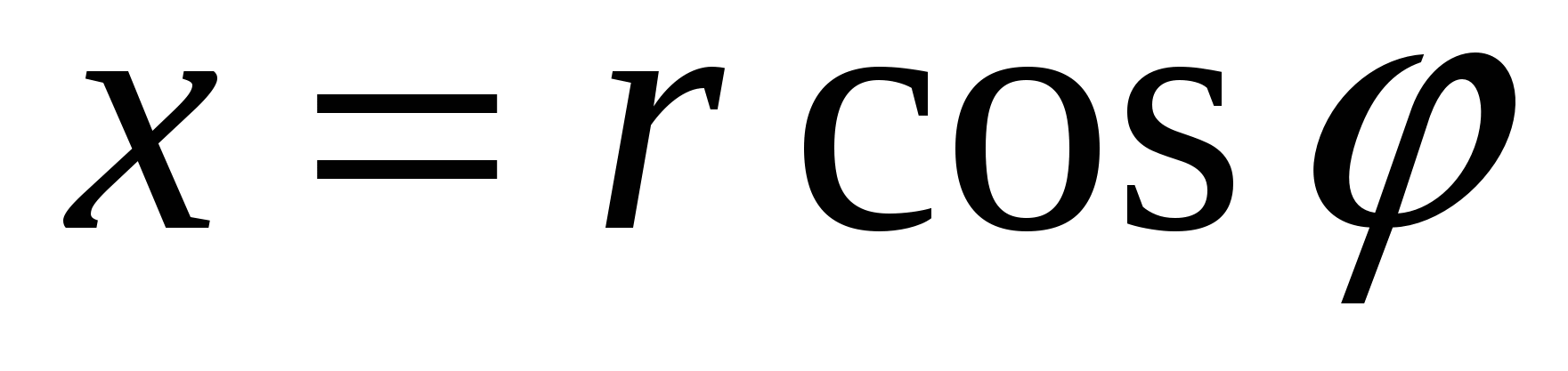 и
и 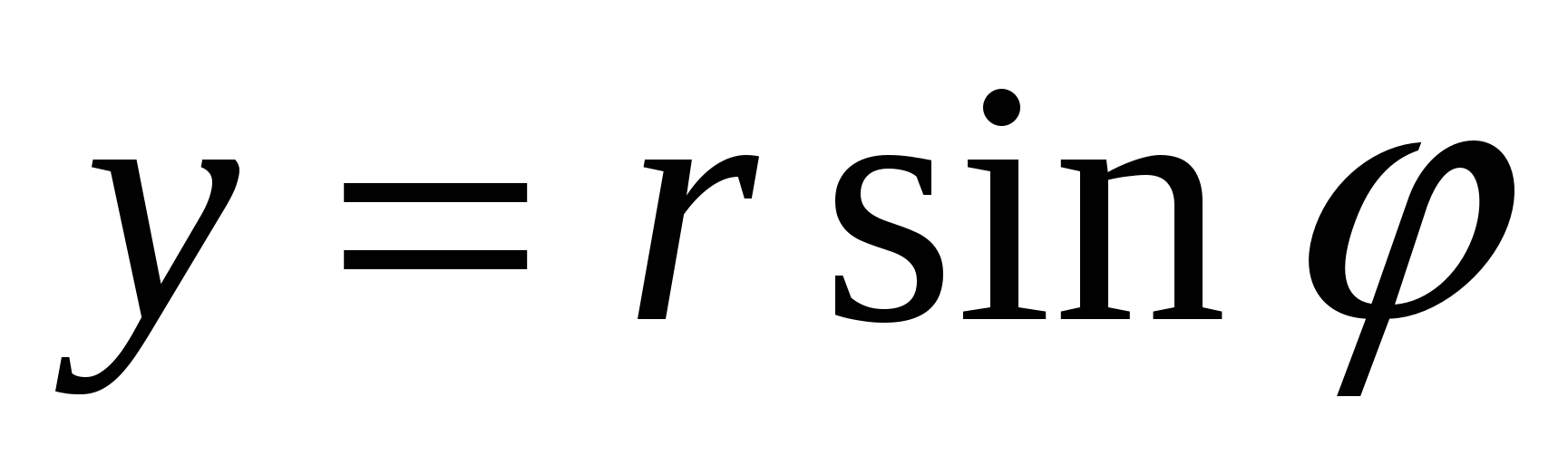 , то
, то 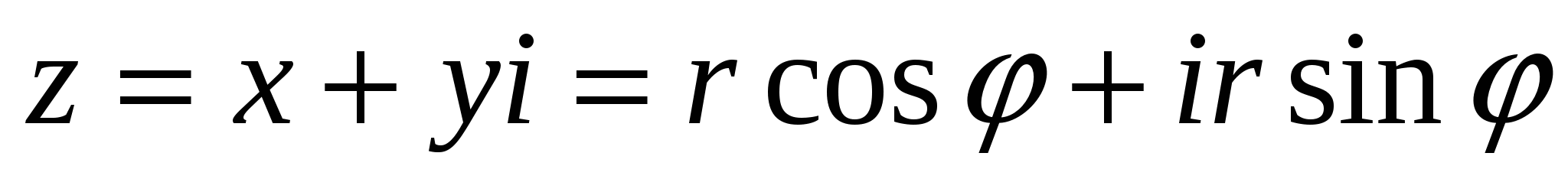 или
или
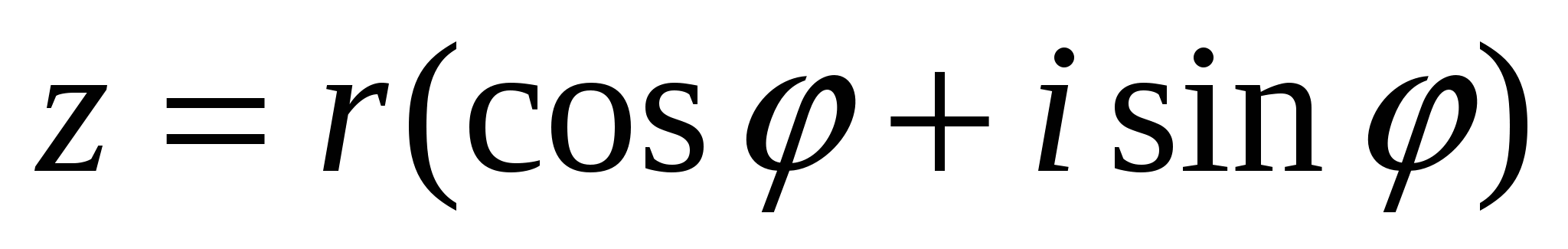 . (13)
. (13)
Правая часть (13) называется тригонометрической формой комплексного числа.
Запись комплексного числа z в виде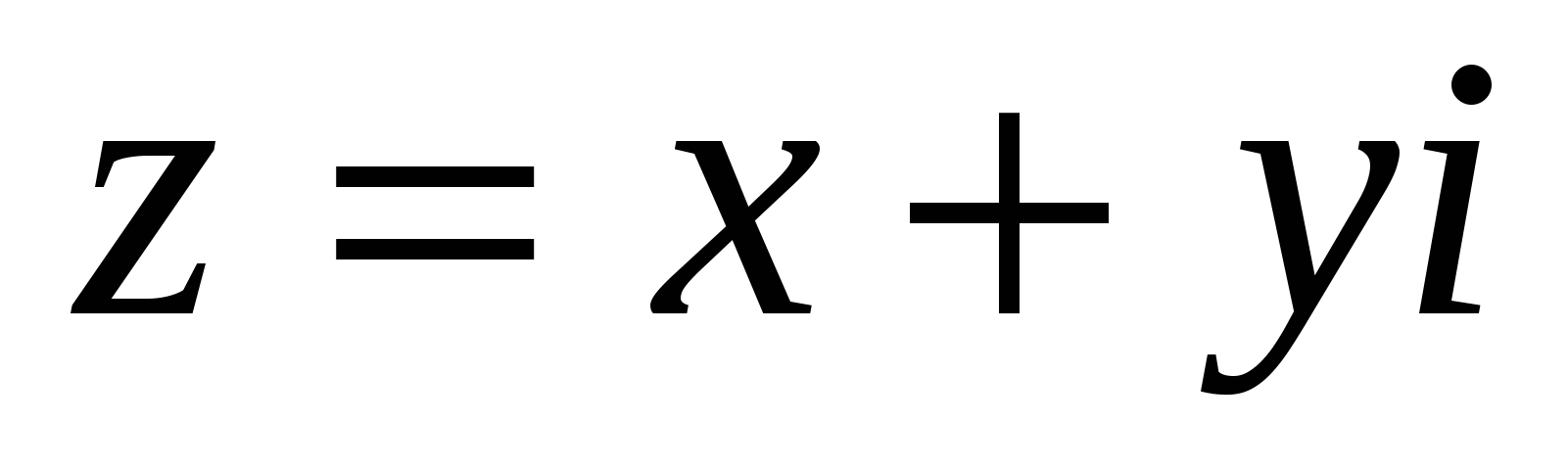 называется алгебраической формой комплексного числа. Переход от алгебраической формы записи к тригонометрической и обратно осуществляется по формулам
называется алгебраической формой комплексного числа. Переход от алгебраической формы записи к тригонометрической и обратно осуществляется по формулам
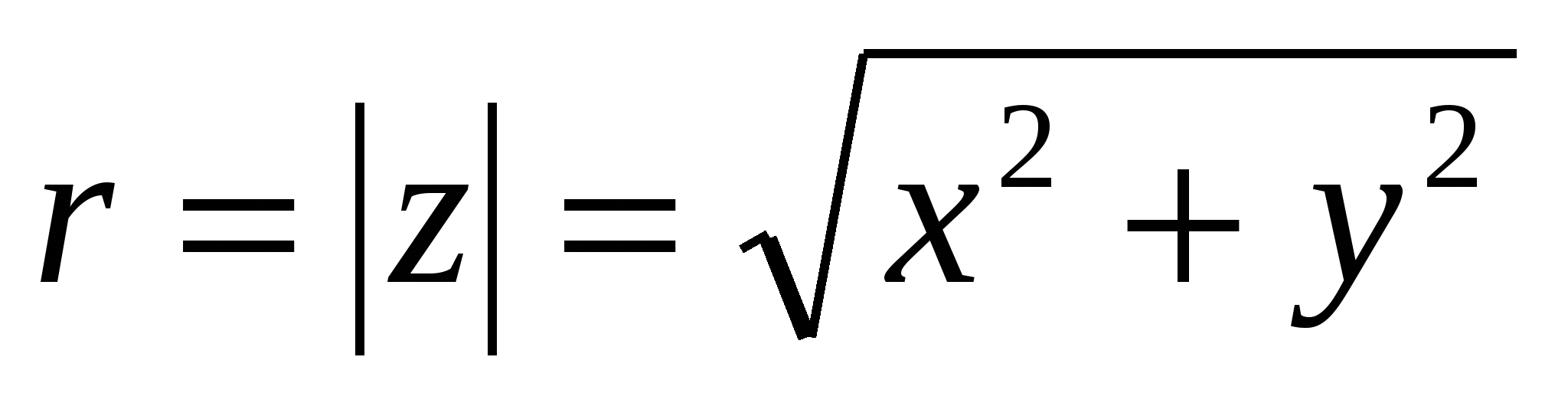 ;
; 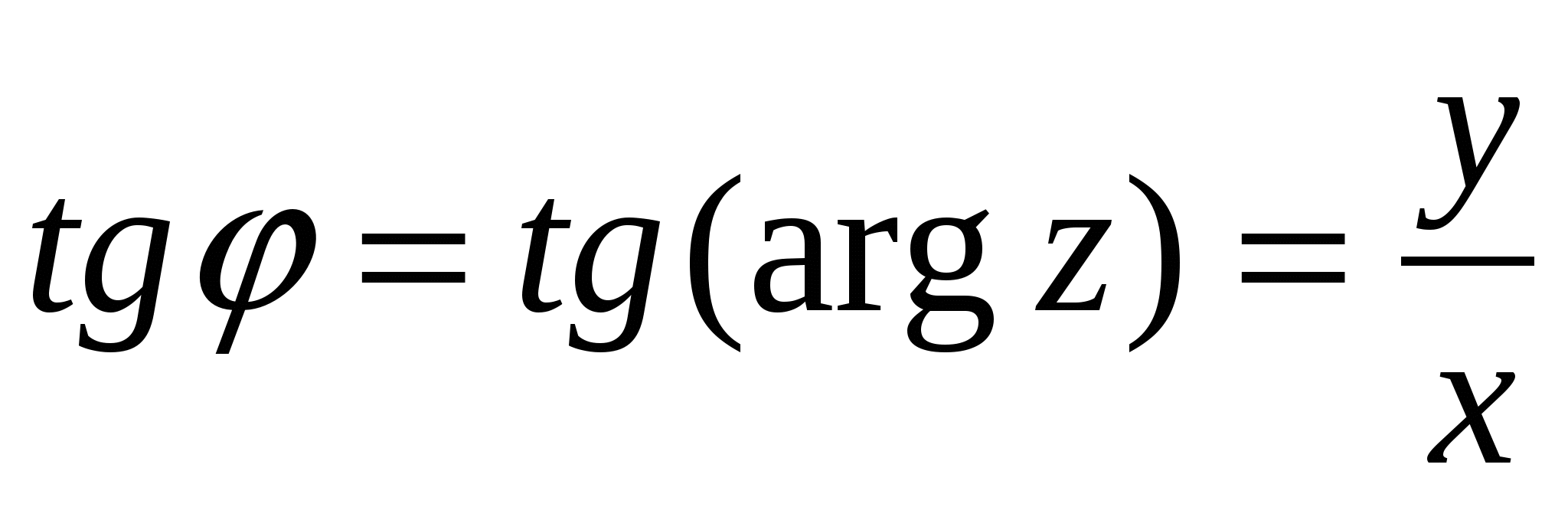 ;
;
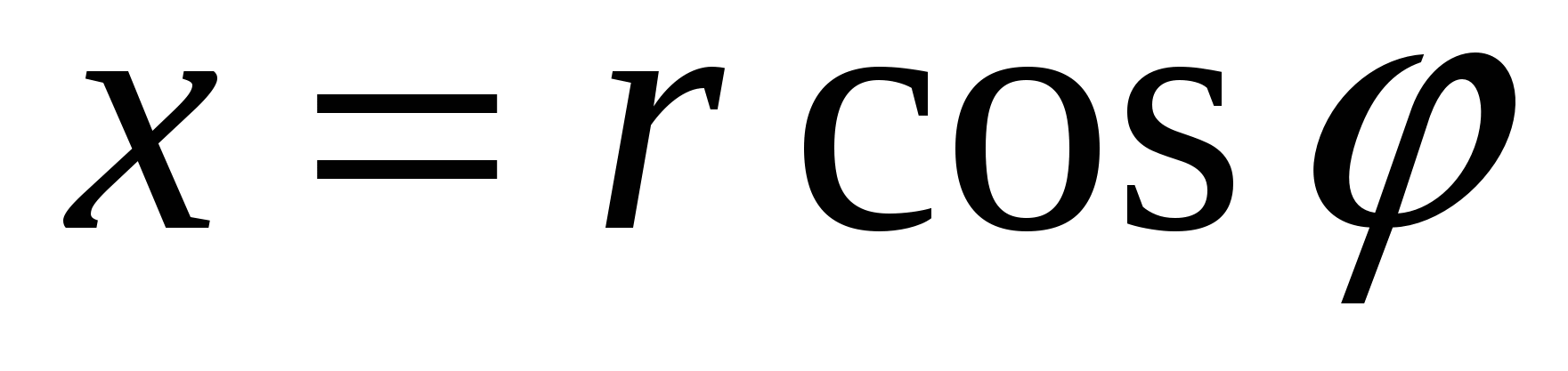 ;
; 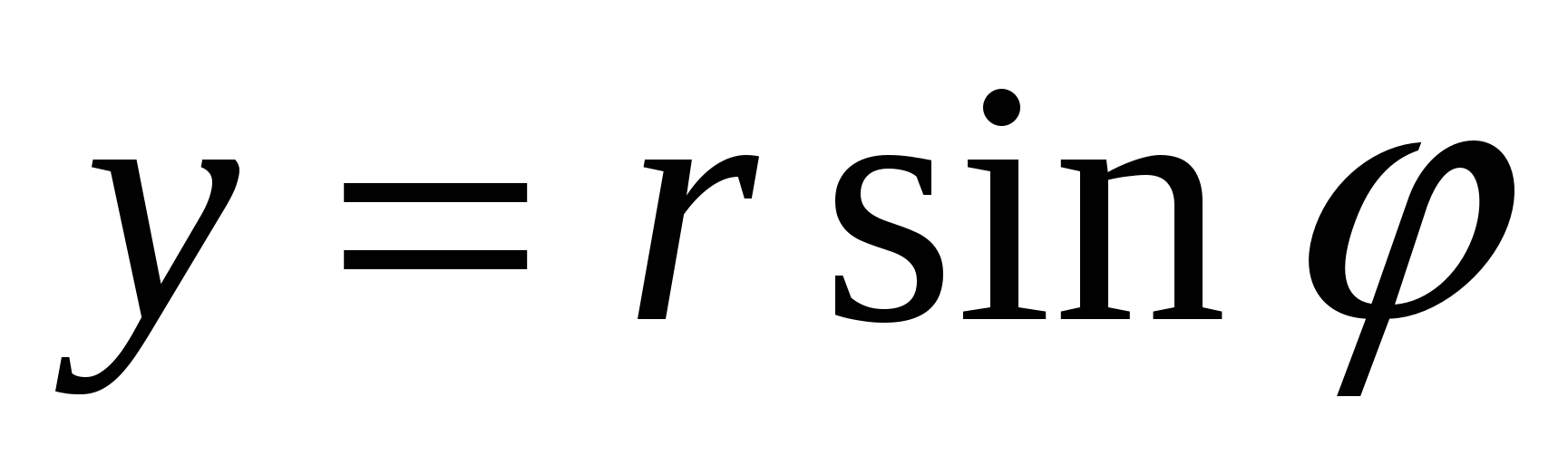 .
.
Пример 1. Составить тригонометрическую форму записи комплексного числа 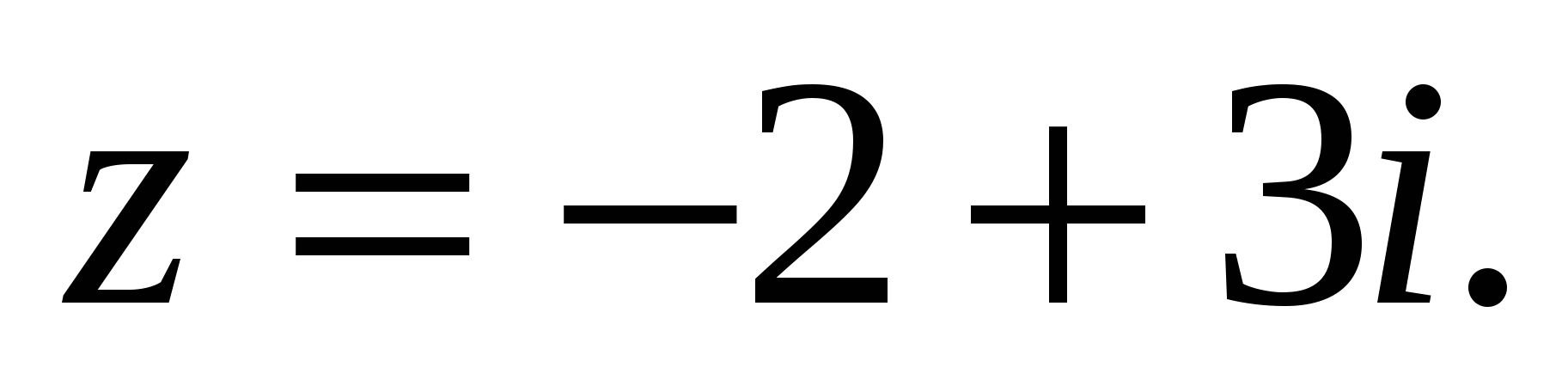
Решение. Имеем: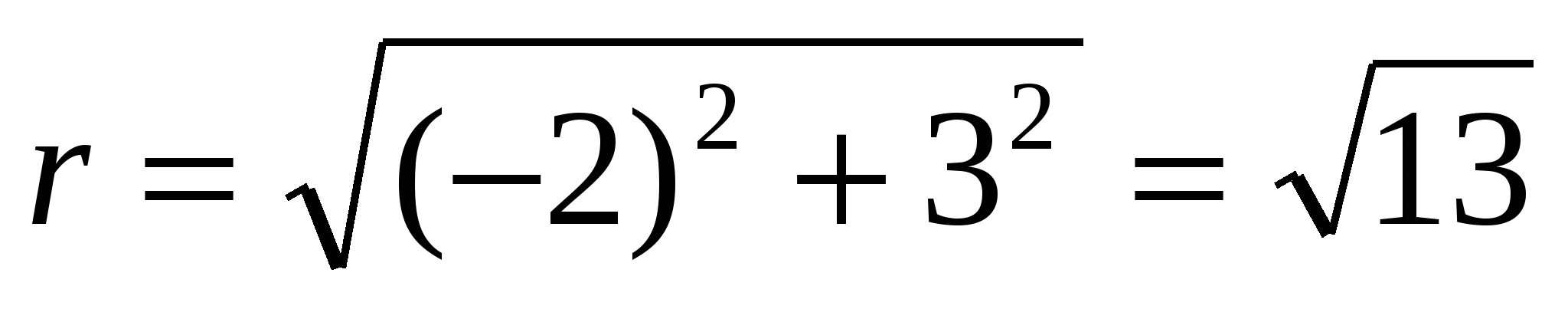
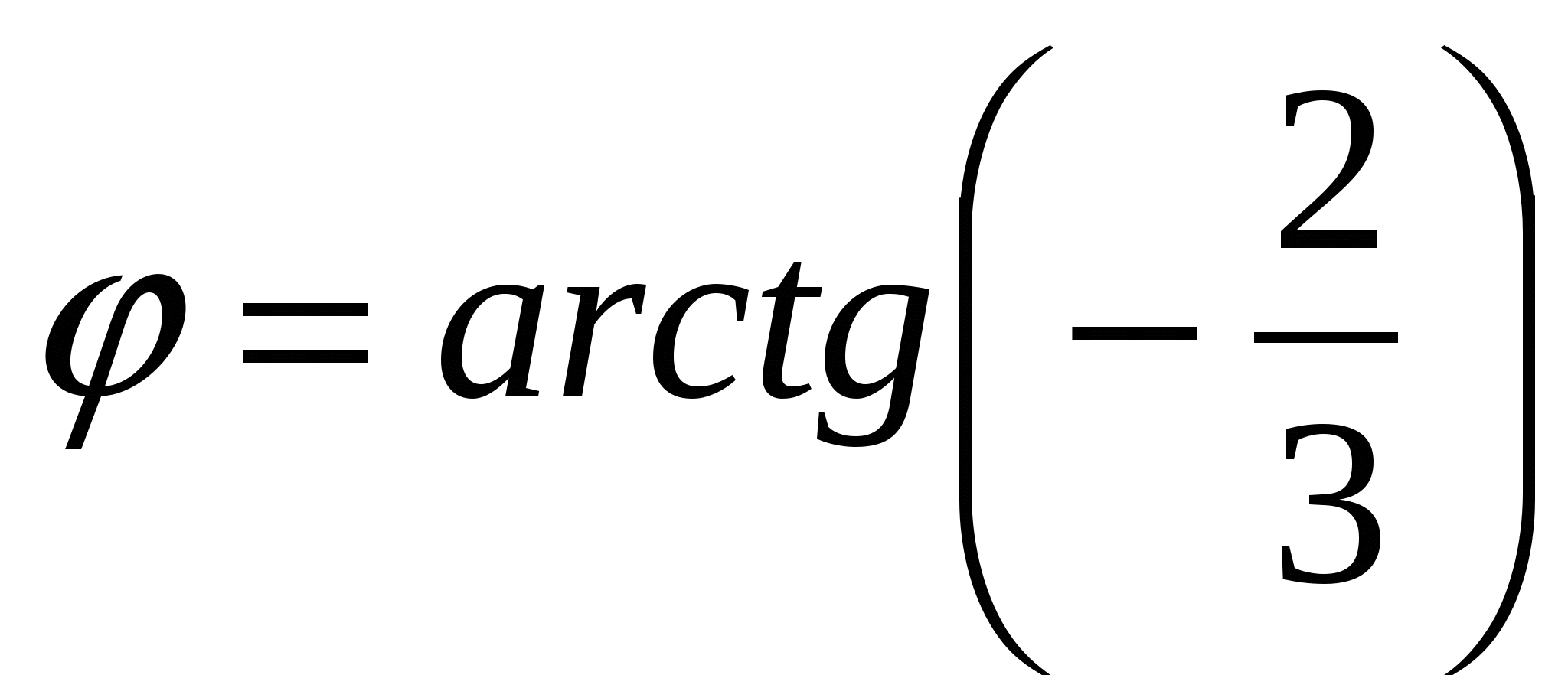 ,
, 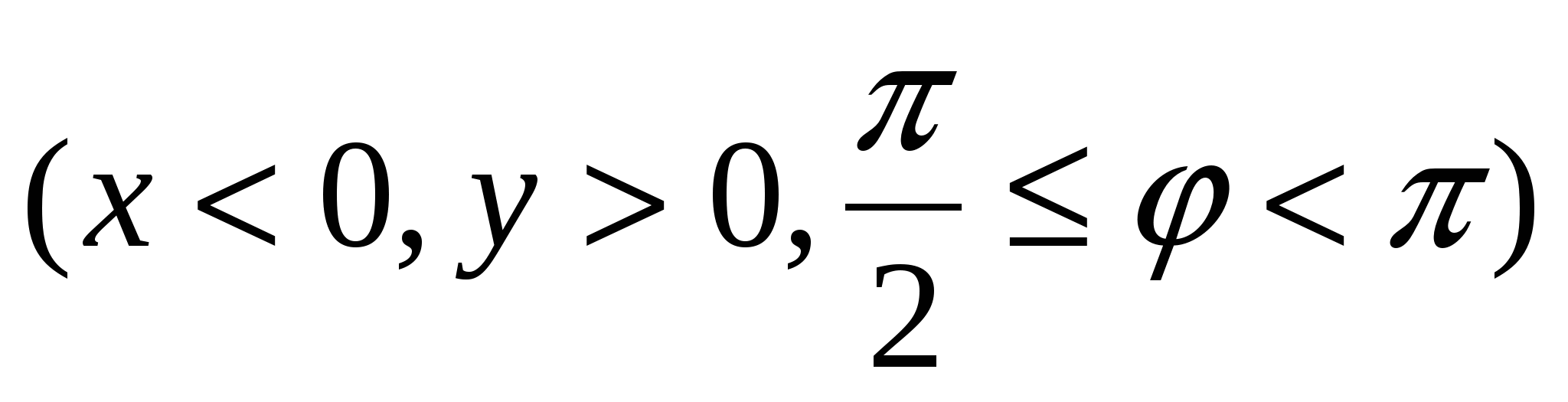 .
.
По таблице тригонометрических функций или на калькуляторе находим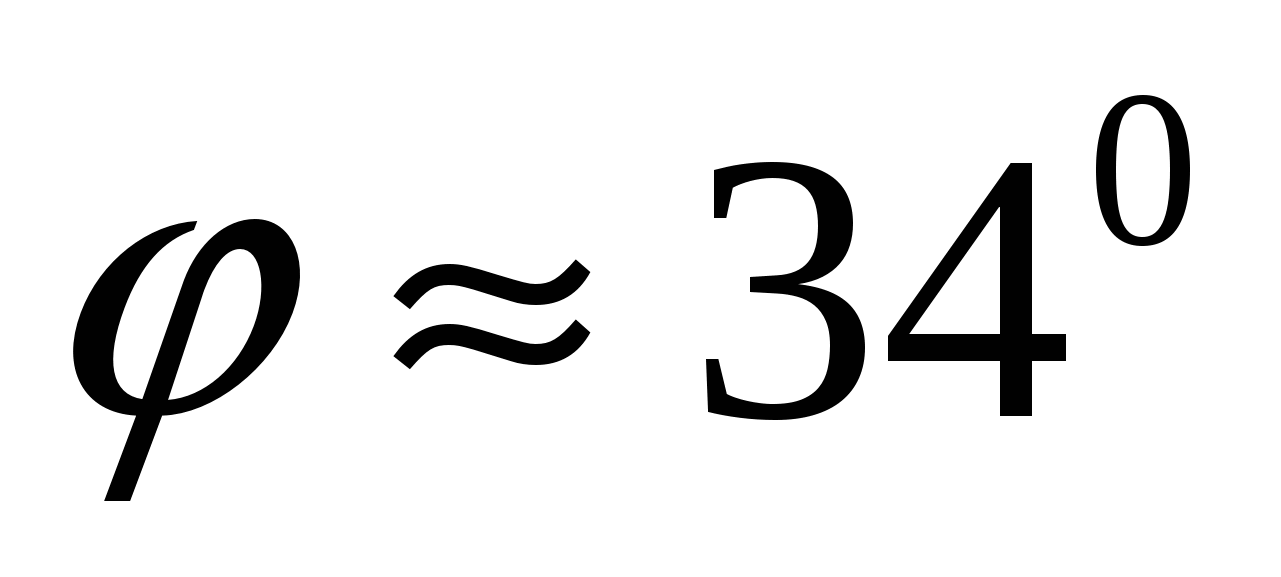 .
.
Следовательно,![]() .
.
Пример 2. Доказать, что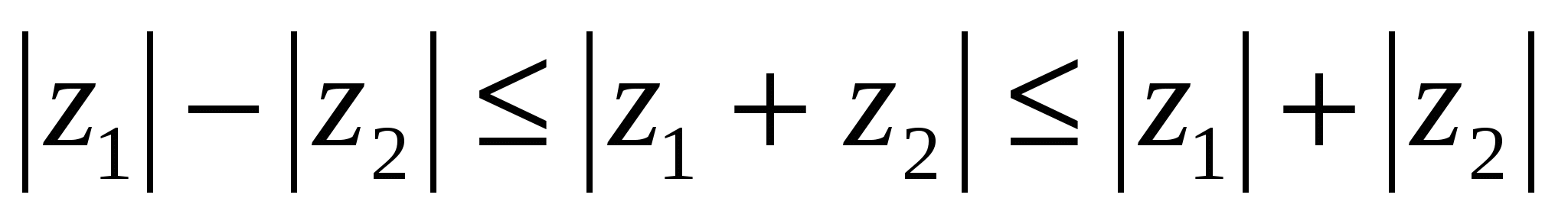 .
.
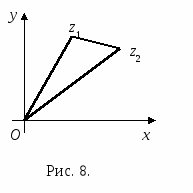
Решение. На комплексной плоскости построим числа z1 и z2 (рис. 8). Неравенства, подлежащие доказательству, вытекают из известной теоремы геометрии о сторонах треугольника (разность двух сторон треугольника не больше третьей стороны, а сумма двух сторон не меньше третьей стороны).
Следует заметить, что для комплексных чисел понятия «больше» и «меньше» лишены смысла, так как эти числа, в отличие от действительных, располагаются на плоскости, точки которой нельзя линейно упорядочить, в то время как точки прямой могут быть линейно упорядочены.
5.1. Действия над комплексными числами, заданными в тригонометрической форме
Пусть даны два комплексных числа в тригонометрической форме:
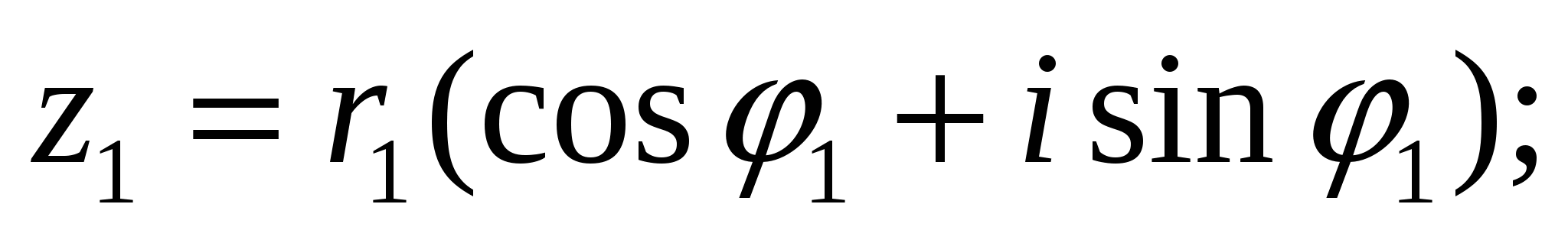
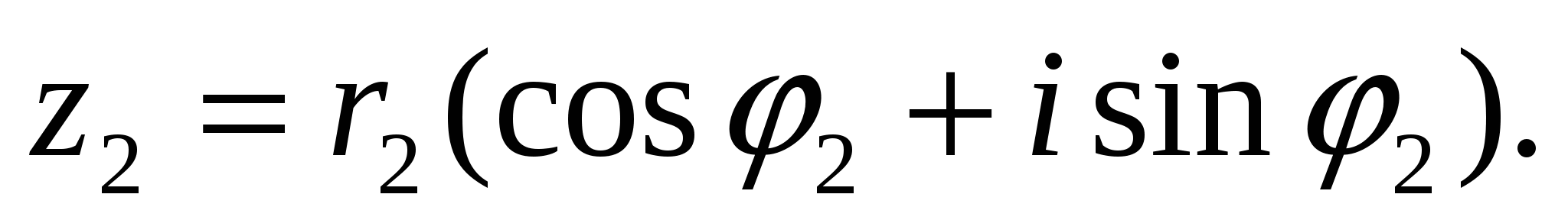 (14)
(14)
Перемножая их, получим
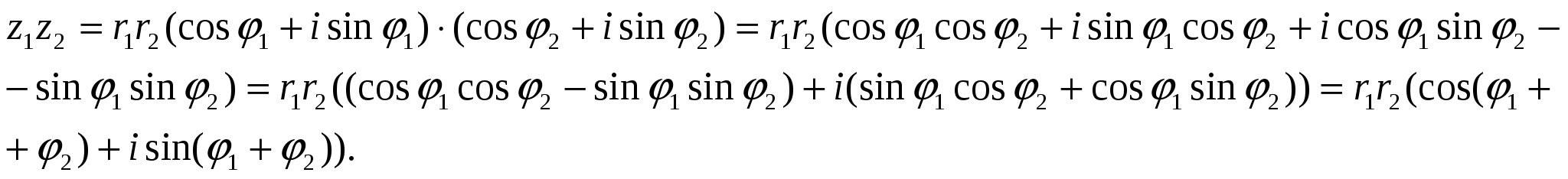
т. е.
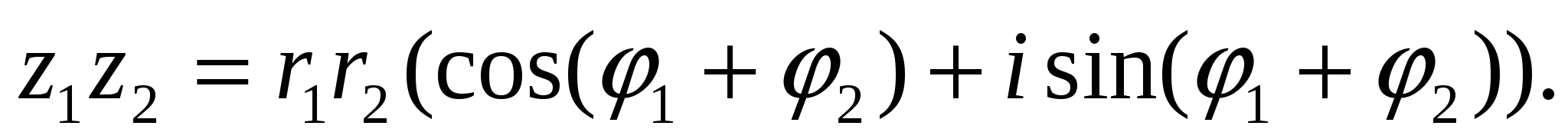 (15)
(15)
Таким образом, при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются:
Пример 1. Дано 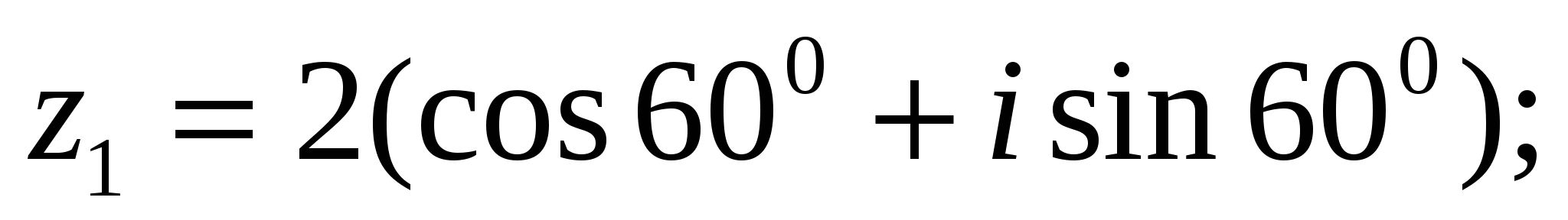
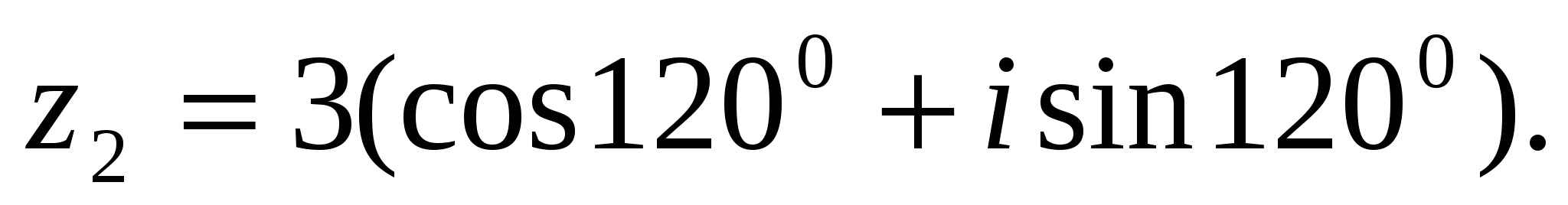
ВЫЧИСЛИТЬ 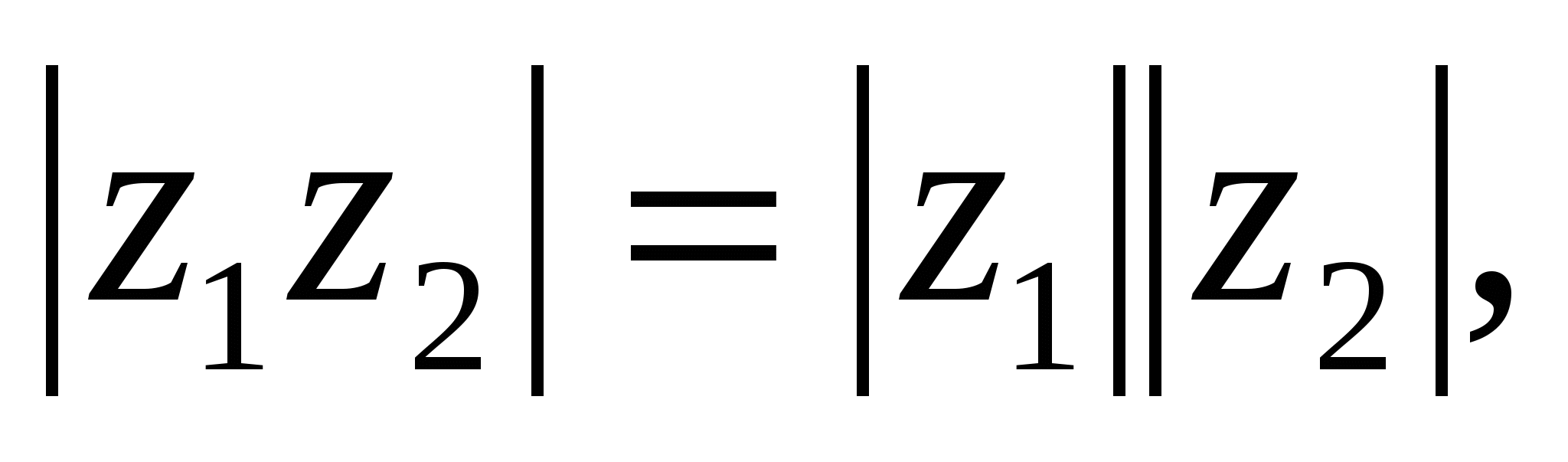
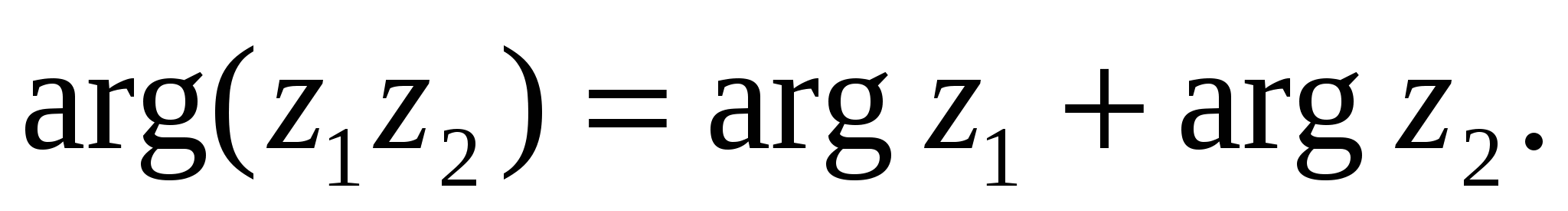
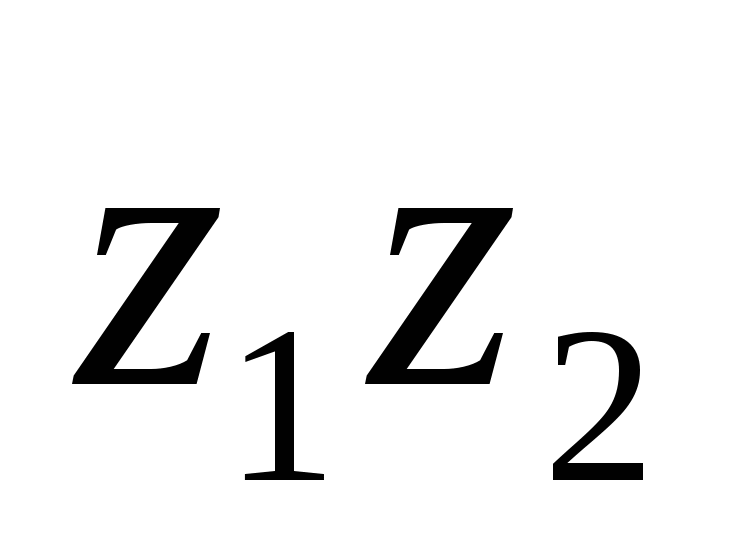
Решение. Применяем формулу (15):
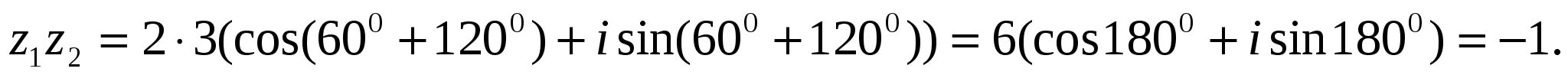
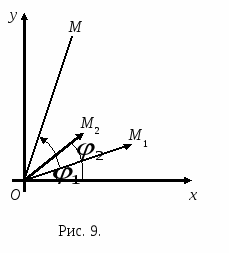
На комплексной плоскости числа z1 и z2 представим, соответственно, векторами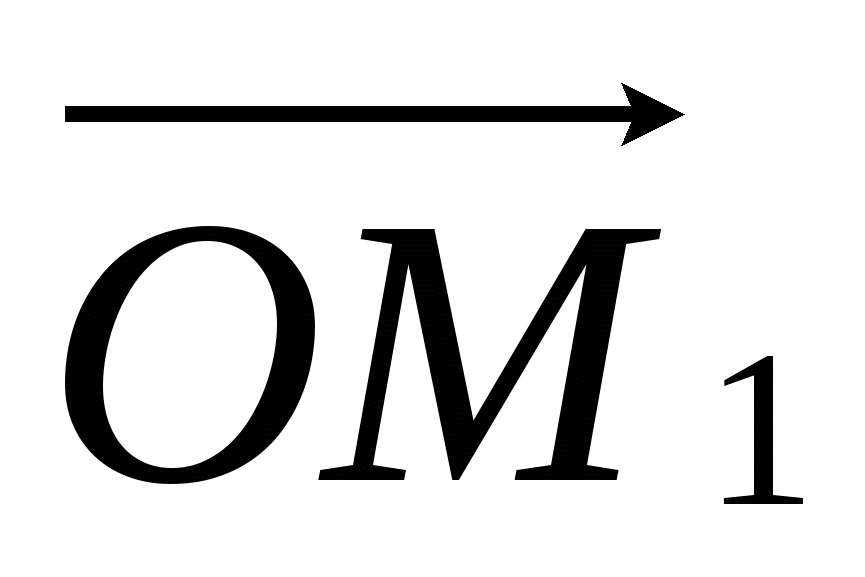 и
и 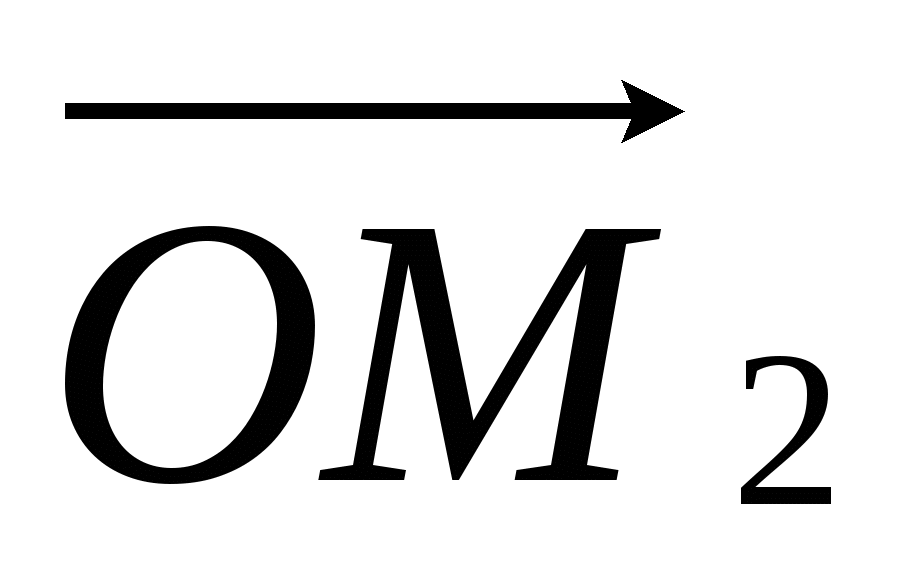 (рис. 9). Чтобы построить вектор
(рис. 9). Чтобы построить вектор 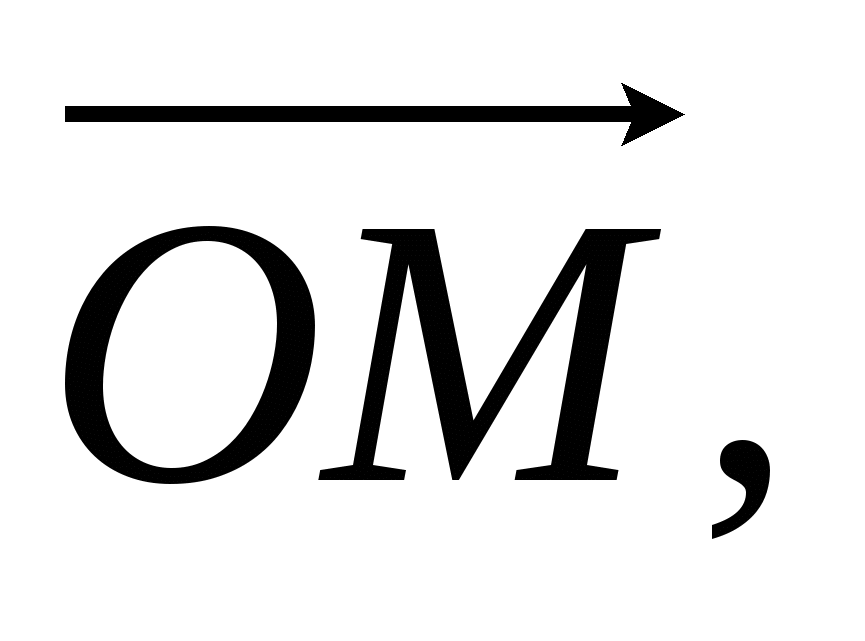 изображающий комплексное число z = z1z2 надо (см. равенство (11)) вектор
изображающий комплексное число z = z1z2 надо (см. равенство (11)) вектор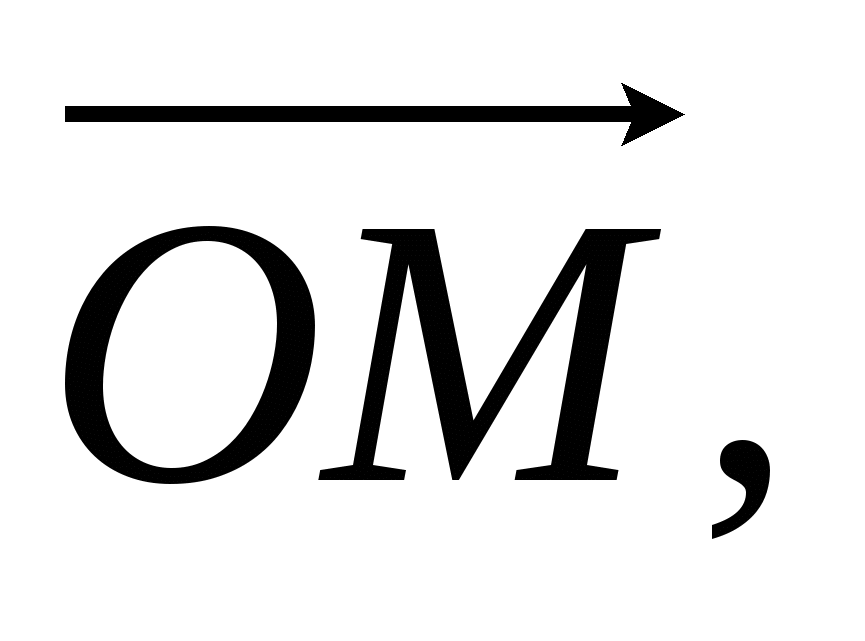 повернуть на угол
повернуть на угол  против часовой стрелки, затем умножить его длину на числоr. Это есть геометрическая интерпретация умножения комплексных чисел.
против часовой стрелки, затем умножить его длину на числоr. Это есть геометрическая интерпретация умножения комплексных чисел.
В частности, так как 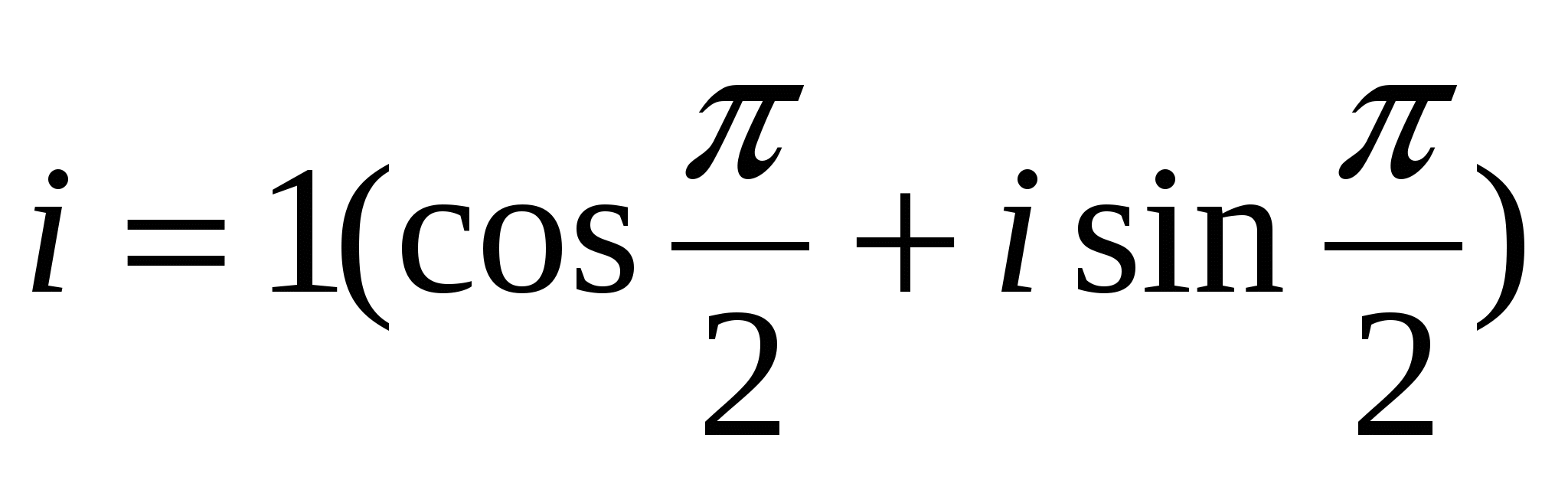 , то умножение любого комплексного числа z на число i с геометрической точки зрения можно рассматривать как операцию поворота вектора, изображающего число z, на угол
, то умножение любого комплексного числа z на число i с геометрической точки зрения можно рассматривать как операцию поворота вектора, изображающего число z, на угол 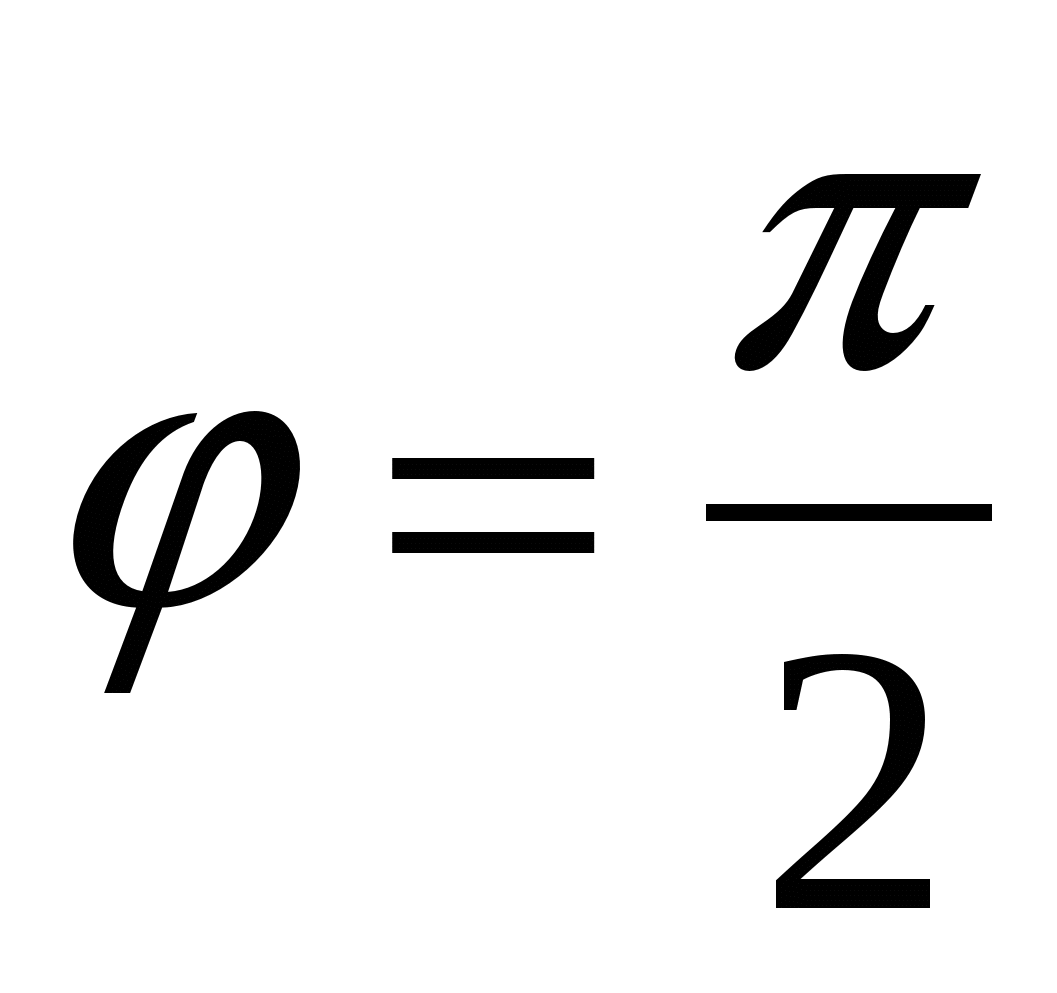 в положительном направлении (против движения часовой стрелки).
в положительном направлении (против движения часовой стрелки).
Разделим теперь первое комплексное число (14) на второе:
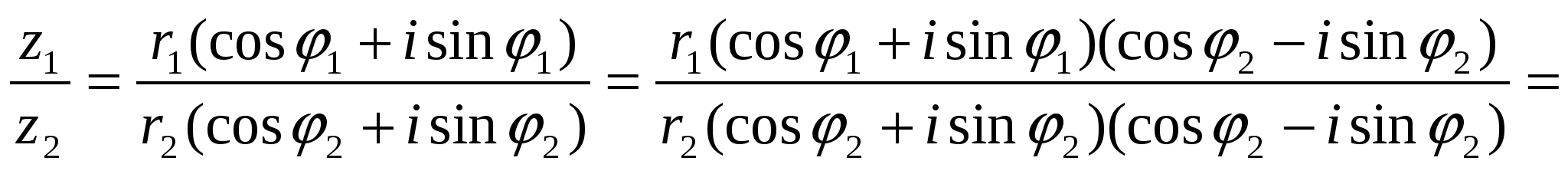
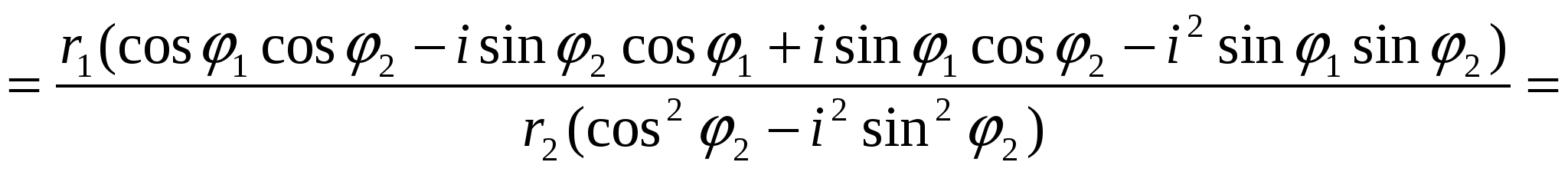 (имея i2= -1, получим:)
(имея i2= -1, получим:)
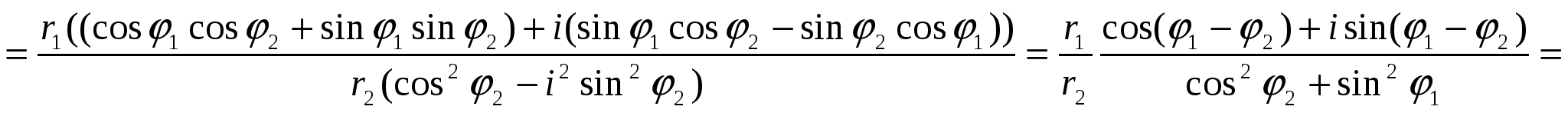
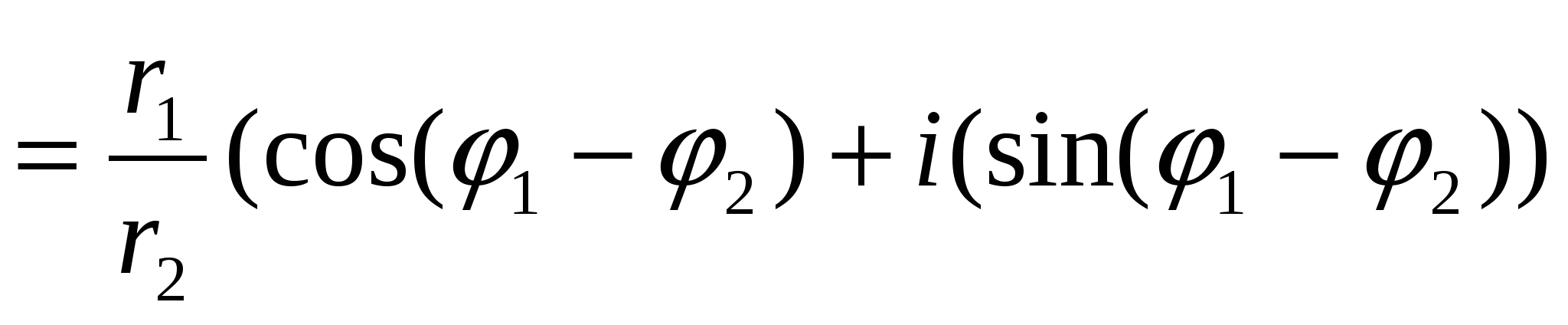 , где
, где 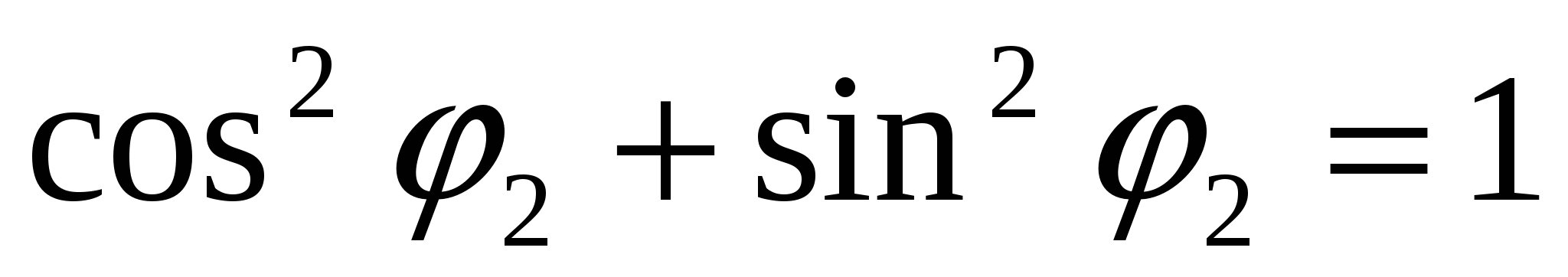
Итак, 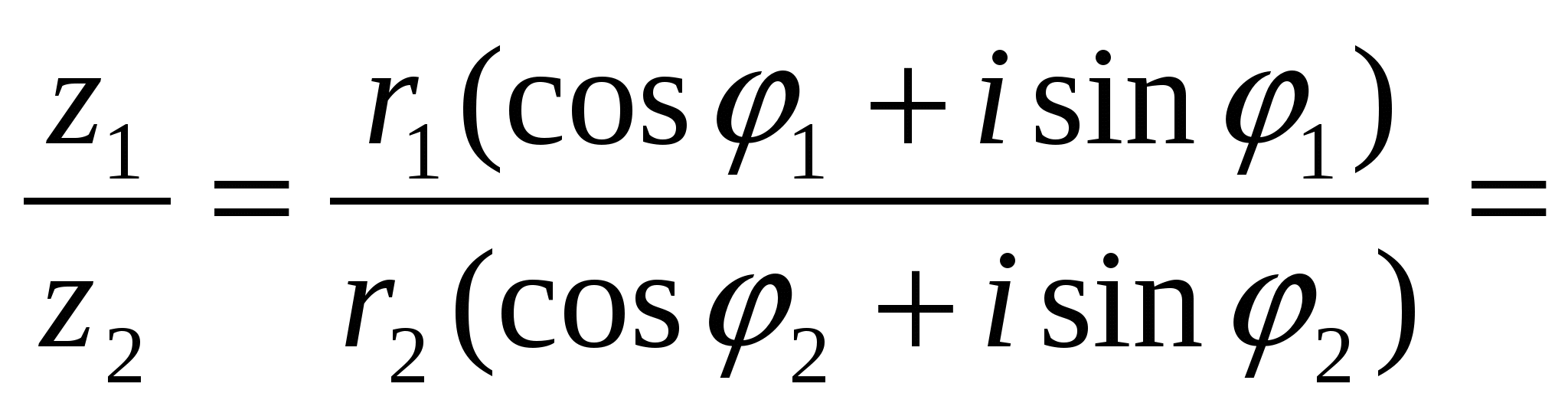
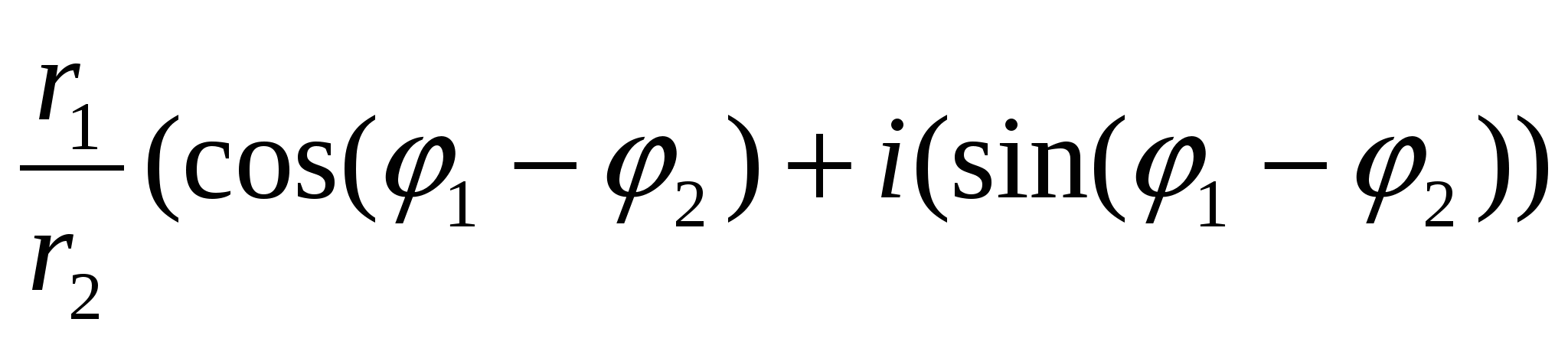
Таким образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются:
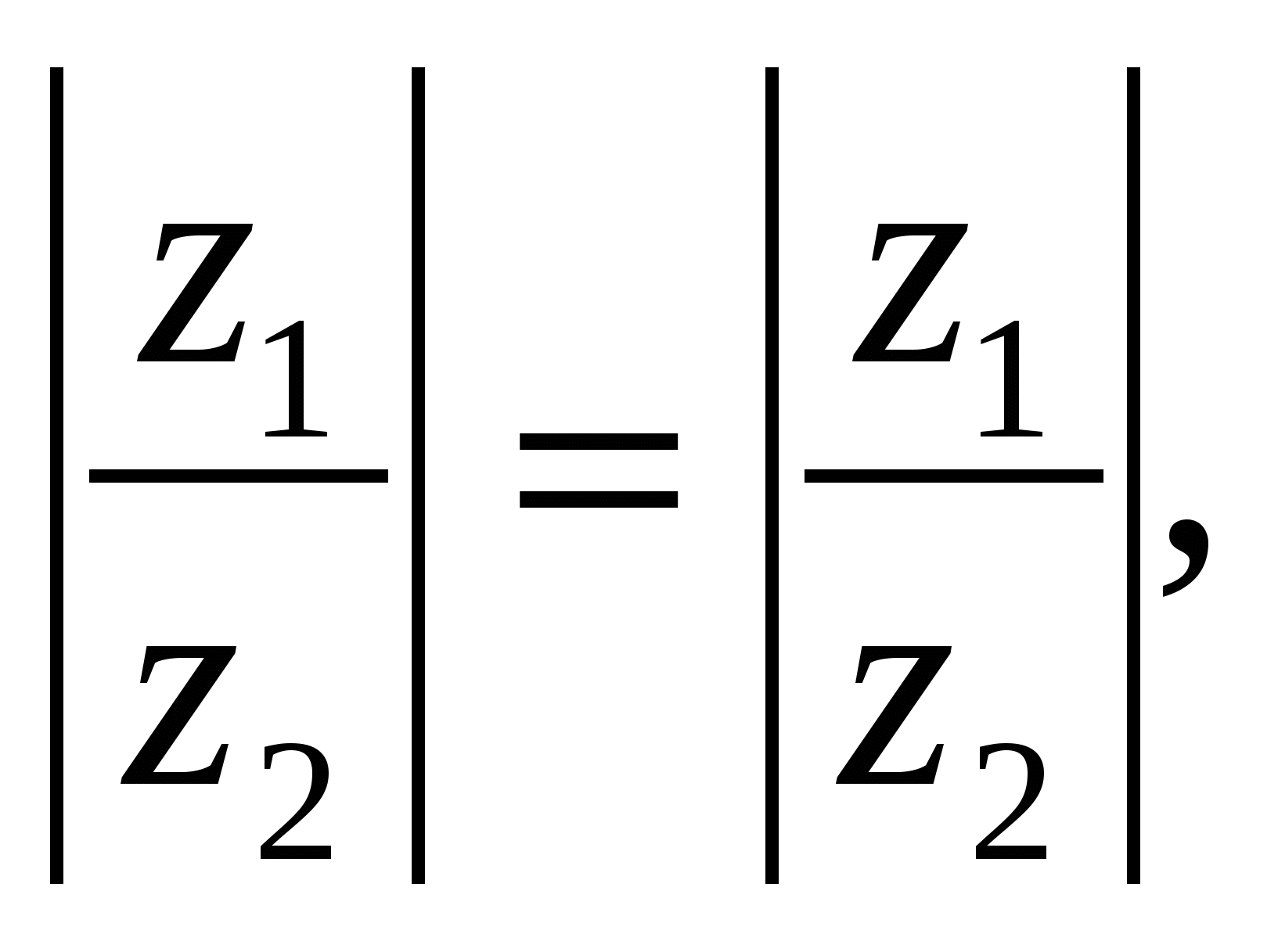
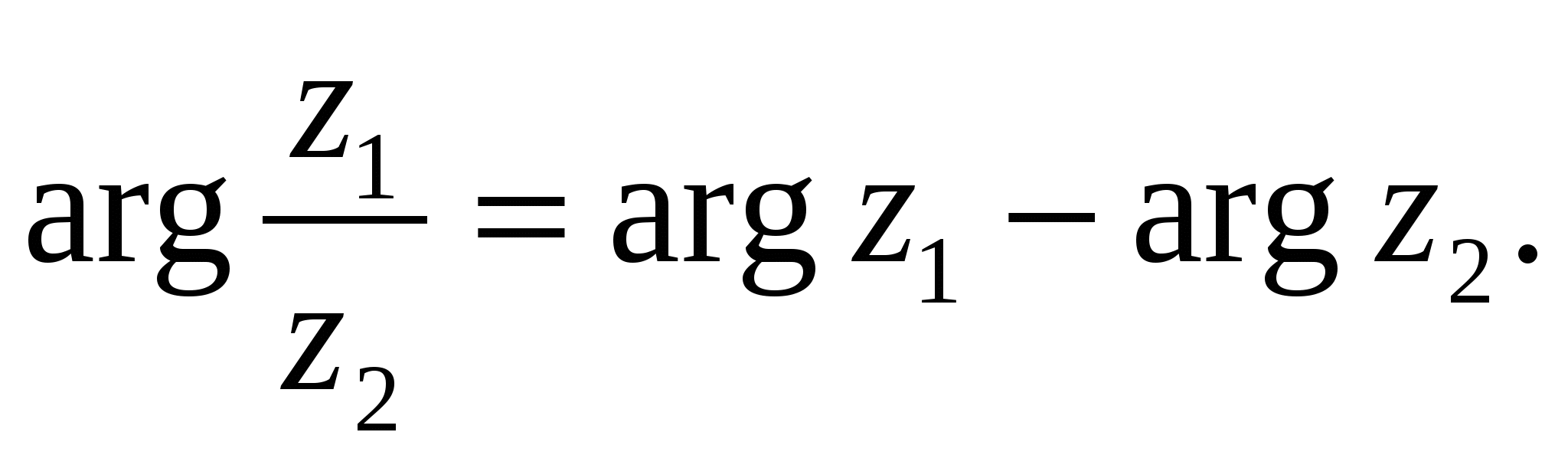
Пример 2. Дано 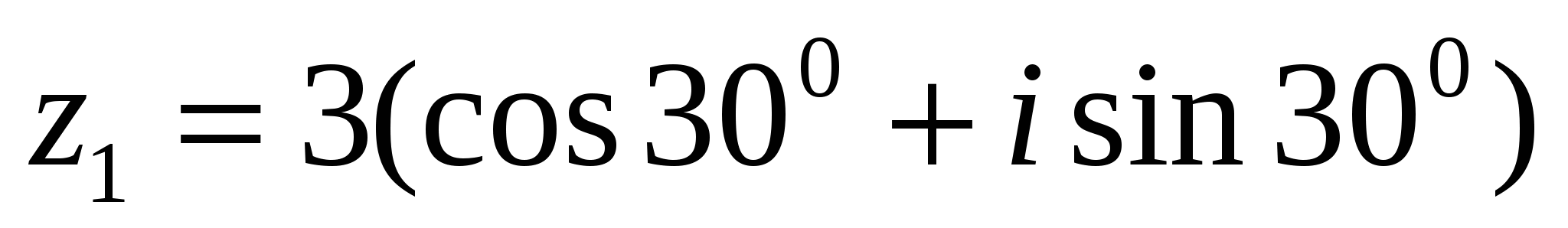 ,
, 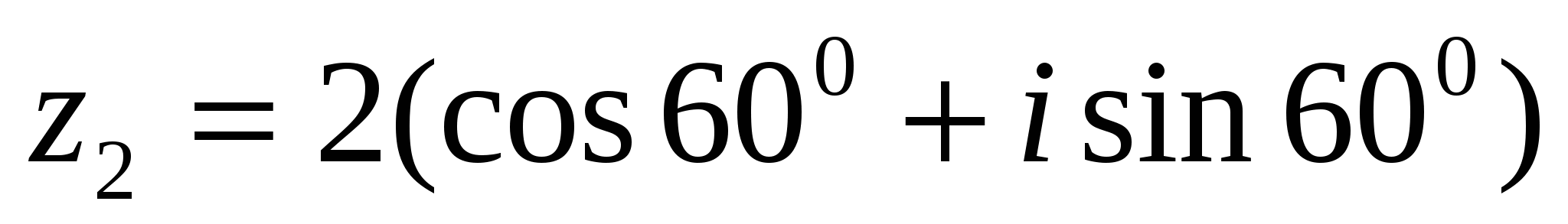 . Вычислить
. Вычислить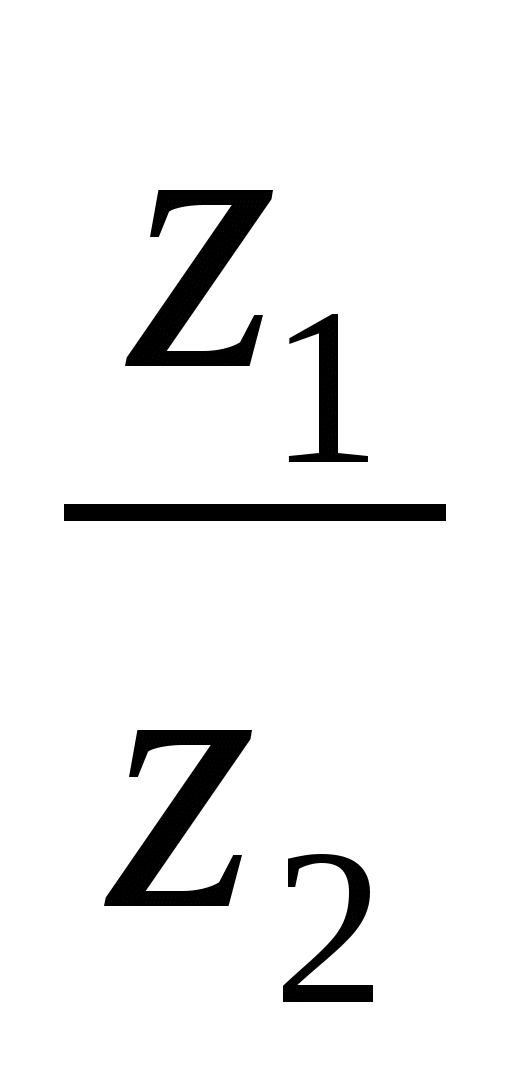 .
.
Решение. Имеем:
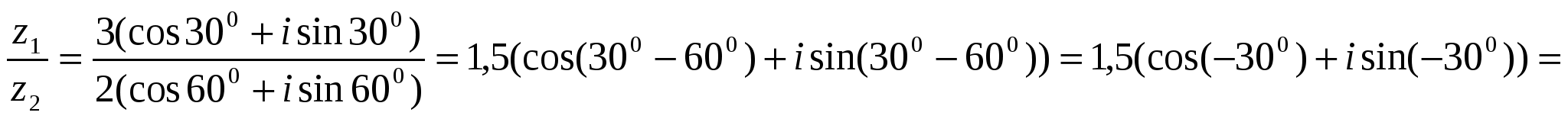
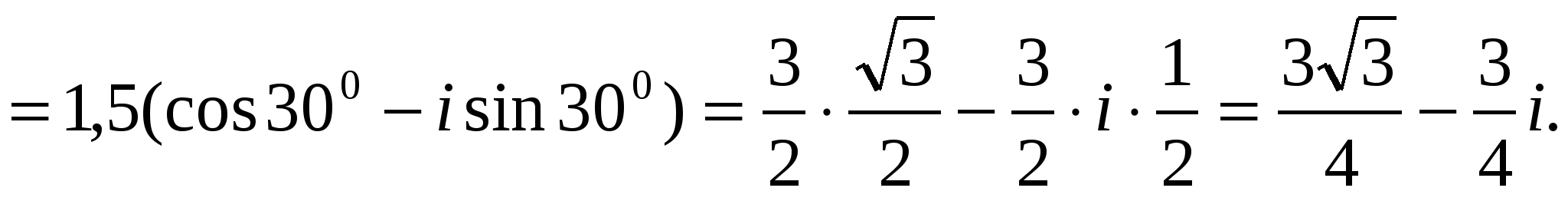
Для построения вектора 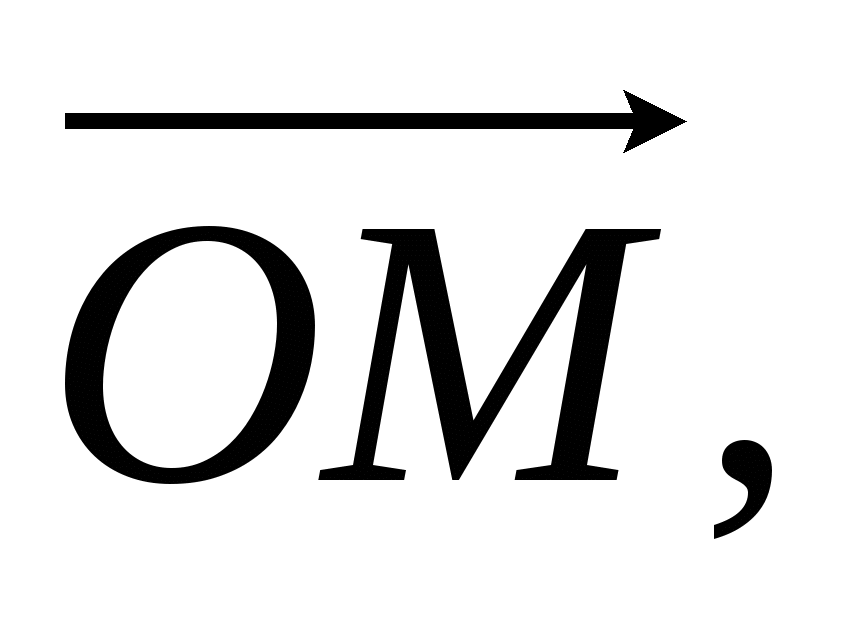 изображающего комплексное число
изображающего комплексное число 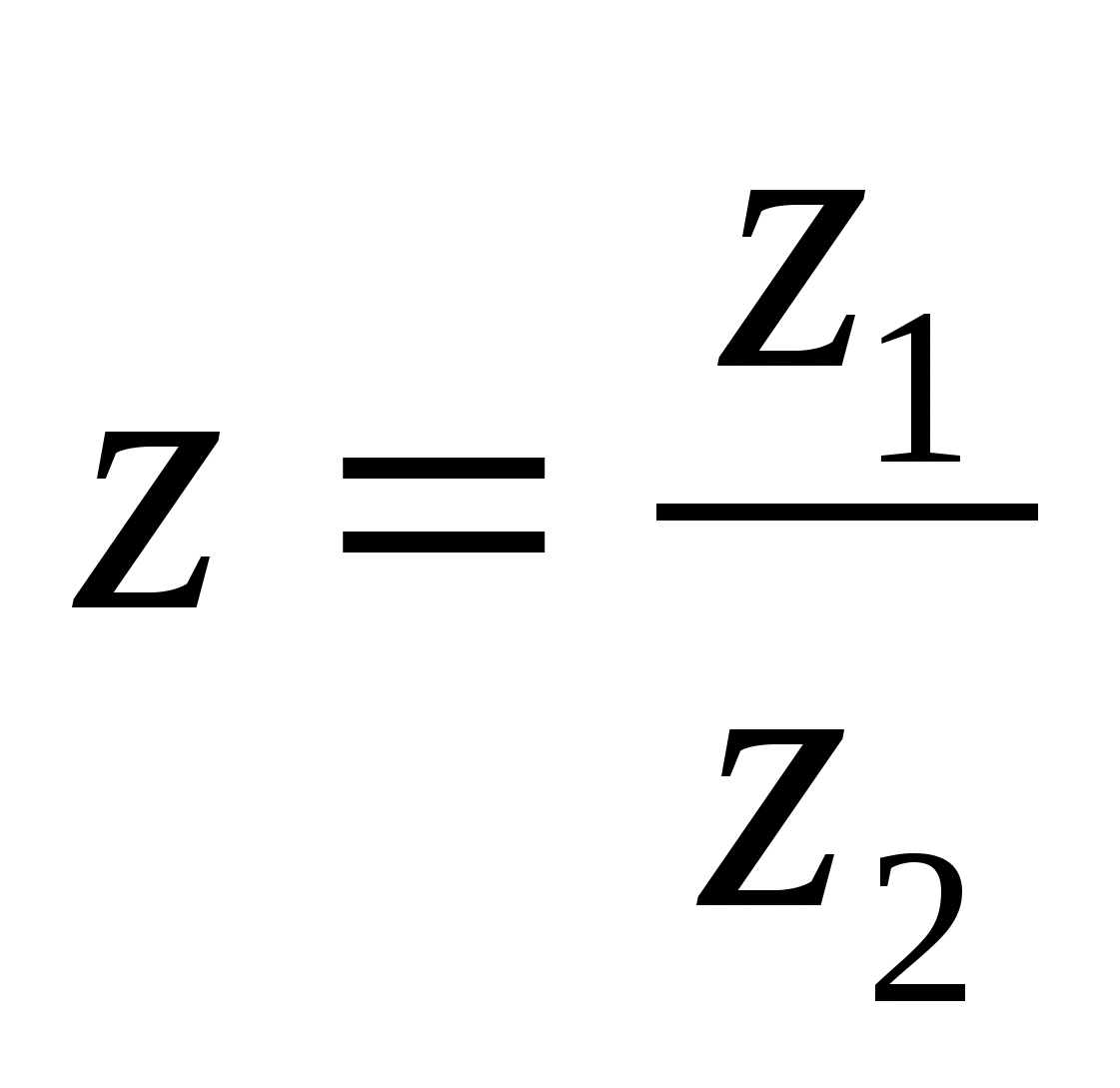 , нужно вектор
, нужно вектор![]() изображающий комплексное число z1, повернуть на угол
изображающий комплексное число z1, повернуть на угол  по часовой стрелке и уменьшить его длину в r2 раз.
по часовой стрелке и уменьшить его длину в r2 раз.
Деление комплексного числа z на i с геометрической точки зрения можно рассматривать как операцию поворота радиус-вектора точки z на угол 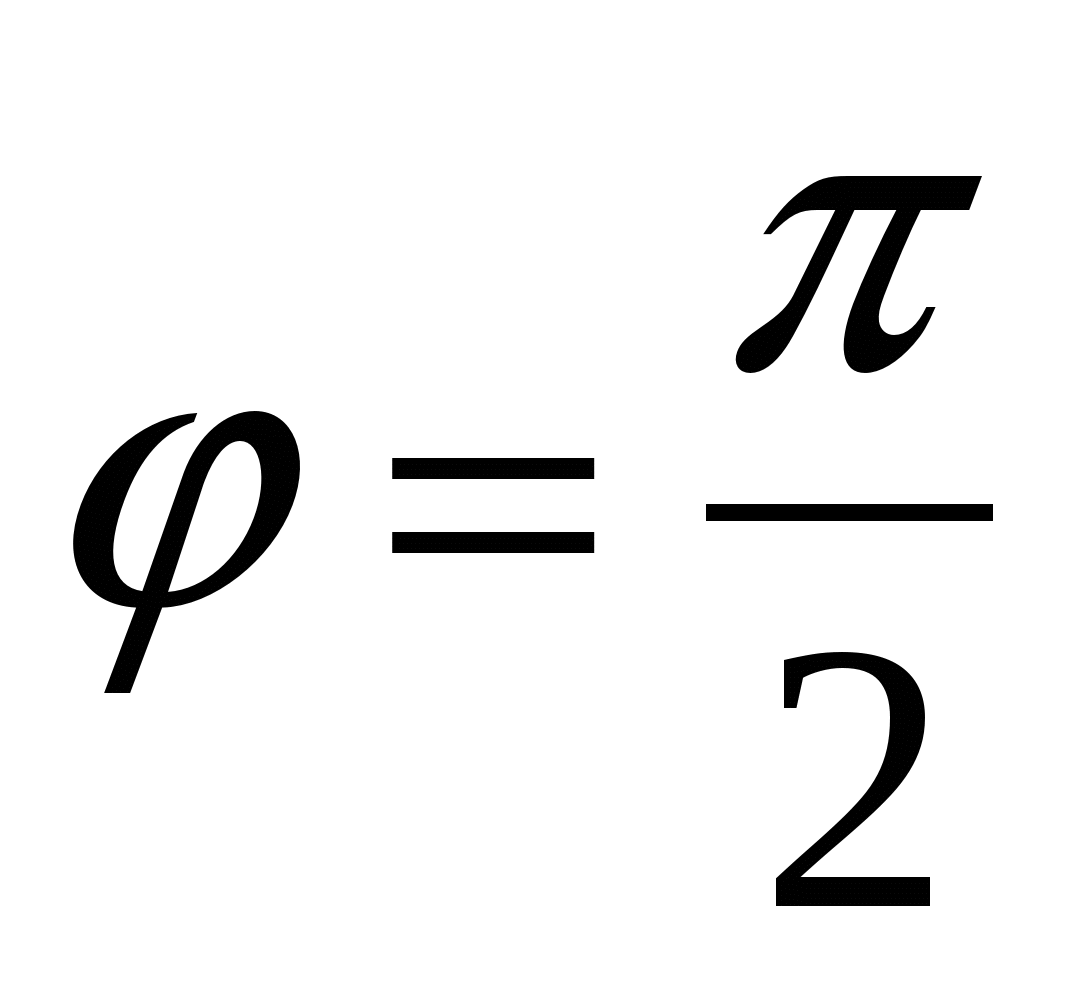 по часовой стрелке.
по часовой стрелке.
Возведение комплексного числа 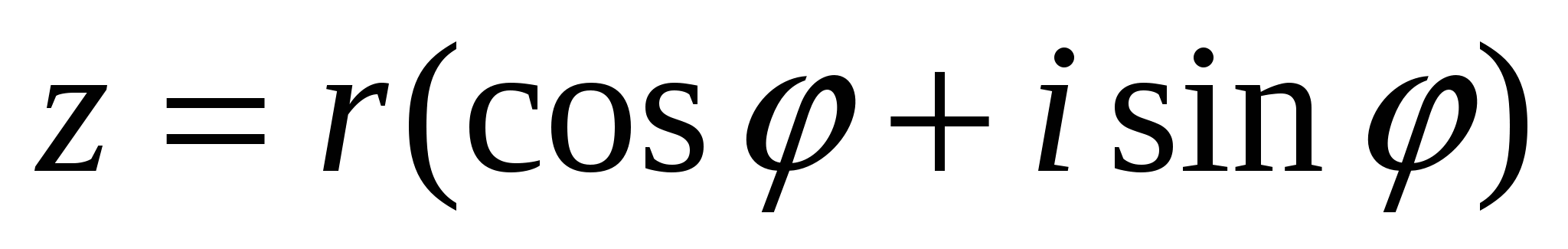 в натуральную степень п рассматривается как и-кратное умножение z на самое себя:
в натуральную степень п рассматривается как и-кратное умножение z на самое себя:
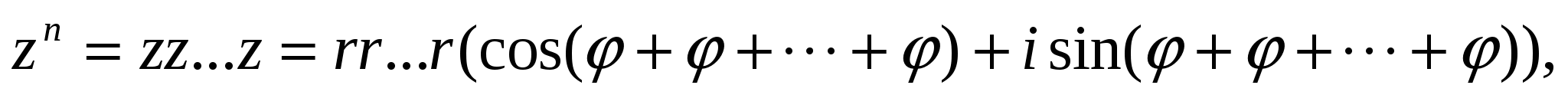
т. е.
![]() (16)
(16)
Таким образом, при возведении комплексного числа в степень п модуль этого числа возводится в степень п, а аргумент умножается на п:
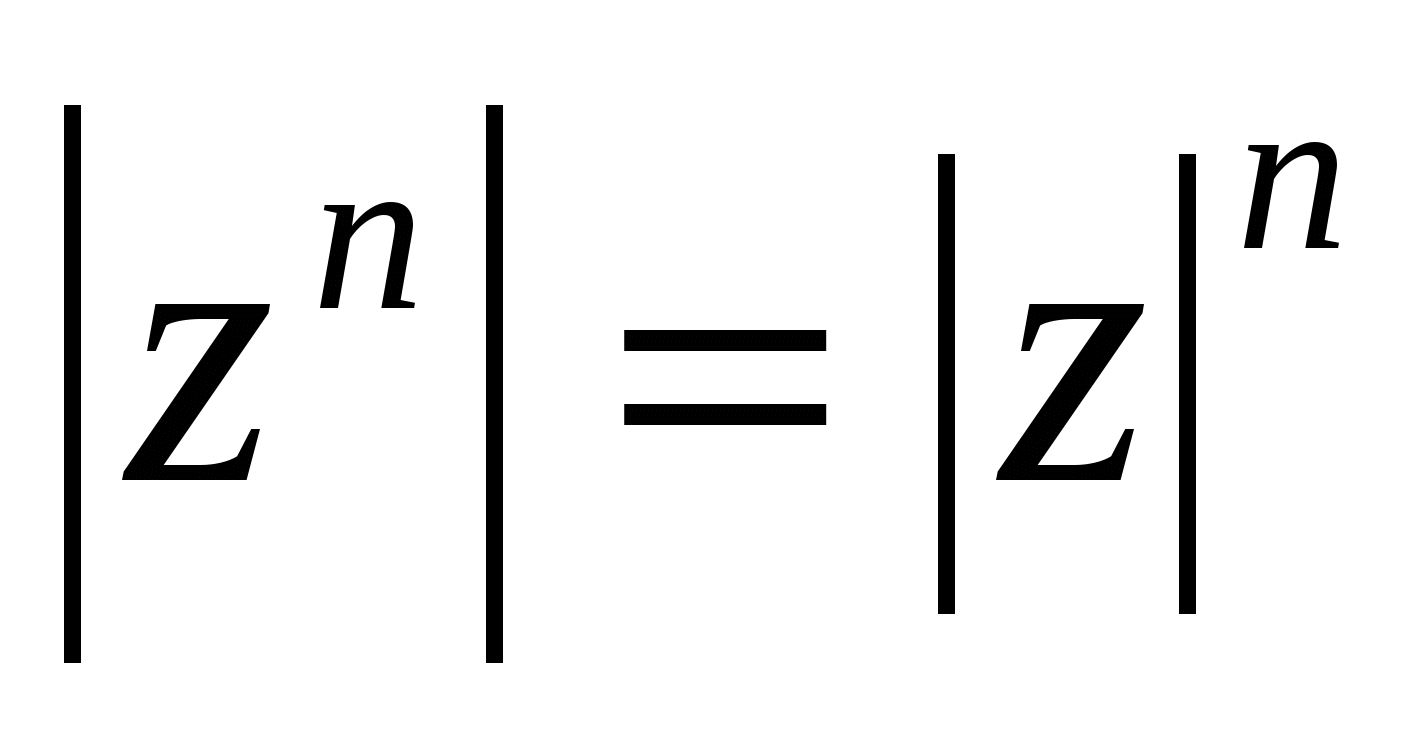 ;
; 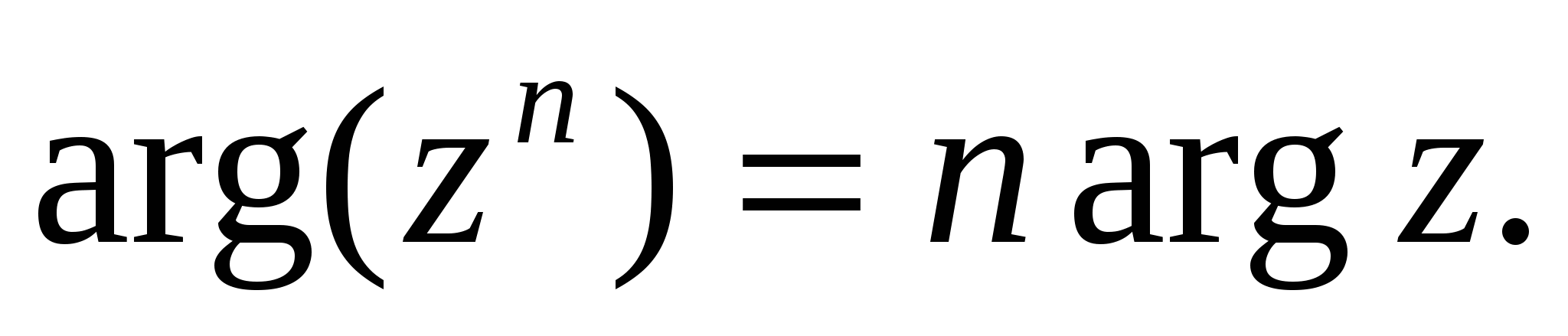
Формулу (16) можно записать в виде
![]() (17)
(17)
В частности, при r = 1 из равенства (17) следует формула Муавра, имеющая широкое применение в математике:
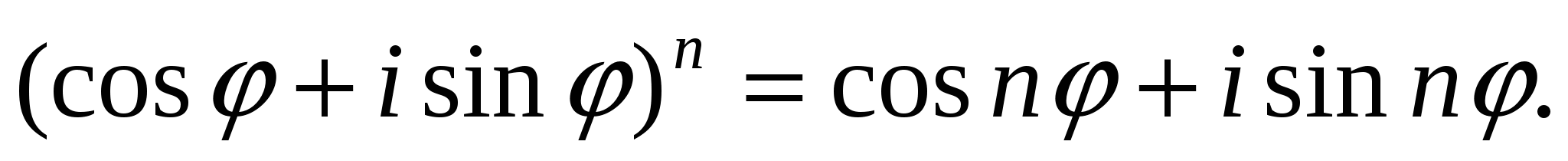
Пример 3. Выразите sin 4φ и cos 4φ через sin φ и cos φ.
Решение. Применяя формулу Муавра при п = 4, получим:
![]() (18)
(18)
Но
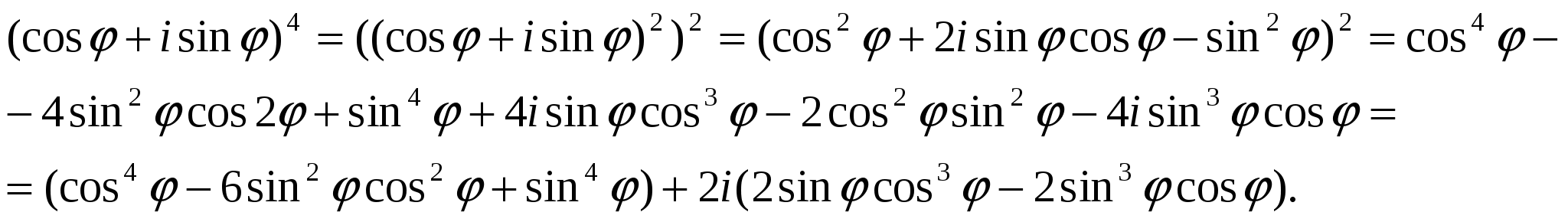 (19)
(19)
Сравнивая действительные и мнимые части равенств (18) и (19), получим
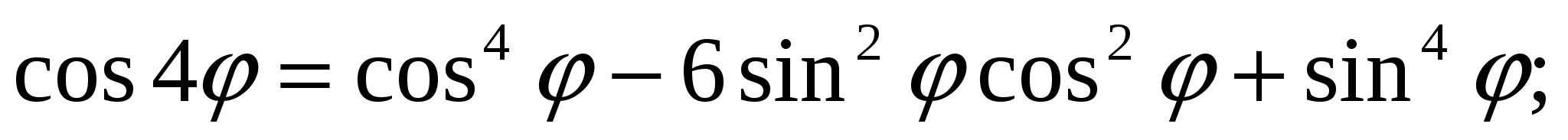
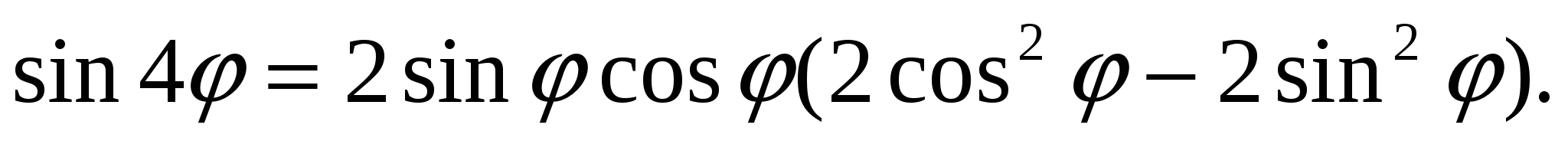
Пусть п - натуральное число.
Корнем п-й степени из комплексного числа 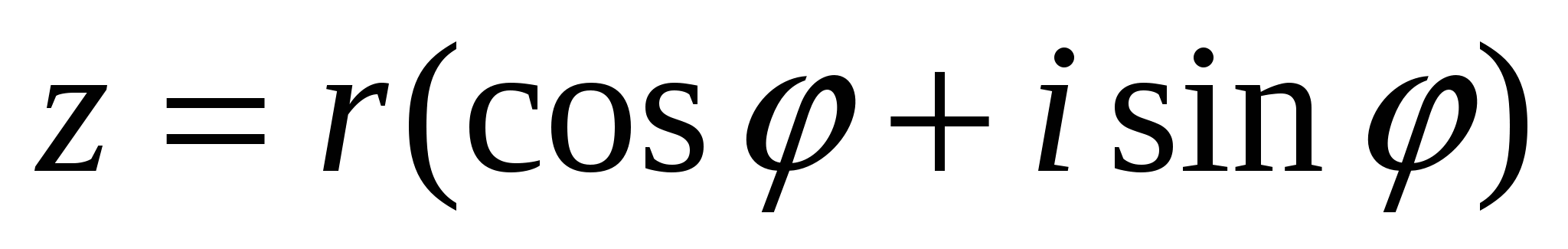 называется комплексное число
называется комплексное число 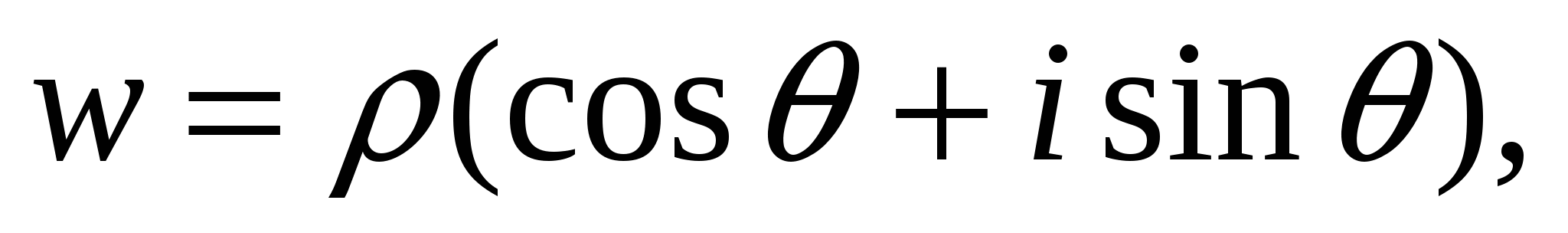 для которого wn = z. Это число обозначается
для которого wn = z. Это число обозначается 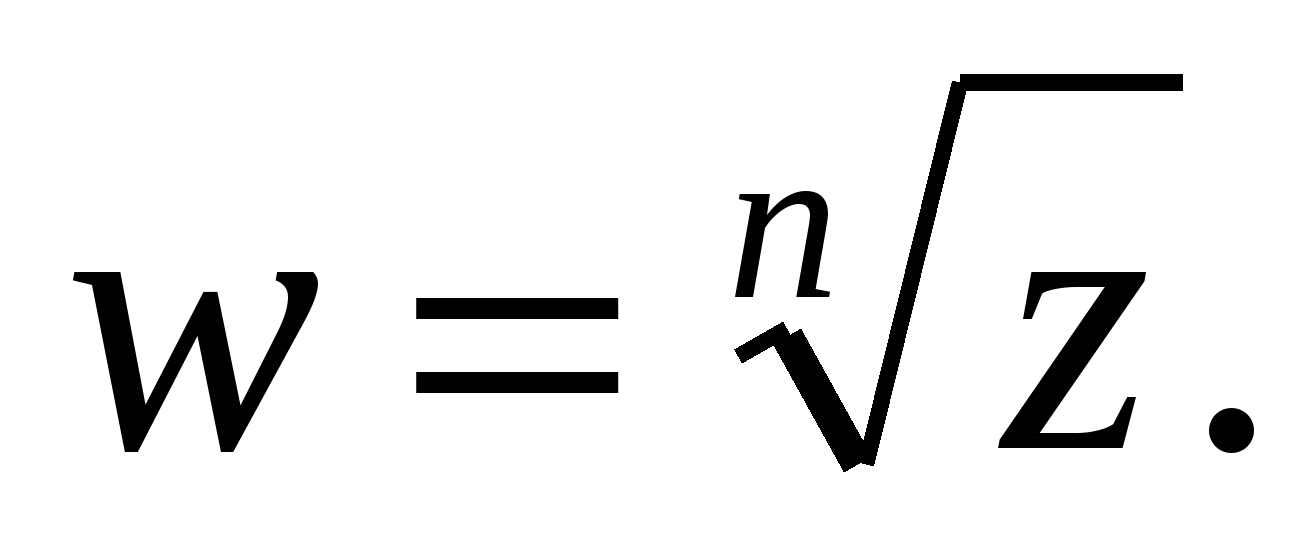
Так как два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются на целое число, кратное 2л, то
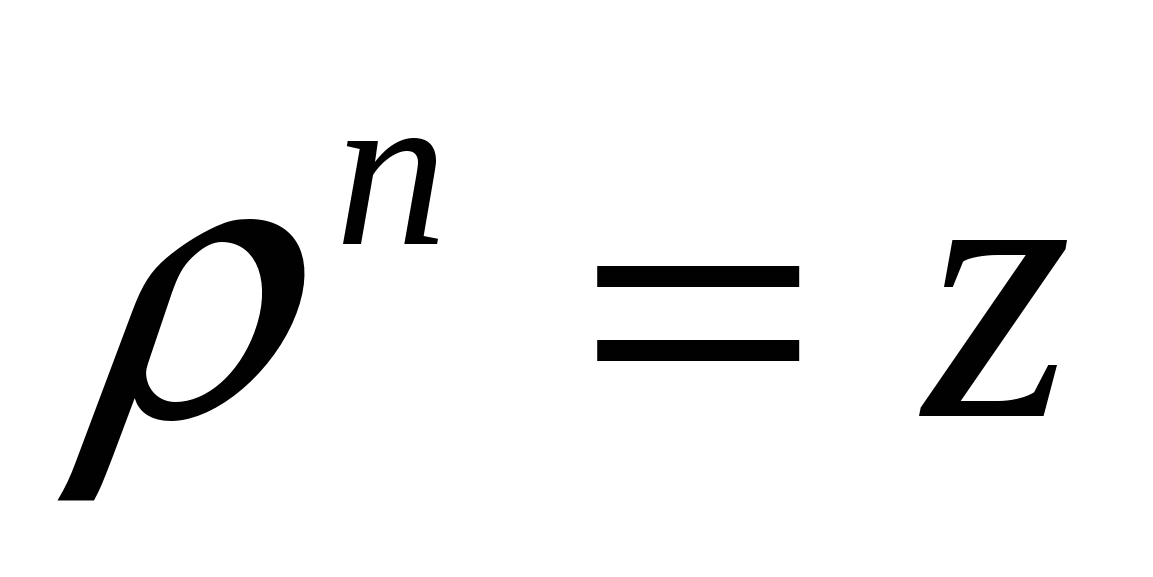 ,
, 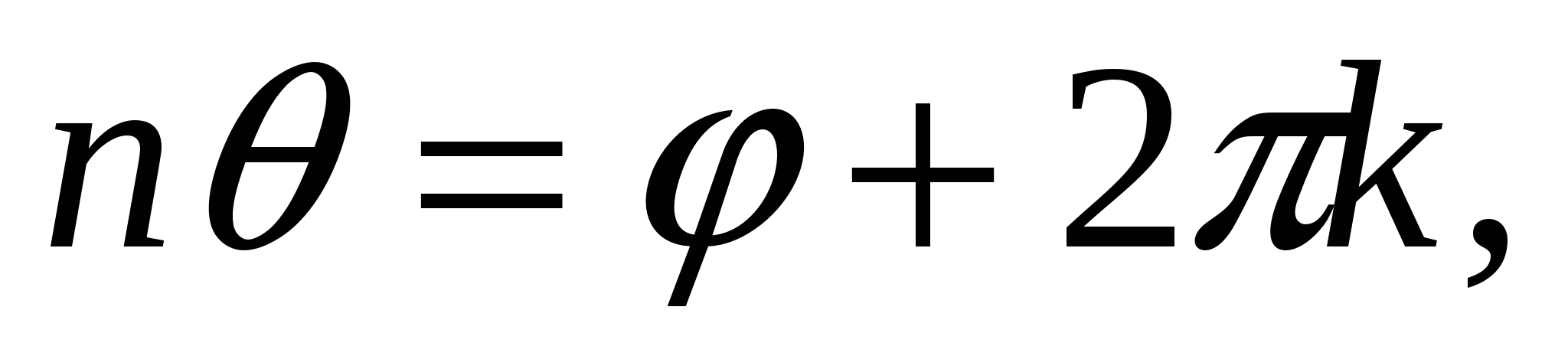
откуда
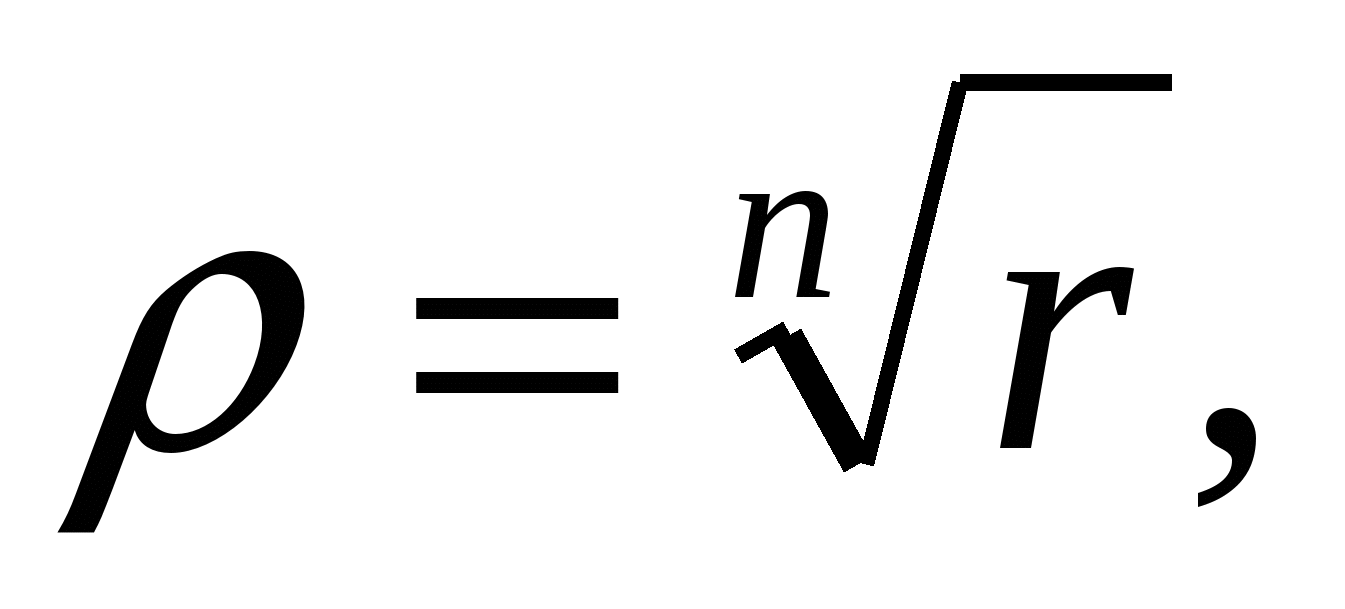
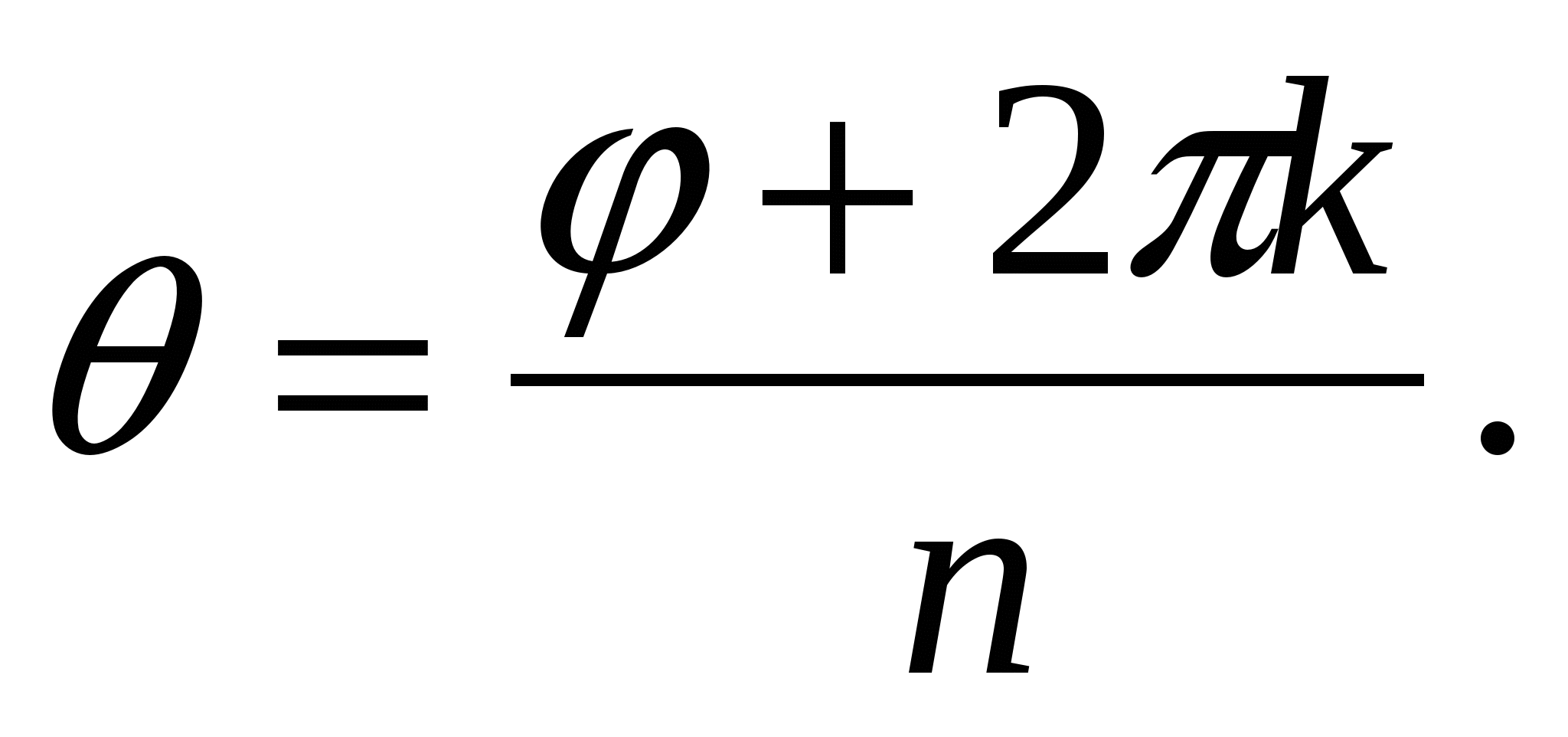
Таким образом,
![]() (20)
(20)
Подставляя вместо к значения 0, 1, 2, ..., п - 1, получим п различных значений корня. Для k = п, п + 1, п + 2, ... или k = -1, -2, ... корни будут принимать полученные ранее значения.
Так, например, при k = 2 имеем: 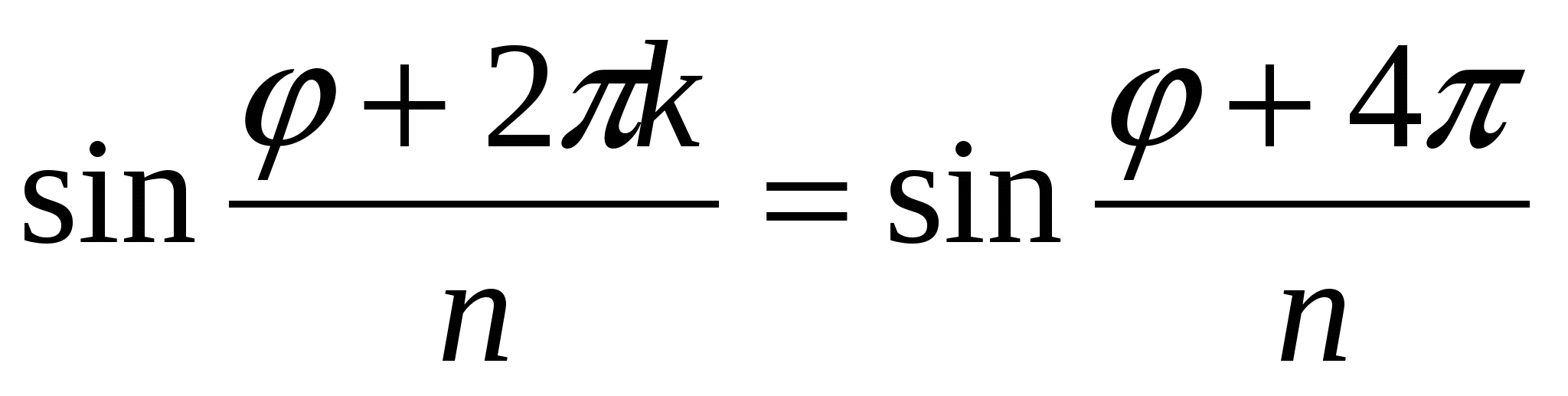 и при k = п + 2
и при k = п + 2
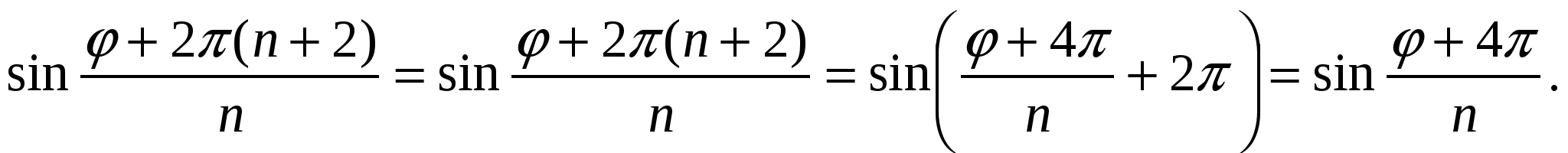
Читатель может проверить, что и для функции косинуса получается то же самое.
Пример 4. Найти все значения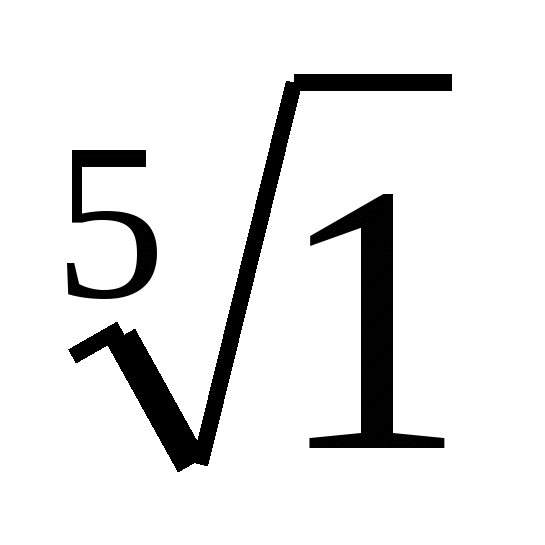
Решение. Так как 1 = l(cos 0 + i sin 0), то
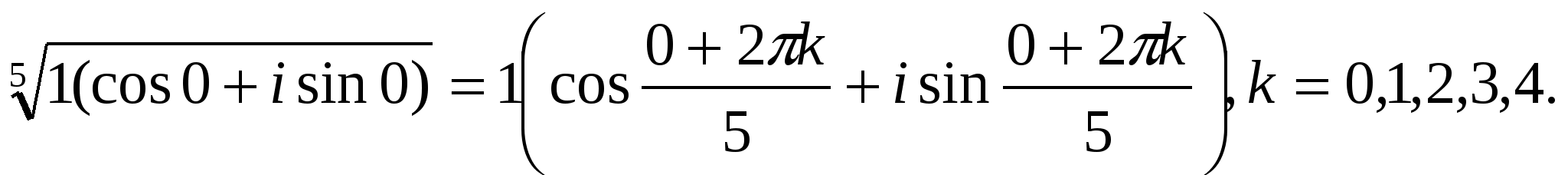
Придавая k последовательно значения 0, 1, 2, 3, 4, соответственно, получим:
z1 = 1 при k = 0;
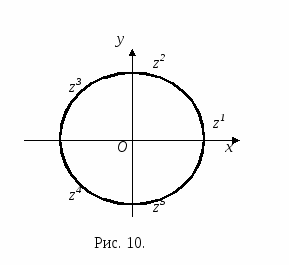
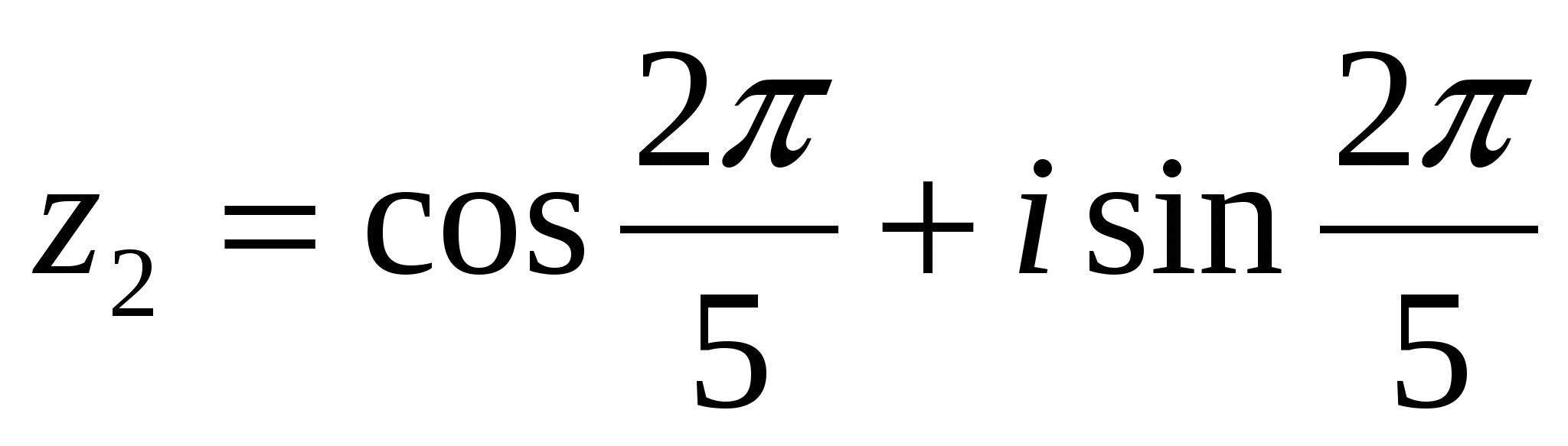 при k = 1;
при k = 1;
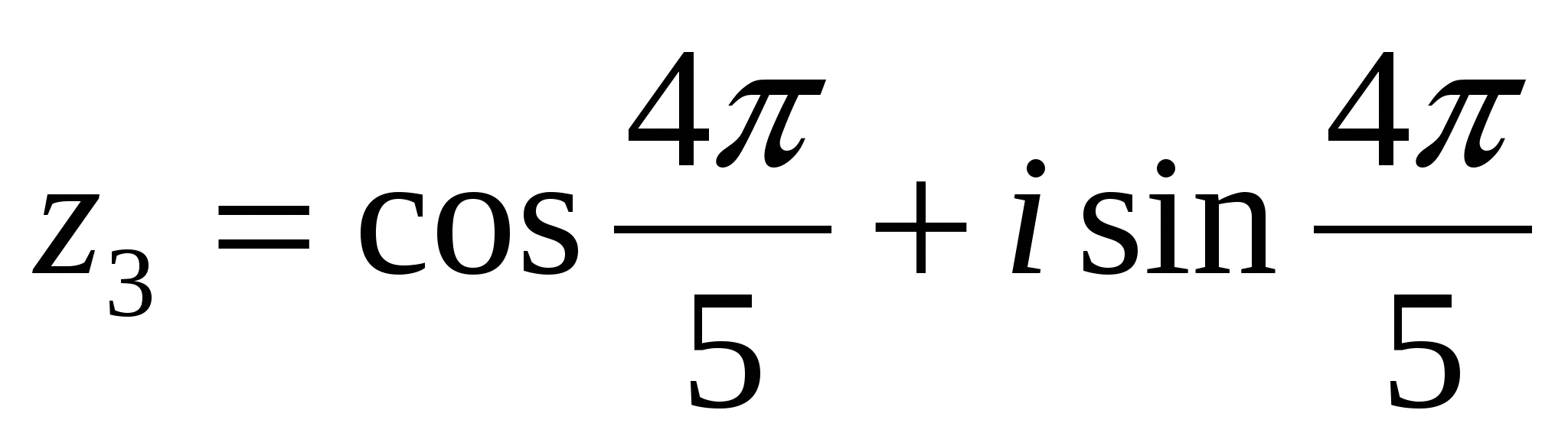 при k = 2;
при k = 2;
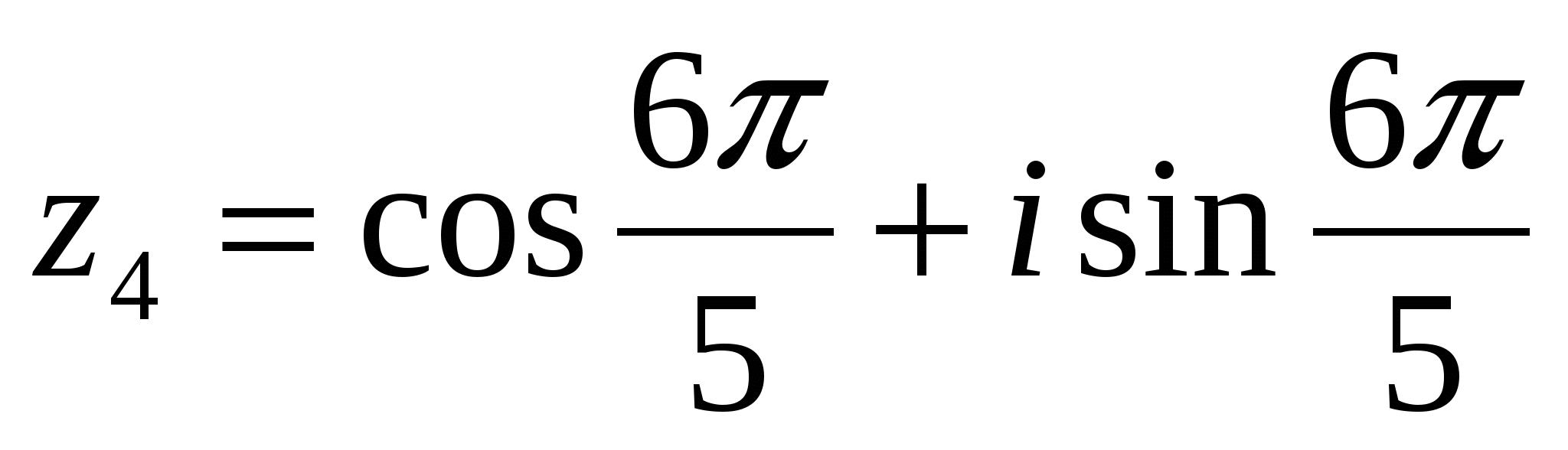 при k = 3;
при k = 3;
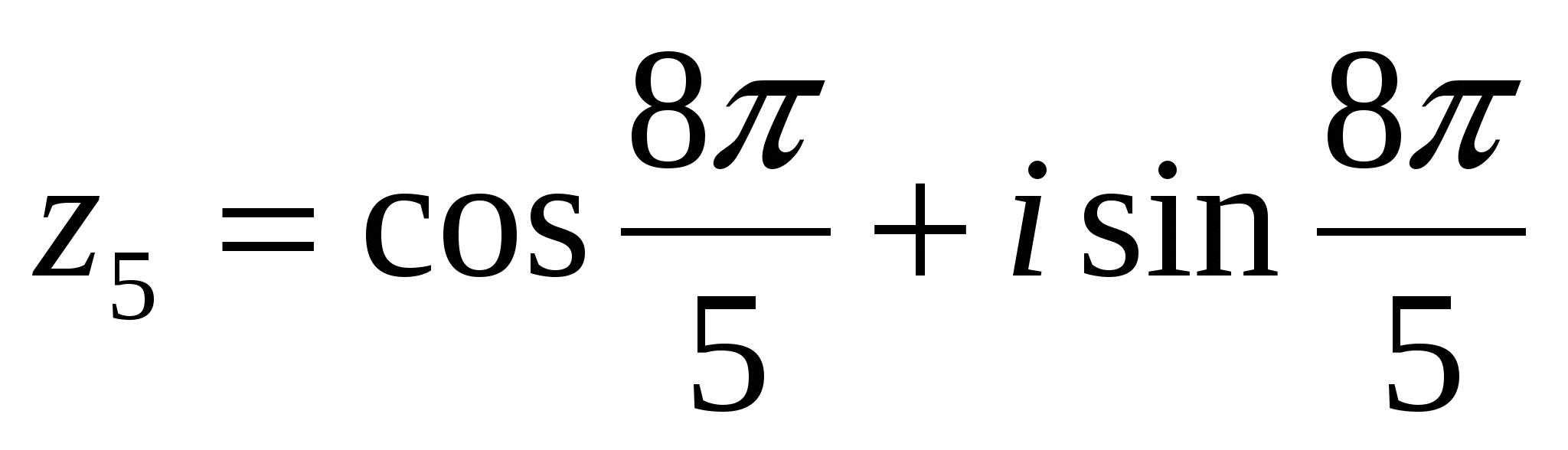 при k = 4.
при k = 4.
Дадим геометрическую интерпретацию полученных значений 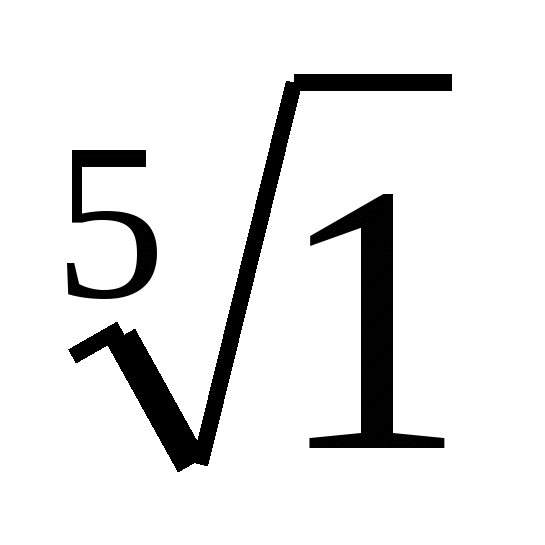 . Модули всех этих значений равны 1. Следовательно, точки z1, z2, z3, z4, z5 лежат на окружности радиуса 1 с центром в начале координат. Построив аргументы значений z1, ... , z5 (рис. 10), заметим, что точки, изображающие числа z1,..., z5, являются вершинами правильного пятиугольника.
. Модули всех этих значений равны 1. Следовательно, точки z1, z2, z3, z4, z5 лежат на окружности радиуса 1 с центром в начале координат. Построив аргументы значений z1, ... , z5 (рис. 10), заметим, что точки, изображающие числа z1,..., z5, являются вершинами правильного пятиугольника.
Исходя из формулы (20) можно показать, что геометрически точки, соответствующие различным значениям корня n-й степени из комплексного числа 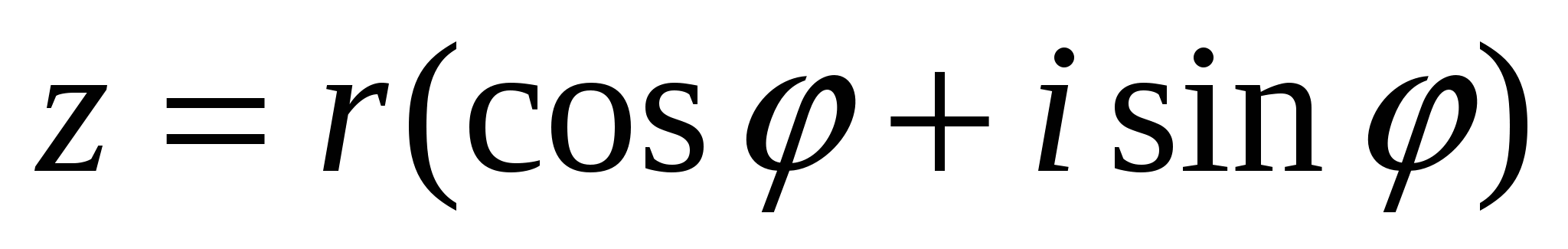 располагаются в вершинах правильного п-угольника с центром в точке О, причем одна из вершин (соответствующая k = 0) имеет полярные координаты
располагаются в вершинах правильного п-угольника с центром в точке О, причем одна из вершин (соответствующая k = 0) имеет полярные координаты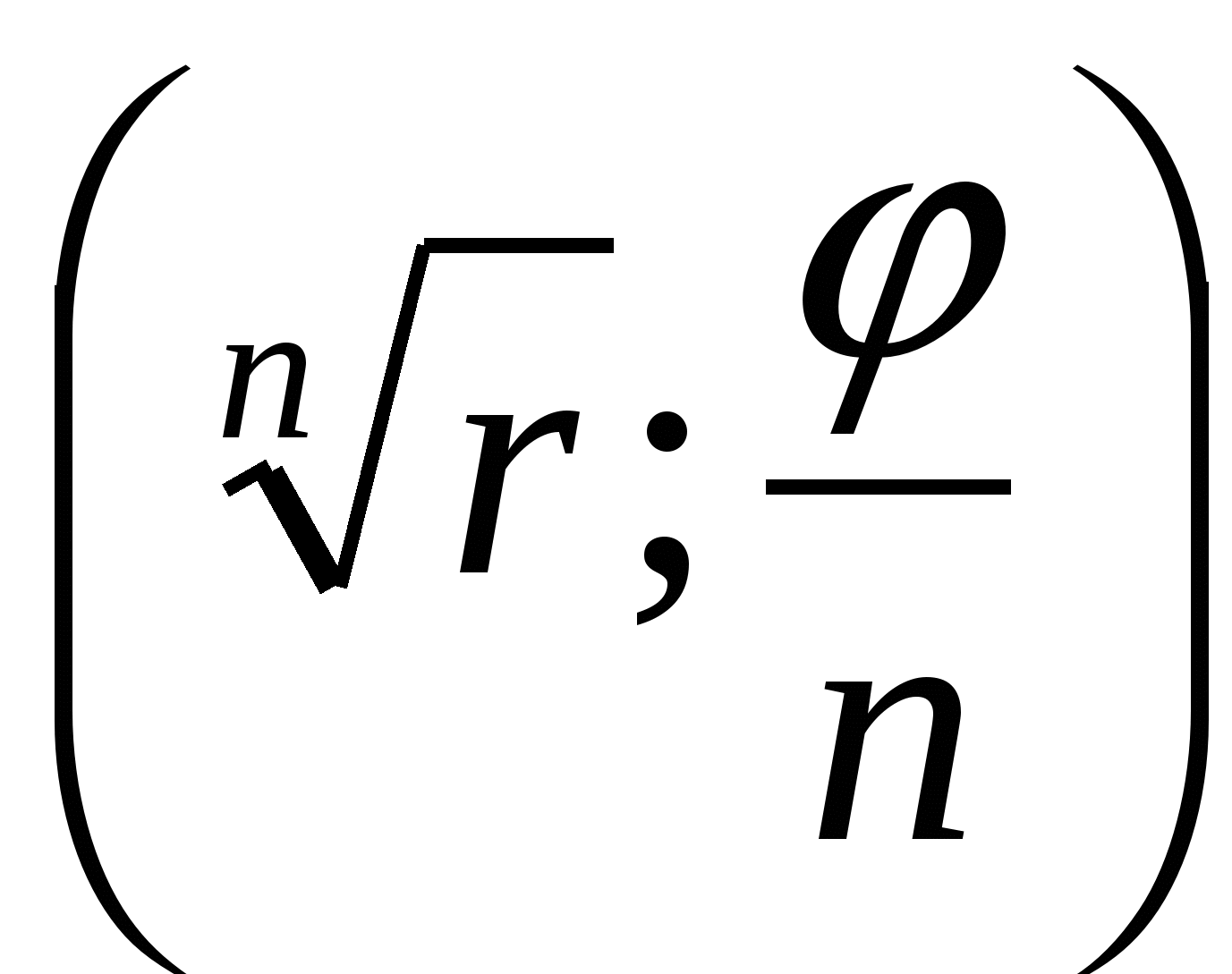 .
.
6. Показательная форма комплексного числа. Формула Эйлера
Найдем тригонометрическую форму комплексного числа z, если 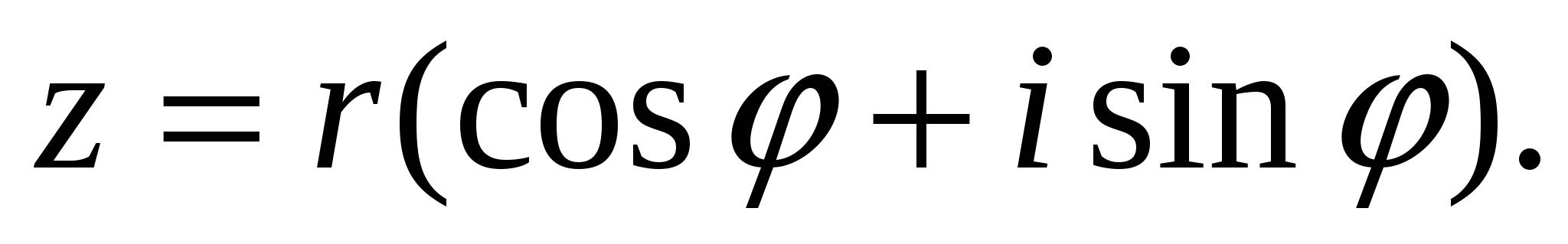 Так как в записи
Так как в записи ![]() выражение
выражение
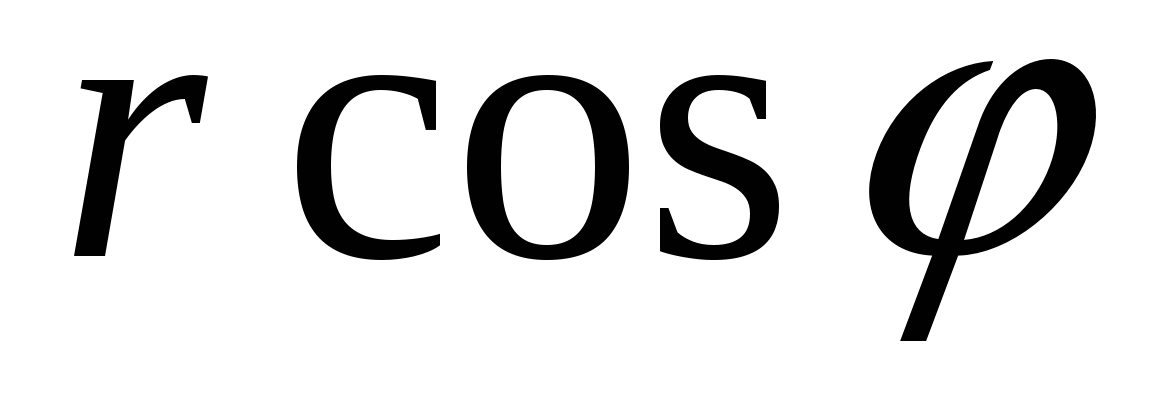 есть действительная, а
есть действительная, а ![]() - мнимая часть и комплексно-
- мнимая часть и комплексно-
сопряженные числа отличаются знаком мнимых частей, то
![]() (21)
(21)
Функция косинус - четная, а синус - нечетная, поэтому соотношение (21) можно записать в виде
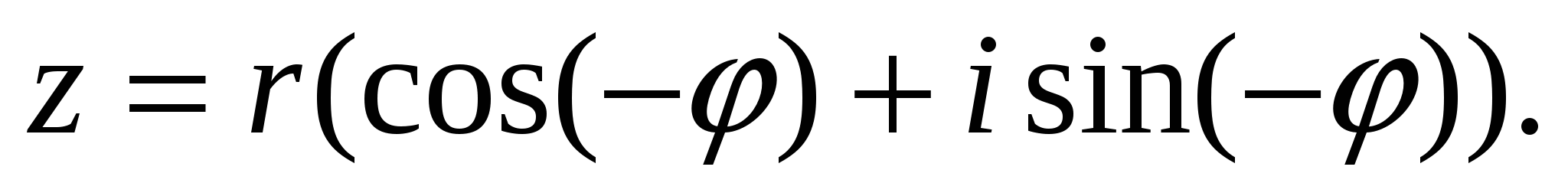
Из геометрических соображений можно заключить, что точка, изображающая комплексное число 1, получается из точки, изображающей число z, в результате ее симметричного отображения относительно оси абсцисс. Значит,
![]()
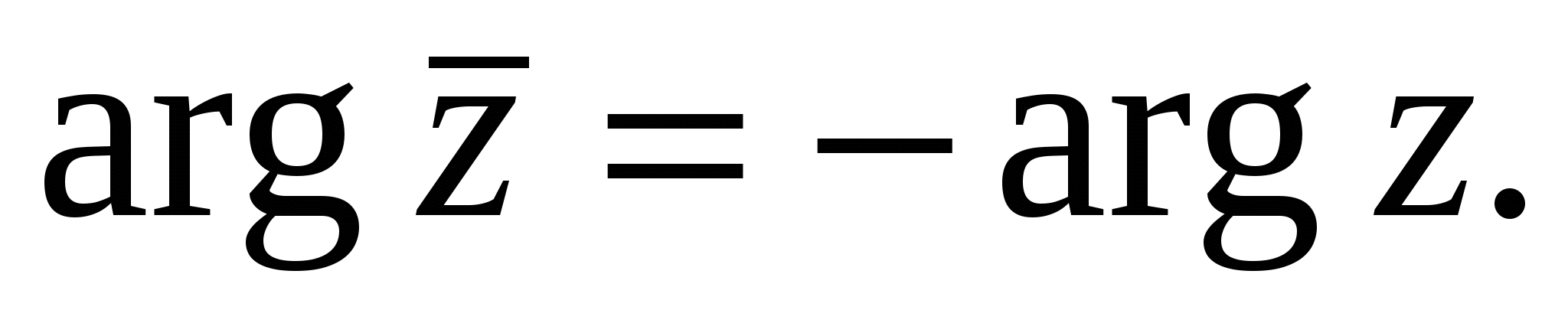
Из правил умножения и деления комплексных чисел в тригонометрической форме следует, что аргумент комплексного числа ведет себя так же, как показатель степени при умножении степеней с одинаковыми основаниями: 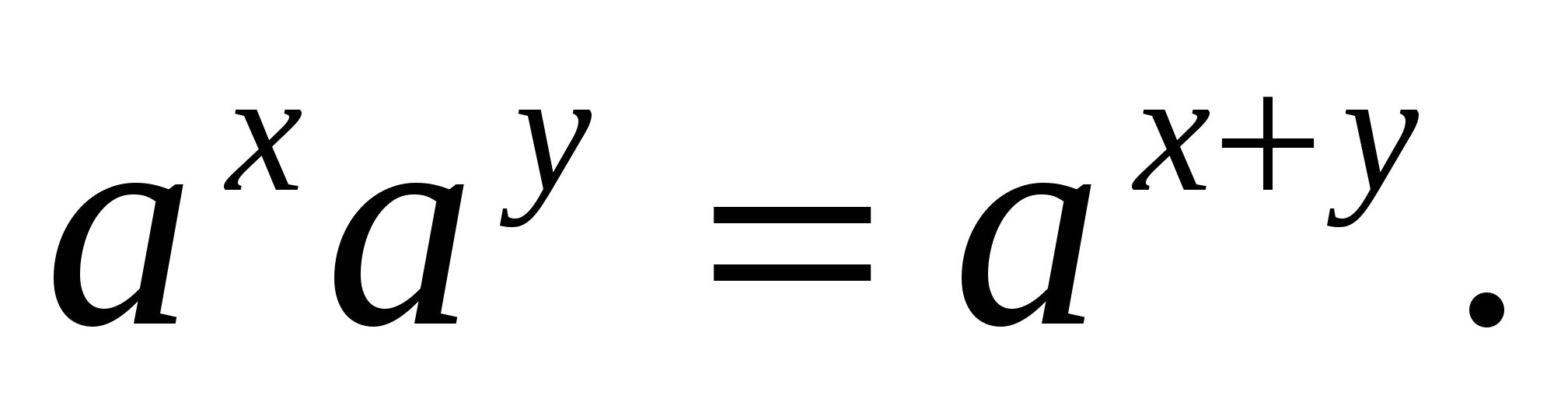 Это обстоятельство навело Л. Эйлера на
Это обстоятельство навело Л. Эйлера на
мысль представлять комплексные числа в виде
![]() (22)
(22)
где е - основание натурального логарифма.
К комплексным числам, записанным в форме (22), применимы правила действий над степенью. А именно, если 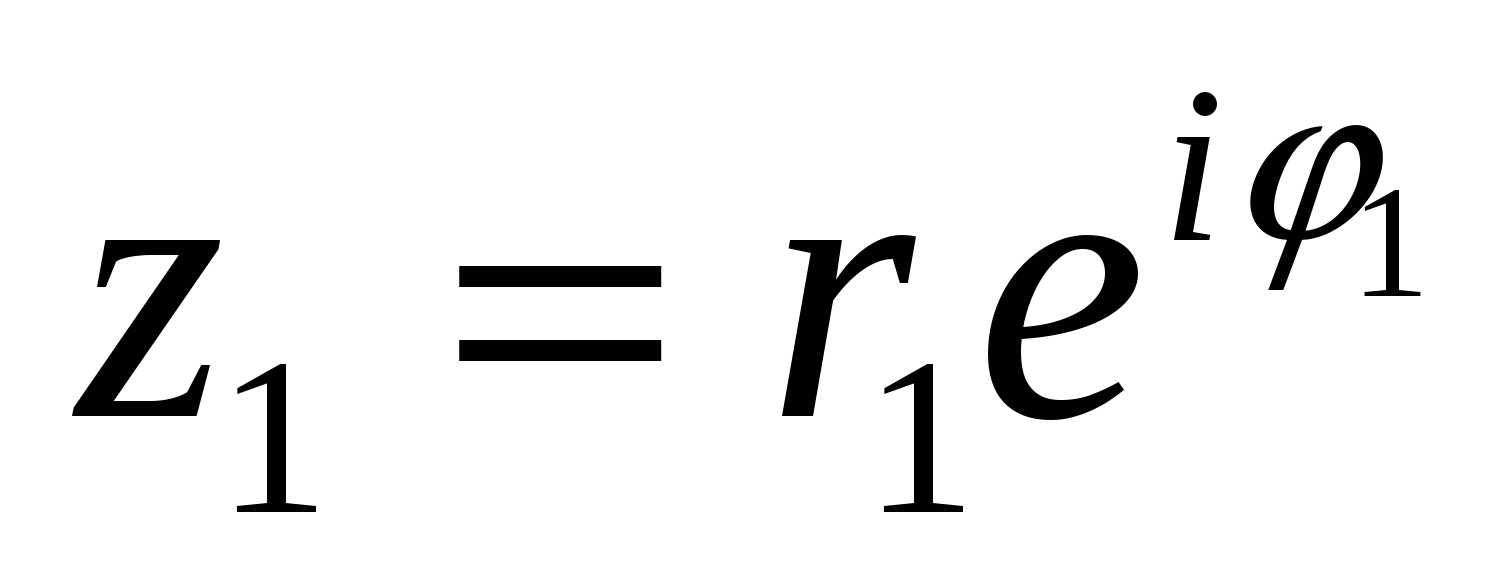 ,
, 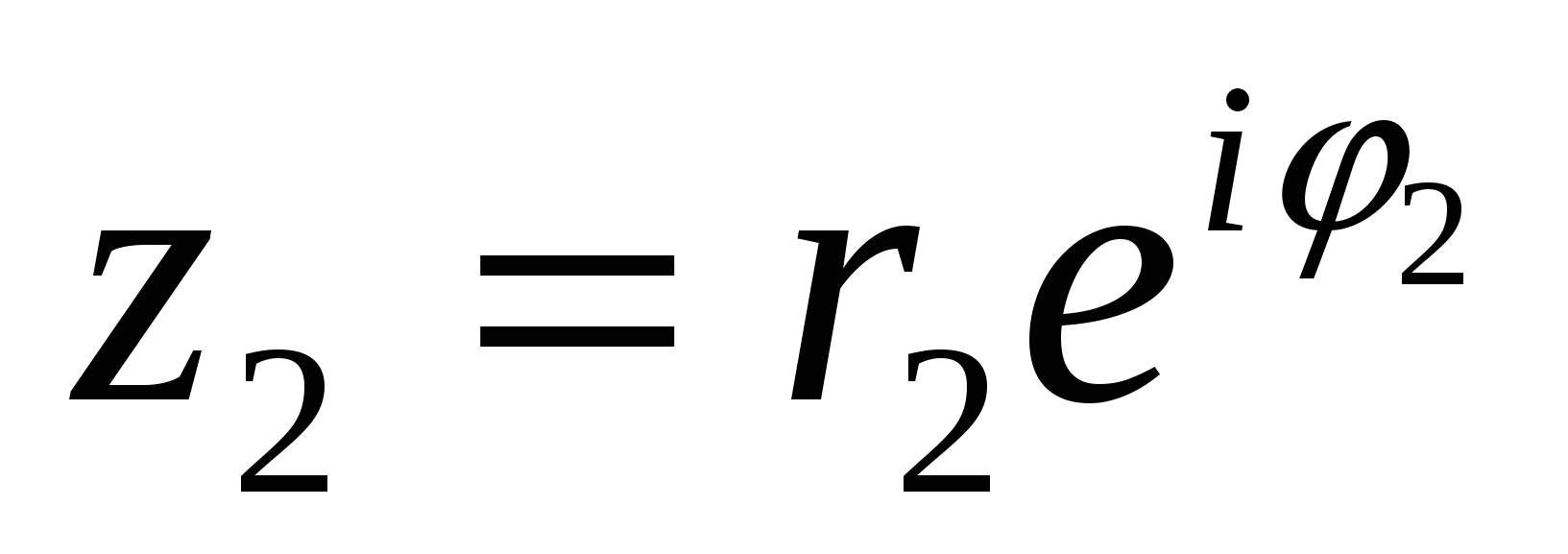 , то
, то
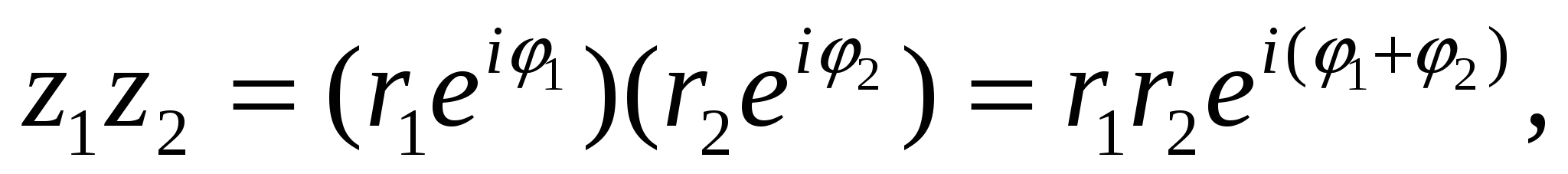 откуда следуют известные нам правила:
откуда следуют известные нам правила:
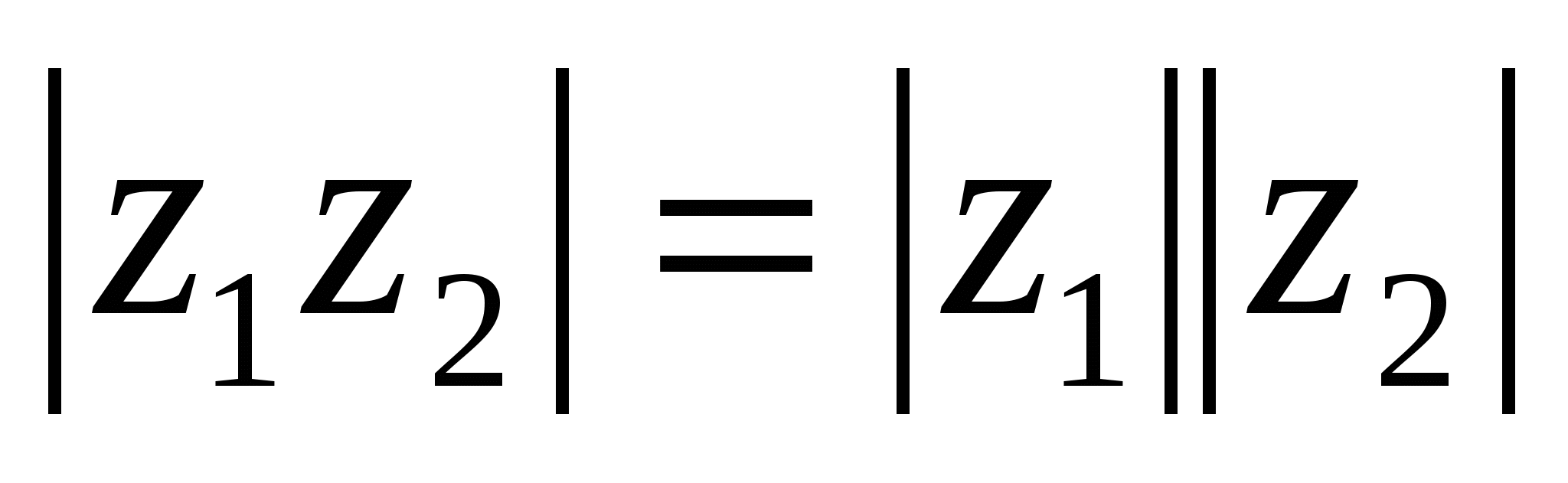 ,
, 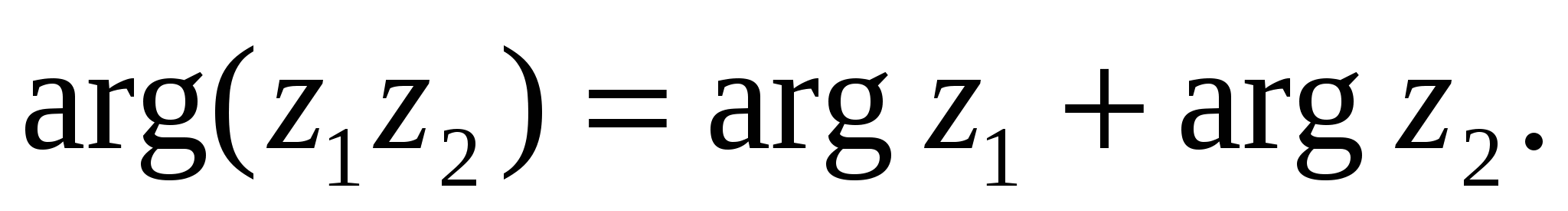
Аналогично получаем
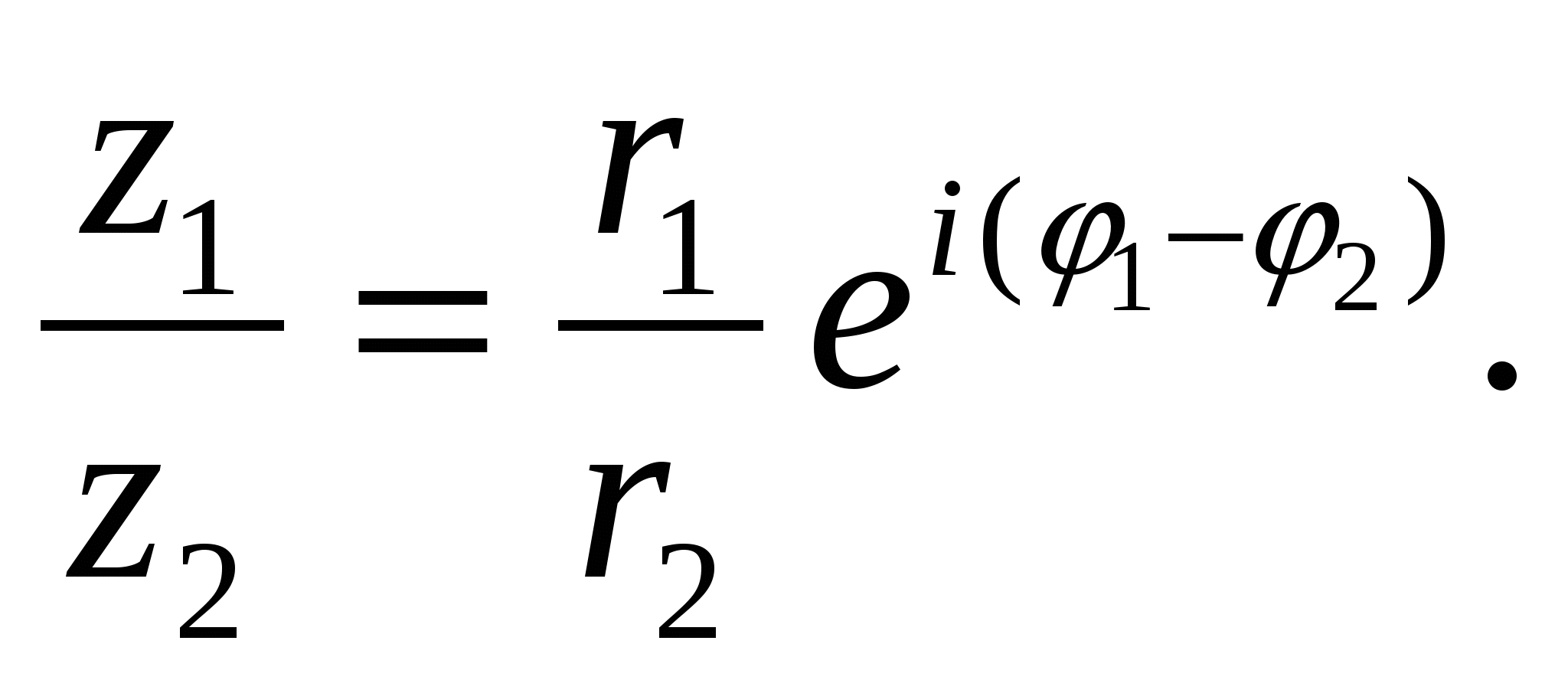
т. е. при делении комплексных чисел справедливы равенства 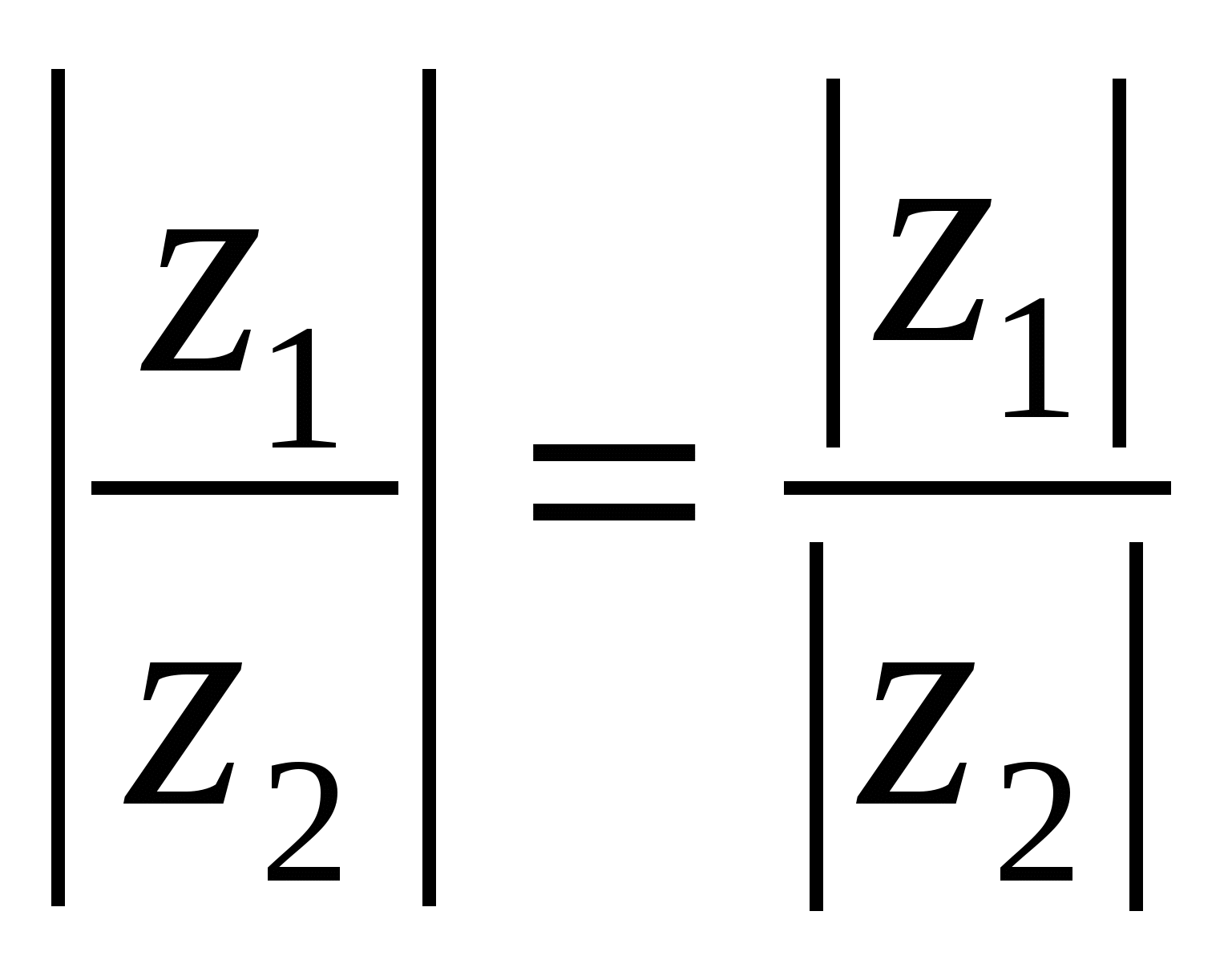 и
и 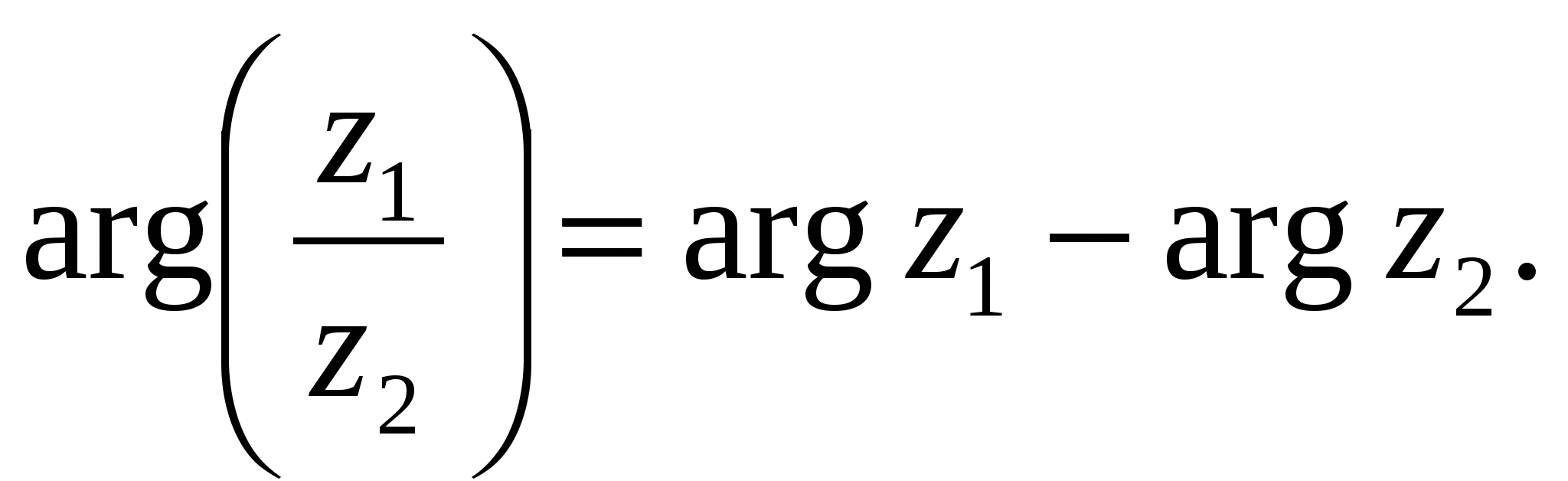
Далее, возведя комплексное число (22) в степень п, получим
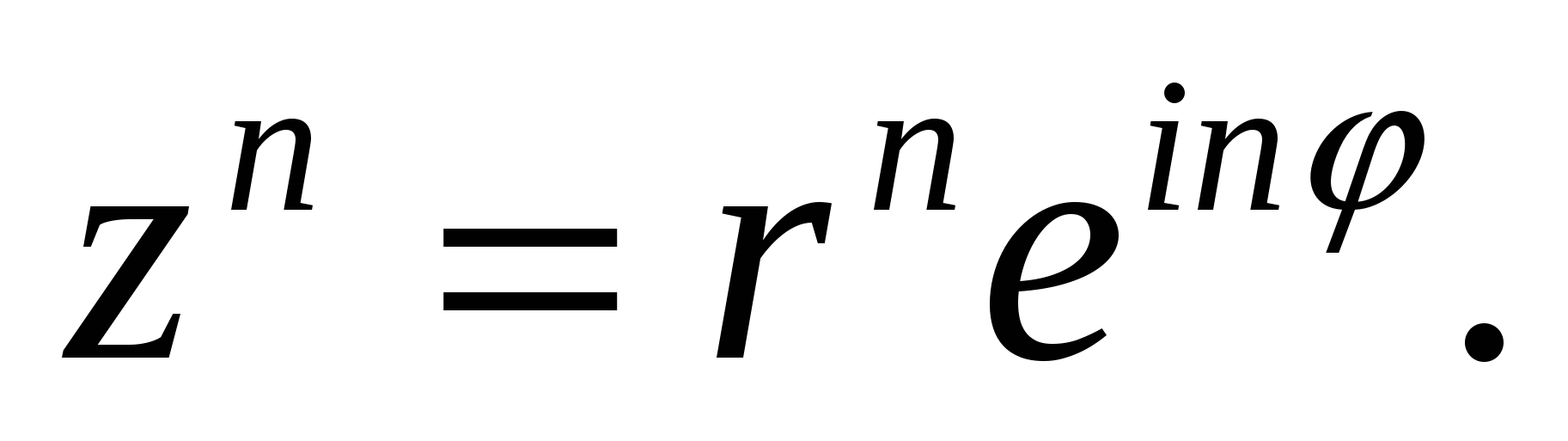
Следовательно, при возведении комплексного числа в степень |zn| = |z|n,arg(zn) = n arg z.
Таким образом, представление комплексного числа в виде (22) формально находит оправдание. Запись (22) называется показательной или экспоненциальной формой комплексного числа.
Если z представлено в форме (22), то комплексно-сопряженное число
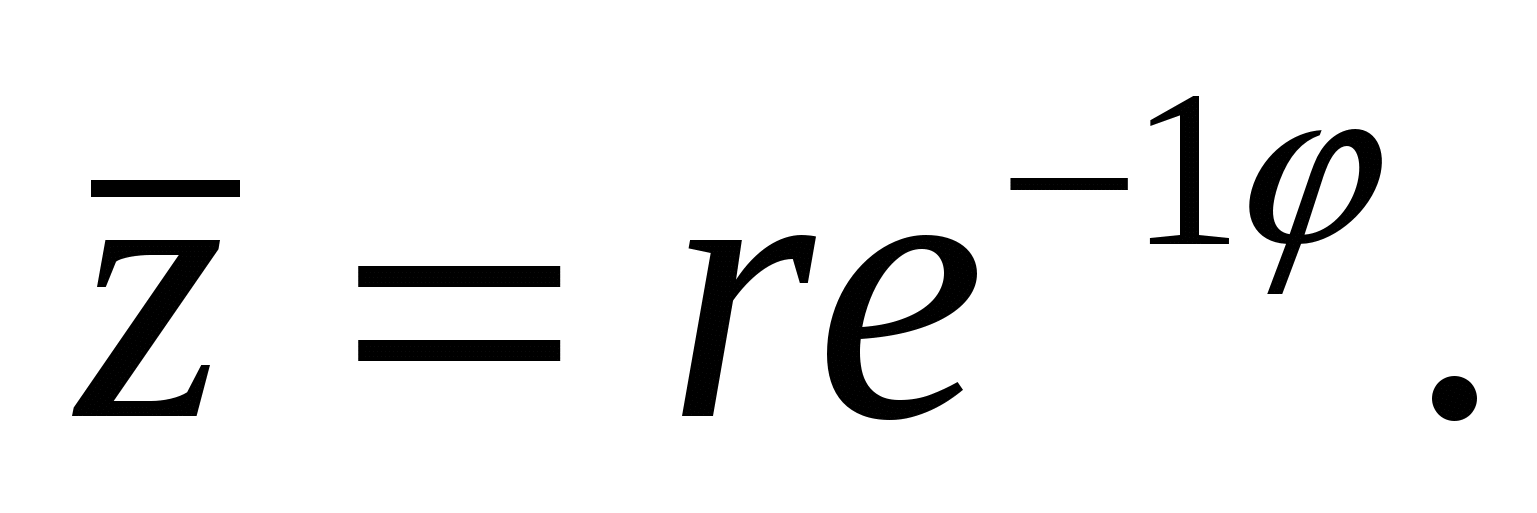
Сравнивая записи комплексного числа в известных нам формах, будем иметь 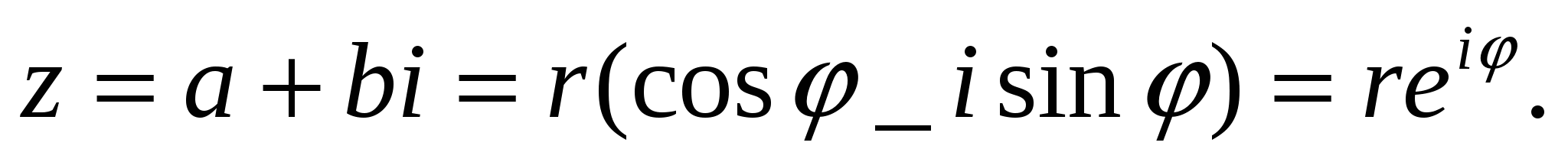 При r = 1
При r = 1
![]() (23)
(23)
Это соотношение называется тождеством Эйлера. Аналогично можно записать
![]() (24)
(24)
Путем сложения и вычитания равенств (23) и (24), соответственно, получаем
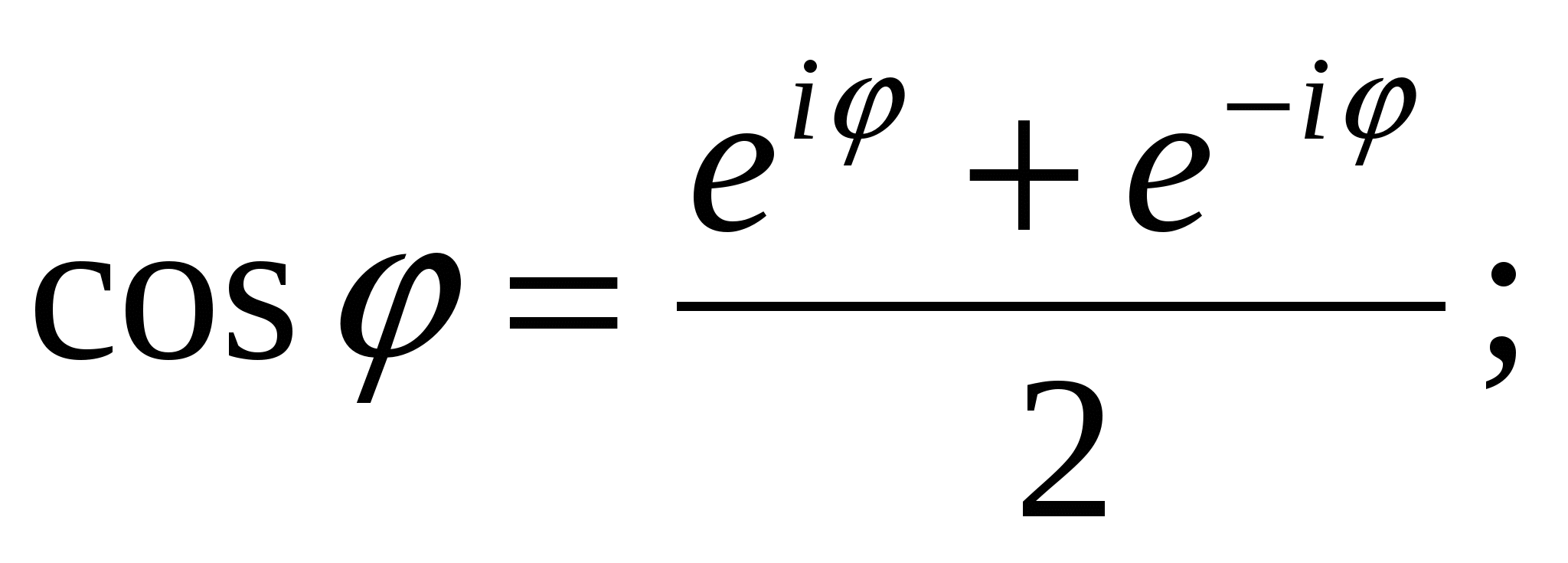
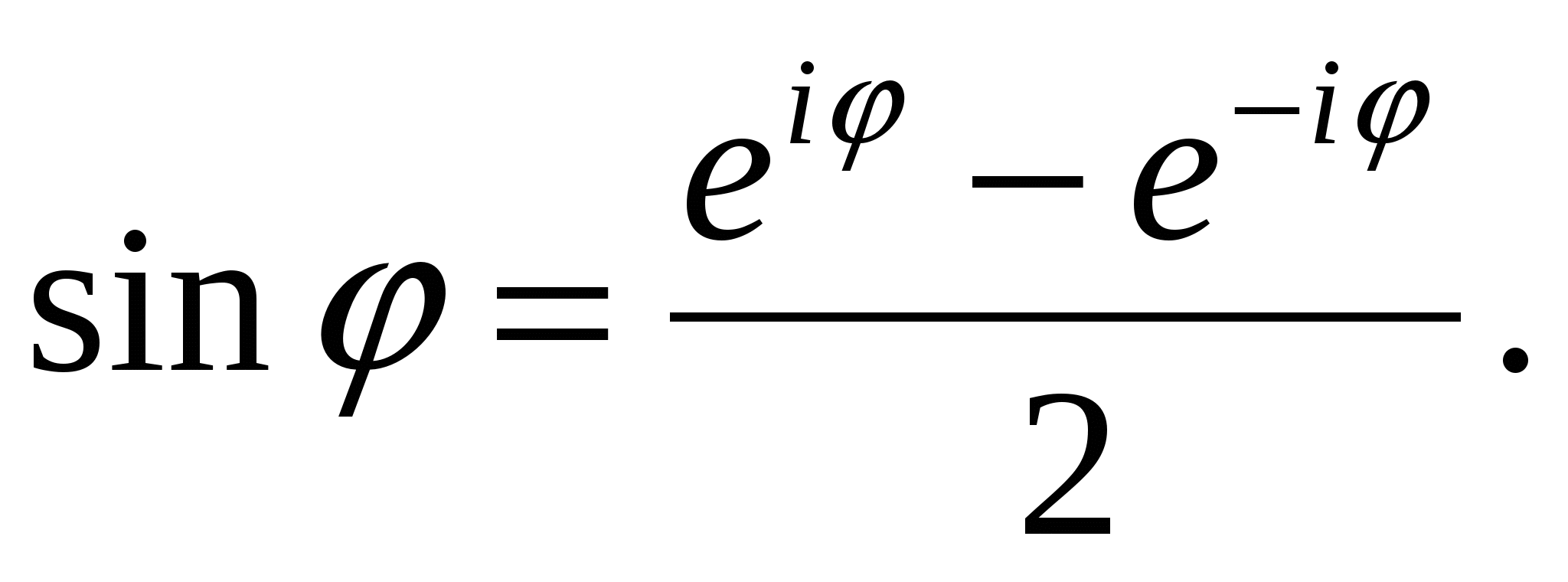
Эти равенства находят широкое применение в различных вопросах математики.
Пример 5. Представить в экспоненциальной форме комплексное число 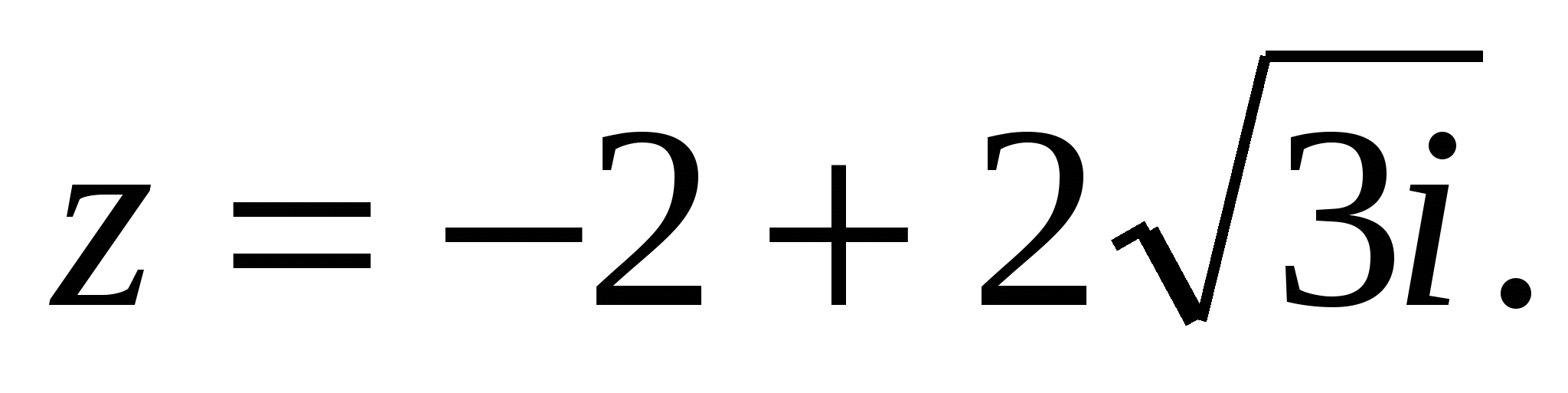
Решение. Находим 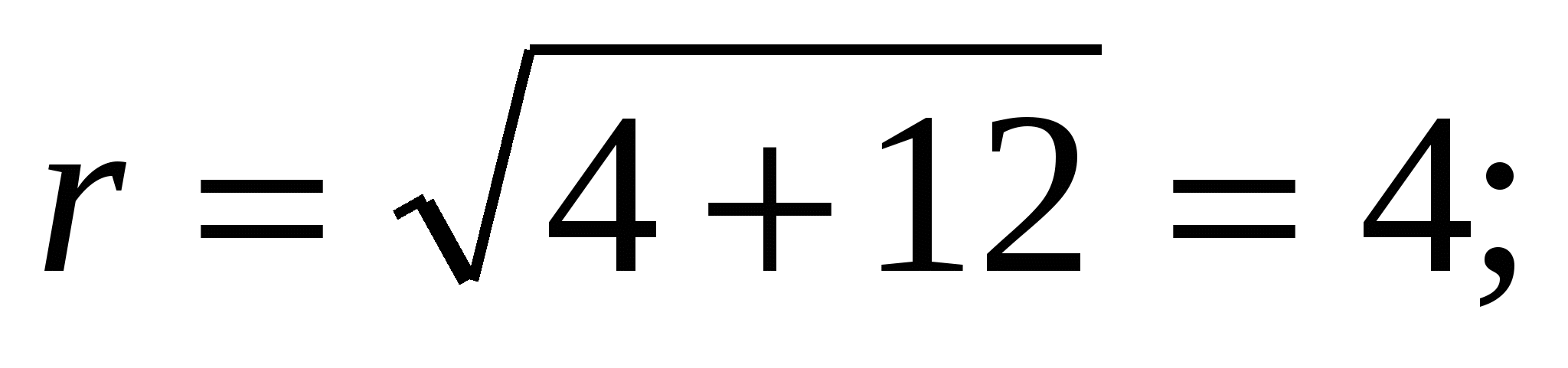
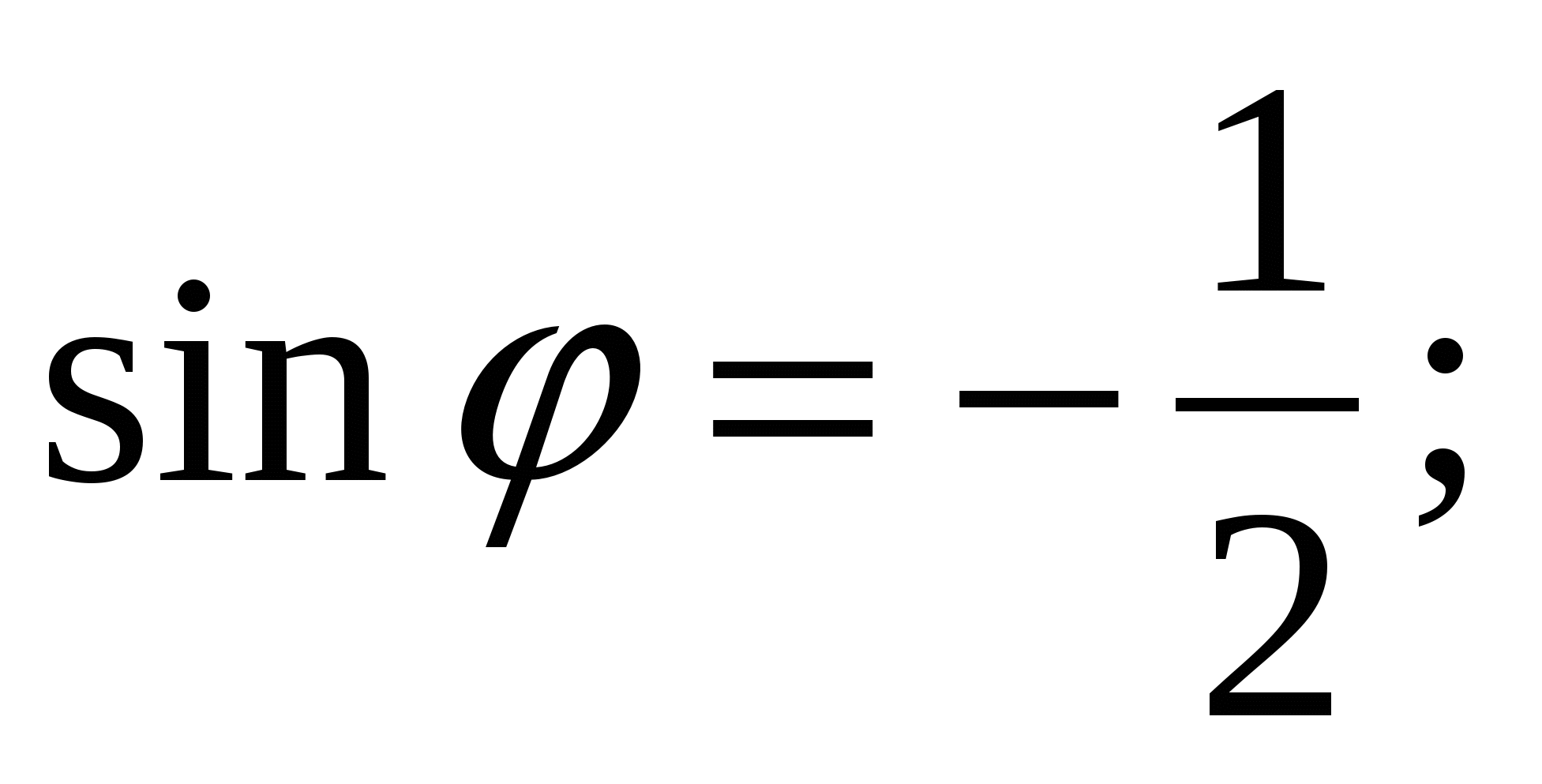
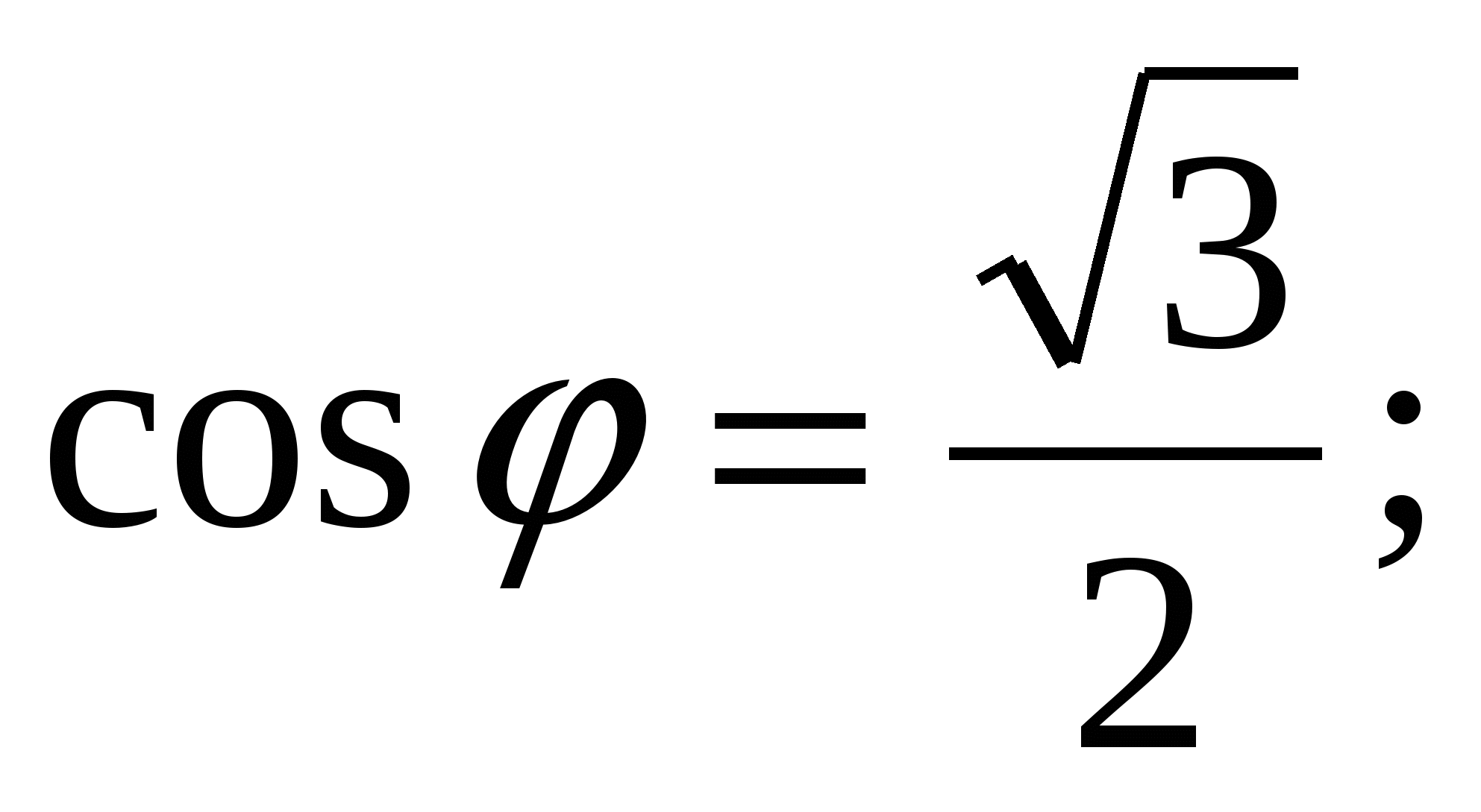
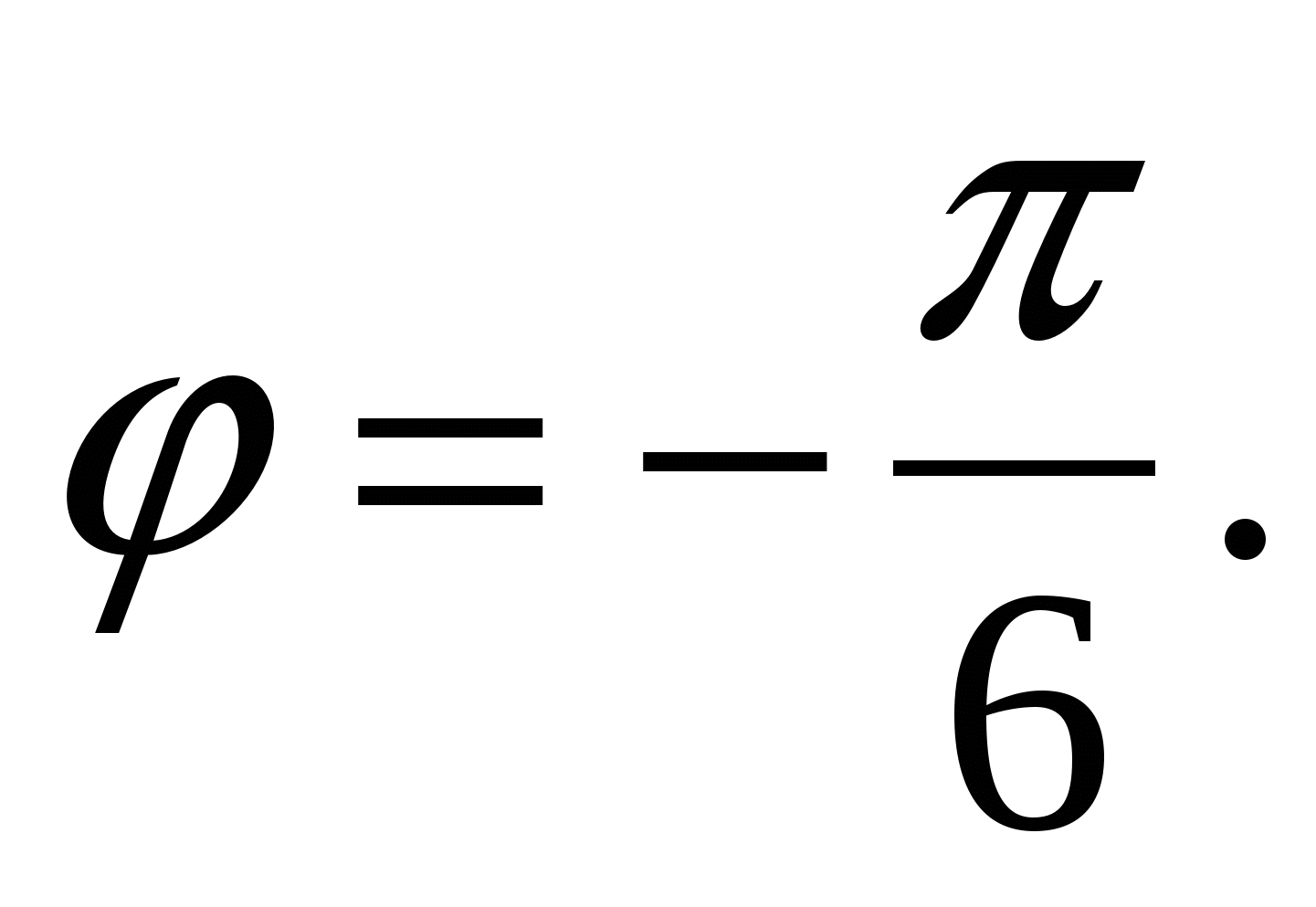 Следовательно,
Следовательно,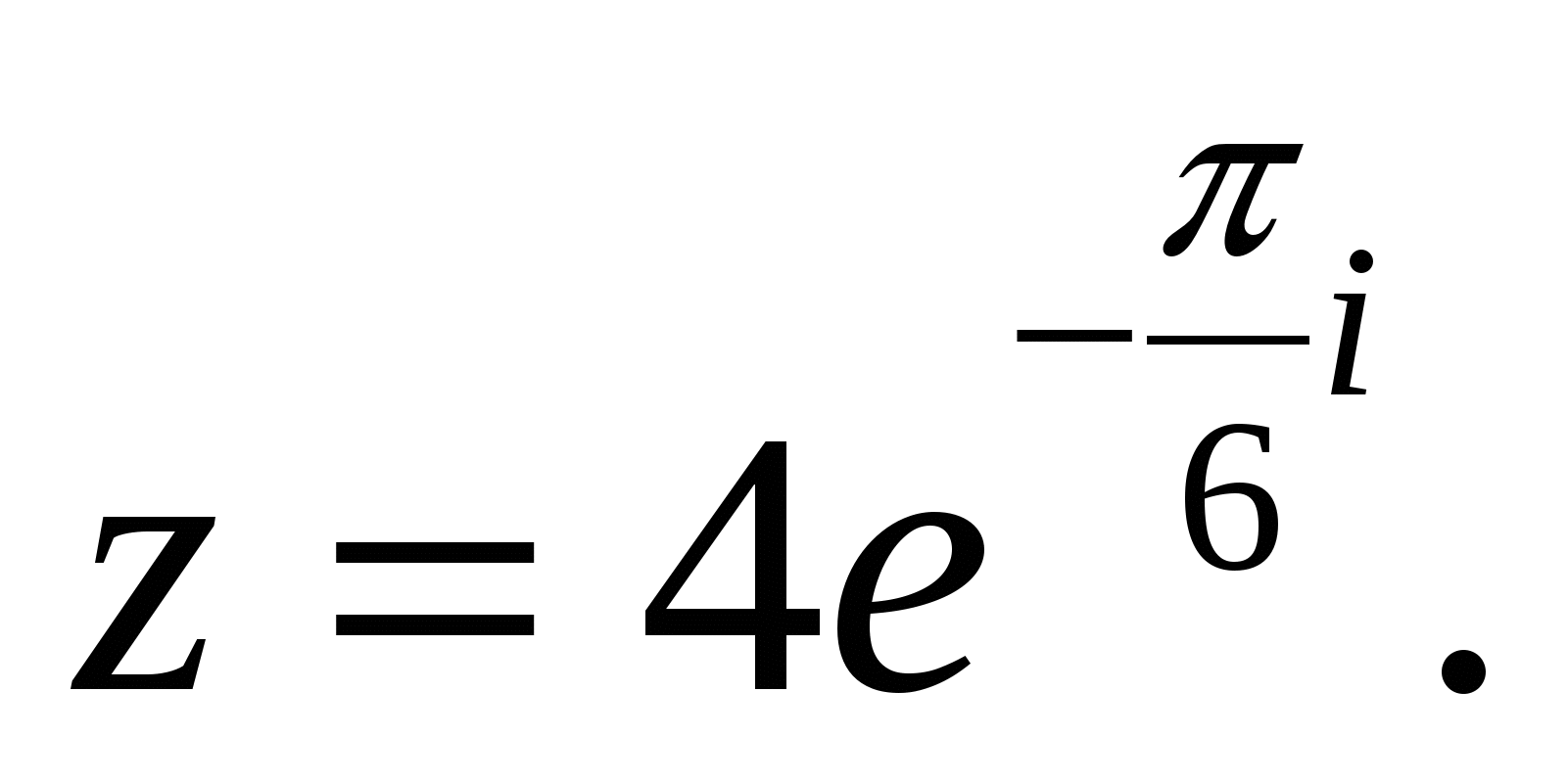
7. Понятие функции комплексной переменной
Пусть даны две комплексные плоскости Оху (плоскость z) и O'uv (плоскость w).
Определение. Если каждой точке (числу) z D (D - множество точек плоскости z ) по некоторому закону f ставится в соответствие единственная точка w
D (D - множество точек плоскости z ) по некоторому закону f ставится в соответствие единственная точка w  Е (Е - множество точек плоскости w), то говорят, что w есть функция от z (однозначная):
Е (Е - множество точек плоскости w), то говорят, что w есть функция от z (однозначная):
w = f (z), (25)
с областью определения D, значения которой принадлежат множеству Е (рис. 11). Т.е. говорят, что на множестве определена однозначная функция комплексного переменного w = f(z), отображающая множество D в множество Е. Если множество значений функции f (z) исчерпывает все множество Е, то Е называется множеством значений (областью изменения) функции f (z). В этом случае пишут
Е = f (D).(26)
Если каждому z ![]() D соответствует несколько значений w, то функция w = f(z) называется многозначной.
D соответствует несколько значений w, то функция w = f(z) называется многозначной.
Множества D и Е можно изображать на одной комплексной плоскости.
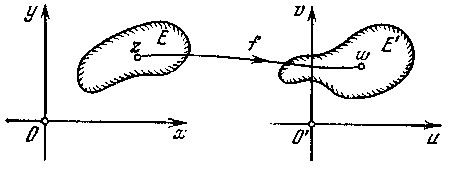
Рис. 11.
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
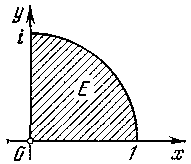
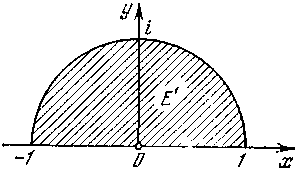
a) б)
Рис. 12.
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
Пример6. Во что переходит сектор Е
![]() ,
, 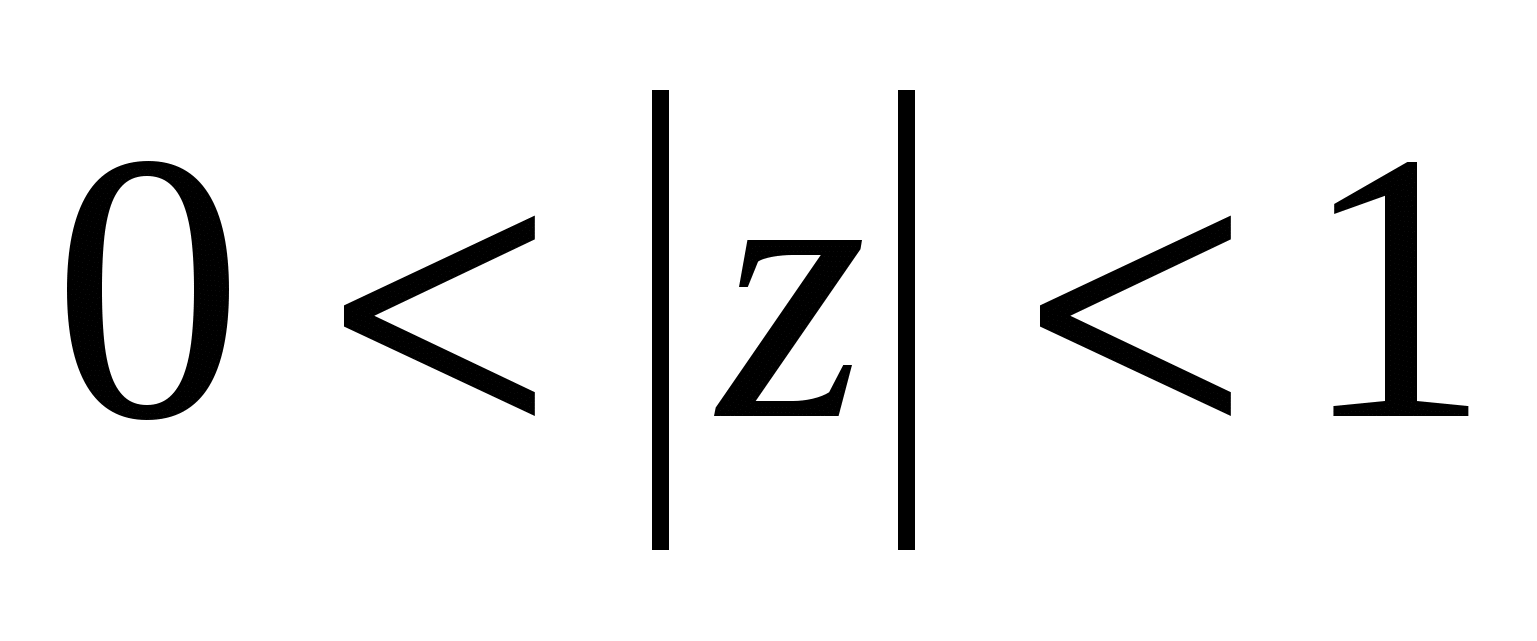
(рис. 12, а) при отображении w = z2?
Имеем
arg w = 2argz < π и |w| = |z|2 < 1.
Поэтому отображенная область E ' представляет собой полукруг (рис. 12, б).
Далее, как правило, будем рассматривать такие функции w = f(z), для которых множества D и Е1 являются областями. Областью комплексной плоскости называется множество точек плоскости, обладающих свойствами открытости и связности.
Функцию w = f(z) можно записать в виде
u + iv = f(x + iy),
т. е.
f(x + iy) = и(х; у) + iv(x; у),
где
и = и(х;у) = Ref(z), v = v(x;у) = Imf(z), (х; у)  D.
D.
Функцию и(х;у) при этом называют действительной частью функции f(z), a v(x;y) - мнимой.
Таким образом, задание функции комплексного переменного равносильно заданию двух функций двух действительных переменных.
Пример 7. Найти действительную и мнимую части функции w = z2.
Решение: Функцию w = z2 можно записать в виде и + iv = (х + iy)2,
т.е.
и + iv = х2 - у2 + i 2ху.
Отсюда следует: и = х2 -у2, v = 2ху.


