- Преподавателю
- Математика
- Задачи с параметрами и методы их решения
Задачи с параметрами и методы их решения
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Гутнова Д.К. |
| Дата | 15.12.2015 |
| Формат | docx |
| Изображения | Есть |
Задачи с параметрами и методы их решения
(Д.К. Гутнова, учитель математики МБОУ СОШ с.Фиагдон
Ардонского района РСО-Алания, e-mail: [email protected])
Задачи с параметром часто встречаются в заданиях ЕГЭ по математике с развернутым ответом, а также в олимпиадах по математике различной степени сложности. В программах математики для неспециализированных школ таким задачам отводится незначительное место.
К задачам с параметрами, рассматриваемым в школьном курсе, можно отнести, например, поиск решений линейных и квадратных уравнений в общем виде, исследование количества их корней в зависимости от значений параметров.
Но большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках.
Задачи с параметрами очень многообразны.
В данной работе рассматриваются:
-
задачи, которые решаются аналитически с использованием равносильных переходов, основанных на монотонности функций;
-
задачи, решаемые геометрически, с помощью графиков функций.
Построение графиков функций - задача сама по себе не простая. Умение строить графики позволяет существенно облегчить решение многих с виду сложных задач с параметрами. В школьном курсе сначала исследуют линейную, квадратичную и другие функции и уравнение окружности. В приведенных ниже примерах графики функций строятся без применения производной.
Основной принцип решения параметрических уравнений можно сформулировать так: необходимо разбить область изменения параметра на участки такие, что при изменении параметра в каждом из них получающиеся уравнения можно решить одним и тем же путем. Ответ задачи состоит из списка участков изменения параметра с указанием ответов каждого участка.
Ниже приведены решения нескольких задач, отобранных из списка заданий ЕГЭ прошлых лет и задачи из XI командной олимпиады по математике и информатике математического факультета СОГУ 2015.
Пример 1. При каких значениях параметра 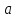 уравнение
уравнение
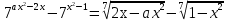
имеет два действительных корня?
Решение
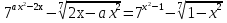
Исходное уравнение принимает вид 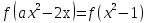 , где
, где 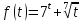 - возрастающая функция на
- возрастающая функция на 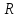 (как сумма двух возрастающих функций).
(как сумма двух возрастающих функций).
Таким образом, используя равносильный переход при условии монотонности функции, получим уравнение
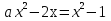 .
.
Перепишем его в виде:
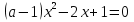 .
.
При 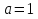 имеем один корень
имеем один корень 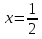 .
.
При 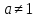 уравнение является квадратным и имеет 2 корня при
уравнение является квадратным и имеет 2 корня при 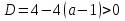 , т.е. при
, т.е. при 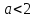 .
.
Итак, при 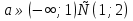 исходное уравнение имеет два действительных решения.
исходное уравнение имеет два действительных решения.
Ответ: 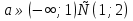 .
.
Пример 2. При каких значениях 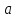 система имеет ровно одно решение:
система имеет ровно одно решение:
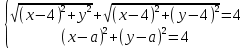
Решение (геометрический способ)
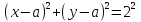 - уравнение окружности с центром в точке с координатами
- уравнение окружности с центром в точке с координатами 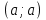 , лежащей на биссектрисе
, лежащей на биссектрисе 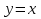 .
.
Рассмотрим точки 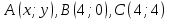 , тогда первое уравнение системы это сумма расстояний
, тогда первое уравнение системы это сумма расстояний 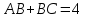 .
.
Так как длина отрезка 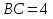 , то в силу неравенства треугольника точка
, то в силу неравенства треугольника точка 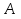 должна лежать на
должна лежать на  .
.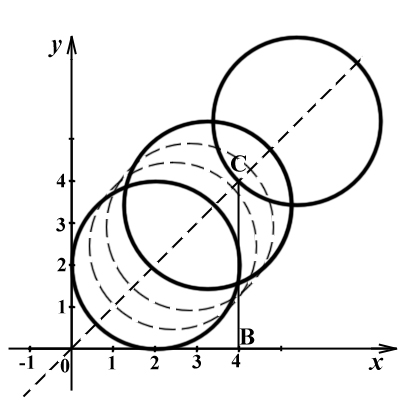
Итак, первое уравнение системы - это отрезок  :
: 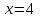 ,
, 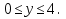
При 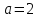 окружность касается отрезка, и система имеет ровно одно решение.
окружность касается отрезка, и система имеет ровно одно решение.
Окружность проходит через точку 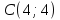 при
при 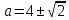 .
.
Причем при 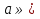 окружность пересекает отрезок в двух точках, а при
окружность пересекает отрезок в двух точках, а при 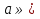 - в одной точке.
- в одной точке.
При 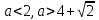 отрезок и окружность не пересекаются.
отрезок и окружность не пересекаются.
Итак, система имеет ровно одно решение при 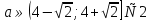 .
.
Ответ: 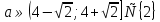 .
.
Пример 3. При каких значениях 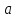 система имеет ровно одно решение:
система имеет ровно одно решение:
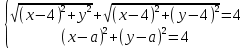
Решение (аналитический способ)
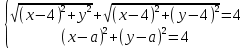
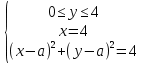
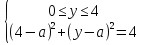
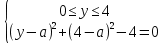
f(y)
(3)
(2)
(1)
1
1
2
3
4
y
-1
-2
2
Графиком функции 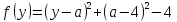 является парабола, ветви которой направлены вверх, а вершина находится в точке
является парабола, ветви которой направлены вверх, а вершина находится в точке 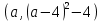 .
.
Т.к. 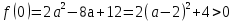 , то нули функции будут одного знака.
, то нули функции будут одного знака.
Уравнение 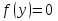 имеет одно решение на
имеет одно решение на 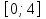 в трех случаях:
в трех случаях:
1) 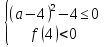
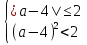
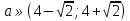 ;
;
2) 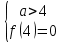
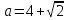 ;
;
3) 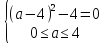
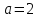 .
.
Ответ: при 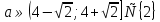 система имеет ровно одно решение.
система имеет ровно одно решение.
Пример 4. При каких значениях 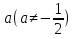 система
система
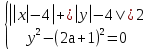
имеет 4 решения?
Решение
Рассмотрим второе уравнение системы. Нетрудно получить, что
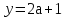 или
или 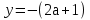 .
.
Графиками данных функций являются параллельные прямые, расположенные симметрично относительно оси абсцисс.
Первое уравнение системы удобно рассматривать отдельно в каждой из четырех четвертей координатной плоскости. В I четверти получаем
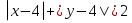 .
.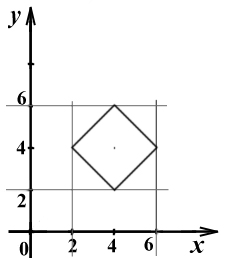
Графиком полученной функции является ромб.
Аналогичным образом получаем ромбы во II, III и IV четвертях.
Следовательно, график исходной функции
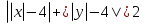
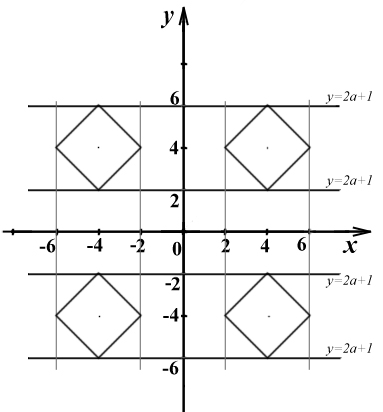
будет выглядеть следующим образом:
Из рисунка видно, что система будет иметь 4 решения при 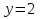 ,
, 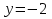 ,
, 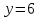 ,
, 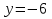 . Таким образом, получаем совокупность
. Таким образом, получаем совокупность
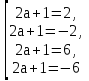
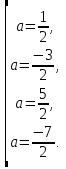
Ответ: при 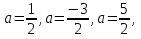
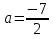 исходная система имеет 4 решения.
исходная система имеет 4 решения.


