- Преподавателю
- Математика
- Методические указания к теме Дифференциальное и интегральное исчисление
Методические указания к теме Дифференциальное и интегральное исчисление
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Кормачева Е.Е. |
| Дата | 09.08.2015 |
| Формат | docx |
| Изображения | Есть |
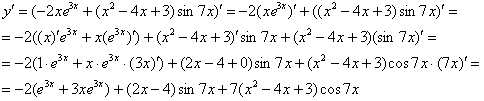
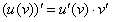
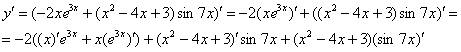
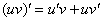
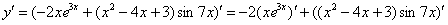
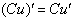
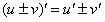
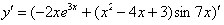
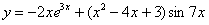
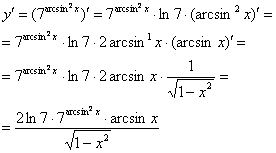
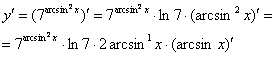
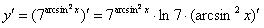
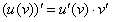
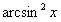
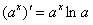
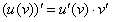
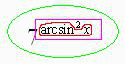
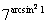
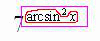
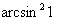
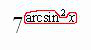
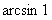
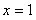
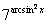

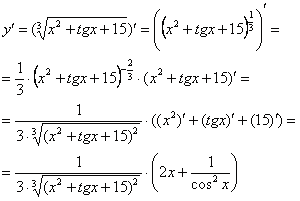
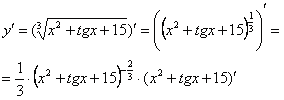
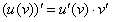
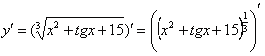
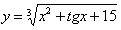
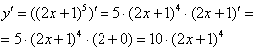
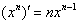
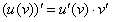
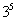
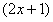
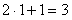
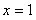
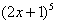
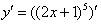
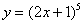
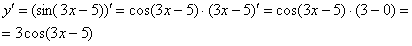
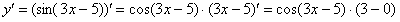
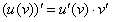
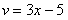
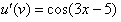
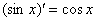
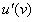
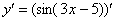
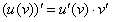
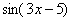
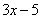
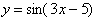
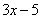
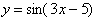
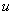
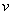
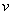
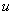
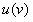
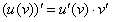
Бюджетное образовательное учреждение
среднего профессионального образования
Вологодской области
«Кадуйский политехнический техникум»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для самостоятельной работы по математике
по теме «Дифференциальное и интегральное исчисление»
КАДУЙ
2013
ОДОБРЕНЫ
МЦК по ООД БОУ СПО ВО «Кадуйский политехнический техникум»
Протокол № от
Методические указания для самостоятельной работы по математике по теме «Дифференциальное и интегральное исчисление»
Методические указания предназначены для студентов очного отделения 2 курса для всех специальностей СПО. Указания содержат сведения о требованиях к написанию и оформлению контрольных работ, краткую теорию по данной теме, примеры решений и задания для внеаудиторной самостоятельной работы по теме «Дифференциальное и интегральное исчисление».
Составитель: Е.Е.Кормачева, преподаватель математики
Рецензент: В.И. Лукина, методист
Содержание
Введение ………………………………………………………………………….4
1. Требования к выполнению и оформлению контрольных работ ...................5
2. Теоретическая часть …………………………………………………………..5
3. Задания для самостоятельной работы……………………………………...11
4. Литература……………………………………………………………………13
Введение
Методические указания предназначены для студентов 2 курса всех специальностей для внеаудиторной самостоятельной работы по математике по теме «Дифференциальное и интегральное исчисление».
Данные указания содержат требования к выполнению контрольных работ по математике, теоретическую часть изучаемого материала, знание которого необходимо по указанной теме. В теоретической части содержатся примеры с решениями производных сложных функций.
Для более глубокого изучения производной сложной функции можно воспользоваться литературой, приведенной в методических указаниях, другими учебниками, а также конспектами лекций по курсу «Математика».
4
1. Требования к выполнению и оформлению контрольных работ
При выполнении контрольной работы необходимо строго придерживаться следующих требований:
-
Контрольная работа должна быть выполнена на отдельном двойном
листе в клетку пастой синего или фиолетового цвета.
-
Работы, содержащие задачи не своего варианта, не рецензируются.
-
Решение каждой задачи начинается с её условия.
-
Решение задач следует излагать подробно и аккуратно, объясняя все
действия по ходу решения.
-
Компьютерное оформление работы не рецензируется.
-
Незачтенная работа переписывается студентом, исправления
записывается в конце работы. Вносить исправления в текст работы
запрещается.
-
Контрольная работа сдается в установленные сроки.
2. Теоретическая часть по теме
«Дифференциальное и интегральное исчисление»
Цель работы: овладение методами вычисления производной сложной и обратных тригонометрических функций.
Умение и навыки, которые должны приобрести студенты: самостоятельно вычислять производные сложных функций, осуществлять поиск информации с использованием компьютерной техники и Интернета
Формирование компетенций:
Рекомендации по выполнению.
1.Разобрать решение примеров.
2.Выполнить задания, используя указания.
3.Оформить решение задач в тетради.
1.Разберите решение примеров:
Вычисление производных сложных функций осуществляется по правилу дифференцирования сложной функции:
5
Прежде всего, обратим внимание на запись . Здесь у нас две функции - и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Пример 1
Найти производную функции
Под синусом у нас находится не просто  , а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
, а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
Функция - это сложная функция, причем многочлен является вложенной функцией , а - внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является вложенной, а какая - внешней.
После того, как определены вложенная и внешняя функции применяют правило дифференцирования сложной функции .
Вычислим производную:
Сначала находят производную внешней функции , по формуле . Все табличные формулы применимы и в том, случае, если  заменить сложным выражением, в данном случае:
заменить сложным выражением, в данном случае:
При выполнении вычислений вложенная функция не изменилась.
По формуле получаем:
Постоянный множитель обычно выносят в начало выражения:
Пример 2
Найти производную функции
Запишем
Определим где внешняя функция, а где вложенная. Для этого пробуем вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен - и есть вложенная функция. И, только потом выполняется возведение в степень , следовательно, степенная функция - это внешняя функция.
По правилу дифференцирования сложной функции , сначала нужно найти производную от внешней функции, в данном случае, от степени. По формуле вычисляем производную:
Пример 3
Найти производную функции
Для того чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
7
Анализируя функцию, приходим к выводу, что сумма трех слагаемых - это вложенная функция, а возведение в степень - внешняя функция.По правилу дифференцирования сложной функции :
Степень снова представляем в виде радикала , а для производной вложенной функции применяем простое правило дифференцирования суммы:
Пример 4
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение подставив значение . Если использовать для вычислений калькулятор, то сначала нужно найти , значит, арксинус - самое глубокое вложение.
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой вложенной функцией является арксинус, а самой внешней функцией - показательная функция.
По правилу сначала нужно взять производную от внешней функции. Вычислим производную показательной функции: .Вместо  рассмотрим сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:
рассмотрим сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:
Теперь опять необходимо вычислить производную сложной функции взяв за вложенную функцию - арксинус, а за внешнюю функцию - степень. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени:
Далее находим по таблице производную арксинуса:
9
Пример 5
Найти производную функции
Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :
Далее дважды необходимо применить правило :
Согласно правилу , получаем:
Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.
3. Задания для самостоятельной работы
1) 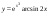 ,
,
16) 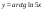 .
.
2) 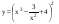 ,
,
17) 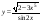 .
.
3) 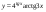 ,
,
18) 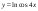 .
.
4) 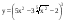 ,
,
19) 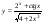 ,
,
5) 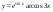 ,
,
20) 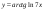 .
.
6) 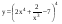 ,
,
21) 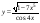 .
.
7) 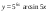 ,
,
22) 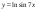 .
.
8) 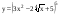 ,
,
23) 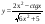 ,
,
9) 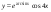 ,
,
24) 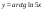 .
.
10) 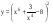 ,
,
25) 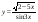 .
.
11) 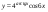 ,
,
26) 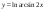 .
.
12) 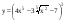 ,
,
27) 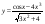 ,
,
13) 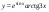 ,
,
28) 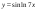 .
.
14) 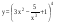 ,
,
29) 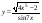 .
.
15) 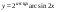 ,
,
30) 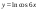 .
.
Оформить решение примеров в тетради.
По результатам решения примеров выставляется оценка.
Шкала оценки образовательных достижений
Процент результативности
(правильных ответов)
Оценка уровня подготовки
Балл (оценка)
Вербальный аналог
90-100
5
отлично
80-89
4
хорошо
70-79
3
удовлетворительно
менее 70
2
неудовлетворительно
12
Литература
-
Григорьев С.Г., Задулина С.В. Под редакцией В.А. Гусева Математика. - М.: Образовательно-издательский центр «Академия», 2011
-
Пехлецкий И.Д. Математика. - М.: Образовательно-издательский центр «Академия», 2011.
Дополнительная литература:
-
Н.В. Богомолов. Практические занятия по математике. - М., ВШ,1990.
-
Н.В. Богомолов, П.И. Самойленко. Математика.-М., Дрофа,2006.
Интернет ресурсы:
-
www/mathematics.ru
-
tutoronline.ru/
-
exponenta.ru
13


