- Преподавателю
- Математика
- Олимпиадные задачи по математике с решениями 9-11 класс
Олимпиадные задачи по математике с решениями 9-11 класс
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Конспекты |
| Автор | Антропова В.Ю. |
| Дата | 24.10.2015 |
| Формат | doc |
| Изображения | Есть |
13
МАТЕМАТИЧЕСКИЙ БЛОК
1. Решите относительно х уравнение: 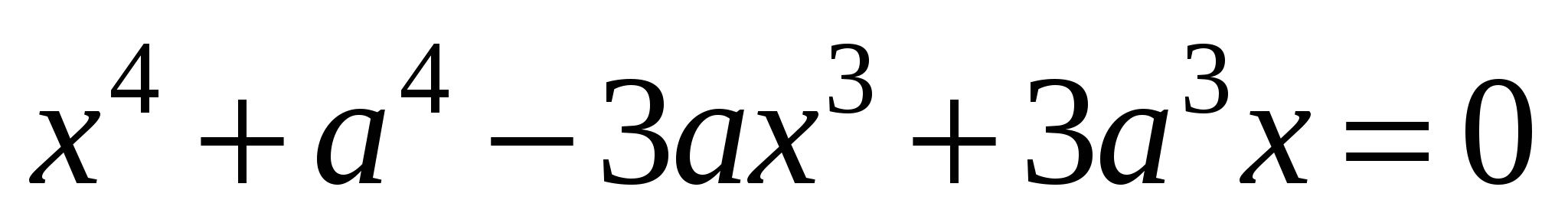 , где
, где 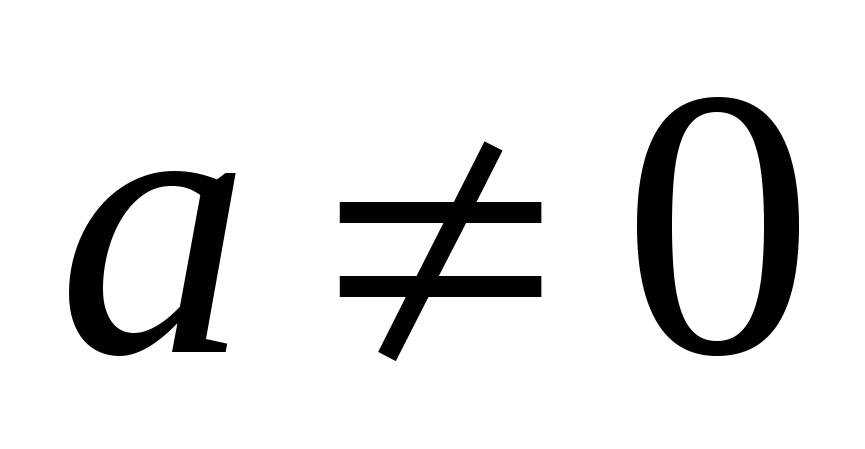
РЕШЕНИЕ:
Преобразуем левую часть уравнения, сгруппировав и разложив на множители:
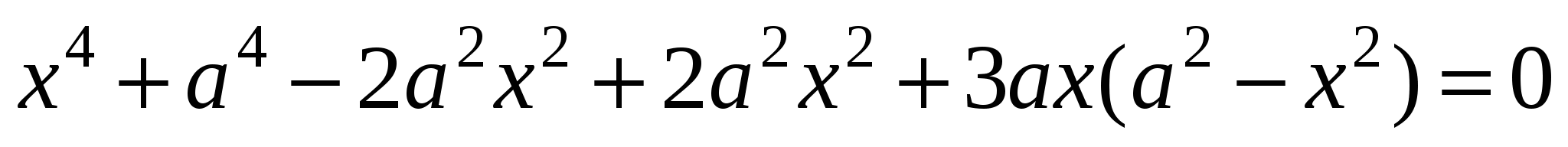

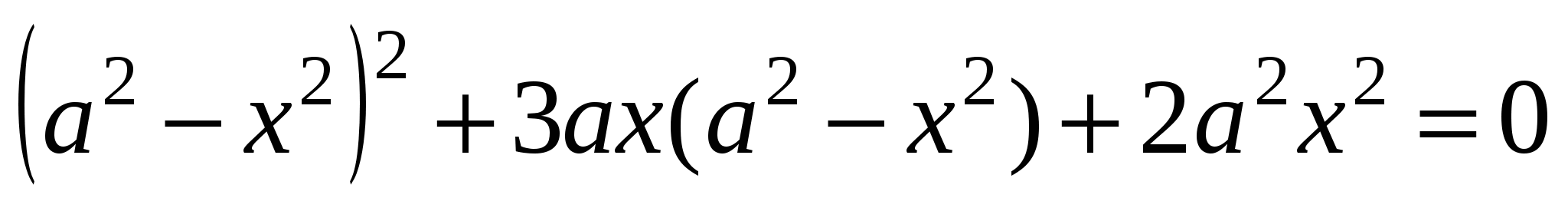

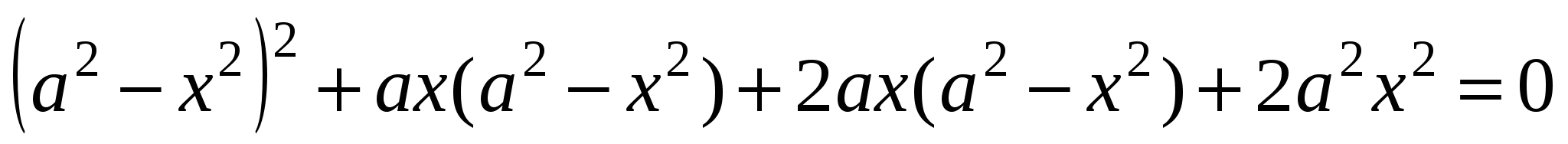

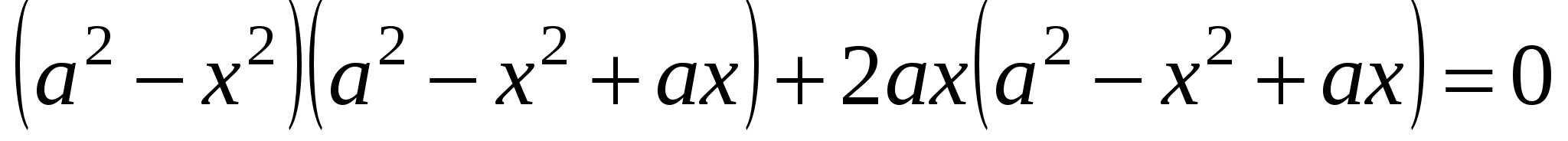

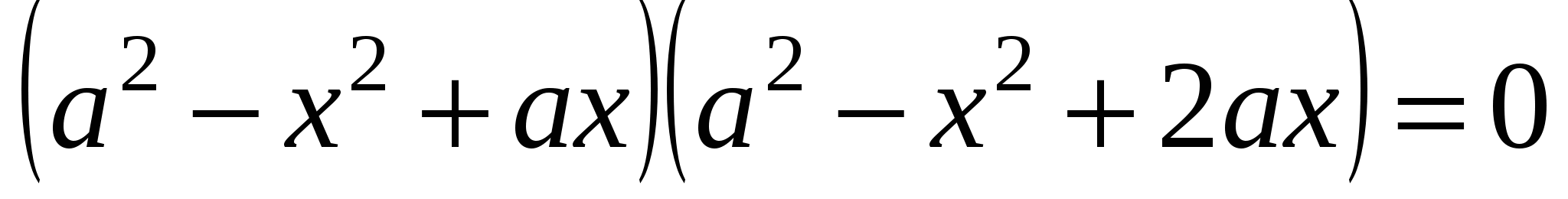

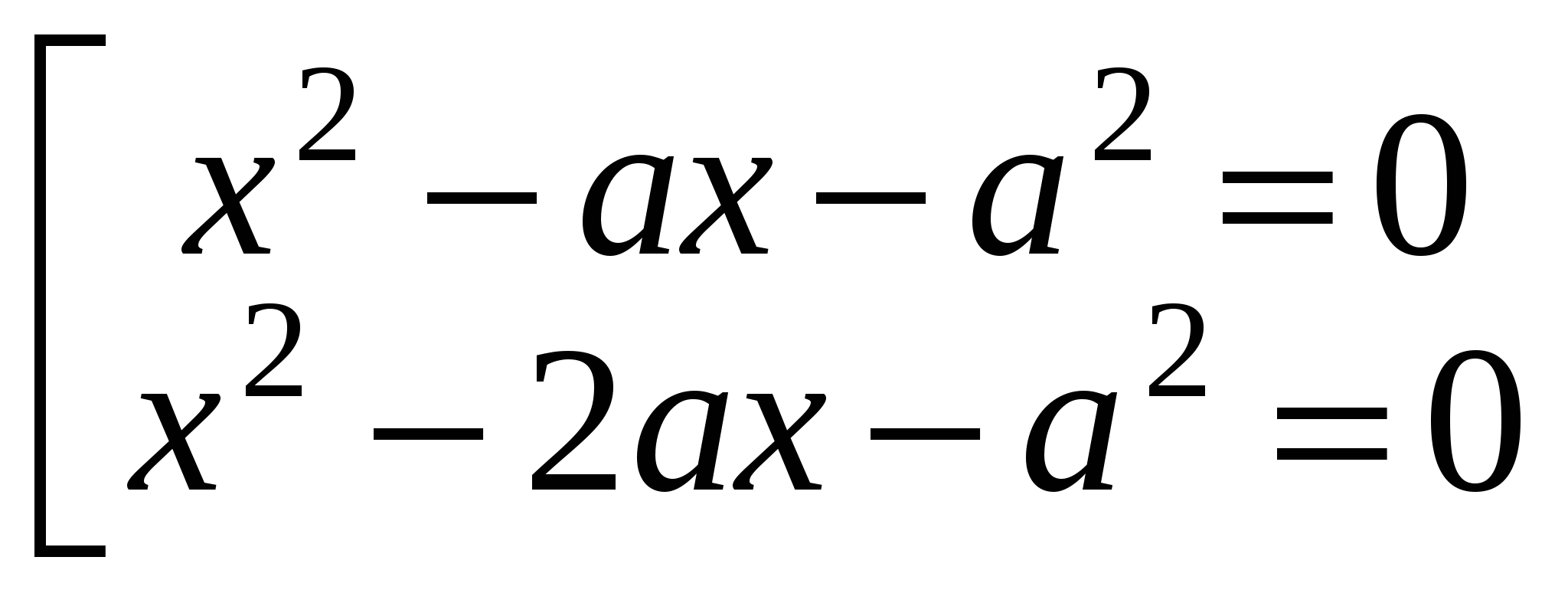

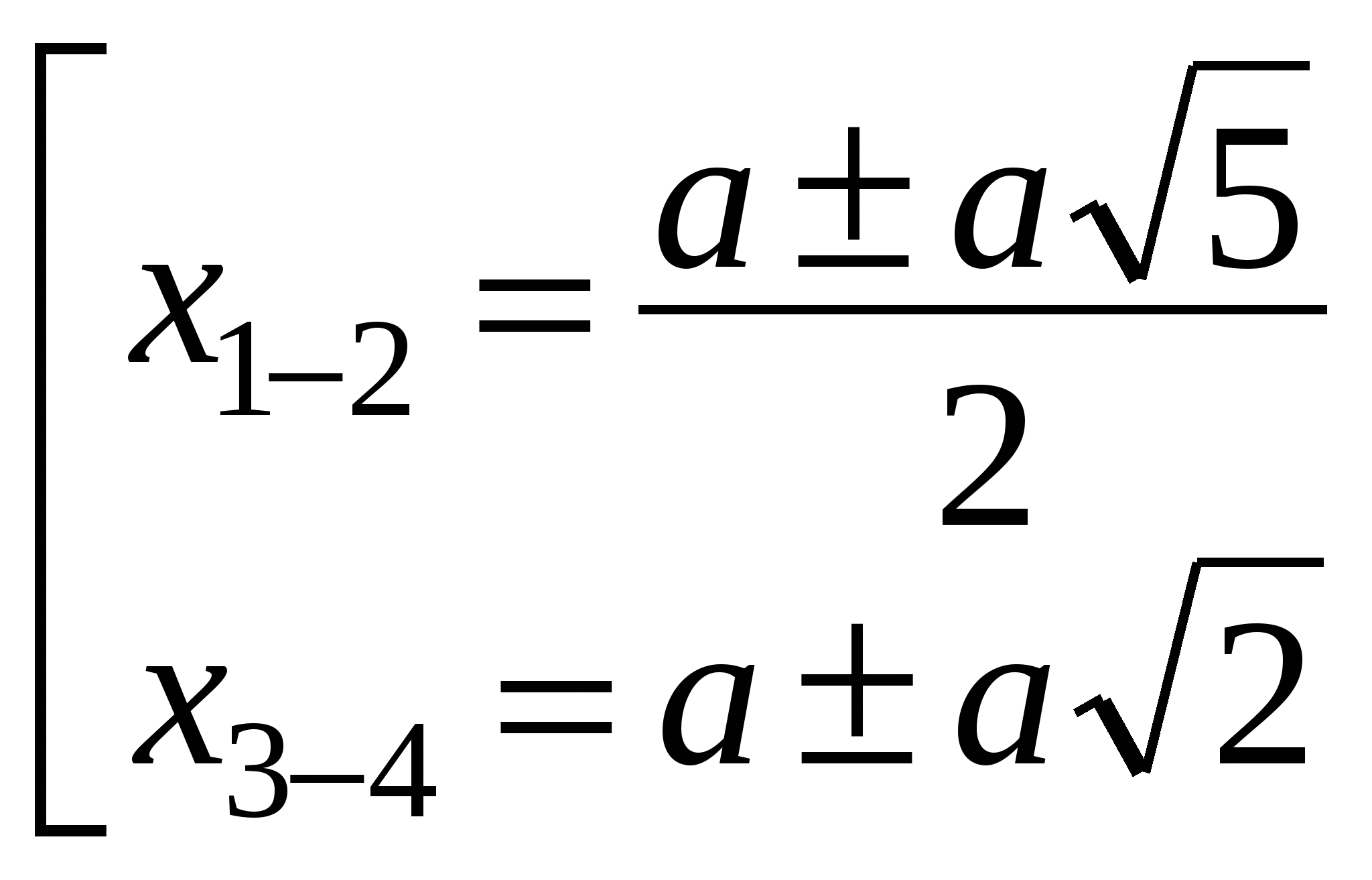
ОТВЕТ: 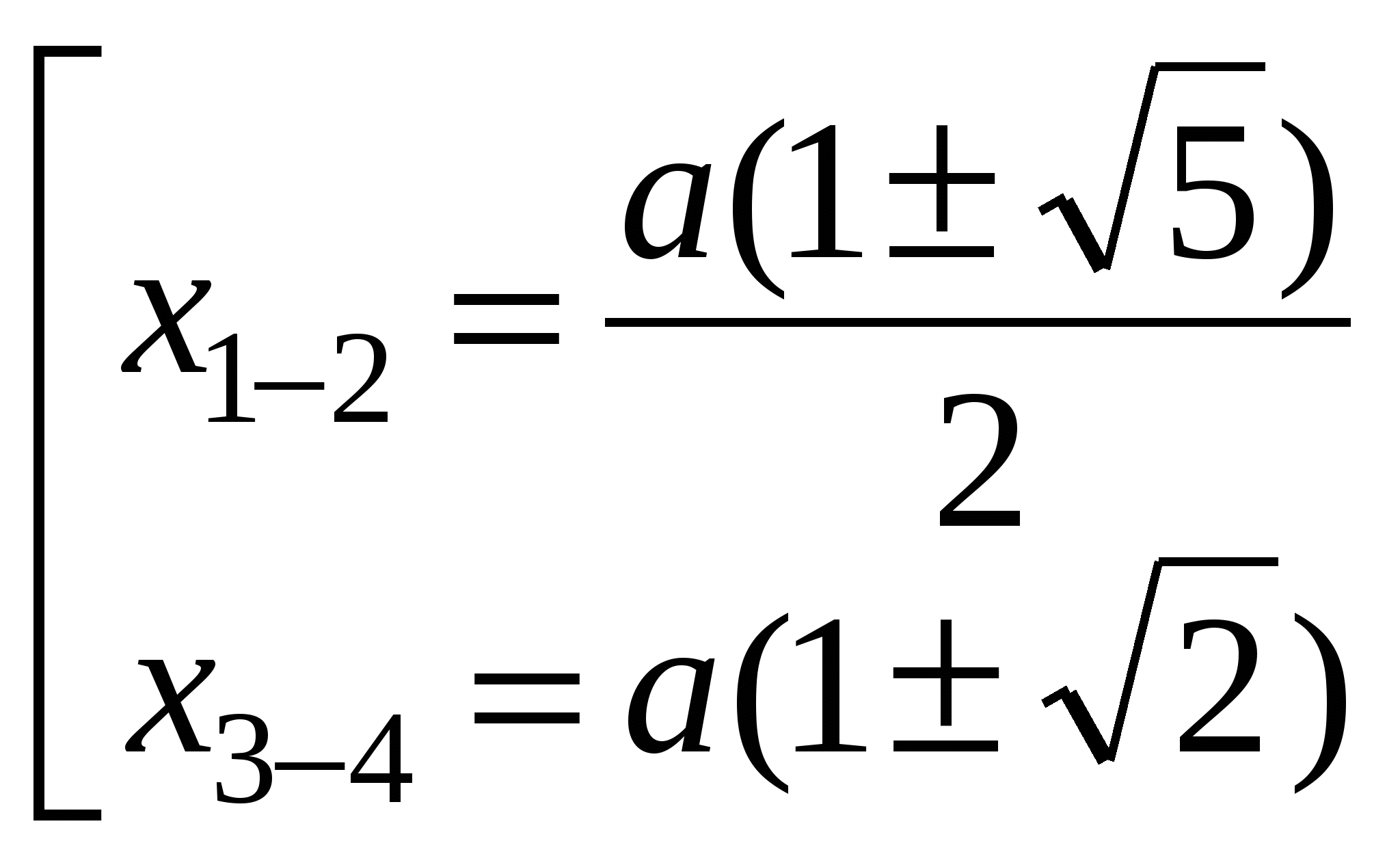
2. Решите в натуральных числах неравенство: 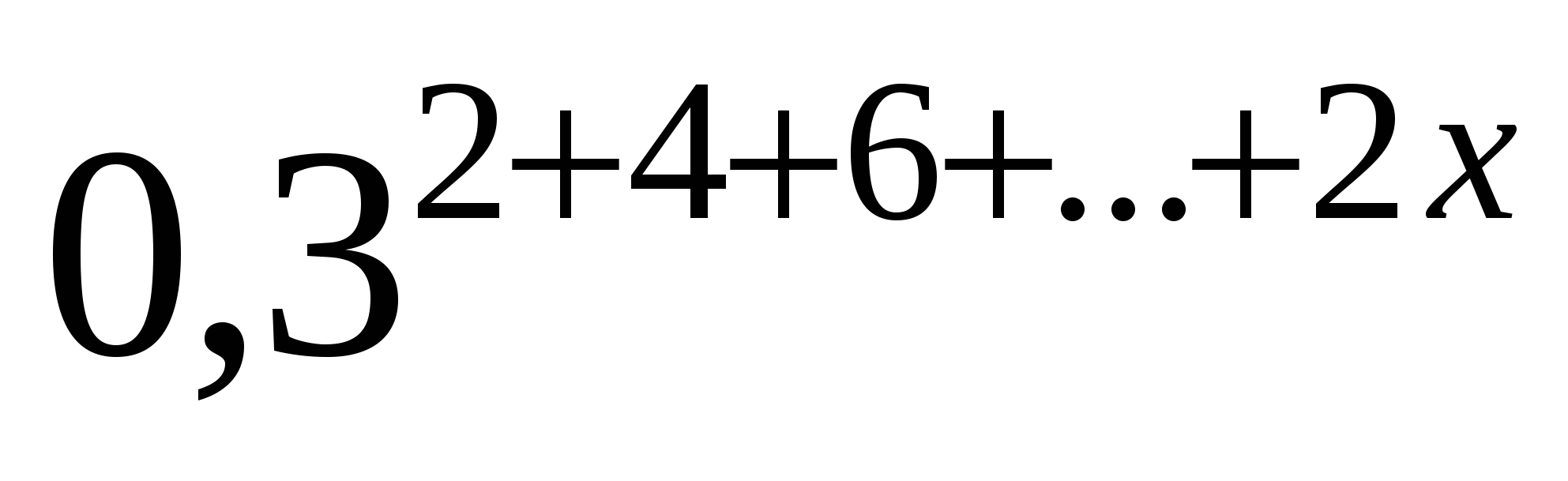 >
>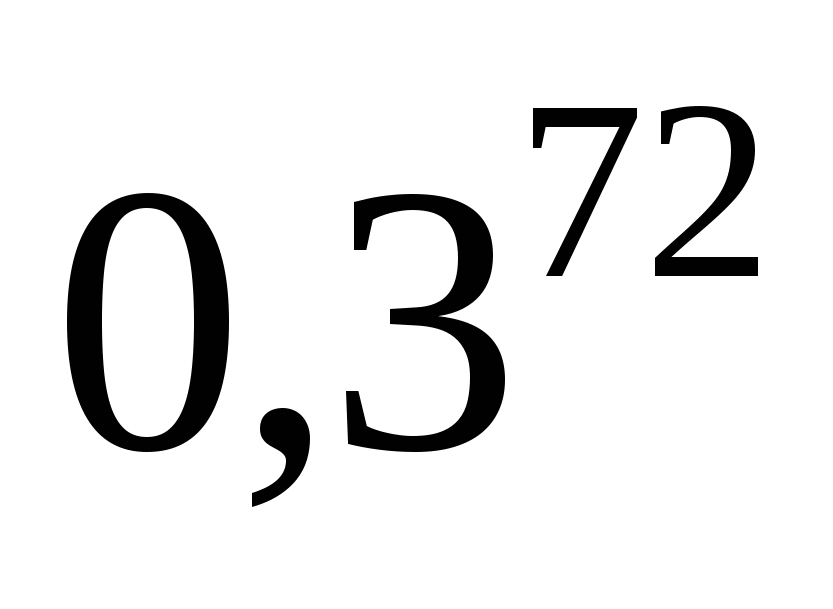
РЕШЕНИЕ:
Найдем сумму арифметической прогрессии из х слагаемых, используя формулу:
![]() : 2 + 4 + 6 + ….+ 2х = 2·(1 + 2 + 3 + … + х) =
: 2 + 4 + 6 + ….+ 2х = 2·(1 + 2 + 3 + … + х) = 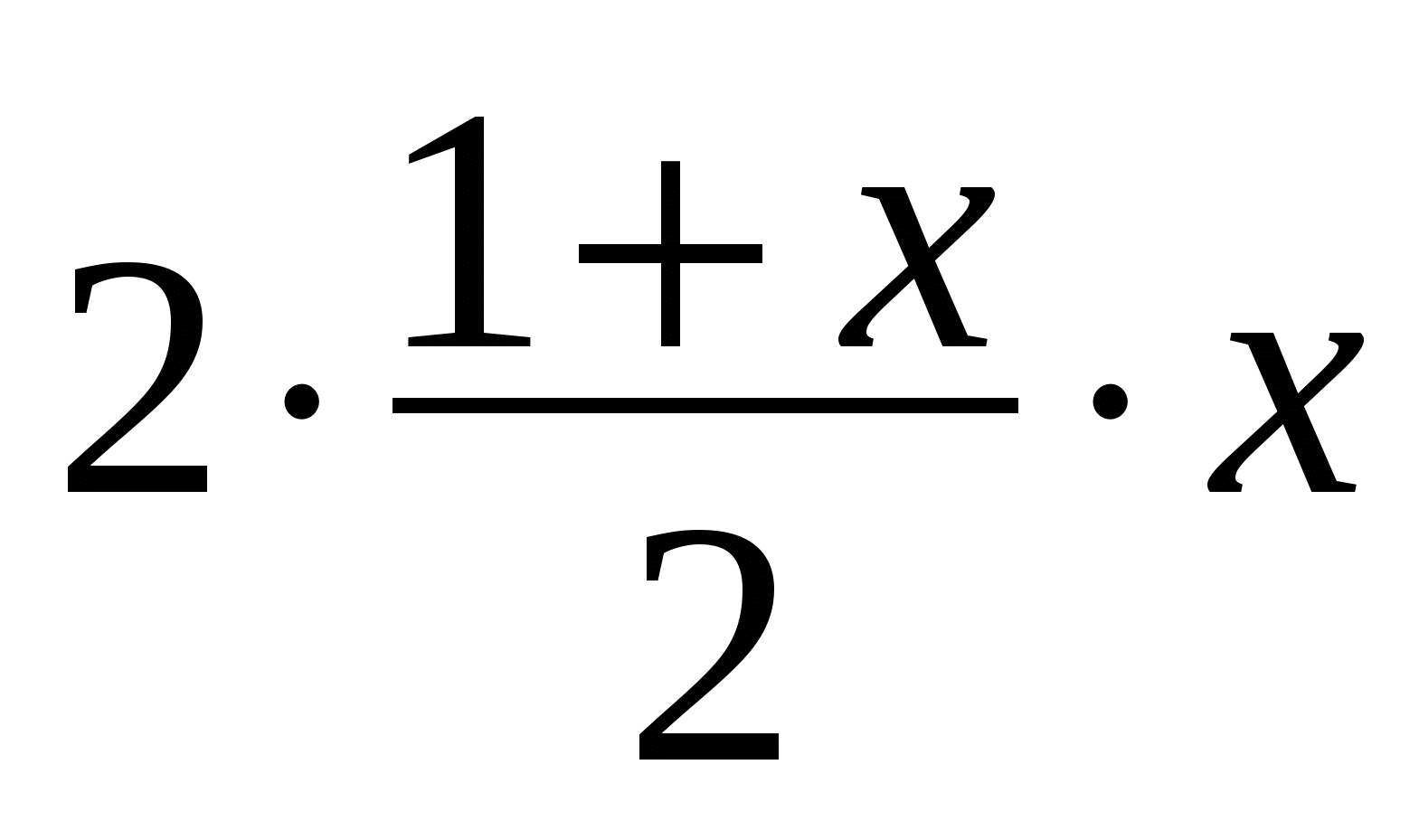 = х2 + х
= х2 + х
Неравенство примет вид: 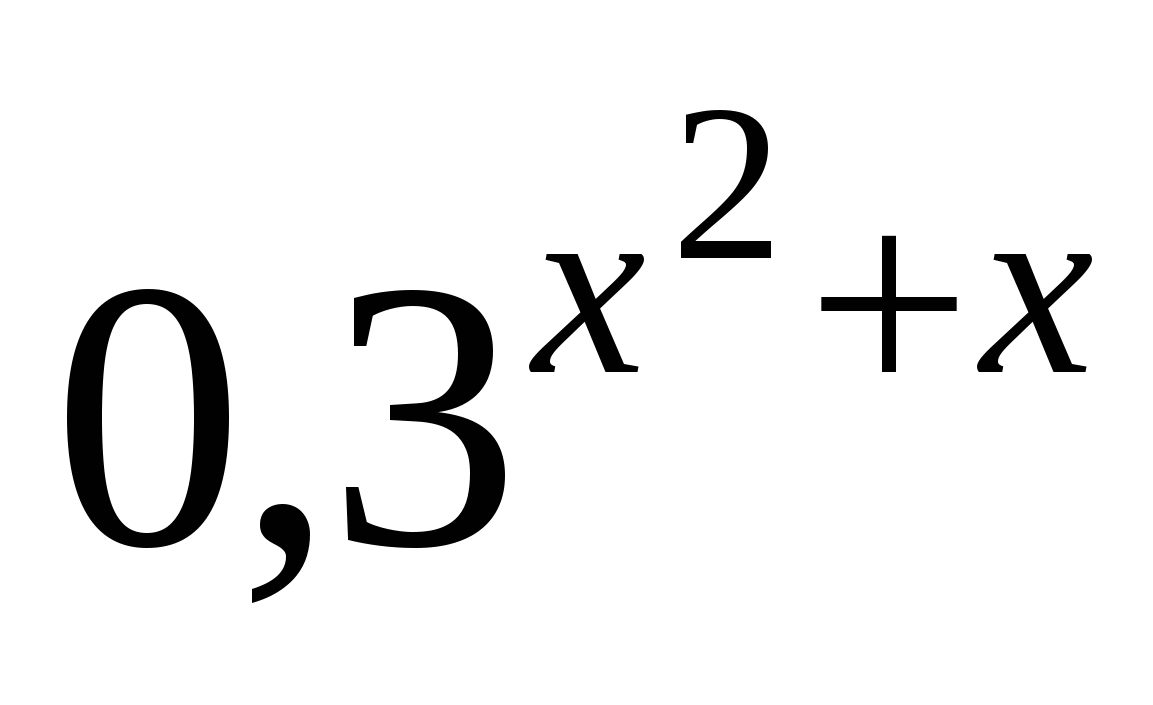 >
>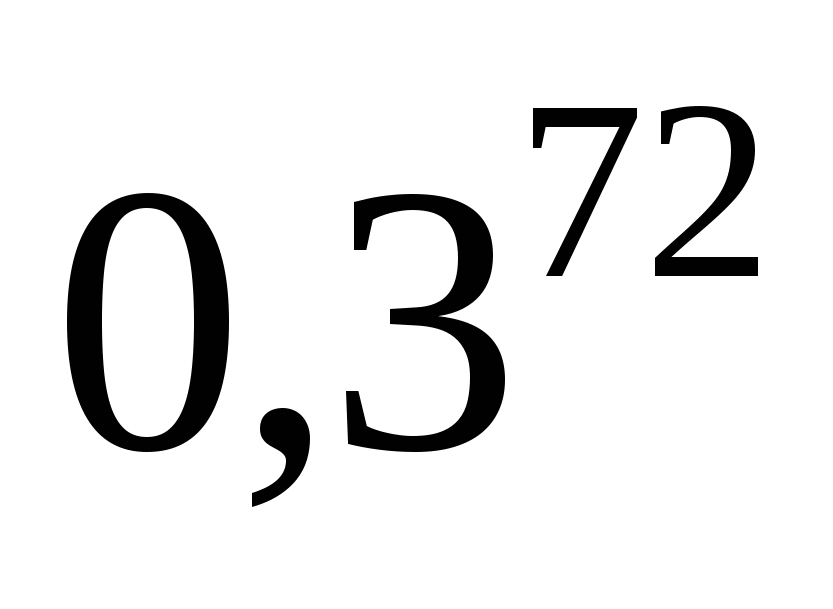 ,
,
т.к. основание 0,3 < 1, имеем 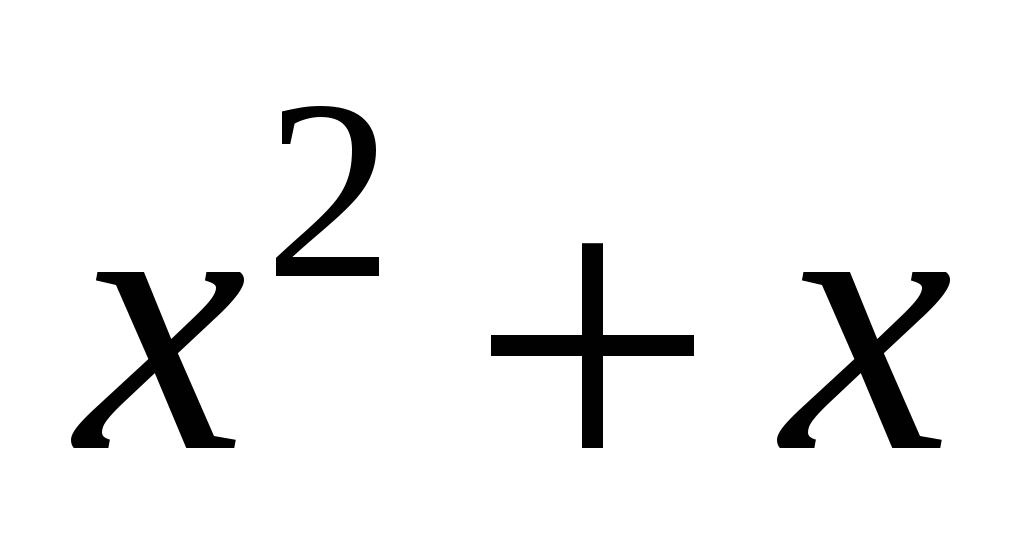 < 72
< 72

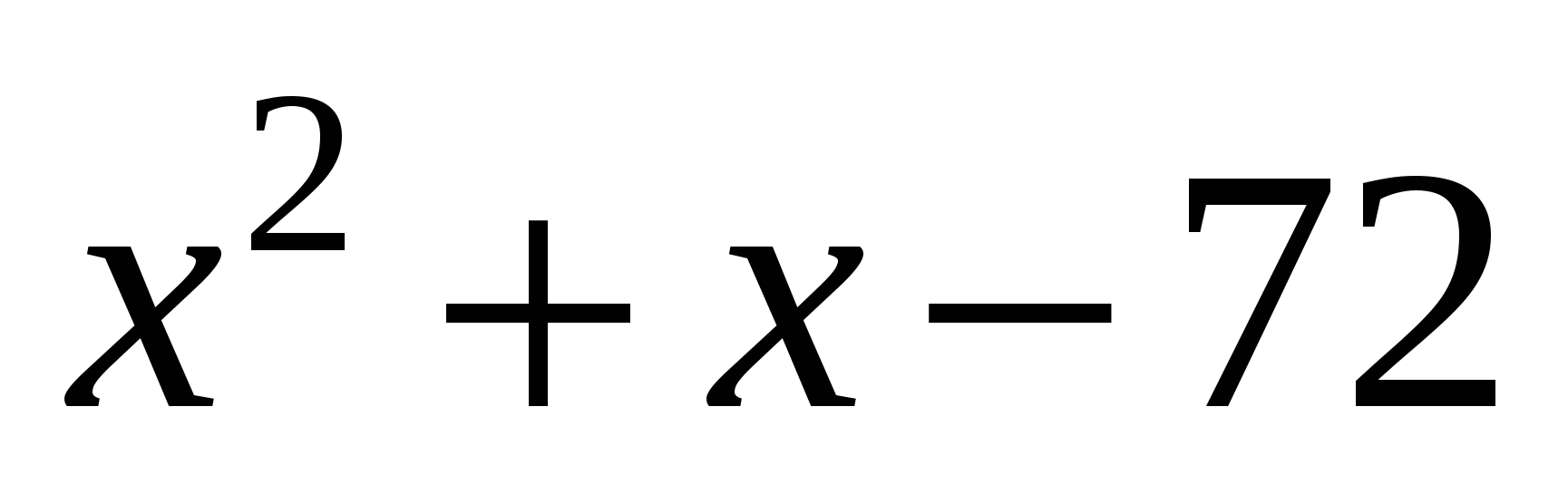 < 0
< 0 
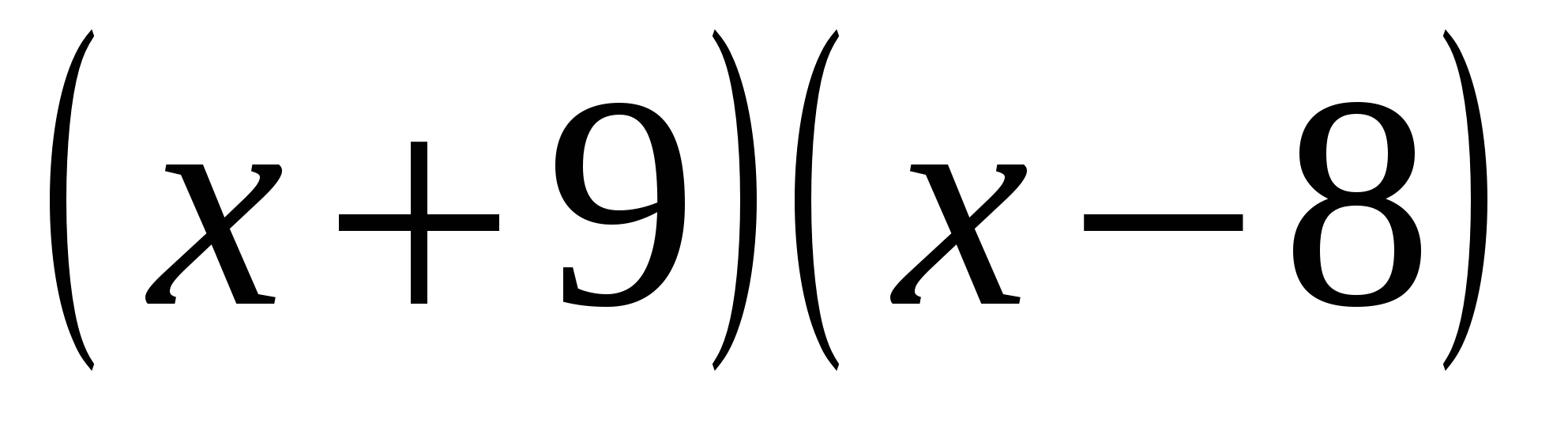 < 0.
< 0.
Откуда получаем, что 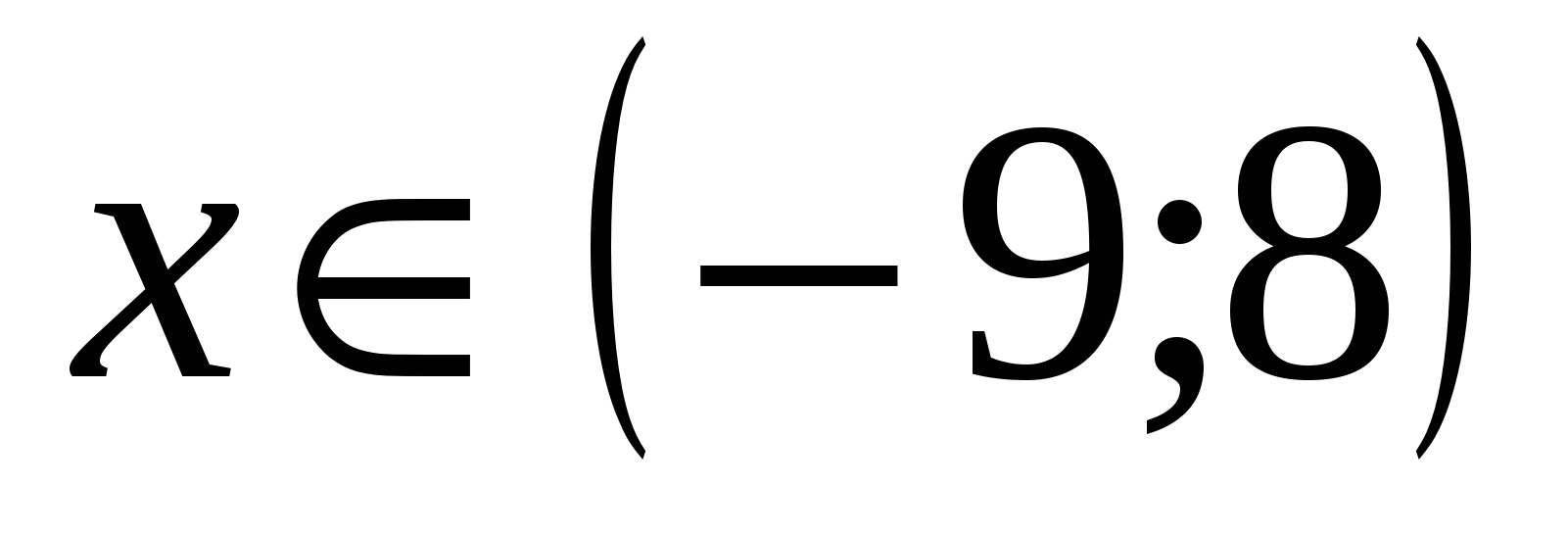 .
.
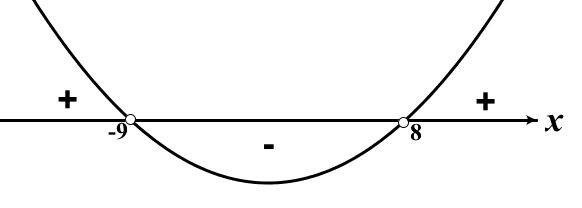
Перечислим натуральные числа, попадающие в указанный интервал: 1; 2; 3; 4; 5; 6; 7.
ОТВЕТ:![]()
3. Докажите тождество: 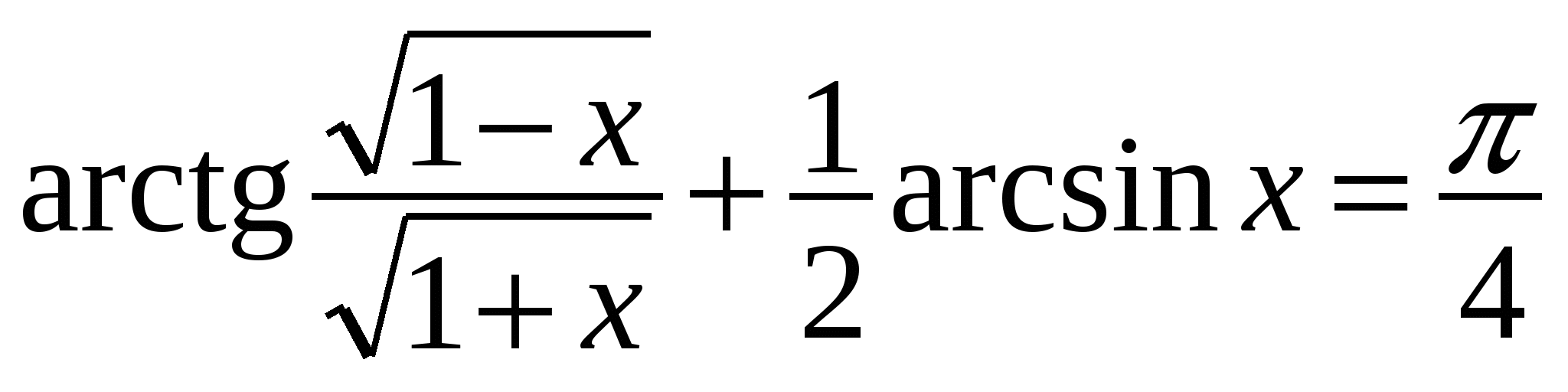 ,
, 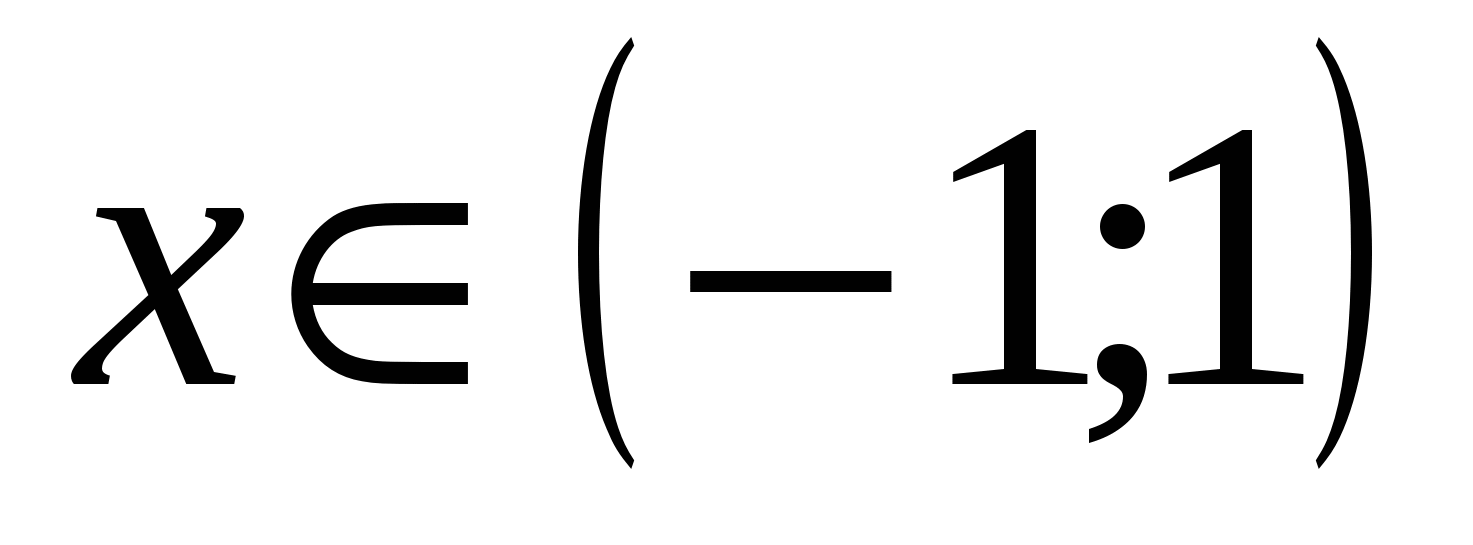
РЕШЕНИЕ:
Выполним для удобства простейшие преобразования: 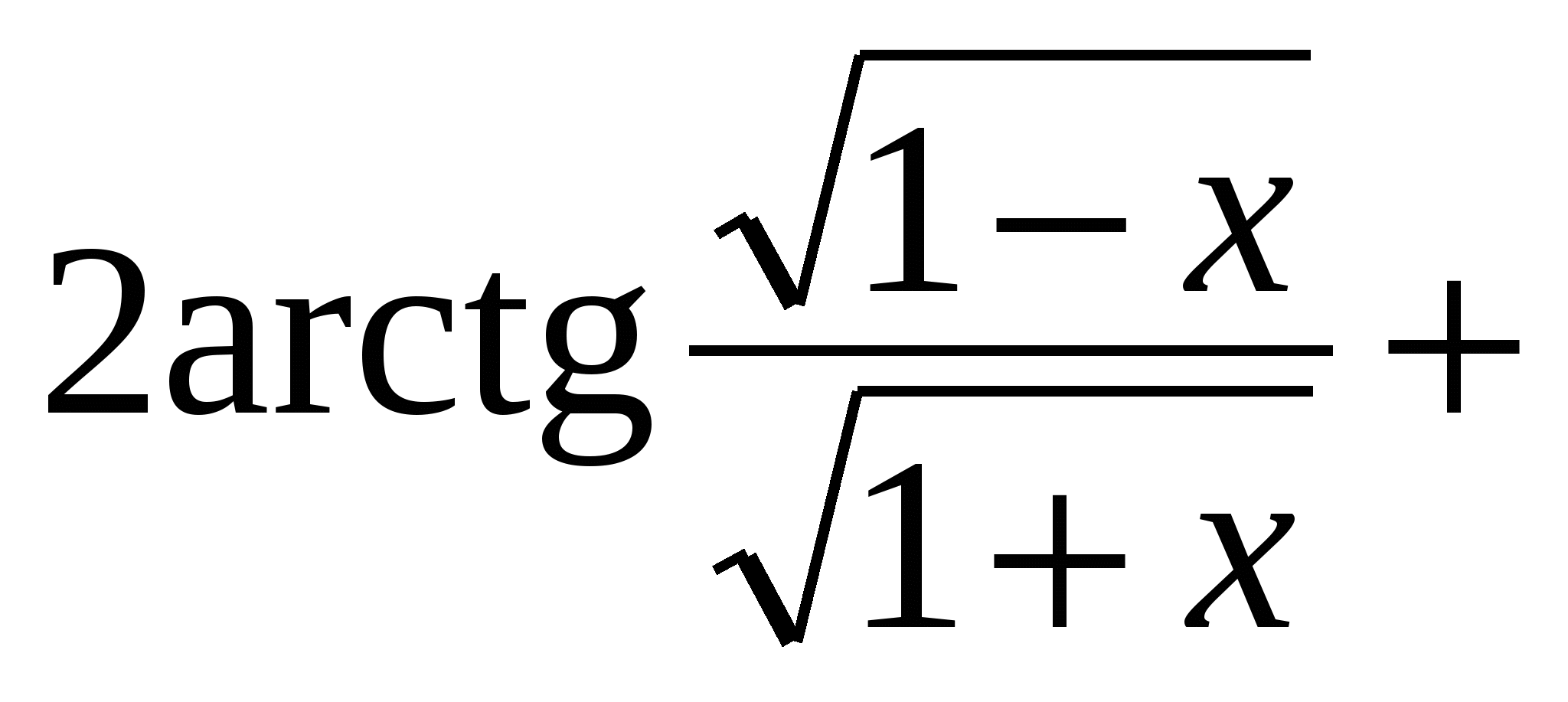 arcsin x =
arcsin x = 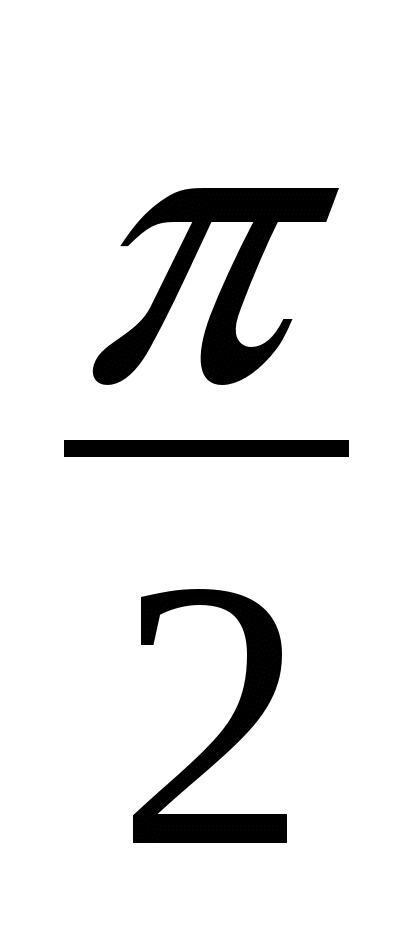
а) При х = 0 имеем верное равенство: 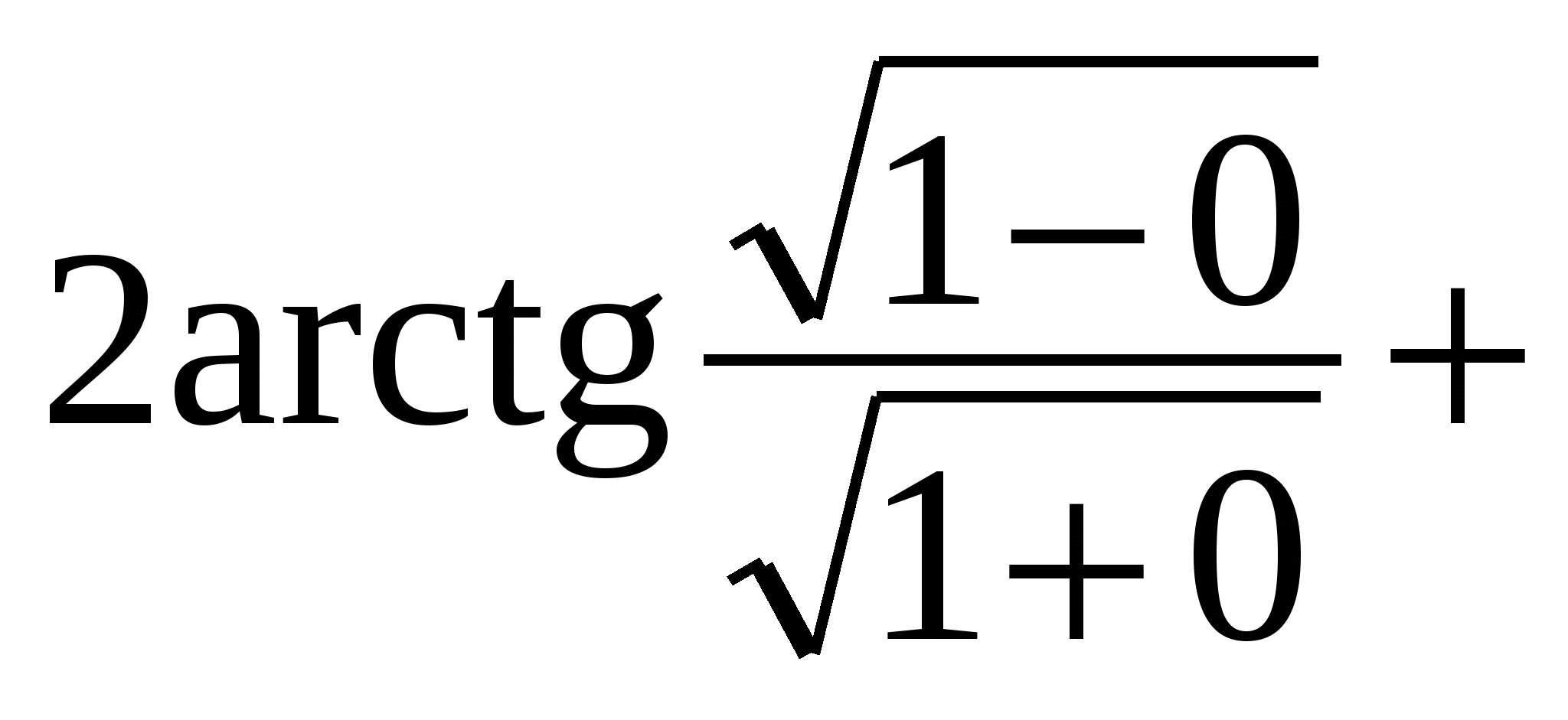 arcsin 0 =
arcsin 0 = 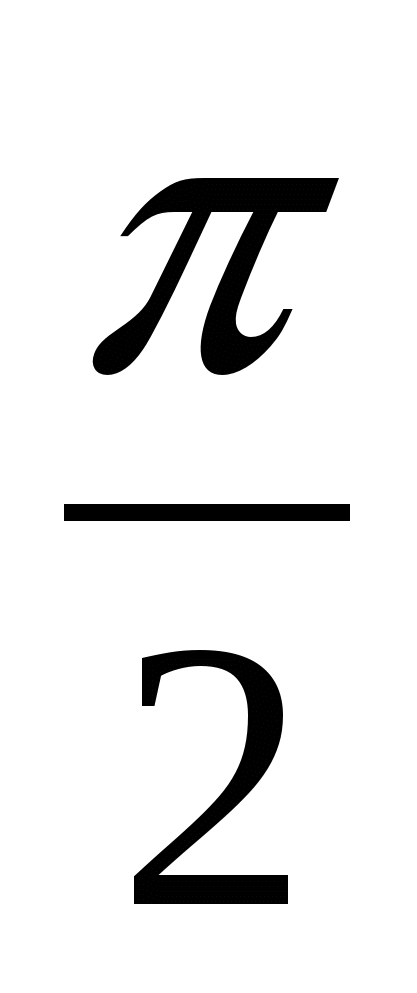

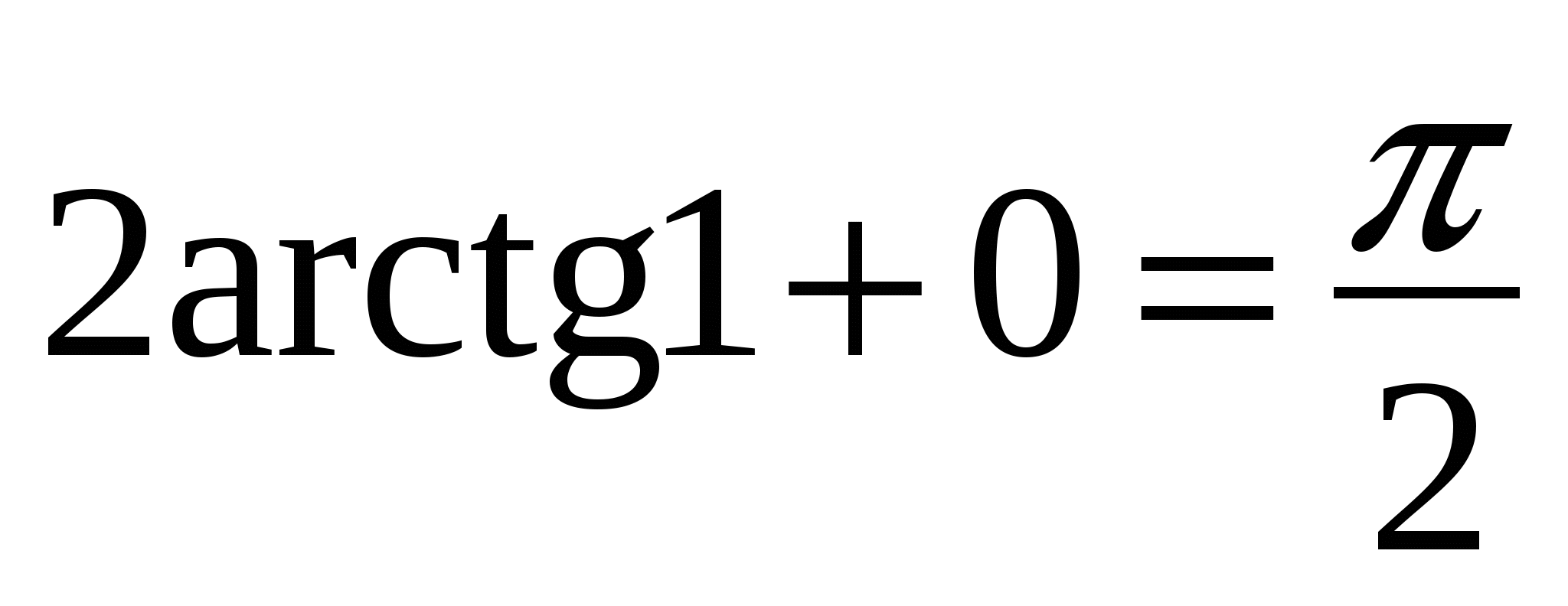

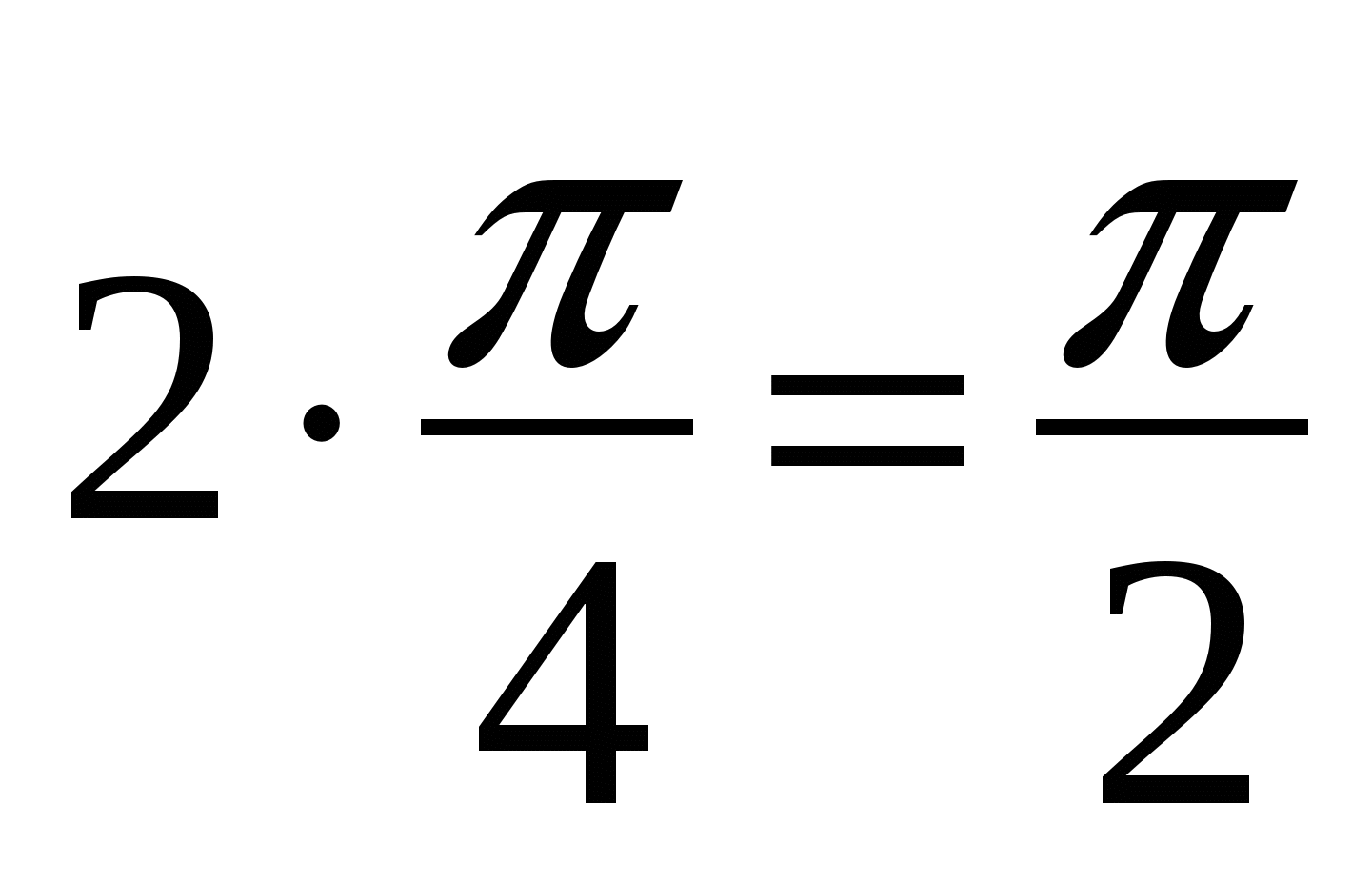 ;
;
б) При 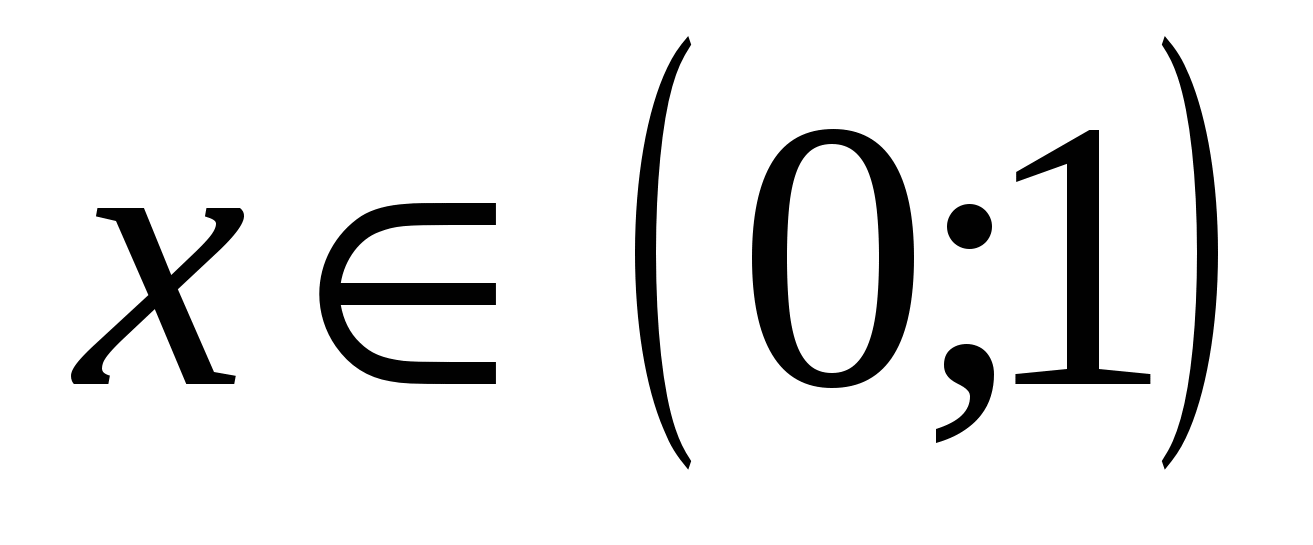 0 <
0 <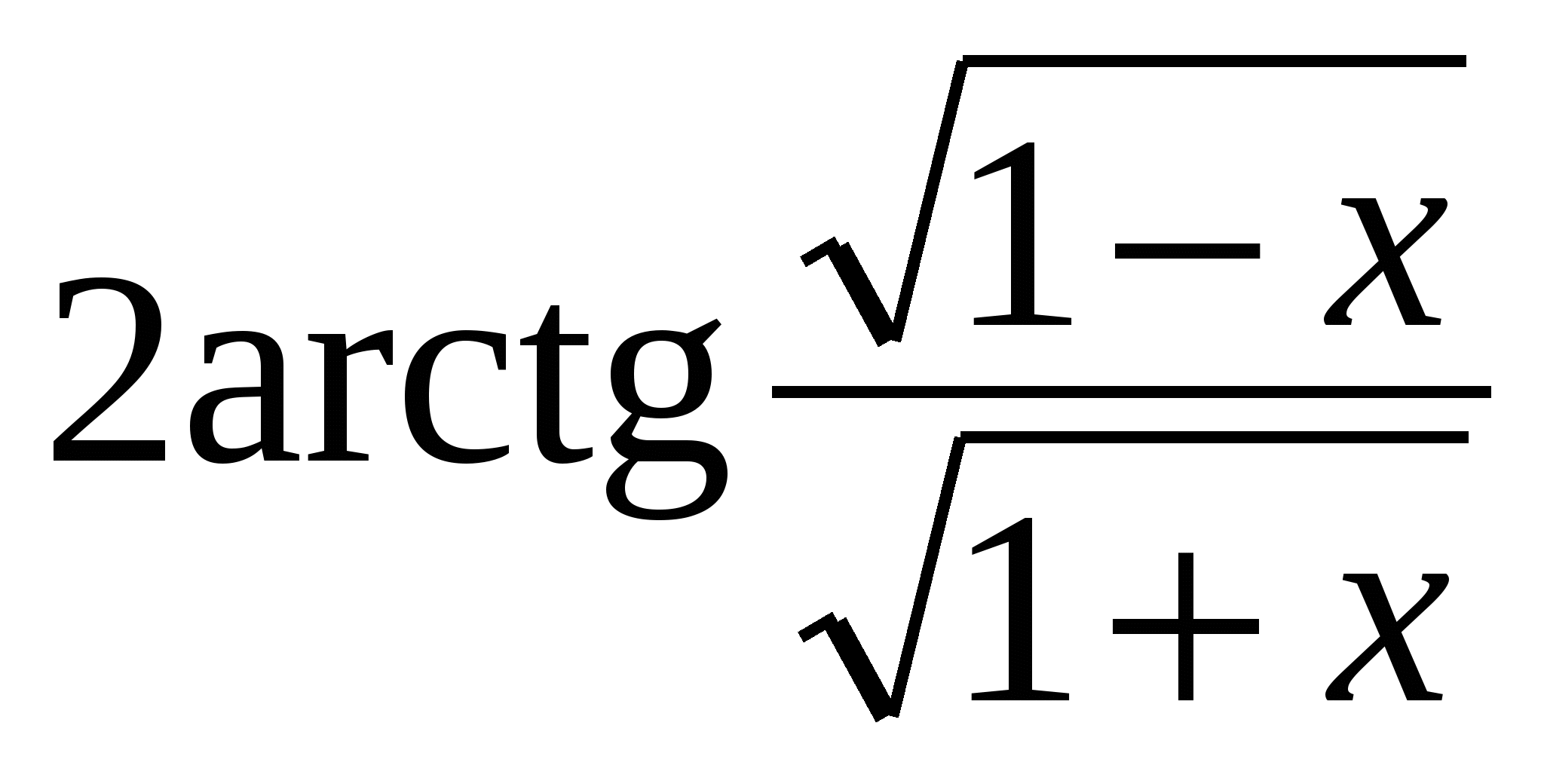 <
< 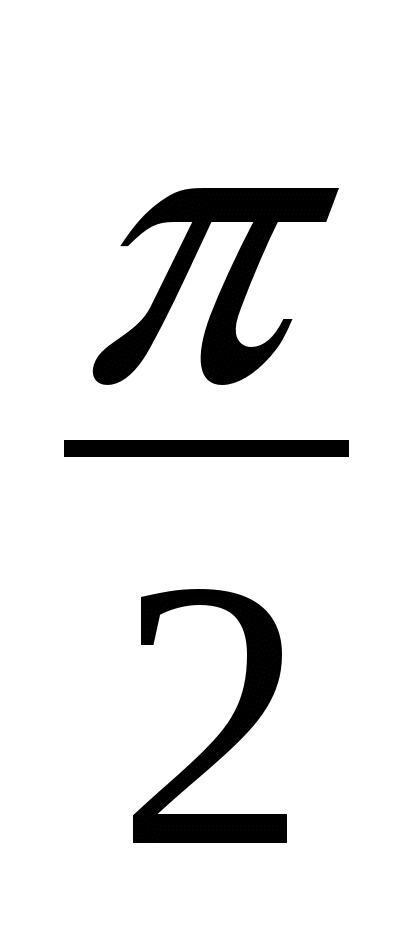 и 0 < arcsin x <
и 0 < arcsin x < 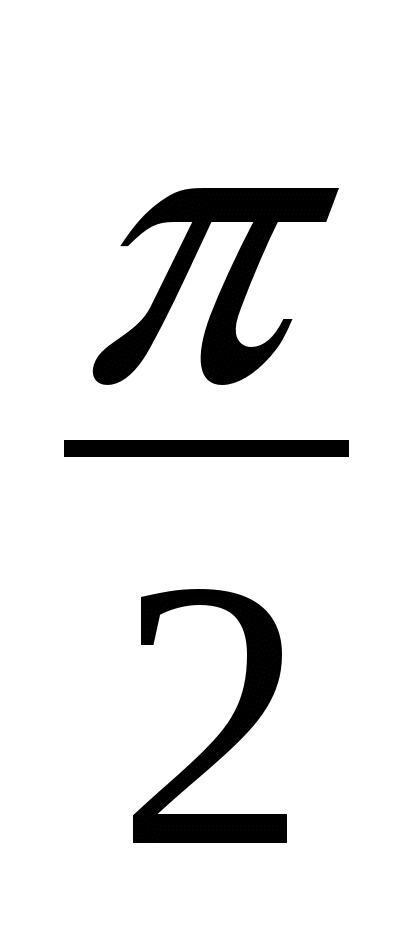 .
.
Докажем равенство 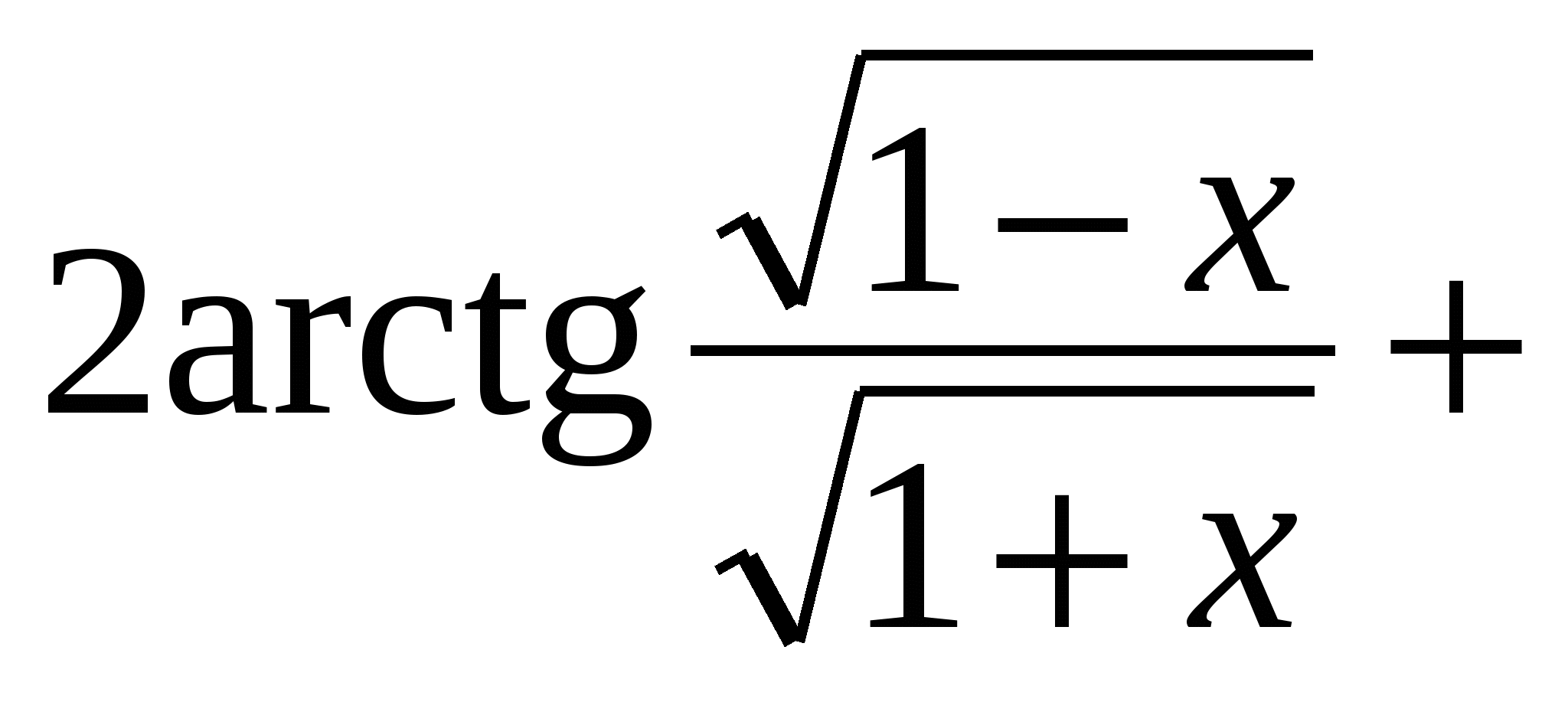 arcsin x =
arcsin x = 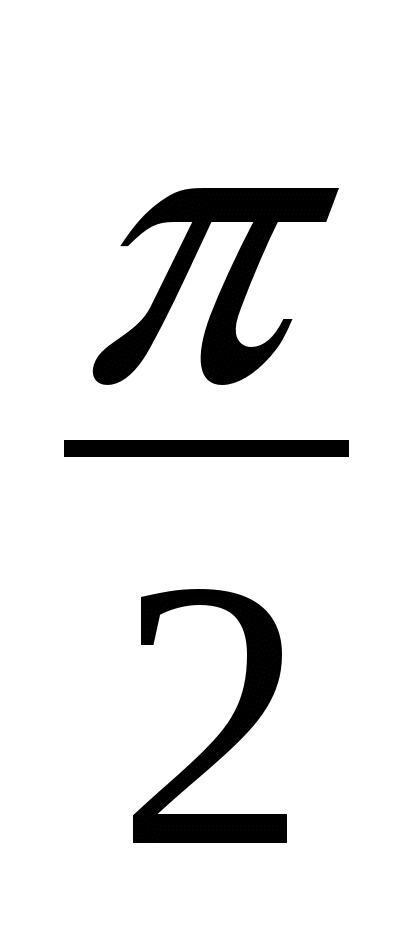 геометрически.
геометрически.
Пусть  АВС - прямоугольный и АВ = 1, ВС = х, BD - биссектриса. Тогда по теореме Пифагора АС =
АВС - прямоугольный и АВ = 1, ВС = х, BD - биссектриса. Тогда по теореме Пифагора АС = 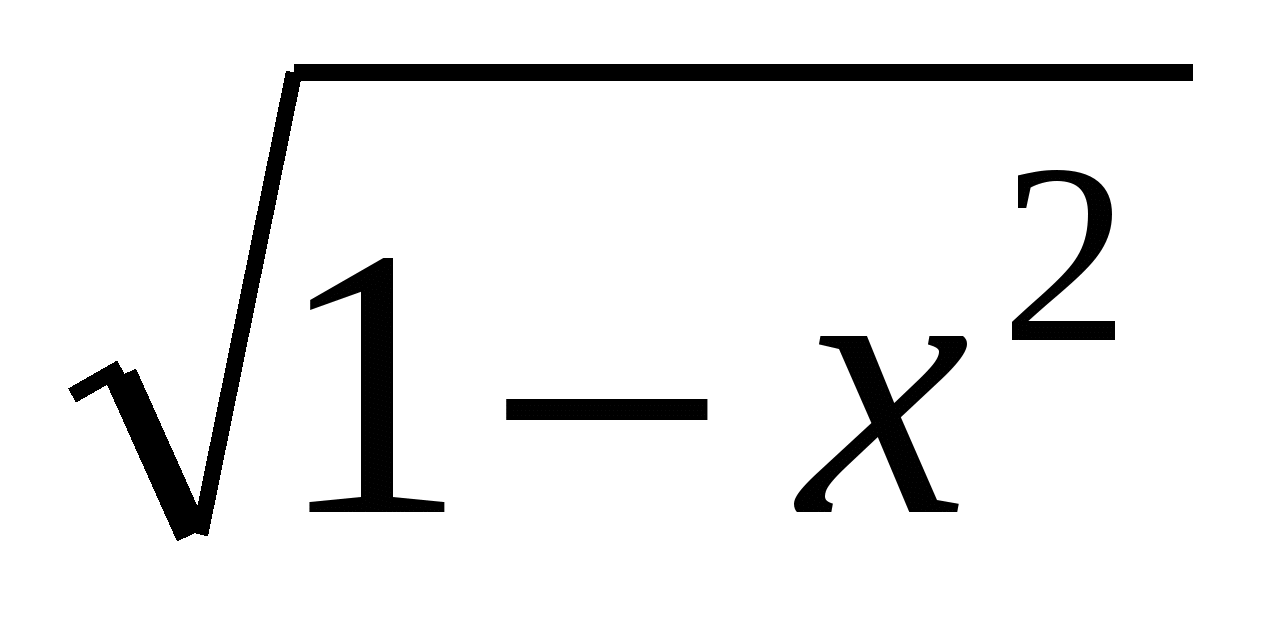 . Пусть
. Пусть 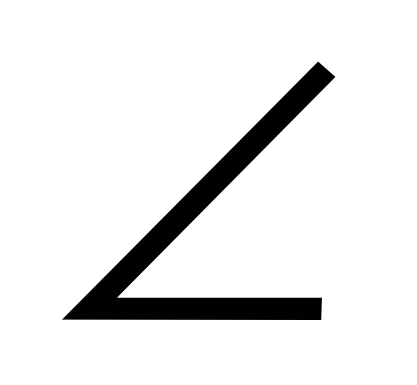 А =
А =  , а
, а 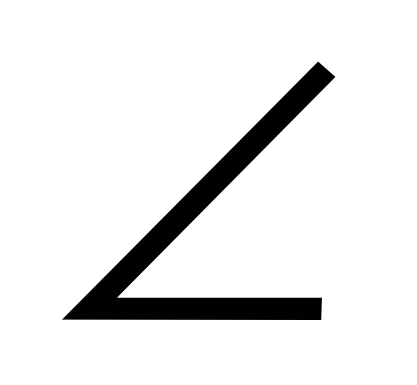 В =
В =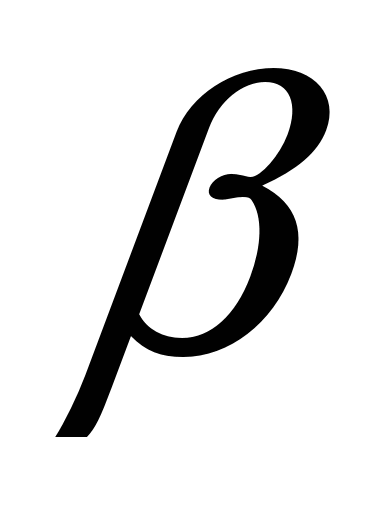 . Очевидно, что 2
. Очевидно, что 2![]() +
+ =
= 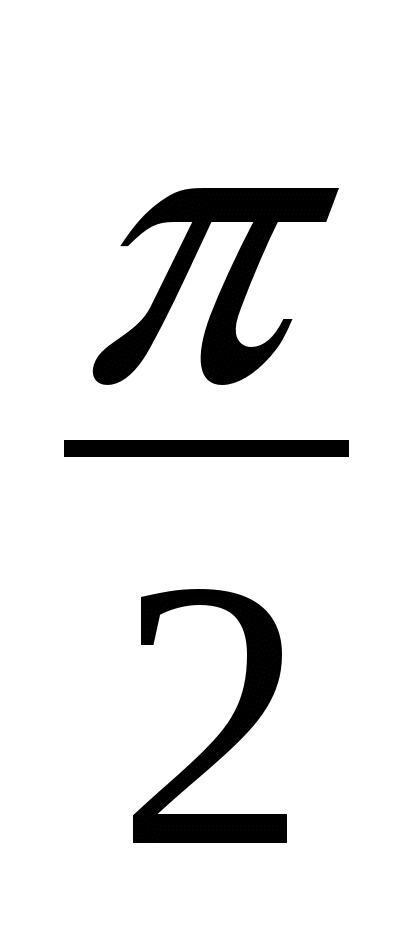 .
.
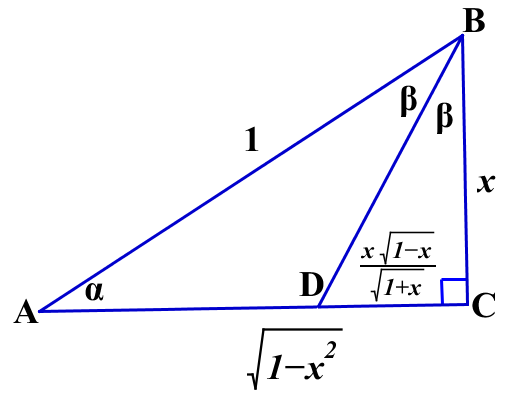
По свойству биссектрисы имеем 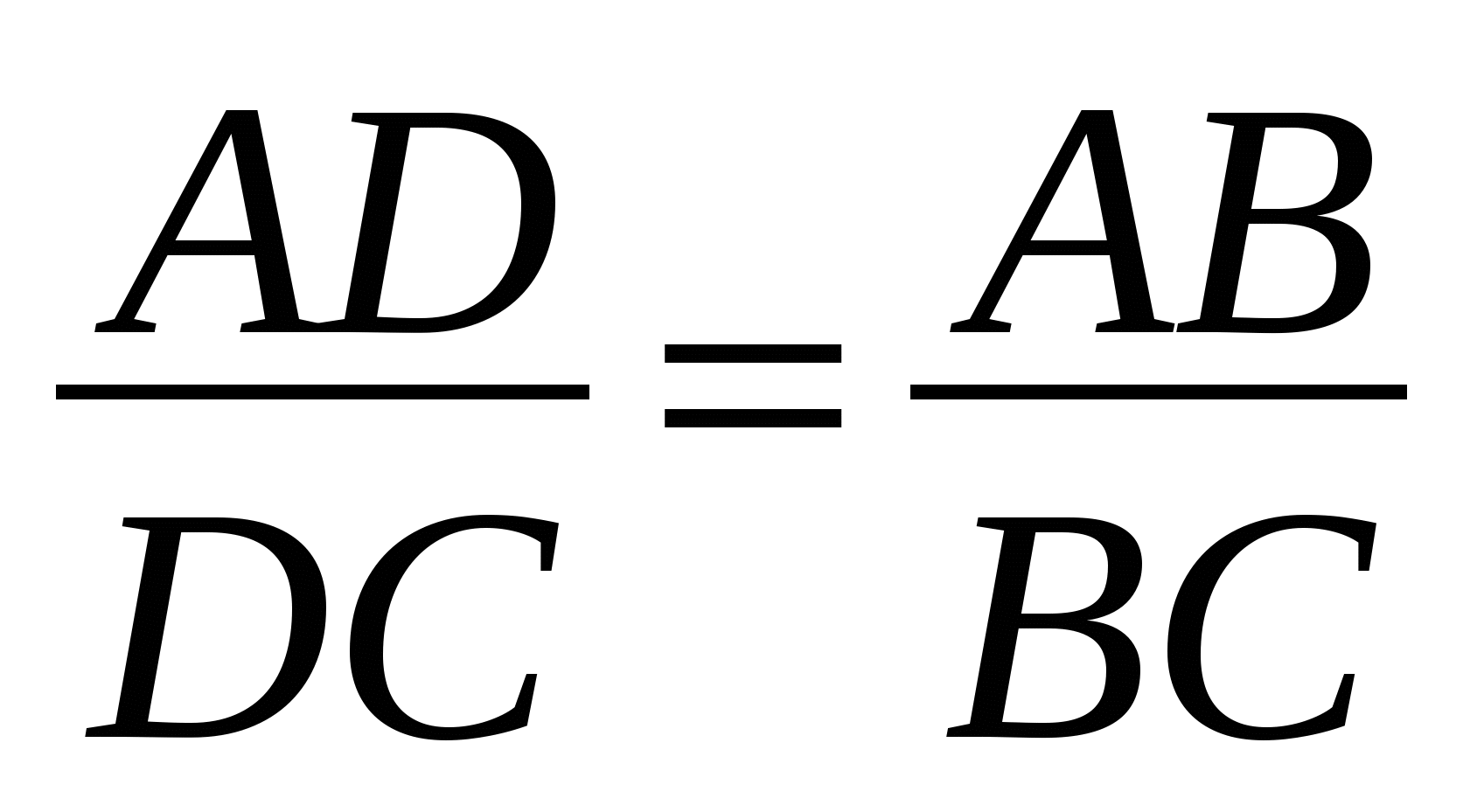 .
.
По свойству производных пропорций 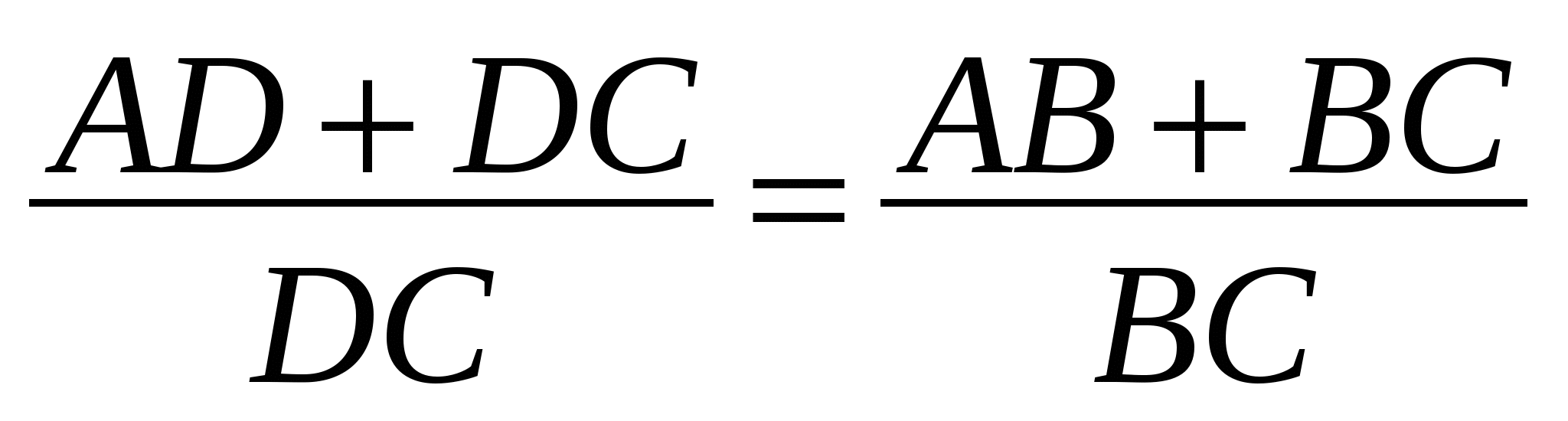

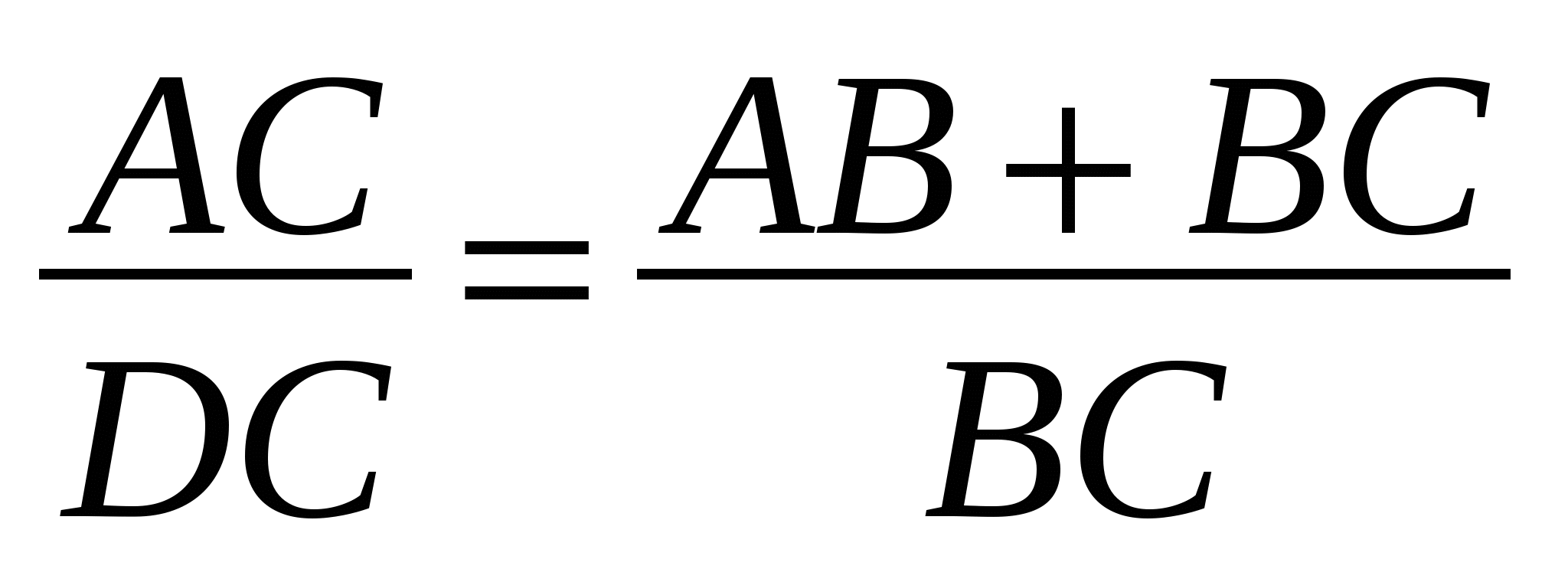

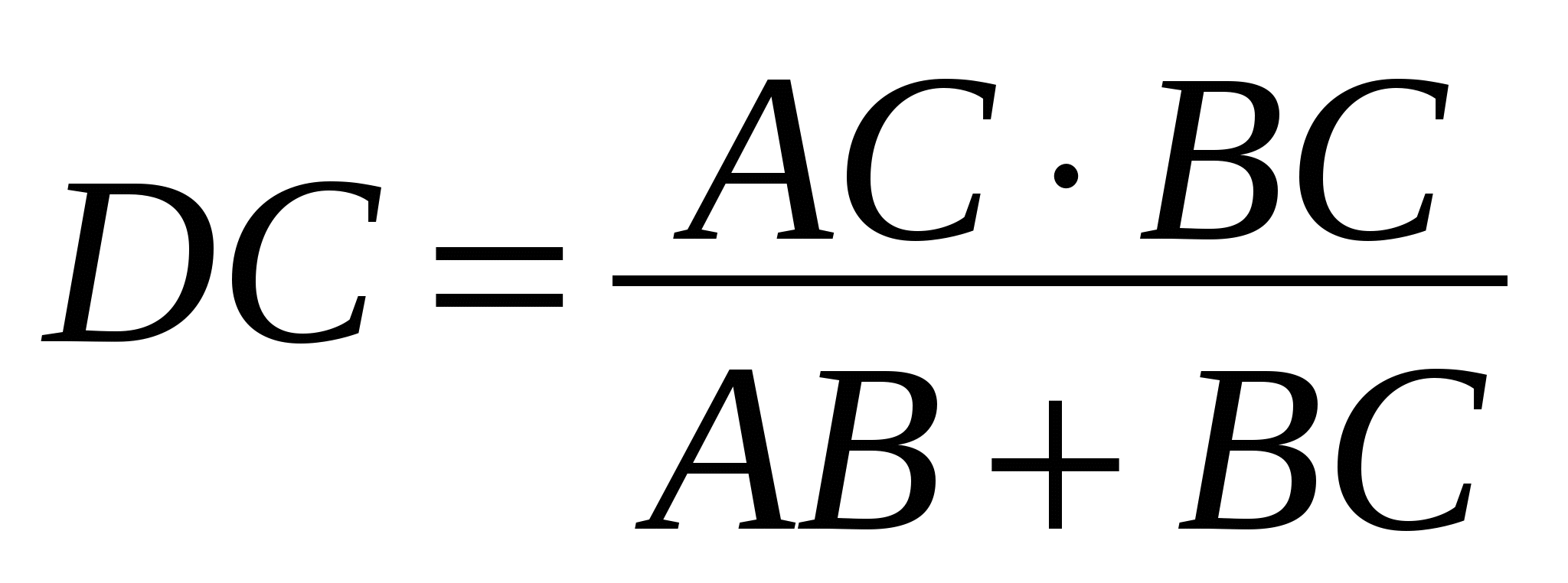 =
= 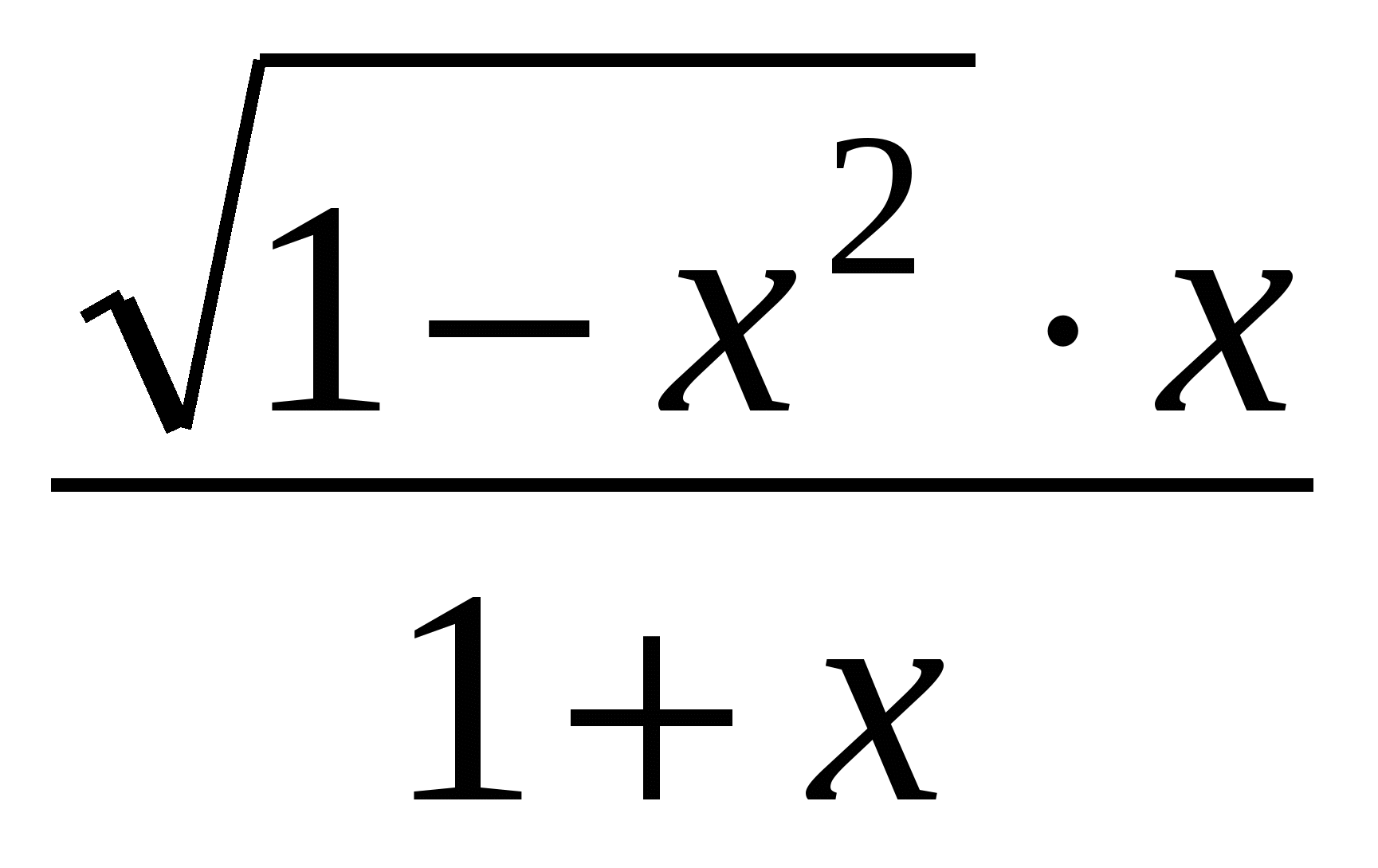 =
= 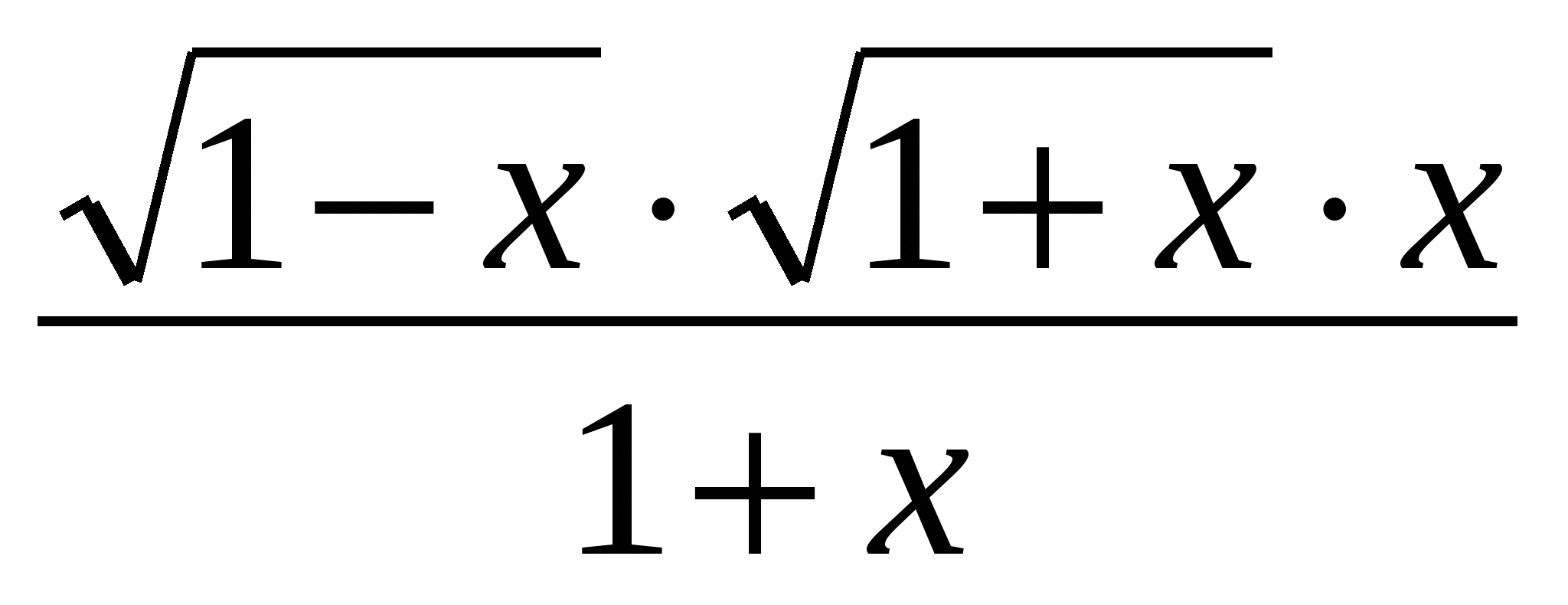 =
= 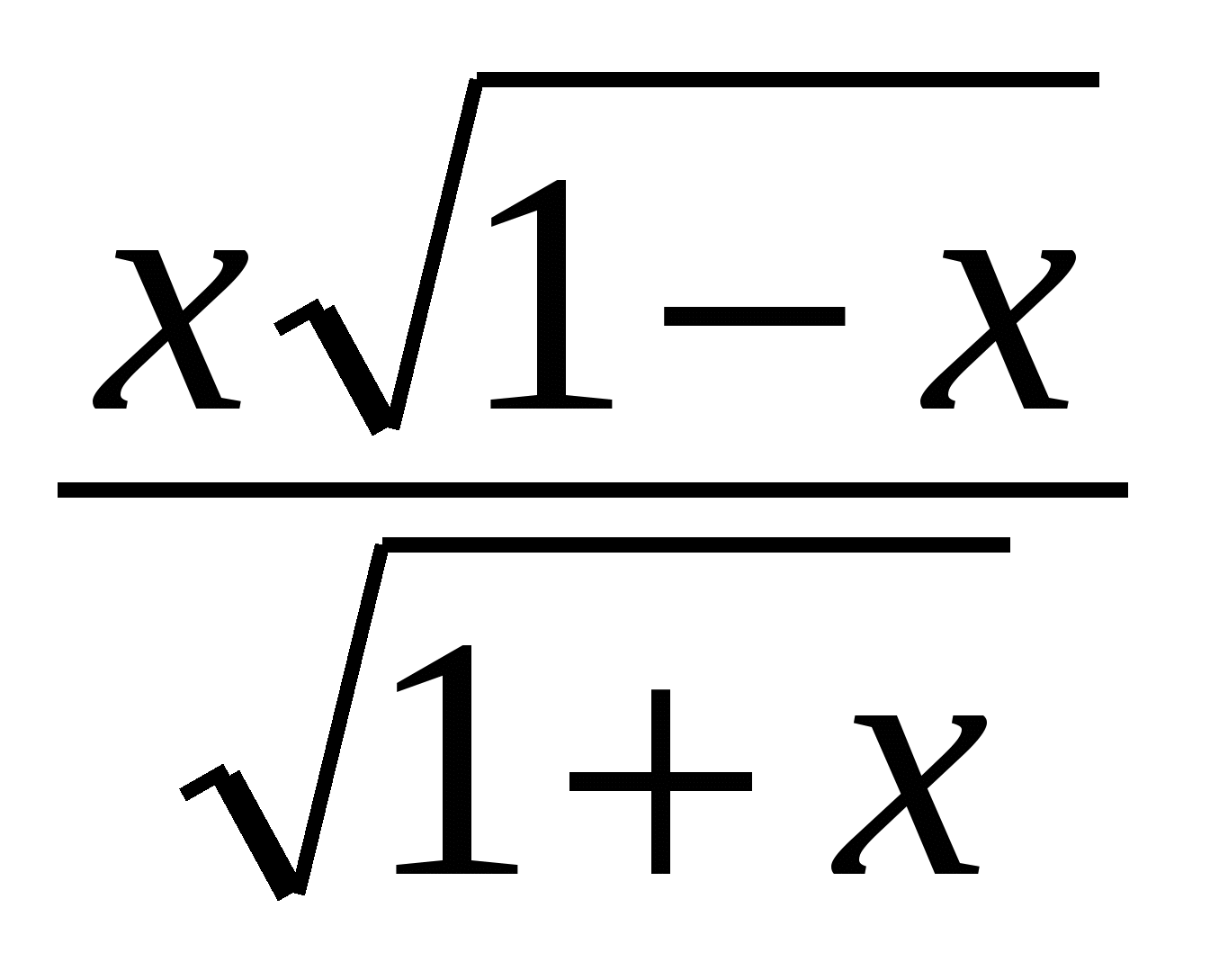
По определению ![]()
 arcsin x =
arcsin x =  , а
, а 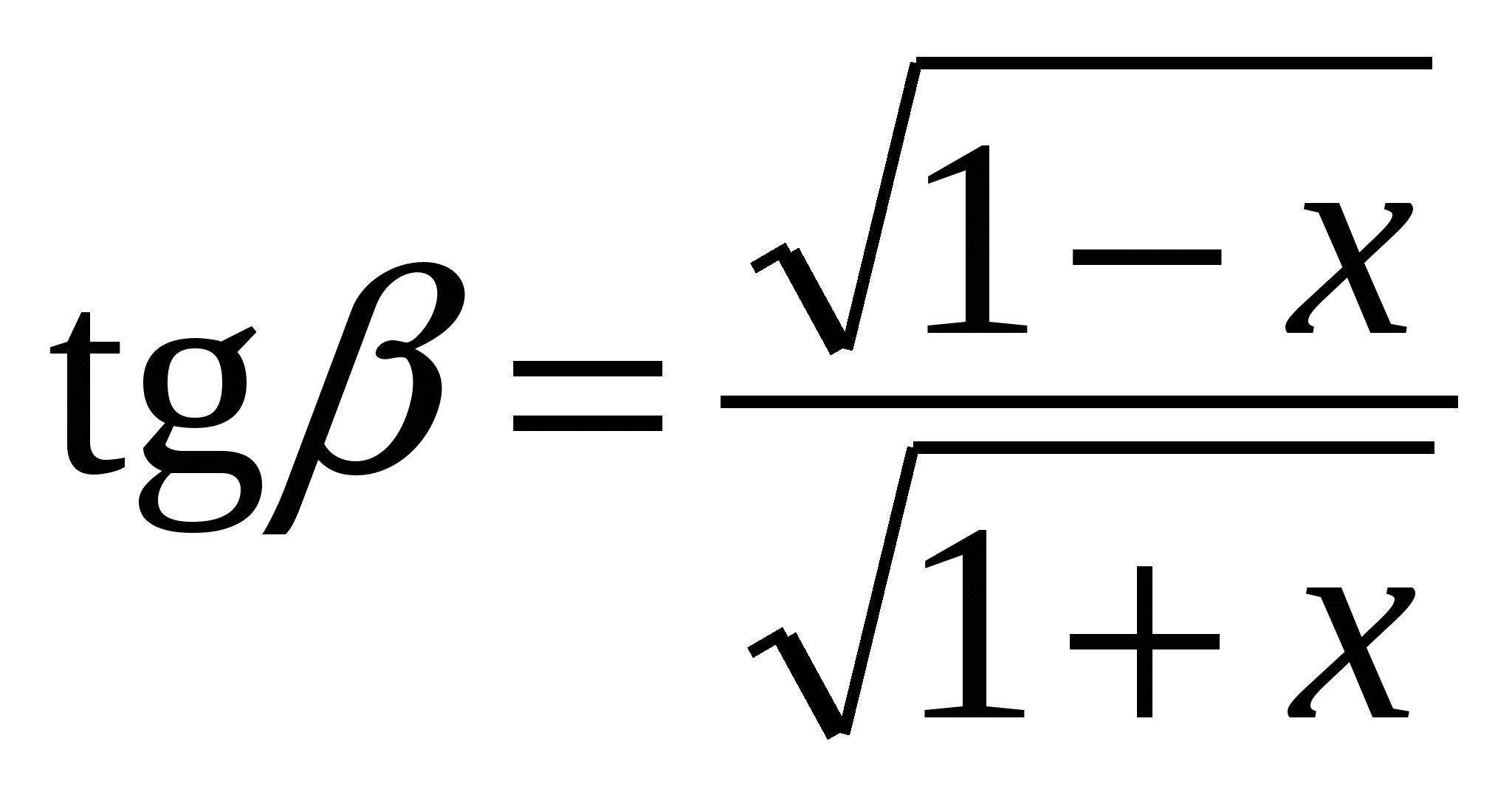

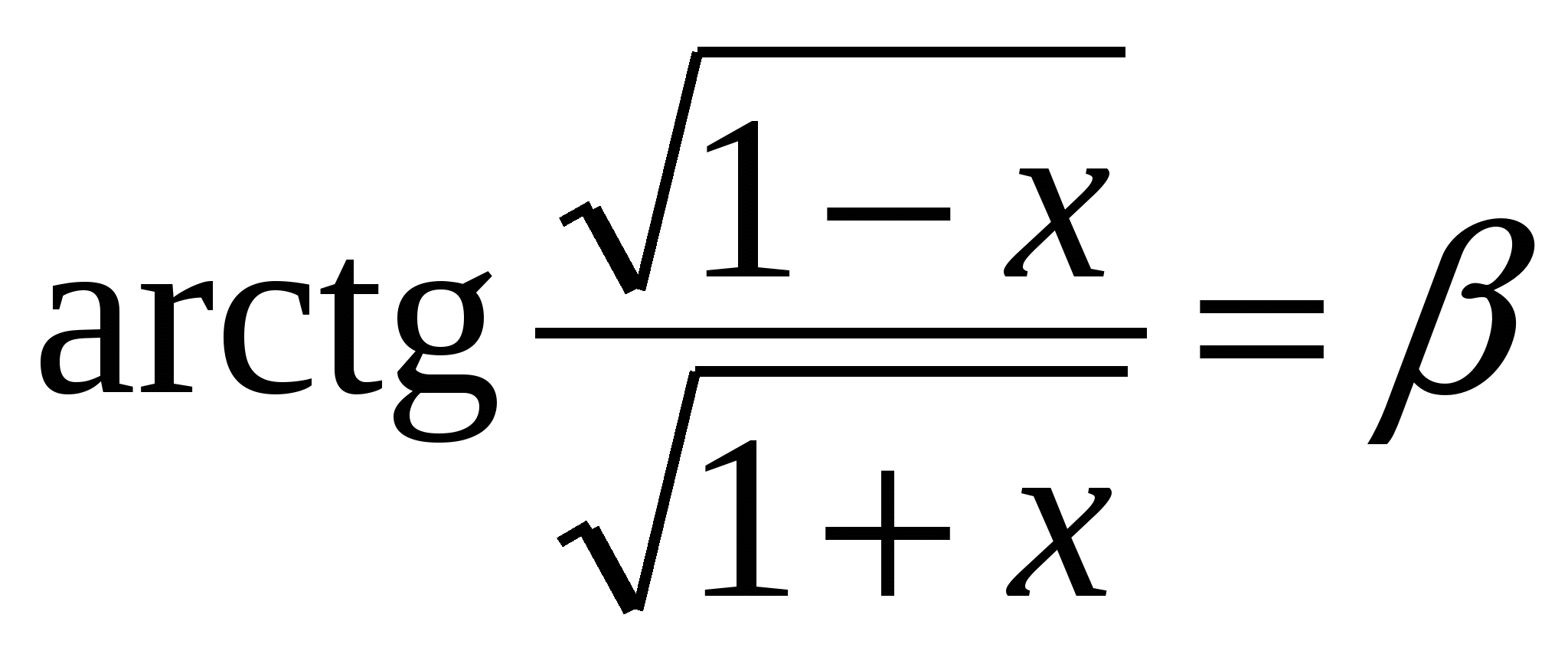 .
.
И т.к. 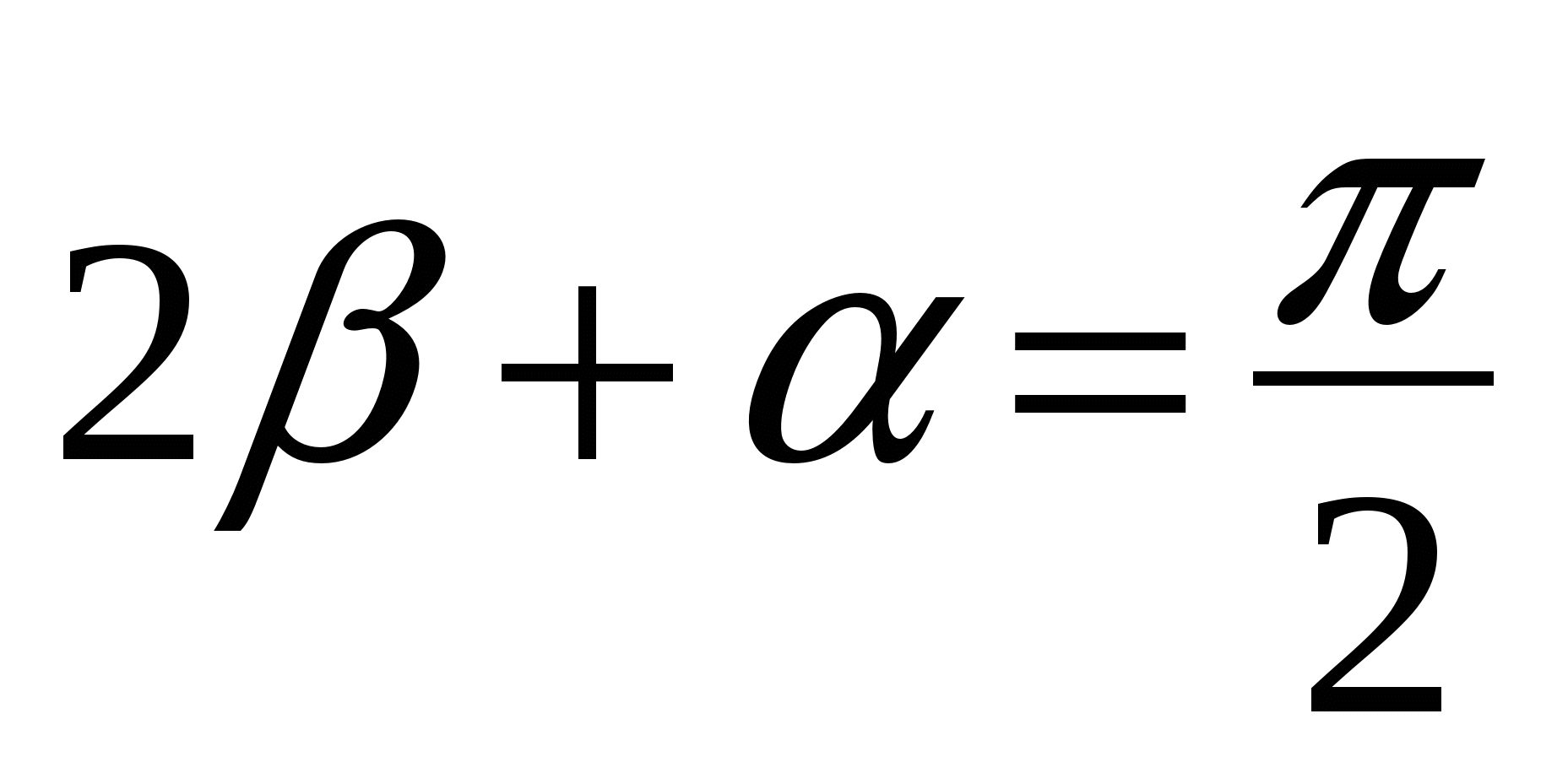

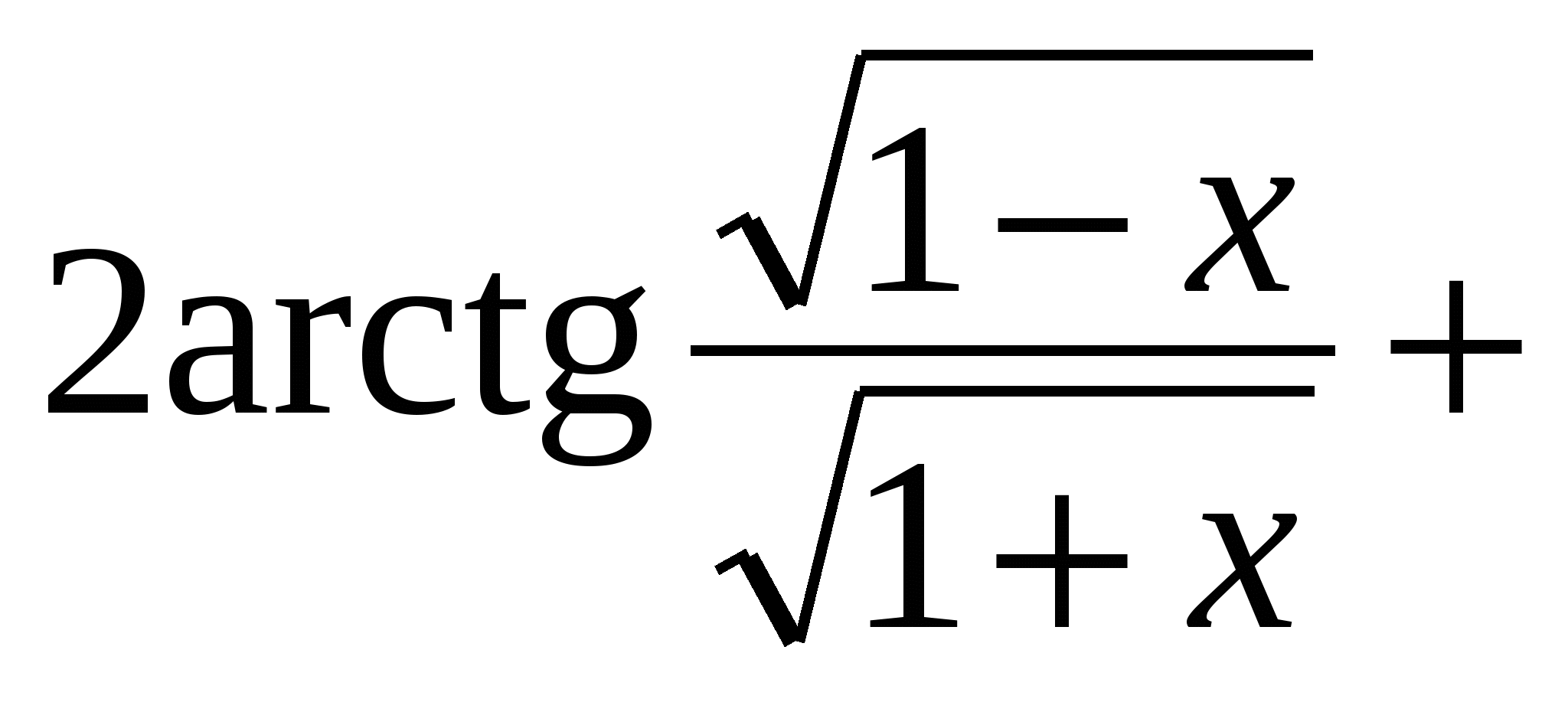 arcsin x =
arcsin x = 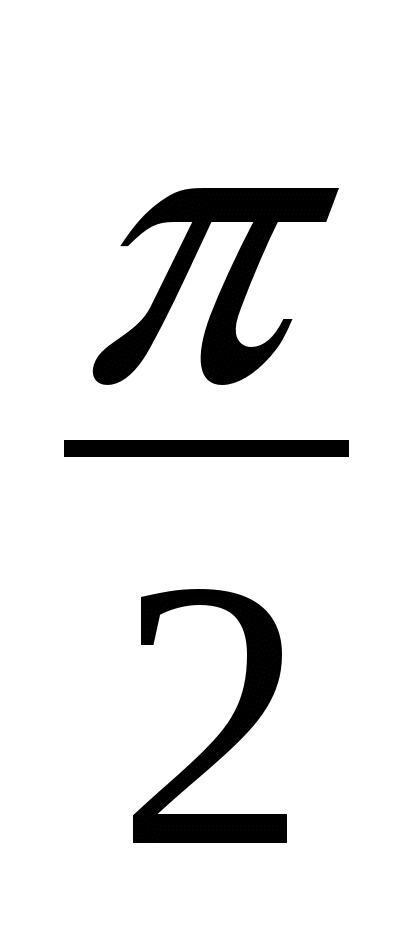 . Что и требовалось доказать.
. Что и требовалось доказать.
в) При 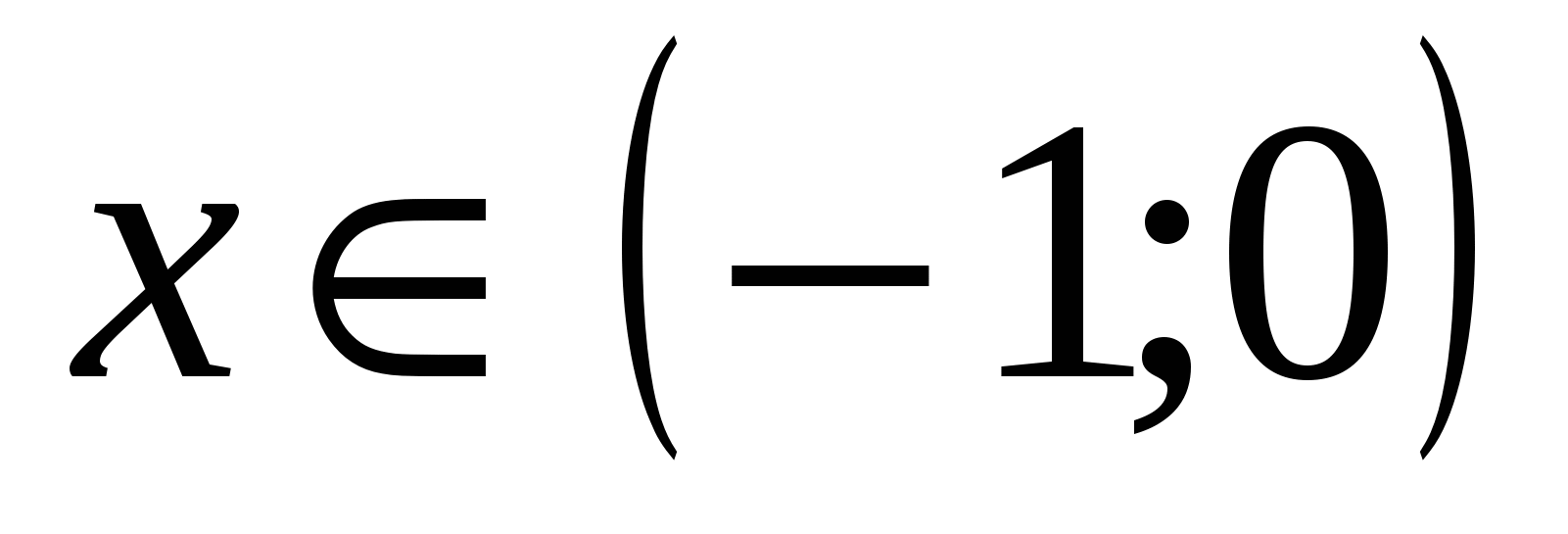
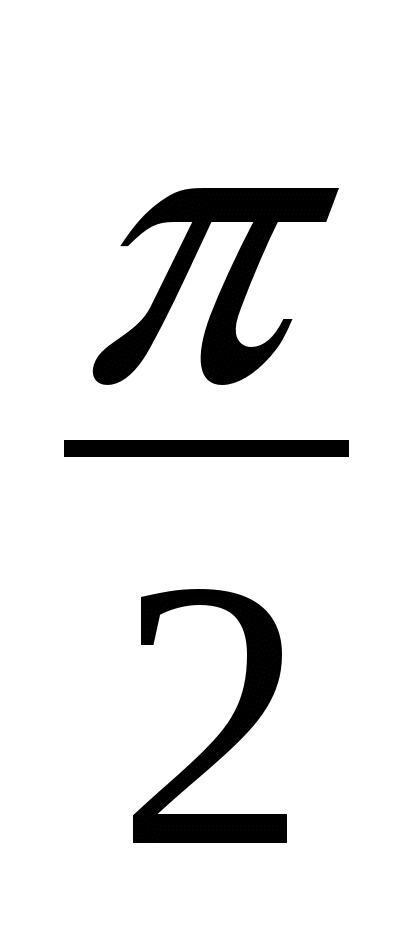 <
<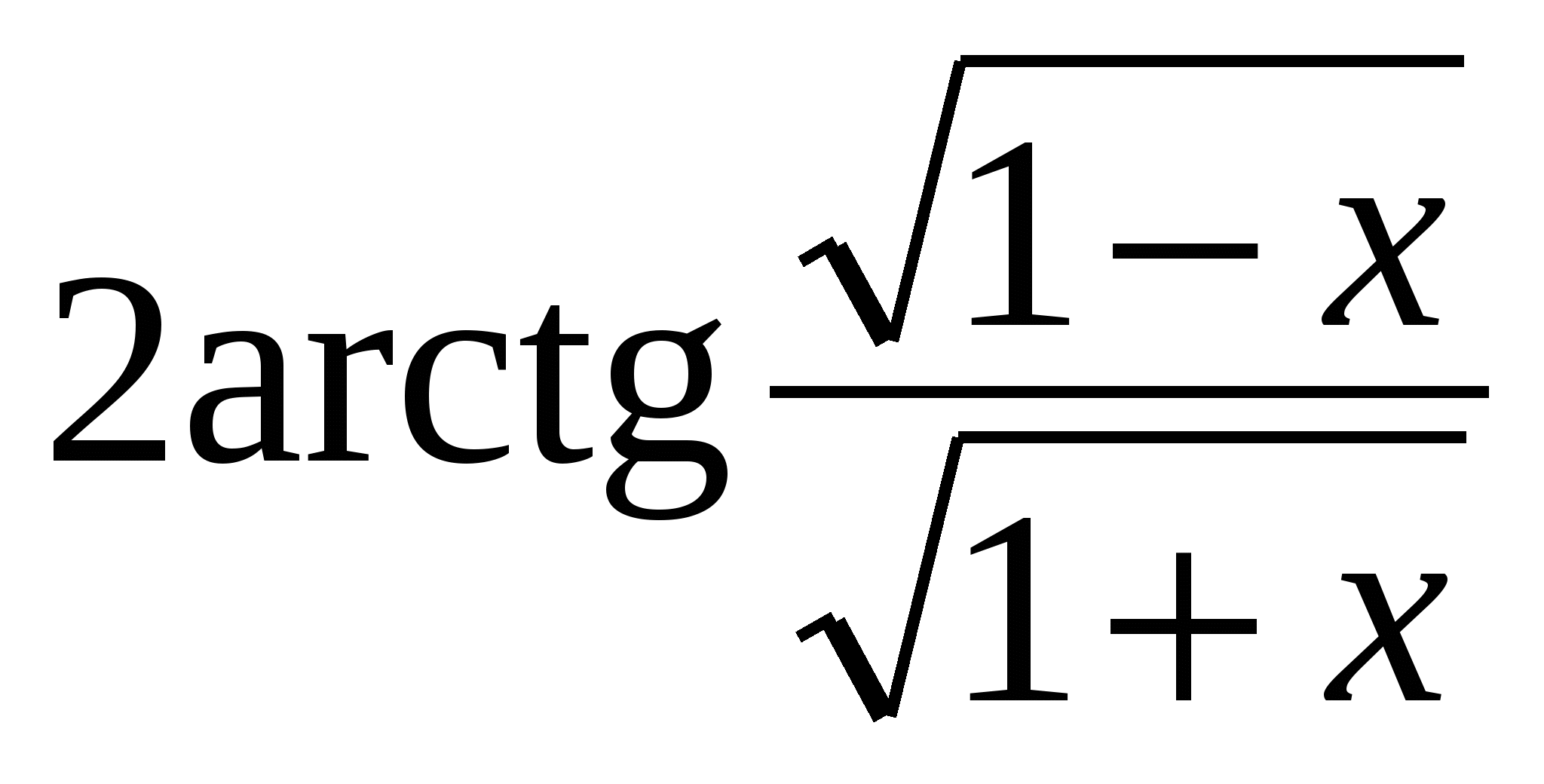 <
<  и -
и -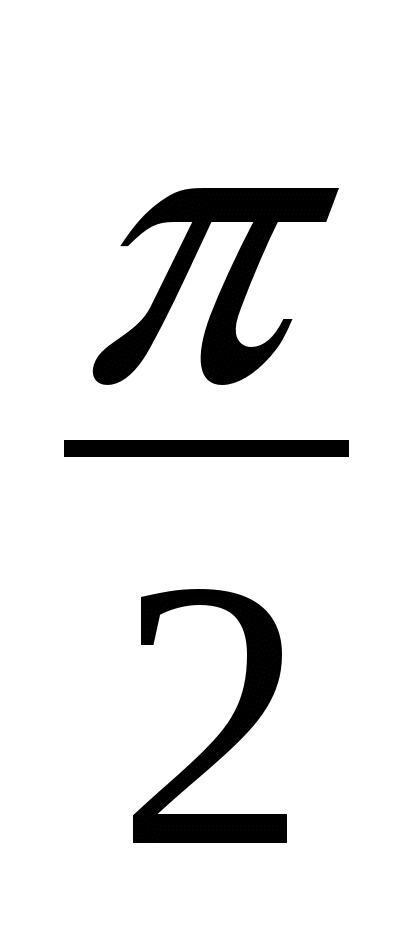 < arcsin x < 0
< arcsin x < 0
Преобразуем тождество: 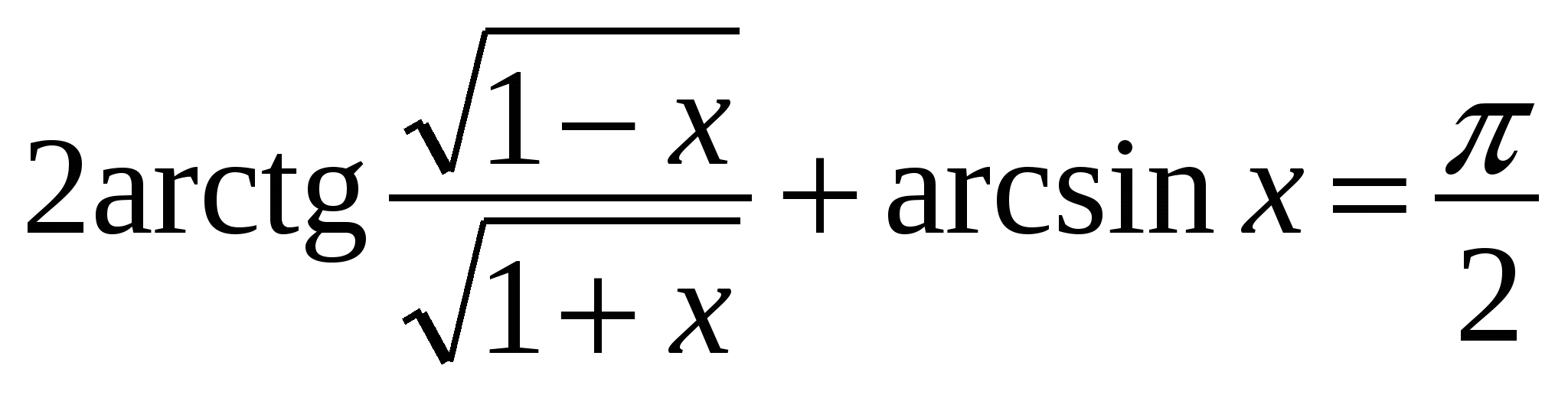

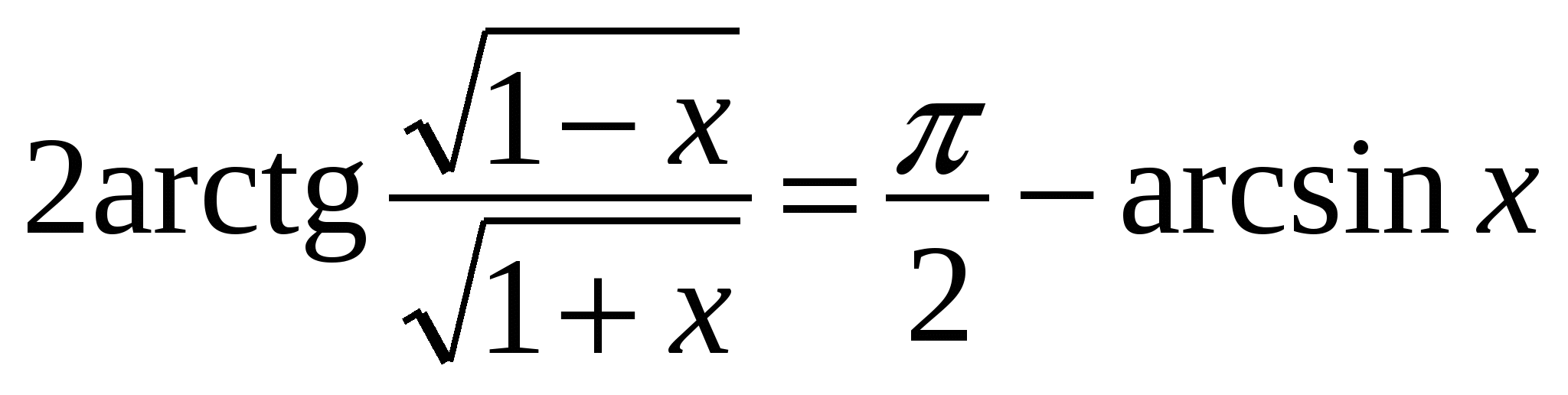 . Заметим, что
. Заметим, что 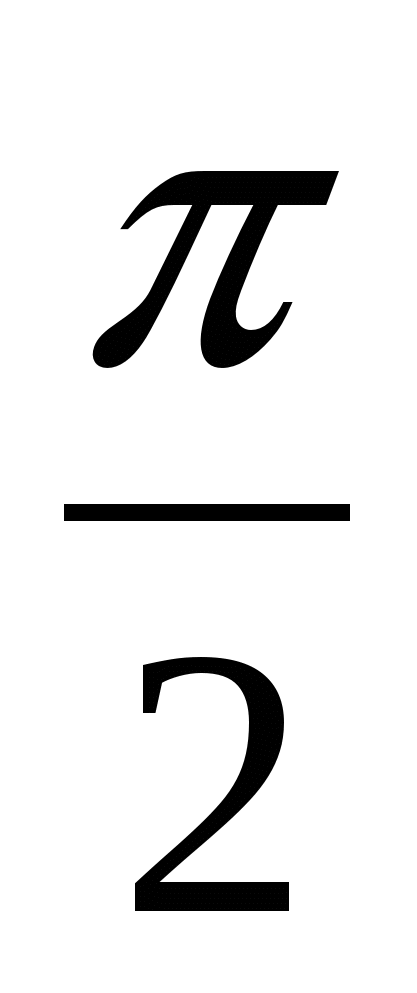 <
<  <
< . При
. При 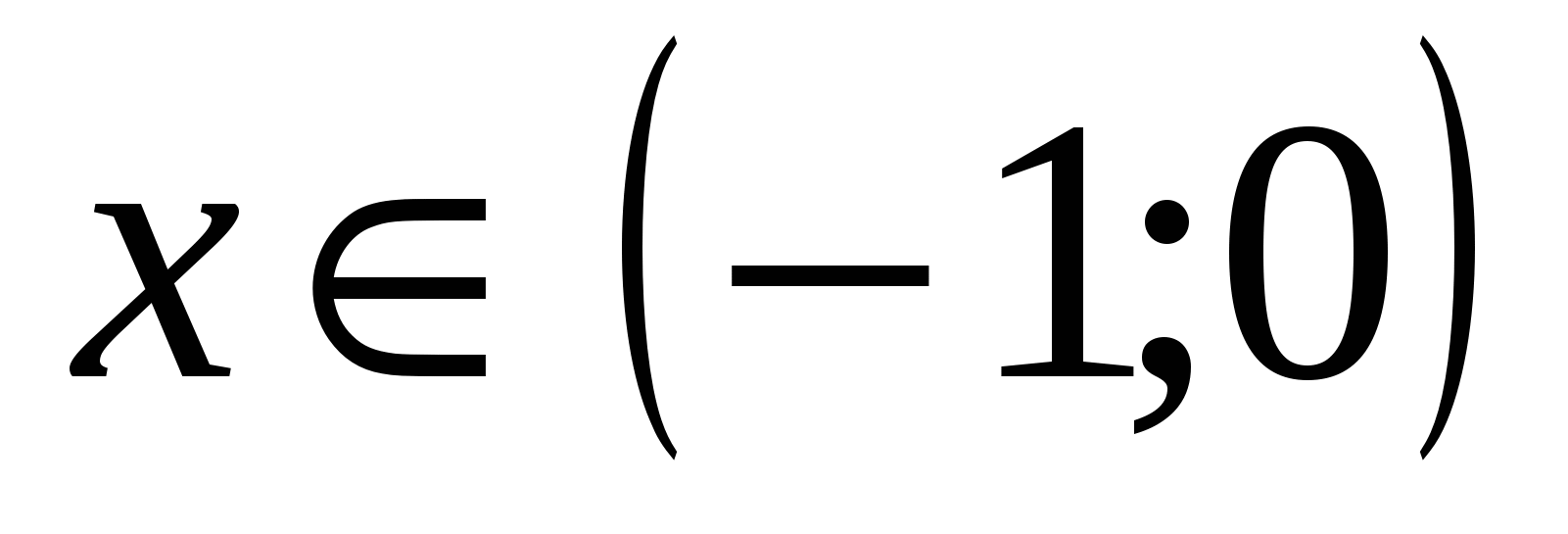 , если равны косинусы данных углов, то будут равны и углы. Поэтому докажем равенство
, если равны косинусы данных углов, то будут равны и углы. Поэтому докажем равенство 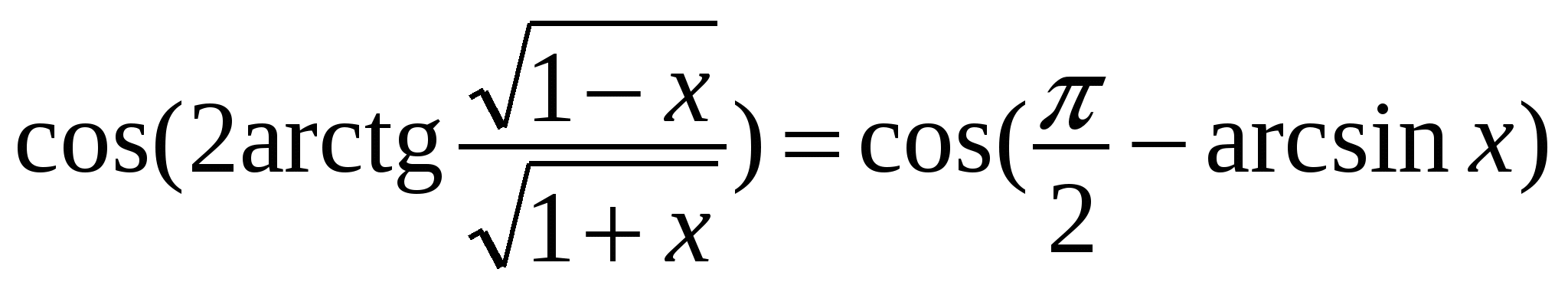 , из которого будет следовать и равенство углов
, из которого будет следовать и равенство углов 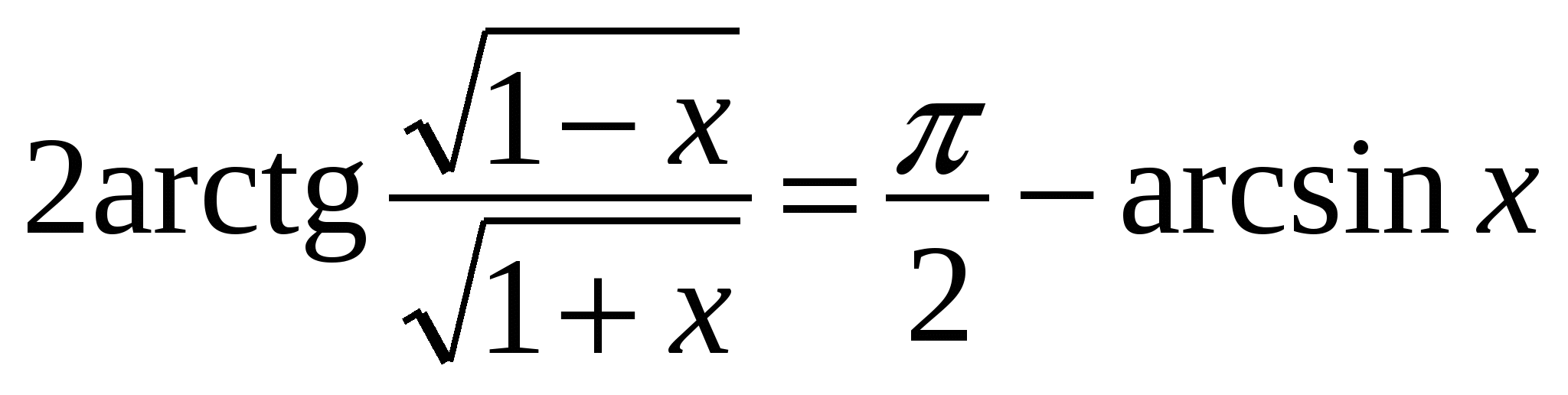 .
.
Воспользуемся универсальной тригонометрической подстановкой 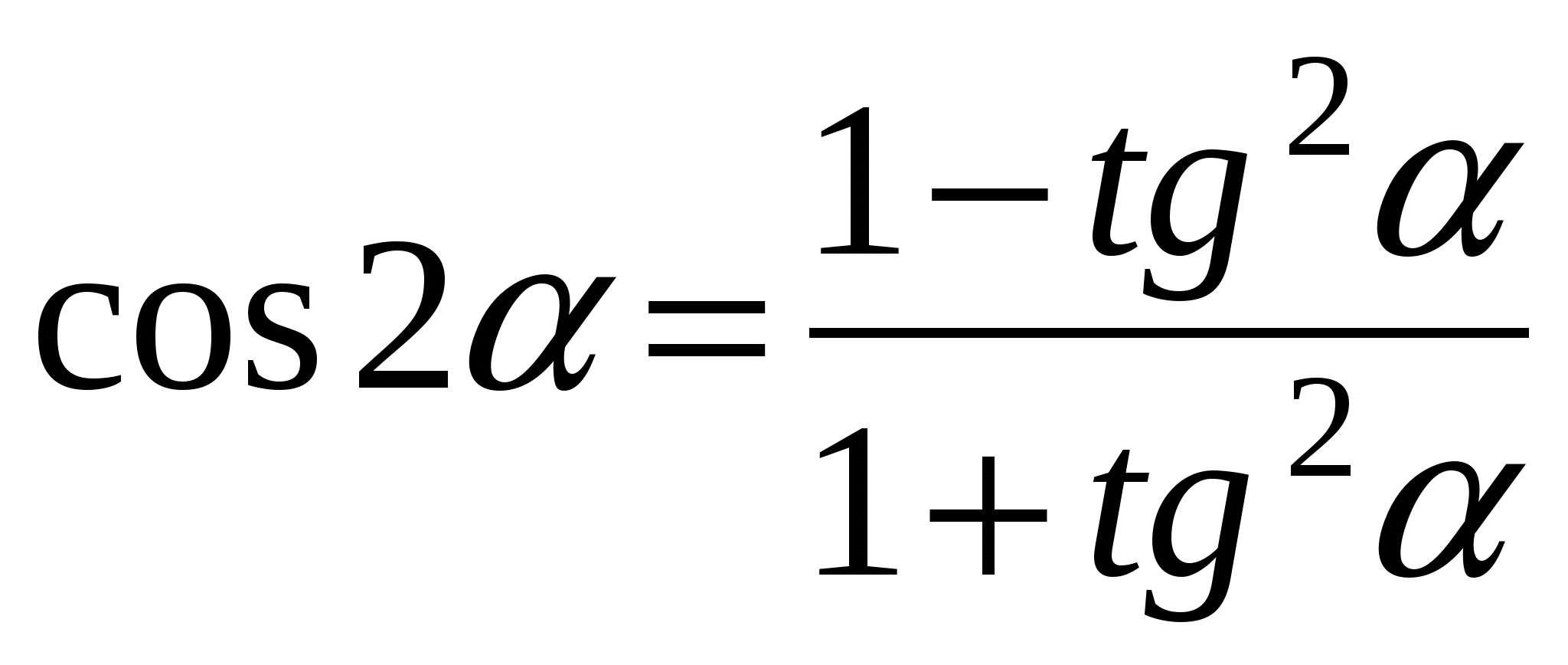 справедливой при данных значениях х, и формулой приведения
справедливой при данных значениях х, и формулой приведения 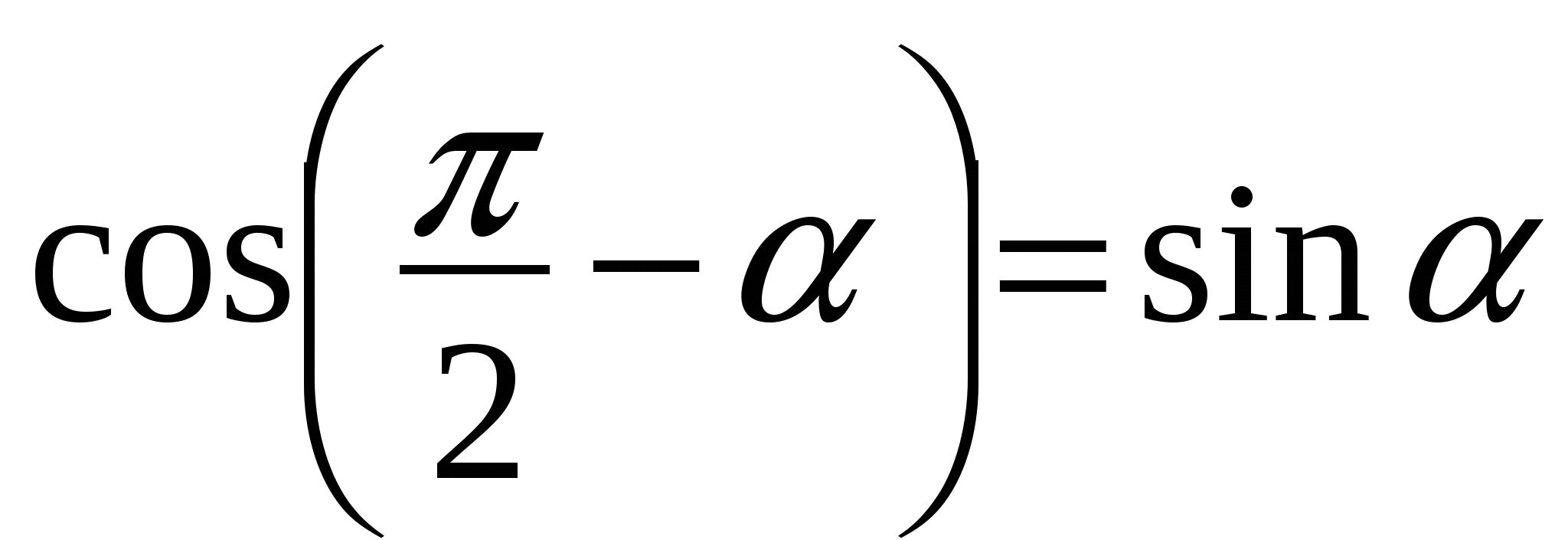 :
: 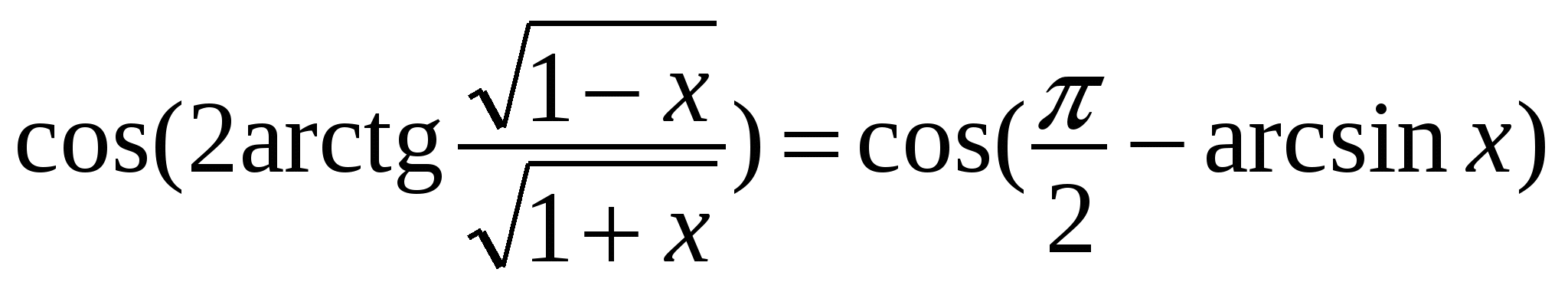

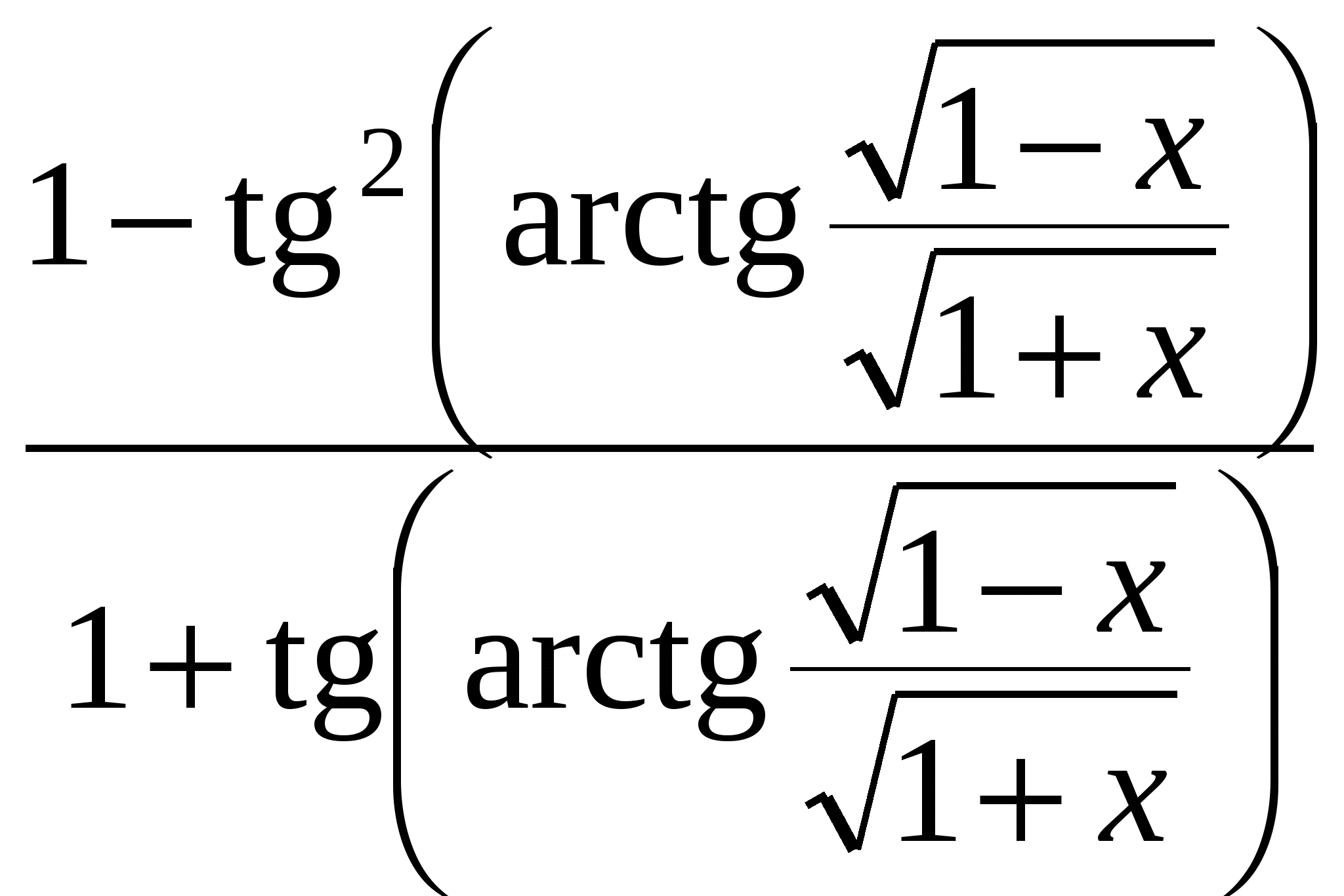 = sin(arcsin x).
= sin(arcsin x).
По определению арксинусов и 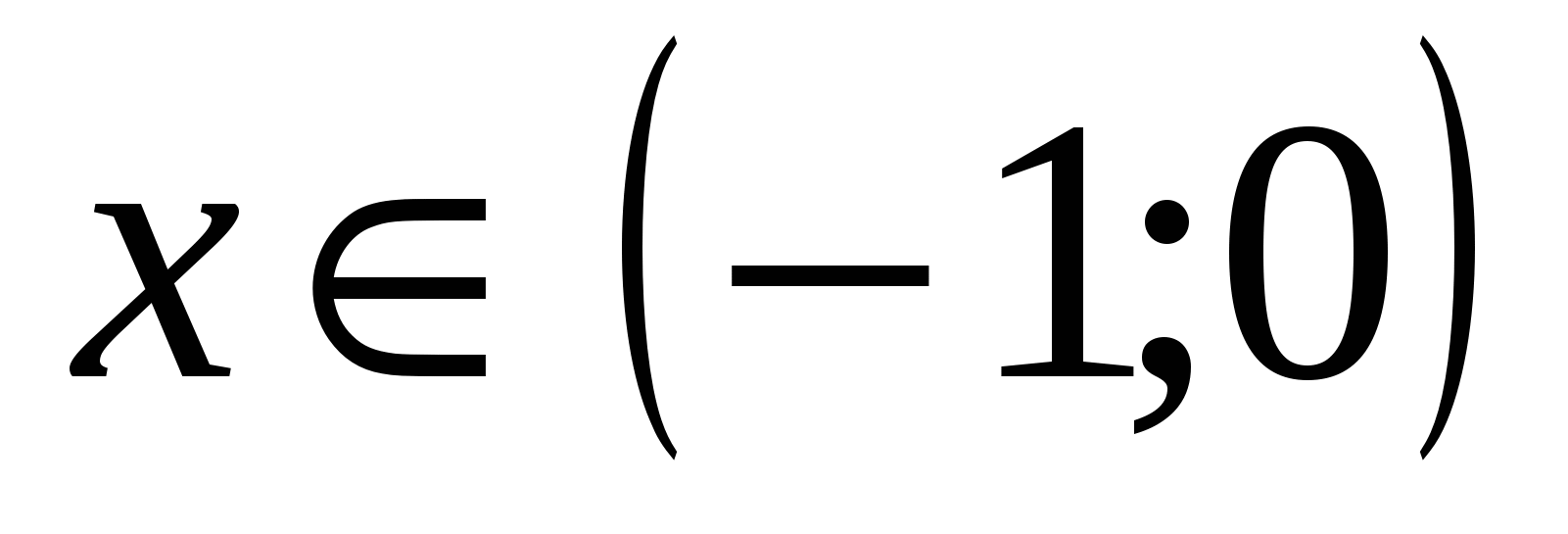 имеем:
имеем: 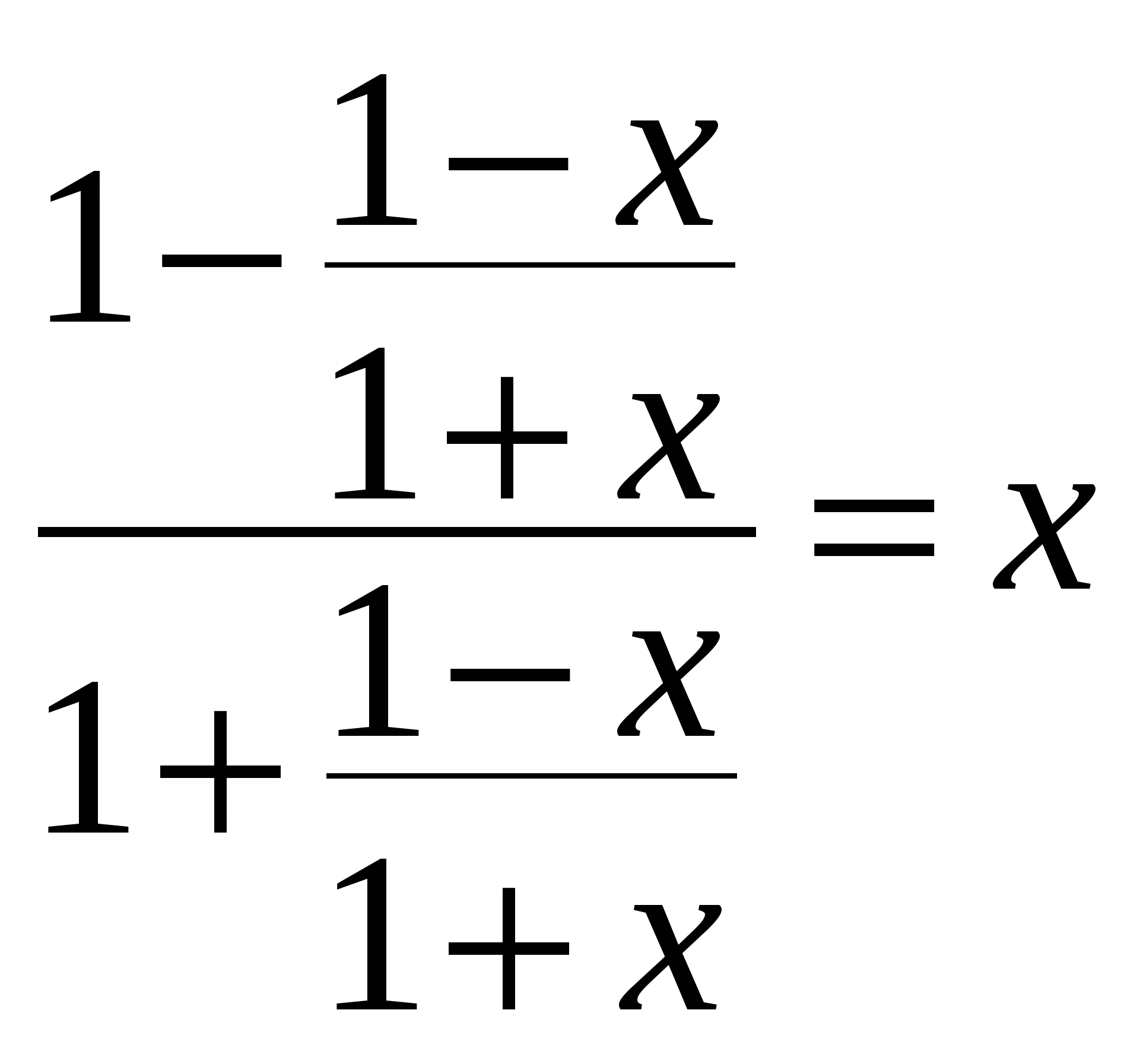

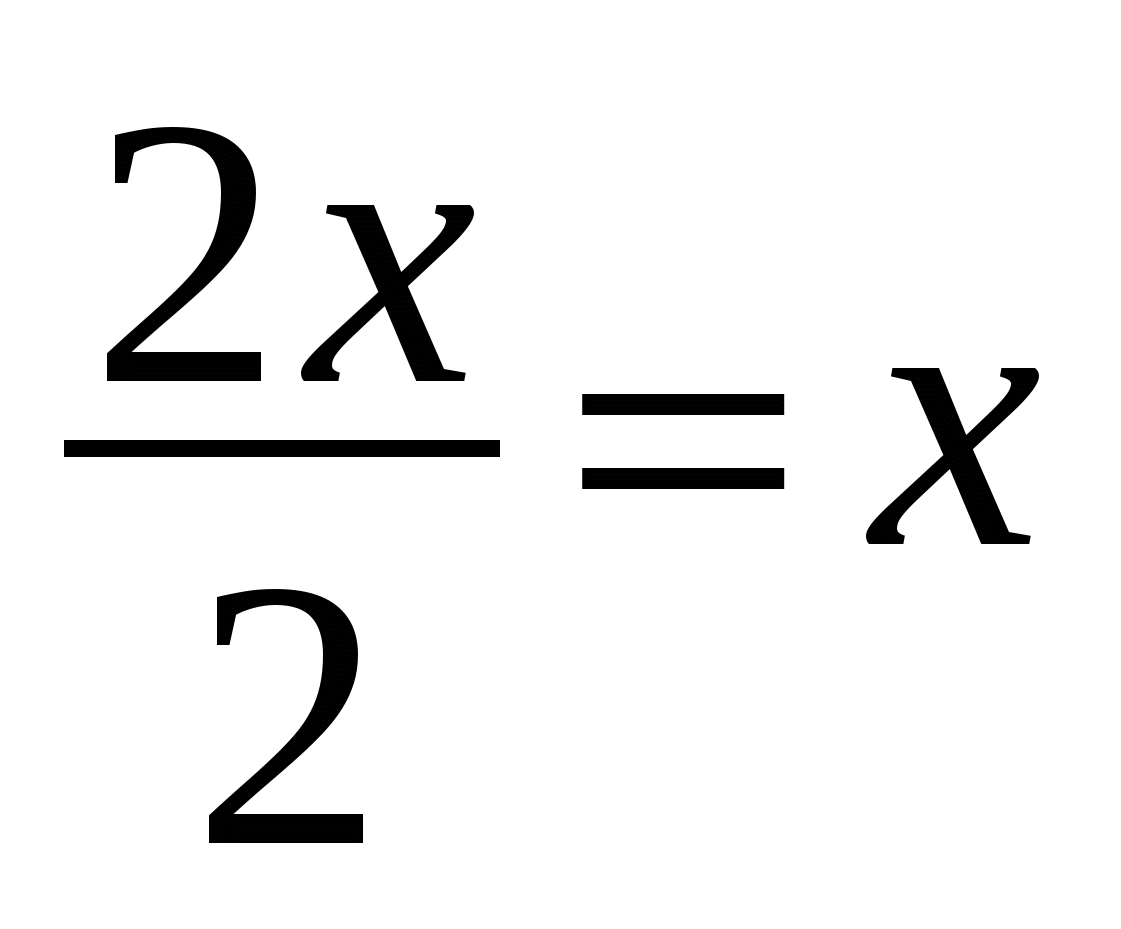 . Что и требовалось доказать.
. Что и требовалось доказать.
Итак, тождество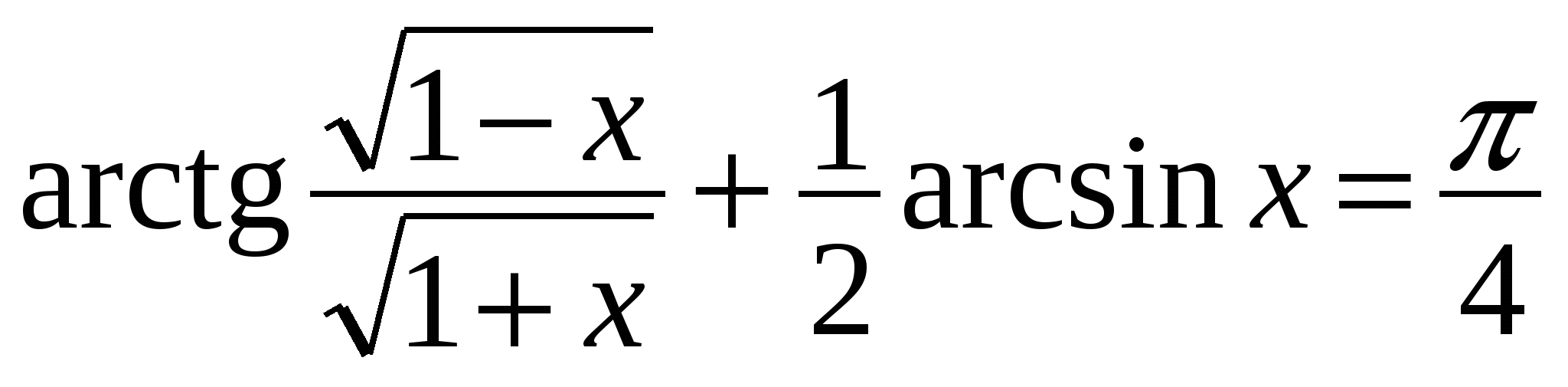 доказано для всех
доказано для всех 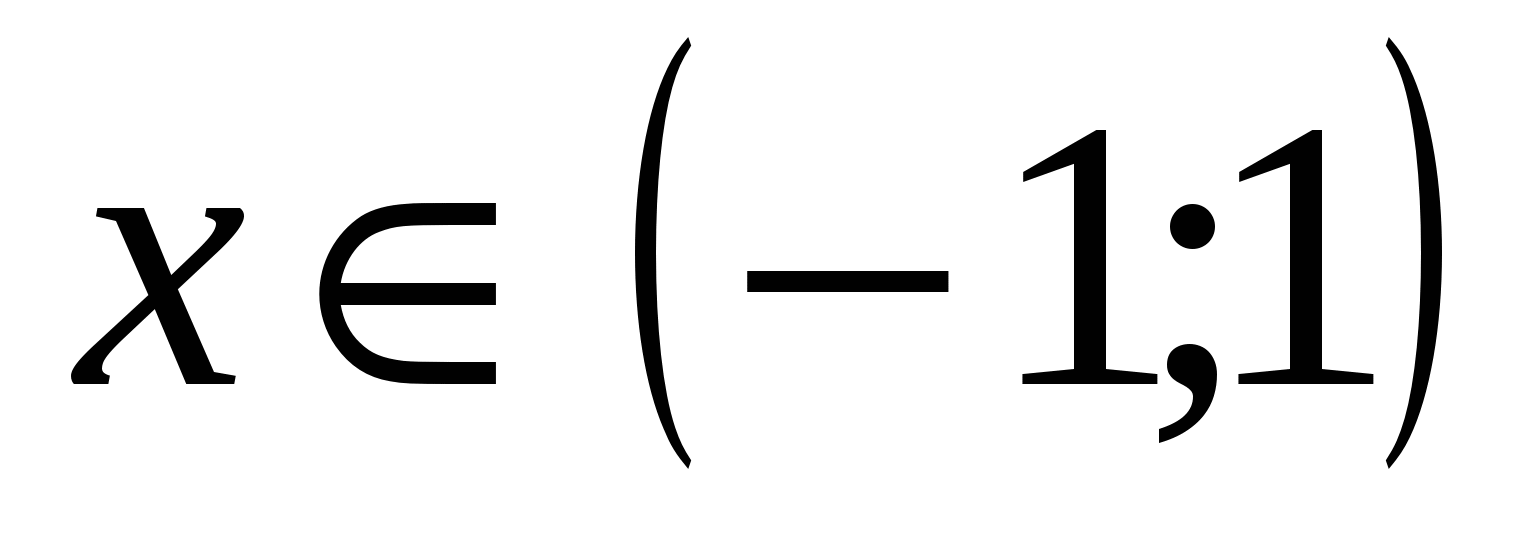
4. Боковую сторону трапеции с основаниями 15 и 2015 разделили на 1000 равных частей. Через каждую точку деления провели прямые, параллельные основаниям. Найдите длины всех параллельных отрезков, заключенных между боковыми сторонами трапеции.
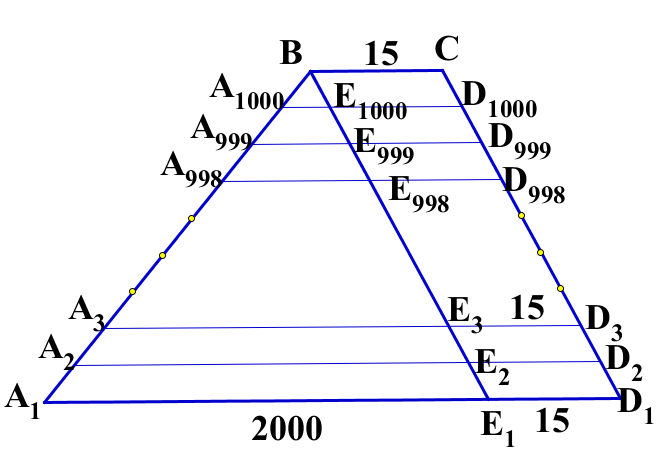
Дано: A1BCD1 - трапеция, ВС ║ A1D1,
ВС = 15, A1D1 = 2015.
А1А2 = А2А3 = …= А999А1000;
A2D2 ║ A3D3 ║ … ║ A1000D1000
Найти: A2D2, A3D3,…, A1000D1000
РЕШЕНИЕ:
1) Проведем ВЕ1 ║СD1.
ВСD1Е1, ВСD2Е2, ВСD3Е1, …., ВСD1000Е1000 - параллелограммы по определению.
D1Е1= D2Е2= D3Е3 = … = D1000Е1000 =15, А1Е1 = 2000
2) Треугольники А1ВЕ1, А2ВЕ2, А3ВЕ3, …, А1000ВЕ1000- подобны по равным углам.
Треугольники А1ВЕ1, А2ВЕ2, А3ВЕ3, …, А1000ВЕ1000- подобны по равным углам.

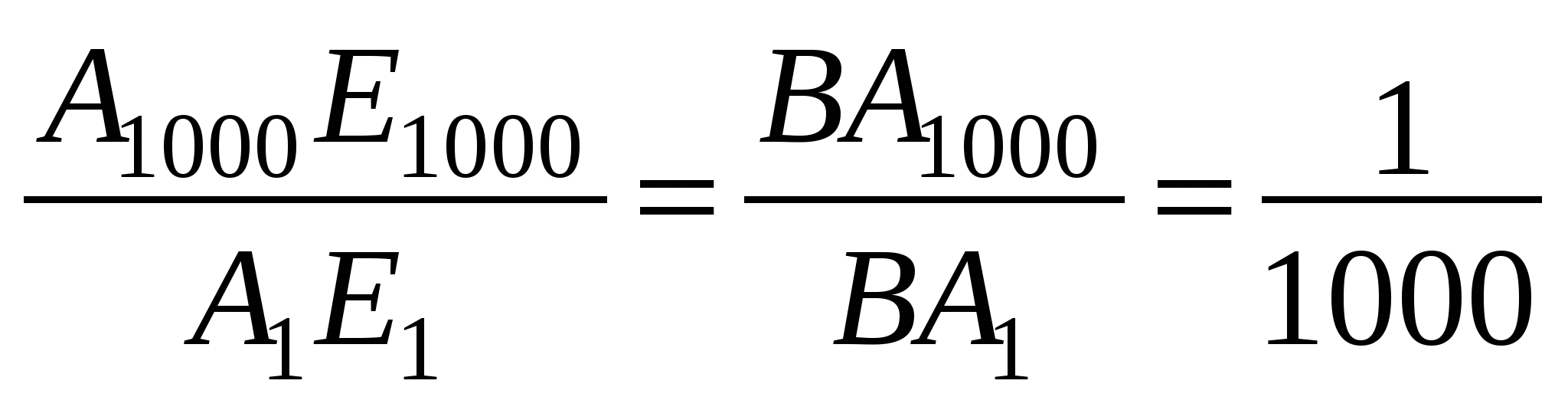

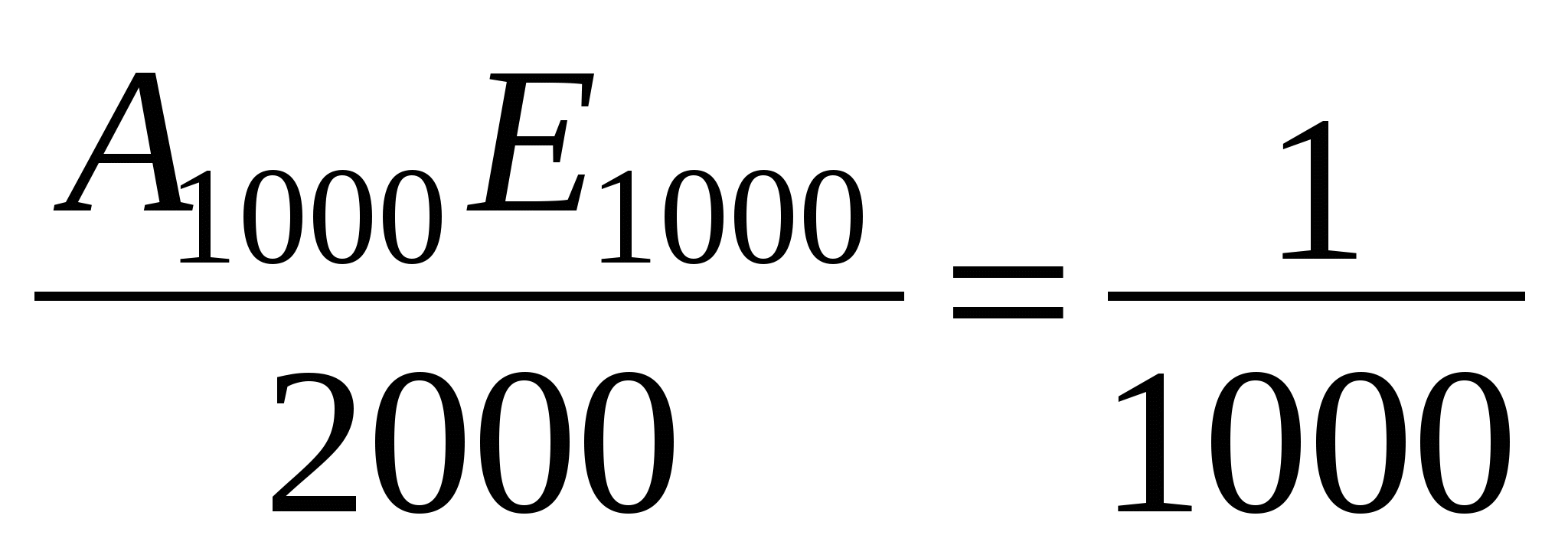

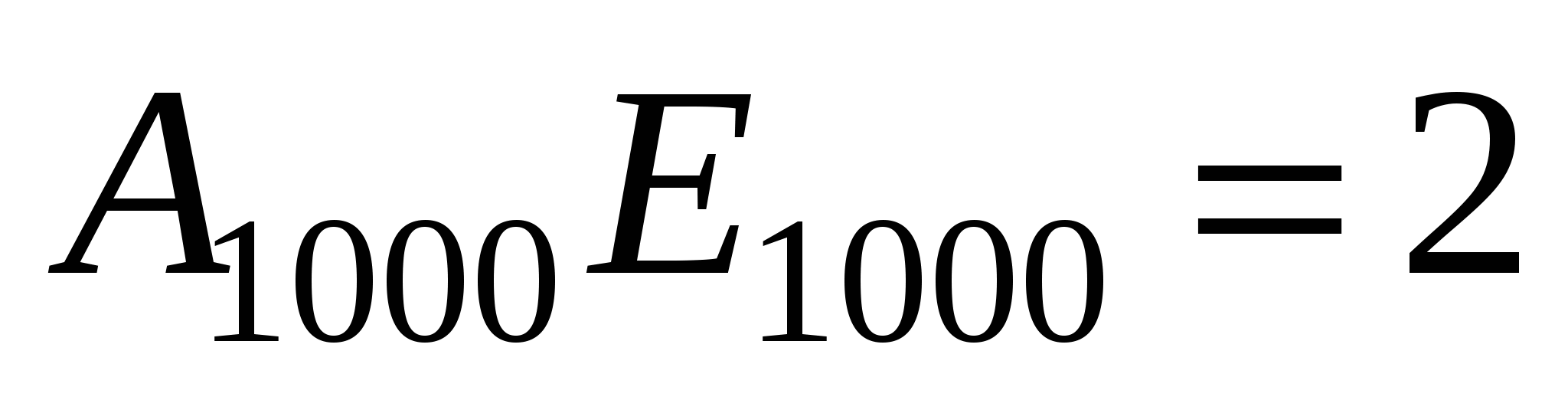

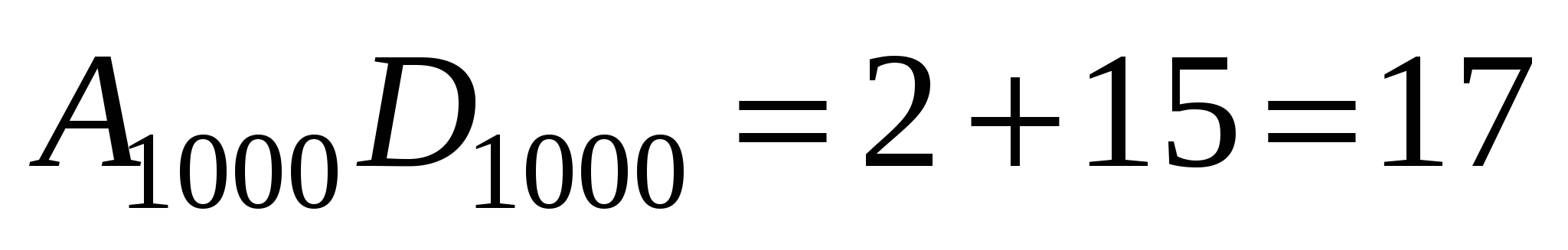 (см. чертеж)
(см. чертеж)
Аналогично, ![]()

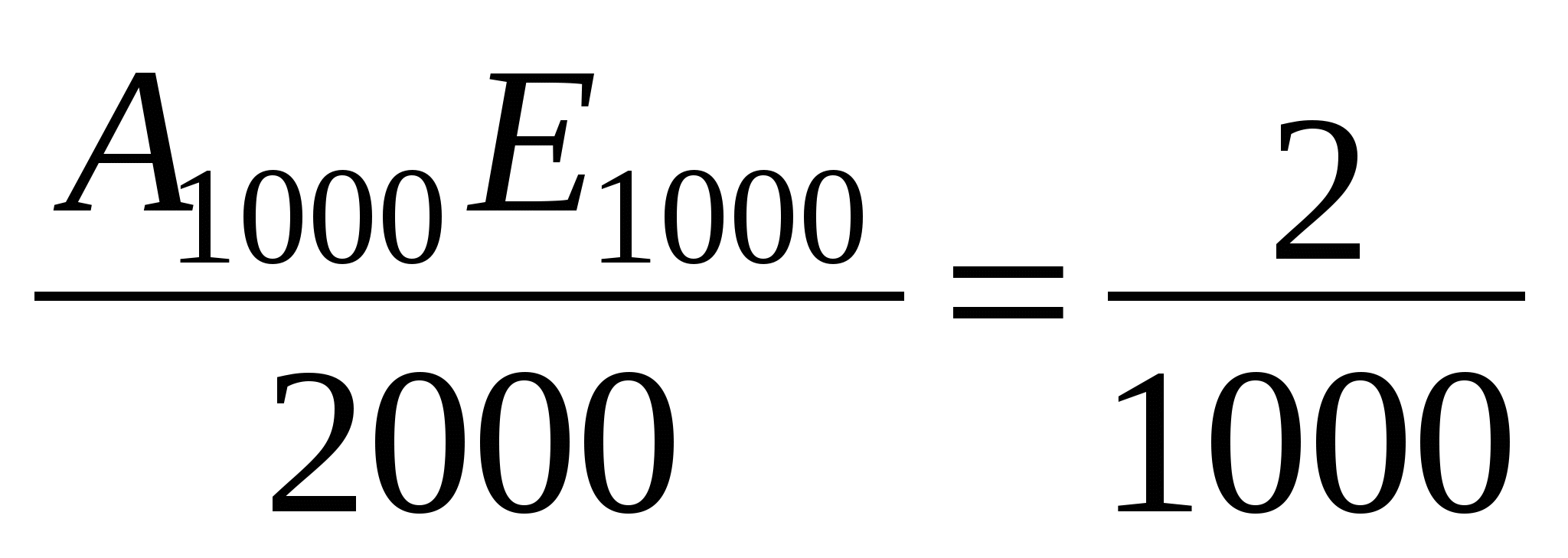

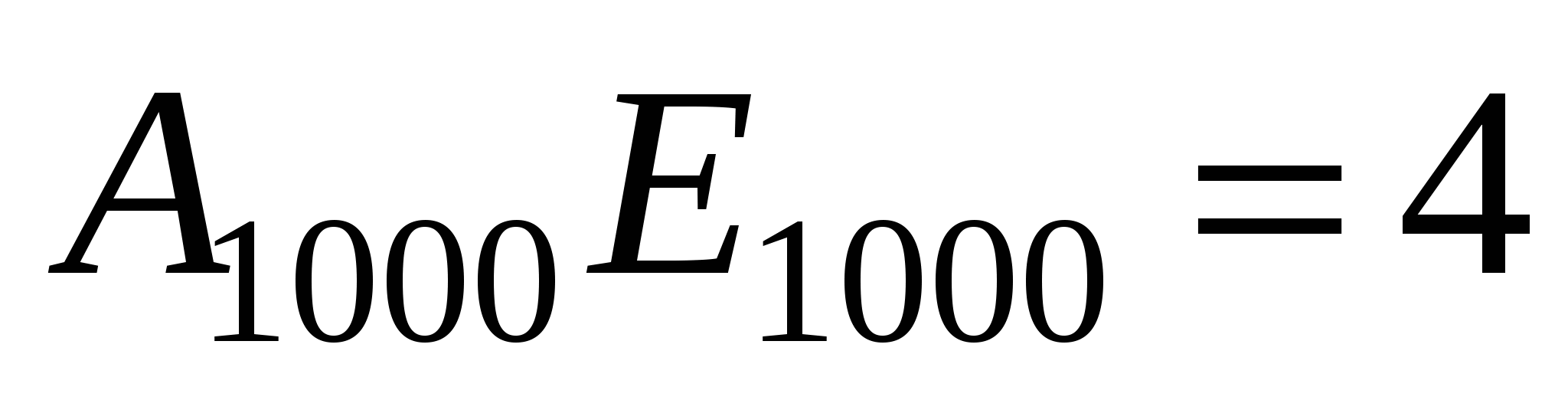

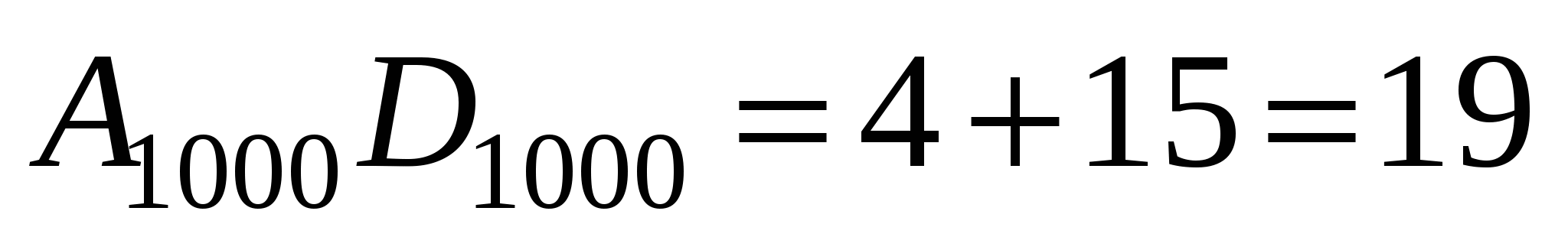 (см. чертеж) и т.д.
(см. чертеж) и т.д.
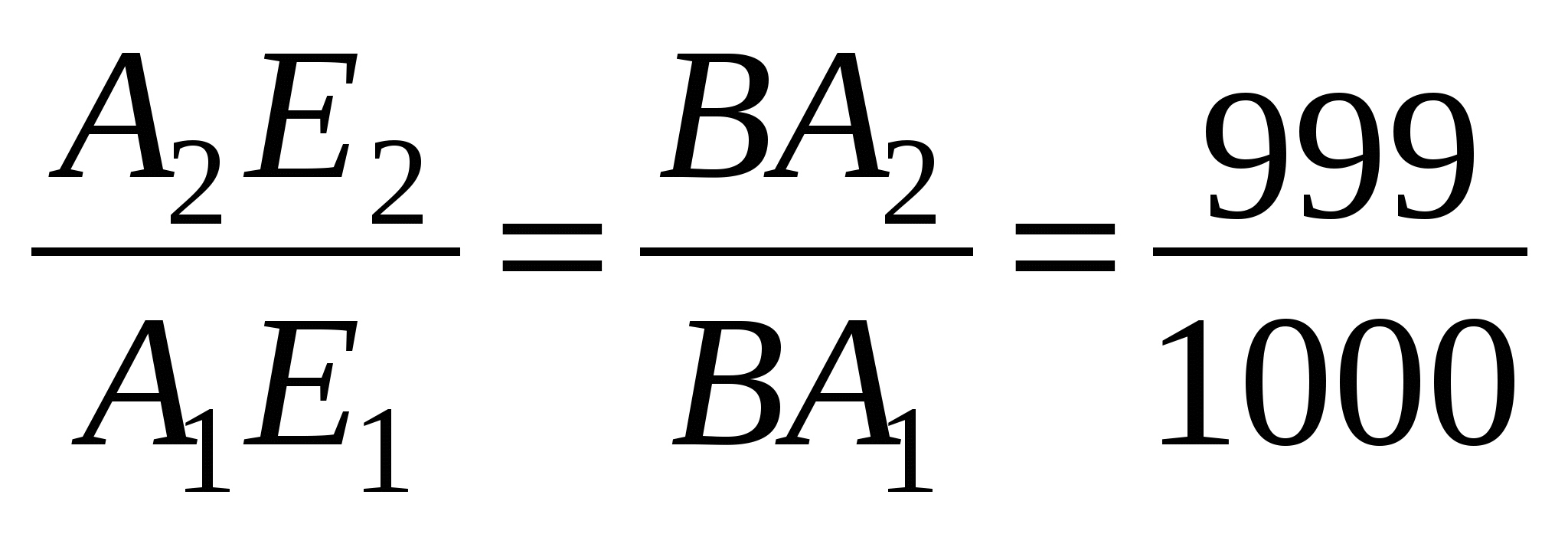

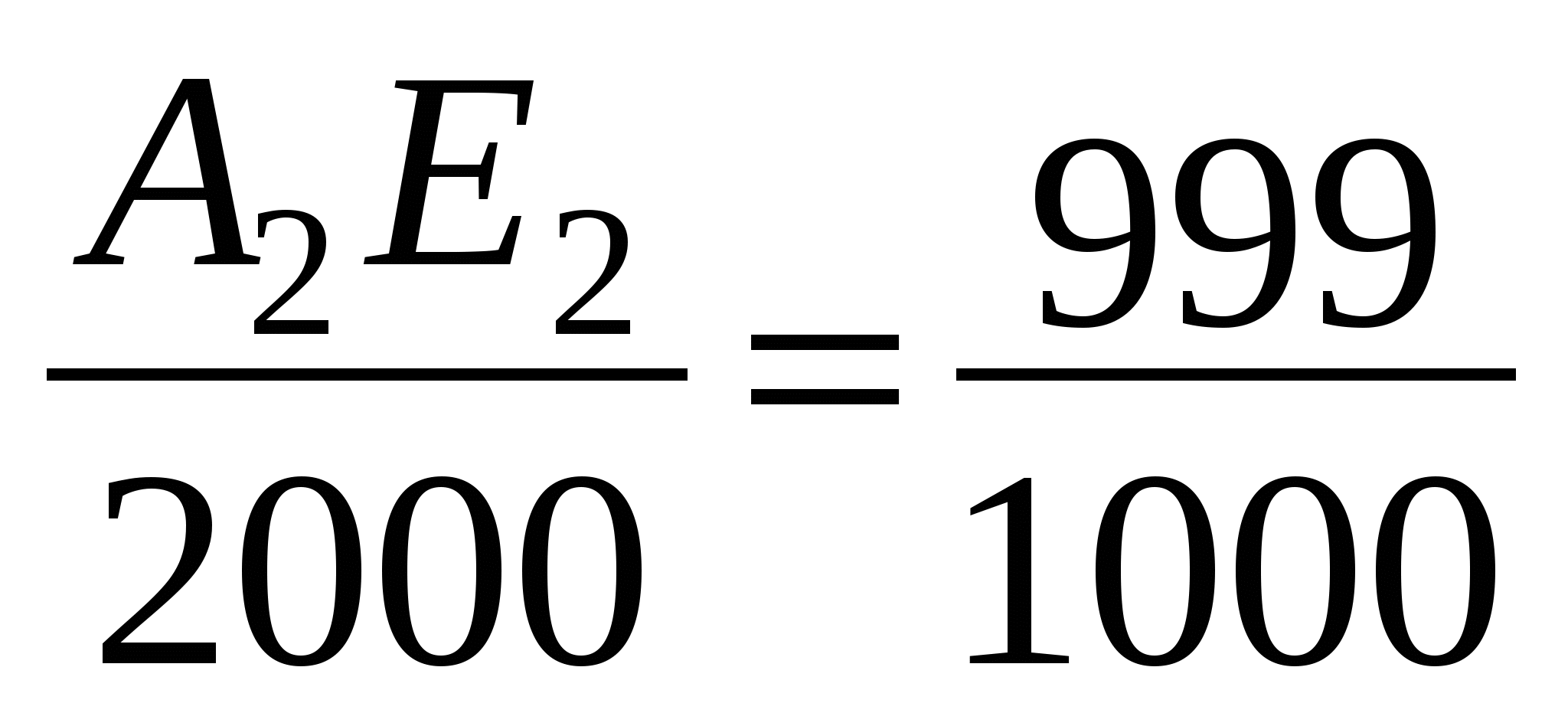

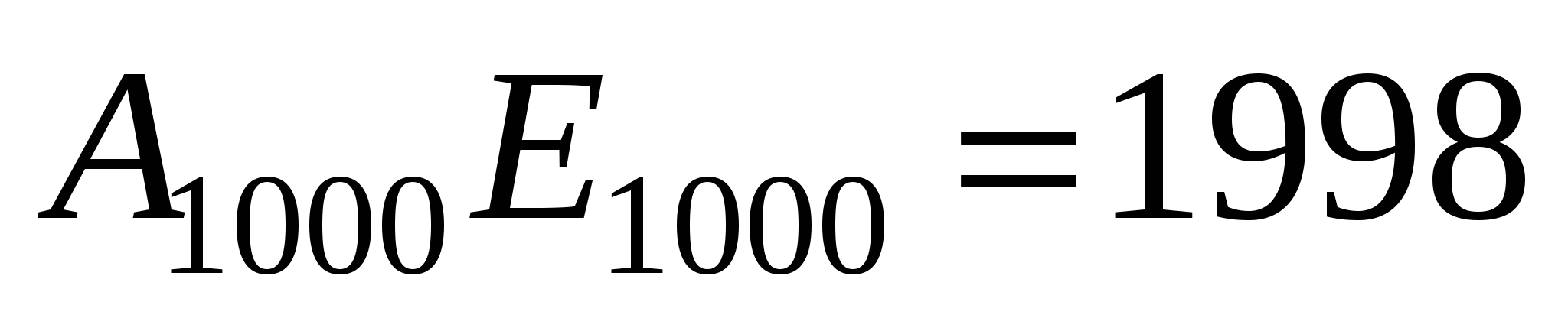

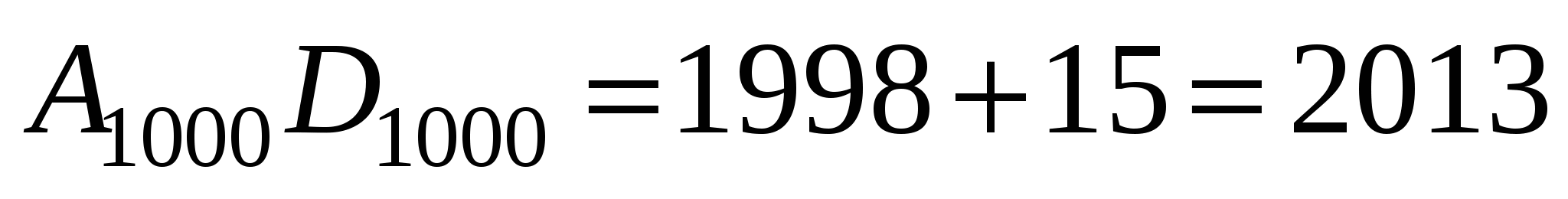
(см. чертеж).
Итак, длины 999 искомых отрезков составляют арифметическую прогрессию с первым членом 17 и разностью 2.
ОТВЕТ: 17, 19, 21, …., 2011, 2013.
5. Найти все значения параметра а, при которых система 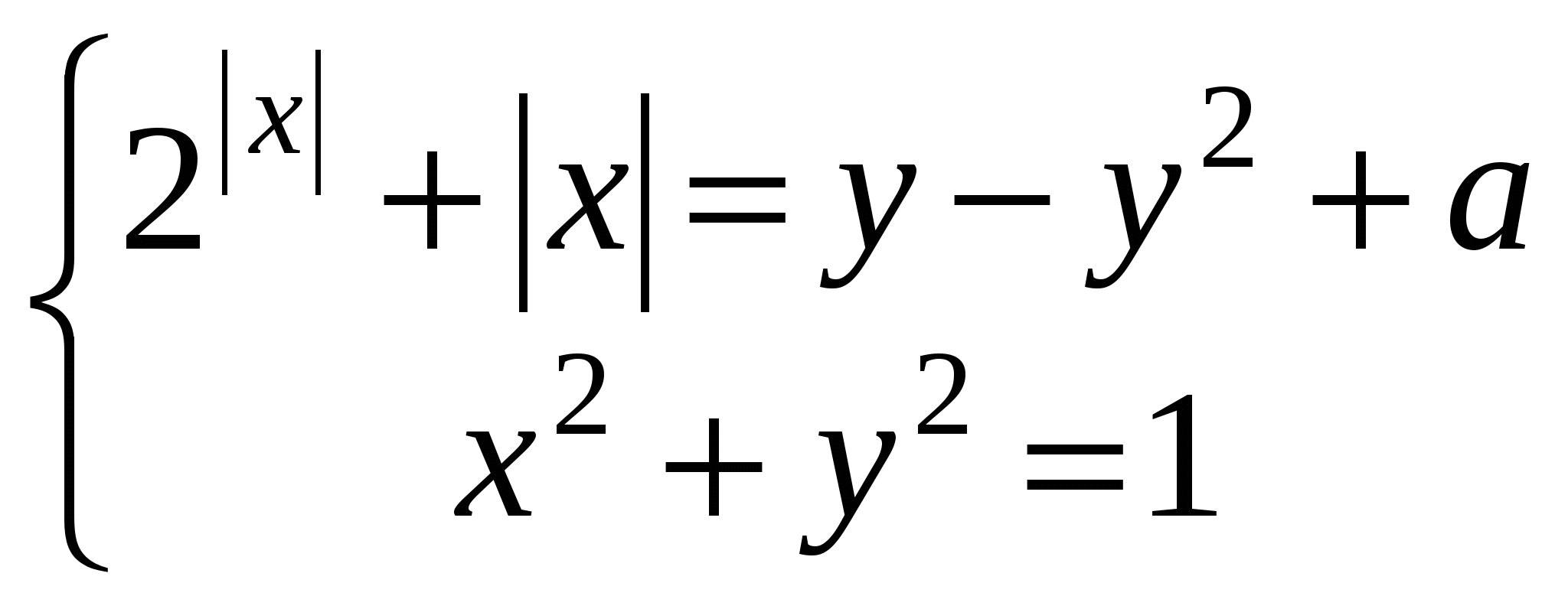
имеет только одно решение в вещественных числах.
РЕШЕНИЕ:
1 способ. Заметим, что если данной система будет удовлетворять пара чисел (в; с), то ей будет удовлетворять и пара чисел (- в; с) в силу ее четности относительно переменной х.
Поэтому данная система может иметь единственное решение вида (0; с) в вещественных числах. Но если х = 0, то из второго уравнения системы у = ![]() .
.
Итак, у нас всего два варианта (0; 1) и (0; -1).
а) Найдем, при каких значениях параметра а система имеет решение (0; 1).
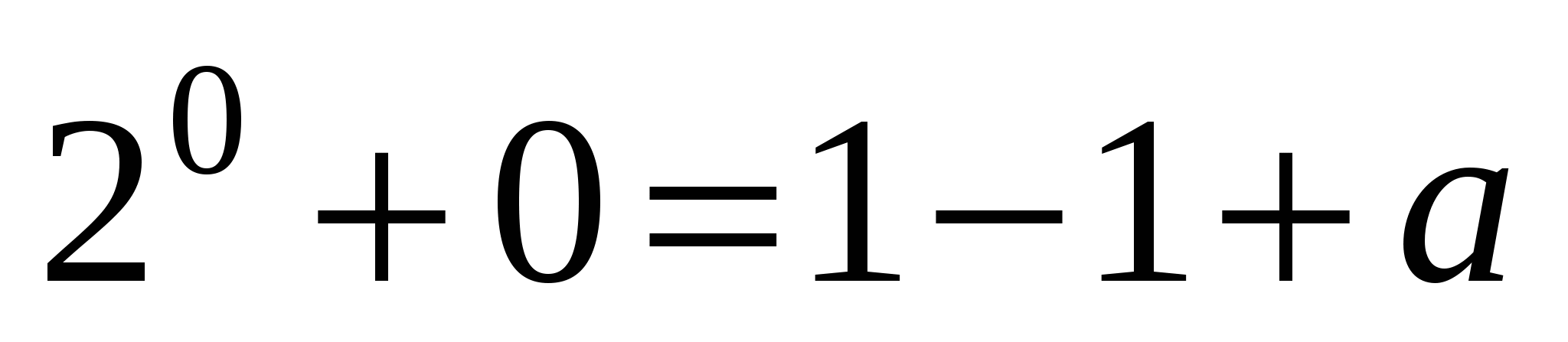
 а = 1
а = 1
Докажем, что при а = 1 система не имеет других решений, кроме (0; 1).
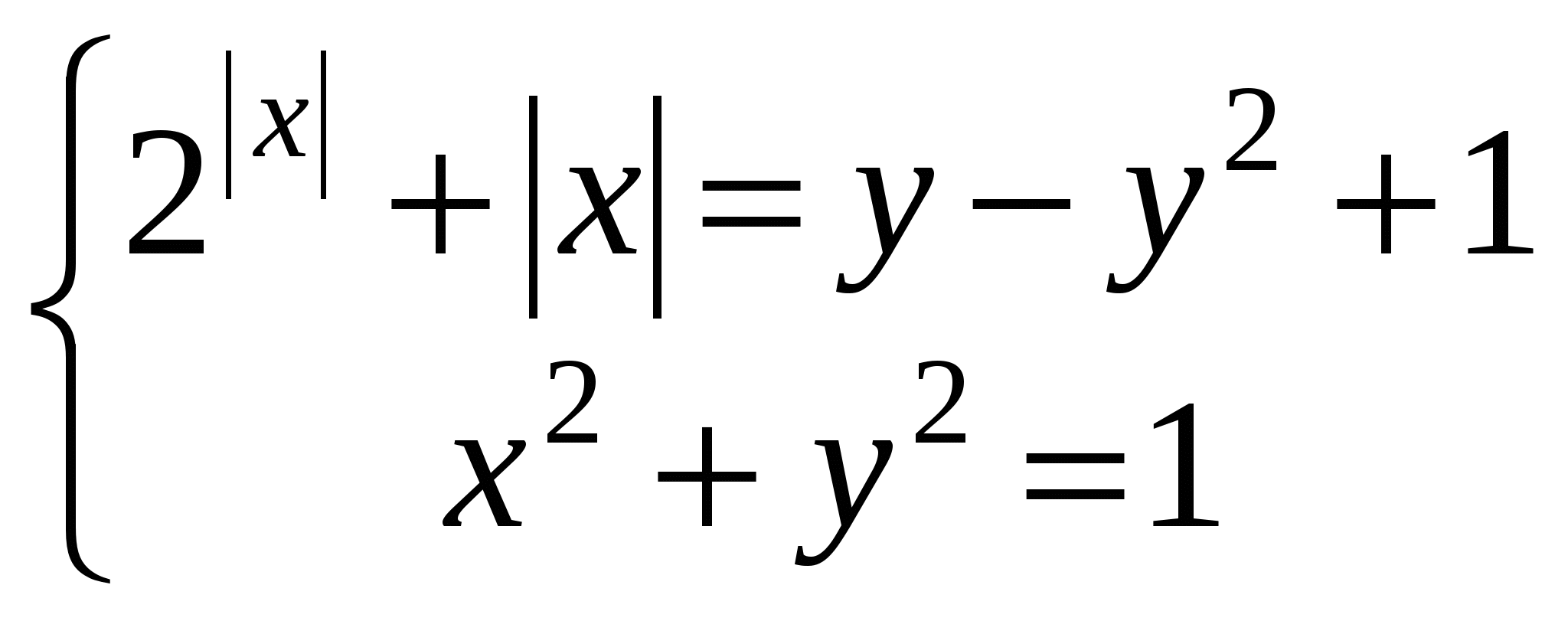

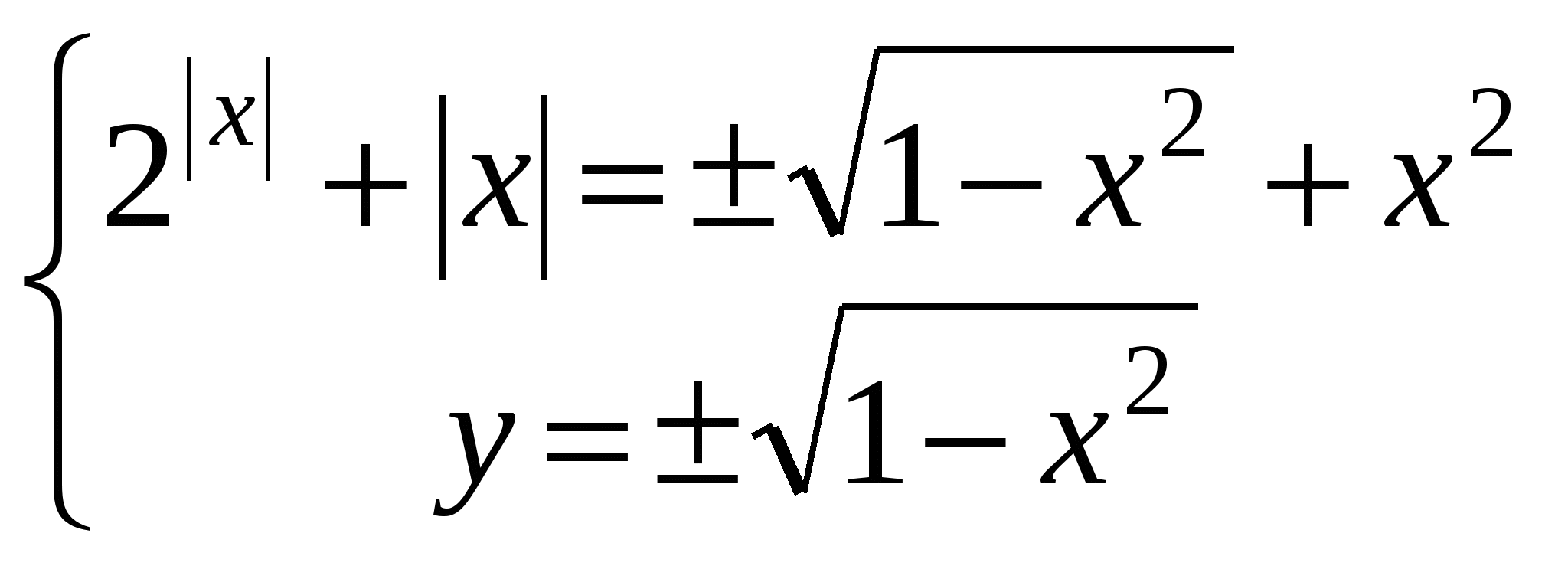
Докажем, что первое уравнений системы имеет единственный вещественный корень х = 0.
Поскольку уравнение четно, относительно переменной х, то достаточно доказать,
что уравнение ![]() имеет единственный корень х = 0, при
имеет единственный корень х = 0, при 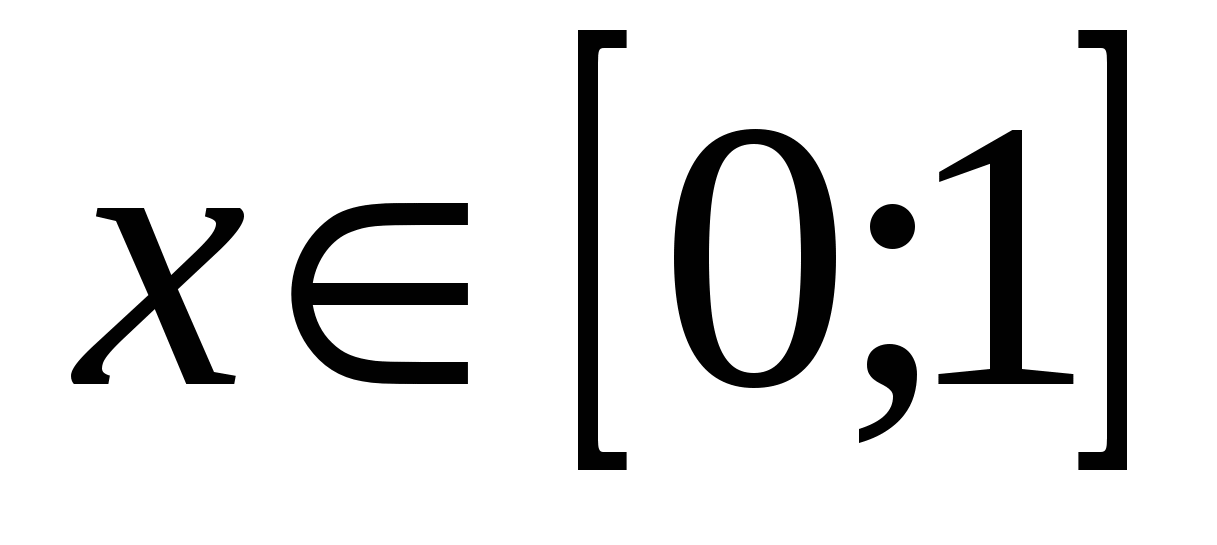
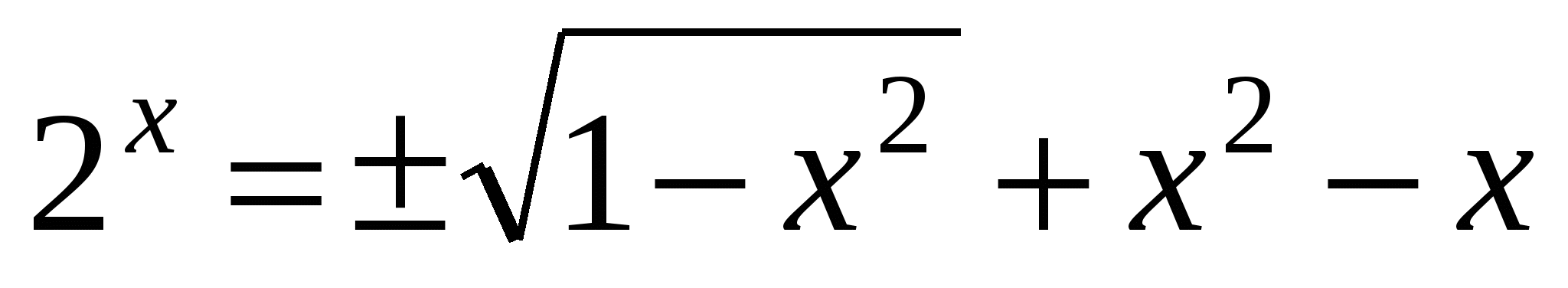 . Заметим, что 2х
. Заметим, что 2х  1, а
1, а 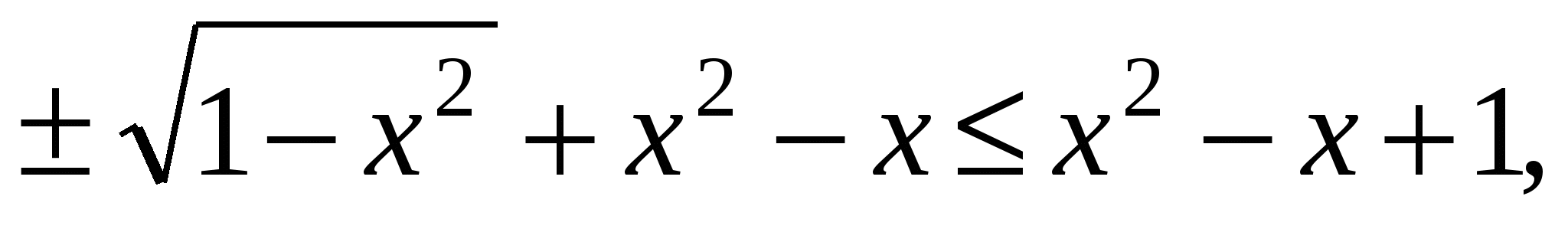 т.к.
т.к. 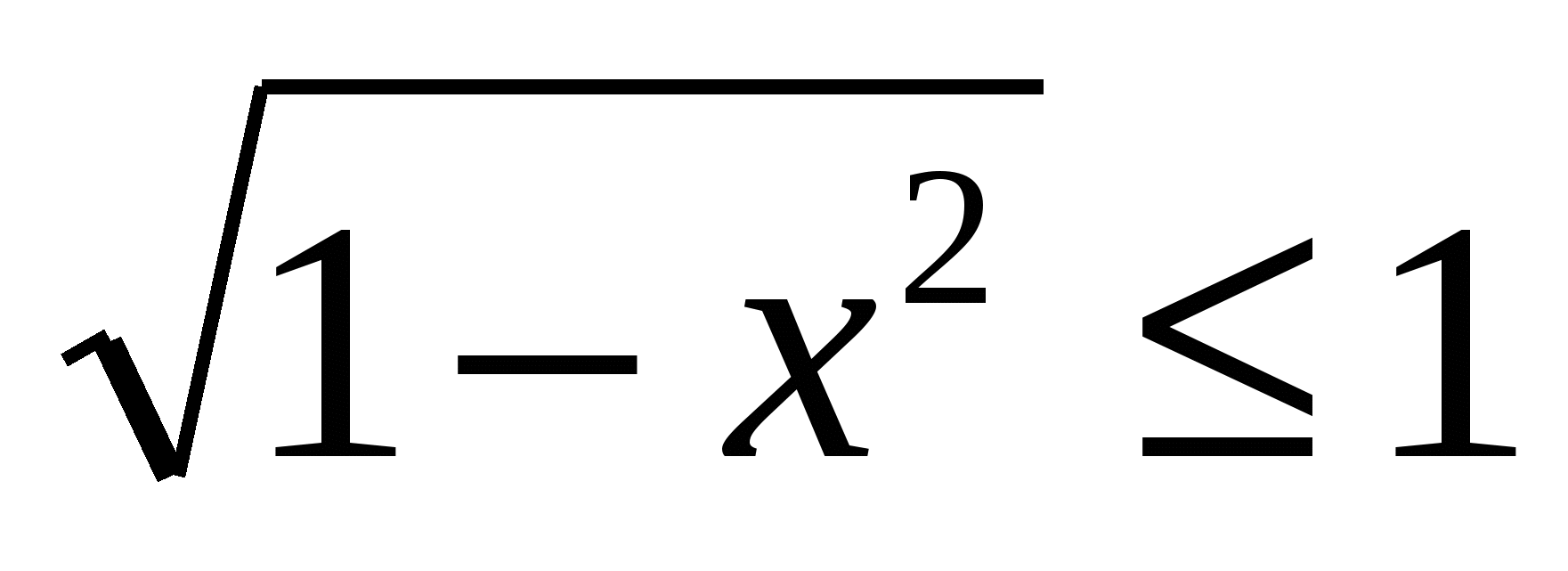 ,
, 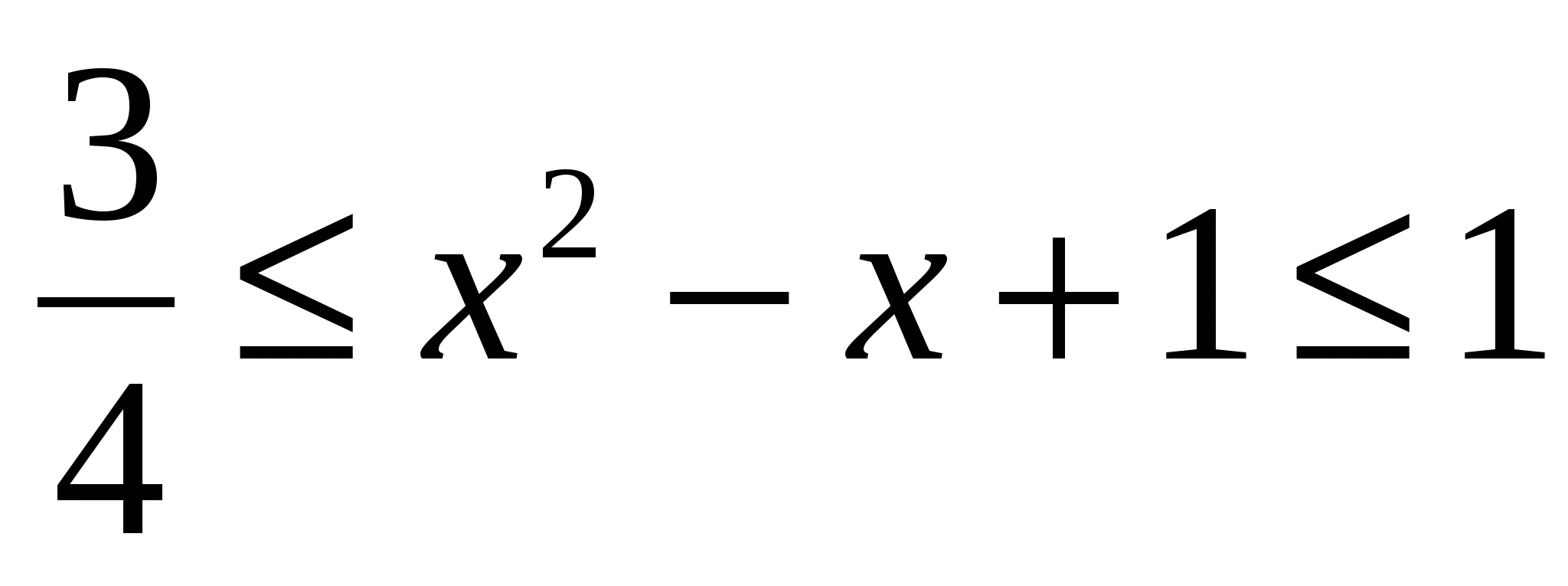 , при
, при 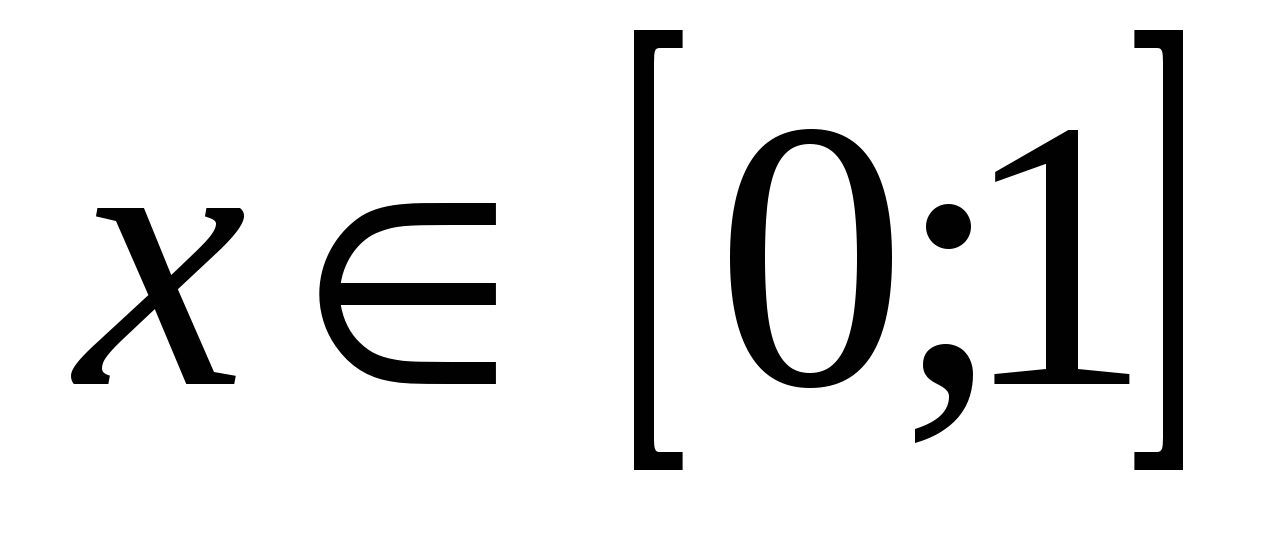 . Т.е. уравнение
. Т.е. уравнение 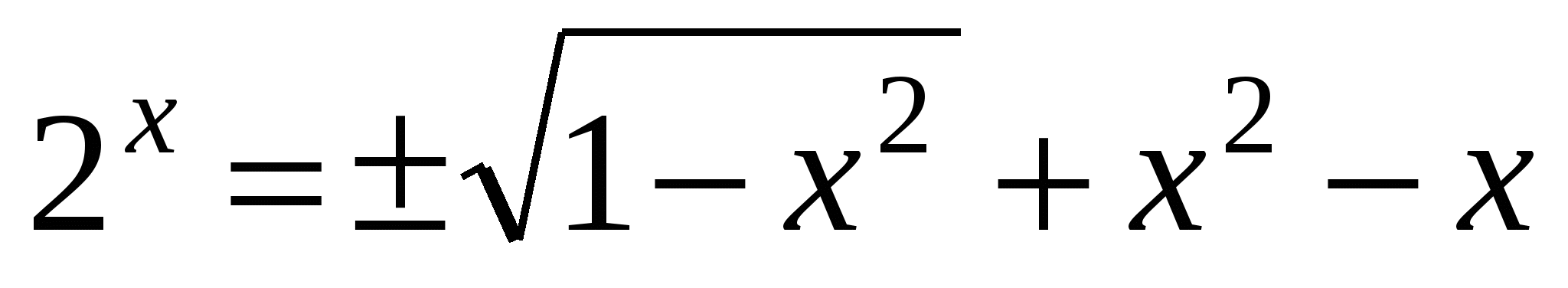 имеет решение
имеет решение
при 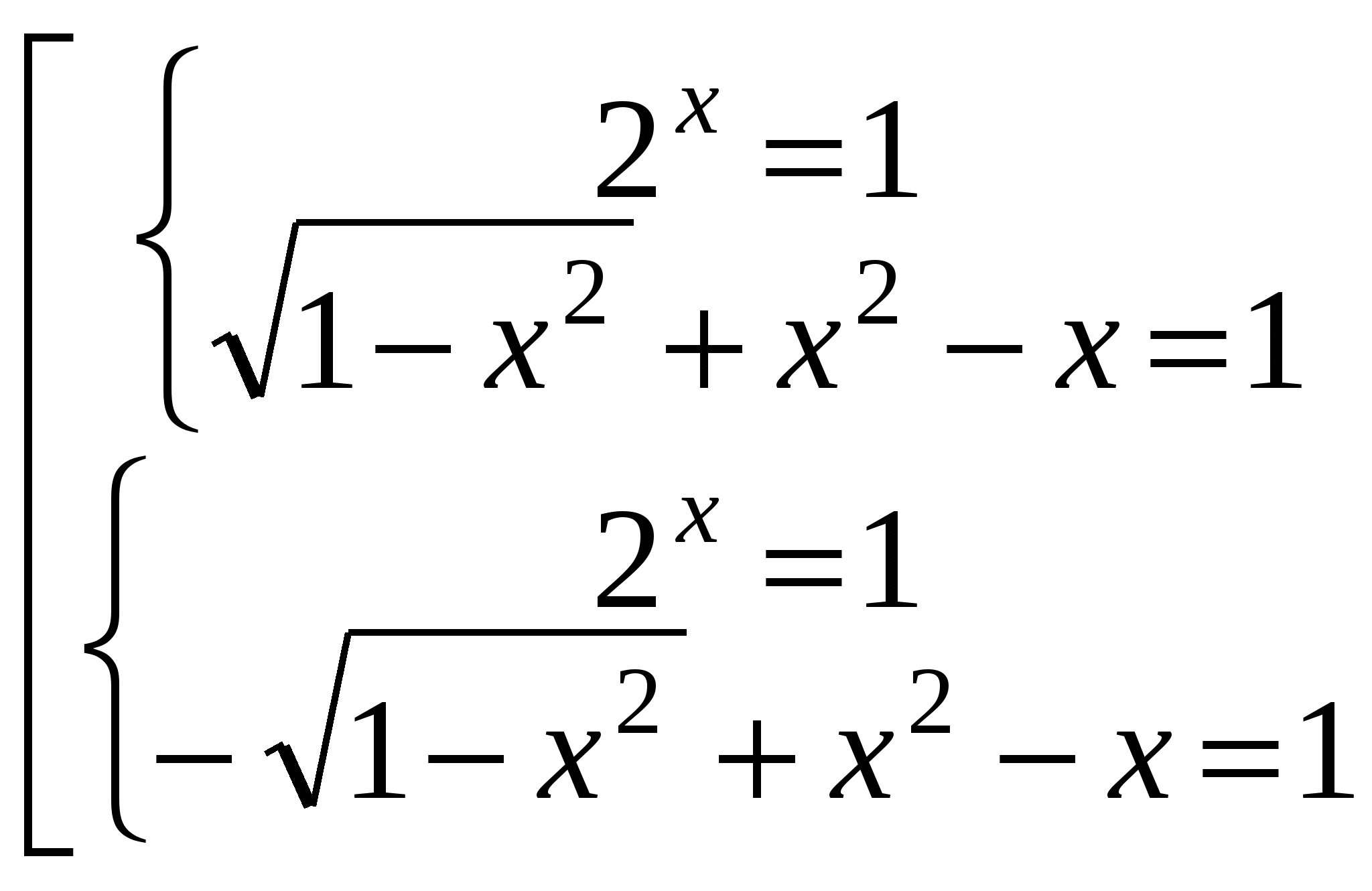 , а, значит, х =0 - единственное решение первой системы данной совокупности, при этом вторая система решений не имеет. Это означает, что система уравнений
, а, значит, х =0 - единственное решение первой системы данной совокупности, при этом вторая система решений не имеет. Это означает, что система уравнений 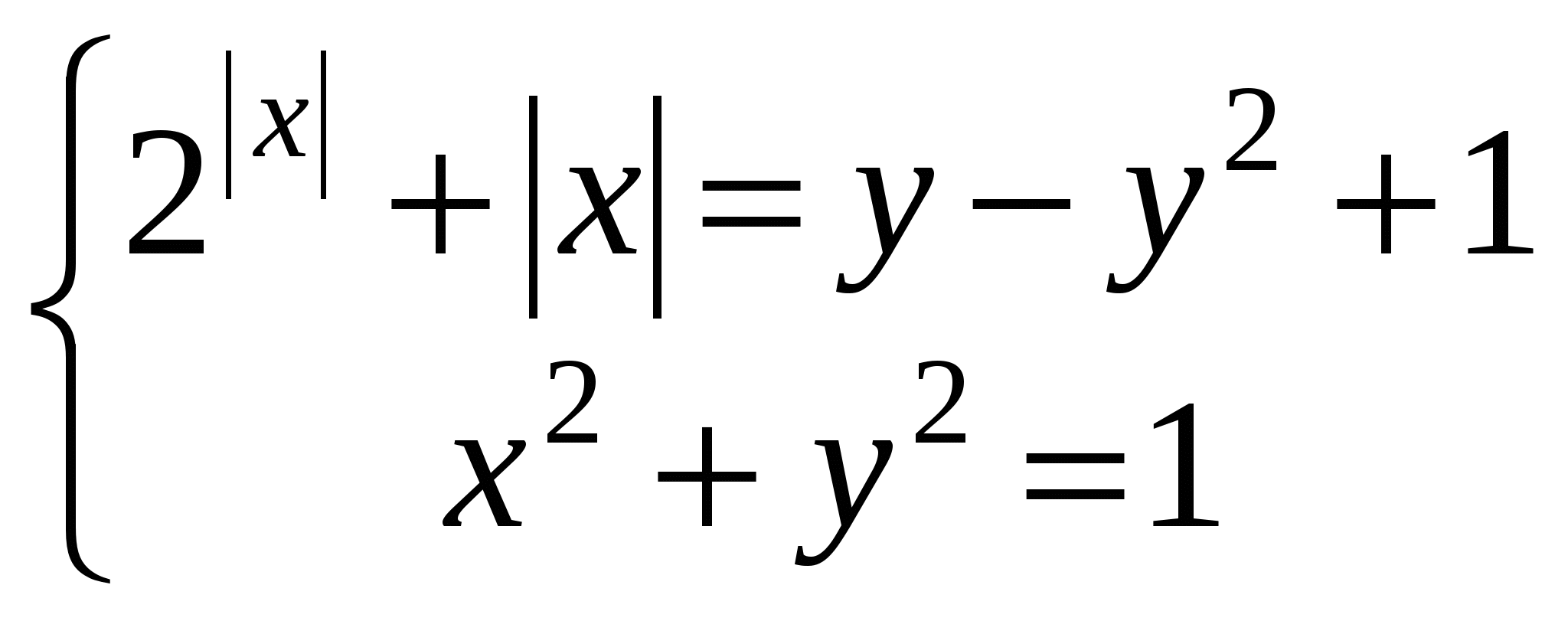 имеет единственное решение (0;1), т.е. значение параметра
имеет единственное решение (0;1), т.е. значение параметра
а = 1 удовлетворяет заданному условию.
б) Найдем, при каких значениях параметра а система имеет решение (0; -1).
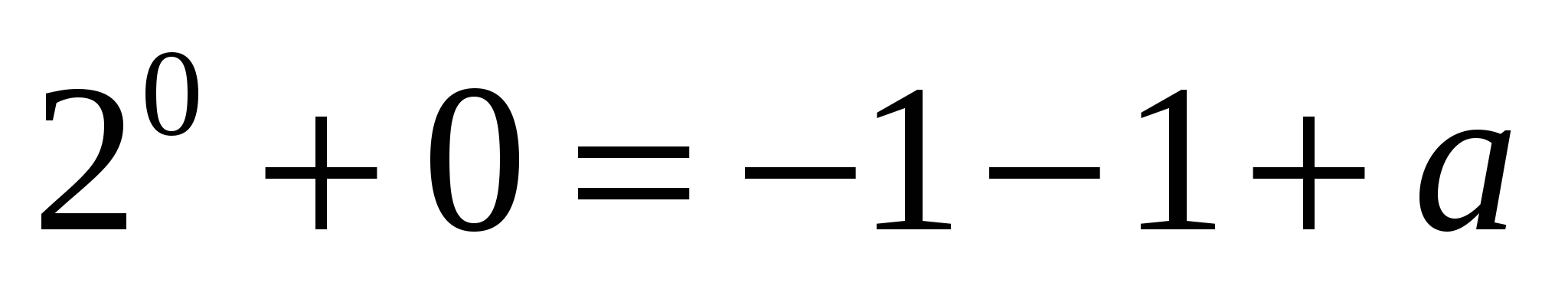
 а = 3
а = 3
Исследуем систему при а = 3 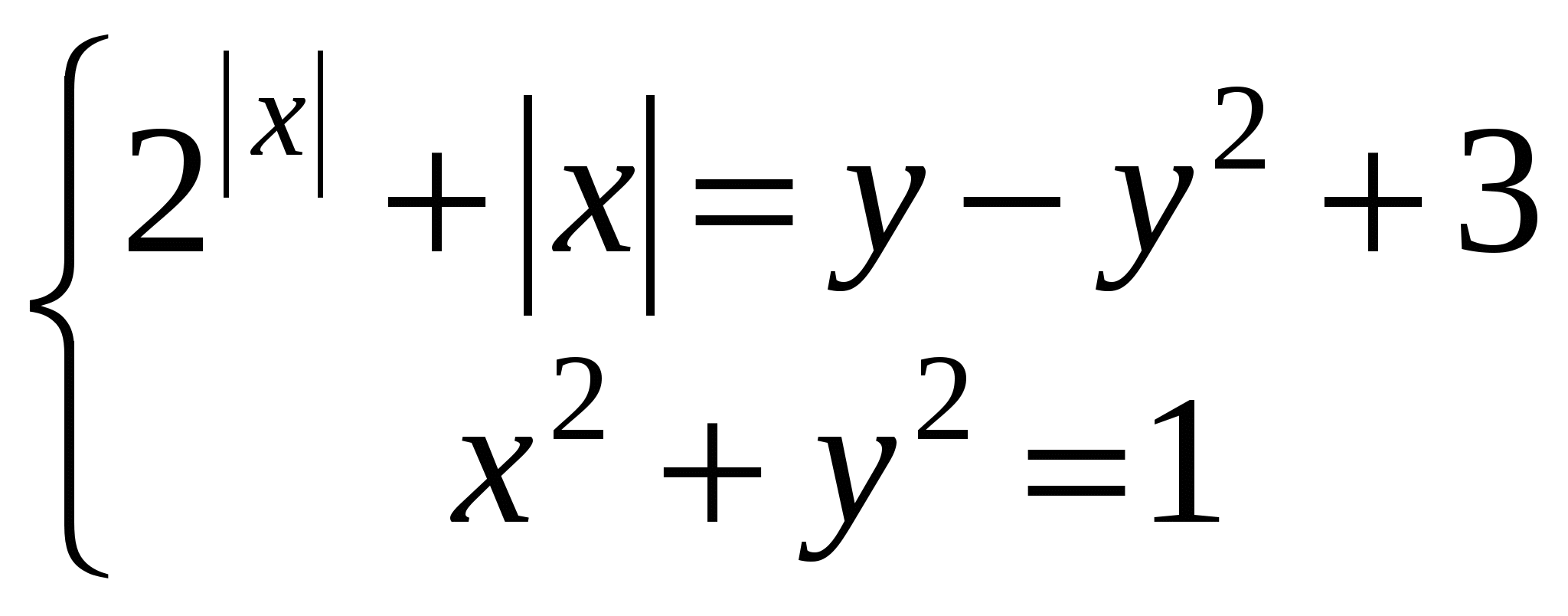
Заметим, что данная система имеет как минимум 2 решения
(0; -1) 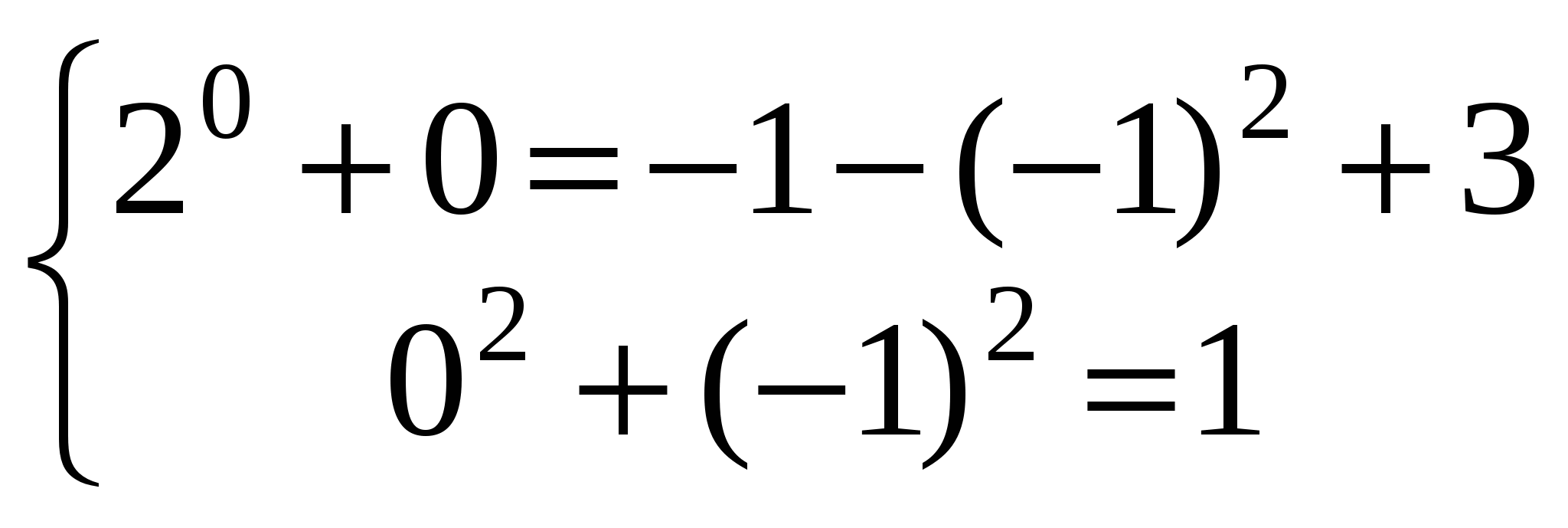 и (1;0)
и (1;0) 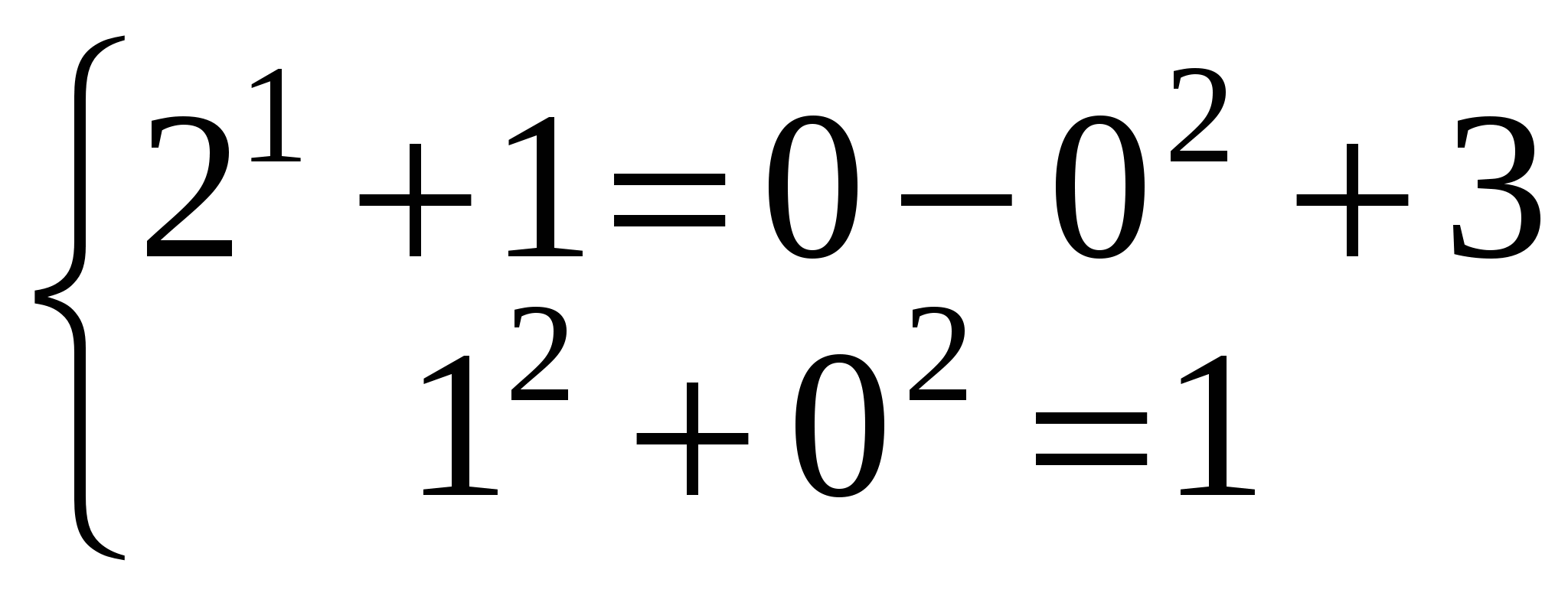
т.е. значение параметра а = 3 не удовлетворяет условию задачи.
2 способ. Выразим из второго уравнения у и подставить в первое: 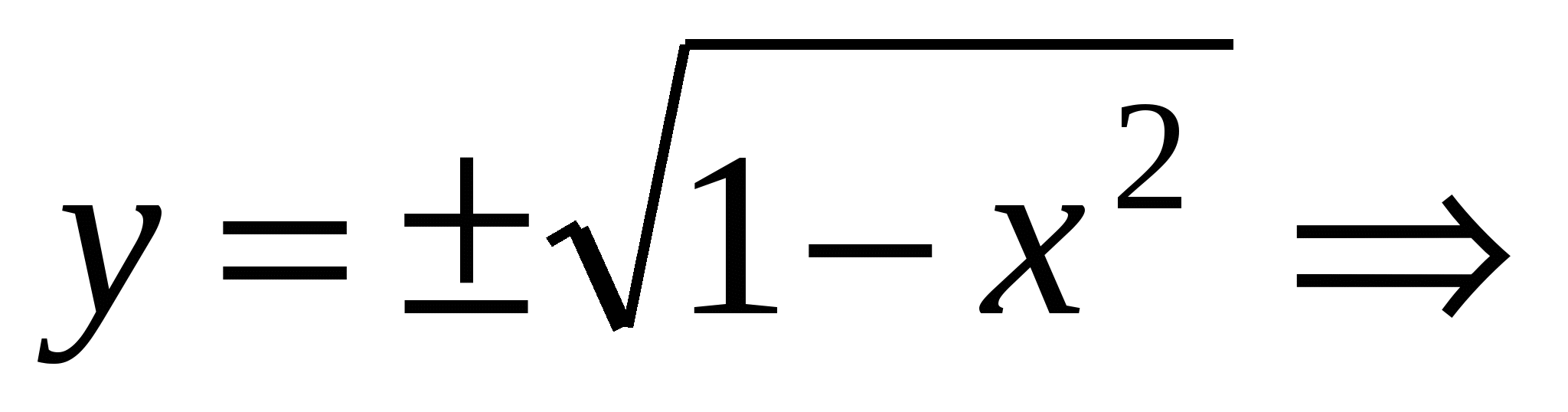
а) 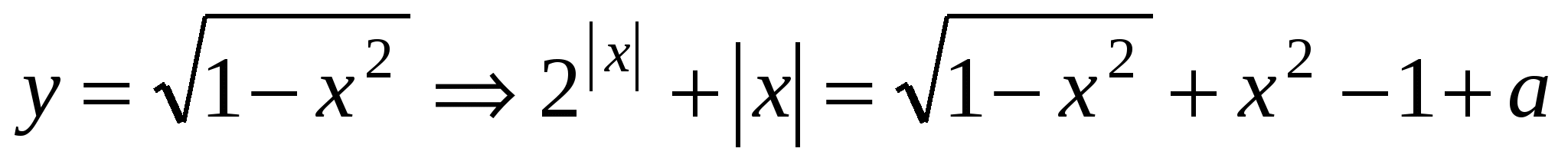 , получили четное относительно х уравнение. Известно, что это уравнение может иметь нечетное количество нулей, только если один из этих нулей х = 0.
, получили четное относительно х уравнение. Известно, что это уравнение может иметь нечетное количество нулей, только если один из этих нулей х = 0.
Пусть х = 0, подставим во второе уравнение нашей системы, тогда 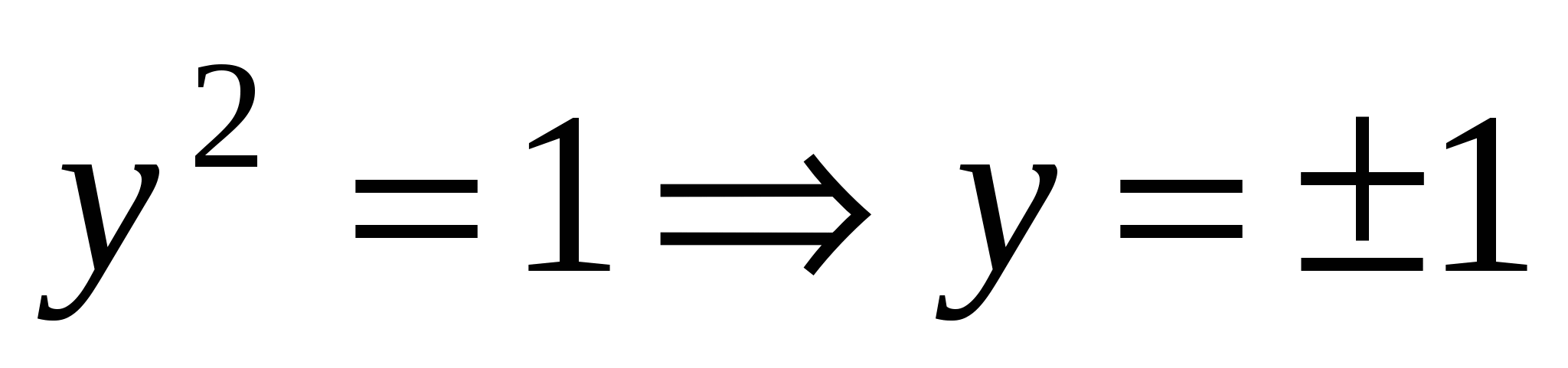 . Подставляем найденные у в первое уравнение системы:
. Подставляем найденные у в первое уравнение системы: 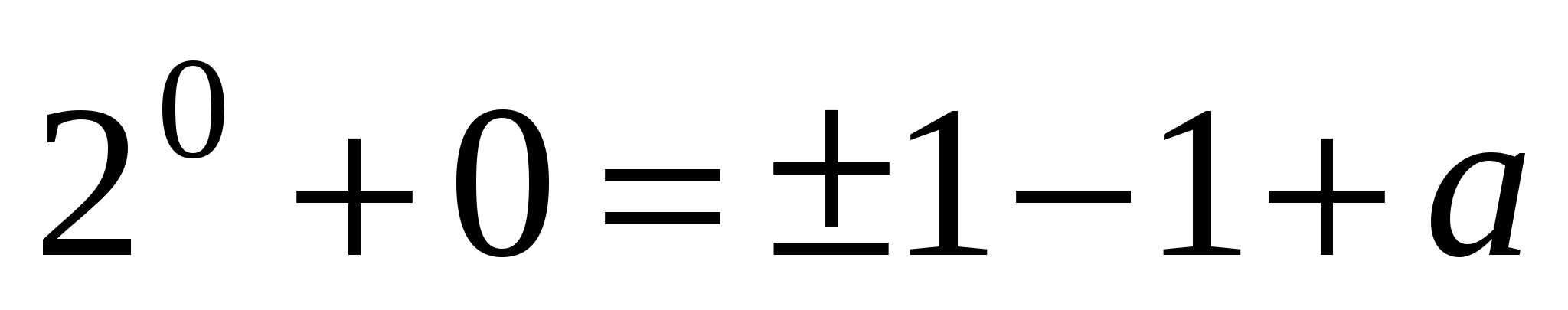 , т.е.
, т.е. 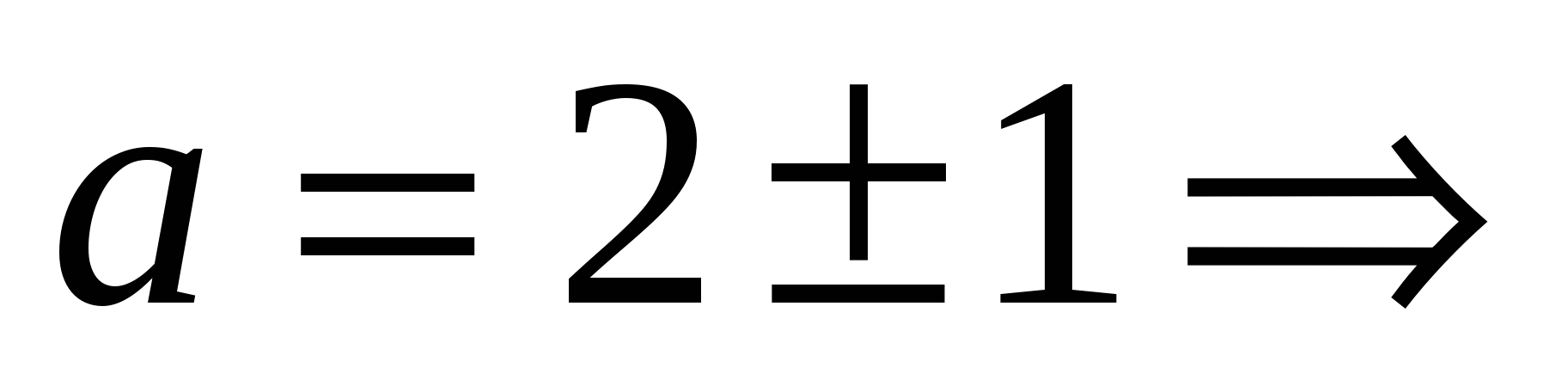 а = 3 или а = 1. Теперь проверим, будет ли при этих параметрах не просто нечетное количество нулей, а один единственный.
а = 3 или а = 1. Теперь проверим, будет ли при этих параметрах не просто нечетное количество нулей, а один единственный.
В случае а = 3 получаем 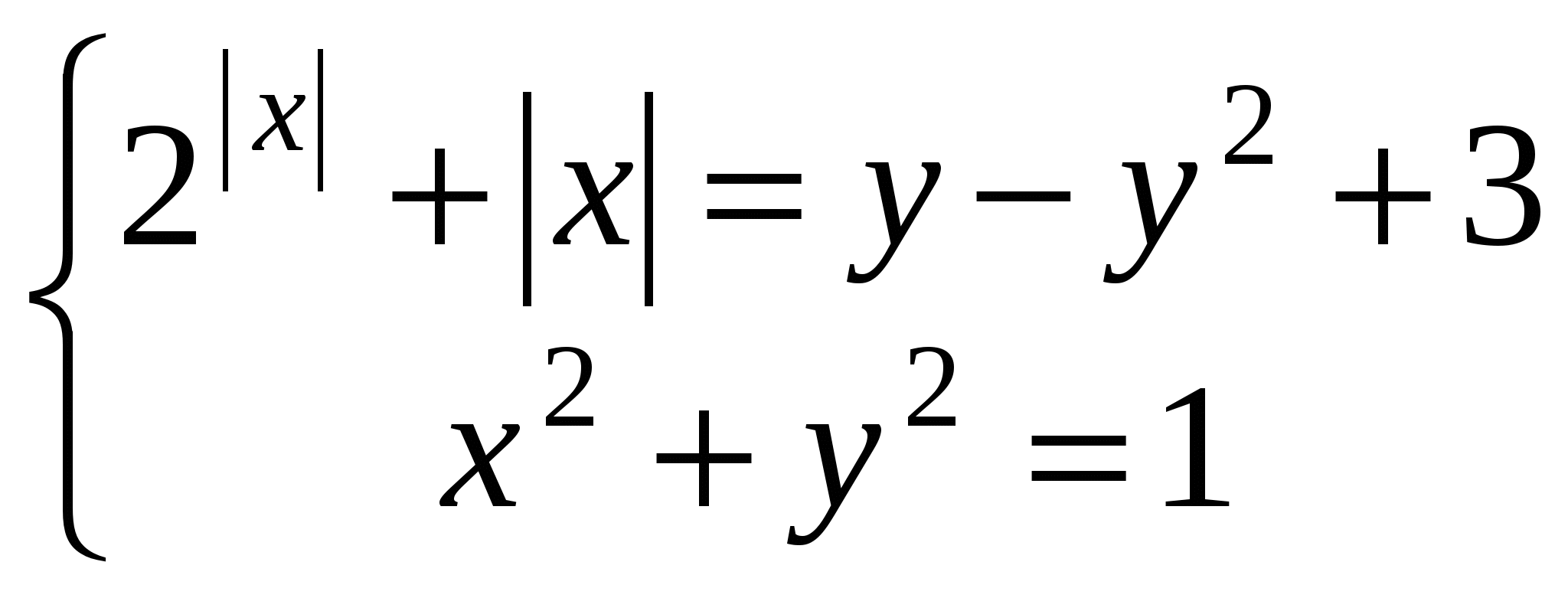 . При у = 0, из второго уравнения системы получаем
. При у = 0, из второго уравнения системы получаем 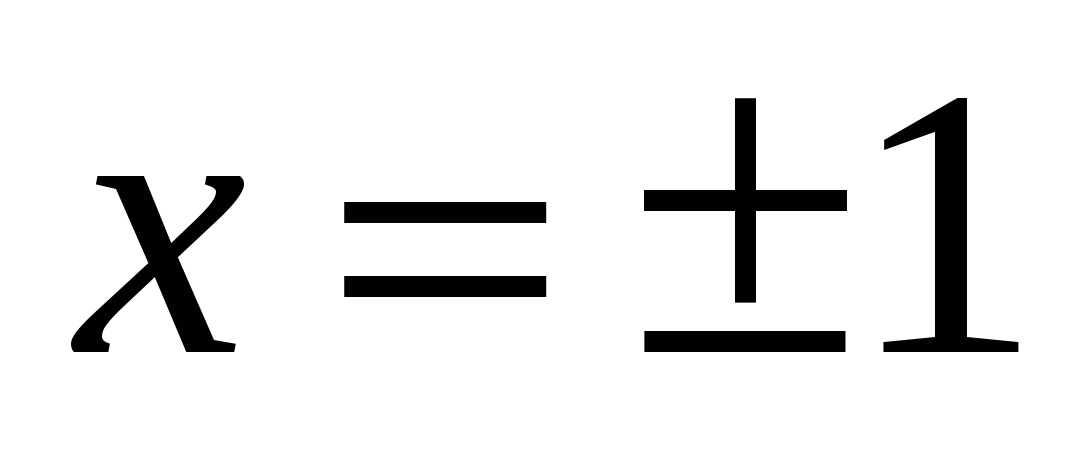 , подставим в первое уравнение:
, подставим в первое уравнение: 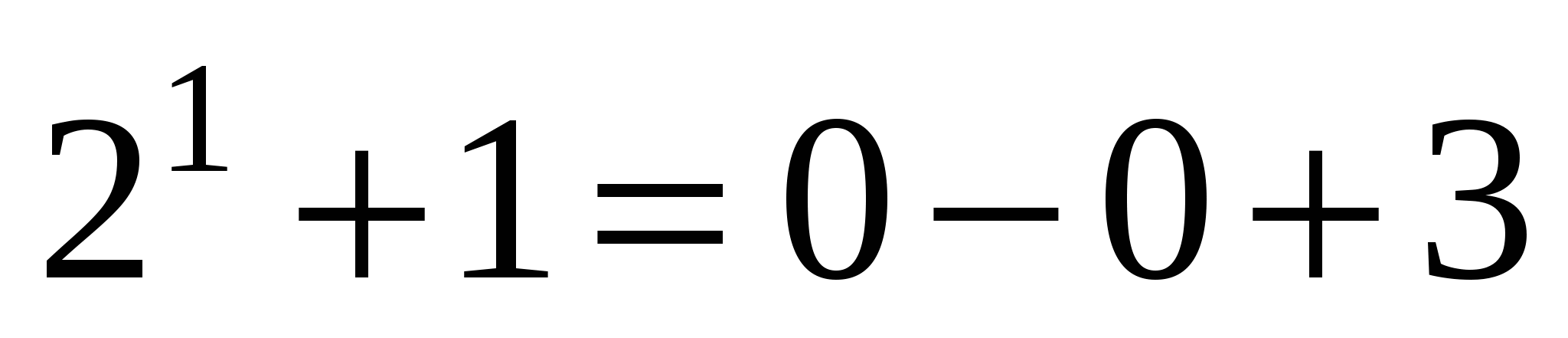 , т.е. 3 = 3. Получили ещё 2 корня, а значит это значение параметра нам не подходит.
, т.е. 3 = 3. Получили ещё 2 корня, а значит это значение параметра нам не подходит.
Если а = 1 получаем 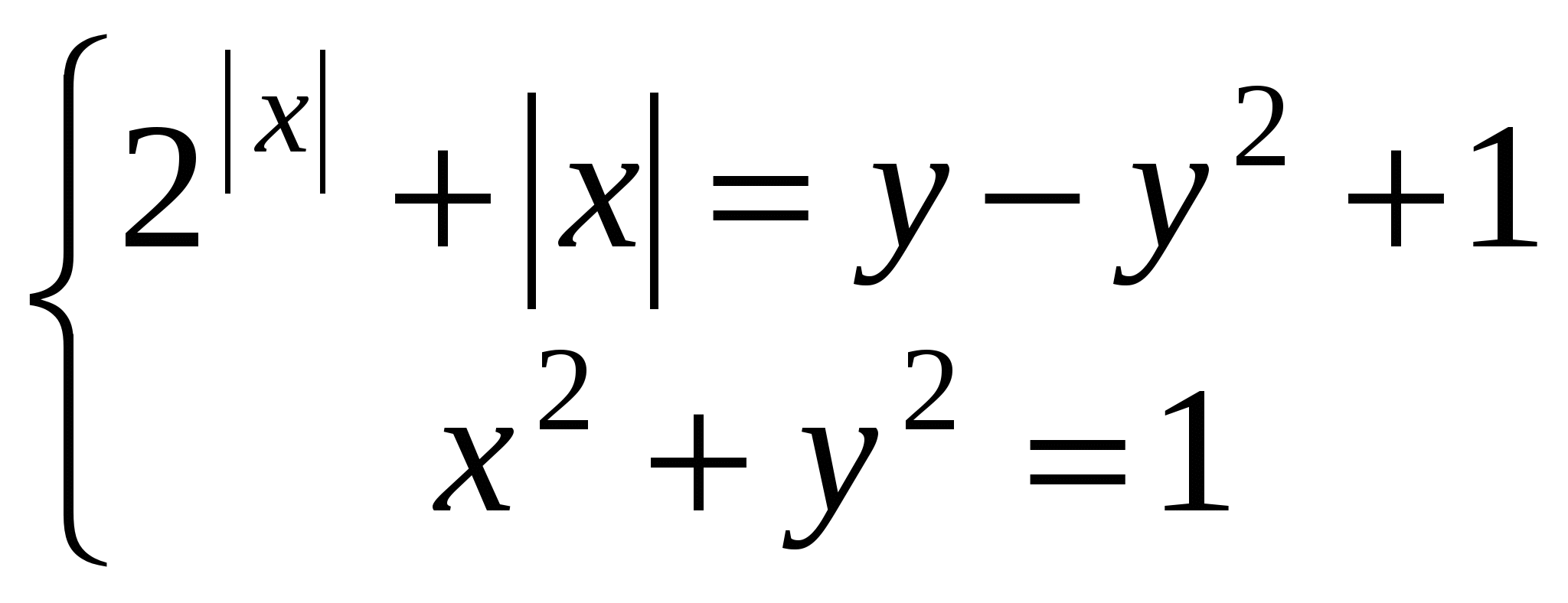 .
.
Если 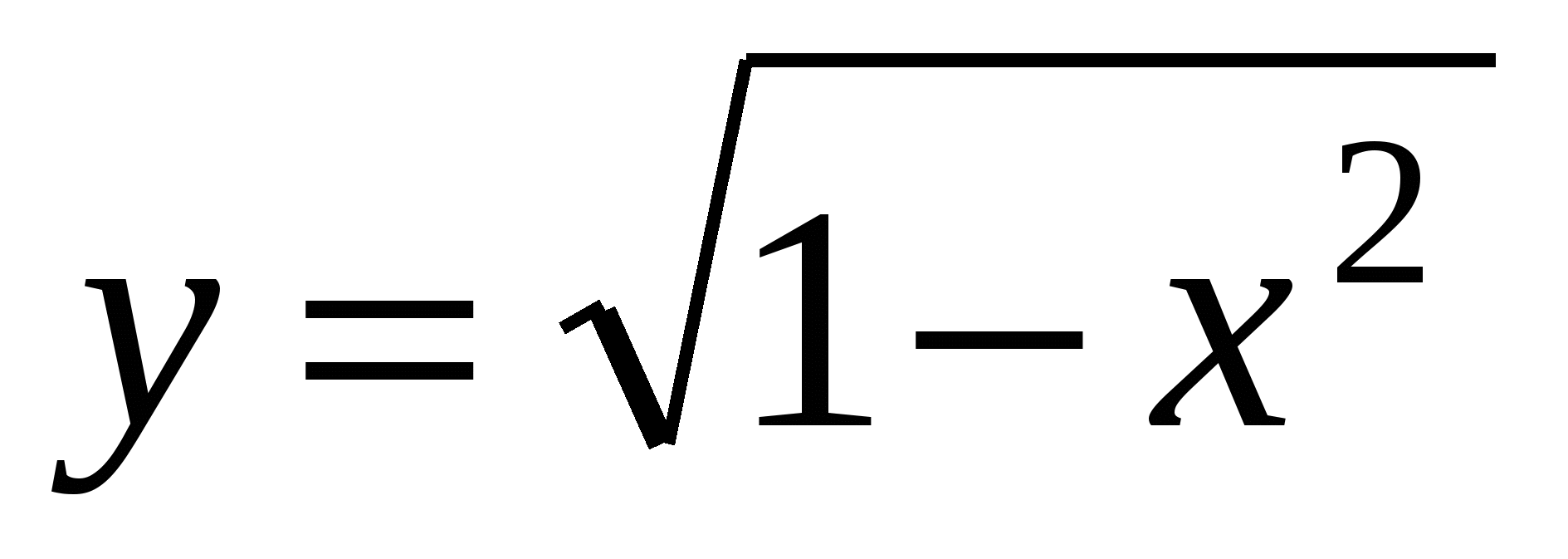 , то
, то 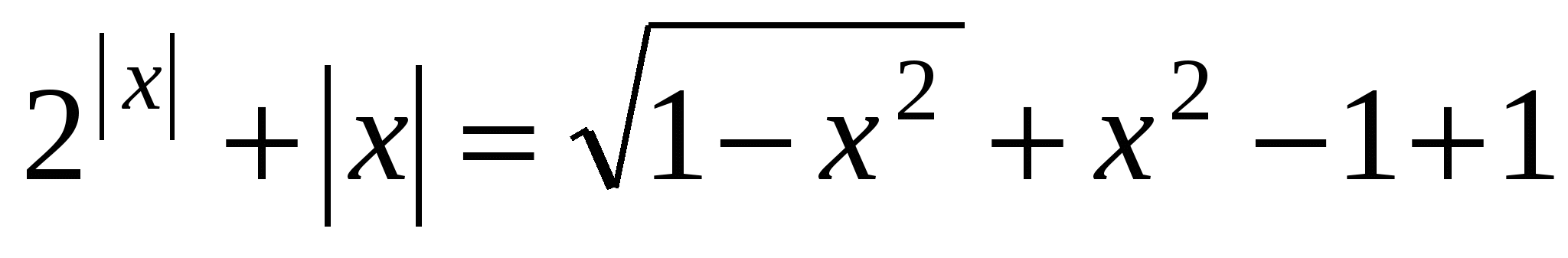
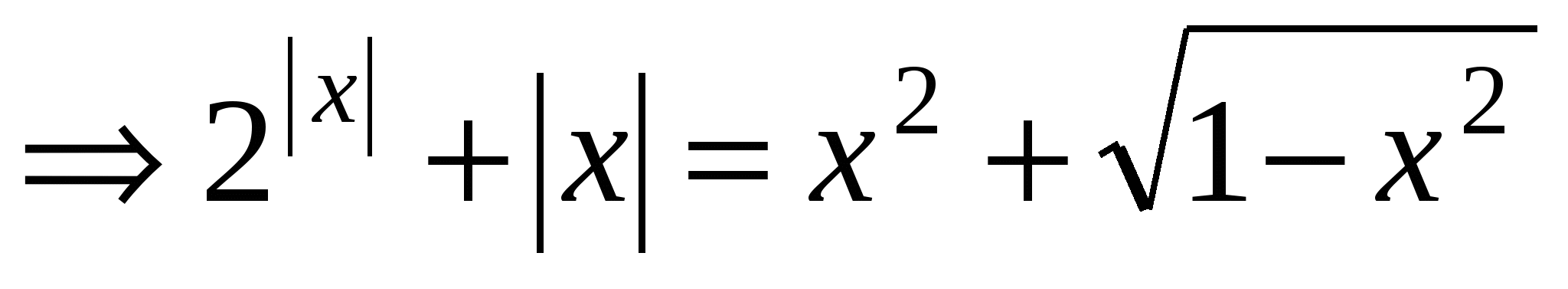 . Если корней не будет при
. Если корней не будет при 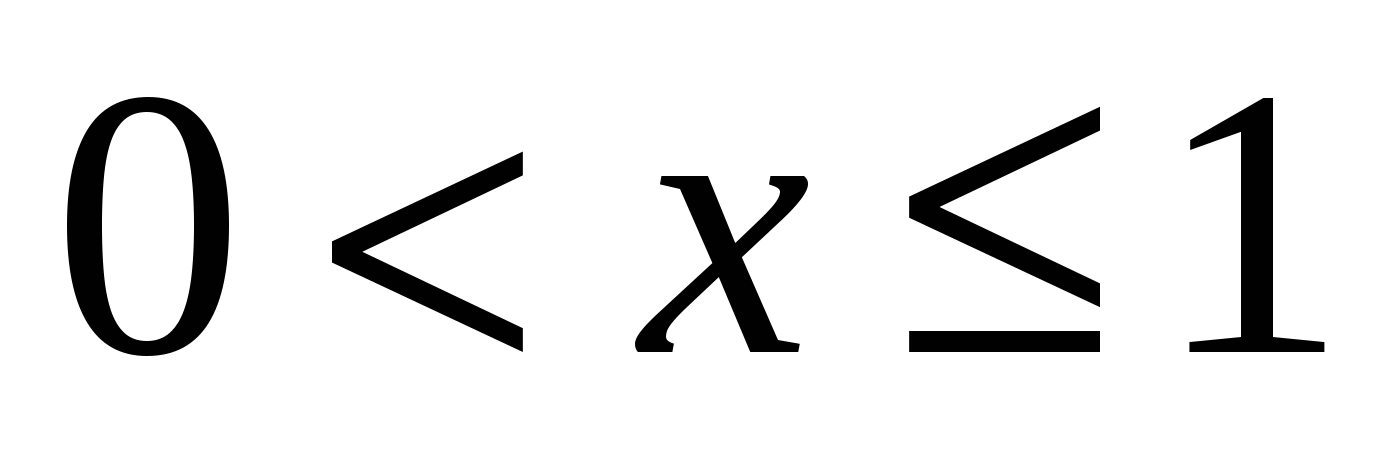 , то в силу четности функции их не будет и при
, то в силу четности функции их не будет и при 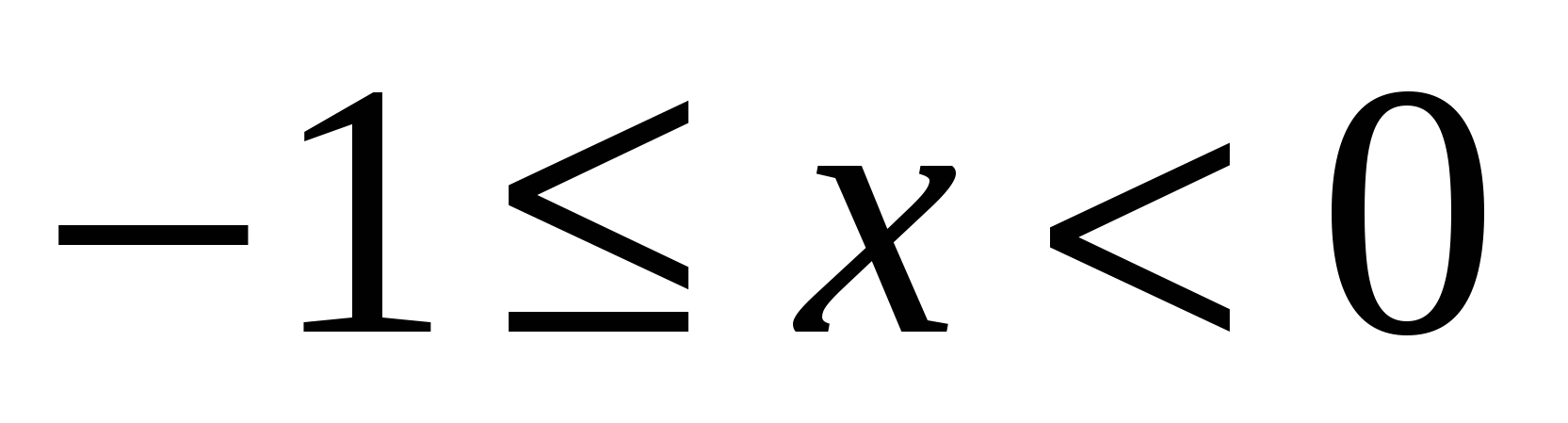 .
.
При 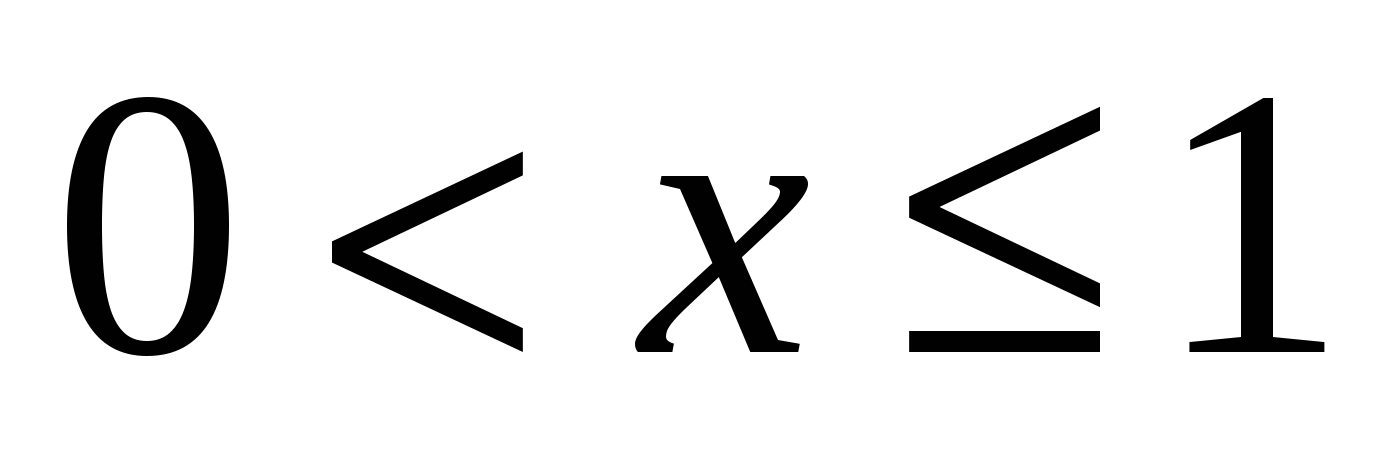 функция
функция 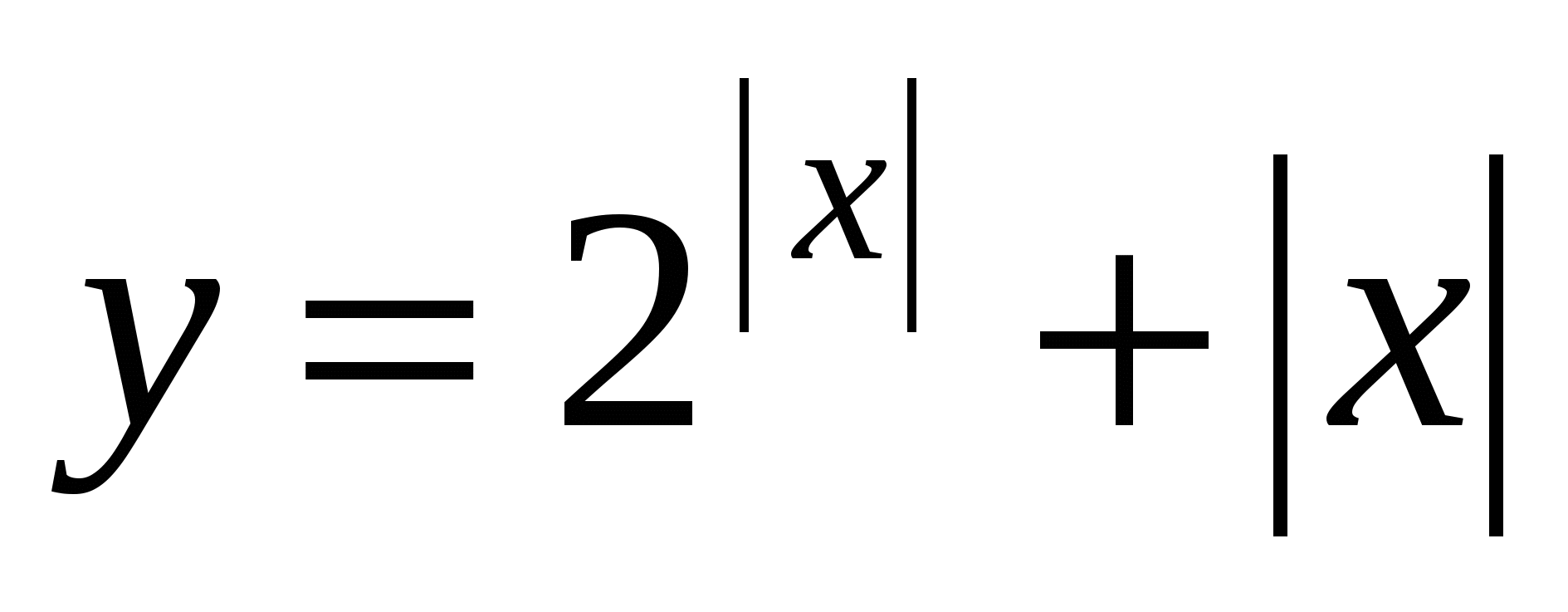 монотонно возрастает. Проверим возрастание функции
монотонно возрастает. Проверим возрастание функции 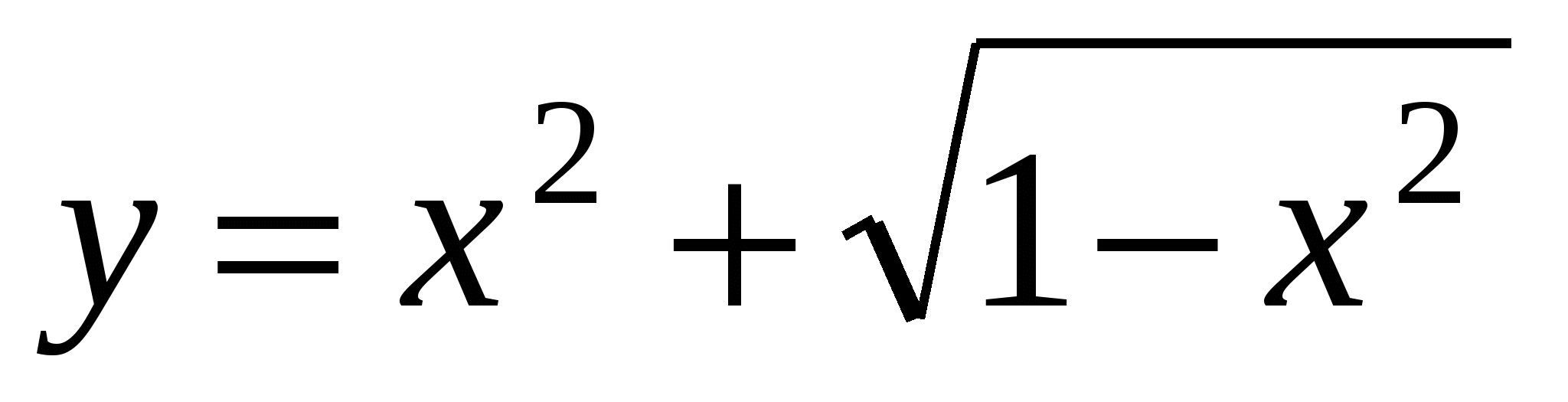 в правой части при помощи производной:
в правой части при помощи производной:
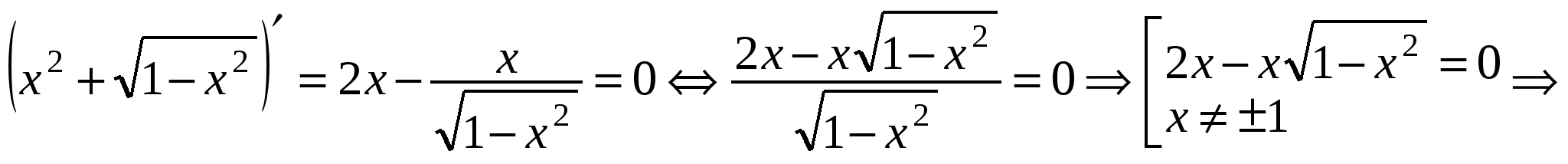
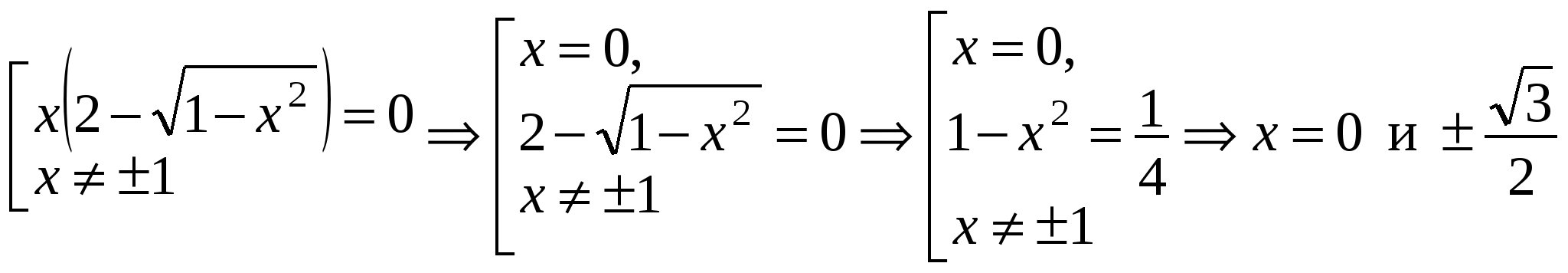 .
.
В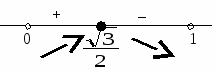 рассматриваемый полуинтервал
рассматриваемый полуинтервал 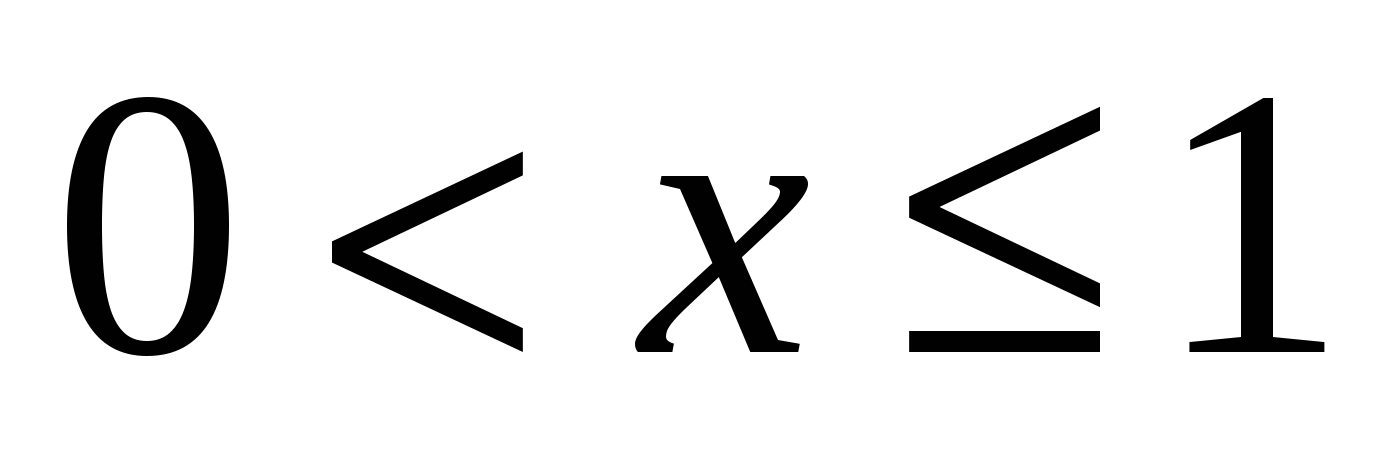 входит только значение
входит только значение ![]() . Причем видим, что в нём достигается максимум функции. Наибольшее значение равно
. Причем видим, что в нём достигается максимум функции. Наибольшее значение равно 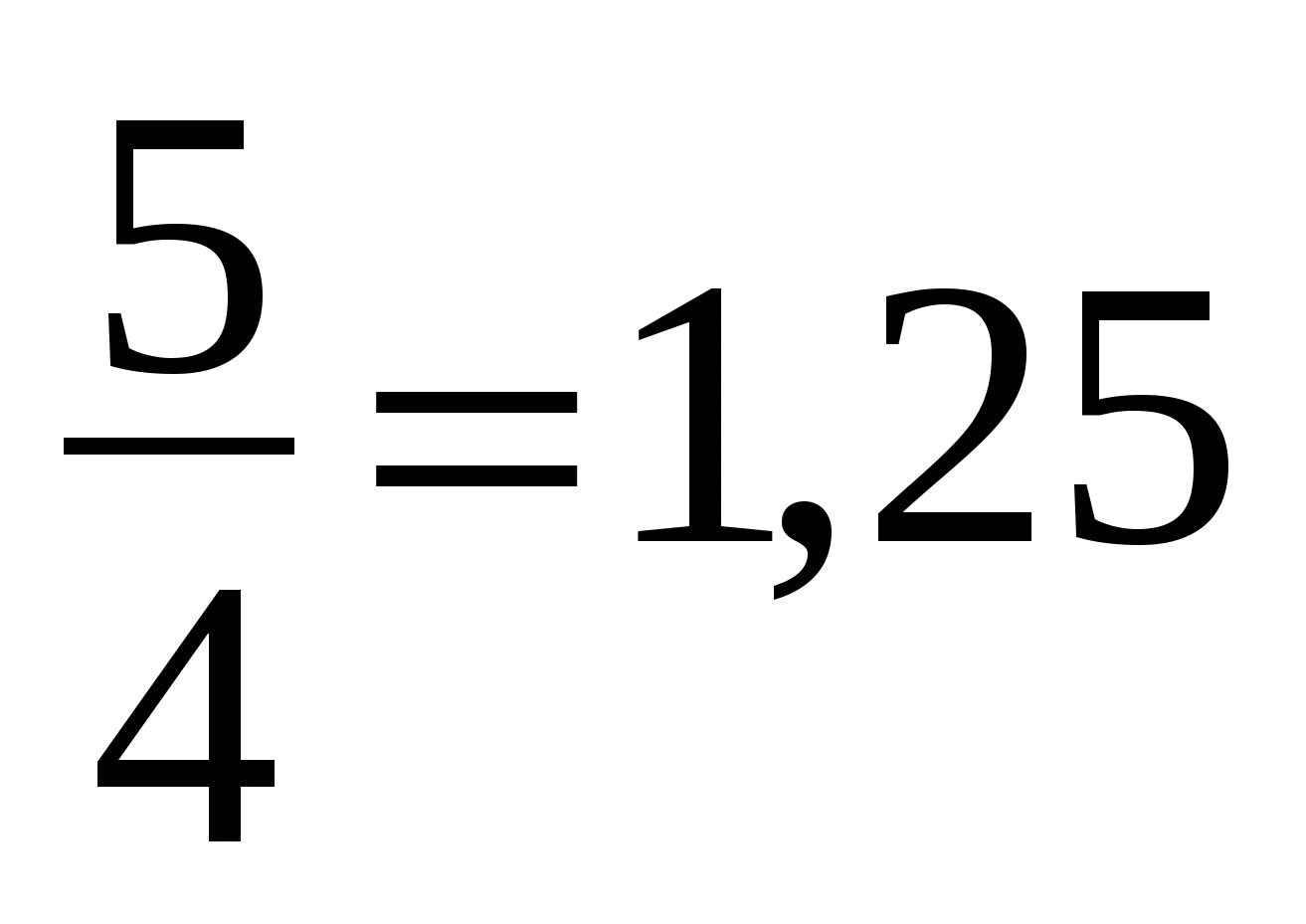 и оно меньше, чем значение левой части в этой же точке (
и оно меньше, чем значение левой части в этой же точке (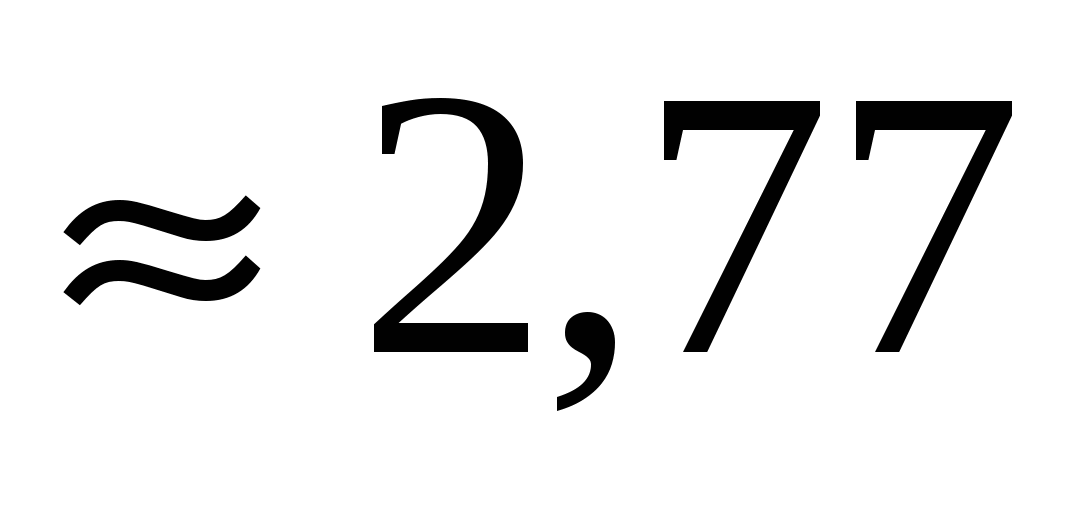 ).
).
А значит, других корней кроме х = 0 нет.
б) Если 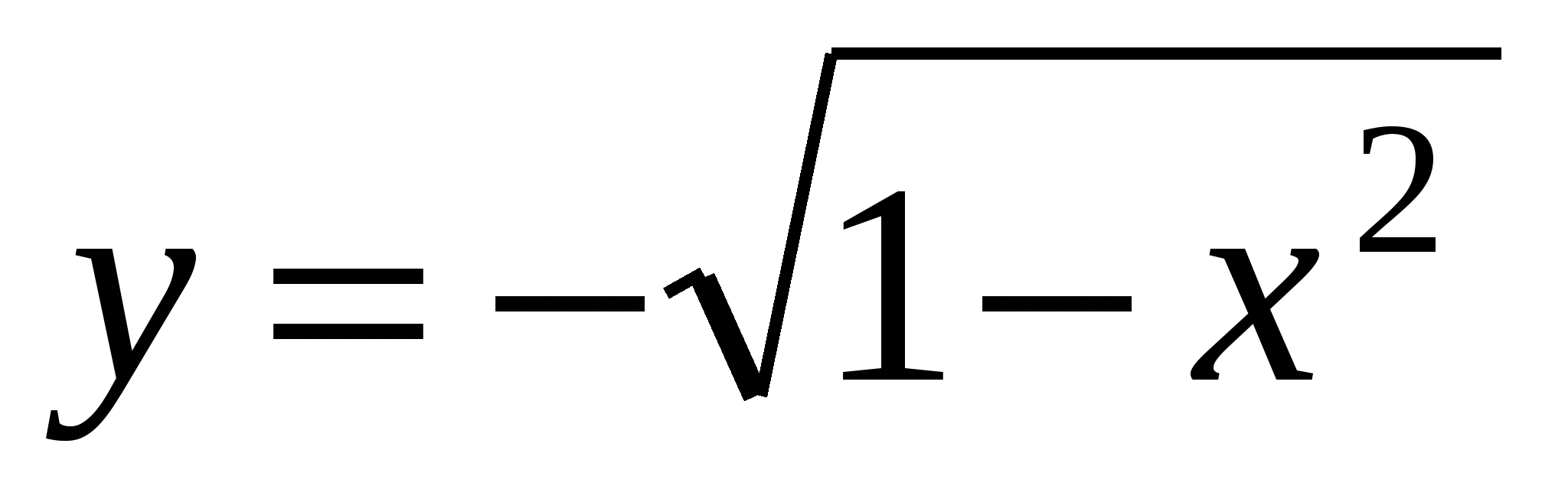 , аналогично рассуждая, находим производную:
, аналогично рассуждая, находим производную:
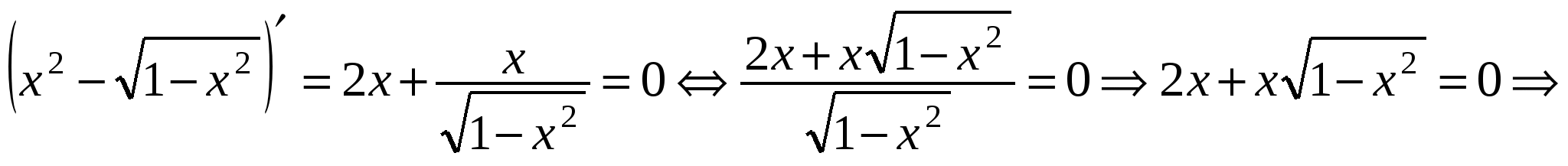
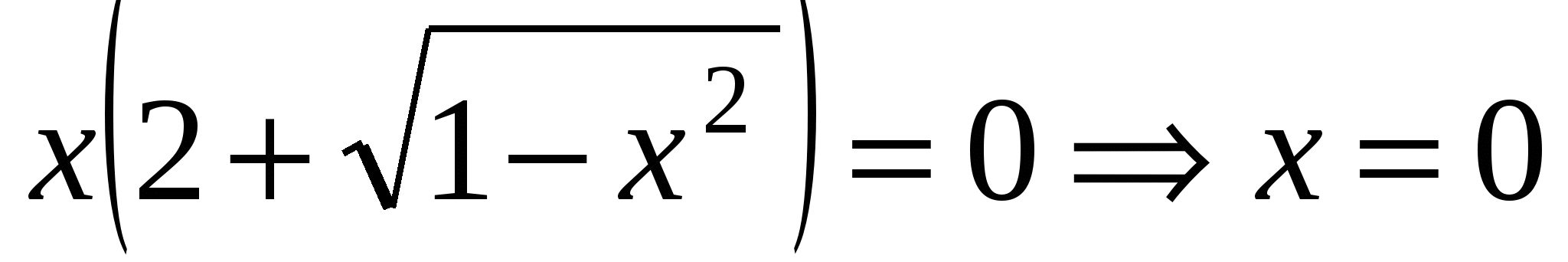
 - единственная критическая точка. Т.е. обе функции на
- единственная критическая точка. Т.е. обе функции на 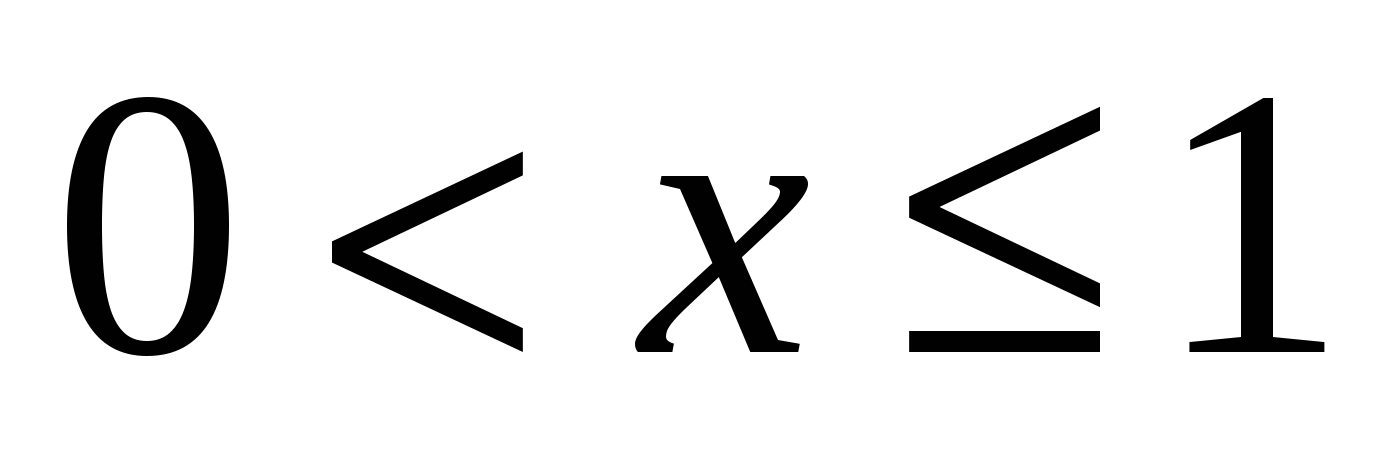 возрастают, но у левой функции область значения в этом полуинтервале от 0 до 1, а у правой от 1 до 3, поэтому эти функции не пересекутся.
возрастают, но у левой функции область значения в этом полуинтервале от 0 до 1, а у правой от 1 до 3, поэтому эти функции не пересекутся.
А значит, других корней кроме х = 0 нет.
ОТВЕТ: а = 1
6. В правильной четырехугольной пирамиде ABCDS точка S - вершина. Через середины ребер AB, AD, CS проведена плоскость. В каком отношении эта плоскость делит объем пирамиды?
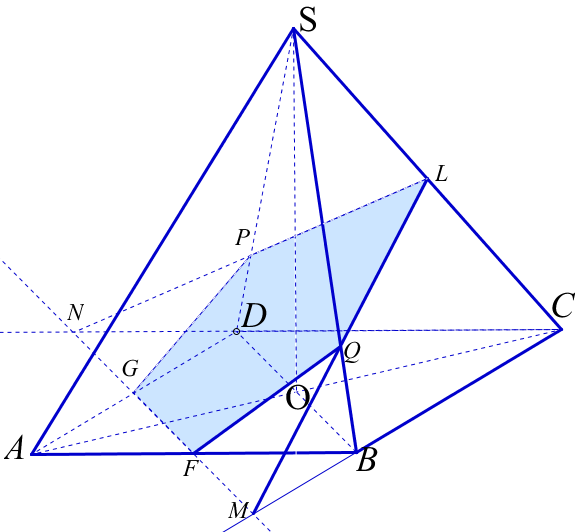
Дано: SABCD - правильная четырехугольная пирамида. G, F, L - середины ребер AD, AB,
CS - соответственно.
РЕШЕНИЕ:
а) Построим сечение.
GF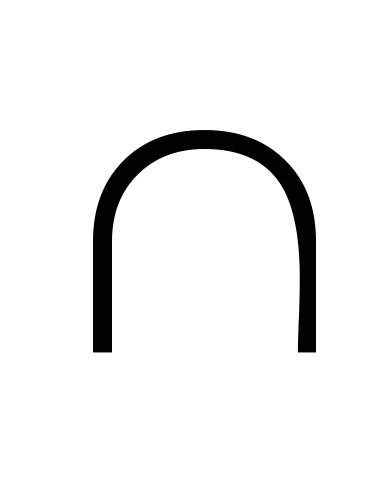 BC= M, GF
BC= M, GF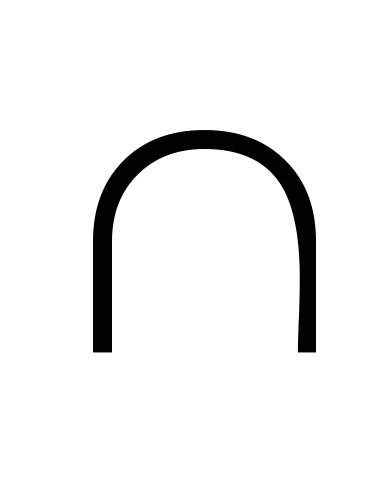 DC=N, ML
DC=N, ML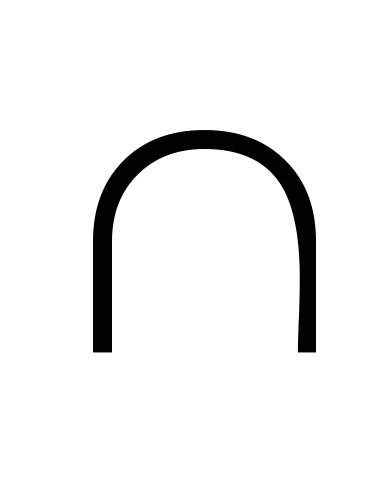 SB=Q, NL
SB=Q, NL SD=P. GFQLP - искомое сечение.
SD=P. GFQLP - искомое сечение.
б) Найдем SQ:QB. Для этого спроецируем все вершины пирамиды на некоторую координатную прямую ОZ, пересекающую плоскость сечения и с началом координат в этой плоскости.
Тогда координаты проекций точек, лежащих в плоскости сечения, будут равны 0.
ZG = ZF = ZQ = ZL = ZP = 0. Пусть ZA = 1, тогда ZB = ZD = -1. 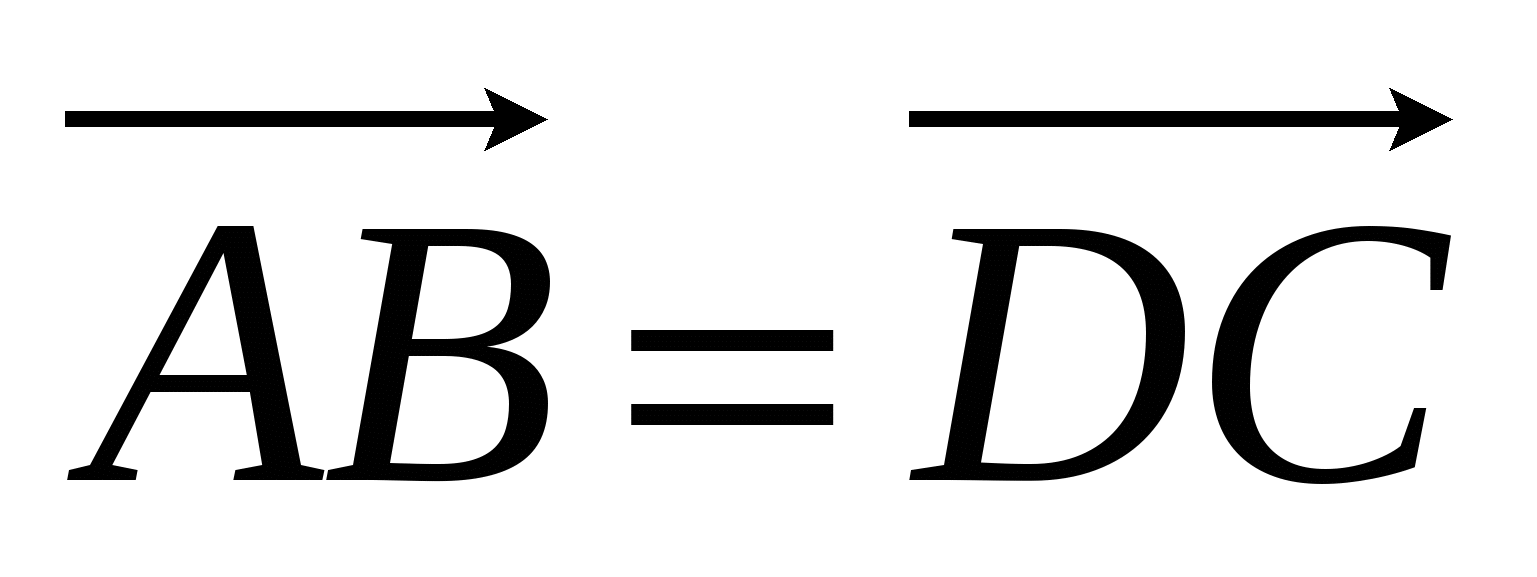
 ZB - ZA = ZC - ZD
ZB - ZA = ZC - ZD  -2 = ZC +1
-2 = ZC +1 ![]() ZC = -3
ZC = -3  ZS = 3. Отсюда имеем, SO : OB =SP : PD = 3 : 1.
ZS = 3. Отсюда имеем, SO : OB =SP : PD = 3 : 1.
в) Найдем какую часть составляет объем многогранника SAFQLPG от объема данной пирамиды. Для этого разобьем многогранник на 4 тетраэдра SAGF, SGFQ, SGQP и SPQL.
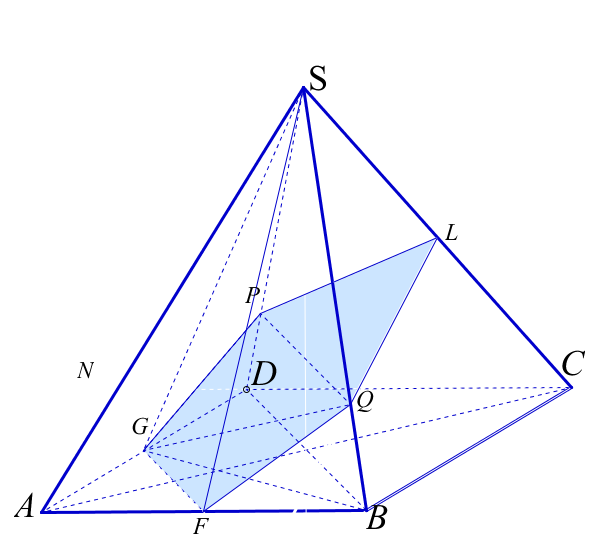
Сравним объемы этих тетраэдров с объемом пирамиды. Для этого воспользуемся теоремой из школьного курса: объемы тетраэдров с общим трехгранным углом относятся как произведение длин ребер, исходящих из вершины трехгранного угла. (Аналог теоремы об отношении площадей треугольников с общим углом).
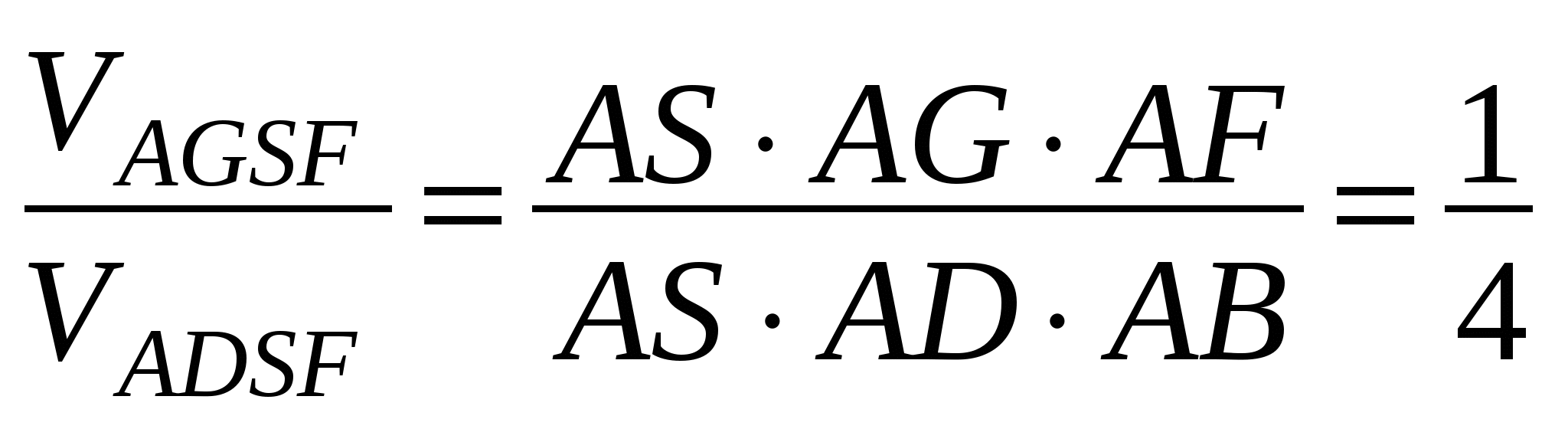 , т.к. VSADB=
, т.к. VSADB= ![]() (площади оснований пирамид относятся как 1 : 2, высота пирамид общая)
(площади оснований пирамид относятся как 1 : 2, высота пирамид общая)  VAGSF =
VAGSF = 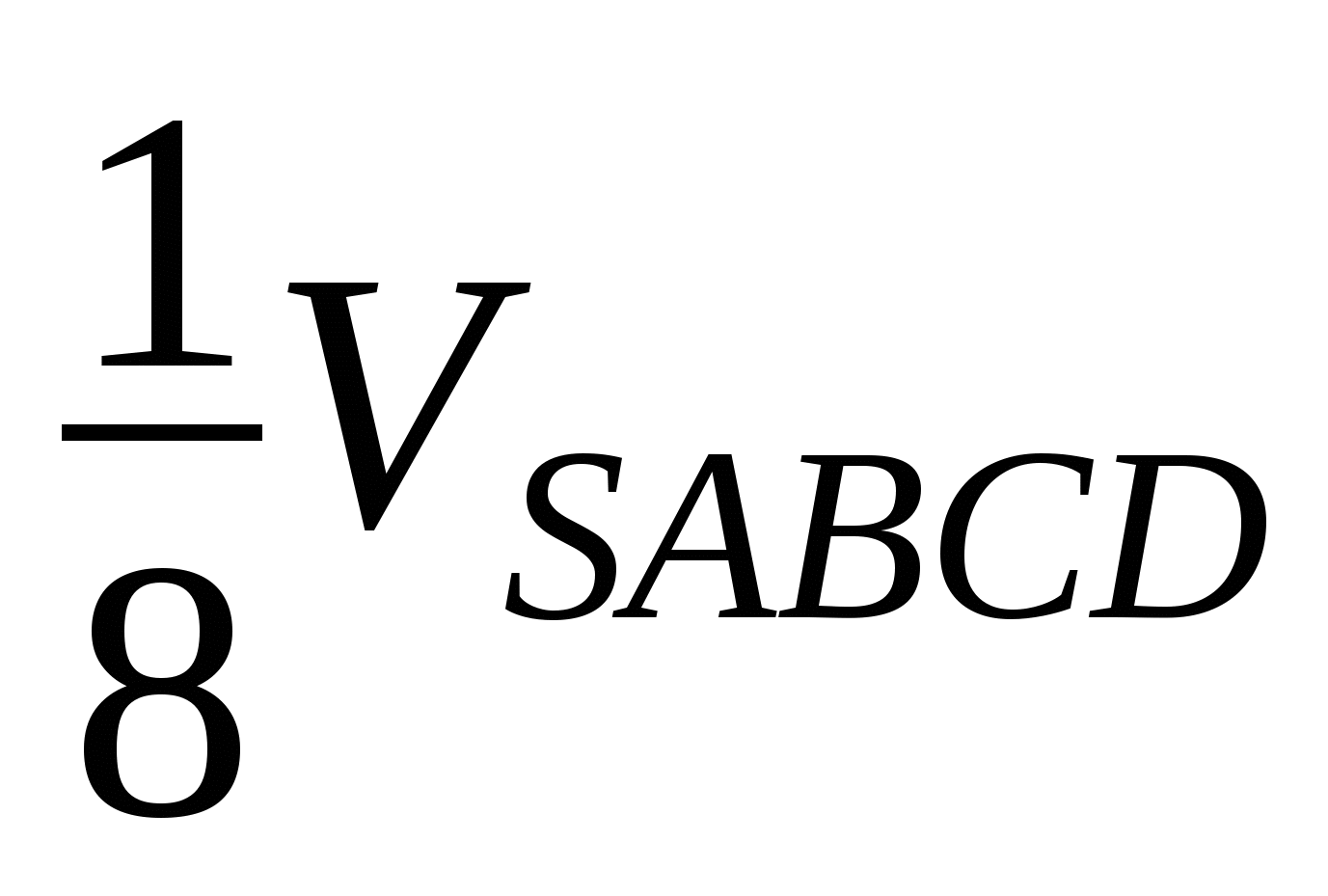 ;
;
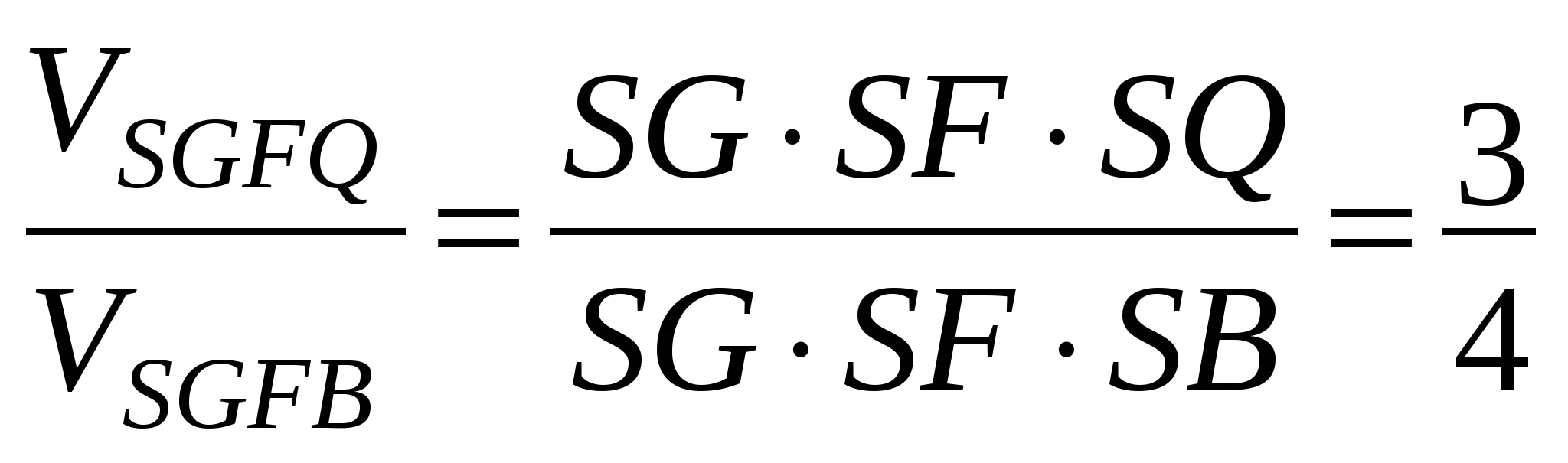 ;
; 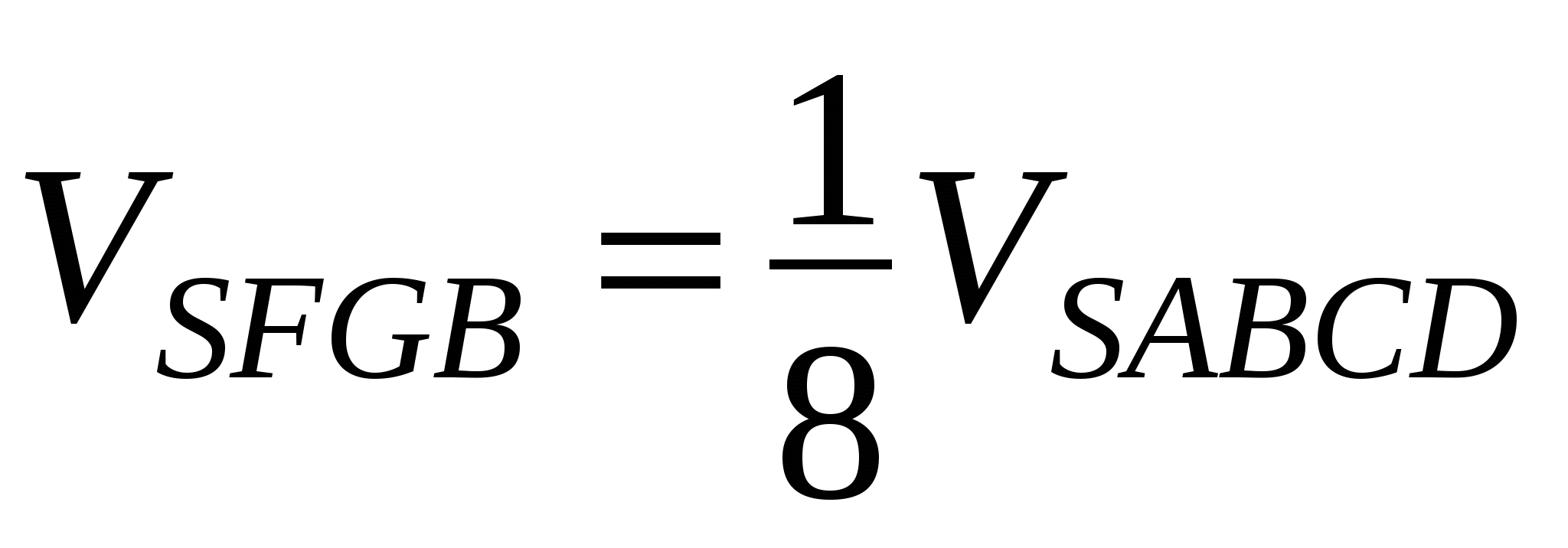 (площади оснований пирамид относятся как 1 : 8, высота пирамид общая)
(площади оснований пирамид относятся как 1 : 8, высота пирамид общая) 
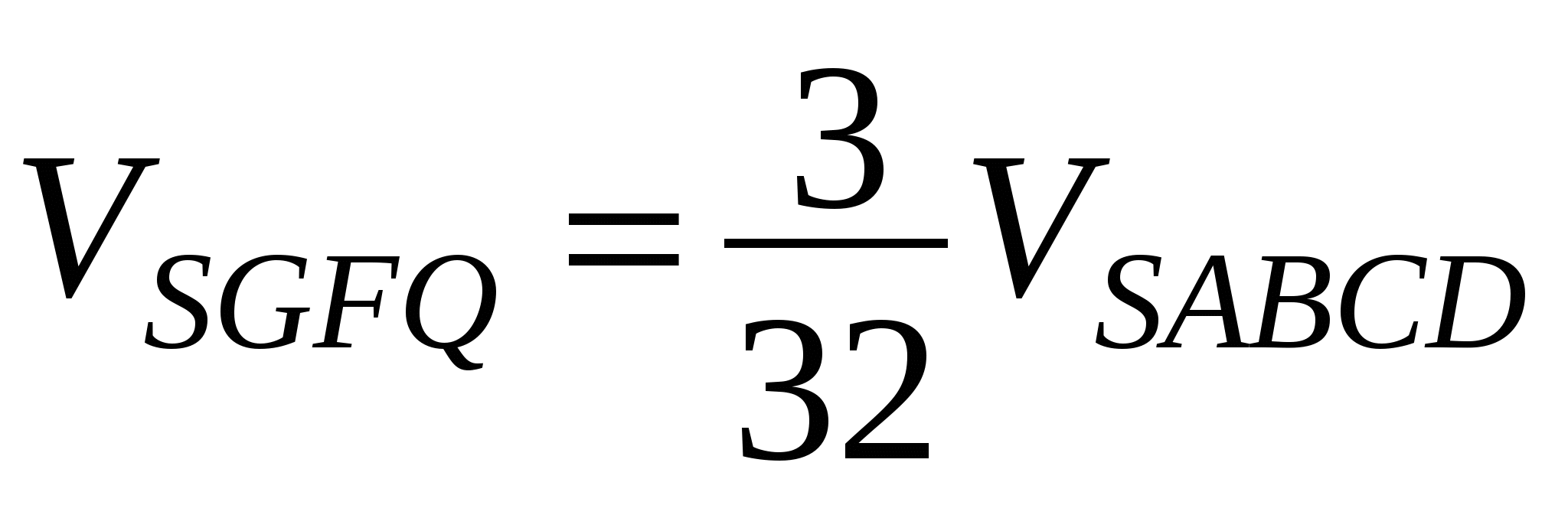 ;
;
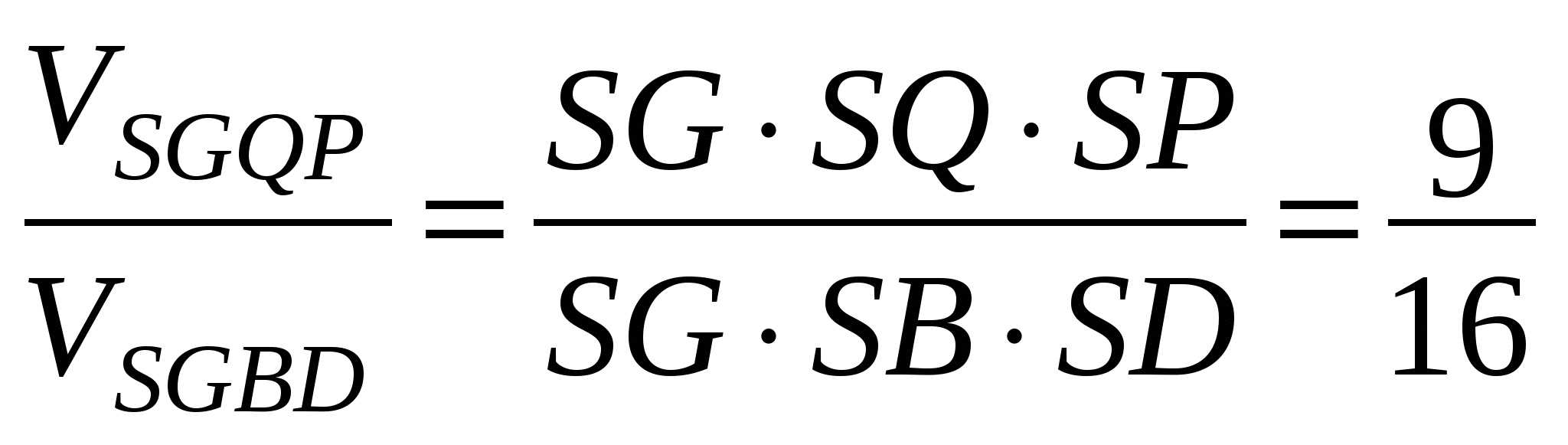 ;
;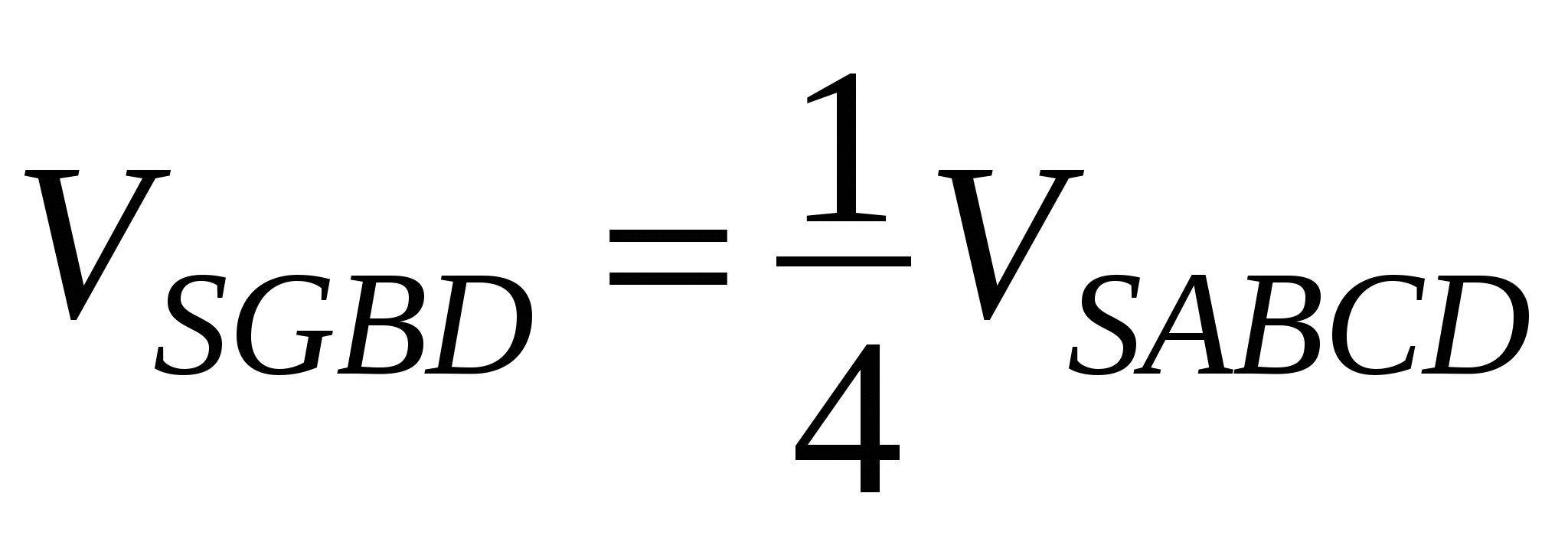 (площади оснований пирамид относятся как 1 : 4, высота пирамид общая)
(площади оснований пирамид относятся как 1 : 4, высота пирамид общая) 
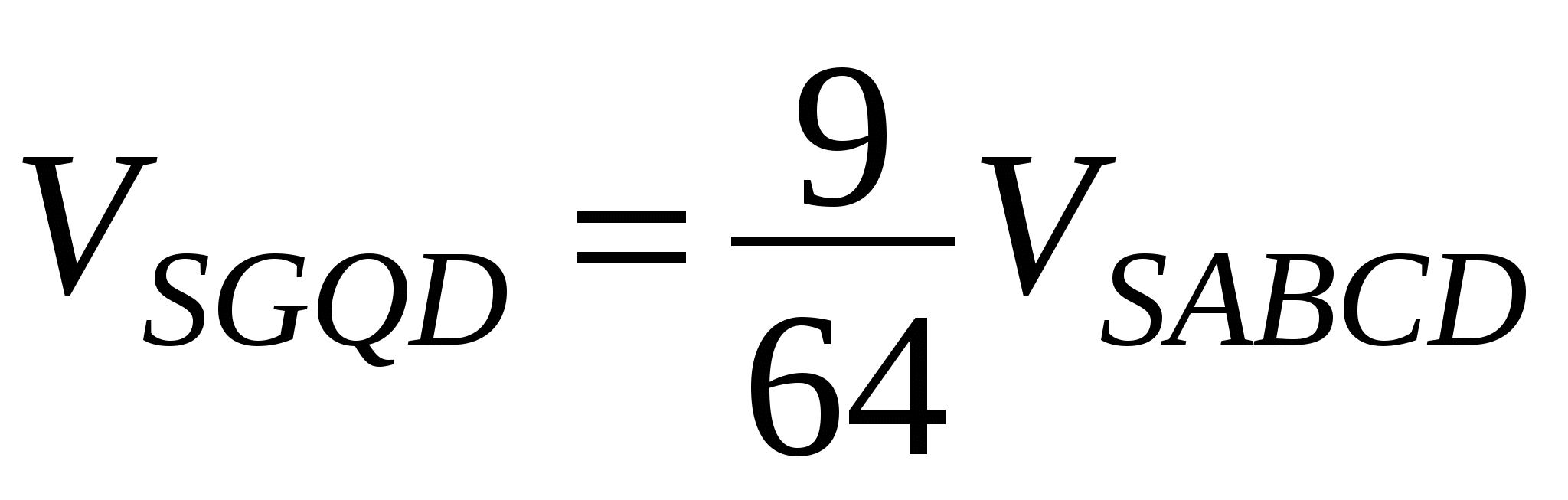 ;
;
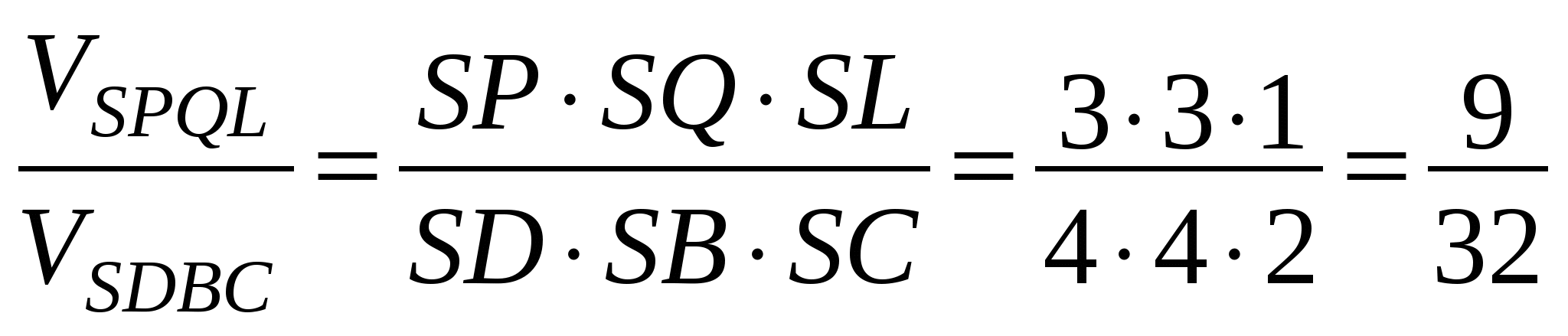 ;
;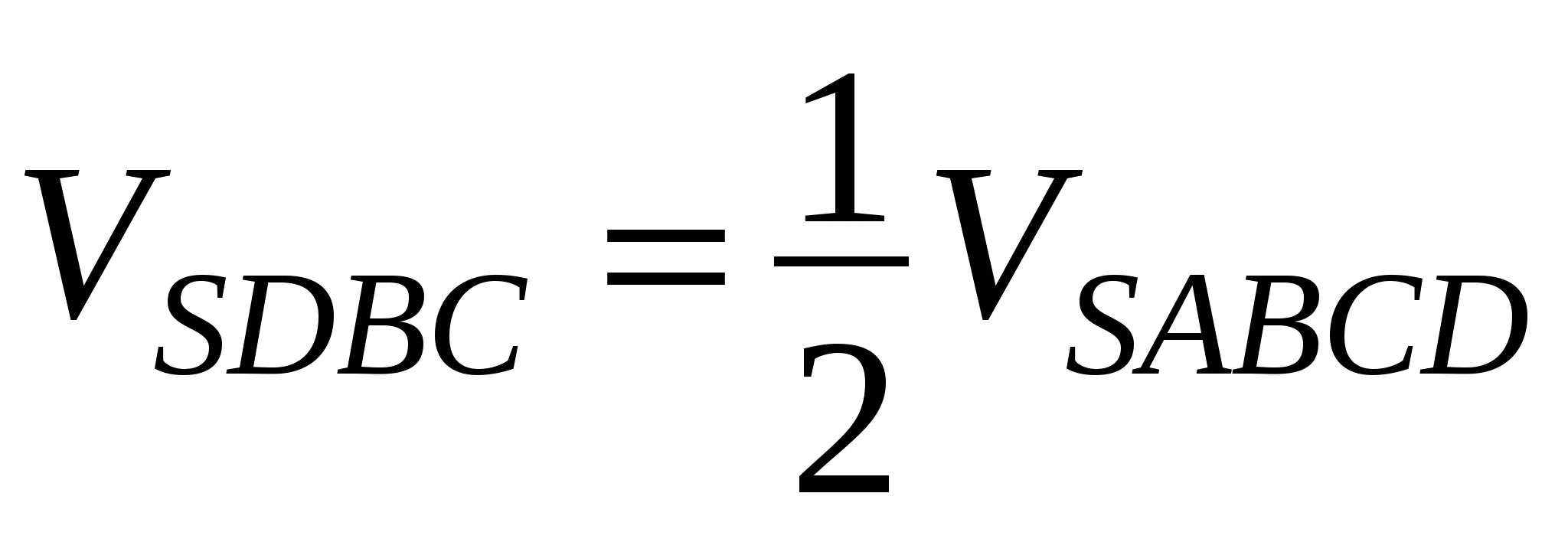 (площади оснований пирамид относятся как 1 : 2, высота пирамид общая)
(площади оснований пирамид относятся как 1 : 2, высота пирамид общая) 
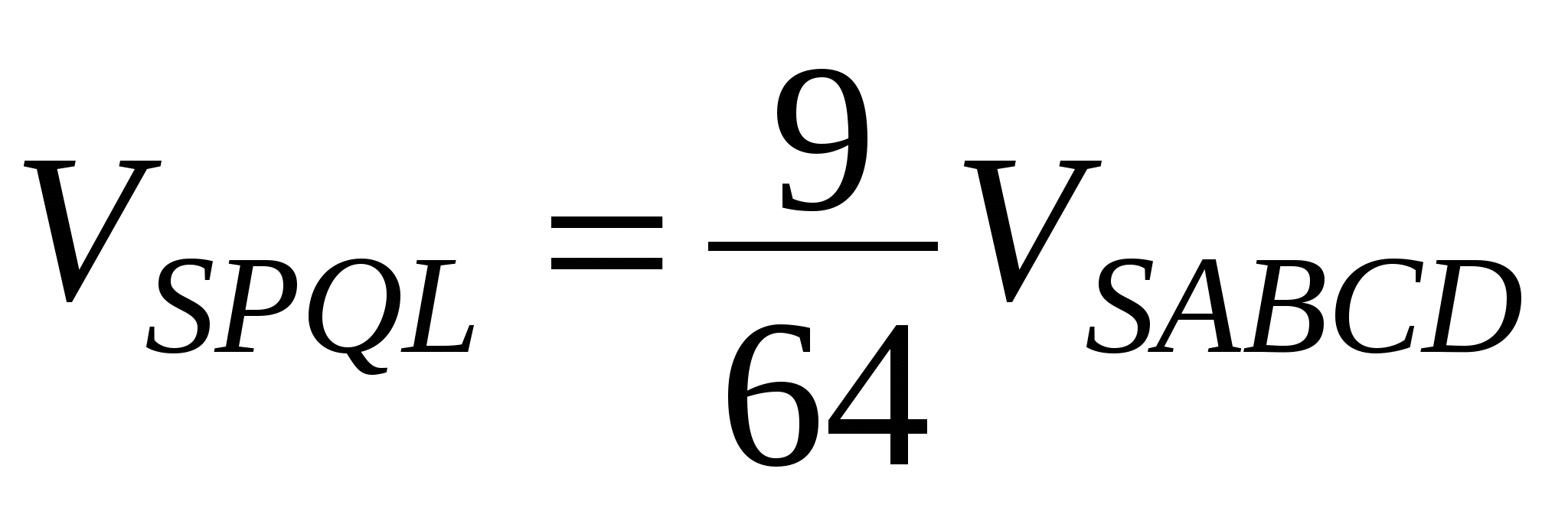 ;
;
Итак, VSAFQLPG = 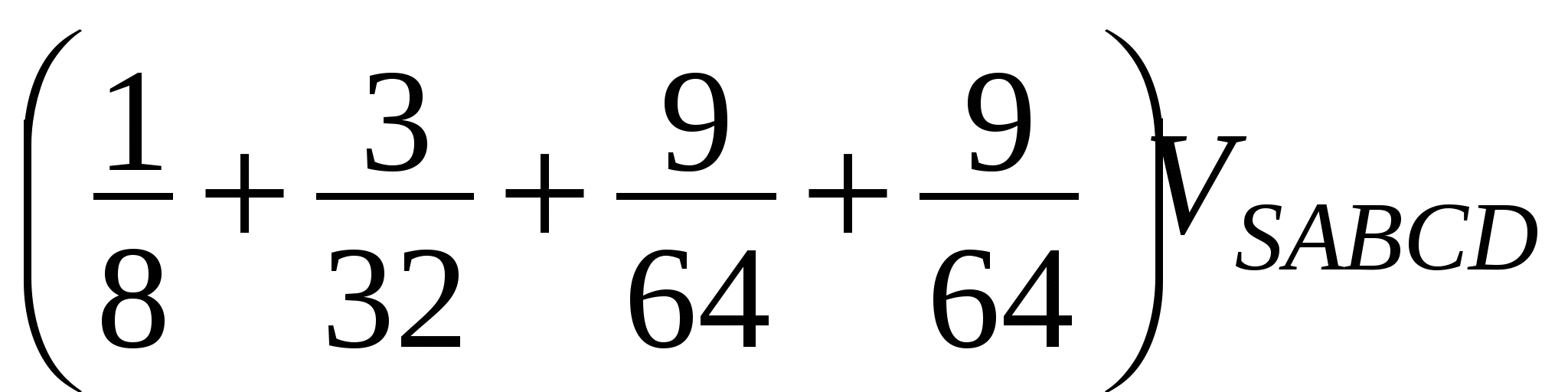 =
= 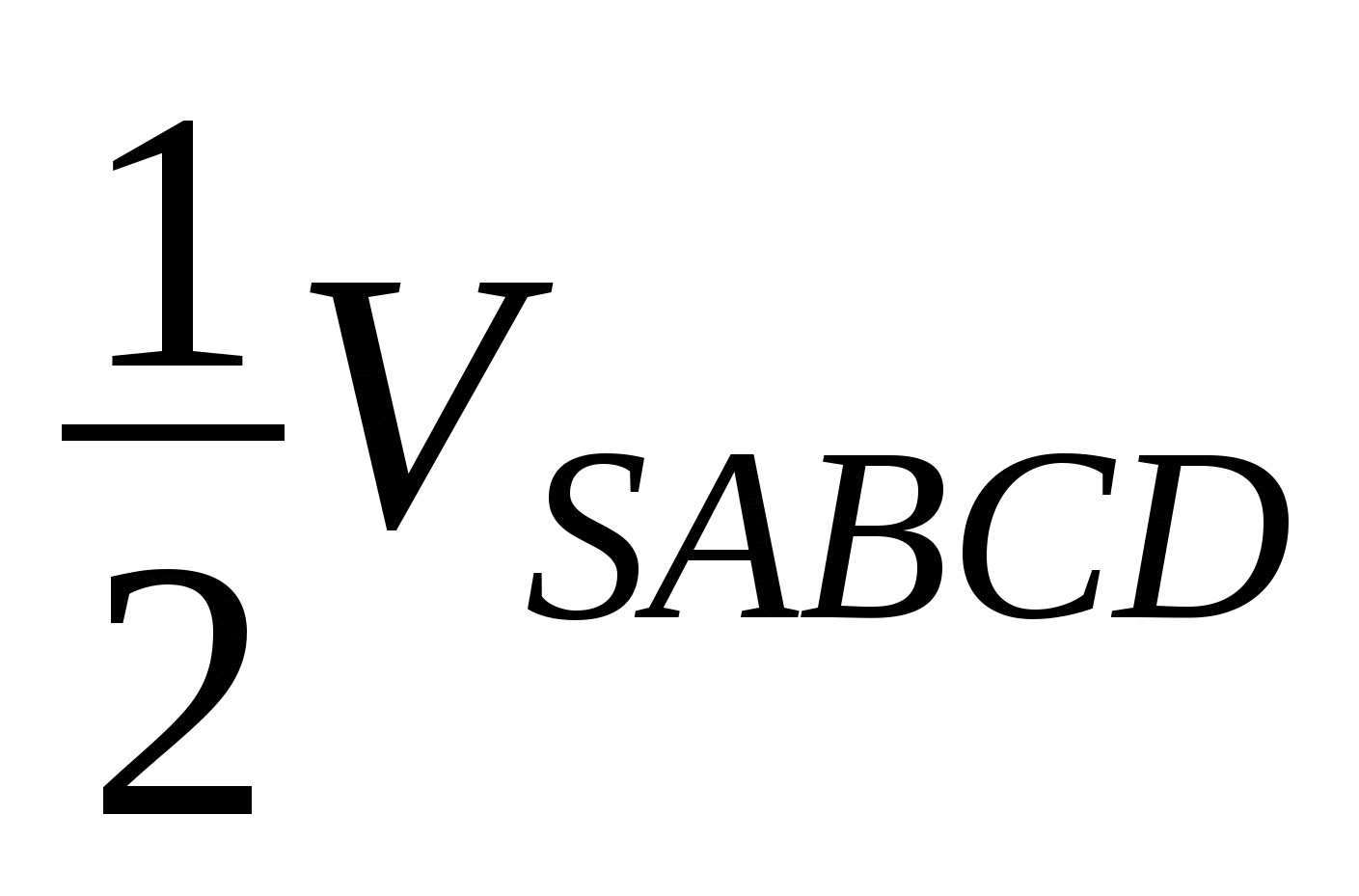 , т.е. сечение разбивает объем пирамиды в отношении 1 : 1.
, т.е. сечение разбивает объем пирамиды в отношении 1 : 1.
Заметим, что при решении данной задачи не использовались линейные размеры пирамиды и ее правильность. Решение не изменится, если в основании будет лежать параллелограмм, а высота пирамиды не будет проектироваться в точку пресечения диагоналей.
ОТВЕТ: 1 : 1
7. Незнайка хочет забраться на крышу своего дома по приставной лестнице. В чулане лежит много лестниц, но у большинства из них не хватает ступенек. По лестницам, у которых отсутствуют две ступеньки подряд, Незнайка забраться не может. Все его лестницы изначально были с N ступенями. У всех лестниц четко определен верх и низ. Причём нет одинаковых лестниц, и все возможные лестницы, имеются в наличии. Какова вероятность, что Незнайка сможет забраться на крышу по случайно выбранной лестнице.
РЕШЕНИЕ:
По классическому определению вероятности: 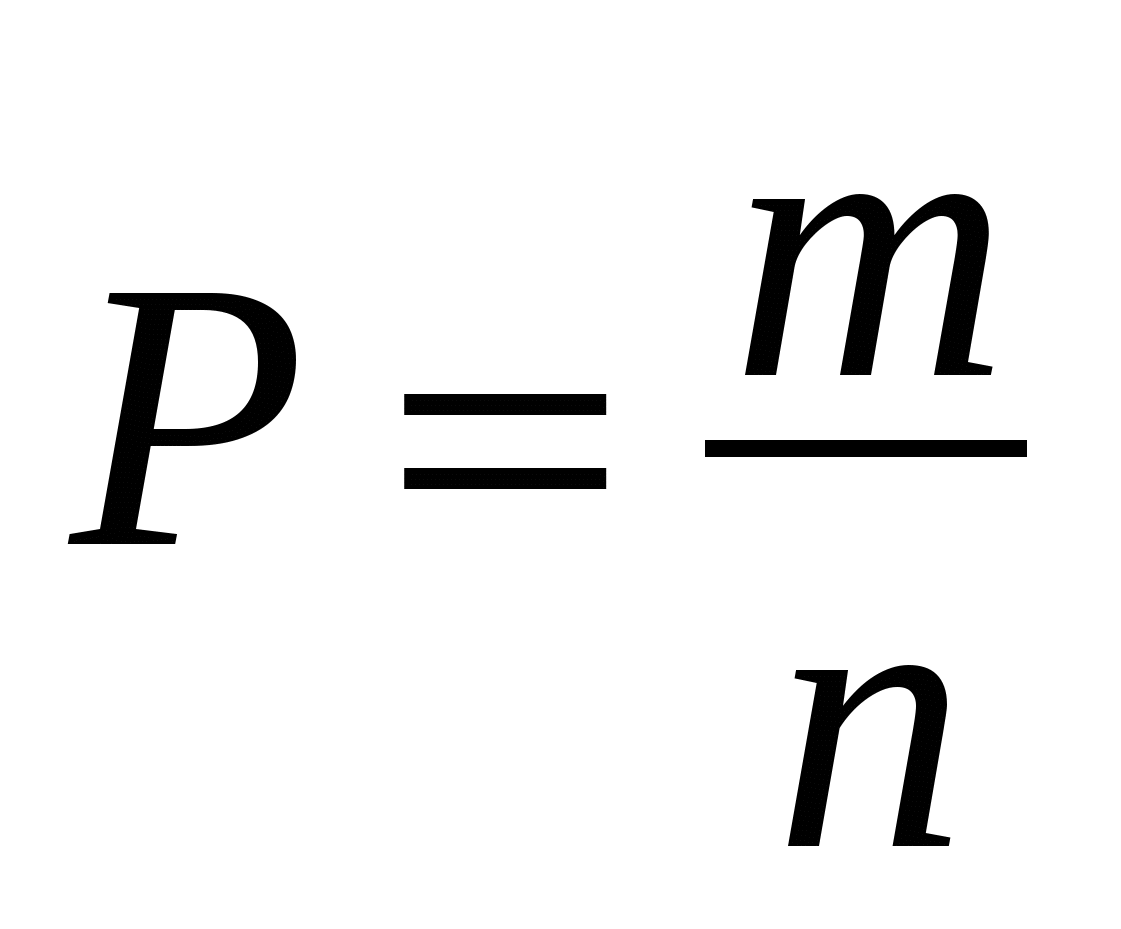 , где
, где
n - общее количество всех возможных лестниц;
m - количество лестниц по которым Незнайка сможет забраться на крышу (те, у которых нет отсутствующих двух подряд ступенек).
Найдем сначала n.
Обозначим за 1 - ступенька есть, 0 - ступенька отсутствует.
Тогда лестницы превращаются в некоторую последовательность из 0 и 1. Изначально на каждой лестнице было по N ступенек, причём каждая ступенька может принимать только два значения: 0 или 1 (есть или отсутствует), даже крайние  всех возможных вариантов лестниц будет
всех возможных вариантов лестниц будет 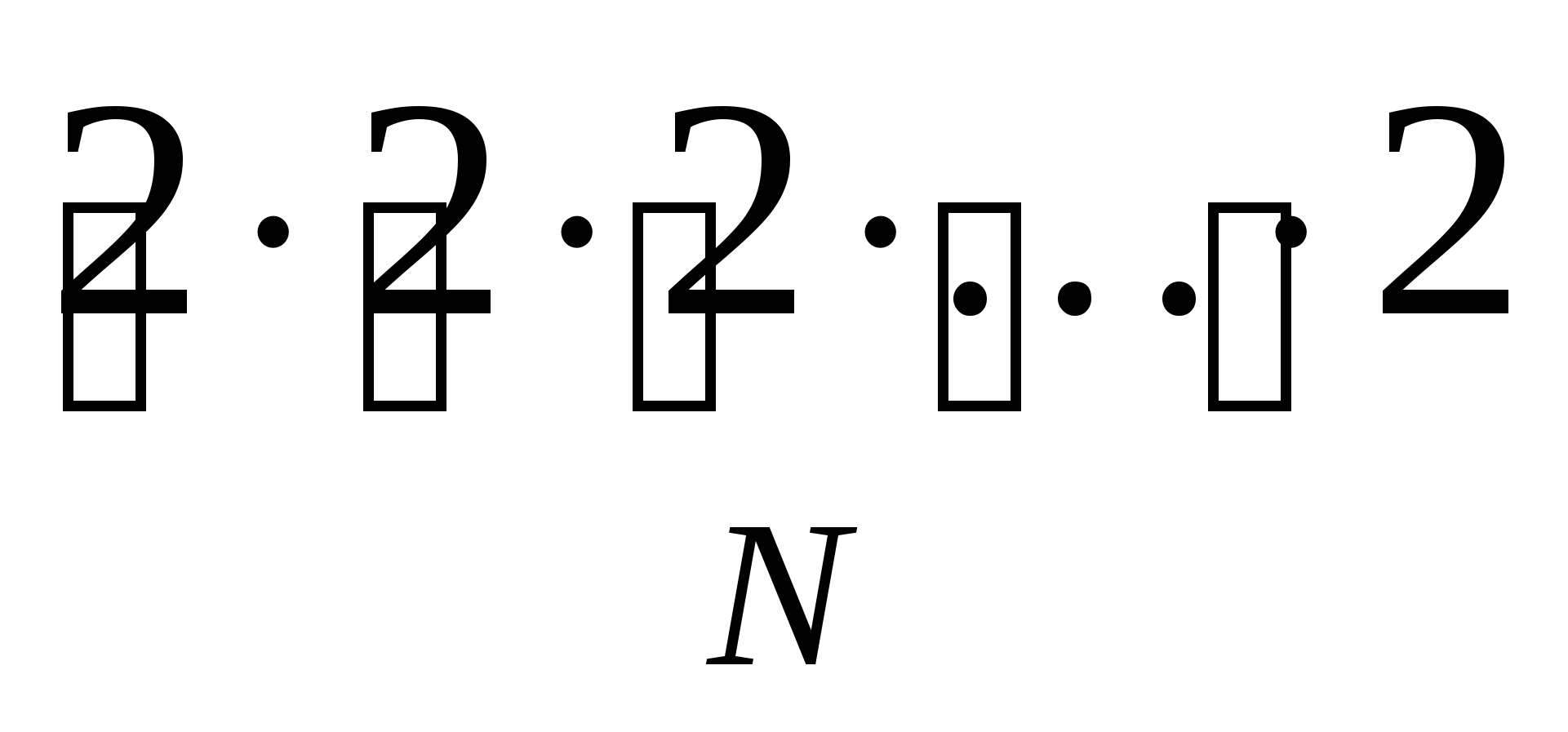
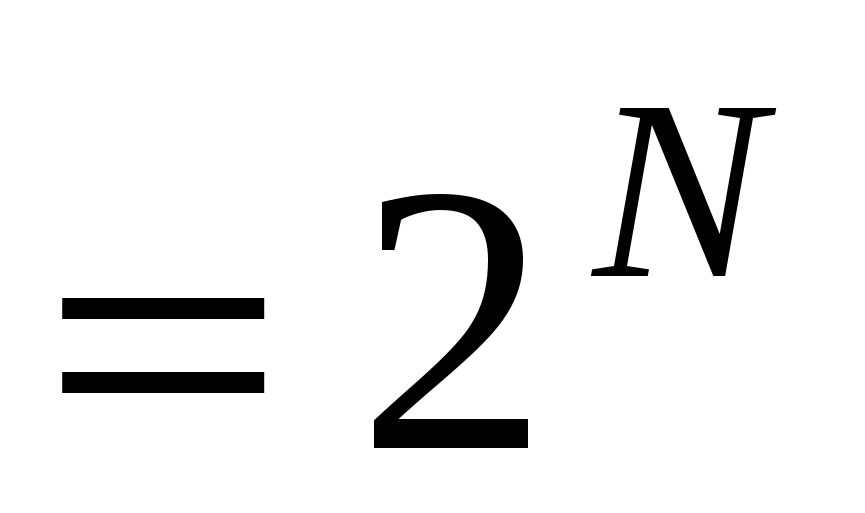 (по правилу произведения).
(по правилу произведения).
Получили, что n![]() . Найдём теперь m.
. Найдём теперь m.
Сколько может быть таких последовательностей из 0 и 1, чтобы не было двух нулей подряд?
Пусть таких последовательностей 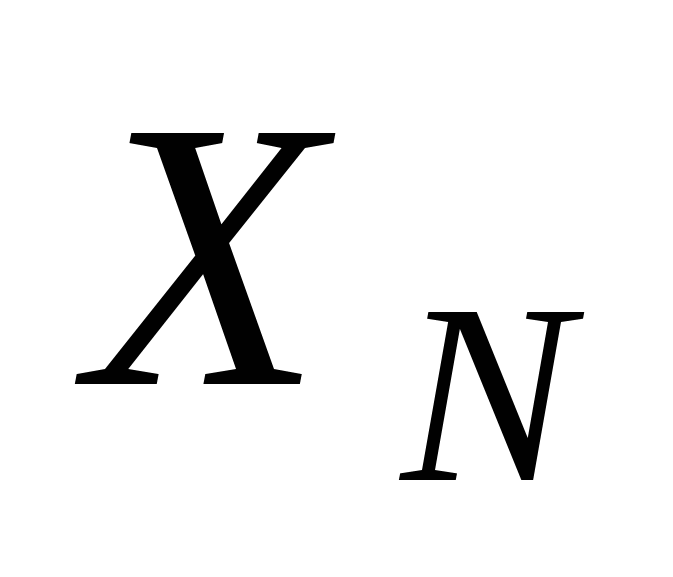 , тогда
, тогда 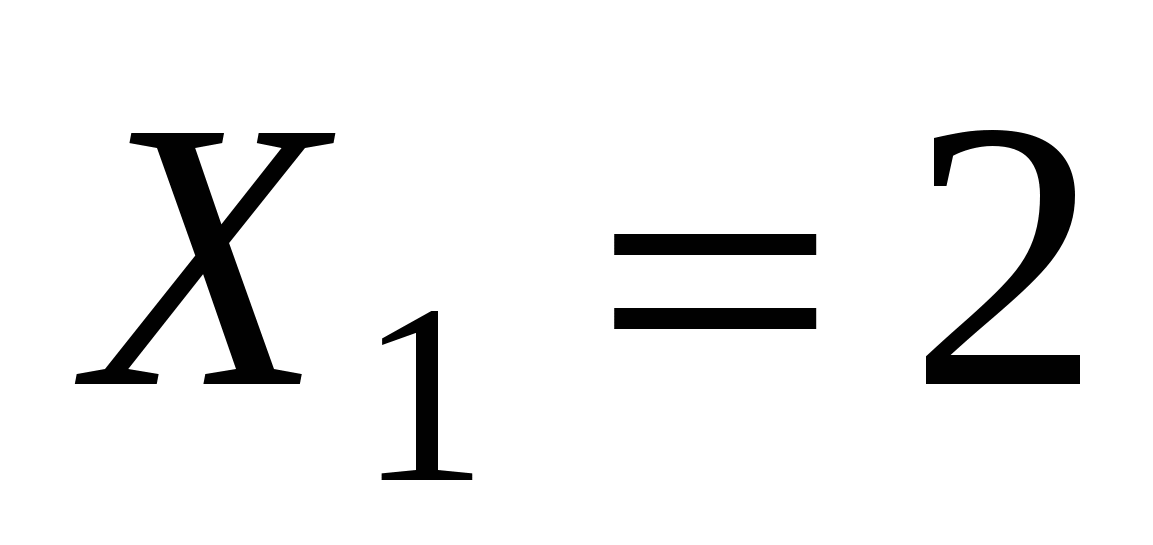 (0 или 1),
(0 или 1), 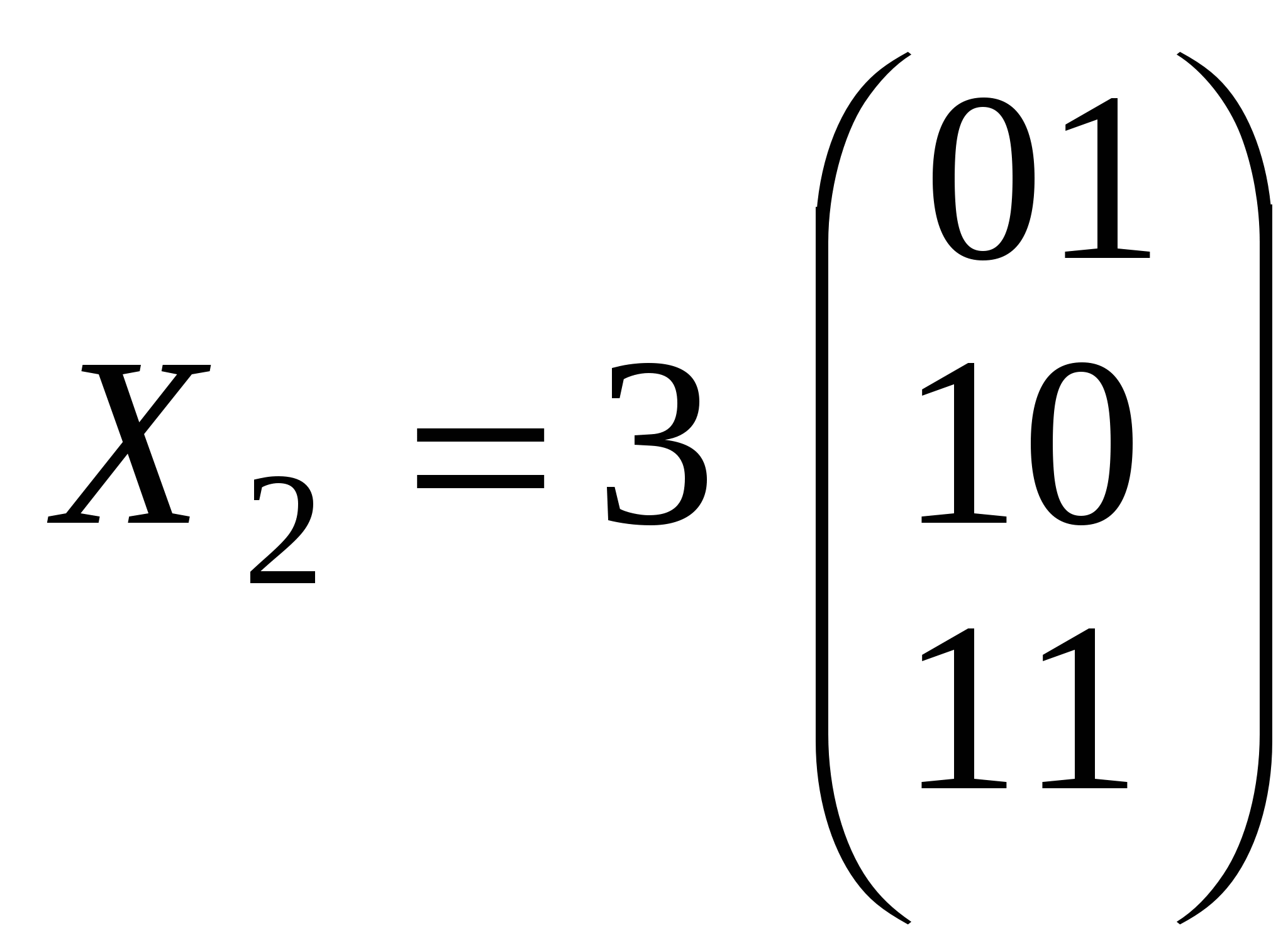 , т.к. вариант 00 нам не подходит.
, т.к. вариант 00 нам не подходит.
Рассмотрим теперь последовательность длины N:
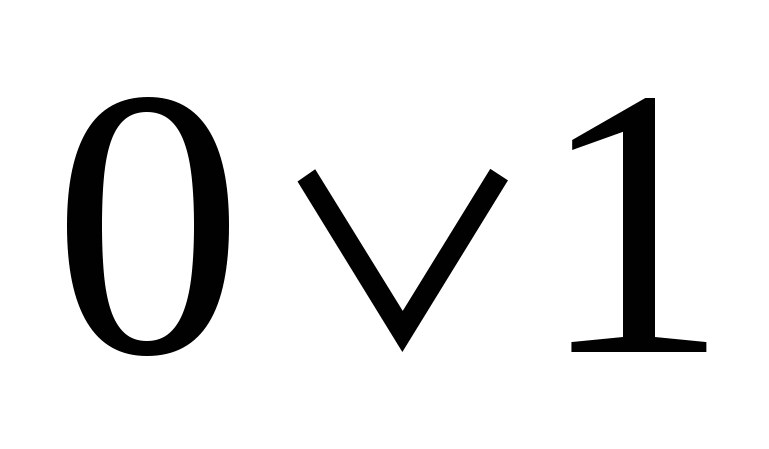
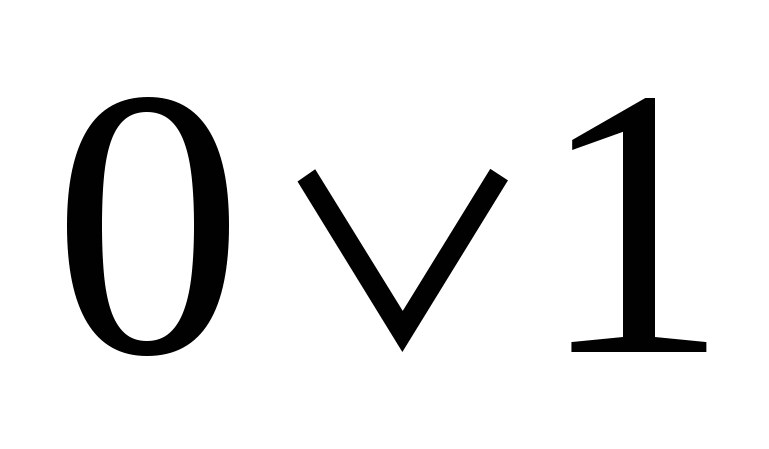
…
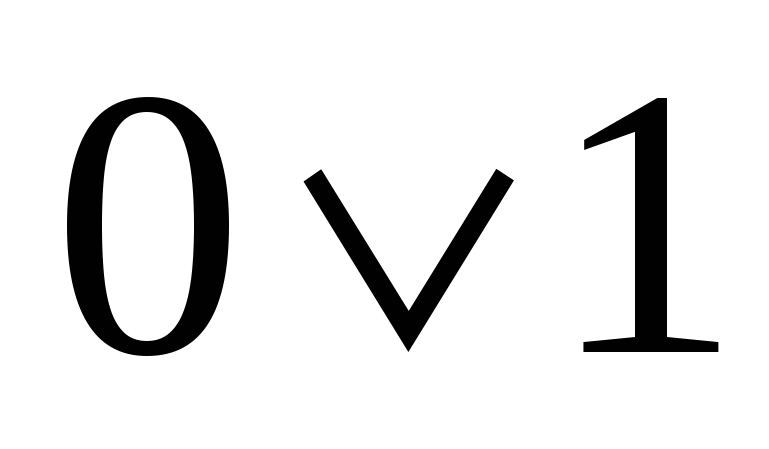
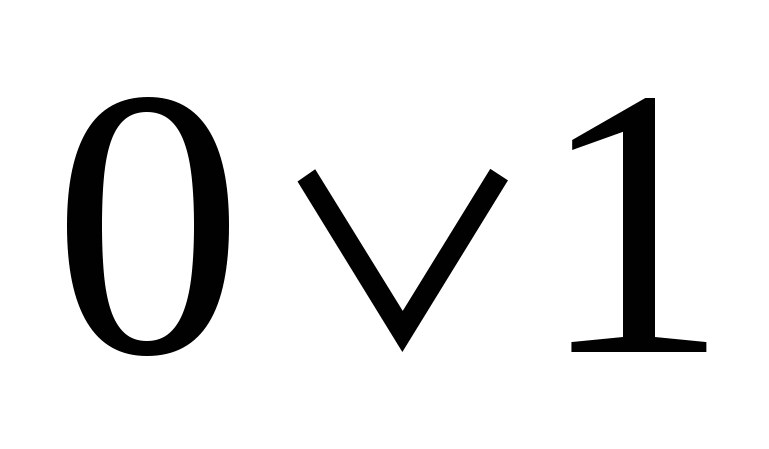
11) Если последняя цифра в этой последовательности 1 (т.е. ступенька есть), то перед ней может быть любая последовательность из 0 и 1, удовлетворяющая условию, что нет двух подряд нулей.

N-1
Т аких вариантов последовательностей будет
аких вариантов последовательностей будет 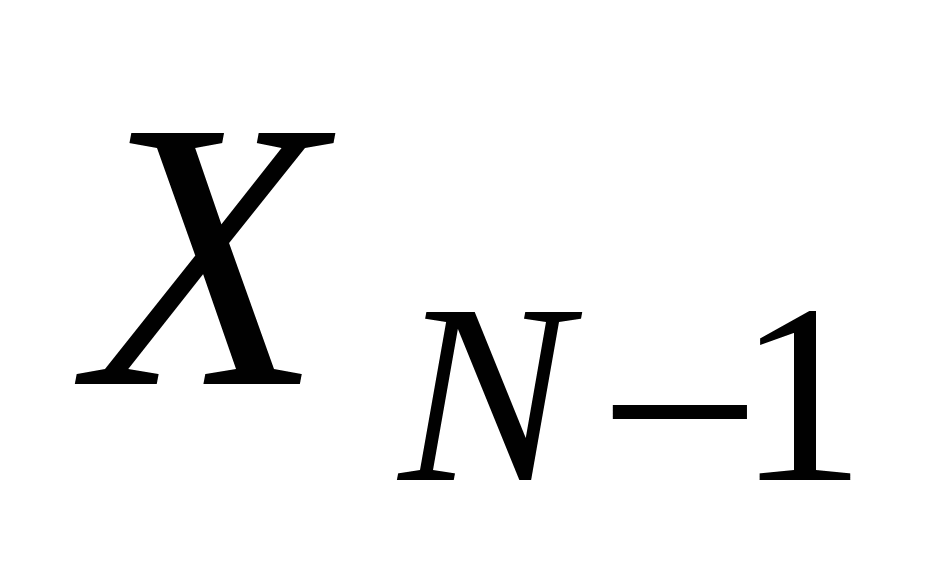 (из
(из 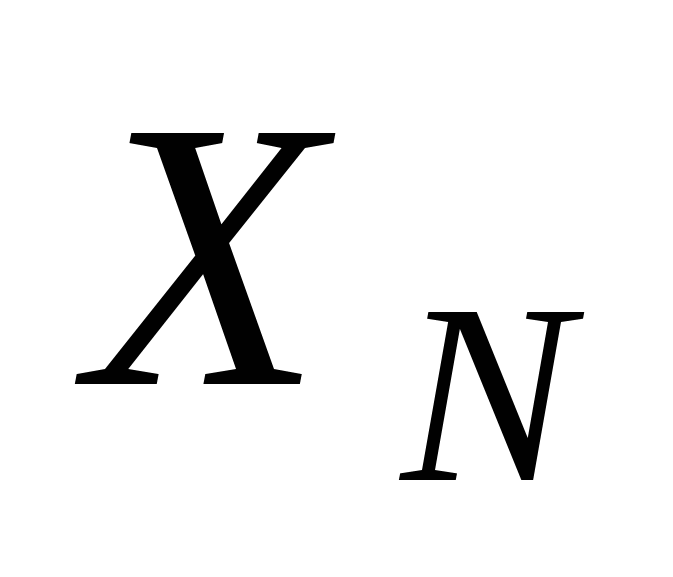 убрали последнюю ступеньку).
убрали последнюю ступеньку).
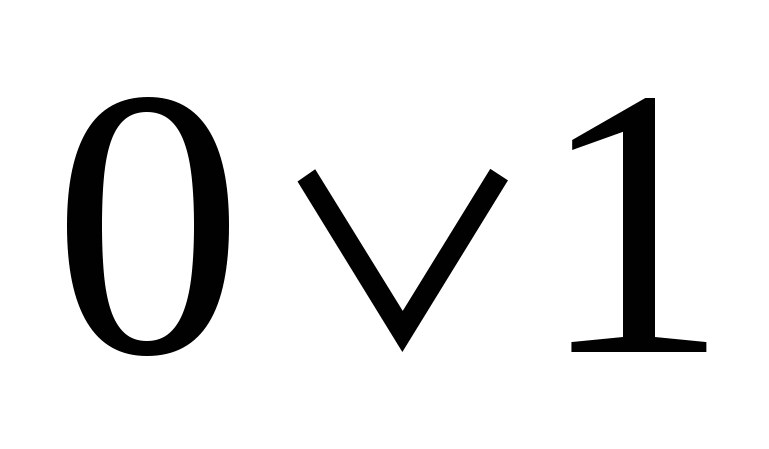
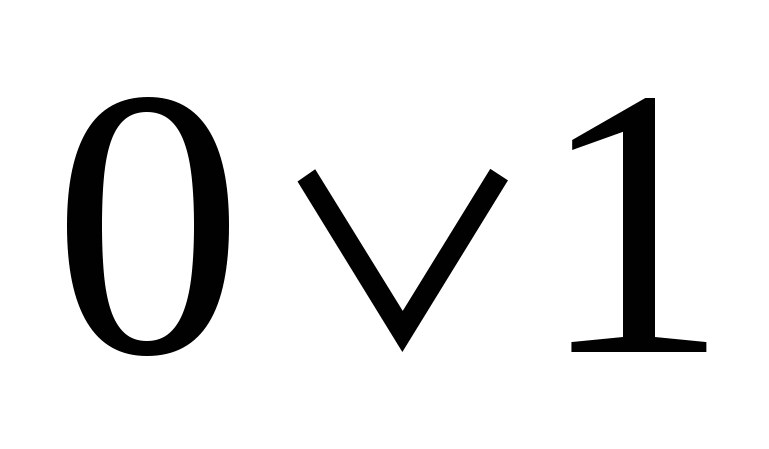
…
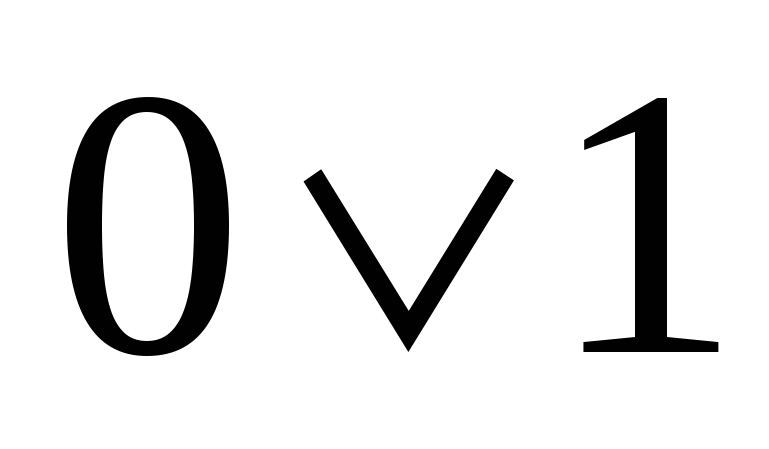
1
02) Если последняя цифра в этой последовательности 0 (т.е. ступенька отсутствует), то перед ней может быть только 1, т.к. не должно быть двух подряд нулей. А перед этой 1 опять может быть любая последовательность из 0 и 1, удовлетворяющая условию, что нет двух подряд нулей.
N-2
Таких вариантов последовательностей будет 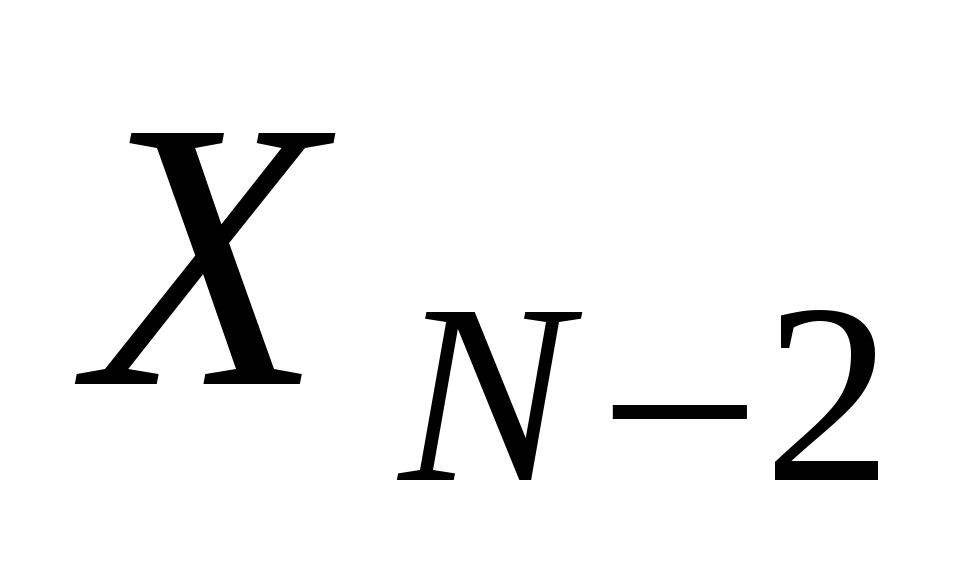 (из
(из 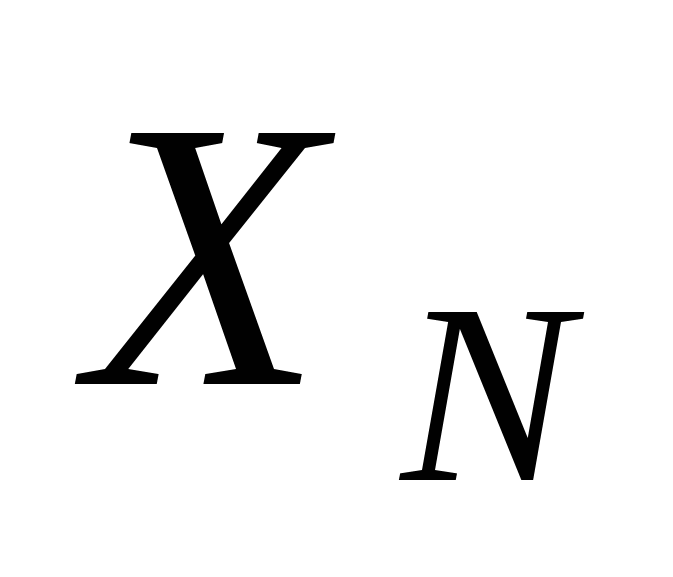 убрали две последних ступеньки).
убрали две последних ступеньки).
А всё вместе - это все возможные последовательности длины N. Тогда по правилу суммы:
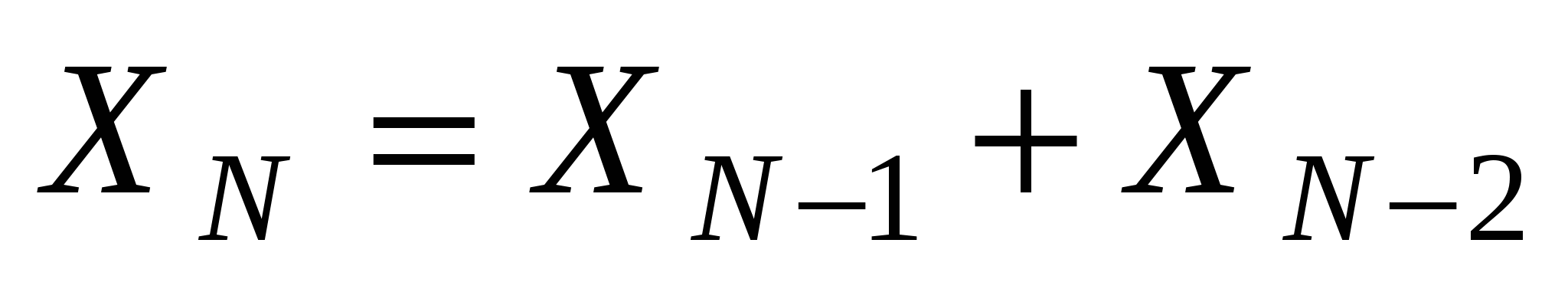 , а это известный ряд чисел Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34, …), начиная с N + 2.
, а это известный ряд чисел Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34, …), начиная с N + 2. ![]()
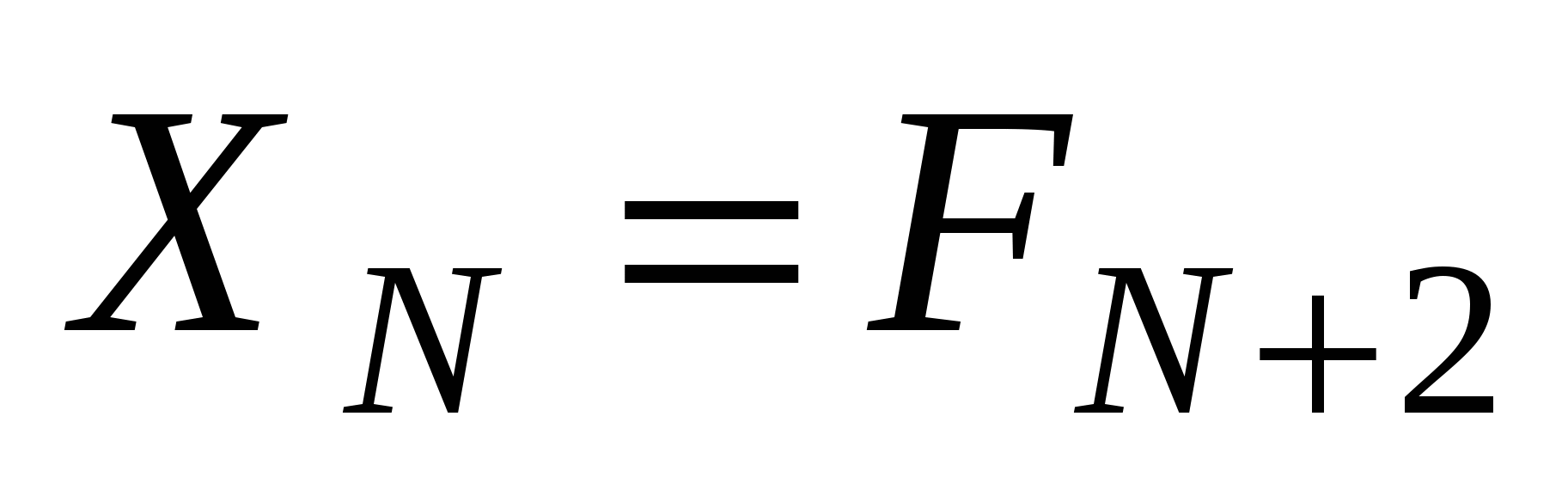 , т.е.
, т.е. 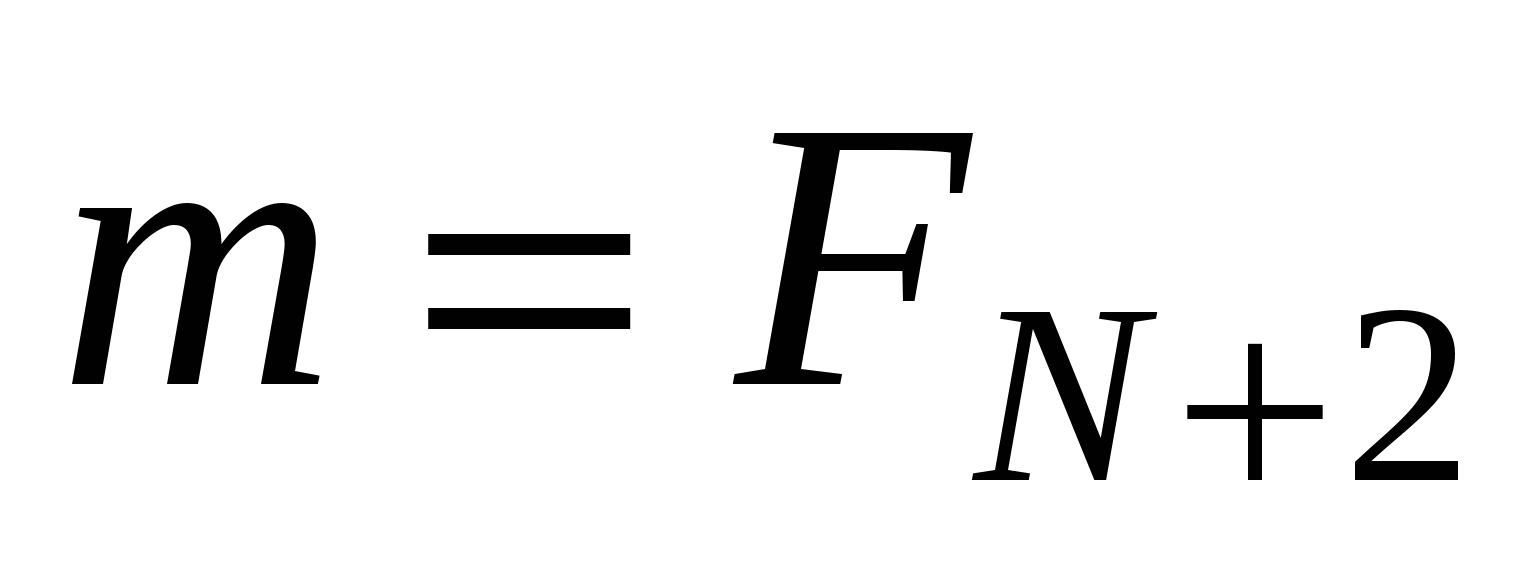 .
.
Тогда искомая вероятность 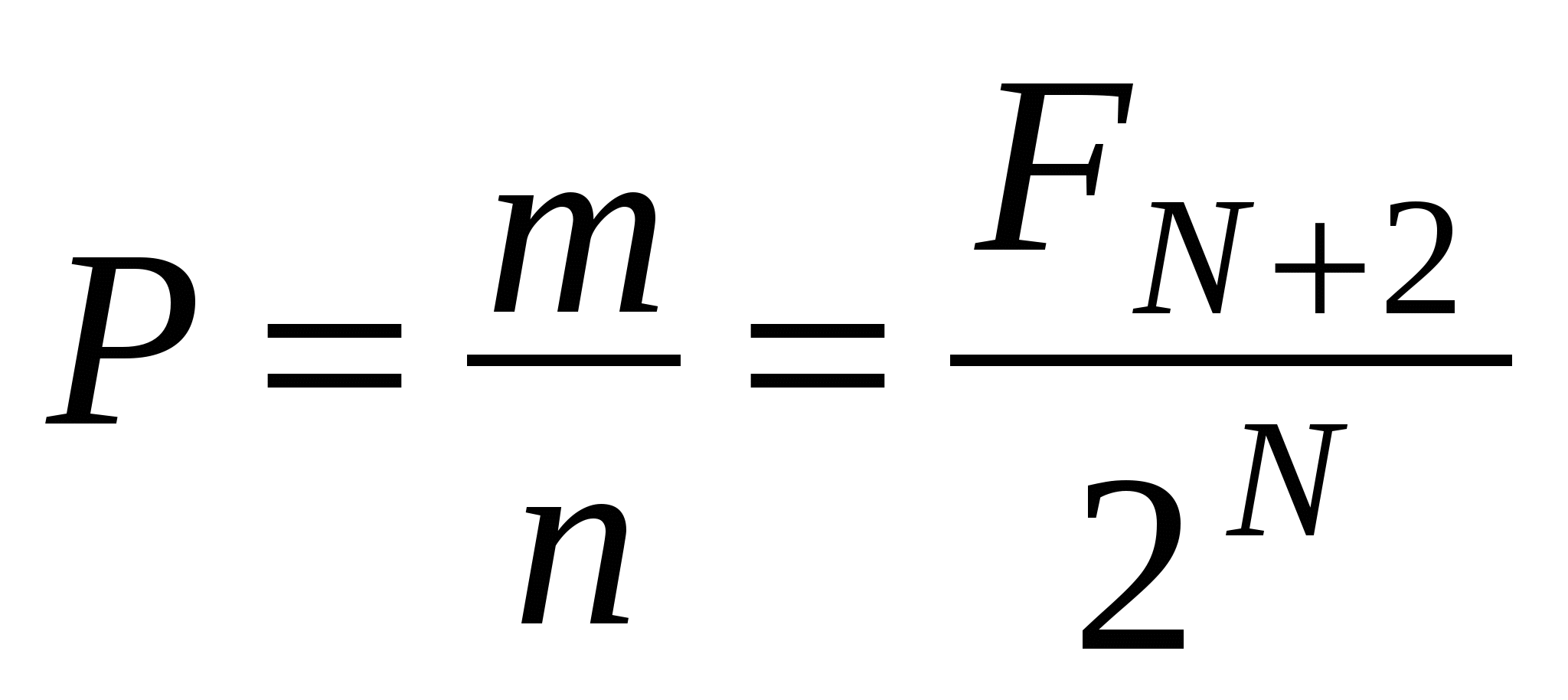 .
.
Итак, получили, что если N = 1, то 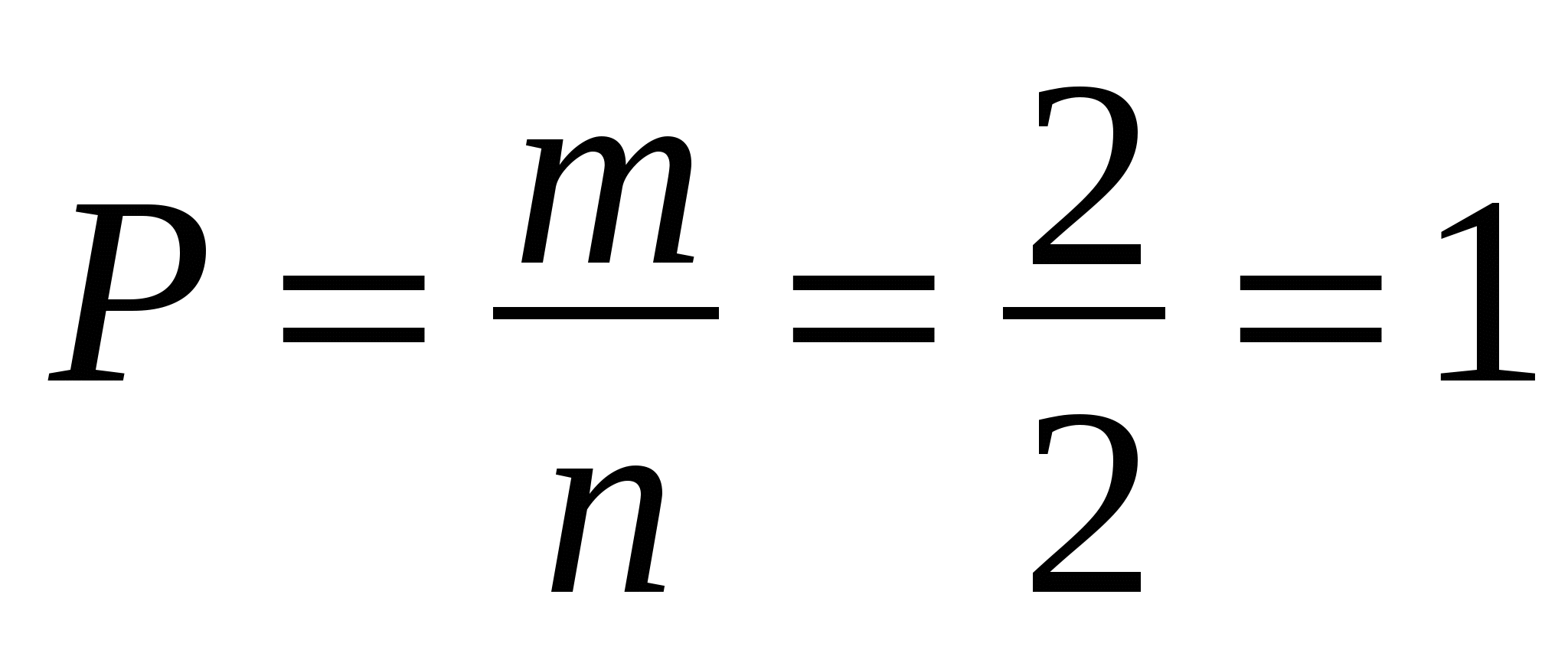 . Для N = 2,
. Для N = 2, 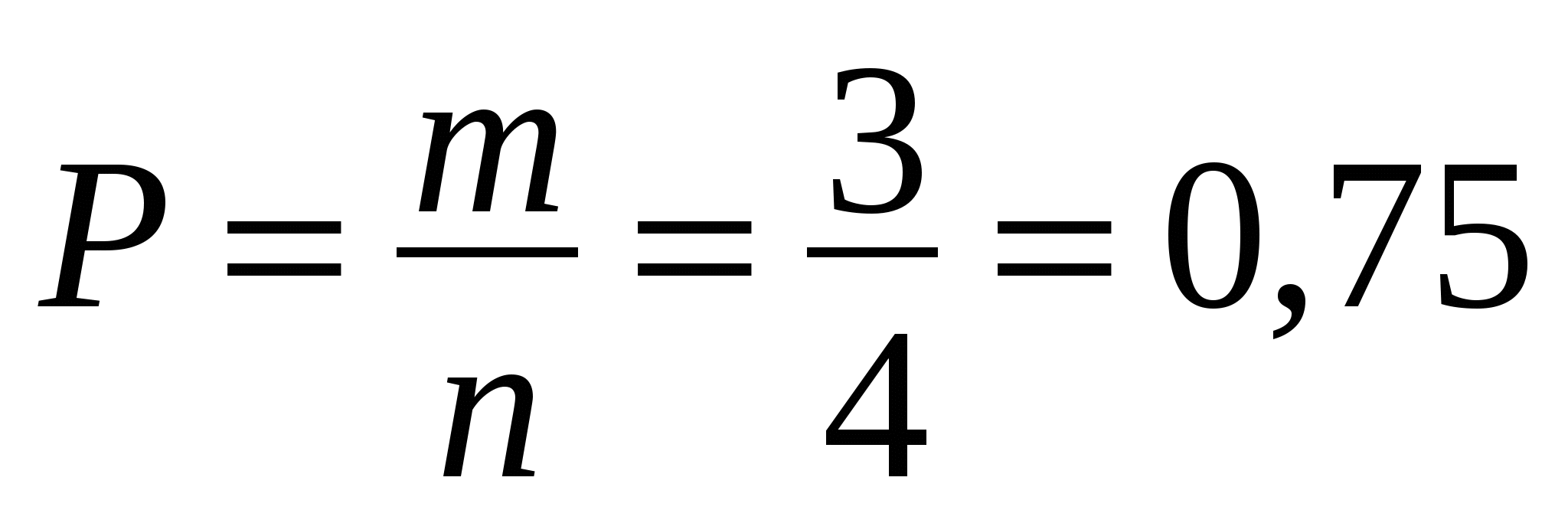 .
.
Для 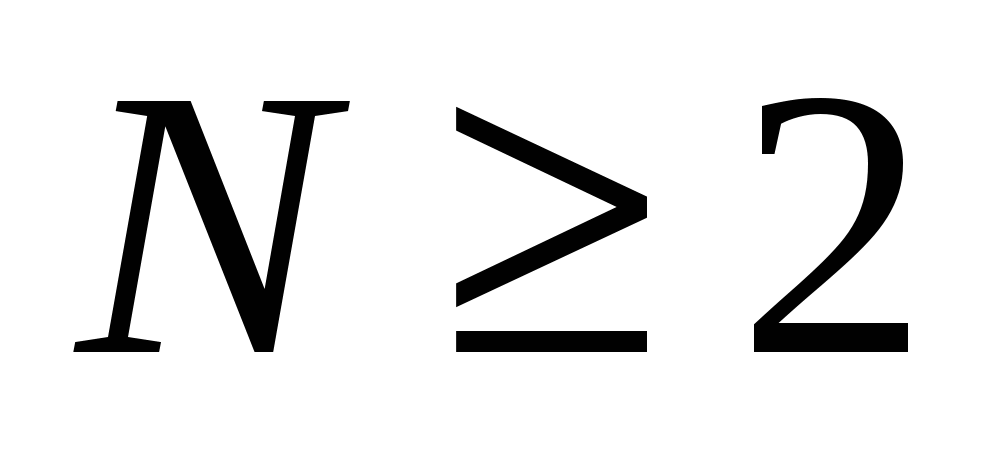 ,
,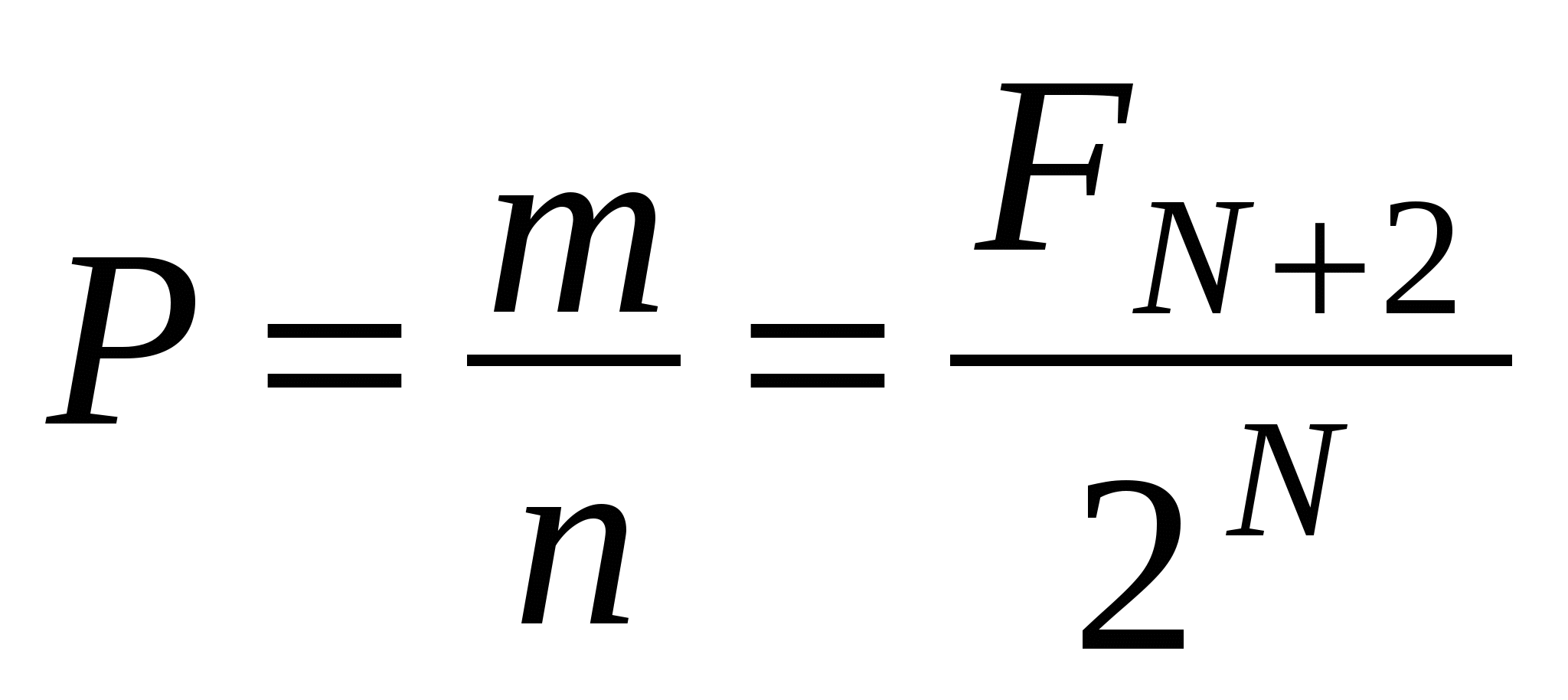 .
.
Проверим для примера формулу вероятности для N = 3.
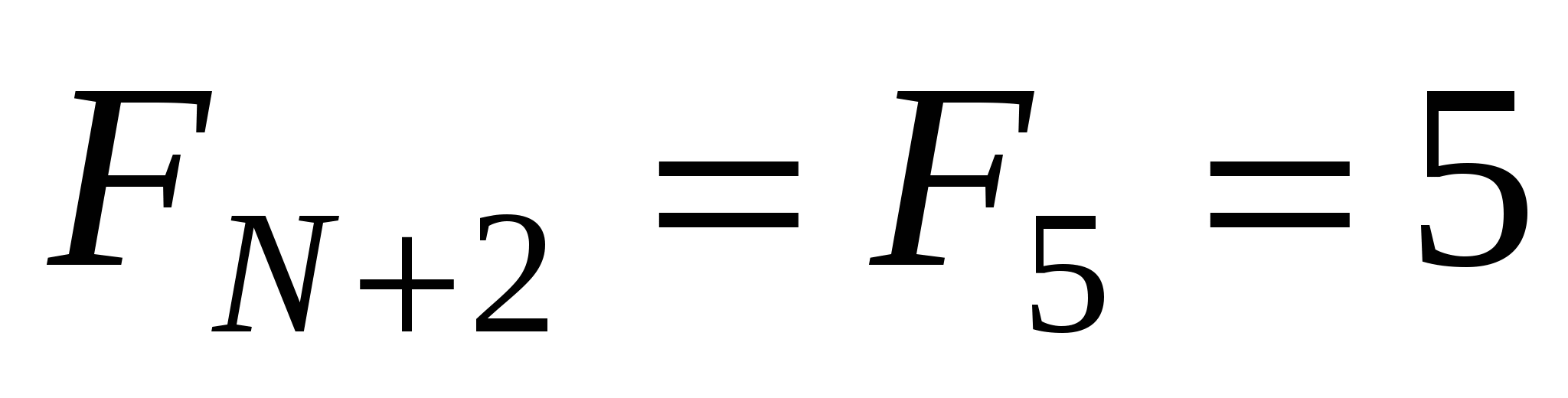 ,
, 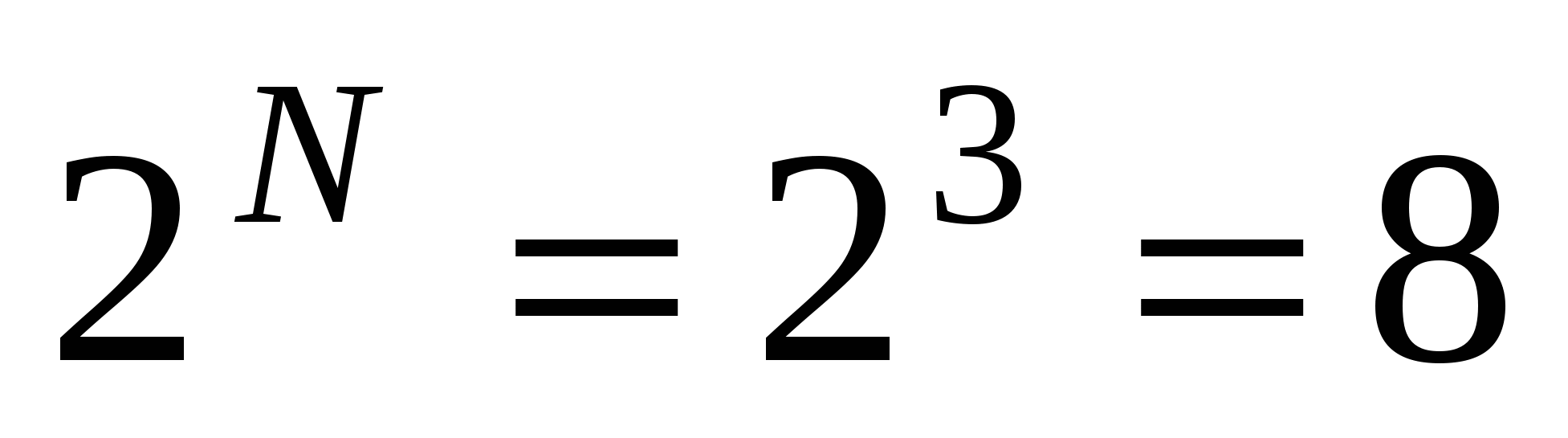

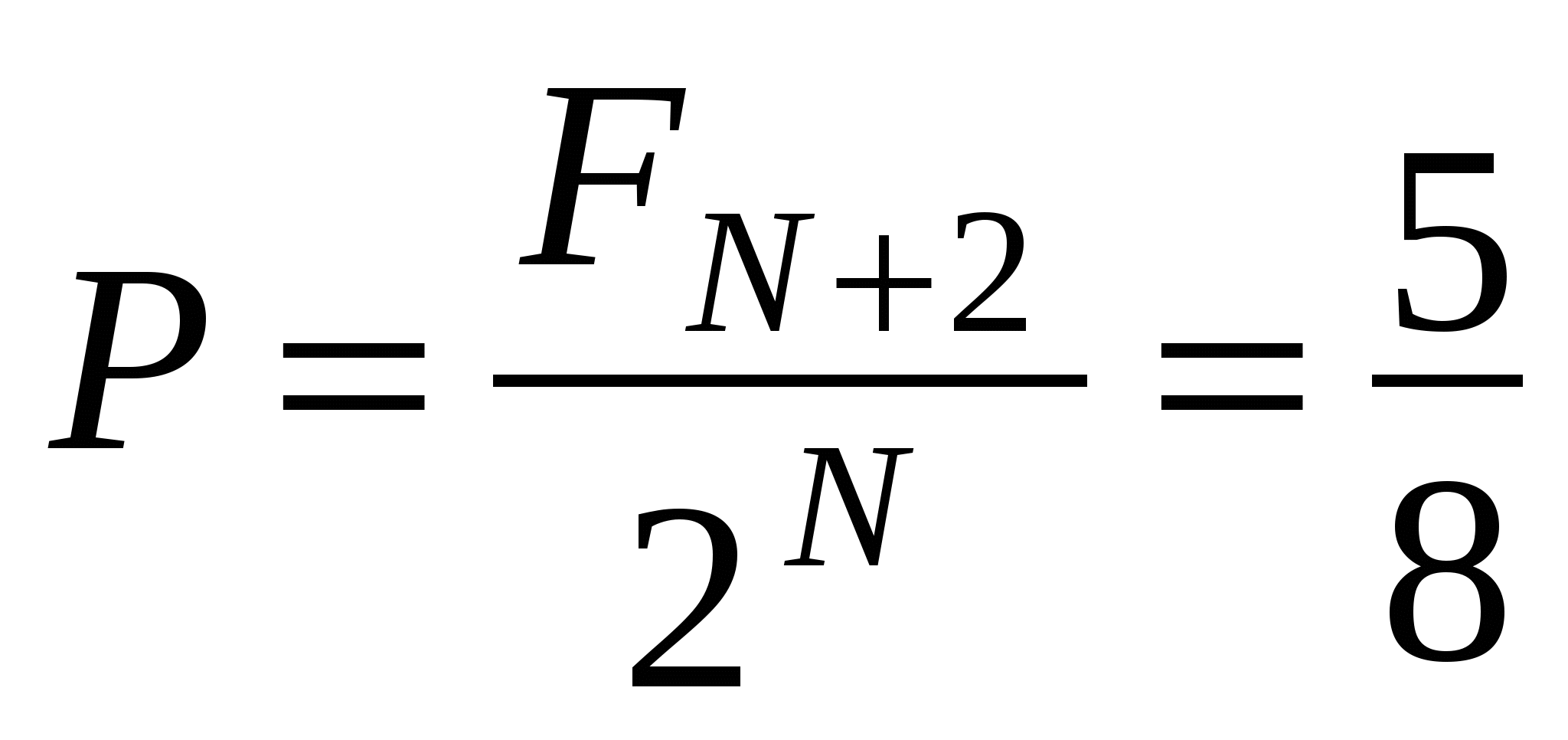 .
.
Действительно: всего вариантов лестниц будет n = 8 (111, 011, 101, 110, 010, 001, 100, 000), причем подходят Незнайке только 5 из них (последние 3 не подходят, т.к. содержат 00 подряд), т.е. m = 5. 
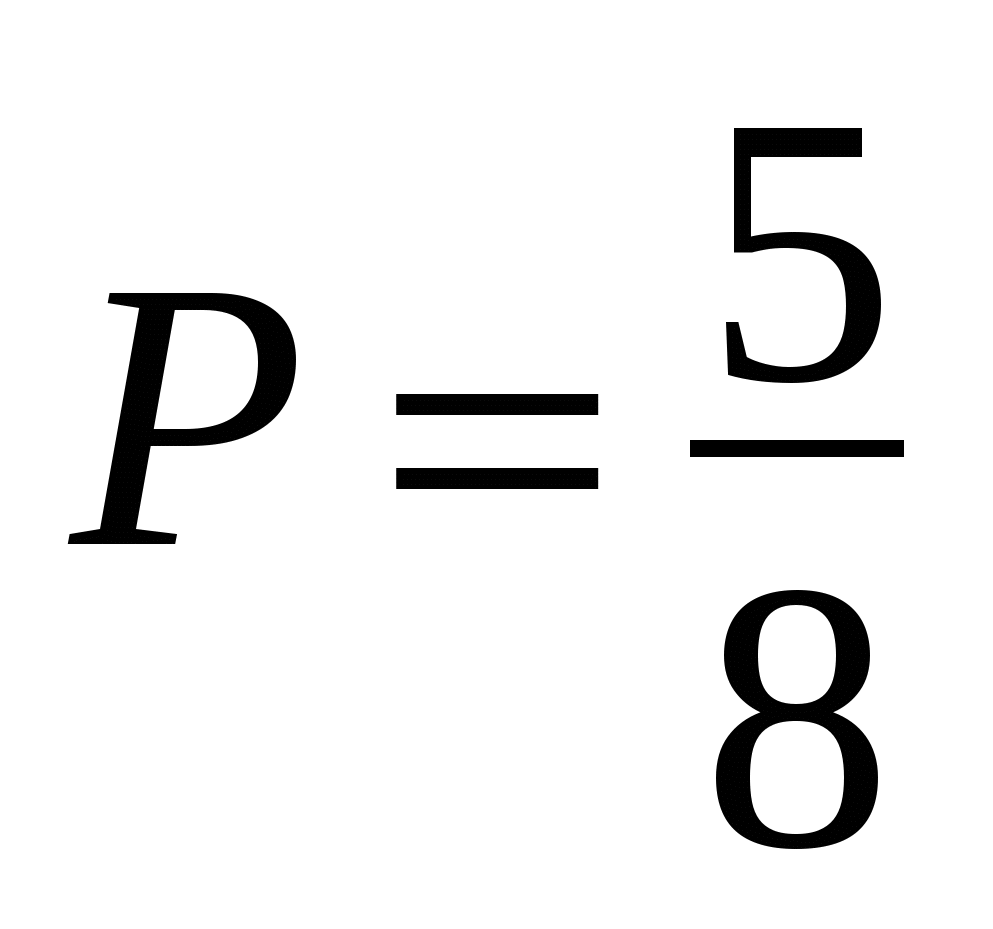 .
.
ОТВЕТ: Если N = 1, то 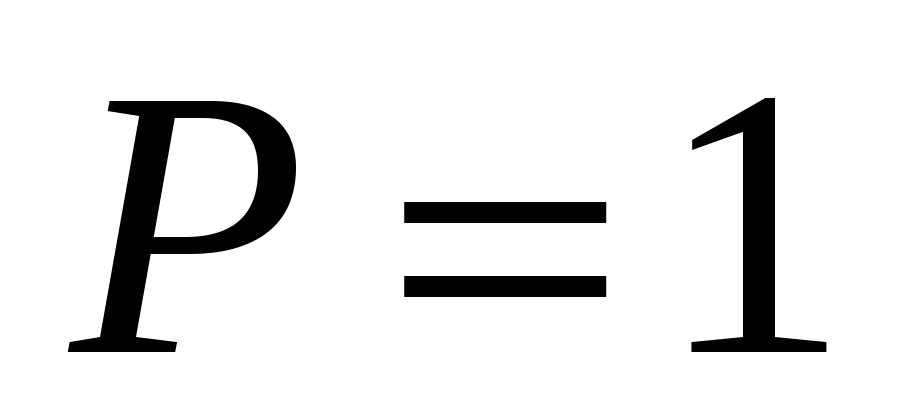 . Для N = 2,
. Для N = 2, 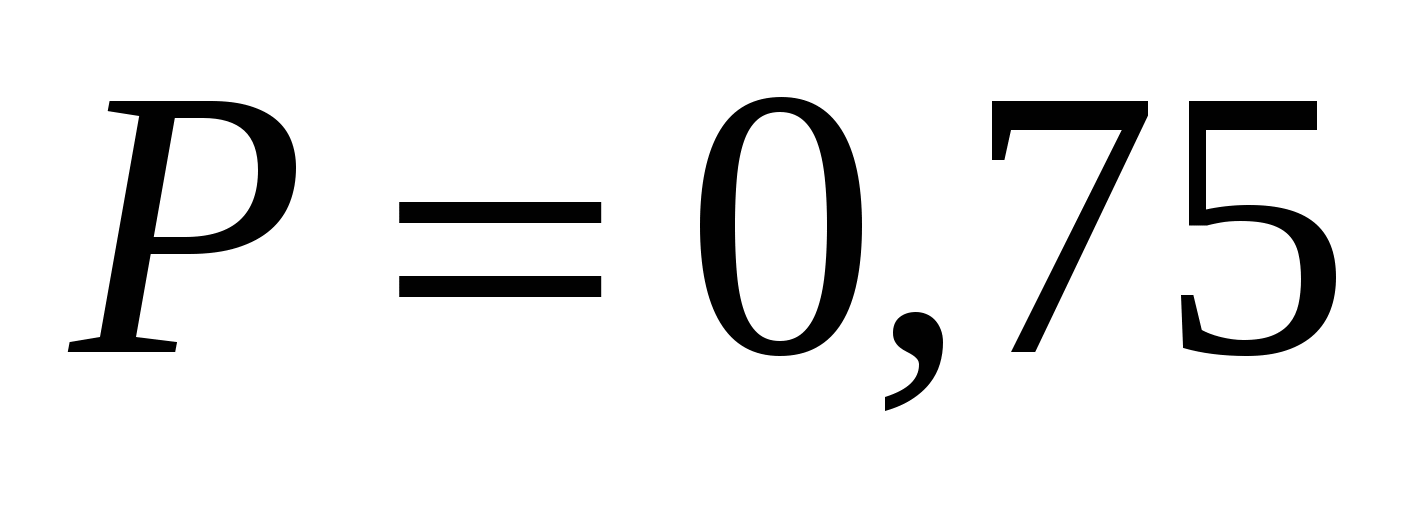 , а для
, а для 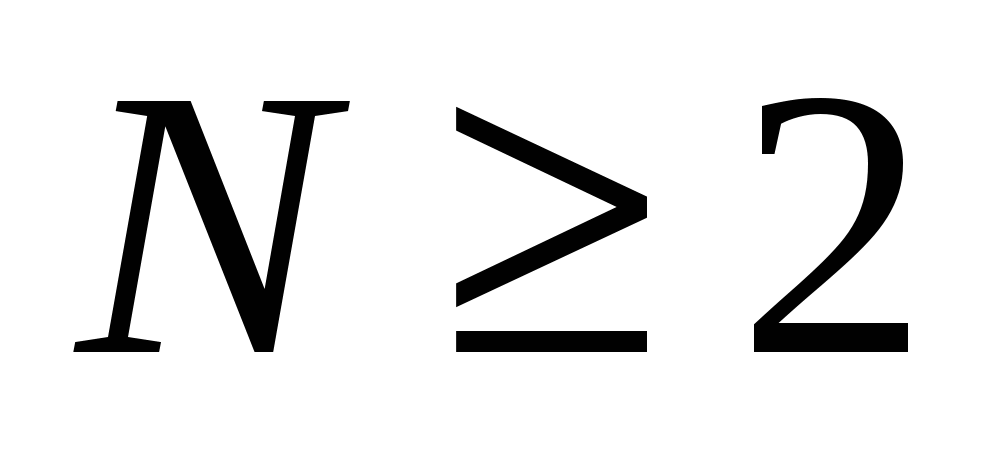 ,
,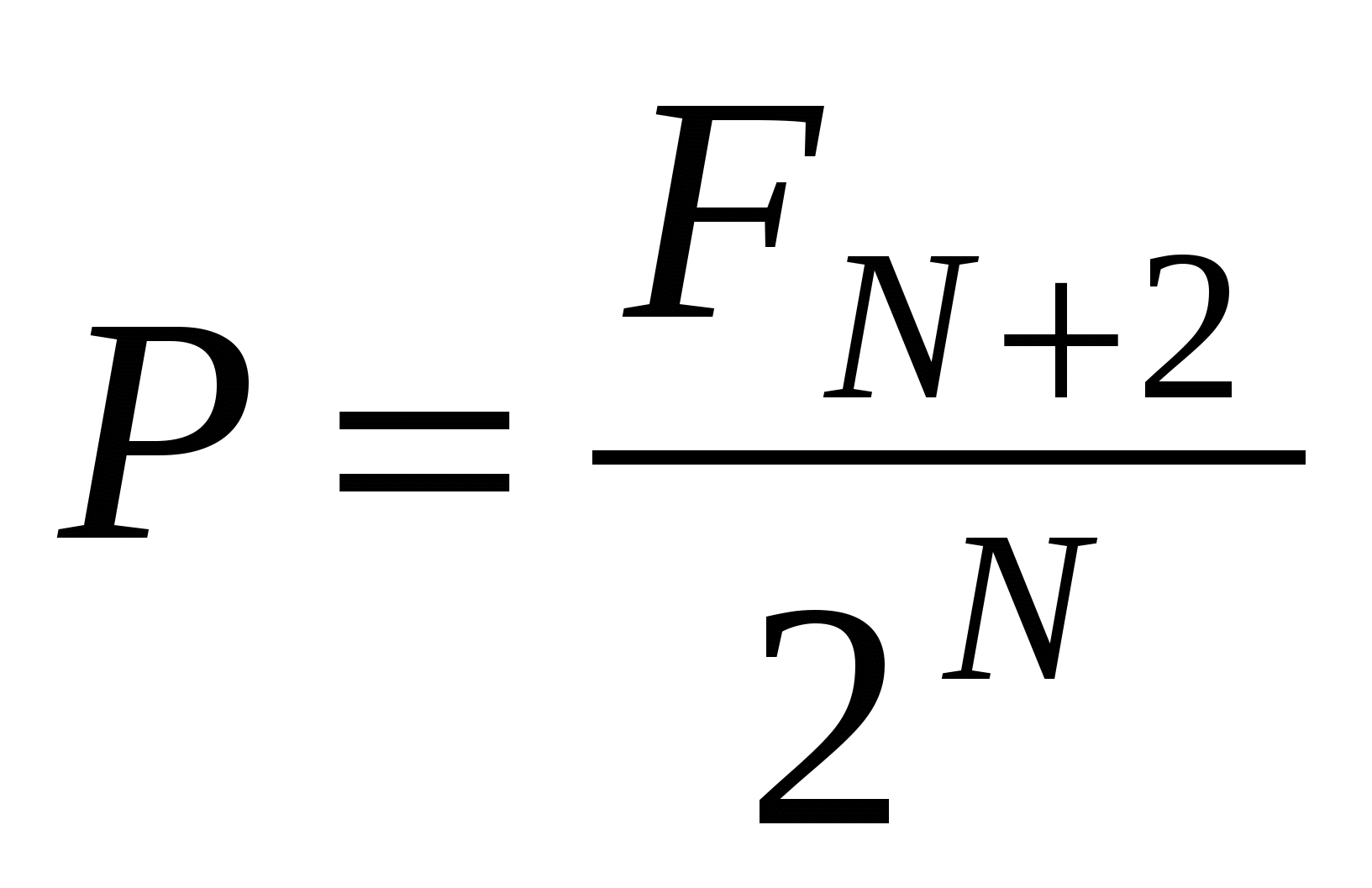 .
.
8. Игральную кость подбросили 12 раз. Что больше - вероятность того, что каждая из цифр 1, 2, 3, 4, 5, 6 выпадет ровно 2 раза или вероятность того, что на всех 12 костях будут только четные числа.
РЕШЕНИЕ:
Вычислим сначала вероятность того, что на всех 12 костях будут только четные числа.
При одном бросании кости количество всех возможных исходов n = 6 (выпала 1 или 2, 3, 4, 5, 6). Благоприятными для наступления нашего события будут только 3 исхода: выпала 2, 4 или 6, т.е. m = 3. По классическому определению вероятности находим, что вероятность выпадения четной цифры при одном броске 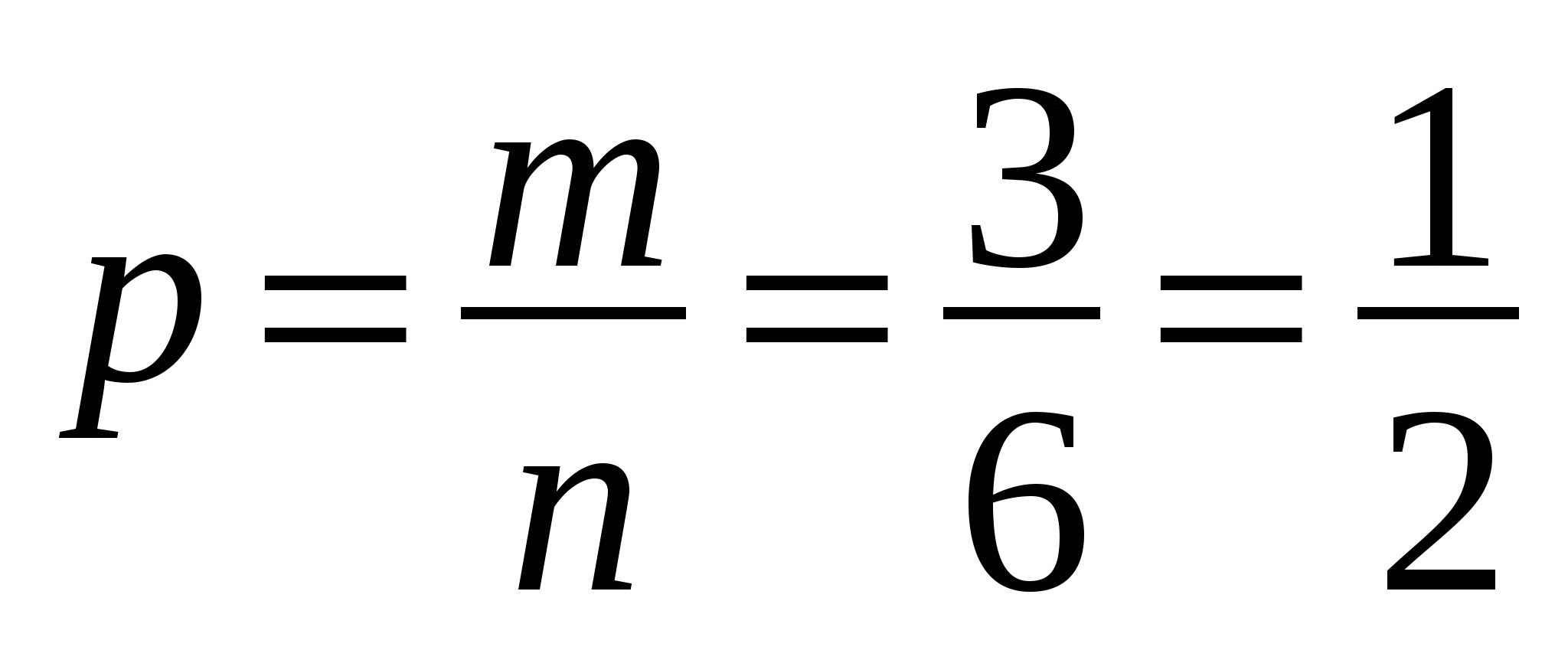 . При 12 бросках, т.к. это независимые испытания, вероятность того, что на всех костях будут только четные числа
. При 12 бросках, т.к. это независимые испытания, вероятность того, что на всех костях будут только четные числа 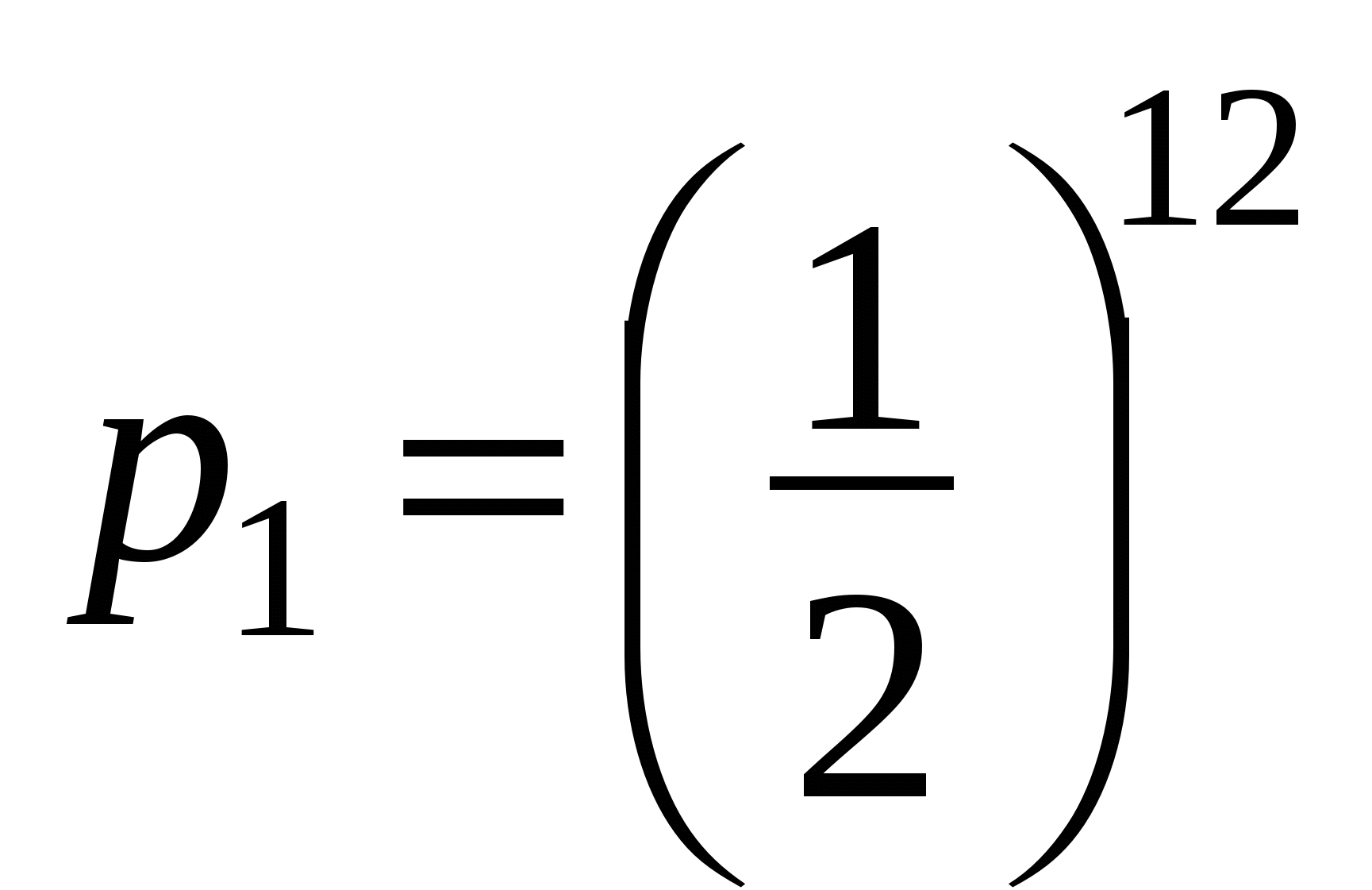 .
.
Найдём теперь вероятность того, что каждая из цифр 1, 2, 3, 4, 5, 6 выпадет ровно по 2 раза.
Количество всех возможных исходов при 12 бросках: n = 612.
При этом благоприятными для нас исходами будут (т.е. каждая из цифр выпадет ровно по 2 раза): m = 6·6·5·5·4·4·3·3·2·2·1·1 = (6!)2, т.к. события независимые, то порядок выпадения цифр не имеет значения.
Тогда по классическому определению вероятности находим, что 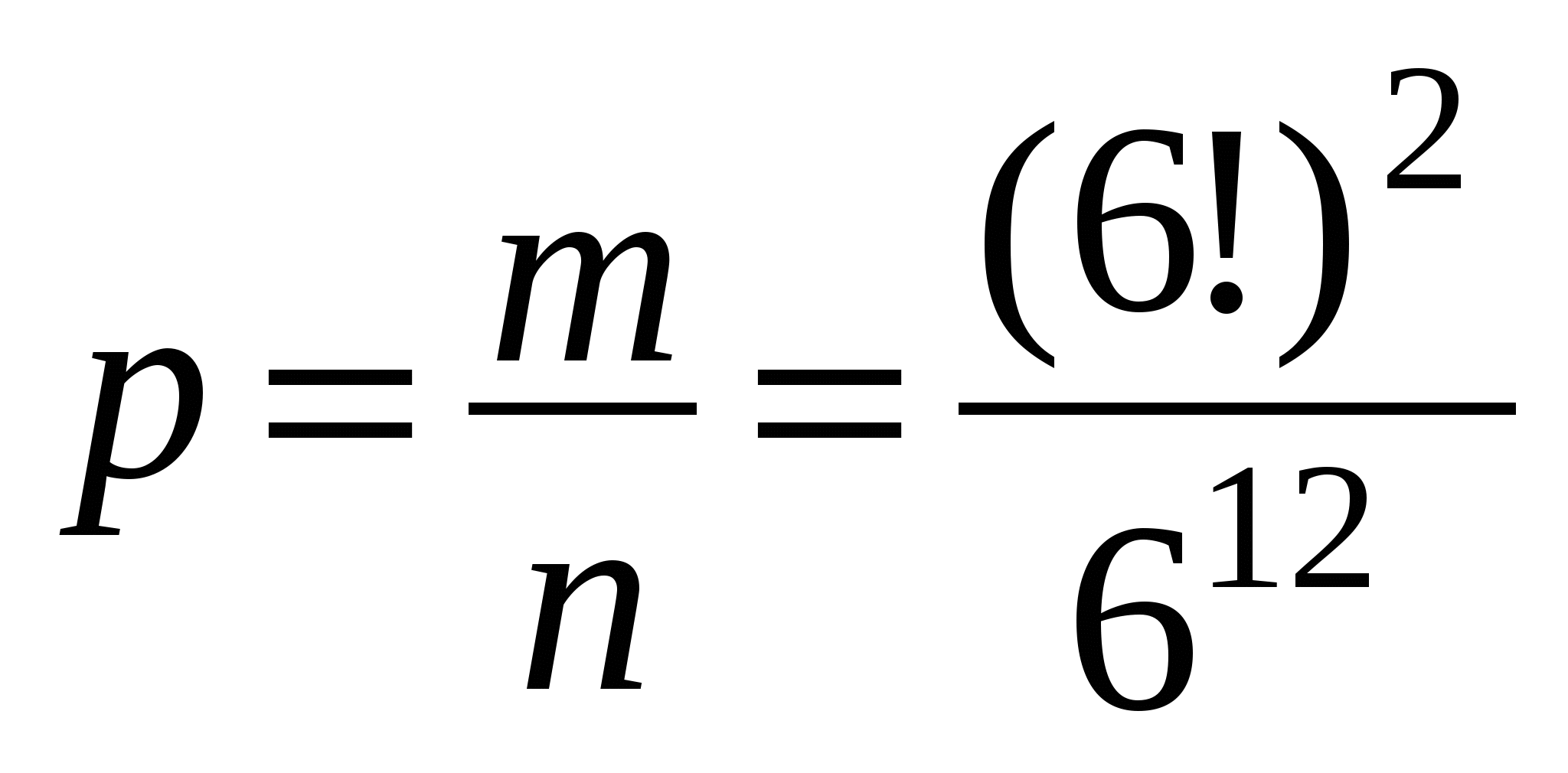 .
.
Сравним эти вероятности: 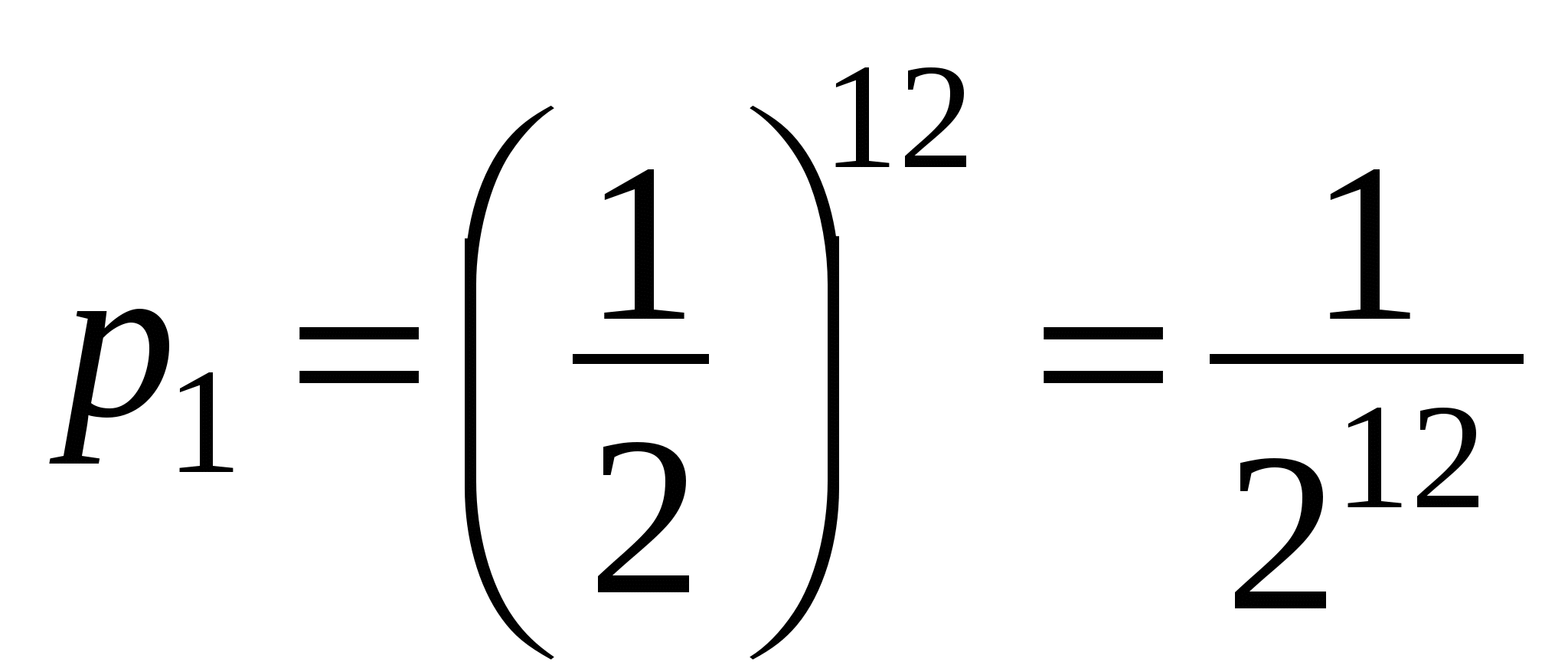 и
и 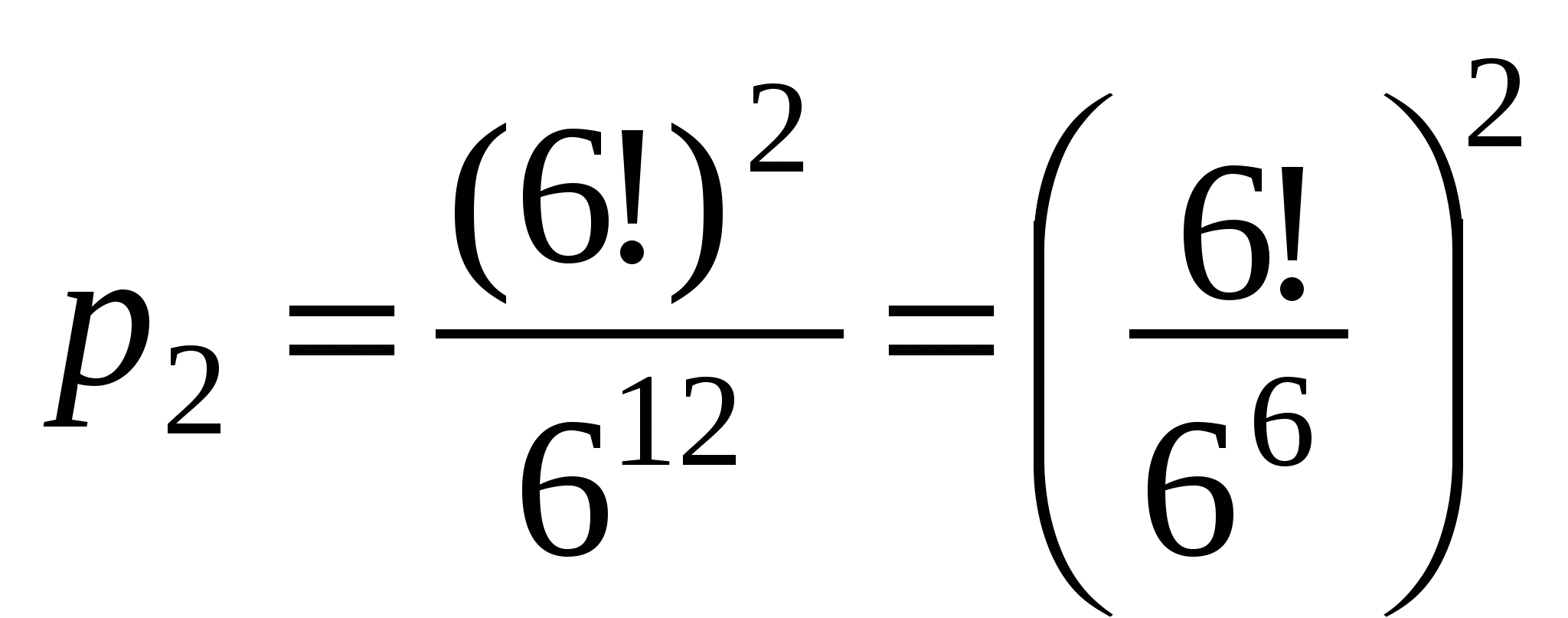 .
.
6! = 6·5·4·3·2·1 = 720 = 36·20 = 62·20
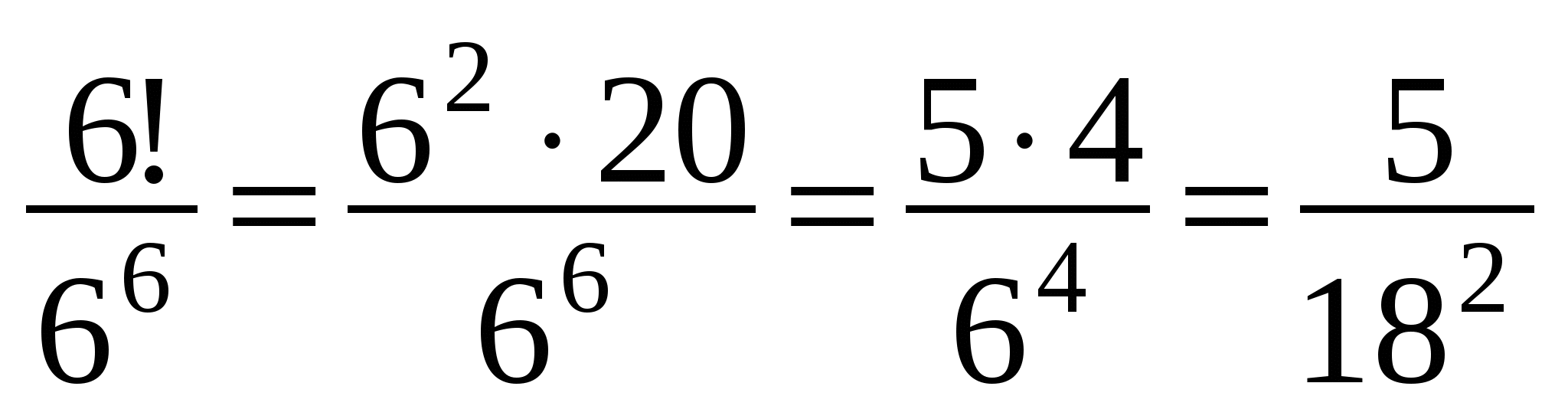 ,
, 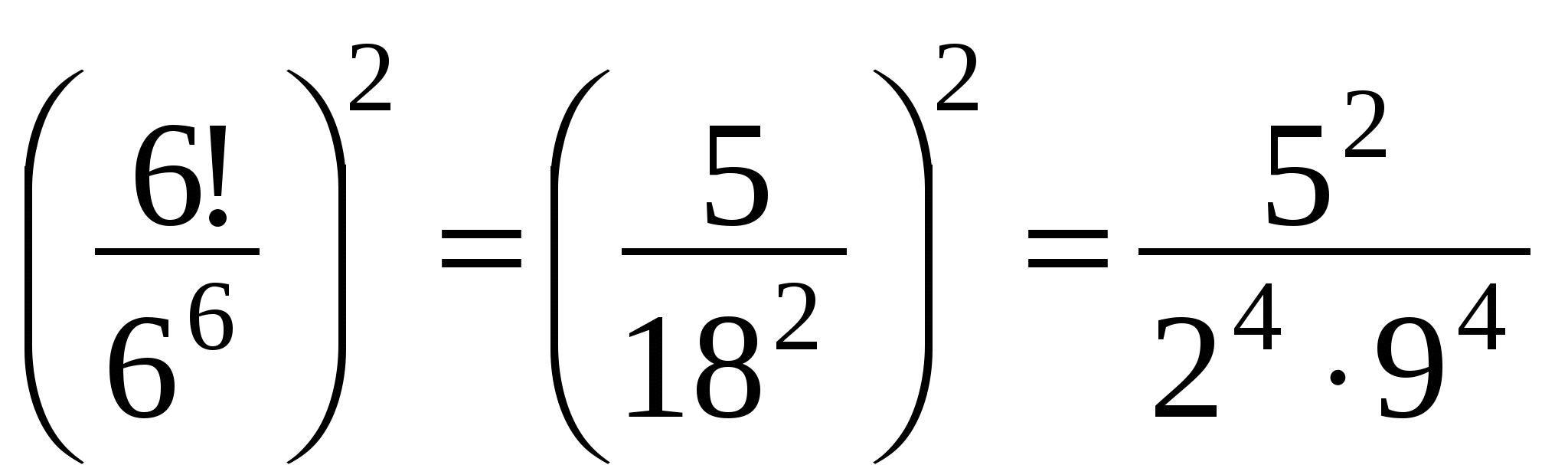 . Сравним числа
. Сравним числа 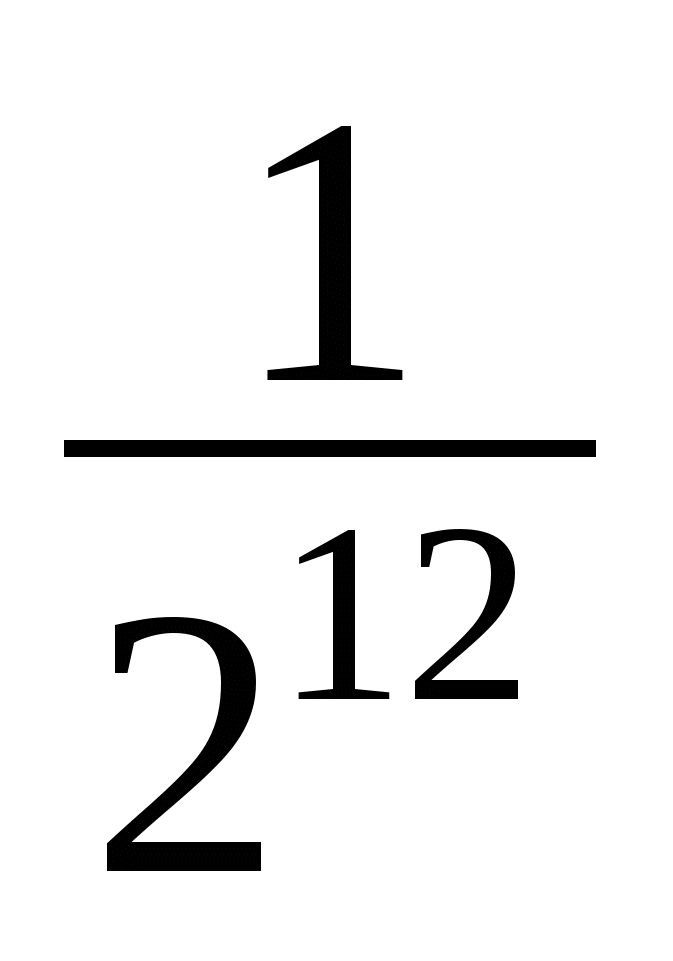 и
и 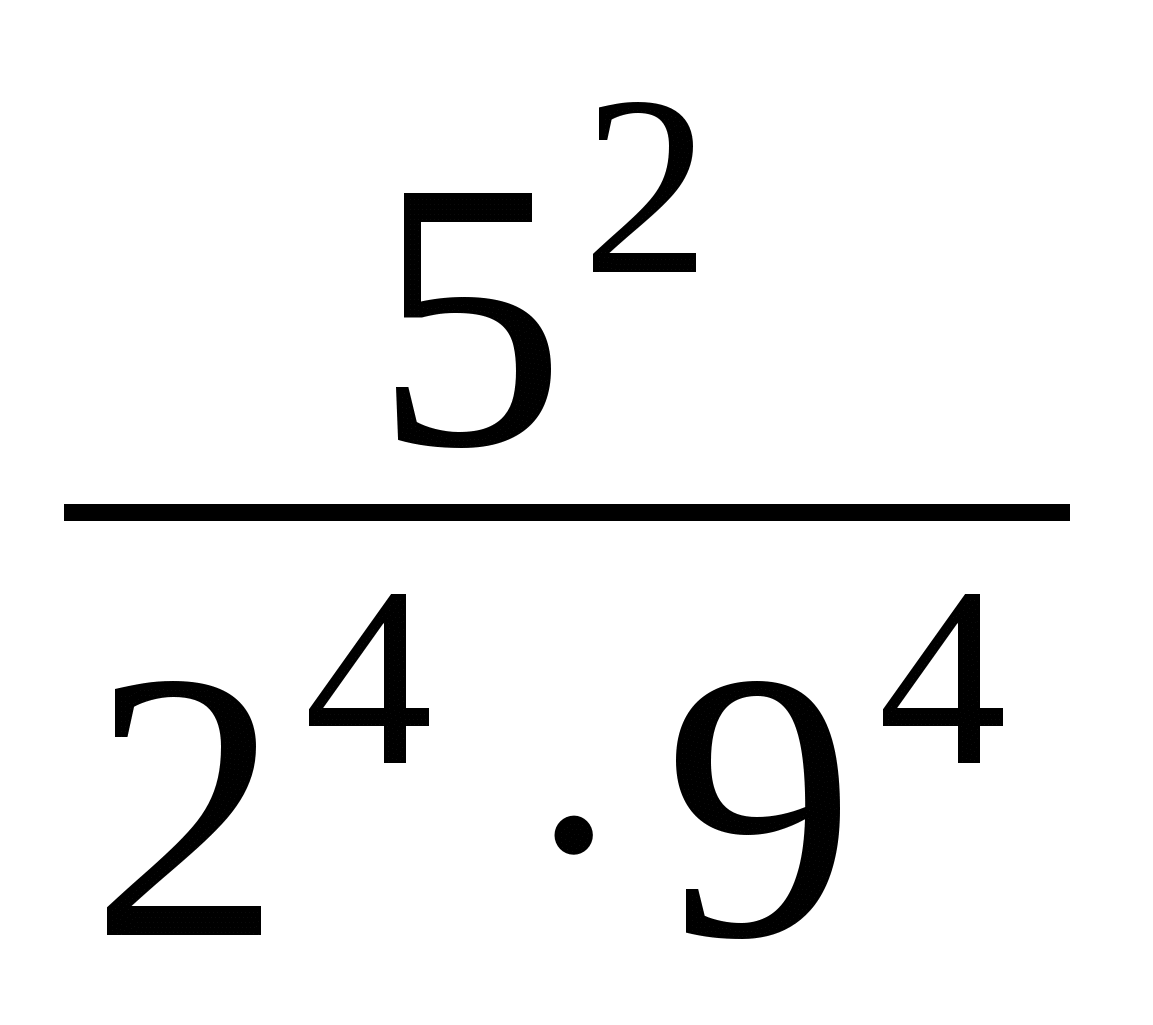 .
.
Умножим оба числа на 24
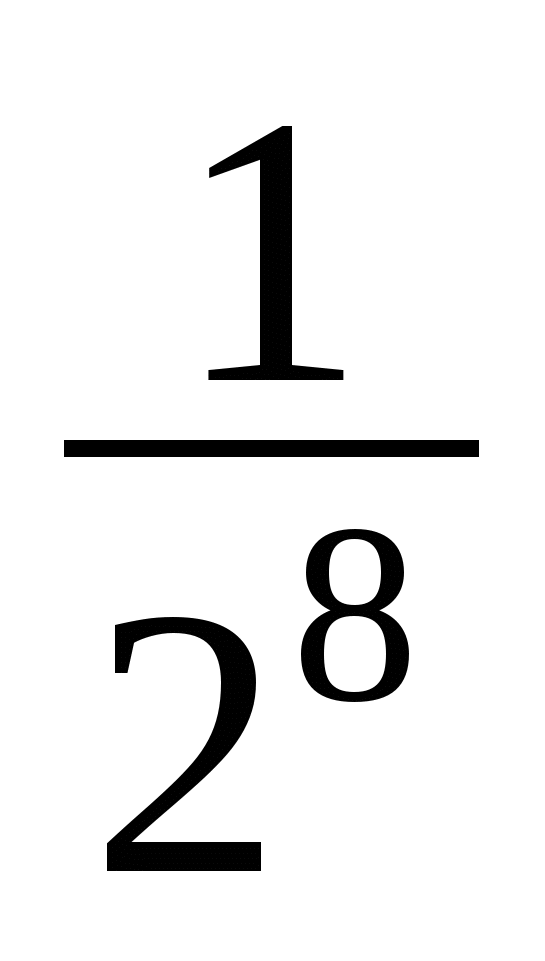 и
и 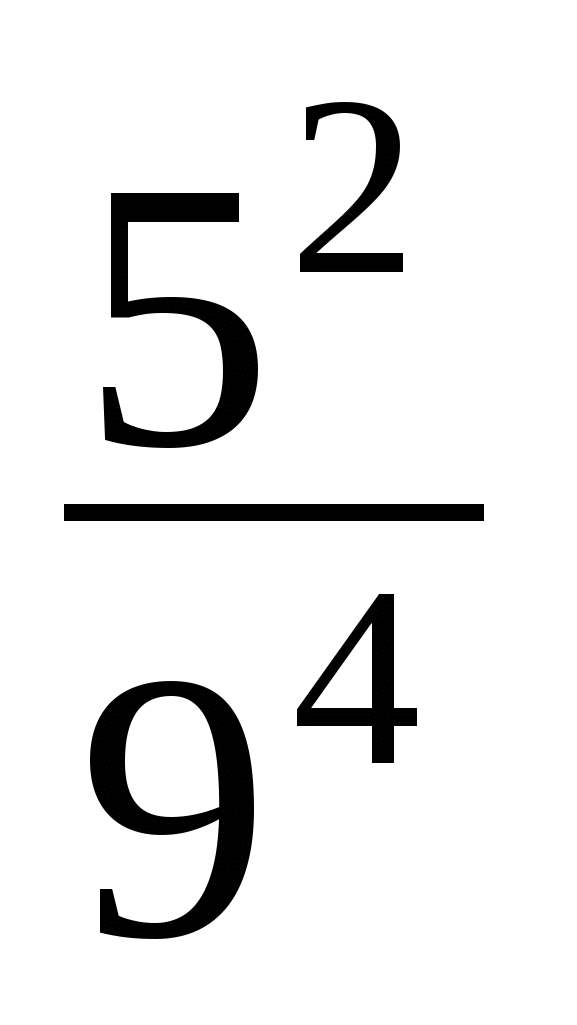 .
.
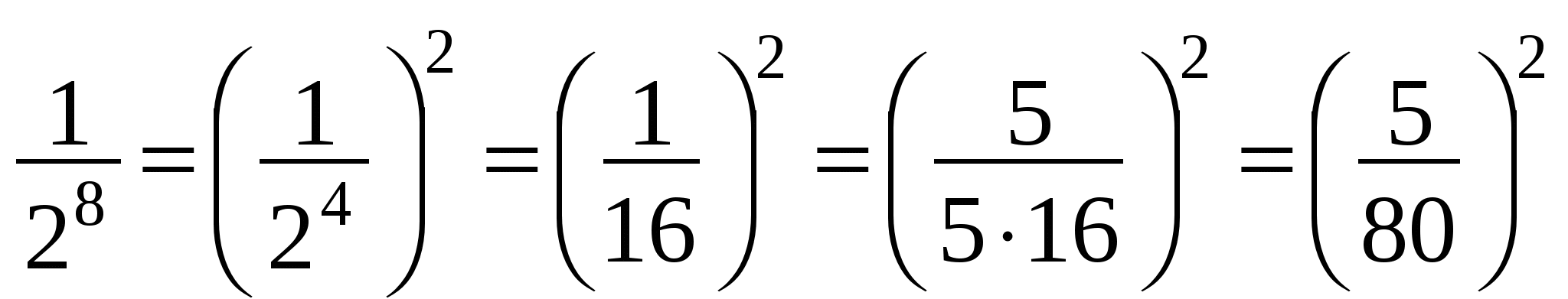 и
и 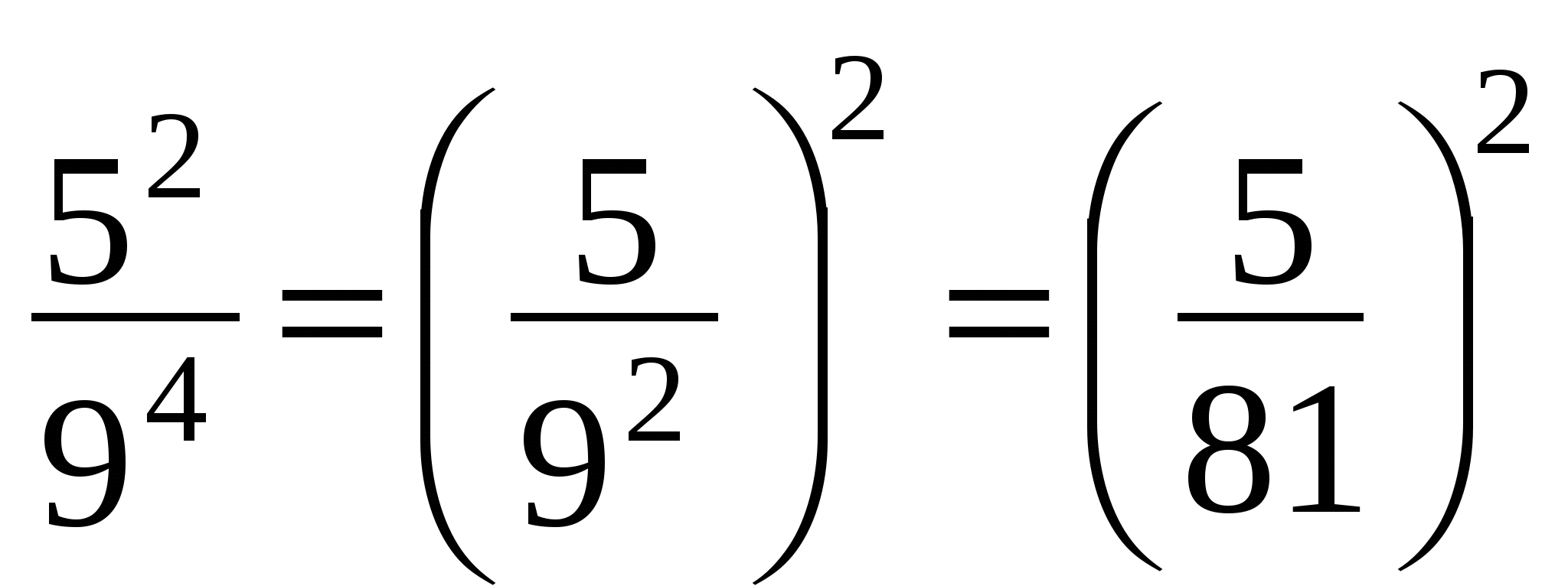 ;
; 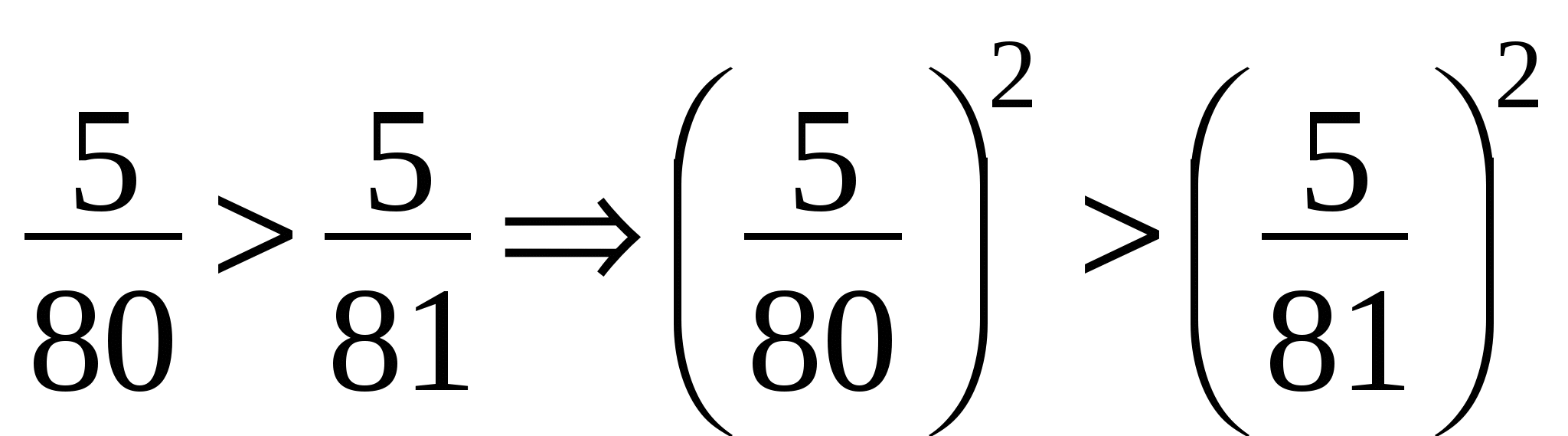
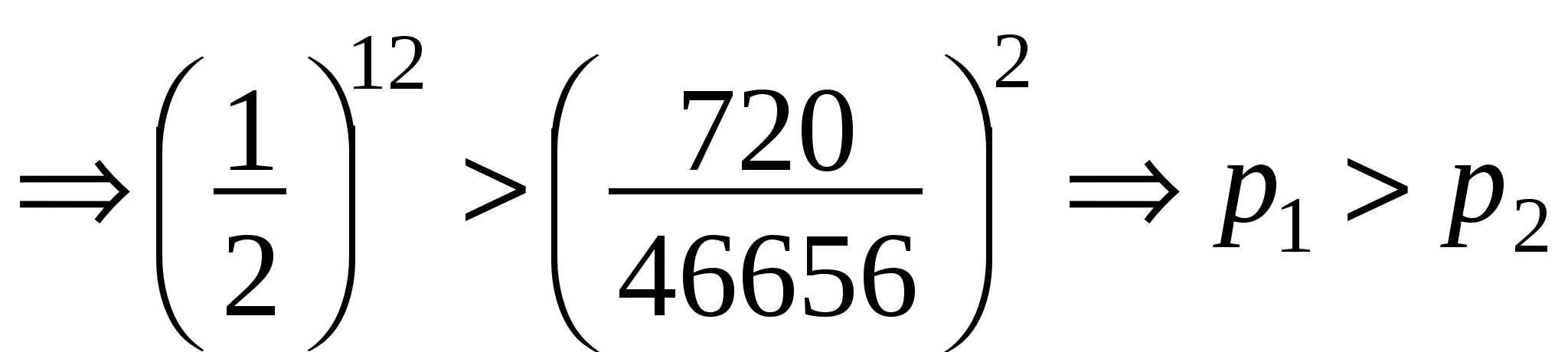 .
.
Получили, что вероятность выпадения на всех 12 костях четных цифр больше (хоть и не намного), чем вероятность того, что каждая из цифр выпадет ровно по 2 раза.
ОТВЕТ: вероятность того, что на всех 12 костях будут только четные числа больше.
9. Имеется неограниченное количество одинаковых кирпичей в форме прямоугольного параллелепипеда. Кирпичи кладутся друг на друга с некоторым сдвигом так, чтобы они не падали. Какой длины «крышу» можно таким образом получить?
РЕШЕНИЕ:
Положим первый кирпич длиной L, на него второй так, чтобы центр тяжести верхнего кирпича попал точно на ребро нижнего, т.е. со сдвигом на 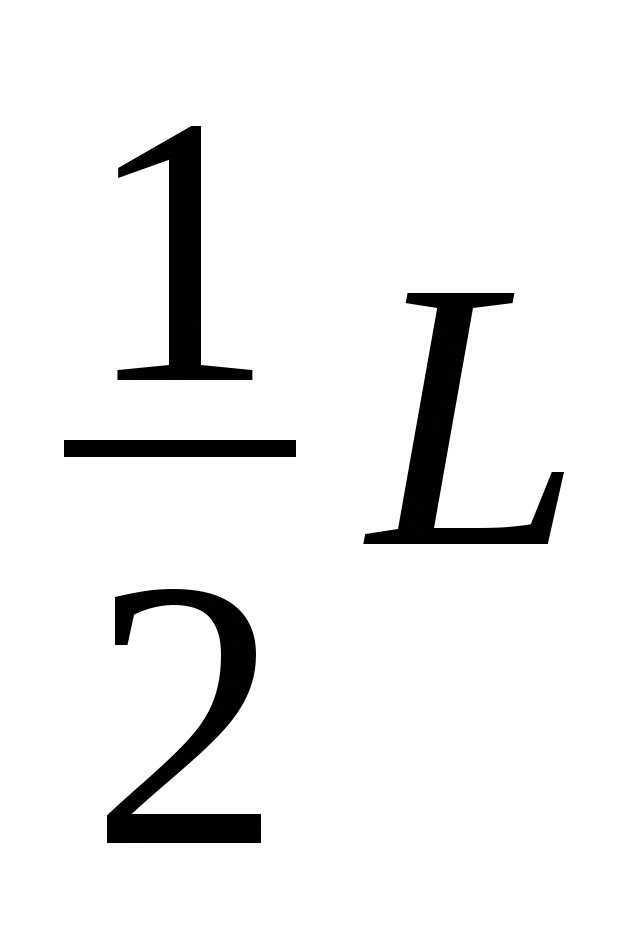 . У получившейся системы снова ищем центр тяжести, его проекция тоже должна попасть не ребро уже следующего кирпича
. У получившейся системы снова ищем центр тяжести, его проекция тоже должна попасть не ребро уже следующего кирпича  третий кирпич ложим со сдвигом
третий кирпич ложим со сдвигом 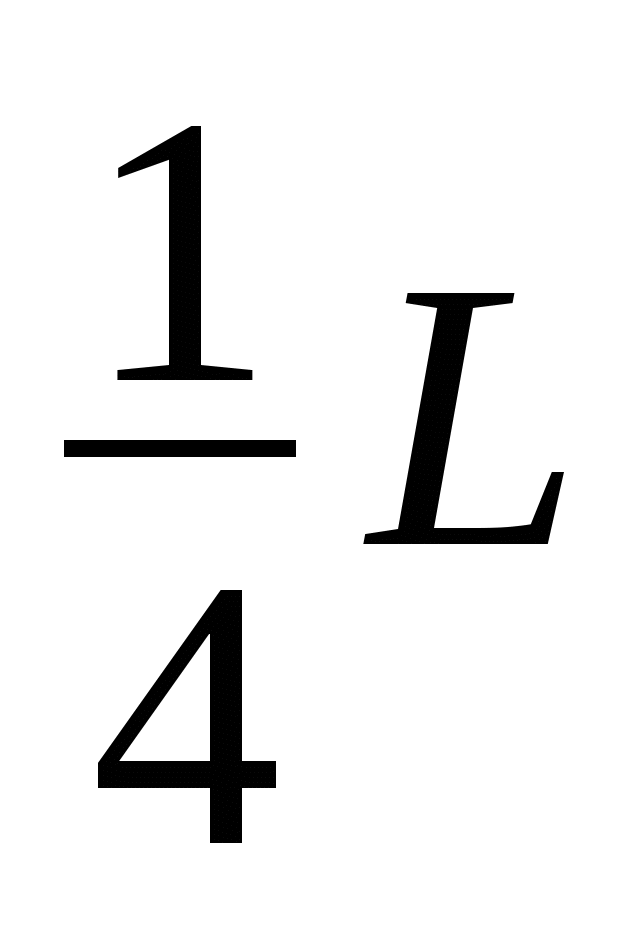 относительно второго. И так далее, т.е. по индукции
относительно второго. И так далее, т.е. по индукции 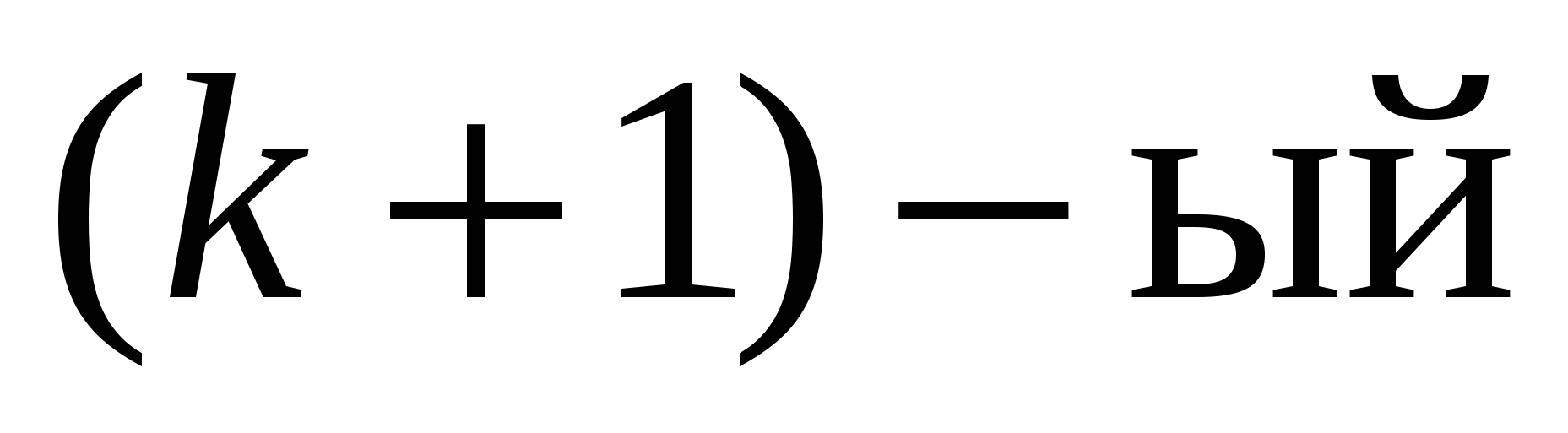 кирпич можно сдвинуть относительно k-го на
кирпич можно сдвинуть относительно k-го на 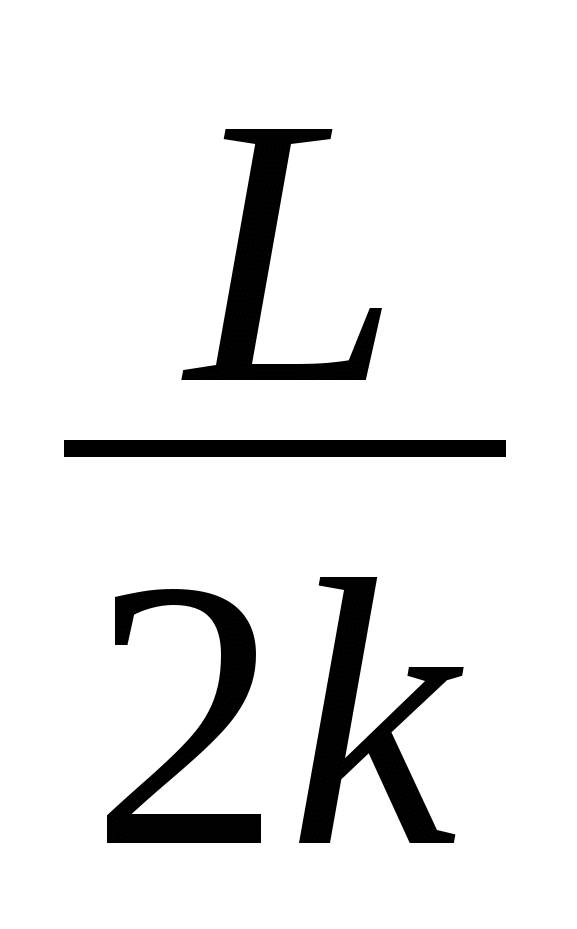 .
.
Получаем последовательность 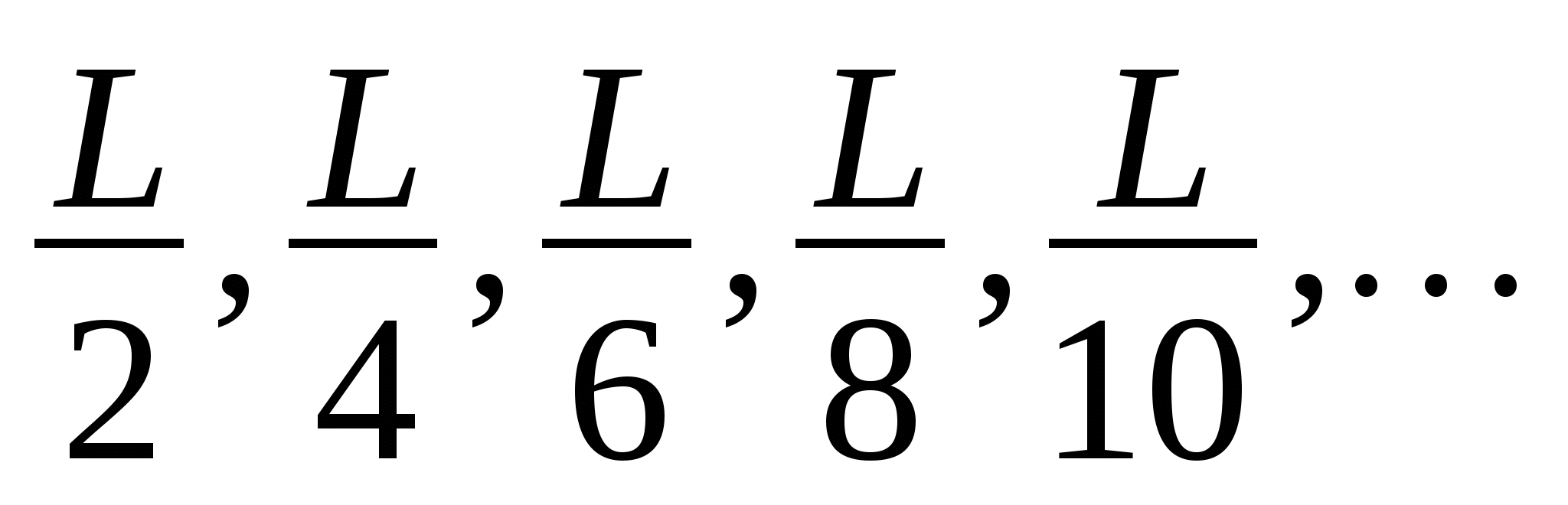 Т.е.
Т.е. 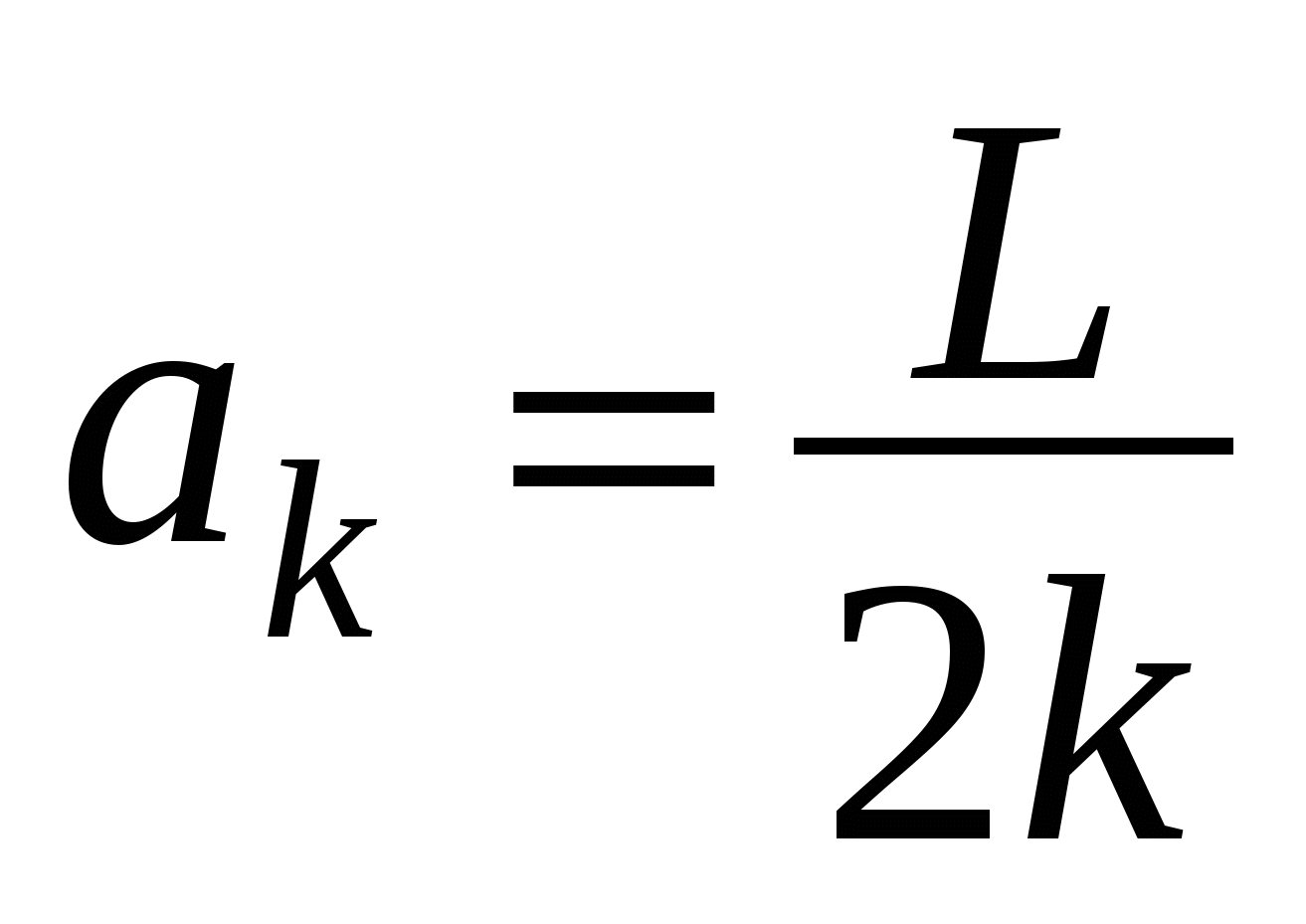 .
.
Пусть xn - смещение центра масс стопки из n кирпичей относительно центра кирпича, на котором эта стопка лежит, тогда:
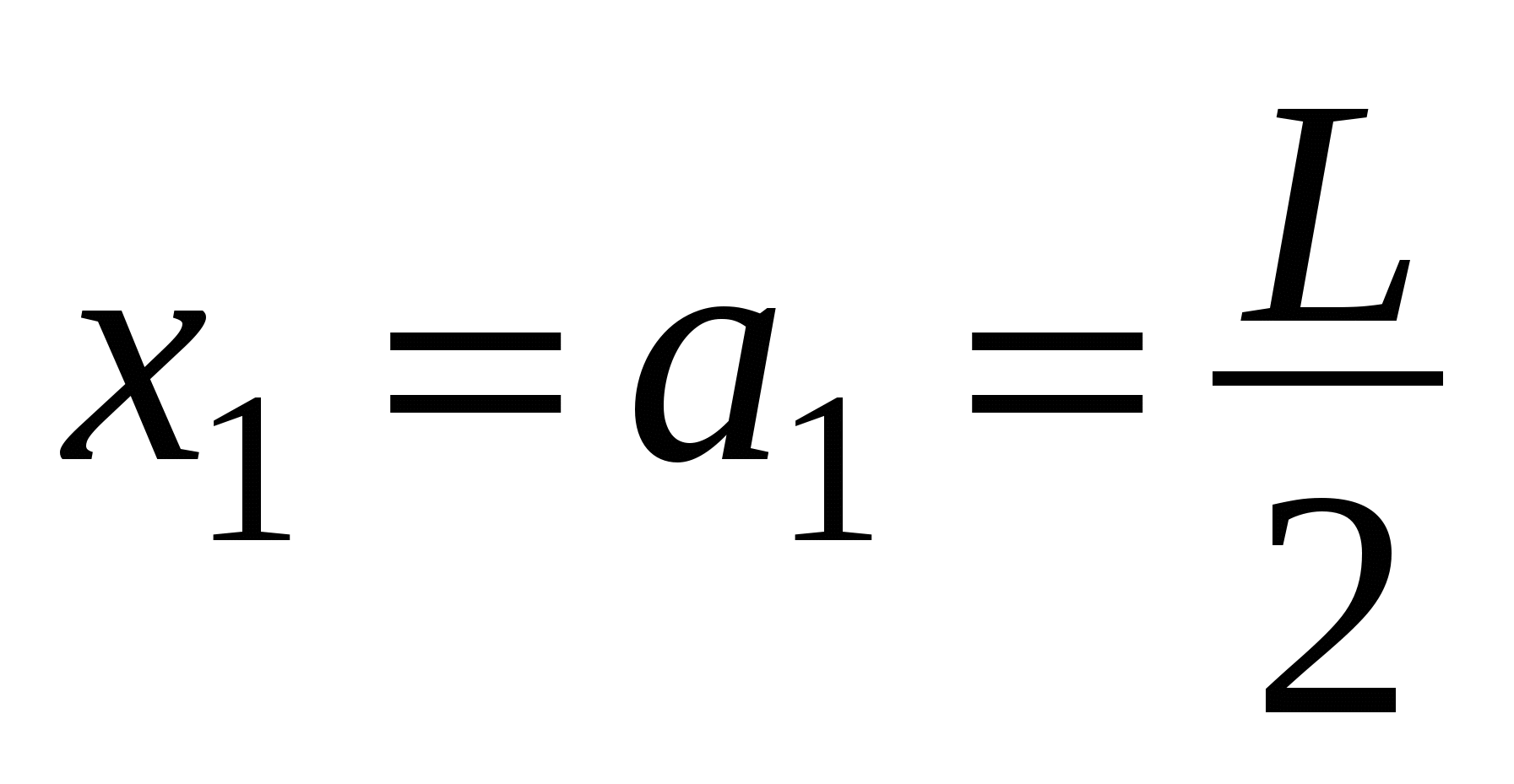 ;
;
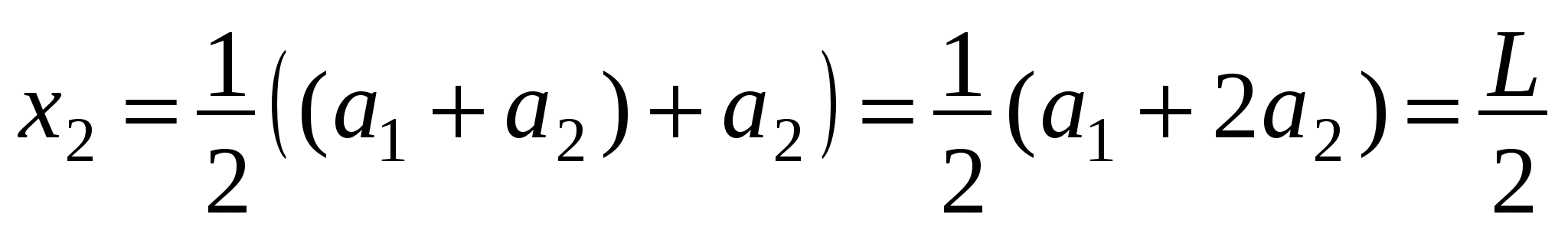 ;
;
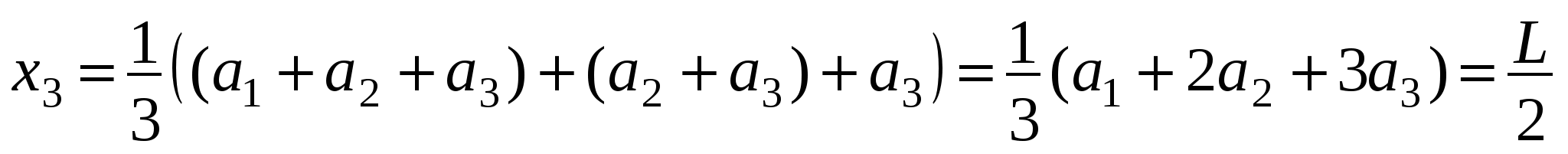 ; и т.д.
; и т.д.
Получили, что смещение самого верхнего кирпича относительно самого нижнего (сумма всех ak) - это частичная сумма гармонического ряда. Известно, что он расходится.
Система 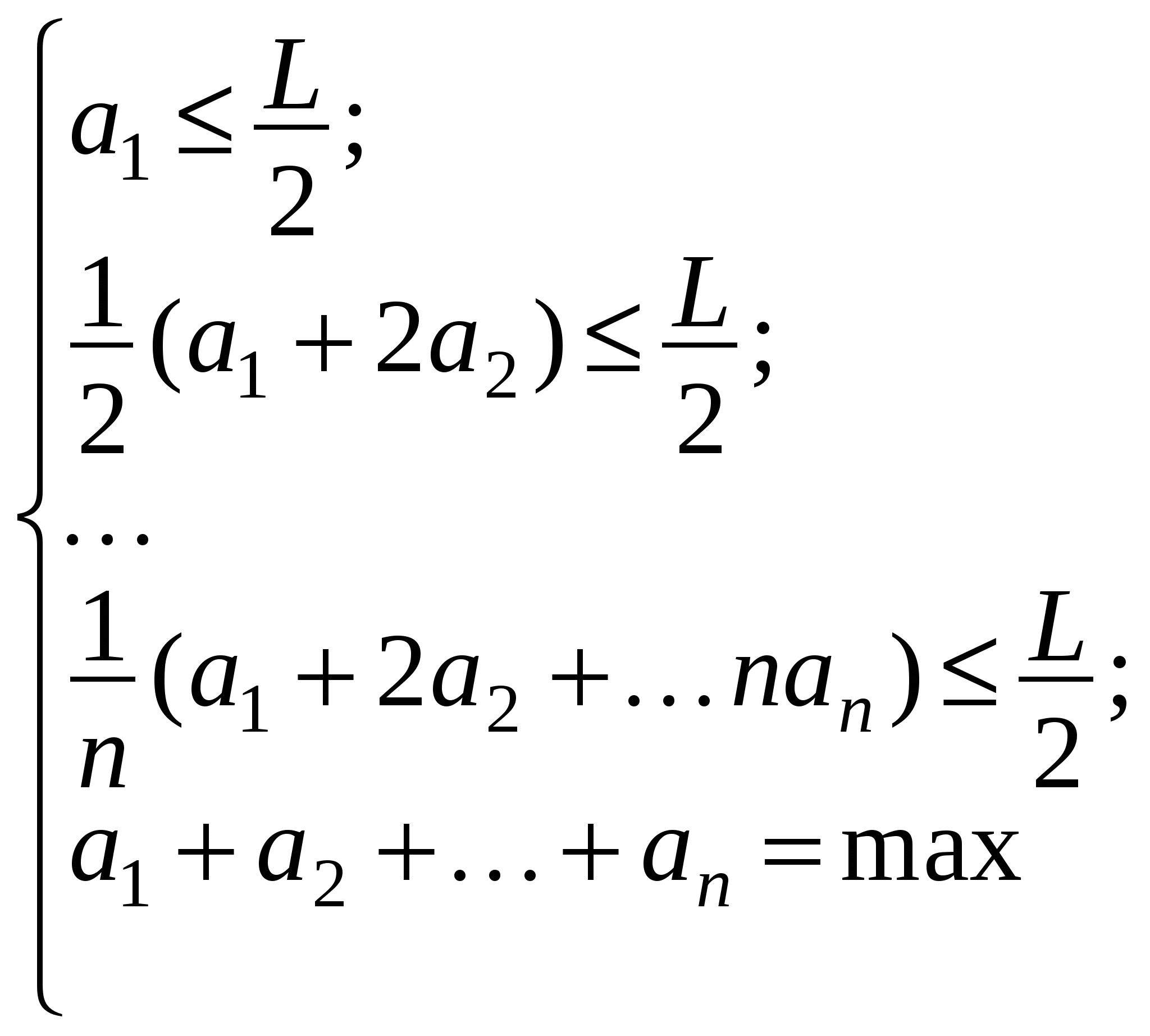 достигает максимума в вершине, где все неравенства превращаются в равенства. А, значит, по лесенке можно забраться бесконечно далеко.
достигает максимума в вершине, где все неравенства превращаются в равенства. А, значит, по лесенке можно забраться бесконечно далеко.
ОТВЕТ: крышу можно сделать как угодно длинной.
МЕТОДИЧЕСКИЙ БЛОК
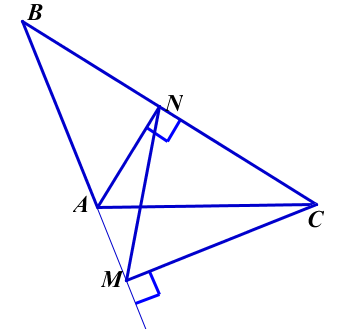
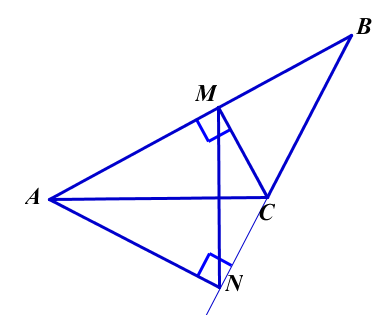
10. В 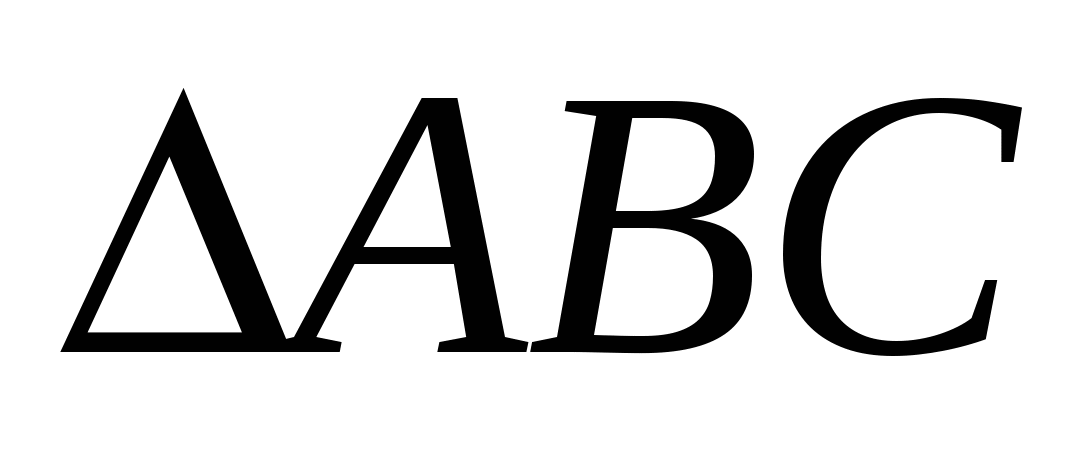
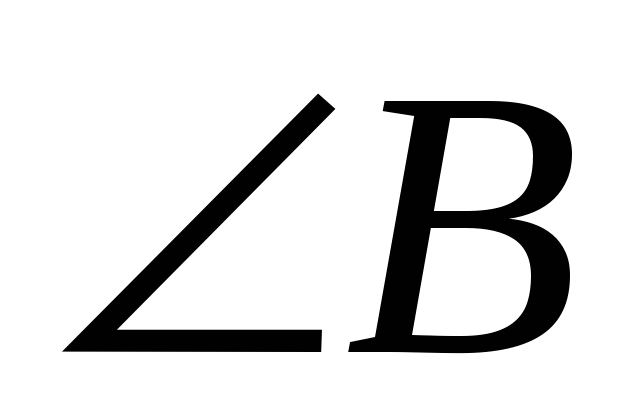 =300, АС = 2, АМ и СN -высоты
=300, АС = 2, АМ и СN -высоты  . Найти длину MN.
. Найти длину MN.
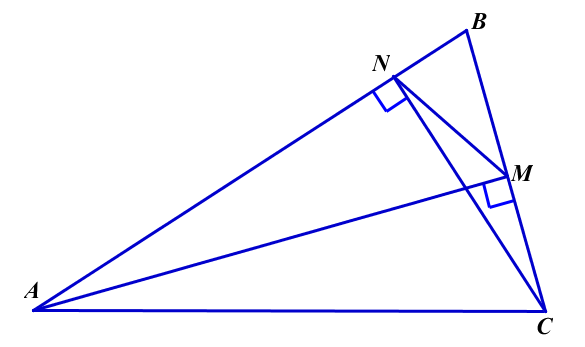
Ошибки: В условии задачи сказано, что АМ и СN -высоты ![]() , а на предложенном Вами чертеже высоты АN и СМ. В дальнейшем решение задачи выполнено по чертежу. Если же рассматривать решение в соответствие с условием, то
, а на предложенном Вами чертеже высоты АN и СМ. В дальнейшем решение задачи выполнено по чертежу. Если же рассматривать решение в соответствие с условием, то  и
и  - вырожденные, а не прямоугольные. Рассматривать нужно прямоугольные
- вырожденные, а не прямоугольные. Рассматривать нужно прямоугольные 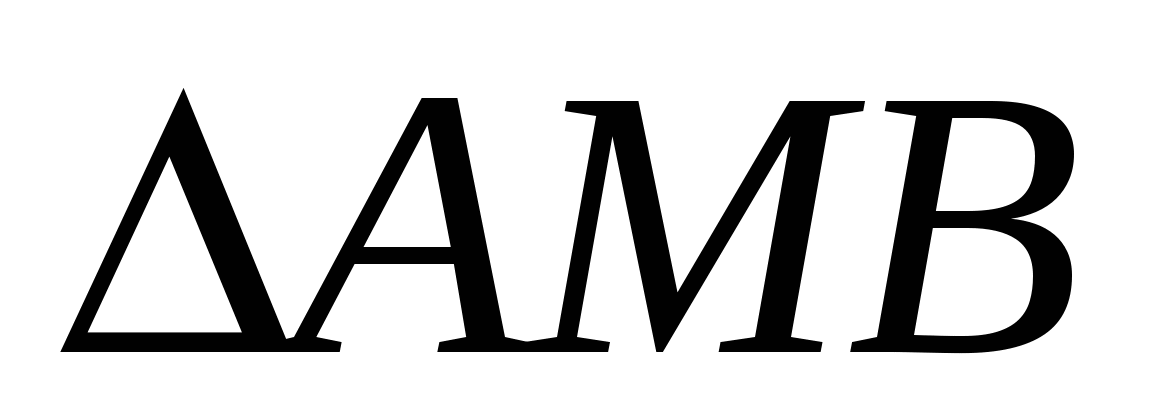 :
: 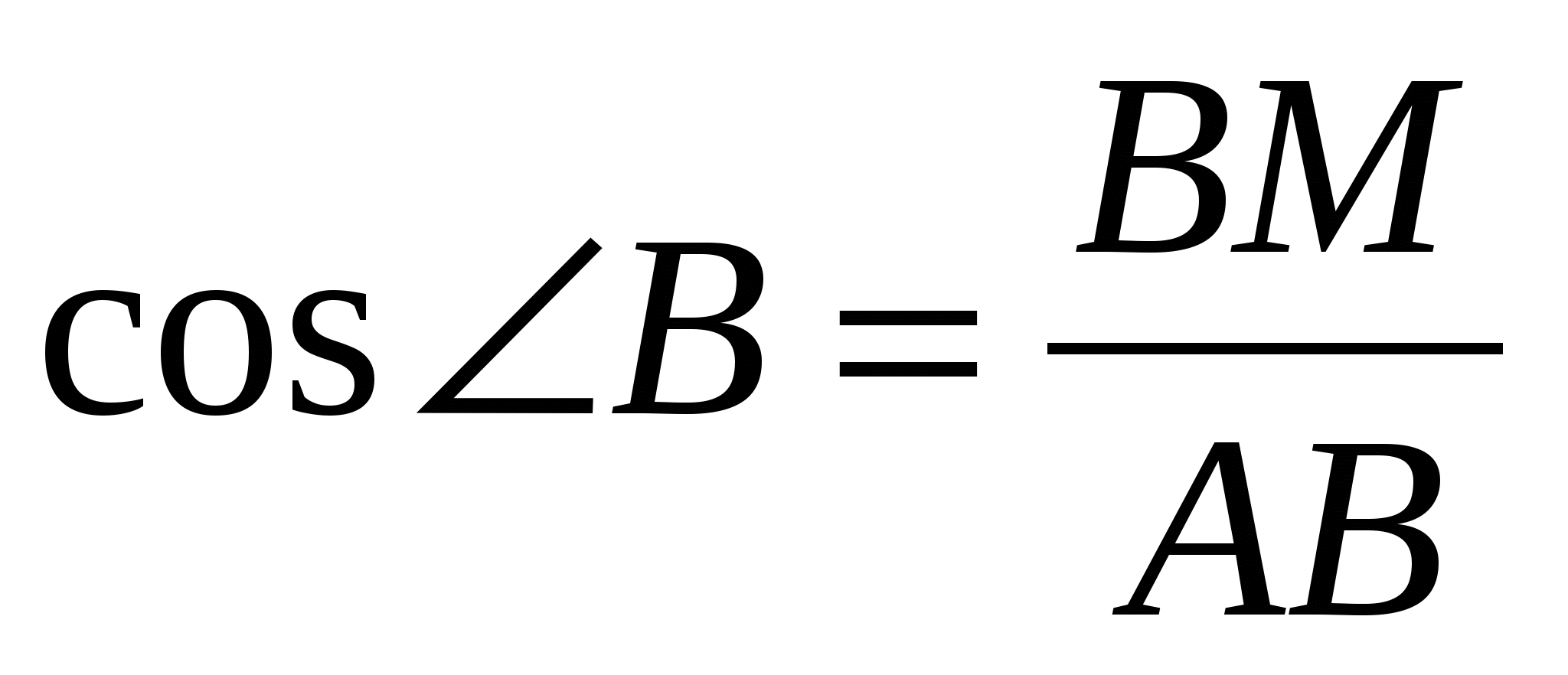 и
и  :
: 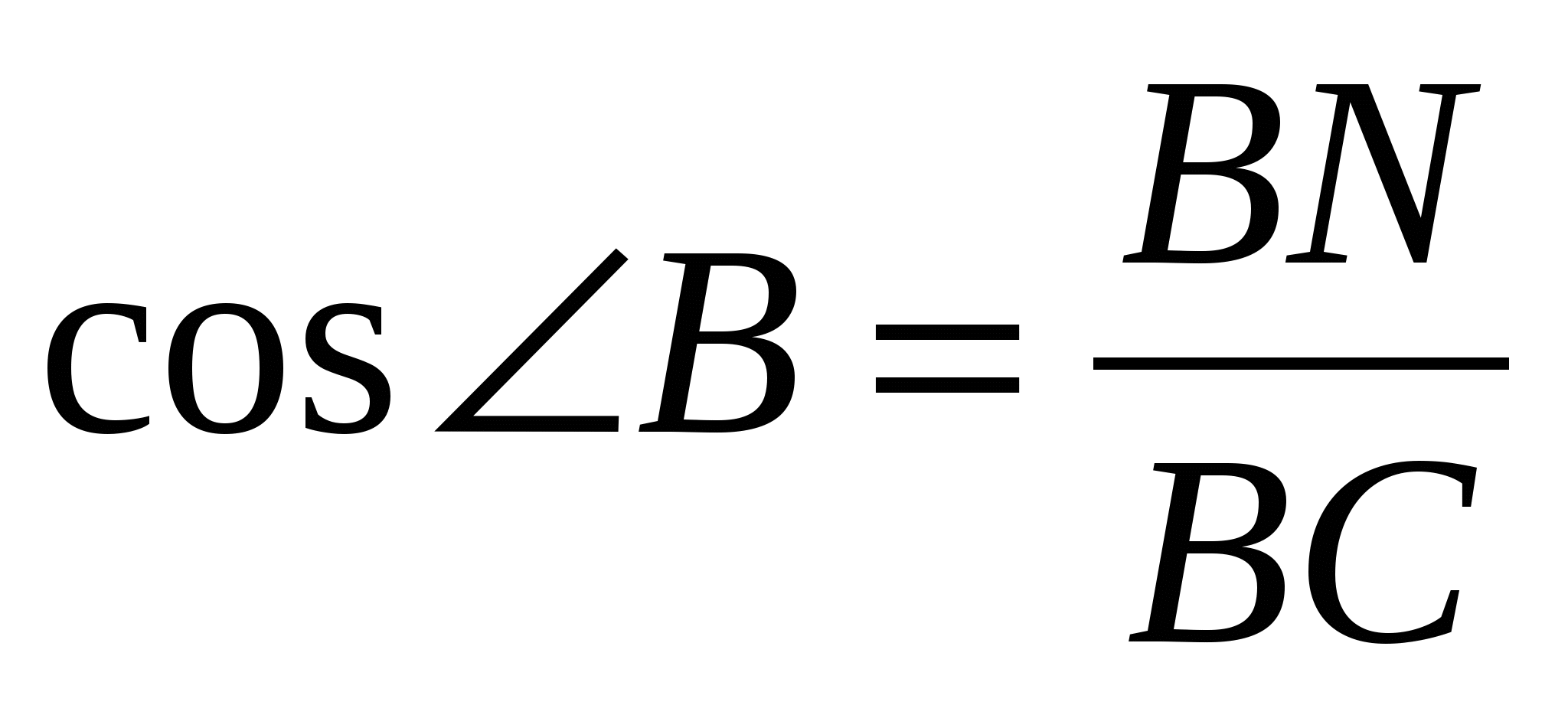 .
.
Далее, в решении сказано, что треугольники подобны по 2 признаку. Но классически подобие по пропорциональности 2-х сторон и общему углу, считается 1 признаком подобия. Поэтому при доказательстве подобия лучше указывать не номер признака, а равные углы или (и) пропорциональность сторон. В остальном решение, приведенное для чертежа, верно и для случая, если один из углов А или С - тупой или прямой.
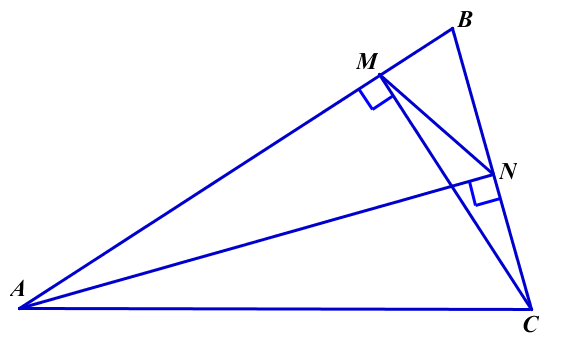
Обычно, ошибки допускаются, в решении обратной к данной задаче, когда даны длины АС и MN, а найти надо 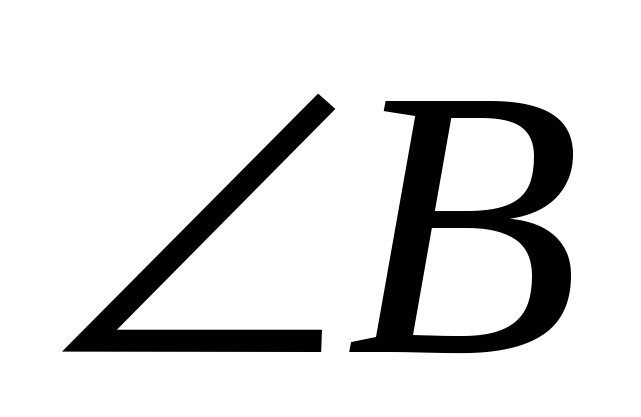 , который может оказаться тупым.
, который может оказаться тупым.
Ученики приходят к выводу: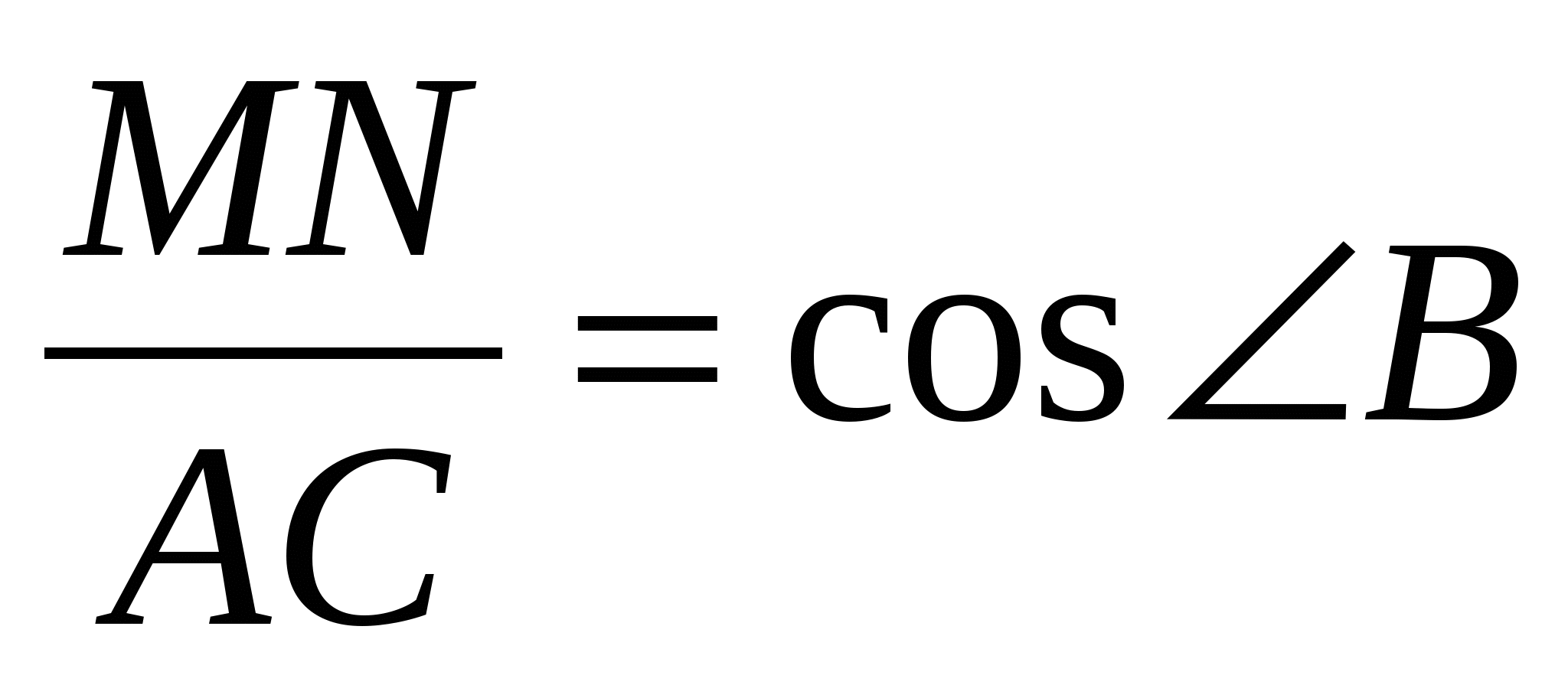 , вместо правильного
, вместо правильного 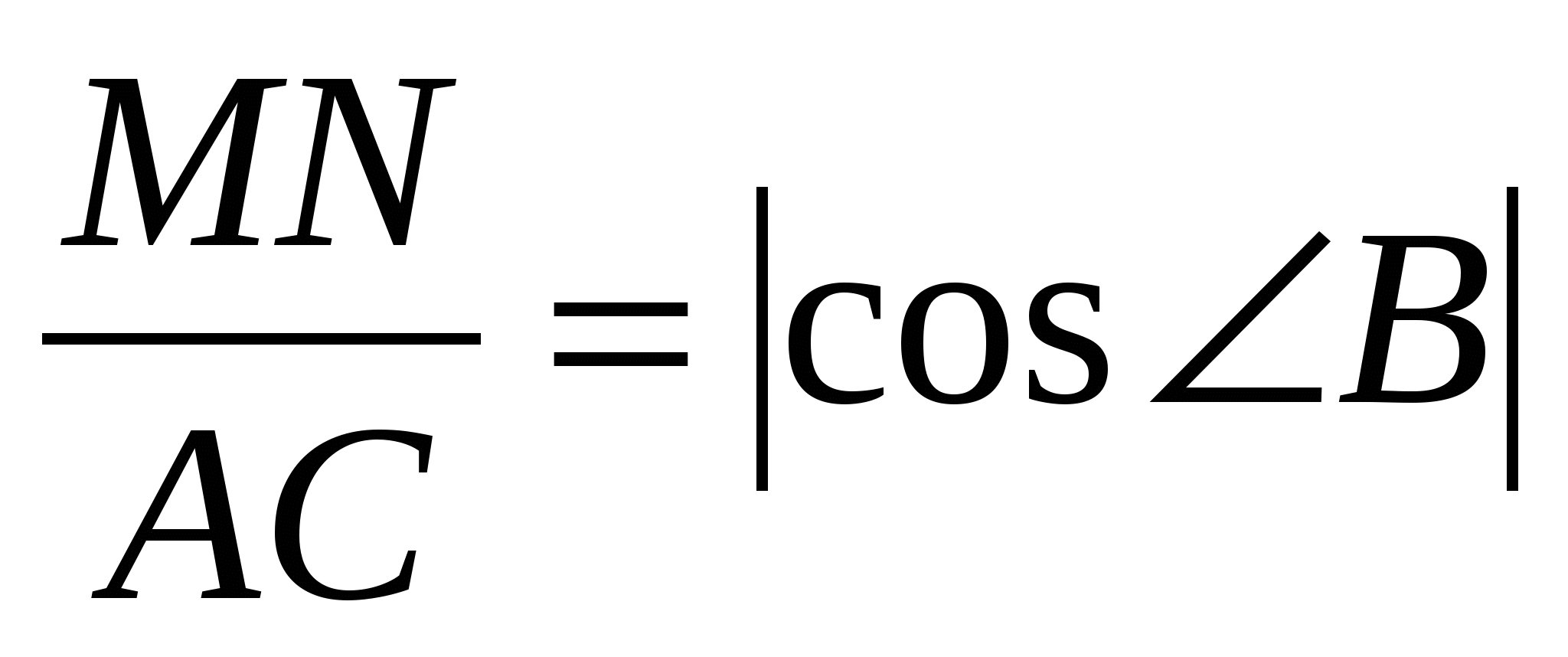 . Тем самым теряя второе значение
. Тем самым теряя второе значение ![]() .
.
11. Решить уравнение: (х2 +2х-5)2 + 2(х2 +2х-5) - 5 = х
1 способ. Группировка. Учит искусственным приемам группировки, введению новой переменной, упрощающей преобразования, развивает интуицию, аккуратность и упорство в преобразованиях. Место применения: факультативные занятия в 8 классе.
(х2 +2х+1-6)2 + 2(х2 +2х+1-6) - 4 = х+1 ((х+1)2-6)2 + 2((х+1)2-6) - 4 = х+1.
((х+1)2-6)2 + 2((х+1)2-6) - 4 = х+1.
Пусть х + 1 = у. Уравнение примет вид: (у2 - 6)2 + 2(у2 - 6) - 4 = у
![]() у4 - 12у2 + 36 + 2у2 - 12 - 4 = у
у4 - 12у2 + 36 + 2у2 - 12 - 4 = у  у4 - 10у2 - у + 20 = 0
у4 - 10у2 - у + 20 = 0
у4 + у3 - 4у2 - у3 - у2 + 4у- 5у2 - 5у + 20 = 0 у2(у2 + у - 4) - у(у2 + у - 4) -5(у2 + у - 4) = 0
у2(у2 + у - 4) - у(у2 + у - 4) -5(у2 + у - 4) = 0 
(у2 + у - 4)( у2 -у - 5) = 0
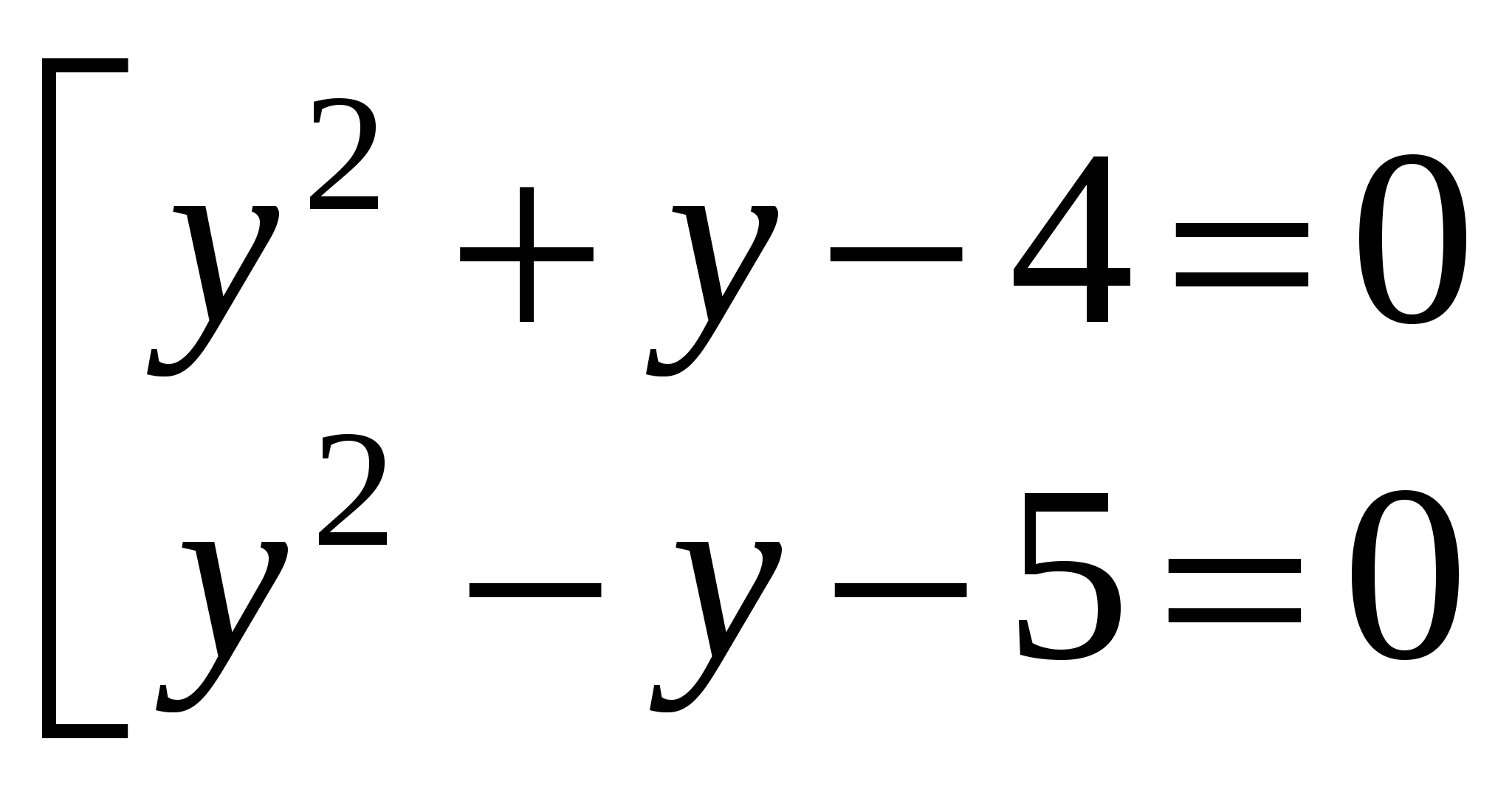

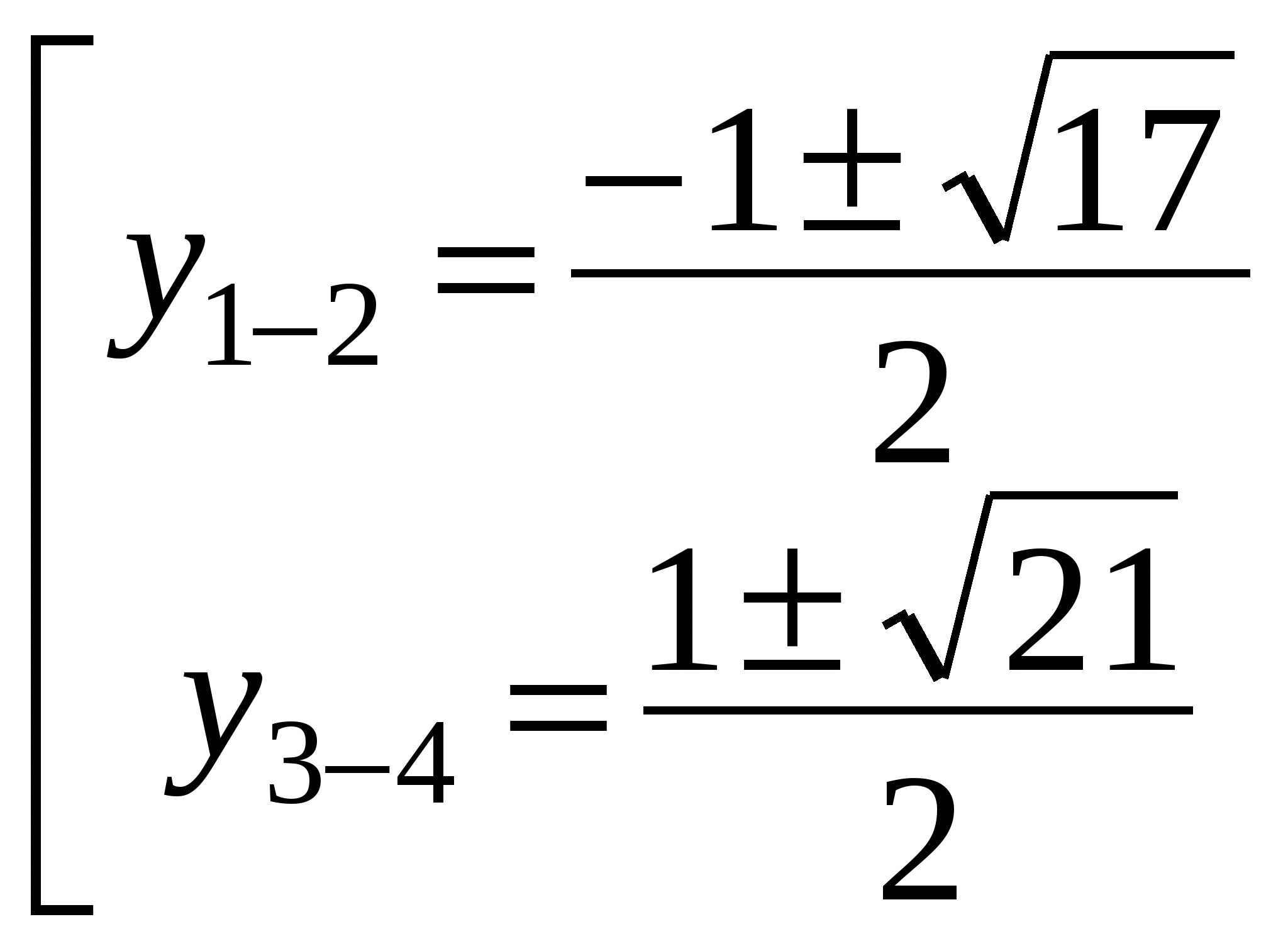

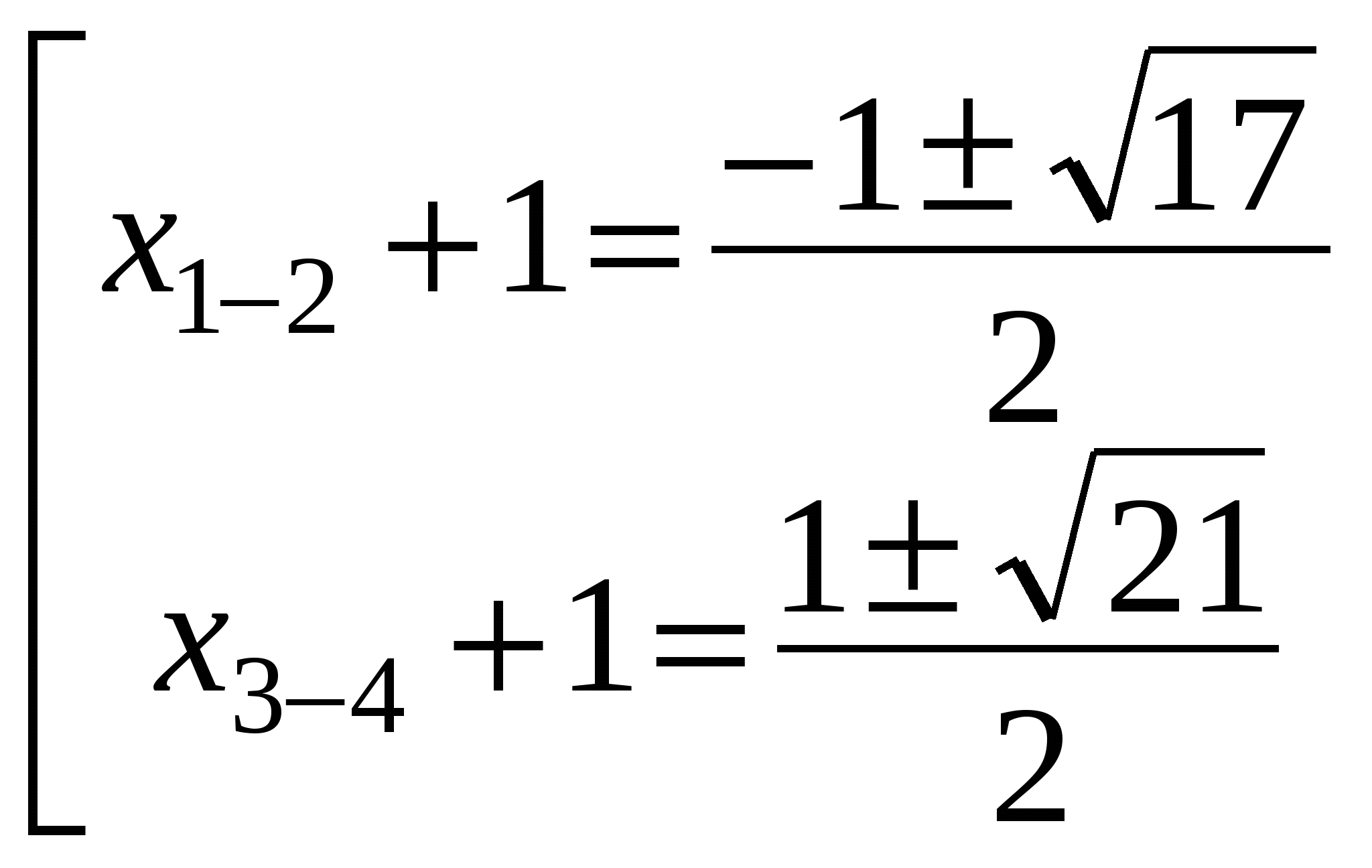
ОТВЕТ: ![]() ;
; 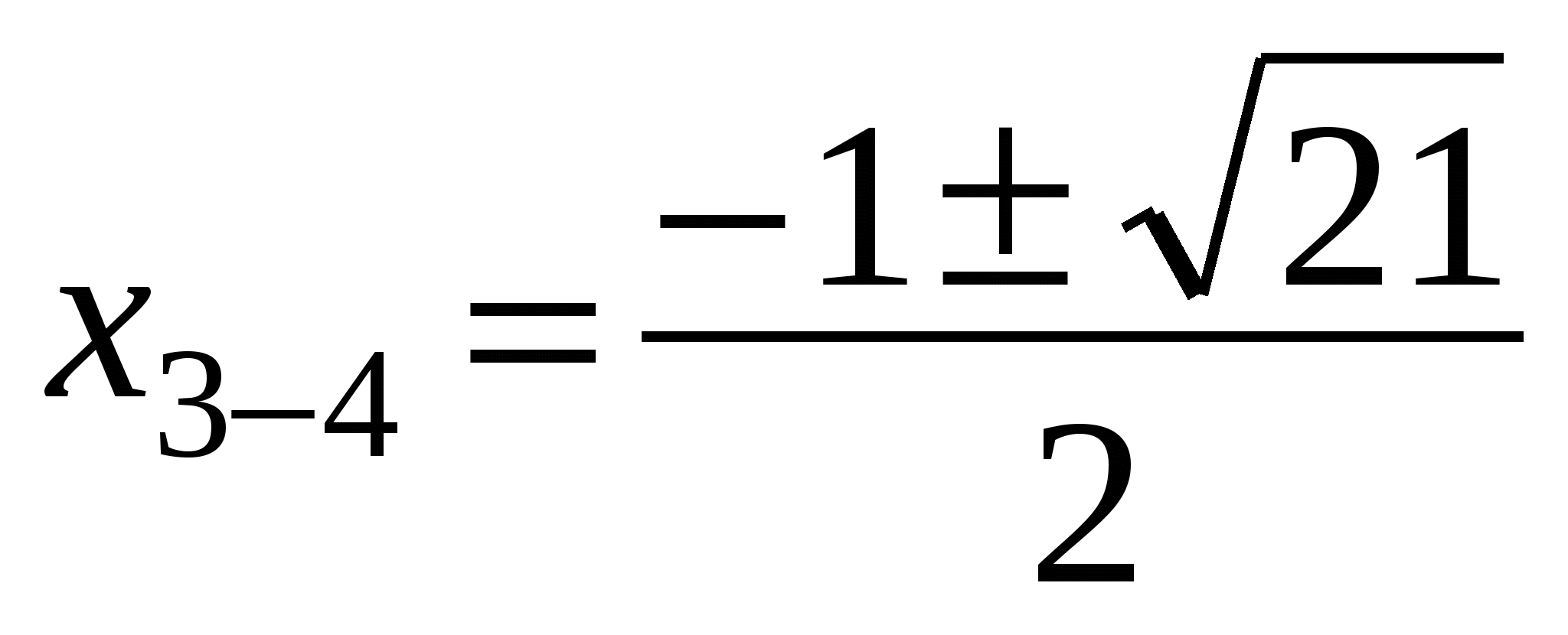
2 способ. Изменение роли переменной и числа. Место применения: факультативные занятия в 8 классе. Учит решать уравнения высших степеней, сведением к квадратным. Полезно, когда не находится нужное разложение на множители. Также полезно для развития навыков выделения полного квадрата.
(х2 + 2х - 5)2 + 2(х2 + 2х - 5) - 5 = х (х2 + 2х - 5)2 + 2(х2 + 2х - 5) +1 - 6 = х
(х2 + 2х - 5)2 + 2(х2 + 2х - 5) +1 - 6 = х
(х2 + 2х - 5 + 1)2 = х + 1 + 5![]() ((х + 1)2 - 5) = (х + 1) + 5.
((х + 1)2 - 5) = (х + 1) + 5.
Пусть х + 1 = у. Уравнение примет вид: (у2 - 5)2 = у + 5. Пусть а = 5.
Уравнение примет вид: у4 - 10у2 + а2 = у + а. Это уравнение квадратное относительно а.
а2 - (2у2 + 1)а + у4 - у = 0; D = (2у2 + 1)2 - 4(у4 - у) = 4у4 + 4у2 + 1 - 4у4 + 4у = (2у + 1)2;
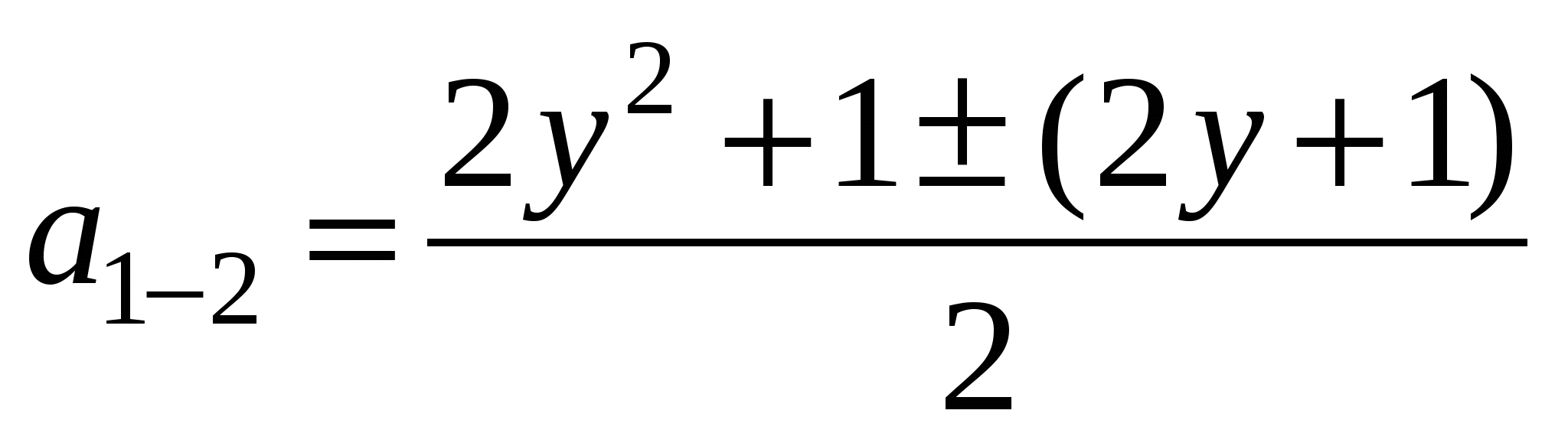 ;
; 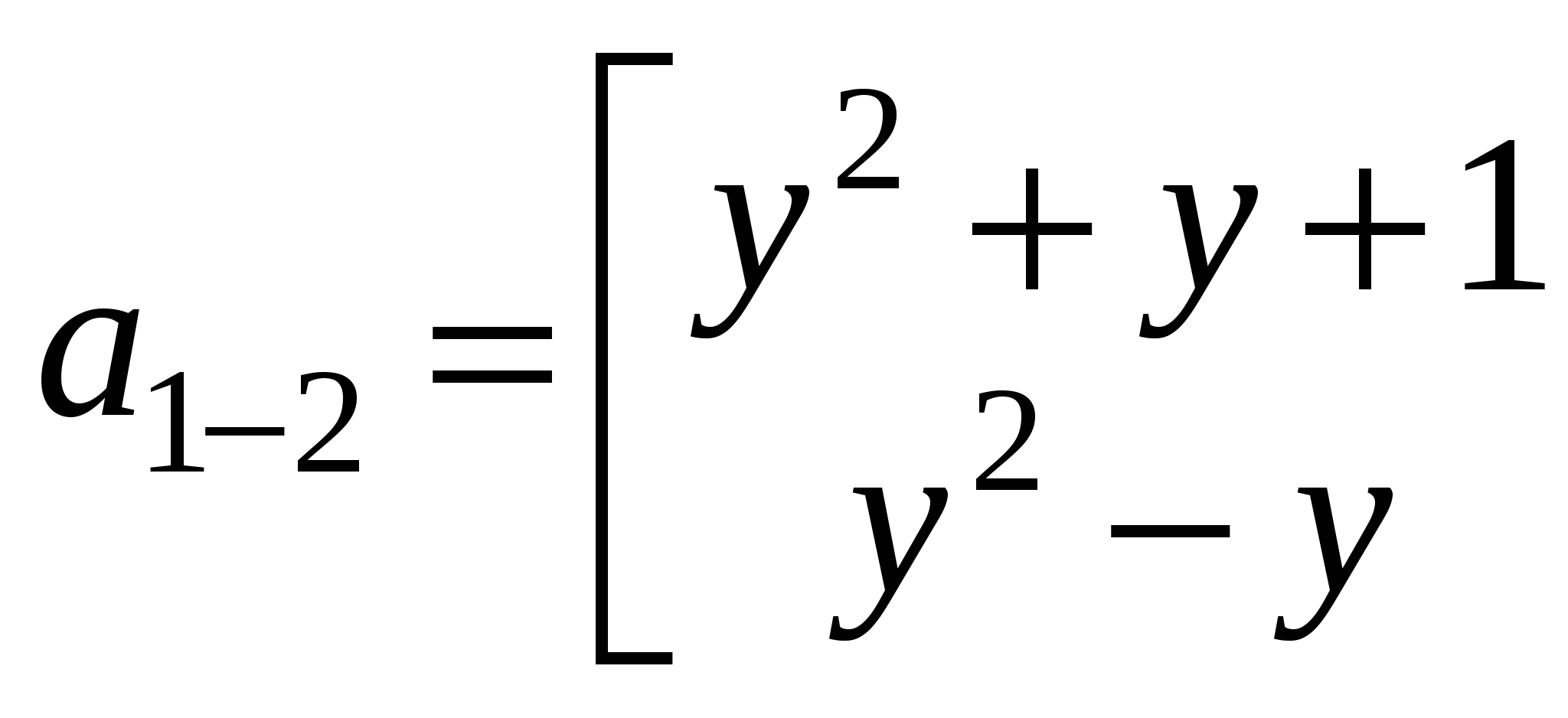


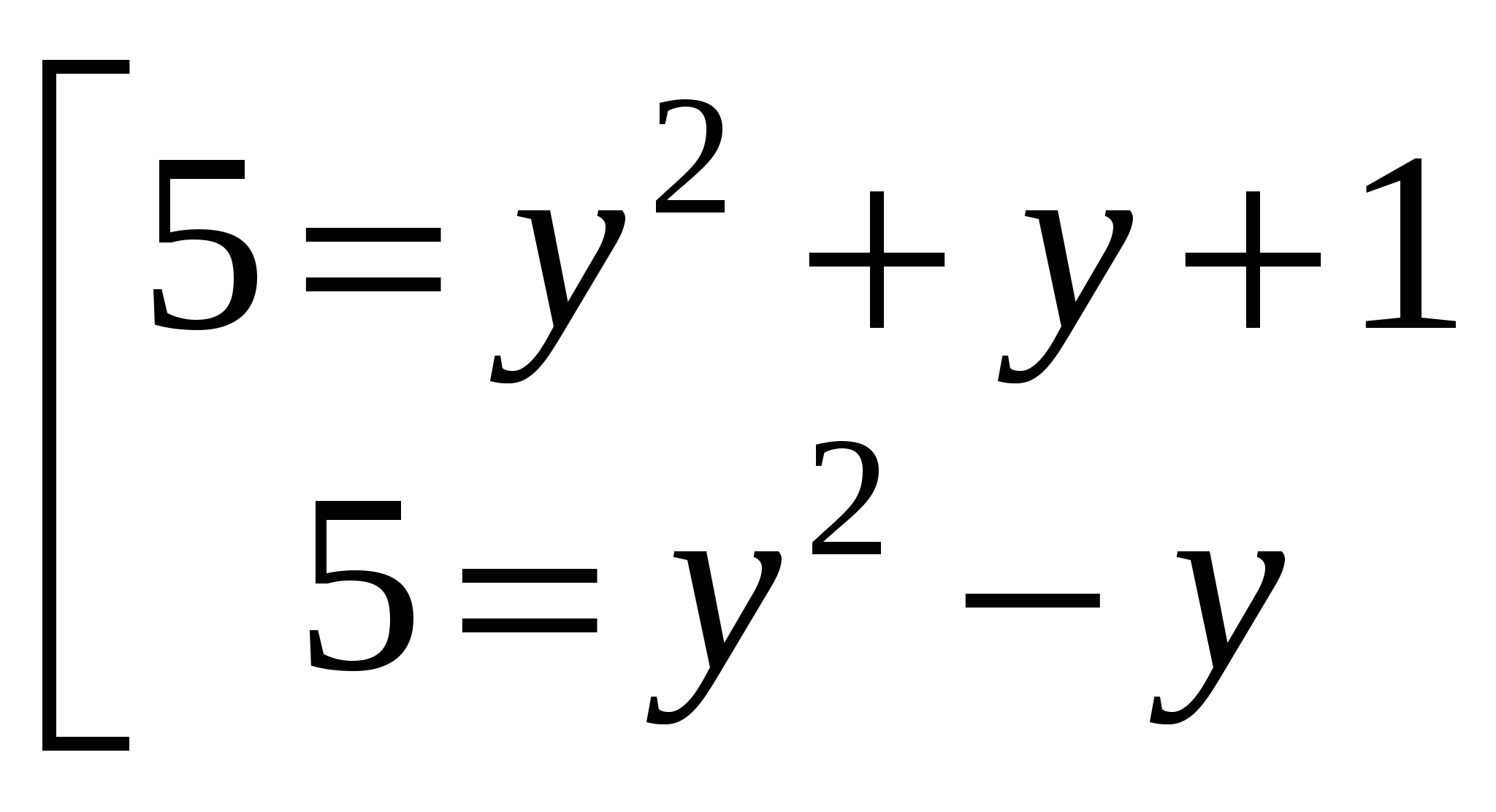

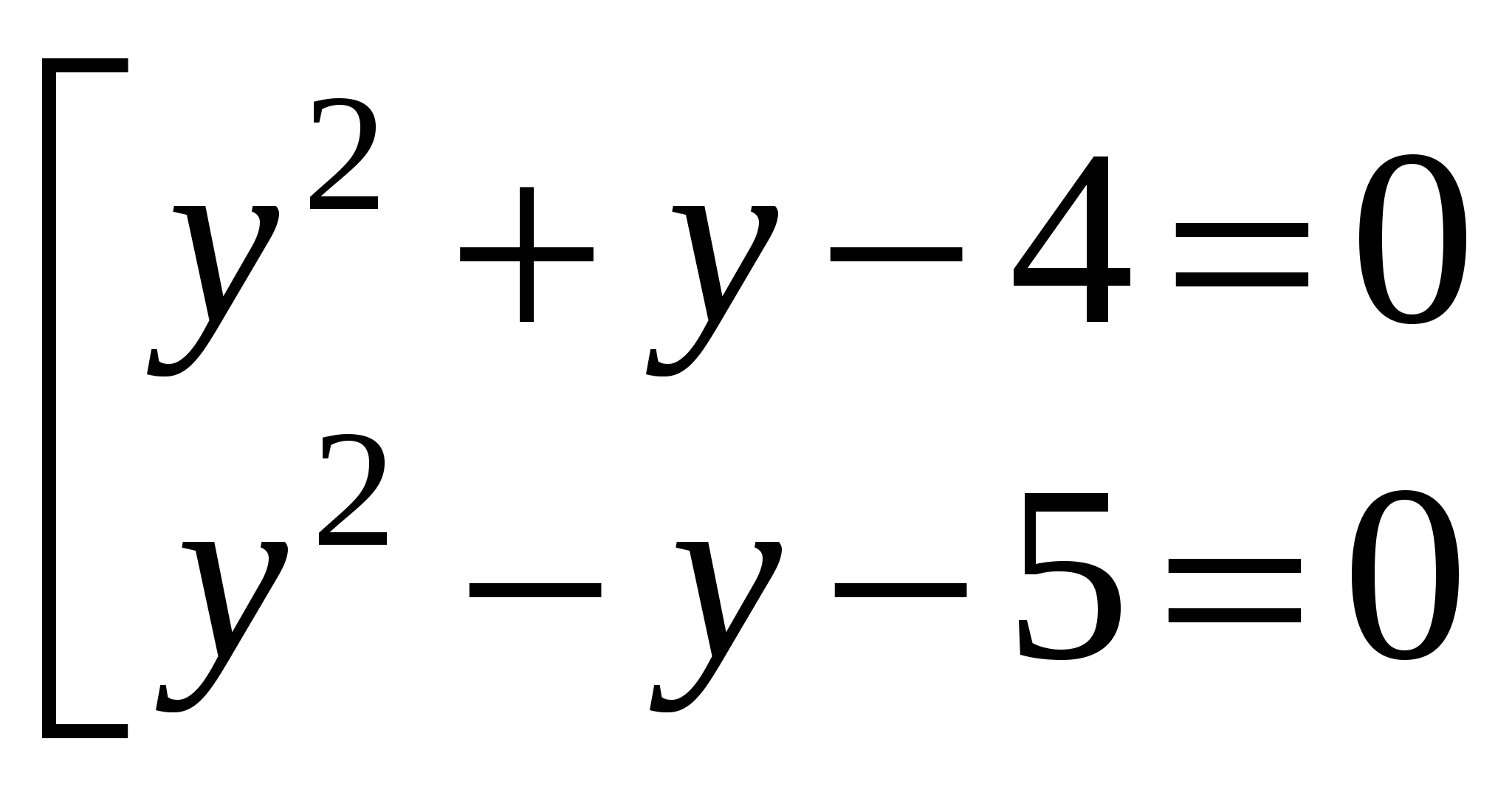

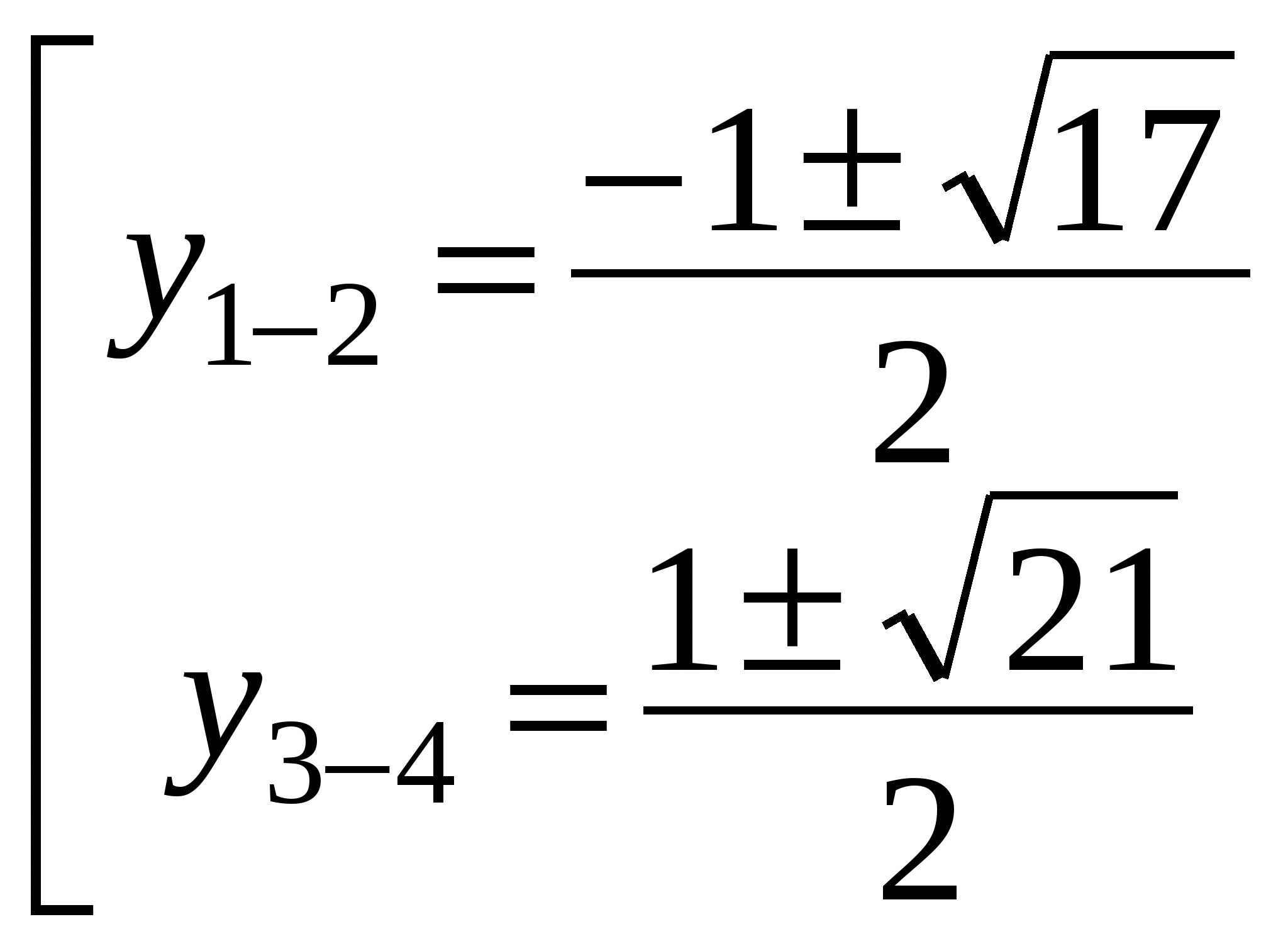

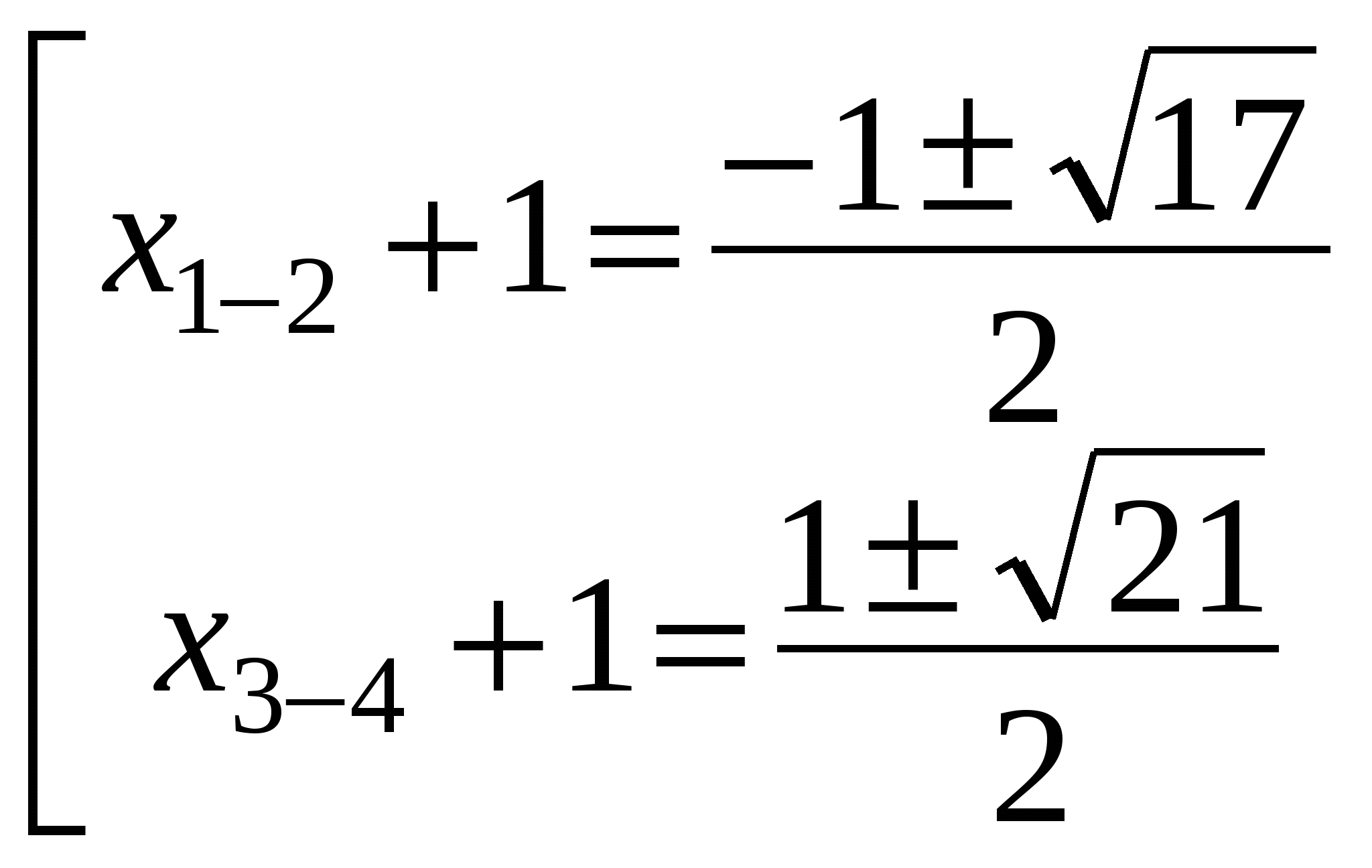
ОТВЕТ: 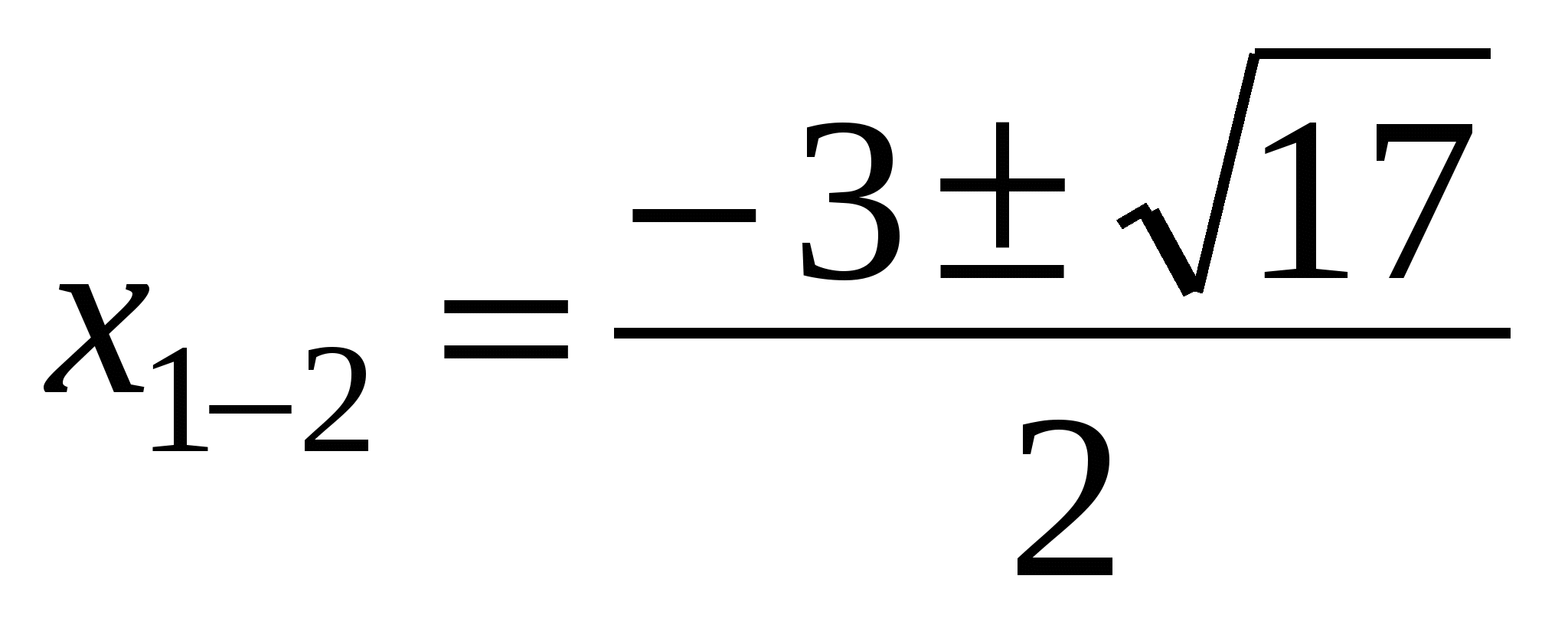 ;
; 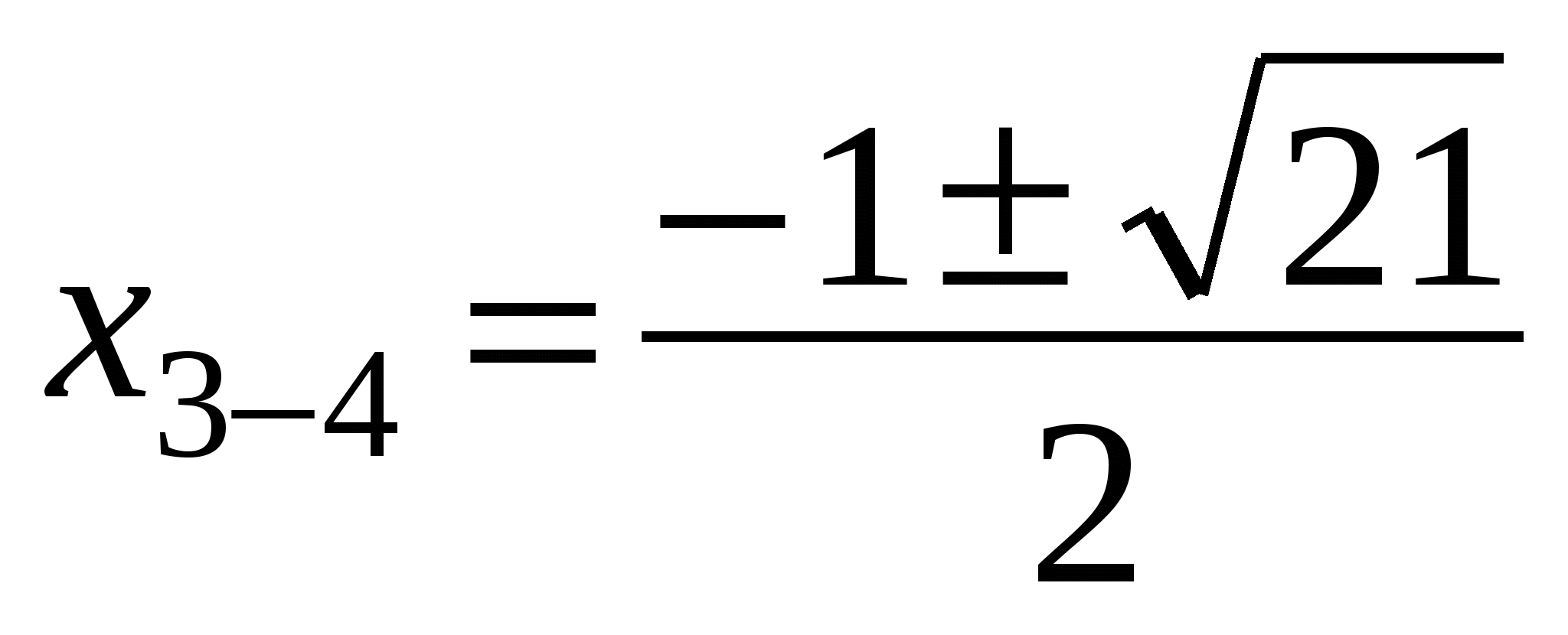
12. Разобьем задачу на 2 этапа: доказательство и вычисления .
1 способ
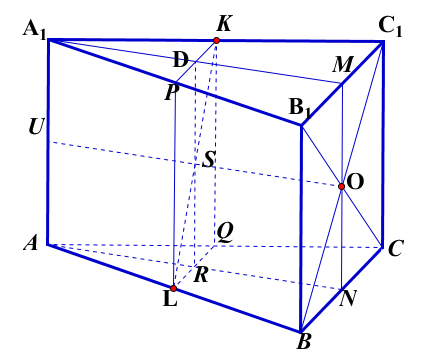
Дано: АВСА1В1С1 -правильная треугольная призма. L, K -середины ребер АВ и А1С1 соответственно.
О- точка пересечения диагоналей грани ВВ1С1С.
Доказать: пл-ть(LKO)![]() пл-ти (ВВ1С1С)
пл-ти (ВВ1С1С)
Доказательство: MN ║РL║KQ║AA1.
Пл-ть (LPKQ)![]() пл-ть (AA1MN) = DR║MN.
пл-ть (AA1MN) = DR║MN.
S - середина DR(из равенства треугольников DSK и LRS. S пл-ти (LKO), т.к.
пл-ти (LKO), т.к.  отрезку LK.
отрезку LK.
OS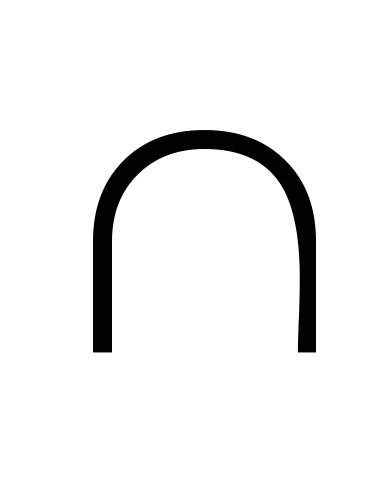 АА1 в точке U - середине АА1.
АА1 в точке U - середине АА1.
Отрезок UO лежит в плоскости сечения и является перпендикуляром к плоскости (ВВ1С1С) по признаку перпендикулярности прямой и плоскости. UO║AN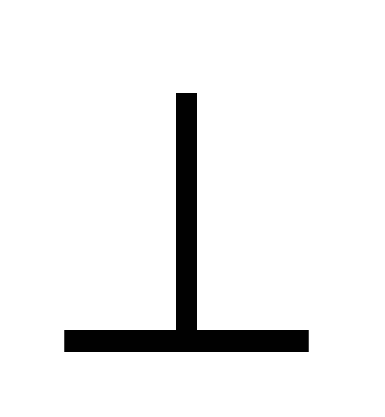 BC и ВВ1
BC и ВВ1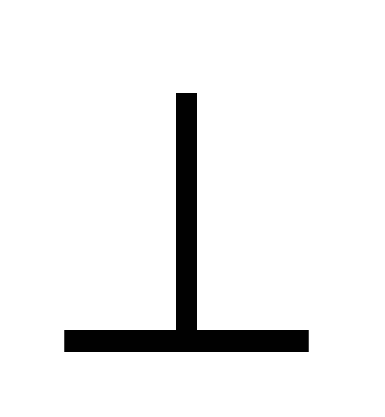 AN║ UO. Плоскость сечения (LKO)проходит через UO, являющимся перпендикуляром к плоскости (ВВ1С1С). Следовательно, по признаку перпендикулярности плоскостей плоскости (LKO) и (ВВ1С1С) перпендикулярны, что и требовалось доказать.
AN║ UO. Плоскость сечения (LKO)проходит через UO, являющимся перпендикуляром к плоскости (ВВ1С1С). Следовательно, по признаку перпендикулярности плоскостей плоскости (LKO) и (ВВ1С1С) перпендикулярны, что и требовалось доказать.
Данный способ доказательства применяется при решении задач на доказательство перпендикулярности прямой и плоскости и перпендикулярности плоскостей и связи между параллельностью и перпендикулярностью в 10 классе. Заметим, что построение сечения не требуется, достаточно доказать принадлежность перпендикуляра одной из плоскостей.
Вычисление:
Поскольку доказано, что секущая плоскость проходит через UO║AN UO║ пл-ти (АВС) по признаку параллельности прямой и плоскости. Т.к. секущая плоскость проходит через прямую, параллельную основаниям призмы, то она пересекает основания по прямым LH и KG параллельным UO. Следовательно, GH
UO║ пл-ти (АВС) по признаку параллельности прямой и плоскости. Т.к. секущая плоскость проходит через прямую, параллельную основаниям призмы, то она пересекает основания по прямым LH и KG параллельным UO. Следовательно, GH секущей плоскости. LH
секущей плоскости. LH пл-ти ВВ1С1С. LH- линия пересечения секущей плоскости и плоскости основания.
пл-ти ВВ1С1С. LH- линия пересечения секущей плоскости и плоскости основания.
Следовательно ![]()
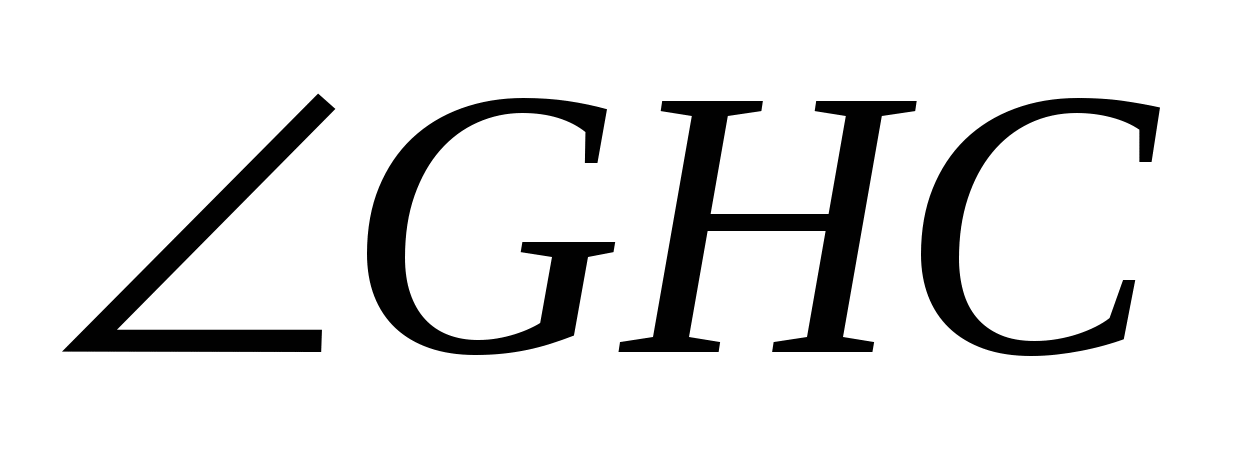 - линейный угол между секущей плоскостью и плоскостью основания. Очевидно, что ВН = 0,5 ВN= 0,25 ВС = С1G.
- линейный угол между секущей плоскостью и плоскостью основания. Очевидно, что ВН = 0,5 ВN= 0,25 ВС = С1G.
Угол найдем из следующей планиметрической задачи.
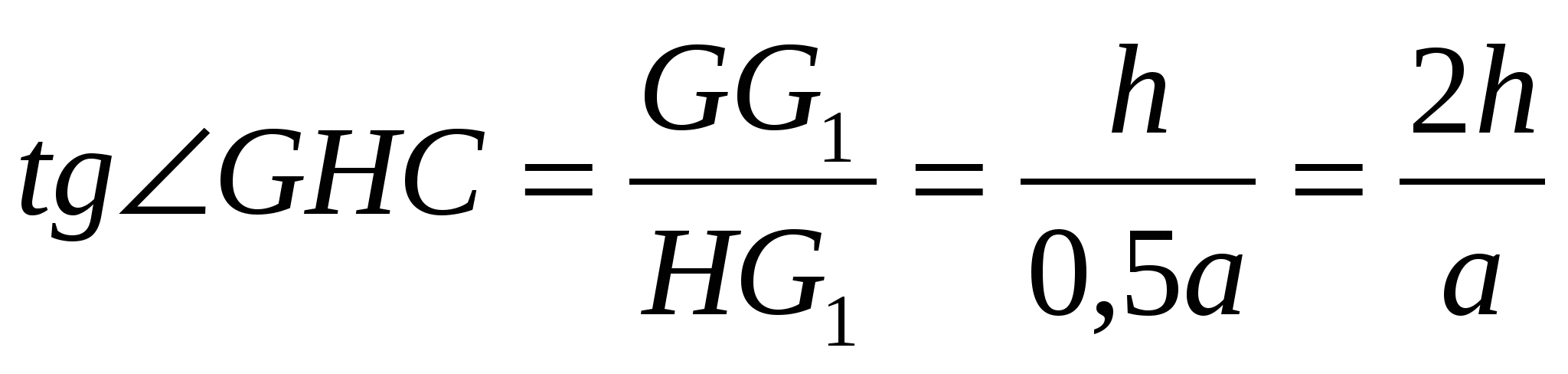
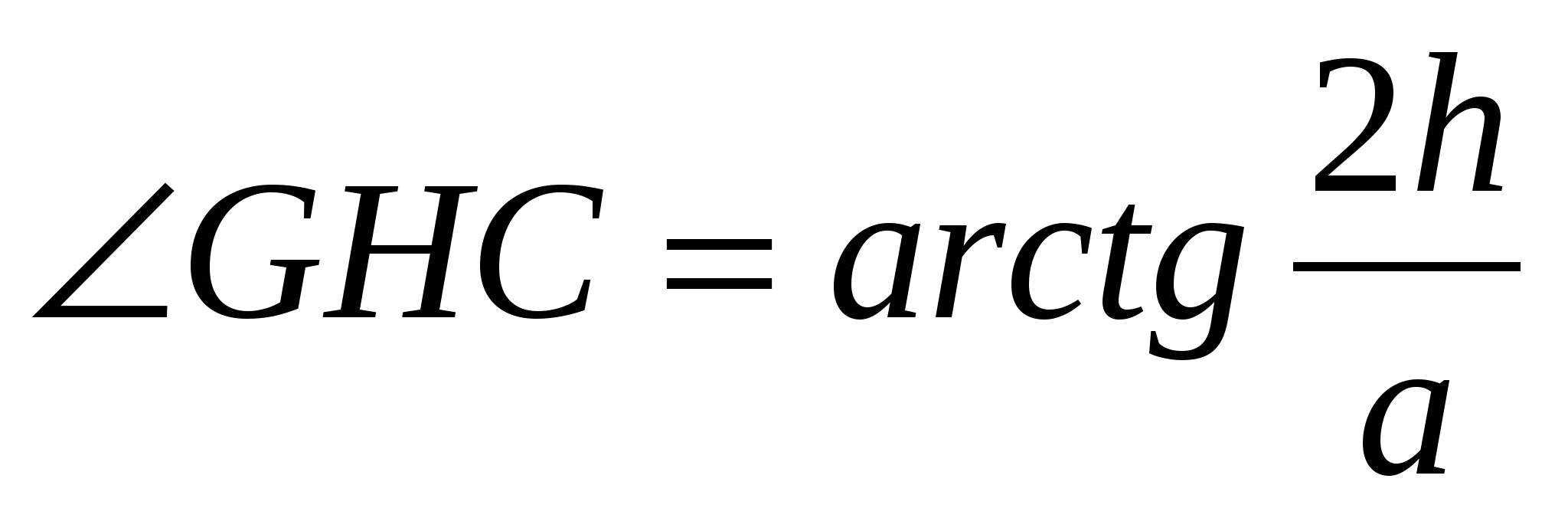 , где h - длина бокового ребра, а - длина ребра основания.
, где h - длина бокового ребра, а - длина ребра основания.
ОТВЕТ: ![]() , где h - длина бокового ребра,
, где h - длина бокового ребра,
а - длина ребра основания.
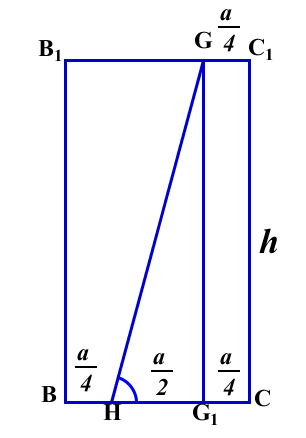
Данный способ применяется при отработке теорем, связанных с параллельностью в пространстве, а также полезен при повторении планиметрии. Само сечение при этом не строится, а строятся только следы секущей плоскости.
2 способ
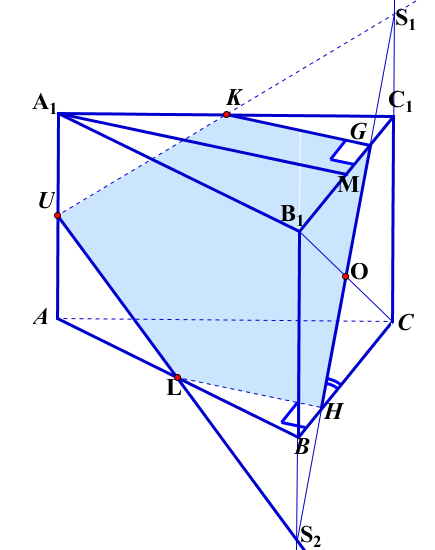
Доказательство: Построим сечение, используя уже доказанный факт принадлежности точки U -середины ребра АА1 данному сечению. UK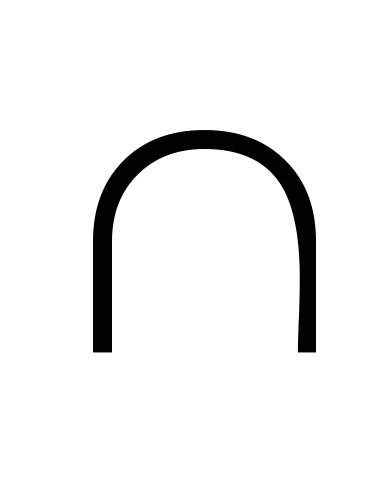 CC1=S1, UL
CC1=S1, UL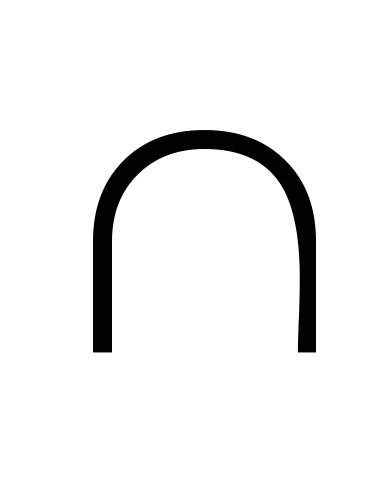 CC1=S2, S1S2
CC1=S2, S1S2 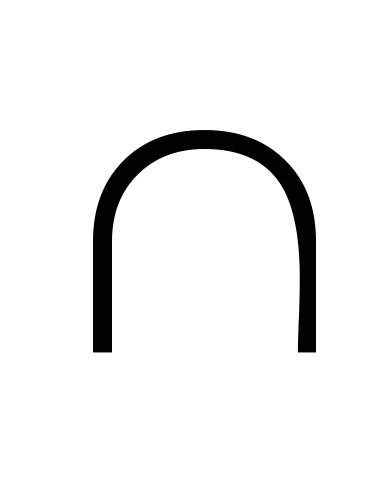 B1C1=G,
B1C1=G,
S1S2 ![]() BC=H. LUKGH - искомое сечение.
BC=H. LUKGH - искомое сечение.
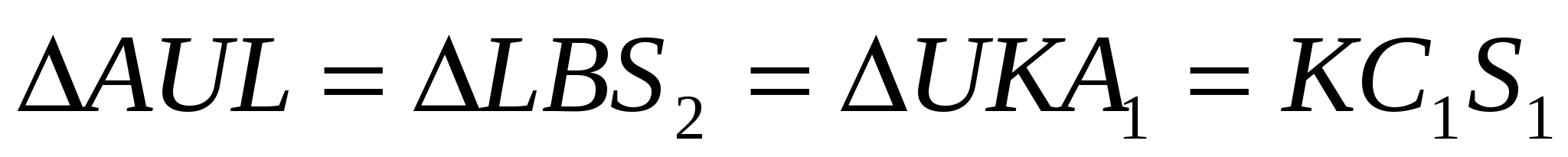 как прямоугольные, с равными катетами AL=LB=A1K=KC1 и равными острыми углами.
как прямоугольные, с равными катетами AL=LB=A1K=KC1 и равными острыми углами.
Отсюда следует ВS2=C1S1 = 0,5АА1 и соответственно равенство треугольников BHS2 и S1C1G -прямоугольных по катету и острому углу.
Далее,  GS1C1 подобен
GS1C1 подобен  HS1C с коэффициентом подобия
HS1C с коэффициентом подобия 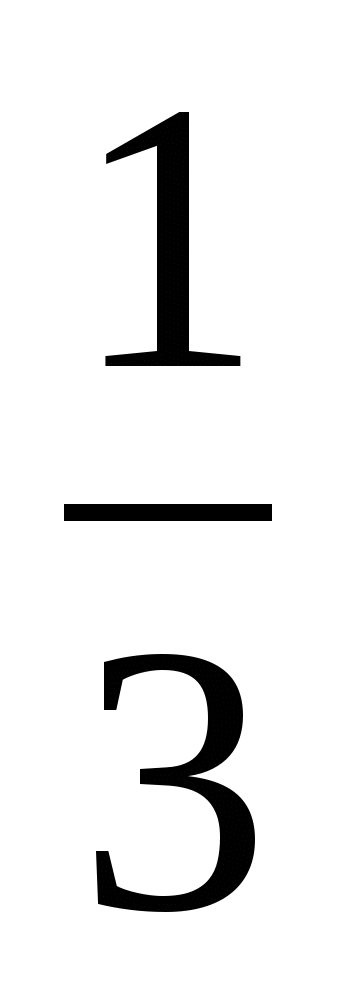 . Тогда GC1=BH=x, HC =3x, МС1=2х.
. Тогда GC1=BH=x, HC =3x, МС1=2х.  C1KS подобен
C1KS подобен  С1А1М . Тогда KG║А1М
С1А1М . Тогда KG║А1М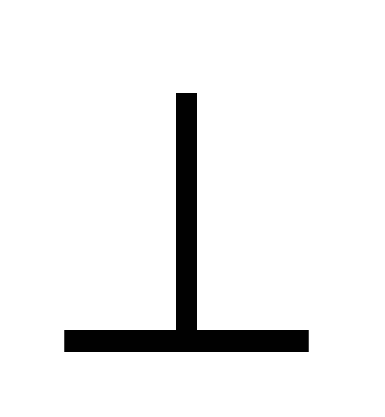 пл-ти (ВВ1С1С). Док-во приведено в 1 способе. Пл-ть ( LUKGH) проходит через KG
пл-ти (ВВ1С1С). Док-во приведено в 1 способе. Пл-ть ( LUKGH) проходит через KG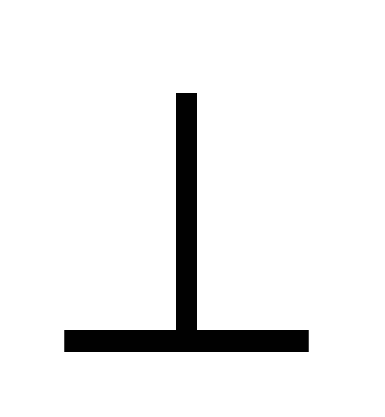 пл-ти (ВВ1С1С). По признаку перпендикулярности плоскостей пл-ть ( LUKGH)
пл-ти (ВВ1С1С). По признаку перпендикулярности плоскостей пл-ть ( LUKGH) 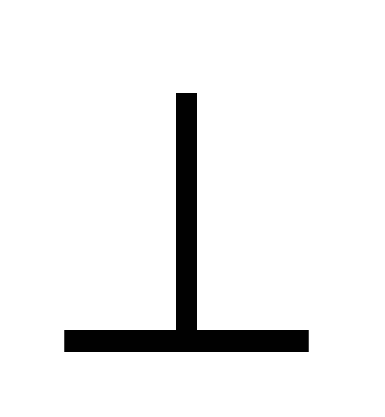 пл-ти (ВВ1С1С), что и требовалось доказать.
пл-ти (ВВ1С1С), что и требовалось доказать.
Данный способ доказательства применяется при решении задач на доказательство перпендикулярности прямой и плоскости и перпендикулярности плоскостей и связи между параллельностью и перпендикулярностью в 10 классе. Разница с 1 способом в том, что построено сечение.
Вычисление: LH - линия пересечения секущей плоскости и плоскости основания.
KG║LH 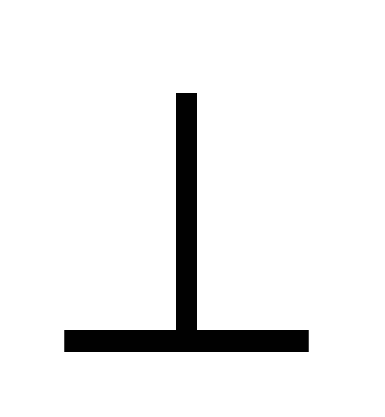 пл-ти (ВВ1С1С).
пл-ти (ВВ1С1С). 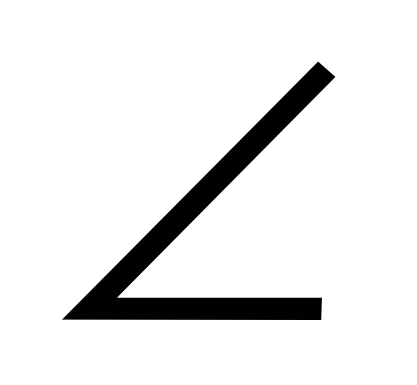 S1HC - линейный угол угла между плоскостями по определению.
S1HC - линейный угол угла между плоскостями по определению. 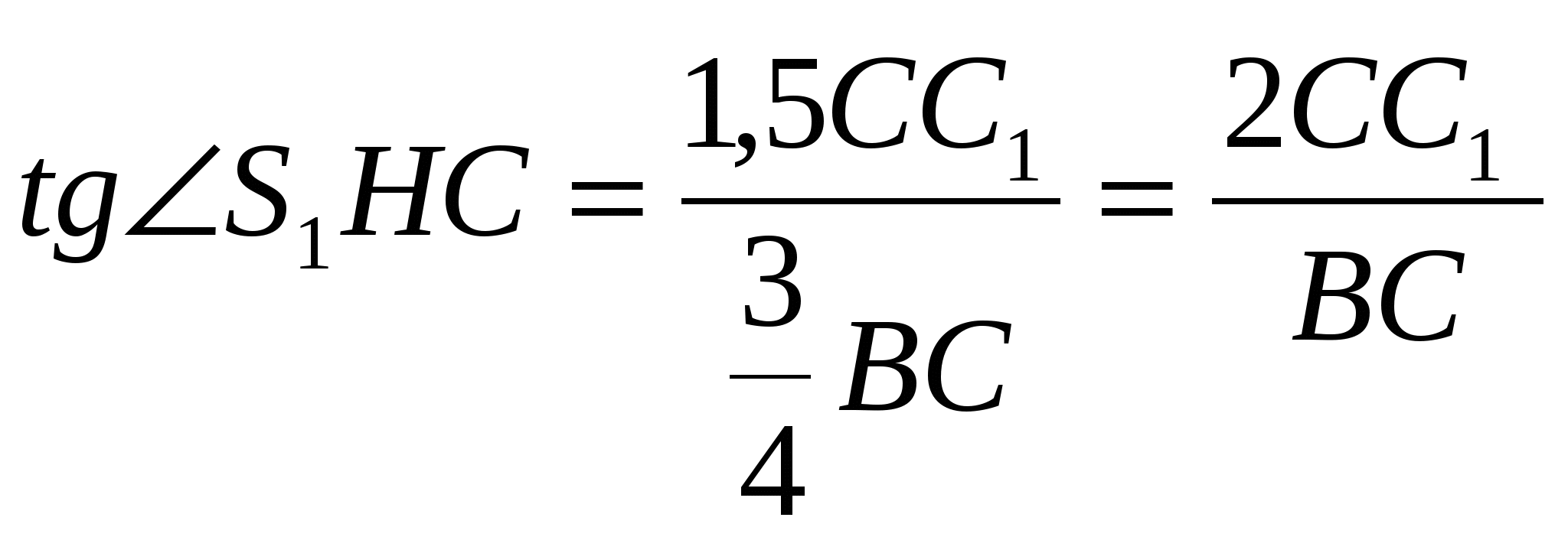 . Откуда угол между плоскостью основания и секущей плоскостью равен арктангенсу отношения удвоенной длины бокового ребра к длине ребра основания.
. Откуда угол между плоскостью основания и секущей плоскостью равен арктангенсу отношения удвоенной длины бокового ребра к длине ребра основания.
ОТВЕТ: 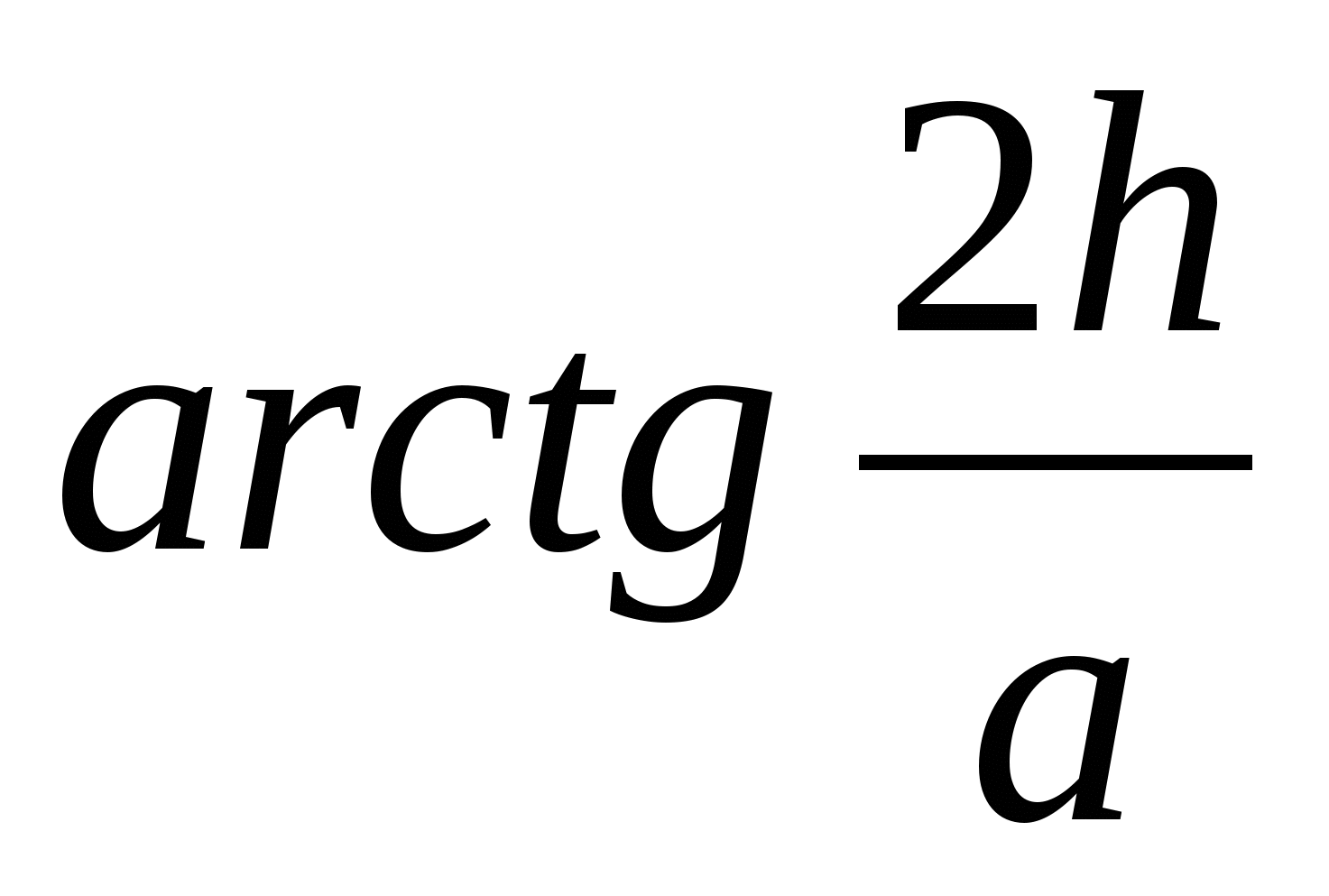 , где h - длина бокового ребра, а - длина ребра основания.
, где h - длина бокового ребра, а - длина ребра основания.
Этот способ применяется при изучении темы Построение и вычисление угла между плоскостями в 10 классе.
3 способ
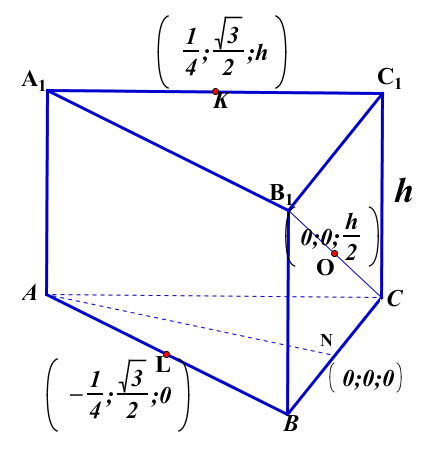
Пусть АА1 : АВ = h . Поместим призму в декартову систему координат так, чтобы плоскость основания совпала с плоскостью ХОУ, начало координат с точкой N. Тогда координаты точек, через которые проходит сечение, будут иметь координаты, указанные на чертеже.
Нормальный вектор пл-ти (ВВ1С1С) будет иметь координаты ![]() (0; 1; 0).
(0; 1; 0).
Найдем координаты нормального вектора
пл -ти (LOK).
Для этого составим уравнение этой плоскости:
ах + ву + сz + d =0.
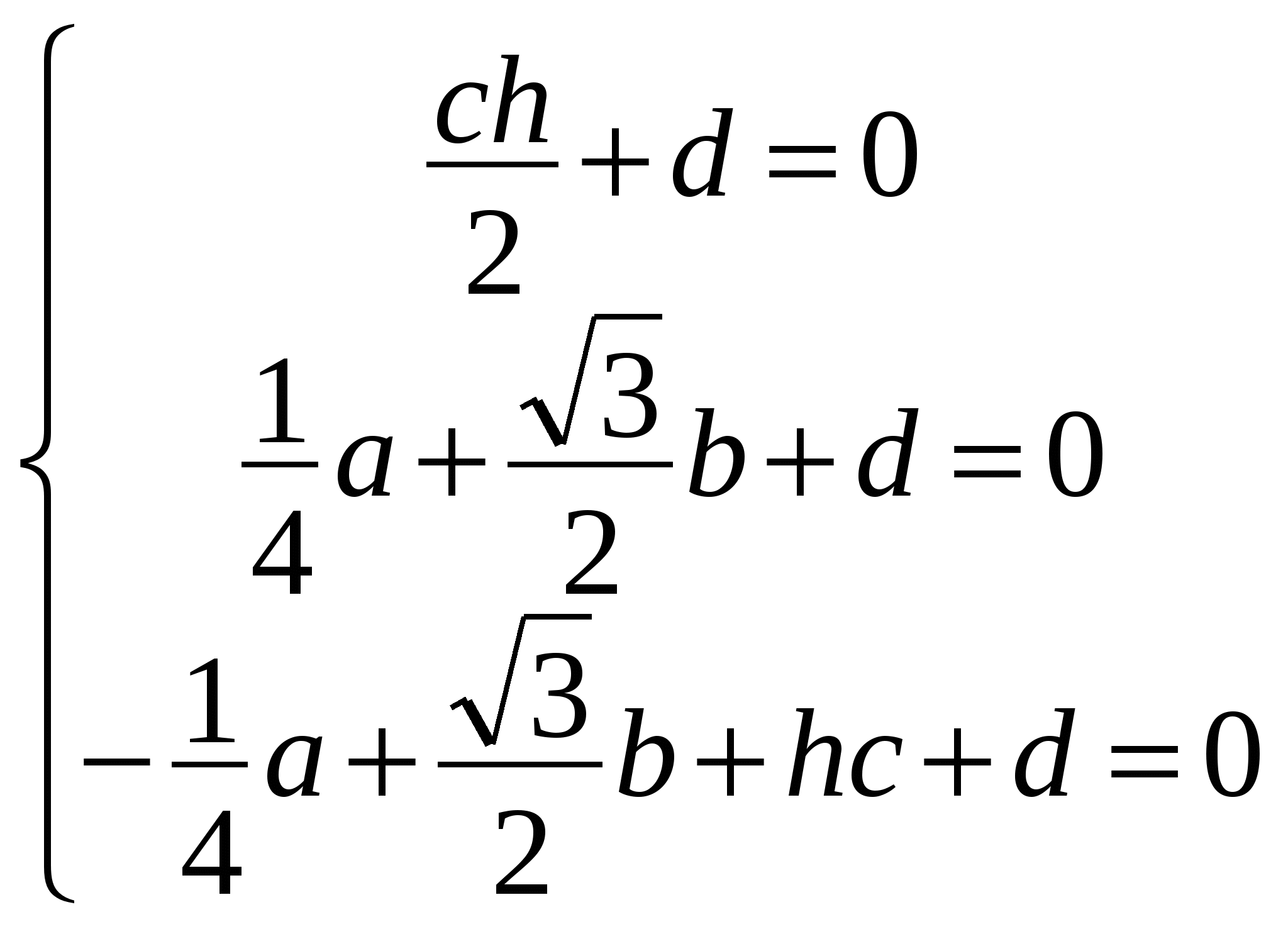 сложим 2 и 3 уравнения и подставим с из 1 уравнения
сложим 2 и 3 уравнения и подставим с из 1 уравнения

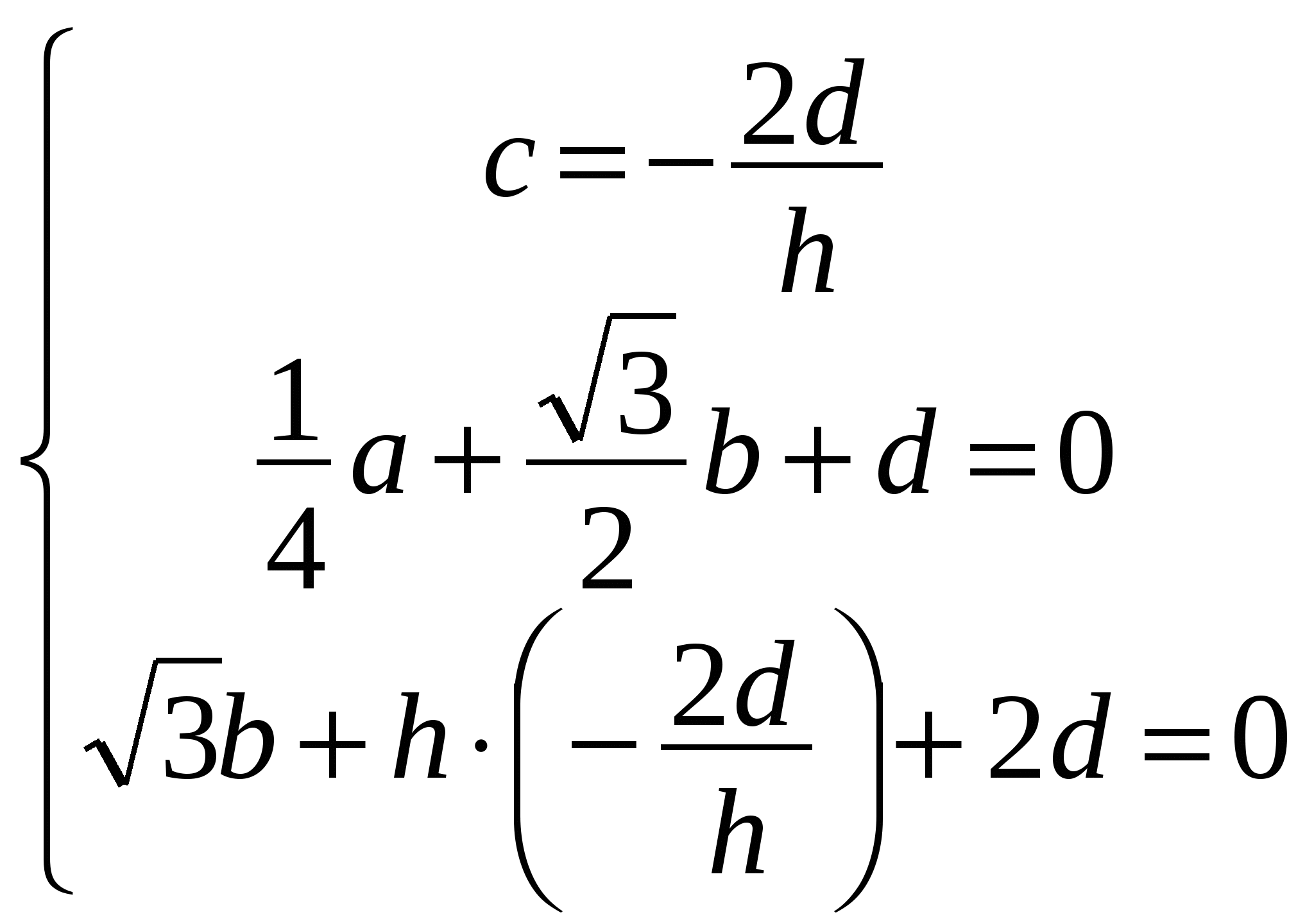

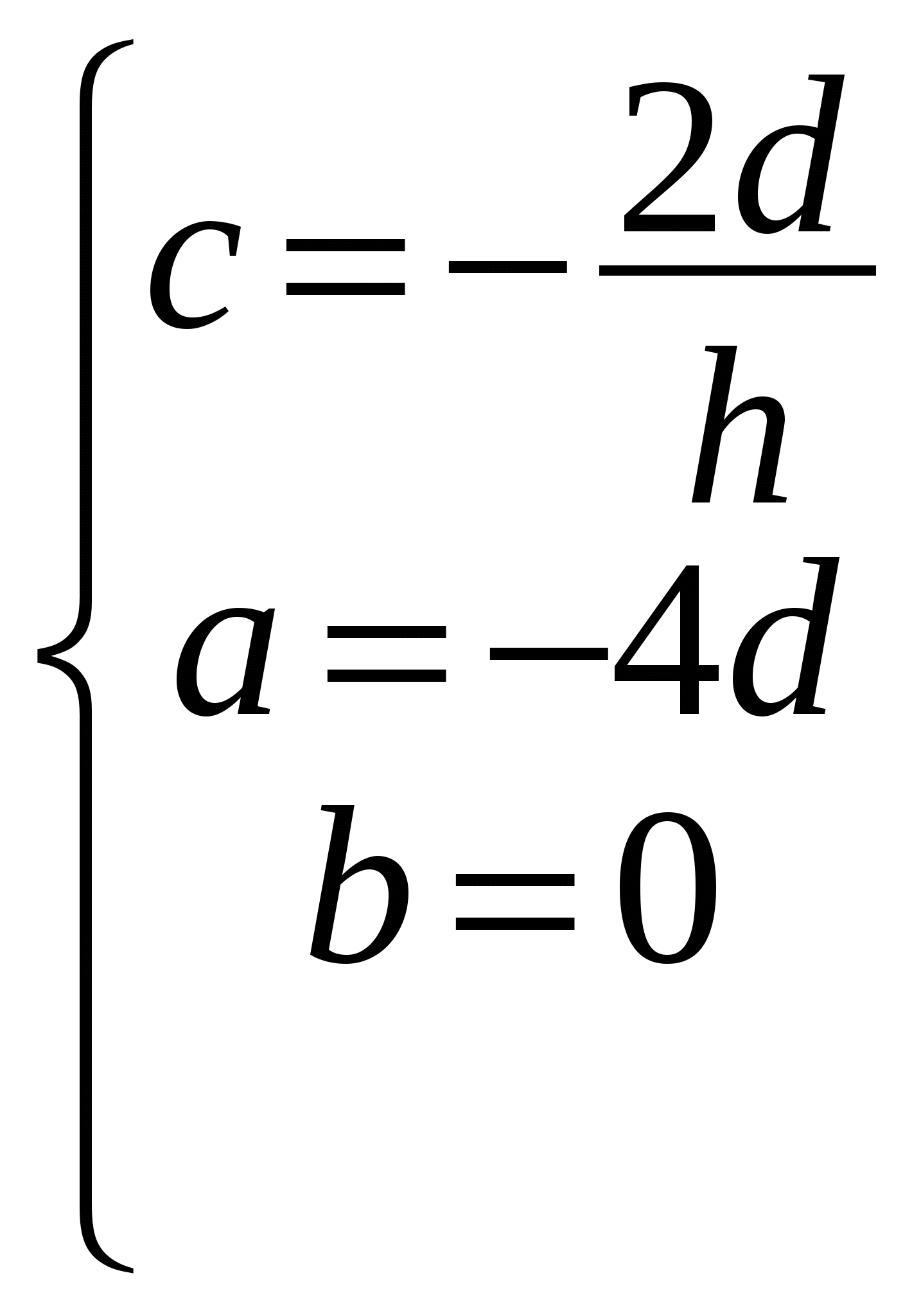
Итак, нормальный вектор пл -ти (LOK) 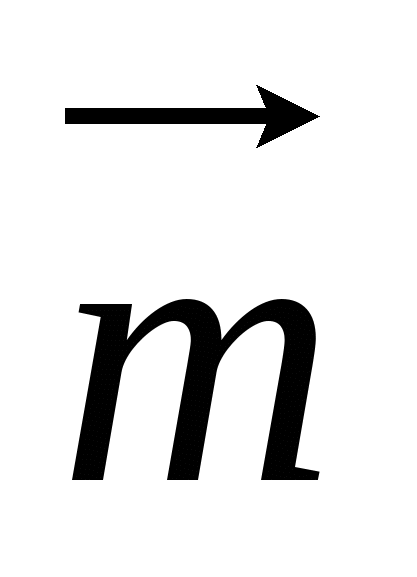
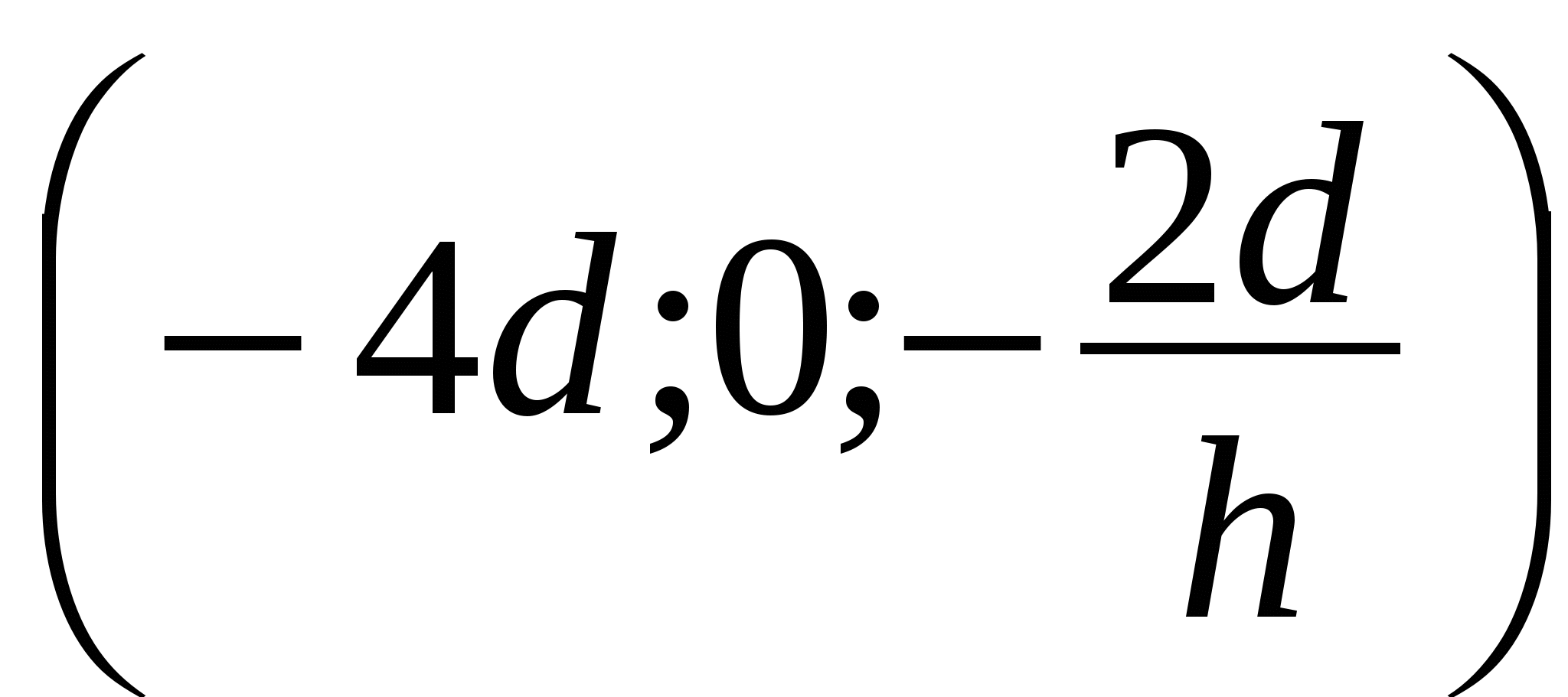 .
.
Найдем скалярное произведение векторов 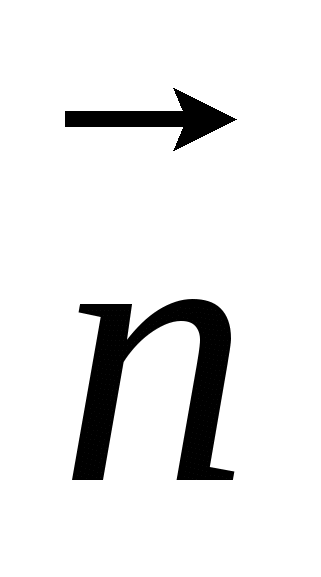 (0; 1; 0) и
(0; 1; 0) и 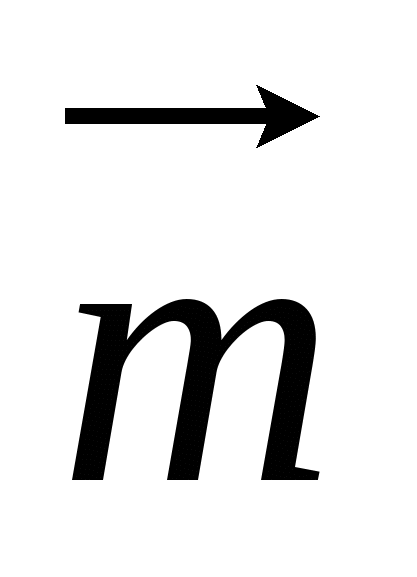
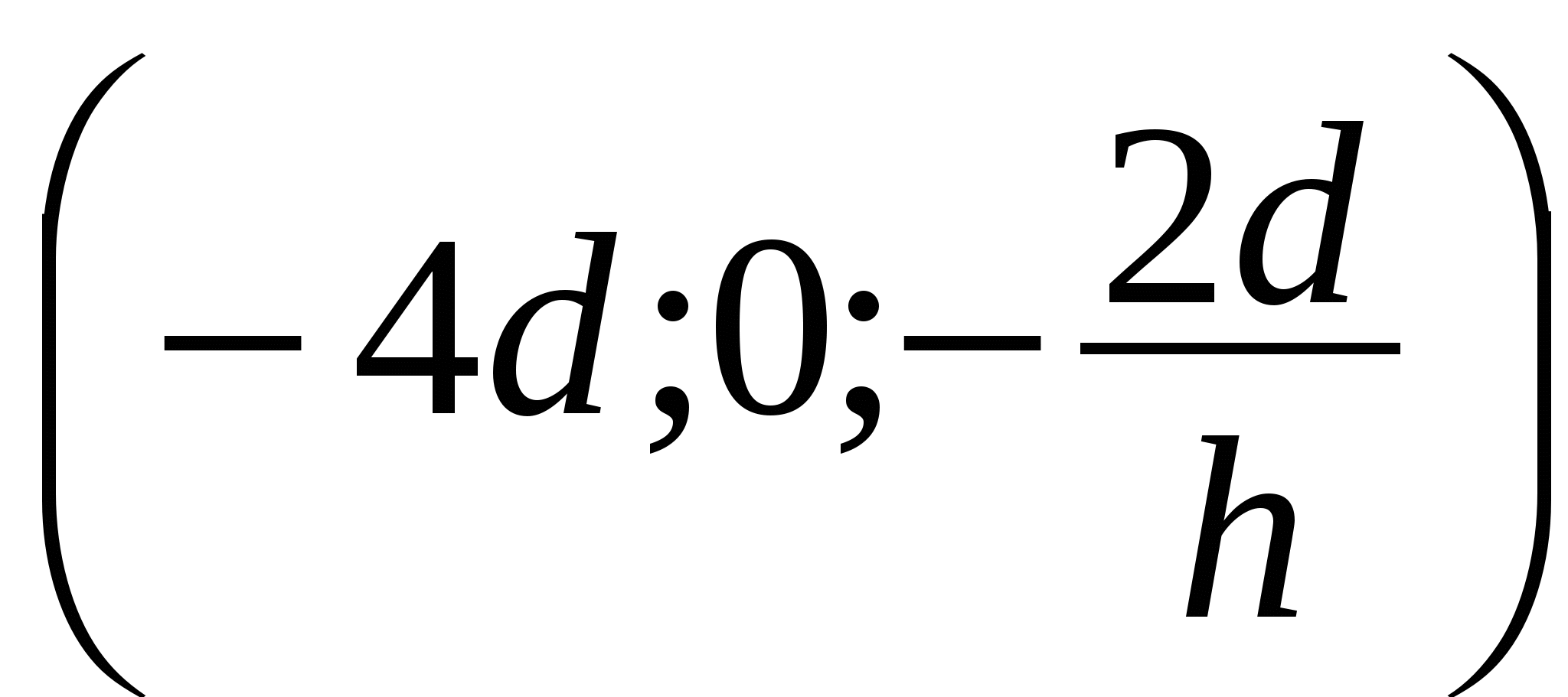 .
.
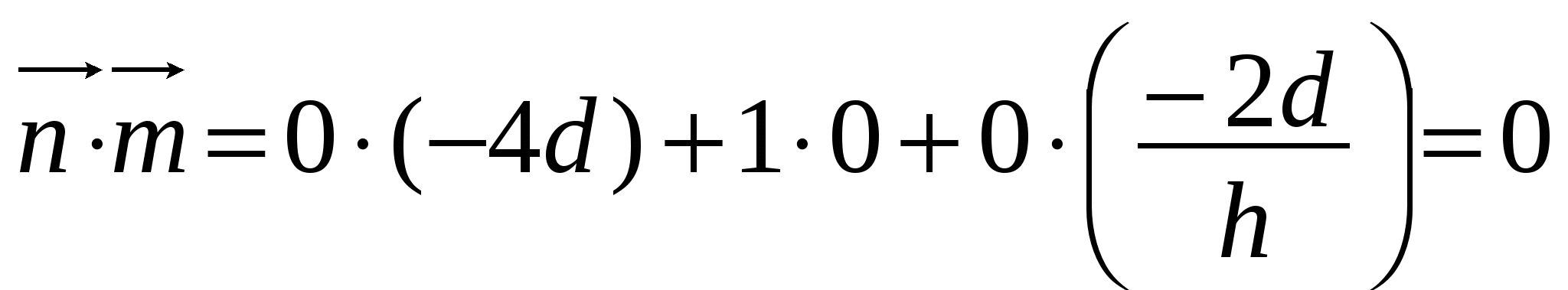 . Откуда следует, что
. Откуда следует, что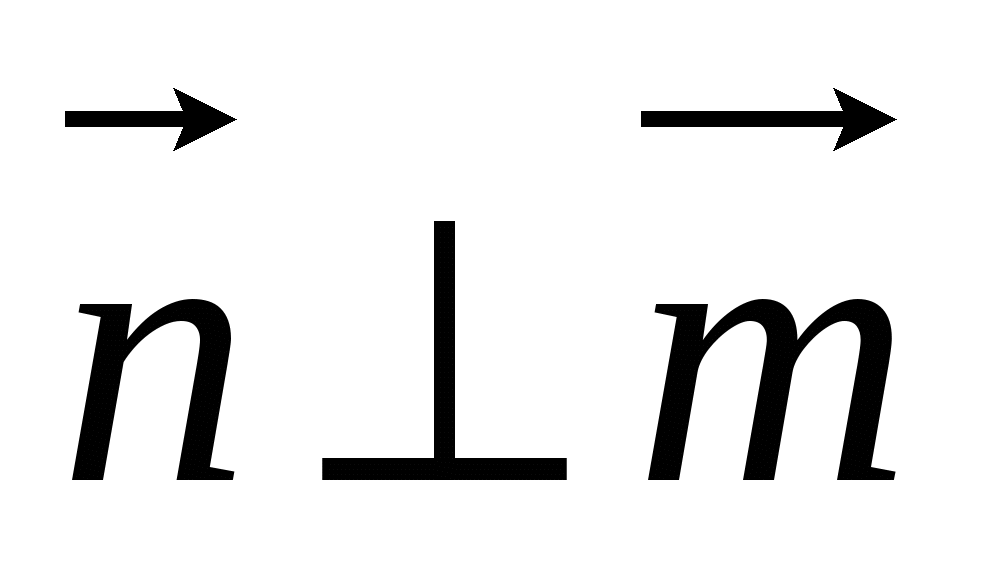 . Из перпендикулярности нормальных векторов следует перпендикулярность плоскостей, что и требовалось доказать.
. Из перпендикулярности нормальных векторов следует перпендикулярность плоскостей, что и требовалось доказать.
Вычисление:
Угол между секущей плоскостью и плоскостью основания с нормальным вектором 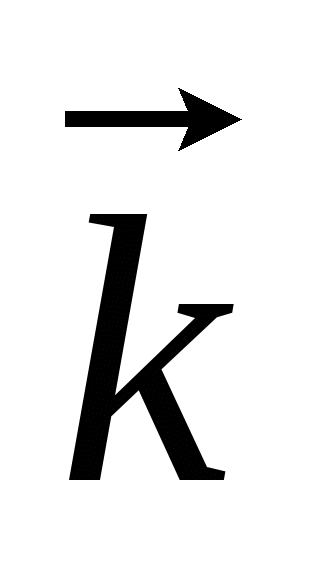 (0; 0; 1) вычислим с помощь скалярного произведения.
(0; 0; 1) вычислим с помощь скалярного произведения.
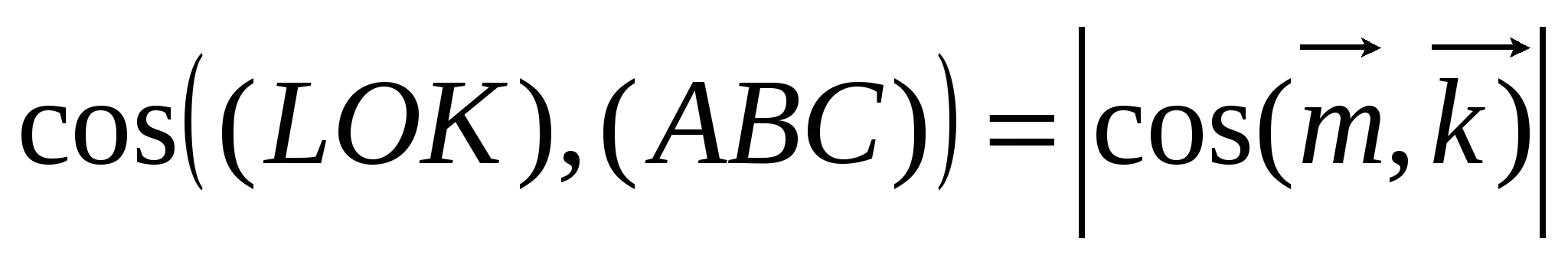 =
=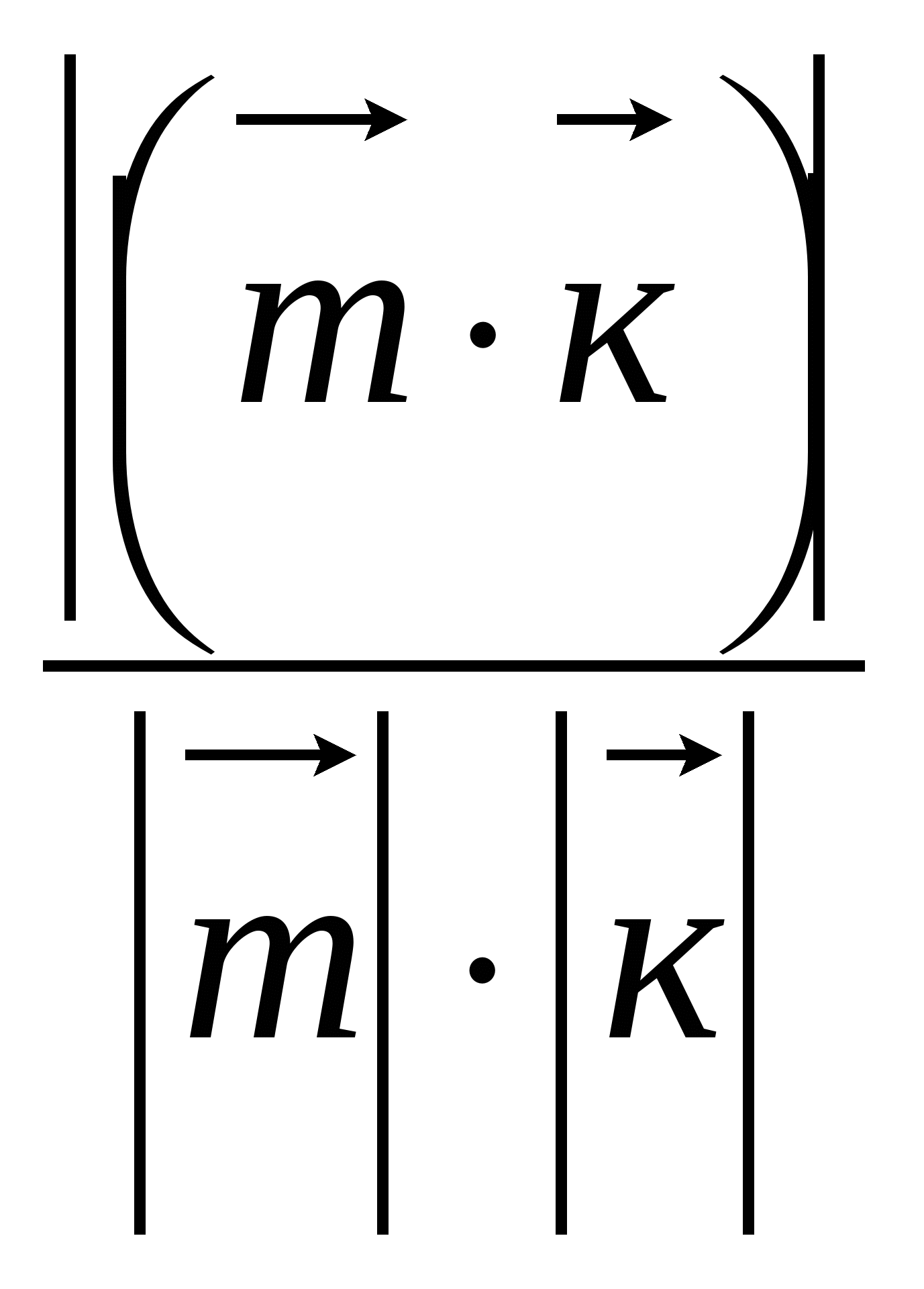 =
= 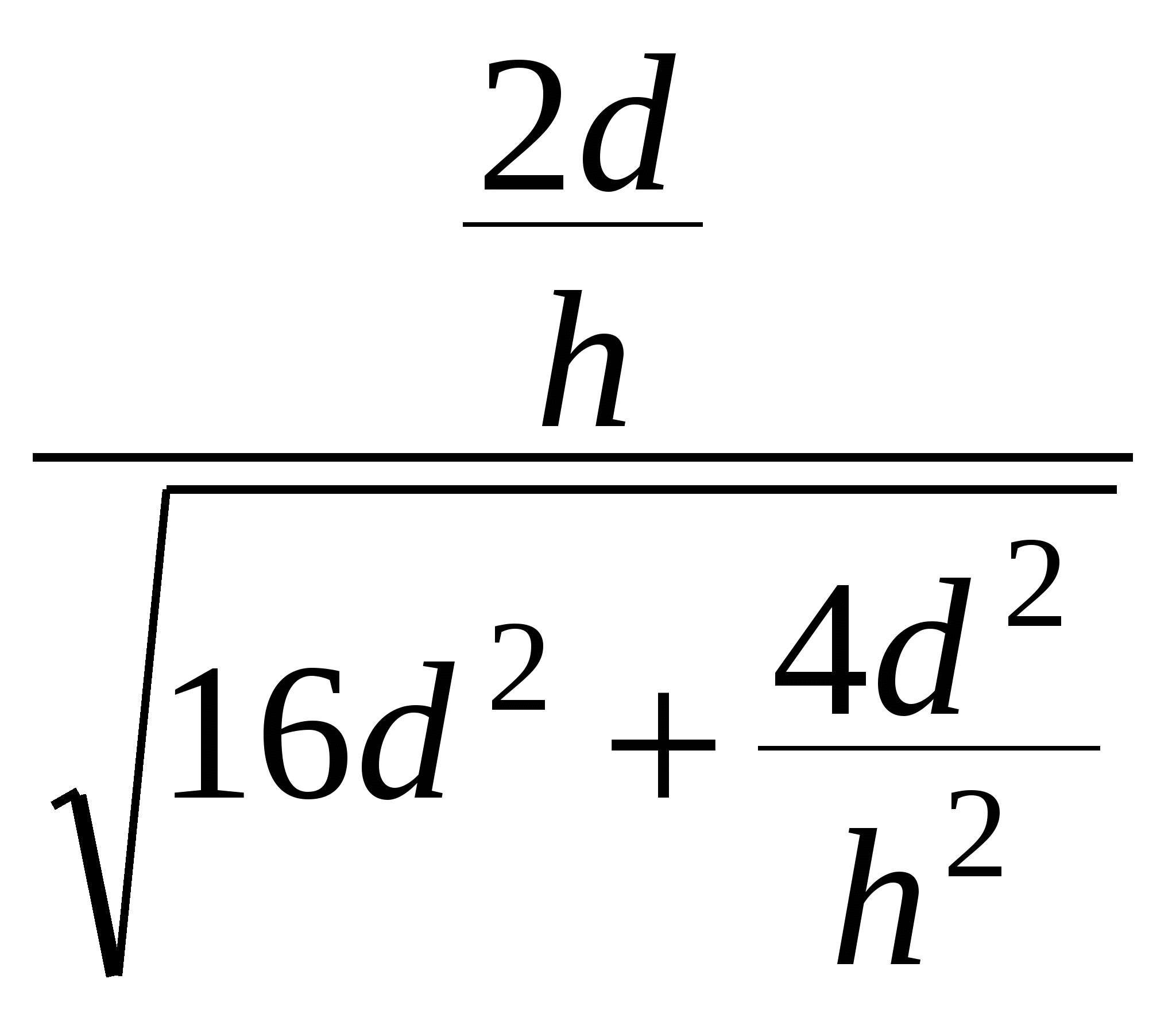 =
=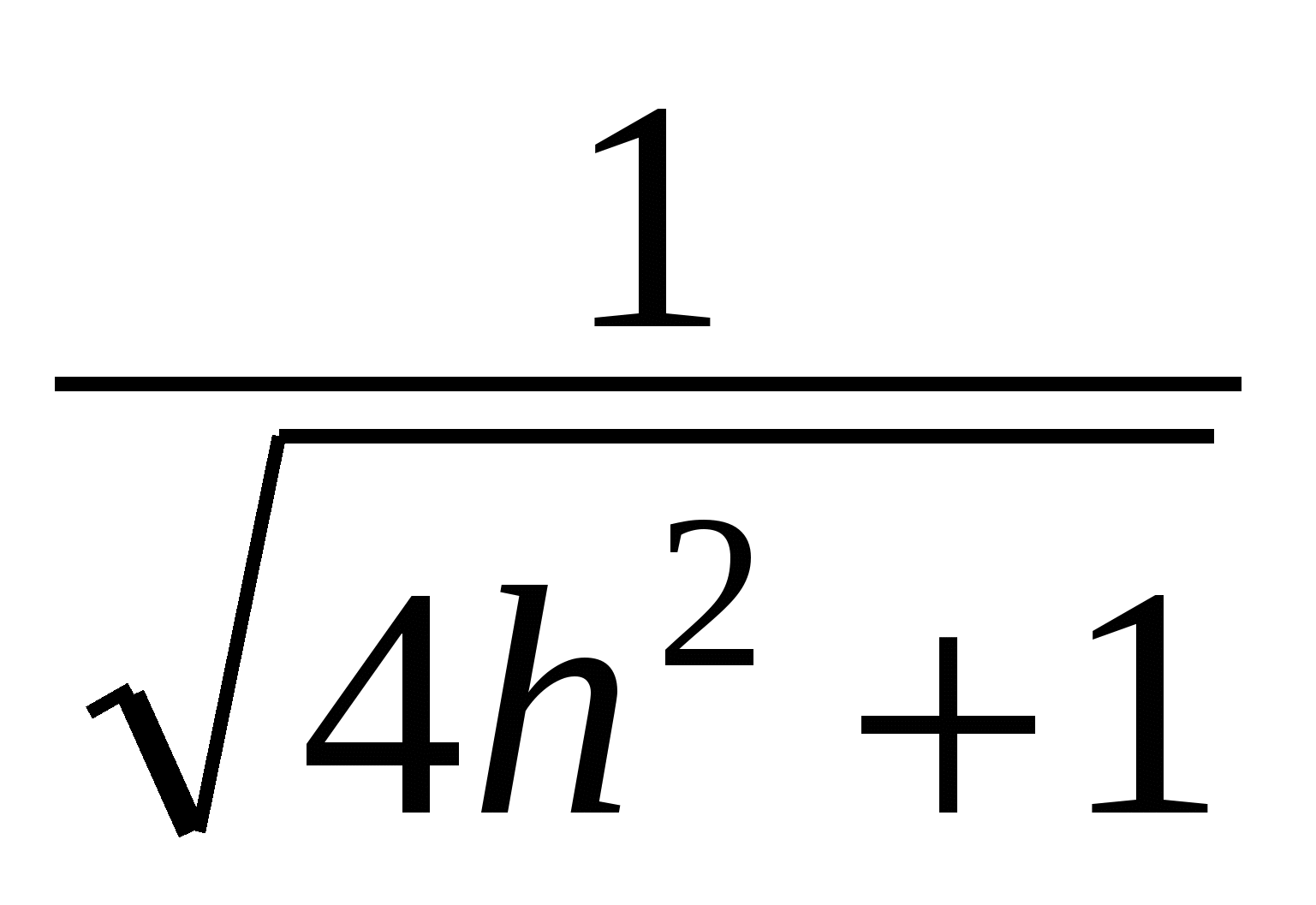
 угол между секущей плоскостью и плоскостью основания равен
угол между секущей плоскостью и плоскостью основания равен 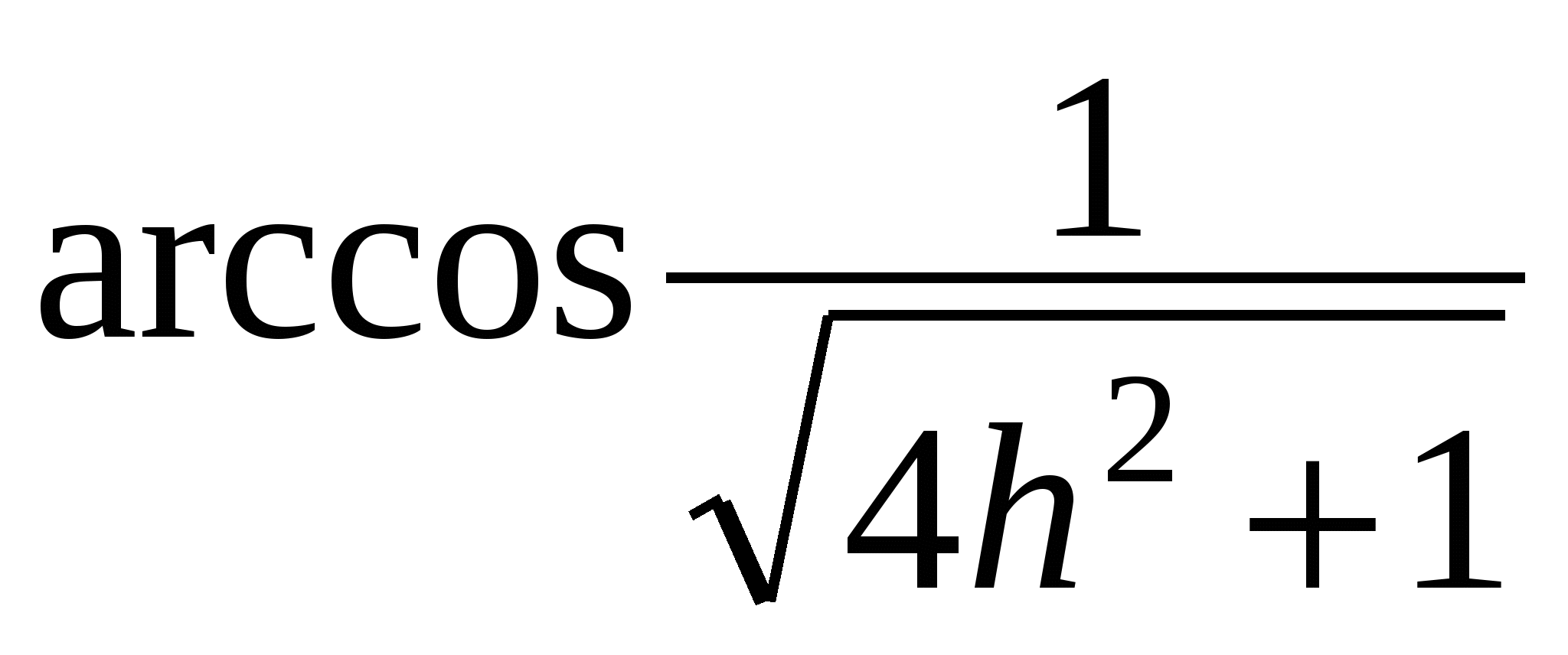 , где h - отношение высоты призмы к длине ребра основания.
, где h - отношение высоты призмы к длине ребра основания.
Данный метод, как универсальный, рассматривается при изучении темы Декартовы координаты в пространстве в 11 классе. В базовом курсе математики уравнение плоскости не вводится. Поэтому данный метод рассматривается в рамках факультативных занятий. В классах математического профиля данный метод рассматривается в 11 классе. Полезно знакомить с этим методом на курсах подготовки к ЕГЭ.
ОТВЕТ: ![]() , где h - отношение высоты призмы к длине ребра основания.
, где h - отношение высоты призмы к длине ребра основания.
Решение конкурсных задач МФ УдГУ для учителей математики, участник antropo4ka.


