- Преподавателю
- Математика
- Методические указания к практическим работам
Методические указания к практическим работам
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Каменская Е.П. |
| Дата | 22.12.2015 |
| Формат | doc |
| Изображения | Есть |
ГАОУ СПО СТСПО
Методические рекомендации
для выполнения практических работ
по теме «Функция»
по дисциплине «Математика»
Преподаватель:
Каменская Е.П.
2015 г.
Данная работа содержит методические указания к практическим работам по дисциплине «Математика» и предназначена для обучающихся специальностям среднего профессионального образования.
Цель разработки: оказание помощи обучающимся в выполнении практических работ по предмету «Математика» по теме «Функция и её сврйства».
Разработчик:
ГАОУ СПО СТ СПО преподаватель Каменская Е.П.
(место работы) (занимаемая должность) (инициалы, фамилия)
Одобрено на заседании методической комиссии общеобразовательных дисциплин
Протокол №_______ от «_____» _________ 20____г.
Председатель МК ________________________ /______________/
Пояснительная записка
Практические занятия служат связующим звеном между теорией и практикой. Они необходимы для закрепления теоретических знаний, полученных на уроках теоретического обучения, а так же для получения практических знаний, при предэкзаменационном повторении. Практические задания выполняются студентом самостоятельно, с применением знаний и умений, полученных на уроках, а так же с использованием необходимых пояснений, полученных от преподавателя при выполнении практического задания.
Практические задания разработаны в соответствии с учебной программой. В зависимости от содержания они могут выполняться студентами индивидуально или фронтально. Данные задания удобно использовать при предэкзаменационном повторении по теме «Функция, её свойства, производные и интеграл».
Содержание
Практическая работа №1 Функции одной переменной и их свойства…5
Практическая работа №3 Непрерывность функции, точки разрыва…..16
Практическая работа №4 Производная и ее геометрический смысл….
Рекомендуемая литература………………………………………………….79
Практическая работа №1
Тема: Функции одной переменной и их свойства.
Цель: сформировать умение использовать свойства функции для ее исследования, решать задачи и упражнения по данной теме.
Теоретические сведения к практической работе
Если каждому элементу х из множества Х по некоторому правилу f поставлен в соответствие элемент у множестваY, то говорят, что на множестве Х определена функция со значениями в множестве Y, и записывают y=f(х).
Множество Х называется областью определения функции D(f), а множество Y - областью значений функции E(f).
Пример 1. Найти область определения функции
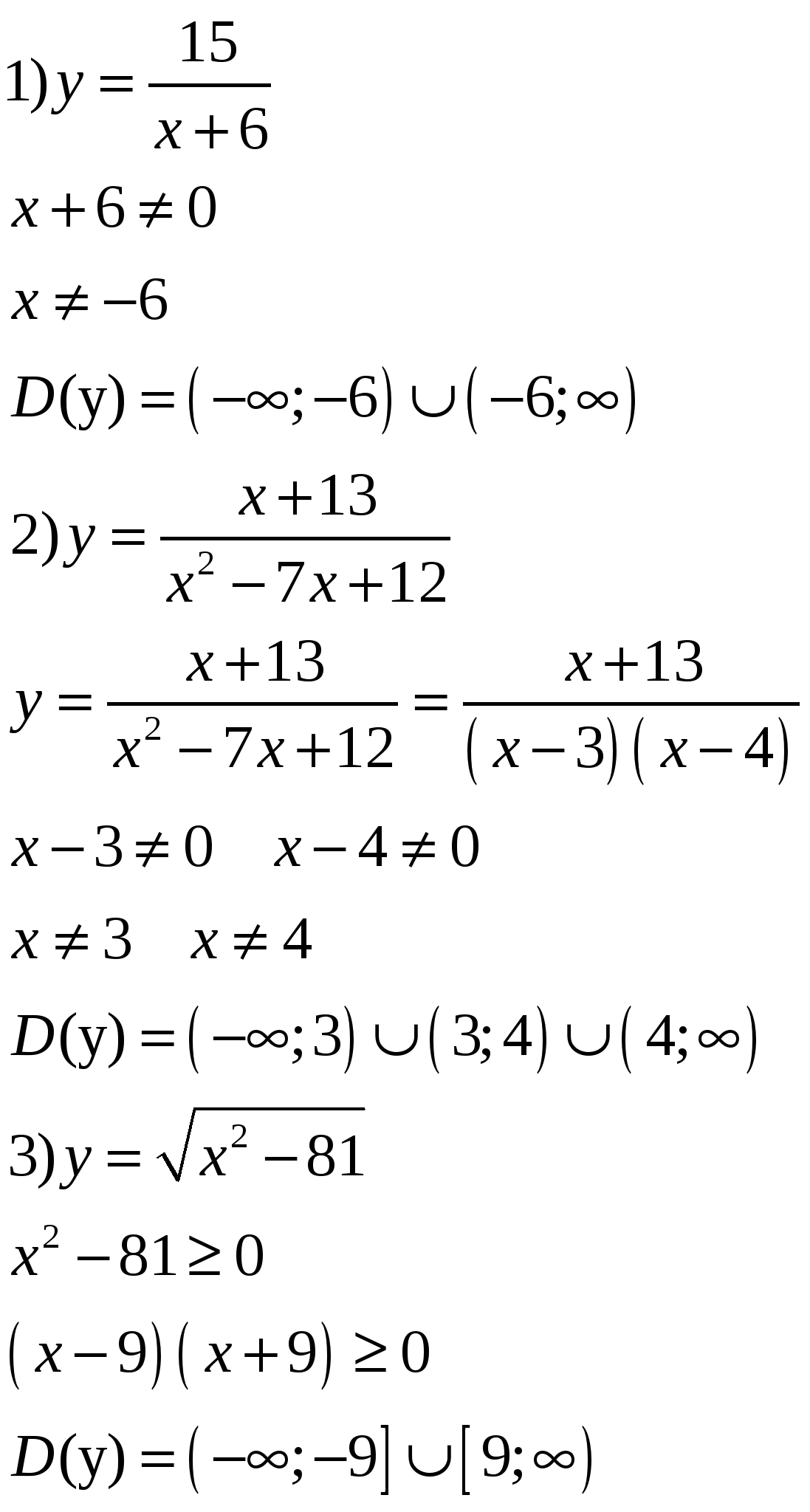
Основные свойства функции:
-
Четность и нечетность. Функция y=f(x) называется четной, если для любых значений х из области определения f(-x)=f(x), и называется нечетной, если f(-x)=-f(x). В противном случае функция y=f(x) называется функцией общего вида.
График четной функции симметричен относительно координатной оси у, график нечетной функции симметричен относительно начала координат (0;0).
Пример 2. Установить четность или нечетность функции.
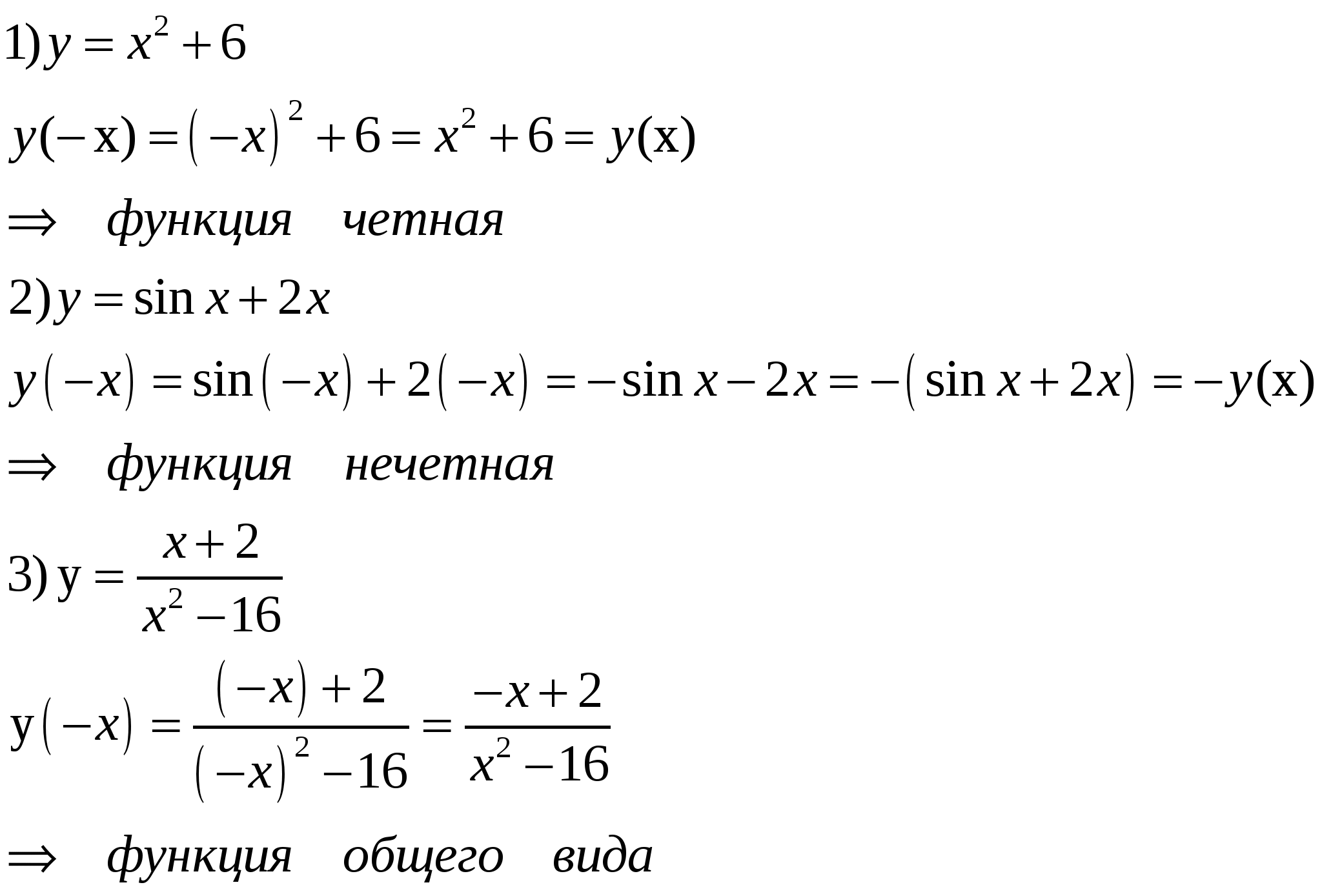
-
Монотонность. Функция y=f(x) называется возрастающей (убывающей) на некотором промежутке Х из области определения, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
-
Ограниченность. Функция y=f(x) называется ограниченной на некотором промежутке Х из области определения, если существует число М>0, такое, что
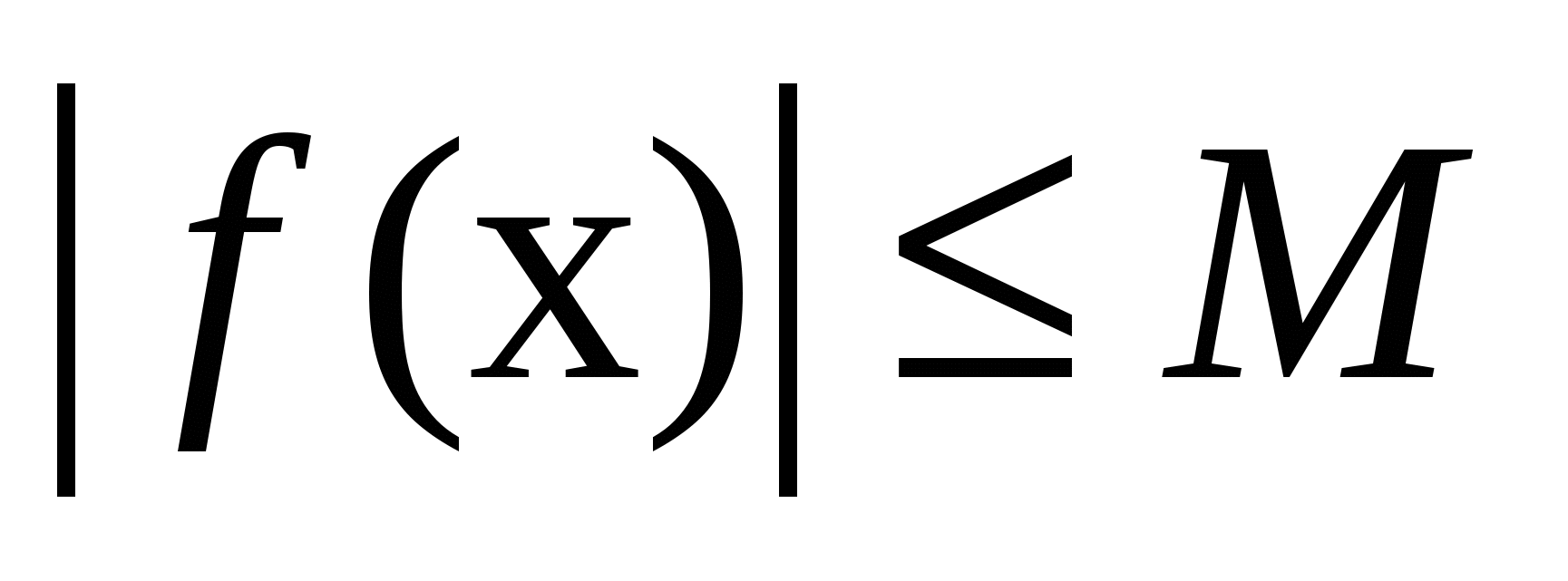 для любого
для любого 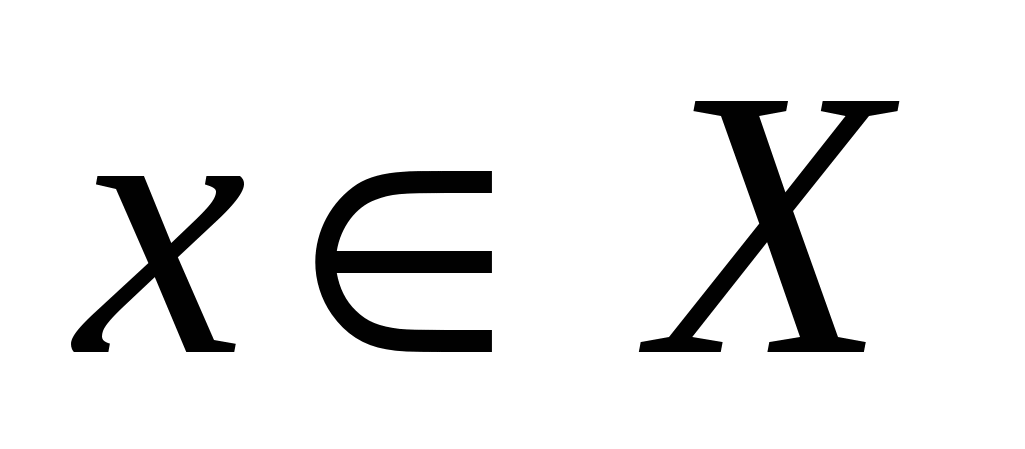 .
. -
Периодичность. Функция y=f(x) называется периодической с периодом Т>0, если для любых значений х из области определения f(x+T)=f(x-T)=f(x).
Пример 3.
Содержание практической работы:
Задание 1. Найти область определения функции
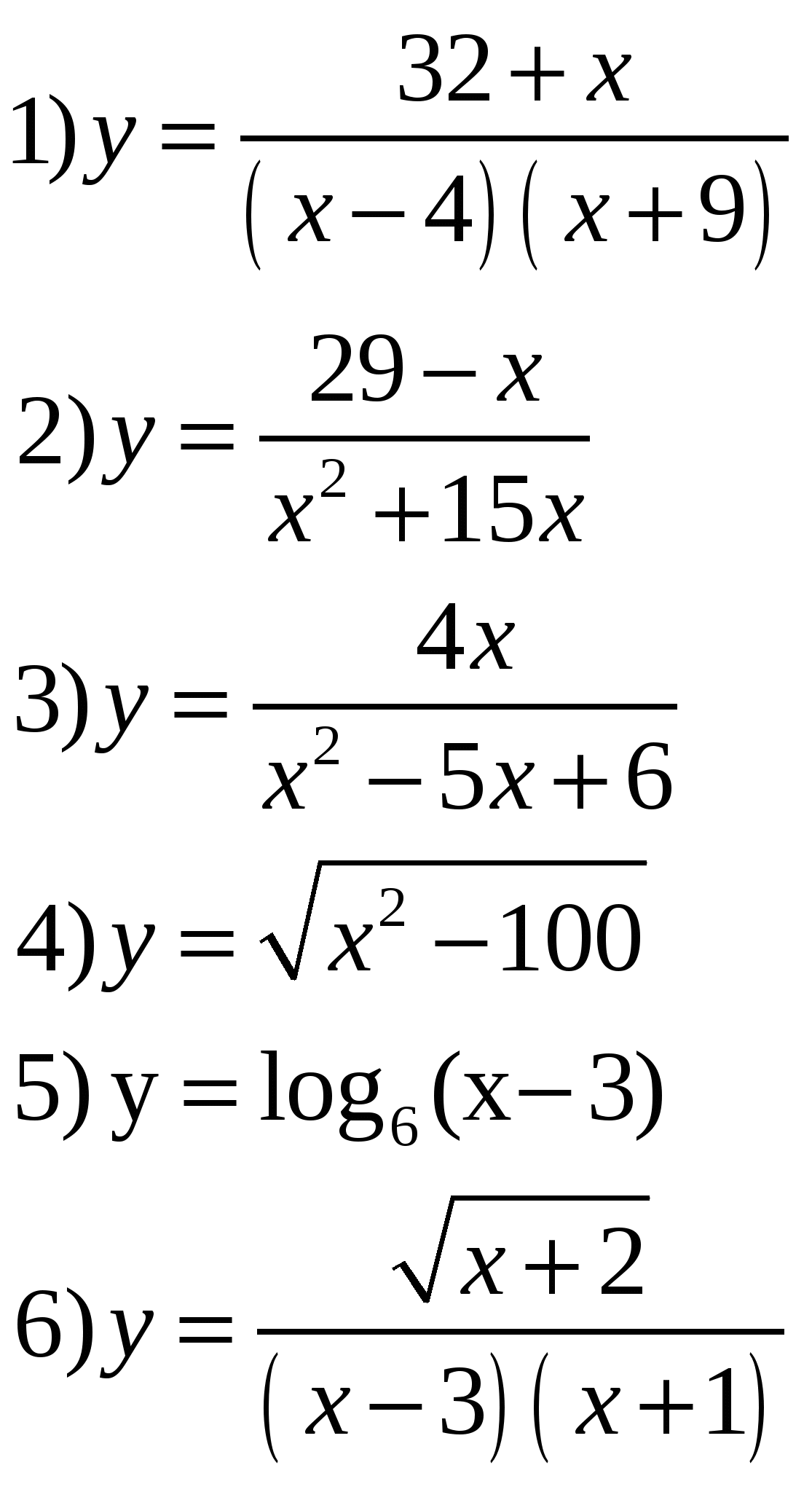
Задание 2. Установить четность или нечетность функции.
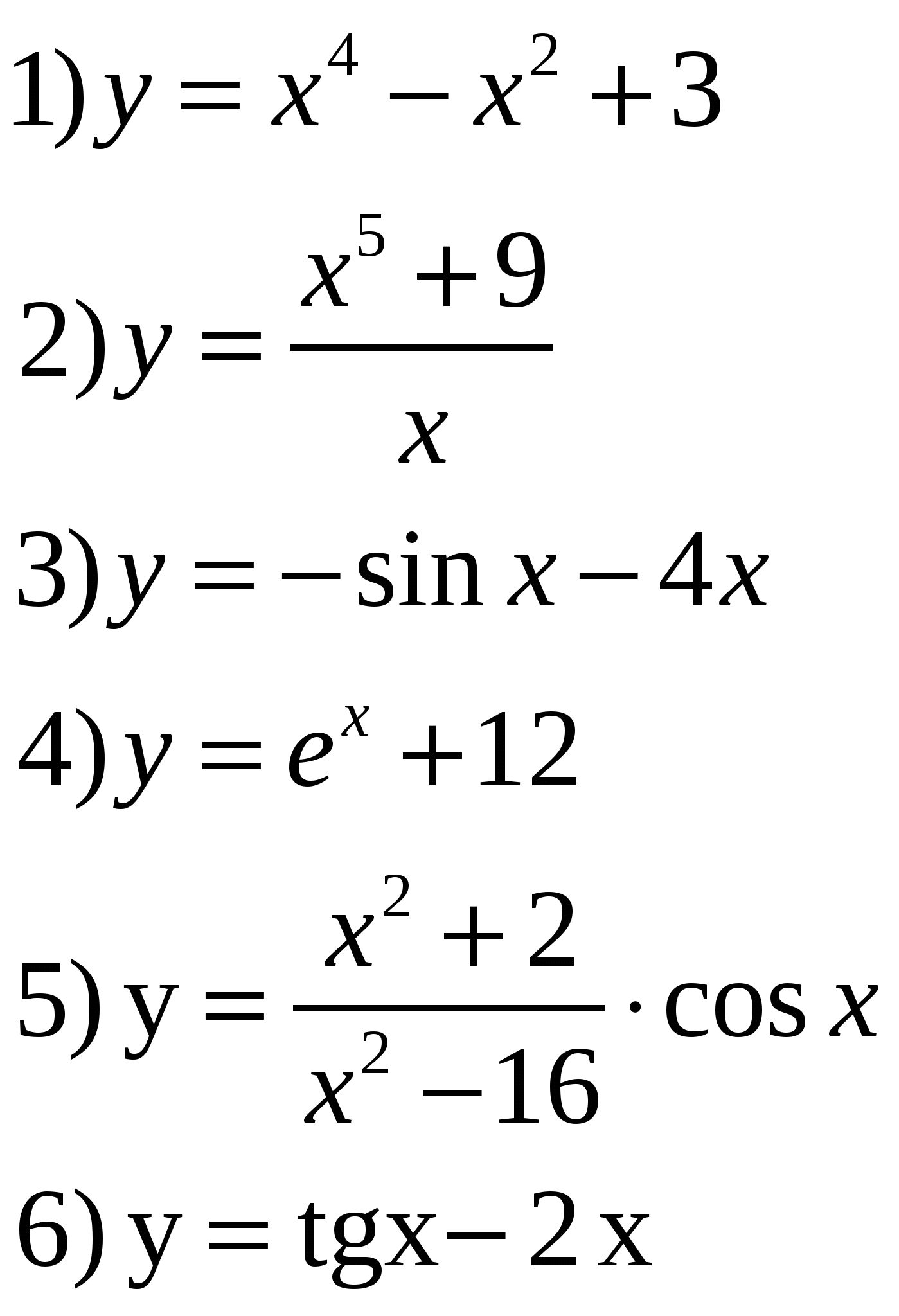
З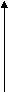
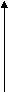 адание 3. Описать основные свойства функции по графику:
адание 3. Описать основные свойства функции по графику:
1
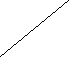
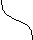
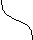 )
)





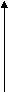
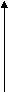
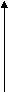
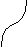
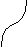
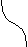 4)
4)




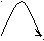
Практическая работа №2
Тема: Непрерывность функции, точки разрыва.
Цель: сформировать умение исследовать функцию на непрерывность и наличие точек разрыва, определять род точек разрыва.
Теоретические сведения к практической работе
Функция 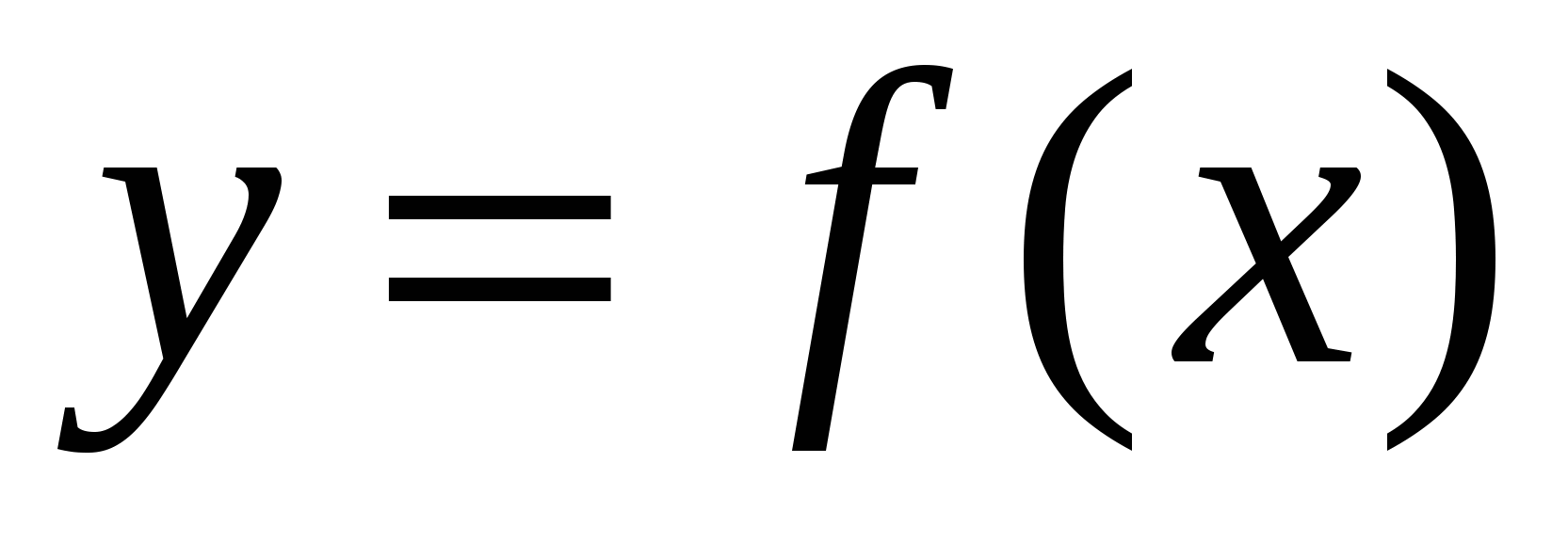 называется непрерывной
называется непрерывной
в точке х0, если она: 1) определена в точке х0; 2) имеет конечный предел при 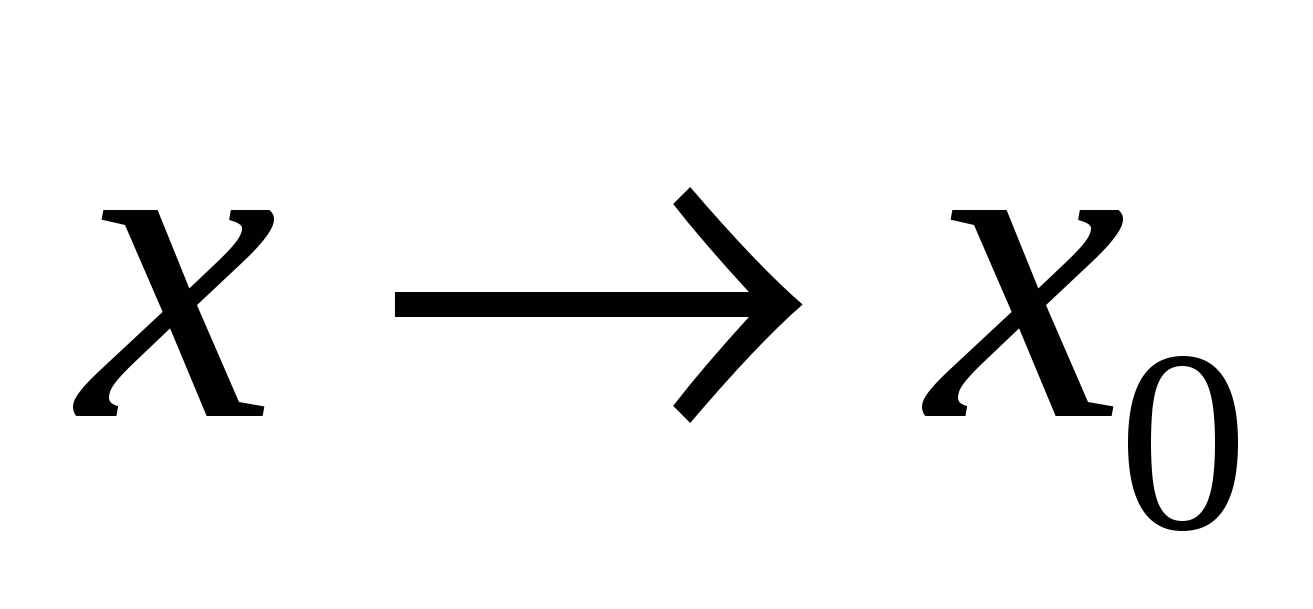 ; 3) этот предел равен значению функции в этой точке
; 3) этот предел равен значению функции в этой точке 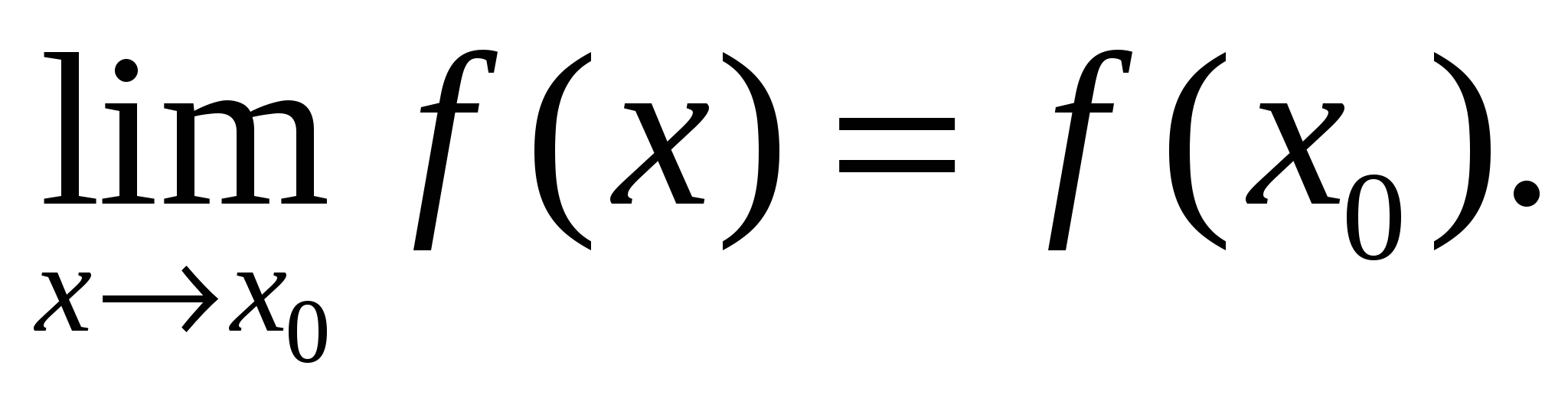
Функция называется непрерывной на некотором промежутке Х, если она непрерывна в каждой точке этого промежутка.
Все элементарные функции непрерывны во всех точках, где они определены.
Содержание практической работы
Задание 1. Доказать, что функция является непрерывной
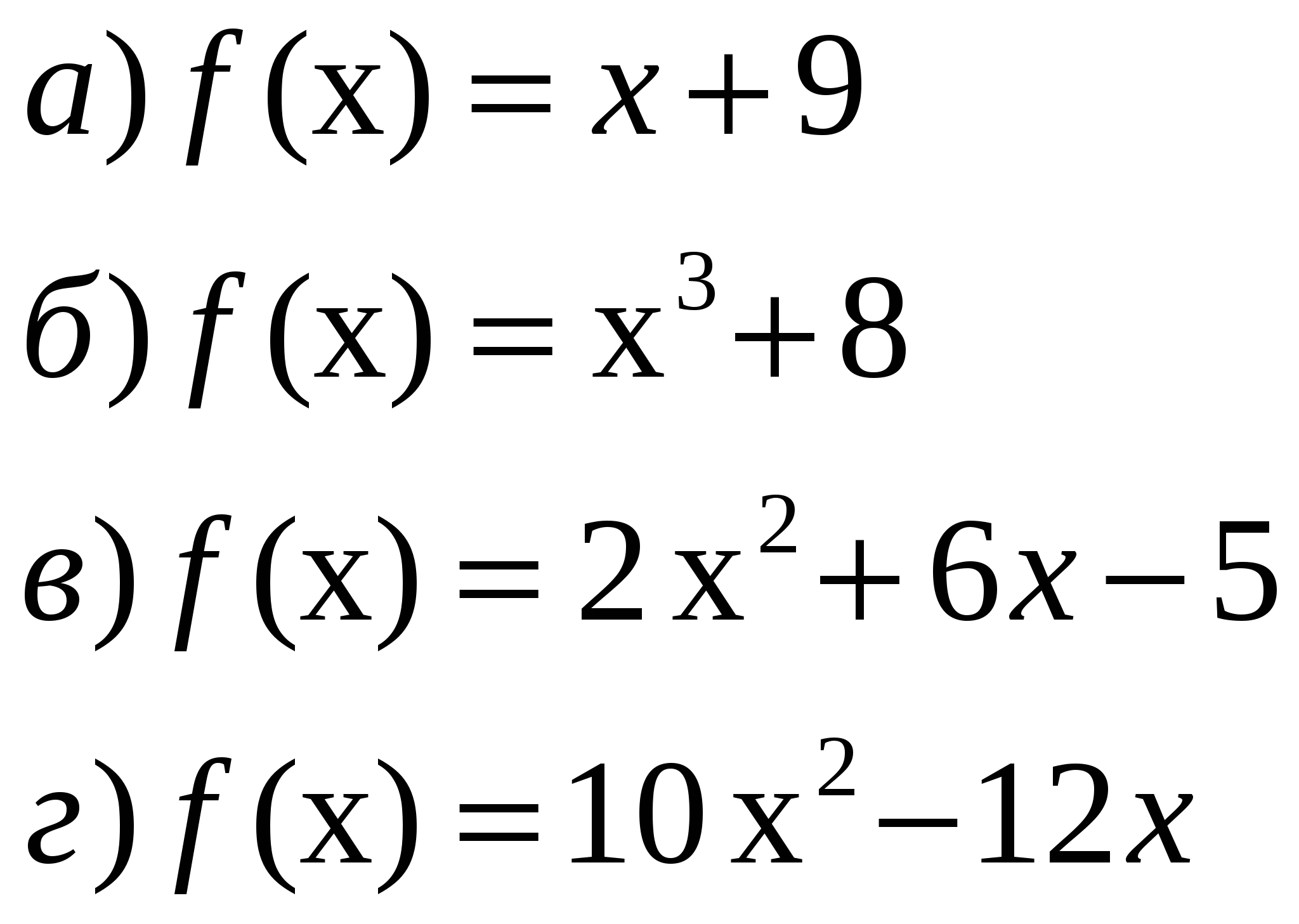
Задание 2. Найдите точки разрыва функции:
Практическая работа №3
Тема: Производная и ее геометрический смысл.
Цель: сформировать умение находить производные функций, находить производные сложных функций, знать геометрический смысл производной. применять правило Лопиталя для нахождения пределов.
Теоретические сведения к практической работе
Производной функции 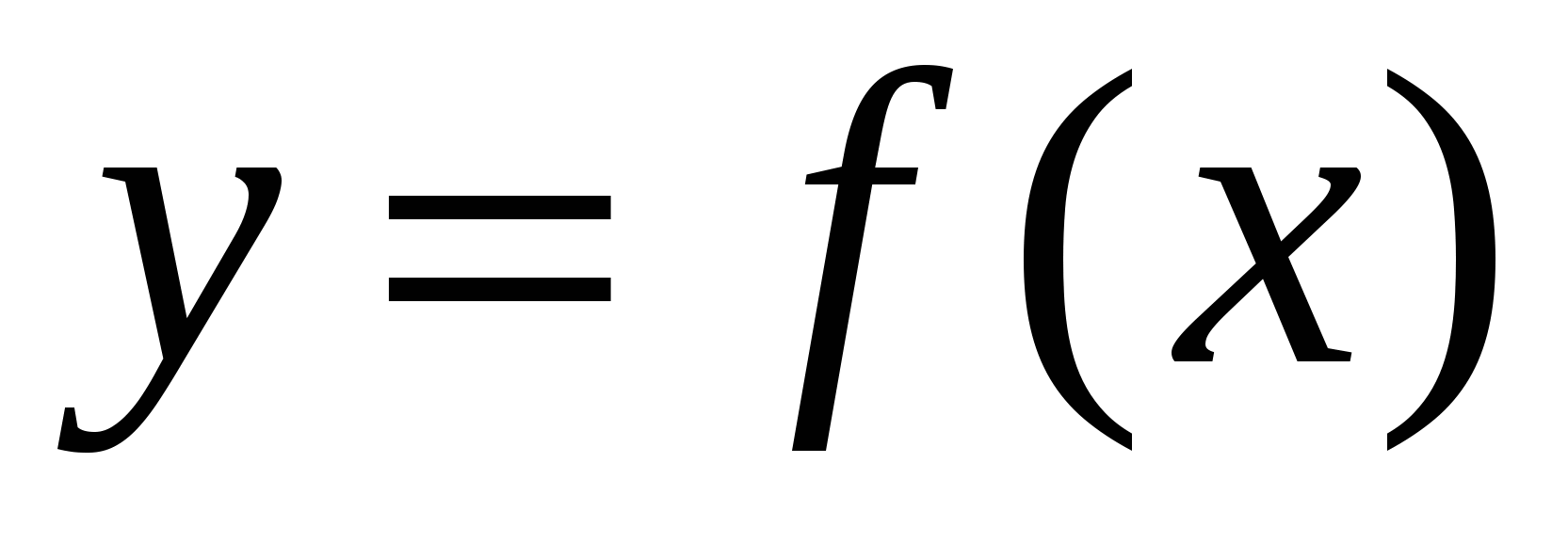 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 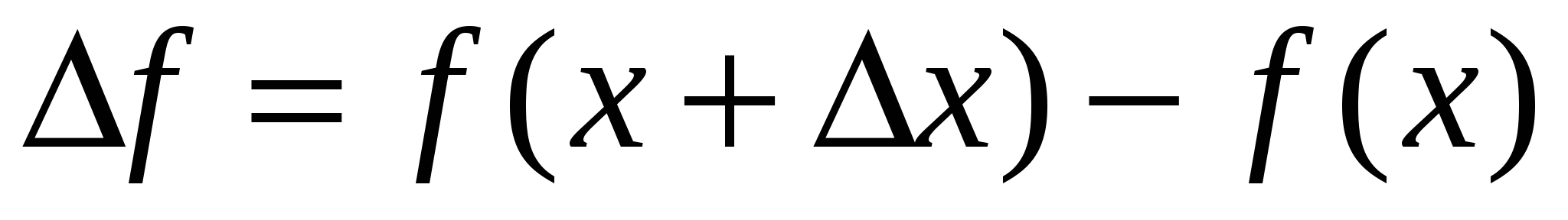 к приращению независимой переменной
к приращению независимой переменной 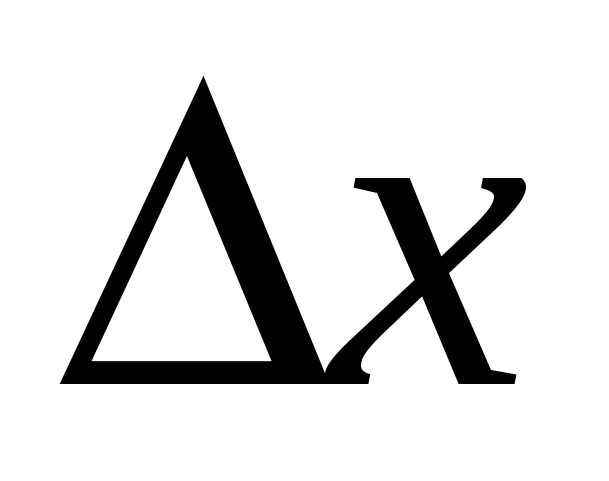 при стремлении последнего к нулю:
при стремлении последнего к нулю:
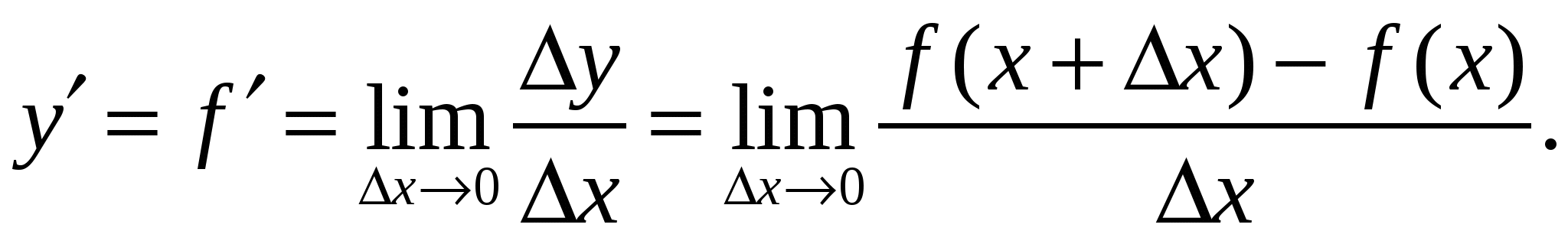
Если функция в точке х0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.
Г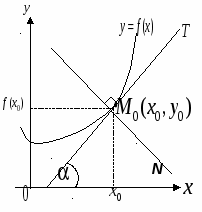 еометрический смысл производной.
еометрический смысл производной.
Если кривая задана уравнением 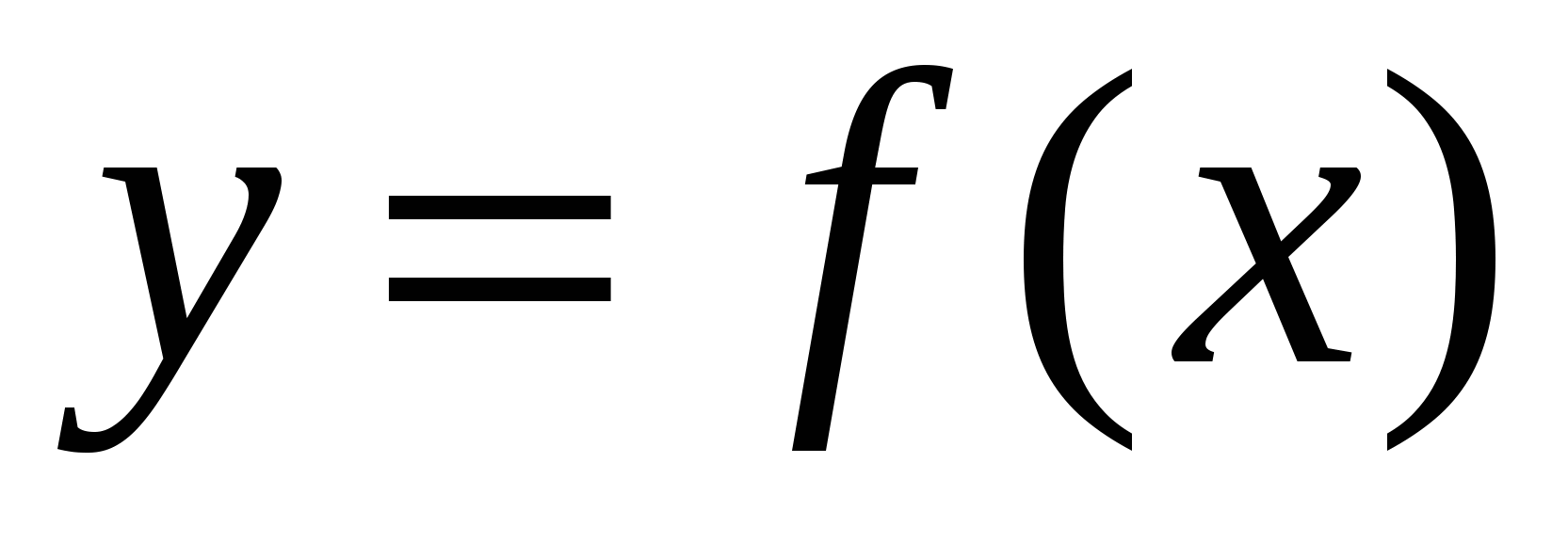 ,
,
то 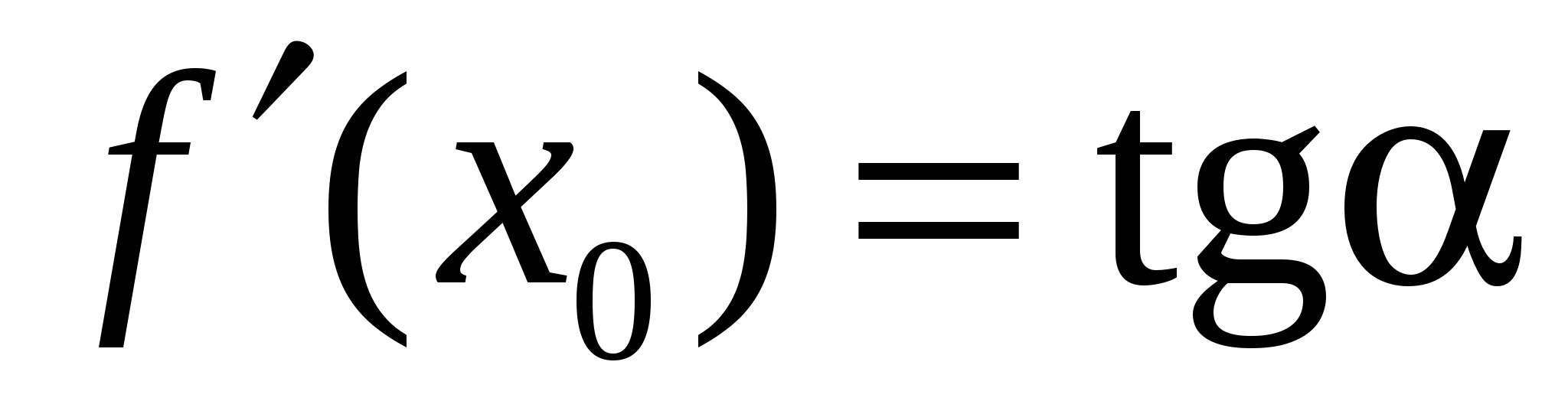 - угловой коэффициент касательной к графику функции в этой точке (
- угловой коэффициент касательной к графику функции в этой точке (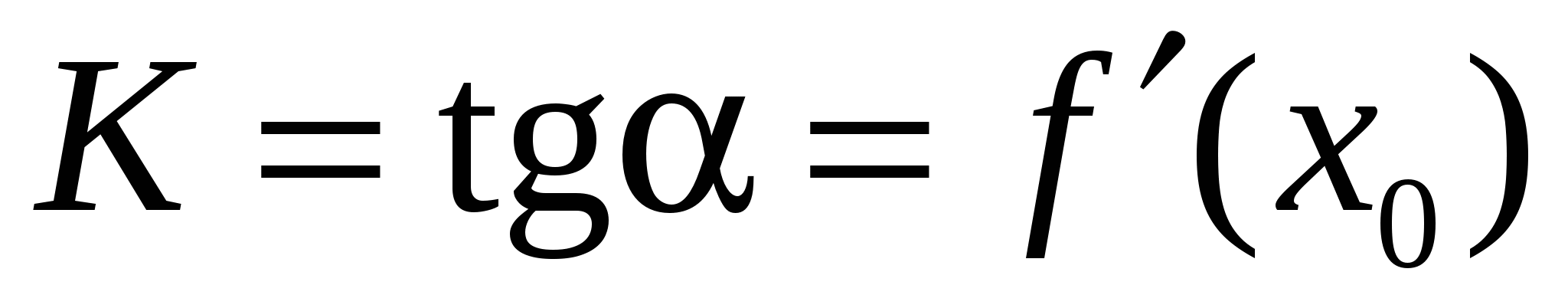 ).
).
Уравнение касательной к кривой 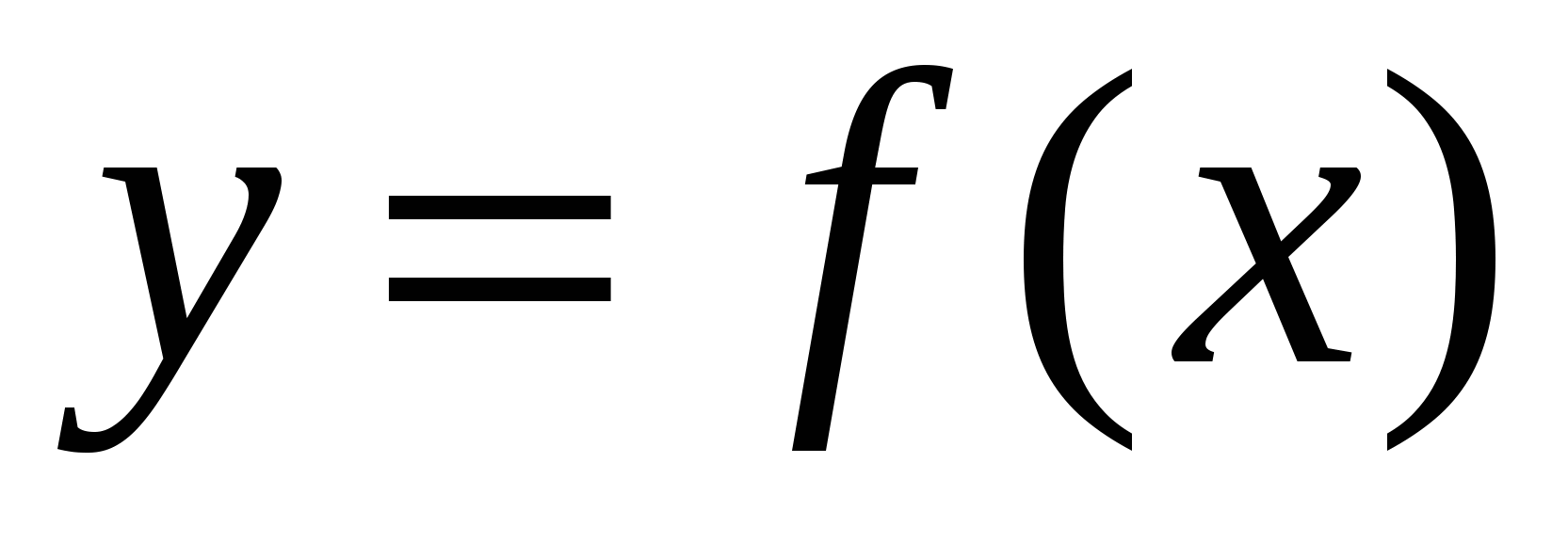
в точке х0 (прямая М0Т) имеет вид:
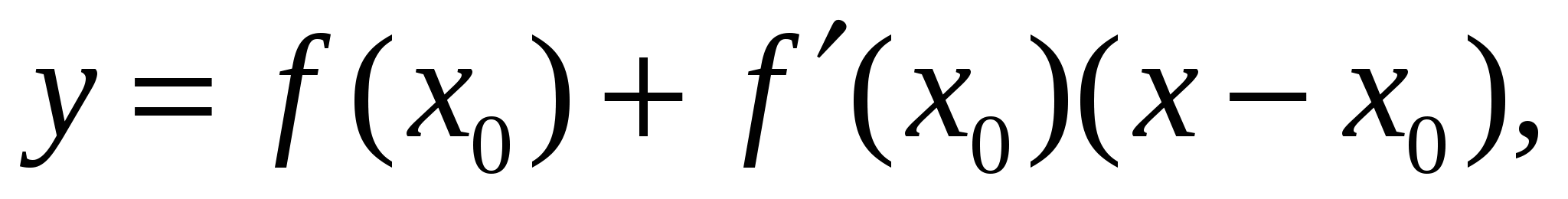
Правила дифференцирования
№ пп
U = u(x), V=V(x) -
дифференцируемые функции
№ пп
U = u(x), V=V(x) -
дифференцируемые функции
I
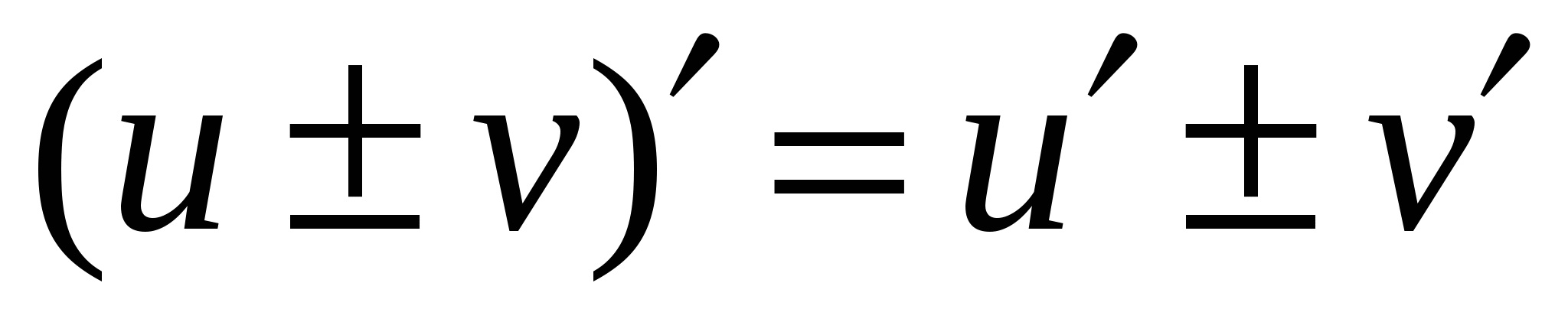
V
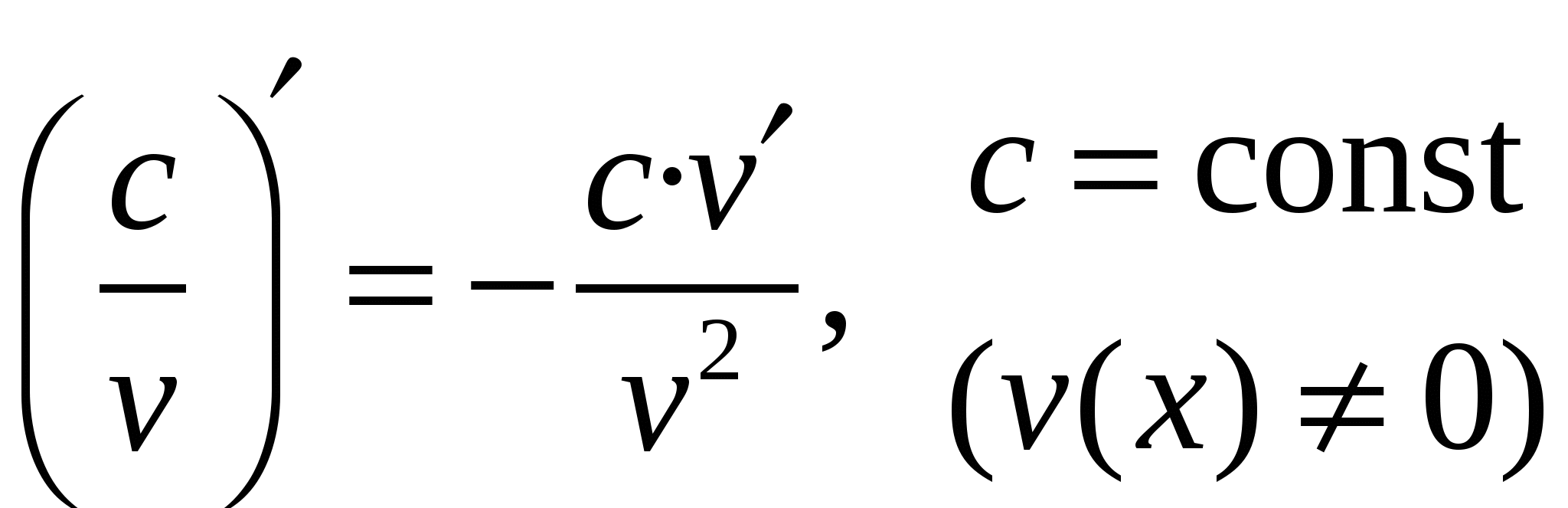
II
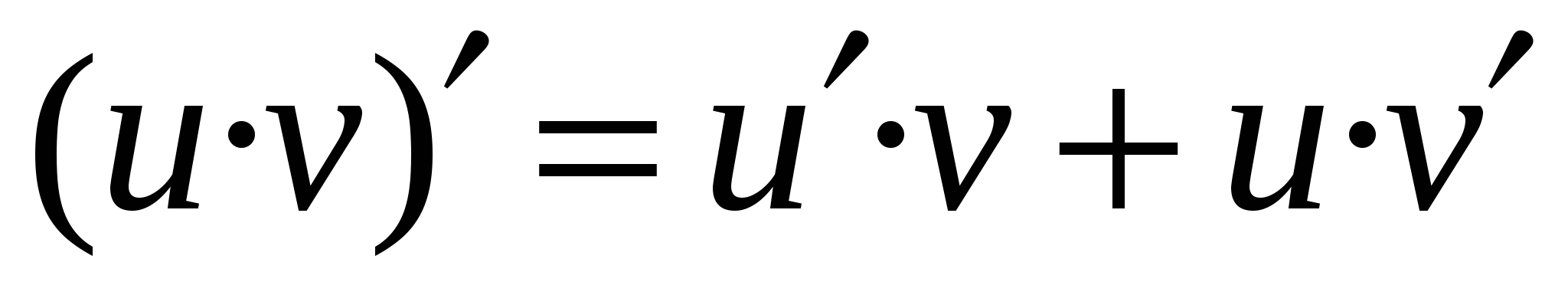
VI
Производная сложной функции 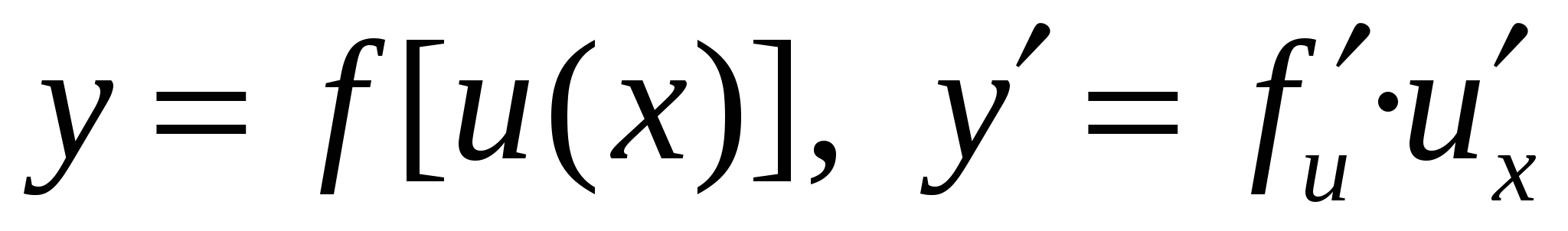
III
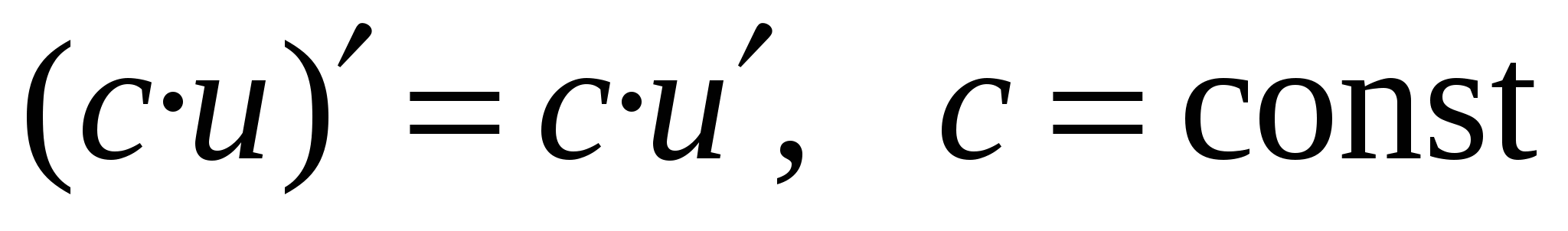
IV
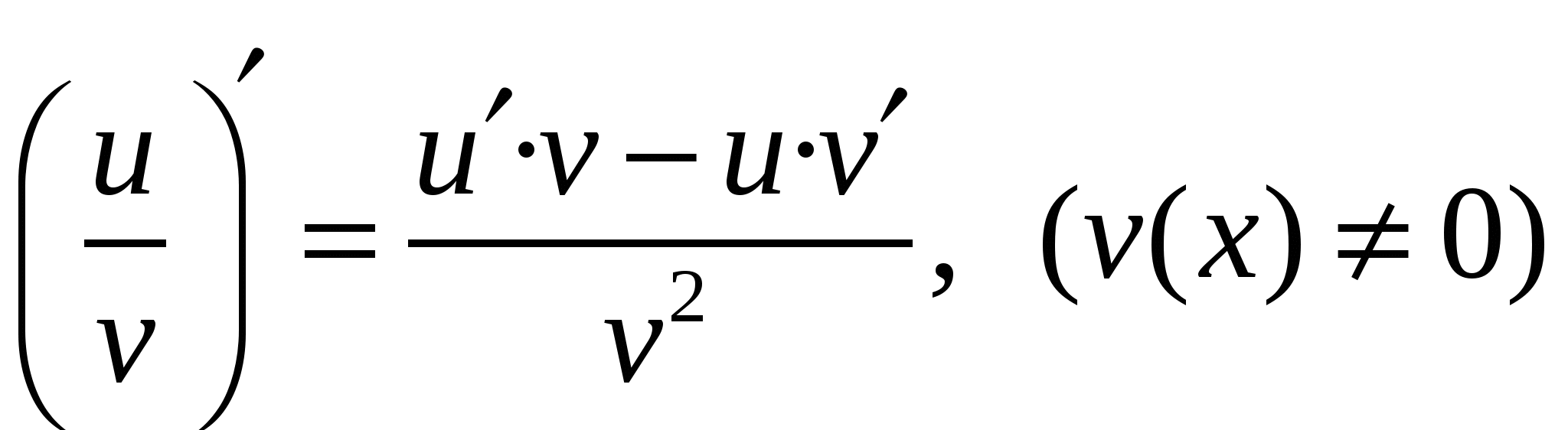
Формулы дифференцирования основных элементарных функций
№ пп
с=const, х - независимая переменная,
u = u(x) - дифференцируемая функция
1
С'= 0
9
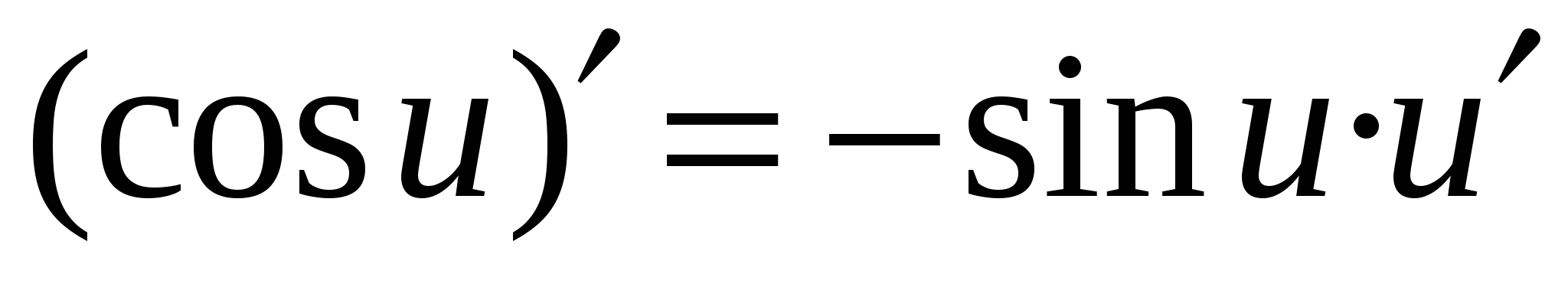
2
x'= 1
10

3
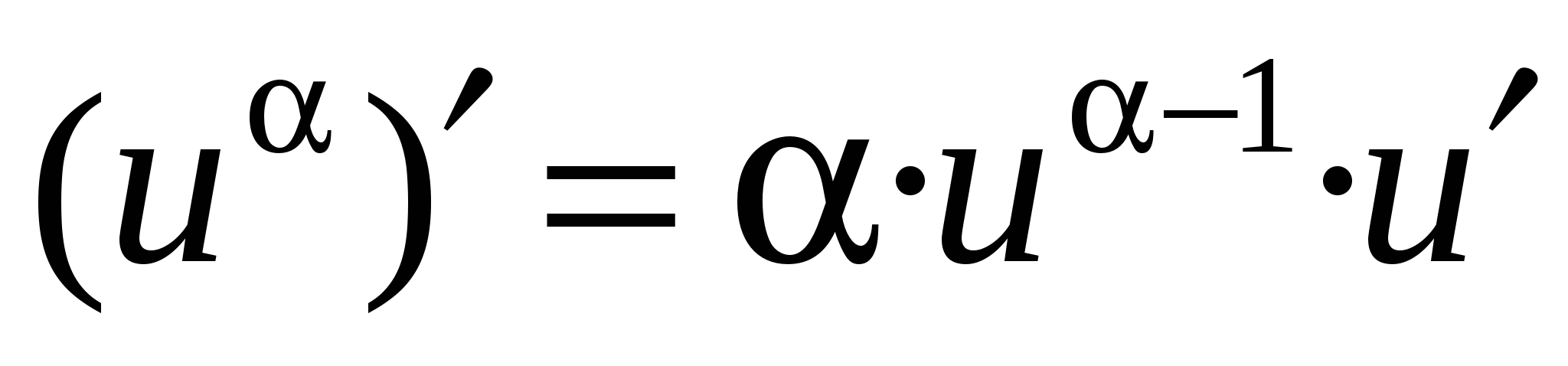
11
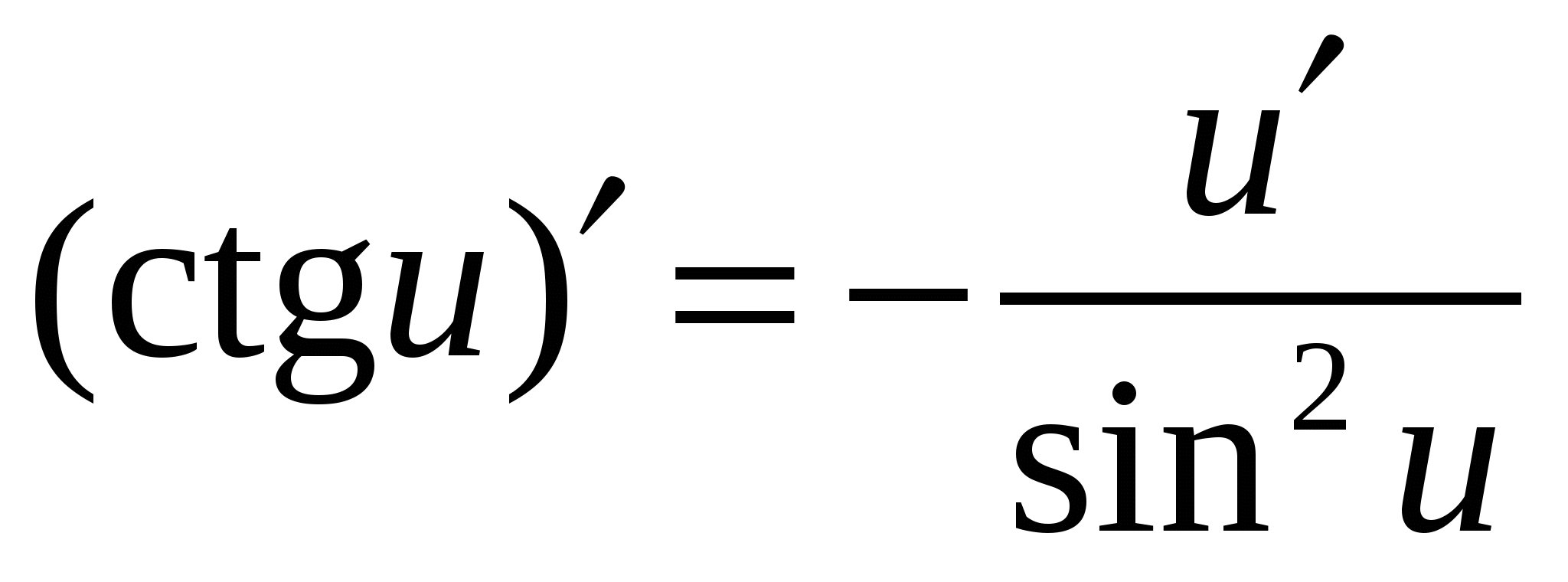
4
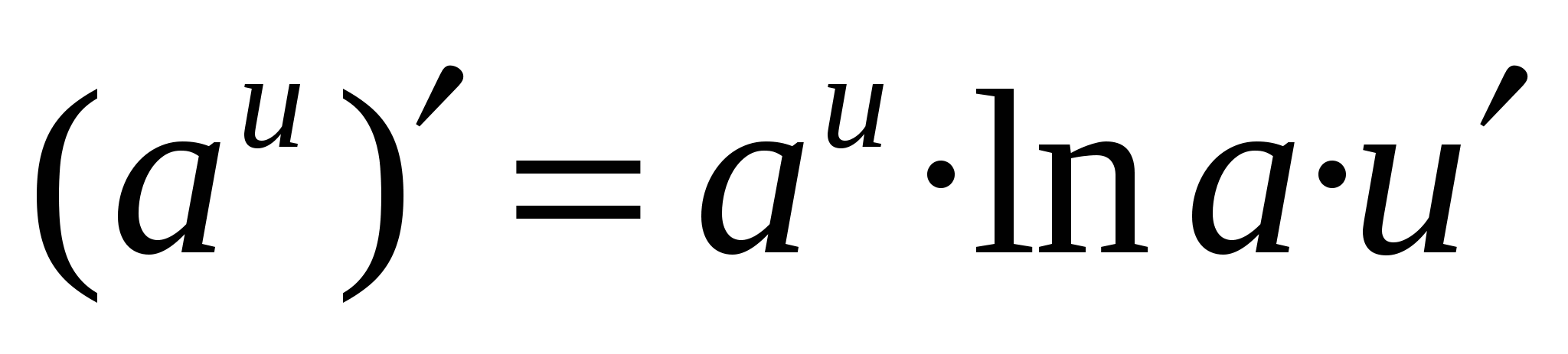
12
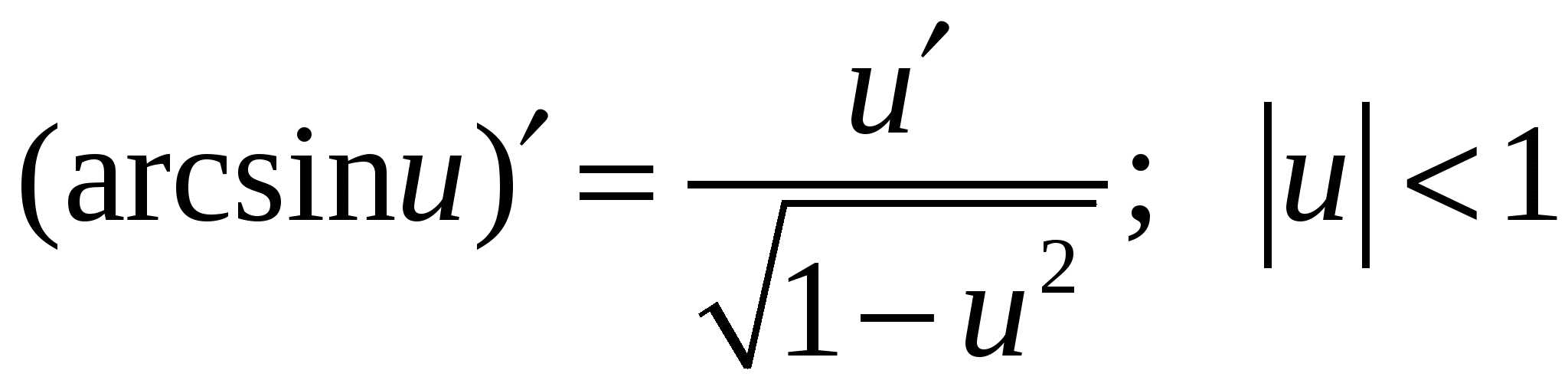
5
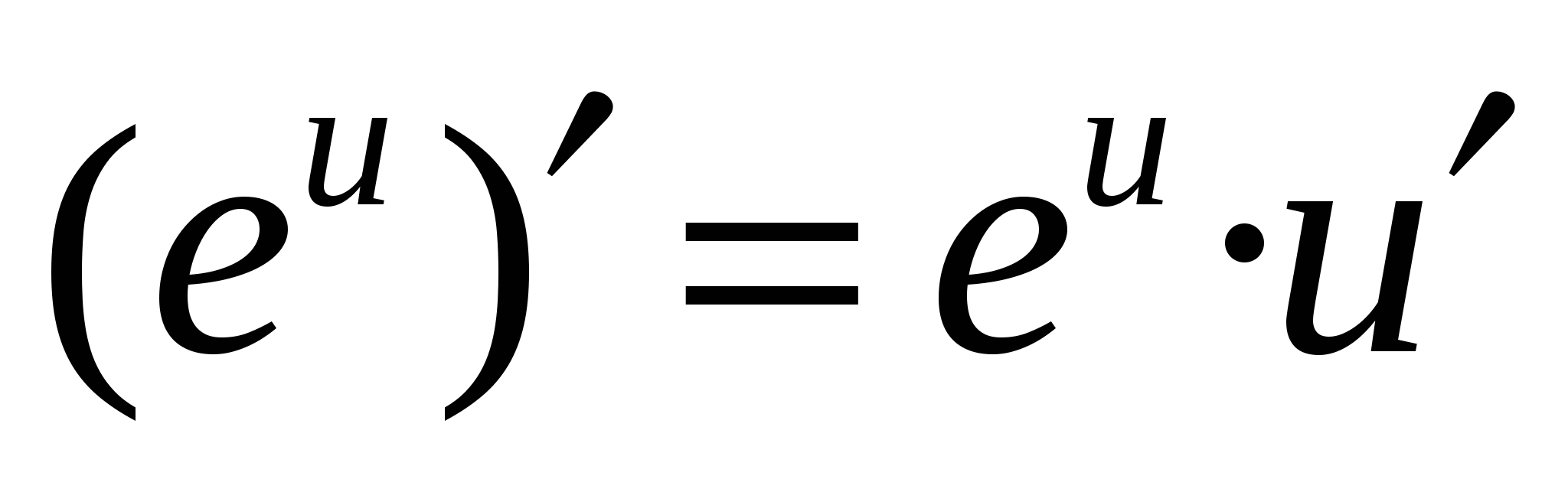
13
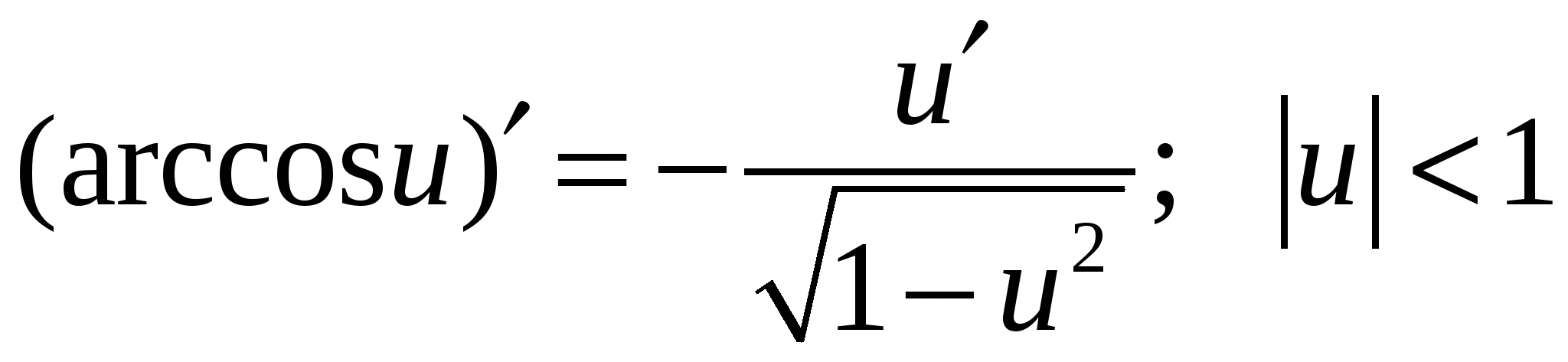
6
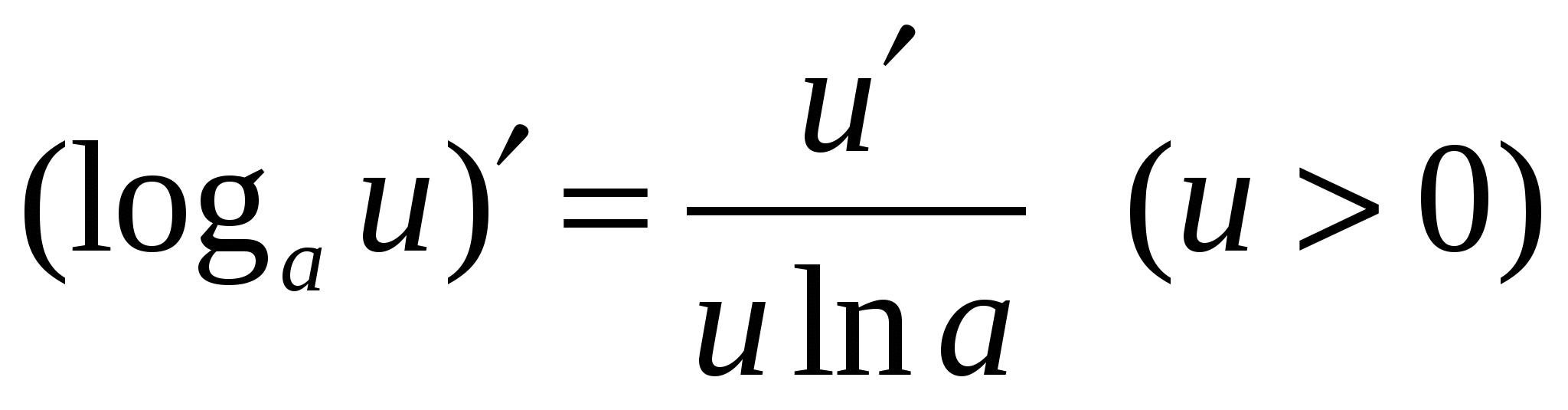
14
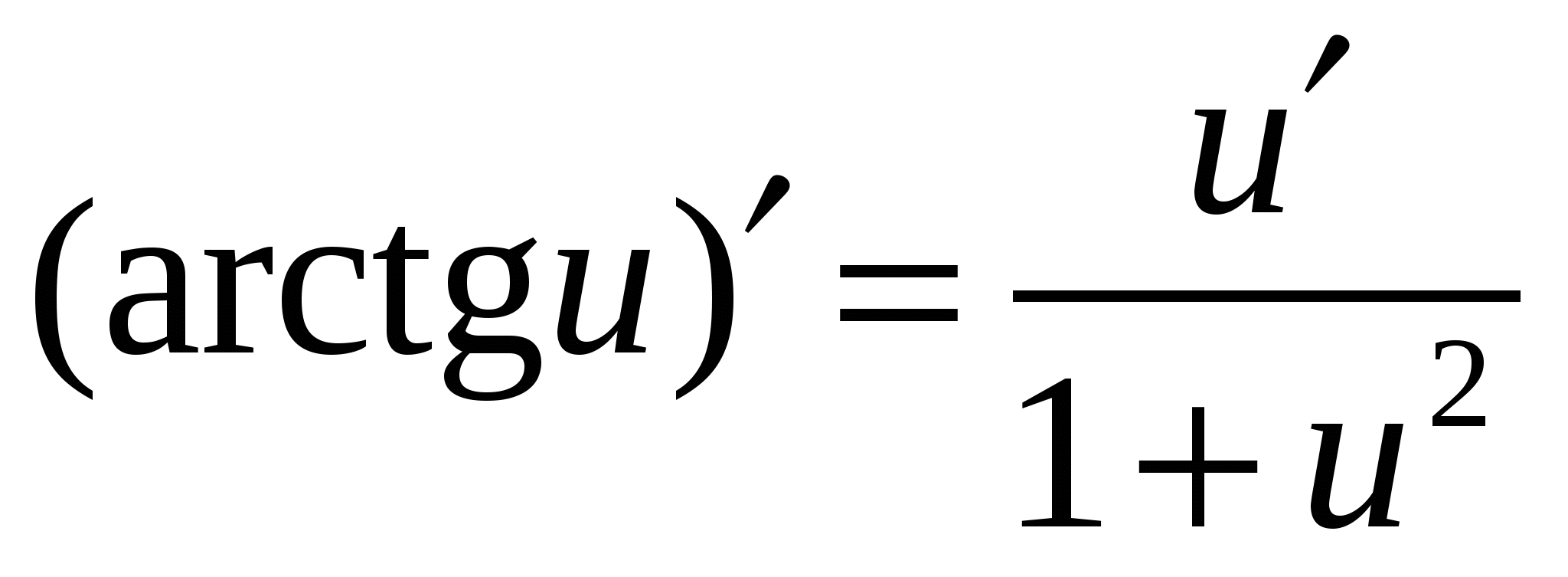
7
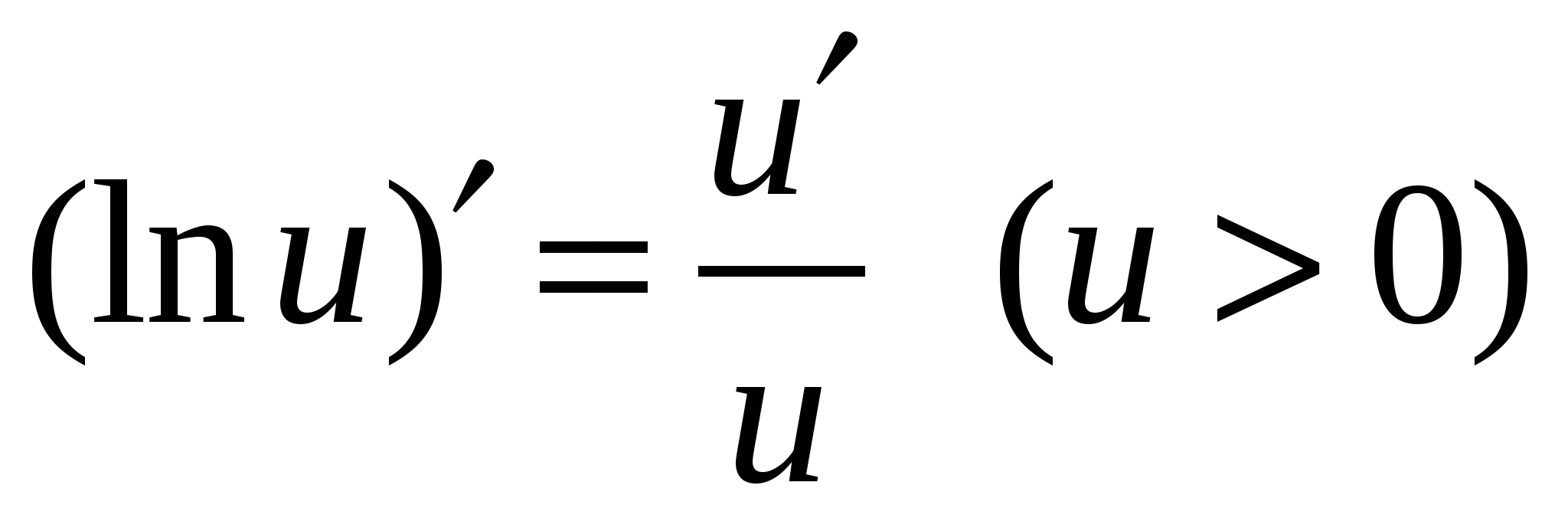
15
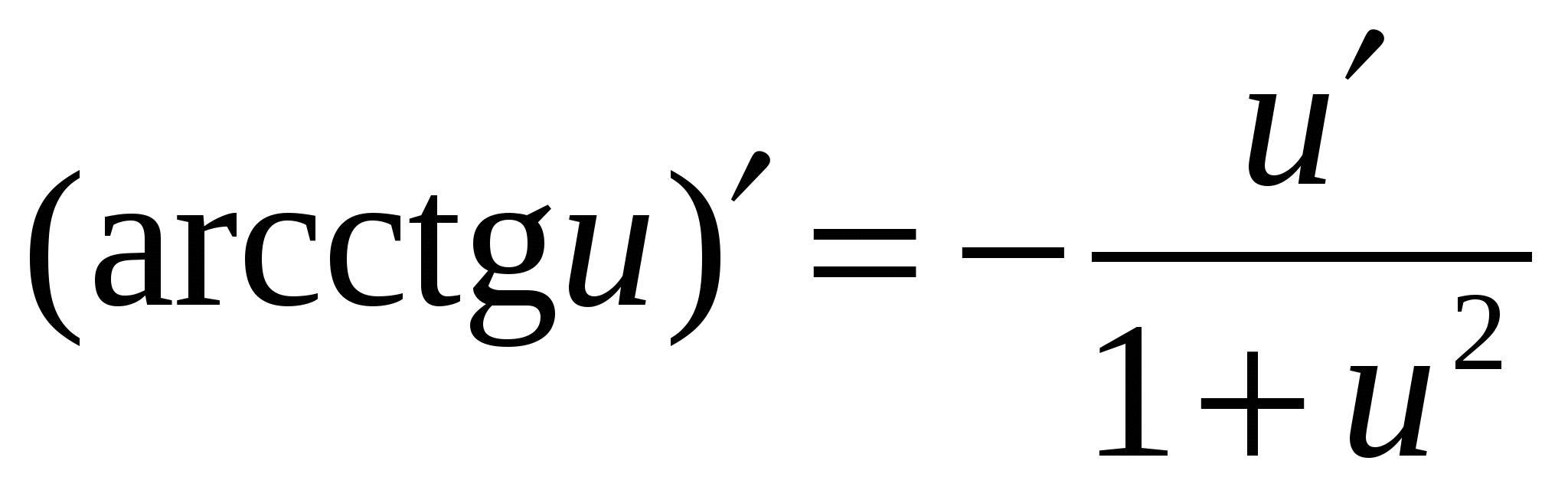
8
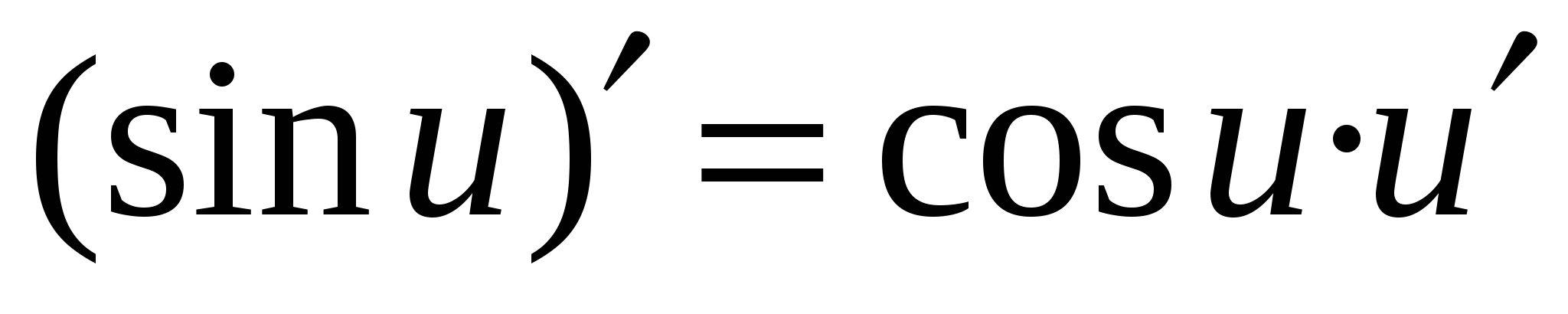
Производной n-го порядка называется производная от производной (n-1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции.
Производная второго порядка 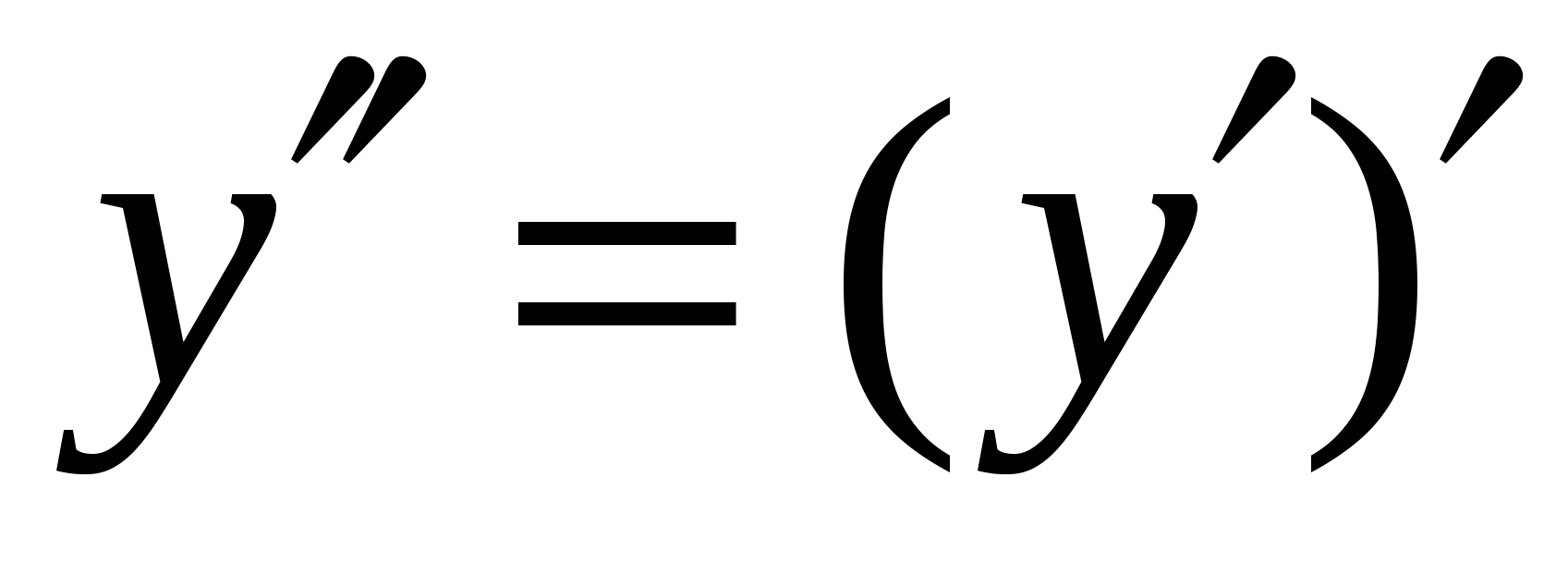 или
или 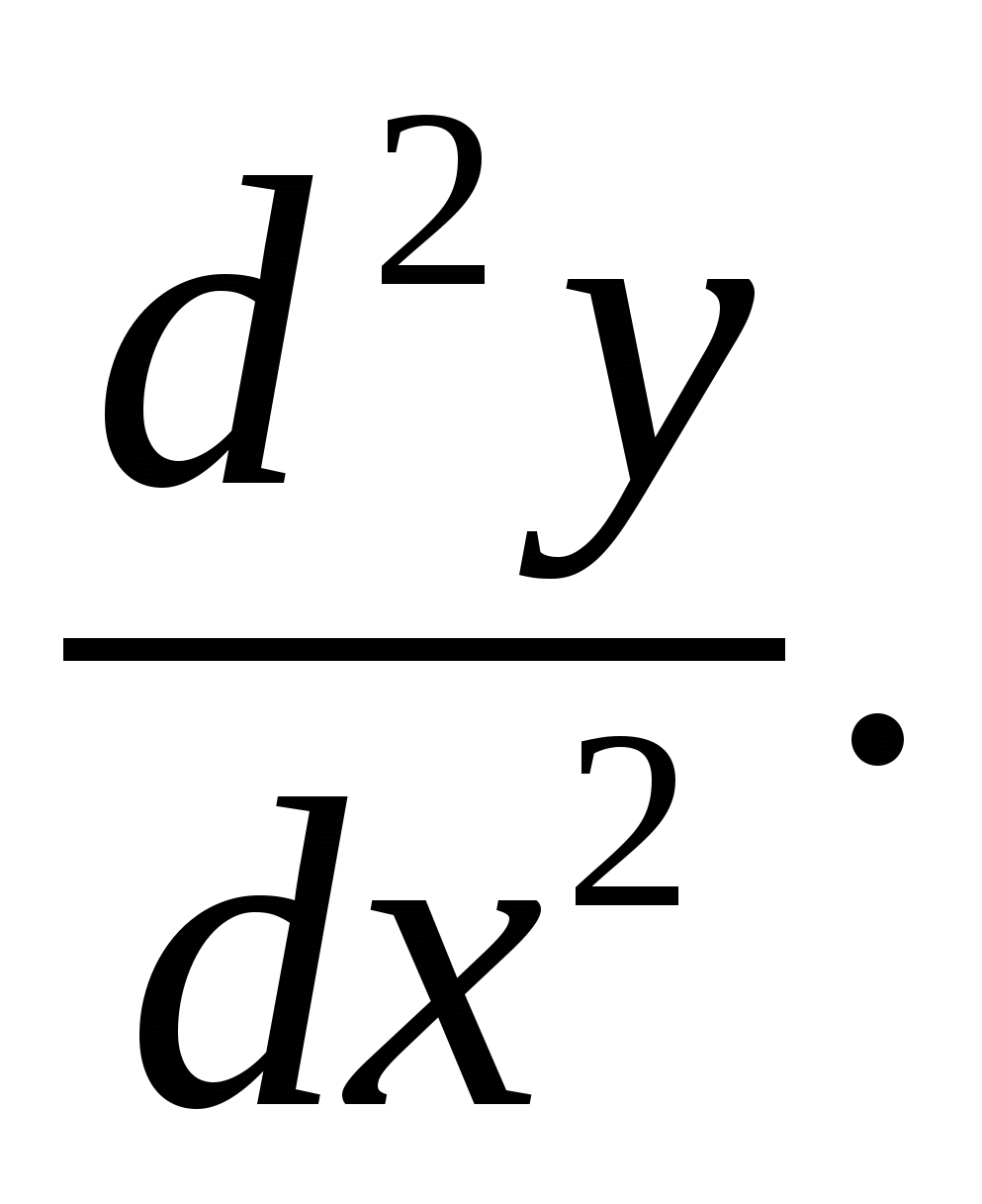
Производная третьего порядка 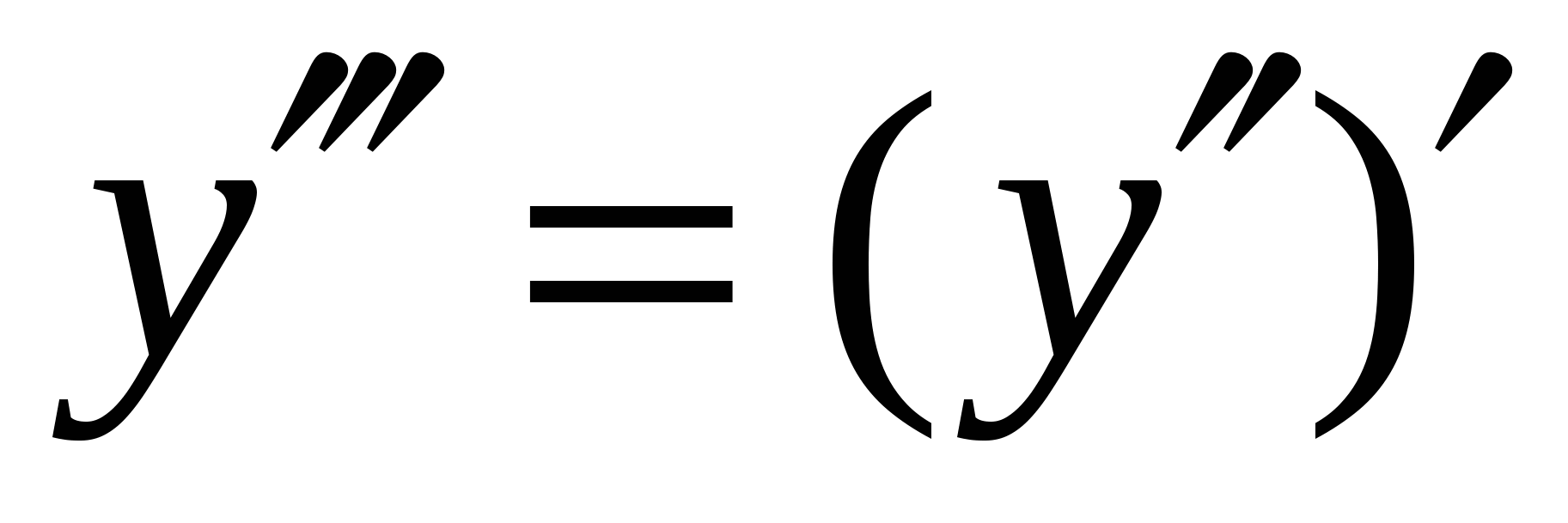 или
или 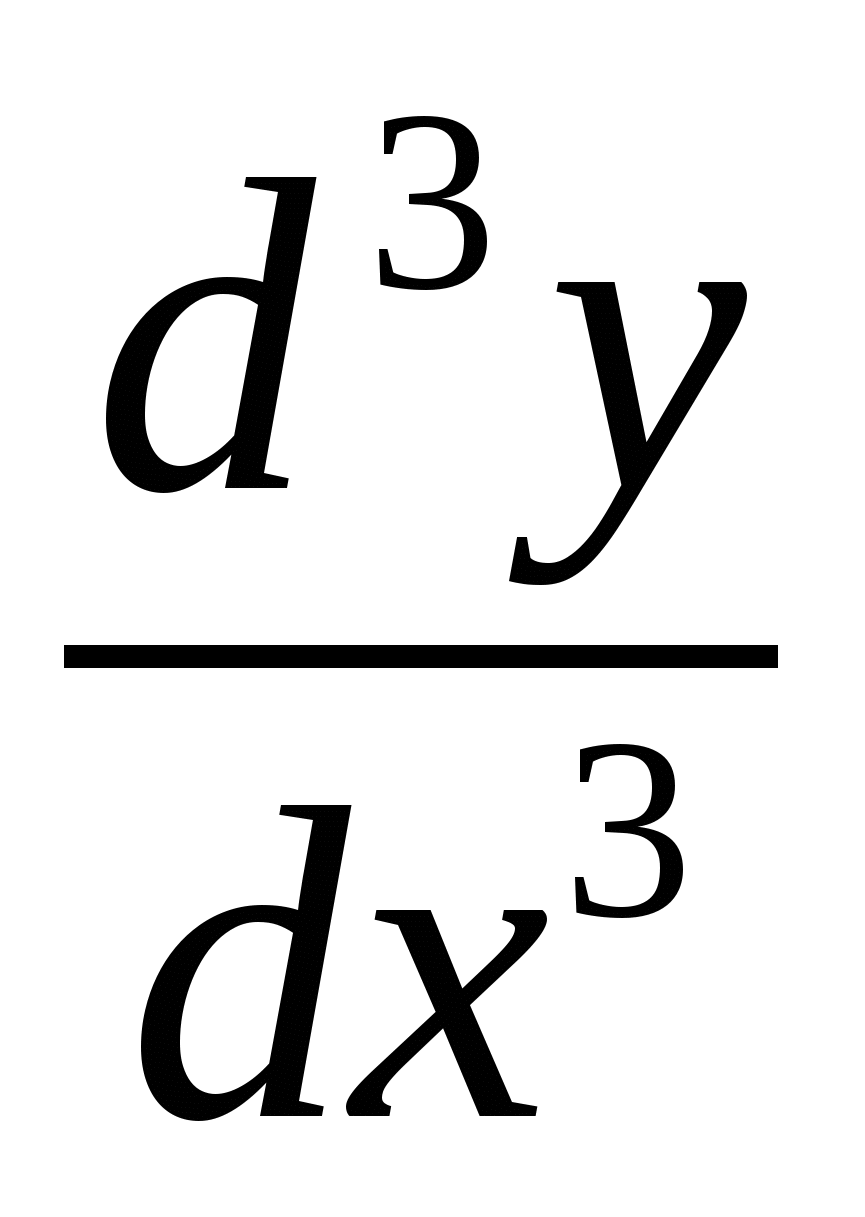 и т. д.
и т. д.
Пример 1. Найти производные функций:
а) 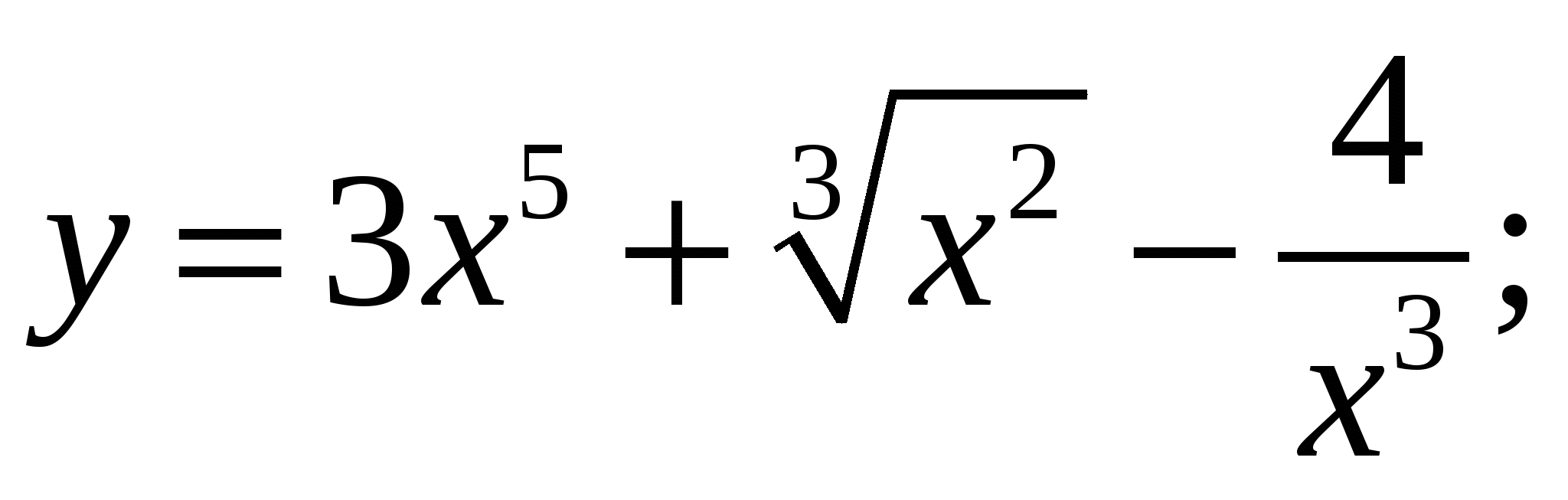 б)
б) 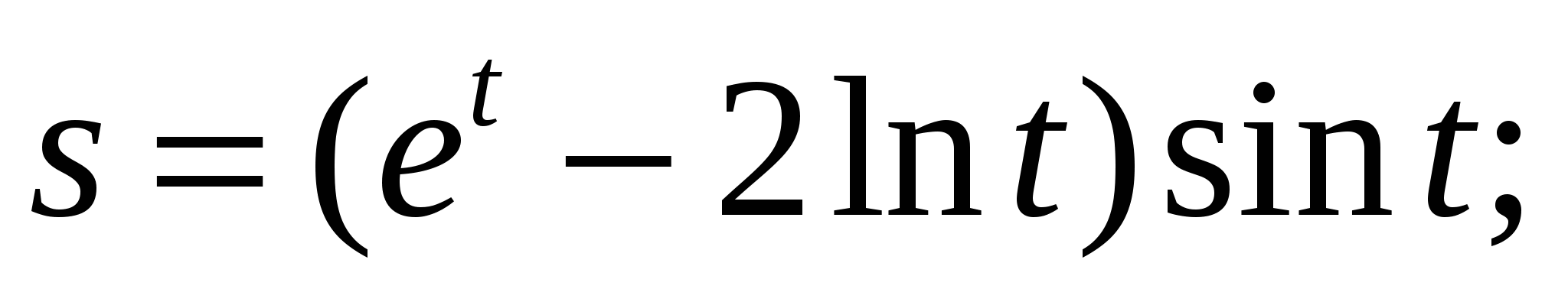
Решение.
а) Используя правила I, III и формулу (3), получим:
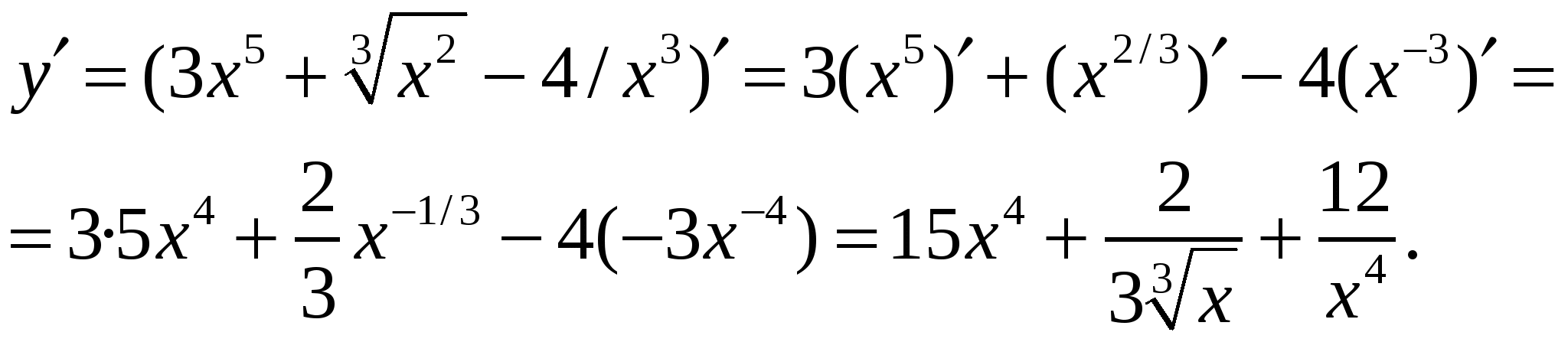
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) получим:
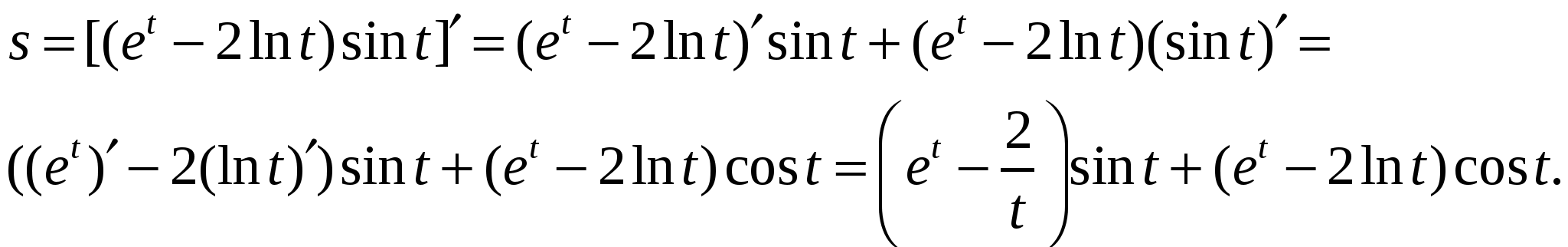
Пример 2. Составить уравнение касательной к кривой  в точке с абсциссой х0=2.
в точке с абсциссой х0=2.
Используем уравнения касательной:
1) 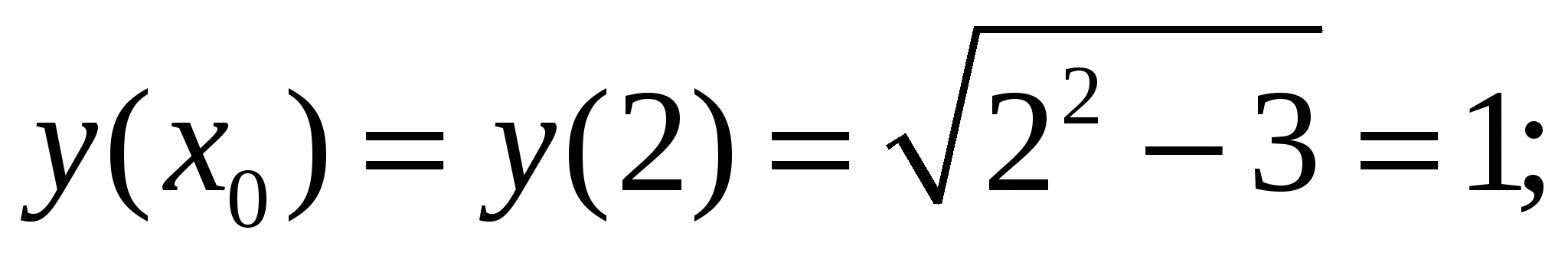
2) 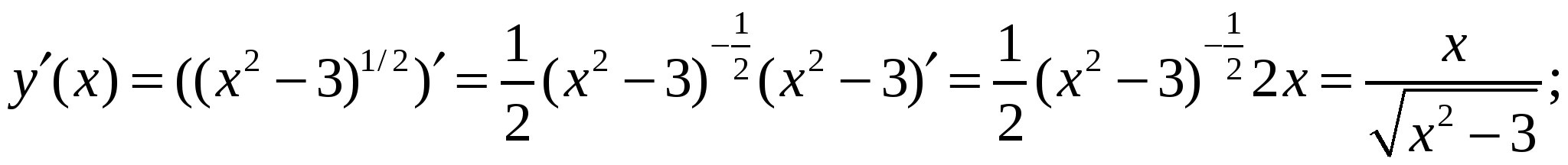
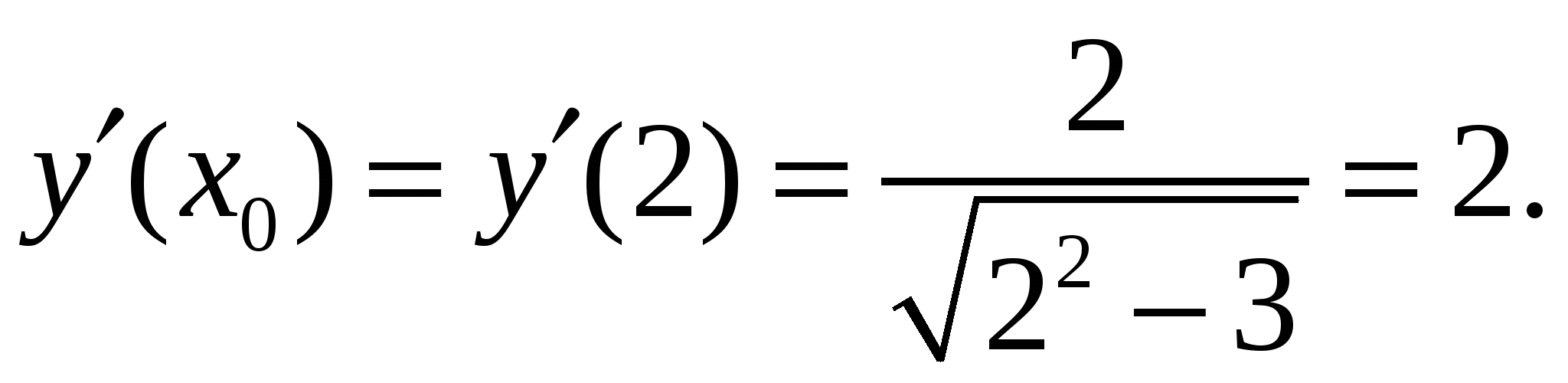
Подставим 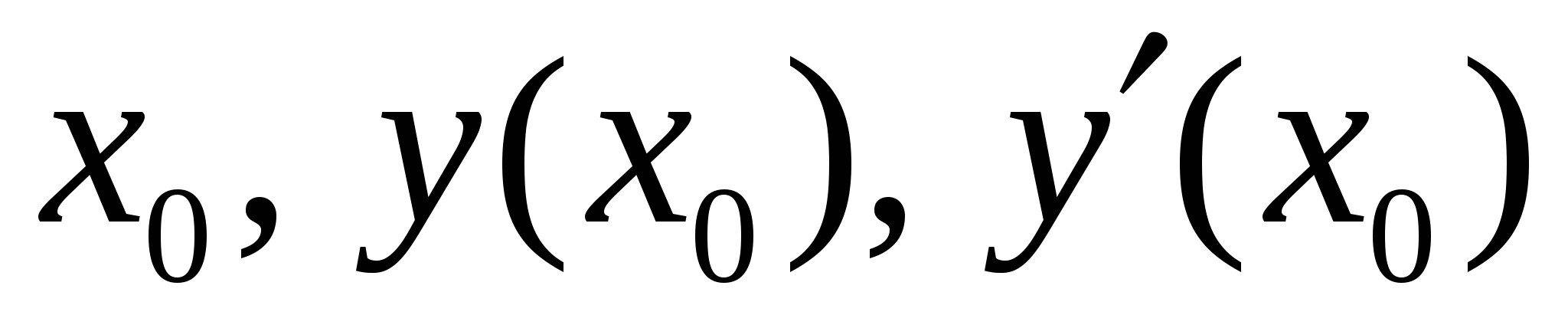 в уравнения и получим:
в уравнения и получим: 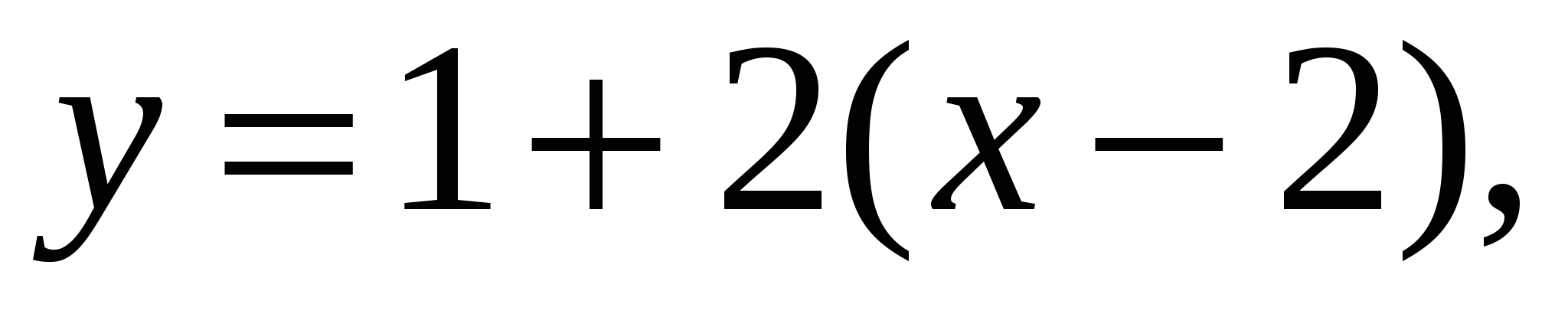
или 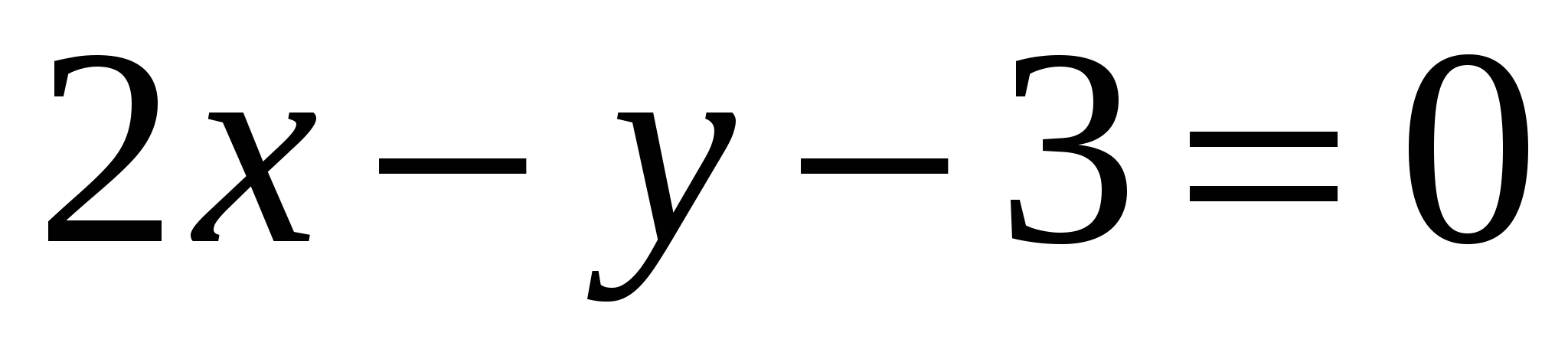 - уравнение касательной.
- уравнение касательной.
Пример 3. Найти производную второго порядка функции 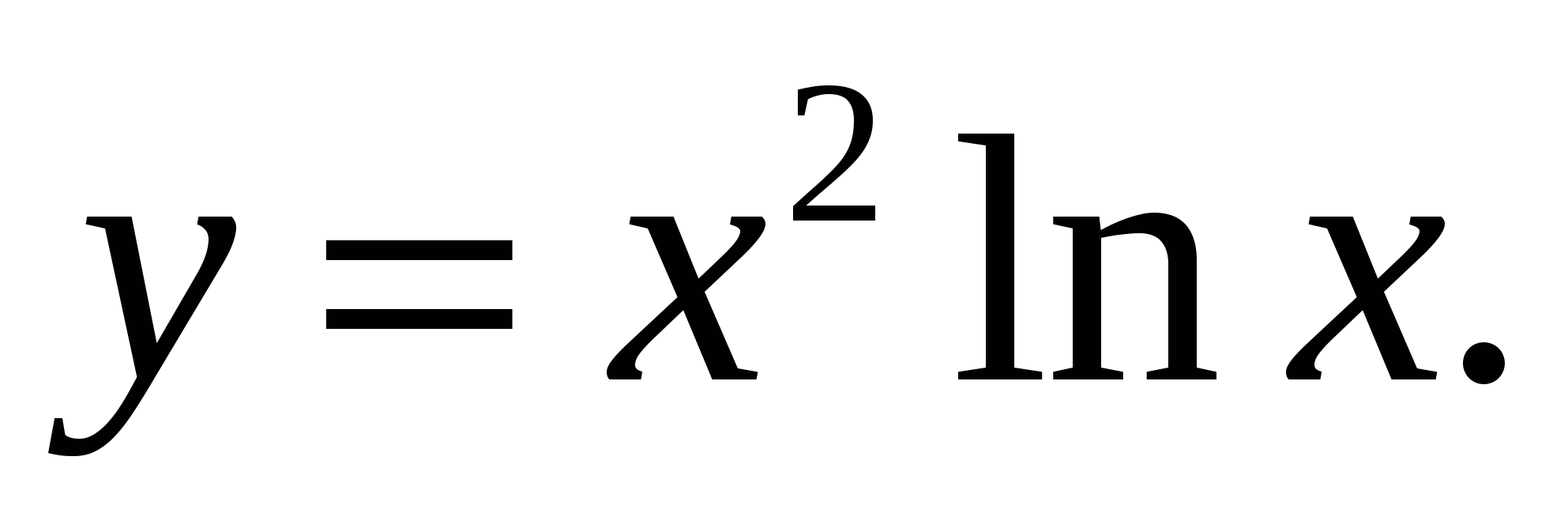
Решение. 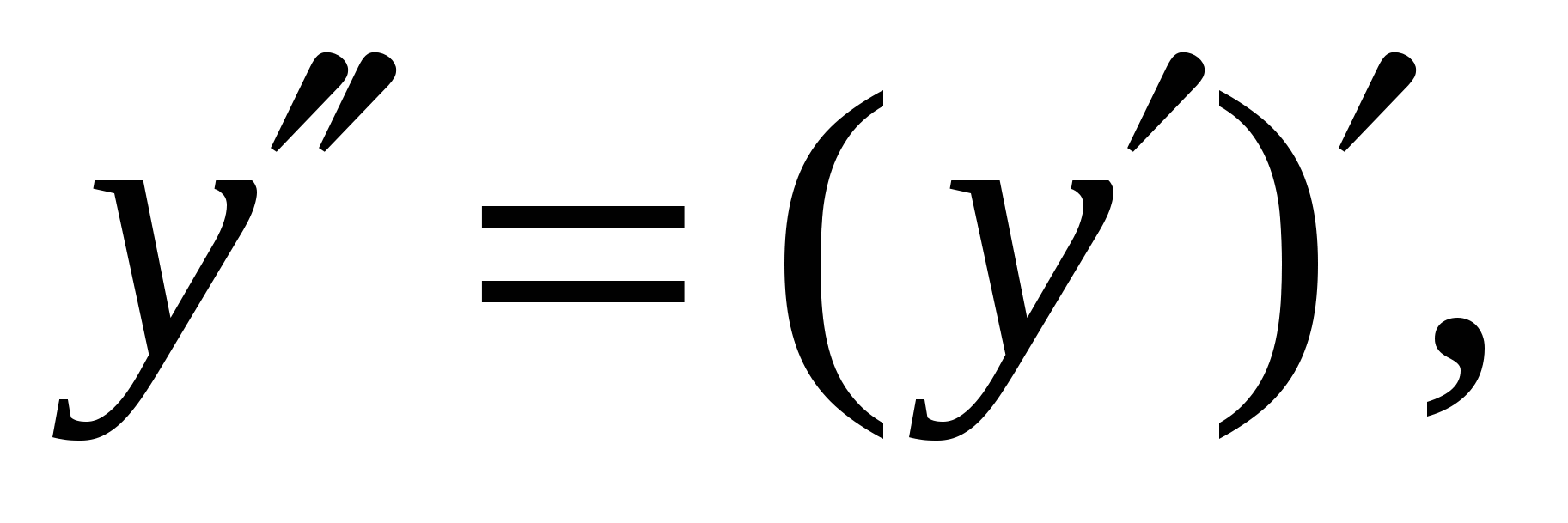 поэтому найдём производную первого порядка,
поэтому найдём производную первого порядка,
а затем второго.
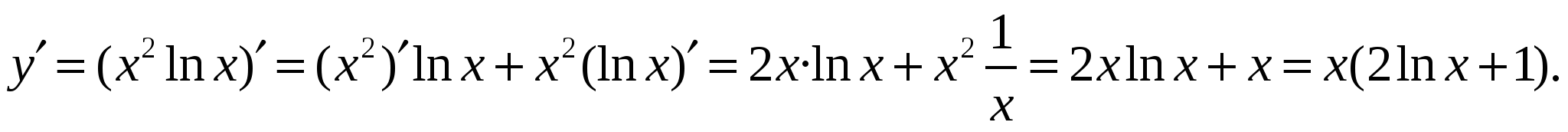
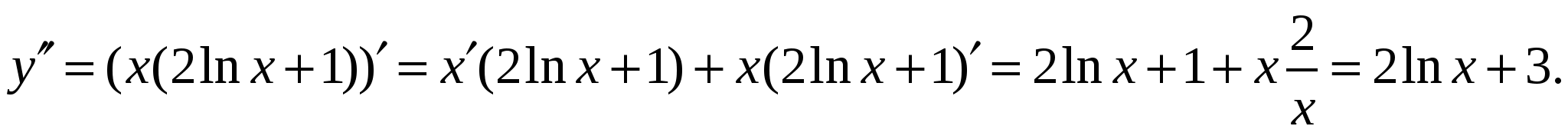
Содержание практической работы
Задание 1. Найти производные 1-го порядка данных функций
1) 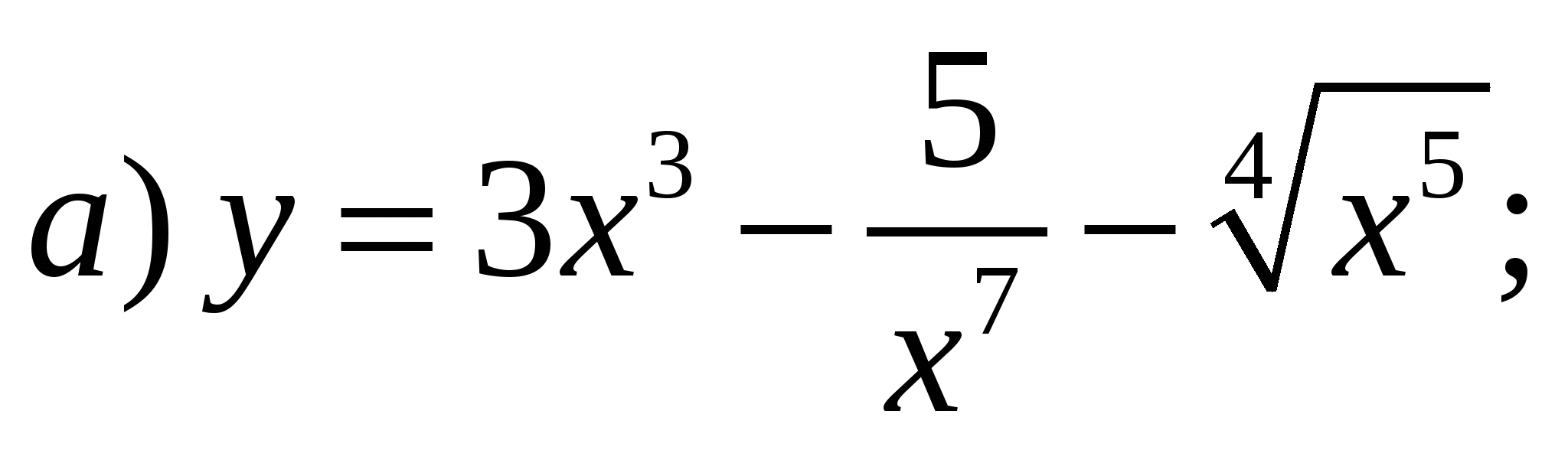
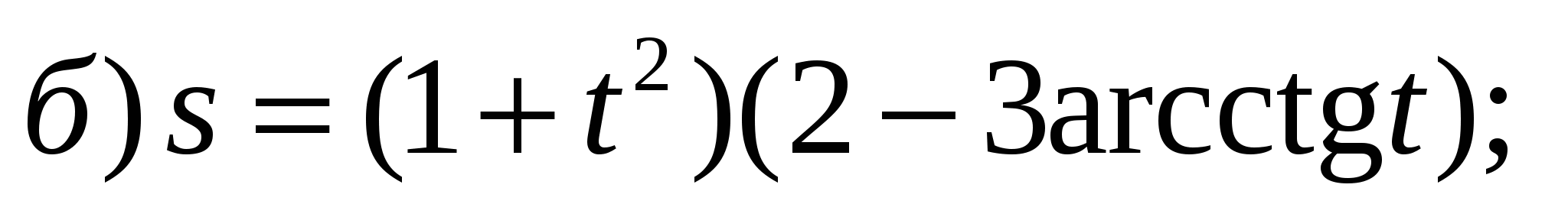
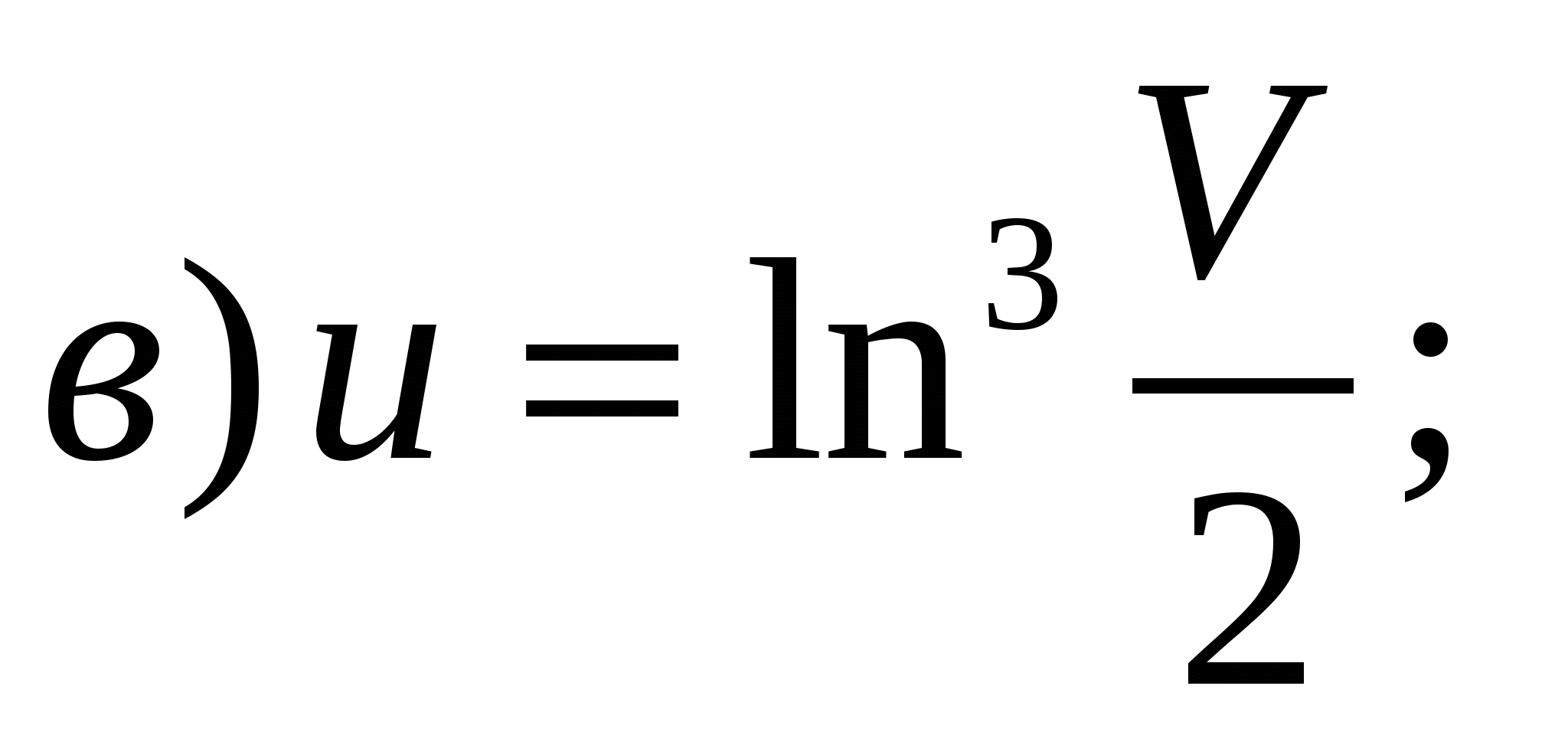
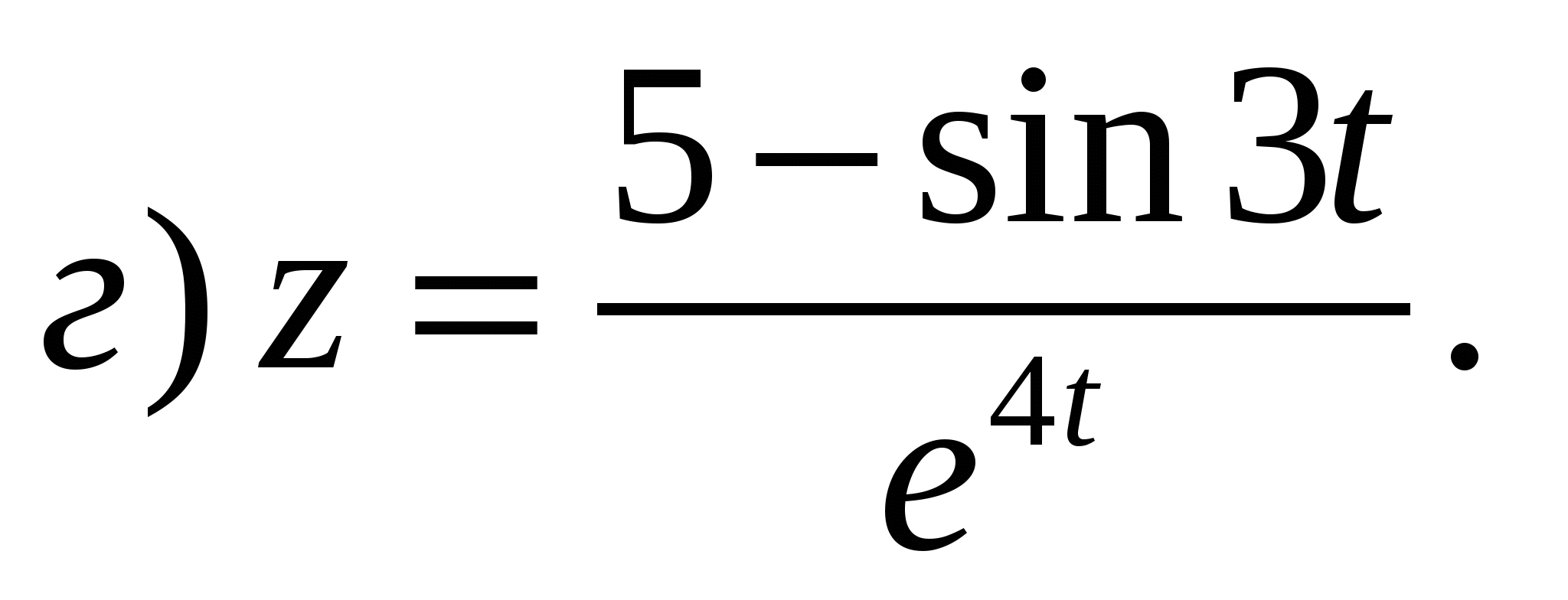
2) 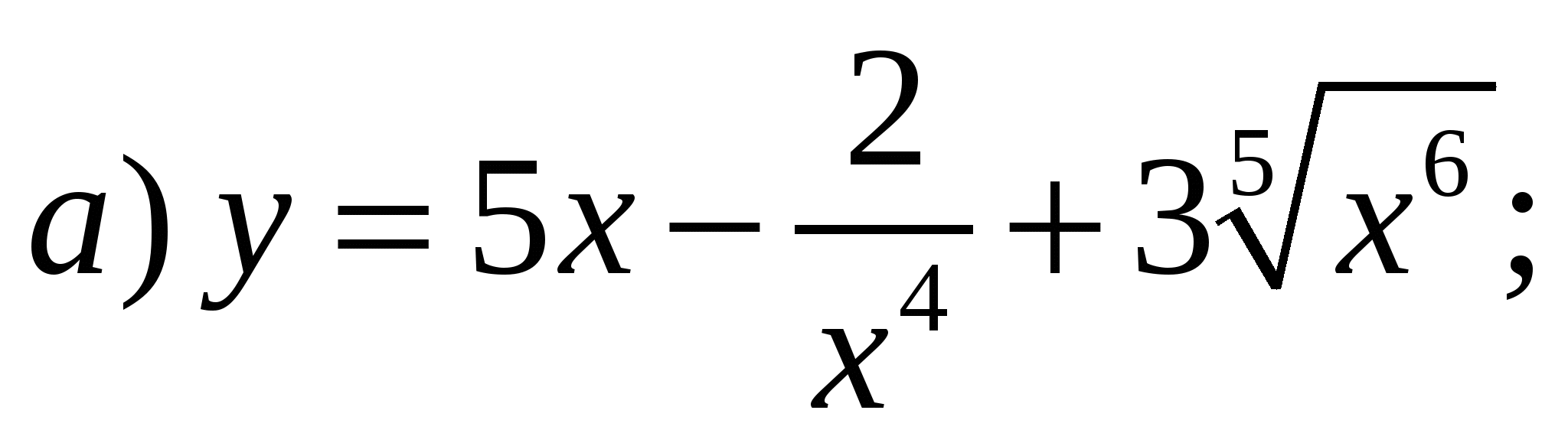
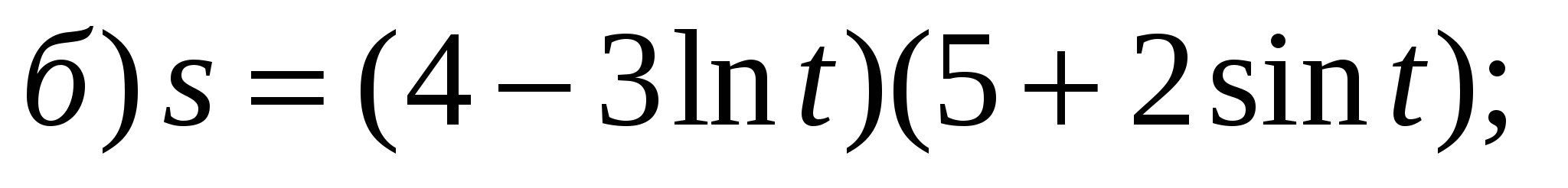
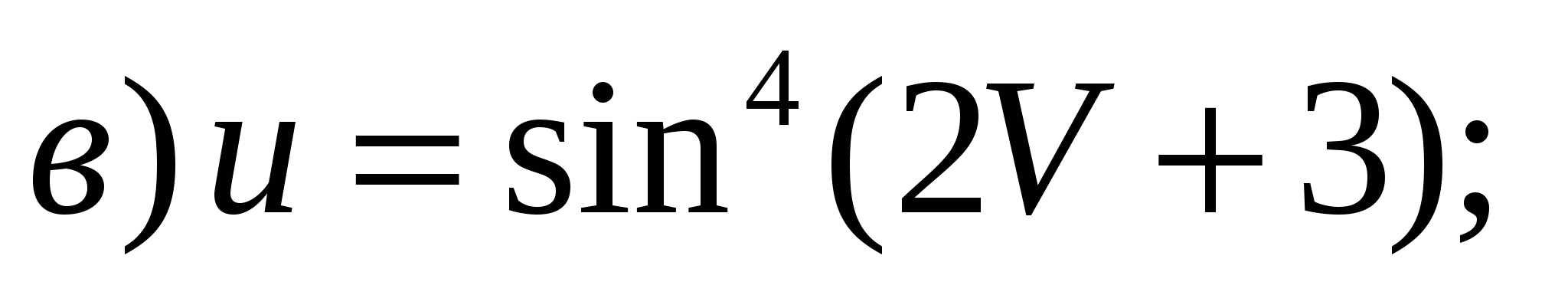
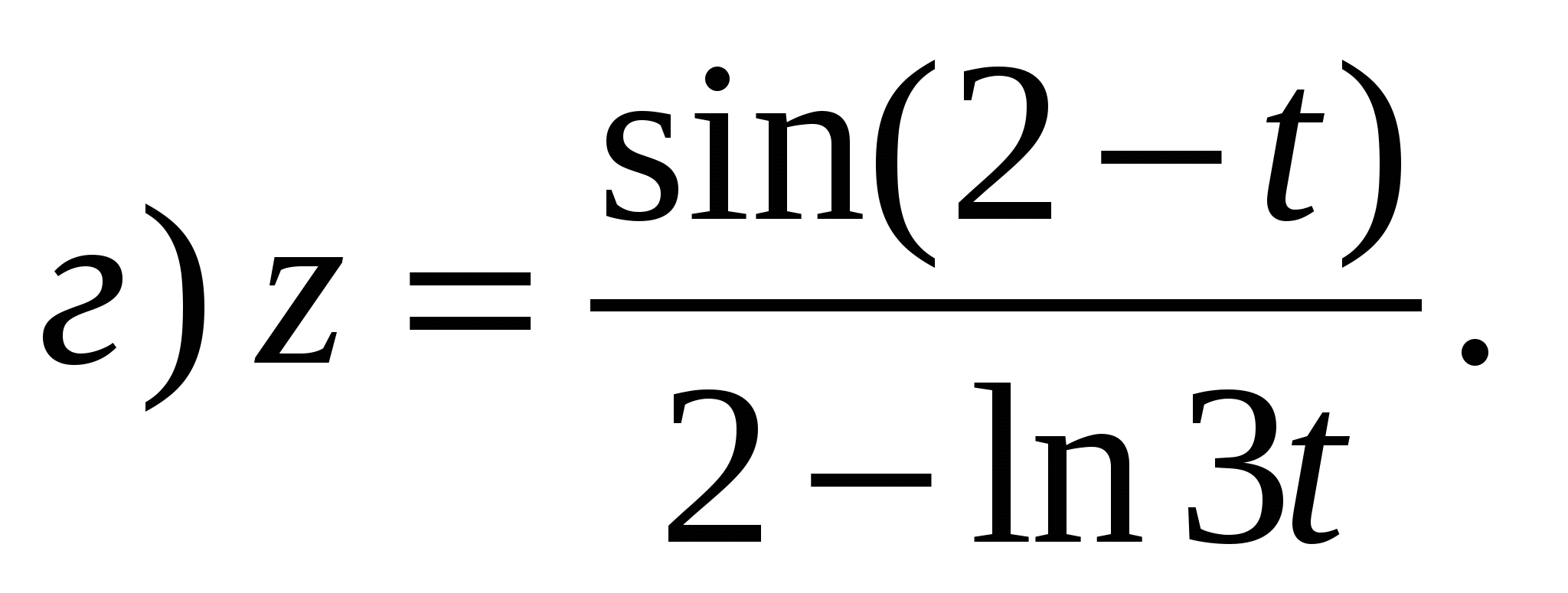 3) 3)
3) 3)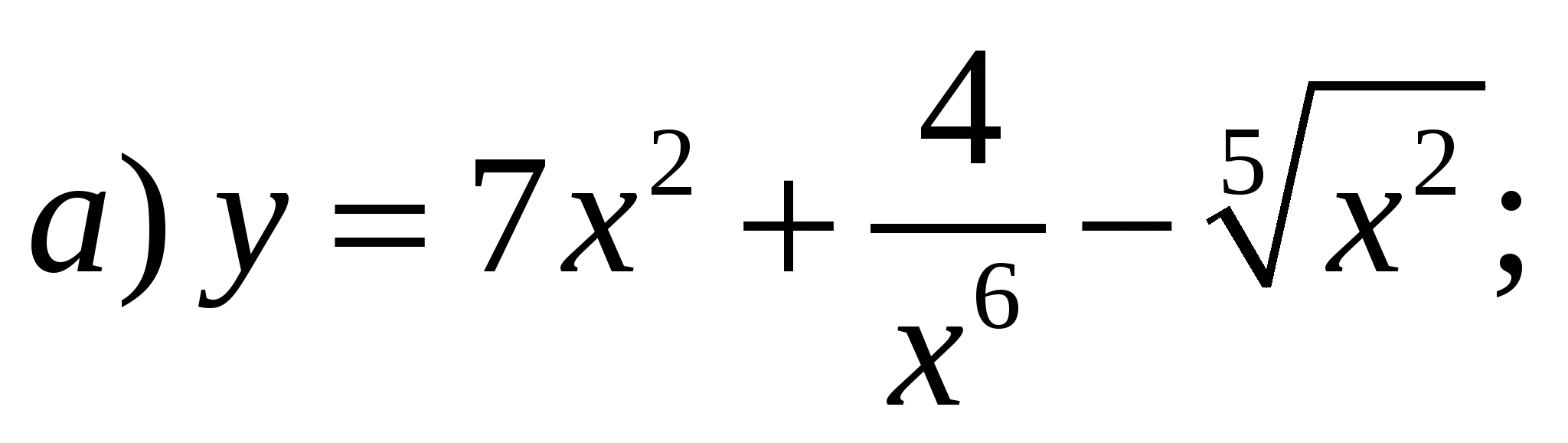
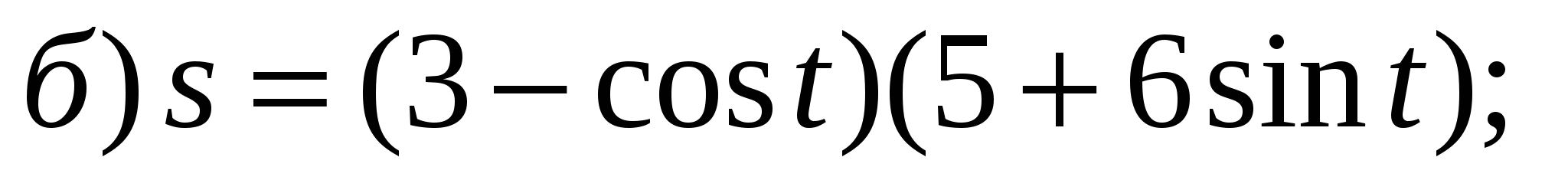
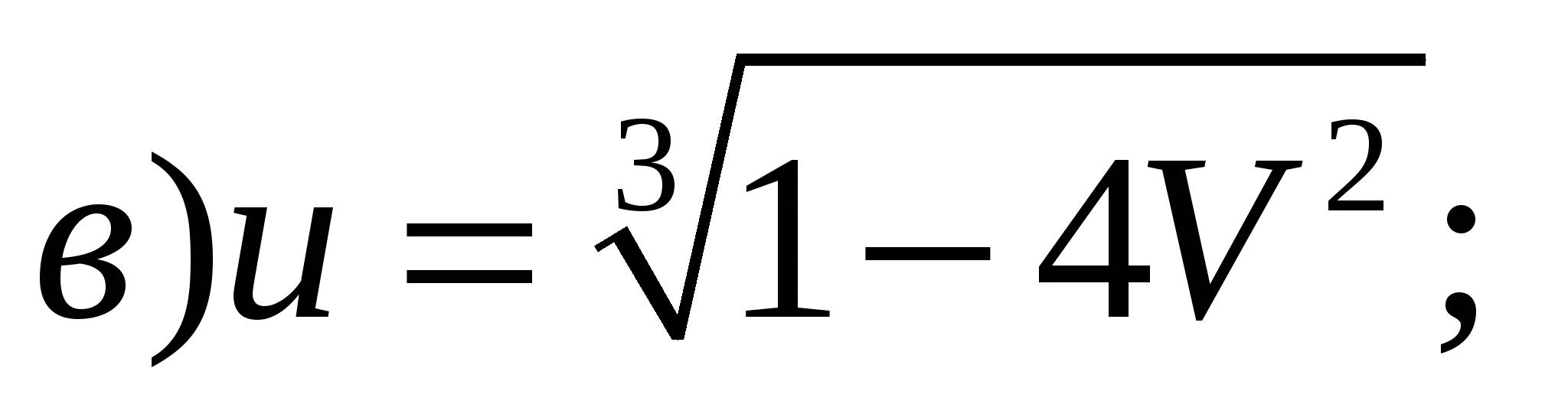
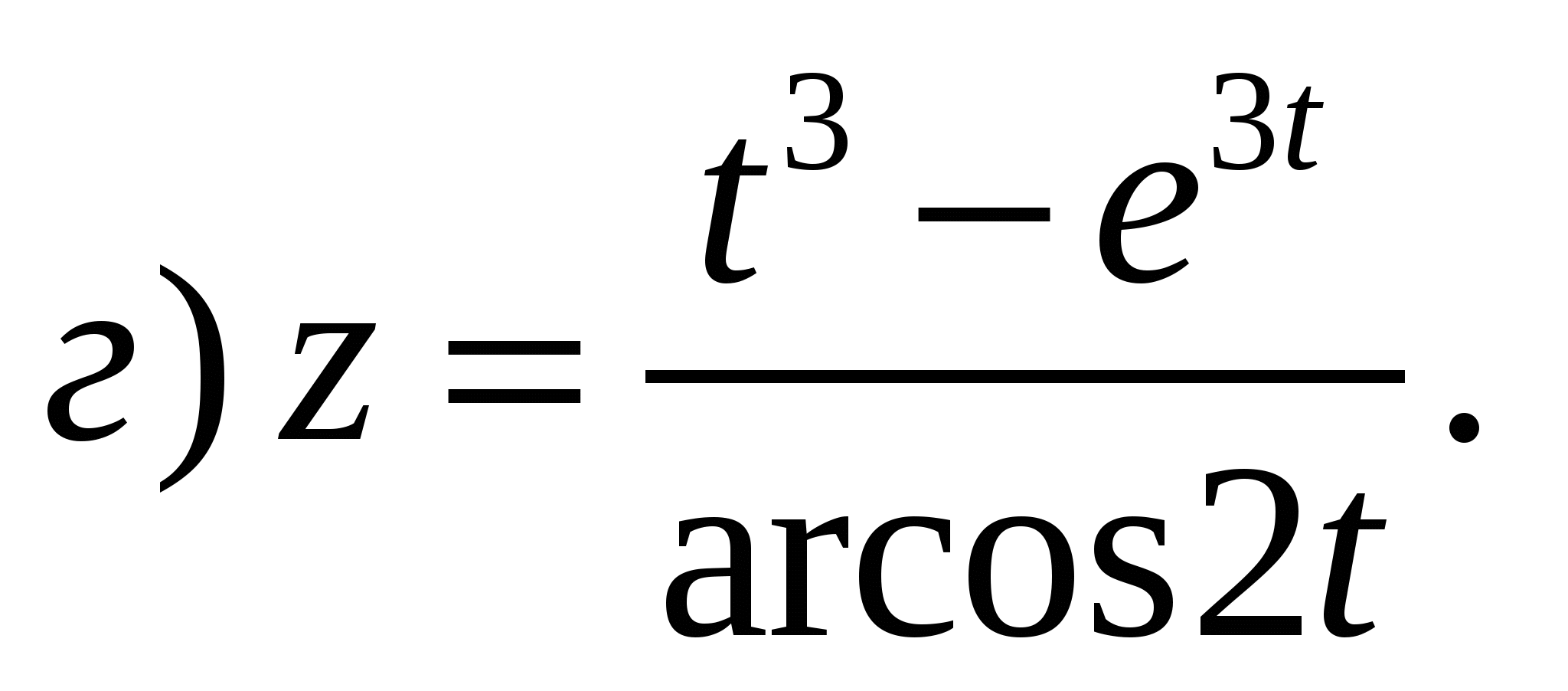
4) 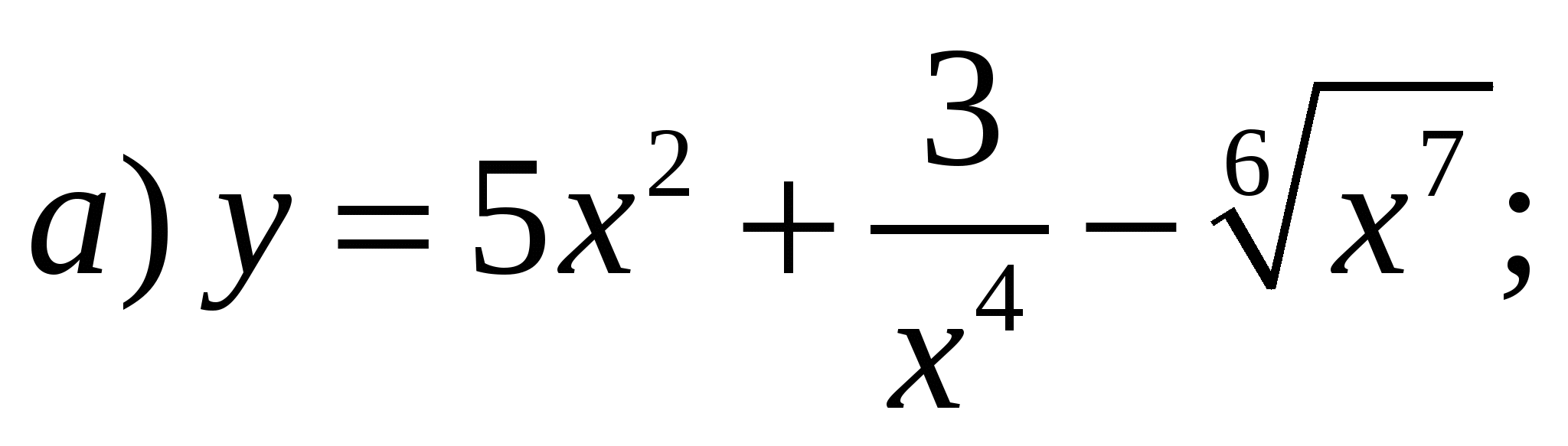
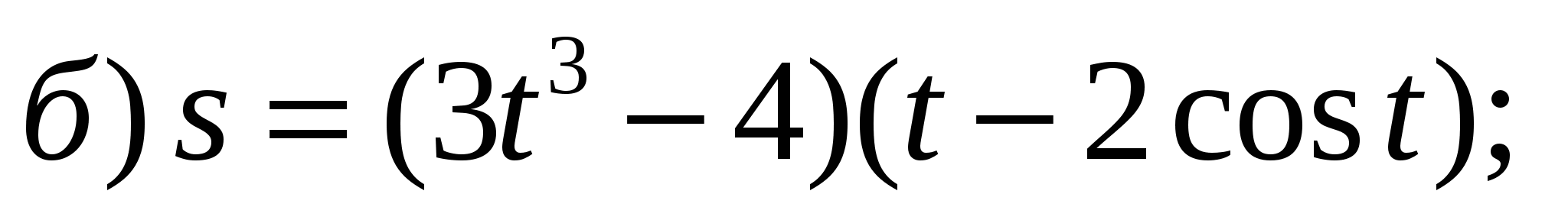
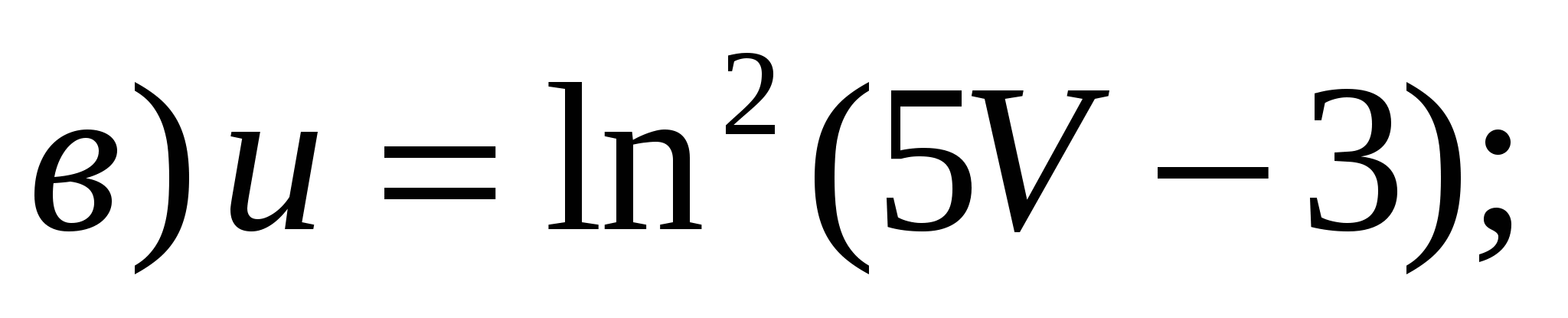
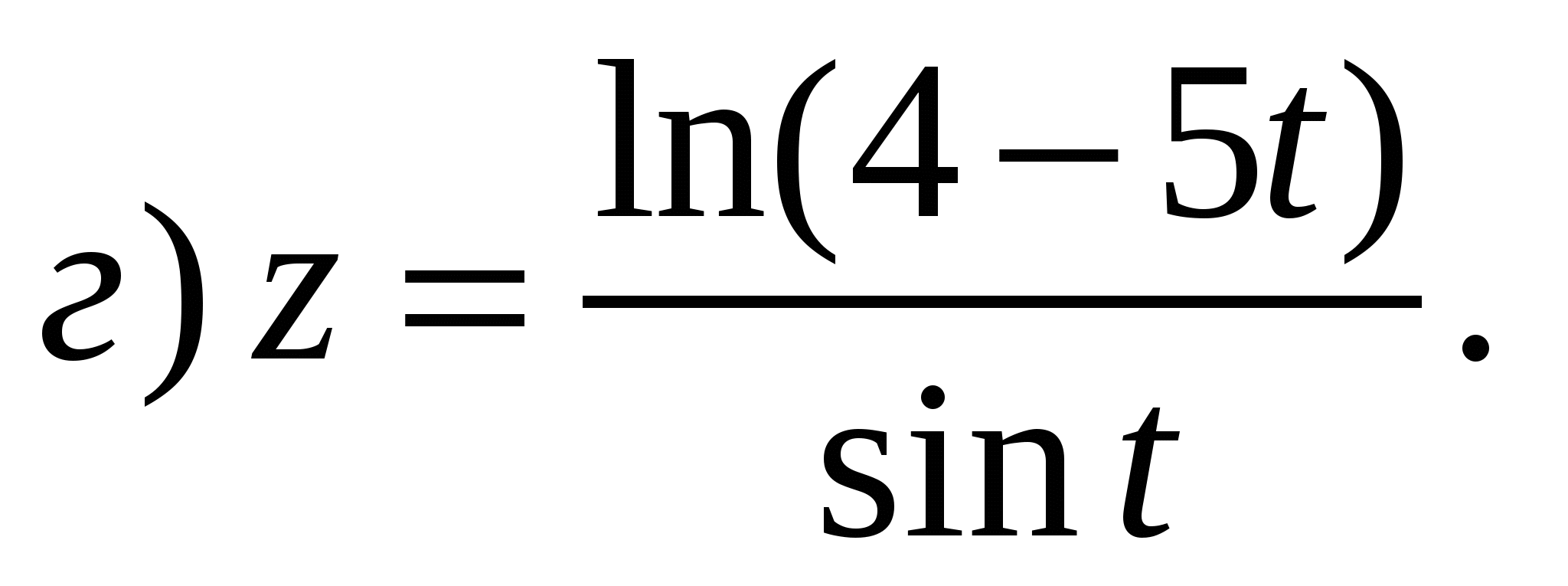
5) 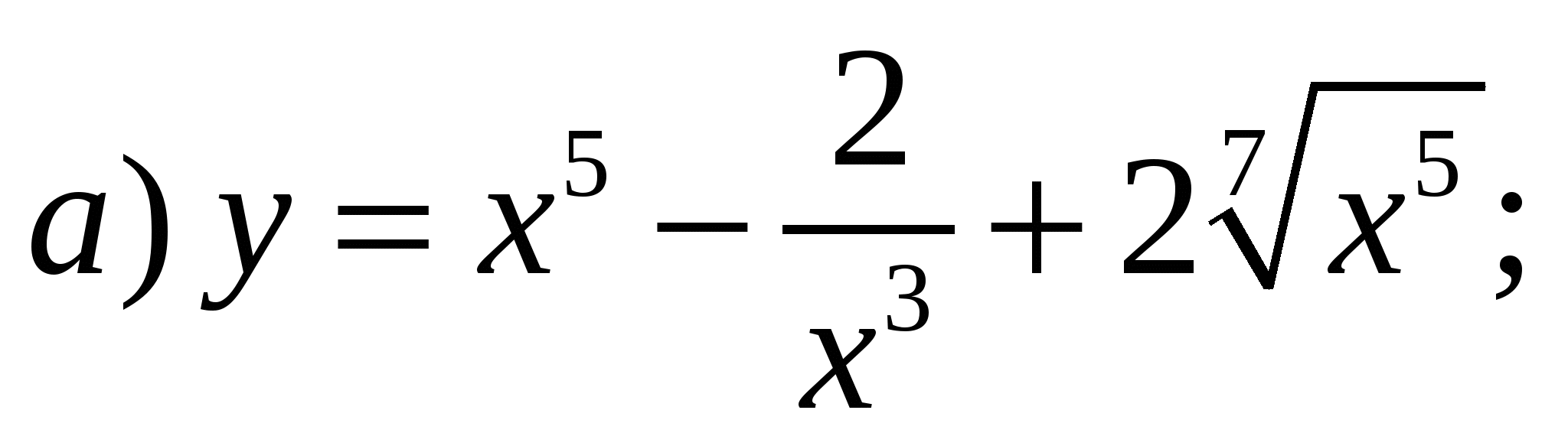
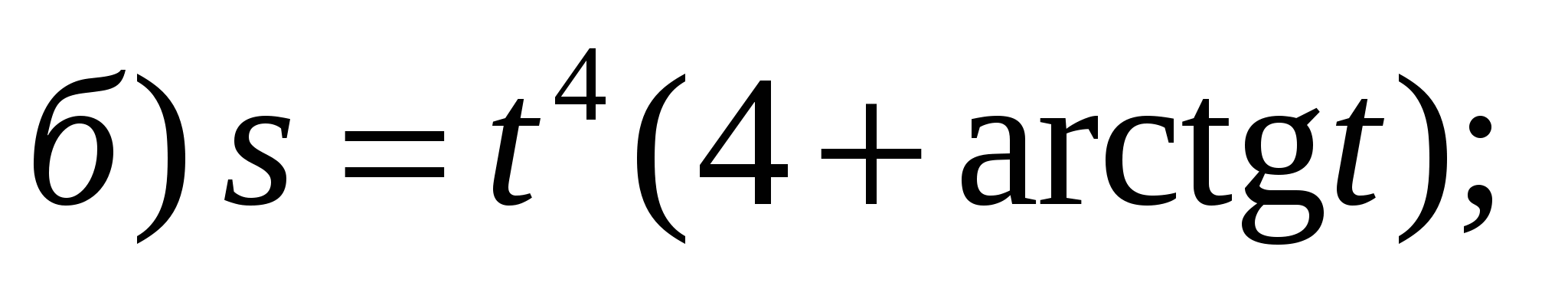
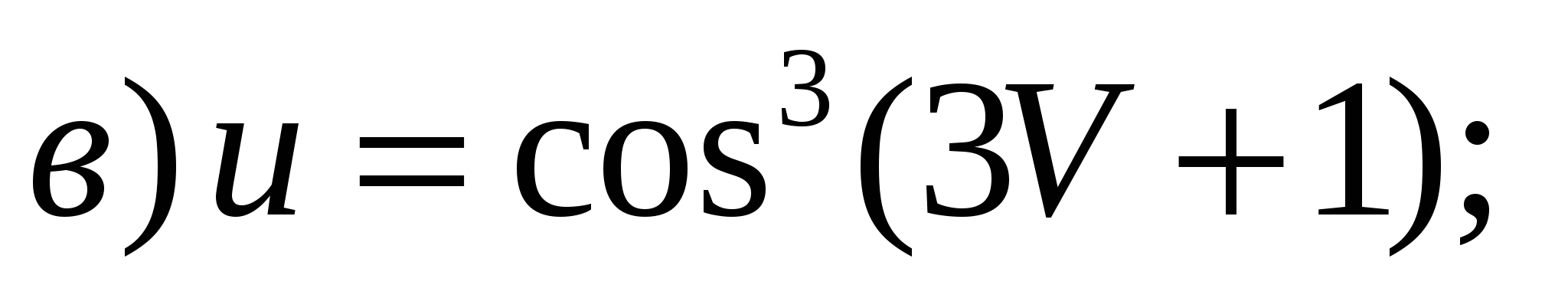
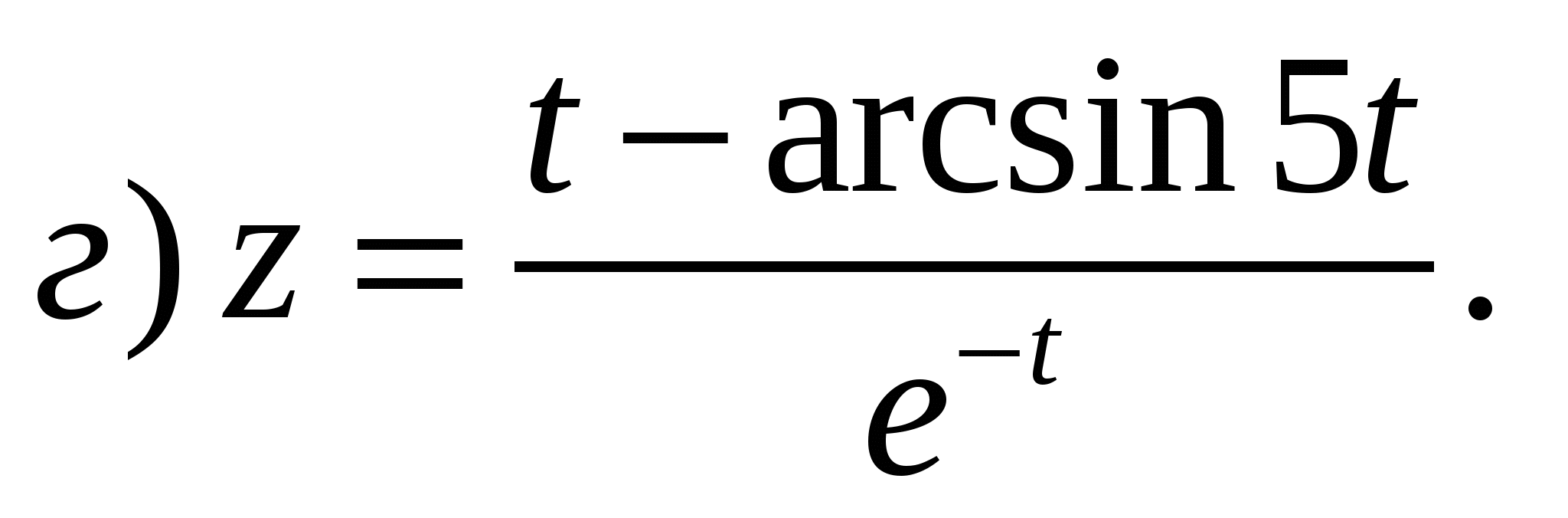
6) 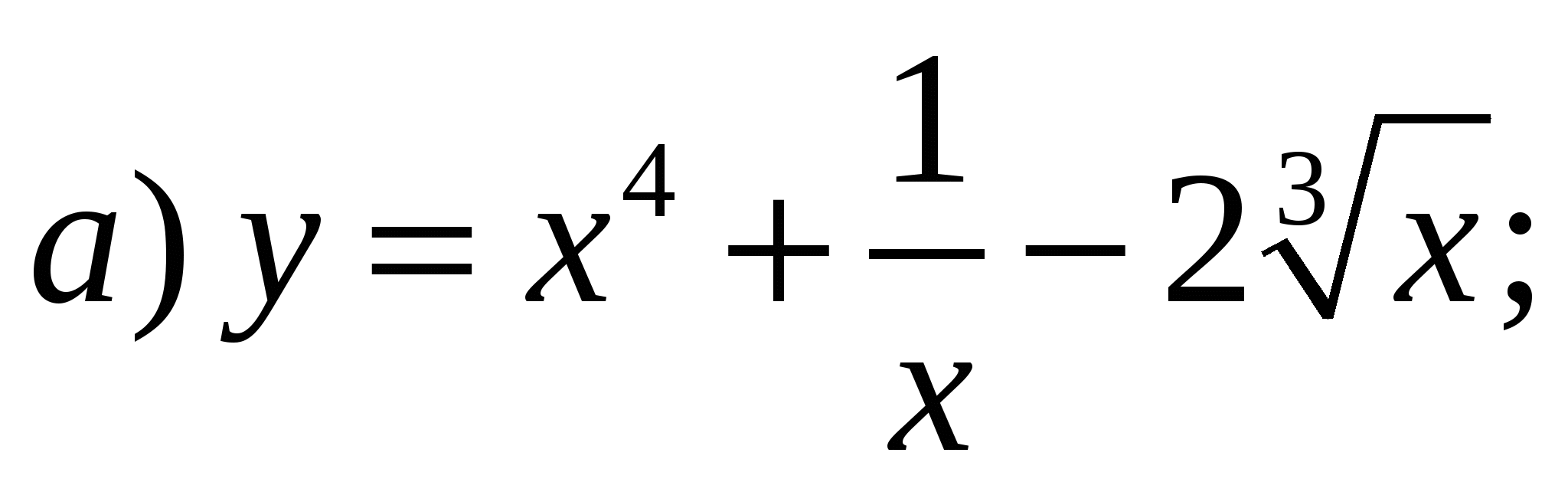
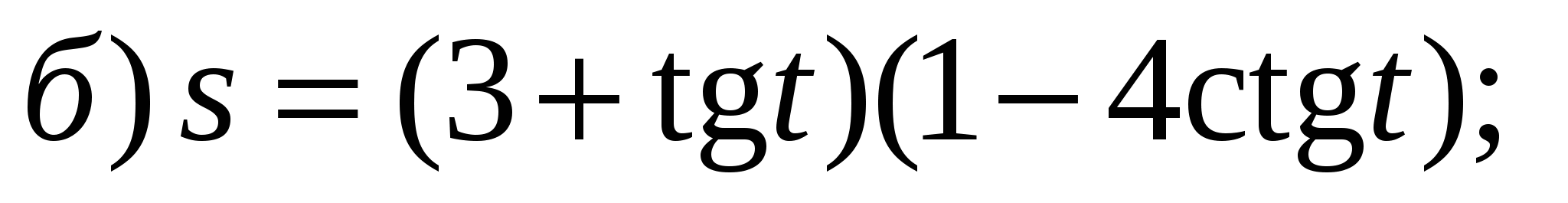
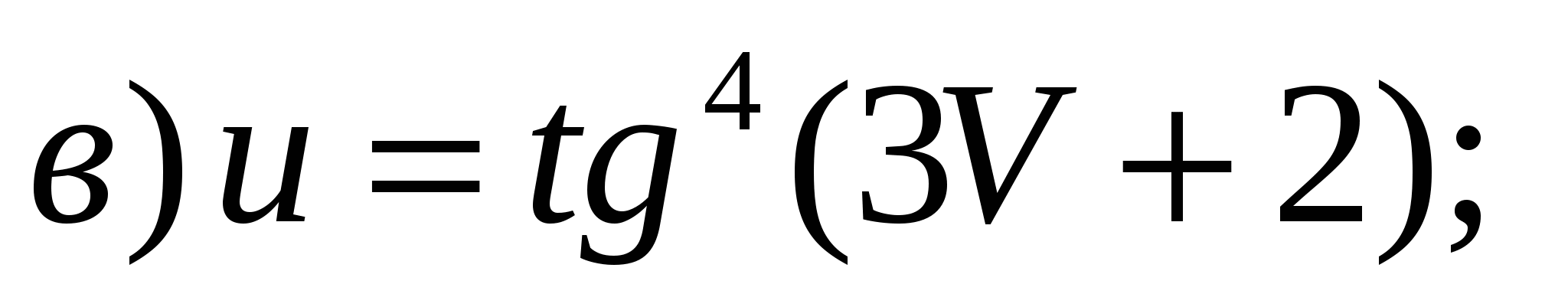
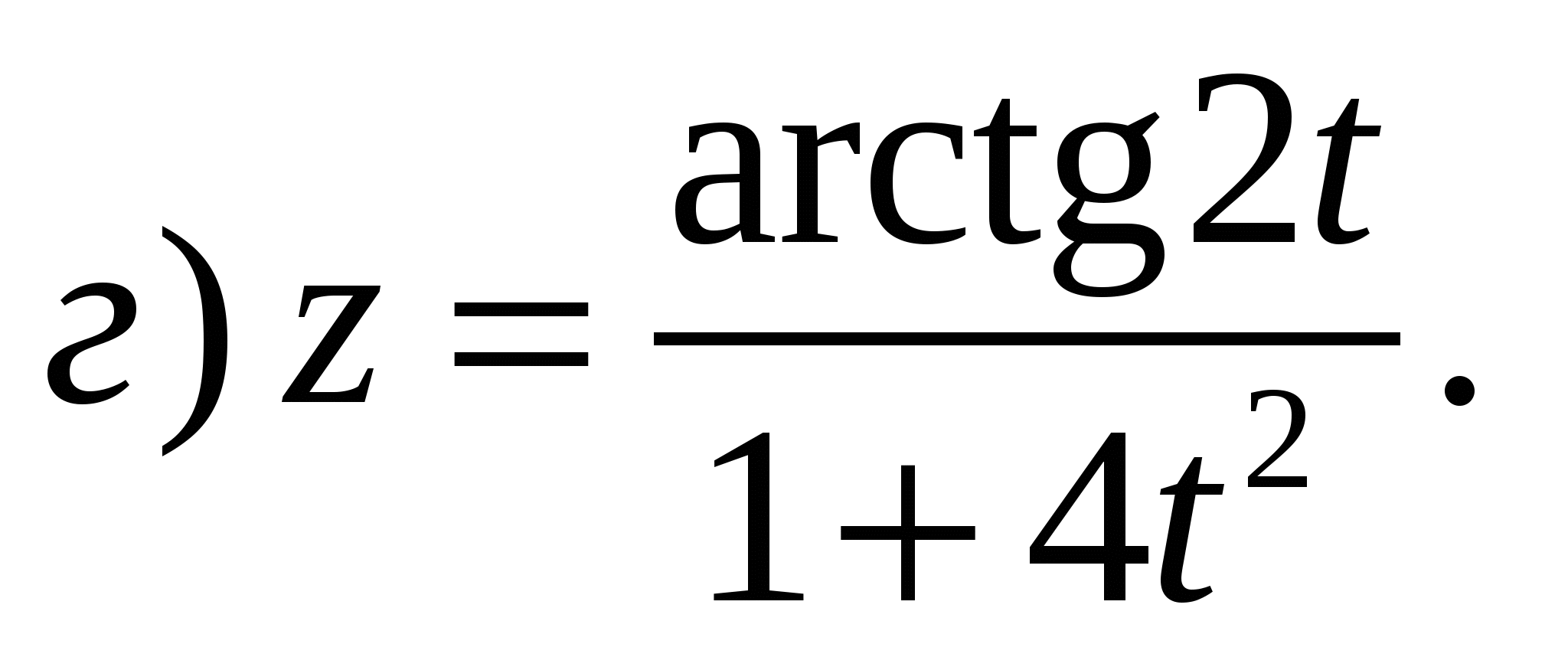
Задание 2. Составить уравнение касательной к кривой y=f(x) в точке с абсциссой х0.
1) 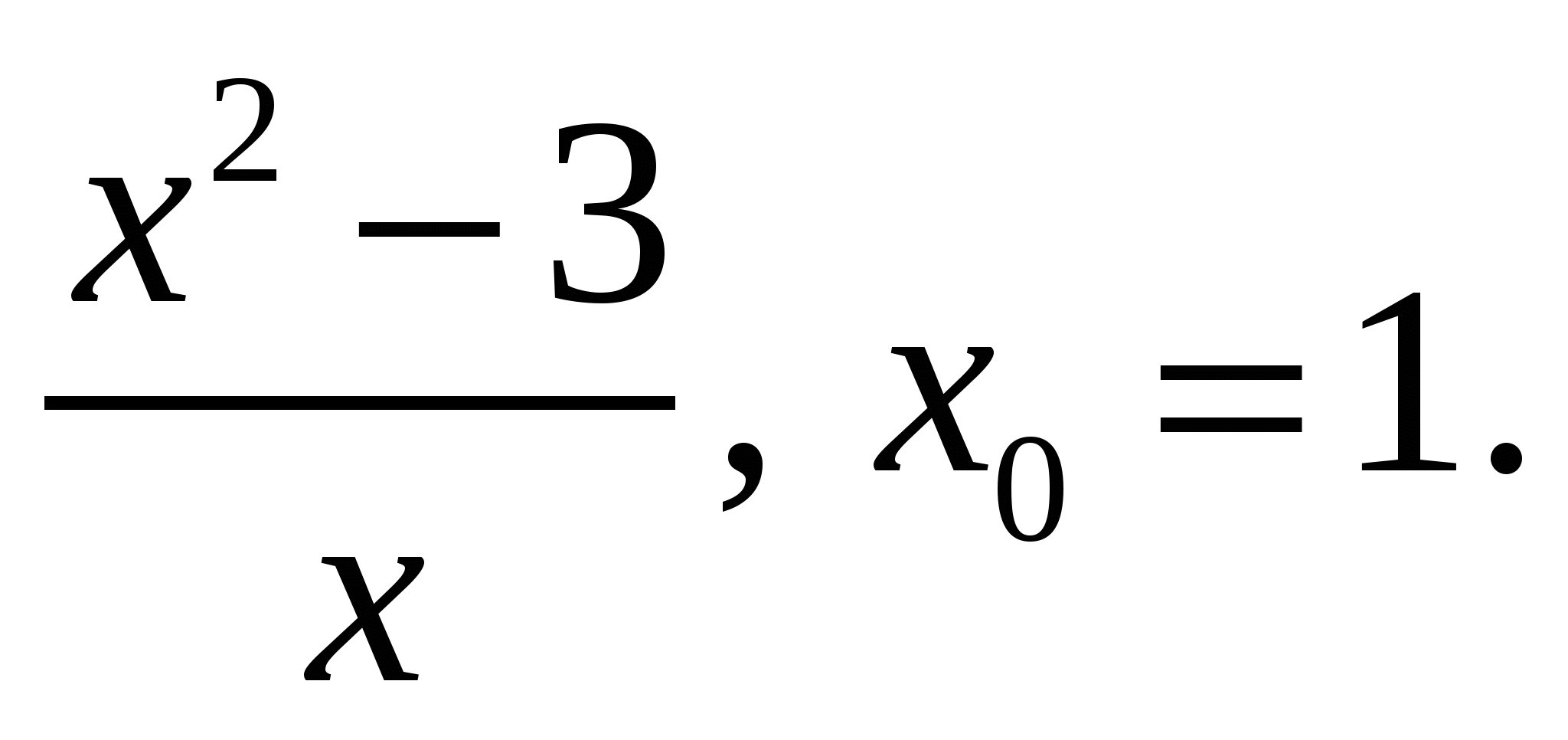
2) 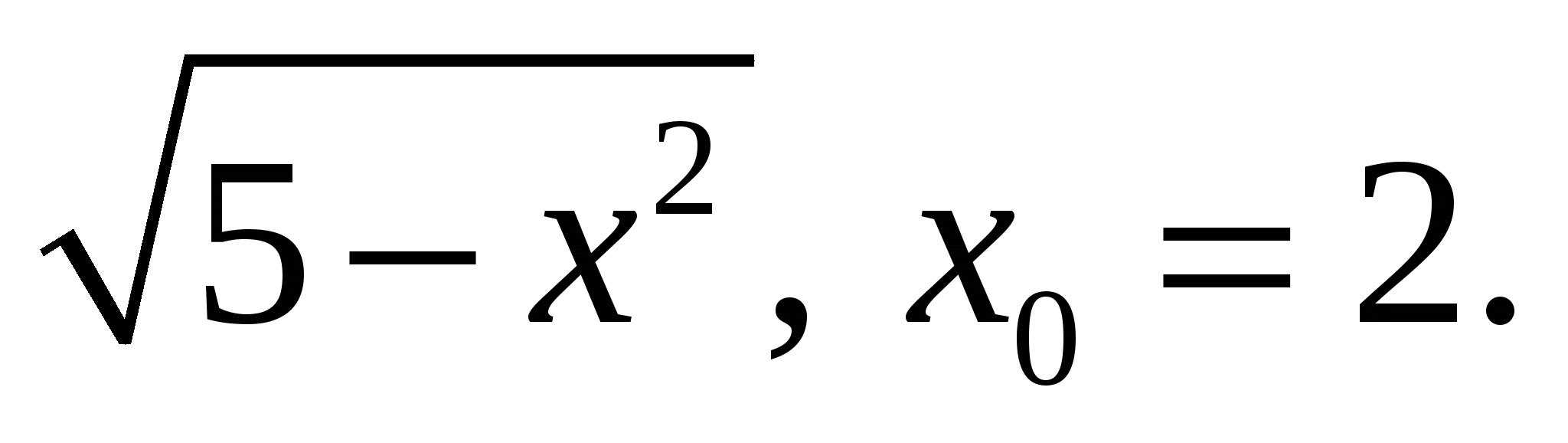
3) 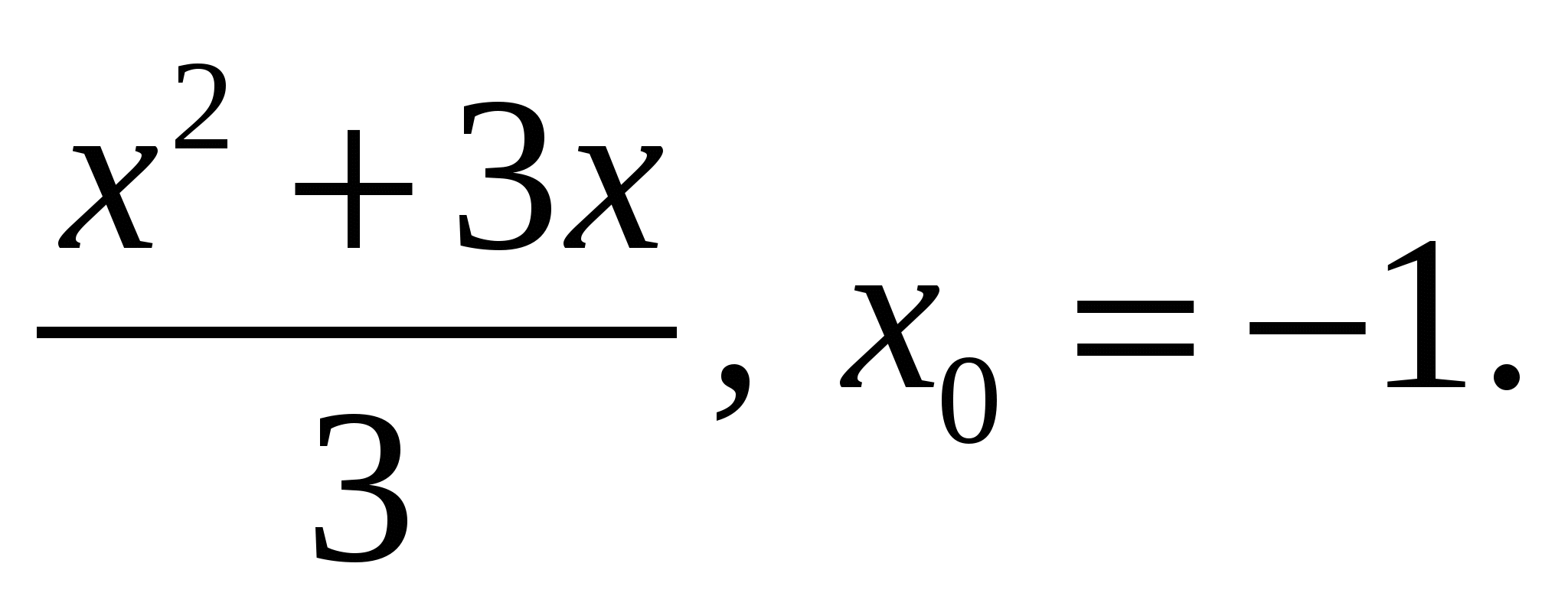
4) 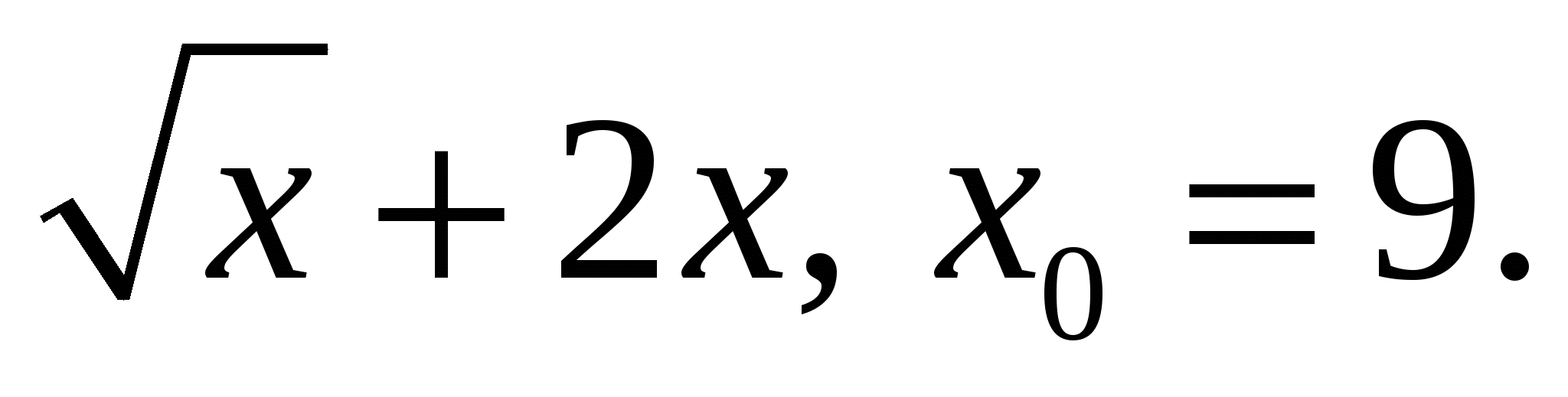
5) 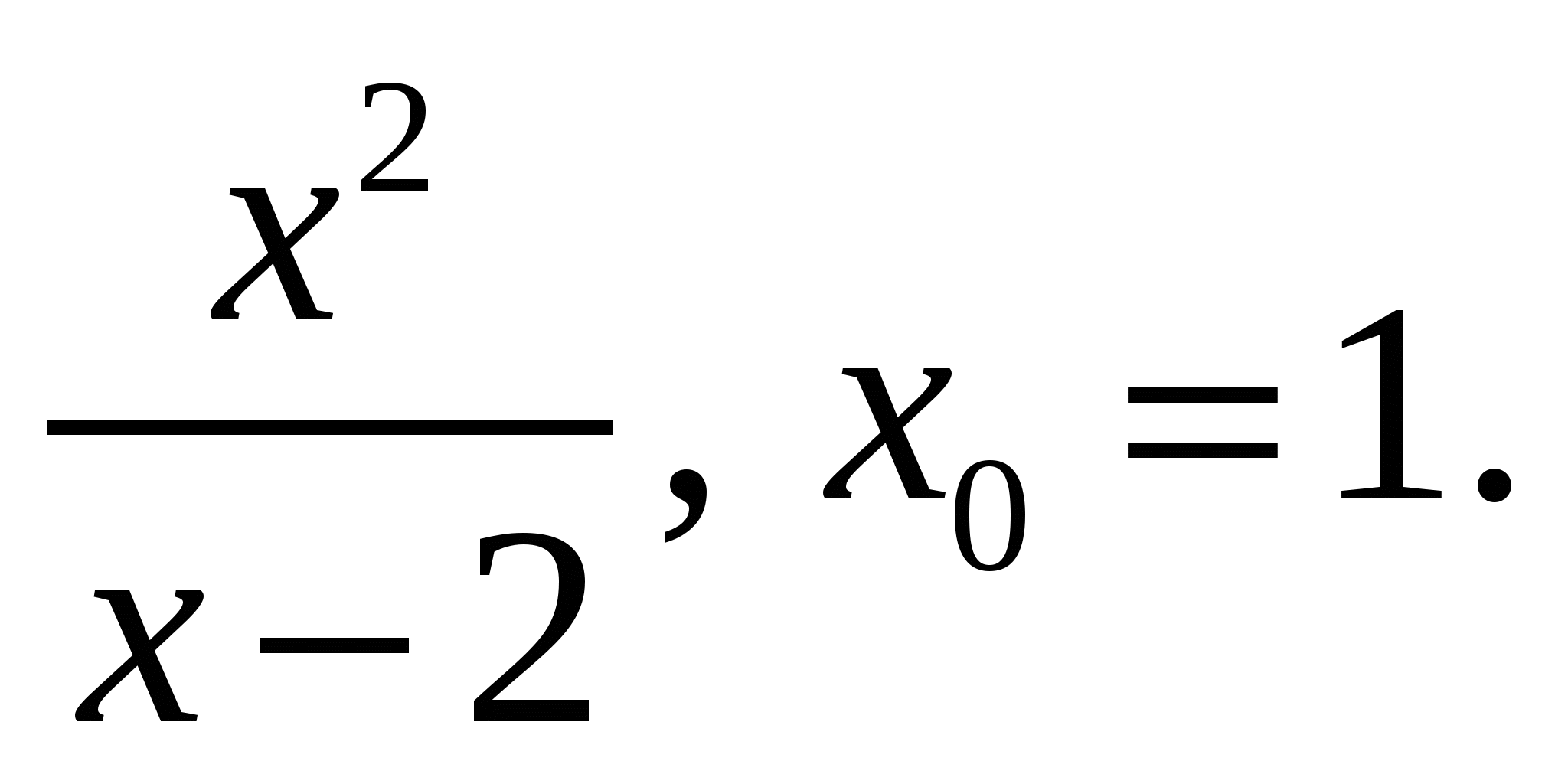
6) 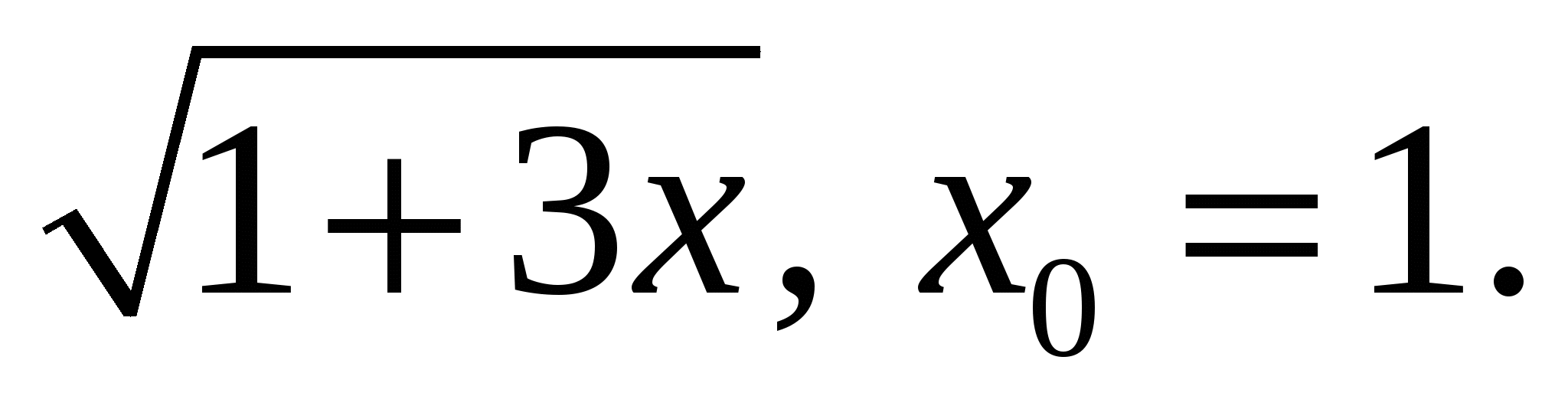
Задание 3. Найти производную второго порядка функции y=f(x).
1) 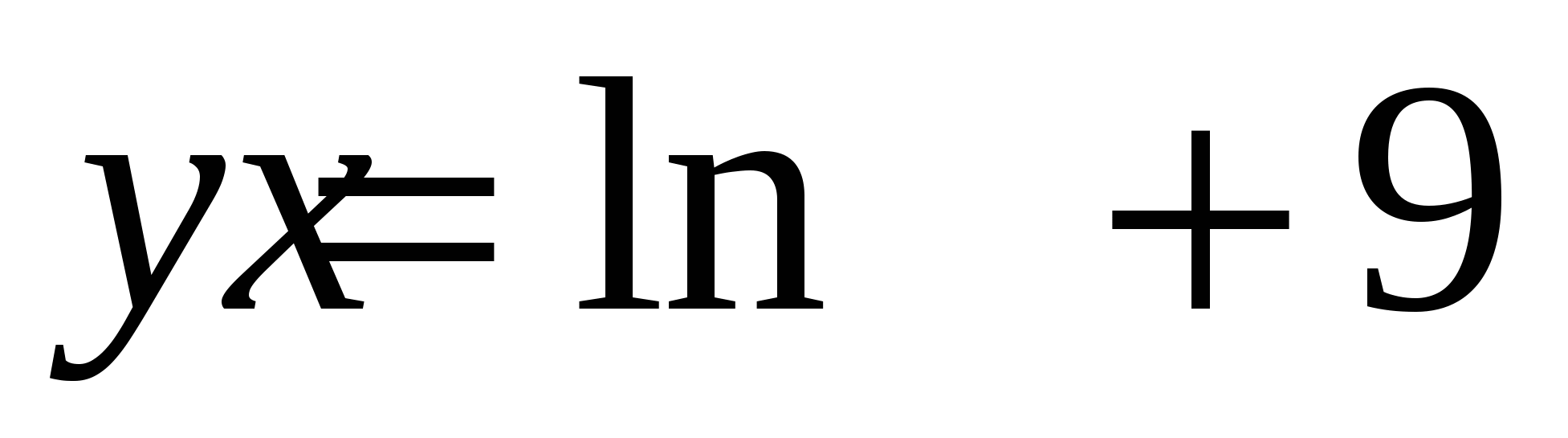
2) 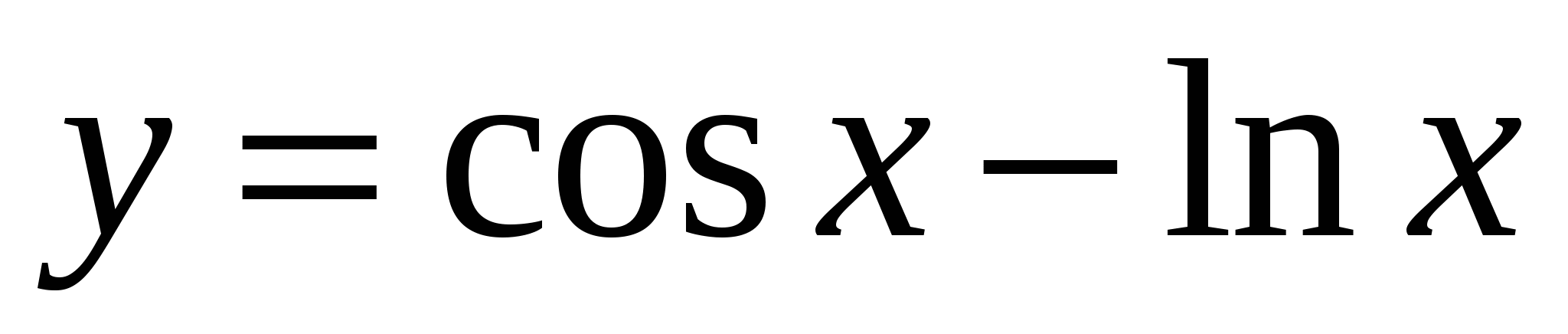
3) 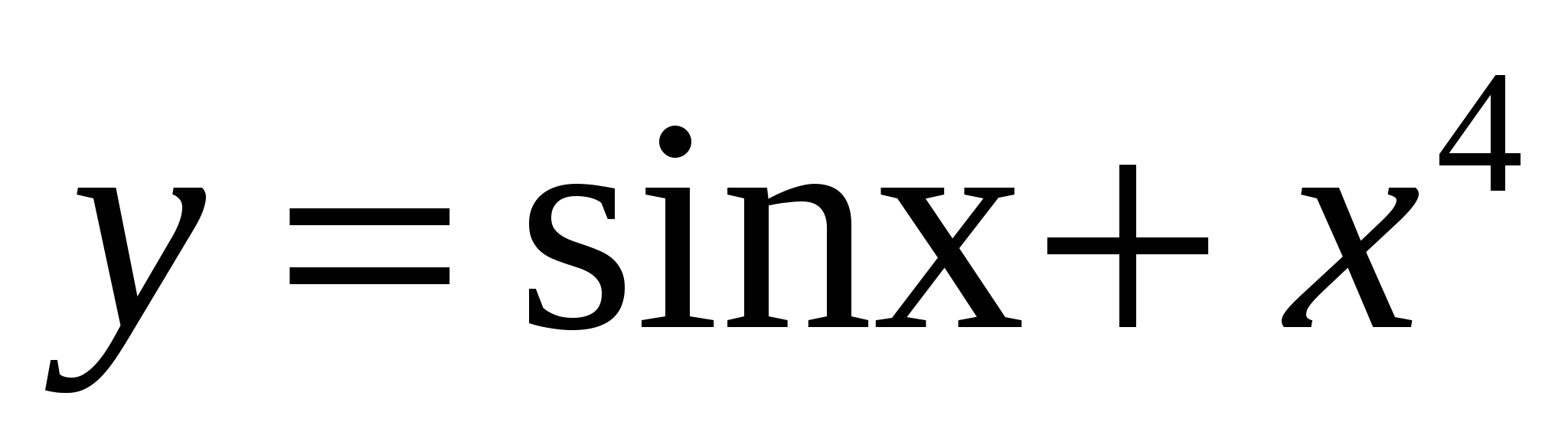
4) 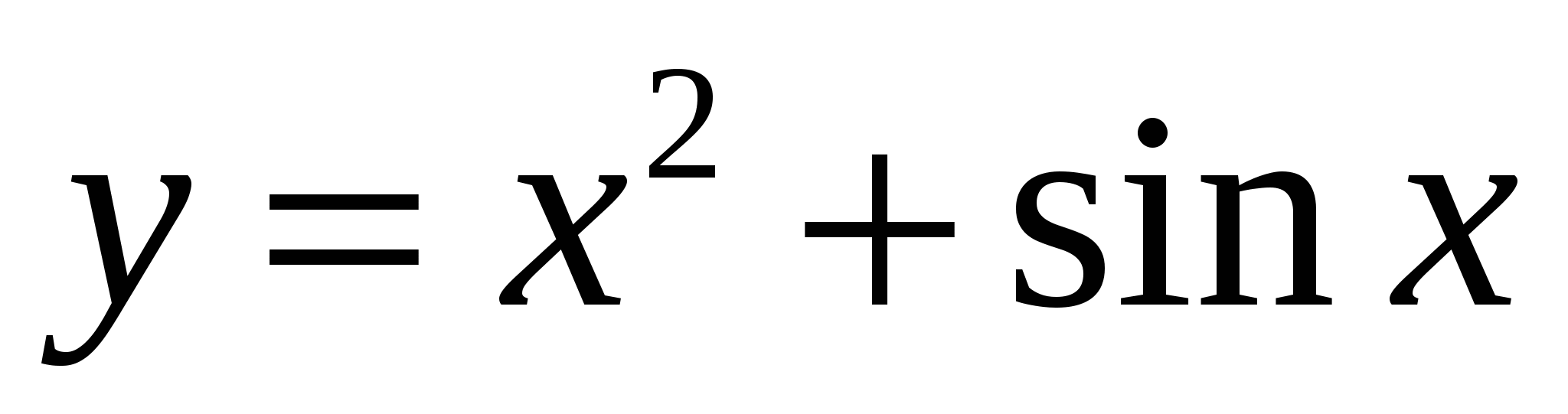
5) 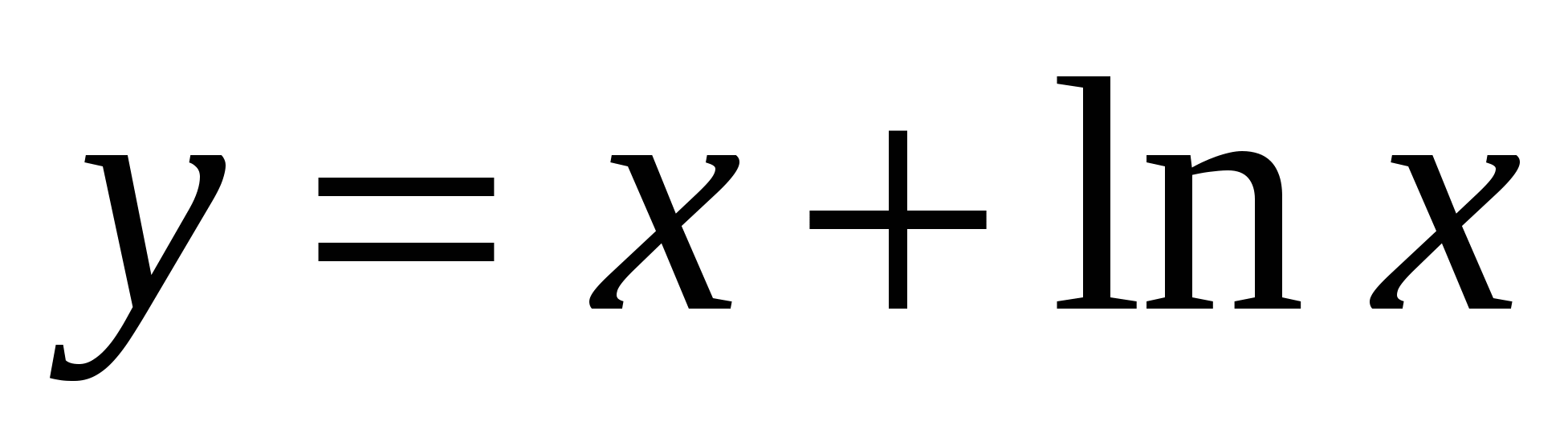
6) 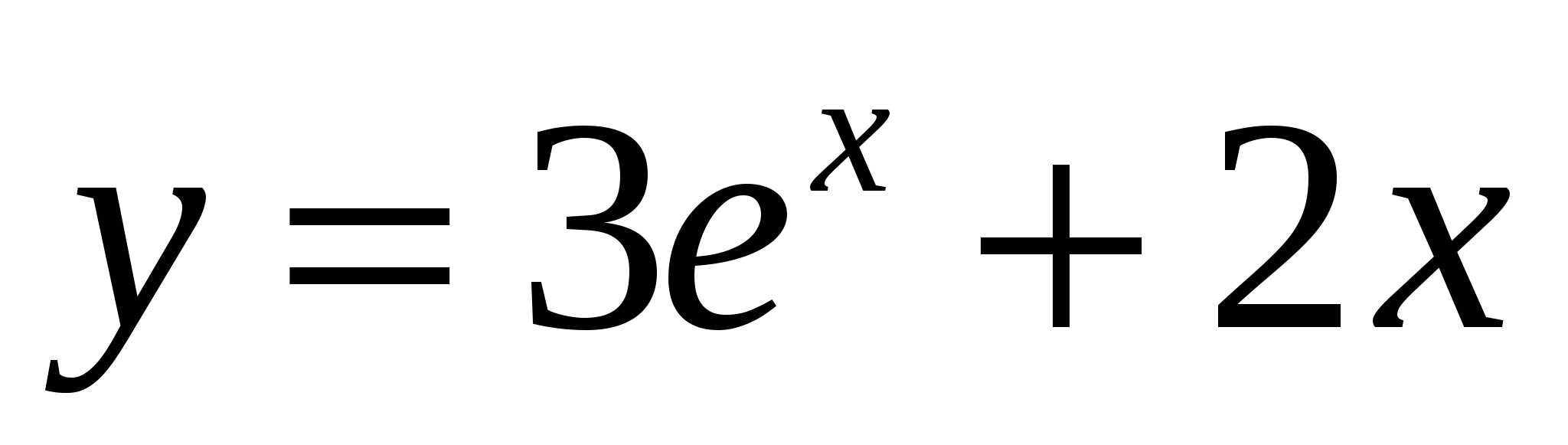
Практическая работа №4
Тема: Интеграл. Методы интегрирования. Определенный интеграл.
Цель: сформировать умение вычислять неопределенные и определенные интегралы, используя различные методы интегрирования.
Теоретические сведения к практической работе
Функция ![]() , определенная на интервале
, определенная на интервале 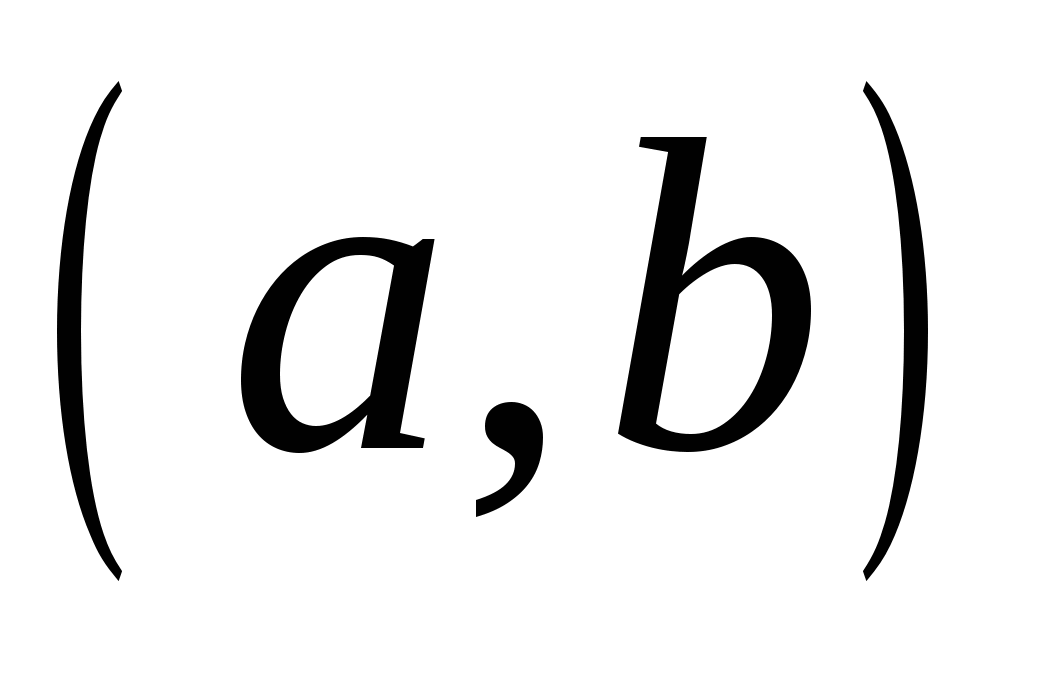 , называется первообразной для функции
, называется первообразной для функции 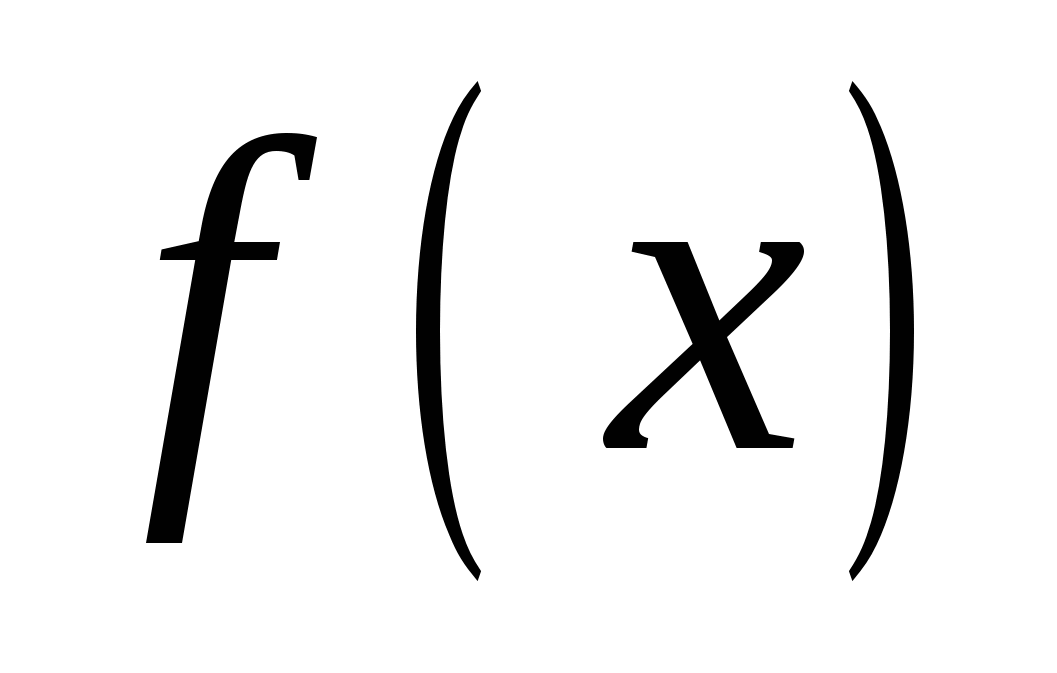 , определенной на том же интервале
, определенной на том же интервале ![]() , если
, если 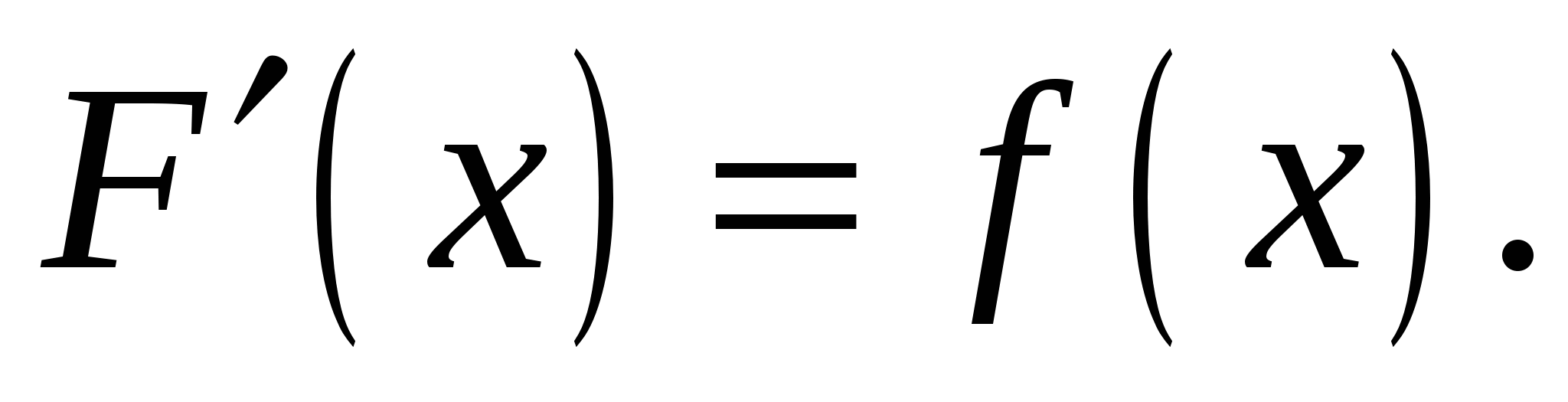
Если 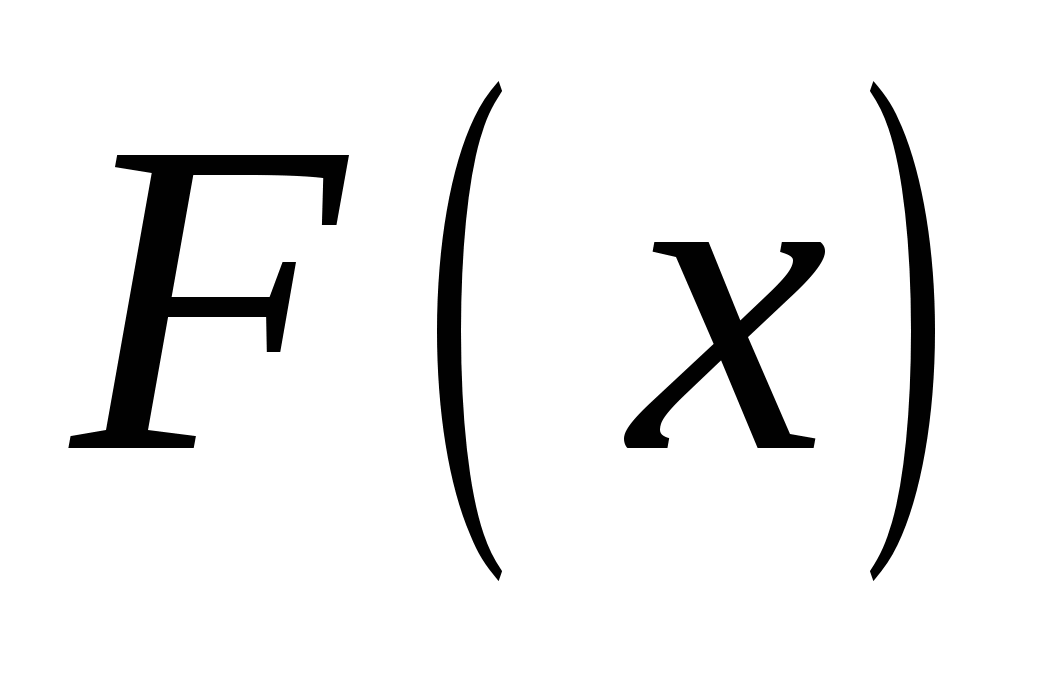 - первообразная для функции
- первообразная для функции 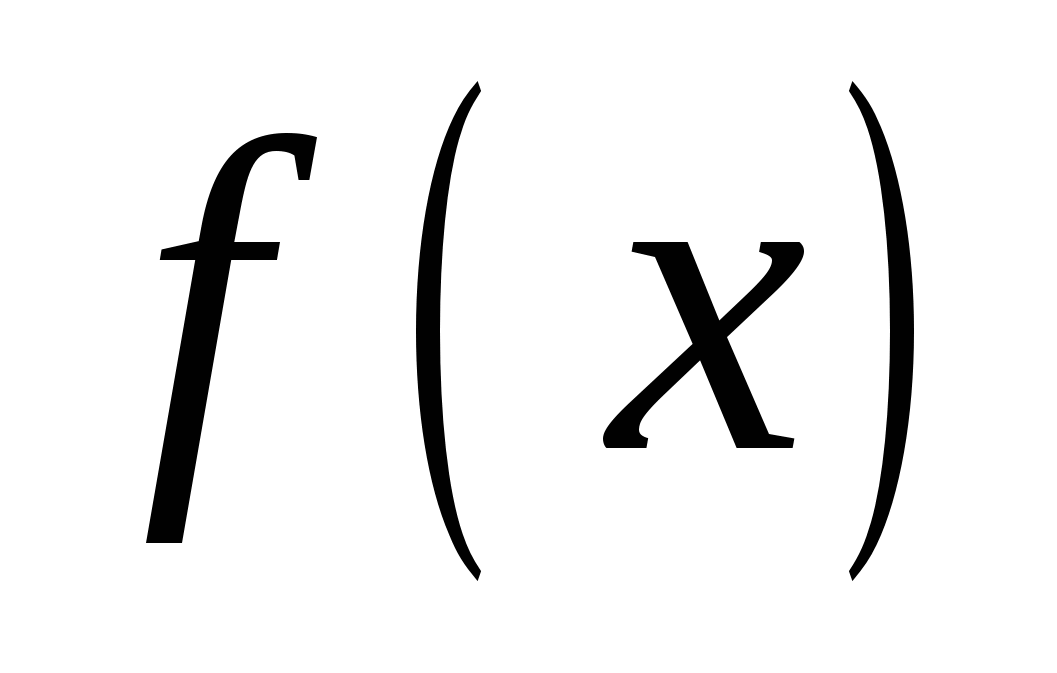 , то любая другая первообразная
, то любая другая первообразная ![]() для функции
для функции 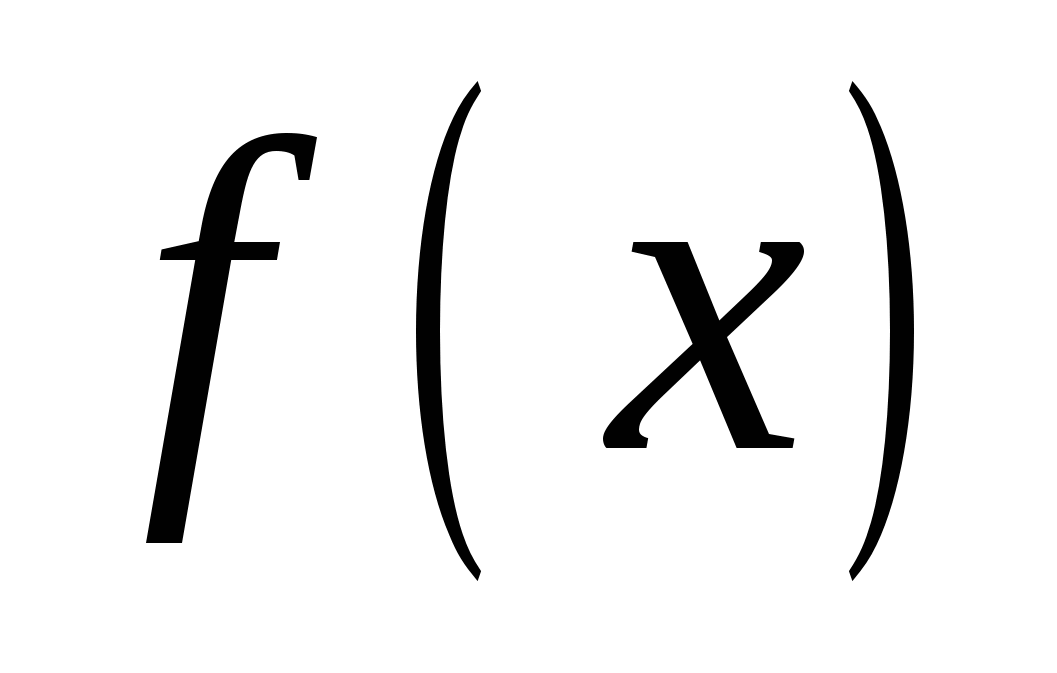 отличается от
отличается от 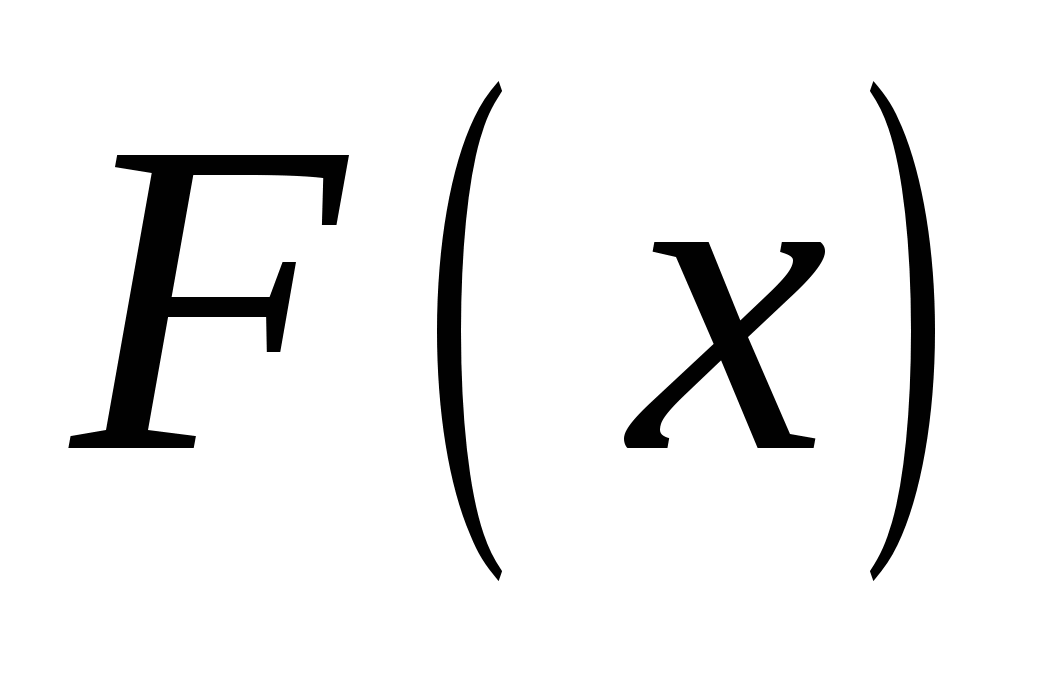 на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е. 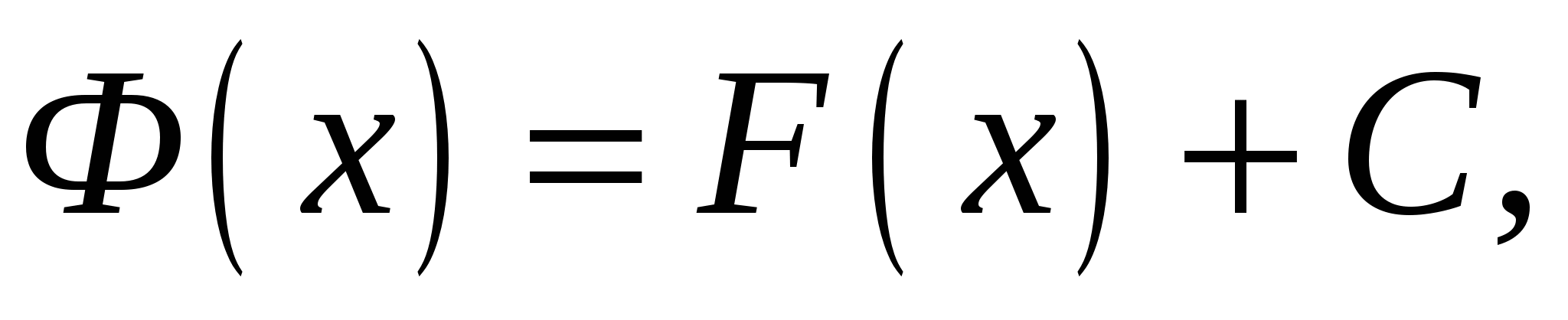 где
где 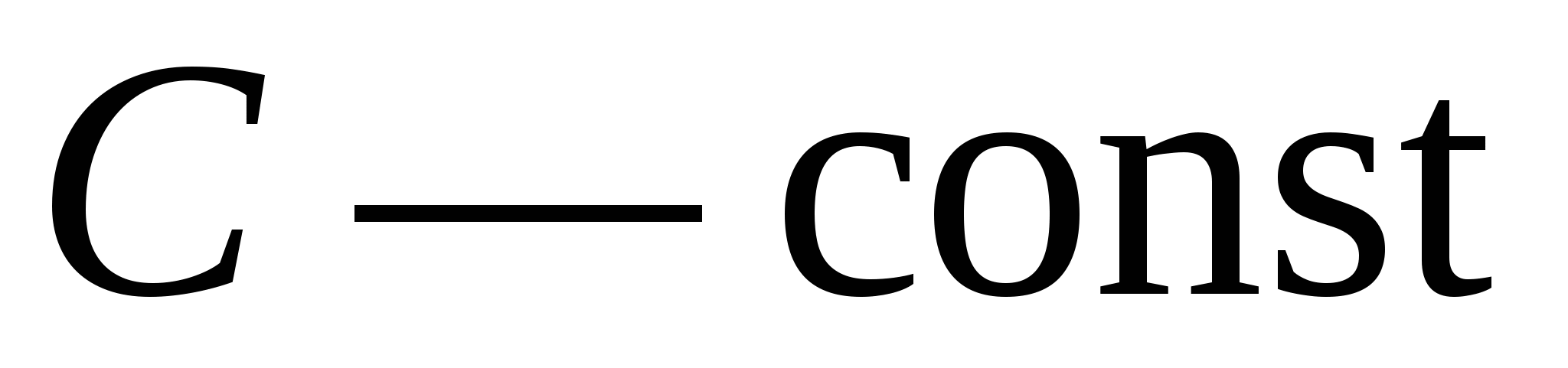 .
.
Неопределенным интегралом от функции 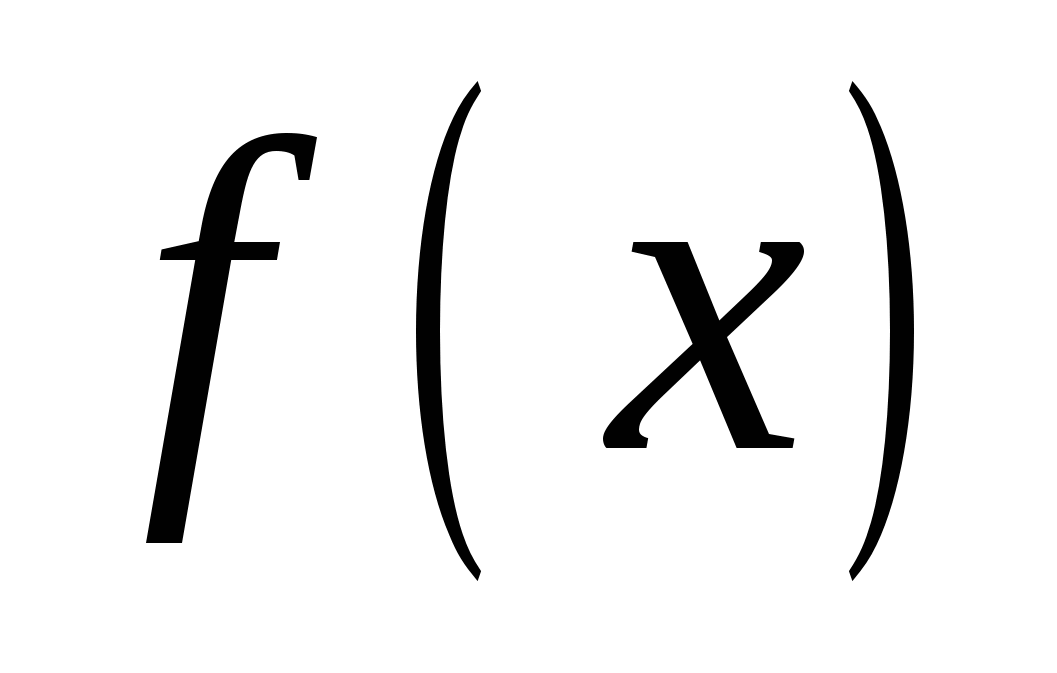 называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 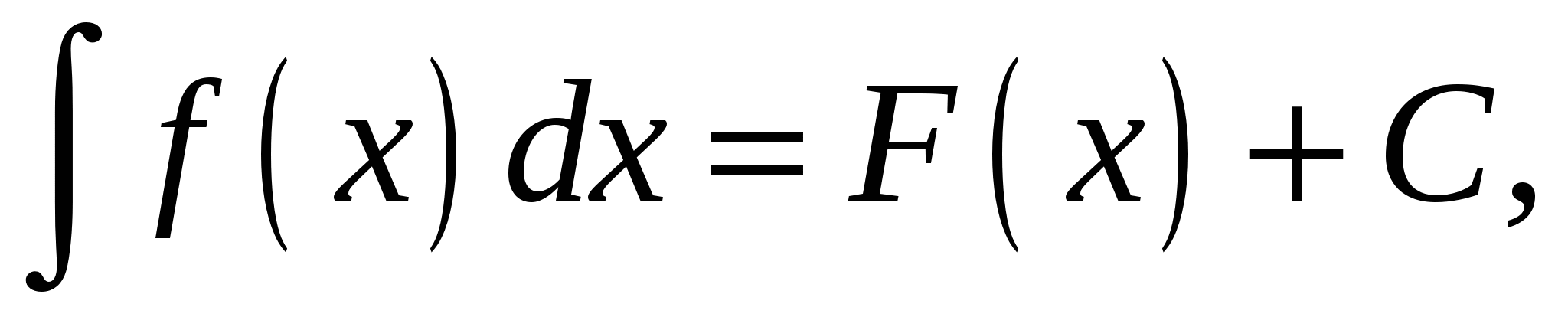 где
где 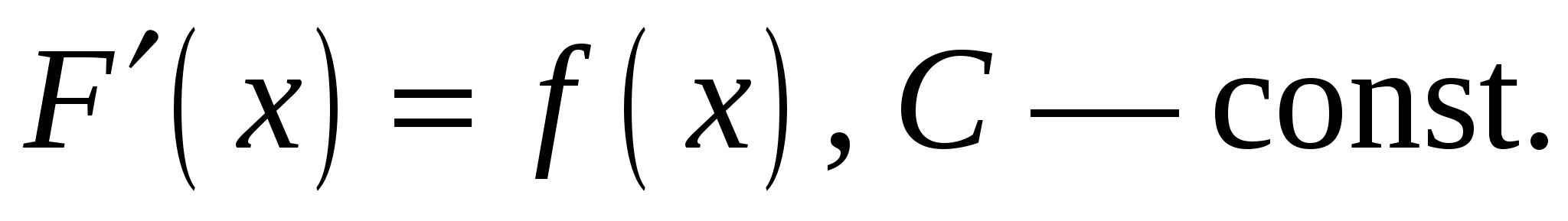
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:
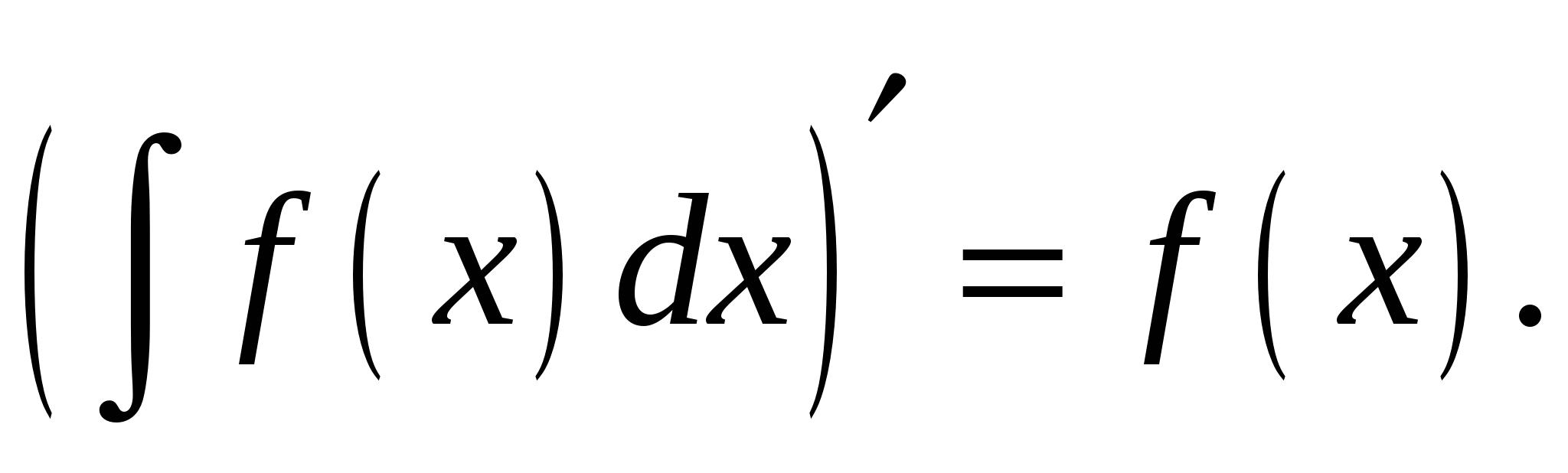
Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1. 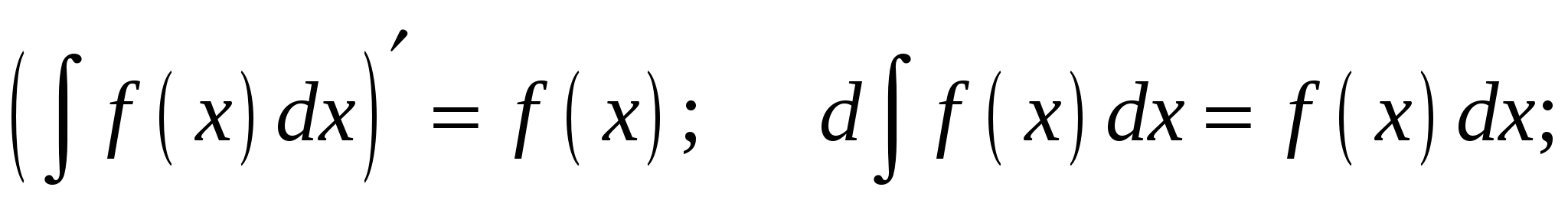
2. 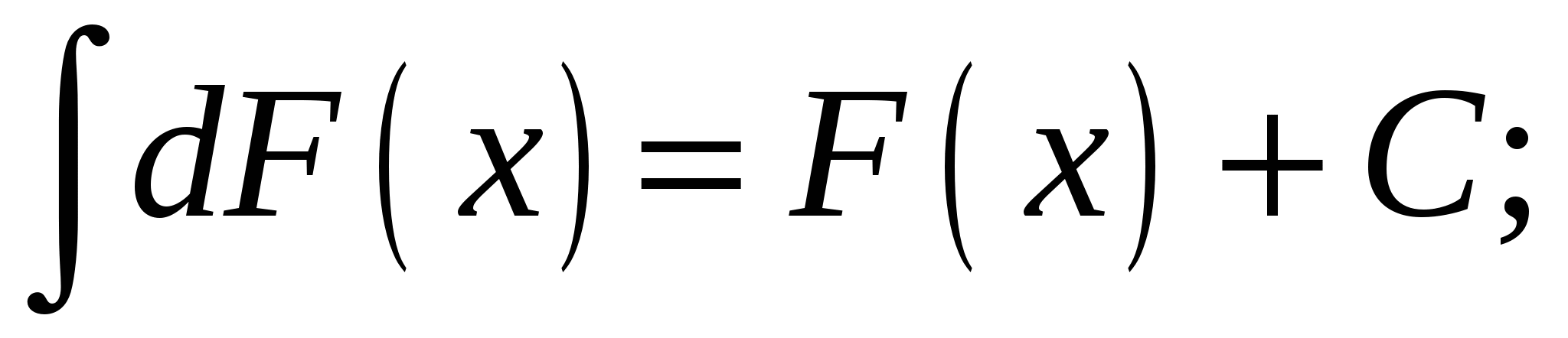
3. 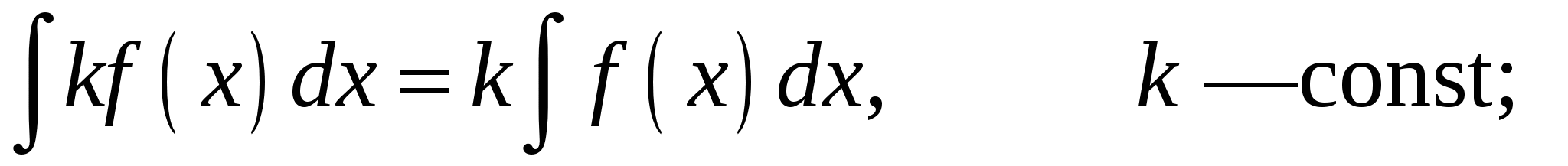
4. 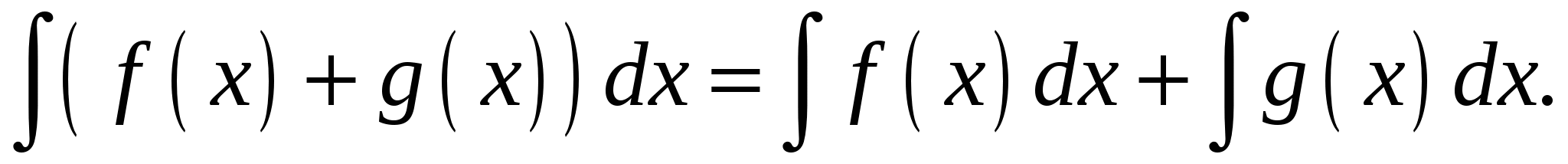
Таблица основных интегралов
1. 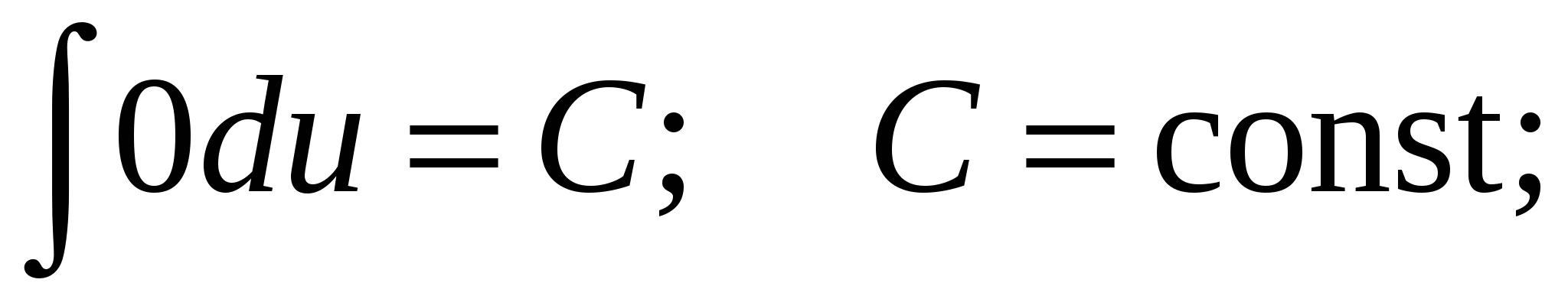 2.
2. 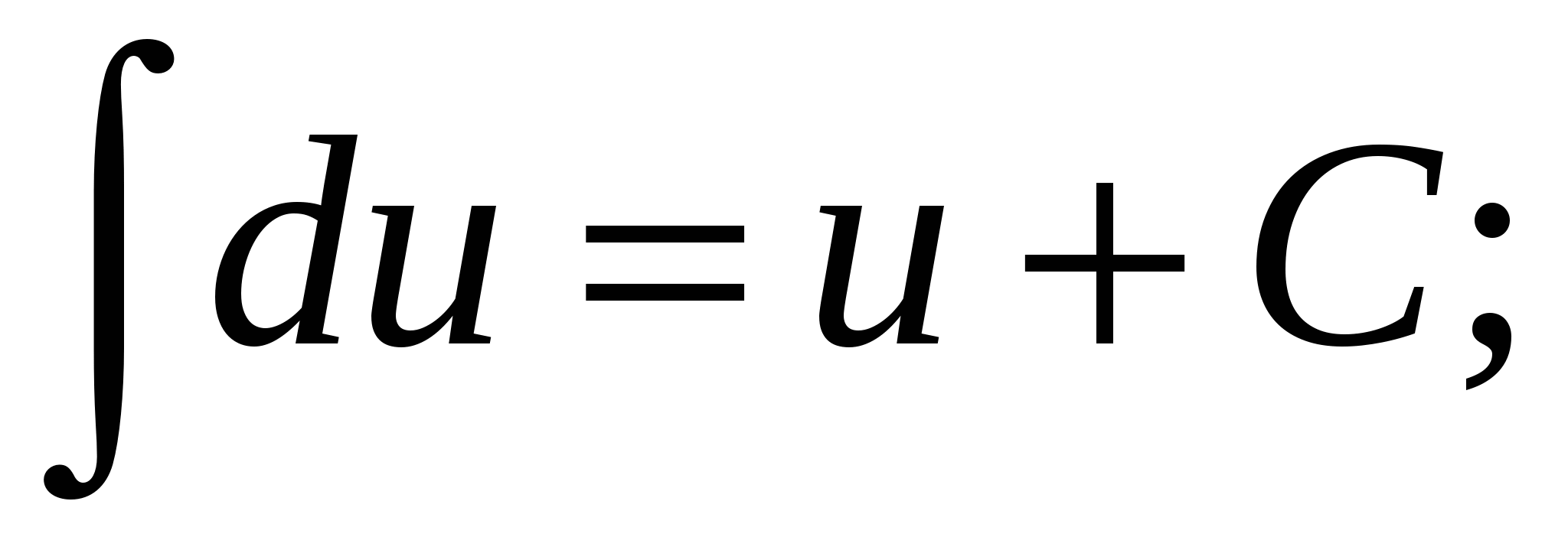
3. 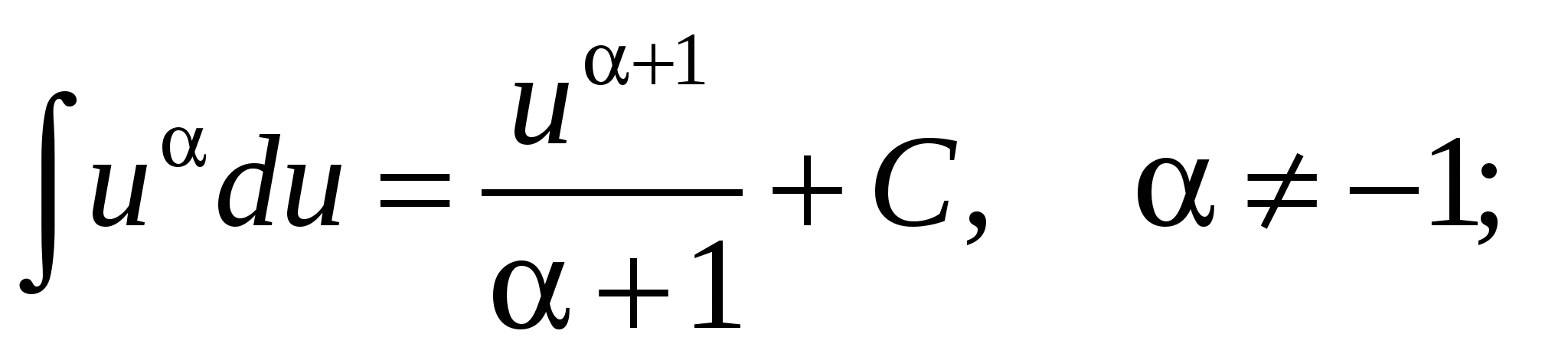
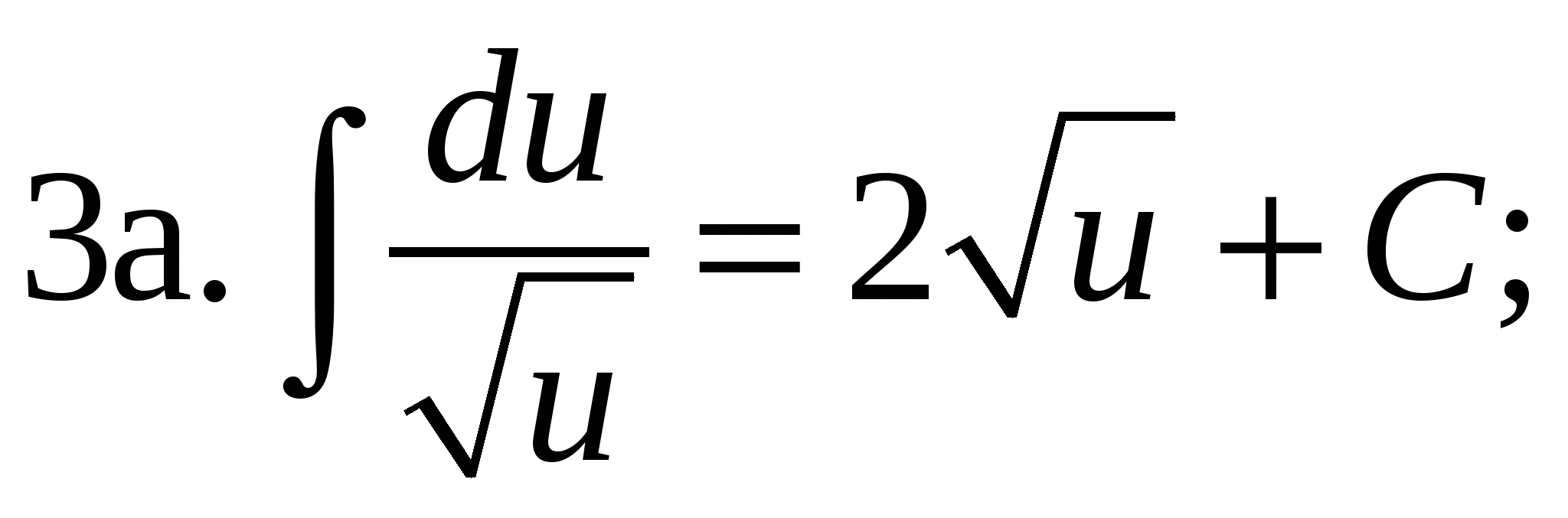
4. 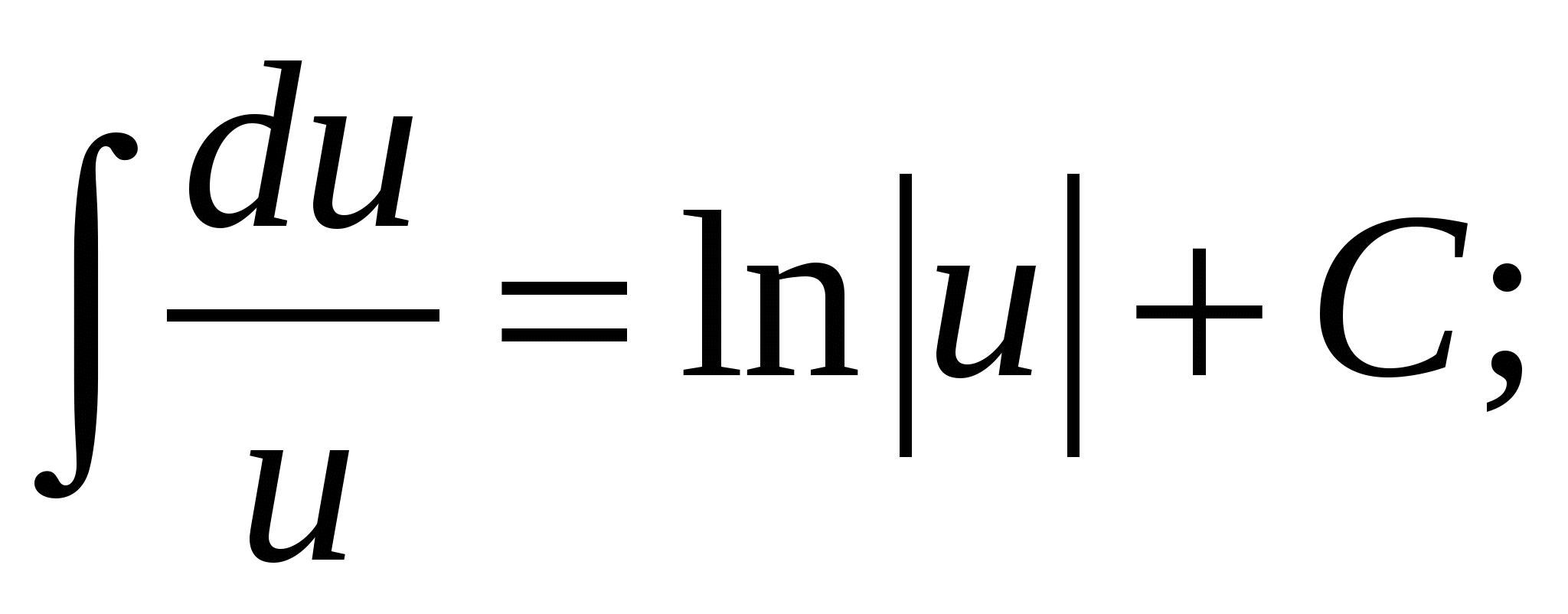 5.
5. 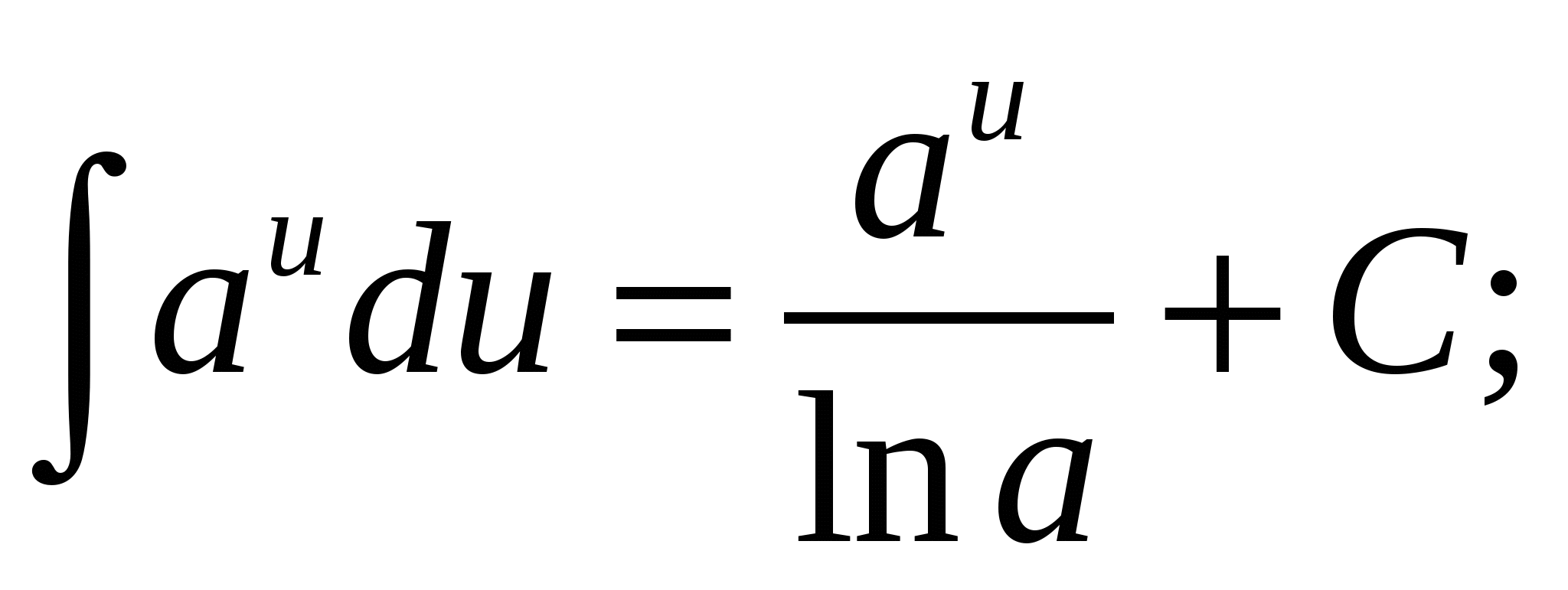
6. 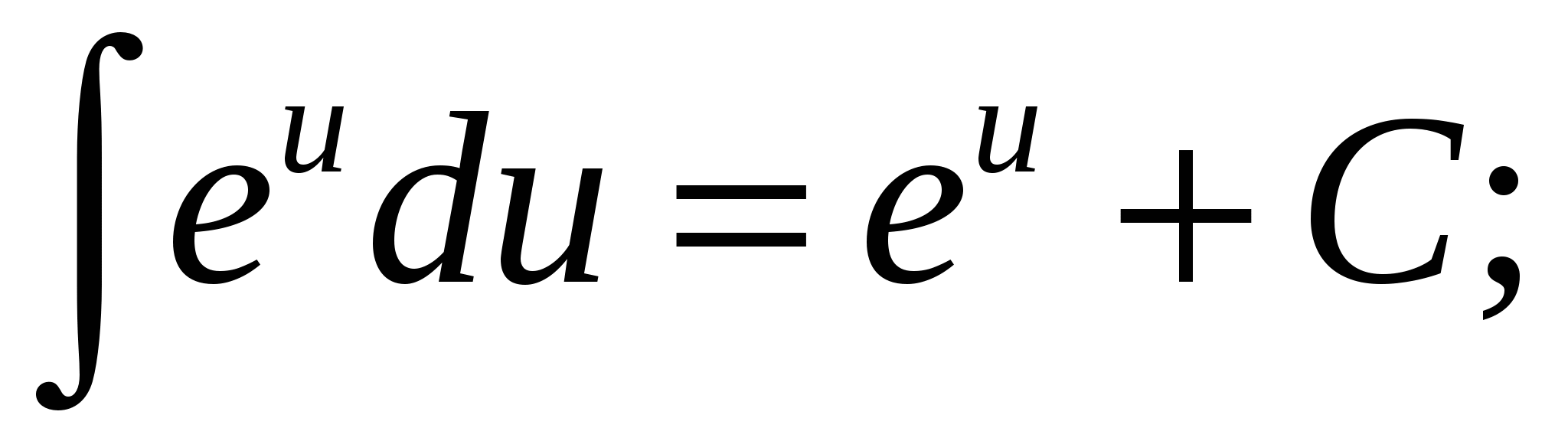 7.
7.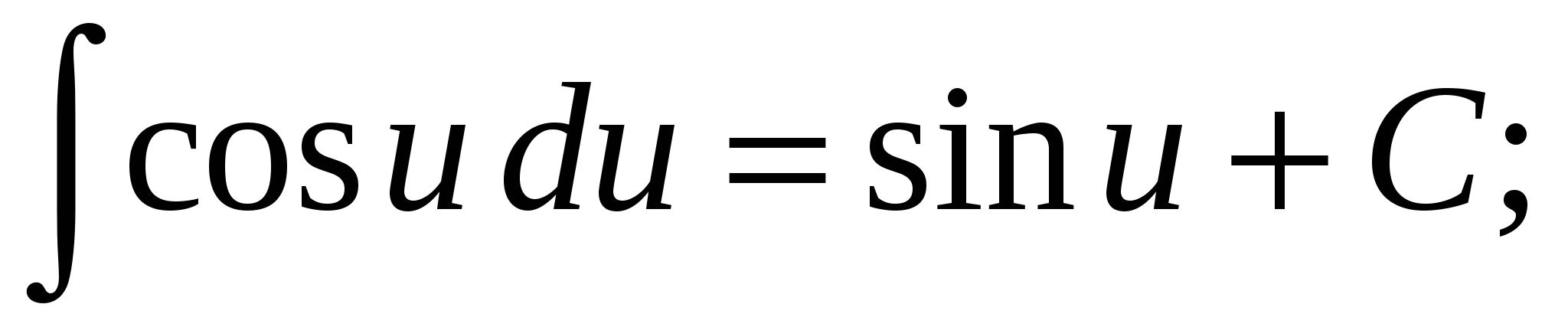
8. 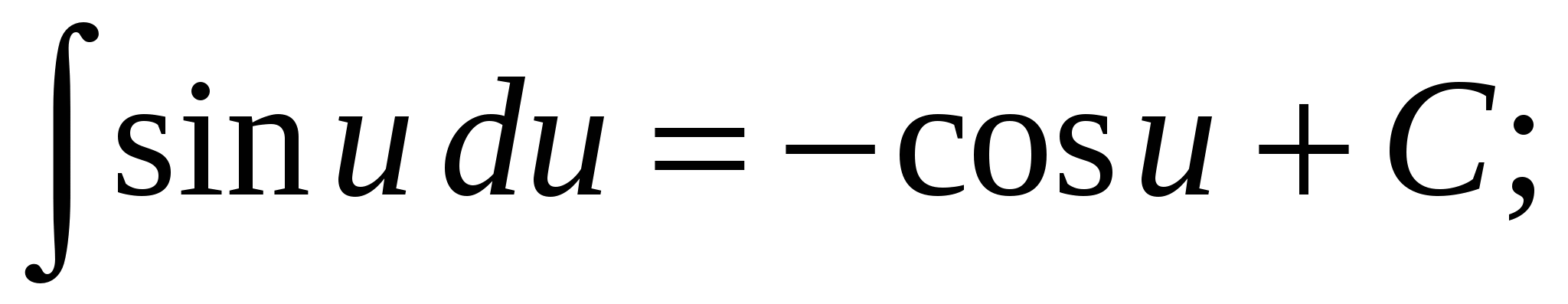 9.
9. 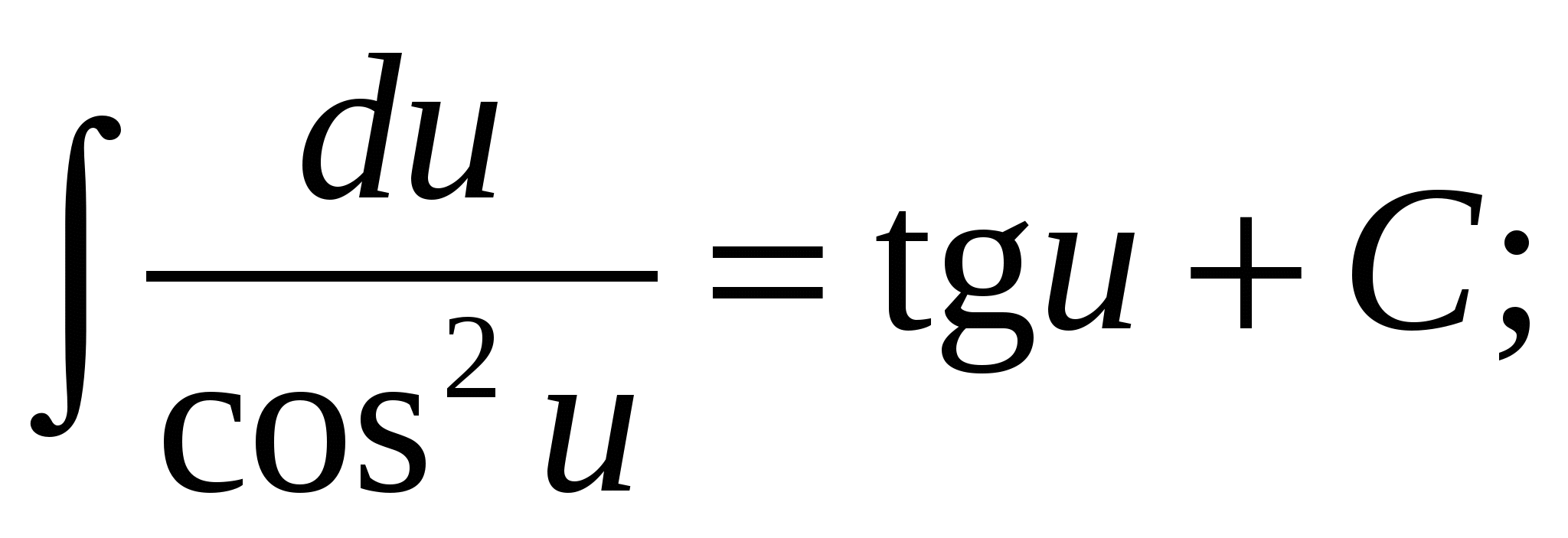
10. 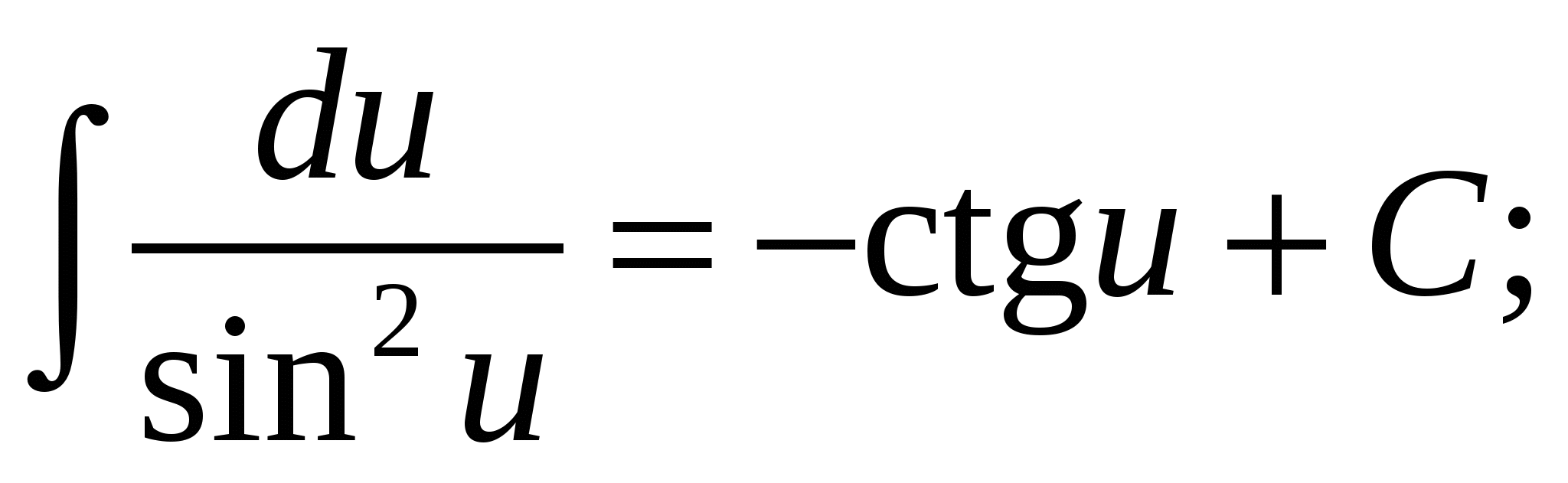 11.
11. 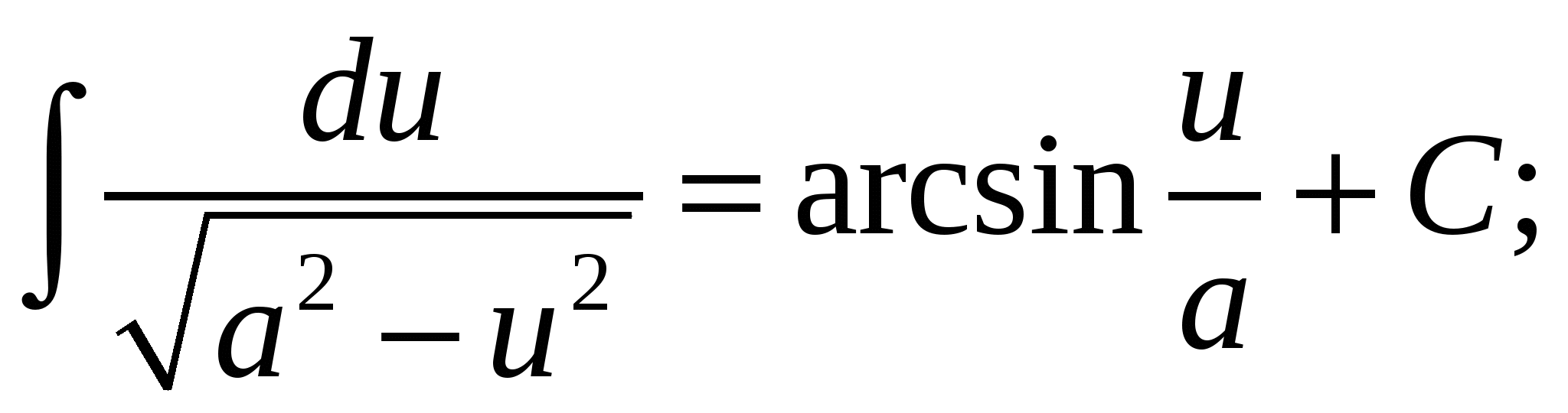
12. 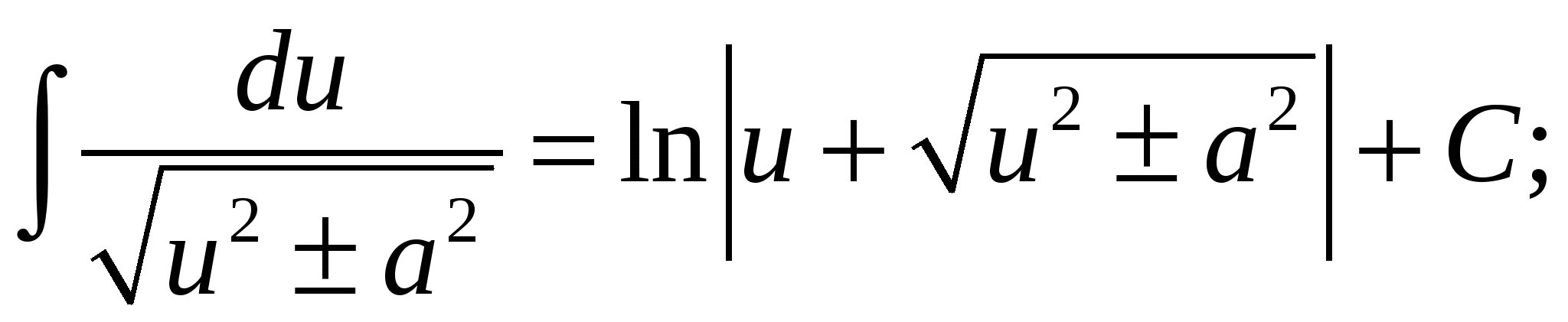 13.
13. 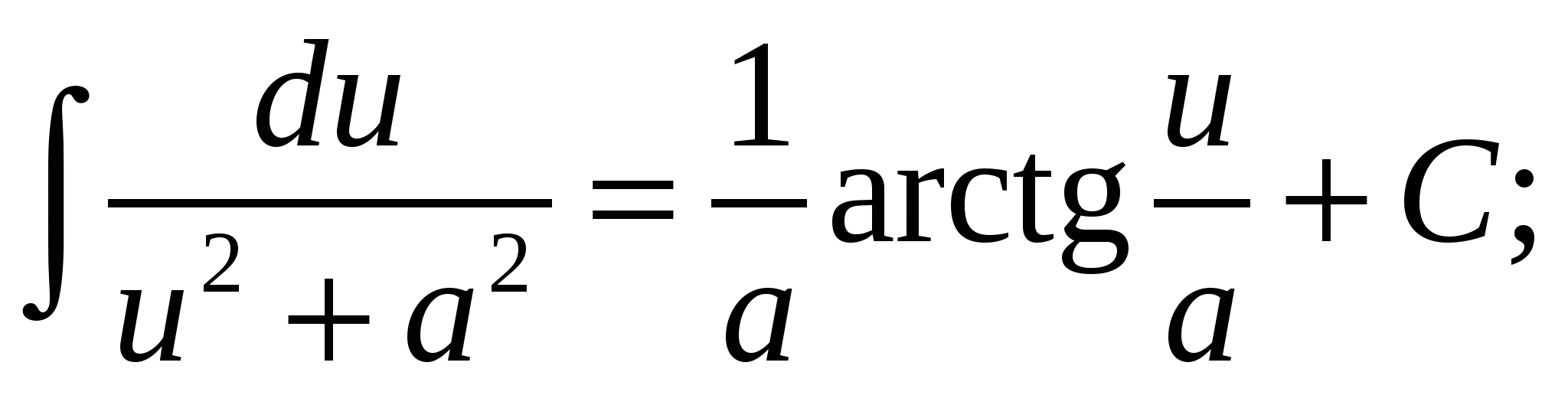
14. 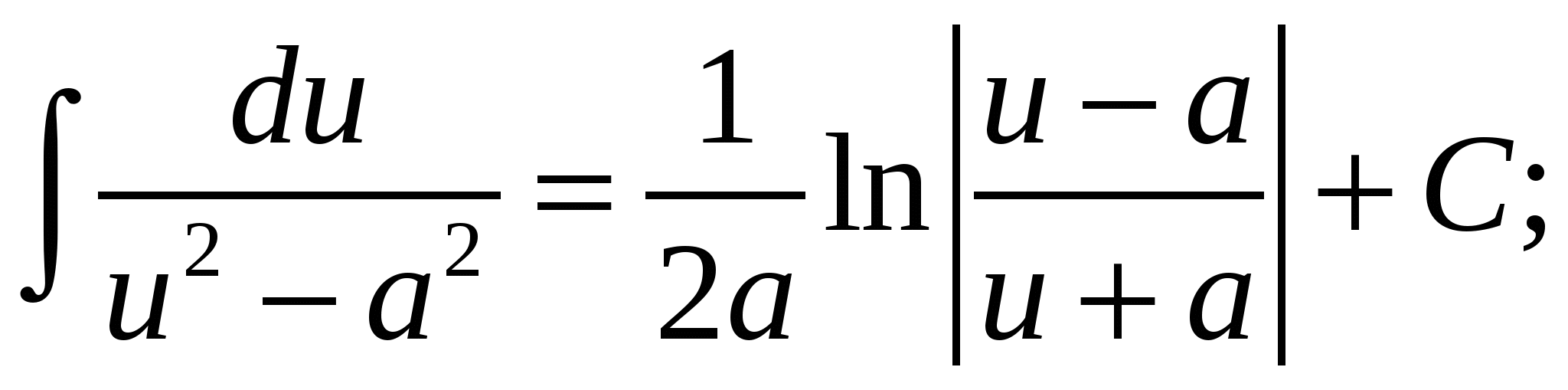 15.
15. 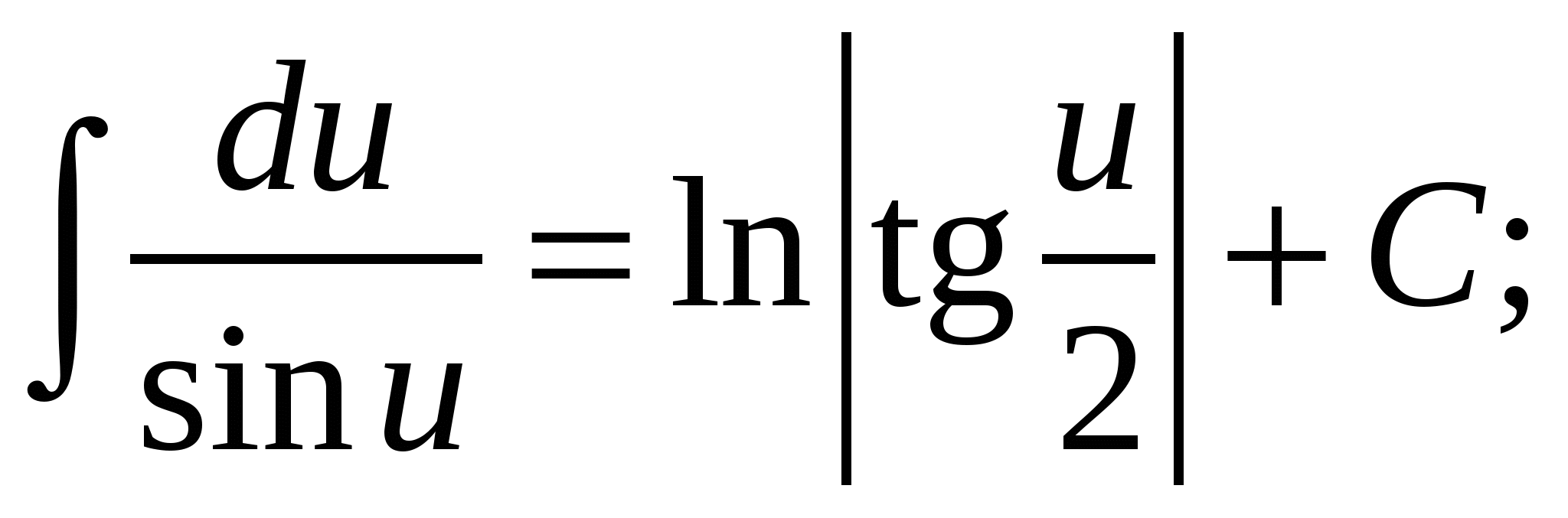
16. 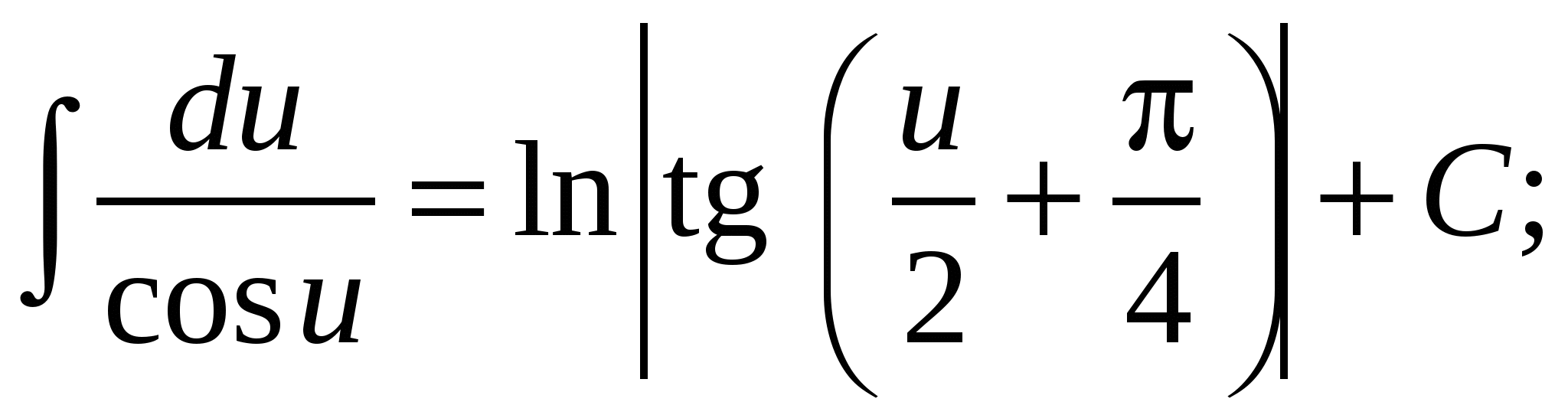 17.
17. 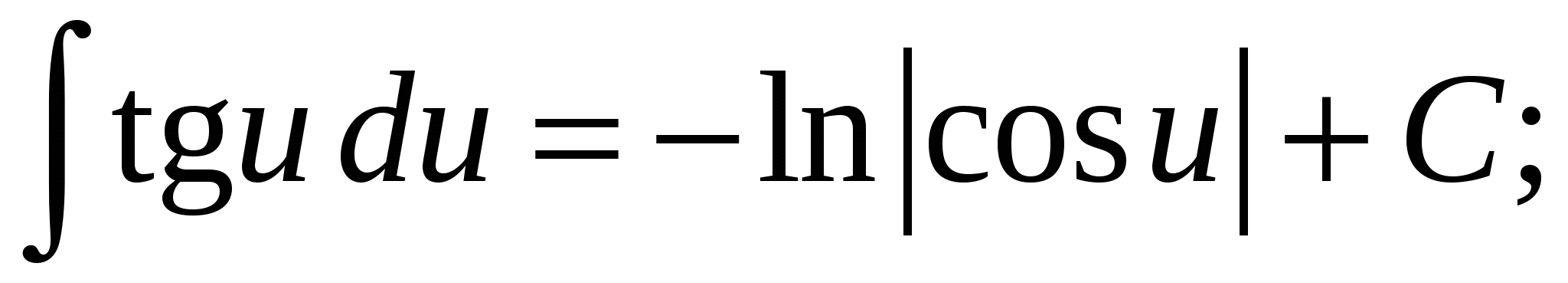
18. 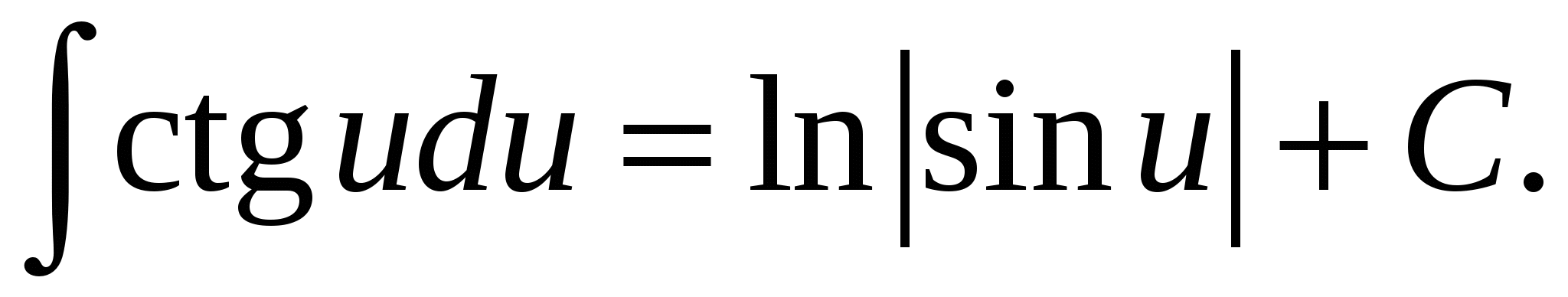
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Пример 1. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы (результат интегрирования проверить дифференцированием):
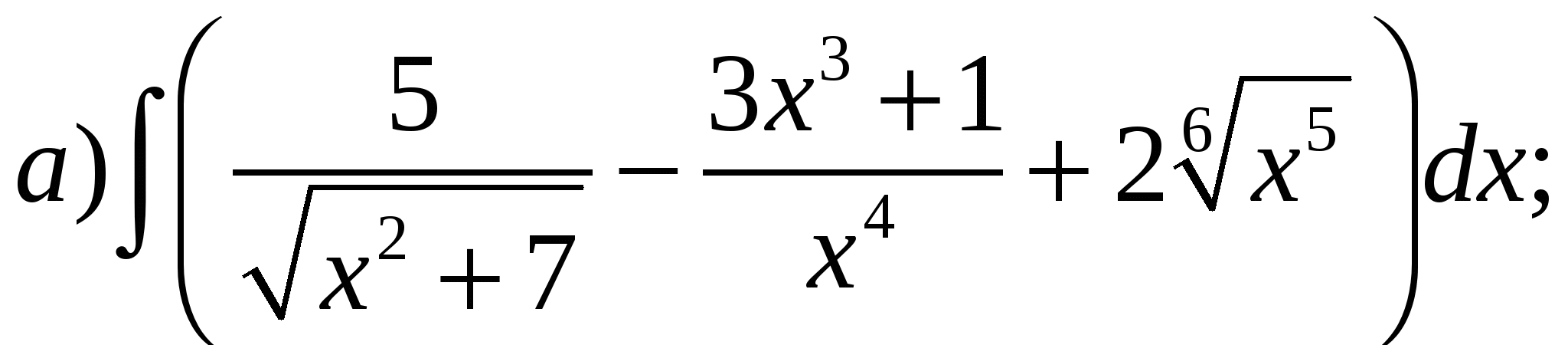
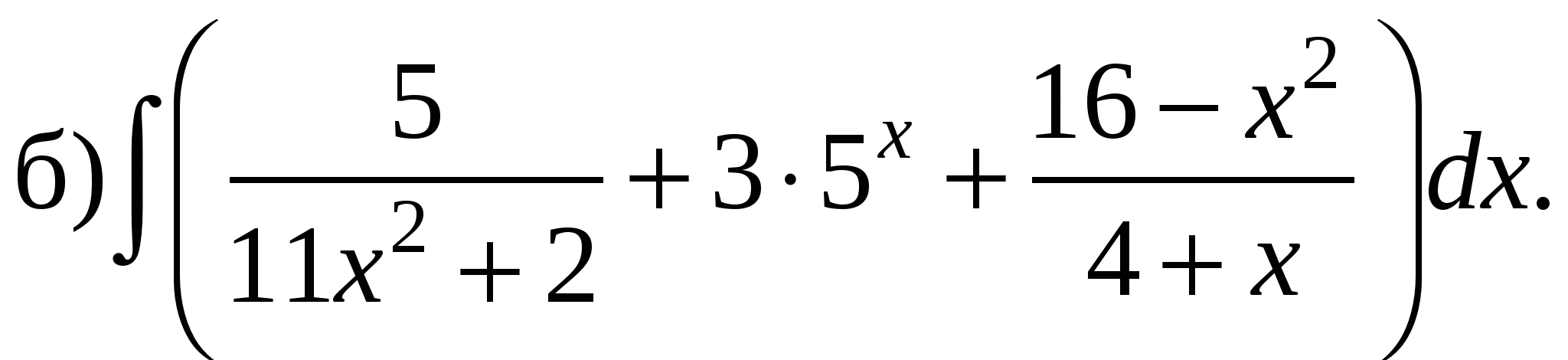
Решение.
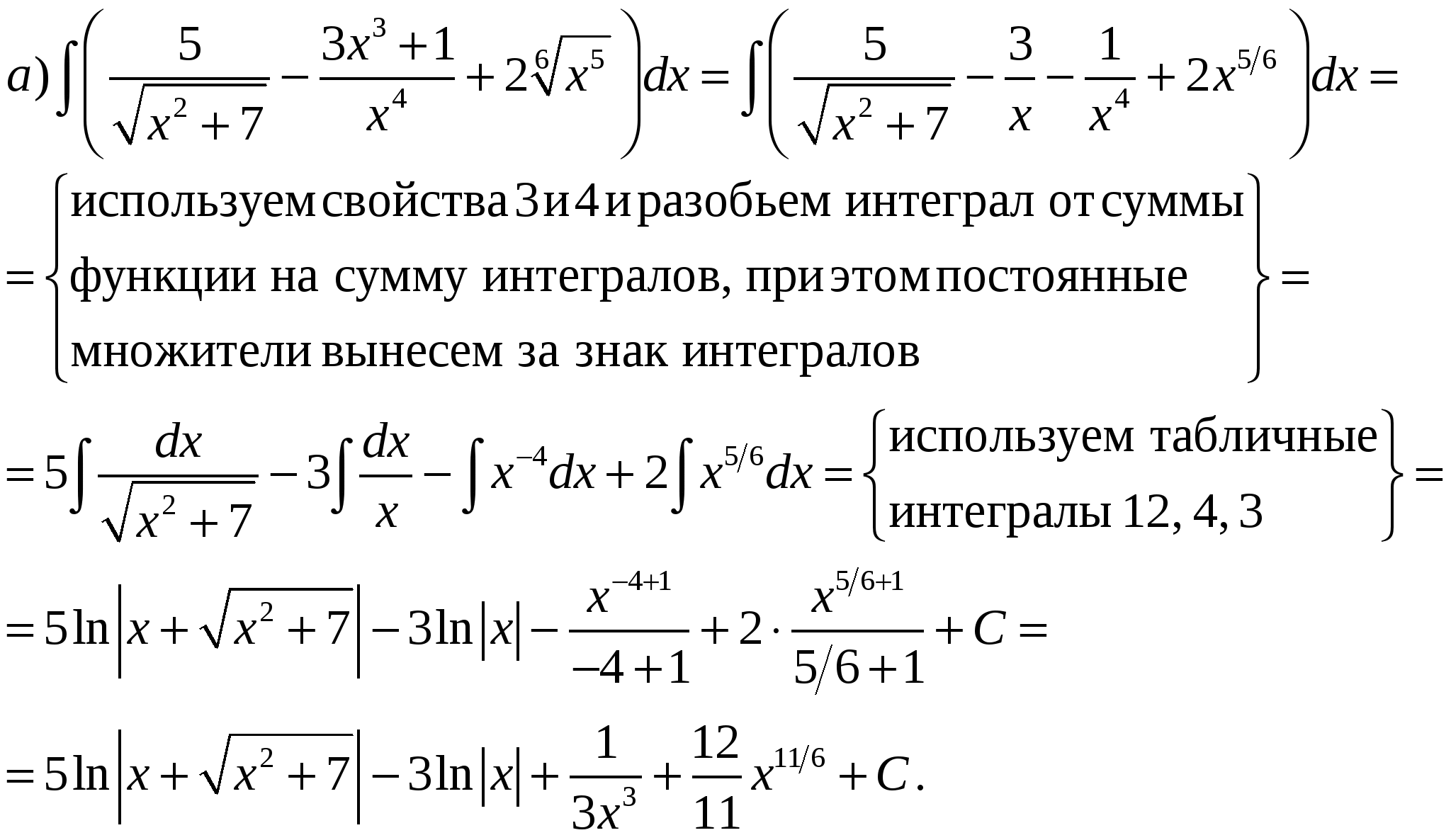 Проверка:
Проверка:
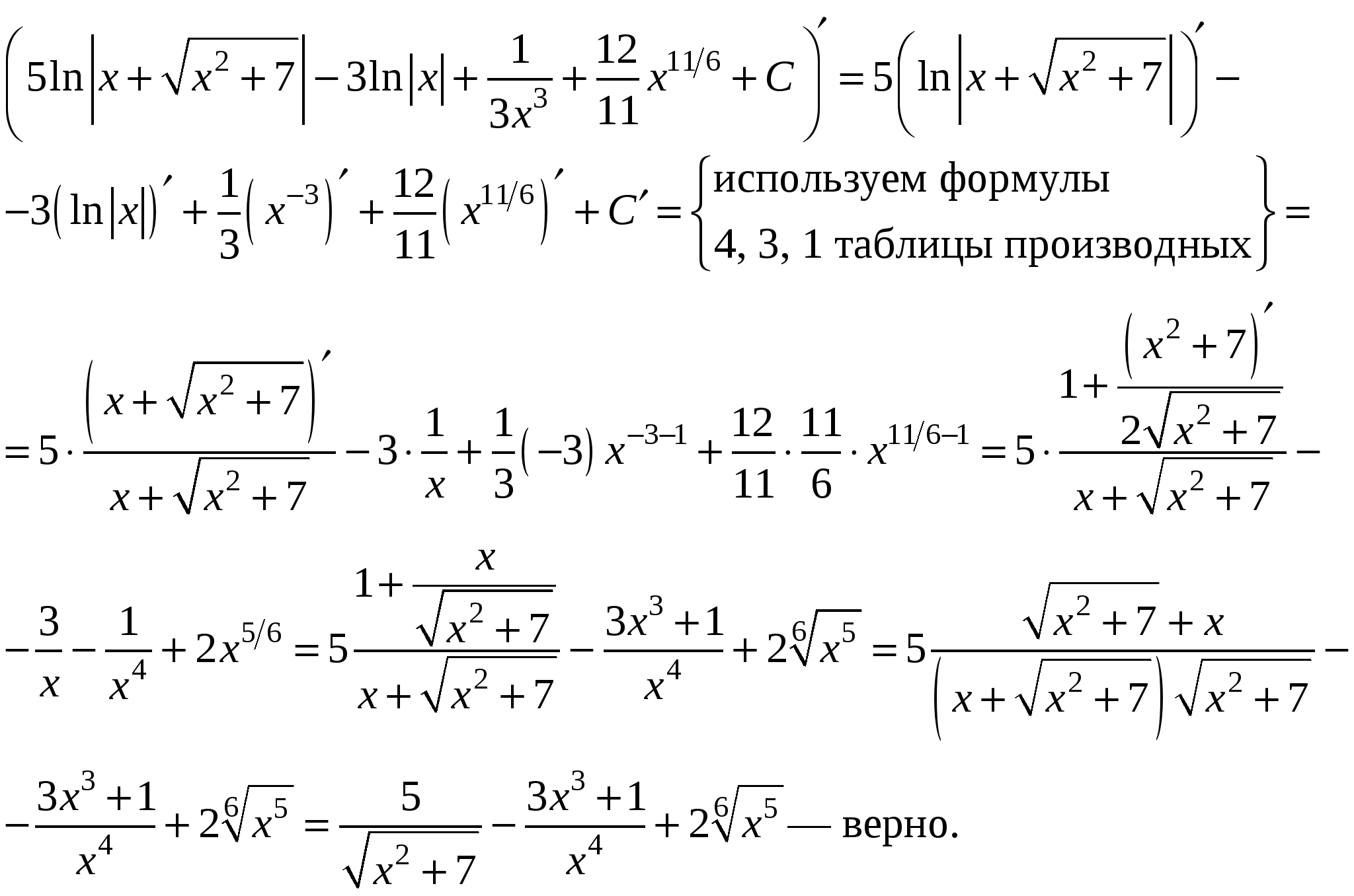
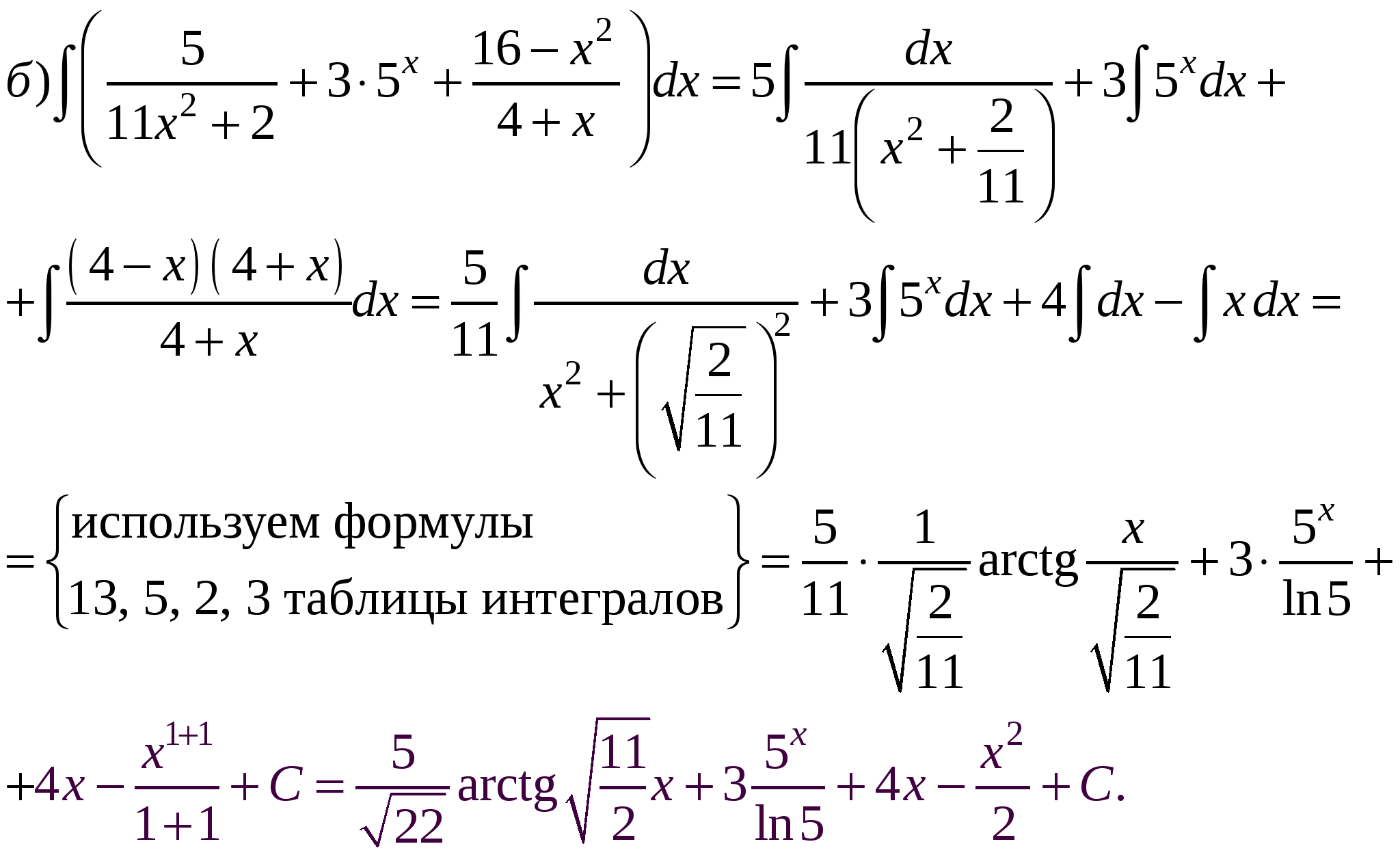
Проверка:
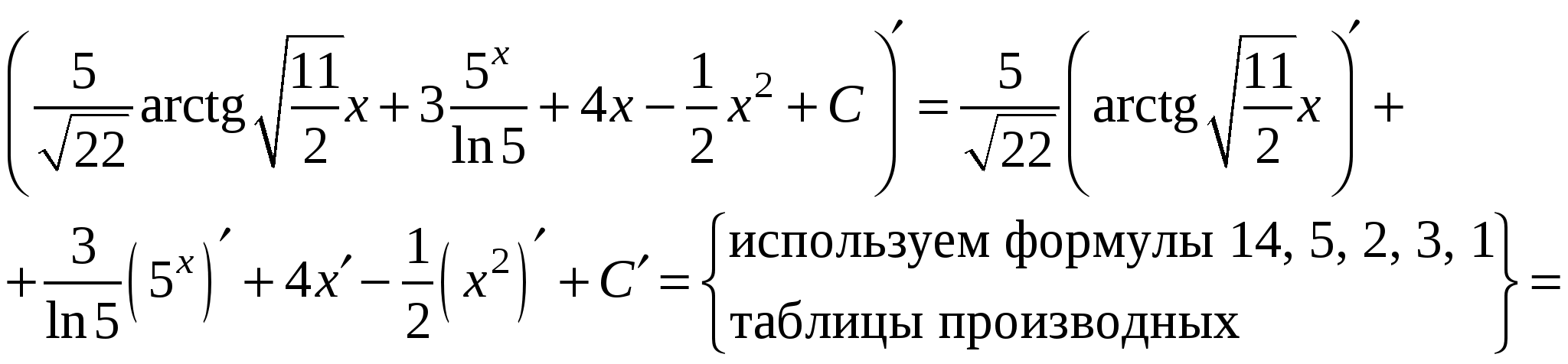
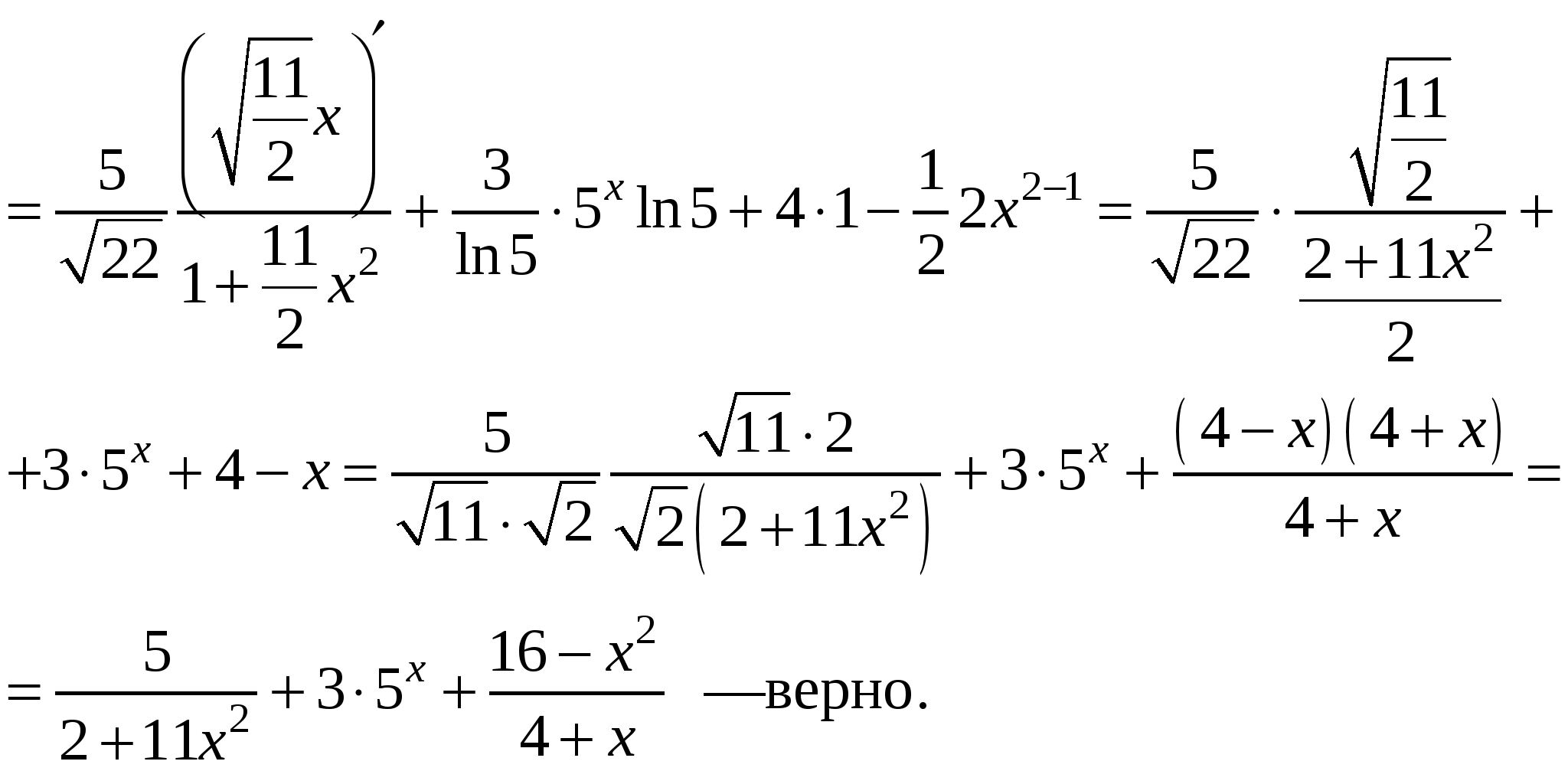
Определенный интеграл, его вычисление и свойства
Определенный интеграл от функции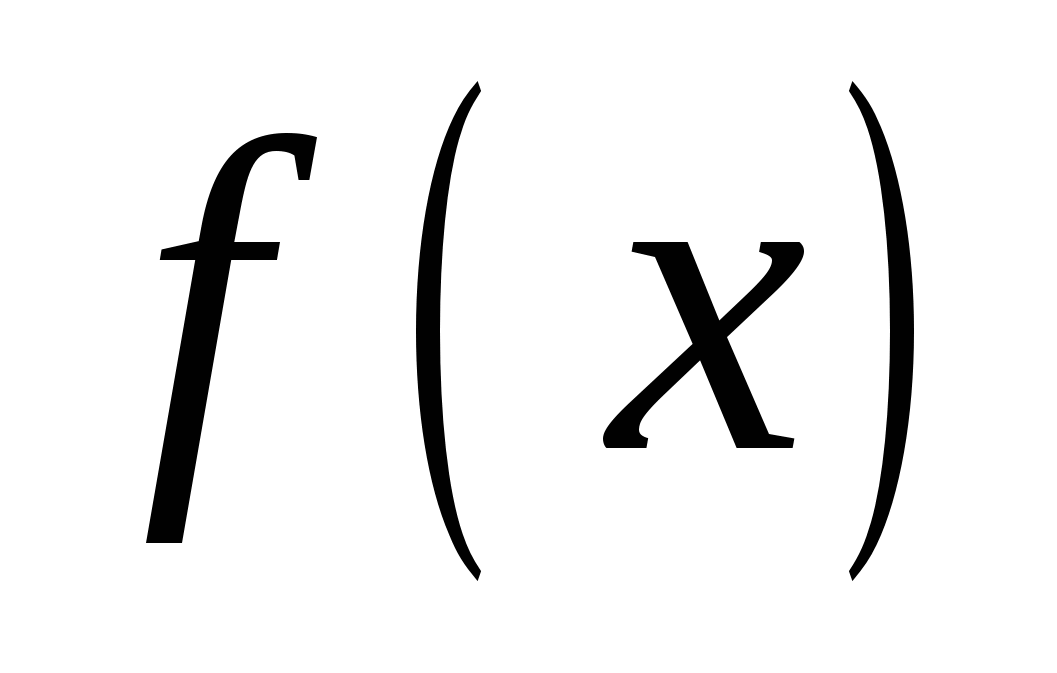 , непрерывной на отрезке
, непрерывной на отрезке 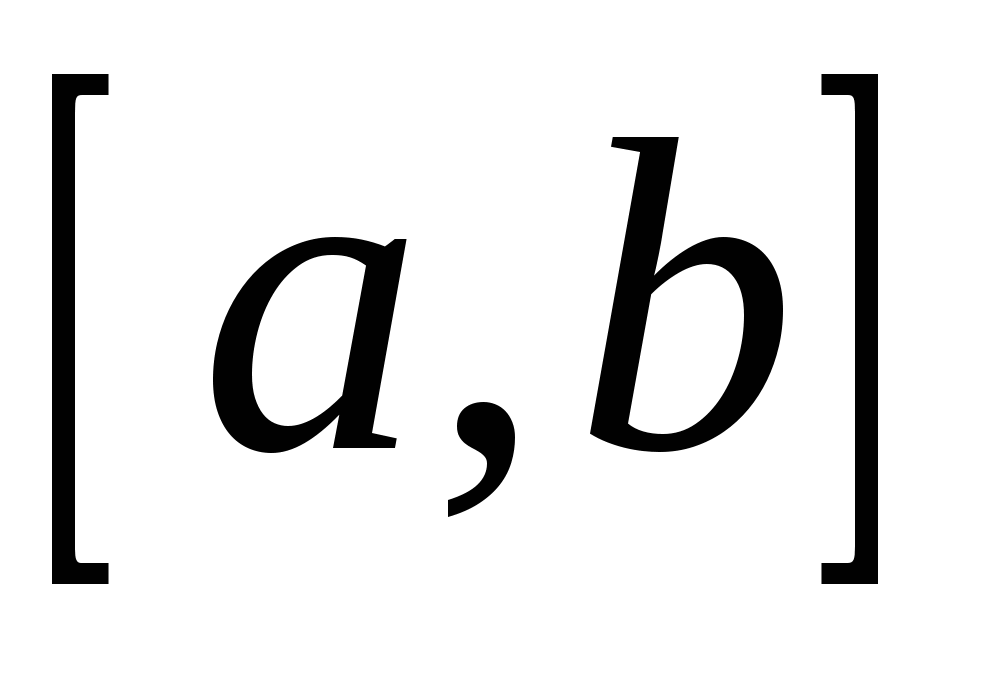 , вычисляется по формуле:
, вычисляется по формуле:
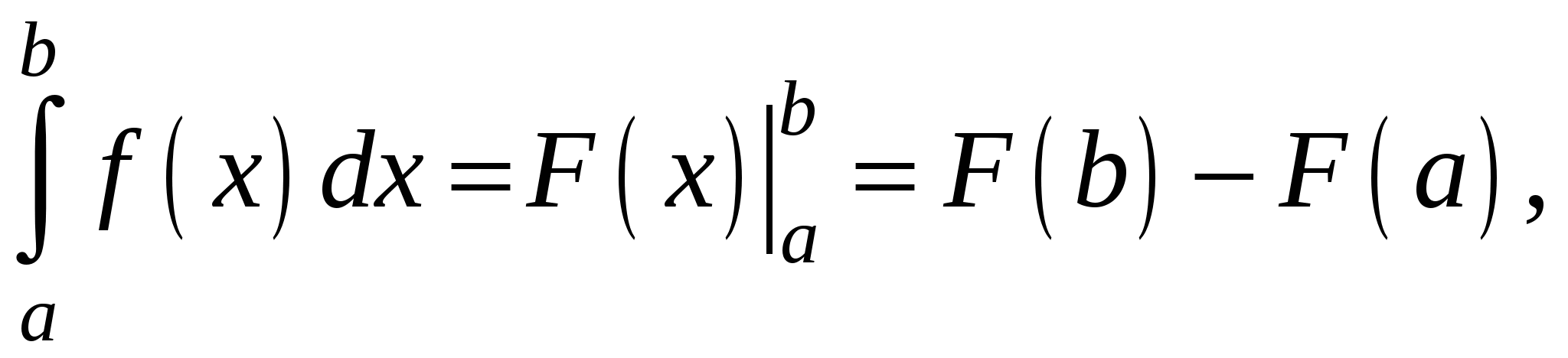 (5)
(5)
где 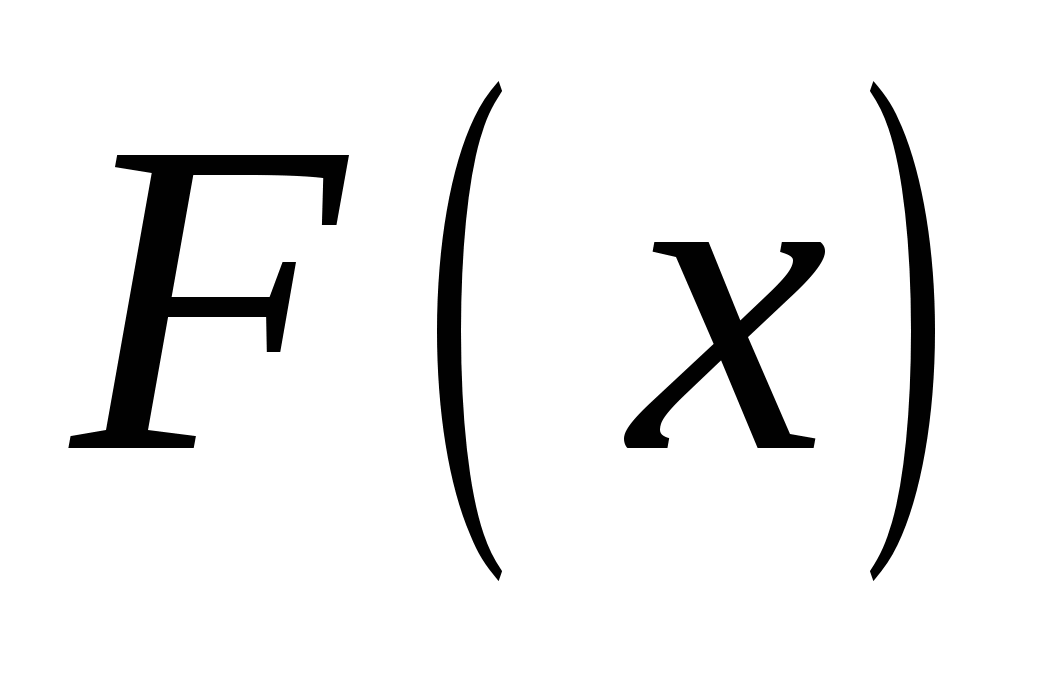 - первообразная для функции
- первообразная для функции 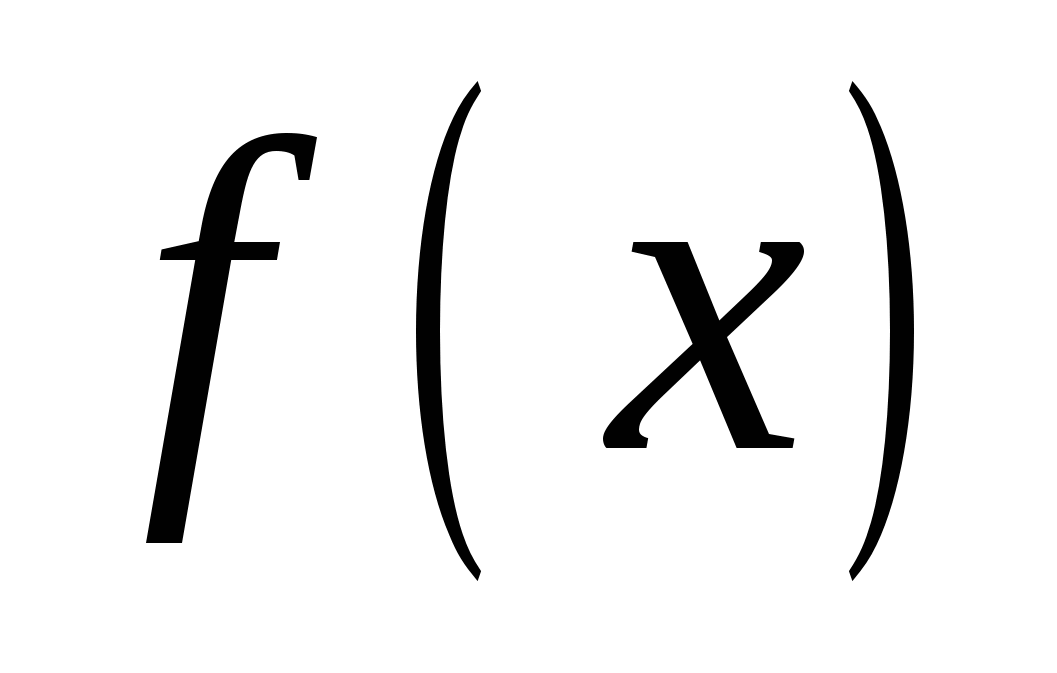 , т. е.
, т. е. 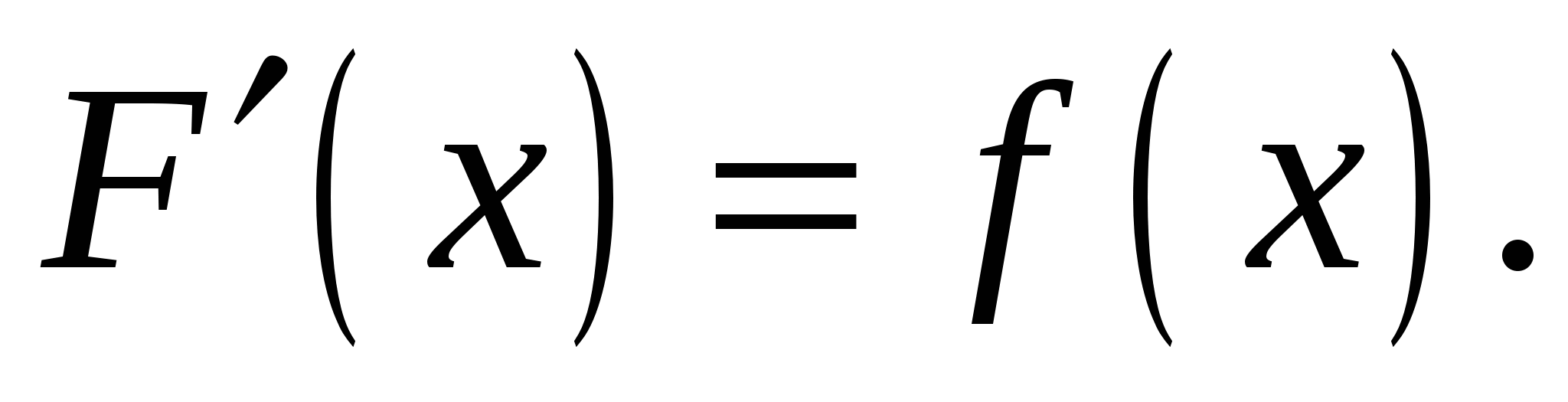
Формула (5) называется формулой Ньютона - Лейбница.
Свойства определенного интеграла:
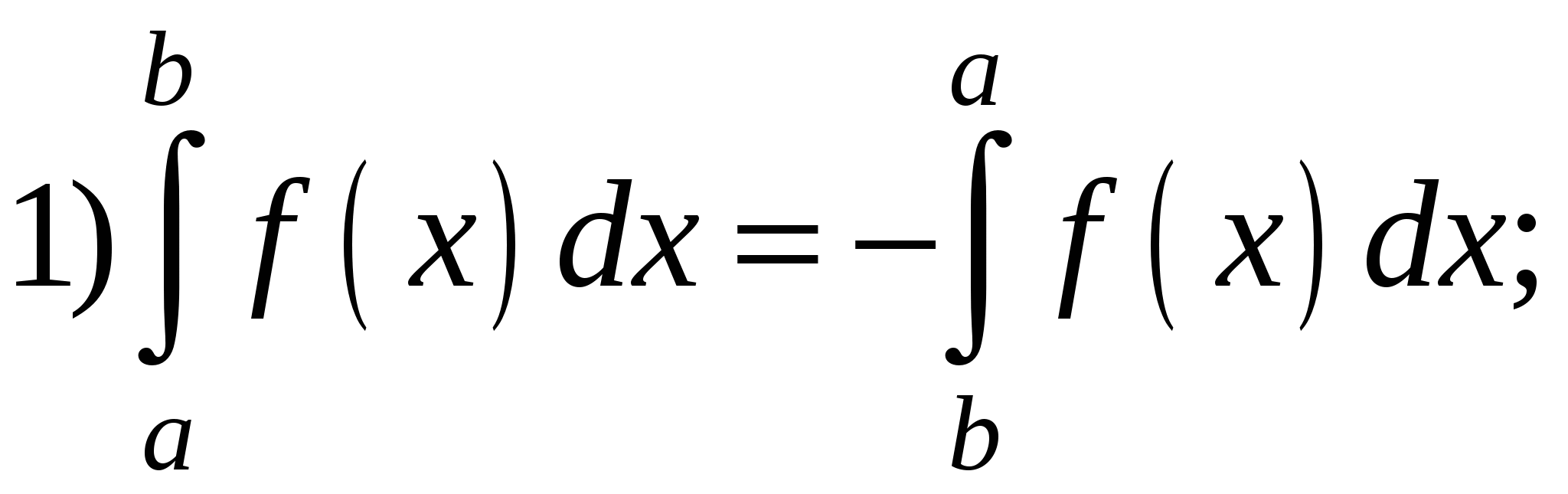
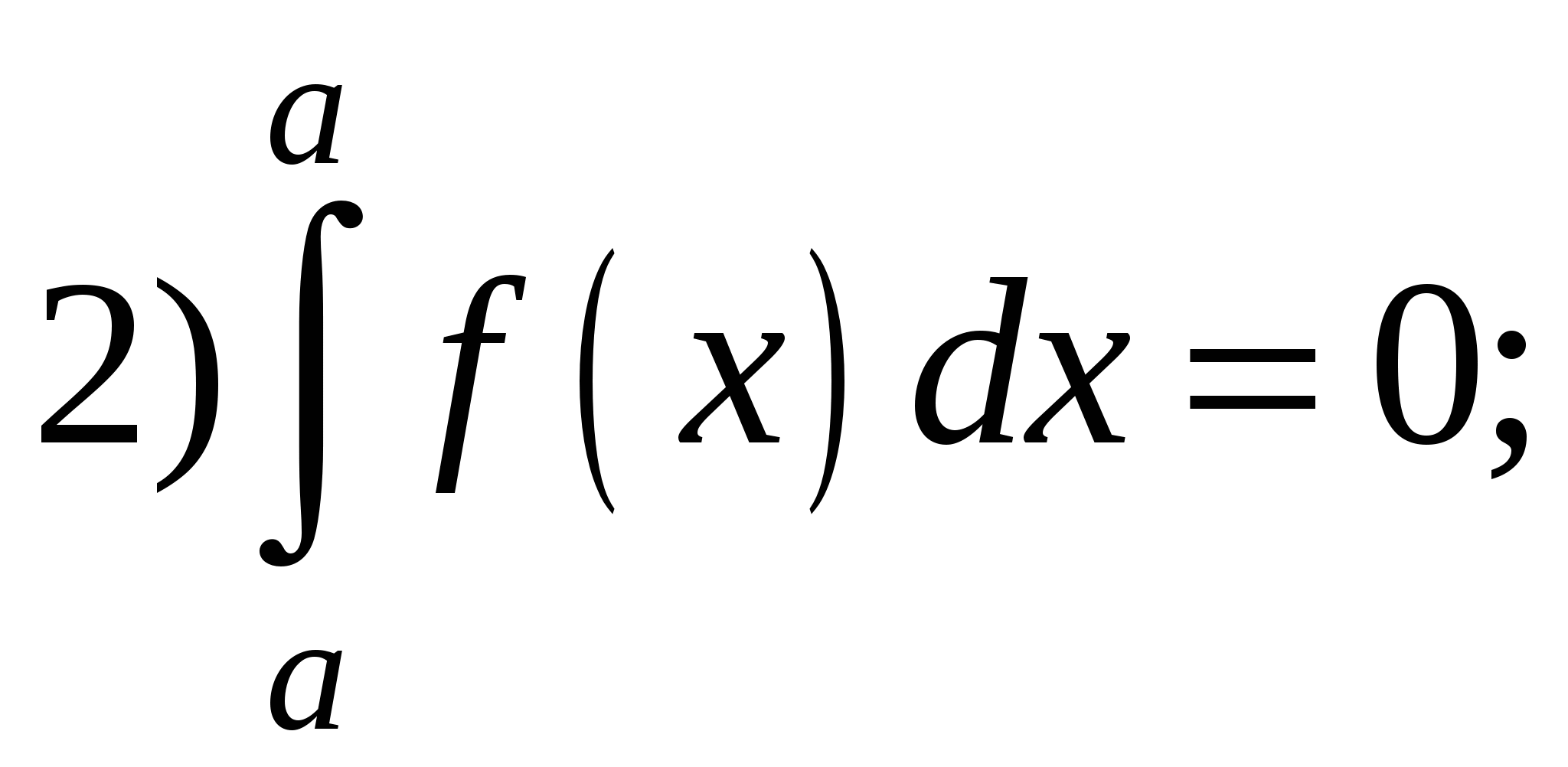
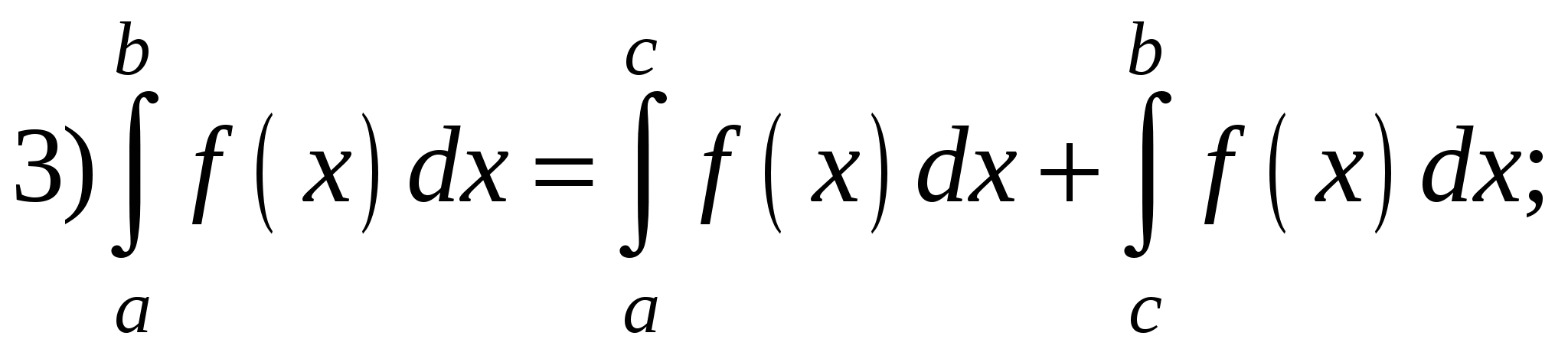
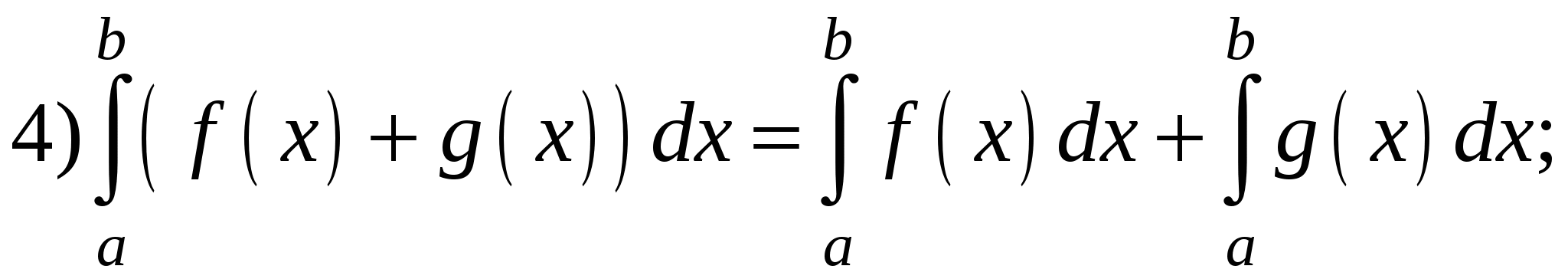
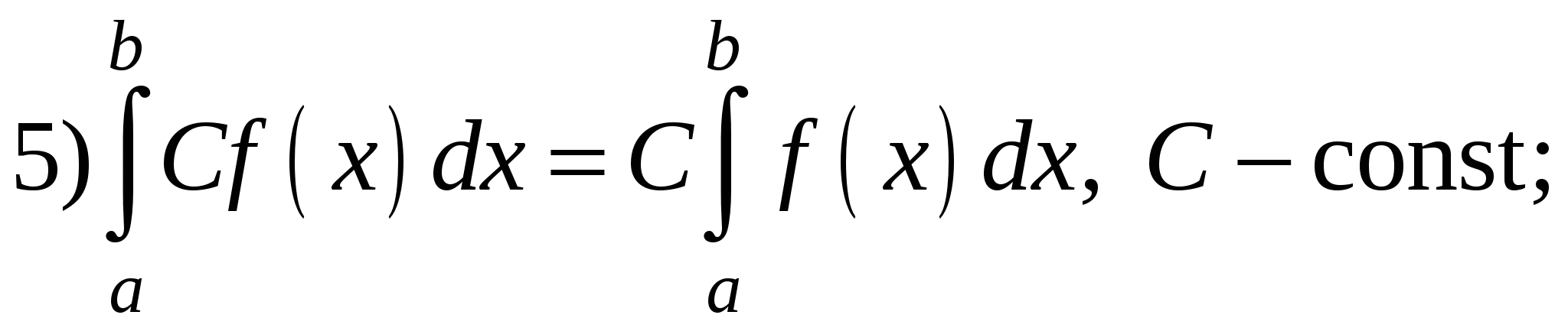
6) Если 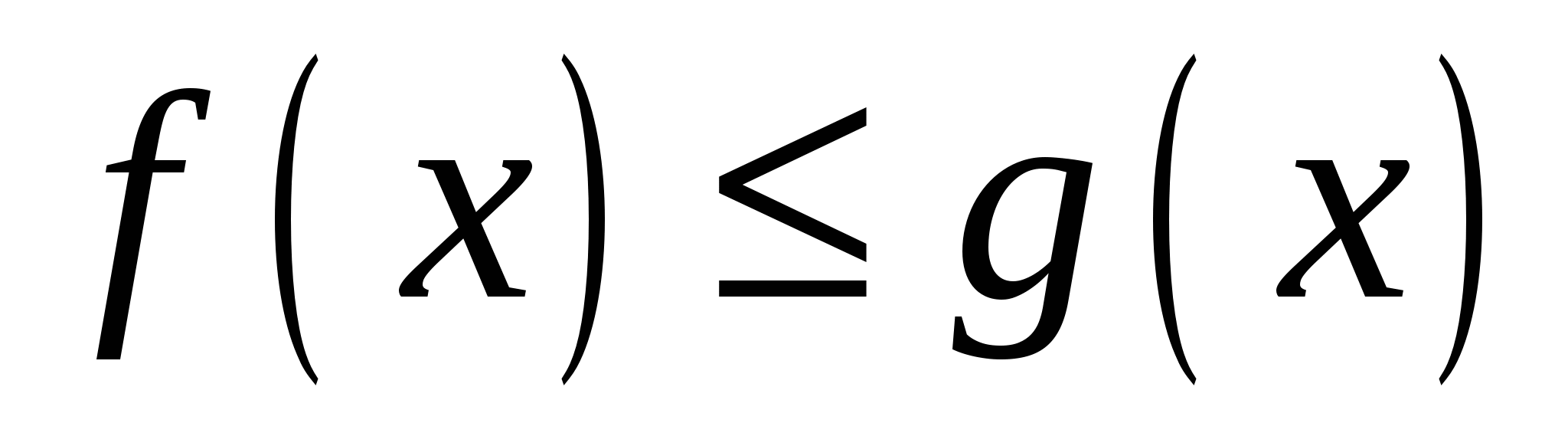 для всех
для всех 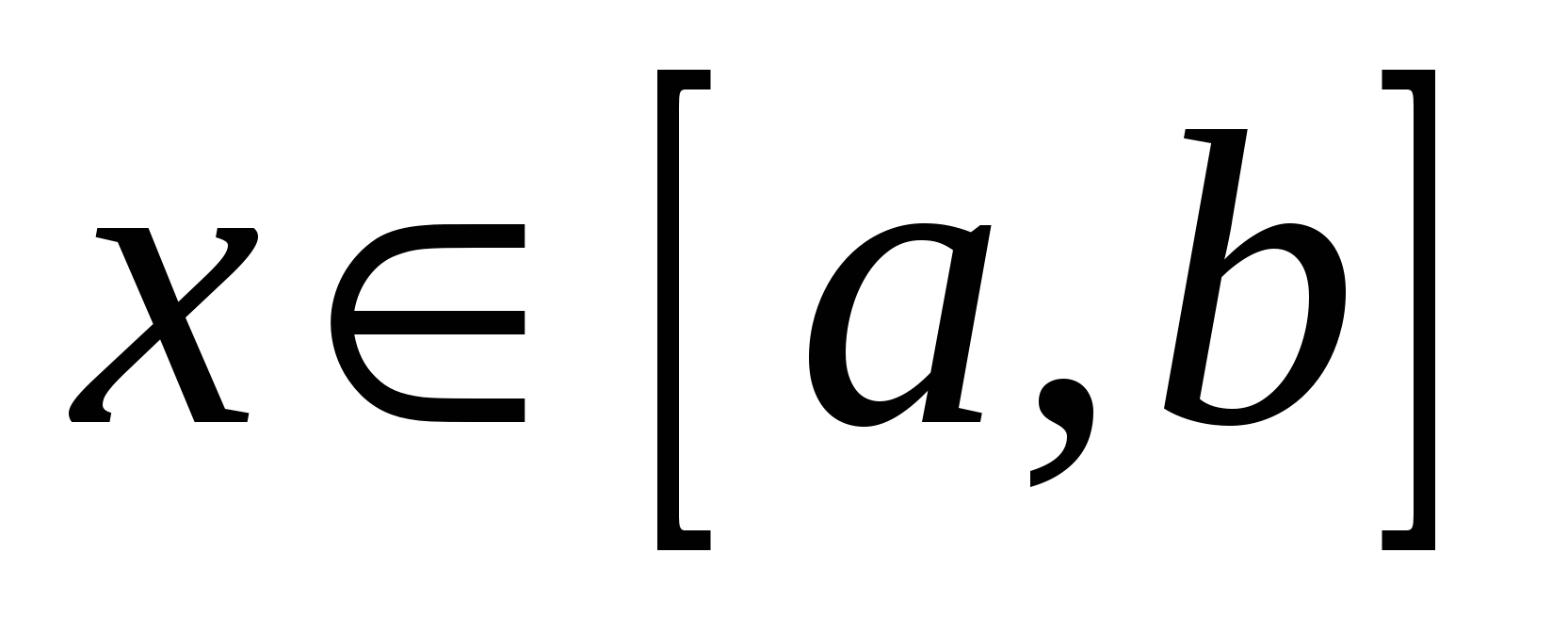 , то
, то 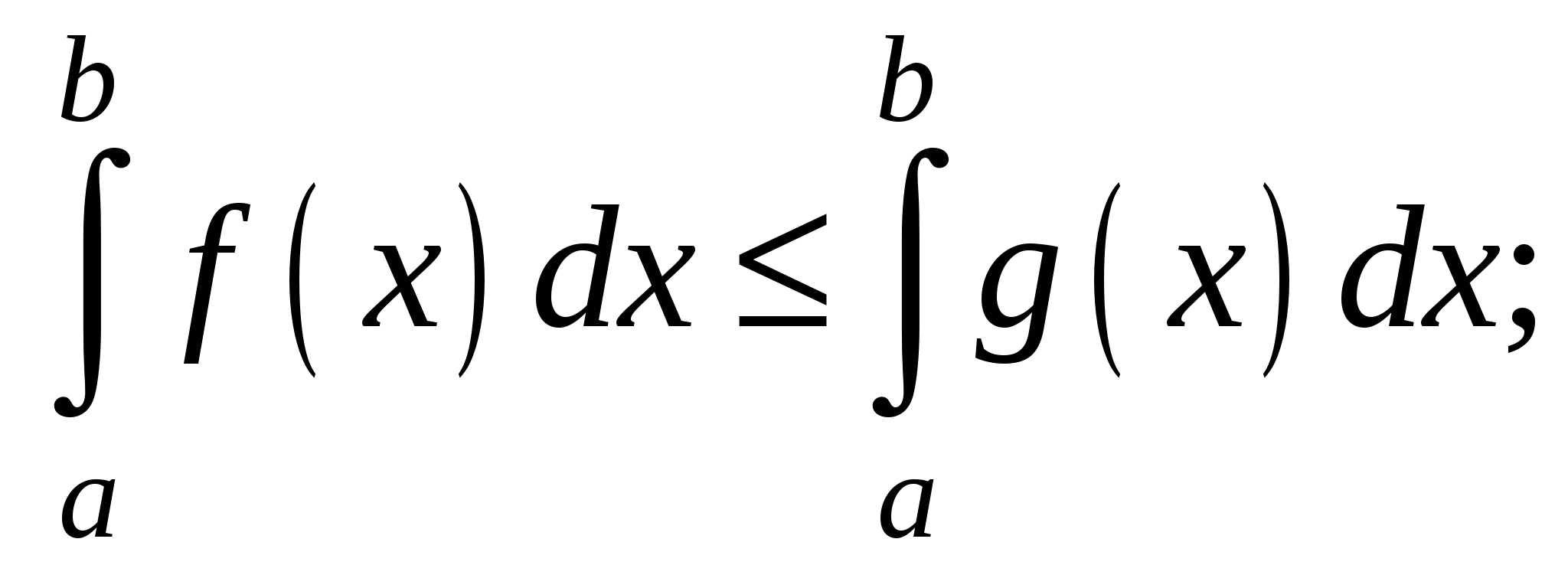
7) Если 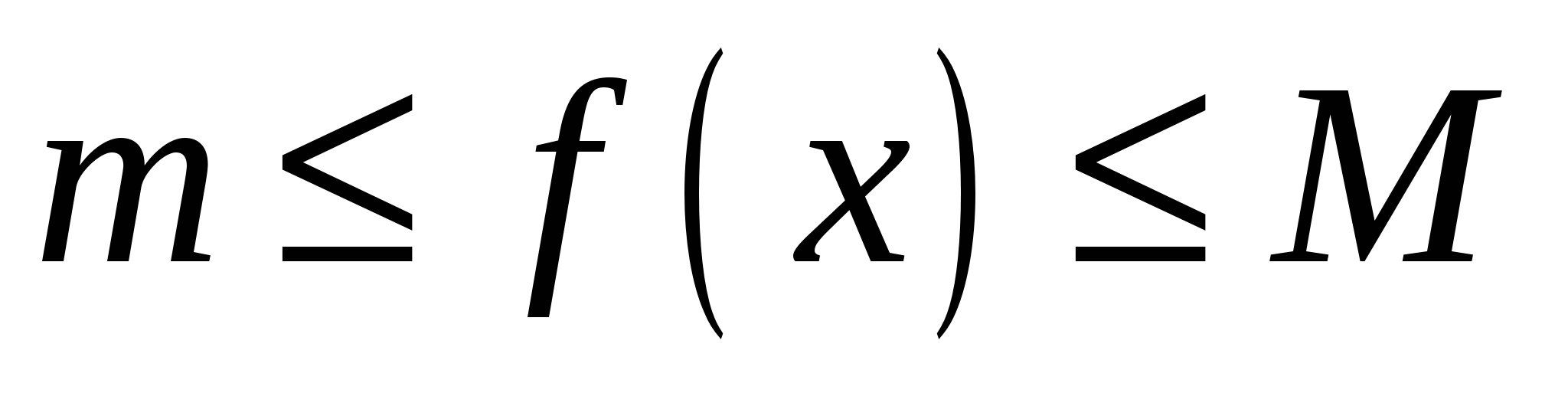 для всех
для всех 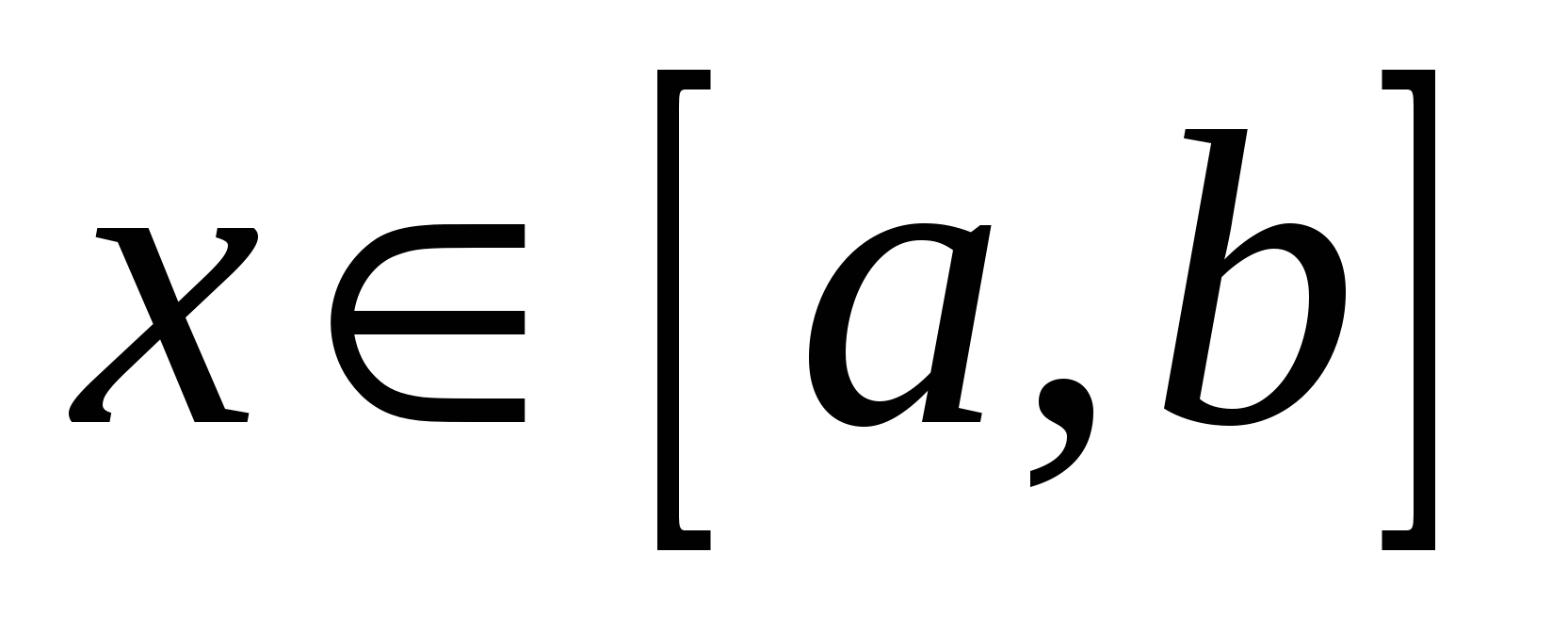 , то
, то 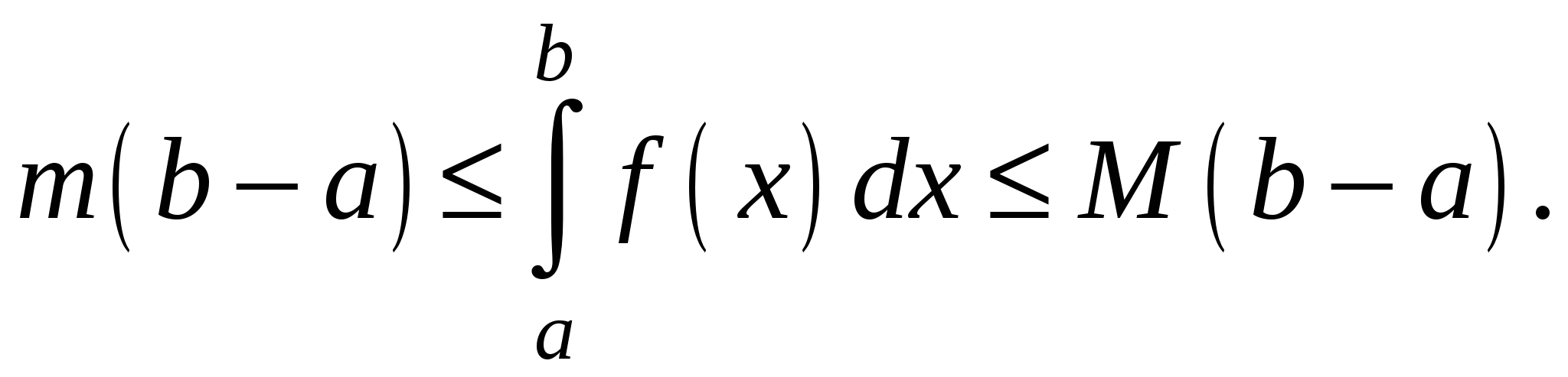
При вычислении определенного интеграла для нахождения первообразной используют те же методы, что и для нахождения неопределенного интеграла, т. е. замену переменной, интегрирование по частям и т. д.
Пример 4. Вычислить определенный интеграл 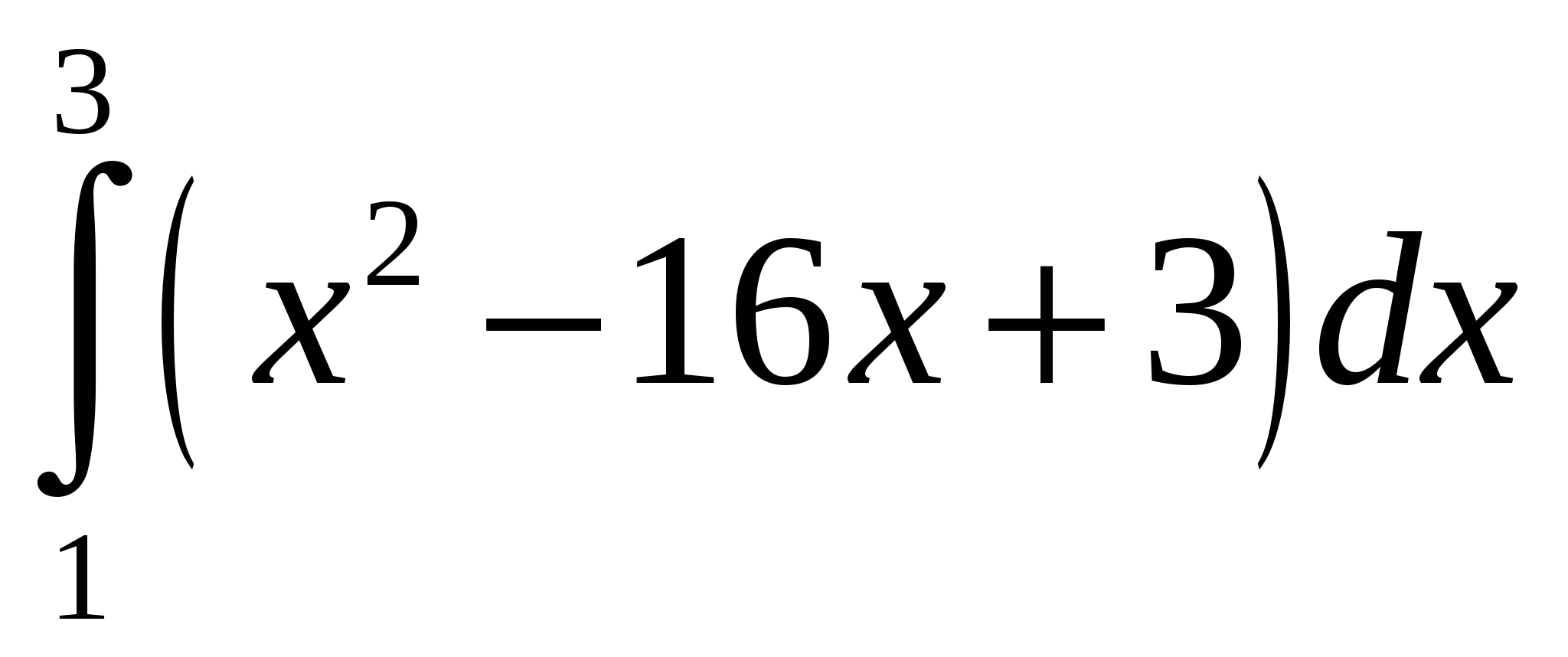
Решение.
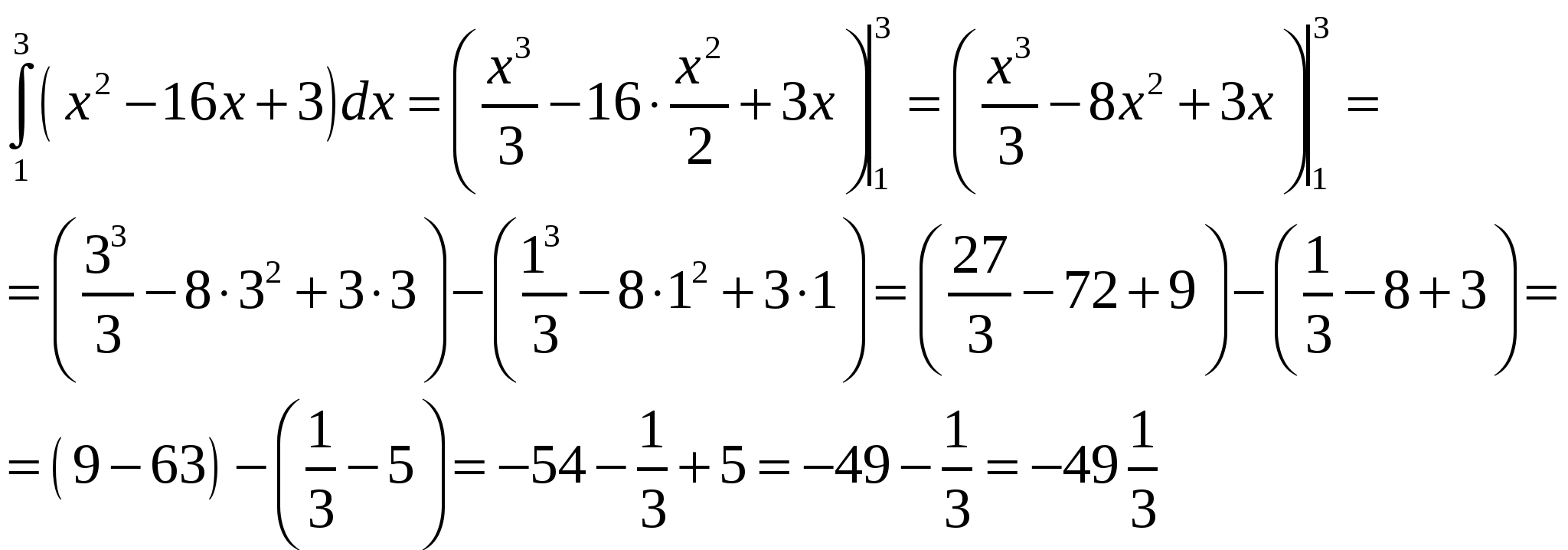
Содержание практической работы
Задание 1. Вычислить интегралы.
1) 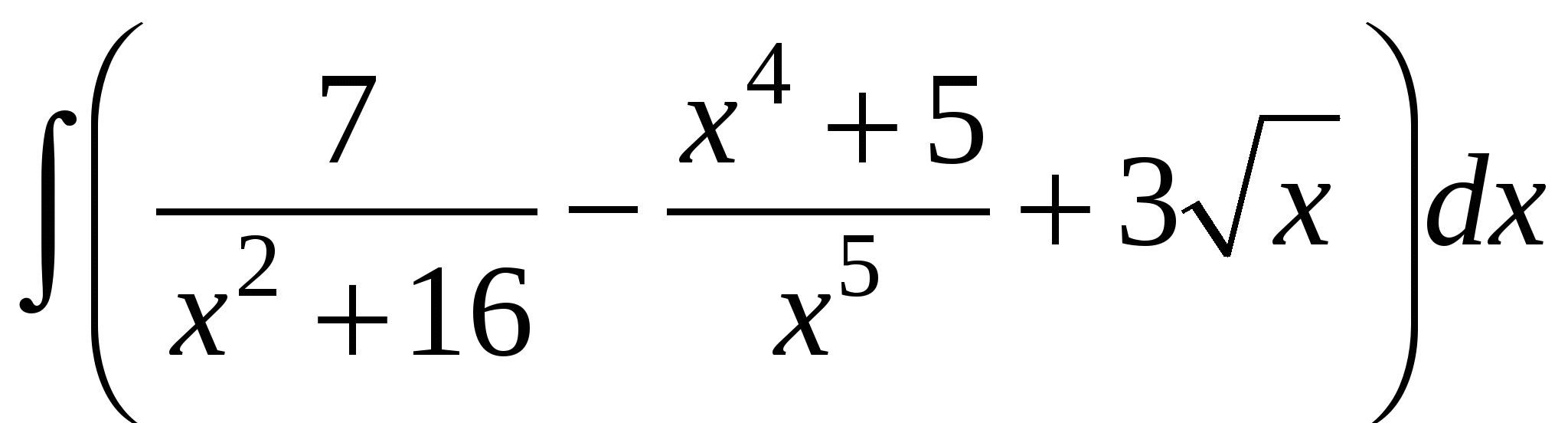
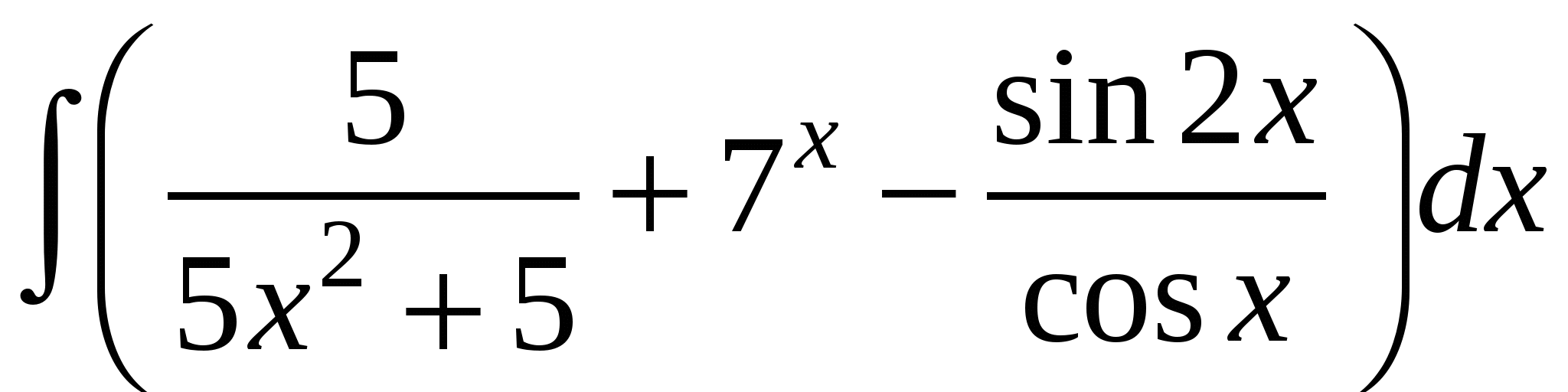
2) 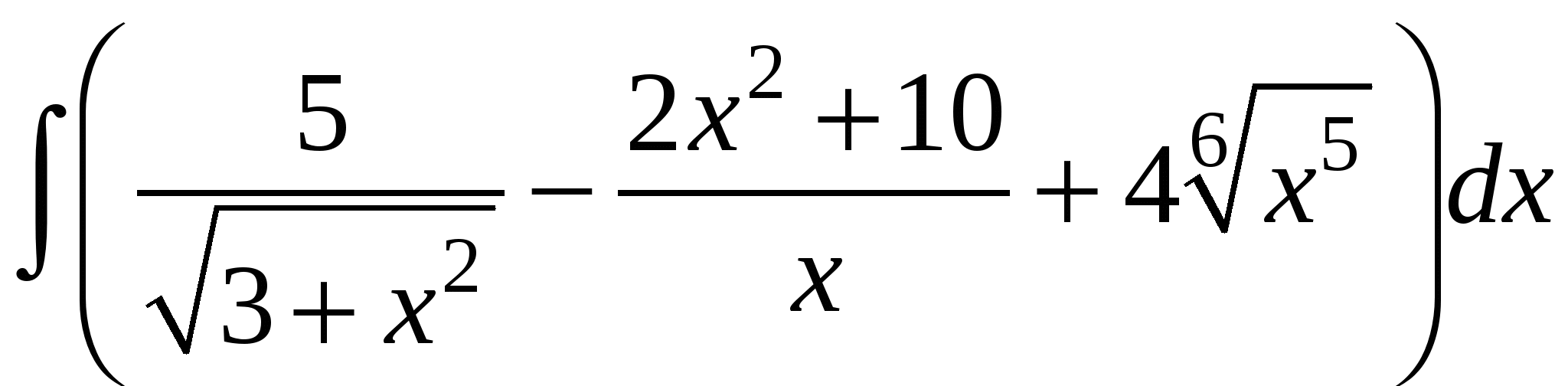
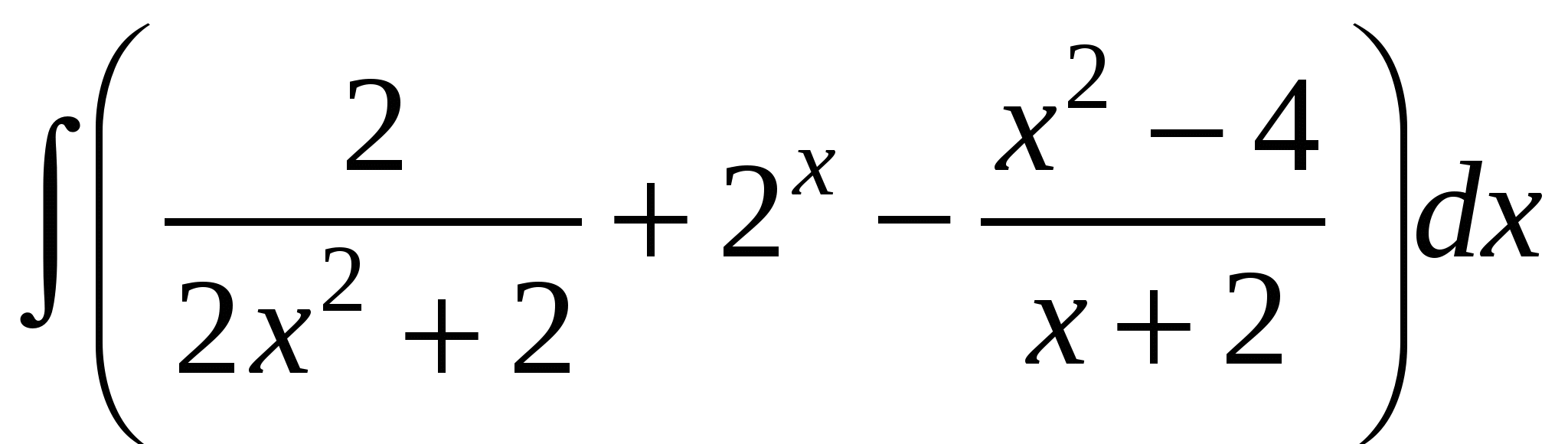
3) 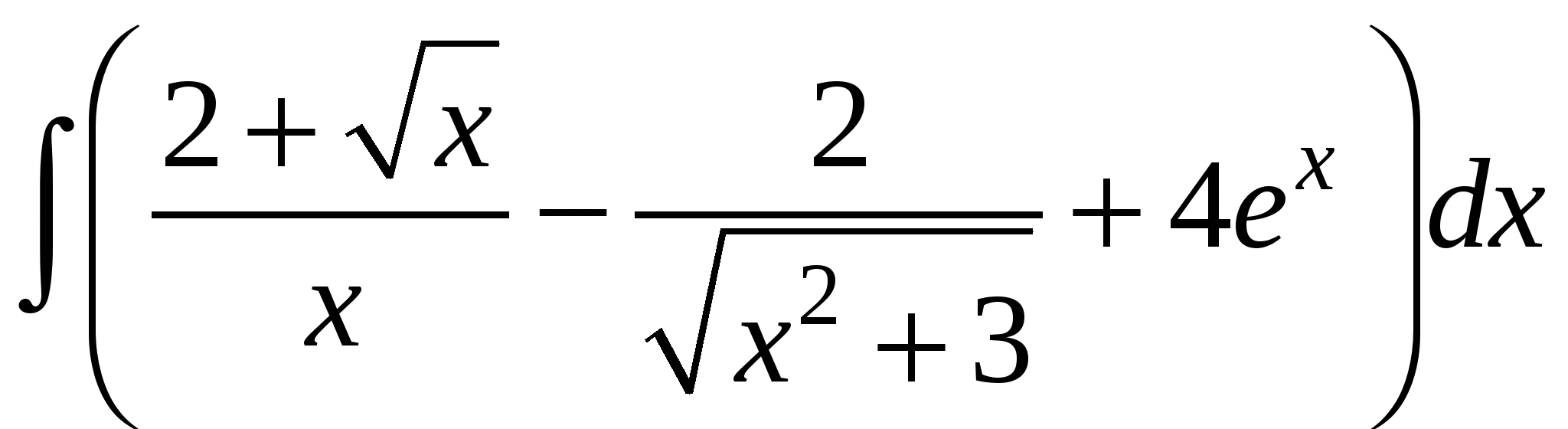
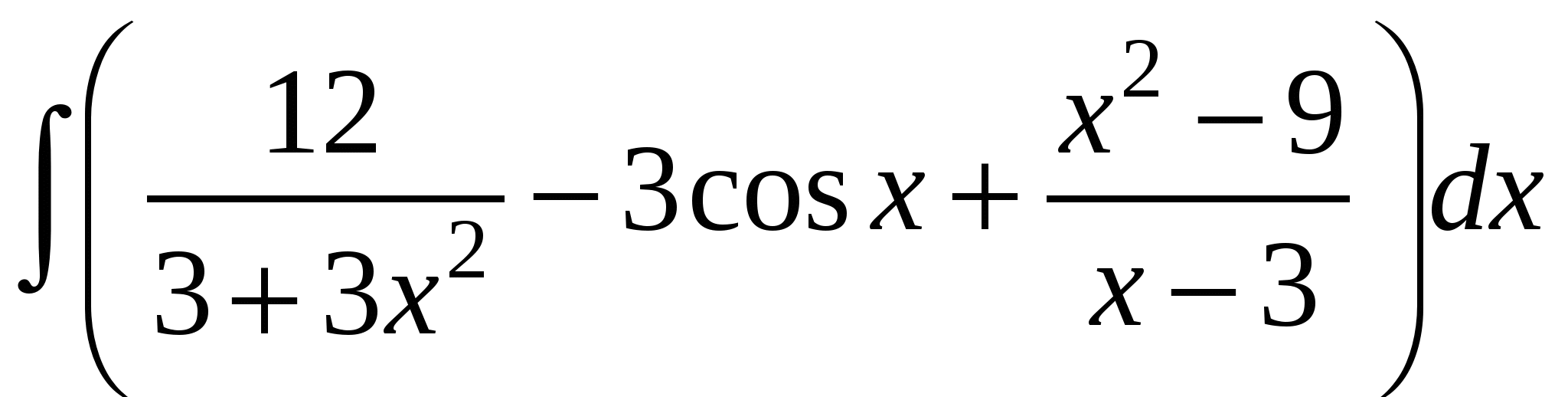
4) 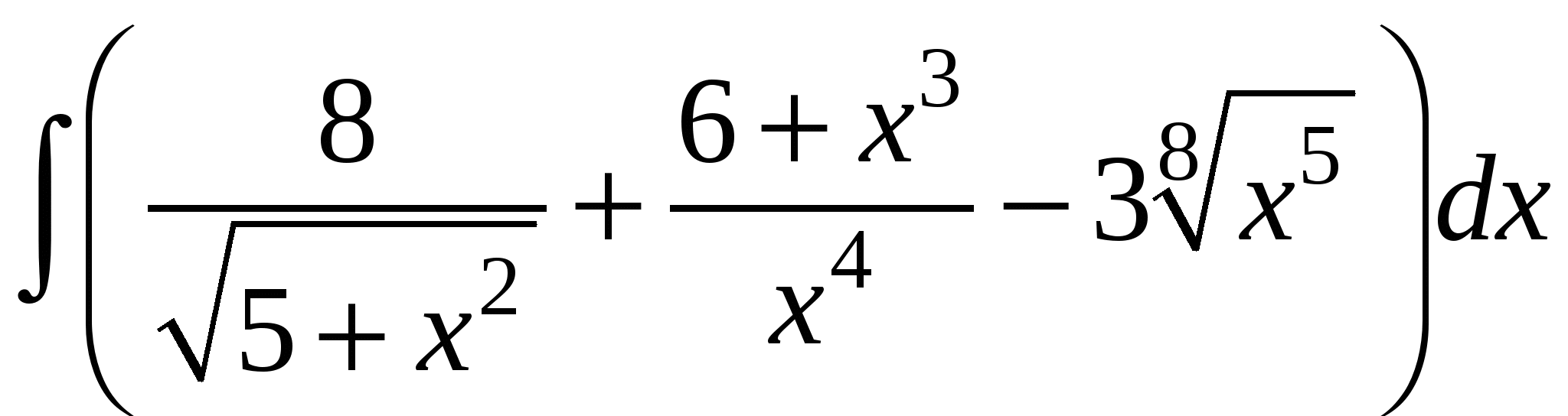
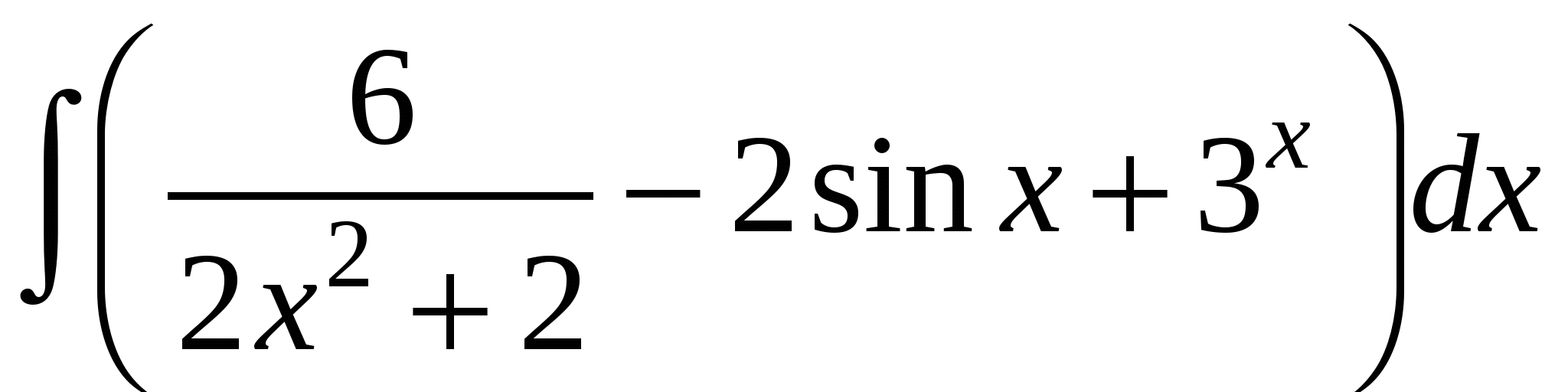
5) 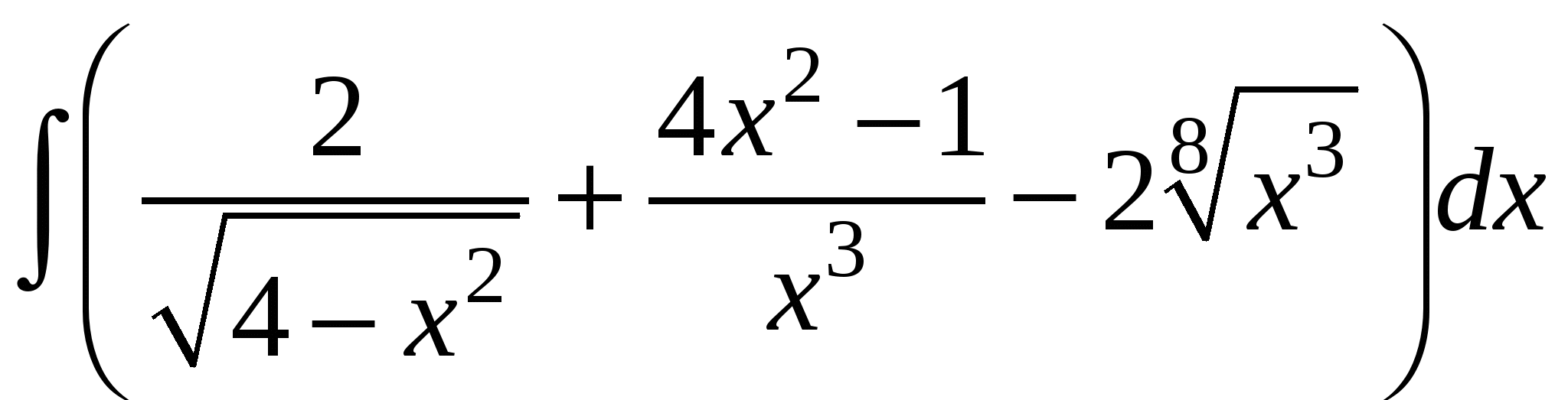
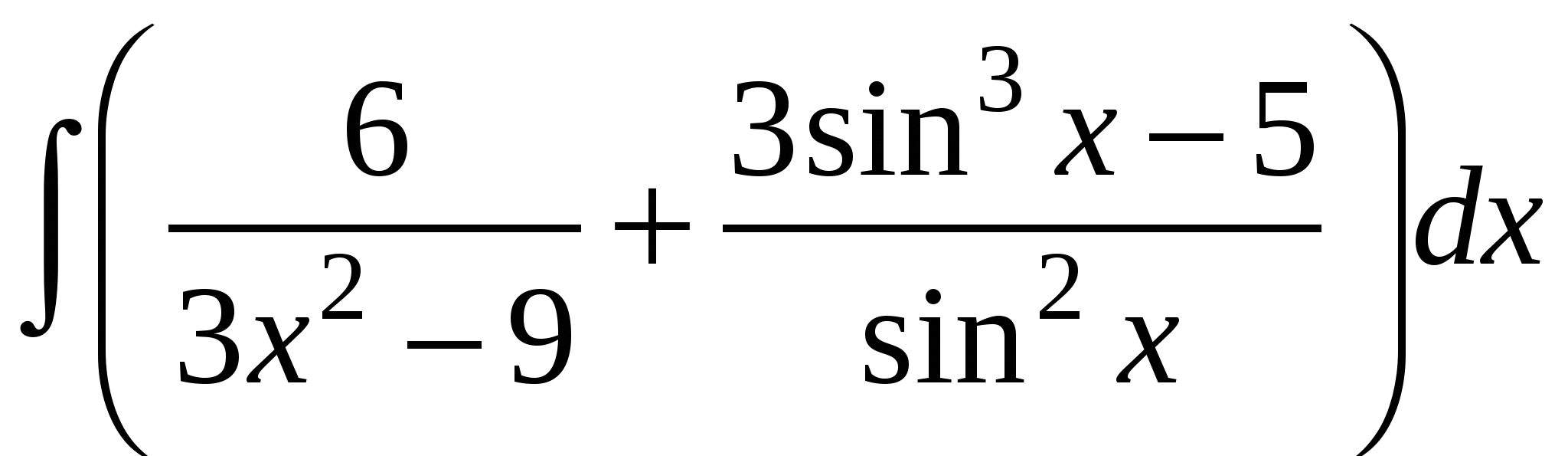
6) 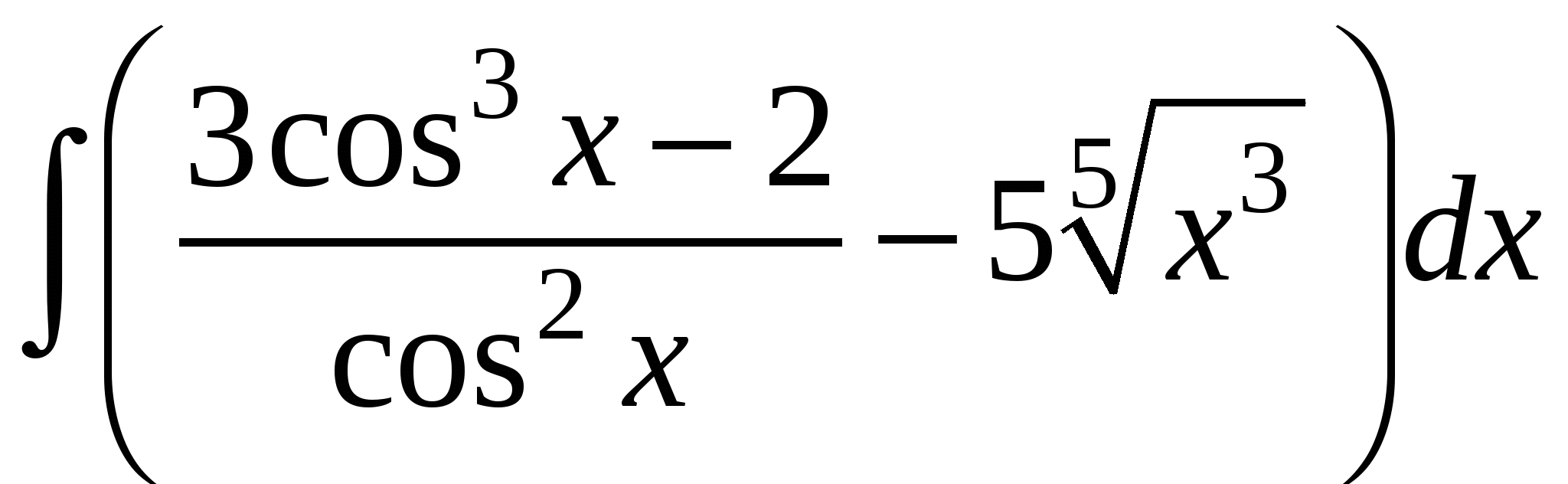
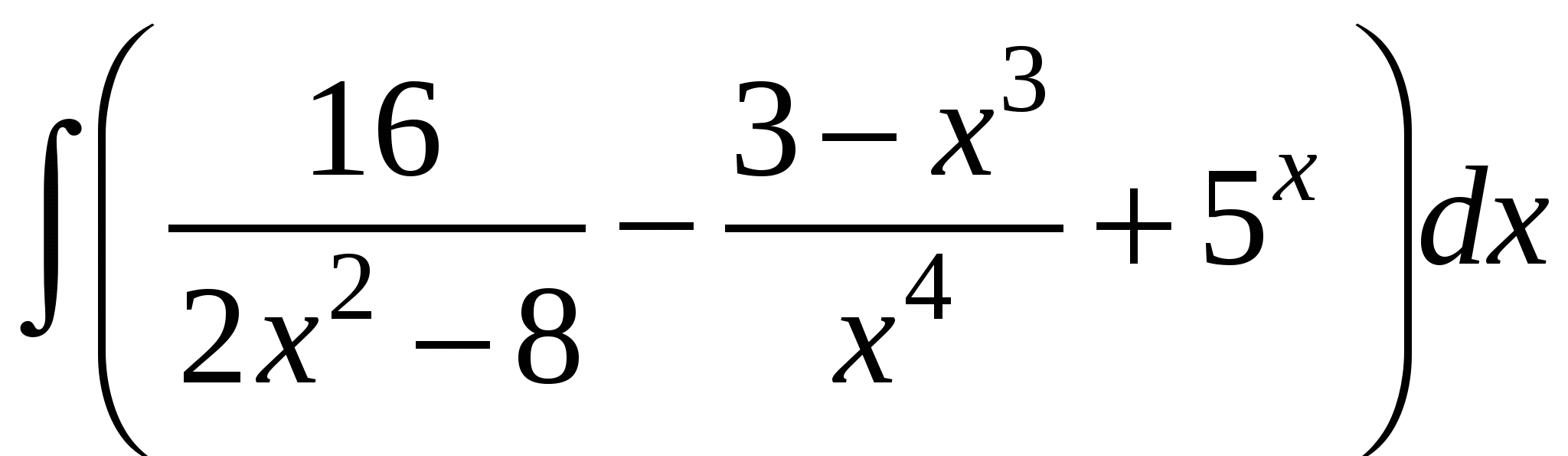
Задание 2. Вычислить определенный интеграл.
1) 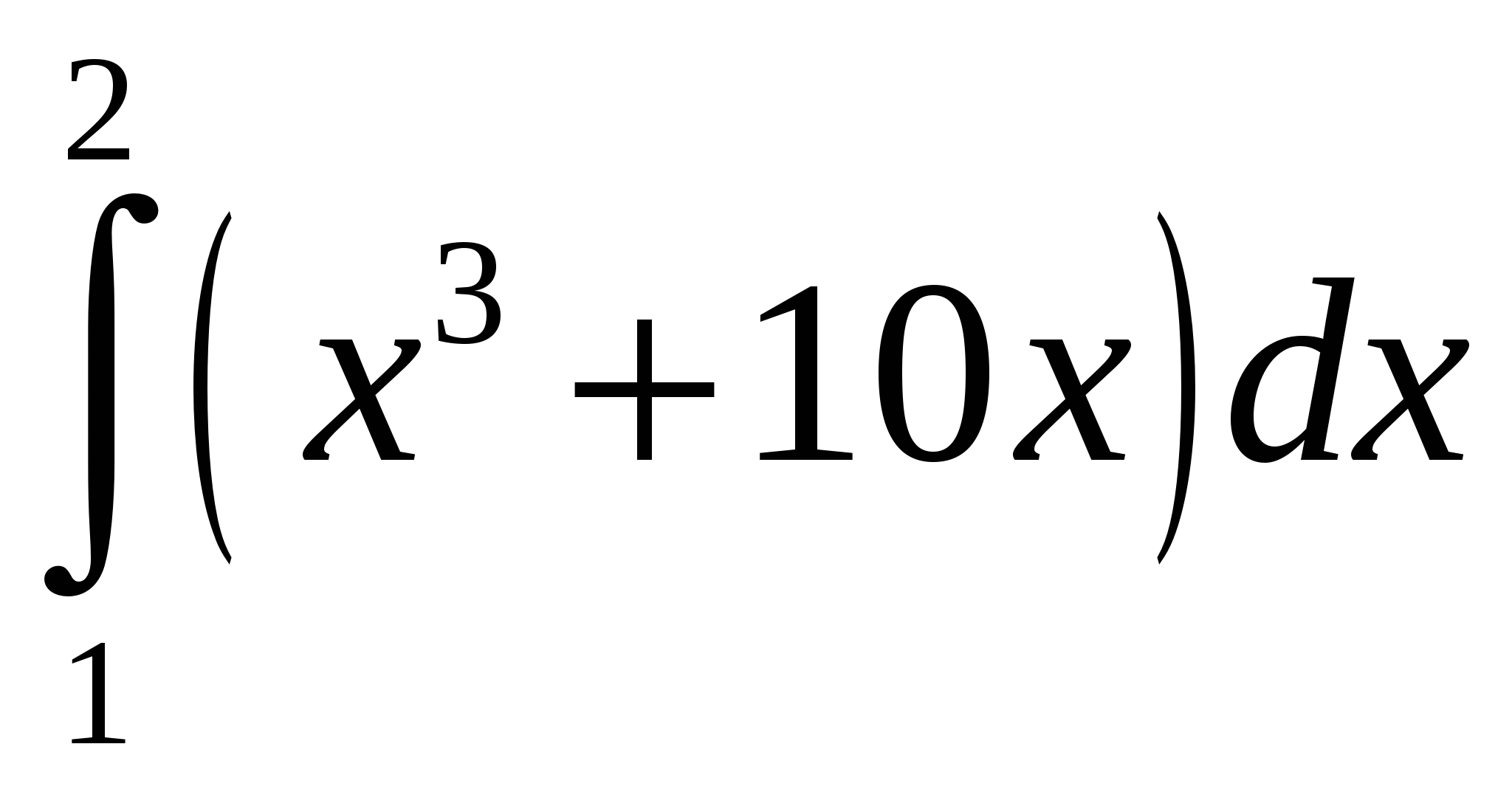
2) 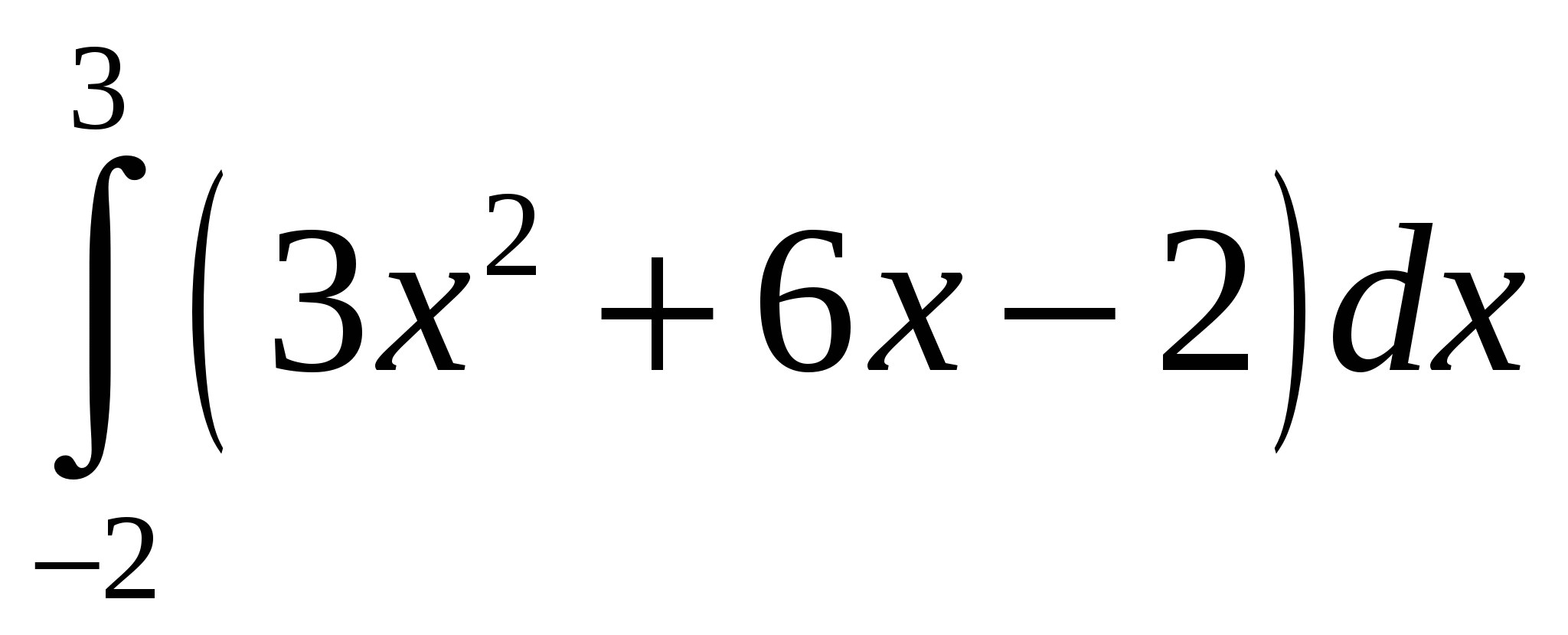
3) 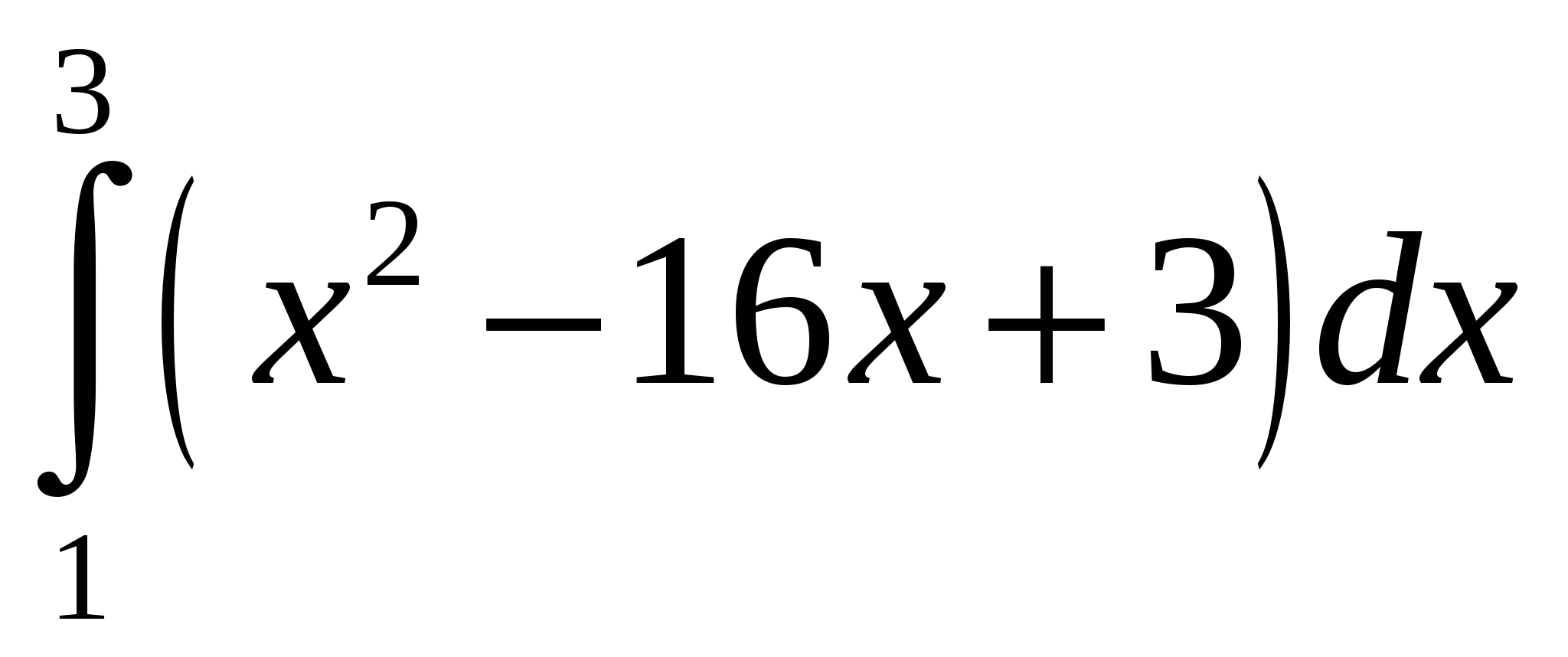
4) 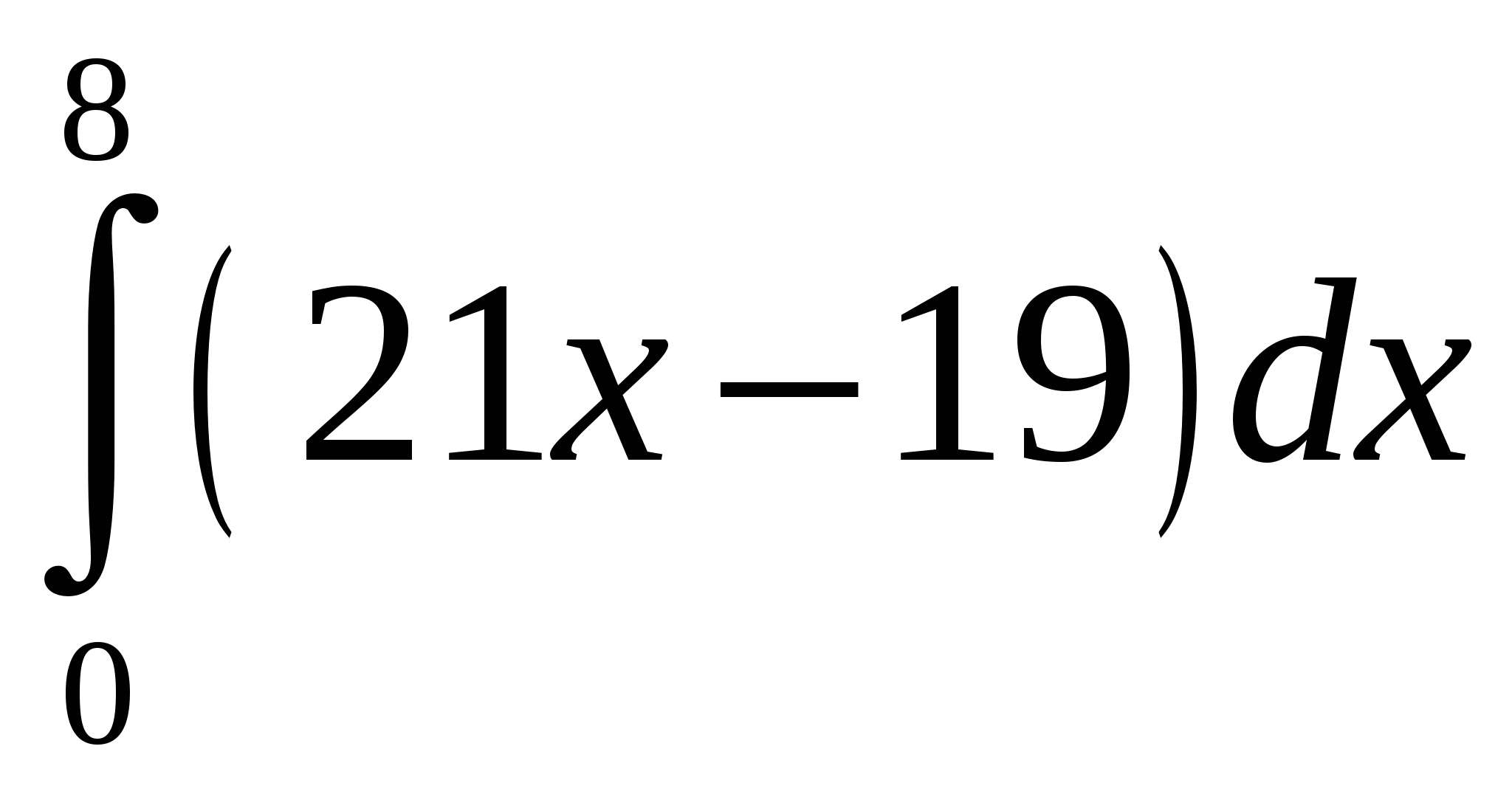
5) 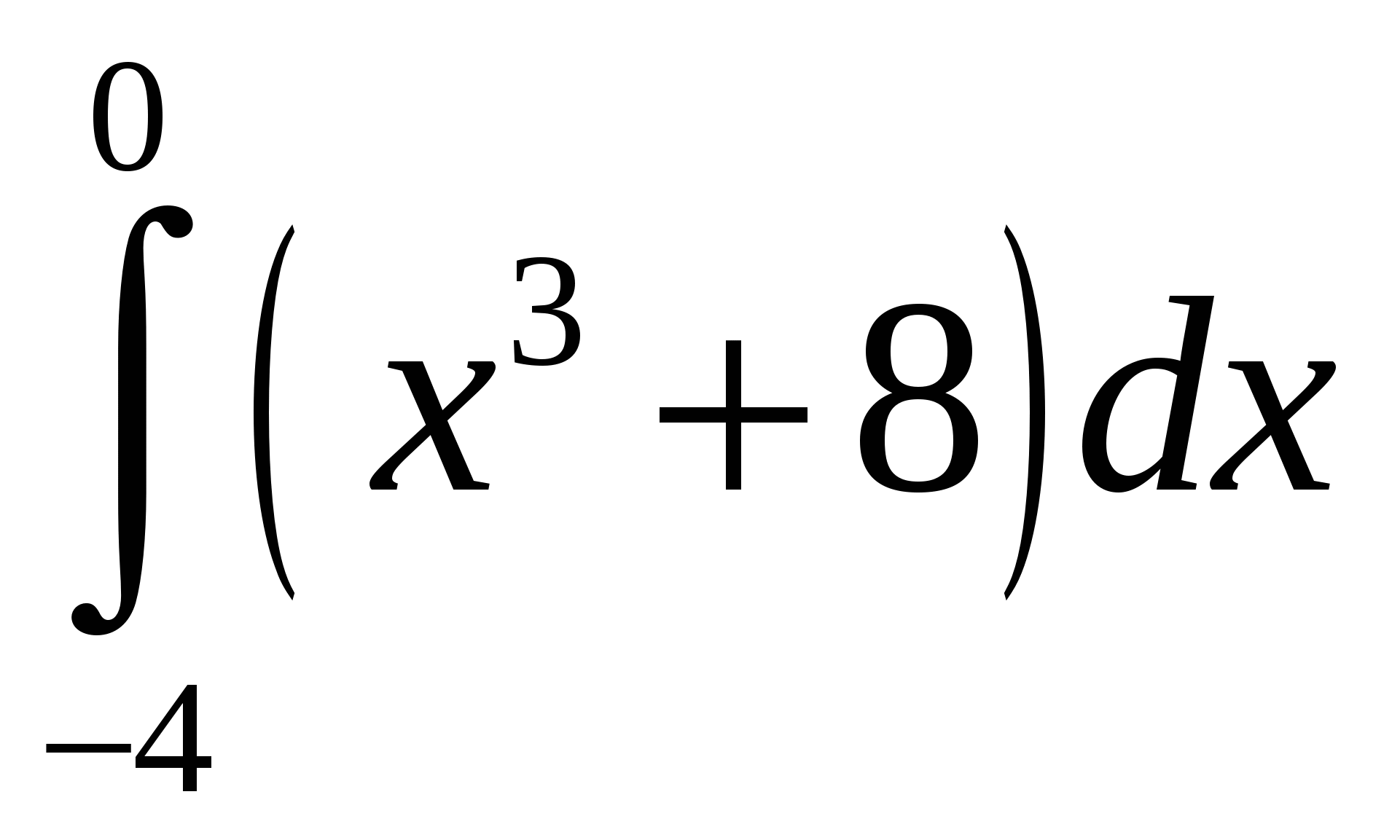
6) 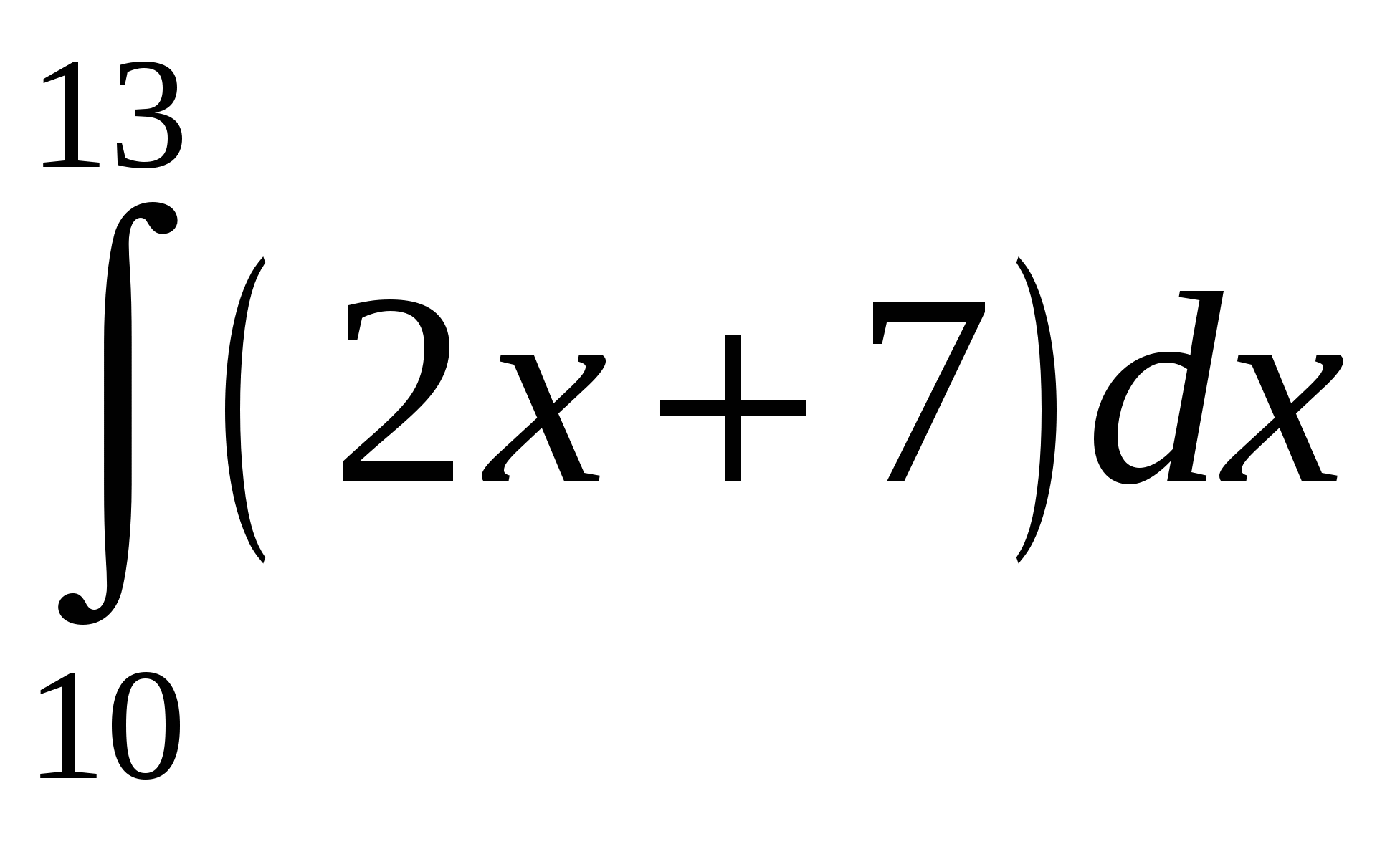
Практическая работа №5
Тема: Применение определенного интеграла для вычисления площадей, длин и объемов фигур.
Цель: сформировать умение применять определенный интеграл для вычисления площадей, длин и объемов фигур.
Теоретические сведения к практической работе
Площади плоских фигур
1. Вычисление площадей плоских фигур в декартовой системе координат
Если плоская фигура (рис. 1) ограничена линиями 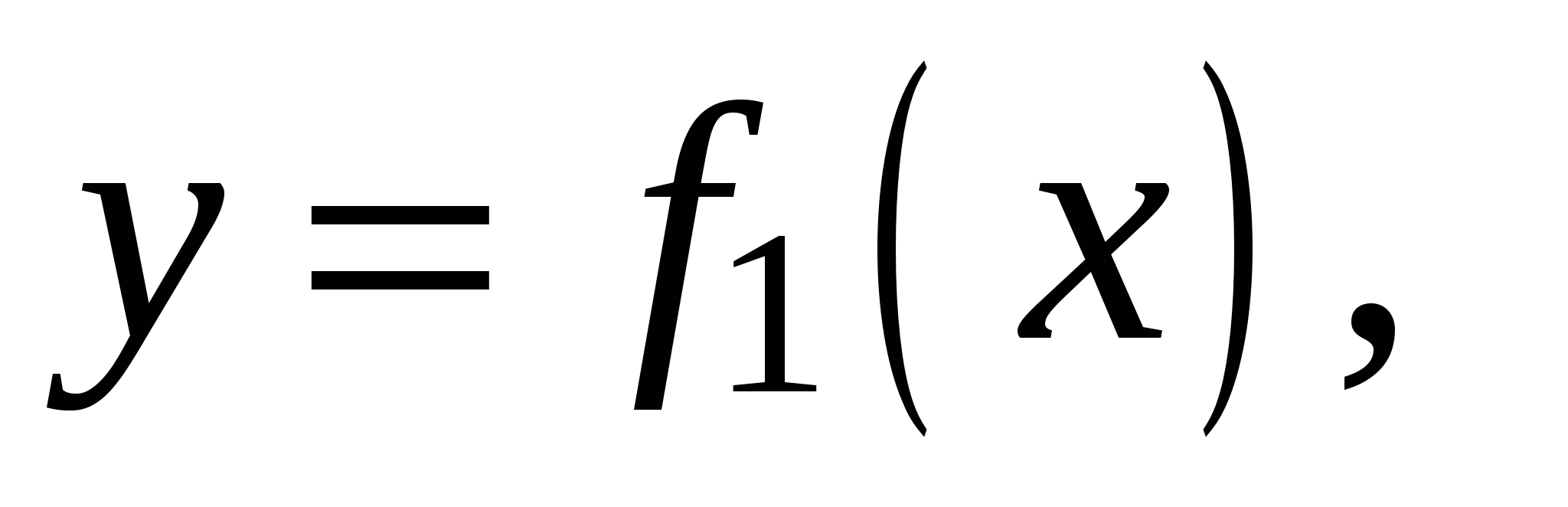
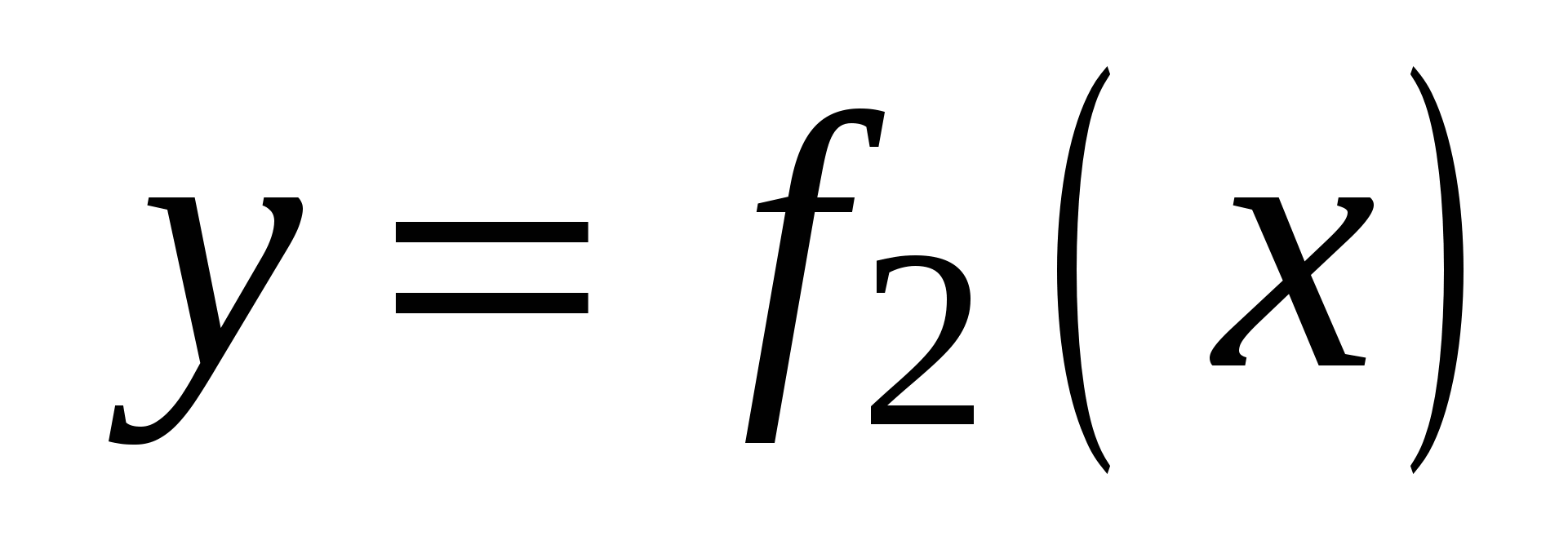 , где
, где 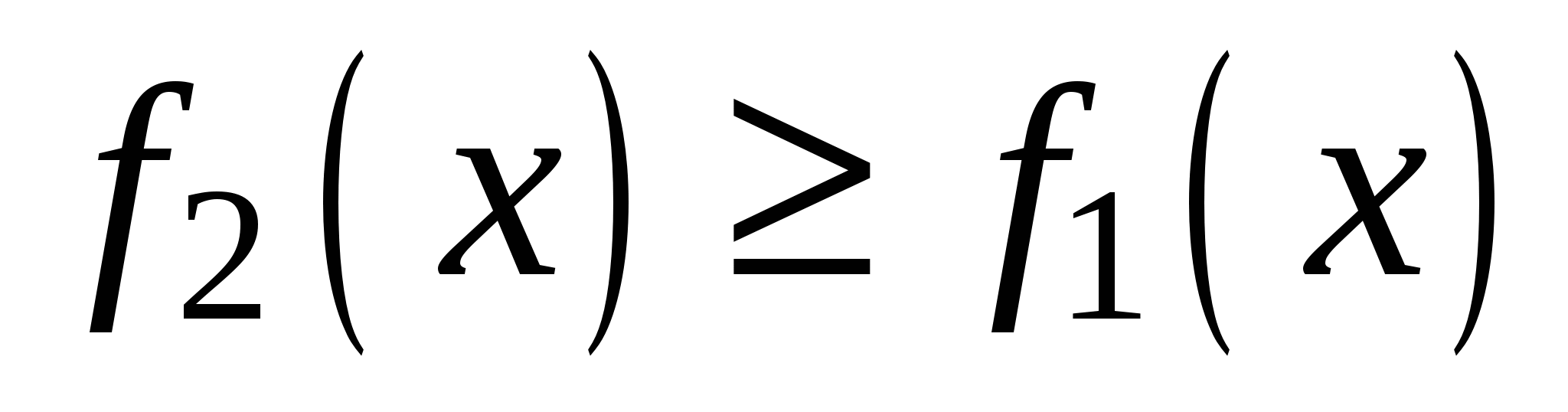 для всех
для всех 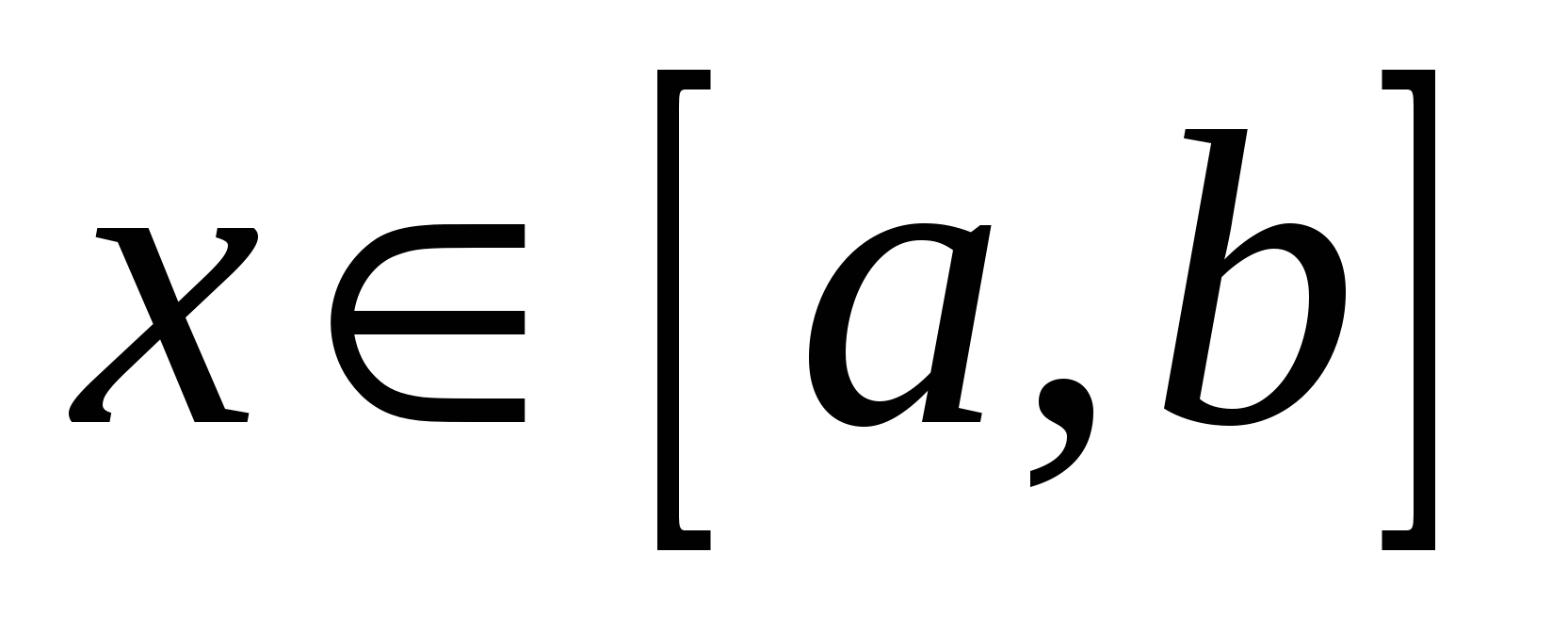 , и прямыми
, и прямыми 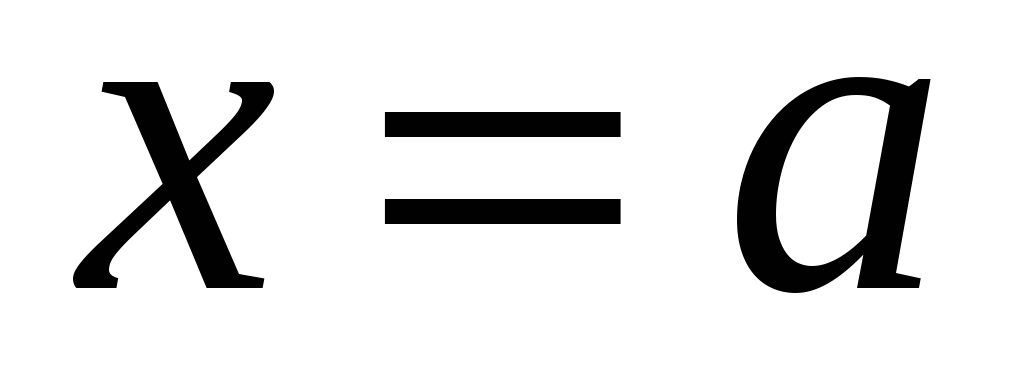 ,
, 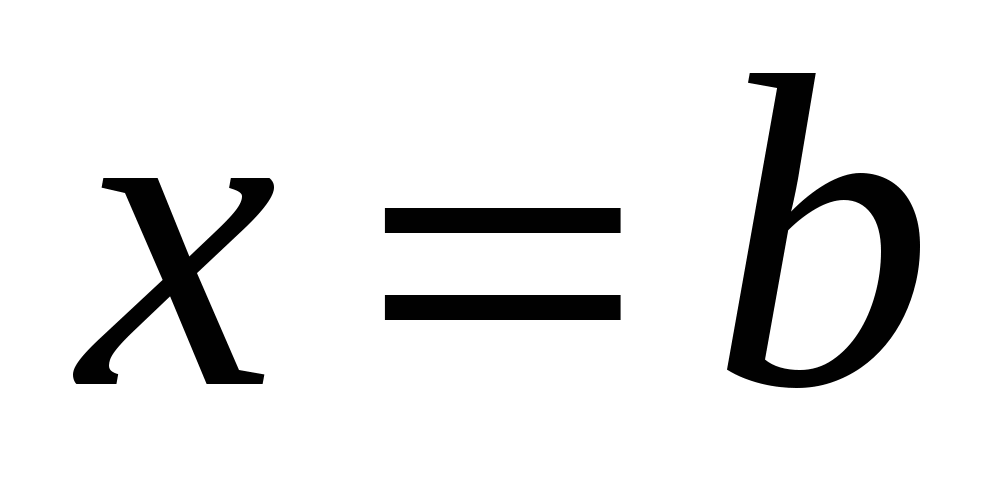 , то ее площадь вычисляется по формуле:
, то ее площадь вычисляется по формуле:
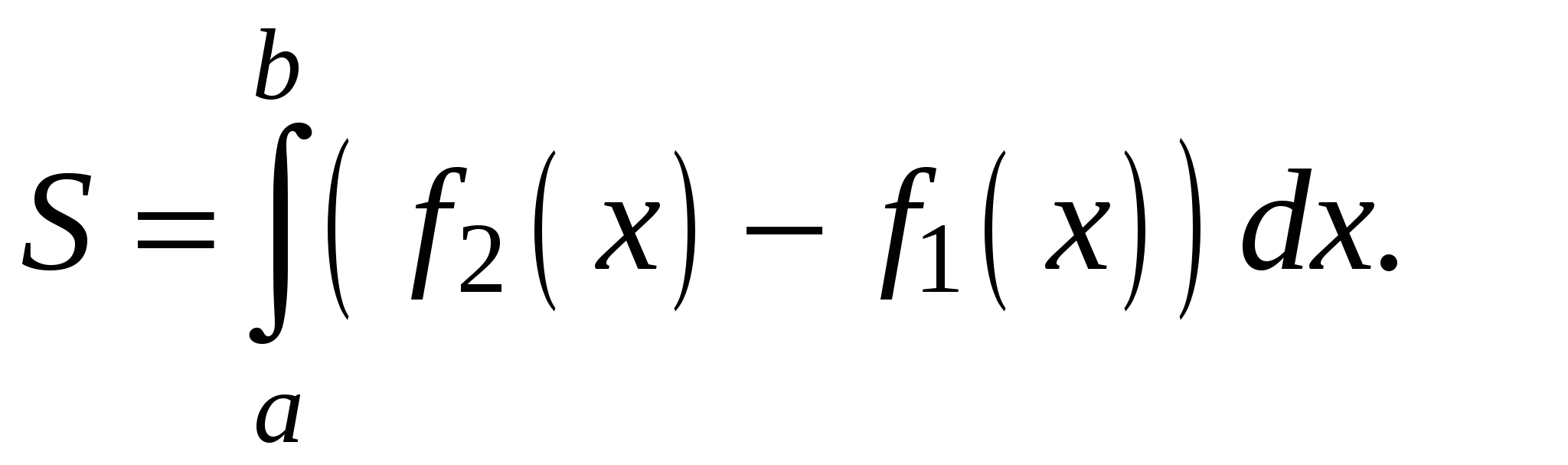 (8)
(8)
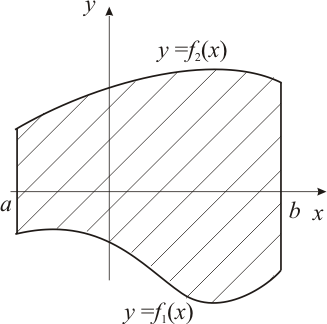
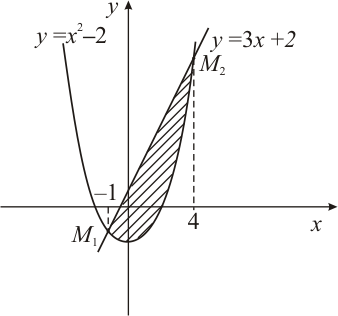
Рис. 1
Рис. 2
Пример. Найти площадь фигуры, ограниченной линиями:
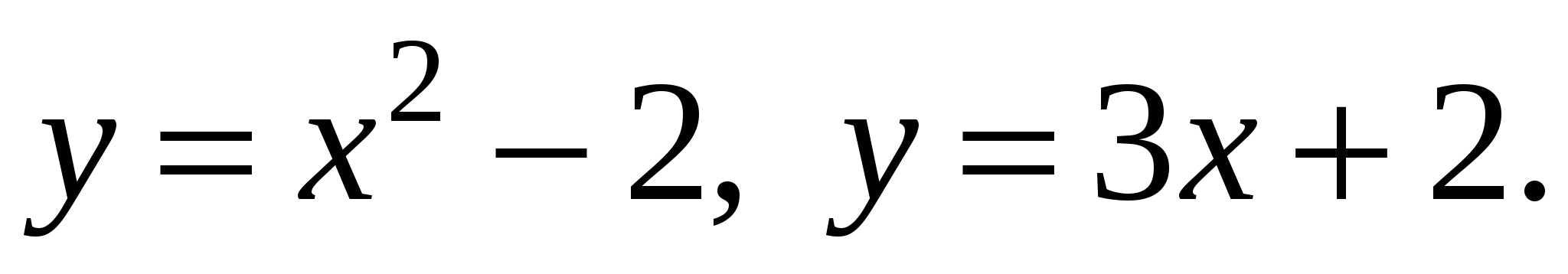
Решение. Построим схематический рисунок (рис. 2). Для построения параболы возьмем несколько точек:
x
0
1
-1
2
-2
3
-3
4
-4
y
-2
-1
-1
2
2
7
7
14
14
Для построения прямой достаточно двух точек, например 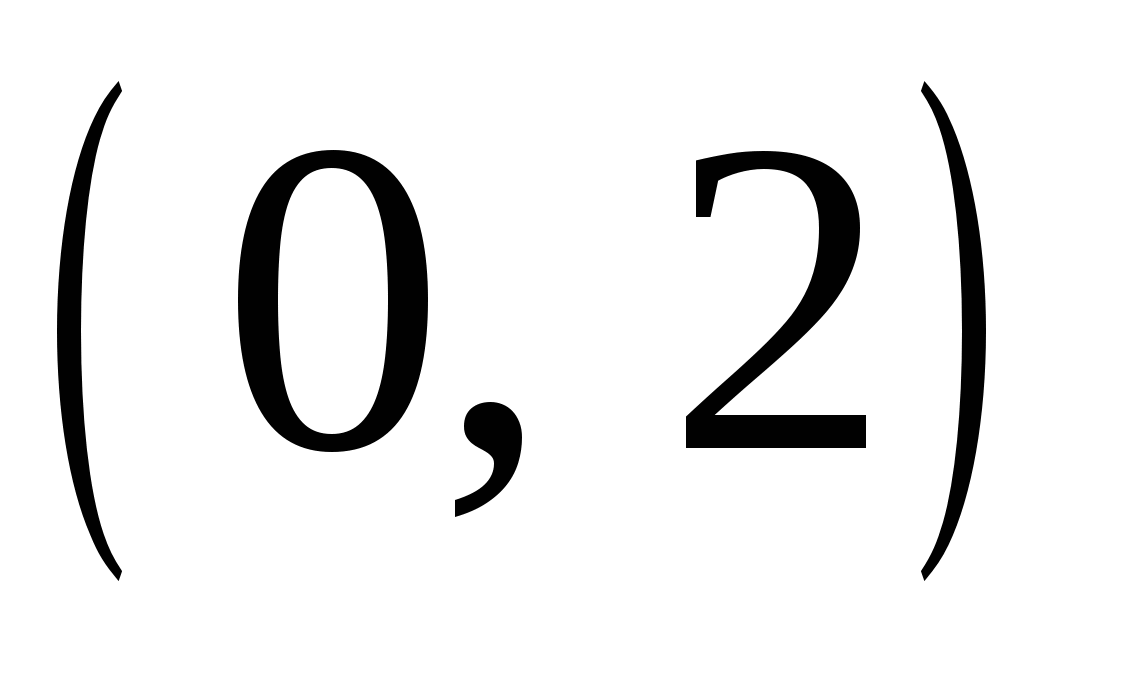 и
и 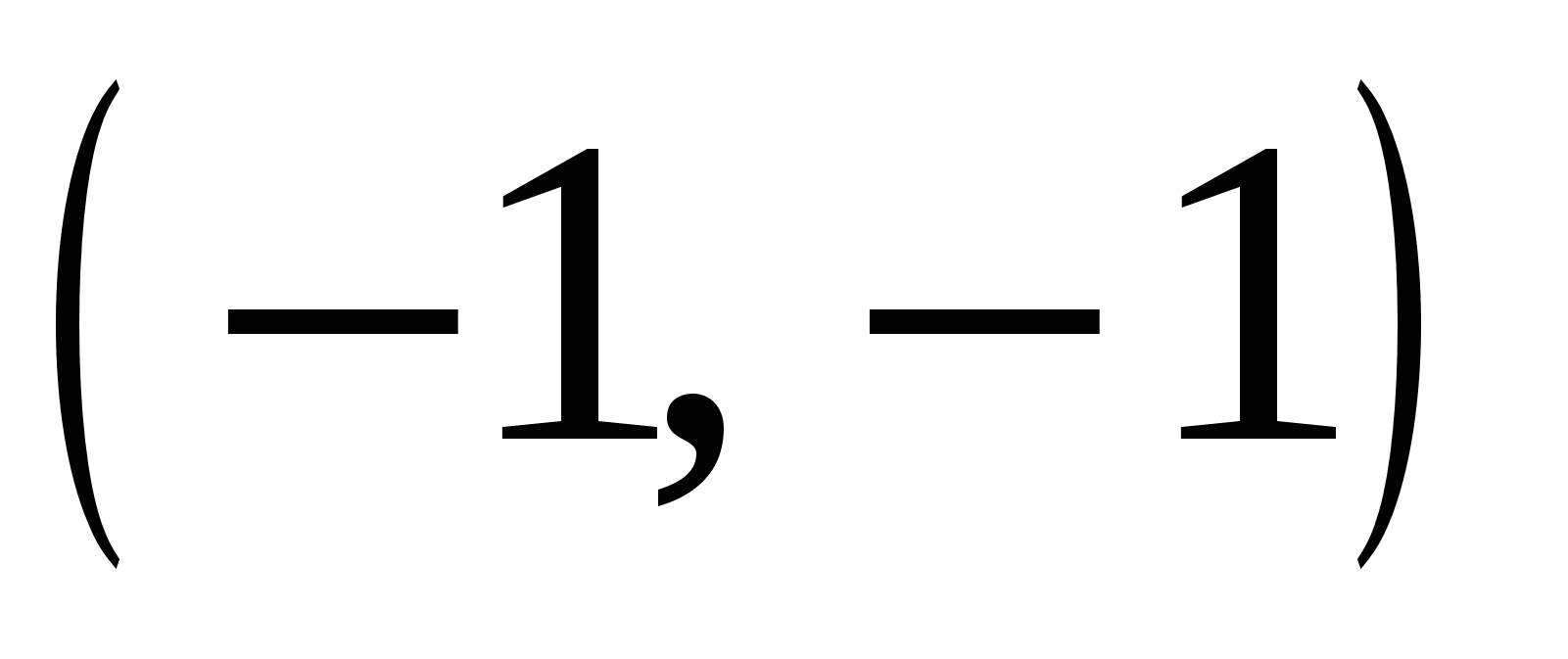 .
.
Найдем координаты точек 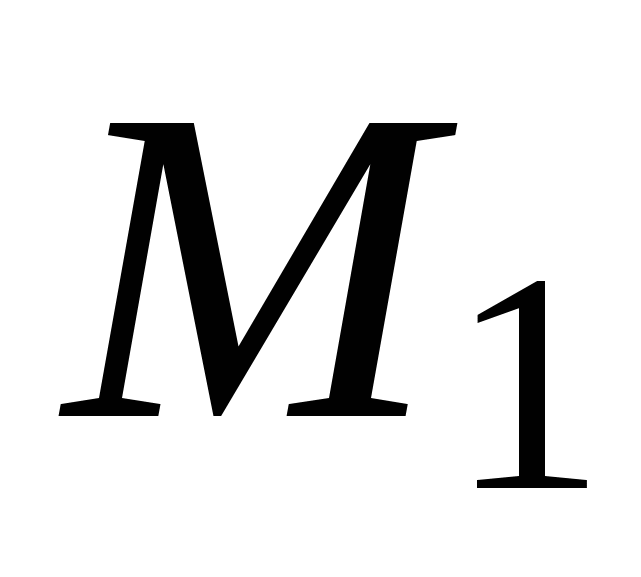 и
и 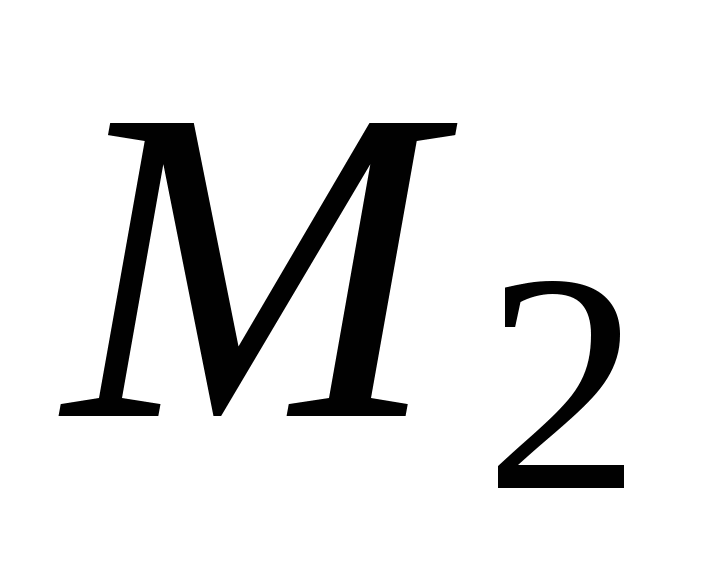 пересечения параболы
пересечения параболы 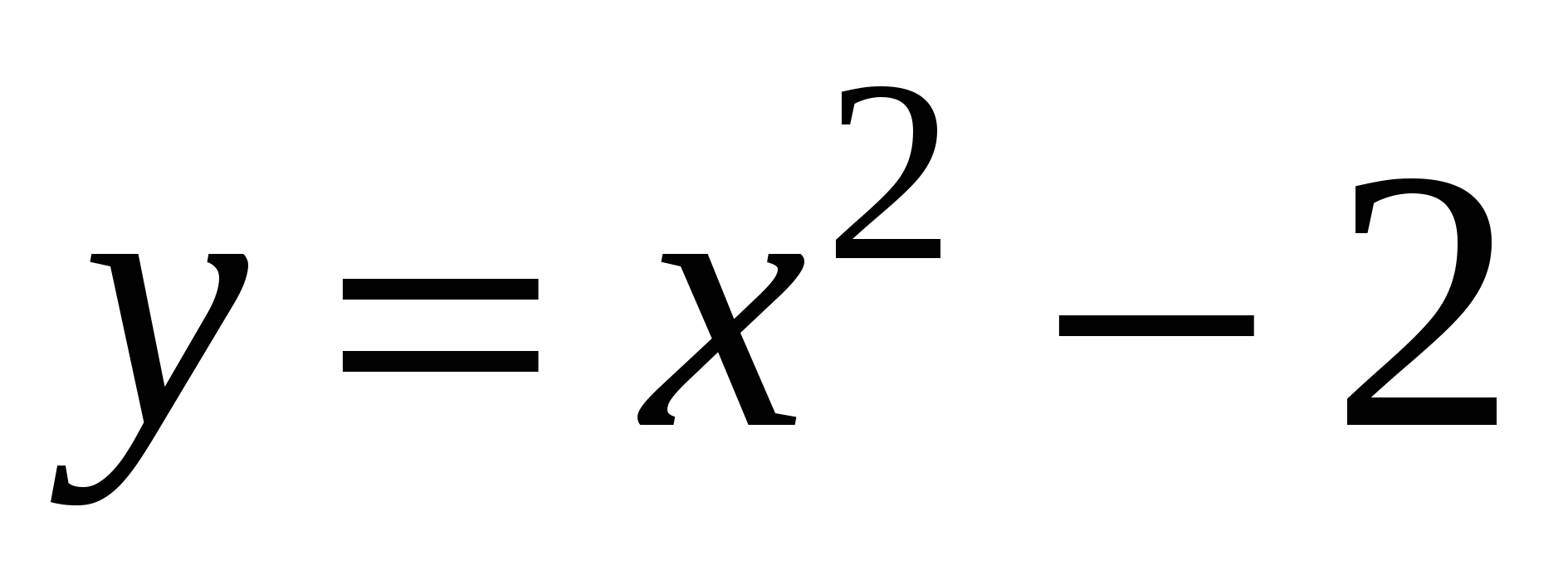 и прямой
и прямой 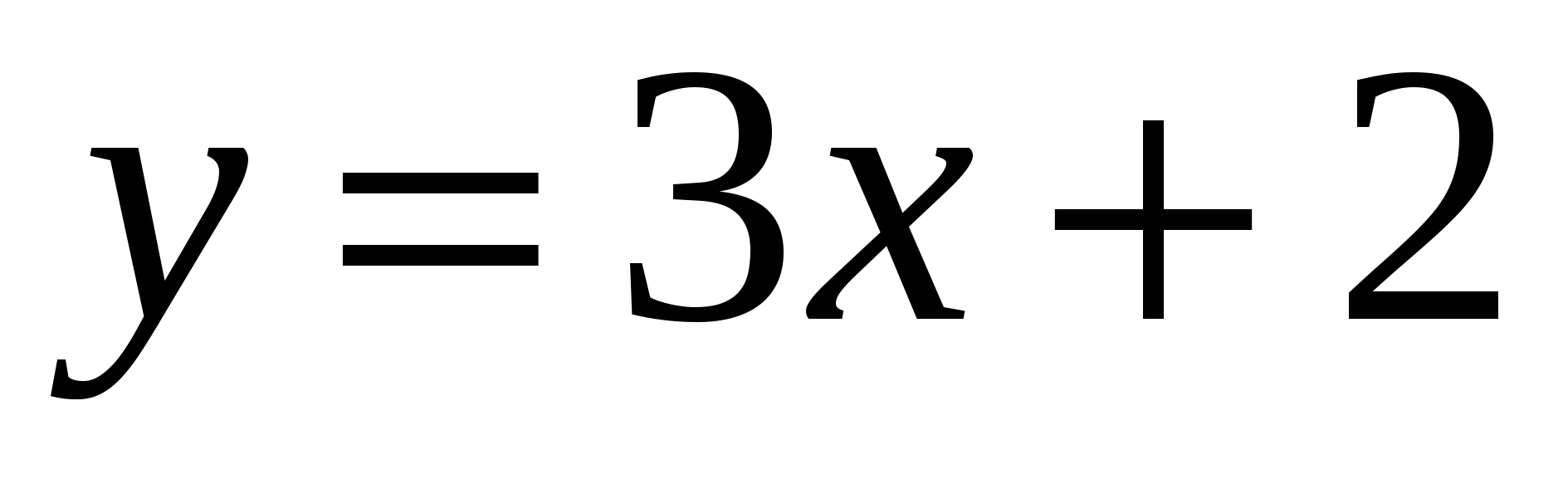 .
.
Для этого решим систему уравнений
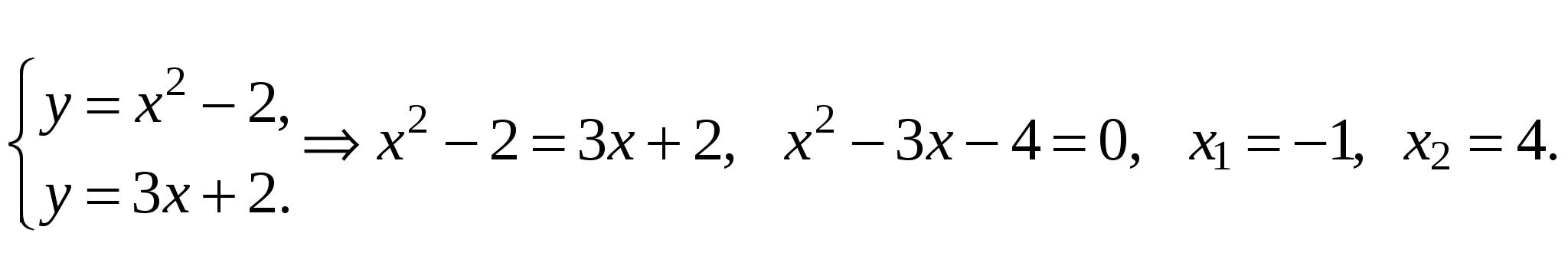
Тогда 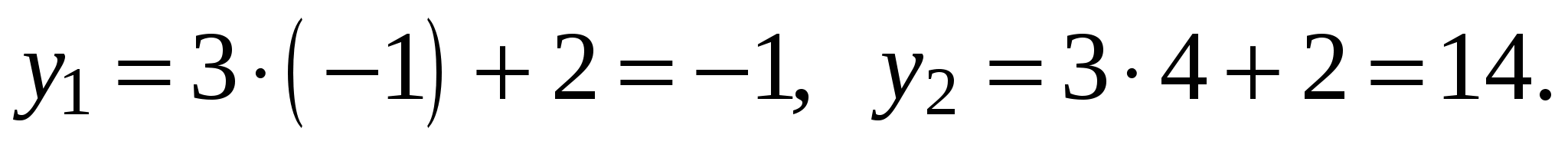 Итак,
Итак, 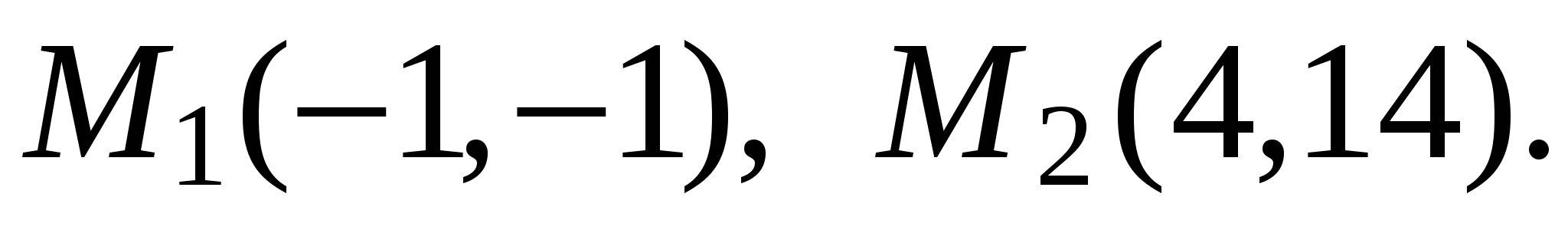
Площадь полученной фигуры найдем по формуле (8), в которой
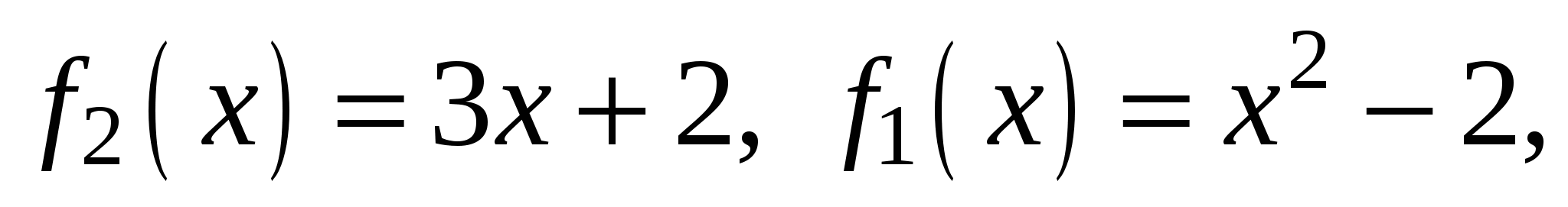 поскольку
поскольку 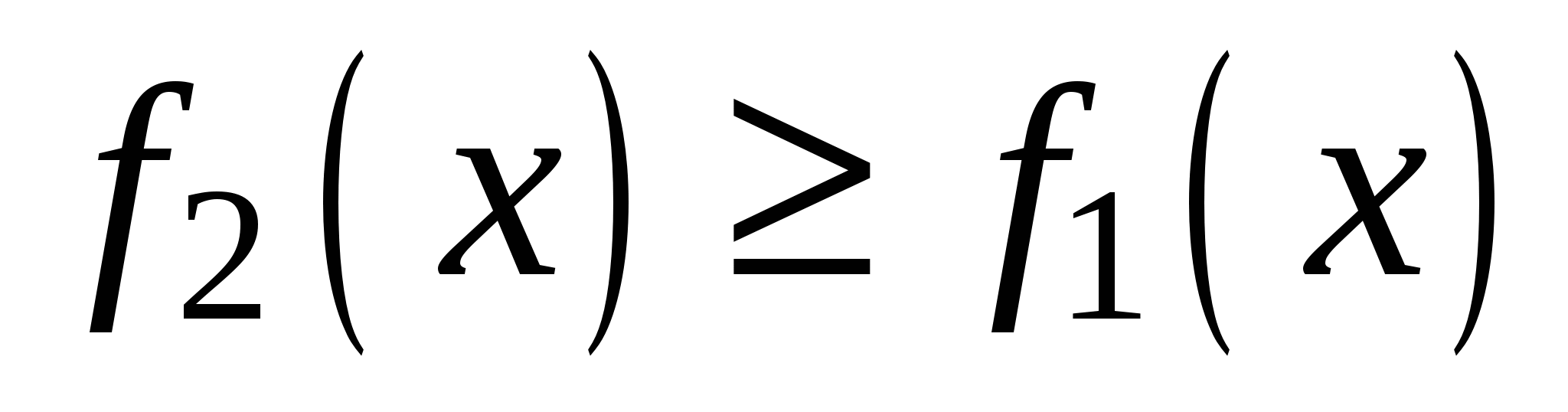 для всех
для всех 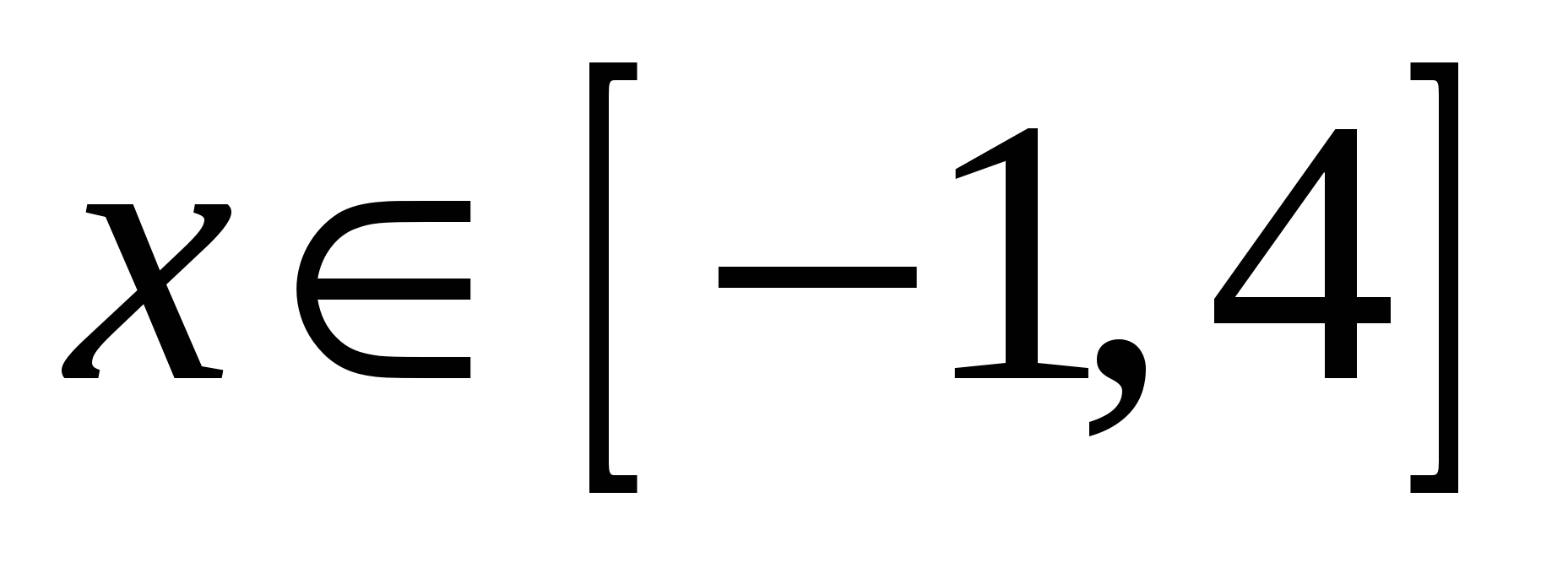 . Получим:
. Получим:
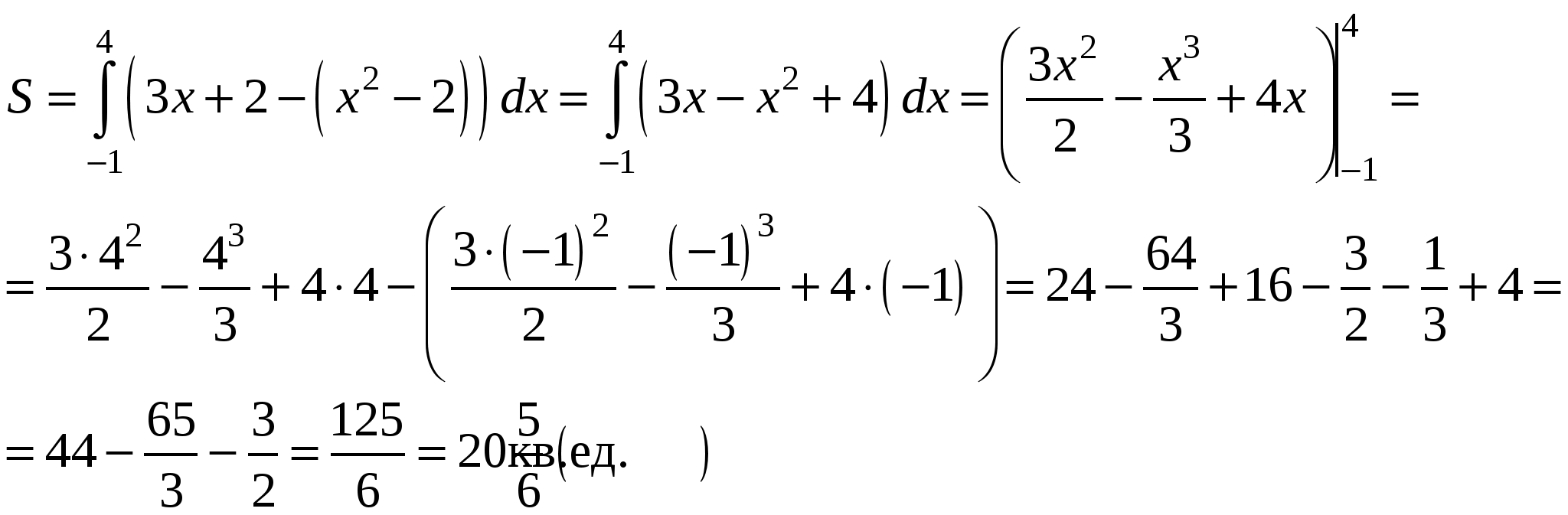
Вычисление объемов тел вращения
Если тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной кривой 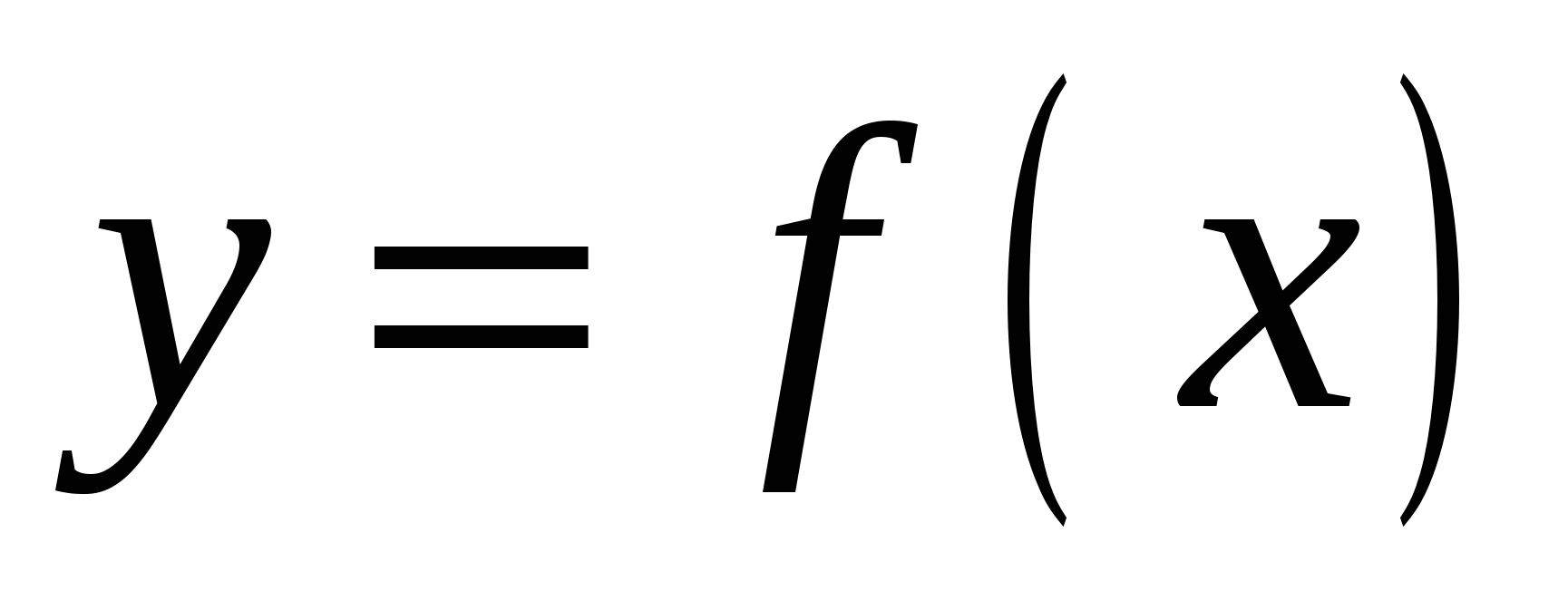 , осью OX и прямыми
, осью OX и прямыми 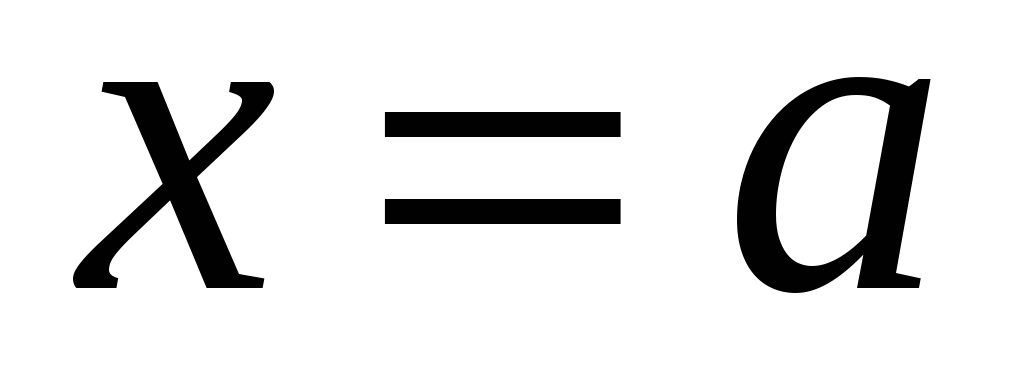 ,
, 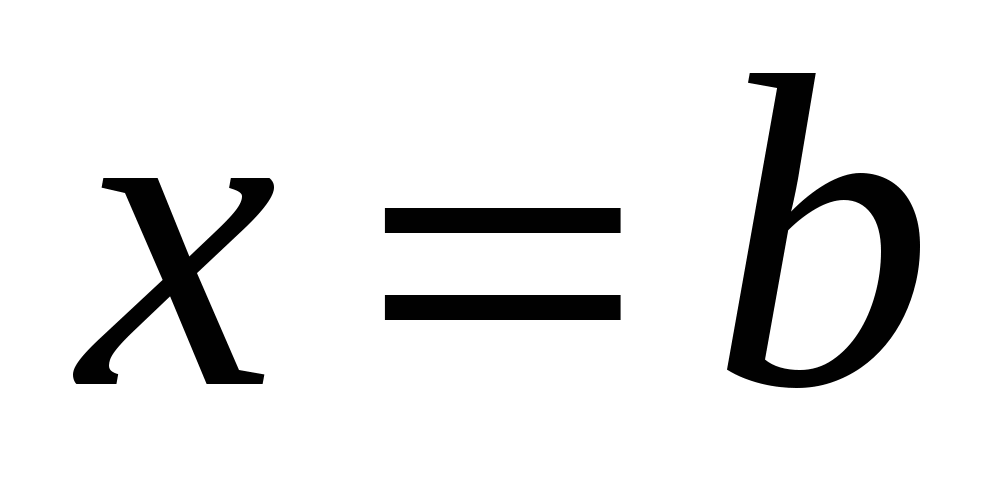 (рис. 5), то его объем вычисляется по формуле:
(рис. 5), то его объем вычисляется по формуле:
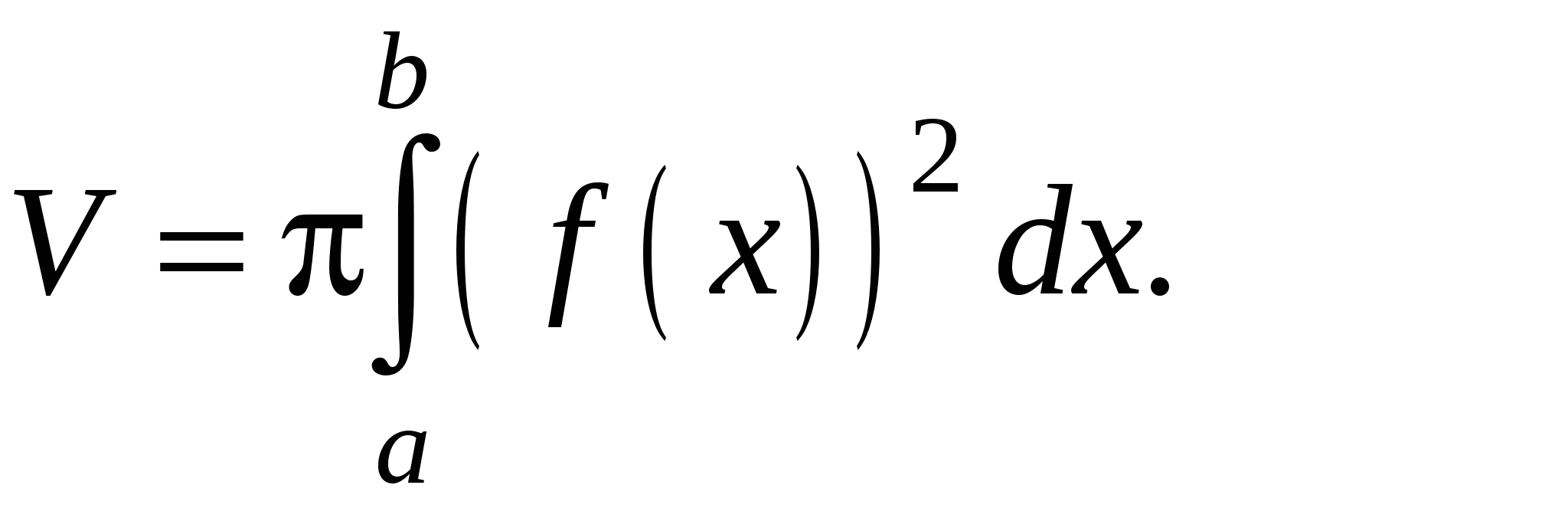 (12)
(12)
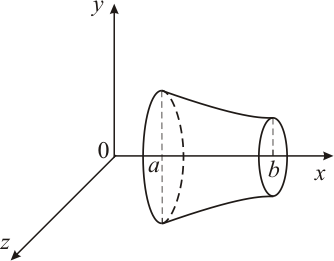
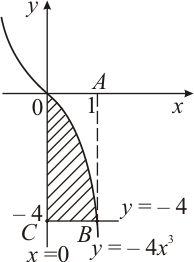
Рис. 5
Рис. 6
Пример. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями: 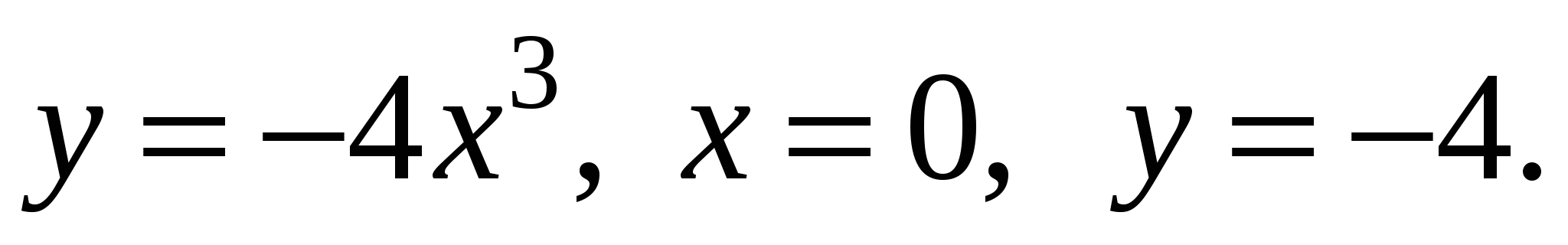
Решение. Построим криволинейную трапецию, вращением которой получается тело вращения (рис. 6).
Чтобы получить объем тела вращения из объема 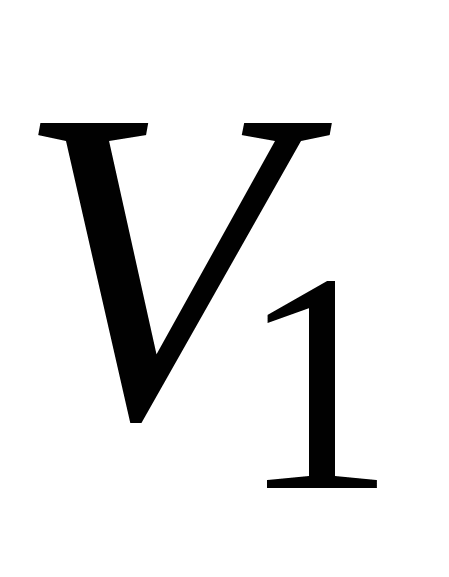 тела, полученного вращением фигуры ОАВС, вычтем объем
тела, полученного вращением фигуры ОАВС, вычтем объем 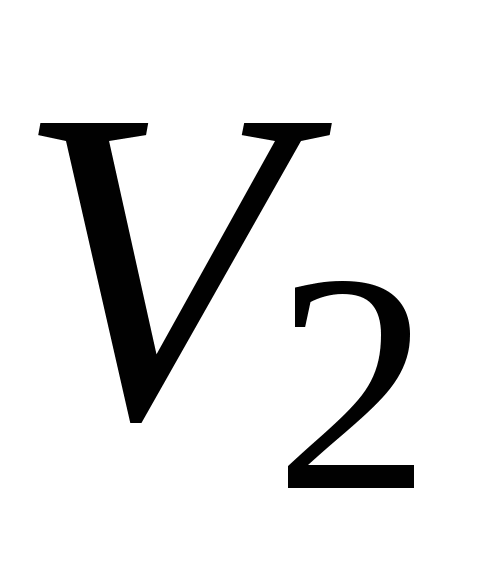 тела, полученного вращением фигуры ОАВ. Тогда искомый объем
тела, полученного вращением фигуры ОАВ. Тогда искомый объем 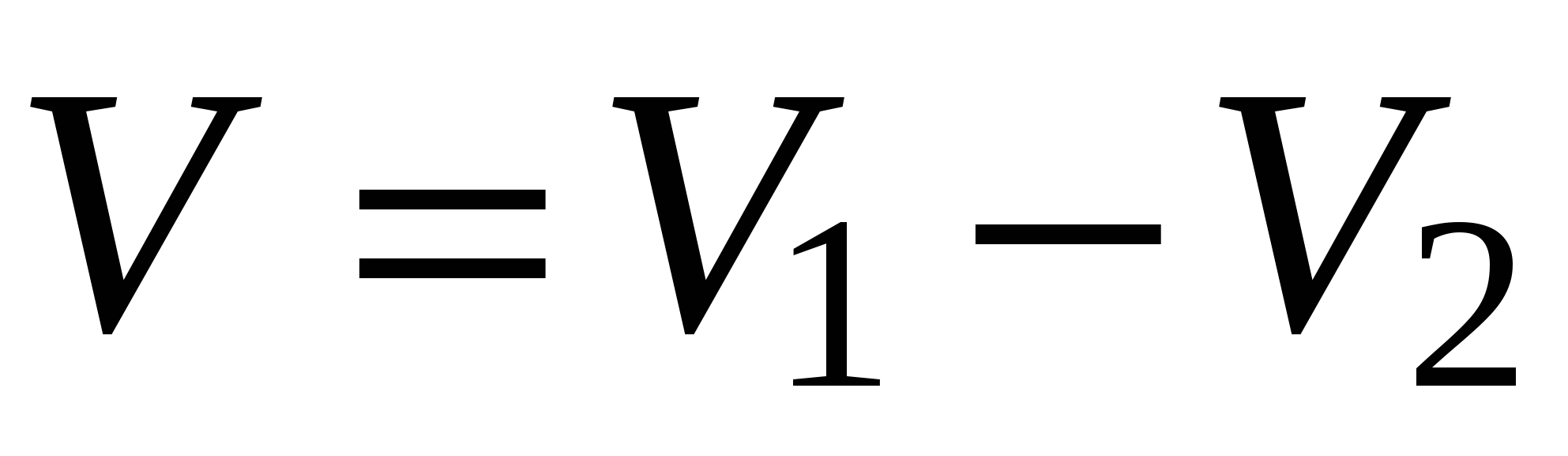 . По формуле (12) найдем
. По формуле (12) найдем 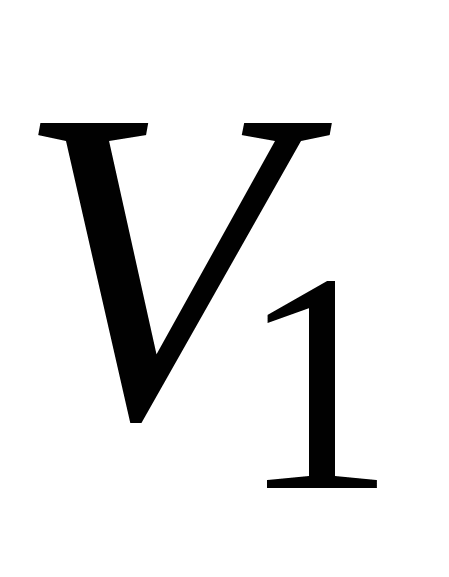 и
и 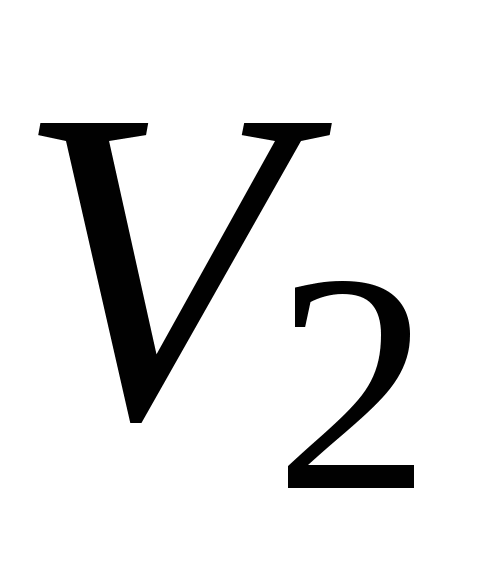 :
: 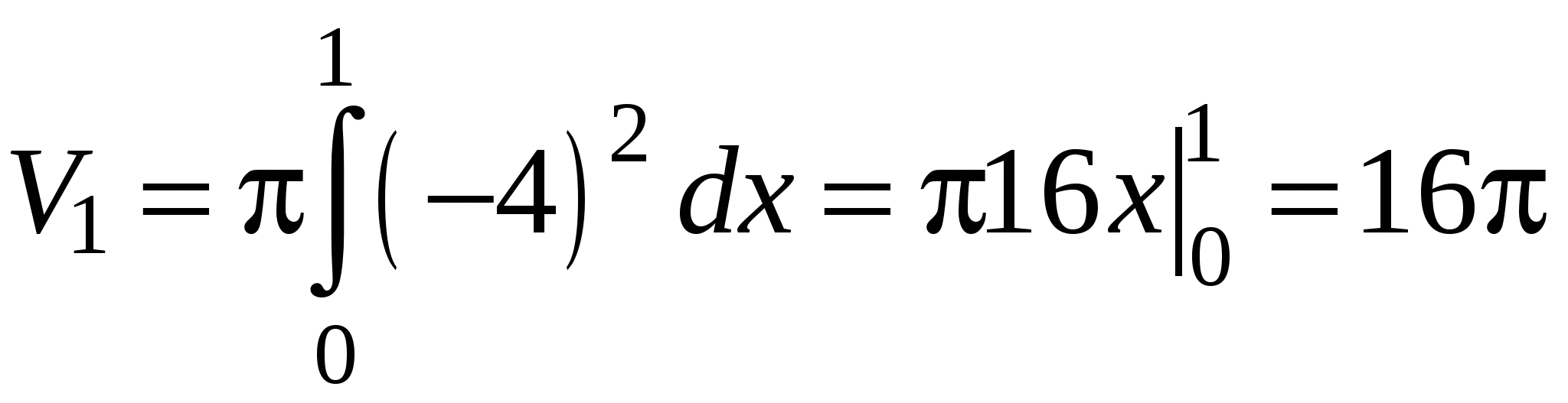 (ед. объема);
(ед. объема);
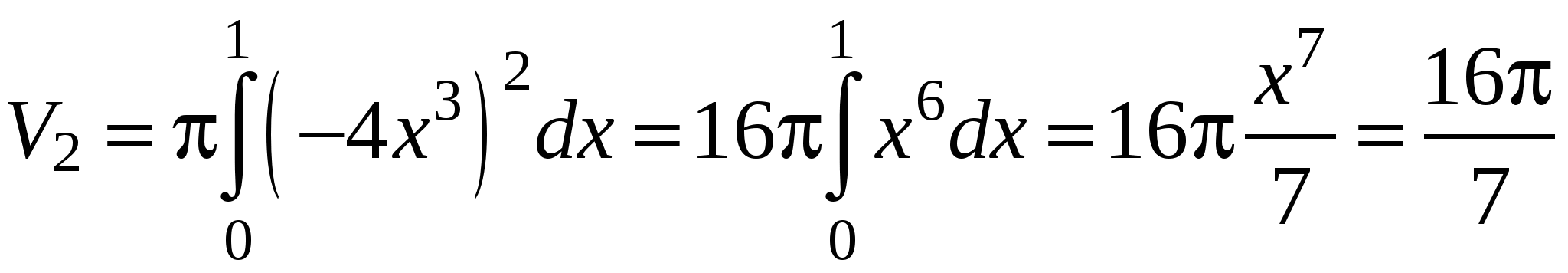 (ед. объема);
(ед. объема);
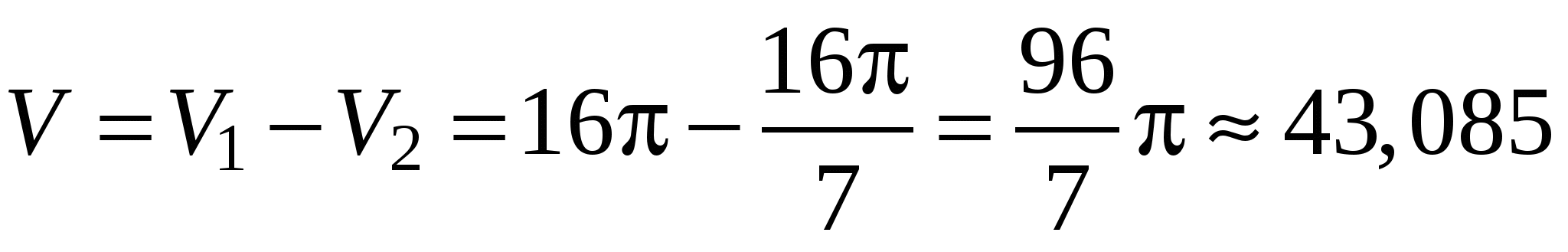 (ед. объема).
(ед. объема).
Содержание практической работы
Задание 1. Найти площадь фигуры, ограниченной линиями.
1) 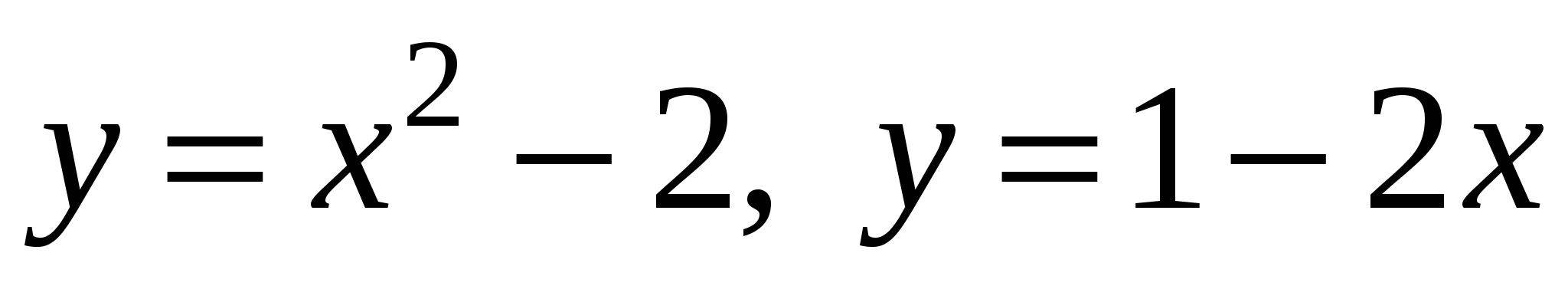
2) 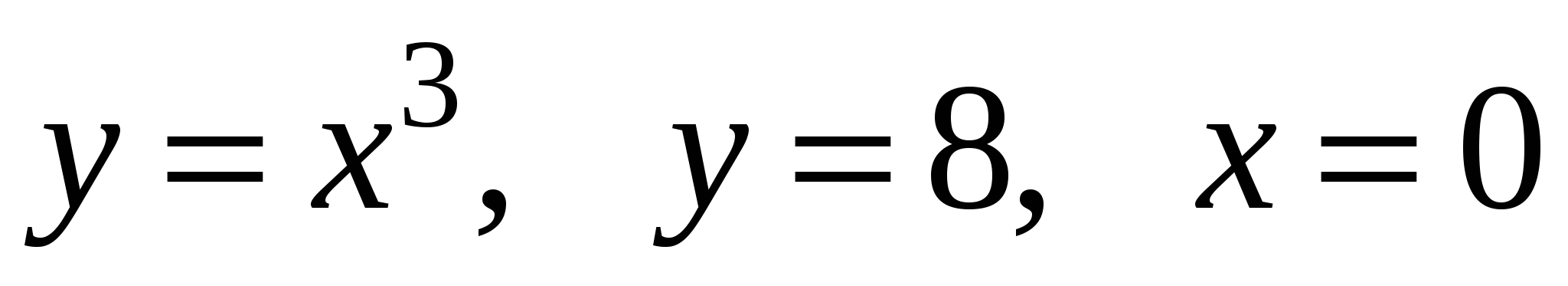
3) 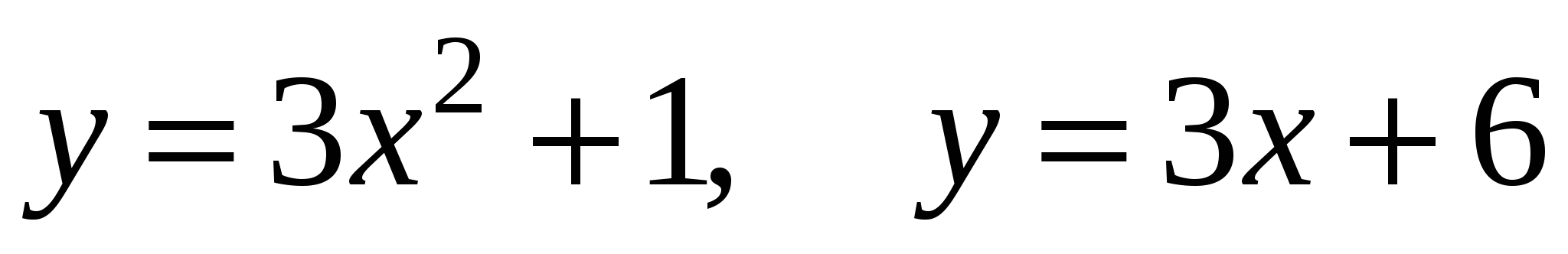
4) 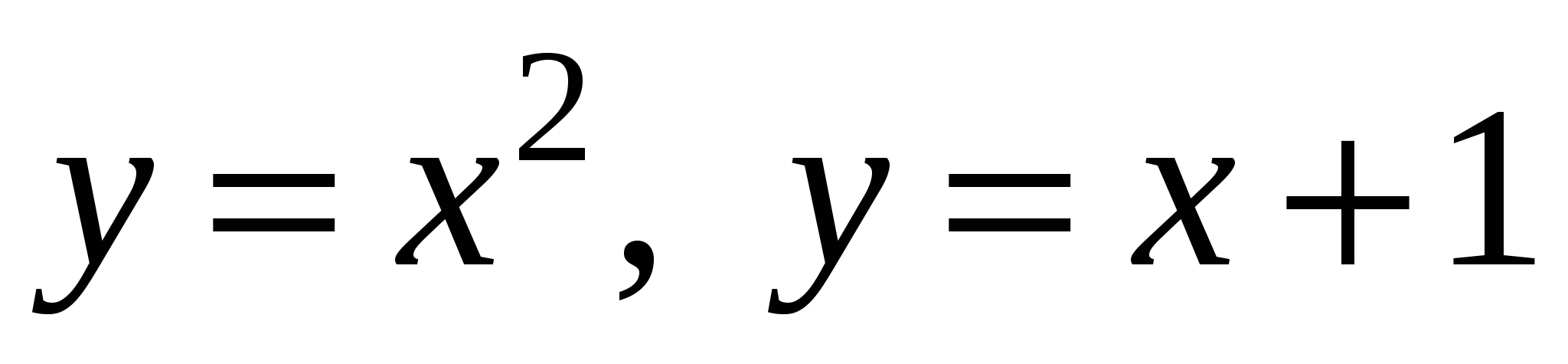
5) 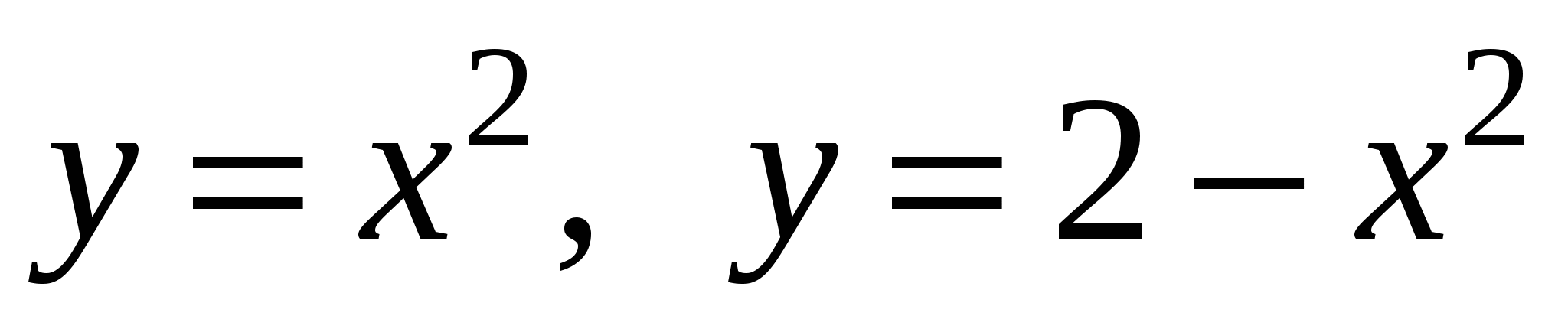
6) 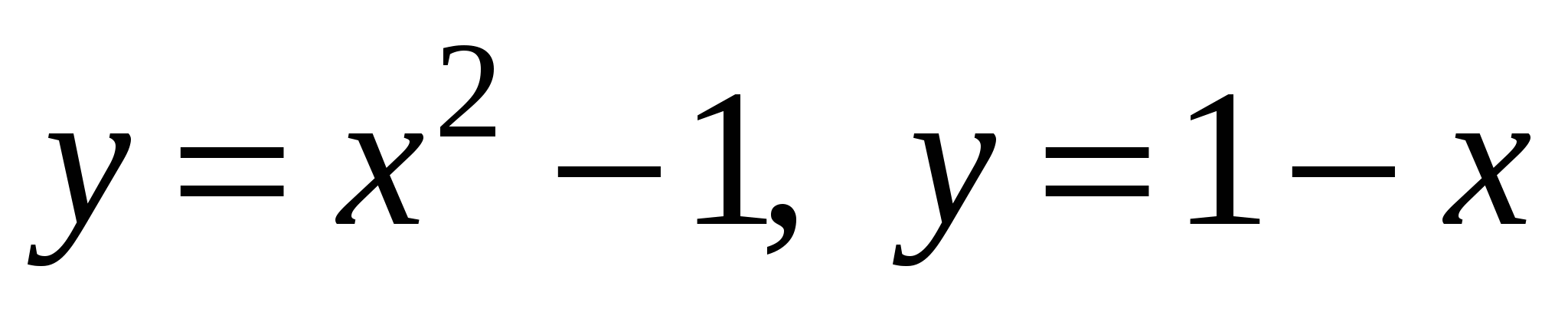
Задание 2. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями.
1) 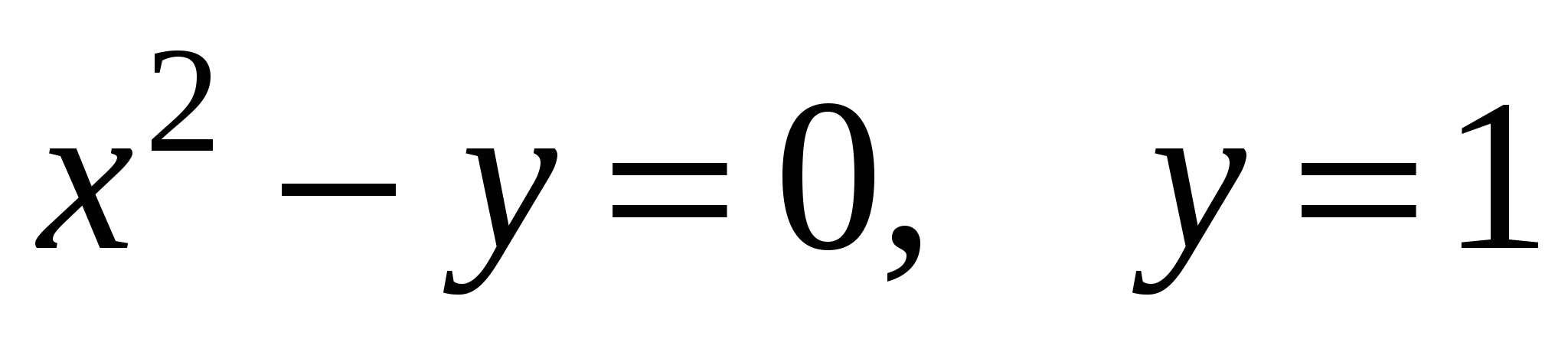
2) 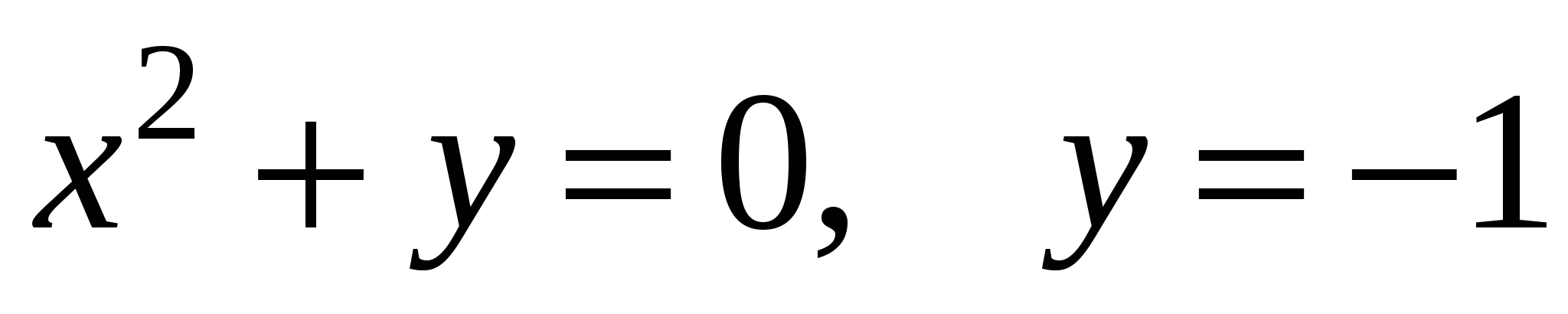
3) 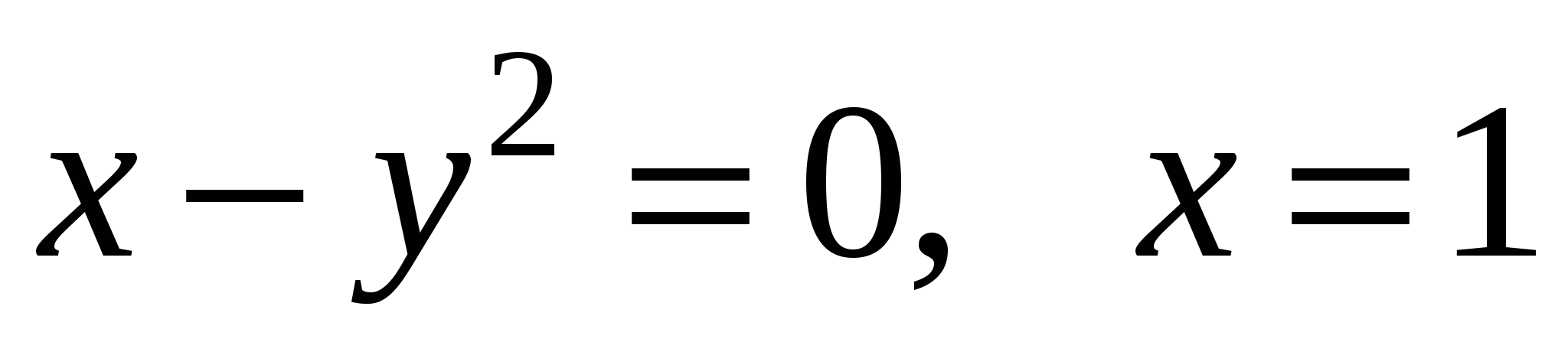
4) 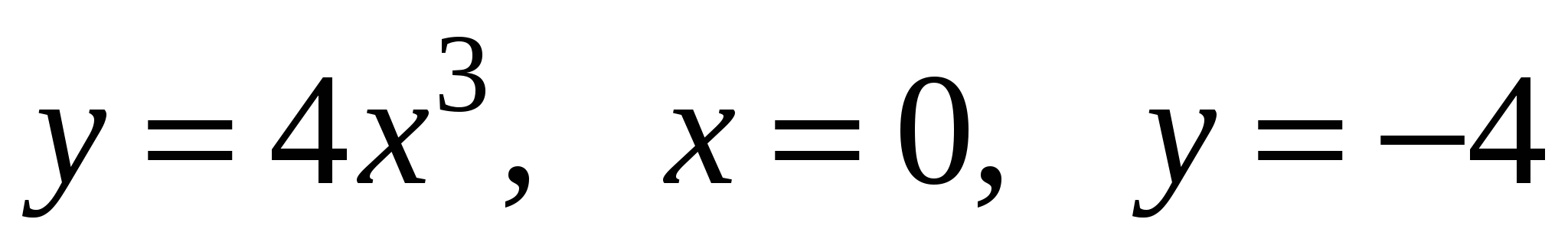
5) 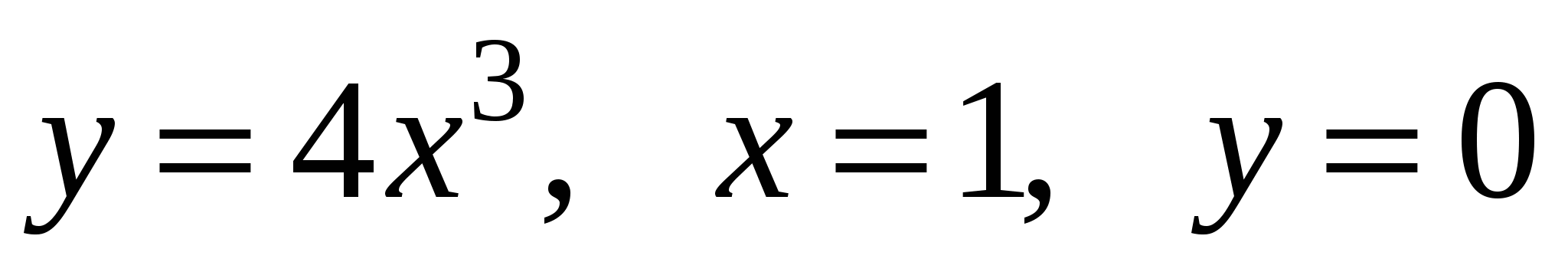
6) 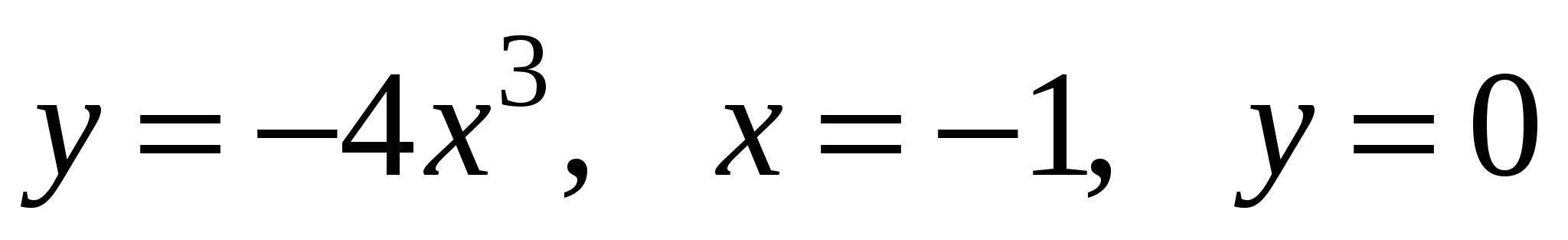
Рекомендуемая литература
Основные источники
-
Григорьев С.Г., Иволгина С.В. Математика. - М.: Образовательно-издательский центр «Академия», 2011
-
Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике. - М: Издательский центр «Академия», 2011
-
Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2009
Дополнительные источники
-
Высшая математика для экономистов. Под ред. Н.Ш. Кремера. - М.: ЮНИТИ, 2007
-
Математика и информатика: учебник для студ. учреждений сред. проф. образования / Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В./ - М.: Издательский центр «Академия», 2009


