- Преподавателю
- Математика
- Статья «Линейные однородные уравнения второго порядка и их свойства»
Статья «Линейные однородные уравнения второго порядка и их свойства»
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Игошкина В.А. |
| Дата | 20.01.2014 |
| Формат | docx |
| Изображения | Есть |
Линейные однородные уравнения второго порядка и их свойства
Теория линейных дифференциальных уравнений является самый простой и разработанной частью теории дифференциальных уравнений, и именно линейные уравнения наиболее часто встречаются в приложениях. Мы будем рассматривать линейные уравнения любого порядка и начнем с уравнений второго порядка.
Линейным однородным уравнением второго порядка называется уравнение вида
P(y)=y"+p(x)y'+q(x)y, (1.1)
где через P(у) мы для краткости обозначили левую часть. Из линейности выражения P(у) относительно функции у и ее производных вытекает, что при произвольных постоянных C, C1 и C2:
P(Cу) = СР(у), Р(С1y1+C2y2) = С1 Р(у1) + С2 Р(у2).
Если y=y1 есть решение уравнения, то есть P(y1)=0, то, очевидно, P(Cy1)=0,то есть и у = Су1 есть также решение уравнения. Точно же, если у1 и у2 суть решения, то
y=C1y1+C2y2, (1.2)
eсть также решение при произвольных постоянных С1 и C2 то есть решения линейного однородного уравнения (1.1) можно умножать на произвольные постоянные и складывать, после чего опять получается решение. Очевидно, это же свойство имеет место и для линейного однородного уравнения любого порядка. Теорема существования и единственности для уравнения (1.1) формулируется особенно просто, как это мы покажем в конце этой главы: если p(x) и q(x) - непрерывные функции в некотором конечном замкнутом промежутке I (a≤x≤b) - любое значение из этого промежутка, то имеется одно и только одно решение уравнения (1.1), удовлетворяющее начальным условиям
y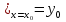 y
y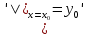 (1.3)
(1.3)
где y0 и y0' - любые заданные числа, и это решение существует на всем промежутке I.
Если фиксировать x0 и придавать y0 и y'0 всевозможные численные значения, то указанные в теореме решения исчерпывают все решения уравнения (1.1). Во всех этих решениях функции у(x), у'(x) и y"(x) непрерывны вплоть до концов промежутка a≤x≤b и предельные значения у' (x) и y'' (x) при x= а суть производные у' (a+0), у" (a+0) - справа, а при x= b производные слева у' (b-0), у"(b-0). В дальнейшем мы в аргументах не будем писать ± 0. Из формулированной выше теоремы непосредственно следует совершенно аналогичное утверждение и для открытого промежутка a<x<b, который может быть как конечным, так и бесконечным. Мы будем всегда рассматривать решения уравнения (1.1) на промежутке непрерывности коэффициентов p(x) и q(x).
Уравнение (1.1) имеет очевидное решение у ≡ 0 (нулевое решение). Ему соответствует y0 = y'0 = 0. В дальнейшем, говоря о решениях уравнения (1.1), мы будем подразумевать, что эти решения отличны от нулевого решения.
Введем одно новое понятие, которое нам понадобится в дальнейшем. Пусть y1 и y2 - два решения уравнения (1.1).Рассмотрим следующее выражение, составленное из них:
∆(y1,y2)=y1y'2-y2y'1. (1.4)
Оно называется определителем Вронского решений y1 и y2 для него имеет место следующая замечательная формула:
∆(y1,y2)=∆0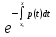 , (1.5)
, (1.5)
где ∆0- постоянная, равная, очевидно, значению ∆(y1,y2) при x=x0. Для доказательства вычисляем производную
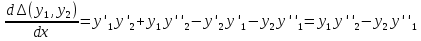 .
.
Принимая во внимание, что y1 и y2 суть решения уравнения (1.1), можем написать
 ,
, 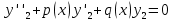 .
.
Умножая первое уравнение на (-y2) второе на y1 и складывая почленно, получим
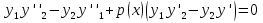
и, следовательно,
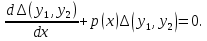
Это есть линейное однородное уравнение относительно 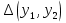 . Из этой формулы непосредственно следует, что определитель
. Из этой формулы непосредственно следует, что определитель 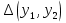 или тождественно на промежутке I равен нулю, если постоянная ∆0 равна нулю или не равен нулю ни при одном x из I, так как показательная функция в нуль не обращается. Напомним, что p (x) считается непрерывной на I функцией.
или тождественно на промежутке I равен нулю, если постоянная ∆0 равна нулю или не равен нулю ни при одном x из I, так как показательная функция в нуль не обращается. Напомним, что p (x) считается непрерывной на I функцией.
Два решения y1 и y2 уравнения (1.1), отличные от нулевого, называются линейно независимыми, если не существует тождественного относительно x на промежутке I соотношения
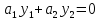 (1.6)
(1.6)
с постоянными коэффициентами a1 и a2, отличными от нуля. Если такое соотношение имеется, то решения y1 и y2 называются линейно зависимыми. Отметим, что если один из коэффициентов, например a20, то из (1.3) следует y2≡0, а это противоречит тому что оба решения отличны от нулевого. Отсюда следует естественность требования того, что оба коэффициента отличны от нуля. Линейная зависимость решений y1 и y2 , выражаемая тождеством (1.6), равносильна, очевидно, тому, что одно из решений отличается от другого лишь постоянным множителем у2=Cy1, где постоянная C отлична от нуля. Продифференцируем это соотношение: у'2 = Cy'1 из двух соотношений
y2(x) = Cy1(x), y'2(x) = Cy'1(x),
непосредственно следует, что определитель Вронского (y1,y2) двух линейно зависимых решений тождественно равен нулю. Положим теперь наоборот, что определитель Вронского (y1,y2) тождественно равен нулю, и покажем, что при этом решения у1(x) и y2(x) -линейно зависимы. Фиксируем такое значение x=x0, при котором y1(x0)0, и напишем два уравнения, содержащие постоянную C, обозначая через y10, y20, y10,y20 значения y1, y2 и их производных при x=x0
y20=Cy10, y20=C y10
Из первого уравнения C=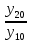 и, подставляя это во второе уравнение,
и, подставляя это во второе уравнение,
убедимся, что оно также удовлетворено в силу того, что (y1,y2) равно 0 тождественно, и в частности при x=x0 . Таким образом, решение y(x)=y2(x)-Cy1(x) уравнения (1.1) удовлетворяет начальным условиям (3) при y0= 0 и y0=0, т. е. у (x) есть нулевое решение и следует, что y2(x)-Cy1(x)0 или y2(x)=Cy1(x). Мы приходим, таким образом, к следующему заключению: равенство нулю определителя Вронского (y1,y2) является необходимым и достаточным условием линейной зависимости решений y1 и y2 т. е. два решения y1 и y2 уравнения (1.1) линейно независимы тогда и только тогда, когда их определитель Вронского отличен от нуля.
Отметим еще следующую очевидную формулу для производной от частного двух решений:
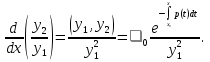 (1.7)
(1.7)
Она, очевидно, теряет смысл в тех точках, где y1 обращается в нуль.
Покажем теперь, что если y1 и у2 - линейно независимых решения уравнения (1.1), то при надлежащем выборе постоянных C1 и С2 формула (1.2) дает нам решение уравнения (1.1), удовлетворяющее любым наперед заданным начальным условиям
y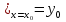 , y
, y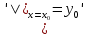 (1.8)
(1.8)
Опять через y10,y20,y10, y20 обозначим значения y1,y2 и их первых производных при x = x0. Чтобы удовлетворить начальным условиям (1.8), надо определить C1 и C2 в формуле (1.2) из системы уравнений
C1 y10+ C2y20= y0, C1 y10+ C2 y20= y0.
Из линейной независимости y 1 и y2 вытекает, что
0= y10 y20- y20 y100,
и следовательно, из написанной системы мы получим определенные значения C1 и C2, что доказывает наше утверждение.
Но в силу теоремы существования и единственности всякое решение уравнения (1.1) вполне определяется своими начальными условиями, и мы можем поэтому высказать следующее предложение: если y1 и y2 -два линейно независимых решения уравнения (1.1), то формула (1.2) дает все решения этого уравнения.
Таким образом, задача интегрирования (1.1) приводится к нахождению его двух линейно независимых решений. Пусть у1 - одно из решений этого уравнения и у2 - какое-либо его решение. Интегрируя соотношение (1.7), получим
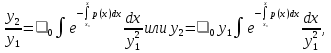 (1.9)
(1.9)
т. е. если известно одно частное решение уравнения (1.1), то второе его решение может быть получено по формуле (1.9), где 0 - постоянная, которую можно положить и равной единице.


