- Преподавателю
- Математика
- Статья Подготовка к ГИА по алгебре (из опыта работы)
Статья Подготовка к ГИА по алгебре (из опыта работы)
| Раздел | Математика |
| Класс | - |
| Тип | Статьи |
| Автор | Мищенко Е.В. |
| Дата | 08.03.2016 |
| Формат | docx |
| Изображения | Есть |
Подготовка к ГИА по алгебре (из опыта работы)
Успешные результаты ГИА обеспечиваются целостной моделью математического образования, сложившейся в нашем образовательном учреждении. Именно она создает условия для последовательной системной подготовки учащихся к новой форме итоговой аттестации, начиная с первого класса.
Мне хотелось бы поделиться опытом по подготовке учеников девятых классов к ГИА. Может что-то с вашей точки зрения покажется неэффективными, а может быть что-то для вас окажется и полезным. Система работы по подготовке к ГИА по математике в 9 классе включает следующие компоненты:
1. Изменение тематического планирования. Составить планирование таким образом, чтобы осталось достаточное число часов на повторение всего учебного материала. Включить в изучение текущего учебного материала задания, соответствующие экзаменационным заданиям.
-
Уравнения и неравенства.
-
Текстовые задачи.
-
Прогрессии: арифметическая и геометрическая.
-
Преобразование выражений. Формулы сокращенного умножения. Рациональные дроби.
-
Элементы комбинаторики и теории вероятностей.
-
Треугольники. Многоугольники. Окружности.
2. В содержание текущего контроля включать экзаменационные задачи.
В контрольные и тестовые работы включаю задания из открытого банка задач. Это дает возможность лучше подготовить учащихся к экзамену. Обязательно добиваюсь того, чтобы ребята отработали задания, в которых допустили ошибки.
3. Изменить систему контроля над уровнем знаний учащихся по математике. Использовать индивидуальный и дифференцированный подход, сконцентрировать усилия на формирование у слабых учащихся базовых математических умений, а у сильных учащихся развивать умения решать задачи повышенного и высокого уровня сложности.
4. Итоговое повторение строится исключительно на отработке умений и навыков, требующихся для получения положительной отметки на экзамене.
-
алгебраические выражения;
-
задачи на проценты;
-
чтение графиков реальных зависимостей, таблиц и диаграмм;
-
функции и их графики;
-
уравнения, системы уравнений; неравенства, системы неравенств;
-
текстовые задачи;
-
вероятность и статистика.
-
решение геометрических задач.
Повторение провожу как на уроках, так и после уроков через системные консультации. На уроке, создав микроклимат в классе, отрабатываю алгоритмизацию действий; удерживая интерес учащихся к предмету, формирую мотивацию к обучению. Учащиеся хорошо усваивают обязательный минимум материала по математике, если пользуются методическими приемами:
- решение задач по образцу;
- рассмотрение различных подходов к решению одной и той же задачи;
- составление опорных схем и применение других наглядных средств обучения;
- правильный подбор тематики и уровня задач, придание им занимательной формы;
На уроках использую карточки-консультанты, с помощью которых повторять изученный материал. В них содержатся все условные моменты изучаемой темы, а так же алгоритм решения заданий.
КАРТОЧКА-КОНСУЛЬТАНТ ПО ТЕМЕ «СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ»
Система линейных уравнений:
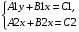 :
:
Способы ее решения
Графический способ
Способ подстановки
Способ сложения
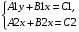
1. В каждом уравнении выразить у через х
2. Построить график функции каждого уравнения
3. Определить координаты точки пересечения
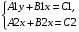
1. Из какого-либо уравнения выразить одну переменную через другую.
2. Подставить полученные выражения и решить его.
3. Подставить найденное значение переменной и вычислить значение второй переменной.
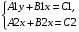
1. Уравнять модули коэффициентов какой-либо переменной.
2. Сложить ( вычесть) получено уравнения системы.
3. Составить новую систему: одно уравнение новое: другое одно из старых.
4. Решить новое уравнение и найти значение одной переменной.
5. Подставить значение найденной переменной в старое уравнение и найти значение другой переменной.
Ответ: х =_______ ; у =_______
В работе со слабоуспевающими детьми использую целый арсенал карточек , которые позволяют отработать алгоритм разнообразных действий и математических операций.
Задания по образцу.
1 выражение
2 выражение
Произведение разности этих выражений на их сумму
Разность квадратов этих выражений
с
3у
0,5 х
ав
с
5в
2у
2с
( с − х) (с + х)
(3у - 5в) (3у + 5в)
с2 − х2
9у2 - 25в2
Произведение разности и суммы двух выражений.
Учащиеся должны выполнять задания с пропусками. Пропускаются ключевые слова, правильное запоминание которых свидетельствует о понимании материала.
Задания с пропусками.
Квадратные корни.
-
При любом а, при котором выражение
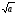 имеет смысл, верно равенство (
имеет смысл, верно равенство (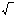 )2 = ___.
)2 = ___. -
Арифметическим квадратным корнем из числа а называется _____________ , квадрат которого равен ______.
-
Выражение
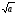 имеет смысл при __________ .
имеет смысл при __________ . -
Корень из произведения неотрицательных множителей равен_____________ корней из этих множителей.
-
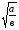 =
= 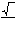 , если а ____; в>0.
, если а ____; в>0.
Использовать тематические таблицы по разным разделам школьного курса. В каждой таблице кратко изложена теория конкретного вопроса (определения, теоремы, следствия, формулы); приводятся рисунки, графики, а так же примеры решения наиболее принципиальных задач.
Таблицы помогают систематизировать знания, быстро и полно повторить основные моменты той или иной темы.
Таблица. Квадратные корни.
Определение арифметического корня
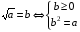
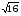 = 4, т.к. 4 > 0, 42 = 16;
= 4, т.к. 4 > 0, 42 = 16;
 ¹ 7, т.к. 72 ¹ 25;
¹ 7, т.к. 72 ¹ 25;
 ¹ −5, т.к. −5 < 0;
¹ −5, т.к. −5 < 0;
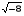 не определён.
не определён.

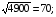
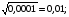
2<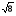 < 3;
< 3;
0,8<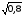 < 0,9.
< 0,9.
Тождества
Основные свойства
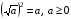
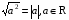
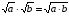
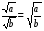
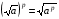
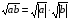
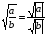
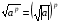
Вынесение из-под корня
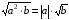 , b ³ 0
, b ³ 0
Внесение под корень
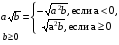
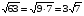 ;
;
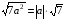 ;
;
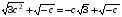 .
.
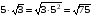 ;
;
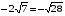 ;
;
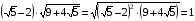 ;
;
Работу учащихся необходимо постоянно контролировать, консультируя их по заданиям, в решении которых они испытывают трудности.
Такая система подготовки позволяет учащимся успешно сдать экзамен, показать высокие результаты.


