- Преподавателю
- Математика
- Некоторые законы распределения случайных величин
Некоторые законы распределения случайных величин
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Рыщанова С.М. |
| Дата | 06.05.2014 |
| Формат | rar |
| Изображения | Есть |
Некоторые законы распределения непрерывных случайных величин
Многие случайные величины, такие как ошибки при измерениях, величины износа деталей некоторых механизмов, отклонения точки попадания от некоторого центра при стрельбе, отклонения размеров от номинальных у животных, растений и т.п., подчиняются нормальному распределению. Нормальный закон распределения вероятностей имеет очень важное значение и широкое распространение.
Широкое распространение нормального распределения объясняется тем, что оно проявляется там, где случайная величина представлена суммой большого числа независимых случайных величин (что чаще всего встречается на практике), влияние каждой из которых на всю сумму не представляется существенным.
Нормальная (гауссовская) случайная величина является предельной для многих случайных величин.
В теории надежности нормальное распределение применяется при оценке надежности элементов, подверженных действию старения и изнашивания, а также разрегулировки, т.е. при оценке постепенных отказов.
Нормальным называется распределение плотностей вероятностей непрерывных случайных величин, которое имеет вид:
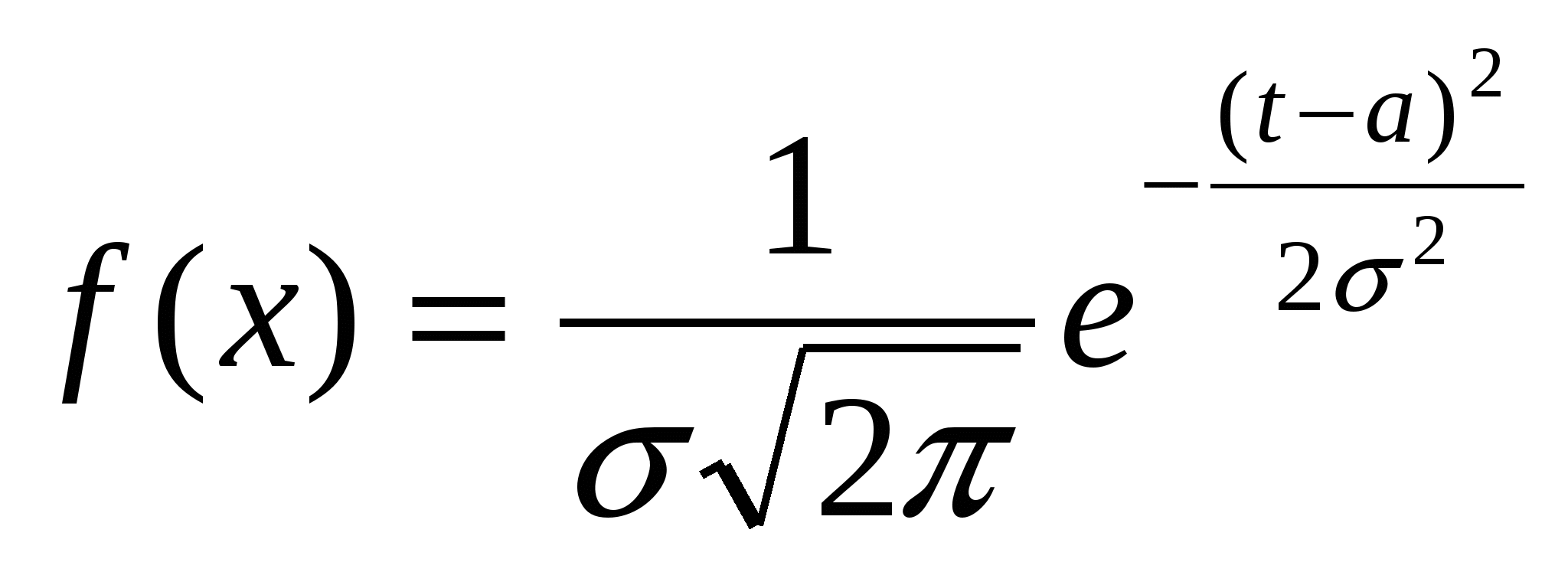
Функция распределения нормального закона имеет вид: 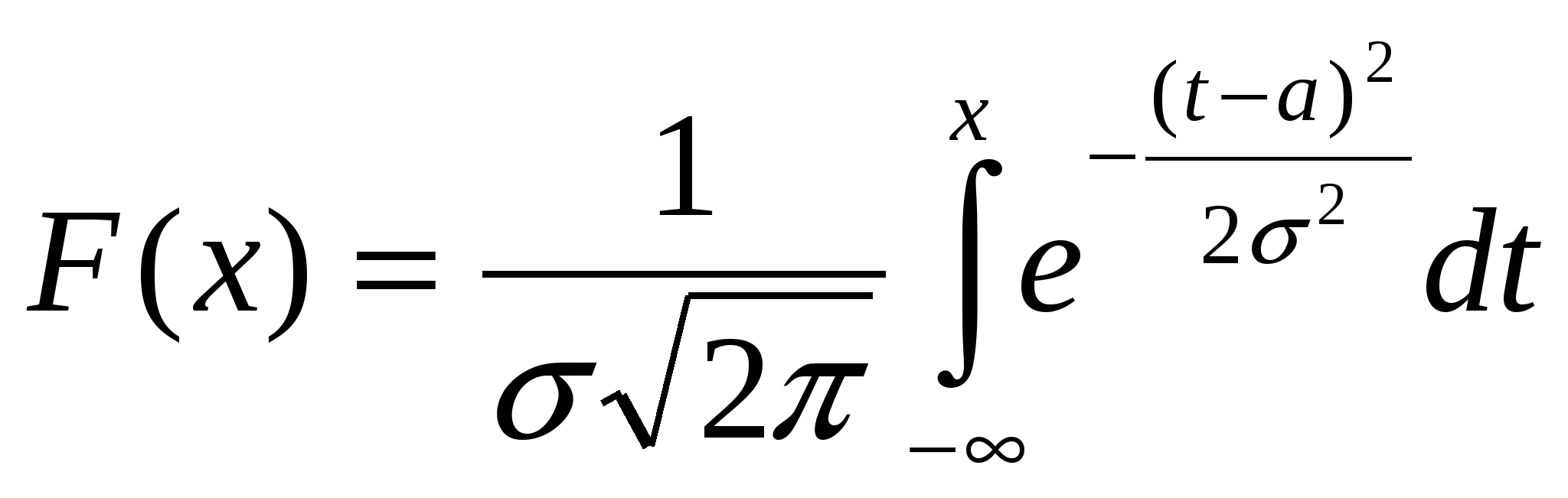
Кривая нормального распределения f(x) имеет колоколообразную форму и называется нормальной кривой или кривой Гаусса. При изменении параметра изменяется форма нормальной кривой. Изменение параметра а (математического ожидания) влияет на положение (увеличение или уменьшение а сдвигает график вправо или влево). Нормальная кривая в точках х = a- и х = a+ имеет перегиб. График функции f(x) симметричен относительно прямой х = а.
Нормальный закон распределения СВ с параметрами а=0 и 2=1 называется стандартным или нормированным, а соответствующая нормальная кривая стандартной или нормированной
Математическое ожидание, дисперсия и среднее квадратическое отклонение:
M(X) = a D(X) = 2 (X) =
Для вычисления вероятности попадания случайной величины в интервал (;) можно воспользоваться функцией Лапласа:
P( Х ) = Ф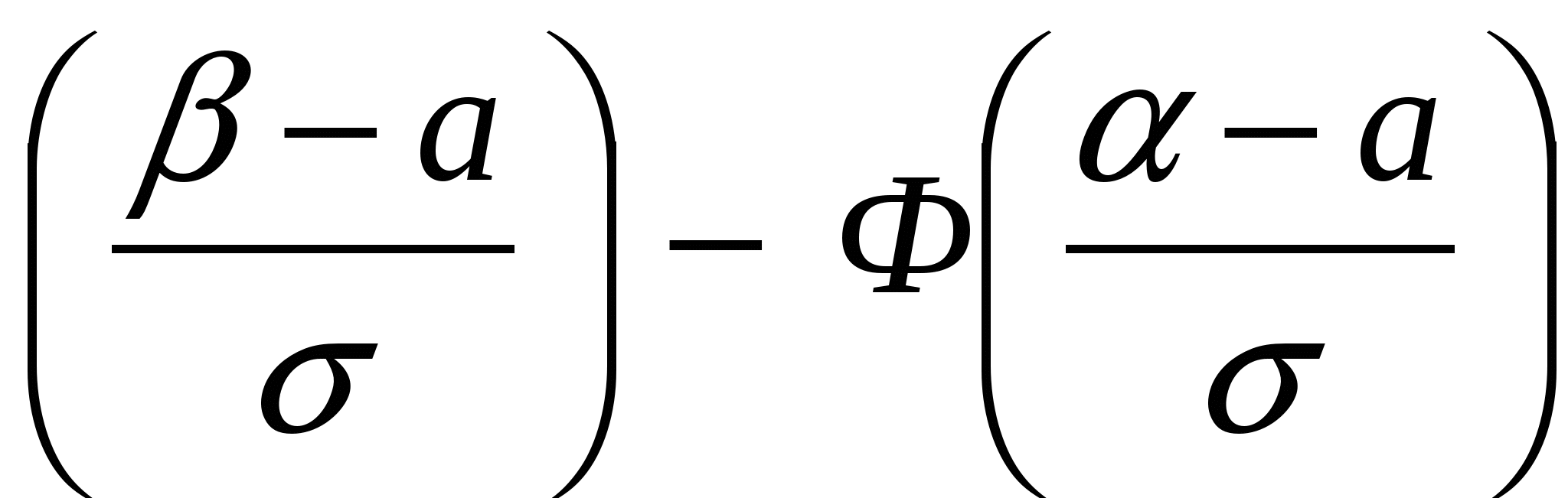 ,
,
где Ф(х) =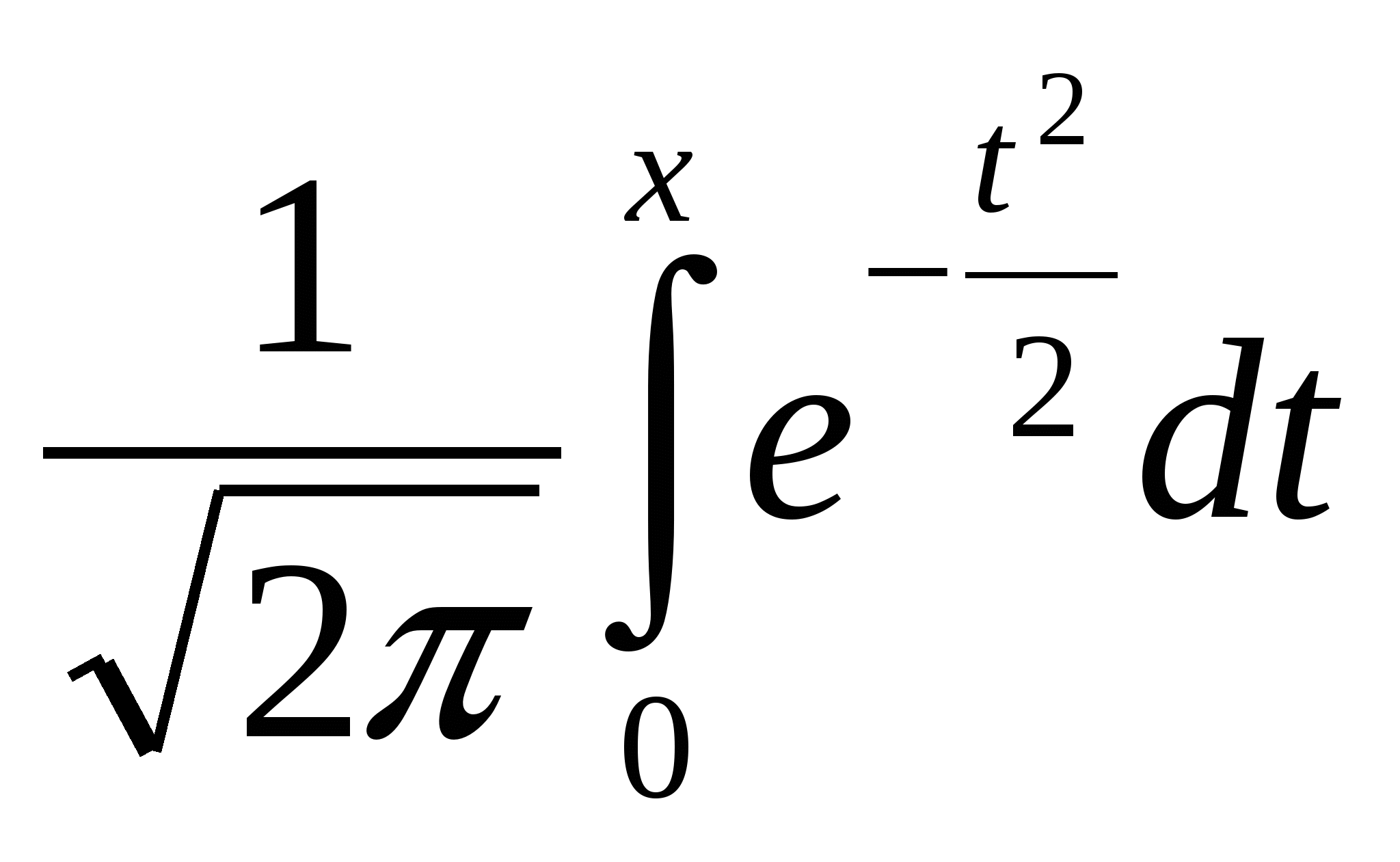 -функция Лапласа (функция Лапласа нечетная, ее значения приведены в таблице)
-функция Лапласа (функция Лапласа нечетная, ее значения приведены в таблице)
Вероятность того, что непрерывная случайная величина отклонится от своего среднего значения не более чем на заданное положительное число , равна:
Р(Х-а ) = 2Ф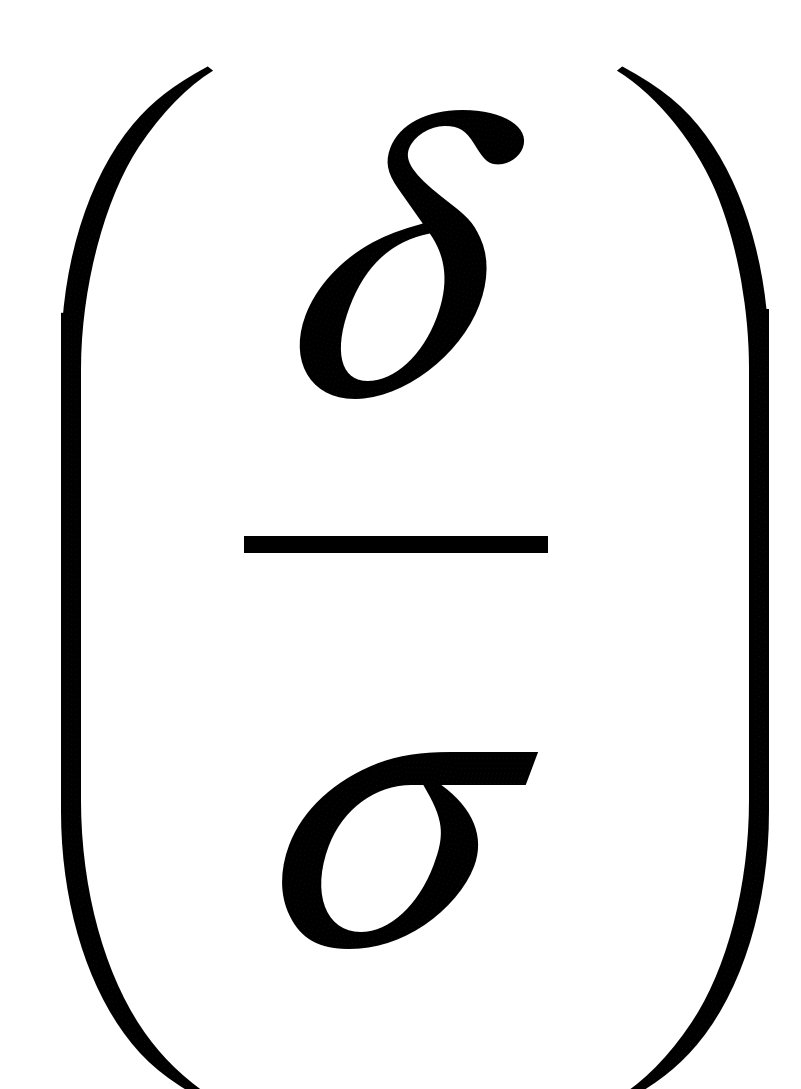
Пример. Затаривание мешков с мукой производится без систематических ошибок. Случайные ошибки подчинены нормальному закону со среднеквадратическим отклонением = 200г. Найти вероятность того, что затаривание будет проведено с ошибкой, не превосходящей по абсолютной величине 100г.
В задаче рассматривается случайная величина-ошибка взвешивания, то есть разность между случайным значением веса мешка муки и его нормативным значением а - математическим ожиданием.
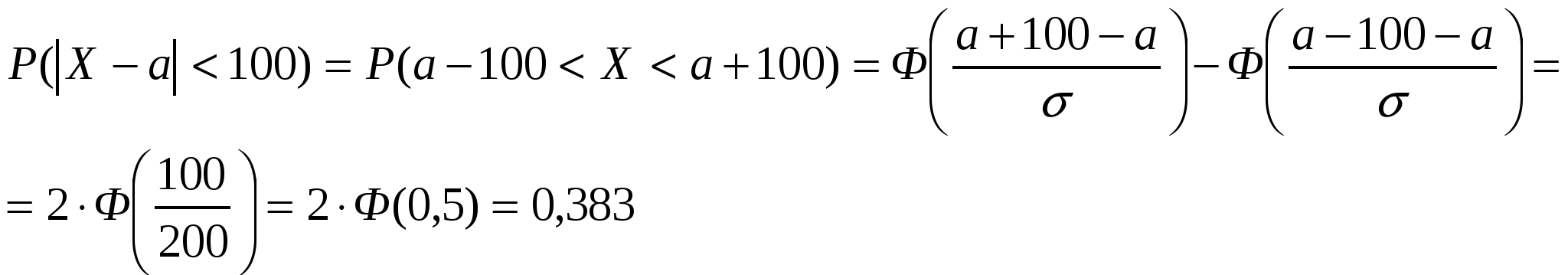
Правило трёх сигм (3): P(X-a 3) = 0.9973 1
2 (хи -квадрат) распределение
Пусть Х1,Х2,Х3, .. Хr распределены с параметрами М(Хi) = 0 и (Xi) =1 (такие величины называются нормированными).
Тогда сумма квадратов этих величин распределена по закону 2 (хи-квадрат) с k степенями свободы:
2 = 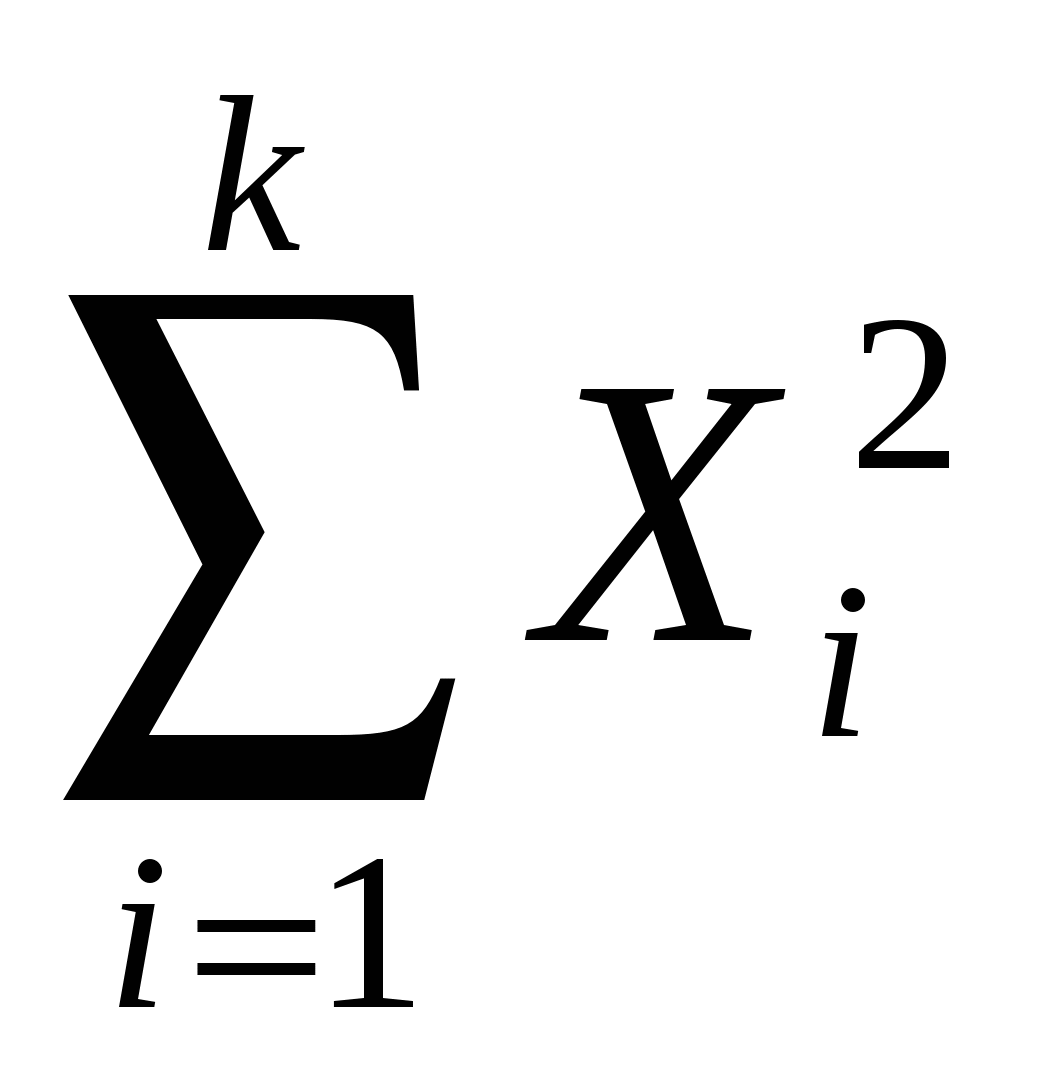
Параметр k называется числом степеней свободы и только от k зависит распределение 2.
Плотность вероятности 2 распределения имеет вид:
f(x) =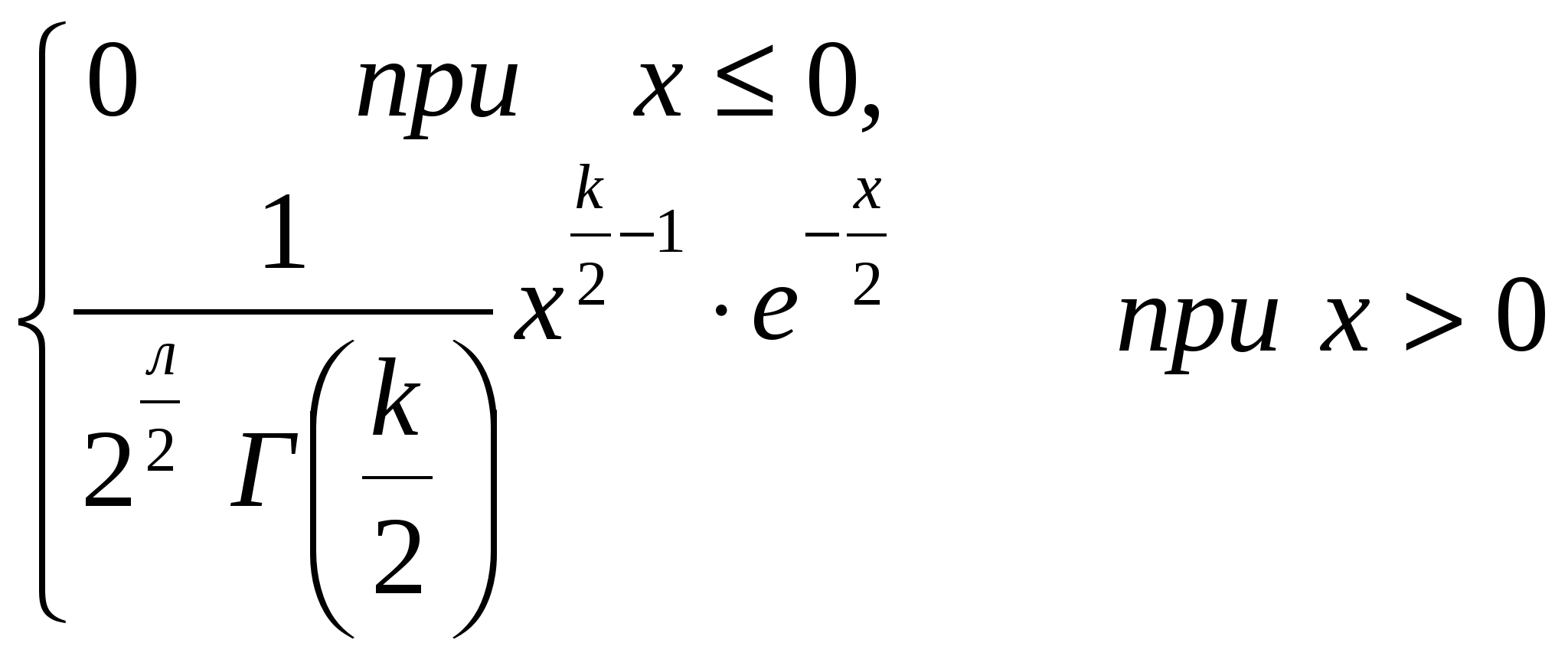
где Г(k/2) - гамма функция.
C увеличением числа степеней свободы распределение медленно приближается к нормальному. При k>30 кривая хи-квадрат сливается с кривой нормального распределения.
Для хи-квадрат распределения:
М(2) = k D(2) = 2k (2) = 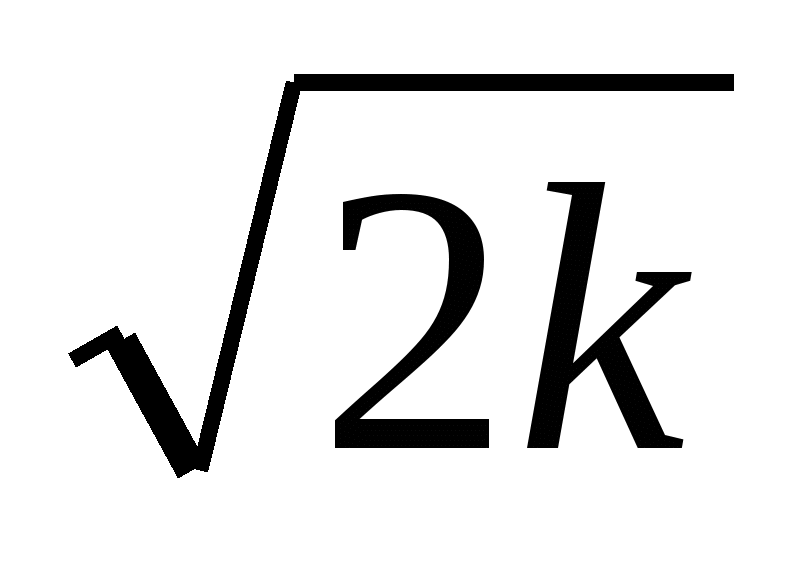
Равномерное непрерывное распределение
Непрерывная случайная величина распределена равномерно в интервале а;b, если все ее возможные значения сосредоточены на этом интервале и если плотность распределения на этом интервале постоянна и равна 1/(b-a).
f(x) =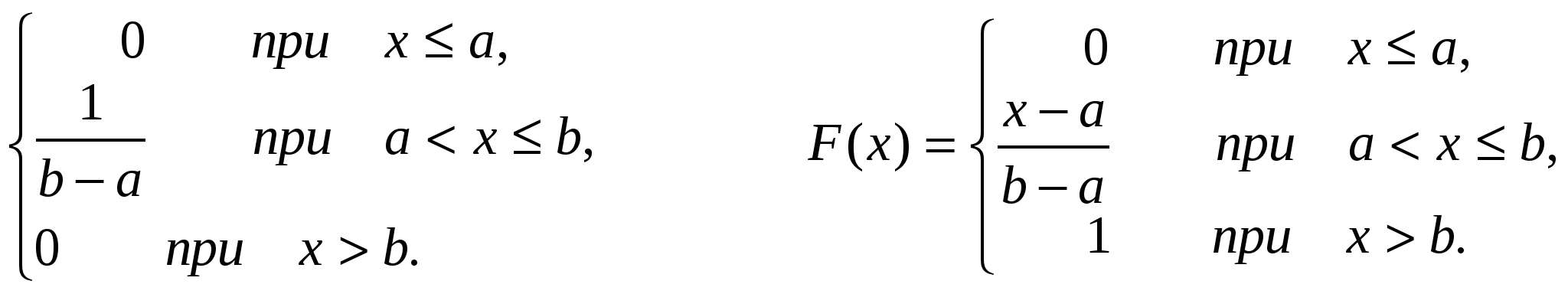
Равномерная случайная величина - это идеальная случайная величина (скорость неизменна), встречается довольно редко.
Каждая случайная величина имеет единственную функцию распределения, но не наоборот. Разные случайные величины могут иметь одну и ту же функцию распределения.
M(Х) = 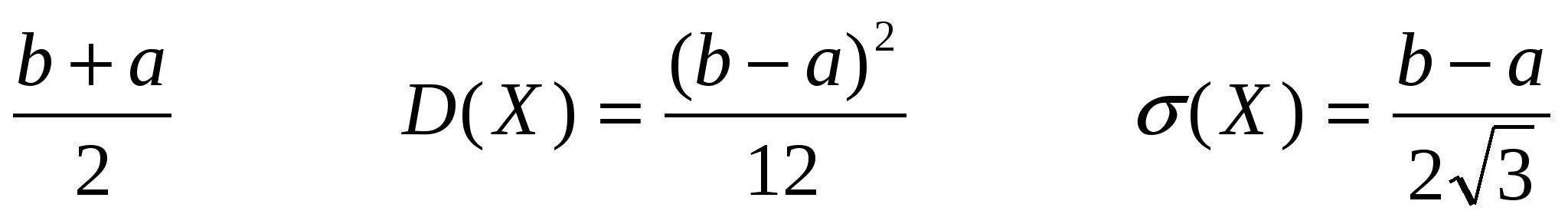
Вероятность попадания СВ Х в интервал [; ] : P( Х ) = 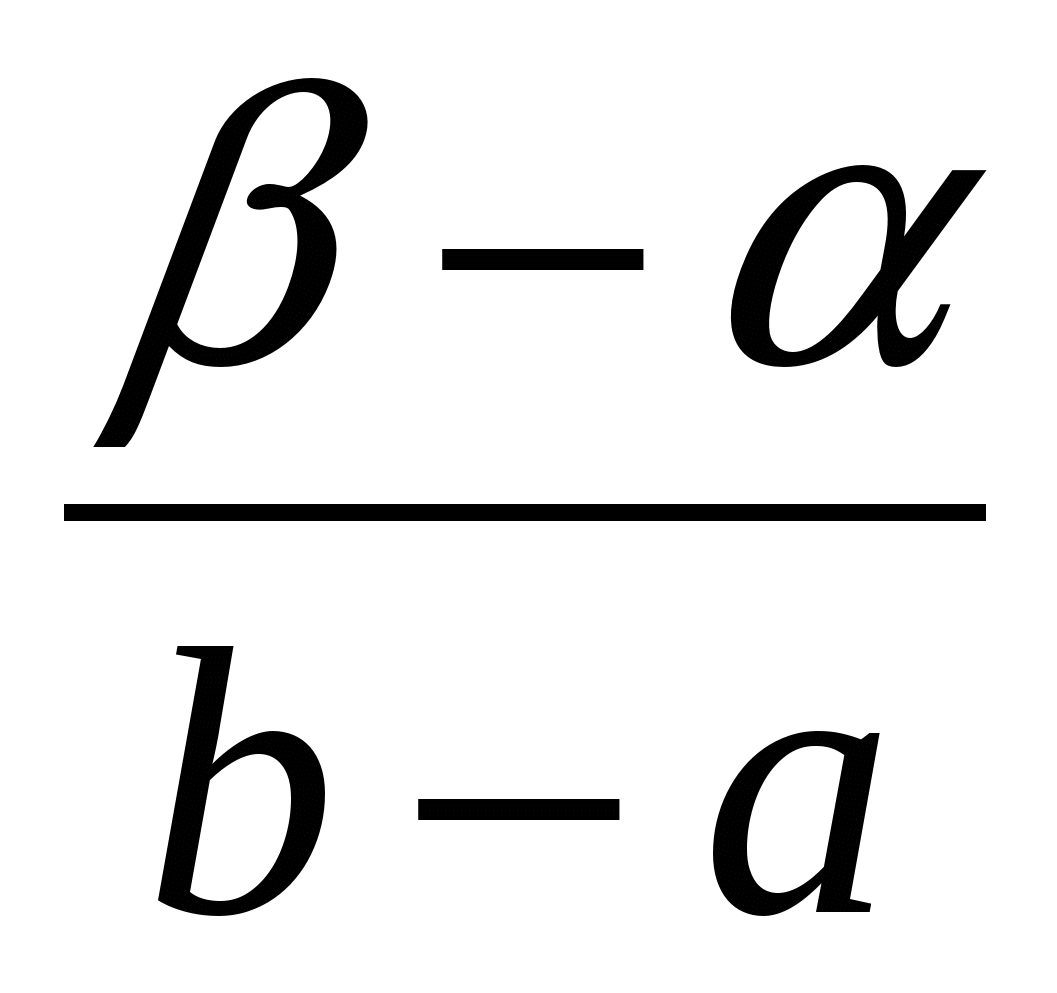
Показательное распределение
Показательное распределение играет важную роль в теории надежности систем, т.к. является основной моделью так называемых внезапных (не связанных с процессом старения и износа) отказов.
Непрерывная случайная величина распределена в интервале 0; по показательному закону, если плотность распределения f(х) имеет вид:

где =const
M(X) = (X)= 1\ D(X) = 1\2
Вероятность попадания СВ Х в интервал [; ] : P( X )= e - - e -
Логарифмически нормальное распределение
Неотрицательная случайная величина Х называется распределенной логарифмически нормально, если логарифм этой величины lnX распределен нормально.
Функция распределения имеет вид:
F(x)=
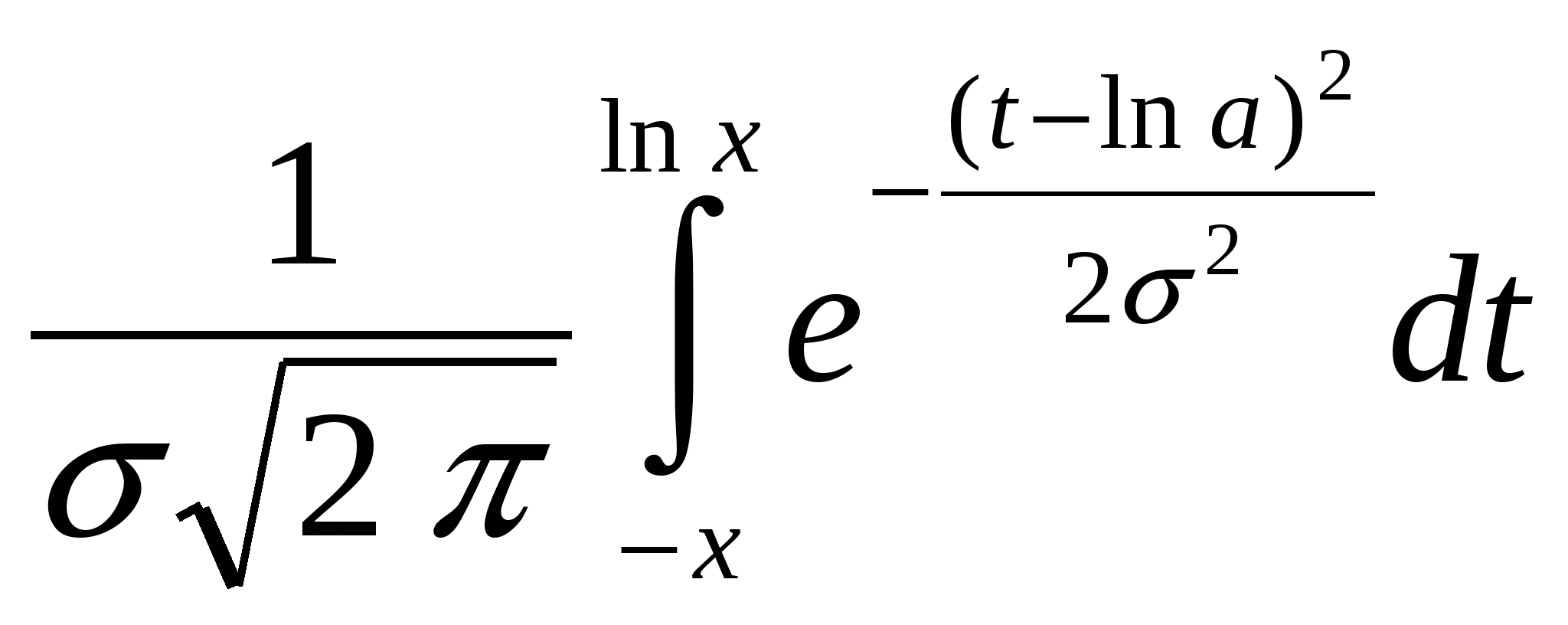
Плотность вероятности:
f (x) =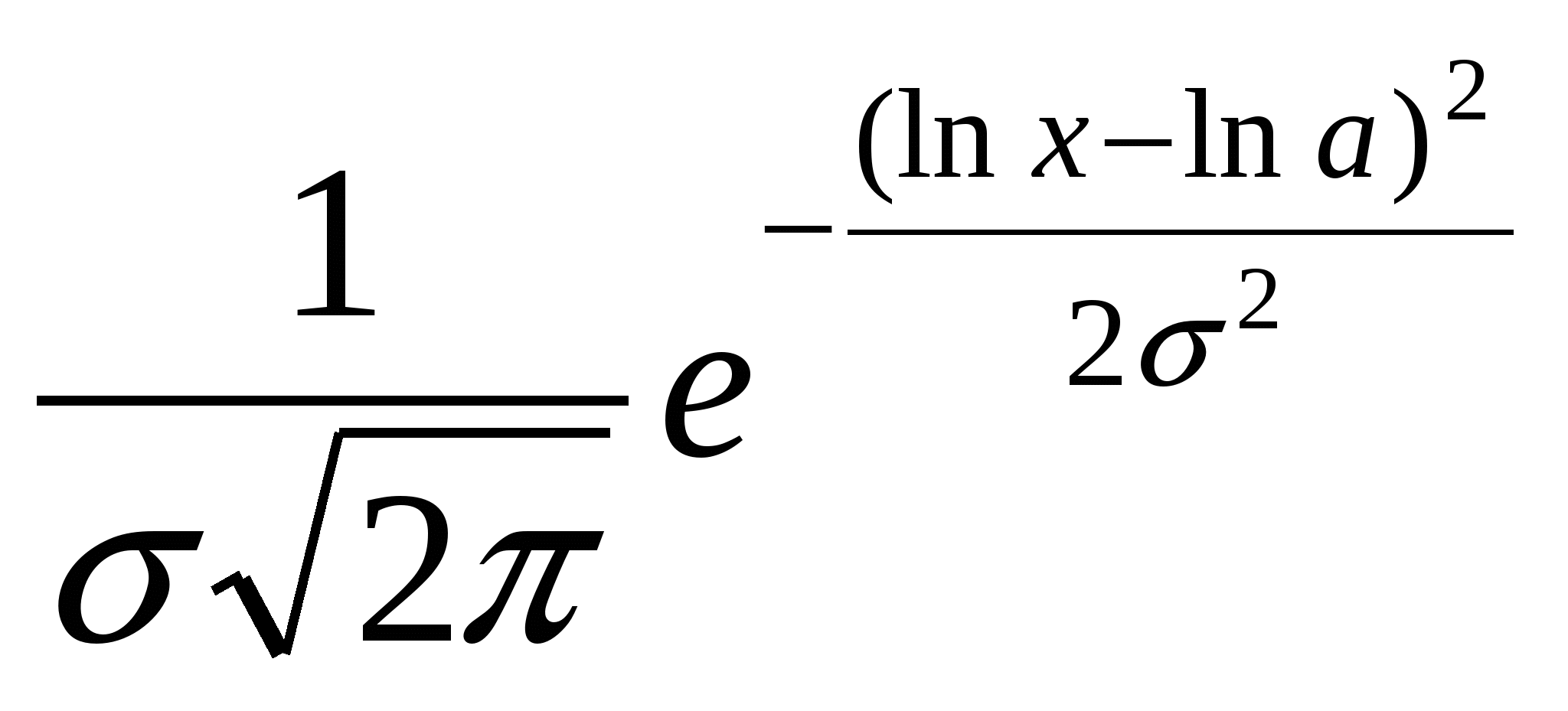
Логарифмически нормальное распределение полностью определяется двумя параметрами а и, где - среднее квадратическое отклонение, а -медиана
Логнормальное распределение используется для описания распределения доходов, банковских вкладов, долговечности изделий в режиме износа и старения.
При малых логарифмически нормальное распределение близко к нормальному.
Гамма - распределение
Гамма - распределением случайной величины Х называется распределение плотности вероятности:
f(x)= 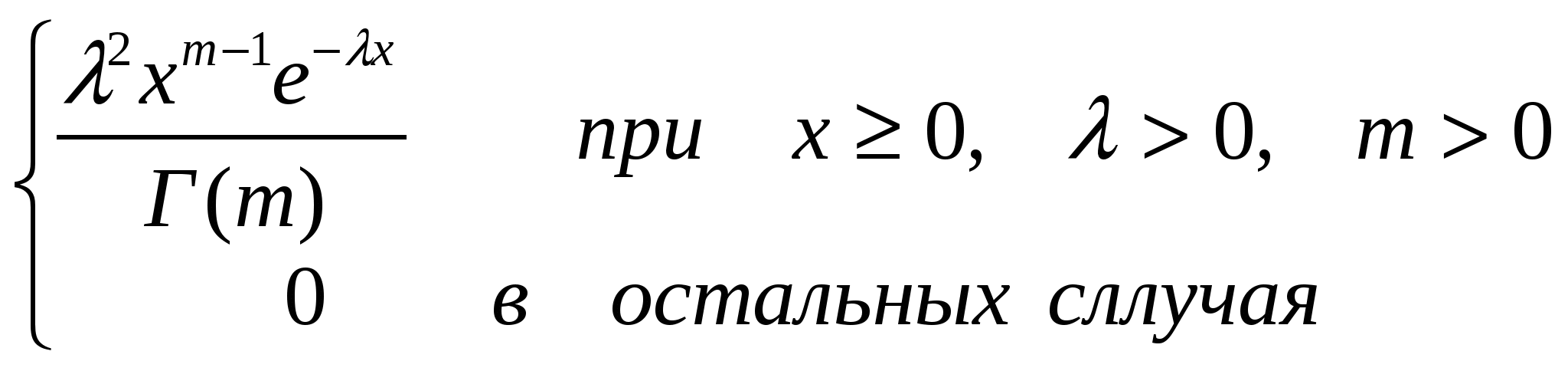
Г(m)= 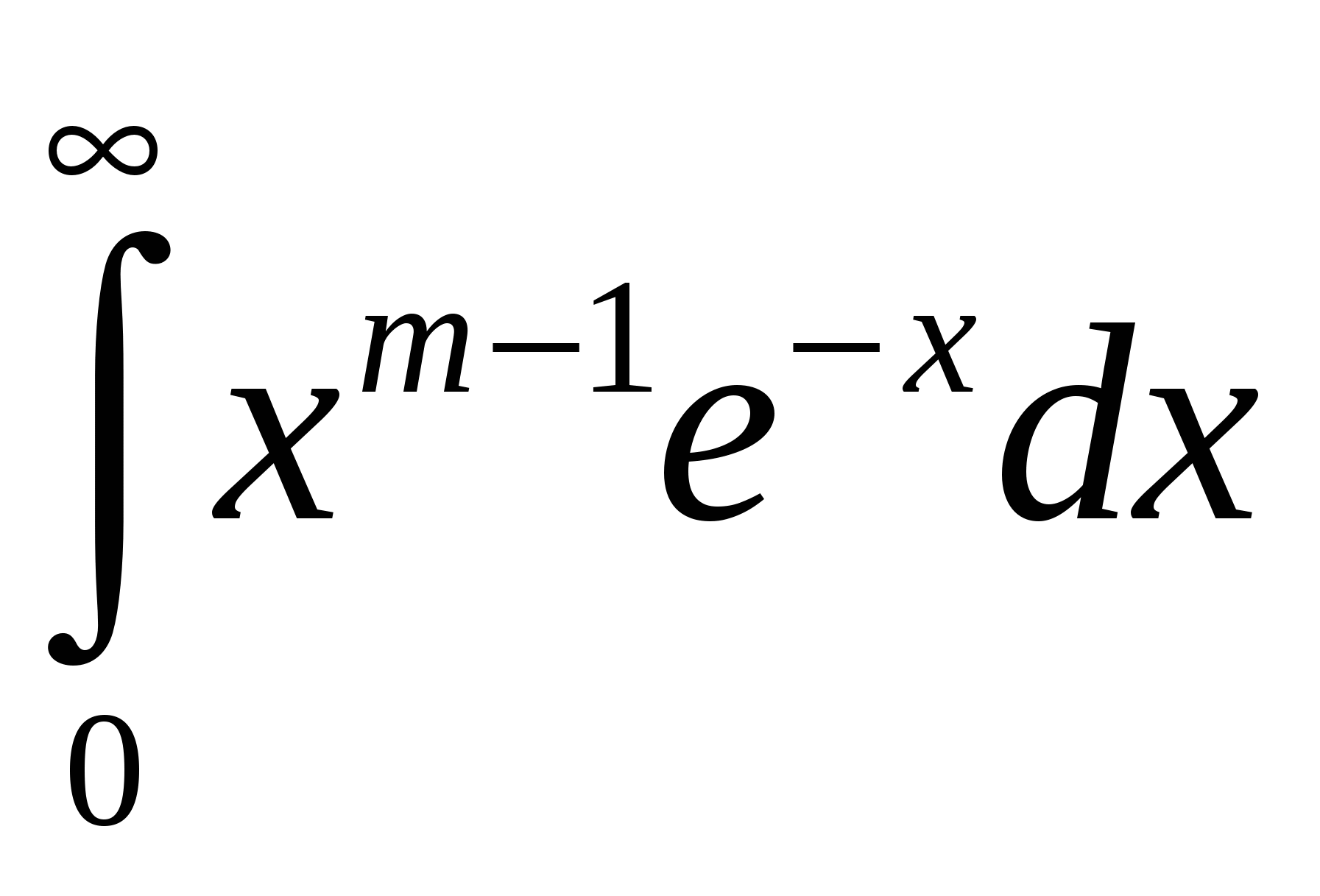 - гамма функция
- гамма функция
Гамма - распределение описывает время, необходимое для появления ровно m независимых испытаний, если эти события происходят с постоянной интенсивностью . Например, если поставка какой-нибудь детали производится партиями объемом m деталей каждая, а заявки на отдельные детали поступают независимо друг от друга с постоянной интенсивностью , то промежуток времени, за который будет израсходована вся партия, является случайной величиной, имеющей гамма-распределение.
При m=1 из гамма -распределения получается показательное распределение. При m=2 гамма-распределение может быть описана нормальным распределением.
Гамма-распределение позволяет описывать широкий класс случайных величин.
Для гамма-распределения: M(X) = 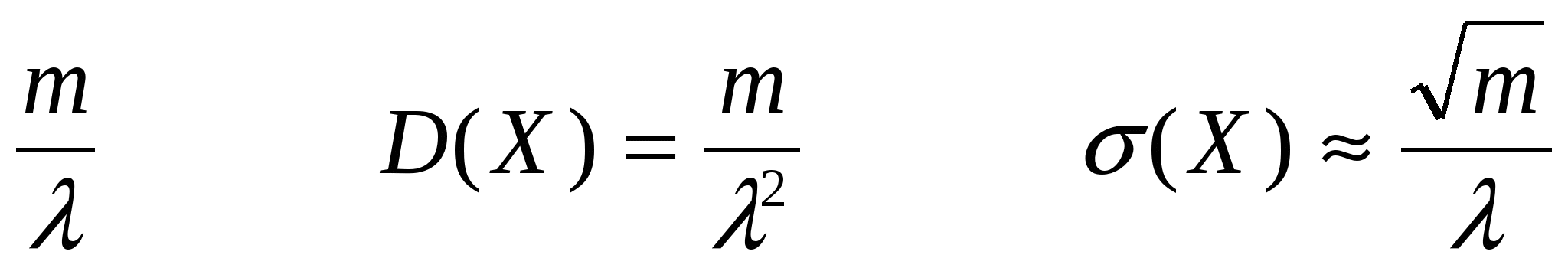
Распределение Вейбулла-Гнеденко
Распределение Вейбулла-Гнеденко имеет следующую плотность распределения:
f (x) = 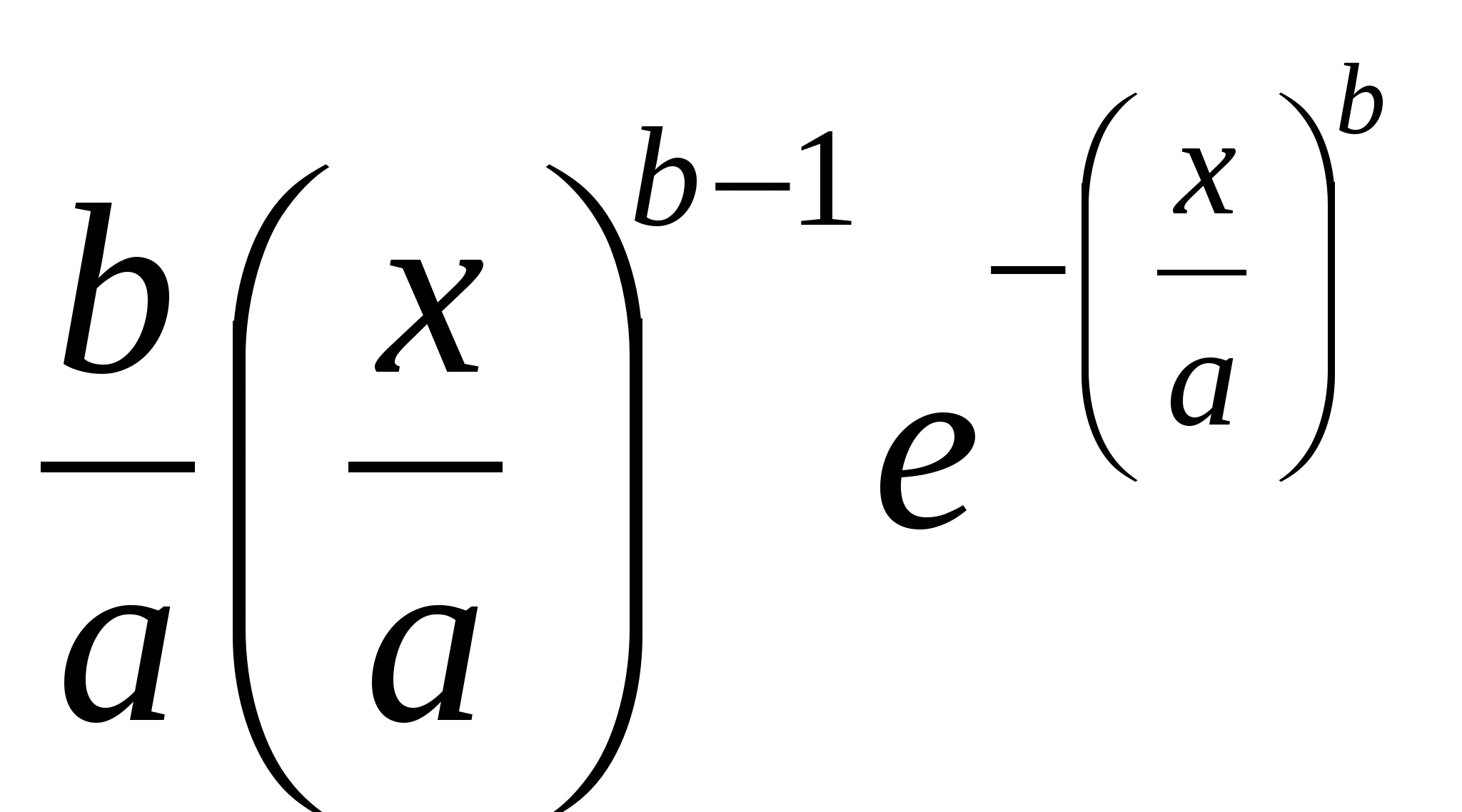 , где b и а- параметры распределения
, где b и а- параметры распределения
При b=1 распределение Вейбулла - Гнеденко совпадает с показательным распределением. Распределение Вейбулла - Гнеденко используется в теории надежности. Функция распределения: F(x) = 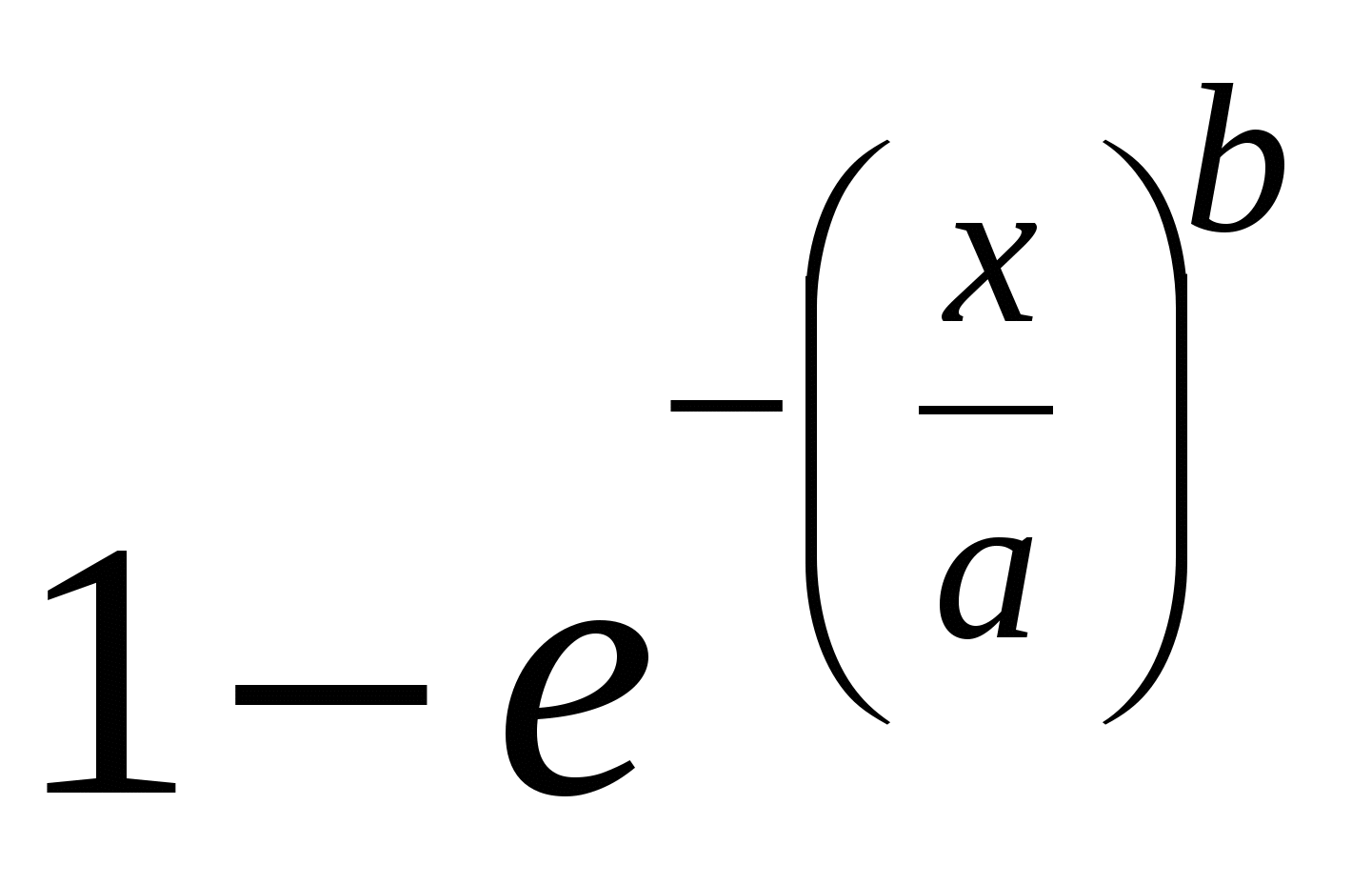
Пример. Автобусы маршрута № 1 идут строго по расписанию. Интервал движения пять минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус этого маршрута не больше трех минут. Найти среднее время ожидания автобуса.
Время ожидания автобуса на временном (в минутах) отрезке [0; 5] можно рассматривать как случайную величину X, которая распределена равномерно: 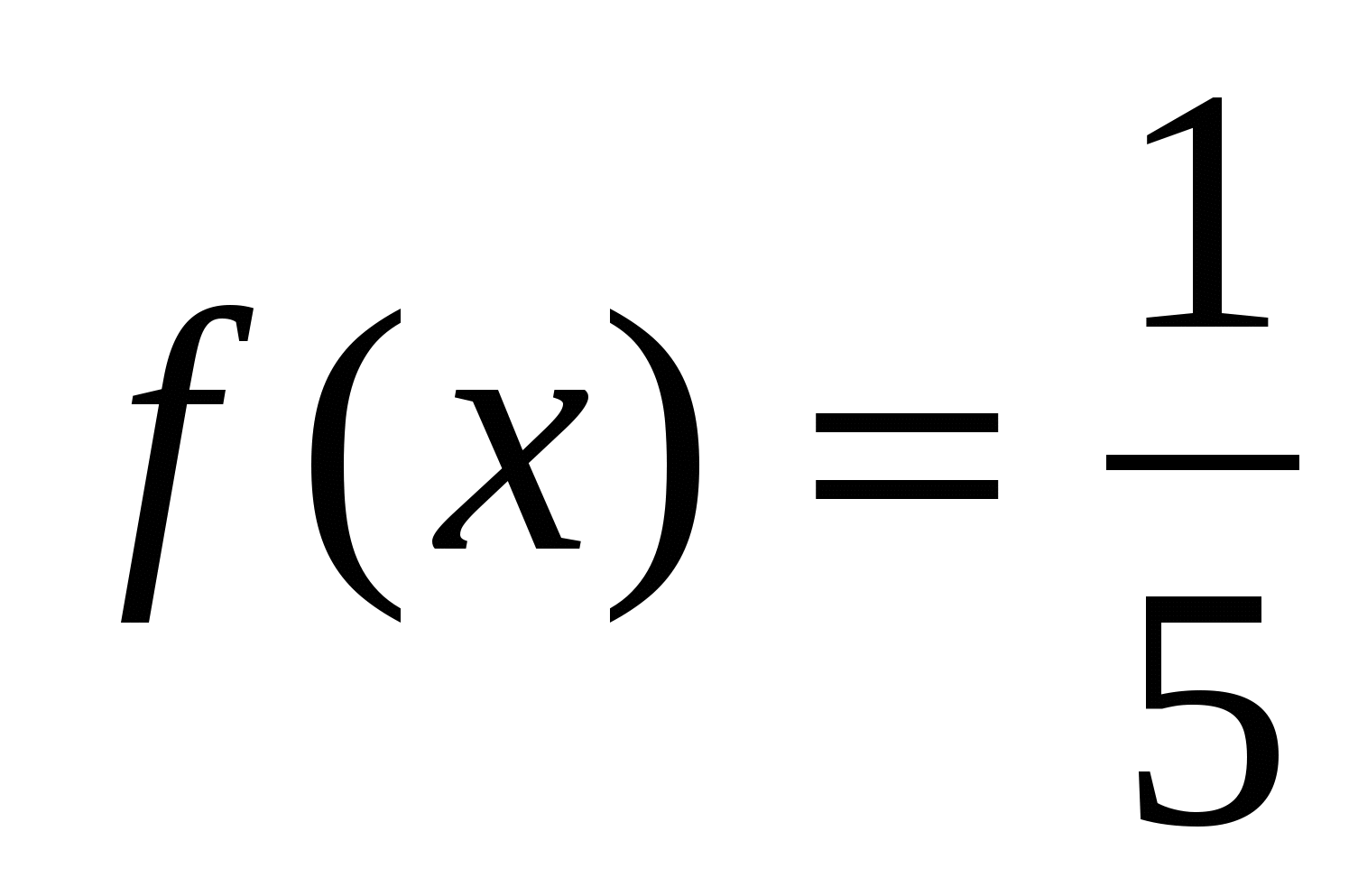
b-a - длина интервала, в котором заключены возможные значения Х. b=5, a=2. P(0<X 3) = 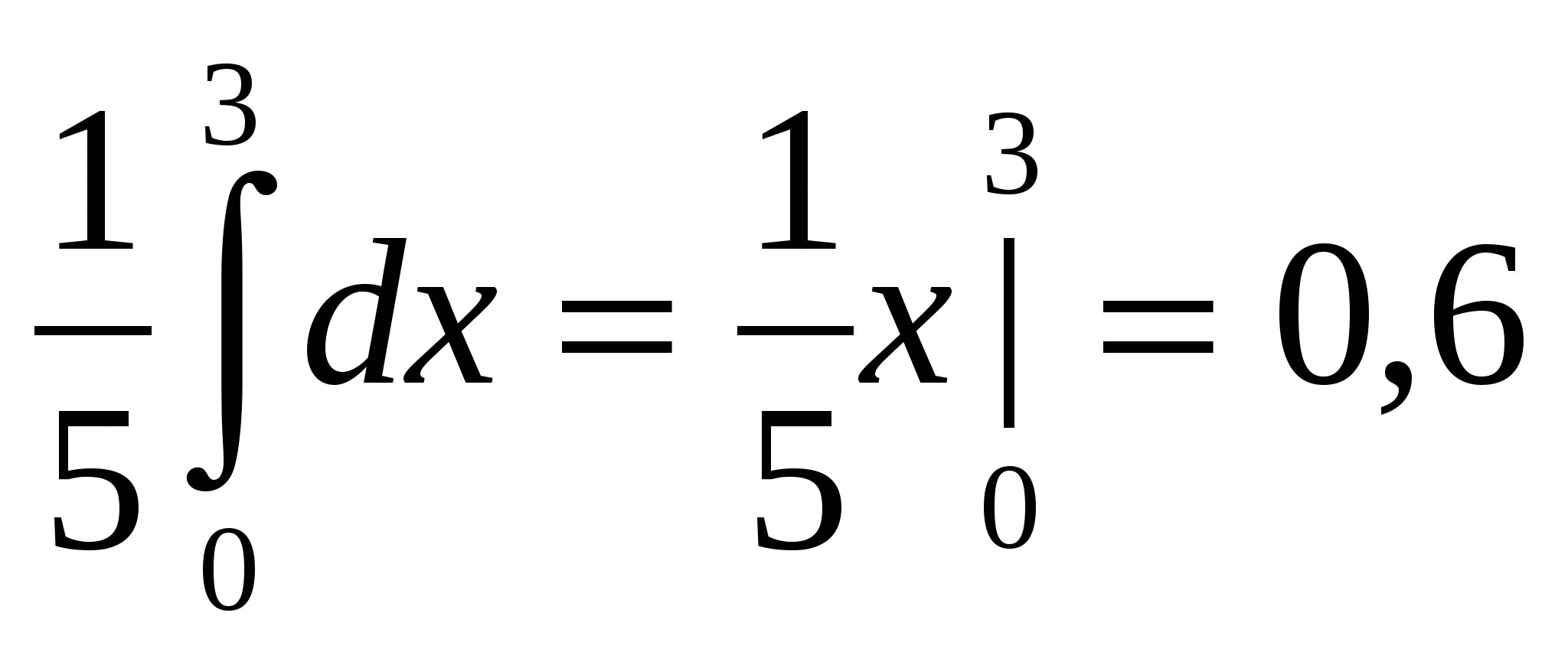
Определим среднее время ожидания автобуса по формуле:
М(Х)=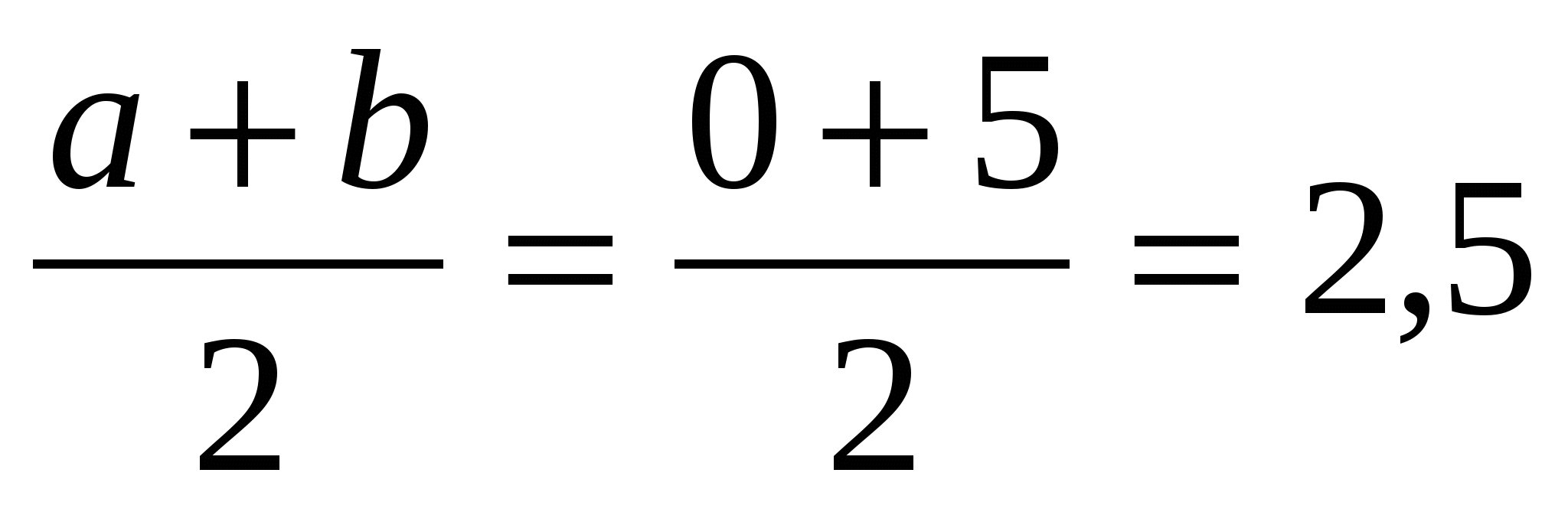
Пример. Перекресток оборудован автоматическим светофором, в котором зеленый и красный свет горят соответственно в течение одной минуты и 0,5 минут. Автолюбитель подъезжает к перекрестку в случайный момент времени, не связанный с работой светофора. Найти вероятность того, что он проедет перекресток не останавливаясь.
Случайная величина Х, обозначающая момент проезда автомашины через перекресток распределена равномерно в интервале 0; 1,5 .
0;1,5 - период смены цветов в светофоре. Для того, чтобы автолюбитель проехал перекресток не останавливаясь, нужно, чтобы момент проезда перекрестка пришелся на интервал времени 0; 1 .
Для случайной величины, распределенной равномерно в 0;1,5 вероятность того, что она примет значение из 0; 1 , равна 2/3, т.к.
P(0<x<1)= 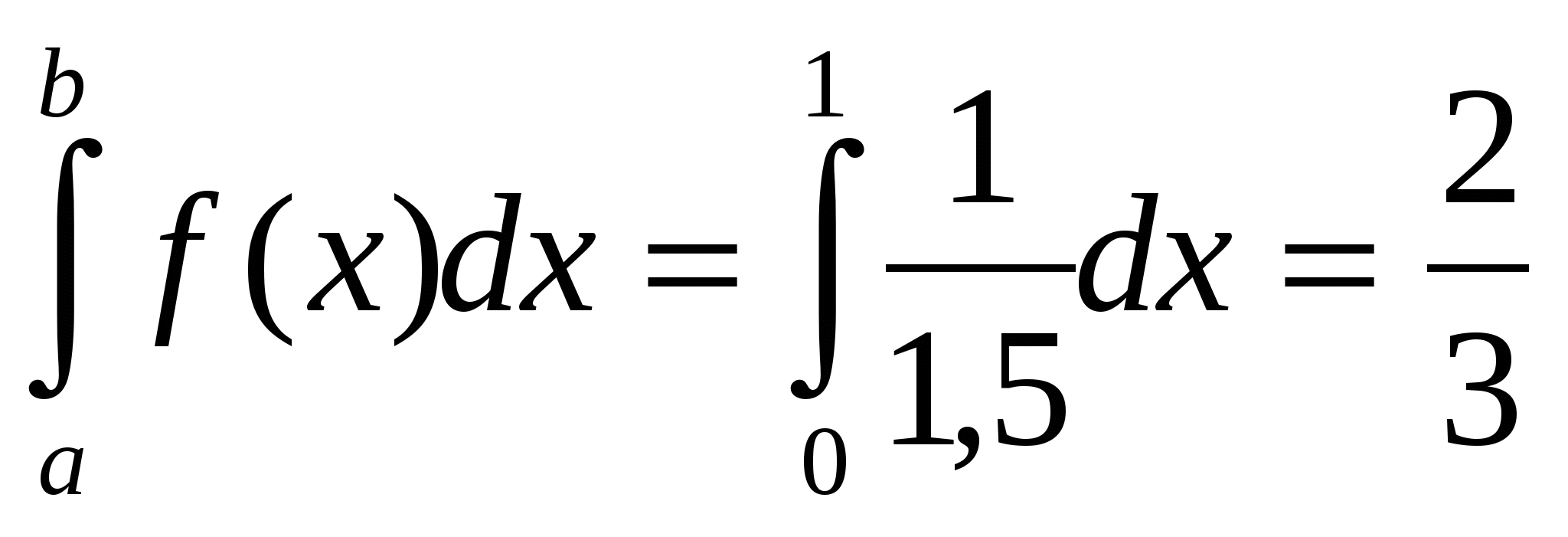 ,
,
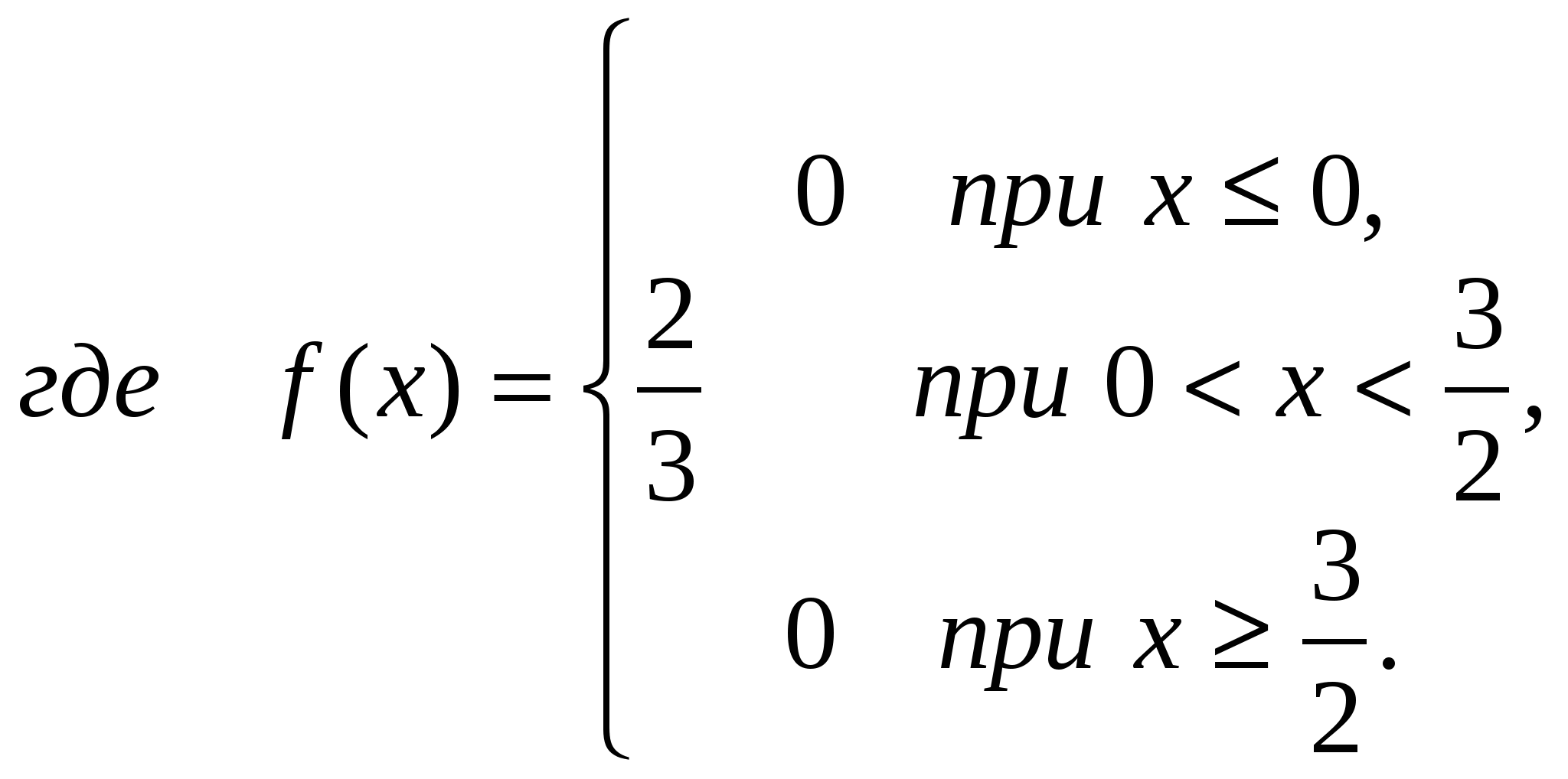
Пример. Время безотказной работы электродвигателя подчинено экспоненциальному (показательному) закону распределения с параметром
=2,5 10-5
Требуется определить среднюю наработку до первого отказа Т1 и вероятность безотказной работы Р(t) за время t = 1000 ч и t = Т1
Функцией надежности Р(t) = e-t называют функцию определяющую вероятность безотказной работы элемента за время длительностью t.
Вероятность безотказной работы элемента не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности интервала t (при заданной интенсивности отказов ).
Если Т - случайная величина времени работы элемента, то
Р(t) = P(T>t)=e-t, тогда Р(1000) = е - 2,510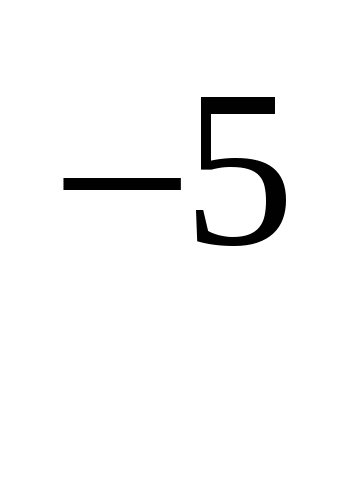 10
10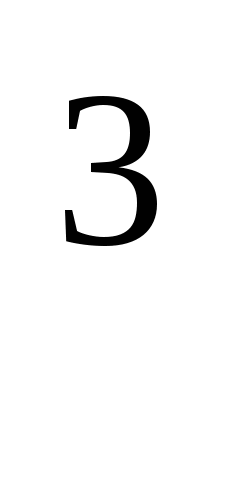 = е - 0,025 = 0,9753
= е - 0,025 = 0,9753
Так как Т1 = m t = 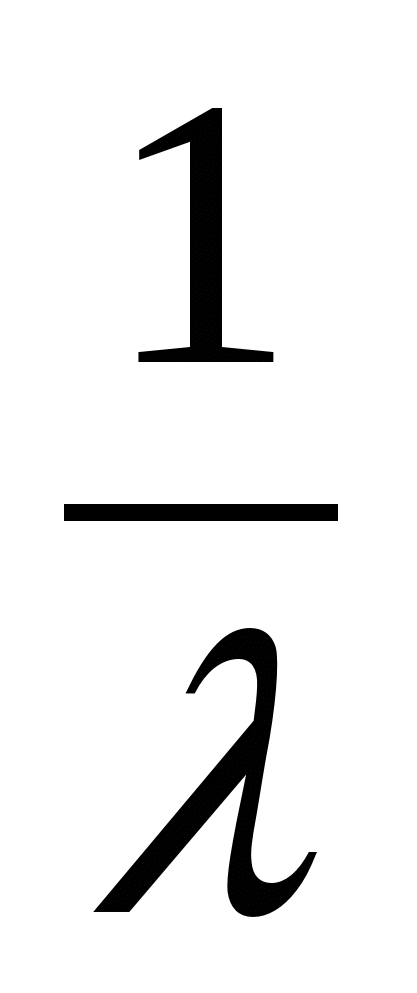 получим: Р(Т)= е -Т1 = е -/= е -1 = 0,3679 0,37
получим: Р(Т)= е -Т1 = е -/= е -1 = 0,3679 0,37
Средняя наработка до первого отказа Т1 определяет время, в течение которого вероятность безотказной работы элемента составляет всего лишь 0,37.
Т1 = 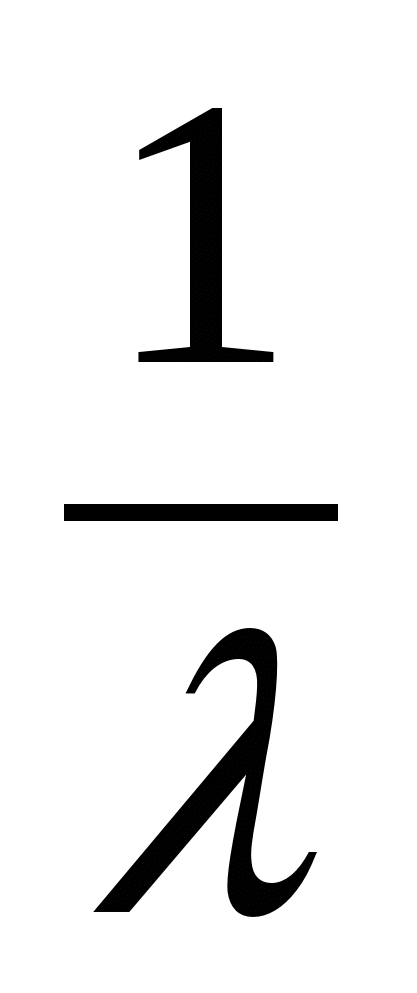 =
= 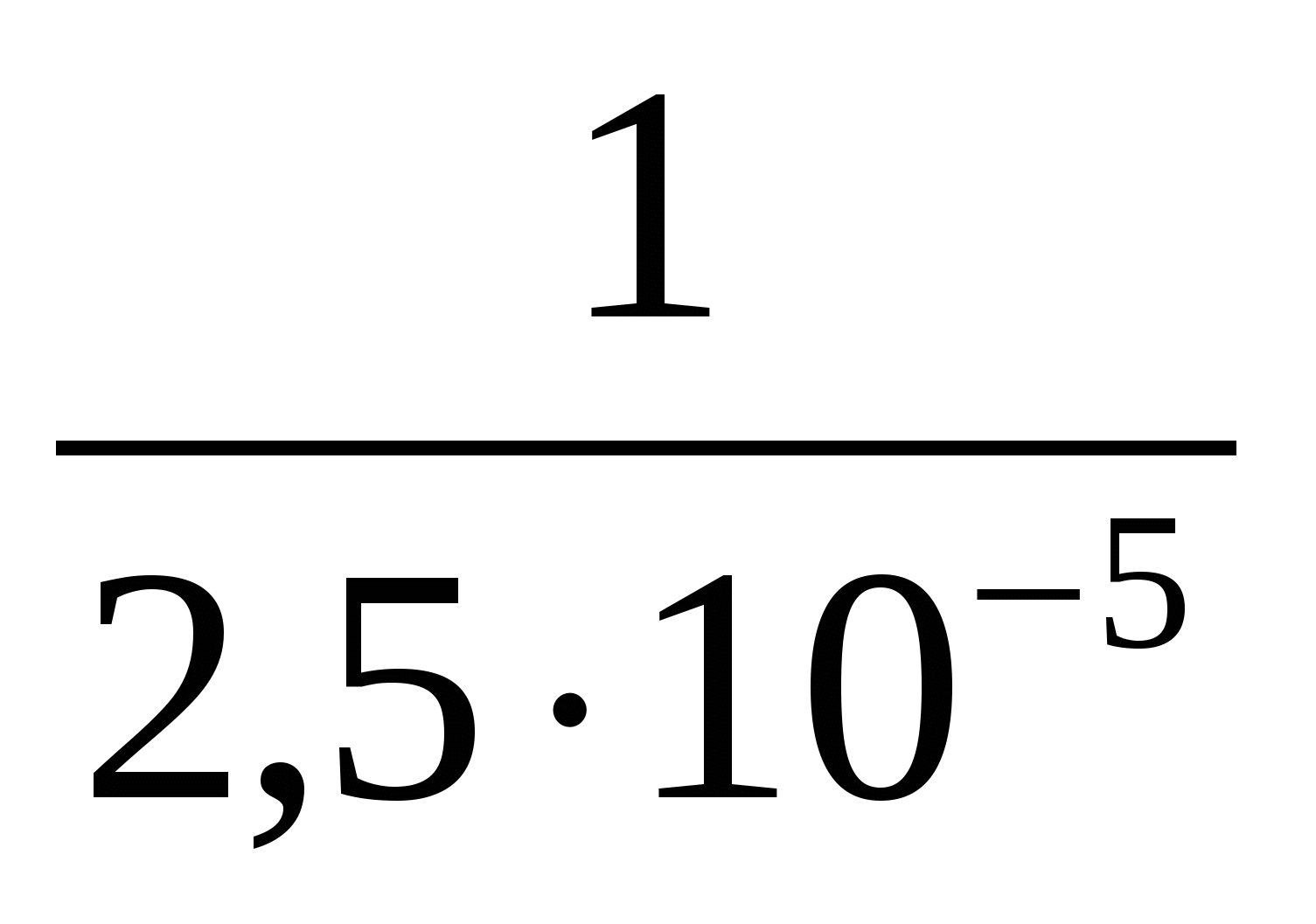 = 40 000 часов
= 40 000 часов
Пример . Длительность времени безотказной работы элемента имеет показательное распределение, интегральная функция которого имеет вид:
F(t) = 1- e -0,02t (t>0). Найти вероятность того, что за время длительностью t= 6 часов элемент откажет.
Так как интегральная функция F(t) = P(T<t) = 1 - e -t определяет вероятность отказа элемента за время длительностью t, то подставив t = 6 в интегральную функцию, получим вероятность отказа.
F(60)= 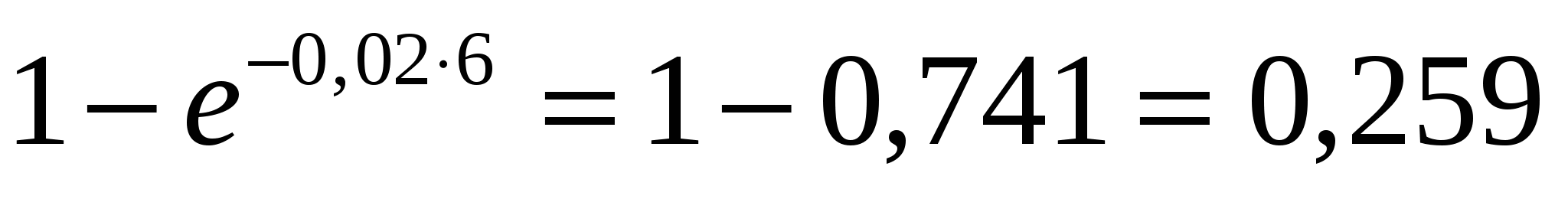
Литература
1.Е.С. Кочетков, С.О. Смерчинская Теория вероятностей в задачах и упражнениях / М. ИНФРА-М 2005.


