- Преподавателю
- Математика
- Квадрат теңдеулерге есептер шығару
Квадрат теңдеулерге есептер шығару
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Имандосова С.А. |
| Дата | 08.01.2014 |
| Формат | doc |
| Изображения | Есть |
Жоспары
Кіріспе бөлім..................................................
-
Мақсаты
-
Қысқаша тарихи мәлімет
Негізгі бөлім...................................................
-
Комплекс сан ұғымы
-
Комплекс сандарға қолданылатын амалдар
-
Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі
-
Муавр формуласы
Қорытынды.................................................
Пайдаланылған әдебиеттер......................
КОМПЛЕКС САНДАР.
Мақсаты: Комплекс сандар қолданбалы математикада орасан зор орын алады, соның ішінде ауыспалы токты есептегенде.Бұл ғылыми жобада комплекс сандарына түрлі амалдар қолдануды үйренеміз. Муавр теоремасын қолданып,комплекс сандардың дәрежесін есептейміз,және де ауыспалы токтың жай есептеріне көз жүгіртеміз.
Қысқаша тарихи мәлімет
Комплекс сан ұғымы тұңғыш рет ХҮІ ғасырда итальяндықтар Дж.Кардано және Р.Бомбелли қарастырған дискриминантты теріс квадрат теңдеулердің, әсіресе кубтық теңдеулердің ,шешімдеріне байланысты шыққан ұғым. 1572 жылы шыққан «Алгебра»
атты кітабында Р.Бомбелли комплекс сандарға арифметикалық операциялар қолданған.
Алғашқы кезде комплекс сандардың іс жүзінде нақты түрде түсінігі (интерпретациясы),болмағандықтан ондай түбірлерді «мүмкін емес», «жорамал» деп санап , ондай түбірлері бар теңдеулерді «түбірі жоқ» теңдеулер қатарына қосатын болған.
Комплекс сандардың жан-жақты қолданылуы тек ХҮІІІ ғасырда басталды. Міне осы кезде комплекс сандардың интегралдық есептеуде механикада және геометрияда қолданулары комплекс аргументті функцияларды қарауға әкеп соқты. Осы мәселелер жайындағы зерттеулерде туған жері Швейцария болса да, отыз жылдан аса Петербург академиясында жұмыс істеп , өзін «орыс ғалымымын» деп атап өткен Леонард Эйлер (1707-1783) мен француз математигі және философы Даланбердің (1717-1783) үлесі көп.
Комплекс сандарға жазықтықтағы нүкте не вектор деп геометриялық түсінікті 1797 жылы даниялық жер өлшеуші К. Вессель (1745-1818) берген ,бірақ тек атақты неміс математигі Карл Фридрих Гаусстың (1777-1855) комплекс сандарды арифметикаға , алгебраға, геометрия және математикалық анализге қолданған еңбектерінен кейін ғана көпшілік комплекс сандардың геометриялық мағынасын қолданып , оны толық пайдалана бастайды. Математикаға «комплекс сан » терминін кіргізген де, жоғарғы алгебраның негізгі теоремасының толық дәлелдеуін тұңғыш рет (1799 ) ұсынған да К.Гаусс.
Нақты сандар жиынында түбірі болмайтын квадрат теңдеуді шешуден бастаймыз, яғни х2+1=0 теңдеуін бір амалын тауып шешуіміз қажет. Демек, квадраты -1 -ге тең жаңа бір сан ұғымын енгізуіміз керек. Ол сан i арқылы белгіленеді, және оны ЖОРАМАЛ БІРЛІК САН деп атайды. Сонымен, х2+1=0, х2= -1 теңдеуінің х1=i, x2= -і түбірлері табылады деп есептейтін боламыз. Бұдан былай 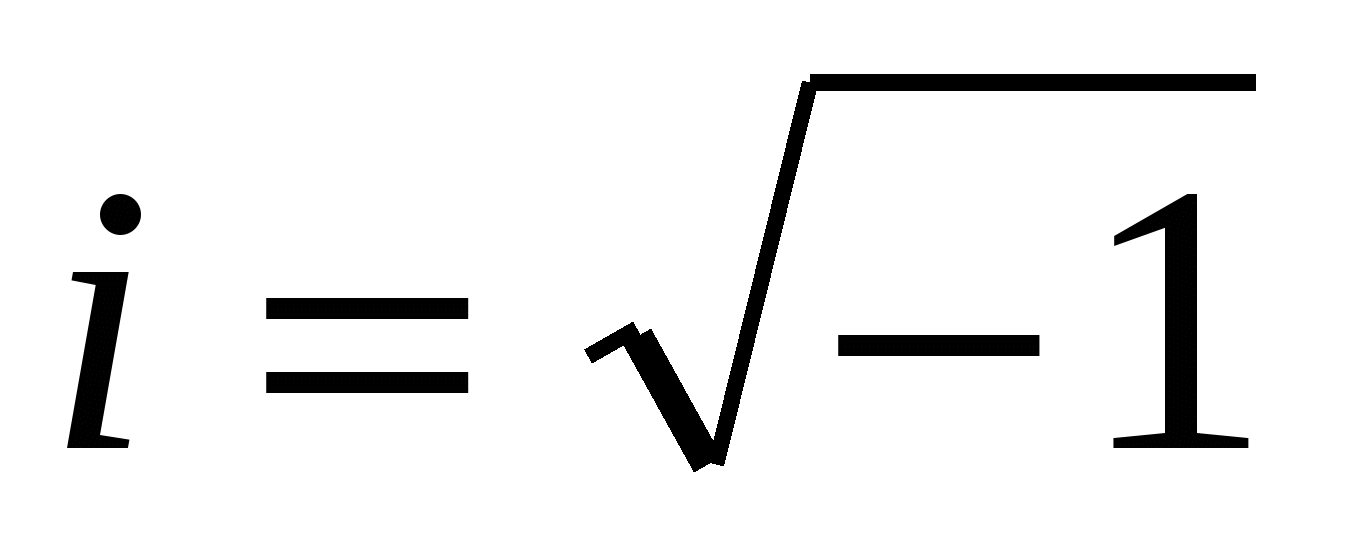 деп қарастырып, бұған жаңа ұғым береміз:
деп қарастырып, бұған жаңа ұғым береміз:
Анықтама: Егер а және b нақты сандар болса, онда a+bi өрнегін комплекс (жорамал) сан деп атаймыз.
Мұнда, а-комплекс санның нақты бөлігі, b-жорамал бөлік деп аталады.
Анықтама 1: комплекс сан деп 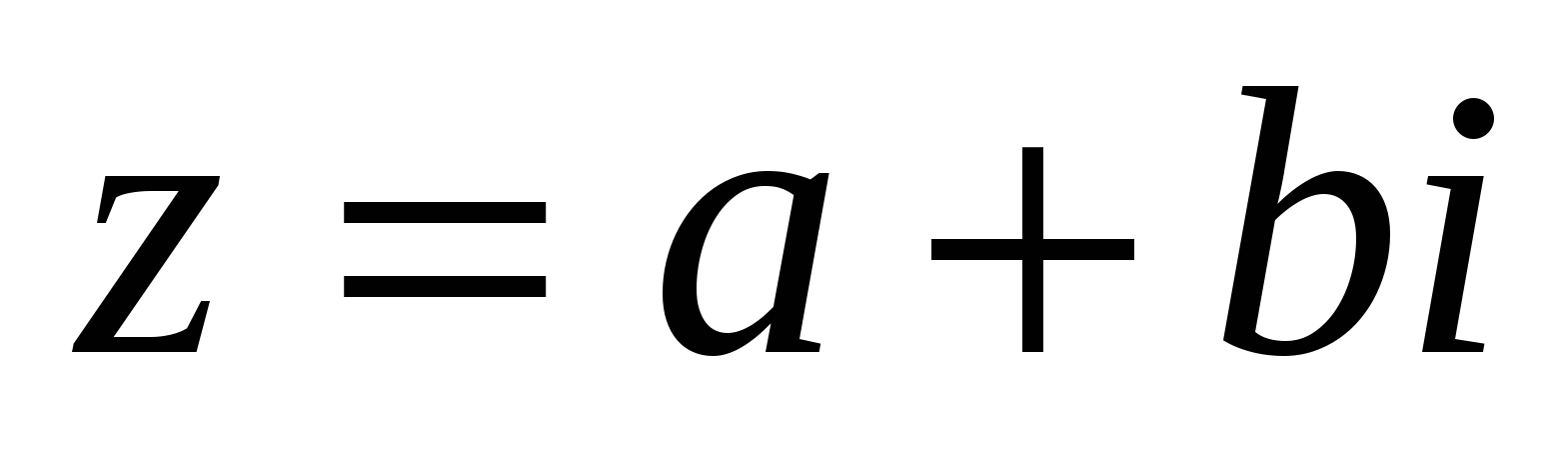 өрнегі аталады. Мұндағы а,b-нақты сандар; i- жорамал бірлік.
өрнегі аталады. Мұндағы а,b-нақты сандар; i- жорамал бірлік.
Егер а=0 болса, онда 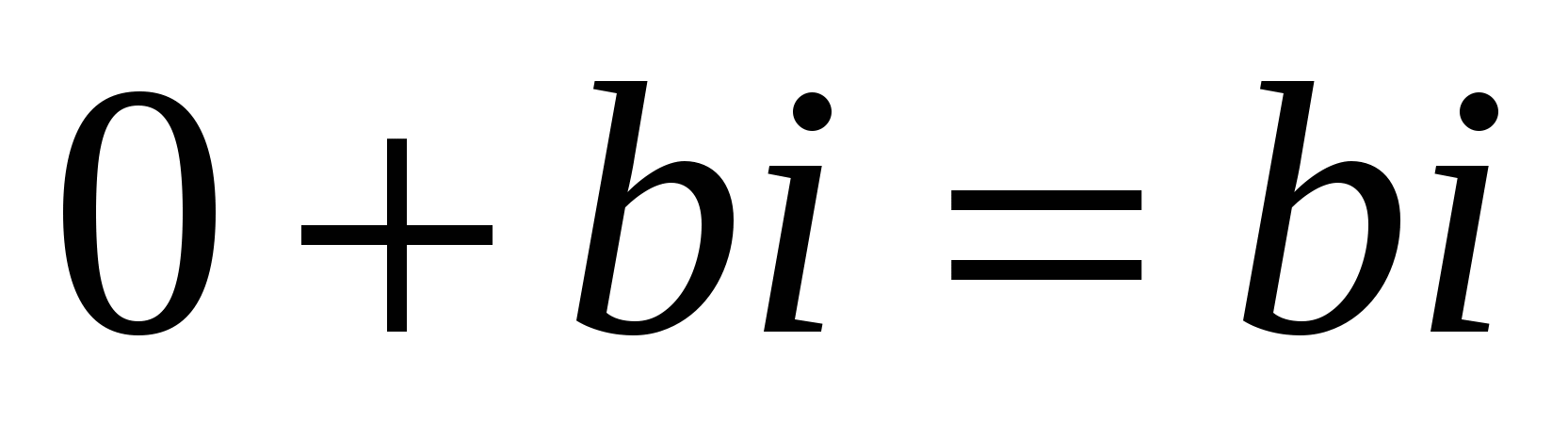 саны таза жорамал сан деп аталады;
саны таза жорамал сан деп аталады;
Егер в=0 болса, онда 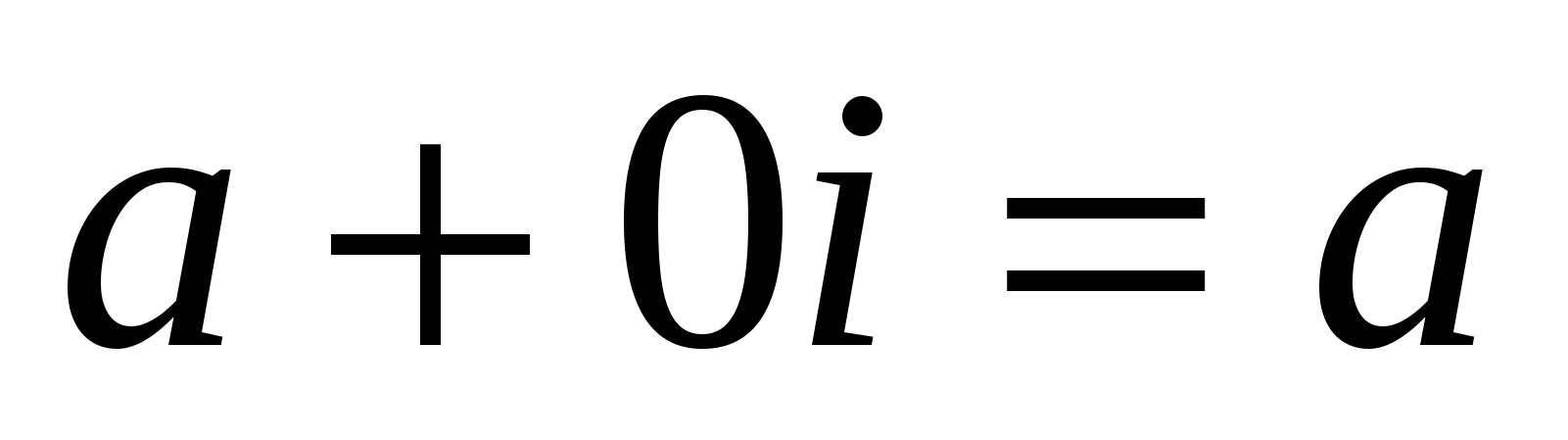 саны нақты сан деп саналады.
саны нақты сан деп саналады.
Анықтама 2: 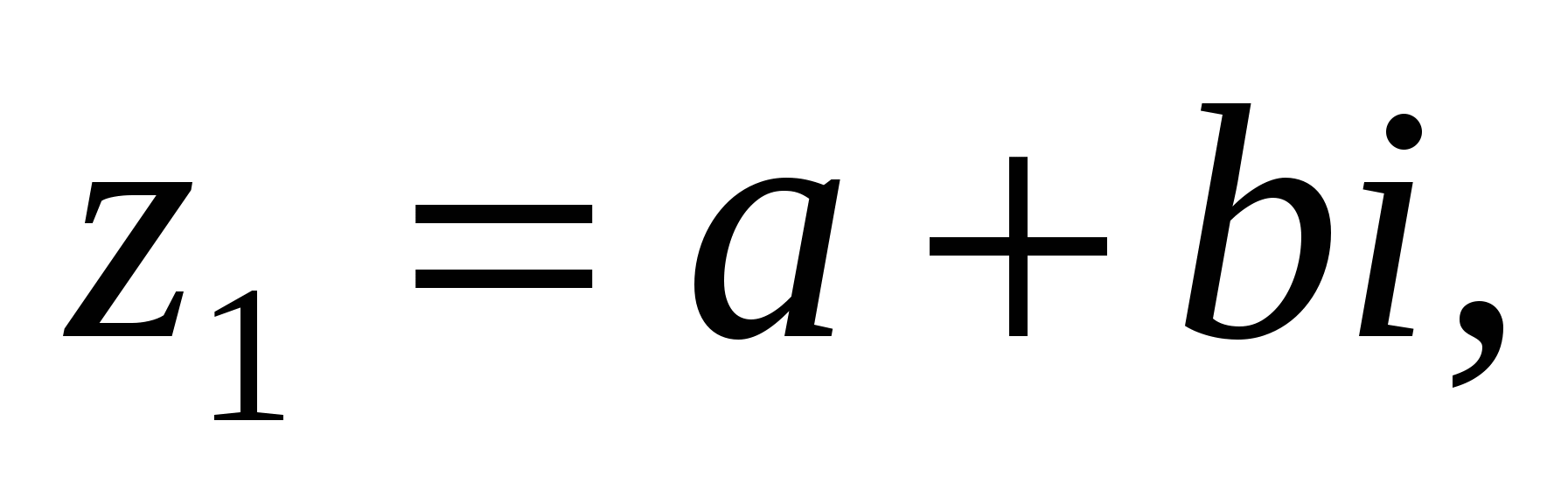
 комплекс сандары тек a=c, b=d болған жағдайда ғана өзара тең деп аталады.
комплекс сандары тек a=c, b=d болған жағдайда ғана өзара тең деп аталады.
Комплекс сандар жиыны С әрпімен белгіленеді;
Комплекс сандарға қолданылатын амалдар.
Анықтама 3: 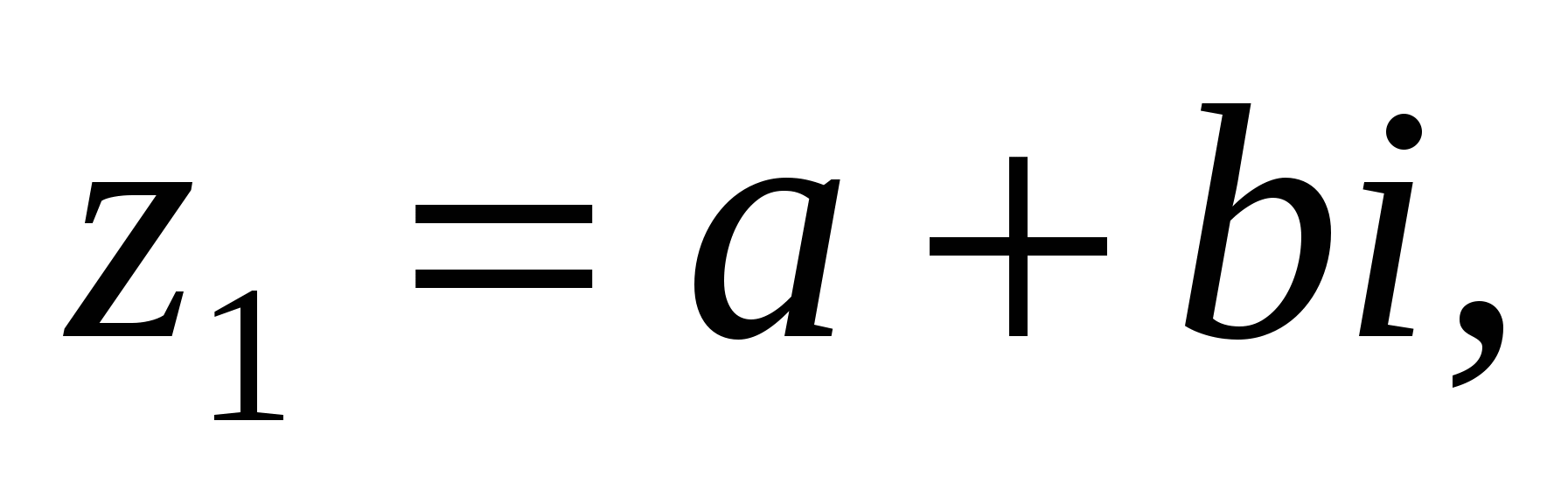
 комплекс сандарының қосындысы деп
комплекс сандарының қосындысы деп 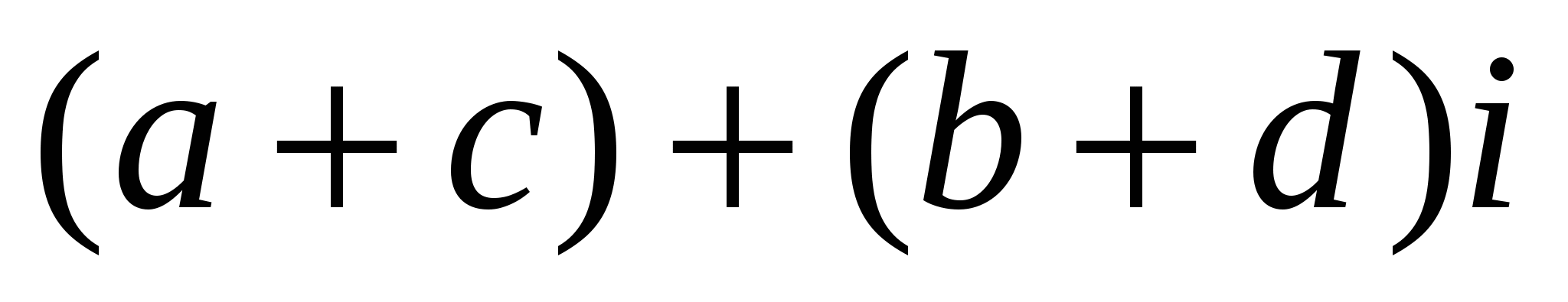 комплекс саны аталады, яғни
комплекс саны аталады, яғни
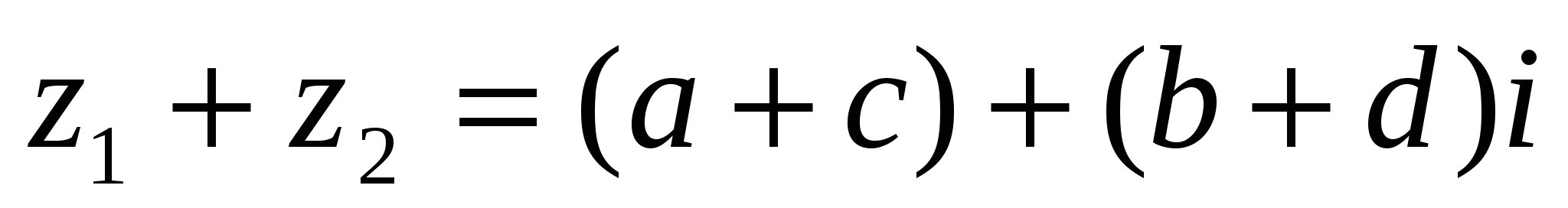 (1)
(1)
1 Мысал: 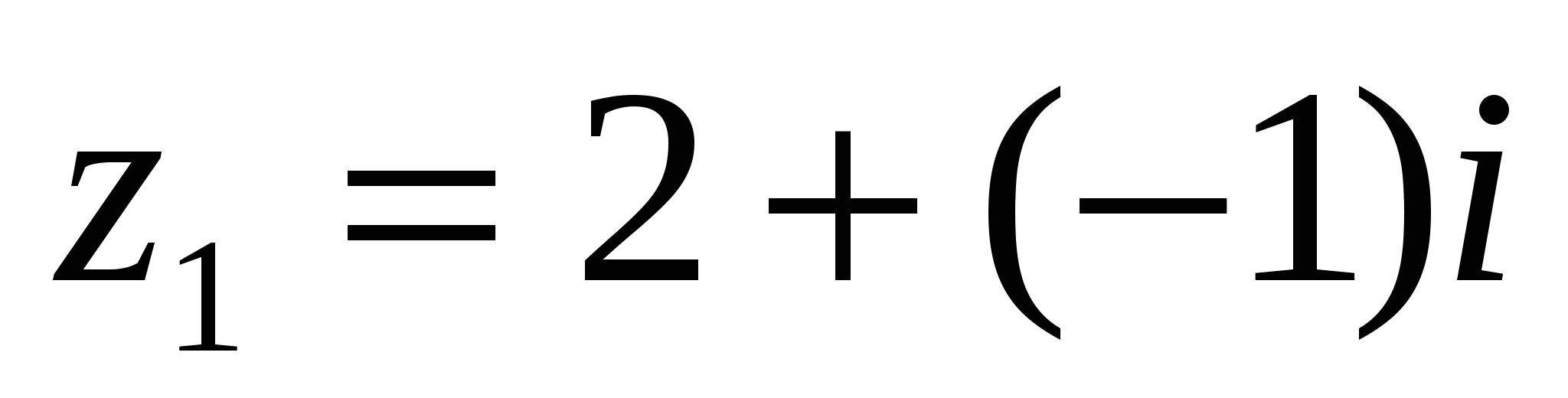 ,
,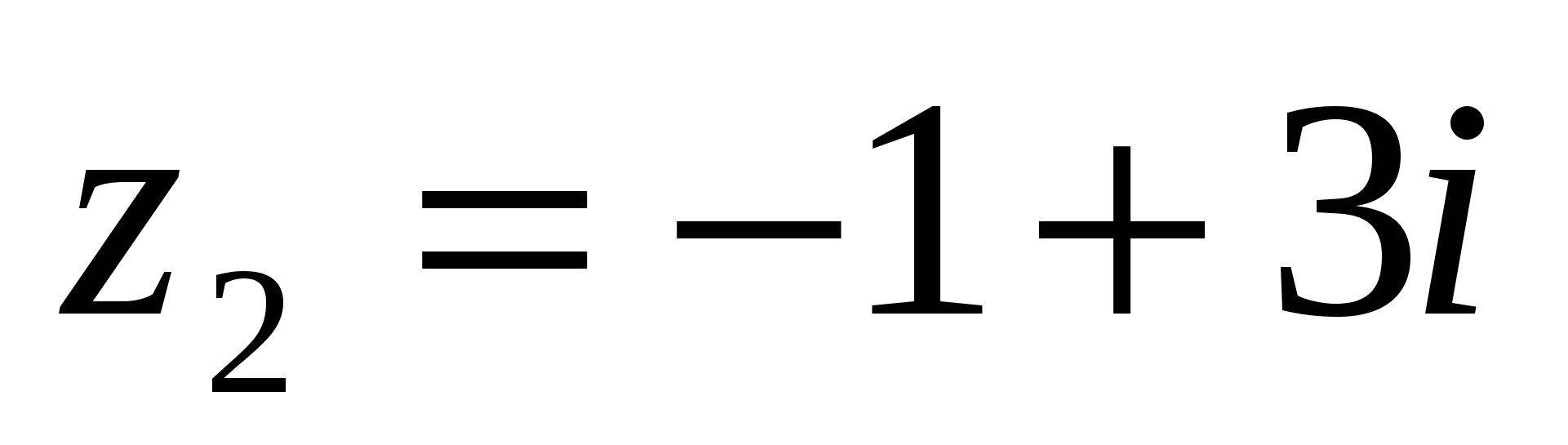 комплекс сандарының қосындысын табу керек.
комплекс сандарының қосындысын табу керек.
Δ 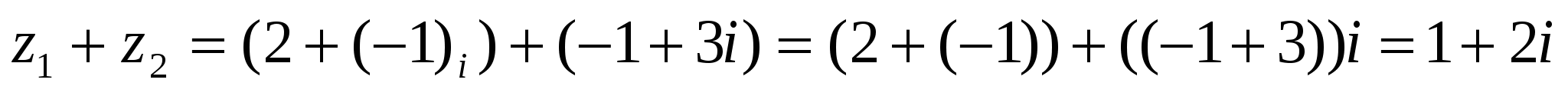 ▲
▲
Комплекс сандарының қосындысының келесі қасиеттері бар:
-
Коммутативтік:
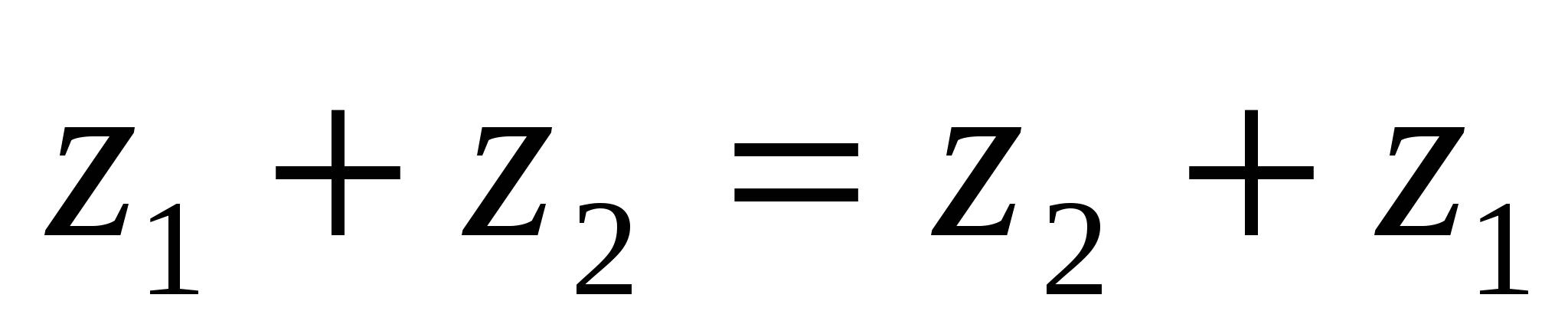 немесе
немесе 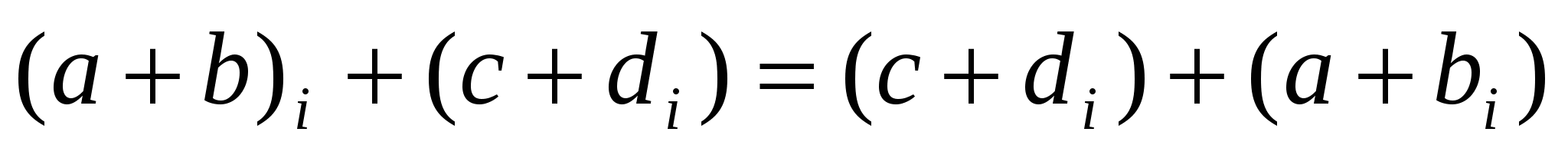
-
Ассоциативтік:
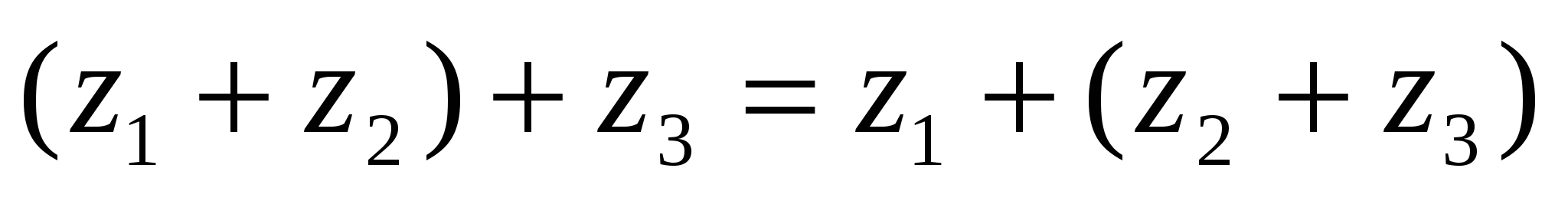 немесе
немесе 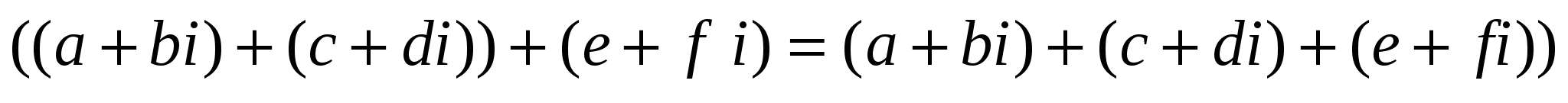
Анықтама 4: 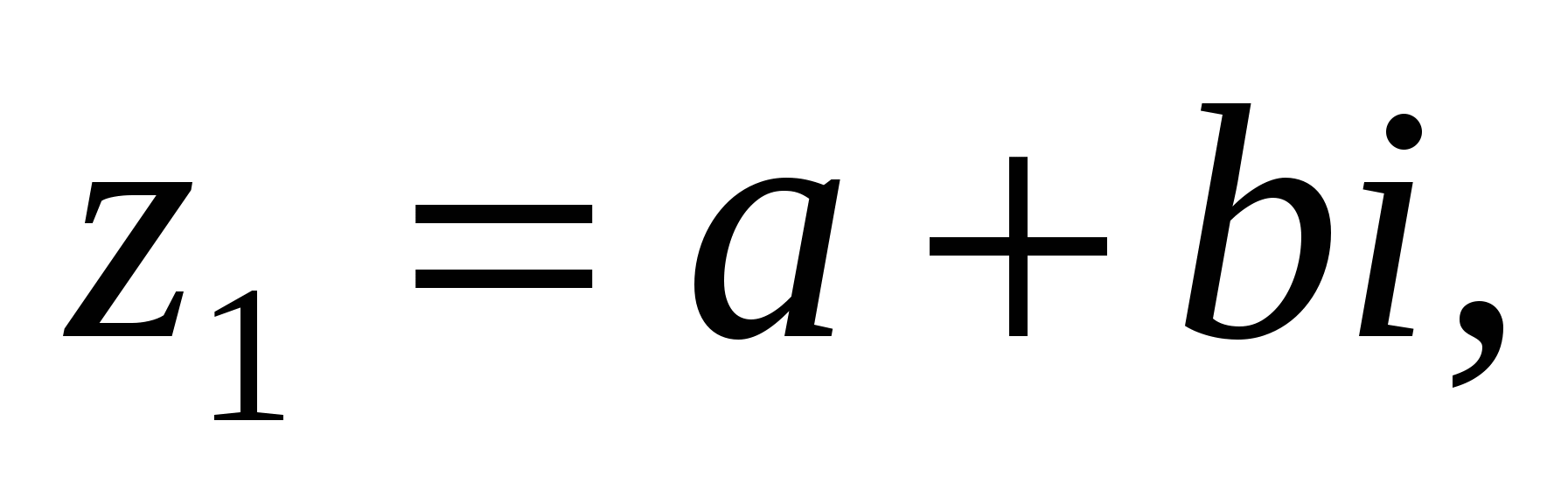
 комплекс сандарының көбейтіндісі деп
комплекс сандарының көбейтіндісі деп 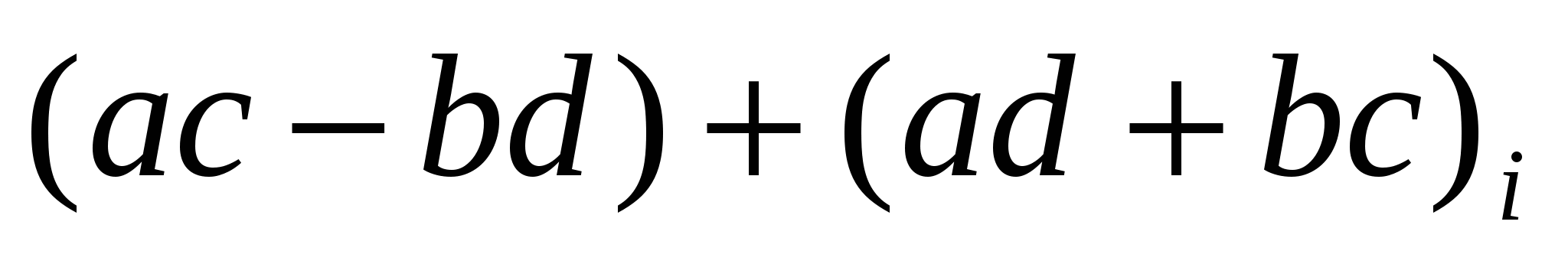 санын атайды, яғни
санын атайды, яғни
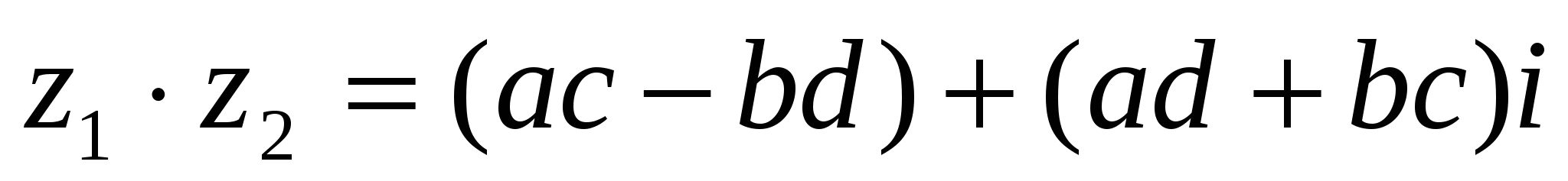 (2)
(2)
2 Мысал: 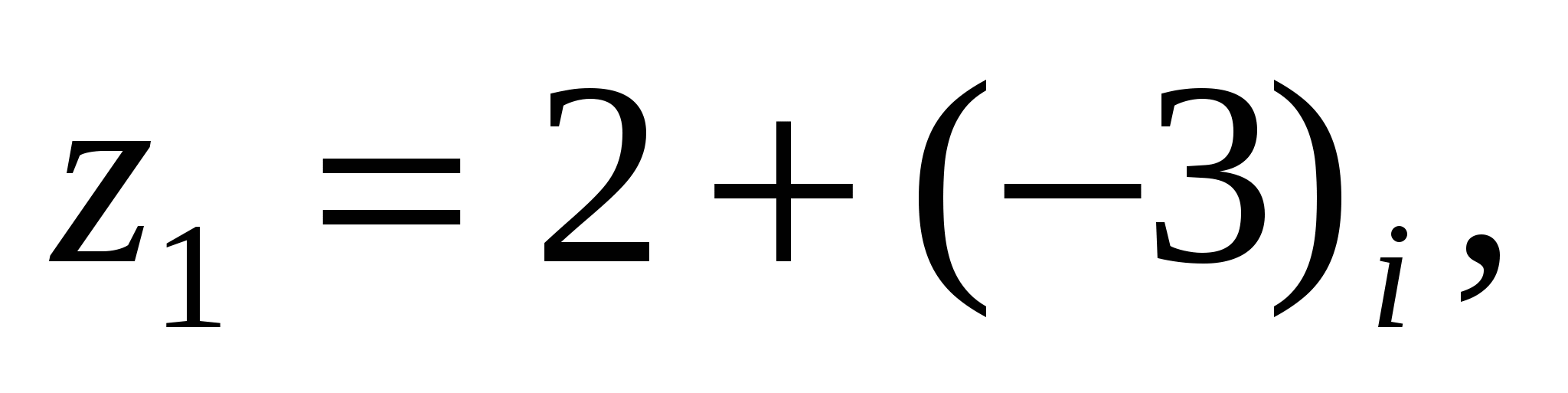
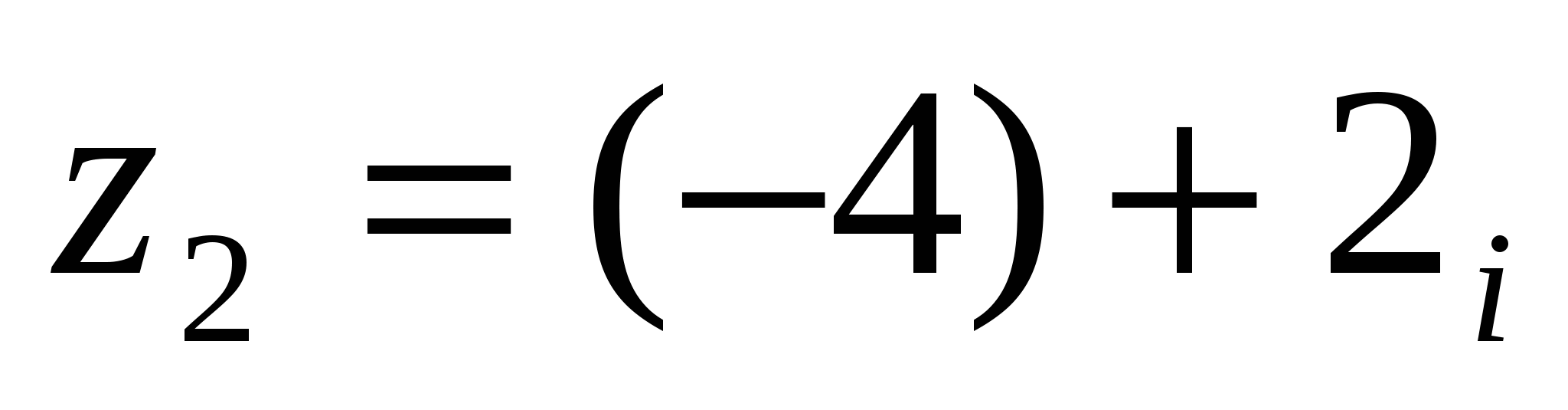 комплекс сандарының көбейтіндісін табу керек.
комплекс сандарының көбейтіндісін табу керек.
Δ 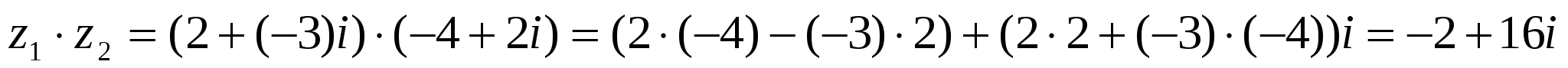 ▲
▲
Комплекс сандарының көбейтіндісінің келесі қасиеттері бар:
-
Коммутативтік:
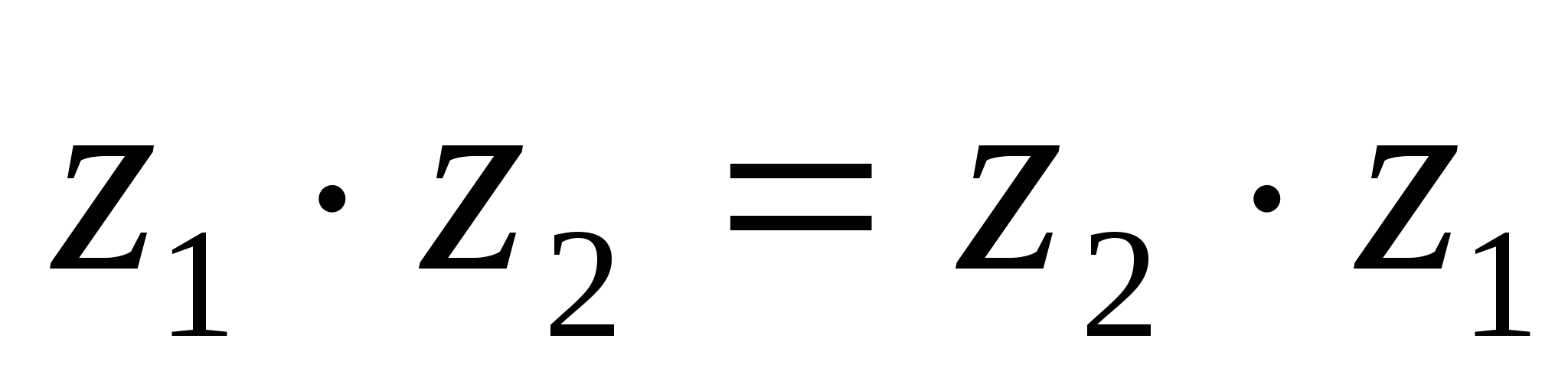 немесе
немесе 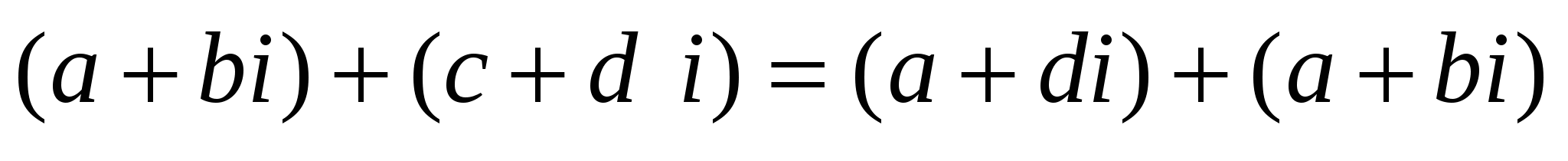
-
Ассоциативтік:
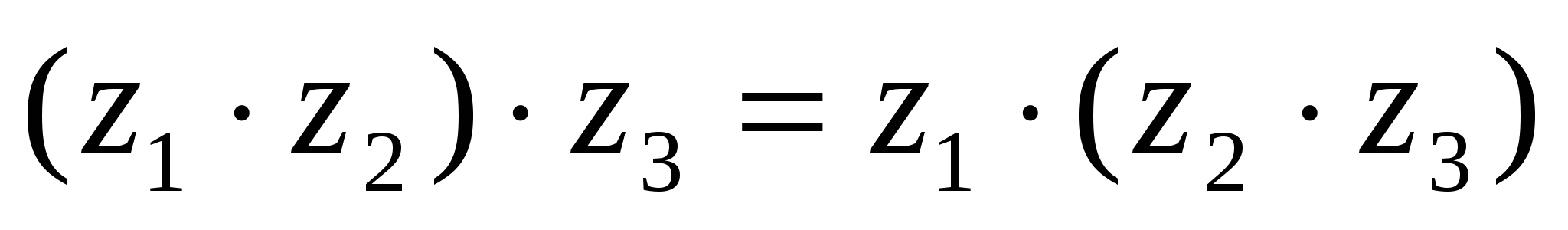 немесе
немесе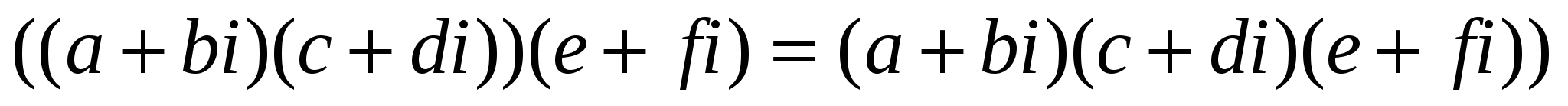
-
Дистрибутивтік:
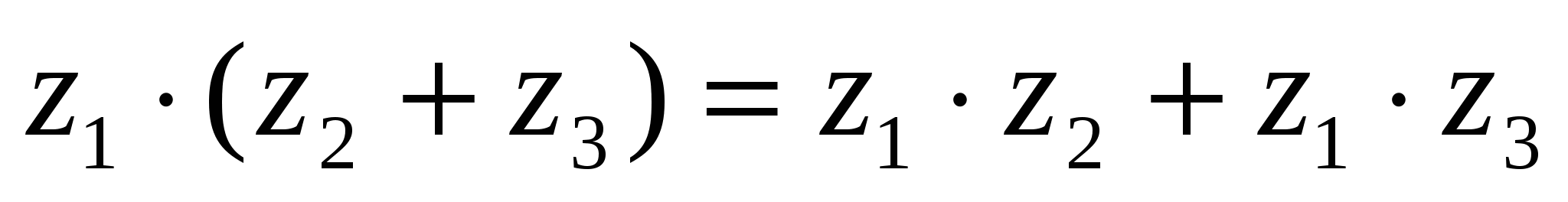 немесе
немесе 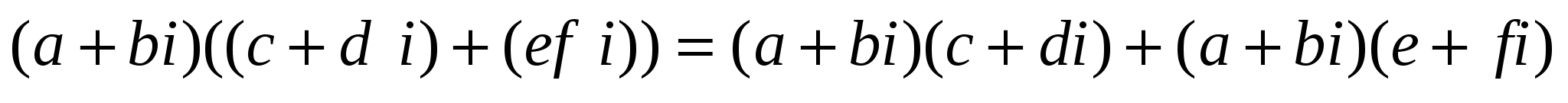
Анықтама 5: 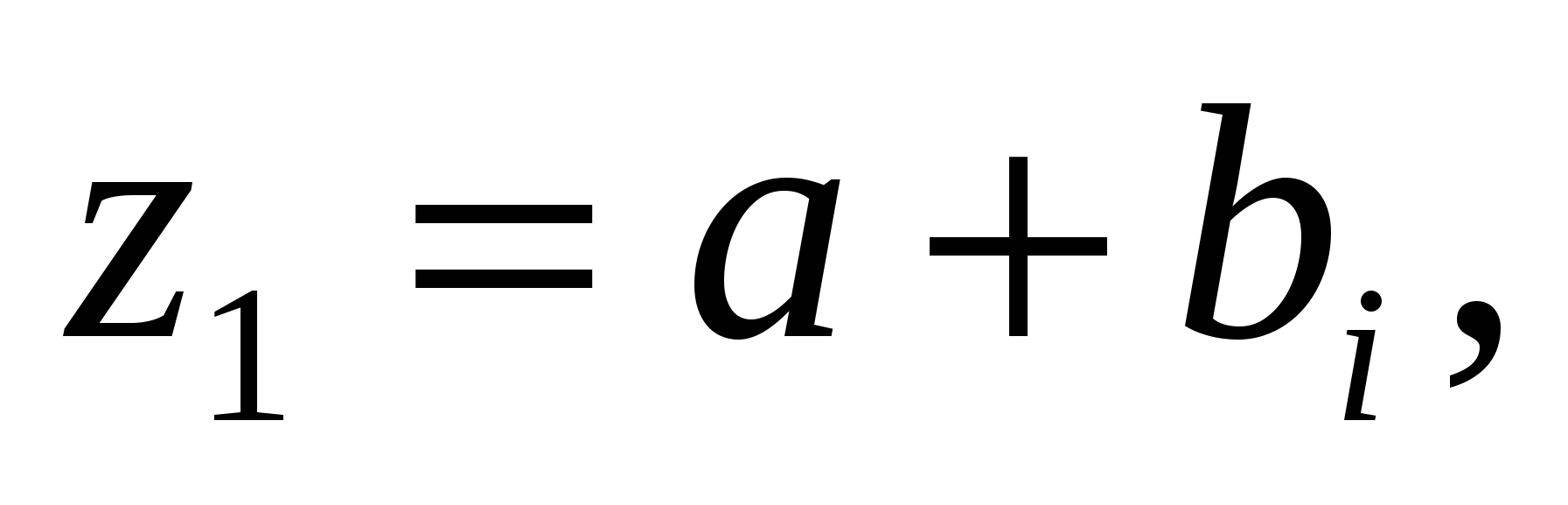
 комплекс сандарының айырмасы деп
комплекс сандарының айырмасы деп 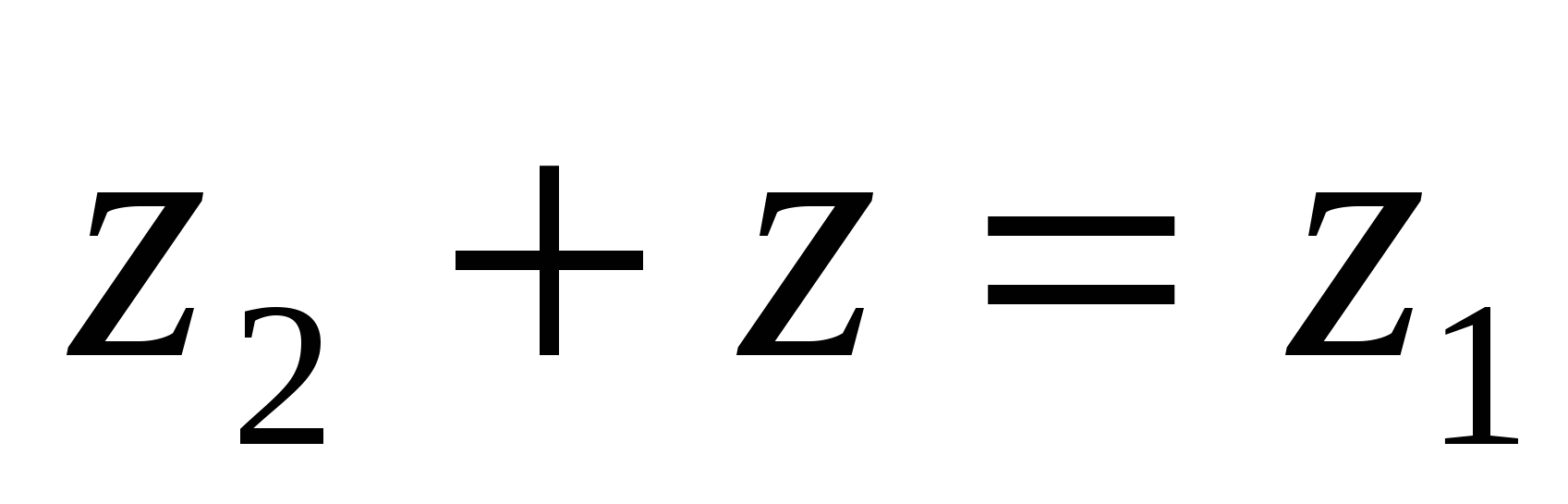 немесе
немесе 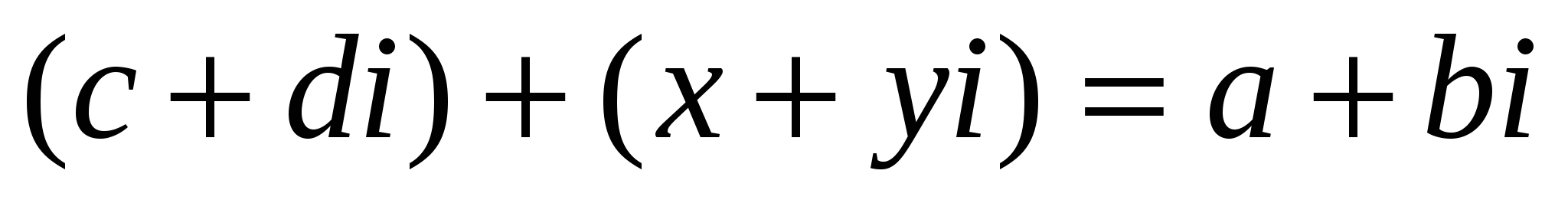 (3) теңдігін қанағаттандыратын
(3) теңдігін қанағаттандыратын ![]() комплекс саны аталады.
комплекс саны аталады.
Комплекс сандарының айырмасының бар болуын және жалғыздығын көрсетейік. (3) формуладан:
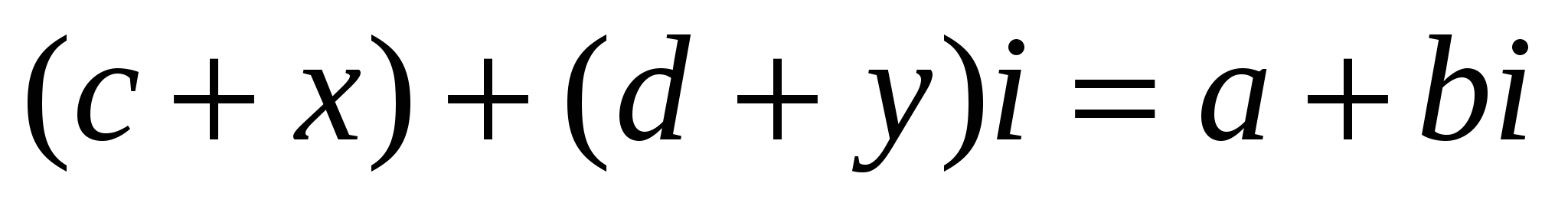
-
анықтаманы ескере отырып, келесі теңдеулер жүйесіне келеміз:
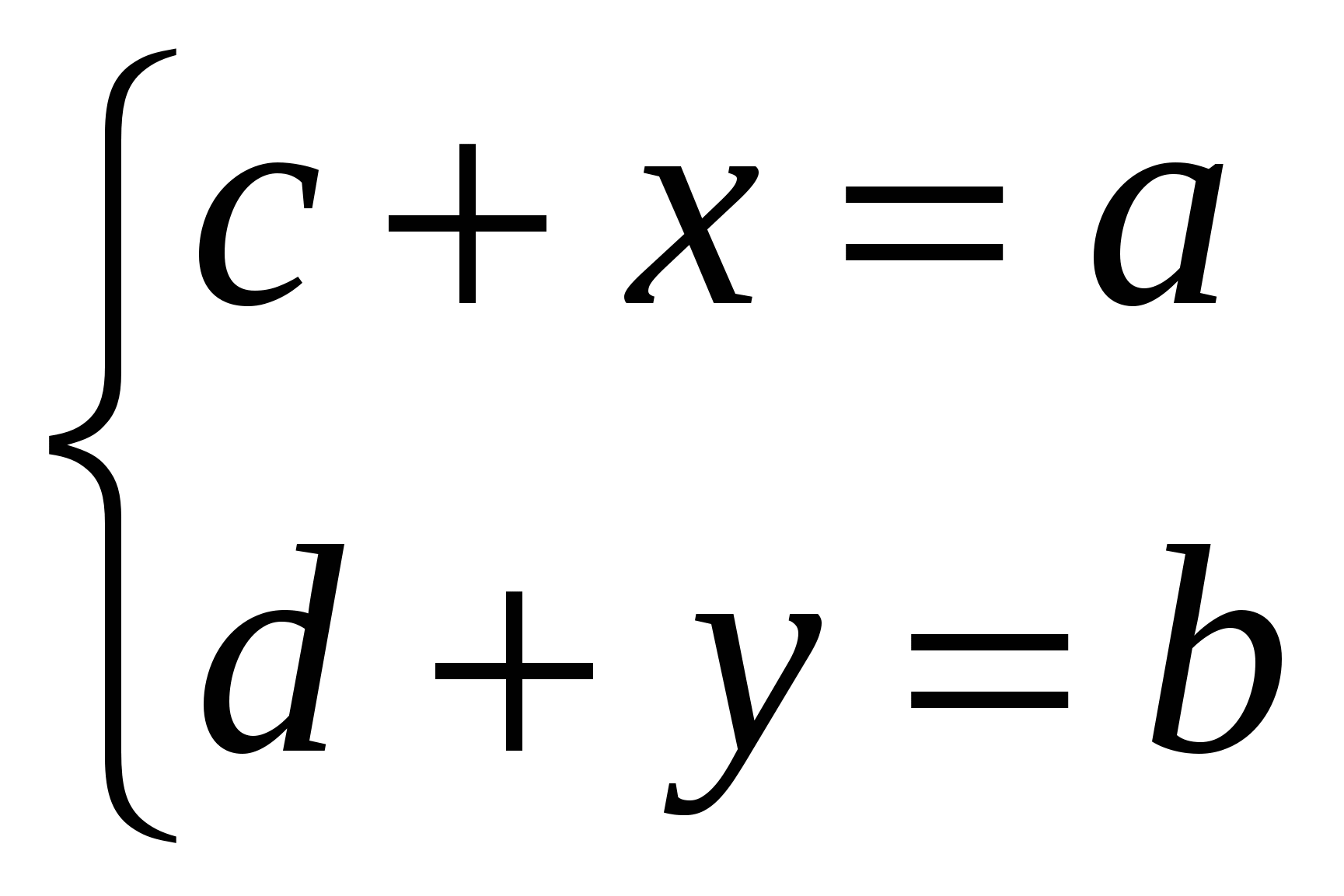 =>
=> 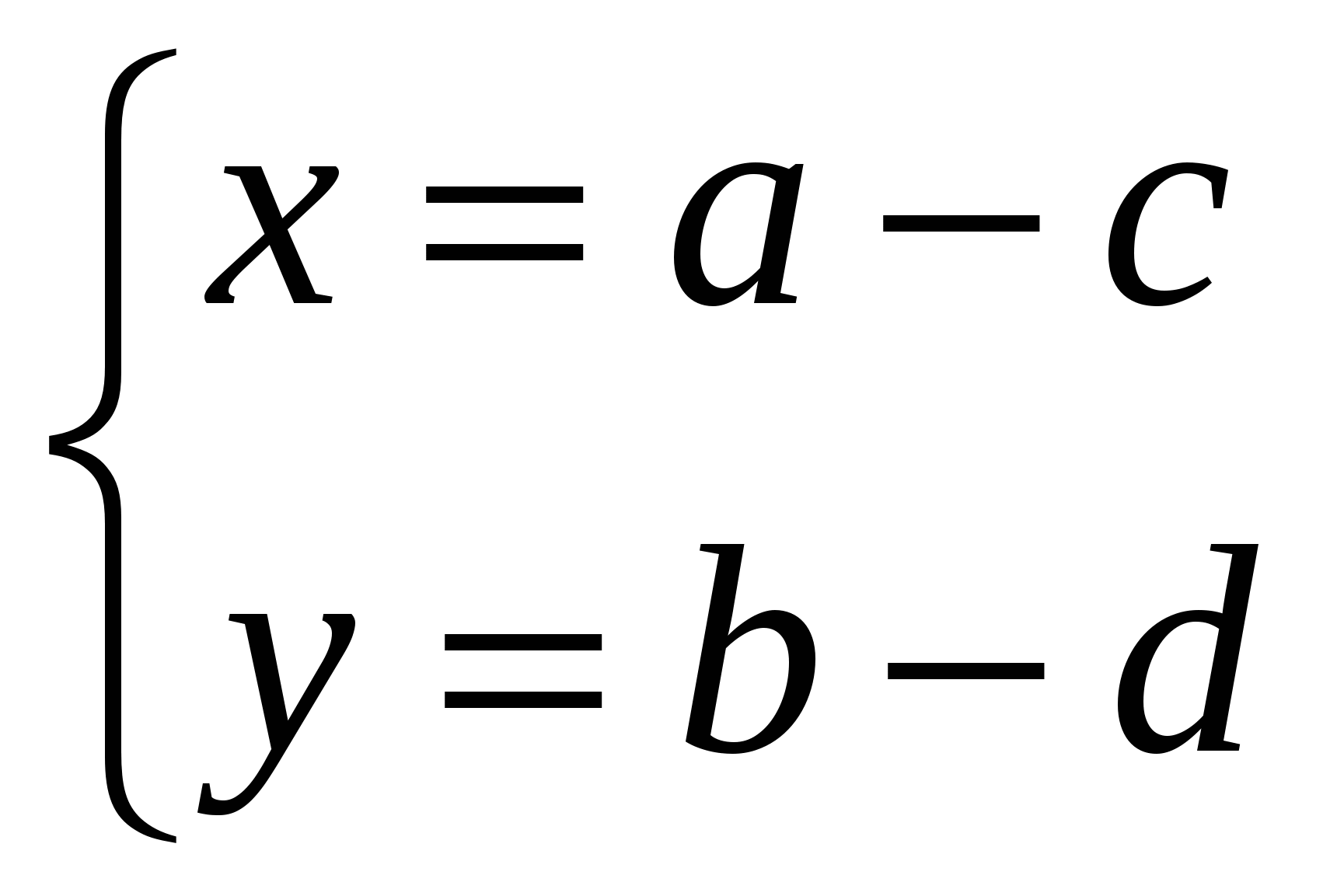
Яғни,  (4)
(4)
Осыдан айырманын бар болуымен жалғыздығы шығады.
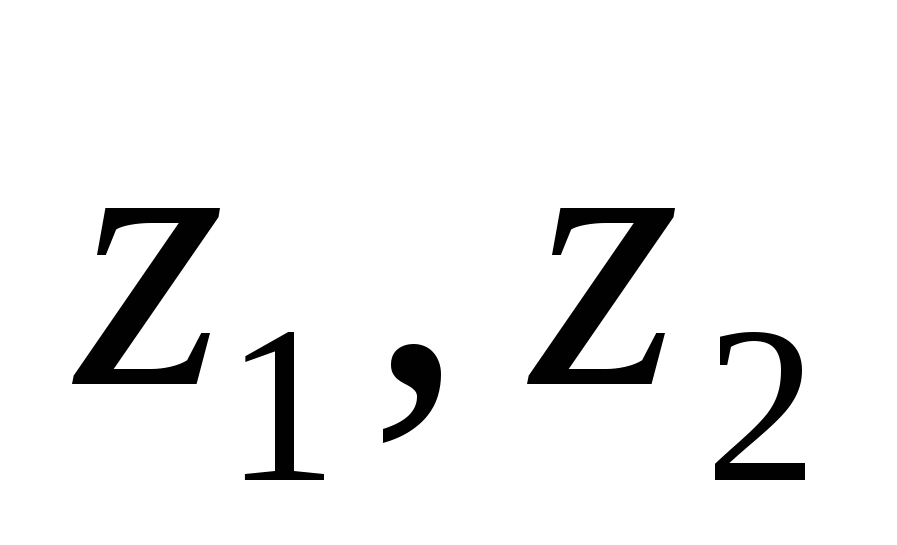 cандарының z айырмасы
cандарының z айырмасы 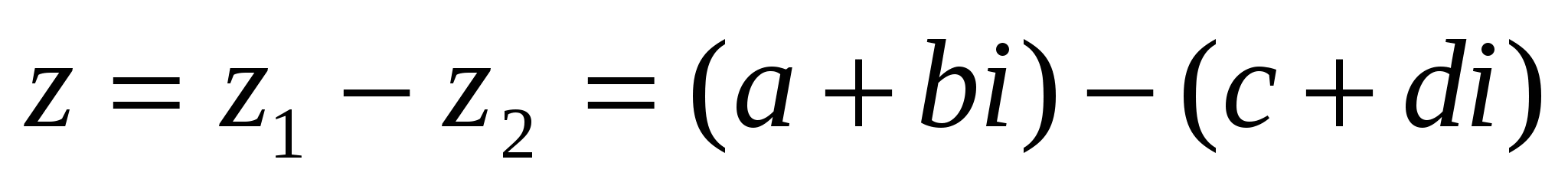 деп белгіленеді.
деп белгіленеді.
-
формуланы келесі түрде жазуға болады:
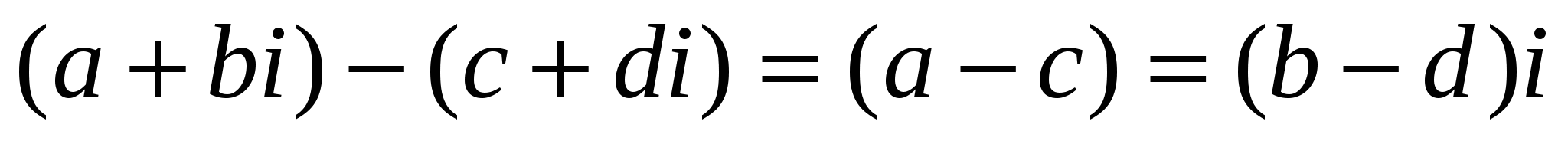 (5)
(5)
3 Мысал: 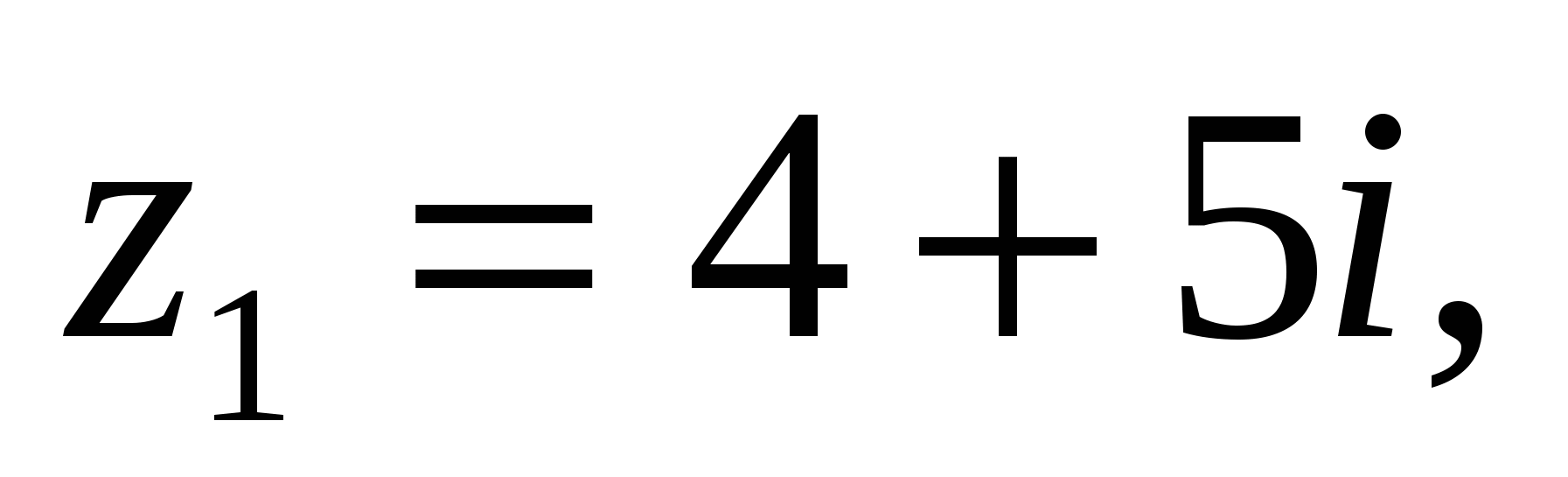
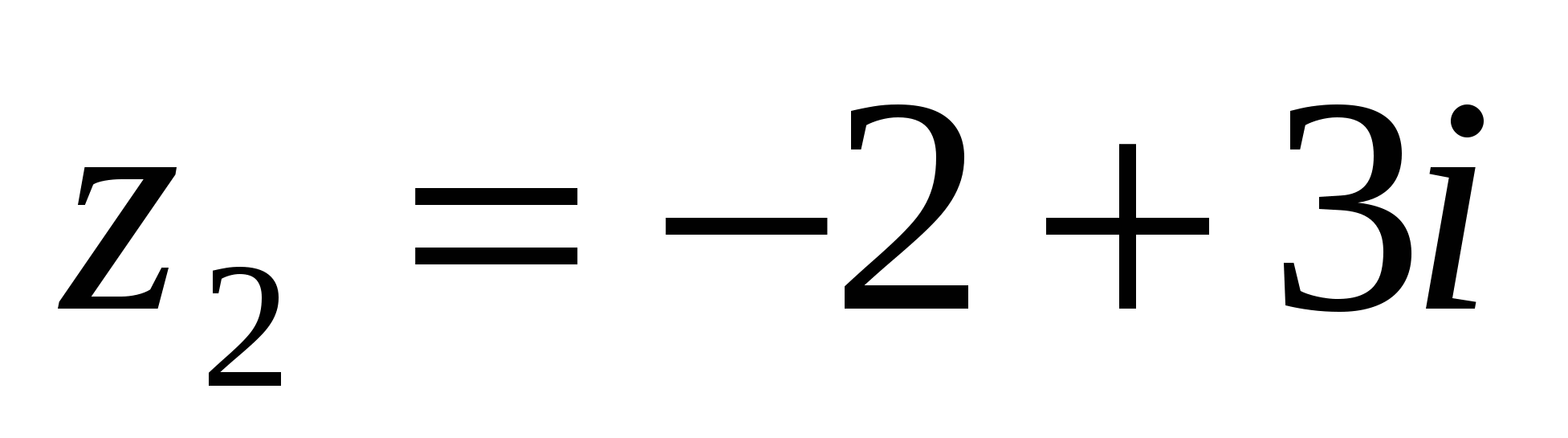 сандарының айырмасын табу керек.
сандарының айырмасын табу керек.
Δ 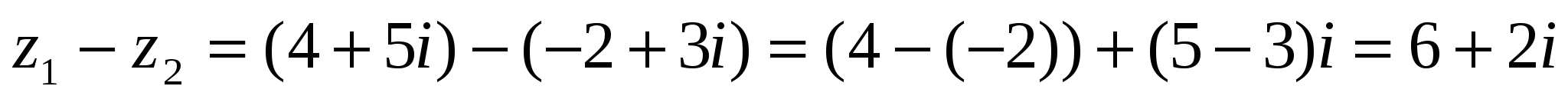 ▲
▲
4 Мысал: 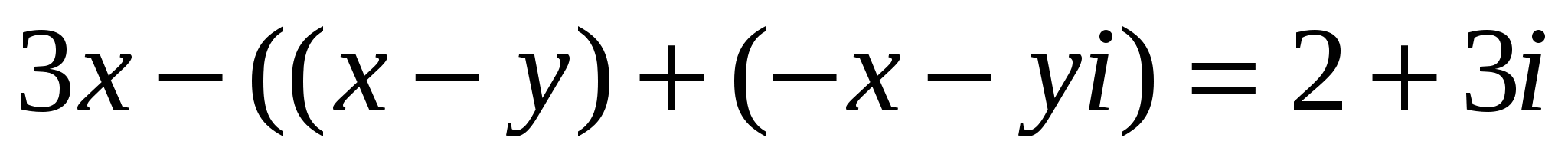 теңдеуін шешу керек.
теңдеуін шешу керек.
Δ көбейтіндіні орындап 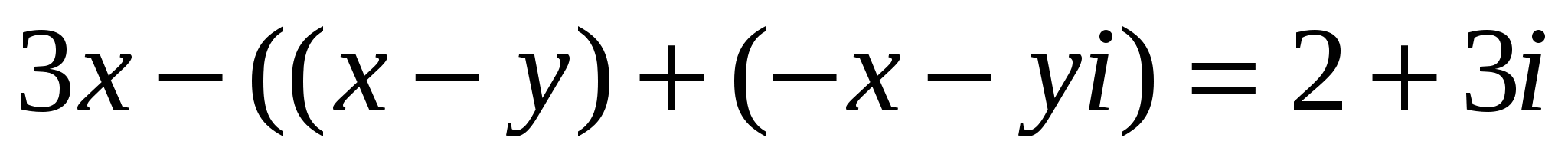 теңдігіне келеміз, осыдан
теңдігіне келеміз, осыдан 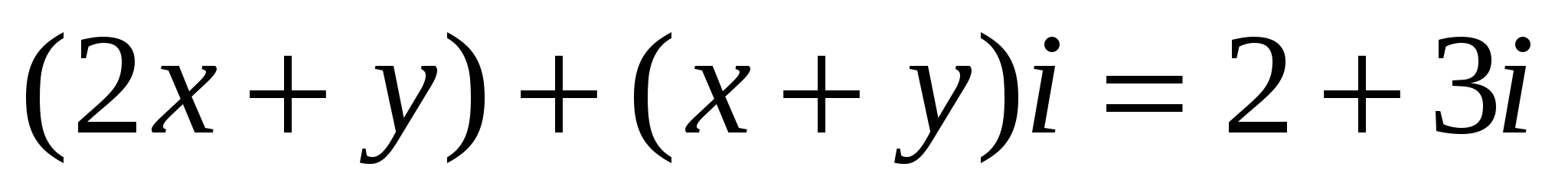
2 анықтама бойынша
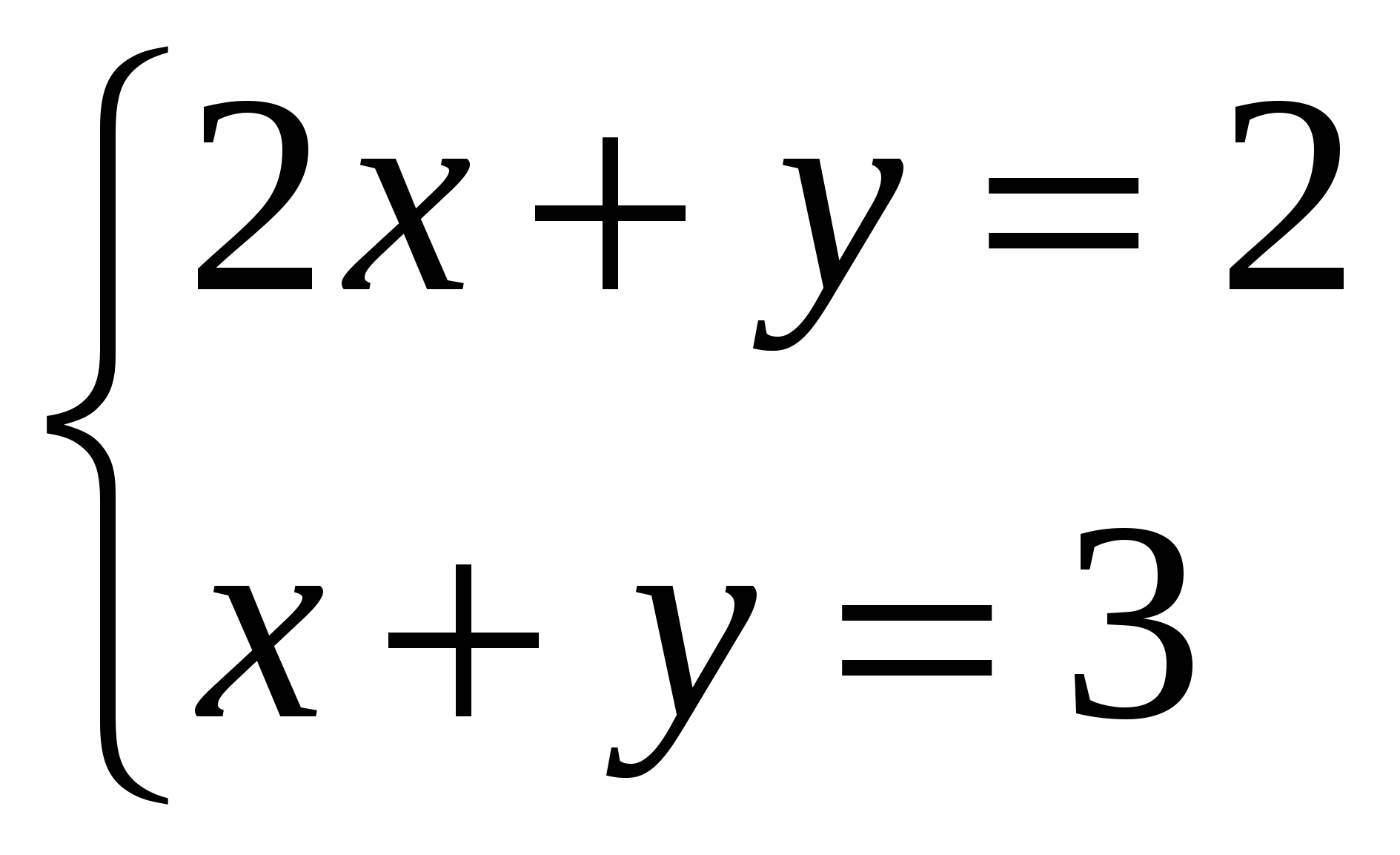
жүйесіне келеміз. Оның шешімі: x=-1, y=4. ▲
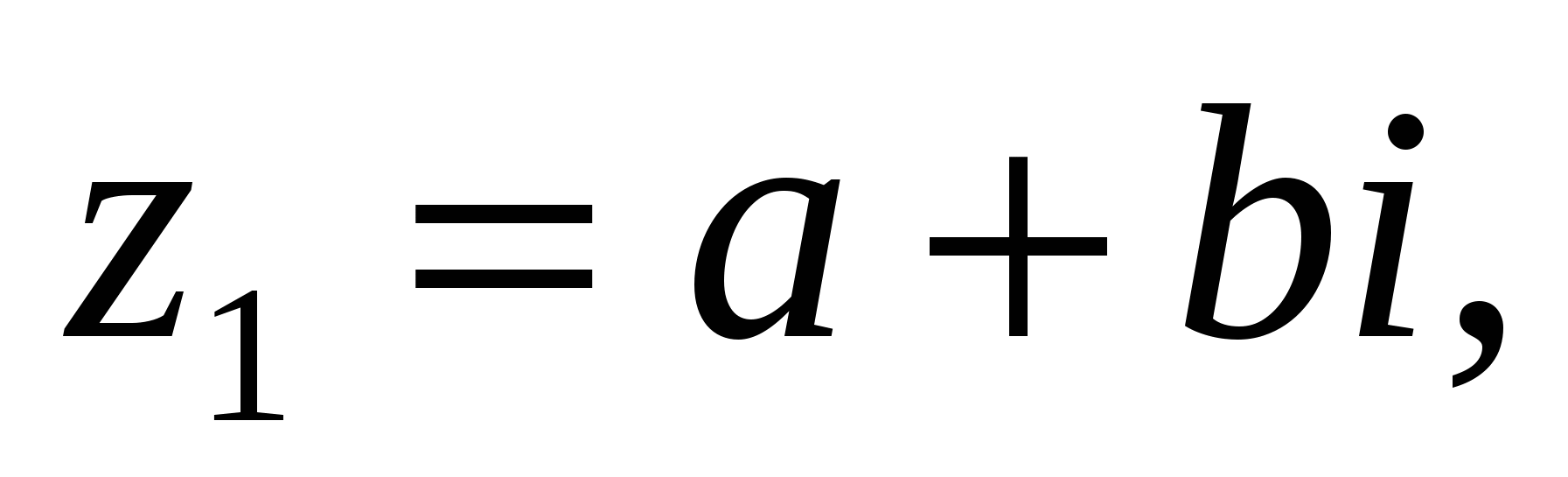 комплекс саны берілген болсын. Онда -z деп белгіленген және
комплекс саны берілген болсын. Онда -z деп белгіленген және 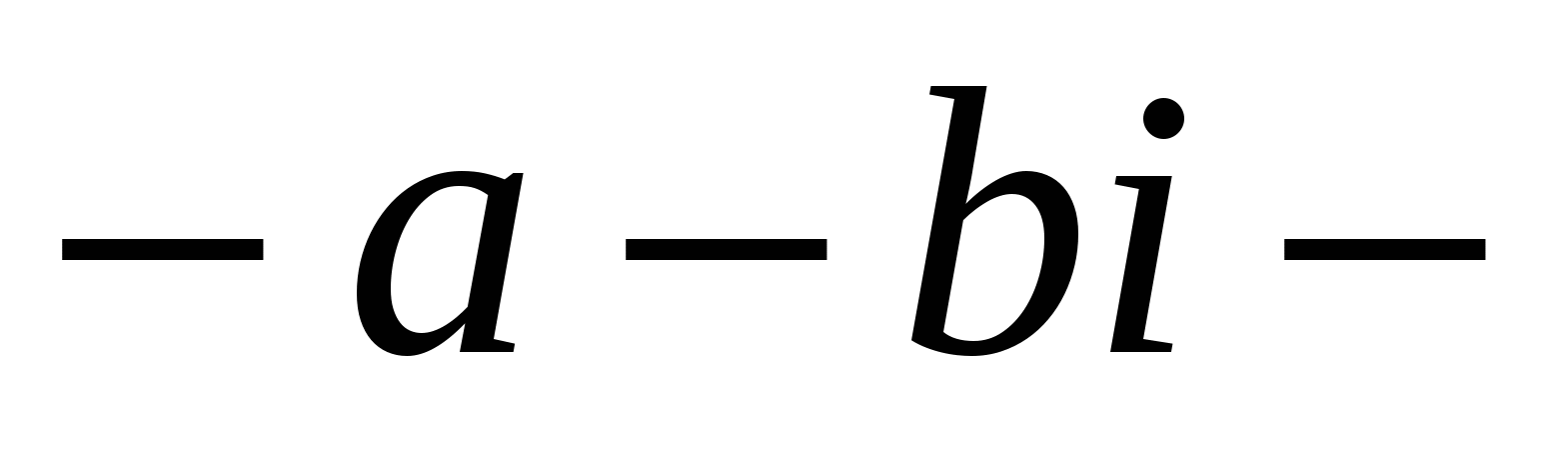 ға тең болатын сан
ға тең болатын сан 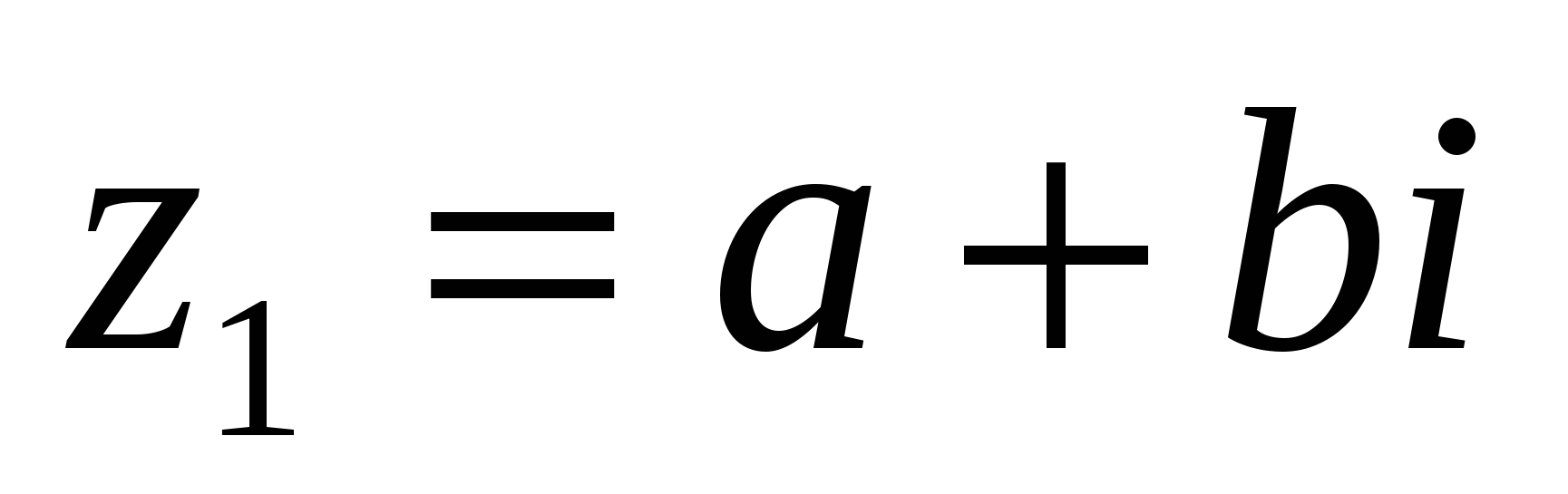 санына қарама-қарсы деп аталады.
санына қарама-қарсы деп аталады.
Сонымен, ![]() комплекс санын
комплекс санын 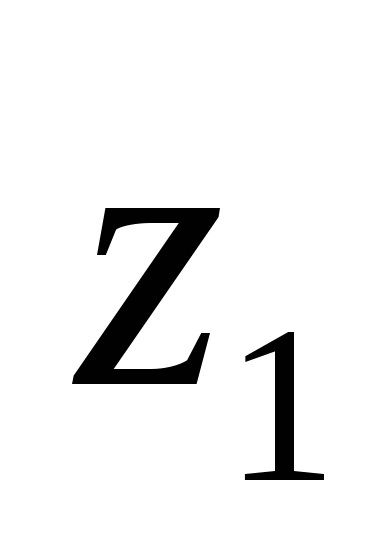 санынан алу үшін
санынан алу үшін 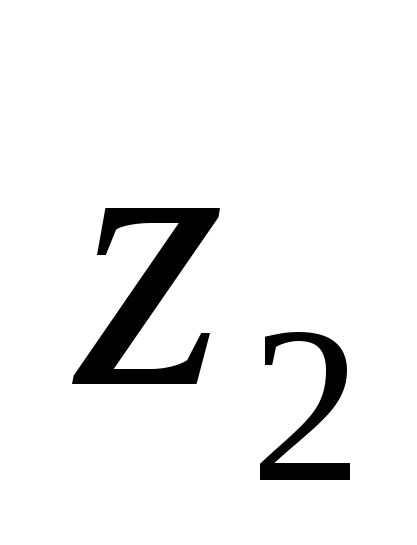 -ні қарама-қарсы -
-ні қарама-қарсы - 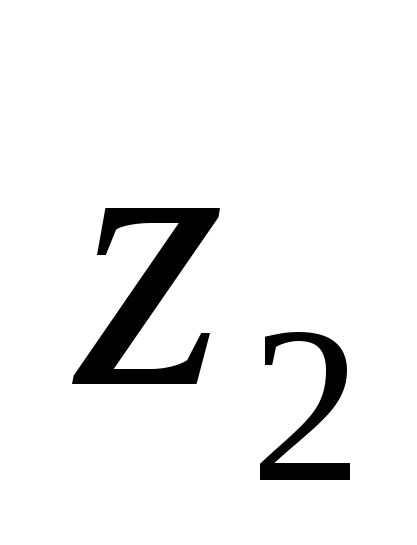 санына қосу керек.
санына қосу керек.
Анықтама 6: 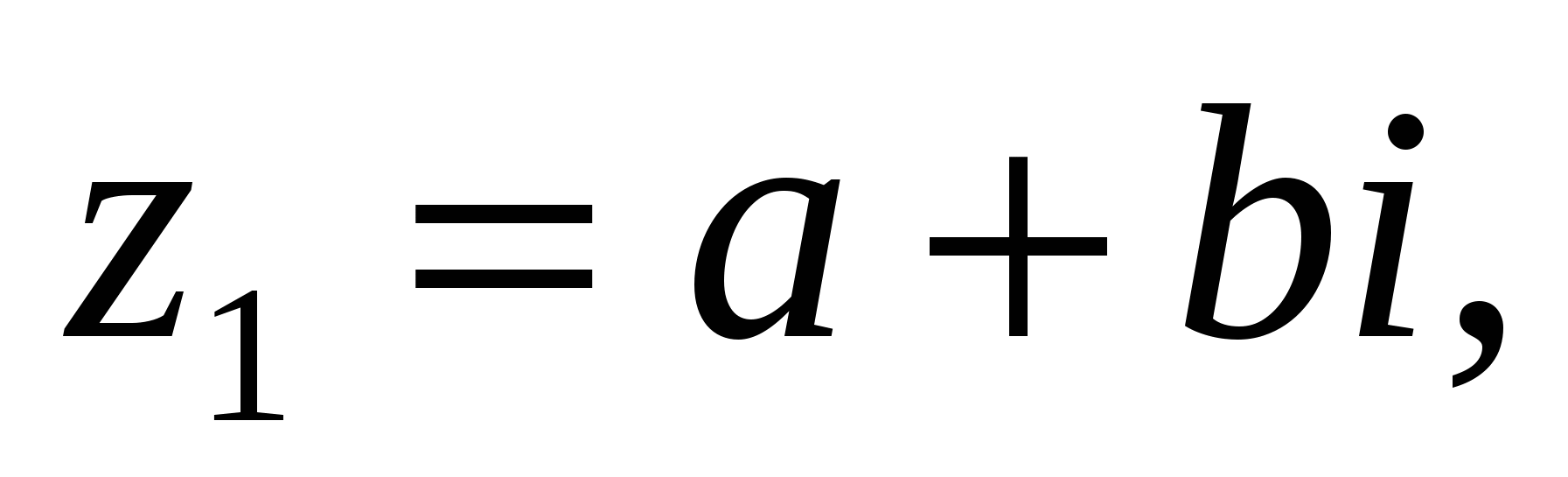
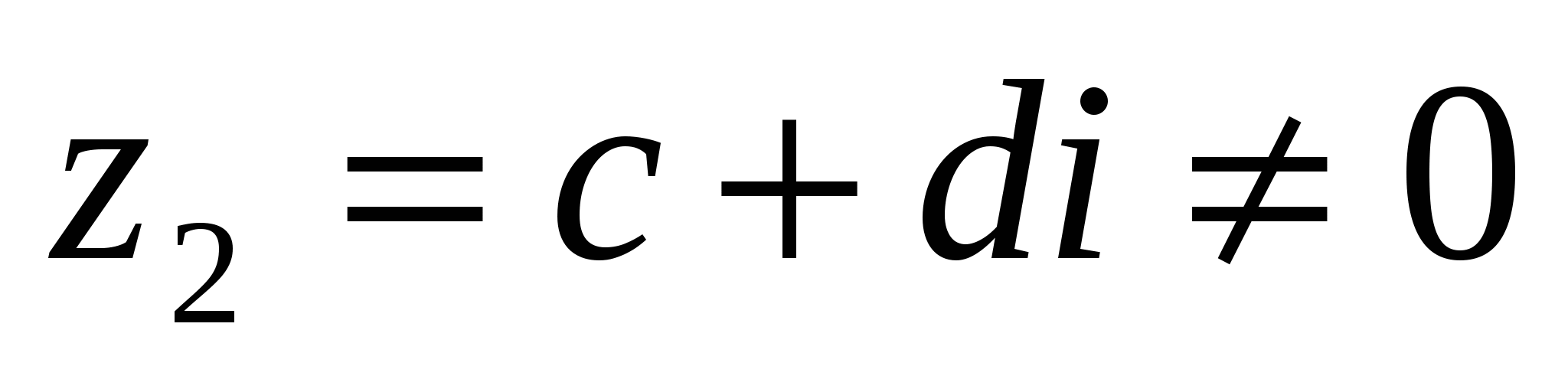 комплекс сандарының бөліндісі деп
комплекс сандарының бөліндісі деп 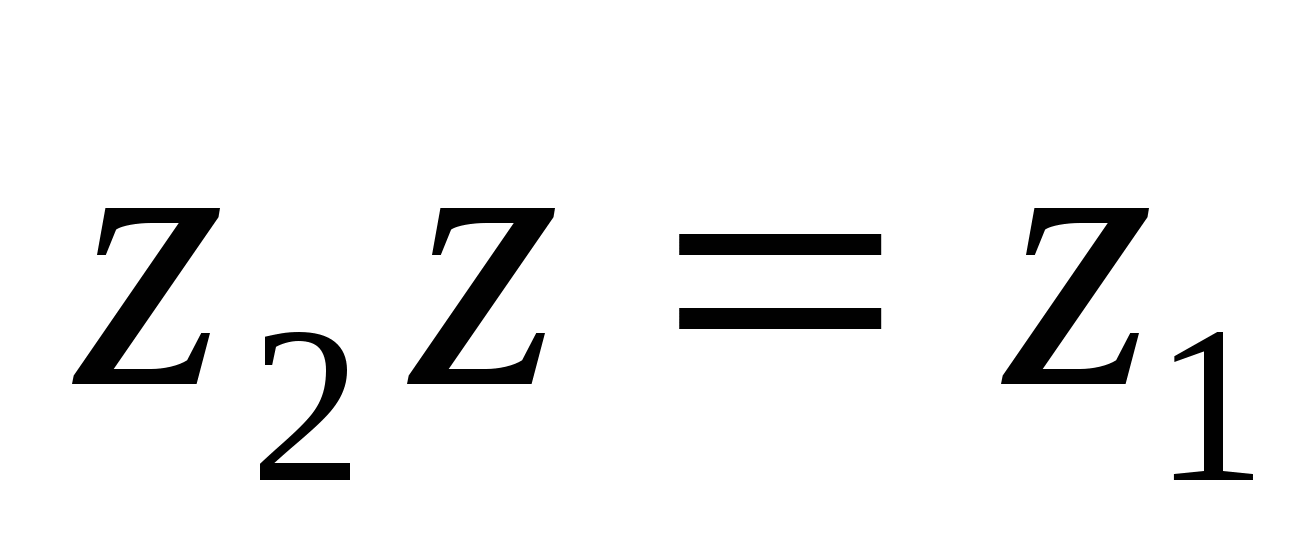 немесе
немесе 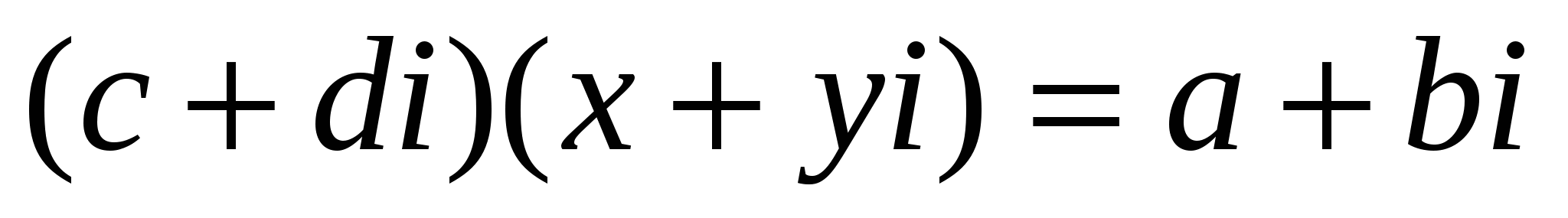 (6) теңдігін қанағаттандыратын
(6) теңдігін қанағаттандыратын ![]() санын атайды.
санын атайды.
Комплекс сандарының бөліндісінің бар болуының және жалғыздығын көрсетейік: (6) формуладан 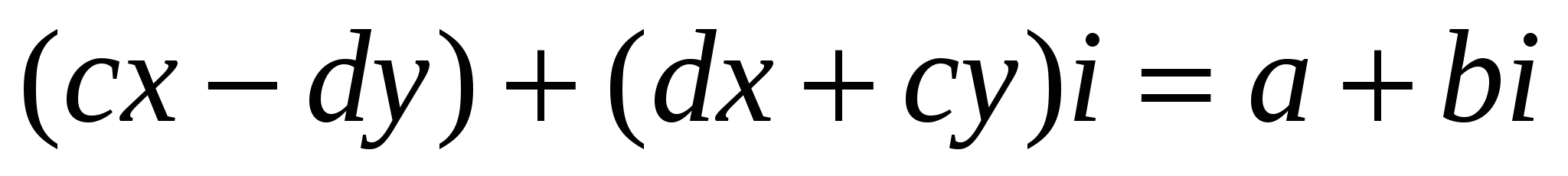 теңдігіне келеміз.
теңдігіне келеміз.
2 анықтама бойынша
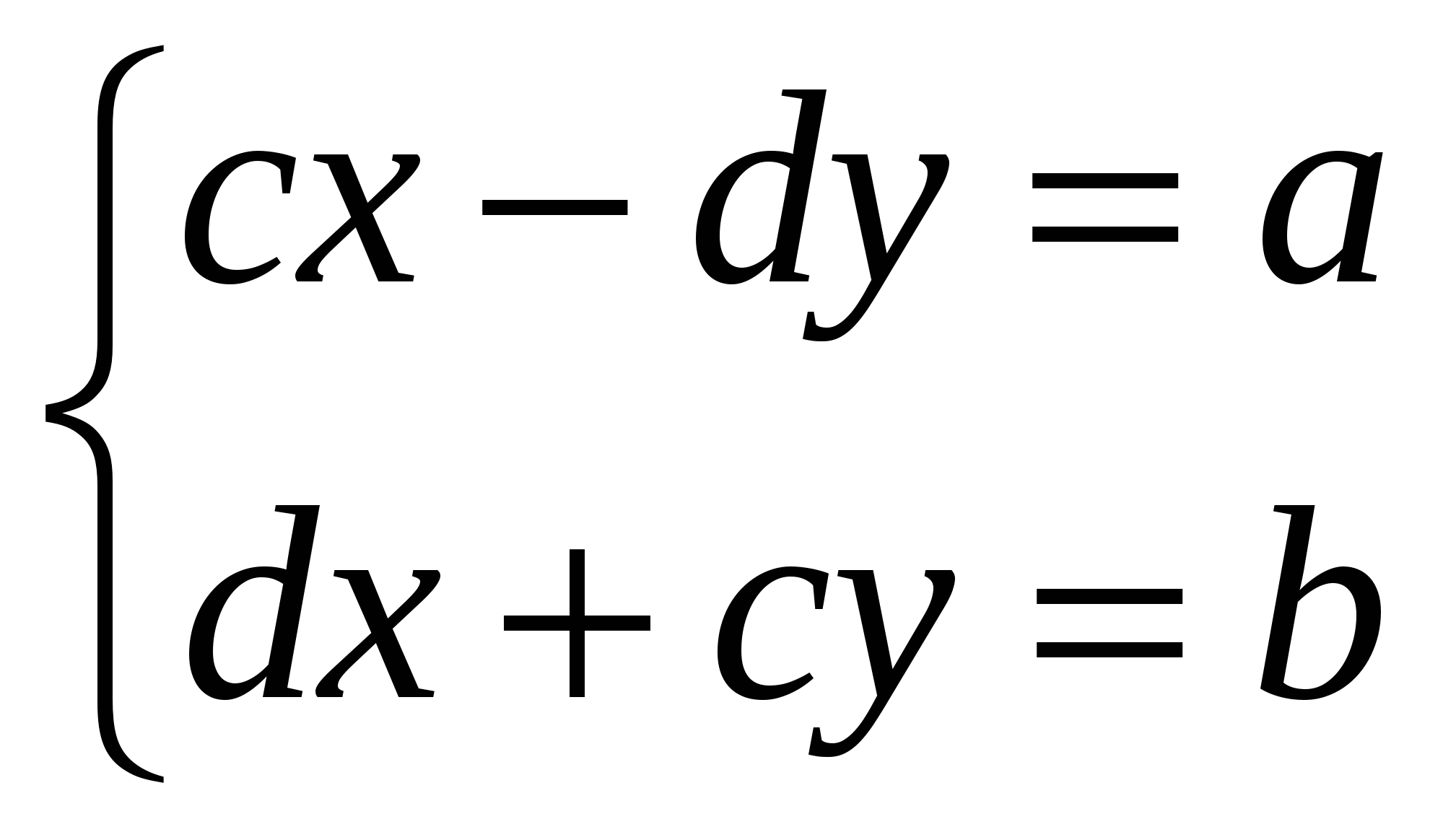
жүйесіне келеміз. Жүйені шешіп х және у үшін жалғыз мәндерін табамыз:
![]()
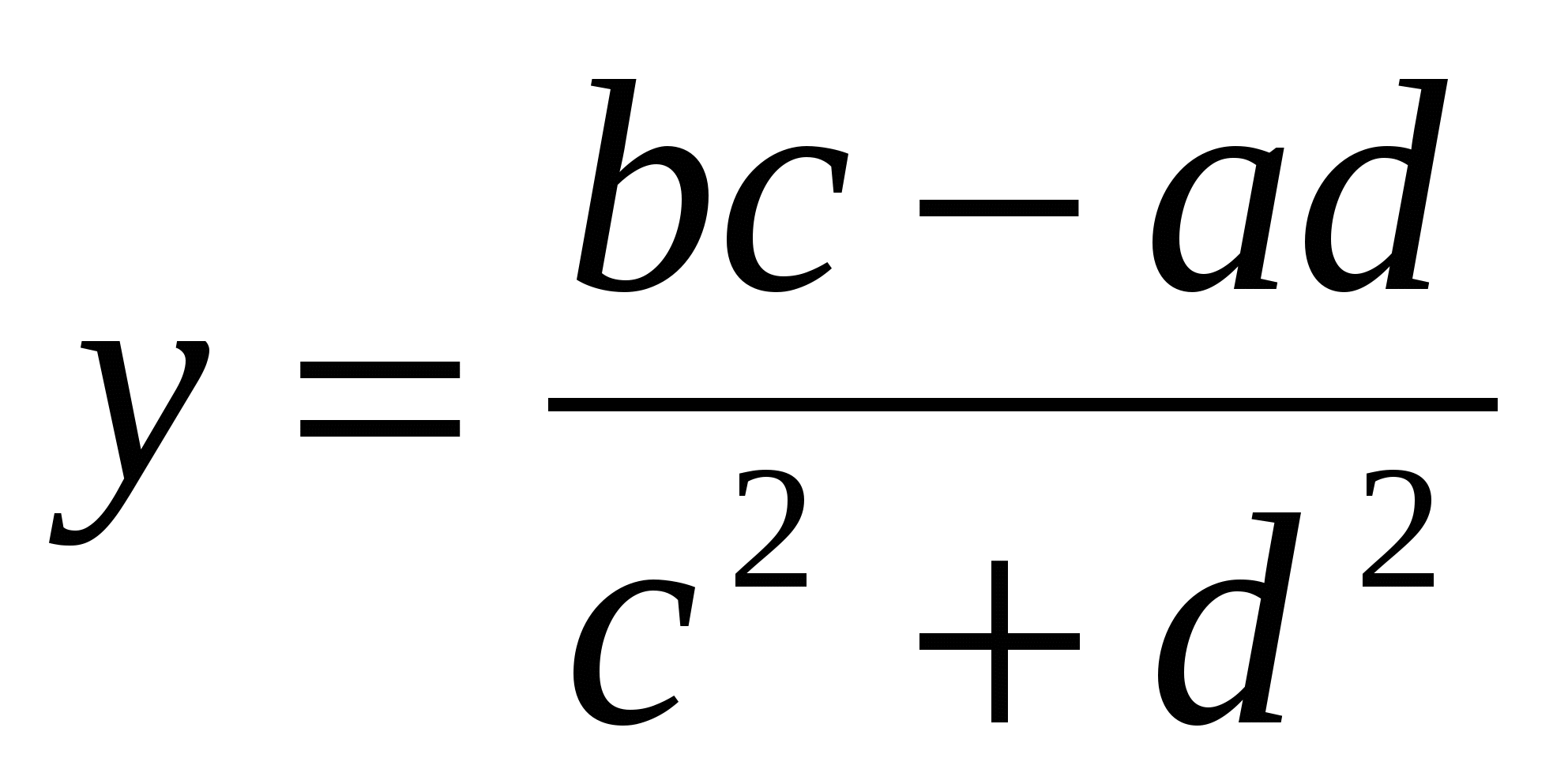
Шыққан өрнектің мағынасы бар, себебі, 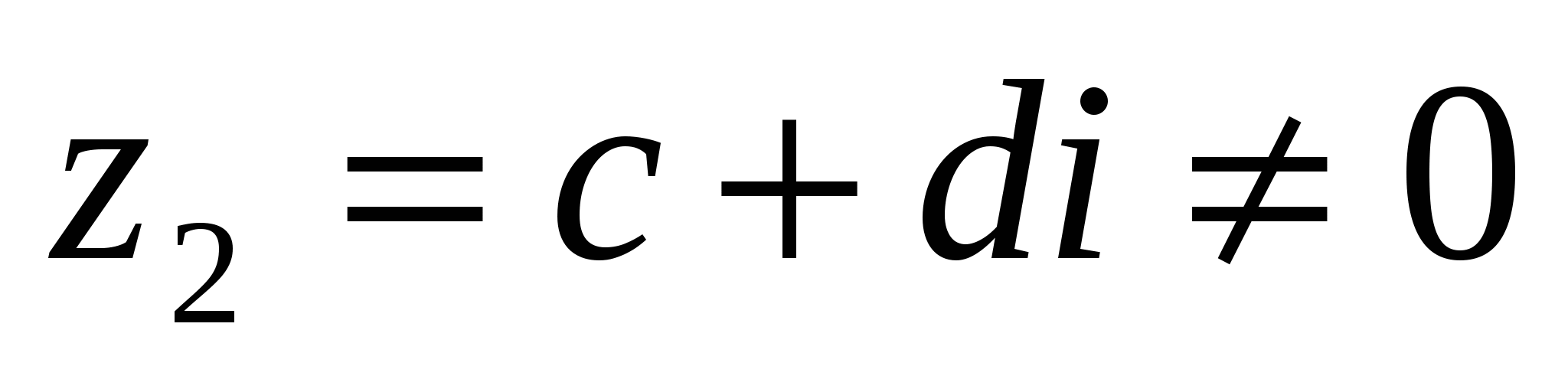 -ден
-ден  екені шығады.
екені шығады.
Сонымен,
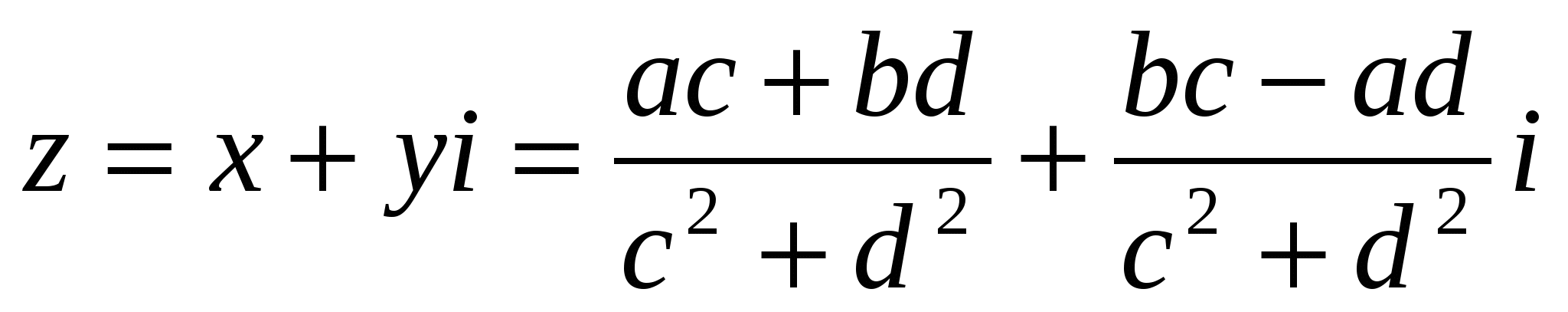 (7)
(7)
Осыдан 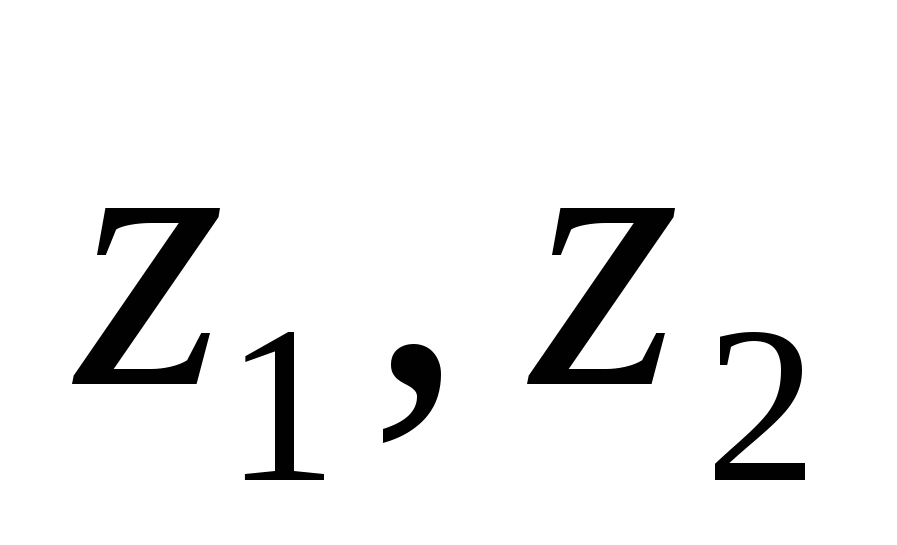 комплекс сандарының бөліндісінің бар болуы және жалғыздығы шығады, бірақ, мұнда
комплекс сандарының бөліндісінің бар болуы және жалғыздығы шығады, бірақ, мұнда 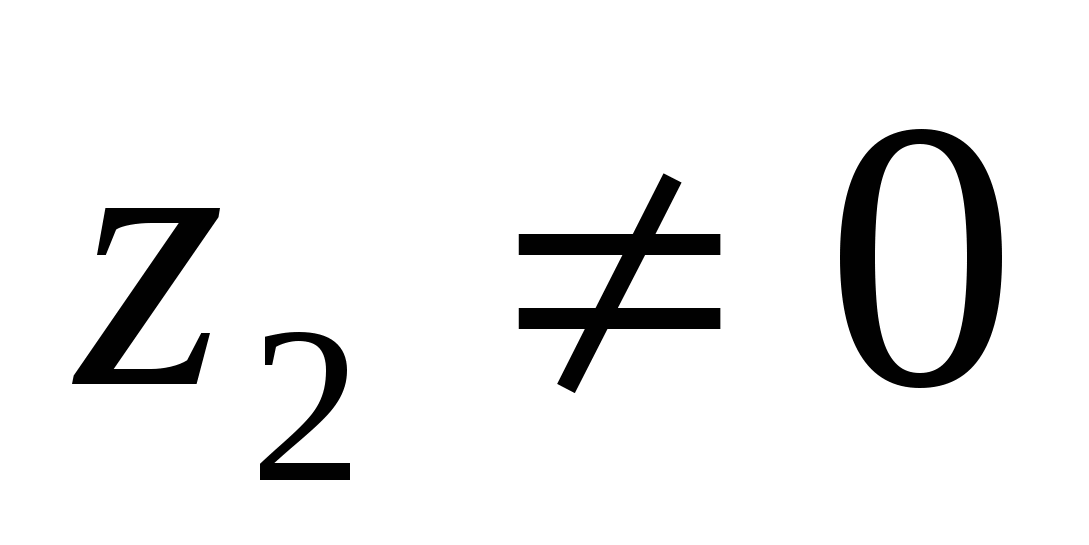 болу керек.
болу керек.
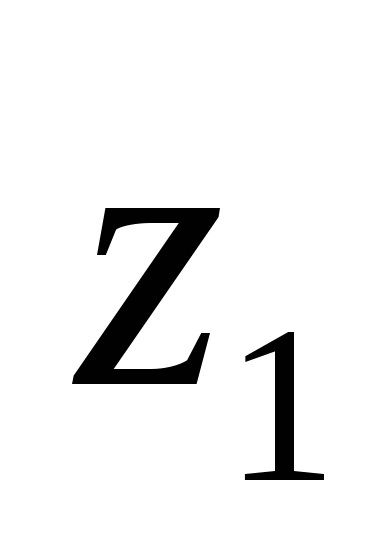 және
және 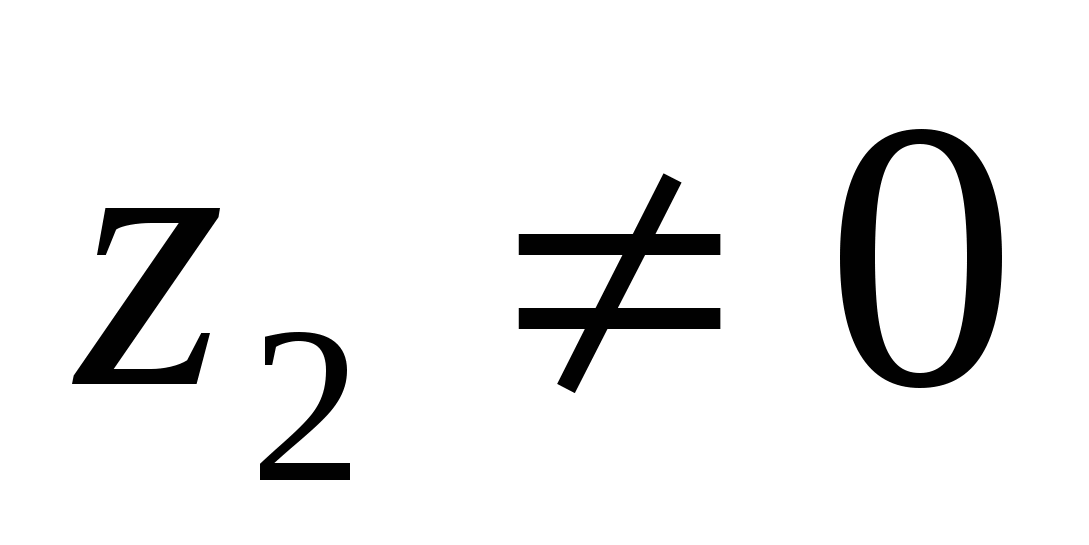 комплекс сандарының бөліндісі
комплекс сандарының бөліндісі
![]()
деп белгіленеді.
5 Мысал: 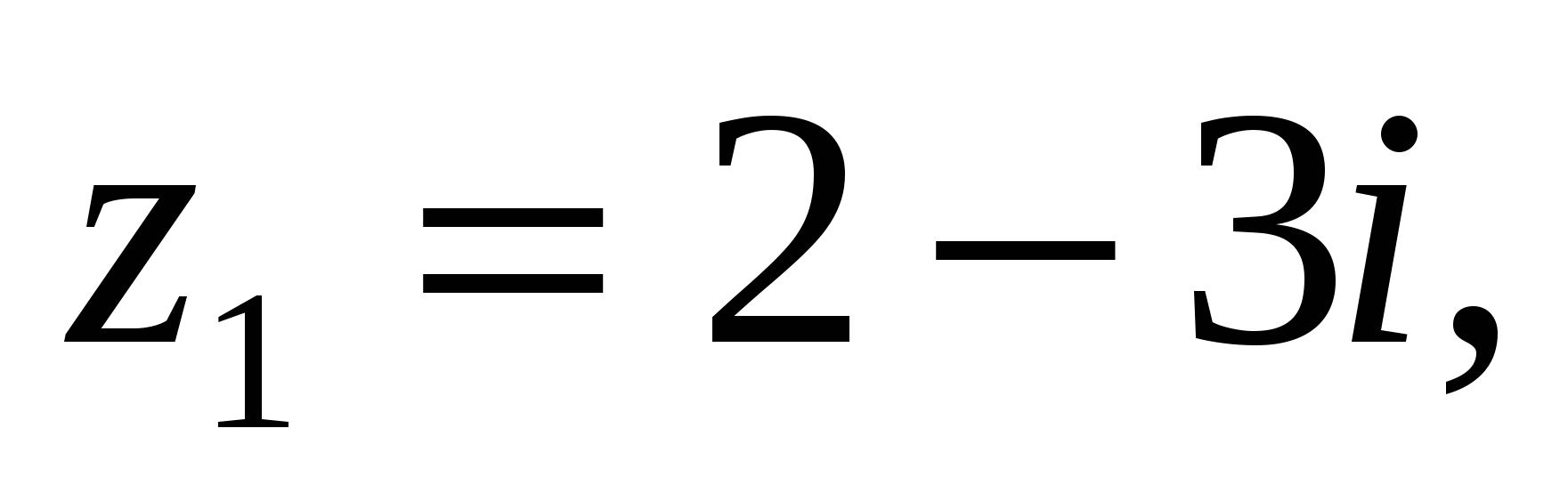
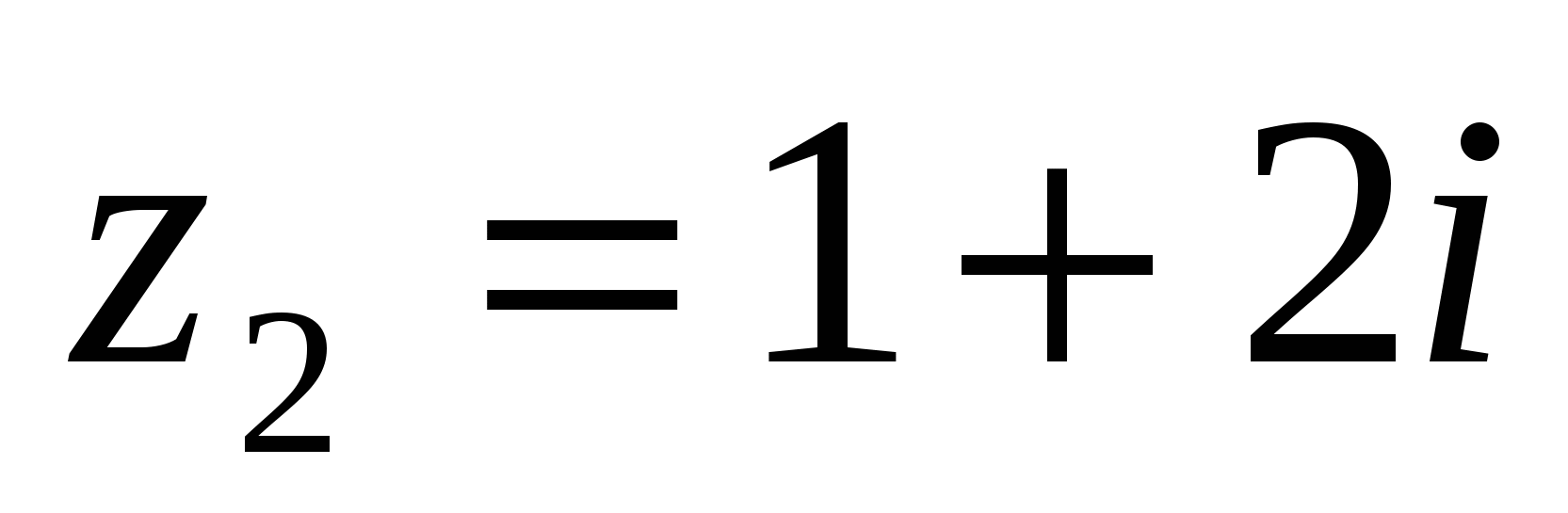 комплекс сандарының z бөліндісін табу керек.
комплекс сандарының z бөліндісін табу керек.
Δ 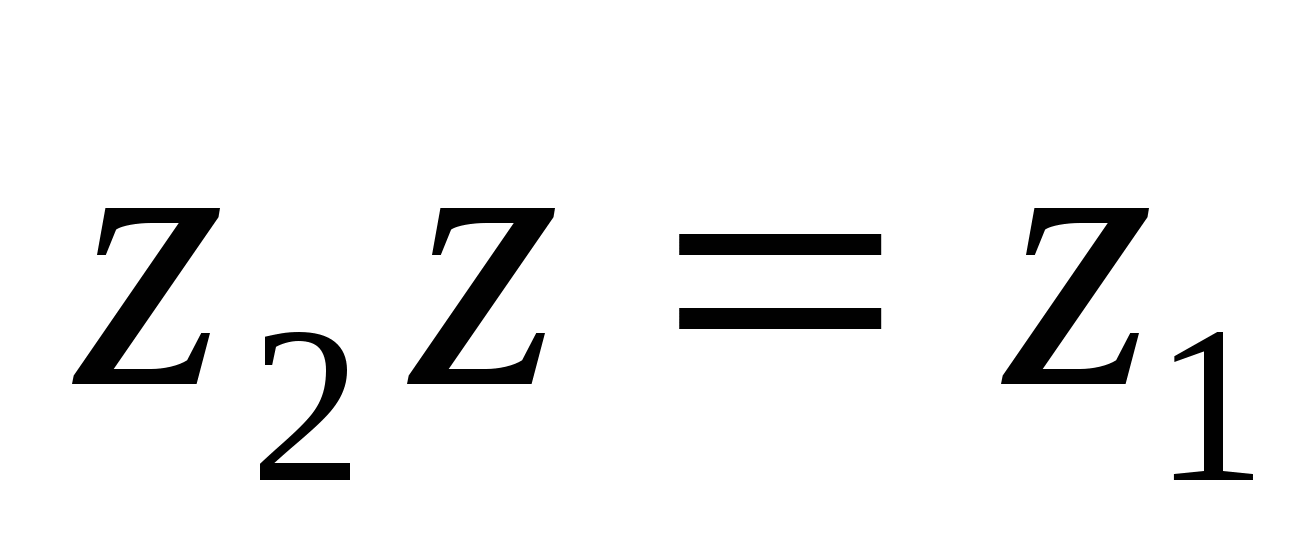 . Айталық,
. Айталық, 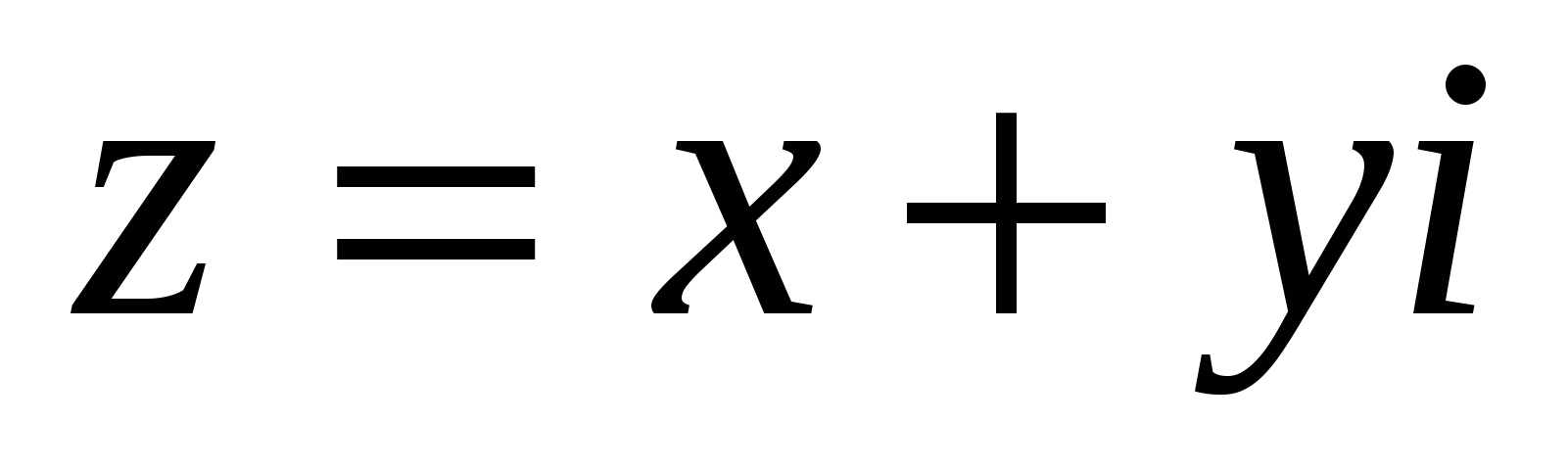 болсын. Онда
болсын. Онда
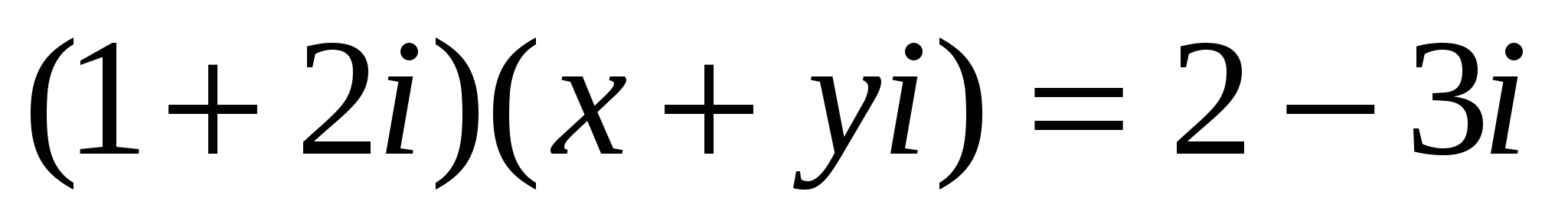
немесе 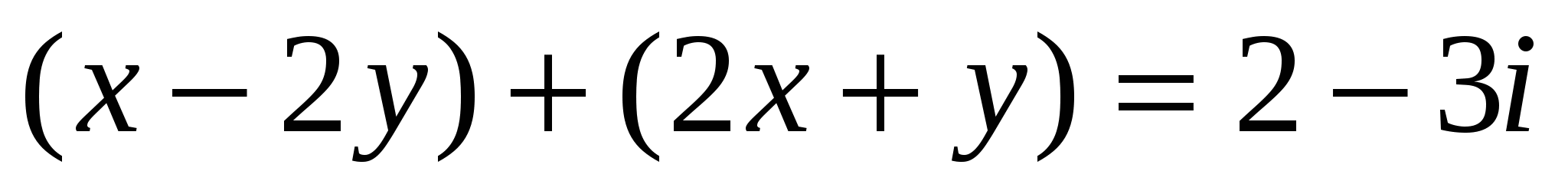
Осыдан келесі жүйеге келеміз
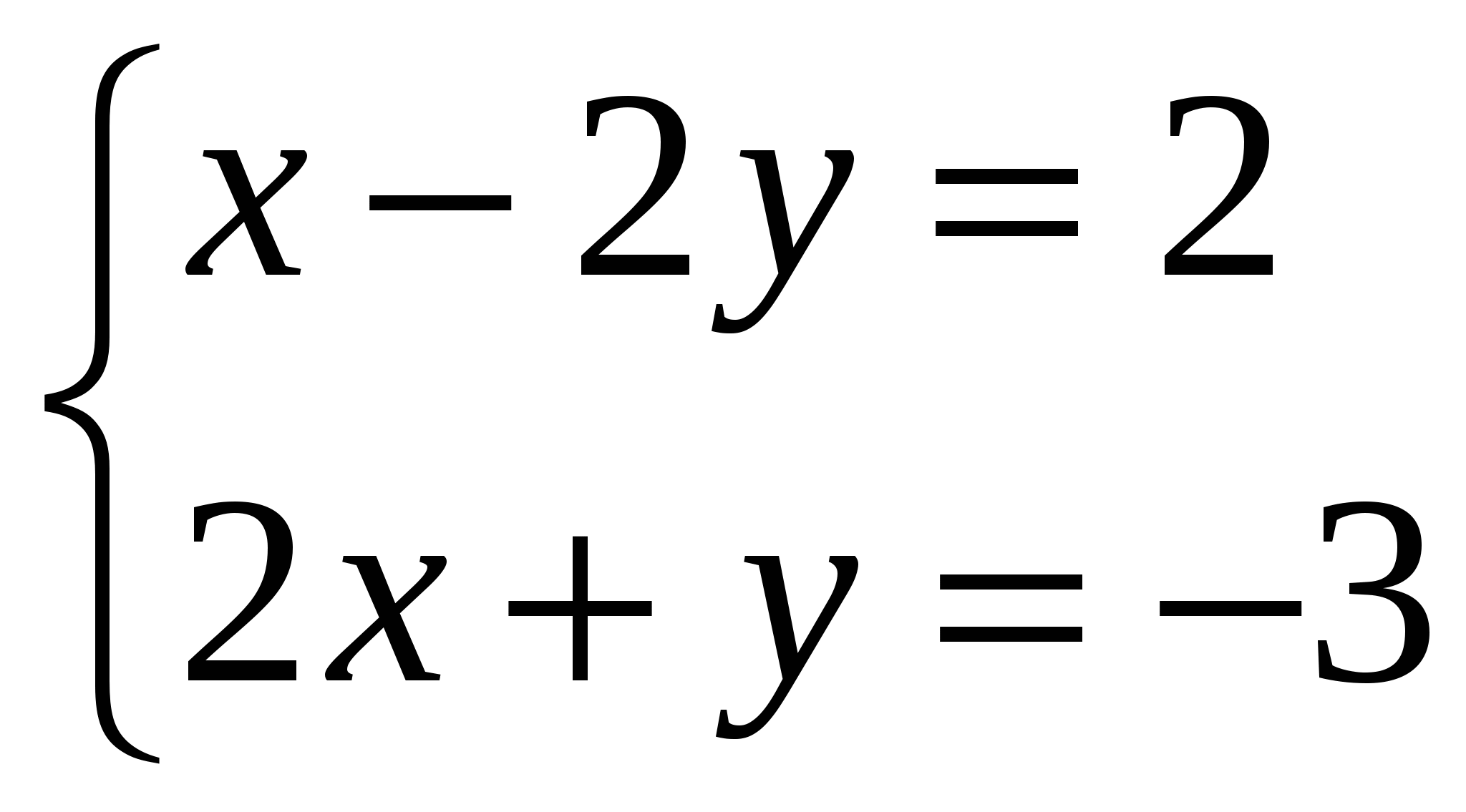
Шыққан жүйені шешіп x=0,8; y=-1,4 екенін табамыз, яғни

Егер 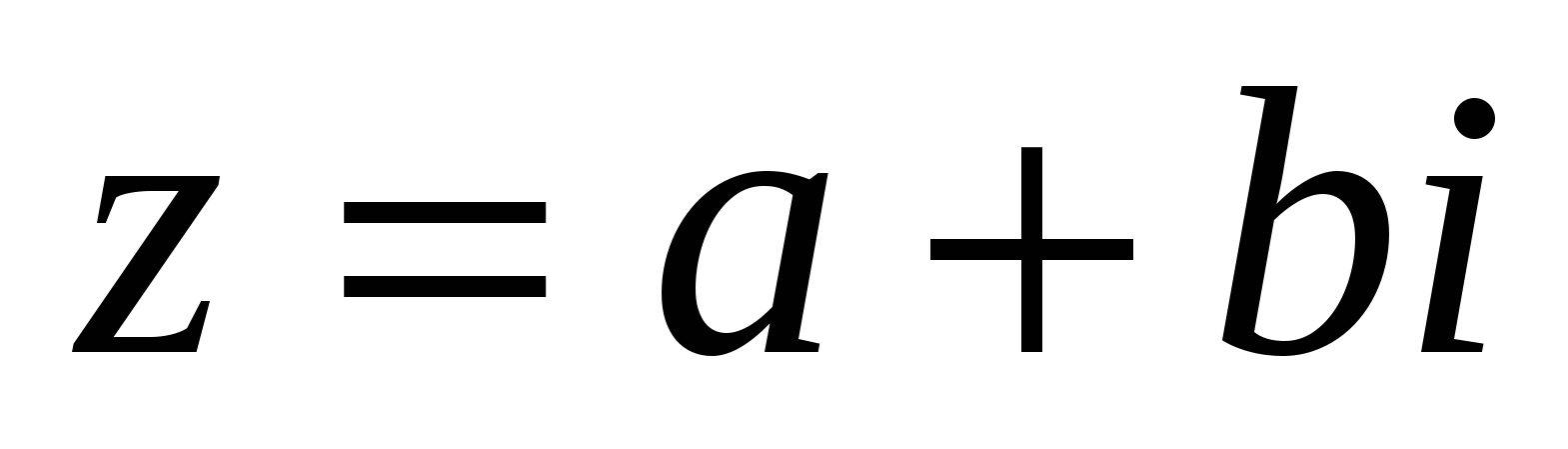 болса, онда
болса, онда 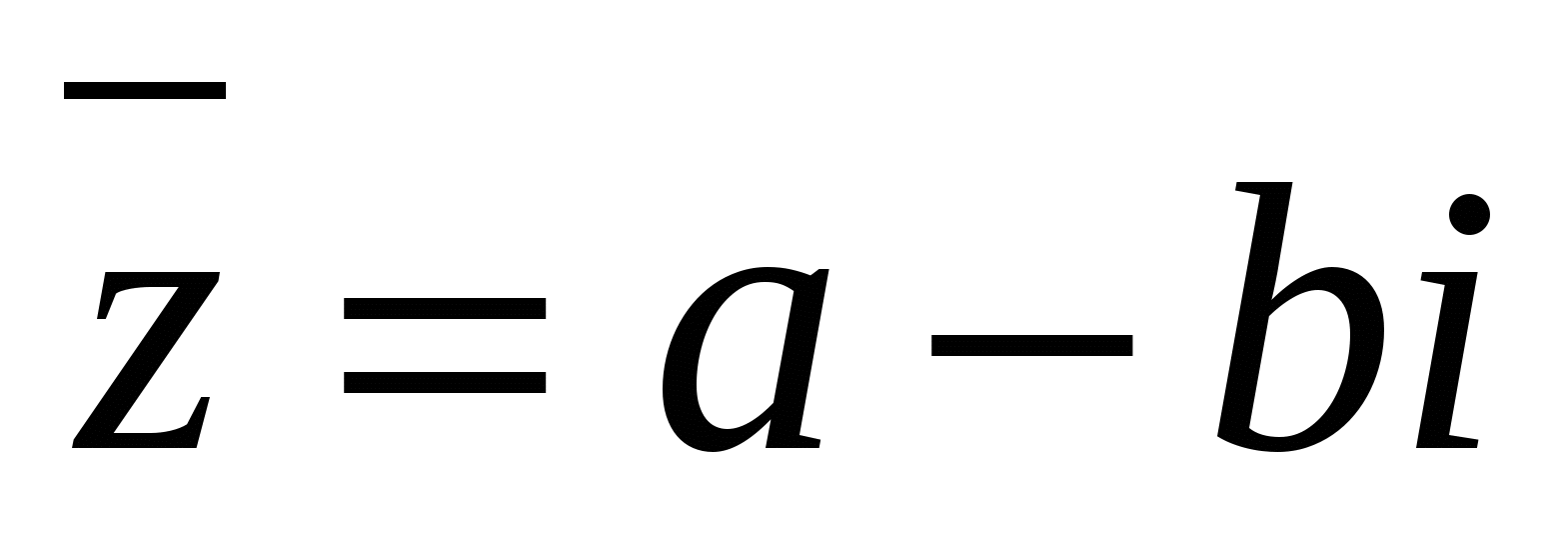 саны z санына түйіндес деп аталады.
саны z санына түйіндес деп аталады.
6 Мысал: 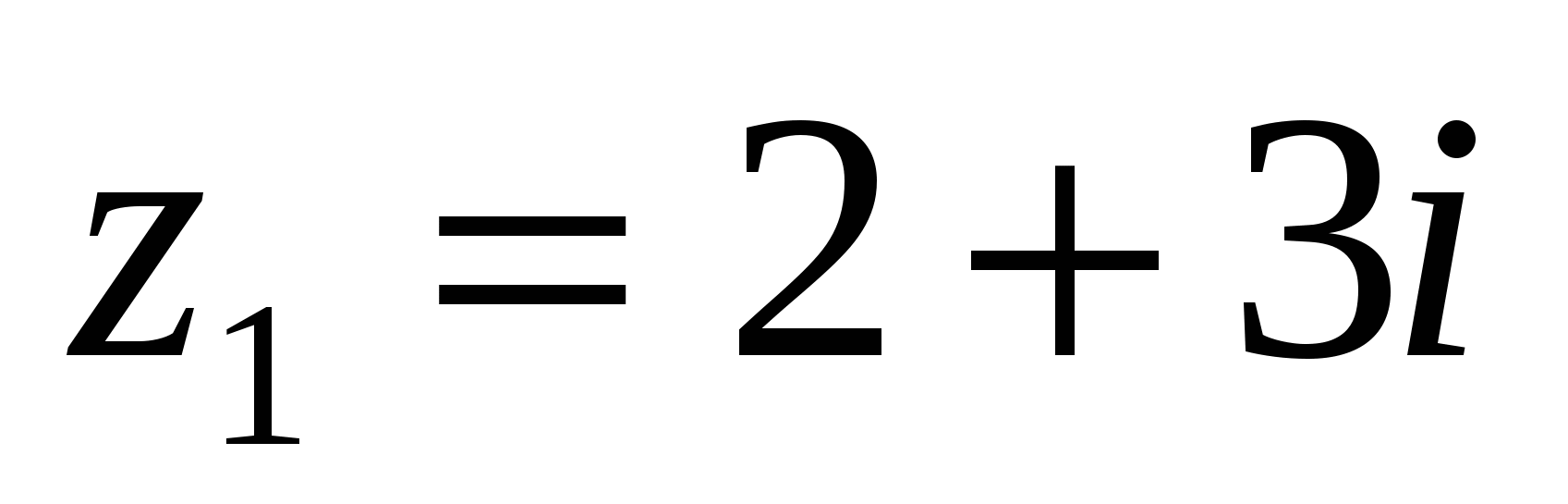 болса, онда
болса, онда 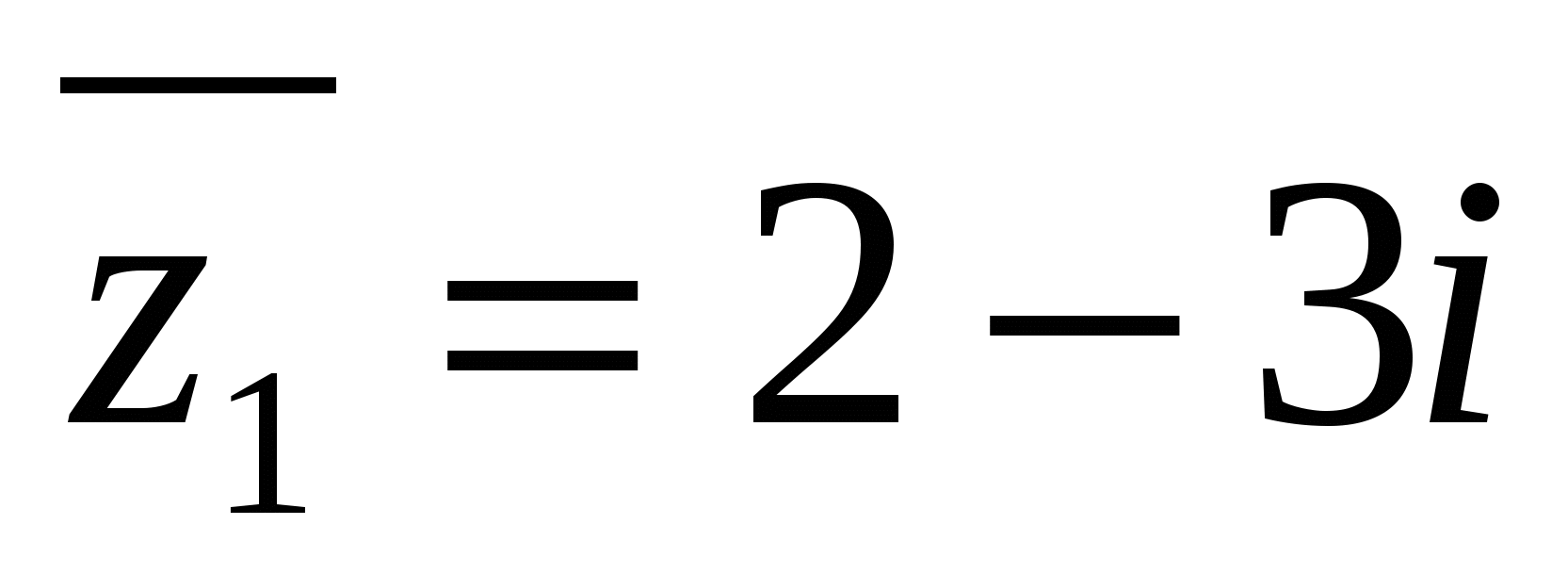 болады.
болады.
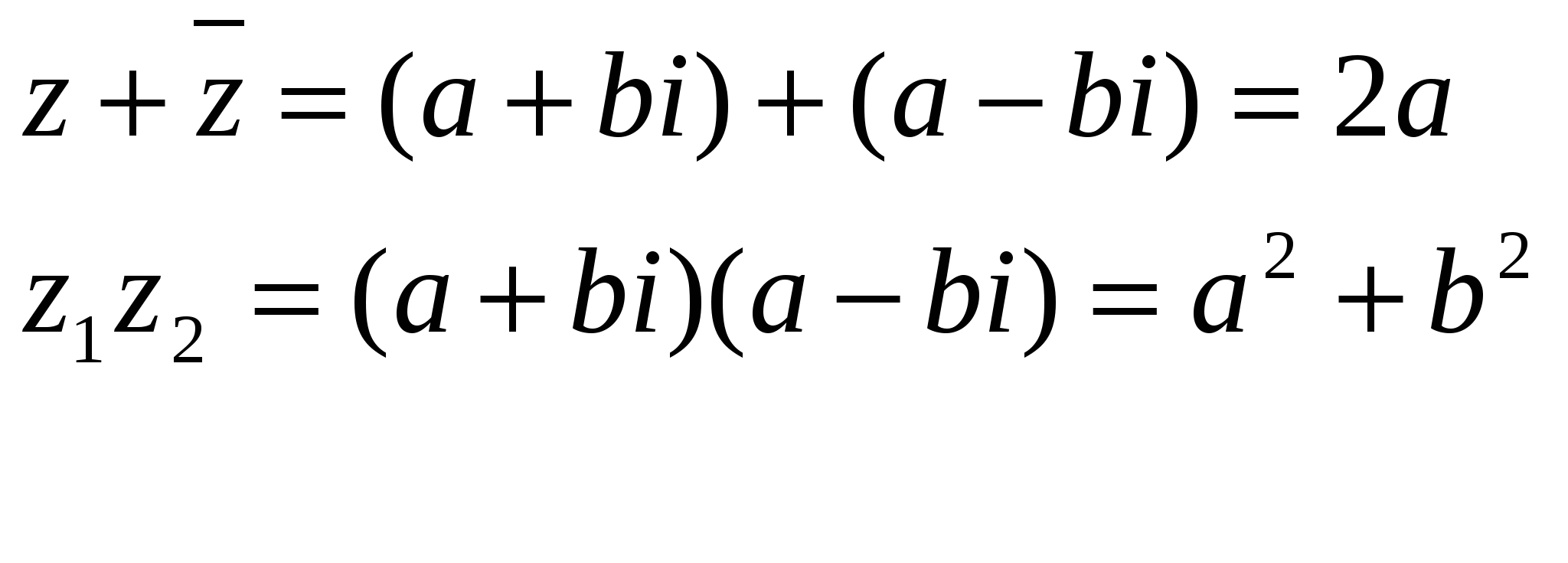
екенің ескере кетейік.
Енді 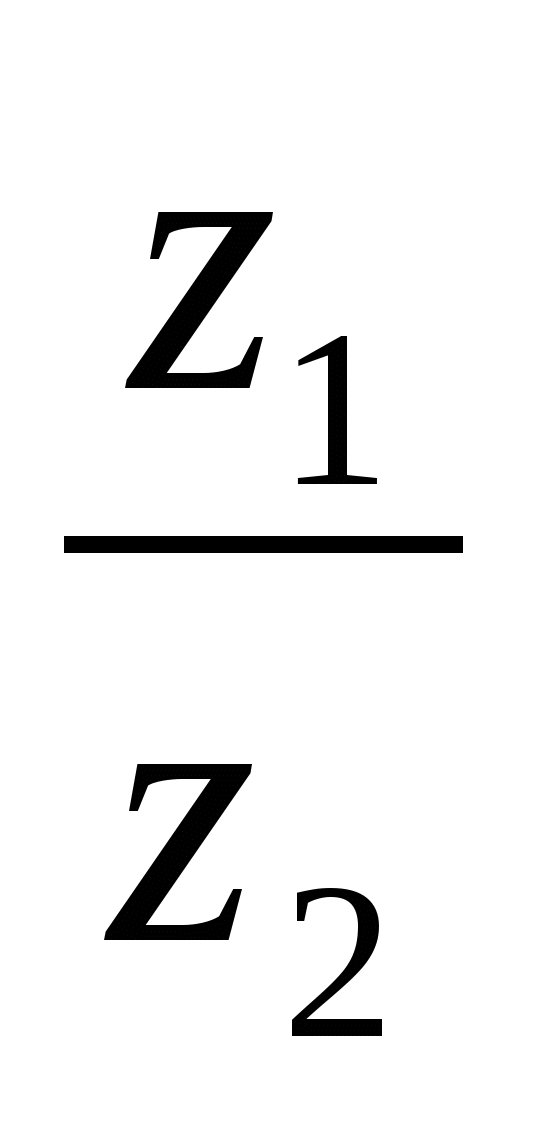 бөлшегі үшін
бөлшегі үшін 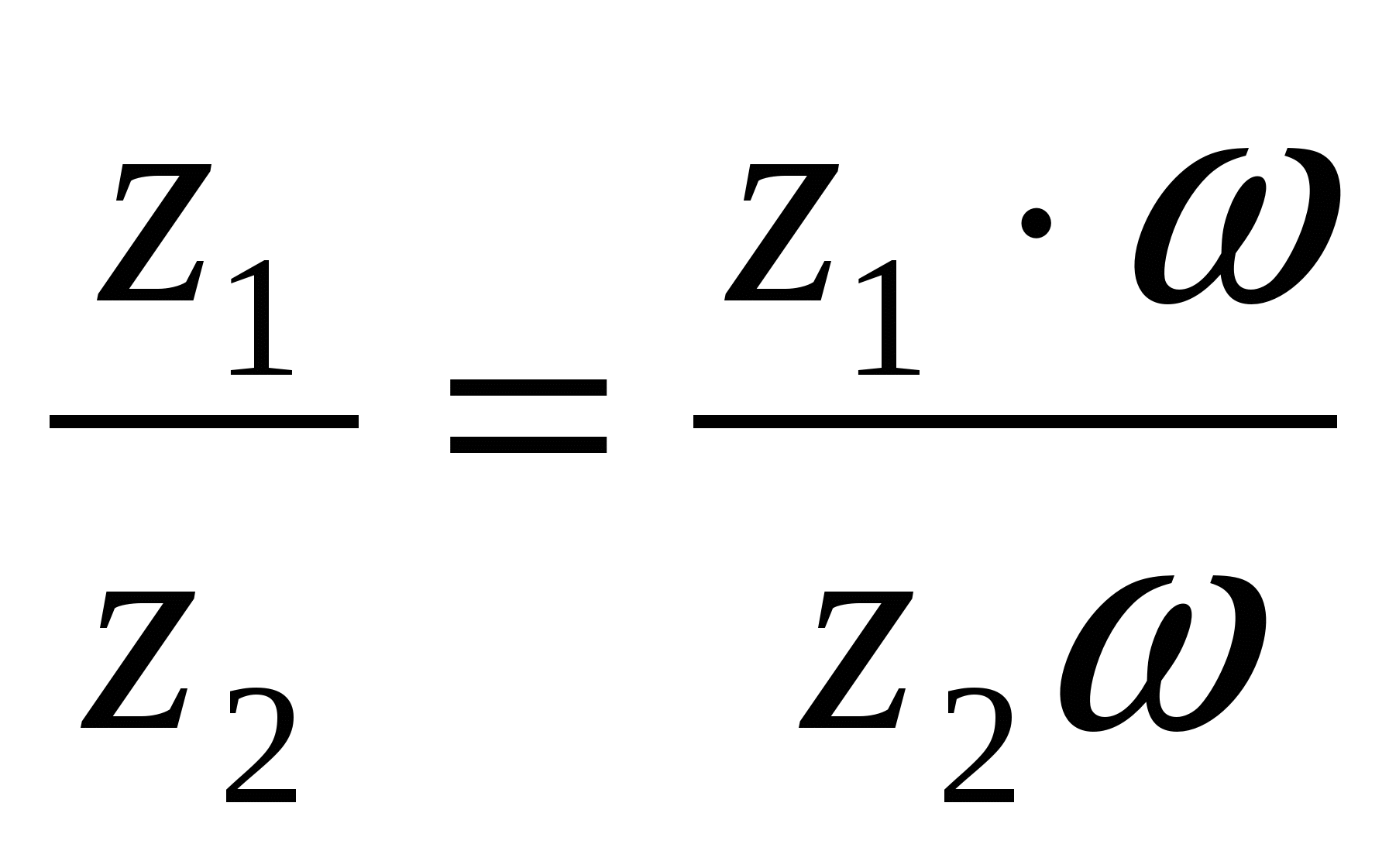 қасиеті орындалатынын көрсетейік. Мұндағы,
қасиеті орындалатынын көрсетейік. Мұндағы, 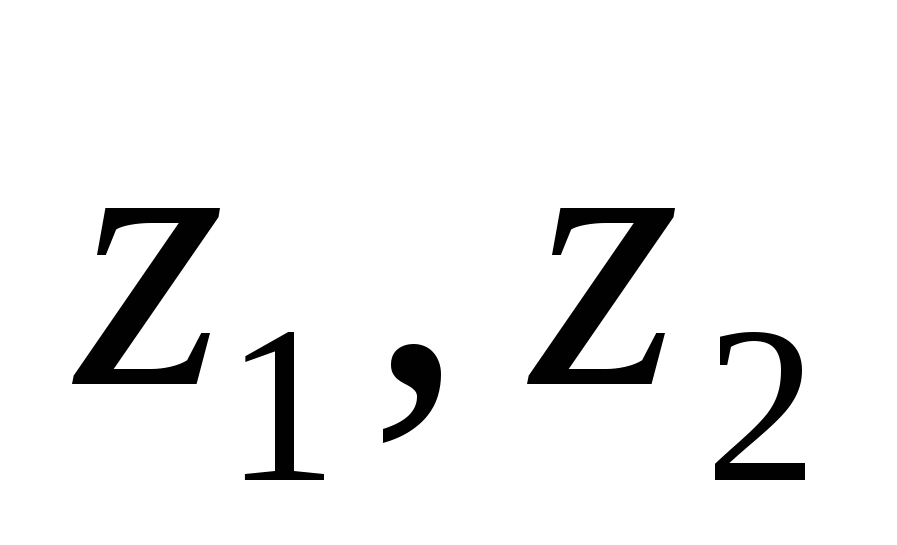 -комплекс сандар,
-комплекс сандар, 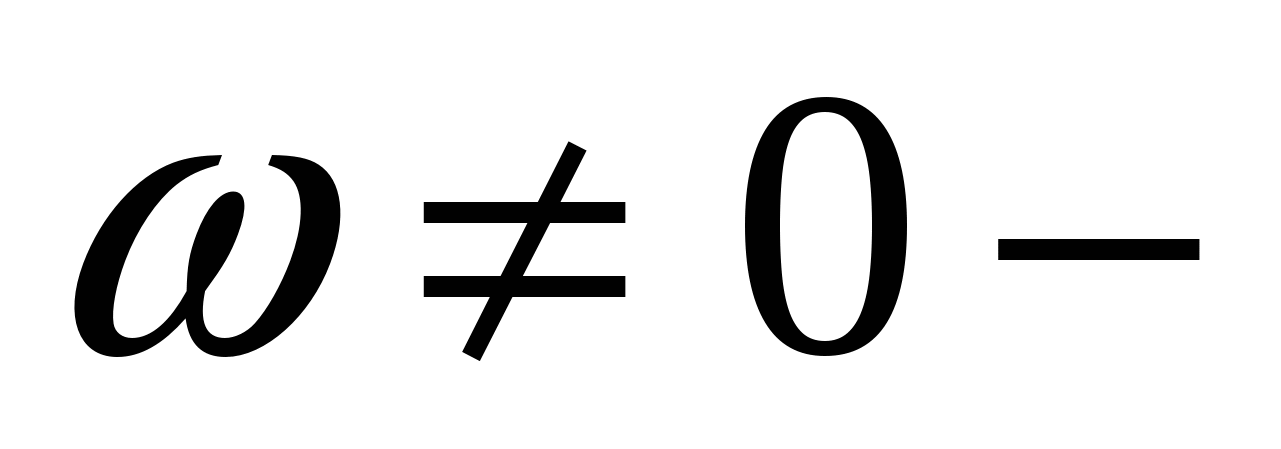 кез келген комплекс сан.
кез келген комплекс сан.
Айталық, ![]() болсын.
болсын.
(7) формула бойынша 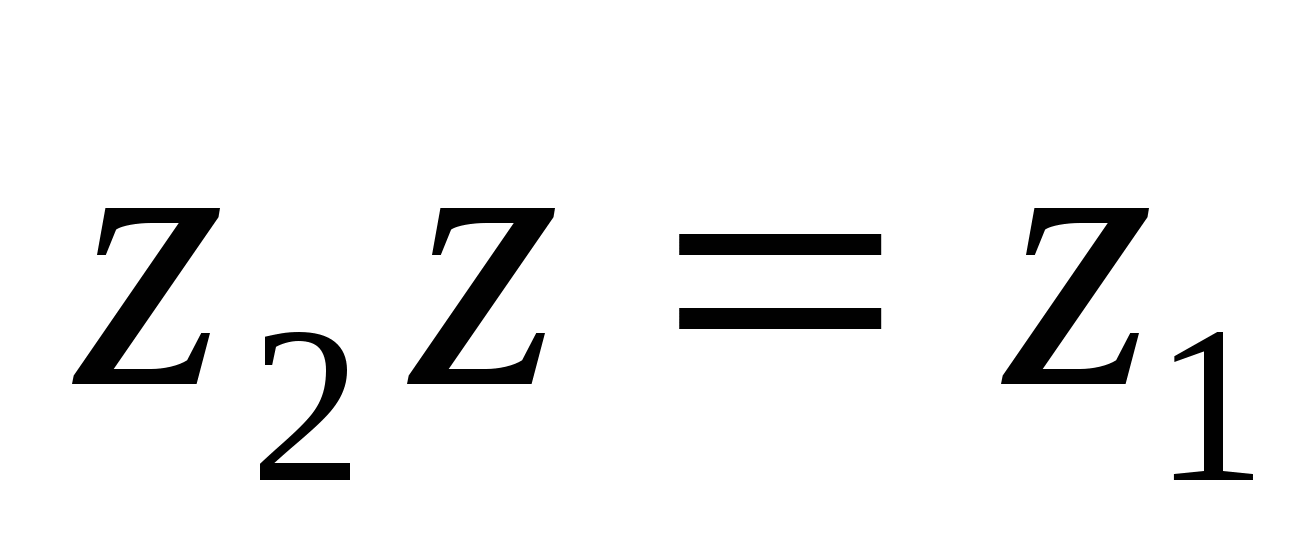 . Сонда
. Сонда 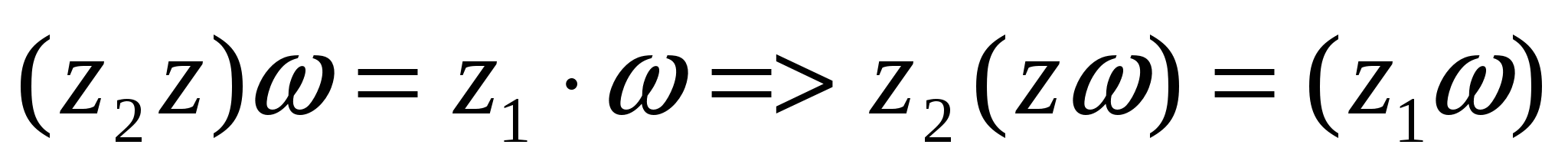 =>
=>
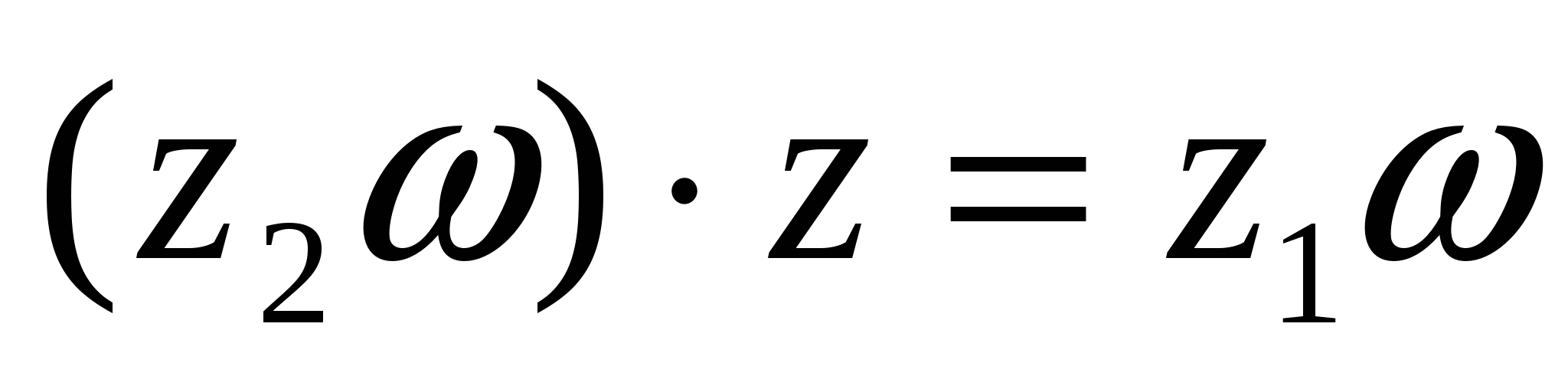
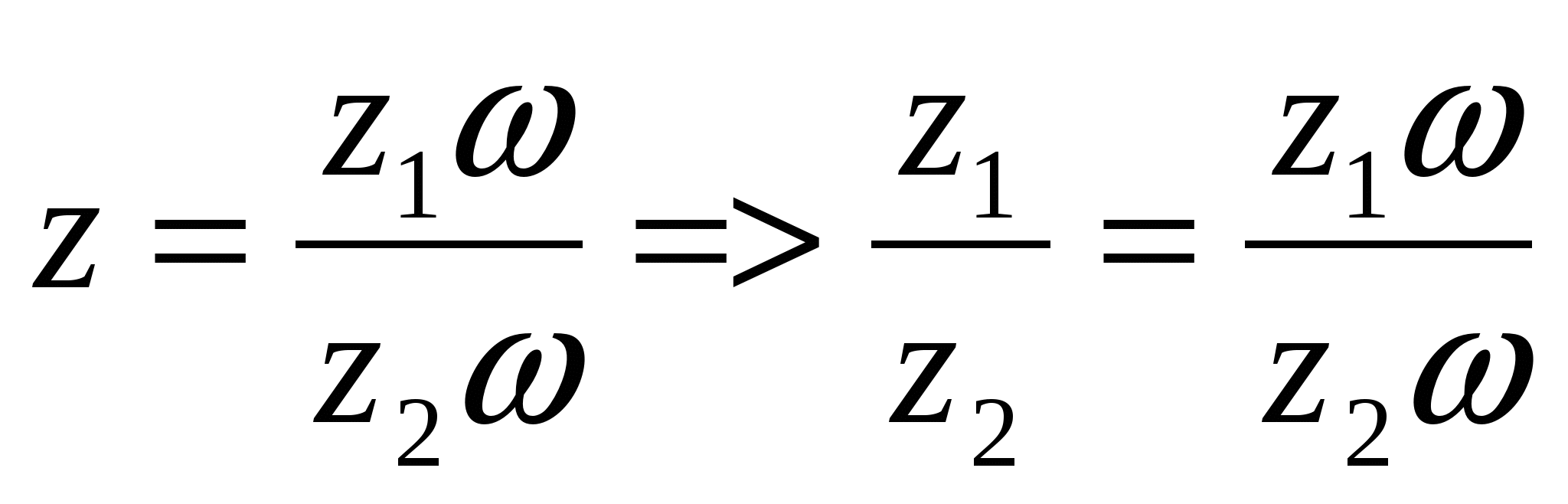
кез келген ![]() үшін.
үшін.
Осы қасиеті бойынша практикалық есептеулерде, екі комплекс санның бөліндісін табу үшін алымы мен бөлімін бірдей бөліміне түйіндес санға көбейту керек.
7 Мысал:  есептеу керек.
есептеу керек.
Δ 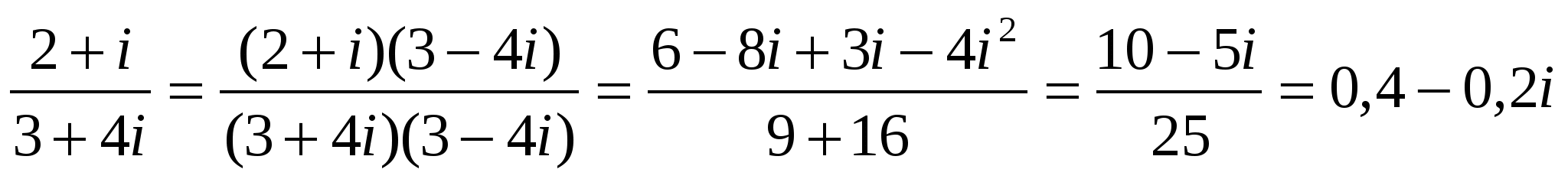 ▲
▲
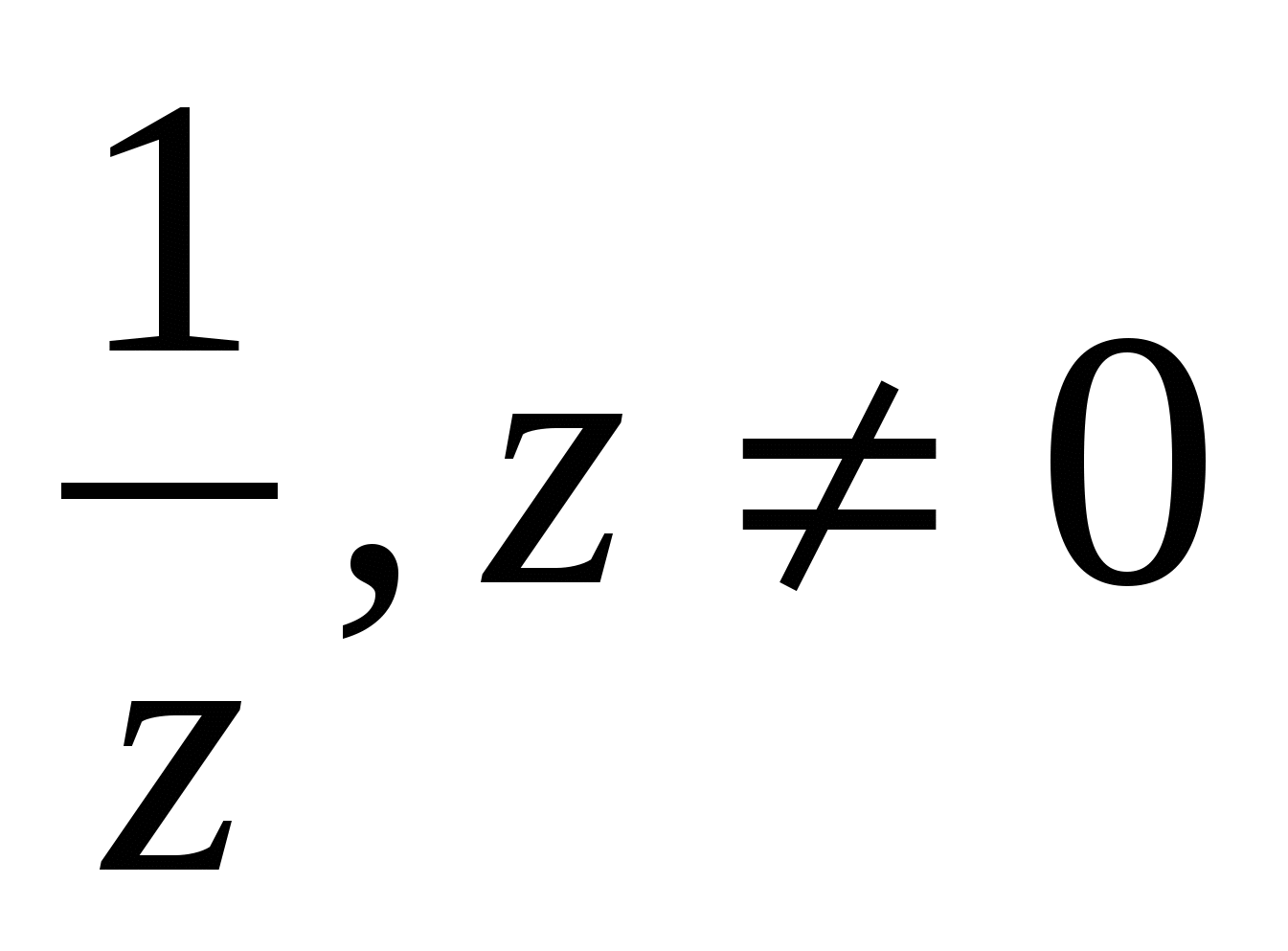 саны
саны  деп белгіленеді де, z санына кері деп аталады.
деп белгіленеді де, z санына кері деп аталады.
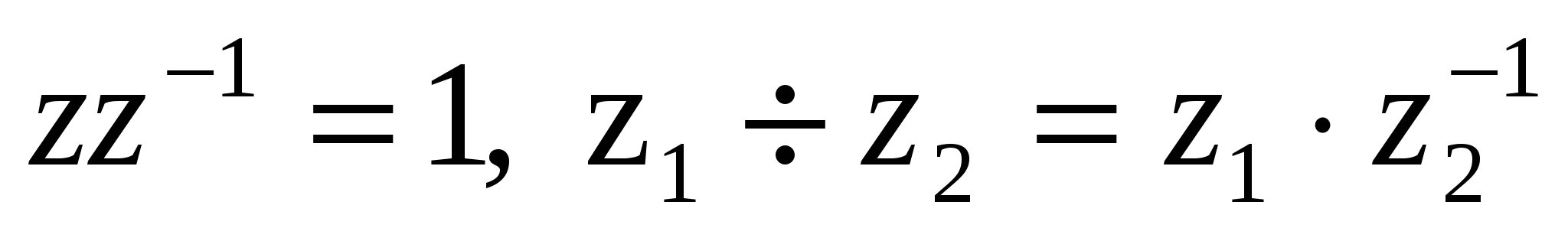 екенің көрсетуге болады. Сонымен, z1 комплекс саның z2 комплекс санына бөлу үшін z1-ді z2 санының кері
екенің көрсетуге болады. Сонымен, z1 комплекс саның z2 комплекс санына бөлу үшін z1-ді z2 санының кері 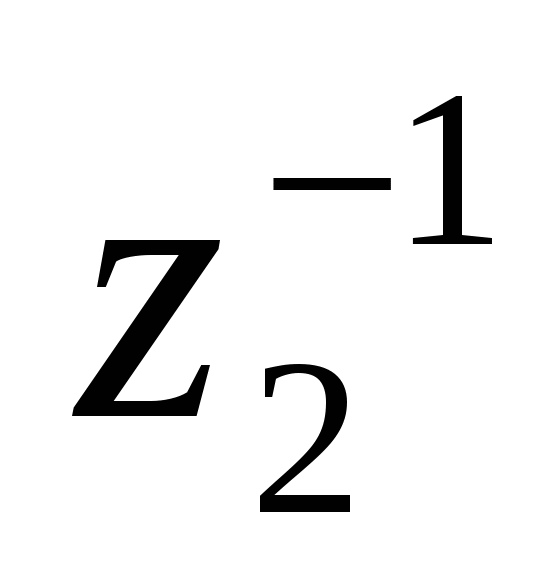 санына көбейту керек.
санына көбейту керек.
8 Мысал: 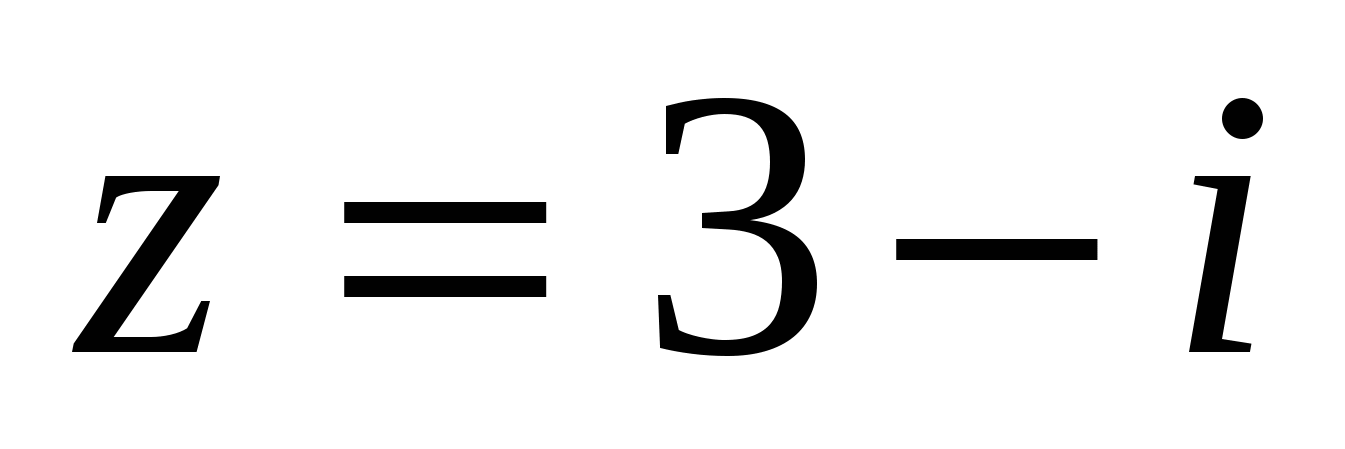 санына кері санын табу керек.
санына кері санын табу керек.
Δ 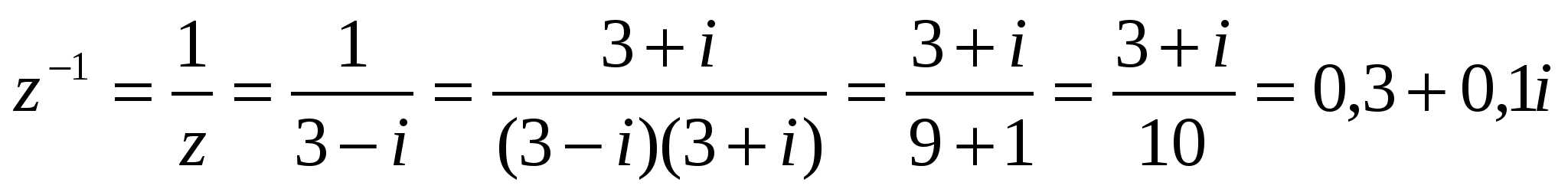 ▲
▲
Кез келген m және n бүтін сандары үшін келесі теңдіктер орындалатының көрсетуге болады:
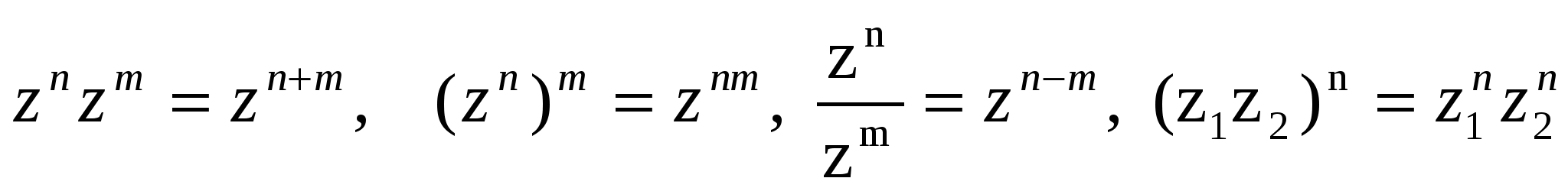 .
.
9 Мысал: есептеу керек:
а) і3, і4, і5, і-1, і-2, і-3, і-4, і-5; б) z-3, егер z=1-і болса.
Δ а) i3=i2 i=-i;
i4=i2 i2=(-1 )(-1)=1
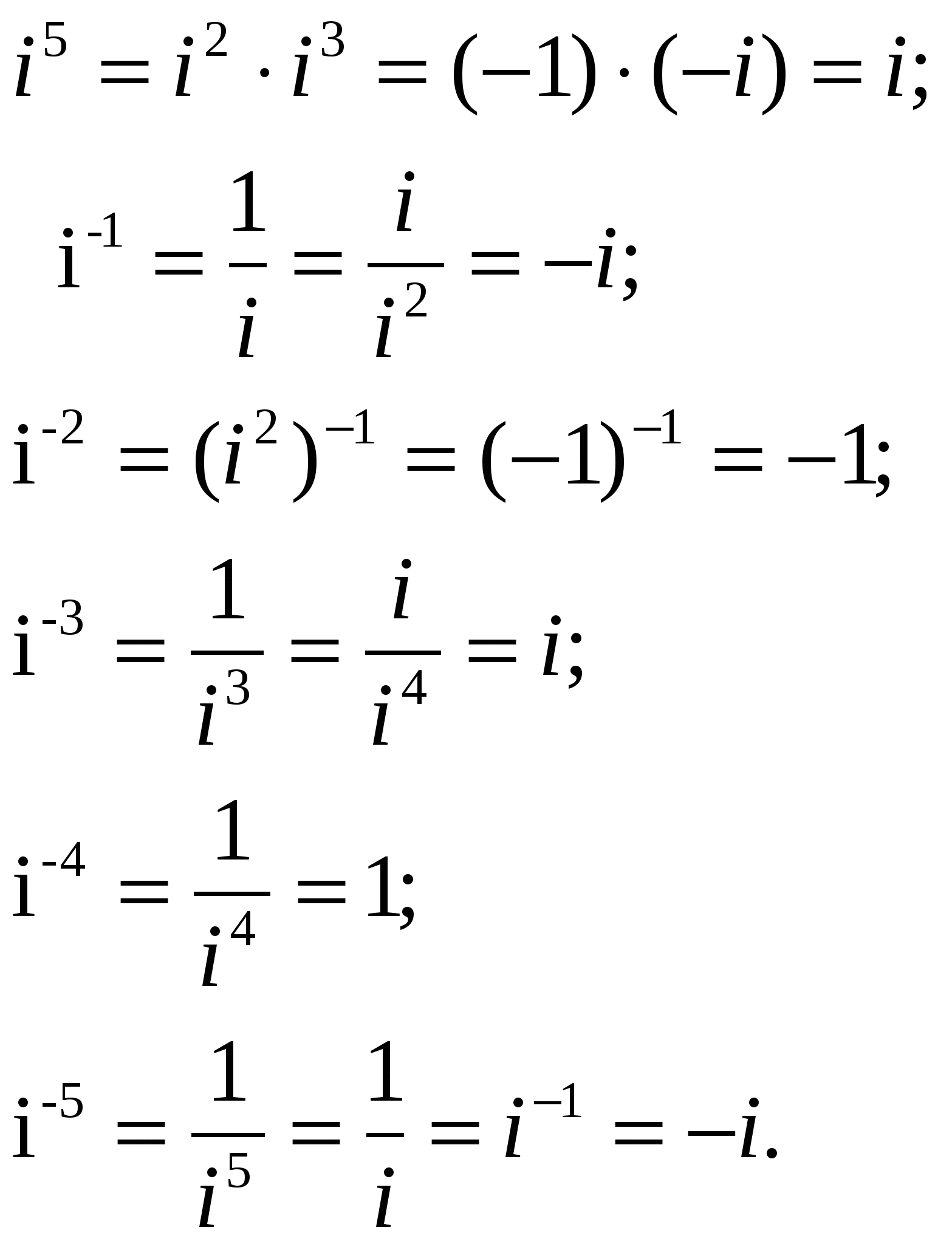
б) 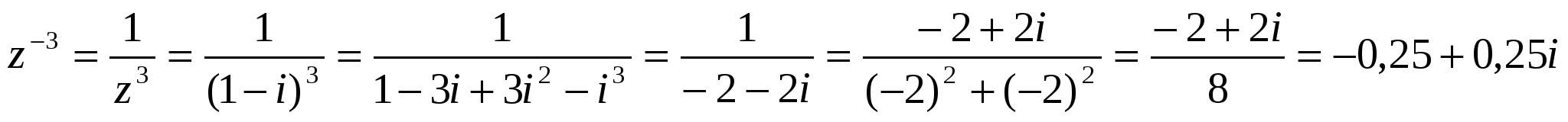 ▲
▲
Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі.
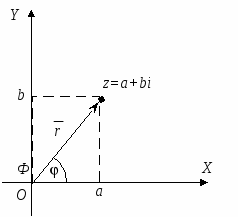
Комплекс сандарды координат жазықтығының көмегімен жазықтықтың нүктелері ретінде өрнектеуге болады. Ox - осінің бойына комплекс санның нақты бөлігін (a=a+0∙i), ал Oy осінің бойына оның жорамал бөлігін орналастырсақ (bi=0+bi) жазықтықта әрбір комплекс сан z(a,b) нүктесі түрінде анықталады. 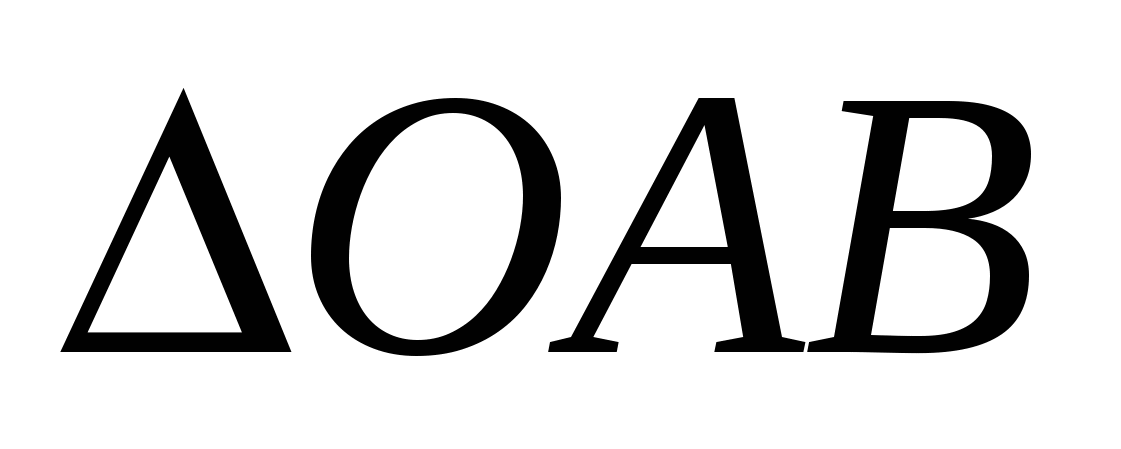 тік бұрышты
тік бұрышты
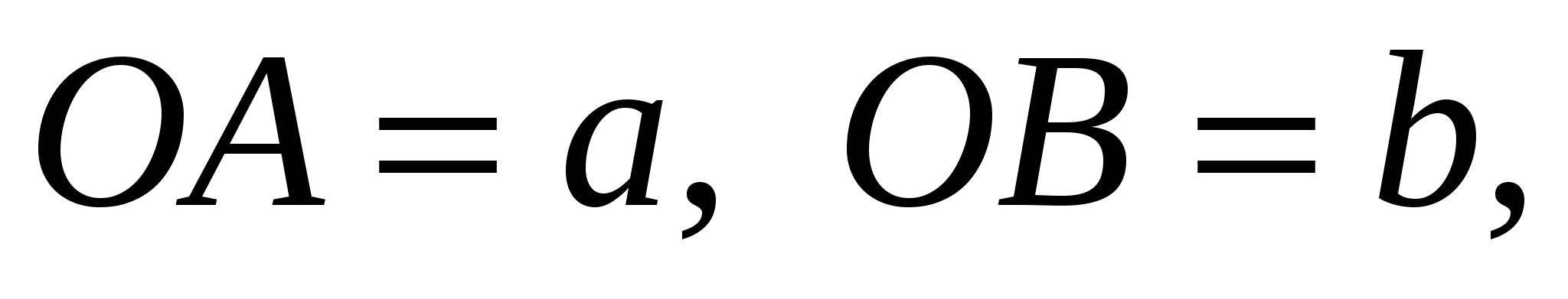 ïzï
ïzï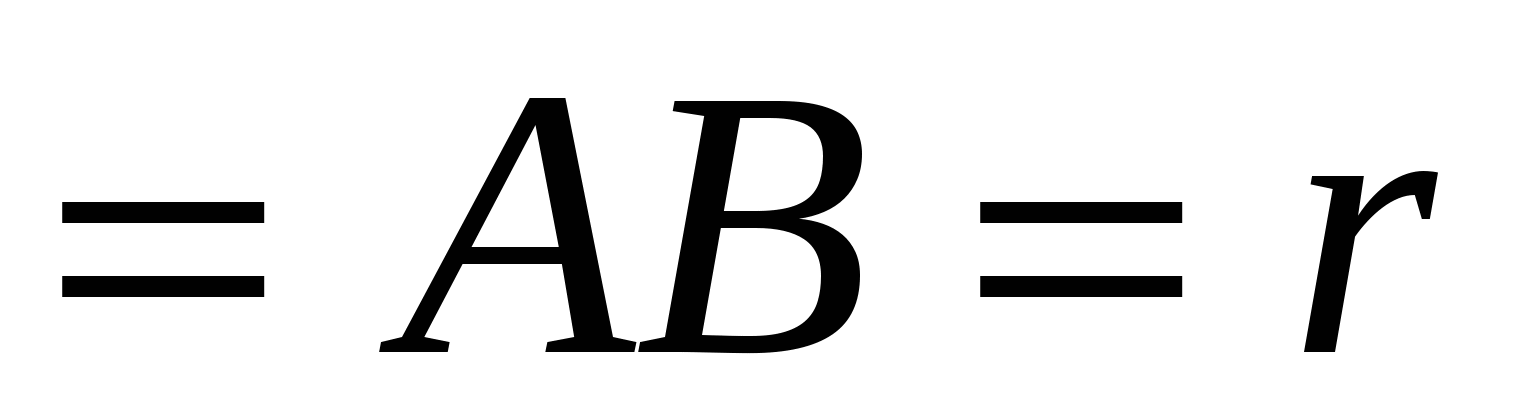 r=ïzï=
r=ïzï=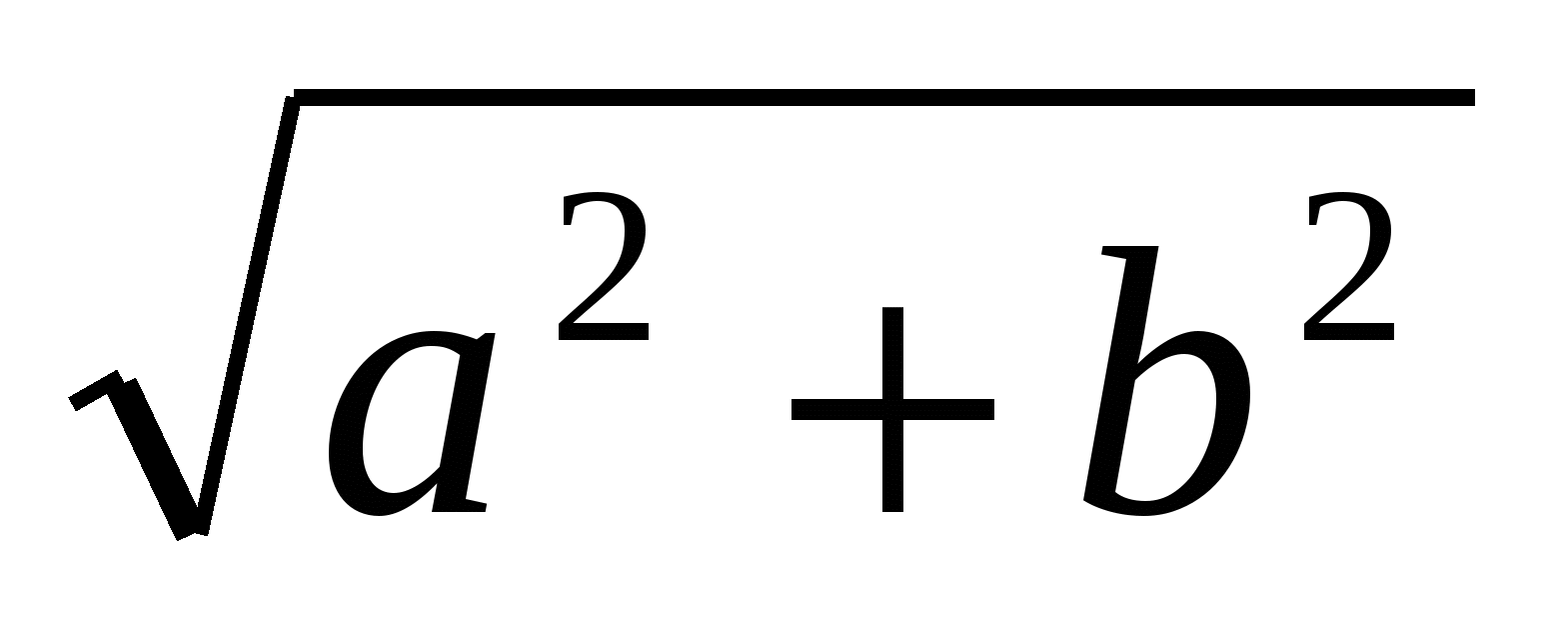 .
.
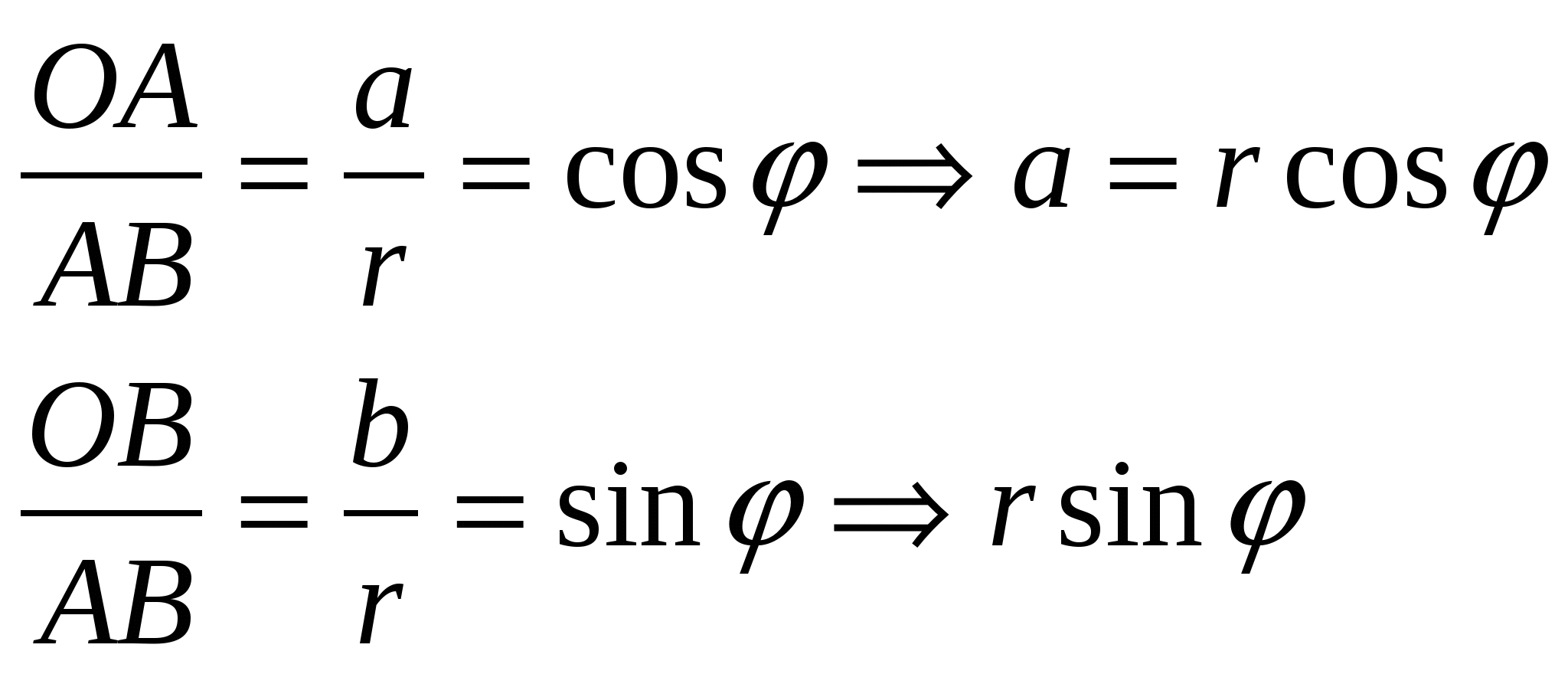
z=a+bi=r(cosφ+isinφ)- комплекс санның тригонометриялық түрі.
 =r - комплекс санның модулі
=r - комплекс санның модулі 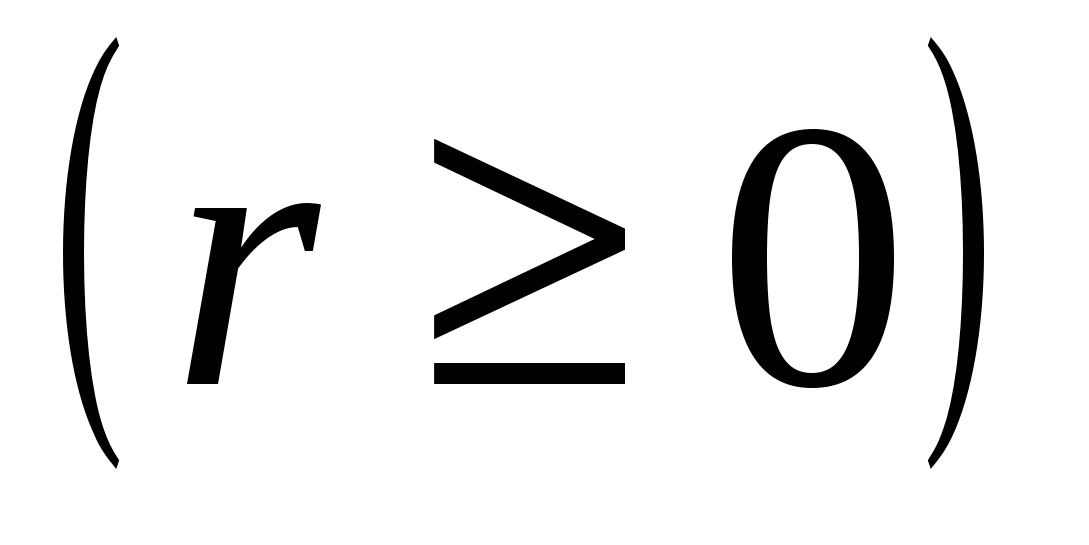 .
.
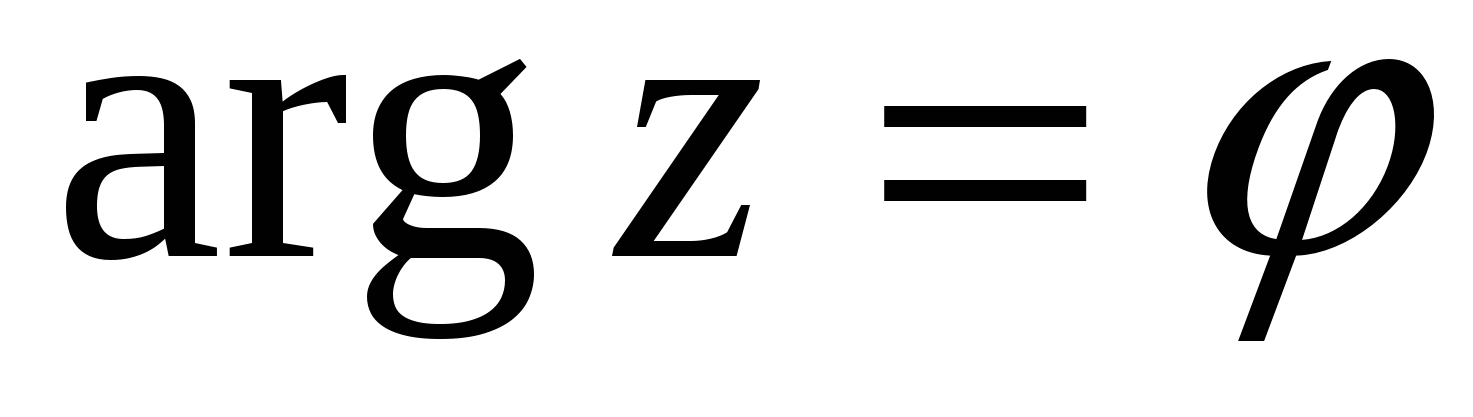 -комплекс санның аргументі.
-комплекс санның аргументі.
Тригонометриялық түрдегі комплекс сандарға амалдар қолдану өте жеңіл.
Айталық,
z1=r1(cosφ1+isinφ1),
z2=r2(cosφ2+isinφ2) болсын.
Онда 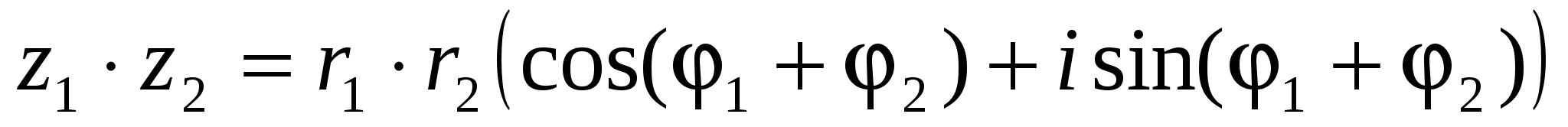
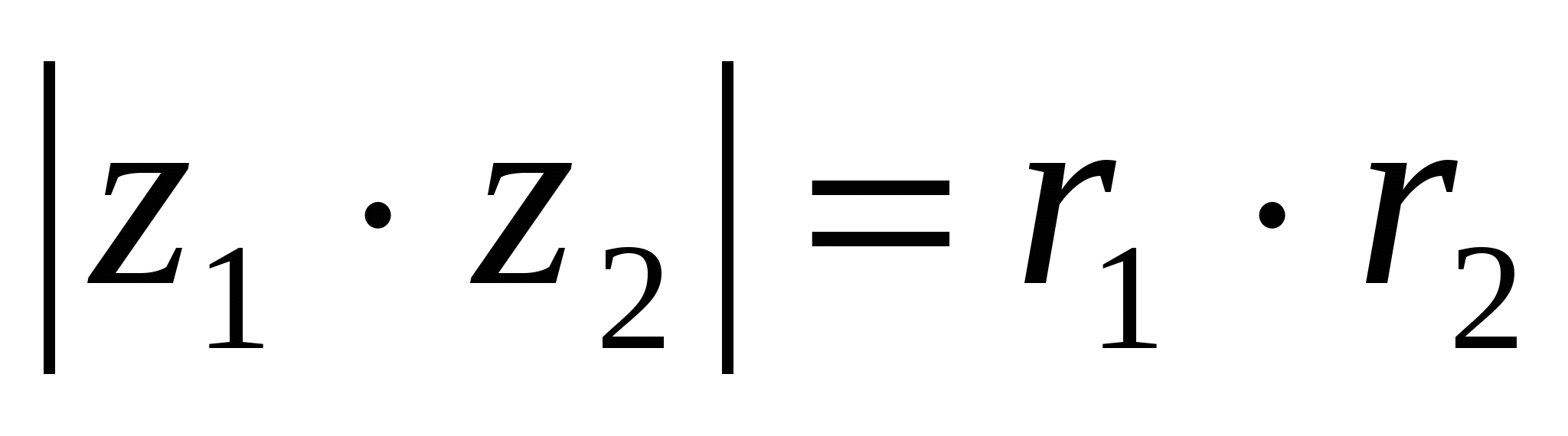
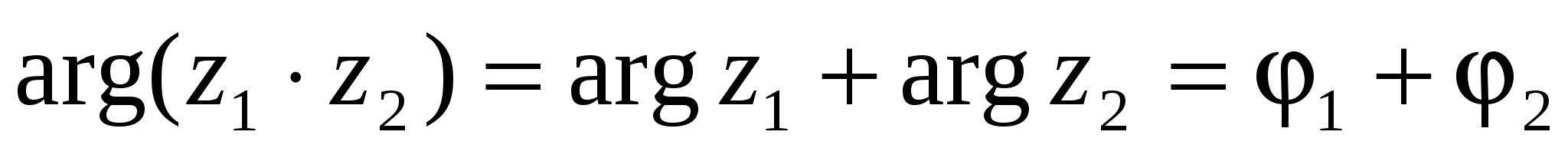
Егер 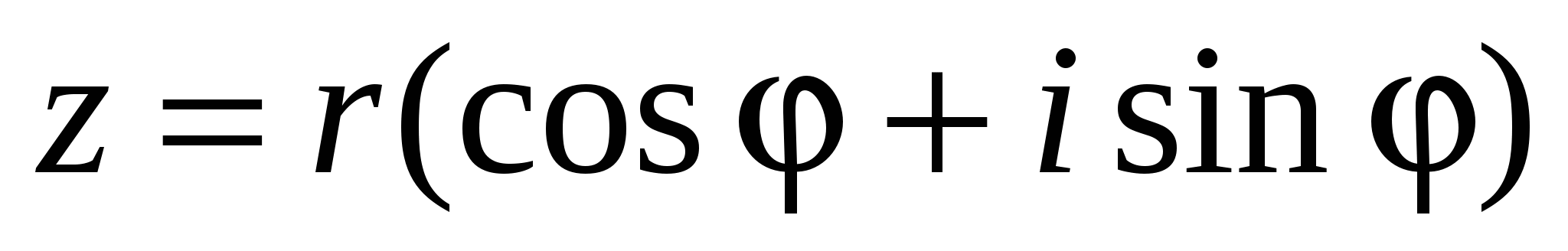 болса, онда
болса, онда
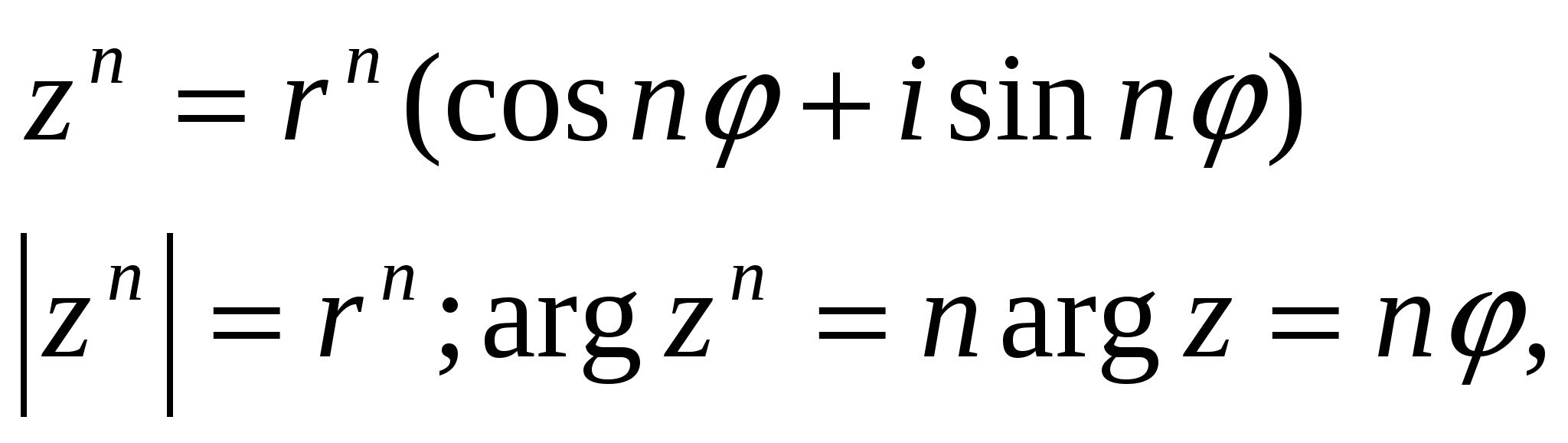
Муавр формуласы 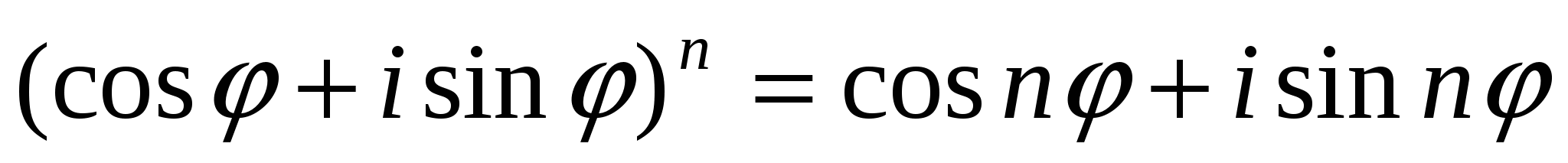
Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі.
Айталық, а=r(cos +isin
+isin ) комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін
) комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін
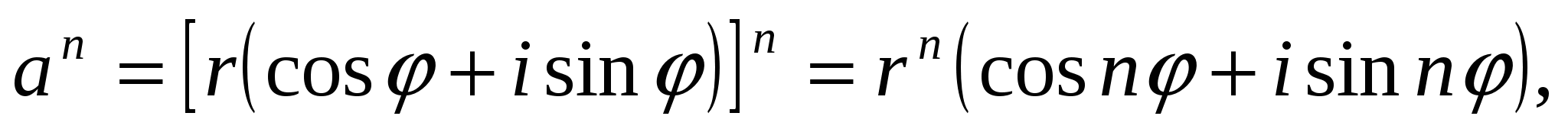
яғни комплекс санды дәрежелегенде оның модулі сол дәрежеге шығарылады, ал аргументі сол дәреже көрсеткішіне көбейтіледі.
![]()
теңдігін пайдаланып , Муавр формуласын бүтін теріс сандар үшін де пайдалануға болады.
a=a+bi комплекс санын оң бүтін n дәрежеге шығару үшін Ньютонның биномын пайдаланған орынды, тек
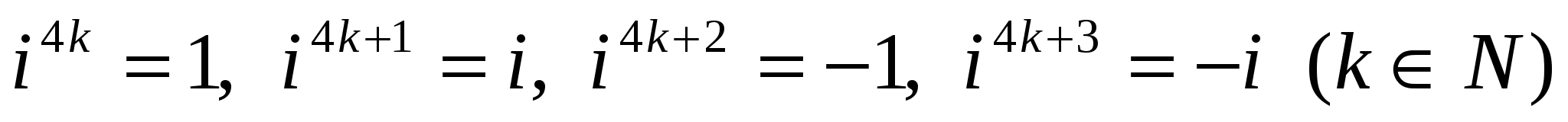
ескерсек жеткілікті.
Муавр формуласының дербес түрін қарастырайық.
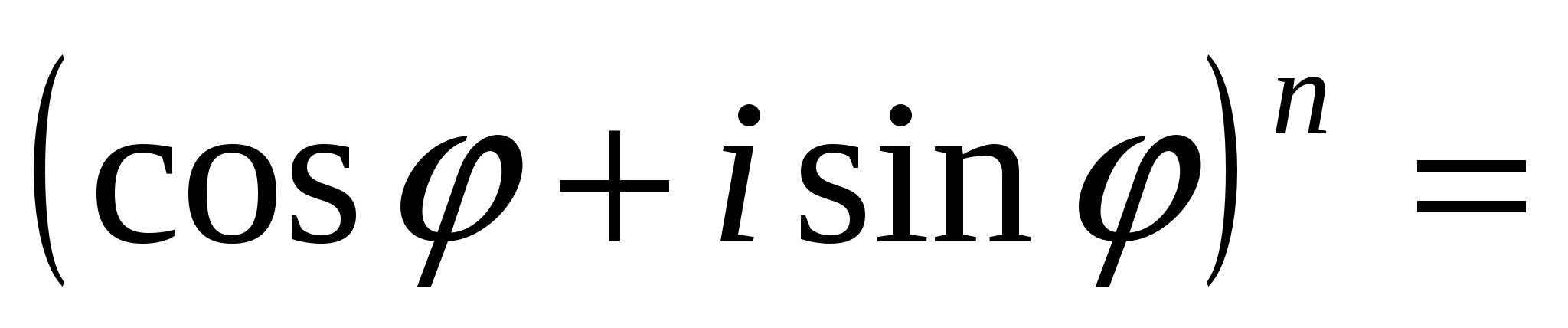 cos n
cos n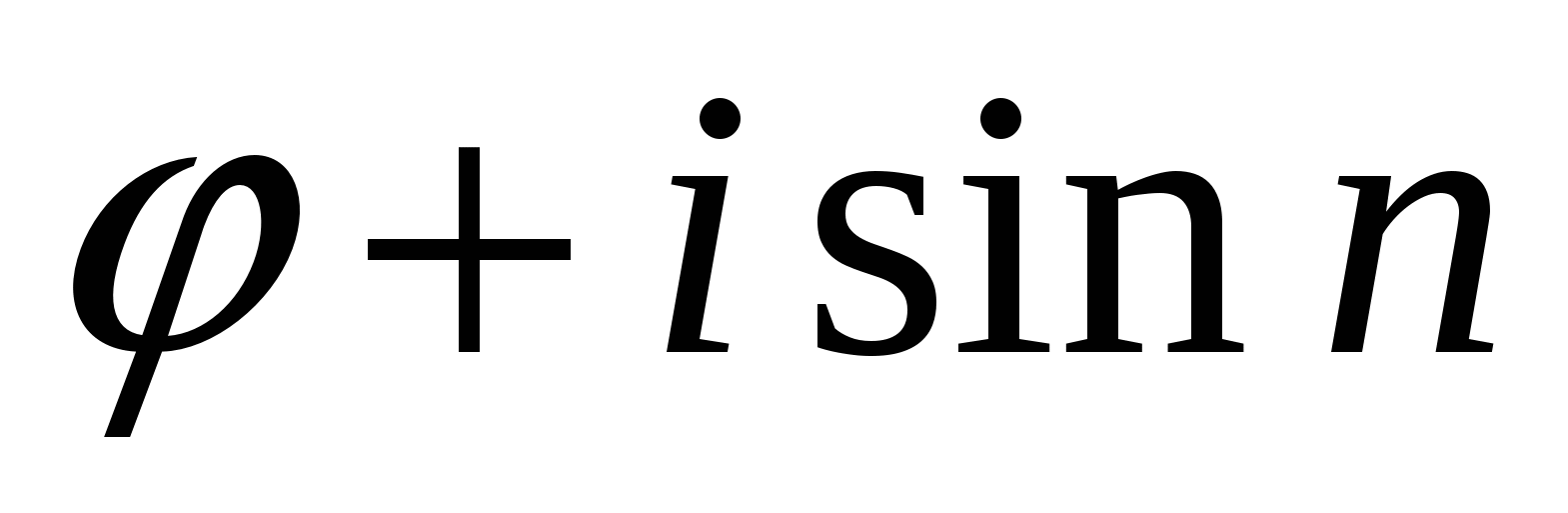

Теңдіктің оң жақ бөлігіне Ньютонның биномды формуласын қолданайық.
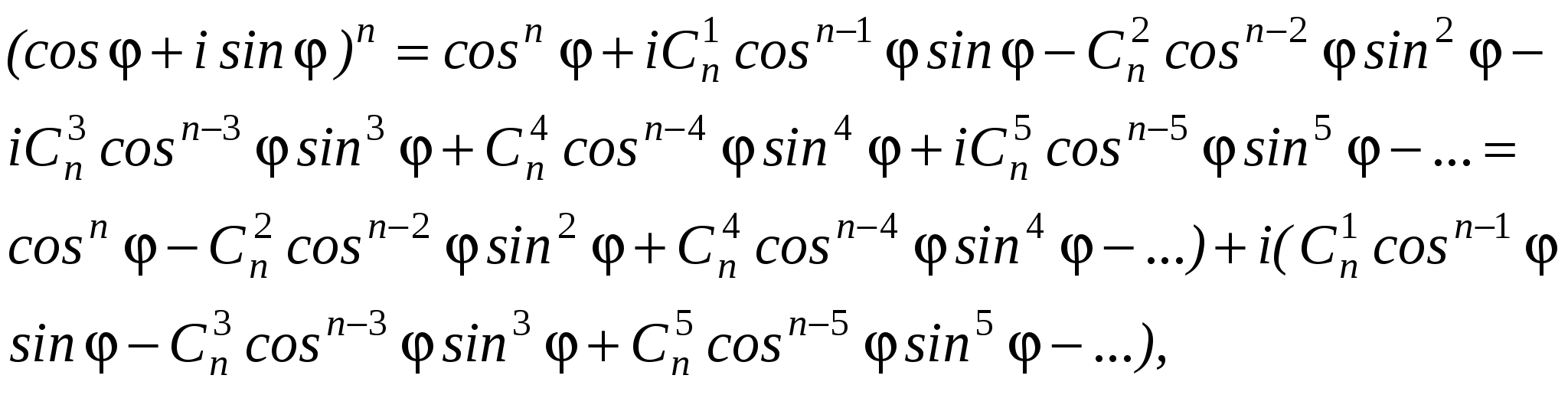
Мұндағы 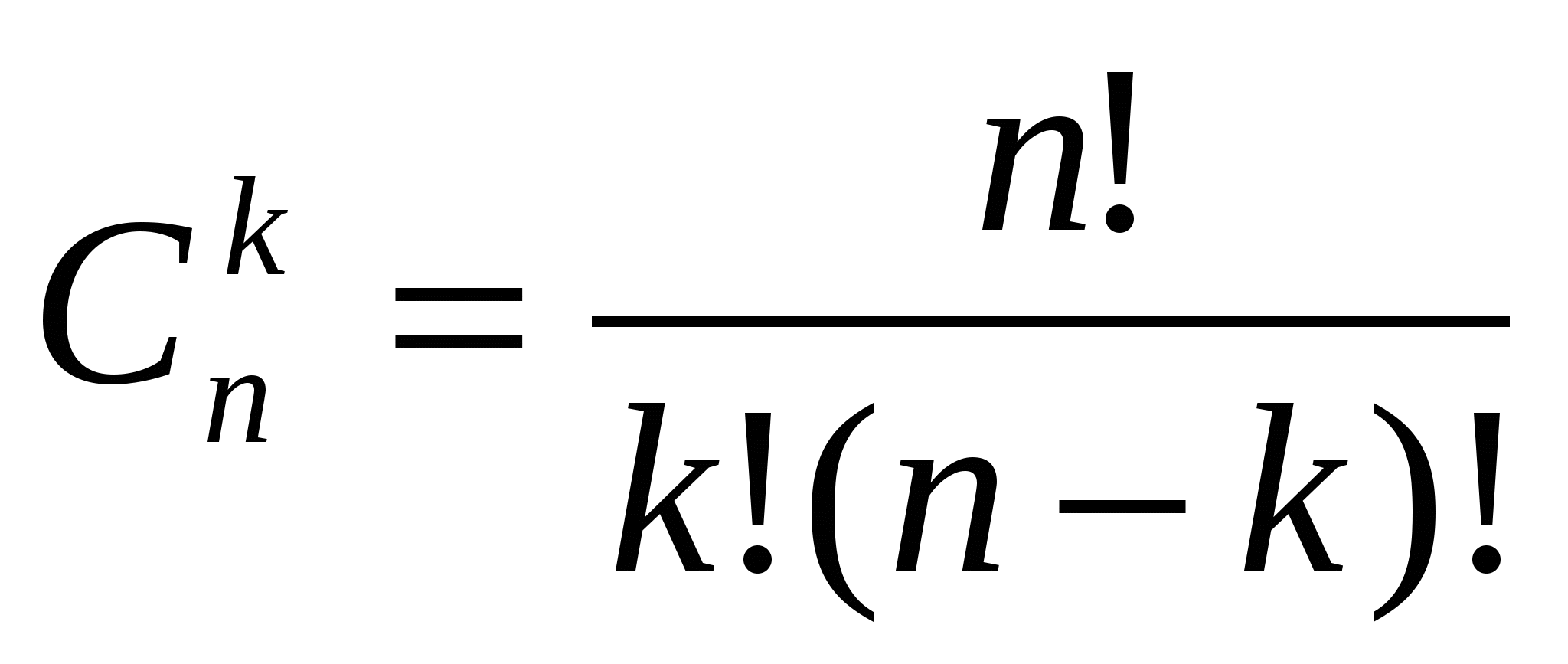
теңдігінің сол және оң жақ бөліктерін салыстырсақ,
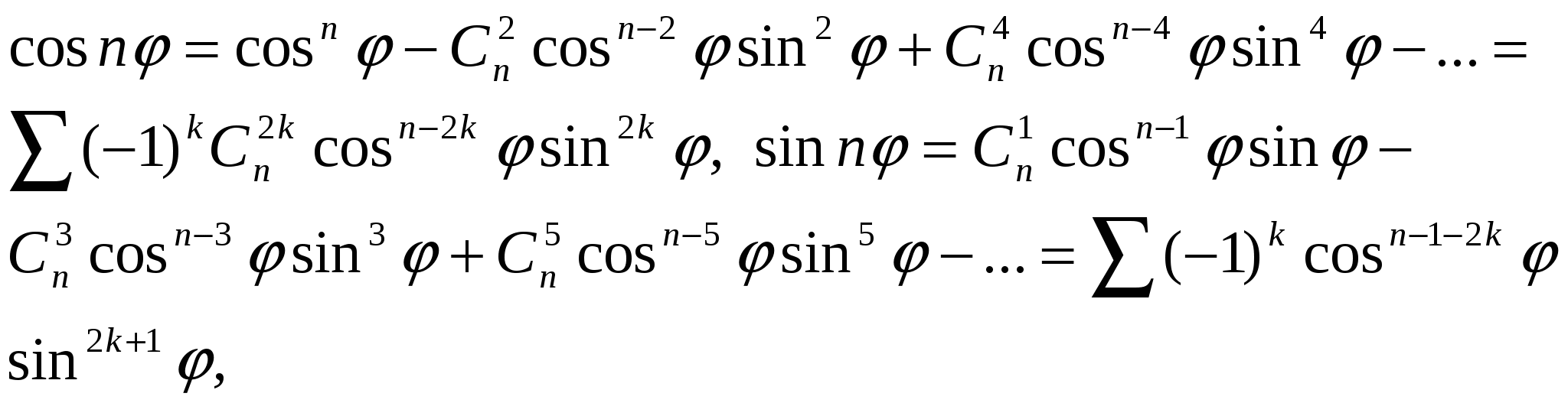
теңдіктерін аламыз.
Сонымен, 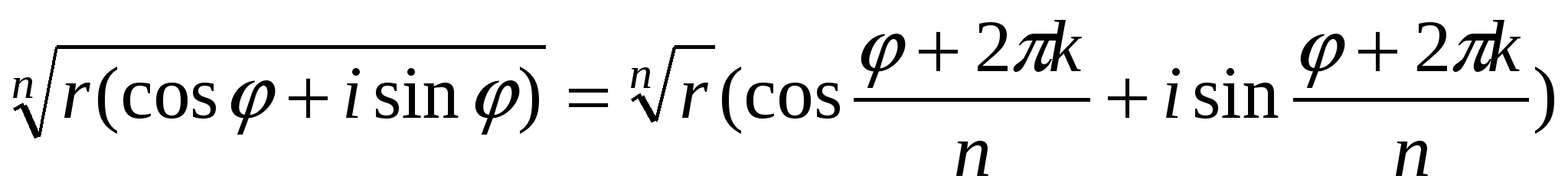 , мұндағы
, мұндағы

ға әртүрлі мәндер беру арқылы түбірдің әртүрлі мәндерін аламыз.
Қортынды. Комплекс сандардан n - ші дәрежелі түбірді әрқашан табуға болады және оның әртүрлі n мәні болады.
Айнымалы ток
Айнымалы қырманның қатарынның көрінісінде үш элемент бар:
1. Өткінші кедергі ,әлуеттің айырымы кедергіге ылғи фаза қырмасы арқылы өтеді.
2. Индуктивты катушка, бұл жерде потенциалдар айрымы 90° токқа акеліп соғады
3. Кешіктірілген кедергі, бұнда потенциалдардың айырымы токты 90° қа тежейді
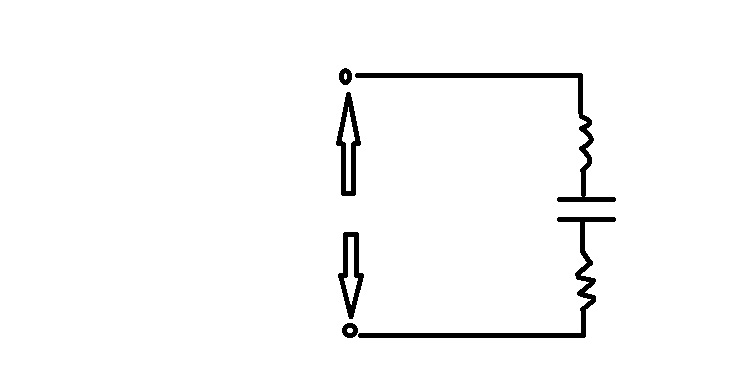
Бұл элементтердің тізбектей жалғануы ( 1 сурет), бірдей ток өтеді, I ,потенциалдар айырымы мынадай жорамалмен беріледі :
![]()
![]()
![]()
Бұл жерде 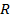 кедергі,
кедергі,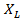 индуктивты кедергі, ал
индуктивты кедергі, ал 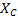 кішіктірілген кедергі ,барлығы Оммен есептеледі .
кішіктірілген кедергі ,барлығы Оммен есептеледі .
V
![]()
![]()
![]()
1 сурет
Кернеу мен жабық токтың формуласы мынадай
![]()
мұндағы 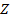 импенданс қатары және кешіктірілген кедергі мен индуктивті қатардағы кедергі.
импенданс қатары және кешіктірілген кедергі мен индуктивті қатардағы кедергі.
Қорытынды:
ХІХ ғасырдың аяғында жиындар теориясының дамуына байланысты комплекс сан 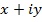 екі нақты сан
екі нақты сан 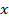 пен
пен 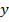 -тің реттелген жұбы
-тің реттелген жұбы 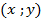 түрінде қаралуы комплекс сандардың геометриялық кекінінен ешбір кем емес екендігі де кейінгі кезде пайда болып отыр.
түрінде қаралуы комплекс сандардың геометриялық кекінінен ешбір кем емес екендігі де кейінгі кезде пайда болып отыр.
Кейінгі жүз жыл ішінде комплекс сандар және комплекс аргументті функциялар теориясы одан әрі дамып ,бұл теория картографияда ,электр және электротехникада , гидромеханикада ,аэромеханикада, сандар теориясында, және басқа да көптеген жаратылыс тану мен техника саласында қолданылады.
Пайдаланылған әдебиеттер
-
Ғали Ұзақов аналитикалық функциялар теориясы,Алматы «Мектеп» 1986
-
Бисадзе А. В. Основы теории аналитических функций комплекснего,
Москва «Наука»,1970
-
Жәутіков О.А. Комплекс сандар және олардың практикалық маңызы, «Мектеп » баспасы,Алматы 1975
-
Привалов И.И. Комплекс айнымалы функциялардың теориясына кіріспе, «Мектеп » баспасы,Алматы 1975


