- Преподавателю
- Математика
- Программа элективного курса по теме «Комплексные числа»
Программа элективного курса по теме «Комплексные числа»
| Раздел | Математика |
| Класс | - |
| Тип | Рабочие программы |
| Автор | Анопова Е.И. |
| Дата | 20.11.2013 |
| Формат | doc |
| Изображения | Есть |
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ГОРОДА ТОМСКА
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ,
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 28 Г. ТОМСКА
Согласовано
на заседании НМС
МОУ СОШ №28
протокол №
«____» __________2013г.
Утверждаю.
Директор МОУ СОШ №28
________________Гринькова Н. А.
« ___» __________2013г
Приказ №
Программа элективного курса по теме
«Комплексные числа»
Составила:
Анопова Елена Ивановна
учитель математики
первой категории
Томск 2013
Пояснительная записка
Понятие числа является основным стержнем всего школьного курса математики, пронизывающим этот курс от первого до последнего класса. Сначала учащиеся знакомятся с натуральными числами и действиями с ними. В пятом классе вводятся дроби, так как невозможно выполнить деление, например 3:4. В шестом классе добавляются отрицательные числа, так как невозможно выполнить вычитание некоторых чисел, например: 3-5. После натуральных, целых, рациональных чисел, добавляются иррациональные, для операции извлечения корней, например, √2. В школьном курсе математики этот вопрос остался не завершённым. Так как при решении квадратных уравнений, если дискриминант отрицательный, то действительных корней не существует. Но если ввести множество комплексных чисел, то квадратное уравнение всегда будет иметь корни. И, конечно, только в старших классах уместен достаточно полный, систематизирующий ретроспективный взгляд на общую картину завершившегося эволюционного процесса.
Данный элективный курс предназначен для предпрофильной и профильной подготовки обучающихся 9-11 класса общеобразовательной школы. Рассчитан на 17 часов.
Он расширяет и углубляет базовую программу по математике, не нарушая её целостности. Каждое занятие направлено на то, чтобы развивать интерес школьников к предмету.
Цель курса:
расширение кругозора учащихся, установление непосредственных связей школьной программы математики с наукой и ее приложениями.
Задачи курса:
-
вооружить учащихся системой знаний по теме «Комплексные числа»;
-
рассмотреть применение комплексных чисел в разных науках, сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;
-
сформировать навыки самостоятельной работы, работы в малых группах;
-
сформировать навыки работы со справочной литературой, с компьютером;
-
сформировать умения и навыки исследовательской работы;
-
способствовать развитию алгоритмического мышления учащихся;
-
способствовать формированию познавательного интереса к математике.
Содержание разделов дисциплины
1 Определение комплексных чисел. Алгебраическая форма записи и арифметические действия над комплексными числами. - 4 часа
История открытия комплексных чисел. Определение множества комплексных чисел.
Арифметические действия с комплексными числами. Сопряжённые комплексные числа. Свойства сопряжённых чисел. Извлечение квадратных корней из отрицательных чисел. Решение квадратных уравнений.
-
Геометрическая интерпретация комплексных чисел. - 2 часа
Изображение комплексных чисел точками на плоскости. Векторная интерпретация действий с комплексными числами.
3. Тригонометрическая форма комплексных чисел. Модуль и аргумент комплексного числа. - 4 часа
Полярные координаты точки и её радиус-вектор. Модуль комплексного числа. Аргумент комплексного числа. Тригонометрическая форма комплексного числа. Свойства модуля и аргумента комплексного числа. Примеры решения уравнений с комплексными переменными.
4. Степени и корни. 4 часа
Возведение в степень комплексного числа. Формула Муавра. Извлечение корней из комплексного числа. Показательная форма комплексного числа.
5 . Применение комплексных чисел в геометрии. - 2 часа
Учебно - тематический план
№ п/п
Раздел дисциплины
Количество часов
Из них
Лекции
Практические
Определение комплексных чисел. Алгебраическая форма записи и арифметические действия над комплексными числами
4
1
3
Геометрическая интерпретация комплексных чисел
2
1
1
Тригонометрическая форма комплексных чисел. Модуль и аргумент комплексного числа
4
2
2
Степени и корни
4
1
3
Применение комплексных чисел в геометрии
2
2
Методы обучения:
Методы преподавания определяются целями и задачами данного курса, направленного на формирование способностей учащихся.
Учащиеся овладевают математическими понятиями, способами математического исследования.
Важнейшим принципом методики изучения курса является постановка вопросов и заданий, позволяющих учителю и учащимся проверить уровень усвоения основных дидактических единиц и степень сформированности умений, приобретённых в процессе изучения курса. Это различные виды тестовых заданий и задания творческого характера.
Технологии обучения:
-
традиционная;
-
элементы проектной, исследовательской технологий;
-
элементы РКМПЧ;
-
интерактивные технологии.
Формы обучения:
-
фронтальная,
-
индивидуальная;
-
групповая;
-
взаимоконтроль.
Требования к уровню освоения содержания дисциплины
-
знать и уметь правильно употреблять термины, связанные с понятием комплексного числа;
-
уметь понимать смысл условий задач;
-
уметь представлять комплексное число в алгебраической, геометрической, тригонометрической и показательной формах;
-
знать и уметь правильно переходить от одной формы записи к другой форме;
-
уметь пользоваться техникой решения задач;
-
уметь пользоваться простейшими приёмами применения арифметических операций над комплексными числами;
-
уметь возводить в степень комплексное число и извлекать из него корень
-
уметь пользоваться справочным материалом для нахождения нужных формул и их использование при решении задач.
Эффективность обучения отслеживается следующими формами контроля:
Задачи для самостоятельного решения, контрольные работы, выполнение проектной или исследовательской работы.
Материально-техническое обеспечение дисциплины
Аудитория, оборудованная мульти-медийными средствами обучения.
Средства обеспечения освоения дисциплины
1) Математика. Комплексные числа 9-11. Предпрофильная и профильная подготовка. Ю.А. Глазков, И.К. Варшавский, М.Я Гаишвили.
2) Единая коллекция Цифровых образовательных ресурсов: school-collection.edu.ru/
Перечень примерных контрольных работ:
1. Определение комплексных чисел. Алгебраическая форма записи и арифметические действия над комплексными числами.


2. Геометрическая интерпретация комплексных чисел




3. Тригонометрическая форма комплексных чисел. Модуль и аргумент комплексного числа


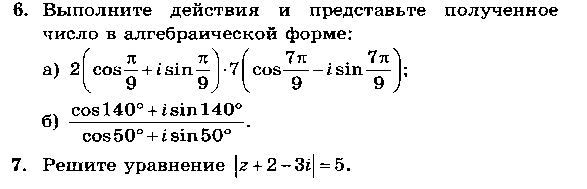
-
Степени и корни

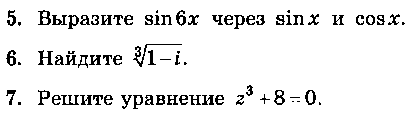
Примерный перечень заданий для самостоятельного решения:
1. Определение комплексных чисел. Алгебраическая форма записи и арифметические действия над комплексными числами
2. Геометрическая интерпретация комплексных чисел
3. Тригонометрическая форма комплексных чисел. Модуль и аргумент комплексного числа
4. Степени и корни
5. Применение комплексных чисел в геометрии
Примерный перечень тем для проектной или исследовательской работы:
-
Калькулятор на комплексные числа.
-
Применение комплексных чисел в электротехнике.
-
Применение комплексных чисел в экономике.
-
Применение комплексных чисел в прикладной математике.
-
Применение комплексных чисел к решению геометрических задач.
-
Применение комплексных чисел для доказательства равенств.
-
Применение комплексных чисел в физике.
-
Применение комплексных чисел для выведения тригонометрических формул.
-
Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней.
-
Уравнение деления круга на пять частей.
-
Определение расстояния между точками на комплексной плоскости.
-
Средства матричного исчисления уравнений и комплексных чисел.
Вычисление комплексных чисел, модуля и аргумента, извлечение кубических корней. Нахождение синусов и косинусов в алгебраическом виде. Решение системы уравнений с помощью формул Крамера, вспомогательных определителей и средствами матричного исчисления. -
Расчет комплексных сопротивлений в электрических цепях переменного тока.
-
Применение комплексных чисел в математических исследованиях.
Занятие №1. Тема «Определение множества комплексных чисел.
Арифметические действия с комплексными числами».
Цель урока: познакомить учащихся с понятием комплексного числа; рассмотреть основные действия над комплексными числами.
Образовательные задачи:
-
Ввести понятие комплексного числа.
-
Показать алгебраическую форму комплексного числа.
-
Познакомить с действиями над комплексными числами в алгебраической
Развивающие задачи:
-
Развивать мышление в процессе выполнения практических заданий.
-
Развивать пространственные представления.
Воспитывающие задачи:
-
Воспитывать культуру записей в тетради.
-
Воспитывать аккуратность, усидчивость, внимательность в процессе прослушивания лекции.
Тип урока: обзорная лекция.
Ход урока
I. Организационный момент.
II. Изложение материала.
-
Историческая справка
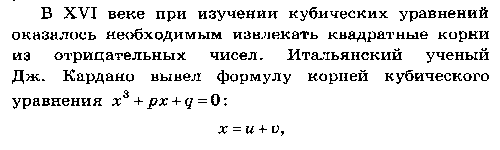

2. Введение понятия комплексного числа.
Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i - мнимая единица, причем i2 = - 1.
Исходя из этого, получим следующее определение комплексного числа.
Определение. Комплексным числом называется выражение вида a + bi, где a и b - действительные числа. При этом выполняются условия:
а) Два комплексных числа a1 + b1i и a2 + b2i равны тогда и только тогда, когда a1=a2, b1=b2.
б) Сложение комплексных чисел определяется правилом:
(a1 + b1i) + (a2 + b2i) = (a1 + a2) + (b1 + b2) i.
в) Умножение комплексных чисел определяется правилом:
(a1 + b1i) (a2 + b2i) = (a1a2 - b1b2) + (a1b2 - a2b1) i.
3. Алгебраическая форма комплексного числа.
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а - действительная часть, bi - мнимая часть, причем b - действительное число.
Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0
Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.
Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.
Два комплексных числа z = a + bi и 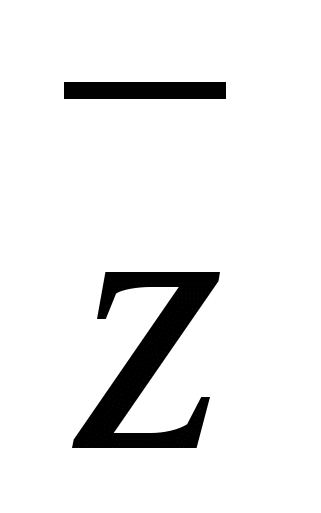 = a - bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
= a - bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
4. Действия над комплексными числами в алгебраической форме.
Над комплексными числами в алгебраической форме можно выполнять следующие действия.
1) Сложение.
Определение. Суммой комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть - сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2)i.
Числа z1 и z2 называются слагаемыми.
Сложение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1 + z2 = z2 + z1.
2º. Ассоциативность: (z1 + z2) + z3 = z1 + (z2 + z3).
3º. Комплексное число -a -bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0
Пример 1. Выполните сложение (3 - i) + (-1 + 2i).
(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Вычитание.
Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 = z1.
Теорема. Разность комплексных чисел существует и притом единственна.
Пример 2. Выполните вычитание (4 - 2i) - (-3 + 2i).
(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.
3) Умножение.
Определение. Произведением комплексных чисел z1=a1+b1i и z2=a2+b2i называется комплексное число z, определяемое равенством: z = (a1a2 - b1b2) + (a1b2 + a2b1)i.
Числа z1 и z2 называются сомножителями.
Умножение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1z2 = z2z1.
2º. Ассоциативность: (z1z2)z3 = z1(z2z3)
3º. Дистрибутивность умножения относительно сложения:
(z1 + z2) z3 = z1z3 + z2z3.
4º. z · ![]() = (a + bi)(a - bi) = a2 + b2 - действительное число.
= (a + bi)(a - bi) = a2 + b2 - действительное число.
На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.
Пример 3. Выполните умножение (2 + 3i) (5 - 7i).
1 способ. (2 + 3i) (5 - 7i) = (2 5 - 3 (- 7)) + (2 (- 7) + 3 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.
2 способ. (2 + 3i) (5 - 7i) = 2 5 + 2 (- 7i) + 3i 5 + 3i (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.
4) Деление.
Определение. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1.
Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i.
На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.
Пусть z1 = a1 + b1i, z2 = a2 + b2i, тогда
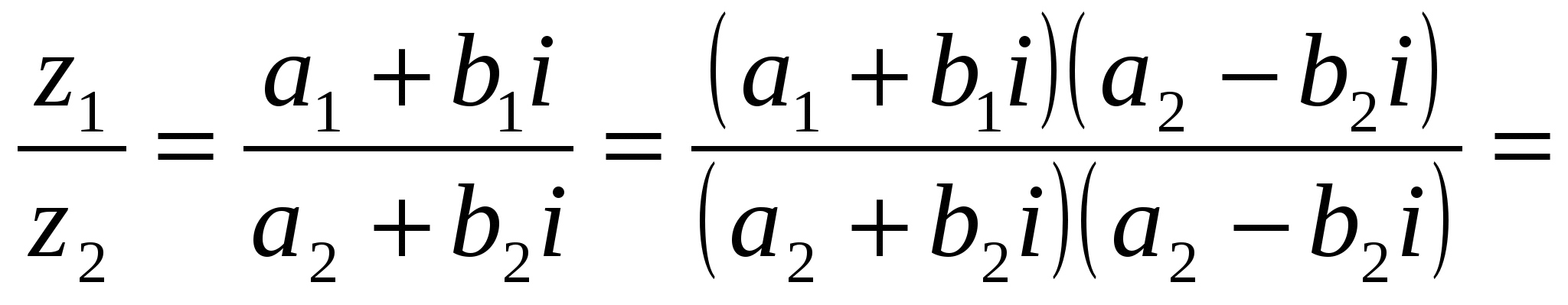
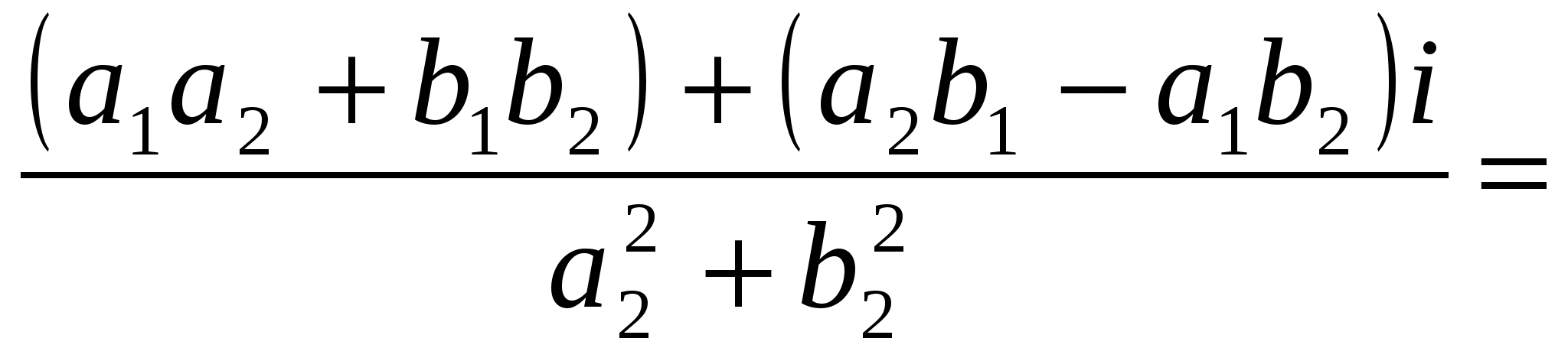
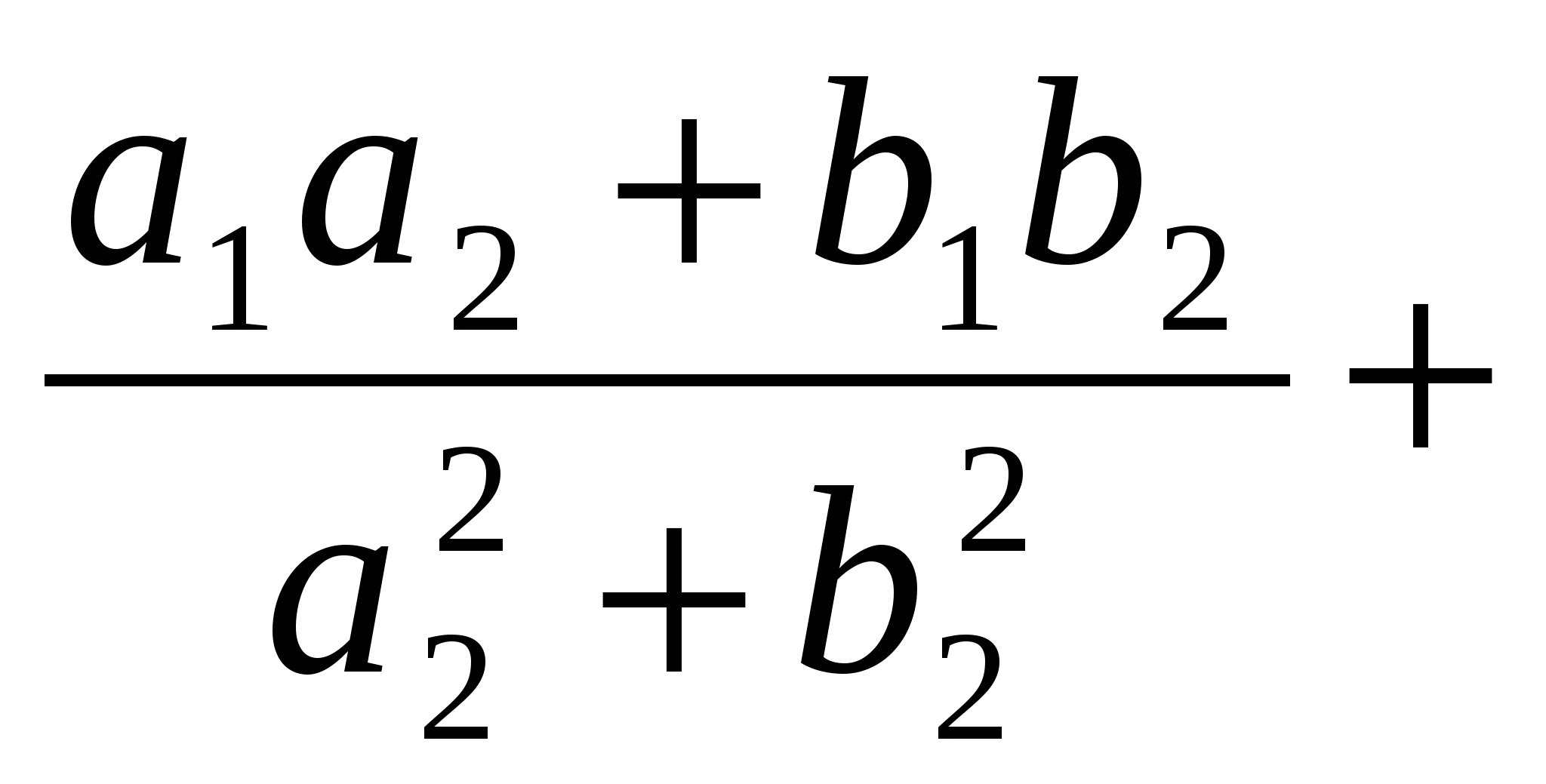
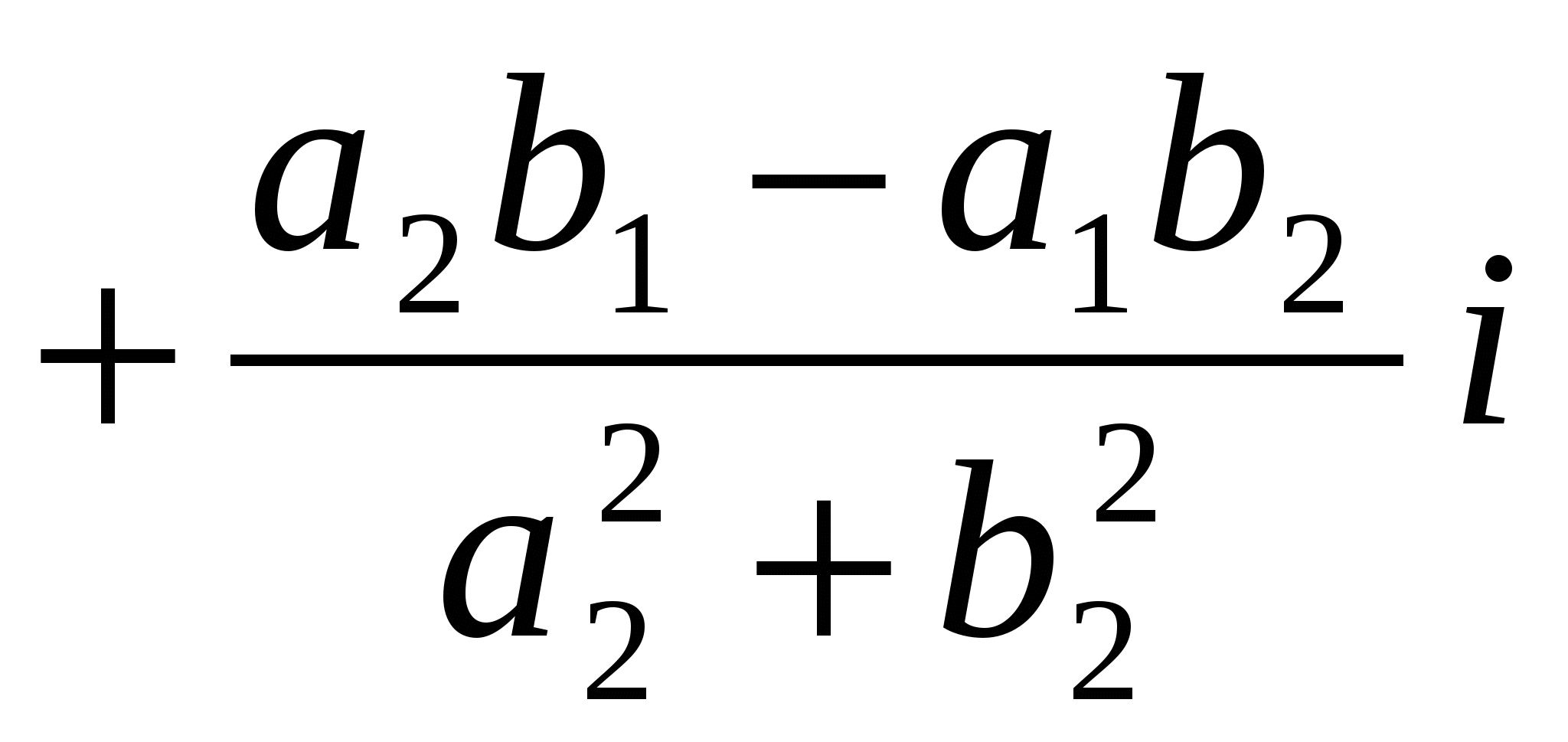 .
.
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.
Пример 4. Найти частное 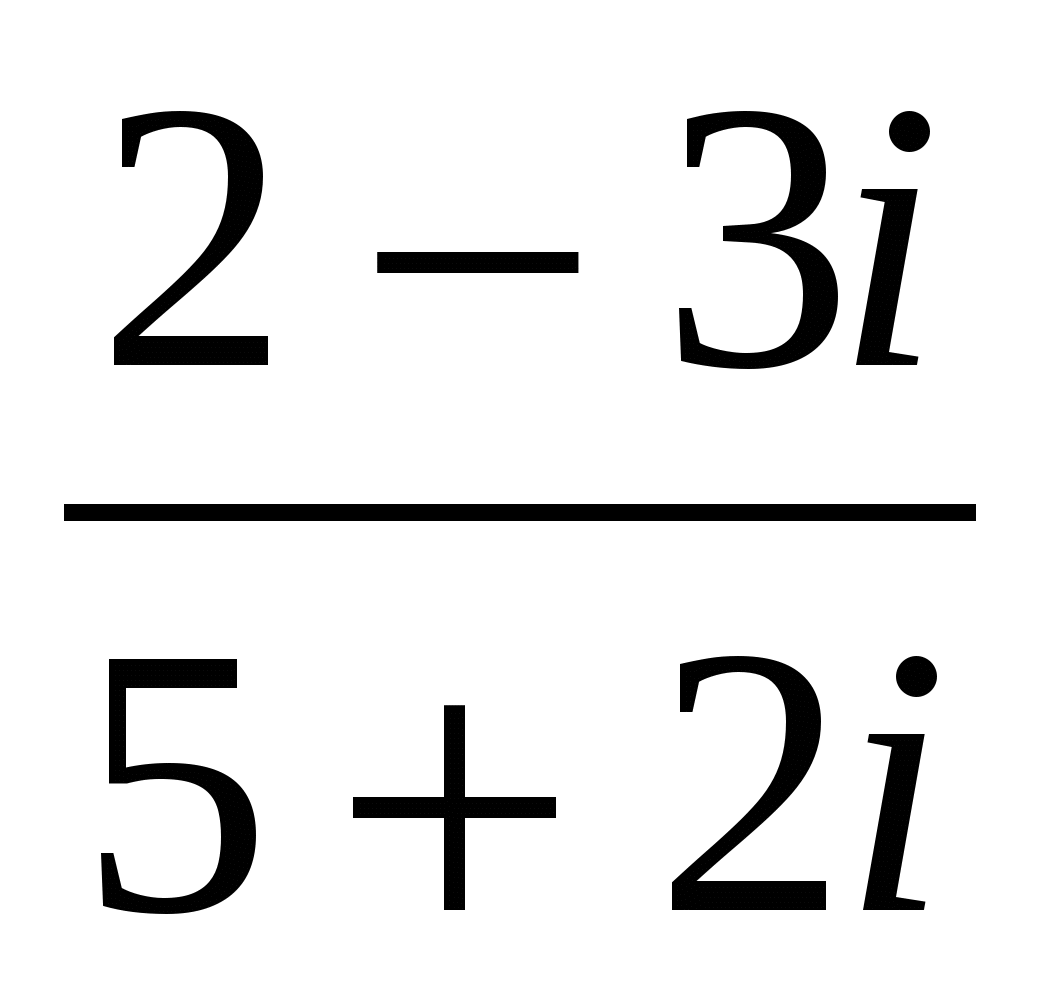 .
.
1 способ.
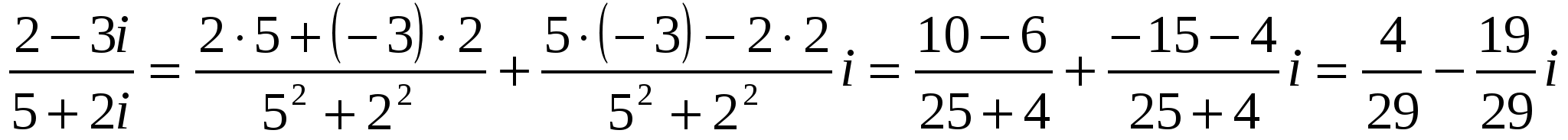 .
.
2 способ.
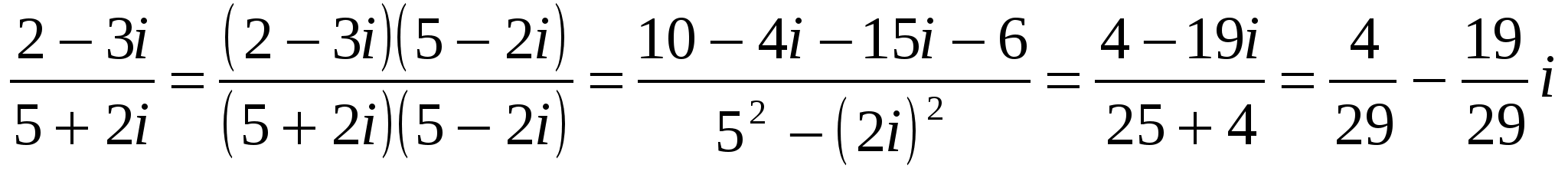 .
.
5) Возведение в целую положительную степень.
а) Степени мнимой единицы.
Пользуясь равенством i2 = -1, легко определить любую целую положительную степень мнимой единицы. Имеем:
i3 = i2 i = -i,
i4 = i2 i2 = 1,
i5 = i4 i = i,
i6 = i4 i2 = -1,
i7 = i5 i2 = -i,
i8 = i6 i2 = 1 и т. д.
Это показывает, что значения степени in, где n - целое положительное число, периодически повторяется при увеличении показателя на 4 .
Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
Пример 5. Вычислите: (i 36 + i 17) · i 23.
i 36 = (i 4)9 = 19 = 1,
i 17 = i 4 4+1 = (i 4)4 i = 1 · i = i.
i 23 = i 4 5+3 = (i 4)5 i3 = 1 · i3 = - i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 - i.
б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.
Пример 6. Вычислите: (4 + 2i)3
(4 + 2i)3 = 43 + 3 42 2i + 3 4 (2i)2 + (2i)3 = 64 + 96i - 48 - 8i = 16 + 88i.
III. Задачи для самостоятельного решения

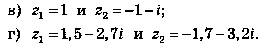
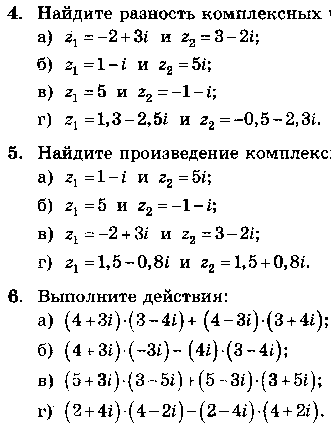
7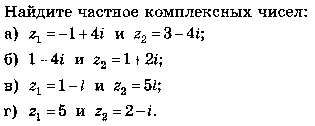 .
.
Список литературы:
-
Алгебра и начала математического анализа. 11 класс: учеб. для общеобр. учрежд.: проф. уровень/М.Я. Пратусевич и др. - М.: Просвещение, 2010 - 463с.
-
Виленкин Н.Я. и др. Алгебра и математический анализ для 11 класса. Учебное пособие для учащихся школ и классов с углубленным изучением курса математики. М.: Просвещение, 1990
-
Избранные вопросы математики: 10 кл. Факультативный курс /А.М. Абрамов, Н.Я. Виленкин, Г.В. Дорофеев и др. Сост. С.И. Шварцбурд. М.: Просвещение, 1980
-
Математика. Комплексные числа 9-11. Предпрофильная и профильная подготовка. Ю.А. Глазков, И.К. Варшавский, М.Я Гаиашвили - М.;Издательства «Экзамен», 2012 - 157с.


