- Преподавателю
- Математика
- Принципы преподавания математики и физики
Принципы преподавания математики и физики
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Тесты |
| Автор | Суслов П.В. |
| Дата | 12.02.2016 |
| Формат | doc |
| Изображения | Есть |
Основные принципы системы преподавания математики и физики
Одиннадцать лет пребывания ученика за партой должны стать годами приобретения жизненного опыта, который создаст условия для их развития, дальнейшей творческой самореализации. Пока ученик находится за партой, необходимо научить его деятельности. Недавно в одной из новостных программ, рассказывали о сельской школе, в которой ввели уроки охоты. Детей учат ставить капканы на различных зверей, строить укрытия, стрелять и т.д. Закадровый текст гласил, что это гораздо полезней, чем заниматься бесполезной тратой времени на уроках математики, перебирая бессмысленные формулы. Честно говоря, обидно такое слушать. Вдумайтесь, нахождение ученика за партой воспринимается как пустое времяпрепровождение. Но ведь очень часто так оно и бывает.
Меня, как учителя, всегда занимала проблема деятельности. Обучая ребёнка на уроке математики, физики и любого другого предмета, мы формируем стереотипы его деятельности. И не важно, чем он будет заниматься мытьём полов или созданием космических кораблей. Таким образом у меня сформировались следующие принципы обучения физике и математике.
-
Принцип самостоятельности.
Мы все помним известное изречение о том что, чтобы избавить человека от голода надо не давать ему кусок хлеба, а надо научить его выращивать его. Главное в учебном процессе научить ученика работать с учебником. Чтение учебного текста это непростой труд, требующий вдумчивой работы, серьёзного напряжения мысли над аксиомами, теоремами, разобранными задачами. Поэтому приоритет в учебном процессе я отдаю самостоятельному добыванию знаний учащимися. После обзорных лекций, абсолютное большинство тем учащиеся изучают по вопросам самоконтроля. Свою роль здесь я вижу чисто консультативную.
Алгоритм действий здесь следующий: Учащийся получает вопросник; начинает разбирать вопросы с кратким составлением конспекта; после разбора 1-2 вопросов идёт к доске и излагает вопросы как понял - эта работа ученика никаким образом не оценивается, цель здесь одна - проконсультировать ученика и выяснить степень понимания учеником вопроса, если понимания нет, то следует ему объяснить вопрос и отправить на дополнительную проработку, в противном случае допустить к разбору следующего задания; после разбора теоретических вопросов предлагается ученику по учебнику самостоятельно разобрать примеры из учебника, после чего ученик приступает к решению закрепляющих упражнений и задач, в течение урока учитель консультирует по мере необходимости ученика; контроль усвоения теории осуществляется на следующем занятии.
-
Принцип поэтапного формирования знаний, умений и навыков.
Невозможно человека с улицы посадить за штурвал реактивного самолёта, дав сложное полётное задание. Его надо обучить очень многому прежде, чем он вообще войдёт в кабину пилота.
Так и ученик. Прежде, чем обучить решению тому или иному типу задач его надо научить выполнять элементарные операции. Например, не стоит вообще разбирать какие-либо темы в математике, если у ученика проблемы с арифметикой.
Чтобы научить решать задачи на применение второго закона Ньютона, необходимо научить: соотношениям в прямоугольном треугольнике, складывать вектора, находить проекции вектора на оси координат, записывать второй закон Ньютона в векторном виде и в проекциях на оси координат, знать формулы равноускоренного движения, уметь переводить единицы измерения в СИ.
-
Принцип развития.
Учебники заполнены в основном упражнениями, а не задачами. Цель упражнения привить определённый навык. Обычно это одноходовки, которые реального развития мышления не дают. Поэтому изучение по любой теме должно подводить под решение задач. Например, изучая квадратичную функцию и квадратные уравнения в 8 классе следует решать задачи с параметрами, причём применяя и аналитические и графические методы решения. Не следует загружать ученика большой по объёму, но несложной работой, но так же не стоит ставить ученика в тупиковое положение, задавая непосильные для него задачи.
Очень важно ученика обучать выдвижению идей и умению их реализовывать при решении задач. Лично я беру задачи из вариантов вступительных экзаменов, ЕГЭ, иногда олимпиад различного уровня по математике и физике. Детей надо приучать к сложным задачам в течение всего учебного процесса, а не перед экзаменами в 11 классе.
-
Принцип вариативности.
Очень важно на примере одной задачи показывать разные методы решения, а затем сравнивать получившиеся решения с различных точек зрения: объём вычислений, оригинальность, эстетическая и практическая ценность.
-
Принцип регулярного и быстрого повторения.
Очень часто, к сожалению, материал забывается на следующий же день после завершающего урока темы. Поэтому, изучая следующую тему, следует включать изученный материал во вновь изучаемый. Например, в учебнике «Алгебра 10», после изучения темы «Логарифмические уравнения и неравенства» следует «Тригонометрические уравнения». Тогда следует дополнить упражнения примерами следующего типа: «Решить уравнение ![]() ».
».
Заканчивая тему по решению уравнений старших степеней и логарифмических уравнений, имеет смысл рассмотреть задачу типа: « Корни уравнения ![]() являются длинами сторон некоторого треугольника, а корни уравнения
являются длинами сторон некоторого треугольника, а корни уравнения 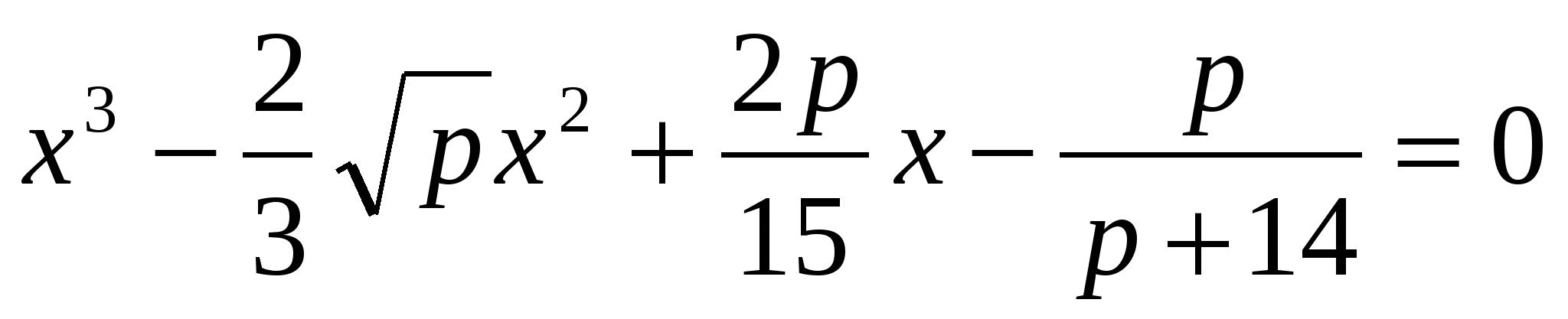 - длинами высот этого же треугольника. Найти p и площадь треугольника.»
- длинами высот этого же треугольника. Найти p и площадь треугольника.»
Суть быстрого повторения заключается в том, чтобы вернуться к решению уже когда-либо разбиравшихся задач. Здесь ученик должен себя отрефлексировать по следующей схеме: я могу решить сейчас эту задачу без труда, или эта задача и сейчас для меня проблемна, хотя и помню основную идею решения, или решение этой задачи я тогда не понял и сейчас решить не могу.
-
Принцип индивидуального прохождения программы.
В процессе изучения программы ученикам в рамках темы даётся выбор скорости и объёма прохождения программы. На итоговую оценку это бесспорно влияет. Но это уже выбор самого ученика.
-
Принцип приоритета теоретического знания над практическим.
Незнание теории приводит ученика к слепой, неосознанной работе. Каждый шаг в практической деятельности ученик должен уметь объяснять почему так, а не иначе он поступает.
-
Принцип взаимоконтроля.
Во время отработки материала полезно осуществлять взаимный контроль учащимися в парах сменного либо постоянного состава. Цели такого вида деятельности: совместное выучивание темы,проверить уровень усвоения материала, помощь товарищу, создать условия психологического комфорта на уроке, получить консультацию учителя, если выяснится, что оба в паре не понимают учебный материал.
Перечисленные базовые принципы во многом формируют практические навыки учащегося, реализуя во многом деятельностный подход в обучении. И хочется верить, что научившись работать за партой, ученик перенесёт основные подходы к работе в любой деятельности.


