- Преподавателю
- Математика
- Концепция Развитие логического мышления на уроках математики
Концепция Развитие логического мышления на уроках математики
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Строков А.В. |
| Дата | 30.07.2015 |
| Формат | doc |
| Изображения | Есть |
Концепция «Развитие логического мышления на уроках математики»
Строков А.В., учитель математики, I КК.
Выше всех добродетелей - рассуждение,
ибо всякая добродетель без разума пуста.
Пётр I.
Введение.
Задача школы - учить мыслить, учиться и действовать. Но этого мало. Необходимо также, чтобы учащиеся приобретали цельное научное мировоззрение, освещающее жизнь и придающее поступкам человека, его работе высокое назначение. Но чтобы полученные при обучении знания превратились в орудие познания и практической деятельности, необходимо, чтобы они были приобретены усилиями собственной мысли, а не только напряжением одной памяти. Заученные формулировки и зазубренные правила не могут служить активным орудием действия и труда и не являются фундаментом для творческого отношения к делу.
Что конкретно дает учащимся изучение математики, помимо «общего развития», которого, в принципе, можно достичь разными путями, а не только изучением математики? Размышляя над этим вопросом, я пришел к выводу, что учителю необходимо передать своим ученикам не только основы математических знаний, но и то, что понадобится им всем, что стоит выше отдельных теорем и формул и что может дать им в школе только математика. Только тогда учитель покажет своим ученикам, что математика глубоко связана с жизнью, привьет им высокий уровень мышления, умение видеть единство в многообразии явлений жизни. Поэтому считаю, что развитие логического мышления на уроках математики очень важно, учитывая его роль в глубоком понимании окружающей действительности, отсюда и научно-методическая проблема: «Развитие логического мышления на уроках математики».
Многие из приобретенных в школе математических знаний понадобятся в жизни всем, кто окончил школу, независимо от выбора ими в будущем той или иной профессии. Однако в отношении логического мышления естественно возникает вопрос: в какой мере обучение логическим рассуждениям на уроках математики помогает нам логически мыслить в жизни? Этот вопрос возникает потому, что в жизни, в быту мы практически никогда не рассуждаем с тем последовательным и тщательным выполнением всех правил логики, как в математике. Более того, даже в школе на уроках биологии, физики, химии, истории и т. д. школьник тоже мыслит логически, но не так, как в математике.
Если в математике школьник имеет дело с аксиомами, определениями и теоремами, то в других науках и в быту никто не устанавливает аксиом, не доказывает теорем, многие понятия не задаются своими определениями, а если последние и даются, то они носят описательный характер. В каждой науке существуют свои общепринятые способы доказательства. Ни физик, ни биолог, ни историк не могут высказать нового положения без его обоснования. Способы обоснований в каждой науке свои, и на первый взгляд бросается в глаза их несхожесть с математическими доказательствами, но при более тщательном анализе выясняется, что во всех методах доказательства есть общая логическая основа.
В житейских рассуждениях мы никогда не исходим из аксиом, наши доказательства никогда не исчерпывают всех возможных случаев, и, тем не менее, мы обычно рассуждаем правильно. В чем же тогда польза школьной математики для тех, кто не собирается в будущем стать математиком? Помимо тех элементарных расчетов, с которыми в быту нам приходится сталкиваться чуть ли не каждый день, например, посещение магазина, математика используется во многих областях науки, например, дифференциальные уравнения - в биологии (проблема борьбы за существование), в медицине (проблема распространения и течения эпидемий), в экономике (прогнозирование развития производства) и во многих других. Но для того чтобы построить математические модели явлений, сами специалисты в этих науках должны прежде всего в достаточной степени владеть математикой. Таким образом, роль математики в жизни любого из нас трудно переоценить.
Развитие логического мышления учащихся на различных этапах урока.
Ян Амос Коменский говорил: «Действительно рассказывают про какого-то философа, что он, имея двух учеников − одного неспособного, а другого шаловливого, − прогнал обоих, так как один, желая учиться, не мог, а другой, имея способности, не желал». В школе мы не можем, как этот философ, просто прогнать своих учеников, если они в чем-то не соответствуют критериям «идеального» ученика - послушного, прилежного, исполнительного, нам приходится иметь дело с различными учениками, с различными характерами, и к каждому из них приходится подбирать «ключик». Просто прогнать - это не интересно, гораздо интереснее попытаться научить чему-либо, пусть даже самого нерадивого ученика.
Очень часто от школьников приходится слышать такие слова: « Я не умею самостоятельно думать, размышлять, у меня не получается делать выводы, решать одну задачу несколькими способами. Получается пересказывать прочитанный текст из учебника, решать задачи по аналогии или по шаблону, используя готовую формулу. Но самого главного - умения мыслить самостоятельно, - у меня нет».
Практика работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить если не все школьники, то, во всяком случае, большая их часть, если развивать у них не столько память, сколько логическое мышление. Необходимо только «заразить» ребят поиском пути решения заданной проблемы. В конце 19 века известный русский методист С. И. Шохор - Троцкий (изобретатель нового метода обучения - «метода целесообразных задач») говорил, что обучение должно проходить не через усвоение учебника или объяснение учителя, а при помощи более или менее самостоятельной работы ученика над искусно подобранными заданиями. С. Л. Рубинштейн, характеризуя психологическую природу мыслительного процесса, указывал: «Всякий мыслительный процесс является по своему внутреннему строению действием, направленным на разрешение определенной задачи. Начальным моментом мыслительного процесса обычно является проблемная ситуация. Мыслить человек начинает, когда у него появляется потребность что-то понять. Мышление обычно начинается с проблемы или вопроса, с удивления или недоумения, с противоречия».
Создание проблемной ситуации - это только лишь начало. Далее учащиеся (под контролем преподавателя) проходят ряд этапов:
-
анализируют ситуацию;
-
формулируют учебно-познавательную проблему;
-
выдвигают гипотезу;
-
проверяют, хватит ли их знаний для решения проблемы.
Следующий шаг - доказательство гипотезы на основе полученных знаний.
Когда результат получен и ученики гордятся своими достижениями, я могу считать свою работу выполненной, ведь каждый школьник почувствовал прелесть открытия, а значит, познакомился с живой математикой.
При изучении нового материала стараюсь использовать метод проблемного обучения и считаю его наиболее успешным на этом этапе урока с точки зрения развития логического мышления. Проблемы, которые ставлю перед учениками, обычно разрешаются на протяжении одного или нескольких уроков. Вот примеры малых проблем-вопросов, которые использую в своей практике:
-
Почему треугольник назван треугольником?
-
Можно ли дать ему другое определение, также связанное с его свойствами?
-
Как можно объяснить название «развернутый угол»?
-
Почему параллелограмм назван параллелограммом?
-
Каким способом можно сравнить два отрезка?
-
Как можно сравнить два угла?
-
Признаки равенства треугольников. Как вы понимаете значение слова «признак»?
-
Основываясь на чем можно утверждать, что треугольники равны?
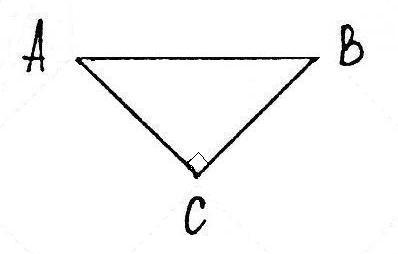 Удобно создавать проблемную ситуацию при помощи эксперимента, исследования частного случая. Например, в 6 классе при изучении темы «Параллельные прямые» предлагаю учащимся такую задачу: «Изобразите все случаи взаимного расположения двух прямых на плоскости. Сколько точек пересечения могут иметь эти прямые?» Учащиеся сами приходят к выводу, что точка пересечения может быть одна (прямые пересекаются), их может быть бесконечно много (прямые совпадают), а может не быть ни одной (прямые параллельны). Можно организовать проблемную ситуацию, предложив ученикам задачу, для решения которой нужны новые знания, при этом поддерживать накал активности цепью проблемных вопросов. Например, перед изучением теоремы Пифагора рассматривается задача, для решения которой нужно уметь вычислить длину гипотенузы по длинам катетов. Построение убеждает, что определенная зависимость между катетами и гипотенузой существует, ибо два катета определяют треугольник, в котором гипотенуза не может быть произвольной. Можно найти приближенное решение графическим путем. Теперь возникает вопрос: «Можно ли выразить формулой зависимость между длинами катетов и гипотенузой?» В поисках ответа рассматриваем удобный частный случай: прямоугольный треугольник с острыми углами по 45° (Рис. 1). Получаем для него формулу:
Удобно создавать проблемную ситуацию при помощи эксперимента, исследования частного случая. Например, в 6 классе при изучении темы «Параллельные прямые» предлагаю учащимся такую задачу: «Изобразите все случаи взаимного расположения двух прямых на плоскости. Сколько точек пересечения могут иметь эти прямые?» Учащиеся сами приходят к выводу, что точка пересечения может быть одна (прямые пересекаются), их может быть бесконечно много (прямые совпадают), а может не быть ни одной (прямые параллельны). Можно организовать проблемную ситуацию, предложив ученикам задачу, для решения которой нужны новые знания, при этом поддерживать накал активности цепью проблемных вопросов. Например, перед изучением теоремы Пифагора рассматривается задача, для решения которой нужно уметь вычислить длину гипотенузы по длинам катетов. Построение убеждает, что определенная зависимость между катетами и гипотенузой существует, ибо два катета определяют треугольник, в котором гипотенуза не может быть произвольной. Можно найти приближенное решение графическим путем. Теперь возникает вопрос: «Можно ли выразить формулой зависимость между длинами катетов и гипотенузой?» В поисках ответа рассматриваем удобный частный случай: прямоугольный треугольник с острыми углами по 45° (Рис. 1). Получаем для него формулу:
АВ2 = АС2 + ВС2 (1). Если принять АВ=c, АС=ВС=a , формула (1) примет вид: c2 = a2 + a2 (2).
(Почти то, что нужно!) Глядя на рисунок 2,
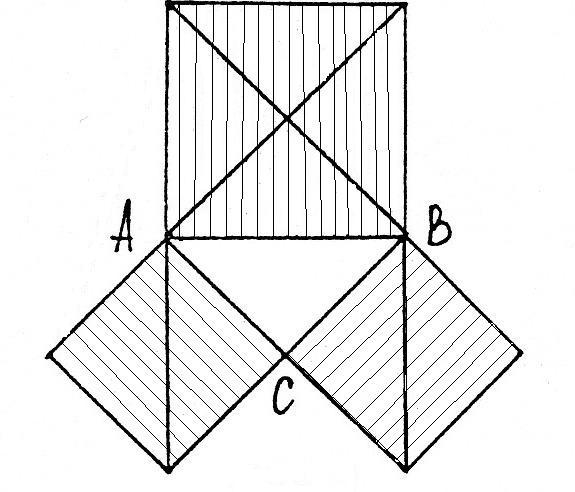 Рис. 1. убеждаемся, что формула верна. Теперь задаемся вопросом: «Верна ли эта формула для произвольного прямоугольного треугольника?» Дальнейшее исследование может быть проведено по такой схеме: поскольку в предлагаемую формулу входят величины АС2, ВС2, АВ2, т.е. площади квадратов со сторонами АС, ВС, АВ, построим эти квадраты. (Рис.2). Первое построение идею доказательства не
Рис. 1. убеждаемся, что формула верна. Теперь задаемся вопросом: «Верна ли эта формула для произвольного прямоугольного треугольника?» Дальнейшее исследование может быть проведено по такой схеме: поскольку в предлагаемую формулу входят величины АС2, ВС2, АВ2, т.е. площади квадратов со сторонами АС, ВС, АВ, построим эти квадраты. (Рис.2). Первое построение идею доказательства не
проясняет. Тогда можно предложить связать величины a, b и c (с = АВ = ВС = СD = AD) в комбинацию прямоугольных треугольников и квадратов таким образом, как показано на рис. 3.
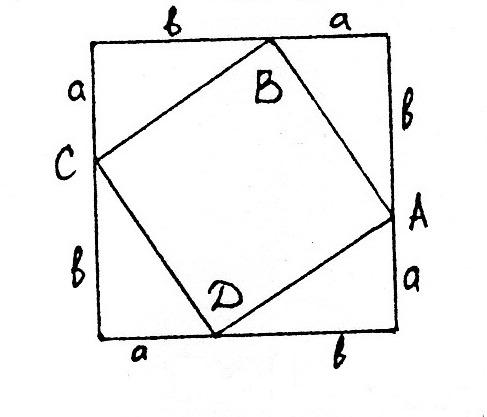 Рис. 2. Здесь площадь малого квадрата равна разности
Рис. 2. Здесь площадь малого квадрата равна разности
площади большого квадрата со стороной (а+b) и учетверенной площади прямоугольного треугольника со сторонами a, b и c, т.е. c2 = (a+b)2 - 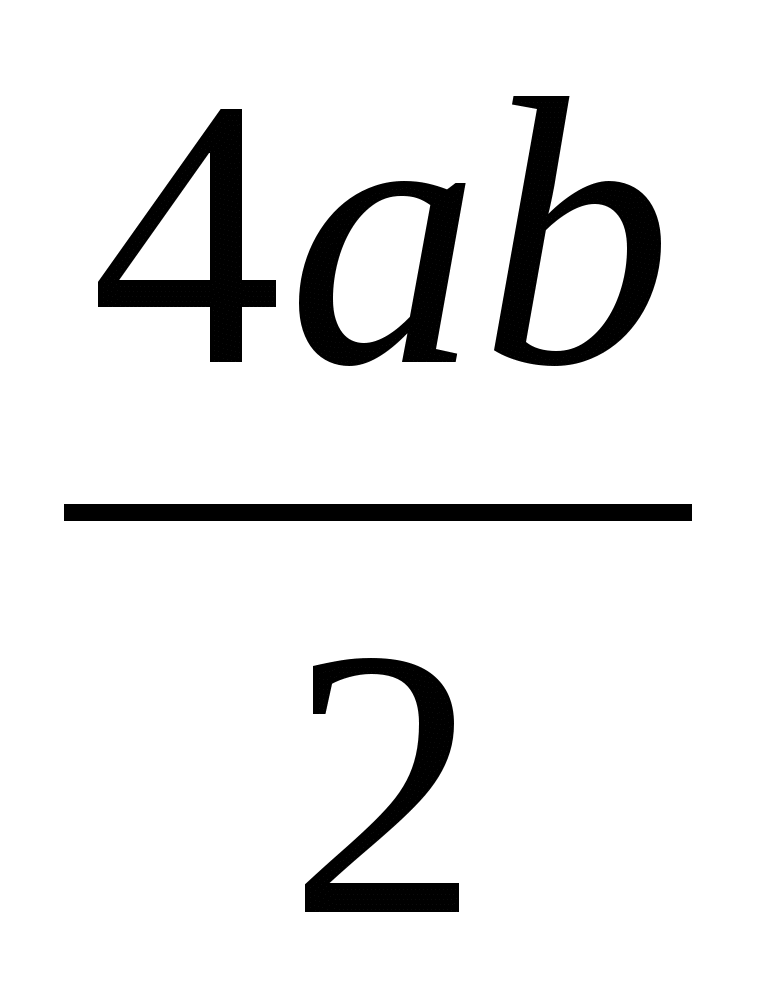 = a2+2ab+b2 - 2ab = a2 + b2 .
= a2+2ab+b2 - 2ab = a2 + b2 .
Можно ли считать формулу доказанной? Если исходить из фигуры, данной на чертеже, то да.
Теперь рассматриваем, всегда ли можно для
любого прямоугольного треугольника провести такое построение. Строим квадрат со стороной a+b и строим прямоугольные треугольники с катетами a и b. Выясняем, почему все такие
Рис.3.
треугольники равны. Остается показать, что фигура, образованная гипотенузами полученных прямоугольных треугольников, является квадратом. Замечаем, что все стороны этой фигуры равны как гипотенузы равных треугольников. Но достаточно ли этого, чтобы фигура ABCD была квадратом? Нет. Доказываем, что все углы этой фигуры прямые, т.к. они равны разности развернутого угла и острых углов данного прямоугольного треугольника. Следовательно, теорему Пифагора можно считать доказанной.
Цепь вопросов, связанных с зависимостью сторон прямоугольного треугольника, может быть продолжена. Справедлива ли теорема Пифагора для непрямоугольного треугольника? Очевидно, нет, т.к. две стороны треугольника a и b не определяют однозначно его форму, а третья сторона меняет свою длину в зависимости от значения угла между сторонами. Следующая проблема: «Верна ли теорема, обратная теореме Пифагора?»
Очень полезно попросить учащихся указать ряд случаев применения теоремы Пифагора. Интересен вопрос: «На чем основан способ построения прямого угла в «египетском» треугольнике со сторонами 3,4 и 5?»
Другой пример. При изучении темы «Прямоугольные треугольники», а в частности, некоторых свойств прямоугольных треугольников (7 класс), удобно создать проблемную ситуацию с помощью чертежа. Делаются чертежи, иллюстрирующие свойства прямоугольных треугольников, и учащимся предлагается самим сформулировать и доказать эти свойства.
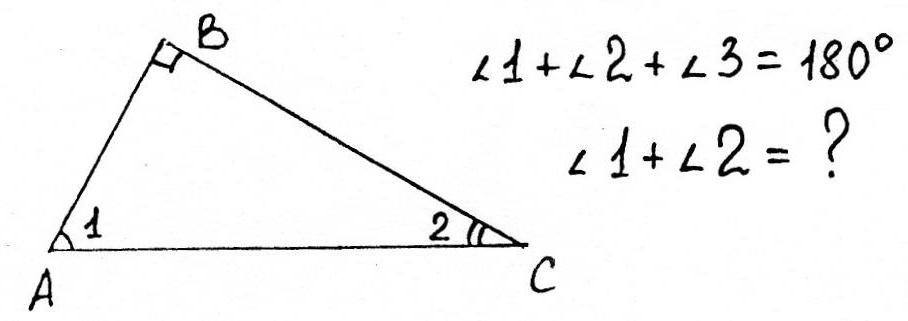
Сумма острых углов прямоугольного треугольника равна 90°.
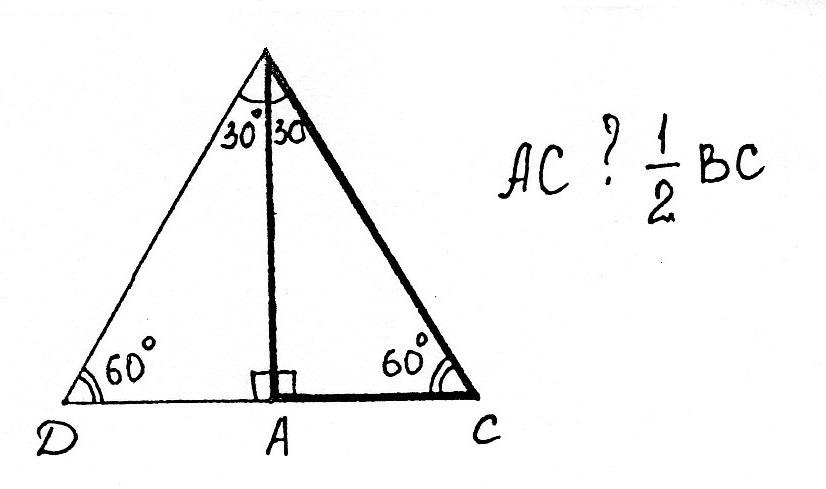
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Е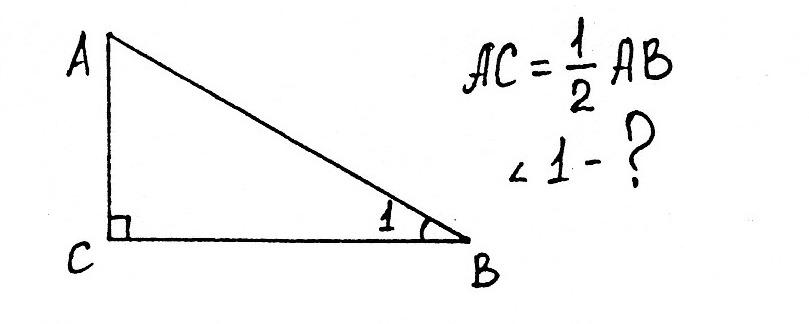 сли катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
сли катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
В процессе рассмотрения этих задач у учащихся формируются навыки «видеть» чертеж, использовать его для доказательства необходимого утверждения.
Проблемные ситуации возникают также в случае необходимости проверить заключение, сделанное на основе интуиции, на основе аналогии или попытки обобщения. Вот несколько примеров таких проблем:
-
Сумма внутренних углов треугольника равна 180°. Равна ли 180° сумма
внутренних углов четырехугольника? Пятиугольника?
-
Чему равна сумма внешних углов треугольника? Четырехугольника?
Пятиугольника?
-
Средняя линия треугольника параллельна основанию. Имеет ли такое же свойство средняя линия ромба? Параллелограмма? Четырехугольника?
-
В треугольнике биссектрисы пересекаются в одной точке. Можно ли то же самое сказать о биссектрисах углов четырехугольника?
-
Можно ли применить формулу площади трапеции к вычислению площади параллелограмма? Прямоугольника? Ромба? Квадрата?
Проблемные ситуации, которые способствуют развитию логического мышления, можно создавать при доказательстве теорем и решении задач на доказательство, ведь именно этот вид работы часто вызывает затруднения у учащихся.
Обучение поиску и построению доказательств направляется тремя вопросами. «Что?» «Откуда?» «Как?»
1. «Что?» - «Что доказывается? Каково доказываемое предложение, для которого мы ищем доказательство? Как оно формируется? Все ли понятия в этой формулировке, нельзя ли иначе сформулировать доказуемое предложение». Это далеко не весь перечень вопросов, которые объединяются в одном вопросе «Что?». Они связаны с изучением доказываемого предложения с возможным его приведением к более удобному для выяснения условий и заключения вида. Например, представление доказуемости предложений с использованием связки «если..., то...», облегчает учащимся выявление того, что едино предложение, записанное после слова «то».
2. «Откуда?» - «Откуда, из каких посылок следует доказываемое предложение? Из каких уже известных истинных предложений данной области можно было бы «вывести» это определение?» Очень важно обратить внимание учащихся на то, что при доказательстве утверждений разрешается пользоваться основными свойствами простейших фигур, т. е. аксиомами, а также свойствами, уже доказанными, т. е. доказанными теоремами. Никакими другими свойствами фигур, даже если они нам кажутся очевидными, пользоваться нельзя. Не разрешается использовать в рассуждении свойства фигуры, видные на чертеже, если мы не можем обосновать их, опираясь на аксиомы и теоремы, доказанные ранее. Это подчеркнуть очень важно, т. к. в первое время учащиеся, самостоятельно доказывая теоремы и решая задачи, очень часто в доказательстве опираются на недоказанные свойства фигур, а также на свойства фигур, явно видные на чертеже, но не обоснованные. Совокупность этих предложений составляет базу для поиска доказательства. Эти совокупности могут быть различными, указывая на различные направления поиска, приводящие к различным доказательствам одного и того же утверждения.
3. «Как?» - «Как доказываемое предложение получается из ранее известных аксиом, определений и теорем». Этот вопрос находит простой ответ: с помощью рассуждения. И именно в рассуждении проявляется умение учеников логически мыслить, раз за разом оттачивая свои навыки.
Развитие логического мышления при закреплении изученного и решении задач.
При закреплении изученного материала, при решении задач очень важным моментом в развитии логического мышления на уроках математики, считаю, является простая проверка ответа, или «взгляд со стороны». Многие знают мультфильм об ученике, который при решении задачи получил в ответе 1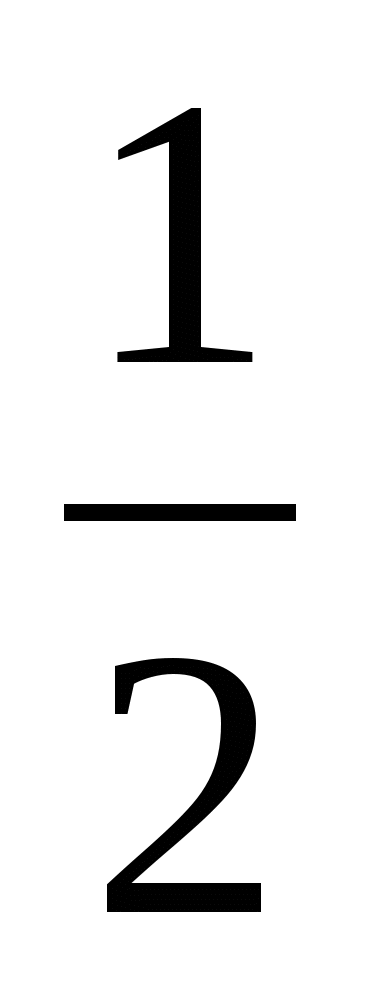 землекопа. На практике это довольно распространенное явление. Например, в задаче, где требовалось найти внутренние углы треугольника, получают ответ: 40°, 120° и 160°. Очень часто встречаются значения синуса, большего единицы, отрицательные площади, отрицательные длины отрезков. В каком бы классе ни учились школьники, допускающие такие ошибки, их объединяет одно - то, что они получили неправдоподобный результат. Предлагаемый ими ответ либо противоречит здравому смыслу, либо не согласуется с известными и многократно повторенными математическими фактами. Естественно, возникает вопрос о том, является ли неправдоподобный ответ забавным казусом, свидетельствующим о крайней невнимательности или малограмотности ученика, или же появление таких ответов представляет собой определенную и стойкую тенденцию, борьба с которой требует постоянного внимания.
землекопа. На практике это довольно распространенное явление. Например, в задаче, где требовалось найти внутренние углы треугольника, получают ответ: 40°, 120° и 160°. Очень часто встречаются значения синуса, большего единицы, отрицательные площади, отрицательные длины отрезков. В каком бы классе ни учились школьники, допускающие такие ошибки, их объединяет одно - то, что они получили неправдоподобный результат. Предлагаемый ими ответ либо противоречит здравому смыслу, либо не согласуется с известными и многократно повторенными математическими фактами. Естественно, возникает вопрос о том, является ли неправдоподобный ответ забавным казусом, свидетельствующим о крайней невнимательности или малограмотности ученика, или же появление таких ответов представляет собой определенную и стойкую тенденцию, борьба с которой требует постоянного внимания.
Чтобы такие ответы не появлялись, важно научить школьников умению находить ошибки в своих решениях, в том числе и путем оценки правдоподобности полученного ответа (например, проверять, не оказался ли искомый катет больше известной гипотенузы), выработать у учащихся навык «прикидки результата» и введение заданий, непосредственно связанных с жизнью. При решении текстовых задач можно выделить следующие виды проверки результата:
-
Установление соответствия между числами, полученными в ходе решения задачи, и данными в условии задачи.
-
Составление и решение задачи, обратной данной.
-
Решение задачи разными способами.
-
Решение задачи различными методами.
-
Прикидка (грубая проверка).
Развитие логического мышления при помощи дифференцированного подхода к процессу обучения.
Опыт моей работы показывает, что в каждом классе учатся разные ученики и по своему уровню развития, и по отношению к предмету. Есть ученики, которые отстают в умственном развитии от своих сверстников, есть невнимательные на уроках, а есть и те, кто пропускает большое количество уроков в силу различных причин, в том числе и из-за болезни. Но есть ребята, которые мгновенно «схватывают» материал.
Многим учащимся математика нужна для того, чтобы окончить школу, и потом они не собираются ей заниматься. Такие ученики ограничиваются обязательным уровнем подготовки, так называемым стандартом. Другие, в соответствии со своими склонностями и способностями, достигают более высоких рубежей. Их не устраивает базисный уровень, им надо изучать математику, чтобы потом поступить в ВУЗ продолжать обучение дальше. Каждой категории учащихся нужна «своя» математика, в зависимости от их склонностей, способностей и целей. И как развиваться «слабому» ученику на уроках, если его уровень не «дотягивает» до некоторой планки? (Ведь то, что не понятно, для них не всегда бывает интересно, а то, что неинтересно, заставить изучить крайне трудно). Учитывая интересы учащихся, работу над развитием их логического мышления веду также и с использованием дифференциального обучения.
В каждом классе я выделяю две группы учащихся: группа базового уровня и группа повышенного уровня. Состав групп в течение года может меняться в зависимости от успехов учащихся. Ученик из группы базового уровня может перейти в группу повышенного уровня, если он свободно выполняет задания обязательного уровня. И наоборот, ученик из группы повышенного уровня может переводиться в группу базового уровня, если он имеет пробелы в знаниях.
На разных этапах учебной работы для каждой группы учащихся использую варианты заданий различной степени сложности. Дифференцированный подход осуществляю на определенных этапах обучения на уроке. На этапе введения нового понятия, т.е. изучении нового материала, знакомства со свойствами, алгоритмами, работаю со всем классом без деления его на группы. Но после того, как несколько упражнений выполнено на доске, учащиеся приступают к дифференцированной самостоятельной работе. Задания группы базового и повышенного уровня получают различные и по содержанию, и по форме подачи.
Задания составляю в двух вариантах: I вариант - для группы базового уровня, II вариант - для группы повышенного уровня. I вариант содержит большое число тренировочных упражнений с постепенным нарастанием трудности. Во II вариант включаю задания комбинированные, такого характера, которые требуют нестандартных приемов решения.
В каждом варианте упражнения начинаются с простейших и располагаются по степени возрастания сложности. I вариант строится так, что переход от одного упражнения к другому связан с незначительными усложнениями формулировки задания. Такой подход предоставляет слабым учащимся возможность на каждом шаге преодолевать только одну какую-нибудь трудность. Во II варианте сложность заданий возрастает в более высоком темпе.
В каждом варианте наряду с тренировочными заданиями включаю задания развивающего характера, решение которых связано с проявлением смекалки, сообразительности. Примеры заданий для дифференцированной самостоятельной работы даны в приложении.
Помимо дифференцированной самостоятельной работы в своей работе использую задания творческого характера и задания, содержащие инструктивный материал, которые тоже разные по уровню сложности. Примеры таких заданий также даны в приложении.
Кроме таких заданий для I варианта составляю обучающие карточки. Обучающие карточки помогают слабым ученикам освоить ранее не понятый материал и хорошо воспринять новые темы. Обучающая карточка состоит из чередования трех блоков:
-
Опорная формула или алгоритм
-
Решенный пример или задача
-
Упражнения , которые ученик должен решить сам.
Пример обучающей карточки дан в приложении.
Такие разноуровневые задания облегчают организацию занятий в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями. Слабые ученики охотно выполняют задания, содержащие инструкции, с помощью обучающих карточек. Творческие задания даю и слабым учащимся, т.к. они стимулируют познавательную активность слабых школьников.
Работа с группами строится так:
-
I вариант решает задание под моим контролем фронтально, а II вариант решает задания самостоятельно. Вариант проверки заранее написан на закрытой части доски.
-
Учащиеся I варианта работают самостоятельно, а учащиеся II варианта работают вместе со мной, разбирая задачи повышенной трудности.
-
Учащиеся, хорошо усвоившие материал, работают самостоятельно, а те, у кого возникли затруднения, выполняют задания под моим наблюдением.
Часто даю дифференцированную домашнюю работу. Слабым учащимся предлагаю задания обязательного уровня, а более сильным ребятам добавляю более сложные задания и упражнения из учебника. Иногда задания одинаковые, но содержат дополнительные вопросы. Например: А - обязательные упражнения (для всех), В - усложненные (добавляются сильным ученикам).
№1. А. Выполните действия: (4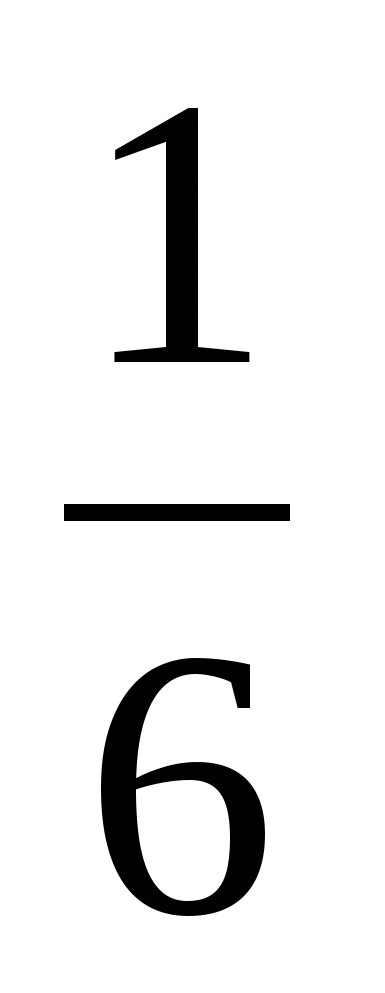 *
*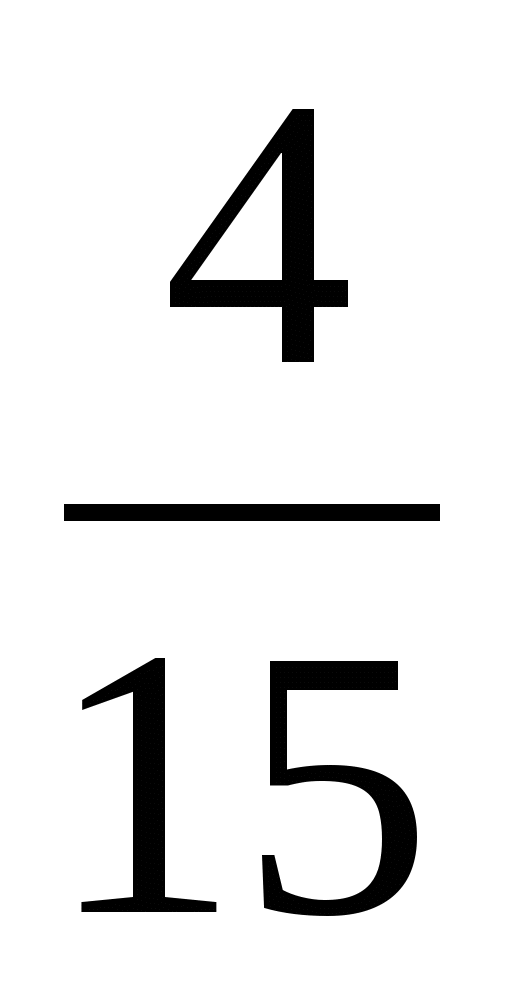 +
+ 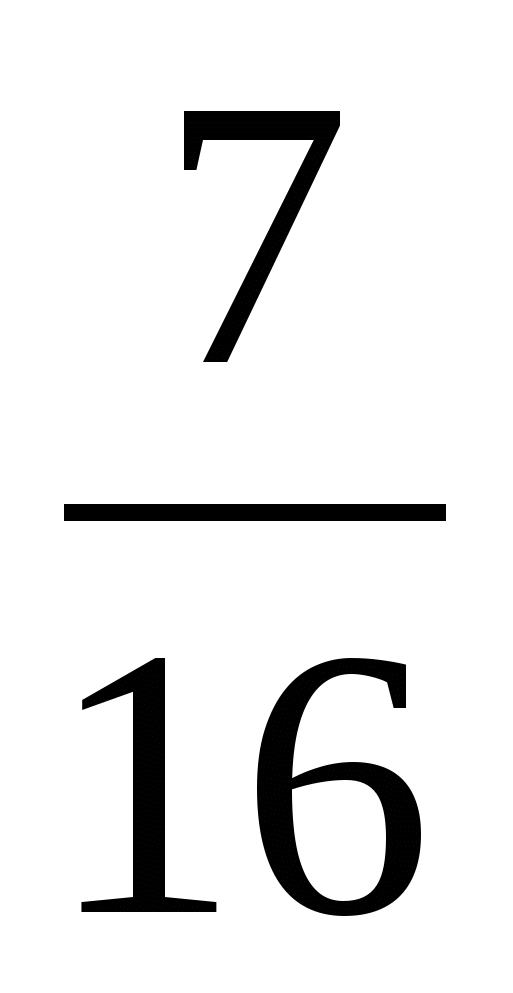 * 2
* 2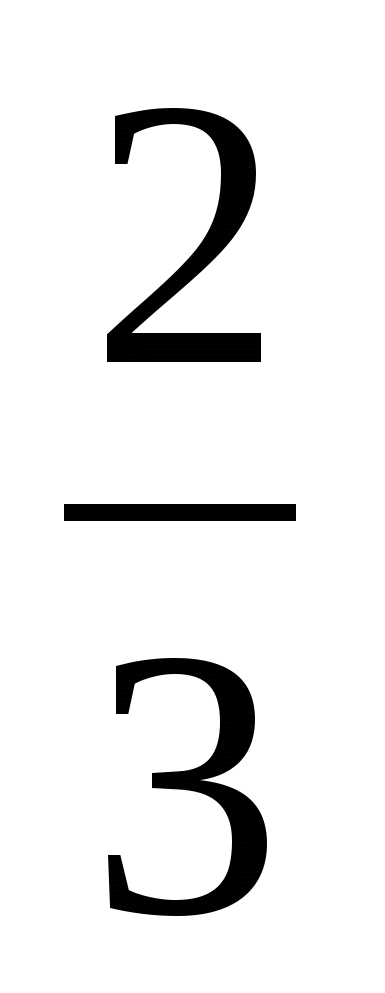 ) : 4
) : 4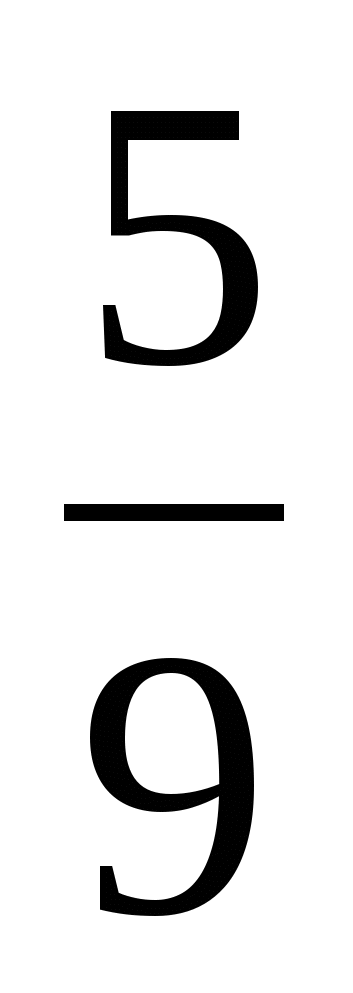 .
.
Б. Выполни указанные выше действия и, используя полученный
результат, вычисли устно: (4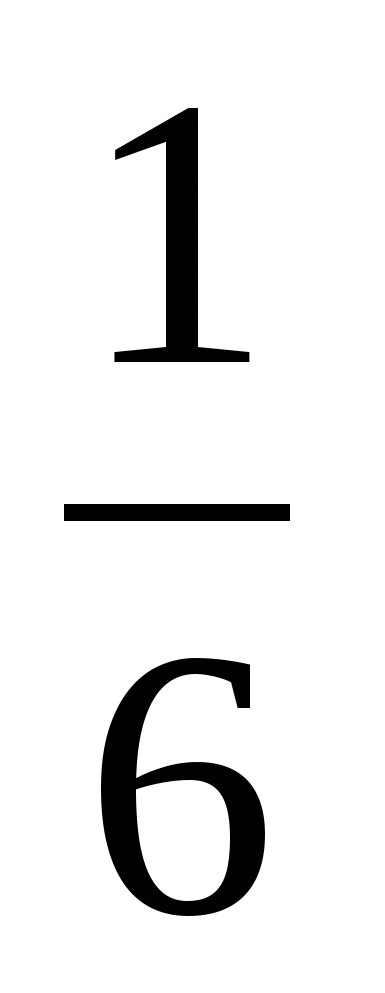 *
* 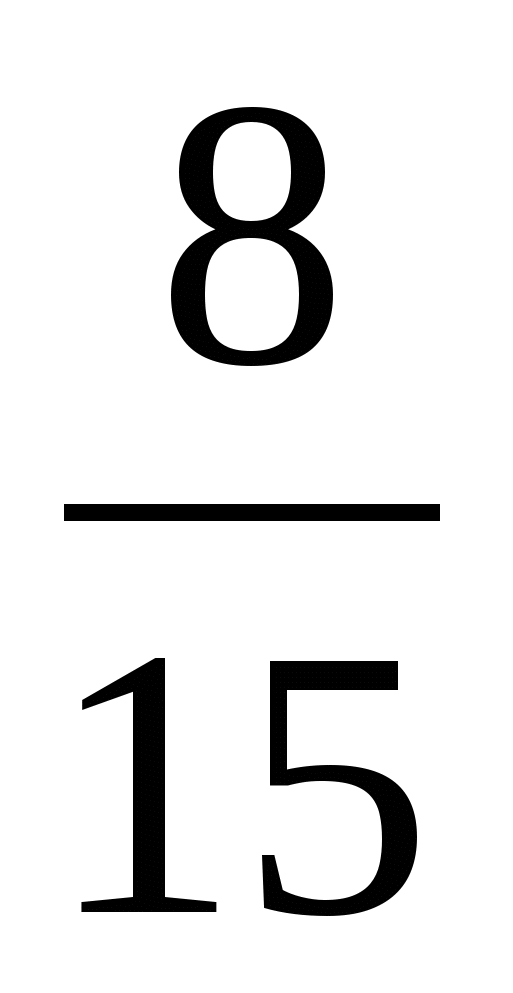 +
+ 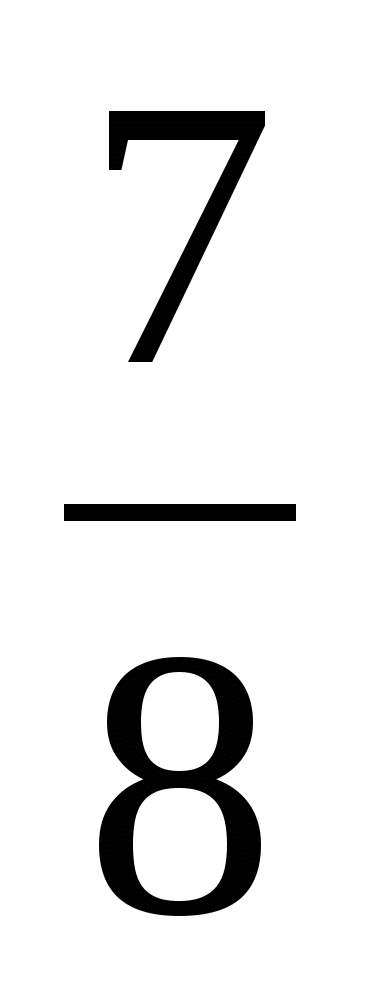 * 2
* 2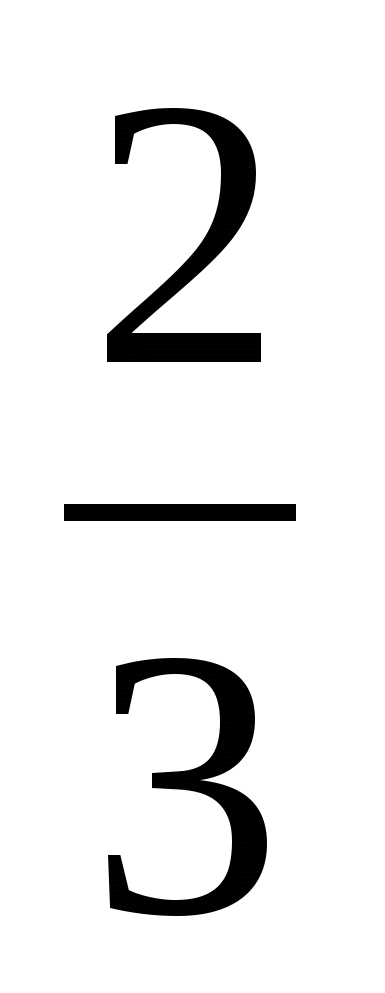 ) : 4
) : 4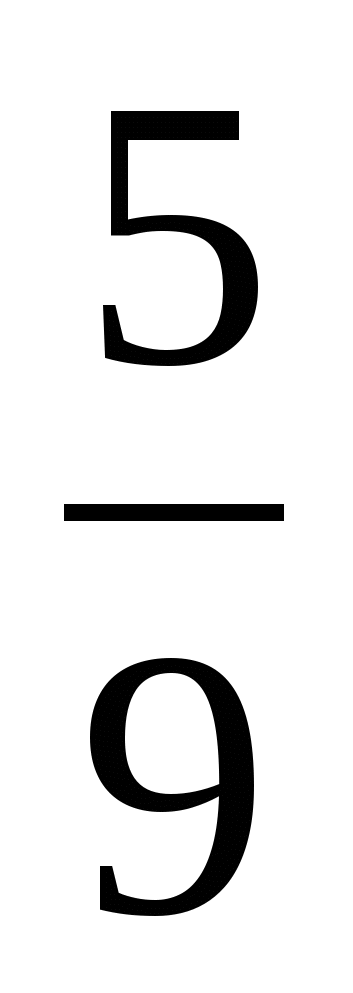 .
.
В упражнении Б учащиеся должны вспомнить, как изменится произведение при увеличении в 2 раза одного из множителей и как изменится сумма при увеличении каждого слагаемого в 2 раза. Проверка такого задания в классе вызывает общий интерес, у ребят появляется желание попробовать свои силы. Разумеется, задания типа Б предлагаются не каждый день, но они вызывают интерес.
Важную роль играет проверка усвоения пройденного материала. Часто учащиеся из сильной группы работают на самоконтроле, а учащиеся из слабой группы поочередно работают у доски по 6-7 человек. В течение урока к такой работе привлекаются все слабые ученики.
Большую роль играют дифференцированные самостоятельные и контрольные работы. При выполнении самостоятельной работы учащиеся сами выбирают, какие задания будут решать, на оценку «3», «4» или «5». Чтобы слабые ученики не списывали у сильных, работы им даю индивидуальные. Ошибки контрольных работ заносятся в специальную тетрадь и выполняется работа по устранению пробелов. Также в своей практике я использую математические диктанты на два варианта с нарастающей степенью сложности. Во время проведения урока-зачета задания также даются дифференцированно, на «3», на «4», на «5». Если зачет не сдан, то после индивидуальной работы с каждым учеником назначается пересдача.
Так как каждый ученик работает над посильным для него заданием, то он лучше осознает свои ближайшие цели и задачи. Наличие в классе сильных учеников позволяет постоянно продумывать работу с ними, учитывать возможность их развития.
Развитие логического мышления через развитие познавательного интереса к предмету и во внеурочной деятельности.
Большую роль в развитии познавательного интереса к математике играет реализация на уроках проектно-исследовательских технологий. Работа над проектами вызывает у учащихся неподдельный интерес и побуждает их к более глубокому изучению материала. Учащиеся не просто знакомятся с новыми понятиями, развивается их творческая активность, умение делать выводы и обобщения на основе данных, полученных в результате исследований, что положительно сказывается на развитии логического мышления. Также во время работы над проектами развивается познавательная деятельность учащихся, которая способствует развитию разносторонней личности. В учащихся воспитывается стремление к самосовершенствованию, удовлетворению своих познавательных потребностей. Пример урока, реализующего проектно-исследовательские технологии, дан в приложении.
Огромную роль при проведении уроков играет использование интерактивной доски - новшества в разряде технических средств обучения, открывающего новые возможности во всех сферах деятельности как учителя, так и ученика. Интерактивная доска позволяет достичь высокую плотность урока и в итоге его результативность.
Также очень важную роль в развитии логического мышления играет внеурочная деятельность. Не только уроки дают учащимся пищу для ума. «Забавляясь, не учатся»,- заявляет в одном из романов А.Франса старая учительница, но автор возражает: «Только забавляясь, и учатся». Нельзя отрицать ни то, ни другое. При любом обучении надо стремиться пробудить интерес у учеников - именно в этом таится секрет многих успехов. Занимательная или развлекательная математика восходит к древним временам. Уже в древнеегипетской арифметической книге Ахмеса встречаются занимательные задачи. Внеурочные занятия по математике призваны решить целый комплекс задач по углубленному математическому образованию, всестороннему развитию индивидуальных способностей школьников, развитию творческой деятельности, максимальному удовлетворению их интересов и потребностей. Для непрерывного обучения и самообразования особое значение имеют развитие самостоятельности и творческой активности учащихся, а также воспитание навыков самообучения по математике. Познавательная деятельность учеников может носить как характер простого воспроизведения, так и преобразовательный, творческий, заставляющий думать, мыслить. При этом под творческой подразумевается такая деятельность, в результате которой учащимся самостоятельно открывается нечто новое, оригинальное, отражающее индивидуальные склонности, способности и индивидуальный опыт школьников.
Внеклассная работа по математике проводится во внеурочное время с учащимися, проявляющими к математике интерес. Активизация внеклассной работы призвана не только возбуждать и поддерживать у учеников интерес к математике, но и желание заниматься ею дополнительно как под руководством учителя, так и при самостоятельной деятельности по приобретению новых знаний. Формами такой работы являются конкурсы, викторины, тематические классные часы, математические вечера. К подготовке этих мероприятий следует привлекать учащихся и их родителей. Большое значение на внеурочных занятиях имеют развитие самостоятельности и творческой активности учащихся. Самостоятельность на уровне поисковой деятельности особенно увлекает ребят.
Внеклассная работа по математике призвана решать три основные задачи:
-
Повысить уровень математического мышления, углубить теоретические знания и развить практические навыки учащихся, проявивших математические способности.
-
Способствовать возникновению интереса у большинства учеников, привлечение некоторых из них в ряды любителей математики.
-
Организовать досуг учащихся в свободное от учебы время.
Контролирующей будет игра, дидактическая цель которой состоит в повторении, закреплении, проверке ранее полученных знаний. Приведу такой пример. При изучении геометрии в 7 классе возникает необходимость повторить все аксиомы, проверить их усвоение учащимися. Обычный опрос не вызывает интереса. Однако, если провести повторение в форме игры, интерес налицо. К «Конкурсу знатоков геометрии» заблаговременно готовлю карточки с заданиями - рисунки к аксиомам. Задание состоит в том, чтобы установить, иллюстрацией к какой аксиоме является каждый рисунок, а также заметить, каких элементов на каждом из них недостает. Необходимо нужный элемент дорисовать, а потом сформулировать соответствующую аксиому. Аналогичные задания предлагаю учащимся при повторении таких понятий, как отрезок, полупрямая, угол, равенство фигур и т.д.
Обобщающие игры требуют интеграции знаний. Они способствуют установлению межпредметных связей, направлены на приобретение умений действовать в разных учебных ситуациях. На первых уроках геометрии в 7 классе ребята знакомятся с различными простейшими фигурами. Появляется новые термины, которые нелегко усваиваются ими. В связи с этим в устные упражнения включаются следующие задания: «Опишите рисунок (чертеж), используя те данные, которые заданы». Запись можно вести символически. В описание рисунка включаются более сложные фигуры, с которыми ученики знакомятся на уроках, то есть рисунок усложняется. Этим способом развивается не только зрительное восприятие, умение видеть чертеж, но и речь. Культура математической речи получает развитие, чего трудно добиться другими методами. Предлагается задание на дом: придумать рисунок и описать его. В начале урока геометрии учащиеся поочередно показывают задание. Они видят творчество других, и это побуждает их творить еще лучше. Для этого необходимо глубоко знать учебный материал.
В процессе игры у детей вырабатывается привычка мыслить самостоятельно и логично, стремление к знаниям, чувство собственного достоинства, чувство сопереживания за друга. Увлекшись, дети не замечают, что учатся познанию, запоминают новое. В свою очередь, дидактические игры в зависимости от содержания материала, способа организации, уровня подготовки школьников, цели урока могут приобретать различный характер. Например, быть продуктивными, репродуктивными, творческими, конструктивными, практическими, воспитывающими. Нельзя считать, что использование игровых ситуаций на уроке дает возможность учащимся овладеть математикой «легко и просто». Легких путей в науке нет. Но необходимо использовать все средства для того, чтобы дети учились с интересом. Дидактическая игра - не самоцель, а средство обучения и воспитания, развития творческой личности. Примеры внеклассных мероприятий по математике даны в приложении.
Считаю, что реализация мною научно-методической проблемы «Развитие логического мышления на уроках математики» с использованием дифференцированной технологии, проектно-исследовательской технологии, технологии развивающего обучения поможет школьнику в его становлении как личности, в преодолении учебных и жизненных преград.
Закончить хочется словами Дмитрия Сергеевича Аничкова: «О математике без сомнения заключить можно, что она острит человеческий разум и делает оный способнейшим к рассматриванию и исполнению правил истинной логики». С этим трудно не согласиться.
10


