- Преподавателю
- Математика
- Программа курса по выбору «Конечные цепные дроби»
Программа курса по выбору «Конечные цепные дроби»
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Никулина В.В. |
| Дата | 11.10.2014 |
| Формат | rar |
| Изображения | Есть |
Приложение 2
Представление рациональных чисел цепными дробями
Определение. Целое число, являющееся делителем каждого целого числа, a1, a2, …, an , называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
Пусть 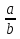 - рациональное число, причем b > 0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:
- рациональное число, причем b > 0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:
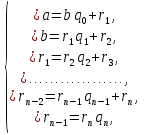 (1)
(1)
где неполным частным последовательных делений q0, q1, …, qn-1 соответствуют остаткам r1, r2,…, rn с условием b > r2 > r3 > … > rn > 0, a - соответствует остаток 0. Системе равенств (1) соответствует равносильная система (2):
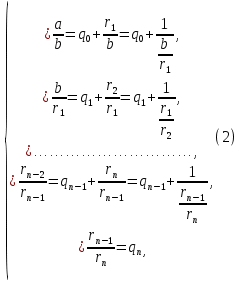
из которой последовательной заменой каждой из дробей 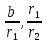 и т.д. ее соответствующим выражением из следующей строки получается представление дроби
и т.д. ее соответствующим выражением из следующей строки получается представление дроби 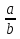 в виде:
в виде:
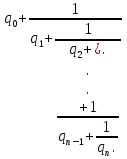
Полученное выражение называется конечной цепной или правильной непрерывной дробью, при этом предполагается, что q0 - целое число, а q1, …, qn - натуральные числа.
Имеются различные формы записи цепных дробей:
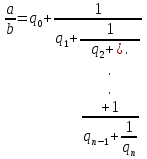 .
.
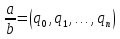 .
.
Согласно последнему обозначению имеем
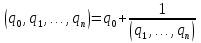 .
.
Числа 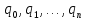 называются элементами цепной дроби.
называются элементами цепной дроби.
Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Разложение рационального числа 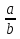 имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.
имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.
Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было qn > 1.
Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, при условии, что qn > 1.
Доказательство:
-
Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при qn > 1:
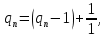
так что представление можно удлинить:
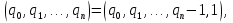
например, (2, 3, 1, 4, 2) = (2, 3, 1, 4, 1, 1).
-
Принимая условие qn > 1, можно утверждать, что целая часть цепной дроби
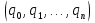 равна ее первому неполному частному q0. В самом деле:
равна ее первому неполному частному q0. В самом деле:
-
если n = 1, то (q0) = q0
-
если n = 2, то
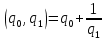 , q1 > 1; поэтому
, q1 > 1; поэтому 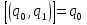 .
. -
если n > 2, то
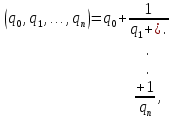
где 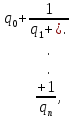 > 1, т.к. q1 ≥ 1.
> 1, т.к. q1 ≥ 1.
Поэтому и здесь 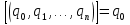 . Докажем то, что рациональное число
. Докажем то, что рациональное число 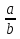 однозначно представляется цепной дробью
однозначно представляется цепной дробью 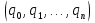 , если
, если
qn > 1.
Пусть 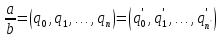 с условием qn > 1,
с условием qn > 1, 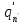 > 1. Тогда
> 1. Тогда 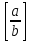 =
= 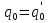 , так что
, так что 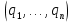 =
= 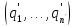 . Повторным сравнением целых частей получаем
. Повторным сравнением целых частей получаем 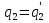 , а следовательно,
, а следовательно, 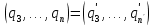 и так далее. Если
и так далее. Если 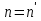 , то в продолжении указанного процесса получим также
, то в продолжении указанного процесса получим также 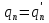 . Если же
. Если же 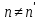 , например
, например 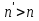 , то получим
, то получим
0 = 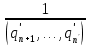 , что невозможно.
, что невозможно.
Теорема доказана.
Вместе с тем мы установили, что при соблюдении условия qn > 1 между рациональными числами и конечными цепными дробями существует взаимно однозначное соответствие.
Замечания:
-
В случае разложения правильной положительной дроби первый элемент
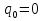 , например,
, например, 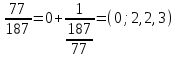 .
. -
При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.
Пример: 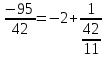 , так как
, так как 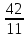 = (3, 1, 4, 2), то
= (3, 1, 4, 2), то 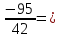 (-2; 3, 1, 4, 2).
(-2; 3, 1, 4, 2).
-
Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.
Пример: 5 = (5); 17 = (17).


