- Преподавателю
- Математика
- Методический кейс Применение производной и интеграла
Методический кейс Применение производной и интеграла
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Конспекты |
| Автор | Кирилюк Н.А. |
| Дата | 28.12.2015 |
| Формат | doc |
| Изображения | Есть |
Городской методический центр
Методический кейс
Применение производной и интеграла
Из опыта работы
учителей математики-
членов городской
динамической группы
руководитель группы
Кирилюк Н.А.
учитель математики высшей категории,
"Старший учитель",
УВК "ОШ І-ІІ ст. №1-лицей "Спектр"
Торез
2011
Применение производной и интеграла
Составители:
Кирилюк Н.А.- учитель математики высшей категории,
"Старший учитель";
Беляева Л.С. - учитель математики высшей категории,
"Учитель-методист";
Захарова З.Т.- учитель математики высшей категории;
Шамдам Н.А. - учитель математики высшей категории,
"Старший учитель";
Беляева Н.А.- учитель математики І категории;
Руденко Е.Г.- учитель математики І категории.
Методический кейс является дидактическим материалом
для 11 профильных классов общеобразовательных учебных заведений. Материал пособия отвечает действующей программе по алгебре и началам анализа. Поможет учителям и учащимся повысить уровень учебных достижений до желаемого результата.
Пояснительная записка
Настоящий кейс является учебно-методическим пособием для профильного обеспечения учащихся 11 классов по развитию навыков применение производной и интеграла к решению, как физических задач, так и математических: исследование функции и построение графиков, вычислению площадей, решению уравнений.
Опираясь на материал школьных учебников, в пособии обсуждаются алгоритмы исследования функции на монотонность, нахождение точек экстремума, наибольшего и наименьшего значения функции, построение графиков функции, вычисление площадей фигур. Приведены образцы решения задач на применение производной и интеграла.
Система практической части по каждой теме представлена для трех уровней: профильного, академического, стандартного. С целью закрепления и контроля предлагается система тестовых заданий.
Содержание
1.Методические рекомендации
1.1.Приложение производной 5
1.2.Интеграл и его приложения 6
-
Практическая часть
2.1. Профильный уровень 11
2.2. Академический уровень 23
2.3. Стандартный уровень 35
3. Тест для самоконтроля 46
1.1. Приложение производной
При построении графиков функций очень важно уметь находить промежутки возрастания, убывания и постоянства функции (то есть промежутки монотонности), а также ее точки экстремума.
1.Для нахождения промежутков возрастания и убывания функции рекомендуется:
-
Найти область определения функции, если она не указана.
-
Найти производную и критические точки функции , т.е. точки из области определения функции , к которых её производная равна нулю или не существует. Критическими точками область определения разбивается на интервалы, на каждом из которых производная сохраняет свой знак.
-
Установить знак производной на каждом из найденных интервалов. Если на рассматриваемом интервале производная функции положительна (отрицательна), то на этом интервале функция возрастает (убывает)
2. Точка x0 называется точкой максимума (минимума) функции у = f(x) ,если для всех х из некоторой окрестности этой точки, кроме х = x0,если выполняется неравенство f(x)<f(x0) (f(x) > f(x0)). Точки максимума и минимума называются точками экстремума.
Для нахождения точек экстремума функции надо:
-
Найти производную и критические точки функции.
-
Исследовать поведение знака производной в некоторой окрестности каждой критической точки. Если функция непрерывна в критической точка x0 , то x0 - точка экстремума функции. При этом, x0 - точка максимума, если знак меняется с плюса на минус, и минимума, если знак меняется с минуса на плюс. Если же знак производной сохраняется при переходе через рассматриваемую точку, то функция не имеет экстремума в этой точке.
3. Решение многих практических задач сводится к определению условий, при которых исследуемая величина принимает своё наибольшее или наименьшее значения. Подобные задачи решаются с помощью производной. Вспомним, прежде всего, понятие наибольшего и наименьшего значений функции.
Значение функции y=f(x) в некоторой точке x0 множества Х называется наибольшим (наименьшим) значением функции на этом множестве, если для каждого х их Х выполняется неравенство f(x) ≤ f(x0 ) (f(x) ≥ f(x0 )).
Обратите внимание на то, что даже ограниченная функция может не иметь на заданном промежутке наибольшего или на наименьшего значения. Так, функция
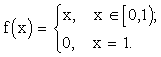 не имеет на отрезке [0;1] наибольшего значения.
не имеет на отрезке [0;1] наибольшего значения.
Ее наименьшее значение на этом промежутке равно 0. (рис.1)

рис.1
Известно, что непрерывная на отрезке функция всегда имеет на этом отрезке наибольшее и наименьшее значения.
Что бы найти наибольшее и наименьшее значения непрерывной функции, имеющий на заданном отрезке конечное число критических точек, нужно вычислить значения функции критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Иногда при нахождении наибольшего и наименьшего значений функции полезно использовать следующий факт.
Если на некотором промежутке непрерывная функция y=f(x) имеет единственную критическую точку x0 и x0 - точка максимума (минимума), то f(x0 ) будет наибольшим (наименьшим) значением функции на этом промежутке.
4. Производная помогает при решении уравнений, неравенств, доказательстве тожеств. При этом мы будем опираться на следующие свойства функций.
-
Если непрерывная функция f возрастает или убывает на некотором промежутку, то на этом промежутке уравнение f(x)=0 имеет не более одного корня.
-
Если f(x)=0 на некотором промежутке, то f(x)=const на этом промежутке.
1.2.Интеграл и его приложения
Часто приходится решать задачи, обратные тем, которые рассматривались при изучении производной: по известной скорости тела восстанавливать закон его движения, по ускорению - скорость, по угловому коэффициенту касательной к кривой- уравнение самой кривой и т.д. Решение каждой из сформулированных задач сводится к нахождению функций по заданной её производной. Восстановление функции по её производной называется интегрированием. Интегрирование - операция, обратная дифференцированию.
1. Допустим, нужно найти функцию F(x) по её производной f(x), т.е. найти такую функцию F(x), что F'(x)=f(x). В этом случае функцию F(x)называют первообразной функции f(x). Таким образом, операция интегрирования состоит в отыскании первообразной данной функции.
В отличие от дифференцирования, операция интегрирования приводит не к одной конкретной функции ,а к целому семейству функций.
Если y=F(x) - первообразная функции y=f(x) на некотором промежутке то функция y=f(x) имеет на этом промежутке бесконечно много первообразных и все они имеют вид y=F(x) + С , где С - произвольная постоянная.
Это свойство первообразных функций имеет простой геометрический смысл:
Графии любых двух первообразных функций можно получить друг из друга параллельным переносом вдоль оси ординат.
Чтобы из множества первообразных выделить одну, нужно задать дополнительные условия, например, значение первообразной в некоторой точке. Геометрически это означает что выделение кривой, проходящей через заданную точку.
2. С понятием первообразной тесно связано другое понятие математики - понятие интеграла. С помощью интеграла можно найти перемещение прямолинейно движущегося тела, площади фигур ,объемы тел, работу переменной силы и многие другие величины.
Интеграл 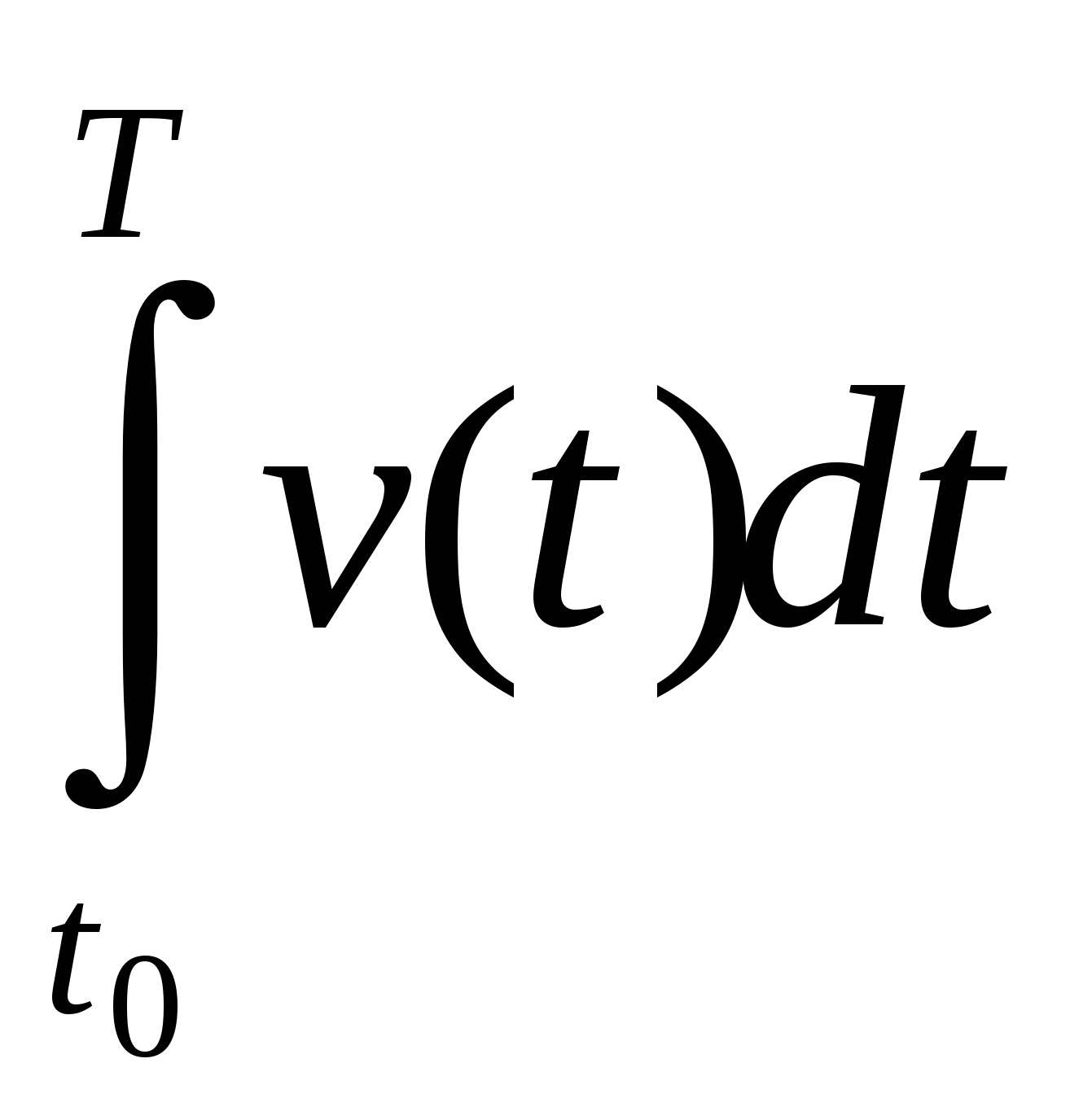 есть перемещение прямолинейно движущейся со скоростью V(t) материальной точки за промежуток времени
есть перемещение прямолинейно движущейся со скоростью V(t) материальной точки за промежуток времени ![]() .
.
Если 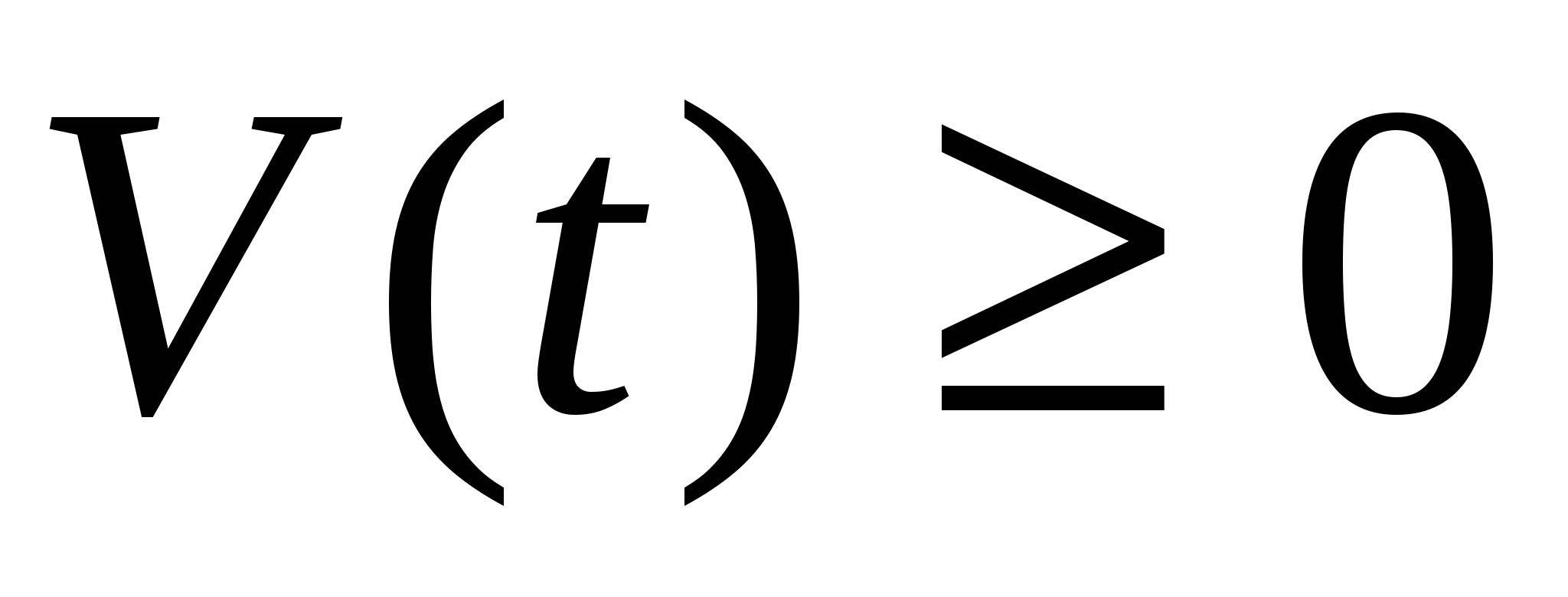 , то этот интеграл можно трактовать как путь, пройденный точкой за промежуток времени
, то этот интеграл можно трактовать как путь, пройденный точкой за промежуток времени 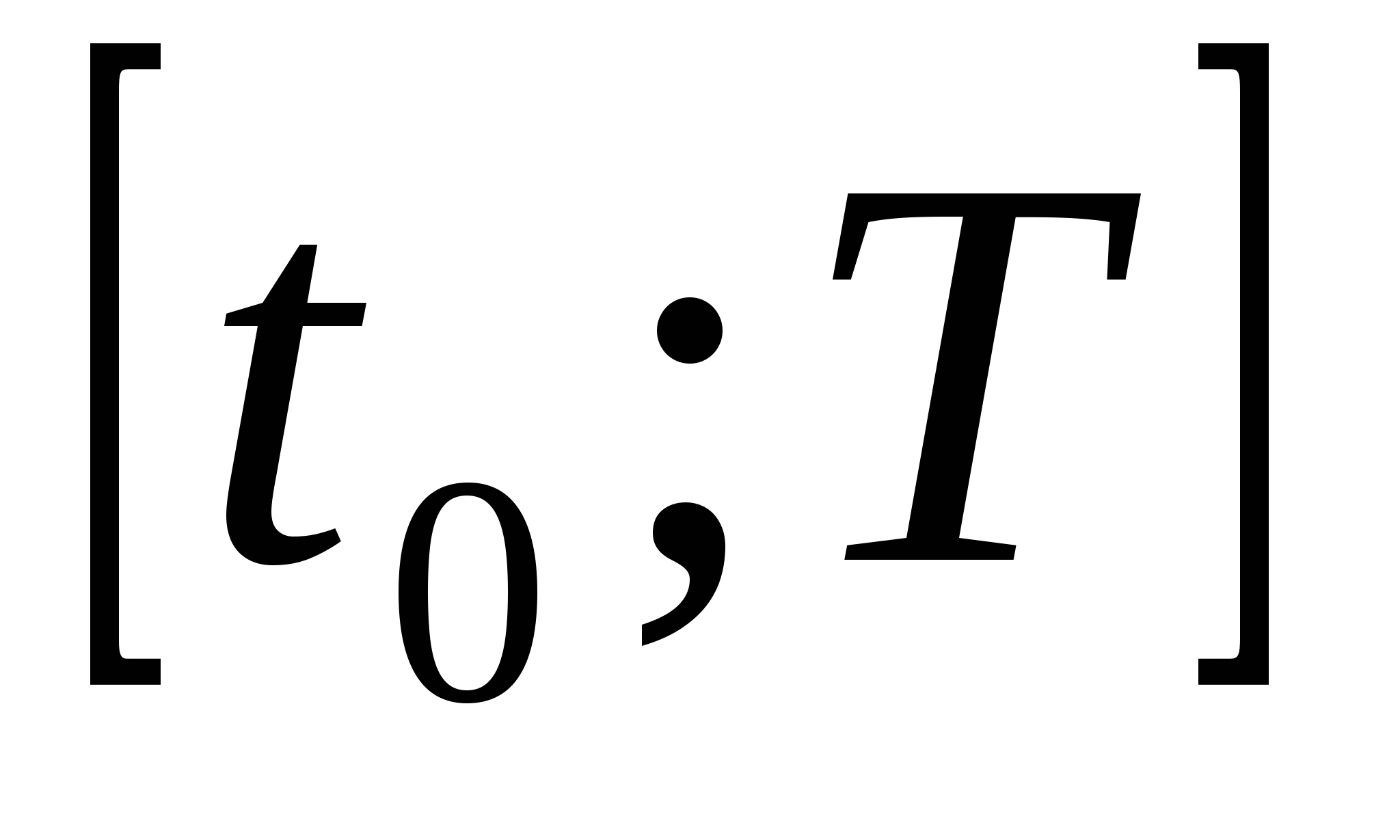 .
.
В этом заключается физический смысл интеграла.
Рассмотрим теперь фигуру, ограниченную графиком непрерывной неотрицательной функции 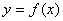 , прямыми
, прямыми ![]()
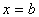 и осью х (рис.2). Эта фигура называется криволинейной трапецией и её площадь равна
и осью х (рис.2). Эта фигура называется криволинейной трапецией и её площадь равна
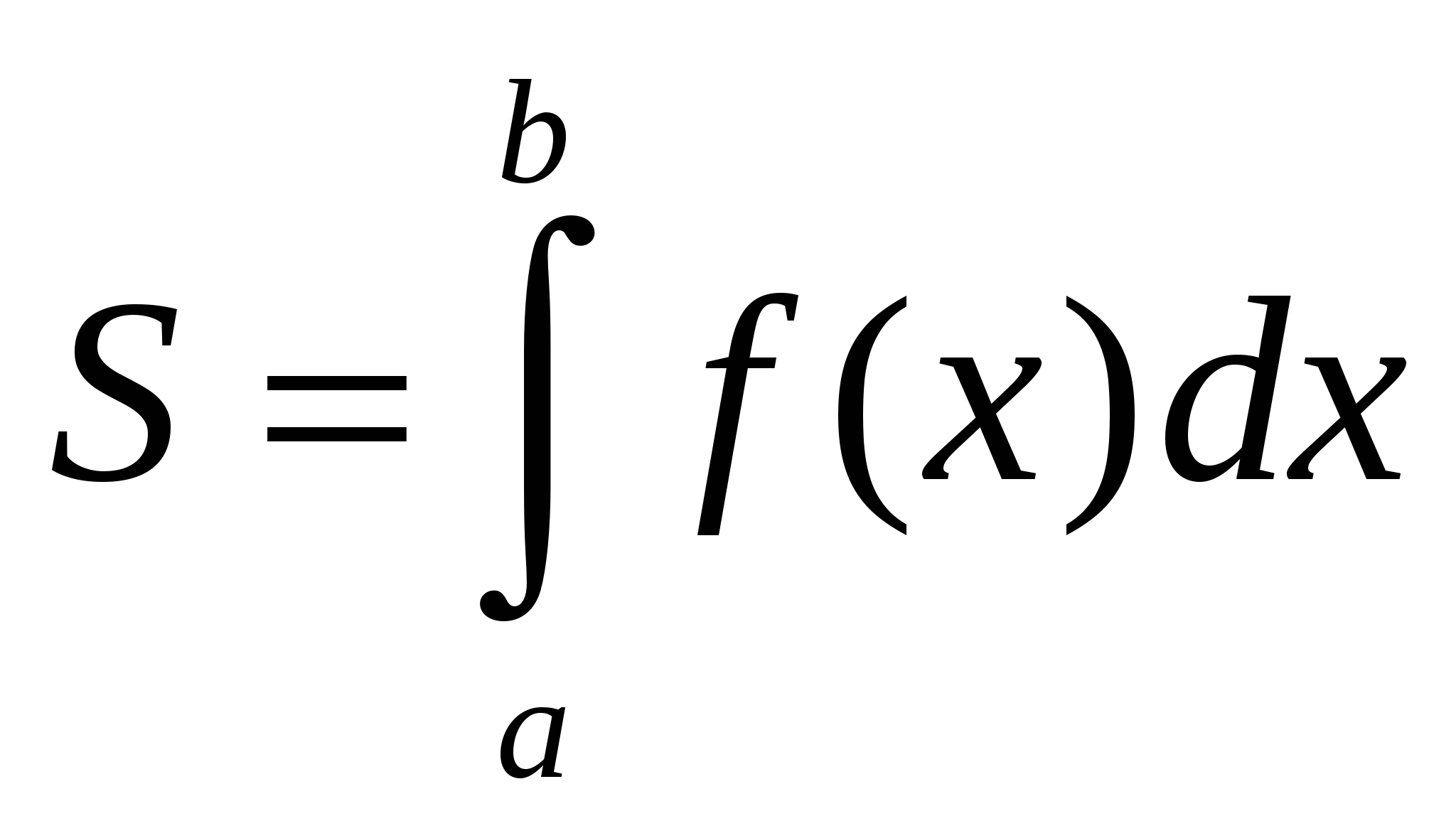
В этом заключается геометрический смысл интеграла.
Для вычисления интеграла обычно используют формулу Ньютона-Лейбница: 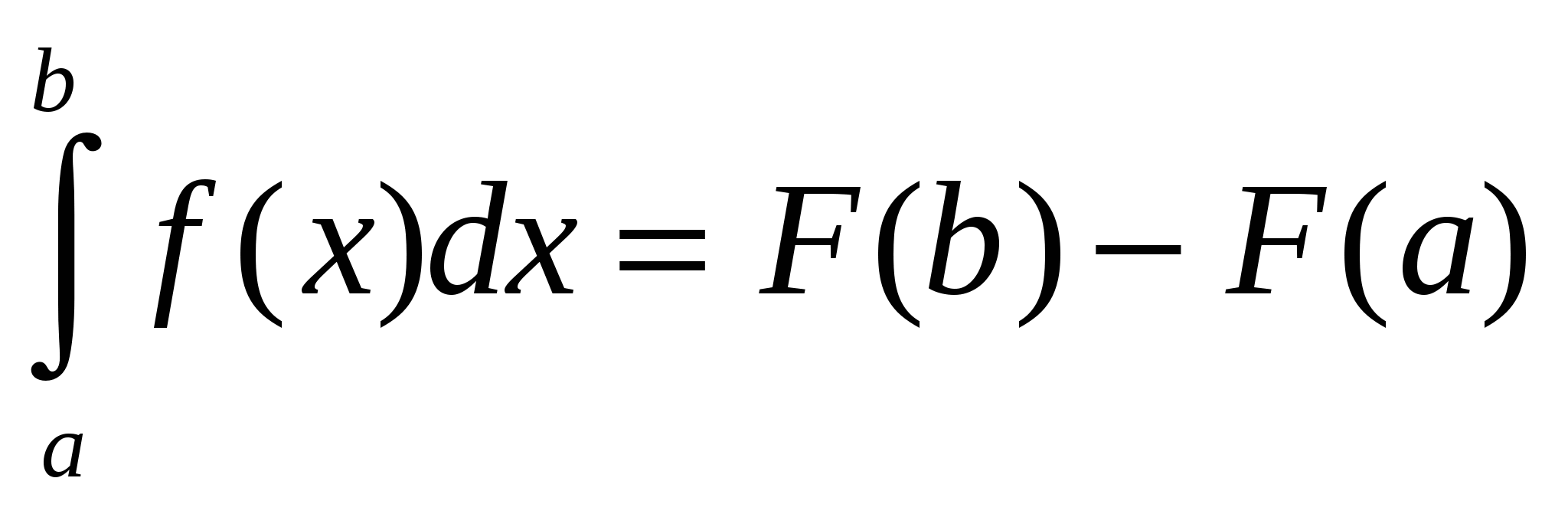
Где 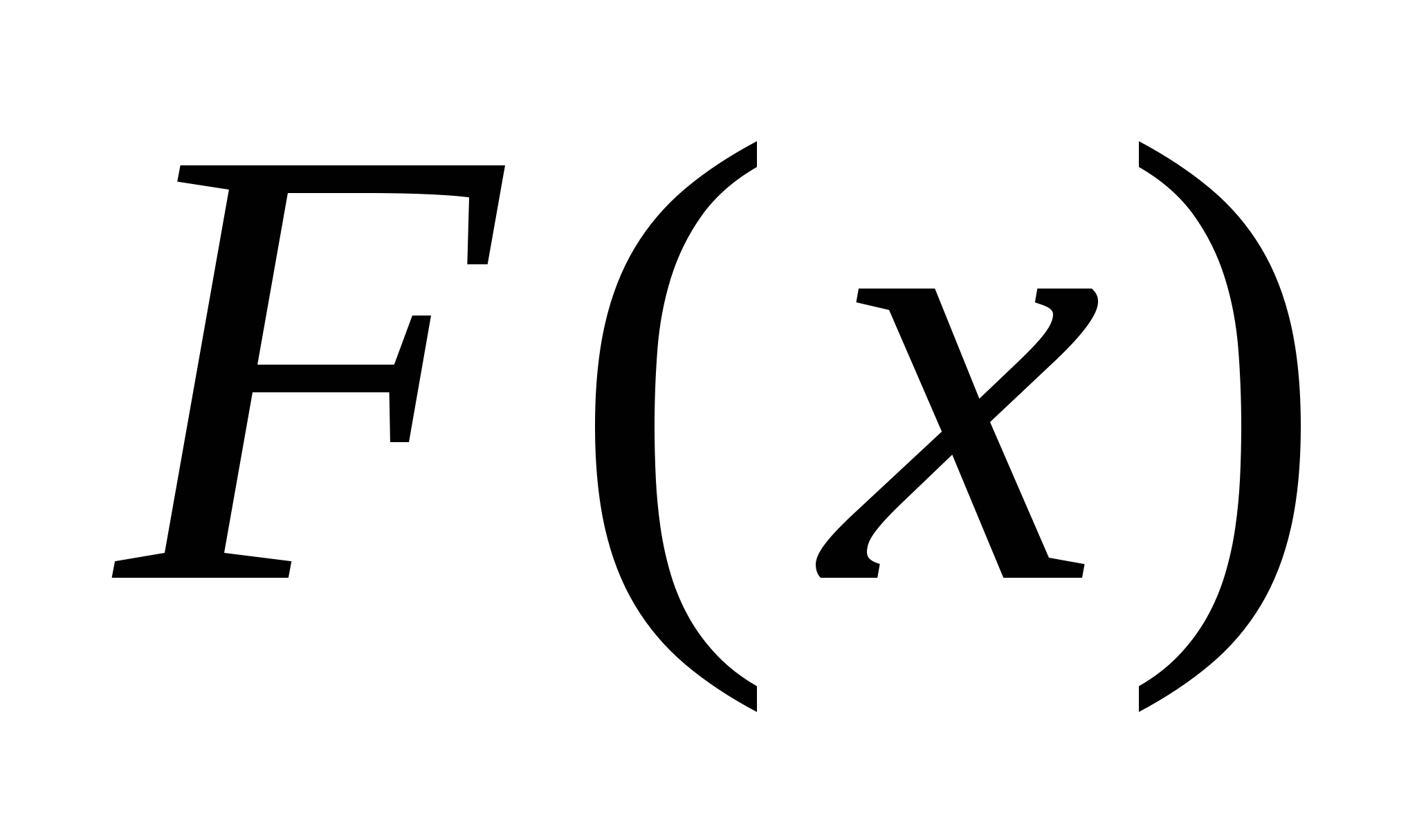 - одна из первообразных функции
- одна из первообразных функции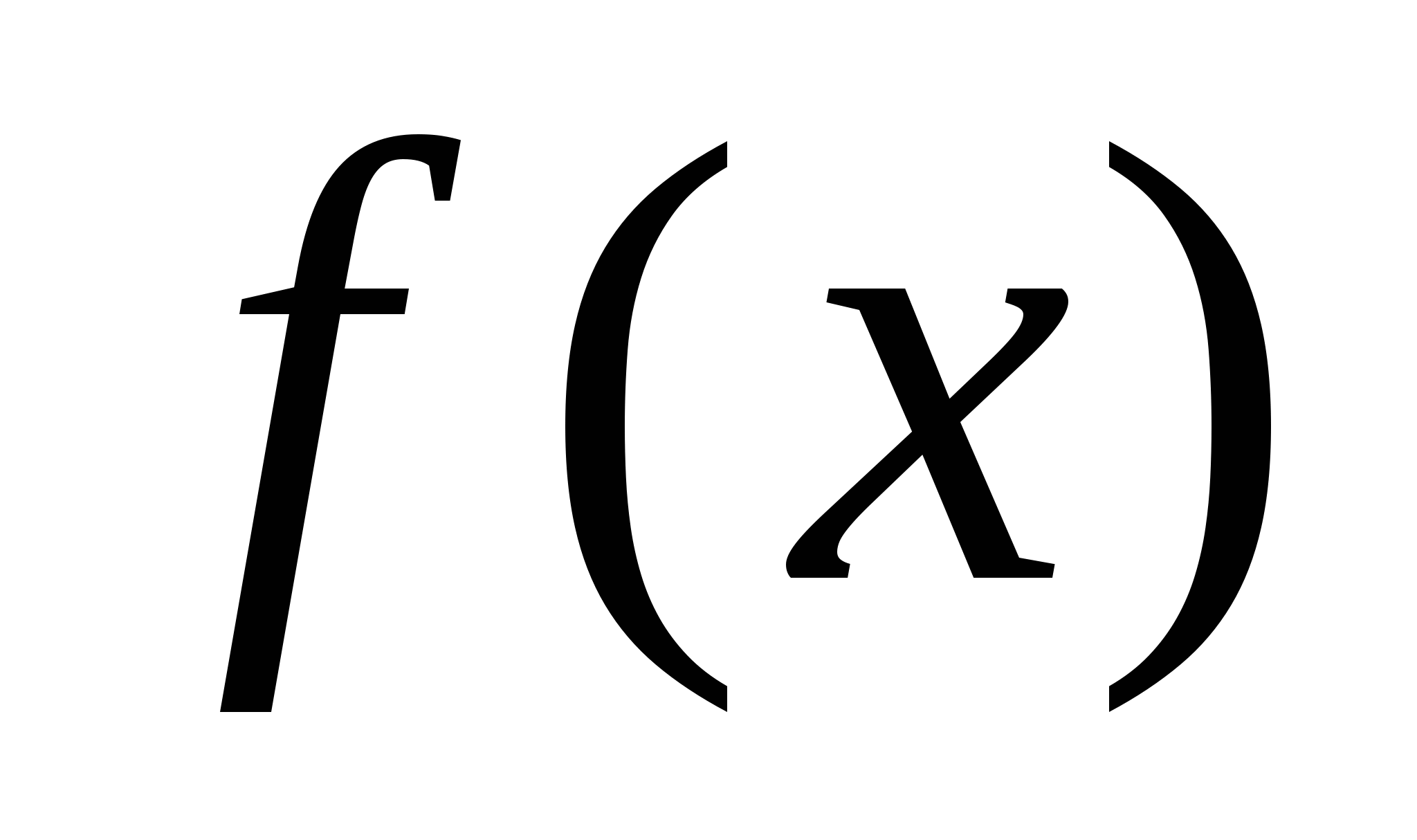 на отрезке
на отрезке 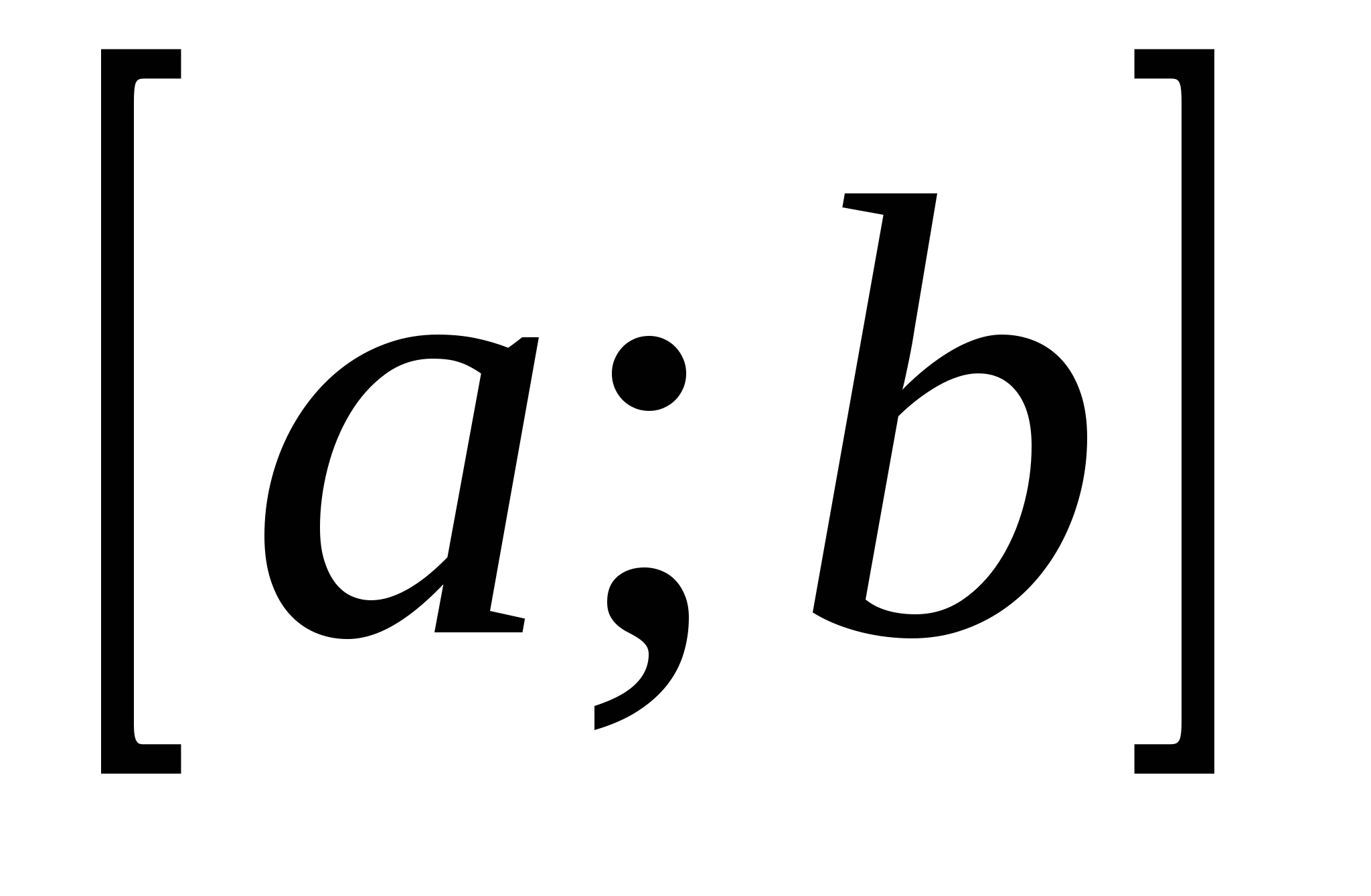 .
.
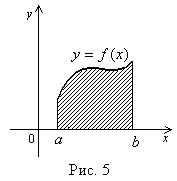
рис.2
Таким образом, интеграл равен приращению первообразной подынтегральной функции на рассматриваемом отрезке.
3. С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и более сложных фигур. В этих случаях обычно используют следующие свойства площадей:
-
Если фигуру разбить на конечное число непересекающихся частей, то её площадь равна сумме площадей этих частей.
-
Площадь фигуры сохраняется при движении, в частности, при параллельном переносе и при преобразовании симметрии.
Так, площадь фигуры AabB, легко найти, если заметить, что эта фигура получена симметричным отображением криволинейной трапеции 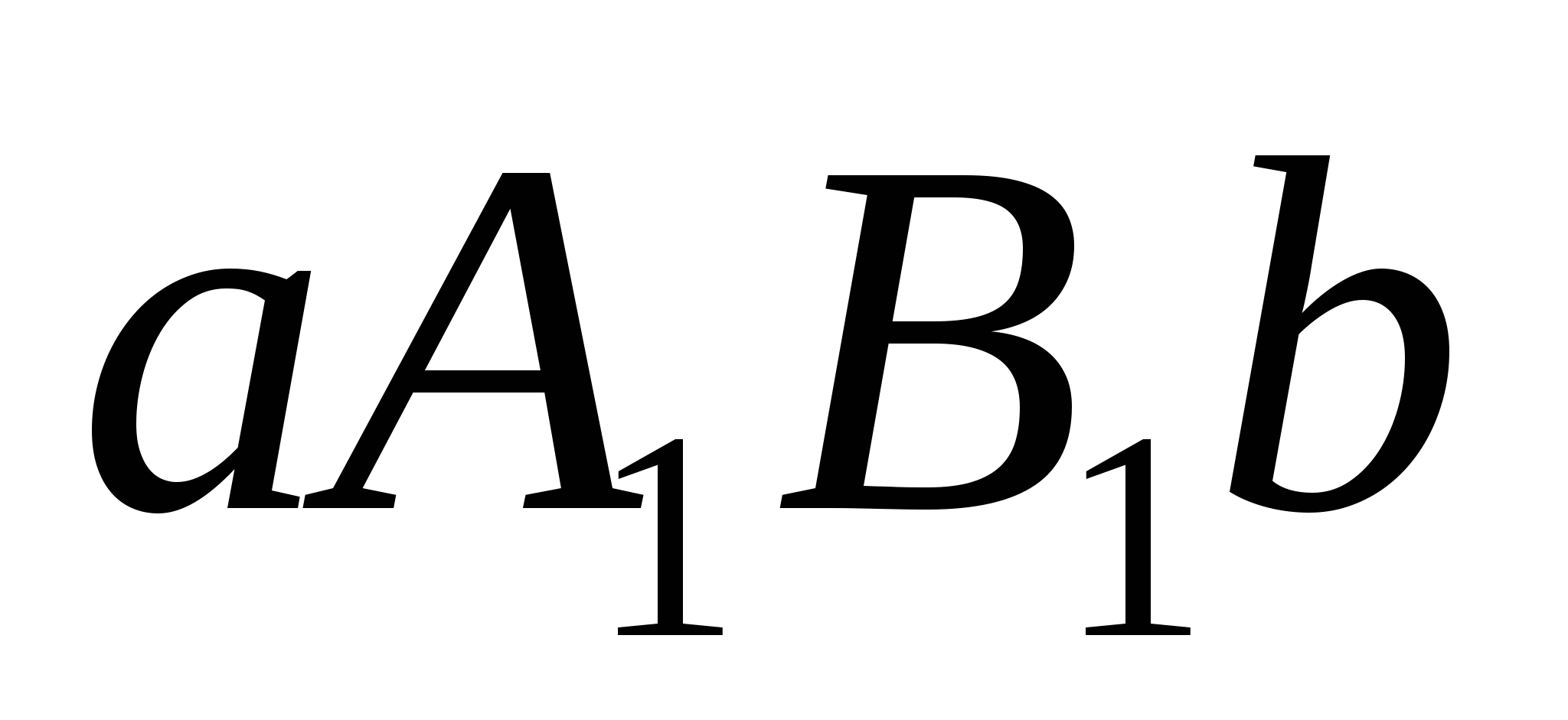 относительно оси х. Таким образом, имеем
относительно оси х. Таким образом, имеем
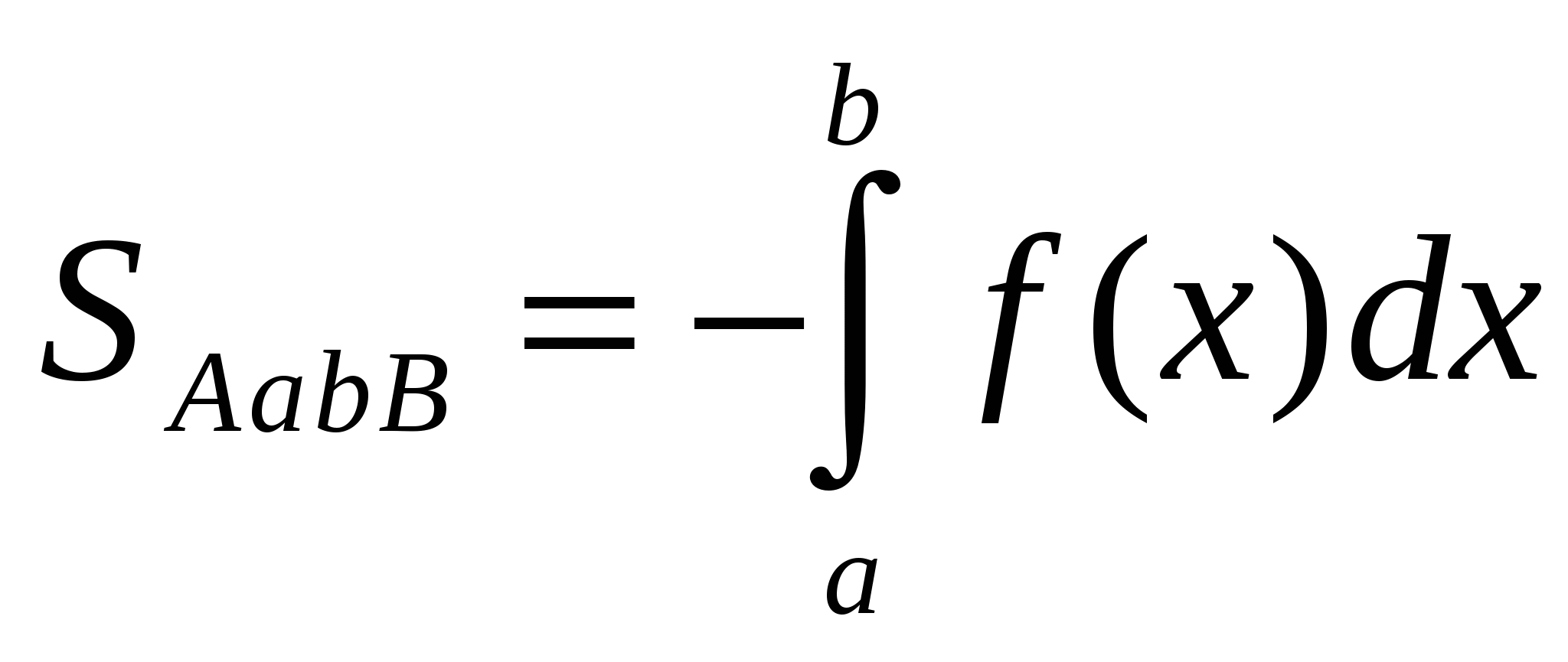
Профильный уровень
Применение производной и интеграла
Задача 1
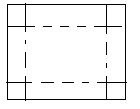
Из прямоугольного листа жести размером 5 на 8 надо изготовить открытую коробку наибольшего объема, вырезая уголки, как показано на рисунке.
Решение
Обозначим через х длину стороны вырезаемого квадрата. Тогда длины сторон прямоугольника уменьшатся на 2х и объем коробки будет равен:
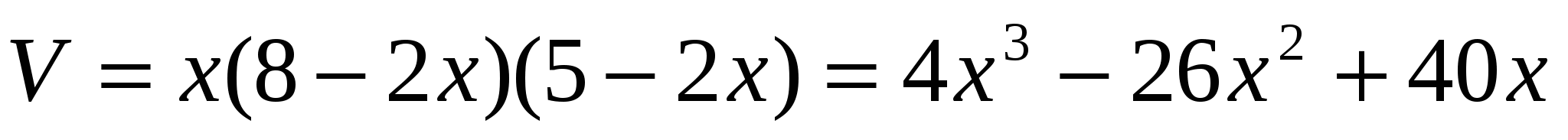 .
.
При этом х может меняться в следующих пределах: 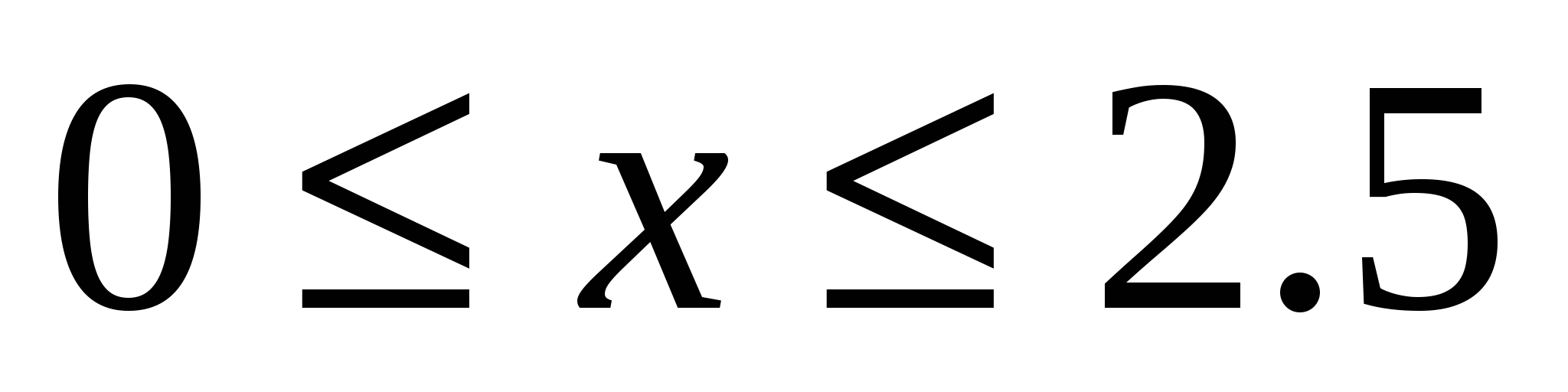 . Заметим сразу, что в крайних точках 0 и 2,5 объем равен 0. Находим критические точки функции:
. Заметим сразу, что в крайних точках 0 и 2,5 объем равен 0. Находим критические точки функции:
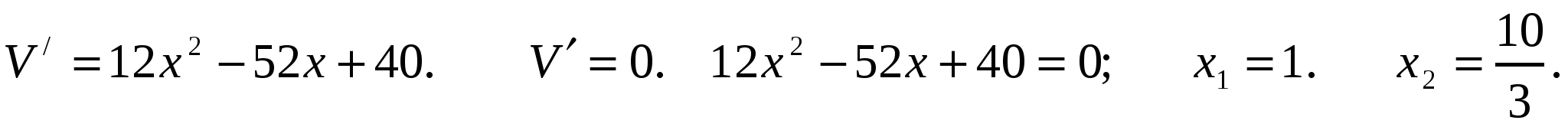
Отметим, что х2 не принадлежит области определения. При х=1 объем максимален: 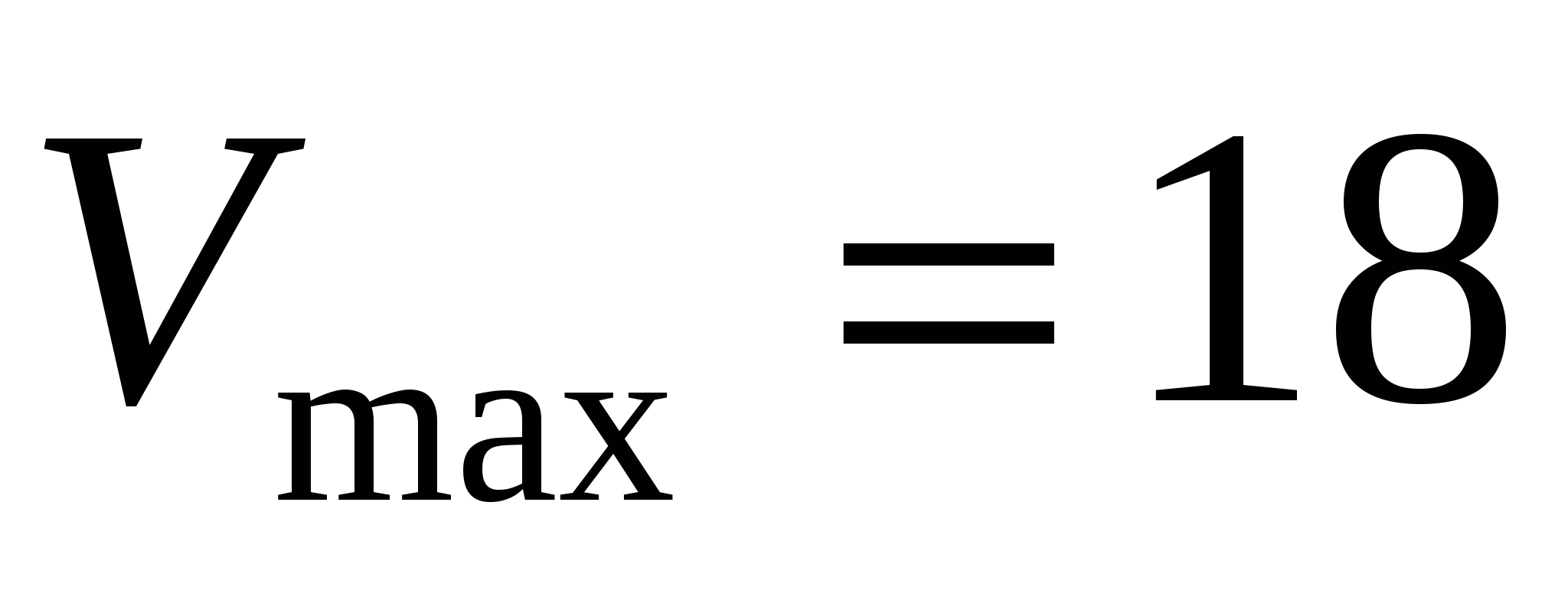 .
.
Ответ: 18.
Задача 2
В данный шар вписать цилиндр наибольшего объема.
Решение
Обозначим через R радиус шара, а через r и h соответственно радиус основания и высоту вписанного цилиндра.
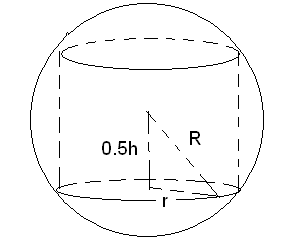
Используя теорему Пифагора, получим равенство : 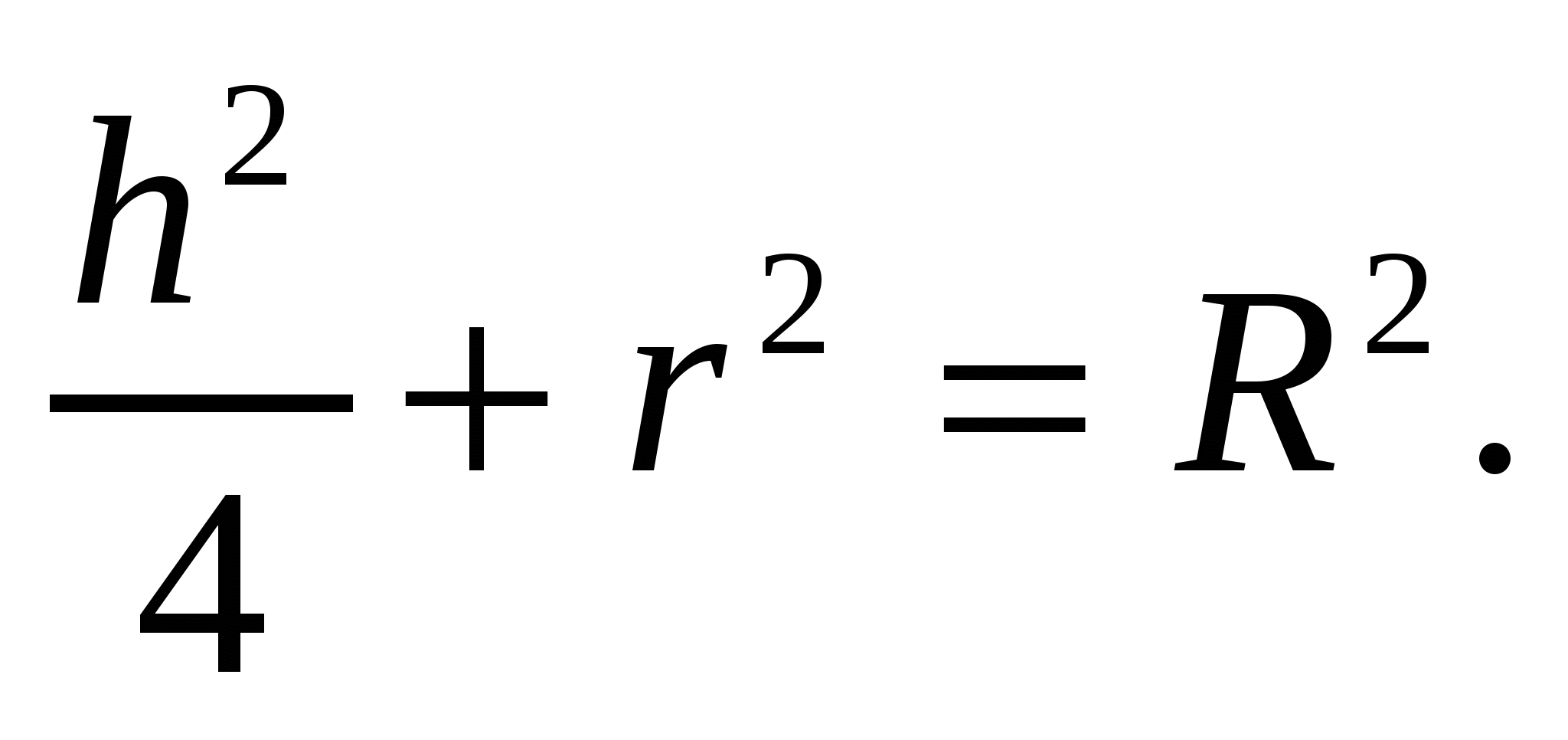
Будем считать h переменной. Тогда 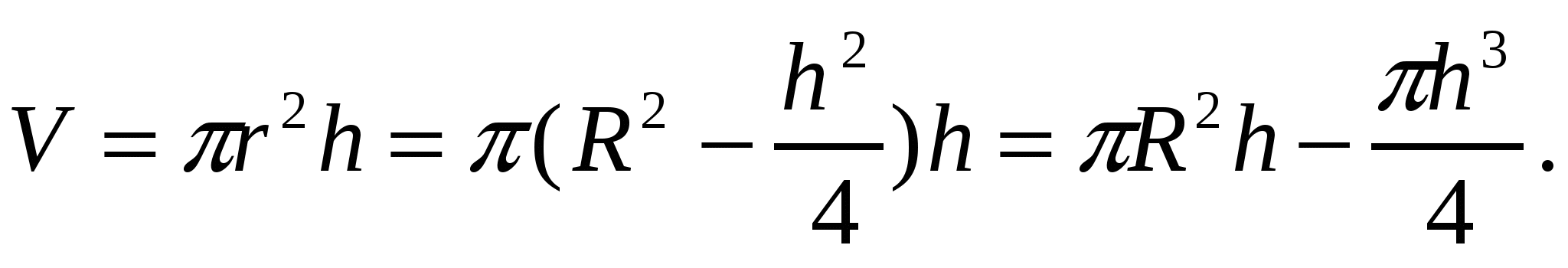
Заметим, что h изменяется в пределах от 0 до 2 R, причем, на концах отрезка цилиндр вырождается, объем его равен 0.
Находим критические точки:
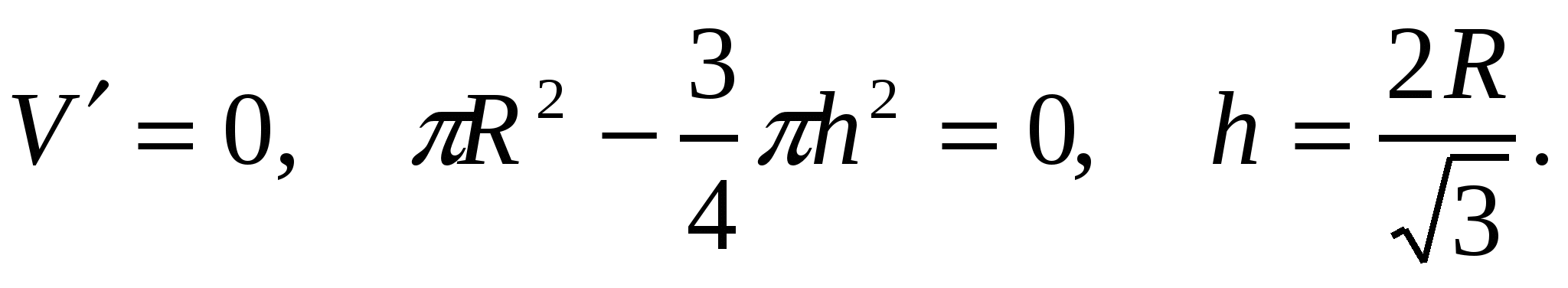
При этом значении h объем будет максимальным:
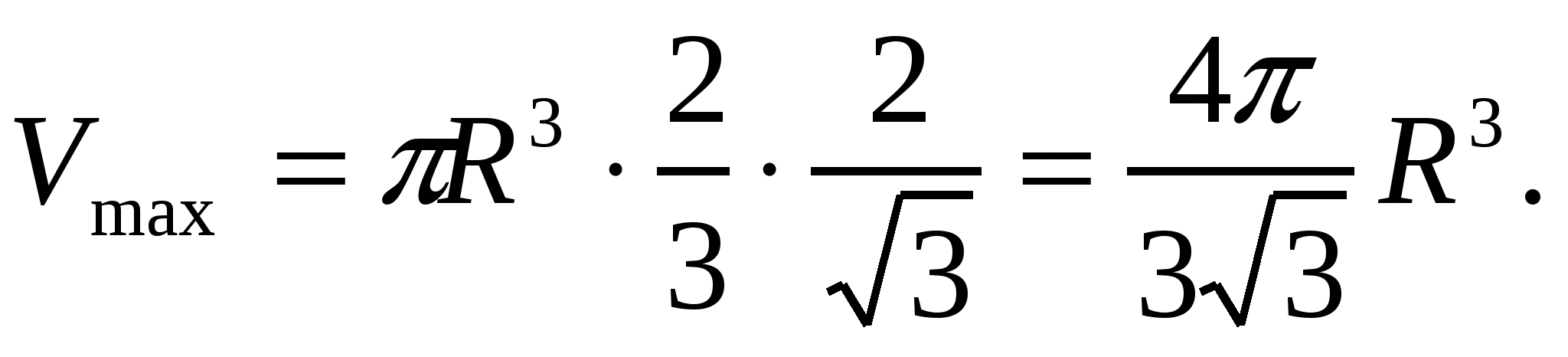
Ответ: 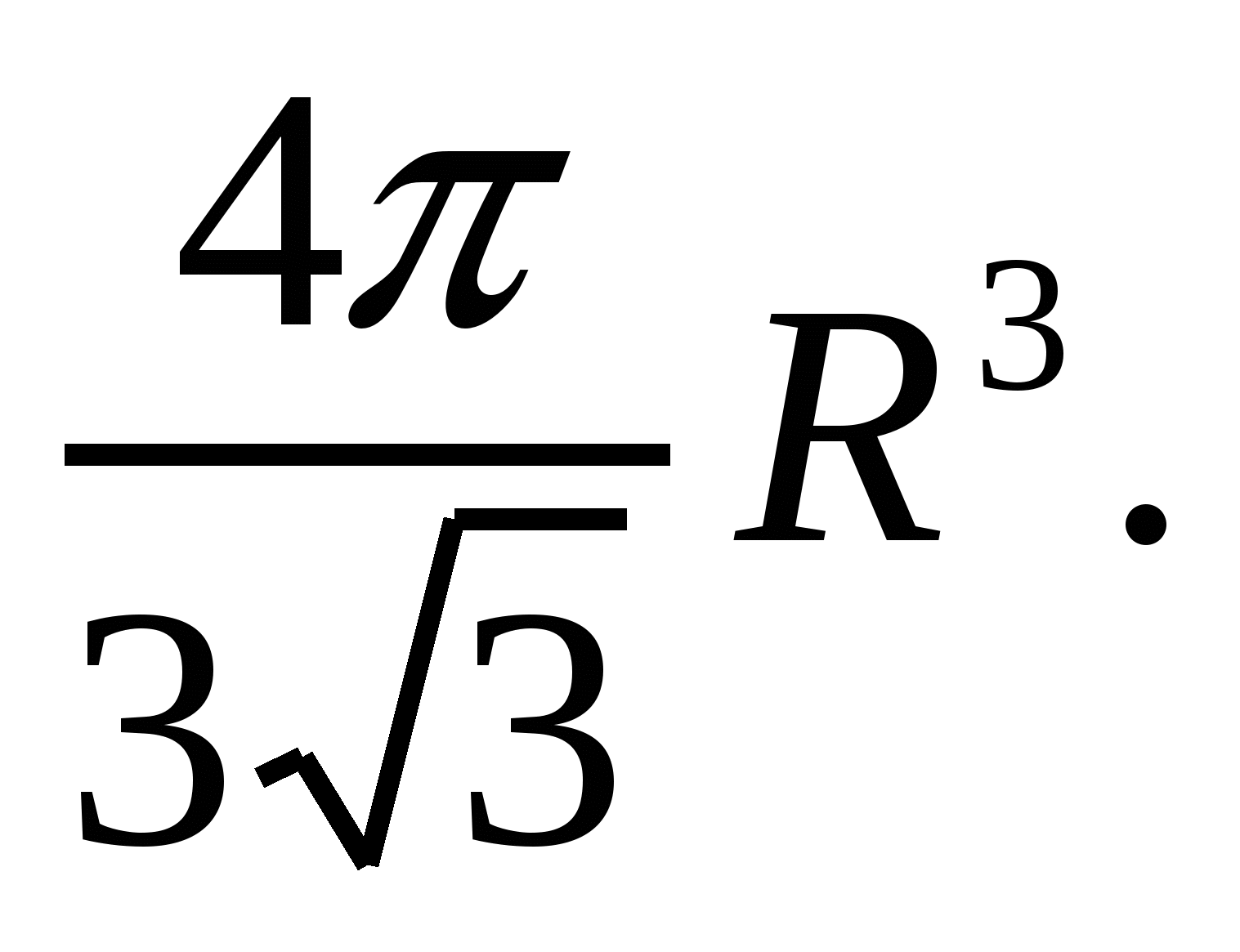
Задача 3
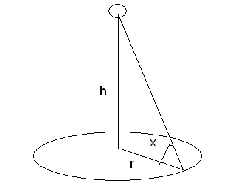
Над центром круглого стола радиуса r висит лампа. На какой высоте следует подвесить эту лампу, чтобы на краях стола получить наибольшую освещенность?
Решение
Из физики известно, что освещенность обратно пропорциональна квадрату расстояния до источника света и пропорциональна синусу угла наклона луча света к освещаемой маленькой площадке.
Иными словами, ![]()
Где Е - освещенность на краю стола, 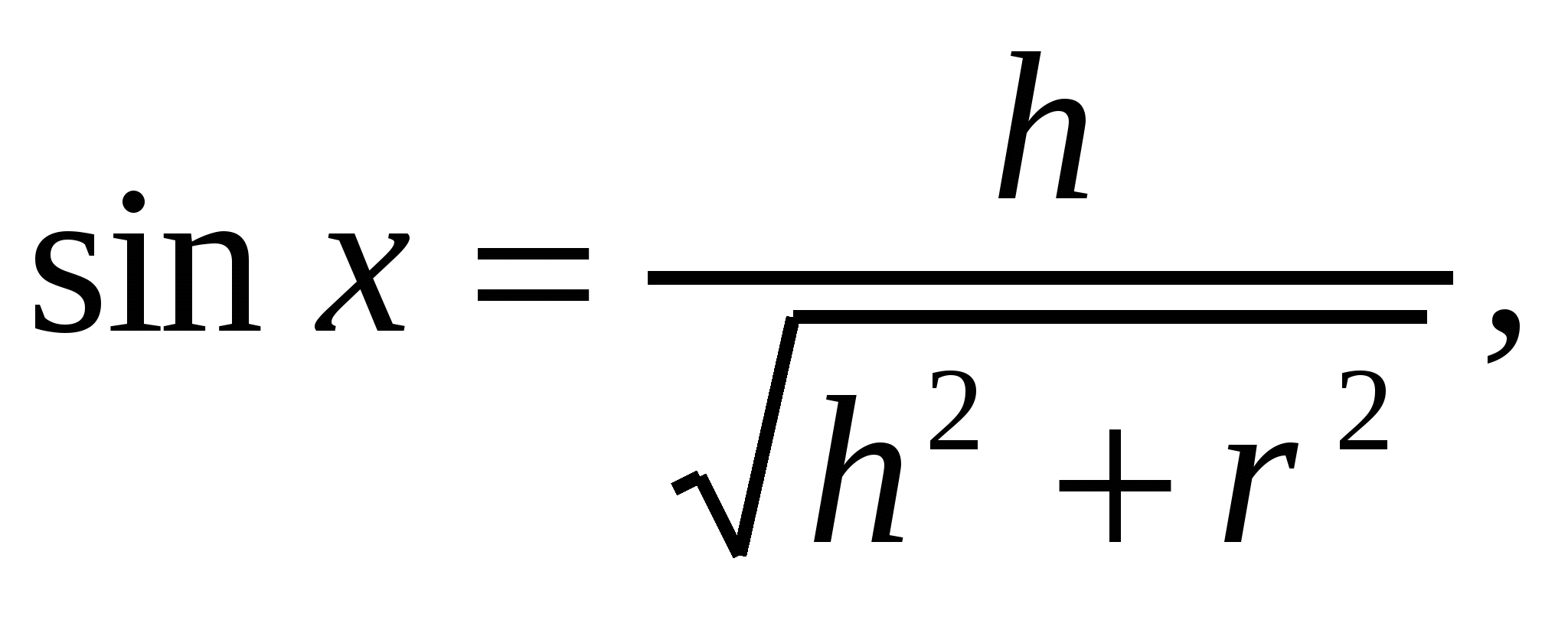 h - расстояние от лампы до стола.
h - расстояние от лампы до стола.
Вместо функции 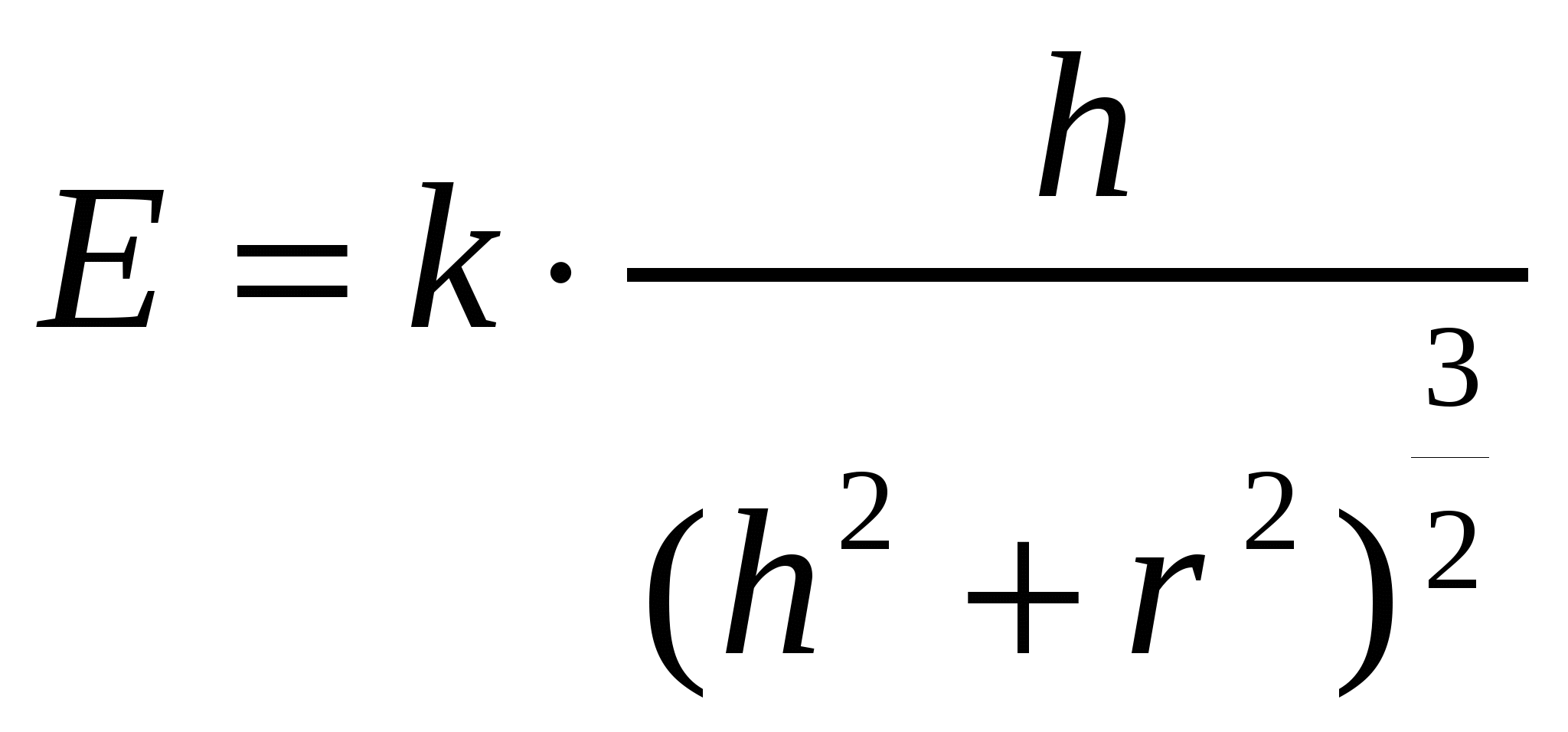 можно рассмотреть функцию
можно рассмотреть функцию 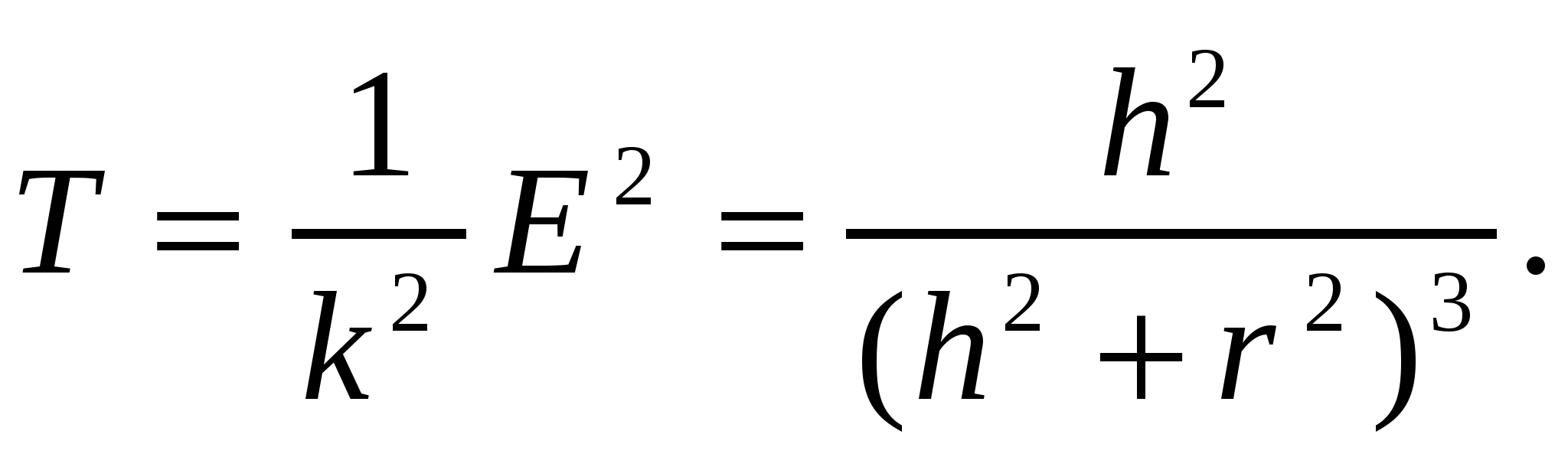 При этом вместо h можно взять переменную z = h2 и найти критические точки Т как функцию от z:
При этом вместо h можно взять переменную z = h2 и найти критические точки Т как функцию от z:
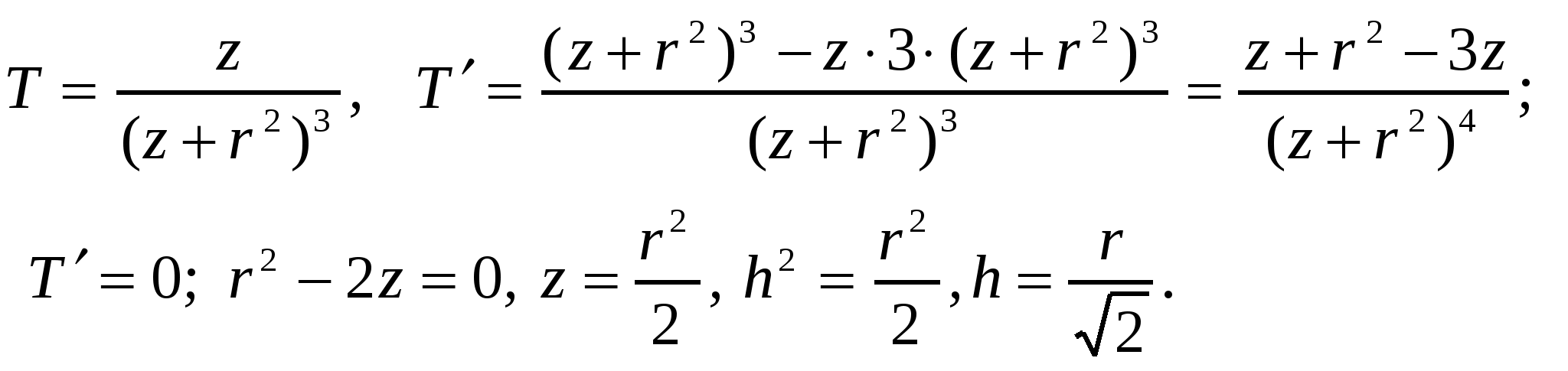
Итак, освещенность максимальна, если 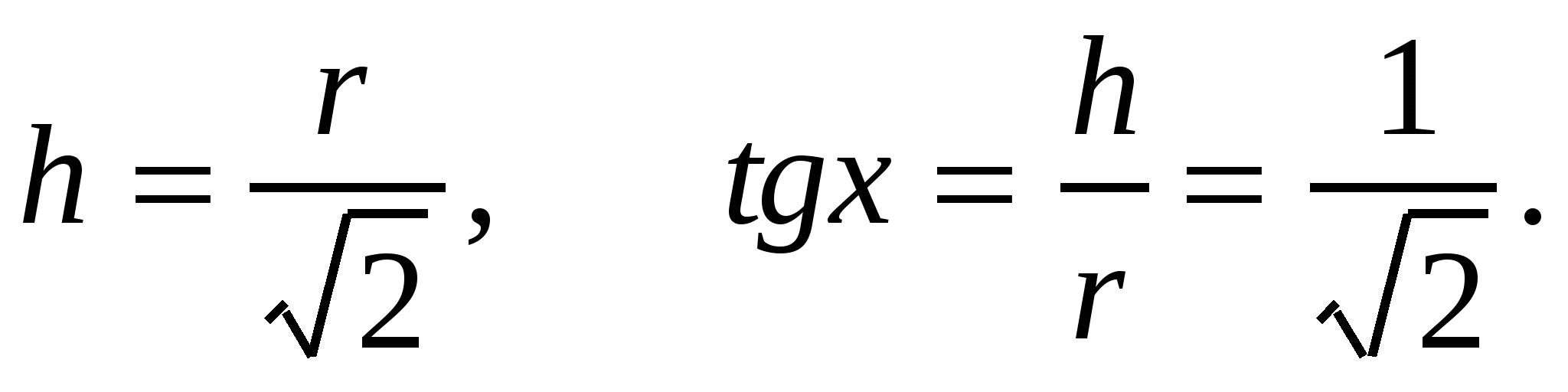
Ответ: 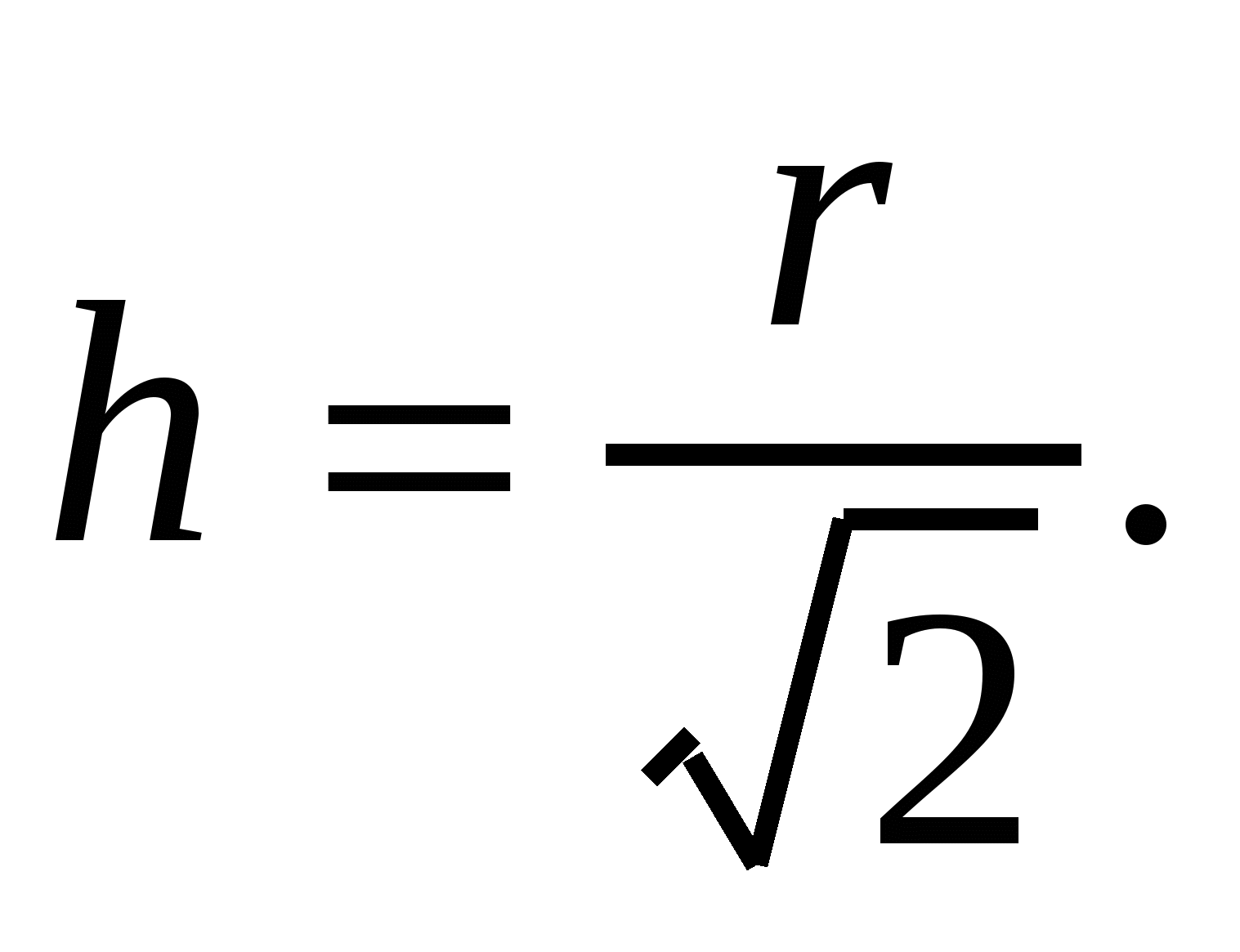
Задача 4
Определить размеры открытого бассейна с квадратным дном и объемом 32м3, чтобы на облицовку его стен и дна было израсходовано наименьшее количество материала.
Решение
Обозначим длину стороны основания бассейна через х, а высоту - через у.
Тогда V(x,y) = x2y= 32.
Площадь боковой поверхности бассейна вместе с площадью его дна равна: S=x2+4xy. Найдем у из равенства x2y= 32, и подставив его значение в последнее равенство, получим такую функцию от х: ![]()
Найдем производную этой функции: 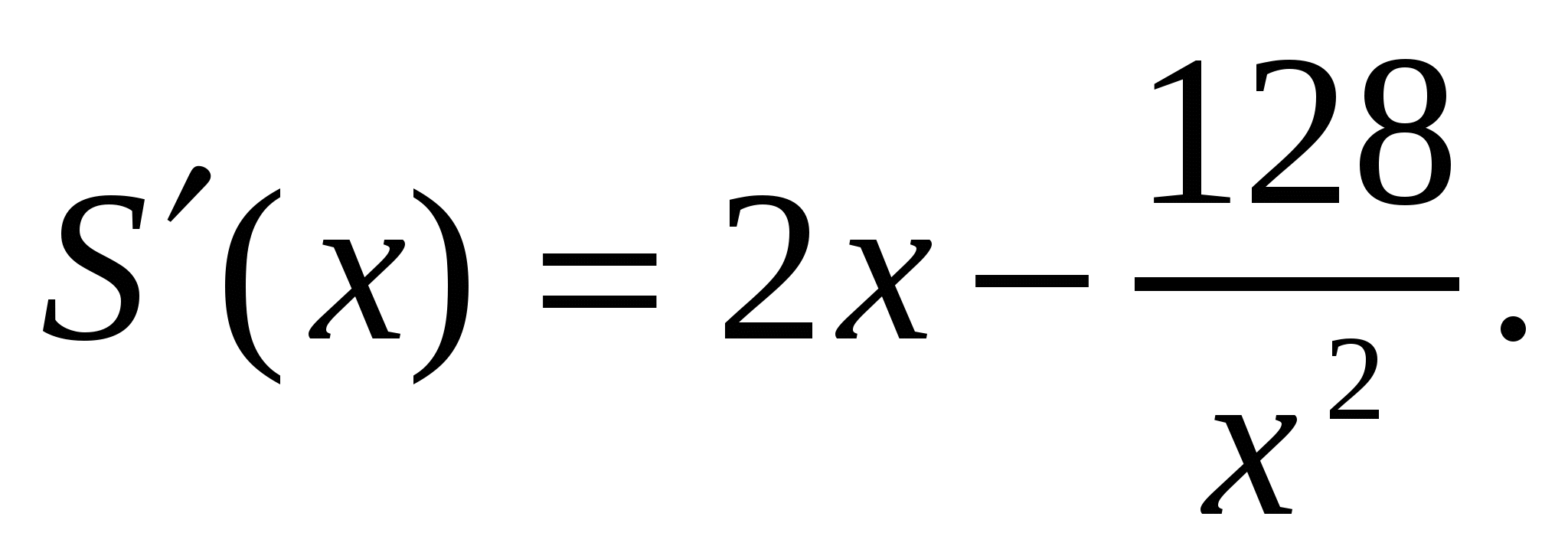 Решим уравнение
Решим уравнение 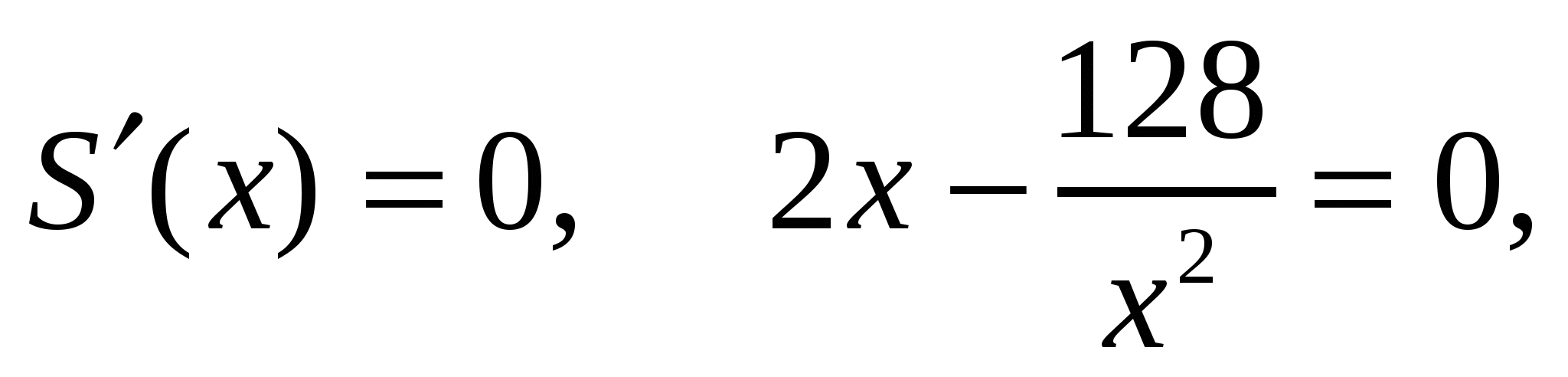 находим критическую точку х=4.
находим критическую точку х=4.
Так как существует только одна критическая точка, то она и является точкой минимума функции S(x). Следовательно, наименьшие размеры бассейна с данным объемом V=32м2 таковы: х=4м, у=2м.
Ответ: х=4м; у=2м.
Задача 5
Сосуд с вертикальной стенкой и высотой h стоит на горизонтальной плоскости. На какой глубине нужно разместить отверстие, чтобы дальность струи из отверстия была наибольшей (скорость вытекающей жидкости, по закону Торричелли, равна 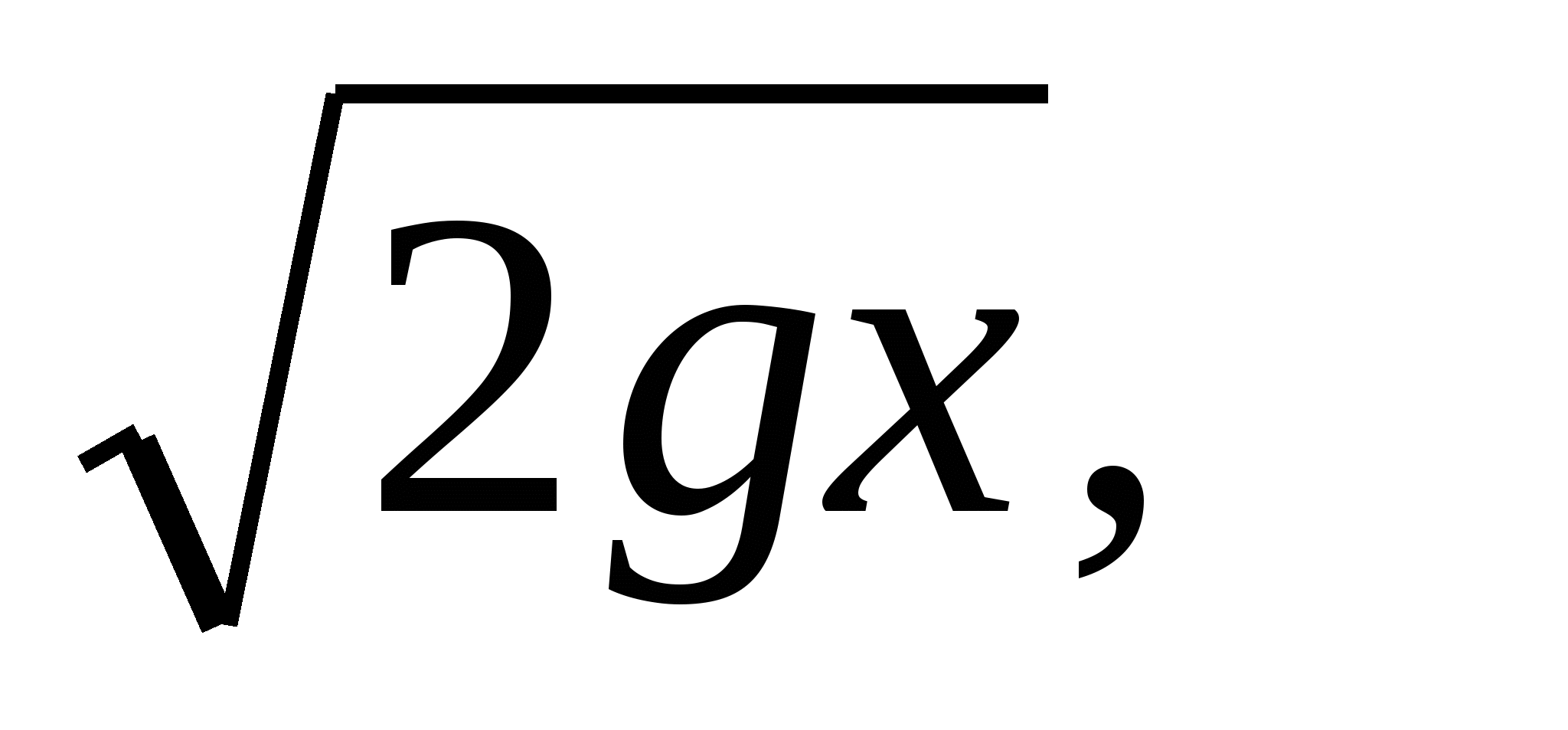 где х - глубина отверстия, g - ускорение свободного падения)
где х - глубина отверстия, g - ускорение свободного падения)
Решение.
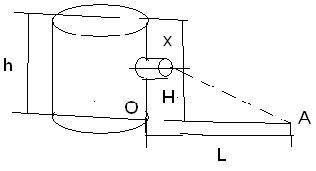
Обозначим через Н расстояние в сосуде от горизонтальной плоскости, а через L -- расстояние точки А от стенки сосуда. Тогда L=vt, где t - время вытекания воды из отверстия на плоскость (в точку А).
Из курса физики известно, что 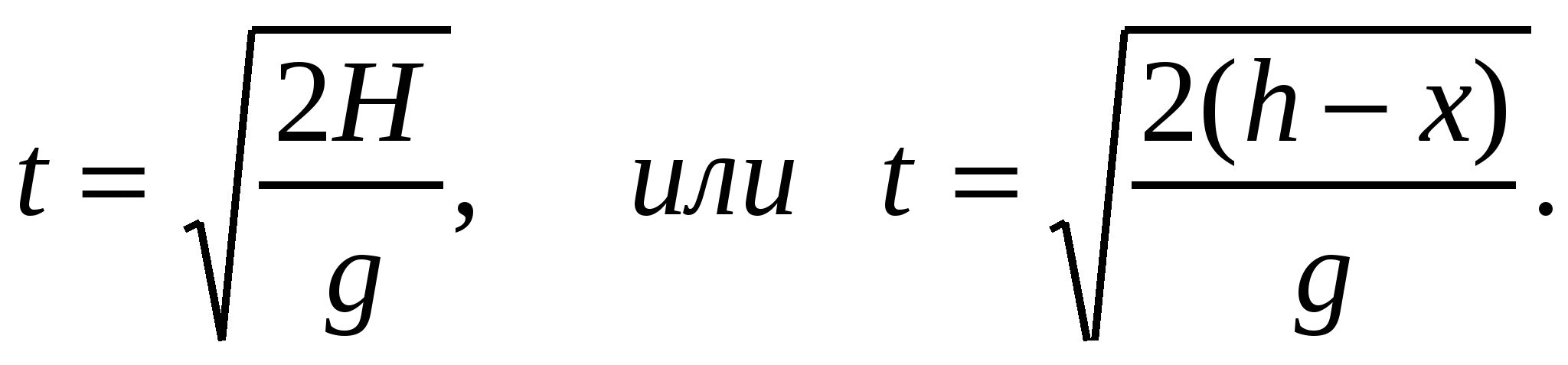
Тогда 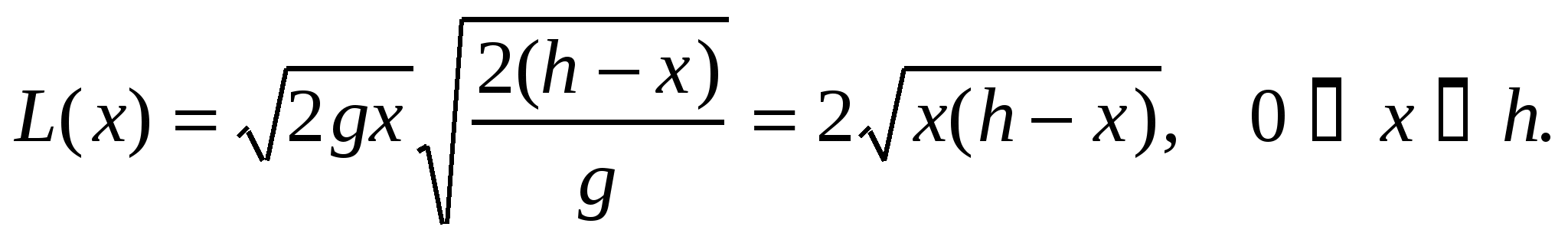
Найдем производную 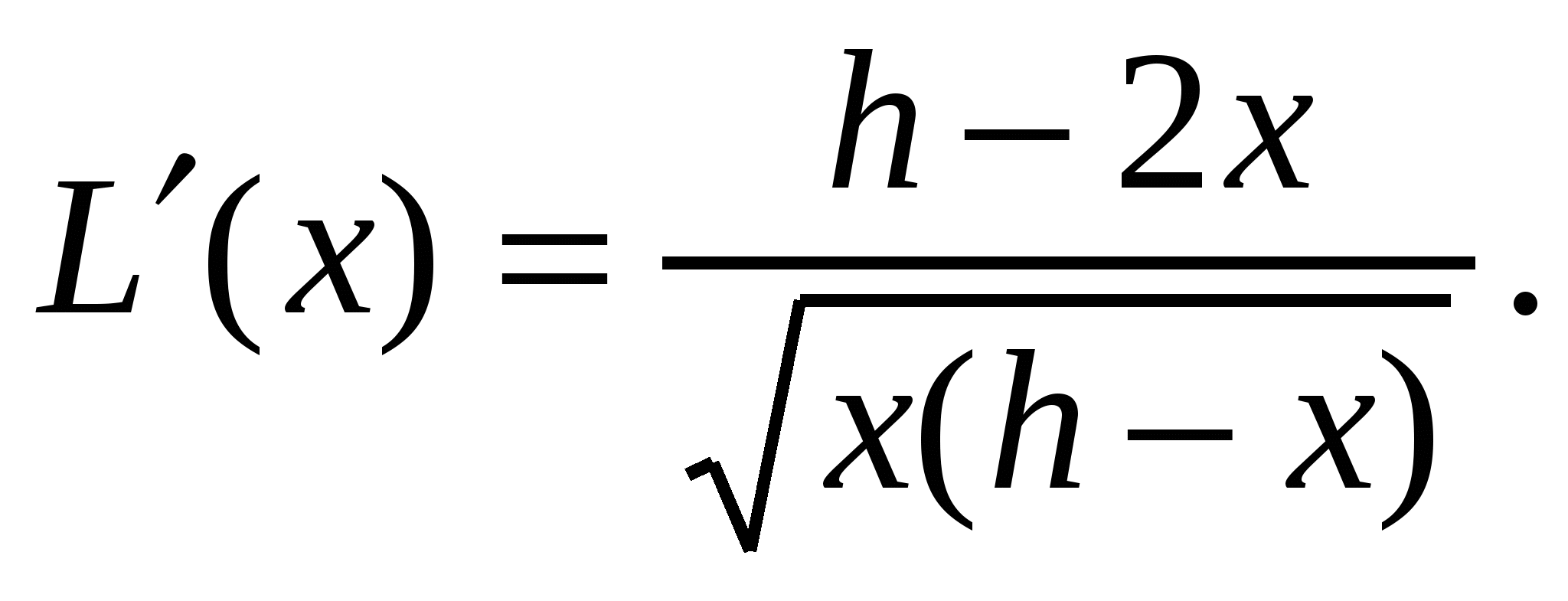 Решим уравнение :
Решим уравнение :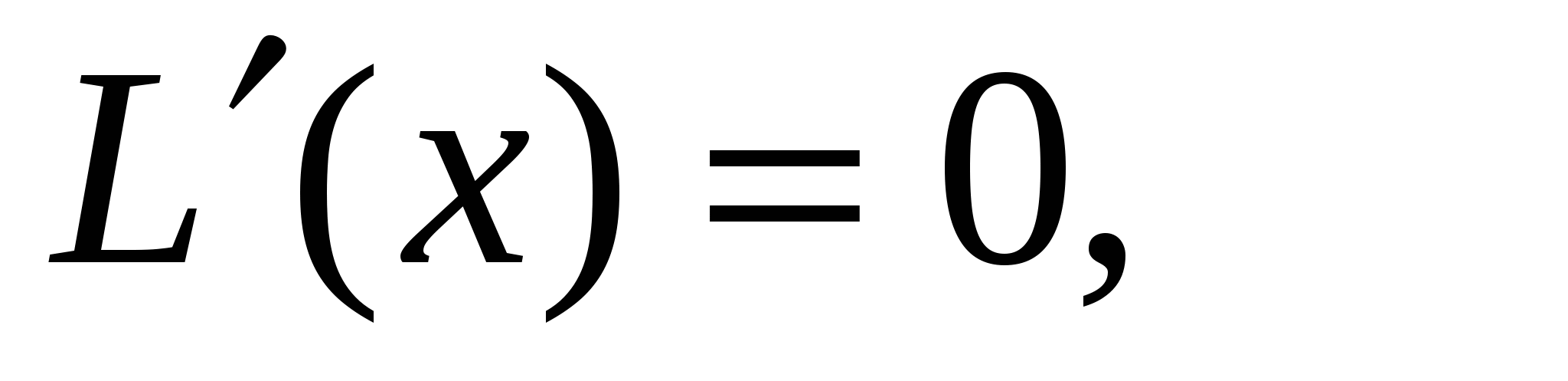
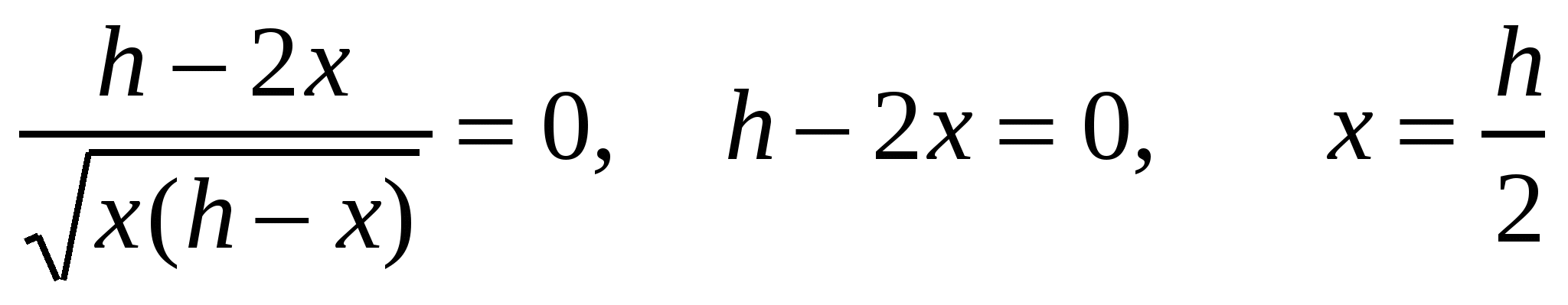 -- критическая точка. Так это единственная критическая точка, то она и есть искомой.
-- критическая точка. Так это единственная критическая точка, то она и есть искомой.
Ответ: 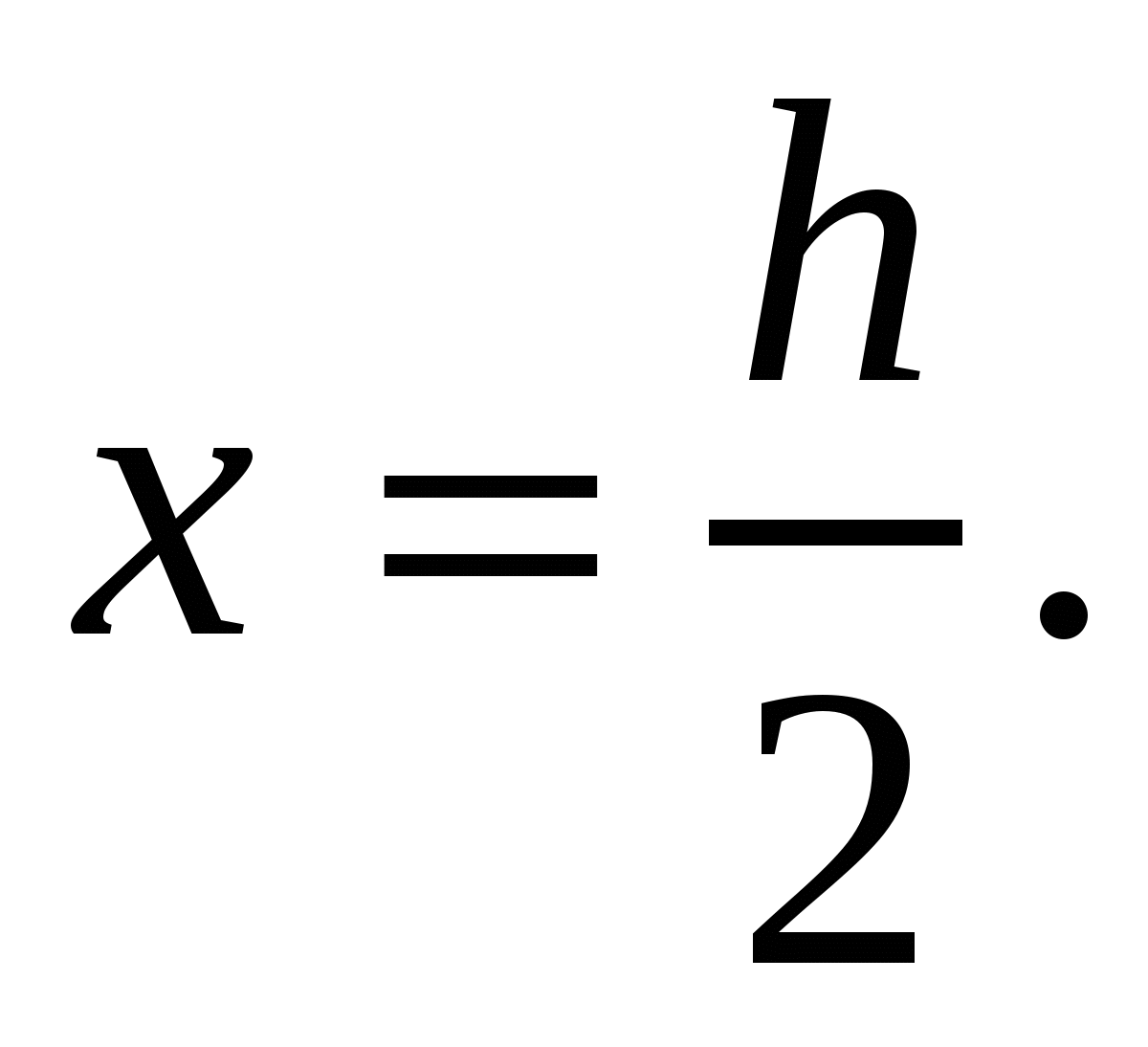
Задача 6
Предположим, что в точку О помещен единичный электрически заряд. Он создает электрическое поле. Известно, что на другой единичный заряд, помещенный в точку х, действует сила, обратно пропорциональная квадрату расстояния, т.е. 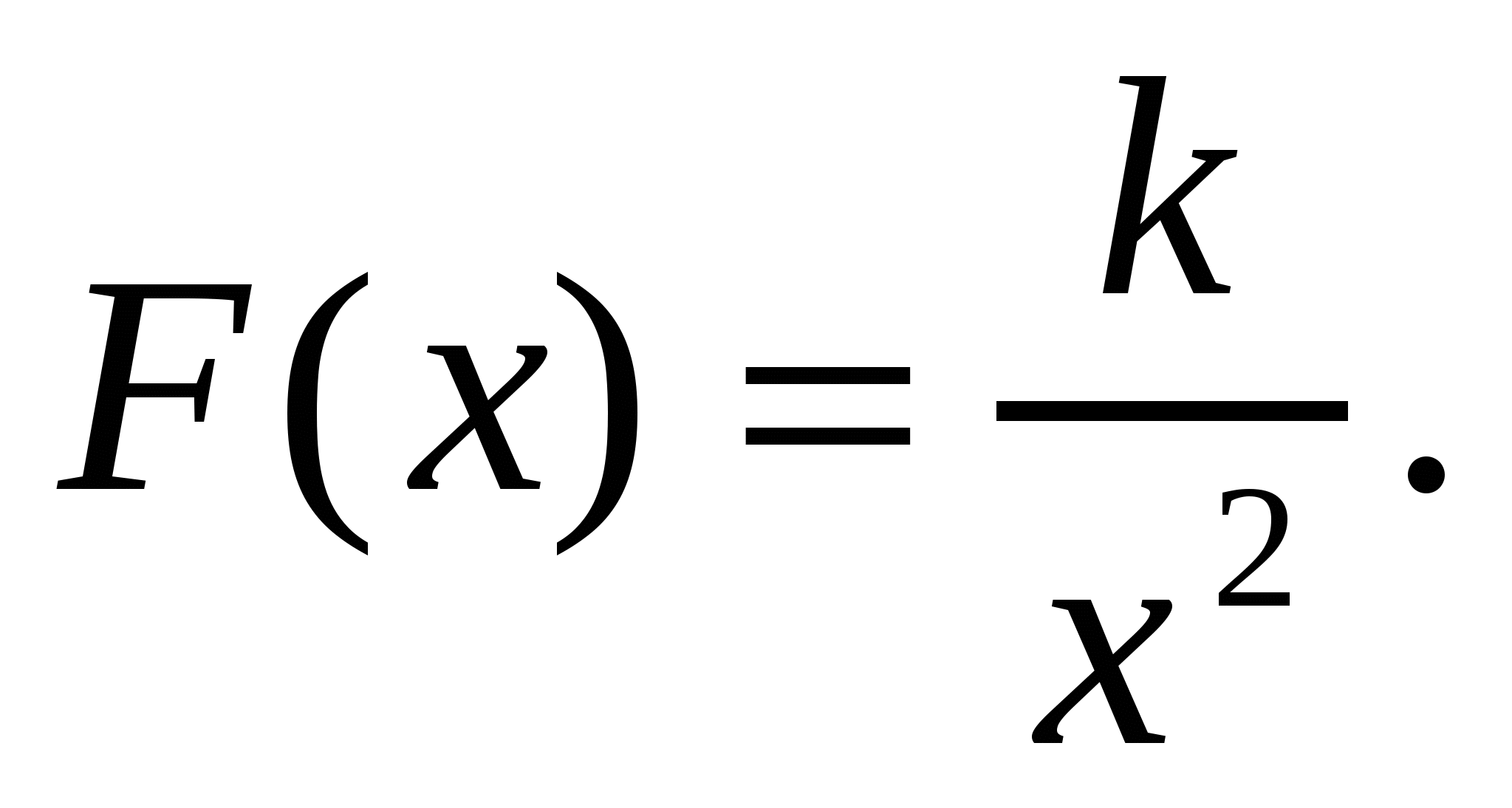 Найти работу электрического поля по перемещению единичного заряда из точки х1 в точку х2.
Найти работу электрического поля по перемещению единичного заряда из точки х1 в точку х2.
Решение
Применяя формулу для работы 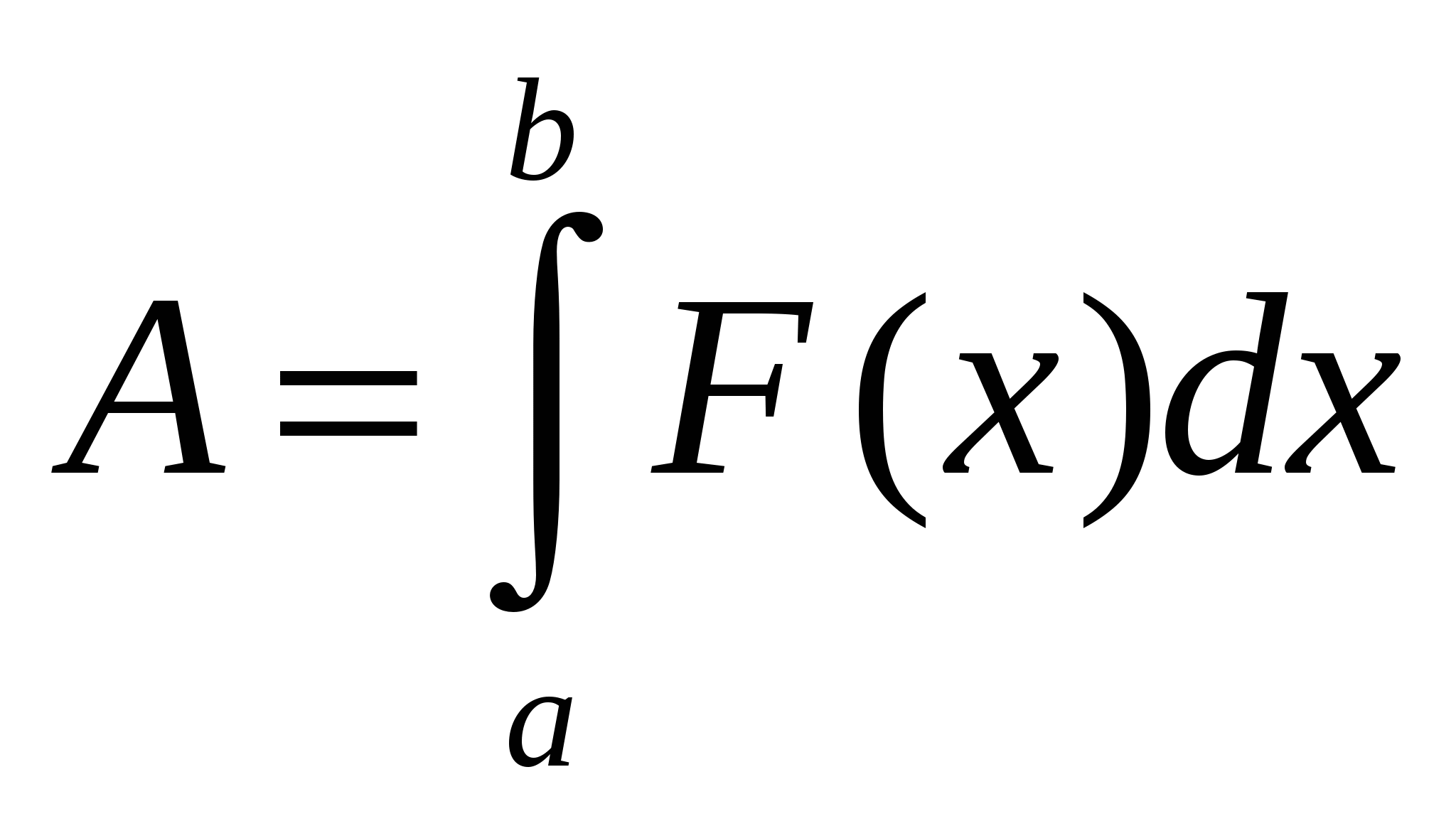 , получим
, получим 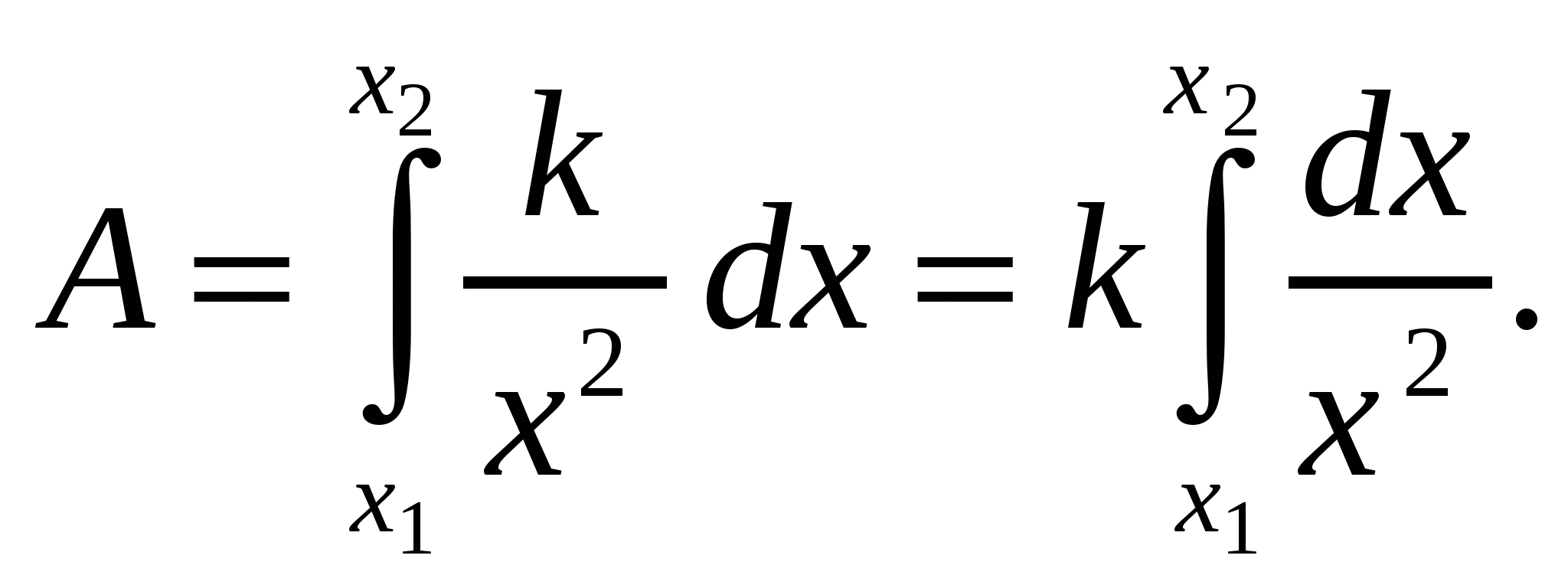
Для функции ![]() , первообразная U(x)=
, первообразная U(x)=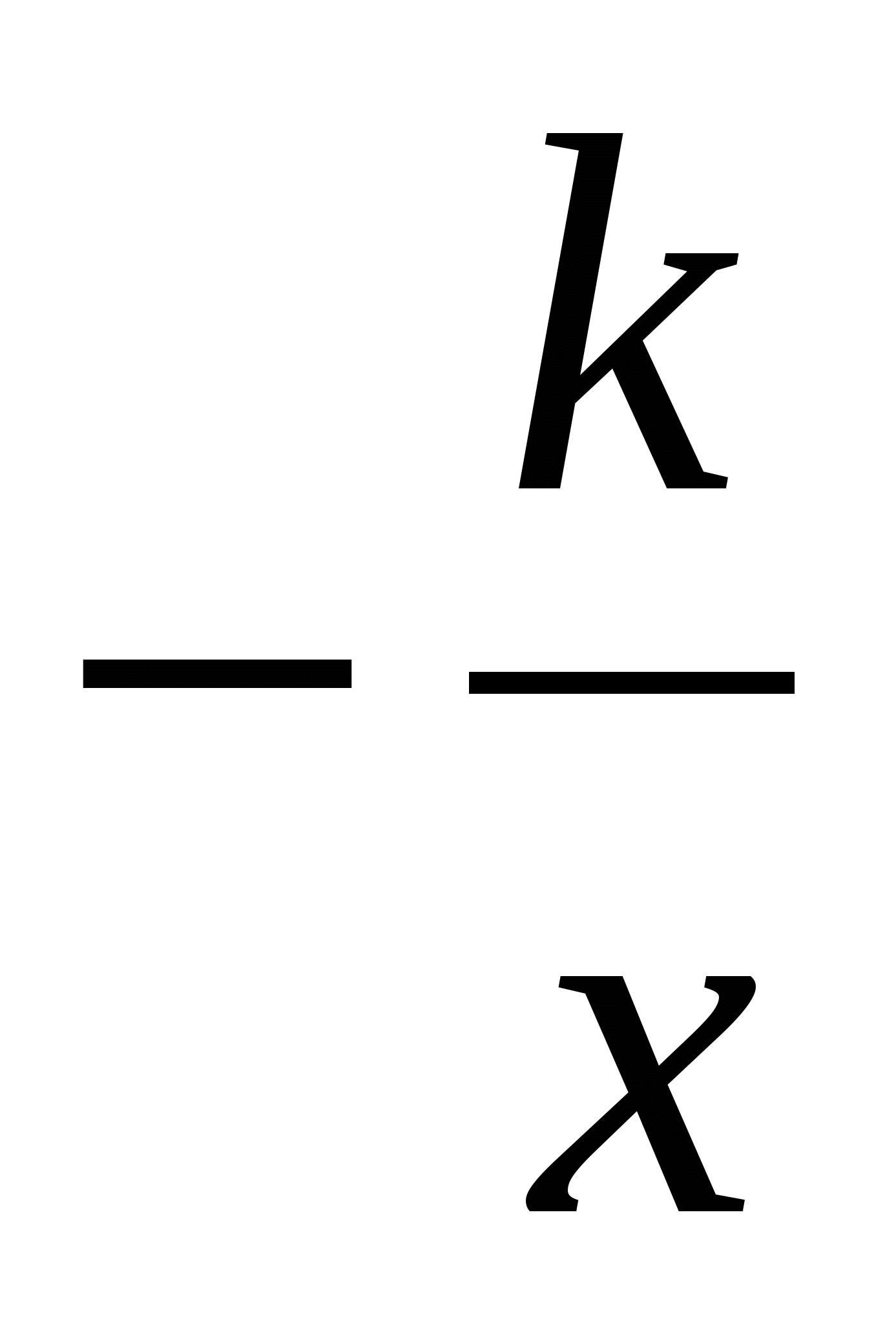 . Получим:
. Получим:
 =
= 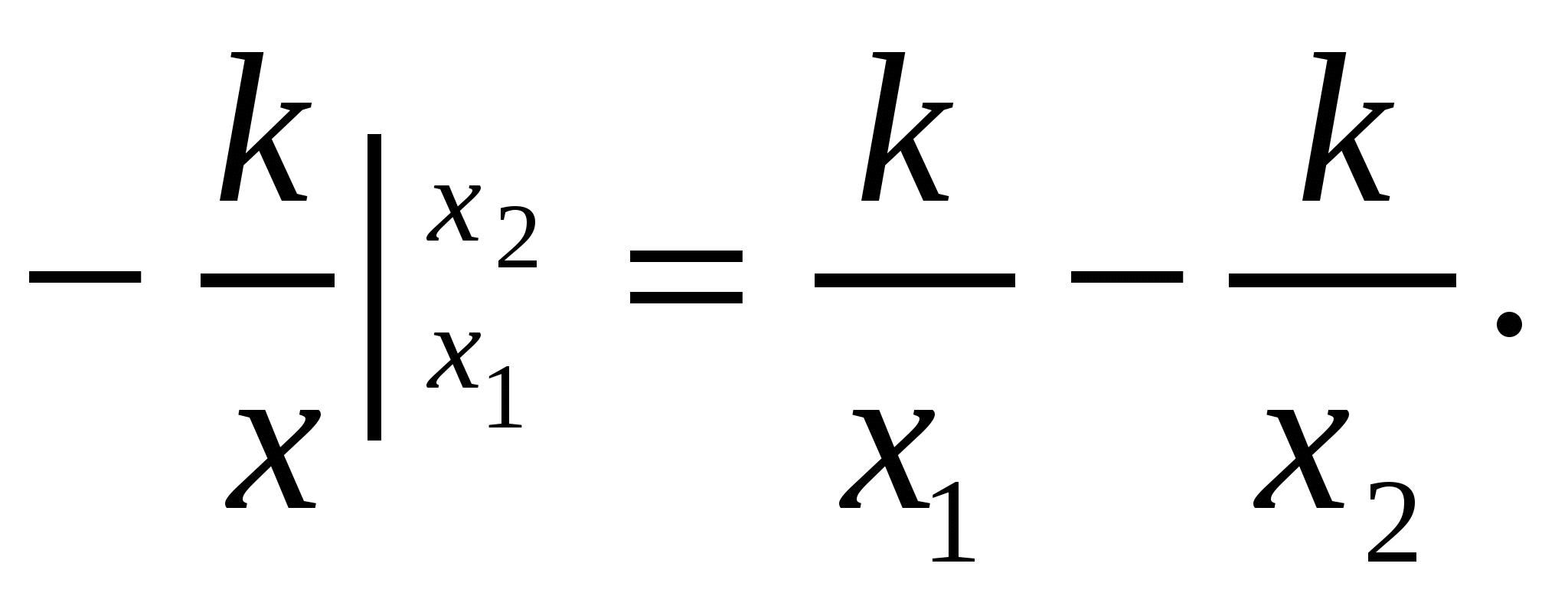
Ответ: 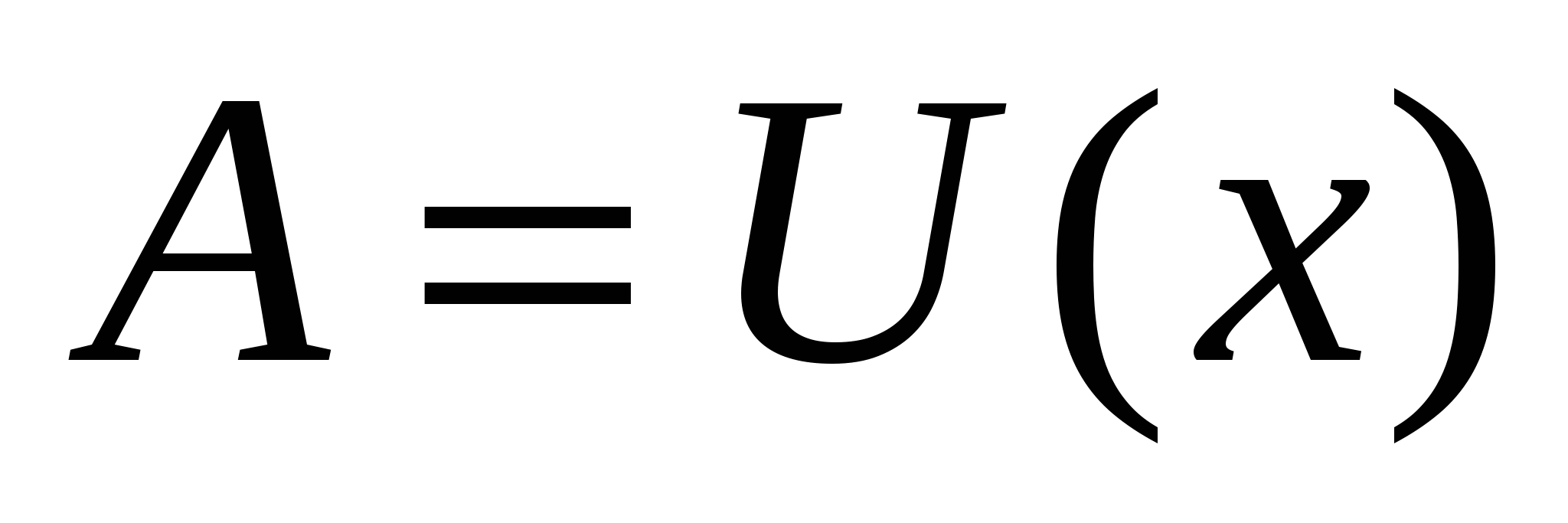
 =
= 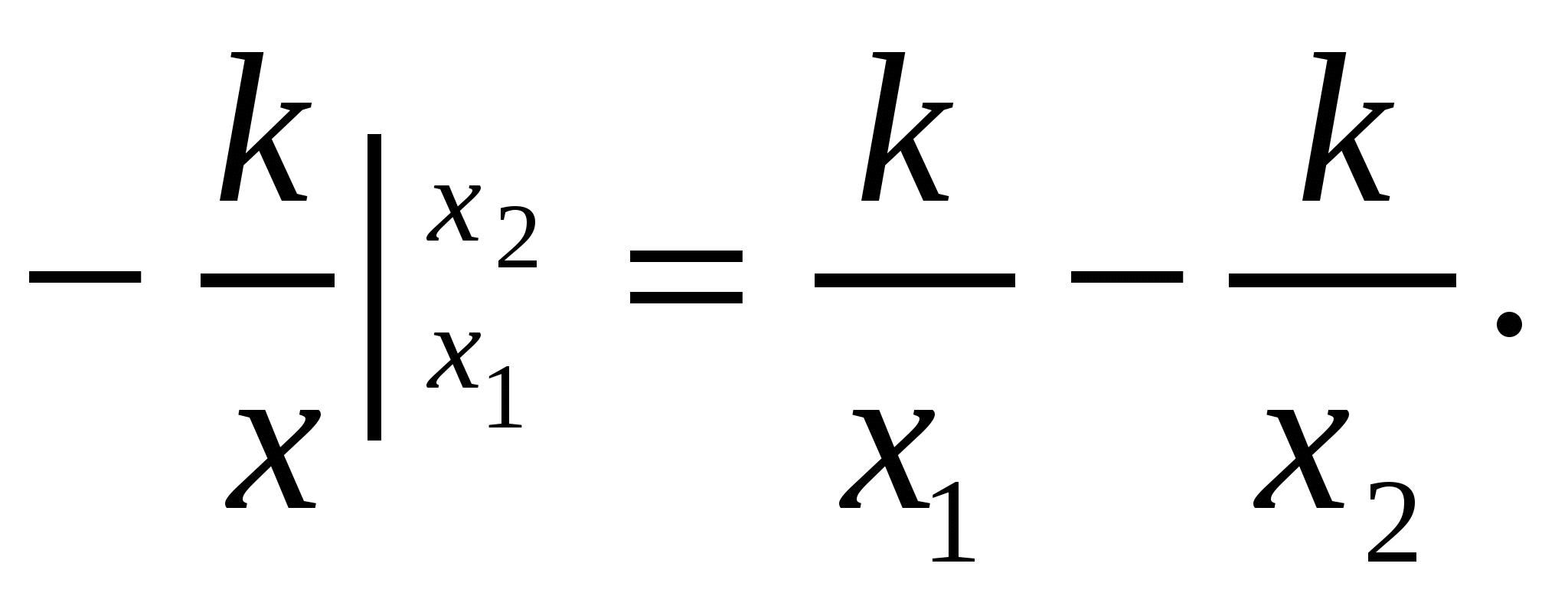
Задача 7
Пирамида Хеопса представляет собой правильную четырехугольную пирамиду высотой 147м, в основании которой квадрат со стороной 232м. Она построена из камня, плотность которого 2,5г/см3. Найти работу против силы тяжести, затраченную при постройке.
Решение.
Проведем вертикально вверх ось х с началом у основания пирамиды. По этой оси будем измерять высоту подъема камней. Пусть высота пирамиды равна Н, сторона основания а, а плотность камня 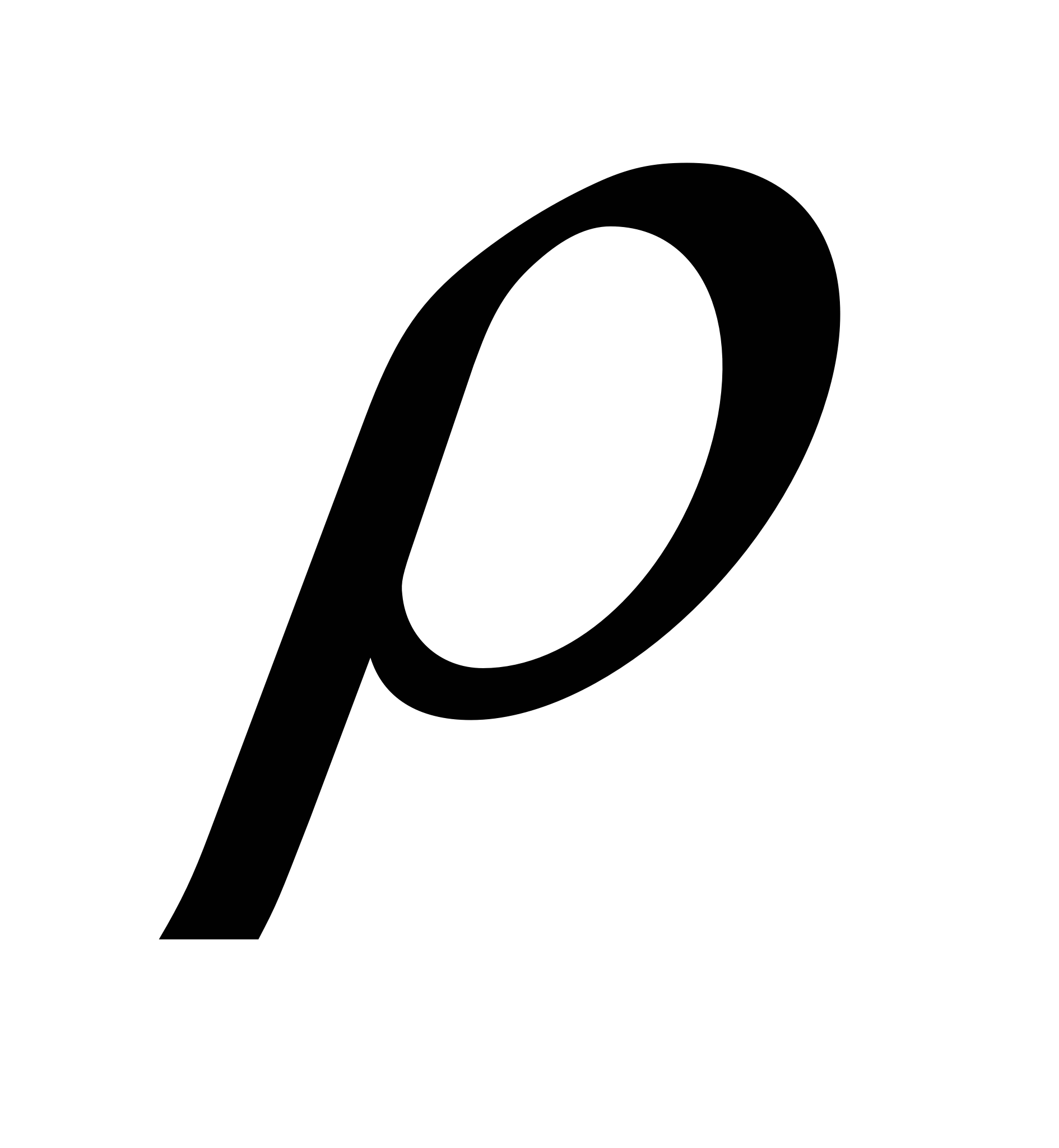 . Обозначим через А(х) работу, которую надо совершить для постройки пирамиды от основания до высоты х. Найдем сначала сторону у квадрата, получающегося в горизонтальном сечении пирамиды на высоте х. из подобия треугольников получаем
. Обозначим через А(х) работу, которую надо совершить для постройки пирамиды от основания до высоты х. Найдем сначала сторону у квадрата, получающегося в горизонтальном сечении пирамиды на высоте х. из подобия треугольников получаем 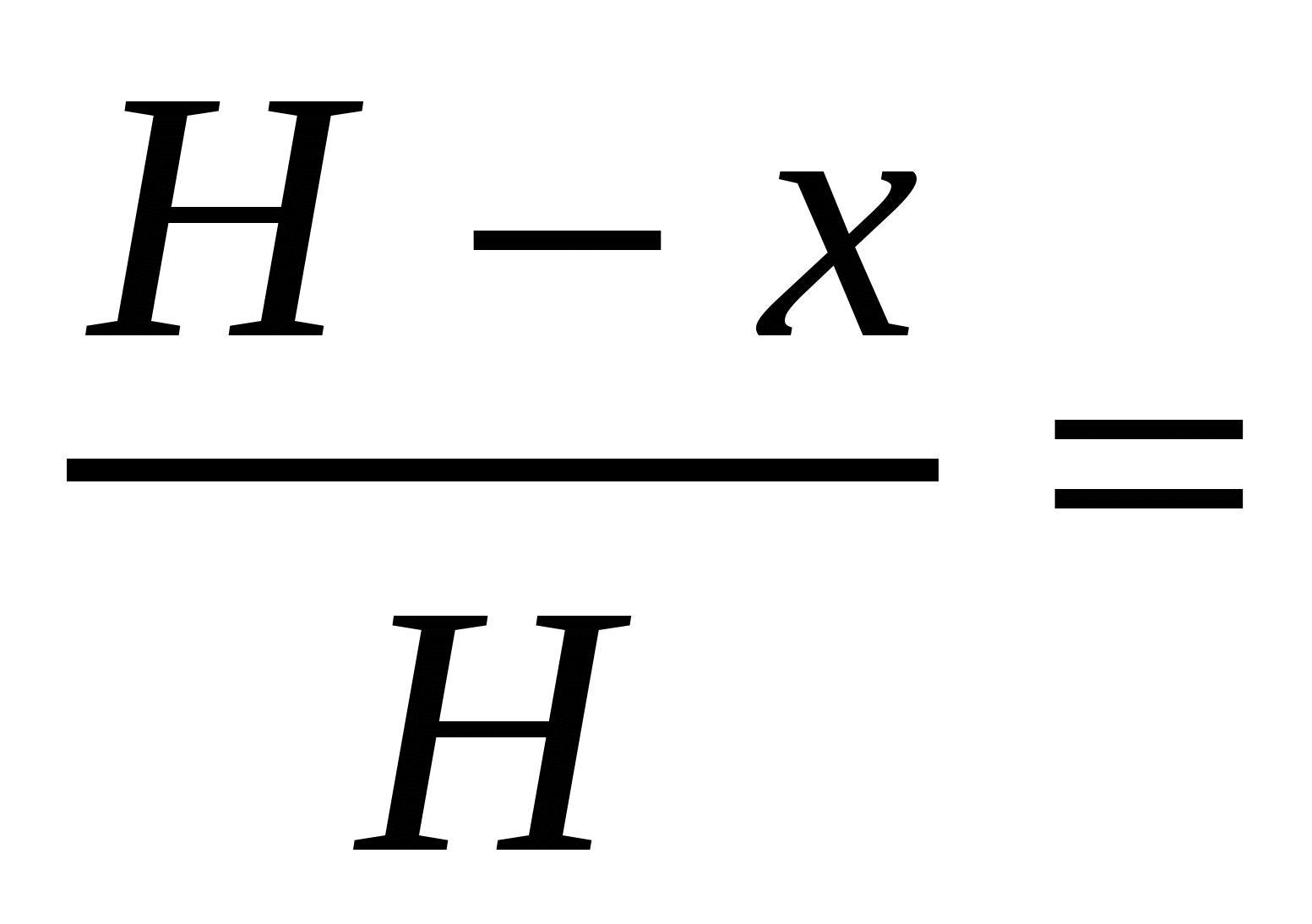
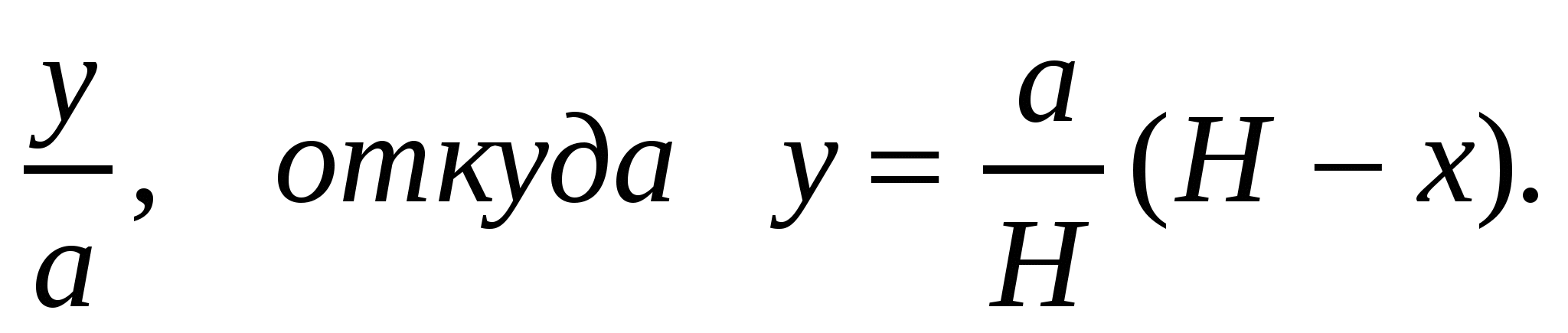
Рассмотрим тонкий слой пирамиды, расположенный на расстоянии х от основания. Пусть толщина слоя равна dx. Слой можно приблизительно считать параллелепипедом. Масса его dm равна: 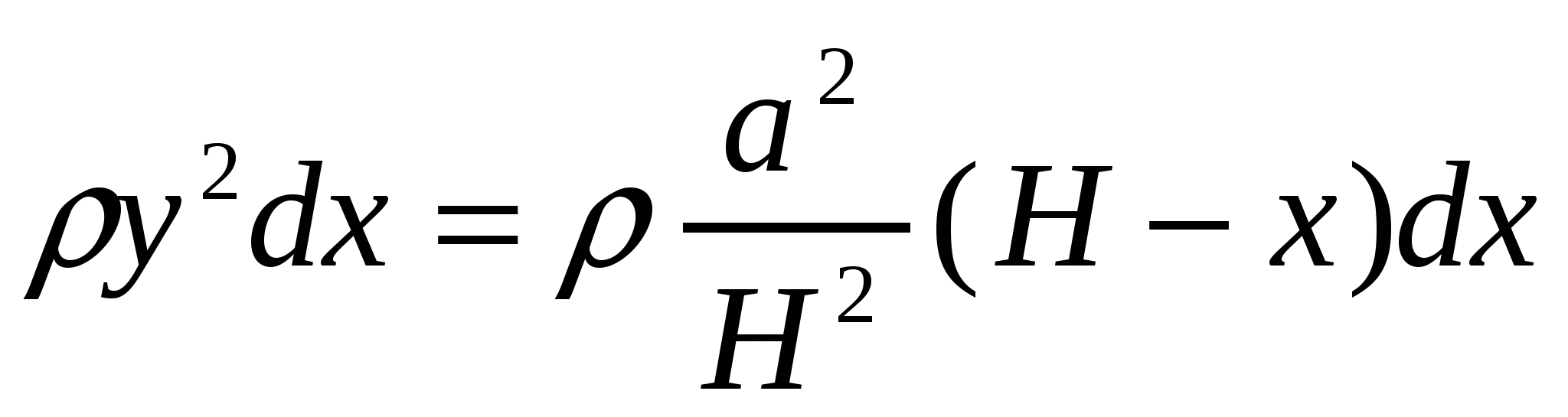 .
.
При подъеме этого слоя на высоту х была проделана работа dA, равная (gdm)x, где g- ускорение силы тяжести, т.е. 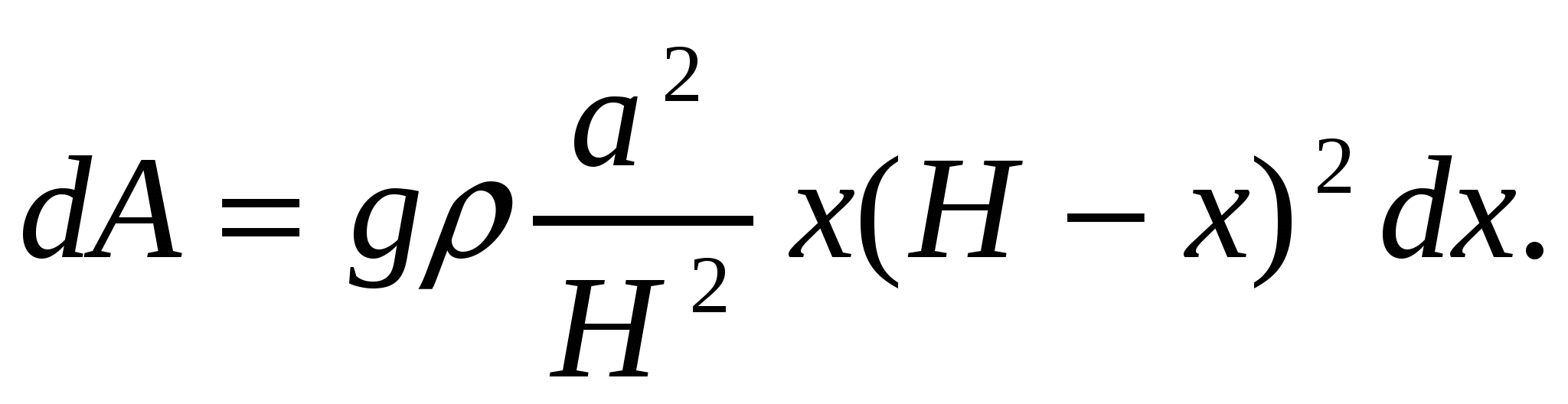
Отсюда 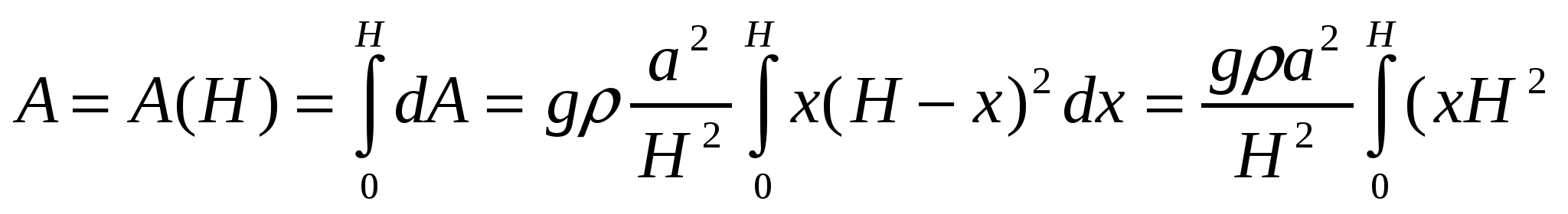
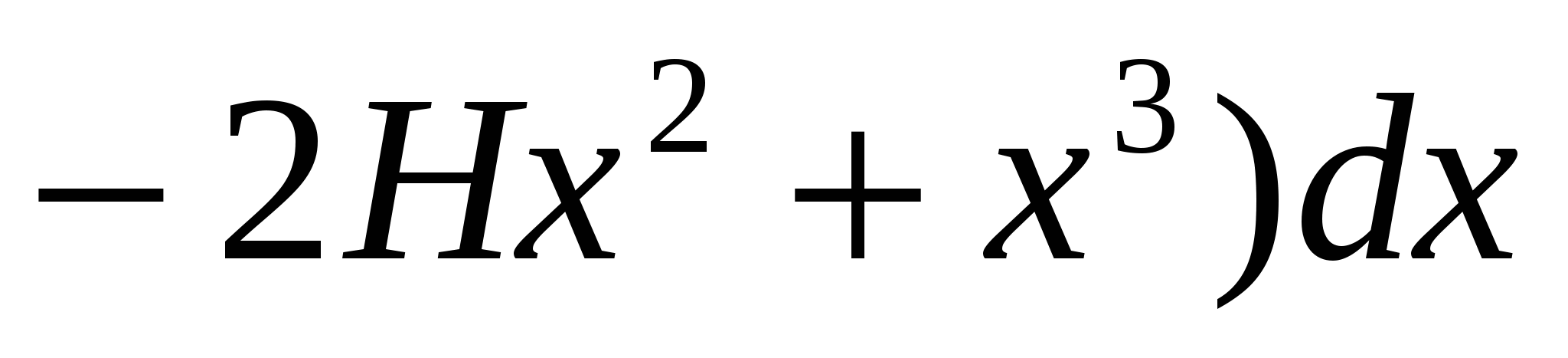 =
=
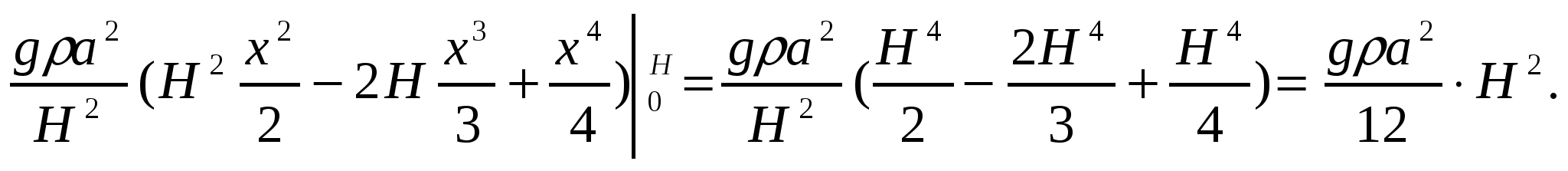
Подставляя числовые данные а=232м, Н=147м, 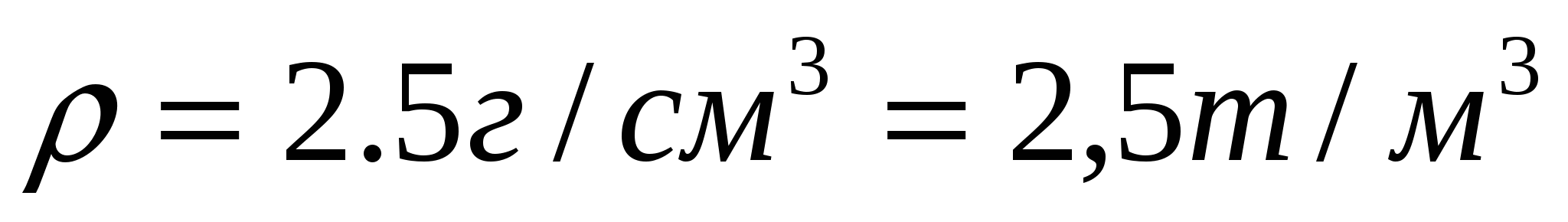 ,
,
получаем А=2,37*1012 Дж=2,4*105тонно-километров.
Ответ: 2,4*105 тонно-километров
Задача 8
Квадратная пластинка со стороной а погружена в воду перпендикулярно ее поверхности, причем верхнее основание пластины находится на поверхности. Найти давление воды на пластину.
Решение
На маленькую площадку площадью dS, расположенную на глубине х от поверхности, давит столб воды в виде цилиндра с основанием dS и высотой х. Давление dp будет при этом равно  , где
, где 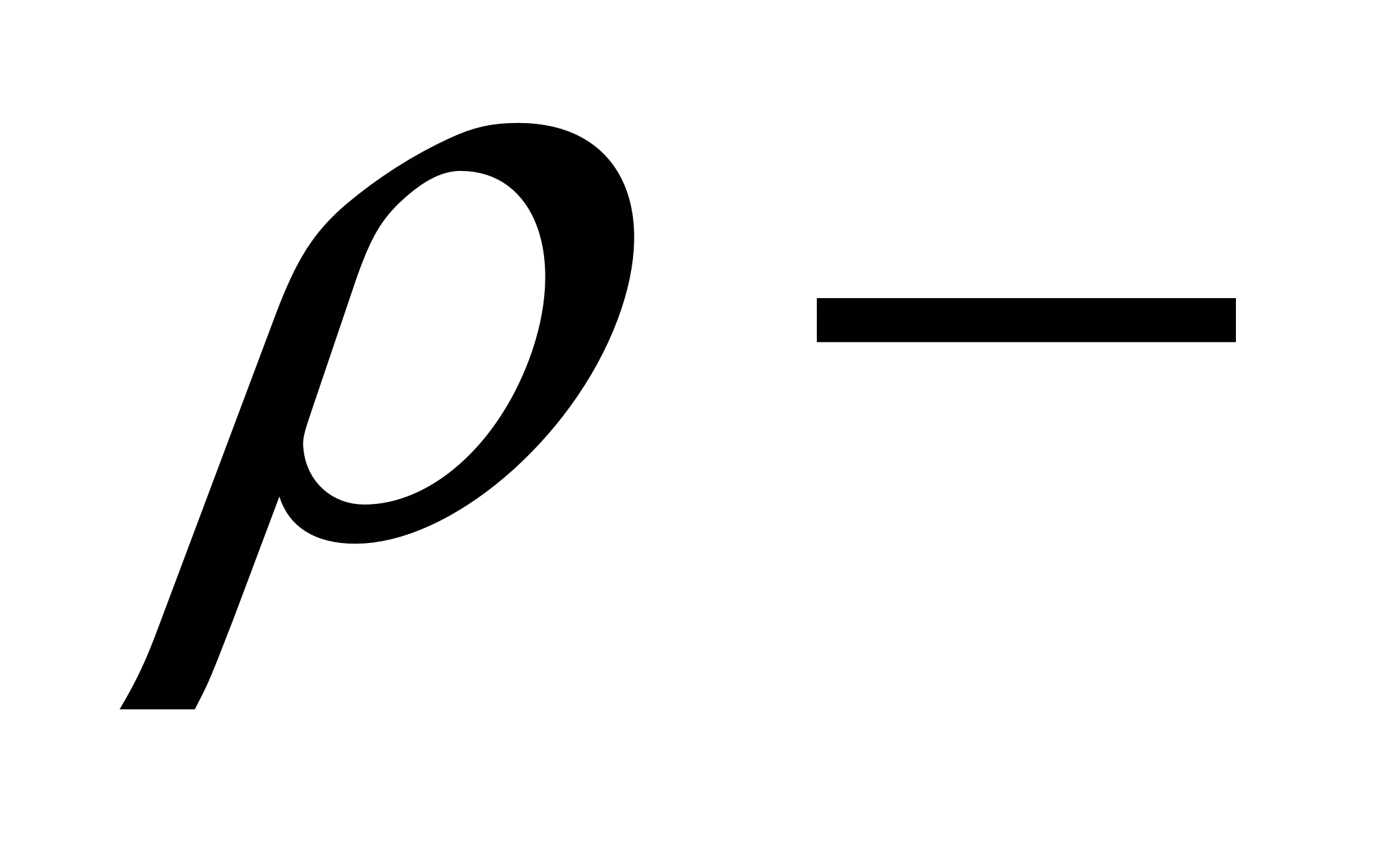 плотность воды,
плотность воды,
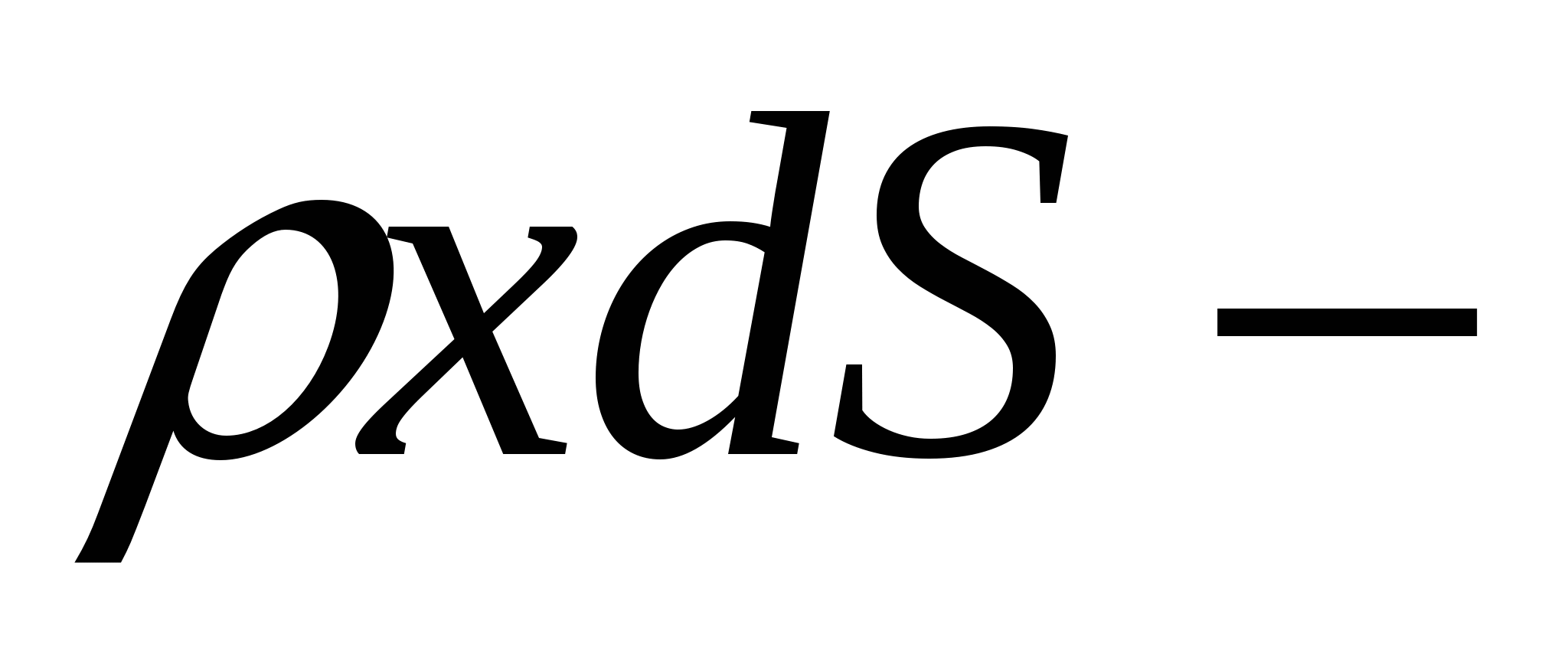 масса цилиндра. Возьмем полоску пластины шириной dx, находящуюся на глубине х. Её площадь dS равна adx. Отсюда dp=
масса цилиндра. Возьмем полоску пластины шириной dx, находящуюся на глубине х. Её площадь dS равна adx. Отсюда dp=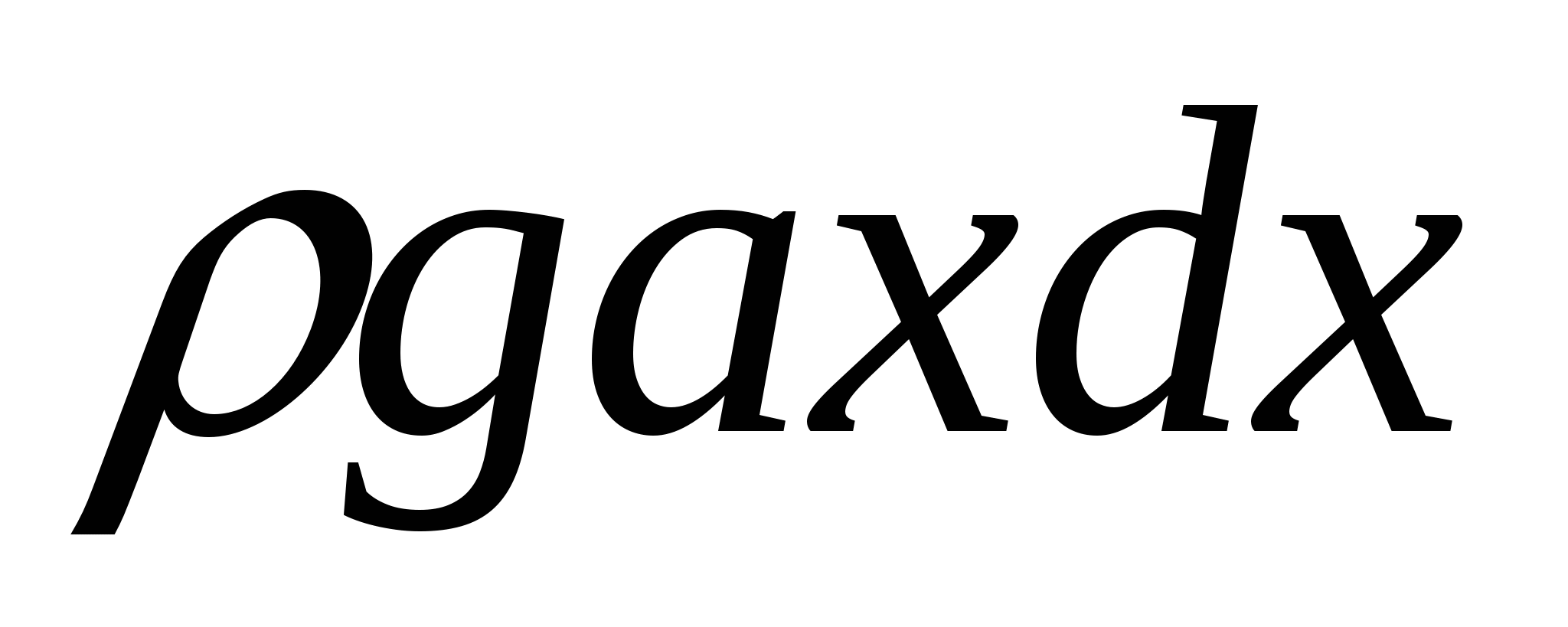 . Получаем
. Получаем 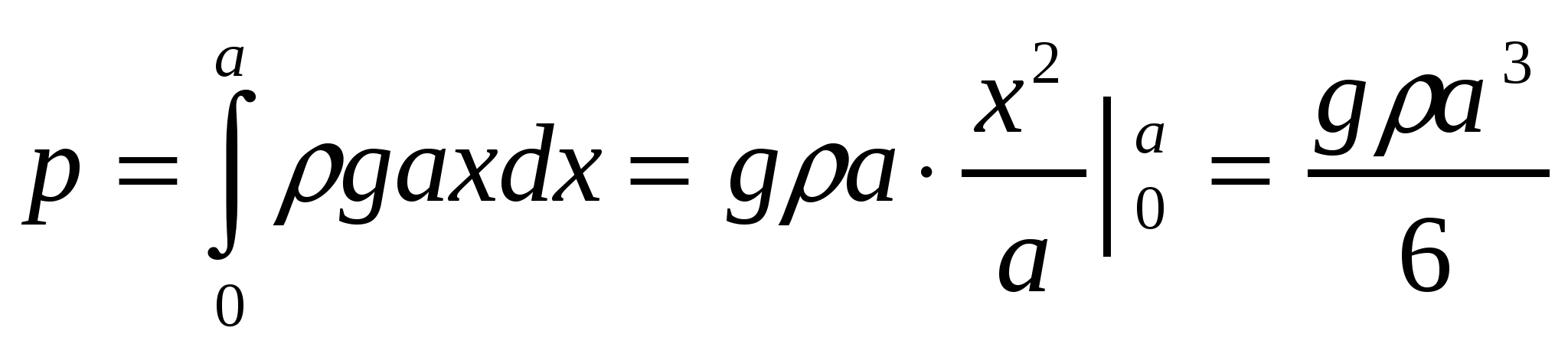 .
.
Ответ: 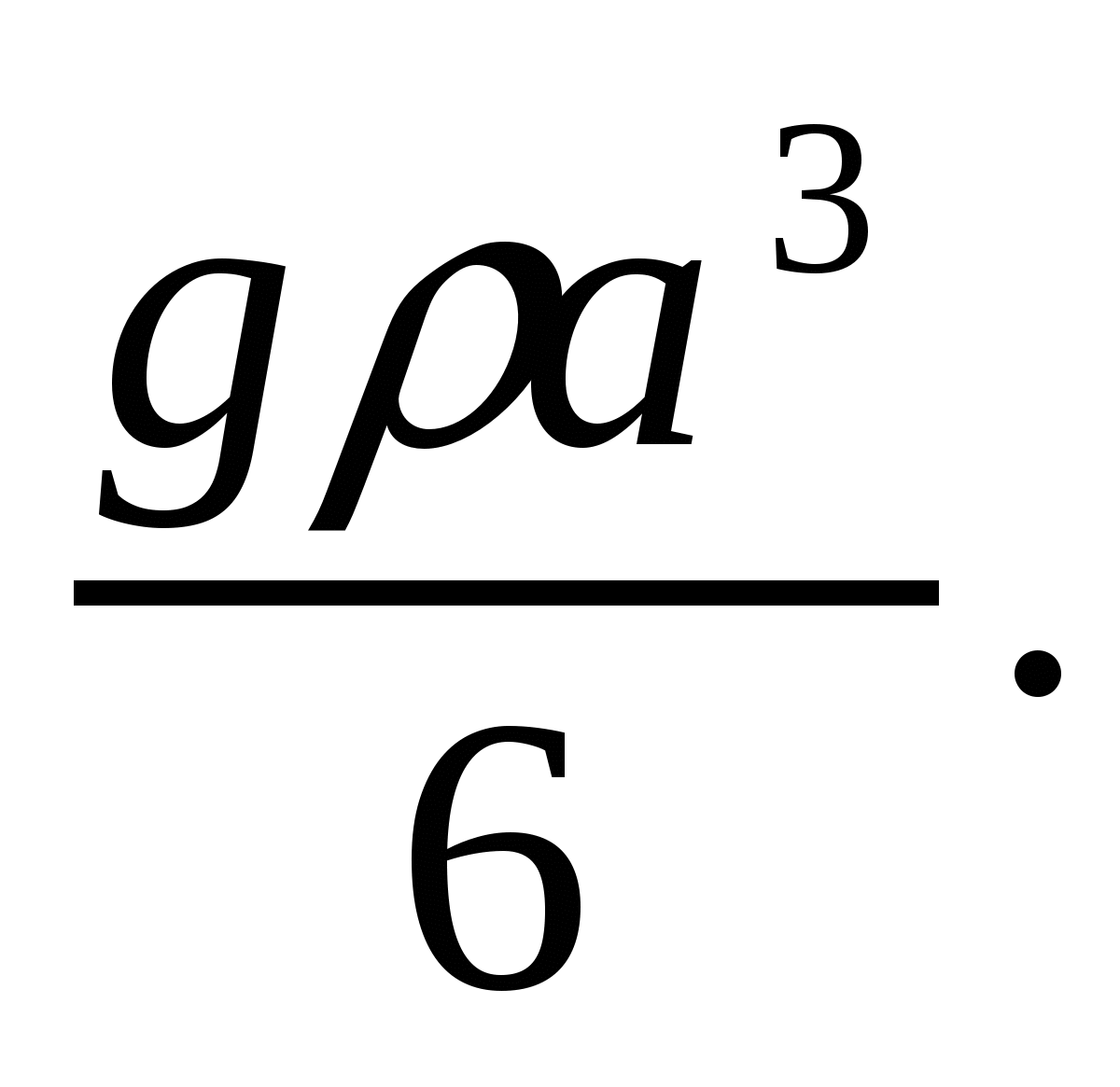
Задача 9
Экспериментально установлено, что продуктивность труда работника приближенно выражается формулой: f(t)= -0,0033t2 -0,089t +20,96, где t -- рабочее время в часах. Вычислите объем выпуска продукции за квартал, считая рабочий день восьмичасовым, а количество рабочих дней в квартале - 62.
Решение.
Объем выпуска продукции в течение смены является первообразной для функции, выражающей продуктивность труда. Поэтому 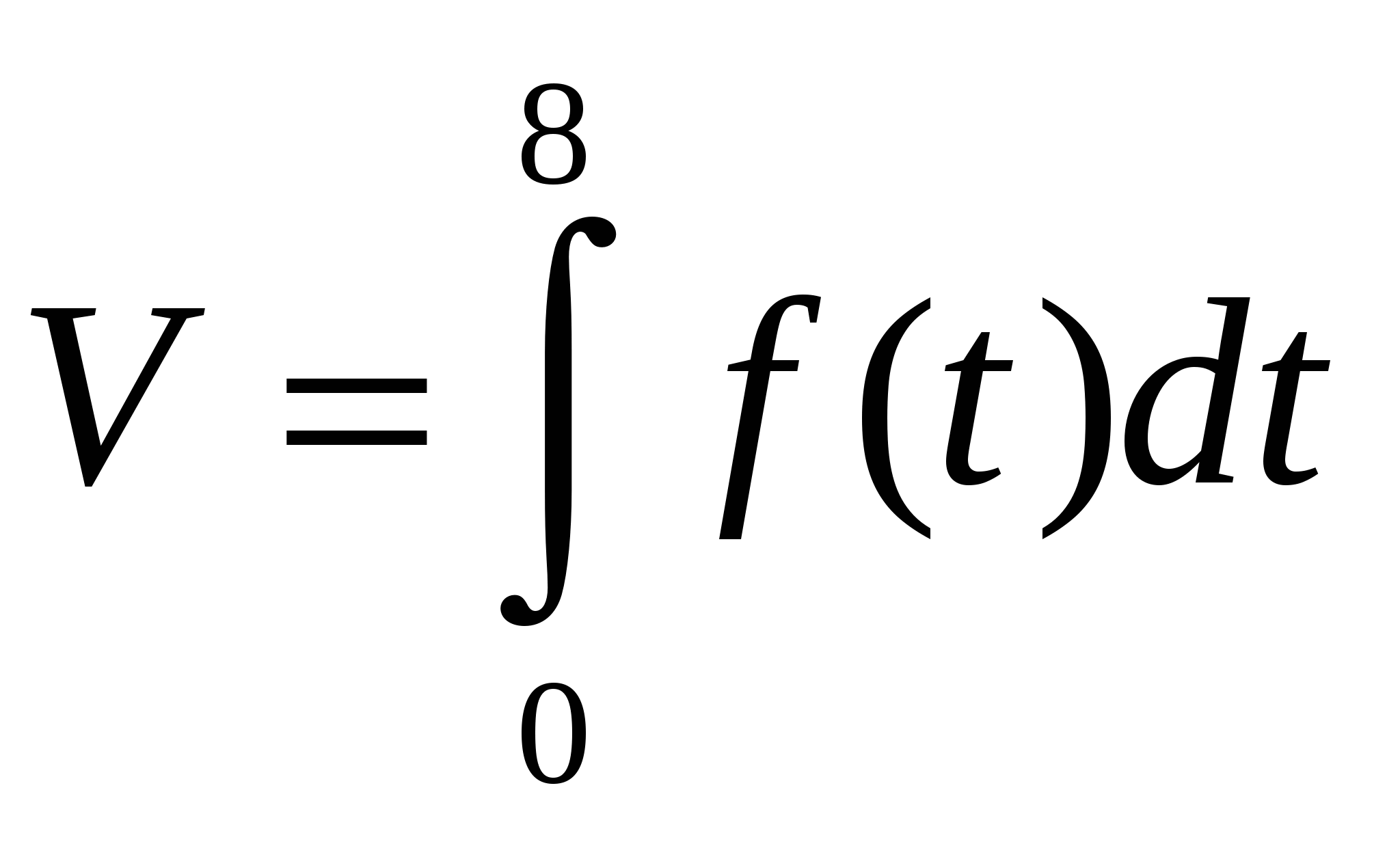 .
.
В течение квартала объем выпуска продукции составит:
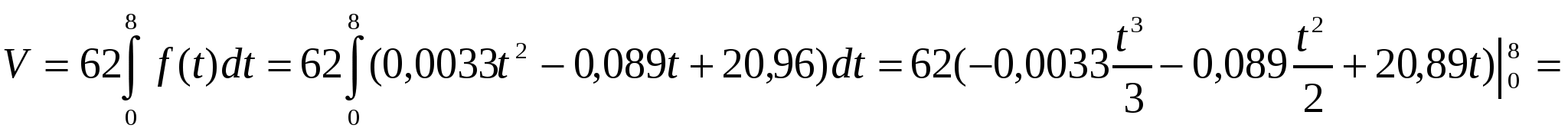
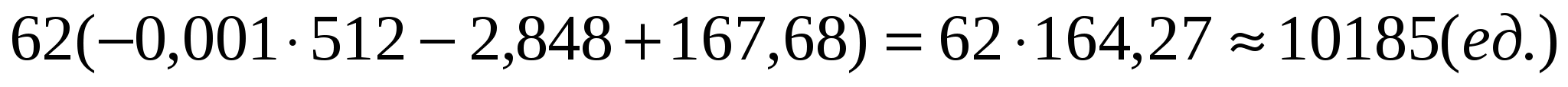
Ответ: 10185 ед.
Задача 10.
Экспериментально установлено, что зависимость расхода бензина автомобиля от скорости на 100км пути выражается по формуле: Q=18 - 0,3v+0,003v2, где 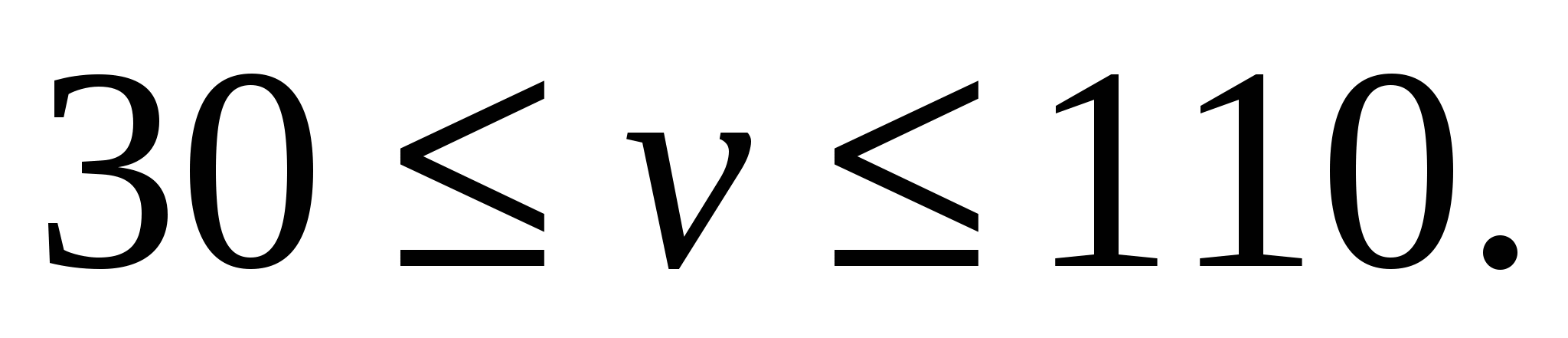 Определить средний расход бензина, если скорость движения 50-60км/час.
Определить средний расход бензина, если скорость движения 50-60км/час.
Решение
Средний расход бензина составляет :
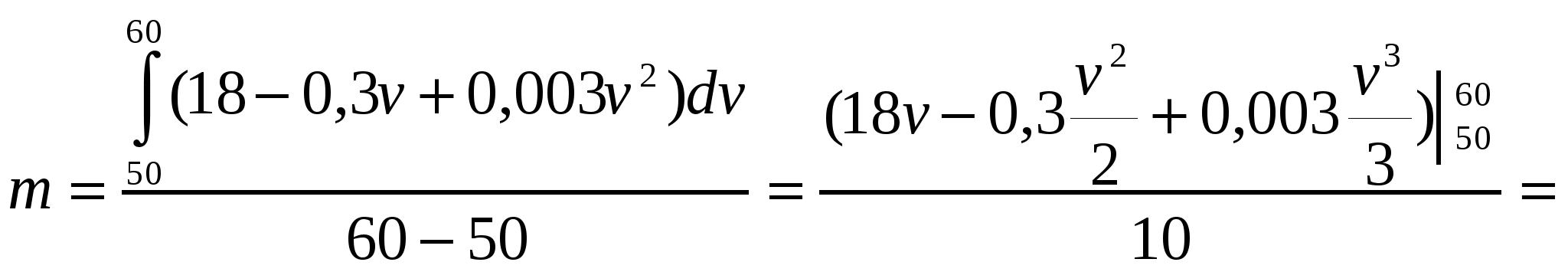
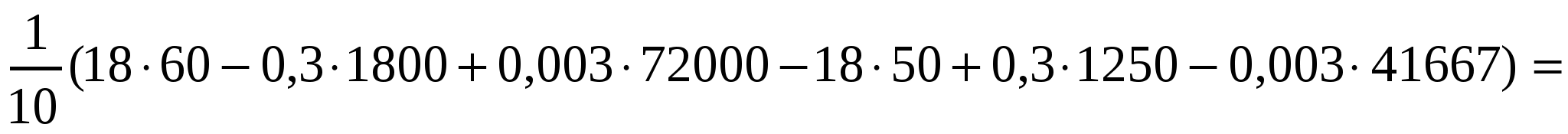
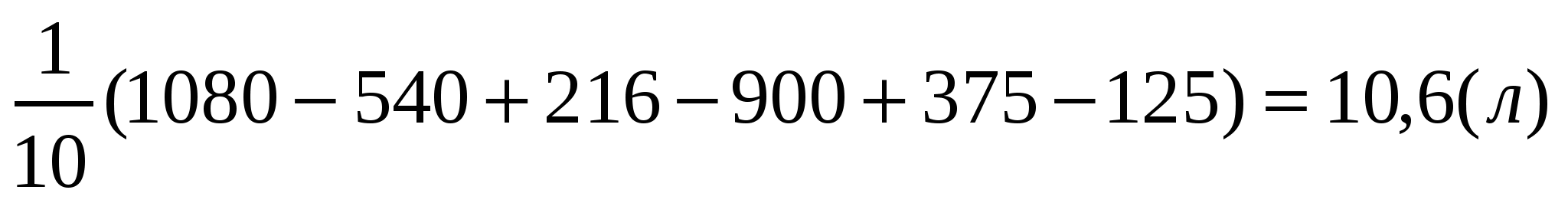
Ответ: 10,6л
Задание 11
Из трёх одинаковых досок шириной а нужно сделать жёлоб наибольшей пропускной способностью, поперечное сечение которого имело бы форму равнобокой трапеции.
Решение
Очевидно, что пропускная способность жёлоба будет наибольшей, если наибольшей будет площадь его поперечного сечения ,где AB > a).Обозначим угол при большем основании трапеции через х. Выразим площадь S трапеции как функцию от х.
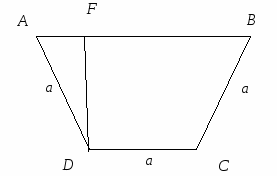
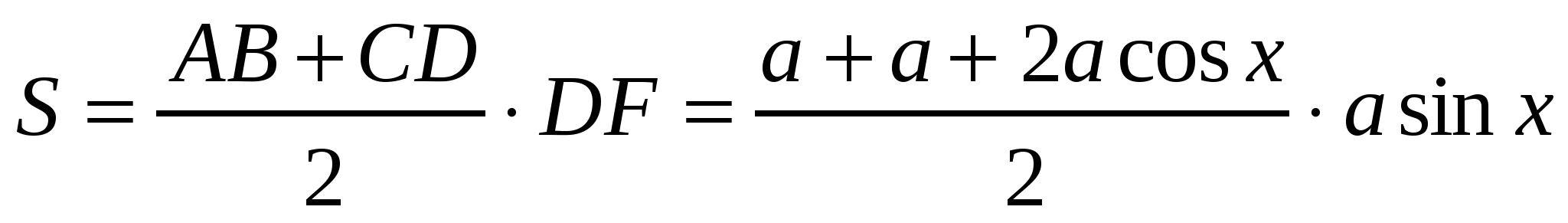
 .
.
Итак, 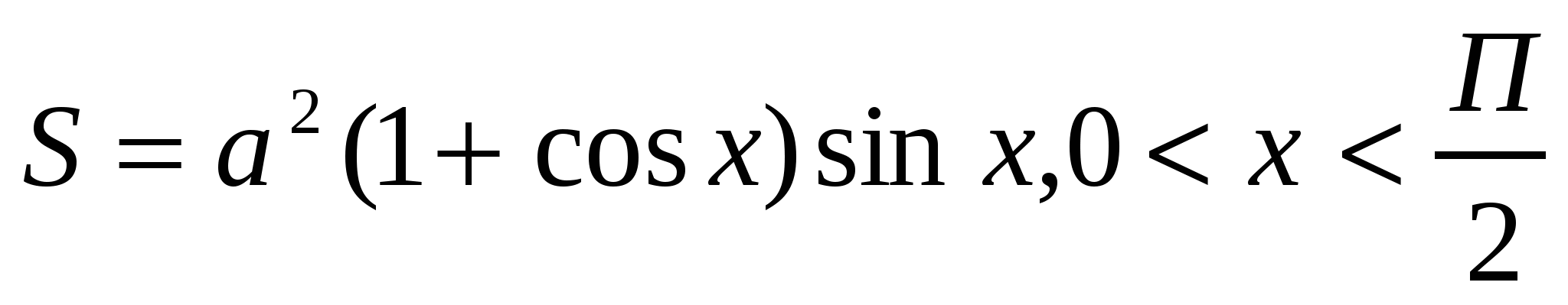 . Найдем производную этой функции:
. Найдем производную этой функции: 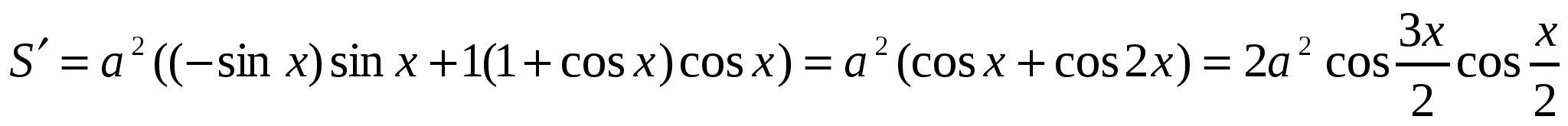 . На интервале
. На интервале 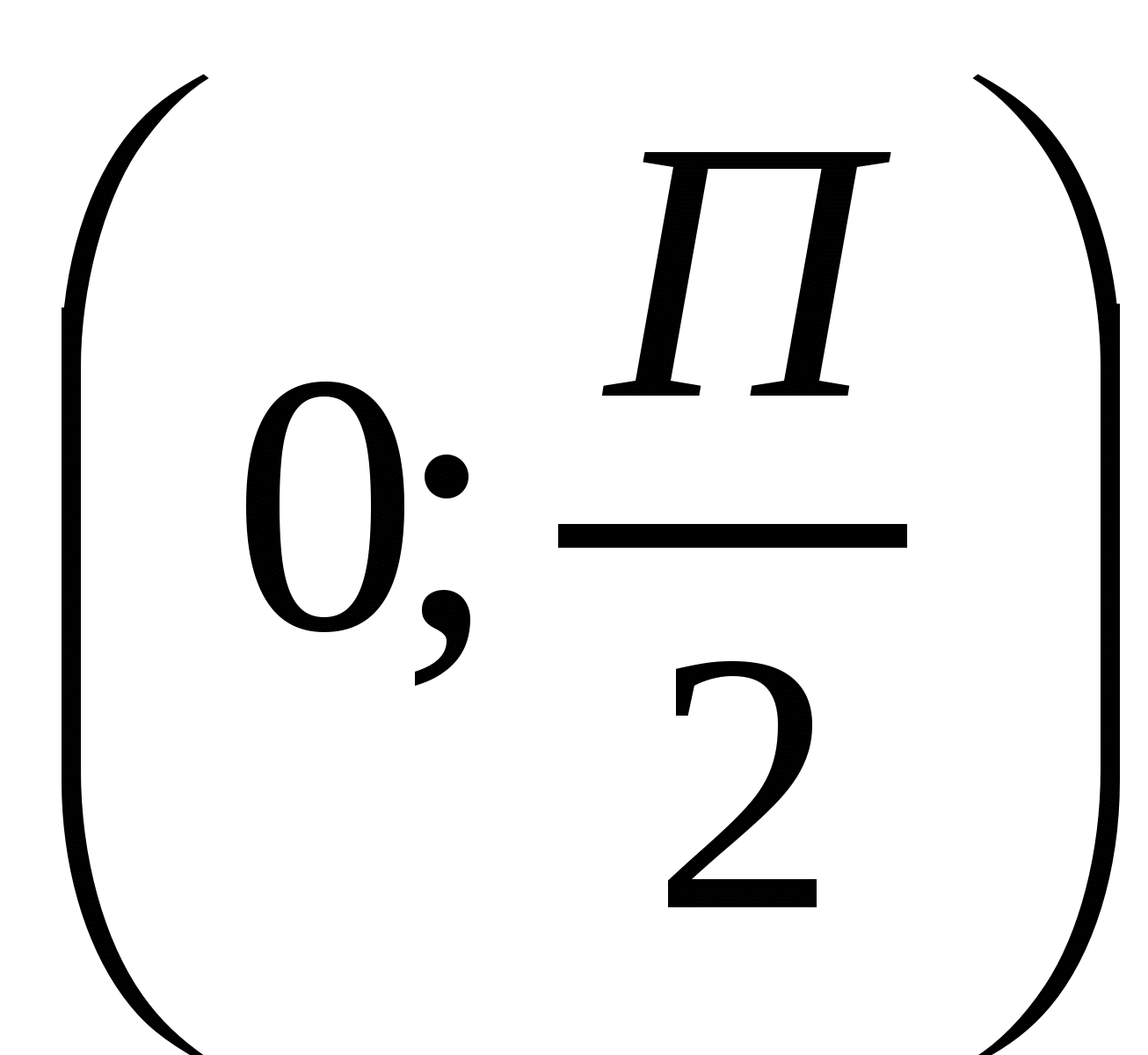
 уравнение
уравнение 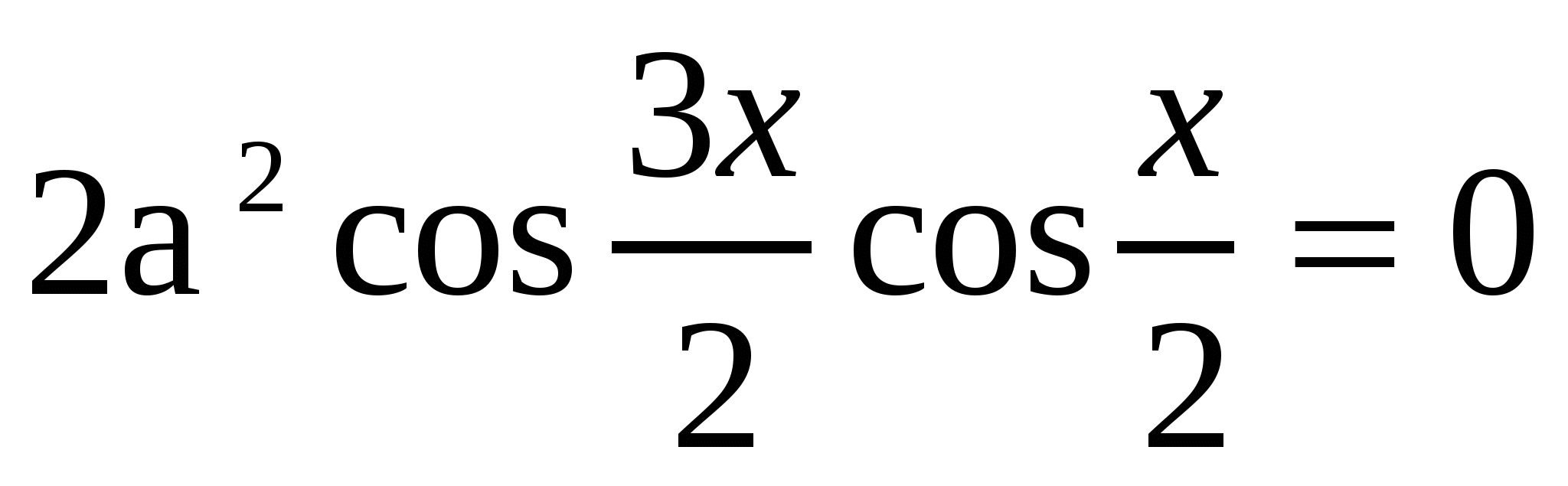 имеет единственное решение
имеет единственное решение 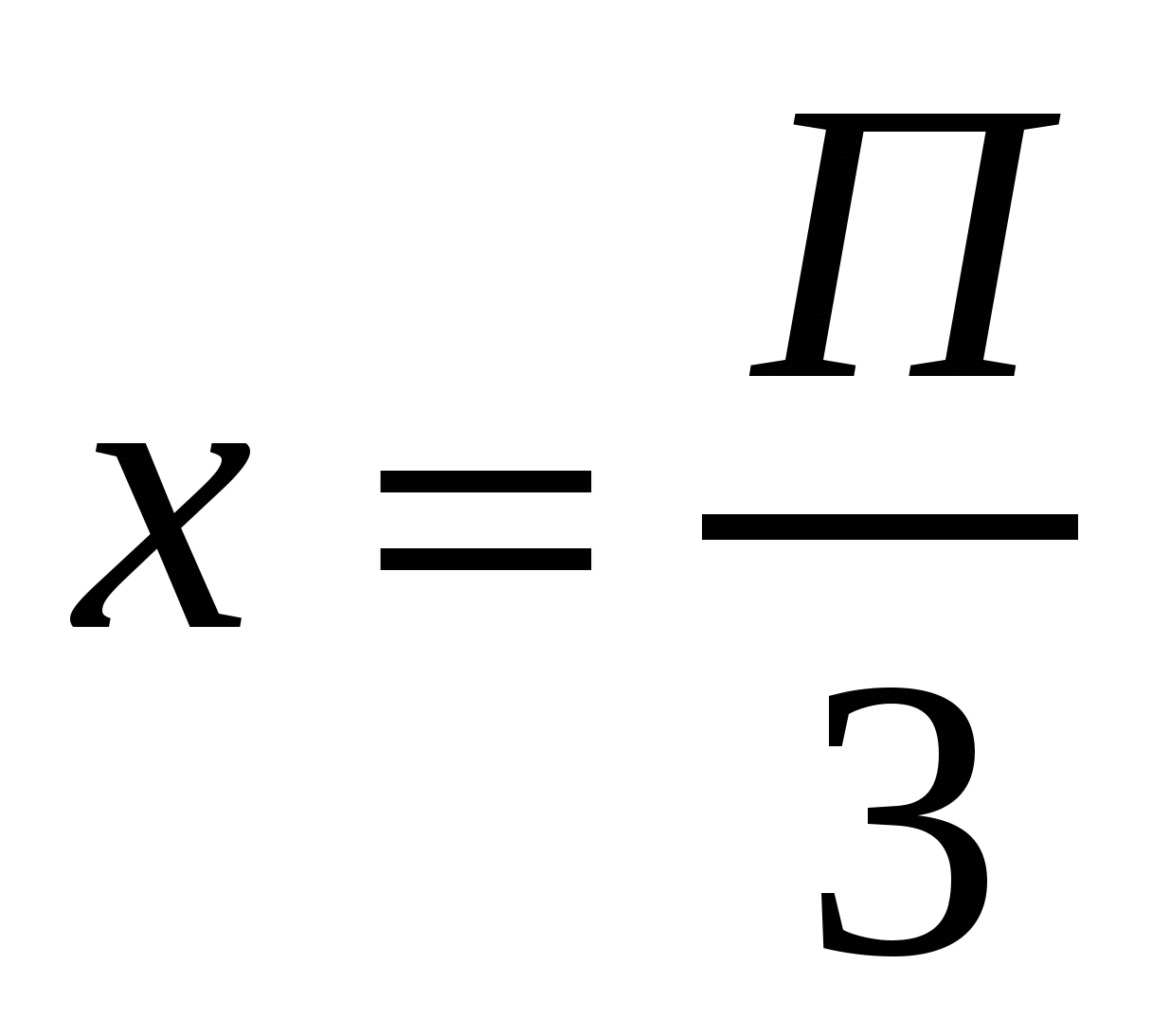 . Следовательно, на этом интервале функция имеет единственную критическую точку
. Следовательно, на этом интервале функция имеет единственную критическую точку ![]() . Так как
. Так как 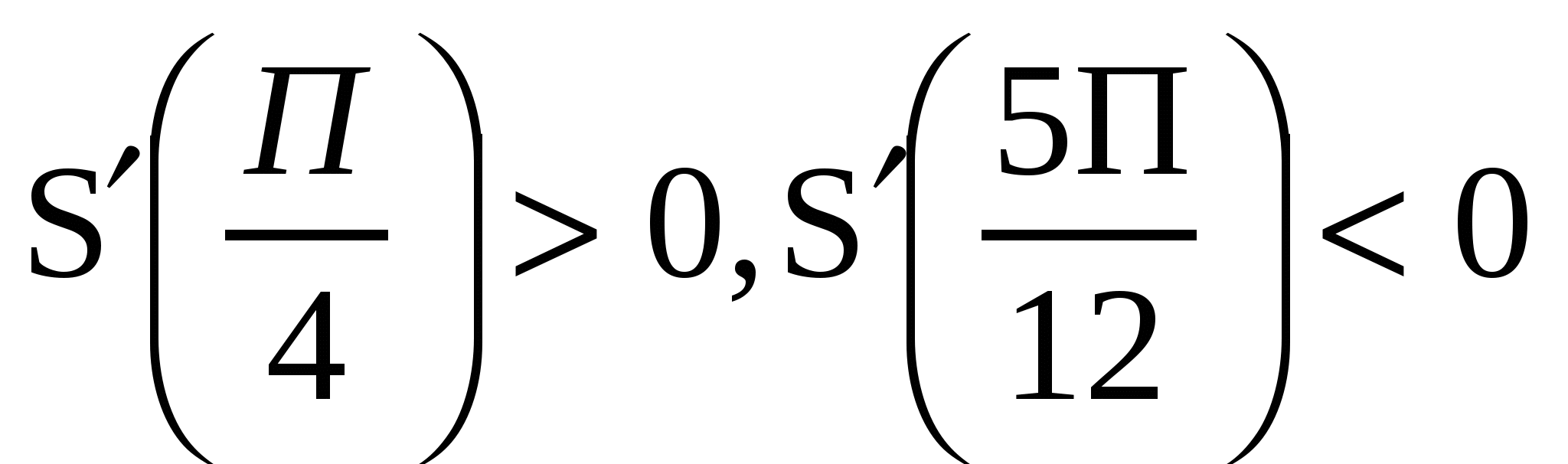 ,то производная переходя через точку
,то производная переходя через точку 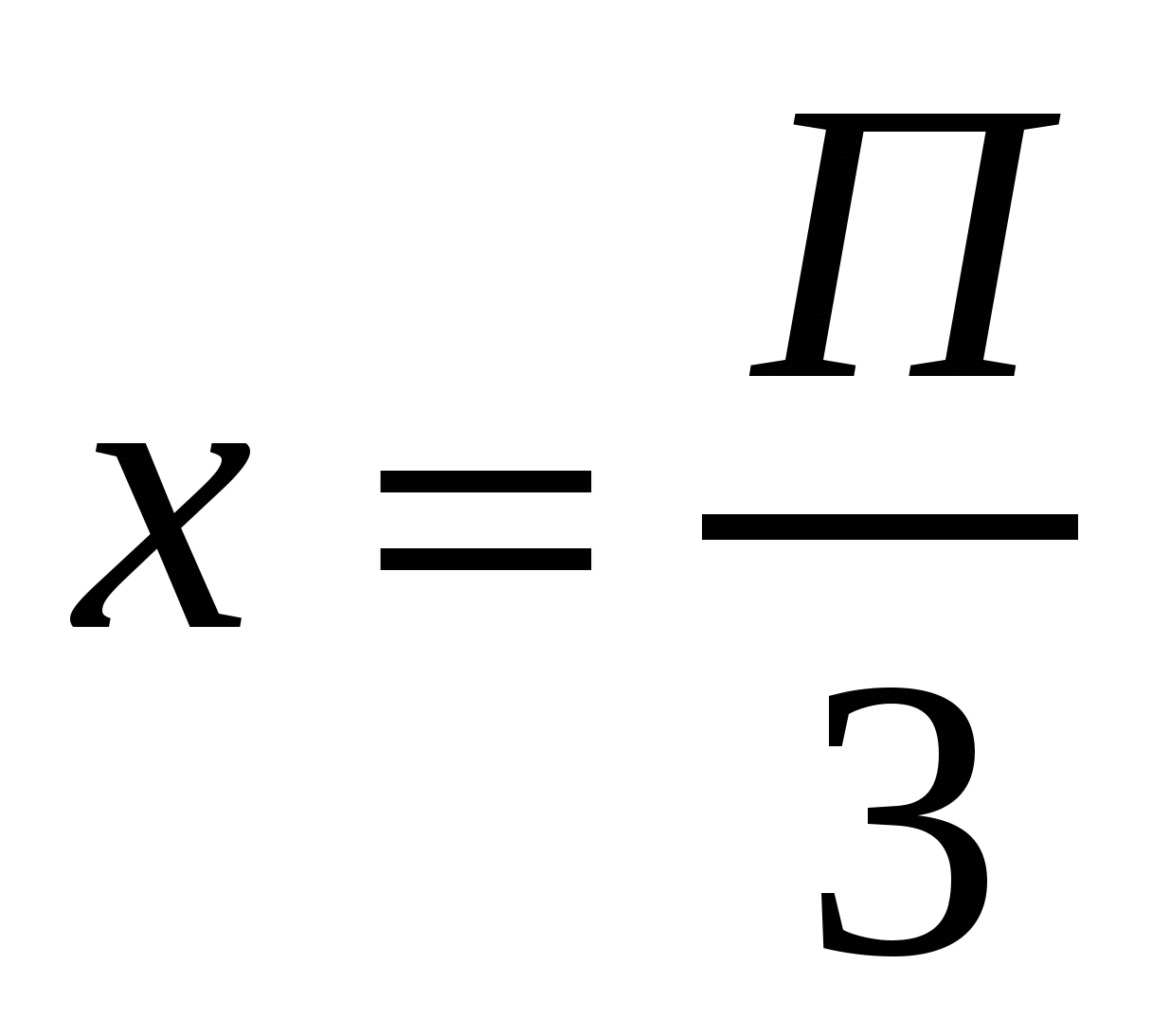 ,меняет знак с плюса на минус, то есть
,меняет знак с плюса на минус, то есть 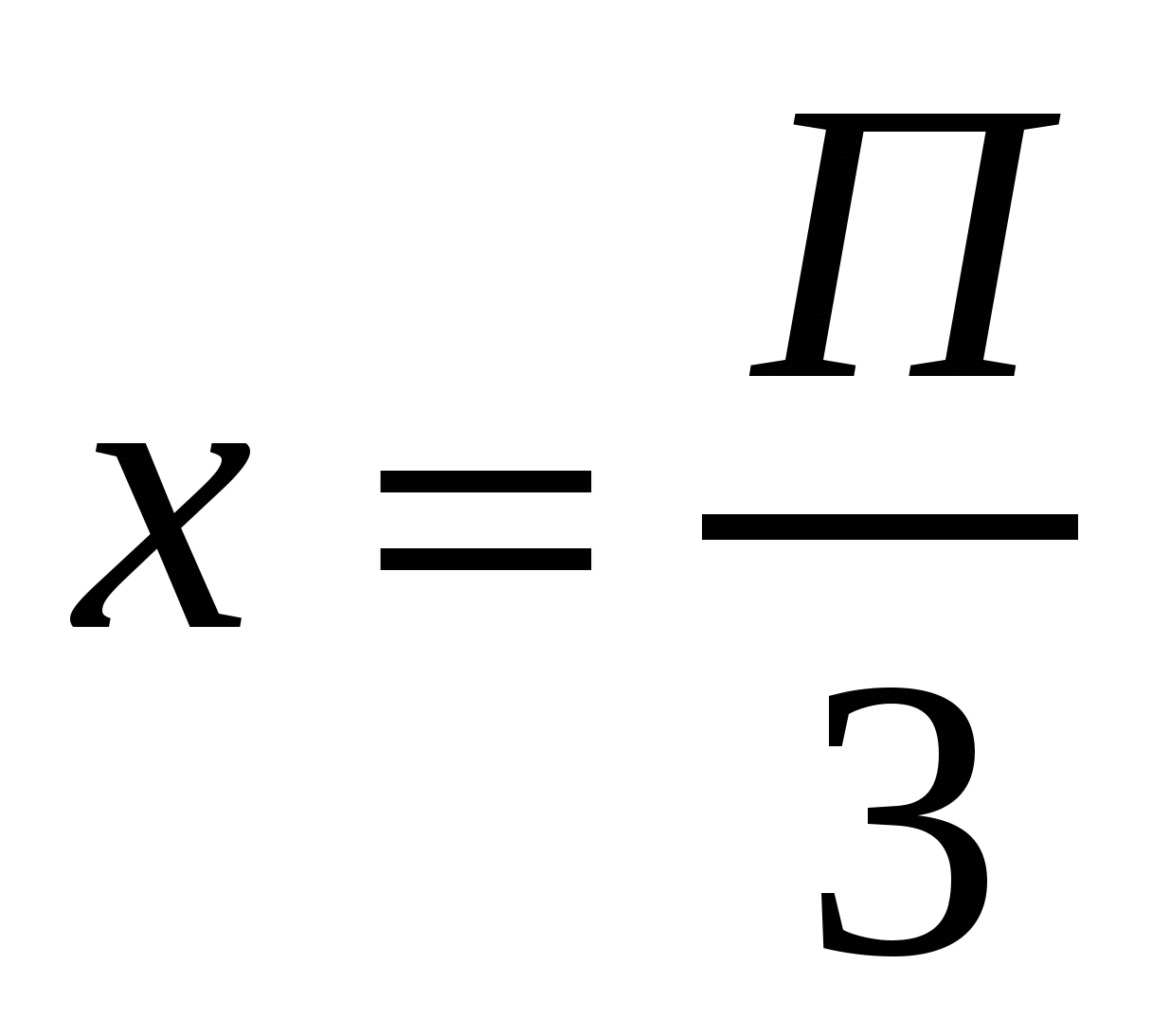 -точка максимума функции, и, следовательно,
-точка максимума функции, и, следовательно, 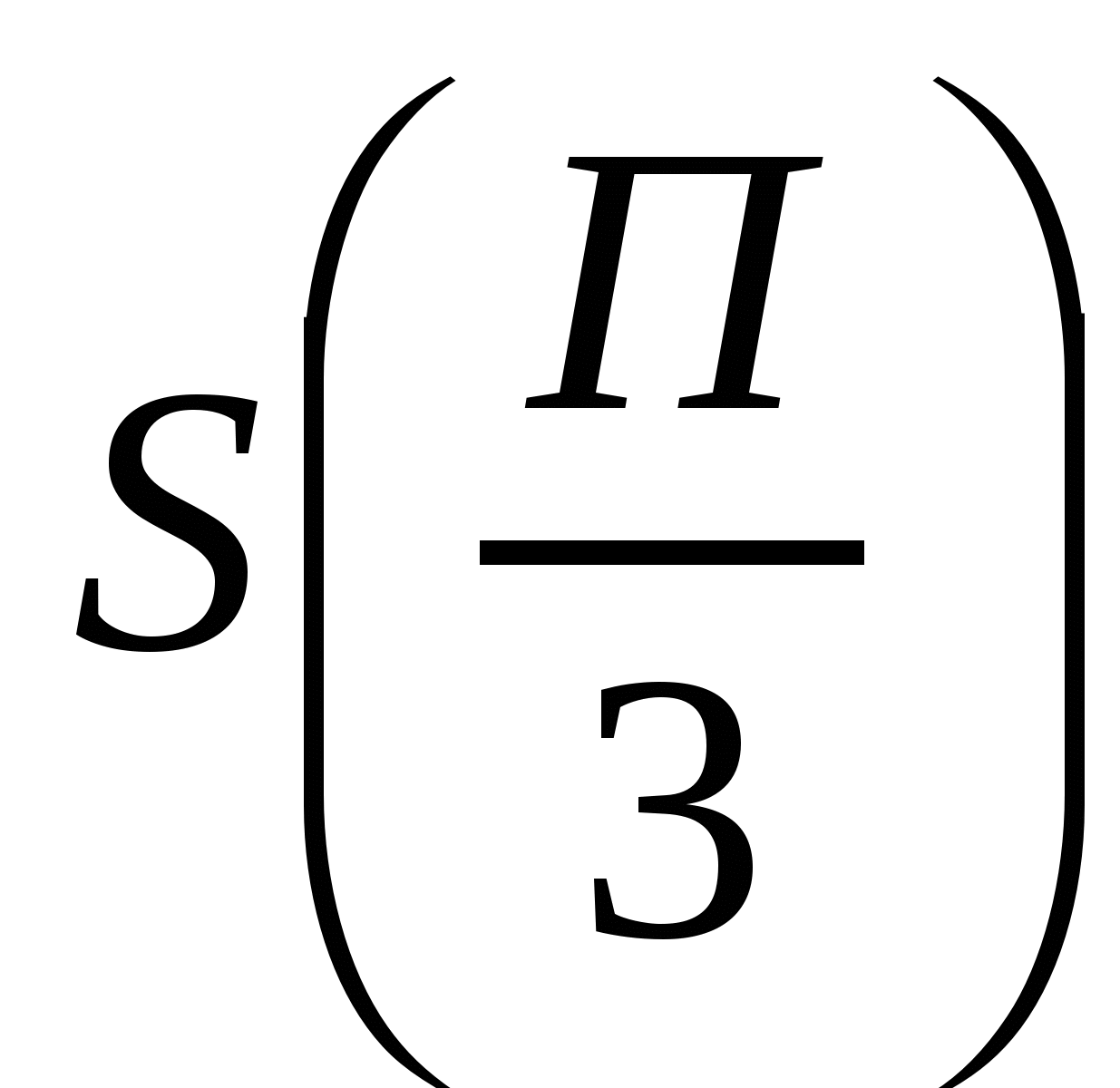 -наибольшее значение функции на промежутке
-наибольшее значение функции на промежутке 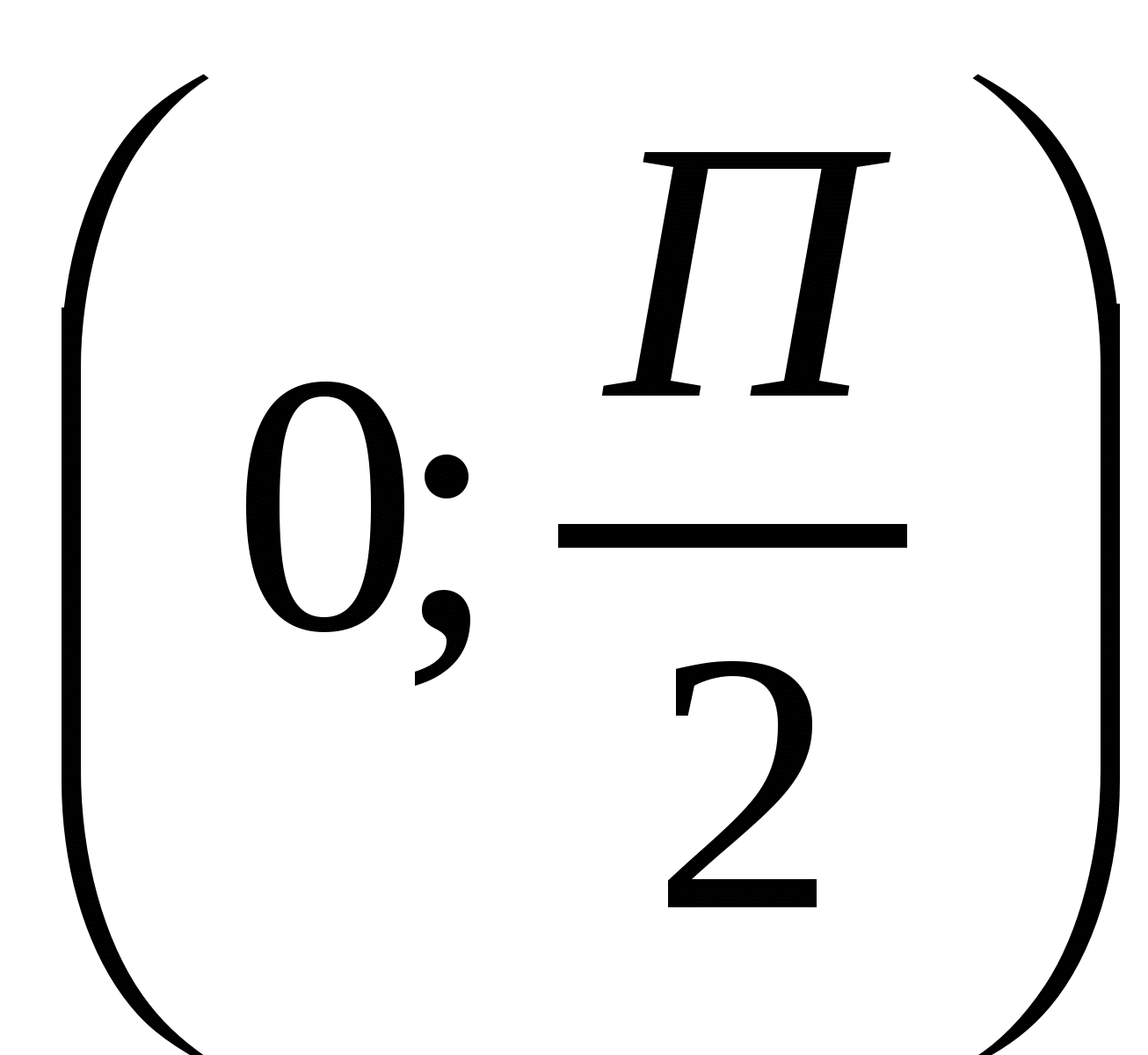 .Итак, доски надо соединить друг с другом под углом 120°.
.Итак, доски надо соединить друг с другом под углом 120°.
Задание 12
Доказать неравенство 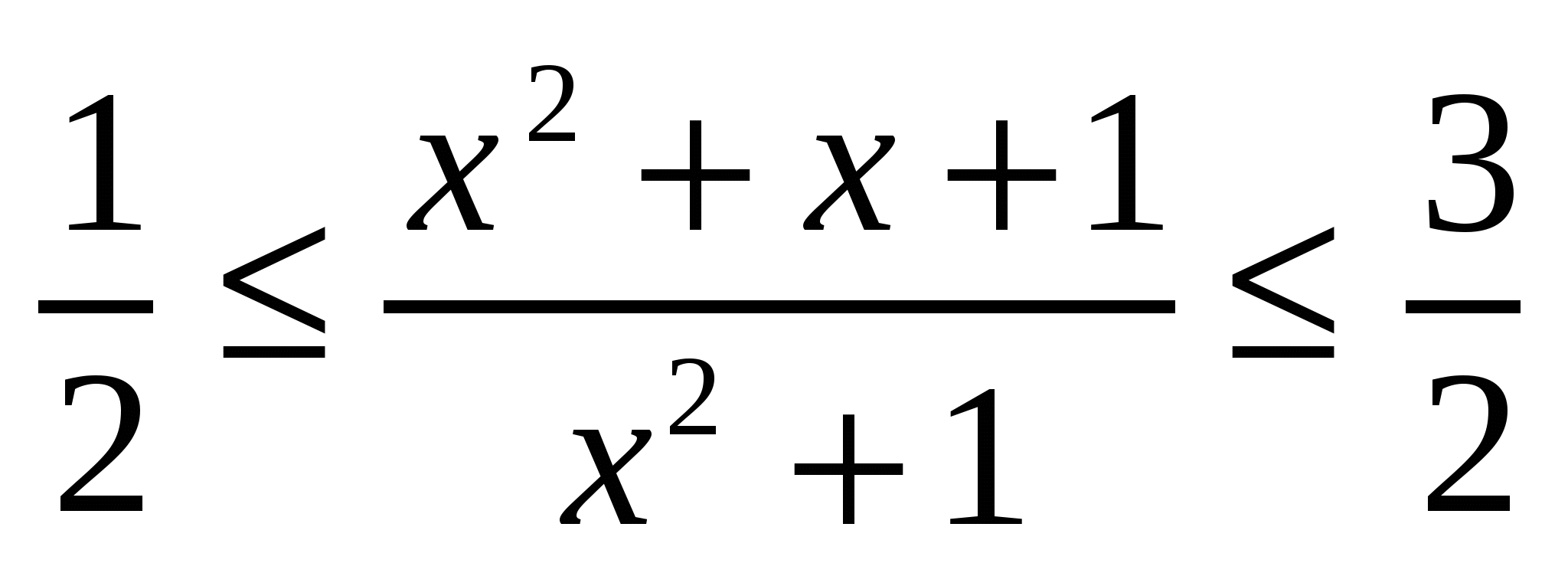 .
.
Решение
Перепишем данное неравенство в виде 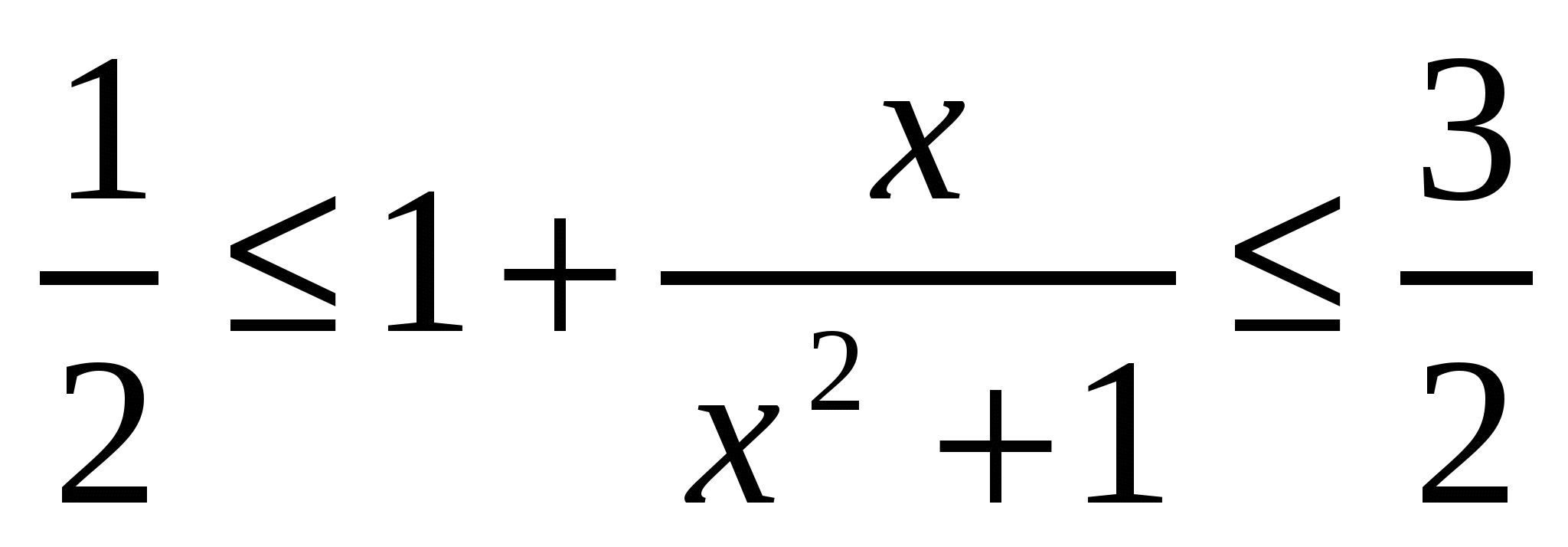 или
или 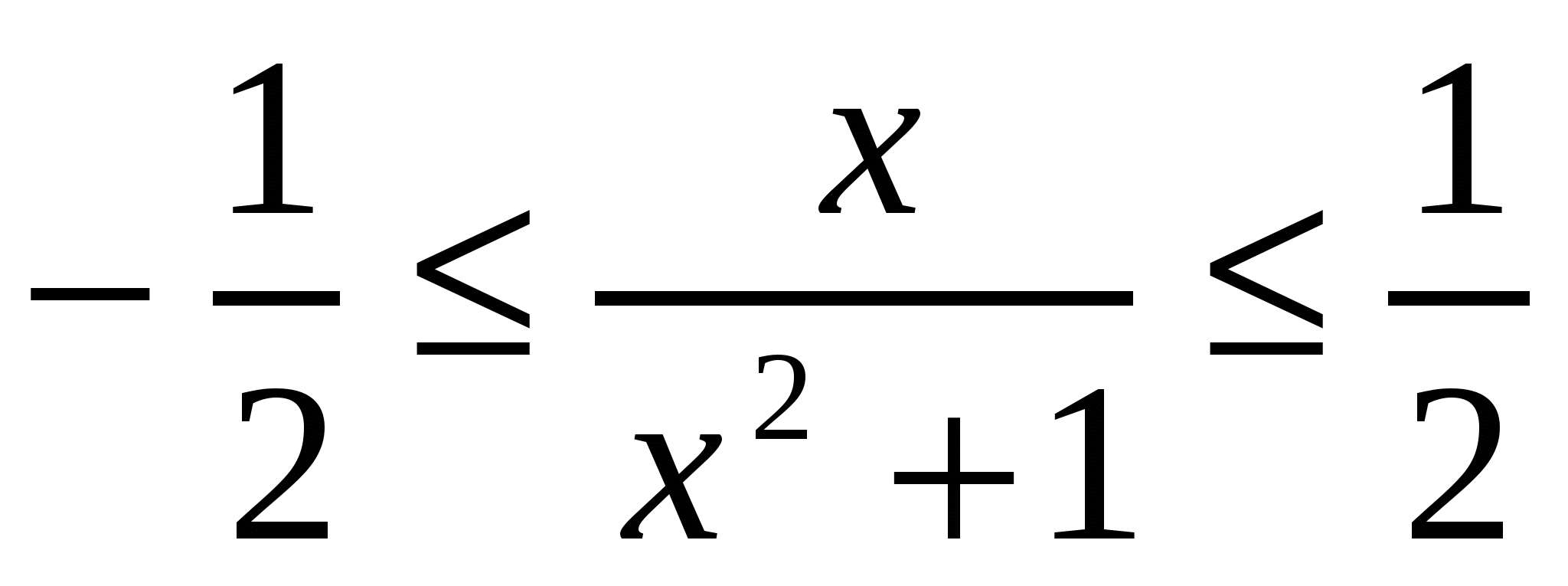 . Найдем наибольшее и наименьшее значение функции f(x)=
. Найдем наибольшее и наименьшее значение функции f(x)=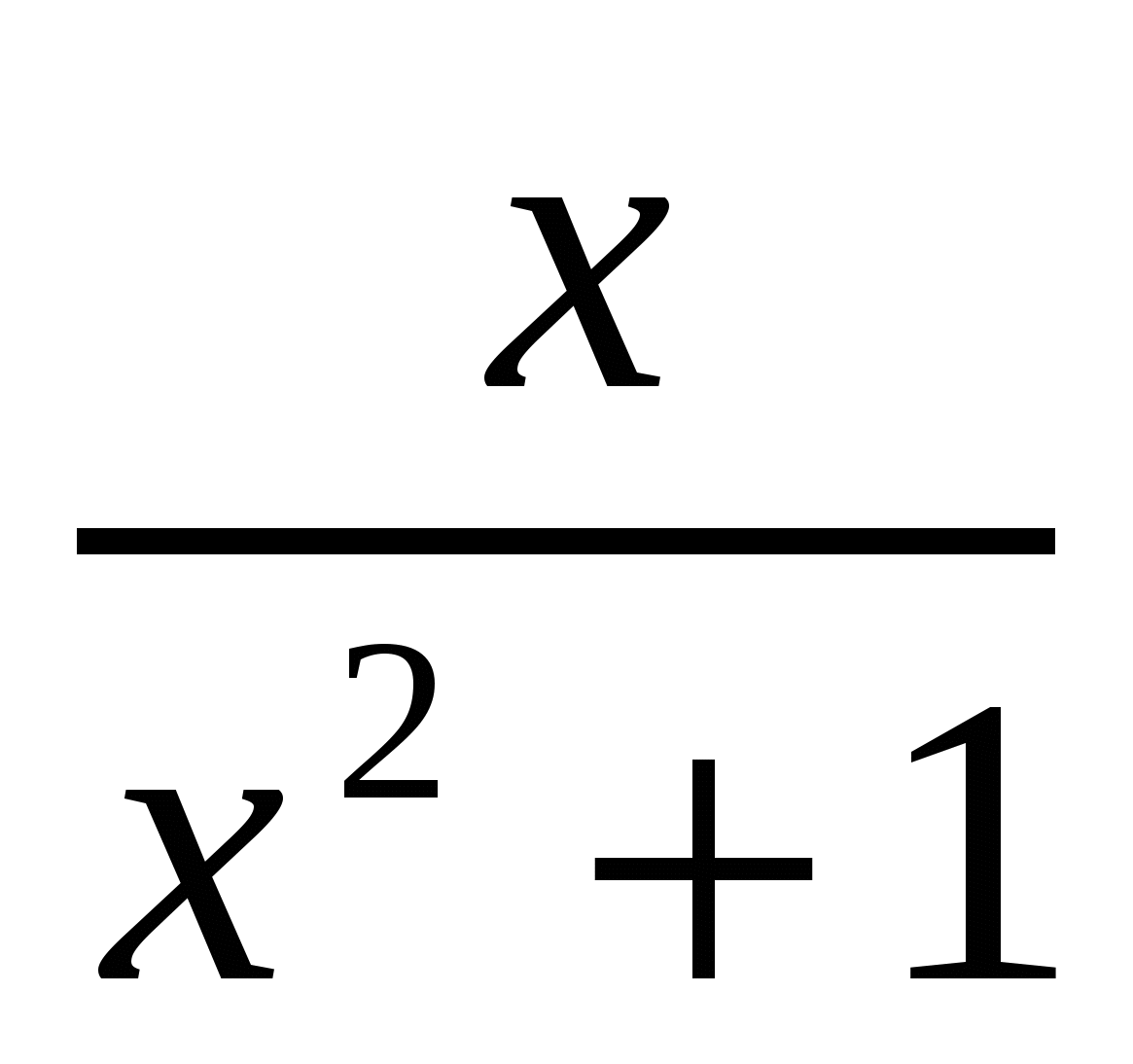 на промежутке
на промежутке 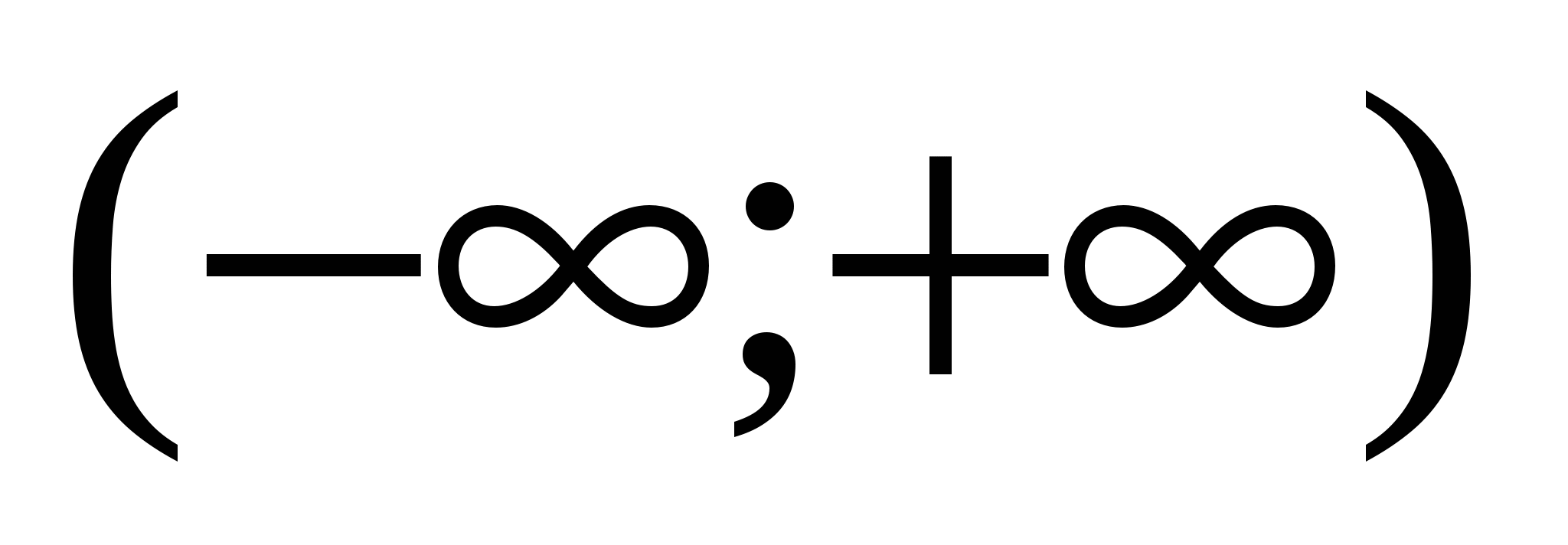 . Так как эта функция нечётная и f(x) >0 при x >0,то достаточно найти наибольшее и наименьшее значение функции на интервале
. Так как эта функция нечётная и f(x) >0 при x >0,то достаточно найти наибольшее и наименьшее значение функции на интервале 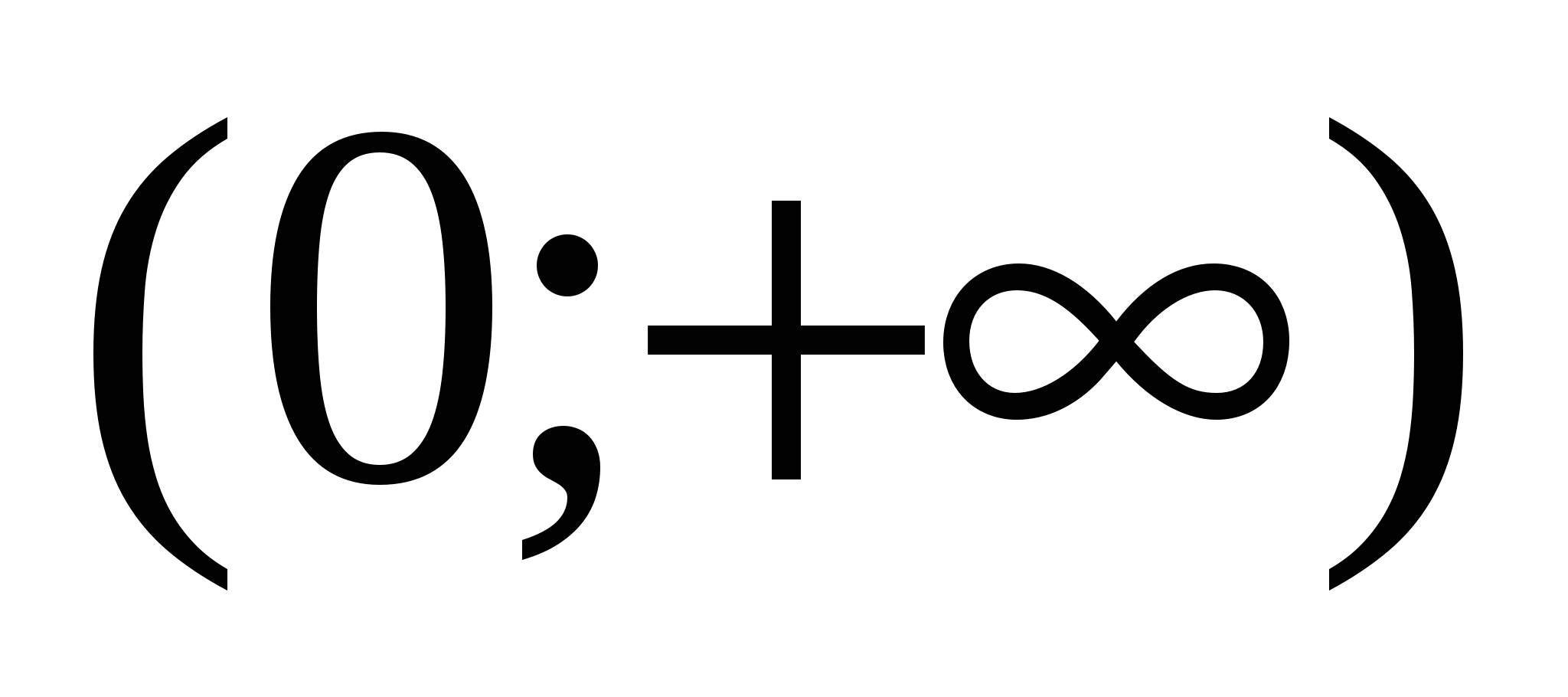 .
.
Найдем производную функции: f(x)=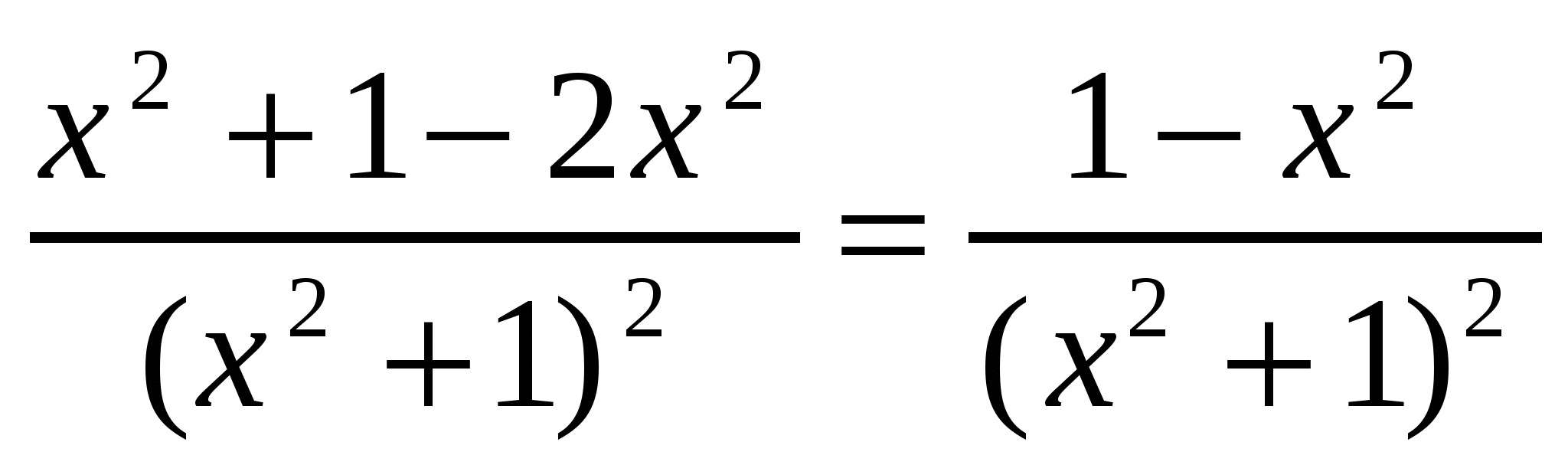 . На интервале
. На интервале 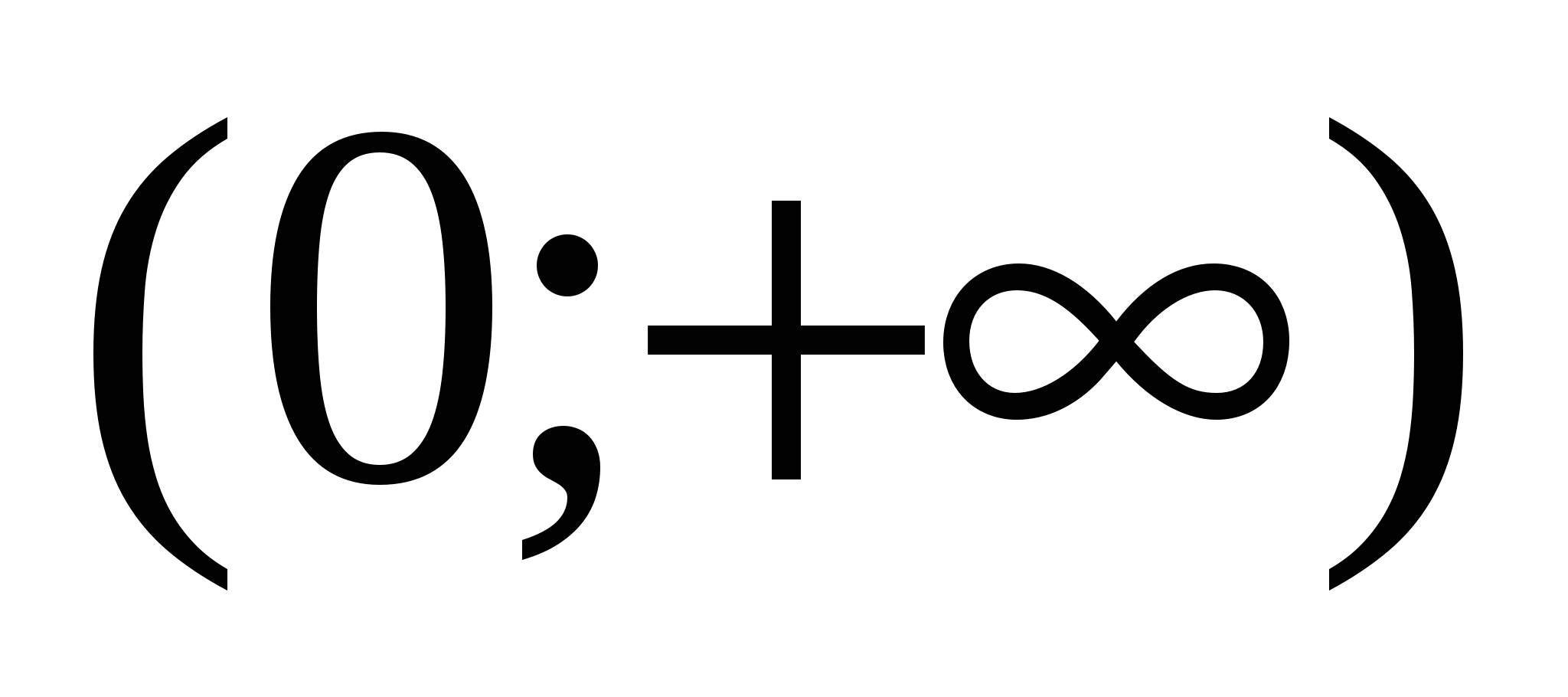
Содержится единственная критическая точка х=1 функции f(x), которая является точкой максимума этой функции. На основании правил нахождения наибольшего и наименьшего значений f(1)=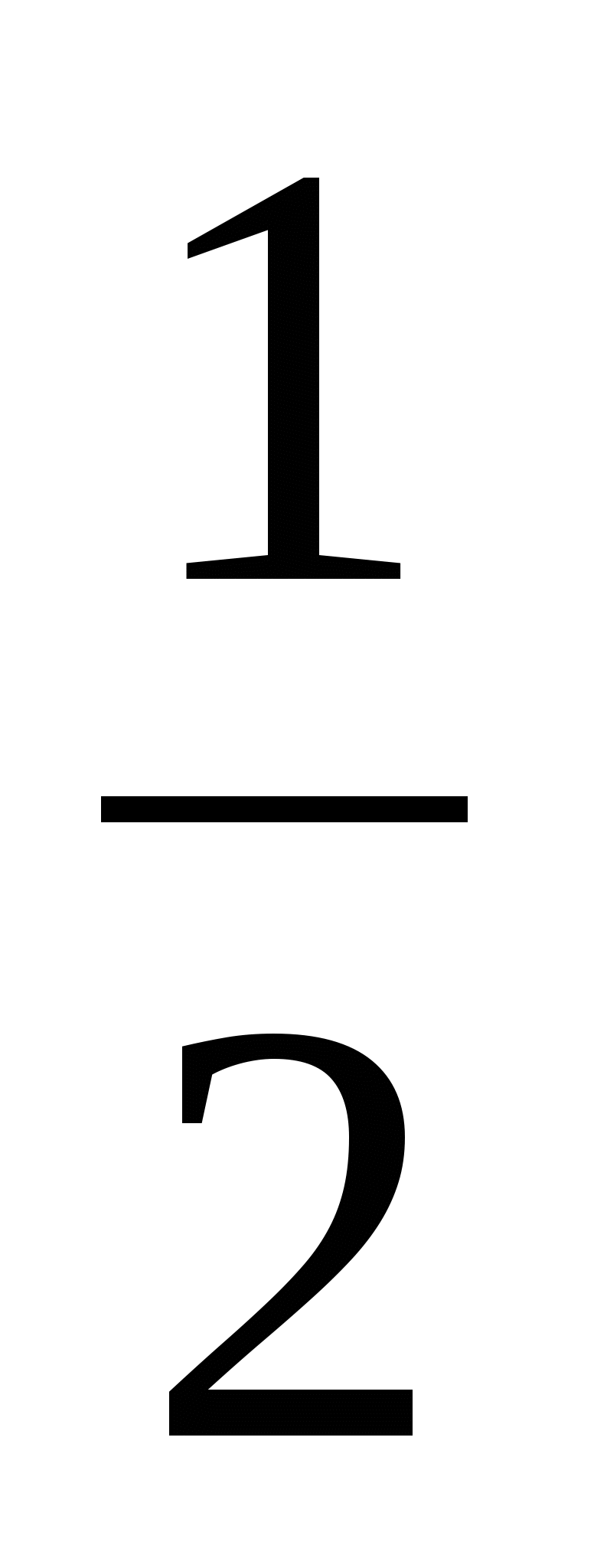 является наибольшим значением функции f(x)=
является наибольшим значением функции f(x)=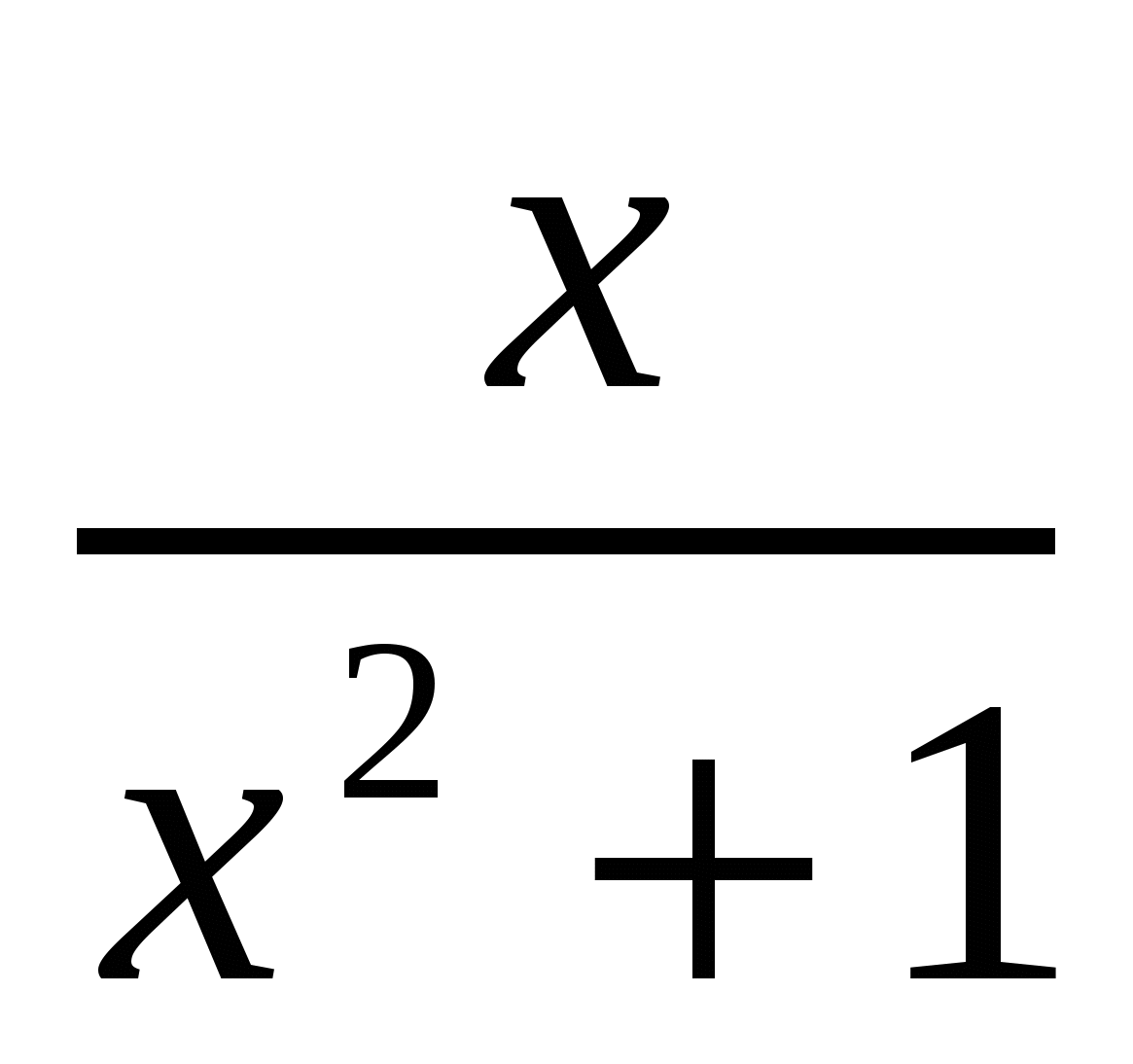 . Тогда f(-1)=
. Тогда f(-1)= 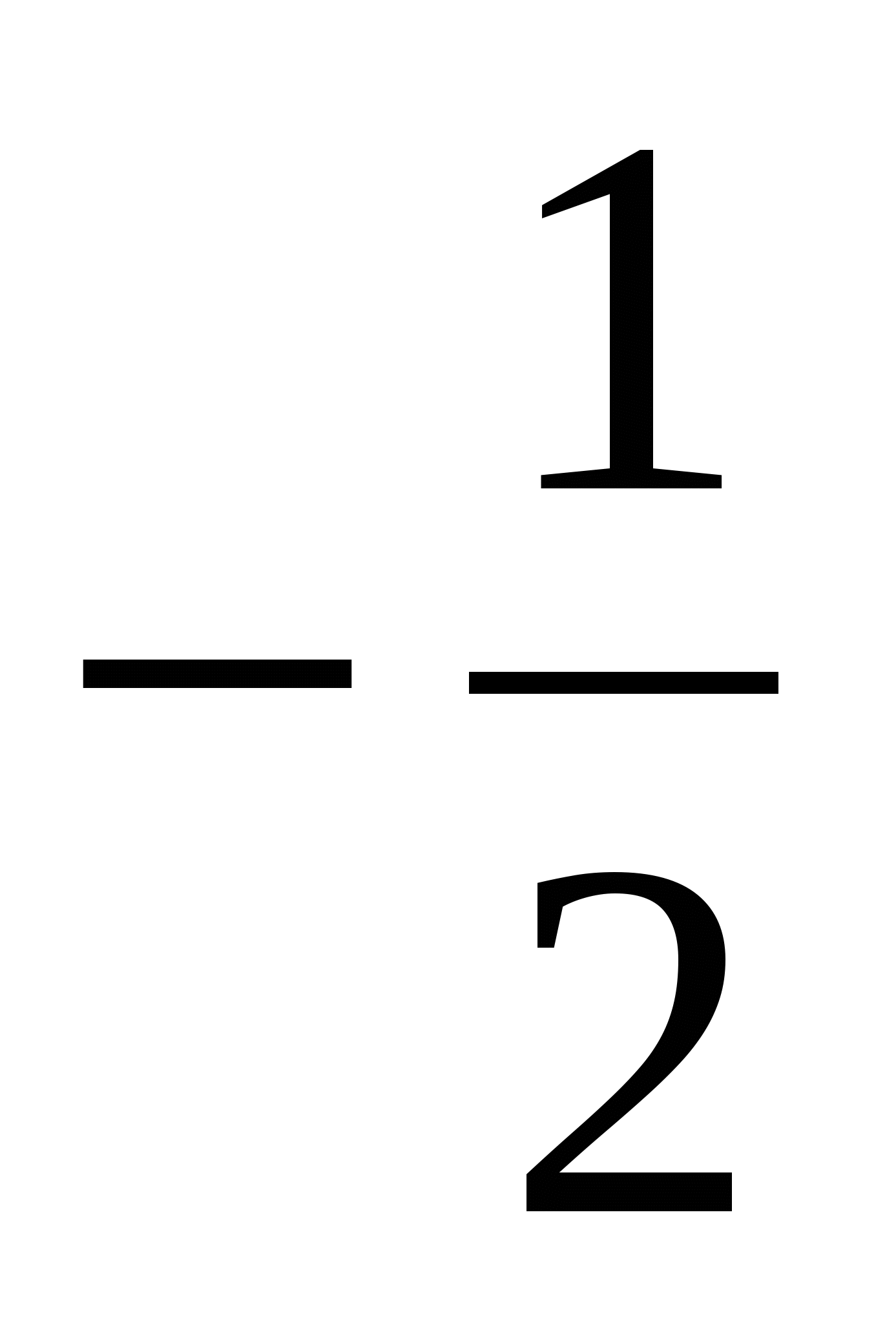 являются её наименьшим значением на интервале
являются её наименьшим значением на интервале 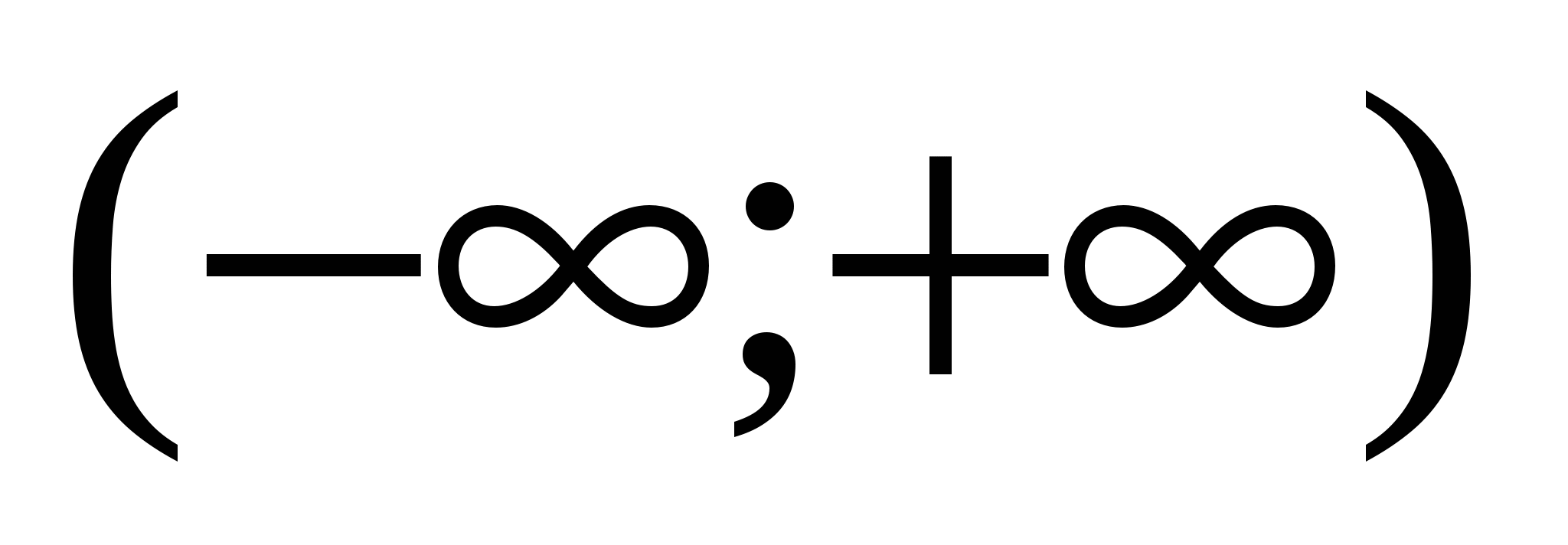 .Отсюда заключаем, что
.Отсюда заключаем, что ![]() , что и требовалось доказать.
, что и требовалось доказать.
Задание 13
Доказать неравенство 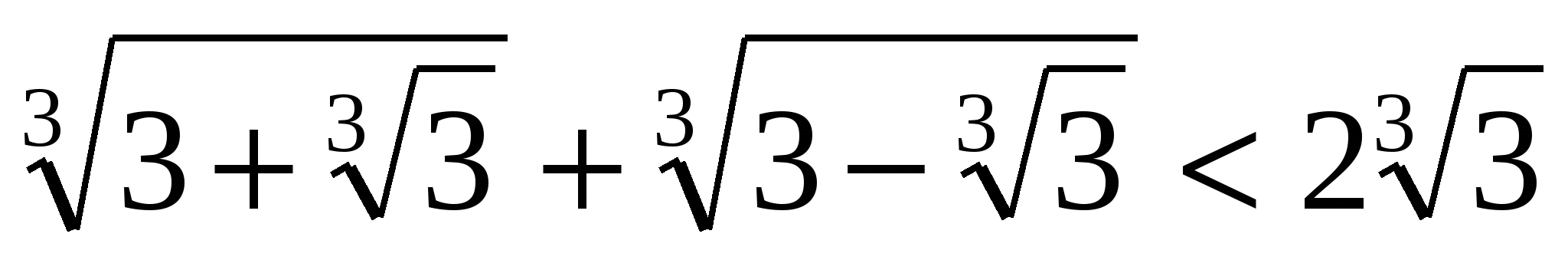 .
.
Рассмотрим функцию f(x)=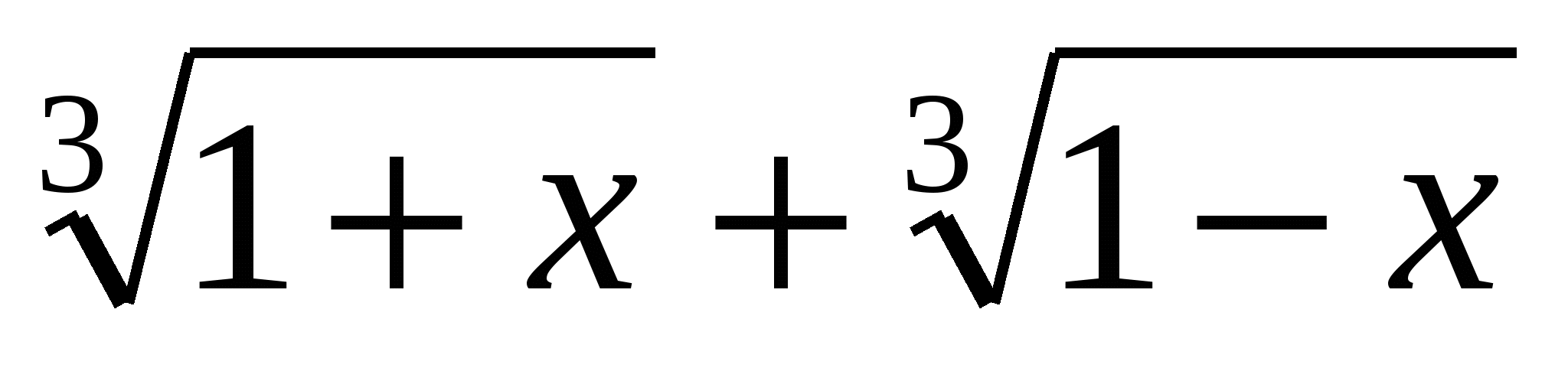 . Она определена на всей числовой оси.
. Она определена на всей числовой оси.
Исследуем её на монотонность. Найдем производную функции:
f(x)=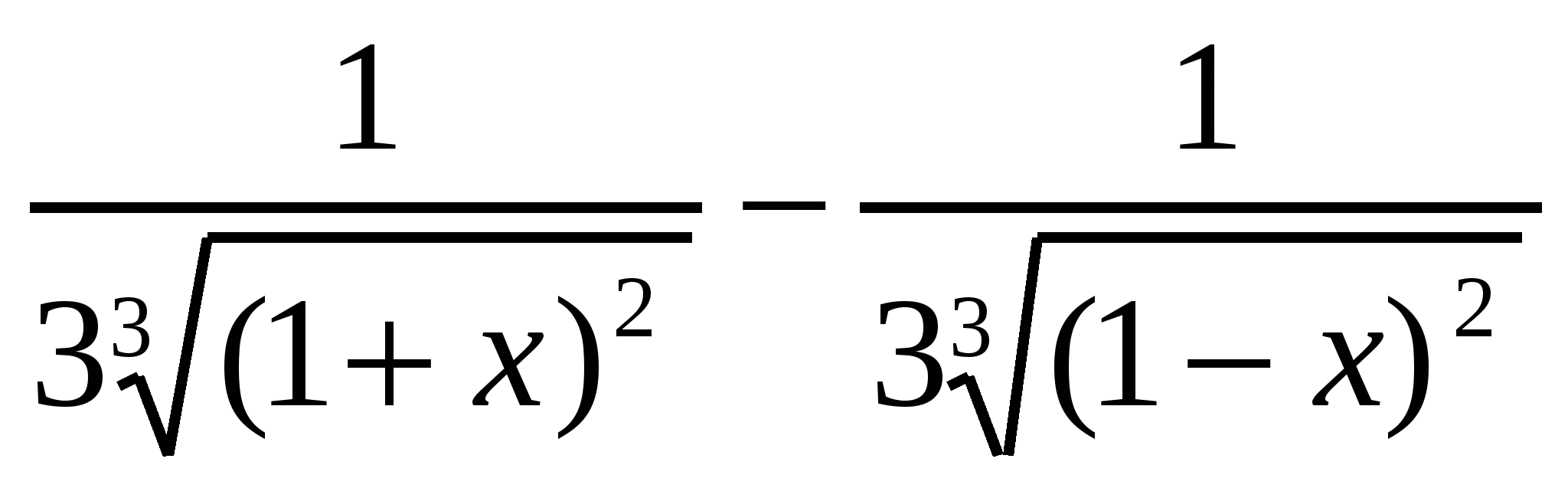 . Так как
. Так как  при x=0,
при x=0, 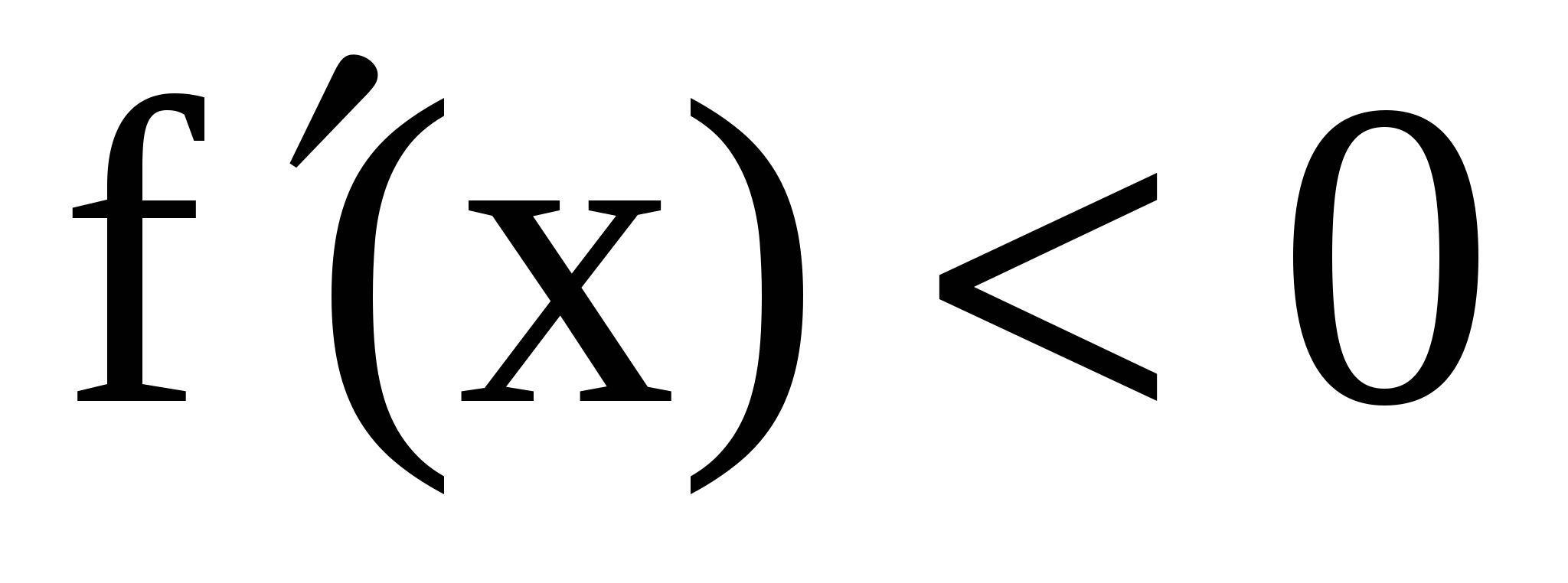 при x>0, то функция f(x) возрастает на промежутке
при x>0, то функция f(x) возрастает на промежутке 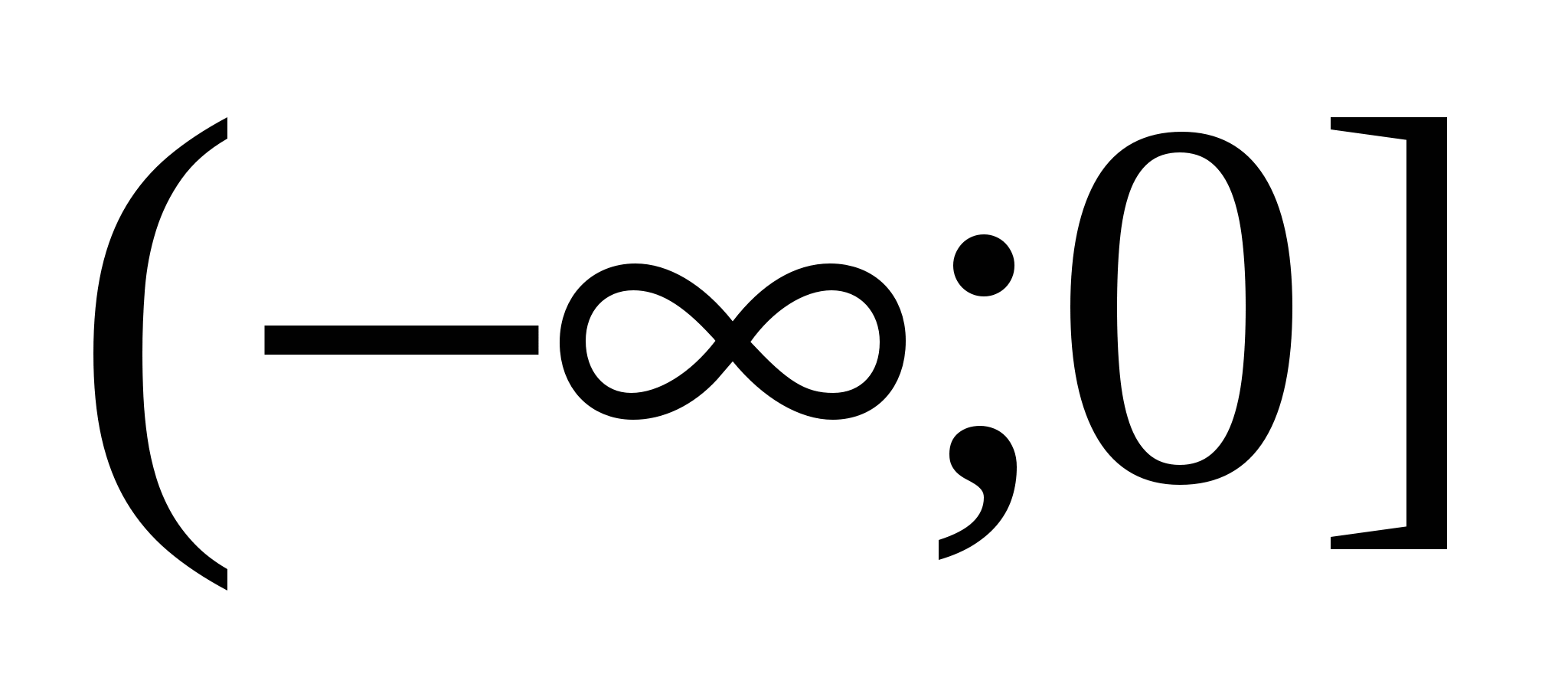 и убывает на промежутке
и убывает на промежутке 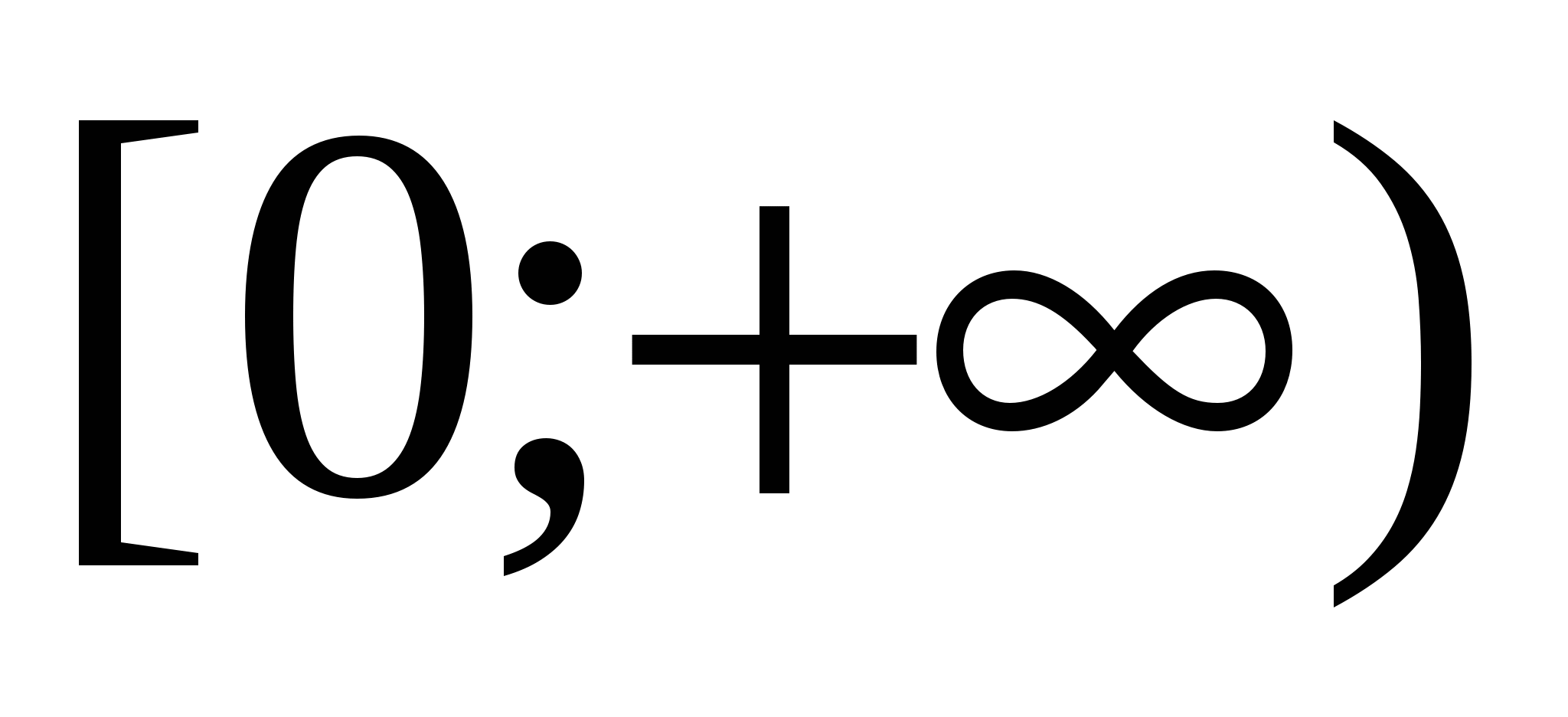 . Следовательно, f(0)=2 - наибольшее значение функции на интервале
. Следовательно, f(0)=2 - наибольшее значение функции на интервале 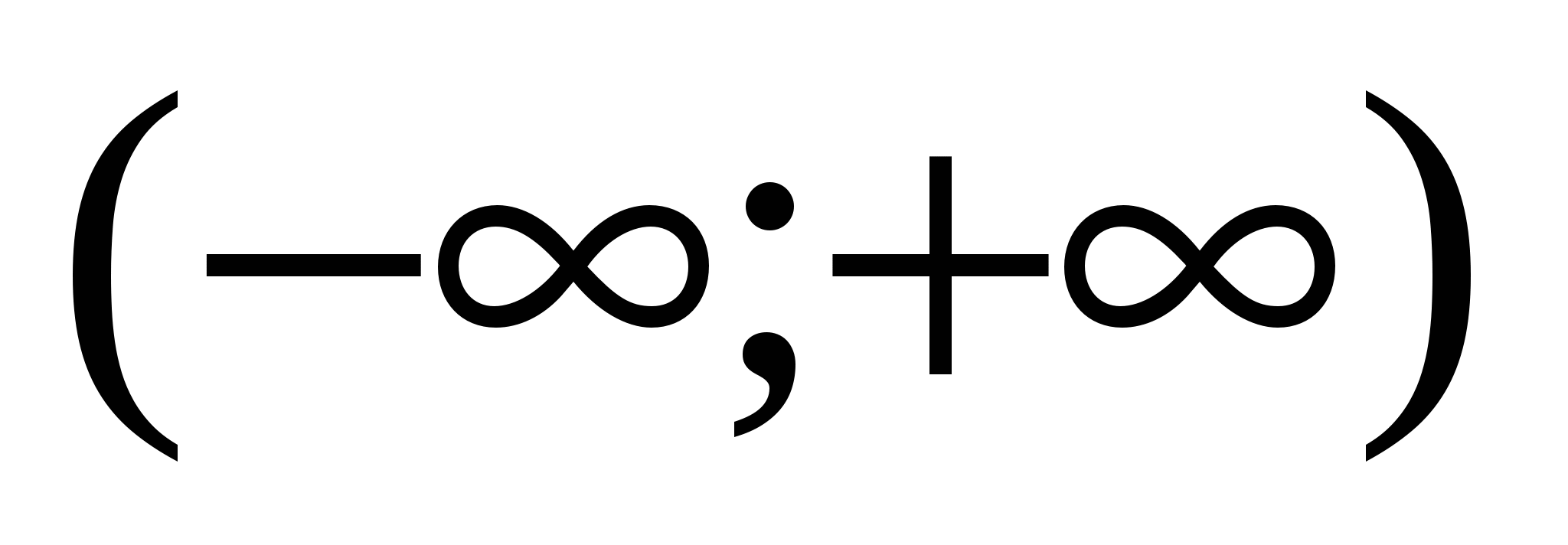 . Поэтому
. Поэтому 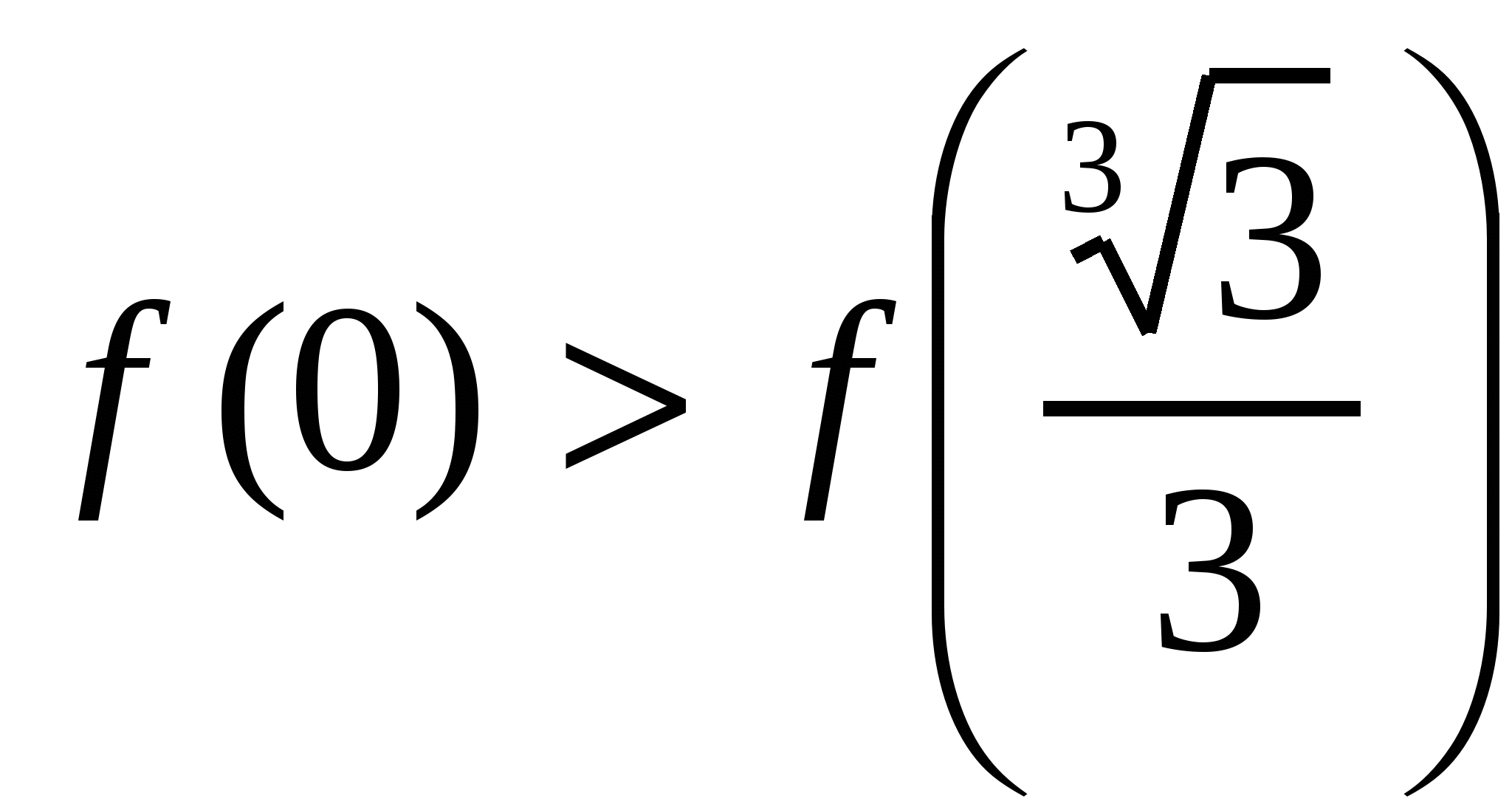 . Так как
. Так как 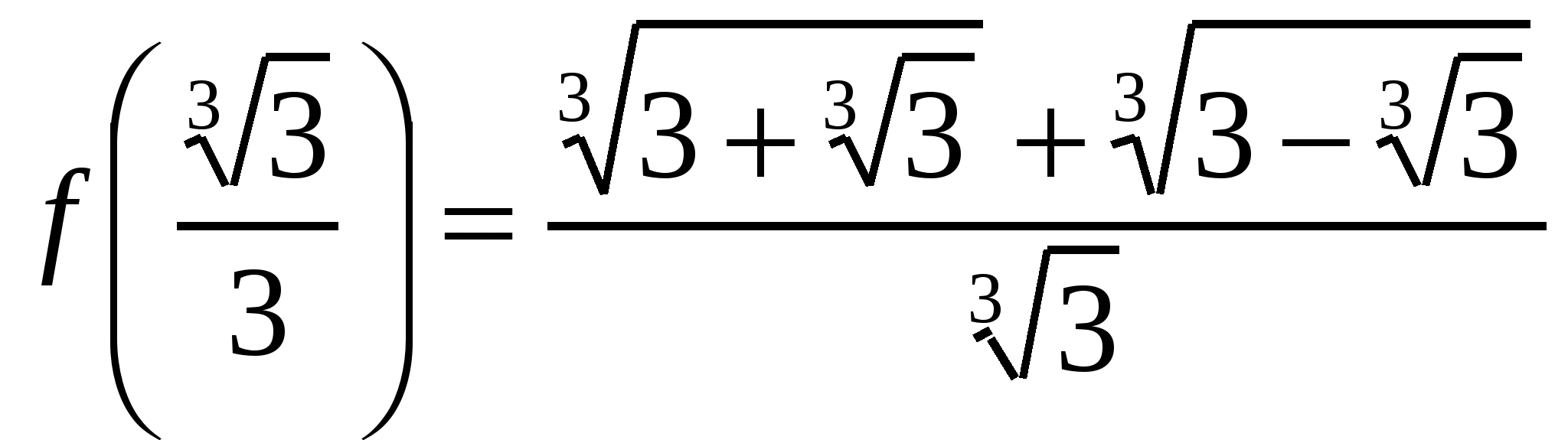 , то последнее неравенство имеет вид
, то последнее неравенство имеет вид 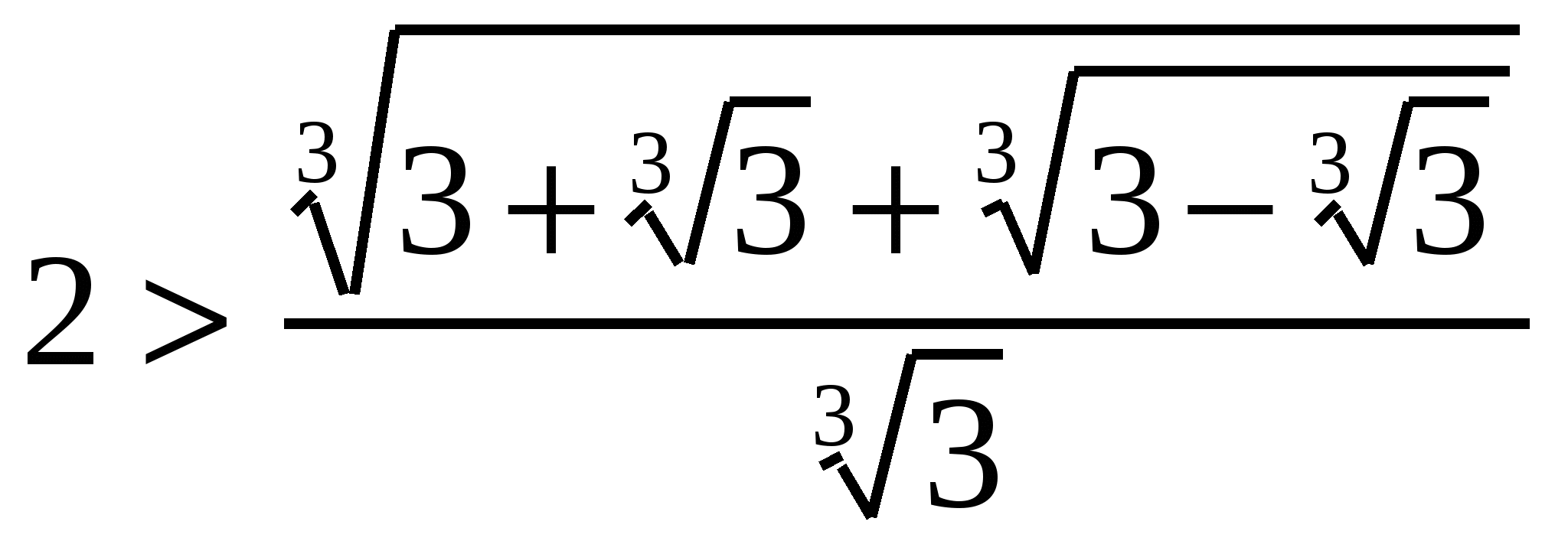 или
или 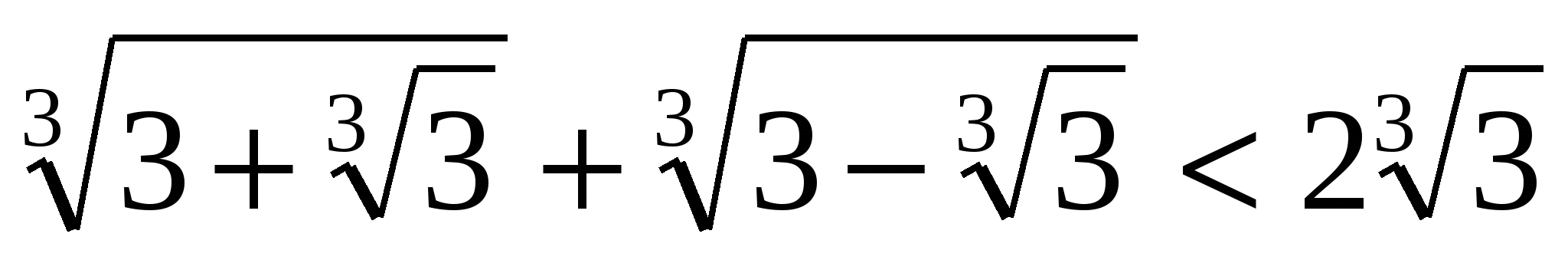 , что и требовалось доказать.
, что и требовалось доказать.
Задание 14
Доказать, что при 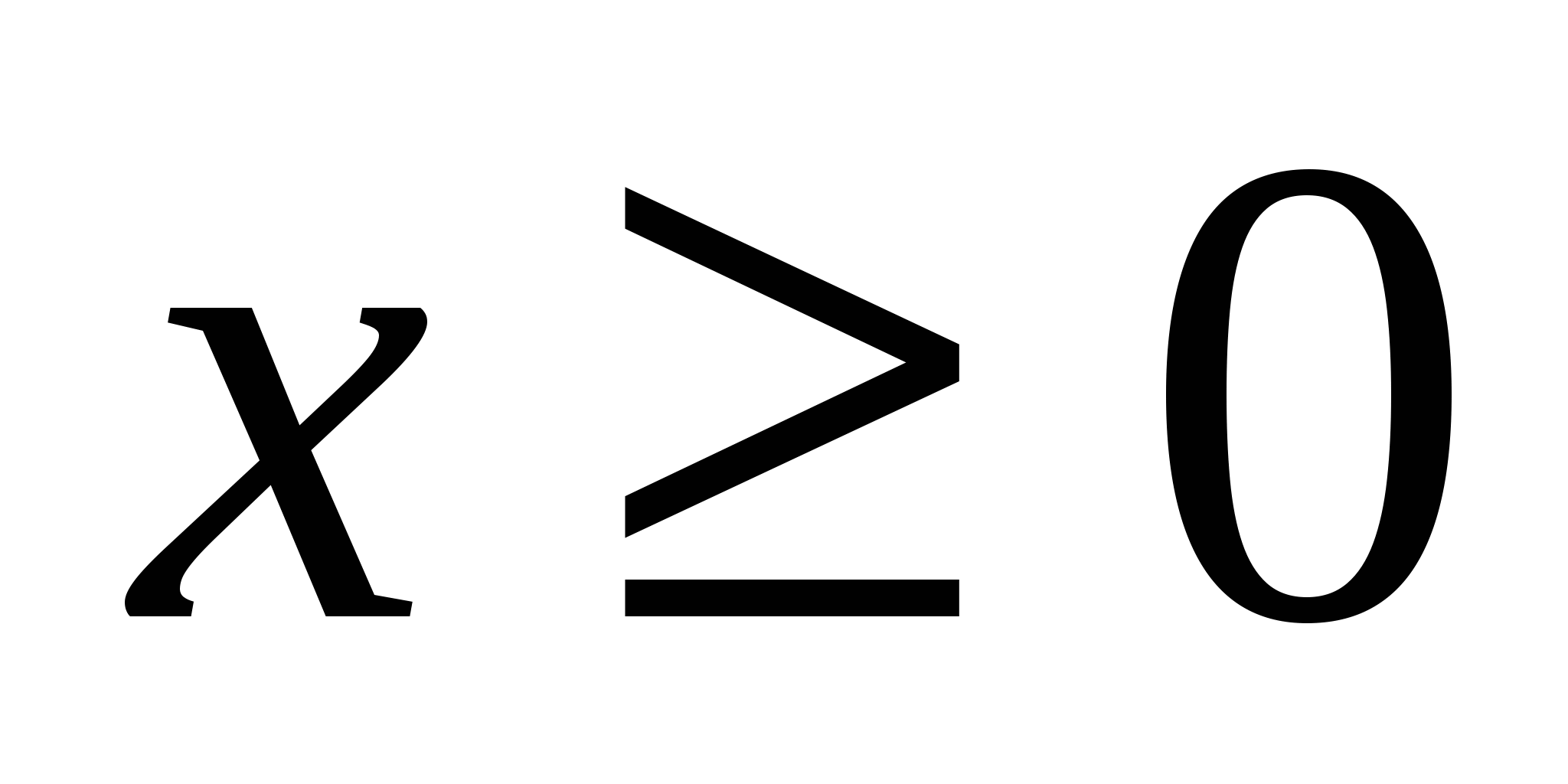 имеют место неравенства:
имеют место неравенства: 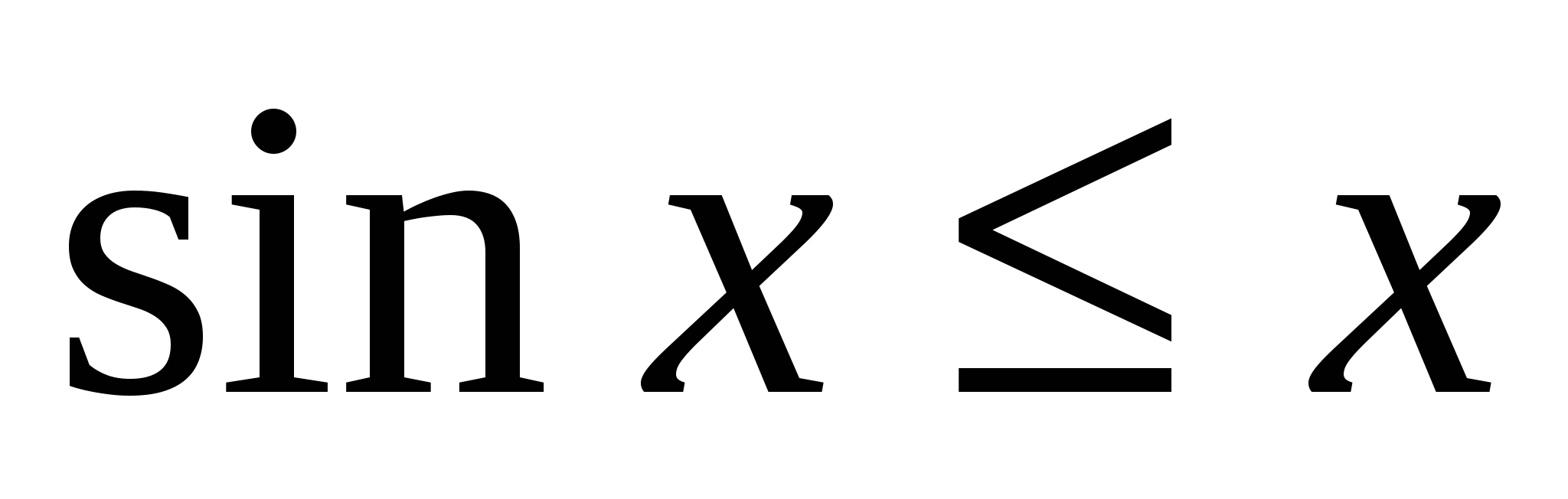 ;
; 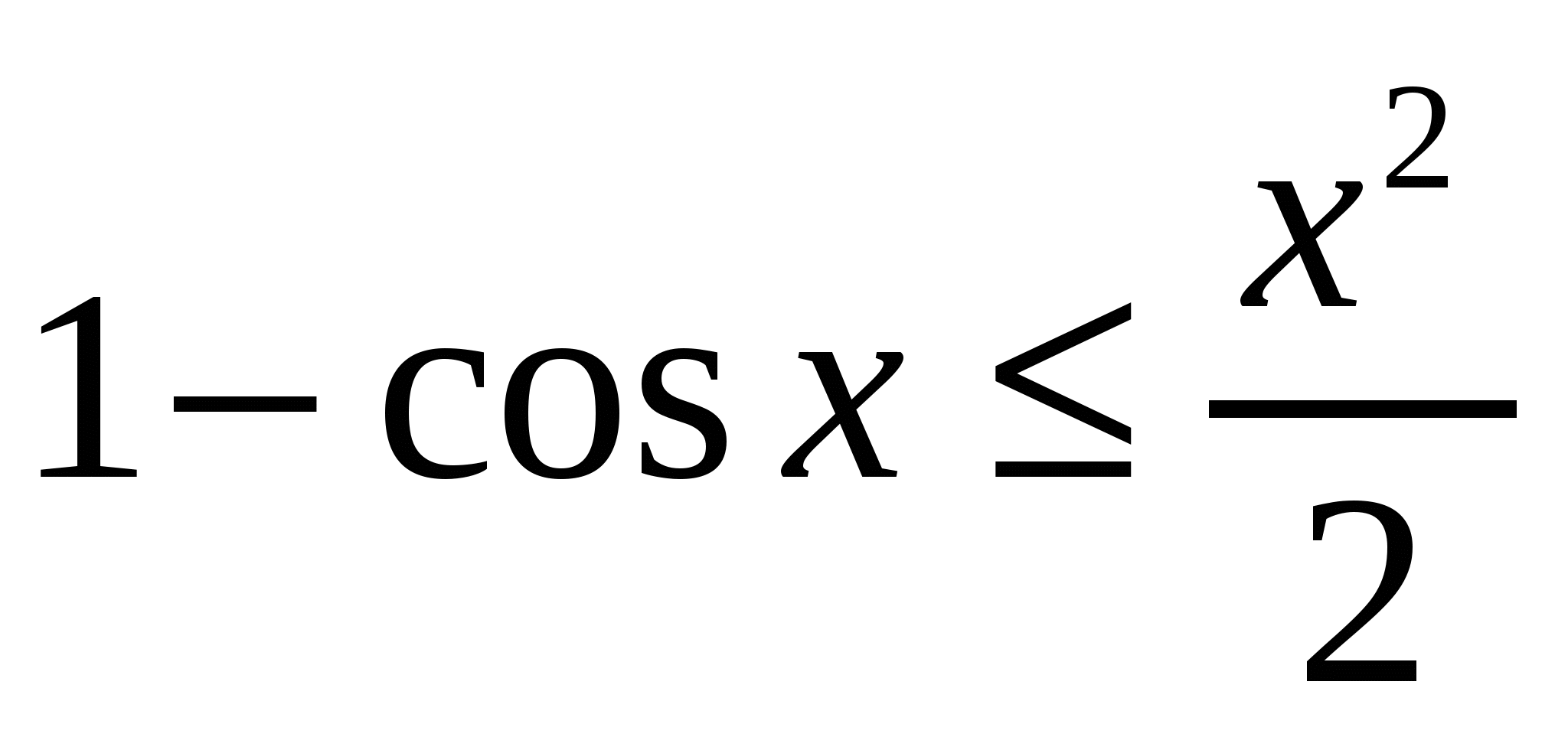 ;
;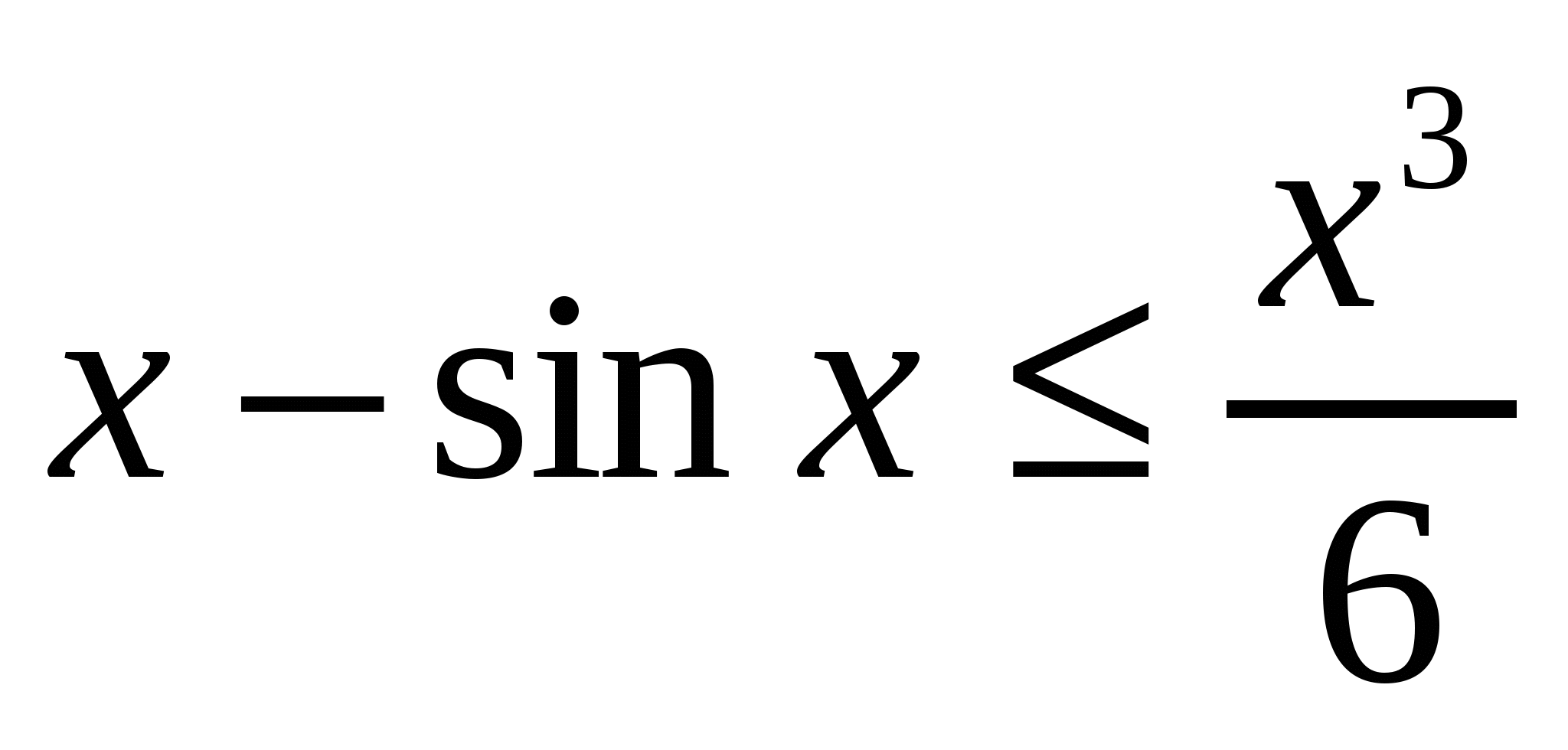 .
.
Решение
При 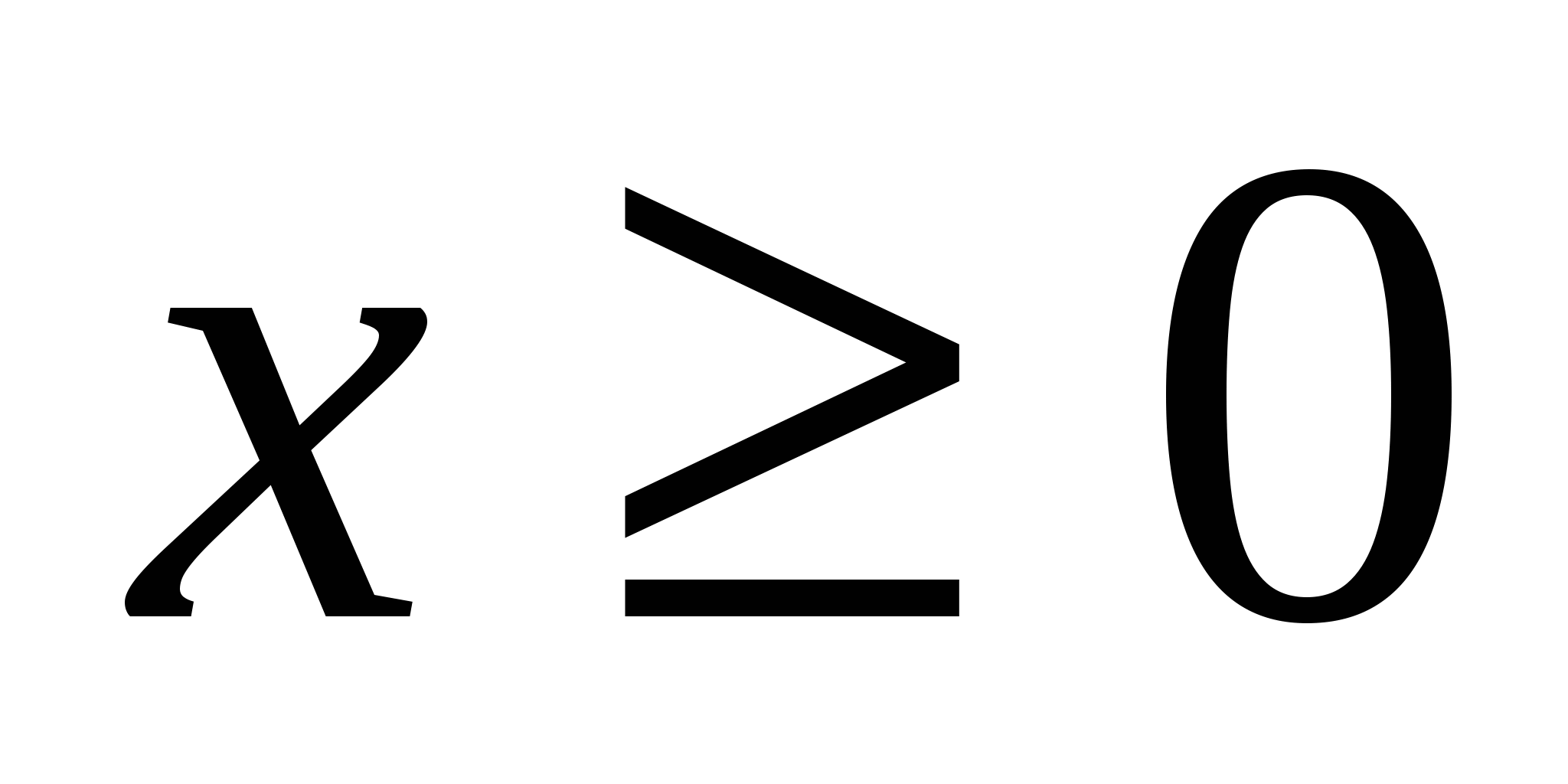 имеем очевидное неравенство
имеем очевидное неравенство 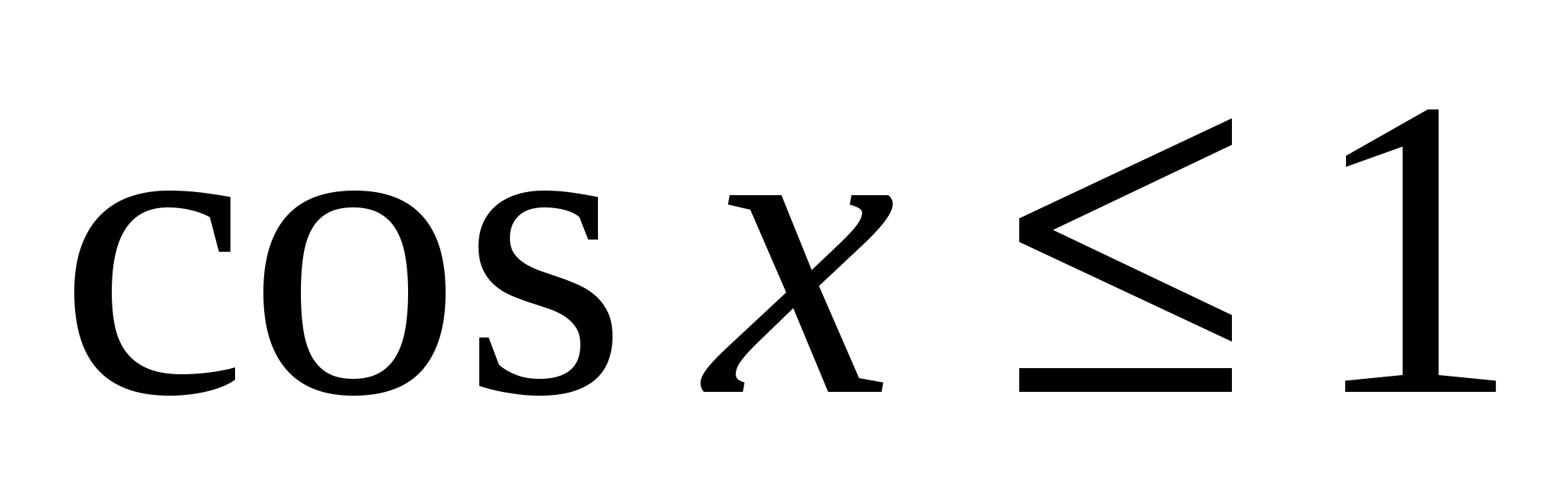 .Применим свойство монотонности интеграла, положив
.Применим свойство монотонности интеграла, положив 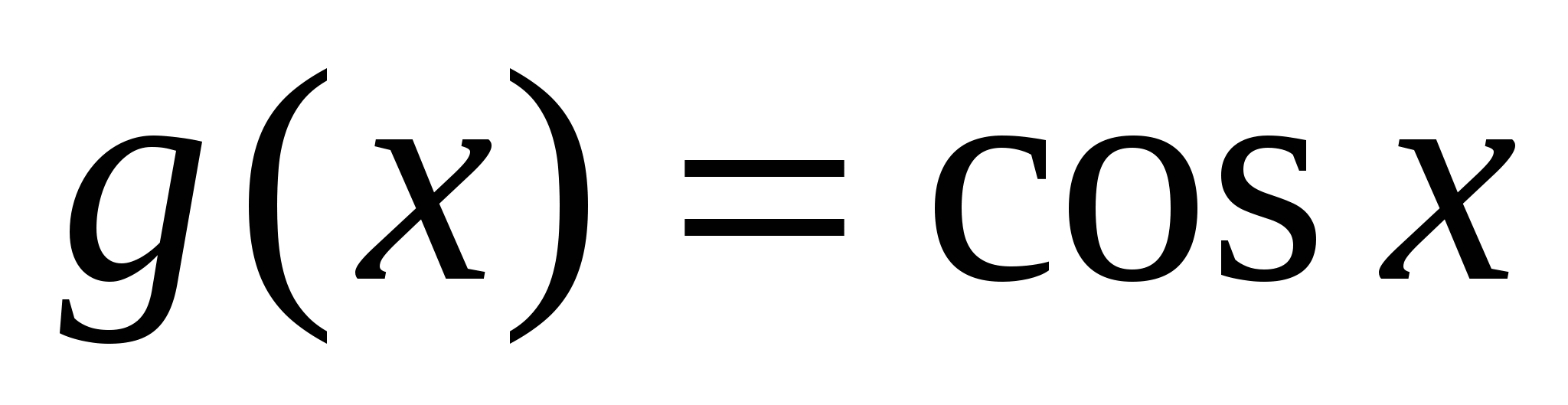 и
и 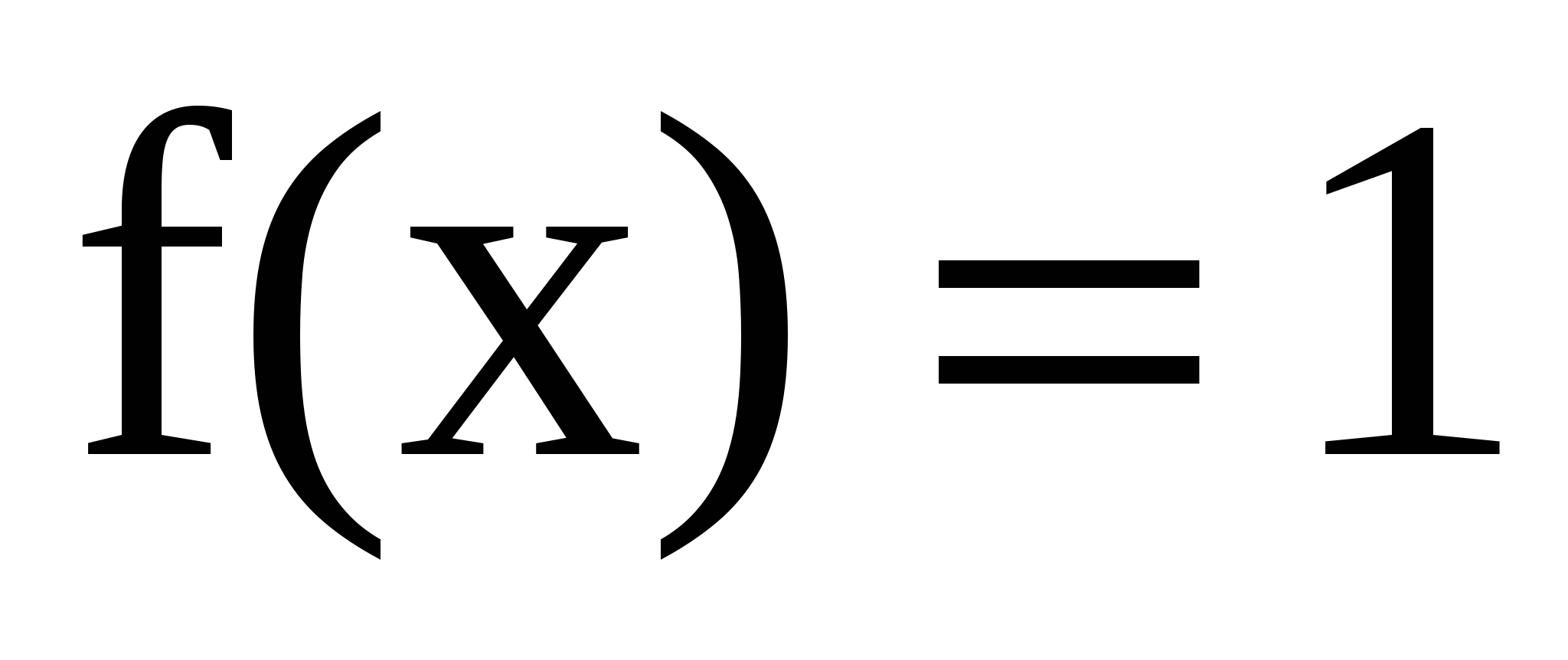 . Функции f и g удовлетворяют всем условиям используемого утверждения на промежутке
. Функции f и g удовлетворяют всем условиям используемого утверждения на промежутке 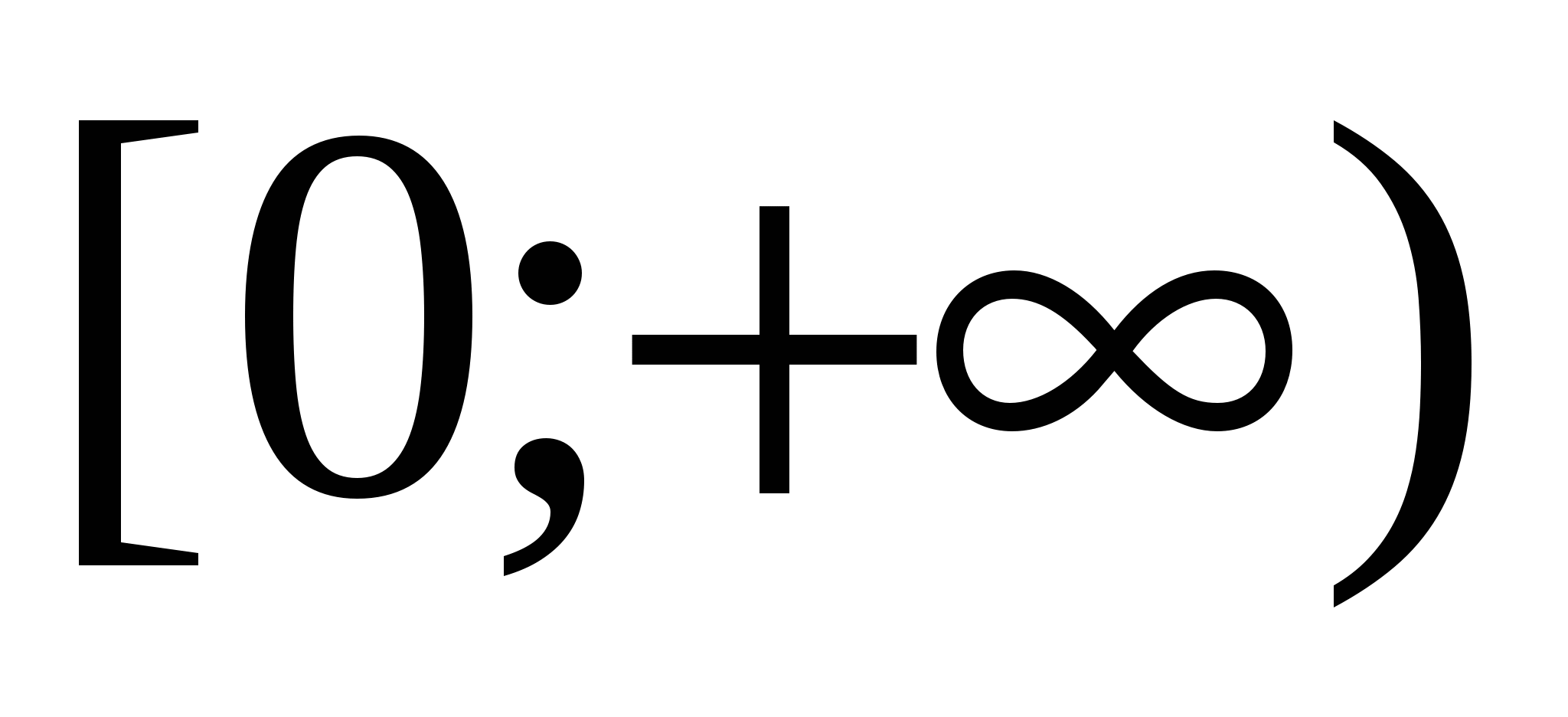 . Поэтому для произвольного x ≥0
. Поэтому для произвольного x ≥0 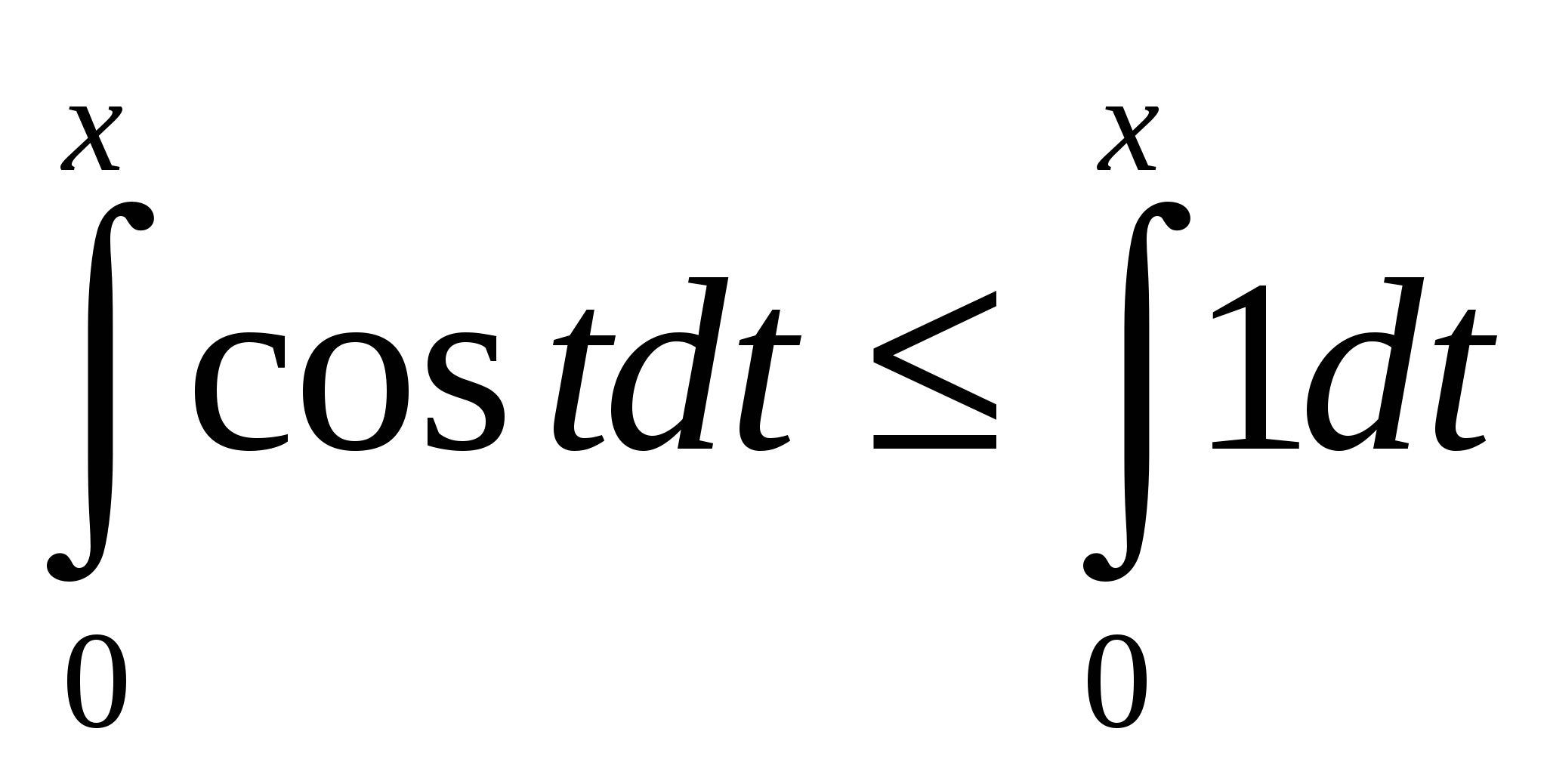 , т. е.
, т. е. 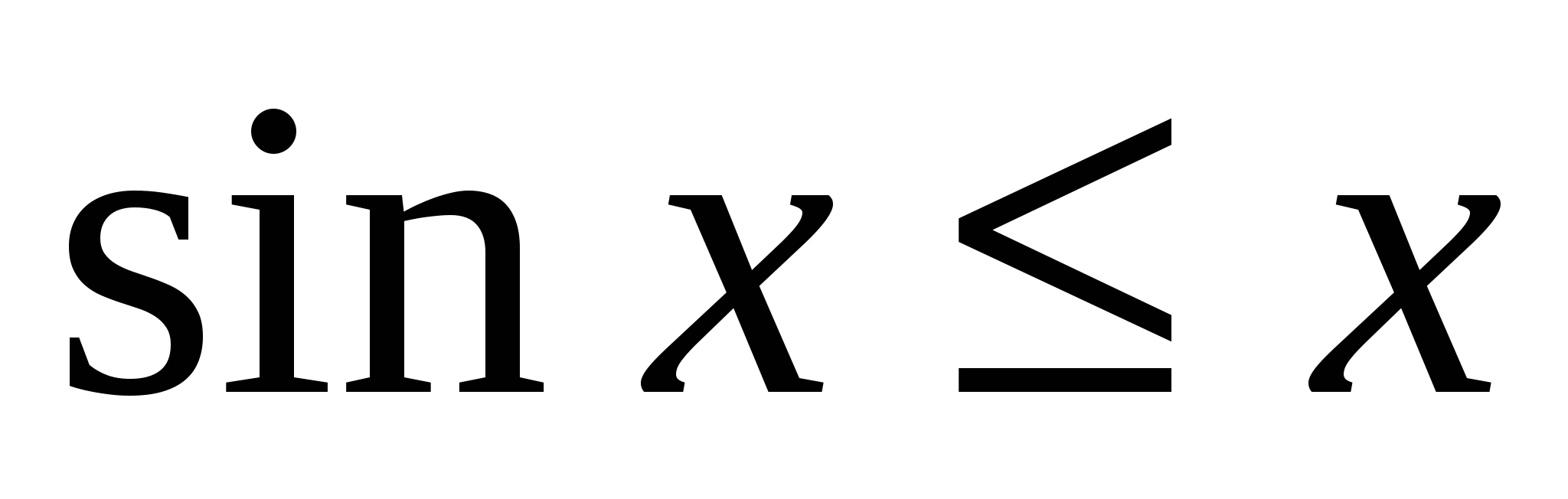 .
.
Применяя тот же метод к полученному неравенству можно записать: ![]() ,или
,или 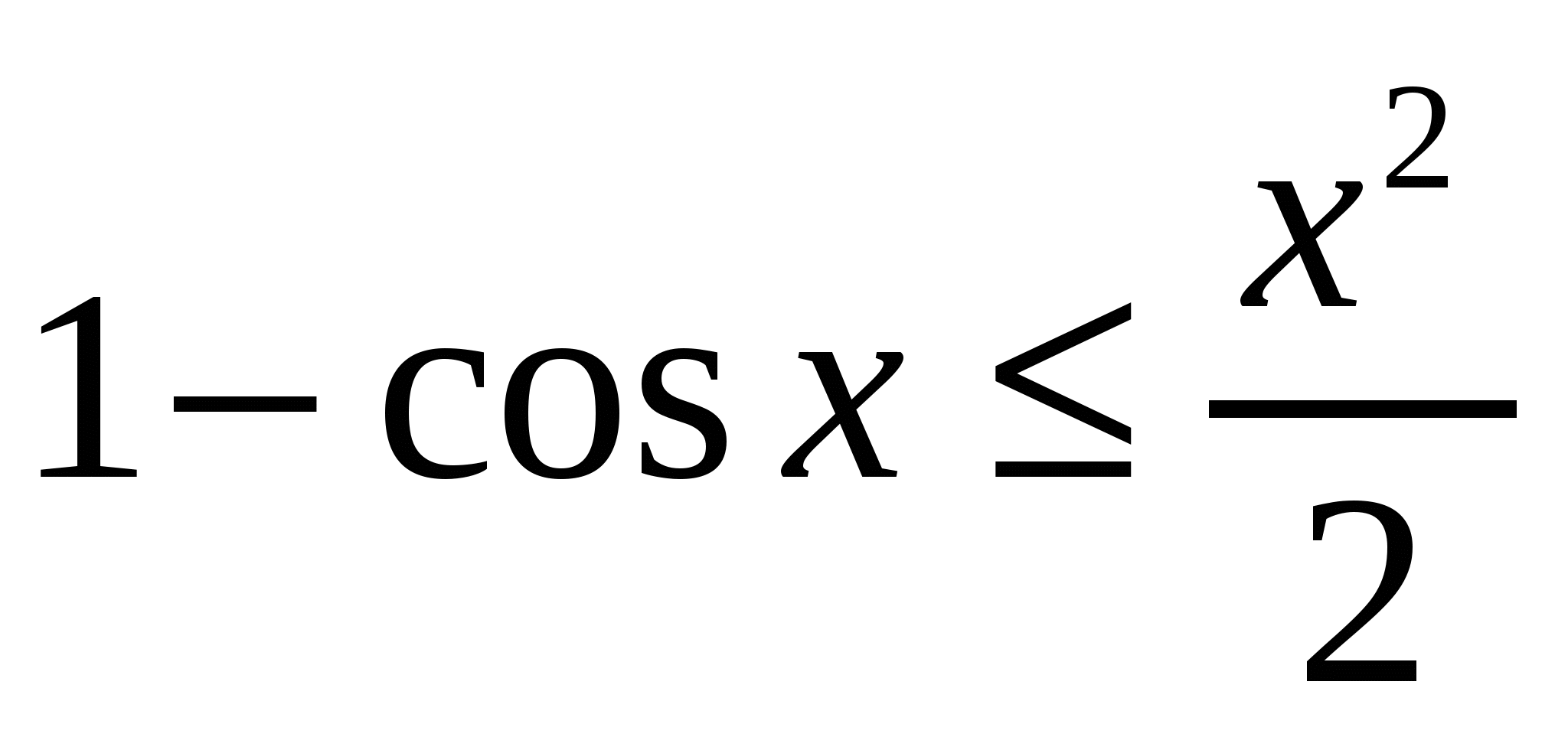 .
.
Ещё раз использую то же утверждение к полученному неравенству, будем иметь 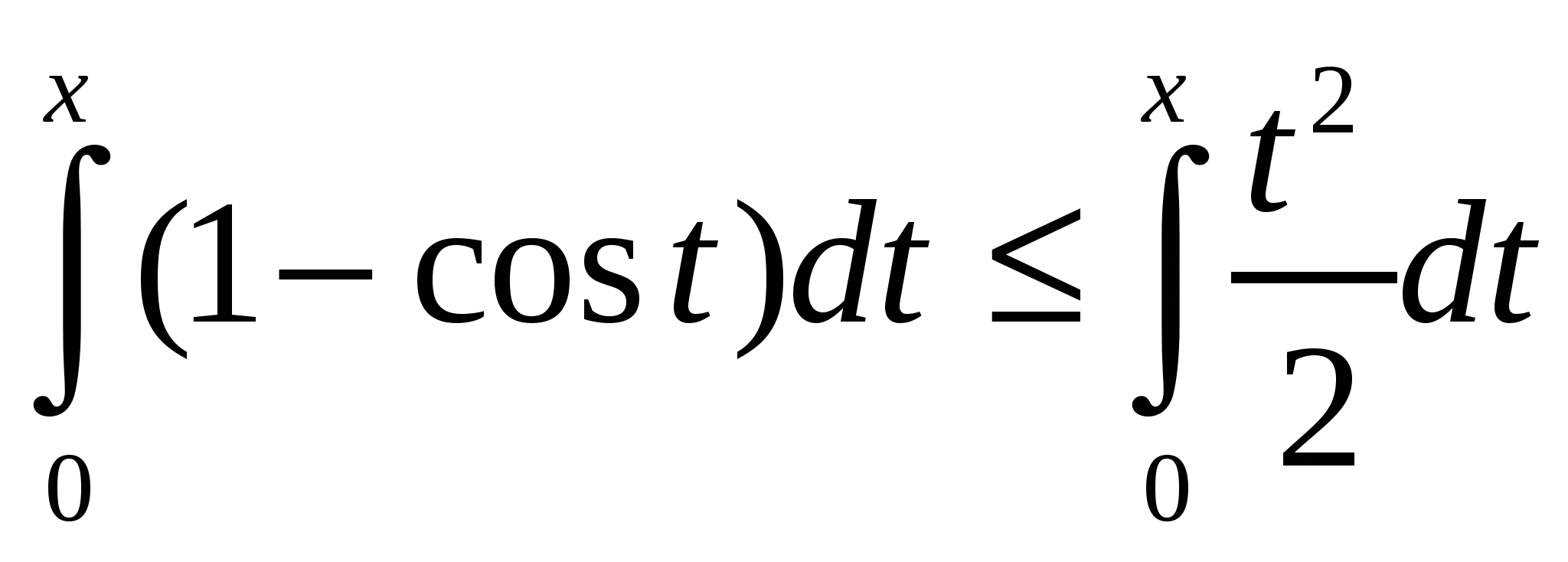 или
или 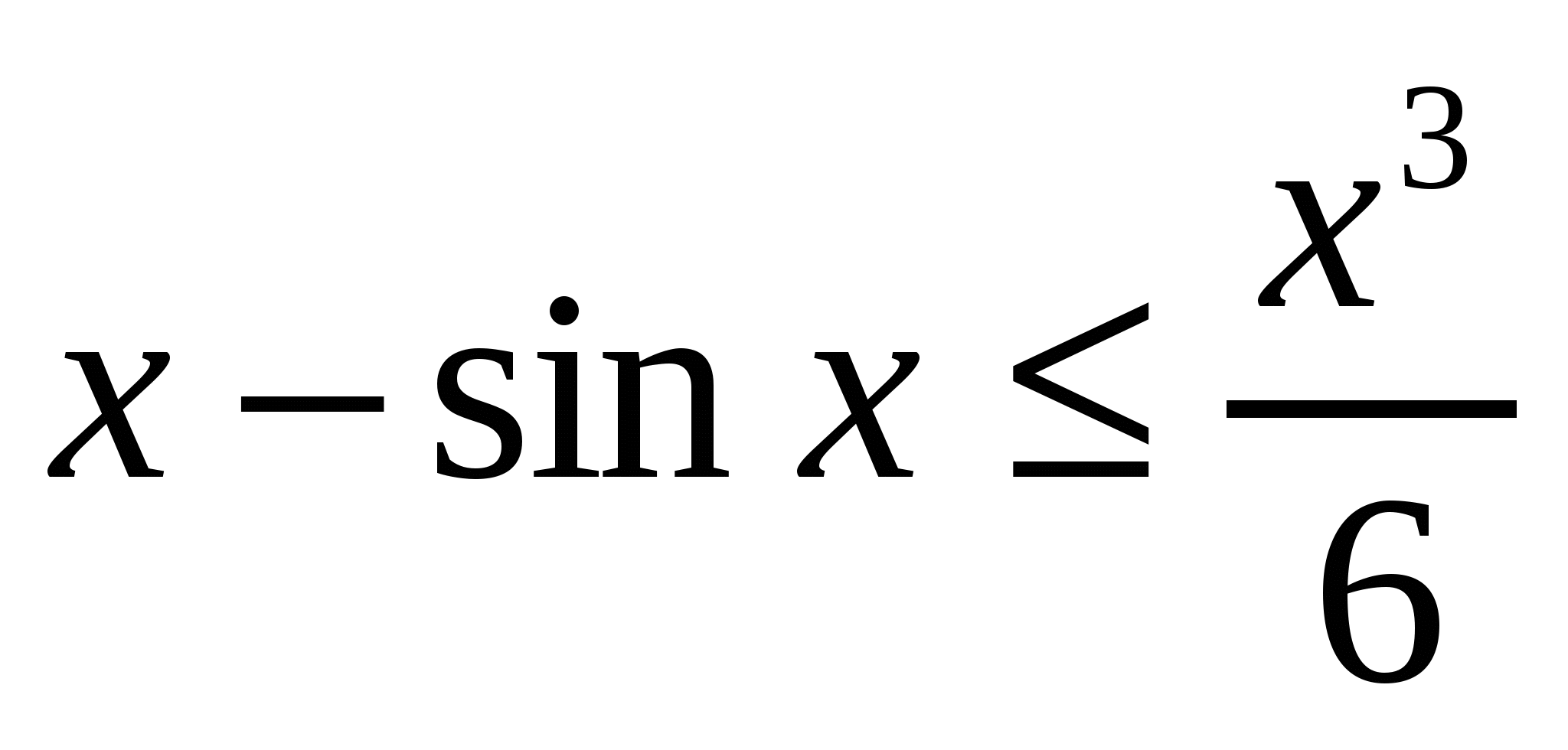 .
.
Задание 15
Два корабля плывут с постоянными скоростями 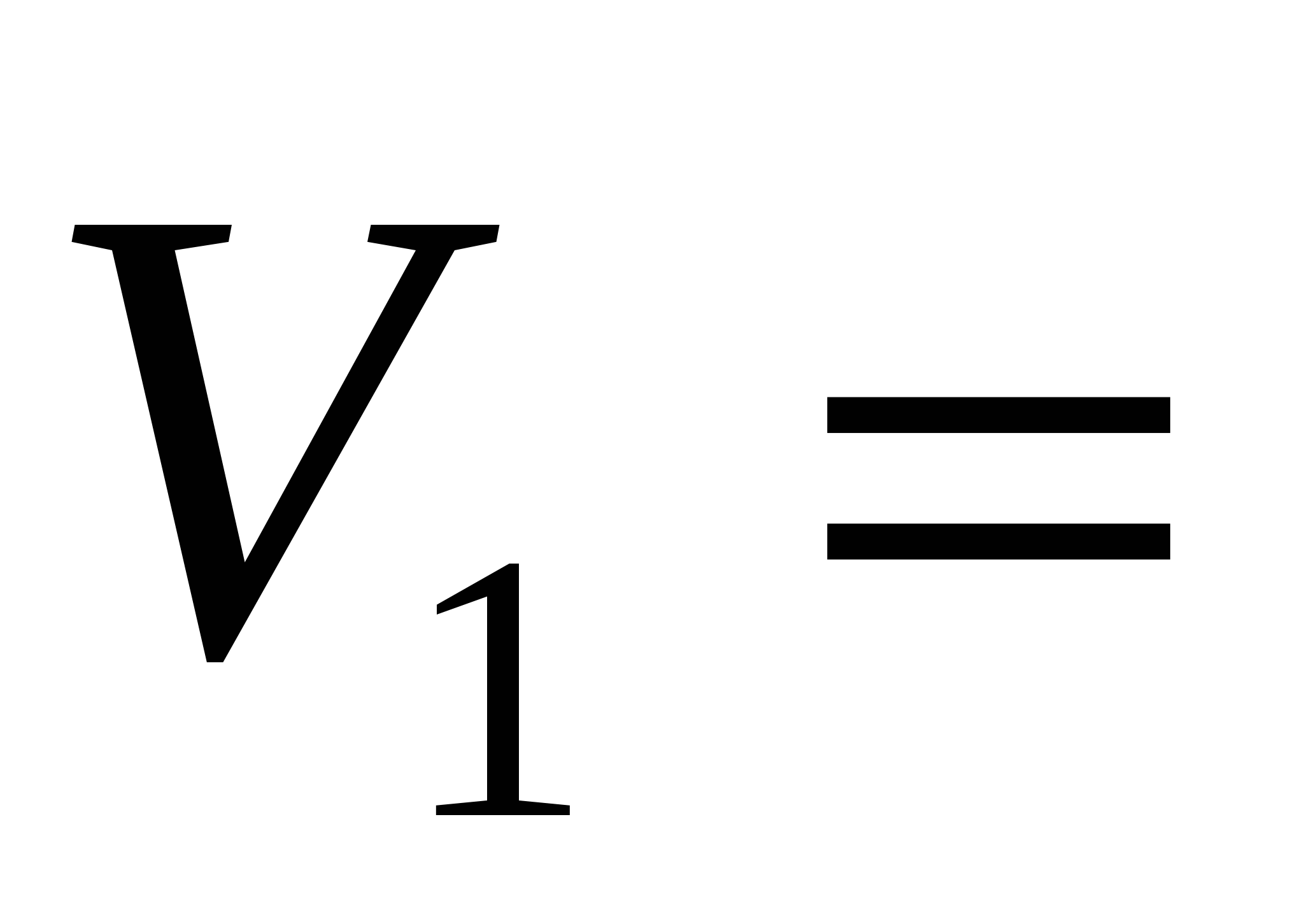 20 км/ч и
20 км/ч и 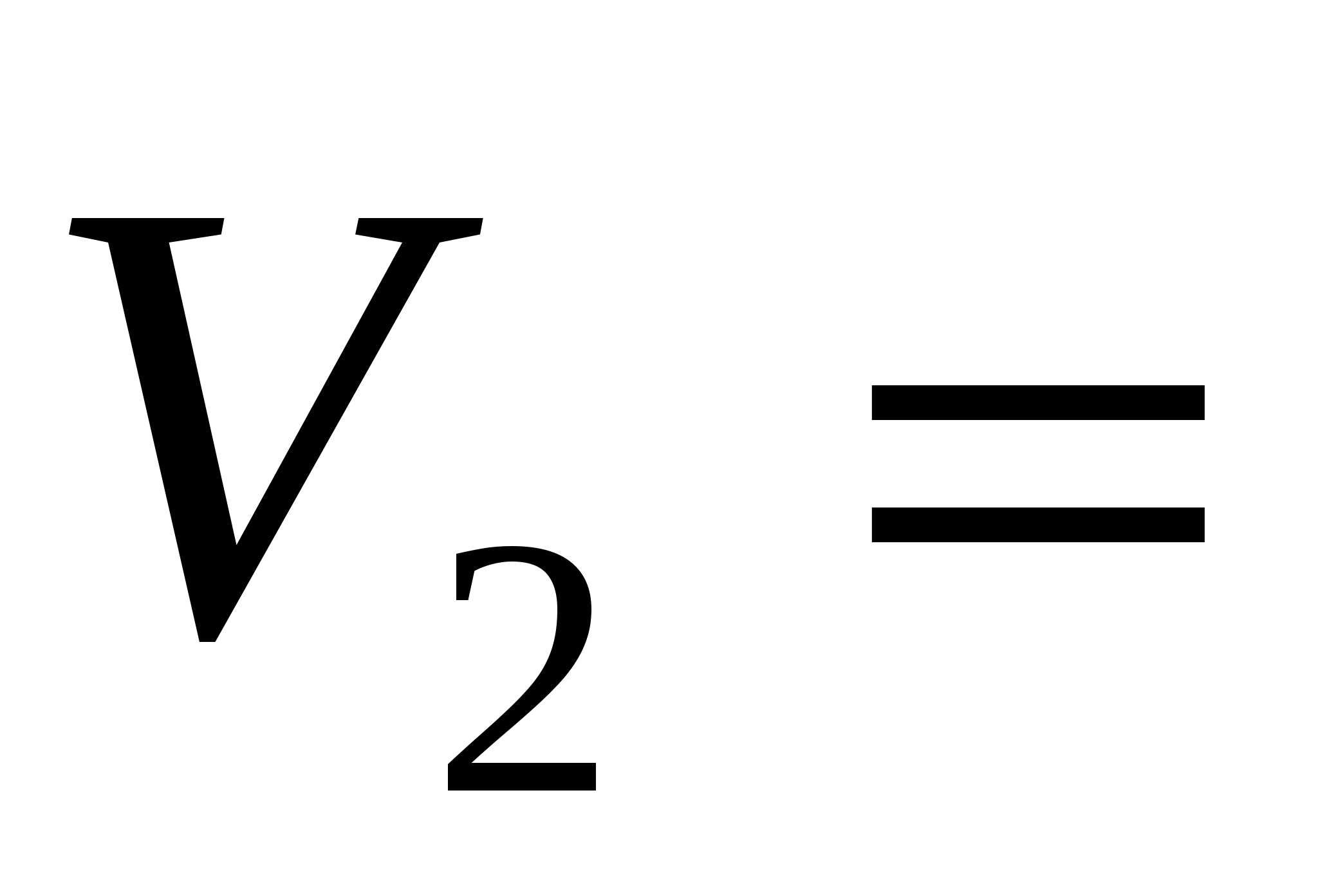 30 км/ч по прямым, угол между которыми 60°, в направлении точки пересечения этих прямых. Найдите наименьшее расстояние между кораблями, если в начальный момент времени расстояние кораблей от точки пересечения прямых были соответственно 10 км и 20 км.
30 км/ч по прямым, угол между которыми 60°, в направлении точки пересечения этих прямых. Найдите наименьшее расстояние между кораблями, если в начальный момент времени расстояние кораблей от точки пересечения прямых были соответственно 10 км и 20 км.
Пусть через t часов от начального момента первый корабль окажется в точке А,
второй - в точке В, R(t) км- расстояние АВ.
По условию ВС=20 - 30t, AC=10-20t. Тогда по теореме косинусов имеем 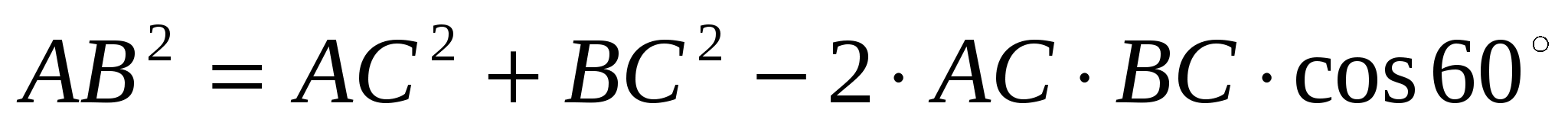 или
или
![]() .
.
Следовательно, 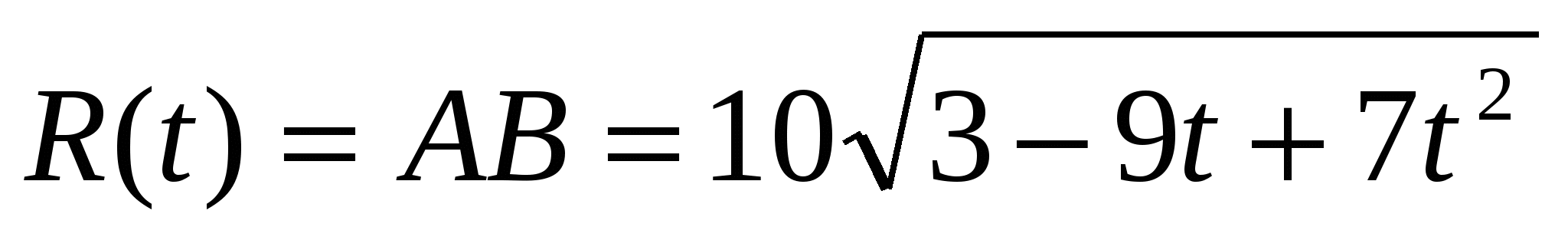 .
.
Требуется найти наименьшее значение этой функции на промежутке 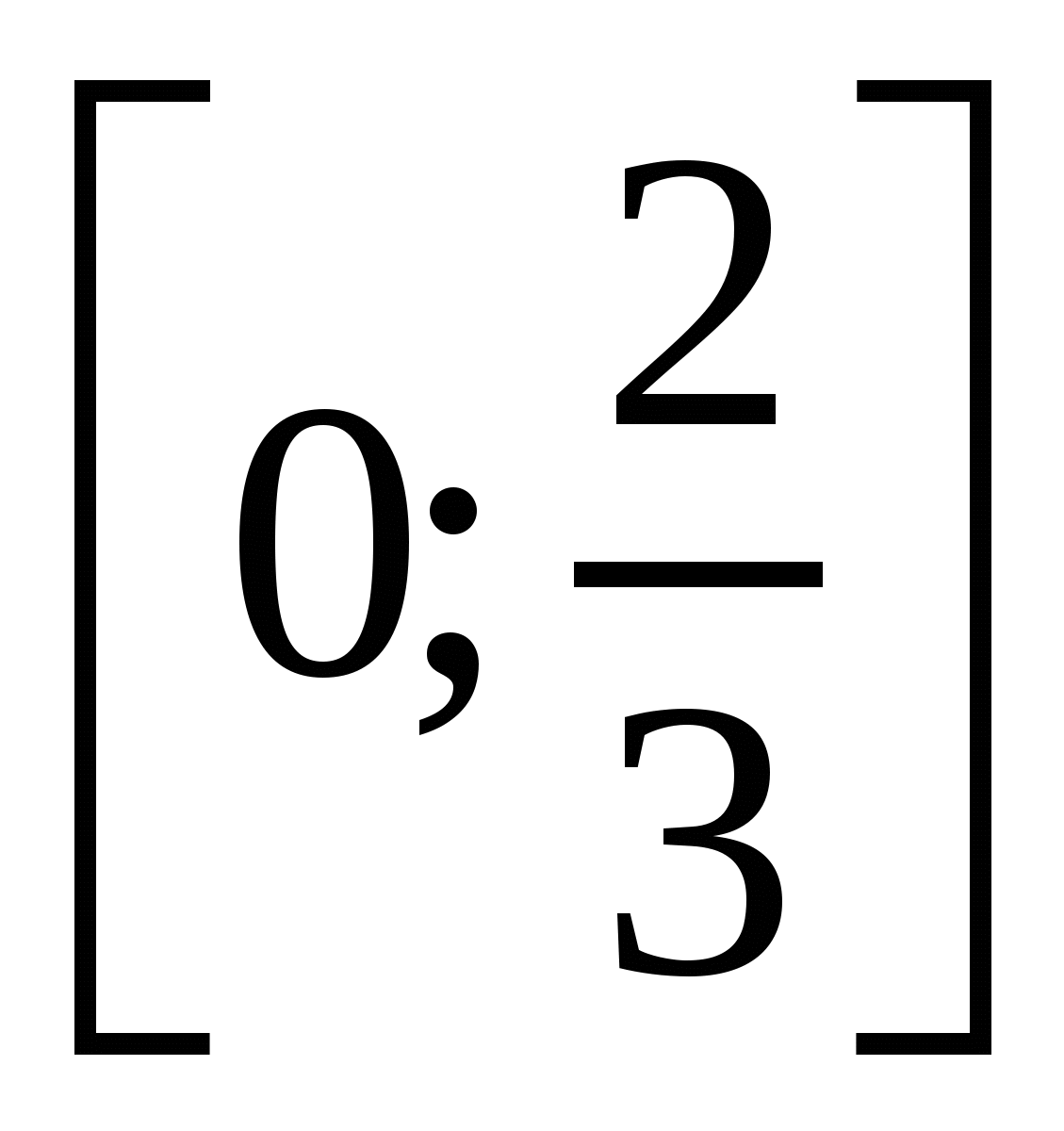 . Функция R(t) определена и дифференцируема на всей числовой оси, причем
. Функция R(t) определена и дифференцируема на всей числовой оси, причем 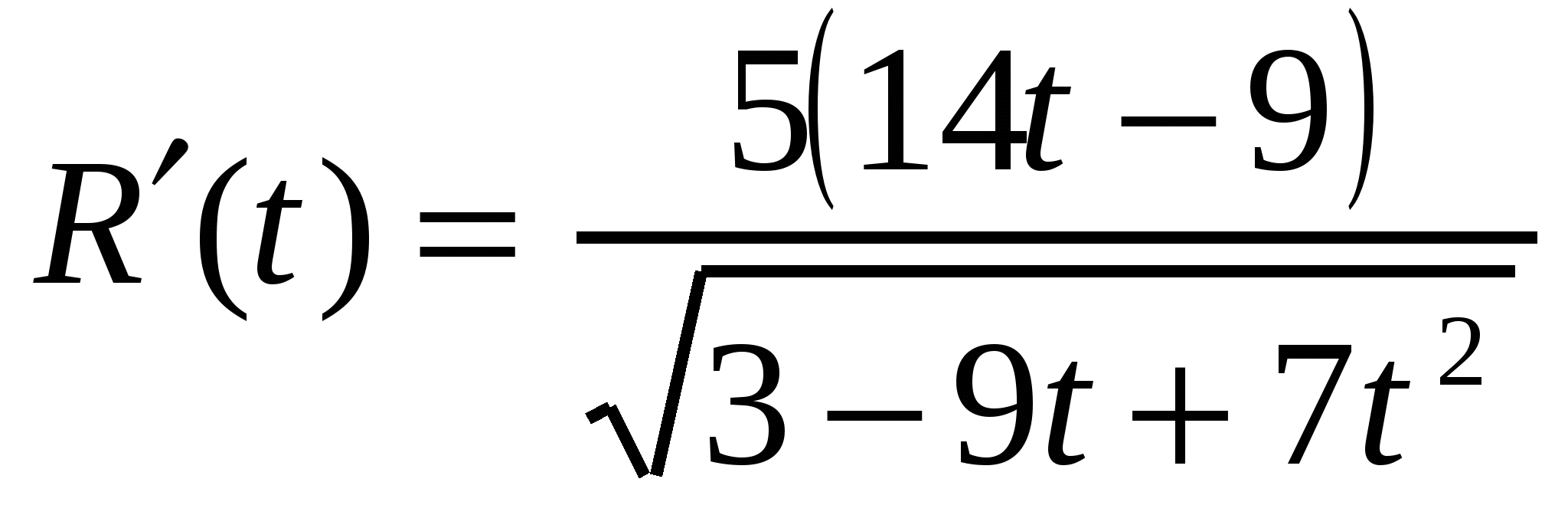 . Следовательно,
. Следовательно, ![]() - единственная на
- единственная на ![]() критическая точка, которая является точкой минимума, так как
критическая точка, которая является точкой минимума, так как 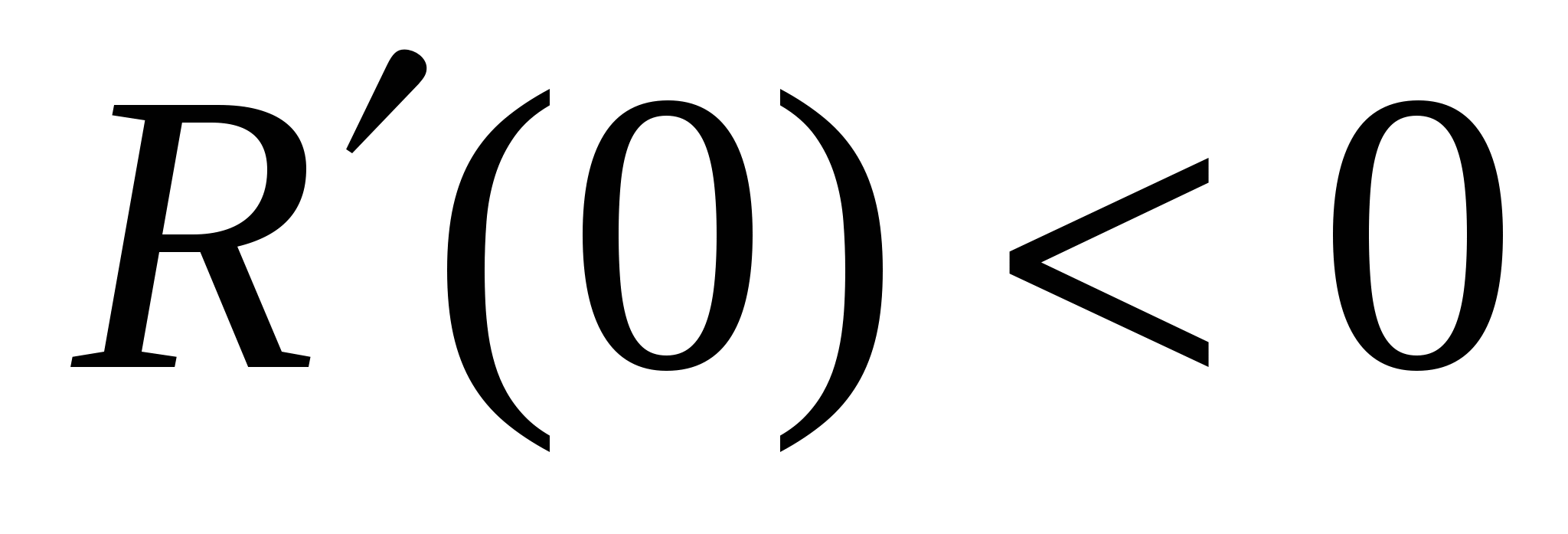 , а
, а 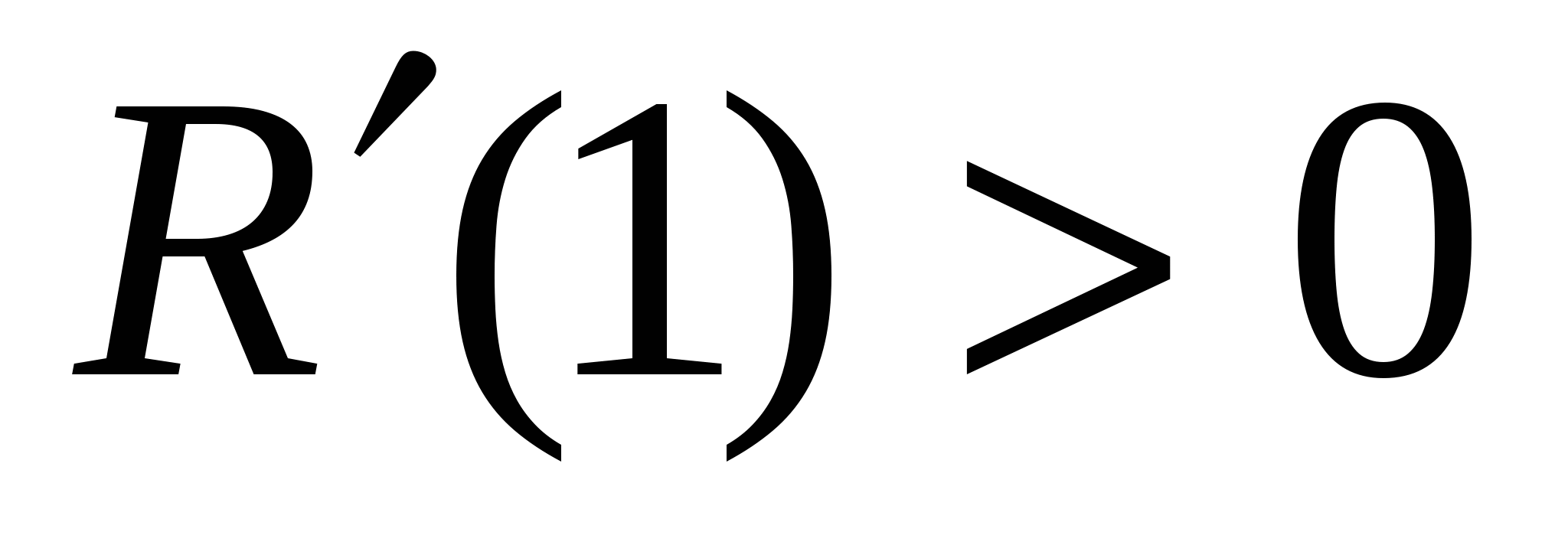 . Значит,
. Значит, 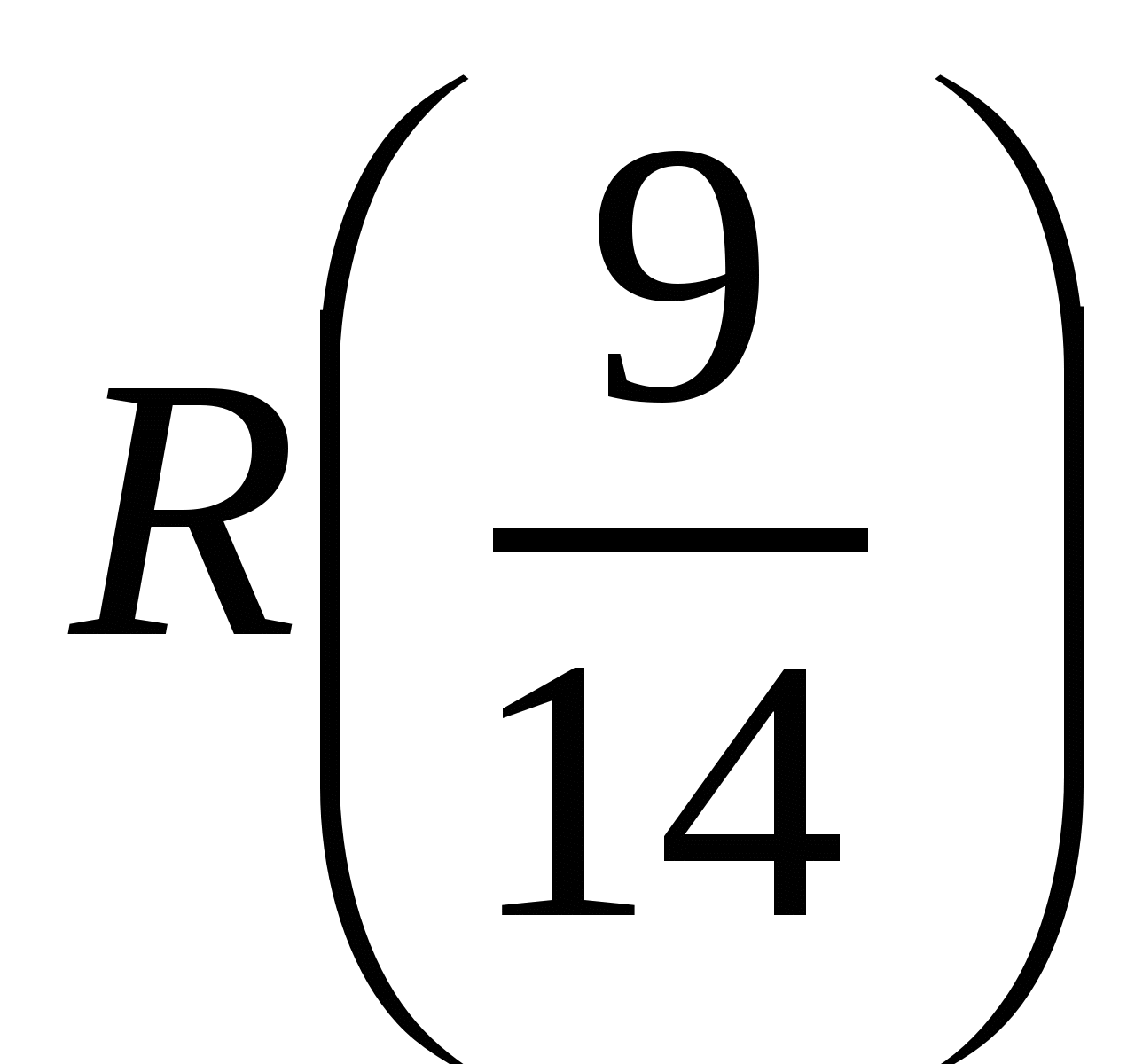 - минимальное расстояние между кораблями,
- минимальное расстояние между кораблями, 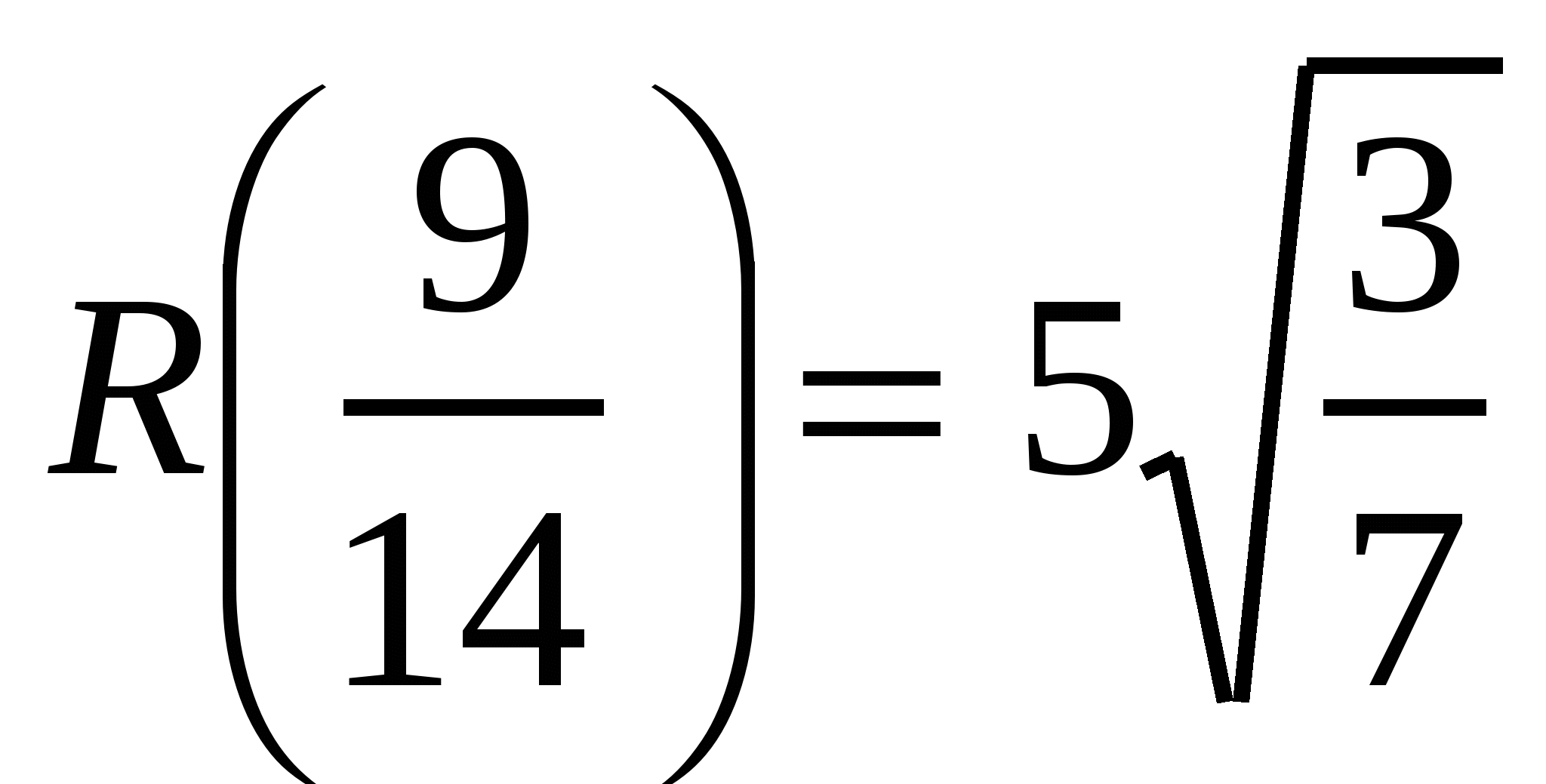 .
.
Ответ: ![]() км.
км.
Академический уровень
Задание 1
Найти промежутки убывания и возрастания функции
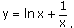
Решение:
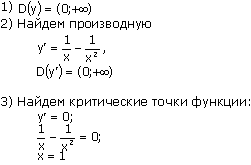
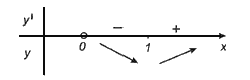
Ответ: при х є(0;1) функція убывает, при х є(1; ∞ ) функція возрастает
Задание 2
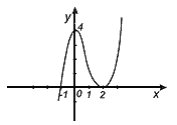
Исследовать функцію f(x)=х3-3х2+4 с помощью производной и построить ее график.
Решение:
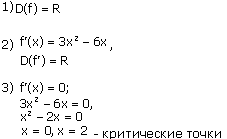
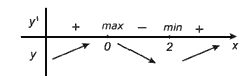
4) х=0-точка максимума, х=2-точка минимума.
5) f(0)=4, f(2)=4
Используя результаты исследования, строим график функции: f(x)=х3-3х2+4
Задание 3
Найти наибольшее и наименьшее значения функции ![]() на отрезке
на отрезке ![]()
Решение:
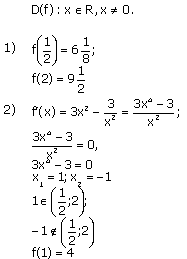
Ответ: 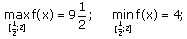
Задание 4
Найти длины сторон прямоугольника с периметром 20 см.,имеющего наименьшую диагональ.
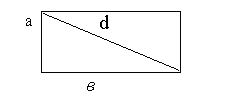
Решение:
Пусть а и в длины сторон прямоугольника, d - его диагональ. Тогда а+в=10. По теореме Пифагора d2=а2+в2. По условию задачи а > 0, в > 0,значит 0 < а < 10.d2=а2+(10-а)2=2а2-20а+100, 0 < а < 10.
Таким образом, задача свелась к нахождению такого значения а, при котором функция d(а)=2а2-20а+100 принимает наименьшее значение на интервале(0;10).
Найдем призводную d'(а)=4а-20.
Критическая точка а=5 є(0;10).
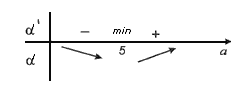
а=5 - точка минимумСледовательно, наименьшее значение функція d(а) на интервале (0;10).принимает в точке а=5.При этом в=5.
Ответ:5см.,5см.
Дифференциальное исчисление - широко применяемый для экономического анализа математический аппарат. Базовой задачей экономического анализа является изучение связей экономических величин, записанных в виде функций. В каком направлении изменится доход государства при увеличении налогов или при введении импортных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? В какой пропорции дополнительное оборудование может заменить выбывающих работников? Для решения подобных задач должны быть построены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления. В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.
По теореме Ферма, если точка является экстремумом функции, то производная в ней либо не существует, либо равна 0. Тип экстремума можно определить по одному из достаточных условий экстремума:
1) Пусть функция f(x) дифференцируема в некоторой окрестности точки x0
. Если производная f '(x) при переходе через точку x0 меняет знак с + на -, то x0 - точка максимума, если с - на +, то x0 - точка минимума, если не меняет знак, то в этой точке нет экстремума.
2) Пусть функция f(x) дважды дифференцируема в некоторой окрестности точки x 0, причем f '(x0) = 0, f ''(x0) ≠ 0, то вточке x0 функция f(x0) имеет максимум, если f ''(x0 ) < 0 и минимум, если f ''(x0) > 0.
Кроме того, вторая производная характеризует выпуклость функции (график функции называется выпуклым вверх [вниз] на интервале (a, b), если он на этом интервале расположен не выше [не ниже] любой своей касательной).
Задание 5
Выбрать оптимальный объем производства фирмой, функция прибыли которой может быть смоделирована зависимостью:
π(q) = R(q) - C(q) = q2 - 8q + 10
Решение:
π'(q) = R'(q) - C'(q) = 2q - 8 = 0 → qextr = 4
При q < qextr = 4 → π'(q) < 0 и прибыль убывает
При q > qextr = 4 → π'(q) > 0 и прибыль возрастает
При q = 4 прибыль принимает минимальное значение.
Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) = p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и / или оборудования. Если же фирма способна производить больше 8 единиц, то оптимальным для фирмы будет выпуск на пределе своих производственных мощностей.
Пример: Извлечь квадратный корень из 3654
Решение: 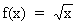 , x0=3654. Легко вычисляются значения f(x) и
, x0=3654. Легко вычисляются значения f(x) и 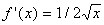
при x = 3600. Формула при a = 3600, b=54 дает:
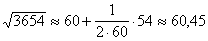
Ответ: √3654≈60,45
Ответ: 35Дж.
Задача 6
Найти площадь фигуры, ограниченной линиями
х-2у+4=0 и х+у-5+0 и у=0.
Решение:
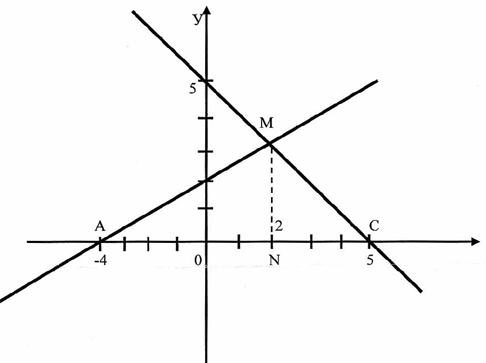
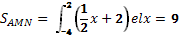
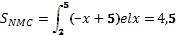
Тогда площадь фигуры равна 9+4,5=13,5
Ответ: 13,5
Пример 2. Скорость движения точки 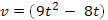 м/с. Найти путь, пройденный точкой за 4-ю секунду.
м/с. Найти путь, пройденный точкой за 4-ю секунду.
Решение:
Согласно условию,  . Следовательно,
. Следовательно, 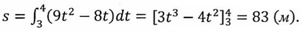
Ответ: 83м.
Задание 7
Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью 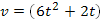 м/с, второе - со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?
м/с, второе - со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?
Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:
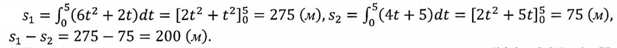
Ответ: 200м.
Задание 8
Тело брошено с поверхности земли вертикально вверх со скоростью v = (39,2-9,8t) м/с. Найти наибольшую высоту подъема тела.
Решение: тело достигнет наибольшей высоты подъема в такой момент времени t, когда v = 0, т.е. 39,2-9,8t = 0, откуда I = 4 с. По формуле (1) на ходим

Ответ: 78,4 м.
Задание 9
Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,22 до 0,32 м?
Решение: используя равенство (3), имеем 50=0,01k, т. е. kК = 5000 Н/м. Находим пределы интегрирования: а = 0,22 - 0,2 = 0,02 (м), b=0,32- 0,2 = 0,12(м). Теперь по формуле (2) получим
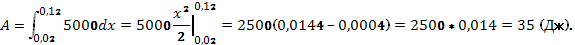
Ответ: 35Дж.
Задание 10
Доказать, что из всех прямоугольников, имеющих данный периметр 2р, наибольшую площадь имеет квадрат.
Решение 1. Обозначим длину одной стороны прямоугольника через х. 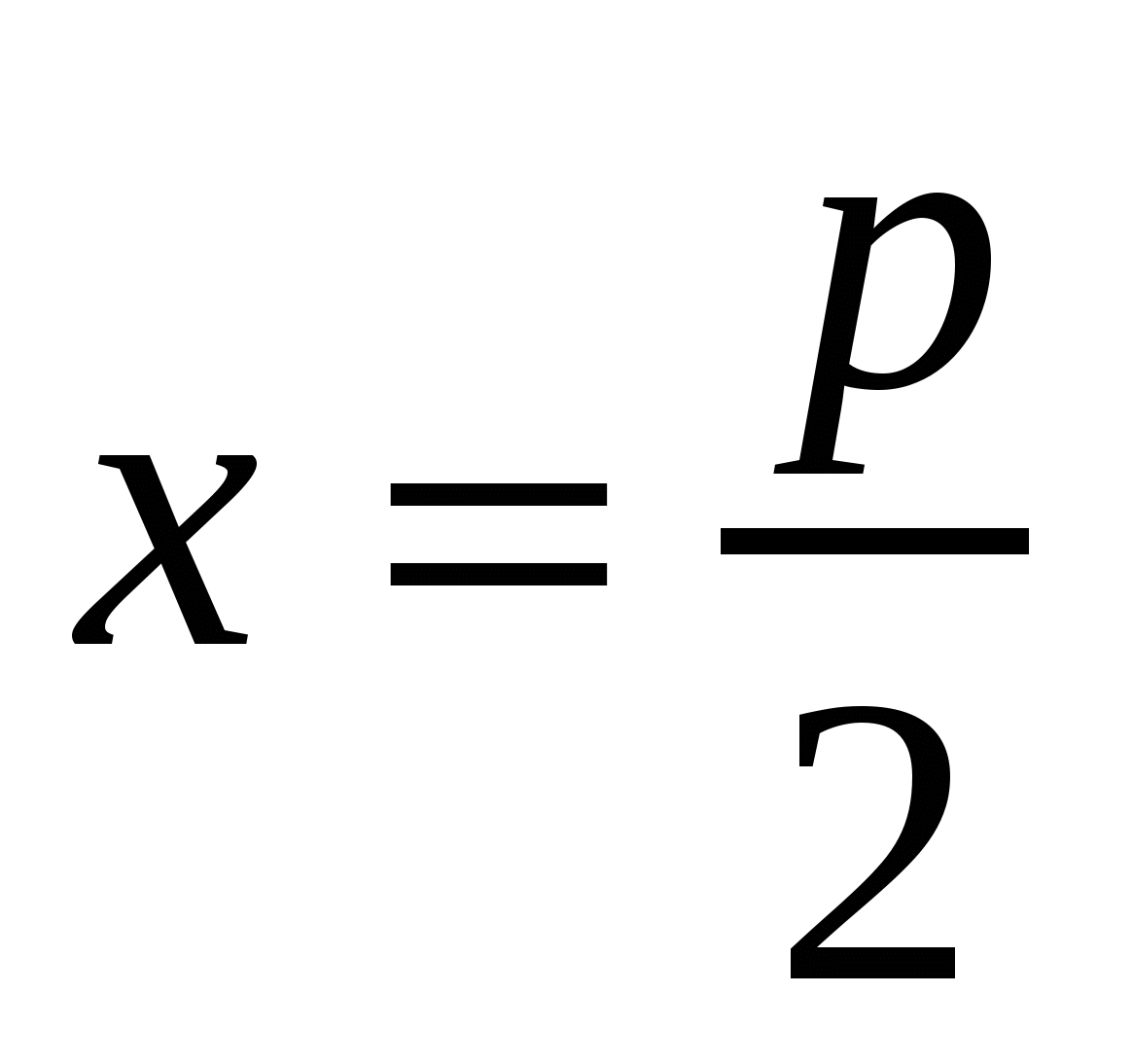 .
. 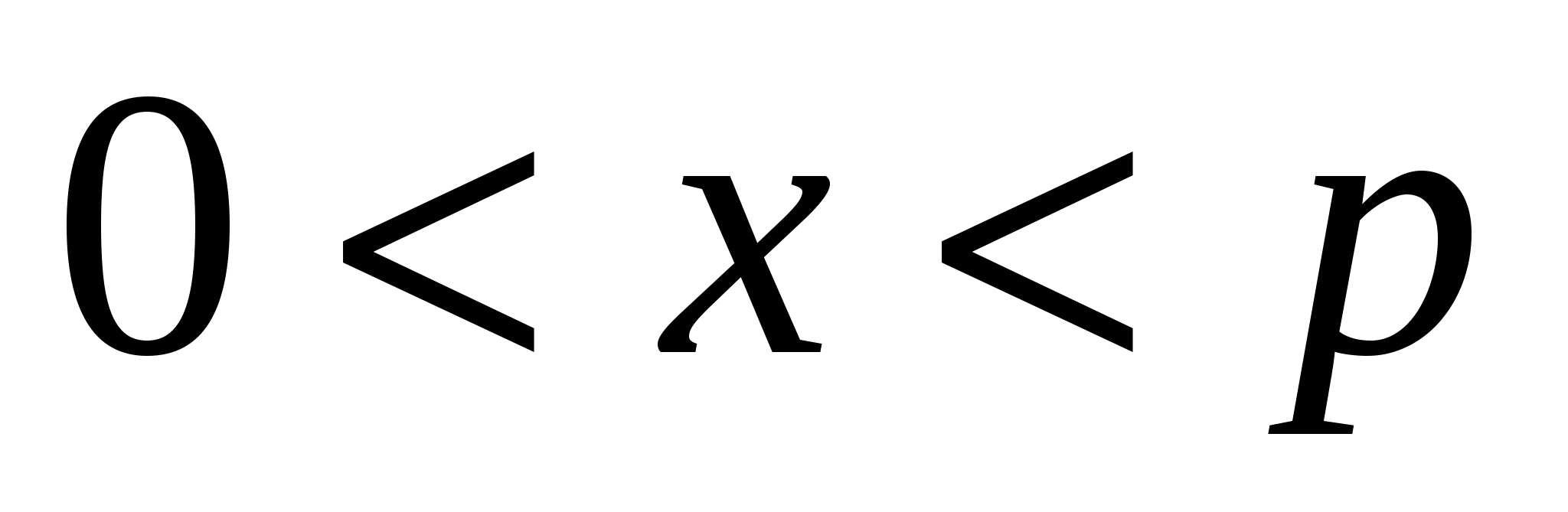 максимум, то он будет и наибольшим значением функции в этом интервале. Другая сторона
максимум, то он будет и наибольшим значением функции в этом интервале. Другая сторона 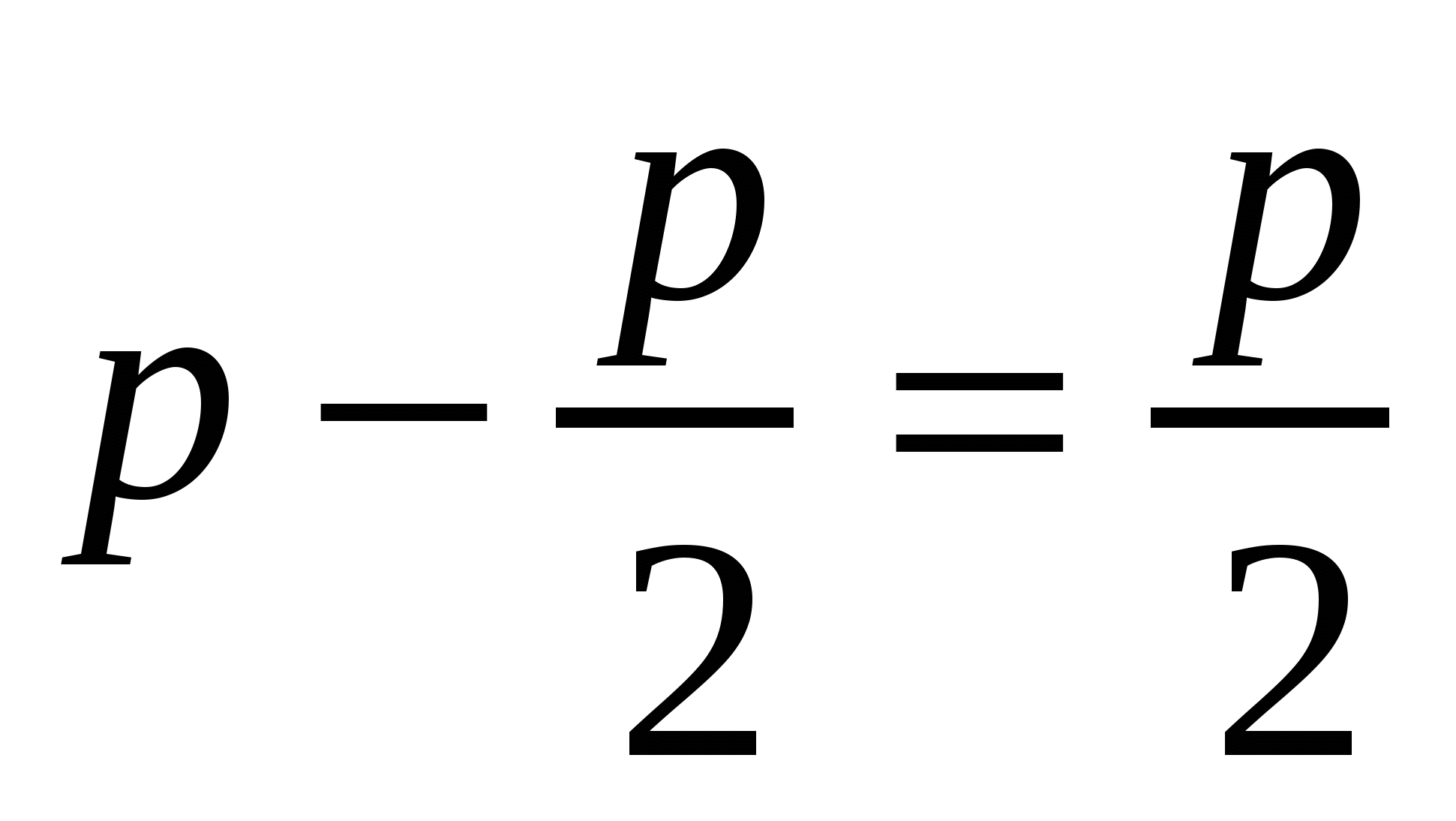 т.е. прямоугольник-квадрат.
т.е. прямоугольник-квадрат.
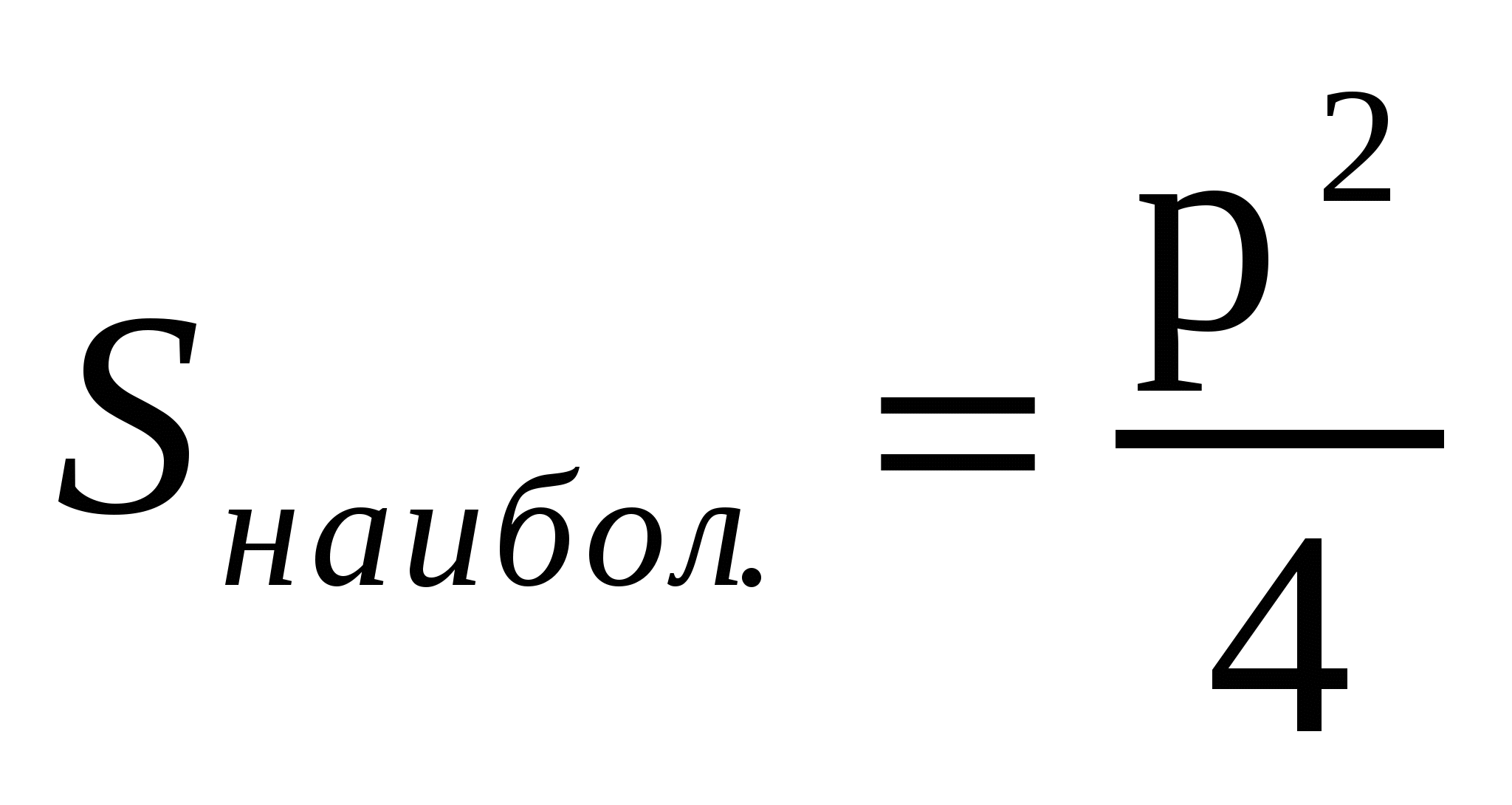
Ответ: ![]()
Решение 2. Имеет: 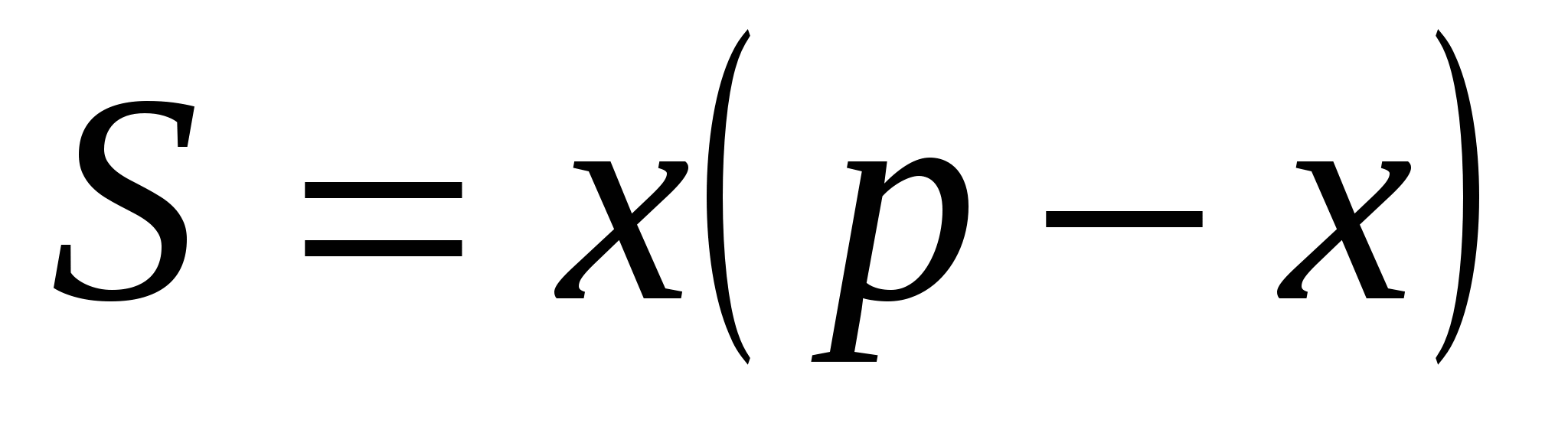 .На основание теоремы о средних
.На основание теоремы о средних 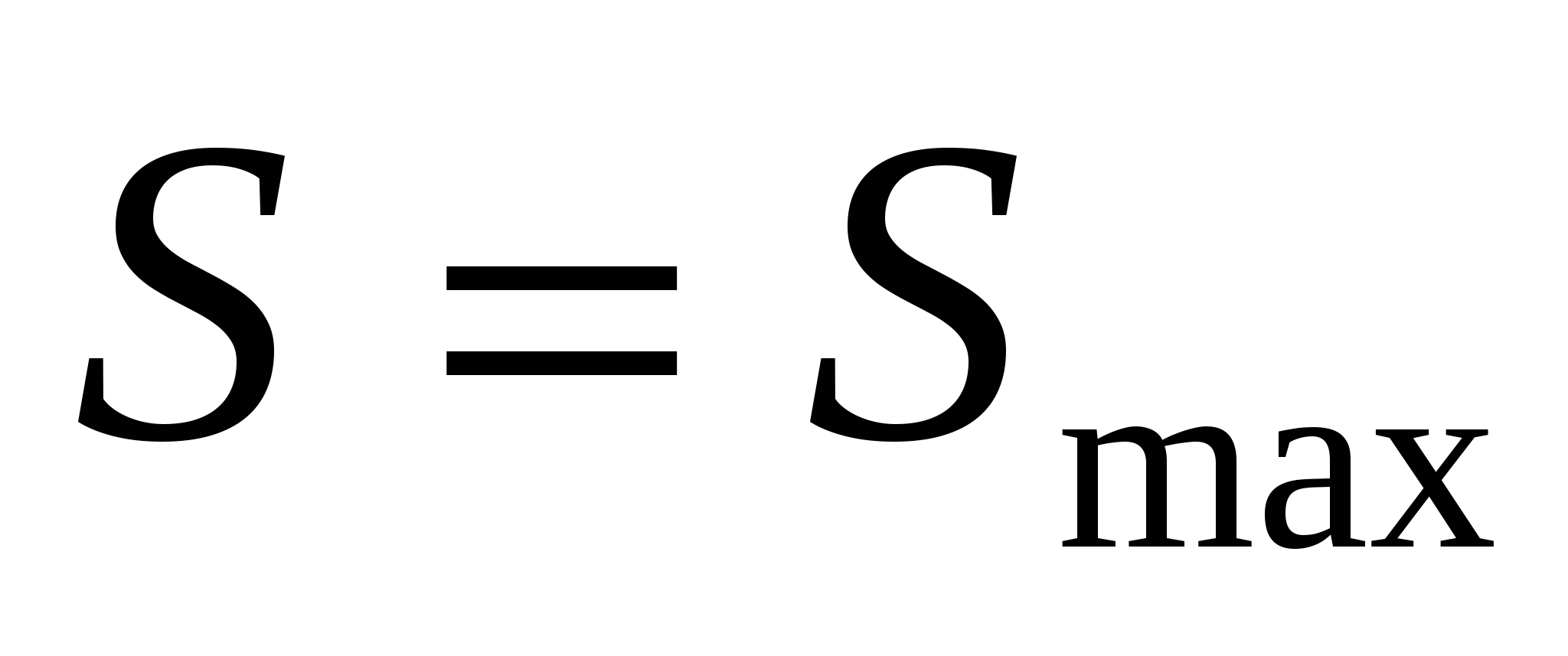 при х=р-х; 2х=р;
при х=р-х; 2х=р; 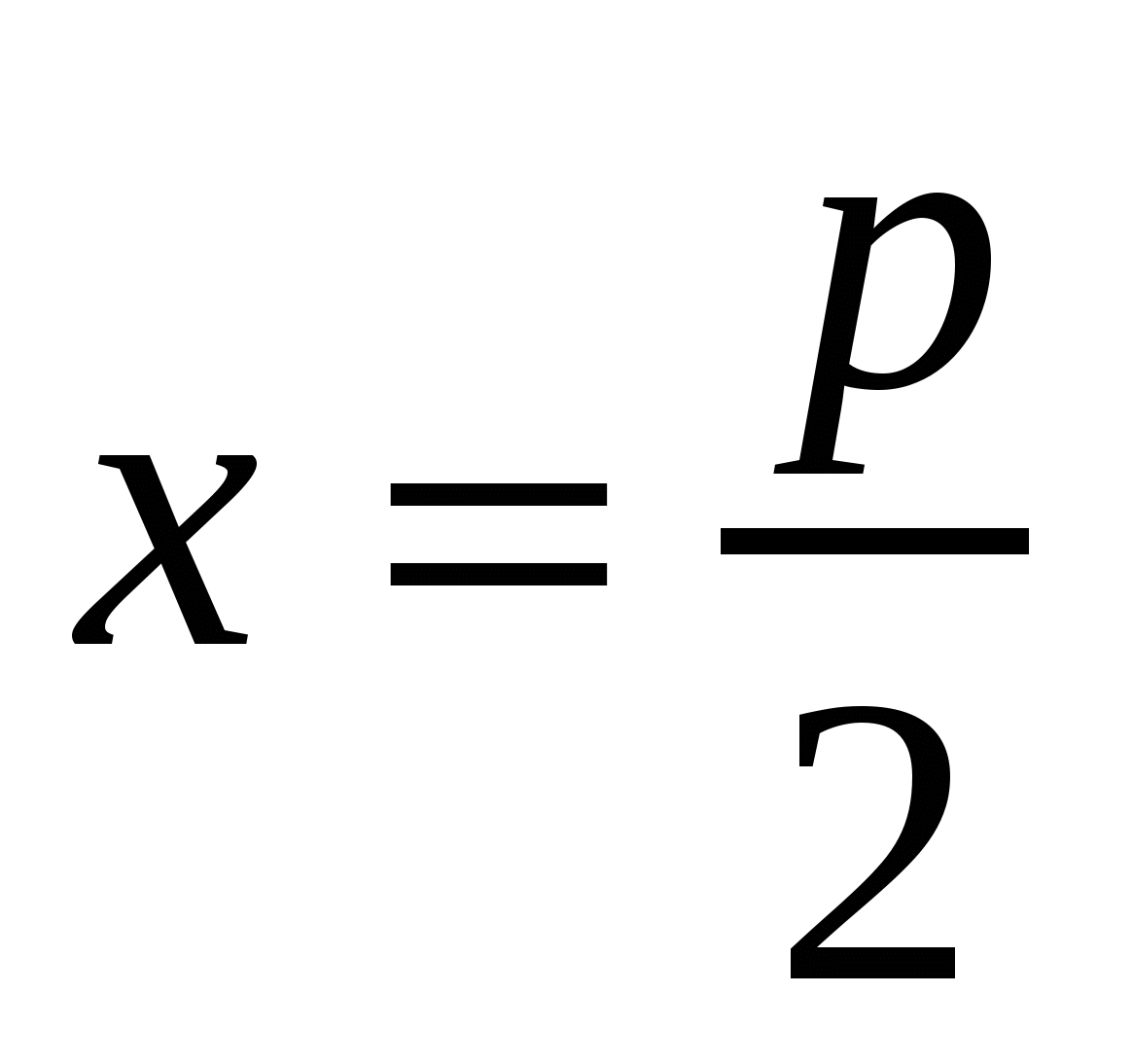 и т.д. как решении 1.
и т.д. как решении 1.
Ответ: ![]()
Задание 11
Основание треугольника равно а, его периметр 2р. Определить его две других стороны так, чтобы его площадь была наибольшей.
Решение 1. Пусть вторая сторона b=x ,третья c=2p-a-x.По формуле Герона имеем: ![]() ,тогда
,тогда 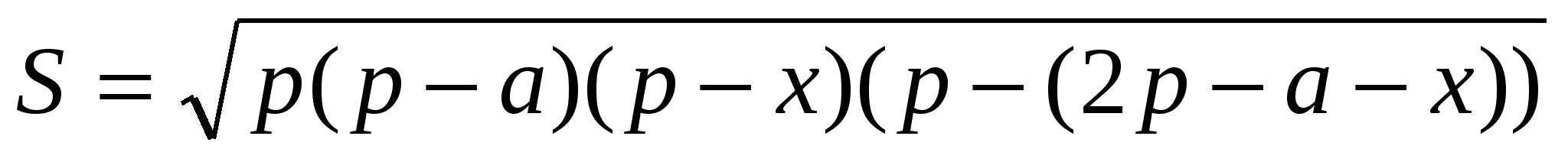 ;
; 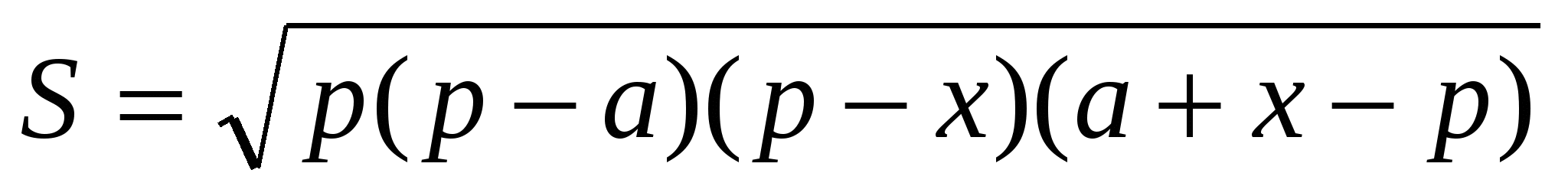 ;
; 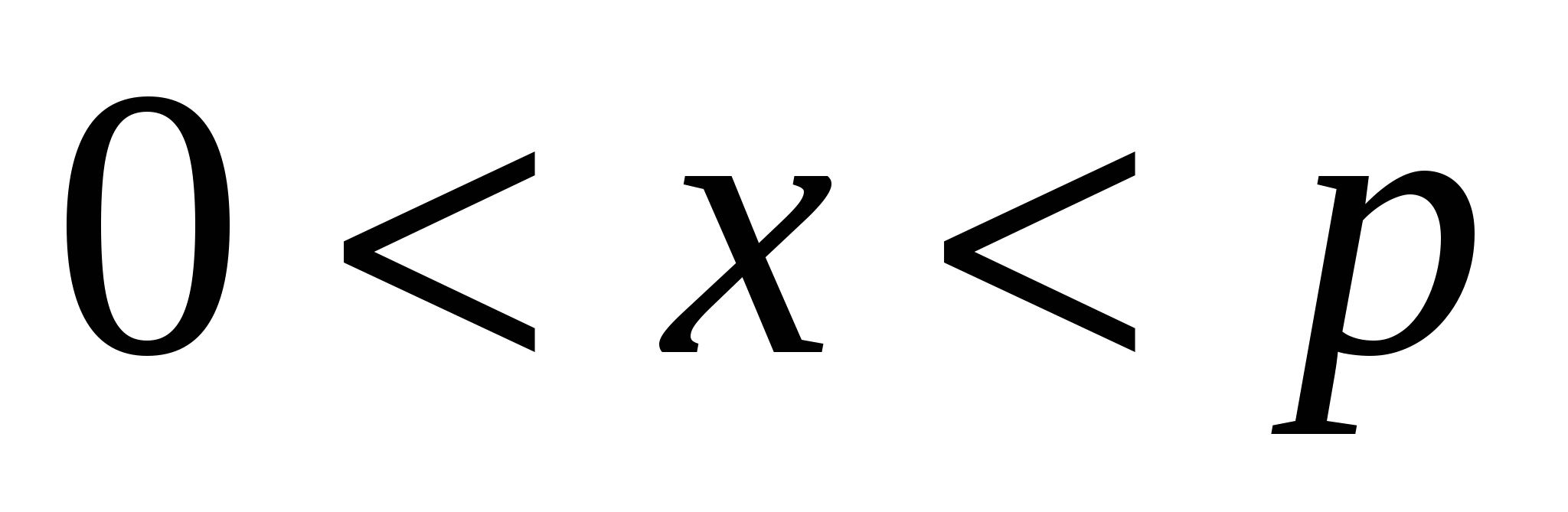 . Функция S достигает наибольшего значения, когда ее подкоренное выражение будет наибольшим. В нем первые два множителя постоянны, поэтому их можно не учитывать и определить наибольшее значение
. Функция S достигает наибольшего значения, когда ее подкоренное выражение будет наибольшим. В нем первые два множителя постоянны, поэтому их можно не учитывать и определить наибольшее значение 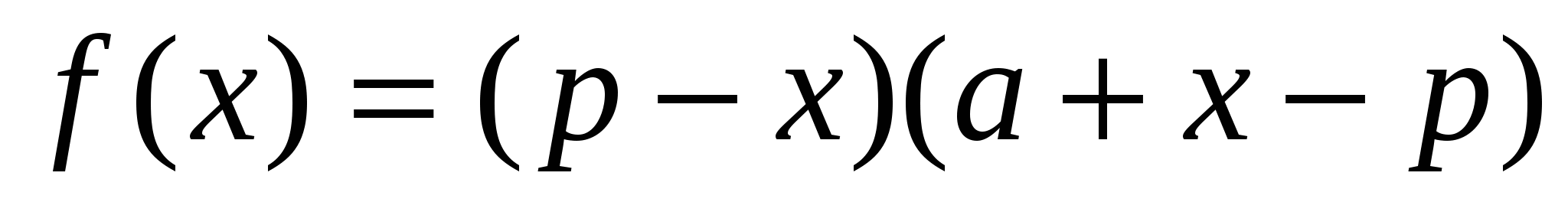 ,тогда
,тогда 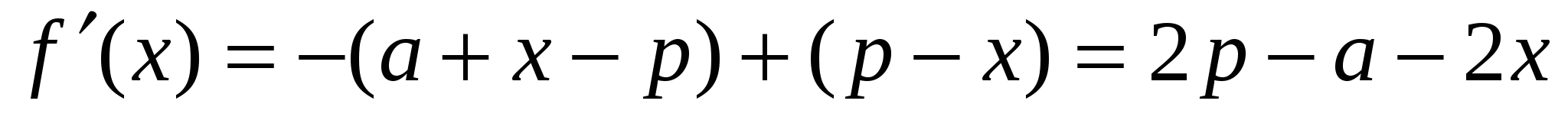 .Решая уравнение
.Решая уравнение 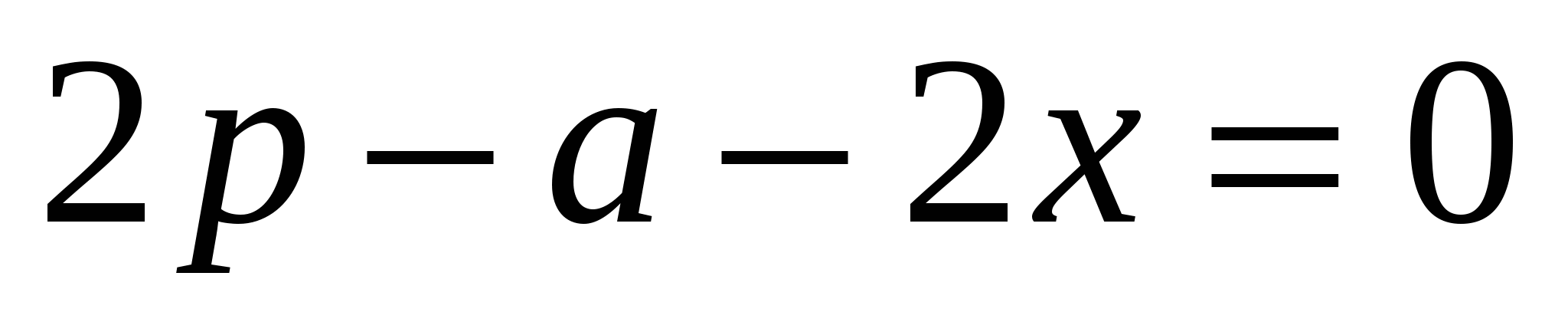 ,находим
,находим 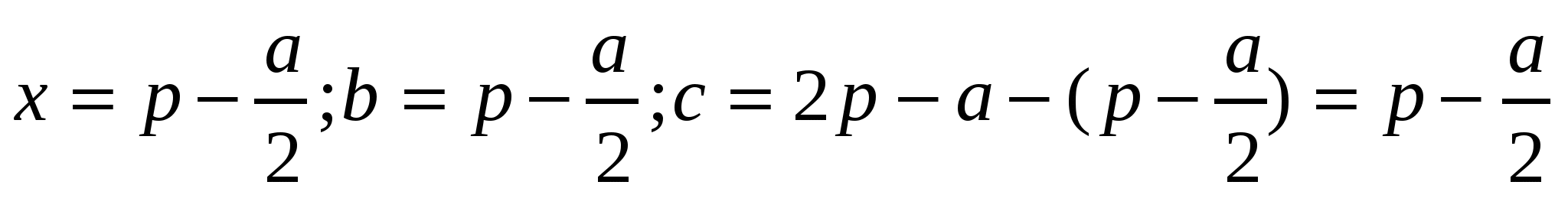 .Поскольку b=с, то рассматриваемый треугольник - равнобедренный. Так как
.Поскольку b=с, то рассматриваемый треугольник - равнобедренный. Так как 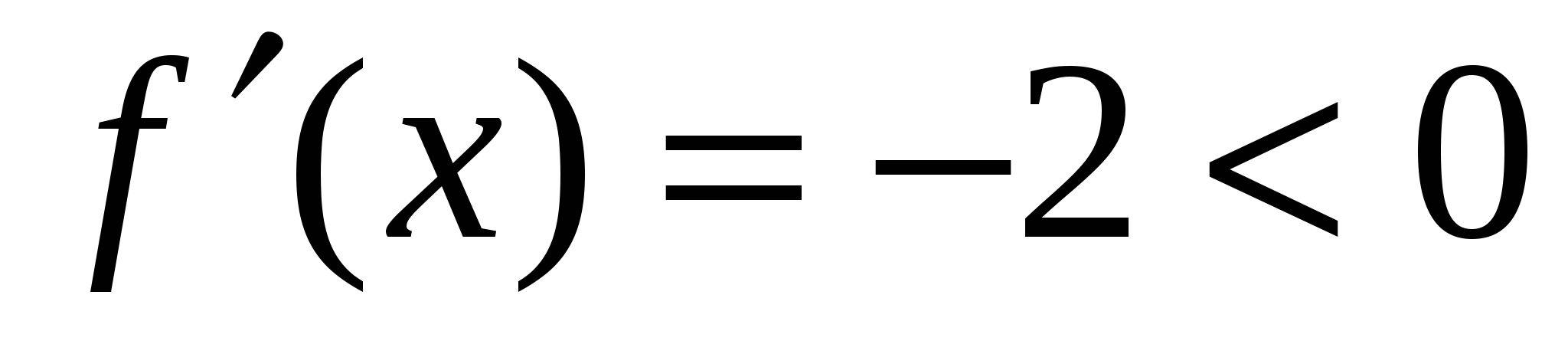 ,то при
,то при 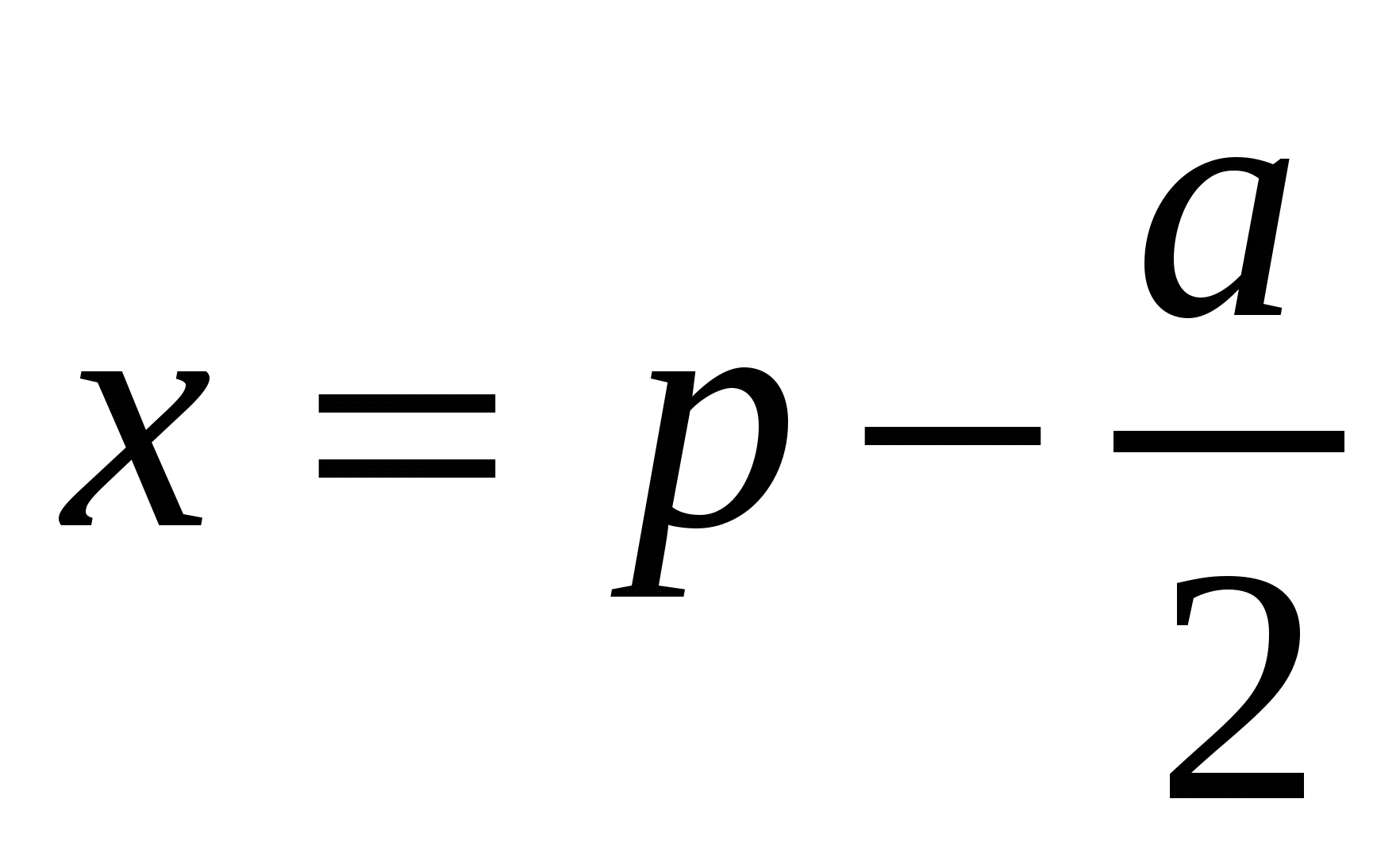 функции S максимальна, а так как в интервале
функции S максимальна, а так как в интервале 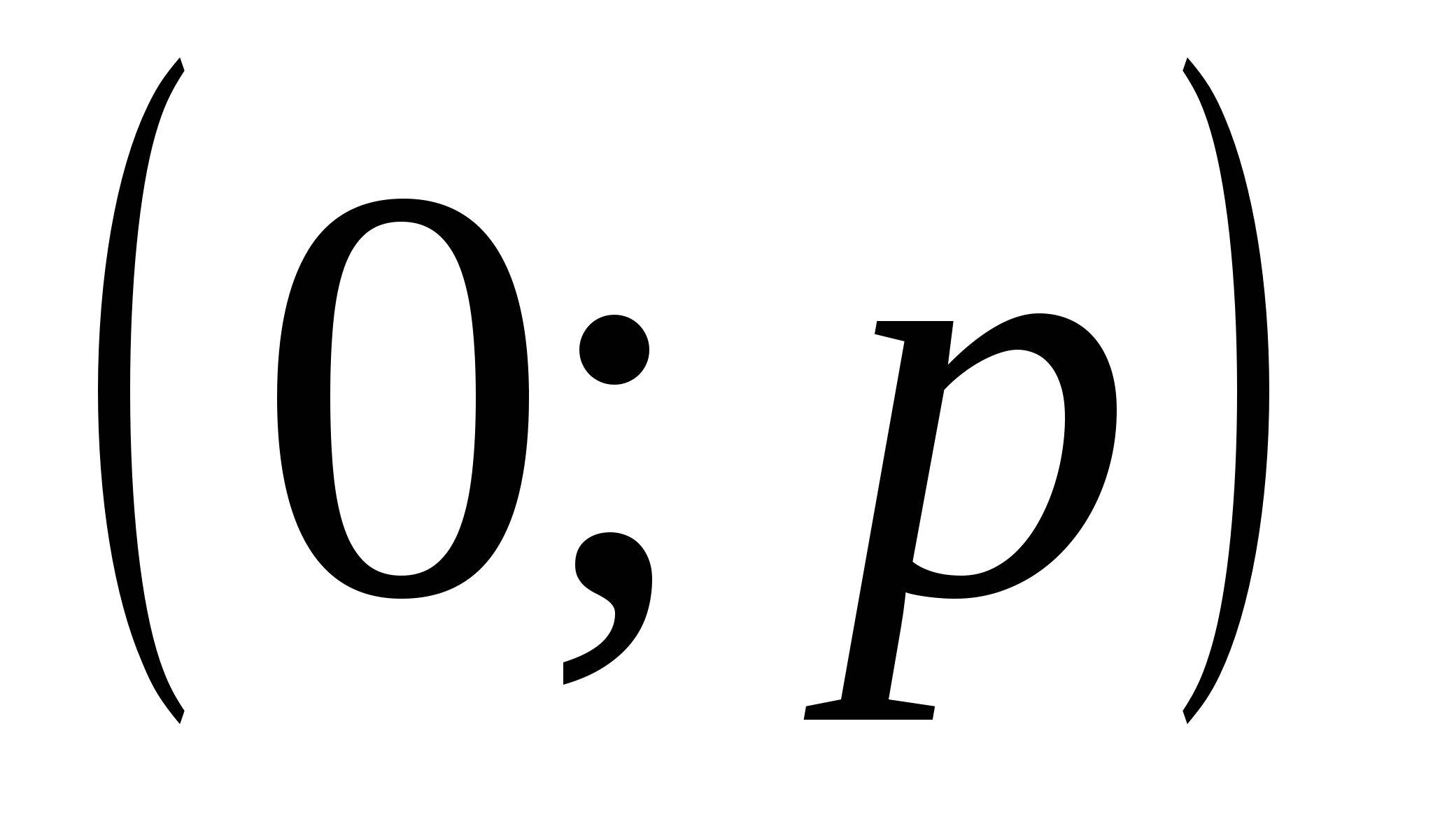 этот максимум единственный, то он совпадает с наибольшим значением.
этот максимум единственный, то он совпадает с наибольшим значением.
Ответ: 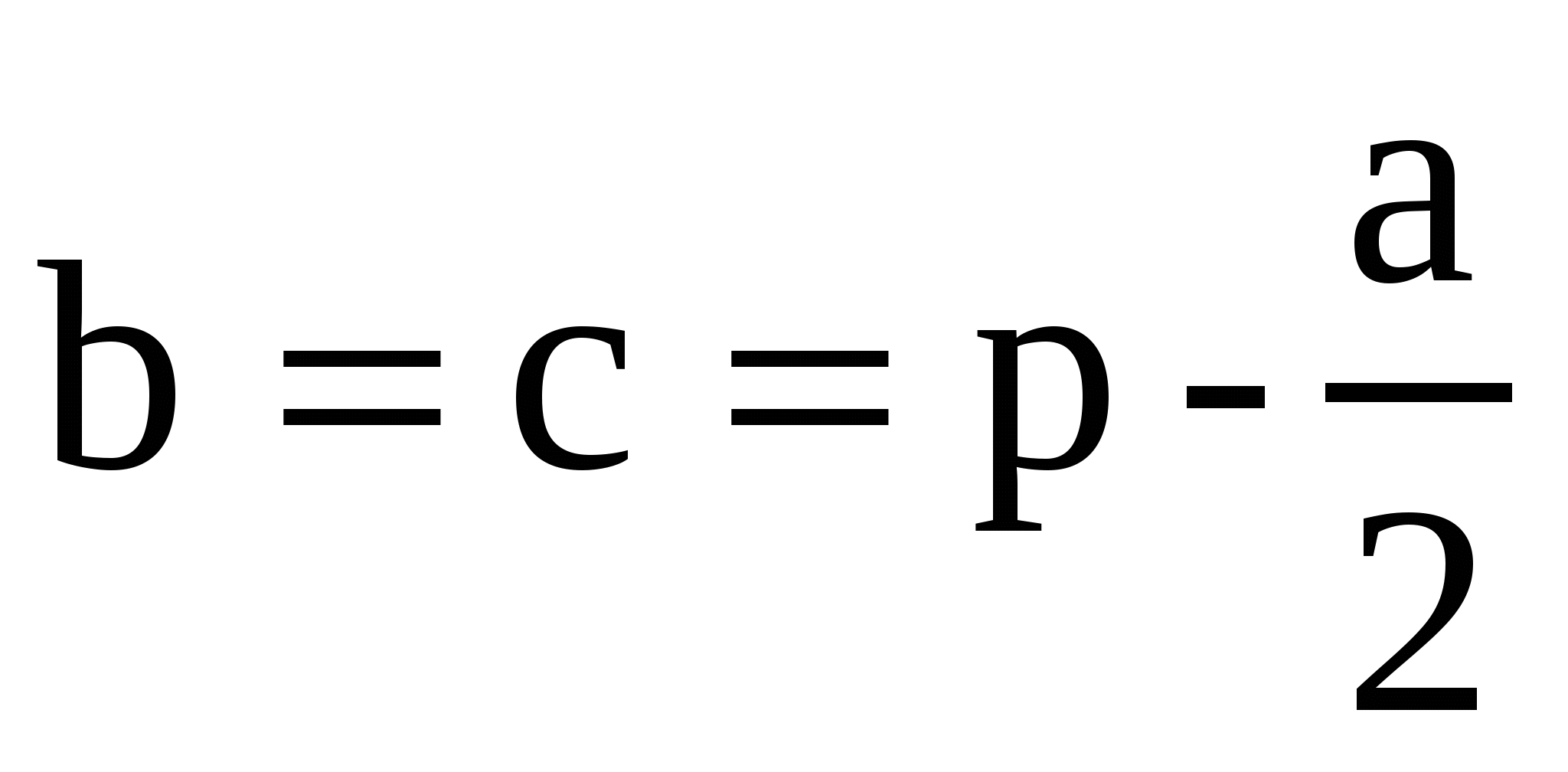
Решение 2. Имеем: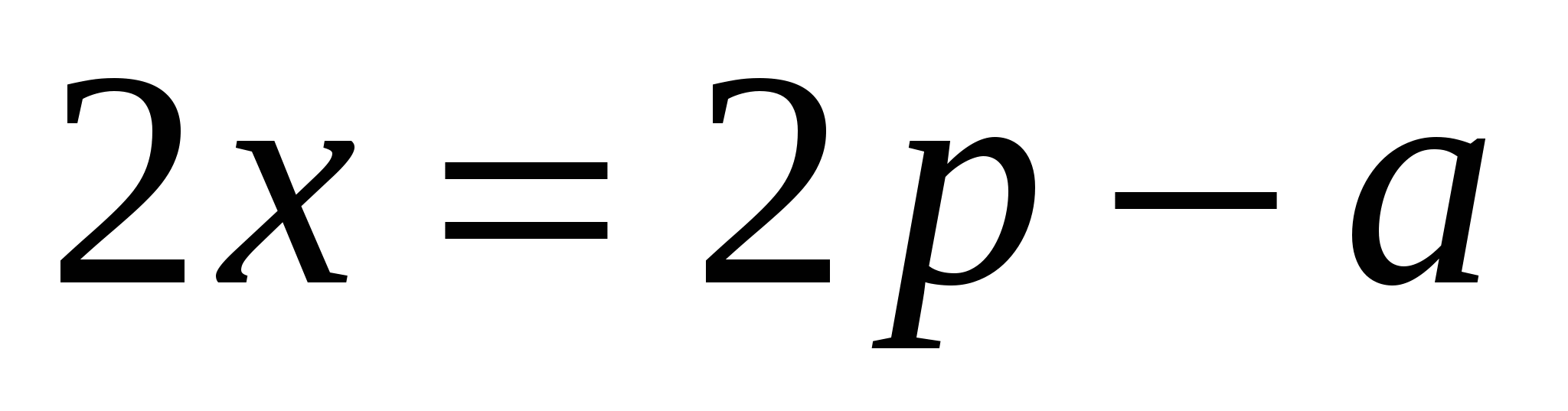 ,откуда
,откуда 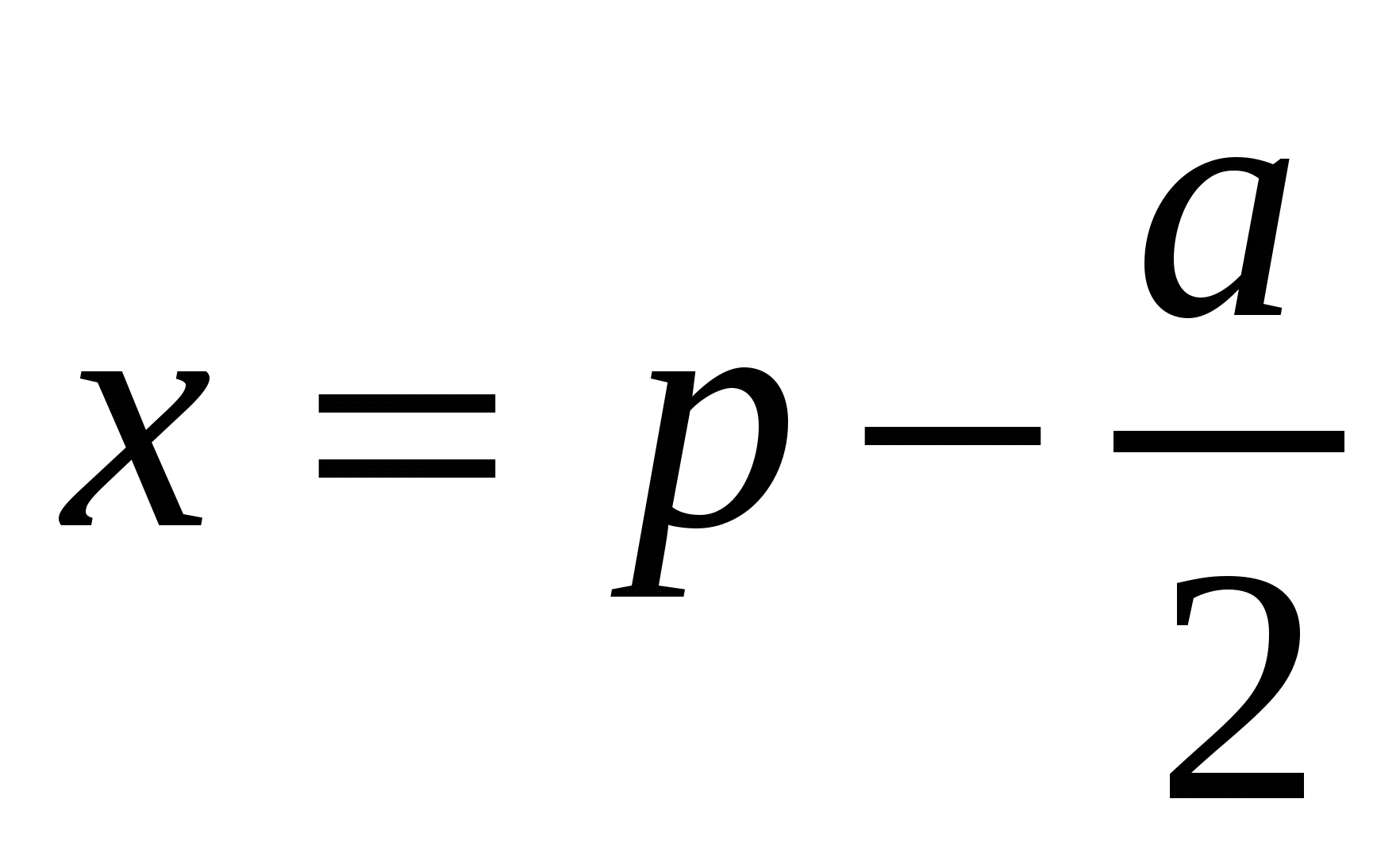 и т.д. как в решении 1.
и т.д. как в решении 1.
Ответ: 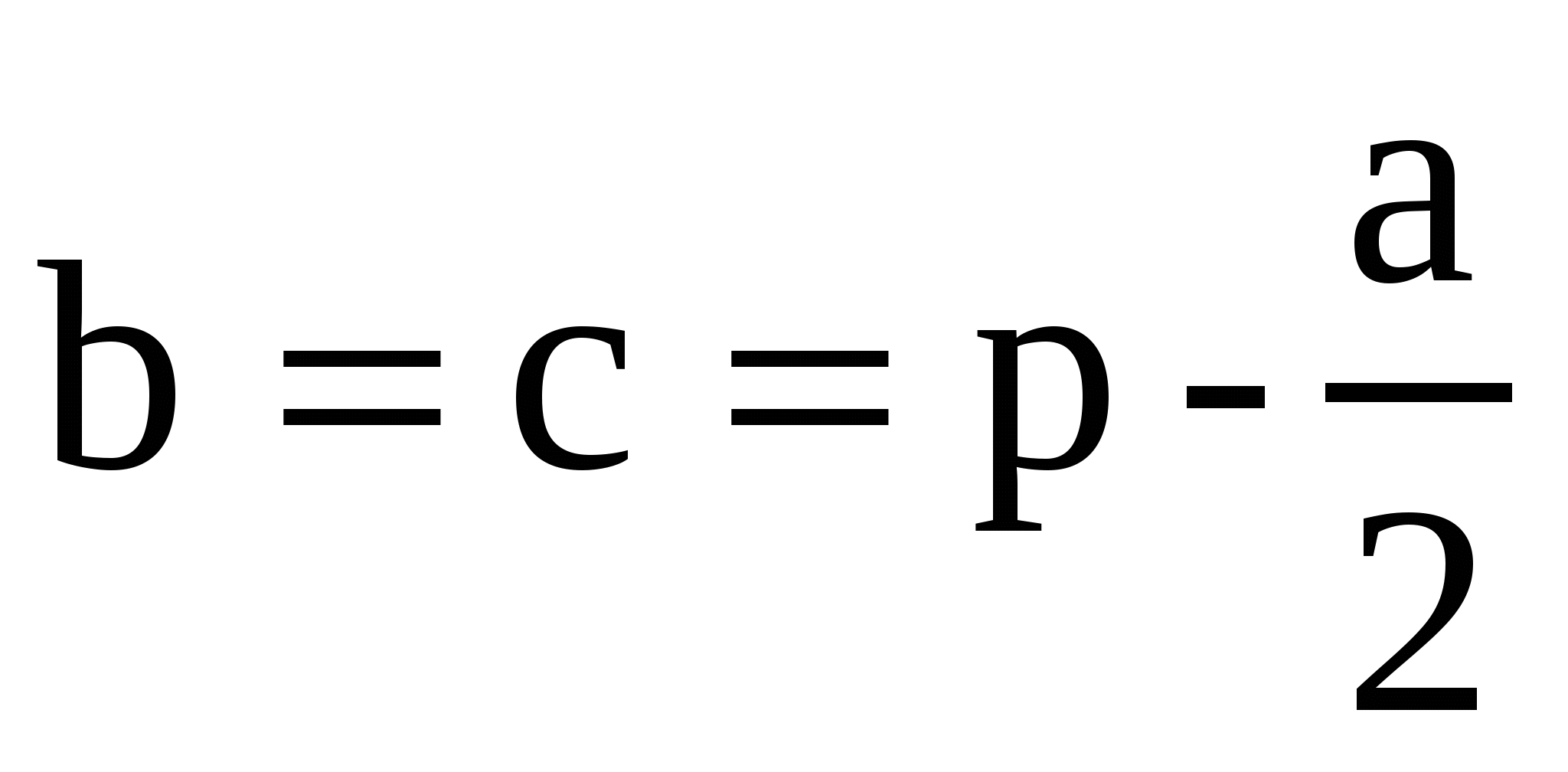
Задание 12
Найти хотя бы одну из первообразных для функции  .
.
Решение 1.
Если F есть первообразная для f, а G- первообразная для g, то F+G есть первообразная для f+g. Поэтому, так как  есть первообразная для
есть первообразная для ![]() ,а
,а 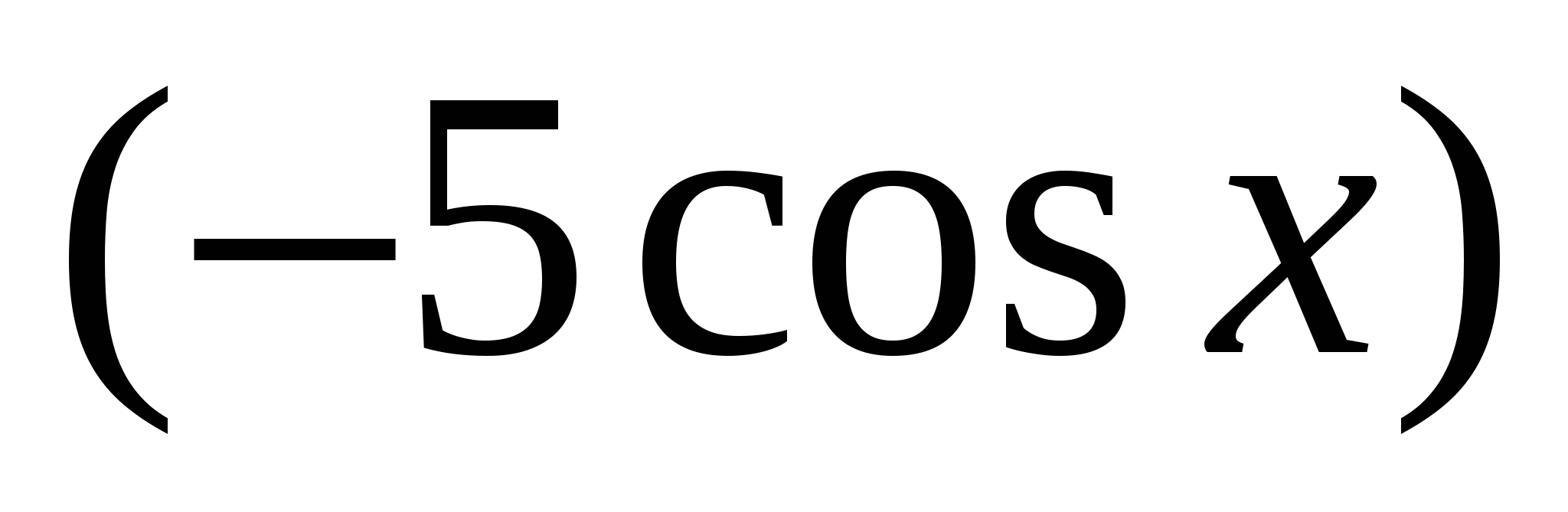 - первообразная для
- первообразная для ![]() , то
, то 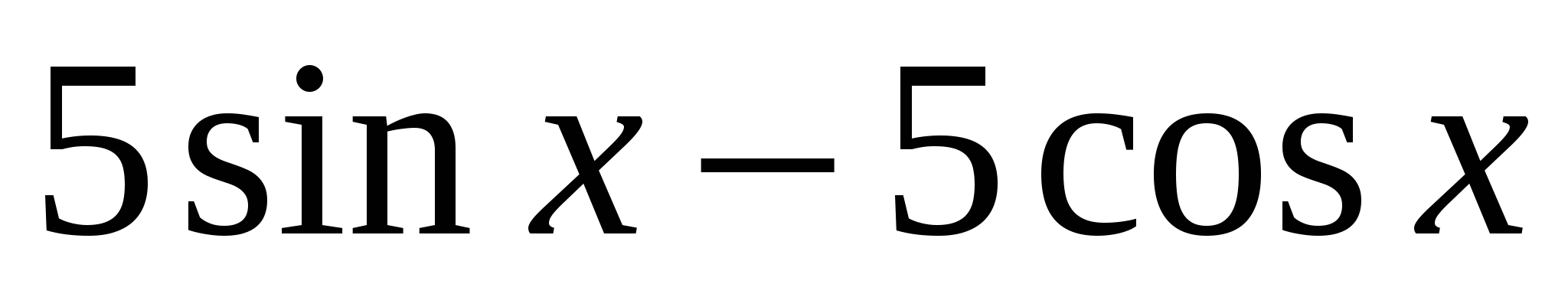 есть первообразная для
есть первообразная для 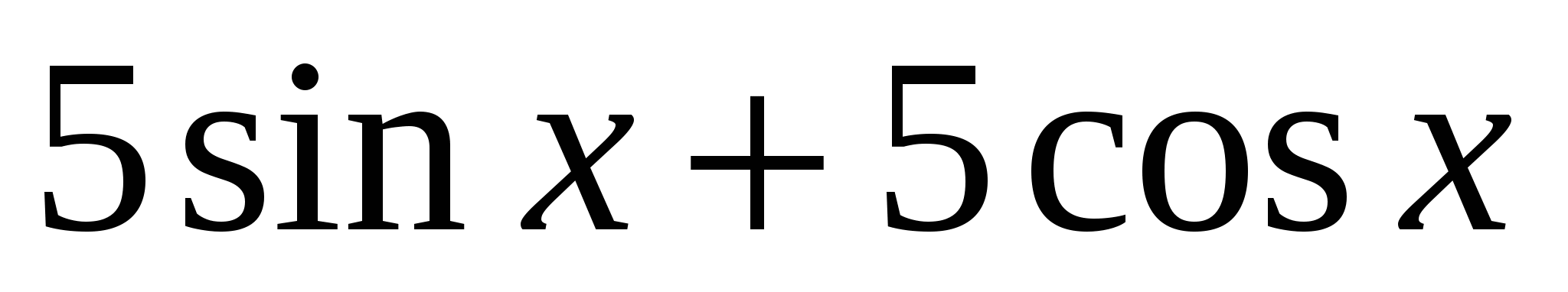 .
.
Ответ: 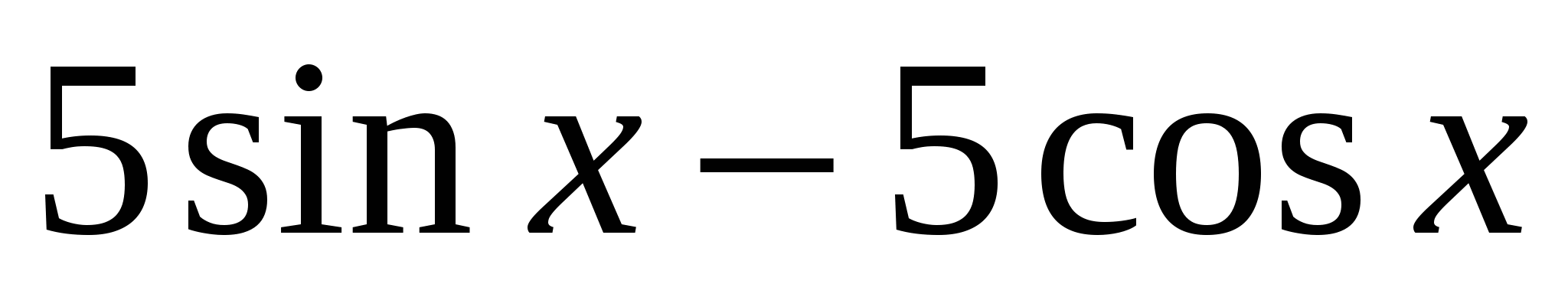
Решение 2. Если F есть первообразная для f, а k - постоянная, то функция kF - первообразная для kF.Поэтому, так как 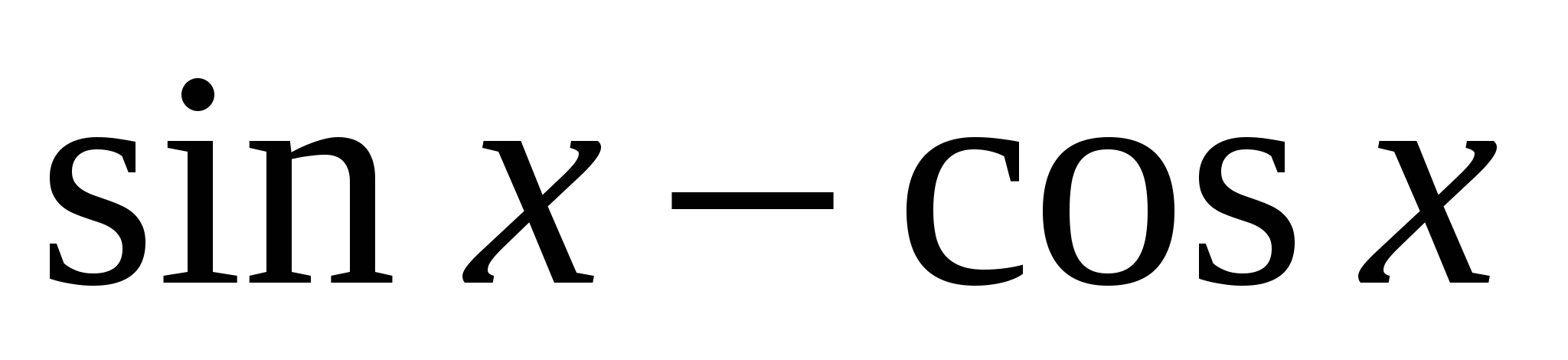 , есть первообразная для
, есть первообразная для ![]() , то функция
, то функция 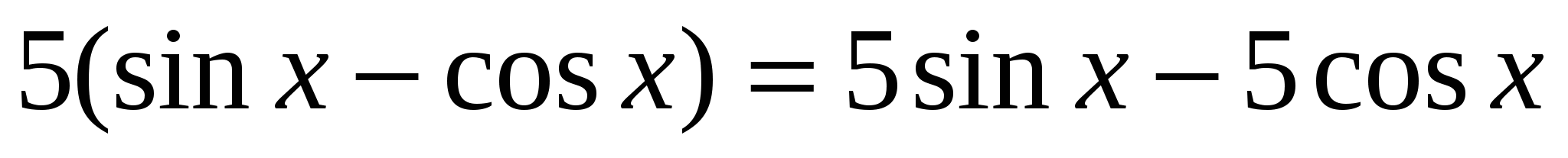 ,- первообразная для
,- первообразная для 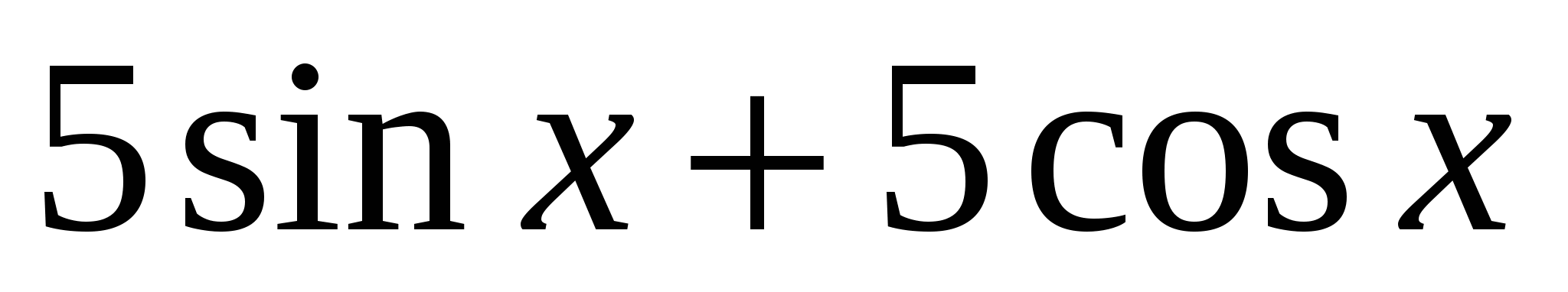 .
.
Ответ: 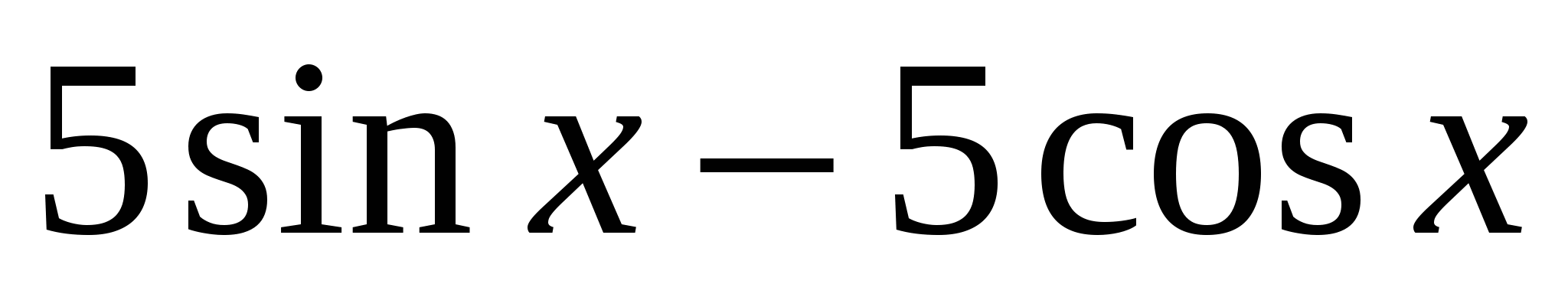
Решение 3. Если F есть первообразная для f, а k и b- постоянные 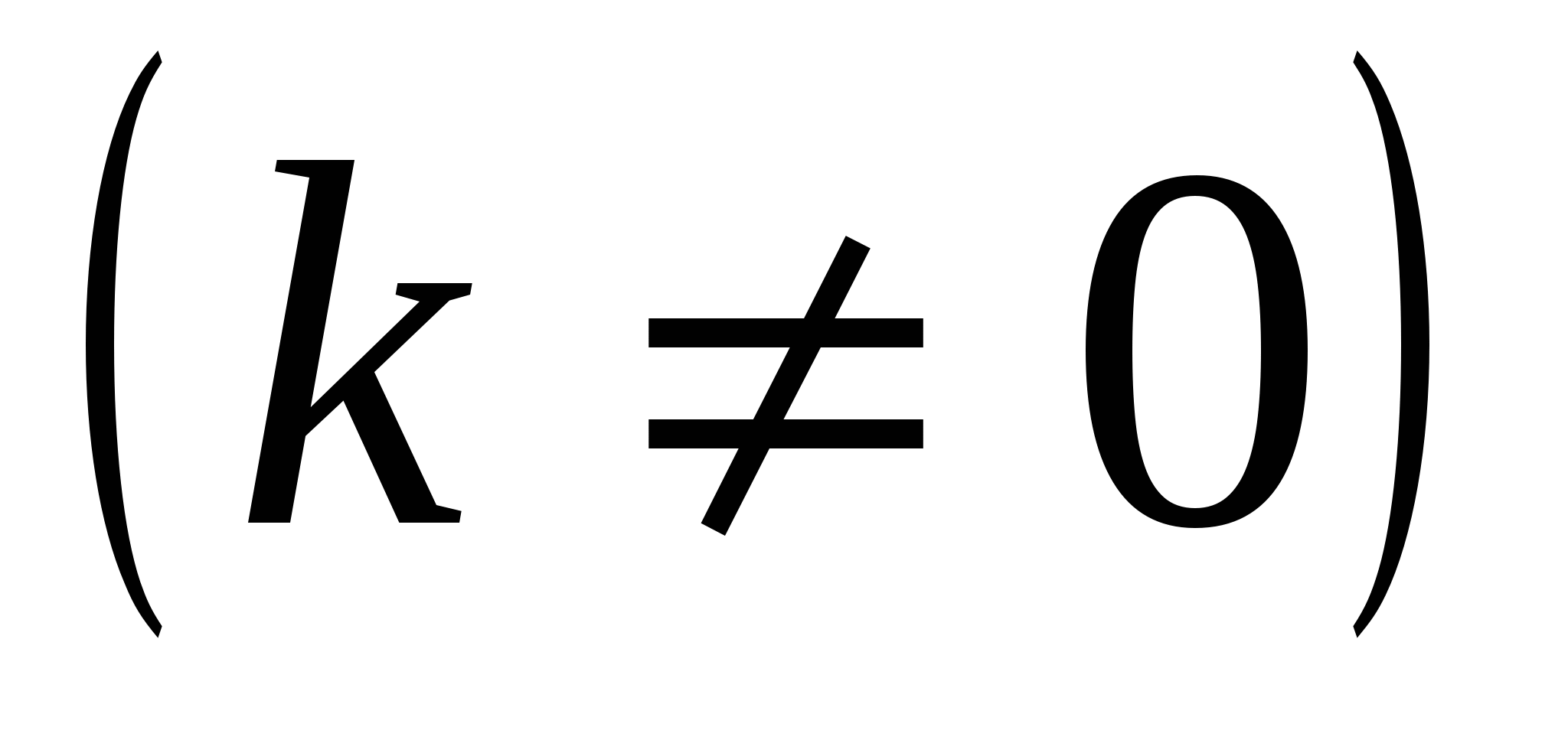 ,то
,то 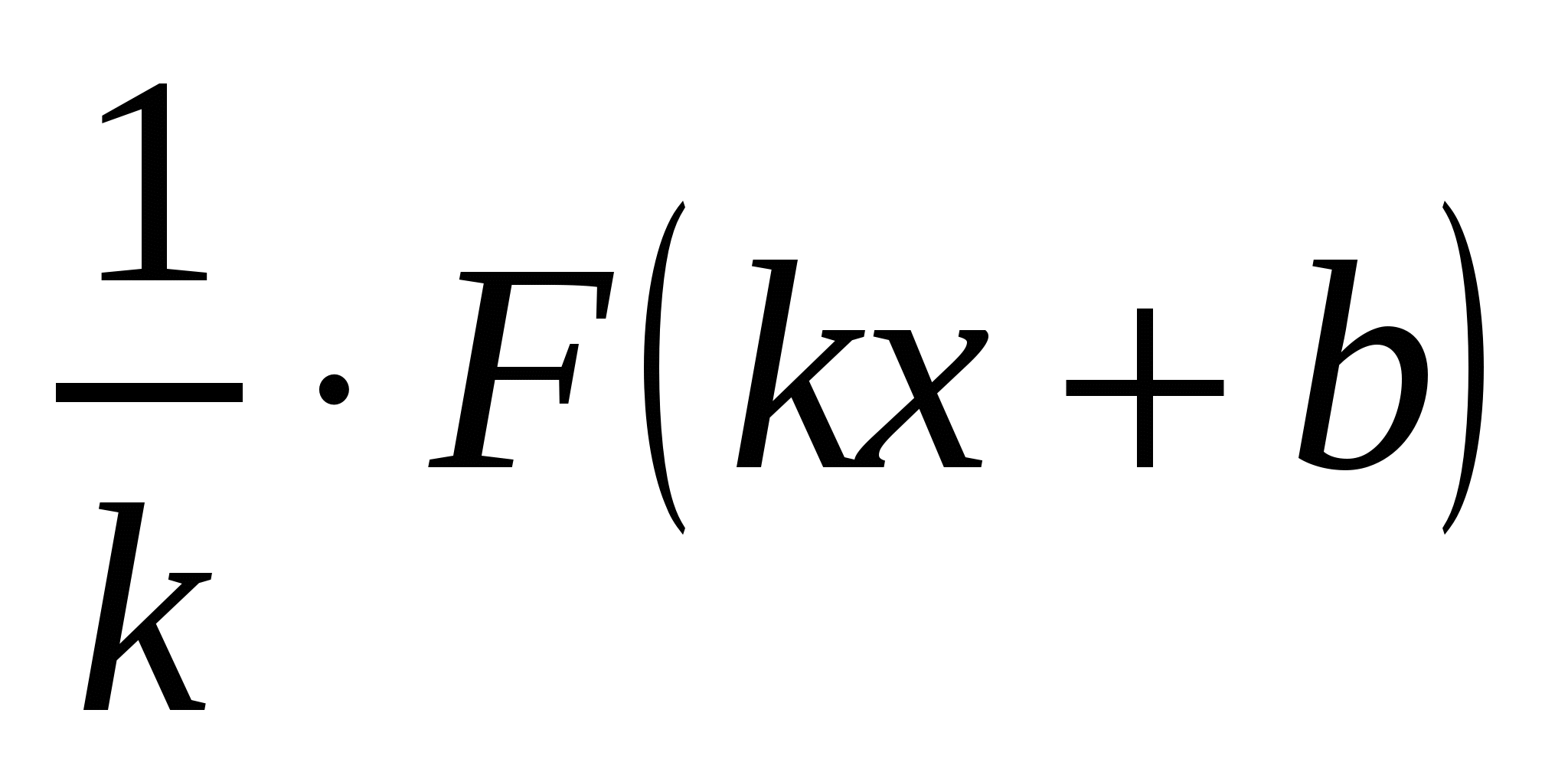 есть первообразная для
есть первообразная для ![]() ,поэтому, так как
,поэтому, так как 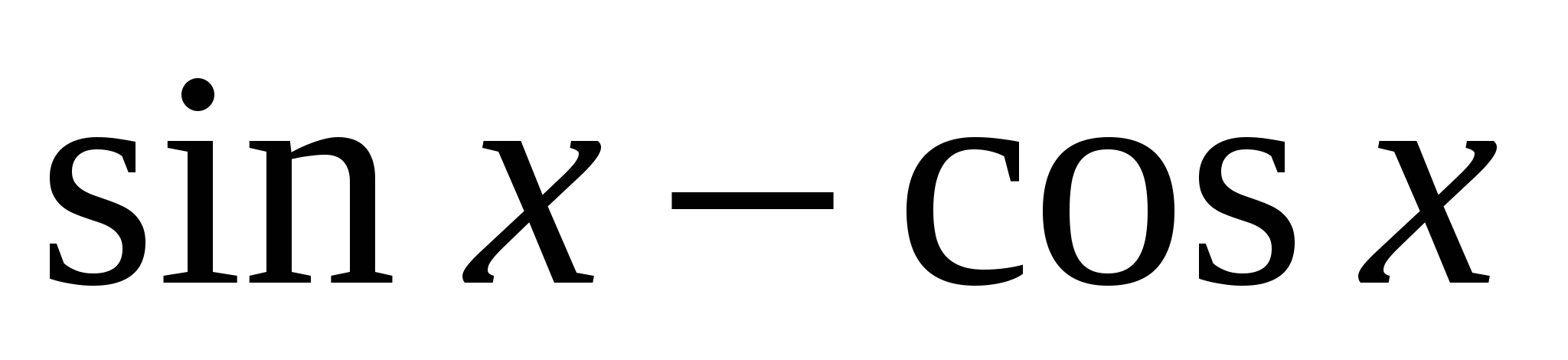 есть первообразная для
есть первообразная для ![]() ,то и функция
,то и функция 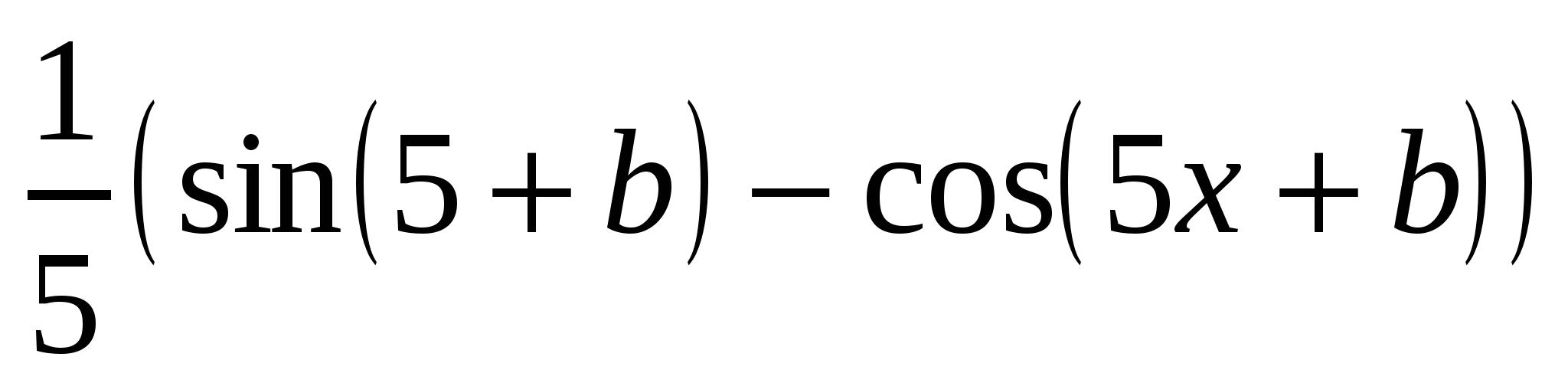 ,кроме функции
,кроме функции 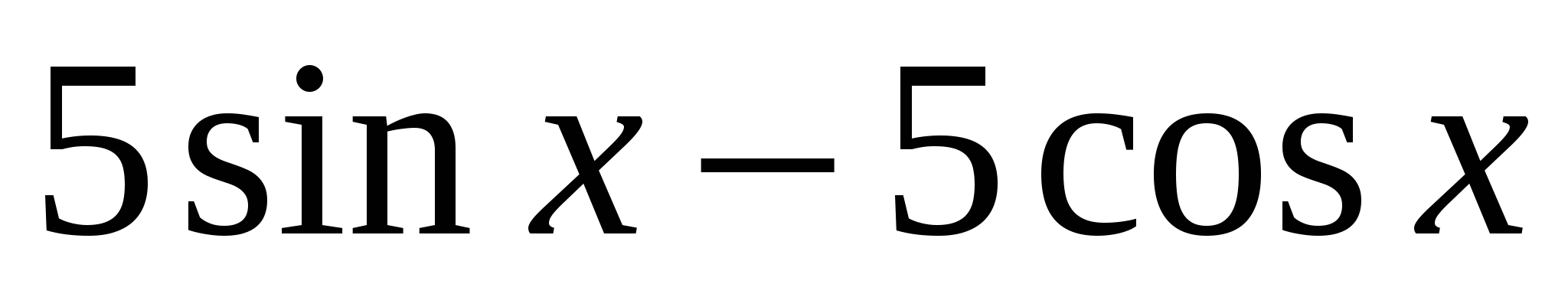 ,найденной в решении 1 и 2,также является первообразной для
,найденной в решении 1 и 2,также является первообразной для 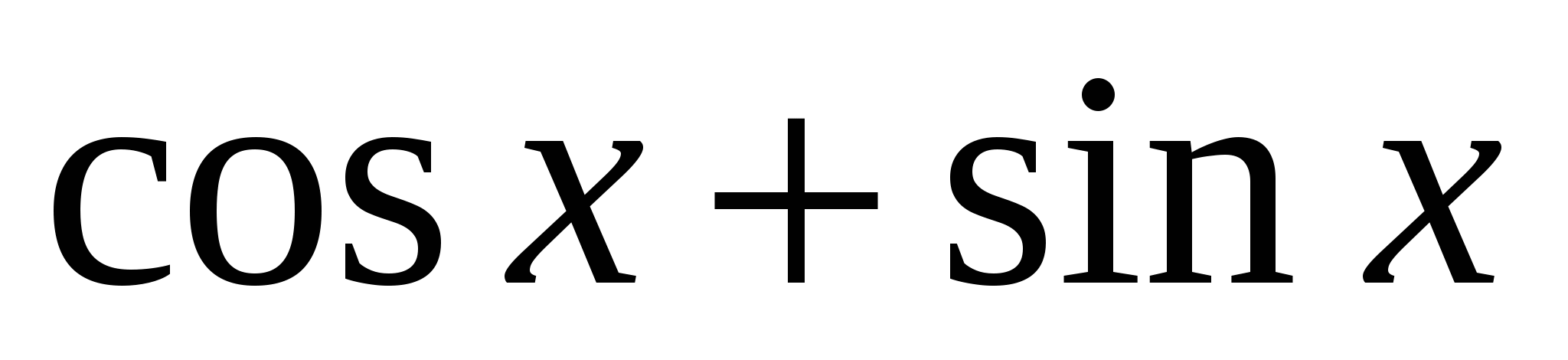 .
.
Ответ: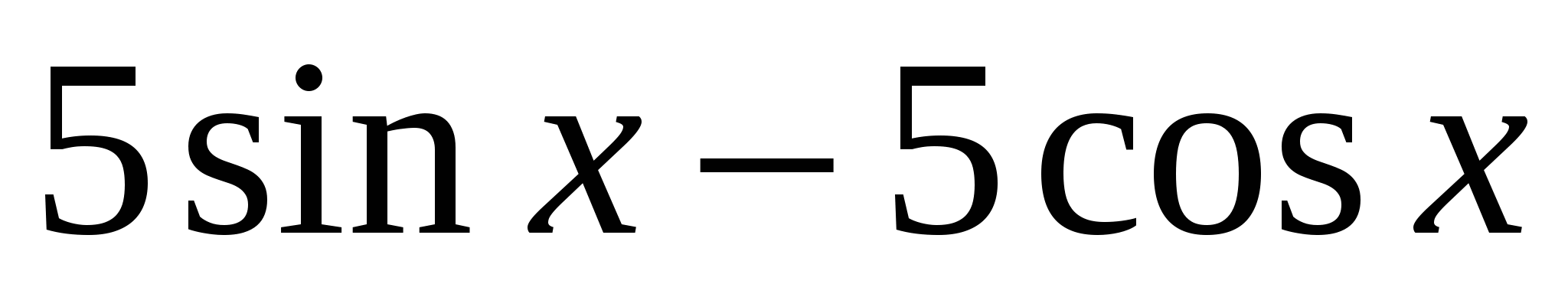
Задача 13
Мощность Р, отдаваемая электрическим элементом, определяется по формуле 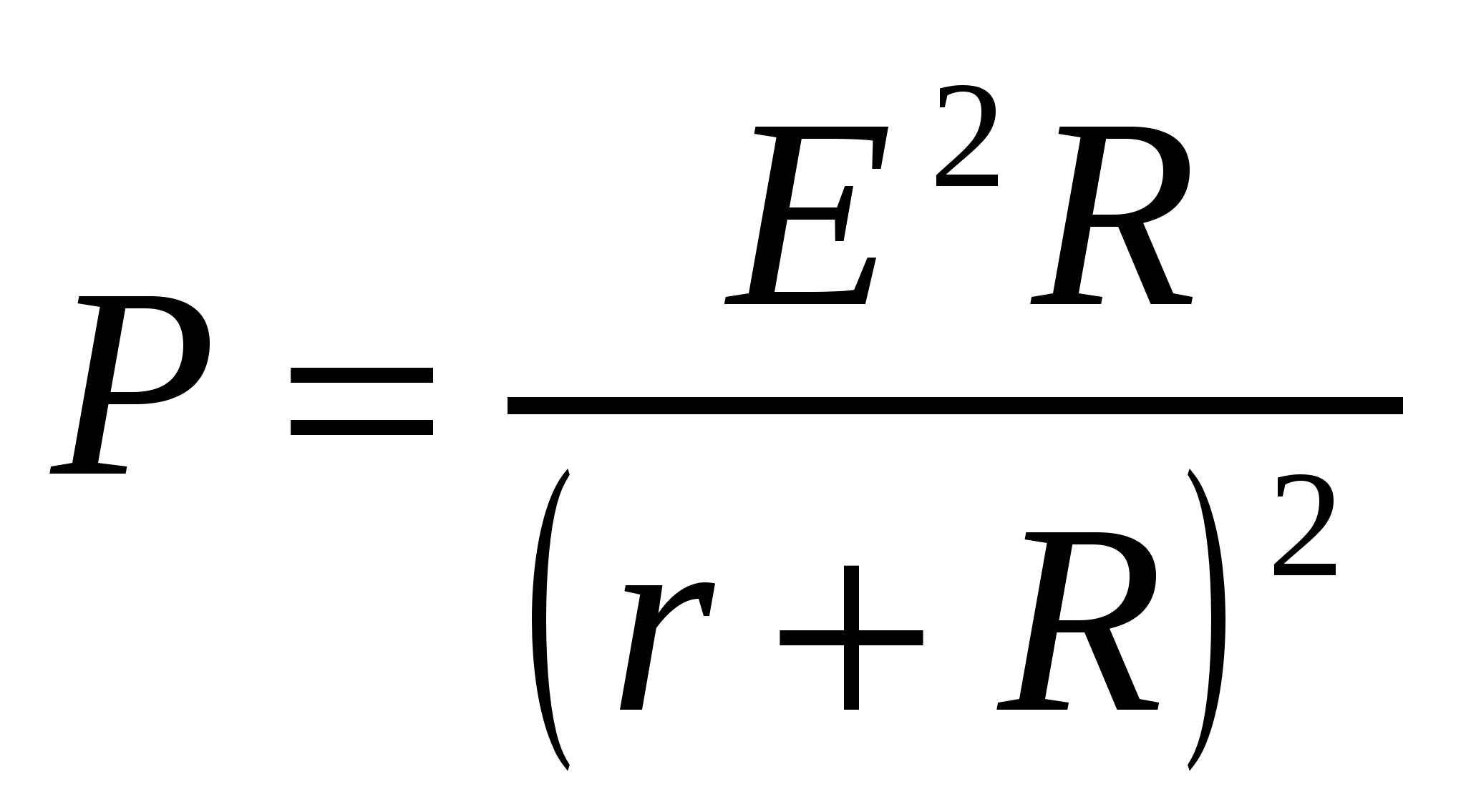 ,
,
где Е - постоянная электродвижущая сила элемента;
r - постоянное внутреннее сопротивление;
R - внешнее сопротивление.
Каким должно быть внешнее сопротивление R,чтобы мощность Р была наибольшей?
Решение 1. Приравняем нулю производную : 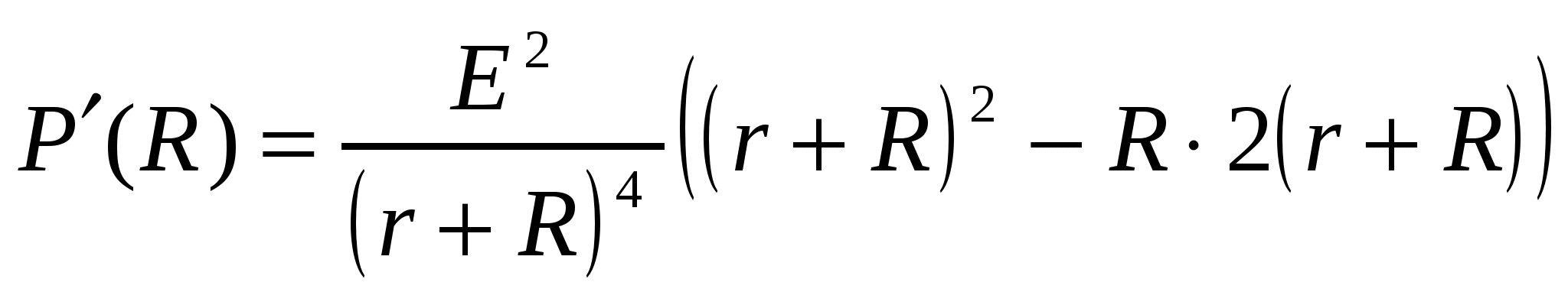 ;
;
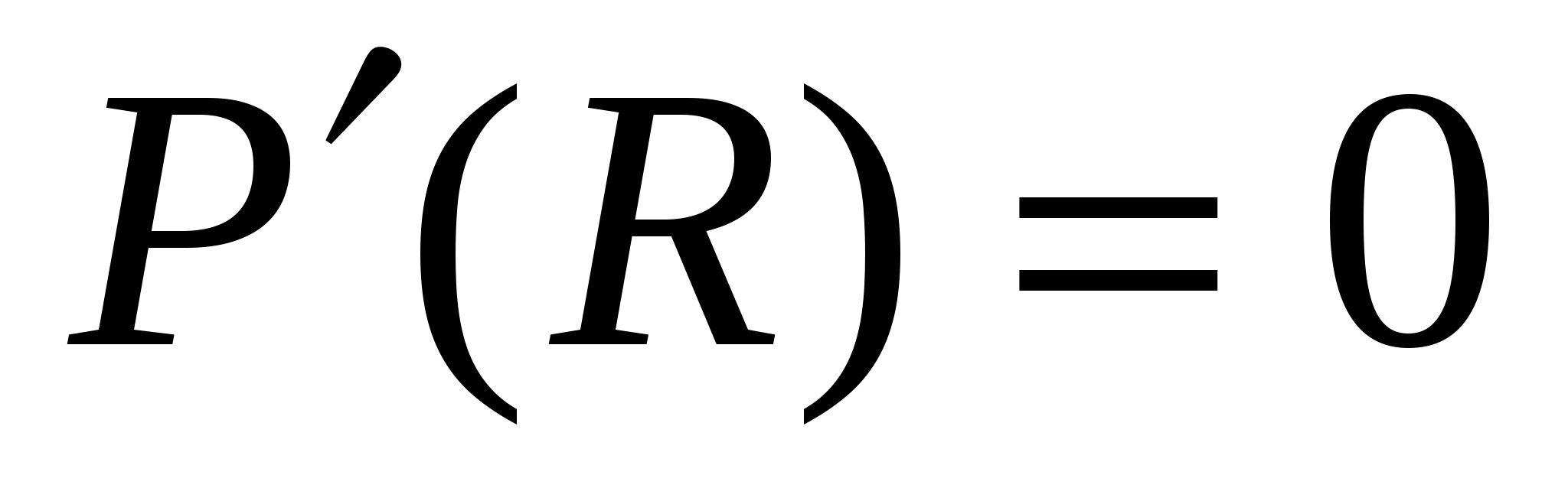 ,откуда,
,откуда, 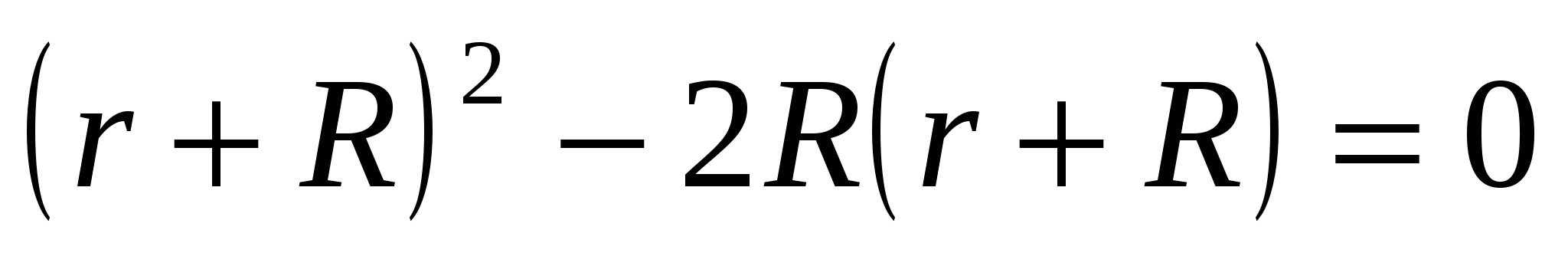 , но
, но 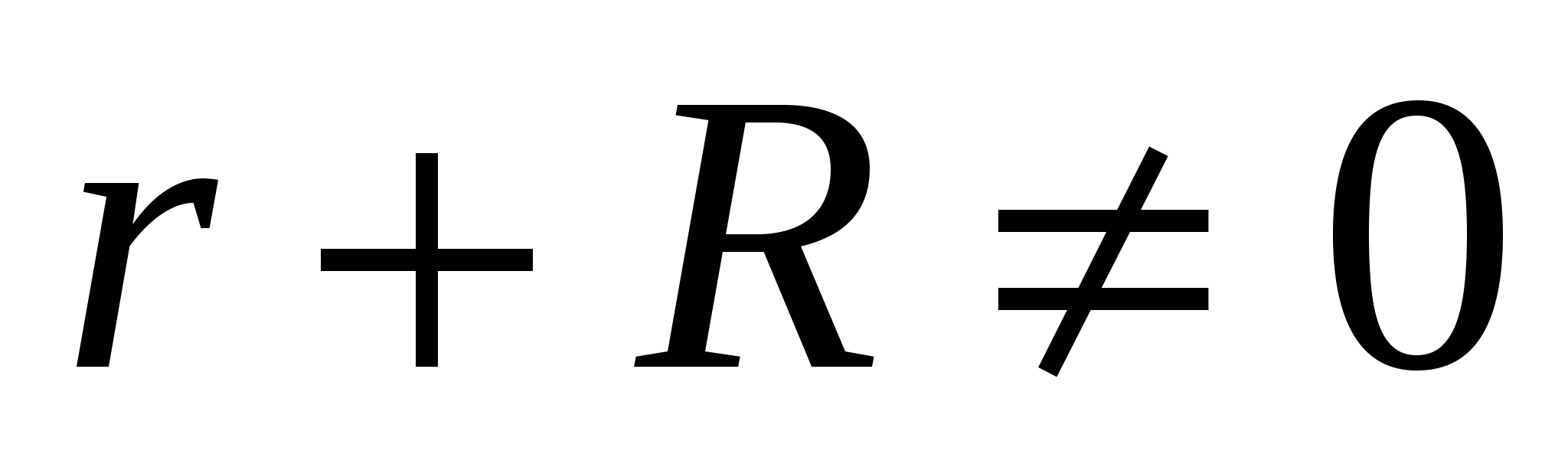 , значит,
, значит, 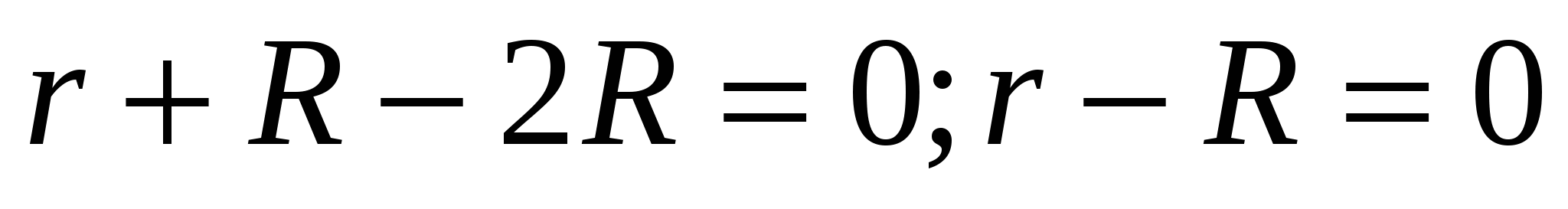 откуда
откуда 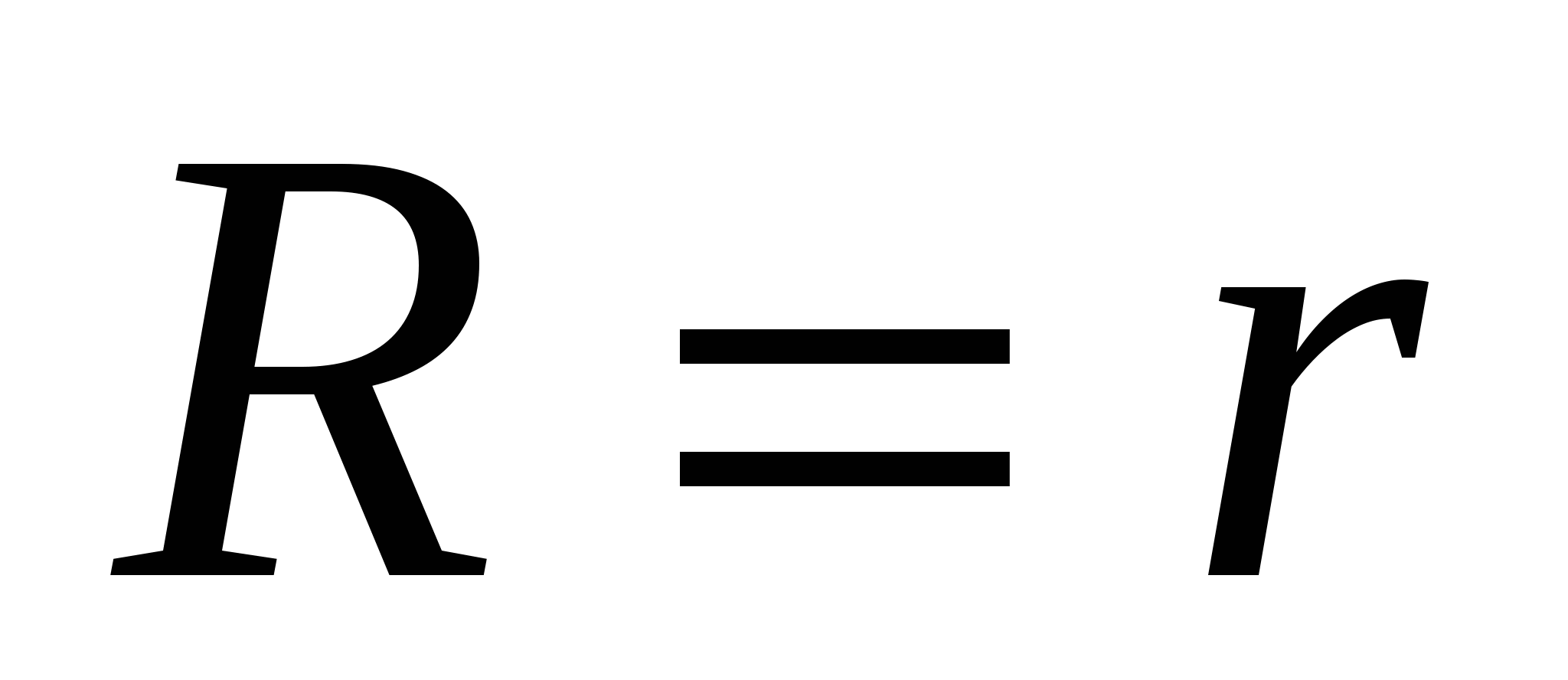 .
.
Ответ: ![]() .
.
Решение 2.
Преобразуем формулу мощности следующим образом 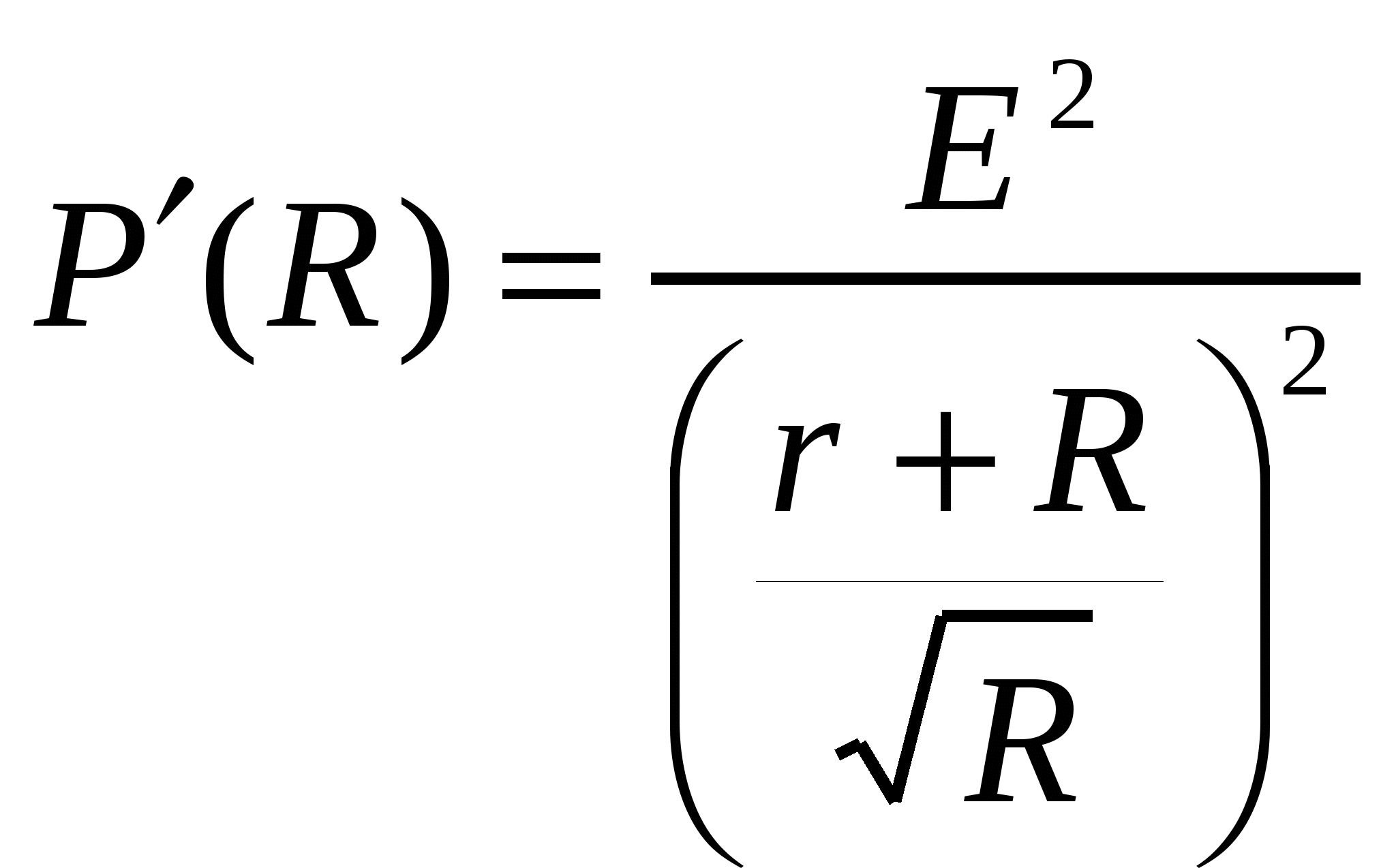 . Поскольку
. Поскольку 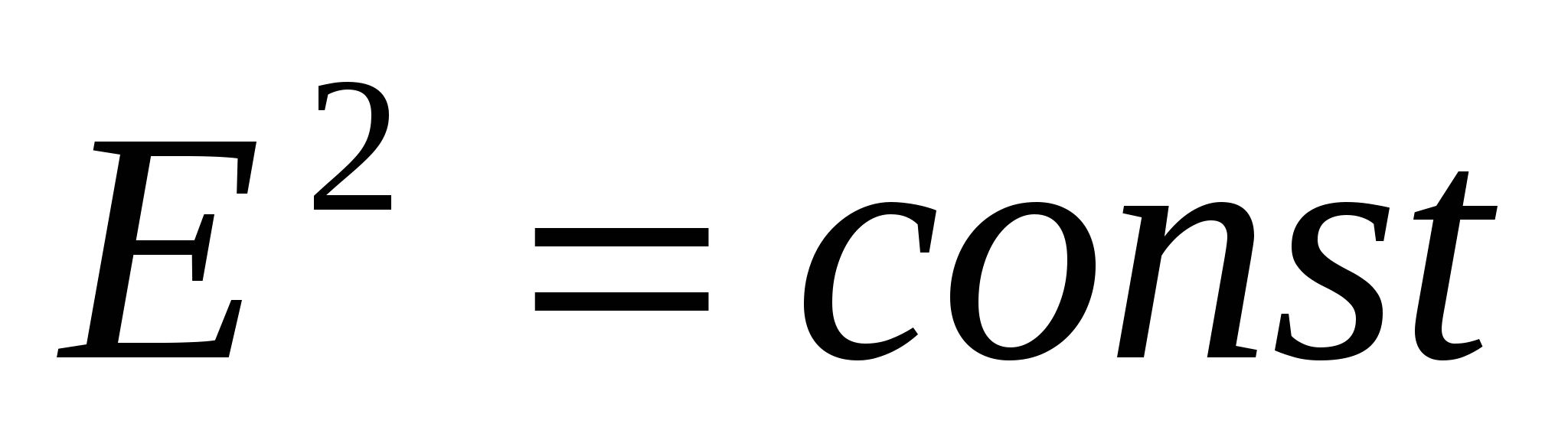 ,то P(R) достигает максимума, если
,то P(R) достигает максимума, если 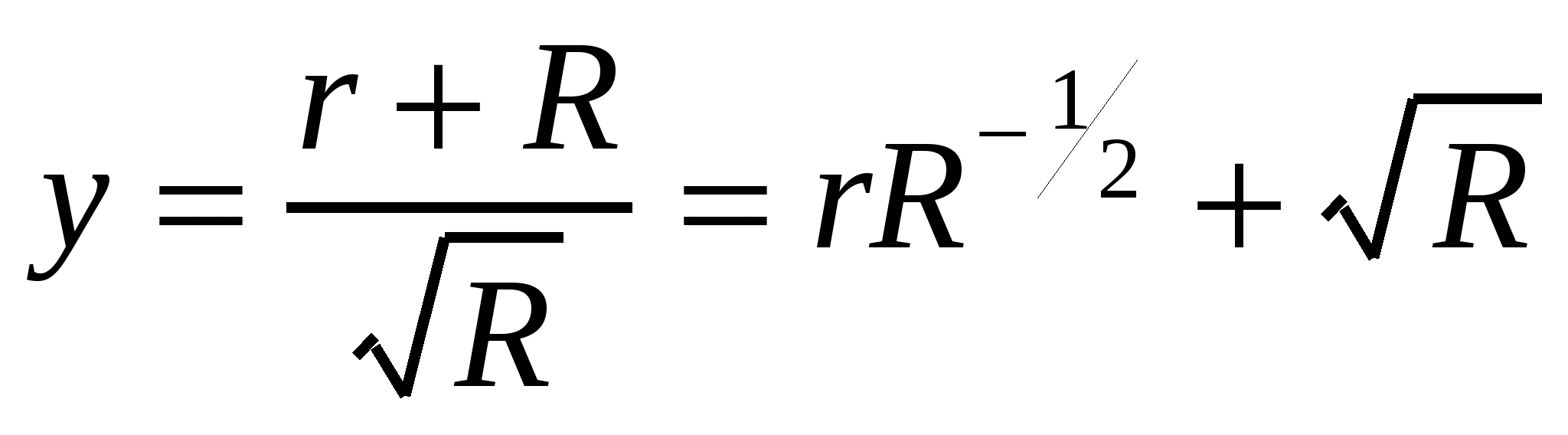 достигает минимума.
достигает минимума. 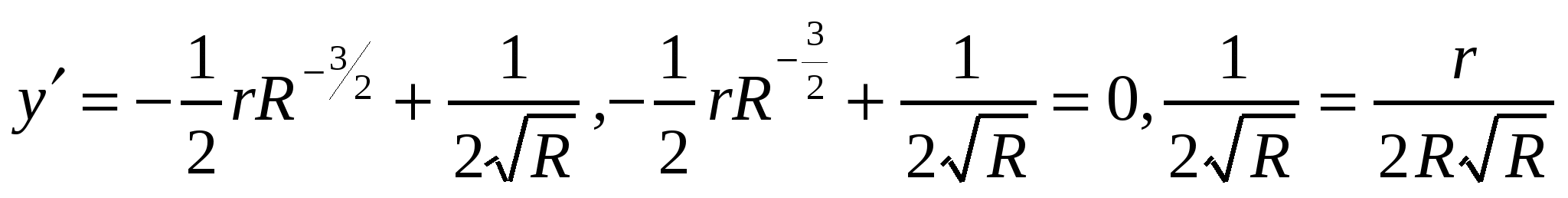 , значит
, значит 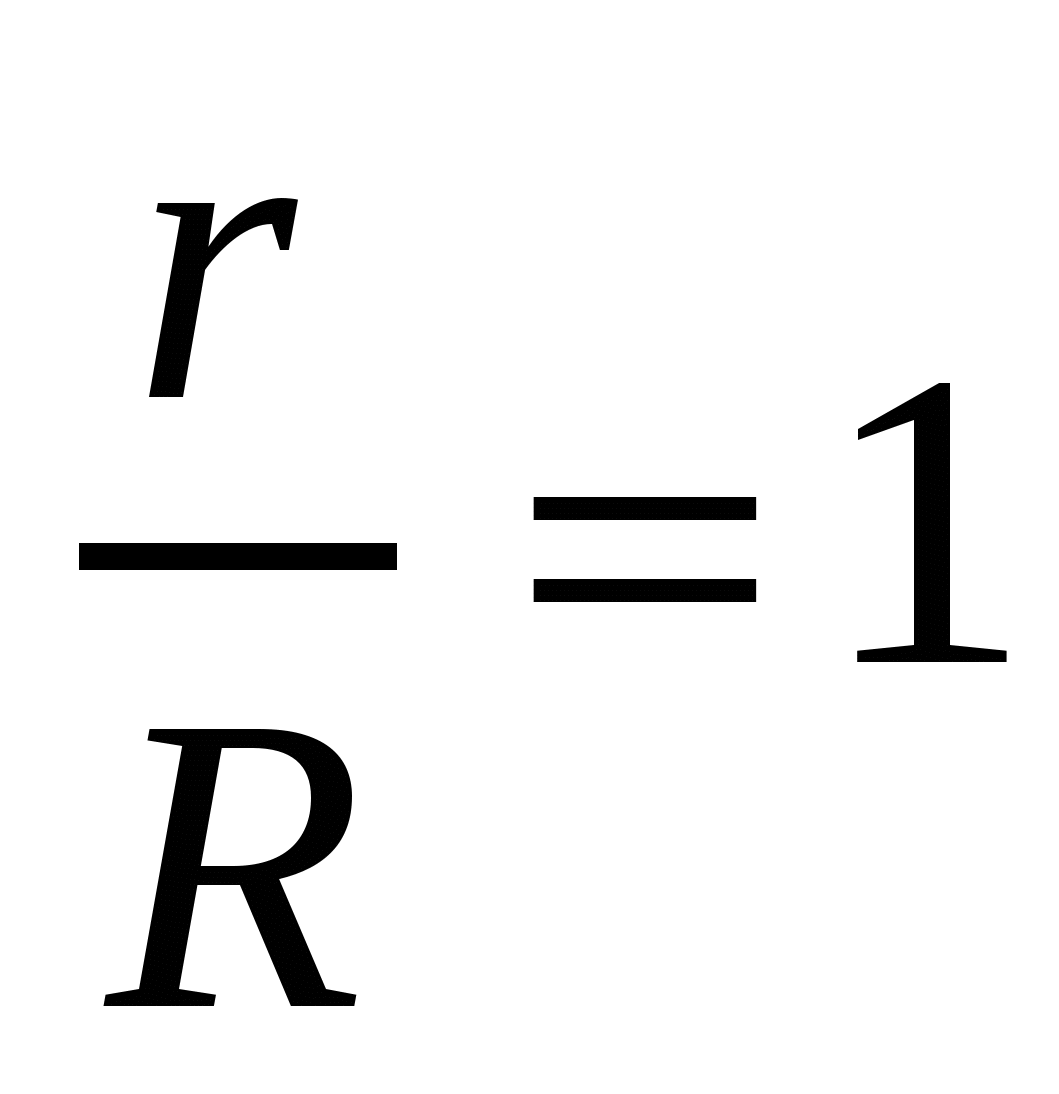 , откуда
, откуда 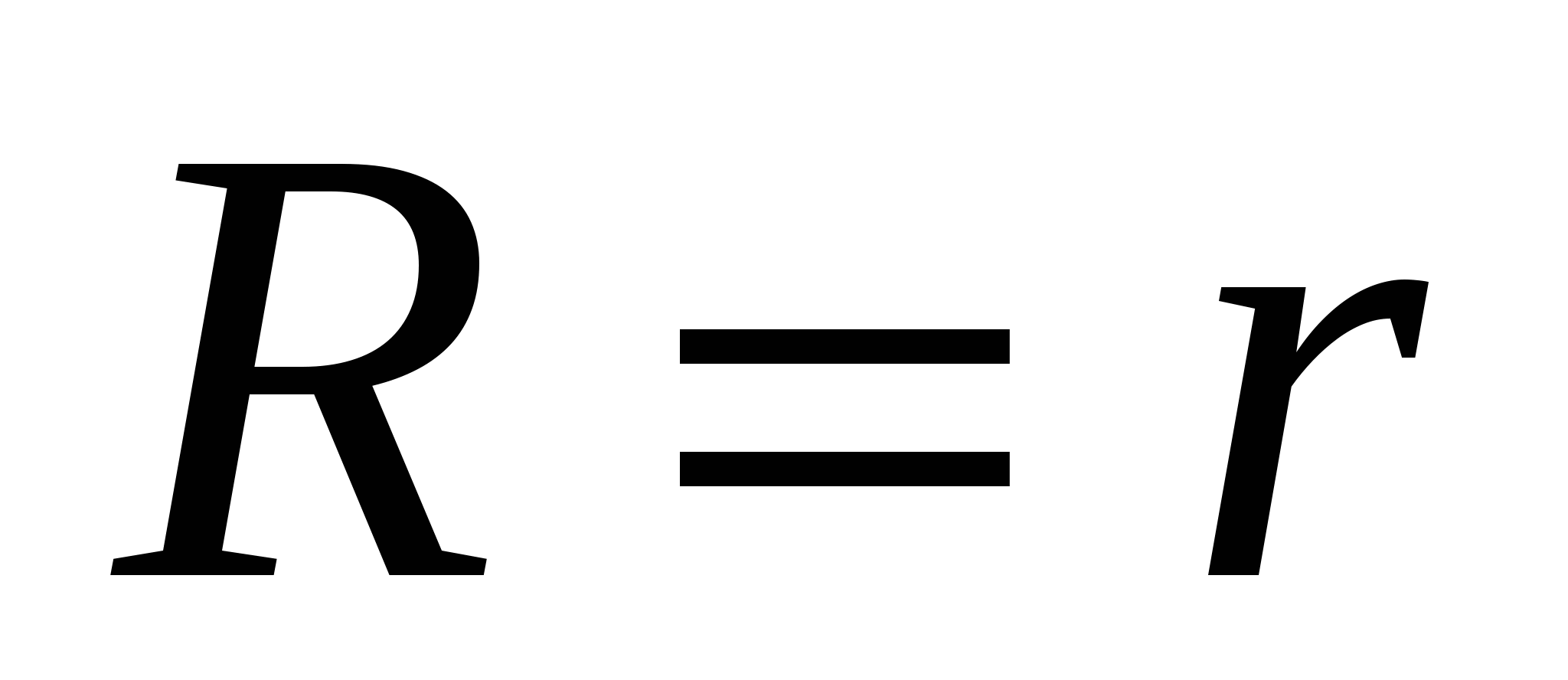 .
.
Ответ: ![]() .
.
Задача 14
Определить размеры открытого бассейна с квадратным дном объемом 32 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение 1. Пусть сторона основание х, а высота у, у >0. Объем бассейна 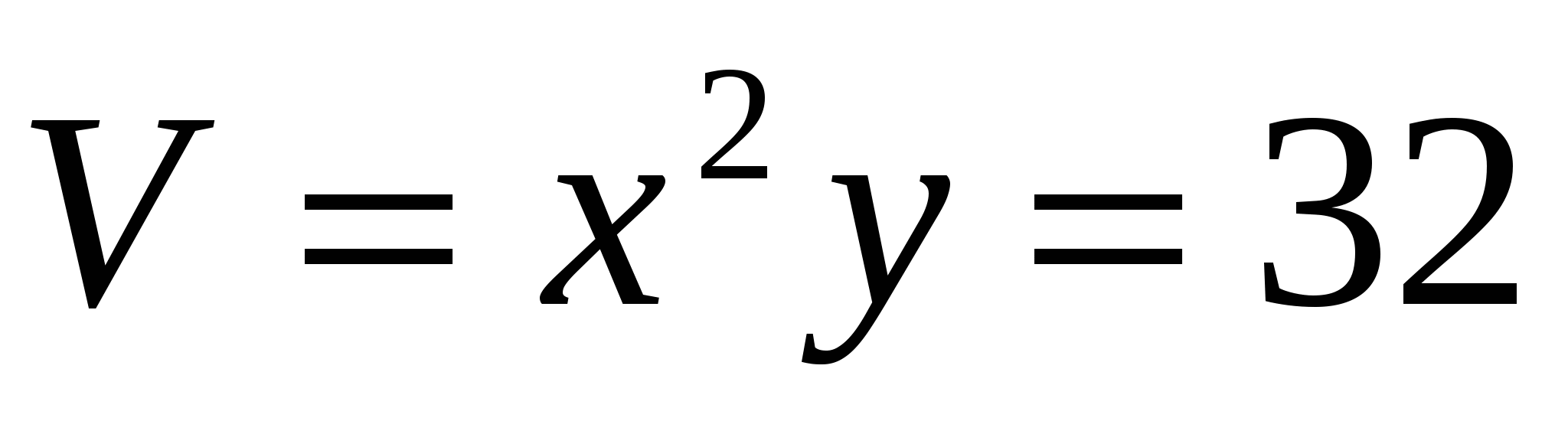 ,(1). Облицовываемая поверхность,
,(1). Облицовываемая поверхность, 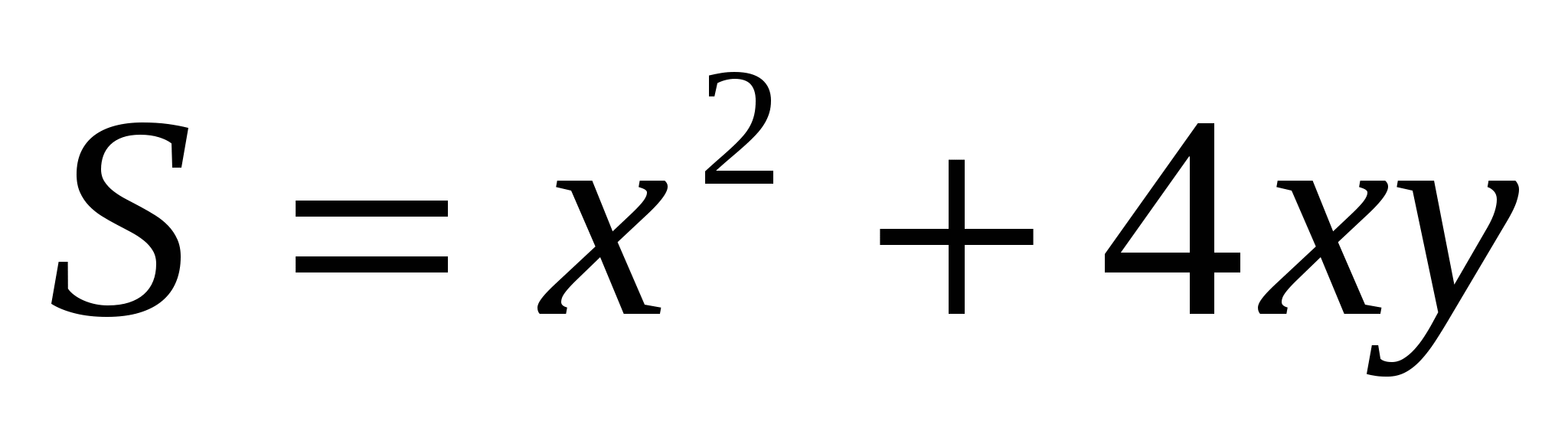 ,(2). Из (1) имеем
,(2). Из (1) имеем 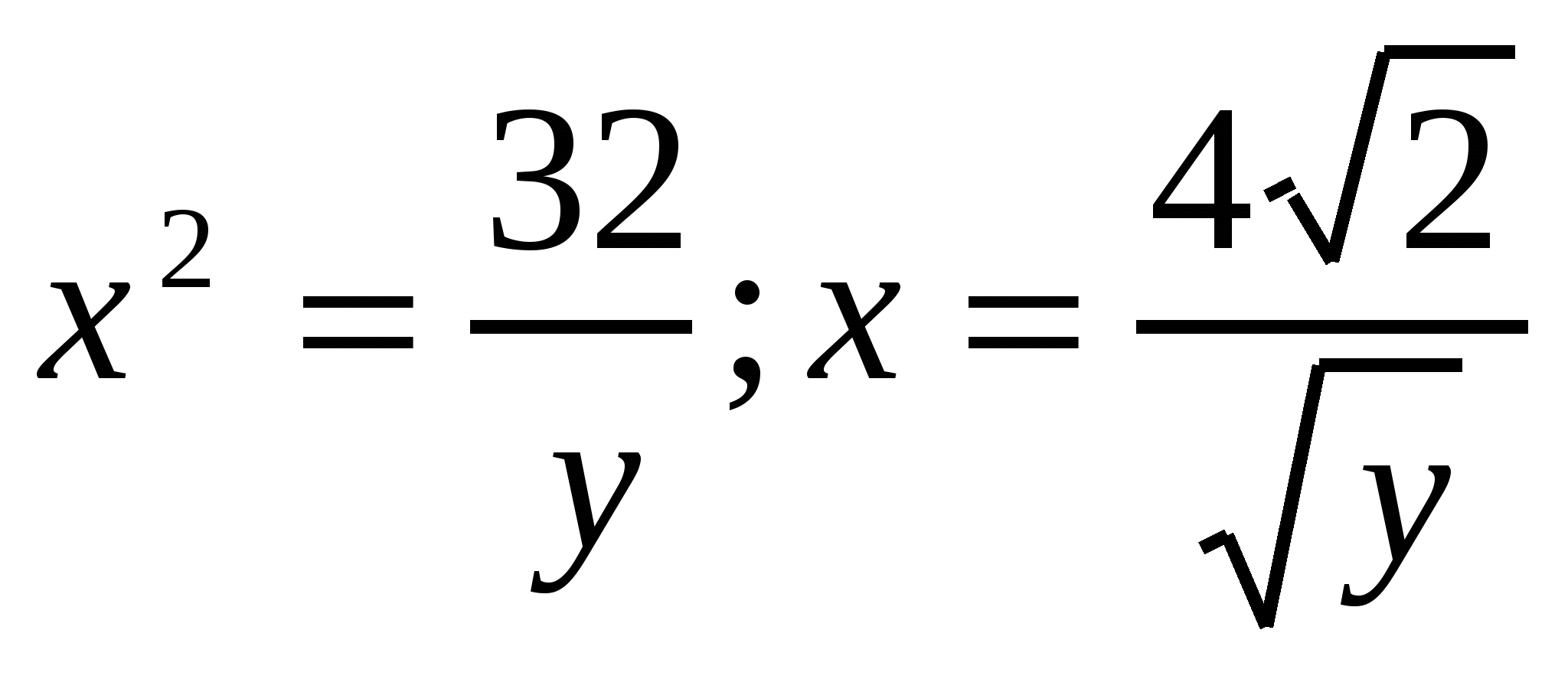 ,(3). Поставим (3) в (2).
,(3). Поставим (3) в (2). 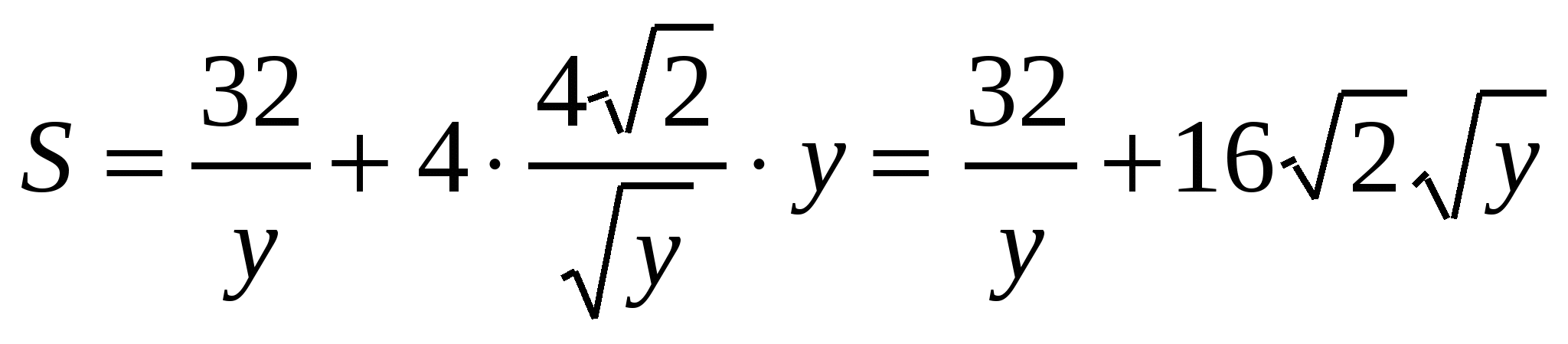 . Приравняем нулю производную
. Приравняем нулю производную ![]() .Имеем:
.Имеем: 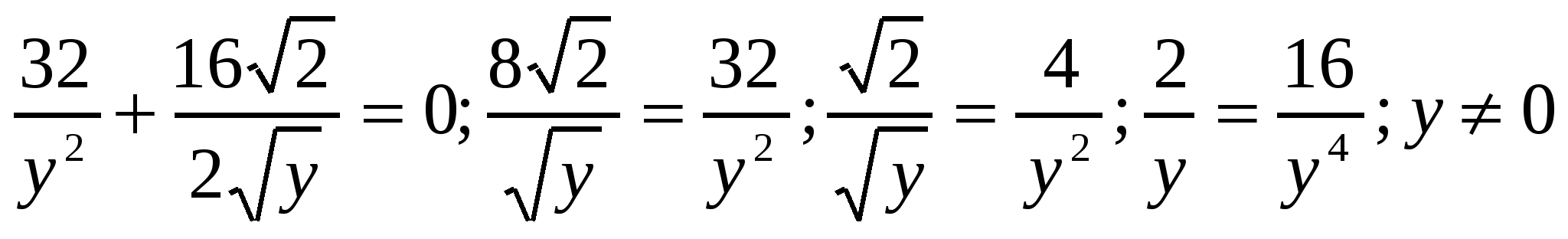 .
.
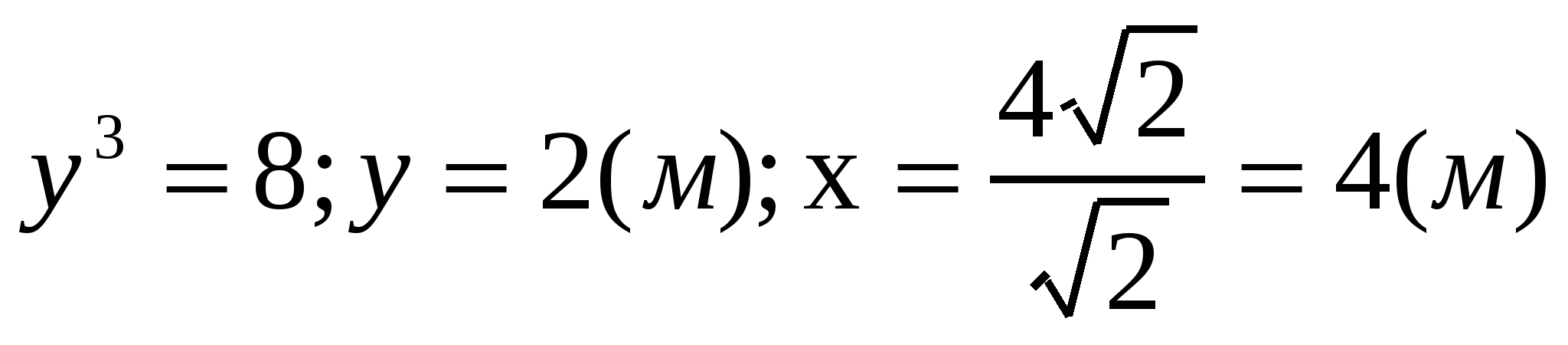 .
.
Ответ: 2 м; 4 м.
Решение 2.Так как 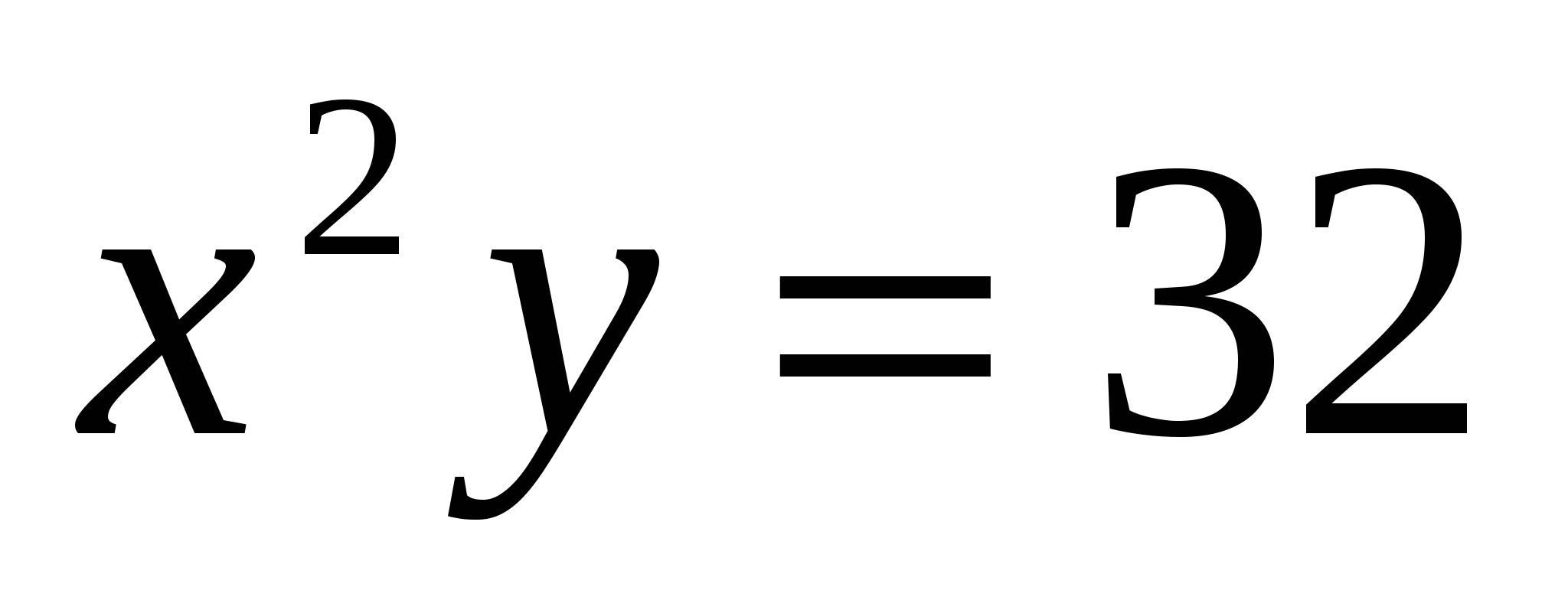 ,то
,то 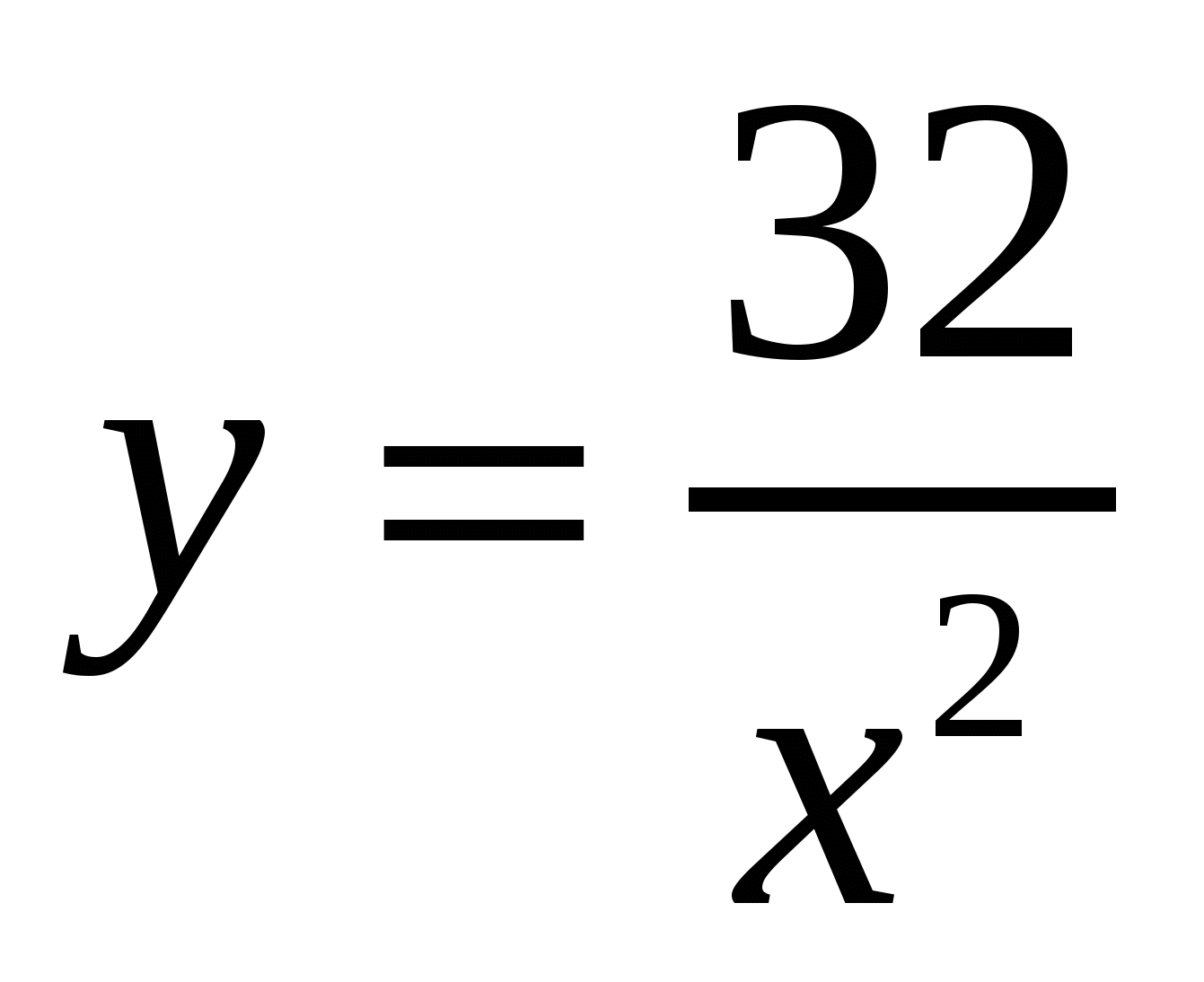 ,тогда
,тогда 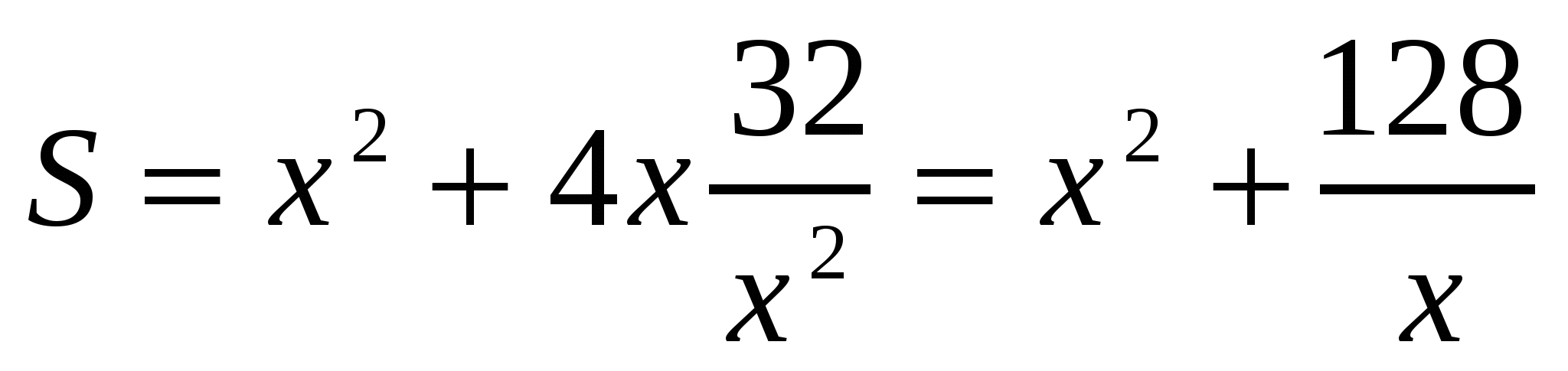 .
. 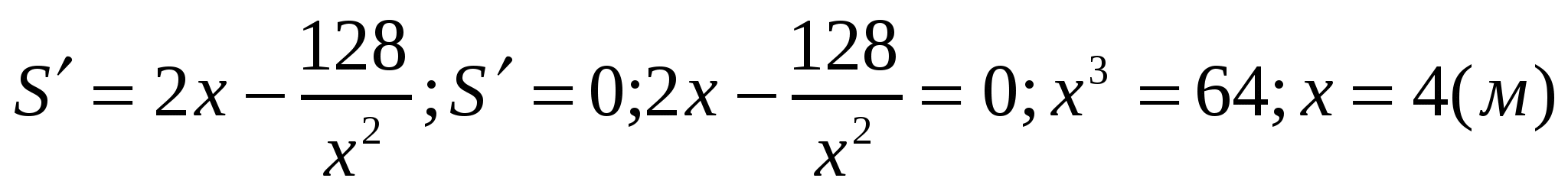 .
. 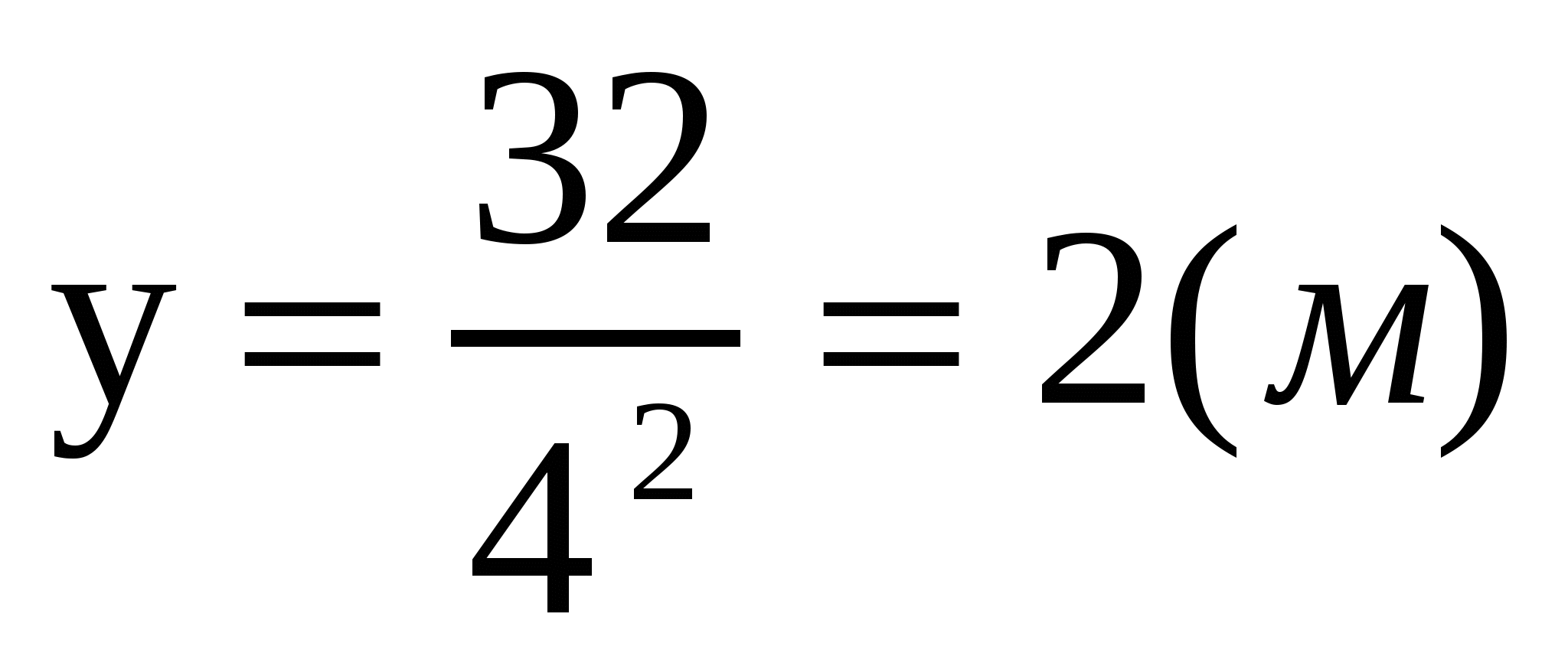 . Часто соображение физического или геометрического характера от исследования функции на экстремум.
. Часто соображение физического или геометрического характера от исследования функции на экстремум.
Ответ: 2 м; 4 м.
Задание 15
Вращая четверть круга, радиуса R вокруг оси х, получим половину шара.
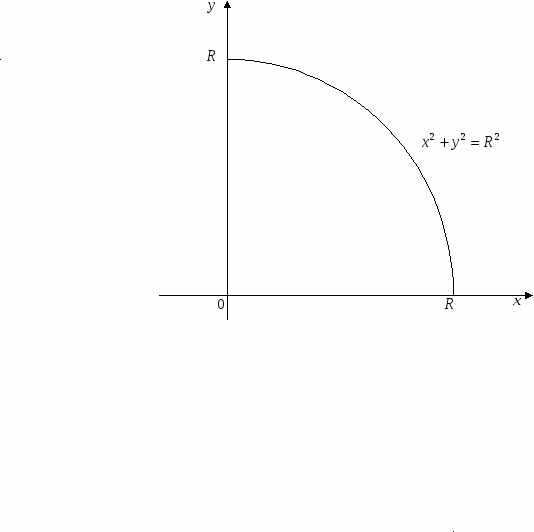
Поэтому, 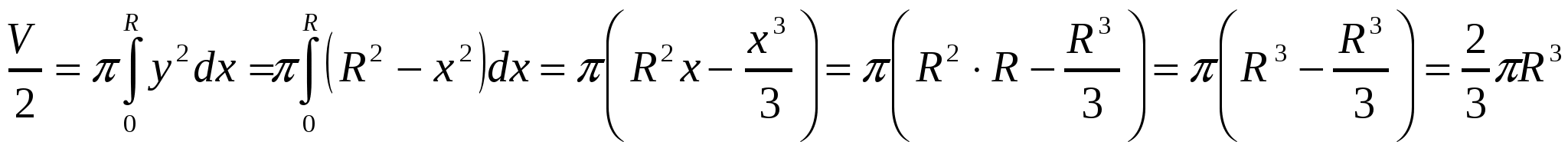 . Откуда,
. Откуда, 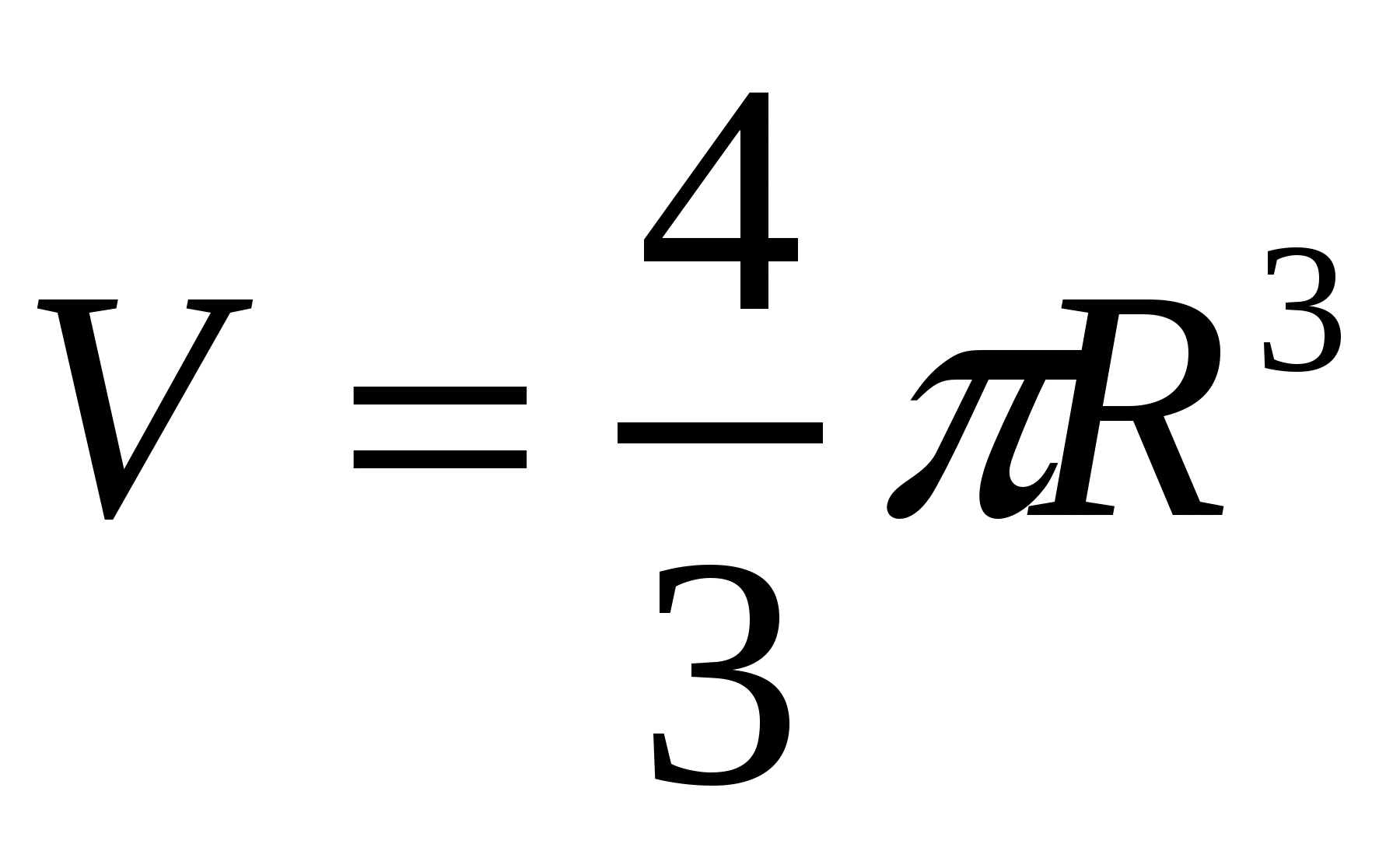 .
.
Ответ: 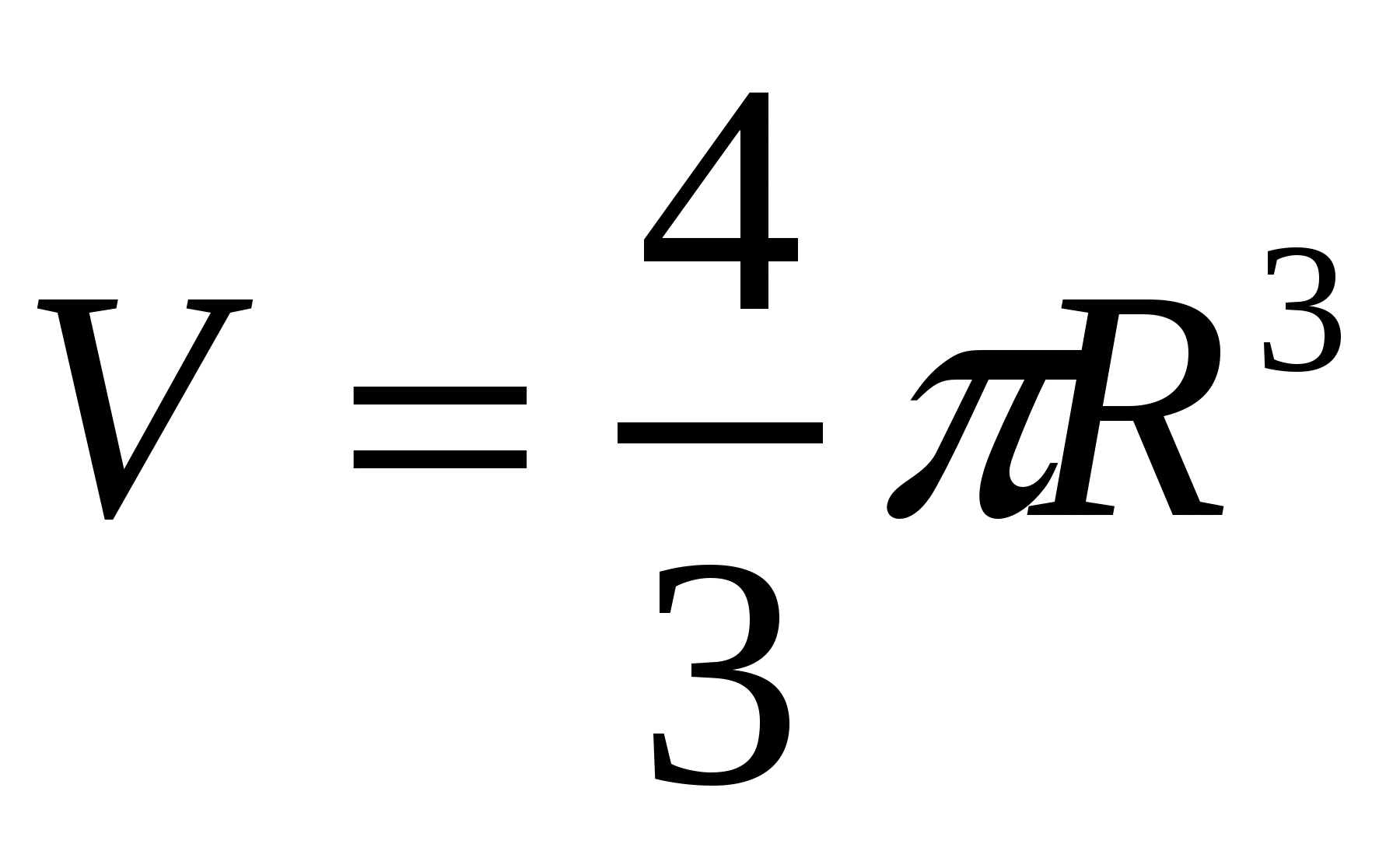 .
.
Решение 2. Вращая четверть круга, радиус R вокруг оси у, получим половину шара. Поэтому, 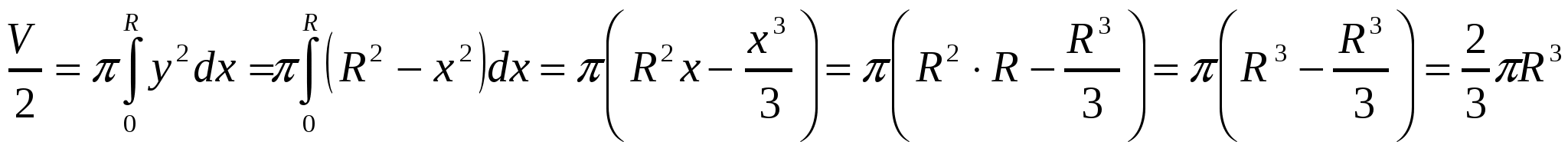 . Откуда,
. Откуда, 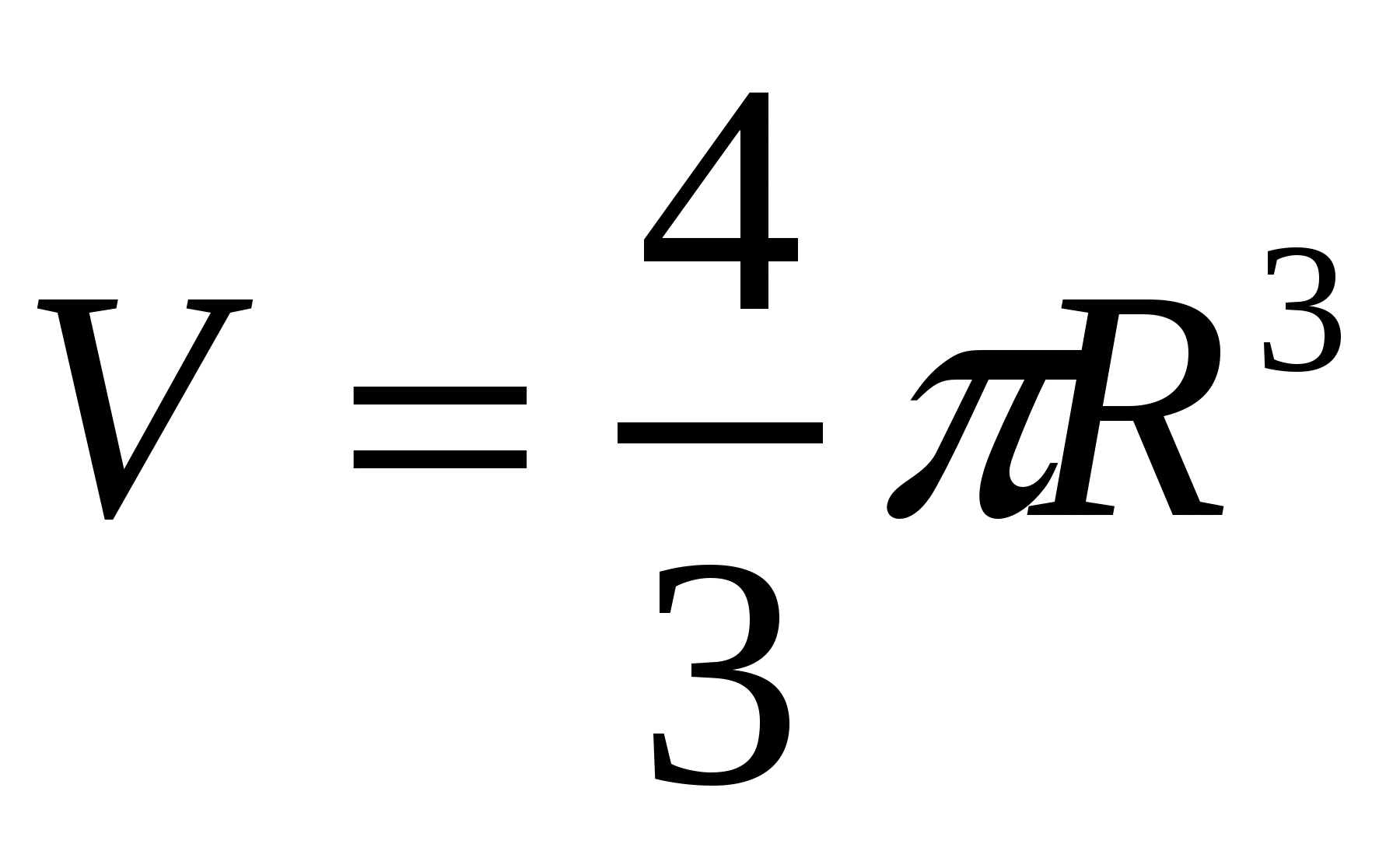 .
.
Ответ: 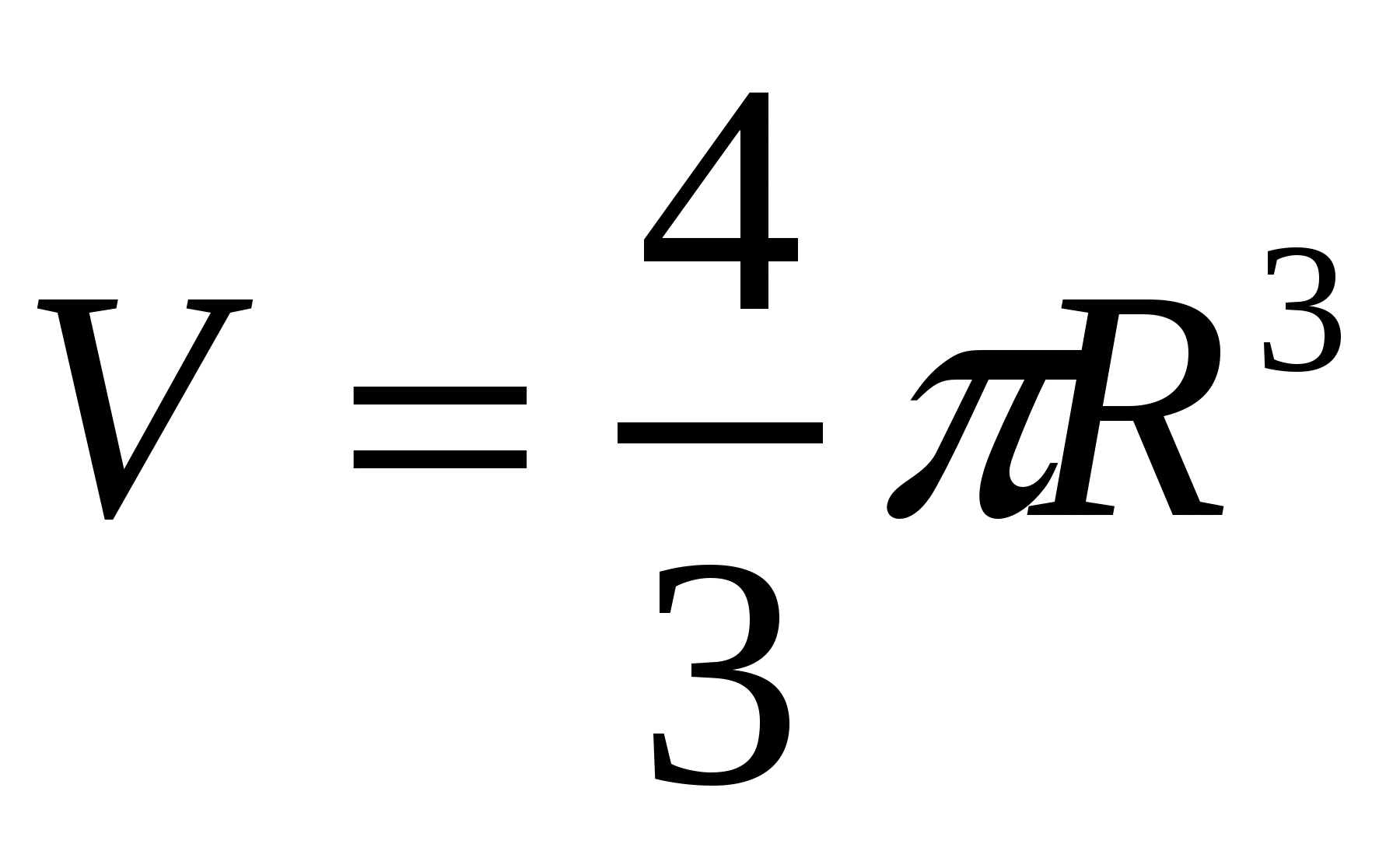 .
.
Решение 3. Применим формулу 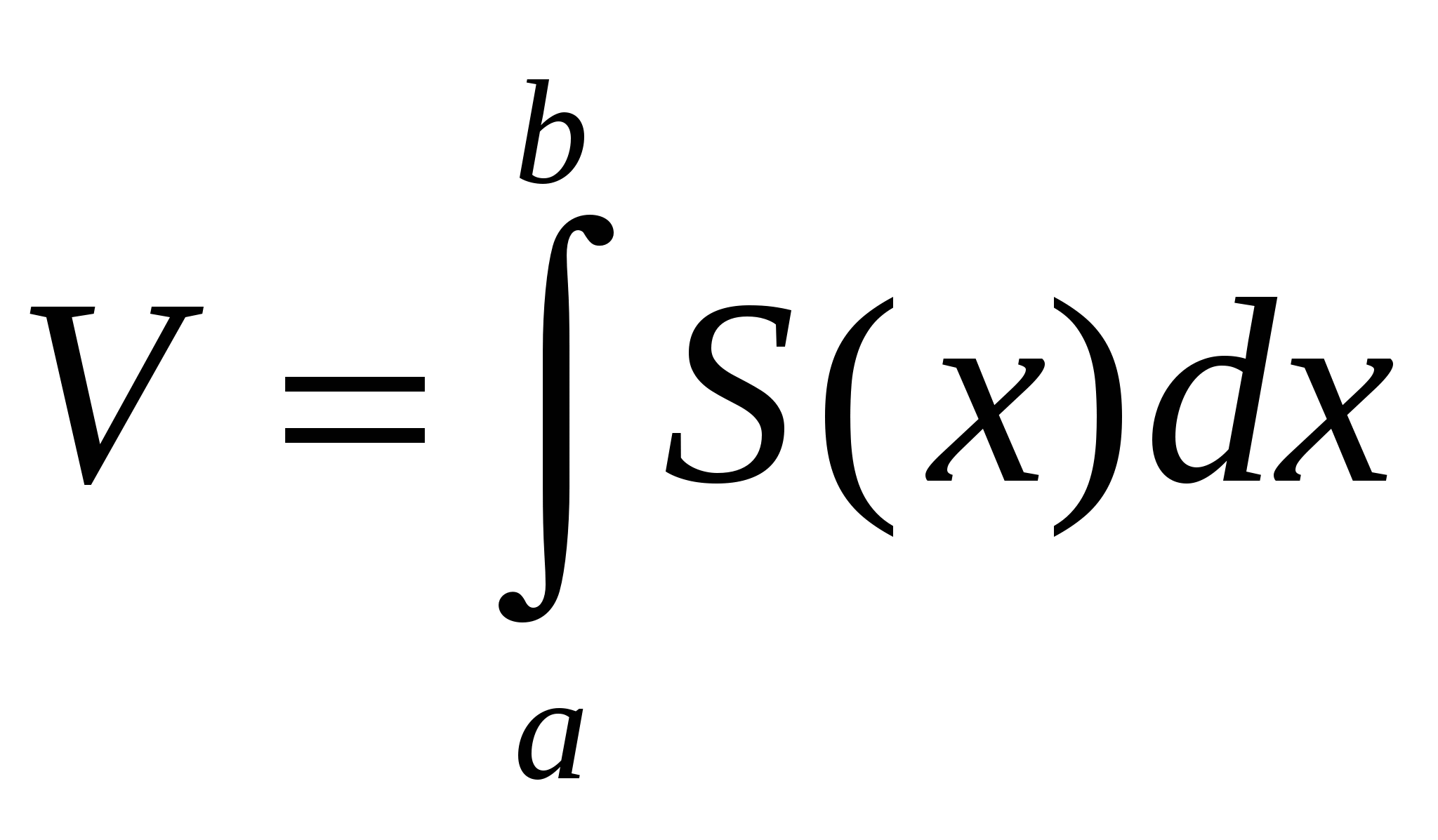 , тогда
, тогда 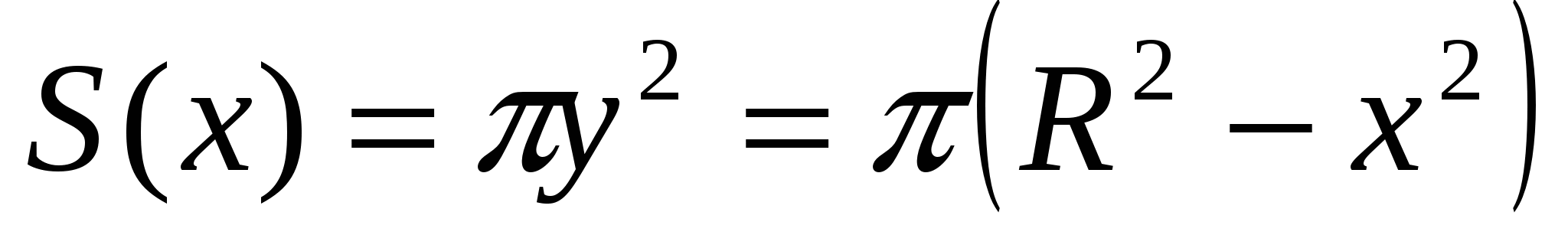 .
.
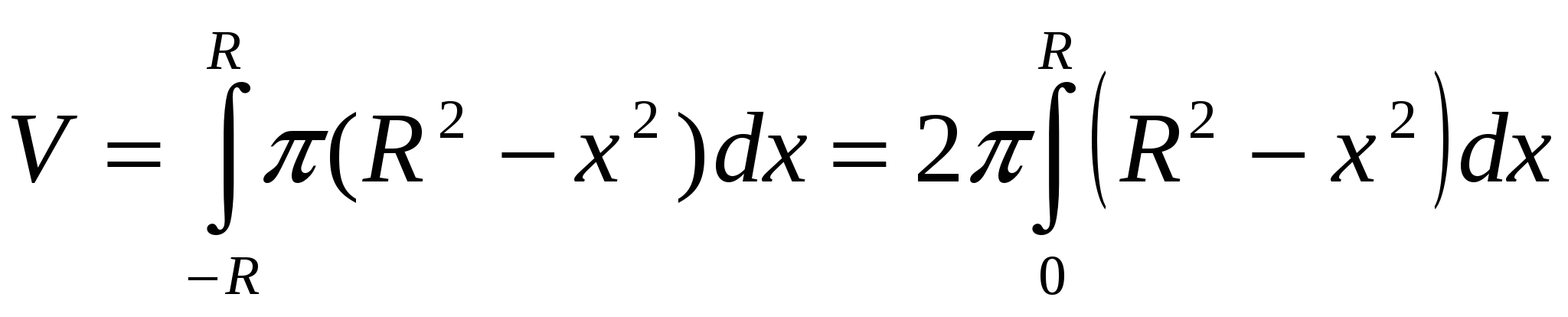 и т.д. как в решении 1.
и т.д. как в решении 1.
Ответ: 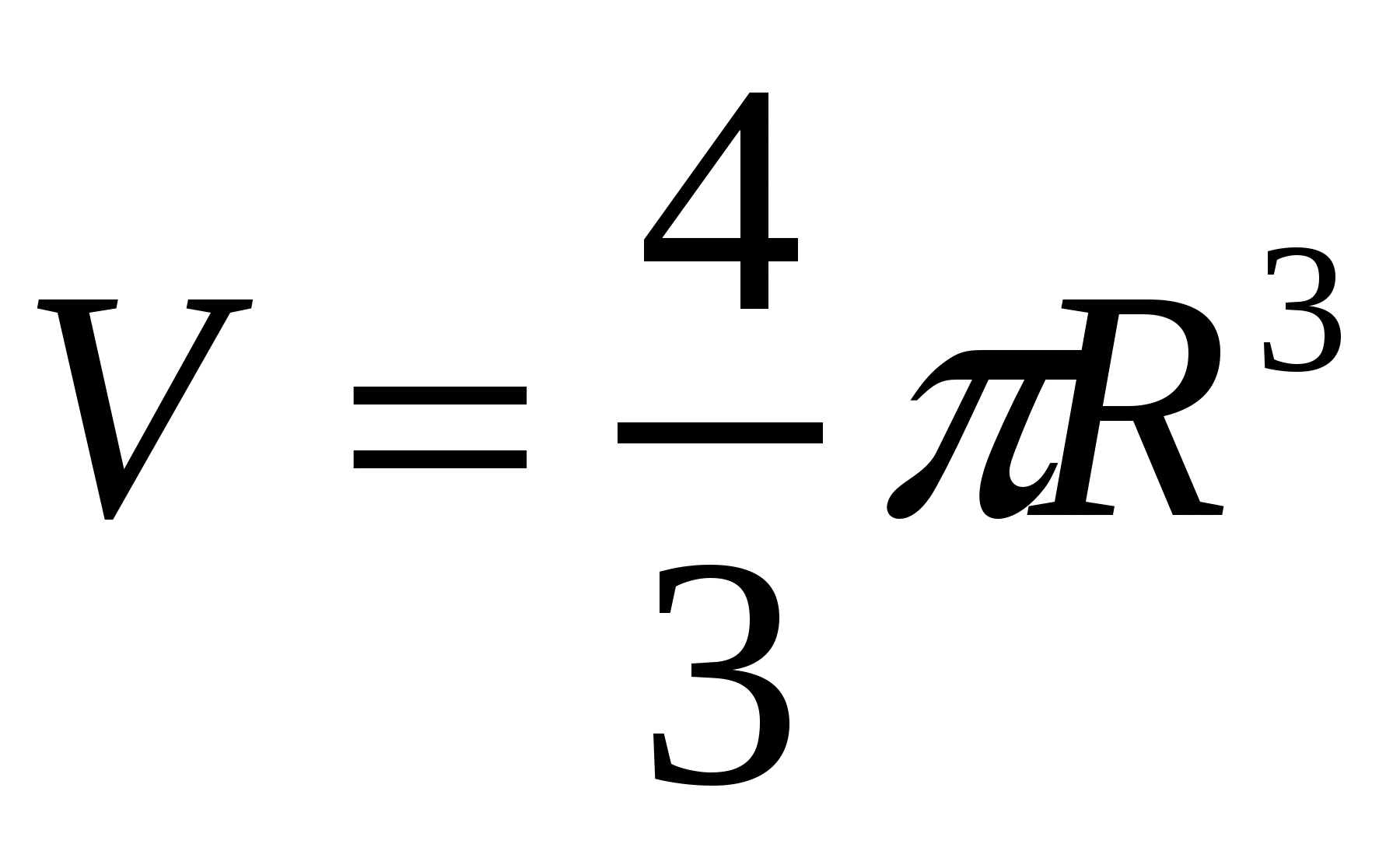 .
.
Стандартный уровень
Завдання 1
Для функції у=(2х+3)4 знайти первісну, графік якої проходить через точку А(-1; 1).
Розв'язування:
Загальний вигляд первісних F(х)=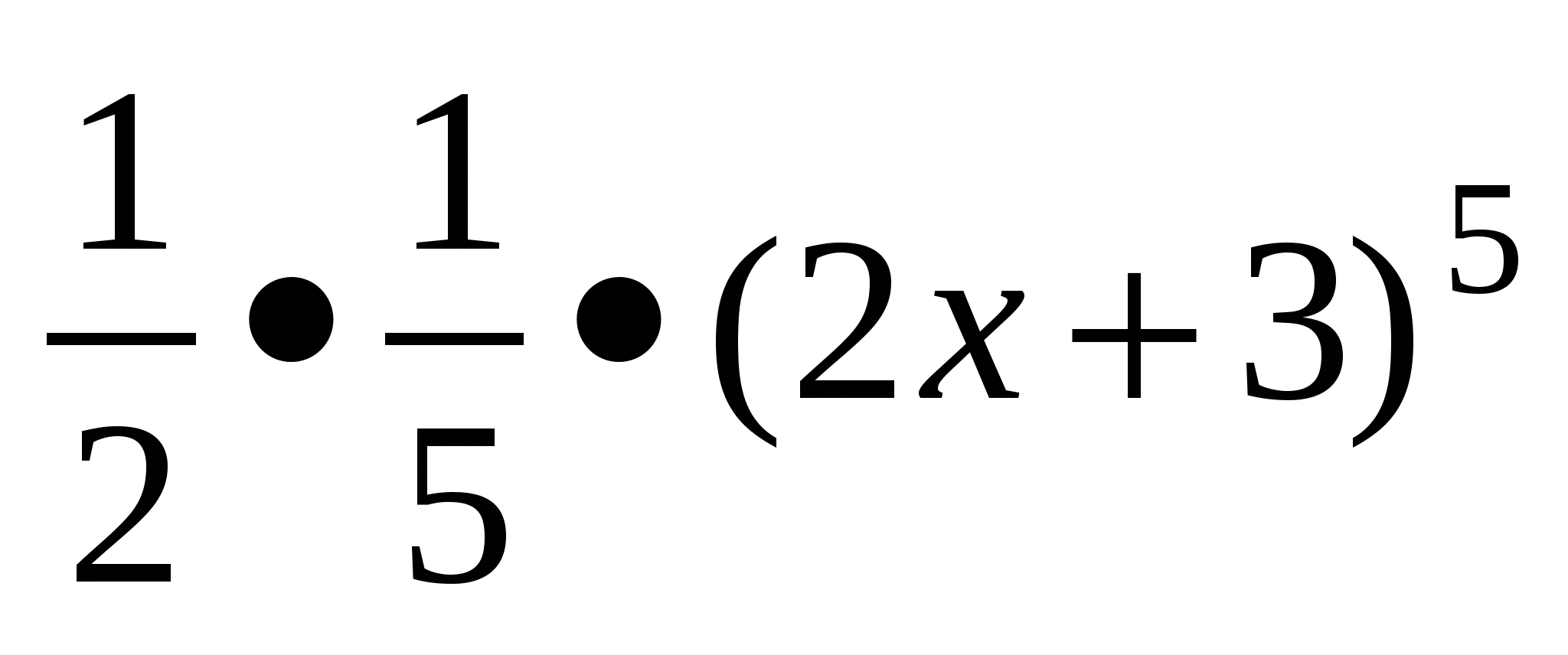 +
+ =
=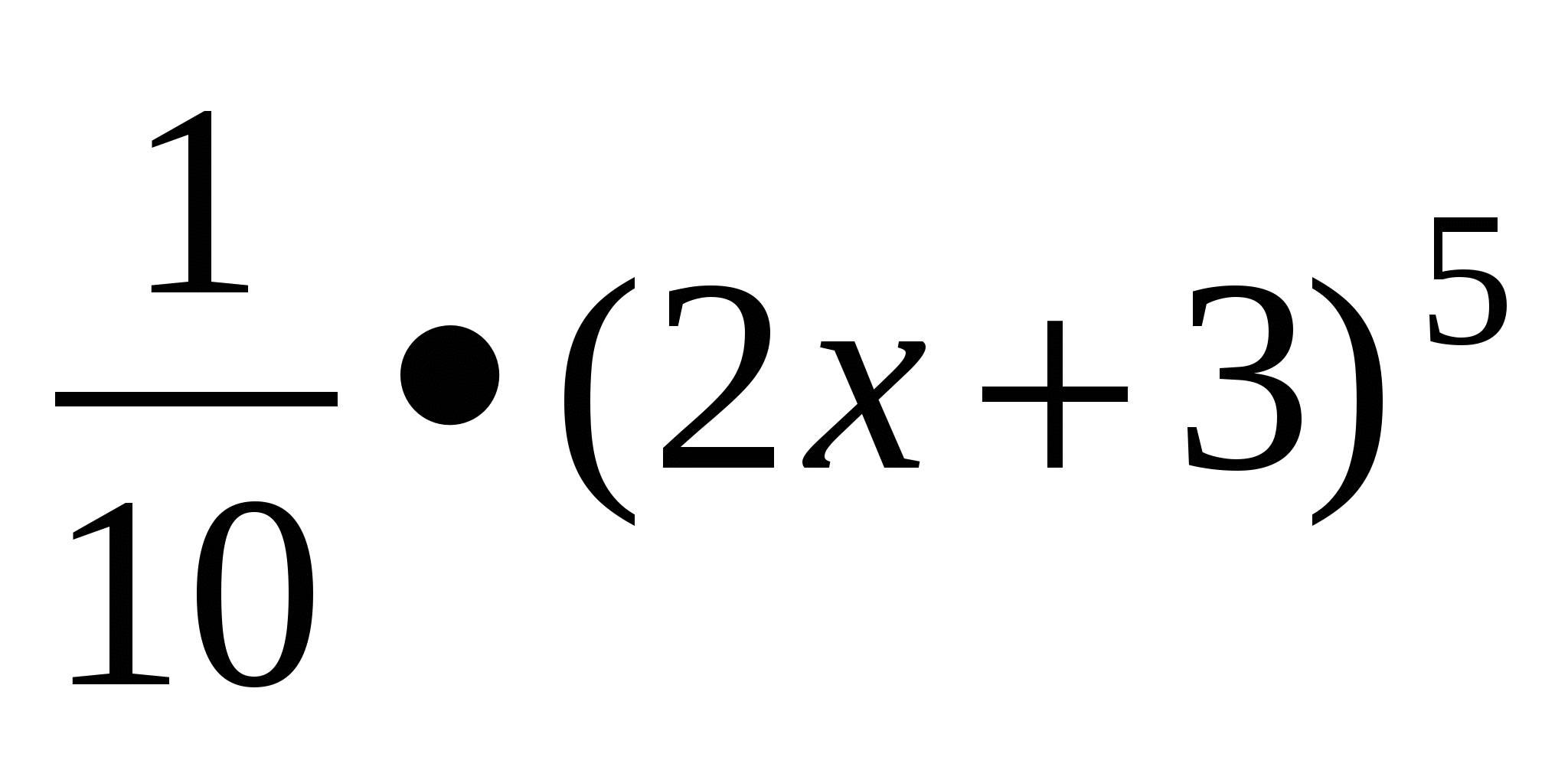 +
+ . Графік первісної проходить через точку А(-1; 1), тому F(-1)=1. Знайдемо значення С за вказаної умови. F(-1)=
. Графік первісної проходить через точку А(-1; 1), тому F(-1)=1. Знайдемо значення С за вказаної умови. F(-1)=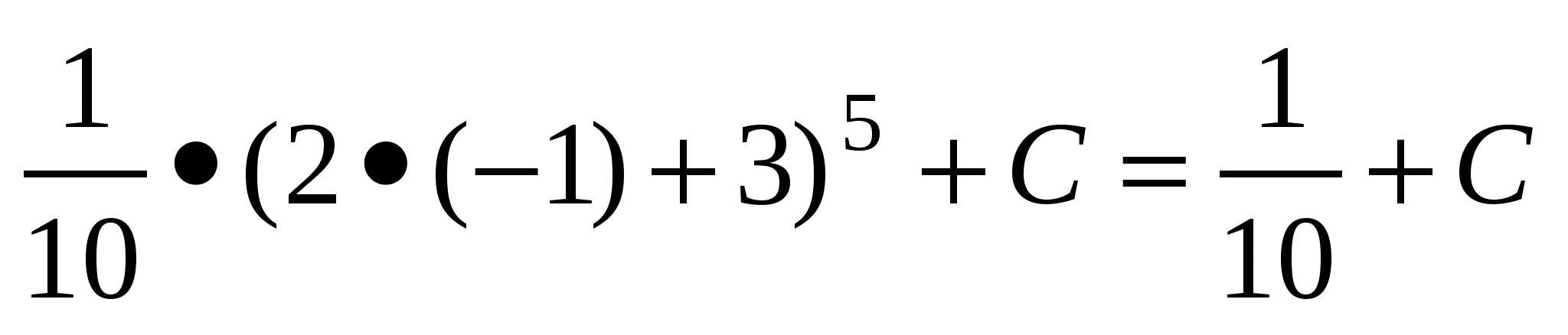 =1,
=1,  =
=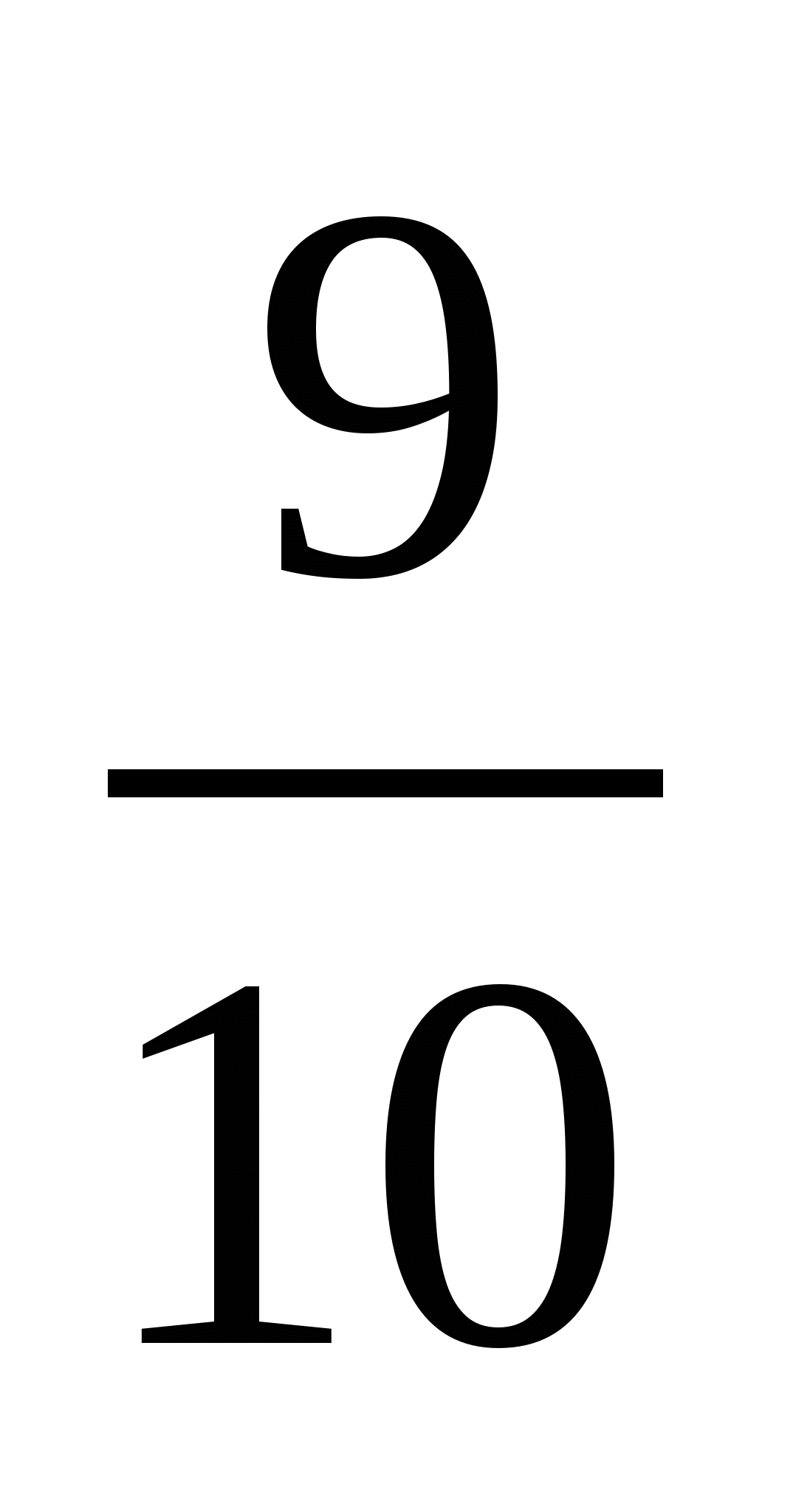 .
.
Отже, F(х)= 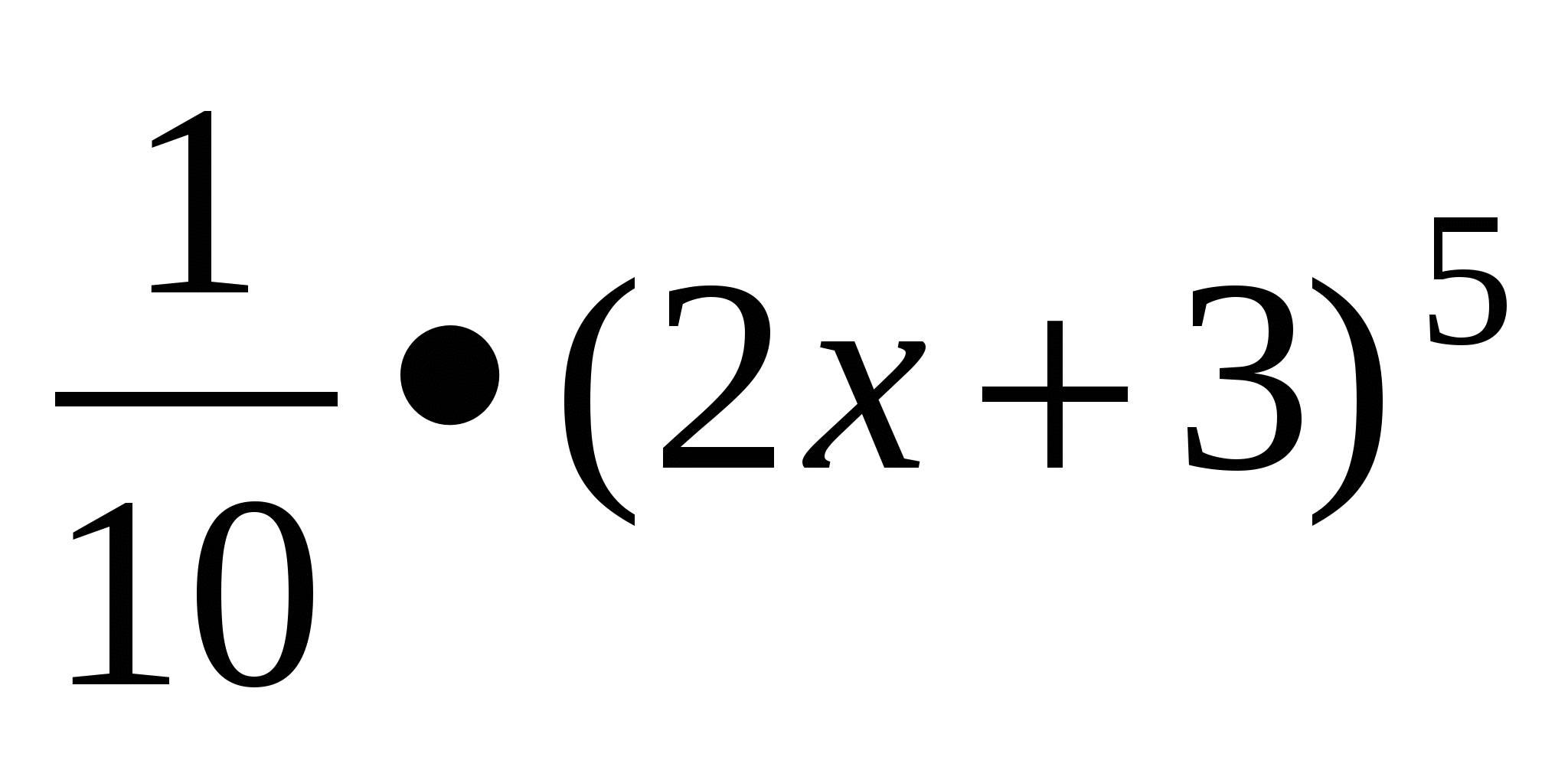 +
+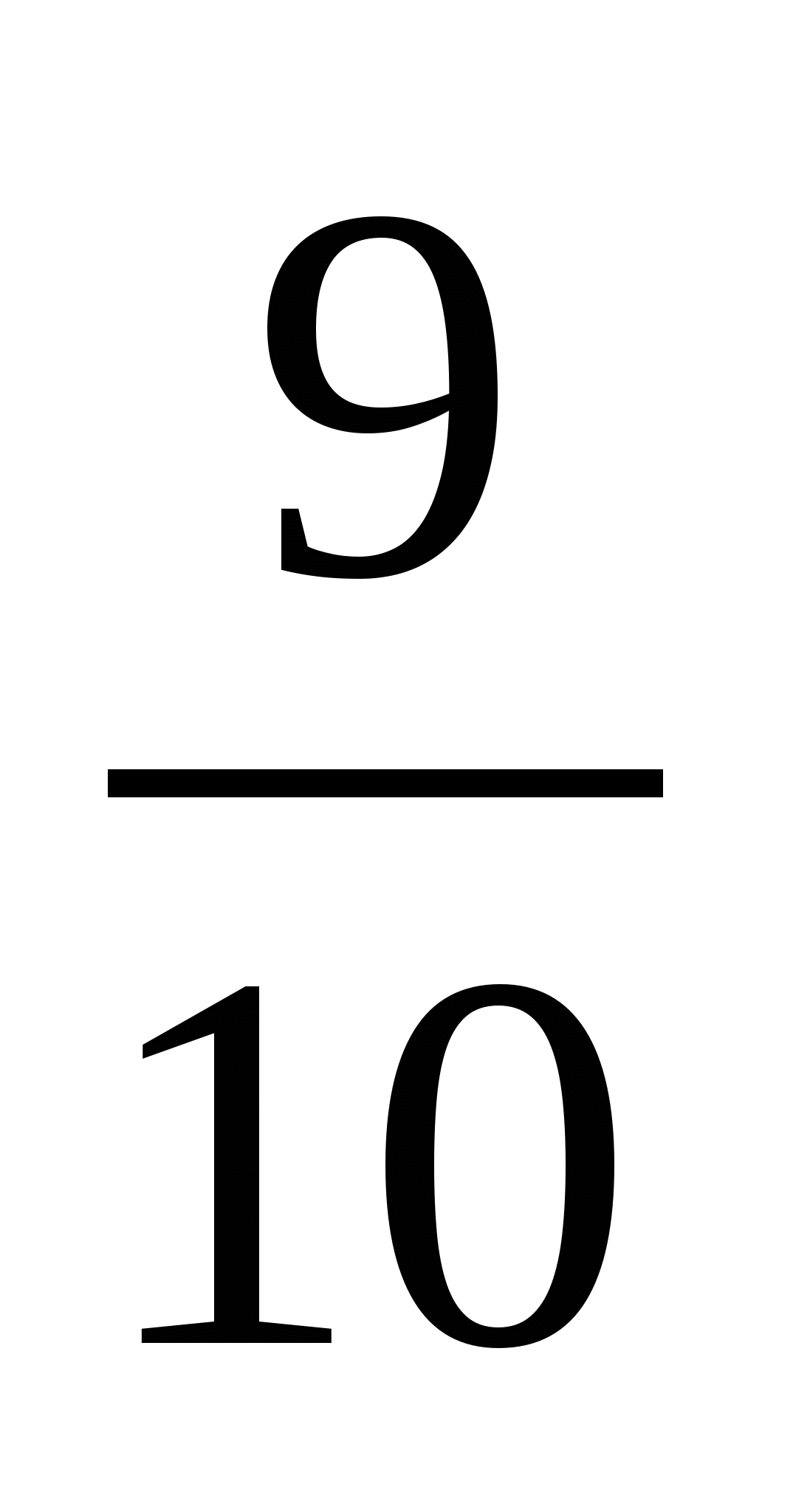 .
.
Відповідь: F(х)= 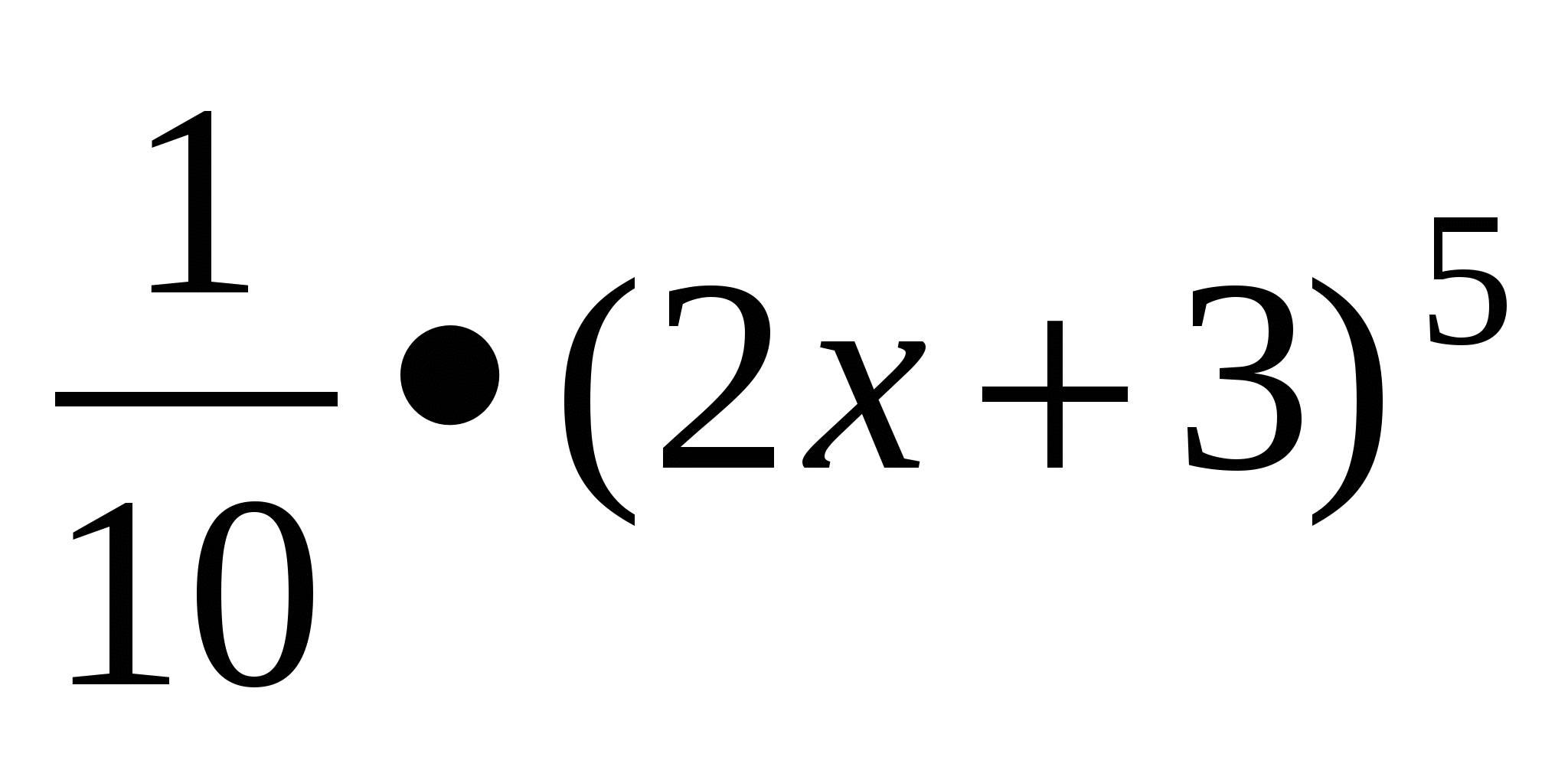 +
+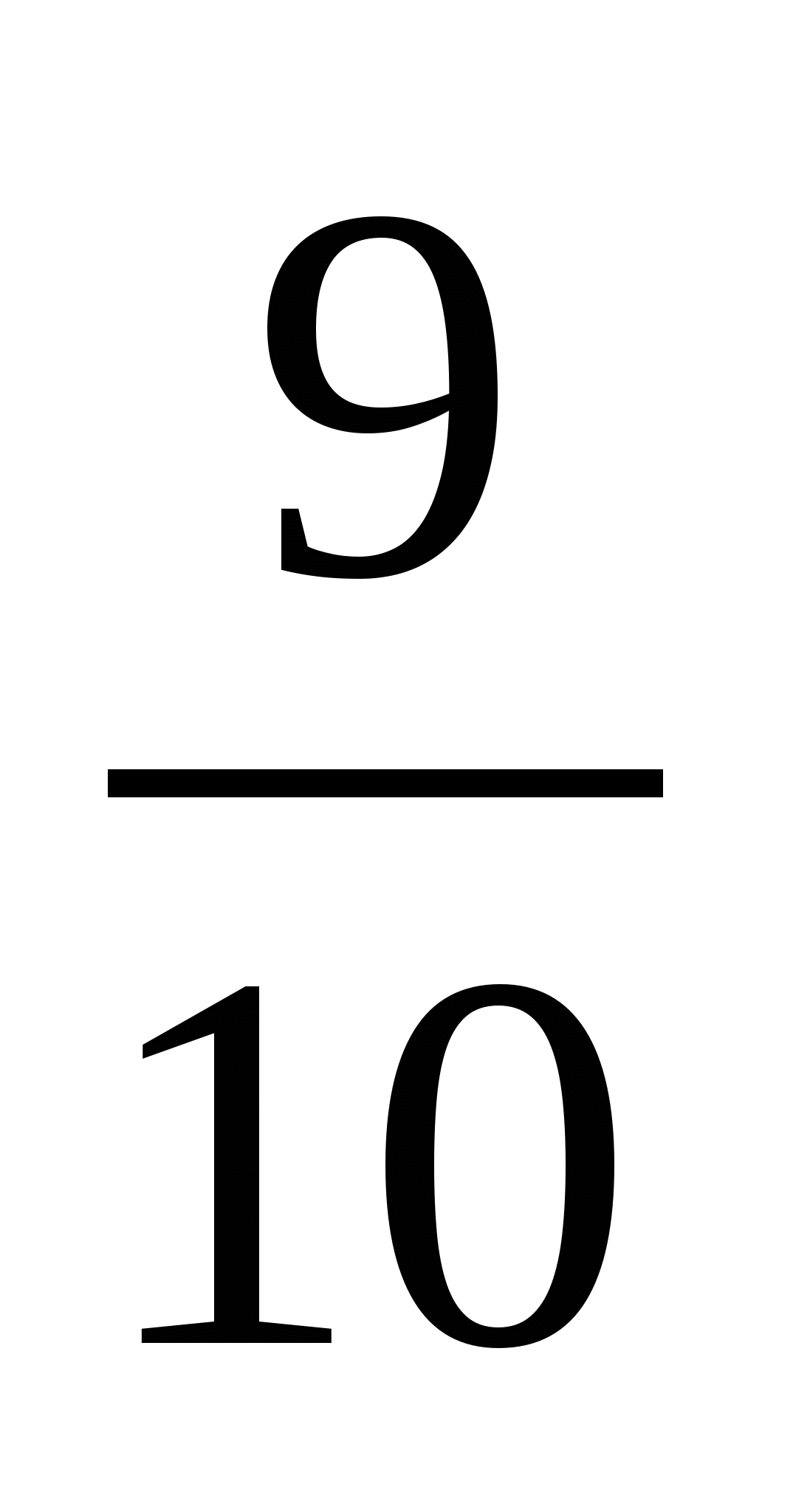 .
.
Завдання 2
Швидкість прямолінейно рухаючейся точки задана формулою v(t)=t2+2t-1. Записати формулу залежності її координати х від моменту часу t, якщо відомо, що у початковий момент (t=0) точка знаходилася у початку відліку.
Розв'язування:
х(t) - це первісна швидкості v(t), тому х(t)=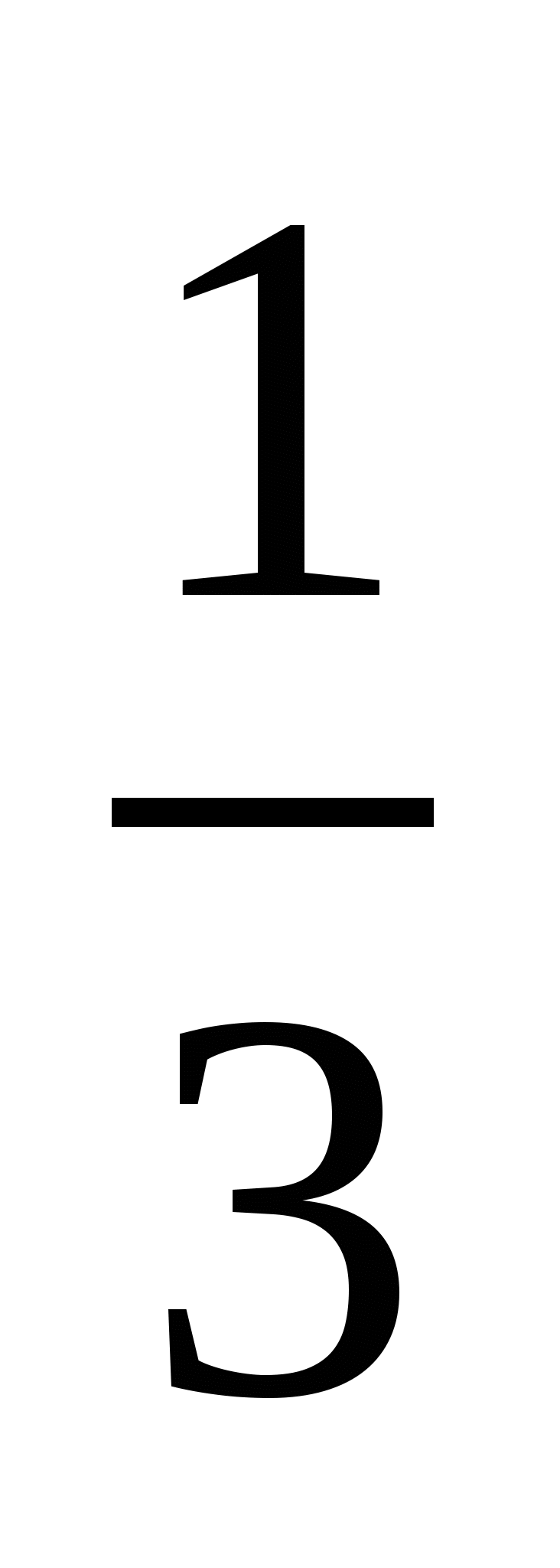 t3+2
t3+2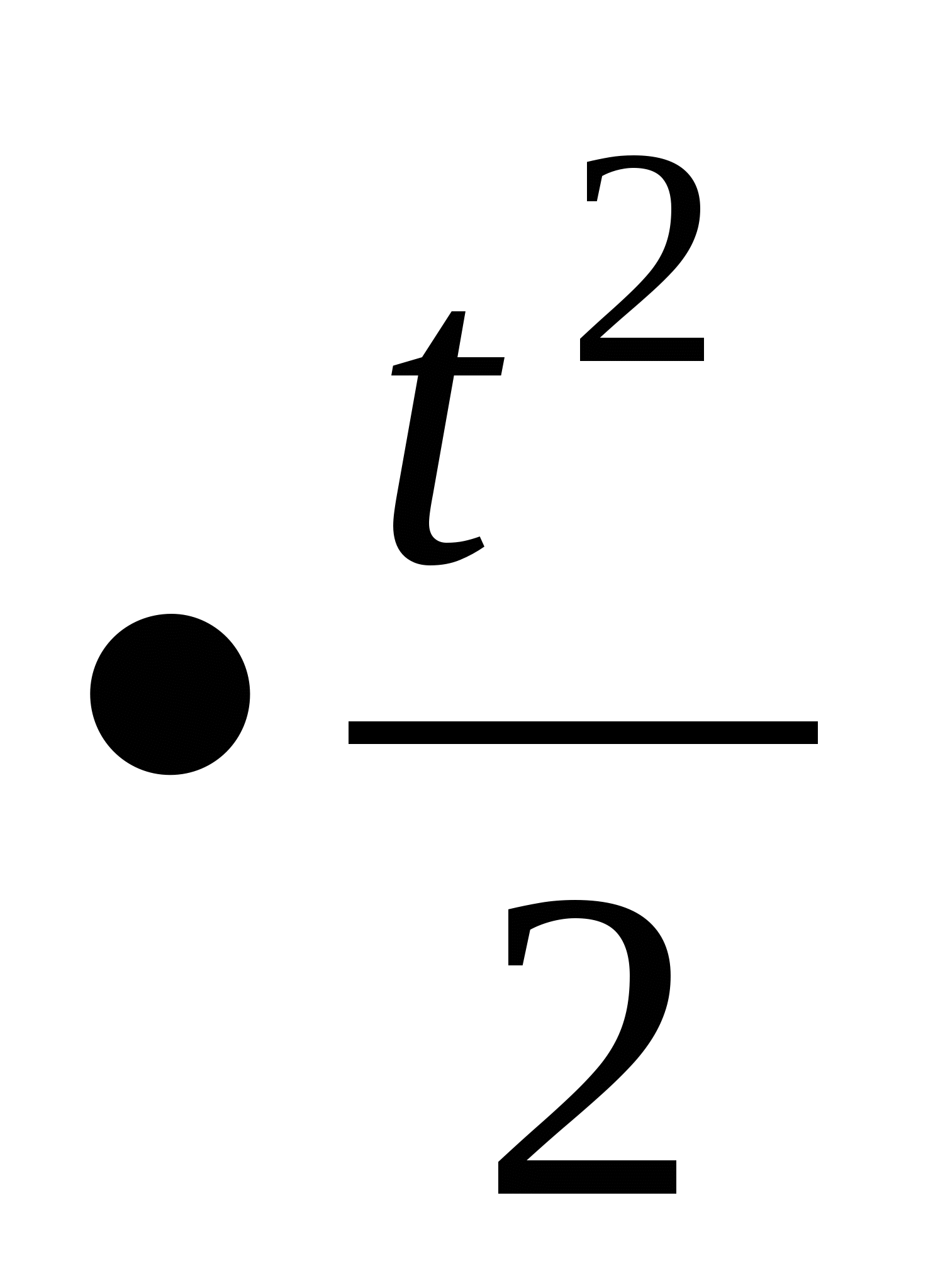 - t + C=
- t + C=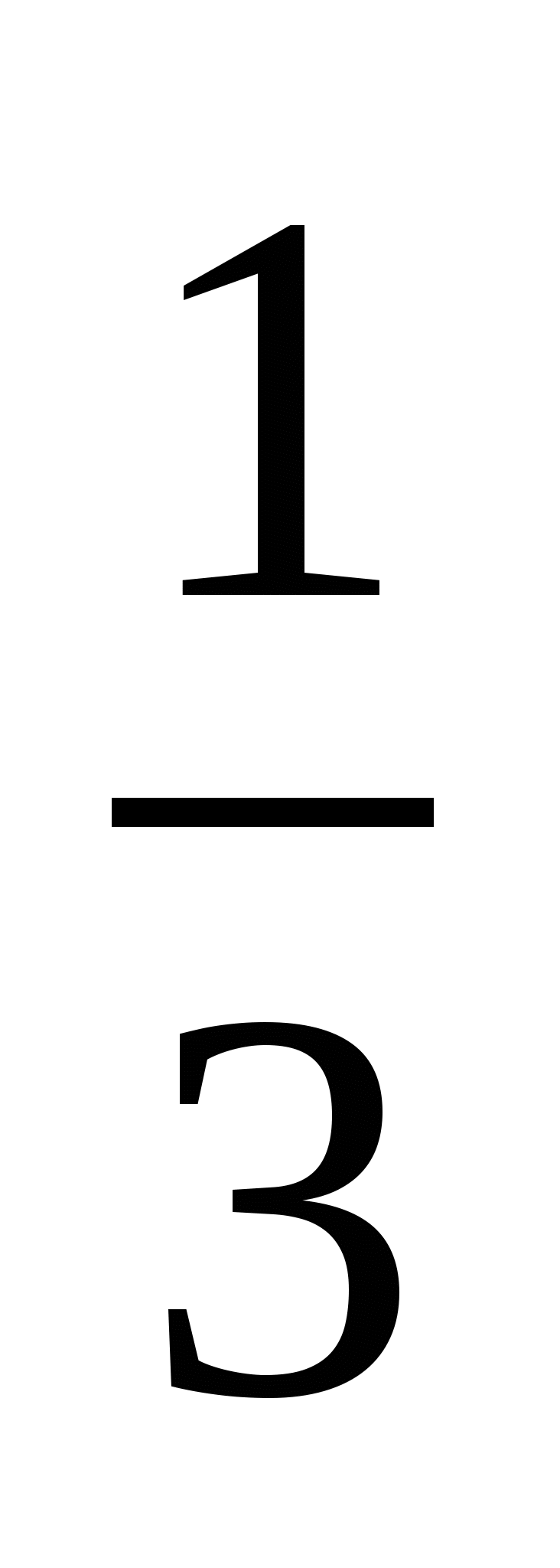 t3 + t2- t + C. За умовою завдання х(0)=0, тому х(0)=0+С=0, маємо С=0.
t3 + t2- t + C. За умовою завдання х(0)=0, тому х(0)=0+С=0, маємо С=0.
Отже, х(t) =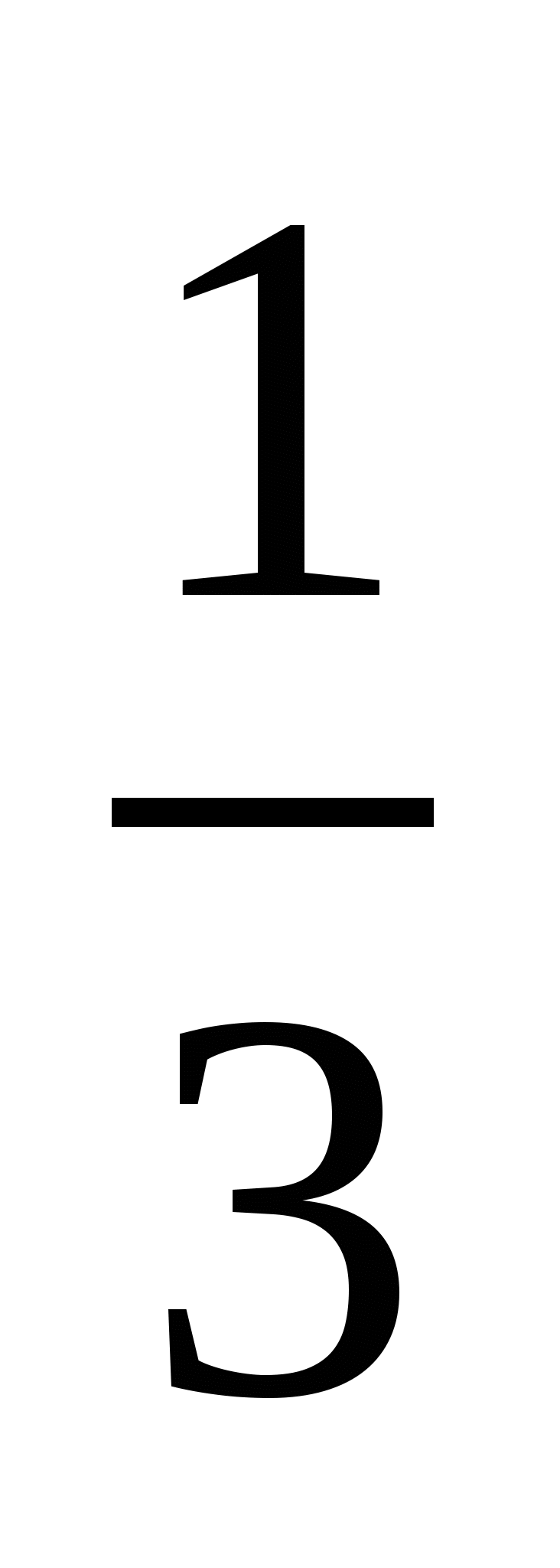 t3 + t2- t.
t3 + t2- t.
Відповідь: х(t) =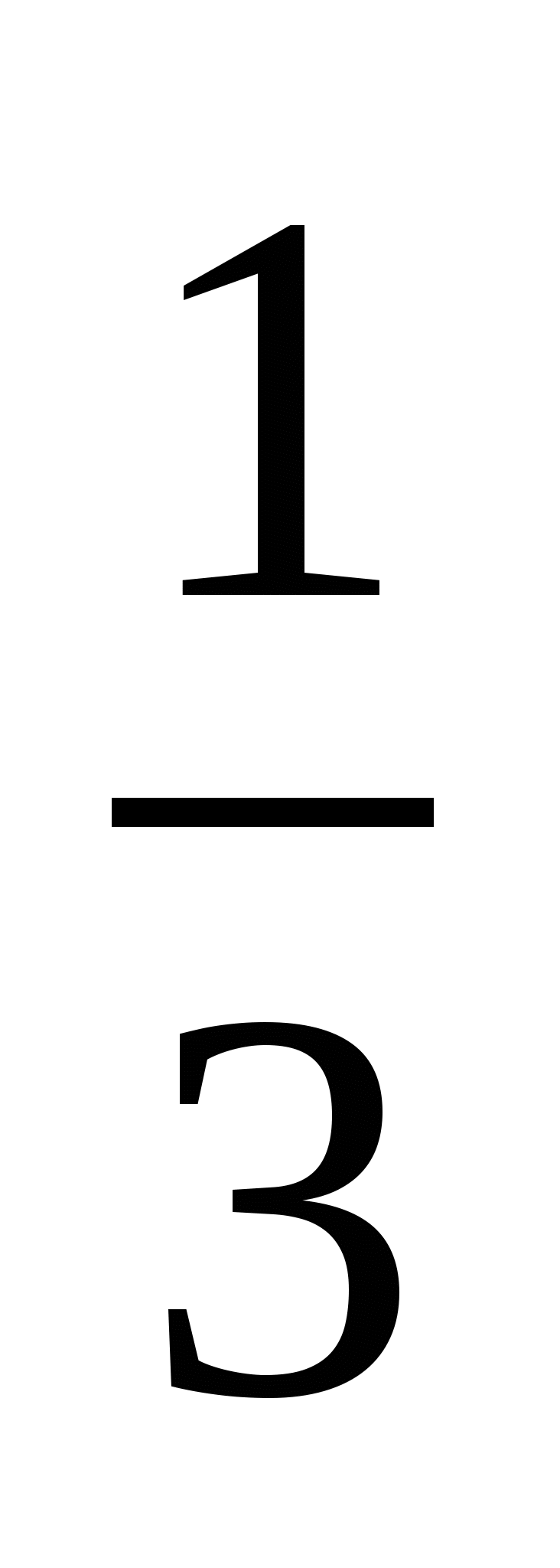 t3 + t2- t.
t3 + t2- t.
Завдання 3
Матеріальна точка масою 3кг рухається вздовж вісі Ох під дією сили, яка направлена вздовж цієї вісі. В момент часу t сила дорівнює F(t). Знайти формулу залежності х(t) від часу t, якщо х(1)=-5, v(1)=4, F(t) =6 - 9t
Розв'язування:
Згідно другому закону Ньютона F=ma, де a - прискорення. Маємо
a(t) = 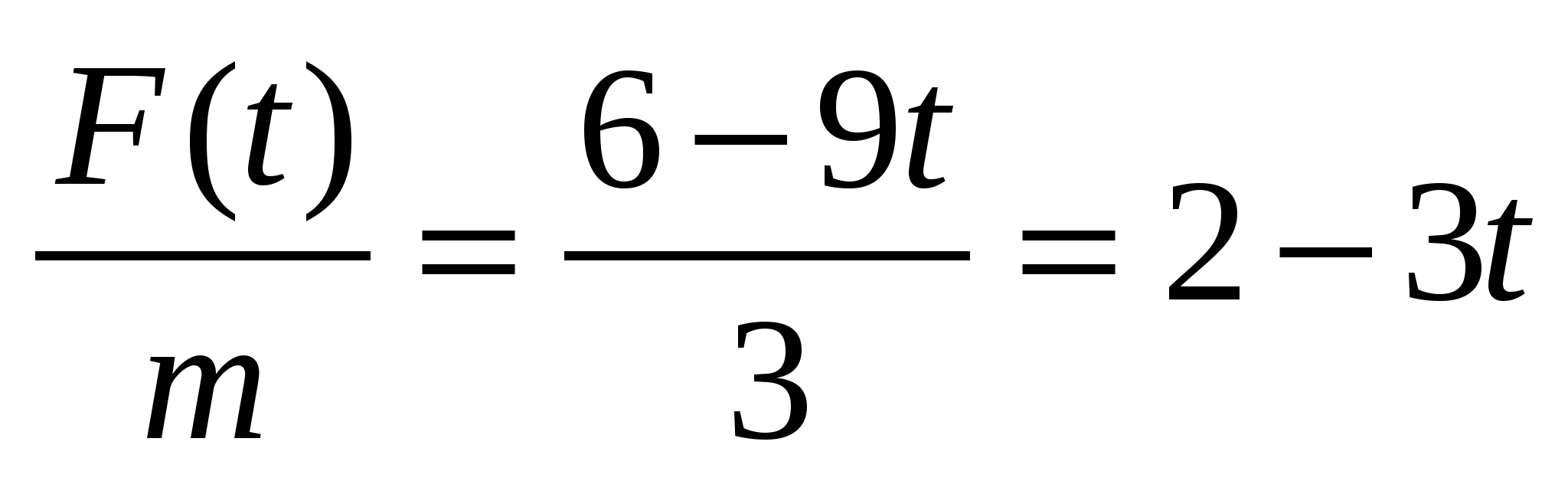 . v(t) - первісна прискорення a(t). Тому v(t)=2t-
. v(t) - первісна прискорення a(t). Тому v(t)=2t-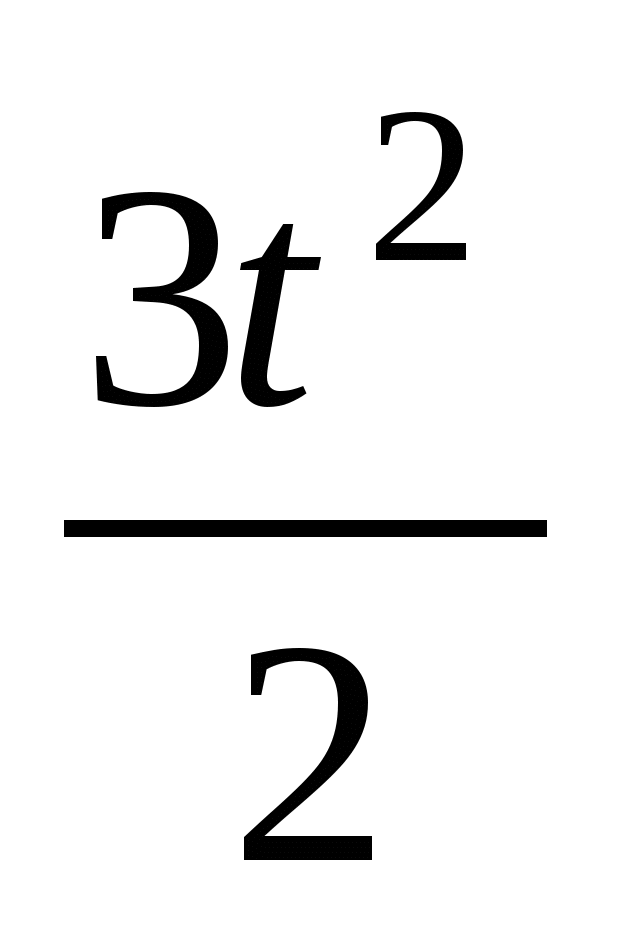 +C1. За умовою v(1)=4, маємо v(1)=2-
+C1. За умовою v(1)=4, маємо v(1)=2-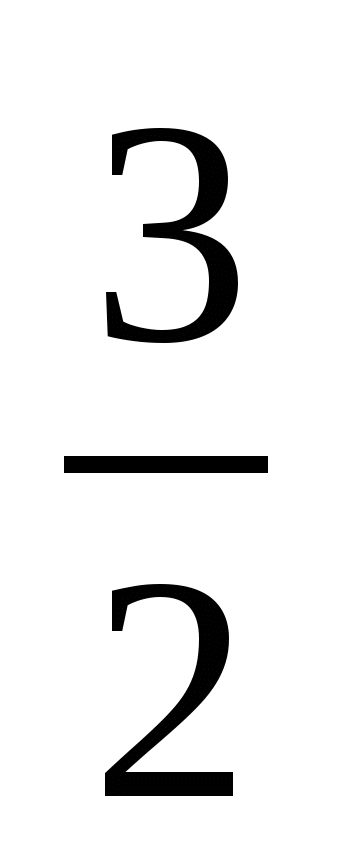 +С1=0,5+ С1, тому С1=3,5, отже
+С1=0,5+ С1, тому С1=3,5, отже
v(t)=2t-![]() +3,5.
+3,5.
Аналогічно х(t)=t2 - 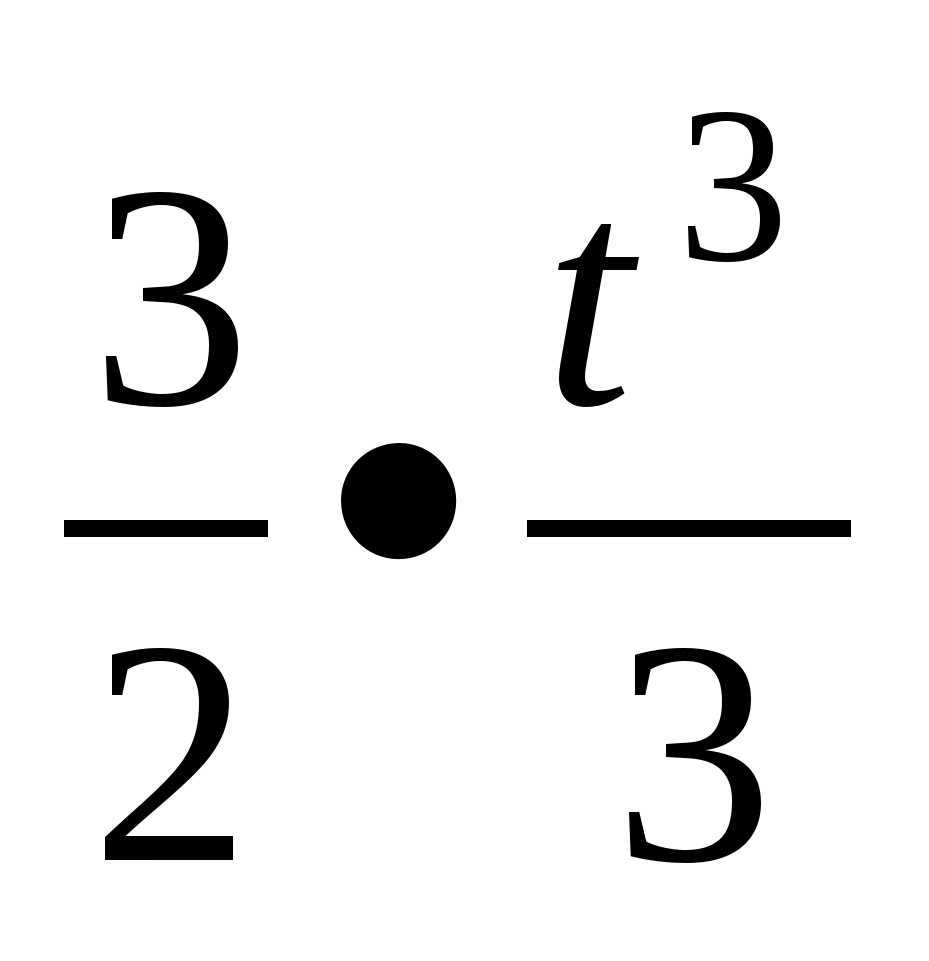 +3,5t+C2= -
+3,5t+C2= - 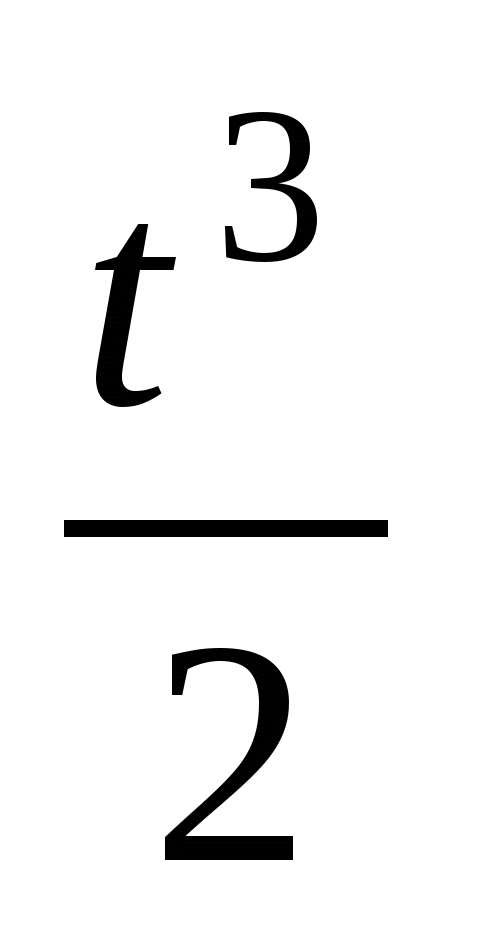 + t2+3,5t+C2. За умовою х(1)=-5, тому х(1)=-
+ t2+3,5t+C2. За умовою х(1)=-5, тому х(1)=- 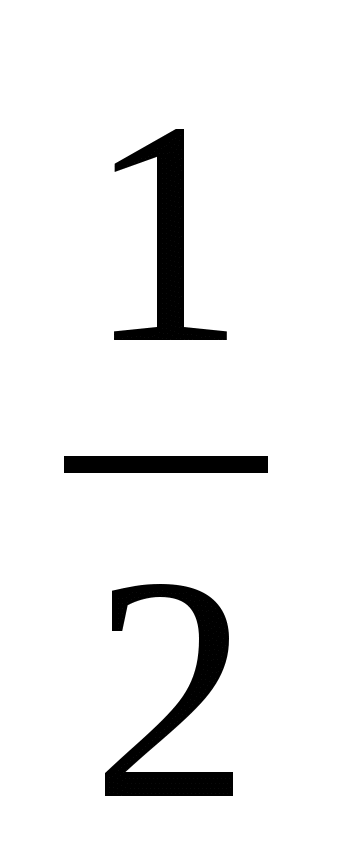 +1+3,5+С2=4+С2=-5, тому С2=-9.
+1+3,5+С2=4+С2=-5, тому С2=-9.
Отже, залежність між координатою та часом задається формулою
х( t)= - ![]() + t2+3,5t-9.
+ t2+3,5t-9.
Відповідь: х( t)= - 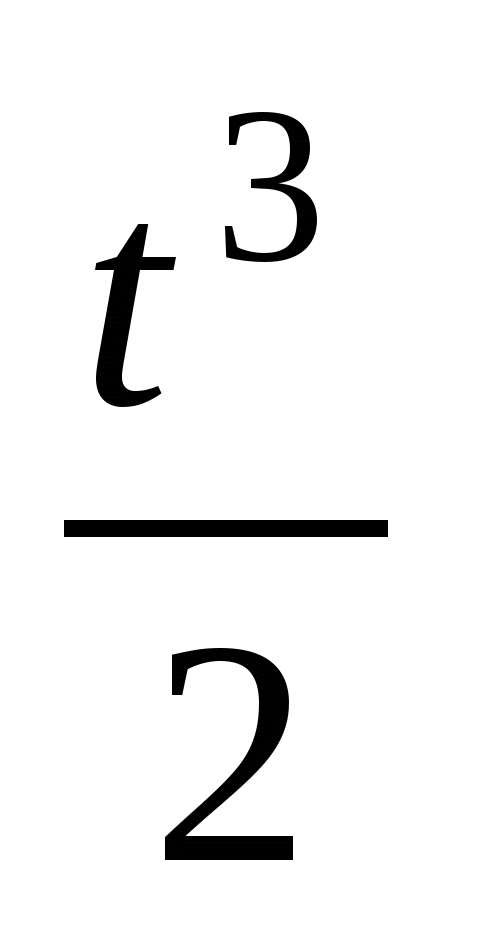 + t2+3,5t-9.
+ t2+3,5t-9.
Завдання 4
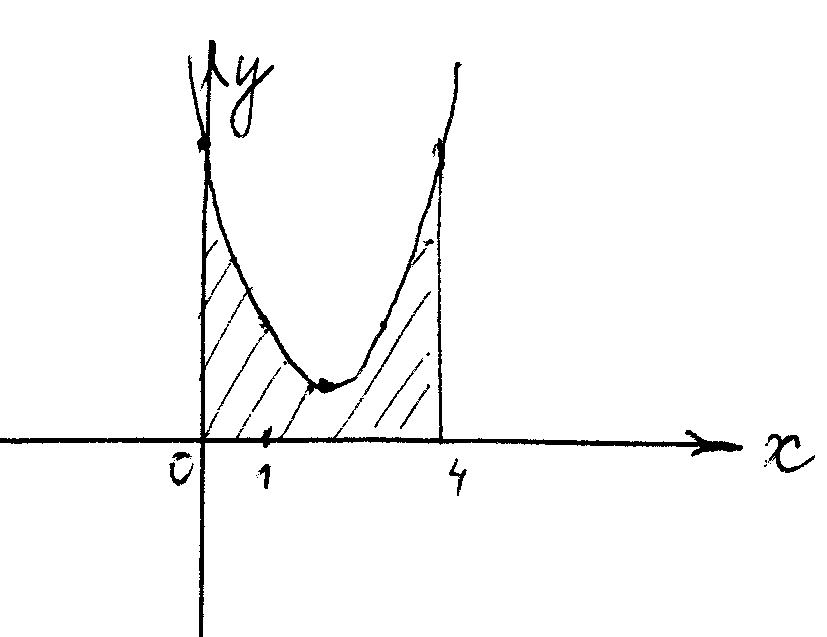
Знайти об'єм тіла, що буде отримано при обертанні навколо віссі абсцис криволінійної трапеції, яка обмежена лініями у=1-х2, у=0.
Розв'язування:
Об'єм тіла обчислюється за формулою V=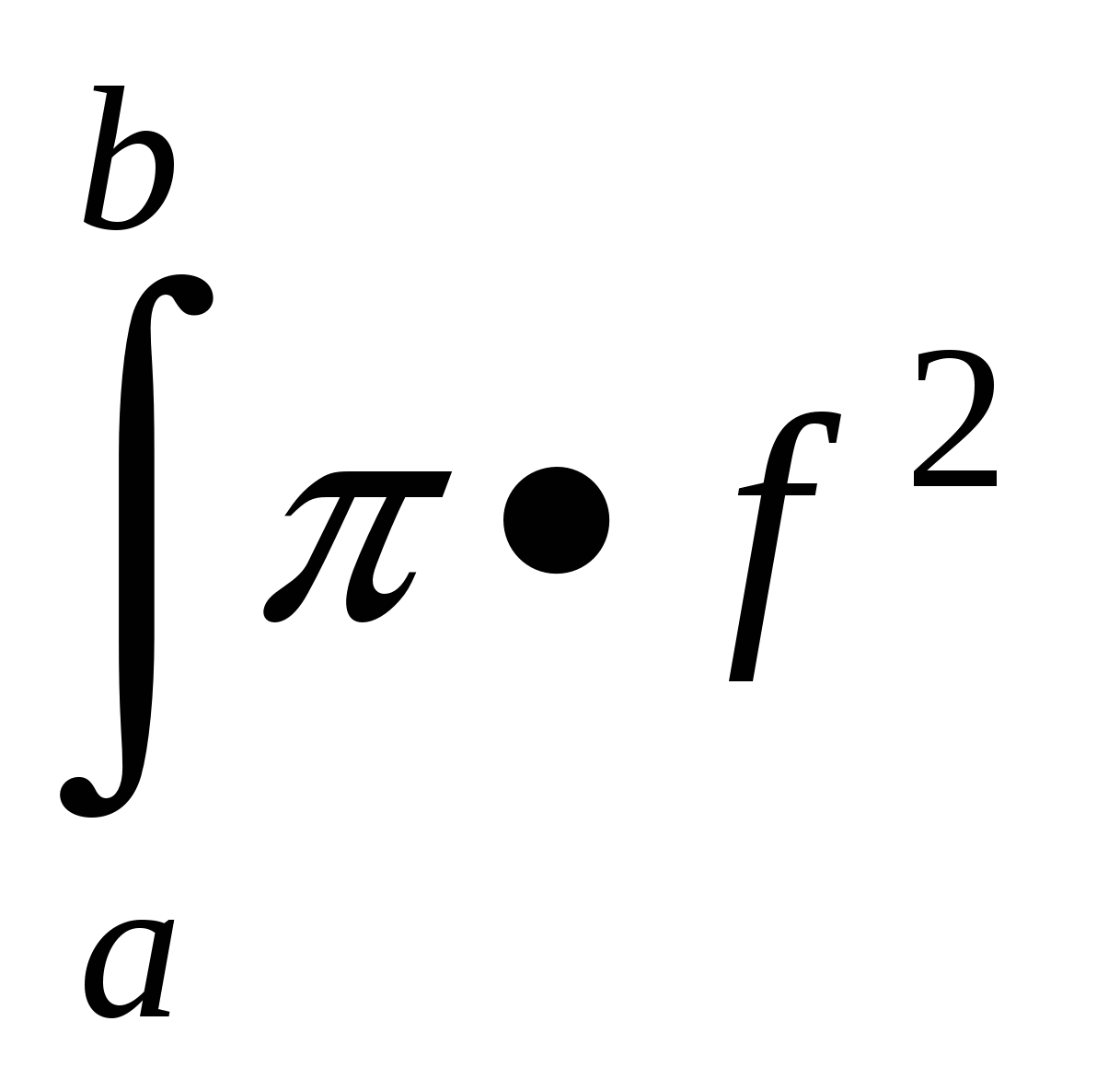 (x)dx. Знайдемо проміжок інтегрування 1-х2=0, маємо х1=1 та х2=-1. Тому V=
(x)dx. Знайдемо проміжок інтегрування 1-х2=0, маємо х1=1 та х2=-1. Тому V=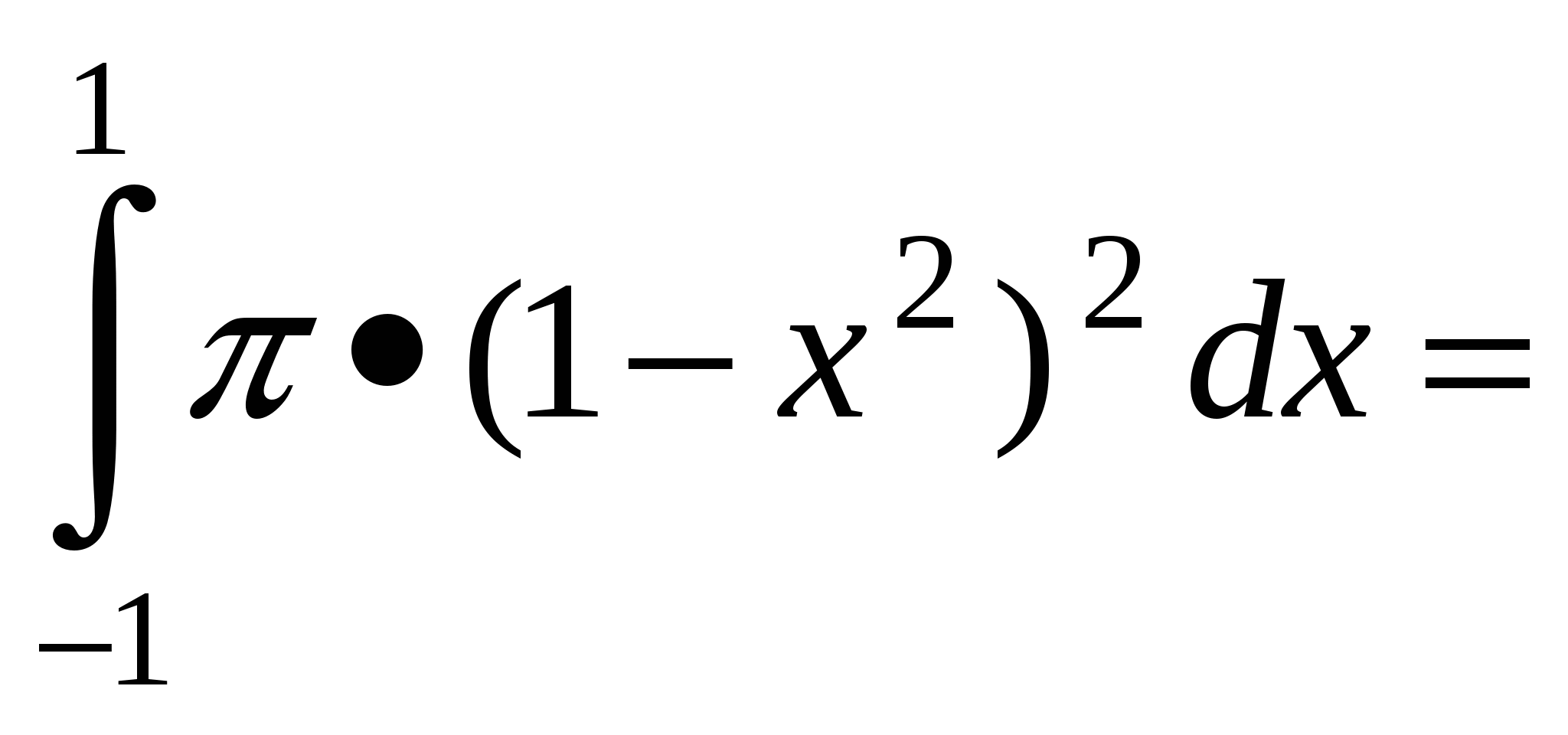
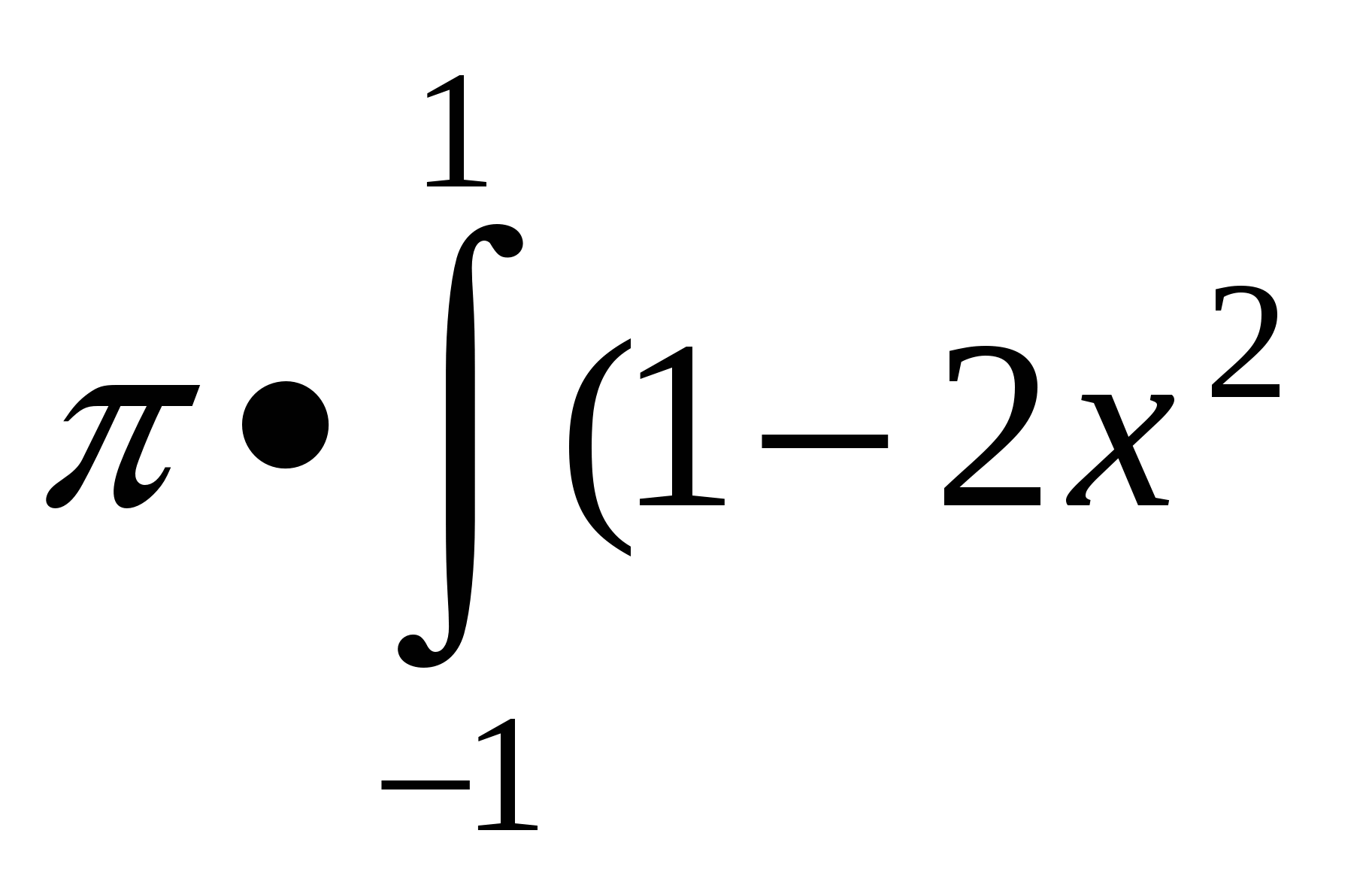 +
+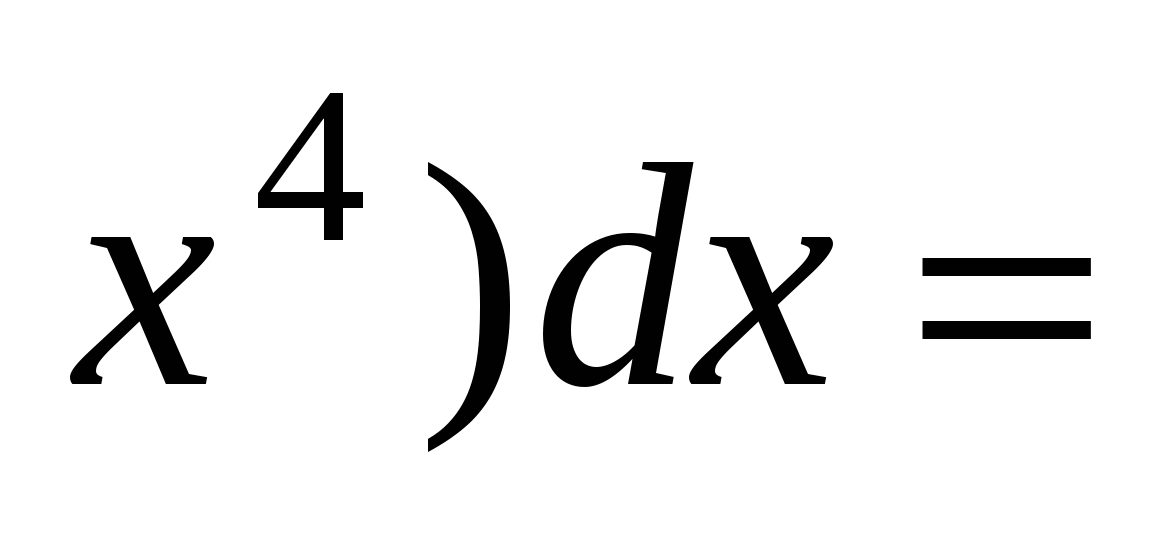
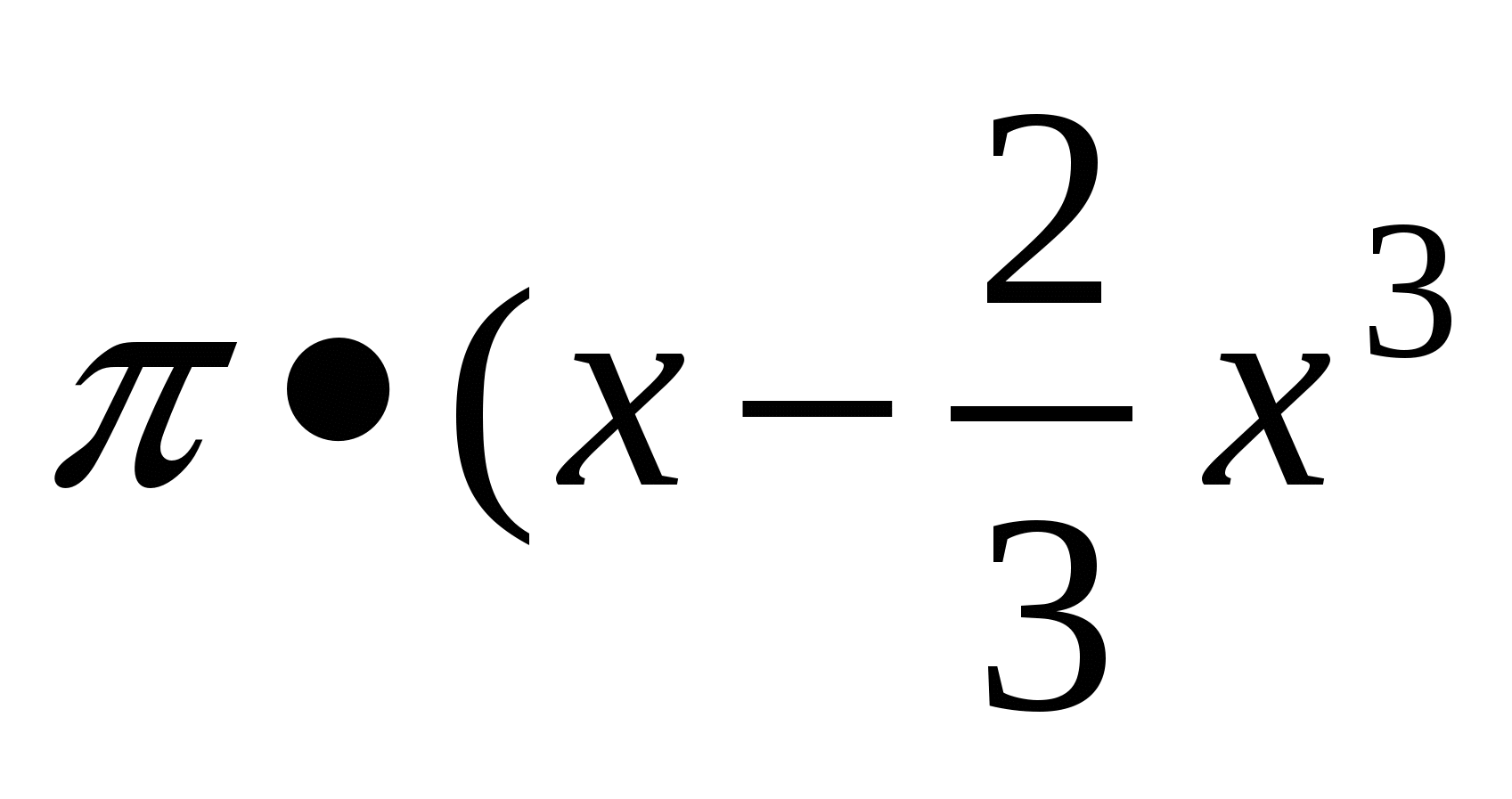 +
+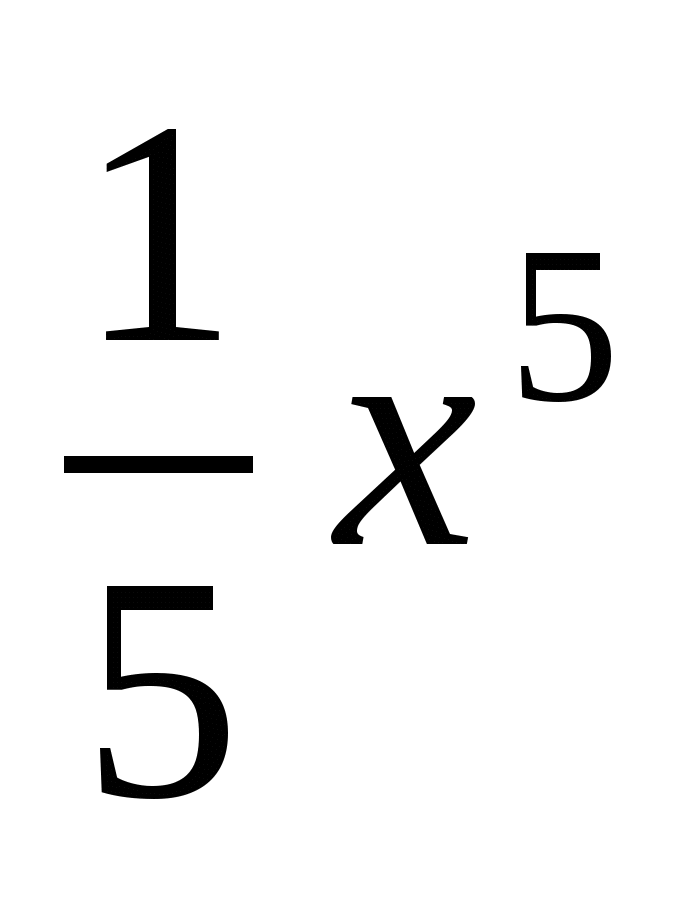
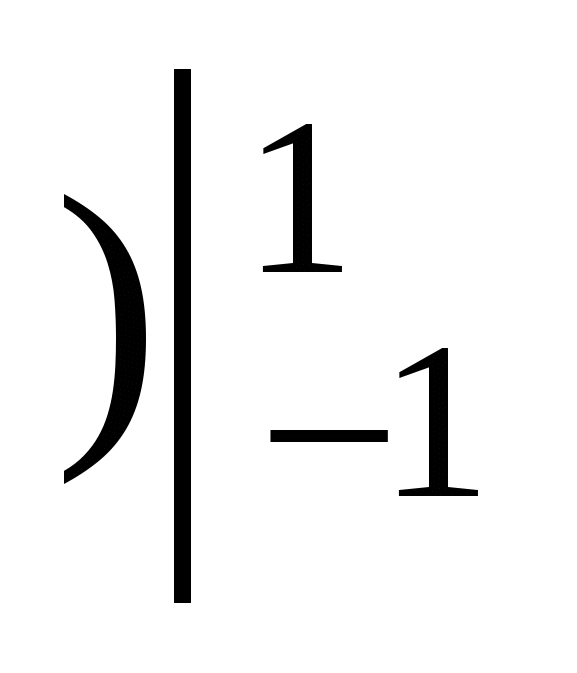 =
=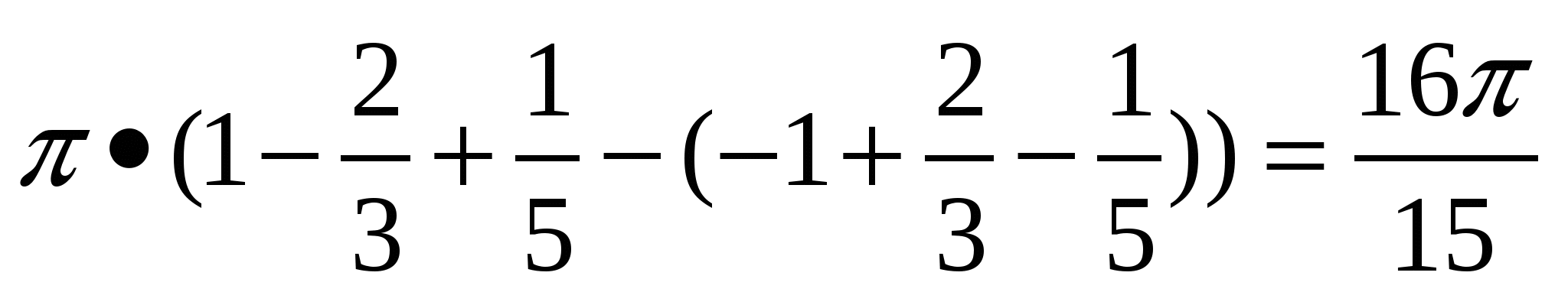 куб.од.
куб.од.
Відповідь: V=![]() куб.од.
куб.од.
Завдання 5
Знайти площу фігури, що обмежена лініями :
а) у=х2-4х+5, у=0, х=0, х=4,
б) у=х2-4х+4, у=4-х2.
Розв'язування:
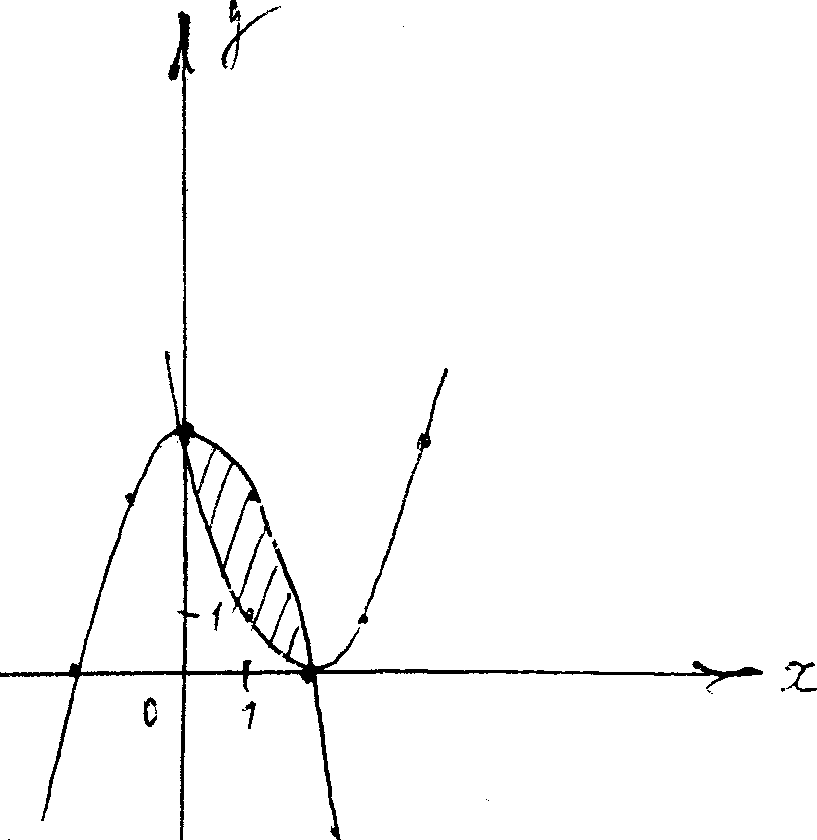
а) Виконаємо малюнок. у=х2-4х+5 - квадратична функція, тому її графіком є квадратна парабола. Знадемо координати вершини параболи:
х0= , у0=4-8+5=1, Тому (2; 1)- координати вершини параболи. Точок перетину графіку даної квадратичної функції із віссю Ох немає, тому що дискримінант є від'ємним числом. Знайдемо декілька додаткових точок:
, у0=4-8+5=1, Тому (2; 1)- координати вершини параболи. Точок перетину графіку даної квадратичної функції із віссю Ох немає, тому що дискримінант є від'ємним числом. Знайдемо декілька додаткових точок:
у(0)=4, у(1)=2, у(3)=2, у(4)=4.
S=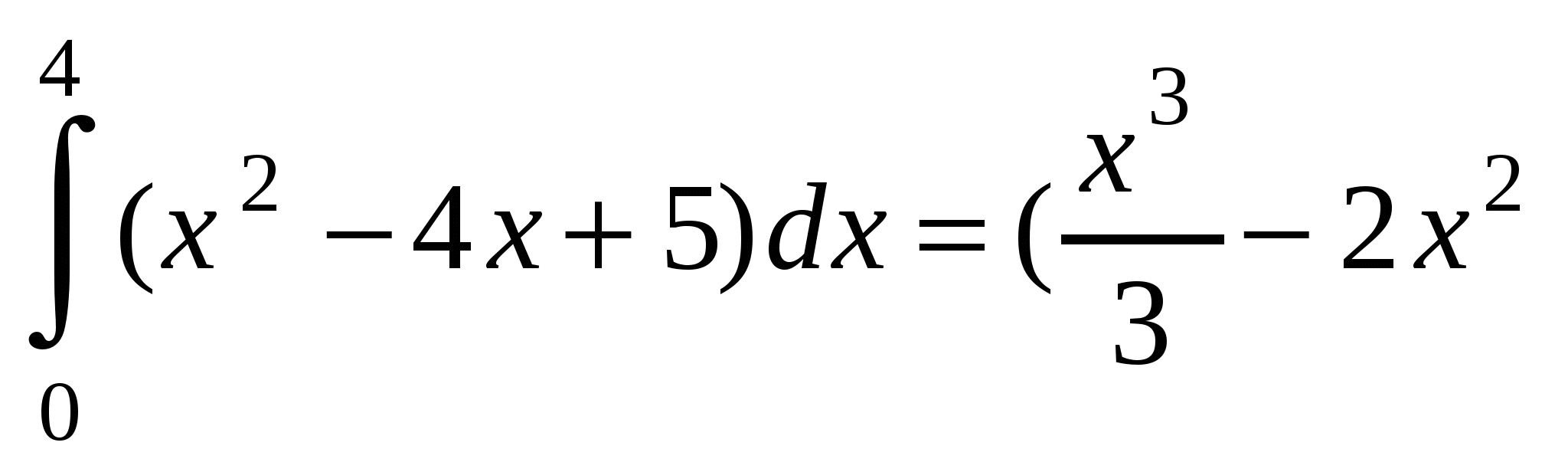
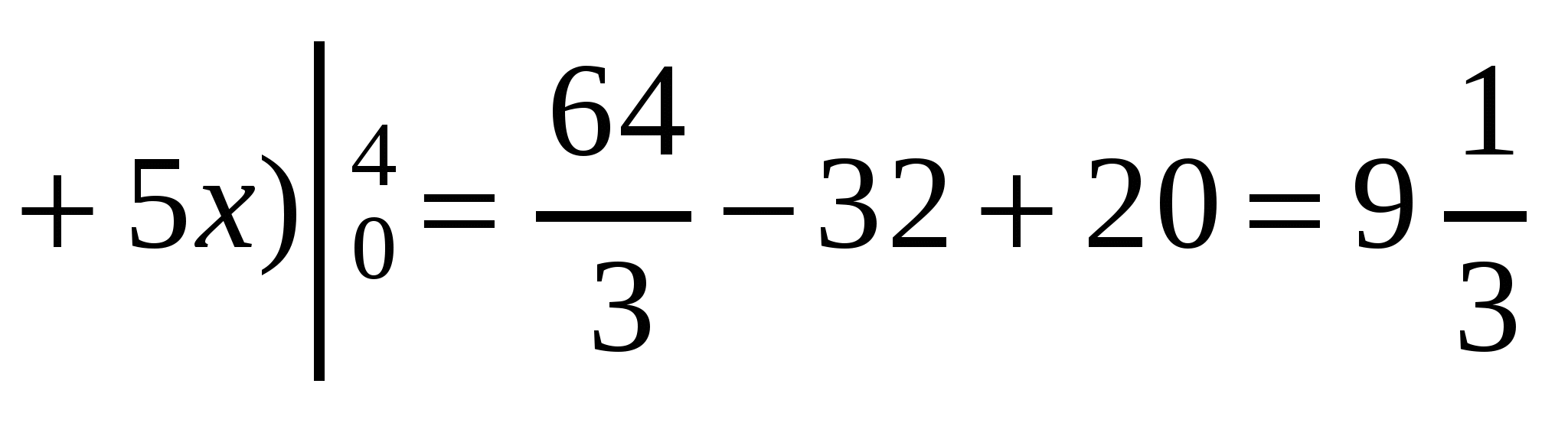 кв.од.
кв.од.
б) Знайдемо абсциси точок перетину графіків функцій.
х2-4х+4=4-х2,
2х2-4х=0,
2х (х-2)=0, отже, х1=0, х2=2.
(х-2)=0, отже, х1=0, х2=2.
S= 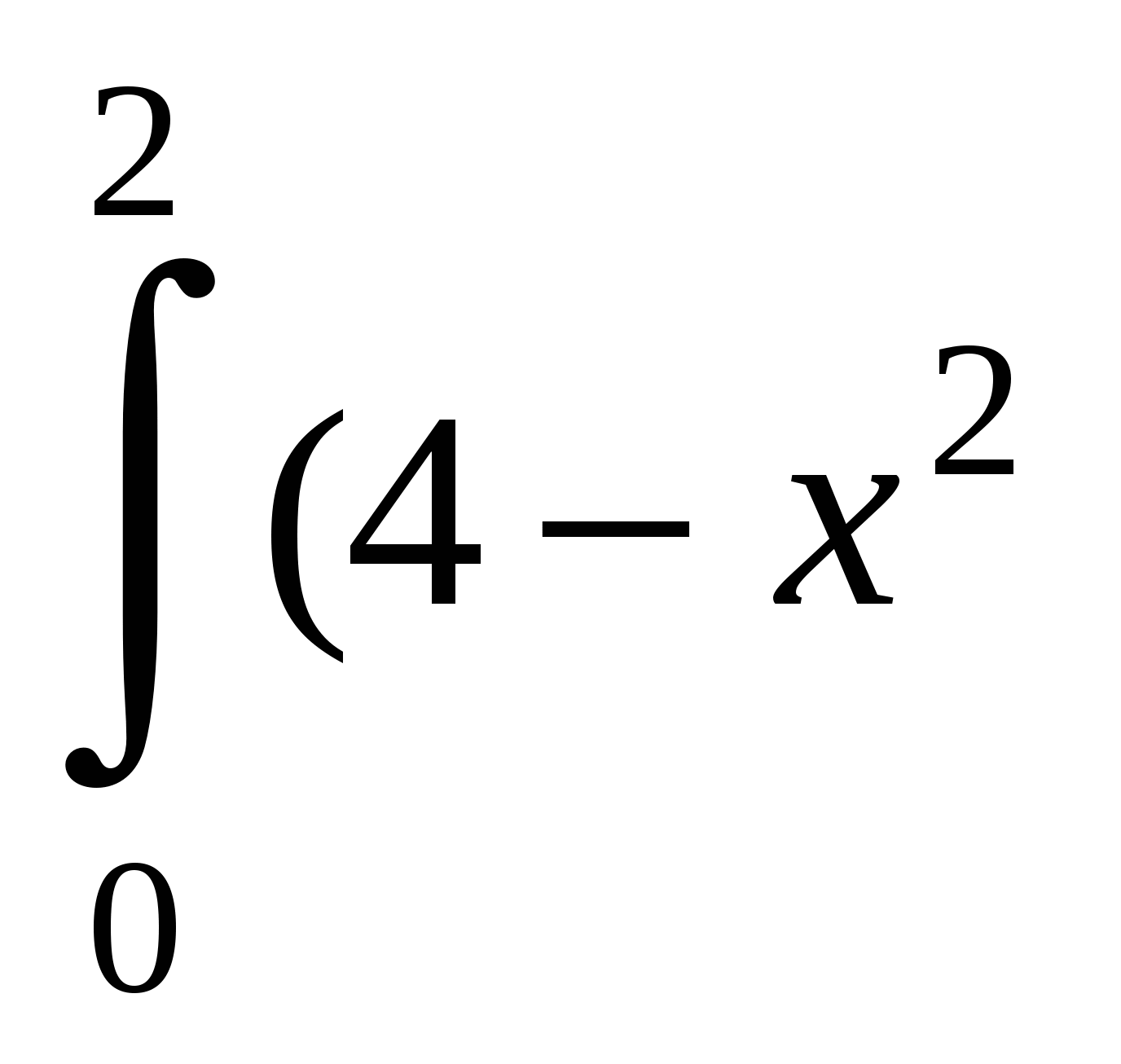 -(
-(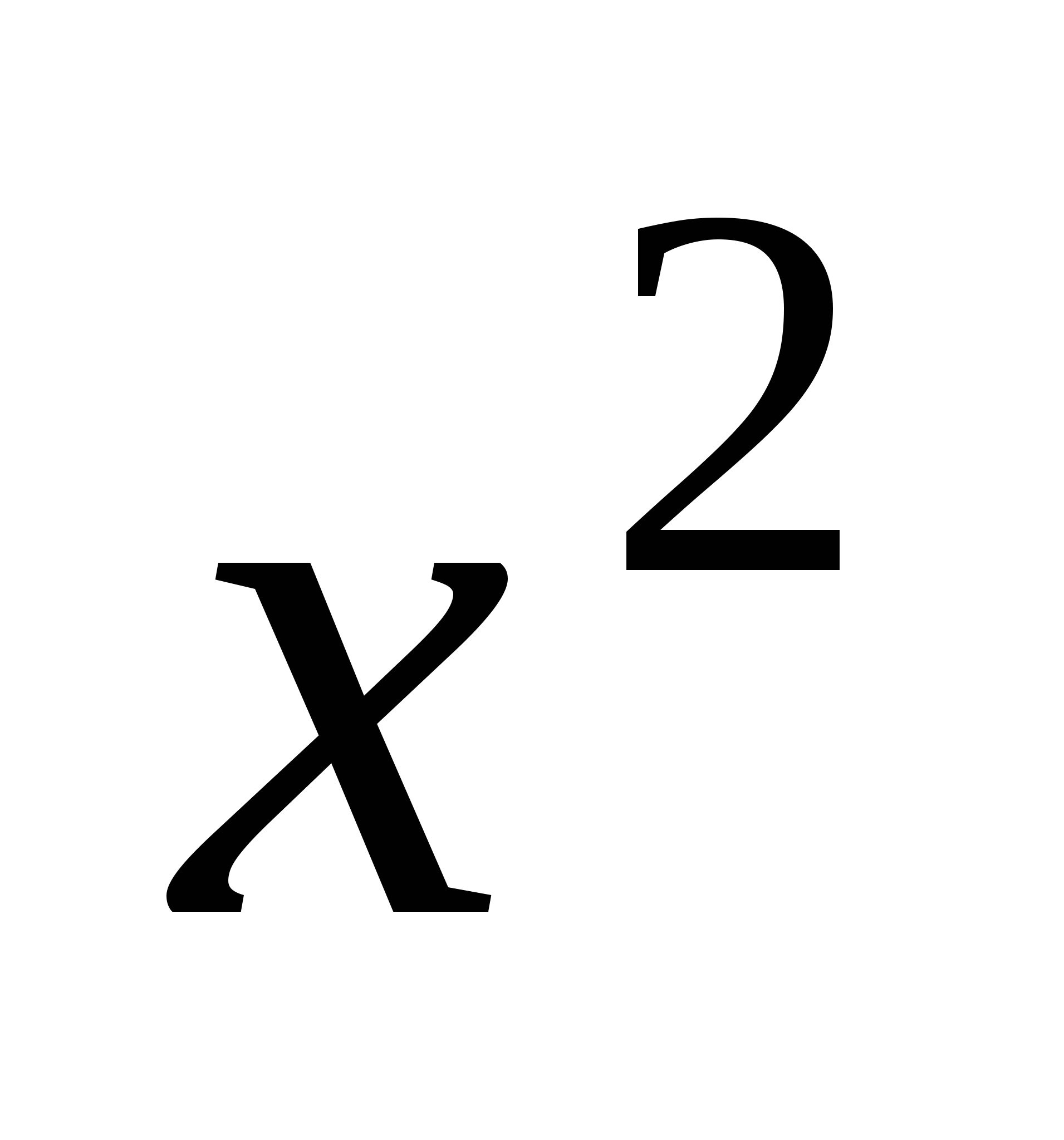 -4
-4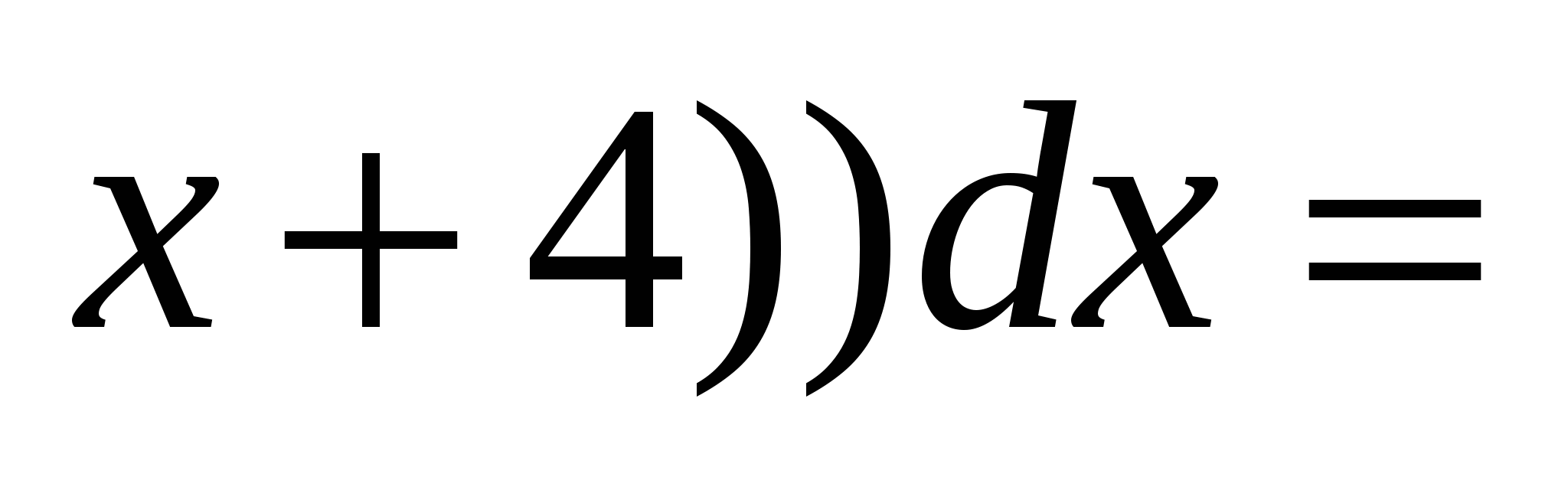
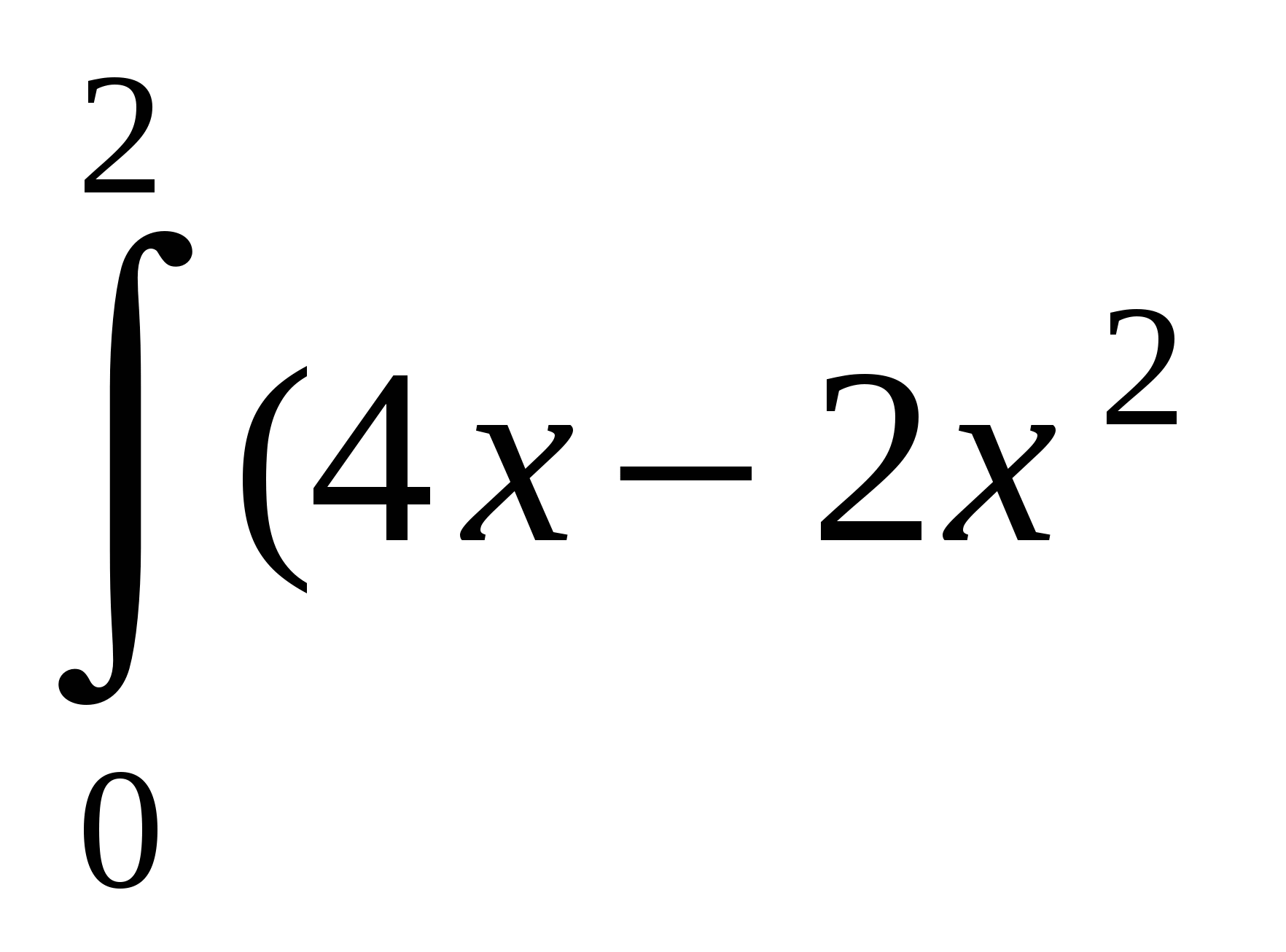
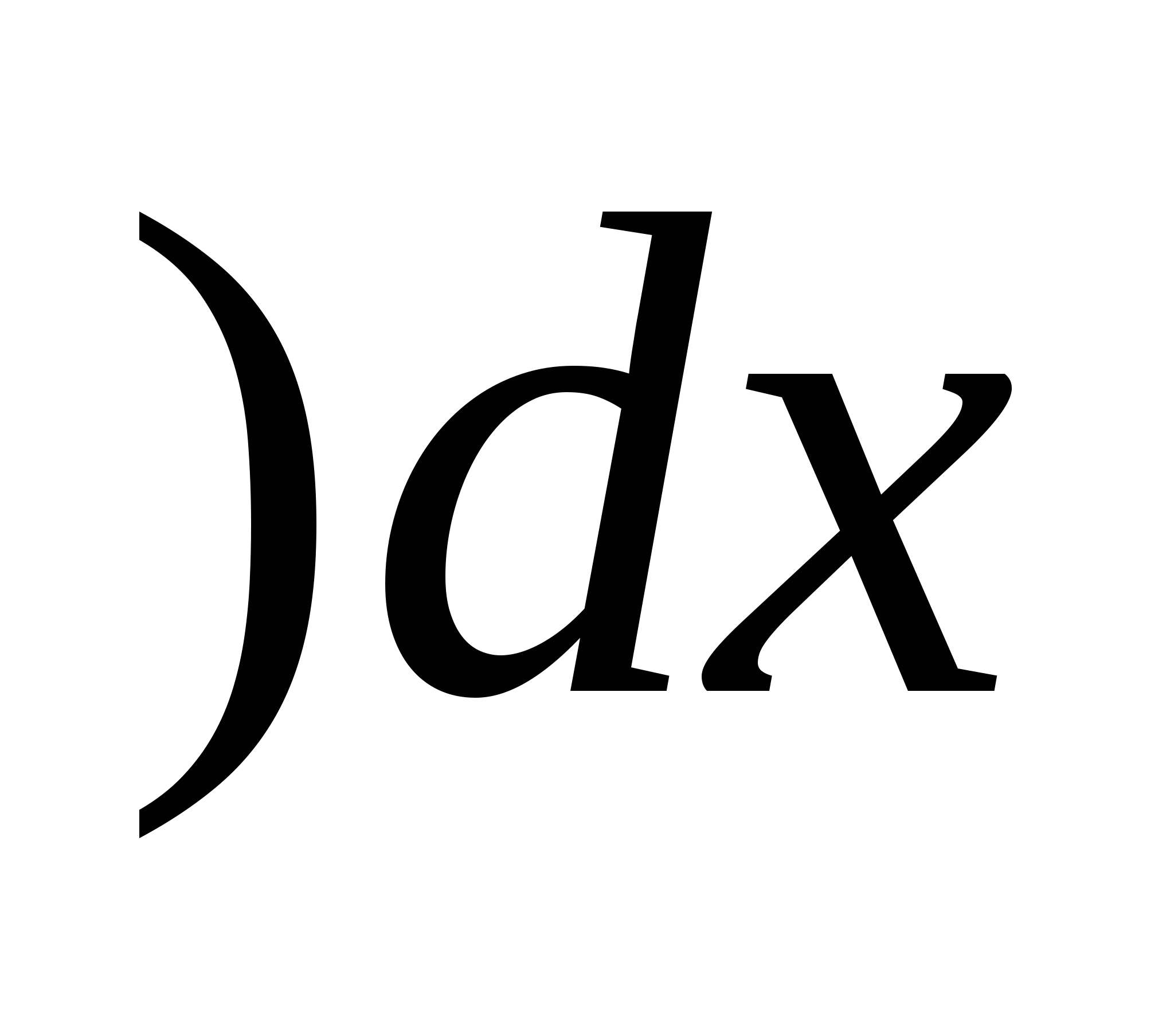 =
=
=(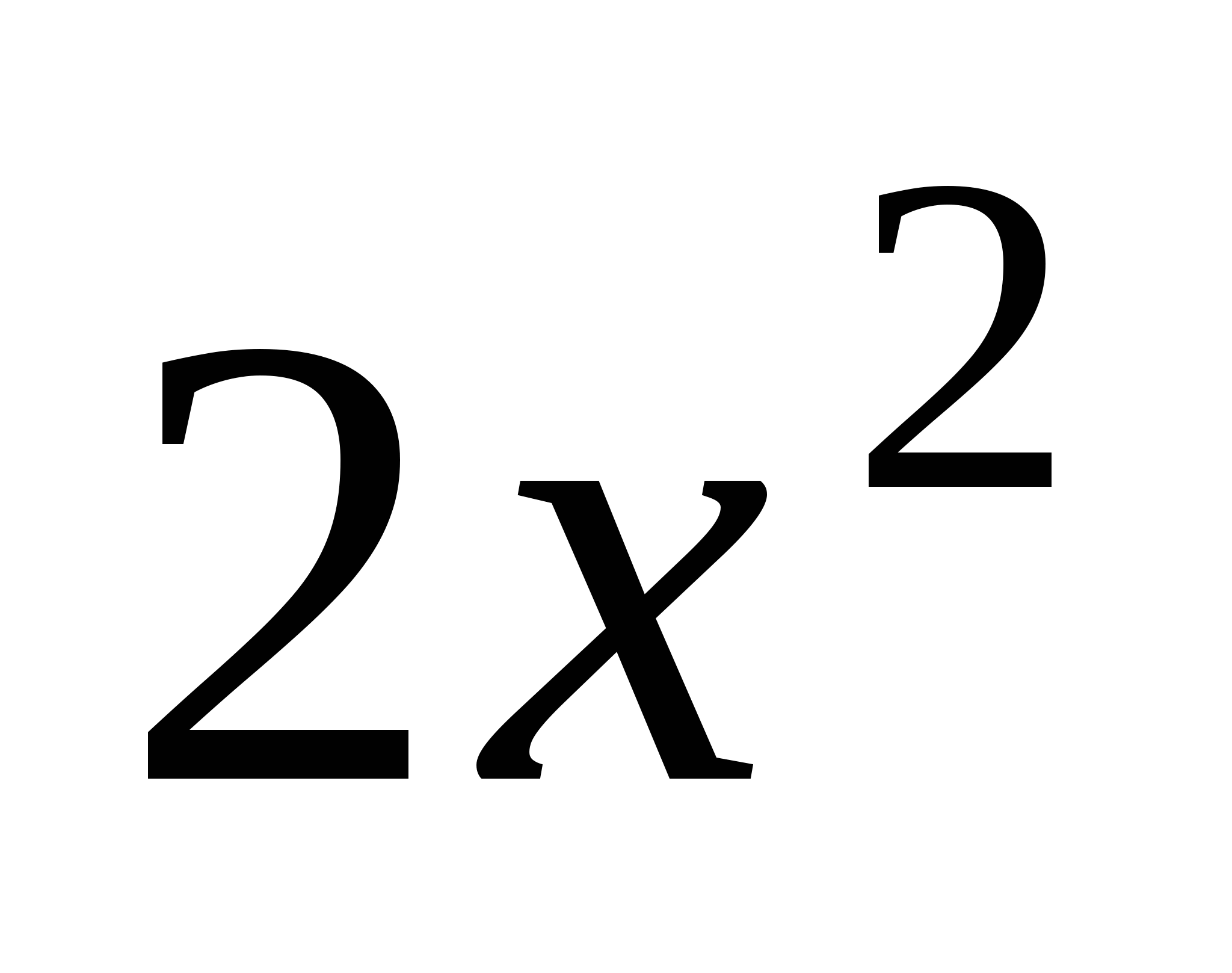 -
-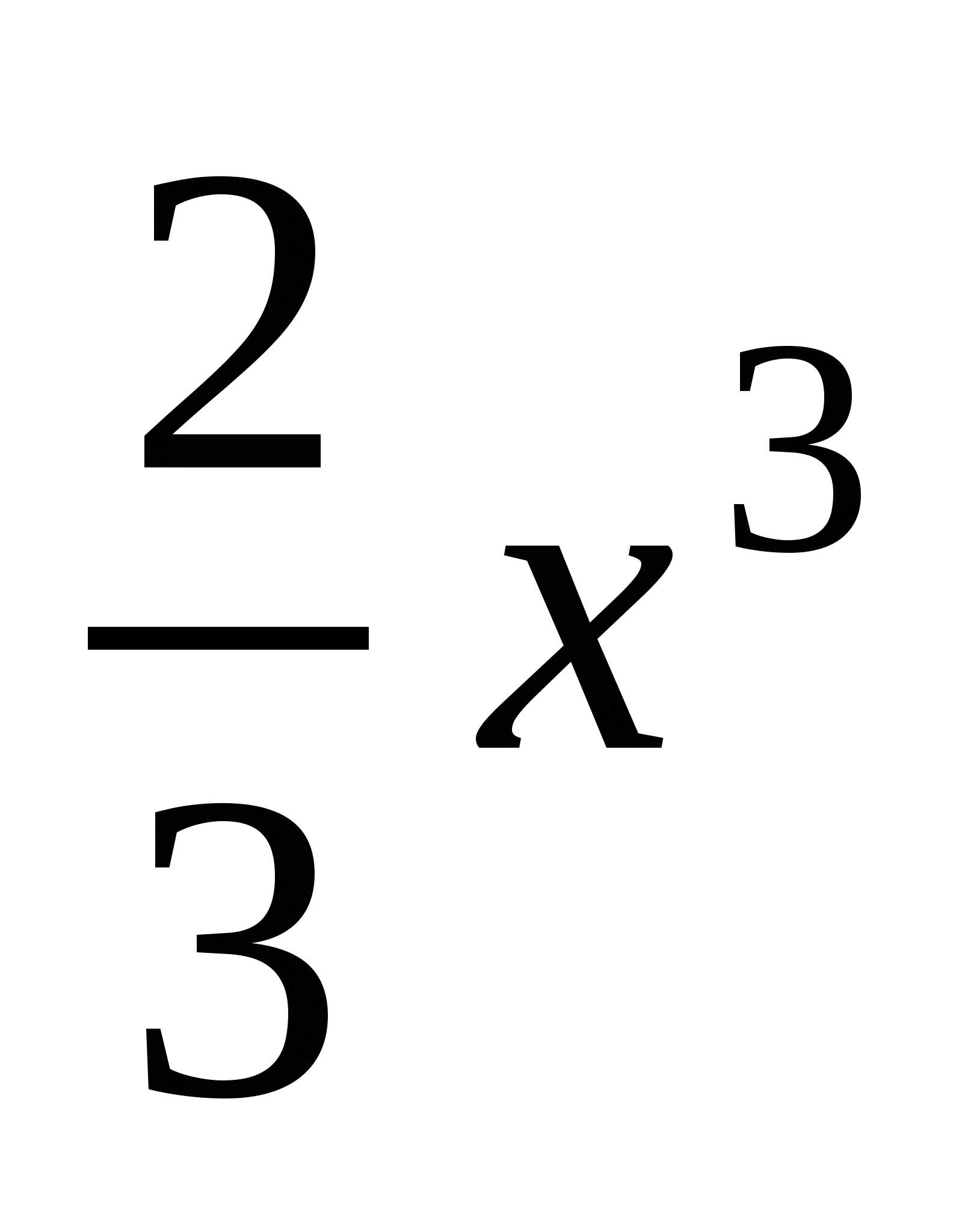 )
)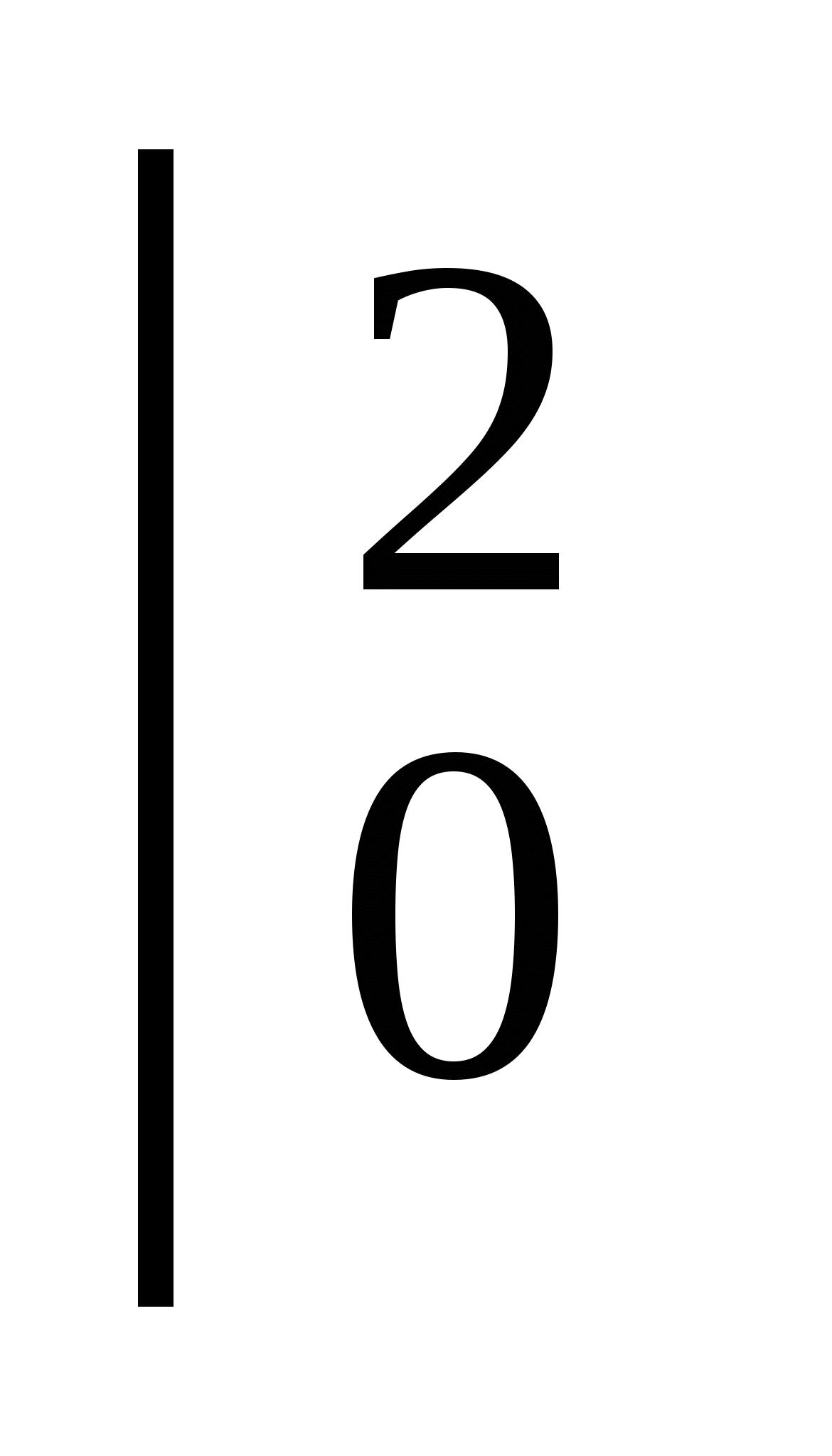 =8-
=8-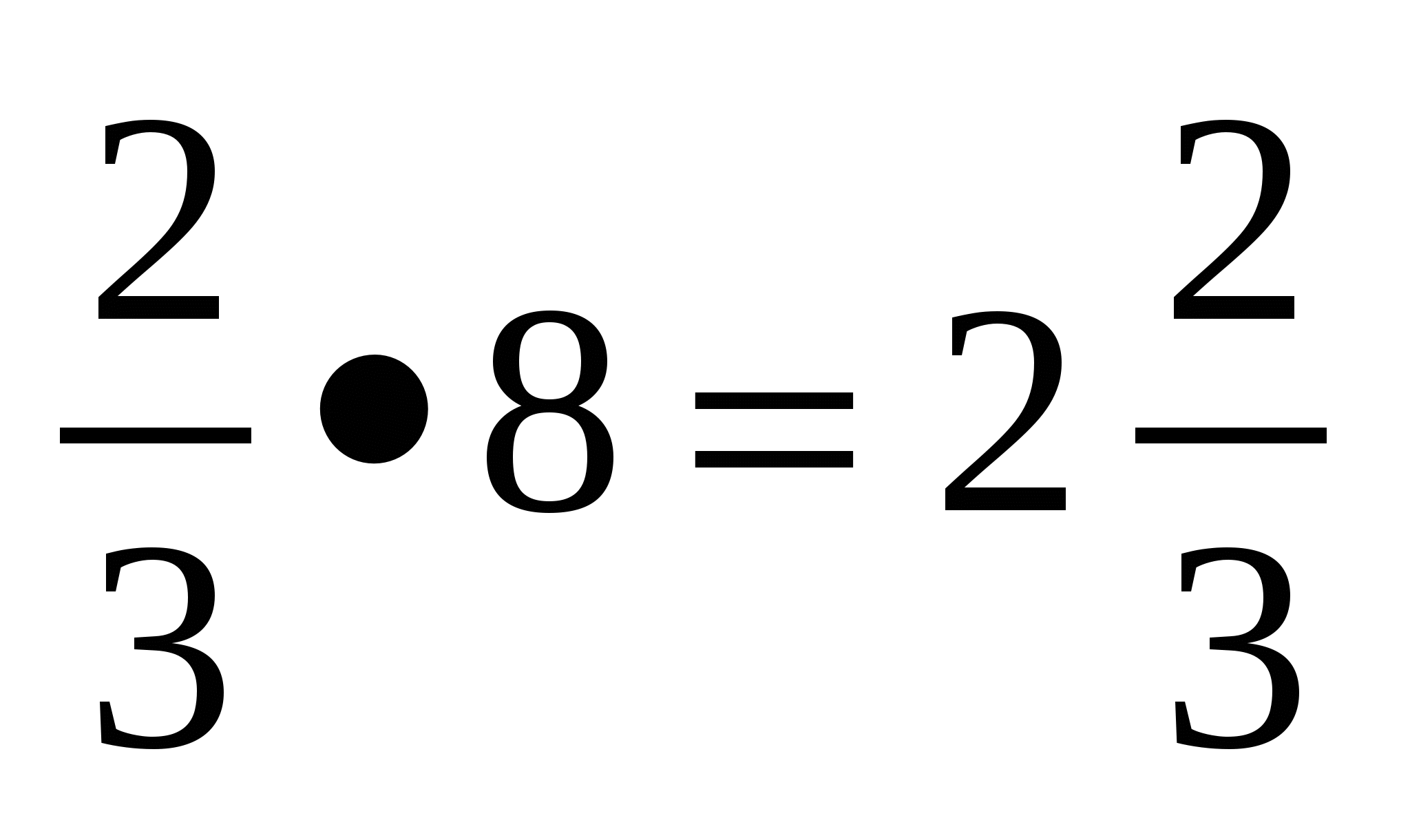 кв.од.
кв.од.
Відповідь: а)S =9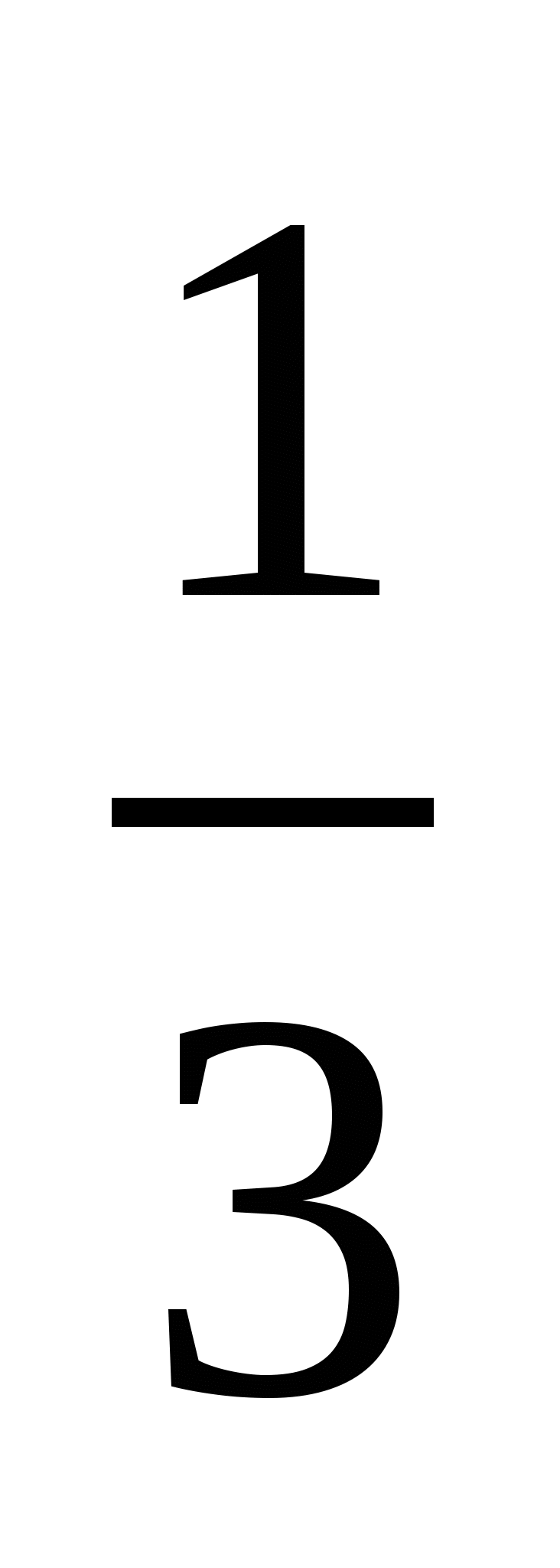 кв.од., б) S=2
кв.од., б) S=2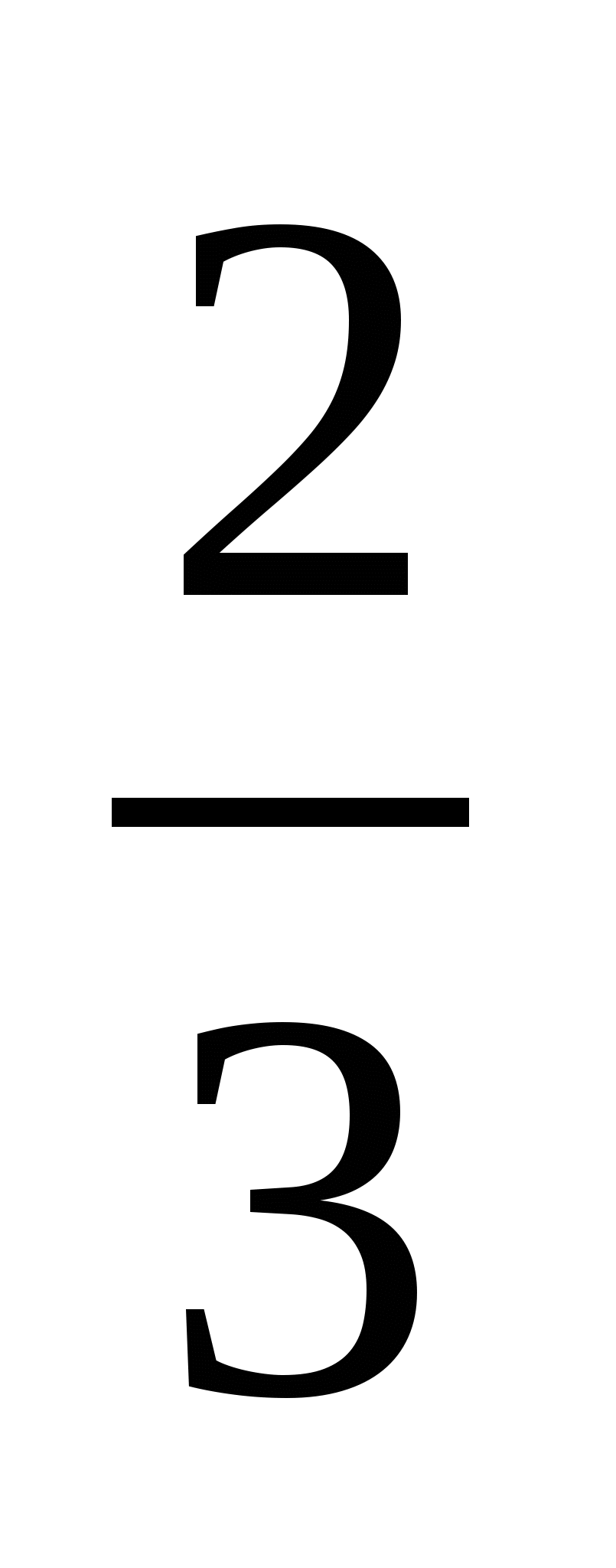 кв.од.
кв.од.
Завдання 6
Знайти критичні точки функції у=2х3-9х2-24х-18.
Розв'язування:
Функція визначена та диференційована на всій числовій прямій.
у'=6х2-18х-24, розв'яжемо рівняння у'=0. 6х2-18х-24=0, х2-3х-4=0, х1=-1, х2=4. Корені рівняння у'=0 і є критичними точками функції.
Відповідь: критичні точки функції х1=-1, х2=4.
Завдання 7
Знайти проміжки зростання та спадання функції:
а) у=х2-4; б)у=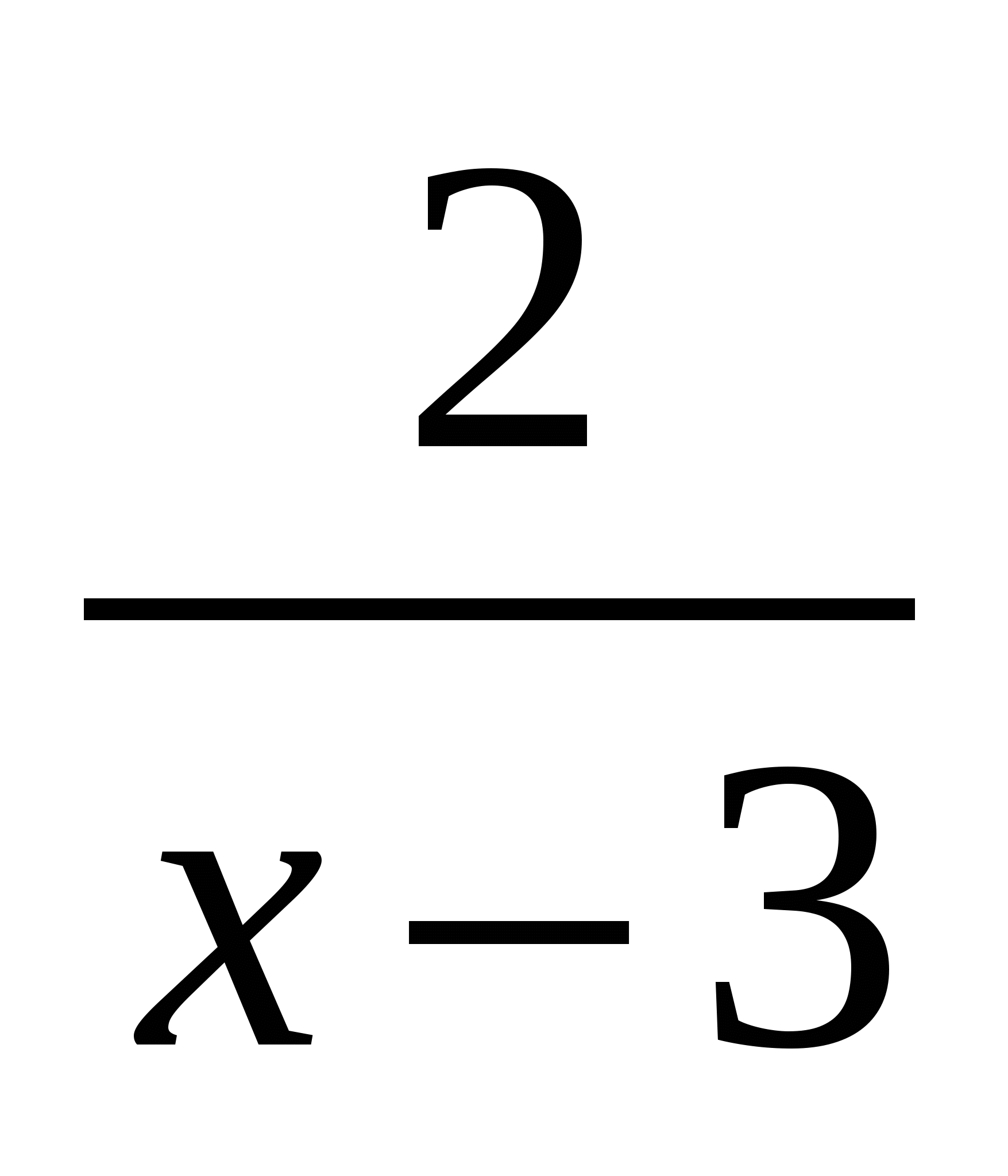 .
.
Розв'язування:
а) Функція визначена та диференційована на всій числовій прямій.
у'=2х, розв'яжемо рівняння у'=0, тобто 2х=0, х=0 - критична точка функції, яка розбиває область визначення функції на два інтервали (-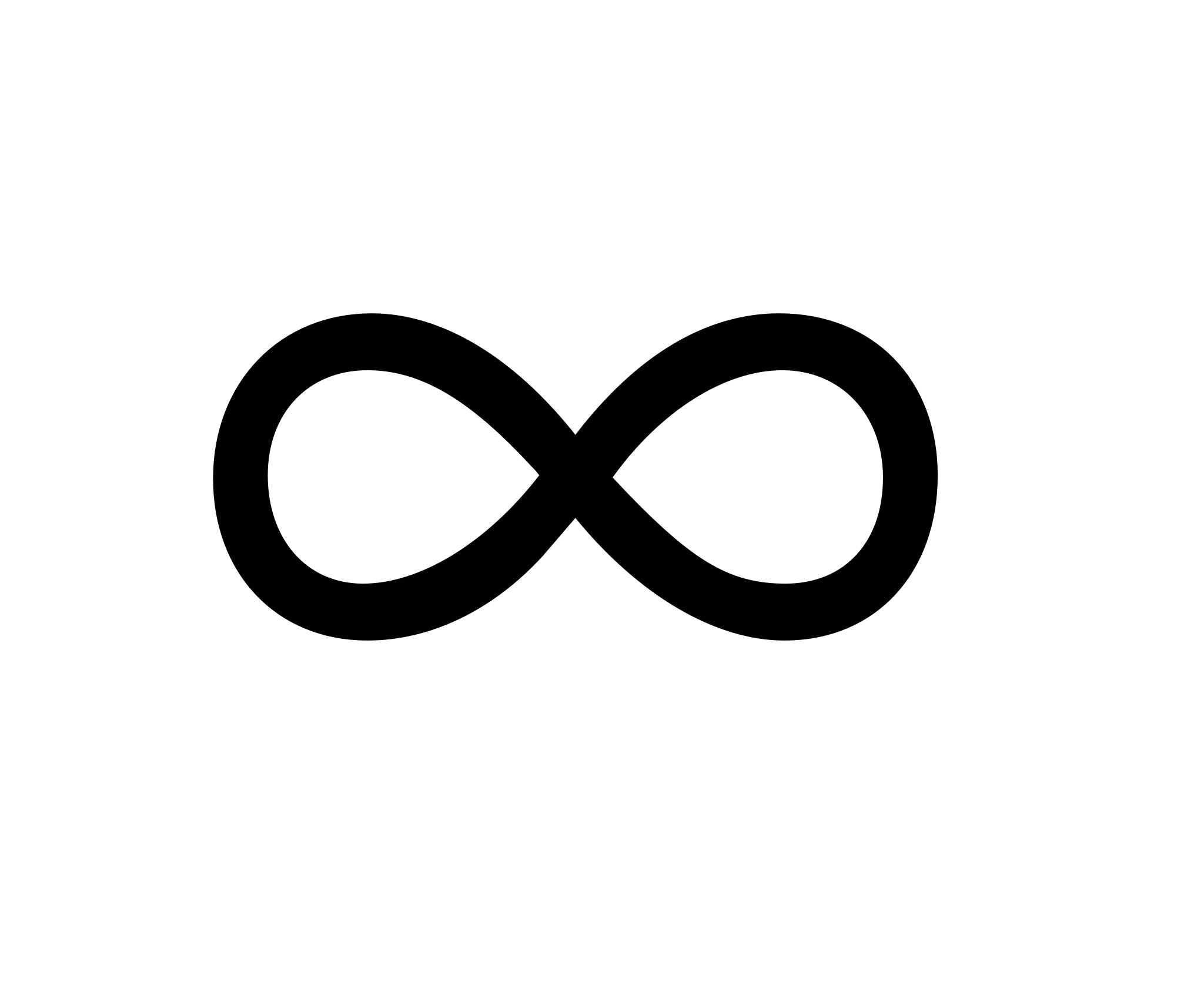 ;0) та (0; +
;0) та (0; + ), на кожному з яких похідна зберігає свій знак. у'(-1)=-2<0, у'(1)= 2>0.
), на кожному з яких похідна зберігає свій знак. у'(-1)=-2<0, у'(1)= 2>0.
Отже, на інтервалі (- ;0) похідна приймає від'ємні значення, на (0; +
;0) похідна приймає від'ємні значення, на (0; + ) - додатні значення. Тому на інтервалі (-
) - додатні значення. Тому на інтервалі (-![]() ;0) функція спадає, а на (0; +
;0) функція спадає, а на (0; +![]() ) - зростає.
) - зростає.
Відповідь: на інтервалі (- ;0) функція спадає, а на (0; +
;0) функція спадає, а на (0; +![]() ) - зростає.
) - зростає.
б) Область визначення даної функції - всі числа, крім х=3.
у'=-2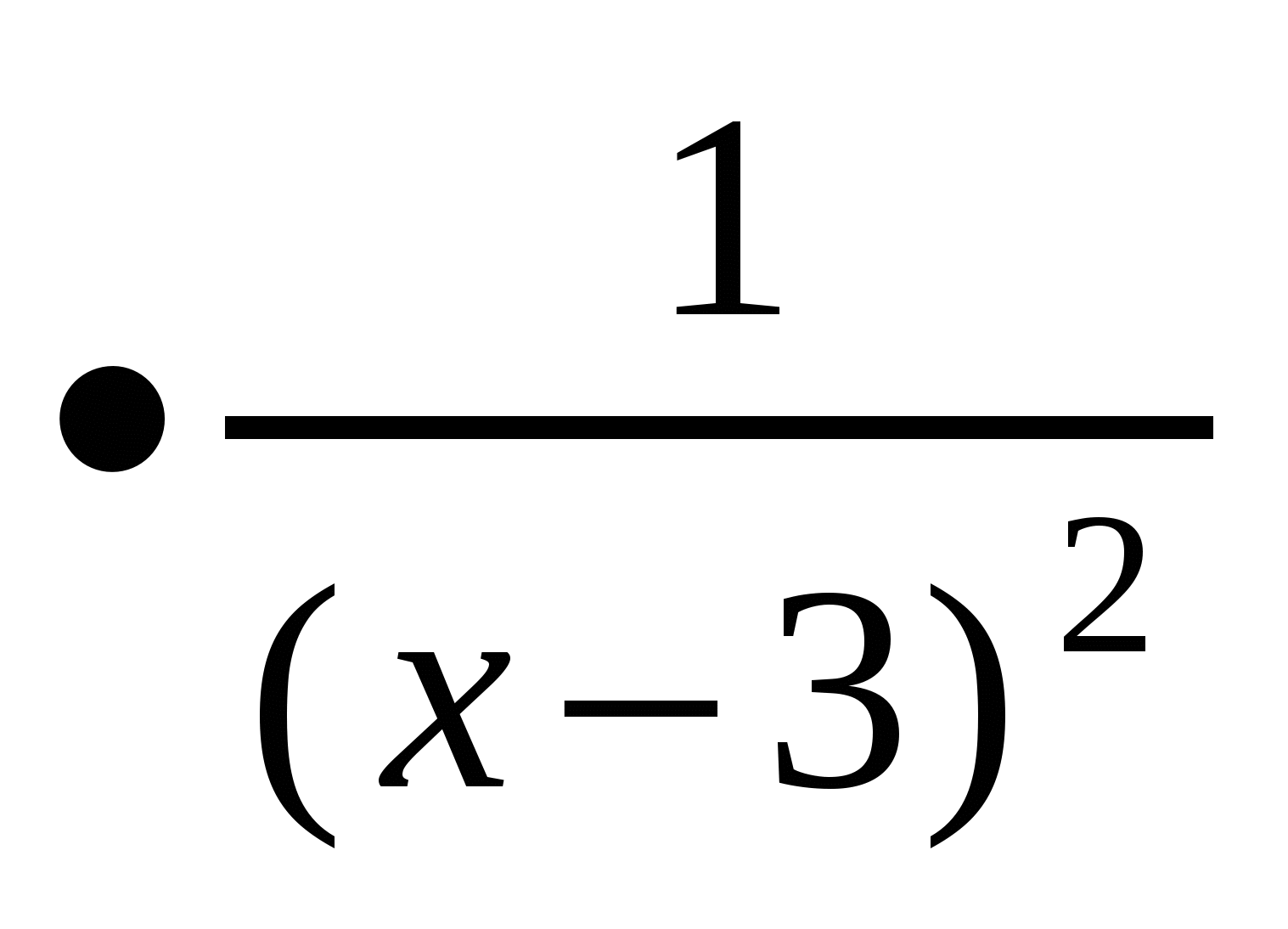 =
=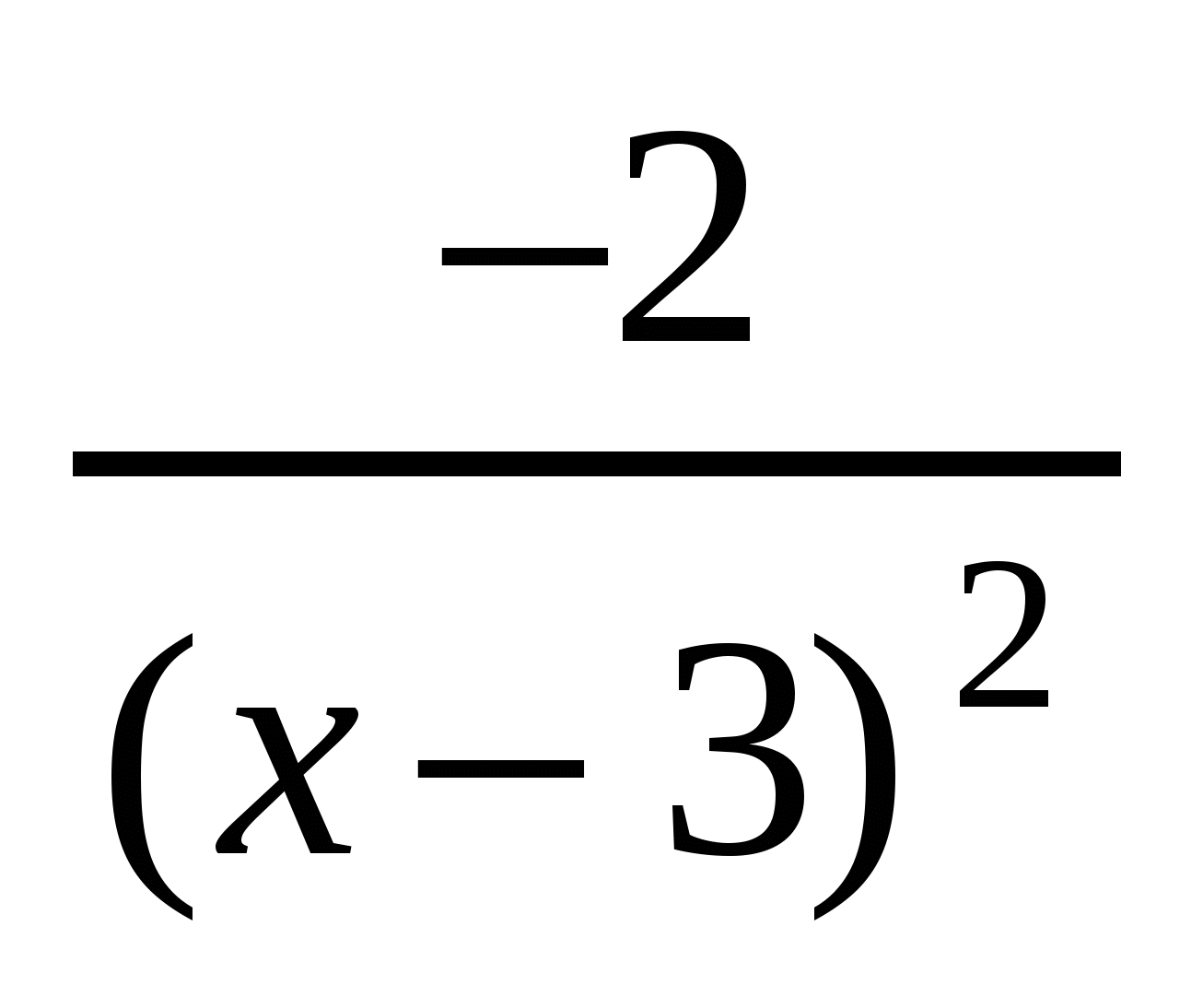 , рівняння у'=0 немає коренів. Тому критичною точкою функції є лише точка х=3, яка розбиває область визначення функції на два інтервали (-
, рівняння у'=0 немає коренів. Тому критичною точкою функції є лише точка х=3, яка розбиває область визначення функції на два інтервали (-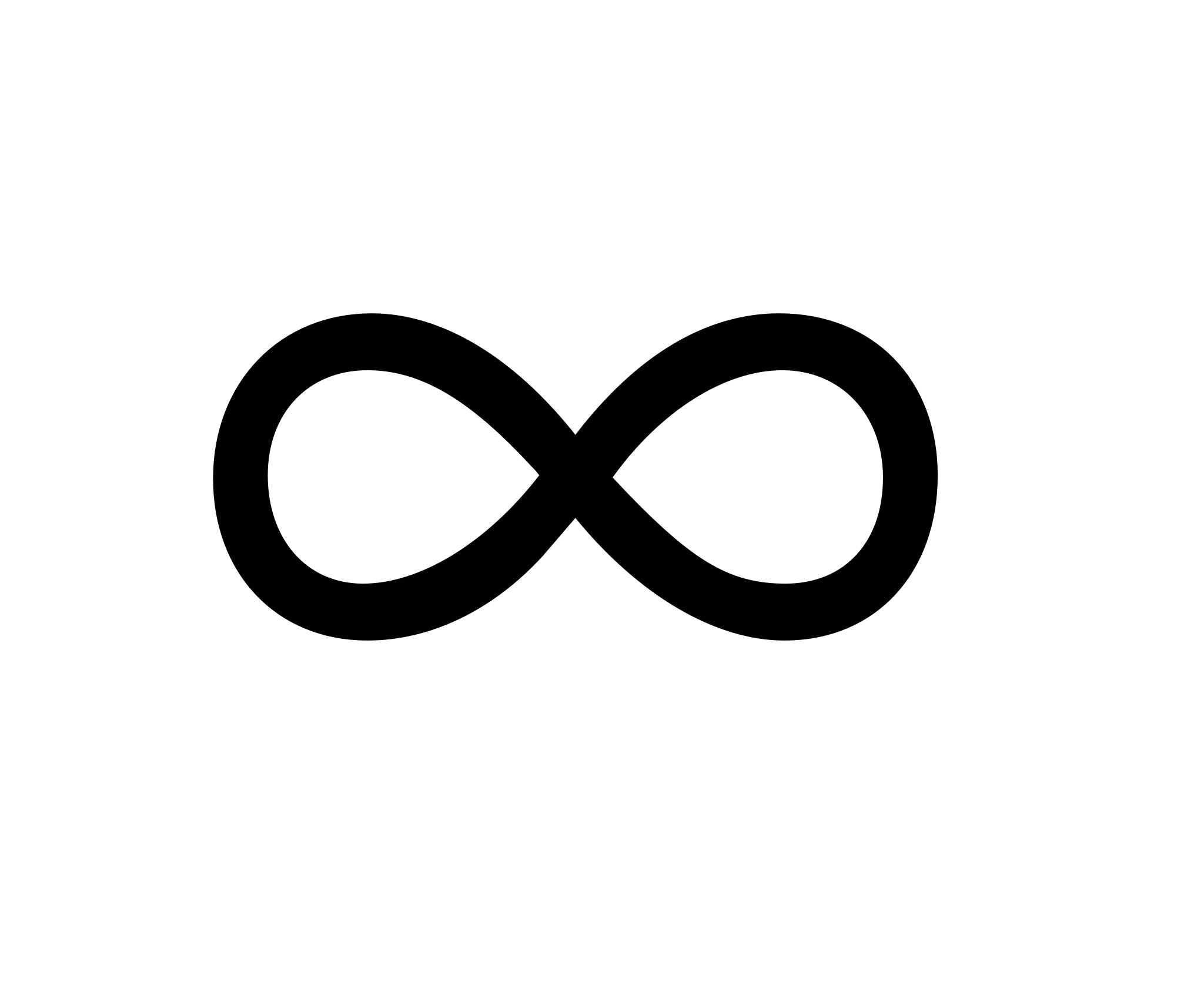 ;3) та (3; +
;3) та (3; +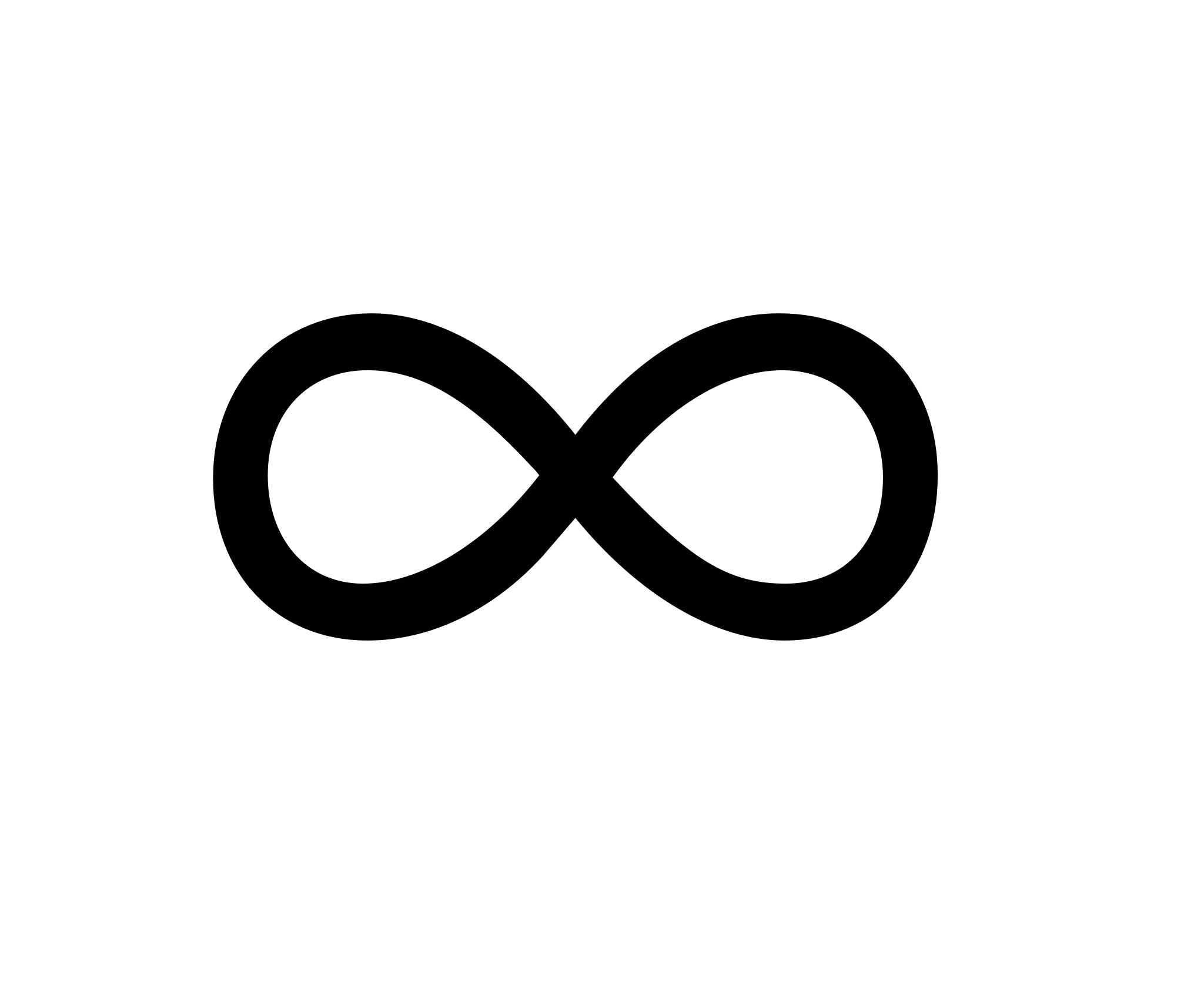 ), на кожному з яких похідна зберігає свій знак. у'(2)=-2<0, у'(4)=-2<0.
), на кожному з яких похідна зберігає свій знак. у'(2)=-2<0, у'(4)=-2<0.
Отже, на інтервалах (- ;3) та (3; +
;3) та (3; + ) похідна приймає від'ємні значення. Тому на інтервалах (-
) похідна приймає від'ємні значення. Тому на інтервалах (- ;3) та (3; +
;3) та (3; + ) функція спадає.
) функція спадає.
Відповідь: на інтервалах (- ;3) та (3; +
;3) та (3; + ) функція спадає.
) функція спадає.
Завдання 8
Який кут (гострий чи тупий) утворює із додатнім напрямом осі Ох та дотичної до графіку функції у=х4-2 у точках -1, 1, 2.
Розв'язування:
Згідно геометричному змісту похідної k=у'(х0), де k - кутовий коефіцієнт дотичної до графіку функції. у'=4х3.Отже, k1=у'(-1)=-4<0, k2=у'(1)=4>0, k3=у'(2)=32>0.
З іншого боку, k=tg α, де α - кут між дотичною та додатнім напрямом віссі Ох. Отже, α1- тупий кут, α2 та α3 - гострі кути.
Відповідь: α1- тупий кут, α2 та α3 - гострі кути.
Завдання 9
Скласти рівняння дотичної до графіку функції f(х)= 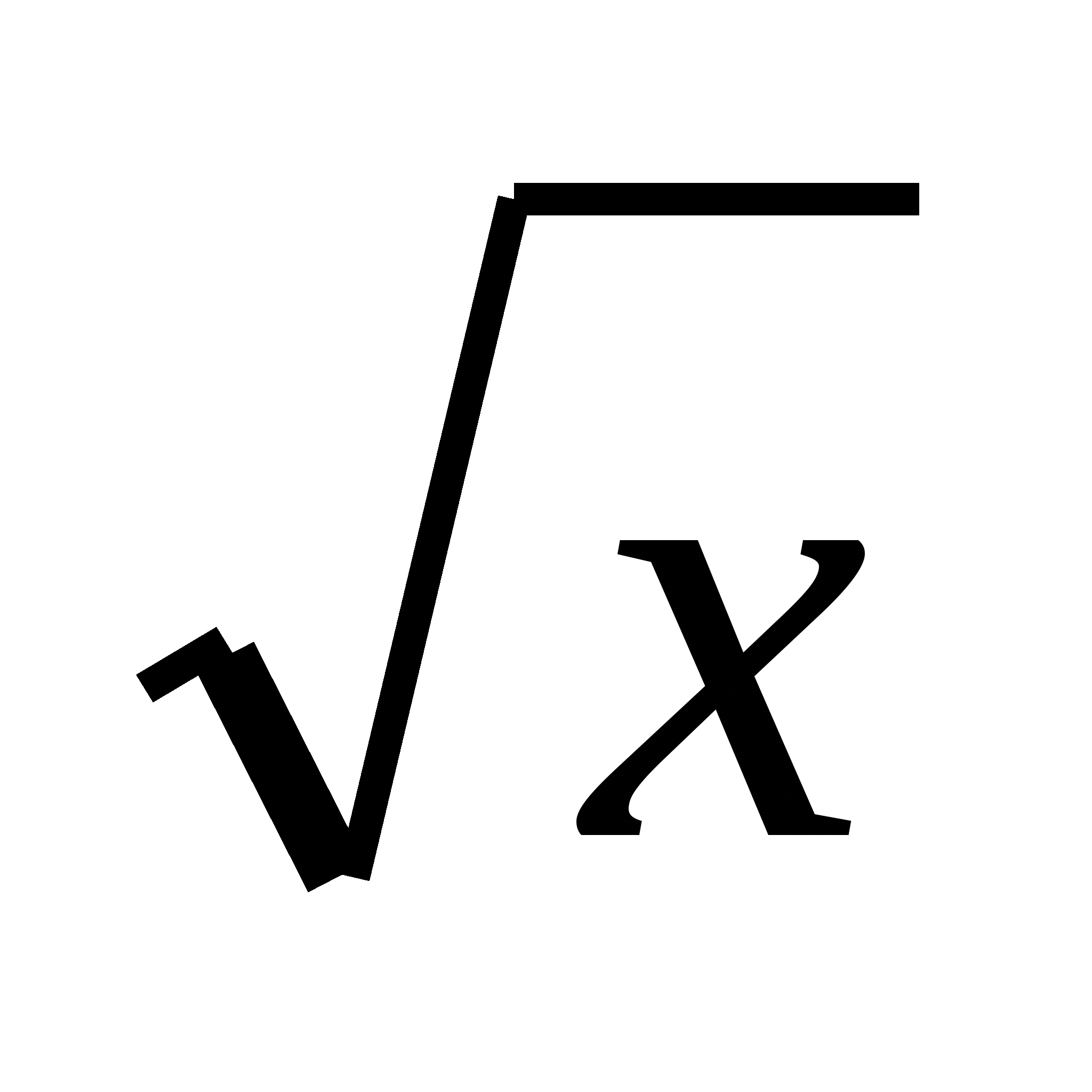 -8 у точці х0=4.
-8 у точці х0=4.
Розв'язування:
Загальний вигляд рівняння дотичної має вигляд у= f(х0)+ f'(х0)(х-х0).
f(х0)= f(4)=-6, f'(х)=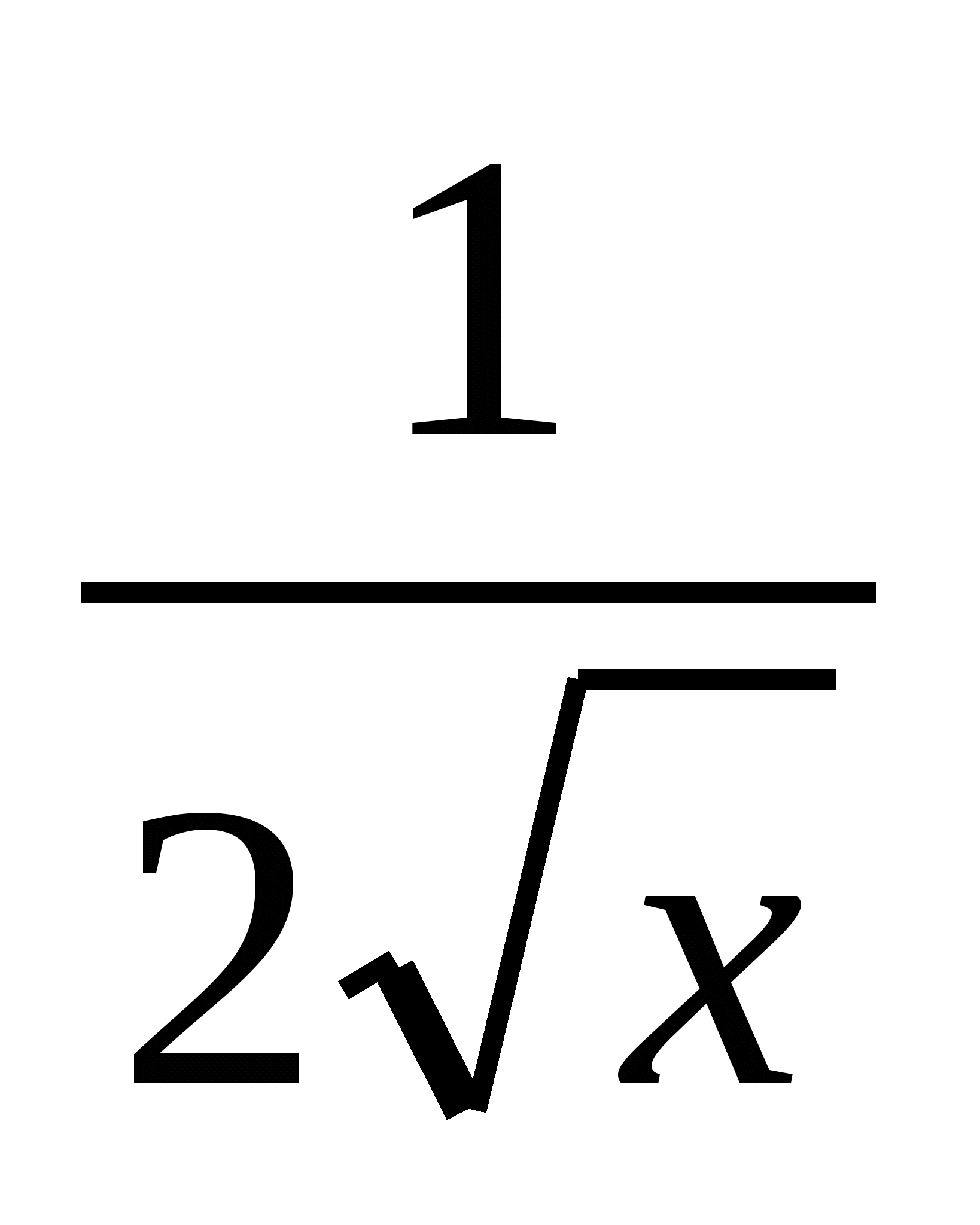 , f'(х0)= f'(4)=0,25.
, f'(х0)= f'(4)=0,25.
Тому загальний вигляд дотичної має вигляд у=-6+0,25 (х-4)=-6+0,25х-1= =0,25х - 7.
(х-4)=-6+0,25х-1= =0,25х - 7.
Відповідь: у=0,25х - 7.
Завдання 10
Знайти найбільше та найменше значення функції у=4х2-48х на проміжку [1;4].
Розв'язування:
Функція визначена та диференційована на всій числовій прямій.
Похідна у'=8х-48, знайдемо нулі похідної : 8х-48=0, х=6 - критична точка функції, але вона не належить даному проміжку. Тому знайдемо значення функції у кінцях даного проміжка, тобто у(1)=-44, у(4)= -128.
Отже, max у(х)= у(1)=-44, min у(х)= у(4)= -128.
[1;4] [1;4]
Відповідь: max у(х)= у(1)=-44, min у(х)= у(4)= -128.
Задание 11
Найти производную функции 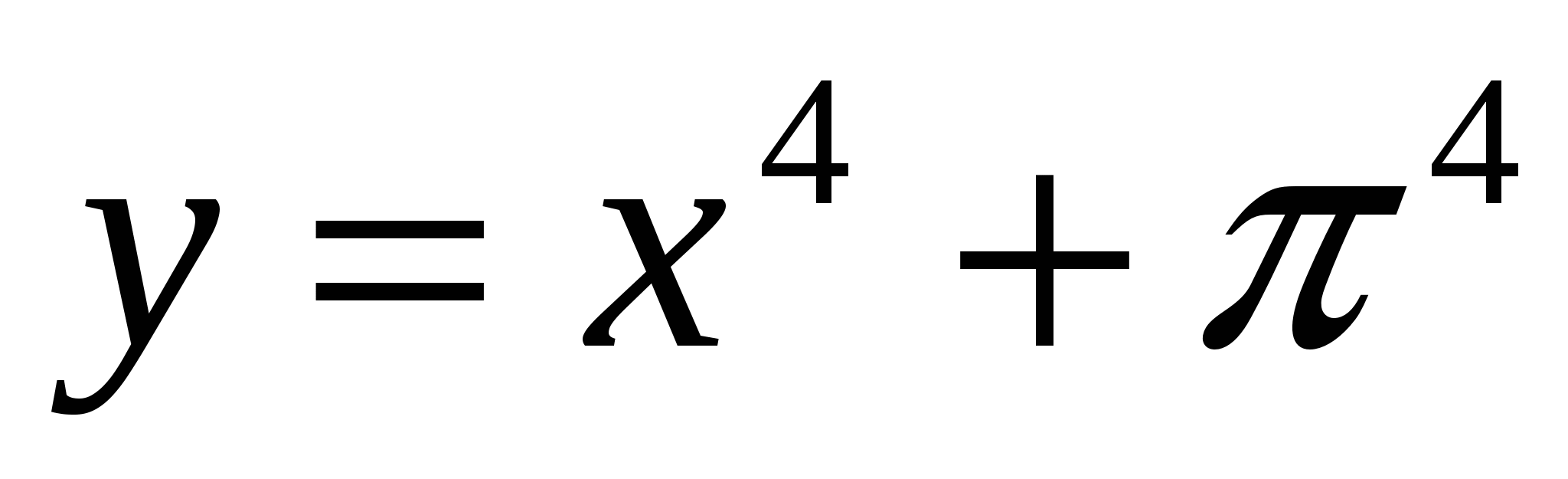 .
.
Решение 1. ![]() .Поскольку
.Поскольку  -постоянная величина, то
-постоянная величина, то 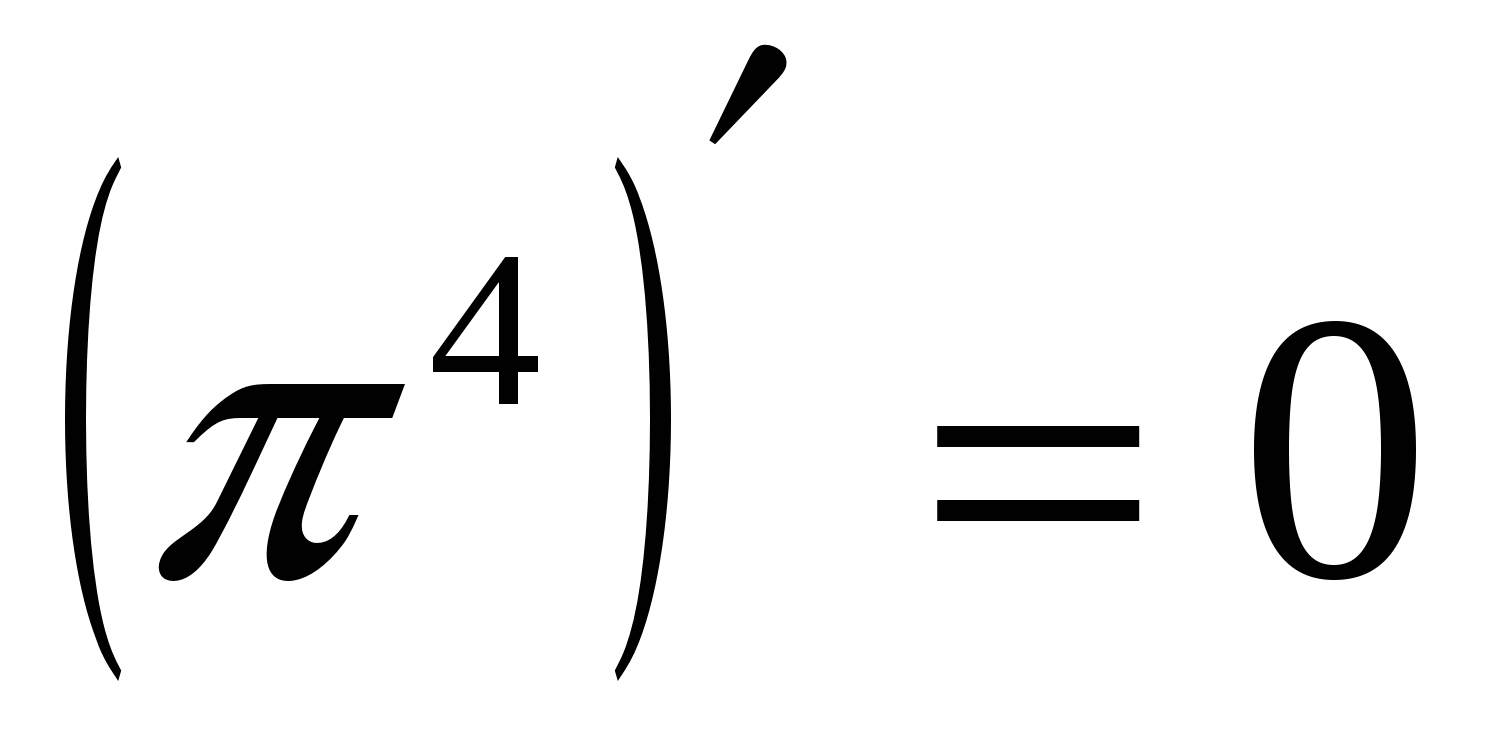 ,поэтому
,поэтому 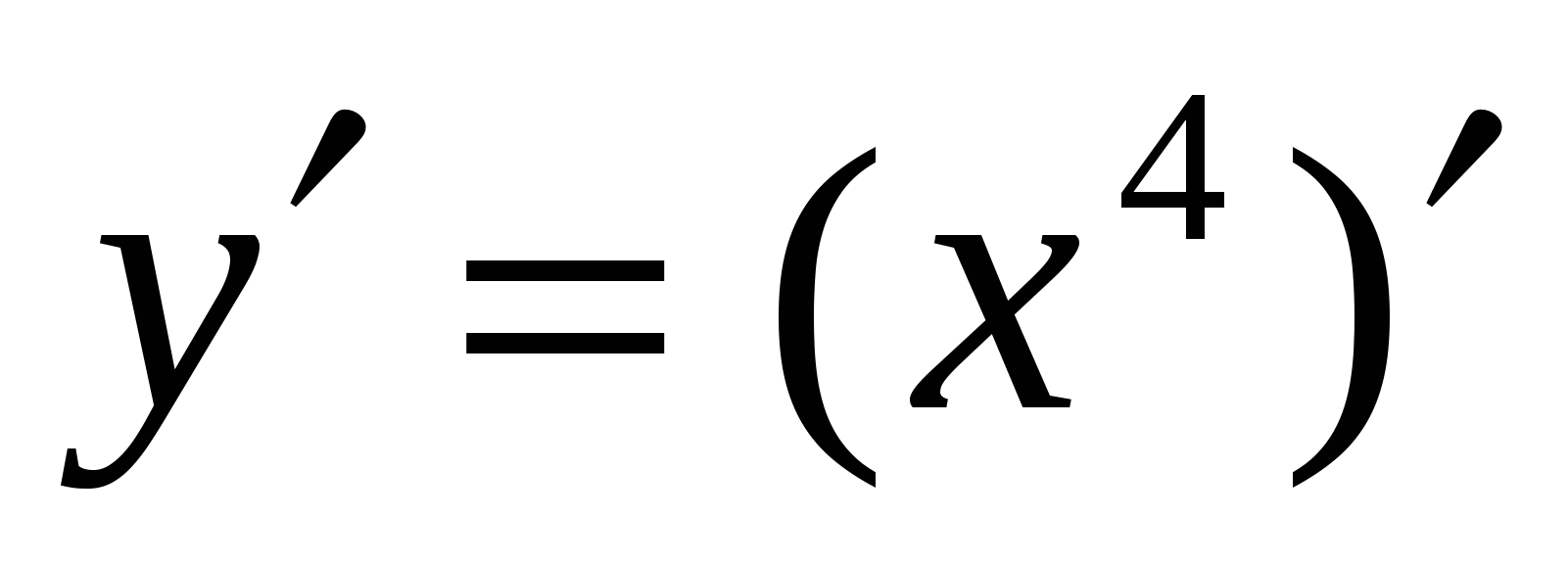 . Применим формулу
. Применим формулу 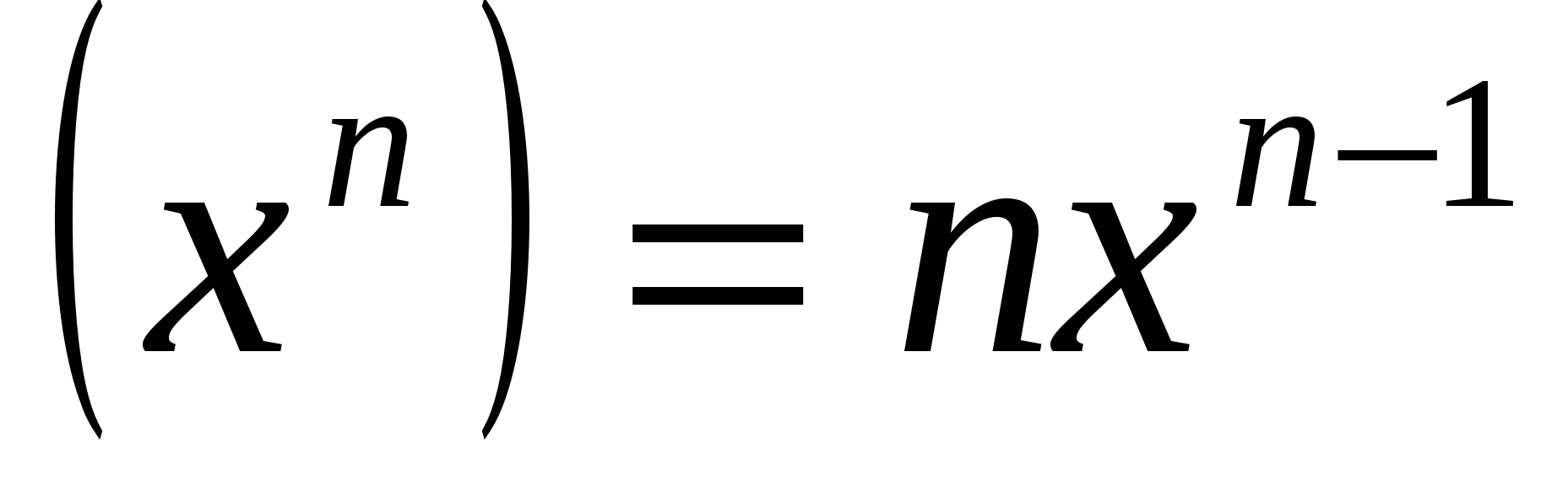 пологая что в ней
пологая что в ней 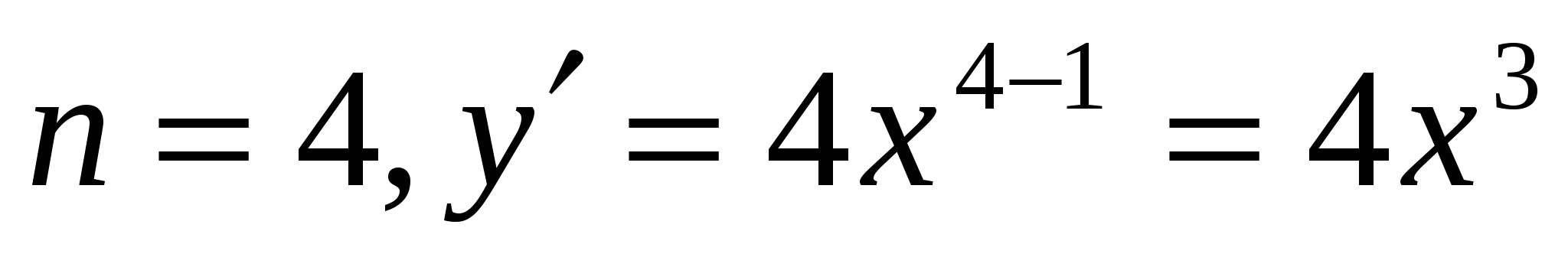 .
.
Ответ: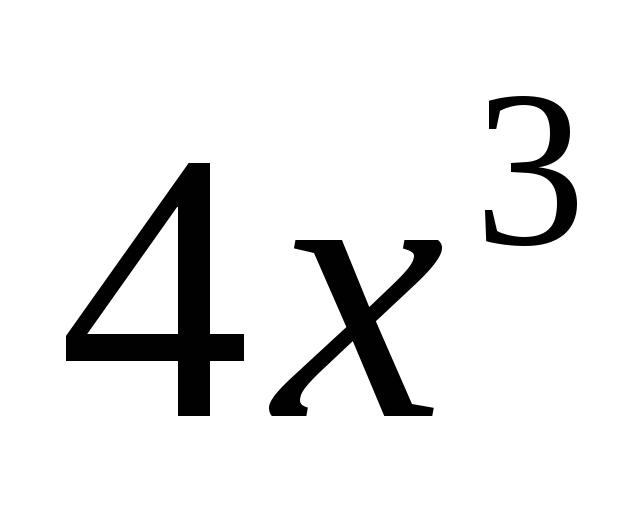
Решение 2. Вычислите  по определению
по определению 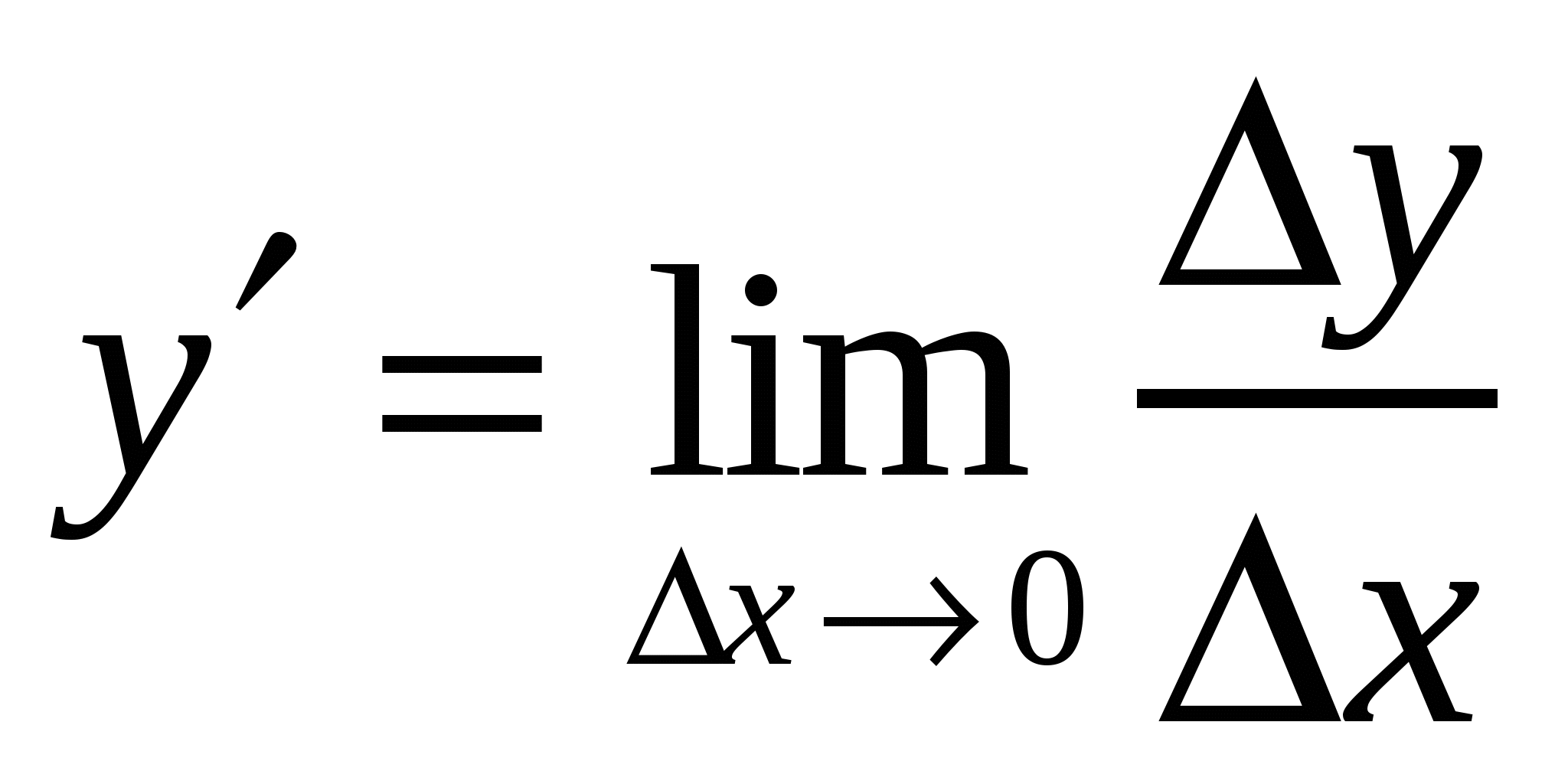 здесь громоздко, поэтому представим что у(х) как произведение:
здесь громоздко, поэтому представим что у(х) как произведение: 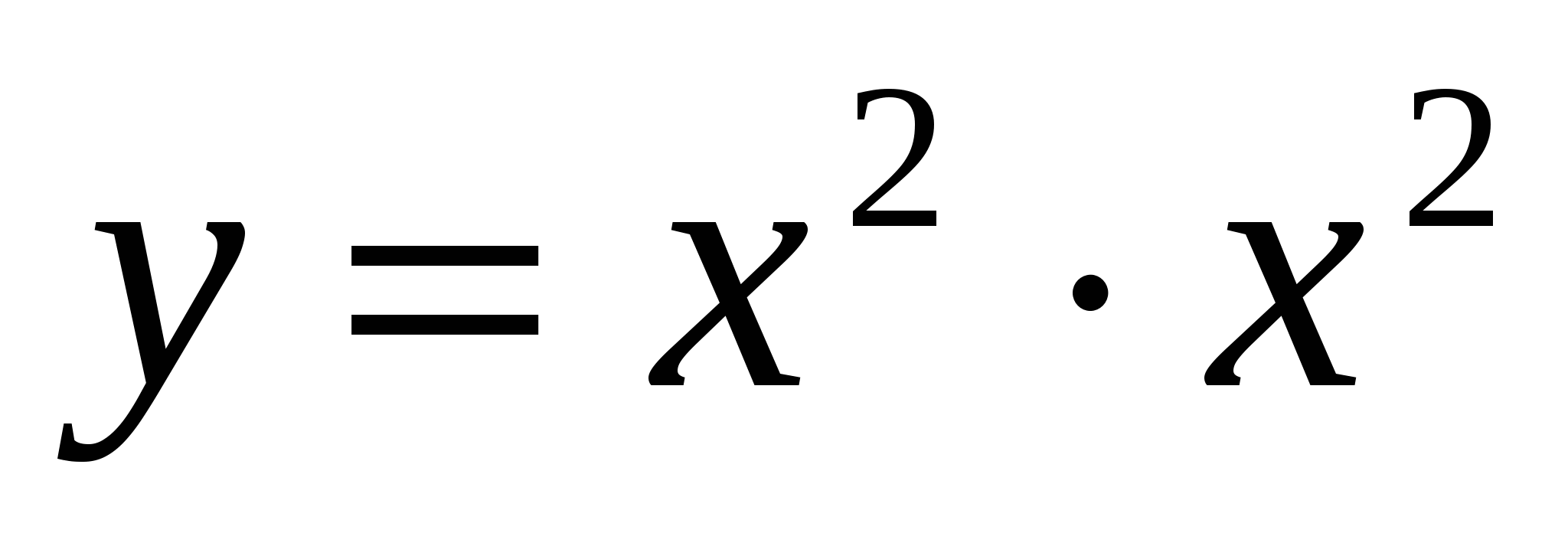 .
.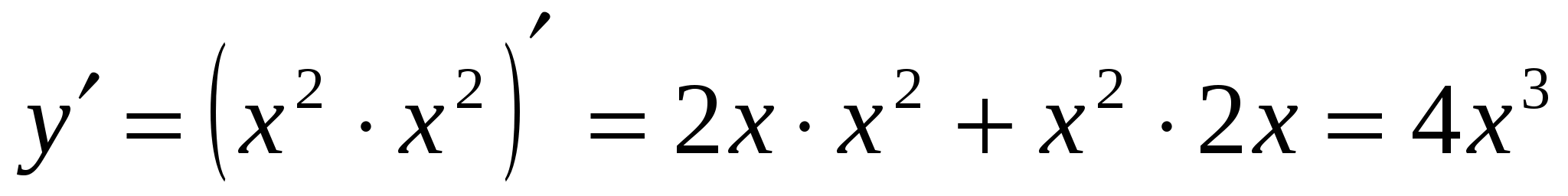 .
.
Ответ: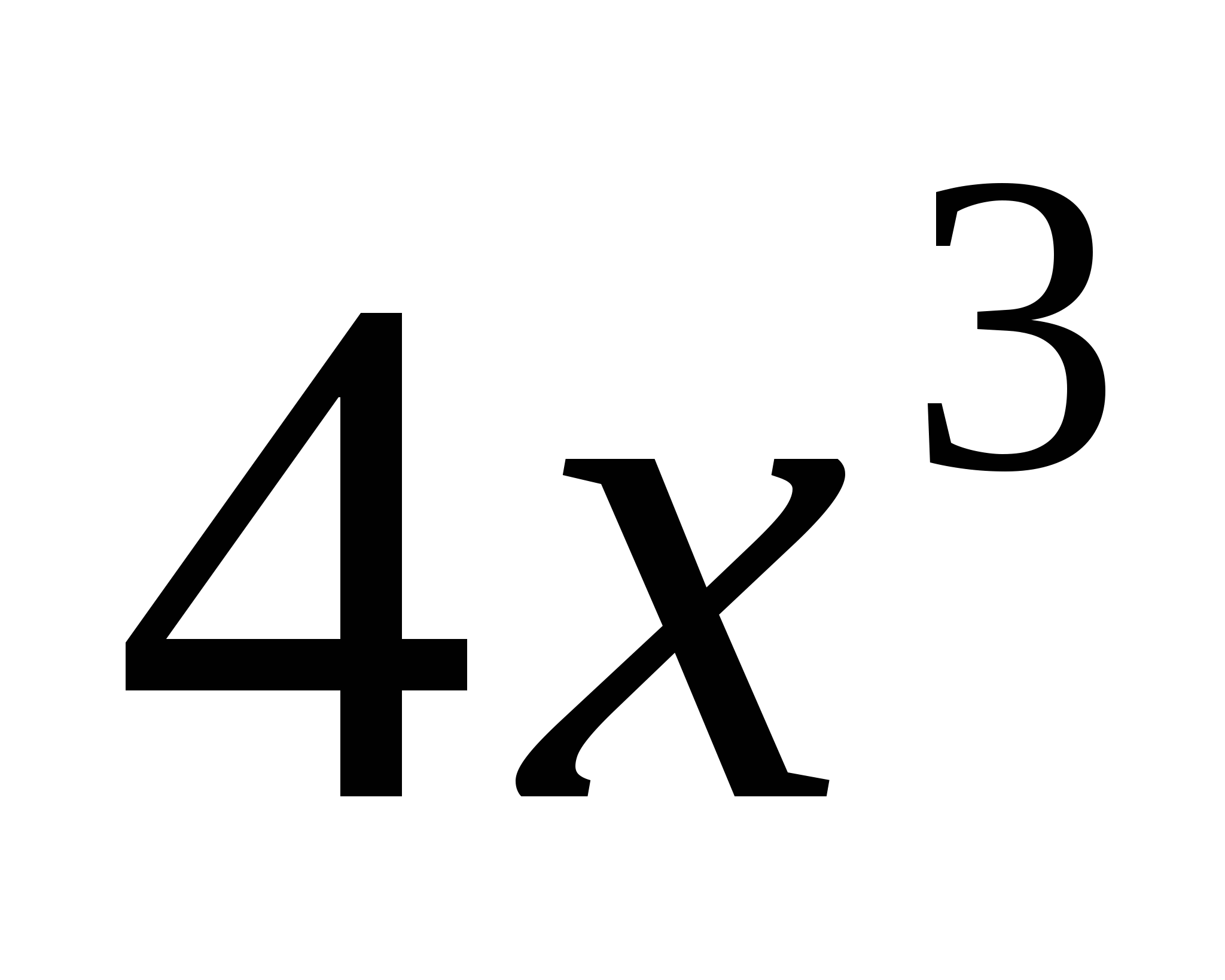
Решение 3. Учтем, что  ,
, 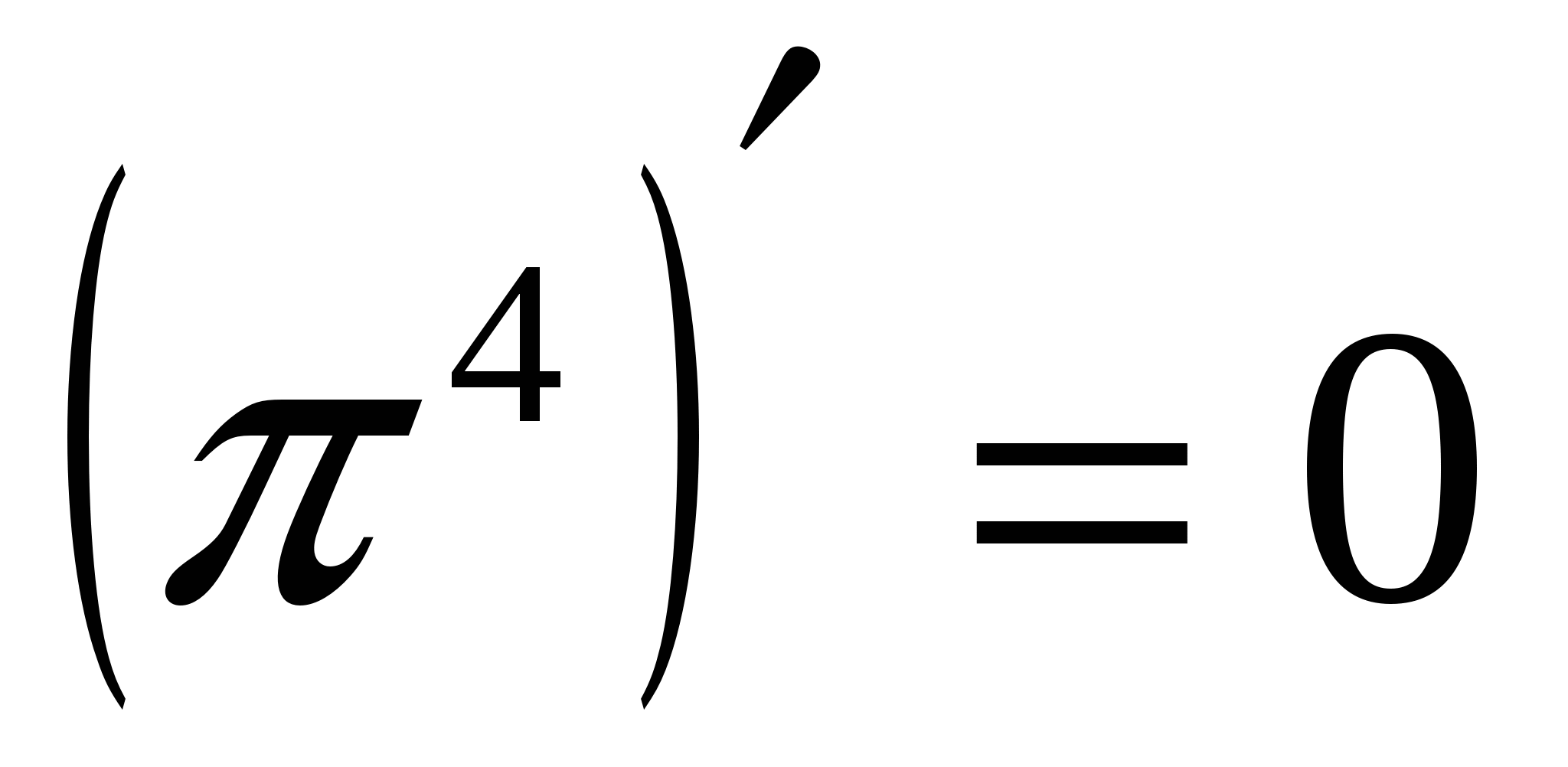 . Применим логарифмическое дифференцирование для определения производной функции
. Применим логарифмическое дифференцирование для определения производной функции 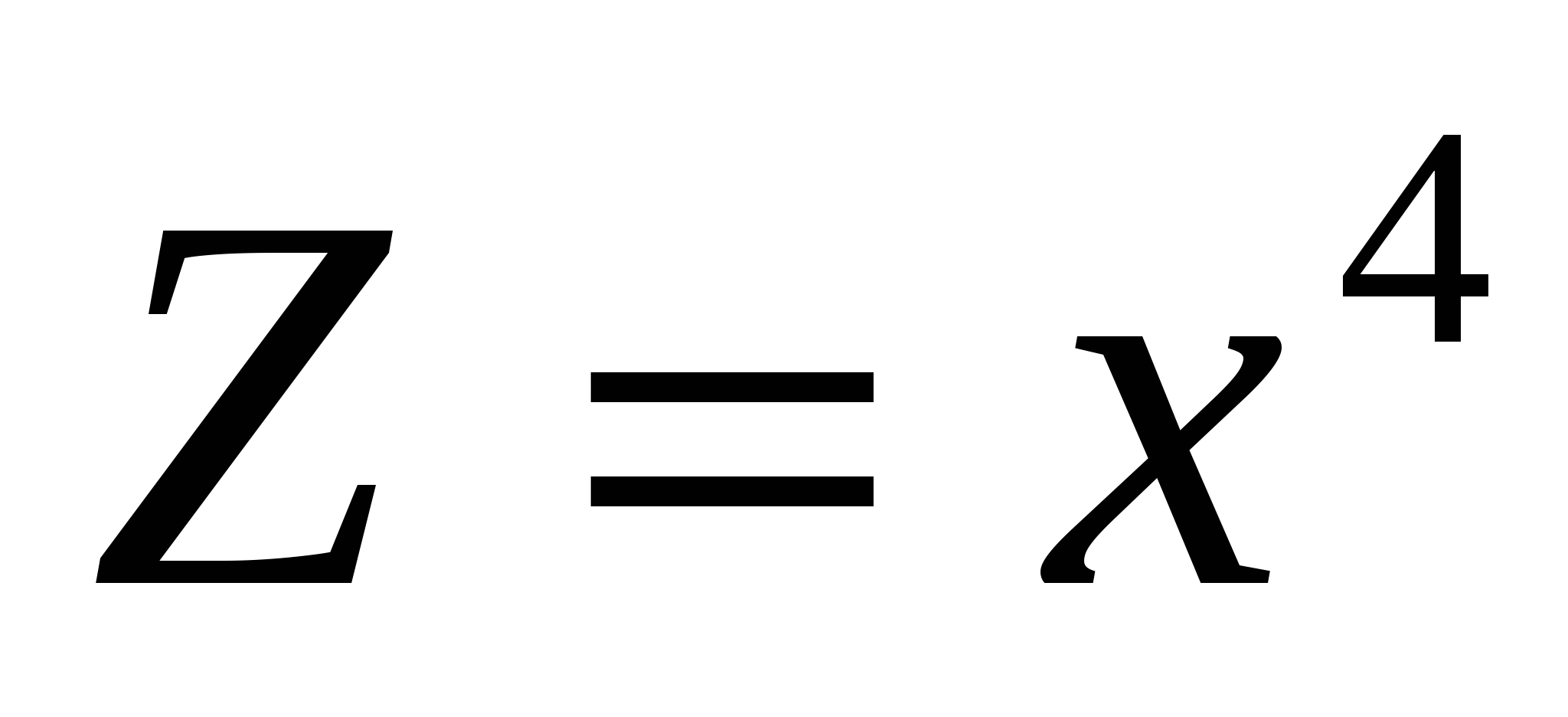 . Имеем:
. Имеем: 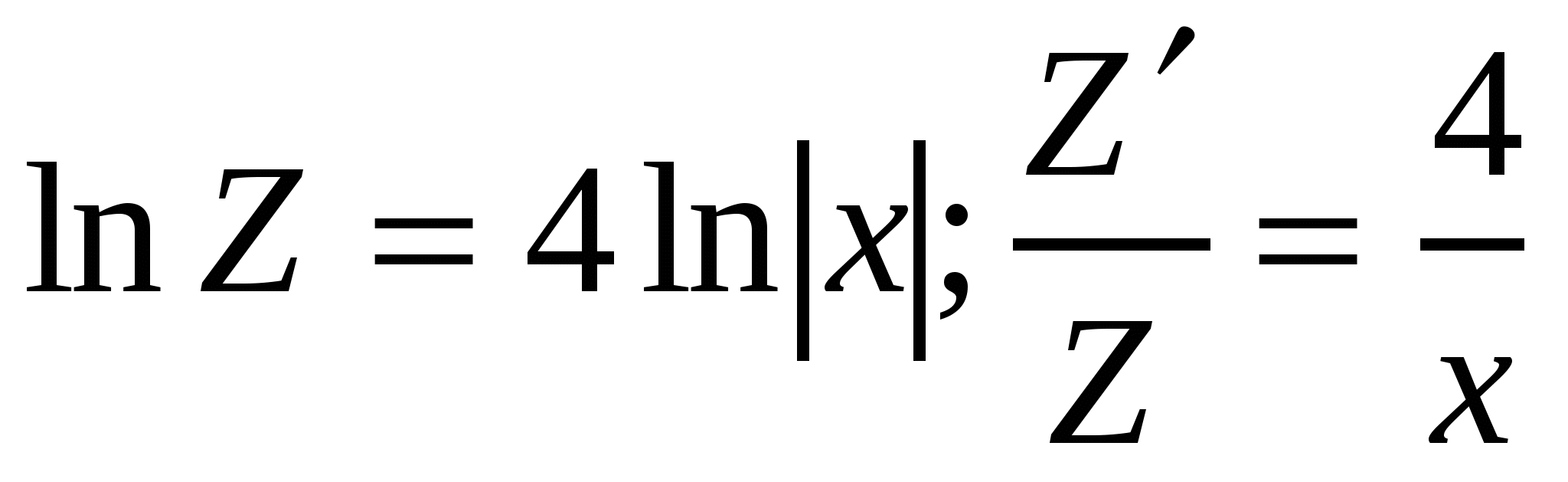 ;
; 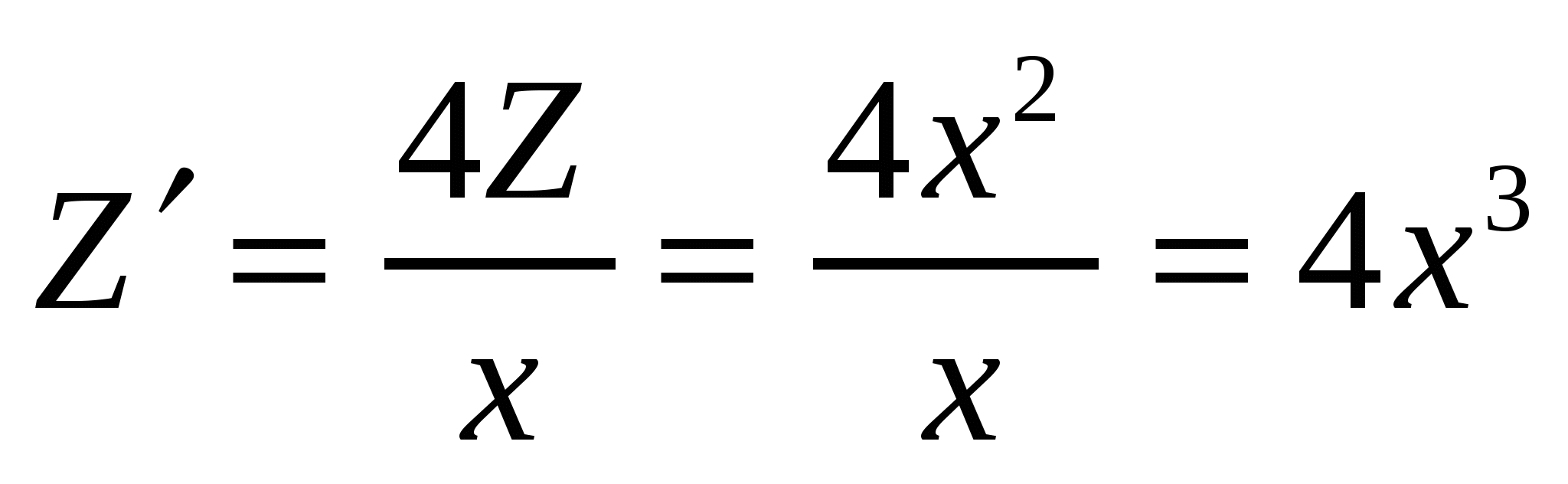 .
.
Ответ: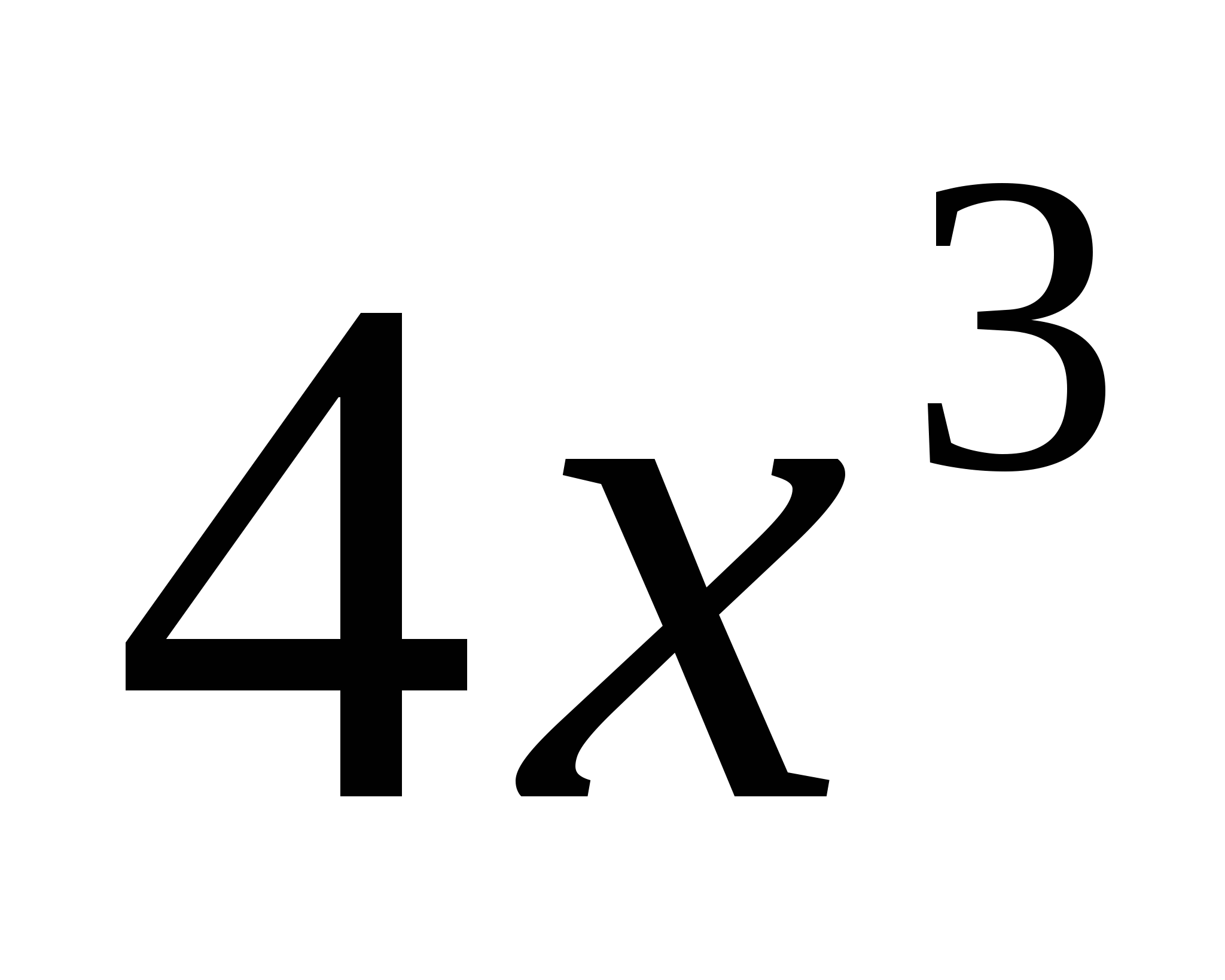
Решение 4. Имеем: 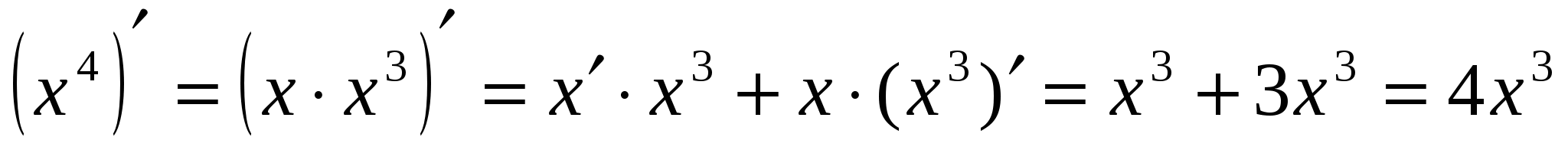 .
.
Ответ: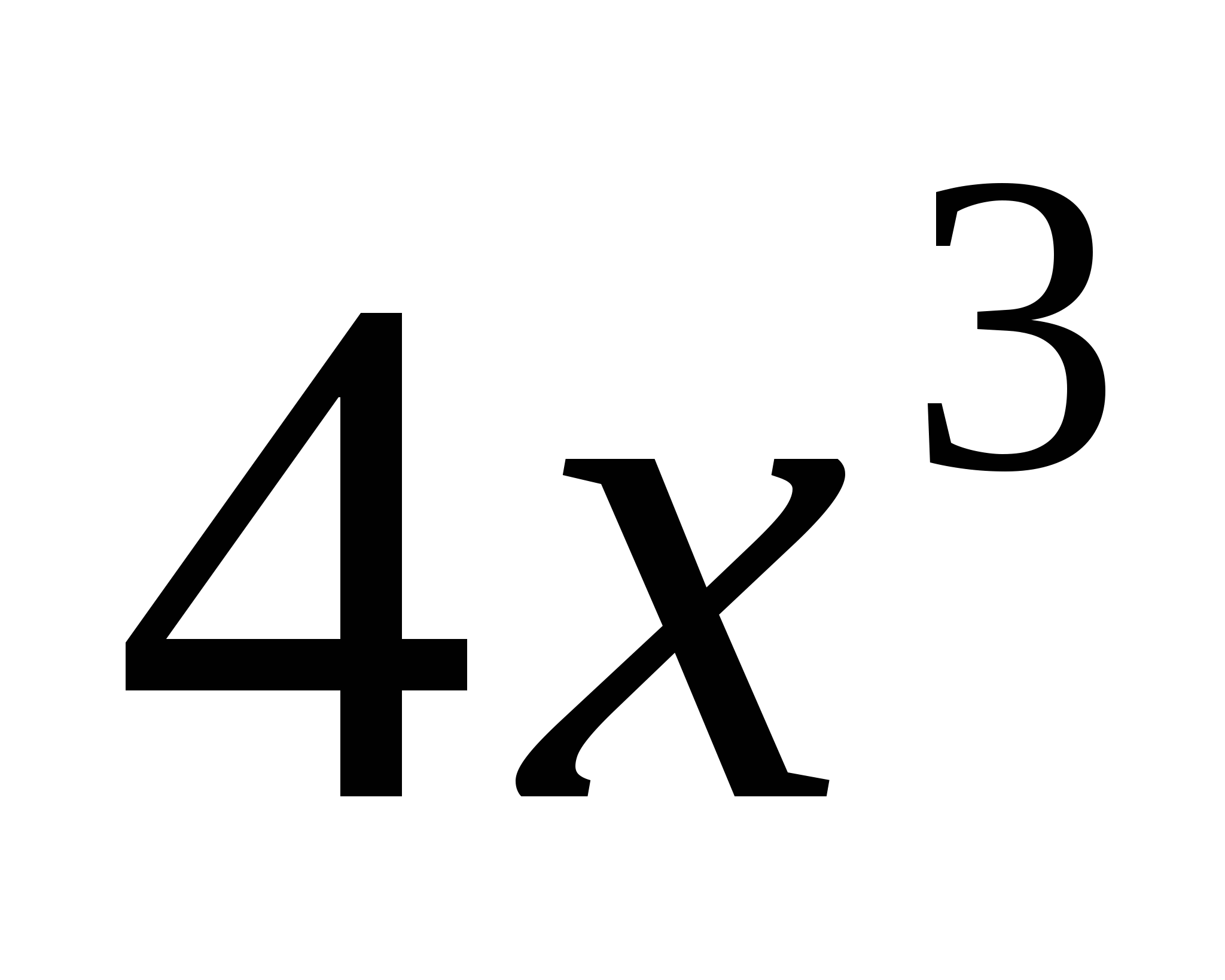
Задание 12
Найти производную функции 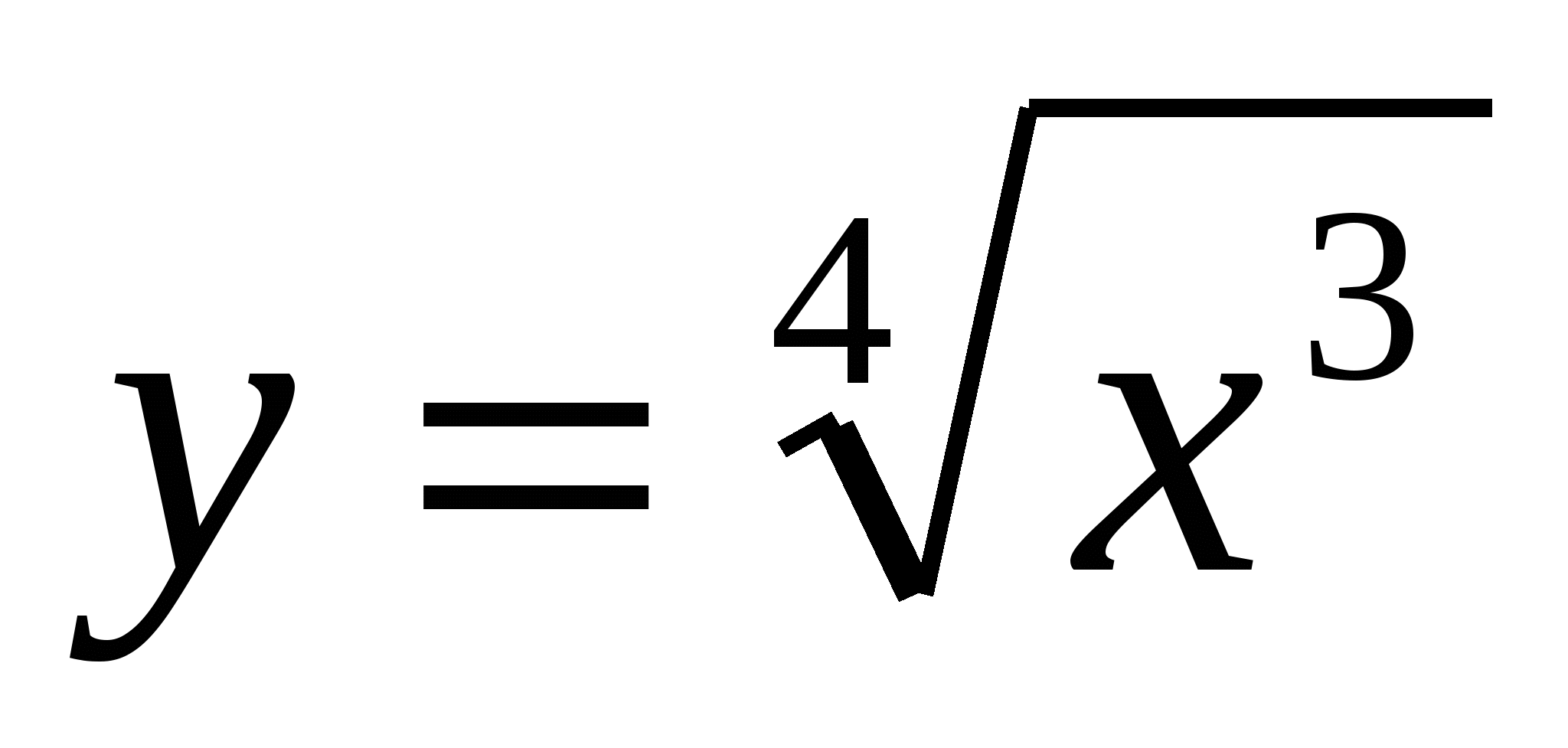 .
.
Решение 1. 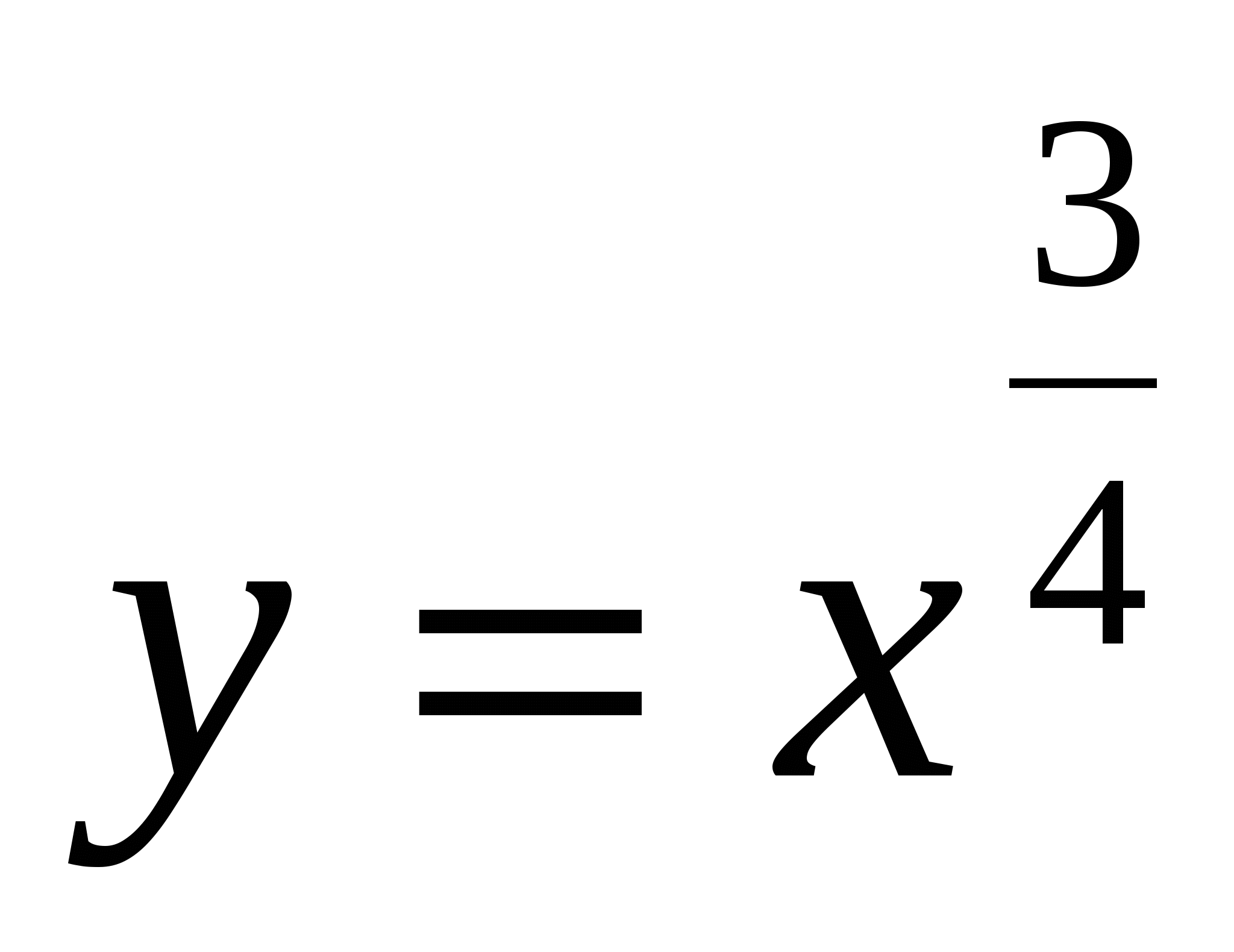 , найдем производную степенной функции:
, найдем производную степенной функции: 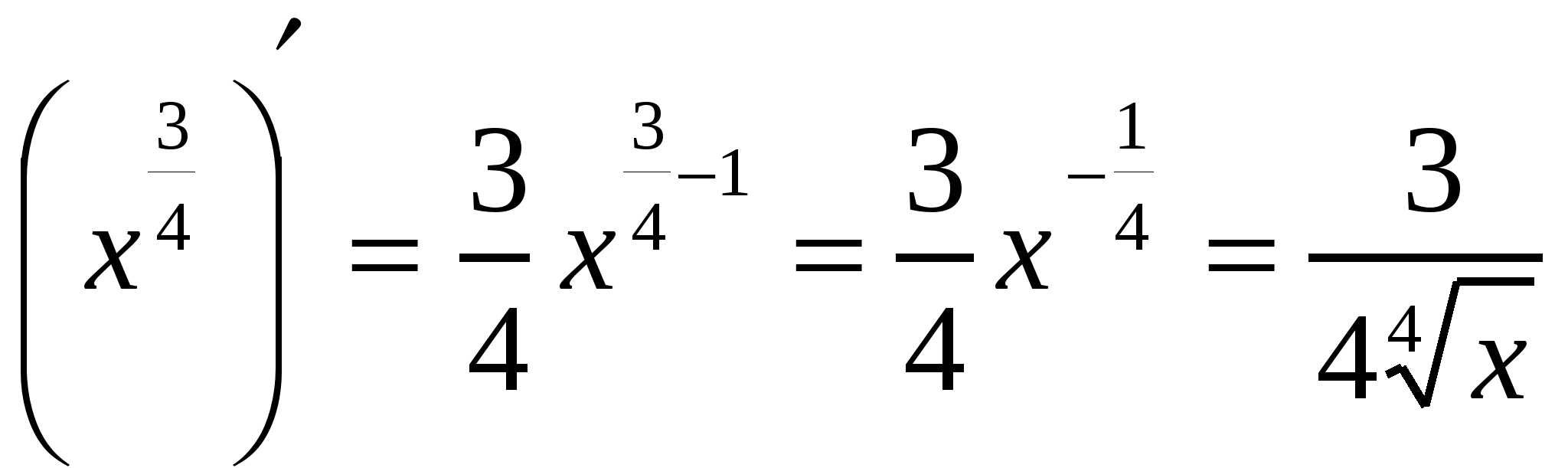 .
.
Ответ: 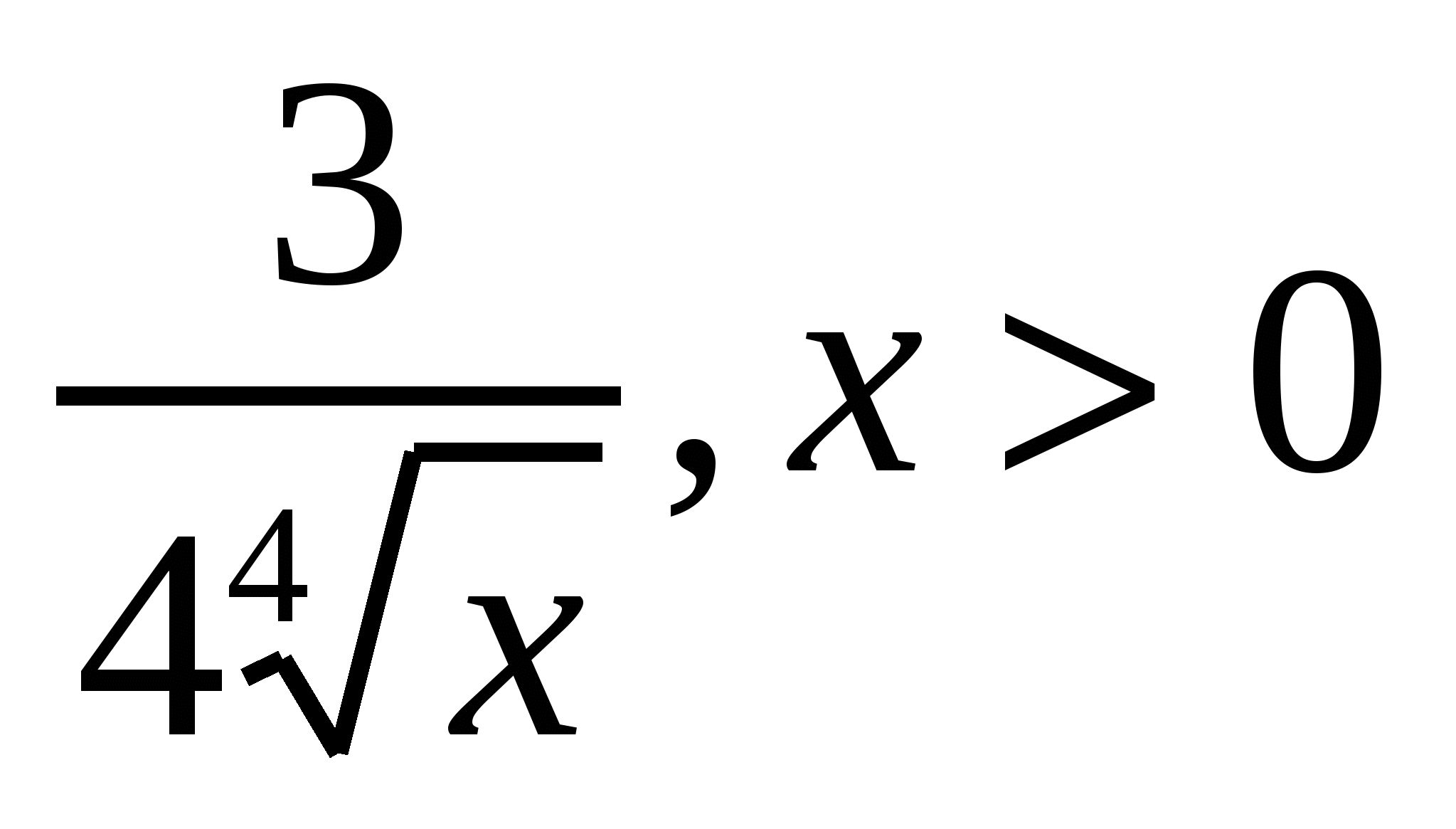
Решение 2. 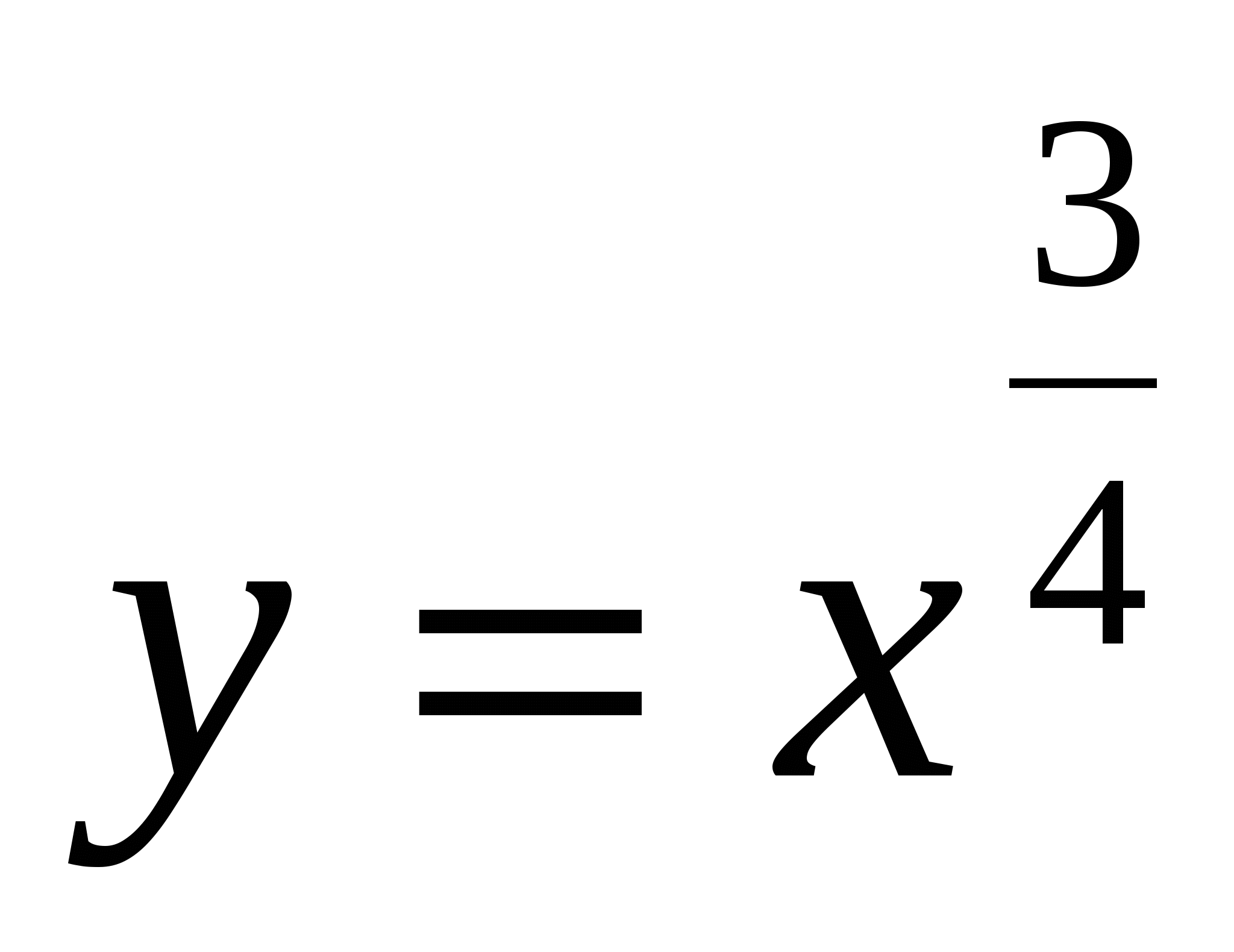 ,используем логарифмическое дифференцирование:
,используем логарифмическое дифференцирование:
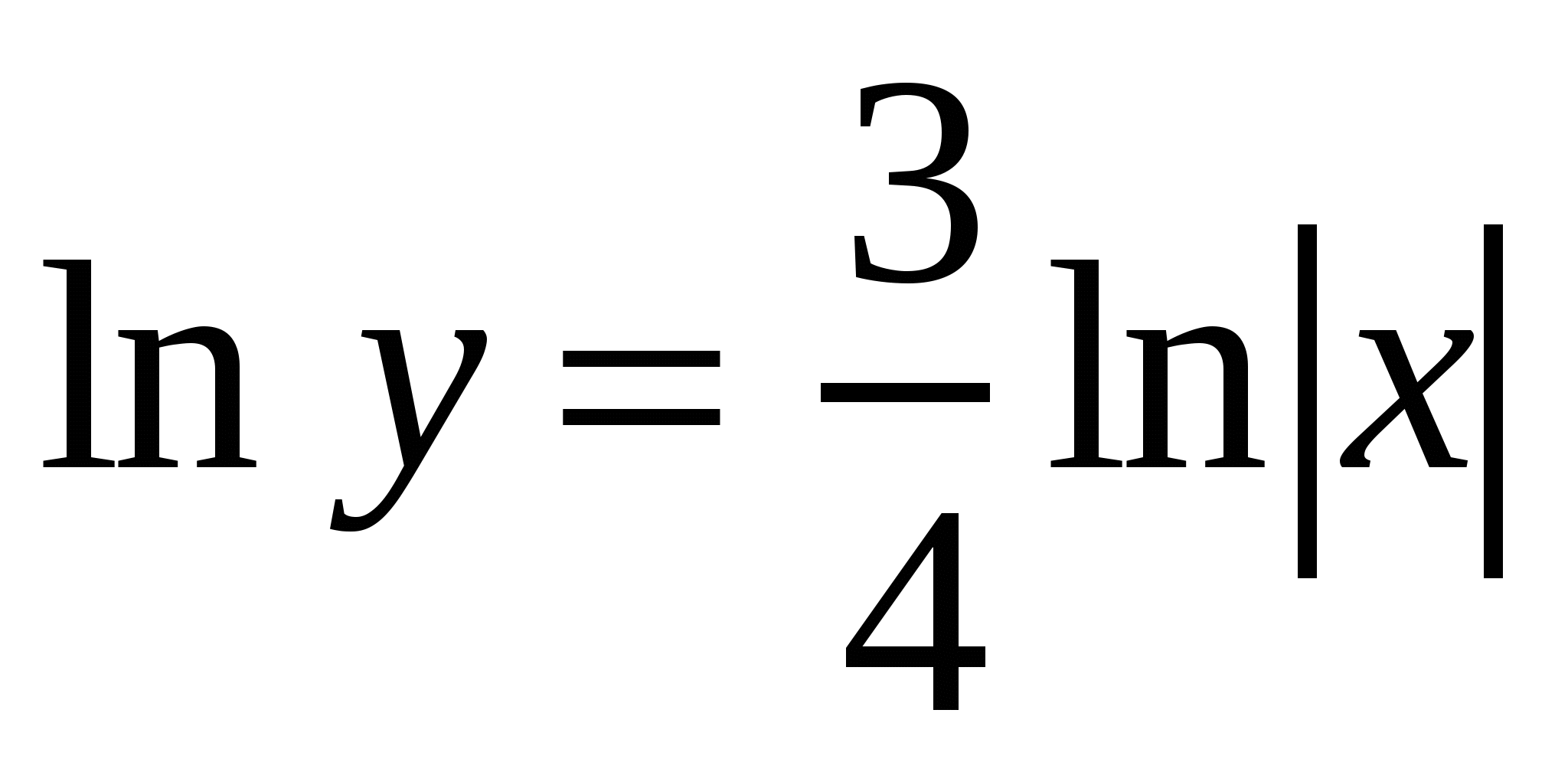 ;
; 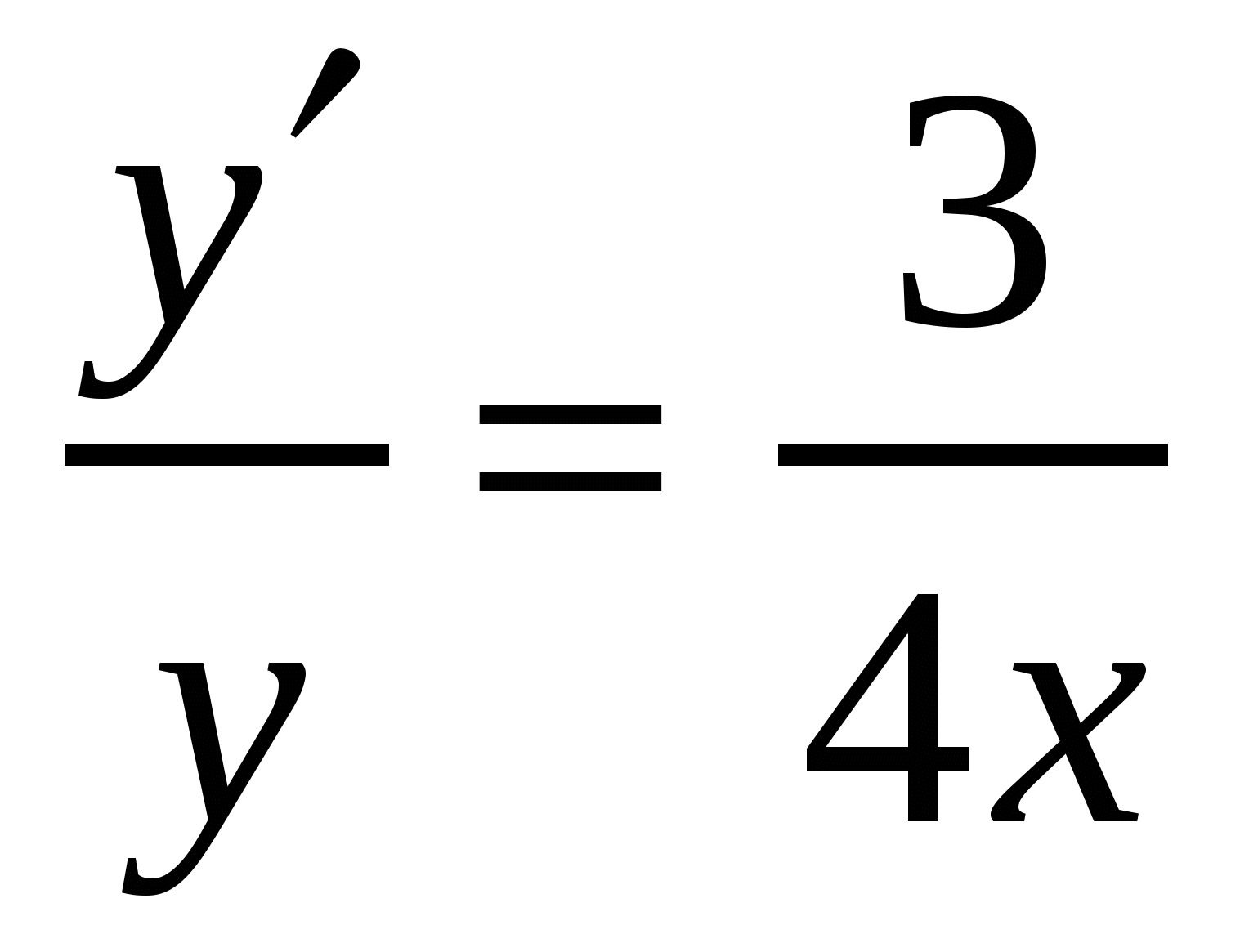 ;
; 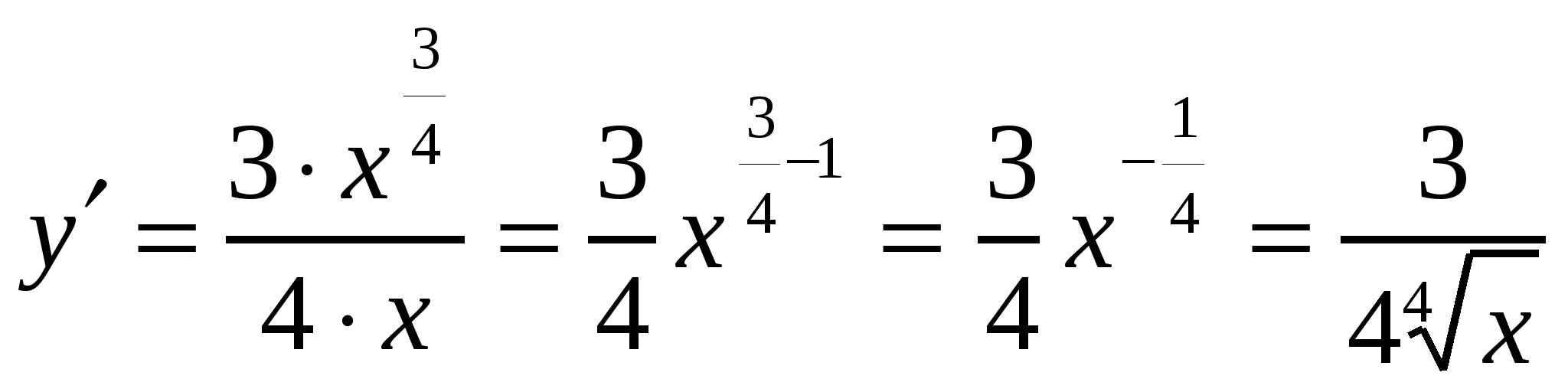 .
.
Ответ: 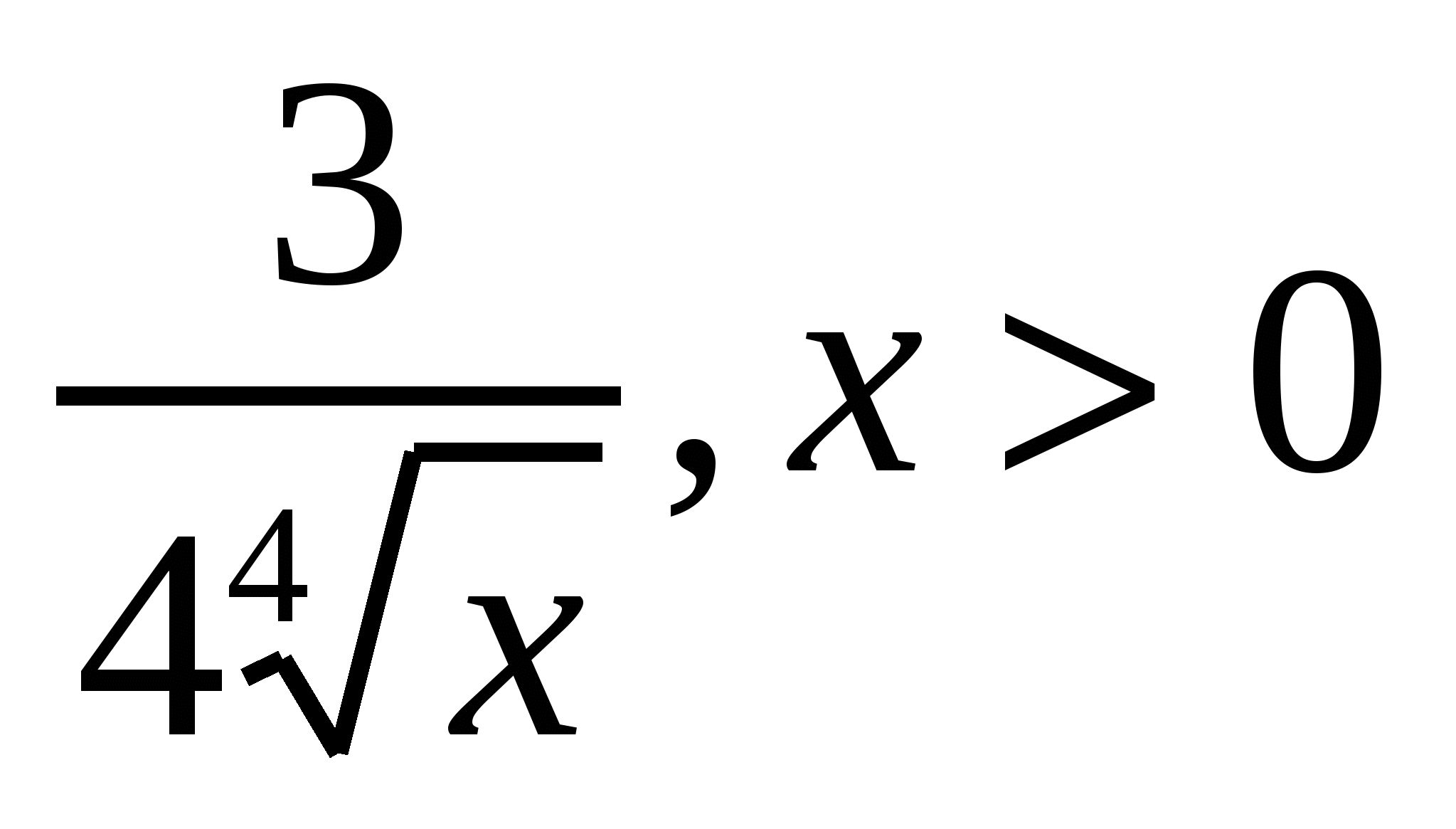
Задание 13
Точка движется по закону 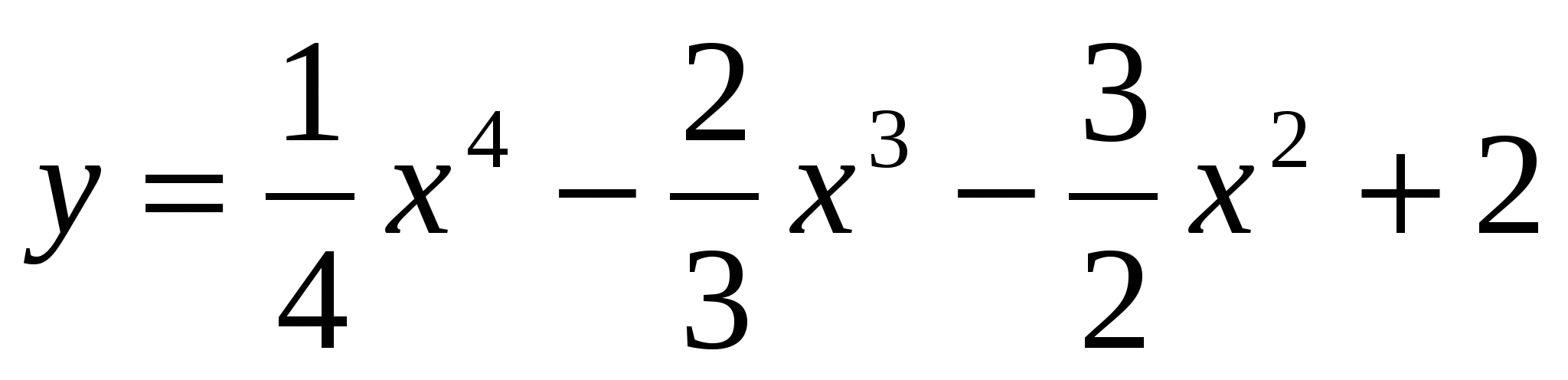 , где х - время, у - путь точки. Найти скорость ускорения точки, экстремумы данной функции.
, где х - время, у - путь точки. Найти скорость ускорения точки, экстремумы данной функции.
Решение 1. Областью существования функции является интервал 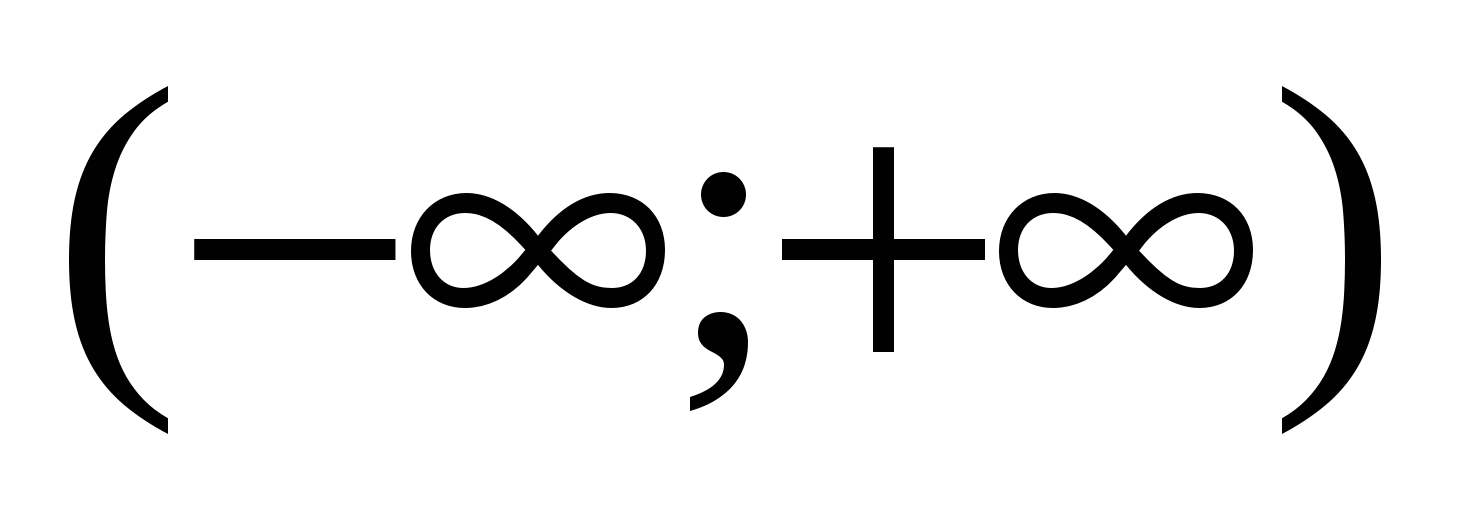 .Находим
.Находим  скорость, точка:
скорость, точка: 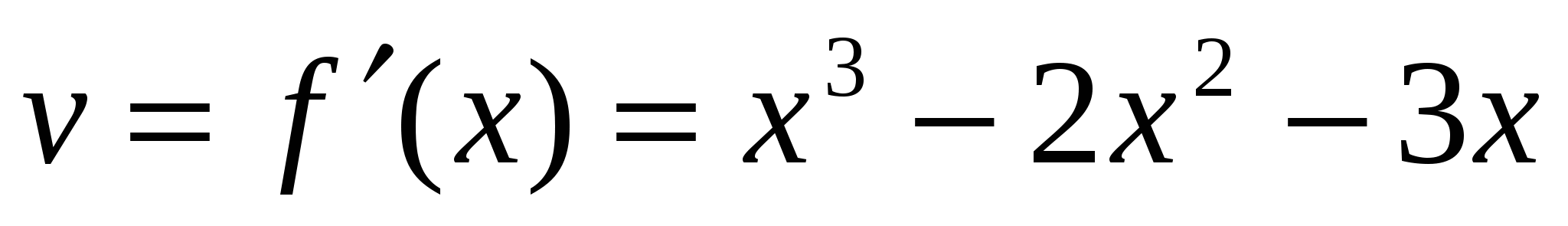 .Решаем уравнение
.Решаем уравнение 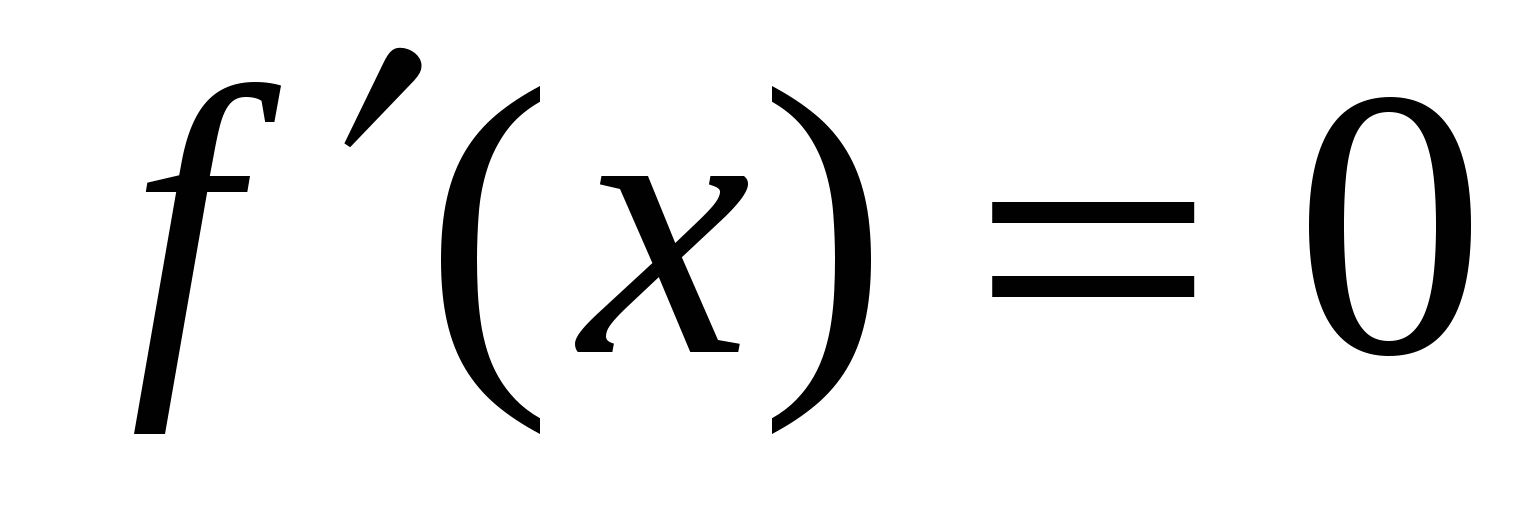 или
или 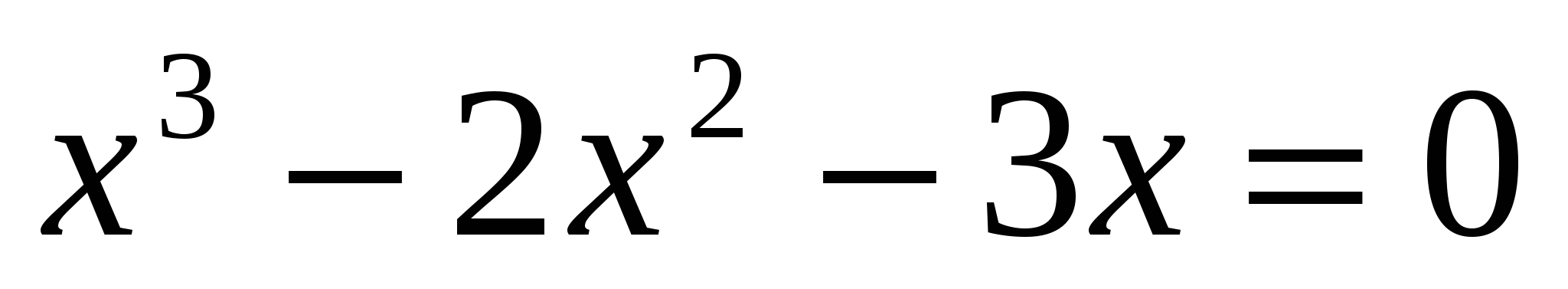 . Разлагаем левую часть на множители:
. Разлагаем левую часть на множители: 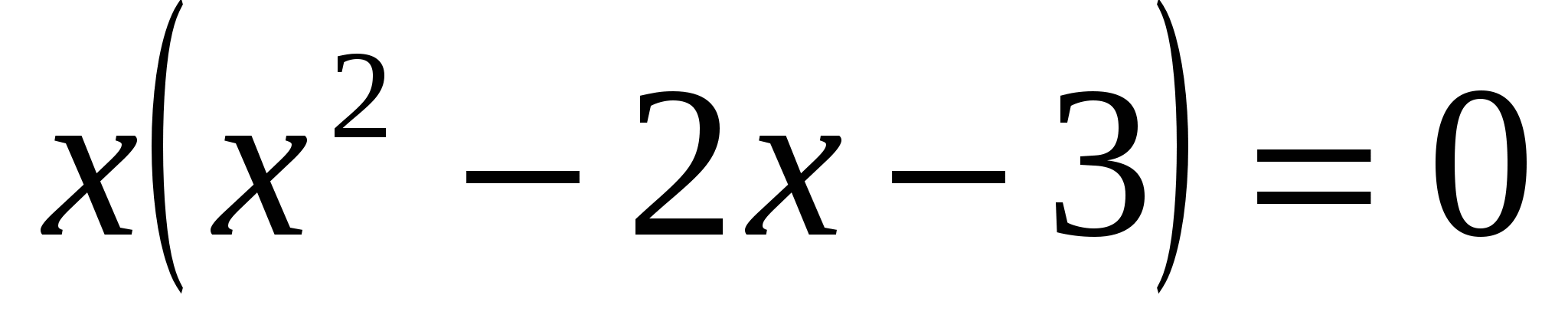 откуда
откуда  или
или 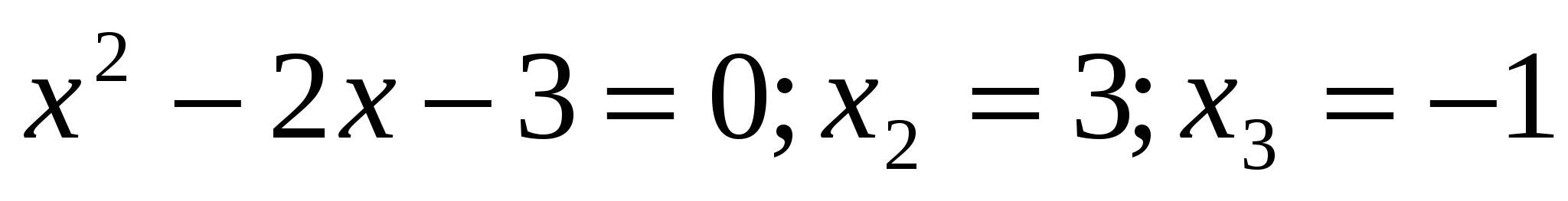 .Производная непрерывна при любом ч. Поэтому только эти точки будут критическими. Располагаем критические точка в порядке возрастания их абсцисс:-1;0;3. Рассмотрим интервалы
.Производная непрерывна при любом ч. Поэтому только эти точки будут критическими. Располагаем критические точка в порядке возрастания их абсцисс:-1;0;3. Рассмотрим интервалы 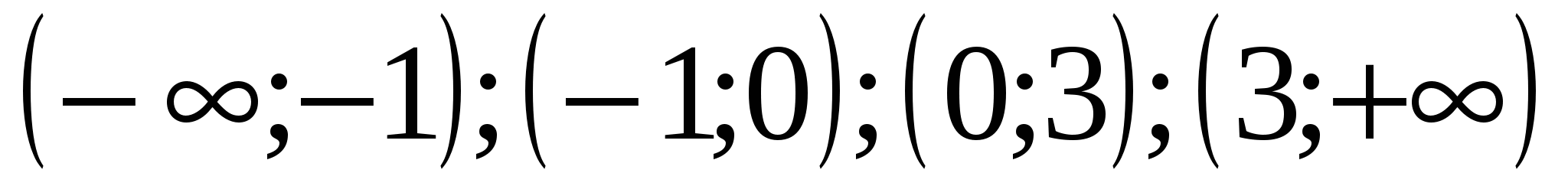 . Выберем внутри каждого их этих интервалов произвольную точку и определим этой точке знак первой производной. В интервале
. Выберем внутри каждого их этих интервалов произвольную точку и определим этой точке знак первой производной. В интервале 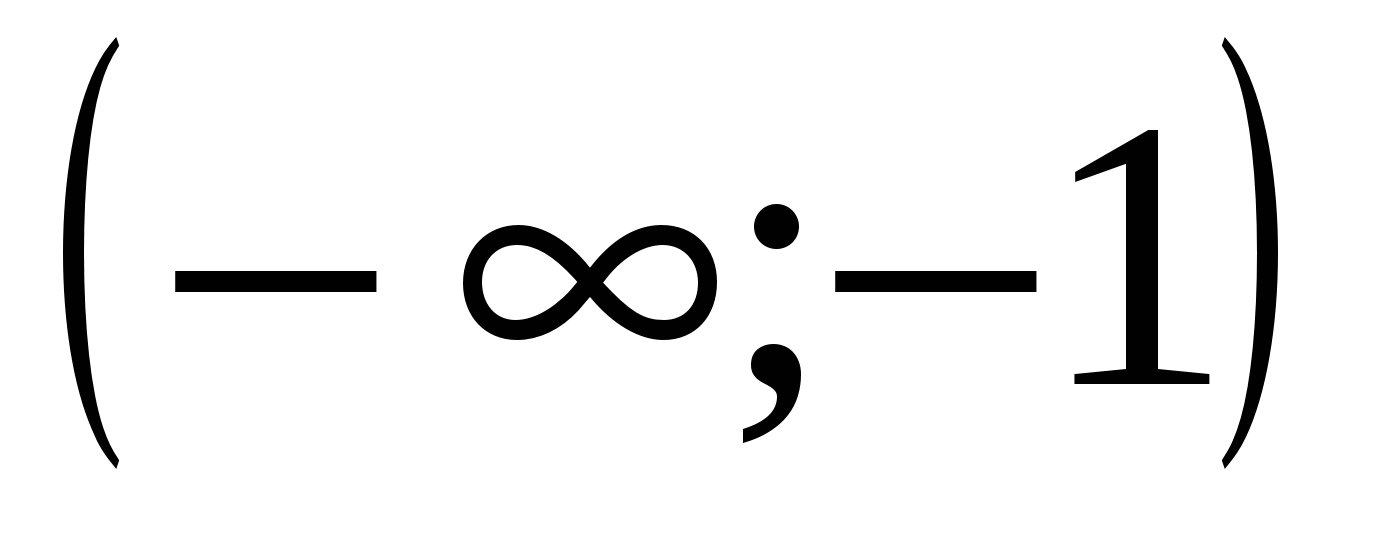 возьмем, например точку х=-2 и найдем
возьмем, например точку х=-2 и найдем 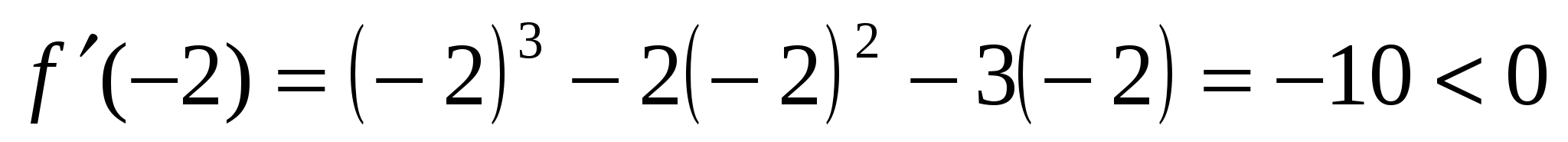 . В интервале
. В интервале 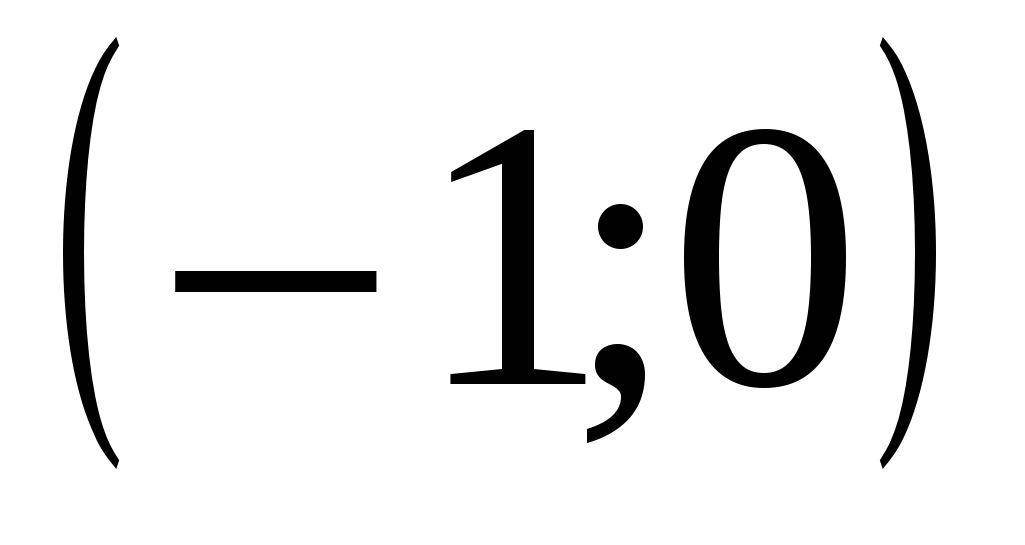 возьмем точку
возьмем точку 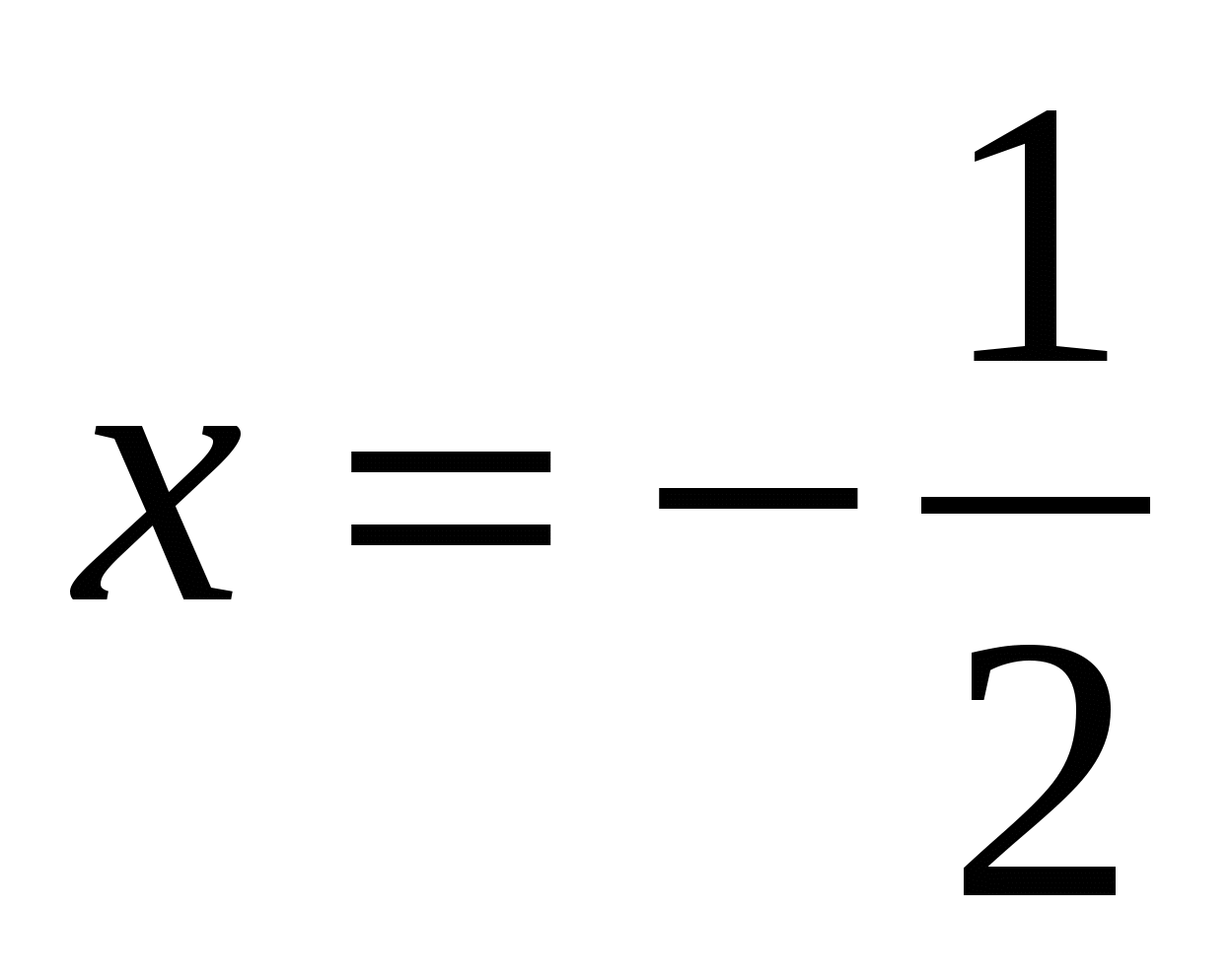 , тогда
, тогда 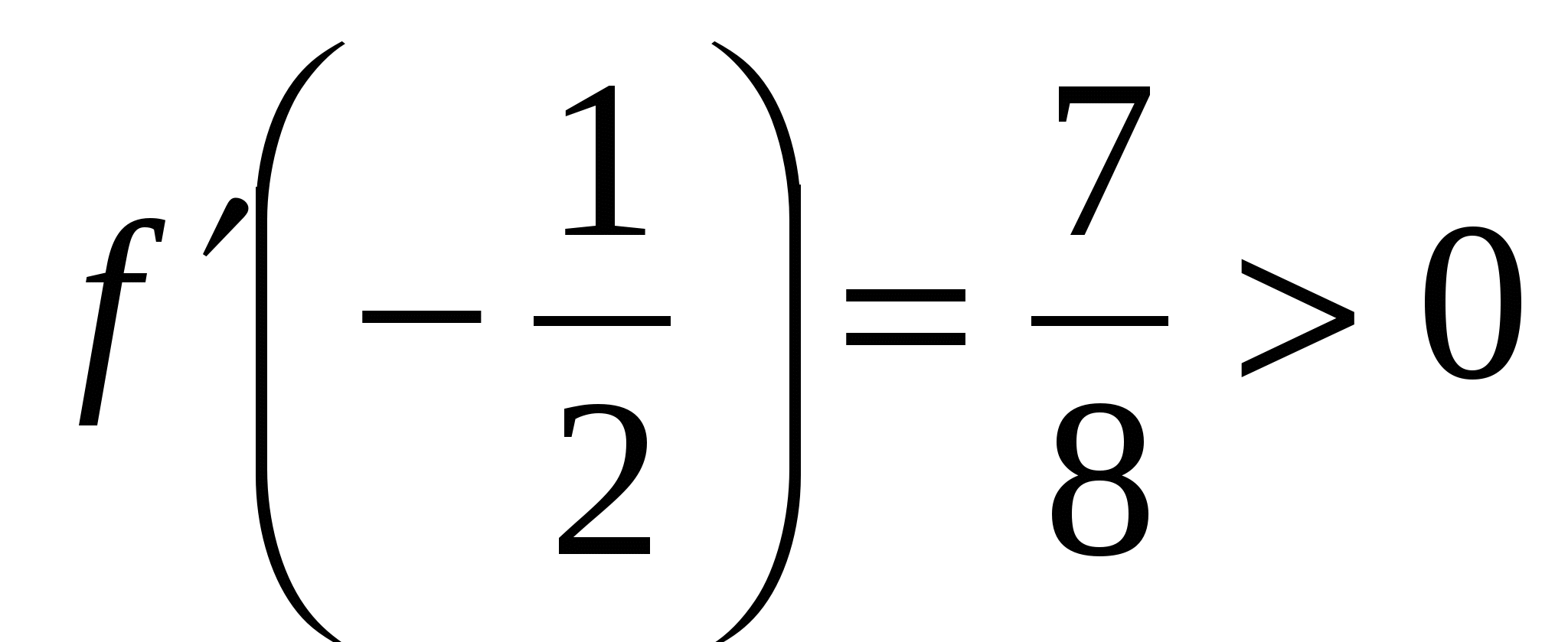 ; в интервале
; в интервале 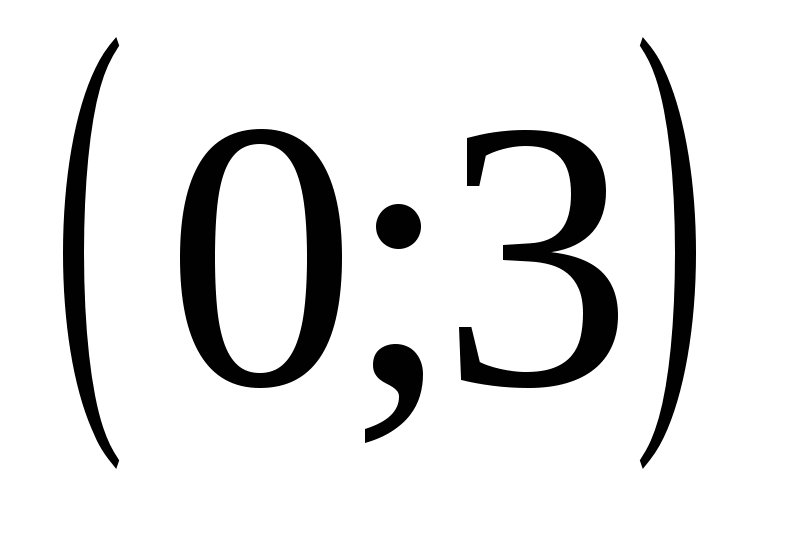 возьмем точку х=1,тогда
возьмем точку х=1,тогда ![]() .В интервале
.В интервале 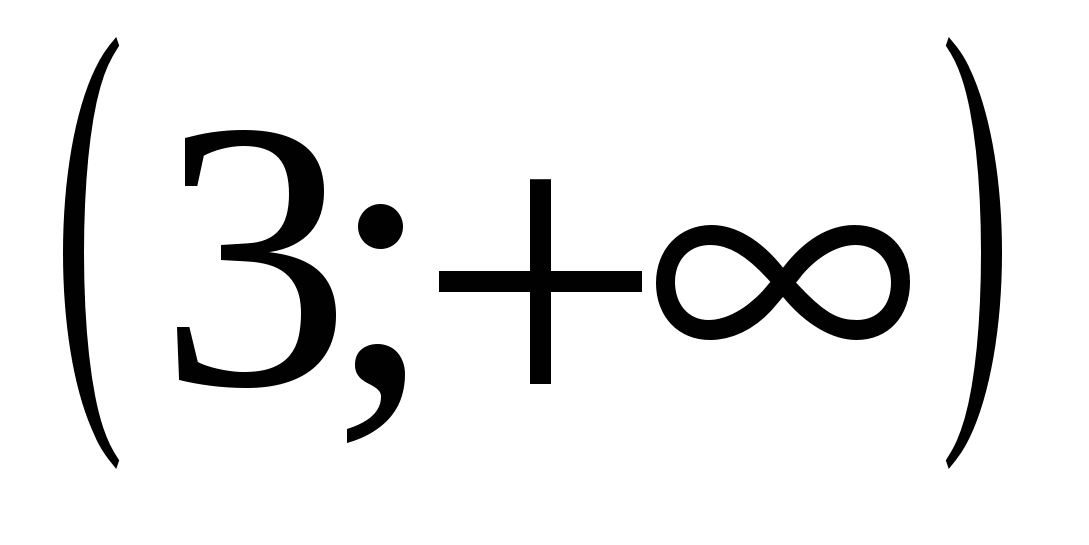 возьмем точку х=4 и получим
возьмем точку х=4 и получим 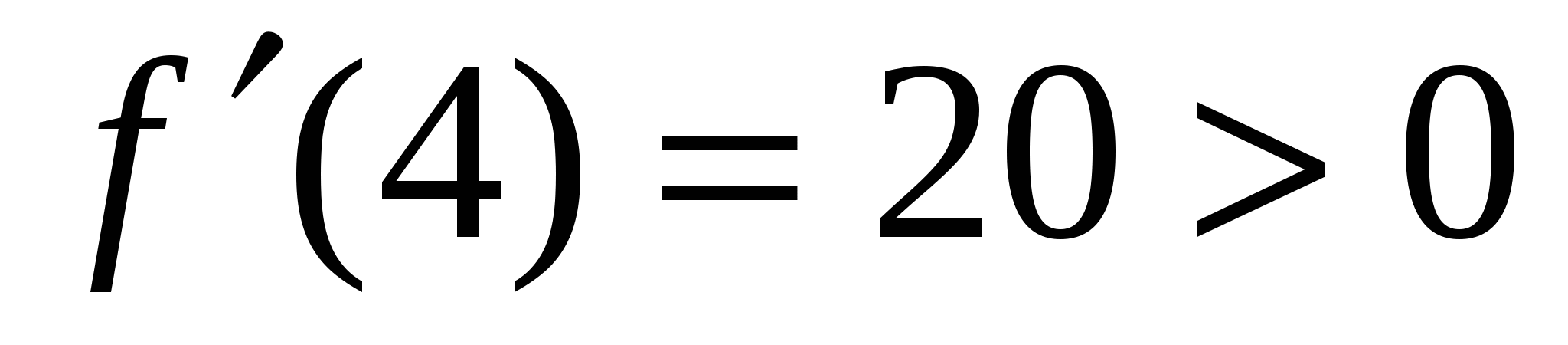 .Строим таблицу поведения функции, находим max и min.
.Строим таблицу поведения функции, находим max и min.
x
![]()
-1
![]()
0
![]()
3
![]()
y'
-
0
+
0
-
0
+
y
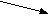
min
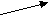
max
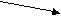
min
Найдем экстремальные значения функции 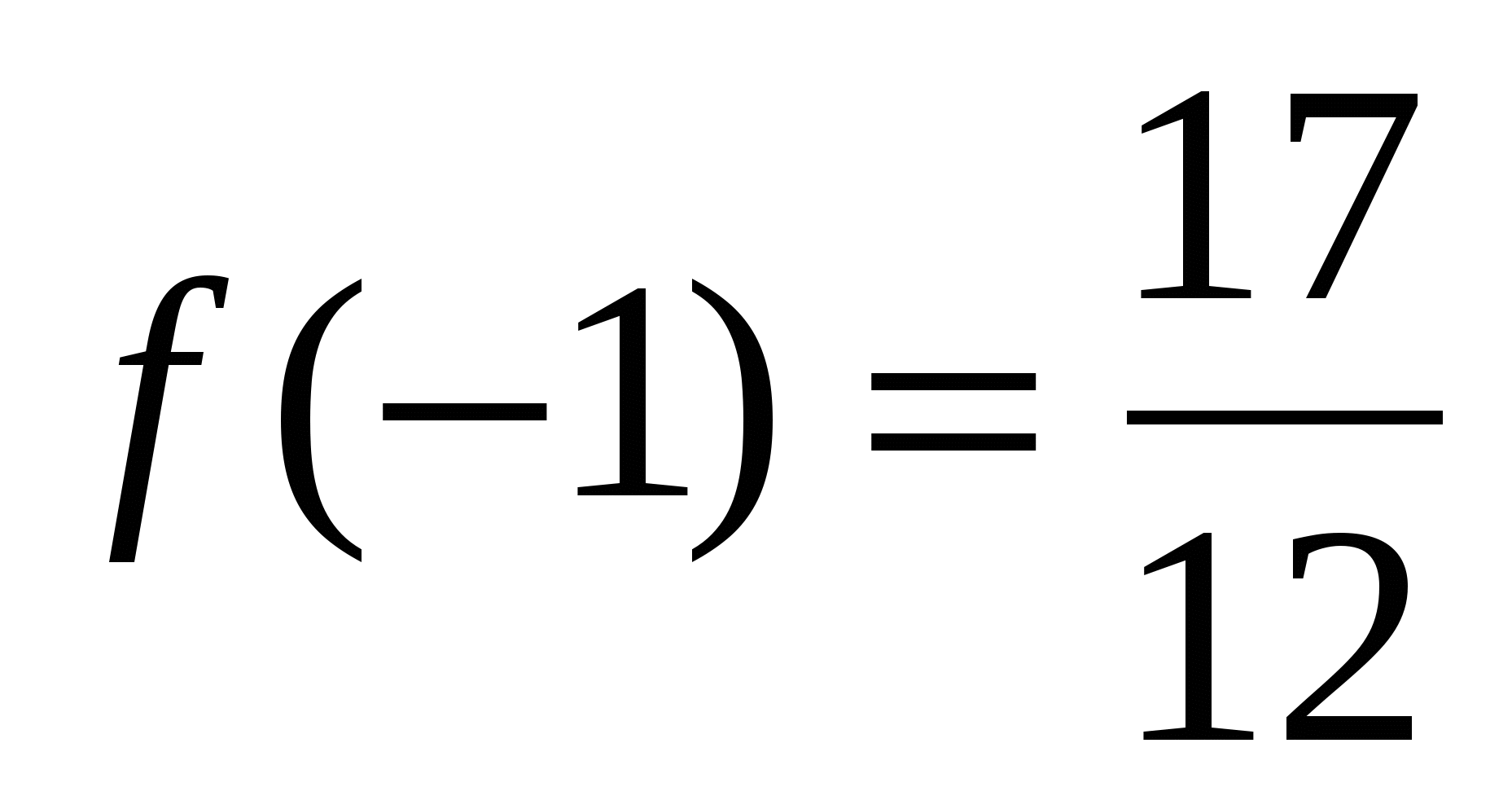 ;
; 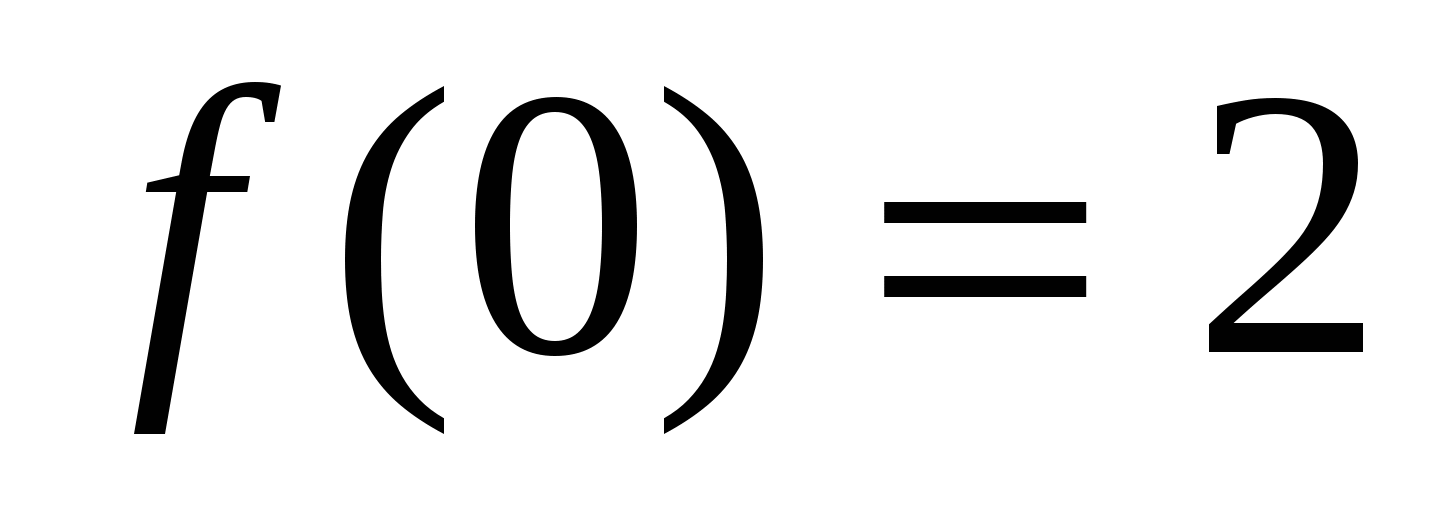 ;
; 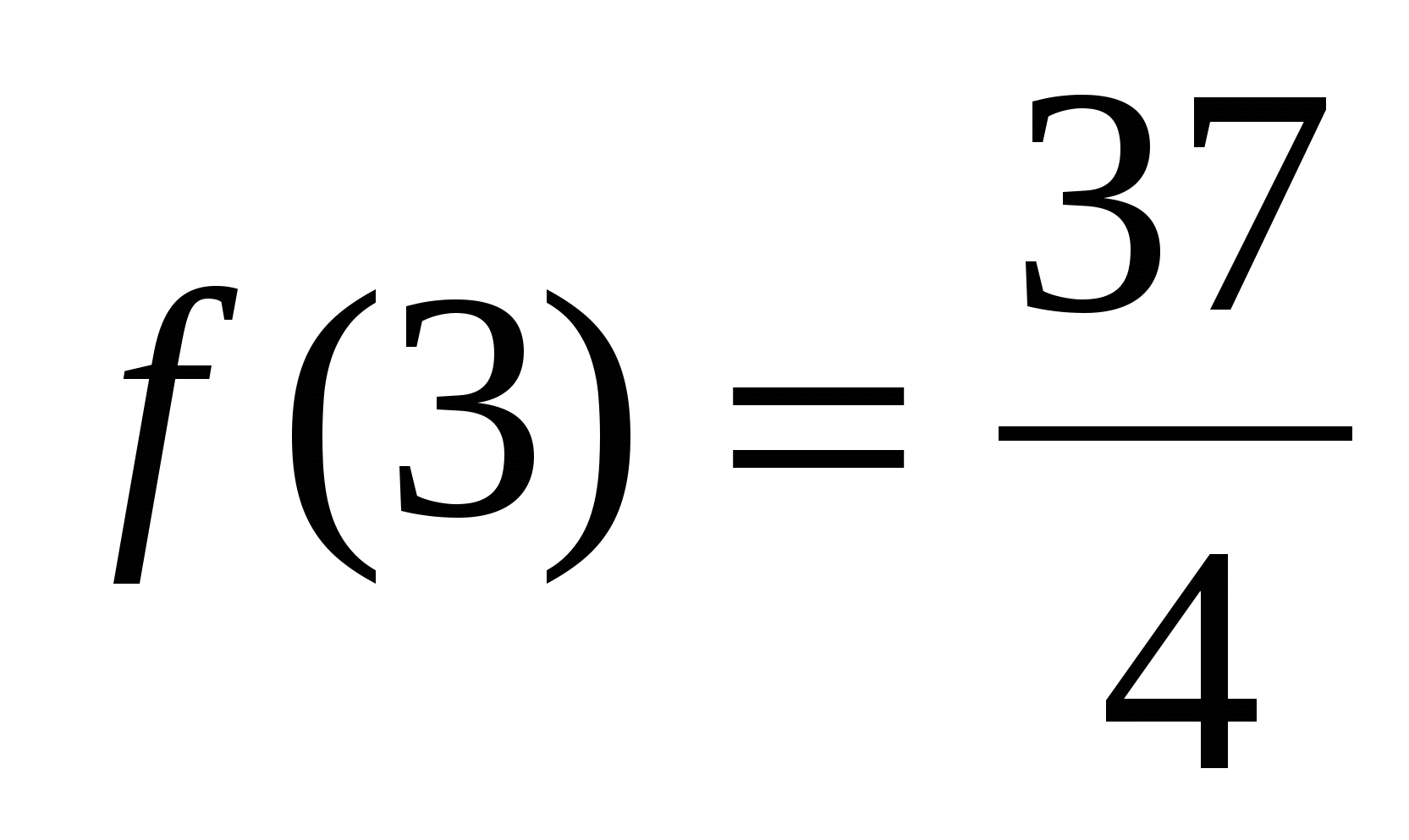 . Ускорение точки:
. Ускорение точки:
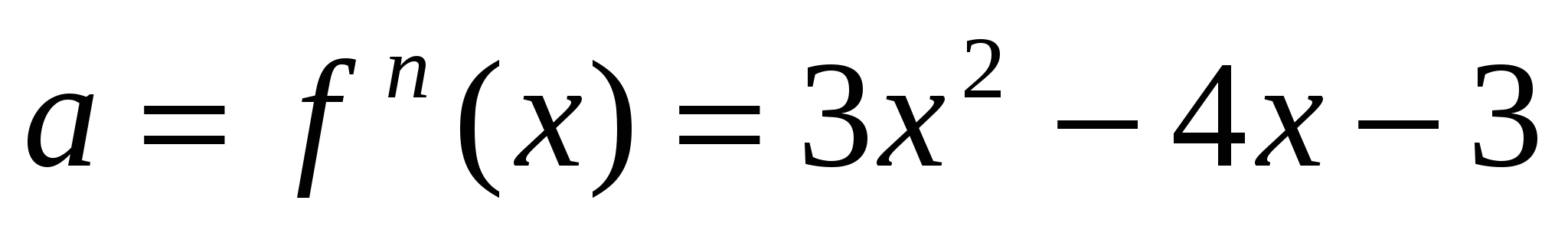 .
.
Ответ: ![]() ;2;
;2; 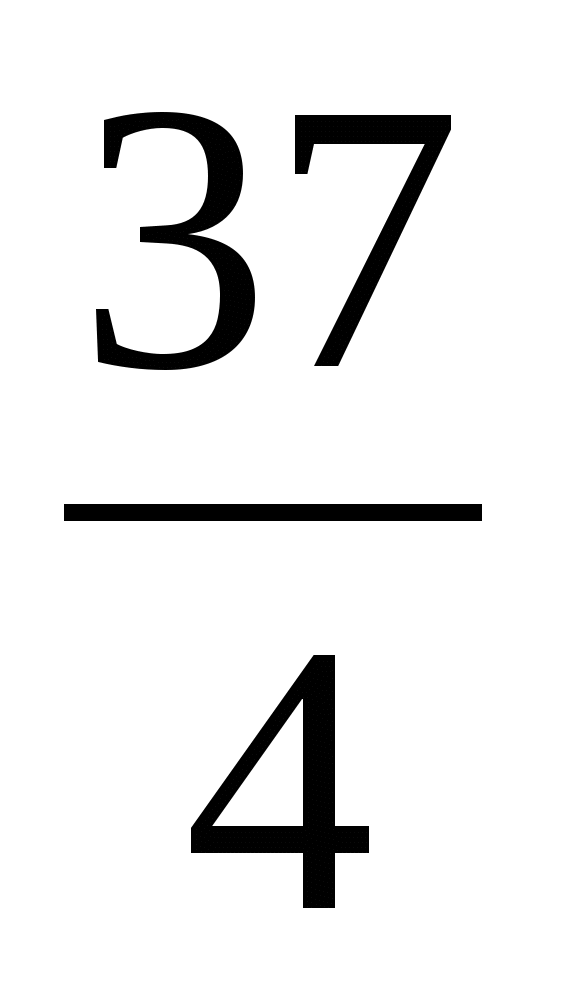 .
.
Решение 2. Исследуем функцию на экстремум по второй производной 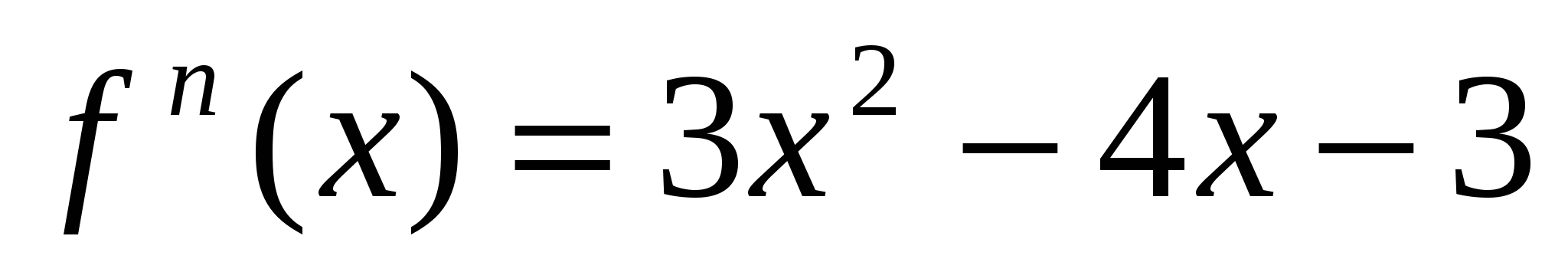 .Определяем знак второй производной в каждой критической точке.
.Определяем знак второй производной в каждой критической точке. 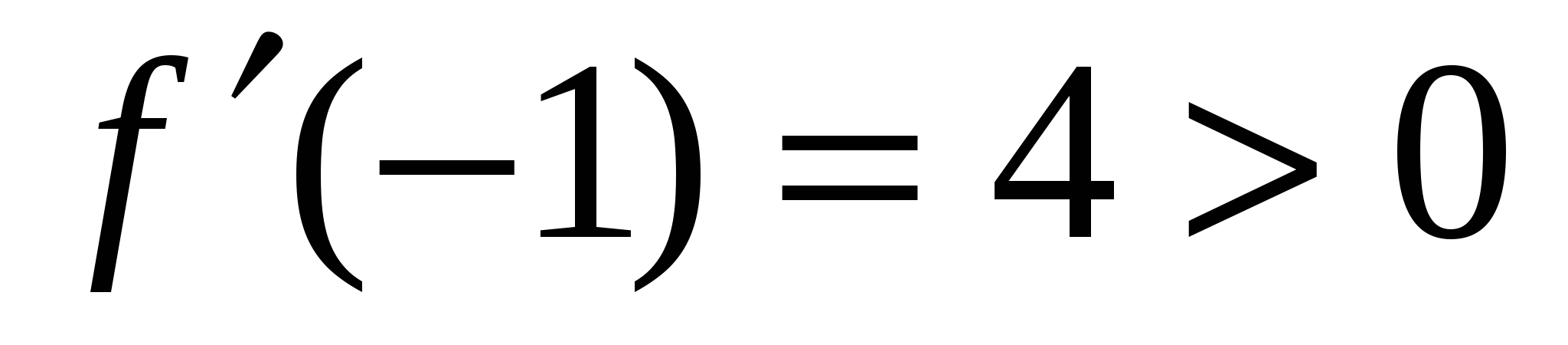 ,при х=-1 функция имеет минимум
,при х=-1 функция имеет минимум 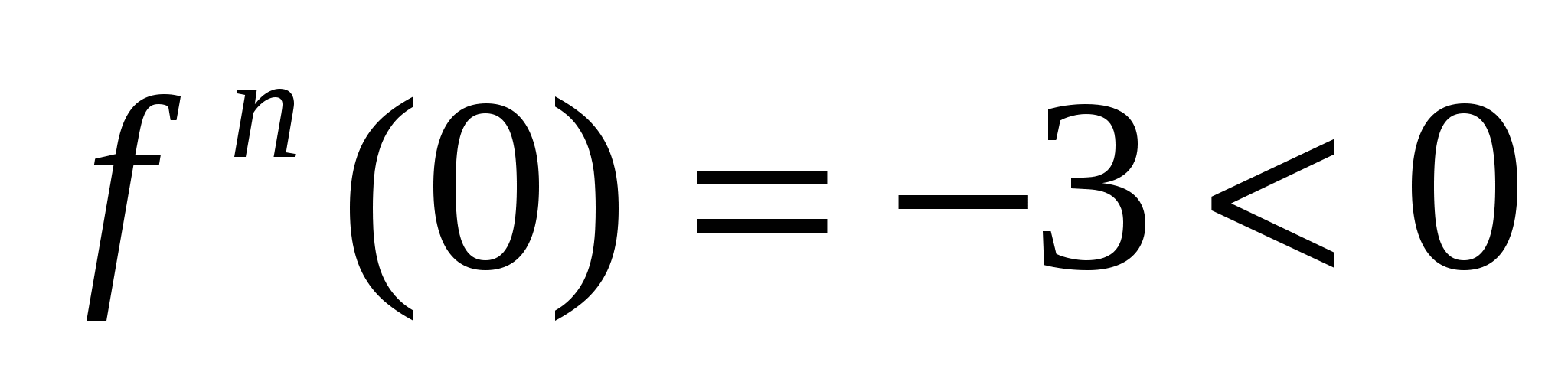 ,при х=0 функция имеет максимум;
,при х=0 функция имеет максимум; 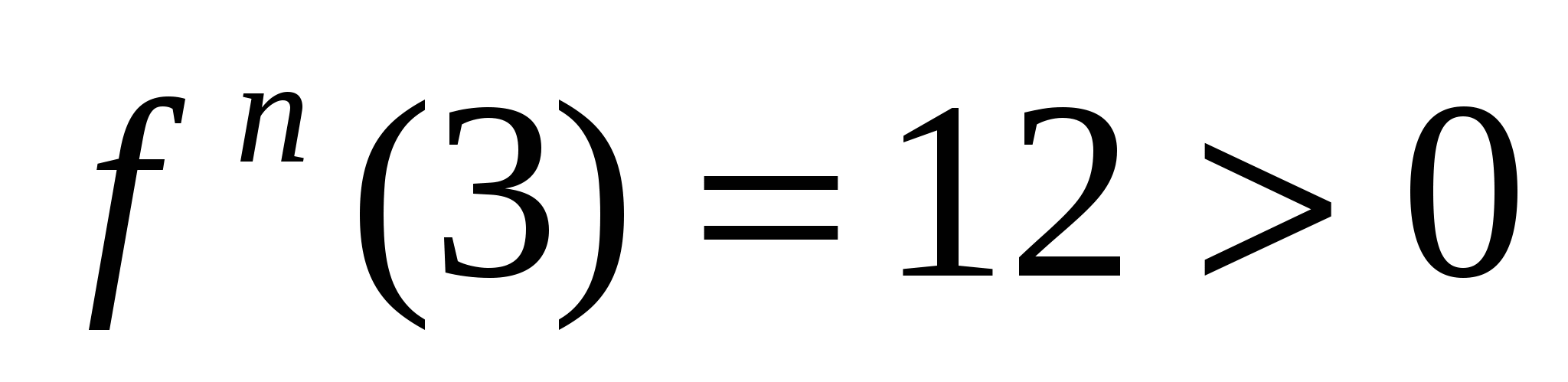 ,при х=3 функция имеет минимум и т.д. как в решении1.Исследования по второму решению проще, однако, от исследования функции на экстремум по первому решению отказываться не следует, т.к. может оказаться, что в критической точке вторая производная окажется равной нулю, а в этом случае нельзя сделать никакого заключения о наличии экстремума.
,при х=3 функция имеет минимум и т.д. как в решении1.Исследования по второму решению проще, однако, от исследования функции на экстремум по первому решению отказываться не следует, т.к. может оказаться, что в критической точке вторая производная окажется равной нулю, а в этом случае нельзя сделать никакого заключения о наличии экстремума.
Ответ: ![]() ;2;
;2; 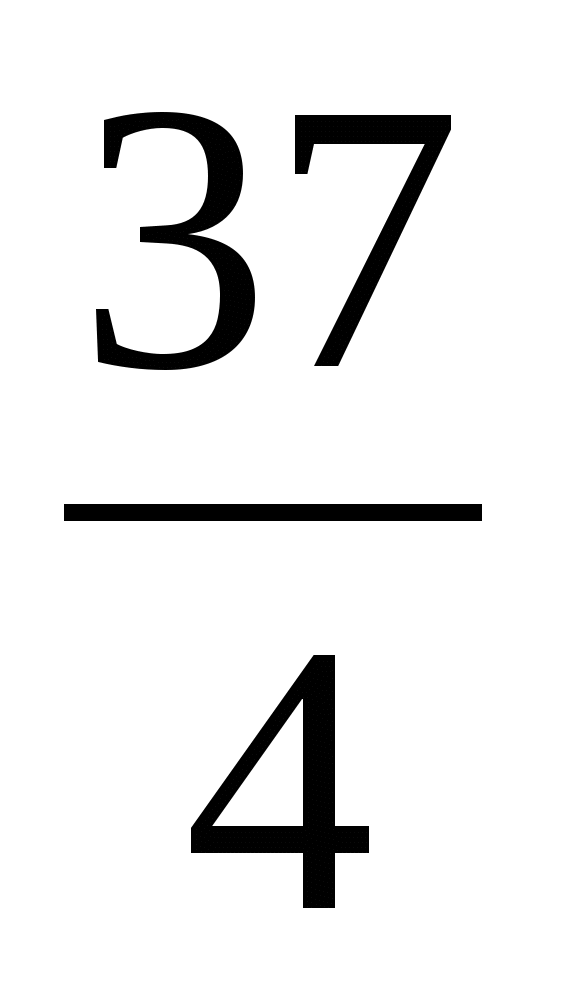 .
.
Задание 14
Определить экстремумы функции 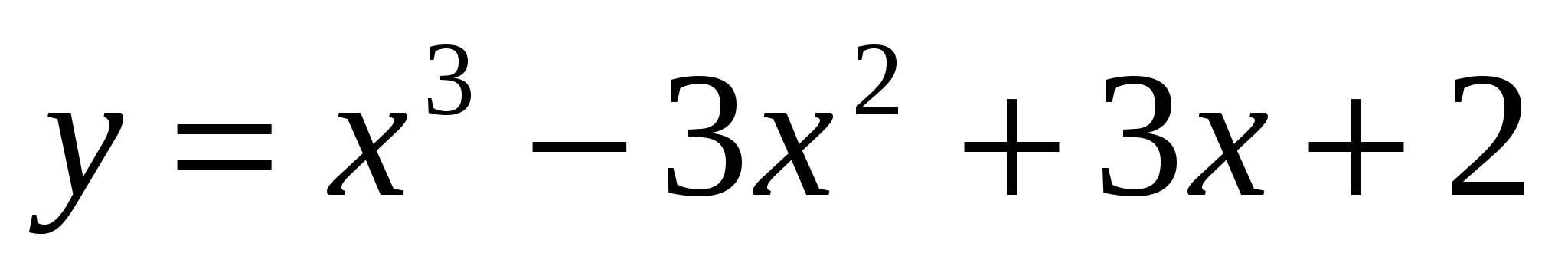 .Найти ее наименьшее и наибольшее значение на отрезке
.Найти ее наименьшее и наибольшее значение на отрезке 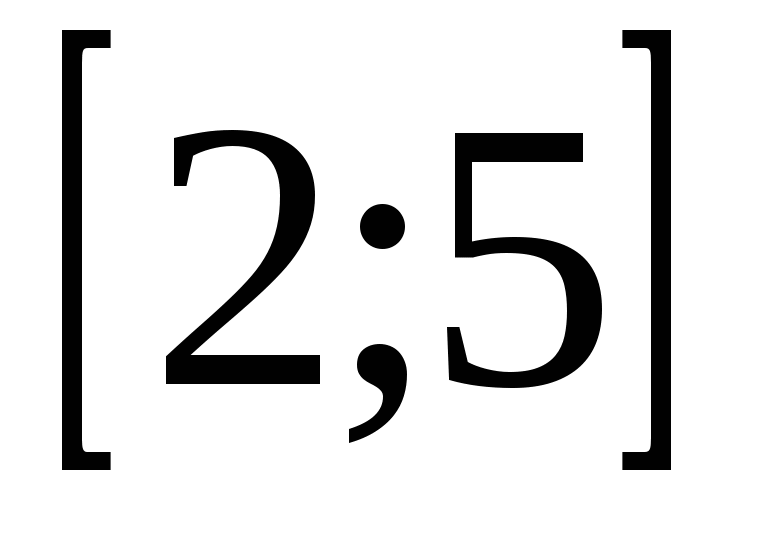 .
.
Решение 1
Областью существования функции является интервал 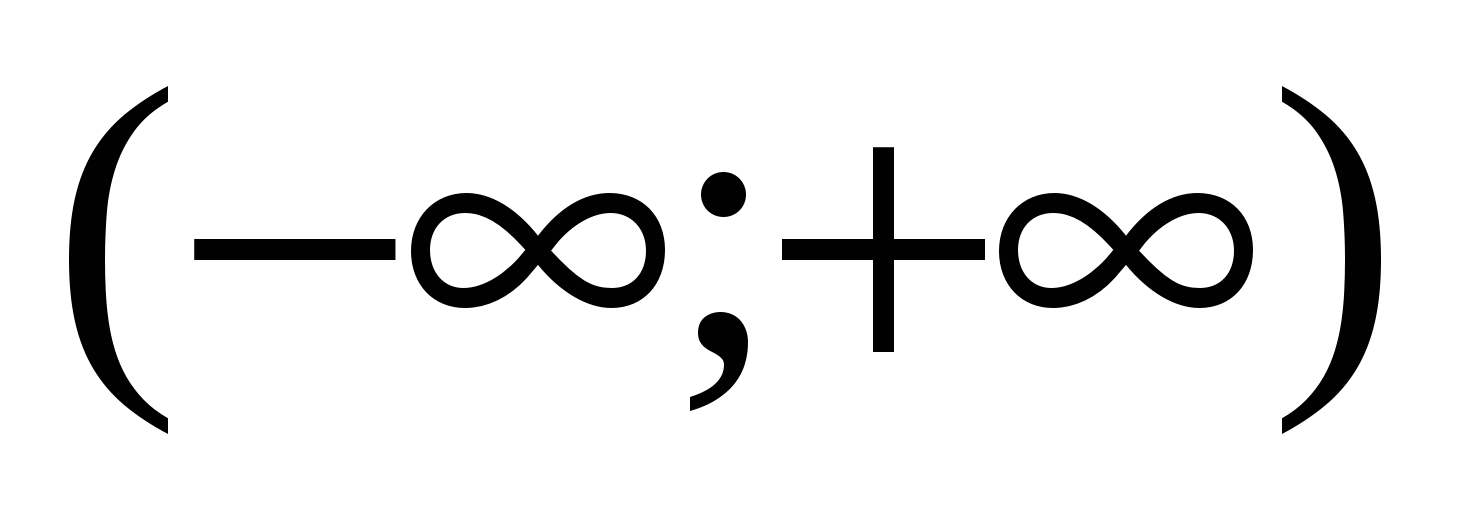 . Находим первую производную функции ее критические точка
. Находим первую производную функции ее критические точка 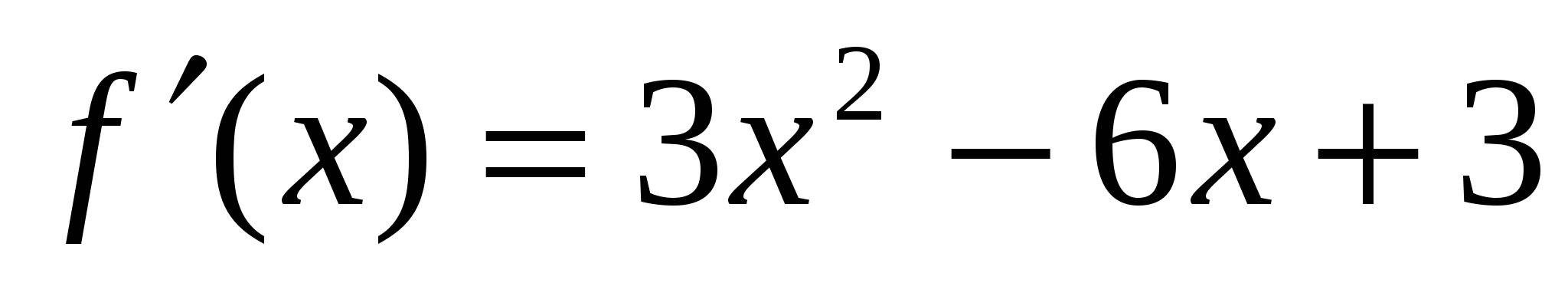 . Решим уравнение
. Решим уравнение 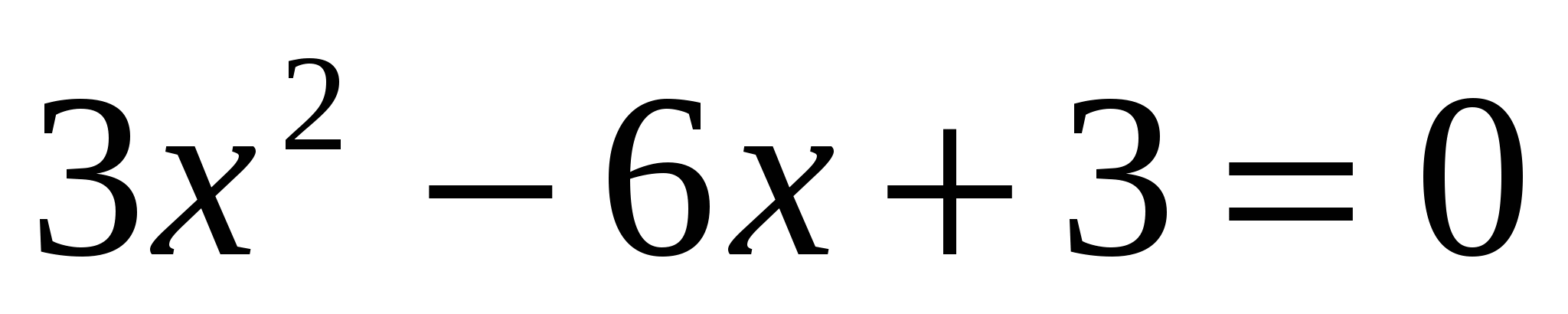 ,
, 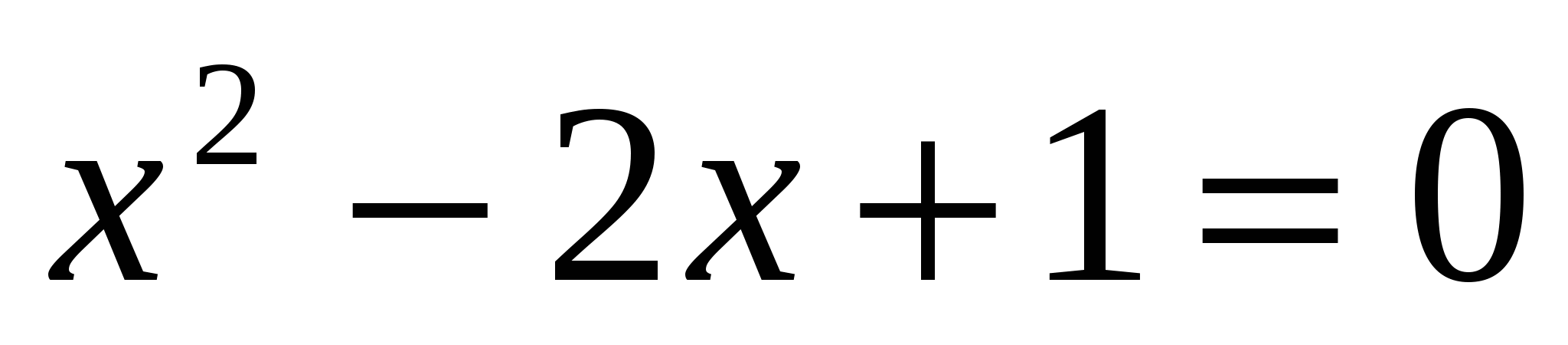 .
. 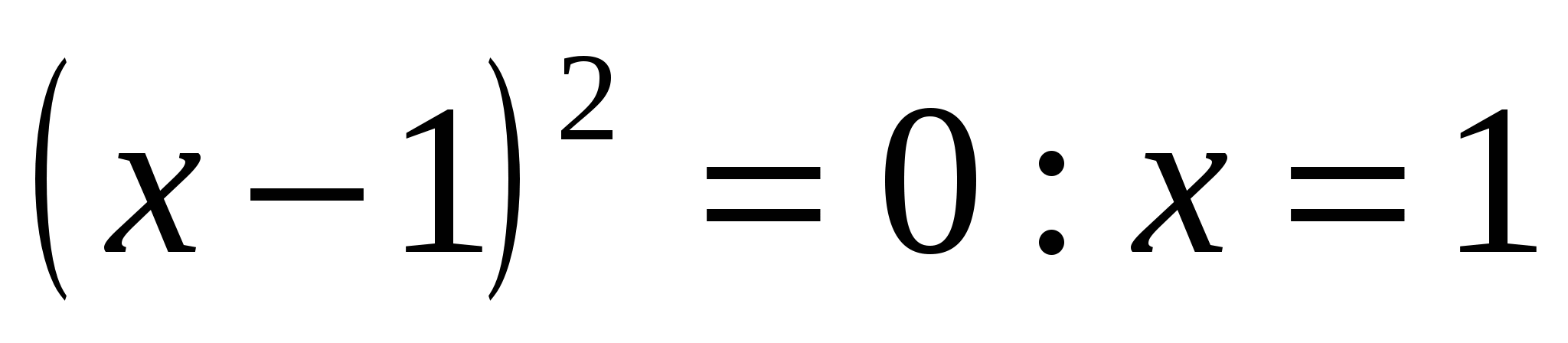 .Производная конечна при любом значении ч, поэтому ч=1 является единственной критической точкой. Рассмотрим интервалы
.Производная конечна при любом значении ч, поэтому ч=1 является единственной критической точкой. Рассмотрим интервалы 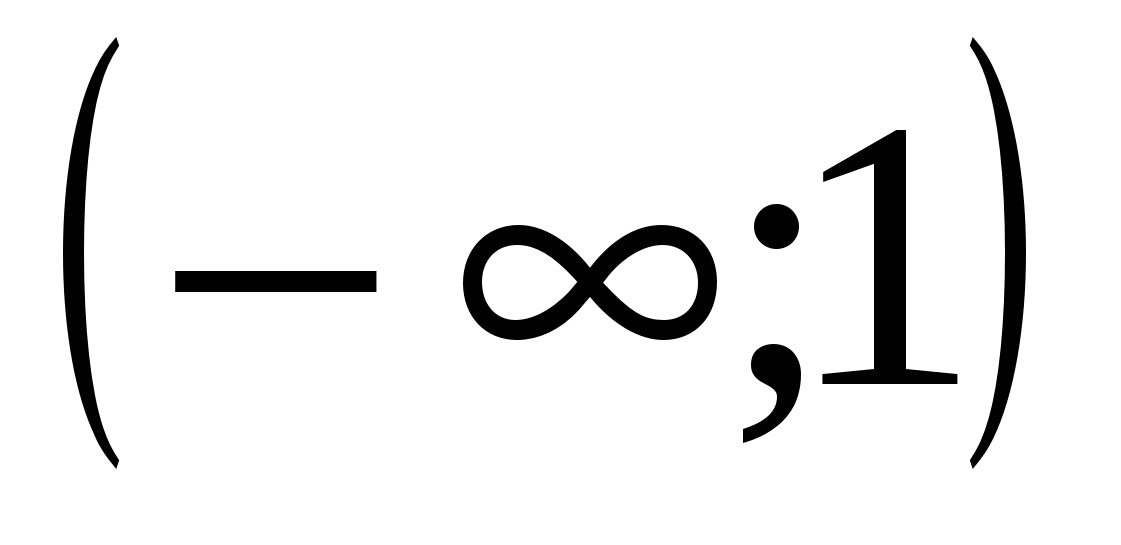 и
и 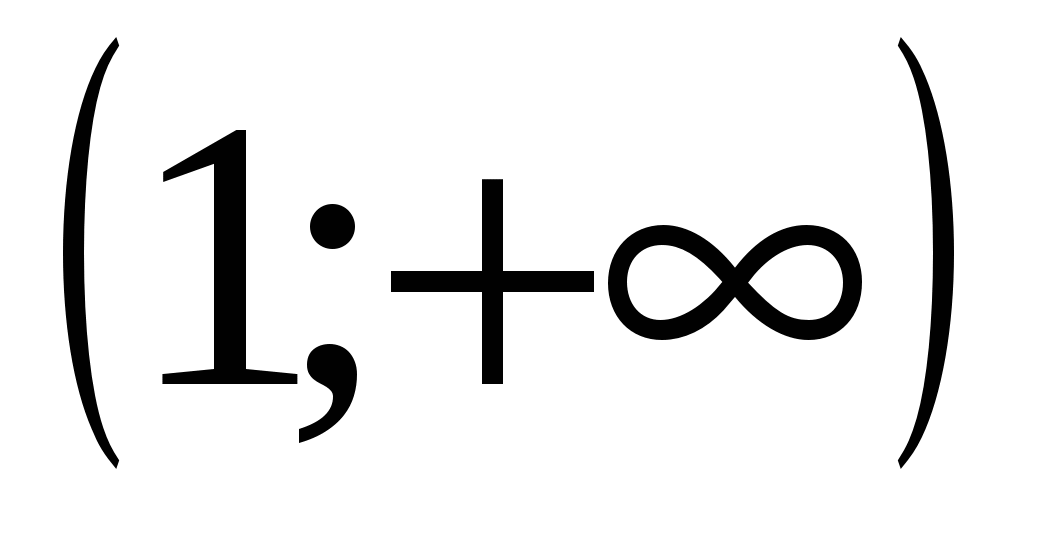 .Внутри каждого из этих интервалом выберем произвольную точку и определим в ней знак первой производной ,например, в первом интервале возьмем точку х=0, во втором, х=2.
.Внутри каждого из этих интервалом выберем произвольную точку и определим в ней знак первой производной ,например, в первом интервале возьмем точку х=0, во втором, х=2. 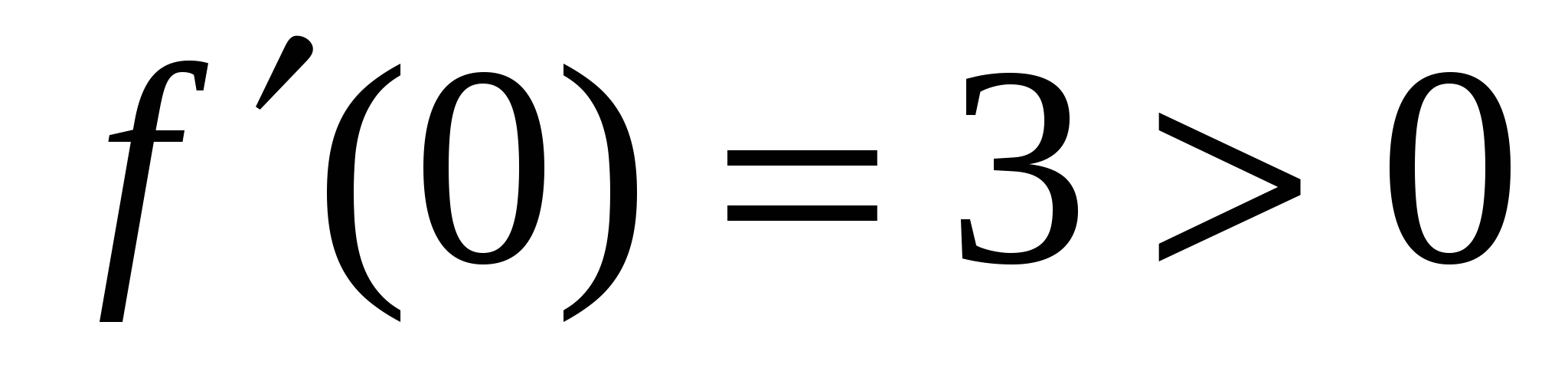 ;
; 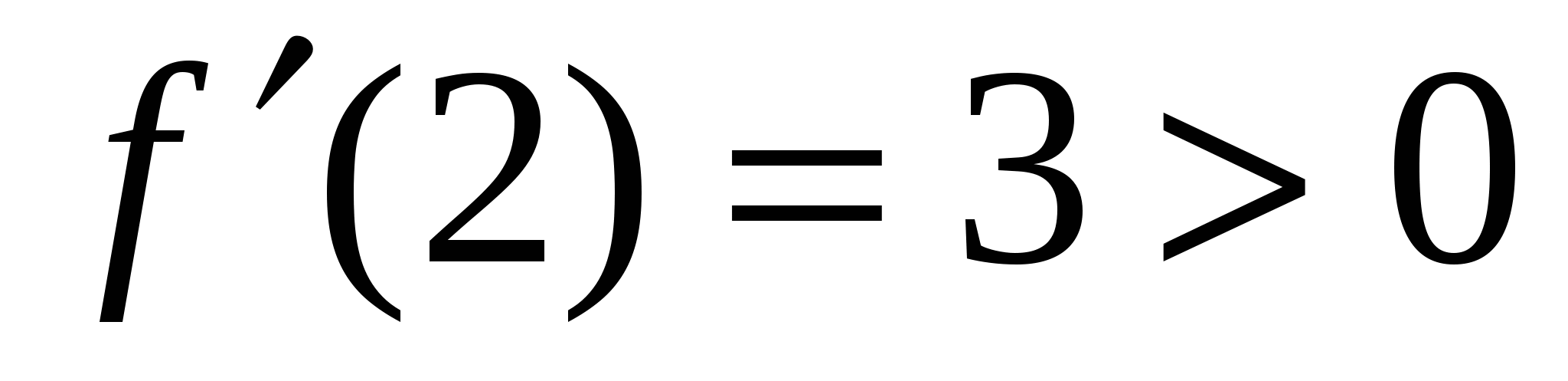 ,т.е. при переходе через критическую точку первая производная знака не поменяла, поэтому в точке х=1 экстремума нет. По второй производной такое исследование провести нельзя. Действительно,
,т.е. при переходе через критическую точку первая производная знака не поменяла, поэтому в точке х=1 экстремума нет. По второй производной такое исследование провести нельзя. Действительно, 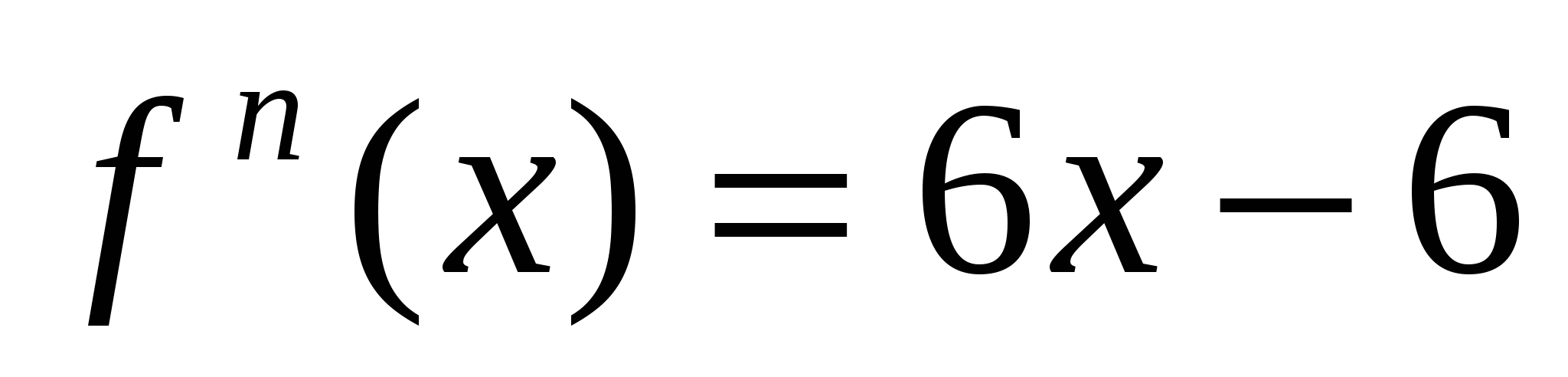 ,и в критической точке х=1 имеем
,и в критической точке х=1 имеем 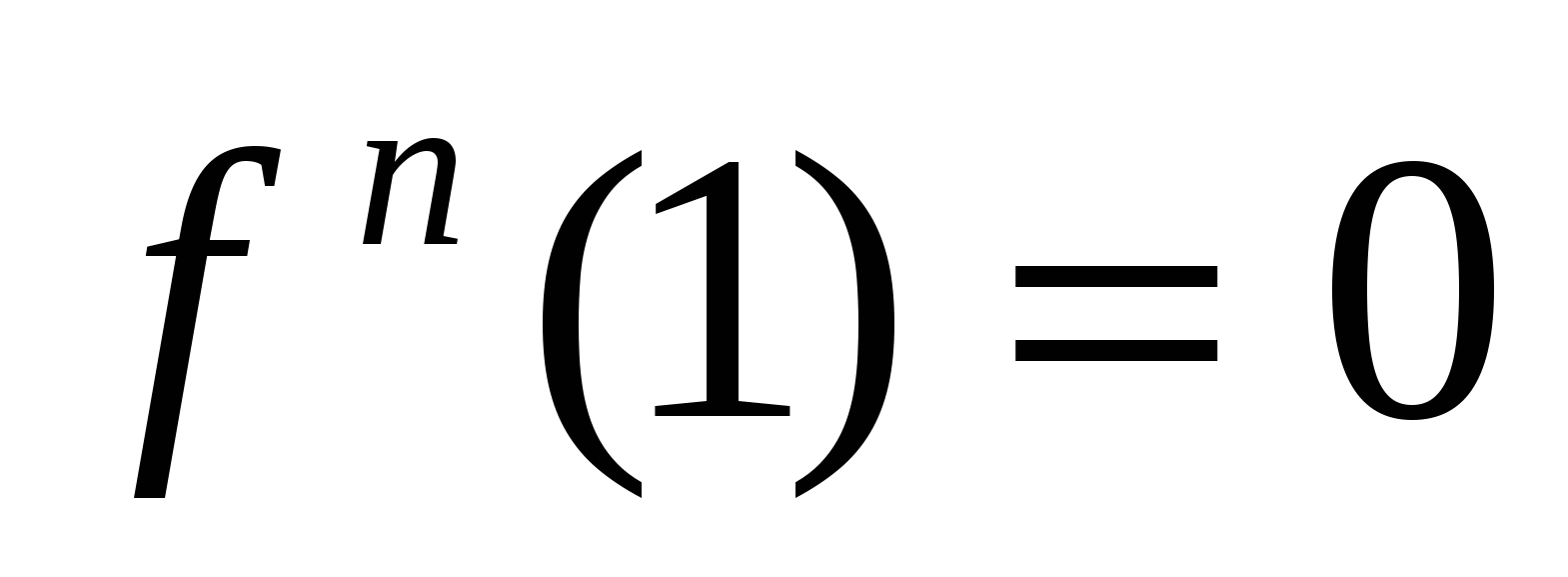 .Поскольку отрезок
.Поскольку отрезок 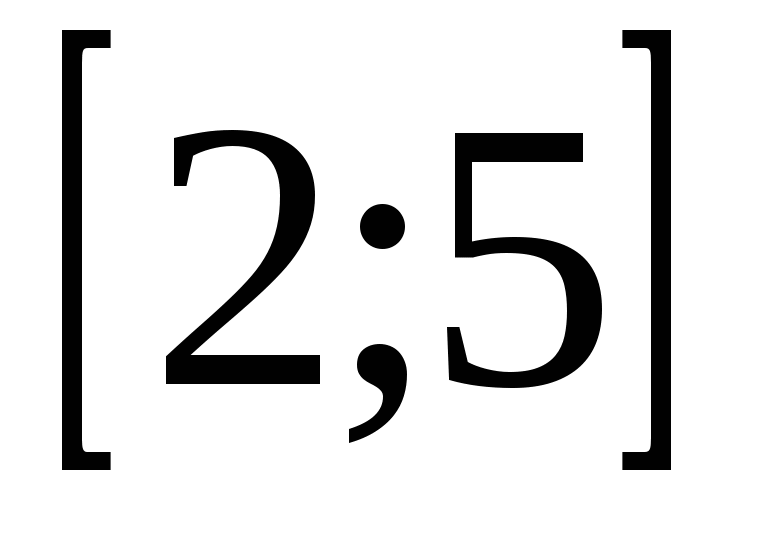 не содержит критической точки, то для определения наименьшего и наибольшего значения функции на этом отрезке следует определить только значения ее на концах отрезка:
не содержит критической точки, то для определения наименьшего и наибольшего значения функции на этом отрезке следует определить только значения ее на концах отрезка: 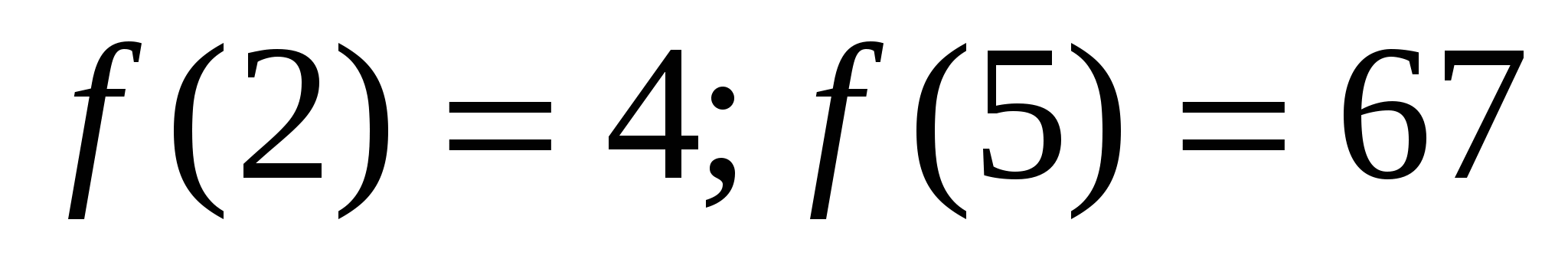 . Наименьшего значения на отрезке
. Наименьшего значения на отрезке 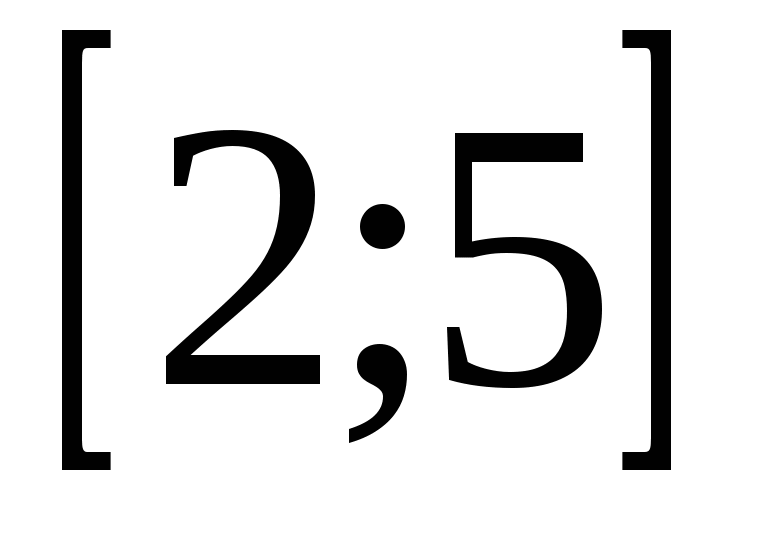 функция достигает на левом конце при х=2 и это наименьшее значение
функция достигает на левом конце при х=2 и это наименьшее значение 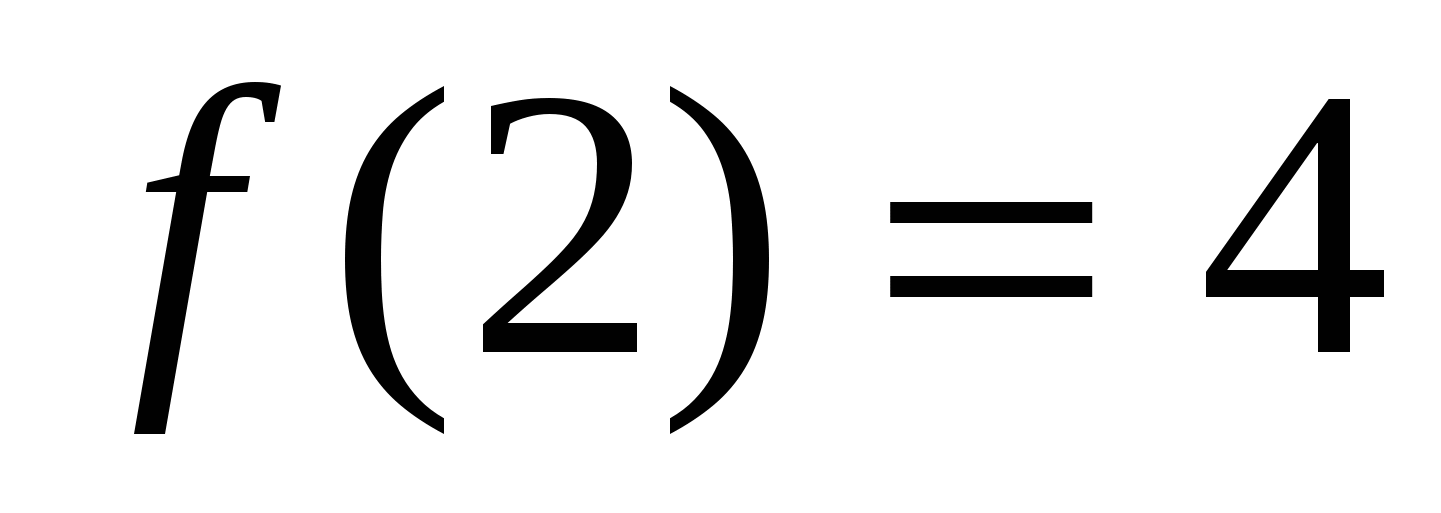 . Наибольшего значения функция достигает при х=5-на правом конце отрезка; это значение
. Наибольшего значения функция достигает при х=5-на правом конце отрезка; это значение 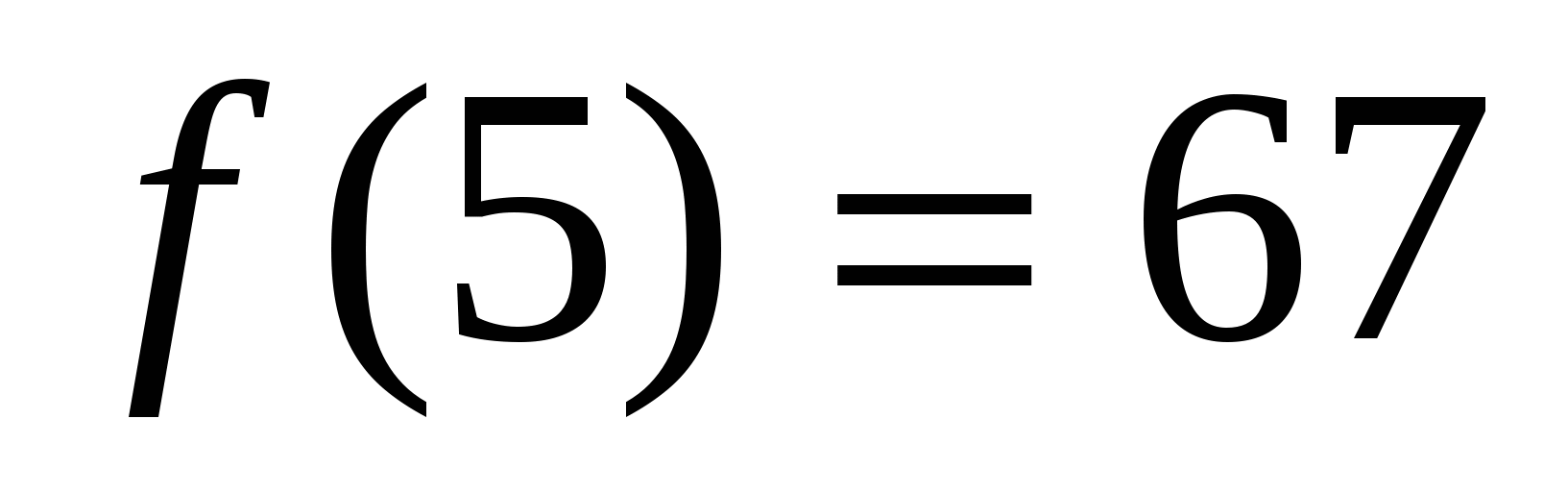 .
.
Ответ: 4;67.
Решение 2
Первую производную 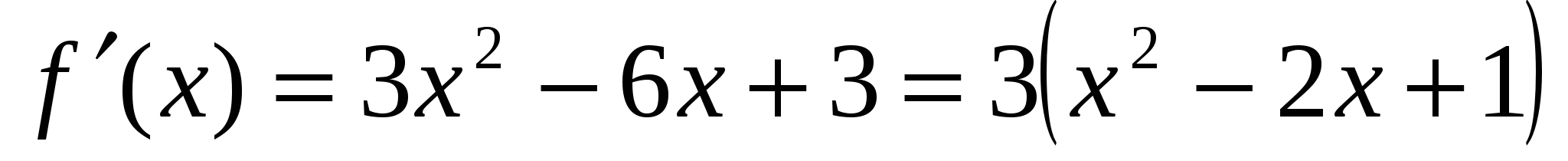 можно записать в виде
можно записать в виде ![]() ,поэтому можно сказу заключить, что в поле действительных чисел она положительна при любом значении
,поэтому можно сказу заключить, что в поле действительных чисел она положительна при любом значении 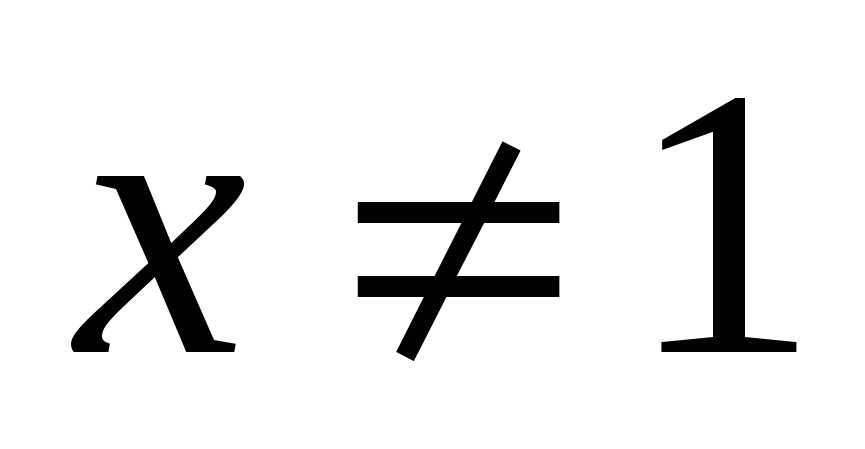 ,поэтому рассматриваемая функция возрастает на всем интервале
,поэтому рассматриваемая функция возрастает на всем интервале 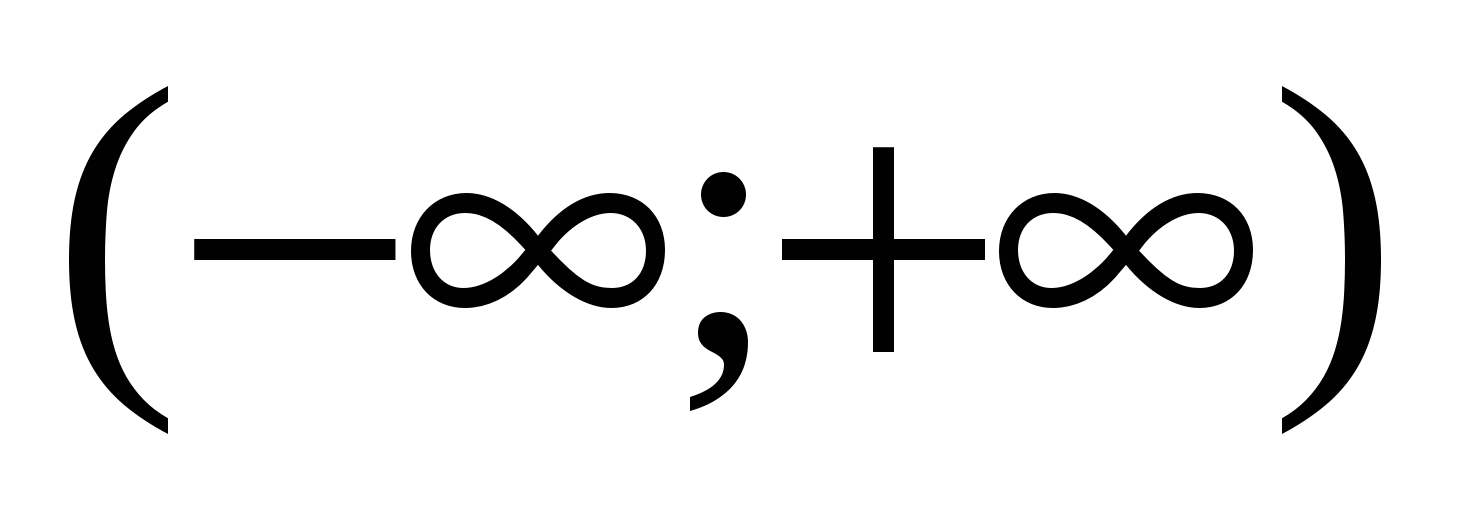 ,и т.д. как в решении 1. Ответ: 4;67
,и т.д. как в решении 1. Ответ: 4;67
Задание 15
Найти одну из первообразных для функции 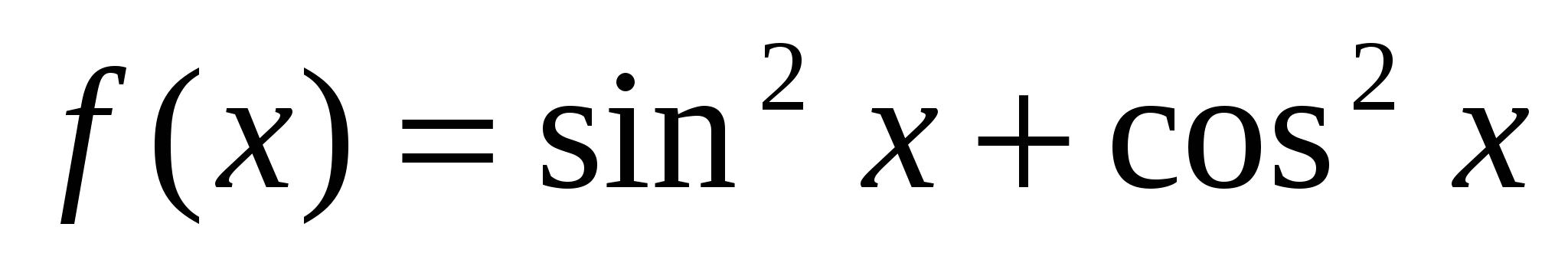 на R.
на R.
Решение 1. имеем: 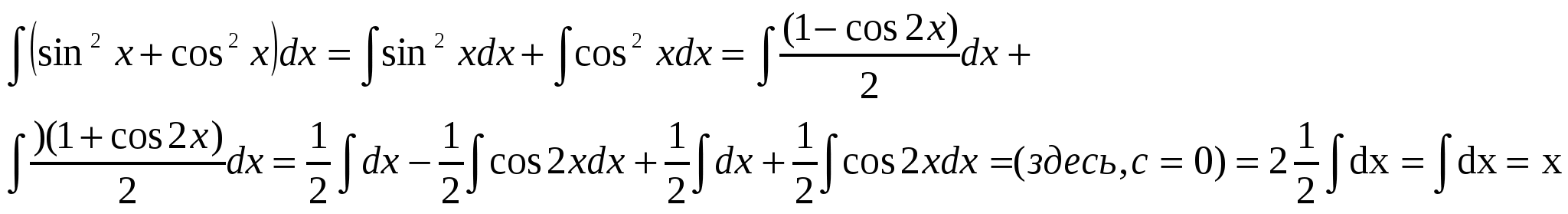
Ответ: х
Решение 2.Имеем 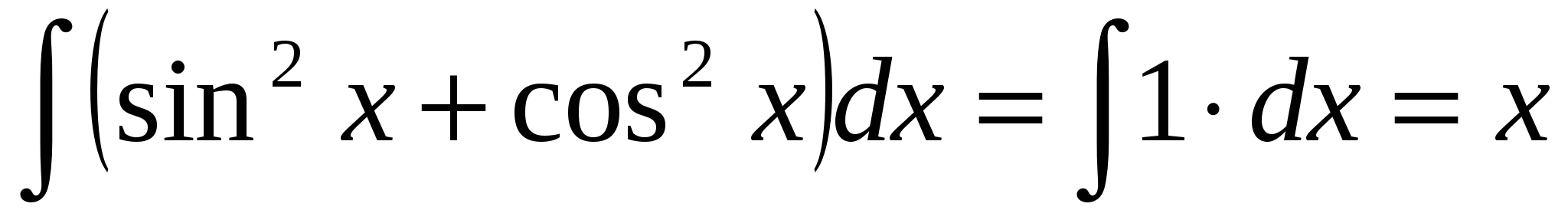
Ответ: х
Задание 16
Найти интеграл 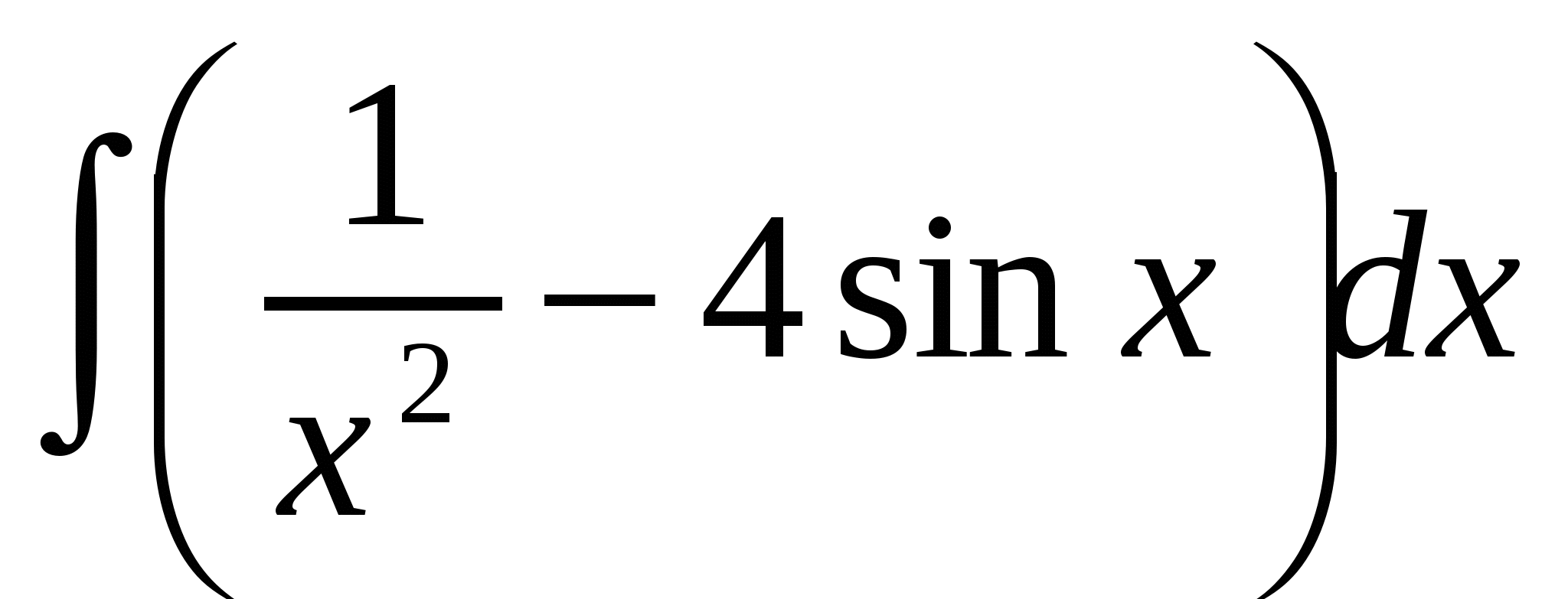 .
.
Решение 1. ![]() ,где с - произвольная постоянная.
,где с - произвольная постоянная.
Ответ: 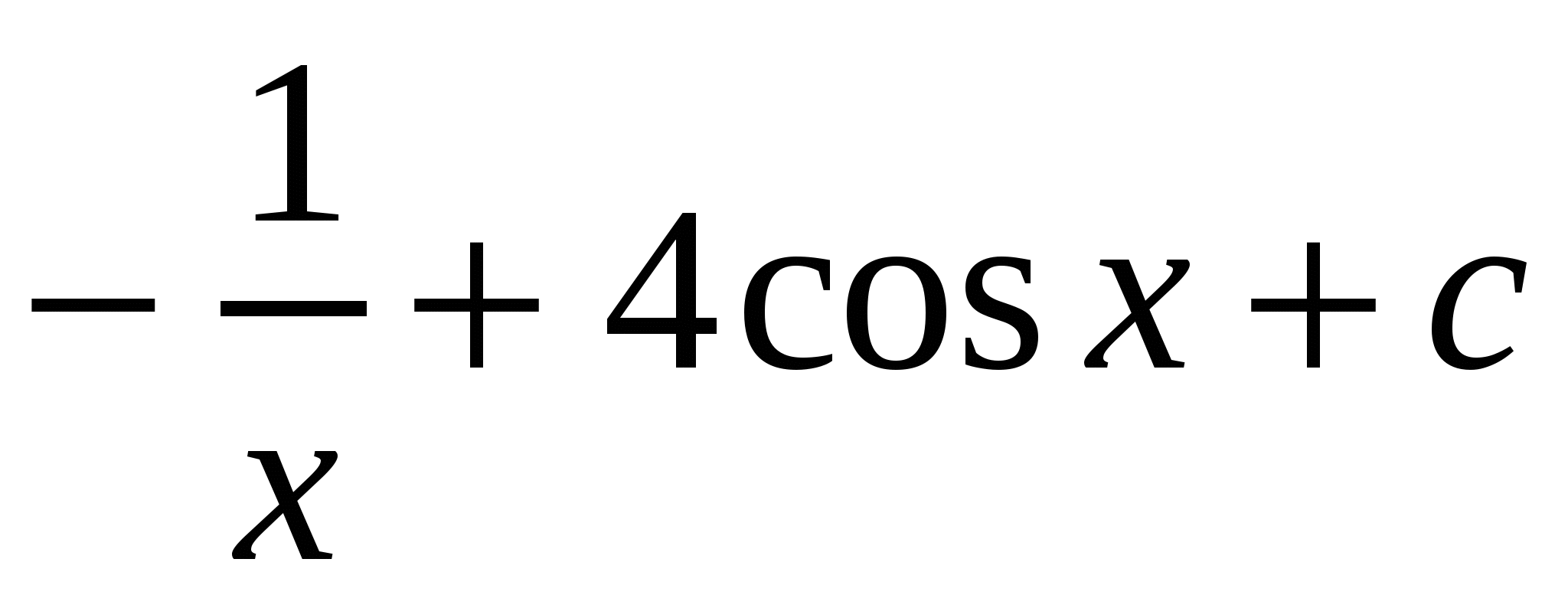
Решение 2.
Первообразными для функций 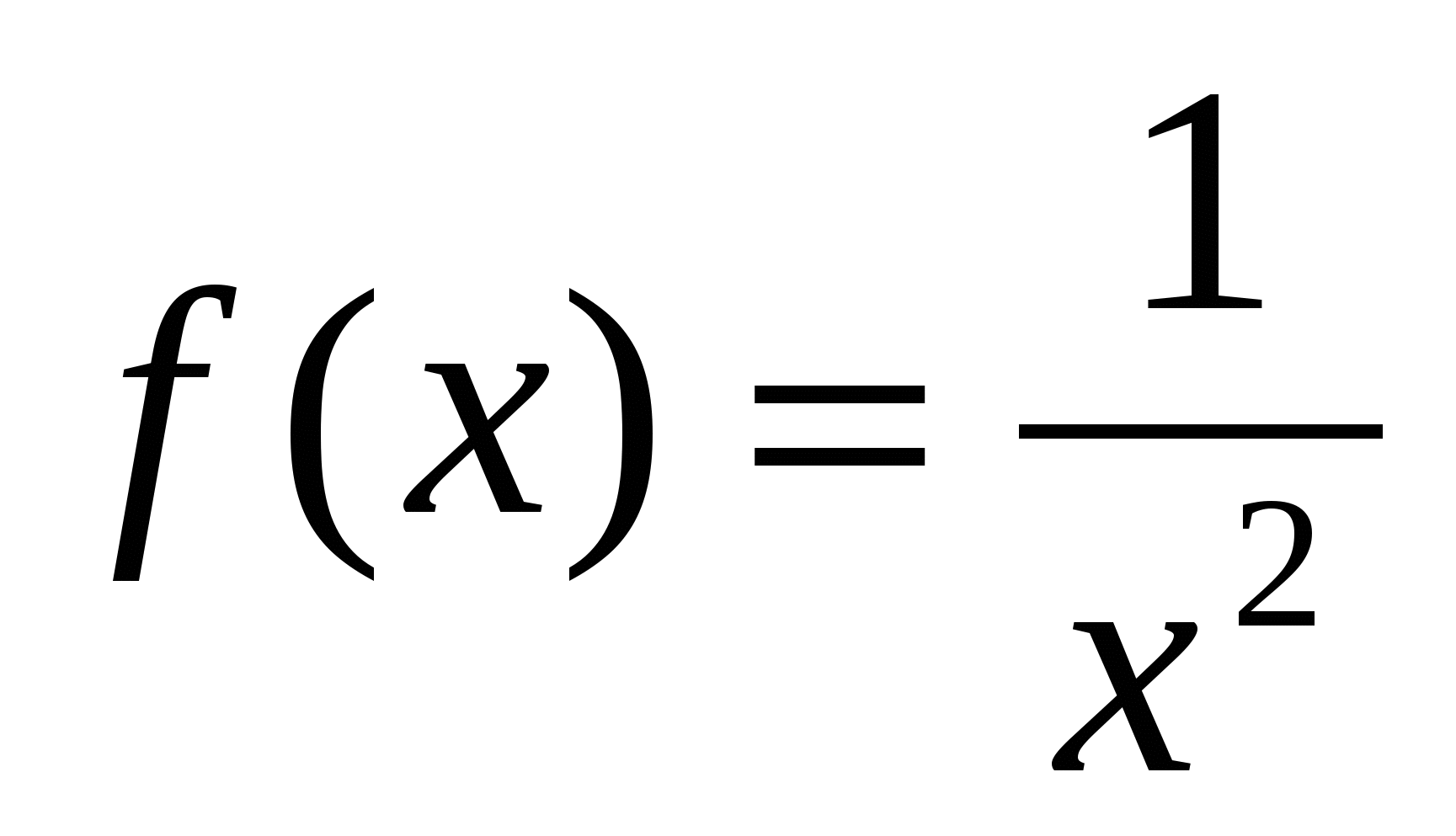 и
и 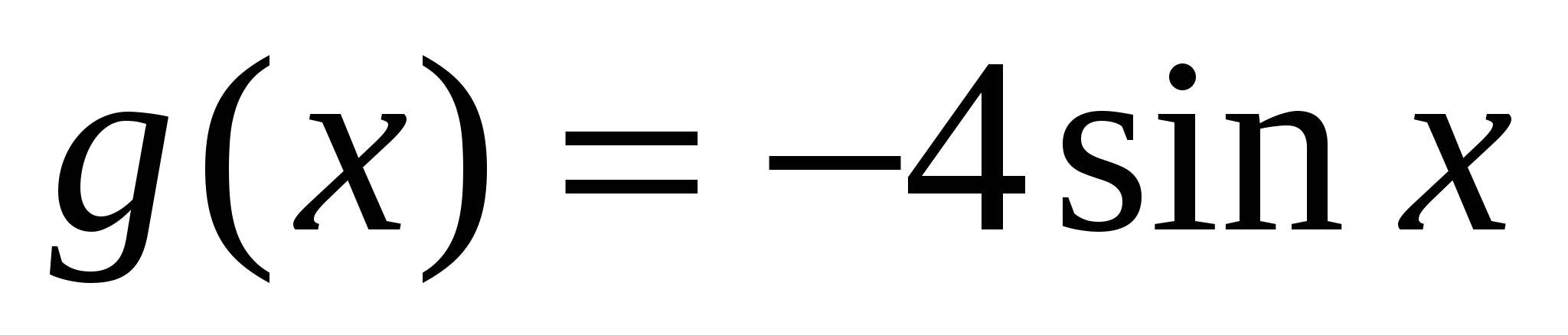 является, например, функции
является, например, функции ![]() и
и 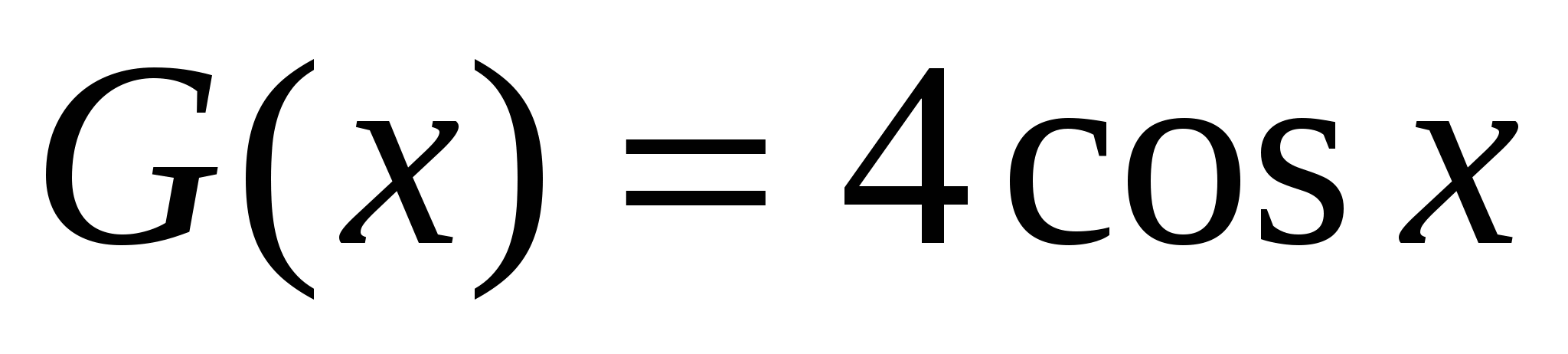 . Поэтому функции
. Поэтому функции 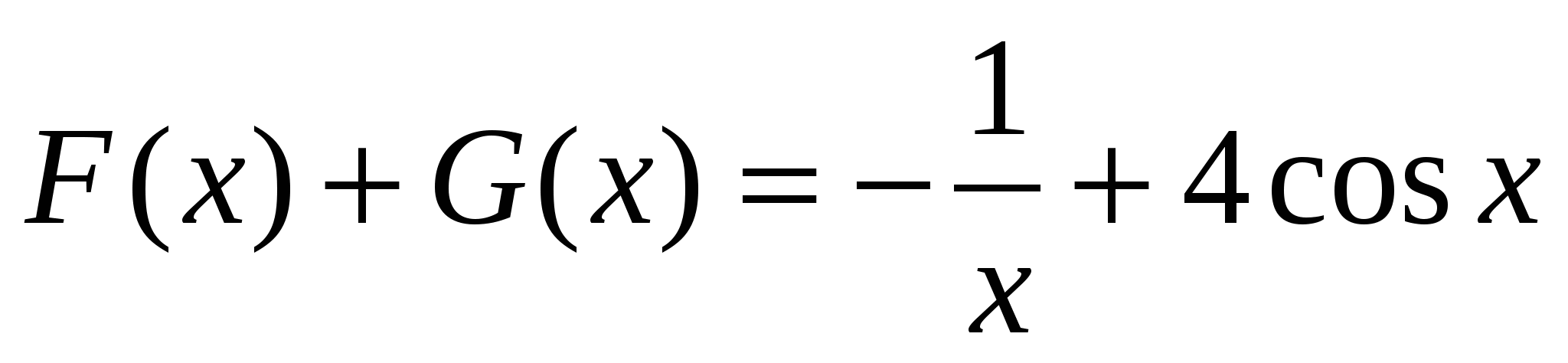 является первообразной для функции
является первообразной для функции 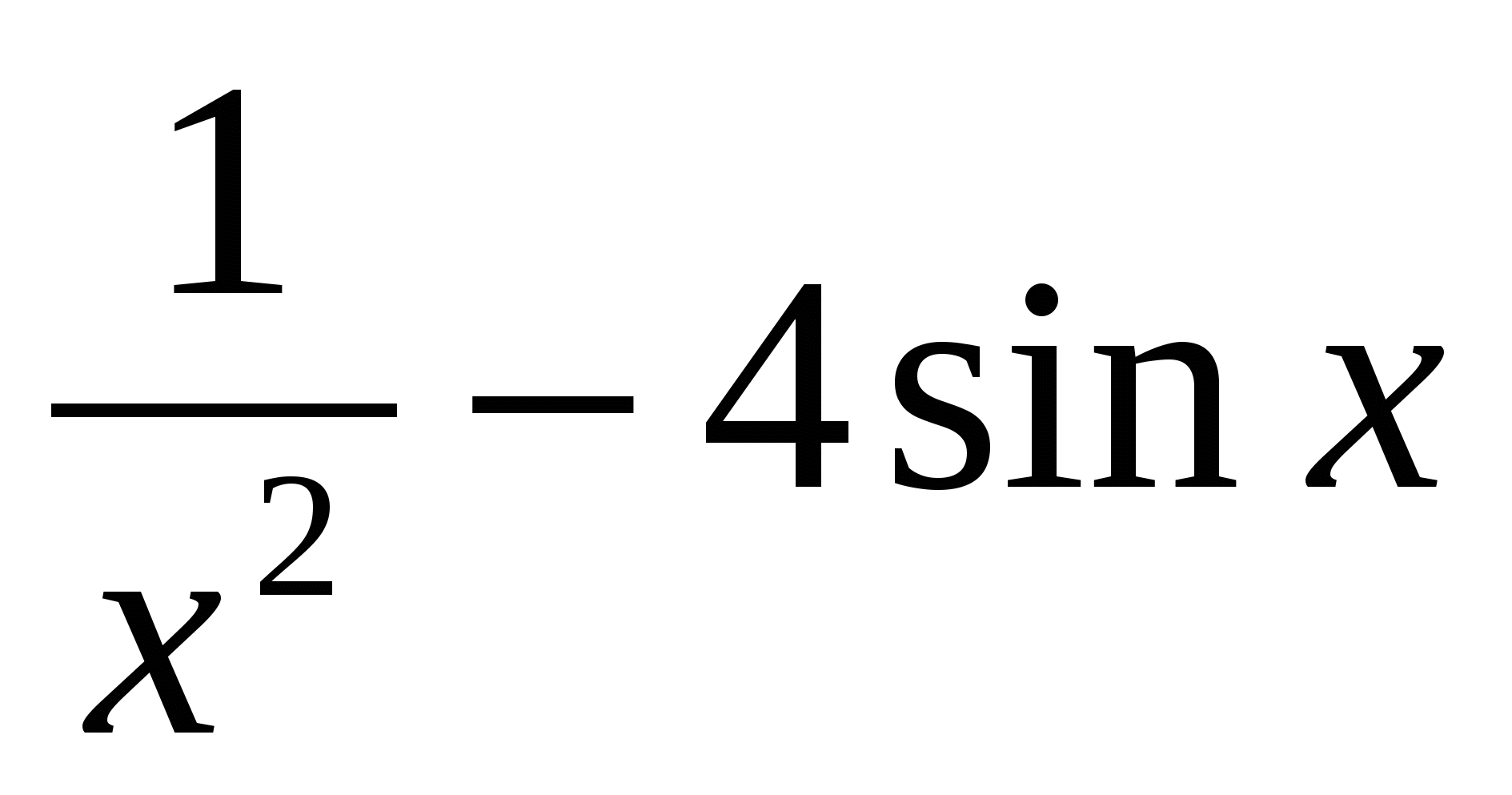 .Следовательно,
.Следовательно, 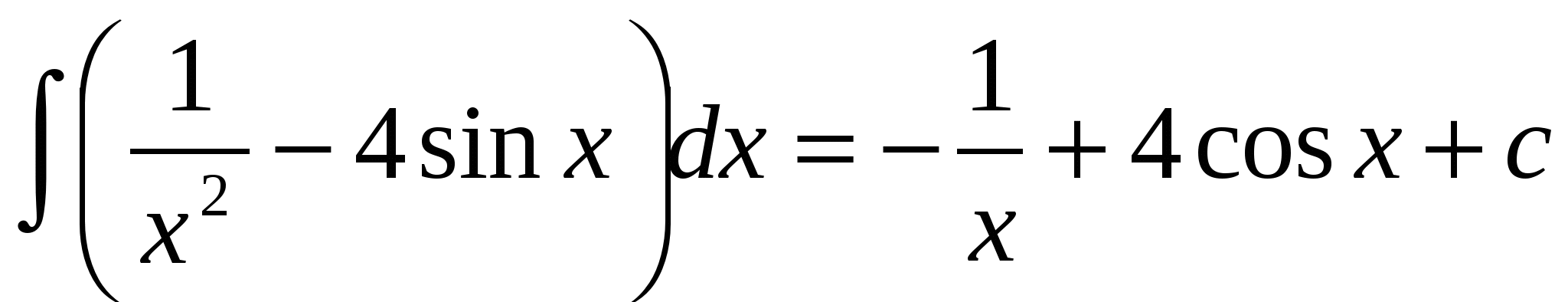 ,где с - произвольная постоянная.
,где с - произвольная постоянная.
Ответ: 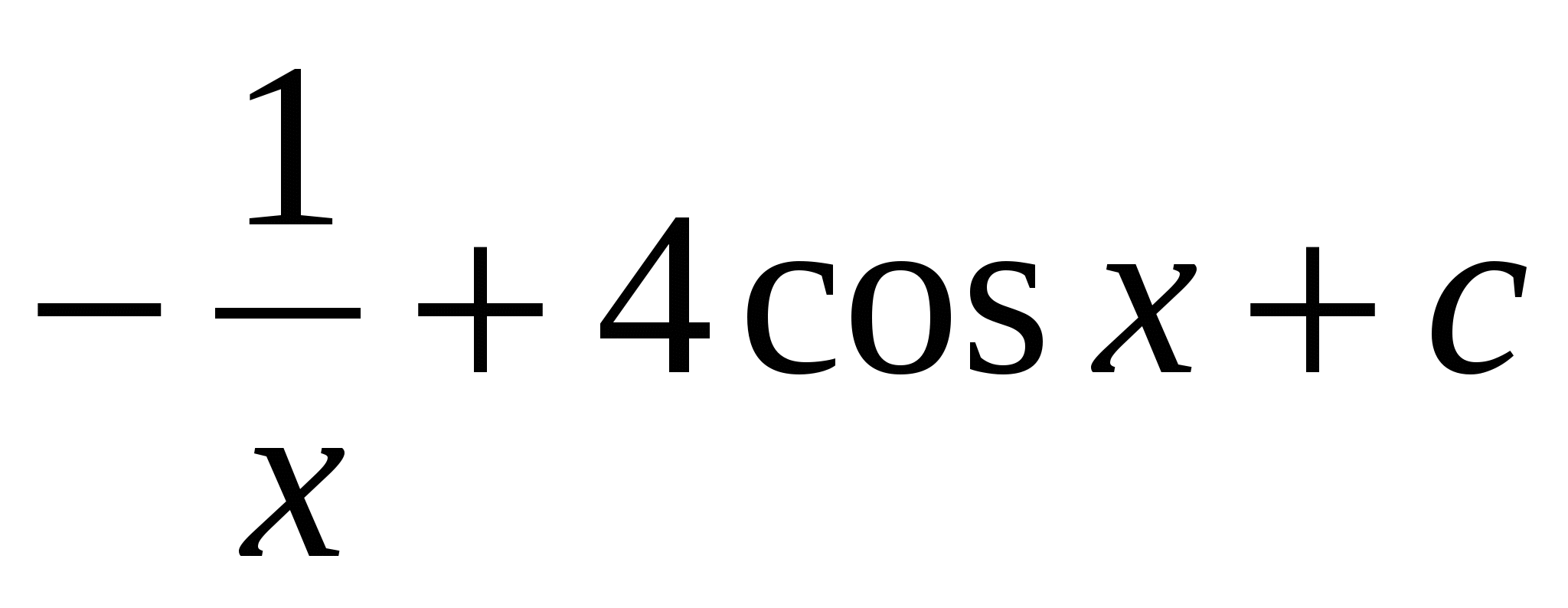
Тест для самоконтроля
1. В какой из точек A. 1; B. 10; C. 20; D. 100; E. 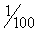 наиболее быстро растёт функция
наиболее быстро растёт функция  ?
?
2. Мяч брошен вертикально вверх. Если ось х направлена вверх, то закон движения мяча 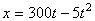 A. Опускается или поднимается мяч в момент времени
A. Опускается или поднимается мяч в момент времени 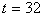 с?
с?
3. Материальная точка движется по закону 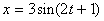 . Какова наибольшая скорость движения?
. Какова наибольшая скорость движения?
A. 1; B. 2; C. 3; D. 4; E. 6.
4. Неравномерно, в зависимости от переменной t изменяется величина:
A. 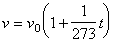 ; B.
; B. 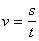 ; C.
; C. 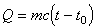 ; D.
; D. 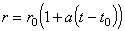 ; E.
; E. 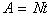 .
.
5. Для какой из следующих функций ось х является касательной в начале координат?
A. 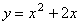 ; B.
; B. 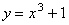 ; C.
; C. 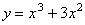 ; D.
; D. 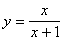 .
.
6. Касается ли прямая 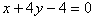 гиперболы
гиперболы ![]() в точке
в точке 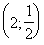 ?
?
A. Да; B. Нет.
7. Укажите функцию, критическая точка которой не является точкой экстремума:
A. 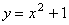 ; B.
; B. 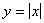 ; C.
; C. 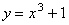 ; D.
; D. 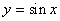 .
.
8. Производная функции 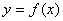 равна
равна 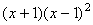 . Сколько точек экстремумов имеет функция?
. Сколько точек экстремумов имеет функция?
A. Одну; B. Две; C. Три; D. Ни одной.
9. На всей числовой оси возрастает функция ...
А. 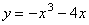 ; B.
; B. 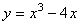 ; C.
; C. 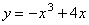 ; D.
; D. 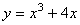 .
.
10. Какое наибольшее число точек экстремумов может иметь функция 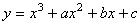 ?
?
A. 0; B. 1; C. 2; D. 3; Е. 4.
11. Укажите неверное утверждение:
A. Не все критические точки являются точками экстремума функции
B. Значение функции в точке минимума может быть больше значения функции в точке максимума
C. Если функция возрастает, то она не имеет точек экстремума
D. Если 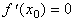 , то
, то 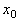 является точкой экстремума функции
является точкой экстремума функции
E. Касательная к графику функции может пересекать его в нескольких точках .
12. На рис. 7 изображён график производной функции  . Укажите промежутки убывания функции
. Укажите промежутки убывания функции  .
. 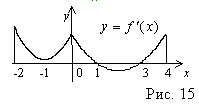
A. 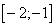 ,
, 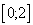 ; B.
; B. 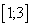 ; C.
; C. 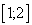 ; D. Верного ответа нет.
; D. Верного ответа нет.
13. Какая из прямых на рис.16 является графиком производной квадратичной функции, изображённой на рис. 17?
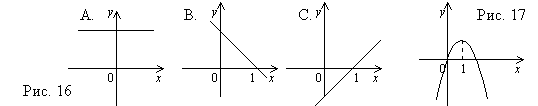
14. Производная функции 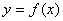 положительна на отрезке
положительна на отрезке 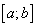 . Каково наименьшее значение
. Каково наименьшее значение 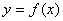 на этом промежутке?
на этом промежутке?
А. 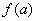 ; B.
; B. 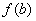 ; C. Наименьшего значения нет;
; C. Наименьшего значения нет;
D. Правильный ответ отличен от приведённых.
15. Какое из следующих утверждений неверно:
А. Наименьшее значение функции может и не быть минимумом.
В. Наибольшее и наименьшее значения функция может принимать только в своих точках экстремума.
С. Если функция не имеет критических точек на 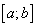 , то наибольшее и наименьшее значения она примет только на концах этого отрезка.
, то наибольшее и наименьшее значения она примет только на концах этого отрезка.
D. Существует функция, у которой совпадают её набольшее и наименьшее значения.
16. Пусть 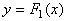 и
и 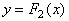 - первообразные одной функции. Какой вид (см. рис. 8) может иметь график функции
- первообразные одной функции. Какой вид (см. рис. 8) может иметь график функции 
17. Могут ли графики первообразных одной функции пересекаться?
А. Да; В. Нет; С. Ответ зависит от вида функции.
18. Тело совершает гармонические колебания с ускорением 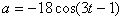 . Амплитуда колебания точки равна ...
. Амплитуда колебания точки равна ...
А. -2; В. 6; С. -6; D. 2;
19. Точка движется прямолинейно со скоростью 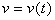 , график которой изображён на рис. 9. За промежуток времени
, график которой изображён на рис. 9. За промежуток времени 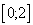 она прошла путь, равный ...
она прошла путь, равный ...
А. 2; В. 0,5; С. 1; D. 4; Е. 3 . Е. 54. 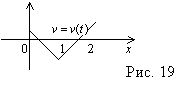
20. Какая из фигур, изображённных на рис. 20-24, является криволинейной трапецией?
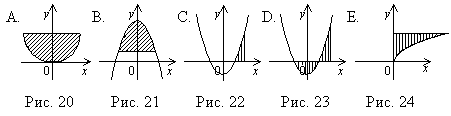
21. Какой из формул Вы воспользуетесь при вычислении площади фигуры, изображённой на рис. 23?
А. 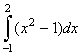 ; В.
; В. 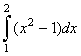 ; С.
; С. 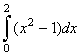 ; D.
; D. 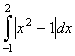 .
.
22. Колесо вращается с угдовой скоростью 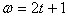 . Сколько оборотов оно сделает за промежуток времени
. Сколько оборотов оно сделает за промежуток времени 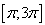 ?
?
А. 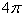 ; В.
; В. 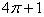 ; С.
; С. 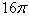 ; D.
; D. 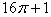 .
.
Ответы и указания к тестам
1. Е. Скорость изменения функции характеризуется её производной.
2. А. Если тело движется в направлении оси, то его скорость положительна.
3. Е.
4. В. Любой равномерно протекающий процесс описывается линейной функцией.
5. С. Для того, чтобы ось х была касательной для функции 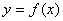 в точке
в точке  , необходимо и достаточно выполнение следующих условий:
, необходимо и достаточно выполнение следующих условий: 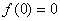 и
и 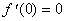 .
.
6. А. Проверьте, проходит ли заданная прямая 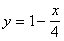 и гипербола
и гипербола ![]() через точку
через точку 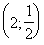 и совпадают ли в этой точке их производные.
и совпадают ли в этой точке их производные.
7. С. Обращение в нуль производной функции в некоторой точке является необходимым, но не достаточным условием существования экстремума.
8. А. Проверьте, меняет ли производная знак в критической точке.
9. D.
10. С. Обратите внимание на то, что производная заданной функции является квадратным трёхчленом.
11. D. См. вопрос № 7.
12. В. Вспомните условие убывания функции.
13. В. Подумайте, как отразится на знаке производной поведение функции на интервалах 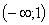 и
и 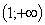 .
.
14. А.
15. В. См. вопрос № 14.
16. С. Вспомните, что первообразные одной функции отличаются друг от друга только некоторым постоянным слагаемым.
17. В.
18. D. Восстановите по ускорению закон движения тела.
19. С. Используйте геометрический и физический смысл интеграла.
20. С.
21. D.
22. В. Обратите внимание, что угол поворота колеса за промежуток времени 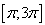 равен
равен 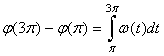 .
.
Литература
-
С.И. Шварцбург; О.С. Ивашев-Мусатов Алгебра и начала анализа Москва "Высшая школа" 1977г.
-
М. Титаренко; А.А. Роганин Задачник по математики (для учащихся и абитуриентов)
-
Сборник всех конкурсных задач по математики под редакцией М.И. Сканави Киев "Українська енциклопедія" 1996г.
-
Н.И. Шкиль; З.И. Слепкань; Е.С. Дубинчук Алгебра и начала анализа Киев "Вежа" 1996г.
-
М.И. Басимов Алгебра и начала анализа Москва "Просвещение"1992г.
-
Афанасьева О.Н.; Бродский Л.С. Применение производной и нитеграла, - Донецк: ДонНУ,2007 - 24с.
-
Т.П. Савенко, В.Г. Паньков, Ю.Н. Попов Задачи по алгебре и началам анализа.
57


