- Преподавателю
- Математика
- Методическое пособие по линейной алгебре для студентов
Методическое пособие по линейной алгебре для студентов
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Сыровая И.С. |
| Дата | 22.08.2015 |
| Формат | doc |
| Изображения | Есть |
16
Министерство образования Иркутской области

Государственное бюджетное
профессиональное образовательное учреждение
Иркутской области
«Иркутский авиационный техникум»
Методическое пособие
для студентов
по дисциплине «Математика»
Тема: «Линейная алгебра»
Иркутск, 2015
Методическое пособие по теме «Линейная алгебра» выполнено для использования его студентами при самостоятельных занятиях по теме «Линейная алгебра» с целью углубления знаний по этой теме и отработки практических навыков решения систем n линейных уравнений с n неизвестными.
УТВЕРЖДЕНО
цикловой комиссией
ГБПОУИО «ИАТ»
Протокол № 10
от «25» июня 2015 г.
Составитель: преподаватель ИАТ Сыровая И.С.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Методическое пособие по теме «Линейная алгебра» выполнено для использования его студентами при самостоятельных занятиях по теме «Линейная алгебра» с целью углубления знаний по этой теме и отработки практических навыков решения систем n линейных уравнений с n неизвестными.
Пособие состоит из 7 разделов.
-
В этом разделе даны определения матрицы, видов матриц и определителей
2-го и 3-го порядков., рассмотрены примеры их вычисления.
-
Приведена информация о системах линейных уравнений и их решении.
3. Решение систем линейных уравнений по формулам Крамера.
4. Решение систем линейных уравнений методом Гаусса.
5. Решение систем линейных уравнений в матричной форме.
6. Задания для самостоятельной работы.
7. Литература.
-
МАТРИЦЫ.
1.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Матрицей размера m х n называется прямоугольная таблица чисел
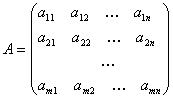 ,
,
содержащая m строк и n столбцов.
Каждый элемент матрицы аik имеет два индекса: i - номер строки и k - номер столбца.
Краткая форма записи матрицы:
А = (аik)m,n
Матрица называется квадратной порядка n, если она состоит из n строк и n столбцов.
Матрица размера 1хn называется матрицей-строкой, матрица размера mх1 называется матрицей-столбцом.
Нулевой матрицей заданного размера называется матрица, все элементы которой равны нулю.
Треугольной матрицей n-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:
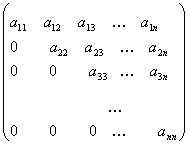 .
.
Единичной называется квадратная матрица n-го порядка, у которой элементы главной диагонали равны 1, а все остальные элементы - нули:
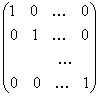 .
.
Матрицы А = (аik)m,n и В = (вik)m,n называются РАВНЫМИ, если аik = вik (i = 1,…,m;
k = 1,…,n).
-
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
Суммой матриц А = (аik)m,n и В = (вik)m,n называются матрица А + В = (аik + вik)m,n.
Произведением матрицы А = (аik)m,n на число l называется матрица lА = (lаik)m,n.
Для любых матриц одинакового размера выполняются свойства:
1) А + В = В +А 2) А + (В + С) = (А + В) + С
3) А + 0 = А
Транспонированной для матрицы А называется матрица АТ, строки которой являются столбцами матрицы А, а столбцы - строками матрицы А.
Пример 1. Даны матрицы
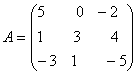 и
и 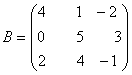
Построить матрицу С = 2А - 3В + АТ.
Решение:
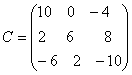 -
-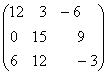 +
+
+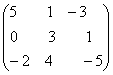 =
=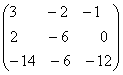 .
.
1.3 УМНОЖЕНИЕ МАТРИЦ
Произведением матрицы А = (аik)m,р на матрицу В = (вik)р,n называется матрица D
размера mхn с элементами
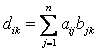
Иными словами, для получения элемента, стоящего в i-ой строке результирующей матрицы и в k-ом ее столбце, следует вычислить сумму попарных произведений элементов
i-ой строки матрицы А на k-ый столбец матрицы В.
Пример 2. Найти произведение матрицы А на матрицу В:

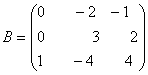 .
.
Решение.
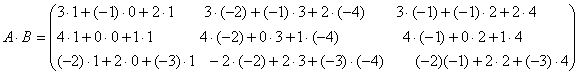
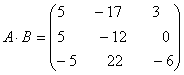 .
.
Число столбцов первой матрицы равно числу строк второй. Это - условие согласования матриц при умножении. Если оно нарушено, матрицы перемножить нельзя.
-
ОПРЕДЕЛИТЕЛИ
Определитель второго порядка.
Пусть матрица А - квадратная матрица 2-го порядка:
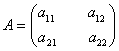 .
.
Определителем 2-го порядка (матрицы а) называется число
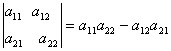
Пример. Вычислить определитель матрицы
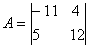
Решение:
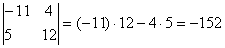
Определитель третьего порядка.
Пусть матрица А - квадратная матрица 3-го порядка:

Определителем 3-го порядка (матрицы А) называется число
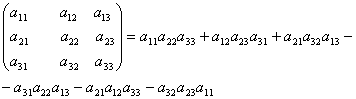
Правило треугольника:



Пример. Вычислить определить
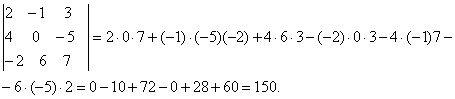
Разложение определителя по строке или столбцу.
Минором элемента aik называется определитель Мik, составленный из элементов, оставшихся после вычеркивания из матрицы А i-ой строки и k-го столбца.
Алгебраическим дополнением элемента aik называется число 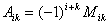 .
.
Определителем 3-го порядка (матрицы А) называется сумма произведений элементов первой строки матрицы на их алгебраические дополнения:
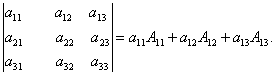
Данную формулу называют разложением определителя по первой строке.
Пример. Вычислить определитель матрицы
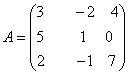 .
.
Решение. Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:
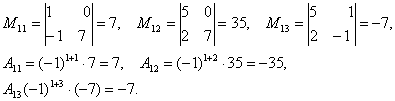
Вычисляем искомый определитель:
D(А) = 3.7 + (-2).(-35) + 4.(-7) = 63.
Свойства определителей.
1. Определитель не меняется при транспонировании, т.е. D(АТ) = D (А).
2. Если две строки определителя поменять местами, то определитель меняет знак.
3. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен нулю.
4. Если все элементы какой-либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
5. Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен нулю.
6. Определитель не изменяется, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.
-
Системы линейных уравнений
Система линейных уравнений с переменными x, y и z имеет вид:
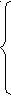
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2 (1)
a3x + b3y + c3z = d3
Решением системы уравнений называется упорядоченная тройка чисел
x, y, z, являющаяся решением каждого уравнения системы.
Для системы уравнений можно составить матрицу А - матрицу коэффициентов при неизвестных и матрицу D - матрицу-столбец свободных коэффициентов.
 a1 b1 c1 d1
a1 b1 c1 d1
A = a2 b2 c2 D = d2
a3 b3 c3 d3
Составим и вычислим определитель матрицы А:


 a1 b1 c1
a1 b1 c1
∆ = a2 b2 c2 = a1b2c3+ b1c2 a3 + a2b3c1 - a3b2c1 - c2b3a1 - a2b1c3
a3 b3 c3
-
Решение систем линейных уравнений по формулам Крамера.
Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: Значение каждого из неизвестных равно дроби, знаменатель которой равен главному определителю системы, а числитель получается из главного определителя путём замены столбца коэффициентов при искомом неизвестном на столбец свободных членов.
Для системы (1) запишем определители ∆, ∆x, ∆y, ∆z.
a



 1 b1 c1 d1 b1 c1 a1 d1 c1
1 b1 c1 d1 b1 c1 a1 d1 c1
∆ = a2 b2 c2 ∆x = d2 b2 c2 ∆y = a2 d2 c2
a3 b3 c3 d3 b3 c3 a3 d3 c3









 a1 b1 d1
a1 b1 d1
∆z = a2 b2 d2
a3 b3 d3
По формулам Крамера: x = ∆x/ ∆ y = ∆y / ∆ z = ∆z/ ∆
Пример: x - y + 3z = 3
3x + y - z = 17
2x -7y + z = - 4
Вычислим главный определитель системы:
1 -1 3
∆ = 3 1 - 1 = 1 + 2 - 63 -6 -7 + 3 = -70
2 -7 1
Заменив столбец коэффициентов при переменной x столбцом свободных коэффициентов, получим определитель ∆x:
3 -1 3
∆х = 17 1 -1 = 3 - 4 - 357 + 12 - 21 + 17 = -350
-4 -7 1
Заменив столбец коэффициентов при переменной y столбцом свободных коэффициентов, получим определитель ∆y:
1 3 3
∆y= 3 17 -1 = 17 - 6 - 36 - 102 - 9 - 4 = -140
2 -4 1
Заменив столбец коэффициентов при переменной z столбцом свободных коэффициентов, получим определитель ∆z:
1 -1 3
∆z = 3 1 17 = -4 - 34 - 63 - 6 + 119 - 12 = 0
2 -7 -4
По формулам Крамера вычислим значения x, y и z:
x = ∆x/ ∆ = 5 y = ∆y / ∆ =2 z = ∆z/ ∆=0
Ответ: (5; 2; 0).
-
Решение систем методом Гаусса.
При решении систем линейных уравнений используют метод Гаусса, который заключается в приведении заданной системы к треугольному виду (прямой ход). Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
При выполнении прямого хода используют следующие преобразования:
-
умножение или деление коэффициентов свободных на одно и то же число;
-
сложение и вычитание уравнений;
-
перестановку уравнений системы;
-
исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.
Пример:
 x - y + 3z = 3
x - y + 3z = 3
3x + y - z = 17
2x -7y + z = - 4
З
 апишем расширенную матрицу:
апишем расширенную матрицу:
1 -1 3 3
3 1 -1 17
2 -7 1 -4
Чтобы в первом столбце получить a2= a3= 0, умножим первую строку соответственно на -3 и -2 и сложим результаты с первой строкой.
1 -1 3 3
0 4 -10 8
0 -5 -5 -10
Первую и вторую строки запишем без изменения, а затем вторую строку умножим на 5, третью - на 4, полученные значения сложим и запишем результаты в качестве третьей строки:
 1 -1 3 3
1 -1 3 3
0 4 -10 8
0 0 -70 0
Запишем новую эквивалентную систему, которой соответствует расширенная матрица:
 x - y + 3z = 3
x - y + 3z = 3
4y - 10z = 8
-70z = 0
Выполняя обратный ход, найдём переменные:
Z = 0;
4y - 10 0 = 8; 4y = 8; y = 2;
x - 2 + 3 0 = 3; x = 3 + 2 = 5.
Итак, получаем ответ: (5; 2; 0).
5 Решение систем линейных уравнений в матричной форме.
Для системы (1) рассмотрим матрицы
 a1 b1 c1 d1 x1
a1 b1 c1 d1 x1
A = a2 b2 c2 D = d2 X = x2
a3 b3 c3 d3 x3
Используя правило умножения матриц, систему (1) запишем в виде:
 a1 b1 c1 x1 d1
a1 b1 c1 x1 d1
a2 b2 c2 x2 = d2
a3 b3 c3 x3 d3
или AX = D.
Это равенство называется простейшим матричным уравнением.
Умножив обе части матричного уравнения на A-1, получим: A-1(AX) = A-1D Так как (A-1A)X = EX = X, ═ X = A-1D.
Таким образом, чтобы решить матричное уравнение, нужно:
1). Найти обратную матрицу А-1.
2). Найти произведение А-1D.
3). Пользуясь определением равных матриц, записать ответ.
П
 ример. Решить матричное уравнение:
ример. Решить матричное уравнение:
 3 -1 0 5
3 -1 0 5
-2 1 1 X = 0
2 -1 4 15
Найдём обратную матрицу A-1.
Вычислим определитель матрицы A:
 3 -1 0
3 -1 0
∆ = -2 1 1 = 12 - 2 + 3 - 8 = 5
2 -1 4
Вычисляя алгебраические дополнения элементов матрицы, получим:
А11= 5; А12= 10; А13= 0; А21= 4; А22= 12; А23= 1; А31= - 1; А32 = - 3; А33= 1.
Запишем новую матрицу:
5 4 -1
10 12 -3
0 1 1
Транспонируем её:
5 10 0
4 12 -3
-1 -3 1
Запишем обратную матрицу:
1 4/5 -1/5
2 12/5 -3/5

 0 1/5 1/5
0 1/5 1/5

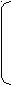
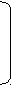 1 4/5 -1/5 5 1 5 + 4/5 0 + (-1/5) 15 2
1 4/5 -1/5 5 1 5 + 4/5 0 + (-1/5) 15 2
Х = 2 12/5 -3/5 0 = 2 5 + 12/5 0 + (-3/5) 15 1
0 1/5 1/5 15 0 5 + 1/5 0 + 1/5 15 3
Итак, можно записать:
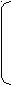
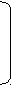
 х1 2
х1 2
х2 = 1 т. е. х1 = 2, х2 = 1, х3 = 3.
х3 3
Ответ: (2; 1; 3).
-
Задания для самостоятельной работы:
-
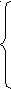 x + 2y + z = 8 2. x + 3y - 6z = 12
x + 2y + z = 8 2. x + 3y - 6z = 12
3x + 2y + z = 10 3x + 2y + 5z = -10
4x + 3y -2z = 4 2x + 5y - 3z = 6
Ответ: ( 1; 2; 3 ) Ответ: (0; 0; -2 )
3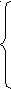 . 5x - y - z = 0 4. 3x - y + 2z = 2
. 5x - y - z = 0 4. 3x - y + 2z = 2
x + 2y + 3z = 14 x + 2y + z = -7
4x + 3y + 2z = 16 2x + y - z = 1
Ответ: (1; 2; 3 ) Ответ: (1; -3; -2 )
7 Литература
-
Лисичкин В.Т., Соловейчик И.Л. Математика- Учебное пособие для техникумов. - М.: Высшая школа, 2012.- 463с.
-
Мордкович А.Г.Алгебра и начала анализа: В 2 ч.: Ч. 2: Учебник для 10-11 классов общеобразовательных учреждений. Изд. 3-е, испр.-М., Мнемозина, 2005.-375с.
-
Филимонова Е.В. Математика: Уч. пособие для сред. спец. уч. завед. - 3-е изд доп. и перераб. - Ростов Н/Д: Феникс, 2005.- 416с.


