- Преподавателю
- Математика
- НОУ по математике Интересные свойства чисел
НОУ по математике Интересные свойства чисел
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Вихорева Н.Н. |
| Дата | 19.12.2015 |
| Формат | docx |
| Изображения | Есть |
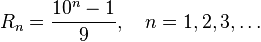
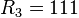
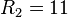
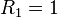
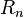
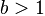
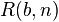
Интересные свойства чисел.
Работу выполнила:
ученица 10«Б» класса
МБОУ СОШ №103
Коперина А.И.
Руководитель: Вихорева Н.Н.
г. Нижний Новгород
2014г.
Содержание.
-
Введение
-
Загадка числа 196
-
Перемножение чисел чуть меньше 100
-
Интересное число 50
-
Число 13223140496
-
Экономные числа
-
Репдигит время
-
Постоянная Капрекара
-
Числа Армстронга
-
Число Смита время
-
Интересные свойства числа 9
-
100 чисел
-
Заключение
Введение.
Всё мы со школьной скамьи изучаем математику: цифры, числа, выражения… Мы привыкли решать всё по заданным алгоритмам, по правилам, и ни когда не задумывались о свойствах чисел. Ведь в любой закономерности есть исключение, в любом законе найдётся лазейка и про каждое число можно рассказать что-то интересное. Каждое число чем-то отличается от других, а чем-то и похоже.
Цель: Я поставила перед собой цель найти такие числа, которые объединены между собой интересными закономерностями или наоборот, не подчиняются каким-либо правилам.
Задачи:
-
Найти такие числа
-
Изучить их свойства
-
Произвести проверку
-
Сделать вывод
Загадка числа 196.Возьмём любое натуральное число, например, 12. Переставим в нём цифры в обратном порядке и сложим с исходным числом.
12 + 21 = 33.
Мы получили число-палиндром, одинаково читающееся как справа налево, так и слева направо. Иногда, чтобы получить палиндром, требуется больше шагов. Вот, например, для числа 192:
192 + 291 = 483
483 + 384 = 867
867 +768 = 1545
1545 + 5451 = 6996
Сделано 4 шага и палиндром, 6996, получен.
И так происходит почти с любым числом, с какого бы ни начать процесс. А вот с числом 196 что-то странное. Сколько ни продолжали переставлять цифры и складывать - палиндрома не выходило
196 + 691 = 887
887 + 788 = 1675
1675 + 5761 = 7436
7436 + 6347 = 13783
13783 + 38731 = 52514
52514 + 41525 = 94039
94039 + 93049 = 187088
187088 + 880781 = 1067869
Само число уже превышает миллион, а палиндром не получен! И до сих пор не найдено ни на каком шагу из числа 196 получится палиндром (а таких шагов разными исследователями с помощью компьютера сделано более семисот миллионов), ни строгого доказательства, что палиндром не будет получен никогда. Числа, которые, как и 196, не дают палиндром после некоторого числа шагов, называются числами Лишрел.
Перемножение чисел чуть меньше 100.
Перемножим 2 числа, чуть меньшие сотни:
(100 - a)(100 - b) = 10000 - 100(a + b) + ab = 100(100 - (a + b)) + ab
Например:
81*97
a = 19, b = 3, a + b = 22, ab = 57, 100 - (a + b) = 78.
Результат: 7857
Следует быть внимательным в случае, когда ab окажется трёхзначным:
88*89
a = 12, b = 11, a + b = 23, ab = 132, 100 - (a + b) = 77.
В этом случае нужно будет первую цифру от 132 прибавить к 77, а уже двуциферное окончание приписать к полученному результату.
Получим: 7832
Интересное число 50.
С математической точки зрения число 50 интересно тем, что это - наименьшее натуральное число, которое представляется в виде суммы двух квадратов натуральных чисел двумя способами.
50 = 49 + 1 = 25 + 25.
Если заменить слово "натуральных" словом "целых", то наименьшим числом такого рода будет 25: 25 = 16 + 9 = 0 + 25.
Оказывается, есть простой способ определить, представимо ли число в виде суммы двух квадратов двумя способами. Для этого оно должно иметь в своём разложении как минимум 2 (не обязательно различных) простых множителя, дающих остаток 1 при делении на 4. А количество простых множителей, дающих остаток 3 при делении на 4 должно быть чётным. Например, число 305 = 5 х 61. И 5 и 61 дают остаток 1 при делении на 4. Множителей, дающих остаток 3 в его разложении нет, т.е. их 0 штук - чётное число. Значит, 305 представляется в виде 305=42+172=72+162.Зная это, подобные числа можно конструировать. Возьмём простое число 5, умножим его на простое число 13, и дважды умножим на простое число 3. Полученный результат 585 представляется как:
585=32+242=122+212.
Число 13223140496 - это наименьшее натуральное число, которое, будучи написанным дважды подряд, образует полный квадрат.
1322314049613223140496 = 3636363636422
Экономные числа
Разложим натуральное число на простые множители. Запись его разложения может иметь как больше цифр, чем само число (например, 2013 = 3*11*61), столько же цифр (27=33) или даже быть короче (1701 = 37*7)
Числа первого вида в занимательной математике называются избыточными. Это уже третье определение избыточного числа (первое относится к базовому свойству числа - сумме делителей, а второе - к названию числа в определённом языке).
Числа, в разбиение которых на простые множители используется (с учётом больших единицы показателей степеней) столько же цифр, сколько их в самом числе, называются равноциферным. В частности, все простые числа - равноциферны в любой системе счисления.
А те же числа, факторизация которых имеет меньше цифр, чем само число, называются экономными. Наименьшее экономное число для десятичной системы - это 125 = 53.
Репдигит - это число, которое состоит из повторяющихся цифр. Например, 111 или 5555. Иногда к репдигитам относят и однозначные числа: 1, 2, ... 9.
Поскольку здесь мы имеем дело с цифрами, то в разных системах счисления разные числа окажутся репдигитами. Например, число 26 будет репдигитом в троичной системе, ведь там оно выглядит как 222.
Репдигитом в тринадцатеричной системе счисления является число 2013. А некоторые числа являются репдигитами в нескольких системах. Сразу заметим, что любое число n записывается как 11 в системе счисления с основанием n-1 и является однозначным в системах с основанием n+1 и более.
Если рассматривать только системы счисления с основанием менее n-1, первым нетривиальным множественным репдигитом будет число 15. В двоичной системе оно запишется как 1111, а в четверичной - как 33.
Следующее - число 24: (24)10 = (44)5 = (33)7 = (22)11.
Постоянная Капрекара. Это число равное 6174.
Получение: выбрать любое четырехзначное число, в котором все цифры разные. Расположить цифры сначала в порядке убывания, затем, переставив их в обратном порядке, образовать новое число. Вычесть новое число из старого. Повторяя этот процесс с получающимися разностями (не более чем за семь шагов) получим число 6174 , которое будет затем воспроизводить самого себя. Производя вычитания, нули следует сохранять.
Примеры: 4321 - 1234 = 3087 8730 - 0378 = 8352 8532 - 2358 = 6174.
1100 - 0011 = 1089 9810 - 0189 = 9621 9621 - 1269 = 8352 8532 - 2358 = 6174.
Числа Армстронга. Числа 153, 370, 371, 407
А что, если вместо суммы квадратов вычислять сумму кубов цифр числа? Оказывается, "орбиты" получаются гораздо интереснее. Некоторые числа "вырождаются" - приходят к единице. Другие - "стабилизируются": через несколько шагов цепочка приводит к одному из чисел 153, 370, 371 или 407 . Эти четыре числа обладают замечательным свойством: они равны сумме кубов своих цифр.
Числа 153, 370, 371 и 407 имеют специальное название - числа Армстронга (в честь математика, который их впервые исследовал). Строгое математическое определение таково: n-значное число называется числом Армстронга, если оно равно сумме n-ых степеней своих цифр.
n
Числа Армстронга
3
153; 370; 371; 407
4
1634; 8208; 9474
5
54748; 92727; 93084
6
548834
7
1741725; 4210818; 9800817; 9926315
8
*24678050; 24678051; 88593477
9
146511208; 472335975; 534494836; 912985153
10
4679307774
11
32164049650; 32164049651; 40028394225; 42678290603; 44708635679; 49388550606; 82693916578; 94204591914
14
28116440335967
Число Смита
4937775 = 3 х 5 х 5 х 65837-разложение на простые множители
Сумма цифр числа - 42 Сумма цифр разложения - 42
Числа Смита: 4, 22, 27, ...
На интервале (0, 10 000) - 376 чисел Смита
На интервале (0, 100 000) - около 3300 чисел Смита
На интервале (0, 1 000 000) - 29928 чисел Смита
Число чисел Смита бесконечно
Наибольшее известное число Смита - 9 x R1031(104594 + 3 x 102297 + 1) x 103913210 имеет 10694985 знаков в своей записи в десятичной системе счисления. Здесь R1031 - репьюнит.(англ. repunit, от repeated unit - повторённая единица) - натуральные числа , запись которых в системе счисления с основанием состоит из одних единиц. В десятичной системе счисления репьюниты обозначаются : ,
и т. д., и общий вид для них:
Известно также родственное понятию числа Смита, понятие Братья Смита - это числа Смита стоящие рядом друг с другом. Например, (728; 729) или (2964; 2965). Однако неизвестно, сколько существует таких пар.
Интересные свойства числа 9 часто применяются в арифметике как для теоретических изысканий и практических действий, так и для составления различных занимательных задач или так называемых «головоломок». Распространено также практическое применение девятки для проверки умножения и деления. Основано оно на том свойстве всякого числа, что остаток, получаемый от деления числа на девять, всегда равен остатку от деления на 9 суммы цифр этого числа. Укажем здесь еще несколько интересных применений этого числа. Прежде всего нетрудно убедиться, что если мы напишем произвольное двузначное число, а затем напишем цифры этого же числа в обратном порядке и возьмем разность полученных чисел, то эта разность всегда разделится на 9. Например,72 − 27 = 45; 92 − 29 = 63; 63 − 36 = 27 и т. д.
Вообще ясно, что (10a + b) − (10b + a) = 9(a − b), т. е. получается число, делящееся на 9. (Кроме того разность эта равна произведению 9 на разность цифр данного двузначного числа.) Знание этой особенности может принести практическую пользу, например, многим бухгалтерам.
100 чисел
-
0 (нуль) Величайшее изобретение человеческого разума, давшего исходный импульс развитию математике как таковой. Согласитесь - невероятно трудно придумать «ничего», дать ему имя и использовать в вычислениях. Самые интересные свойства - на нуль нельзя делить, нуль, будучи показателем степени, приравнивает любое число к единице. Умножение на нуль дает нуль. Сложение и вычитание его результат не меняет. Использование нуля позволяет создавать позиционные системы счисления (в отличие, например, от римских цифр, обходившихся без нуля). О следующих числах предельно кратко.
-
1 Дает тождество при умножении. Равно любому числу в нулевой степени.
-
2 Единственное четное простое число.
-
3 Число размерностей пространства, в которых мы живем. Единственное число, равное сумме всех меньших чисел - естественно, речь все время идет о целых числах. Имеет горизонтальную ось симметрии.
-
4 Наименьшее число цветов для раскраски карты на плоскости. Тетраэдальное число.
-
5 Число Платоновых многогранников. Пятое число из последовательности Фибоначчи. Пирамидальное число.
-
6 =3! Наименьшее совершенное число. Треугольное число.
-
7 Наименьшее число сторон многоугольника, которым нельзя замостить плоскость. Шестиугольное число.
-
8 Наибольший куб в последовательности Фибоначчи. Имеет горизонтальную и вертикальную оси симметрии.
-
9 Максимальное число кубов, необходимое для представления в виде их суммы любого положительного целого числа.
-
10 Основание нашей системы счисления. Число топологически различных фигур из 5 спичек. Тетраэдальное и треугольное число.
-
11Наибольшее количество кусков, на которые делят круг 4 прямые линии. Имеет горизонтальную ось симметрии.
-
12 Наименьшее число, имеющее 4 делителя. Количество плиток пентамино.
-
13 Число Архимедовых многогранников. Число из последовательности Фибоначчи. Перестановочное (с 31) простое число.
-
14 Четвертое число Каталана. Пирамидальное число.
-
15 Четвертое число последовательности Белла. Треугольное число. Произведение первых трех нечетных чисел. Количество сочетаний четырех чисел из шести.
-
16Единственное число (кроме 1), выражаемое в форме xy=yx , а именно 24=42.
-
17 Количество вариантов узоров, построенных с использованием сдвигов, поворотов и отражений. Перестановочное (с 71) простое число.
-
18 Единственное число, равное удвоенной сумме его цифр.
-
19 Максимальное число четвертых степеней чисел, с помощью суммы которых можно выразить любое число. Шестиугольное число.
-
20 Число топологически различных фигур из 6 спичек. Тетраэдальное число. Количество сочетаний трех чисел из шести.
-
21 Число из последовательности Фибоначчи. Треугольное число. Количество сочетаний двух или четырех чисел из шести.
-
22 Количество кусков, на которые делят круг 6 прямых линий.
-
23 Количество деревьев с восемью звеньями.
-
24 =4! Самое большое число, которое делится на все числа, меньшие корня из него.
-
25 Наименьшее число, которое можно представить как сумму двух квадратов.
-
26 Наименьшее число не-палиндром, квадратом которого является палиндром.
-
27 Единственное (возможно?) число, у которого сумма цифр (9) суммы кубов цифр (8+343=351) с суммой цифр (18) куба суммы цифр (729) равна самому числу.
-
28 Второе совершенное и одновременно треугольное число.
-
29 Седьмое число Люка. Наибольшее количество кусков, на которые делят круг 7 прямых линий.
-
30 Самое большое число, у которого все числа меньшие его и взаимно простые с ним простые. Пирамидальное число.
-
31 Простое число Мерсенна. Перестановочное (с 13) простое число.
-
32 Наименьшая 5-ая степень числа (исключая 1)
-
33 Самое большое число, не равное сумме разных треугольных чисел. Имеет горизонтальную ось симметрии.
-
34 Наименьшее число такое, что имеет равное количество делителей с ближайшими соседними числами. Число из последовательности Фибоначчи
-
35 Количество плиток гексамино. Тетраэдальное число. Количество сочетаний трех или четырех чисел из семи.
-
36 Наименьшее число (кроме 1), которое одновременно и квадратное и треугольное.
-
37 Максимальное количество 5х степеней чисел, необходимое для выражения их суммой любого числа. Количество кусков, на которые делят круг 8 прямых линий. Шестиугольное число. Перестановочное (с 73) простое число.
-
38 Наибольшее римское число (по длине) в лексикографической записи (XXXVIII).
-
39 Три делителя этого числа пишутся одними и теми же цифрами.
-
40 Максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в пятимерном пространстве. Количество расстановок 7 ферзей на доске 7*7 не угрожающих друг другу.
-
41 Наименьшее число, не выражаемое в форме |2x - 3y|. А его квадрат содержит в написании два квадрата.
-
42 Пятое число Каталана. Количество вариантов плоскостей гексагексафлексагона.
-
43 Количество гептиамондов. (Фигуры из 7 правильных треугольников)
-
44 Количество вариантов перемешивания пяти предметов.
-
45 число Капрекара. Треугольное число. Количество сочетаний двух или восьми чисел из десяти.
-
46 Количество участков, на которые делят круг 9 прямых линий.
-
47 Наибольшее число кубов, из которых нельзя сложить куб. Количество деревьев с девятью звеньями.
-
48 Наименьшее число, имеющее 10 делителей.
-
49 Наименьшее число такое, что оно само и его ближайшие соседи имеют среди делителей квадраты.
-
50 Наименьшее число, которое можно представить как сумму квадратов двумя способами. Число вариантов складывания полоски из 5 марок.
-
51 Шестое число Мотзкина.
-
52 Это пятое число Белла.
-
53 Является одним из чисел n, которые служат делителем суммы n первых простых чисел.
-
54 Наименьшее число, которое может быть представлено суммой трех квадратов тремя способами.
-
55 Наибольшее треугольное число среди чисел Фибоначчи. Пирамидальное число.
-
56 Количество вариантов Латинских квадратов. Тетраэдальное число.
-
57 = 111 по основанию 7.
-
58 Половина, сумма цифр и сумма квадратов цифр - простые числа.
-
59 Наименьшее число, представляемое четвертыми степенями чисел в форме a4+b4-c4.
-
60 Наименьшее число, имеющее своими делителями все числа от 1 до 6.
-
61 Это шестое число Эйлера. Шестиугольное число.
-
62 Наименьшее число, которое может быть представлено суммой трех квадратов двумя способами.
-
63 Количество вариантов упорядочивания множества из 5 элементов.
-
64 Наименьшее число, имеющее 7 делителей.
-
65 Еще одно (как и 50) число, которое можно представить как сумму квадратов двумя способами.
-
66 Треугольное число. Количество сочетаний двух или десяти чисел из двенадцати.
-
67 Наименьшее число, которое будет палиндромным, если его представить по основанию 5 или 6.
-
68 Попытка проследить последовательные суммы квадратов цифр сразу обрывается, так как ряд замыкается.
-
69 интересно тем, что n2 и n3 вместе содержат все цифры.
-
70 Количество сочетаний четырех элементов из восьми.
-
71 Делитель суммы всех простых чисел, меньших его самого. Перестановочное (с 17) простое число.
-
72 Максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в шестимерном пространстве.
-
73 Наименьшее из чисел (исключая 1), которое меньше удвоенного числа с перевернутыми цифрами (37*2=74). Перестановочное (с 37) простое число.
-
74 Одно из чисел с таким свойством, что сумма его с перевернутым числом равна квадрату суммы его цифр (74+47=11^2). Число областей, на которые делят плоскость 9 пересекающихся окружностей.
-
75 Если сложить сумму цифр с их произведением и повторять эту операцию, то вскоре зациклимся на числе 39.
-
76 Количество треугольников, которые можно сложить из зубочисток 6 цветов.
-
77 Наибольшее число, которое не может быть представлено суммой ряда чисел, начиная с 1.
-
78 Наименьшее число, которое может быть представлено суммой четырех квадратов тремя вариантами. Треугольное число. Количество сочетаний двух или одиннадцати чисел из тринадцати.
-
79 Перестановочное простое число, так как 97 тоже простое.
-
80 Наименьшее число n такое, что n и n+1 оба являются произведениями четырех и более простых чисел.
-
81 Квадрат суммы цифр.
-
82 Пятиугольное число.
-
83 Еще одно из чисел с таким свойством, что сумма его с перевернутым числом равна квадрату суммы его цифр.
-
84 Тетраэдальное число. Количество сочетаний трех или шести чисел из девяти. Количество областей, на которые делят пространство 7 сфер.000
-
85 Если взять сумму квадратов цифр и повторять эту операцию, то вскоре попадем в замкнутое кольцо, в котором, что самое интересное, число 85 не участвует.
-
86 = 222 по основанию 6.
-
87 Единственное ничем не примечательное число в первой сотне, этим и интересно :) 03.01.2002 Василий Данилов прислал сообщение о том, что 87 - сумма квадратов первых 4 простых чисел 87 = 22 + 32 + 52 + 72 с сылкой на источник! Зайдите - это интересно!
-
88 Единственное число из двух одинаковых цифр, квадрат которого содержит две пары одинаковых цифр. Имеет горизонтальную и вертикальную оси симметрии.
-
89 = 81 + 92 Число из последовательности Фибоначчи.
-
90 Число десятков равно количеству делителей (не считая 1)
-
91 Запишется как 10101 по основанию 3. Шестиугольное число. Самое большое число, для которого выполняется равенство 12+22+32+...+n2 = 1+2+3+...+m, поэтому оно пирамидальное и еще и треугольное число.
-
92 Число расстановок восьми ферзей на шахматной доске так, чтобы они не угрожали друг другу. Число областей, на которые делят плоскость 10 пересекающихся окружностей.
-
93 = 333 по основанию 5.
-
94 Половина, сумма цифр и сумма квадратов цифр - простые числа.
-
95 Количество вариантов разделения плоскости на 10 областей.
-
96 Наименьшее число, которое можно представить как сумму квадратов четырьмя способами.
-
97 Наименьшее из чисел, три первых кратных которого содержат цифру 9. Перестановочное (с 79) простое число.
-
98 Наименьшее из чисел, пять первых кратных, которого содержат цифру 9.
-
99 Число Капрекара, так как 992=9801, а 98+01=99.
-
100 Наименьший квадрат, равный сумме кубов четырех последовательных чисел.
Заключение
Вывод: В своей работе я постаралась узнать свойства чисел, которые в школьном курсе математики не рассматриваются, произвела вычисления и доказала, что эти числа действительно подчинятся заданным критериям.


