- Преподавателю
- Математика
- ВКР по теме: МЕТОД КООРДИНАТ И ЕГО ИЗУЧЕНИЕ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
ВКР по теме: МЕТОД КООРДИНАТ И ЕГО ИЗУЧЕНИЕ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Перевалова О.А. |
| Дата | 21.01.2015 |
| Формат | doc |
| Изображения | Есть |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Дальневосточный государственный гуманитарный университет»
Кафедра математики и информационных технологий
МЕТОД КООРДИНАТ И ЕГО ИЗУЧЕНИЕ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
выпускная квалификационная работа
по специальности 050201.65 «Математика»
Хабаровск, 2015
СОДЕРЖАНИЕ
Введение 3
Глава 1. Теоретические основы темы: Метод координат и его изучение в школьном курсе геометрии. 5
1.1 Основные положения изучения метода координат в школе 5
1.2 Суть метода координат 7
1.3 Метод координат на плоскости 10
1.4 Метод координат в пространстве 17
1.5 Уравнения геометрических мест точек 25
1.6 Применение и значение метода координат 28
Глава 2. Методические основы темы: Метод координат и его изучение в школьном курсе геометрии 31
2.1 Анализ школьных учебников 31
2.2 Этапы решения задач методом координат 35
2.3 Задачи, обучающие координатному методу 37
2.4 Опытное преподавание 44
Глава 3. Использование ЭВМ при изучении темы: Метод координат и его изучение в школьном курсе геометрии 52
3.1 Роль и место компьютера в учебном процессе 52
3.2 Применение УМК «Живая математика» 57
3.3 Применение программы «GeoGebra» 64
Заключение 69
Библиографический список 71
Приложение ……………………………………………………………………74
ВВЕДЕНИЕ
В геометрии применяются различные методы решения задач - это синтетический (чисто геометрический) метод, метод преобразований, векторный, метод координат и другие. Они занимают различное положение в школе. Основным методом считается синтетический, а из других наиболее высокое положение занимает метод координат потому, что он тесно связан с алгеброй. Изящество синтетического метода достигается с помощью интуиции, догадок, дополнительных построений. Координатный метод этого не требует: решение задач во многом алгоритмизировано, что в большинстве случаев упрощает поиск и само решение задачи.
Можно с уверенностью говорить о том, что изучение данного метода является неотъемлемой частью школьного курса геометрии. Но нельзя забывать, что при решении задач координатным методом необходим навык алгебраических вычислений и не нужна высокая степень сообразительности, а это в свою очередь негативно сказывается на творческих способностях учащихся. Поэтому необходима методика изучения метода координат, позволяющая учащимся научиться решать разнообразные задачи координатным методом, однако не показывающая этот метод как основной для решения геометрических задач. Этим и определяется актуальность выбранной темы: «Изучение метода координат в школьном курсе геометрии основной школы».
Объект исследования данной работы - это процесс изучения учащимися геометрии.
Предметом исследования является изучение метода координат в курсе геометрии основной школы.
Цель работы - разработать методику изучения и использования метода координат в школьном курсе геометрии.
Гипотеза: изучение метода координат в школе будет более эффективно, если:
-
в 5-6 классе проведена пропедевтическая работа по формированию основных умений и навыков;
-
в системном курсе планиметрии учащиеся знакомятся со структурой этого метода;
-
используется продуманная система задач для формирования отдельных компонентов метода.
-
используется компьютеризация процесса обучения в целом.
Предмет, цель и гипотеза исследования определяют следующие задачи:
-
Анализ вариантов изучения метода координат в некоторых из действующих учебников, а также содержание программы по математике по данной теме.
-
Описание метода координат и способов его применения на примере конкретных математических задач.
-
Выделение умений, необходимых для успешного овладения методом координат и подбор задач, формирующих данные умения.
-
Опытная проверка.
-
Применение ЭВМ при изучении темы.
Для достижения целей работы, проверки гипотезы и решения поставленных выше задач были использованы следующие методы:
-
анализ программы по математики, учебных пособий, методических материалов, касающихся метода координат;
-
наблюдение за ходом образовательного процесса, за деятельностью учащихся при использовании в обучении новых компьютерных технологий.
Основной опытной базой являлась средняя общеобразовательная школа п.Обор.
ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕМЫ: МЕТОД КООРДИНАТ И ЕГО ИЗУЧЕНИЕ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
1.1 ОСНОВНЫЕ ПОЛОЖЕНИЯ ИЗУЧЕНИЯ МЕТОДА КООРДИНАТ В ШКОЛЕ
Придавая геометрическим исследованиям алгебраический характер, метод координат переносит в геометрию наиболее важную особенность алгебры - единообразие способов решения задач. Если в арифметике и элементарной геометрии приходится, как правило, искать для каждой задачи особый путь решения, то в алгебре и аналитической геометрии решения проводятся по общему для всех задач плану, легко приспособляемому к любой задаче. Перенесение в геометрию свойственных алгебре и поэтому обладающих большой общностью способов решения задач составляет главную ценность метода координат.
Другое достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений.
Можно выделить следующие цели изучения метода координат в школьном курсе геометрии:
-
дать учащимся эффективный метод решения задач и доказательства ряда теорем;
-
показать на основе этого метода тесную связь алгебры и геометрии;
-
способствовать развитию вычислительной и графической культуры учащихся.
В школе изучение координатного метода и обучение его применению для решения различных математических задач происходит в несколько этапов. На первом этапе вводится основной понятийный аппарат, который хорошо отрабатывается в 5-6 классах и систематизируется в курсе геометрии. В 5 классе учащиеся знакомятся с координатным лучом, который в последствии, при изучении отрицательных чисел, дополняется до координатной прямой. И уже после введения рациональных чисел в 6 классе учащиеся изучают координатную плоскость. На втором этапе ученики знакомятся с уравнениями прямой и окружности. Данные понятия изучаются ими как в алгебре, так и в геометрии с разной содержательной целью, поэтому учащиеся часто не видят связи между ними, а, значит, и плохо усваивают суть метода. Так, в курсе алгебры VII класса графики основных функций вводятся путем построения ряда точек, координаты которых вычисляются по аналитическому заданию функции. В курсе геометрии уравнение прямой и окружности вводится на основе геометрических характеристических свойств, как множество точек, обладающих определенным свойством (равноудаленности от 2 точек - для прямой, от одной точки - для окружности). Обучение применению самого метода координат для решения задач происходит в курсе геометрии 9 класса. Для этого сначала раскрываются основные этапы применения метода, а затем на примере ряда задач показывается непосредственное применение метода координат.
Но не следует принимать координатный метод за основной метод решения задач и доказательства теорем. Шарыгин И. Ф. в своей статье [19] говорит о вреде метода координат, как для сильных, так и для слабых учеников. Что касается слабых учеников, то «большей частью в этой группе находятся дети, которые плохо считают, с трудом понимают и запоминают формулы. Для этих детей Геометрия могла бы стать предметом, за счет которого они могли бы компенсировать недостатки общематематического развития. А вместо этого она ложится на них дополнительным грузом… Координатный метод оставляет в стороне геометрическую суть изучаемой геометрической ситуации. Воспитывается исполнитель, решающий заданную конкретную задачу. Не меньше, но и не больше. Не развивается геометрическая, и даже математическая интуиция, столь необходимая математику-исследователю», что в свою очередь составляет опасность для сильных учеников.
1.2 СУТЬ МЕТОДА КООРДИНАТ
Немного из истории координатного метода.
В настоящее время уже очень большое число специалистов из разных областей науки имеют представление о прямоугольных декартовых координатах на плоскости, так как эти координаты дают возможность наглядно при помощи графика изобразить зависимость одной величины от другой. Название «декартовы координаты» наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры. Древний математик александрийской школы Аполлоний Пергский (живший в III-II веке до н. э.) уже фактически пользовался прямоугольными координатами. Он определял и изучал с их помощью хорошо известные в то время кривые: параболу, гиперболу и эллипс.
Аполлоний задавал их уравнениями: у2 =рх (парабола)
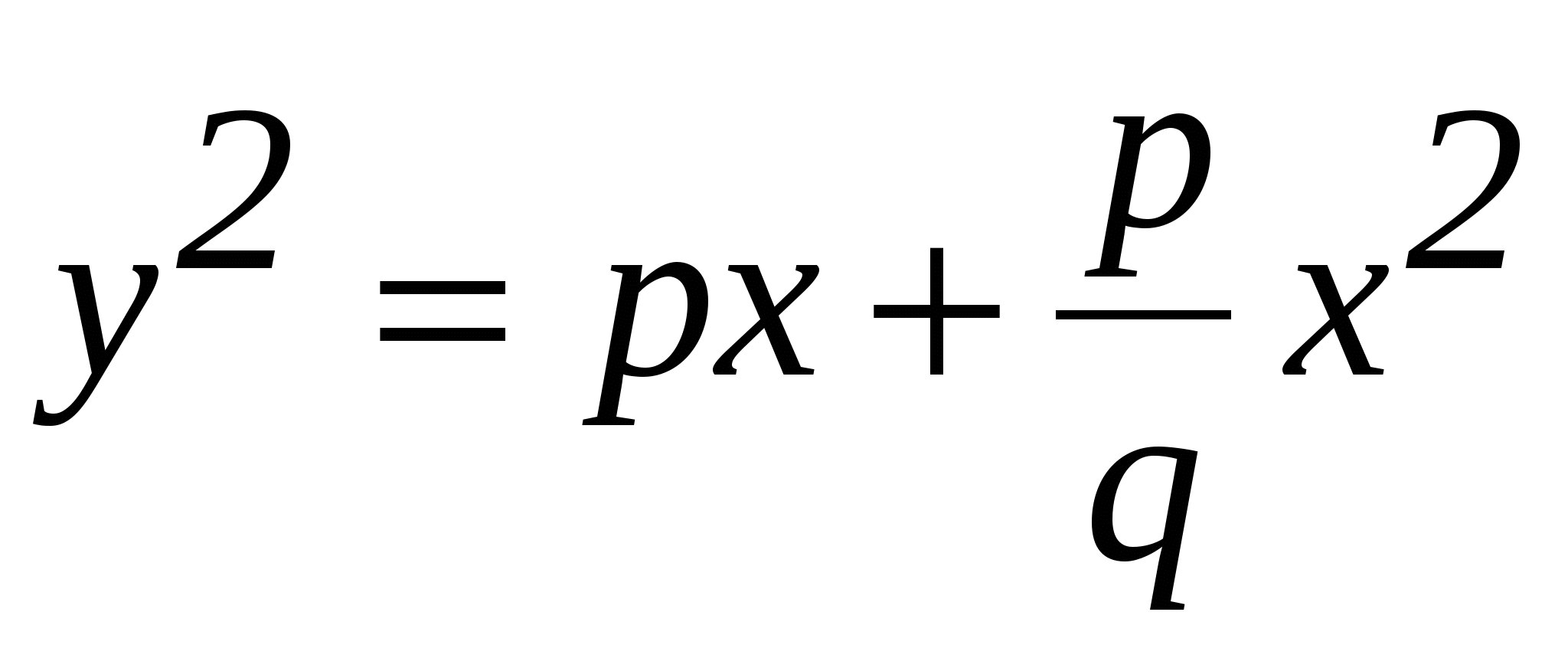 (гипербола)
(гипербола)
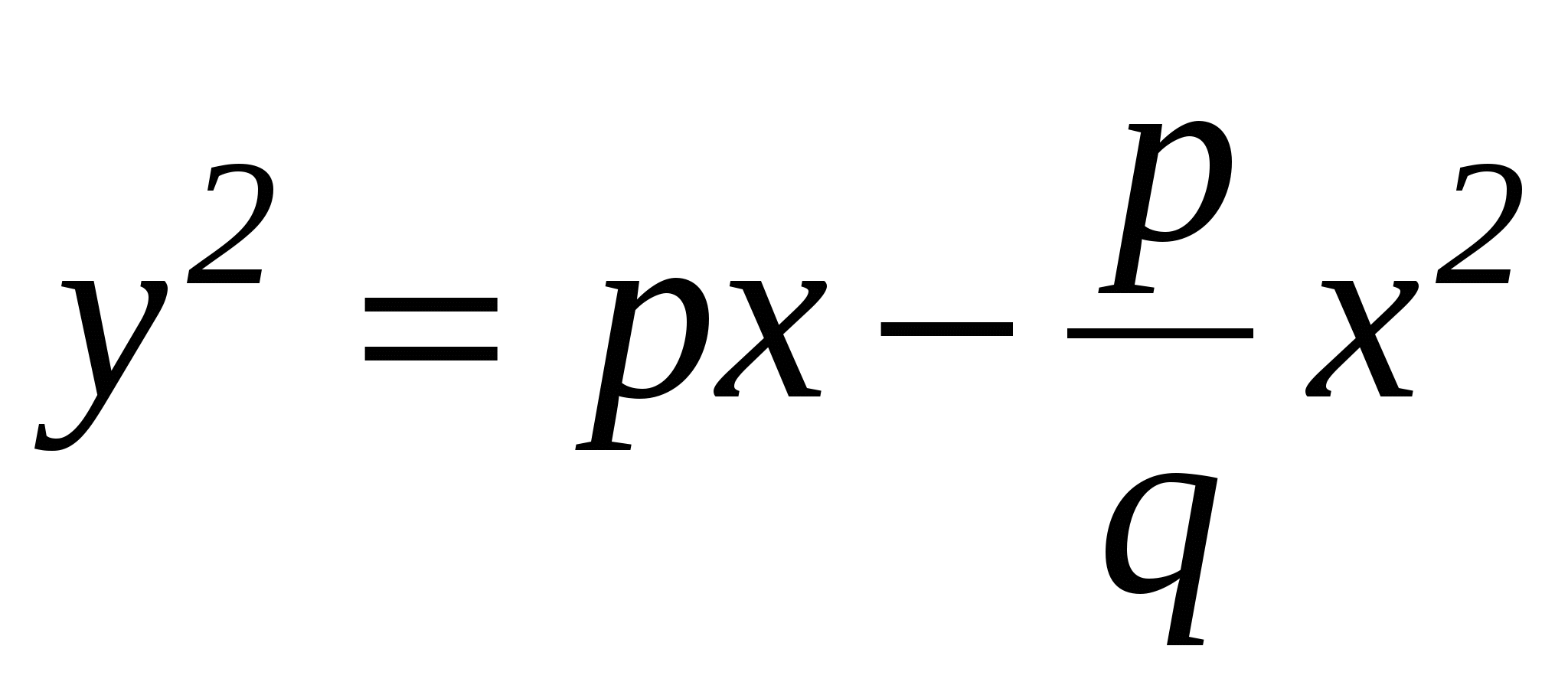 (эллипс, где р и q положительны)
(эллипс, где р и q положительны)
Он, конечно, не выписывал уравнения в этой геометрической форме, так как в те времена не существовало еще алгебраической символики, а описывал уравнения, пользуясь геометрическими понятиями; у2 в его терминологии есть площадь квадрата со стороной у; рх - площадь прямоугольника со сторонами р и х и т.д. С этими уравнениями связаны названия кривых. Парабола по-гречески обозначает равенство: квадрат имеет площадь у2 равную площади рх прямоугольника. Гипербола по-гречески обозначает избыток: площадь квадрата у2 превосходит площадь рх прямоугольника. Эллипс по-гречески обозначает недостаток: площадь квадрата меньше площади прямоугольника.
Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру. Нужно сказать, однако, что одновременно с Декартом построил аналитическую геометрию и другой французский математик, Ферма.
Значение аналитической геометрии состоит, прежде всего, в том, что она установила тесную связь между геометрией и алгеброй. Эти две ветви математики ко времени Декарта достигли уже высокой степени совершенства. Но развитие их в течение тысячелетий шло независимо друг от друга, и ко времени появления аналитической геометрии между ними намечалась лишь довольно слабая связь.
К оординаты позволяют определять с помощью чисел положение любой точки пространства или плоскости. Это дает возможность «шифровать» различного рода фигуры, записывая их при помощи чисел. Соотношения между координатами чаще всего определяет не одну точку, а некоторое множество (совокупность) точек. Например, если отметить все точки, у которых абсцисса равна ординате, т. е. точки, координаты которых удовлетворяют уравнению х=у, то получится прямая линия - биссектрисы первого и третьего координатных углов.
оординаты позволяют определять с помощью чисел положение любой точки пространства или плоскости. Это дает возможность «шифровать» различного рода фигуры, записывая их при помощи чисел. Соотношения между координатами чаще всего определяет не одну точку, а некоторое множество (совокупность) точек. Например, если отметить все точки, у которых абсцисса равна ординате, т. е. точки, координаты которых удовлетворяют уравнению х=у, то получится прямая линия - биссектрисы первого и третьего координатных углов.
И
Рис.1ногда, вместо «множество точек», говорят «геометрическое место точек». Например, геометрическое место точек, координаты которых удовлетворяют соотношению х=у - это, как было сказано выше, биссектрисы первого и третьего координатного угла. Установление связей между алгеброй, с одной стороны, и геометрией - с другой, было по существу, революцией в математике. Оно восстановило математику как единую науку, в которой нет «китайской стены» между отдельными ее частями.
Суть метода координат
Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.
Метод координат - это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.
В отношении школьного курса геометрии можно сказать, что в некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами. Метод координат связан, правда, с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. И только достаточный опыт позволяет выбирать систему координат наиболее целесообразно.
1.3 МЕТОД КООРДИНАТ НА ПЛОСКОСТИ
-
Аффинная система координат на плоскости.
Определение. Аффинная система координат (или аффинным репером) на плоскости называется упорядоченная тройка точек этой плоскости не лежащих на одной прямой: R={О, Е1, Е2}.
Рассмотрим тогда векторы: е1= ОЕ1 и е2 = ОЕ2 (рис. 2). Поскольку точки О, Е1, Е2, не лежат на одной прямой, поэтому векторы е1и е2 не коллинеарны, следовательно, они образуют базис совокупности V2 всех векторов плоскости. Таким образом, мы приходим к упорядоченной тройке R={О, е1, е2}, состоящей из точки О и двух неколлинеарных векторов е1и е2.
О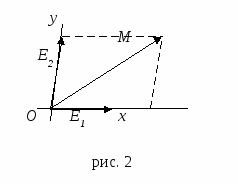 братно если дана упорядоченная тройка R={О, е1, е2}, состоящая из точки О и двух неколлинеарных векторов е1и е2, то от неё легко перейти к тройке R={О, Е1, Е2}, отложив векторы е1и е2 от точки О и взяв соответственно концы этих векторов Е1 и Е2: е1= ОЕ1 и е2 = ОЕ2. Ясно, что точки О, Е1, Е2, не будут лежать на одной прямой, так как векторы е1и е2 не коллинеарны.
братно если дана упорядоченная тройка R={О, е1, е2}, состоящая из точки О и двух неколлинеарных векторов е1и е2, то от неё легко перейти к тройке R={О, Е1, Е2}, отложив векторы е1и е2 от точки О и взяв соответственно концы этих векторов Е1 и Е2: е1= ОЕ1 и е2 = ОЕ2. Ясно, что точки О, Е1, Е2, не будут лежать на одной прямой, так как векторы е1и е2 не коллинеарны.
Таким образом, мы приходим к выводу, что задание на плоскости системы координат как упорядоченной тройки точек R={О, Е1, Е2}, не лежащих на одной прямой, равносильно заданию её как упорядоченной тройки R={О, е1, е2}, состоящей из точки О и двух неколлинеарных векторов е1и е2. В результате в геометрическую картину, составленную из точек, вводятся векторы.
Первая точка О в системе координат R называется началом системы координат, а векторы е1 и е2 - её базисными или координатными векторами. Прямая ОЕ1 с направляющим вектором е1 называется координатной осью Ох, или осью абсцисс, а прямая ОЕ2 с направляющим вектором е2 называется координатной осью Оу, или осью ординат.
Пусть на плоскости задана система координат R={О, е1, е2} и произвольная точка М. Вектор ОМ = rм называется радиус-вектором точки М относительно точки О (или системы координат R).
Определение. Координатами точки М в системе координат R={О, е1, е2} называются координаты её радиус-вектора ОМ в базисе е1, е2, то есть коэффициенты х, у в его разложении в линейную комбинацию векторов базиса: М(х, у)R ОМ = хе1+ уе2.
Итак, понятие координат точки тесно связывается с понятием координат вектора, а понятие системы координат для точек - с понятием базиса векторов. «Привязывая» векторный базис к фиксированной точке плоскости (началу координат), мы приходим к системе координат для точек. Если тот же векторный базис «привязать» к другому началу, мы получим другую систему координат для точек.
Векторы а и в коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Каждой точке М плоскости поставим в соответствие вектор ОМ. Координаты вектора ОМ называются координатами точки М в данной аффинной системе координат. При этом если ОМ = (х, у), то пишут: М (х, у).
Пусть прямые, проведенные через точку М параллельно осям координат, пересекают оси координат соответственно в точках М1 и М2 (рис. 3).
Тогда имеем ОМ = ОМ1 + ОМ2.
С другой стороны, ОМ = хе1+ уе2.
Следовательно, х =ОМ1 / е, у = ОМ2 / е2.
Точки Е1 и Е2имеют координаты: Е1 (1; 0), Е2 (0;1).
Если на плоскости даны две точки А (х1, у1) и В (х2, у2), то координаты вектора АВ вычисляются так: АВ = ОВ - ОА = (х2 - х1, у2 - у1).
Пусть точка С делит отрезок АВ в данном отношении: 
Т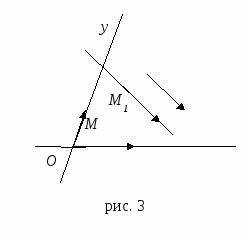 огда
огда  . Из правил действии над векторами в координатах следует, что координаты точки С определяются формулами:
. Из правил действии над векторами в координатах следует, что координаты точки С определяются формулами:
 ,
, 
В частности, если С - середина отрезка АВ, то
 ,
, 
Рассмотрим различные способы задания прямой на плоскости.
Пусть требуется написать уравнение прямой l, заданной в некоторой аффинной системе координат точкой М1 (х1, у1) и ненулевым вектором  , параллельным прямой l (рис. 2).
, параллельным прямой l (рис. 2).
Вектор а будет называться направляющим вектором прямой l .
Пусть М (х, у) - произвольная точка прямой l . Тогда, согласно условию, векторы  и а коллинеарны тогда и только тогда, когда выполняется равенство
и а коллинеарны тогда и только тогда, когда выполняется равенство  , или ОМ = ОМ1 + tа,
, или ОМ = ОМ1 + tа,
где t - некоторое число (параметр). Это соотношение в координатах запишется так: 
Полученные уравнения называют параметрическими уравнениями прямой. При  и
и  эти уравнения равносильны следующему уравнению первой степени:
эти уравнения равносильны следующему уравнению первой степени: 
Если прямая задана двумя различными точками: А (х1, у1) и В (х2, у2), то вектор АВ = (х2 - х1, у2 - у1) является направляющим вектором прямой l. Следовательно, при х1 х2 и у1
х2 и у1 у2 получаем уравнение
у2 получаем уравнение

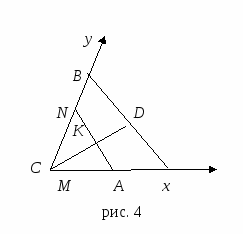 , которое называется уравнением прямой, проходящей через две точки.
, которое называется уравнением прямой, проходящей через две точки.
В частности, если прямая l проходит через точки А (а, 0) и В (0, b), отличные от начала координат, то уравнение прямой принимает вид
частности, если прямая l проходит через точки А (а, 0) и В (0, b), отличные от начала координат, то уравнение прямой принимает вид
Это уравнение называется уравнением прямой в отрезках.
Исключая из параметрических уравнений прямой параметр t. При  получим уравнение: у - у1 = k (х - х1),
получим уравнение: у - у1 = k (х - х1),
где  . Число k называют угловым коэффициентом прямой. В частном случае, при х1 = 0 и у1 = b, уравнение принимает вид
. Число k называют угловым коэффициентом прямой. В частном случае, при х1 = 0 и у1 = b, уравнение принимает вид 
Если же  , то прямая l параллельна оси Оy, а её уравнение запишется так: х = х1.
, то прямая l параллельна оси Оy, а её уравнение запишется так: х = х1.
Таким образом, всякую прямую на плоскости можно задать уравнение первой степени Ах + Ву + С = 0, где хотя бы одно из чисел А и В отлично от нуля. Верно и обратное предложение: всякое уравнение первой степени Ах + Ву + С = 0 есть уравнение некоторой прямой в аффинной системе координат на плоскости.
При  уравнение Ах + Ву + С = 0 приводится к виду у = kх + b, где
уравнение Ах + Ву + С = 0 приводится к виду у = kх + b, где
 ,
, 
Если же В = 0 и  , то оно принимает вид х = а, где
, то оно принимает вид х = а, где  .
.
-
Декартова система координат на плоскости. Прямая и окружность.
О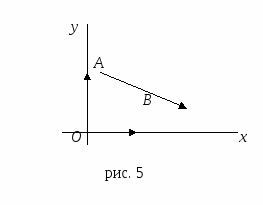 пределение. Декартовой (или ортонормированной, или прямоугольной) системой координат на плоскости называется такая аффинная система координат, базисные векторы которой ортонормированны, то есть имеют единичные длины и ортогональны (перпендикулярны). Обозначение R = {O, i, j}; так что |i| = |j| = 1, i перпендикулярен j.
пределение. Декартовой (или ортонормированной, или прямоугольной) системой координат на плоскости называется такая аффинная система координат, базисные векторы которой ортонормированны, то есть имеют единичные длины и ортогональны (перпендикулярны). Обозначение R = {O, i, j}; так что |i| = |j| = 1, i перпендикулярен j.
При решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.
Пусть даны две точки: А (х1, у1) и В (х2, у2). Тогда, как известно,
 .
.
Пользуясь формулой, запишем уравнение окружности с центром в точке С (a, b) и радиусом r:  .
.
Вышеизложенная теория прямой справедлива и для прямоугольной системы координат. В частности, при решении задач пользуются уравнением прямой с угловым коэффициентом k, проходящей через точку А (х1, у1):
 .
.
О тсюда следует, что угловой коэффициент прямой, заданной двумя точками А (х1, у1) и В (х2, у2), вычисляется по формуле
тсюда следует, что угловой коэффициент прямой, заданной двумя точками А (х1, у1) и В (х2, у2), вычисляется по формуле
Угловой коэффициент в прямоугольной системе координат имеет следующий геометрический смысл:  , где
, где  - величина угла от оси абсцисс до прямой l.
- величина угла от оси абсцисс до прямой l.
Пусть прямые l1 и l2 заданы своими уравнениями с угловыми коэффициентами: у = k1х + b1 и у = k2х + b2.
Если l1 || l2, то  , поэтому k1 = k2, и обратно, т.е. условие k1 = k2 выражает признак параллельности прямых l1 и l2.
, поэтому k1 = k2, и обратно, т.е. условие k1 = k2 выражает признак параллельности прямых l1 и l2.
В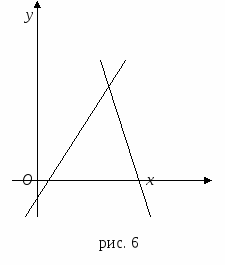 ведем формулу для вычисления угла
ведем формулу для вычисления угла  между пересекающимися прямыми l1 и l2 (рис. 6).
между пересекающимися прямыми l1 и l2 (рис. 6).
Так как  и
и  ,
,  , то
, то


или
Полученную формулу для вычисления угла от прямой l1 до прямой l2 можно записать и так: 
Отсюда следует, что  тогда и только тогда, когда k1k2 = - 1, т.е. условие k1k2 = - 1 выражает признак перпендикулярности прямых l1 и l2.
тогда и только тогда, когда k1k2 = - 1, т.е. условие k1k2 = - 1 выражает признак перпендикулярности прямых l1 и l2.
Приступая к решению геометрической задачи, следует рационально выбрать систему координат, присоединить её к данной фигуре наиболее естественным образом. Желательно, чтобы данные точки располагались на осях координат, тогда среди координат будут нули. Это позволит упростить вычисления.
3. Полярная система координат на плоскости
У равнения многих кривых удобно задавать не в декартовой системе, а в других системах координат. Координатами называются числа, при помощи которых можно определить положение точки. Например, положение точки на поверхности земного шара определяются ее географическими координатами - шириной и долготой. Одной из важных систем координат на плоскости является полярная система координат.
равнения многих кривых удобно задавать не в декартовой системе, а в других системах координат. Координатами называются числа, при помощи которых можно определить положение точки. Например, положение точки на поверхности земного шара определяются ее географическими координатами - шириной и долготой. Одной из важных систем координат на плоскости является полярная система координат.
Полярная система координат задается точкой О и лучом ОА с началом в этой точке. Точка О называется полюсом, ось ОА - полярной осью. Полярными координатами точки М называются ее расстояние r от полюса и угол  , который направленный отрезок ОМ образует с полярной осью.
, который направленный отрезок ОМ образует с полярной осью.
Координата r называется полярным радиусом, а координата  - полярным углом точки М. При этом употребляют запись М(r,
- полярным углом точки М. При этом употребляют запись М(r,  ) . Из определения полярных координат следует, что r
) . Из определения полярных координат следует, что r![]() 0. Координата
0. Координата  определяется неоднозначно, так как координатам (r,
определяется неоднозначно, так как координатам (r,  ) и (r,
) и (r,  ), соответствует одна и та же точка. Если наложить на
), соответствует одна и та же точка. Если наложить на  условие 0
условие 0
 или
или  , то координата
, то координата  становится однозначной. При
становится однозначной. При  точка
точка  совпадает с полюсом, а координата
совпадает с полюсом, а координата  не определена. Кривые могут задаваться уравнениями в полярных координатах так же, как они задаются уравнениями в декартовых координатах [24].
не определена. Кривые могут задаваться уравнениями в полярных координатах так же, как они задаются уравнениями в декартовых координатах [24].
1.4 МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
1. Декартова прямоугольная система координат в пространстве
Координаты точек и векторов.
Декартова прямоугольная система координат в пространстве задается тремя попарно перпендикулярными осями координат с общим началом:
Ох - ось абсцисс, Оу - ось ординат, Оz - ось аппликат.
Плоскости Оху, Оуz, Ozx называются плоскостями координат. Система координат Охуz называется правой, если для наблюдателя, стоящего на плоскости Оху и расположенного так, что ось Оz направлена от ног к голове, кратчайший поворот, совмещающий положительное направление оси Ох с положительным направлением оси Оу, происходит против часовой стрелки. Если же такой поворот происходит по часовой стрелке, то система называется левой. Названия "правая система" и "левая система" объясняются тем, что оси координат правой системы направлены как большой, указательный, средний палец правой руки, расположенные попарно перпендикулярно друг другу, а оси левой системы - как пальцы левой руки [31].
Радиус-вектором точки М относительно декартовой прямоугольной системы координат Охуz называется вектор  . Координатами точки М относительно декартовой прямоугольной системы координат называются проекции ее радиус-вектора на оси координат:
. Координатами точки М относительно декартовой прямоугольной системы координат называются проекции ее радиус-вектора на оси координат:
х=Прх  , у=Пру
, у=Пру  , z=Прz
, z=Прz  , т.е. скалярные величины направленных отрезков
, т.е. скалярные величины направленных отрезков  на осях Ох, Оу, Оz: х=(ОР)х, у=(ОQ)y, z=(OR)z,
на осях Ох, Оу, Оz: х=(ОР)х, у=(ОQ)y, z=(OR)z,
где P, Q, R - проекции точки М на оси Ох, Оу, Оz соответственно. При этом пишут ![]()
Существует определения координат вектора.
Определение. Координатами вектора  относительно декартовой прямоугольной системы координат Охуz называются его проекции на оси координат: ах=Прх
относительно декартовой прямоугольной системы координат Охуz называются его проекции на оси координат: ах=Прх , ау=Пру
, ау=Пру , аz=Прz
, аz=Прz . При этом употребляется запись
. При этом употребляется запись  =( ах ,ау, аz).
=( ах ,ау, аz).
Координаты вектора равны разностям между координатами его конца и начала: если ![]() , то
, то  ,
,  ,
,  выражение координат вектора через координаты его начала и конца. Действительно,
выражение координат вектора через координаты его начала и конца. Действительно,  . Следовательно,
. Следовательно,
 .
.
Аналогичным образом можно найти выражения для  ,
,  .
.
2. Цилиндрическая система координат в пространстве [31].
Цилиндрические координаты - трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем (r,θ,h). В терминах декартовой системы координат,
-
 (радиус) - расстояние от оси z к точке P,
(радиус) - расстояние от оси z к точке P, -
 (азимут или долгота) - угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость
(азимут или долгота) - угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость -
h (высота) - расстояние (с учетом знака) от xy-плоскости до точки P.
Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 2x + 2y = 2c, тогда как в цилиндрических оно выглядит как r = с
П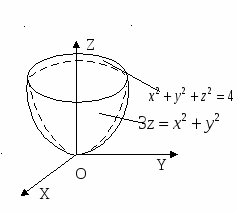 ример: Найти центр тяжести однородного тела, ограниченного сферой
ример: Найти центр тяжести однородного тела, ограниченного сферой  и параболой
и параболой  .
.
Воспользуемся формулами  ,
,
 ,
,  ,
,
где ρ - плотность тела в точке (x,y,z), а m - масса тела: . в которых положим ρ=1. Тело симметрично, центр тяжести лежит на оси Oz, поэтому
. в которых положим ρ=1. Тело симметрично, центр тяжести лежит на оси Oz, поэтому  и необходимо найти аппликату центра тяжести тела, т.е.
и необходимо найти аппликату центра тяжести тела, т.е.  . Т.к. тело симметричное, то в цилиндрической системе координат определяющие неравенства запишем в виде (рассмотрим первую четверть координатной системы.):
. Т.к. тело симметричное, то в цилиндрической системе координат определяющие неравенства запишем в виде (рассмотрим первую четверть координатной системы.):
(V1):  ,
,  ,
,  , а интеграл в виде
, а интеграл в виде 
 Следовательно,
Следовательно,  . Таким образом, центр тяжести данного тела находится в точке
. Таким образом, центр тяжести данного тела находится в точке  .
.
Замечание. Неравенства, определяющие область V1 получены следующим образом. Уравнение  определяется пересечением параболоида
определяется пересечением параболоида  и сферы
и сферы ![]() . Откуда,
. Откуда,  , z=1 и в цилиндрической системе координат
, z=1 и в цилиндрической системе координат  . Следовательно,
. Следовательно,  ; функции
; функции ![]() ,
,  ; а
; а  .
.
Необходимо отметить, что при решении данной задачи не было необходимости выполнять чертеж. Достаточно записать неравенства, определяющие область V.
3. Сферическая система координат
Сферическая система координат определяется так [24]:
Для любой точки А, с прямоугольными координатами (x ; у, z) не совпадающий с началом координат, проводится радиус- вектор ОА, затем проецируется на плоскость xOy, тогда ОА1 =пр(хоу)ОА = угол отсчитывается от оси Ох, а угол в плоскости ZOA от оси Оz. Тогда три параметра ( , , ) образуют сферическую систему координат.
Величину называют сферическим радиусом, - широтой, - долготой. Для 0 широта и долгота неопределенна.
При =90 сферическая система координат вырождается в полярную.
Если полюс и полярная ось совпадают соответственно с началом O и осью Ox прямоугольной системы координат, то при условии, что для измерения , x, y, z использованы равные единицы масштаба, декартовы и сферические координаты связаны соотношениями.

 .
.
Стереографической проекцией называется проекция сферы из одного полюса (скажем южного) на касательную плоскость к другому полюсу (северному). Стереографическая проекция является взаимно однозначным отображением сферы с выколотой точкой на плоскость. С ее помощью можно получать плоское изображение сферы (например, земной поверхности или « небесной сферы»), и поэтому ею с давних времен пользуются астрономы и картографы.
И зобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы
зобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы
астролябии.
Первое свойство сферической проекции - оно сохраняет углы между линиями. Рассмотрим, например, пересечение линий Г1 и Г2 на сфере. Угол ( Г1, Г2) измеряется углом между большими окружностями сферы, касающимися кривых Г1, Г2 в точке их пересечения или углом между касательными к этим окружностям прямыми. Пусть Г1 и Г2 перешли при проекции в 12 . Нужно доказать равенство. (Г1 ;Г2) = ( 1 ; 2).
Не нарушая общности, можно предположить, что Г1 проходит через полюсы сферы. Тогда нужно доказать равенство углов UPW и UP'W.
Для этого рассмотрим плоскость = (МSV), параллельную и проходящую через полюс S, и плоскость (MPV), касающуюся сферы в точке Р. Эти плоскости пересекаются по прямой МV и значит, они симметричны относительно плоскости МОV. Отсюда следует равенство углов UPW и TSR. Но из параллельности плоскостей и сразу следует UP'W =TSR, откуда UPW=UP'W.
 Второе свойство стереографической проекции: окружности на сфере переходят в прямые или окружности на плоскости .
Второе свойство стереографической проекции: окружности на сфере переходят в прямые или окружности на плоскости .
Сразу видно, что окружность на сфере, проходящая через полюс S, отображается на прямую. Покажем, что все другие окружности на сфере стереографическая проекция переводит в окружности на . Для этого вспомним, что плоская кривая, составляющая прямые углы со всевозможными лучами, исходящими из одной точки, является окружностью.
Пусть окружность l проектируется на кривую l', Pl и P' - образ Р. Пусть Q - точка пересечения перпендикуляра к плоскости окружности l , проходящего через ее центр I, и касательной QP к сфере в точке P. Пусть Q' - точка пересечения SQ с . Ясно, что QP l;
значит, по первому свойству, QP l' и в силу замечания из предыдущего абзаца это значит, что l' - окружность.
 Третье свойство стереографической проекции: при вращении сферы относительно оси, проходящей через точки S и N, стереографическая проекция произвольной точки P на сфере будет вращаться около (SN). Другими словами, параллели сферы проектируются в концентрические окружности плоскости , и проекция вращающейся по параллели точки станет вращаться по такой окружности.
Третье свойство стереографической проекции: при вращении сферы относительно оси, проходящей через точки S и N, стереографическая проекция произвольной точки P на сфере будет вращаться около (SN). Другими словами, параллели сферы проектируются в концентрические окружности плоскости , и проекция вращающейся по параллели точки станет вращаться по такой окружности.
Четвертое свойство стереографической проекции; если Р' - проекция точки Р, то |SP| |SP'| = d2 , где d/2 - радиус сферы. Доказательство легко получить из подобия прямоугольных треугольников SP'N и SPN.
Стереографическая проекция и её свойства лежат в основе конструкции и принципа действия астролябии. Название этого прибора означает «схватывают звезды». Схватывание это состоит в измерении координат интересующего нас светила. Сам прибор - сложная металлическая конструкция; он состоит из «паука», вращающегося по криволинейной координатной сетке - «паутине».
1.5. УРАВНЕНИЯ ГЕОМЕТРИЧЕСКИХ МЕСТ ТОЧЕК
1. Определение геометрического места точек
Геометрическое место точек - это множество всех точек, удовлетворяющих определённым заданным условиям.
Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d. Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример2. Окружность - это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек - А).
Тогда отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности AmB, называется дугой. Прямая PQ, проходящая через точки M и N окружности, называется секущей, а её отрезок MN, лежащий внутри окружности - хордой. Хорда, проходящая через центр круга например, BC называется диаметром и обозначается d или D. Диаметр - это наибольшая хорда, равная двум радиусам (d = 2r). Предположим, дана точка А (7; 3; 5); эта запись означает, что точка А определяется координатами х = 7, у = 3, z = 5. Если масштаб для построения чертежа задан или выбран, то откладывают на оси х от некоторой точки О отрезок ОАХ, равный 7 единицам, и на перпендикуляре к этой оси, проведенном из точки Ах, отрезки АХА' = 3 ед. и АХА" = 5 ед. Получаем проекции А' и А". Для построения достаточно взять только ось х. Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Например, отрезок ОАХ - выражает абсциссу точки А, отрезок АХА' - ее ординату, отрезок АХА" - аппликату. Если задается лишь абсцисса, то этому соответствует плоскость, параллельная плоскости, определяемой осями у и z. Действительно, такая плоскость является геометрическим местом точек, у которых абсциссы равны заданной величине. Если задаются две координаты, то этим определяется прямая, параллельная соответствующей координатной оси.
Например, имея заданными абсциссу и ординату, получаем прямую, параллельную оси z (это прямая АВ). Она является линией пересечения двух плоскостей _ и _, где _ - геометрическое место точек с равными ординатами. Прямая АВ служит геометрическим местом точек, у которых равны между собой абсциссы и равны между собой ординаты. Если задаются все три координаты, то этим определяется точка. Точка К, полученная в пересечении трех плоскостей, из которых _ есть геометрическое место точек по заданной абсциссе, _ - по заданной ординате и _ - по заданной аппликате. Точка может находиться в любом из восьми октантов. Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это расстояние отложить; для этого координаты точек выражают относительными числами.
2. Определение уравнения геометрического места точек
Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.
Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные - параметрами.
Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:
1) взять произвольную (текущую) точку M(x, y) линии;
2) записать равенством общее свойство всех точек M линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки M(x, y) и через данные в задаче.
В прямоугольных координатах уравнение прямой на плоскости задается в одном из следующих видов:
1. Уравнение прямой с угловым коэффициентом y = kx + b, (1)
где k - угловой коэффициент прямой, т. е. тангенс того угла, который прямая образует с положительным направлением оси Ox, причем этот угол отсчитывается от оси Ox к прямой против часовой стрелки, b - величина отрезка, отсекаемого прямой на оси ординат. При b = 0 уравнение (1) имеет вид y = kx и соответствующая ему прямая проходит через начало координат.
Уравнением (1) может быть определена любая прямая на плоскости, не перпендикулярная оси Ox.
Уравнение прямой с угловым коэффициентом разрешено относительно текущей координаты y.
2. Общее уравнение прямой Ax + By + C = 0. (2)
Частные случаи общего уравнения прямой:
а) Если C = 0, уравнение (2) будет иметь вид
Ax + By = 0,
и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.
б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид
Ax + С = 0, или 

 .
.
Уравнение не содержит переменной y, а определяемая этим уравнением прямая параллельна оси Oy.
в) Если в общем уравнении прямой (2) A = 0, то это уравнение примет вид
By + С = 0, или 

 ;
;
уравнение не содержит переменной x, а определяемая им прямая параллельна оси Ox.
Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.
г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.
Это уравнение оси Ox.
д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.
Это уравнение оси Oy.
3. Уравнение прямой в отрезках на осях 



 (3)
(3)
где a - величина отрезка, отсекаемого прямой на оси Ox; b - величина отрезка, отсекаемого прямой на оси Oy.
Каждый из этих отрезков отложен от начала координат.
Особенности этого уравнения такие: в левой части уравнения между дробями сосит знак плюс, величины a и b могут быть как положительными, так и отрицательными, правая часть уравнения равна единице.
4. Нормальное уравнение прямой ![]()




 (4)
(4)
Здесь p - длина перпендикуляра, опущенного из начала координат на прямую, измеренная в единицах масштаба, а  - угол, который этот перпендикуляр образует с положительным направлением оси Ox. Отсчитывается этот угол от оси Ox против часовой стрелки. Для приведения общего уравнения прямой (2) к нормальному виду обе его части надо умножить на нормирующий множитель:
- угол, который этот перпендикуляр образует с положительным направлением оси Ox. Отсчитывается этот угол от оси Ox против часовой стрелки. Для приведения общего уравнения прямой (2) к нормальному виду обе его части надо умножить на нормирующий множитель:




 (5)
(5)
причем перед дробью следует выбрать знак, противоположный знаку свободного члена C в общем уравнении прямой (2).
Особенности нормального уравнения прямой: сумма квадратов коэффициентов при текущих координатах равна единице, свободный член отрицателен, а правая его часть равна нулю.
1.6 ПРИМЕНЕНИЕ И ЗНАЧЕНИЕ МЕТОДА КООРДИНАТ
Мысль о возможности систематического применения метода координат в научных исследованиях зародилась несколько тысяч лет тому назад. Известно, например, что астрономы древнего мира, используя специальные системы координат на воображаемой небесной сфере, определяли положение наиболее ярких звёзд, составляли карты звёздного неба, вели отличавшиеся большой точностью наблюдения за перемещением Солнца, Луны и планет относительно неподвижных звёзд. В более позднюю эпоху широко развилось использование системы географических координат для составления карт земной поверхности и определения местонахождения корабля в открытом море. Однако до XVII века применение метода координат имело односторонний характер: им пользовались, по сути, только для указания положения определённого объекта - неподвижного (гора, мыс) или движущегося (корабль, планета).
Метод координат представляет собой глубокий и мощный аппарат, позволяющий привлекать для исследования геометрических объектов. Благодаря универсальности подхода к решению различных задач, метод аналитической геометрии стал основным методом геометрических исследований и широко применяется в других областях точного естествознания - механике, физике.
Сферическая система координат широко применяется в астрономии, в частности при расчетах траектории движения спутников и других объектов. Пример ее использования астролябия.
Стереографическая проекция является взаимно однозначным отображением сферы с выколотой точкой на плоскость. С ее помощью можно получать плоское изображение сферы (например, земной поверхности или « небесной сферы»), и поэтому ею с давних времен пользуются астрономы и картографы.
Изобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы астролябии.
Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физических системы - такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра - гораздо проще моделировать в полярных координатах. Причиной создания полярной системы координат было исследование орбитального и движения по кругу.
Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. 
Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, так и системы с точечными источниками энергии, такие как радиоантенны.
Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических полярных координатах при шести частотах. Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в  полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность.
полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность.
В инженерной деятельности при изучении свойств геометрических объектов используют прямоугольную систему координат, отличающуюся от декартовой системы координат, применяемой в математике, направлением осей.
ГЛАВА II. МЕТОДИЧЕСКИЕ ОСНОВЫ ТЕМЫ: МЕТОД КООРДИНАТ И ЕГО ИЗУЧЕНИЕ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
2.1 АНАЛИЗ ШКОЛЬНЫХ УЧЕБНИКОВ
Хорошо известно, что, как бы ни строился школьный курс геометрии, в нем обязательно присутствуют различные методы доказательства теорем и решения задач. Среди таких методов важное место занимают такие методы, как метод геометрических преобразований, метод координат, векторный метод. Сами эти методы тесно связаны между собой. В зависимости от концепции, раскрываемой авторами учебников геометрии для средней школы, тот или иной метод может занимать доминирующее значение. Так в учебнике [23] активную роль играет метод координат, который весьма плодотворен.
В школьной программе по математике методу координат уделяется сравнительно мало внимания. В разделе «Цели изучения курса геометрии» говорится: «При доказательстве теорем и решении задач… применяются геометрические преобразования, векторы и координаты». Следовательно, программа не ставит целью изучение метода координат как метода решения задач. В программе говорится, что «в результате изучения курса геометрии учащиеся должны уметь использовать координаты для решения несложных стандартных задач». Ни слова не говориться об овладении учащимися методом координат для доказательства теорем и решении задач. Упор делается на «несложные стандартные задачи», тогда как метод координат лучше проявляет свои достоинства при решении нестандартных и довольно сложных (если не решать их другими способами) задач.
В соответствии с программой по математике для средней общеобразовательной школы координаты впервые появляются в 5 классе. При этом, ребята знакомятся с изображением чисел на прямой и координатами точек. Причем введение этих понятий в учебниках различно. Так в учебнике [3] в пятом параграфе первой главы рассматривается координатный луч, с его помощью в дальнейшем происходит сравнение натуральных и дробных чисел, а так же иллюстрация действий сложения и вычитания над натуральными числами. С понятием координатной прямой авторы учебника [4] знакомят учащихся в 6 классе. В учебнике же [6] нет определения «координатный луч». Авторы в начале 5 класса вводят понятие координатной прямой, хотя, до изучения отрицательных чисел, которое происходит в 6 классе, работа идет только с правой частью координатной прямой, представляющей собой координатный луч. Это не совсем удобно, так как могут возникнуть не нужные пока вопросы о другой части этой координатной прямой. В целом, учебники [3], [4] содержат больше заданий, связанных с определением координатного луча, (координатной прямой, а затем и координатной плоскости) и чаще обращаются к нему для введения других понятий или рассмотрения действий над числами, чем учебники [6], [7].
Согласно программе в геометрии координаты изучаются в следующем объеме: «Координатная плоскость. Формула расстояния между двумя точками плоскости с заданными координатами. Уравнение прямой и окружности».[27]
Так, в учебнике [2] координатам посвящена отдельная глава в 9 классе. Причем этот материал изучается после изучения темы «Векторы», но до изучения скалярного произведения векторов. На рассмотрение темы отводиться 18 часов. В данном учебнике метод координат выделен в отдельную главу, в которой изучаются координаты вектора, уравнение окружности и прямой, решаются простейшие задачи в координатах. В этой главе дается понятие метода координат как метода изучения геометрических фигур с помощью средств алгебры. Школьники учатся решать задачи путем введения системы координат. Автор ставит целью научить школьников владеть методом координат не только в применении к задачам на построение фигур по их уравнению, но и при решении задач на доказательство, а также для вывода геометрических формул.
В отличие от других школьных учебников по геометрии в учебнике [23] координаты заняли одно из центральных мест. Они вводятся, начиная с 8 класса после изучения тем «Четырехугольники» и «Теоремы Пифагора». На изучение темы отводится 19 часов. Сразу, после рассмотрения основных понятий, связанных с введением координат на плоскости, уравнений окружности и прямой, с учащимися изучаются такие вопросы, как пересечение двух окружностей, пересечение прямой и окружности, определение синуса, косинуса и тангенса любого угла от 0° до 180°. Это и есть первые приложения метода координат, с которыми знакомятся учащиеся.
В курсе алгебры, исходя из уравнения y=f(x), где f(x) заданная функция, строили кривую, определяемую этим уравнением, т. е. строили график функции y=f(x) . Таким образом, шли как бы «от алгебры к геометрии». При изучении метода координат в геометрии мы выбираем обратный путь: исходя из геометрических свойств некоторых кривых, выводим их уравнение, т. е. идем как бы «от геометрии к алгебре». В 8 классе по учебнику [23] и в 9 по учебнику [2] рассматривается уравнение прямой и окружности. При этом обращается внимание на общее понятие «уравнение фигуры»: «Уравнением фигуры на плоскости в декартовых координатах называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие данному уравнению, являются координатами некоторой точки фигуры»[23]. Уравнение фигуры на плоскости в общем виде можно записывать так: F(х,у)=0, где F(х,у) функция двух переменных х и у.
Учебник [28] реализует авторскую концепцию построения школьного курса геометрии, в нем больше внимания по сравнению с традиционными учебниками уделяется методам решения геометрических задач. Метод координат по данному учебнику является предпоследней темой 9 класса. При его изучении учащиеся знакомятся с декартовыми координатами на плоскости, рассматривают два уравнения «плоских линий: прямой и окружности», которые в дальнейшем будут необходимы при решении задач. В процессе этого отрабатываются некоторые умения, необходимые для решения задач координатным методом. Следует отметить, что в учебнике сравнительно небольшой теоретический материал по данной теме. Так, например, единственной доказанной формулой (причем только для одного случая когда х1≠х2 и у1≠у2), если не считать уравнений линий, является формула расстояния между точками. В отличие от учебников [23] и [2] формула середины отрезка в теоретическом материале не рассматривается, хотя в практических заданиях присутствует задача «Рассмотрим на координатной прямой точки А(-2,5) и В(4,3). Найти координаты точки М, если М - середина АВ», таким образом учащимся предлагается самим вывести формулу координат середины отрезка, рассматривая данный конкретный случай и используя понятия координат и формулу расстояния между точками.
Автор не предлагает учащимся как такового понятия фигуры, но подробно рассматривает уравнения «плоских линий», которые понадобятся учащимся при решении задач. Это уравнения окружности и прямой.
А после изучения векторов рассматривается параграф «Координатный метод», в котором на примере двух разобранных задач, в одной из которых рассматривается окружность Аполлония, а в другой обращается внимание на выбор системы координат, учащимся предлагается ряд задач, решаемых данным методом. Это довольно сложные задачи, в основном связанные с нахождением геометрического места точек.
Автор данного учебника признает, что «координатный метод является одним их самых универсальных методов», но отмечает, что «метода на все случаи жизни нет».
2.2.ЭТАПЫ РЕШЕНИЯ ЗАДАЧ МЕТОДОМ КООРДИНАТ
Чтобы решать задачи как алгебраические, так и геометрические методом координат необходимо выполнение 3 этапов:
1) перевод задачи на координатный (аналитический) язык;
2) преобразование аналитического выражения;
3) обратный перевод, т. е. перевод с координатного языка на язык, в терминах которого сформулирована задача.
Для примера рассмотрим алгебраическую и геометрическую задачи и проиллюстрируем выполнение данных 3 этапов при их решении координатным методом.
№1. Сколько решений имеет система уравнений.
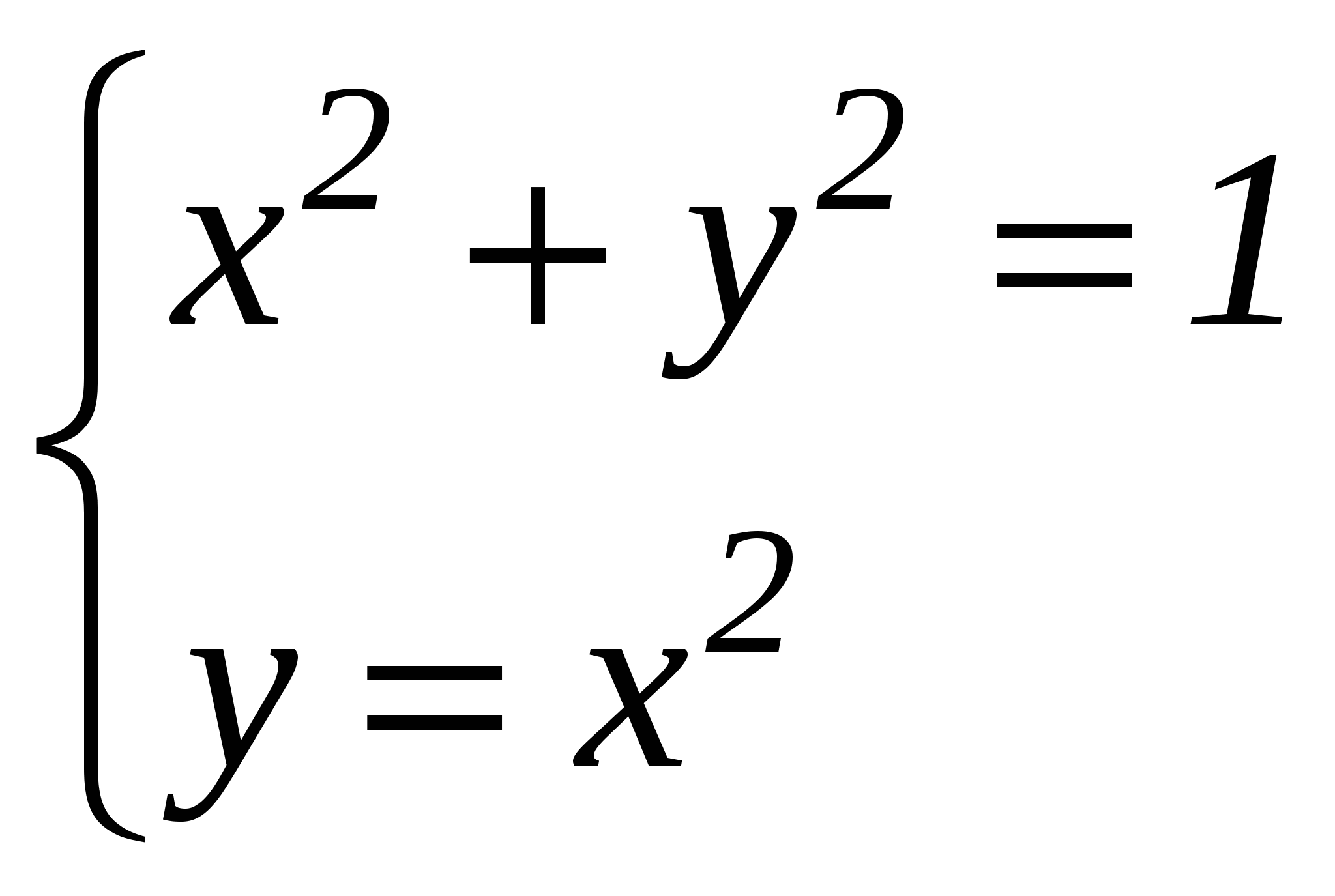
Решение:
1 этап: на геометрическом языке в данной задаче требуется найти, сколько точек пересечения имеют фигуры, заданные данными уравнениями. Первое из них является уравнением окружности с центром в начале координат и радиусом, равным 1, а второе - уравнением параболы.
2 этап: построение окружности и параболы; нахождение точек их пересечения.
3 этап: количество точек пересечения окружности и параболы является ответом на поставленный вопрос.
№2. Найдите множество точек, для каждой из которых расстояния от двух данных точек равны.
Решение:
Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А Предположим далее, что АВ=а, тогда в выбранной системе координат А(0,0) и В(а,0). Точка М(х,у) принадлежит искомому множеству тогда и только тогда, когда АМ=МВ, или, что то же самое, АМ2=МВ2. Используя формулу расстояния от одной точки координатной плоскости до другой, получаем АМ2=x2+y2, MB2=(x-a)2+y2. Тогда х2+у2=(х-а)2 + у2
Равенство х2+у2=(х-а)2+у2и является алгебраической моделью ситуации, данной в задаче. На этом заканчивается первый этап ее решения (перевод задачи на координатный язык).
На втором этапе осуществляется преобразование полученного выражения, в результате которого получаем соотношение 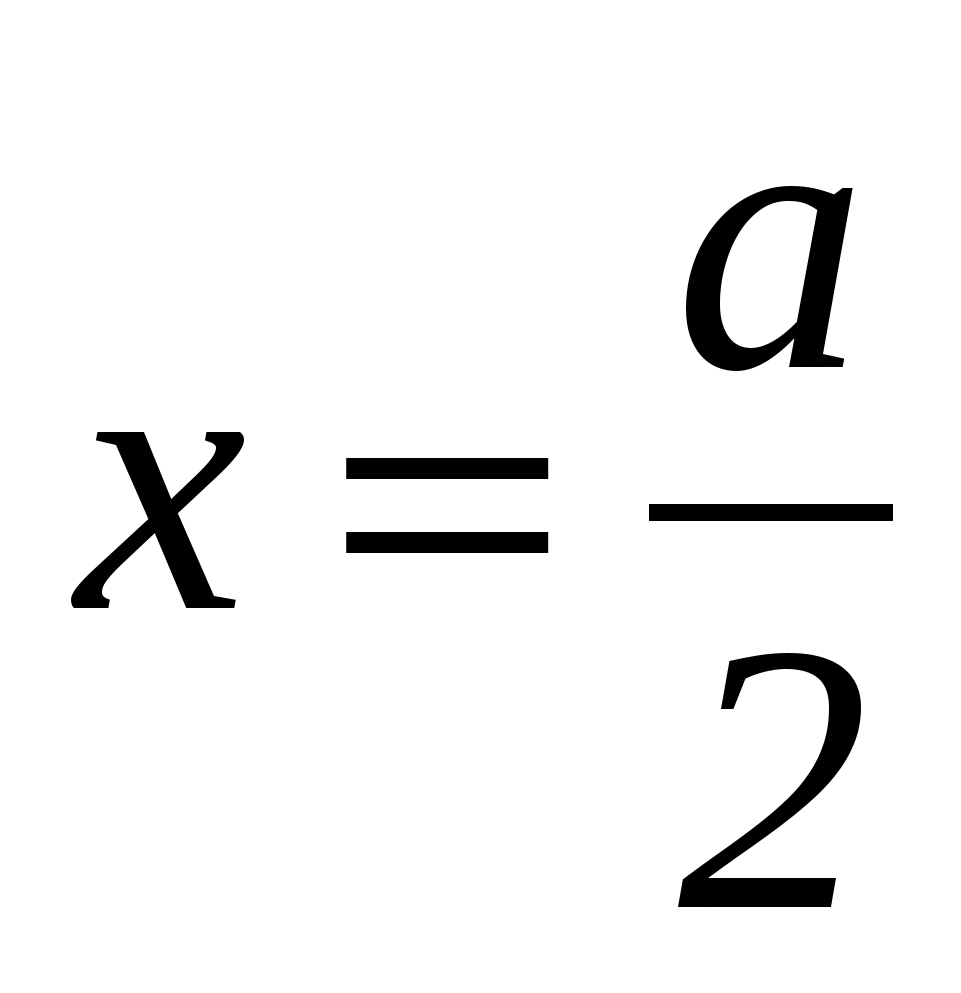 .
.
На третьем этапе осуществляется перевод языка уравнения на геометрический язык. Полученное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние 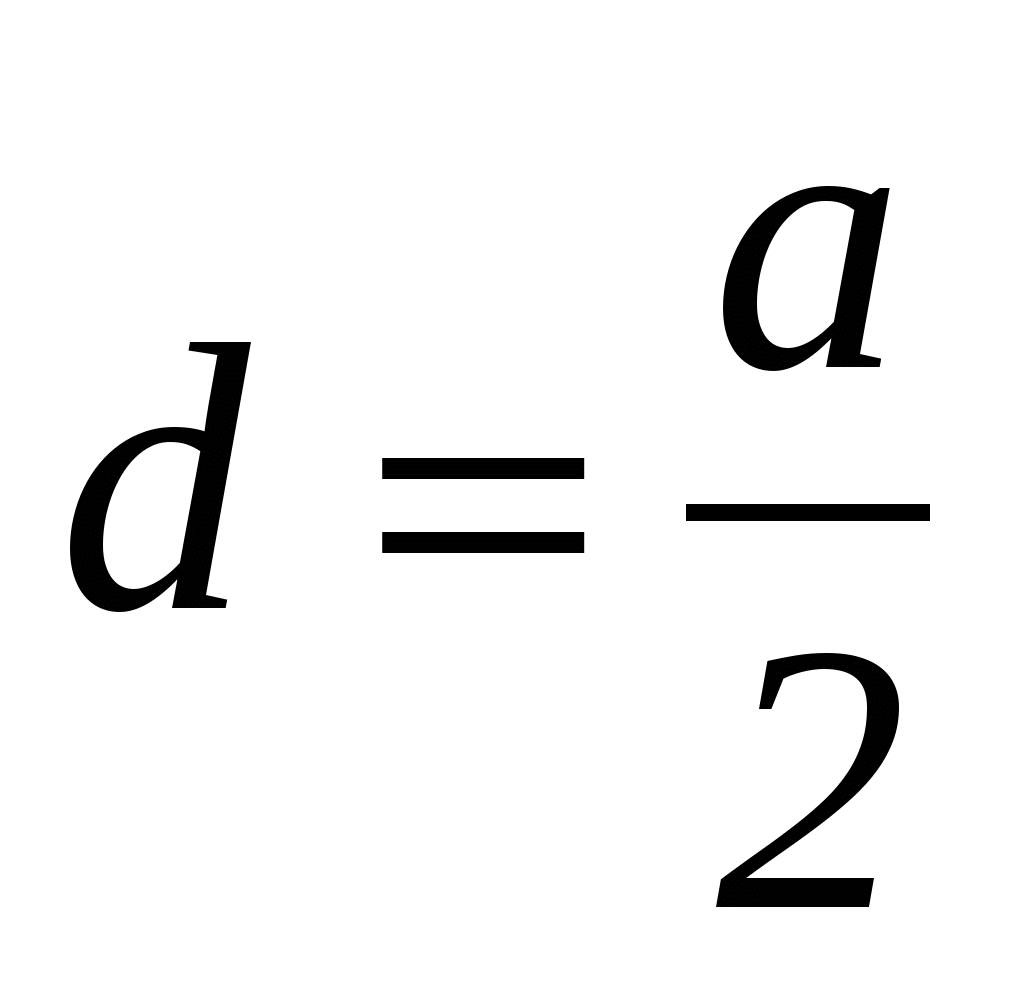 , т.е. серединного перпендикуляра к отрезку АВ.
, т.е. серединного перпендикуляра к отрезку АВ.
2.3 ЗАДАЧИ, ОБУЧАЮЩИЕ КООРДИНАТНОМУ МЕТОДУ
Для разработки методики формирования умения применять координатный метод важно выявить требования, которые предъявляет логическая структура решения задач мышлению решающего. Координатный метод предусматривает наличие у обучающихся умений и навыков, способствующих применению данного метода на практике. Проанализируем решение нескольких задач. В процессе этого анализа выделим умения, являющиеся компонентами умения использовать координатный метод при решении задач. Знание компонентов этого умения позволит осуществить его поэлементное формирование.
Задача №1 . В треугольнике ABC: AC=b, AB=c, ВС=а, BD - медиана. Докажите, что 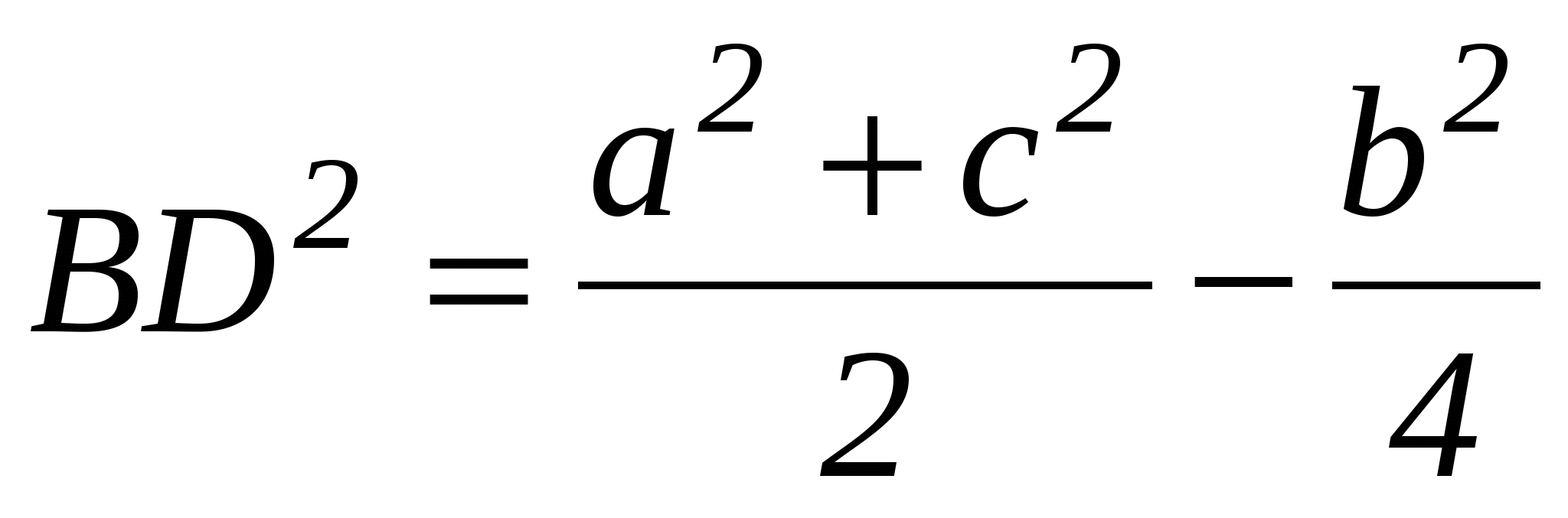 .
.
Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох - прямая АС (рис. 7).
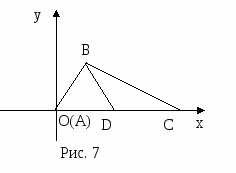 (умение оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).
(умение оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).
В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(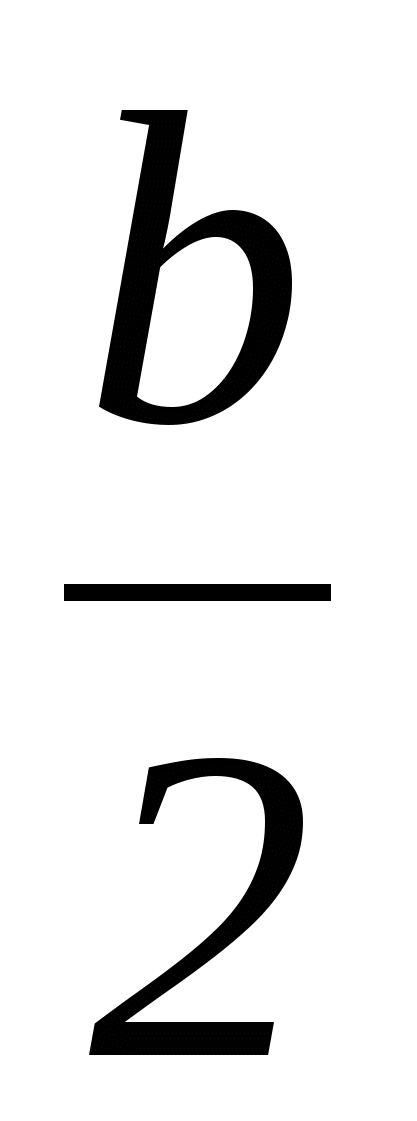 ,0) и С(b,0)
,0) и С(b,0)
(умение вычислять координаты заданных точек). Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:
х2+у2=с2 , (x-b)2+y2=a2 (1)
(умение находить расстояние между двумя точками, заданными координатами)
По той же формуле 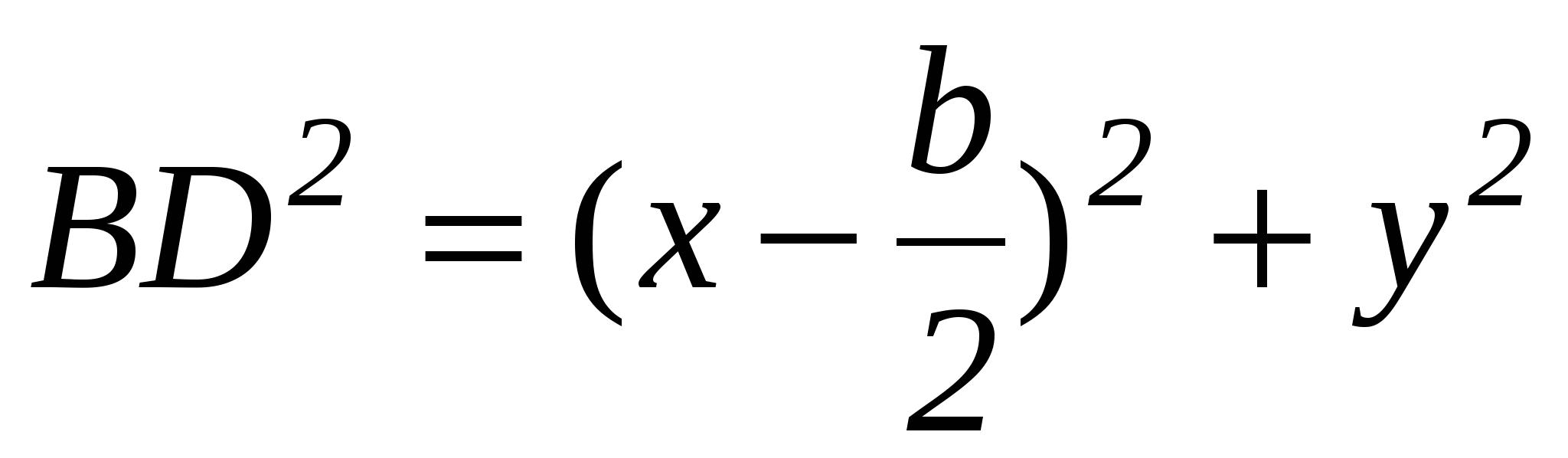 . (2)
. (2)
Используя формулы (1) находим х и у.
Они равны:
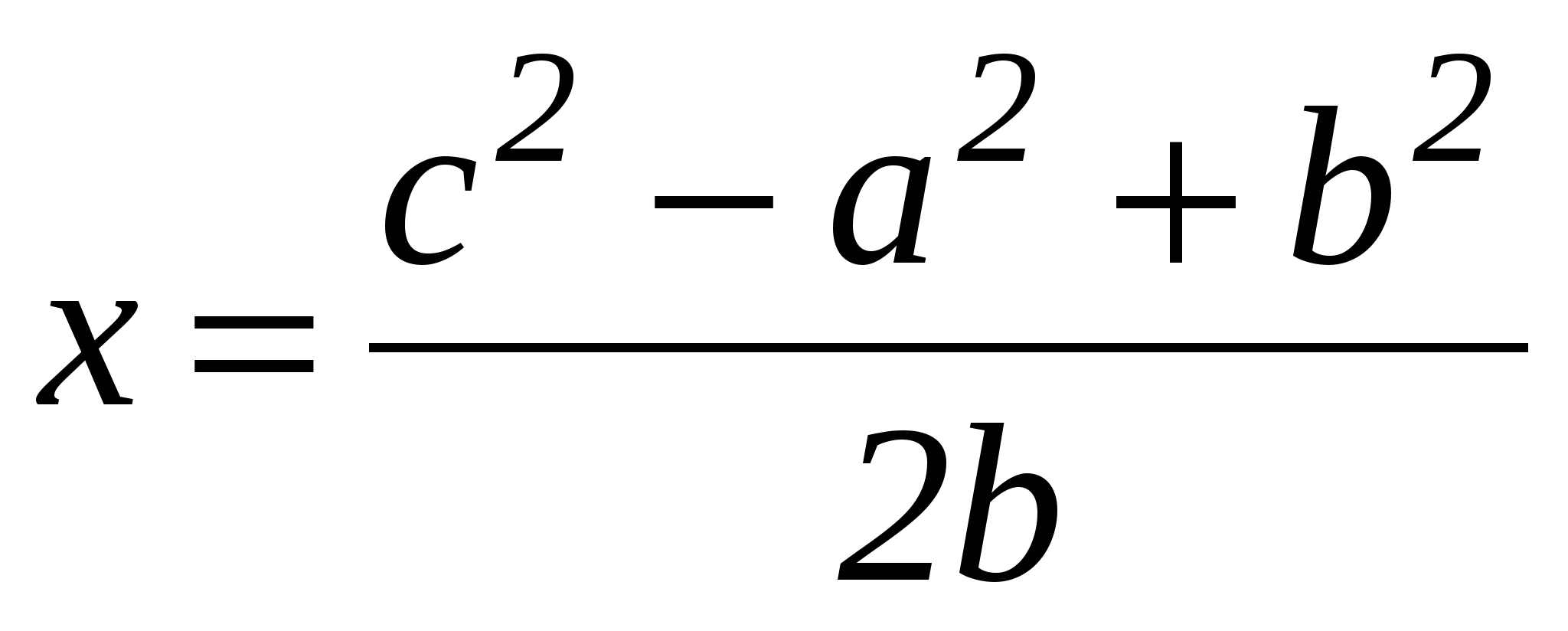 ;
; 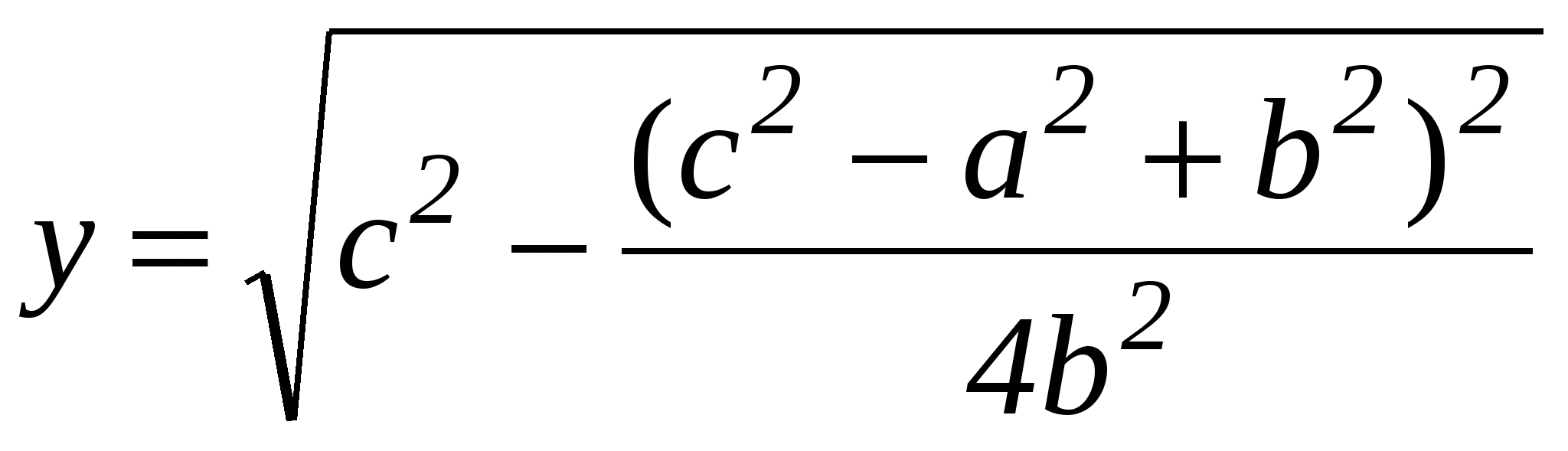 .
.
Далее, подставляя х и у в формулу (2), находим 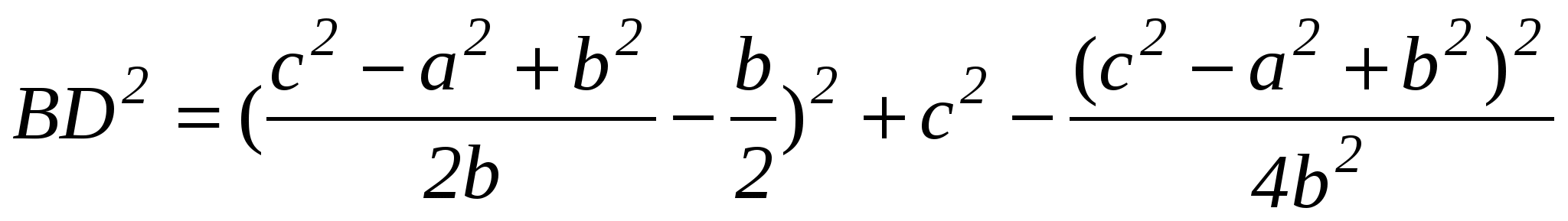 .
.
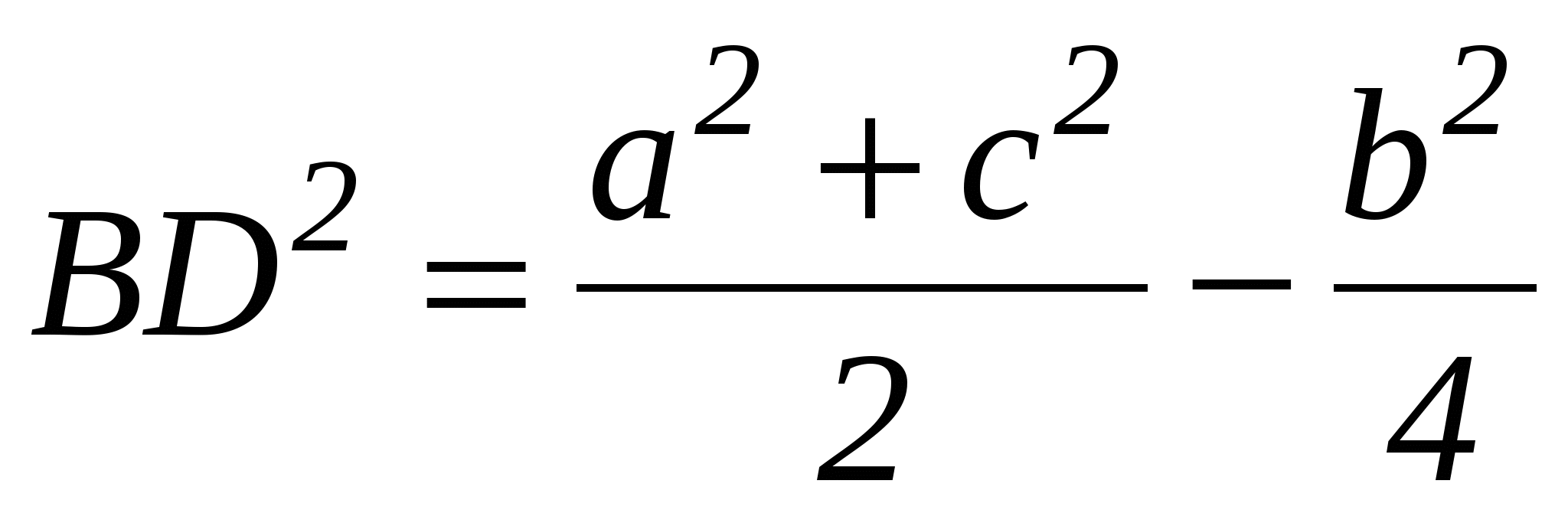 .
.
(умение выполнять преобразования алгебраических выражений)
Задача №2. Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная.
Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А.
(умение оптимально выбирать систему координат).
Предположим АВ=а, тогда в выбранной системе координат А(0,0), В(а,0). (умение находить координаты заданных точек)
Точка М(х,у) принадлежит искомому множеству тогда только тогда, когда AM2-MB2=b2 где b - постоянная величина (умение переводить геометрический язык на аналитический, составлять уравнения фигур).
Используя формулу расстояний между двумя точками, получаем:
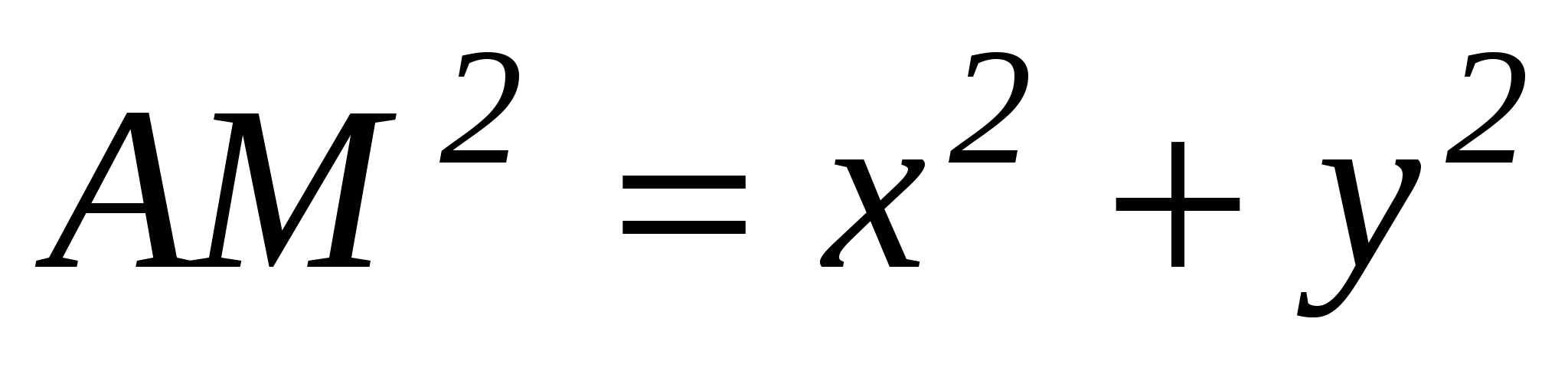 ,
, 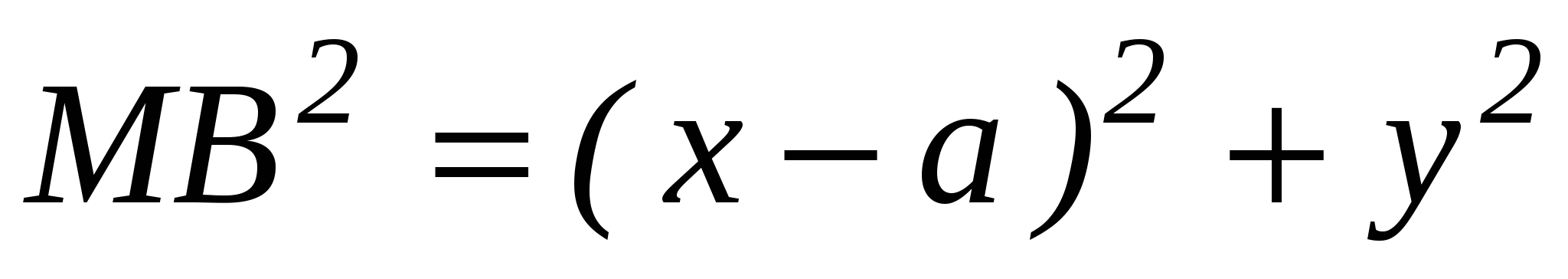 ,
,
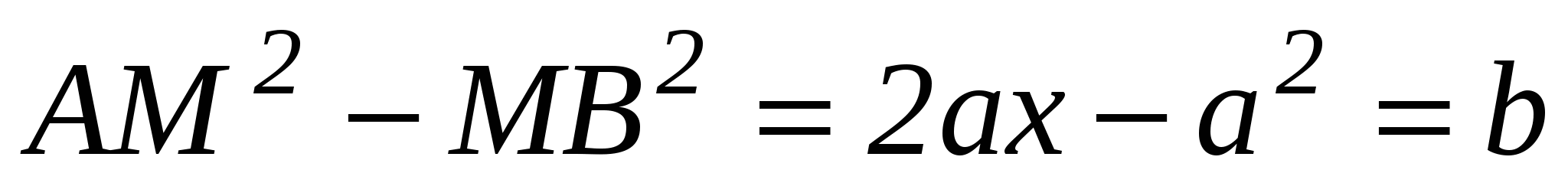
(умение вычислять расстояние между точками, заданными координатами), или 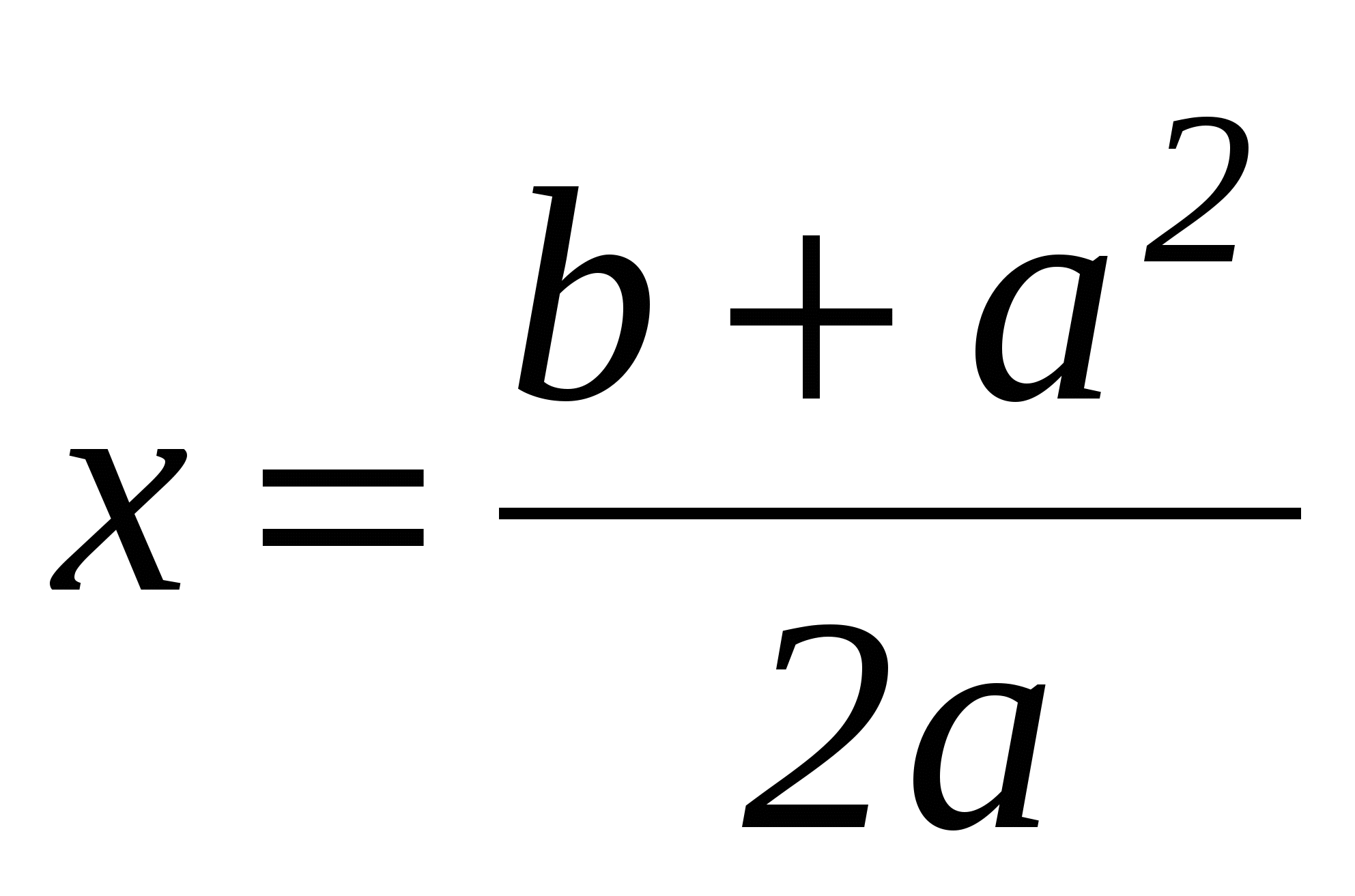 . Данное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние
. Данное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние 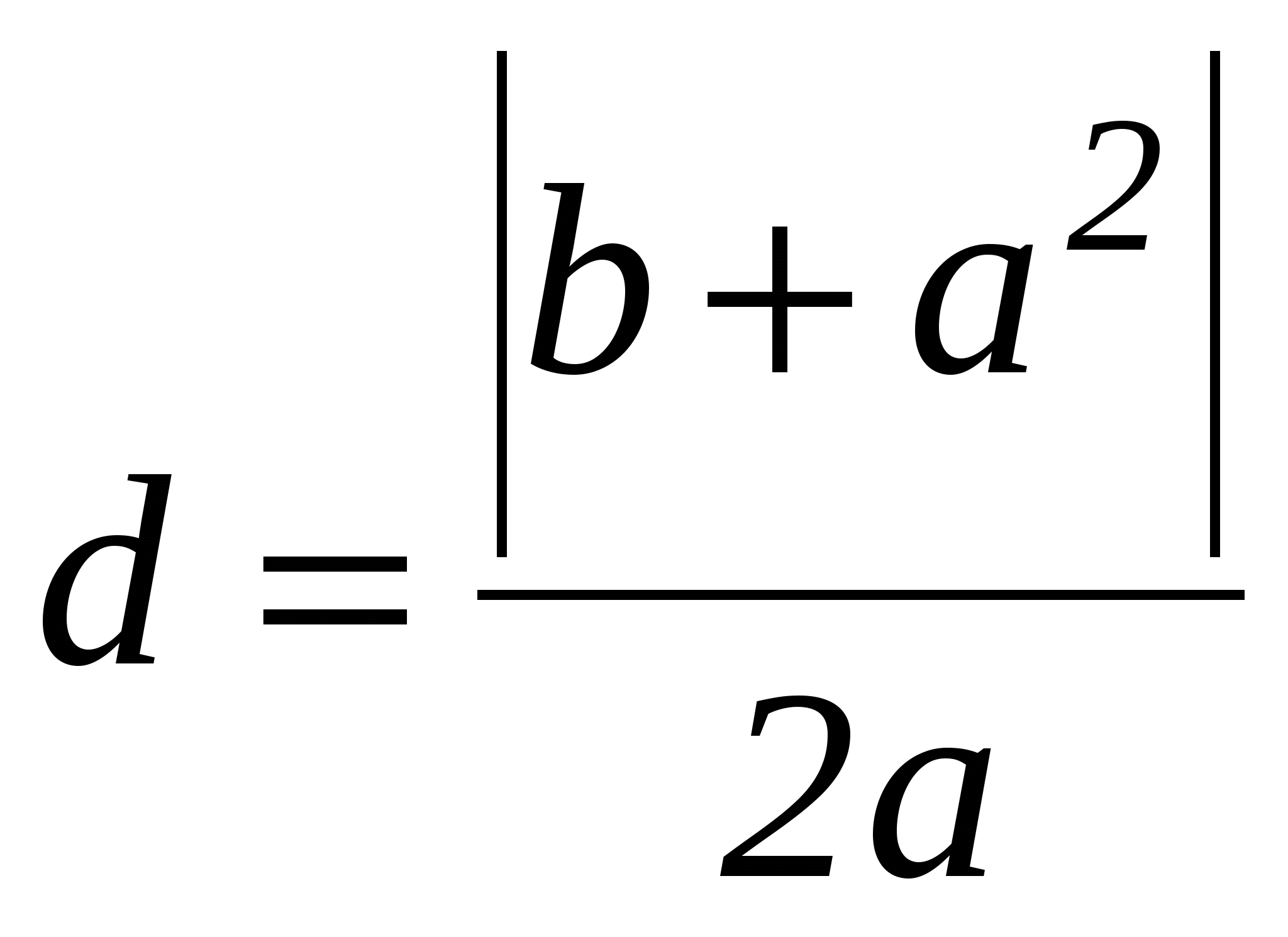 . (умение видеть за уравнением конкретный геометрический образ)
. (умение видеть за уравнением конкретный геометрический образ)
Нетрудно видеть, что и для решения этой задачи необходимо овладение перечисленными выше умениями. Кроме того, для решения приведенной задачи, а также и других задач важно умение «видеть за уравнением» конкретный геометрический образ, которое является обратным к умению составлять уравнения конкретных фигур.
Выделенные умения являются основой при решении и более сложных задач.
Задача №3. В трапеции меньшая диагональ перпендикулярна основаниям. Найти большую диагональ, если сумма противоположных углов равна ![]() , а основания равны а и b.
, а основания равны а и b.
Направим оси координат по меньшей диагонали и одному из оснований (рис. 8).
(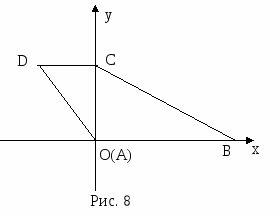 умение оптимально выбирать систему координат).
умение оптимально выбирать систему координат).
Тогда точка А имеет координаты (0,0), точка В - (а,0), точка С - (0,c), точка D - (b,c).
(умение находить координаты заданных точек)
Пусть 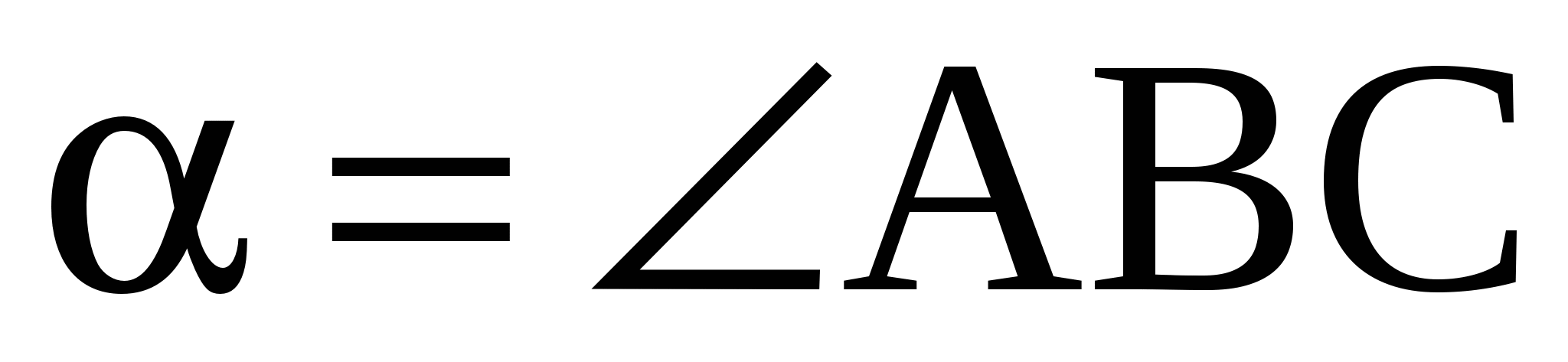 и
и  острые углы в трапеции АВСD, тогда их сумма равна
острые углы в трапеции АВСD, тогда их сумма равна 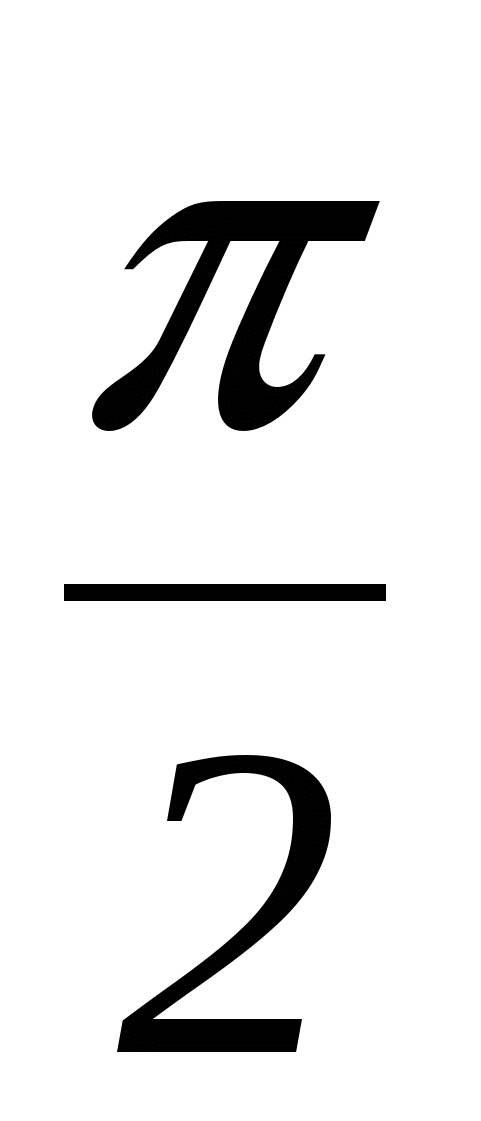 . Для вычисления длины большей диагонали BD надо найти значение с. Его можно вычислить 2 способами. Первый - из прямоугольного треугольника АВС по формуле
. Для вычисления длины большей диагонали BD надо найти значение с. Его можно вычислить 2 способами. Первый - из прямоугольного треугольника АВС по формуле 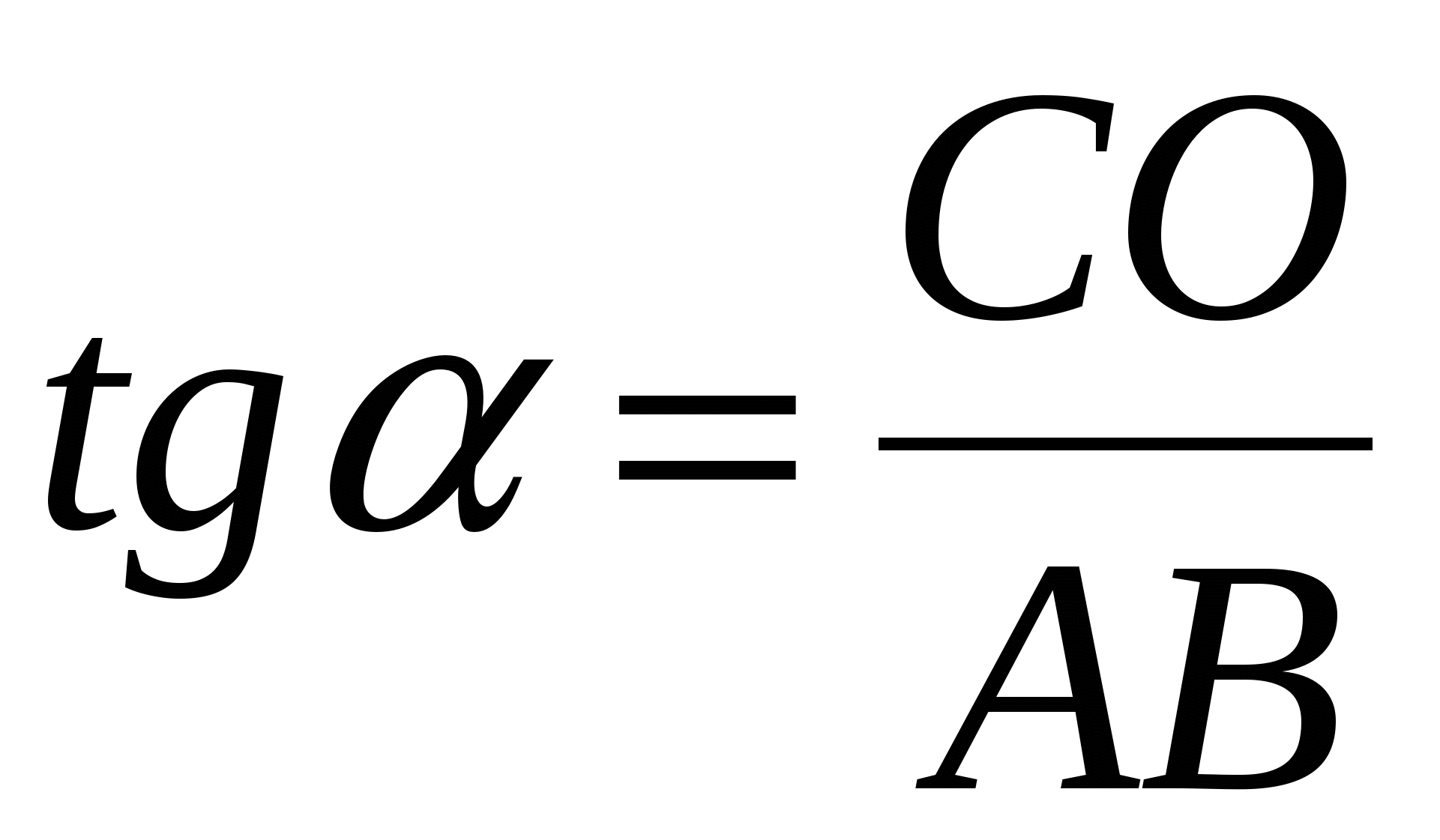 находим
находим 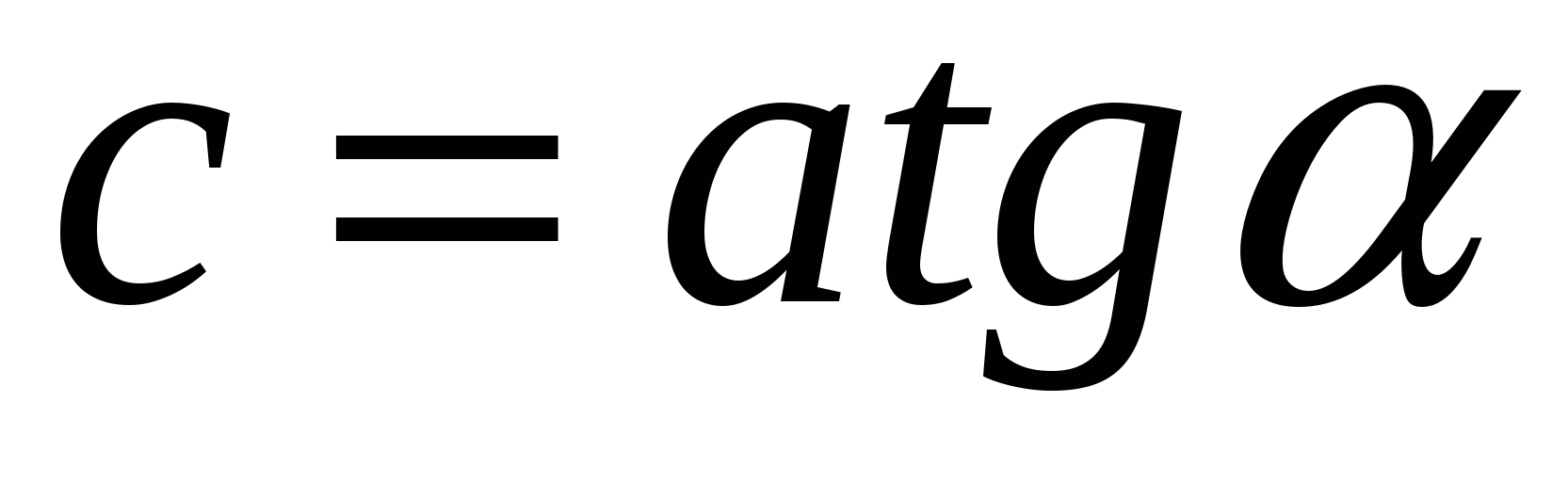 . Второй способ из прямоугольного треугольника ACD:
. Второй способ из прямоугольного треугольника ACD: 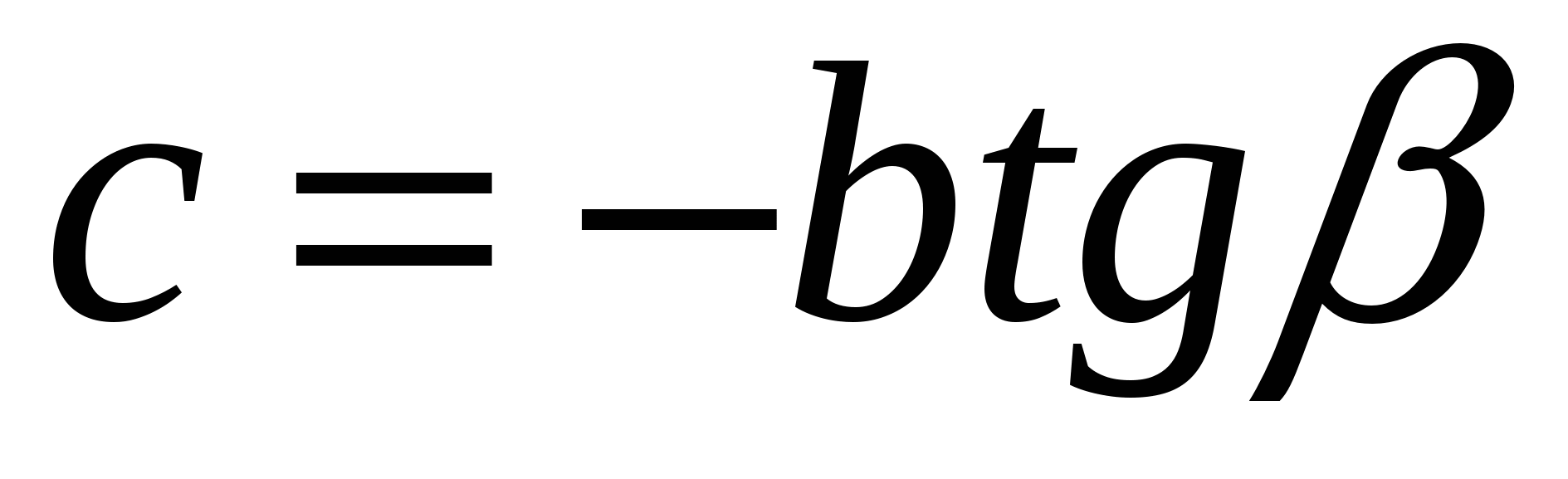 . Отсюда получили, что
. Отсюда получили, что
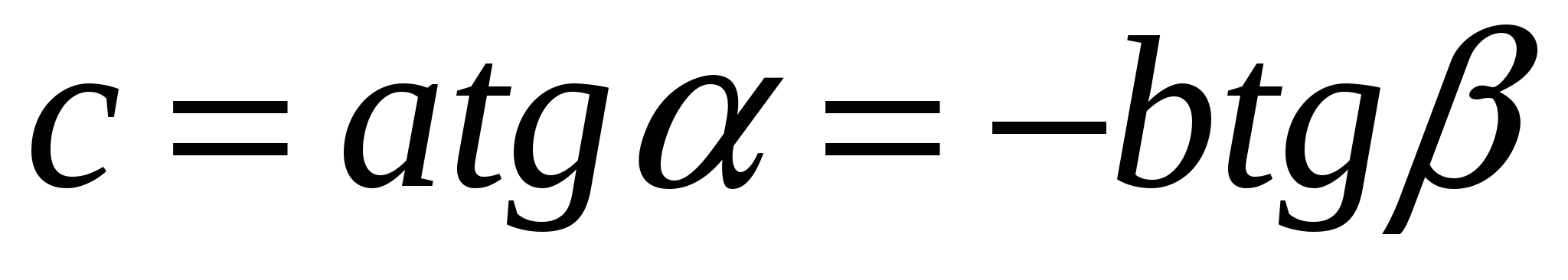 (1)
(1)
Из равенства (1) находим отношение 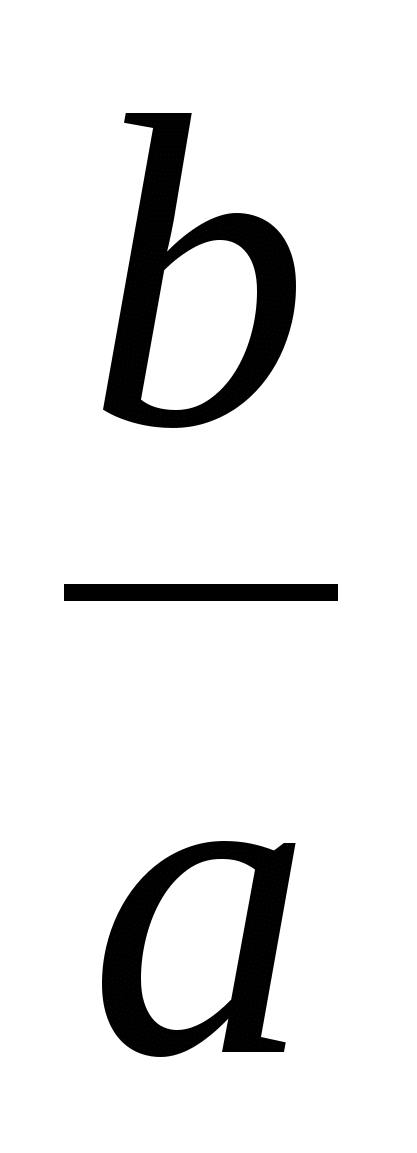 : оно равно -
: оно равно -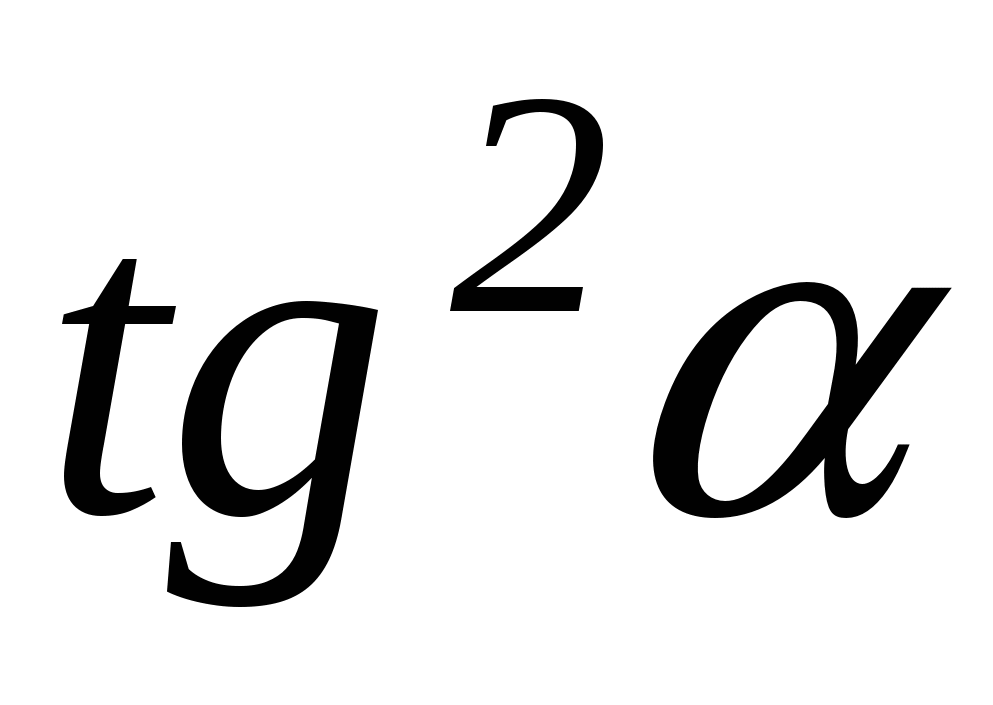 , так как
, так как 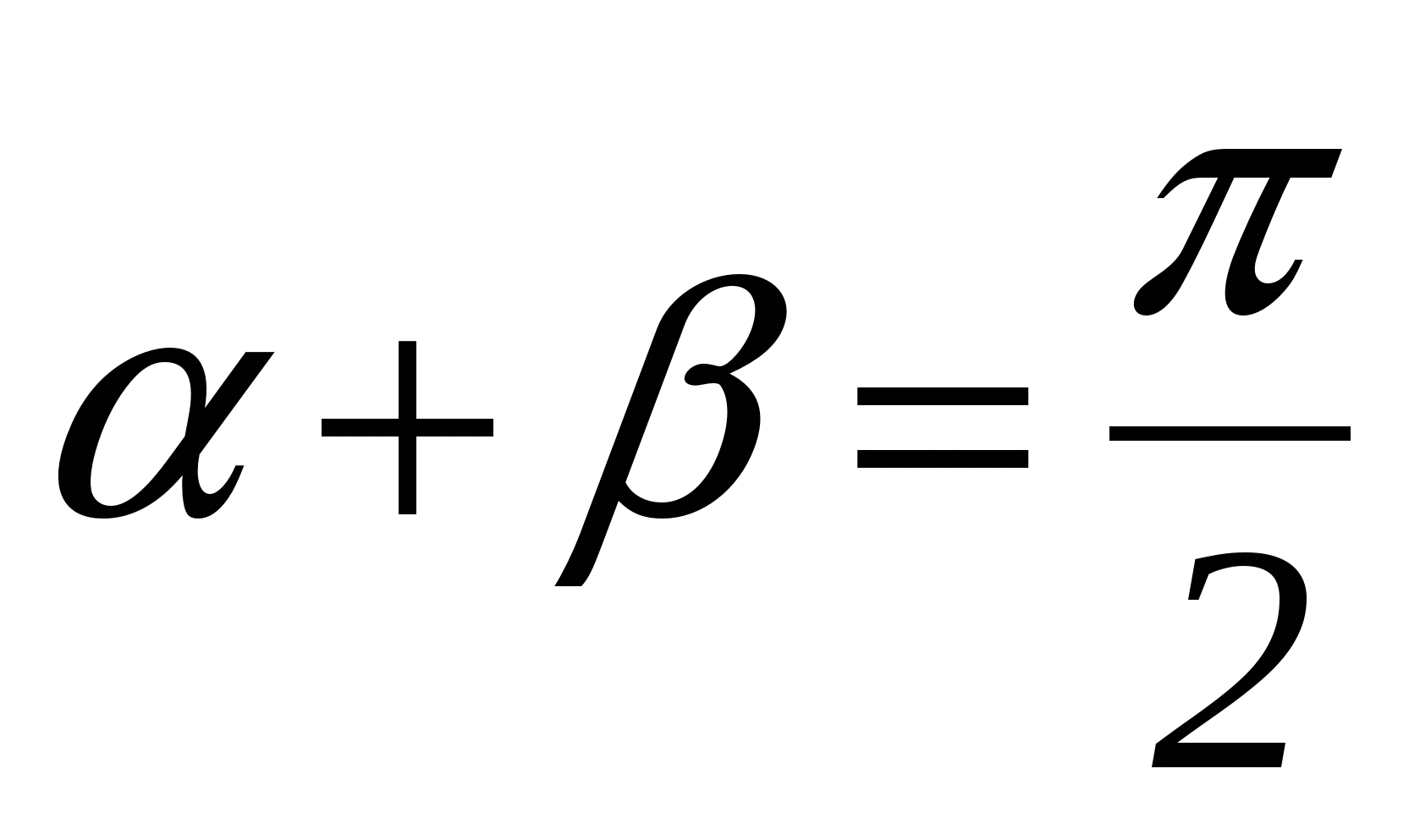 . Выразим
. Выразим 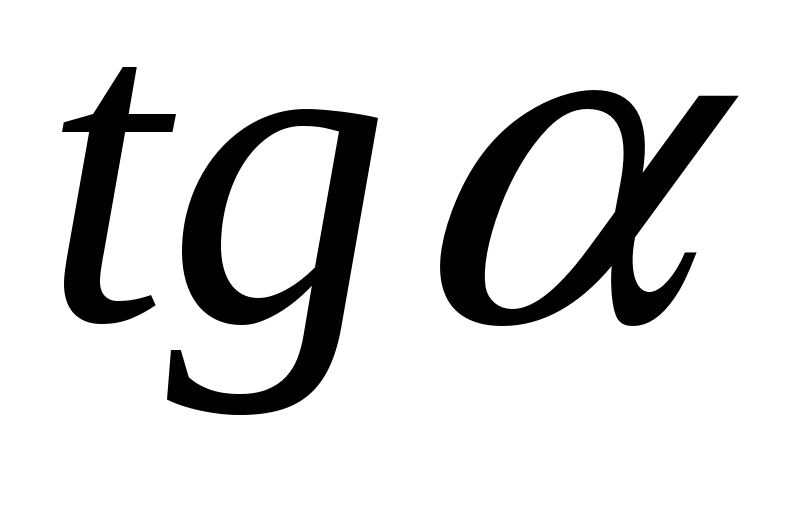 . Он равен
. Он равен 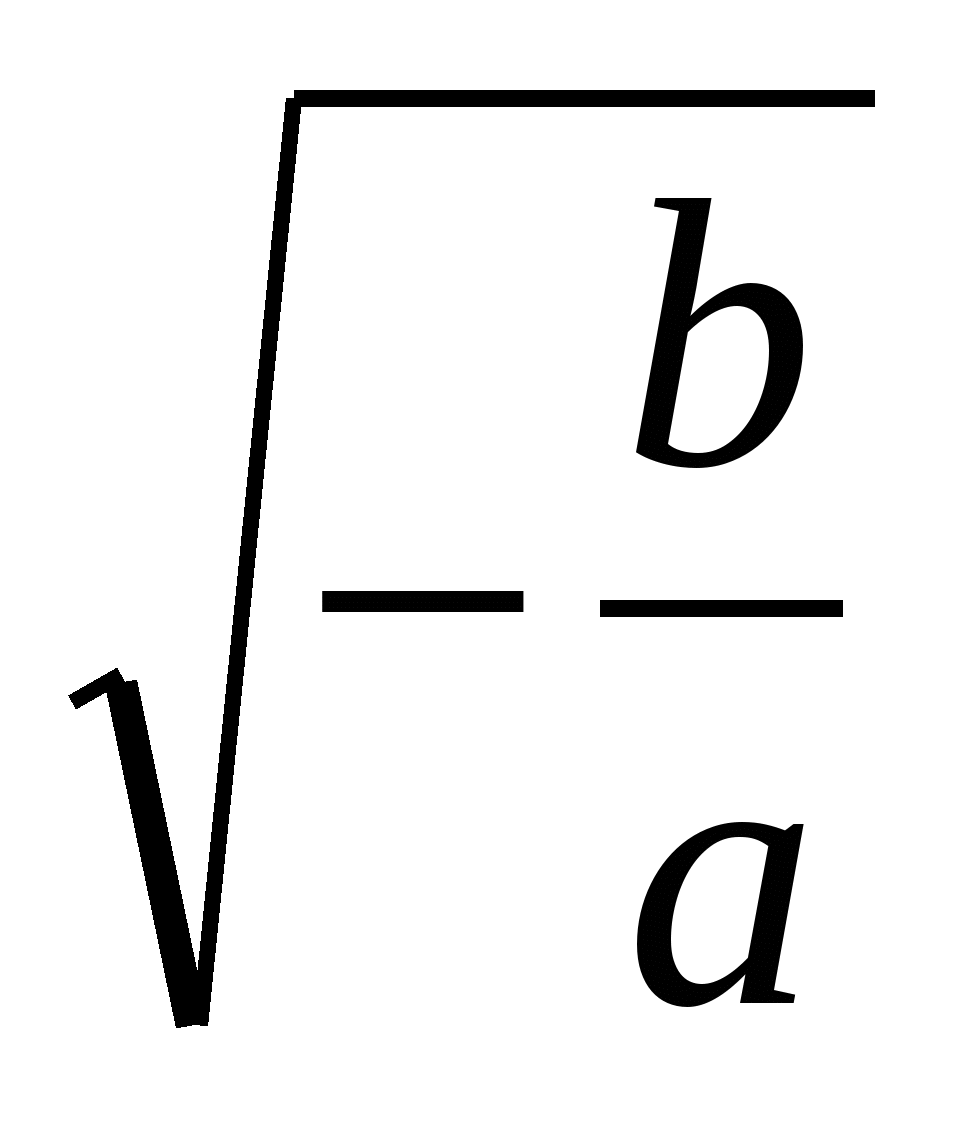 , исходя из этого, пользуясь зависимостью (1), получаем
, исходя из этого, пользуясь зависимостью (1), получаем 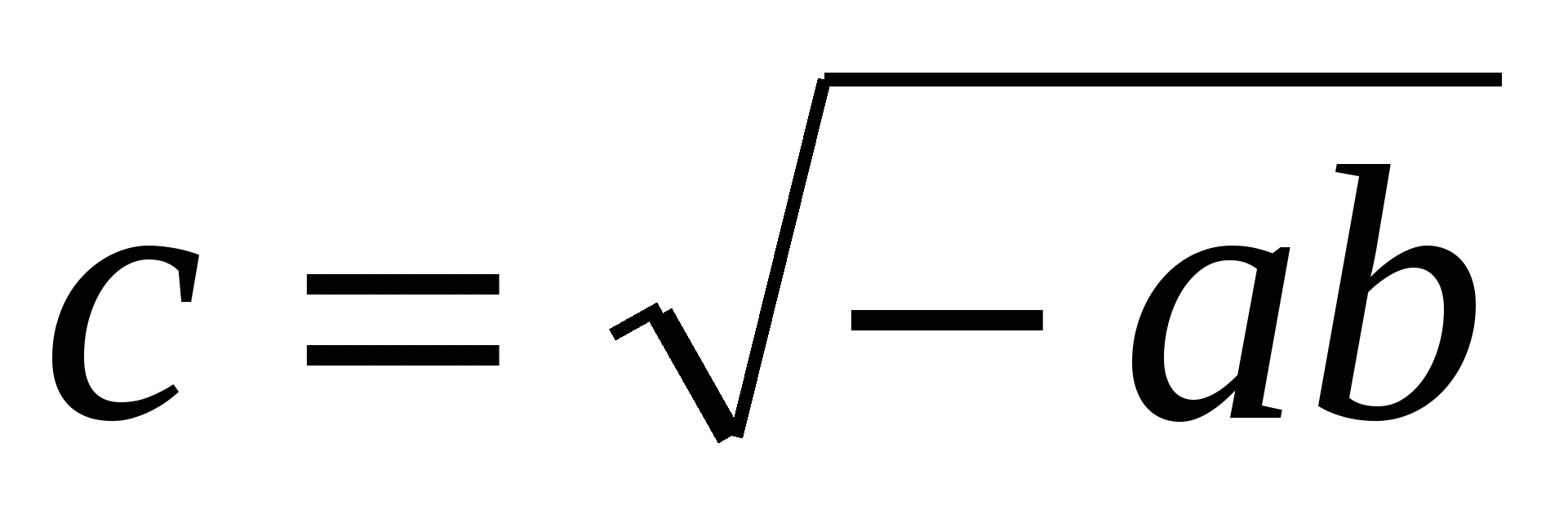 .
.
(умение выразить недостающие координаты через уже известные величины)
Далее воспользовавшись координатной формулой расстояния между двумя точками, найдем длину BD.
(умение вычислять расстояние между точками, заданными координатами)
Она равна 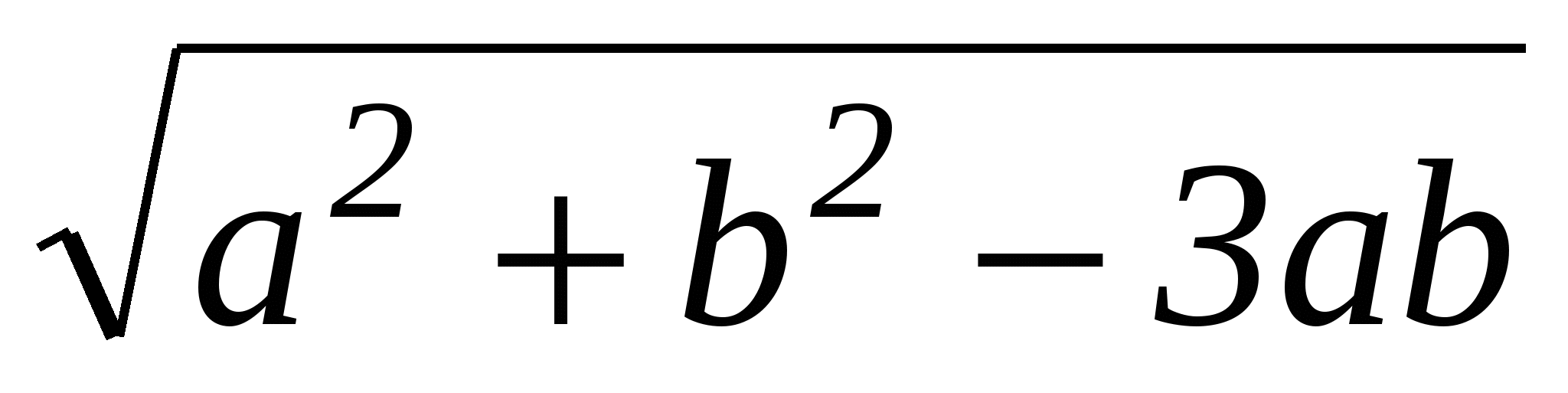 .
.
Итак, компонентами умения применять координатный метод в конкретных ситуациях являются следующие умения:
-
переводить геометрический язык на аналитический для одного типа задач и с аналитического на геометрический для другого;
-
стоить точку по заданным координатам;
-
находить координаты заданных точек;
-
вычислять расстояние между точками, заданными координатами;
-
оптимально выбирать систему координат;
-
составлять уравнения заданных фигур;
-
видеть за уравнением конкретный геометрический образ;
-
выполнять преобразование алгебраических соотношений.
Данные умения можно отработать на примере следующих задач, формирующих координатный метод:
-
задачи на построение точки по ее координатам;
-
задачи на нахождение координат заданных точек;
-
задачи на вычисление расстояния между точками, заданными координатами;
-
задачи на оптимальный выбор системы координат;
-
задачи на составление уравнения фигуры по ее характеристическому свойству;
-
задачи на определение фигуры по ее уравнению;
-
задачи на преобразование алгебраических равенств;
Приведу примеры таких задач.
С координатной прямой, а затем и с координатной плоскостью учащиеся знакомятся в 5-6 классах при изучении математического материала. При этом удобно использовать мультимедийные презентации, которые позволяют в динамике излагать необходимый материал, использовать всевозможные иллюстрации и звуковые эффекты, тем самым, заинтересовывая учащихся и являясь хорошим наглядным средством. Одним из примеров является презентация «Метод координат», опирающаяся на учебник [7]. (см. приложение). Приведем несколько примеров задач, которые можно использовать при изучении координатной плоскости. Эти задачи могут быть использованы:
-
для оттачивания навыков построения точек по их координатам со всем классом;
-
для дополнительных заданий отстающим ученикам;
-
для развития интереса к изучаемой теме.
-
На координатной плоскости постройте точки А(7,2), B(-2,1), C(0,2).
-
Отметьте на плоскости несколько точек. Начертите произвольную систему координат и найдите в ней координаты заданных точек.
-
Постройте фигуры по координатам их узловых точек. Указание: узловыми будем называть точки, служащие концами отрезков, образующих фигуры. Точки, координаты которых записаны подряд через запятую, соединяйте последовательно друг с другом. Если же координаты разделяются знаком «;», то соответствующие точки не следует соединять. Они нужны для изображения вспомогательных элементов.
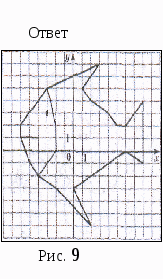 А) Камбала (Рис. 9)
А) Камбала (Рис. 9)
(3,7), (1,5), (2,4), (4,3),
(5,2), (6,2), (8,4), (8,-1),
(6,0), (0,-3),(2,-6),(-2,-3),
(-4,-2),(-5,-1),(-6,1),(-4,1);
(-6,1), (-6,2), (-3,5), (3,7);
(-4,-2),(-2,0),(-2,2),(-3,5);(-3,3).
Б) Найдите координаты выделенных на рисунке точек, двигаясь по часовой стрелке от самой жирной точки. (Рис. 10 и 11)
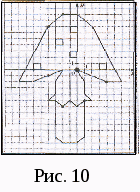
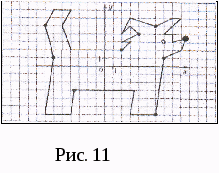
Выбор системы координат имеет очень важное значение при применении метода координат.
Для примера возьмем задачу, которая рассмотрена в учебнике [2] «Середина гипотенузы прямоугольного треугольника равноудалена от его вершин».
П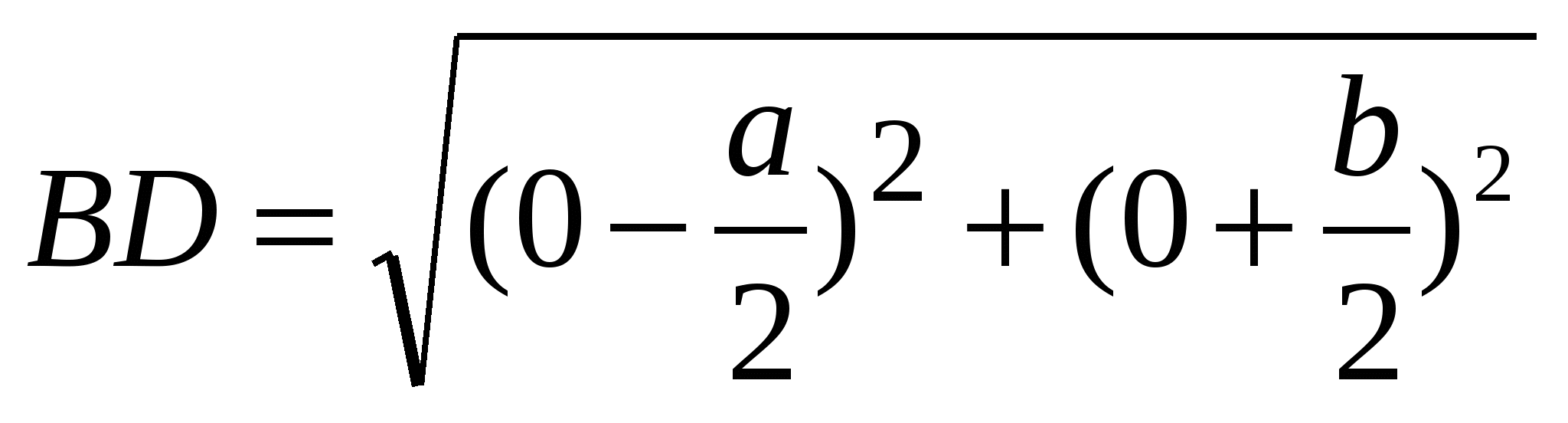
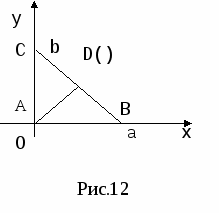
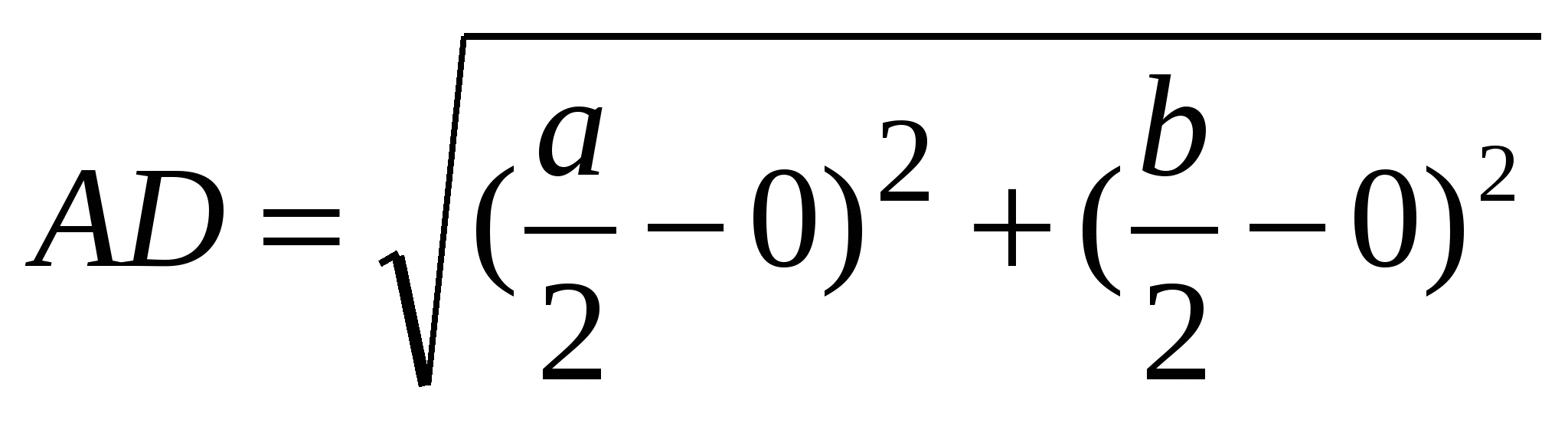 ервым шагом при применении метода координат является такой выбор осей и системы координат, при котором алгебраические выкладки становятся более простыми. Для данной задачи удачный выбор системы координат показан на рисунке 12. Таким образом, начало координат помещаем в точку А, а оси проводим через точки В и С так, чтобы эти точки лежали на положительных лучах осей. Следовательно, В(а,0) и С(0,b). Поэтому по формуле середины отрезка D(
ервым шагом при применении метода координат является такой выбор осей и системы координат, при котором алгебраические выкладки становятся более простыми. Для данной задачи удачный выбор системы координат показан на рисунке 12. Таким образом, начало координат помещаем в точку А, а оси проводим через точки В и С так, чтобы эти точки лежали на положительных лучах осей. Следовательно, В(а,0) и С(0,b). Поэтому по формуле середины отрезка D(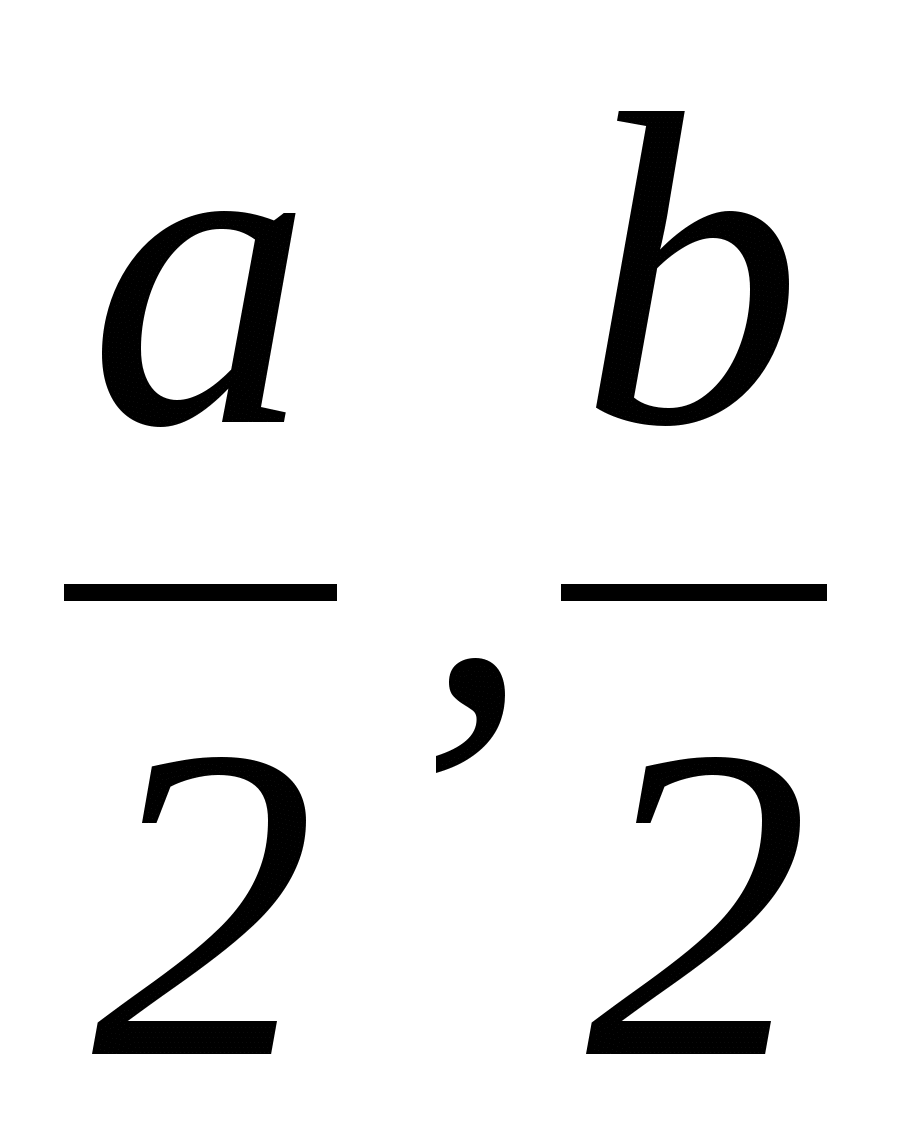 ). Теперь ,
). Теперь ,
Поэтому AD=BD. А так как по определению середины отрезка BC=CD, то теорема доказана.
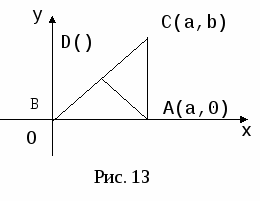
Можно выбрать систему координат и по-другому (рис.13, рис.14). Если выбрать оси совсем случайно, то легкую задачу можно превратить в очень трудную. Чтобы начать доказательство исходя из рисунка 15, нужно найти способ, позволяющий выразить алгебраически, что треугольник ABC имеет при вершине А прямой угол. Сделать это можно, но будет это не очень просто.
C(c,d)
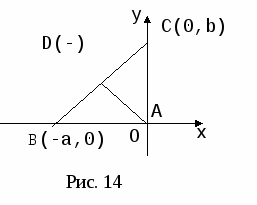
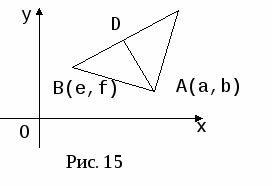
Поэтому необходимо вырабатывать у учащихся, начиная с 6 класса, представления о возможности произвольного выбора системы координат. Эту работу целесообразно вести в процессе решения задач. В целях пропедевтической работы можно рекомендовать в 6 классе задачи из учебника на нахождение координат точек по рисунку, разнообразя их с помощью изменения направления осей и начала координат (см. приложение)
2.4 ОПЫТНОЕ ПРЕПОДАВАНИЕ
Опытное преподавание проводилось в 9 классе средней общеобразовательной школы п.Обор. Перед его проведением была изучена математическая и методическая литература и разработана методика проведения факультатива. Было проведено 2 занятия. В данном классе изучение геометрии ведется по учебнику [2], поэтому в качестве основного теоретического и практического источника я выбрала данный методический комплект.
I. Занятия проводились по теме «Простейшие задачи в координатах», до ознакомления с которыми учащиеся изучали тему «Векторы», познакомились с понятием «координаты вектора», а также узнали формулу середины отрезка.
1 занятие: «Простейшие задачи в координатах»
Образовательная цель урока - рассмотреть задачи о вычислении длины вектора по его координатам и по координатам его начала и конца; показать, как они используются при решении других задач.
Содержание урока:
-
Вначале урока был проведен устный счет для проверки усвоения материала, разобранного на прошлом уроке, а также для проведения пропедевтической работы по повторению тех понятий и фактов, которые будут использованы при объяснении нового материала.
Устный счет:
-
Координаты точек А(-2, 3) и В(2, -4). Найдите координаты векторов
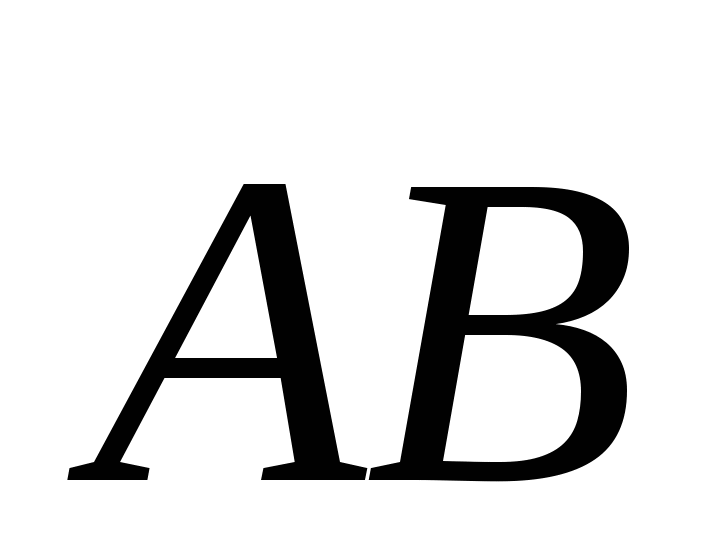 и
и 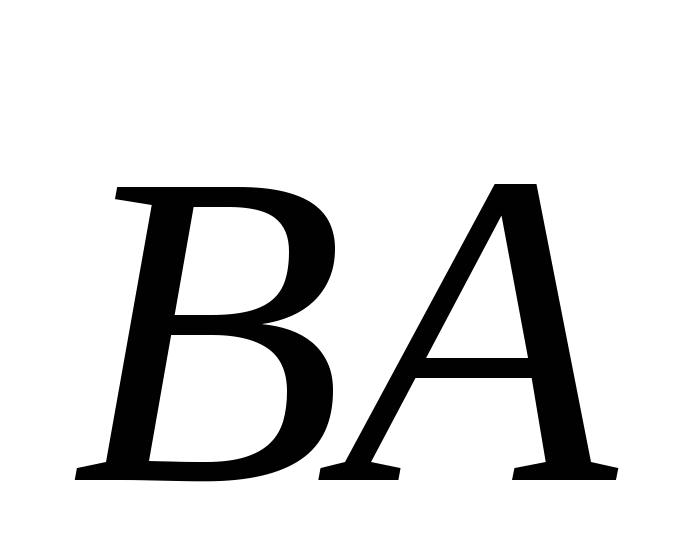 .
. -
Координаты точек М(5,-8) и Р(-3, 4). Найдите координаты точки О (О - середина отрезка МР).
-
СР - диагональ окружности; С(-2, -1), Р(5, 7). Найдите координаты центра окружности - точки Е.
-
ABCD - прямоугольник, АD=7, АВ=5. Найдите АС.
-
Новый материал:
-
Вычисление длины вектора по его координатам.
-
В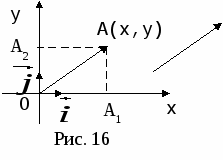
 Oывод формулы опирается на теорему Пифагора и на то, что расстояние между двумя точками оси координат находится по формулам
Oывод формулы опирается на теорему Пифагора и на то, что расстояние между двумя точками оси координат находится по формулам 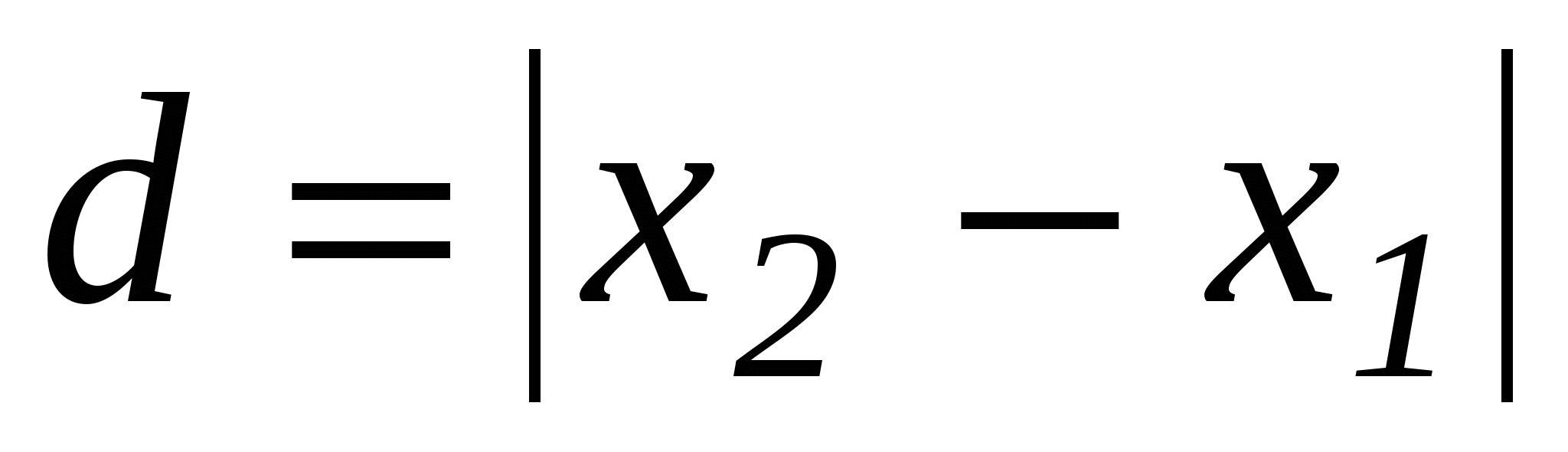 (для точек
(для точек 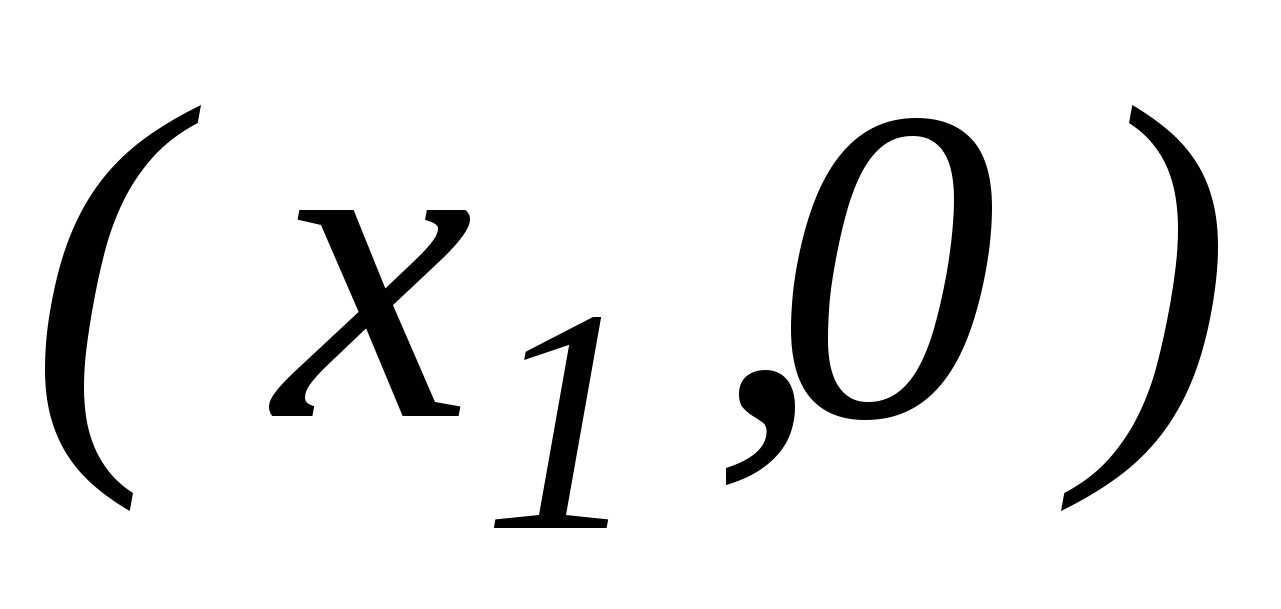 ;
; 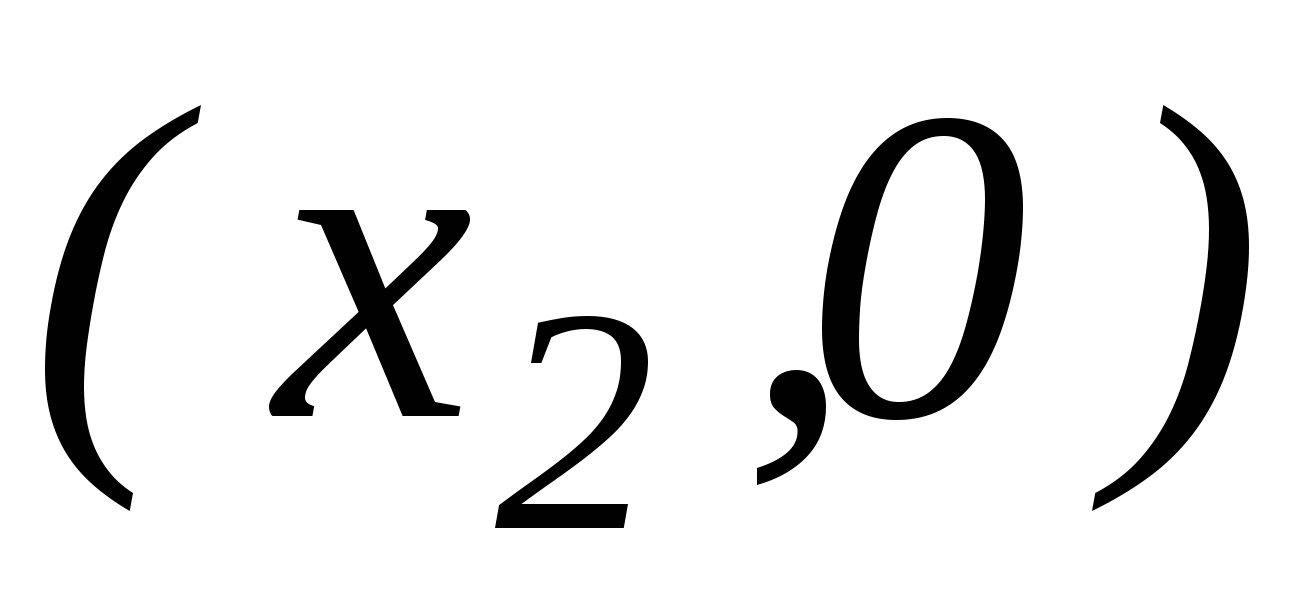 оси х) и
оси х) и 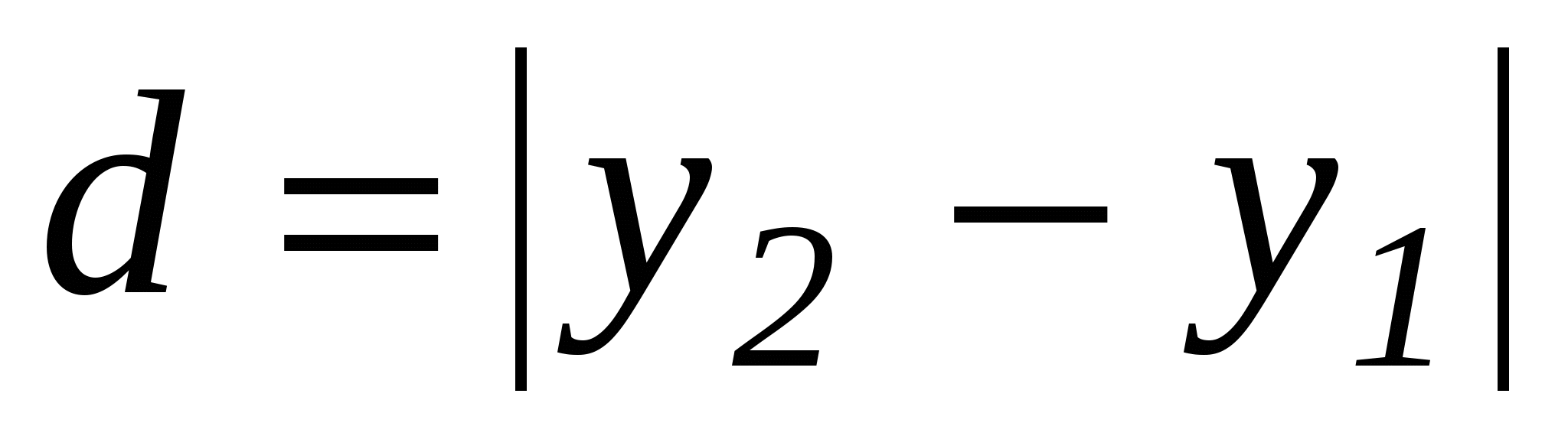 (для точек
(для точек 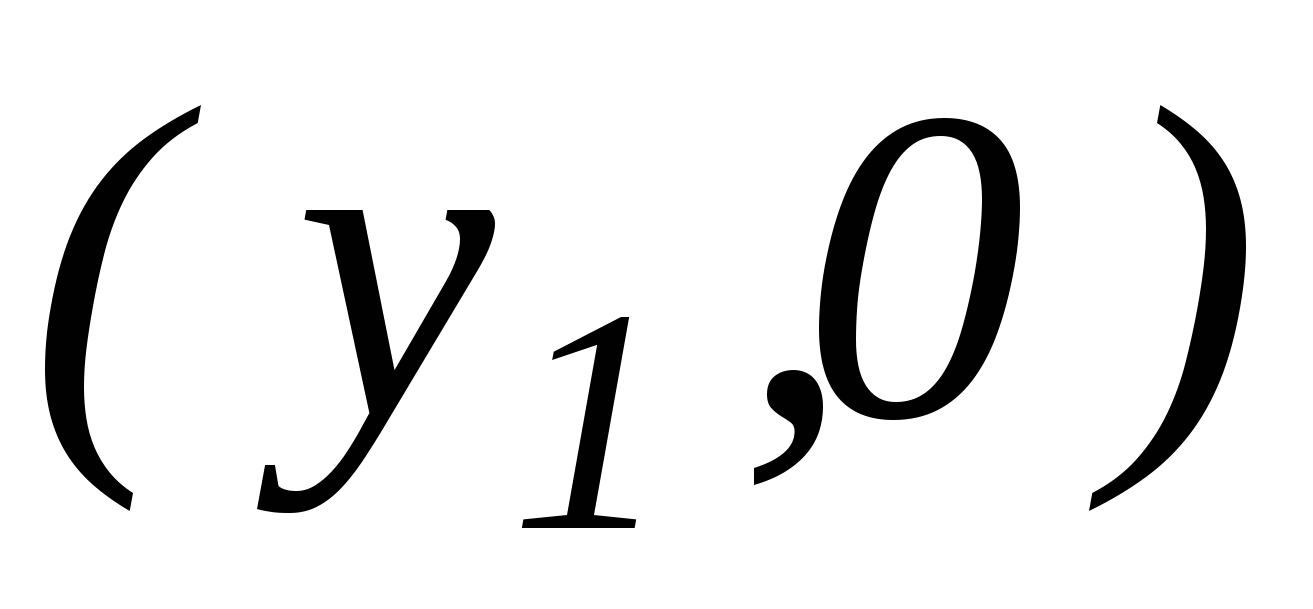 ;
; 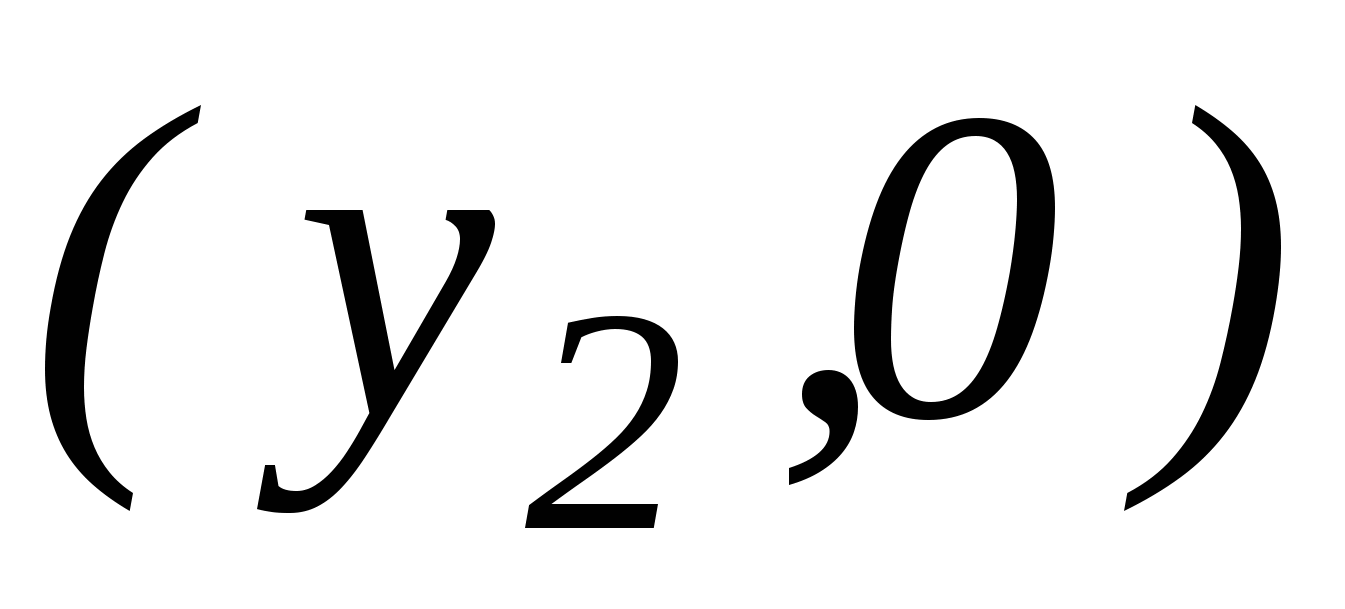 оси у). Покажем, что длина вектора
оси у). Покажем, что длина вектора 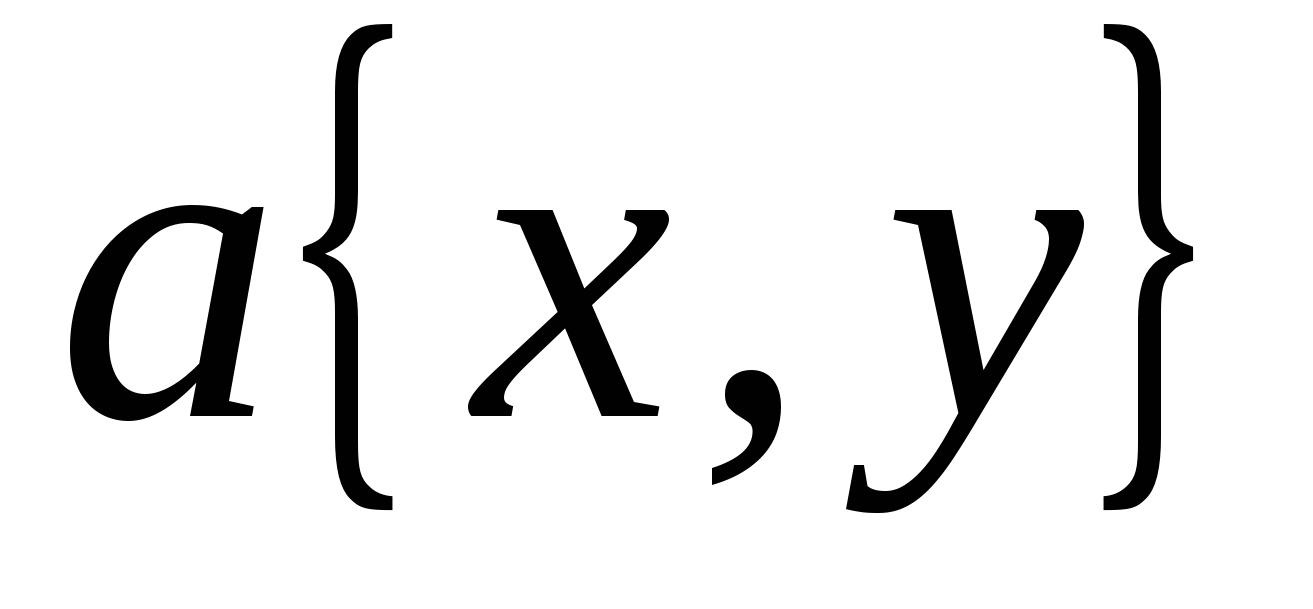 равна
равна 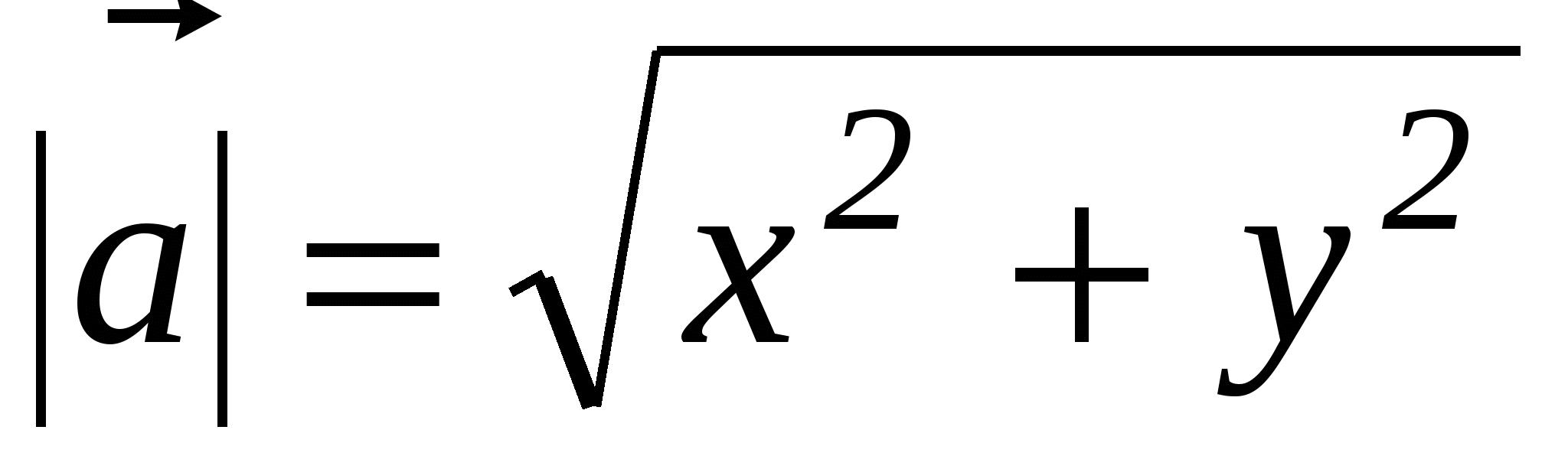 . Данная формула доказывается только для случая, когда х≠0 и у≠0, в достоверности других случаев учащимся предоставляется убедиться самостоятельно. Для доказательства задаем координатную плоскость и рассматриваем вектор
. Данная формула доказывается только для случая, когда х≠0 и у≠0, в достоверности других случаев учащимся предоставляется убедиться самостоятельно. Для доказательства задаем координатную плоскость и рассматриваем вектор 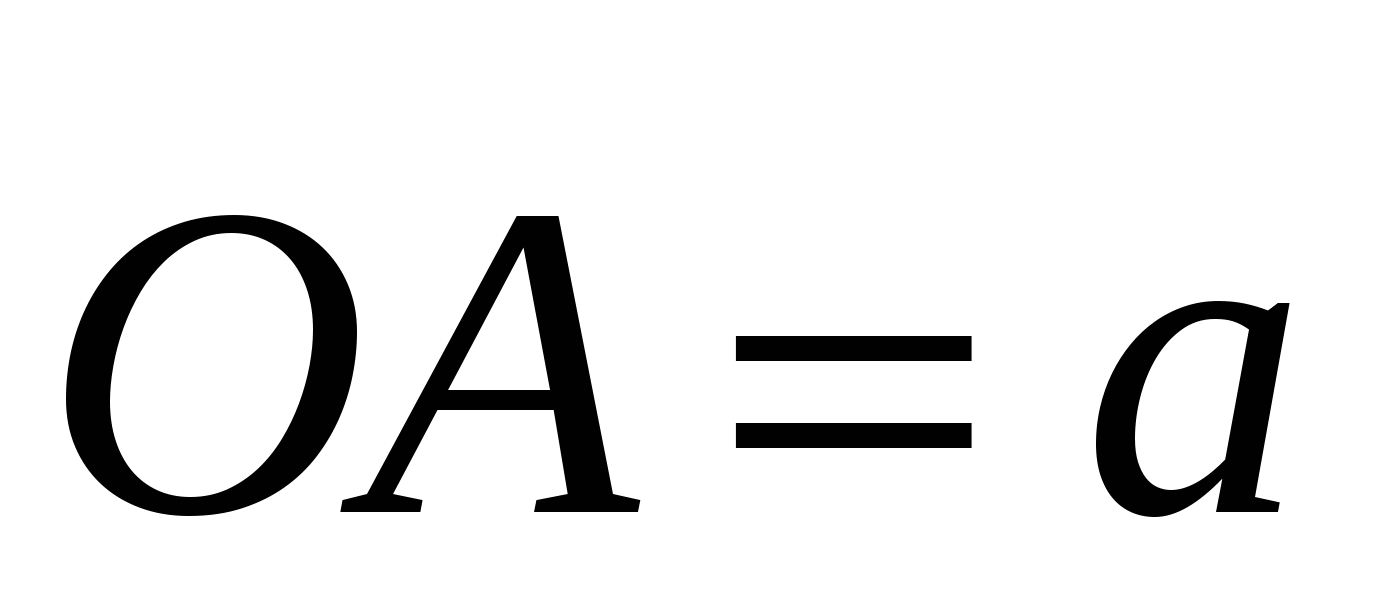 с началом в начале координат (по теореме: от любой точки можно отложить вектор, равный данному и притом единственный). Используя формулу для нахождения координат вектора по координатам его начала и конца, можем найти координаты точки А. Далее с помощью теоремы Пифагора находим длину отрезка ОА=
с началом в начале координат (по теореме: от любой точки можно отложить вектор, равный данному и притом единственный). Используя формулу для нахождения координат вектора по координатам его начала и конца, можем найти координаты точки А. Далее с помощью теоремы Пифагора находим длину отрезка ОА=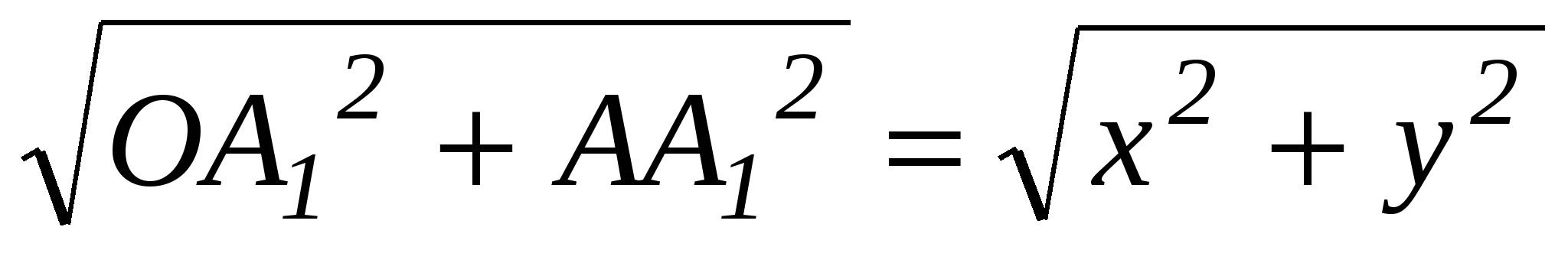 .
. 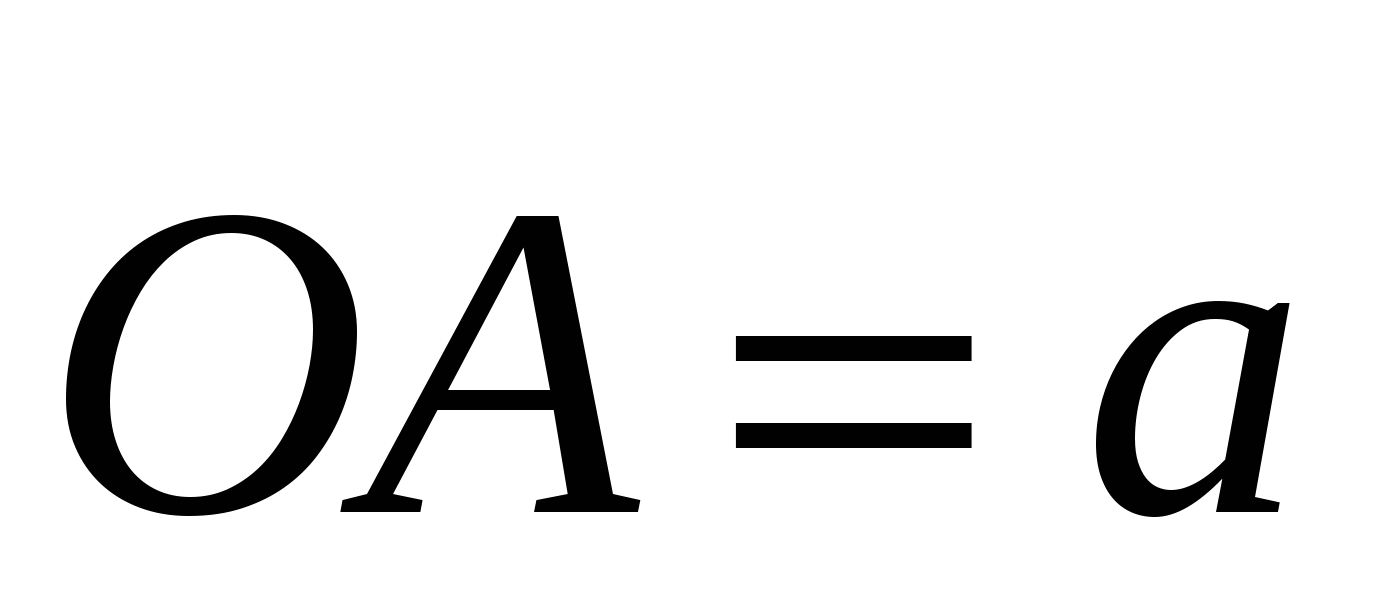 следовательно, их длины раны, т.о.
следовательно, их длины раны, т.о. 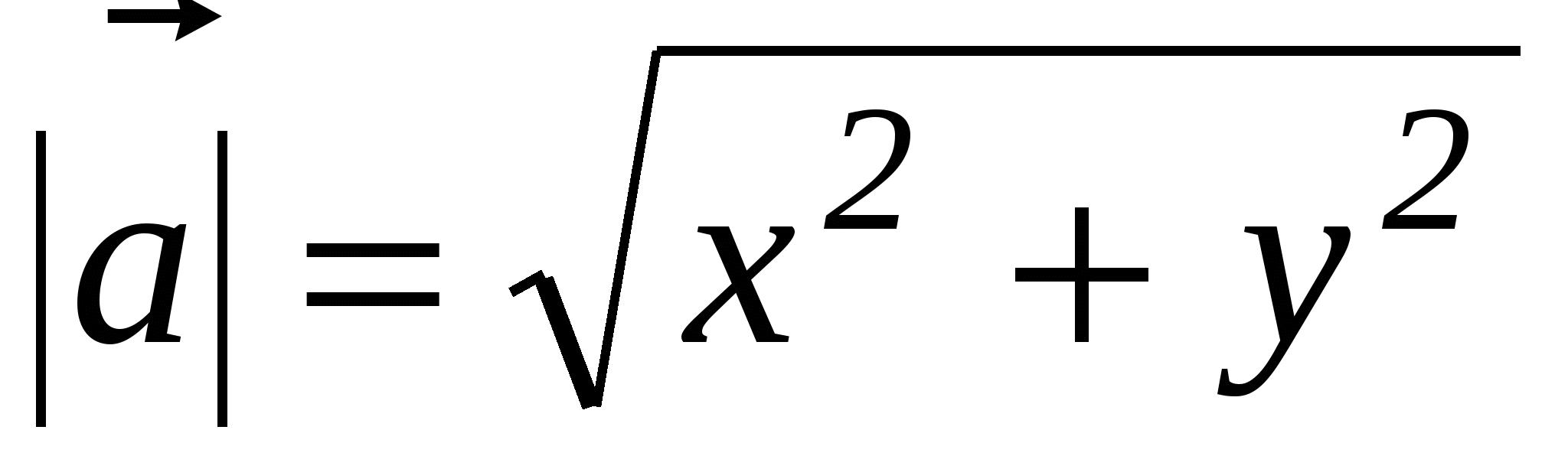 .
.
Далее показывается применение данной формулы.
-
-
Расстояние между двумя точками.
-
Нахождение данной формулы опирается на использование предыдущей. Пусть имеются точки М1(х1,у1)и М2(х2,у2), необходимо найти расстояние между этими точками. Рассмотрим вектор М1М2. Его координаты равны 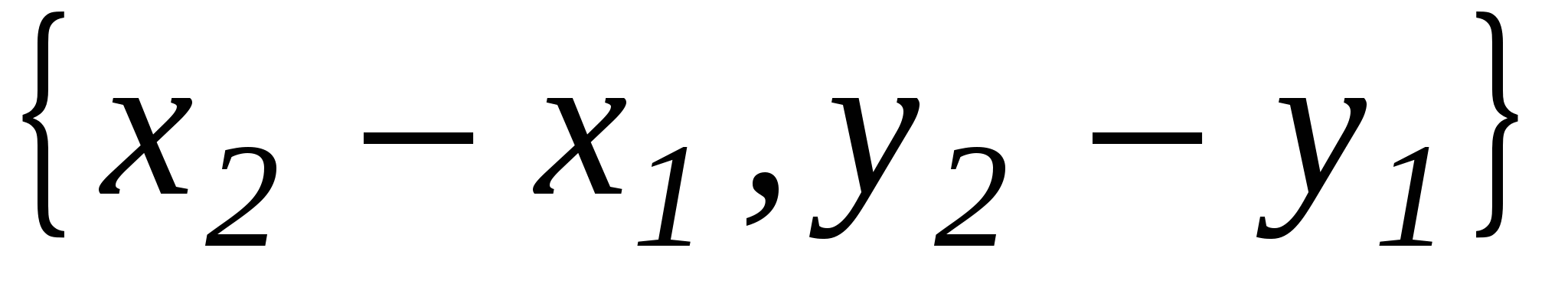 . Находим длину вектора по его координатам:
. Находим длину вектора по его координатам: 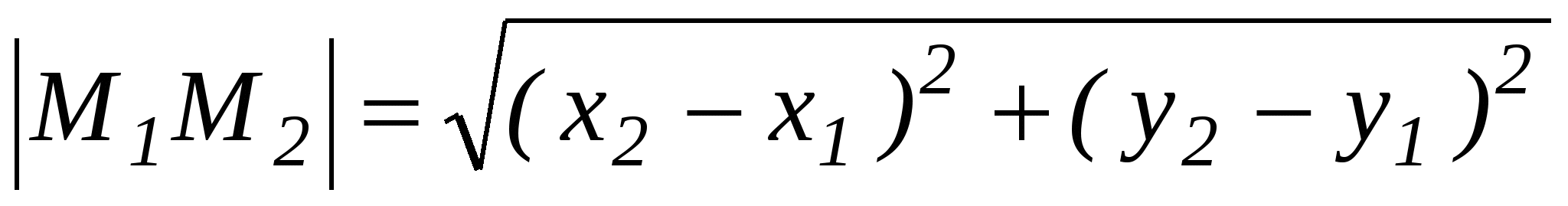 , а расстояние между М1 и М2 это длина вектора
, а расстояние между М1 и М2 это длина вектора 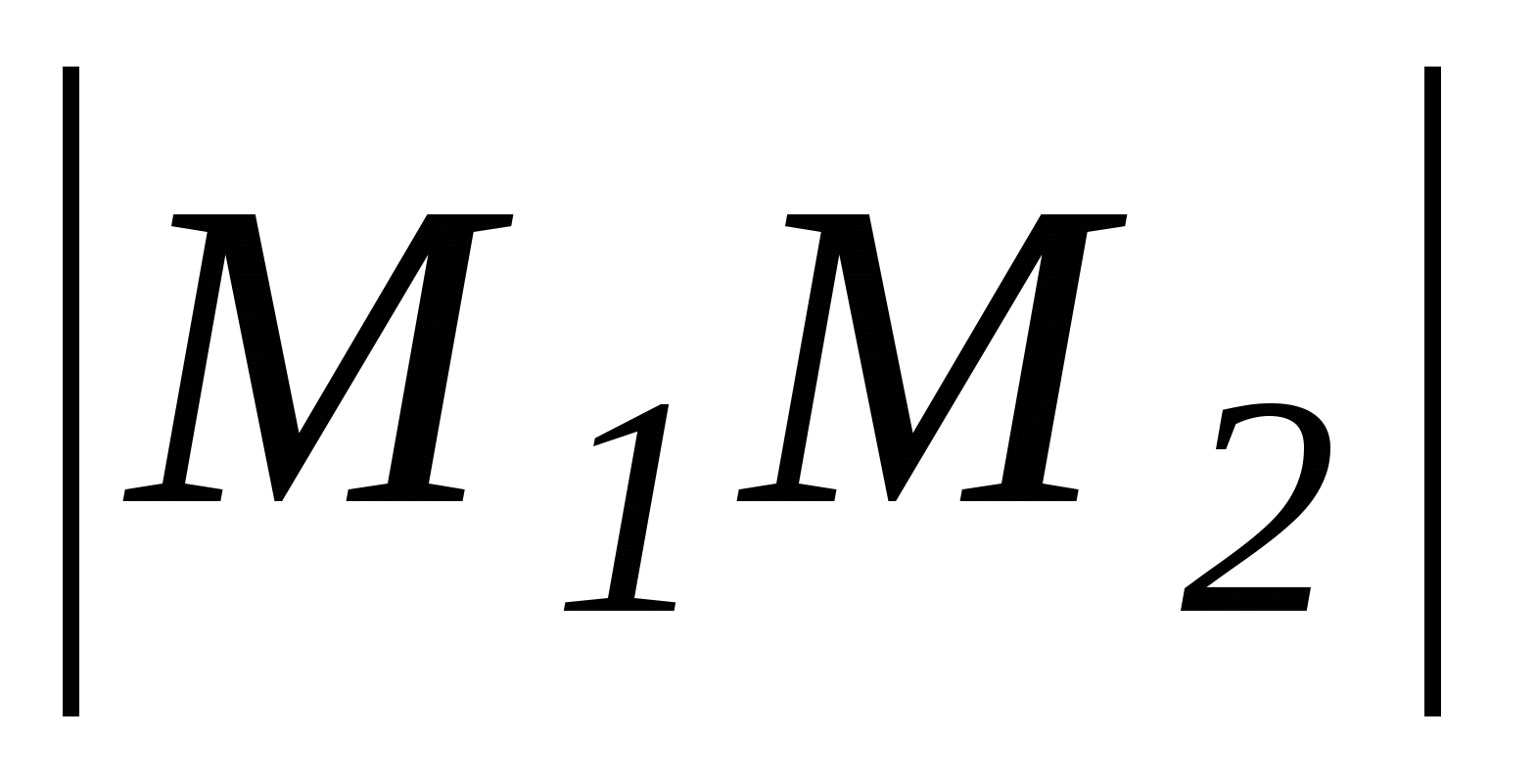 . После выведения данной формулы можно записать формулу
. После выведения данной формулы можно записать формулу 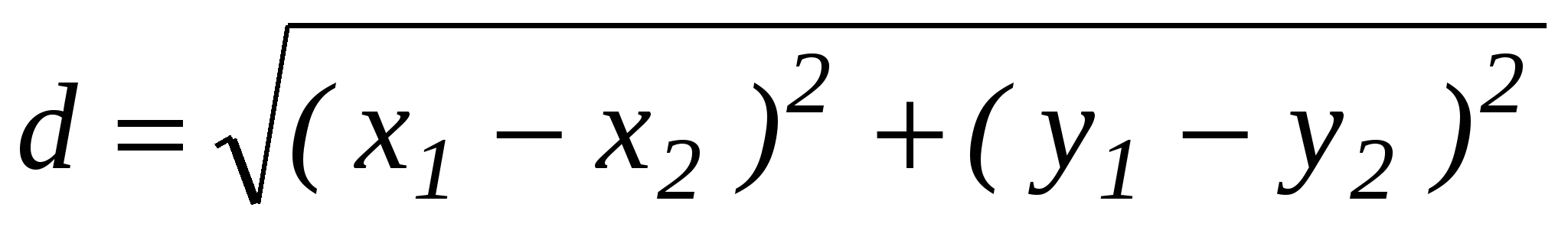 и показать, что они эквивалентны.
и показать, что они эквивалентны.
-
Закрепление: для закрепления используется ряд задач на применение данных формул.
-
Найдите длины векторов: а)
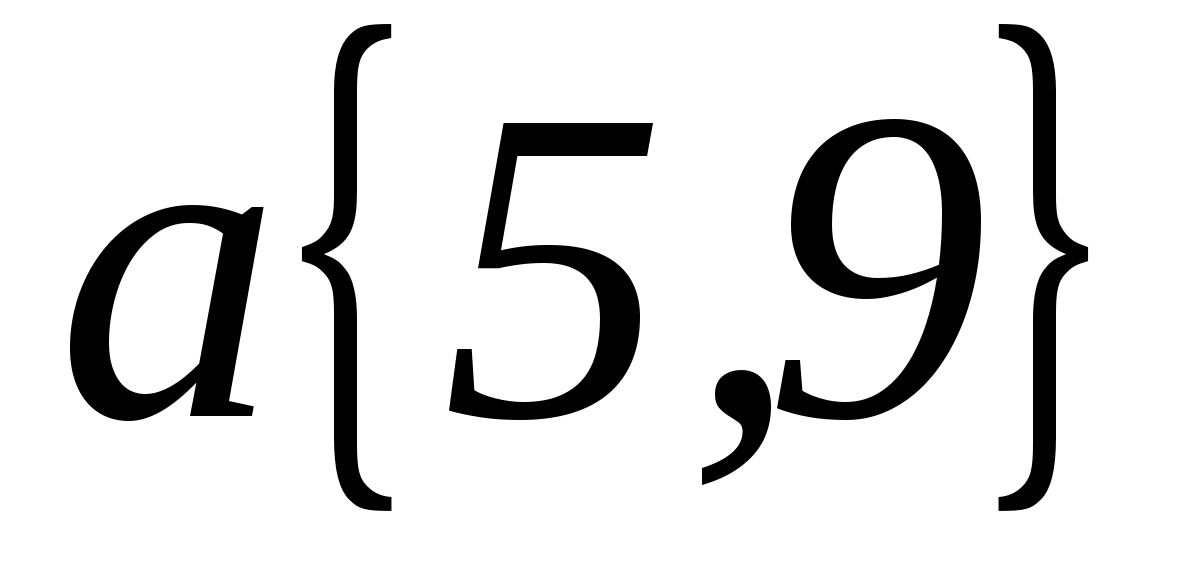 ; b)
; b) 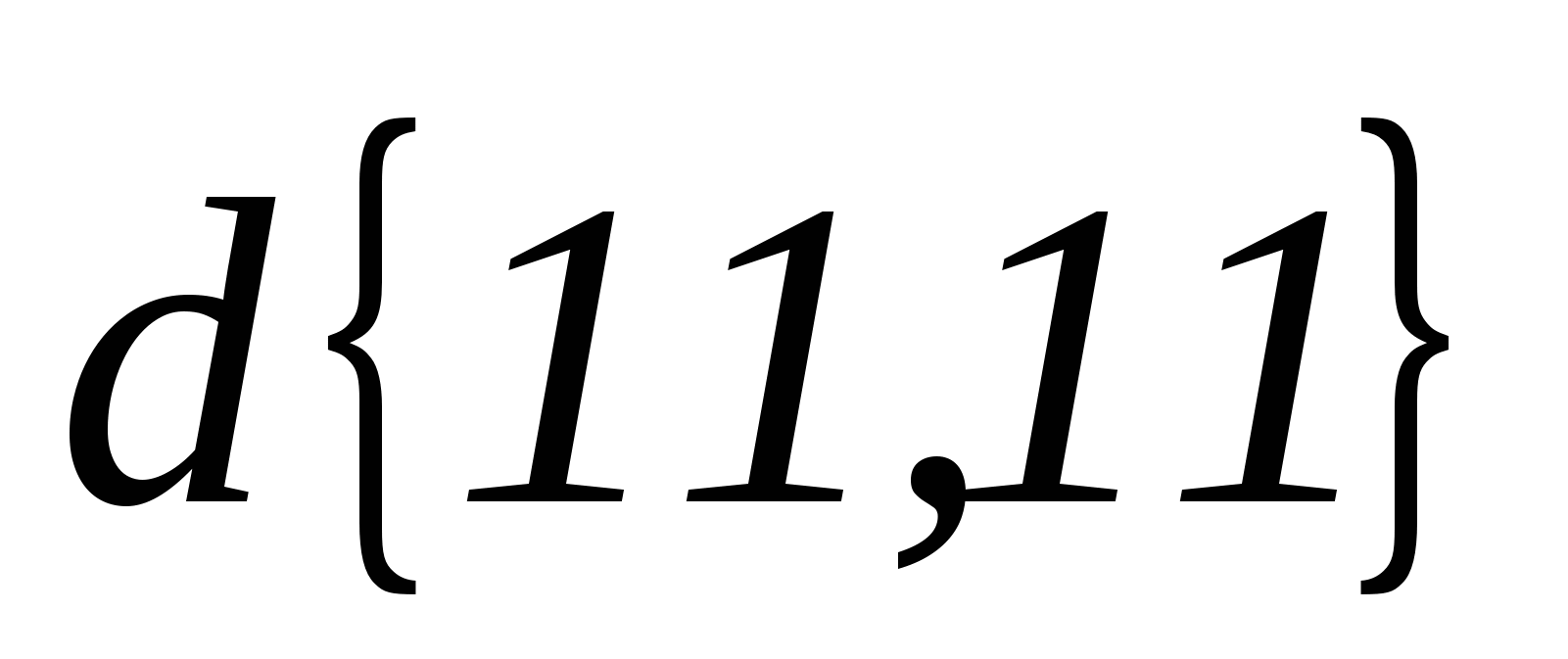 [2: № 938]
[2: № 938] -
Найдите медиану АМ треугольника АВС, вершины которого имеют координаты: А(0,1), В(1, -4), С(5,2). [2: № 942]
-
Вершина А параллелограмма ОАСВ лежит на положительной полуоси Ох, вершина В имеет координаты (b, c), а ОА=а. Найдите а)координаты вершины С; b)сторону АС и диагональ СО. [2: № 944].
-
Домашнее задание № 939, 941 [2]
-
2 занятие: «Простейшие задачи в координатах». (урок - закрепление)
Общеобразовательная цель урока: показать, как «простейшие задачи» используются при решении более сложных и проверить усвоение знаний, полученных на прошлом уроке.
Содержание урока:
-
В начале урока был проведен устный счет для проверки усвоения материала, разобранного на прошлом уроке.
Устный счет: записать координаты
●Середины отрезка ●К оординаты вектора
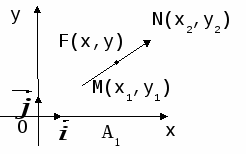
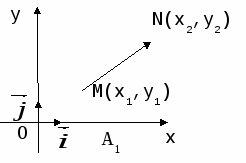
y =
Рис. 18
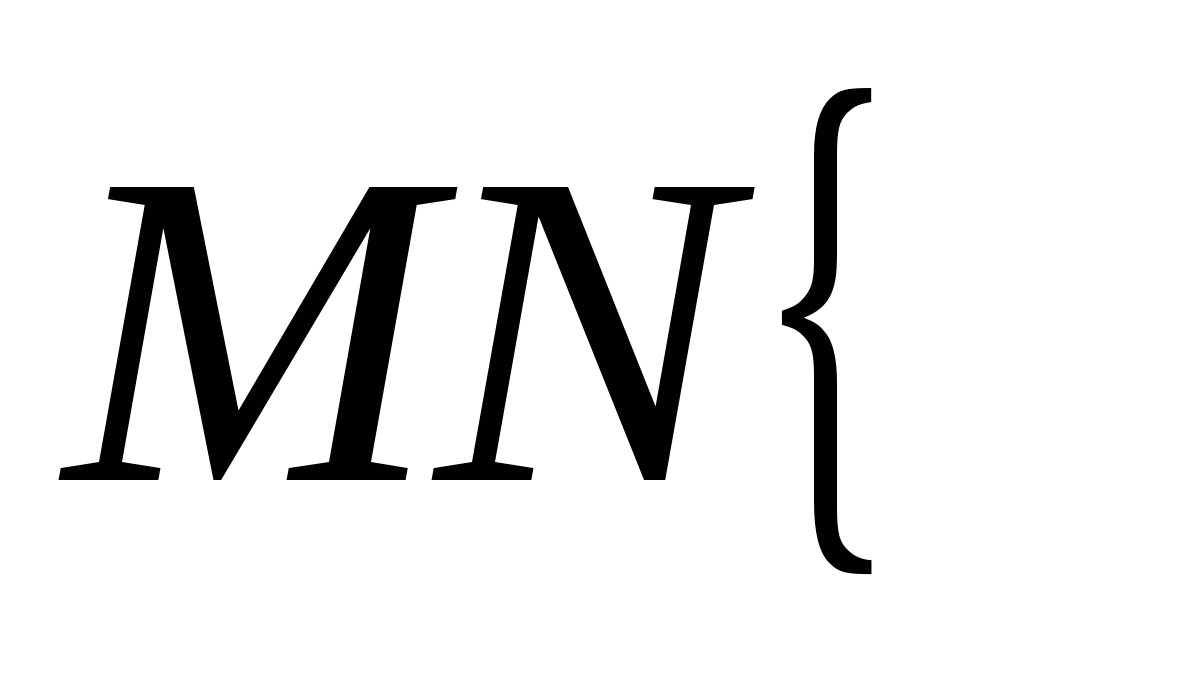
x =
Рис. 17
-
Длины вектора
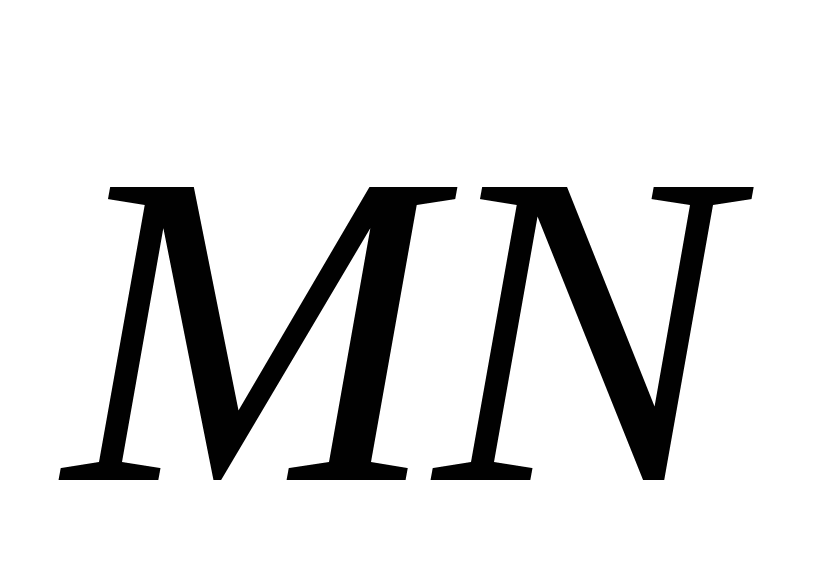
-
Расстояние между точками М и N.
-
Решение задач.
-
Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если А(0,1), В(1,-4), С(5,2).
-
Докажите, что четырехугольник MNPQ является параллелограммом, и найдите его диагонали, если N(6,1), P(7,4), Q(2,4), М(1,1). [2: № 950(а)]
-
Самостоятельная работа.
I. Вариант I
1. Найдите координаты и длину вектора
 , если
, если 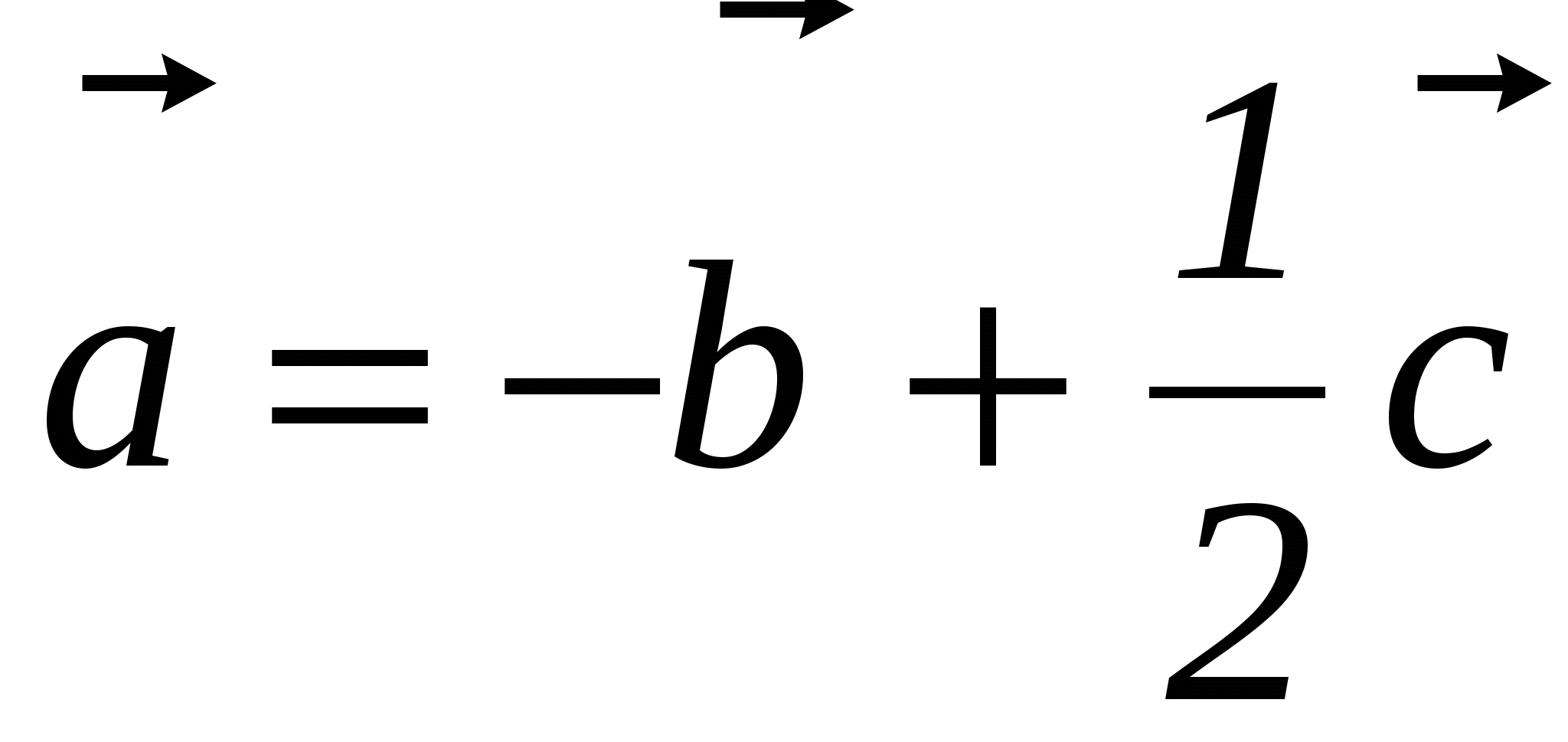 ,
, 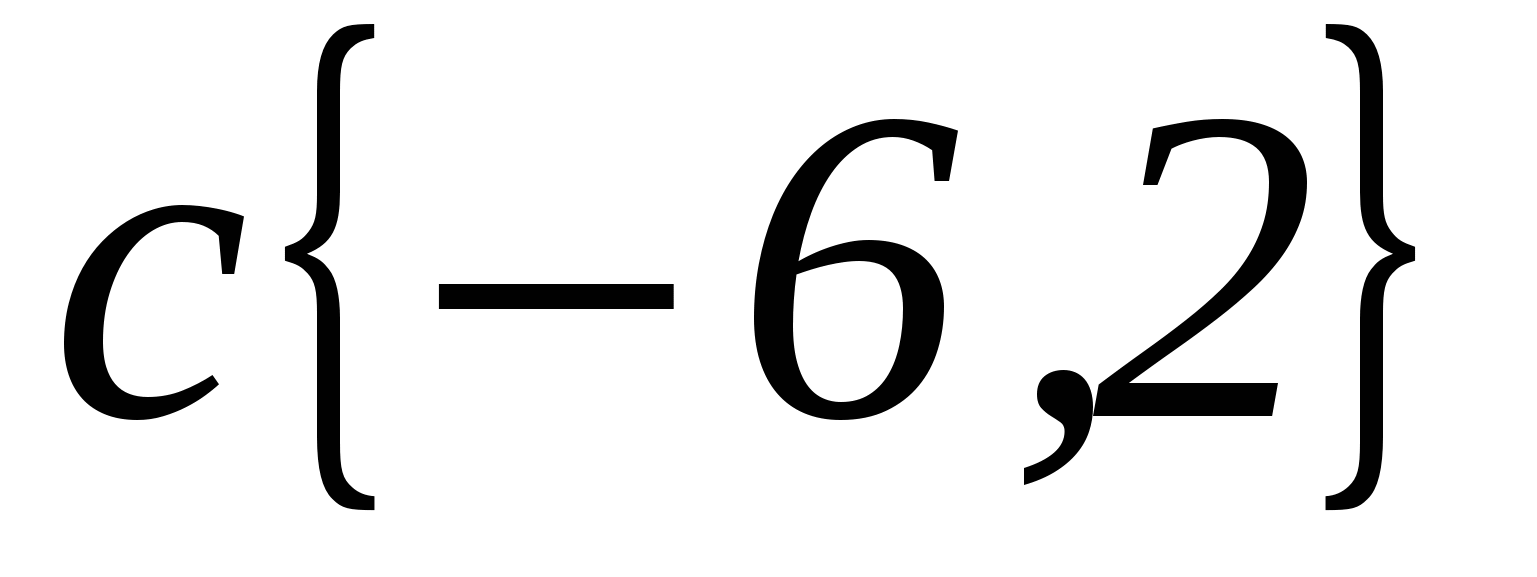 ,
, 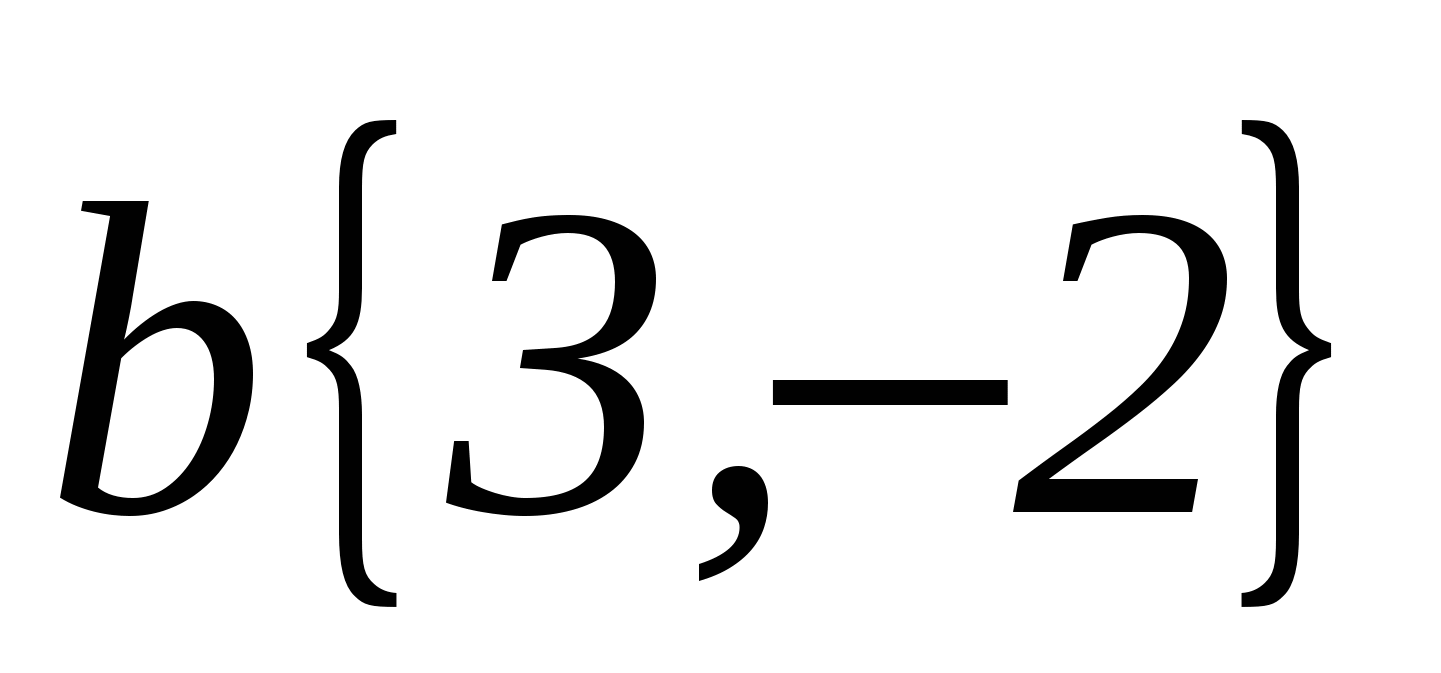 .
. 2. Даны координаты вершин треугольника АВС А(-6,1), В(2,4), С(2,-2). Докажите, что треугольник АВС равнобедренный и найдите высоту проведенную из вершины А.
Дополнительно для обоих вариантов: Даны координаты вершин треугольника АВС А(-4,3), В(2,7), С(8,-2). Доказать, что треугольник прямоугольный.
Вариант II.
1. Найдите координаты и длину вектора
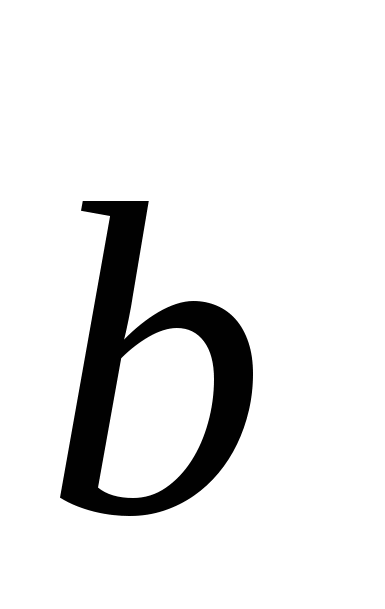 , если
, если 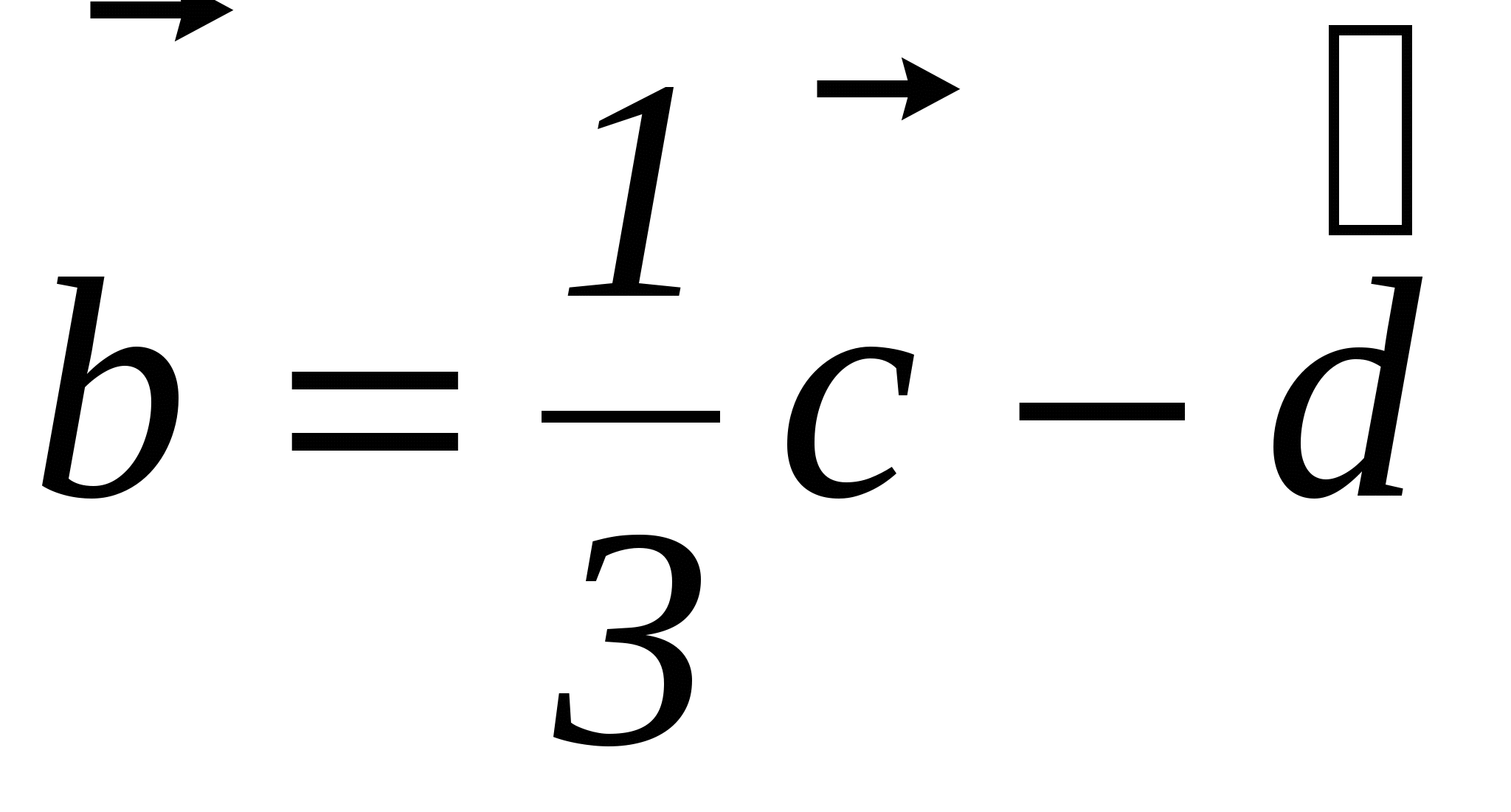 ,
, 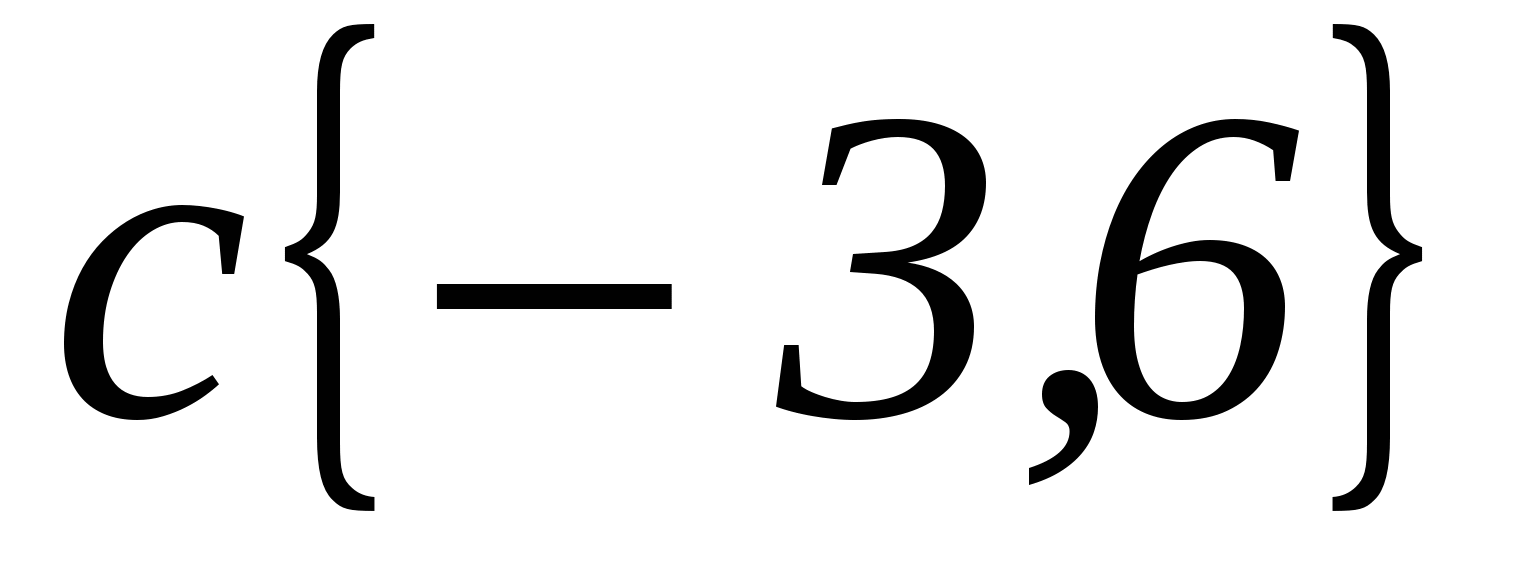 ,
, 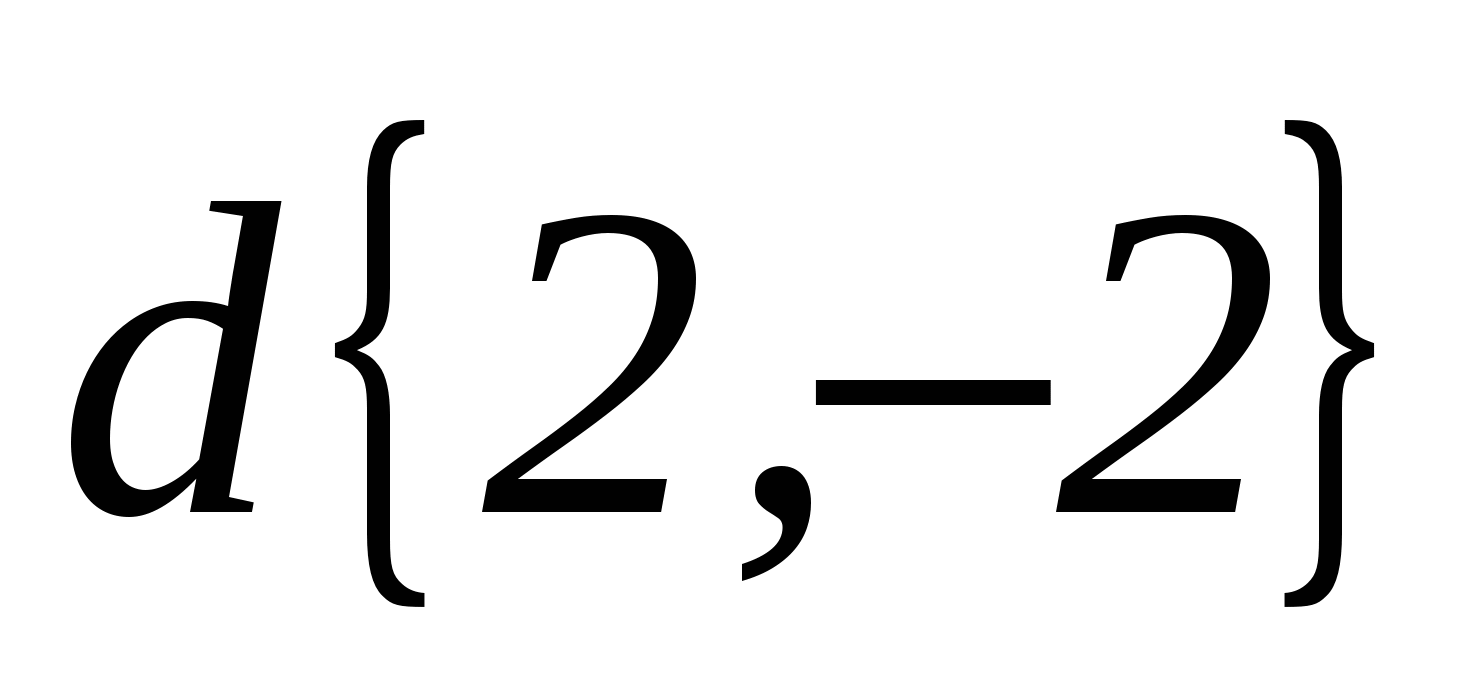 .
. 2. Дано А(-6,1), В(0,5), С(-6,4), Р(0,-8). Докажите, что АВСР прямоугольник и найдите координату точки пересечения его диагоналей.
-
Домашнее задание №945, 948(а)
II. Факультатив.
Для проведения факультатива предлагается ряд более сложных нестандартных задач, при решении которых используется метод координат.
Задача 1. Два предприятия А и В производят продукцию с одной и той же ценой m за одно изделие. Однако автопарк, обслуживающий предприятие А, оснащен более современными и более мощными грузовыми автомобилями. В результате транспортные расходы на перевозку одного изделия составляют для предприятия А 10 р. на 1 км, а для предприятия В 20 р. на 1 км. Расстояние между предприятиями 300 км. Как территориально должен быть расположен рынок сбыта между двумя предприятиями для того, чтобы расходы потребителей при покупке изделий были минимальными.
Решение:
Д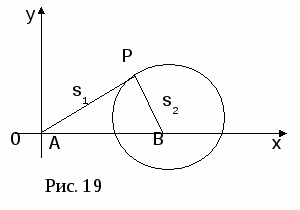 ля решения данной задачи воспользуемся методом координат. Систему координат выберем так, чтобы ось Ох проходила через пункты А и В, а ось Оу через точку А. Пусть Р произвольная точка, s1 и s2 расстояния от точки до предприятий А и В (рис.17). Тогда А(0, 0), В(300, 0), Р(х, у).
ля решения данной задачи воспользуемся методом координат. Систему координат выберем так, чтобы ось Ох проходила через пункты А и В, а ось Оу через точку А. Пусть Р произвольная точка, s1 и s2 расстояния от точки до предприятий А и В (рис.17). Тогда А(0, 0), В(300, 0), Р(х, у).
При доставке груза из пункта А расходы равны m+10s1. При доставке груза из пункта В расходы равны m+20s2. Если для пункта Р выгоднее доставлять груз с предприятия А, то m+10s1< m+20s2, откуда s1<2s2, в обратном случае получим s1>2s2.
Таким образом, границей области для каждой точки, до которой расходы на перевозку груза из пунктов А и В равны, будет множество точек плоскости, удовлетворяющих уравнению
s1=2s2 (1)
Выразим s1 и 2s2 через координаты:
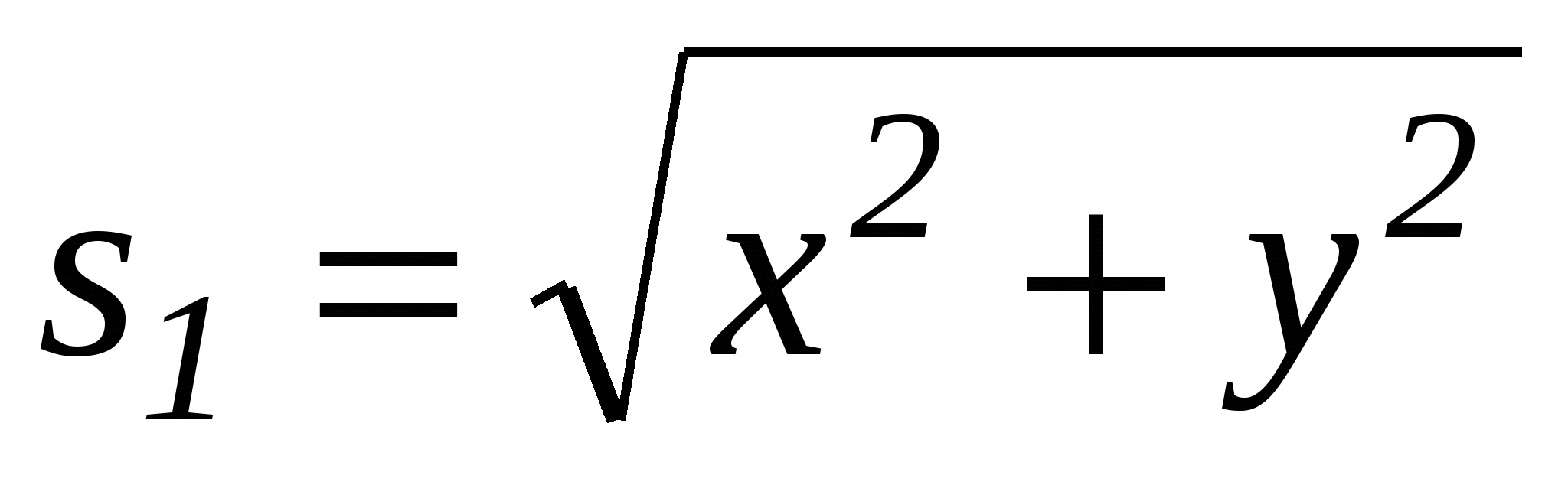 ,
, 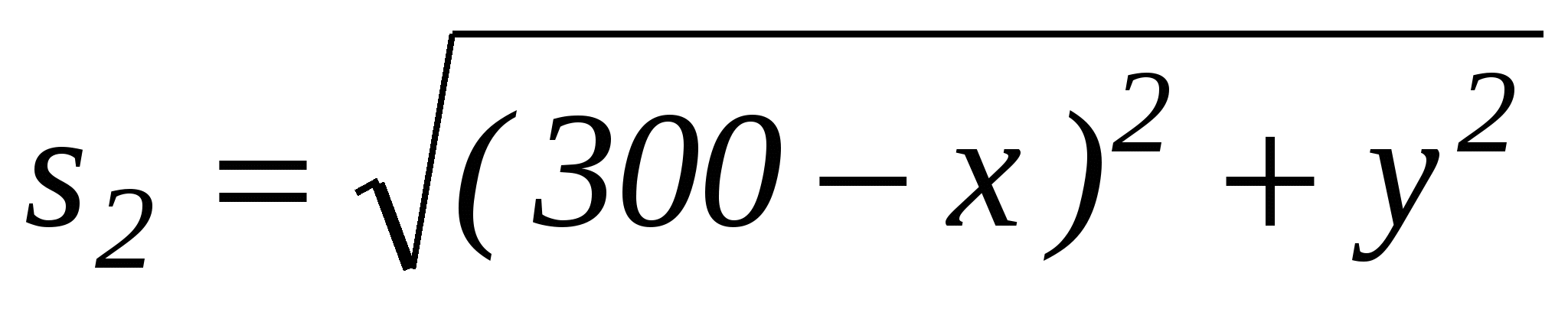 .
.
Имея в виду (1), получим 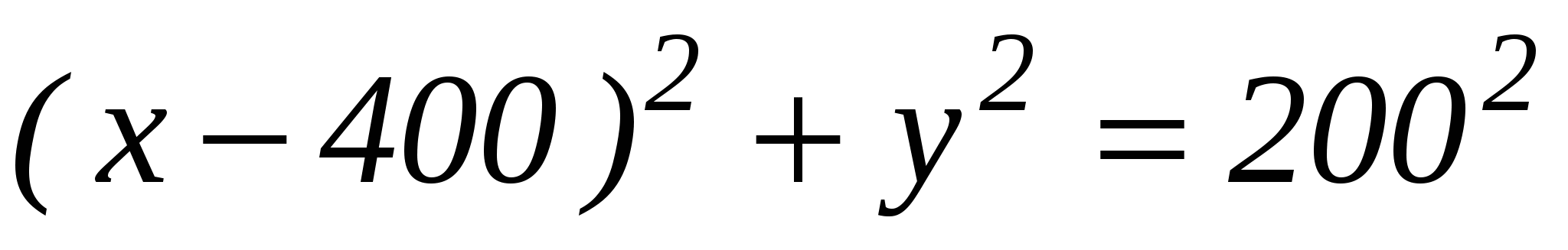 .
.
Это и есть уравнение окружности. Следовательно, для всех пунктов, попадающих во внутреннюю область круга, выгоднее привозить груз из пункта В, а для всех пунктов, попадающих во внешнюю часть круга, - из пункта А.
Задача 2. На плоскости даны точки А и В; найти геометрическое место точек М, удаленных от А в двое больше, чем от В.
Решение:
В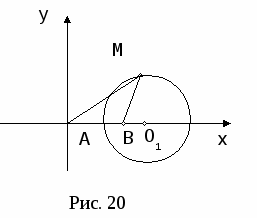 ыберем систему координат на плоскости так, чтобы начало координат попало в точку А, а положительная полуось абсцисс пошла по АВ. За единицу масштаба возьмем отрезок АВ. Точка А будет иметь координаты (0,0), точка В координаты (1,0). Координаты точки М обозначим через (х,у). Условие
ыберем систему координат на плоскости так, чтобы начало координат попало в точку А, а положительная полуось абсцисс пошла по АВ. За единицу масштаба возьмем отрезок АВ. Точка А будет иметь координаты (0,0), точка В координаты (1,0). Координаты точки М обозначим через (х,у). Условие 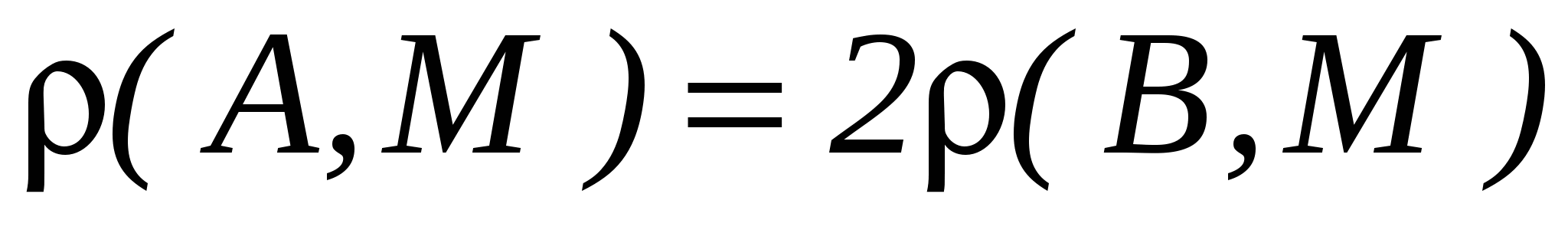 записывается в координатах так:
записывается в координатах так:
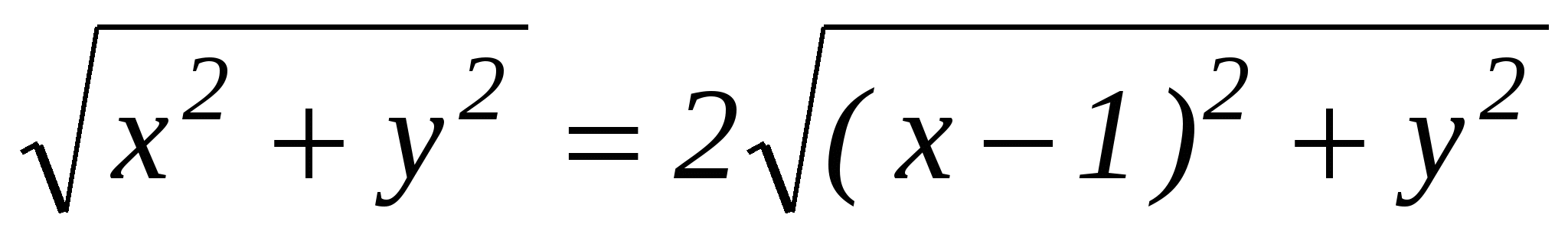 .
.
Мы получили уравнение искомого геометрического места точек. Чтобы понять, какое множество описывается этим уравнением, мы преобразуем его так, чтобы оно приняло знакомый нам вид. Возведя обе засти в квадрат, раскрывая скобки и приводя подобные члены, получаем равенство: Зх2-8х+4+Зу2=0.
Это равенство можно переписать так: 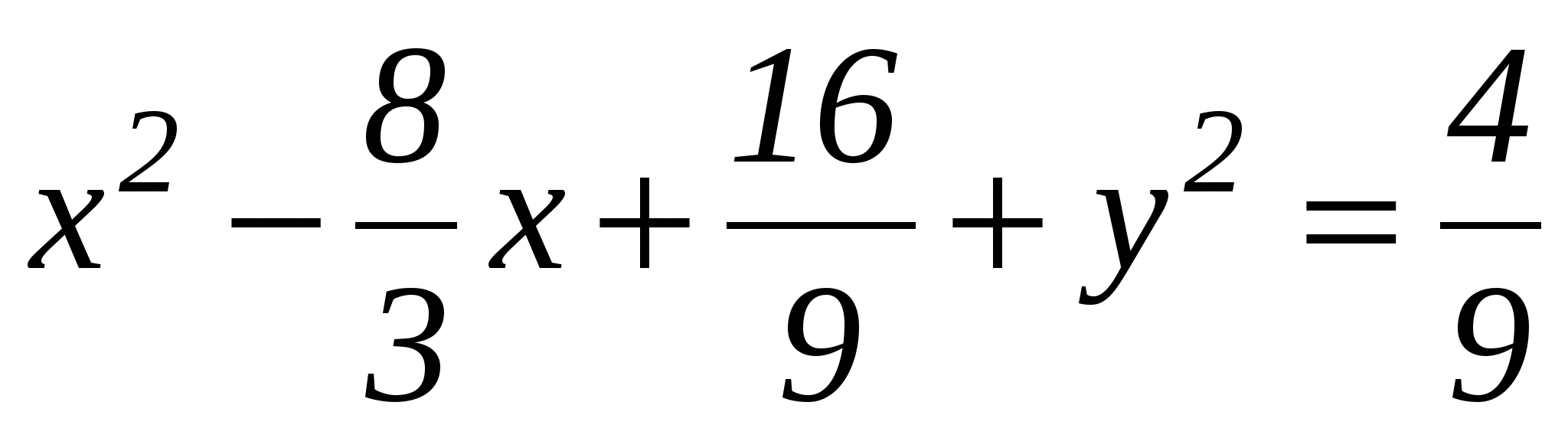
или так: 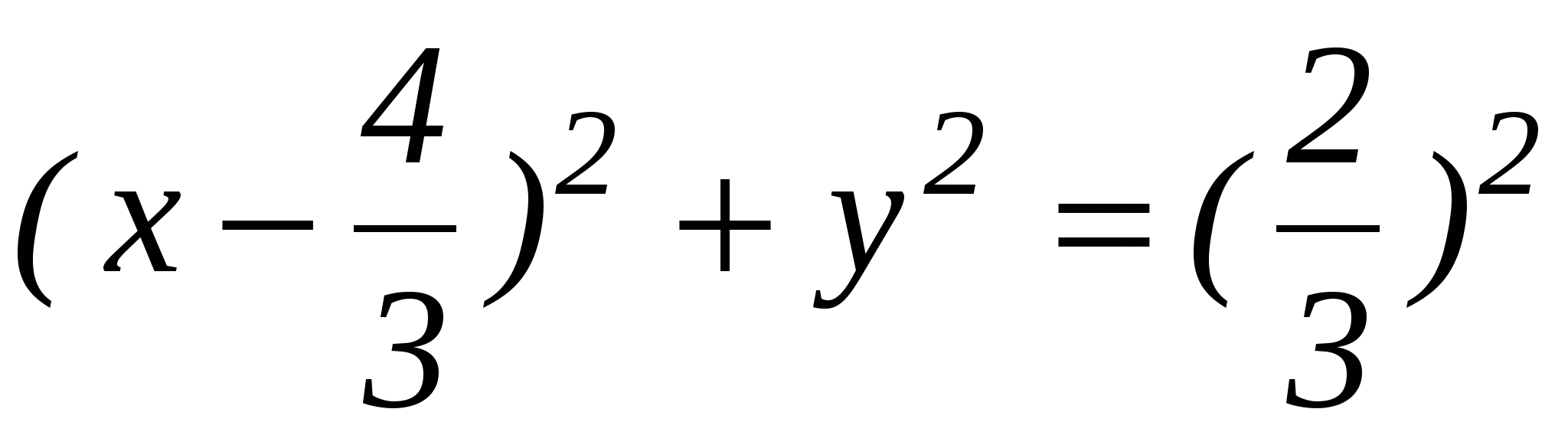 . Это уравнение окружности с центром в точке (
. Это уравнение окружности с центром в точке (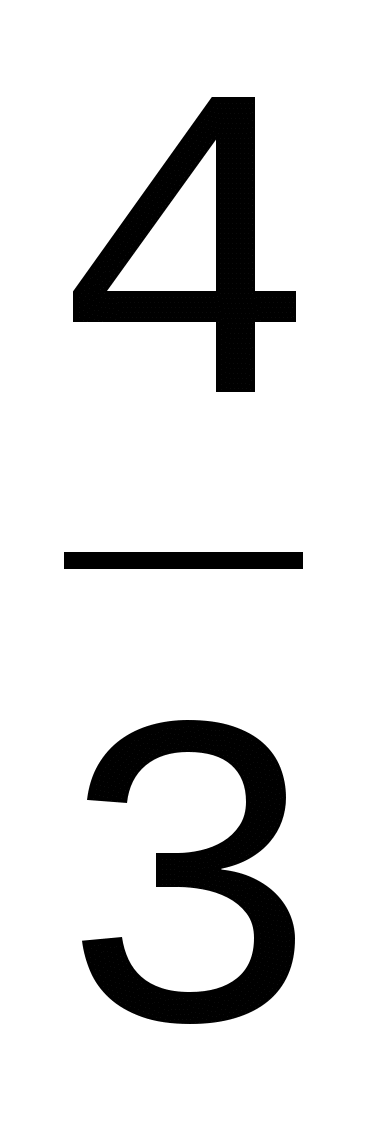 ,0) и радиусом, равным
,0) и радиусом, равным 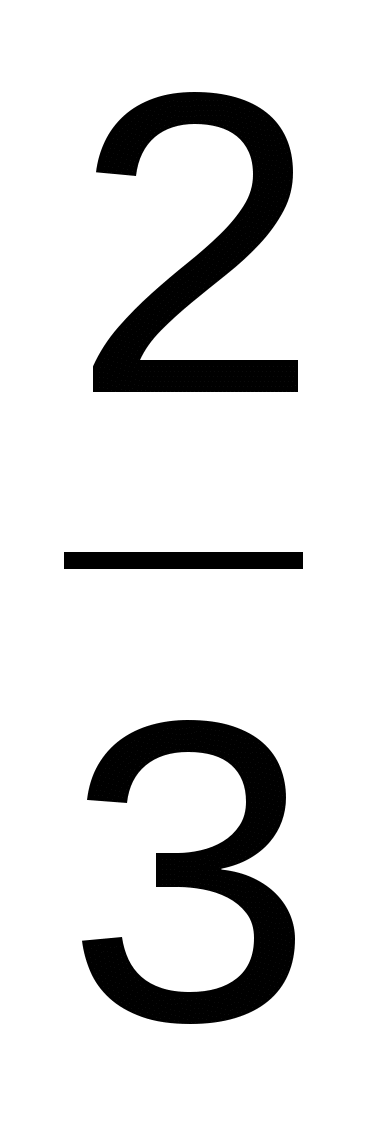 . Это значит, что наше геометрическое место точек является окружностью.
. Это значит, что наше геометрическое место точек является окружностью.
Задача 3. Дан треугольник ABC; найти центр окружности, описанной около этого треугольника.
Решение:
Примем точку А за начало координат, ось абсцисс направим от А к В. Тогда точка В будет иметь координаты (с,0), где с - длинна отрезка АВ. Пусть точка С имеет координаты (q,h), а центр искомой окружности - (а,b). Радиус этой окружности обозначим через R. Запишем в координатах принадлежность точек А(0,0), В(с,0) и C(q,h) искомой окружности:
a2+b2=R2,
(c-a)2+b2=R2,
(q-a)2+(h-b)2=R2.
Каждое из этих условий выражает тот факт, что расстояние точек А(0,0), В(с,0), C(q,h) от центра окружности (а,b) равно радиусу. Эти условия легко получить, если записать уравнение искомой окружности (окружности с центром (а,b) и радиусом R), т. е. (x-a)2+(y-b)2=R2, а затем в это уравнение вместо х и у подставить координаты точек А, В и С, лежащих на этой окружности. Эта система трех уравнений с тремя неизвестными легко решается, и мы получаем:
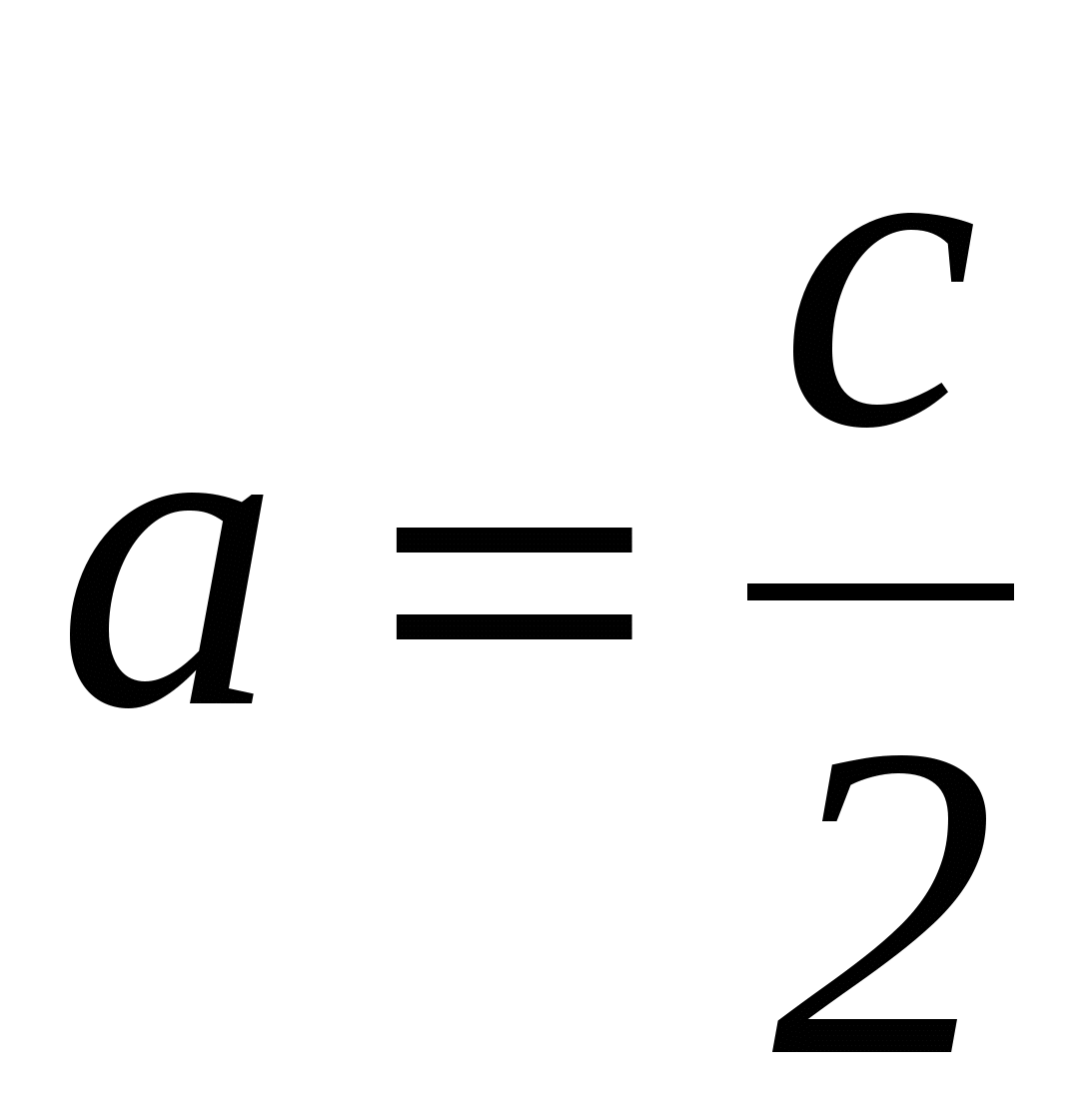 ,
, 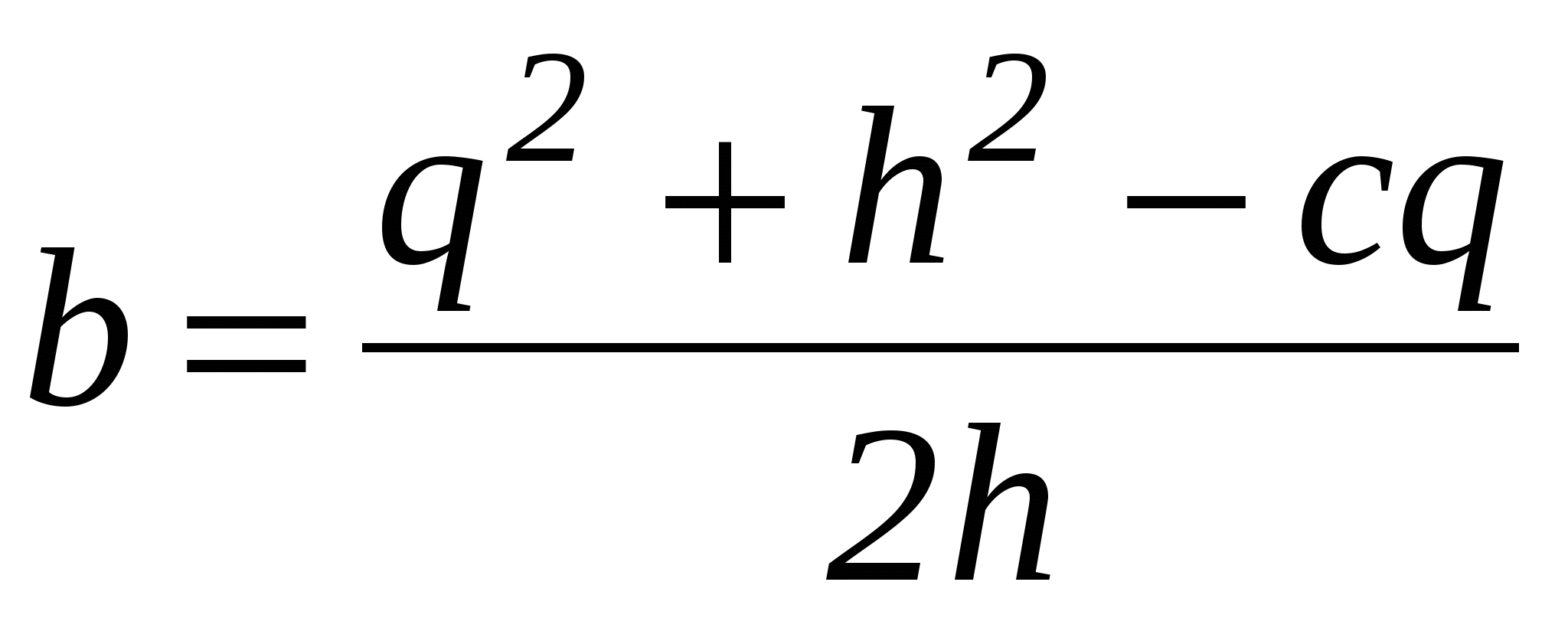 ,
,
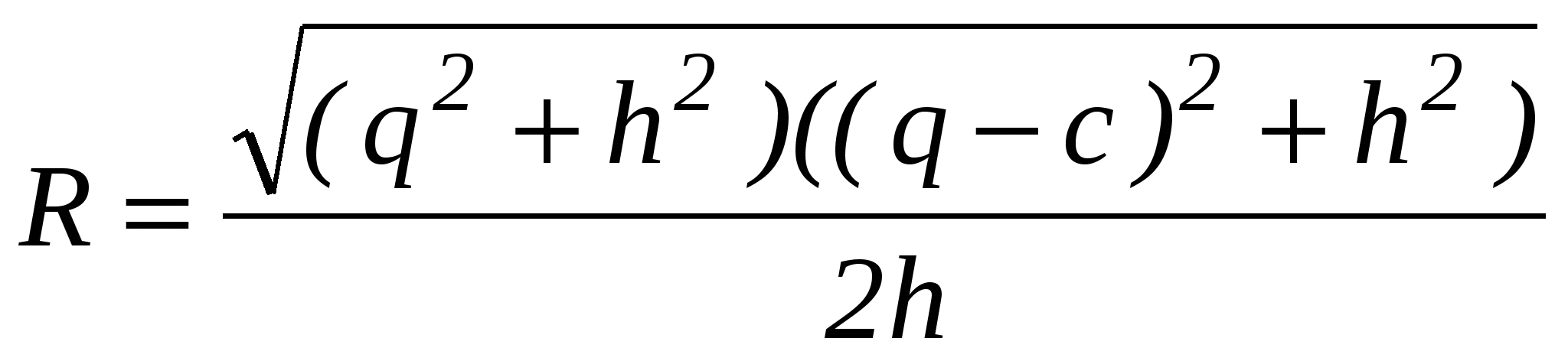 .
.
Задача решена, так как мы нашли координаты центра и радиус. Причем следует заметить, что мы при решении задачи не прибегали к построению чертежа.
Домашнее задание:
-
Лестница, стоящая на гладком полу у стены соскальзывает вниз. По какой линии движется котенок, сидящий на середине лестницы?
-
В квадрат вписана окружность. Доказать, что сумма квадратов расстояний любой точки окружности до сторон квадрата постоянна.
Краткий анализ проведенных занятий: Учащиеся на уроках активно принимали участие, особенно на первом при выводе формул, так как материал не сложный и использует факты и понятия, которые были изучены не так давно и повторены на устном счете. Также на 1 уроке удалось прорешать все запланированные задачи на закрепление, особую трудность вызвала задача № 3, в которой учащиеся долго не могли сделать чертеж и путались в формулах нахождения длины и координат вектора. Проведенная на следующем уроке самостоятельная работа показала, что практически все ученики усвоили материал (с работой не справились 2 человека из 26 учеников этого класса). Наибольшее количество ошибок было сделано в задаче № 2, при использовании формулы нахождения расстояния между 2 точками. Таким образом, можно предположить, что тема «Простейшие задачи в координатах» была успешно усвоена большинством учеников данного класса.
ГЛАВА 3. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ИЗУЧЕНИИ ТЕМЫ: МЕТОД КООРДИНАТ И ЕГО ИЗУЧЕНИЕ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ.
3.1. РОЛЬ И МЕСТО КОМПЬЮТЕРА В УЧЕБНОМ ПРОЦЕССЕ
Появление компьютеров вызвало небывалый интерес к их применению в сфере обучения. Процесс компьютеризации необратим, остановить его ничто не может.
Во-первых, на возрастающей роли компьютеров в жизни современного общества. Сейчас трудно назвать какую-либо ее область - будь то производство, наука, техника, культура, сельское хозяйство, быт, развлечение, где бы применение компьютеров не приносило ощутимых результатов.
Во-вторых, на стремительном росте применения компьютеров всех регионов планеты.
В основе того и другого - впечатляющие (и даже более того - потрясающие ум и воображение, особенно если говорить о перспективах) успехи в развитии компьютерной техники. Возможности компьютеров растут столь стремительно, что прогнозы специалистов об их ближайшем будущем напоминают научную фантастику.
Практически все развитые страны широко разрабатывают компьютерные технологии обучения. Это вызвано тем, что компьютер стал средством повышения производительности труда во всех сферах деятельности человека. Резко возрос объем необходимых знаний, и с помощью традиционных способов и методик преподавания уже невозможно подготовить требуемое количество высокопрофессиональных специалистов.
Умелое использование вычислительной техники приобретает в наши дни общегосударственное значение, и одна из важнейших задач школы - вооружать учащихся знаниями и навыками использования современной вычислительной техники. С компьютеризацией обучения во всем мире связаны надежды повысить эффективность учебного процесса, уменьшить разрыв между требованиями, которые общество предъявляет подрастающему поколению, и тем, что действительно дает школа.
Функции компьютера в системе образования весьма разнообразны - от управления органами народного образования в целом и отдельной школы до средств развлечения учащихся во внеурочное время. Если же говорить об основных функциях компьютера в учебном процессе, то он выступает как объект изучения и средство обучения. Каждой из этих функций соответствует свое направление компьютеризации обучения. Первая из них предполагает усвоение знаний, умений и навыков, которые позволяют успешно использовать компьютер при решении разнообразных задач, или, другими словами, овладение компьютерной грамотностью, которую называют нередко «второй грамотностью». Второе направление видит в компьютере мощное средство обучения, которое способно значительно повысить его эффективность. Указанные два направления и составляют основу компьютеризации обучения.
Указанный аспект компьютеризации обучения охватывает первое ее направление, где компьютер выступает как объект изучения. Наша школа, как общеобразовательная, уже приступила к практической реализации этой задачи. Имеется и второе направление компьютеризации, в рамках которого компьютер рассматривается как средство обучения. С компьютеризацией обучения во всем мире связаны надежды повысить эффективность учебного процесса, уменьшить разрыв между требованиями, которые общество предъявляет подрастающему поколению, и тем, что действительно дает школа.
Когда говорят о достоинствах компьютера в обучении, обычно имеют в виду, прежде всего дисплей. Не только схемы, график, чертежи и прочая "скучная" символика, но и рисунки, движущиеся изображения, словно по мановению волшебной палочки возникают на дисплее - в цвете и со звуковым сопровождением, причем эти изображения может создавать и сам ученик. Часто указывают на возможность для школьника вести содержательную беседу, диалог с компьютером, причем ученик не только отвечает на вопросы электронного педагога, но и сам может их ставить и даже вступать с компьютером в спор. Одно из наиболее плодотворных применений компьютера в обучении - использование его как средств управления учебной деятельностью школьников. Именно в этом качестве он может наиболее существенно повысить эффективность обучения.
Школьный компьютер дает возможность учащемуся выступить в непривычной для него роли пользователя современной вычислительной техники. Эта роль изменяет весь процесс обучения. Школьник, подобно конструктору, может теперь проектировать новые объекты и анализировать их. С помощью компьютера можно решать задачи на поиск и устранение неисправностей в различных технических системах, получить доступ к самой различной информации. Компьютер поможет превратить эту информацию в знания, сделать их средством деятельности ученика, которое он сможет применить в учении и в труде. Чтобы эффективно использовать компьютер в учебном процессе, необходимо решить множество проблем.
Основные цели компьютерной грамотности учащихся состоят в следующем. Прежде всего, надо обеспечить формирование знаний, умений и навыков, которые дают понимание возможностей компьютера и его влияния на общество в целом и на самого обучаемого. Последнее связано с пониманием того, как компьютер поможет решать разнообразные задачи, в том числе и учебные. Важнейшим компонентом компьютерной грамотности является формирование умений практически использовать компьютер при решении разнообразных учебных и трудовых задач с использованием современных средств математического обеспечения. В число этих задач обязательно должны входить задачи автоматизированного поиска информации. Компьютерная грамотность - это отнюдь не какая- то, пусть даже очень важная, добавка к системе знаний и умений, формируемых у учащихся в школе. Она должна входить в единую систему интеллектуального достояния школьника.
Сфера применения и роль вычислительных машин в повышении эффективности деятельности человека должны быть раскрыты учащимся прежде всего в процессе практического использования ЭВМ для решения разного рода задач в ряде учебных предметов. При этом необходимо, чтобы совокупность этих задач охватывала все основные области применения ЭВМ. Школьный компьютер может быть использован учащимися для вычислительной работы в курсах математики, физики, химии, анализа данных учебного эксперимента и поиска закономерностей при проведении лабораторных работ, исследовании функций в курсе алгебры, построении и анализе математических моделей.
Курс математики - научная база изучения информатики. Понятие алгоритма необходимо формировать не только на примере алгоритмов из курса математики, но и на примере алгоритмов из других сфер деятельности человека. Необходимо дать ясные представления ученику о возможности автоматизации деятельности человека на основе алгоритма. Тем самым будет понятна роль техники в решении возникающих перед человеком практических задач.
Формирование навыков работы с компьютером, освоение прикладного программного обеспечения в курсе информатики позволит реализовать вторую важнейшую задачу внедрения ЭВМ в школу. При обучении математике могут найти применения, прежде всего следующие возможности современных компьютеров.
1. Быстрота и надежность обработки информации любого вида. Отметим, что для обработки числовой информации можно использовать не только микро ЭВМ, но и калькулятор.
2. Представление информации в графической форме. По своим графическим (демонстрационным) возможностям микро ЭВМ практически не уступают даже цветному телевидению, но позволяют активно влиять на ход демонстраций, что значительно повышает их методическую ценность.
3. Хранение и быстрая выдача больших объемов информации. Например, все используемые в курсе математики таблицы могут храниться в памяти компьютера. Требуемая информация выдается на экран после одного - двух нажатий клавиш.
Возможность применения микро ЭВМ на уроках зависят от программного обеспечения машин. Все используемые на занятиях программы можно условно разделить на обучающие и учебные. Обучающие программы создаются для того, чтобы заменить учителя в некоторых видах его деятельности (при объяснении нового материала, закреплении пройденного, проверки знаний и т.п.). Цель учебных программ - помочь ученику в его познавательной деятельности, работе на уроке. Использование учебных программ осуществляется при участии и под руководством учителя. С помощью учебных программ можно выполнить разнообразные вычислительные операции, анализировать функции, строить графики и исследовать математические функции, использовать графику машины для повышения наглядности изучаемого материала.
Математических программ в наше время очень много, например, УМК «Живая математика» [8] или свободно распространяющаяся бесплатная программа «GeoGebra» [33]. Данные программы являются учебными, так как направлены на развитие самостоятельности и познавательной деятельности у учащихся, их возможности в познании учащимися самих себя, в осознании своей деятельности, качеств и личностной рефлексии. Значение их в учебной деятельности трудно переоценить. Чтобы сформировать полноценную учебную деятельность, недостаточно выработать у учащегося систему знаний о предметном мире. Он должен овладеть своей деятельностью, знать, как он анализирует условия задачи, каковы его стратегии поиска решения, то есть у него должен выработаться рефлексивный механизм саморегуляции. В конце концов, всё это необходимо для формирования целостного представления о самом себе как о личности, становления устойчивого «образа Я».
3.2 ПРИМЕНЕНИЕ УМК «ЖИВАЯ МАТЕМАТИКА»
Традиционный подход к преподаванию геометрии приводит к малой популярности этого предмета, особенно среди учащихся, далёких от математики. Наиболее очевидная причина этого заключается в том, что формулировки и доказательства теорем заучиваются, но не проверяются. Такой стиль обучения нацелен на развитие некритического, нетворческого мышления и естественно отторгается современными школьниками. Помочь решить возникающие в связи с этим проблемы может учебно-методический комплект (УМК) «Живая Математика» [8], который сформирован на основе программы Geometry's Sketchpad (в русском переводе «Живая Математика»), переведенной на русский язык и адаптированной Институтом новых технологий. Комплект был поставлен в школы-миллионеры Российской Федерации в рамках ПНПО.
Учебно-методический комплект состоит из самой программы «Живая Математика», методического пособия и альбомов готовых динамических чертежей, разделенных на две группы: «Теоремы и задачи школьного курса» и «Дополнительные материалы».
Первая группа «Теоремы и задачи школьного курса» включает альбом «Введение в компьютеризированный курс планиметрии», содержащий 46 уроков по темам: начальные геометрические сведения, треугольники, четырехугольники; площади, подобие, окружность.
Программа «Живая математика» очень удобный продукт для подготовки электронных образовательных ресурсов к урокам математики.
«Живая математика» имеет прозрачный и понятный интерфейс, позволяет создавать красочные чертежи, визуализировать алгебраические операции. Использование данной программы позволяет сделать процесс обучения интересным и наглядным, развивает творческую деятельность учащихся, их абстрактное и логическое мышление. Сама среда не является обучающей и «сама ничего не делает», - все чертежи в ней создаются пользователем, а программа лишь предоставляет для этого необходимые средства, так же как и возможности для усовершенствования чертежей и их исследования.
Применение программы «Живая геометрия» в процессе обучения:
-
-
развивает навыки самостоятельного мышления;
-
формирует положительное и ответственное отношение к учебе;
-
повышается самооценка учащегося, самокритичность;
-
появляется заинтересованность и потребность в получении дополнительных знаний;
-
раскрывается интерес к научной деятельности, что является существенным достижением в период значительного спада интереса к математике;
-
высокий эстетический уровень оформления работ, делает изучение геометрии привлекательным.
-
Сама программа «Живая математика» представляет собой уникальный продукт, позволяющий строить современный компьютерный чертеж, который выглядит как традиционный, однако, представляет собой качественно совершенно новое явление. Чёртёж, построенный на бумаге с помощью карандаша и линейки, имеет важнейшее значение, но обладает двумя недостатками: требует затрат времени и конечный продукт оказывается статичным. Программа «Живая математика» позволяет значительно экономить время, но самое главное: чертёж, построенный с помощью программы, можно тиражировать, деформировать, перемещать и видоизменять. Элементы чертежа легко измерить компьютерными средствами, а результаты этих измерений допускают дальнейшую компьютерную обработку. Возможны также многократные обмены чертежами с учителем, хранение нескольких вариантов одного и того же чертежа и т. п. Появляется возможность добиваться от учащихся точных и грамотных письменных формулировок (по крайней мере, констатирующих то, что они видят); их можно переделывать столько раз, сколько требуется.
УМК может использоваться практически при любых видах учебной деятельности, в том числе, при выполнении домашних работ, творческих проектов и т. д .
.
При работе в рамках данного УМК каждая обсуждаемая фигура изображается на экране монитора. При решении задач учащиеся могут выполнять задание на чертеже, приложенном к программе, а могут создавать собственные чертежи и сверять свои построения с образцом. Если же работа происходит в классе, оснащенном только одним компьютером и проектором, ученикам можно предложить выполнить решение в тетради, пользуясь при этом указаниями и подсказками, данными в задачах, и сверить свои построения с образцом.
Учителю математики, приступающему к работе в УМК, достаточно владеть компьютером на уровне начинающего пользователя. Сама программа «Живая Математика» легко осваивается при помощи руководства, содержащегося в первом разделе данного пособия. Учащиеся могут установить программу на домашний компьютер и работать с ней индивидуально во внеурочное время. Для того чтобы учащиеся получили первоначальные навыки работы в программе, достаточно 2-3 занятий. За это время можно изучить материал первых четырёх уроков сборника методических материалов. Учащиеся, присутствующие на первом занятии, становятся активными помощниками учителя на тех уроках геометрии, когда использзуется программа. Это провоцирует «цепную реакцию»: на следующие занятия учащиеся торопятся, даже те, которые не любят математику и зачастую прогуливают уроки.
При помощи программы УМК «Живая математика» можно:
-
Объяснять сложные темы и изучать теоремы
Учебники геометрии содержат многочисленные определения, постулаты, теоремы, леммы, которые бывает нелегко понять или воспроизвести. При помощи «Живой Математики» удобно создавать конструкции, моделирующие условия теорем, и экспериментировать с ними. Альбом «Теоремы и задачи школьного курса» составлен в соответствии с учебниками Атанасяна Л.С. «Геометрия. 7-9 кл.» и «Геометрия.10-11кл».
Например, при изучении темы «Применение подобия к решению задач и доказательству теорем» в 8 классе рассматривается задача: какая фигура получится, если последовательно соединить середины сторон произвольного четырёхугольника?
Работаем следующим образом:
-
предлагаем учащимся построить произвольные четырёхугольники, причём как выпуклые, так и невыпуклые;
-
через команду «Середина» меню «Измерения» строим середины всех сторон четырёхугольника, последовательно их соединяем;
-
анализируем особенности полученной фигуры; возможно, уже сейчас учащиеся выдвинут предположения, что данная фигура является параллелограммом;
-
предлагаем проверить сохранение свойств внутренней фигуры при любой форме внешнего четырёхугольника - потянем туда-сюда вершины исходной фигуры;
-
для уточнения предположения с помощью меню «Измерения» вычисляем величины отдельных элементов внутренней фигуры и снова изменяем исходную фигуру, наблюдая, что происходит с измерениями;
-
окончательно формулируем гипотезу.
Т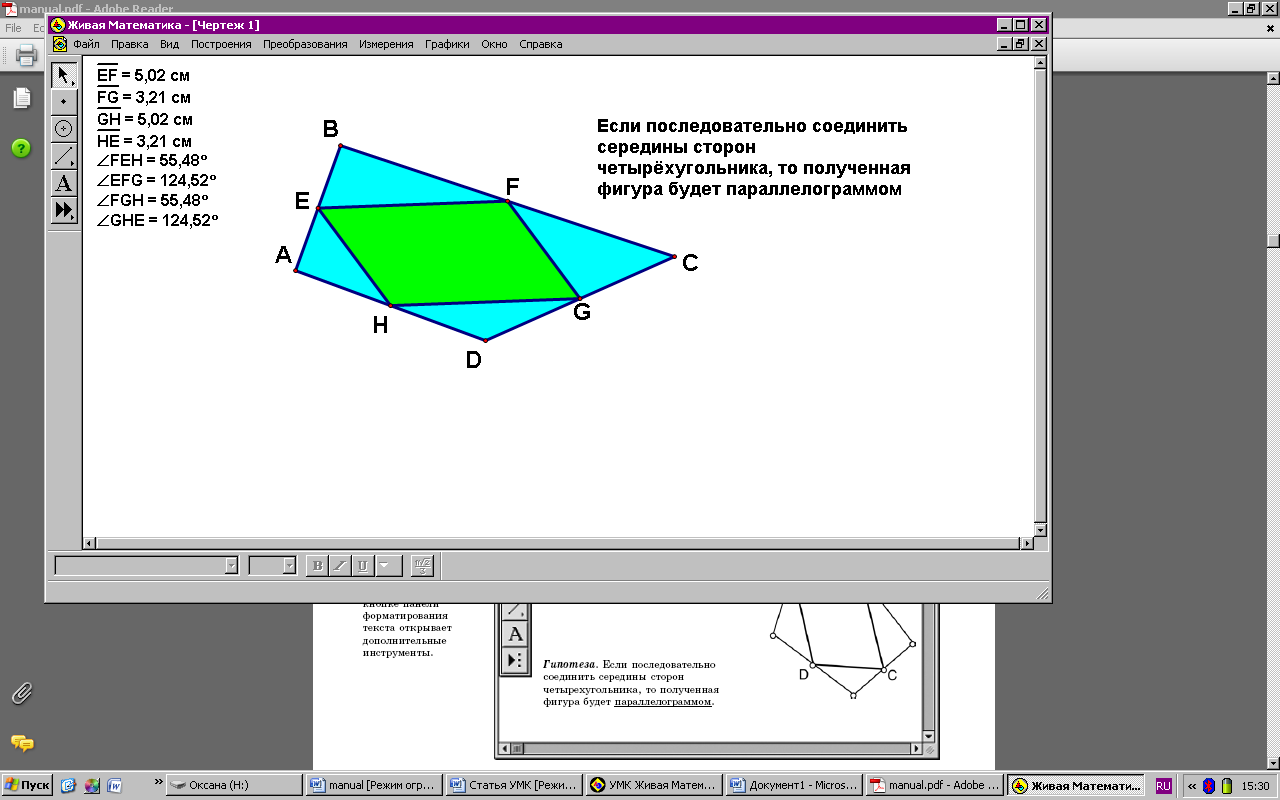 еперь осталось доказать сформулированную гипотезу (рис. 21).
еперь осталось доказать сформулированную гипотезу (рис. 21).
Рисунок 21. Иллюстрация решения задачи на выдвижение гипотезы.
-
Оживлять рисунки из учебника
Получив определенный навык работы в «Живой Математике», нетрудно понять, что проще и быстрее воспроизвести рисунок из учебника на компьютере, чем рисовать его на бумаге. Одному из учеников каждый урок дается задание подготовить чертежи ко всем задачам домашней работы. При этом оценивается динамичность (существование чертежа со всеми своими возможными деформациями) и соответствие чертежа условиям задачи. В качестве дополнительного необязательного задания учащиеся могут подобрать задачи по изучаемой теме из дополнительных источников, подготовить чертежи. Таким образом, каждый учащийся может создать свой собственный электронный учебник (рис.22,23).
Р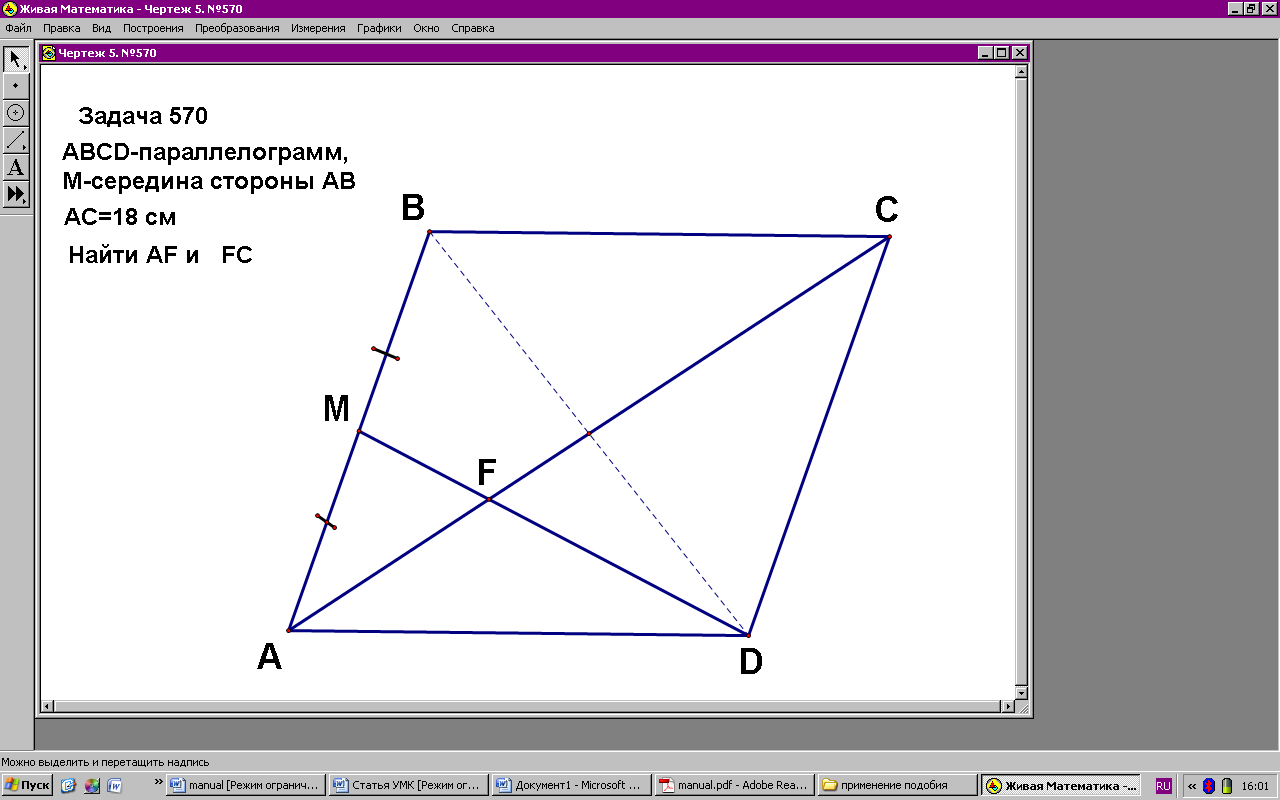
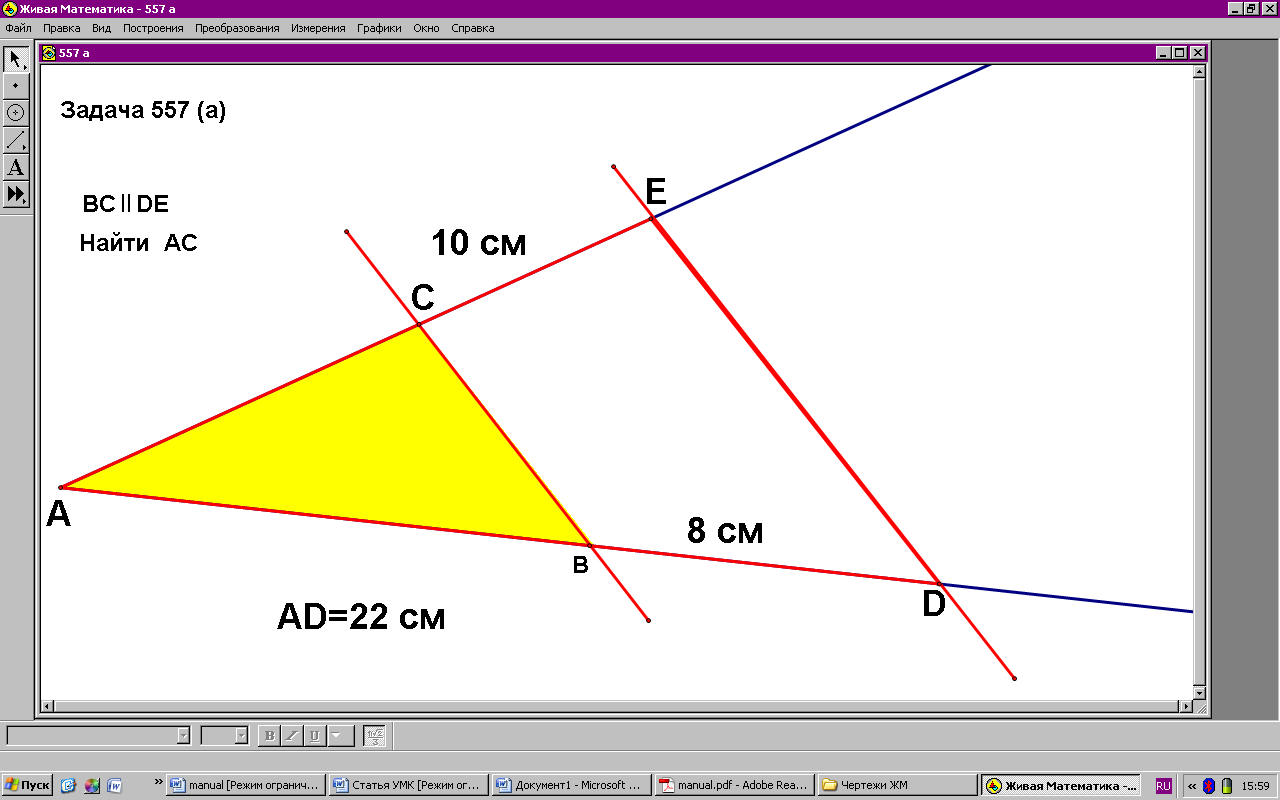 исунок 22-23. Иллюстрация чертежей к задачам из учебника.
исунок 22-23. Иллюстрация чертежей к задачам из учебника.
Решать экспериментальные задачи. Задачи этого типа отличаются от задач на доказательство тем, что утверждение надо не только доказать, но и сформулировать. Экспериментируя с чертежом, учащийся формулирует гипотезы. После этого задача превращается в задачу на доказательство сформулированной гипотезы. Например, при изучении темы «Площадь трапеции» полезно рассмотреть следующую задачу: площади каких трапеций равны полупроизведению их диагоналей. Обычно, таким образом сформулированные задачи ставят учащихся в тупик, они просто не знают с чего начать решение. Программа «Живая математика» позволяет сначала увидеть такую трапецию, а затем установить её свойства и сделать вывод.
Ход решения задачи:
-
строим произвольную трапецию;
-
через команду «Площадь» меню «Измерения» вычисляем площадь трапеции;
-
через встроенный калькулятор меню «Измерения» вычисляем величину, равную полупроизведению диагоналей;
-
двигаем вершины трапеции, добиваясь равенства величин, вычисленных в пунктах 2 и 3;
-
а
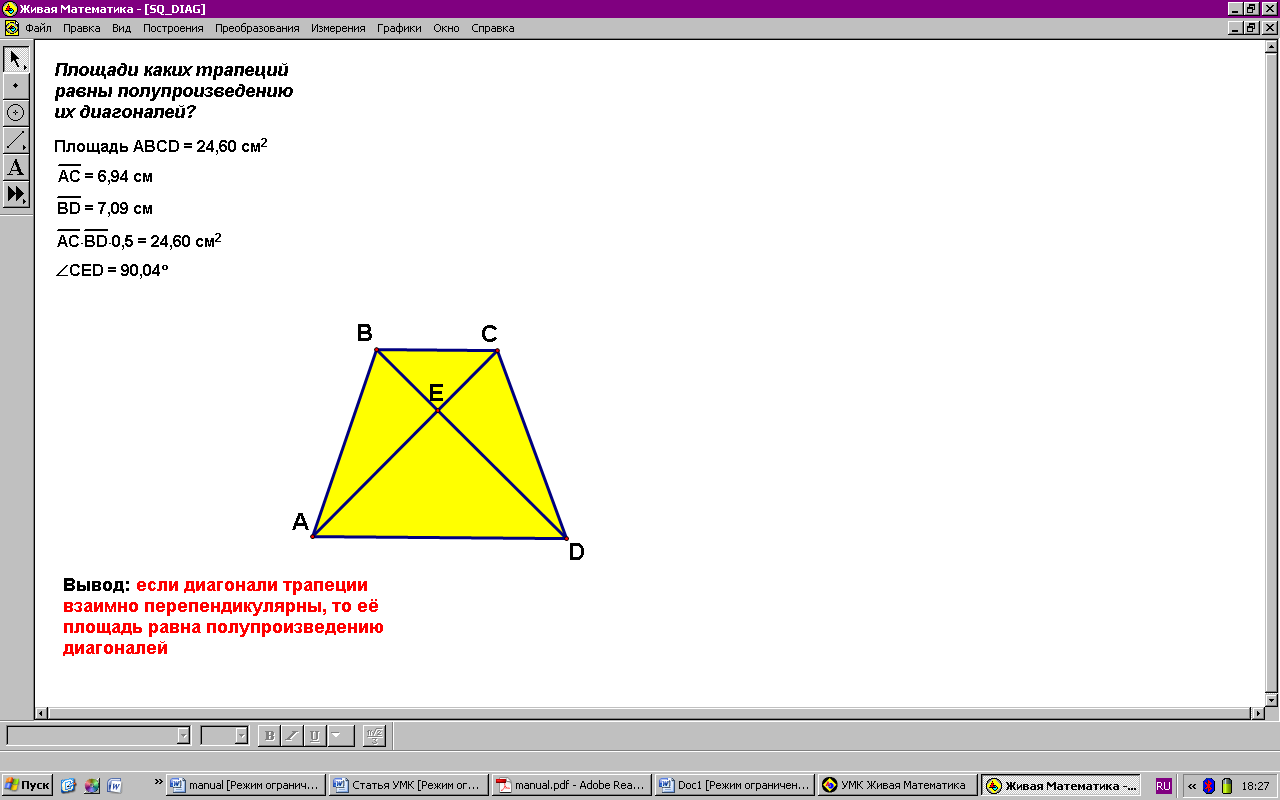 нализируем особенности трапеции, для которой равенство выполняется, выдвигаем предположение: угол между диагоналями прямой;
нализируем особенности трапеции, для которой равенство выполняется, выдвигаем предположение: угол между диагоналями прямой; -
проверяем предположение: с помощью меню «Измерения» вычисляем угол между диагоналями.
При необходимости корректируем чертёж, двигая вершины трапеции, и формулируем ответ на вопрос задачи (рис. 24).
Рисунок 24. Иллюстрация решения задачи.
При изучении темы «Координатная плоскость» в 6 классе, я тоже прибегла к помощи данного УМК. В компьютерной программе есть возможность задать систему координат, построить точки по заданным координатам, и выполнить обратную задачу: найти координаты построенных точек. Очень понравилась ребятам работа по созданию рисунков животных, космических моделей в компьютерной программе. Перед ними ставилась задача придумать свой индивидуальный рисунок на бумаге, затем записать координаты полученных точек для построения фигуры и наконец, воссоздать красочный рисунок на компьютере в системе координат при рассмотрении данной квадратичной функции.
При изучении темы «Построение сечений многогранников». В программе много готовых анимационных задач по данной теме: это и построение сечений параллелепипеда, призмы, пирамиды и др. Есть возможность рассмотреть построенное сечение с разных углов обзора, прийти к выводу, о многоугольнике получившимся в результате сечения в зависимости от заданных точек
-
Применять программу в других разделах математики
Легко убедиться, что «Живая Математика» - незаменимый инструмент для изучения не только геометрии, но и вообще всех математических курсов, например, алгебры (тема «Функции и графики»), так же во внеурочное время.
У дивительные геометрические объекты - фракталы, которые моделируют сложные и красивые явления природы и поэтому являются элементом многих графических компьютерных программ. Фрактал - это самоподобный геометрический объект, который выглядит одинаковым образом при любом увеличении изображения (рис. 25). Построение фрактала включает в себя изготовление простой конструкции, которая формирует все меньшие и меньшие детали фигуры. Команда «Итерации» позволяет построить конструкции такого рода, впрочем, как и другие фигуры с повторяющимся алгоритмом построения элементов. Построение фракталов позволяет иллюстрировать не только интереснейшее геометрическое явление, но и привлечь учащихся к исследовательской работе, заинтересовать их в изучении геометрии на более высоком уровне, что способствует активизации познавательной деятельности учащихся.
дивительные геометрические объекты - фракталы, которые моделируют сложные и красивые явления природы и поэтому являются элементом многих графических компьютерных программ. Фрактал - это самоподобный геометрический объект, который выглядит одинаковым образом при любом увеличении изображения (рис. 25). Построение фрактала включает в себя изготовление простой конструкции, которая формирует все меньшие и меньшие детали фигуры. Команда «Итерации» позволяет построить конструкции такого рода, впрочем, как и другие фигуры с повторяющимся алгоритмом построения элементов. Построение фракталов позволяет иллюстрировать не только интереснейшее геометрическое явление, но и привлечь учащихся к исследовательской работе, заинтересовать их в изучении геометрии на более высоком уровне, что способствует активизации познавательной деятельности учащихся.
Рисунок 25. Фрактал. Снежинка Коха.
Возможности программы поистине уникальны. Чтобы построить грамотный чертёж, нужно знать, как минимум, определения и свойства рассматриваемых фигур.
3.3 ПРИМЕНЕНИЕ ПРОГРАММЫ «GEOGEBRA»
GeoGebra - это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику в одном удобном для использования пакете. Она завоевала несколько образовательных наград в Европе и США [33].
Краткие характеристики:
- графика, алгебра и таблицы связаны между собой и полностью динамичны;
- легкий в использовании интерфейс, обладает мощными возможностями;
- вы можете сами создать интерактивный обучающий материал, такие как веб-страницы;
- доступна на многих языках для миллионов пользователей по всему миру;
- бесплатная программа с открытым кодом.
Решение задач с использованием GeoGebra очень удобно, приведу пример:
Пример (ЕГЭ-2012, С4)
Дан параллелограмм ABCD, AB=2, BC=3, A= 60 . Окружность с центром О касается биссектрисы угла D и двух сторон параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь четырехугольника ABOD.
Н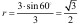 а Рисунке 26 приведено решение задачи в программе GeoGebra. Окружностей две, каждая из них вписана в правильный треугольник. Эти треугольники имеют стороны равные 3 и 2 - соответственно. Поэтому радиусы окружностей равны третьей части высоты правильного треугольника.
а Рисунке 26 приведено решение задачи в программе GeoGebra. Окружностей две, каждая из них вписана в правильный треугольник. Эти треугольники имеют стороны равные 3 и 2 - соответственно. Поэтому радиусы окружностей равны третьей части высоты правильного треугольника.
Д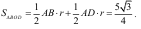 ля треугольника со стороной 3 радиус равен . Найдем площадь невыпуклого четырехугольника как
ля треугольника со стороной 3 радиус равен . Найдем площадь невыпуклого четырехугольника как
с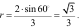 умму площадей треугольников АОВ и AOD:
умму площадей треугольников АОВ и AOD:
Для треугольника со стороной 2 радиус равен
Чтобы найти площадь четырехугольника ABOD, вычтем из площади
параллелограмма площадь треугольников BOC и DOC:
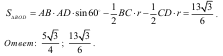
Рис. 26 Решение задачи в GeoGebra (2 случая)
Сравним полученные ответы с результатами GeoGebra:
Результаты, полученные в GeoGebra, совпадают с решением задачи.
Программу GeoGebra [33] можно применять на уроках геометрии для построения чертежей (задача 1) и на уроках алгебры для построения графиков функций, графического решения уравнений и неравенств, а также их систем (задача 2).
З адача № 1
адача № 1
Основание АВ равнобедренного треугольника равно 20. Окружность радиуса 15 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АВ в его середине. Найдите радиус окружности, вписанной в треугольник АВС.
Решение.
Пусть точка О - центр окружности, расположенной
вне  АВС. Радиус окружности, вписанной
АВС. Радиус окружности, вписанной
в треугольник лежит на пересечении его биссектрис. Пусть точка М - центр окружности, вписанной в
 АВС, тогда МТ - радиус вписанной окружности.
АВС, тогда МТ - радиус вписанной окружности.
Рассмотрим 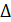 ОАМ. Угол ОАМ прямой, как угол между биссектрисами смежных углов; АТ - высота, опущенная из вершины прямого угла. Следовательно АТ2 = МТ· ТО.
ОАМ. Угол ОАМ прямой, как угол между биссектрисами смежных углов; АТ - высота, опущенная из вершины прямого угла. Следовательно АТ2 = МТ· ТО.
АТ=  АВ = 10; ТО=15; 102 = МТ· 15, отсюда МТ=
АВ = 10; ТО=15; 102 = МТ· 15, отсюда МТ=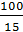 =
=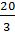 = 6
= 6 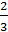 .
.
Ответ: 6  .
.
Задача №2
Для каждого значения a найдите число корней уравнения Iх -2I - 1= а - 3х.
Р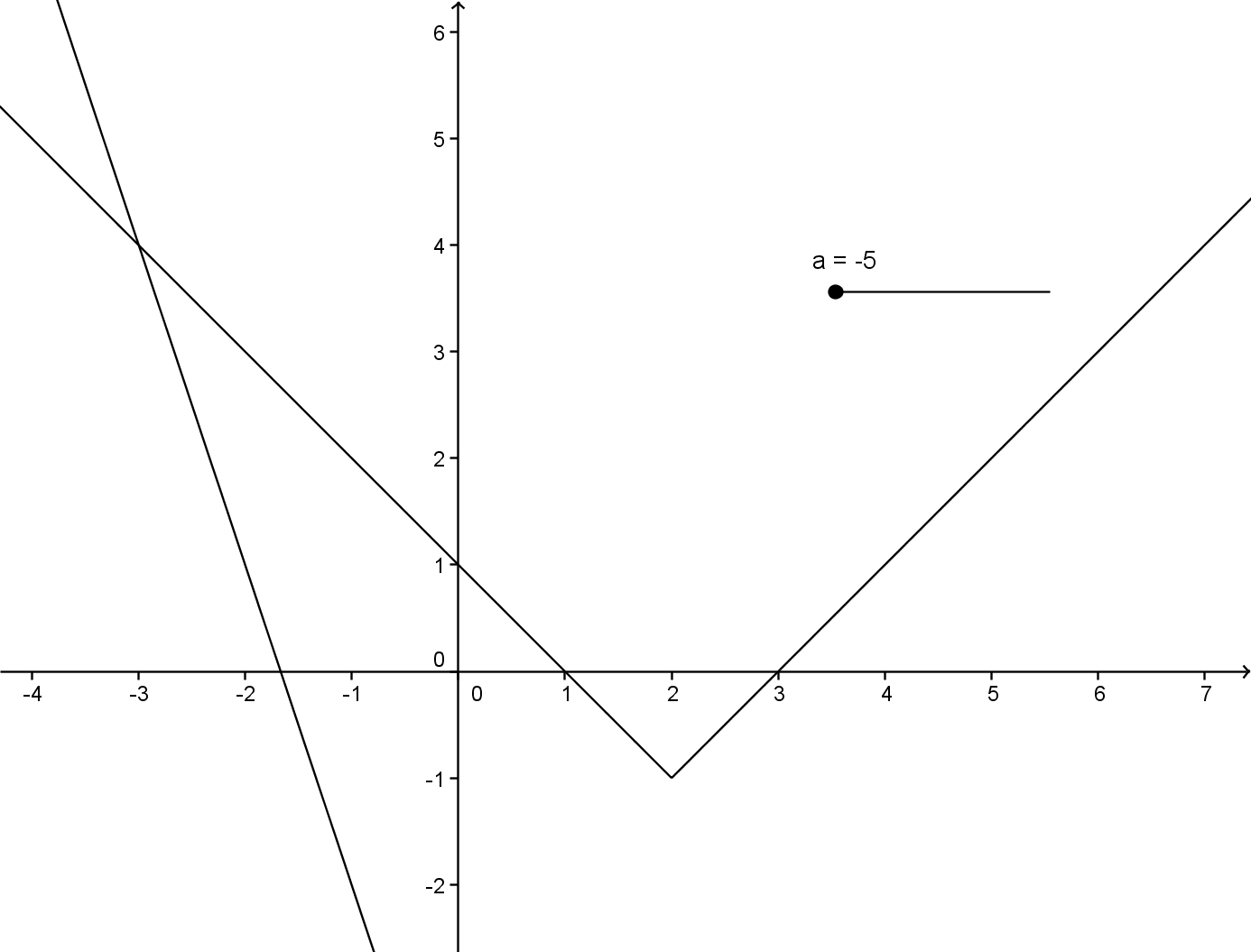 ешение.
ешение.
1 способ.
Решим графически:
Из графика видно, что при любом а уравнение имеет один корень.
Ответ: (-∞; + ∞).
2 способ.
Iх -2I - 1= а - 3х;
Iх -2I = а - 3х +1;
1) х≥2, х≥2, х=(а+3):4 ≥2, значит а+3 ≥ 8. Х - 2= а+1 - 3х; х=(а+3):4;
2) х<2, х<2, х = (а - 1):2<2, значит а<5 - х+2 = а+3 - 3х; х = (а - 1):2;
При всех значениях а решение единственное.
Ответ: (-∞; + ∞).
Аналогично прогамме «Живая математика» [29] в GeoGebra [30] есть возможность задать систему координат, построить точки по заданным координатам, и выполнить обратную задачу: найти координаты построенных точек. Можно создавать рисунки животных, космических моделей в компьютерной программе.
 «Построение сечений многогранников» так же возможно в данной программе. В программе много различный функций, которые помогают достаточно легко построить многогранник и его сечение. Например: построение сечений параллелепипеда, призмы, пирамиды, куба (рис 27/1 и 27/2) и др. Есть возможность рассмотреть построенное сечение с разных углов обзора, прийти к выводу, о многоугольнике получившимся в результате сечения в зависимости от заданных точек
«Построение сечений многогранников» так же возможно в данной программе. В программе много различный функций, которые помогают достаточно легко построить многогранник и его сечение. Например: построение сечений параллелепипеда, призмы, пирамиды, куба (рис 27/1 и 27/2) и др. Есть возможность рассмотреть построенное сечение с разных углов обзора, прийти к выводу, о многоугольнике получившимся в результате сечения в зависимости от заданных точек
Рис.27/1 Построение сечения куба
Рис.27/2 Построение сечения куба
GeoGebra - это программа, которая даёт возможность создавать чертежи в планиметрии, в частности, для построений с помощью циркуля и линейки [33] .
Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т. д.) за счёт команд встроенного языка, который позволяет управлять и геометрическими построениями.
ЗАКЛЮЧЕНИЕ
Достаточно простой в применении, метод координат является необходимой составляющей решения задач различного уровня. Использование данного метода, позволяет учащимся значительно упростить и сократить процесс решения задач, что помогает им при дальнейшем изучении, как школьного курса математики, так и при изучении математики в высших учебных заведениях.
В данной выпускной квалификационной работе:
-
проанализировано несколько действующих школьных учебников относительно темы «Метод координат»;
-
описан сам метод координат, виды и этапы решения задач методом координат;
-
выделены основные умения, необходимые для овладения данным методом и приведен ряд задач, формирующих их;
-
рассмотрены некоторые математические программы, которые возможно применять при обучении теме: «Метод координат» и вообще математике, которые очень сильно облегчат работу учителя и кардинально изменят отношение учащихся к математике.
-
показана целесообразность и возможности компьютерного обучения, рассмотрены проблемы взаимодействия человека и компьютера в сфере образования.
-
рассмотрены предпосылки для подачи учебного материала с применением ЭВМ.
Также было проведено опытное преподавание, которое подтвердило гипотезу о том, что изучение метода координат в школьном курсе геометрии необходимо. Оно будет более эффективно, если в 5-6 классе проведена пропедевтическая работа по формированию основных умений и навыков, в системном курсе планиметрии учащиеся знакомятся со структурой данного метода, и используется продуманная система задач для формирования отдельных компонентов метода. В данной работе, в полное мере, удалось показать все положительные и отрицательные стороны при обучении математике с помощью компьютера.
Библиографический список
-
Автономова, Т. В. Основные понятия и методы школьного курса геометрии: Книга для учителя [Текст]/ Б. И. Аргунов - М. Просвещение, 1988г. - 127с.
-
Атанасян, Л. С. Геометрия для 7-9 классов средней школы [Текст] / В. Ф. Бутузов, С. Д. Кадомцев, Э. Г. Позняк, И. И. Юдина - М. Просвещение, 1992г.- 335с.
-
Виленкин, Н. Я. Математика: Учеб. для 5 кл. сред. шк. [Текст]/ А. С. Чесноков, С. И Шварцбурд.- М. Просвещение, 1989г. - 304с.
-
Виленкин, Н. Я. Математика: Учеб. для 6 кл. общеобразоват. учреждений [Текст] / В. И. Жохов, А. С. Чесноков, С. И Шварцбурд. - М. Мнемозина, 2001г. - 304с.
-
Гельфанд, И. М. Метод координат [Текст]- М. Наука, 1973г. -87с.
-
Дорофеев, Г. В. Математика: Учеб. для 5 кл. общеобразоват. учреждений [Текст] / И. Ф. Шарыгин, С. Б. Суворова - М. Просвещение, 2000г. - 368с.
-
Дорофеев, Г. В. Математика: Учеб. для 6 кл. общеобразоват. учеб. заведений [Текст] / И. Ф. Шарыгин, С. Б. Суворова - М. Дрофа, 1998г. - 416с.
-
Живая Математика: Сборник методических материалов. - М.: Институт новых технологий - 176 с.
-
Изучение координат в III - IV кл. / Л. Г. Петерсон // Математика в школе - 1983г.- №4
-
Индивидуальные карточки по геометрии для 7-9 кл. / Т. М. Мищенко // Математика в школе - 2001г. - № 8
-
Итоги работы в 7 кл. по учебнику Шарыгина И. Ф. 7-9 / О.В. Бощенко // Математика в школе - 2002г. №5
-
К изучению перемещений на координатной плоскости / Г.Б. Лудина // Математика в школе - 1983г.- №2
-
К началу обучения геометрии 1-7 кл. // Математика в школе 1983г. - №6
-
Лускина М. Г. Факультативные занятия по математике в школе: Методические рекомендации [Текст]/ В. И. Зубарева - Киров ВГПУ, 1995г.
-
Лященко, Е. И. Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов [Текст] / К. В. Зобкова, Т. Ф. Кириченко - М. Просвещение, 1988г. - 233с.
-
Метод координат / А. Савин // Квант -1977г. - №9
-
Мишин, В. И. Методика преподавания математики в средней школе: Частная методика: Учеб пособие для студентов пед. ин-тов по физ.-мат. спец. [Текст] / А. Я. Блох, В. А. Гусев, Г. В. Дорофеев - М. Просвещение 1987г. - 416с.
-
Никольская, И. Л. Факультативный курс по математике: Учеб. пособие для 7-9 кл. ср. шк. [Текст] - М. Просвещение, 1991г. - 383с.
-
Новые компьютерные технологии. Координатная плоскость // Математика - Приложение к газ. «Первое сентября» - 2004г. №29
-
Нужна ли школе XXI века геометрия /И. Шарыгин // Математика - Приложение к газ. «1 сентября» - 2004г. №12
-
О конкретном учебнике геометрии для 7-9 кл. / Л.С. Атанасян // Математика в школе - 1989г. - №1
-
Обсуждение одного учебника / И.Е Феоктистов // Математика в школе -2001г. №5
-
Погорелов, А. В. Геометрия для 7-11 классов средней школы - М: Просвещение, 1990г. - 384с.
-
Понтрягин, Л. С. Знакомство с высшей математикой. Метод координат [Текст] - М. Наука, 1987г. - 128с.
-
Понтрягин Л.С., Метод координат. М., Наука, 1977.
-
Постников М.М., Аналитическая геометрия, М., Техника, 2004.
-
Программа по математике для средней школы - М. Просвещение, 1998г. -205с.
-
Саранцев, Г. И. Упражнения в обучении математике [Текст] - М. Просвещение, 1995г. - 240с.
-
Сикорский, К. П. Дополнительные главы по курсу математики. Учебное пособие по факультативному курсу для учащихся 7-8 классов [Текст] - М. Просвещение, 1974г.- 315с.
-
Упражнения по теме «Координатная плоскость» / О.А. Леонова // Математика в школе - 2001г. - №10
-
Шарыгин, И. Ф. Геометрия 7-9 кл.: Учеб для общеоразоват. учеб. заведений [Текст] - М. Дрофа, 2000г. -368с.
-
Энциклопедия элементарной математики. Геометрия, том 4.
-
geogebra.org -официальный сайт GeoGebra.
Приложение 1.
ВИДЫ ЗАДАЧ, РЕШАЕМЫХ МЕТОДОМ КООРДИНАТ
Применяя метод координат, можно решать задачи двух видов.
-
Пользуясь координатами можно истолковать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функции первый пример такого применения метода координат.
-
Задавая фигуры уравнениями и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Например, можно выразить через координаты основную геометрическую величину - расстояние между точками.
В связи с усилением роли координатного метода в изучении геометрии особенно актуальной становиться проблема его формирования. Наиболее распространенными среди планиметрических задач, решаемых координатным методом, являются задачи следующих 2 видов: 1) на обоснование зависимостей между элементами фигур, особенно между длинами этих элементов; 2) на нахождение множества точек, удовлетворяющих определенным свойствам.
Примером задач первого вида может служить следующая:
«В треугольнике ABC, AB=c, AC=b, BC=a, BD - медиана.
Доказать, что 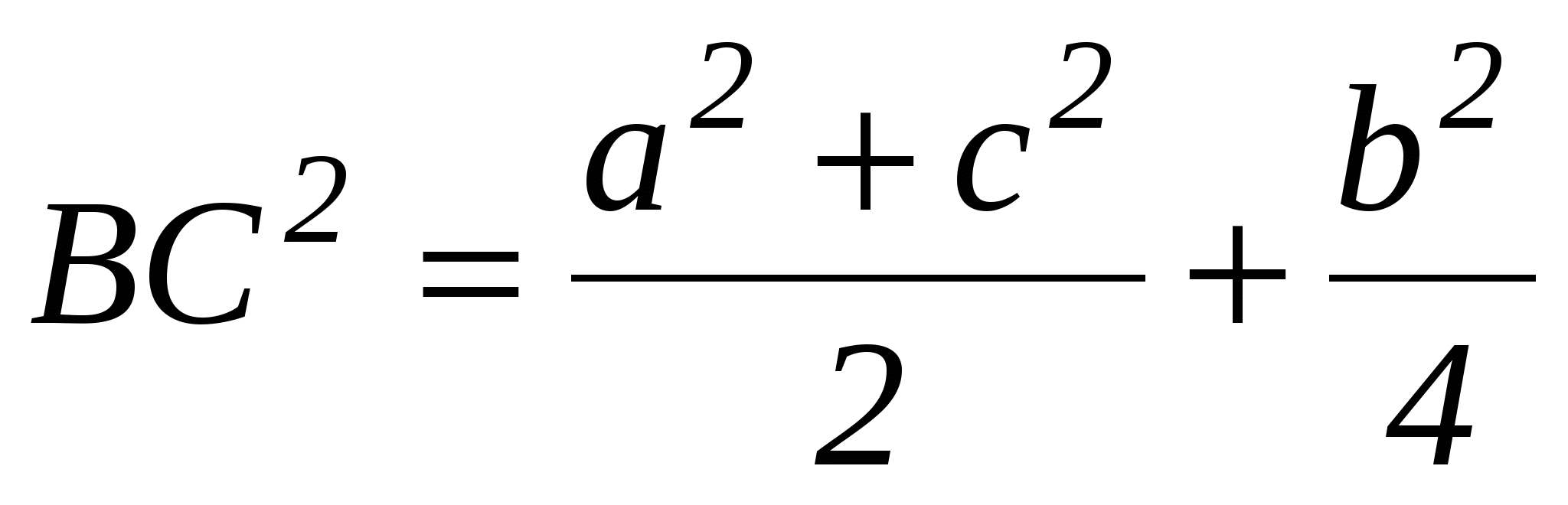 »
»
Задача: «Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная» - является примером задач второго вида.
Решения этих задач были разобраны выше.
Н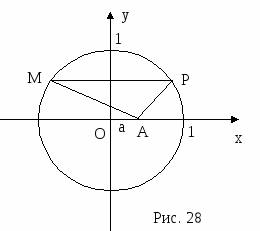 есмотря на недостатки метода координат такие как наличие большого количества дополнительных формул, требующих запоминания, и отсутствие предпосылок развития творческих способностей учащихся, некоторые виды задач трудно решить без применения данного метода. Поэтому изучение метода координат необходимо, однако более детальное знакомство с этим методом целесообразно проводить на факультативных занятиях. Далее приведем ряд задач для факультативов.
есмотря на недостатки метода координат такие как наличие большого количества дополнительных формул, требующих запоминания, и отсутствие предпосылок развития творческих способностей учащихся, некоторые виды задач трудно решить без применения данного метода. Поэтому изучение метода координат необходимо, однако более детальное знакомство с этим методом целесообразно проводить на факультативных занятиях. Далее приведем ряд задач для факультативов.
Пример 1. Докажите, что сумма квадратов расстояний от точки, взятой на диаметре окружности, до концов любой из параллельных ему хорд постоянна.
Решение:
Введем прямоугольную систему координат с началом в центре окружности. Пусть хорда МР параллельна оси Ох, а точка А принадлежит диаметру (рис. 28). Обозначим расстояние ОА через а, а расстояние от точки Р до оси Ох через b. Тогда точка А имеет координаты (а, 0). Точки Р и М принадлежат окружности с центром в начале координат и радиусом равным 1, следовательно их координаты удовлетворяют уравнению данной окружности 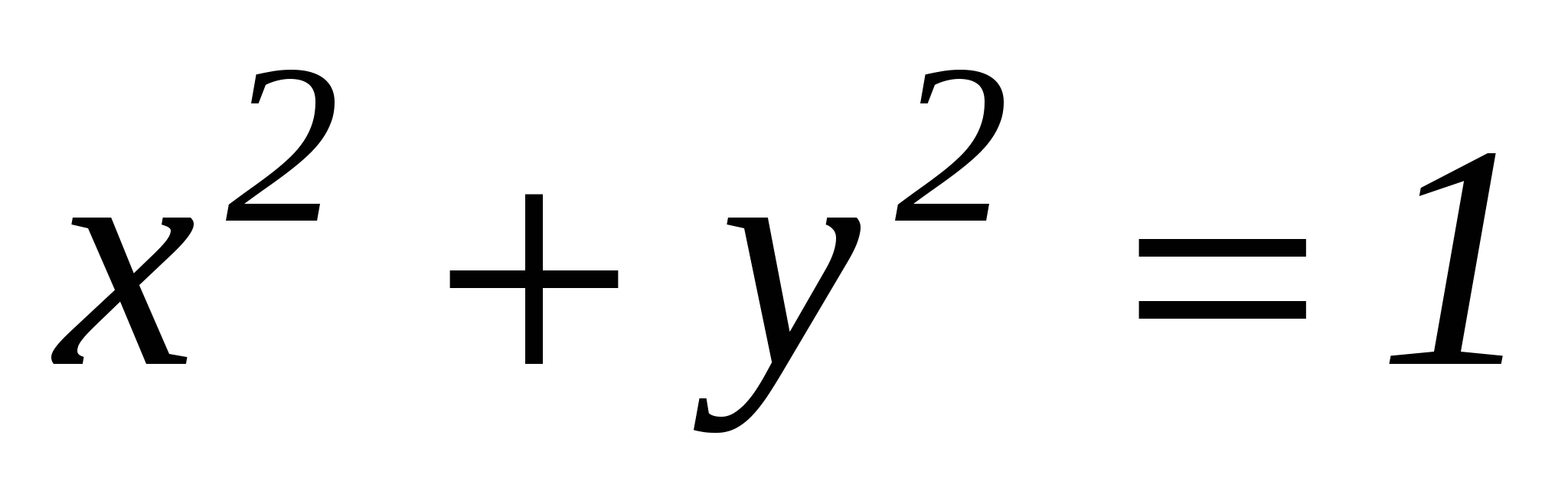 . Используя это уравнение находим координаты точек Р(
. Используя это уравнение находим координаты точек Р(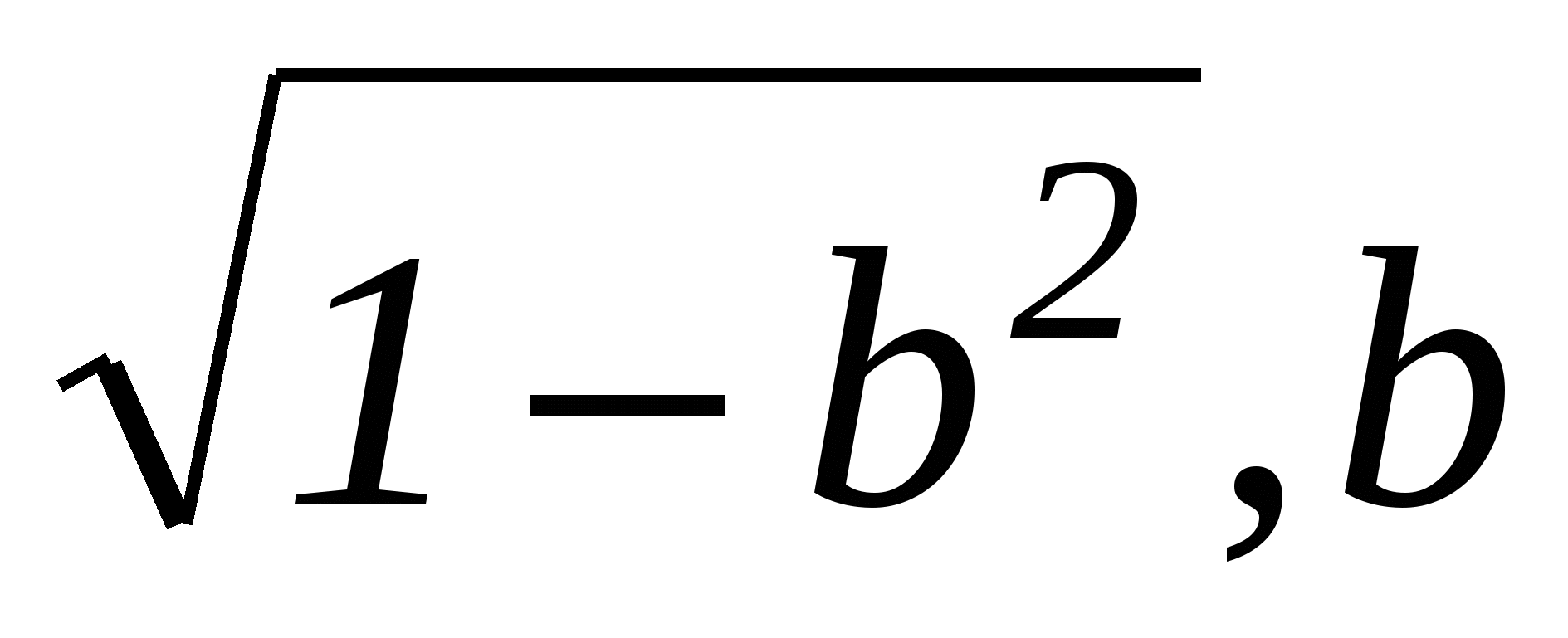 ) и М(
) и М(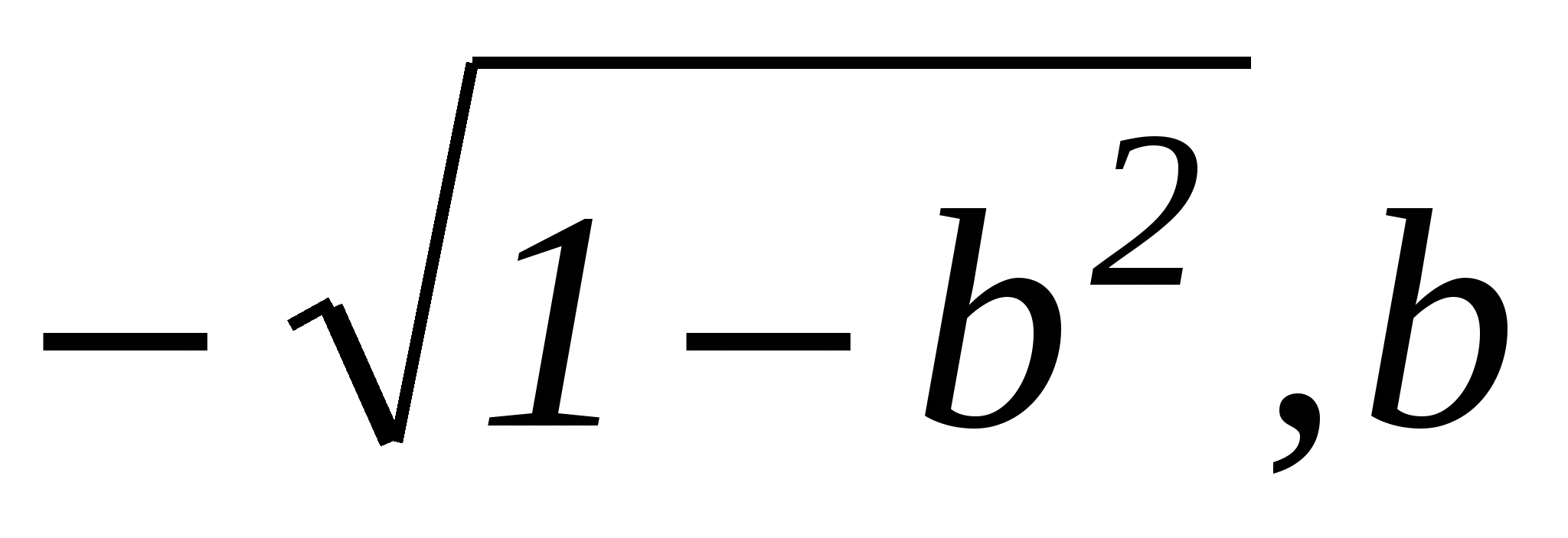 ). Необходимо доказать, что АМ2+АР2 не зависит от переменной b. Найдем АМ2 и АР2 используя формулу нахождения расстояния между двумя точками по их координатам:
). Необходимо доказать, что АМ2+АР2 не зависит от переменной b. Найдем АМ2 и АР2 используя формулу нахождения расстояния между двумя точками по их координатам: 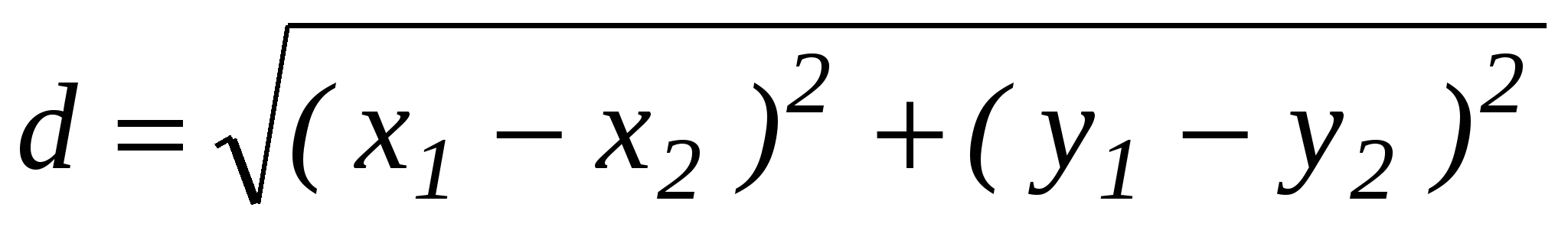 . Они соответственно равны
. Они соответственно равны 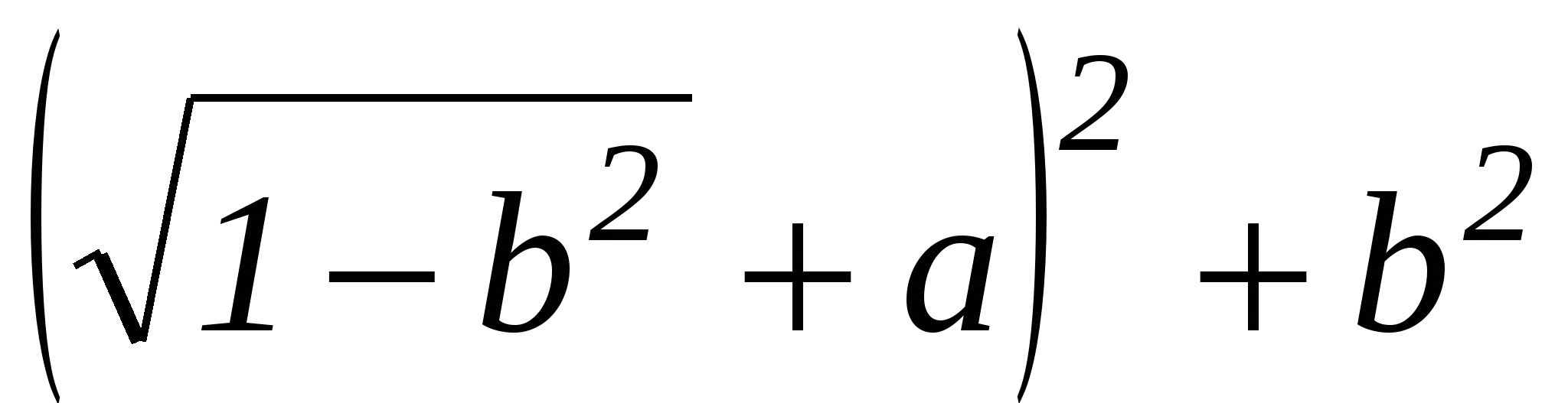 и
и 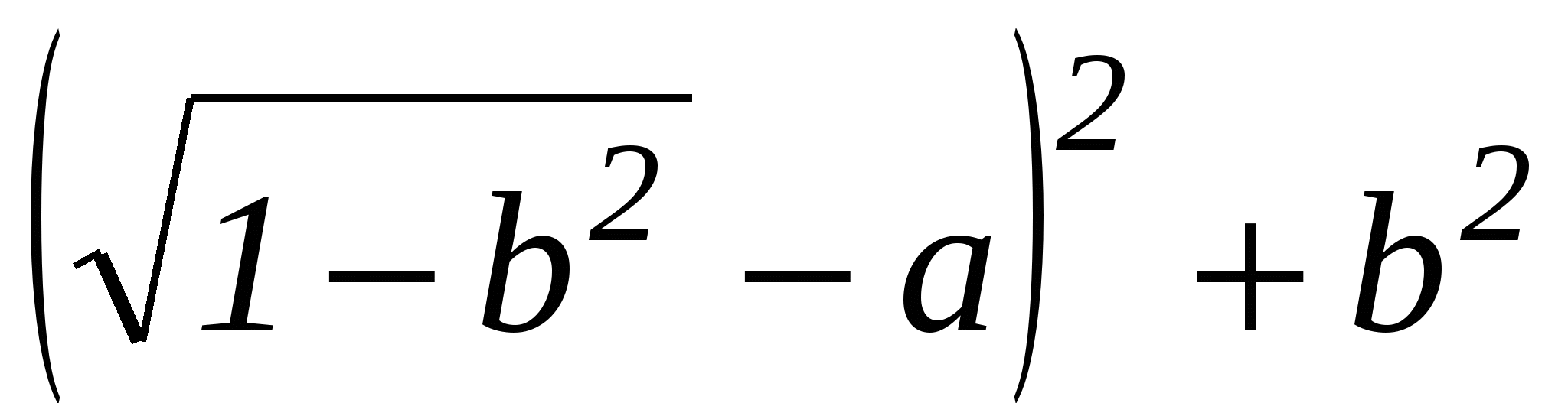 , а их сумма после приведения подобных равна 2а2+2. Это число не зависит от переменной b, что и требовалось доказать.
, а их сумма после приведения подобных равна 2а2+2. Это число не зависит от переменной b, что и требовалось доказать.
Пример 2. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей. (Теорема Эйлера)
Решение:
Введем прямоугольную систему координат как показано на рисунке 29.
П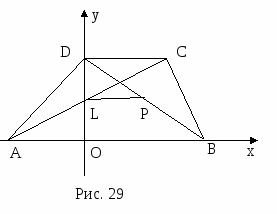 усть точки А, В, С и D имеют координаты (0,0), (d,0), (c,d) и (0,d) соответственно. Следовательно, координаты точек L и P есть (
усть точки А, В, С и D имеют координаты (0,0), (d,0), (c,d) и (0,d) соответственно. Следовательно, координаты точек L и P есть (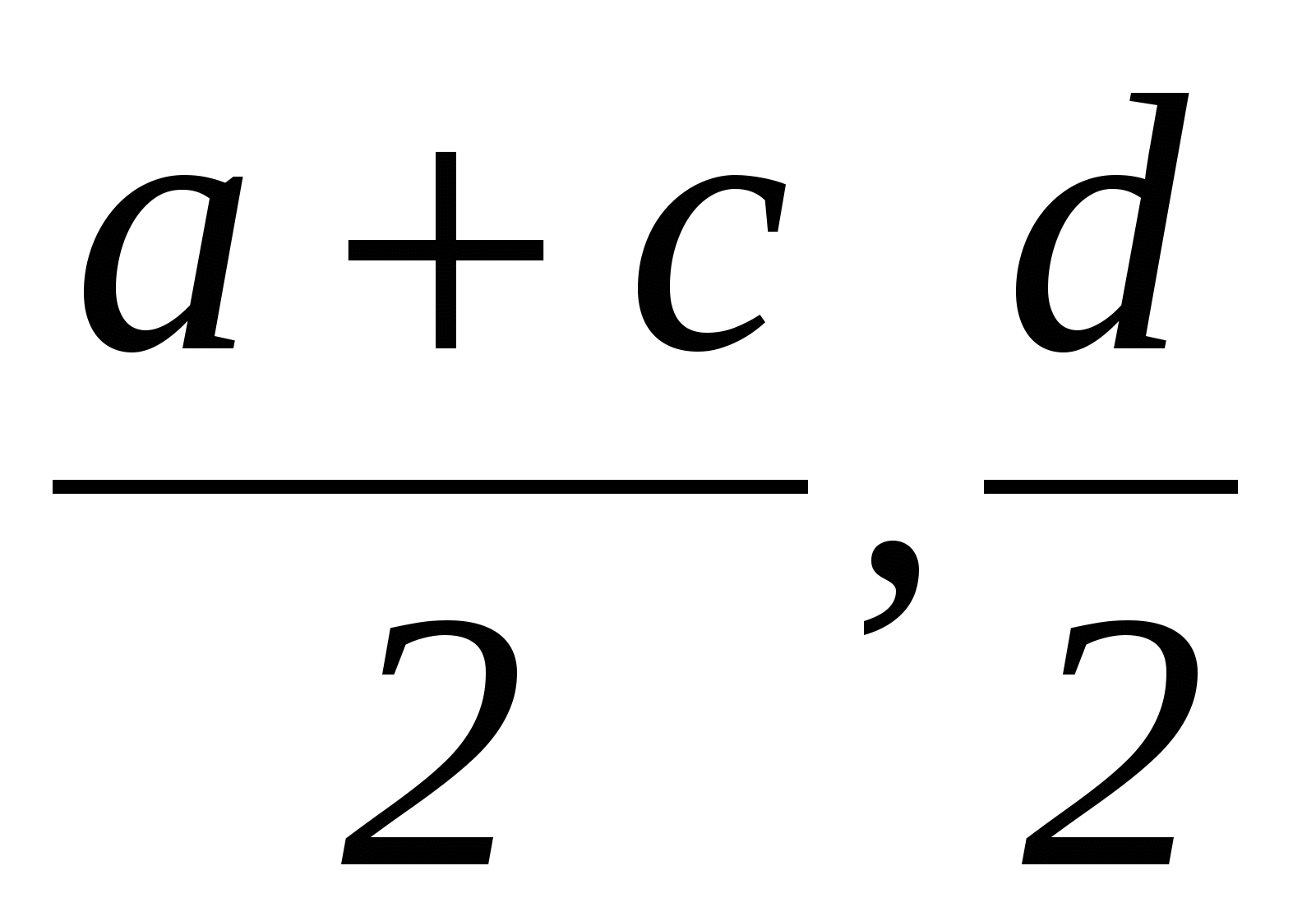 ) и (
) и (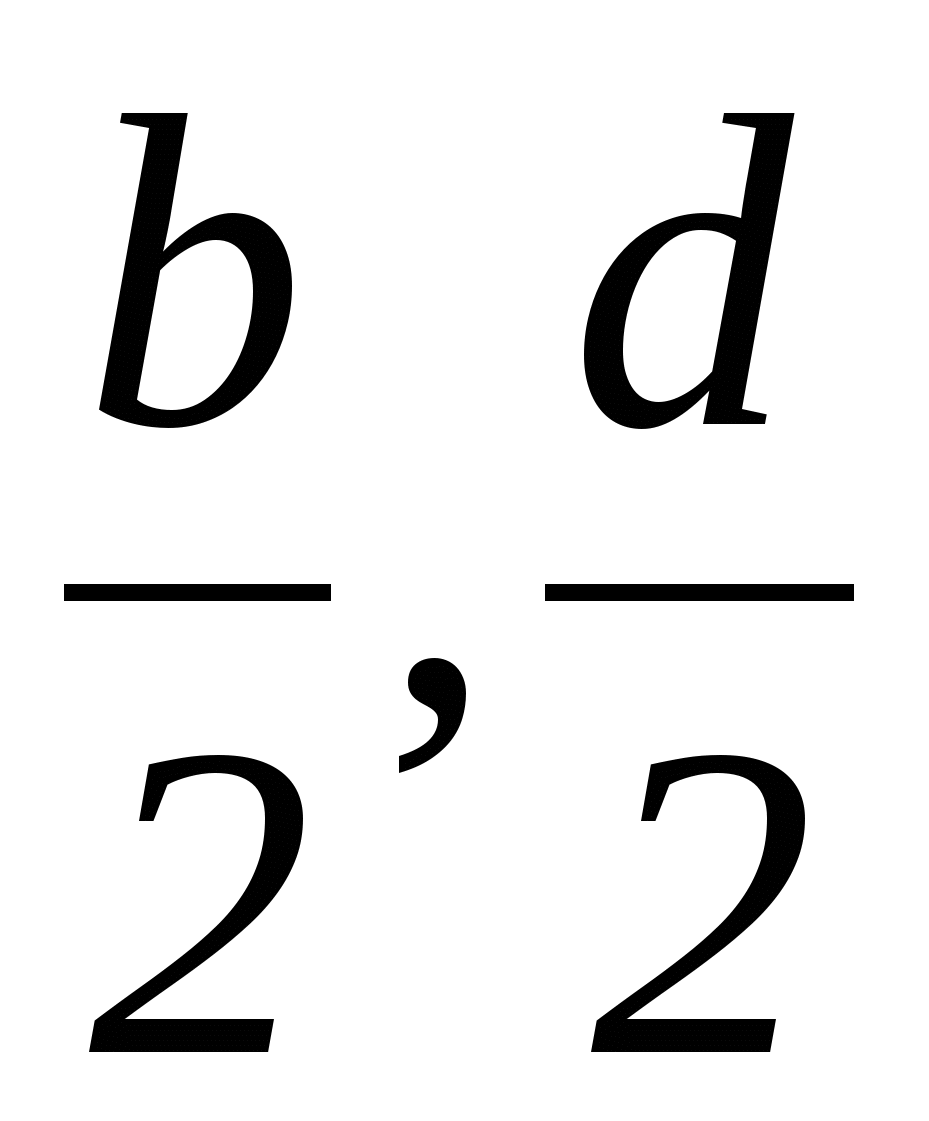 ). Найдем квадраты длин отрезков, с помощью формулы нахождения расстояния между точками по их координатам.
). Найдем квадраты длин отрезков, с помощью формулы нахождения расстояния между точками по их координатам.
AD2=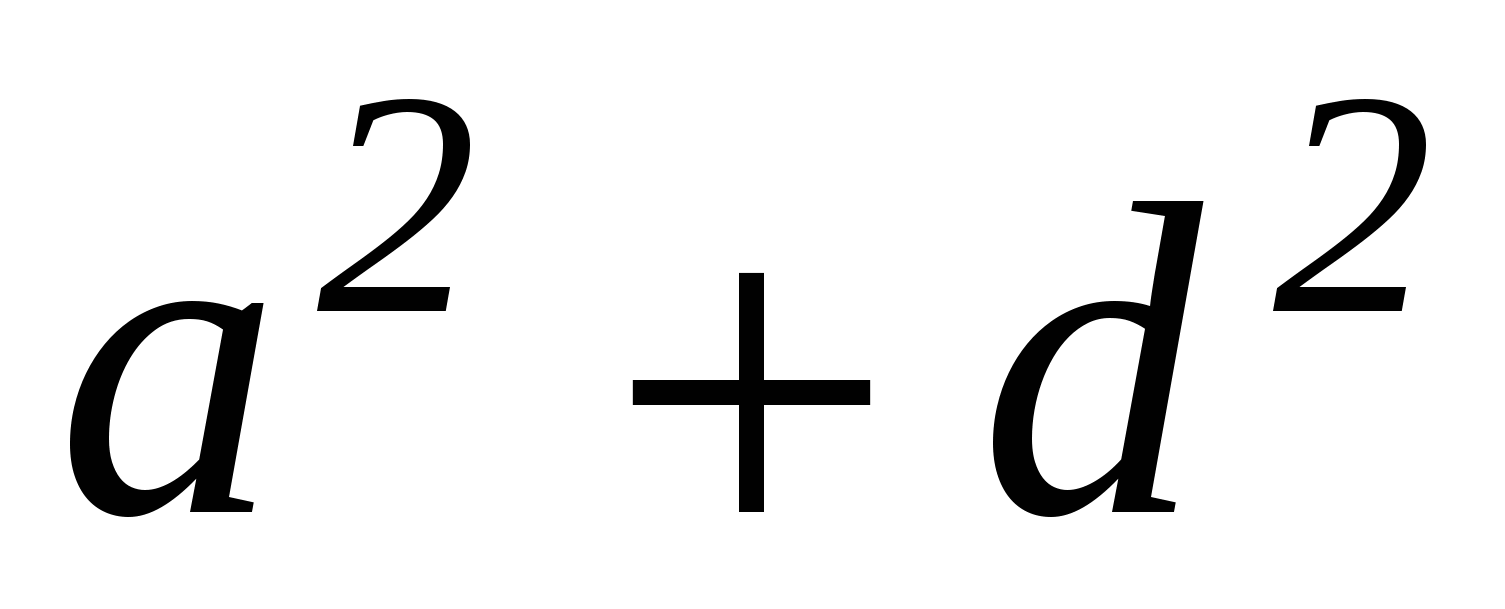 ; BC2=
; BC2=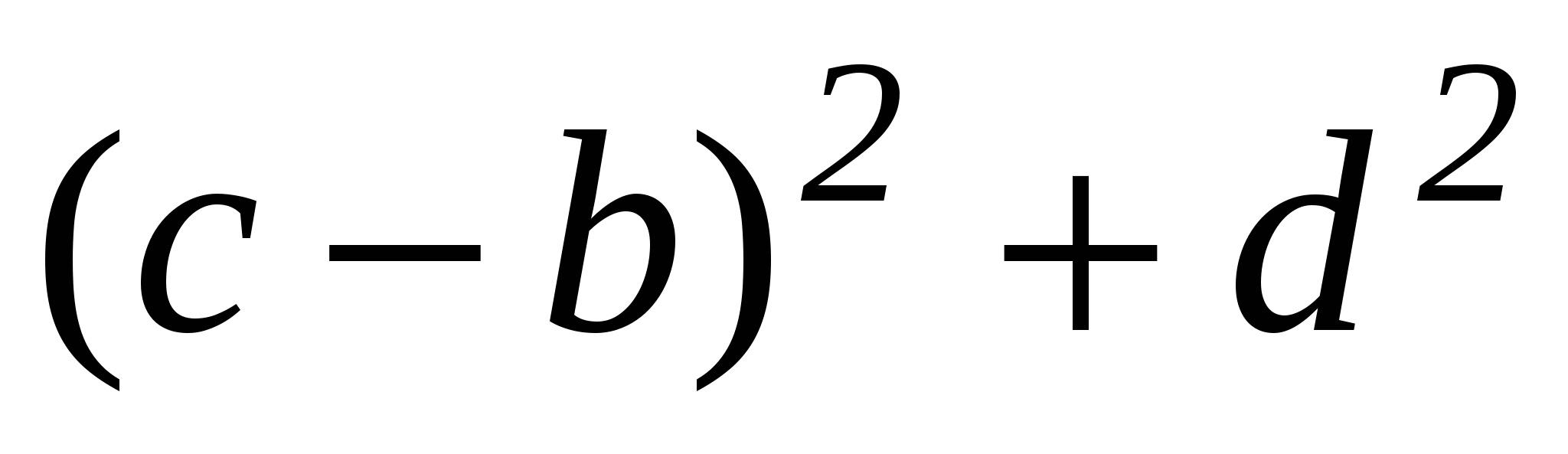 ; DC2=
; DC2=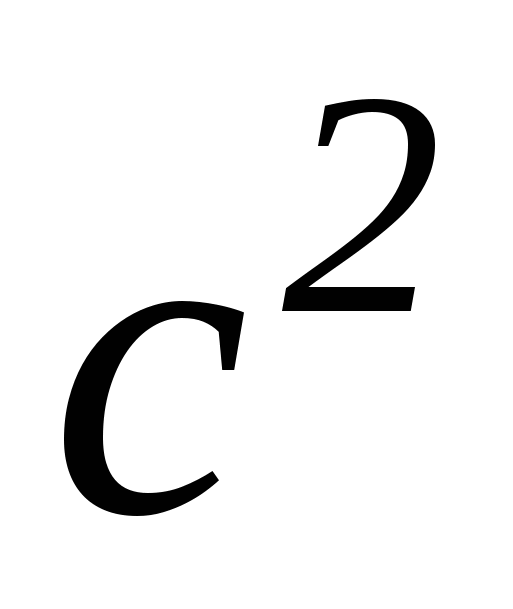 ; AB2=
; AB2=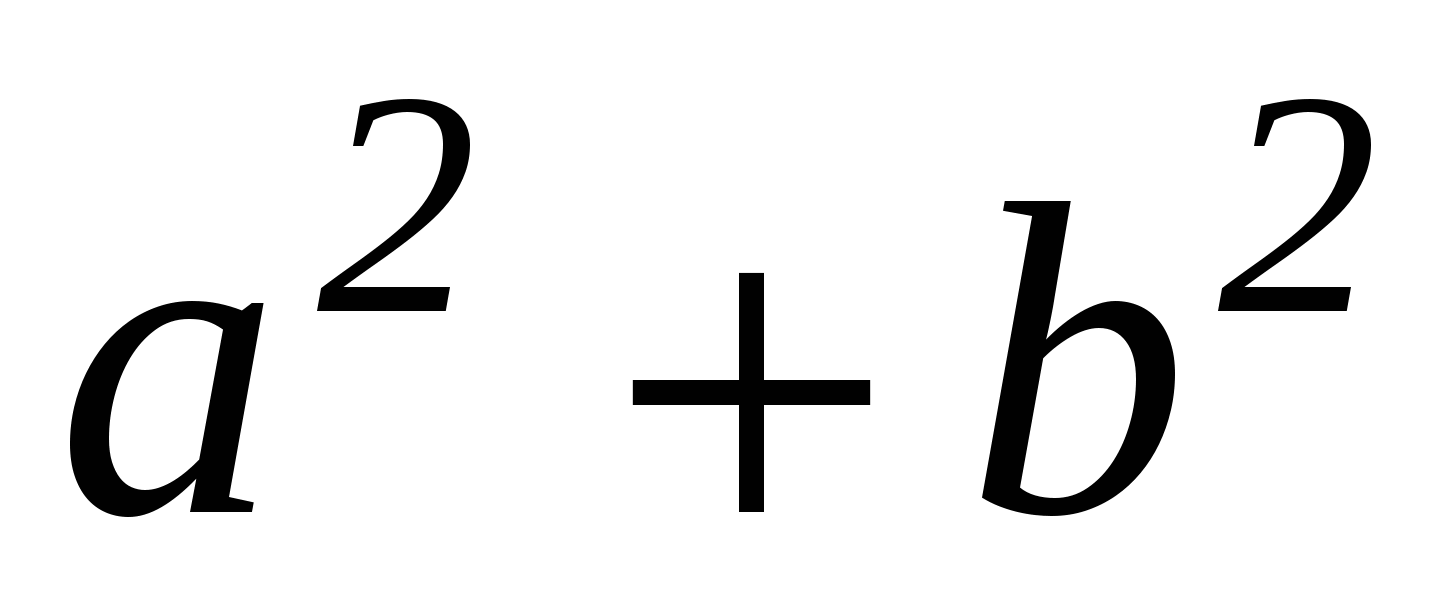 ;
;
AC2=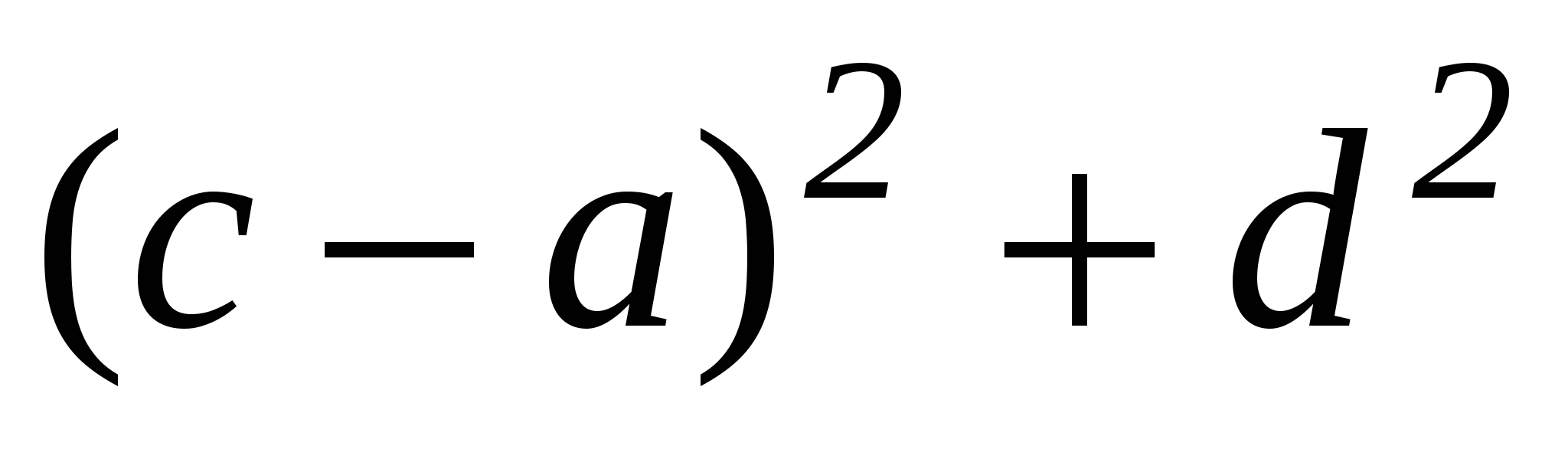 ; BD2=
; BD2=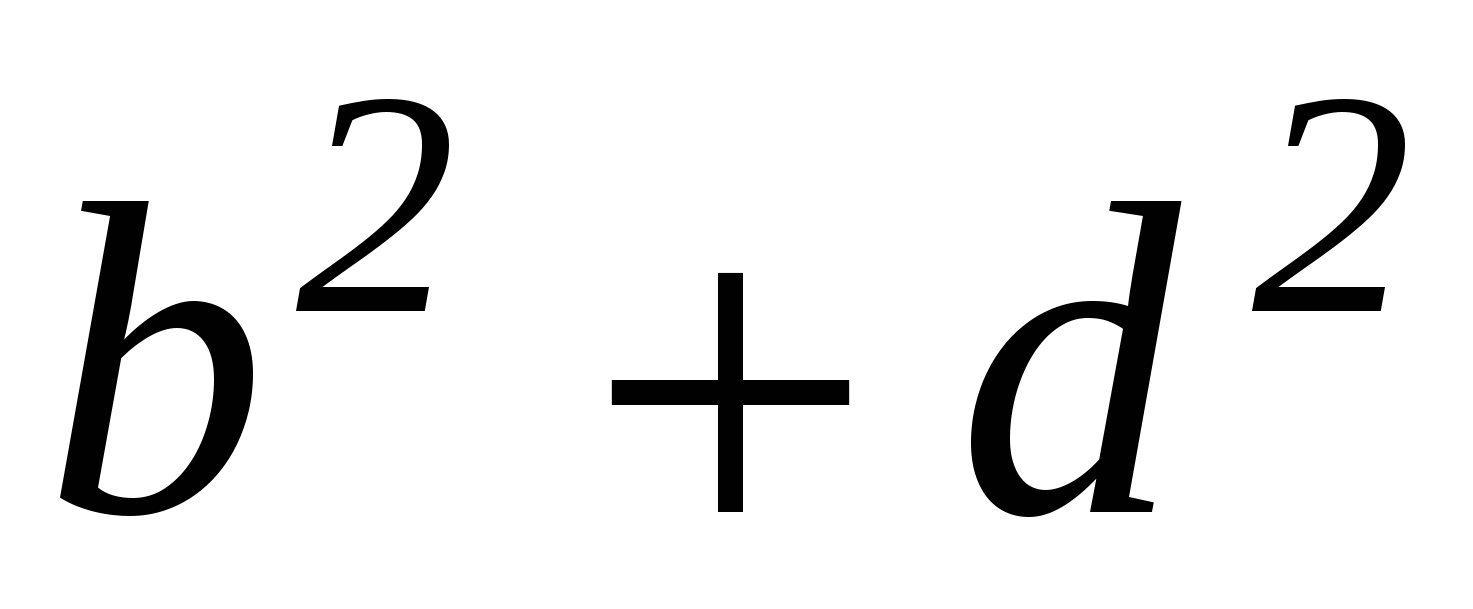 ; LP2=
; LP2=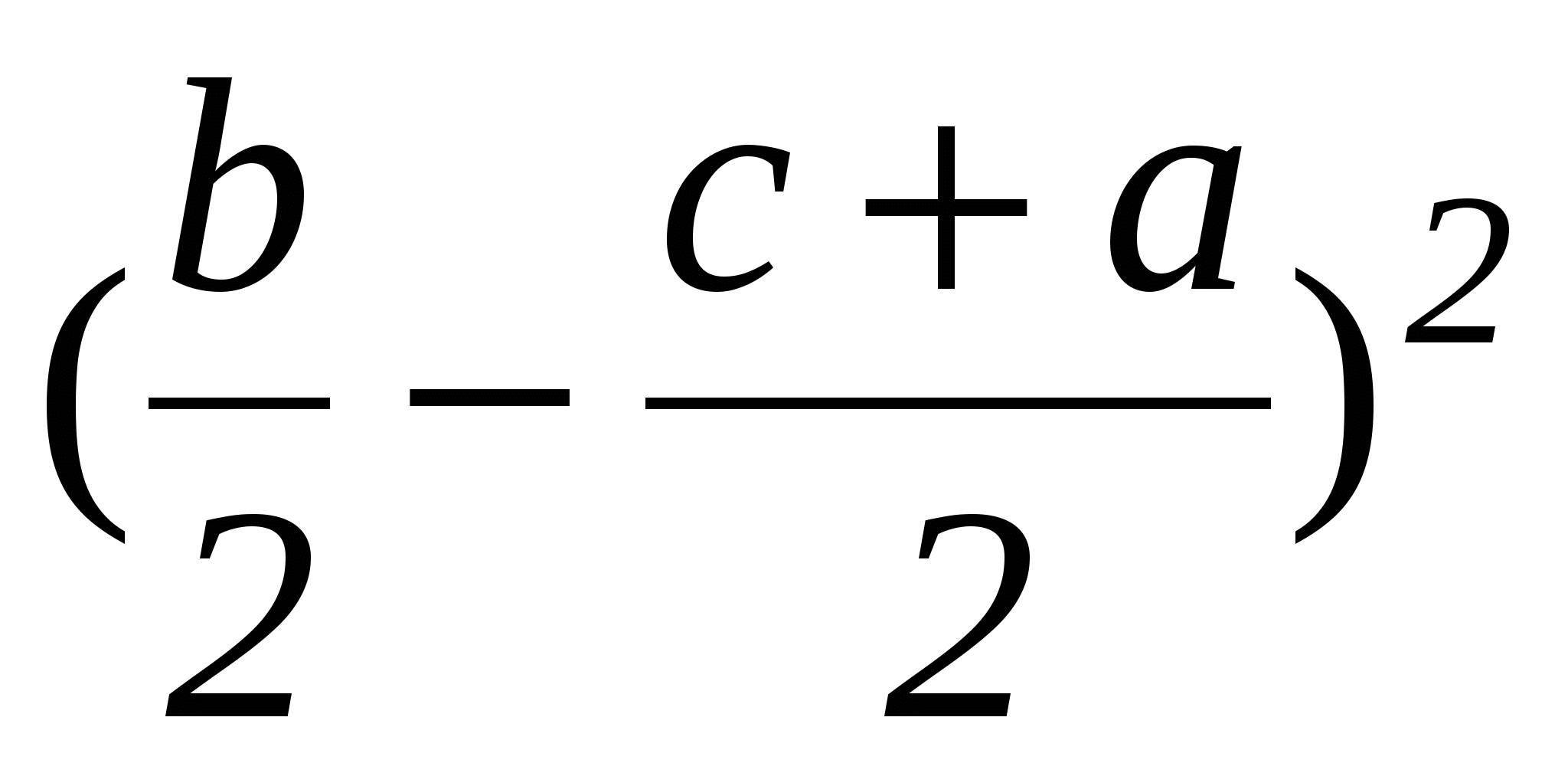 .
.
Запишем выражение, которое необходимо доказать, используя найденные нами значения.
AD2+BC2+DC2+AB2=AC2+BD2+4LP2
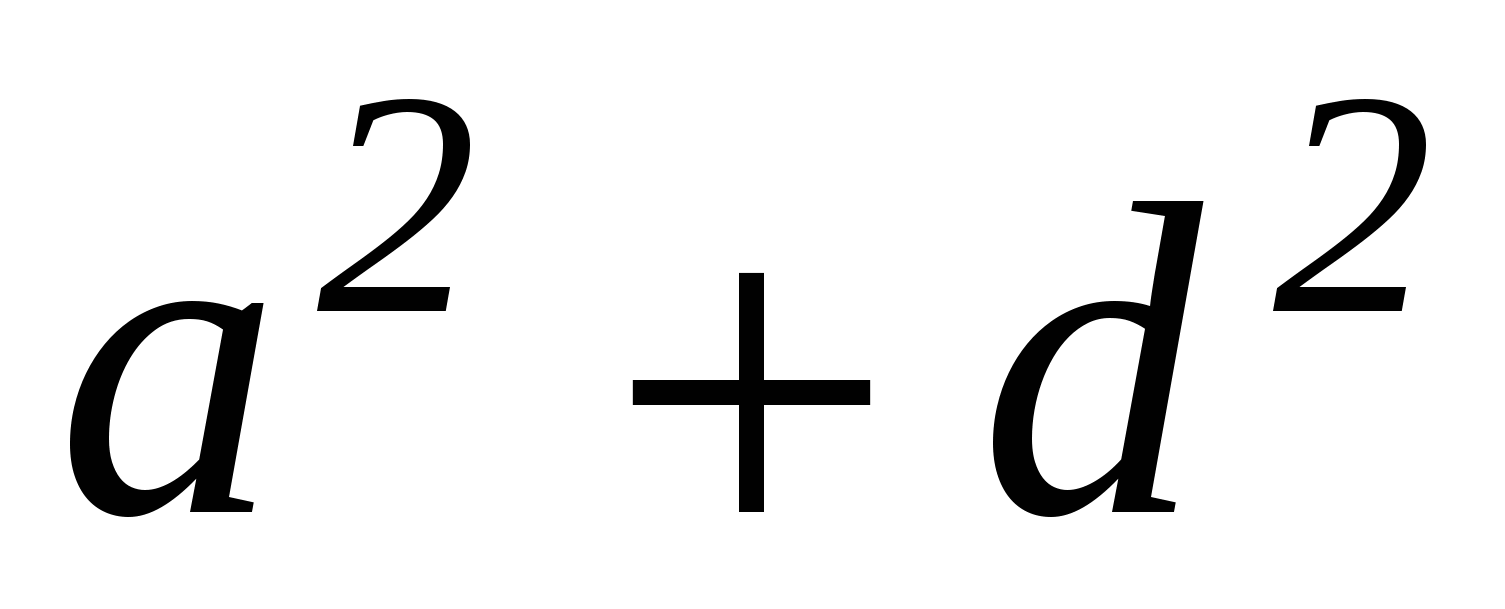 +
+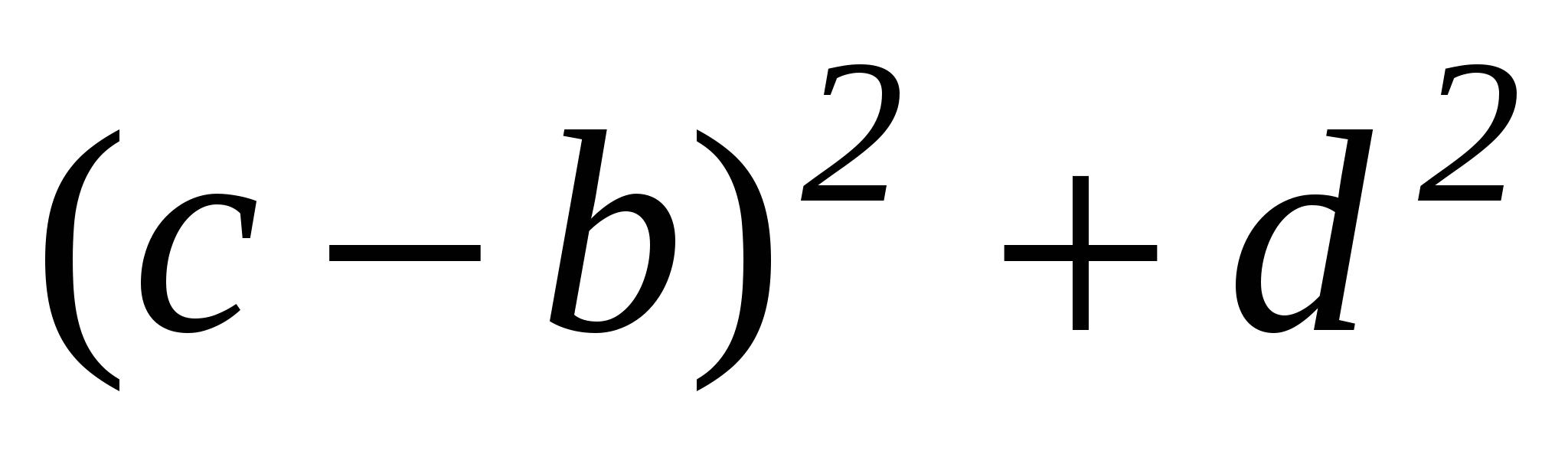 +
+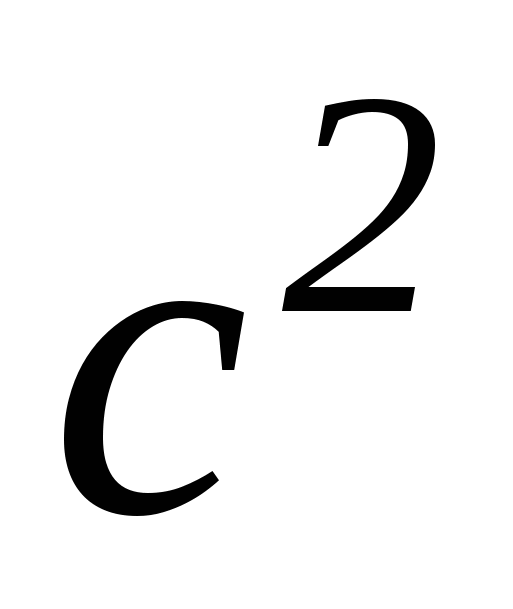 +
+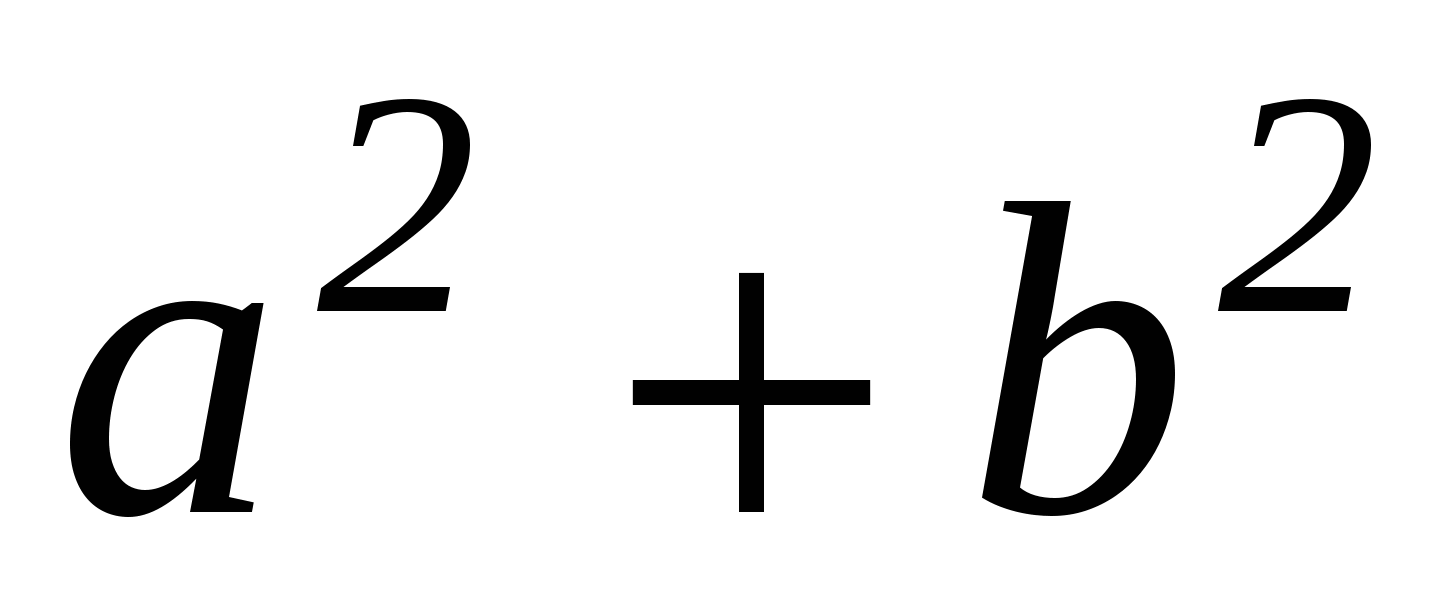 =
=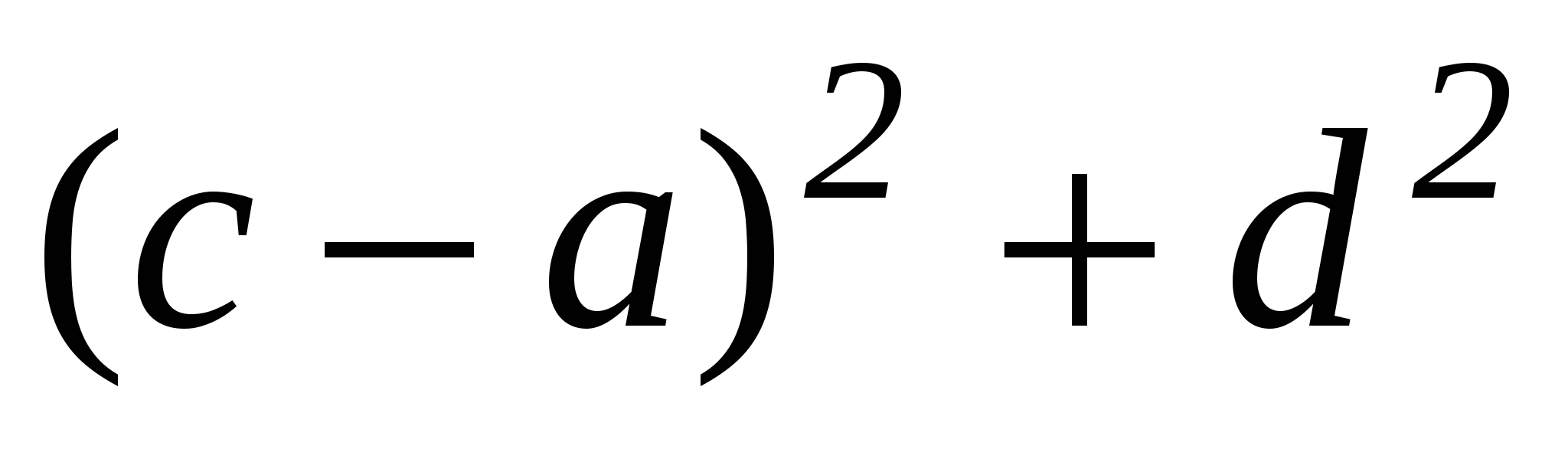 +
+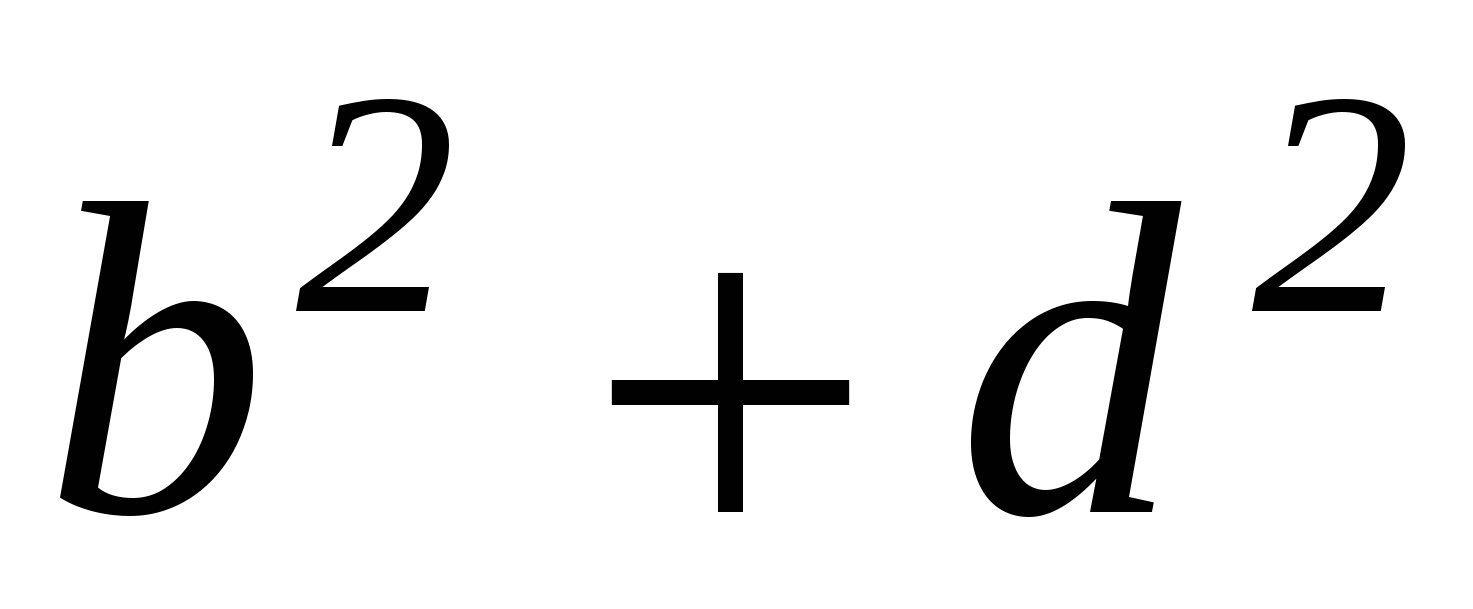 +4
+4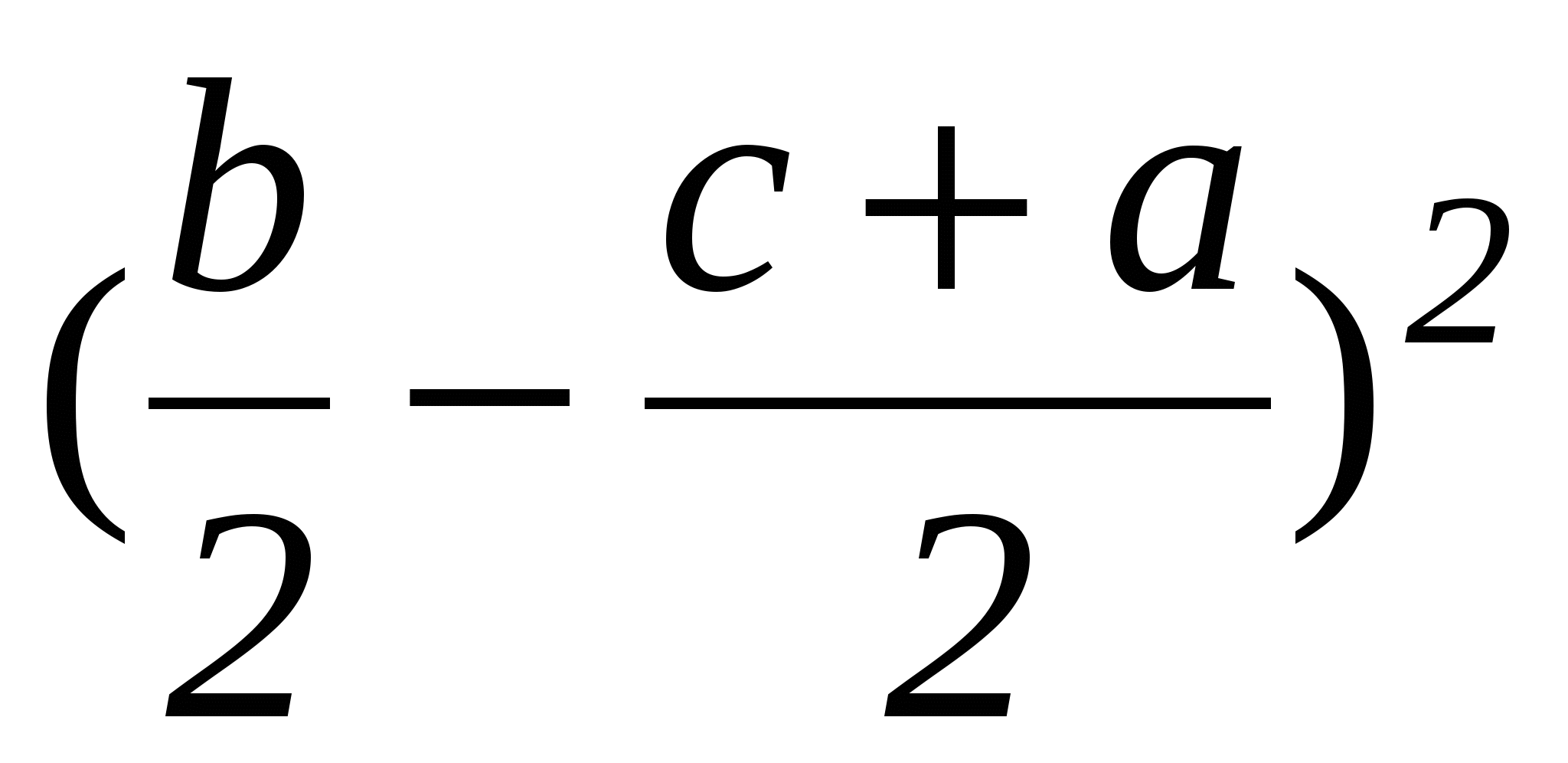
Р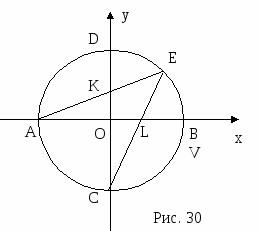 аскроем скобки, приведем подобные и получим верное равенство 0=0. Значит, сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей.
аскроем скобки, приведем подобные и получим верное равенство 0=0. Значит, сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей.
Пример 3. Диаметры AB и CD окружности перпендикулярны. Хорда ЕА пересекает диаметр СD в точке К, хорда ЕС пересекает диаметр АВ в точке L. Докажите, что если СК:KD так же как 2:1, то AL:LB так же как 3:1.
Решение:
Введем прямоугольную систему координат, направив оси по данным диаметрам AB и CD (рис. 30).
Радиус окружности будем считать равным 1. Тогда точки А, В, С, D будут иметь координаты (-1,0), (1,0), (0,-1), (0,1) соответственно. Так как СК:KD=2:1, то точка К имеет координаты (0,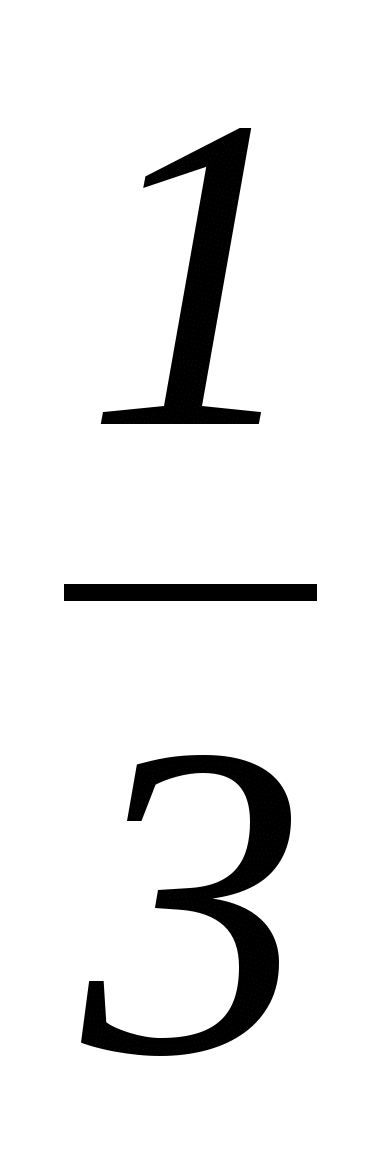 ). Найдем координаты точки Е как точки пересечения прямой АК, имеющей уравнение
). Найдем координаты точки Е как точки пересечения прямой АК, имеющей уравнение 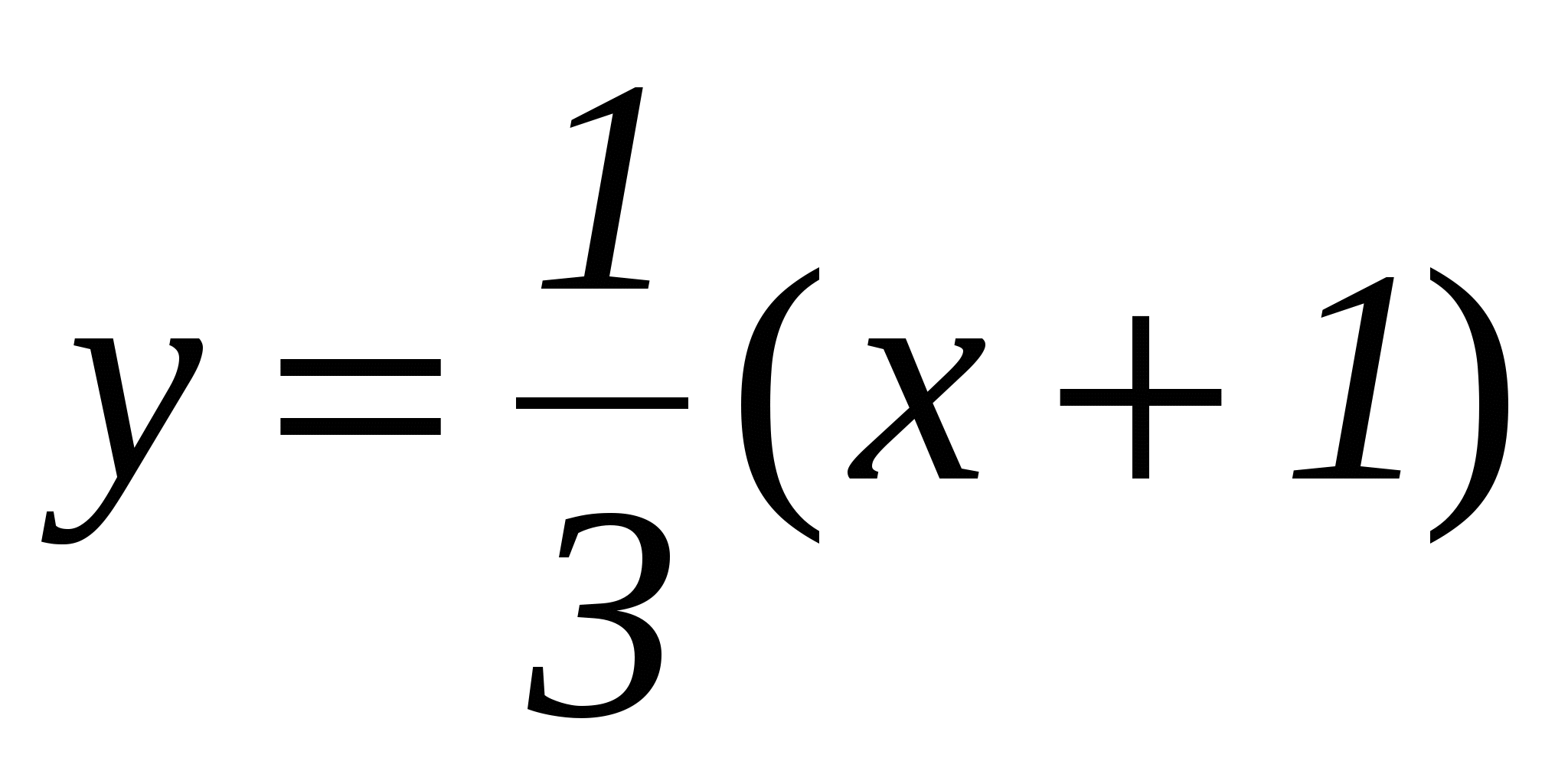 и окружности, заданной уравнением
и окружности, заданной уравнением 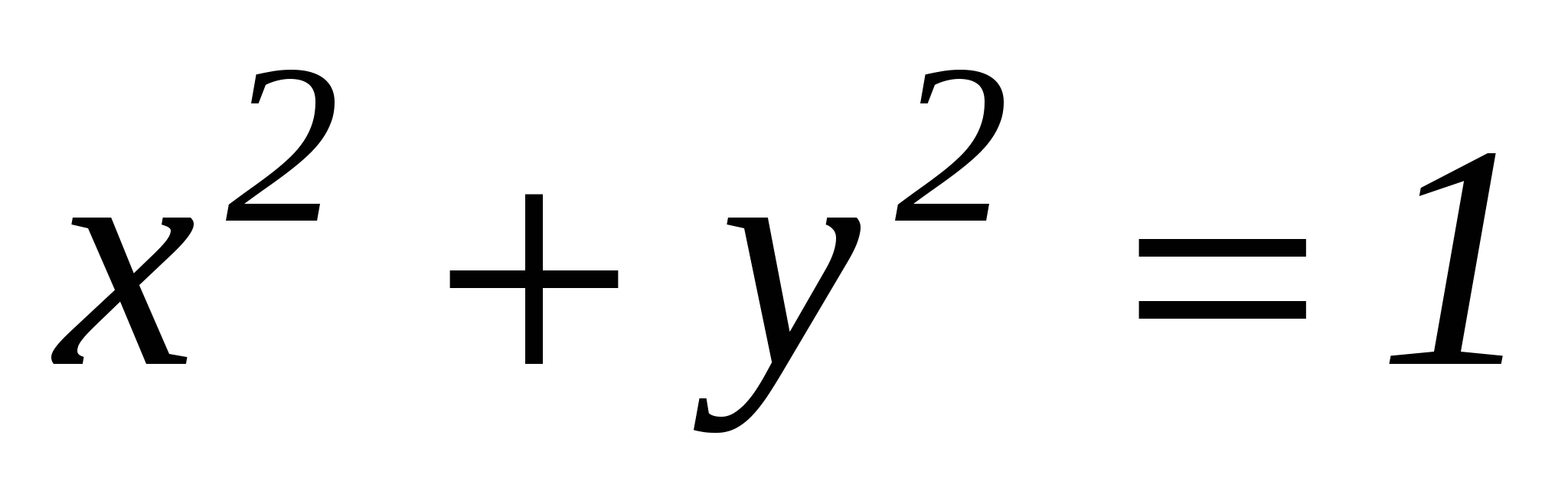 . Получаем, что точка Е имеет координаты (
. Получаем, что точка Е имеет координаты (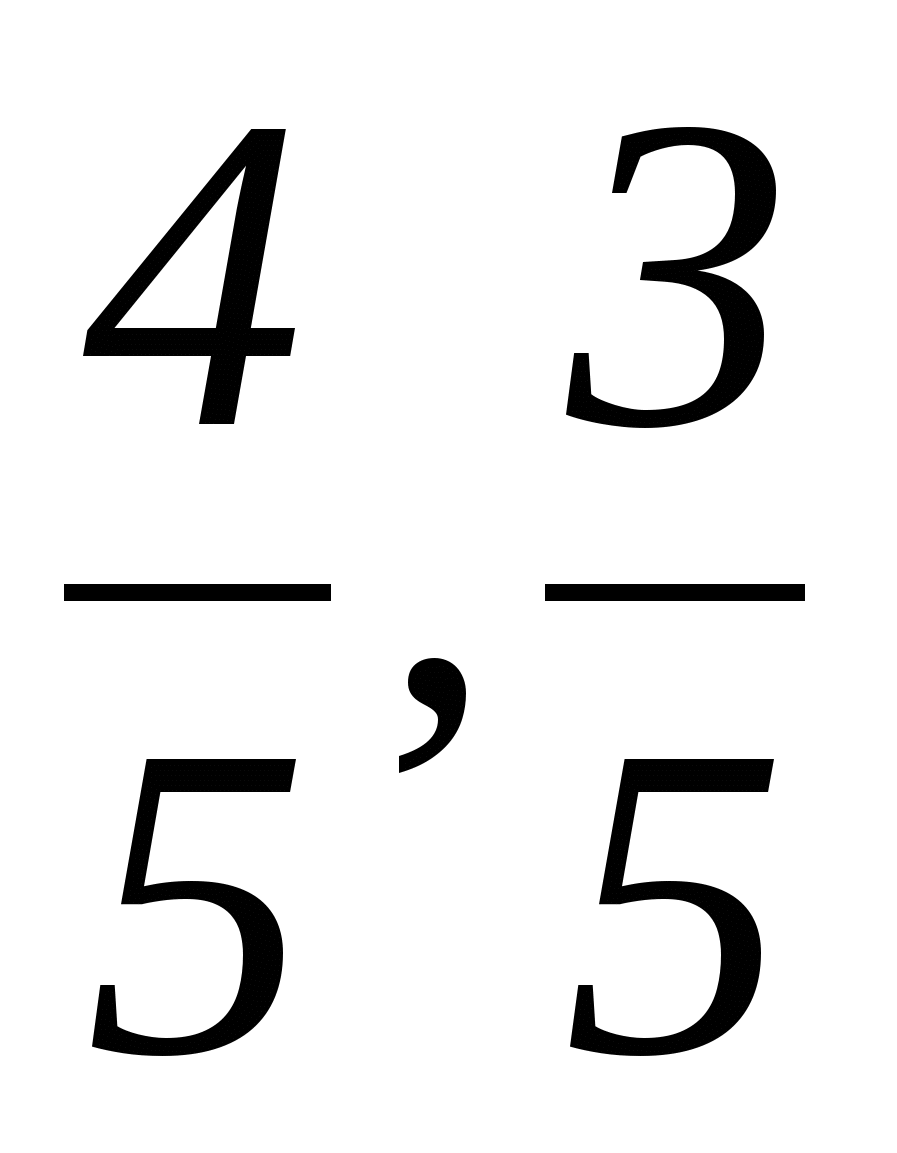 ). Точка L - это точка пересечения прямых СЕ и оси абсцисс, значит ординаты точки L равна 0.
). Точка L - это точка пересечения прямых СЕ и оси абсцисс, значит ординаты точки L равна 0.
Найдем абсциссу точки L. Прямая СЕ задана уравнением 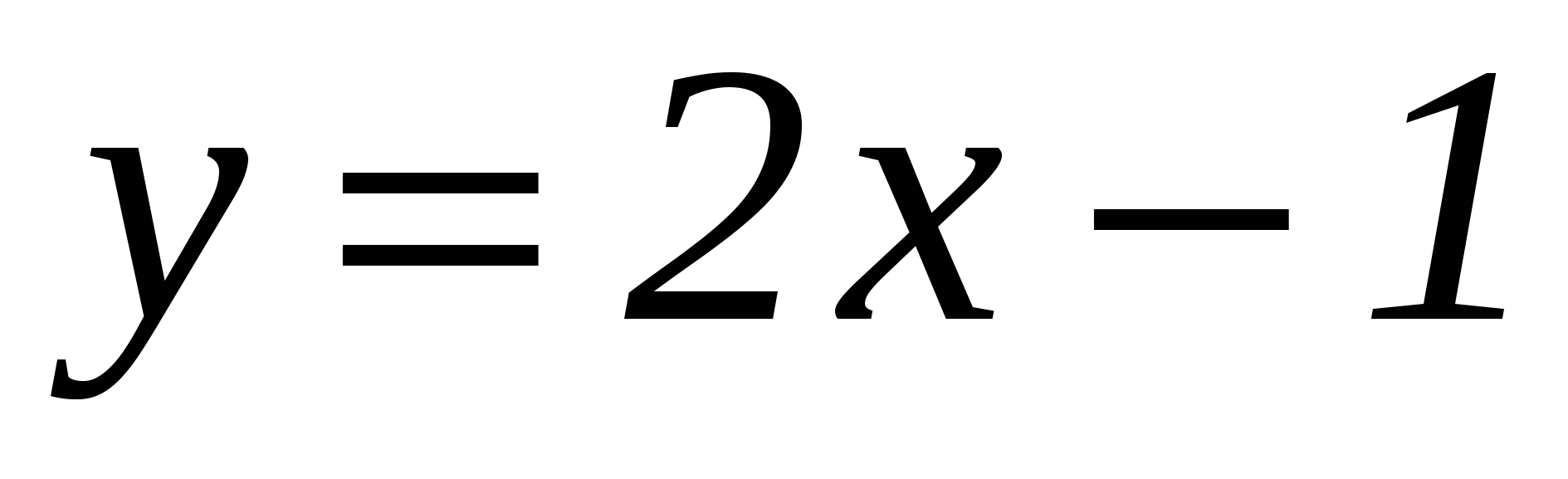 . Она пересекает ось Ох в точке (
. Она пересекает ось Ох в точке (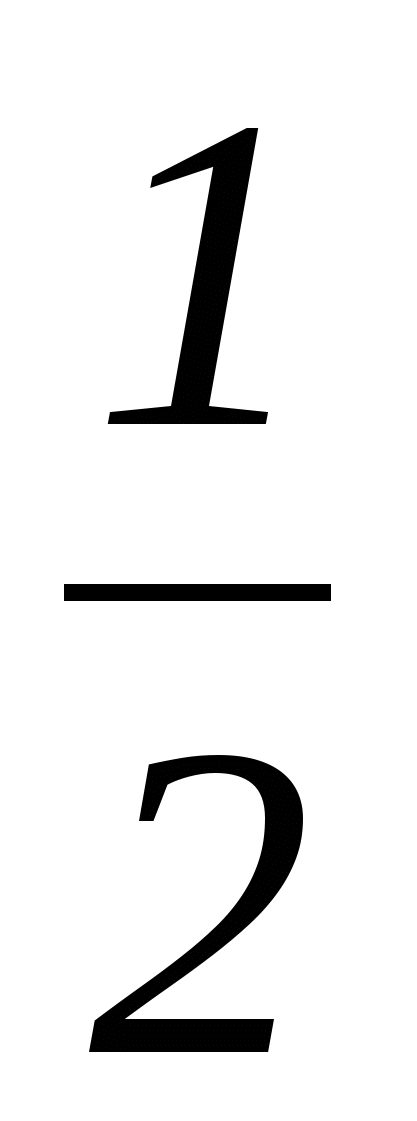 ,0). Отсюда координаты точки L(
,0). Отсюда координаты точки L(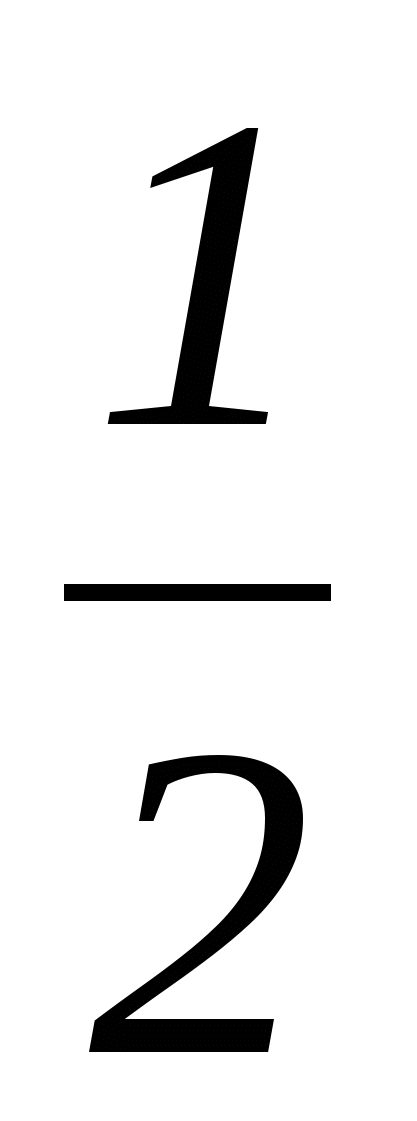 ,0). Найдем отношение AL:LB. Оно равно трем, что и требовалось доказать.
,0). Найдем отношение AL:LB. Оно равно трем, что и требовалось доказать.
Задачи
-
Доказать, что если в треугольнике две медианы конгруэнтны, то треугольник равнобедренный.
-
Найти множество таких точек Р, что отношение расстояний от каждой из них до двух данных точек равно а.
-
Докажите, что уравнение окружности с центром в точке С (а,с) и радиусом r имеет вид: (х-а)2+(у-с)2=r2
-
Найти угол между прямыми Зх-4у+6=0 и 12х+5у+8=0
-
Определите расстояние от точки А(-3,4) до прямой у=х+2.
-
Вычислите площадь треугольника, вершины которого имеют следующие координаты: А (0,-2), В(6,2) и С(2,4) .
-
На прямой с даны три точки А, В, С так, что точка В лежит между точками А и С. В одной полуплоскости с границей а построены равносторонние треугольники АМВ и ВРС. Доказать, что середина отрезка РА, середина отрезка МС и точка В являются вершинами равностороннего треугольника.
-
Доказать, что для любой точки Р лежащей между вершинами В и треугольника ABC, справедливо равенство :
АВ2*РС+АС*ВР-АР2*ВС=ВС*ВР*РС.
-
Дан прямоугольник. Докажите, что сумма квадратов расстояний от произвольной точки, принадлежащей плоскости этого прямоугольника до его вершин, в два раза больше суммы квадратов расстояний от этой точки до сторон прямоугольника.
-
Доказать, что если через некоторую точку М провести прямую, пересекающую окружность в точках А и В, то произведение МА*МВ постоянно и не зависит от положения прямой.
-
Дан прямоугольник ABCD. Найти множество точек М, для которых MA2+MC2=MB2+MD2. (ответ: множество точек М есть плоскость)
-
Дан прямоугольник ABCD. Найти множество точек М, для которых MA+MC=MB+MD. (Ответ: пара прямых)
-
Дан прямоугольный треугольник ABC (C=90°) . Найти множество точек Р, для которых 2РС2=РА2+РВ2. (ответ: множество точек Р есть прямая, содержащая середину М гипотенузы АВ и перпендикулярная к медиане СМ).
Задачи, решаемые методом координат
Задача 1. Даны уравнения одной из сторон ромба х-3у + 10 = 0 и одной из его
д иагоналей х + 4у - 4 = 0; диагонали ромба пересекаются в точке (0; 1). Найти уравнение остальных сторон ромба.
иагоналей х + 4у - 4 = 0; диагонали ромба пересекаются в точке (0; 1). Найти уравнение остальных сторон ромба.


Решение:
Найдем т. пересечения  и
и  :
:


 =>
=>  A(-4;2)
A(-4;2)
Т.к P - середина отрезка AC, то

 => C(4;0). Через точку C направим прямую, параллельную
=> C(4;0). Через точку C направим прямую, параллельную  (т.е. найдем
(т.е. найдем  ).
). 
 =>
=> ![]()
 По свойству ромба:
По свойству ромба: =>
=>  ;
;  =>
=> ![]()
![]()
 ;
;  ;
;  ;
;  =>
=> ![]()

 ; По формуле прямой, проходящей через две точки, найдем
; По формуле прямой, проходящей через две точки, найдем 
 ;
; 
Задача 2. Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенных из вершины А. Вычислить внутренний угол при вершине В.
А (8;0), В(-4; -5); С(-8;-2).
Решение:
1)  ={-12; -5}, |
={-12; -5}, | |=13
|=13
![]() = {-4; 3}, |
= {-4; 3}, |![]() |=5
|=5
![]() = {-16; -2}, |
= {-16; -2}, | |=
|= =
=
2)  =0.5(
=0.5( +
+ )=0.5{-12-16;-5-2}={-28;-7}
)=0.5{-12-16;-5-2}={-28;-7}
|![]() | =
| = 
x +4
=
y + 5
-4
33) Имеем уравнение прямой ВС:
3x + 4y + 32 = 0.
|![]() | = ρ(A, BC) =
| = ρ(A, BC) =
|3∙8+4∙0+32|
=![]()

4) Найдем уравнение прямой AL:
 ;
;  ;
;

Значит,
 .
.
Тогда,  или
или 
Найдем точку L - точку пересечения прямых AL и BC:
 ;
; 
Тогда 
и  .
.
Итак, 
и

5) 

Ответ:  ;
;  ;
; ;
; 
Задача 3. Найти точки пересечения кривой второго порядка ![]() с прямой (а):
с прямой (а):

Решаем систему:  ;
;  ;
;
Подставляем в первое уравнение и получаем: 
 D<0 => нет точек пересечения
D<0 => нет точек пересечения
Ответ: нет точек пересечений
Задача 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось направлена по биссектрисе первого координатного угла. Даны полярные координаты точек  . Определить декартовы прямоугольные координаты этих точек.
. Определить декартовы прямоугольные координаты этих точек.

M(xM; yM), где
xM=ρ1Cos (φ1+π/4) = Cos(25π/12) = Cos(π/12),
yM=ρ1Sin (φ1+π/4) = Sin(25π/12) = Sin(π/12).
N(xN; yN), где
xN=ρ2Cos (φ2+π/4) = 2Cos(π +π/4) =-2Cos(π/4)= ,
,
yN=ρ2Sin (φ2+π/4) = 2Sin(π +π/2) = -2Sin(π/4)=  .
.
Ответ:
Задача 5. Для векторов  , заданных в ортонормированном базисе
, заданных в ортонормированном базисе  найдите:
найдите:
-
направляющие косинусы вектора
 ;
; -
площадь параллелограмма, построенного на векторах
 и
и  , имеющих общее начало;
, имеющих общее начало; -
объем пирамиды, построенной на векторах
 ,
, и
и  , имеющих общее начало.
, имеющих общее начало.

1)  ;
;  ;
; 
2)  ;
; 
 ;
; 
3) 

Ответ:  ;
;  ;
;  ;
; ; 82.
; 82.
Задача 6. С помощью преобразования поворота прямоугольной декартовой системы привести к каноническому виду уравнение кривой второго порядка
29x2 + 144xy + 71y2 - 40x + 30y - 50 = 0.
Написать формулы преобразования и изобразить данную кривую на чертеже.
Решение:
При повороте системы координат на угол φ наблюдается следующая зависимость между старыми и новыми координатами:

 .
.
Тогда общее уравнение кривой второго порядка
Ax2 + 2Bxy + Cy2 + Dx + Ey + F = 0
преобразуется следующим образом:


 +
+
 +
+

Раскроем скобки. Получим

или
 , где
, где




 .
.
Для того, чтобы избавиться от перекрестного члена необходимо повернуть систему координат на такой угол φ, чтобы  , т.е.
, т.е.



Найдем  :
:
 где
где  .
.
Тогда

и  ;
;  .
.
Имеем: 
![]()


 .
.
Получили: 


 , где
, где  .
.
Канонический вид уравнения заданной кривой: 
Это гипербола с вершинами в точках  и
и  ; асимптотами
; асимптотами  и фокусами
и фокусами  и
и
Ответ: 
Задача 7. Привести уравнение кривой к каноническому виду и построить кривую на плоскости:
 .
.
Решение:
Имеем: a11 = 4, a22 = 9, a12 = 0, a1 = −16, a2 = 9, a0 = 37. Тогда
 , то есть уравнение задает кривую эллиптического типа. Так как
, то есть уравнение задает кривую эллиптического типа. Так как  , то выделяем "полный квадрат":
, то выделяем "полный квадрат":

 ;
;
 ;
;

 ;
;

 .
.
Сделаем замену:
 .
.
В системе координат ![]() уравнение имеет вид:
уравнение имеет вид:

 .
.
Таким образом, данное уравнение определяет
эллипс с полуосями  и
и  ,
,
с центром в точке ![]() . Строим чертеж .
. Строим чертеж .

Задача 8.
Решение:

Ответ:

Задача 9.


Ответ: 
Задача 10. Привести уравнение кривой к каноническому виду и построить кривую на плоскости:
 .
.
(1)
Решение:
Имеем: a11 = 9, a12 = −6, a22 = 0, a1 = −21, a2 = 6, a0 = 81. Тогда

то есть уравнение (1) задает кривую гиперболического типа. Далее находим:

Найдем собственные значения:
 .
.
Тогда угол поворота равен ![]()
Далее найдем координаты α, β нового центра О1 системы координат  .
.
 .
.
Уравнение (1) в системе ![]() примет вид:
примет вид:



 .
.
(2)
Уравнение (2) задает гиперболу, у которой  и
и  , фокусы гиперболы лежат на оси О1х1.
, фокусы гиперболы лежат на оси О1х1.
Строим гиперболу на плоскости  по плану :
по плану :
╥ поворачиваем ось ![]() на угол
на угол  против часовой стрелки, для этого строим прямую
против часовой стрелки, для этого строим прямую ![]() (так как
(так как  ); в результате получаем систему координат
); в результате получаем систему координат ![]() ;
;
╥ на плоскости
на плоскости  отмечаем точку
отмечаем точку  , через эту точку проводим две прямые, параллельные осям
, через эту точку проводим две прямые, параллельные осям ![]() и
и  ; получаем систему координат
; получаем систему координат  ;
;
╥ в системе  строим гиперболу, согласно уравнению (2).
строим гиперболу, согласно уравнению (2).
Задача 11. Уравнение прямой x + 3y - 4 = 0 привести к нормальному виду.
Решение.
Нормирующий множитель определяется по формуле




Здесь A = 1; B = 3. Перед корнем надо выбрать знак, противоположный знаку свободного члена в заданном уравнении, т. е. знак плюс. Тогда нормирующий множитель







после умножения обеих частей уравнения на N уравнение примет вид






Задача 12. Общее уравнение прямой 4x - 3y + 12 = 0 представить в виде: 1) с угловым коэффициентом; 2) в отрезках на осях и 3) в нормальном виде. Построить эту прямую.
Решение.
1) Уравнение прямой с угловым коэффициентом имеет вид y = kx + b. Чтобы заданное уравнение преобразовать к этому виду, разрешим его относительно y: 3y = 4x + 12, 


 .
.
Сравнивая с уравнением y = kx + b, видим, что здесь угловой коэффициент прямой ![]()
 , а величина отрезка, отсекаемого прямой на оси ординат, b = 4 (если уравнение прямой дано в общем виде Ax + By + C = 0, то ее угловой коэффициент легко получить, если разделить коэффициент при x на коэффициент при y и взять полученное частное с обратным знаком
, а величина отрезка, отсекаемого прямой на оси ординат, b = 4 (если уравнение прямой дано в общем виде Ax + By + C = 0, то ее угловой коэффициент легко получить, если разделить коэффициент при x на коэффициент при y и взять полученное частное с обратным знаком 

 ).
).
2) В отрезках на осях уравнение прямой имеет вид 



 (1)
(1)
Чтобы определить величины отрезков, отсекаемых заданной прямой 4x - 3y + 12 = 0, поступим так: в уравнении прямой положим y = 0. Получаем 4x + 12 = 0, а x = -3. Значит, наша прямая пересекает ось Ox в точке с координатами (-3, 0) и в уравнении (1) величина отрезка a = -3.
Полагая в нашем уравнении x = 0, определим ординату точки пересечения прямой с осью ординат. Будем иметь
-3y + 12 = 0; y = 4.
Точка пересечения прямой с осью ординат имеет координаты (0, 4), и в уравнении (1) величина отрезка b = 4.
Таким образом, наше уравнение в отрезках на осях будет иметь вид





3) Чтобы привести уравнение к нормальному виду, обе его части следует умножить на нормирующий множитель 


 , выбрав перед корнем знак, противоположный знаку свободного члена в общем уравнении прямой. В нашем случае свободный член в общем уравнении прямой равен +12, а поэтому перед корнем в нормирующем множителе должен быть выбран противоположный знак, т. е. знак минус, и так как A = 4, B = -3, то
, выбрав перед корнем знак, противоположный знаку свободного члена в общем уравнении прямой. В нашем случае свободный член в общем уравнении прямой равен +12, а поэтому перед корнем в нормирующем множителе должен быть выбран противоположный знак, т. е. знак минус, и так как A = 4, B = -3, то 





 .
.
Умножая на  обе части уравнения 4x - 3y + 12 = 0, приведем его к нормальному виду
обе части уравнения 4x - 3y + 12 = 0, приведем его к нормальному виду







Запомнить: В нормальном уравнении прямой сумма квадратов коэффициентов при текущих координатах должна быть равна единице, а свободный член должен быть отрицательным. Эти два требования в полученном нами последнем уравнении, как легко проверить, выполнены. В пункте 2 решения мы получили уравнение прямой в отрезках на осях: a = -3, b = 4. Зная эти отрезки, мы легко построим нашу прямую (см. рисунок).

Задача 13. Найти длину перпендикуляра, опущенного из начала координат на прямую 3x - 6y + 5 = 0, а также координаты основания этого перпендикуляра.
Решение.
Приведем данное уравнение к нормальному виду:









После умножения на нормирующий множитель уравнение примет вид






И з сравнения с
з сравнения с 





 заключаем, что
заключаем, что ![]()
 .
.
Для определения координат основания этого перпендикуляра из рисунка
получим формулы






(эти формулы верны при любом расположении прямой относительно координатных осей).
как видно из уравнения 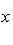

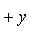











 и искомые координаты основания перпендикуляра равны
и искомые координаты основания перпендикуляра равны 




Задача14.Найти геометрическое место точек, равноудаленных от двух данных точек.
Решение.
В озьмем прямоугольную систему координат, и пусть две данные точки B и C лежат на оси абсцисс и имеют координаты (x1, 0) и (x2, 0) (см. рисунок). Пусть точка A принадлежит искомому геометрическому месту. Обозначим ее координаты через x и y: A(x, y).
озьмем прямоугольную систему координат, и пусть две данные точки B и C лежат на оси абсцисс и имеют координаты (x1, 0) и (x2, 0) (см. рисунок). Пусть точка A принадлежит искомому геометрическому месту. Обозначим ее координаты через x и y: A(x, y).
На основании формулы для определения расстояния между двумя точками 


 , значит, так как по условию AB = AC, можем написать, что
, значит, так как по условию AB = AC, можем написать, что 
 . Это и есть уравнение искомого геометрического места.
. Это и есть уравнение искомого геометрического места.
Возводя в квадрат обе части искомого равенства, будем иметь
(x - x1)2 + y2 = (x - x2)2 + y2.
После очевидных упрощений получим 2x(x2 - x1) = (x2 - x1)(x2 + x1); сокращая на 

 , имеем 2x = x1 + x2, или
, имеем 2x = x1 + x2, или 
 .
.
Это уравнение прямой, перпендикулярной оси Ox и проходящей через середину отрезка BC.
Итак, искомым геометрическим местом является прямая, перпендикулярная к отрезку BC, соединяющему данные точки, и проходящая через его середину.
Замечание. При решении задачи нам пришлось уничтожить радикалы в уравнении искомого геометрического места


 (1)
(1)
в результате чего было получено уравнение 
 (2)
(2)
Из алгебры известно, что возведение обеих частей уравнения в квадрат может привести к уравнению, которое не равносильно (не эквивалентно) исходному. Это значит, что уравнение, полученное от возведения в квадрат обеих частей исходного уравнения, может иметь решения, не удовлетворяющие исходному уравнению, т. е. иметь так называемые "посторонние" корни. Поэтому всегда в тех случаях, когда обе части уравнения приходится возводить в квадрат, следует ставить вопрос об эквивалентности полученного и исходного уравнений.
В интересующем нас случае вопрос ставится так: не содержит ли линия (2) точек, которых нет на линии (1), т. е. таких, координаты которых не удовлетворяют уравнению (1) и таким образом не удовлетворяют исходному условию AB = AC.
Чтобы убедиться в том, что линия (2) не содержит точек, которых нет в линии (1), надо показать, что уравнение (2) может быть преобразовано в уравнение (1).
Произведя в обратном порядке операции, с помощью которых было получено уравнение (2), мы придем к уравнению (x - x1)2 + y2 = (x - x2)2 + y2, откуда следует, что


 (3)
(3)
т. е. что ![]()
 ; отсюда видно, что или AB - AC = 0, или AB + AC = 0.
; отсюда видно, что или AB - AC = 0, или AB + AC = 0.
Но AB > 0 и AC > 0, а следовательно, 
 , так как сумма двух положительных величин не может быть равна нулю, а потому остается только одно равенство AB - AC = 0, т. е. AB = AC, и знак минус перед правой частью уравнения (3) должен быть отброшен. Поскольку из уравнения (1) получается уравнение (2) и обратно - из уравнения (2) следует уравнение (1), то эти уравнения равносильны (эквивалентны). Таким образом, поставленный вопрос решен: линия (2) не содержит таких точек, которых нет на линии (1).
, так как сумма двух положительных величин не может быть равна нулю, а потому остается только одно равенство AB - AC = 0, т. е. AB = AC, и знак минус перед правой частью уравнения (3) должен быть отброшен. Поскольку из уравнения (1) получается уравнение (2) и обратно - из уравнения (2) следует уравнение (1), то эти уравнения равносильны (эквивалентны). Таким образом, поставленный вопрос решен: линия (2) не содержит таких точек, которых нет на линии (1).
Задача 15. Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек A и B есть величина постоянная, равная a2. Длину AB считать равной 2a.
Решение.
Проведем вывод уравнения в прямоугольных координатах. Направим ось Ox по прямой, соединяющей A и B, как обычно, вправо, начало координат поместим в середине отрезка AB, ось Oy направим вверх по перпендикуляру к оси Ox. Длина отрезка AB по условию равна 2a (AB = 2a); тогда точки A и B будут иметь координаты: A(-a, 0); B(a, 0). Пусть точка M принадлежит кривой. Ее координаты обозначим через x и y (см. рисунок).
И з условия задачи AM * BM = a2. По формуле расстояния между двумя точками
з условия задачи AM * BM = a2. По формуле расстояния между двумя точками




Значит, 


Возведем обе части этого уравнения в квадрат:
[(x + a)2 + y2][(x - a)2 + y2] = a4,
Или [(x2 + y2 + a2) + 2ax][(x2 + y2 + a2) - 2ax] = a4;
(x2 + y2 + a2)2 - 4a2x2 = a4.
Упрощая, получаем (x2 + y2)2 = 2a2(x2 - y2).
Это и есть искомое уравнение.
Задача 16. В правильной треугольной призме  , все ребра которой равны 1, найдите расстояние между прямыми
, все ребра которой равны 1, найдите расстояние между прямыми  и
и  :
:
 Как мы помним из геометрического метода решения этой задачи, расстояние между прямыми
Как мы помним из геометрического метода решения этой задачи, расстояние между прямыми  и
и  есть расстояние от точки
есть расстояние от точки  до плоскости
до плоскости  :
:

Решение:
Рассстояние  от точки
от точки  до плоскости
до плоскости  вычисляется по такой формуле:
вычисляется по такой формуле:

Поместим нашу призму в систему координат. Если мы решаем задачу с кубом или прямоугольным параллелепипедом, то выбор системы координат очевиден: мы помещаем начало координат в одну из вершин куба, а оси направляем вдоль ребер. В случае призмы это не столь очевидно.
Нам надо выбрать систему координат таким образом, чтобы координаты точки  и точек
и точек  ,
,  и
и  , задающих плоскость
, задающих плоскость  вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом:
вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом:
З апишем координаты нужных нам точек:
апишем координаты нужных нам точек:




Чтобы найти коэффициенты ![]() ,
,  ,
,  и
и  в уравнении
в уравнении  плоскости
плоскости  , примем коэффициент
, примем коэффициент  , и подставим координаты точек
, и подставим координаты точек ![]() ,
,  и
и  в уравнение плоскости. Получим систему уравнений:
в уравнение плоскости. Получим систему уравнений:


Отсюда:
 ,
,
 ,
,

Подставим значения коэффициентов и координаты точки  в формулу для расстояния. Получим:
в формулу для расстояния. Получим:


О твет:
твет: 
Задача 17. В единичном кубе ![]() найдите расстояние от точки
найдите расстояние от точки  до плоскости
до плоскости  .
.
Решение:
Р ассстояние
ассстояние  от точки
от точки  до плоскости
до плоскости  вычисляется по такой формуле:
вычисляется по такой формуле:

Чтобы воспользоваться этой формулой, поместим куб в систему координат:
В задаче роль точки ![]() играет точка
играет точка  . То есть
. То есть  ,
,  ,
, 
Теперь задача найти коэффициенты ![]() ,
,  ,
,  и
и  в уравнении
в уравнении  плоскости
плоскости  .
.
Плоскость  определяется тремя точками
определяется тремя точками  ,
,  и
и  . Если координаты точек подставим в уравнение плоскости
. Если координаты точек подставим в уравнение плоскости  , то получим верное равенство.
, то получим верное равенство.
Коэффициент ![]() в уравнении плоскости можно принять равным 1.
в уравнении плоскости можно принять равным 1.
Ч тобы найти коэффициенты
тобы найти коэффициенты  ,
,  и
и  , подставим координаты точек
, подставим координаты точек ![]() ,
,  и
и  в уравнение плоскости
в уравнение плоскости  . Получим систему уравнений:
. Получим систему уравнений:

Отсюда:  ,
,  ,
, 
Подставим координаты точки  и значения коэффициентов в формулу для расстояния:
и значения коэффициентов в формулу для расстояния:

Ответ: 


