- Преподавателю
- Математика
- Решение уравнений высших степеней
Решение уравнений высших степеней
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Казанцева Л.В. |
| Дата | 18.10.2014 |
| Формат | doc |
| Изображения | Есть |
СХЕМА ГОРНЕРА
В РЕШЕНИИ УРАВНЕНИЙ С ПАРАМЕТРАМИ
ИЗ ГРУППЫ «С» ПРИ ПОДГОТОВКЕ К ЕГЭ
Казанцева Людмила Викторовна
учитель математики МБОУ «Уярская СОШ № 3»
Содержание текстов Единого государственного экзамена показало, что материал учебника не достаточен для успешной сдачи экзамена. Знаний, полученных на школьных уроках, хватает только для решения примеров из группы «В».
На факультативных занятиях необходимо расширить круг имеющихся знаний за счет решения заданий повышенной сложности группы «С».
Даная работа освещает часть вопросов, рассматриваемых на дополнительных занятиях.
Целесообразно ввести схему Горнера после изучения темы «Деление многочлена на многочлен». Этот материал позволяет решать уравнения высших порядков не способом группировки многочленов, а более рациональным путем, экономящим время.
План занятий.
Решение уравнений высших степеней.
Занятие 1.
1. Объяснение теоретического материала.
2. Решение примеров а), б), в), г).
Занятие 2.
1. Решение уравнений а), б), в), г).
2. Нахождение рациональных корней многочлена
Применение схемы Горнера при решении уравнений с параметрами.
Занятие 3.
-
Задания а), б), в).
Занятие 4.
1. Задания г), д), е), ж), з).
Решение уравнений высших степеней.
Схема Горнера.
Теорема: Пусть несократимая дробь 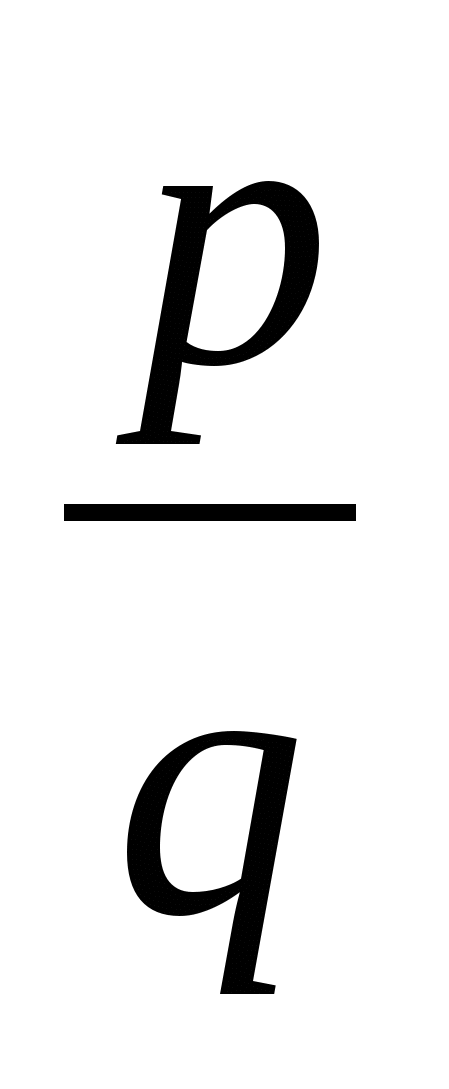 является корнем уравнения
является корнем уравнения
ao xn + a1 xn-1 + … + an-1x1 + an = 0
c целыми коэффициентами. Тогда число р является делителем старшего коэффициента ао.
Следствие: Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.
Следствие: Если старший коэффициент уравнения с целыми коэффициентами равен 1, то все рациональные корни, если они существуют - целые.
Пример 1. 2х3 - 7х2 + 5х - 1 = 0
Пусть несократимая дробь 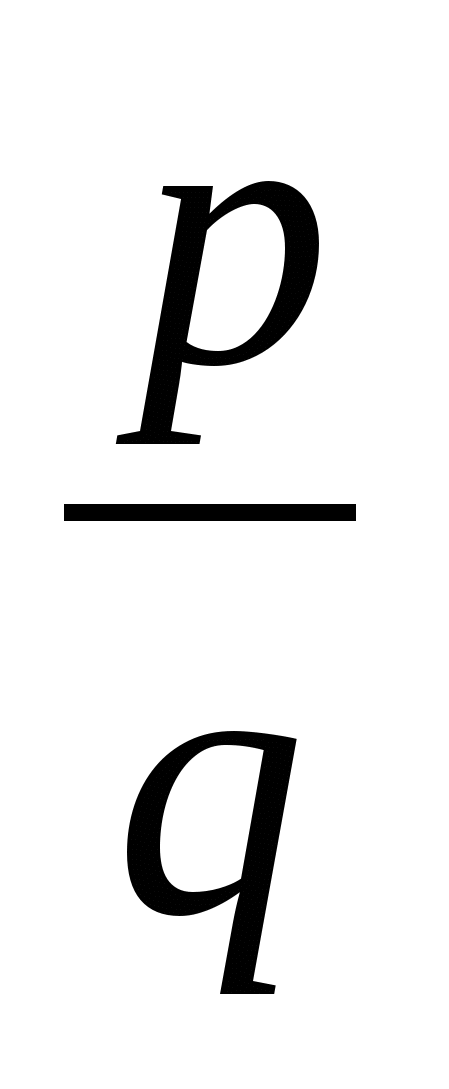 является корнем уравнения, тогда р является делителем числа 1 : ± 1
является корнем уравнения, тогда р является делителем числа 1 : ± 1
q является делителем старшего члена: ± 1; ± 2
Рациональные корни уравнения надо искать среди чисел: ± 1; ± ![]() .
.
f(1) = 2 - 7 + 5 - 1 = - 1 ≠ 0
f(-1) = -2 - 7 - 5 - 1 ≠ 0
f(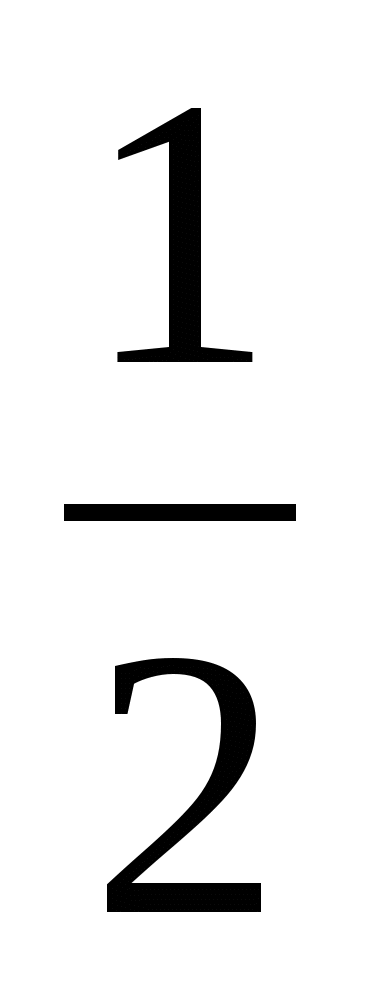 ) =
) = 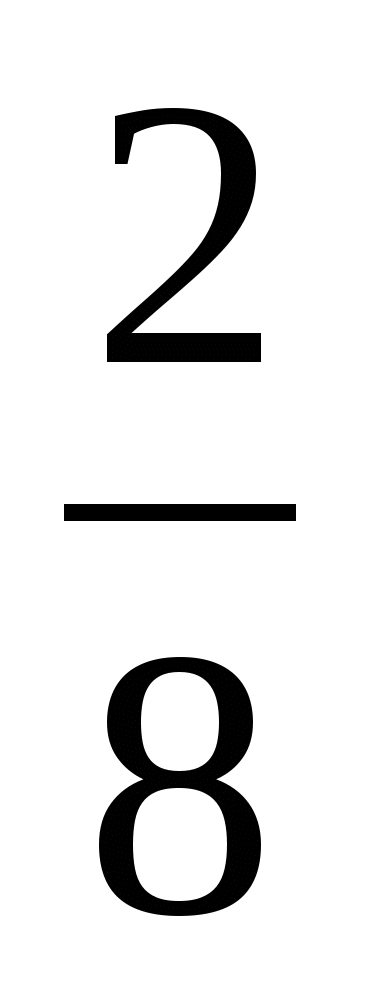 -
- 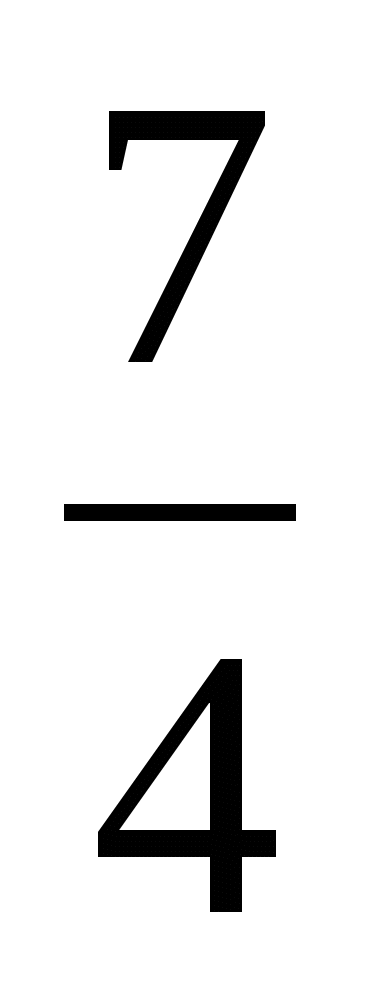 +
+ 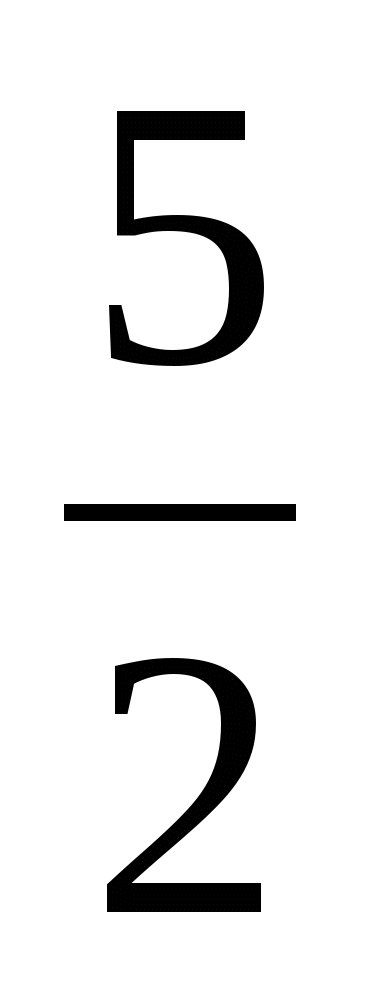 - 1 =
- 1 = 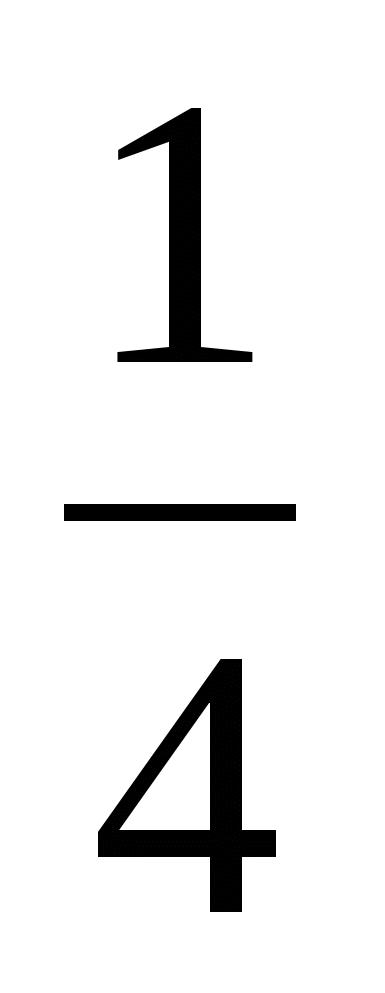 -
- 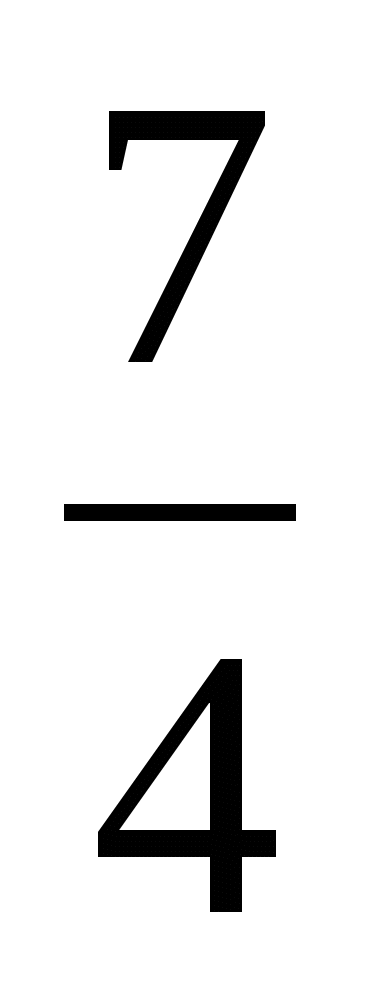 +
+ 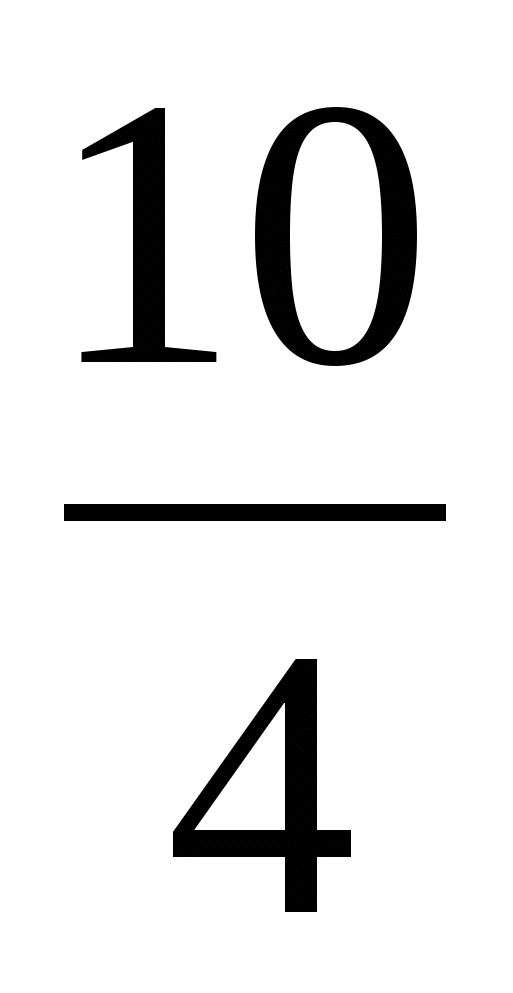 -
- 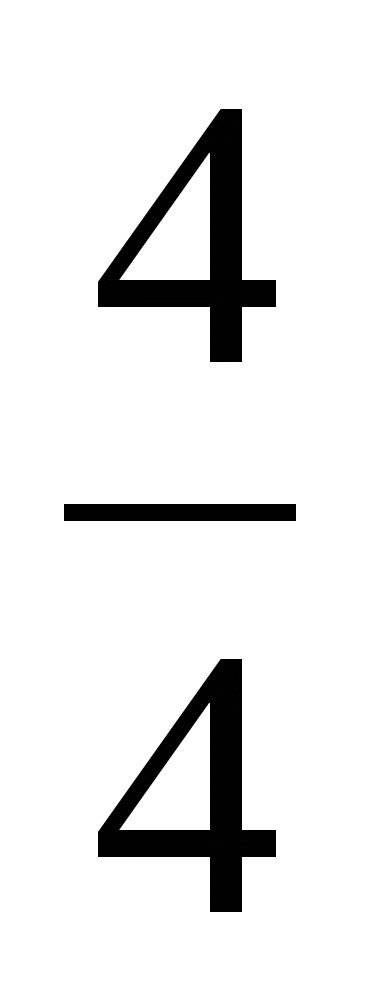 = 0
= 0
Корнем является число 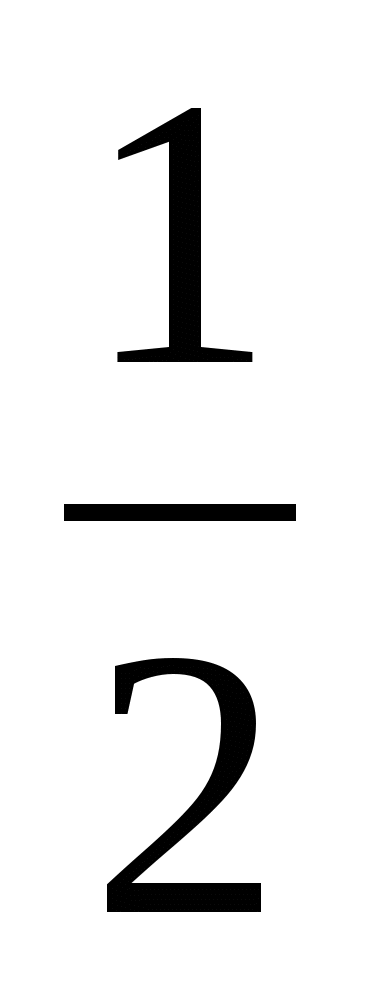 .
.
Деление многочлена Р(х) = аохп + a1 xn-1 + … + an на двучлен (х - £) удобно выполнять по схеме Горнера.
Обозначим неполное частное Р(х) на (х - £) через Q(x) = boxn-1 + b1xn-2 + …bn-1,
а остаток через bn
Р(х) = Q(x) (x - £) + bn , то имеет место тождество
аохп + a1 xn-1 + … + an = (boxn-1 + … + bn-1) (х - £) + bn
Q(x) - многочлен, степень которого на 1 ниже степени исходного многочлена. Коэффициенты многочлена Q(x) определяются по схеме Горнера.
ао
a1
a2
…
an-1
an
£
bo = aо
b1 = a1 + £·bo
b2 = a2 + £·b1
bn-1 = an-1 + £·bn-2
bn = an + £·bn-1
В первой строке этой таблицы записывают коэффициенты многочлена Р(х).
Если какая-то степень переменной отсутствует, то в соответствующей клетке таблицы пишется 0.
Старший коэффициент частного равен старшему коэффициенту делимого (ао = bo). Если £ является корнем многочлена, то в последней клетке получается 0.
Пример 2. Разложить на множители с целыми коэффициентами
Р(х) = 2х4 - 7х3 - 3х2 + 5х - 1
Ищем целые корни среди делителей свободного члена: ± 1.
Подходит - 1.
Делим Р(х) на (х + 1)
2
- 7
- 3
5
- 1
- 1
2
- 9
6
- 1
0
2х4 - 7х3 - 3х2 + 5х - 1 = (х + 1) (2х3 - 9х2 + 6х - 1)
Ищем целые корни среди свободного члена: ± 1
Так как старший член равен 1, то корнями могут быть дробные числа: - 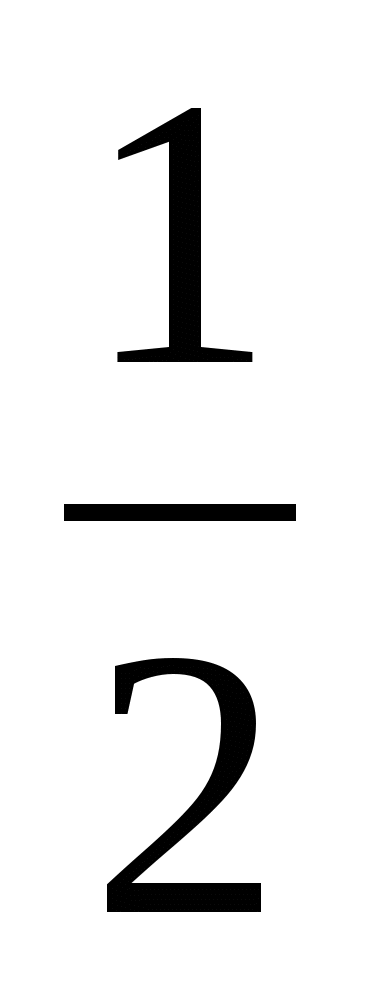 ;
; 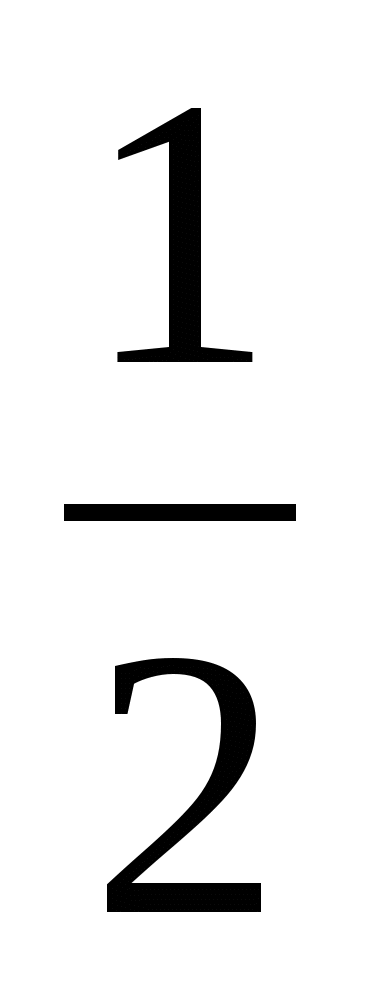 .
.
Подходит 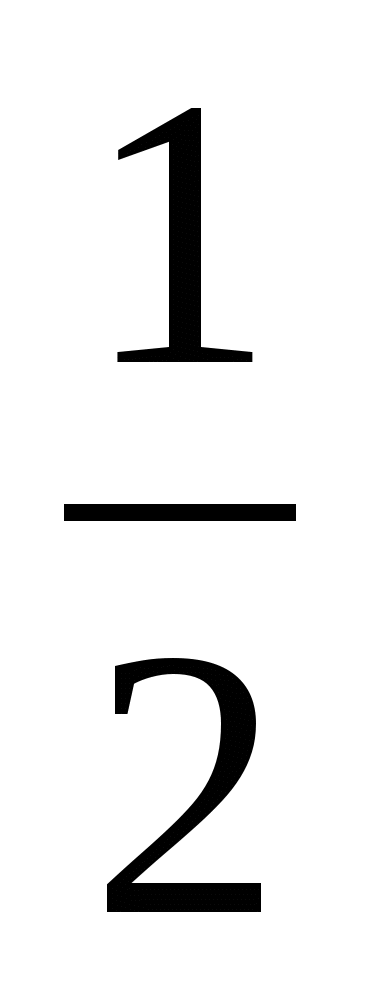 .
.
2
- 9
6
- 1
![]()
2
- 8
2
0
2х3 - 9х2 + 6х - 1 =(х - 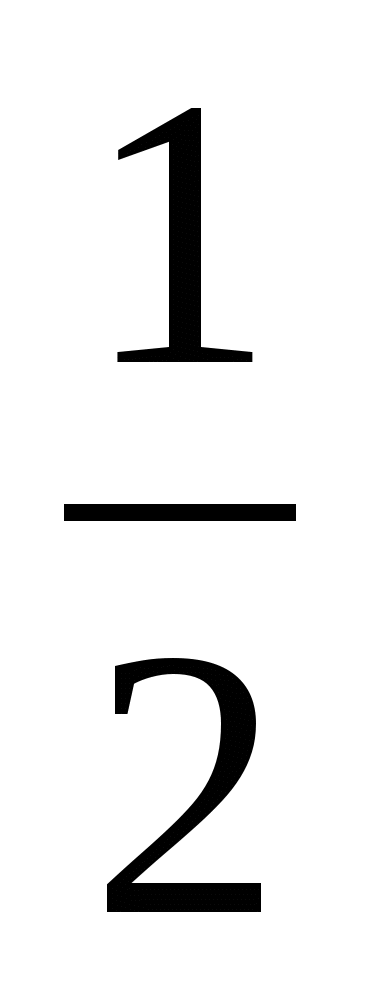 ) (2х2 - 8х + 2) = (2х - 1) (х2 - 4х + 1)
) (2х2 - 8х + 2) = (2х - 1) (х2 - 4х + 1)
Трехчлен х2 - 4х + 1 на множители с целыми коэффициентами не раскладывается.
Задание:
1. Разложите на множители с целыми коэффициентами:
а) х3 - 2х2 - 5х + 6
q: ± 1;
р: ± 1; ± 2; ± 3; ± 6
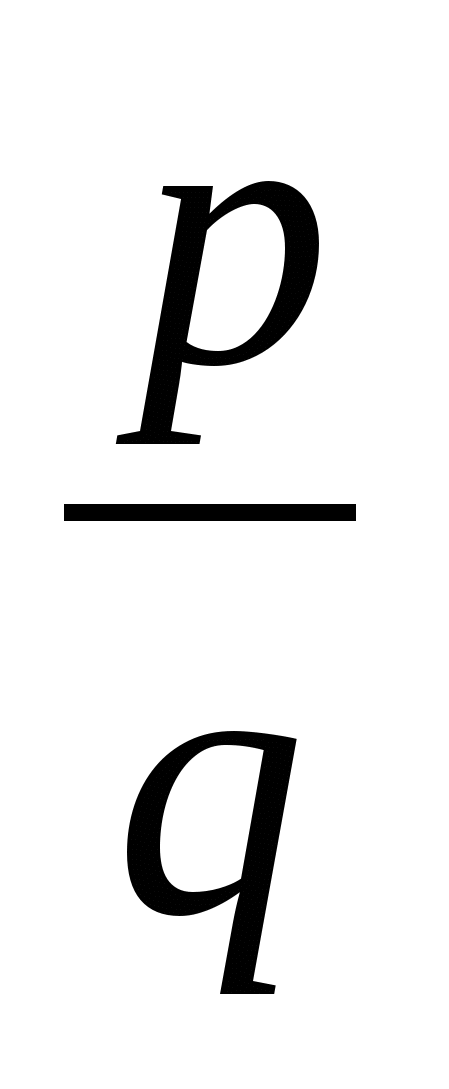 :± 1; ± 2; ± 3; ± 6
:± 1; ± 2; ± 3; ± 6
Находим рациональные корни многочлена f(1) = 1 - 2 - 5 + 6 = 0
х = 1
1
- 2
- 5
6
1
1
- 1
- 6
0
х3 - 2х2 - 5х + 6 = (х - 1) (х2 - х - 6) = (х - 1) (х - 3) (х + 2)
Определим корни квадратного уравнения
х2 - х - 6 = 0
х = 3; х = - 2
б) 2х3 + 5х2 + х - 2
р: ± 1; ± 2
q: ± 1; ± 2
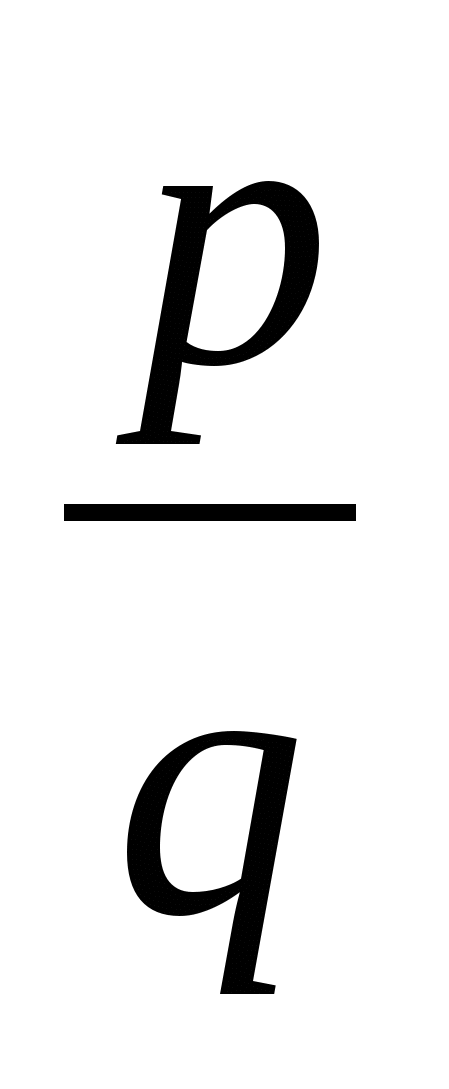 :± 1; ± 2; ±
:± 1; ± 2; ± 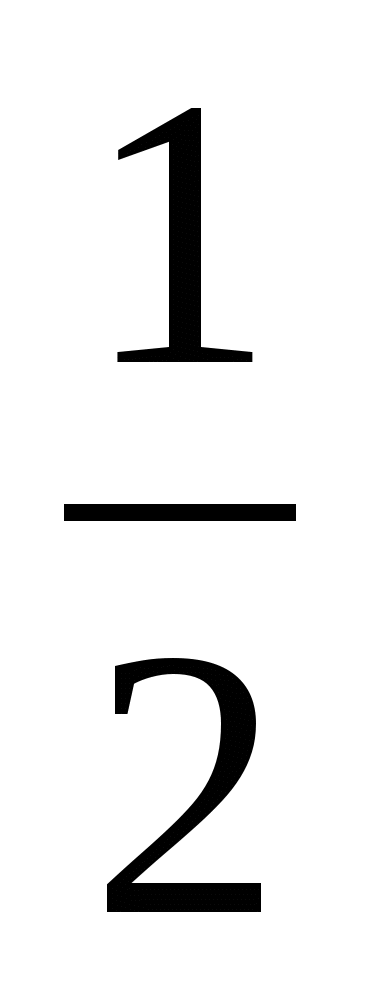
Найдем корни многочлена третьей степени
f(1) = 2 + 5 + 1 - 2 ≠ 0
f(-1) = - 2 + 5 - 1 - 2 = 0
Один из корней уравнения х = - 1
2
5
1
- 2
- 1
2
3
- 2
0
2х3 + 5х2 + х - 2 = (х + 1) (2х2 + 3х - 2) = (х + 1) (х + 2) (2х - 1)
Разложим квадратный трехчлен 2х2 + 3х - 2 на множители
2х2 + 3х - 2 = 2 (х + 2) (х - 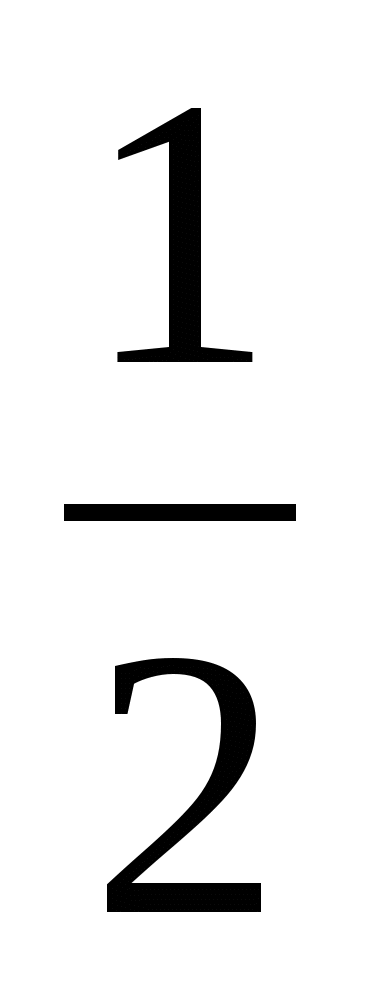 )
)
D = 9 + 16 = 25
х1 = - 2; х2 = 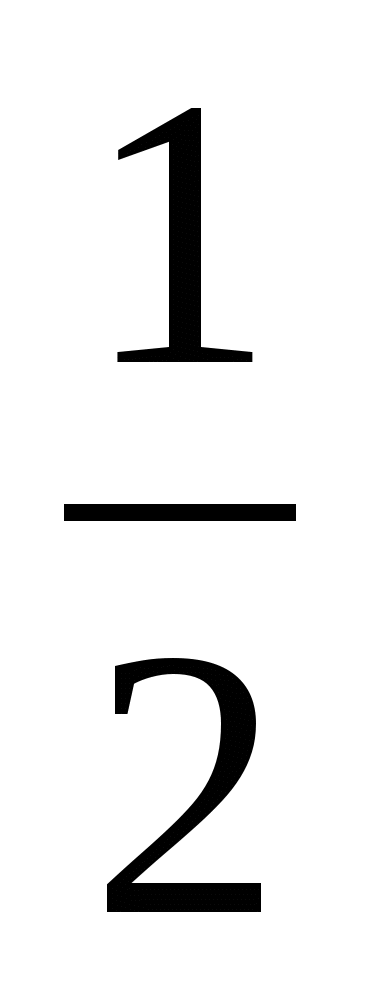
в) х3 - 3х2 + х + 1
р: ± 1
q: ± 1
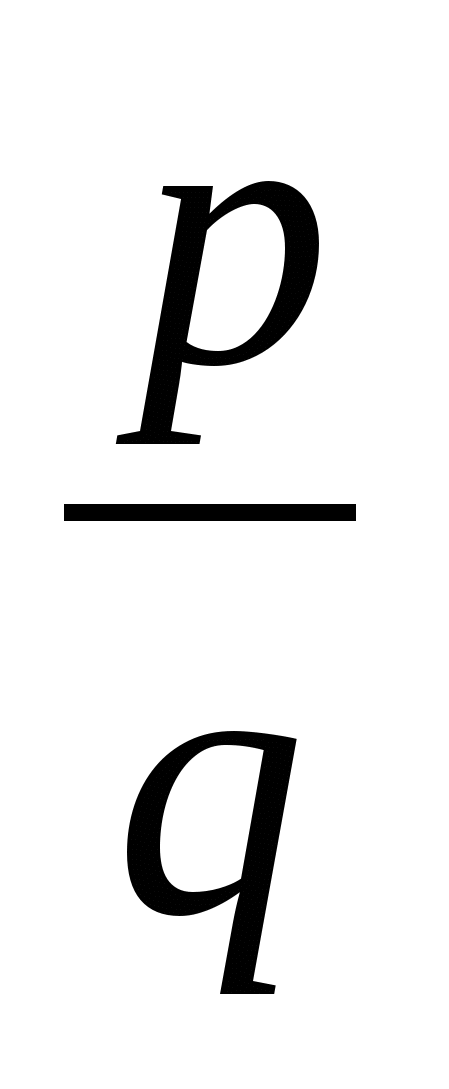 :± 1
:± 1
f(1) = 1 - 3 + 1 - 1 = 0
Одним из корней многочлена третьей степени является х = 1
1
- 3
1
1
1
1
- 2
- 1
0
х3 - 3х2 + х + 1 = (х - 1) (х2 - 2х - 1)
Найдем корни уравнения х2 - 2х - 1 = 0
D = 4 + 4 = 8
х1 = 1 - 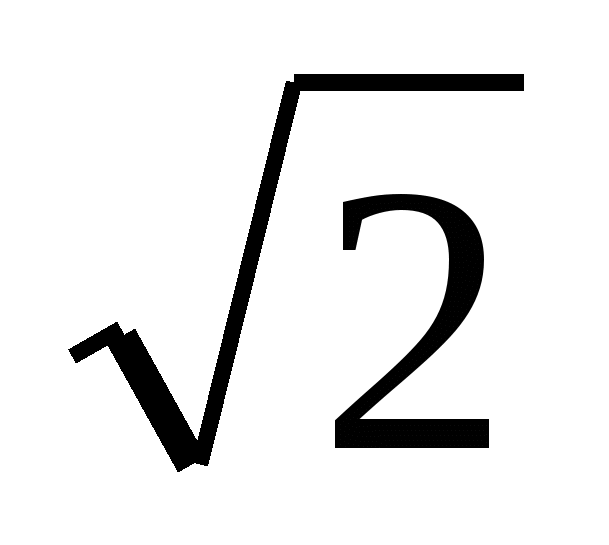
х2 = 1 + 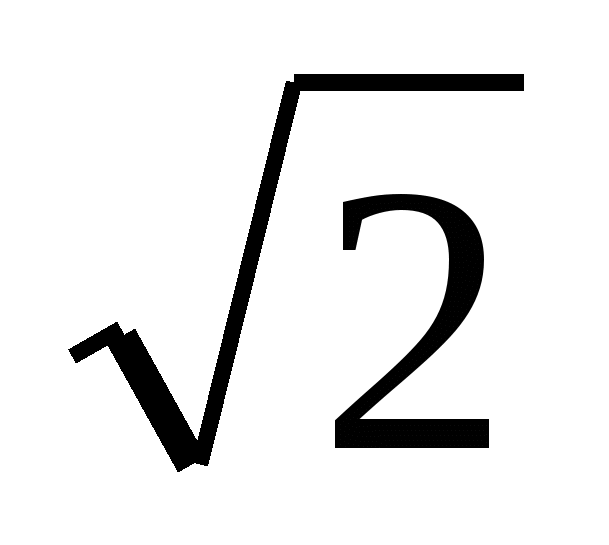
х3 - 3х2 + х + 1 = (х - 1) (х - 1 + 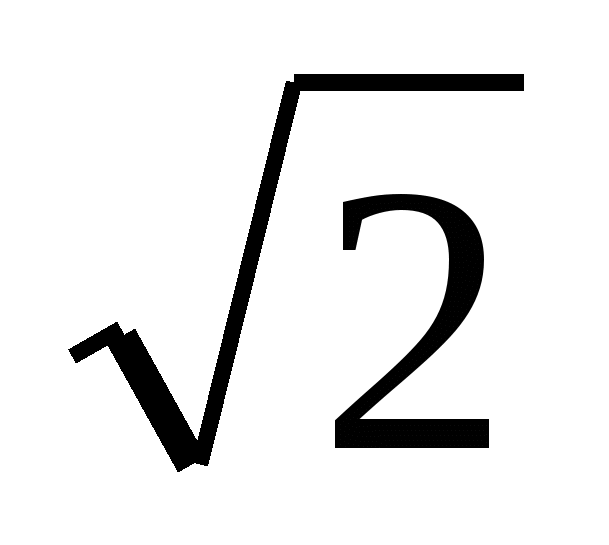 ) (х - 1 -
) (х - 1 - 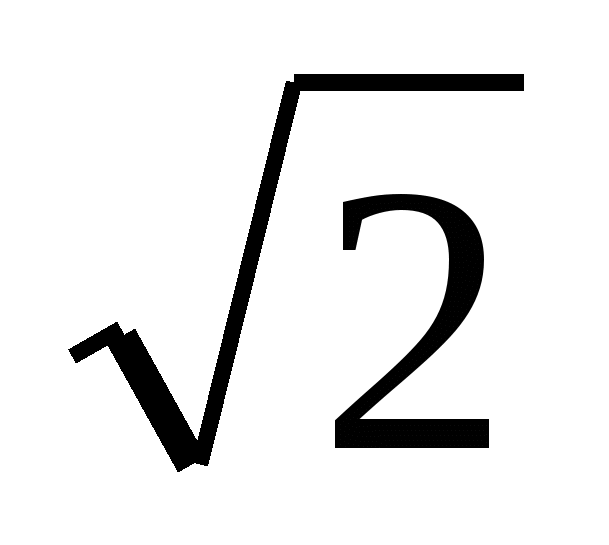 )
)
г) х3 - 2х - 1
р: ± 1
q: ± 1
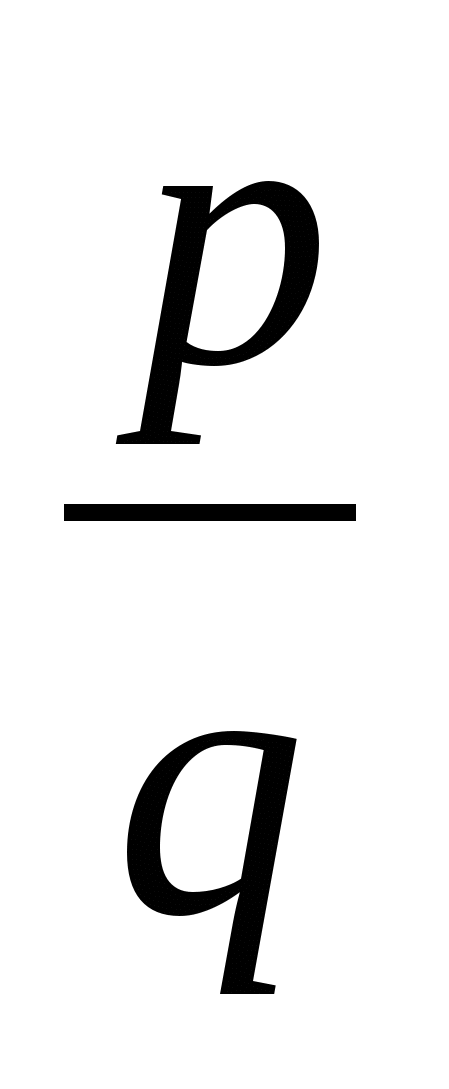 :± 1
:± 1
Определим корни многочлена
f(1) = 1 - 2 - 1 = - 2
f(-1) = - 1 + 2 - 1 = 0
Первый корень х = - 1
1
0
- 2
- 1
- 1
1
- 1
- 1
0
х3 - 2х - 1 = (х + 1) (х2 - х - 1)
х2 - х - 1 = 0
D = 1 + 4 = 5
х1,2 = 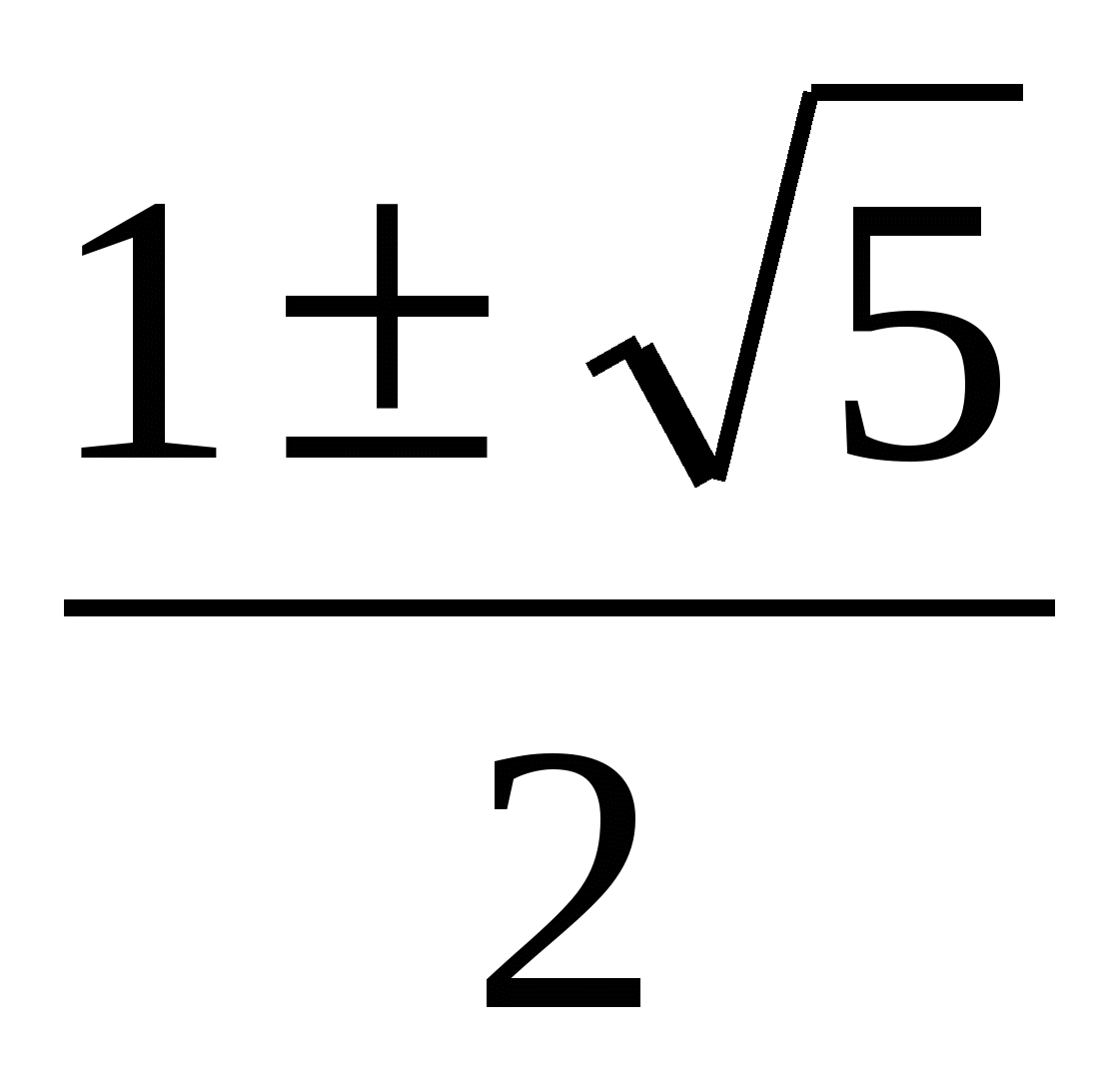
х3 - 2х - 1 = (х + 1) (х - 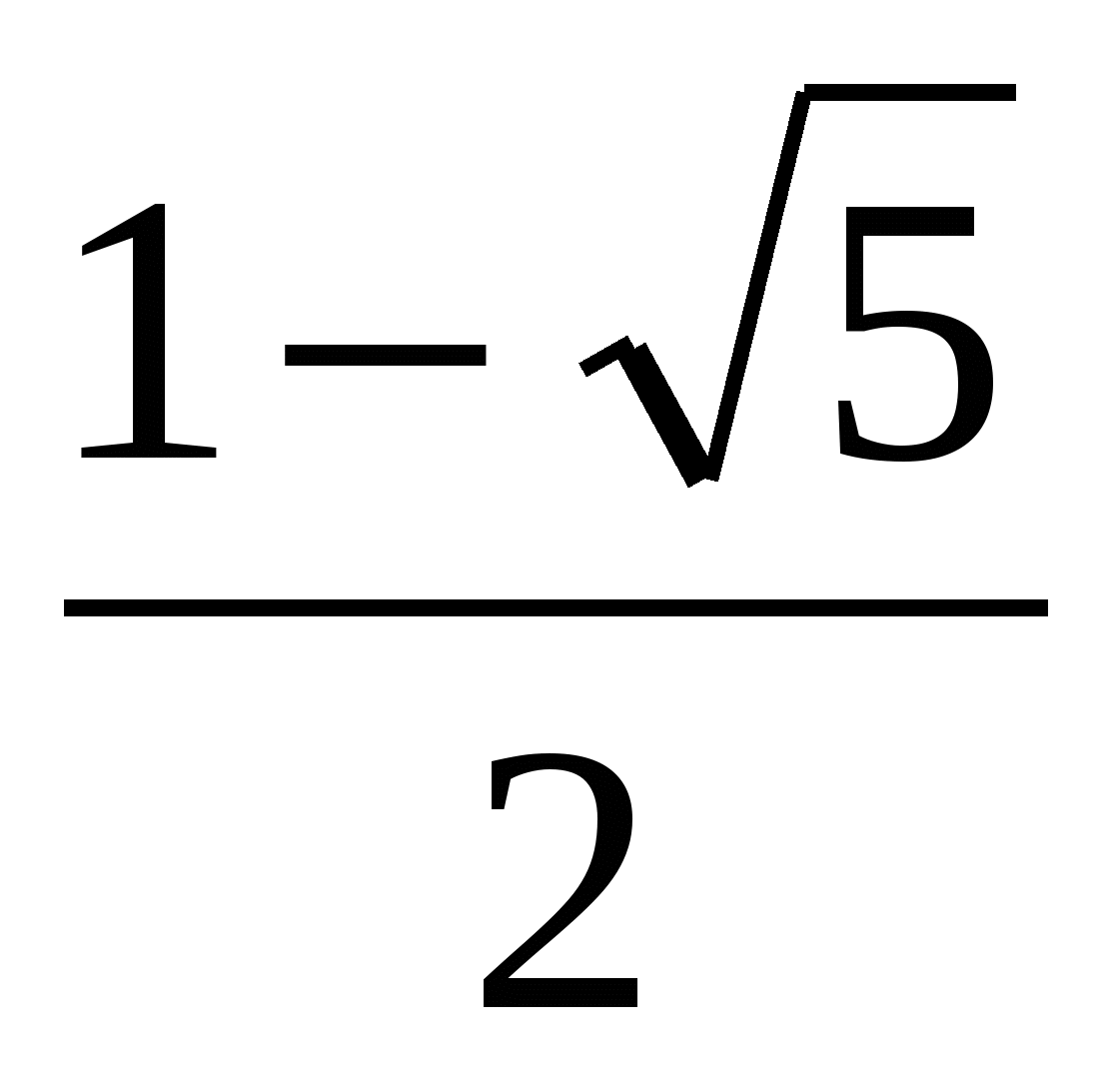 ) (х -
) (х - 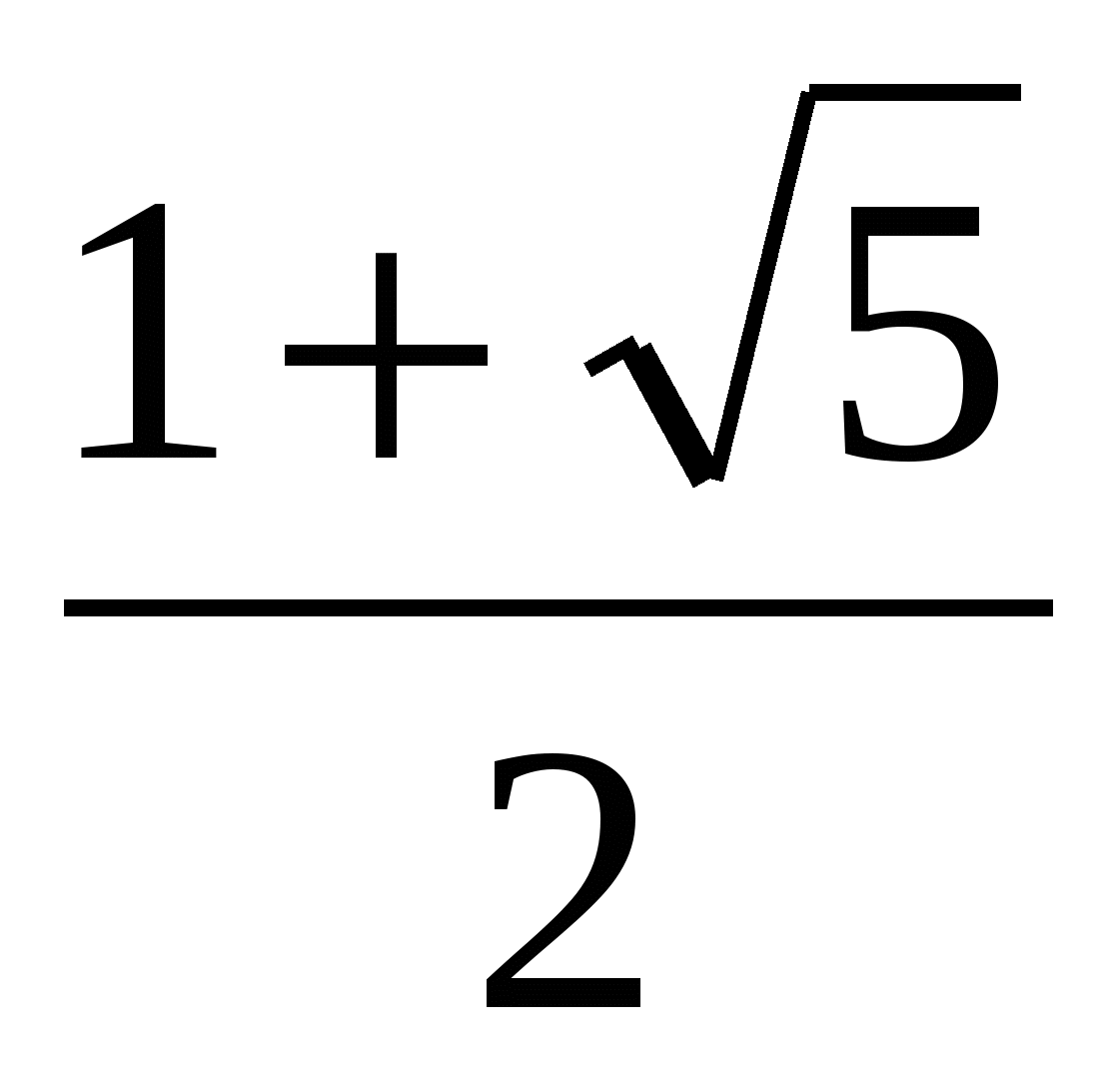 )
)
2. Решить уравнение:
а) х3 - 5х + 4 = 0
Определим корни многочлена третьей степени
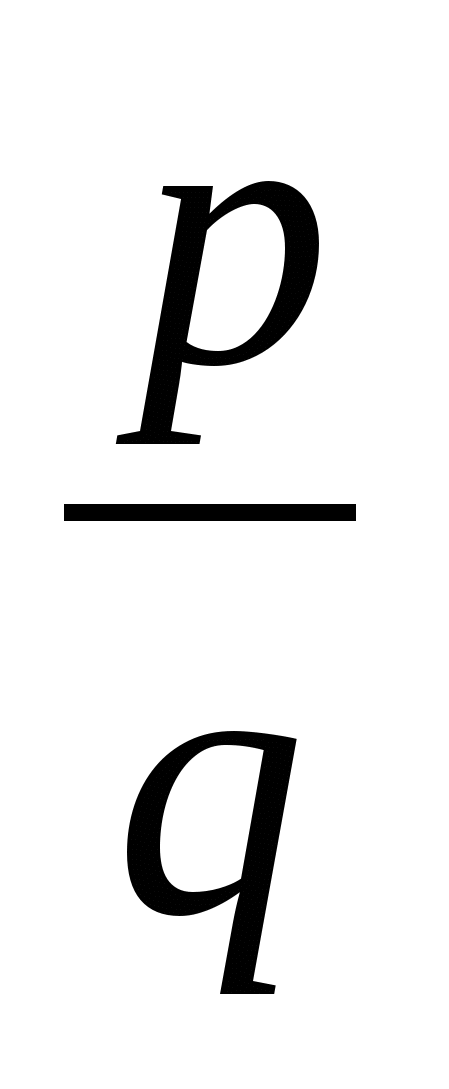 :± 1; ± 2; ± 4
:± 1; ± 2; ± 4
f(1) = 1 - 5 + 4 = 0
Одним из корней является х = 1
1
0
- 5
4
1
1
1
- 4
0
х3 - 5х + 4 = 0
(х - 1) (х2 + х - 4) = 0
Найдем корни квадратного уравнения х2 + х - 4 = 0
D = 1 + 16 = 17
х1 = 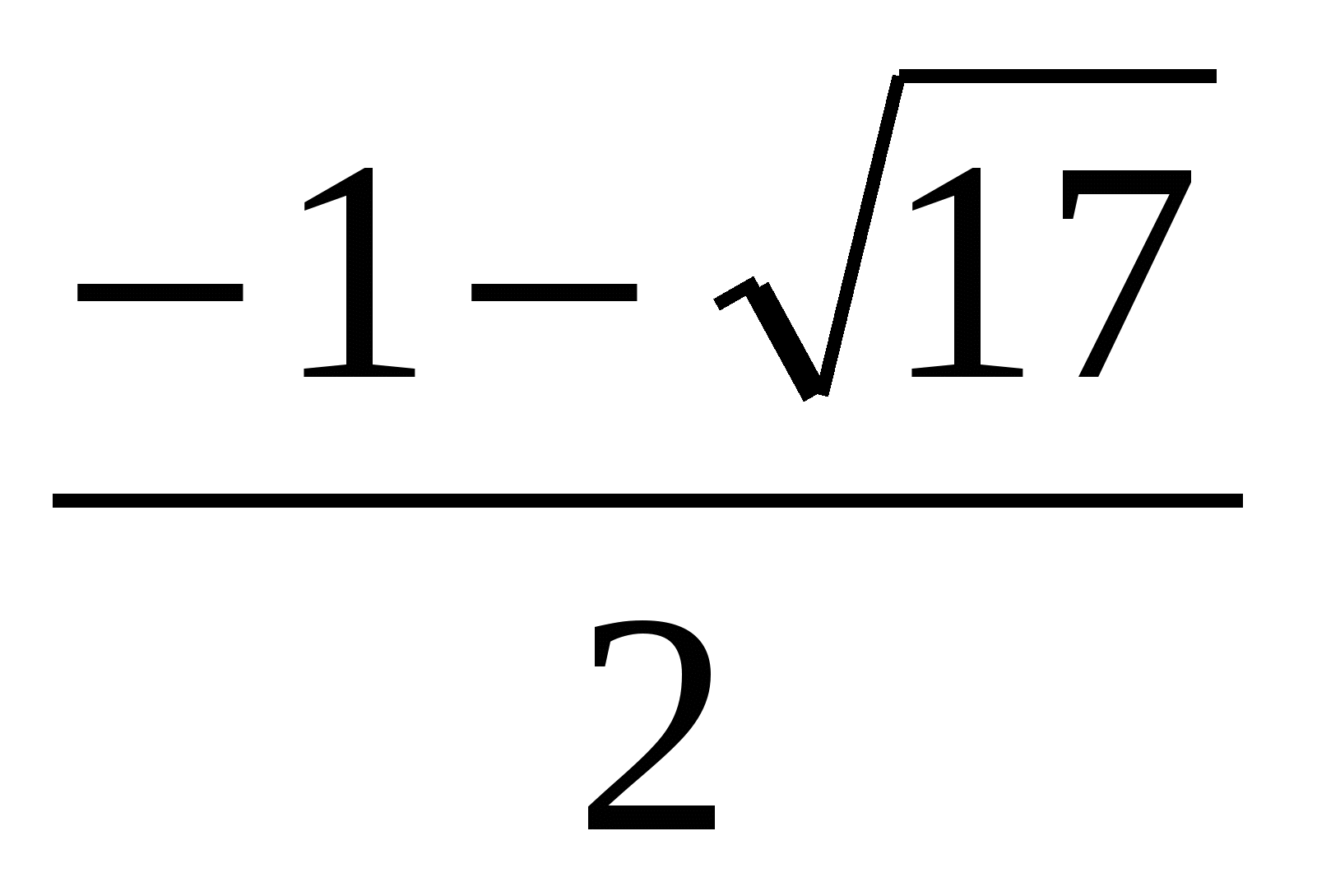 ; х2 =
; х2 = 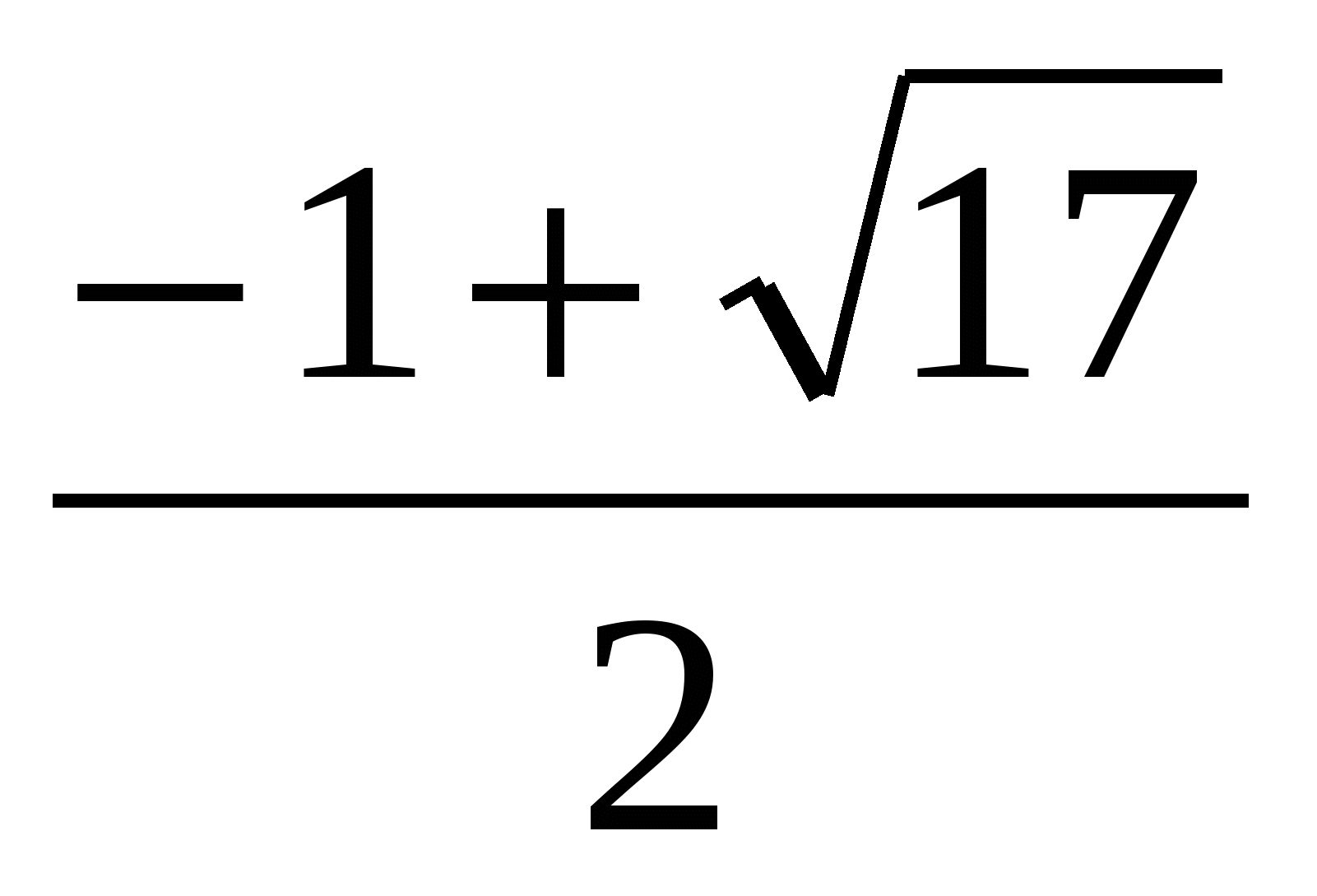
Ответ: 1; 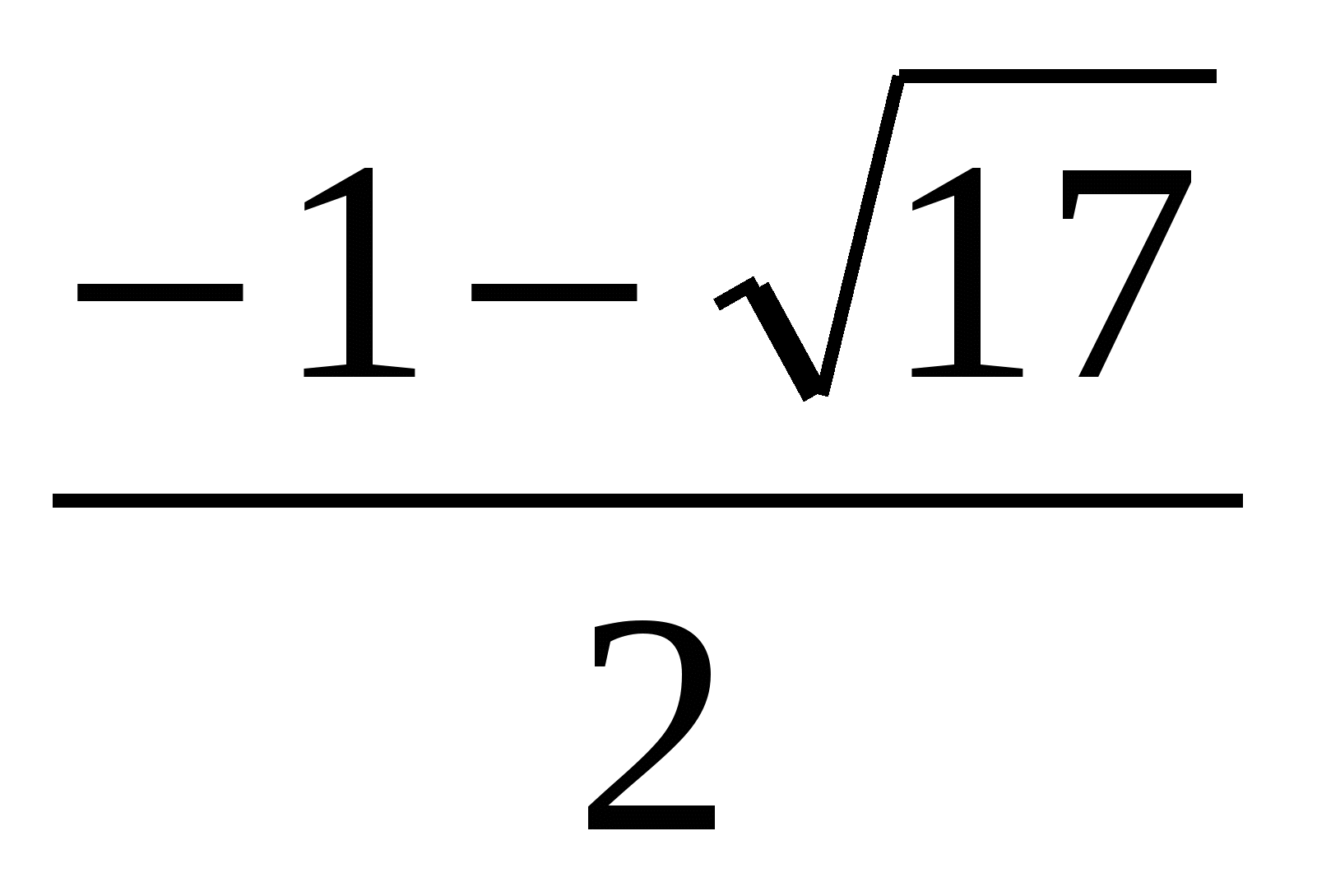 ;
; 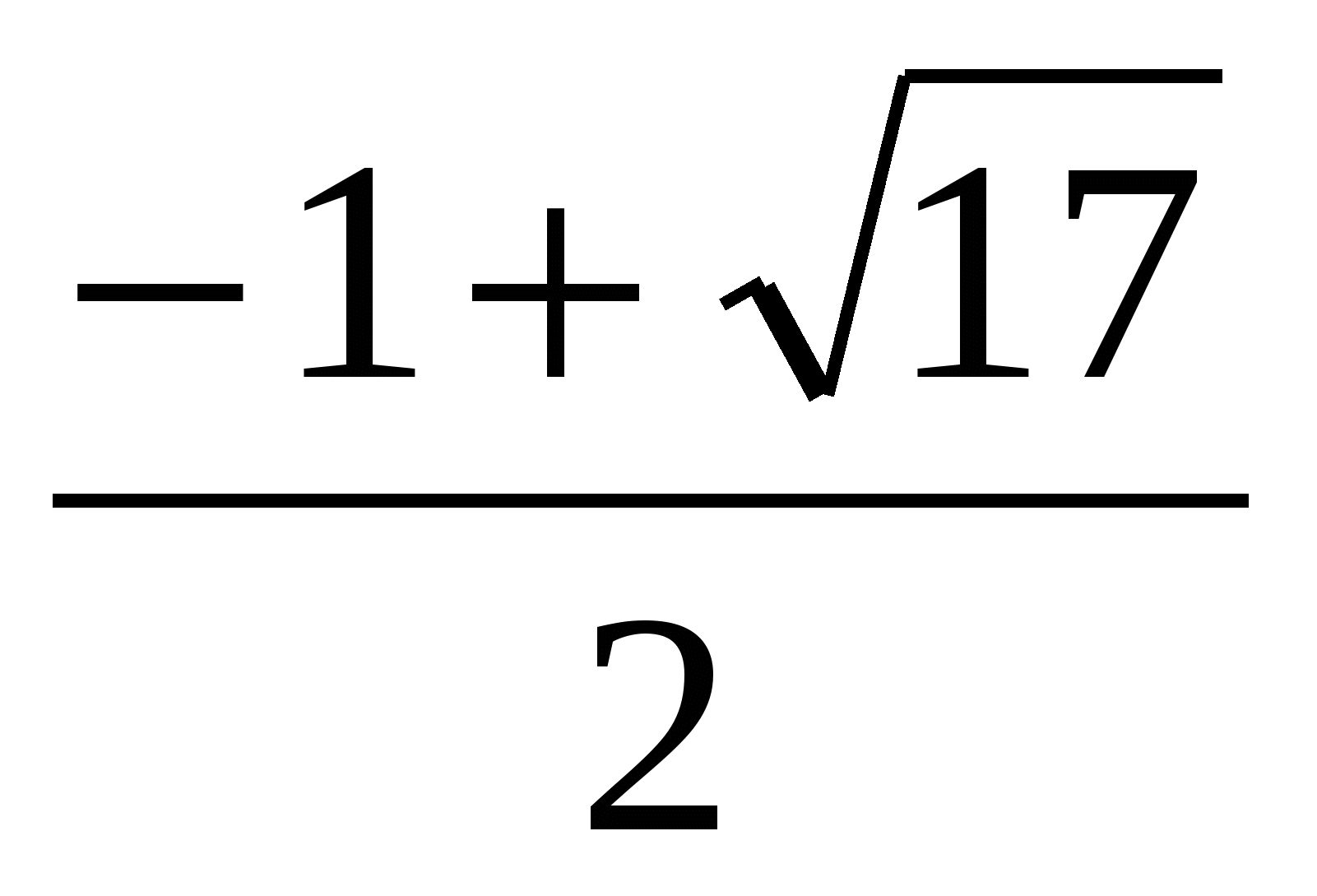
б) х3 - 8х2 + 40 = 0
Определим корни многочлена третьей степени.
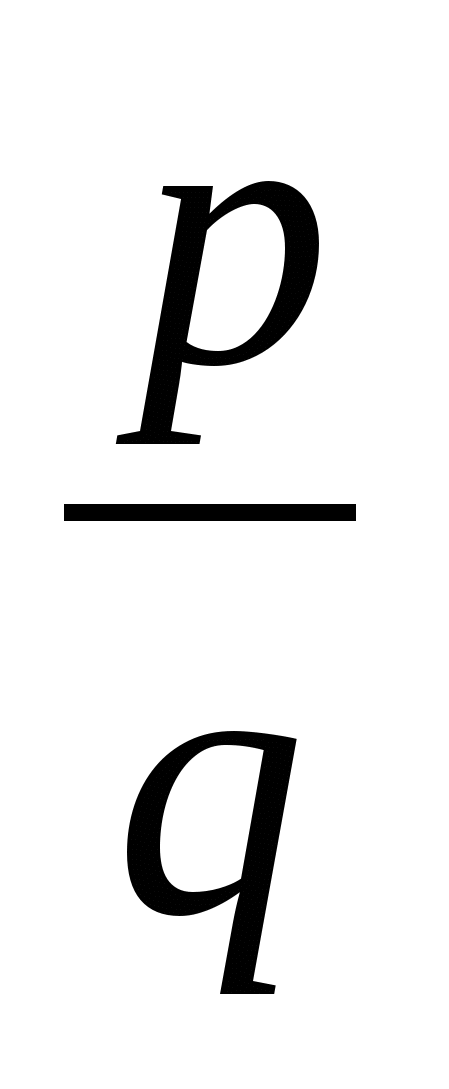 :± 1; ± 2; ± 4; ± 5; ± 8; ± 10; ± 20; ± 40
:± 1; ± 2; ± 4; ± 5; ± 8; ± 10; ± 20; ± 40
f(1) ≠ 0
f(-1) ≠ 0
f(-2) = - 8 - 32 + 40 = 0
Одним из корней является х = - 2
1
- 8
0
40
- 2
1
- 10
20
0
Разложим многочлен третьей степени на множители.
х3 - 8х2 + 40 = (х + 2) (х2 - 10х + 20)
Найдем корни квадратного уравнения х2 - 10х + 20 = 0
D = 100 - 80 = 20
х1 = 5 - 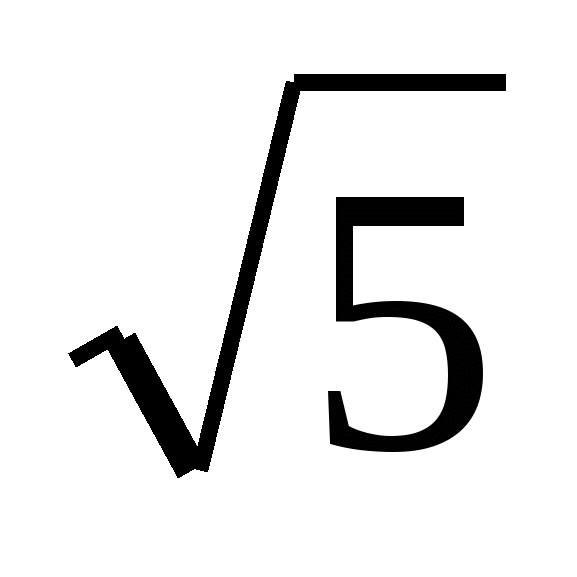 ; х2 = 5 +
; х2 = 5 + 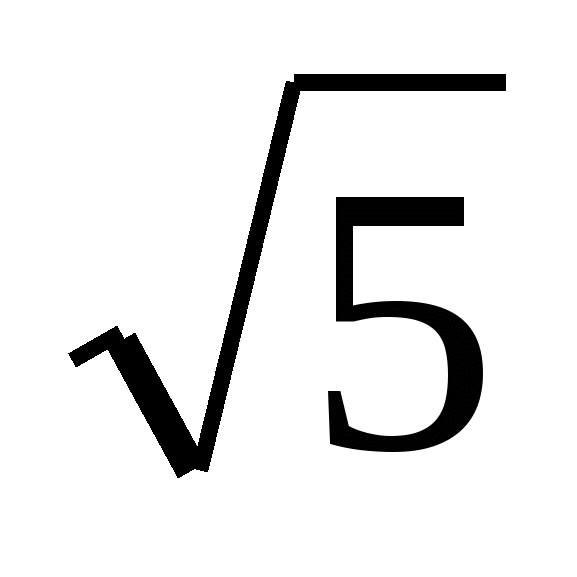
Ответ: - 2; 5 - 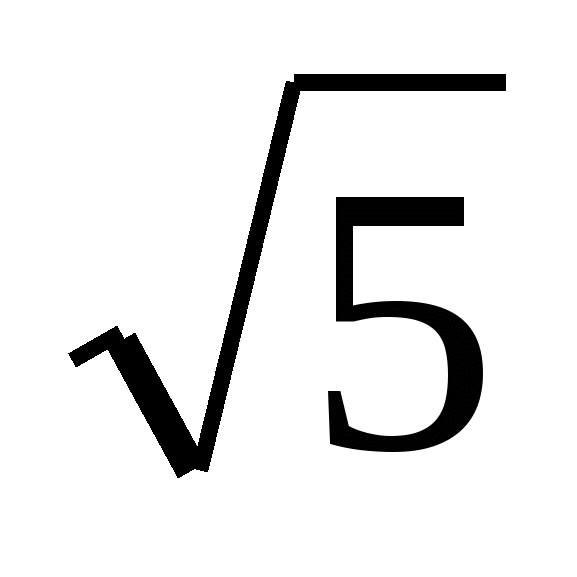 ; 5 +
; 5 + 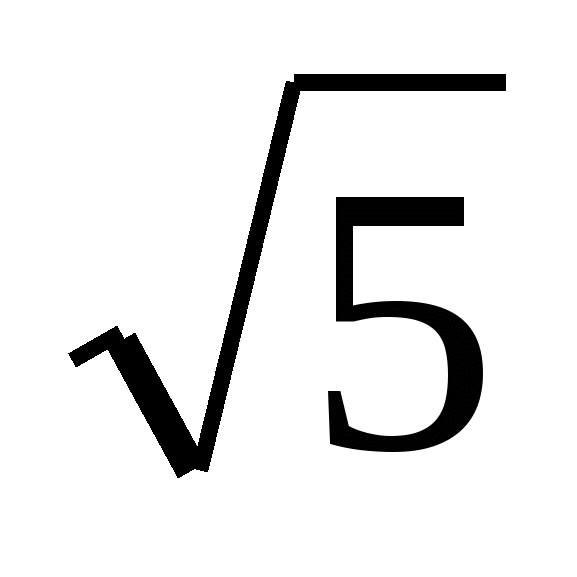
в) х3 - 5х2 + 3х + 1 = 0
Ищем целые корни среди делителей свободного члена: ± 1
f(-1) = - 1 - 5 - 3 + 1 ≠ 0
f(1) = 1 - 5 + 3 + 1 = 0
Подходит х = 1
1
- 5
3
1
1
1
- 4
- 1
0
х3 - 5х2 + 3х + 1 = 0
(х - 1) (х2 - 4х - 1) = 0
Определяем корни квадратного уравнения х2 - 4х - 1 = 0
D = 20
х = 2 + ![]() ; х = 2 -
; х = 2 - 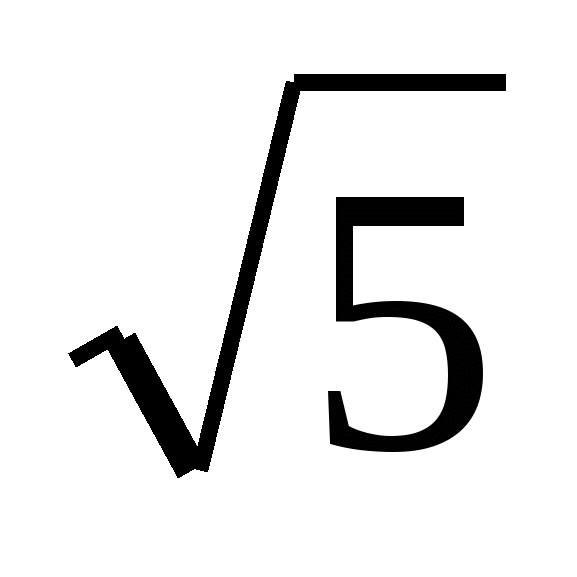
Ответ: 2 - 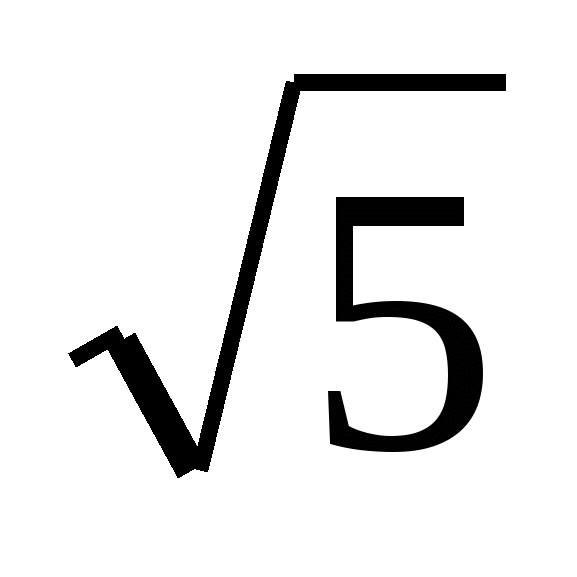 ; 1; 2 +
; 1; 2 + 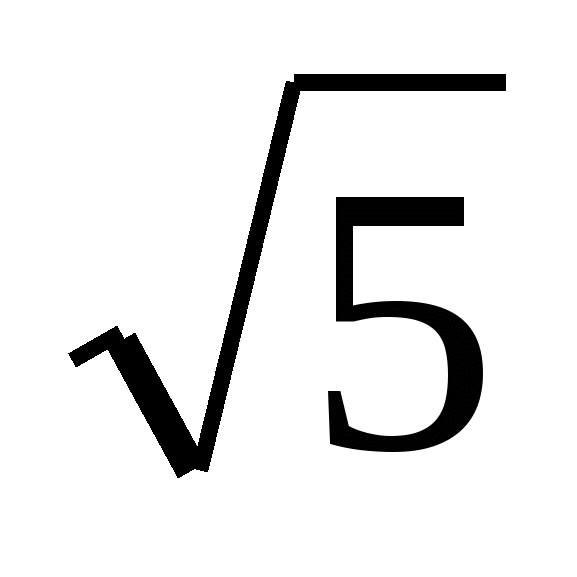
г) 2х4 - 5х3 + 5х2 - 2 = 0
Найдем рациональные корни многочлена
р: ± 1; ± 2
q: ± 1; ± 2
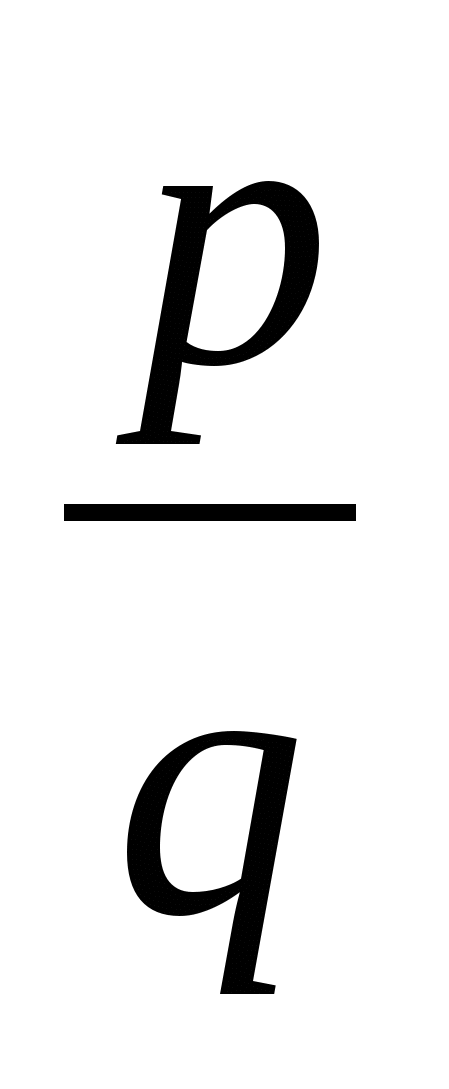 :± 1; ± 2; ±
:± 1; ± 2; ± 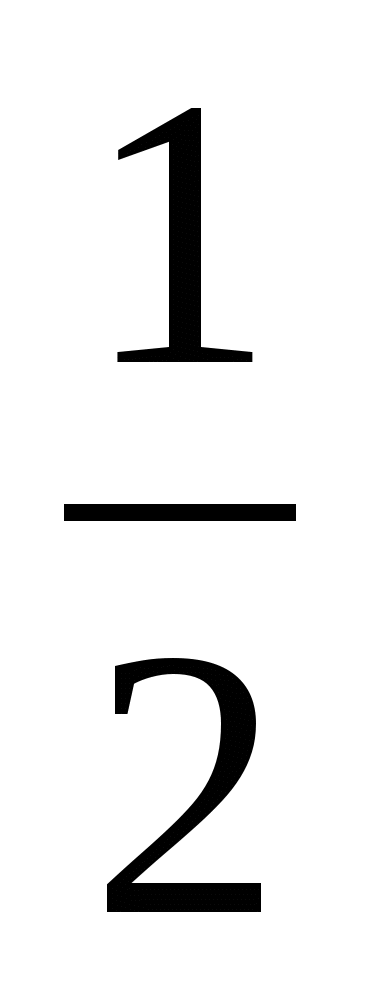
f(1) = 2 - 5 + 5 - 2 = 0
Один из корней уравнения х = 1
2
- 5
5
0
- 2
1
2
- 3
2
2
0
2х4 - 5х3 + 5х2 - 2 = 0
(х - 1) (2х3 - 3х2 + 2х + 2) = 0
Находим по такой же схеме корни уравнения третьей степени.
2х3 - 3х2 + 2х + 2 = 0
р: ± 1; ± 2
q: ± 1; ± 2
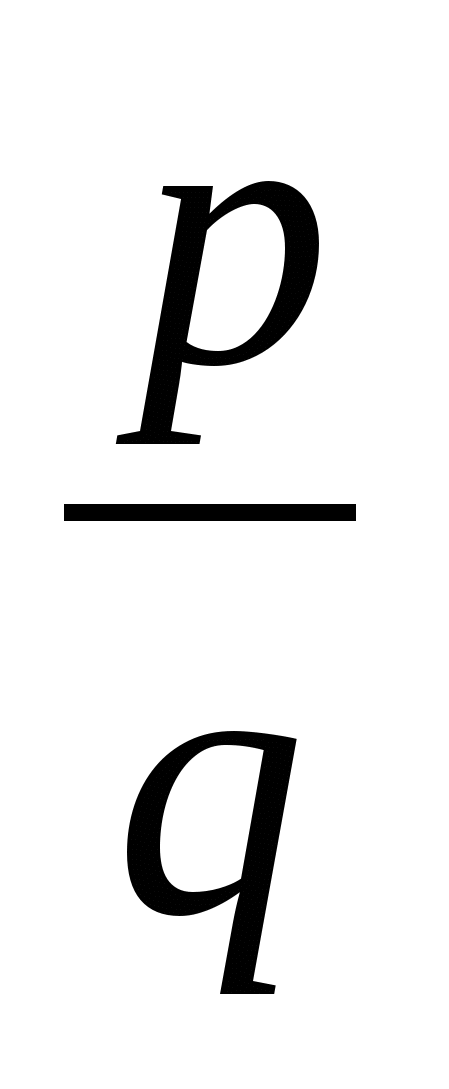 :± 1; ± 2; ±
:± 1; ± 2; ± 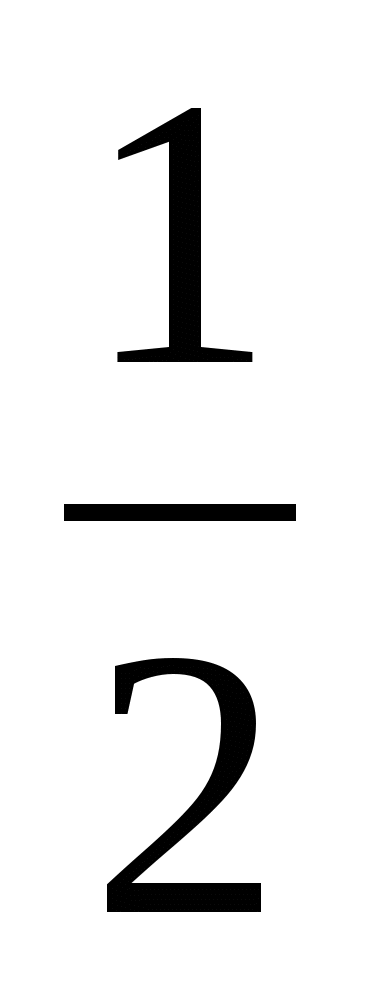
f(1) = 2 - 3 + 2 + 2 ≠ 0
f(-1) = - 2 - 3 - 2 + 2 ≠ 0
f(2) = 16 - 12 + 4 + 2 ≠ 0
f(-2) = - 16 - 12 - 4 + 2 ≠ 0
f(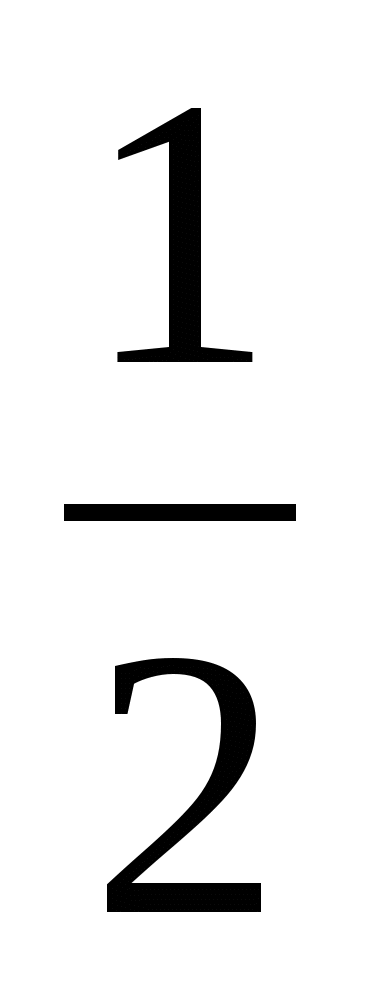 ) =
) = 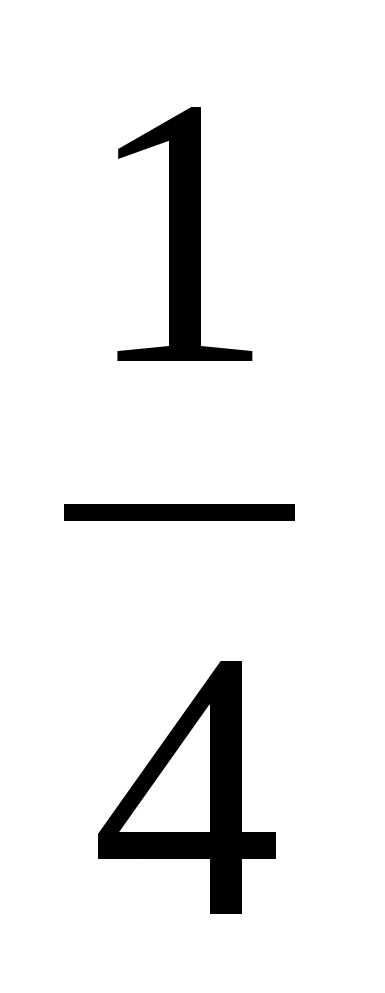 -
- 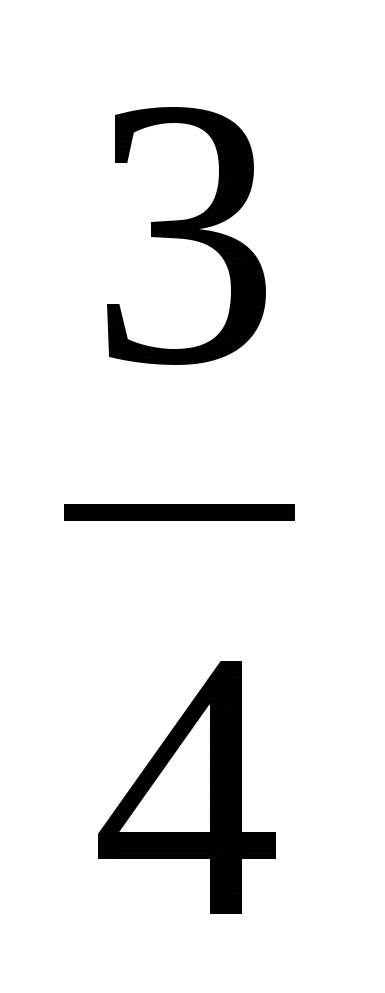 + 1 + 2 ≠ 0
+ 1 + 2 ≠ 0
f(-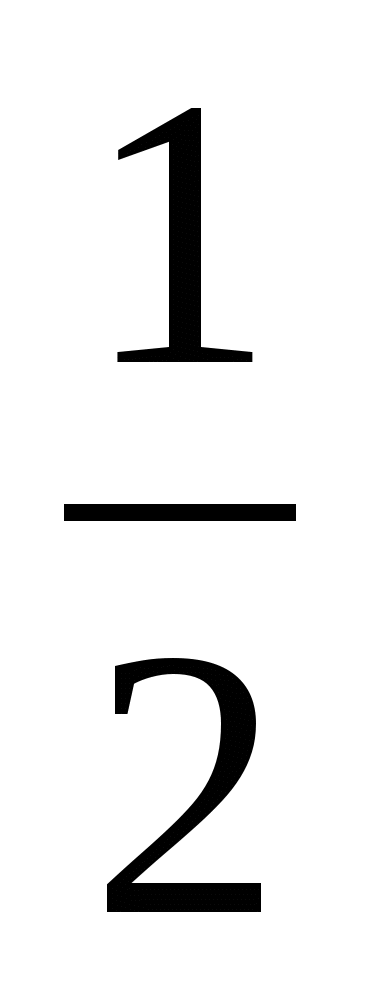 ) = -
) = - 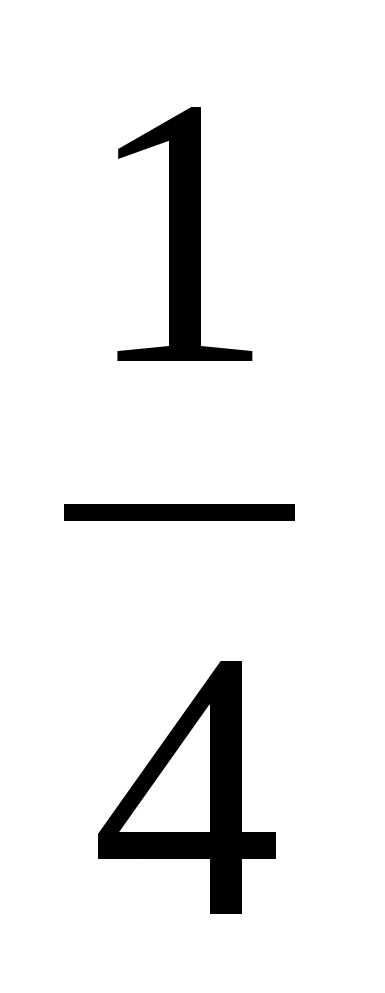 -
- 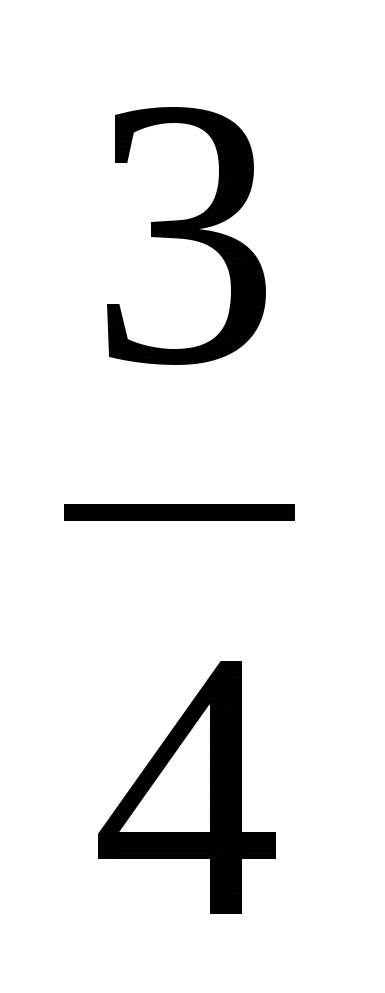 - 1 + 2 ≠ 0
- 1 + 2 ≠ 0
Следующий корень уравнения х = -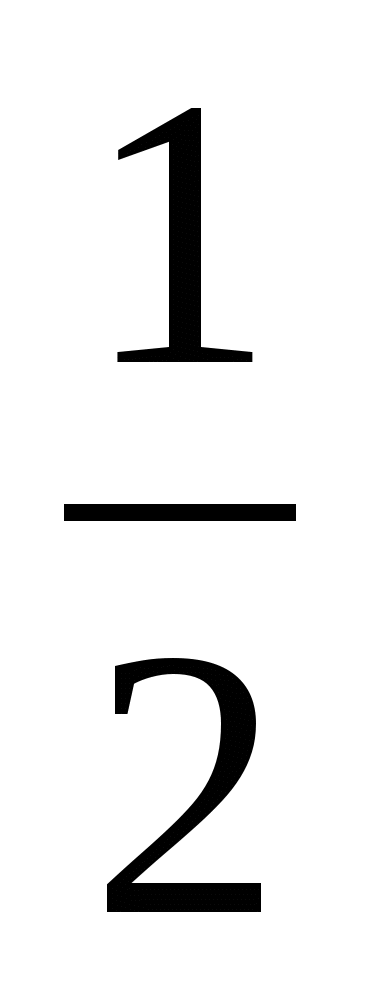
2
- 3
2
2
-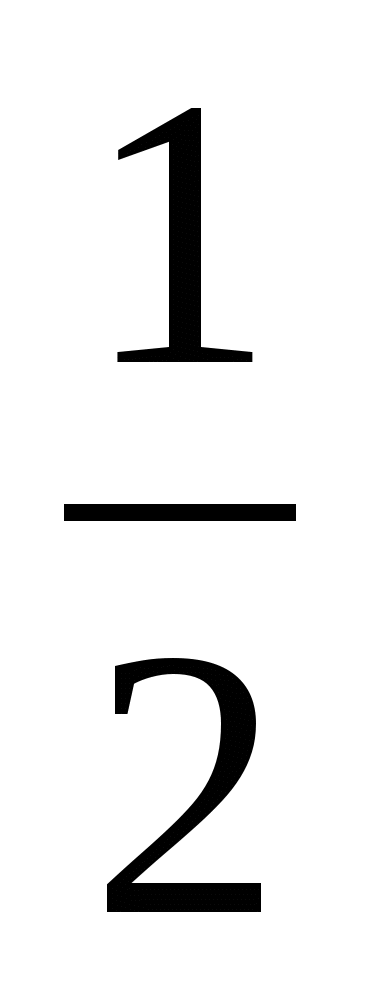
2
- 4
4
0
2х3 - 3х2 + 2х + 2 = 0
(х + 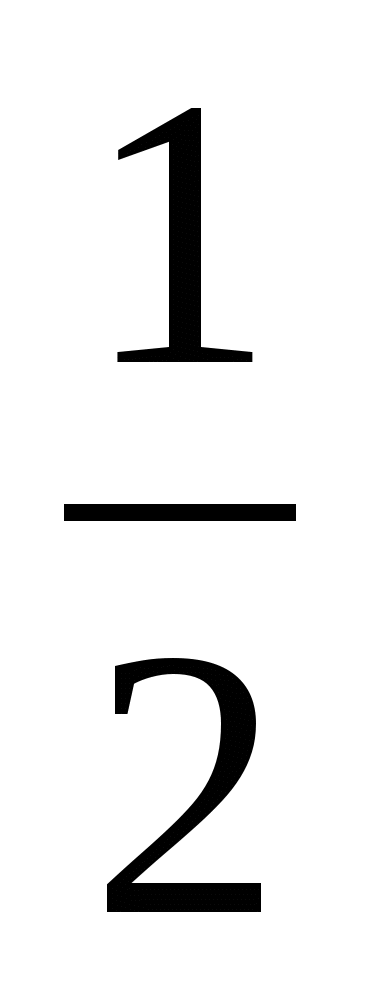 ) (2х2 - 4х + 4) = 0
) (2х2 - 4х + 4) = 0
Определим корни квадратного уравнения 2х2 - 4х + 4 = 0
х2 - 2х + 2 = 0
D = - 4 < 0
Следовательно, корнями исходного уравнения четвертой степени являются
1 и -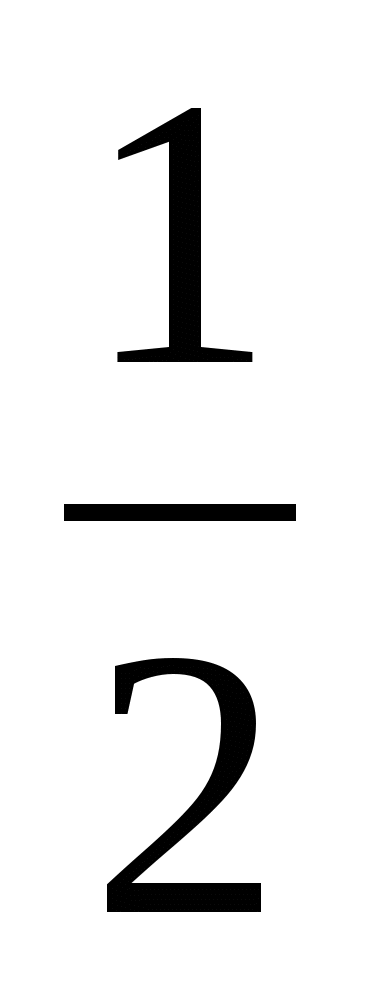
Ответ: -![]() ; 1
; 1
3. Найдите рациональные корни многочлена
а) х4 - 2х3 - 8х2 + 13х - 24
р: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
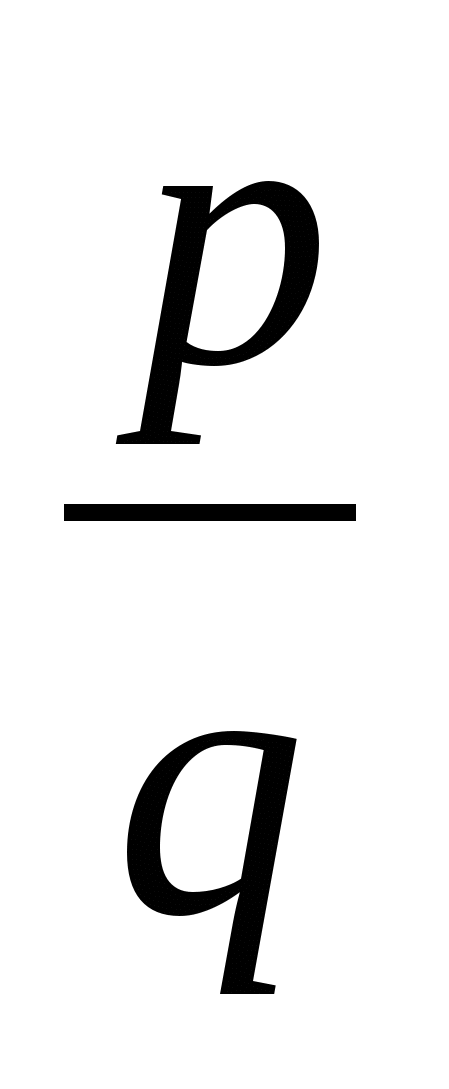 :± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
:± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
Подберем один из корней многочлена четвертой степени:
f(1) = 1 - 2 - 8 + 13 - 24 ≠ 0
f(-1) = 1 + 2 - 8 - 13 - 24 ≠ 0
f(2) = 16 - 16 - 32 + 26 - 24 ≠ 0
f(-2) = 16 + 16 - 72 - 24 ≠ 0
f(-3) = 81 + 54 - 72 - 39 - 24 = 0
Один из корней многочлена х0= - 3.
х4 - 2х3 - 8х2 + 13х - 24 = (х + 3) (х3 - 5х2 + 7х + 8)
Найдем рациональные корни многочлена
х3 - 5х2 + 7х + 8
р: ± 1; ± 2; ± 4; ± 8
q: ± 1
f(1) = 1 - 5 + 7 + 8 ≠ 0
f(-1) = - 1 - 5 - 7 - 8 ≠ 0
f(2) = 8 - 20 + 14 + 8 ≠ 0
f(-2) = - 8 - 20 - 14 + 8 ≠ 0
f(-4) = 64 - 90 - 28 + 8 ≠ 0
f(4) ≠ 0
f(-8) ≠ 0
f(8) ≠ 0
Кроме числа x0 = - 3 других рациональных корней нет.
б) х4 - 2х3 - 13х2 - 38х - 24
р: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
f(1) = 1 + 2 - 13 - 38 - 24 ≠ 0
f(-1) = 1 - 2 - 13 + 38 - 24 = 39 - 39 = 0, то есть х = - 1 корень многочлена
1
2
- 13
- 38
- 24
- 1
1
1
- 14
- 24
0
х4 - 2х3 - 13х2 - 38х - 24 = (х + 1) (х3 - х2 - 14х - 24)
Определим корни многочлена третьей степени х3 - х2 - 14х - 24
р: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
f(1) = - 1 + 1 + 14 - 24 ≠ 0
f(-1) = 1 + 1 - 14 - 24 ≠ 0
f(2) = 8 + 4 - 28 - 24 ≠ 0
f(-2) = - 8 + 4 + 28 - 24 ≠ 0
Значит, второй корень многочлена х = - 2
1
1
- 14
- 24
- 2
1
- 1
- 12
0
х4 - 2х3 - 13х2 - 38х - 24 = (х + 1) (х2 + 2) (х2 - х - 12) =
= (х + 1) (х + 2) (х + 3) (х - 4)
Ответ: - 3; - 2; - 1; 4
Применение схемы Горнера при решении уравнений с параметром.
Найдите наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три различных корня, один из которых х0 .
а) f(х) = х3 + 8х2 + ах + b, х0 = - 3
Так один из корней х0 = - 3 , то по схеме Горнера имеем:
1
8
а
b
- 3
1
5
- 15 + а
0
0 = - 3 (- 15 + а) + b
0 = 45 - 3а + b
b = 3а - 45
х3 + 8х2 + ах + b = (х + 3) (х2 + 5х + (а - 15))
Уравнение х2 + 5х + (а - 15) = 0 должно иметь два корня. Это выполняется только в том случае, когда D > 0
а = 1; b = 5; с = (а - 15),
D = b2 - 4ac = 25 - 4 (a - 15) = 25 + 60 - 4a > 0,
85 - 4a > 0;
4a < 85;
a < 21 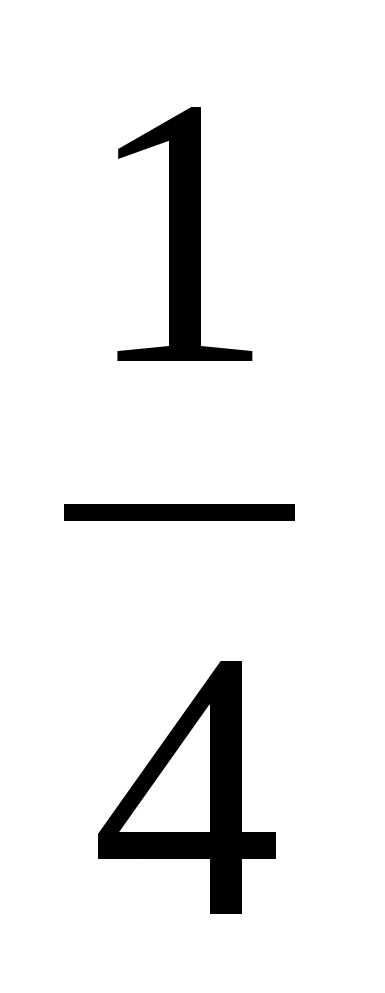
Наибольшее целое значение параметра а, при котором уравнение
f(х) = 0 имеет три корня, а = 21
Ответ: 21.
б) f(x) = x3 - 2x2 + ax + b, x0 = - 1
Так как один из корней х0= - 1, то по схеме Горнера имеем
1
- 2
a
b
- 1
1
- 3
3 + а
0
x3 - 2x2 + ax + b = (x + 1) (x2- 3x + (3 + a))
Уравнение x2 - 3x + (3 + a) = 0 должно иметь два корня. Это выполняется только в том случае, когда D > 0
a = 1; b = - 3; c = (3 + a),
D = b2 - 4ac = 9 - 4 (3 + a) = 9 - 12 - 4a = - 3 - 4a > 0,
- 3 - 4a > 0;
- 4a < 3;
a < - 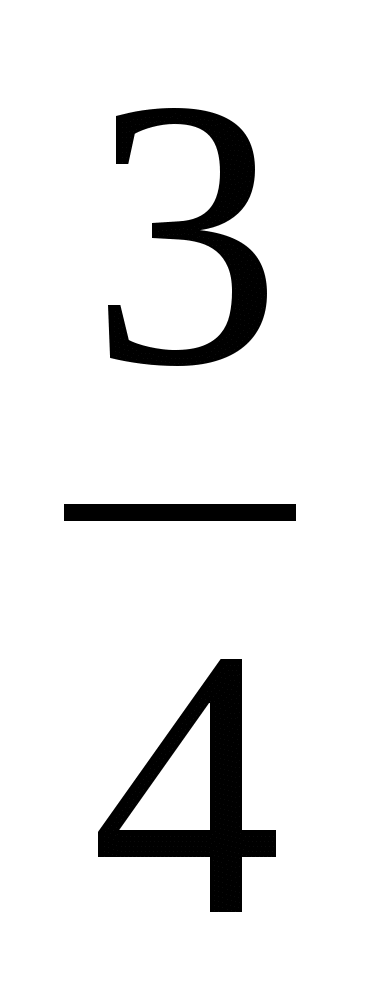
Наибольшее значение а = - 1
Ответ: - 1
в) f(x) = x3 + 11x2 + ax + b, x0 = - 4
Так как один из корней х0 = - 4, то по схеме Горнера имеем
x3 + 11x2 + ax + b = (х + 4) (х2 + 7х + (а - 28))
f(x) = 0, если х = - 4 или х2 + 7х + (а - 28) = 0
Уравнение имеет два корня, если D > 0
D = b2 - 4ac = 49 - 4 (a - 28) = 49 + 112 - 4a = 161 - 4a >0,
161 - 4a > 0;
- 4a < - 161;
a < 40 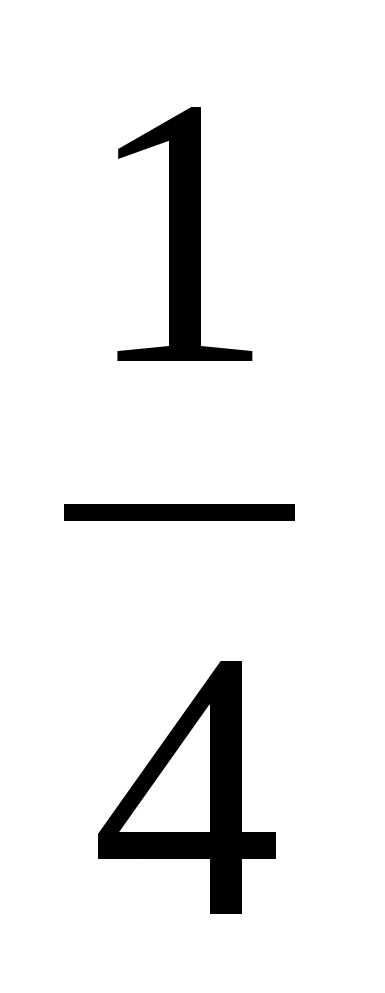
Уравнение имеет три корня при наибольшем целом значении а = 40
Ответ: а = 40
г) f(x) = x3 - 11x2 + ax + b, x0 = 4
Так как один из корней х0 = 4, то по схеме Горнера имеем
1
- 11
a
b
4
1
- 7
- 28 + а
0
x3 - 11x2 + ax + b = (x - 4) ( x2 - 7x + (a - 28))
f(x) = 0, если х = 4 или x2 - 7x + (a - 28) = 0
Второе уравнение имеет два корня, если D > 0, то есть
D = b2 - 4ac = 49 - 4 (a - 28) = 49 + 112 - 4a = 161 - 4a >0,
161 - 4a > 0;
- 4a < - 161;
a < 40 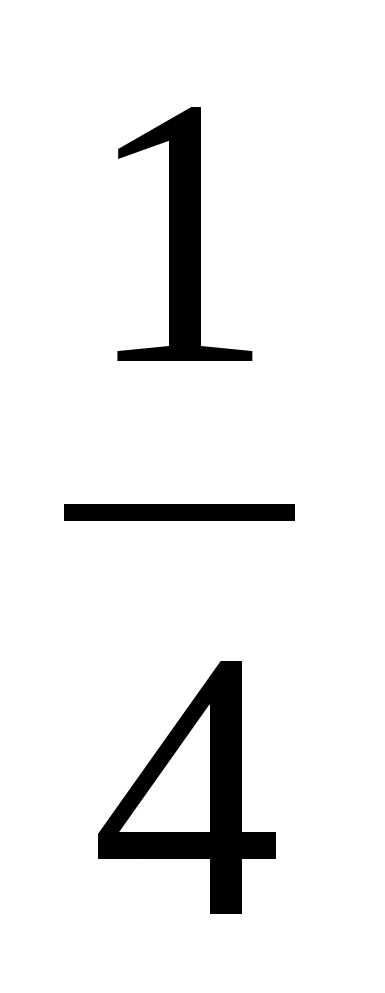
Уравнение имеет три корня при наибольшем целом значении а = 40
Ответ: а = 40
д) f(x) = x3 - 13x2 + ax + b, x0 = 4
Так как один из корней х0 = 4, то по схеме Горнера имеем
1
- 13
a
b
4
1
- 9
- 36 + а
0
x3 - 13x2 + ax + b = (x - 4) ( x2 - 9x + (a - 36))
f(x) = 0, если х = 4 или x2 - 9x + (a - 36) = 0
Второе уравнение имеет два корня, если D > 0, то есть
D = b2 - 4ac = 81 - 4 (a - 36) = 81 + 144 - 4a = 225 - 4a >0,
225 - 4a >0;
- 4a < - 225;
a < 56 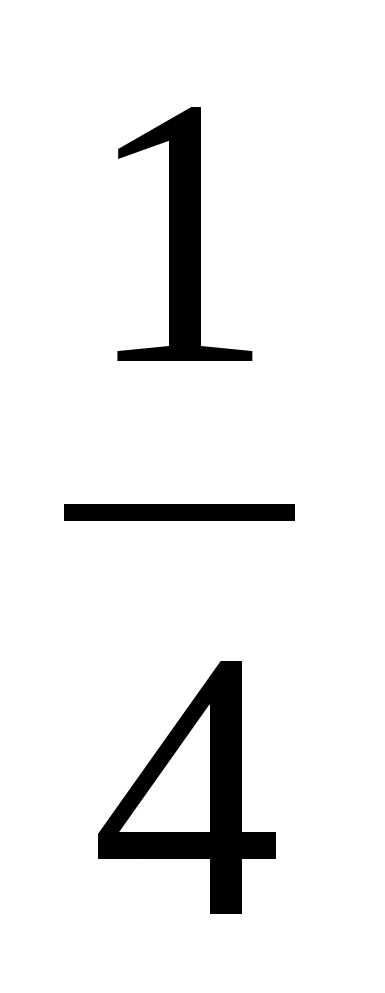
Уравнение f(x) = 0 имеет три корня при наибольшем значении а = 56
Ответ: а = 56
е) f(x) = x3 + 13x2 + ax + b, x0 = - 5
Так как один из корней x0 = - 5, то по схеме Горнера имеем
1
13
a
b
- 5
1
8
- 40 + а
0
x3 + 13x2 + ax + b = (x + 5) ( x2 + 8x + (a - 40))
f(x) = 0, если х = - 5 или x2 + 8x + (a - 40) = 0
Уравнение имеет два корня, если D > 0
D = b2 - 4ac = 64 - 4 (a - 40) = 64 + 160 - 4a = 224 - 4a >0,
224 - 4a >0;
a < 56
Уравнение f(x) имеет три корня при наибольшем значении а = 55
Ответ: а = 55
ж) f(x) = x3 + 19x2 + ax + b, x0 = - 6
Так как один из корней - 6, то по схеме Горнера имеем
1
19
a
b
- 6
1
13
а - 78
0
x3 + 19x2 + ax + b = (x + 6) ( x2 + 13x + (a - 78)) = 0
f(x) = 0, если х = - 6 или x2 + 13x + (a - 78) = 0
Второе уравнение имеет два корня, если D > 0
D = b2 - 4ac = 169 - 4 (a - 78) = 169 + 312 - 4a = 481 - 4a >0,
481 - 4a >0;
- 4a < - 481;
a < 120 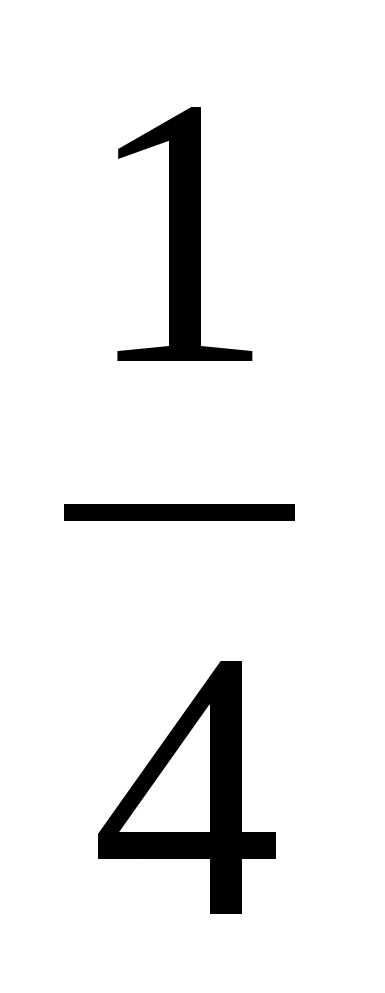
Наибольшее целое значение а, при котором уравнение f(x) = 0 имеет три корня, 120.
Ответ: 120
з) f(x) = x3 + 22x2 + ax + b, x0 = - 7
Так как один из корней x0 = - 6, то по схеме Горнера имеем
1
22
a
b
- 7
1
15
а - 105
0
x3 + 22x2 + ax + b = (x + 7) ( x2 + 15x + (a - 105)) = 0
f(x) = 0, если х = - 7 или x2 + 15x + (a - 105) = 0
Второе уравнение имеет два корня, если D > 0
D = b2 - 4ac = 225 - 4 (a - 105) = 225 + 420 - 4a = 645 - 4a >0,
645 - 4a >0;
- 4a < - 645;
a < 161 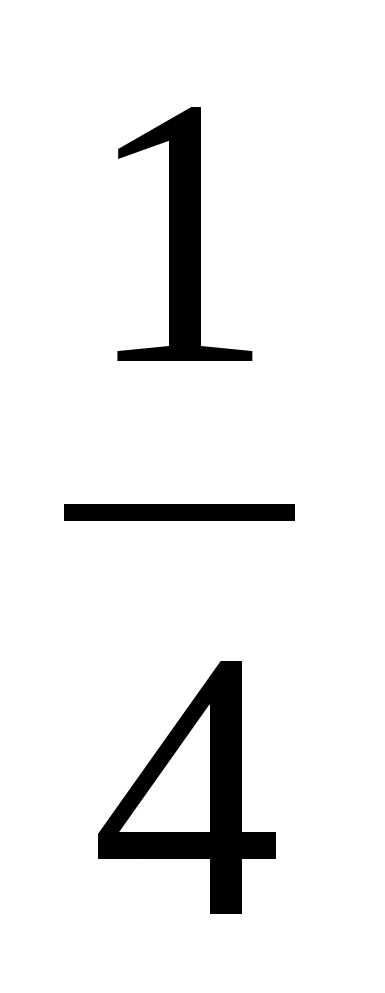
Уравнение имеет три корня при наибольшем целом значении а = 161.
Ответ: 161
13


