- Преподавателю
- Математика
- Методические рекомендации для реализации программы дисциплины «Математика»
Методические рекомендации для реализации программы дисциплины «Математика»
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Спиридонова Е.К. |
| Дата | 14.10.2014 |
| Формат | doc |
| Изображения | Есть |
ОГБОУ СПО «Смоленский техникум железнодорожного транспорта, связи и сервиса»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для реализации программы дисциплины
«Математика»
Задание на контрольную работу №1
по специальности 190623 «Техническая эксплуатация подвижного состава железных дорог».
Смоленск, 2013
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Учебная дисциплина «Математика» является естественнонаучной, формирующей базовые знания для освоения общепрофессиональных и специальных дисциплин.
После изучения материала каждого раздела студент должен выполнить домашнюю контрольную работу. Контрольная работа выполняется в отдельной тетради. Условие задачи переписывается полностью. Решение примеров сопровождается краткими и чёткими пояснениями.
Для подготовки к зачёту необходимо ответить на вопросы, которые указаны в конце методических рекомендаций.
Дисциплина «Математика» изучается на 1 курсе по заочной форме обучения. По учебному материалу выполняется одна контрольная работа.
Контрольная работа выполняется в соответствии с заданным вариантом в сроки, обусловленные учебным планом. Вариант контрольной работы определяется двумя последними цифрами шифра студента по таблице вариантов, которые помещены перед каждым заданием на контрольную работу.
Контрольная работа выполняется в отдельной тетради в клеточку черной или синей пастой. На контрольную работу наклеивается титульный лист с номером работы; наименованием предмета; фамилией, именем и отчеством студента и преподавателя; полным шифром студента и основой обучения. На первом листе контрольной работы записывается вариант студента и перечисляются соответствующие ему задания контрольной работы. Каждое задание выполняется с нового листа через клетку. В конце контрольной работы приводится список используемой литературы, а также дата выполнения и подпись студента.
После проверки работы преподавателем, студент должен выполнить работу над ошибками (если они имеются в работе). Работа над ошибками выполняется в той же тетради после рецензии преподавателя и сдается на повторную проверку.
ТАБЛИЦА ВАРИНТОВ КОНТРОЛЬНОЙ РАБОТЫ №1
Задание на контрольную работу №1 составлено в 50 вариантах. Каждый вариант состоит из 9-и примеров.
В соответствии с таблицей 1 необходимо по двум последним цифрам шифра выбрать номера контрольных вопросов, на которые необходимо дать ответы.
Таблица 1
Две последние цифры шифра
Вариант
Номера примеров
Две последние цифры шифра
Вариант
Номера примеров
1
2
3
4
5
6
01 или 51
1
4,58,66,91,122,
155,182,212,243
26 или 76
26
29,38,87,116,147,156,209,241,267
02 или 52
2
5,53,67,92,130,
161,189,216,250
27 или 77
27
28,31,73,117,150,
160,211,217,268
03 или 53
3
6,49,75,93,127,
157,183,220,244
28 или 78
28
26,37,79,118,148,157,207,227,269
04 или 54
4
7,57,68,94,132,
162, 190,215,252
29 или 79
29
22,43,84,119,151,
153,210,218,270
05 или 55
5
11,48,77,95,126,
154,184,222,254
30 или 80
30
19,53,80,120,149,161,208,230,271
06 или 56
6
17,59,69,96,133,
160,191,225,245
31 или 81
31
25,52,74,91,122,
158,211,224,270
07 или 57
7
2,56,76,97,131,
163,185,221,255
32 или 82
32
20,51,81,92,132,
154,208,219,242
08 или 58
8
3,52,70,98,128,
156,192,214,251
33 или 83
33
26,44,75,93,123,159,206,228,243
09 или 59
9
9,47,78,99,124,
159,186,223,246
34 или 84
34
10,37,76,94,133,
155,210,220,272
10 или 60
10
12,55,71,100134,
153,193,217,253
35 или 85
35
28,36,77,95,124,
180,205,229,271
11 или 61
11
18,51,72,101,129,
164,187,224,247
36 или 86
36
16,54,83,96,134,
152,209,240,270
12 или 62
12
10,54,74,102,125,
158,194,218,249
37 или 87
37
15,36,82,97,125,
181,204,223,266
13 или 63
13
8,50,79,103,135,
165,195,219,248
38 или 88
38
11,55,78,98,135,
176,207,239,267
14 или 64
14
1,60,73,104,123,
152,188,213,242
39 или 89
39
24,35,66,99,126,
178,197,228,268
15 или 65
15
13,42,64,105,138,164,196,234,256
40 или 90
40
29,45,68,100,136,173,196,237,269
16 или 66
16
14,39,61,106,143,
169,199,212,257
41 или 91
41
22,56,67,101,127,
175,203,221,265
17 или 67
17
16,47,63,107,145,
165,201,233,258
42 или 92
42
17,34,72,102,137,
177,195,229,264
Продолжение таблицы 1
Две последние цифры шифра
Вариант
Номера примеров
Две последние цифры шифра
Вариант
Номера примеров
1
2
3
4
5
6
18 или 68
18
21,38,62,108,139,
170,204,214,259
43 или 93
43
21,33,69,103,128,
174,202,238,263
19 или 69
19
24,41,65,109,142,166,197,213,260
44 или 94
44
30,60,63,104,138,170,194,227,262
20 или 70
20
25,32,90,110,137,
163,205,225,261
45 или 95
45
14,32,70,105,129,
171,201,230,261
21 или 71
21
15,40,86,111,144,
171,202,232,262
46 или 96
46
12,59,64,106,139,
167,193,236,260
22 или 72
22
30,48,88,112,141,167,198,215,263
47 или 97
47
13,58,71,107,130,
172,200,222,259
23 или 73
23
20,39,89,113,146,
162,203,226,264
48 или 98
48
23,57,65,108,140,168,192,231,258
24 или 74
24
23,49,85,114,140,172,200,216,265
49 или 99
49
18,46,62,109,131,
169,199,235,257
25 или 75
25
27,50,90,115,136,
168,206,231,266
50 или 100
50
27,32,61,110,141,
166,190,226,256
ПРИМЕРЫ К КОНТРОЛЬНОЙ РАБОТЕ №1
Системы уравнений 1-30
Пользуясь формулами Крамера, решить систему уравнений.



№ 1. x+y-z=36 №2. 2x-4y+9z=28 №3. x+y+z=36 №4. 3x+5y+3z=16
1. x+y-z=36 №2. 2x-4y+9z=28 №3. x+y+z=36 №4. 3x+5y+3z=16
x+z-y=13 7x+3y-6z=-1 2x -3z=-17 x+2y+z=8
y+z-x=7 7x+9y-9z=5 6x -5z=7 x-7y-2z=5




№5. 4x+y-3z=-1 №6. 4x-3y+z=43 №7. 3x+y+2z=11 №8. 2x+3y+4z=15
8x+3y-6z=-1 x+y-z=3 2x+2y-3z=9 x+y+5z=16
x+y-z=-1 2x+y =13 x-5y-8z=23 3x-2y+z=1




№9. 5x-19y-z=26 №10. 6x+3y-5z=0 №11. x+2y+z=4 №12. 2x+y=5
2x-5y-z=6 9x+4y-7z=3 3x-5y+3z=1 x+3z=16
8x-31y-4z=35 14x+6y-11z=6 2x+7y-z=8 5y-z=10




№13. 7x+2y+3z=15 №14. 2x-y+5z=27 №15. x-4y-2z=0 №16. 3x+y-2z=6
5x-3y+2z=15 5x+2y+13z=70 3x-5y-6z=-21 5x-3y+2z=-4
10x-11y+5z=36 3x-z=-2 3x+y+z=-4 4x-2y-3z=-2




№17. 5x+6y-2z=12 №18. 12x-13y-4z=-10 №19. 8x-y+3z=22 №20 . 7x-2y=-24
2x+5y-3z=9 7x-9y-11z=0 4x+y+6z=-1 6x-4y-5z=-37
4x-3y+2z=-15 12x-17y-15z=-7 13x+y+16z=5 4x+3y+6z=13



№ 21. 3x+2y-4z=8 №22. 2x-5y+3z=4 №23. 3x-3y+2z=2 №24. 3x+2y-4z=8
21. 3x+2y-4z=8 №22. 2x-5y+3z=4 №23. 3x-3y+2z=2 №24. 3x+2y-4z=8
2x+4y-5z=11 4x+3y-5z=2 4x-5y+2z=1 2x+4y-5z=11
4x-3y+2z=1 5x+4y-2z=18 5x-6y+4z=3 4x-3y+2z=1
№


 25. 4x-2y-z=3 №26. x+y+z=4 №27. 2x+y-2z=1 №28. x-y+3z=-4
25. 4x-2y-z=3 №26. x+y+z=4 №27. 2x+y-2z=1 №28. x-y+3z=-4
2x+y=8 x+2y+3z=7 x-y+3z=4 2x+y-2z=5
1,5x=4,5 x+y+5z=8 3x+y+z=4 3x+3y+z=6


№29. 4x-y+2z=8 №30. 2x+y-2z=4
3x-2y+5z=14 3x-y-5z=12
5x+3y-3z=2 4x+3y+2z=3
Функции. Последовательности. 31-121
Пределы. Найти пределы.
№31. lim (x+3)2 -9
x→0 x
№32. lim x2+3x
x→0 x2+x
№33. lim x2+x-6
x→2 x-2
№34. lim x2-25
x→5 x+5
№35. lim x2-121
x→11 x-11
№36. lim x2+3x-10
x→-5 x+5
№37. lim x2-1
x→1 2x2-x-1
№38. lim x2+3x+2
x→-1 x+1
№39. lim 49-x2
x→-7 x+7
№40. lim x2-x-6
x→3 x-3
№41. lim x2+x-12
x→3 x-3
№42. lim x2-64
x→8 8-x
№43. lim x3+27
x→-3 2x2-3x-27
№44. lim 2x2+3x-35
x→-5 3x2+16x+5
№45. lim x2-5x+6
x→2 x2-12x+20
№46. lim x2+5x+6
x→-2 x2+x-2
№47. lim x2-4
x→2 x2-2x
№48. lim 2x2+7x+6
x→-2 x+2
№49. lim x2-6x+9
x→3 x2-3x
№50. lim x2-5x+6
x→2 x-2
№51. lim x2-4x
x→0 x2+x
№52. lim x2-5x+6
x→3 x-3
№53. lim (x+4)2-16
x→0 x
№54. lim x2-x-6
x→-2 x+2
№55. lim x2+3x+2
x→-2 x+2
№56. lim x2+2x
x→0 x2+x
№57. lim (x+2)2-4
x→0 x
№58. lim x2-4x+4
x→2 x-2
№59. lim 36-x2
x→-6 x+6
№60. lim x2-5x+25
x→5 x2-5x
№61. lim 10-3x2
x→∞ 2x2+7
№62. lim x+x3
x→∞ x3+2x2
№63. lim 2x2-x+1
x→∞ x+4x2 -3x
№64. lim 6x2+x3
x→∞ 4x3-7
№65. lim 5x2-7x+3
x→∞ 4x2+3x-1
№66. lim x2-1
x→∞ 2+x2
№67. lim 9x2+3x-1
x→∞ x2
№68. lim 3x2-2x3-4
x→∞ 7x3+x2-5x
№69. lim 3x2-4
x→∞ 5x3+x2
№70. lim 8x3-16x
x→∞ 2x+2x3
№71. lim 5x2-3x+6
x→∞ 3-10x2
№72. lim 8x3+16x4-3
x→∞ 2+x-8x4
№73. lim 10x+8x2-4x
x→∞ 2x2-5x+3
№74. lim 6x2+3
x→∞ 2x2-2
№75. lim 8x3-4x2+1
x→∞ 4x3-3
№76. lim 3x2+4x-1
x→∞ 3+6x2-3x
№77. lim x2+1
x→∞ x2
№78. lim 2x
x→∞ x-1
№79. lim x4+x5
x→∞ 3x2-2x5
№80. lim 1-x2
x→∞ 1+2x2
№81. lim x3-3
x→∞ x3
№82. lim 2-x2
x→∞ 3+3x2
№83. lim 8-x+x2
x→∞ 3+2x2
№84. lim 3-x+x3
x→∞ 16+4x3
№85. lim 5+x
x→∞ x2-1
№86. lim x2-1
x→∞ x2+1
№87. lim 3x2+2x3
x→∞ 2x3-5
№88. lim x+x2
x→∞ 3x+2x2
№89. lim x2+x-3
x→∞ 2x2-1
№90. lim -3x2+4x3
x→∞ 2x3+5
№91. lim 3
x-2 x+2
№92. lim 5
x→4 2x-8
№93. lim 2
x→1 x-1
№94. lim 8
x→3 2x-6
№95. lim 5
x→∞ x-2
№96. lim 4
x→∞ x2+x
№97. lim 8
x→∞ x-1
№98. lim 2
x→4 8-2x
№99. lim 3
x→∞ 2x+1
№100. lim 5
x→∞ x+1
№101. lim 3
x→∞ x-1
№102. lim 2
x→∞ 2x+3
№103. lim 3
x→5 10-2x
№104. lim 2
x→5 2x-10
№105. lim 5
x→∞ 6x+1
№106. lim 2
x→3 6-2x
№107. lim 8
x→1 x-1
№108. lim 5
x→3 21-7x
№109. lim 3
x→4 12-3x
№110. lim 3
x→∞ 2x-4
№111. lim 5
x→∞ 6x-8
№112. lim 8
x→1 1-x
№113. lim 4
x→∞ 2x+1
№114. lim 2
x→3 9-3x
№115. lim 3
x→∞ 3x+1
№116. lim 5
x→∞ 2x-4
№117. lim 8
x→∞ 3x+1
№118. lim 3
x→∞ 4x-1
№119. lim 5
x→4 8-2x
№121. lim -3x2+4x3
x→∞ 2x3+5
№120. lim 2
x→6 12-2x
Производная функция. 122-151
Найти производную функцию.
№122. a) y=5x4+3sin x -cos x+9
б) f (x)=(x3-2x+7) 4f ′ (2)-?
№123. а) y=x3*4√x-3* 3√x-2
б) f (x)=3sin2x f ′ ( П/6)-?
№124. а) 3x2-8/3x2+8
б) f (x)=arcos 2x f ′ (1/4)-?
№125. а) y=(5x3-3)*(6x2+1) y′(2)-?
б) f (x)=cos(3x2-1)
№126. а) y=4√x3*x2*√x-1* 5√x-2
б) f (x)=sin23x f ′ (П/18)-?
№127. а) y=x3*√x2/4√x3*√x
б) y=sin25x y′(П/20)-?
№128. а) y=(x3+4)*(x2+x-1) y′(2)-?
б) f (x)=cos(x3-2)
№129. а) y=x4-3/x4+3
б) f(x)=cos3x*(sin3x+1) f ′ (П/24)-?
№130. а) y=x4-3cos x+3sin x-ln x+29
б) f (x)=sin x*tg x f ′ (П/4)-?
№131. а) y=3√x+2/3*3√x2-3/3√x+25
б) y=ctg x-sin3x y′(П/6)-?
№132. а) y=4ln x+x3 y′(2)-?
б) y=5sin3x
№133. а) y=x5+2ln x y′(-2)-?
б) f (x)=3sin(2x2-1)
№134. а) y=(2+sin x)/sin x y′(П/4)-?
б) y=(x2+3)*√(x2-3)
№135. а) y=arcos x+arcsin x y′(1/√2)-?
б) y=ln(4x3+x)5
№136. а) y=2arcsin x+3arccos x y′(1/2)-?
б) f (x)=ln (x2+3)/(x2-3)
№137. а) y=(ln x+2)/(2-ln x)
б) y=52x-1
№138. а) y=(ex-1)/(ex+1)
б) y=tg24x
№139. а) y=(2-sin x)/(2+sin x) y′(П/3)-?
б) y=ln(3x2-2)6
№140. а) y=cos x-sin x y′(П/4)-?
б) y=ln((x3-3)/(x3+3))
№141. а) y=cos x*(2+sin x)
б) f (x)=3*5√(3x2-1)3 f ′(0)-?
№142. а) y=5x4-3sin x+6cos x-ln x+11
б) f (x)=(x3+1)* 3√(x2-1)2 f ′(1)-?
№143. а) y=(3+sin x)*(3-sin x) y′(П/4)-?
б) y=ln(x3+5)4
№144. а) f (x)=(e x+2)/(ex-2)
б) y=sin x*cos x
№145. а) f (x)=2sin x*(1-cos x) f ′(П/3)-?
б) y=ln(x2-4)/(x2+4)
№146. а) f (x)=(x2-3x+1)/(x2+1) f ′(-1)-?
б) y=(sin x+2)*cos x
№147. а) y=10x4-e2x+√2
б) y=(x3-1)/(x3+1) y′(0,5)-?
№148. а) y=x2*ex*x+3xy′(0)-?
б) f (x)=ln 7√x3/(x-1)
№149. а) y=5√(4x2-3)
б) y=5sin2x y′(0)-?
№150. а) y=sin3 (8x2-1)
б) y=(3x2-1)/(2x+1) y′(0)-?
№151. а) y=(8x2-1)*(4x-3) y′(1)-?
б) y=ln (3-x2)/(3+x2)
Дифференциал функции. 152-181
Найти приближенное значение функции.
№152. y=3x2-x+2 при x=2, x=0,01
№153. y=2x2+3x-2 при x=3, x=0,002
№154. y=3x2+2x+10 при x=5, x=0,001
№155. y=3x2+4x при x=10, x=0,001
№156. y=4x2-5x при x=5, x=0,001
№157. y=2x3-x+10 при x=2, x=0,001
№158. y=5x2-3x+5 при x=5, x=0,02
№159. y=4x3-2x при x=5, x=0,001
№160. y=6x2+2x-1 при x=10, x=0,001
№161. y=6x3-2x при x=10, x=0,01
№162. y=4x2+2x при x=2, x=0,001
№163. y=5x3-2x при x=2, x=0,002
№164. y=4x2-3x при x=3, x=0,001
№165. y=5x3-2x при x=2, x=0,002
№166. y=7x3-x при x=2, x=0,002
№167. y=3x2+5x+1 при x=3, x=0,001
№168. y=x3+2x при x=2, x=0,1
№169. y=x2-2x при x=1, x=0,01
№170. y=2x3+5 при x=2, x=0,001
№171. y=x3 при x=10, x=0,03
№172. y=2x2-3x при x=5, x=0,01
№173. y=3x2-2x+4 при x=4, x=0,02
№174. y=2x2+2x-1 при x=3, x=0,02
№175. y=3x2+2x-3 при x=2, x=0,01
№176. y=3x3-2x при x=2, x=0,01
№177. y=2x2-x+3 при x=1, x=0,1
№178. y=3x2+2x-2 при x=3, x=0,02
№179. y=5x3+2x при x=2, x=0,001
№180. y=3x2+2x-1 при x=5, x=0,02
№181. y=2x2+3x-4 при x=3, x=0,01
Дифференциал функции. 182-211
Найти дифференциал функции.
№182. y=7x4-cos(x3+2)+ln x №205. y=e 3x*x-1+sin 4x
№183. y=√(5x3-x+1) +sin(1-10x) №206. y=3x*sin 5x
№184. y=ln(x6-3)+tg x2 №207. y=e cos2x-tg 3x
№185. y=arccos 7x-3ln sin x №208. y=√(3x2-1)+cos 6x
№186. y=e cos x+√(3x2-1) №209. y=√3*x3+sin 3x2
№187. y=cos43x №210. y=e sin x+cos(8x2-1)
№188. y=x4*ctg 2x №211. y=3x4+cos 7x3
№189. y=e sin 3x-ln sin x
№190. y=0,5 arcsin 4x+cos7x
№191. y=√(9x3-x)+4e √x
№192. y=√2*x4+cos 4x2
№193. y= 5x2+sin 8x2
№194. y=√(3x2-1)+cos 8x
№195. y=arctg 2x+5sin x
№196. y=arcsin 3x+3x2-ln x
№197. y=x3*tg 3x
№198. y=sin56x
№199. y=ln(x5+2)+sin 2x
№200. y=3x*x-1+ln cos x
№201. y=3√x+sin 6x
№202. y=tg(3x-1)+ln 2x
№203. y=3sin x+sin 6x2
№204. y=ctg 3x-2tg x
Неопределенный интеграл. 212-241
Найти неопределенный интеграл.
№212. a) ∫(1-6√x +9 5√x4)dx; б) ∫x*dx/√(1-4x2); в) ∫cos 2x*dx/(5+sin 2x).
№213. a) ∫e x*dx/3√(1+e x); б) ∫x*sin(x2+1)dx; в) ∫x*e xdx.
№214. a) ∫e xdx/(e x-2); б) ∫x3*3√(1-3x4)dx; в) ∫cos(3-7x)dx.
№215. a) ∫(x3-1/√x)dx; б) ∫dx/sin23x; в) ∫x*sin x dx.
№216. a) ∫(5/cos2(5x+2))dx; б) ∫(3x2-4x3+3)dx; в) ∫ln x dx.
№217. a) ∫(x/√(1+3x2))dx; б) ∫(sin x+3x2-2)dx; в) ∫(sin x*cos3x)dx.
№218. a) ∫(2x+1)2dx; б) ∫cos x*e sin xdx; в) ∫cos2x*sin x dx.
№219. a) ∫sin5x*cos x dx; б) ∫x*cos x dx; в) ∫(x+√x-2x)dx.
№220. a) ∫√(3x-1)dx; б) ∫x*ln x dx; в) ∫(7x6-1/x+e x)dx.
№221. a) ∫(5x4-3√x2+1)dx; б) ∫(sin 3x/(cos3x-2))dx; в) ∫6x(x2-1)4dx.
№222. a) ∫(5x3-8/x-sin x)dx; б) ∫sin 6x dx; в) ∫sin3x*cos x dx.
№223. a) ∫(2sin x+3cos x)dx; б) ∫x3*sin 3x4 dx; в) ∫(e x/1+e x) dx.
№224. a) ∫((x2+x+5)/2x)dx; б) ∫x2*3√(7+x3) dx; в) ∫sin 2x/(4-cos 2x)dx.
№225. a) ∫(3x+1)2/x dx; б) ∫sin4x/(1+cos 4x)3dx; в) ∫(2x3-2)5*x2 dx.
№226. a) ∫((2+x)/x)2 dx; б) ∫ e x+2dx; в) ∫x*ln x dx.
№227. a) ∫x2*cos x3 dx; б) ∫(x3+2x)/x dx; в) ∫(3x3-2)5*x2dx.
№228. a) ∫(3√x-3/4 3√x2)dx; б) ∫x2*cos(3-x3)dx; в) ∫(2x+1)/(x2+x+1)dx.
№229. a) ∫(x3+2x+3sin x)dx; б) ∫x3*sin3x4dx; в) ∫(ln x)/x2dx.
№230. a) ∫(e x+3x-2√x)dx; б) ∫x/(5-x2) dx; в) ∫(ln x)/x4 dx.
№231. a) ∫(4x-3*3√x2) dx; б) ∫e cos x*sin x dx; в) ∫(ln x)/x3dx.
№232. a) ∫(3x2+4√x3-2)dx; б) ∫x3/(1+x4)dx; в) ∫sin4x*cos x dx.
№233. a) ∫2/√(1-x2)dx; б) ∫cos x/(7-3sin x)dx; в) ∫x9*3√(x10-5)dx.
№234. a) ∫(4x4-2x3+x2)/x2dx; б) ∫sin x/(2-5cos x)dx; в) ∫(3x4-5)6*x3dx.
№235. a) ∫x3*(1+7x)dx; б) ∫(x2+1)/(x3+3x)dx; в) ∫(sin √x)/√x dx.
№236. a) ∫(arctg3x)/(1+x2)dx; б) ∫x5/(1+x6)dx; в) ∫(e x+4x+4sin x)dx.
№237. a) ∫(arcsin2x)/√(1-x2)dx; б) ∫(4x3+3x2+x)/x dx; в) ∫(6x-1)/(3x2-x)dx.
№238. a) ∫x3/(x4+2)dx; б) ∫x4(5x5+5)3dx; в) ∫(3√x+2x-sin x) dx.
№239. a) ∫(cos2x+3)/cos2x dx; б) ∫sin3x*cos x dx; в) ∫(1+x5)7*x4dx.
№240. a) ∫(5x-1/x5+3/cos2x)dx; б) ∫sin x*cos5x dx; в) ∫tg x dx.
№241. a) ∫(2*sin3x+3)/sin2x dx; б) ∫x2/√(x3-1)3 dx; в) ∫ctg x dx.
Определенный интеграл. 242-271
Вычислить определенные интегралы.
0 0
№242. a) ∫(3x2+1)dx; б) ∫sin2x*cos x dx.
-1 -П/2
1 3Π/2
№243. a) ∫(1/2x+4x2)dx; б) ∫ cos x/3 dx.
-1 0
1 1
№244. a) ∫(2x+1)dx; б) ∫x2*e x*x*xdx.
0 0
0 1
№245. a) ∫(√x+1/√x)dx; б) ∫√(1-x) dx.
1 0
1 0
№246. a) ∫(3x2-3√x)dx; б) ∫sin x * e cos x dx.
-1 -П/2
4 П /4
№247. a) ∫(3x2-2x+4)dx; б) ∫sin 8x dx. 1 -П/8
2 2
№248. a) ∫2dx/5x; б) ∫e x/(e x-1) dx.
1 0
8 2
№249. a) ∫(2+x)/x2dx; б) ∫ x4 dx/(1+x5).
2 0
2 П/4
№250. a) ∫(2x2+1)/x dx; б) ∫sin x*cos5 x dx.
1 -П/2
1 0
№251. a) ∫(1-3√x2) dx; б) ∫sin(4x+ П/4) dx.
-1 -П/4
4 2
№252. a) ∫x+1/√x dx; б) ∫(x5-x)/(1-3x2+x6)dx.
1 0
2 2П
№253. a) ∫dx/ 3√x2; б) ∫sin x/(cos x+1) dx.
1 3/2П
4 П/4
№254. a) ∫(0,5x3-3√x) dx; б) ∫ dx/sin22x.
1 П/8
3 П/3
№255. a) ∫(x2-3x) dx; б) ∫cos(3x-П/3) dx.
0 0
2 2
№256. a) ∫2x(1+x2) dx; б) ∫е 2x-1dx.
1 0,5
8 2
№257. a) ∫(x-3√x)/x dx; б) ∫x √(5x2+1) dx.
1 1
2 П/4
№258. a) ∫(x-1)2/x2 dx; б) ∫е sin xcos x dx.
1 0
П/2 3
№259. a) ∫(3cos x+2sin x) dx; б) ∫е 2x /(10-е 2x) dx.
0 0
0,5 П/3
№260. a) ∫2 dx/√(1-x2); б) ∫cos4x*sin x dx.
0 0
П √П
№261. a) ∫(x*cos x+1)/x dx; б) ∫x*sin x2 dx.
П/2 0
П/3 П/2
№262. a) ∫(2/cos2x +sin x) dx; б) ∫sin(П -4x) dx.
0 0
П 0
№263. a) ∫(е x-cos x) dx; б) ∫3x3/4√(1+x4) dx.
0 -1
1 0
№264. a) ∫3 dx/(1+x2); б) ∫x2*еx*x*x-1 dx.
√3/3 1
√3/2 1
№265. a) ∫ dx/2√(1-x2); б) ∫x3/(1+x4) dx.
√2/2 -3
4 2
№266. a) ∫[(x-3)2-4] dx; б) ∫5 dx/√(5x-1).
1 1
1 1
№267. a) ∫(2x+4x2-5) dx; б) ∫(2x3+1)4*x2 dx.
-1 0
2 П/2
№268. a) ∫(3x3-2x+8) dx; б) ∫sin x*cos2x dx.
0 0
1 П/2
№269. a) ∫(2- √x3) dx; б) ∫cos x dx/(2-sin x).
0 0
9 П/6
№270. a) ∫(1-x)/√x dx; б) ∫е sin x*cos x dx.
1 0
4 П/3
№271. a) ∫(2x+3x2-5) dx; б) ∫sin x dx/(3-cos x).
0 0
МЕТОДИЧЕСКИЕ УКЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОРАБОТЫ №1
Системы линейных уравнений
Определителем третьего порядка 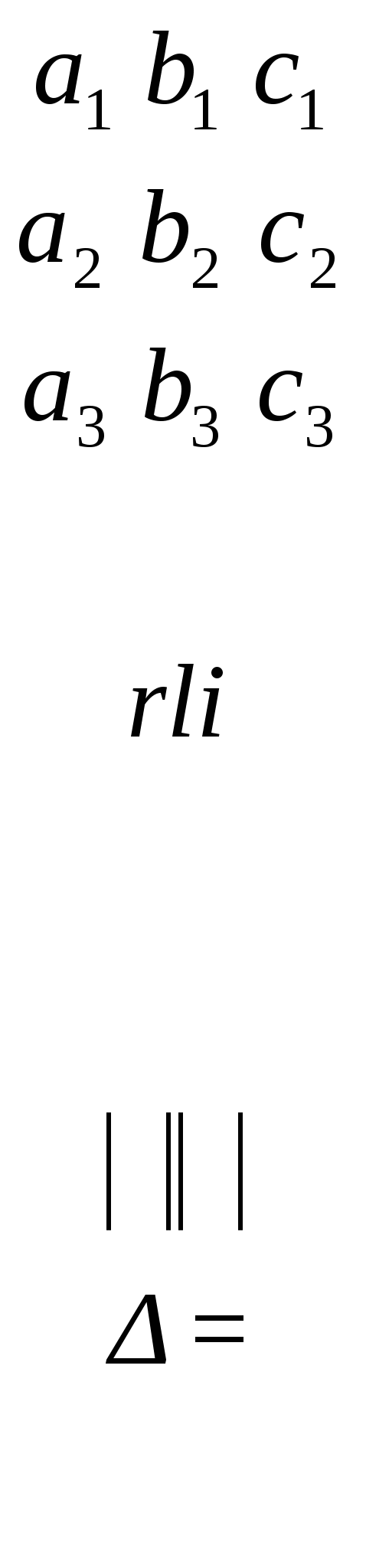 называется число, которое может быть найдено следующими способами:
называется число, которое может быть найдено следующими способами:
1. 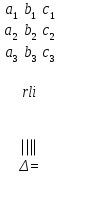 .
.
2. 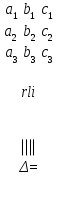
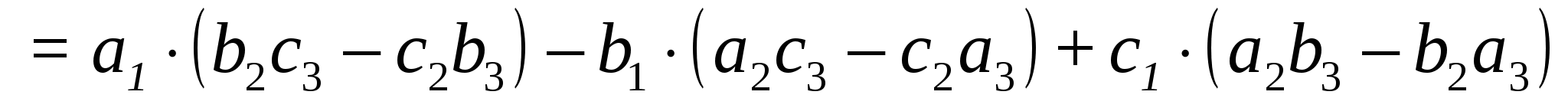 .
.
Решение системы уравнений
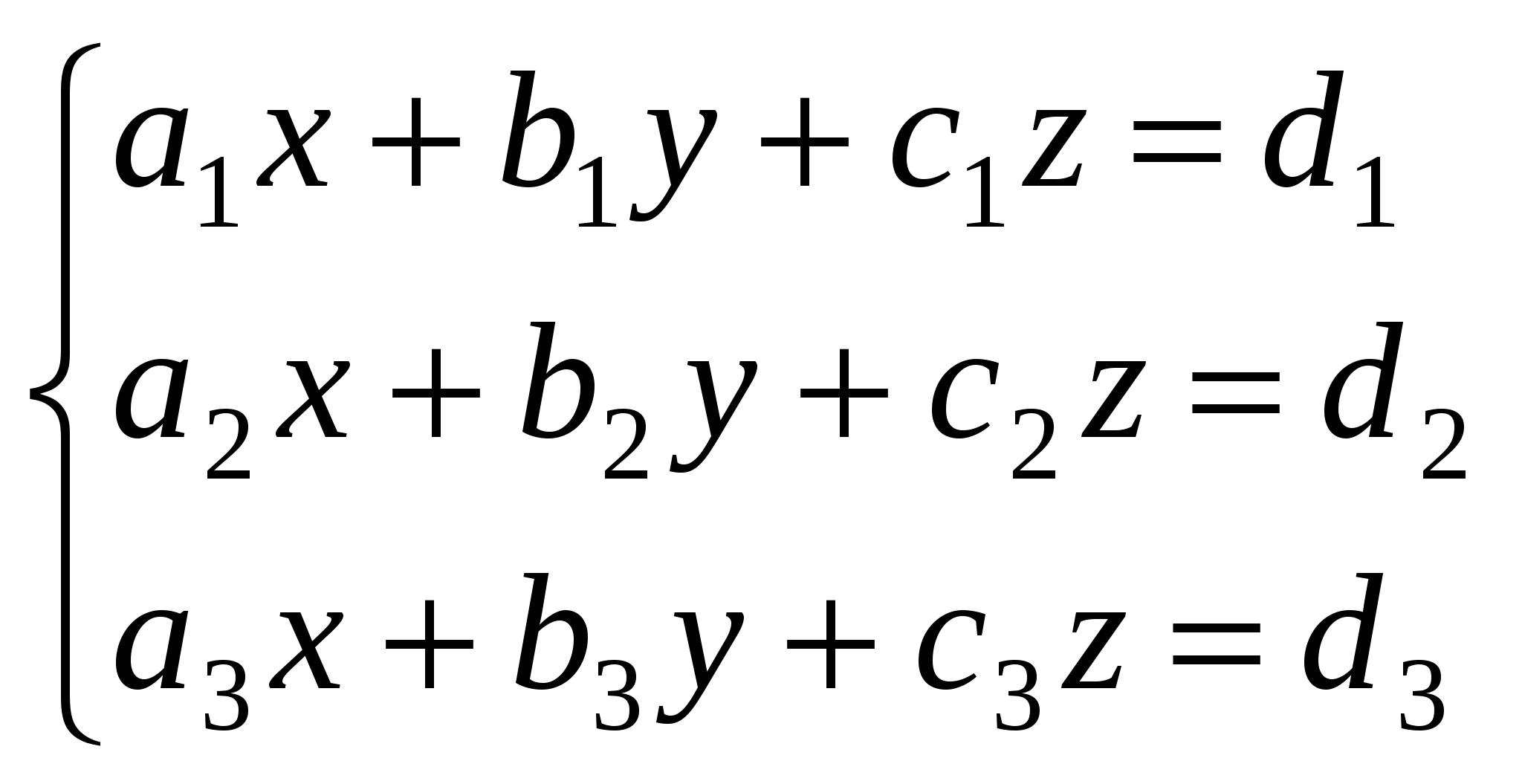
методом Крамера осуществляется по формулам:
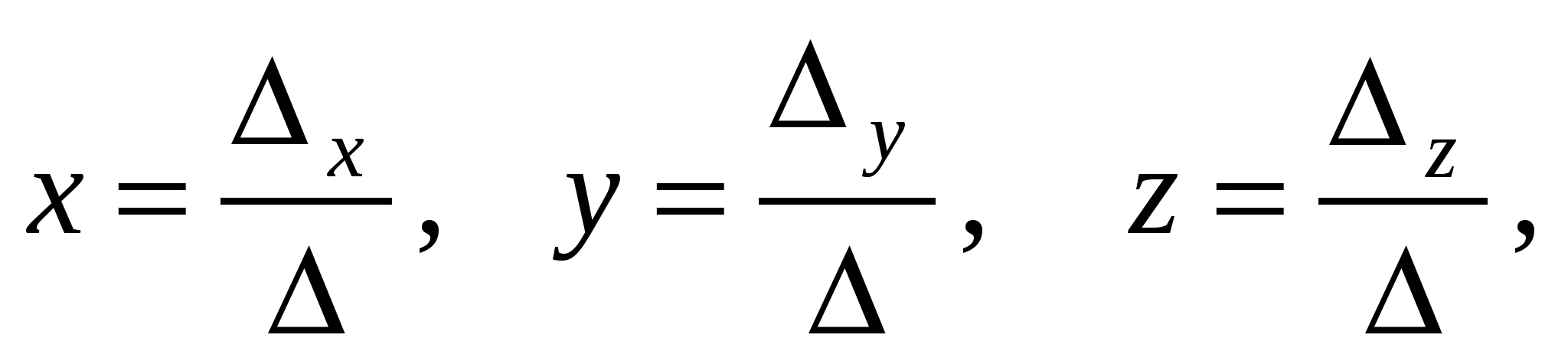 где
где
. 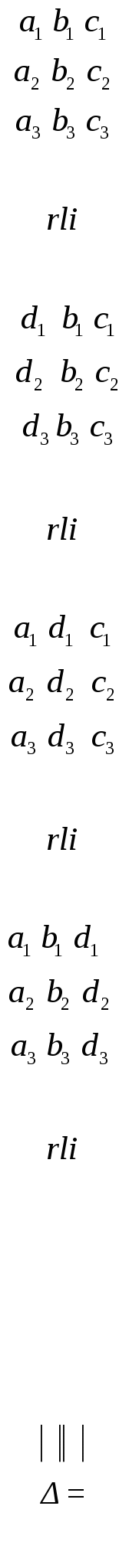
Пример. Решить систему линейных уравнений по формулам Крамера 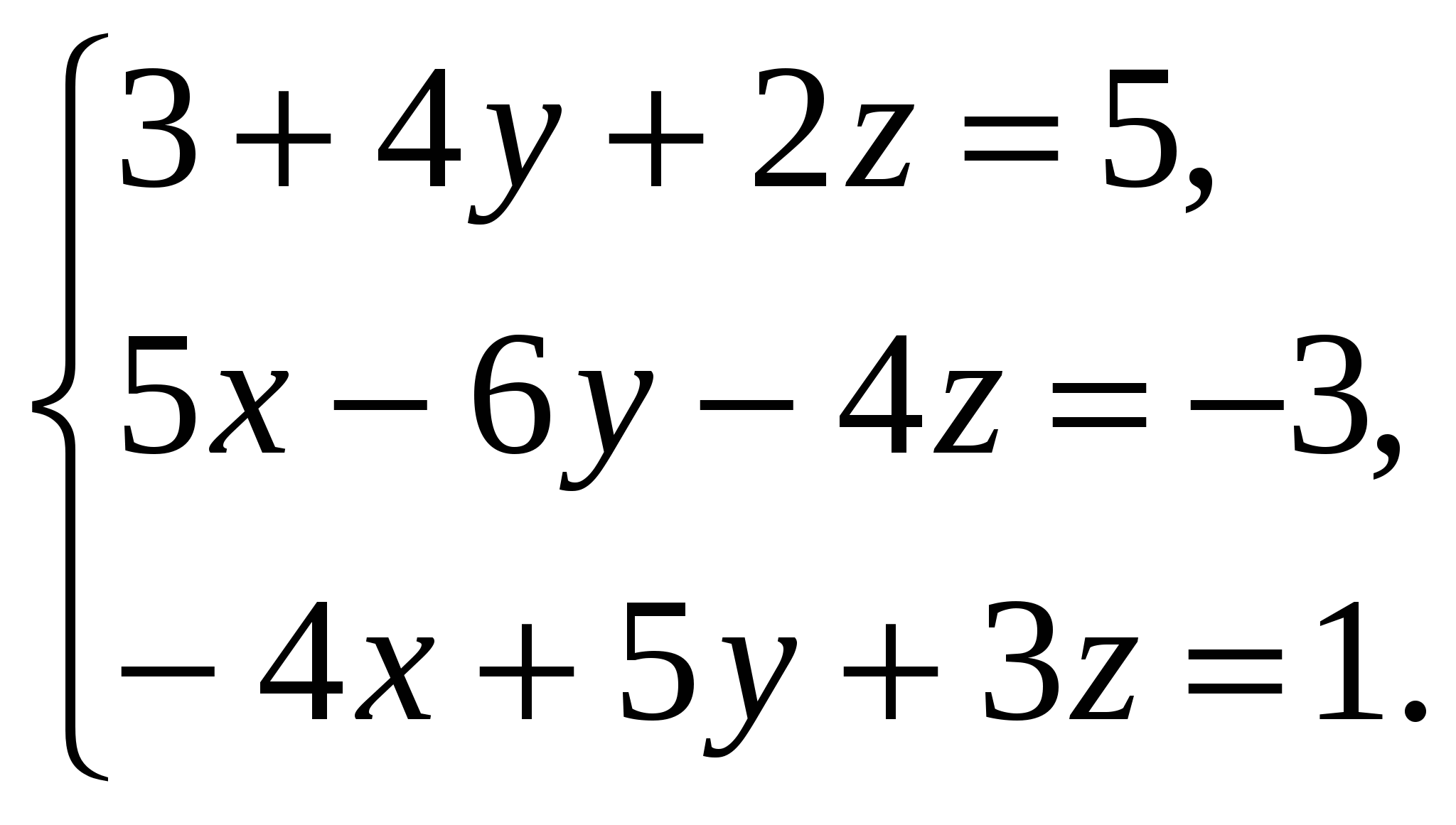
Решение. 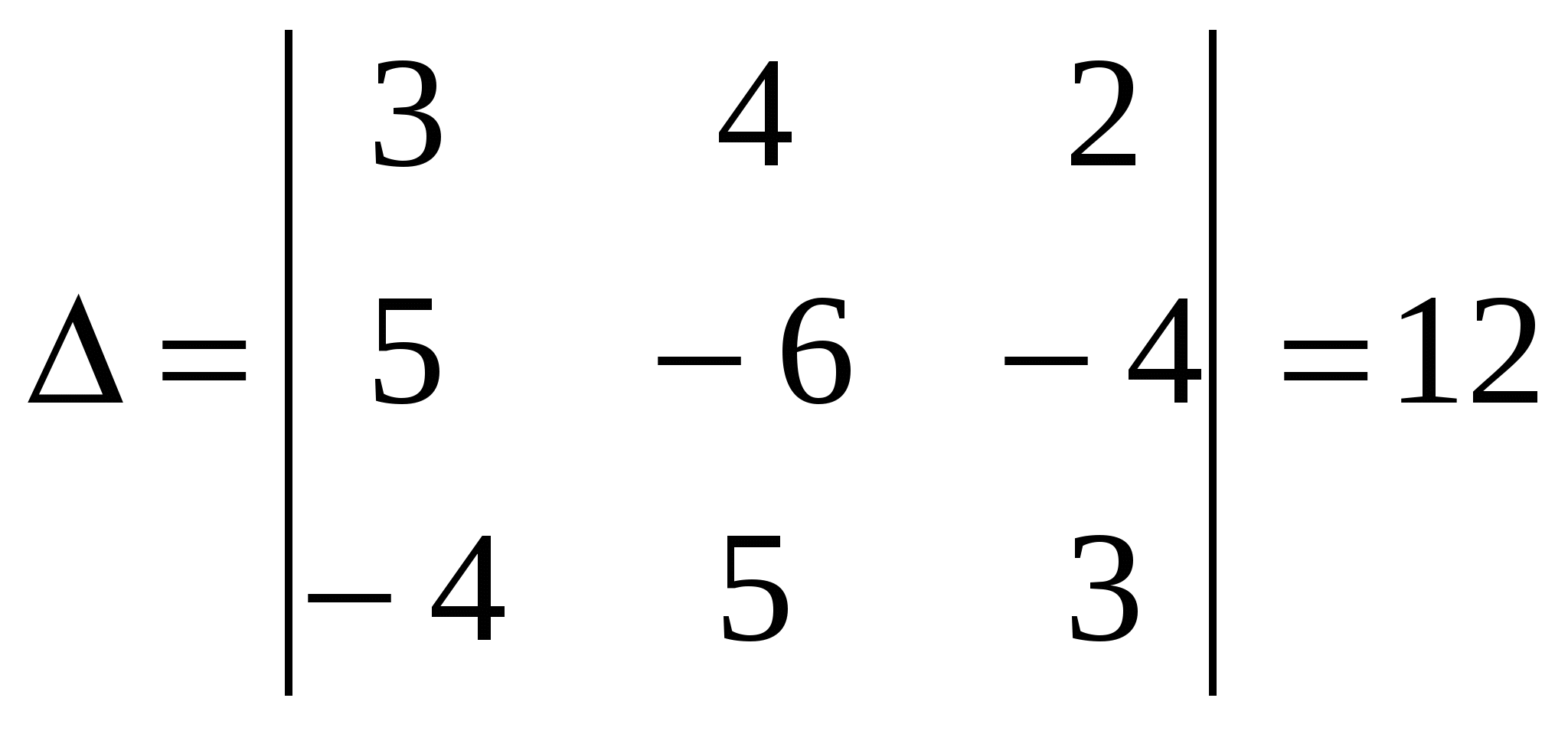 ,
, 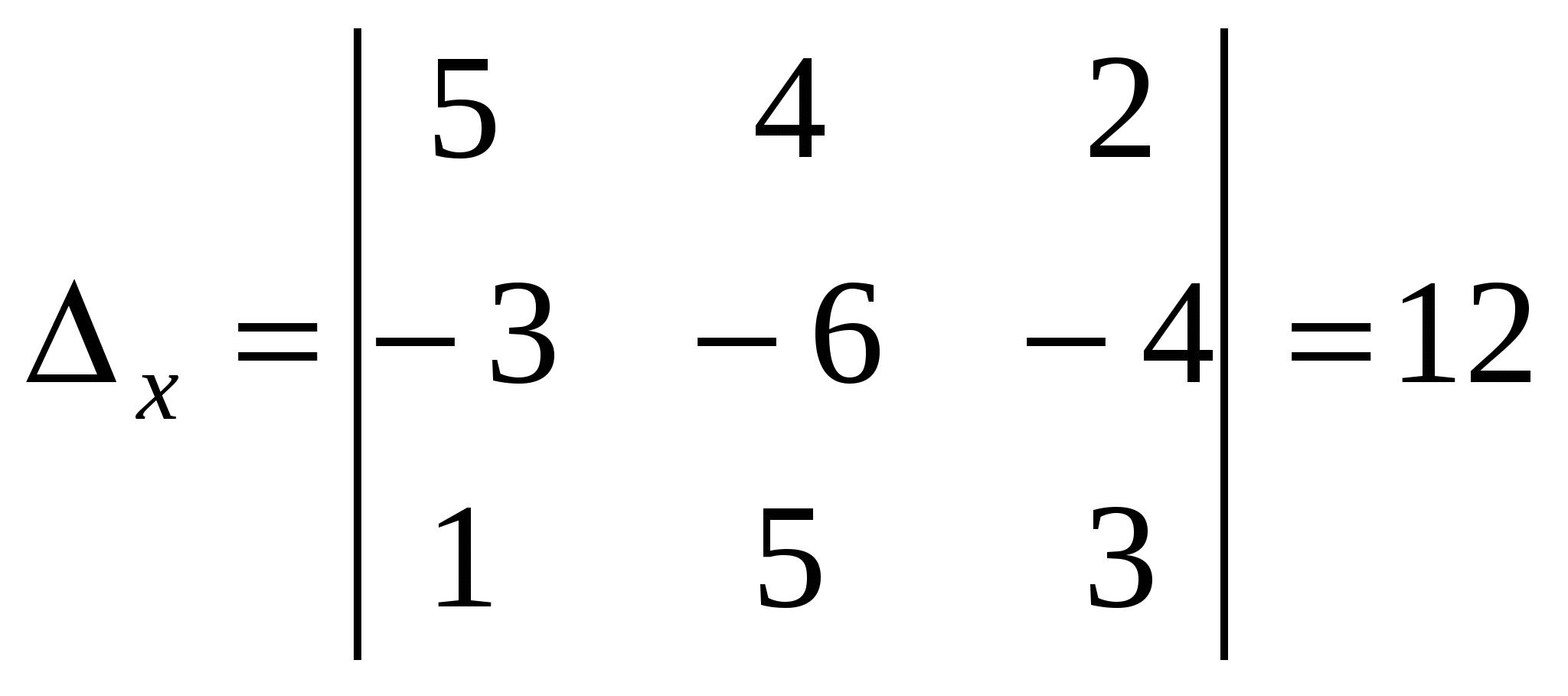 ,
, 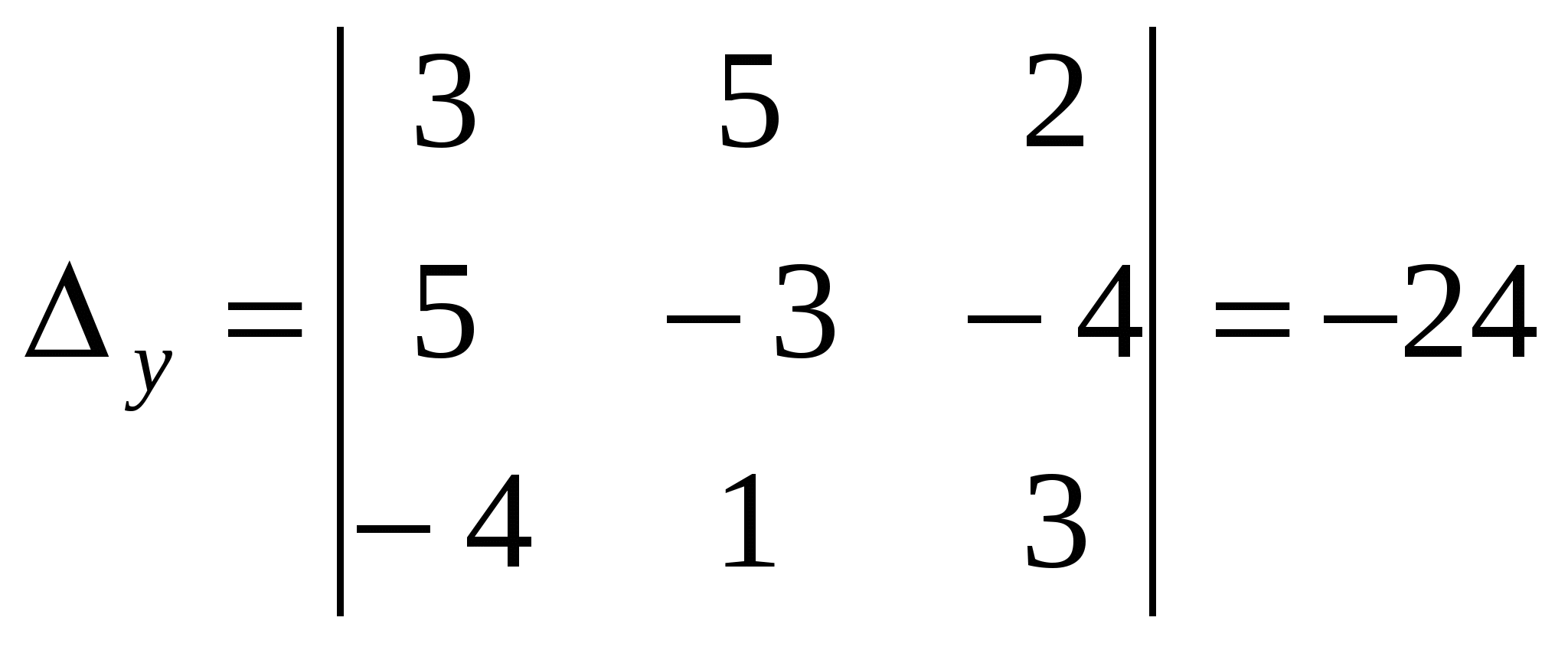 ,
, 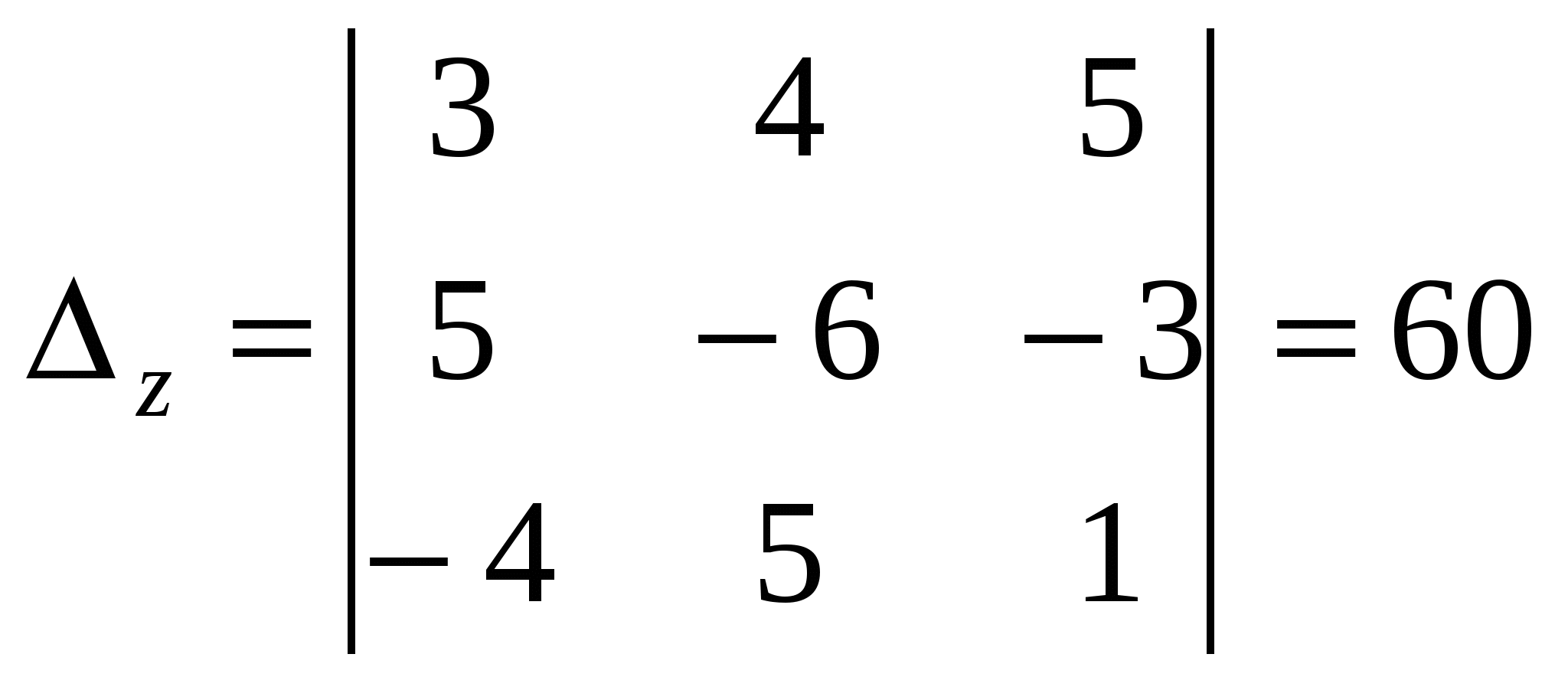 .
.
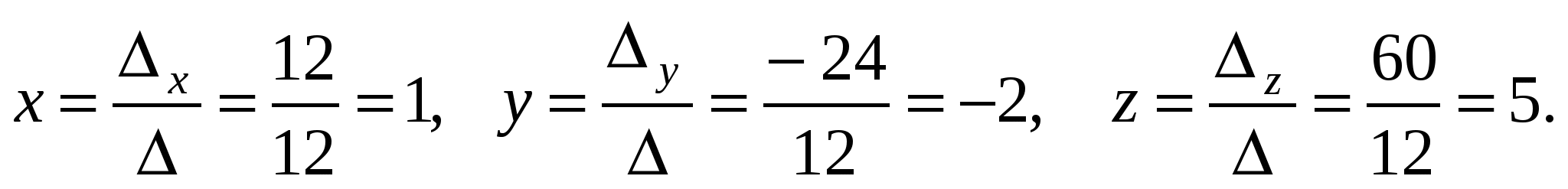
Ответ. 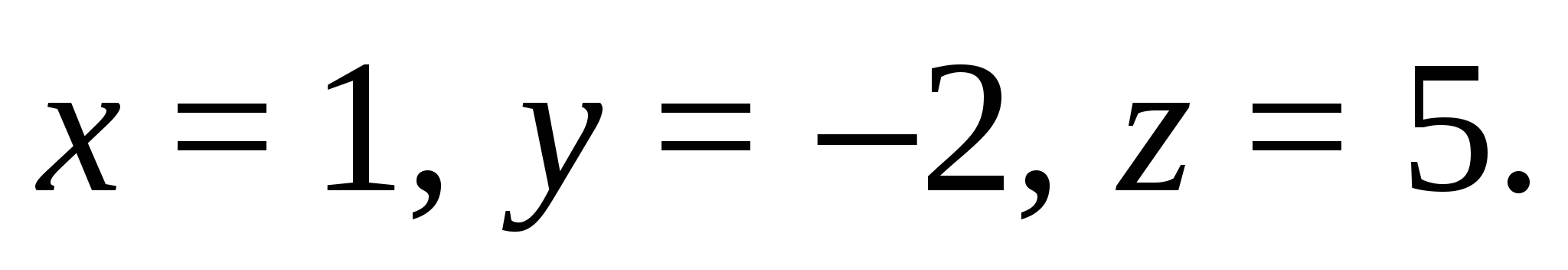
Вычисление пределов функций
Число  называется пределом последовательности x1,х2,…,xn , если для всякого сколь угодно малого положительного числа
называется пределом последовательности x1,х2,…,xn , если для всякого сколь угодно малого положительного числа  найдется такое положительное число N, что
найдется такое положительное число N, что 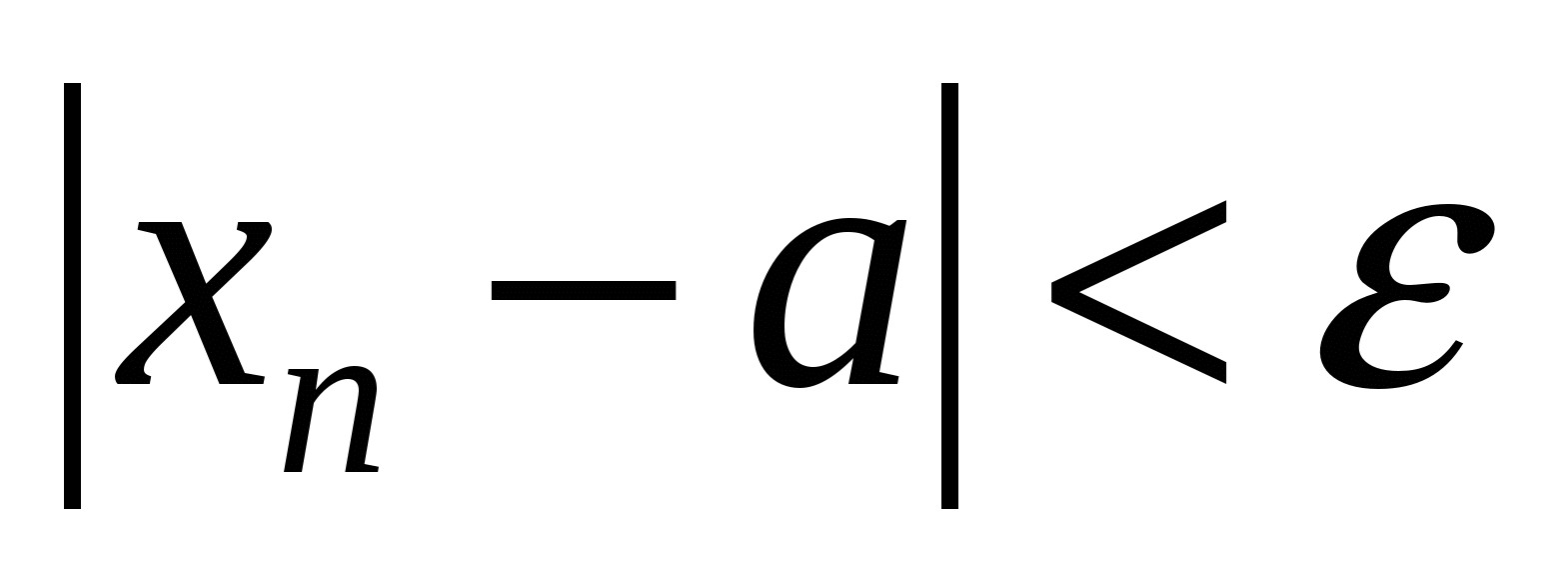 при
при 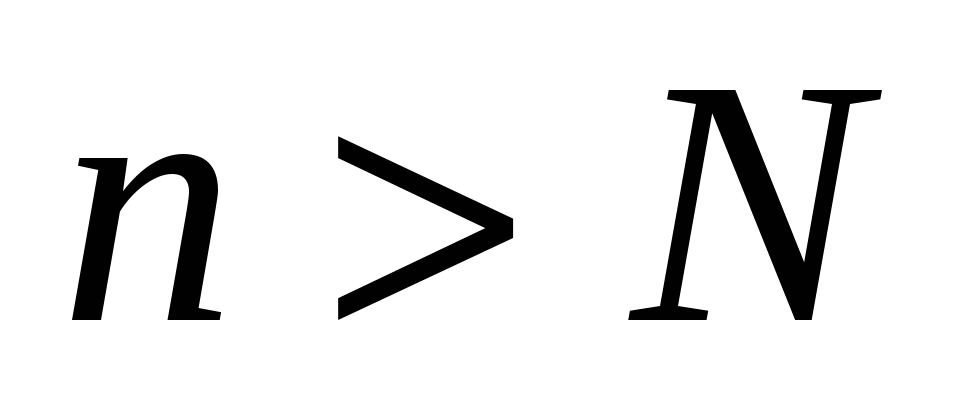 . В этом случае пишут:
. В этом случае пишут: 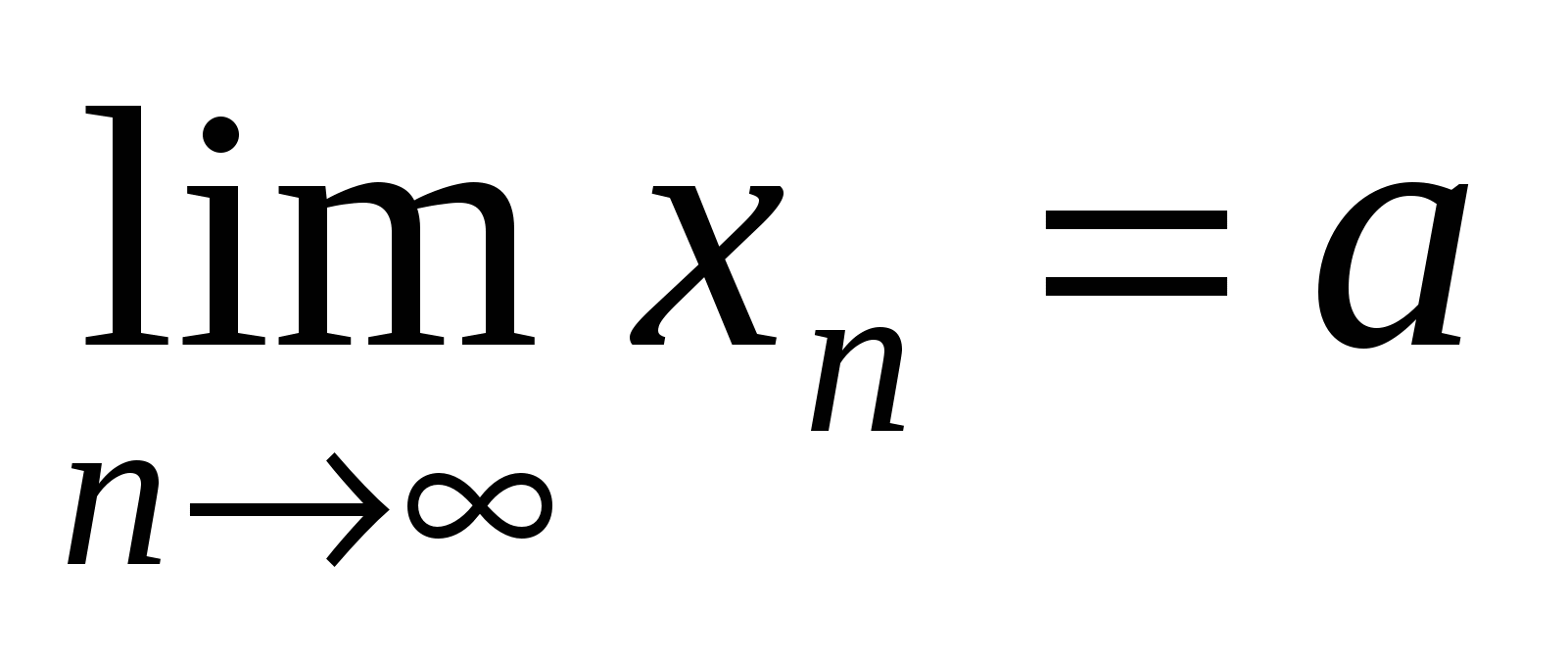 .
.
Число  называется пределом функции
называется пределом функции 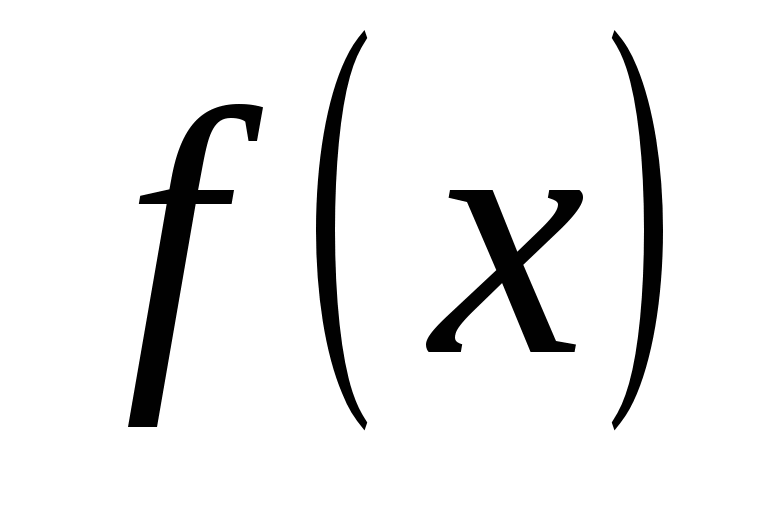 при
при  , если для любого сколь угодно малого
, если для любого сколь угодно малого 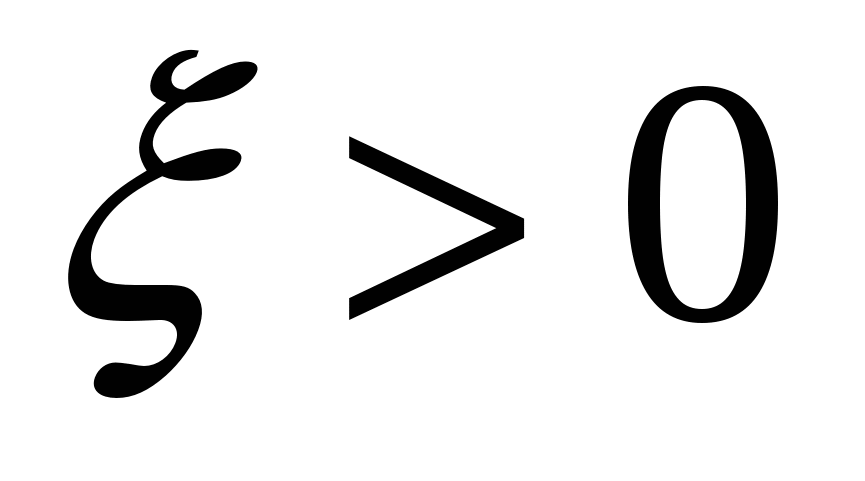 найдется такое
найдется такое ![]() , что
, что 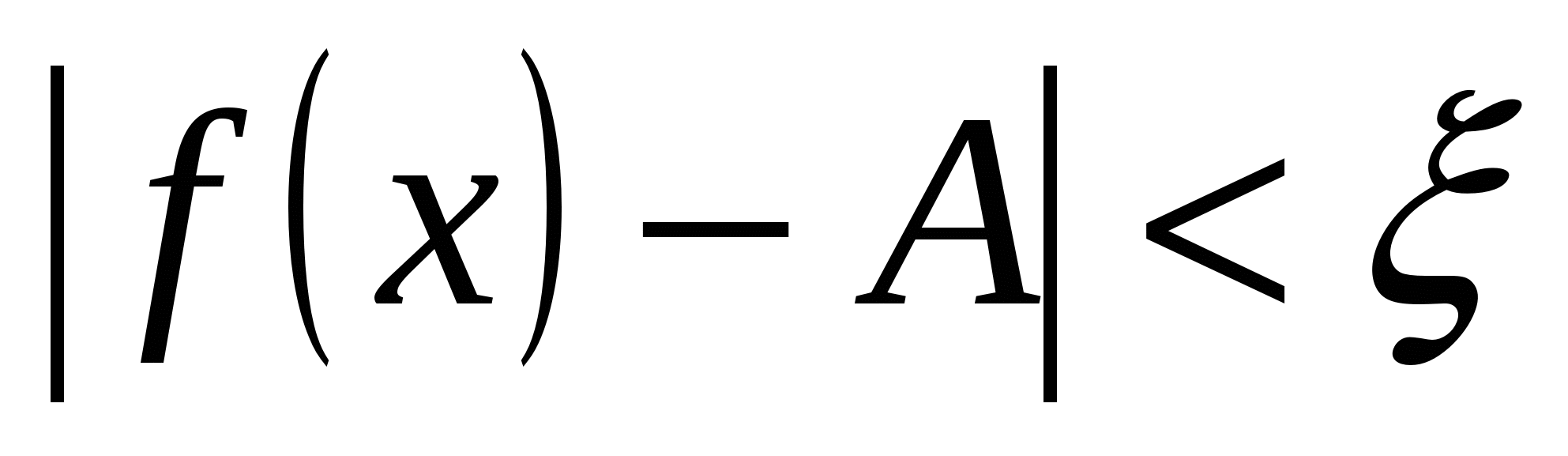 при
при 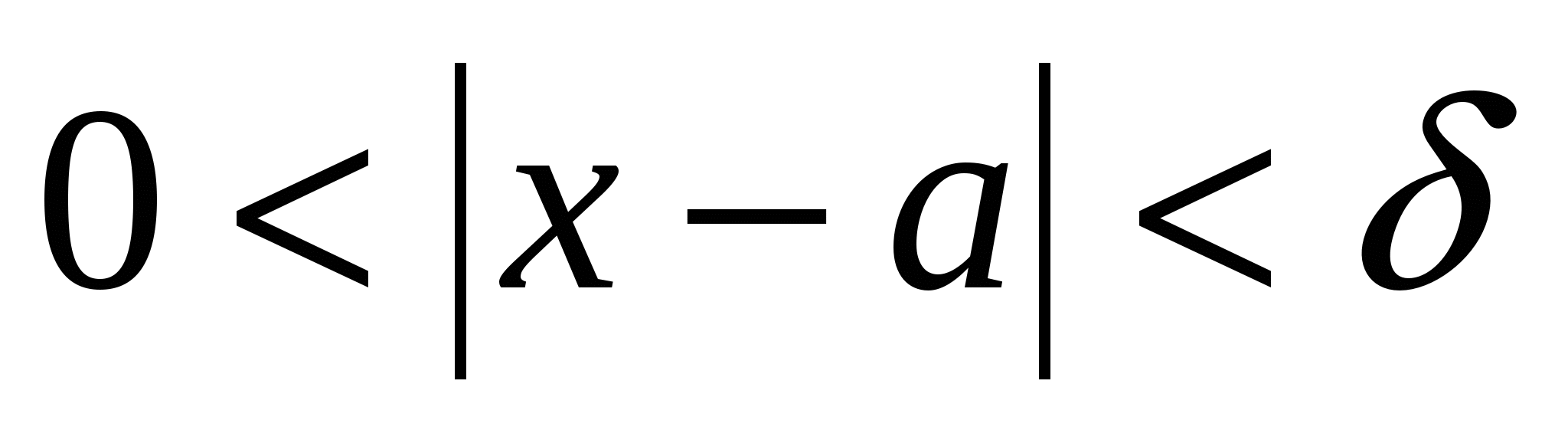 . Это записывают так:
. Это записывают так: 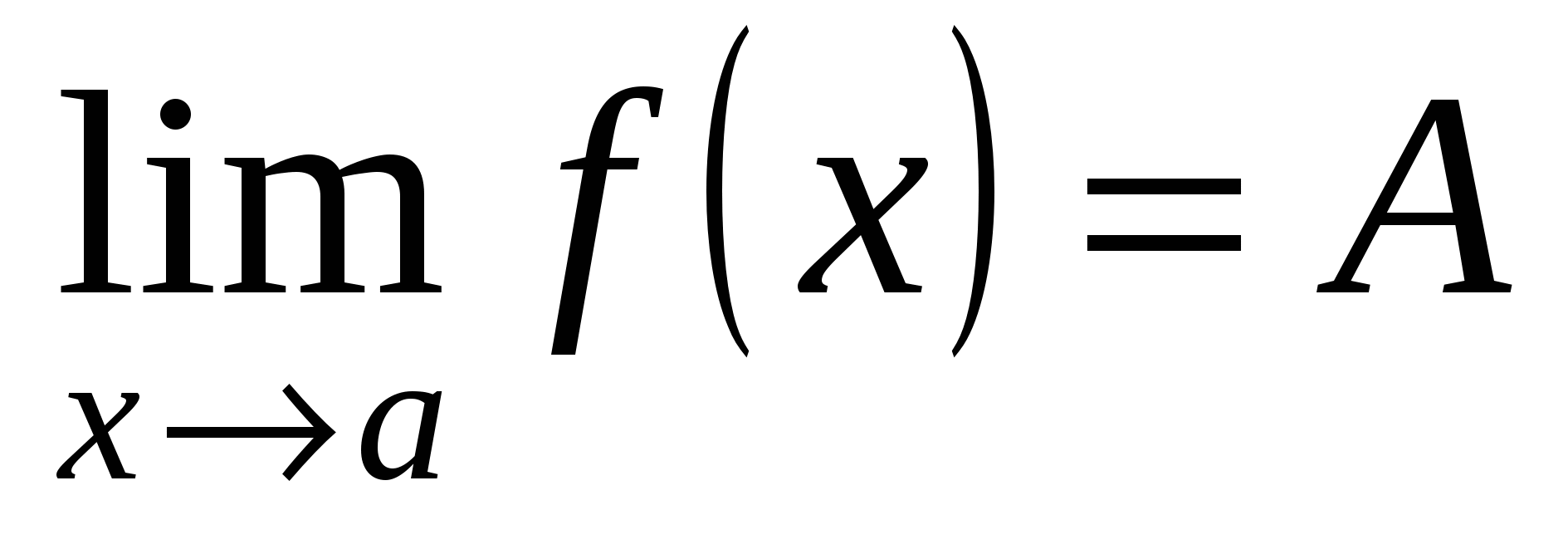
Аналогично 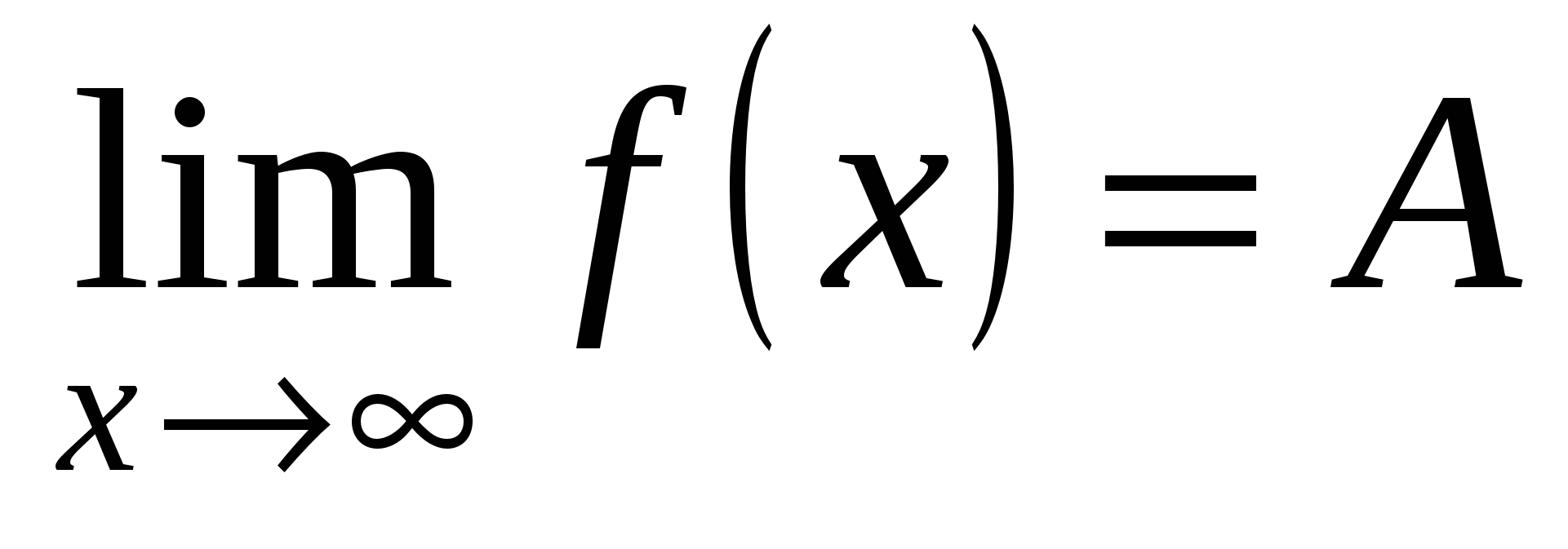 , если
, если 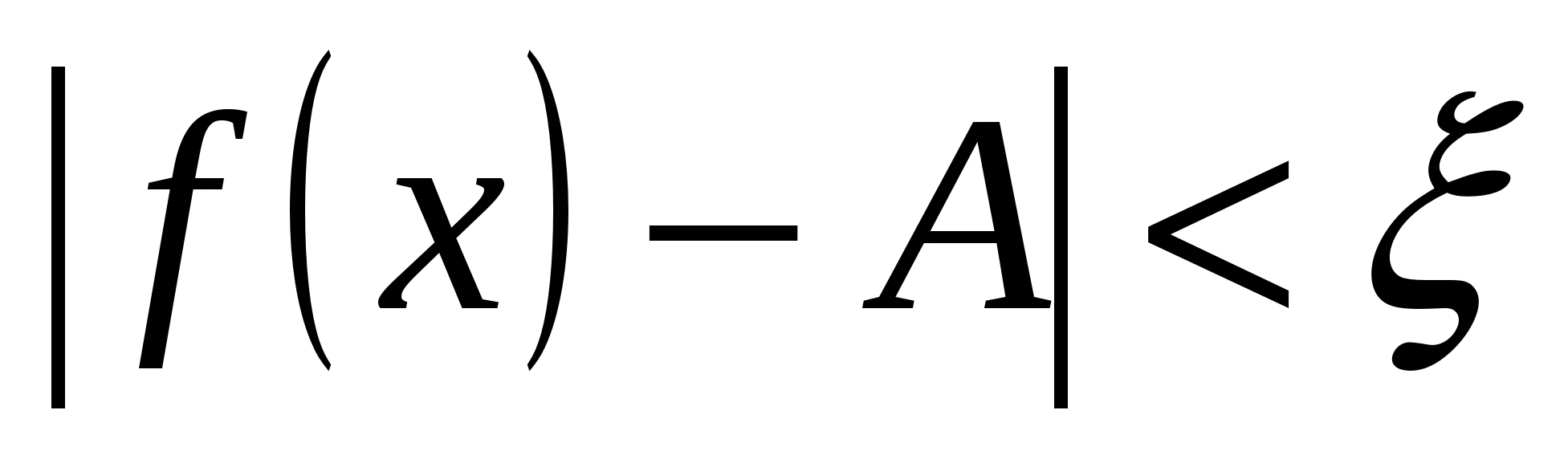 при
при 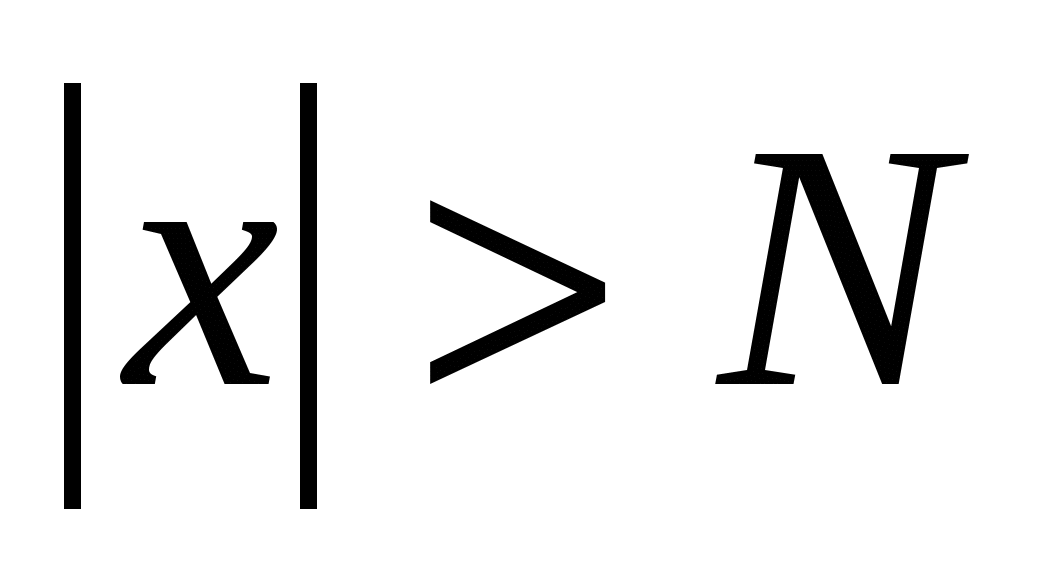 .
.
Условно записывают 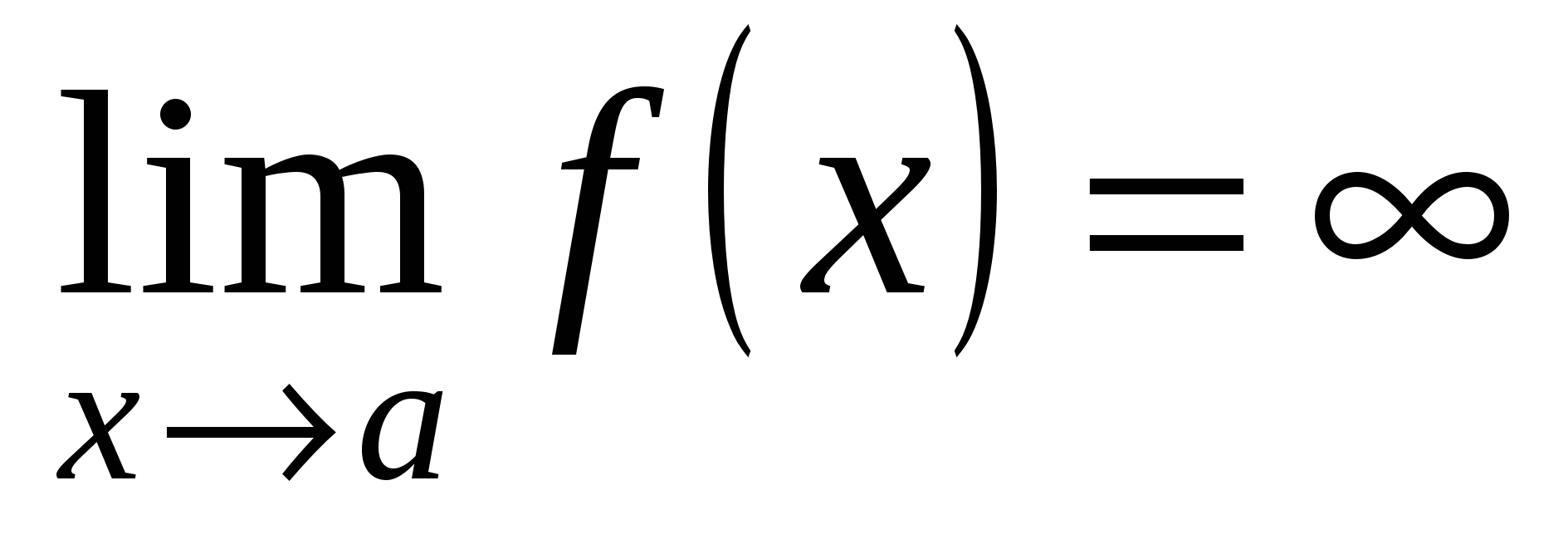 , если
, если 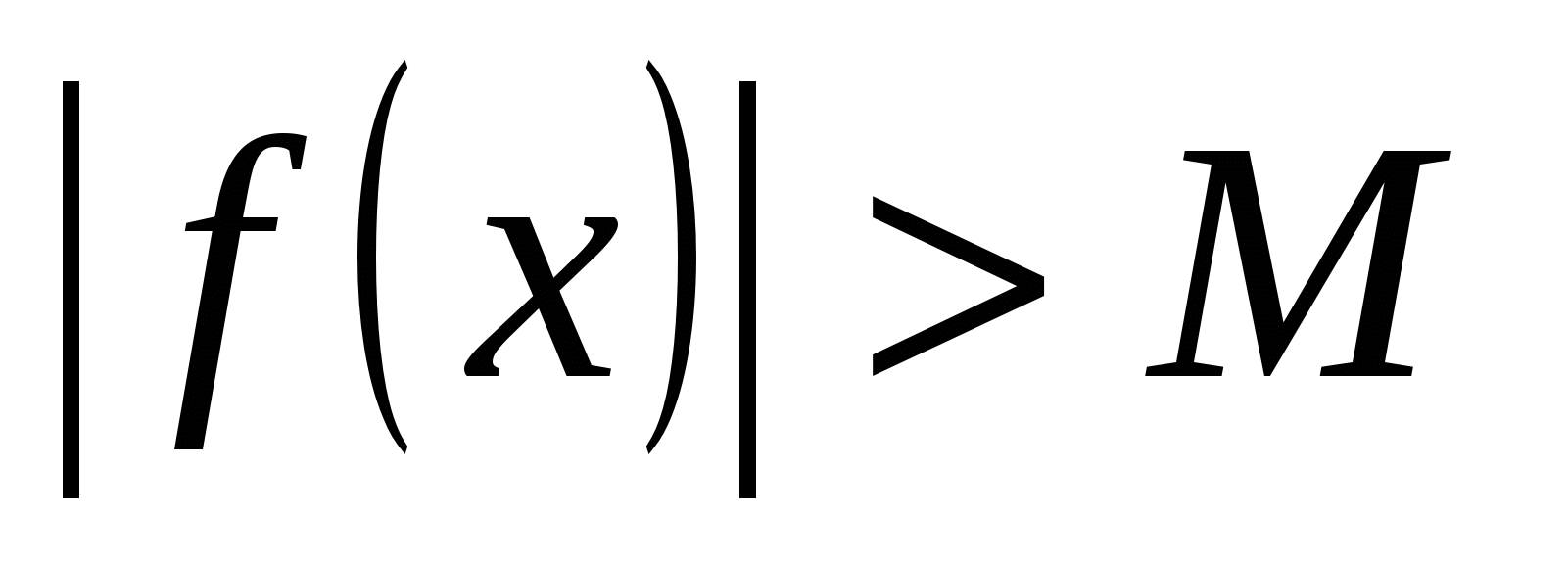 при
при 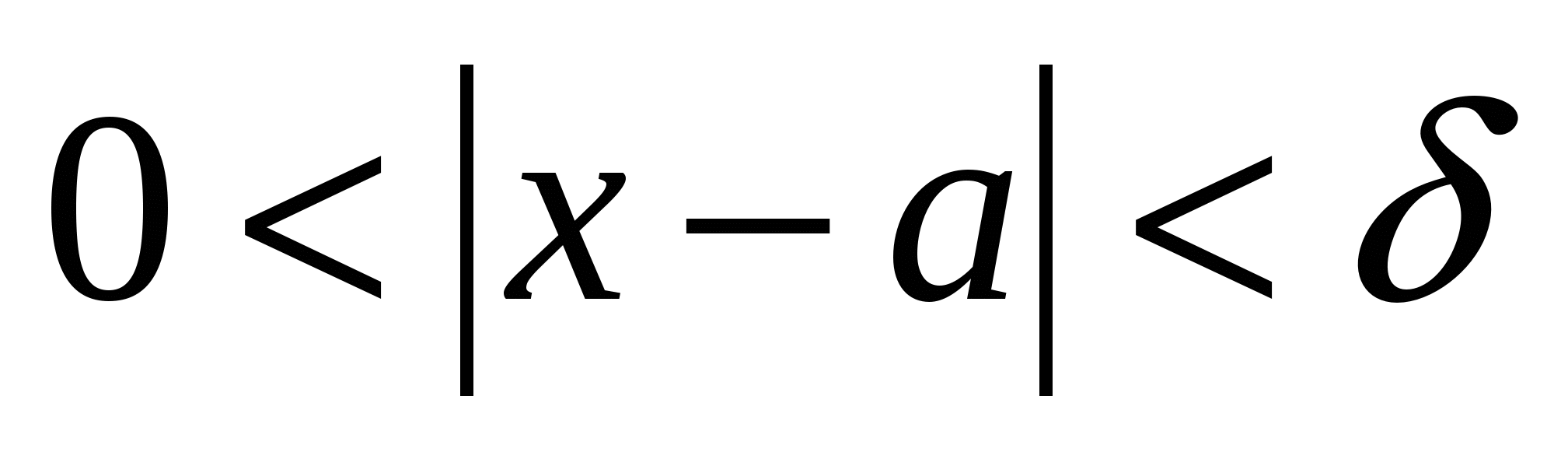 , где М - произвольное положительное число. В этом случае функция
, где М - произвольное положительное число. В этом случае функция 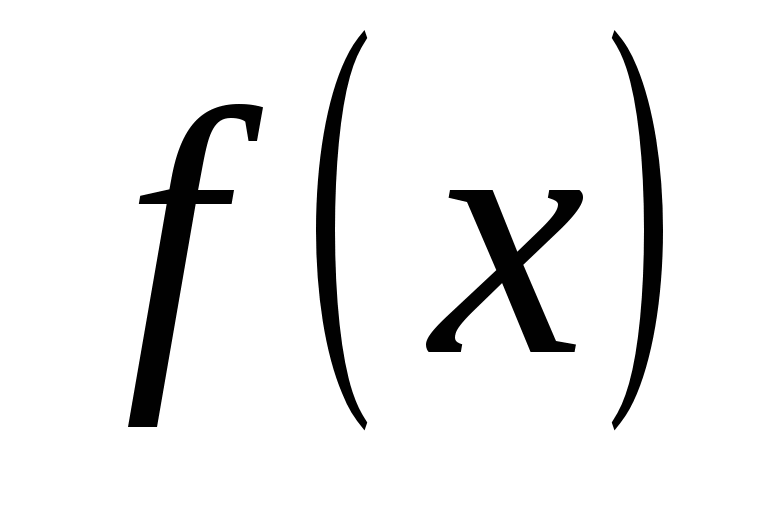 называется бесконечно большой при
называется бесконечно большой при  . Если
. Если 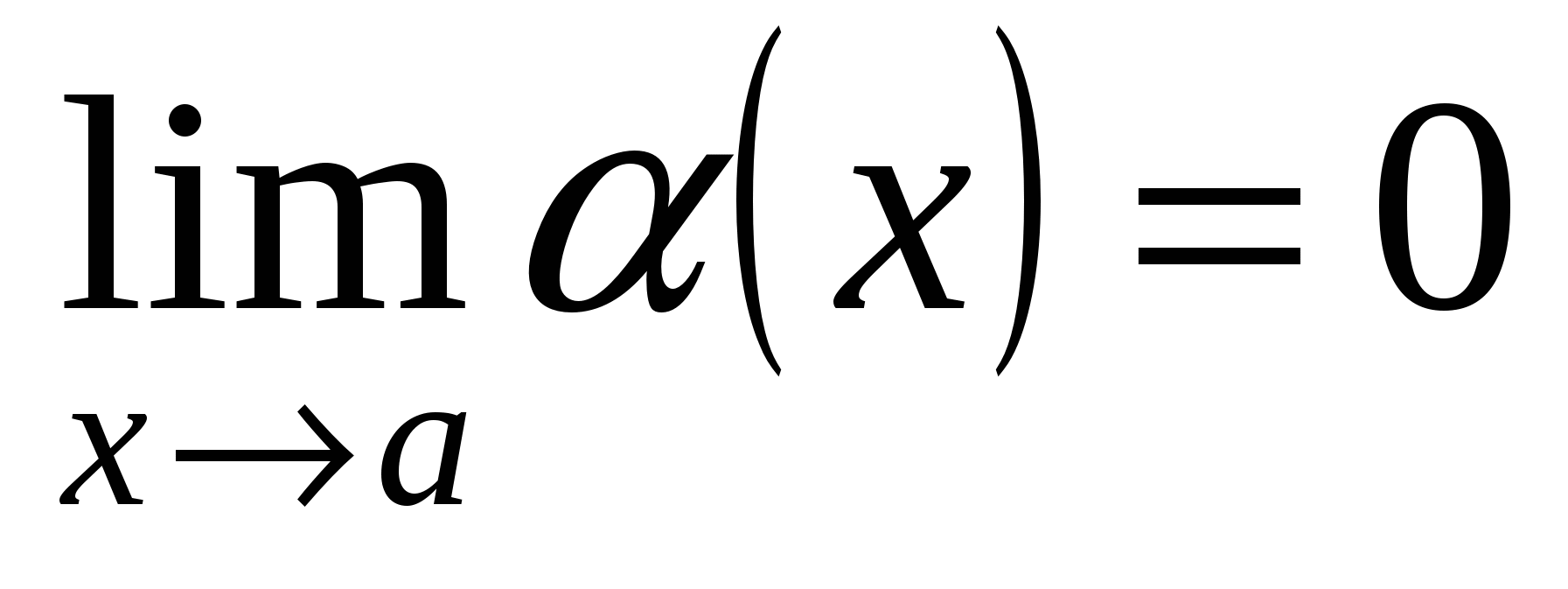 , то функция
, то функция 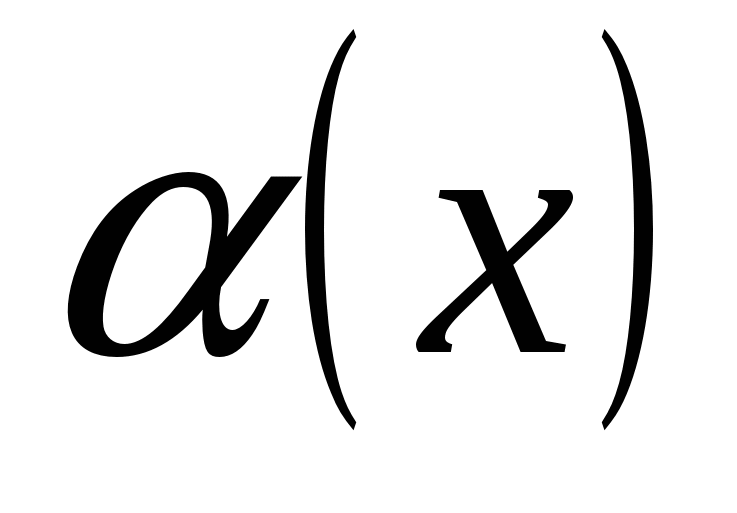 называется бесконечно малой при
называется бесконечно малой при  .
.
Практическое вычисление пределов основывается на следующих теоремах.
Если существуют 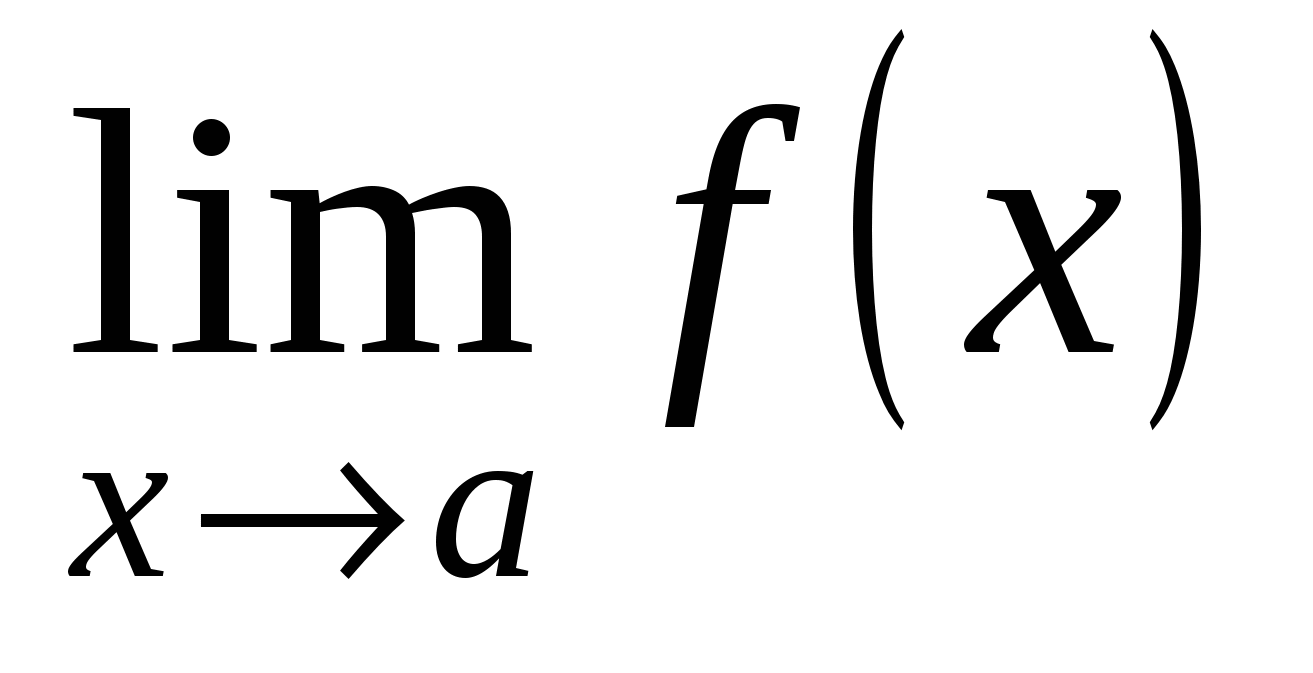 и
и 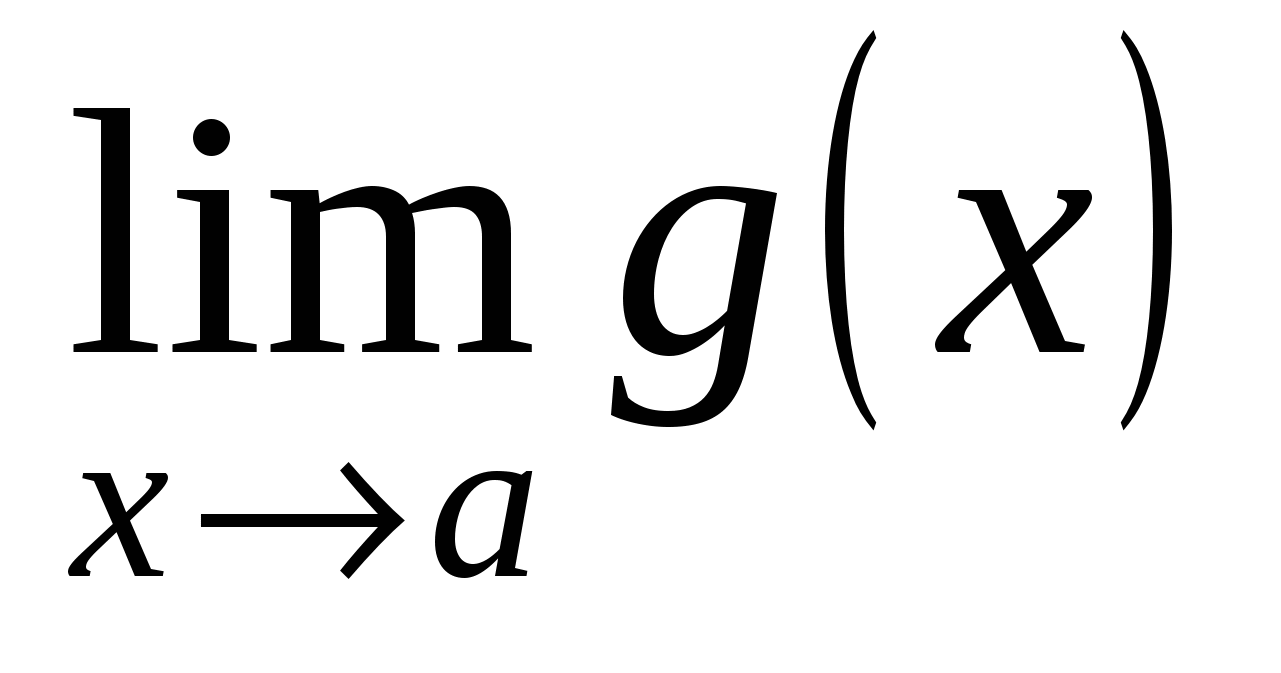 , то
, то
-
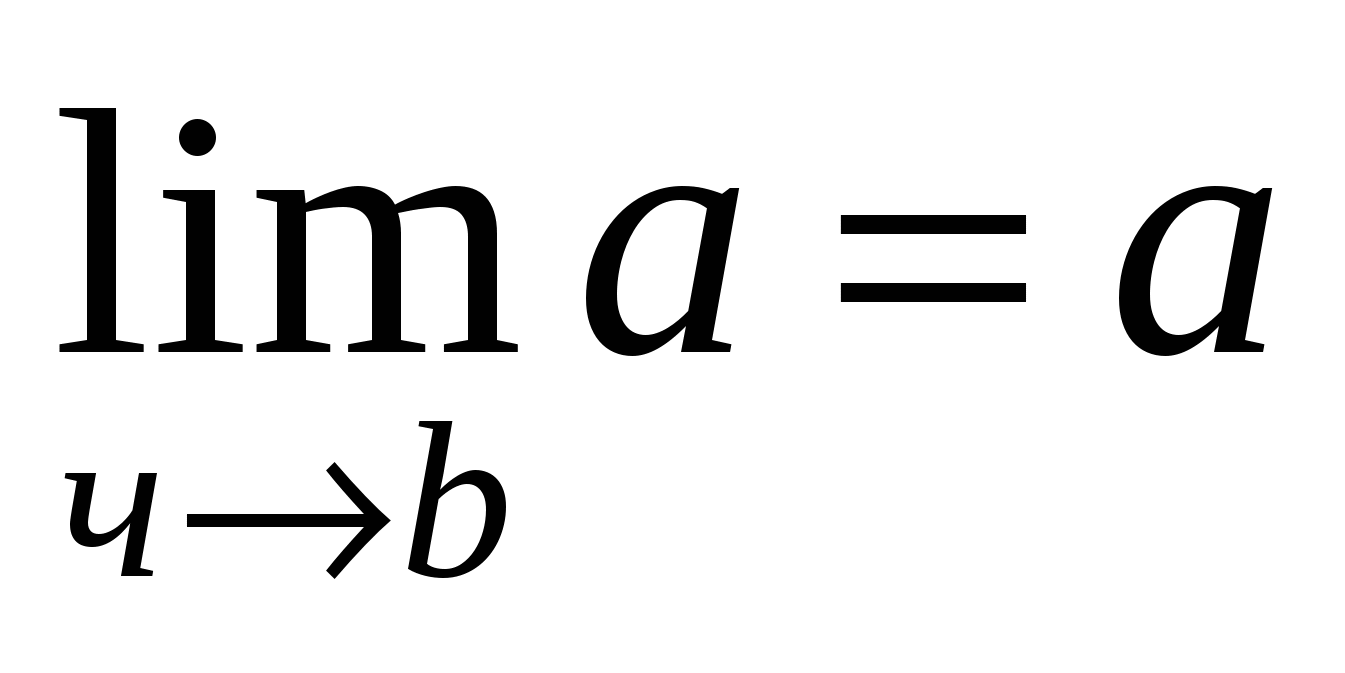
-
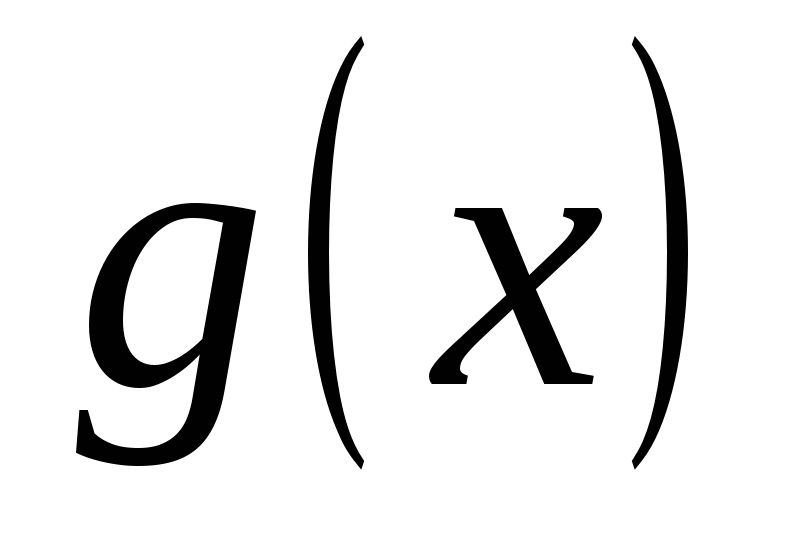 ;
; -
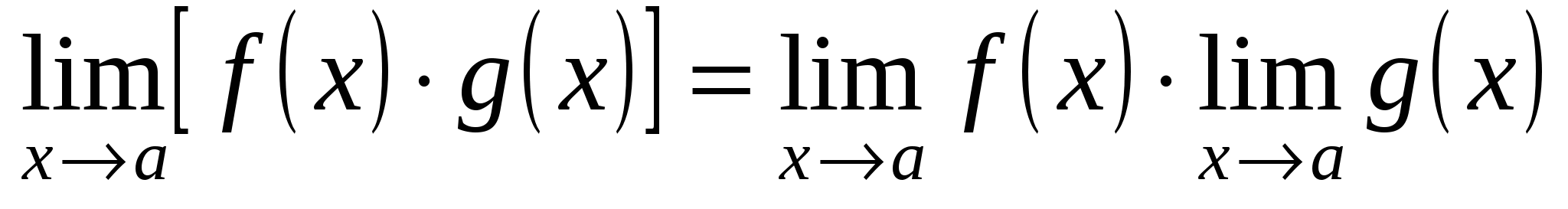 ;
; -
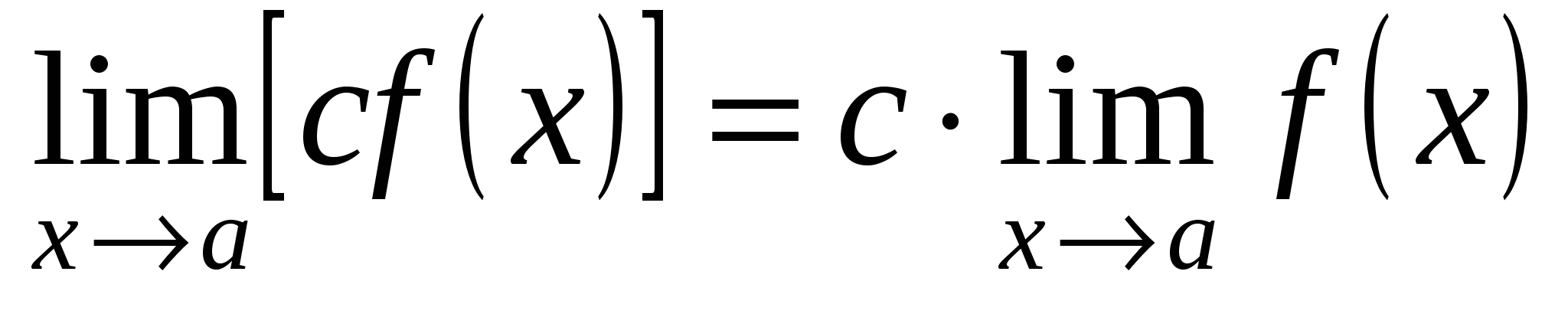
-
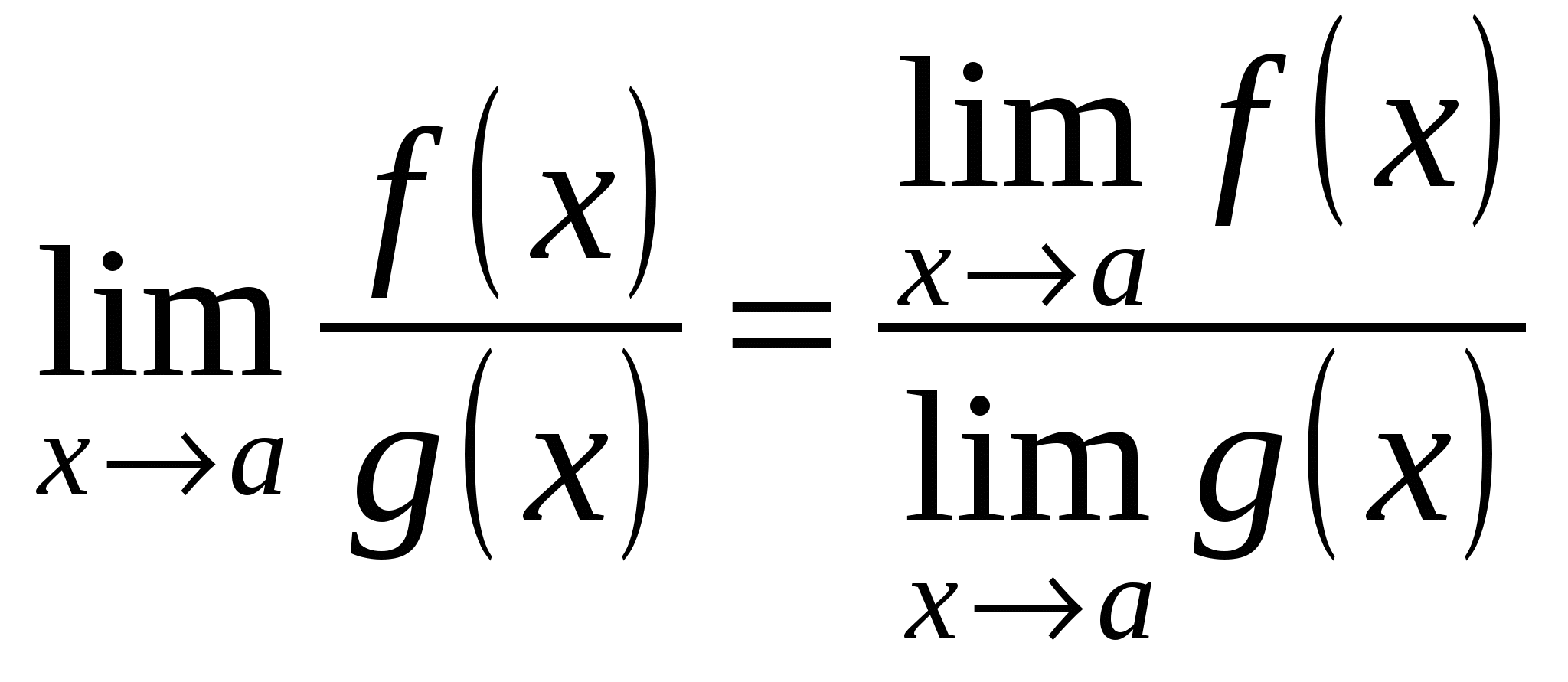 (при
(при 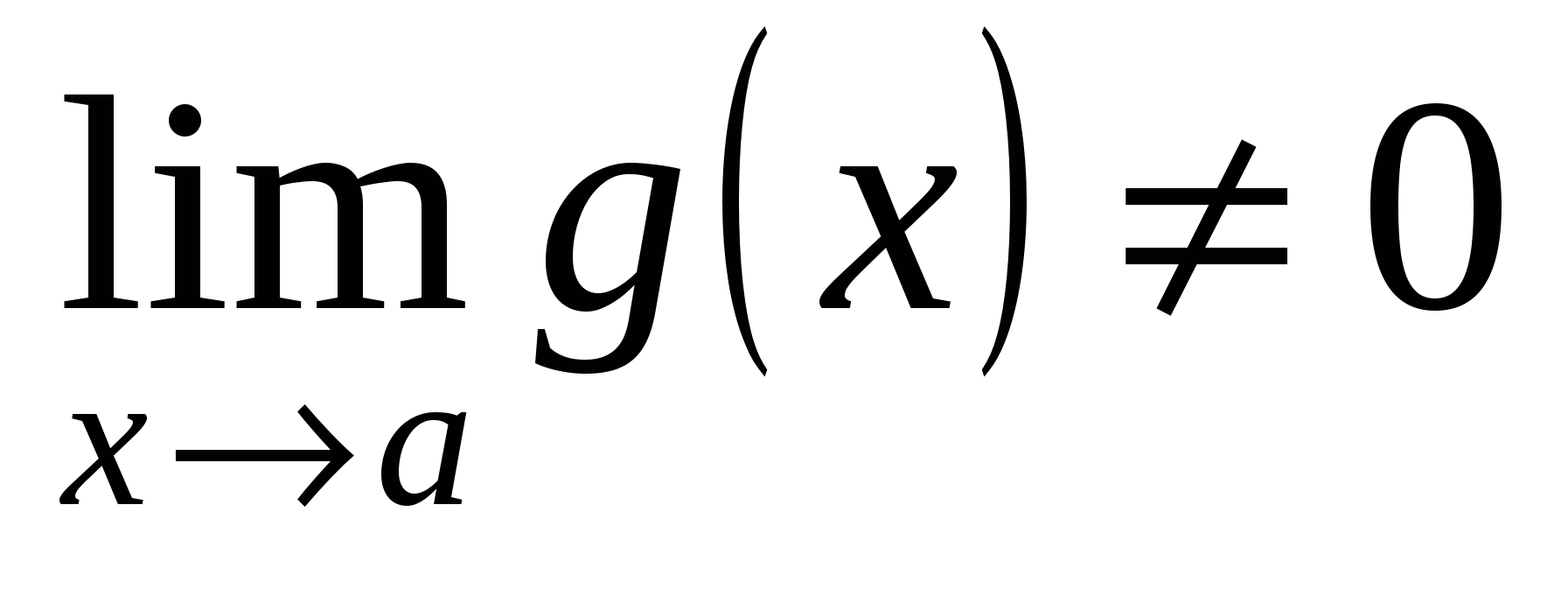 ).
).
Путем элементарных рассуждений, основанных на свойствах пределов, можно получить следующие наиболее часто встречающиеся пределы (постоянная 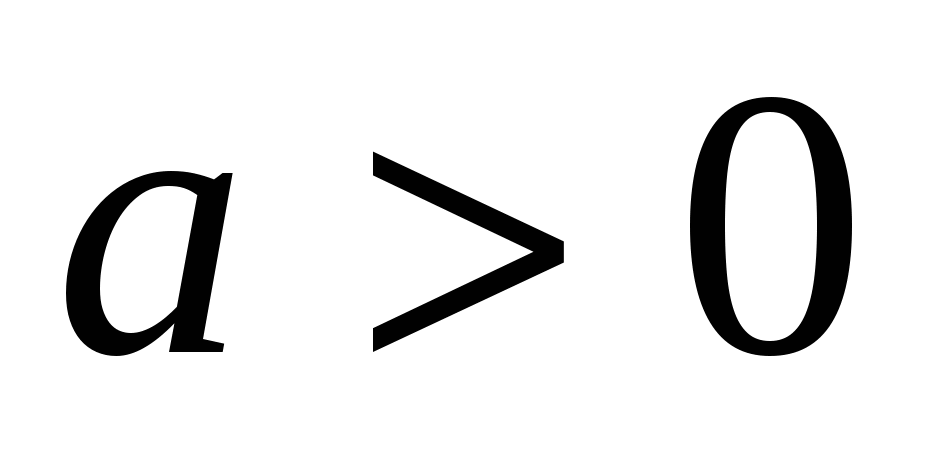 ):
):
1) 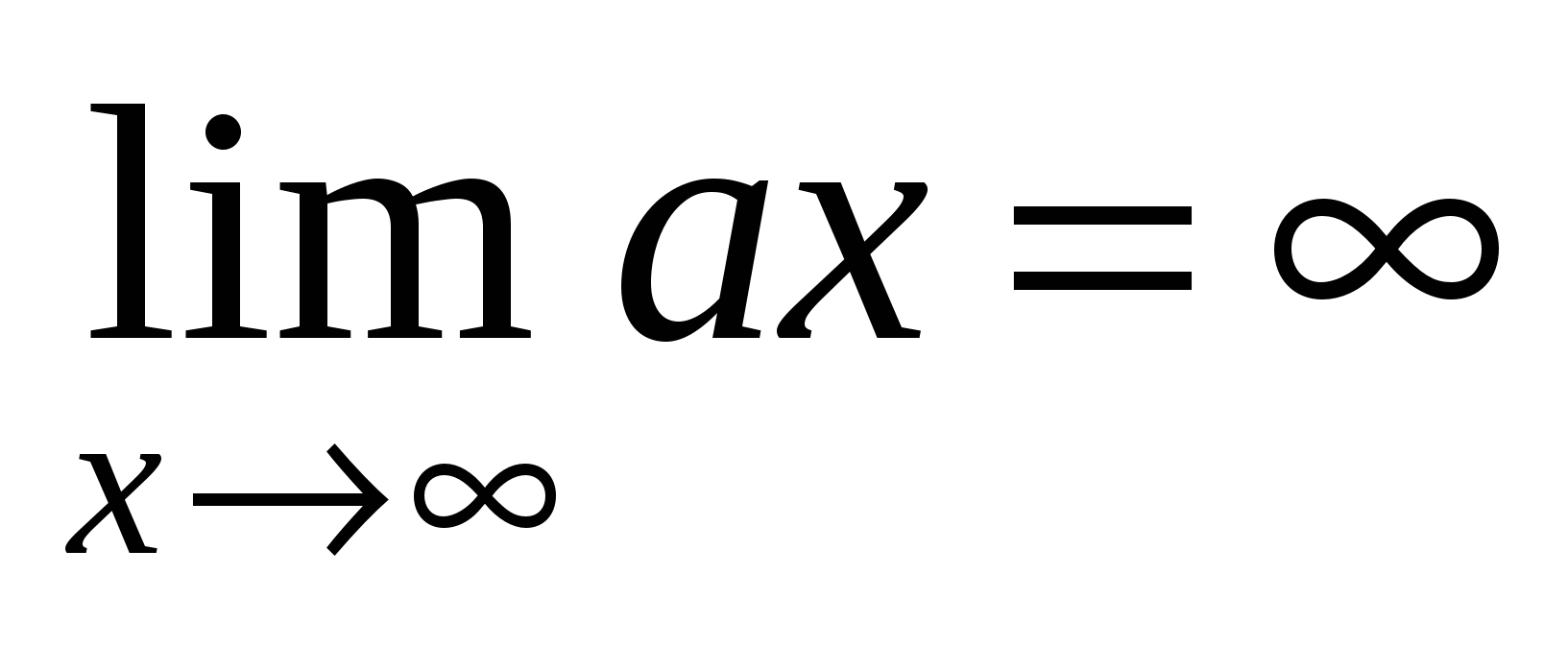
2) 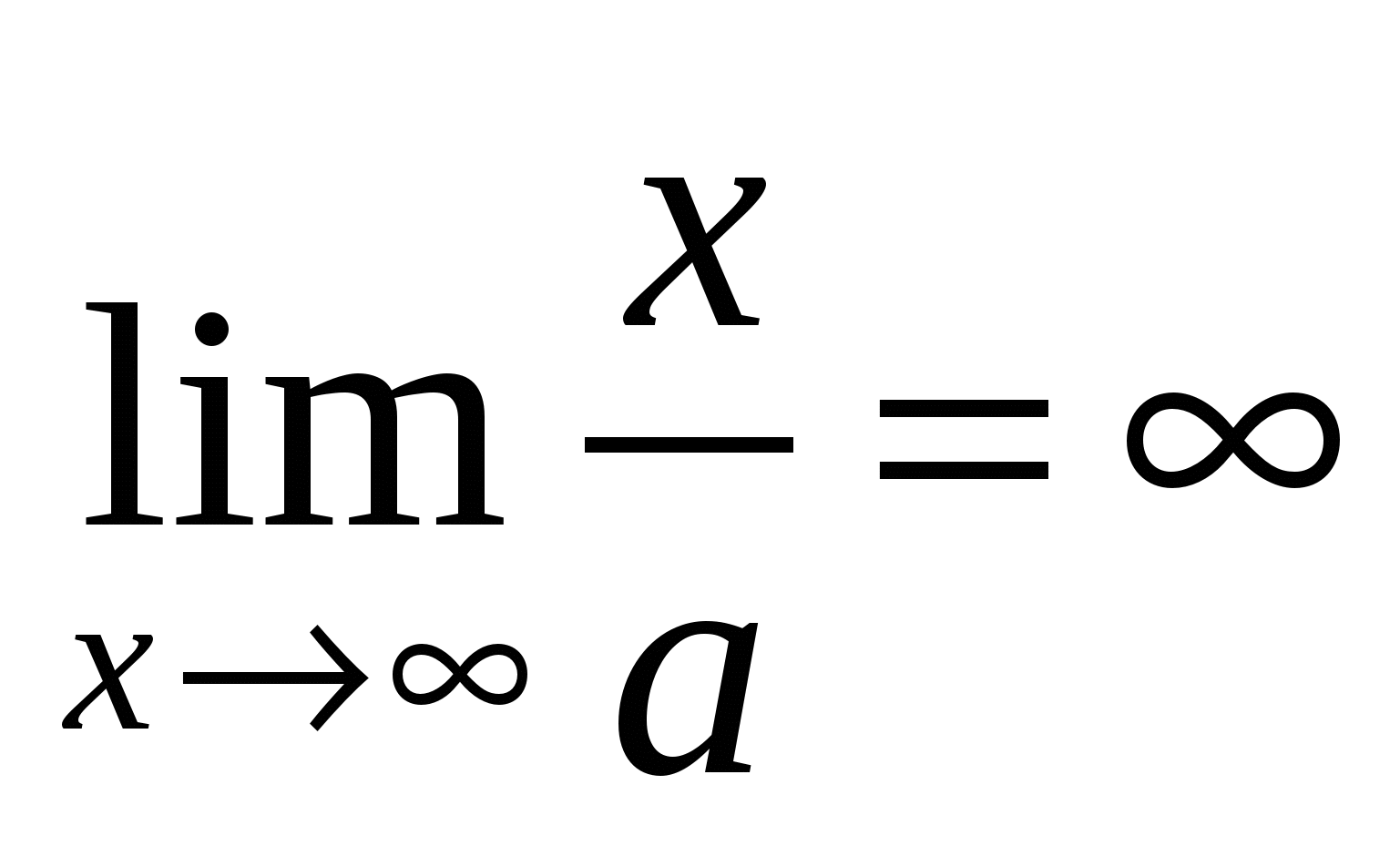
3) 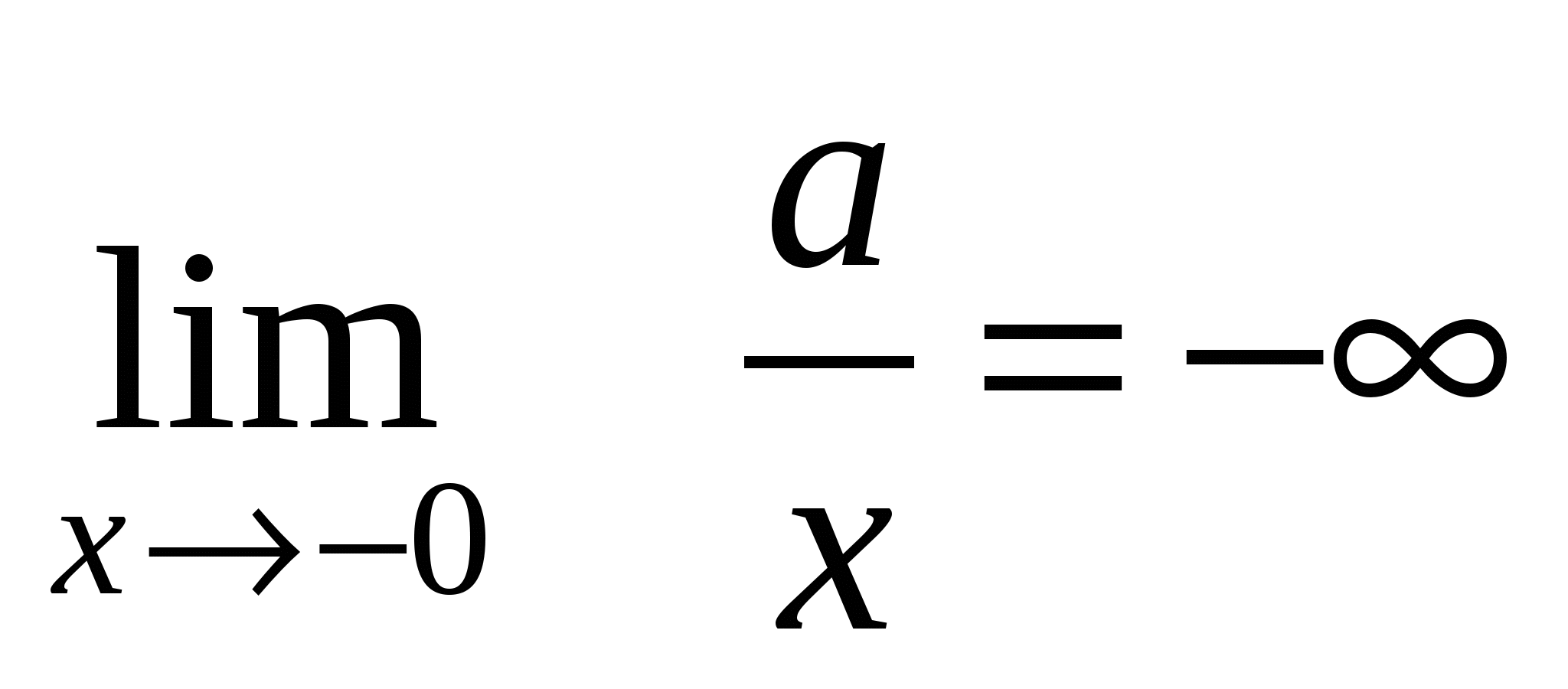
4) 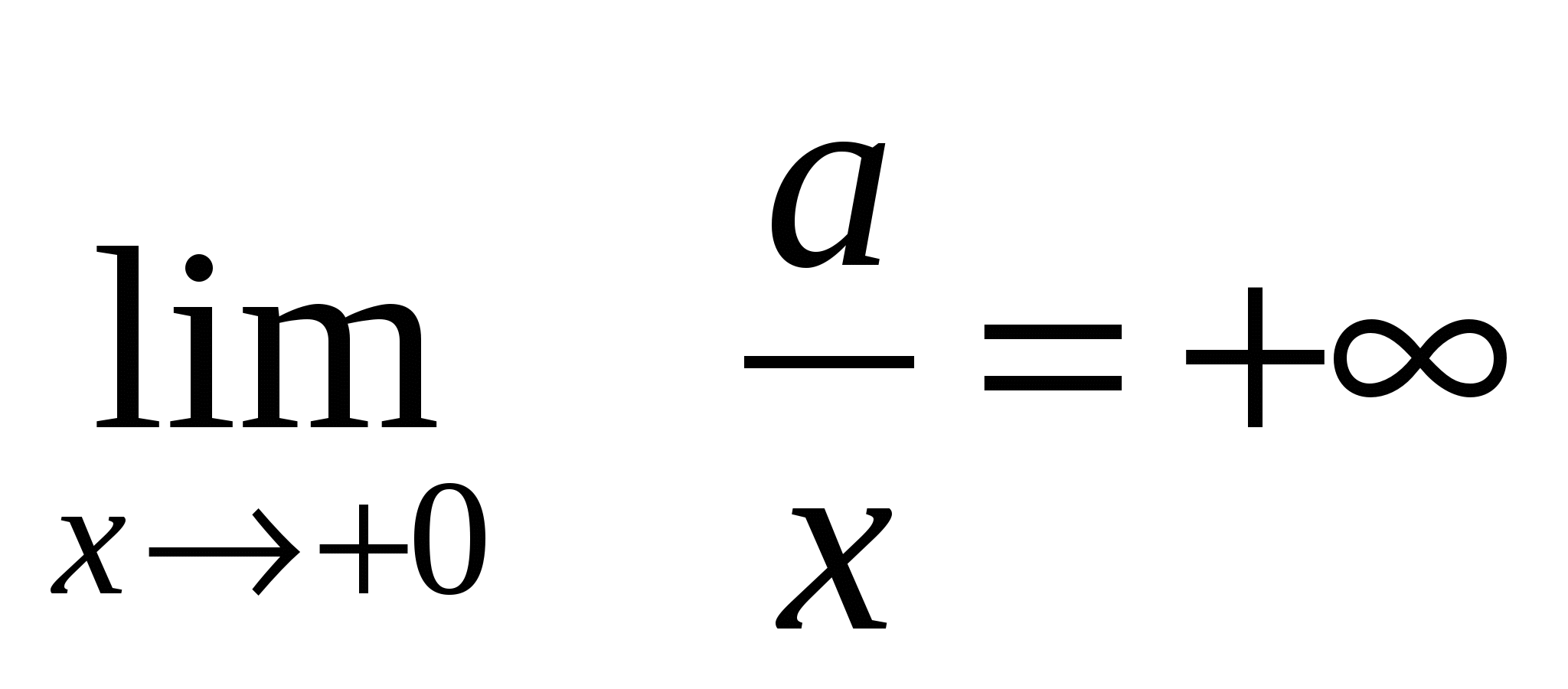
5) 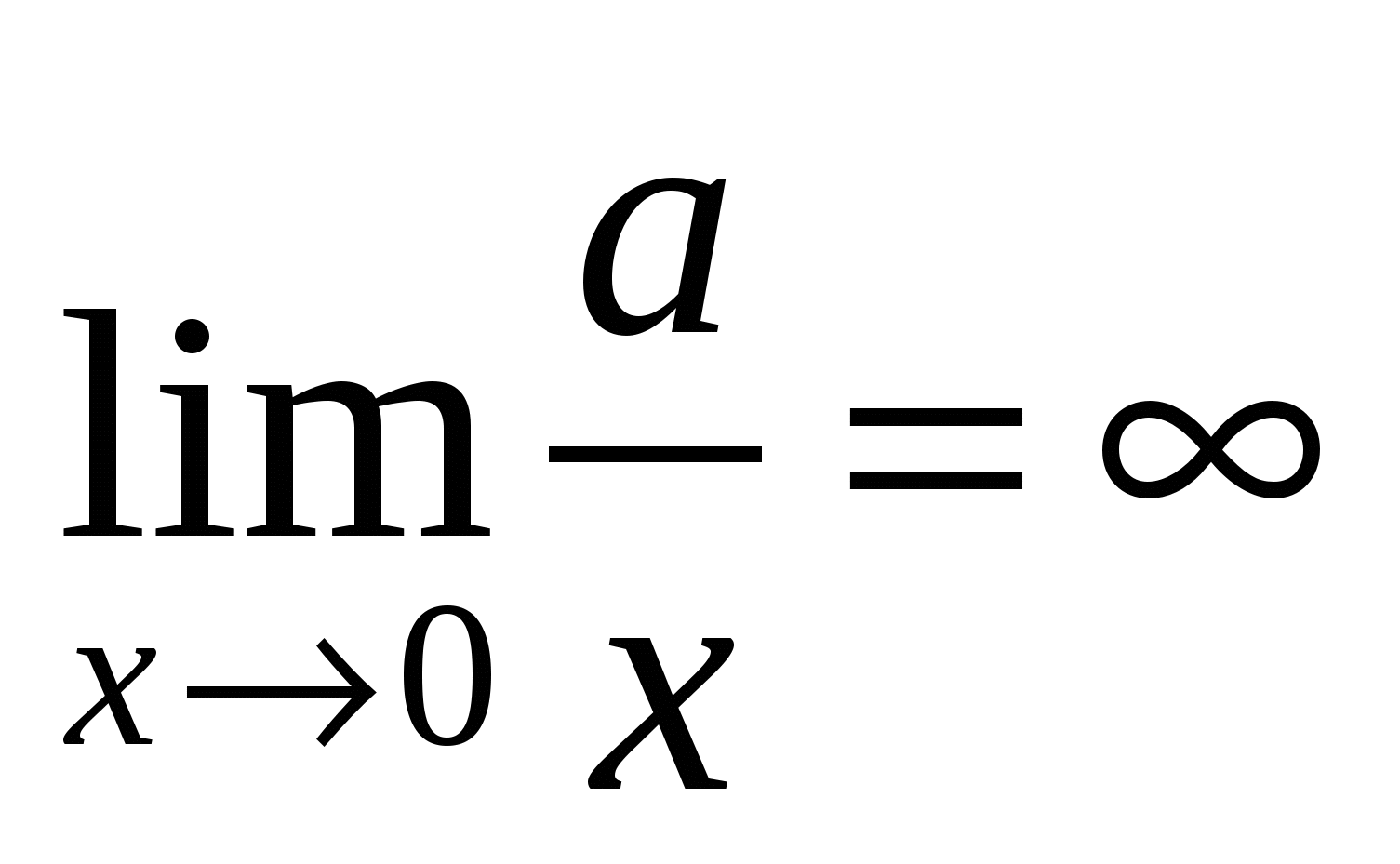
6) 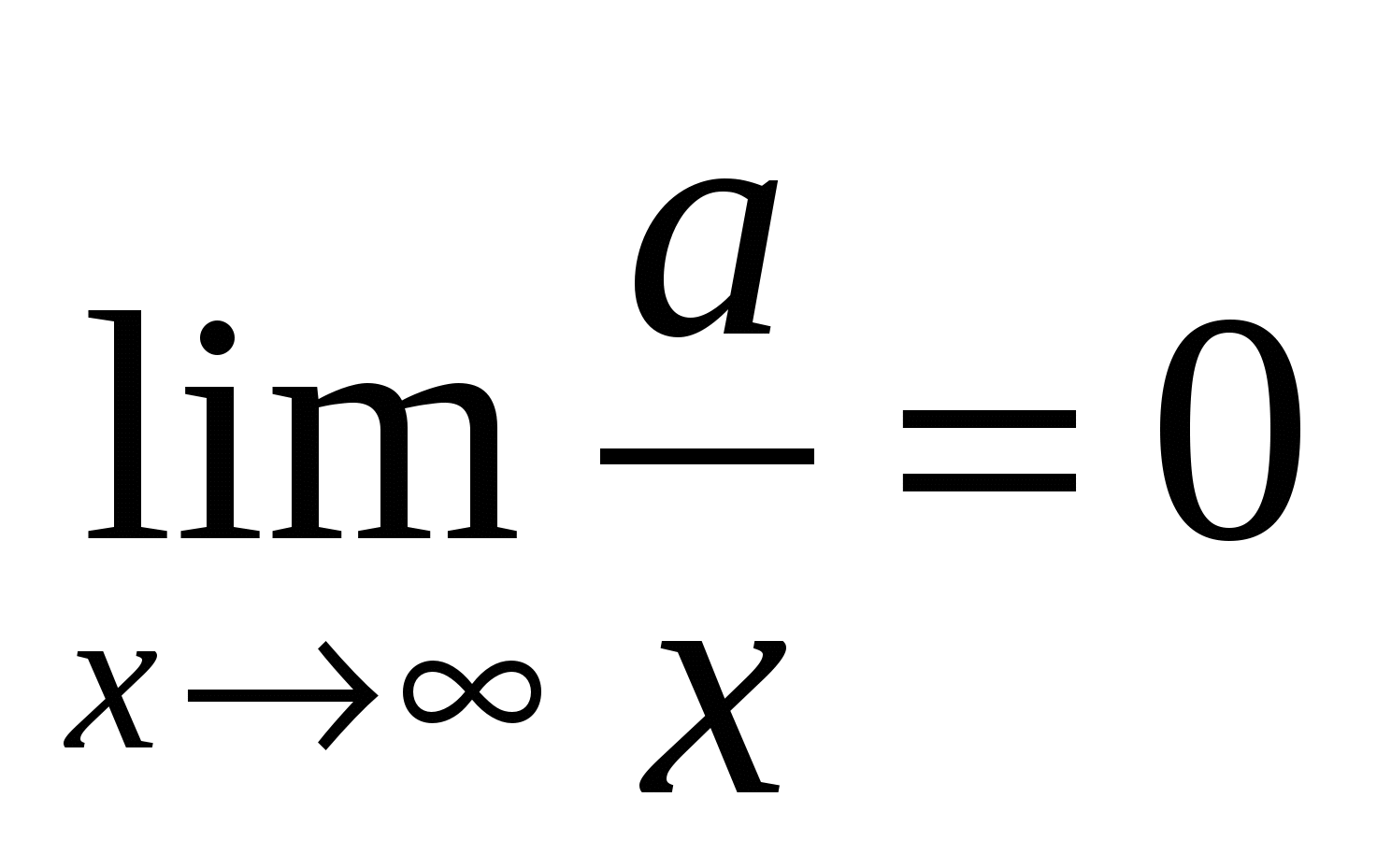
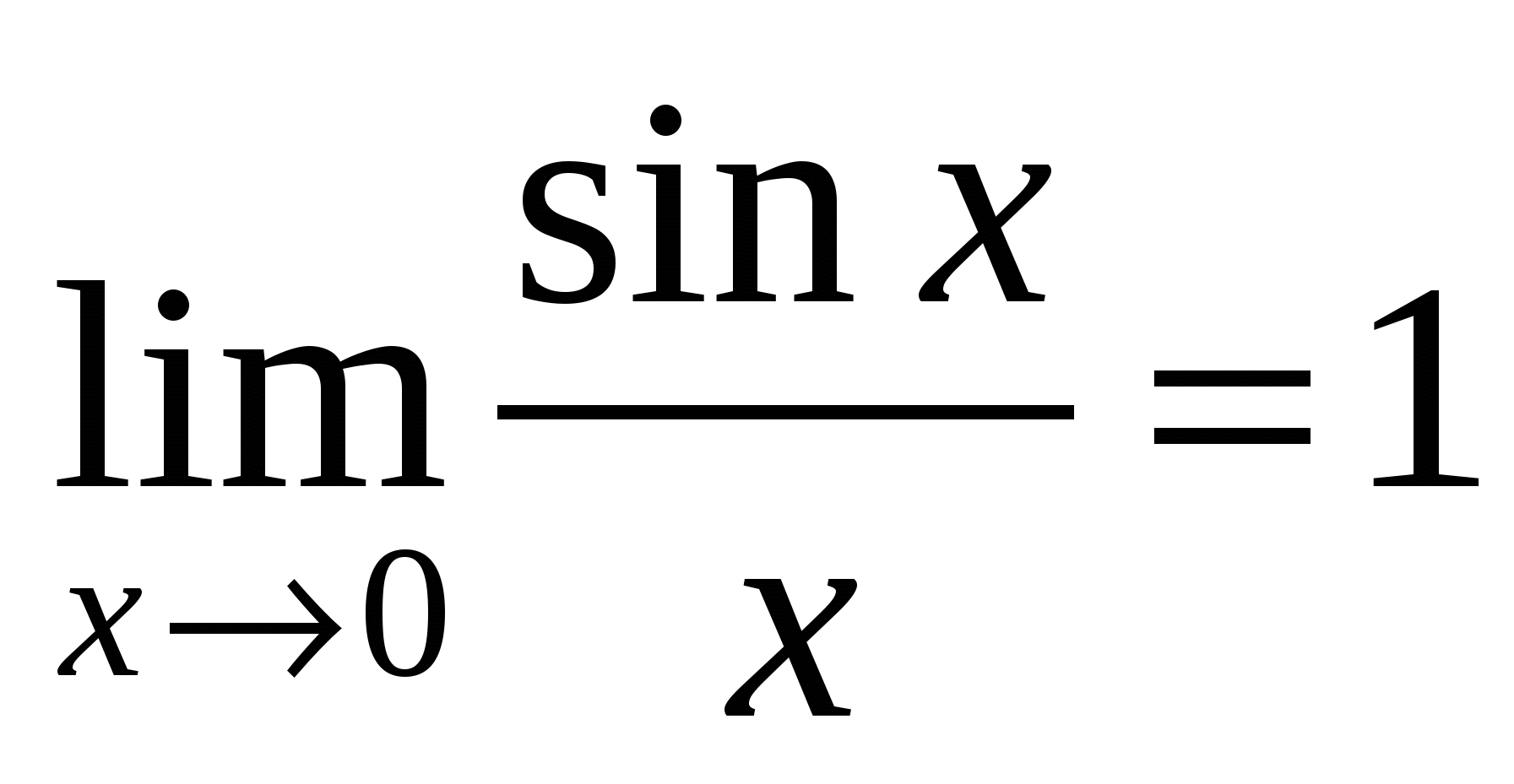 (первый замечательный предел);
(первый замечательный предел);
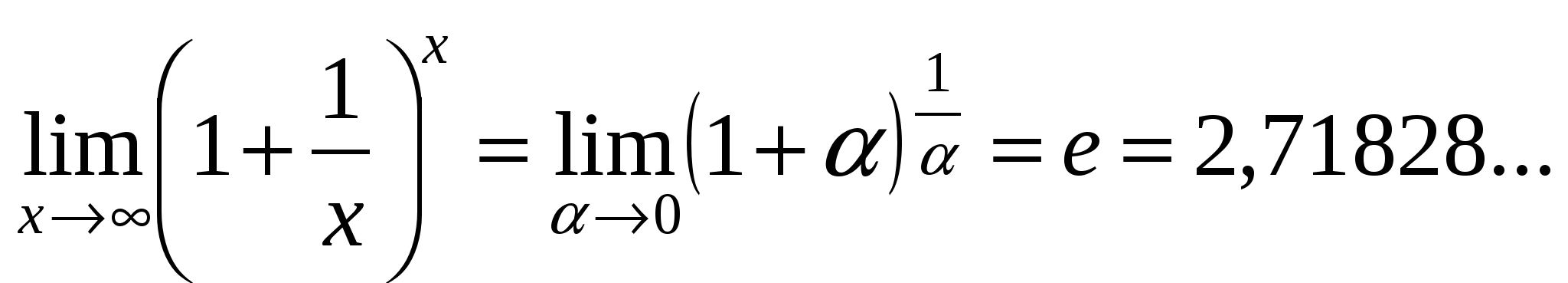 (второй замечательный предел)
(второй замечательный предел)  ,
,
Функция ![]() называется непрерывной в точке если:
называется непрерывной в точке если:
1) эта функция определена в некоторой окрестности и точки  ;
;
2) существует предел 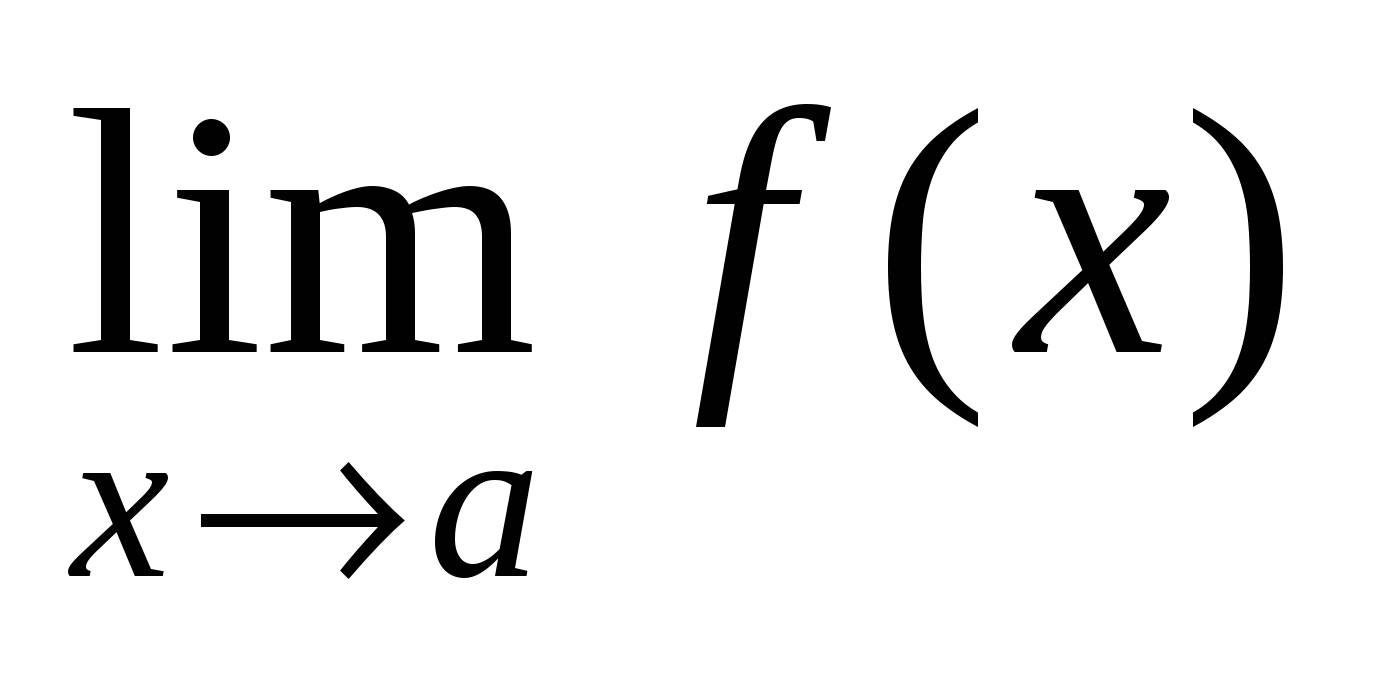 ;
;
3) этот предел равен значению функции в точке  , т.е.
, т.е. 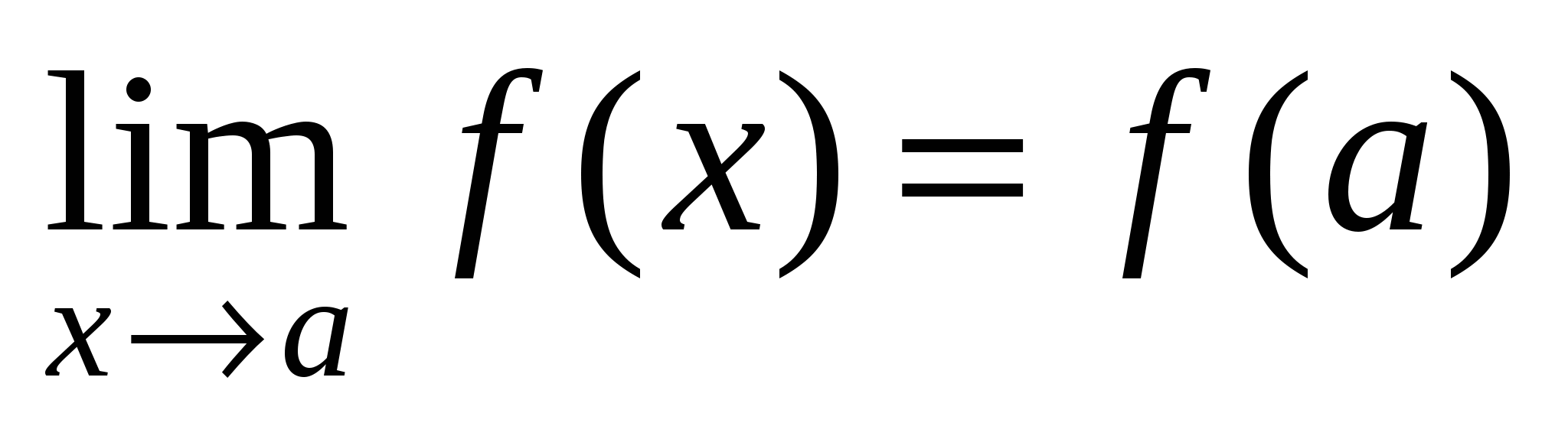 .
.
При нахождении пределов часто используется тот факт, что все основные элементарные функции непрерывны при всех значениях 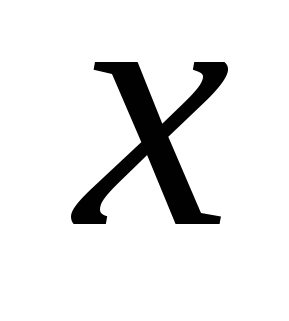 , для которых они определены.
, для которых они определены.
Пример 1. Вычислить 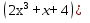 .
.
Решение. 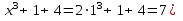
Пример 2. Вычислить 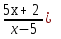 .
.
Решение. Здесь 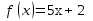 и
и ![]() . Так как
. Так как 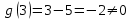 , то
, то
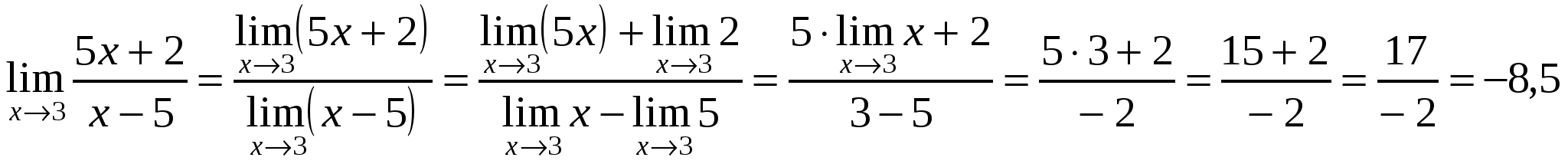 .
.
Пример 3. Вычислить предел 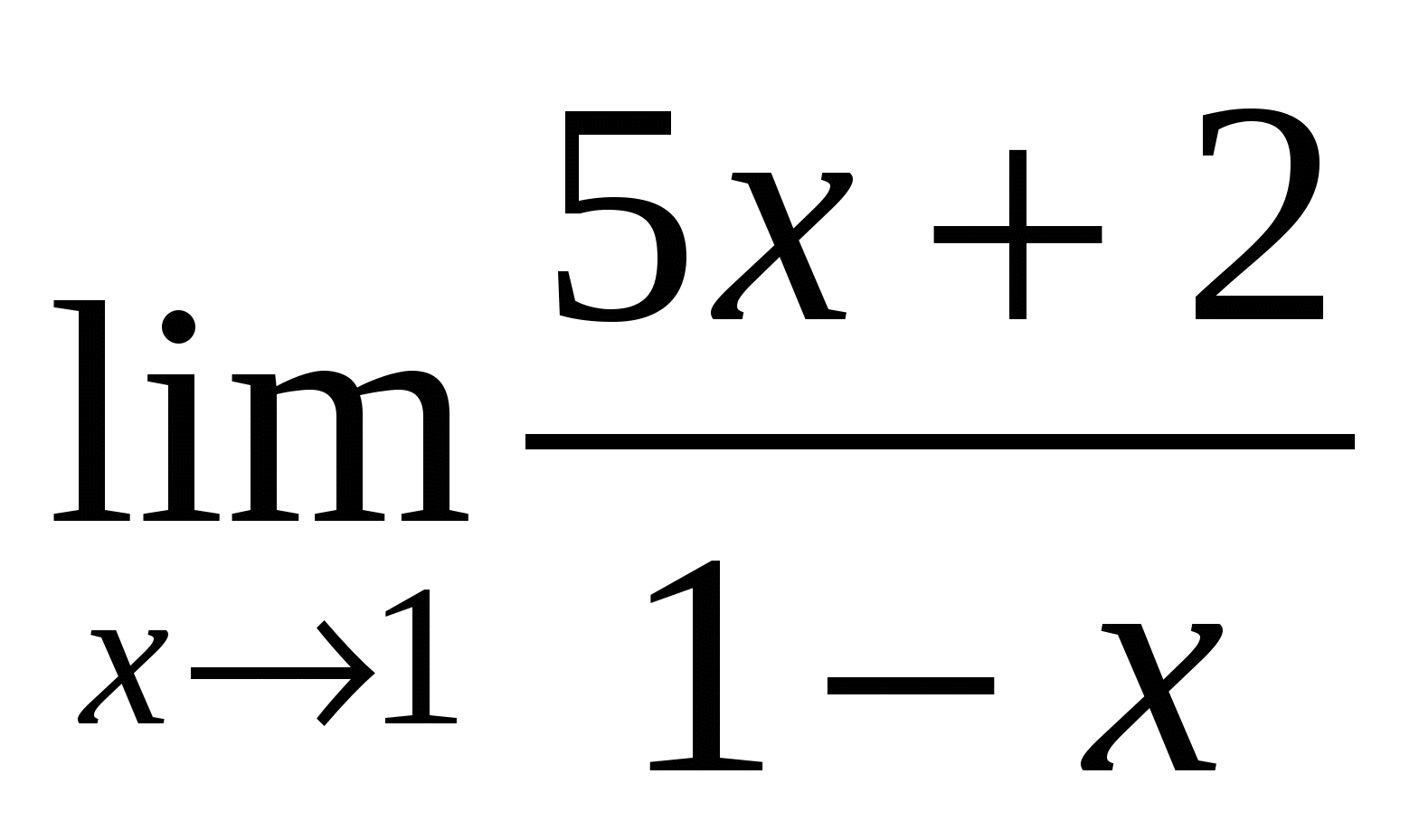 .
.
Решение. Здесь 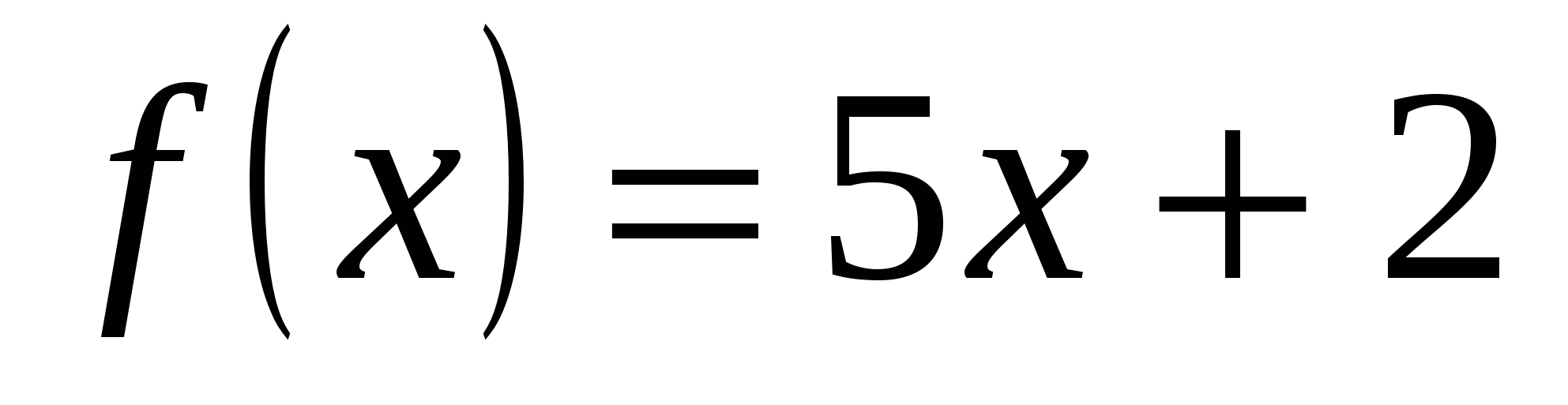 и
и ![]() . Так как
. Так как 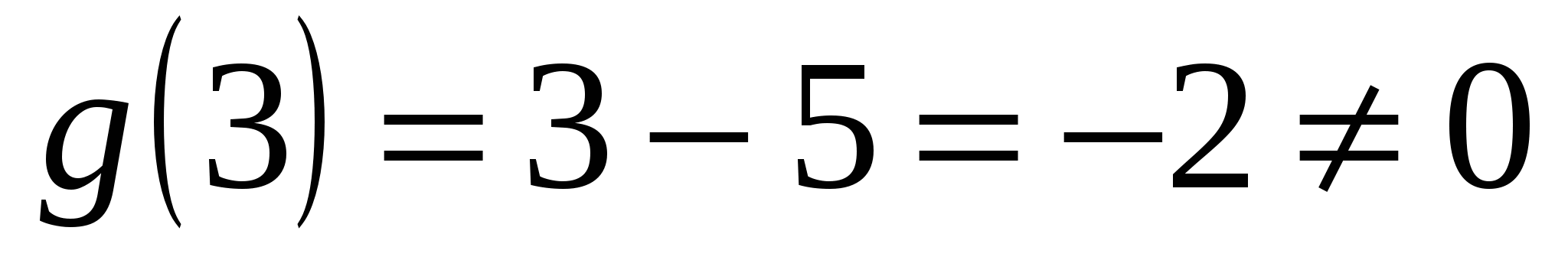 , то
, то
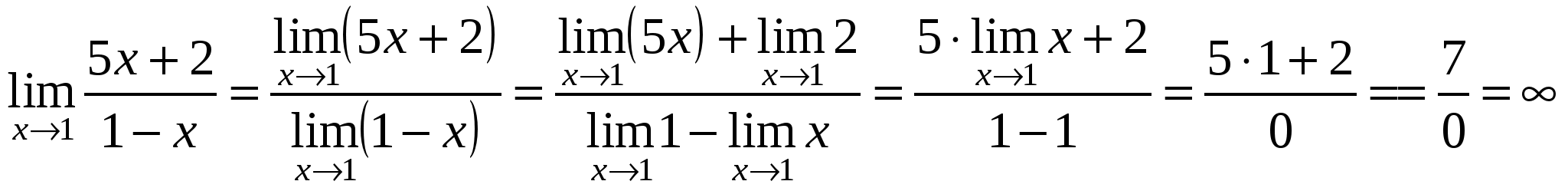
Неопределенность 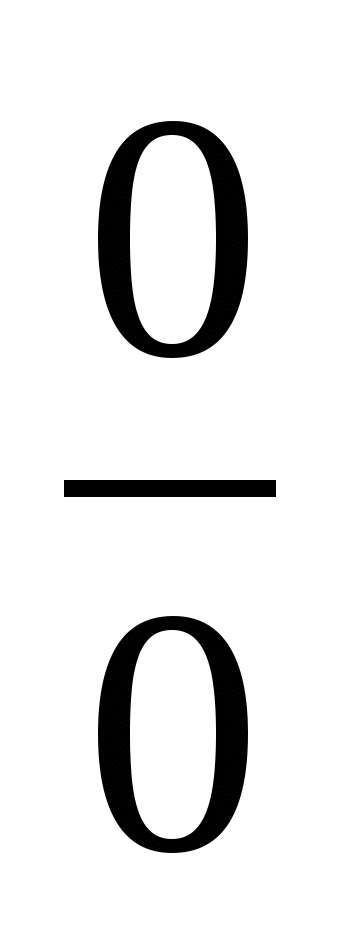 .
.
Неопределенности такого вида возникают при вычислении пределов типа: 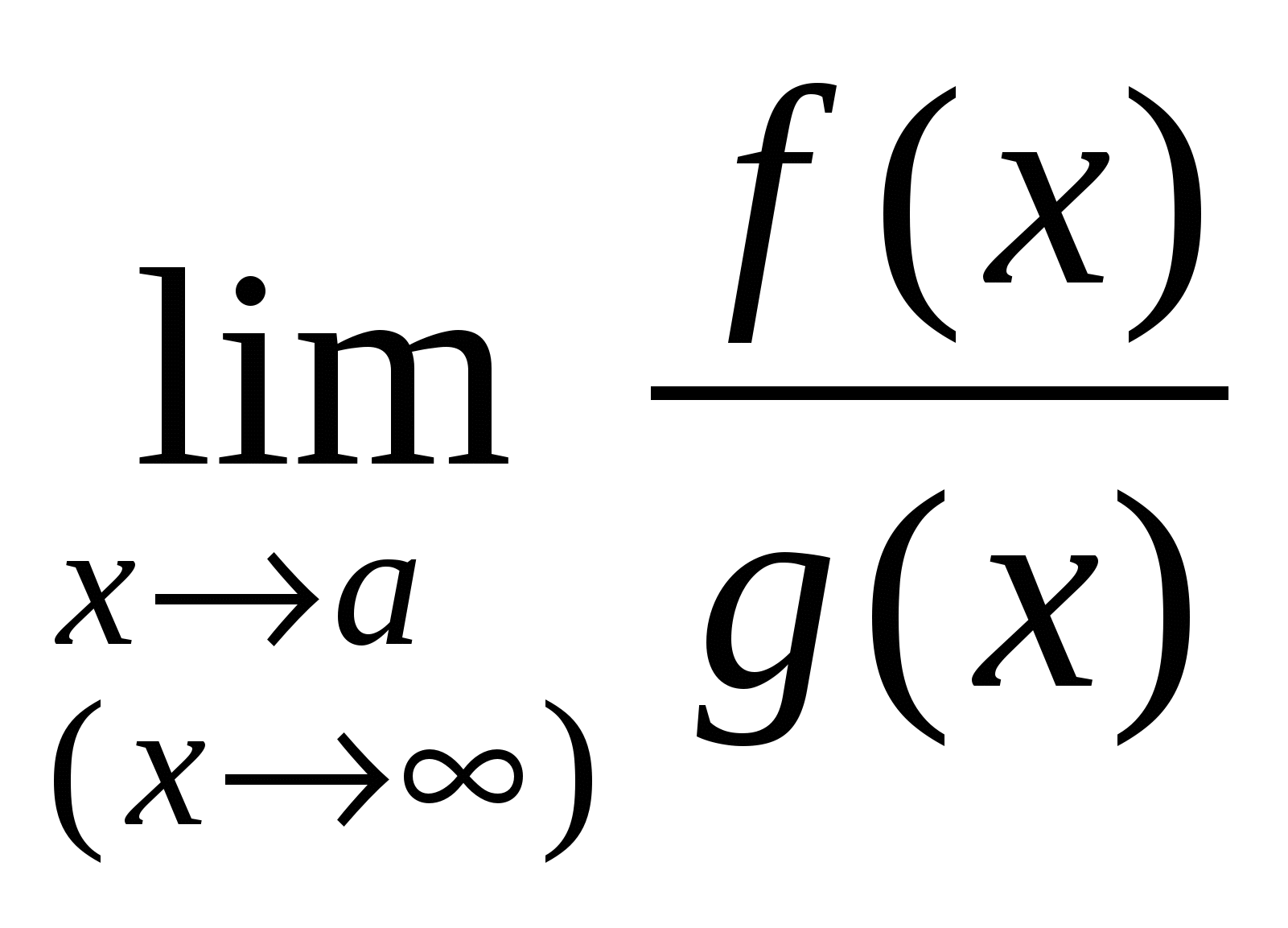 , если
, если 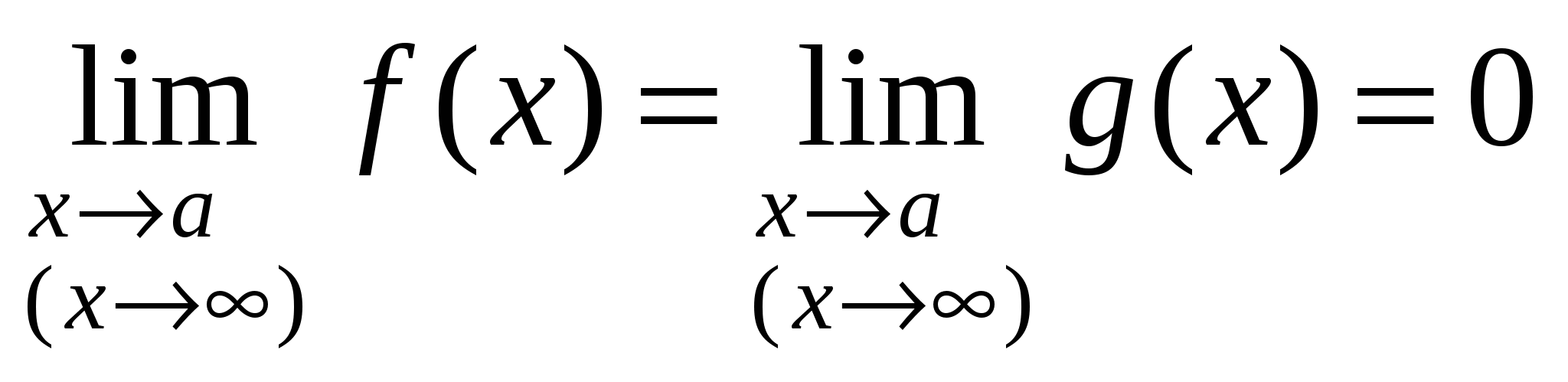
При этом возможны частные случаи:
-
Числитель
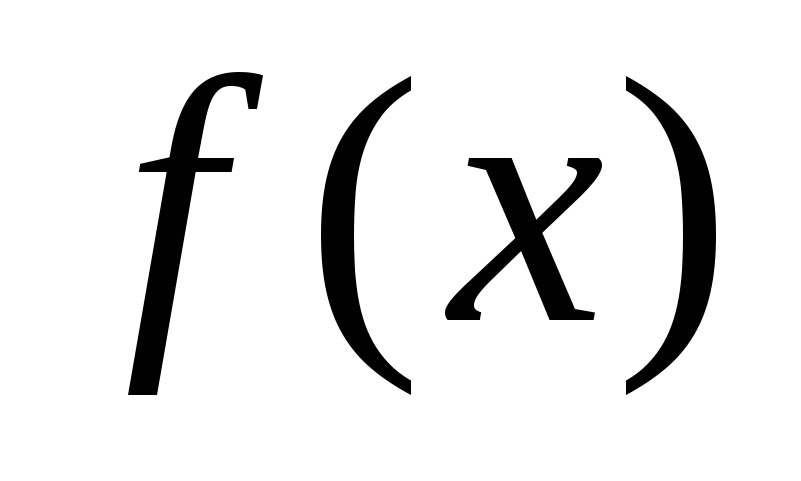 и знаменатель
и знаменатель 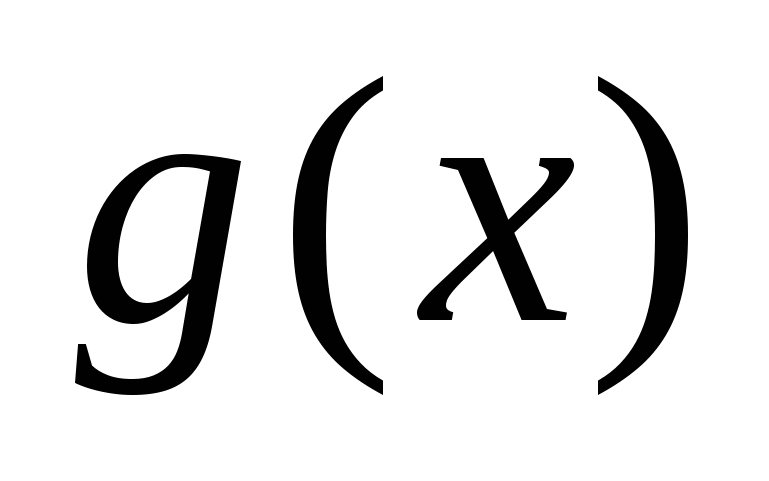 дроби многочлены.
дроби многочлены.
Для вычисления предела необходимо разложить числитель и знаменатель на множители и сократить дробь на множитель, порождающий нуль.
Пример 4. Вычислить предел 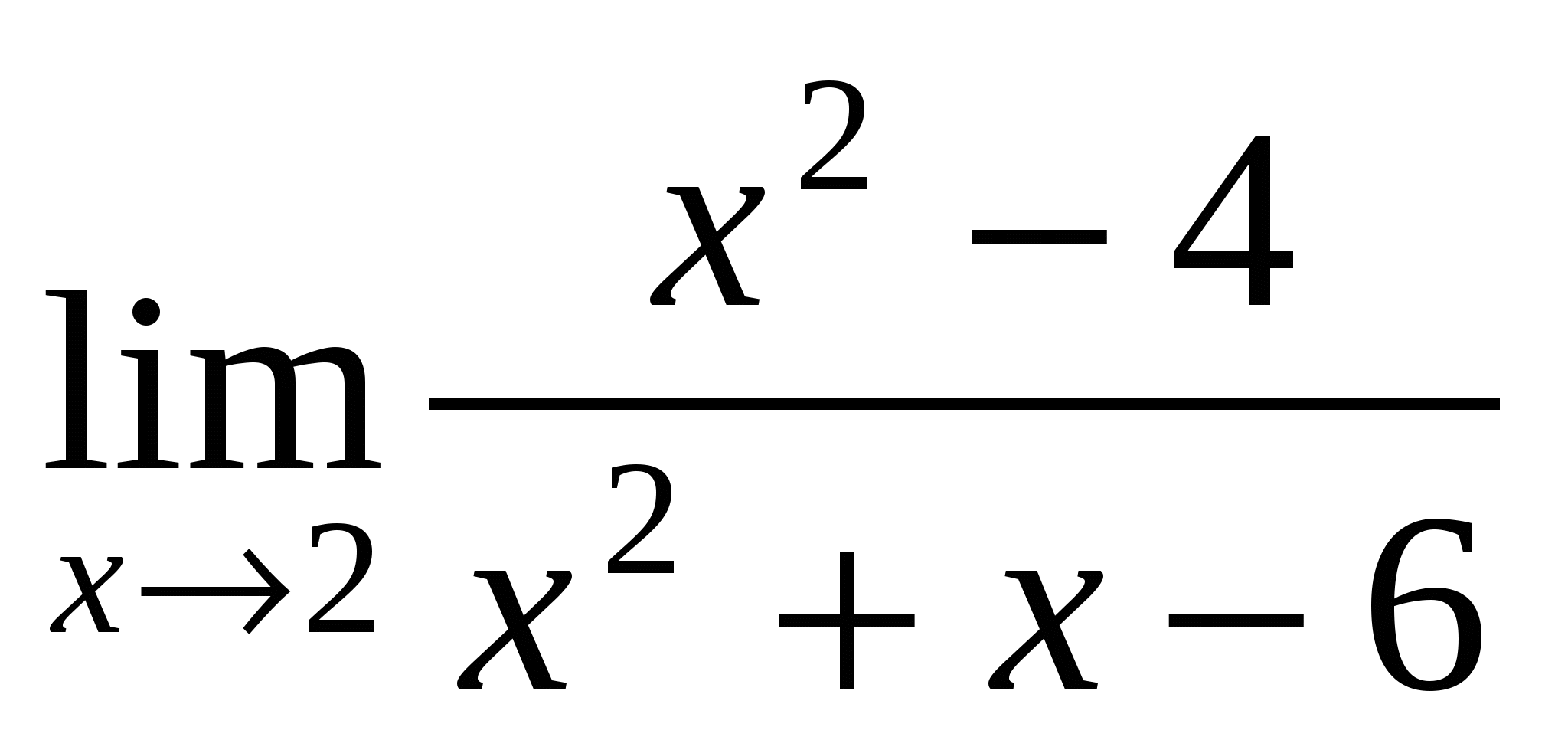 .
.
Решение. Здесь 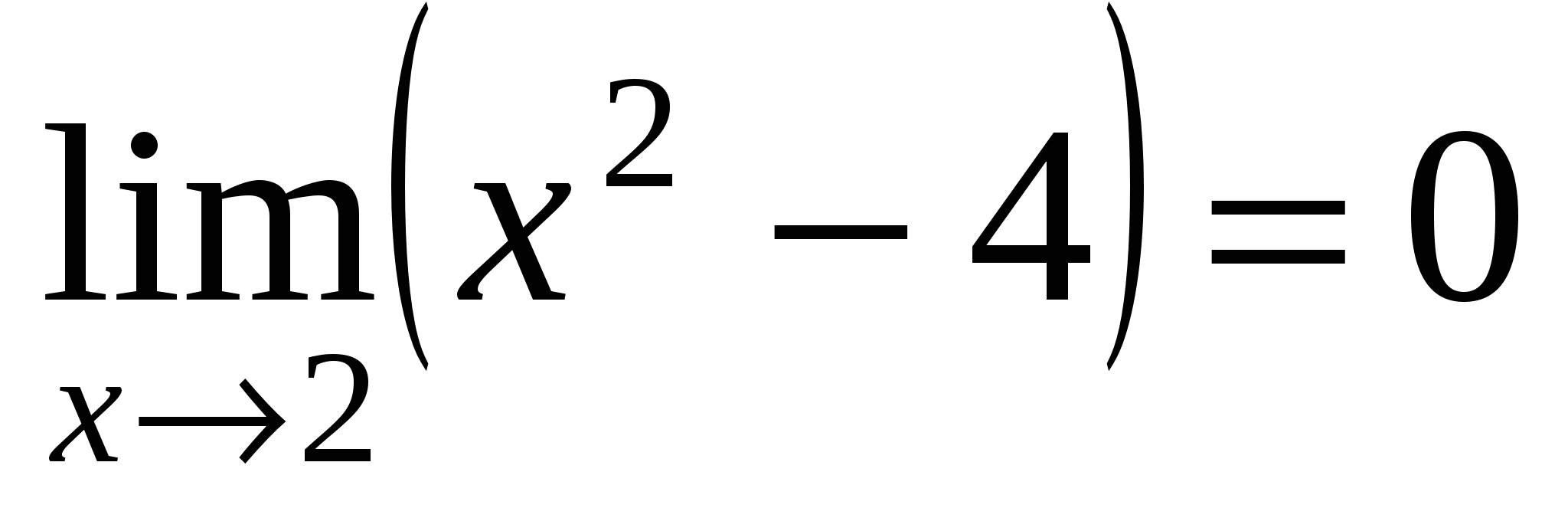 и
и 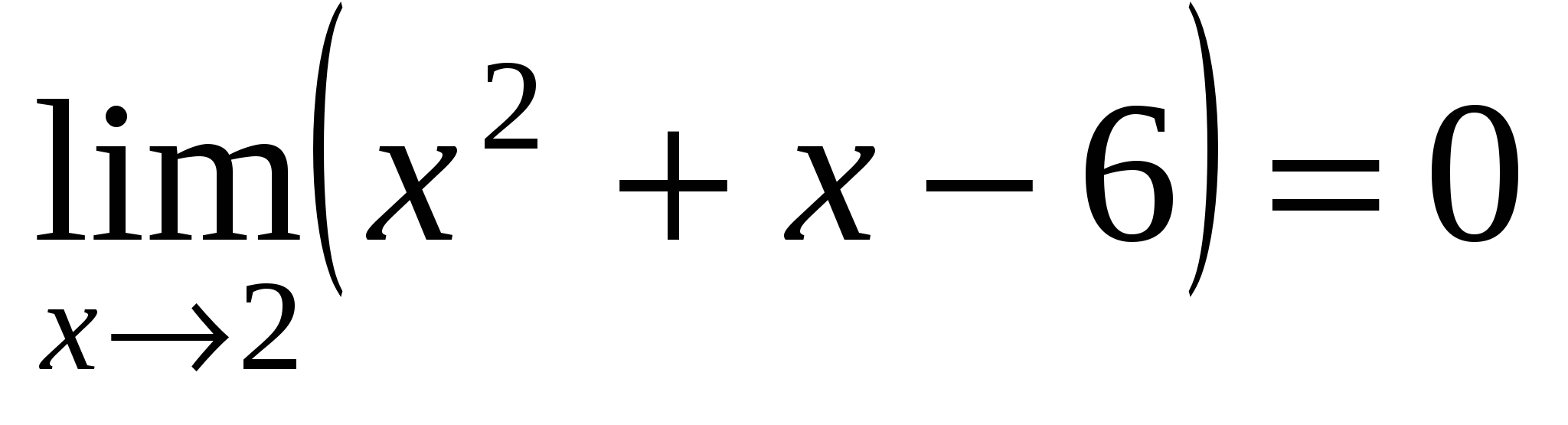 . Имеем неопределенность
. Имеем неопределенность 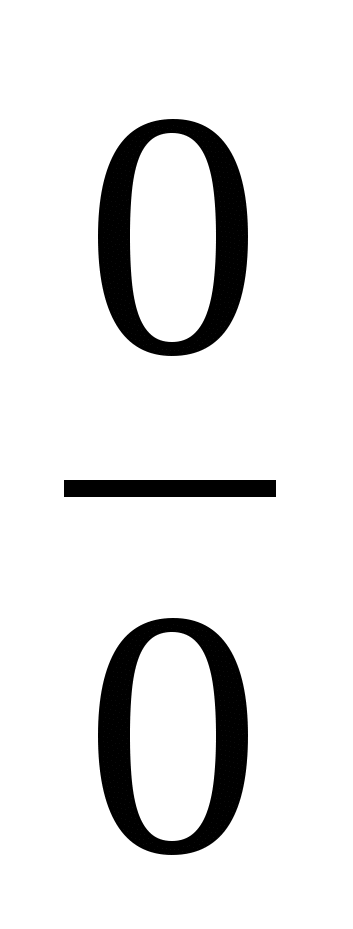 . Разложим числитель и знаменатель на множители.
. Разложим числитель и знаменатель на множители. 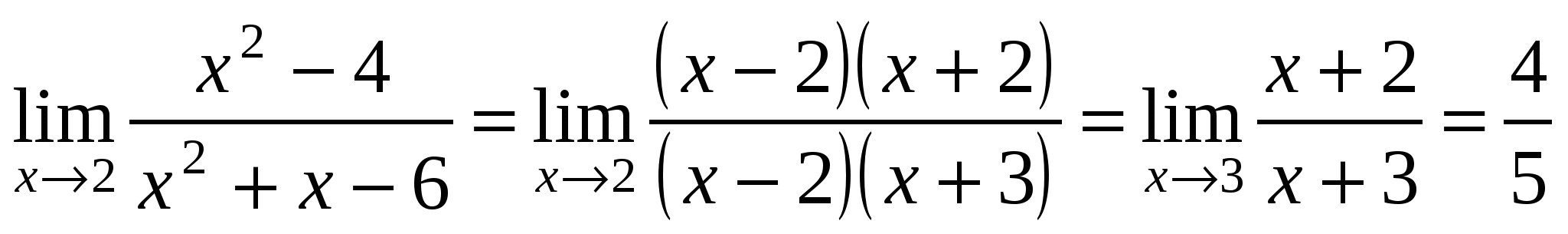
Пример 5. Найти 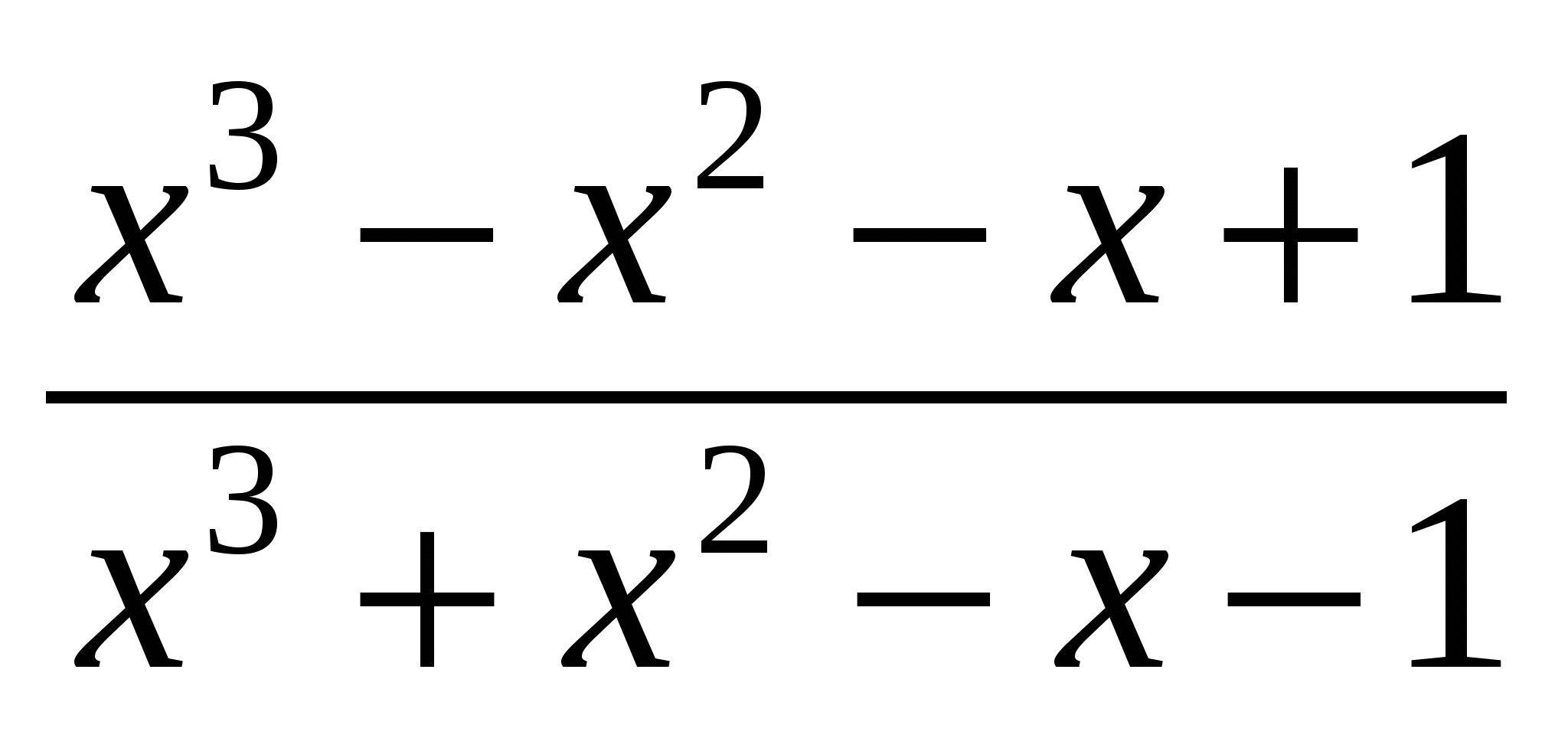
Решение. Разложим на множители числитель и знаменатель дроби:

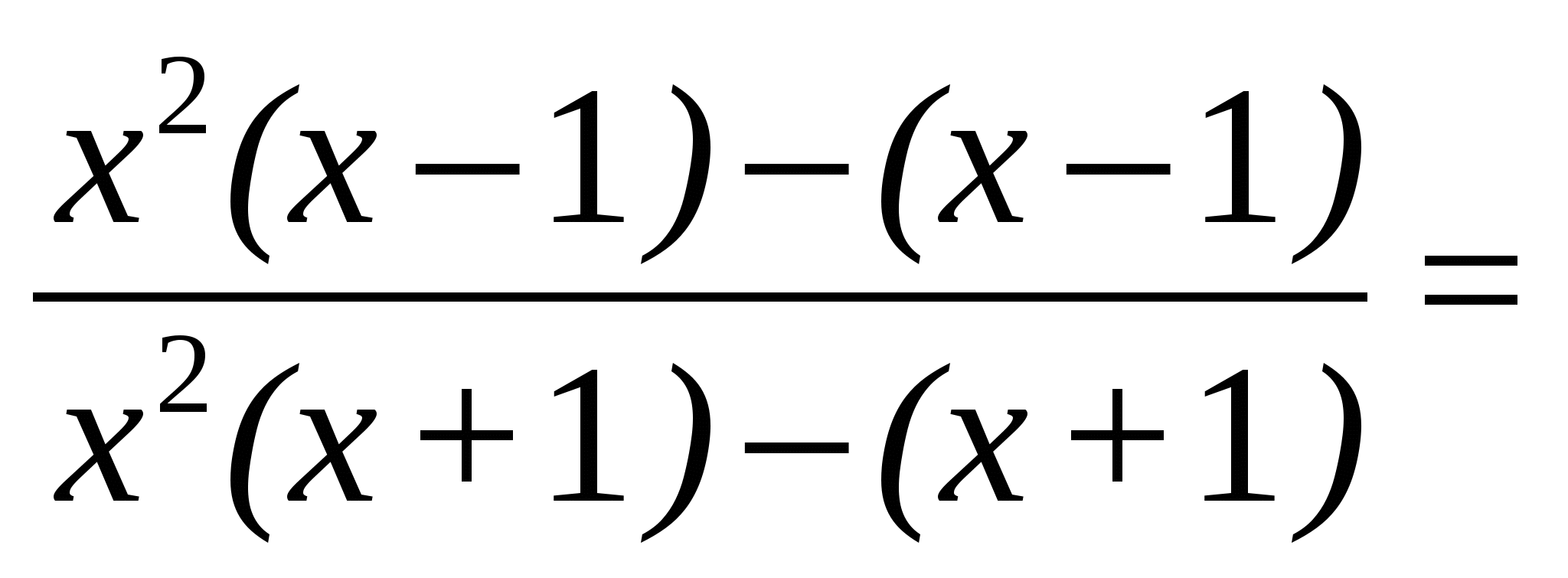
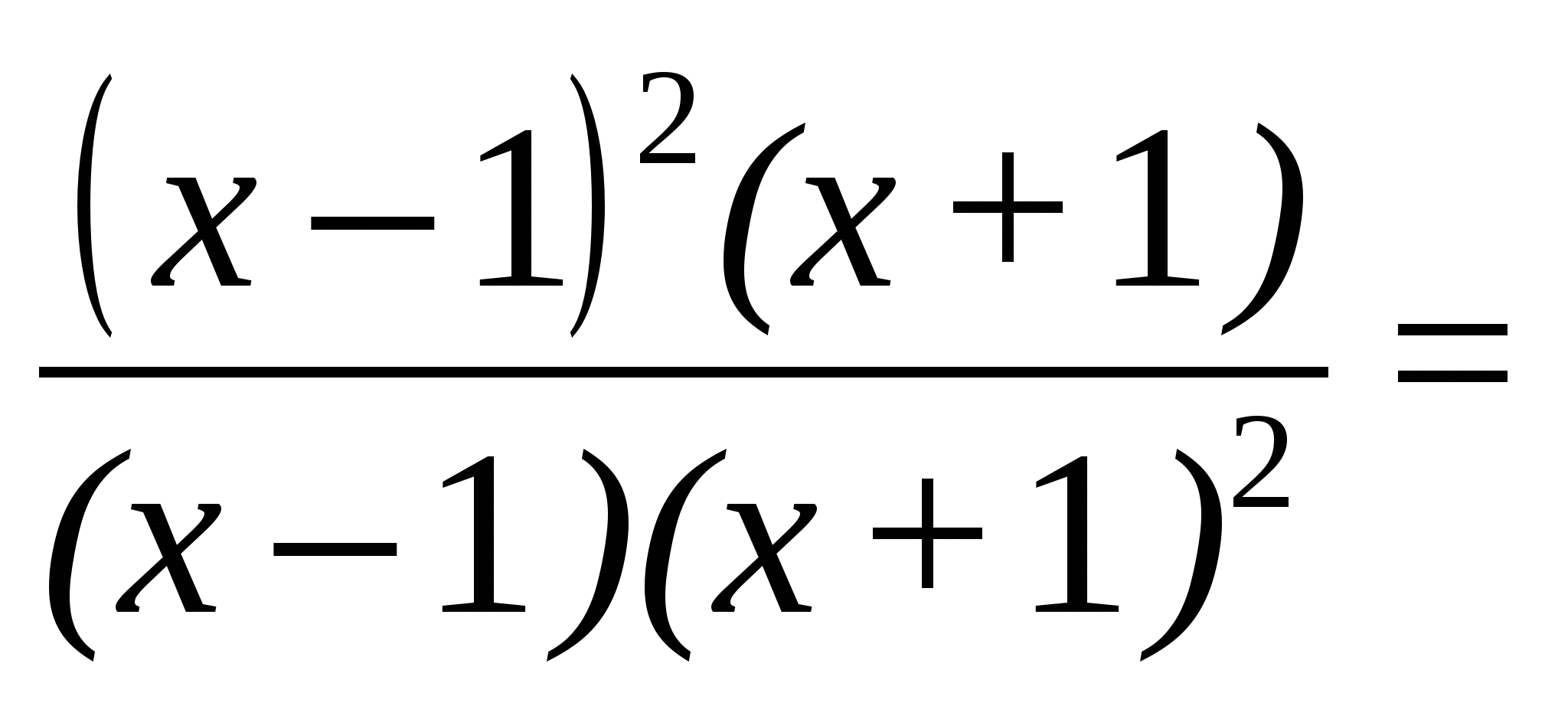
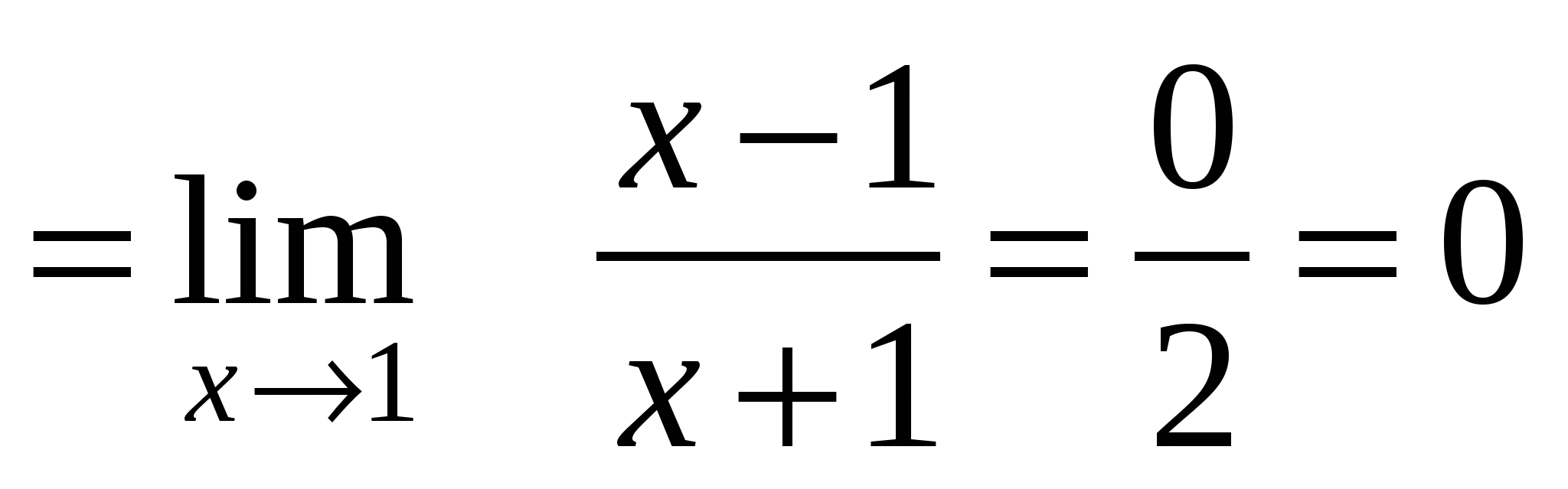
2. Числитель или знаменатель дроби, или оба содержат иррациональность. Для решения примера необходимо освободиться от иррациональности, умножив числитель и знаменатель дроби на сопряженное выражение, сократить дробь на множитель, порождающий нуль.
Пример 6. Вычислить 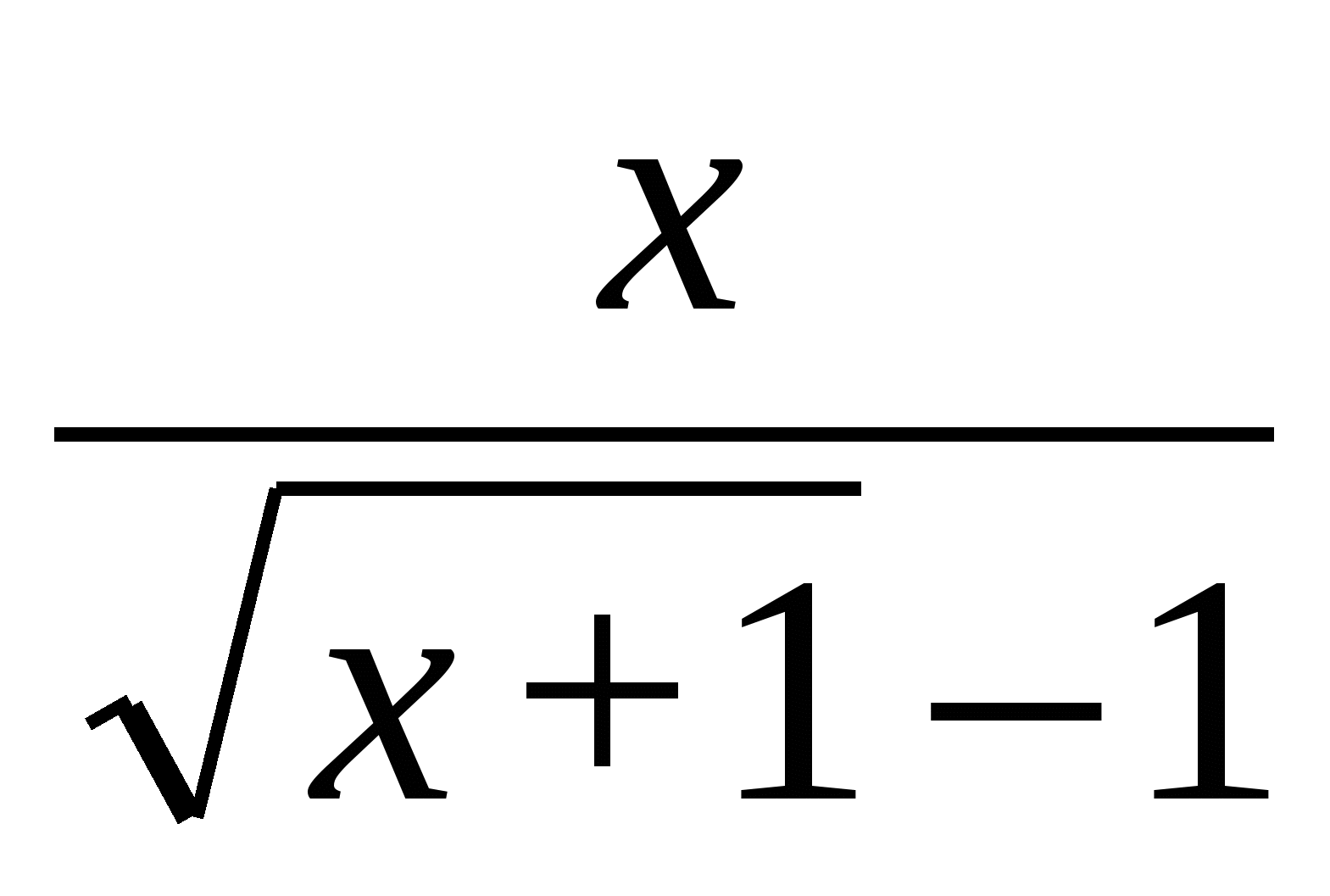
Решение. При  числитель и знаменатель стремятся к нулю. Так как
числитель и знаменатель стремятся к нулю. Так как 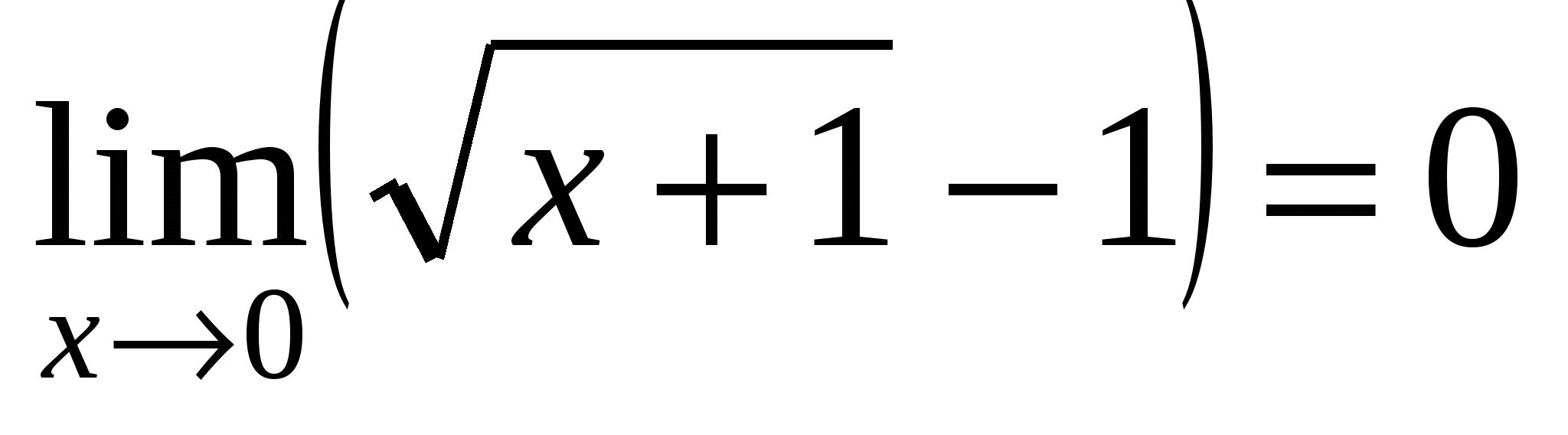 то теорему о пределе частного применять нельзя. Для раскрытия неопределенности
то теорему о пределе частного применять нельзя. Для раскрытия неопределенности ![]() умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, получим:
умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, получим:
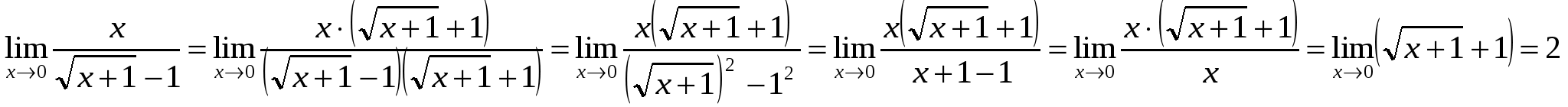 Пример 7. Найти
Пример 7. Найти 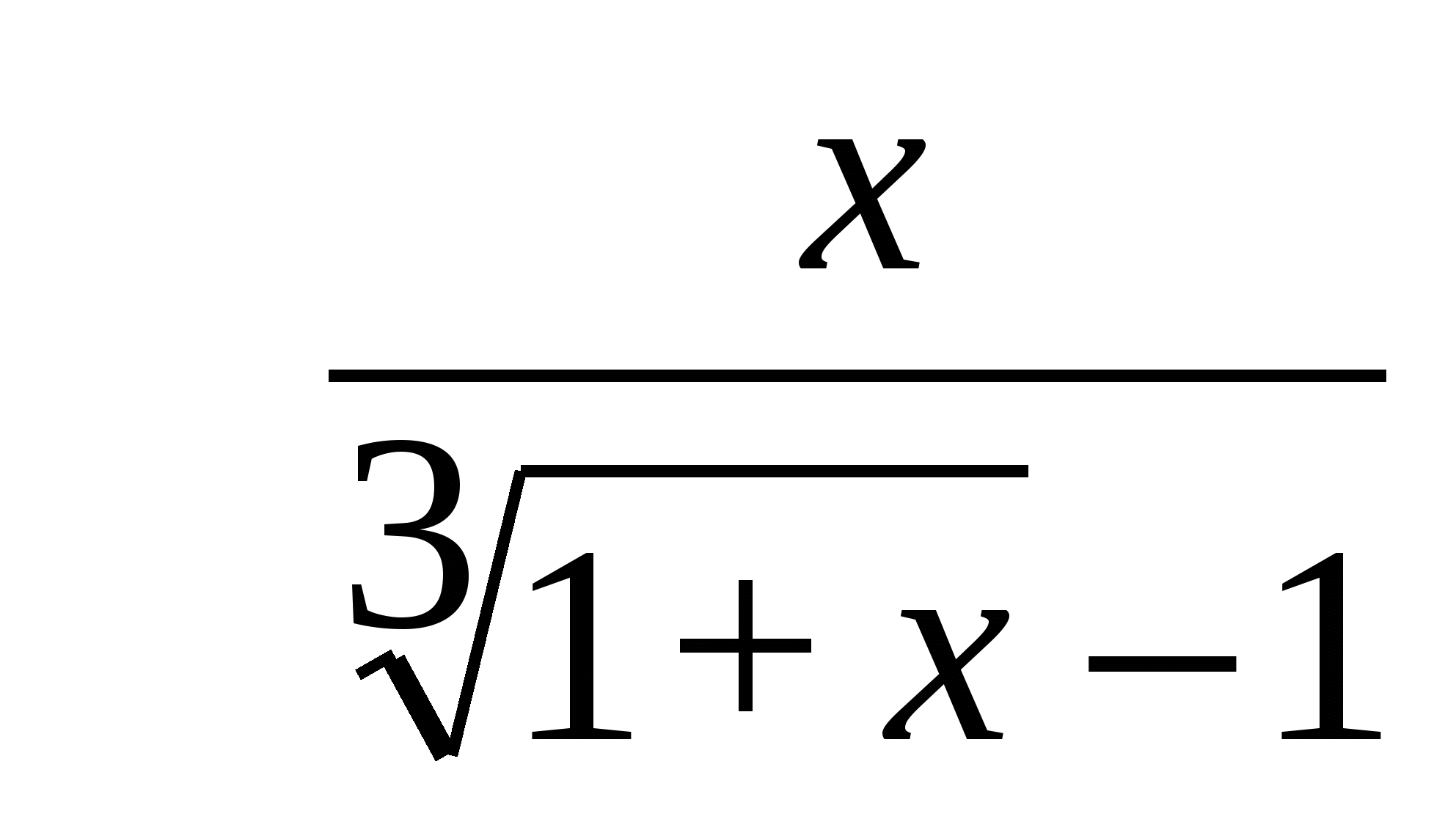
Решение. При  числитель и знаменатель стремятся к нулю. Для раскрытия неопределенности
числитель и знаменатель стремятся к нулю. Для раскрытия неопределенности ![]() умножим числитель и знаменатель на выражение, сопряженное знаменателю по формуле разности кубов. Тогда получим:
умножим числитель и знаменатель на выражение, сопряженное знаменателю по формуле разности кубов. Тогда получим:
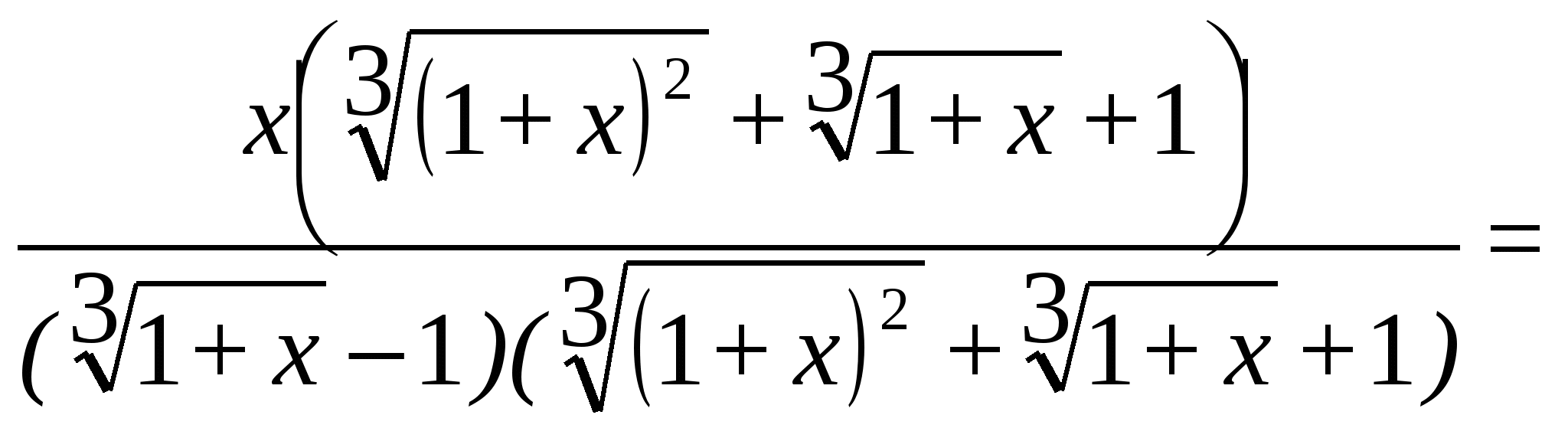
 =
=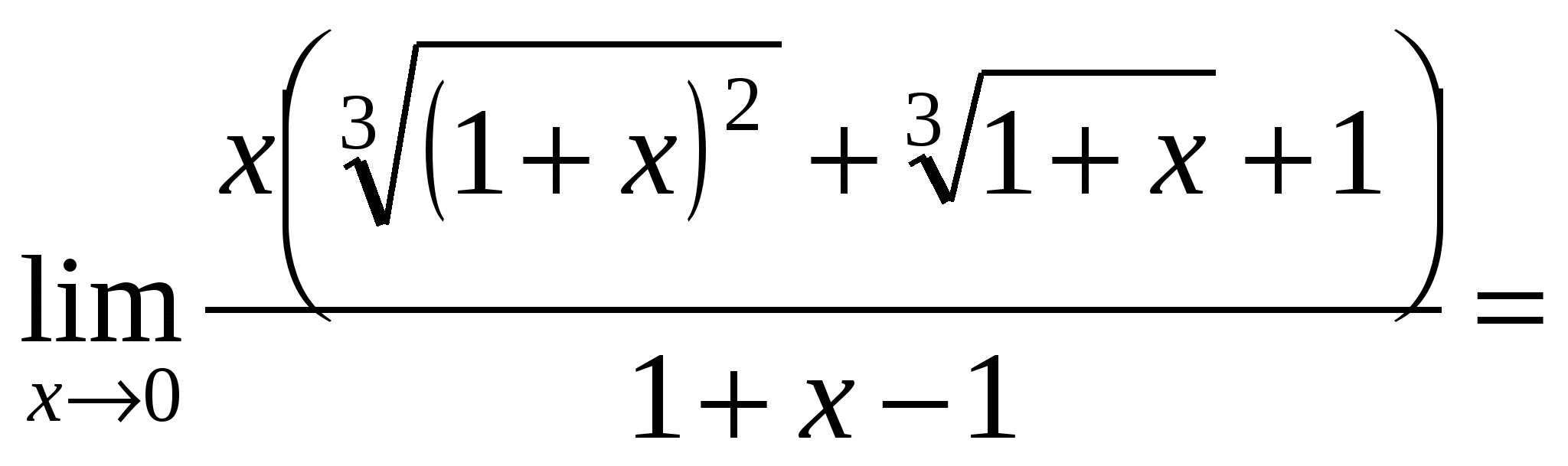
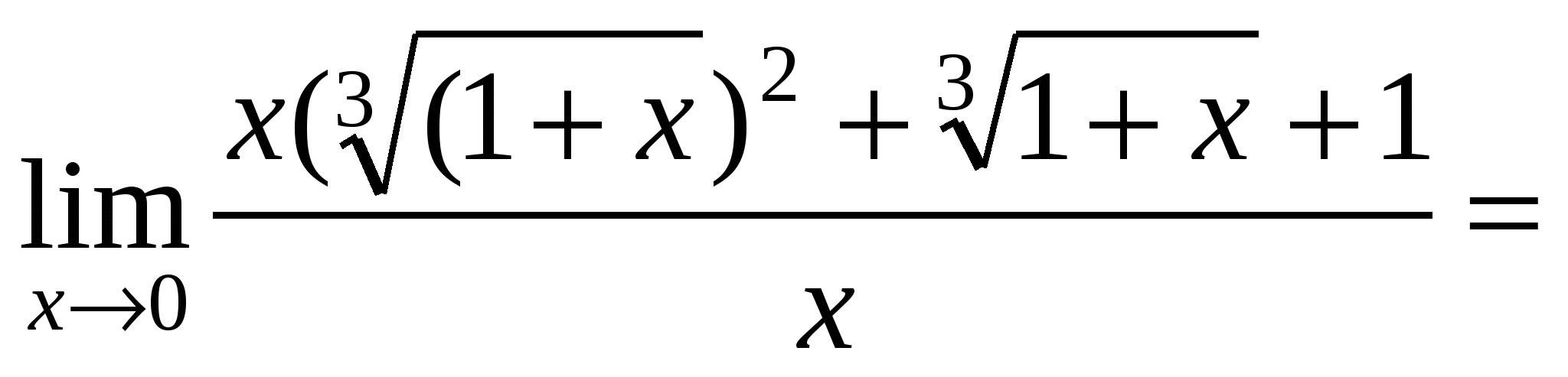
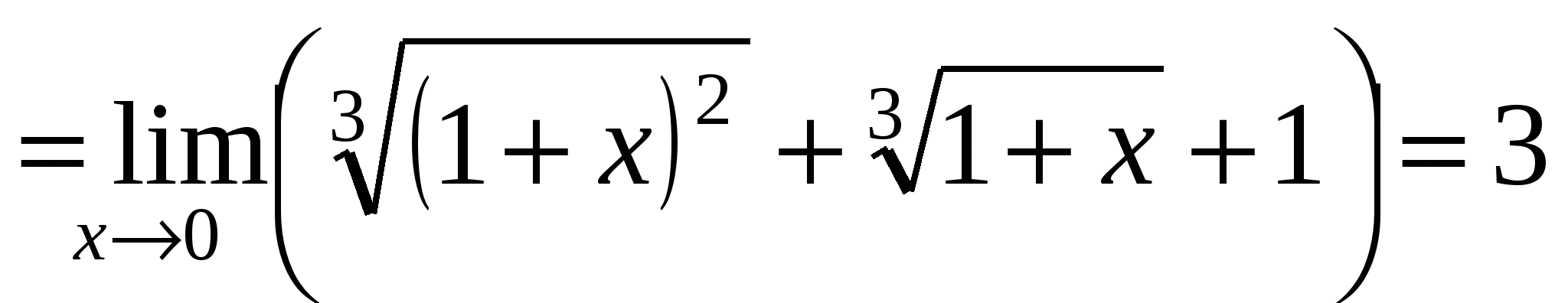
3. Выражение содержит тригонометрические функции. Для решения примера необходимо путем тригонометрических и алгебраических преобразований свести его к первому замечательному пределу.
Пример 8. Найти 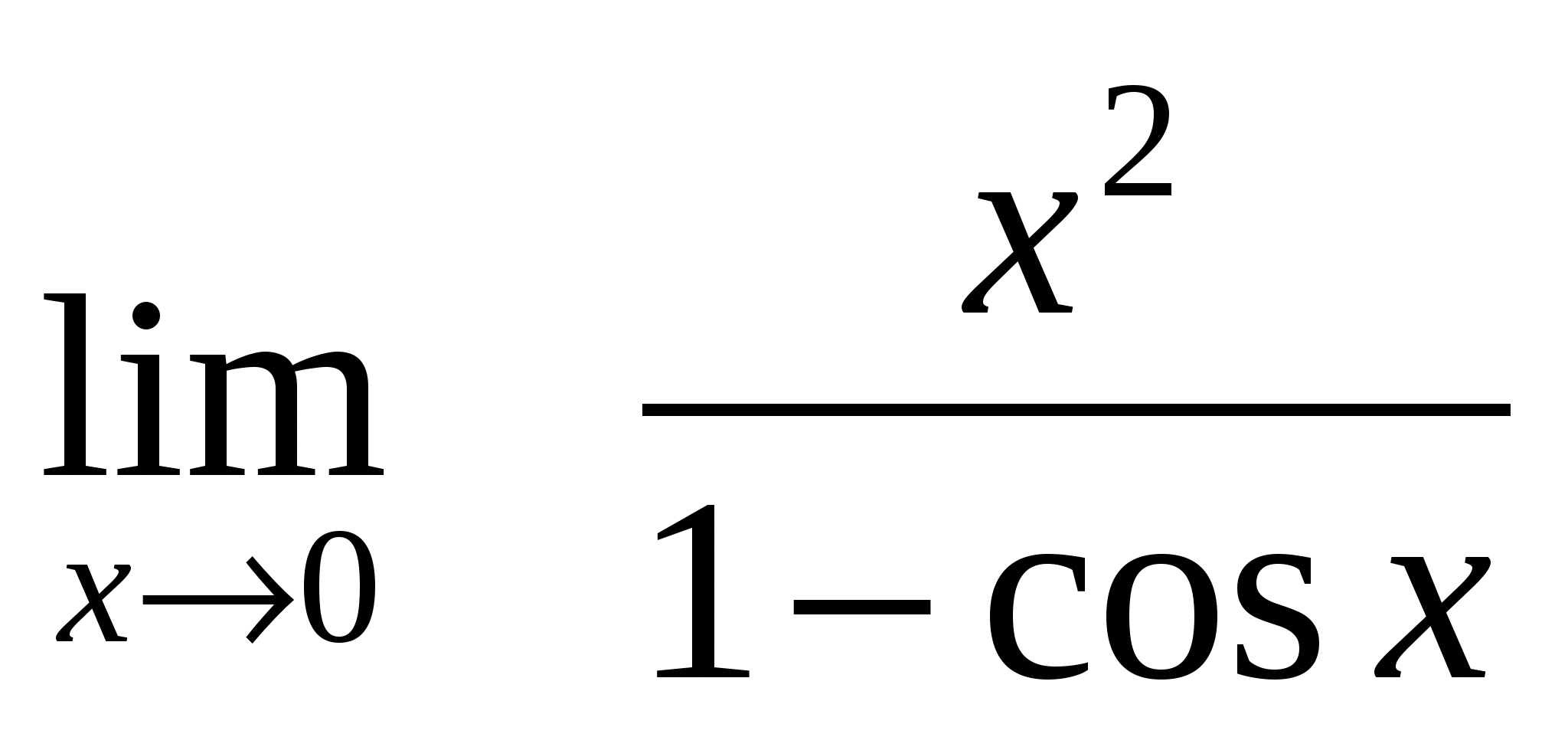
Решение. Подстановкой предельного значения 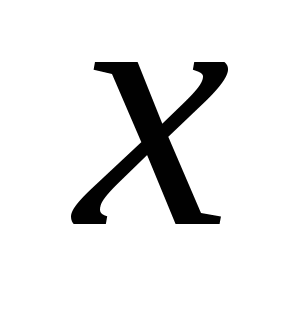 убедимся, что имеем неопределенность
убедимся, что имеем неопределенность 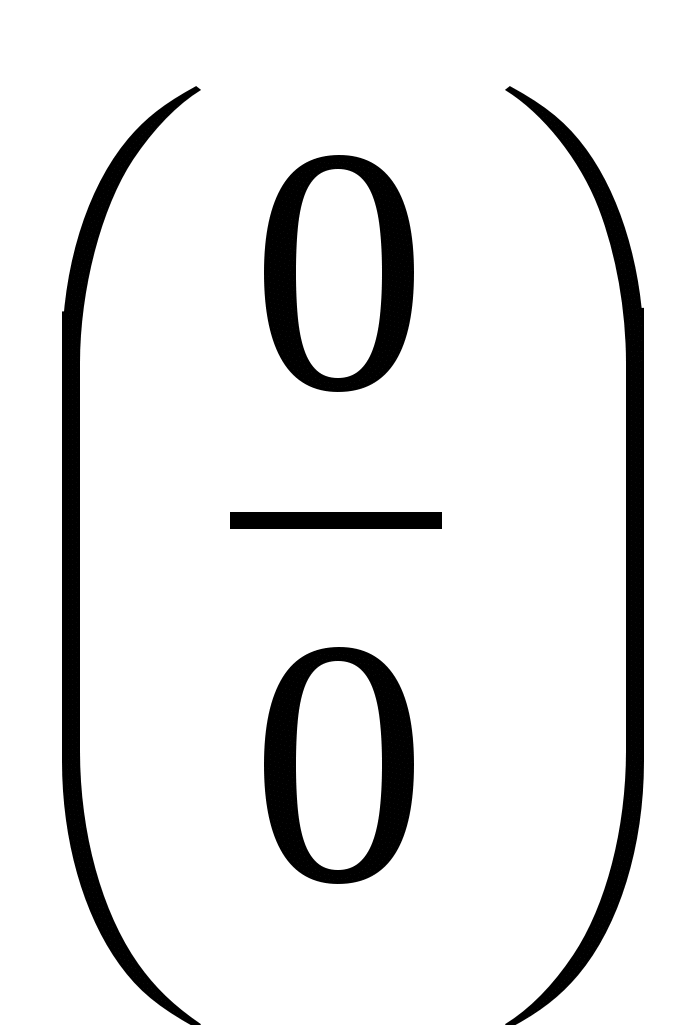 . Применяем тригонометрическую формулу
. Применяем тригонометрическую формулу 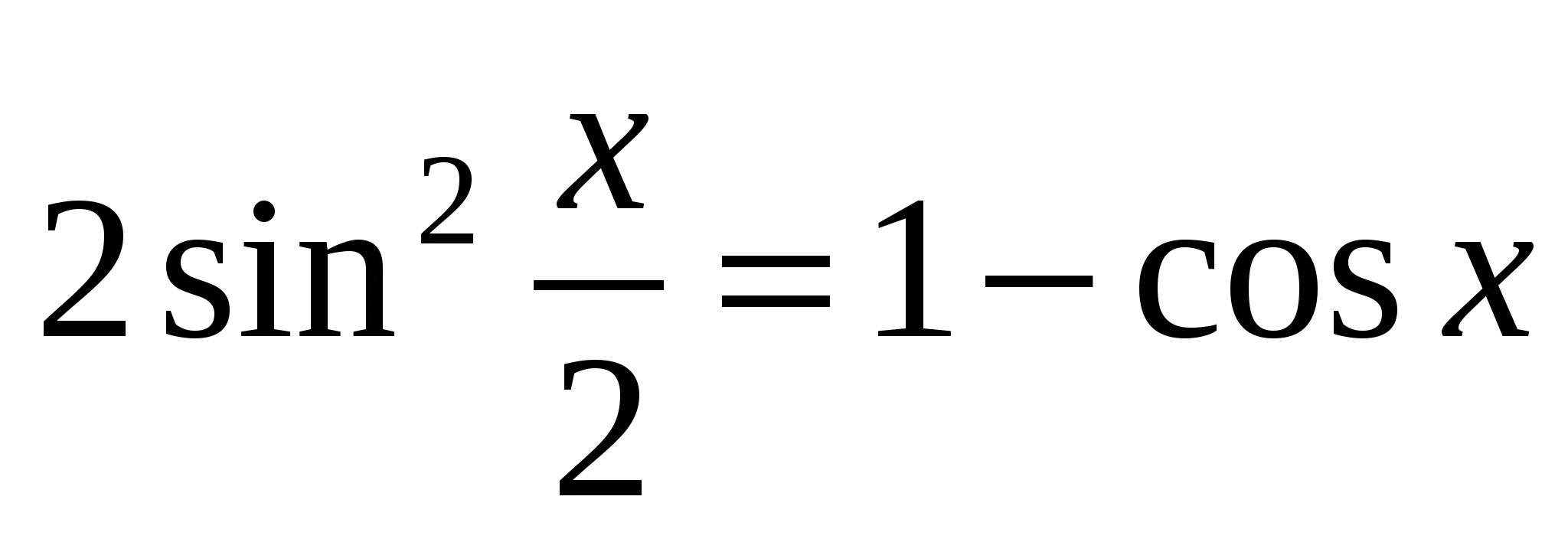 , преобразуем полученное выражение, сводим к первому замечательному пределу.
, преобразуем полученное выражение, сводим к первому замечательному пределу.
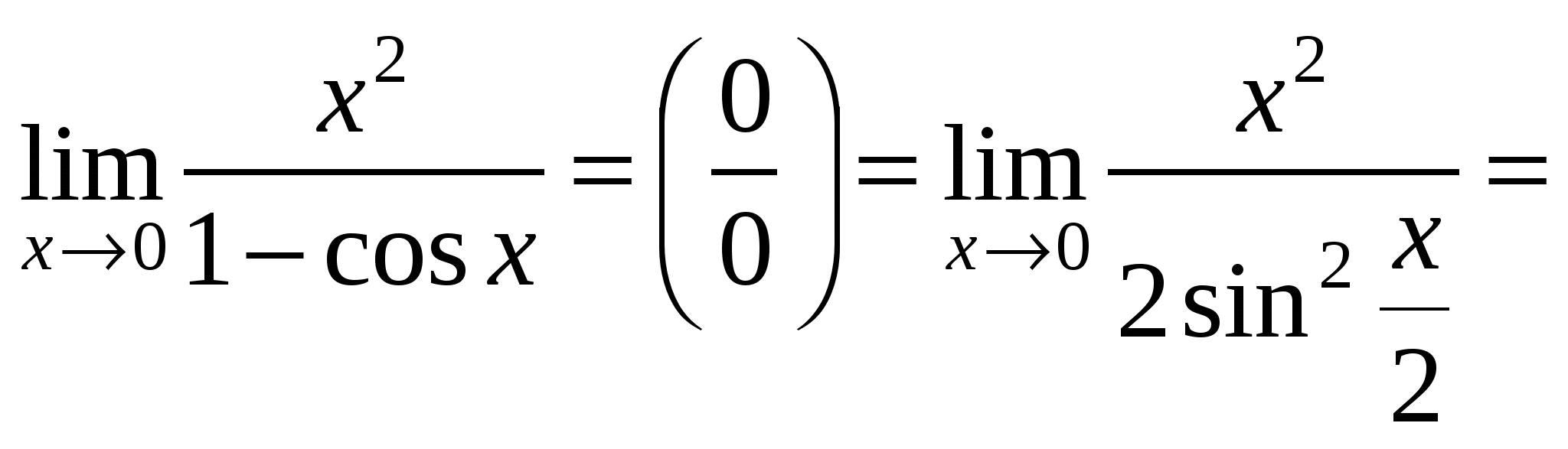
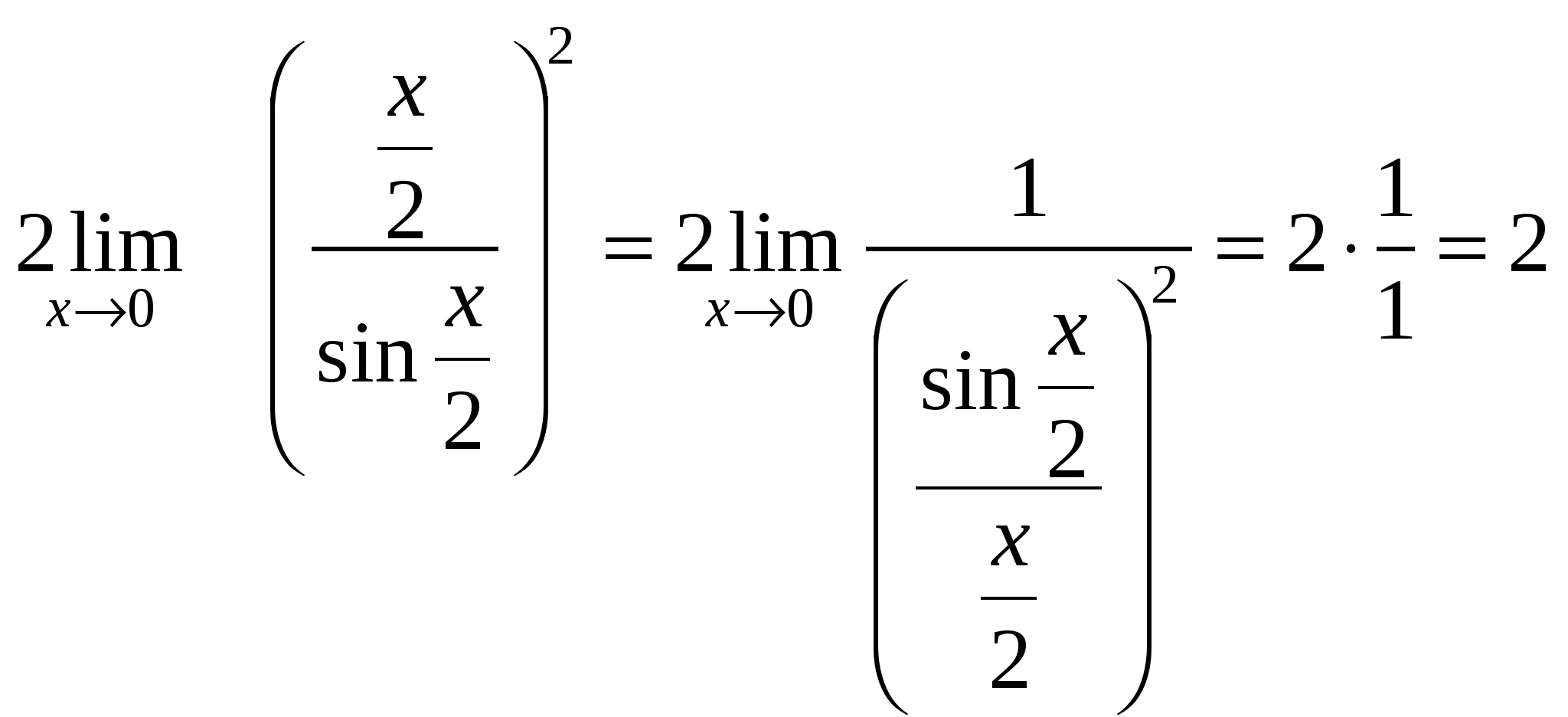
Неопределенность вида 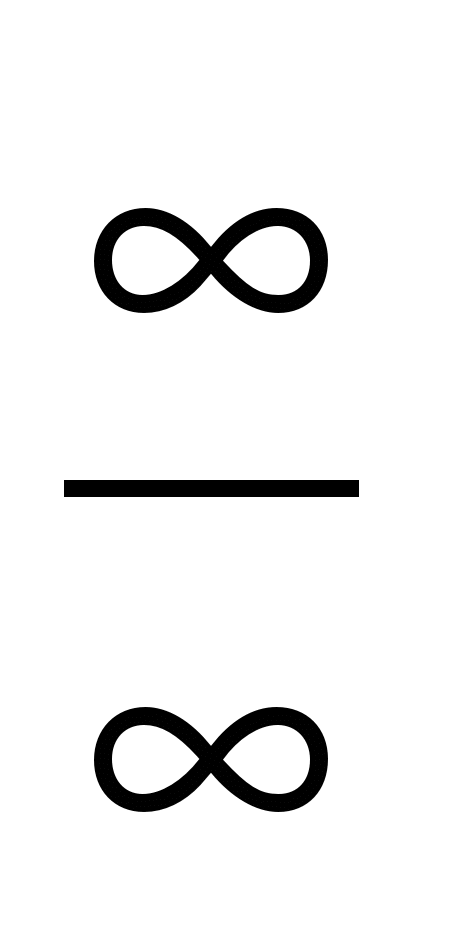
1. Числитель и знаменатель дроби при  - полиномы.
- полиномы.
![]() Для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень с наивысшим показателем, а затем перейти к пределу.
Для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень с наивысшим показателем, а затем перейти к пределу.
Пример 9. Найти 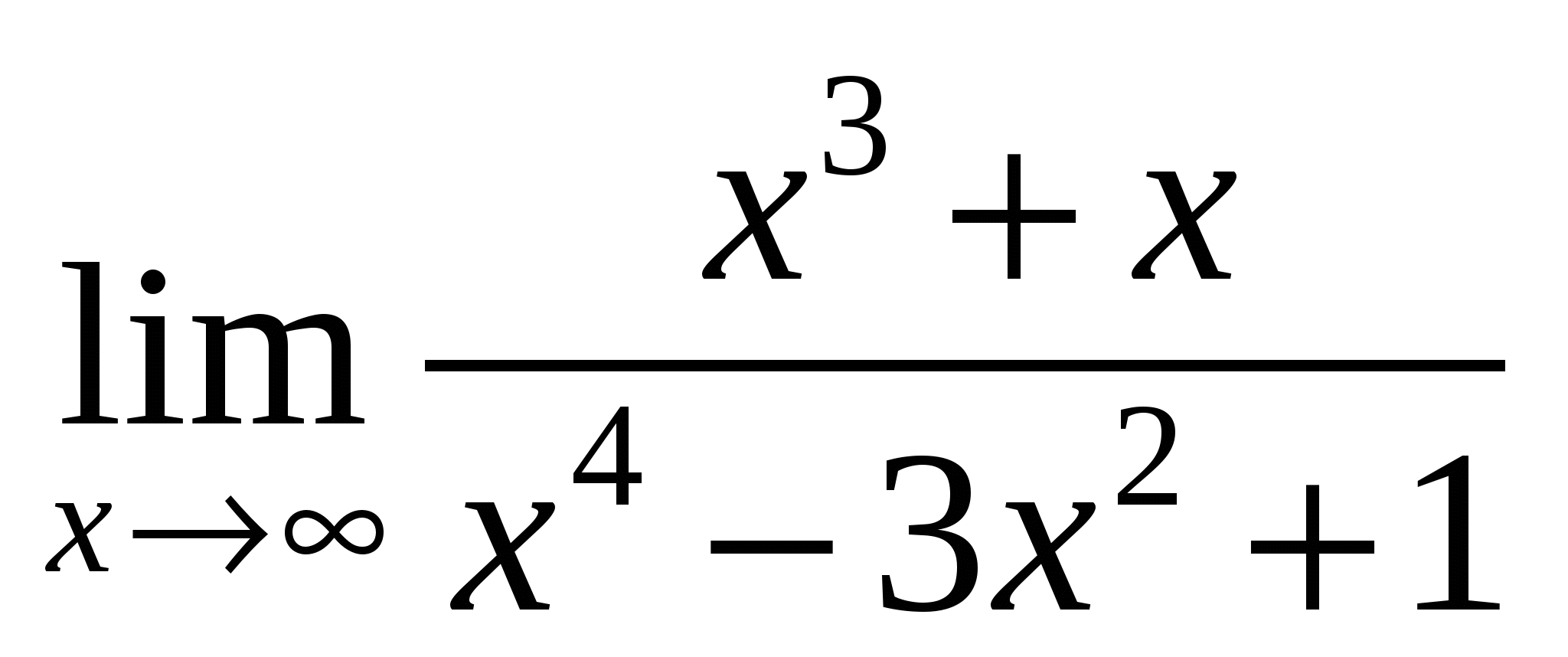
Решение. 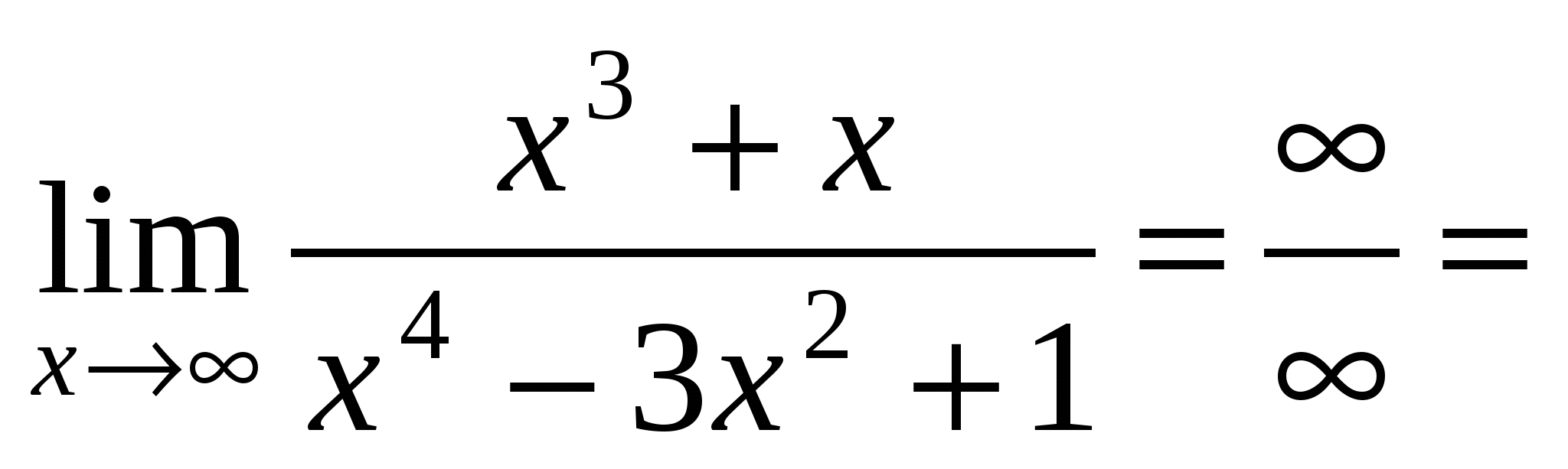
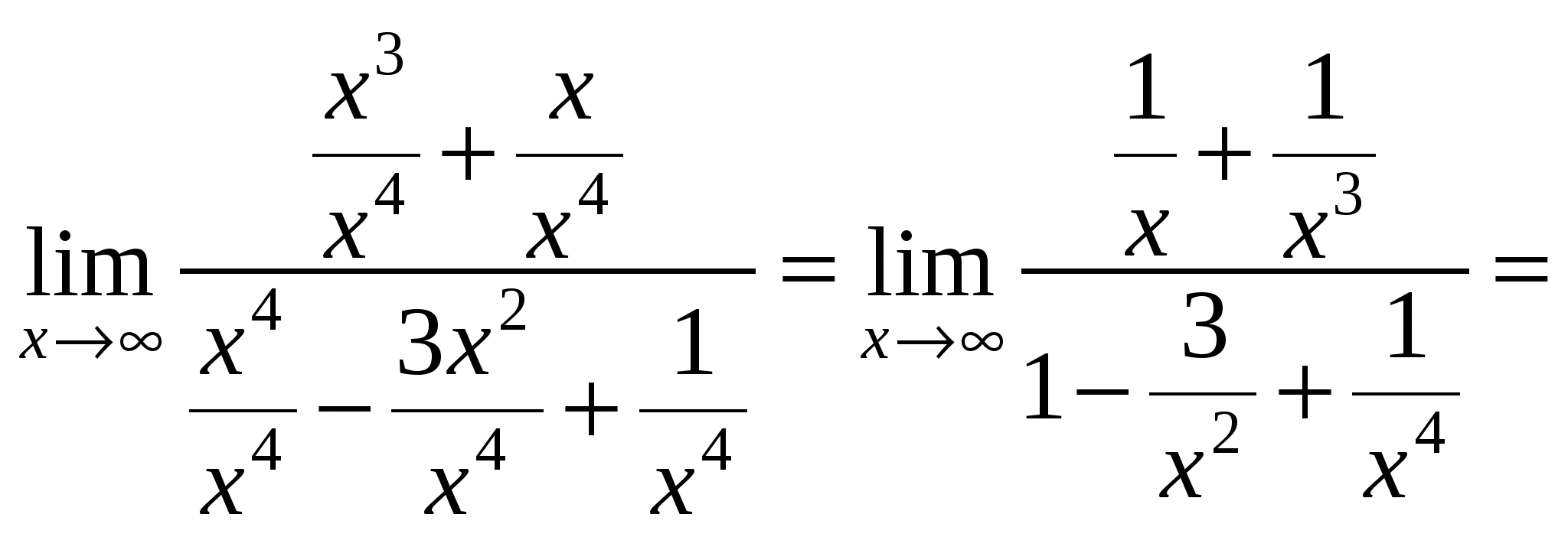
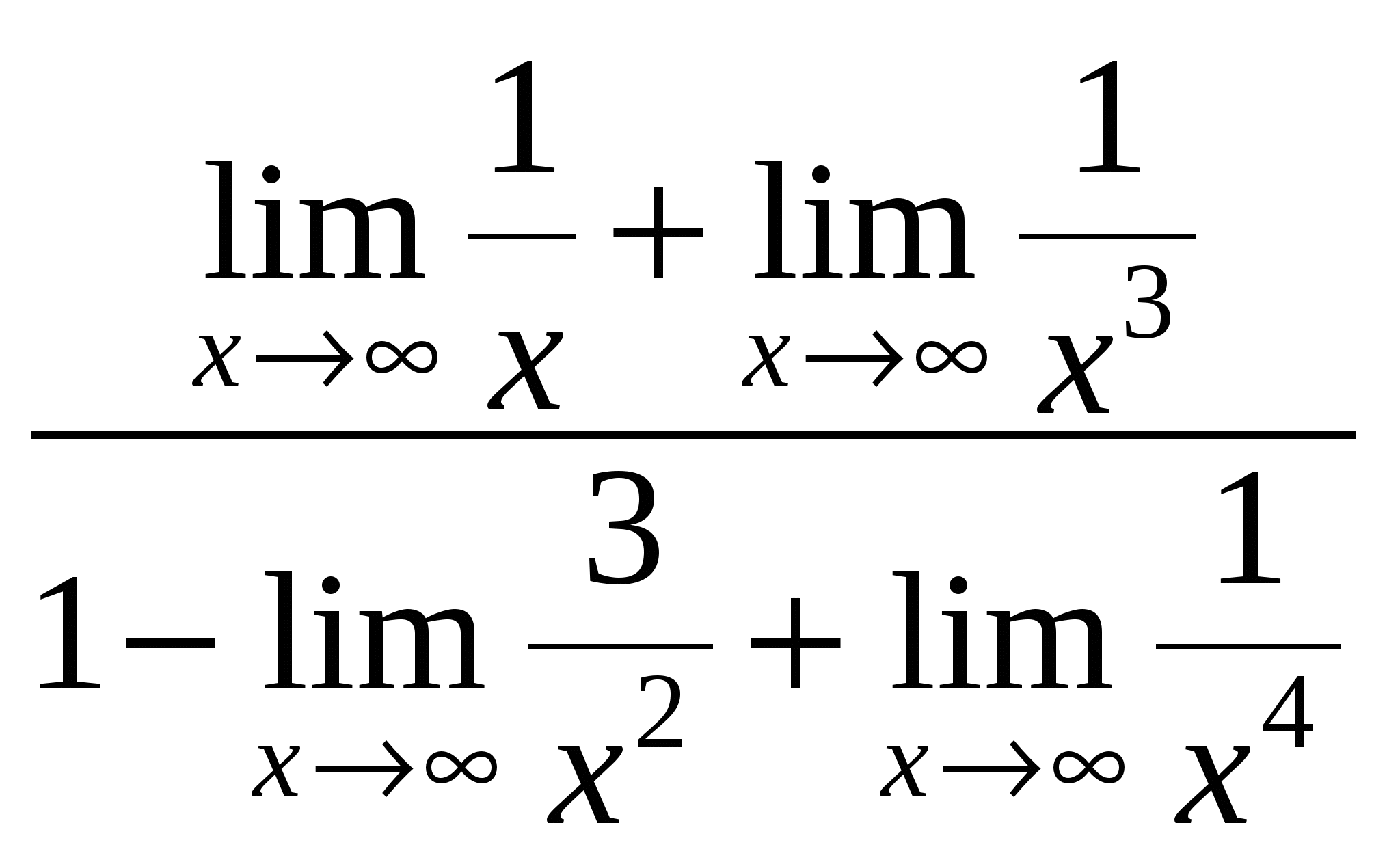
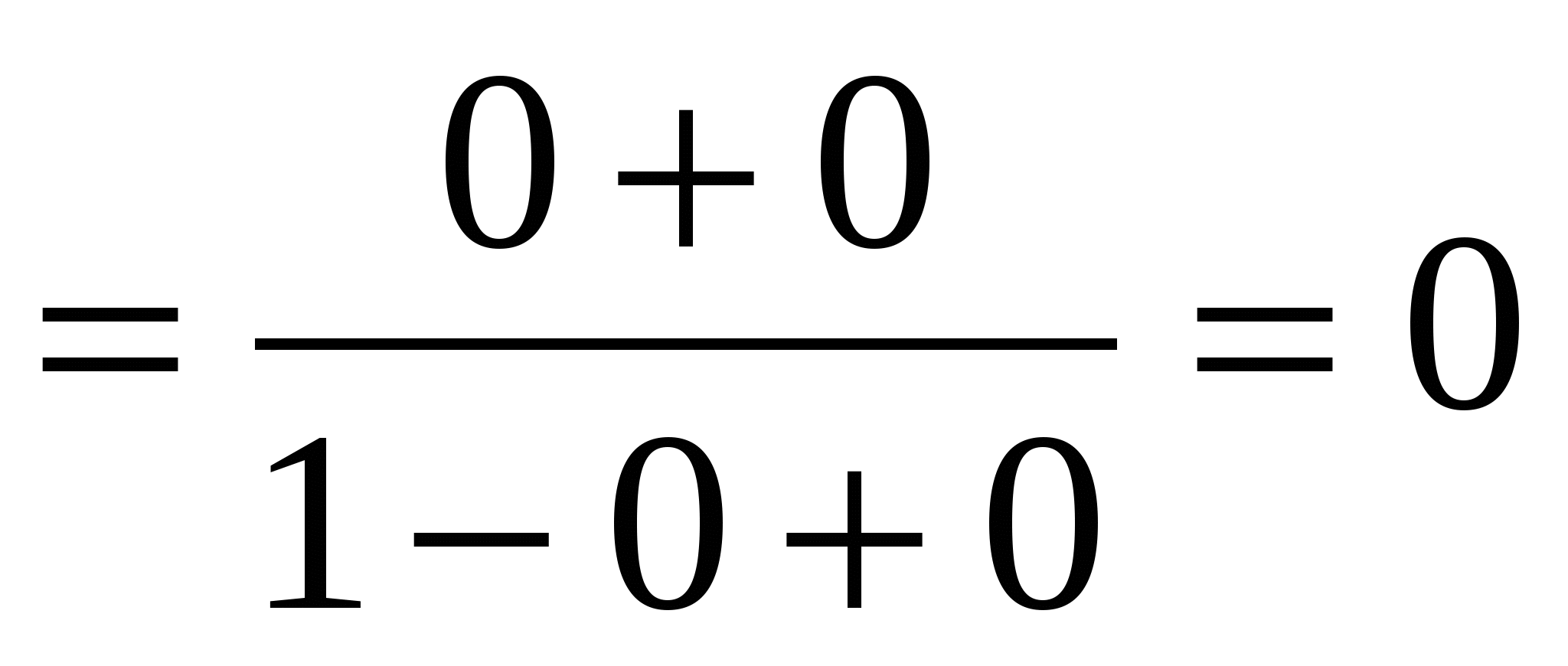
Пример 10. Найти 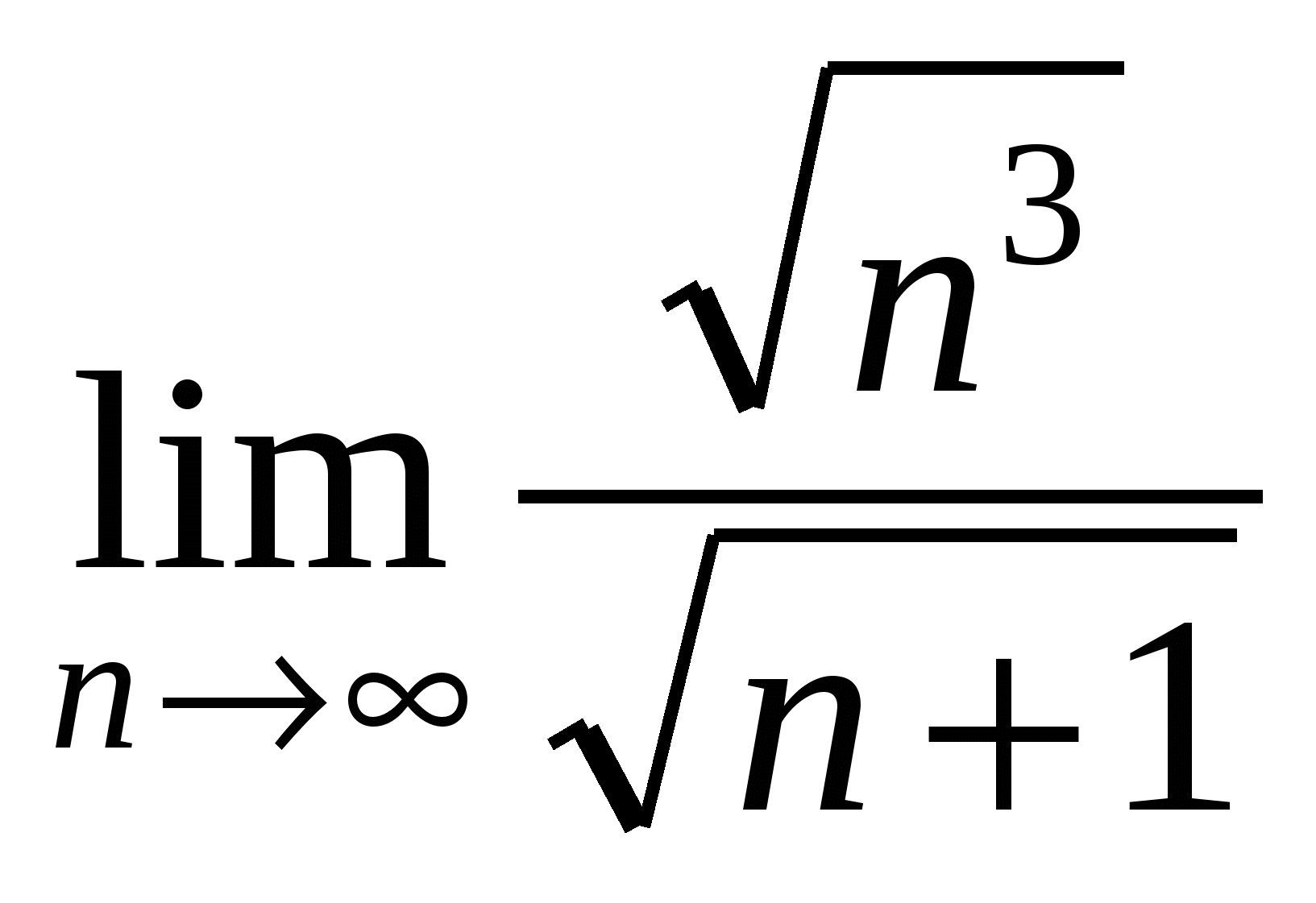
Решение. Поделим числитель и знаменатель дроби на старшую степень 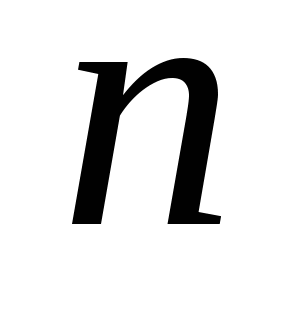 (выбираем из двух вариантов
(выбираем из двух вариантов ![]() и
и 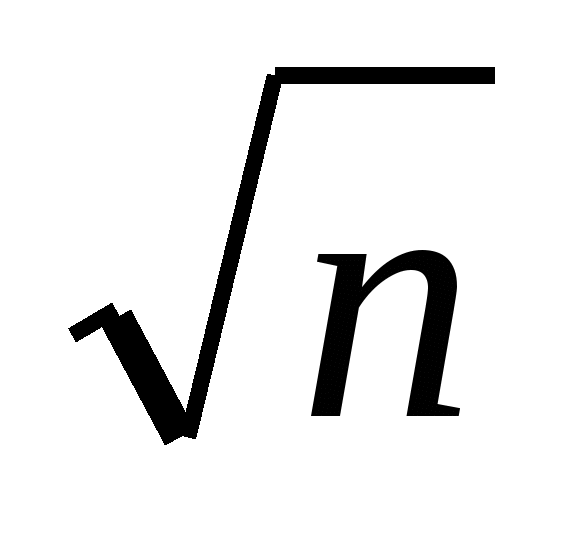 ), т.е на
), т.е на 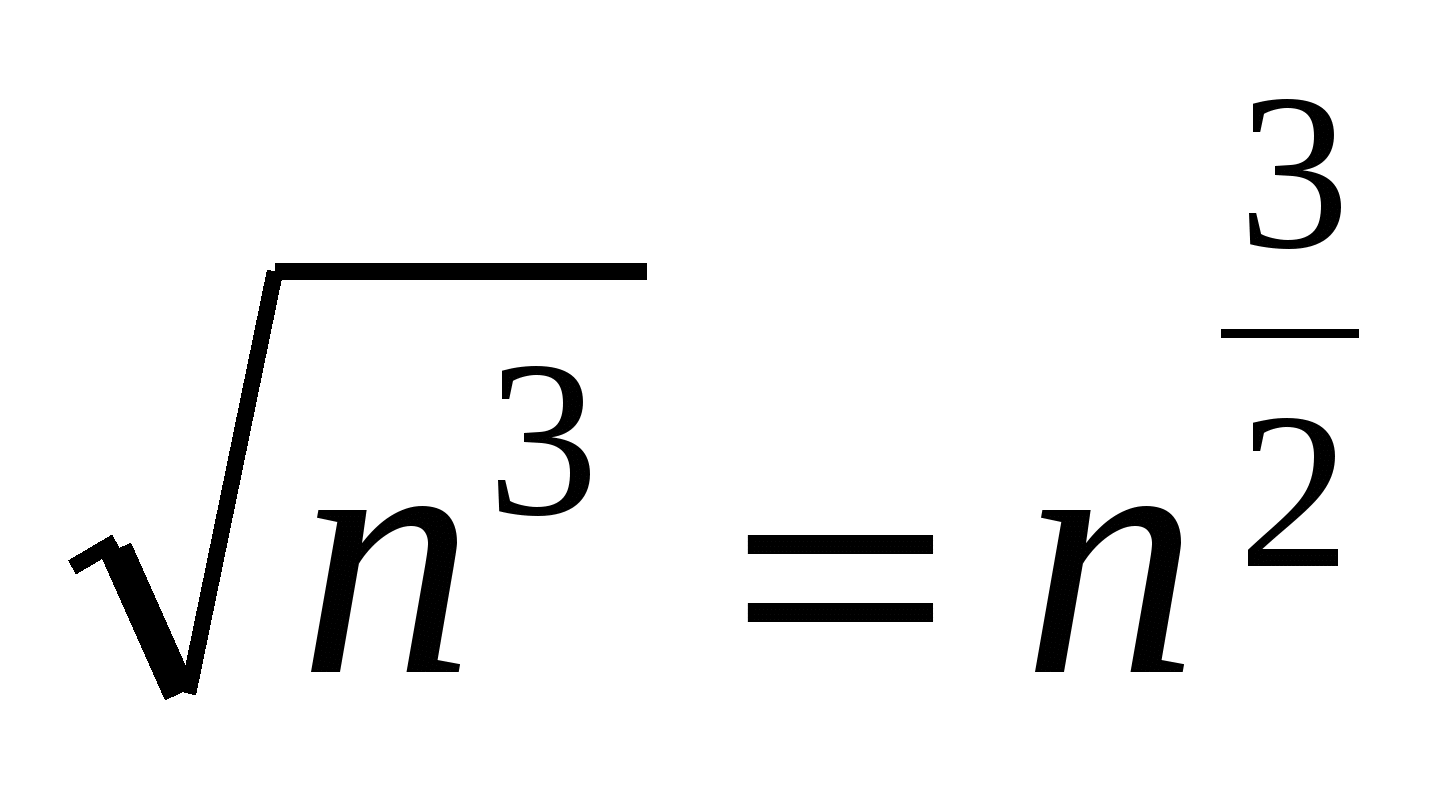
Тогда 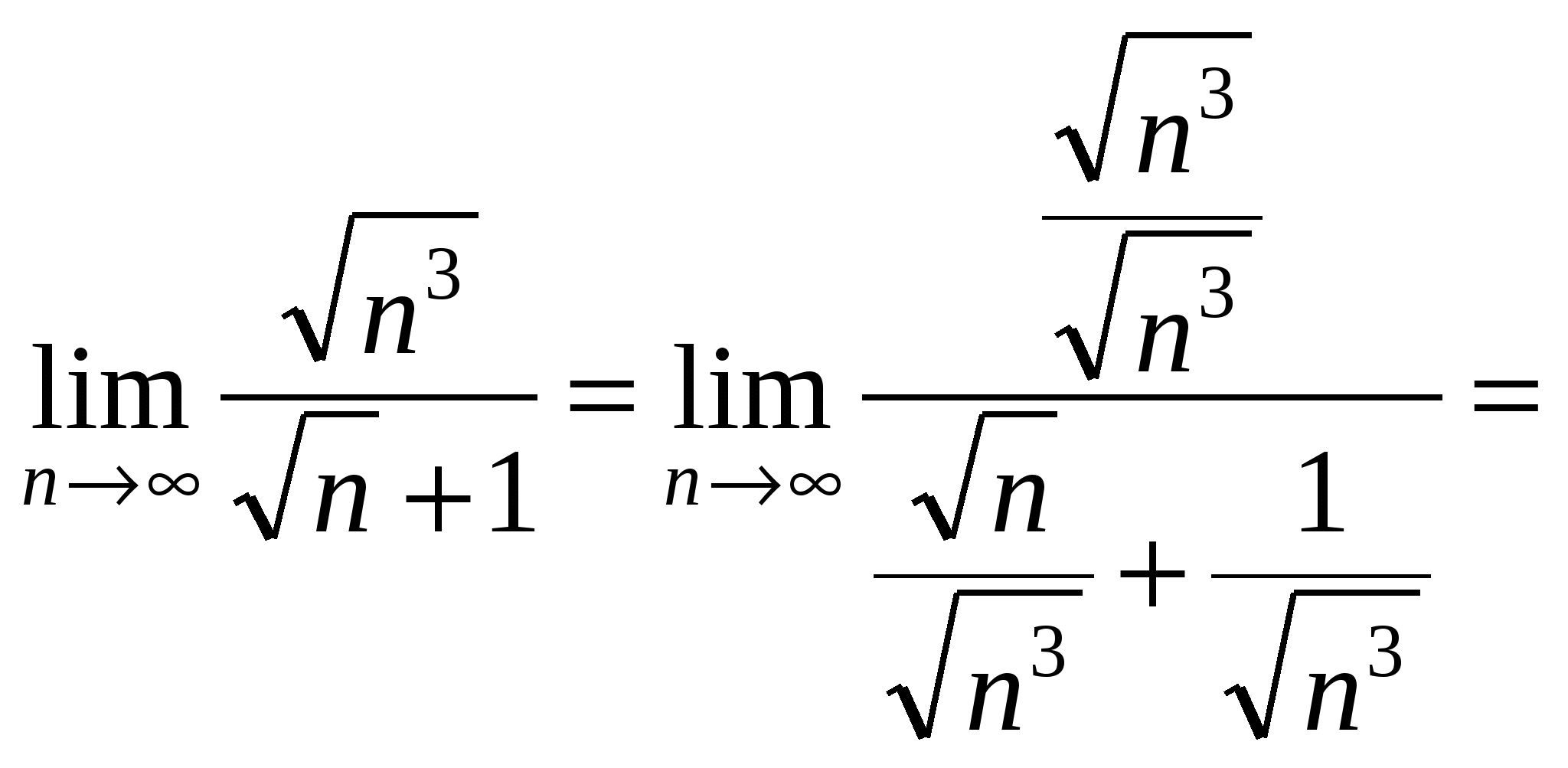
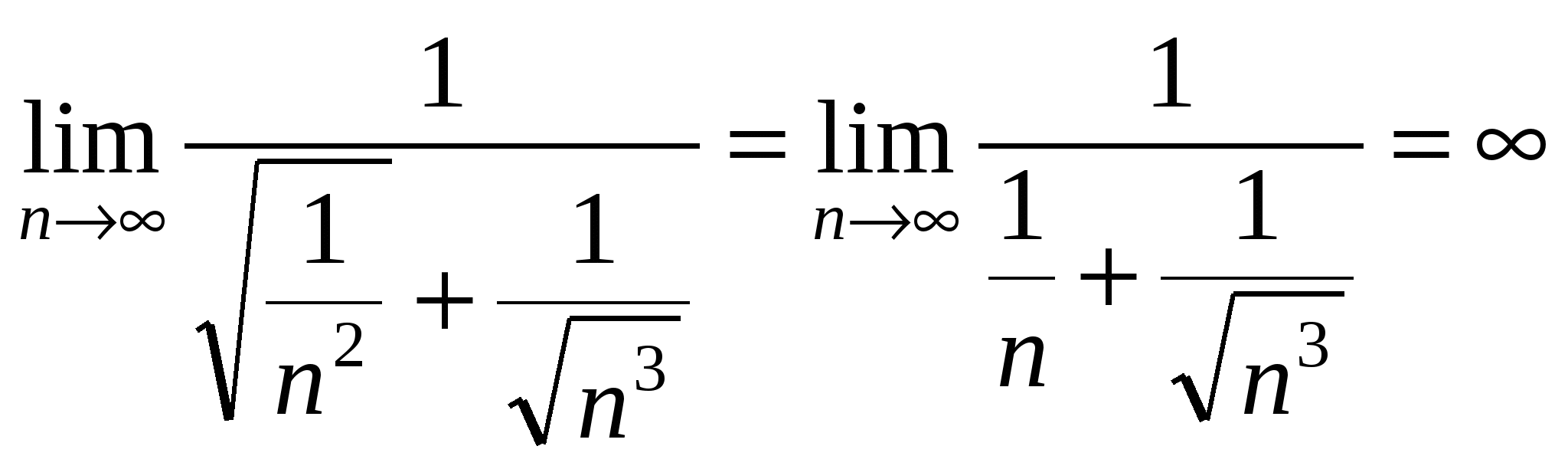
Неопределенность вида 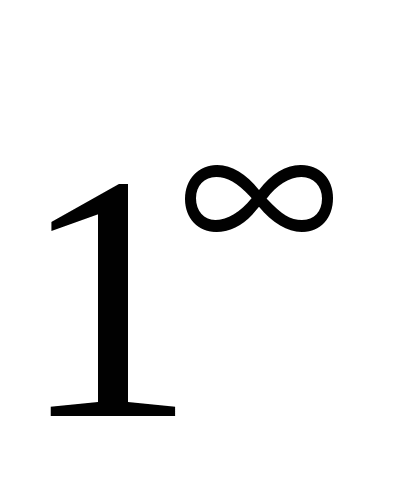
Неопределенности такого вида появляются при решении примеров вида: 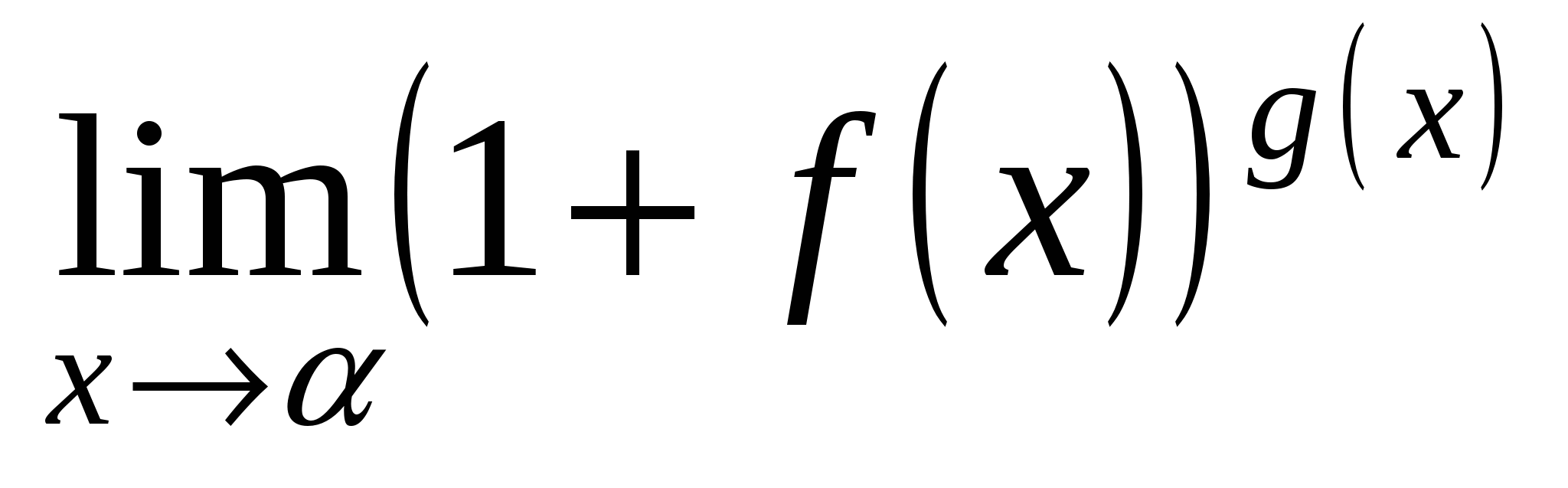 , где
, где 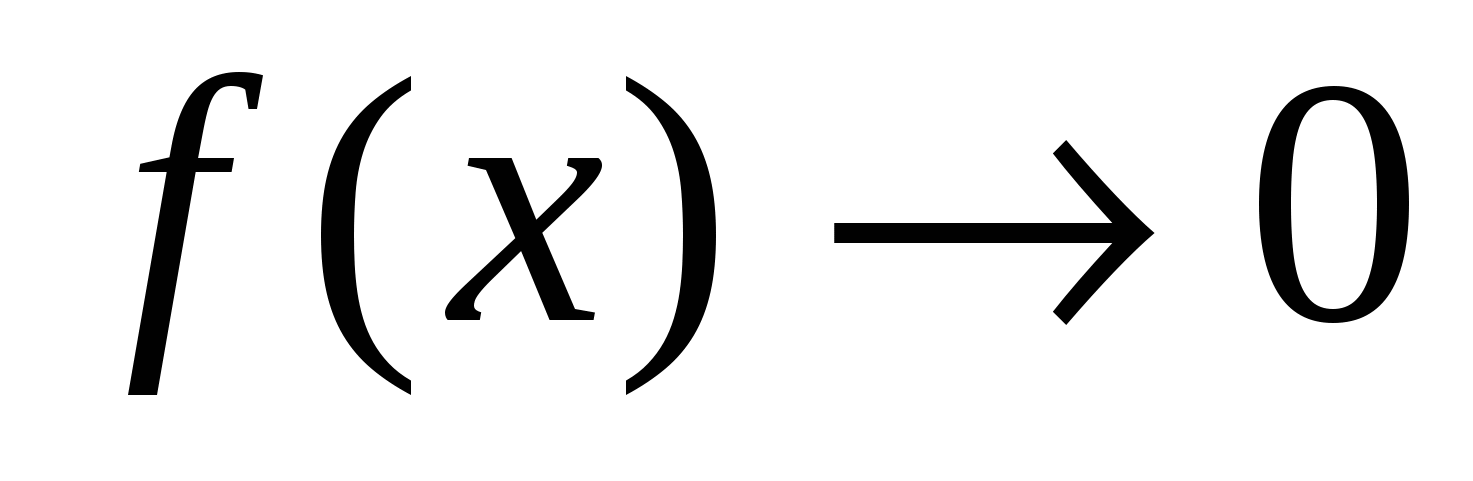 ,
, 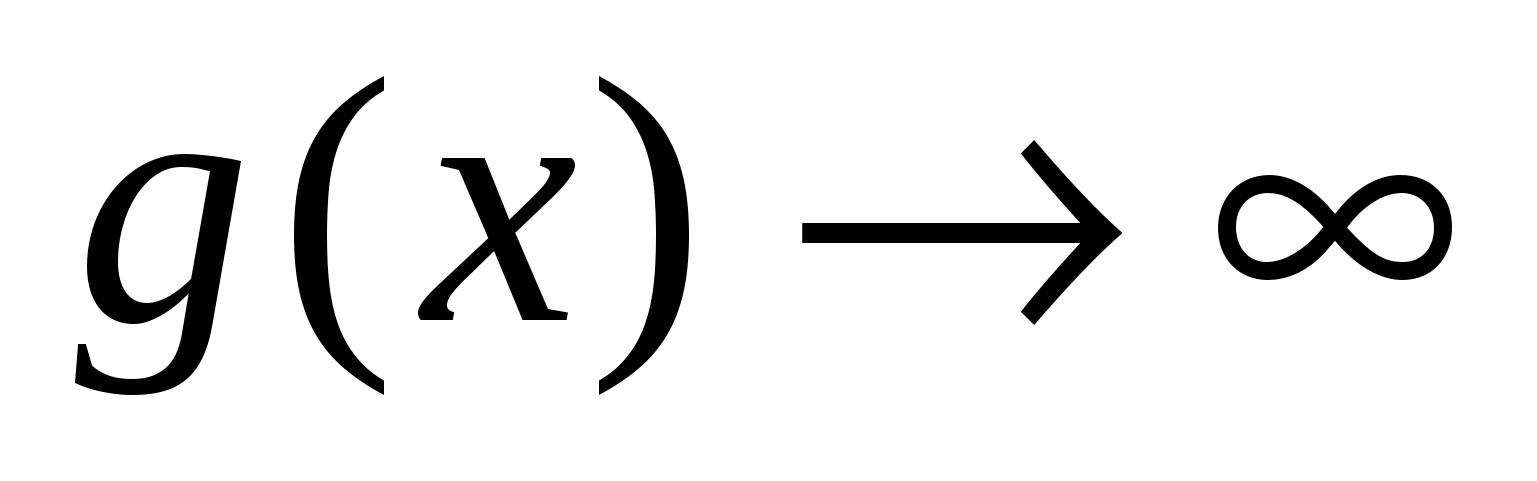 или
или 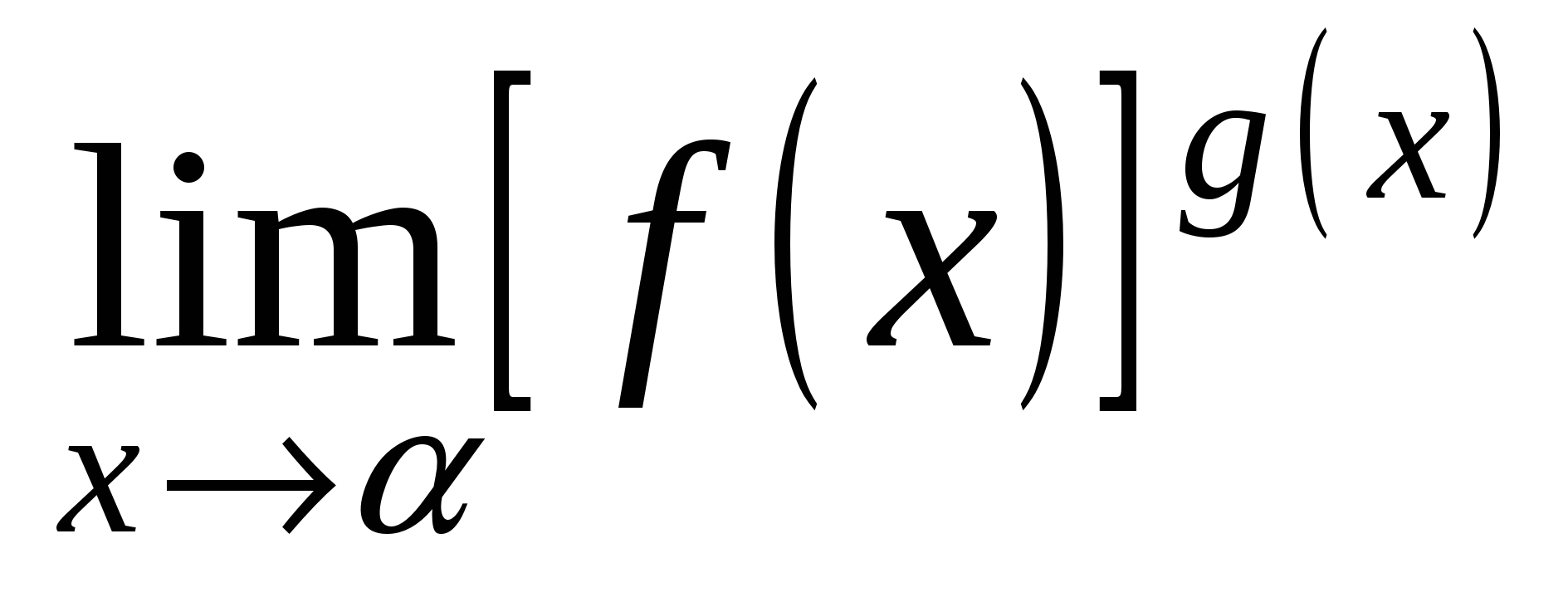 , где
, где 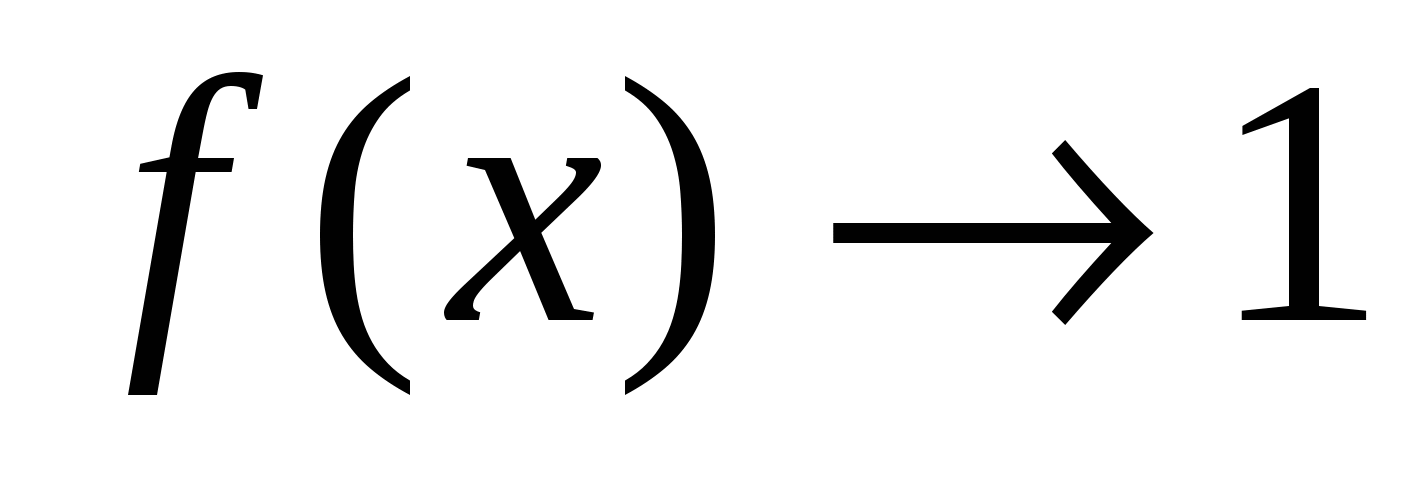 ,
, 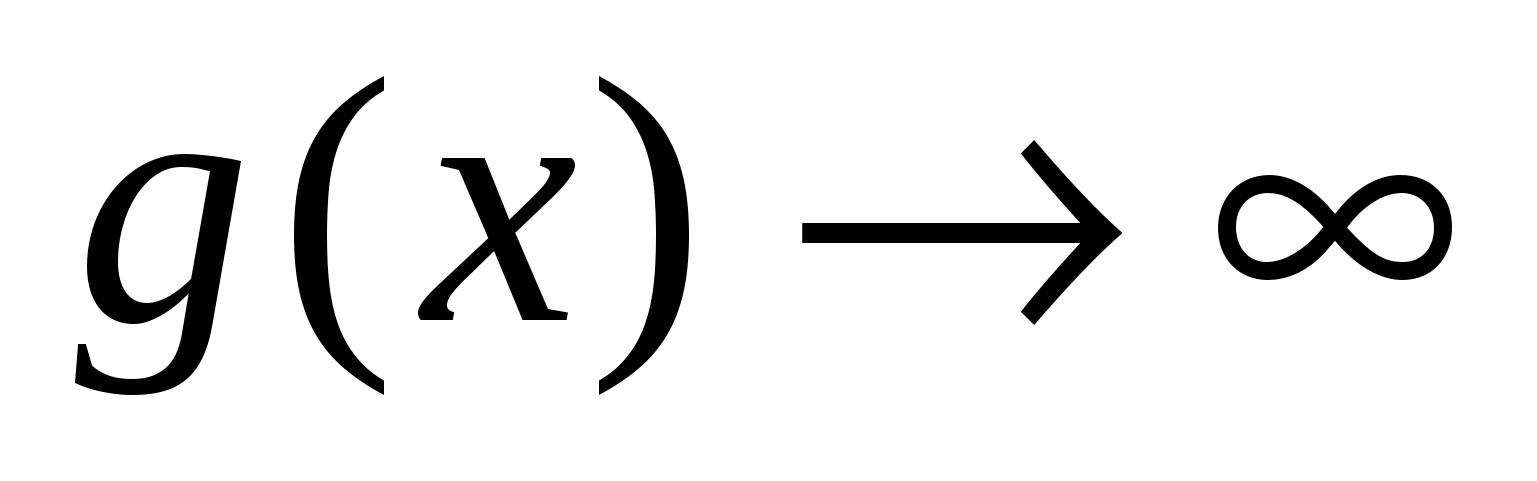 .
.
Преобразуя выражения, сводим их ко второму замечательному пределу.
Пример 11. Найти 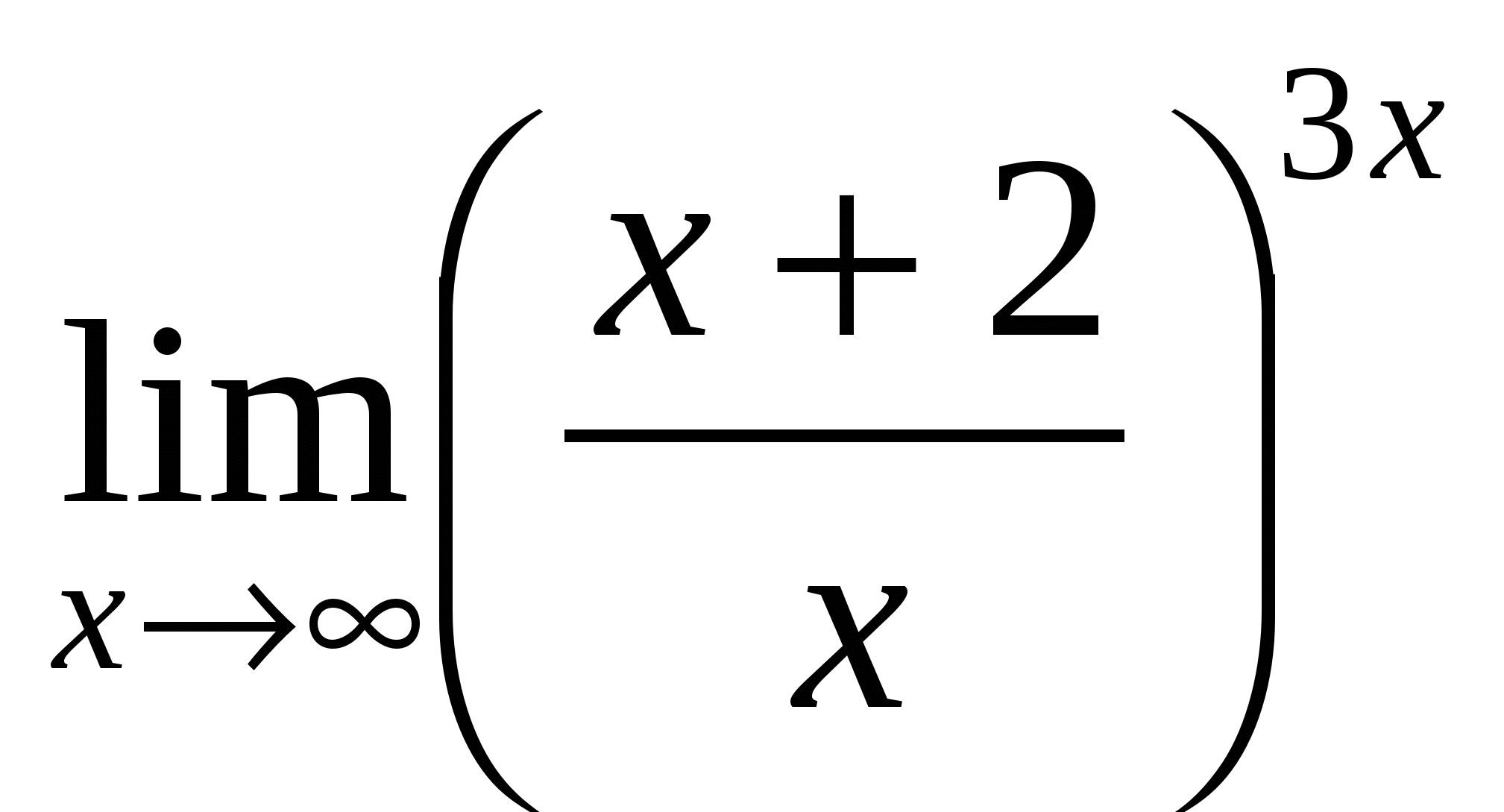 .
.
Решение. 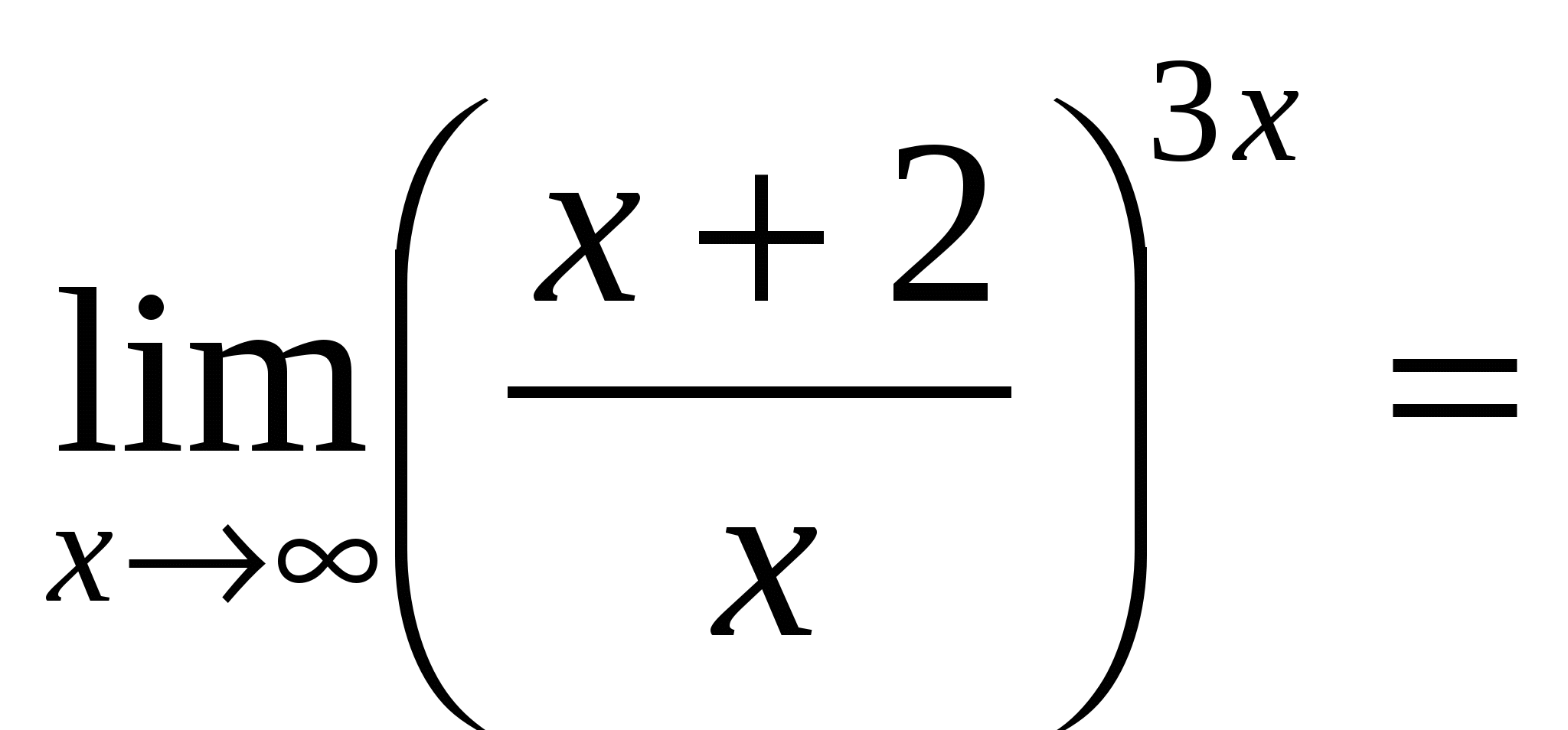
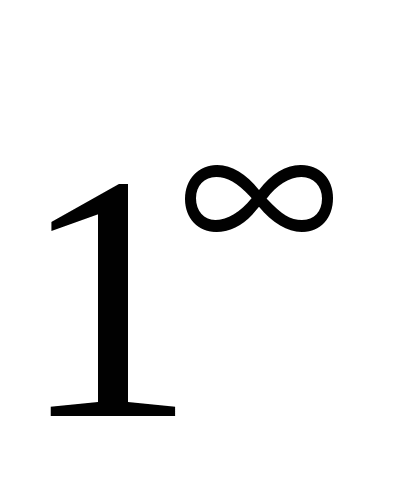
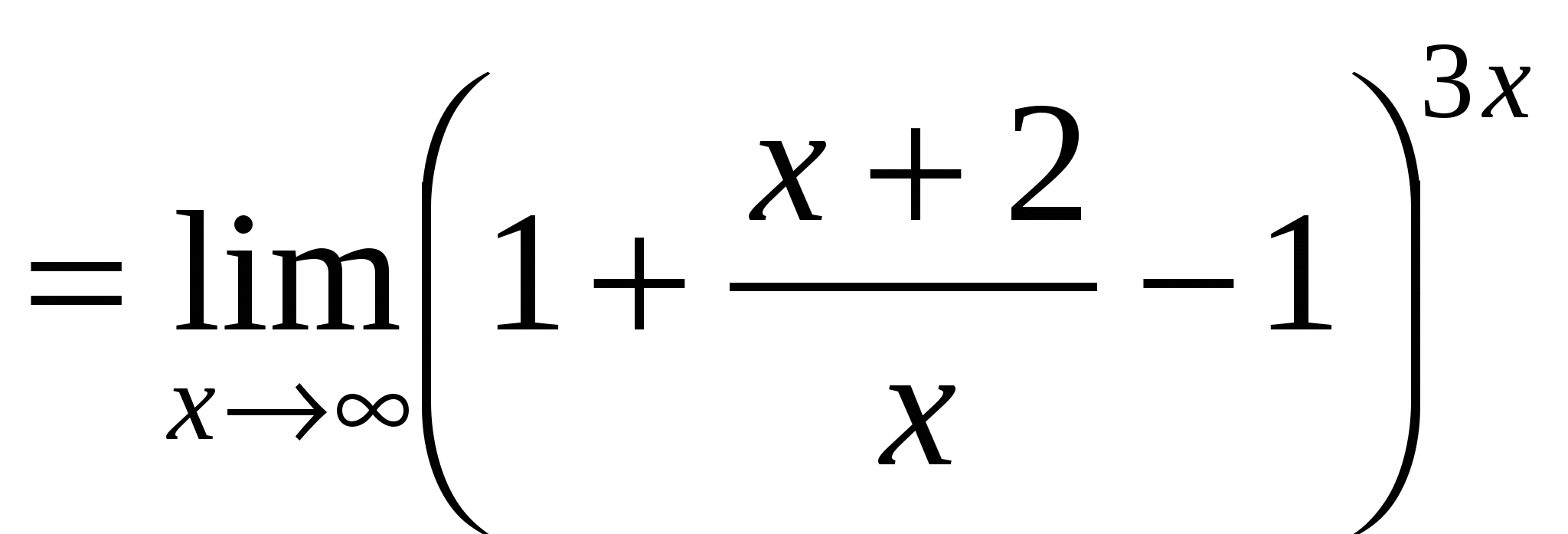
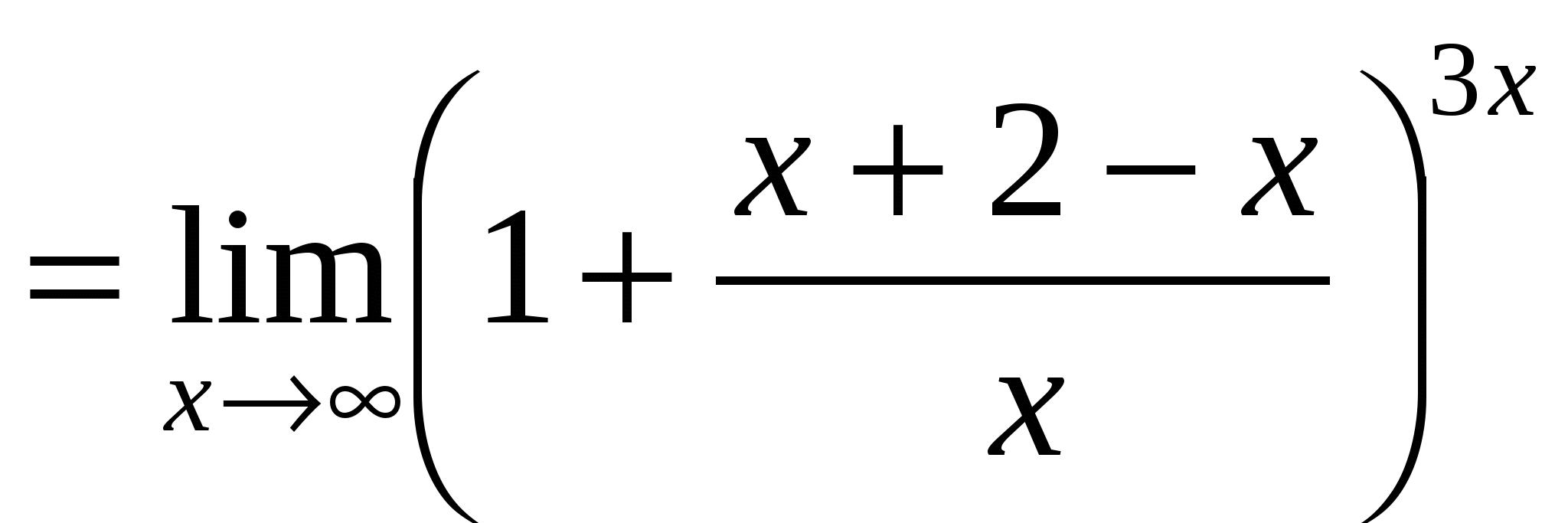
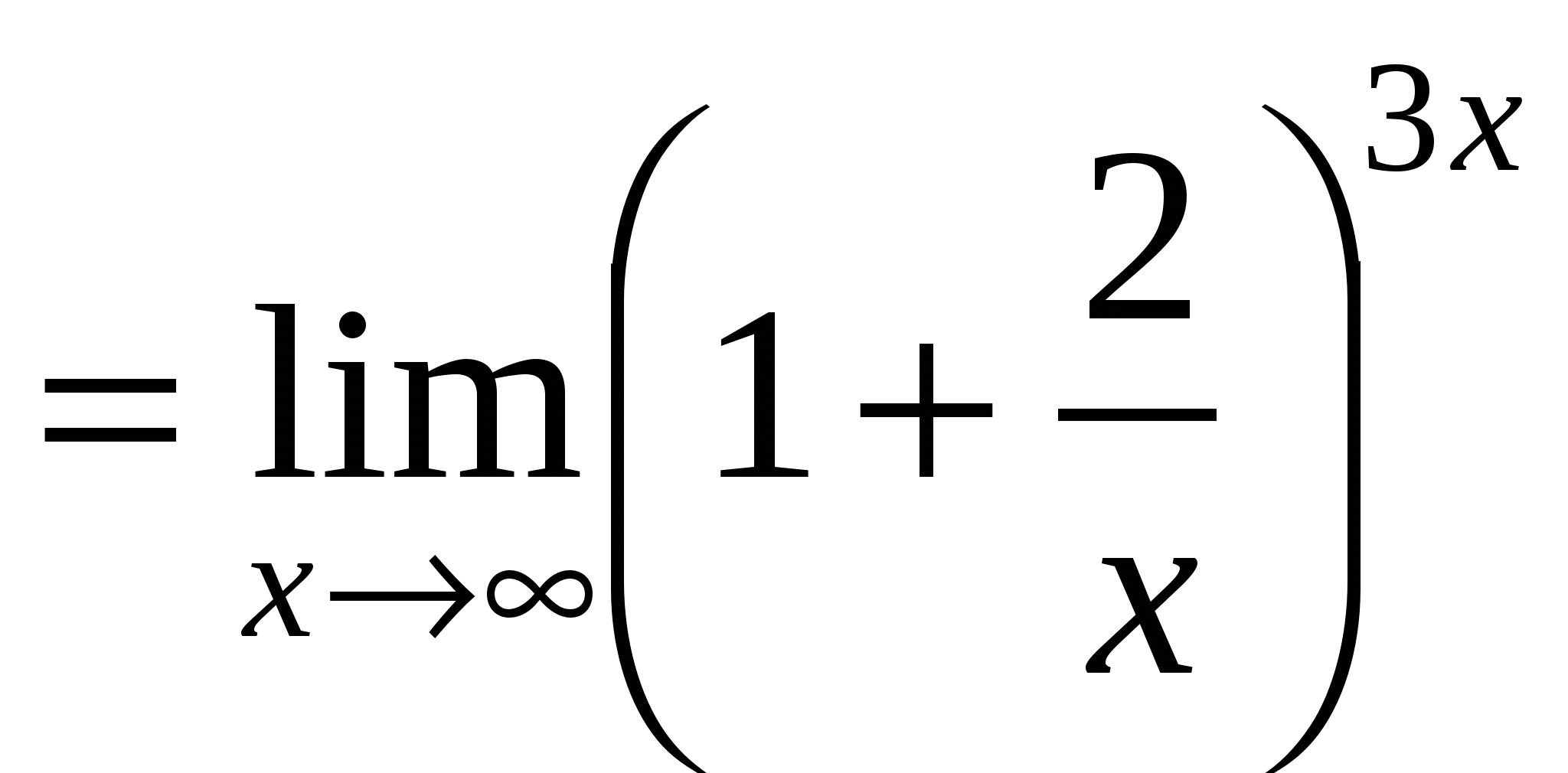
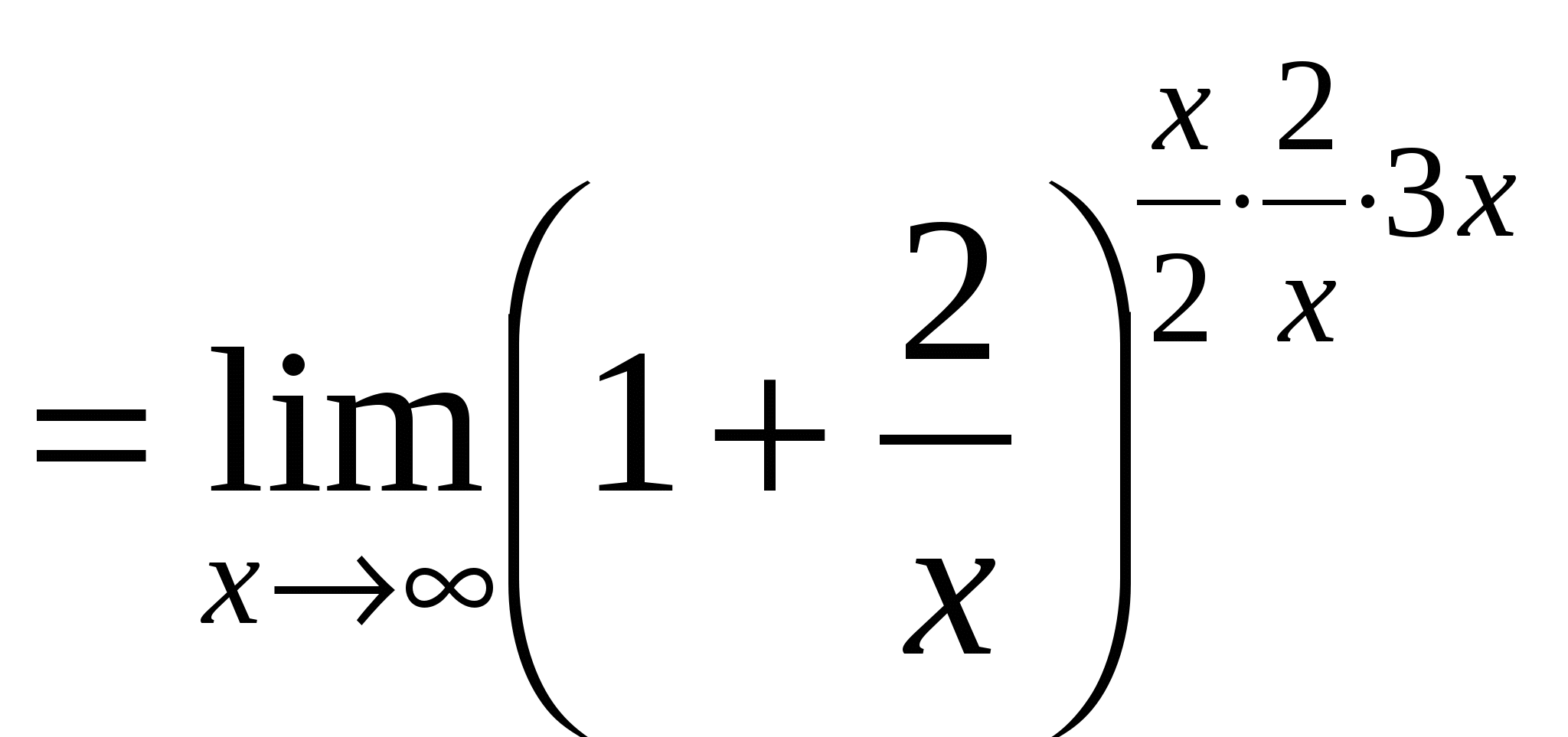
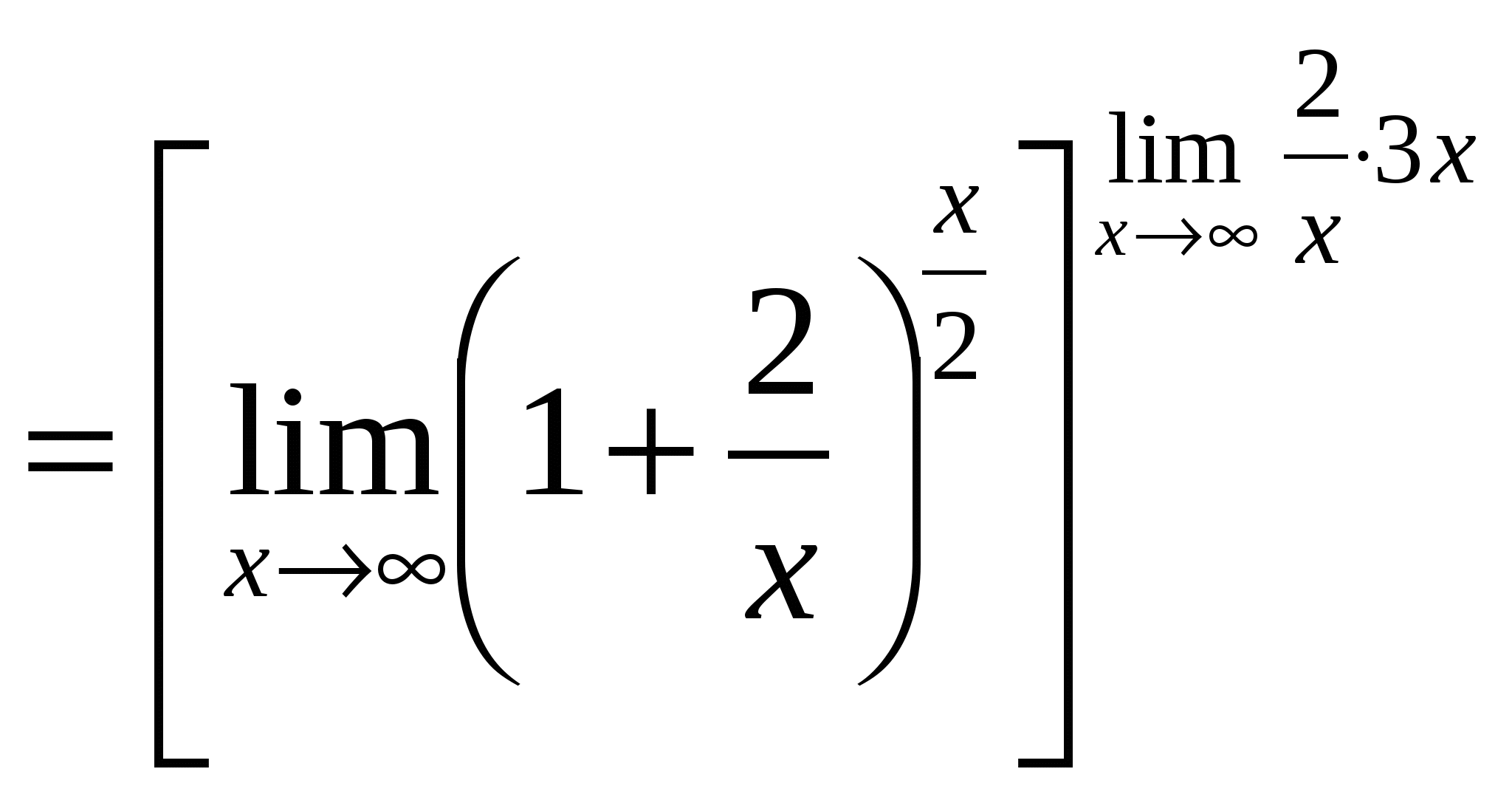
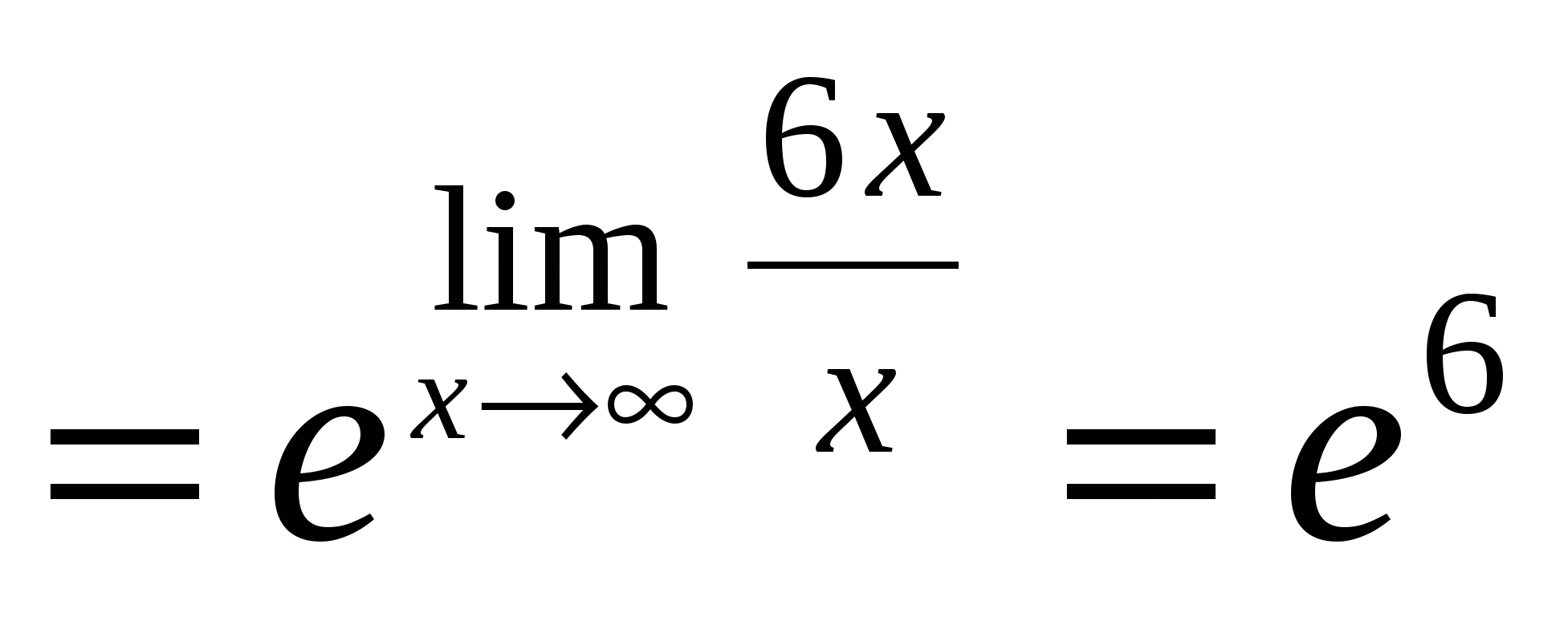
Дифференциальные исчисления функций одной переменной
Функция 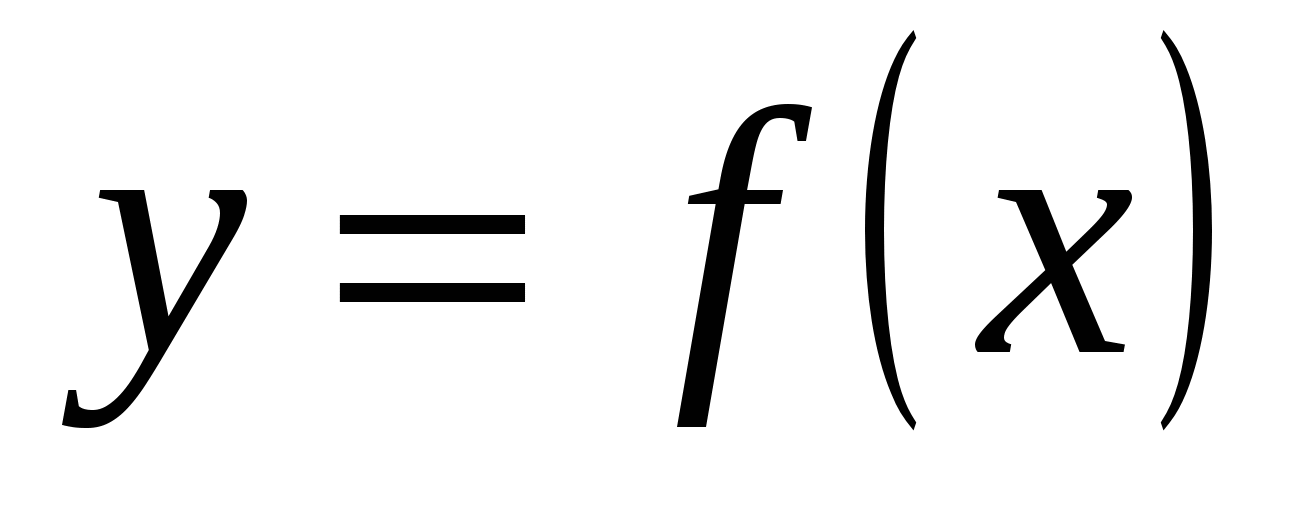 описывает зависимость между двумя переменными величинами
описывает зависимость между двумя переменными величинами 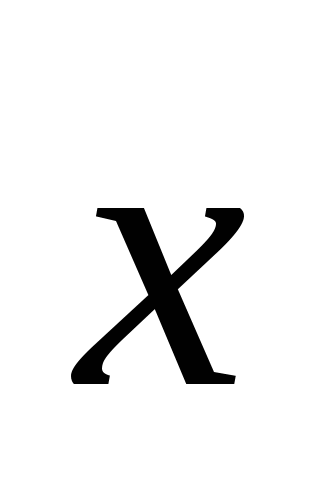 и
и 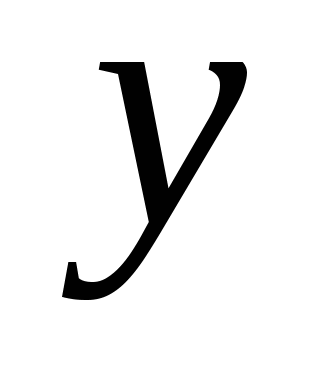 . Если независимая переменная
. Если независимая переменная ![]() в точке
в точке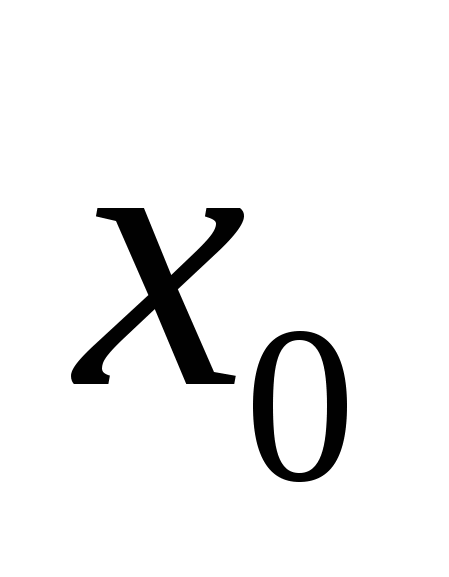 получила приращение
получила приращение 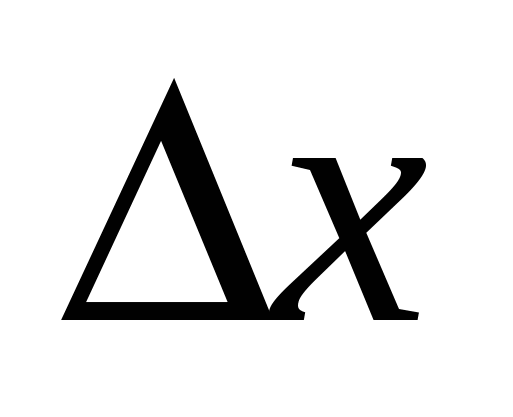 (т.е.
(т.е. 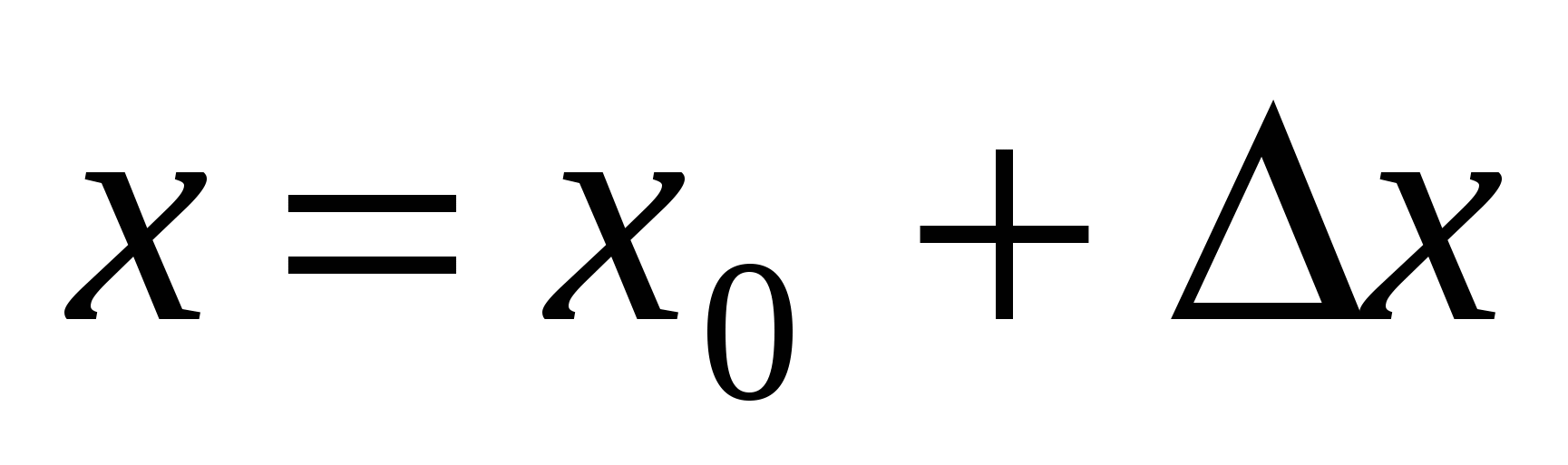 ), то переменная
), то переменная ![]() получит приращение
получит приращение 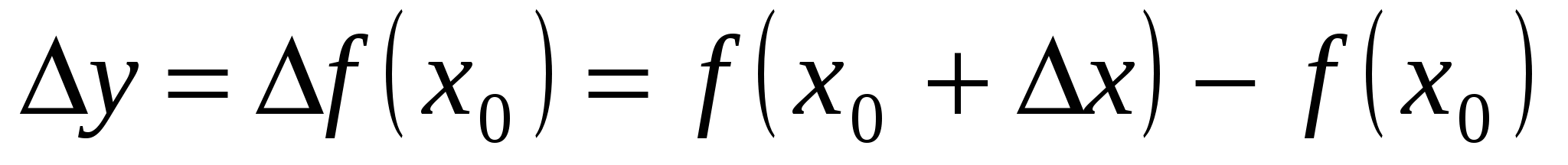 .
.
Предел отношения 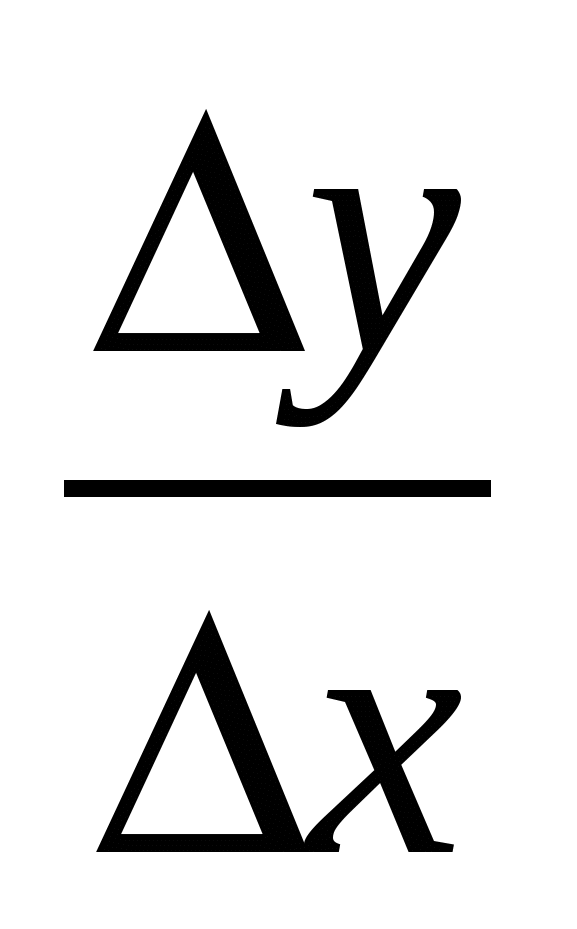 , если
, если 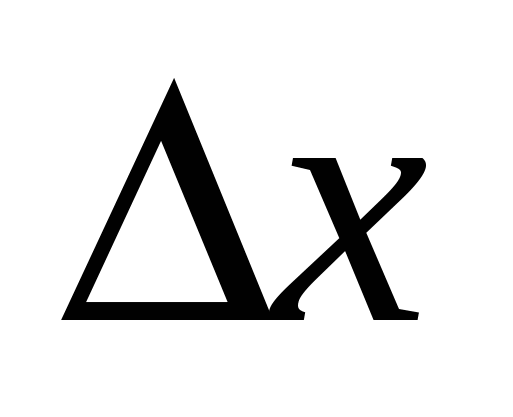 стремится к нулю, называется производной функции
стремится к нулю, называется производной функции 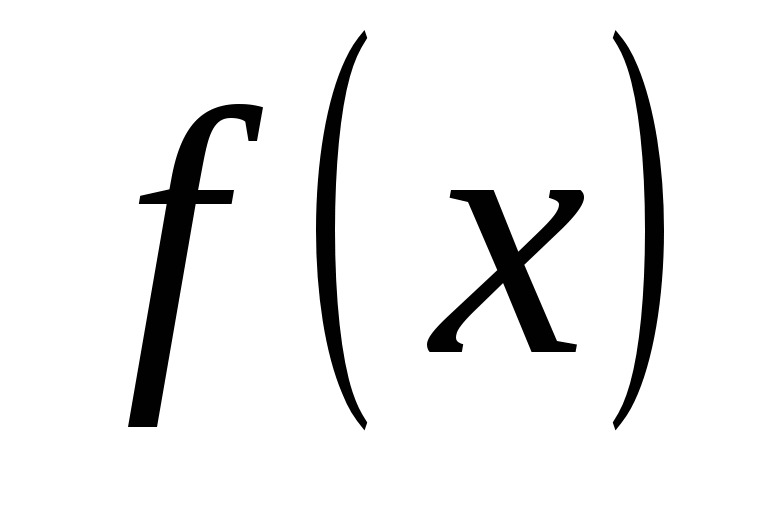 в точке
в точке 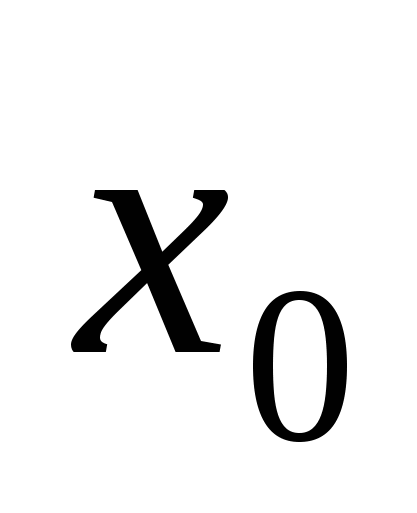 и обозначается
и обозначается ![]() или
или 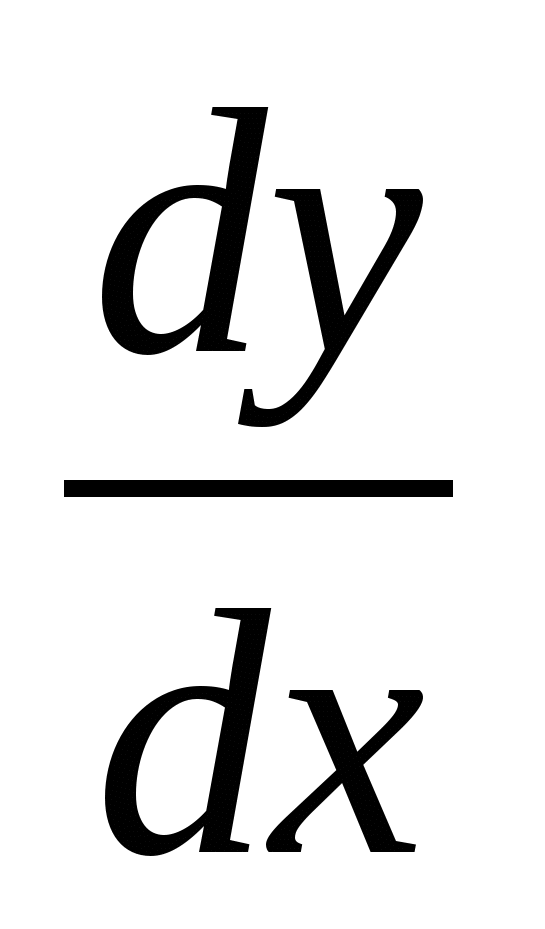 .
. 
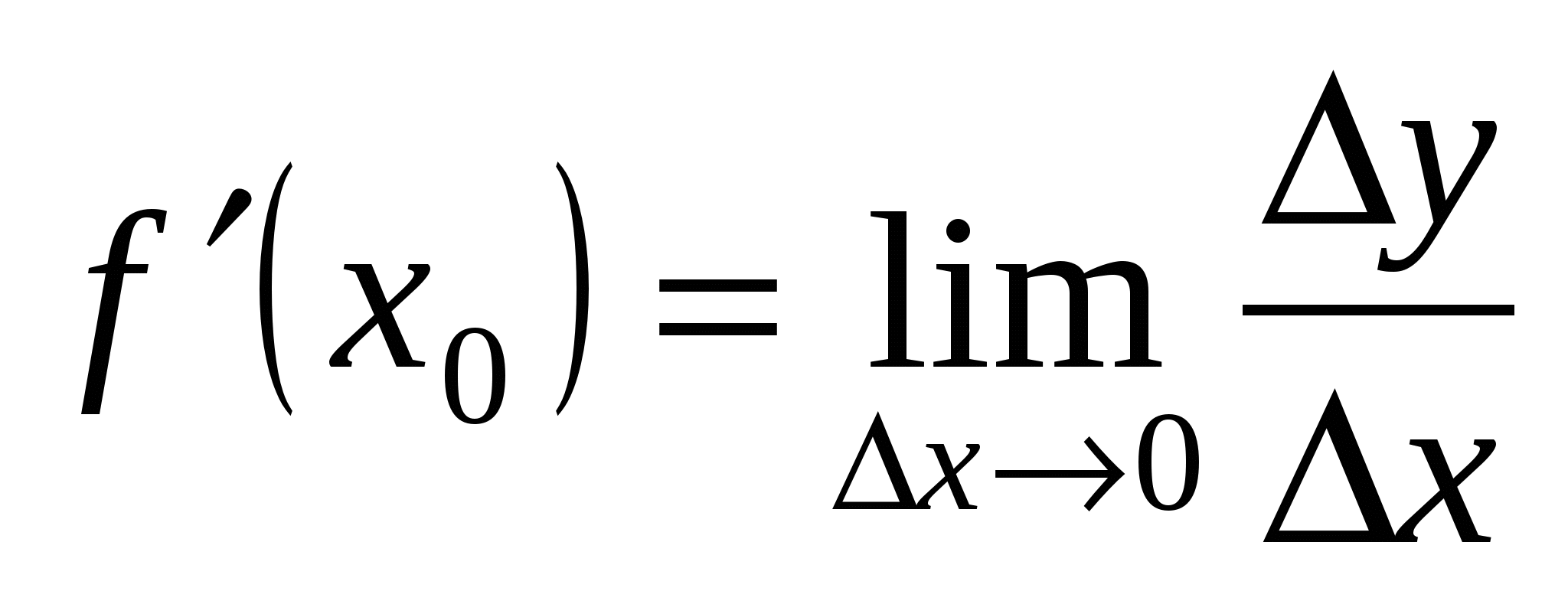
Операция нахождения производной функции называется дифференцированием. Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке.
Производная сложной функции
Пусть 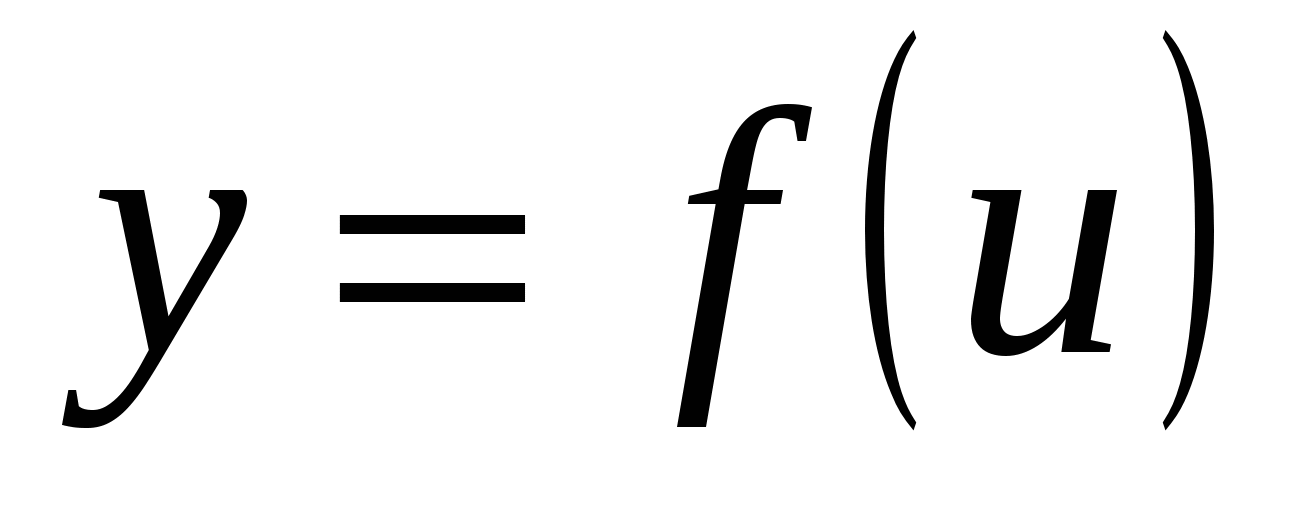 , где
, где  является не независимой переменной, а функцией независимой переменной
является не независимой переменной, а функцией независимой переменной 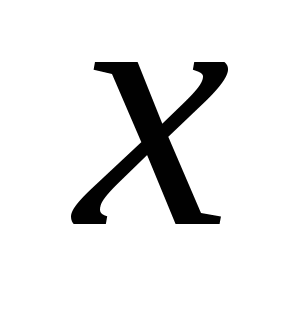 , т.е.
, т.е. 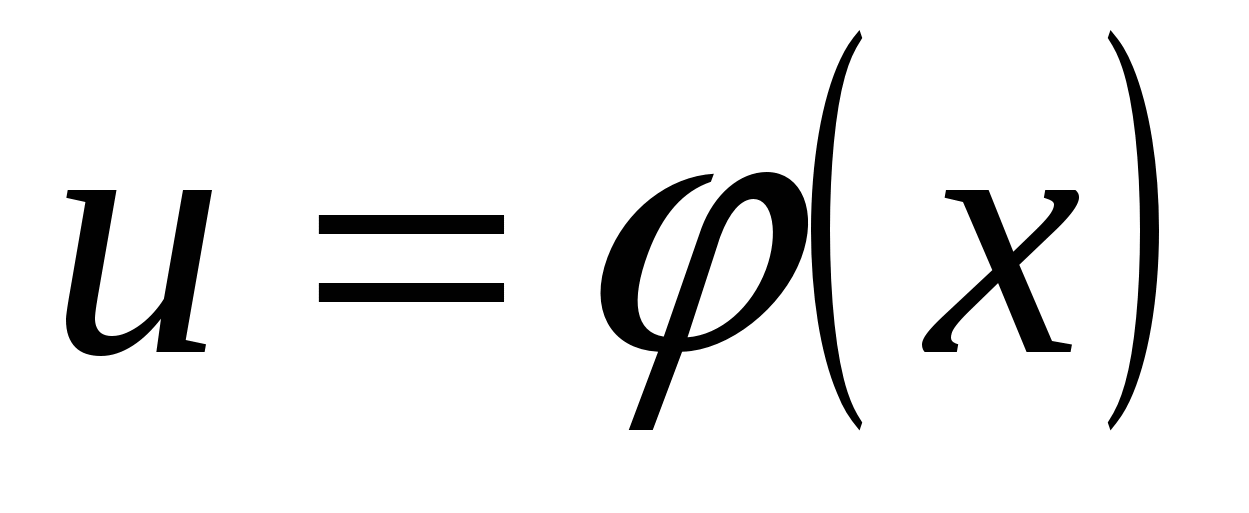 . Таким образом,
. Таким образом, ![]() . В этом случае функция
. В этом случае функция 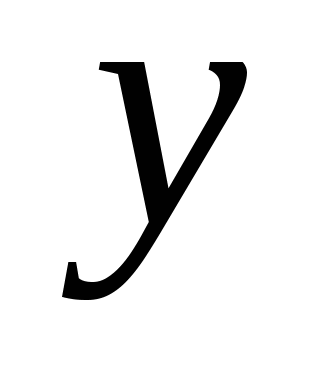 называется сложной функцией
называется сложной функцией ![]() , а переменная
, а переменная ![]() промежуточным аргументом.
промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если 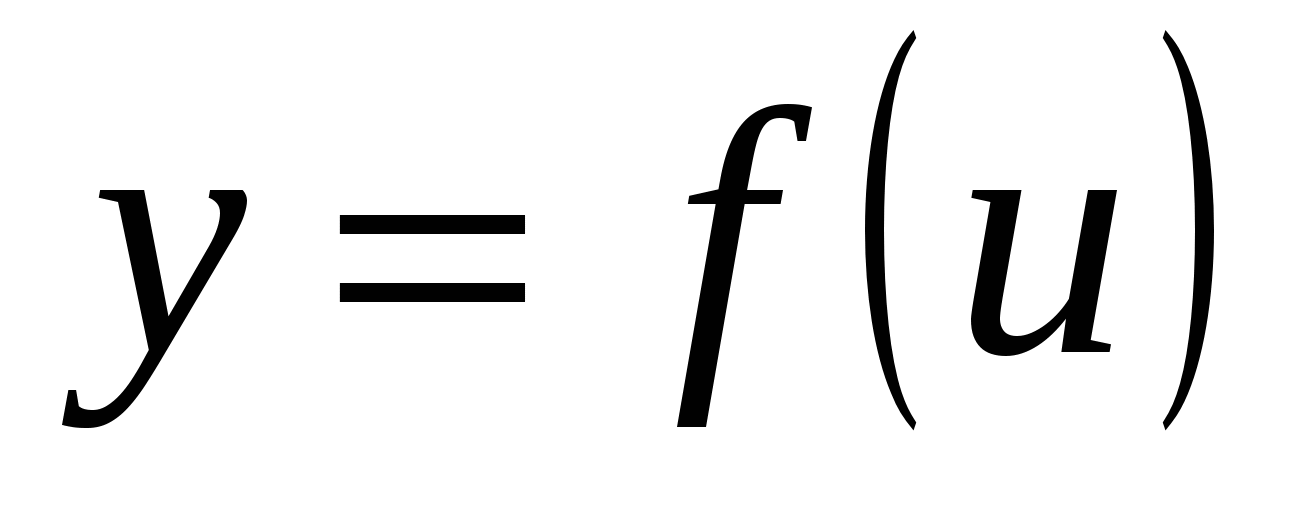 и
и 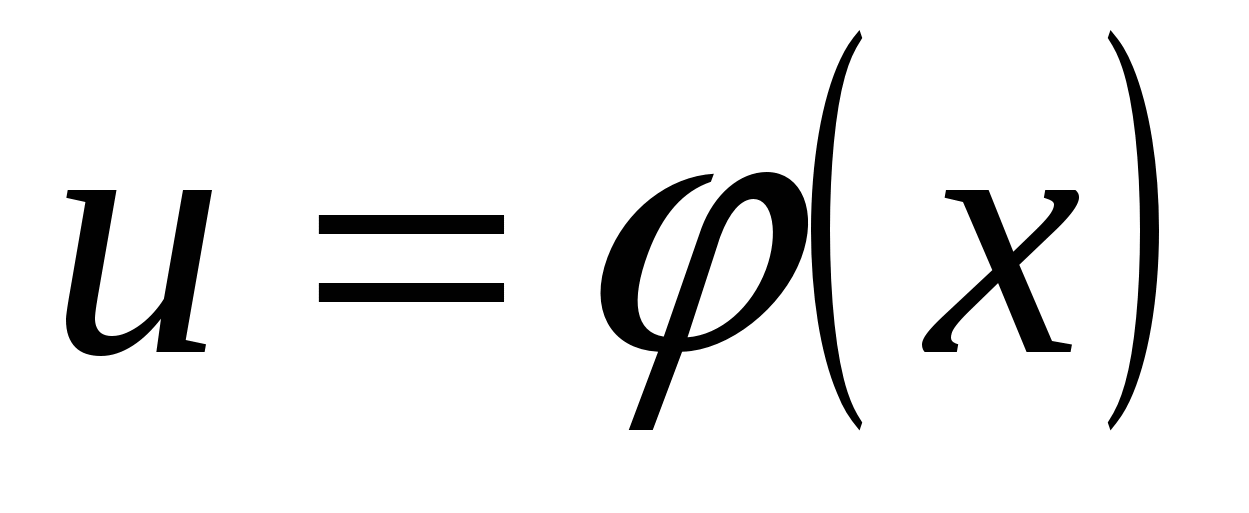 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции ![]() существует и равна произведению производной функции
существует и равна произведению производной функции 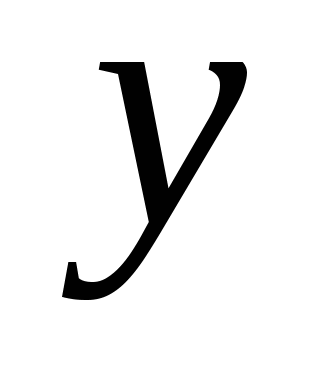 по промежуточному аргументу
по промежуточному аргументу ![]() на производную промежуточного аргумента
на производную промежуточного аргумента  по независимой переменной
по независимой переменной ![]() .
. 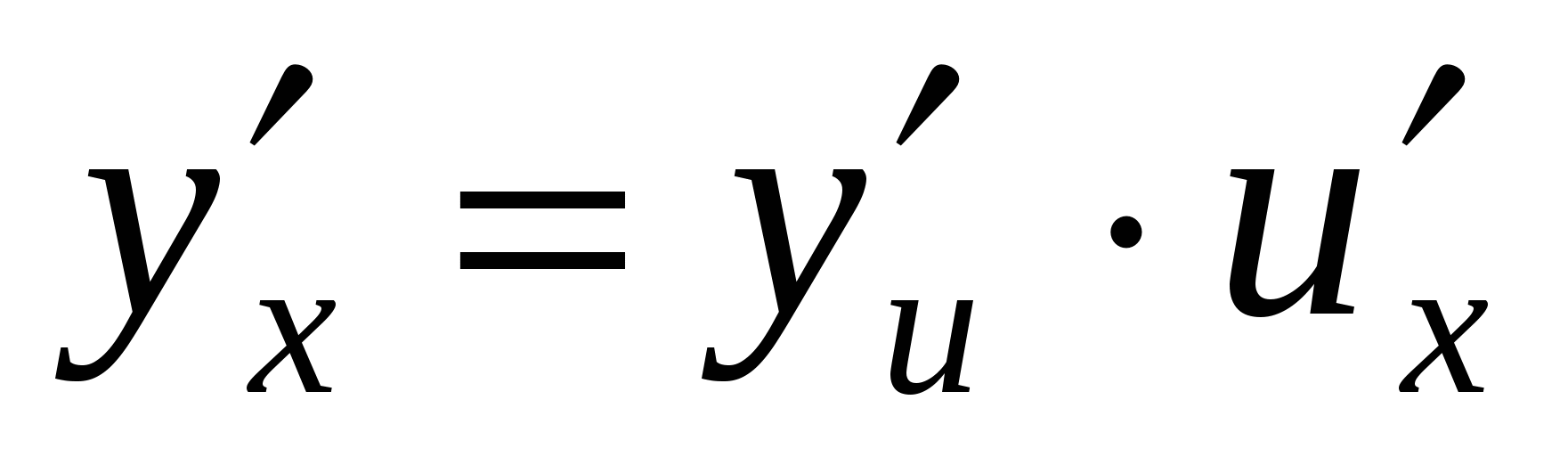
Эта теорема распространяется и несложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Формулы дифференцирования
С - постоянная, 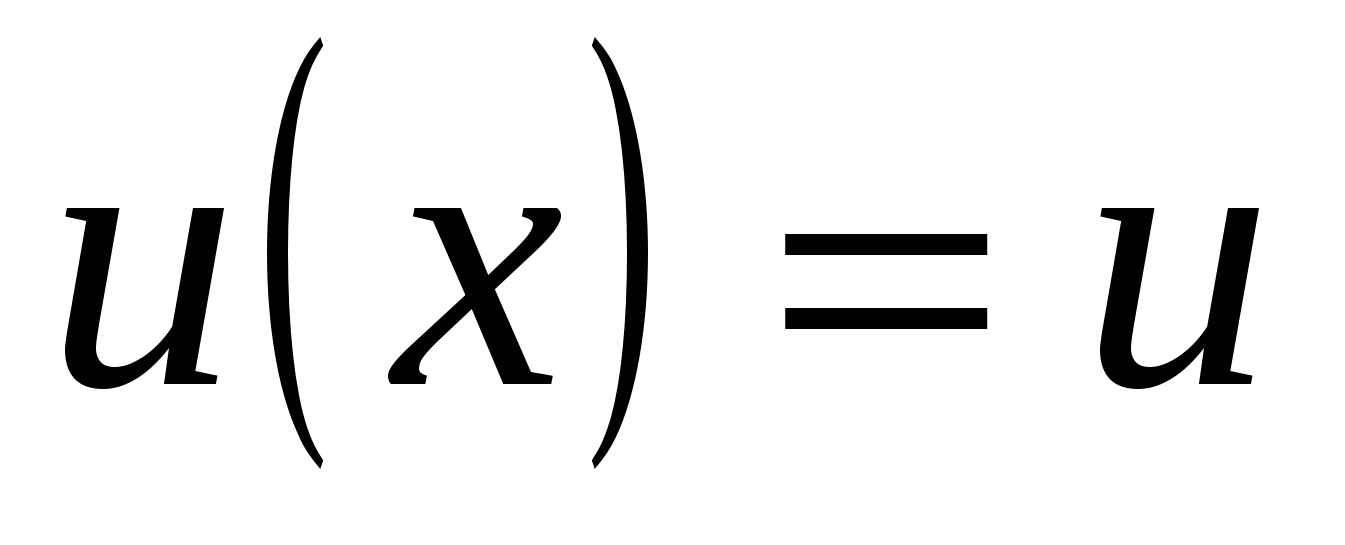 и
и 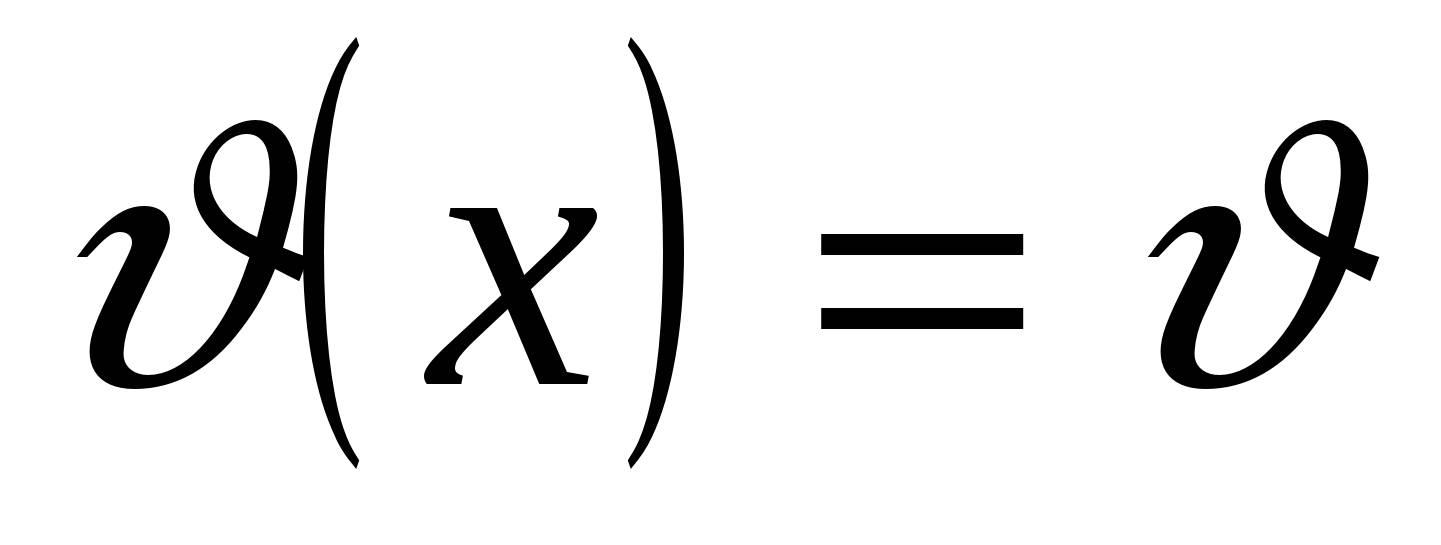 функции аргумента
функции аргумента 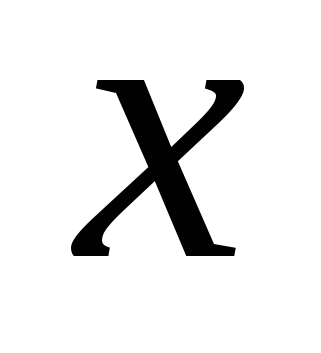
1. 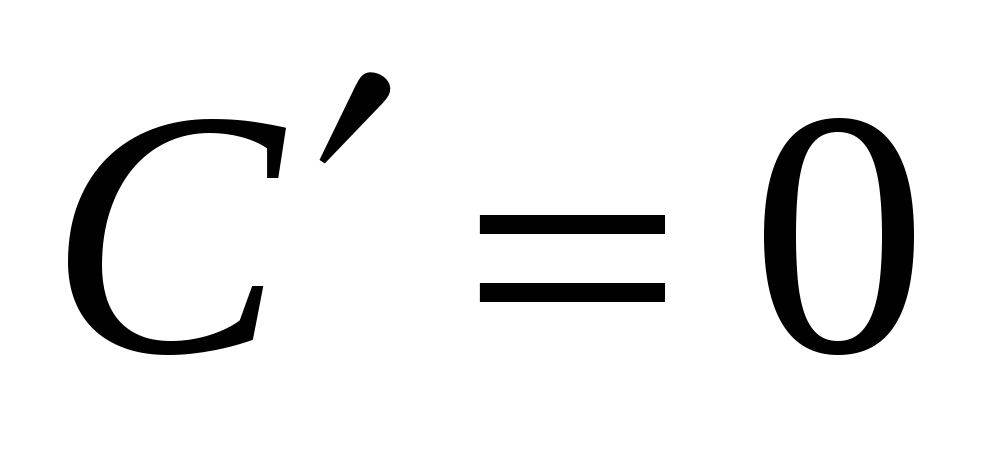
4. 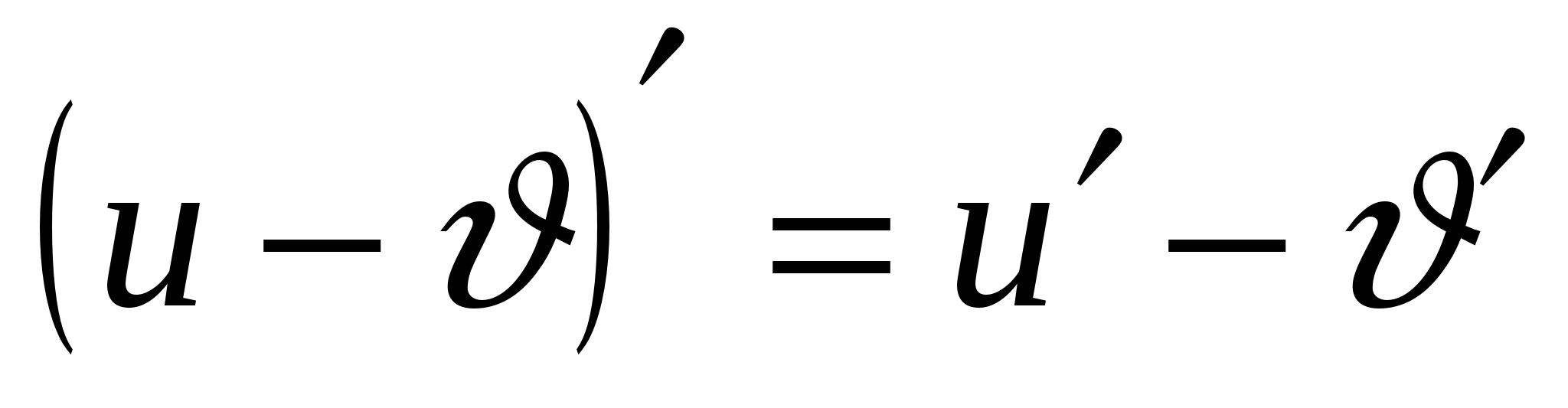
7. 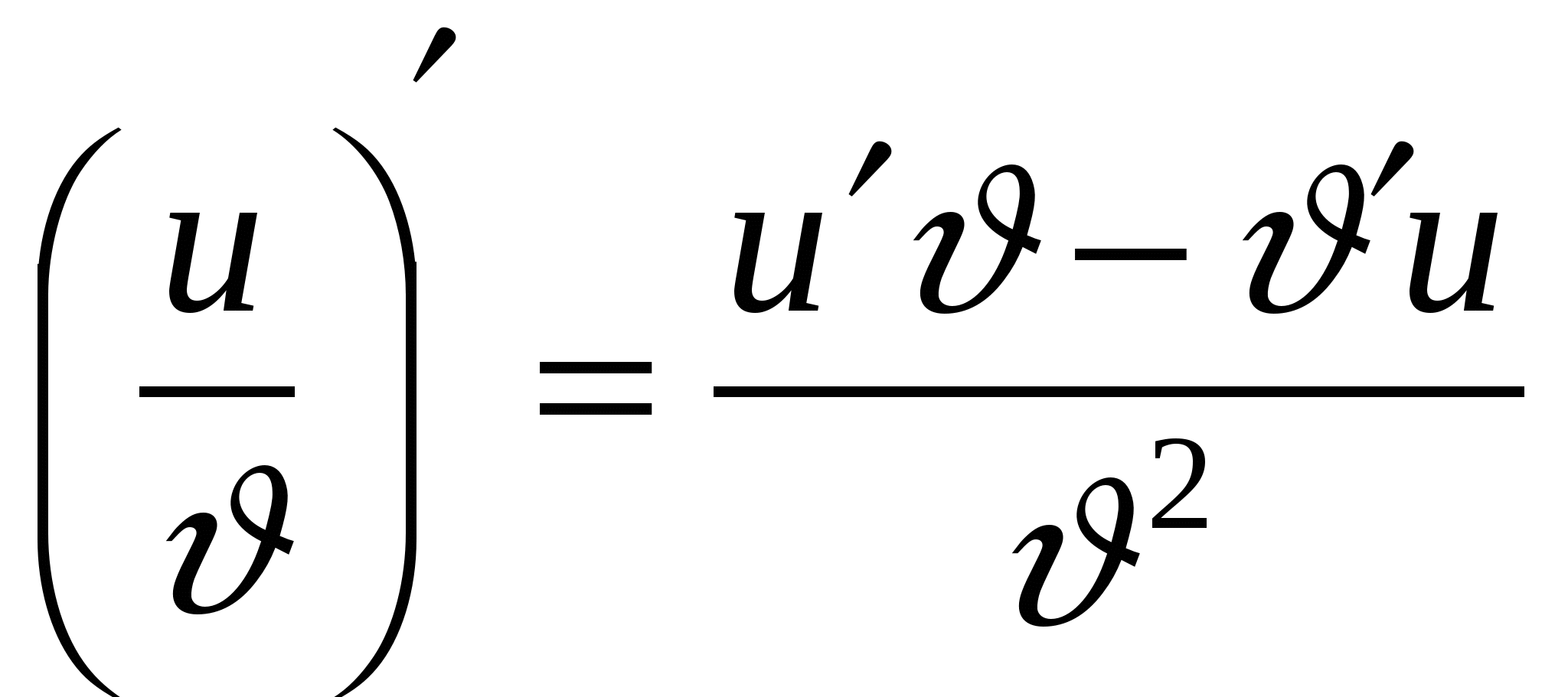
2. 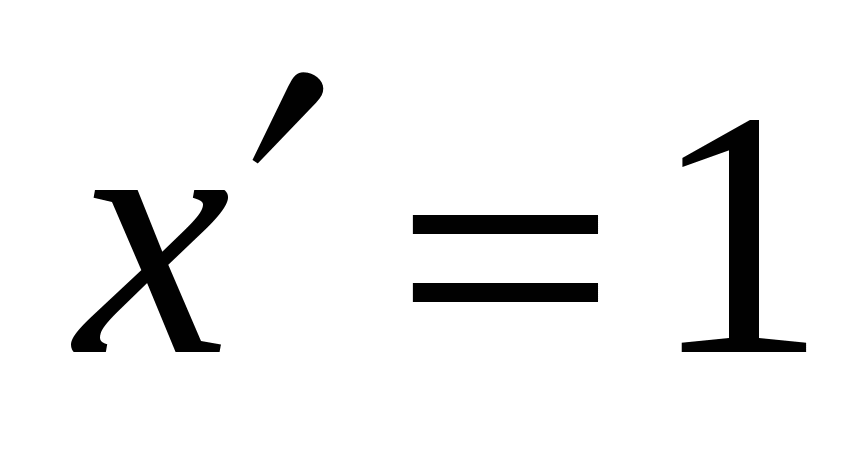
5. 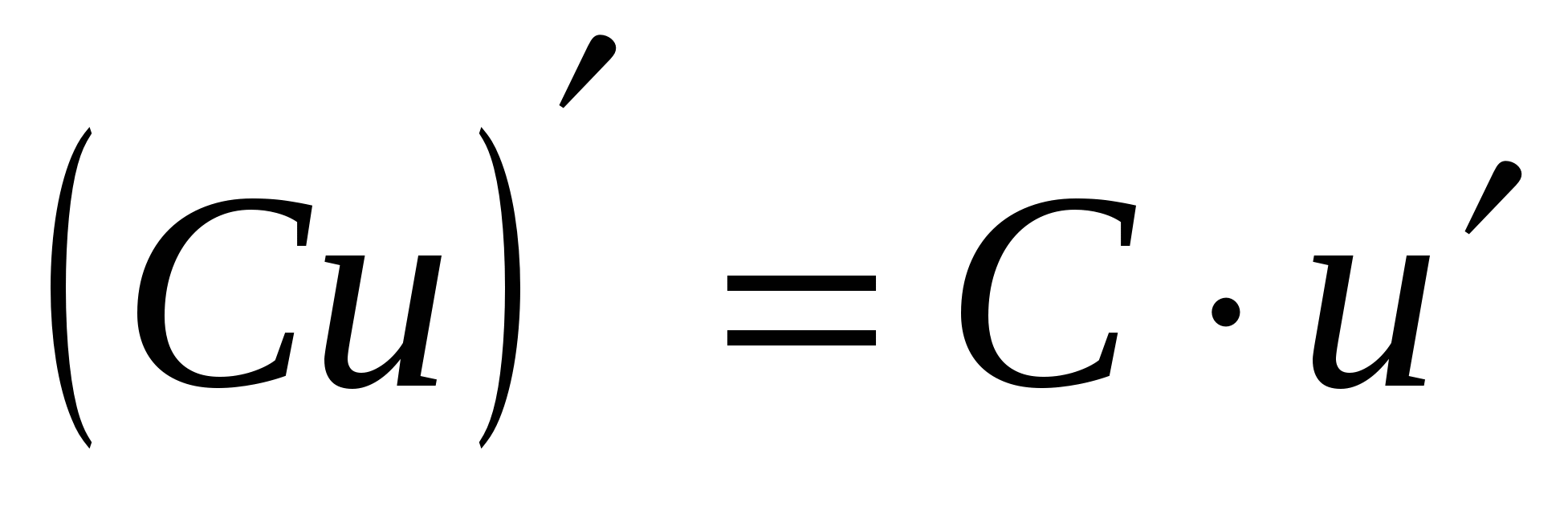
3. 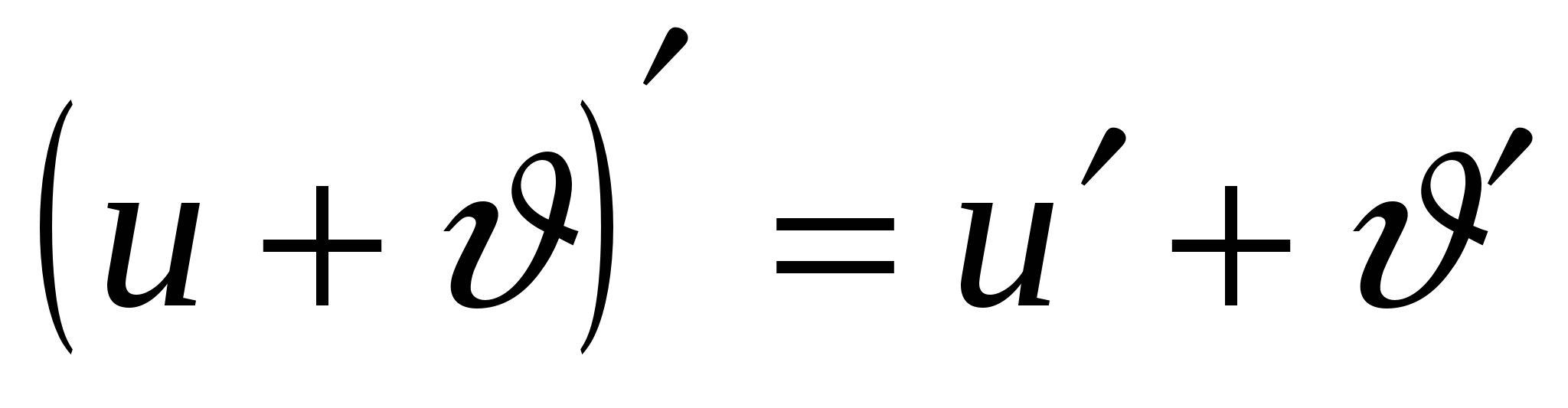
6. 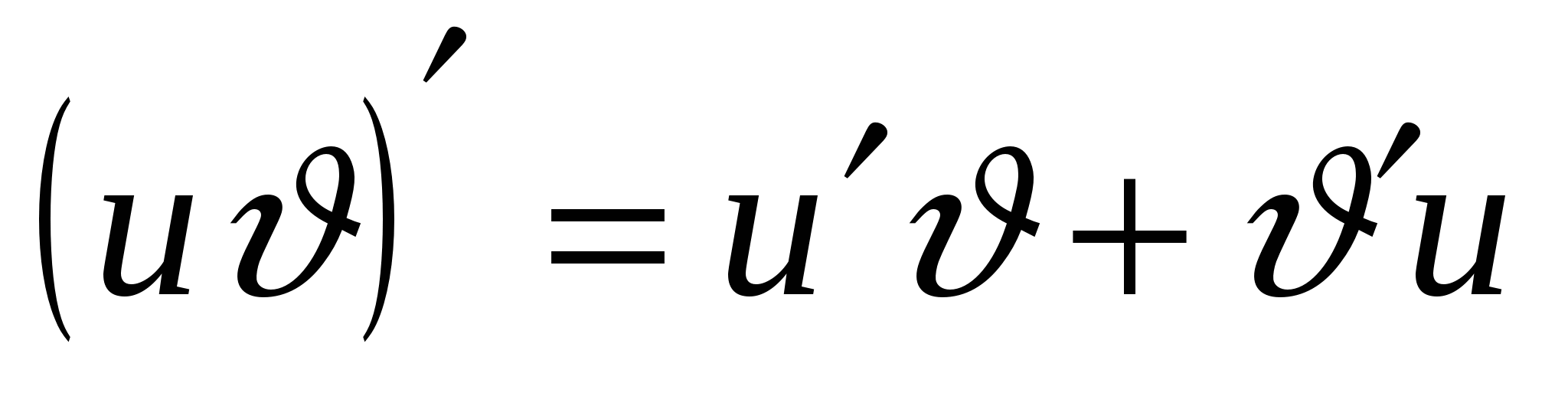
Основные элементарные функции
Сложные функции
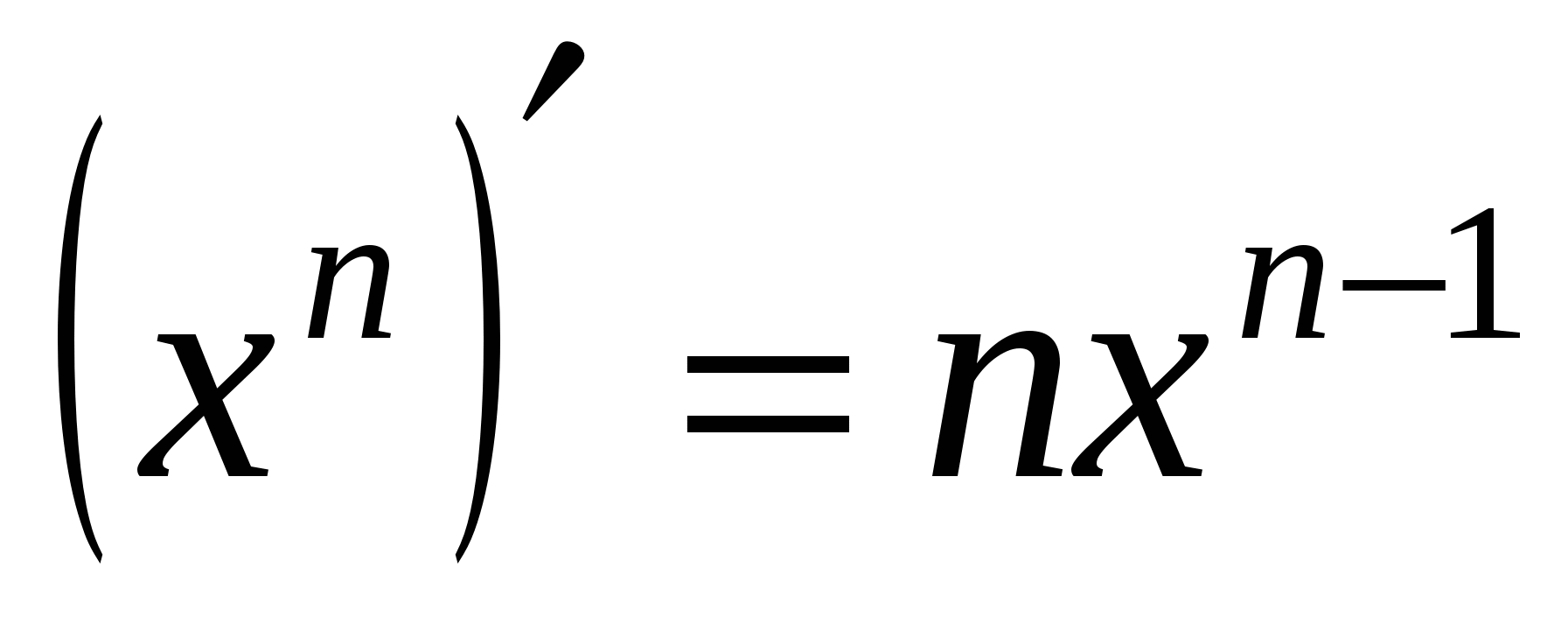
8а
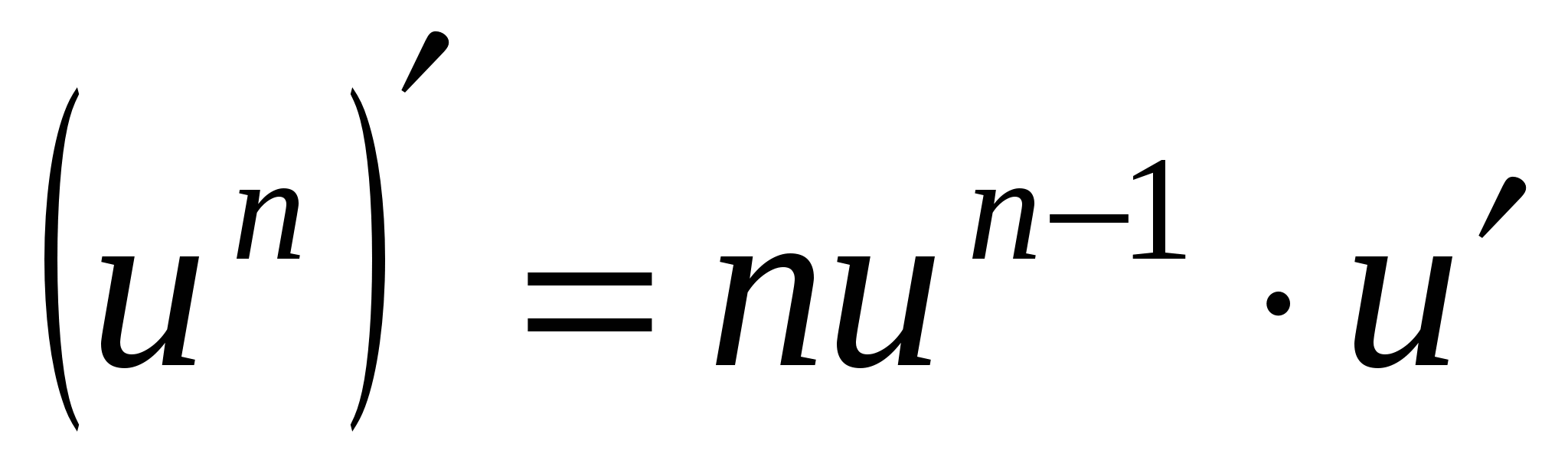
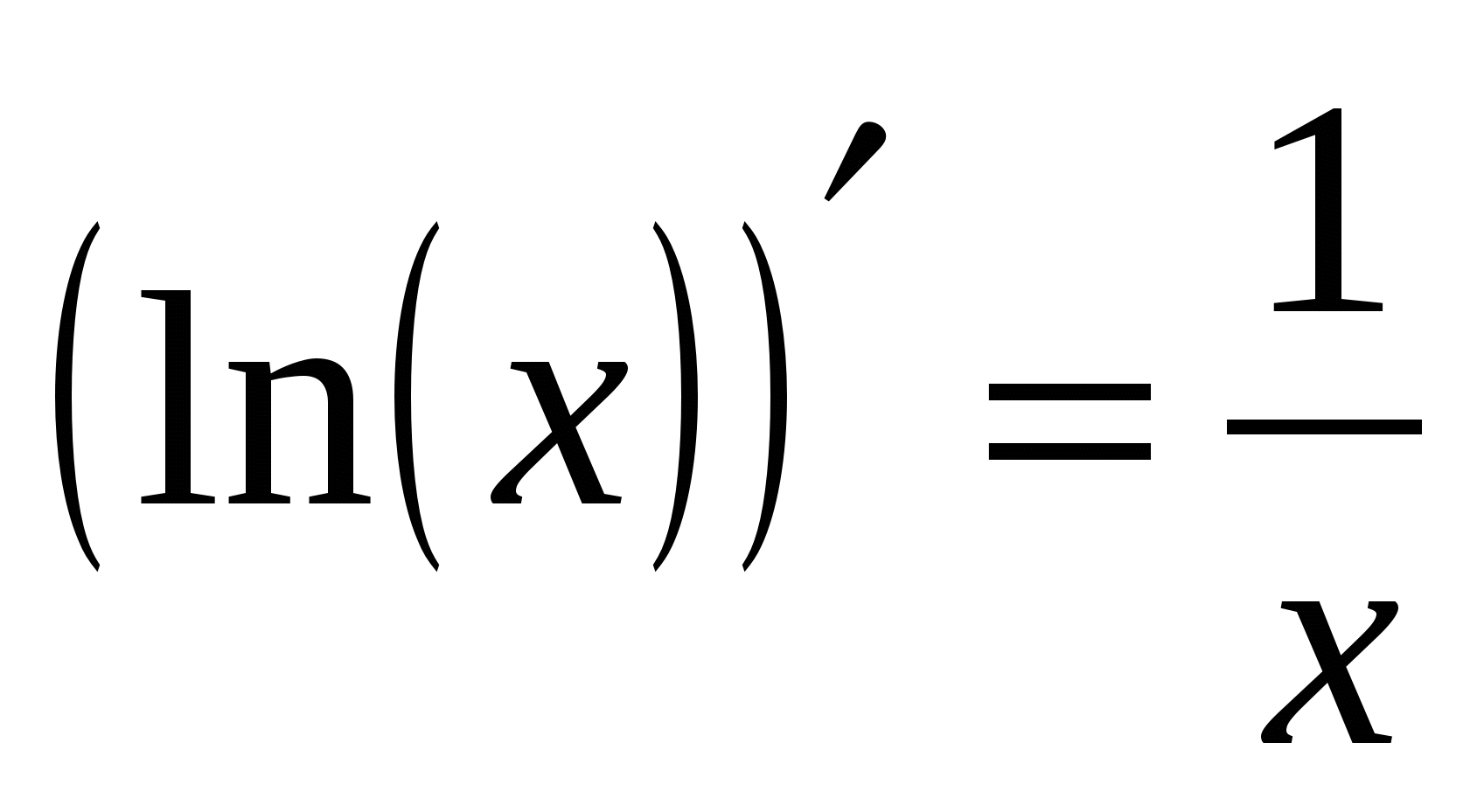
9а
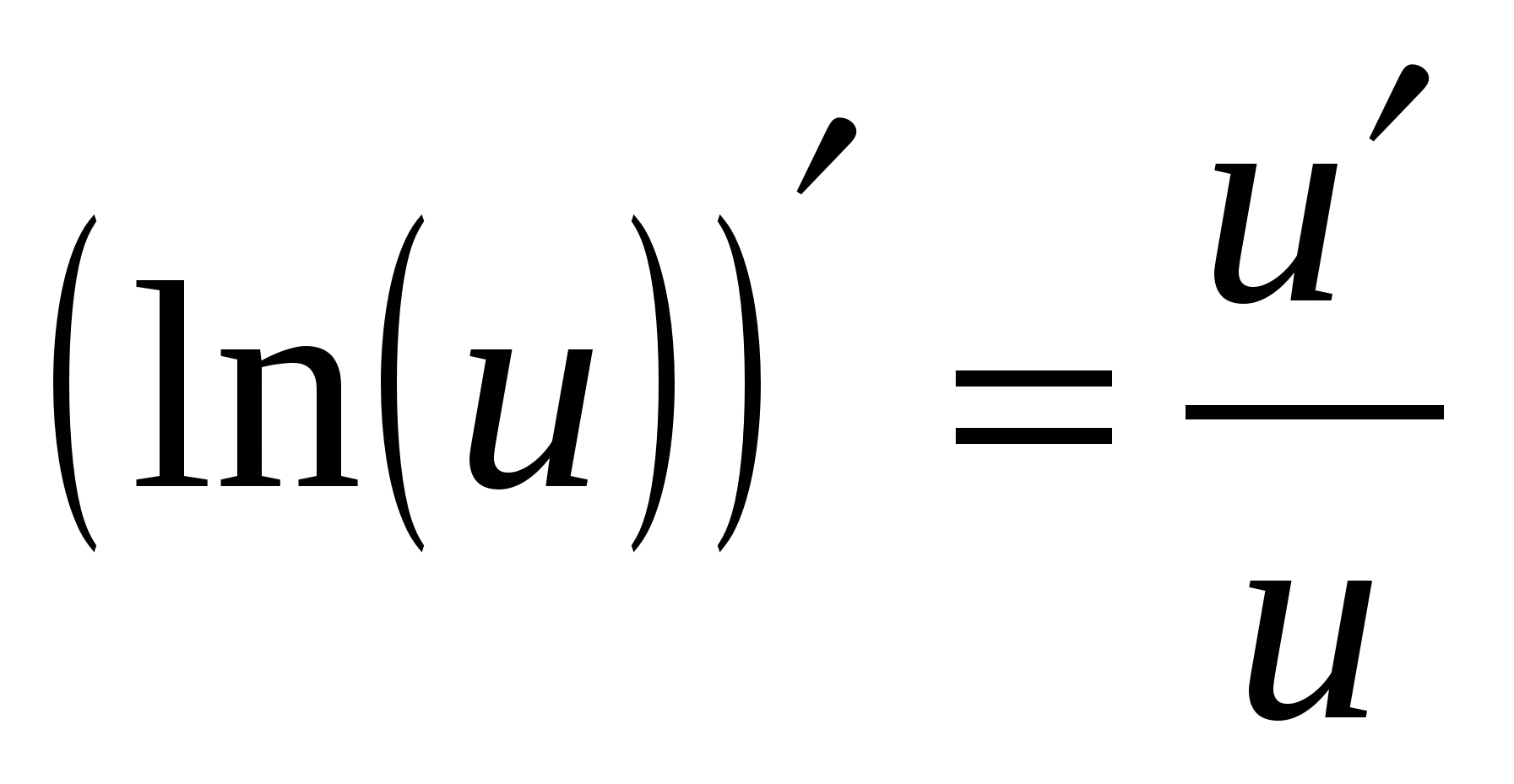
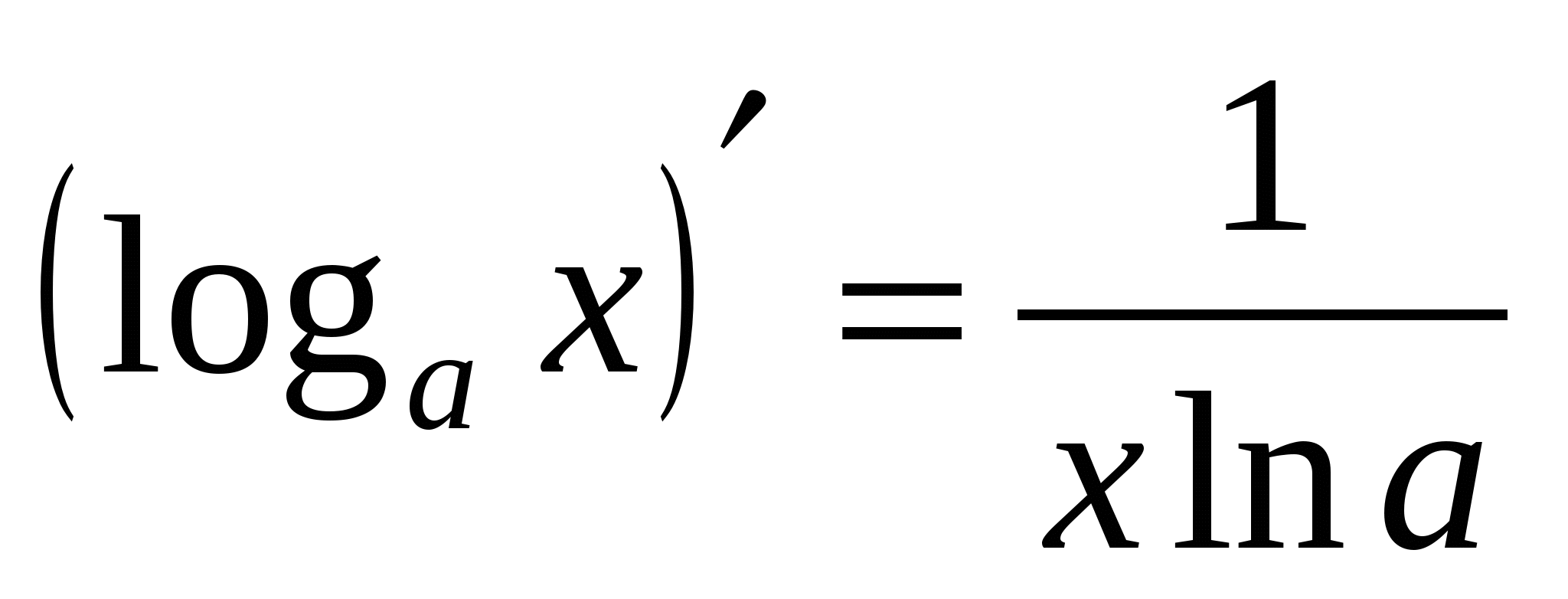
10а
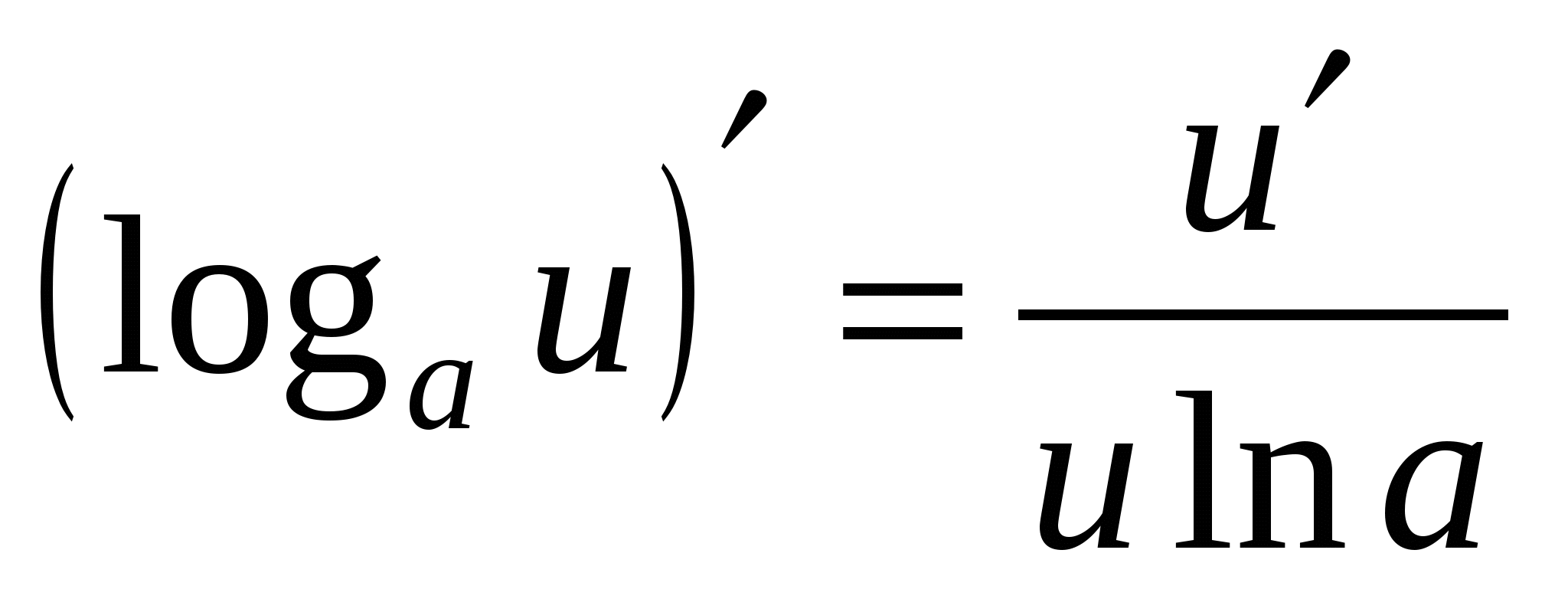
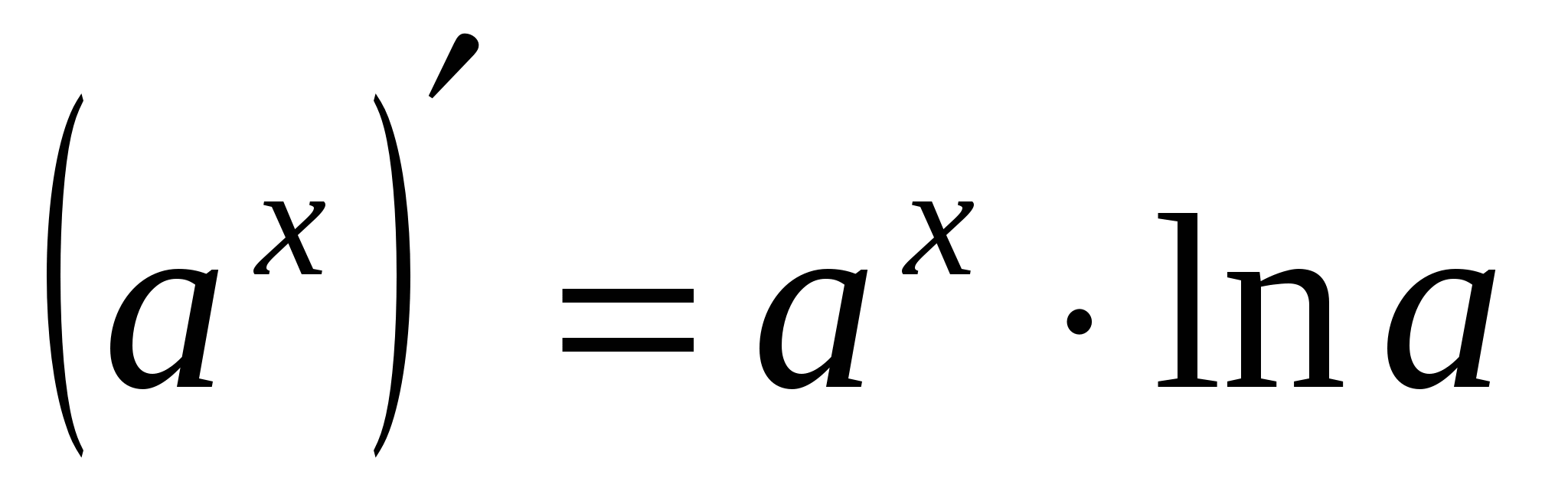
11а
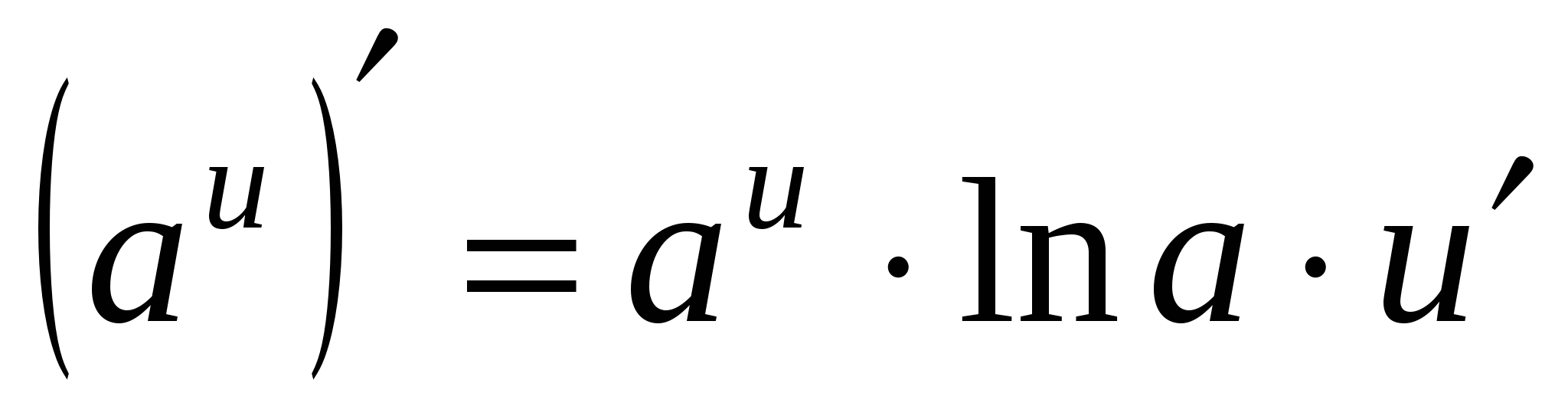
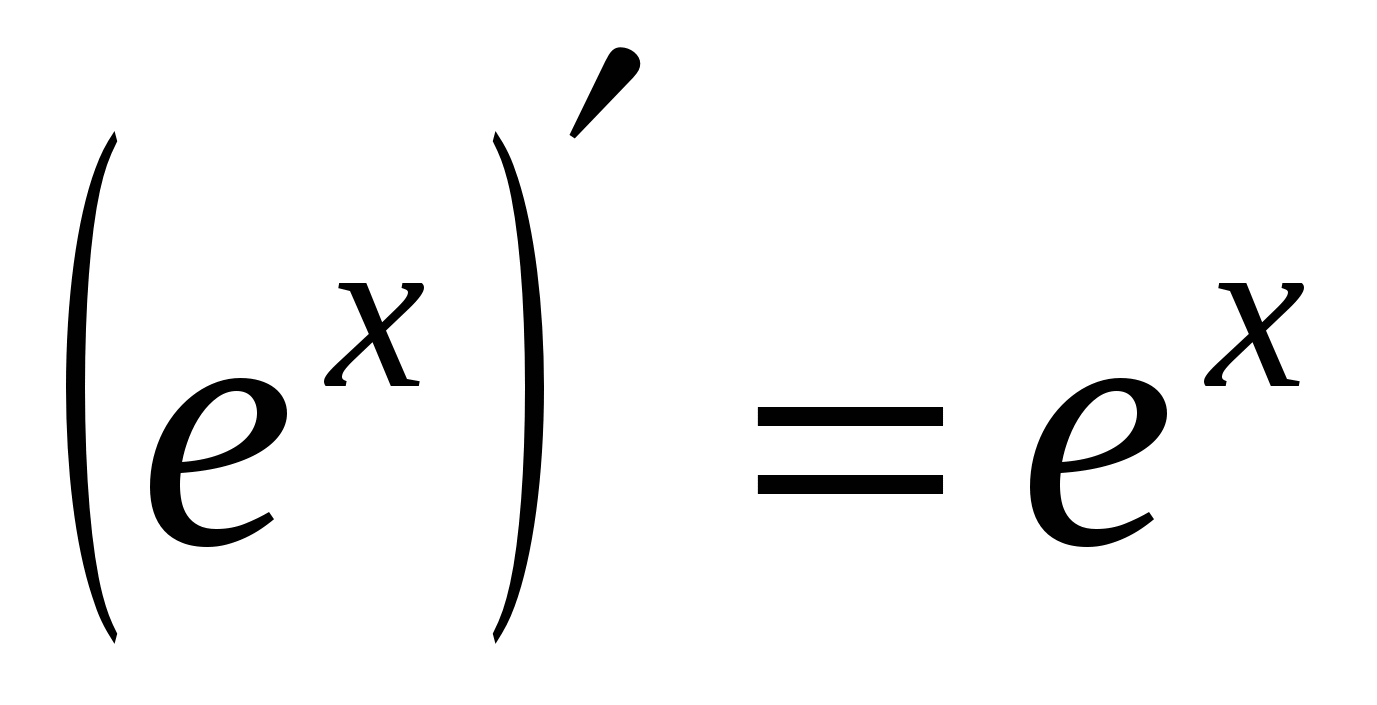
12а
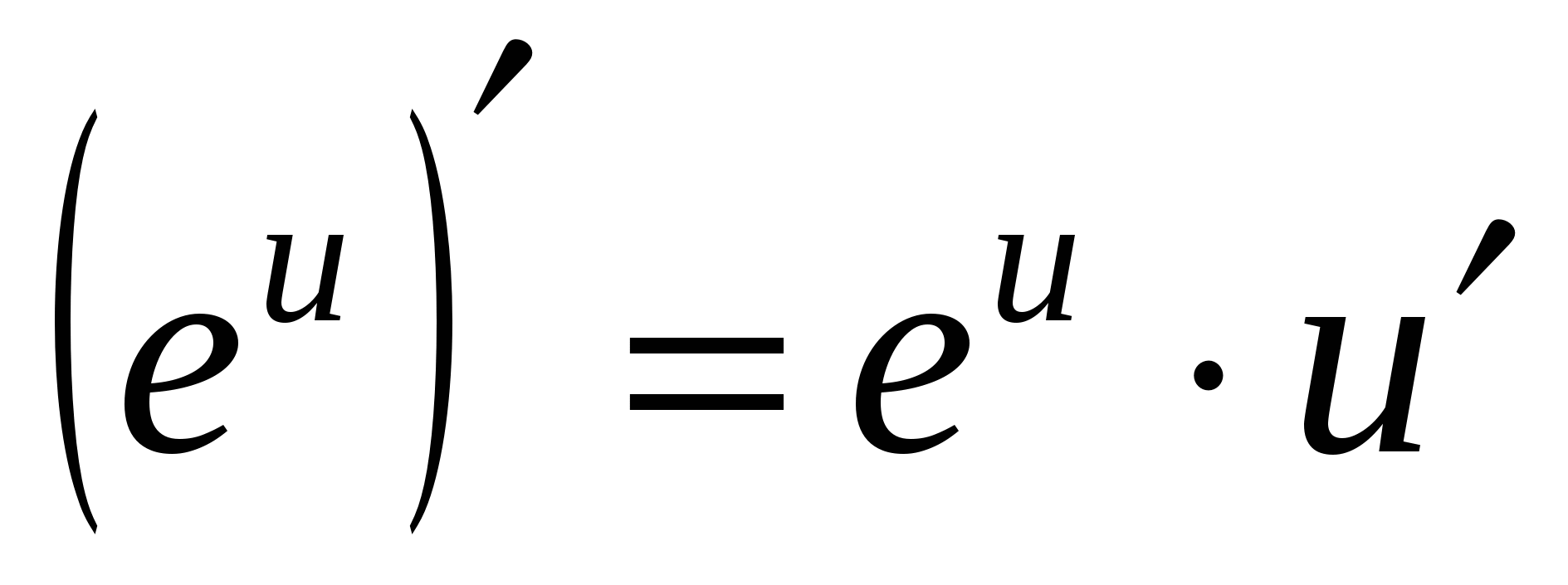
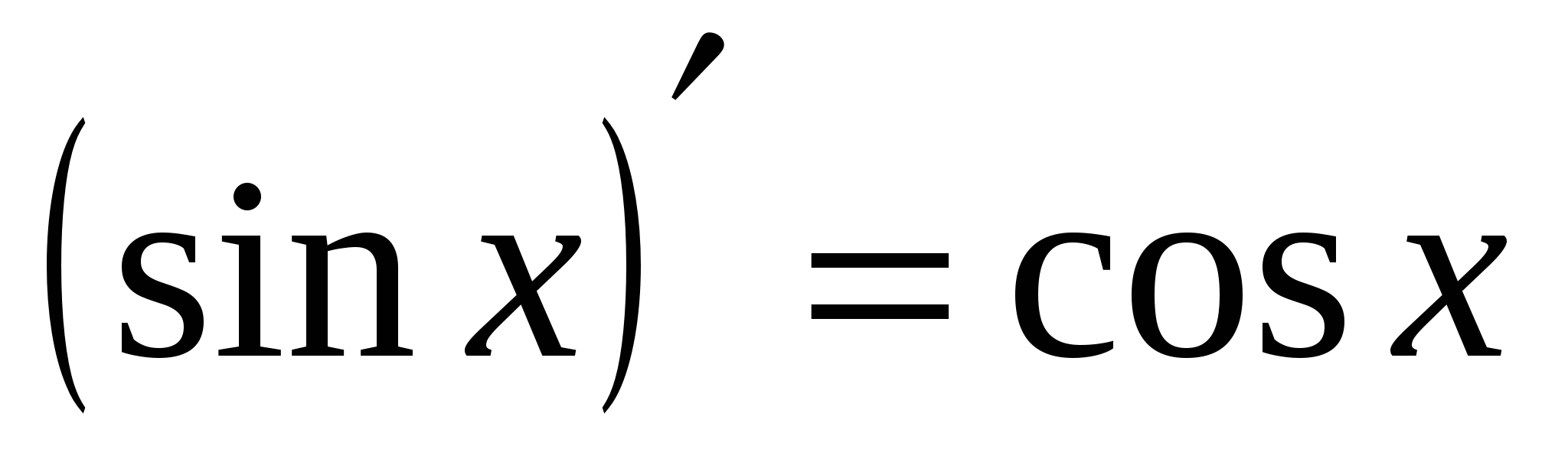
13а
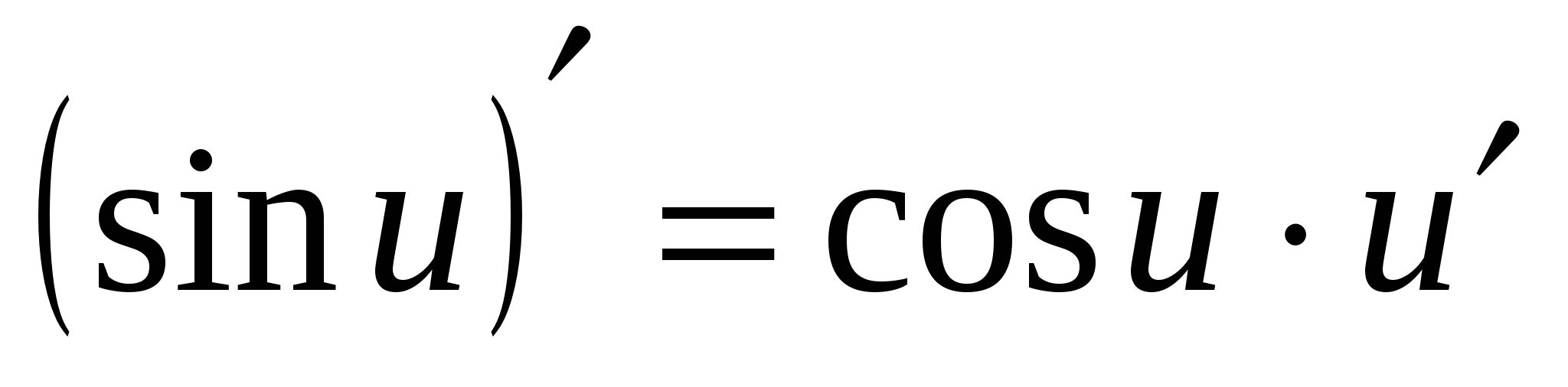
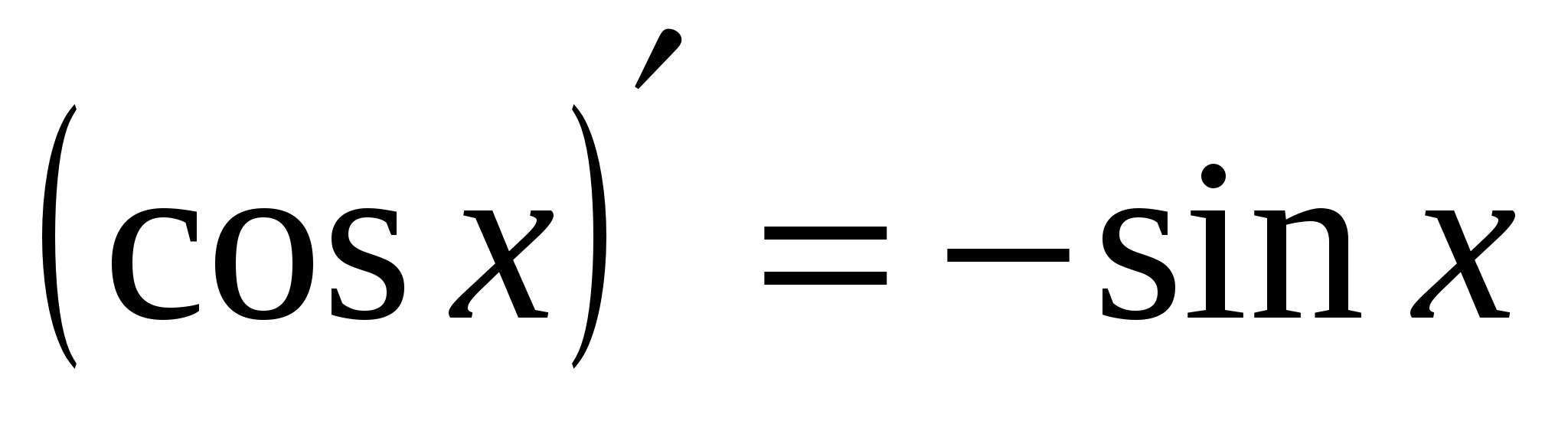
14а
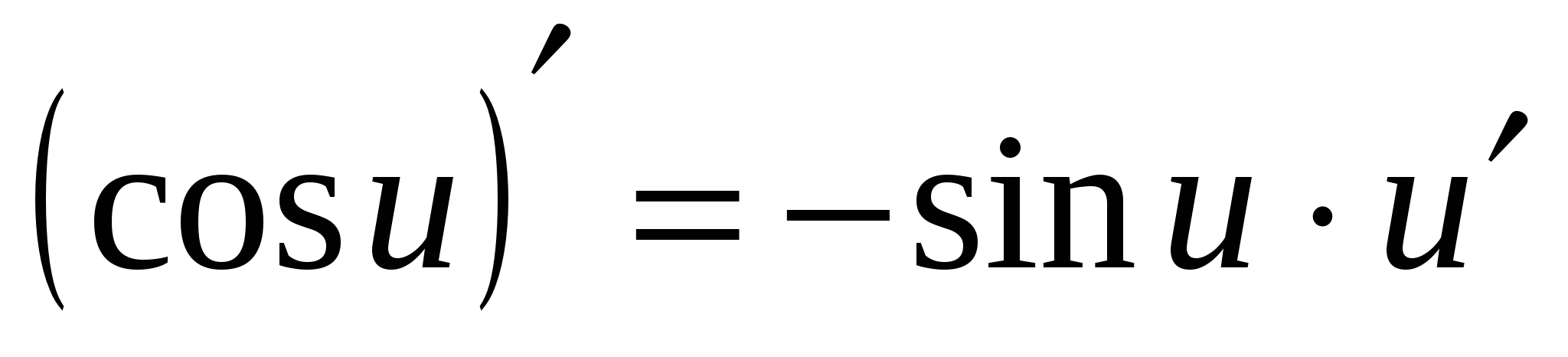
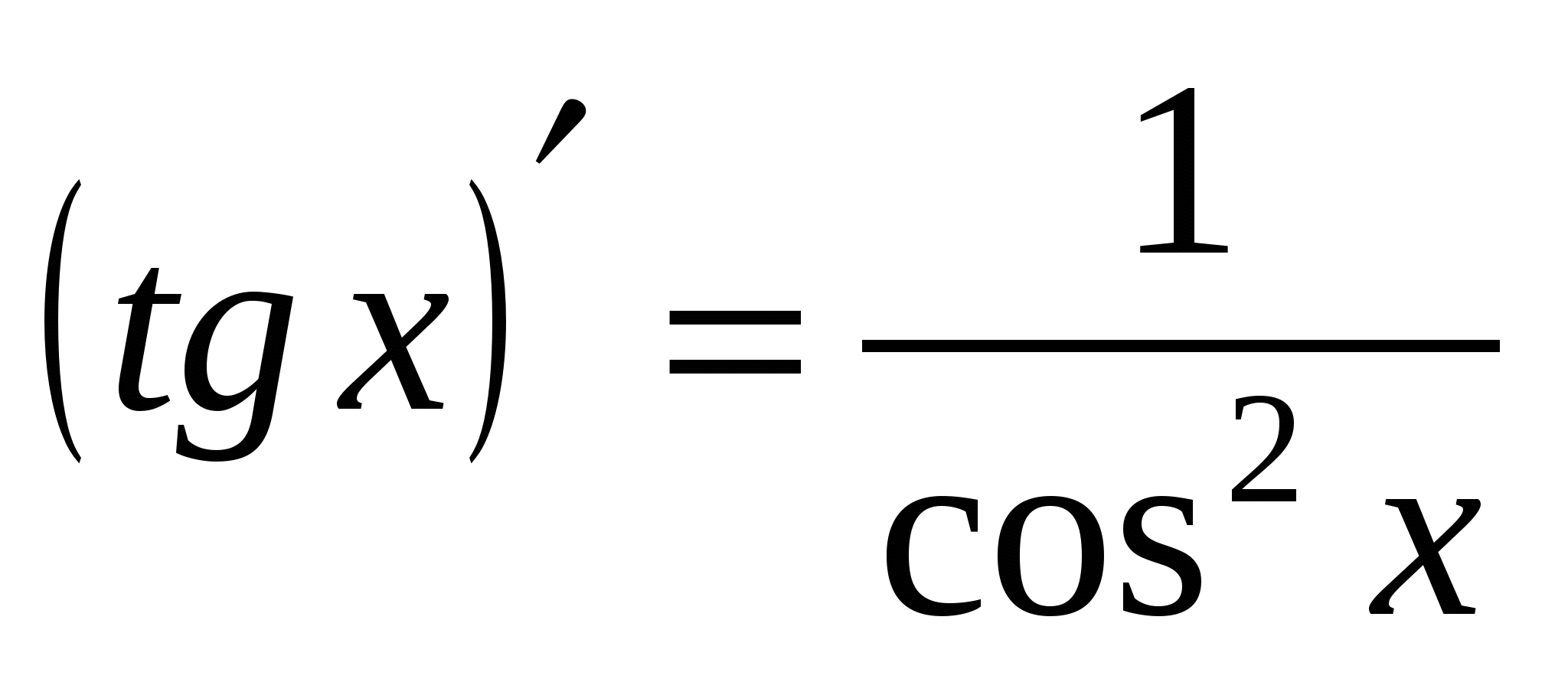
15а
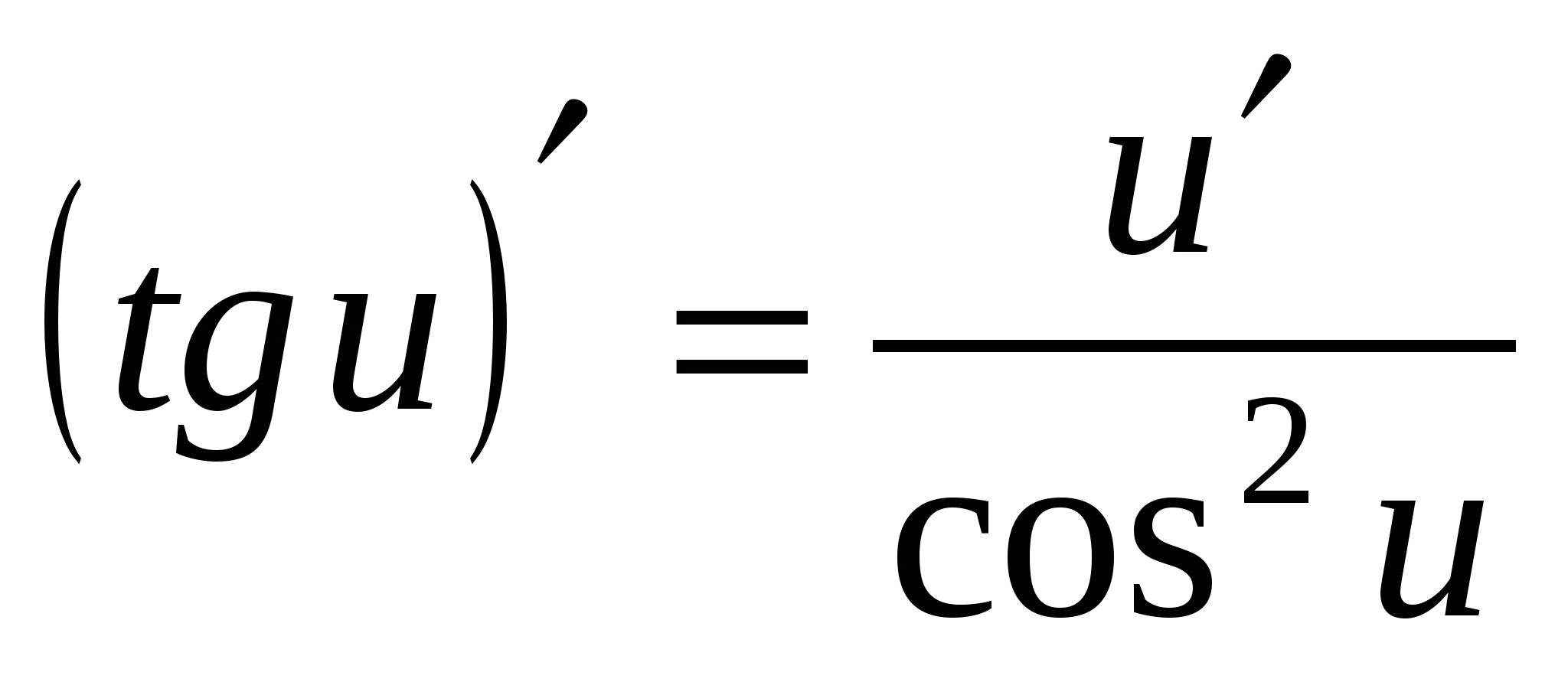
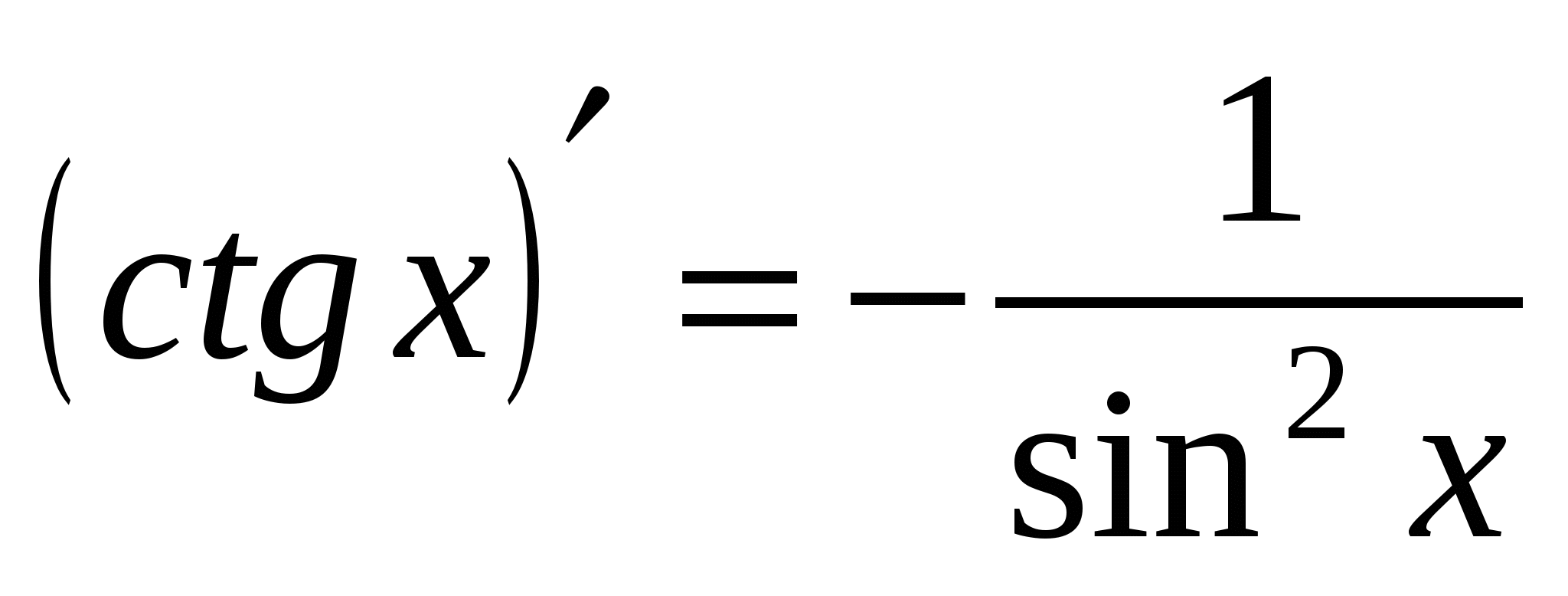
16а
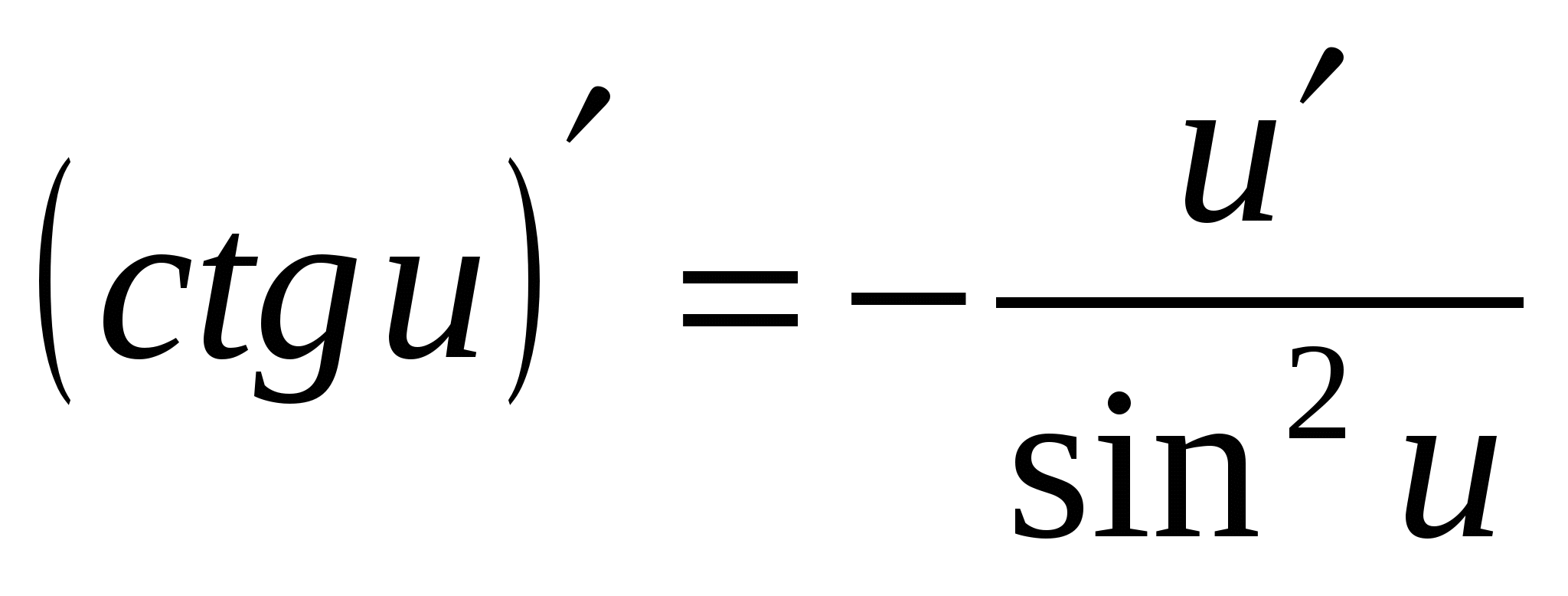
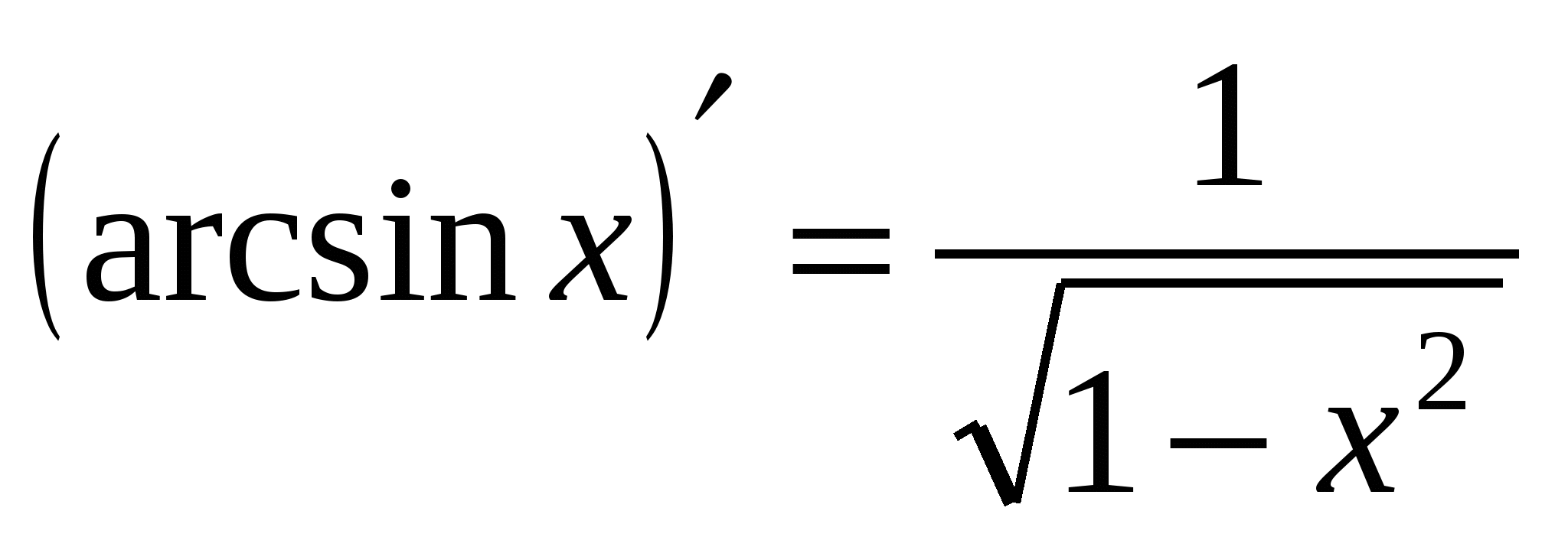
17а
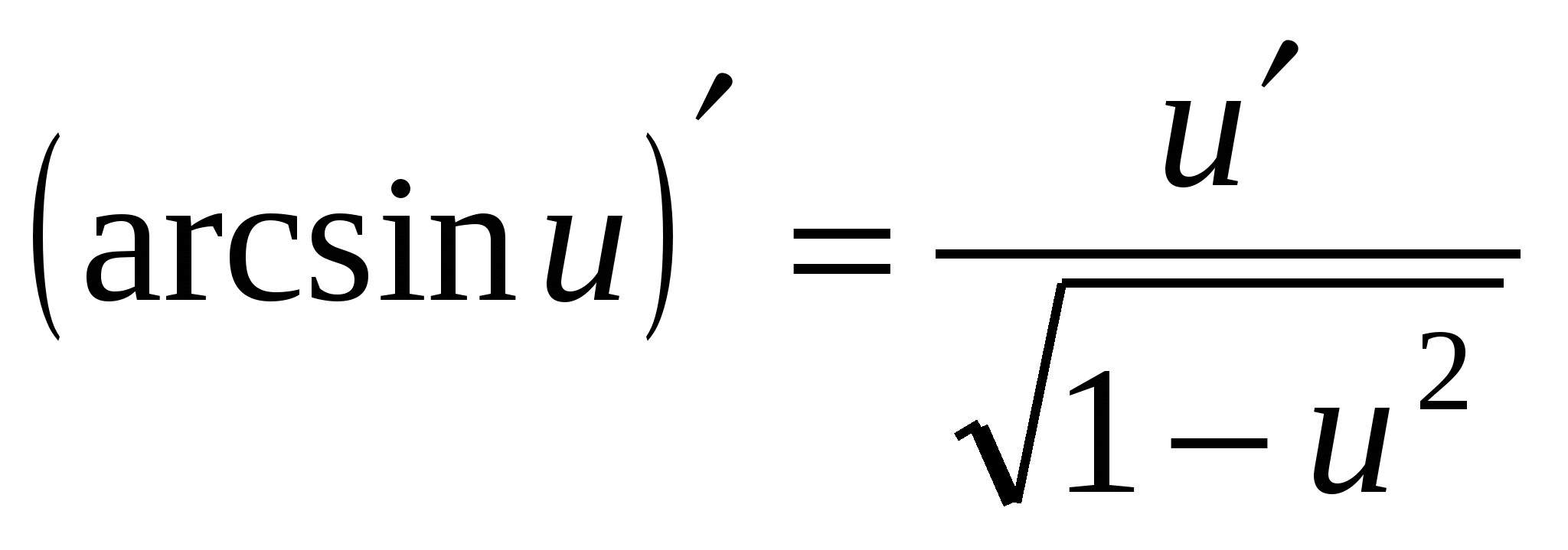
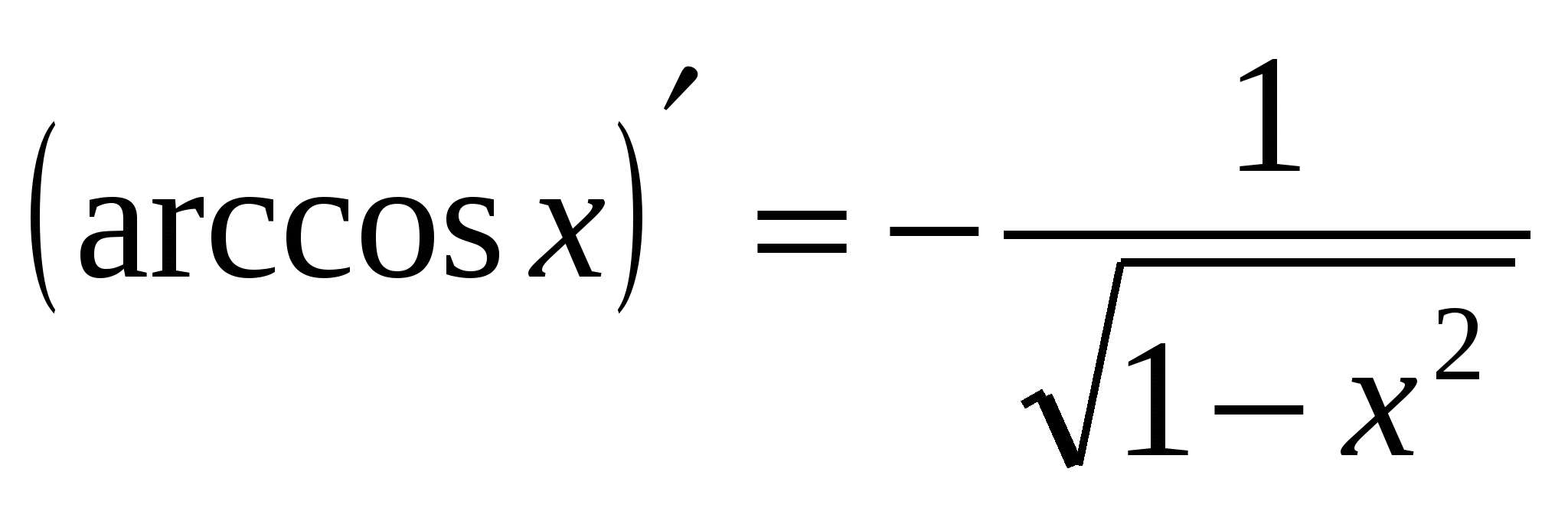
18а
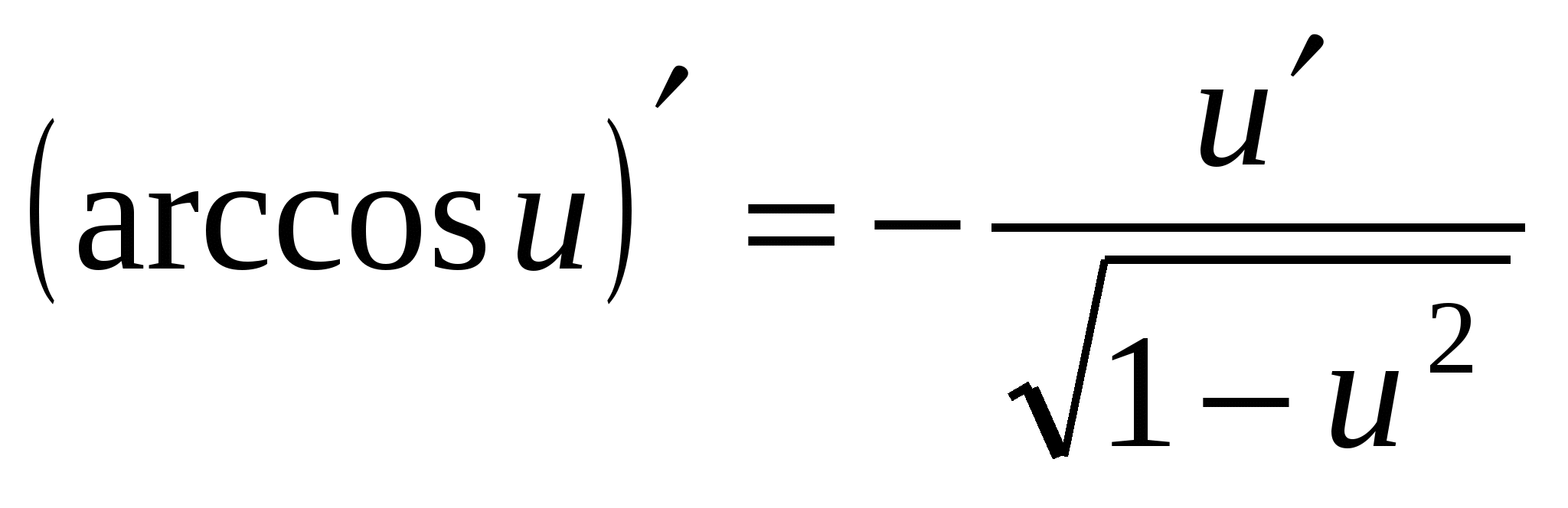
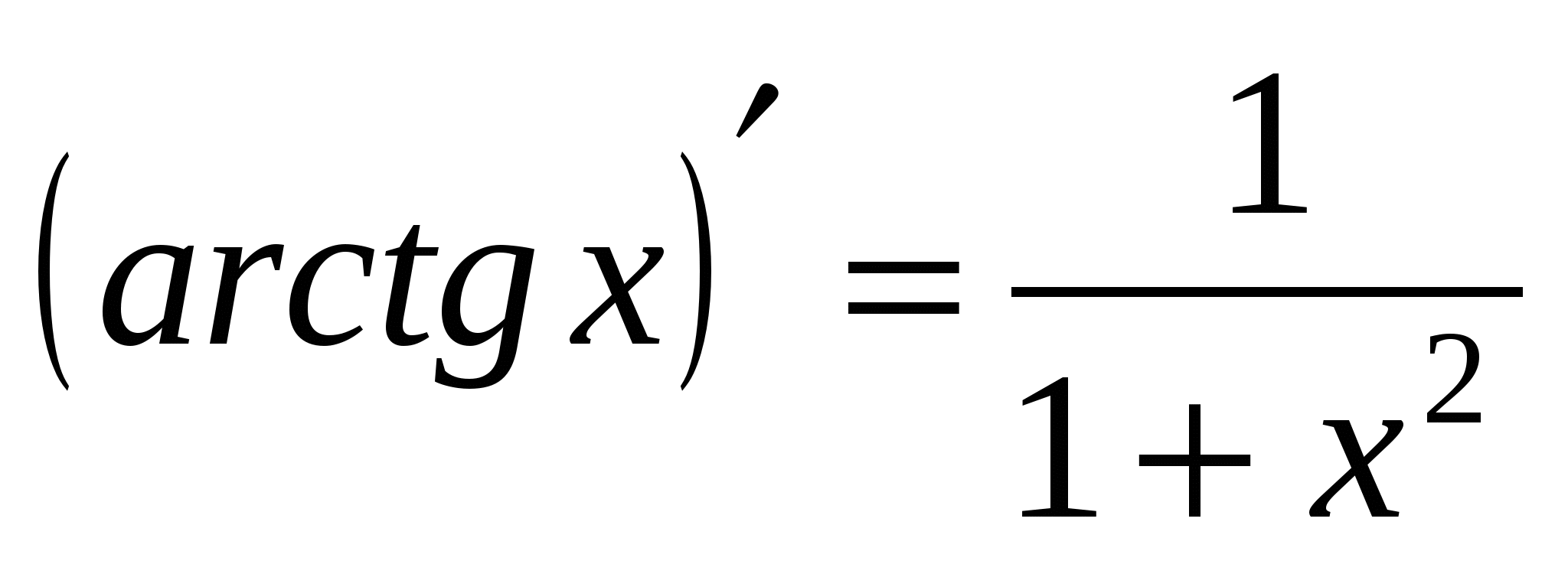
19а
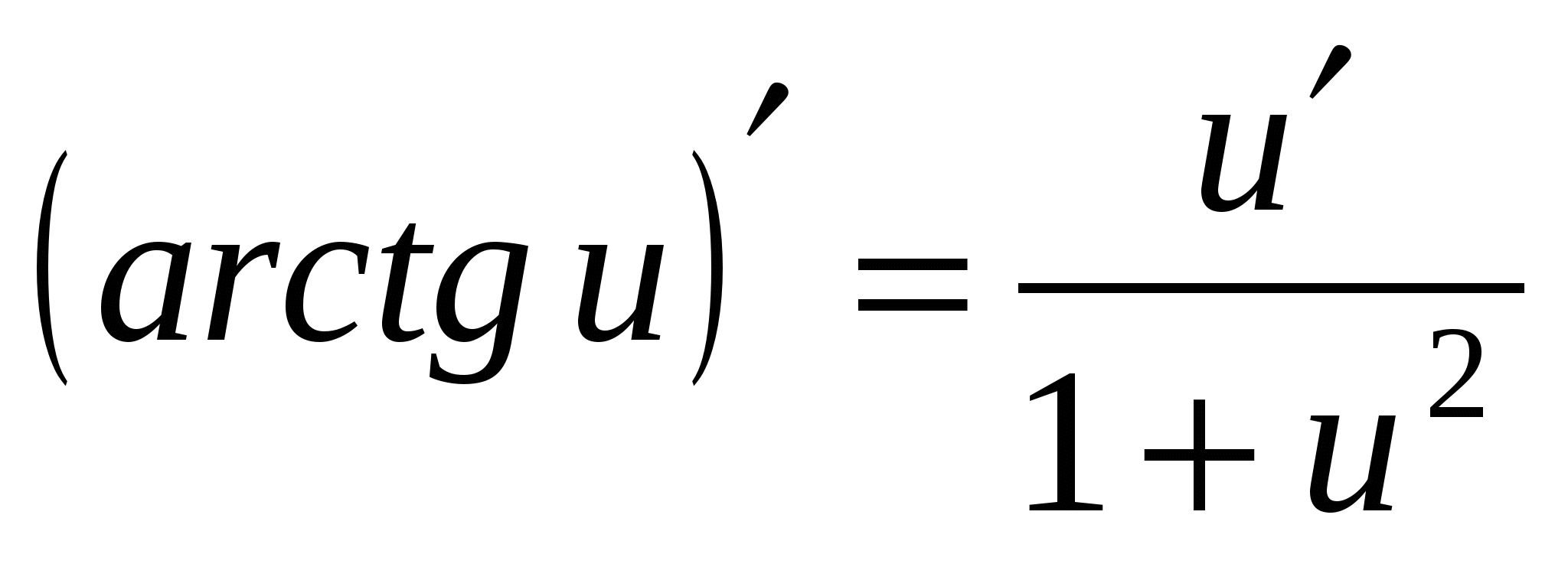
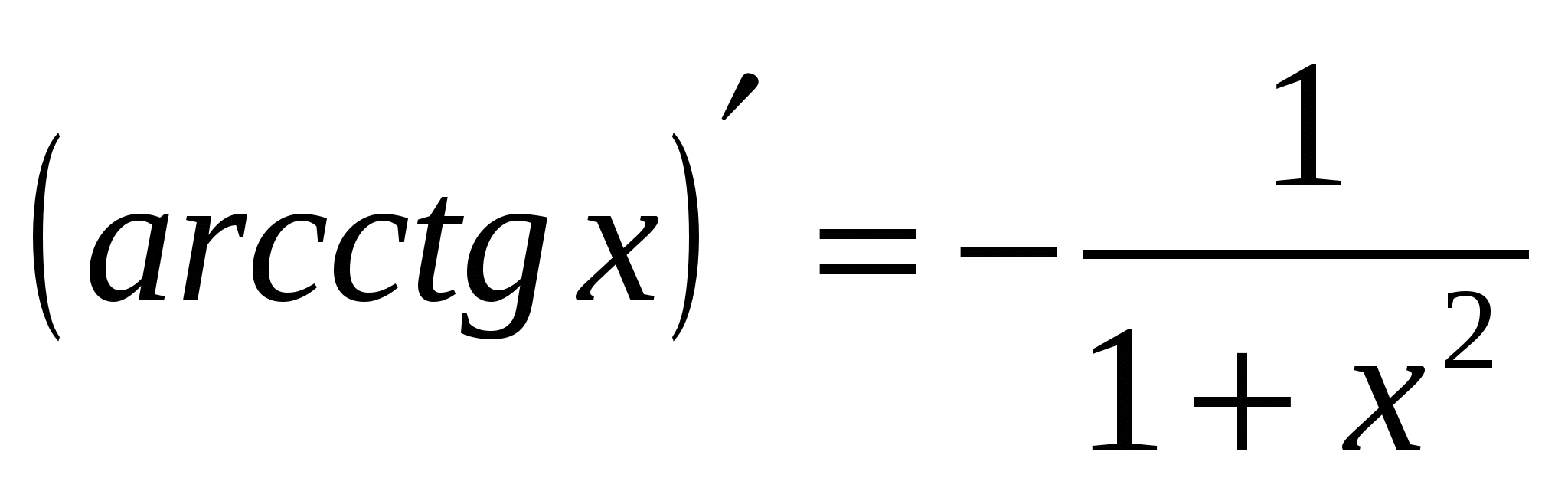
20а
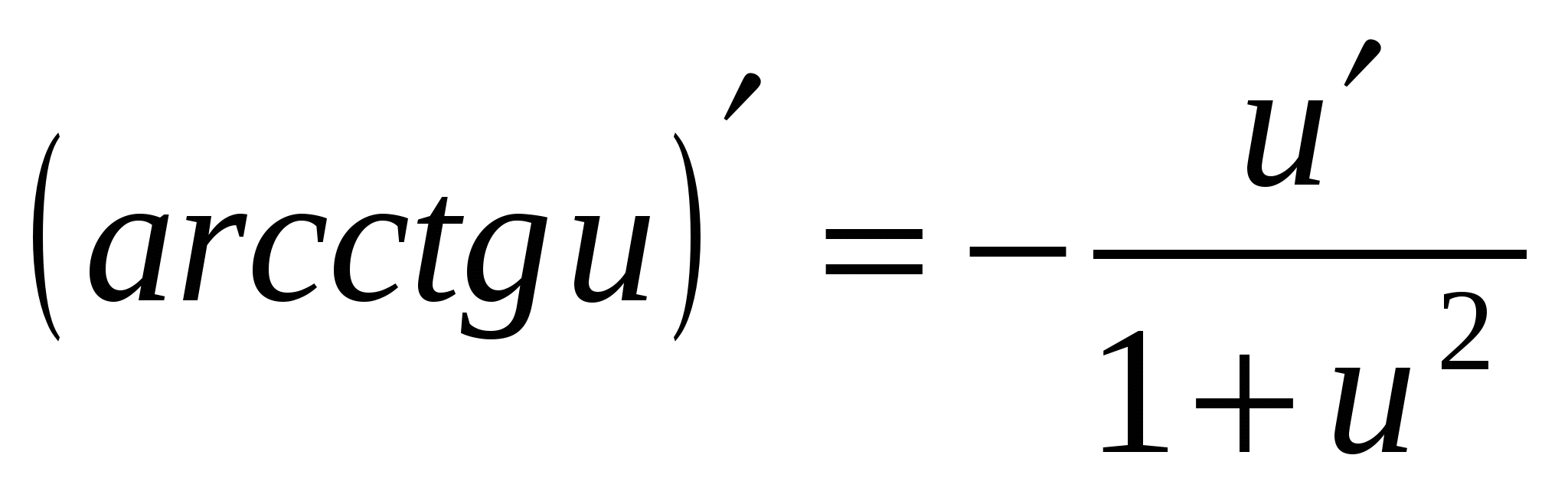
Пример 1. Найти производную функции 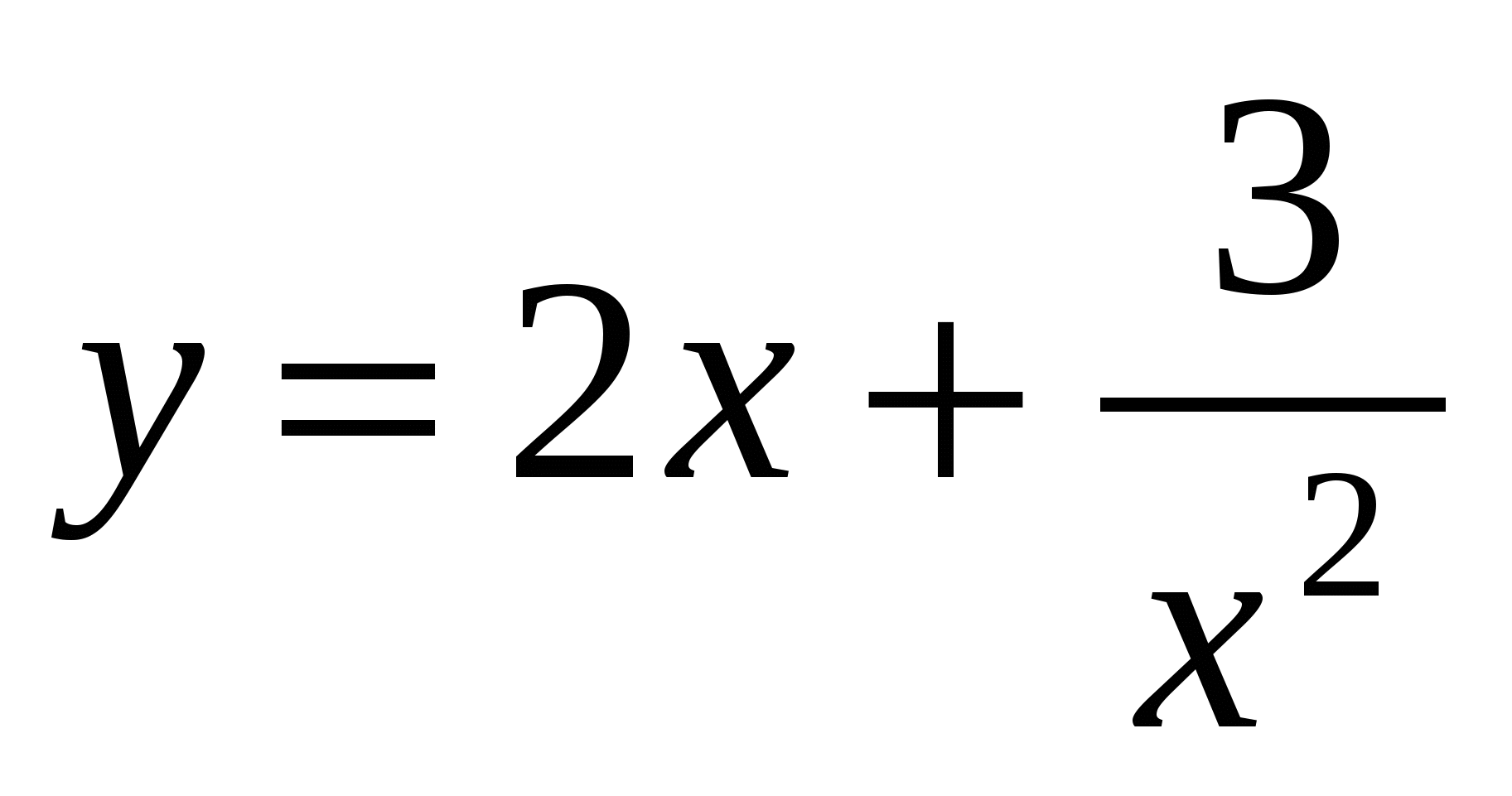 .
.
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5 и 8: 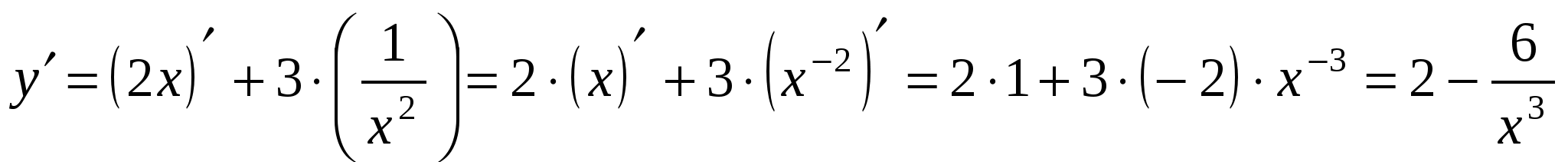
Пример 2. Найти производную функции 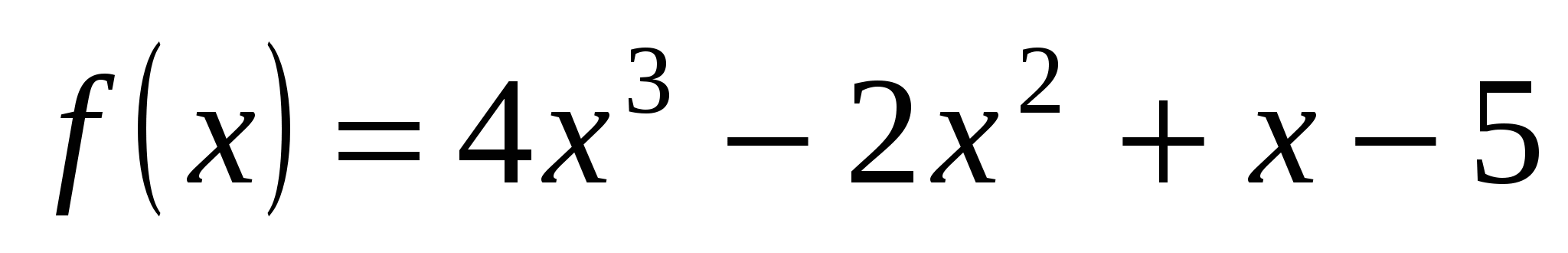 .
.
Решение: применив последовательно формулы 4, 3, 5 и 8, имеем
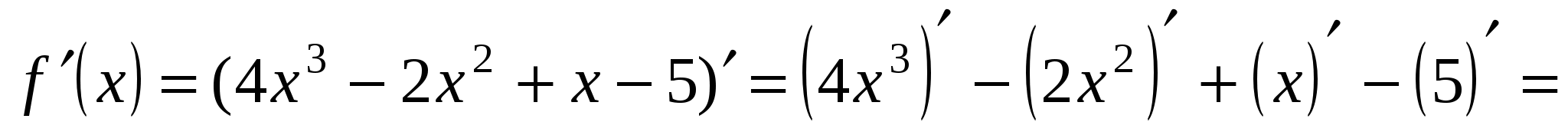
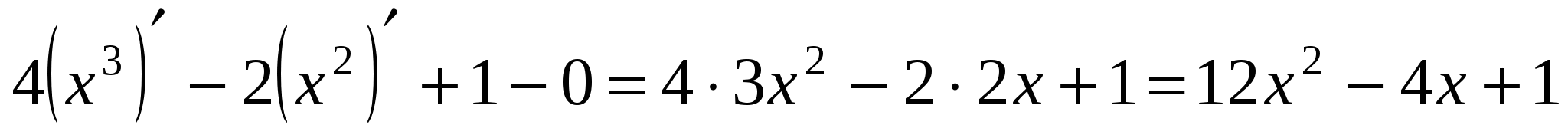 .
.
Пример 3. Найти производную функции 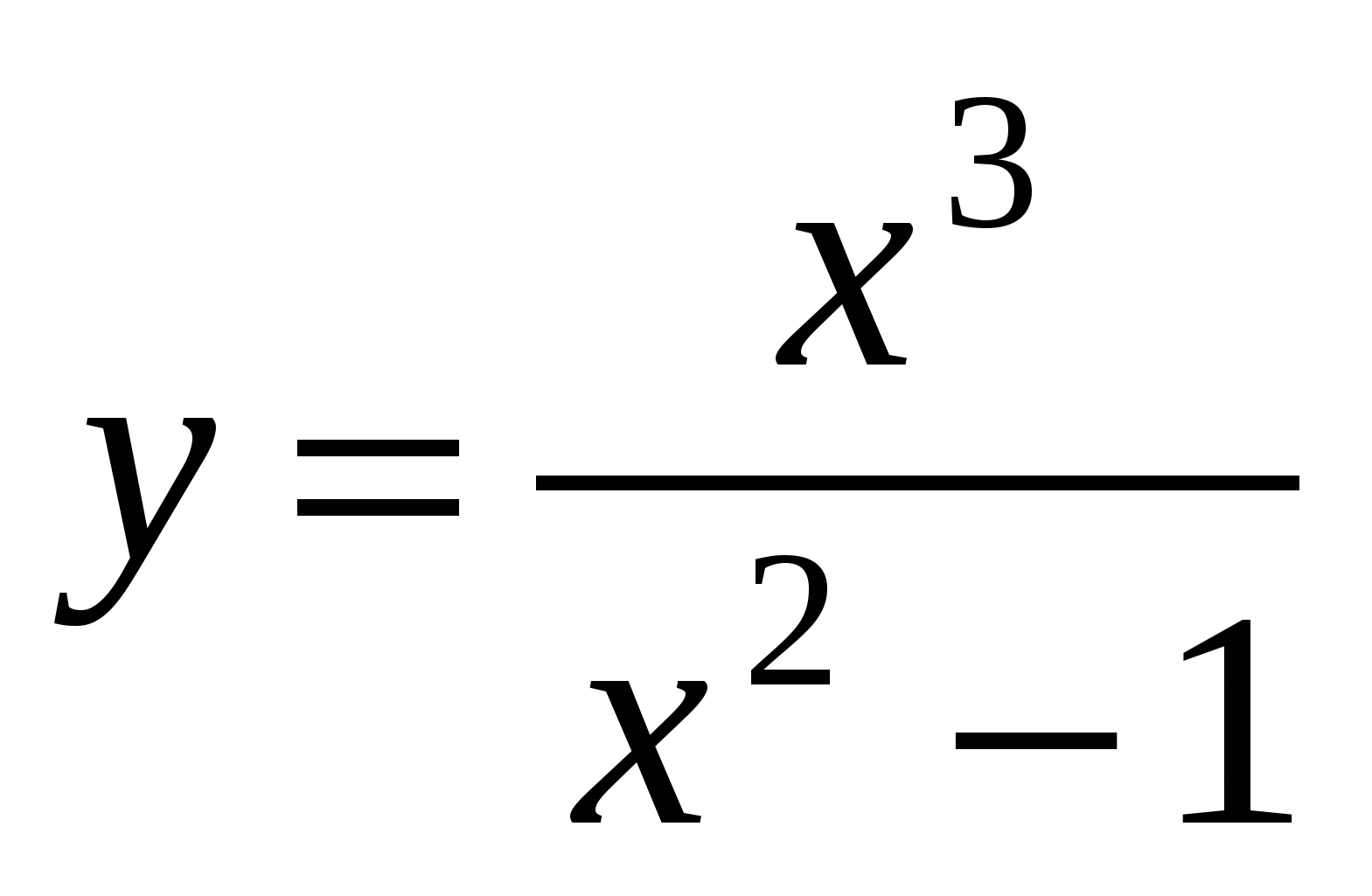 .
.
Решение. Применяя формулы 6, 3, 7 и 1, получим:
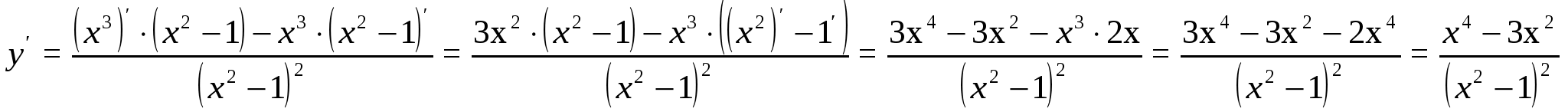
Пример 4. Найти производную функции 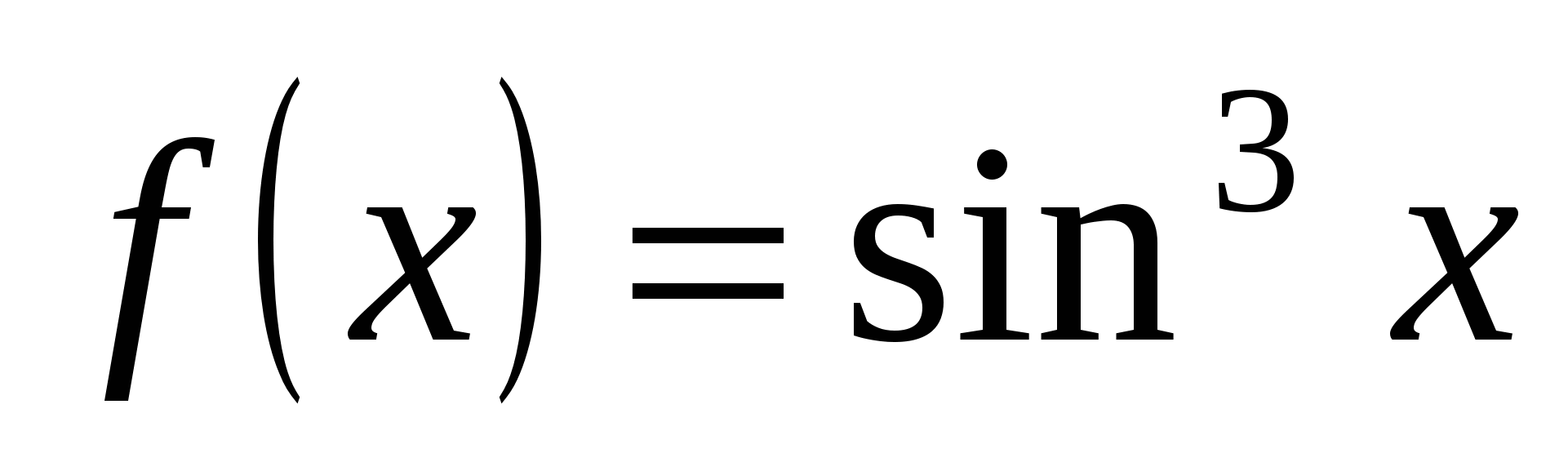 и вычислить ее значение при
и вычислить ее значение при ![]()
Решение. Это сложная функция с промежуточным аргументом 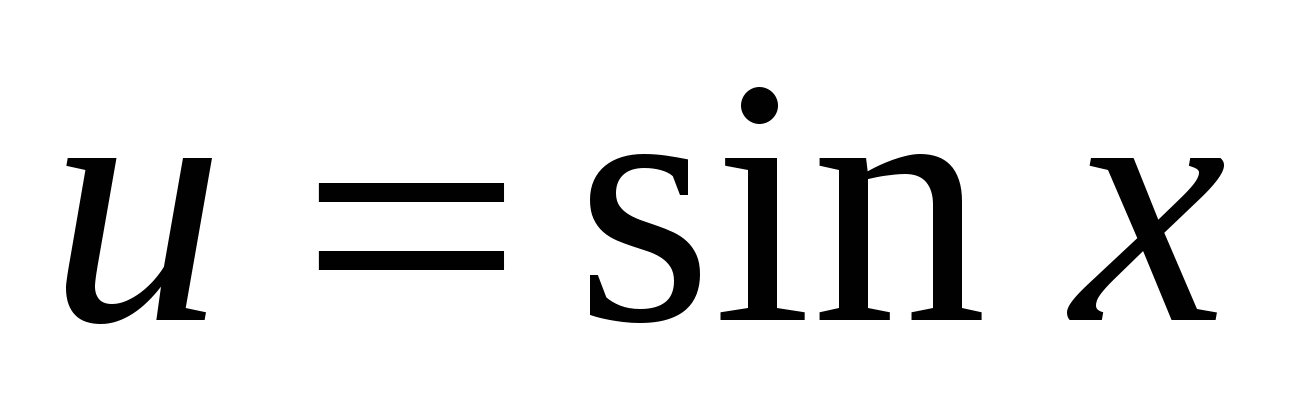 . Используя формулы 8а и
. Используя формулы 8а и 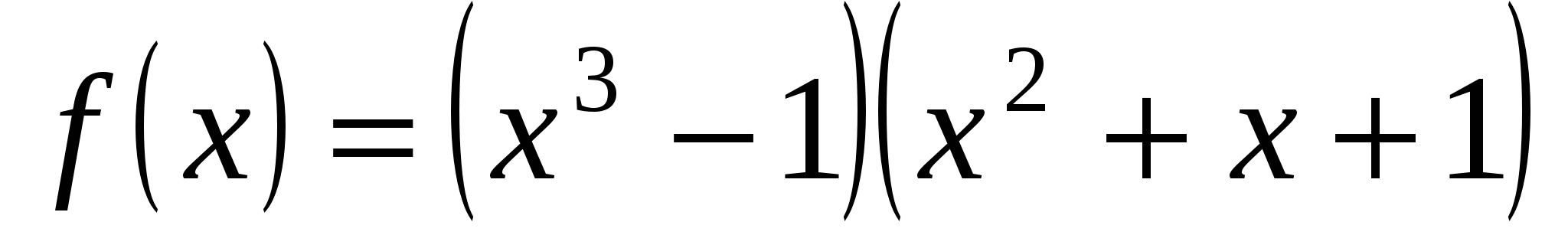 13, имеем:
13, имеем: 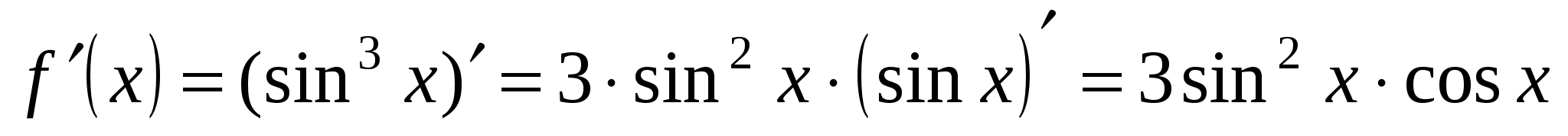 .
.
Вычислим значение производной при 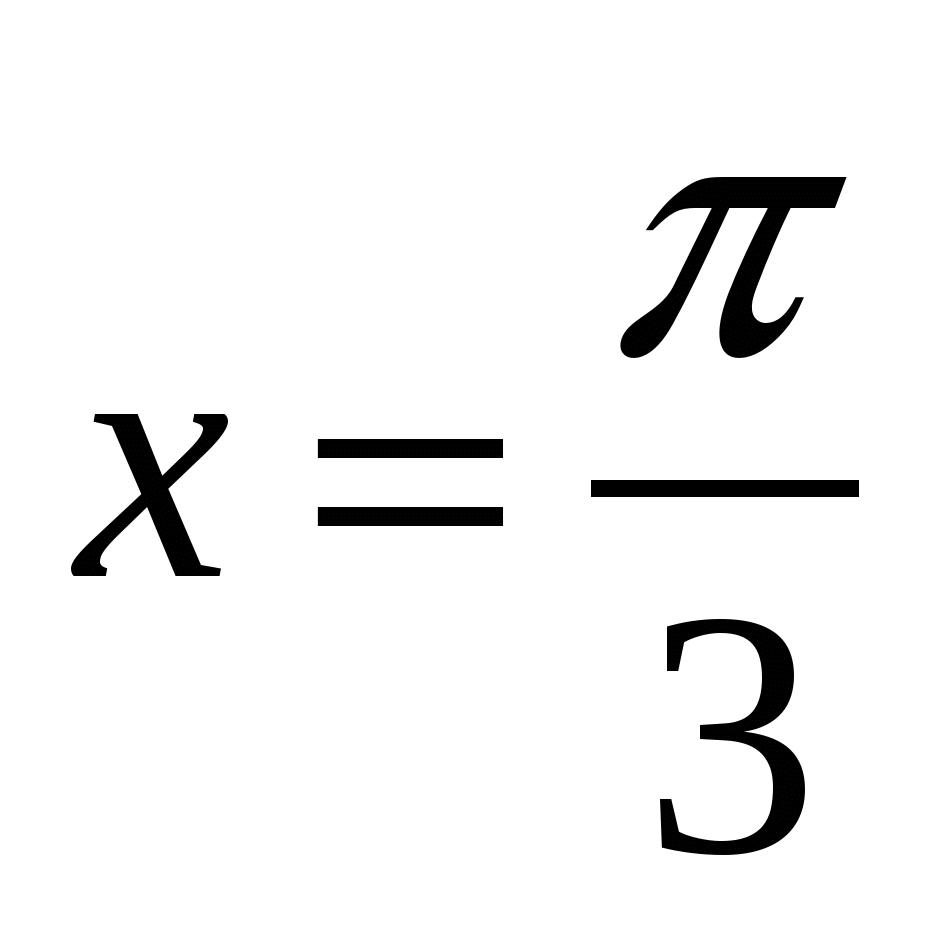 .
.
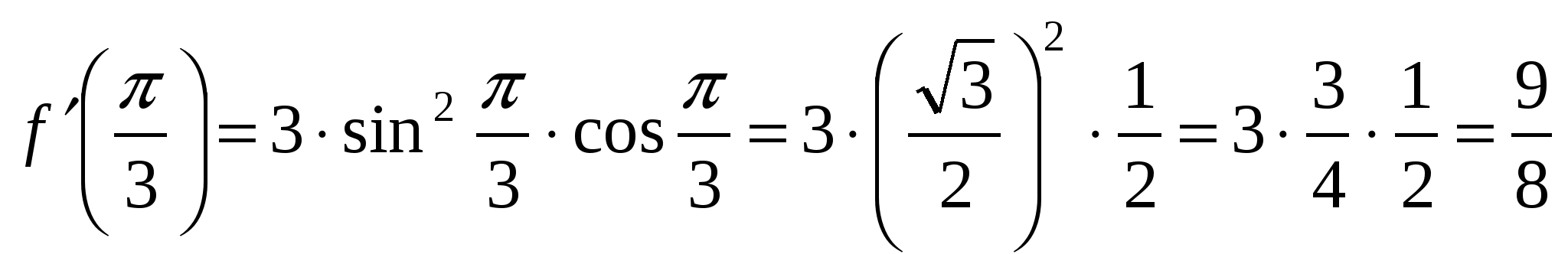 .
.
Пример 5. Найти производную функции 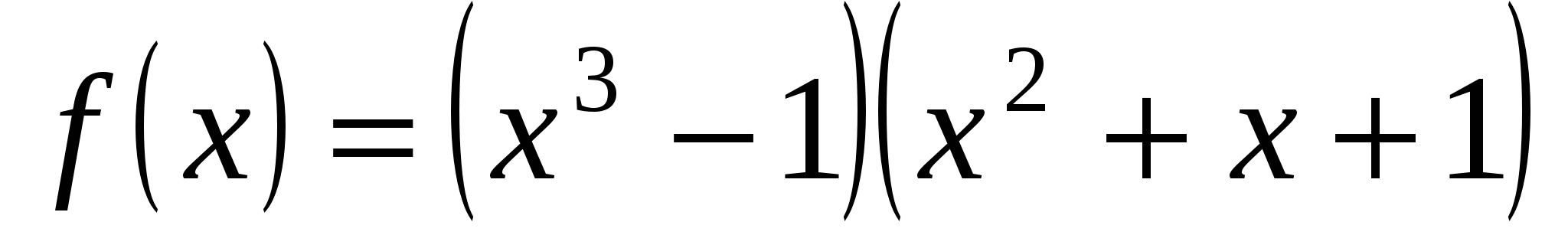 .
.
Решение. Используя правило дифференцирования произведения и соответствующие формулы нахождения производных, получим
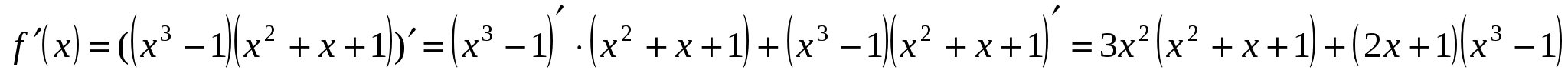 .
.
Пример 6. Найти производную функции 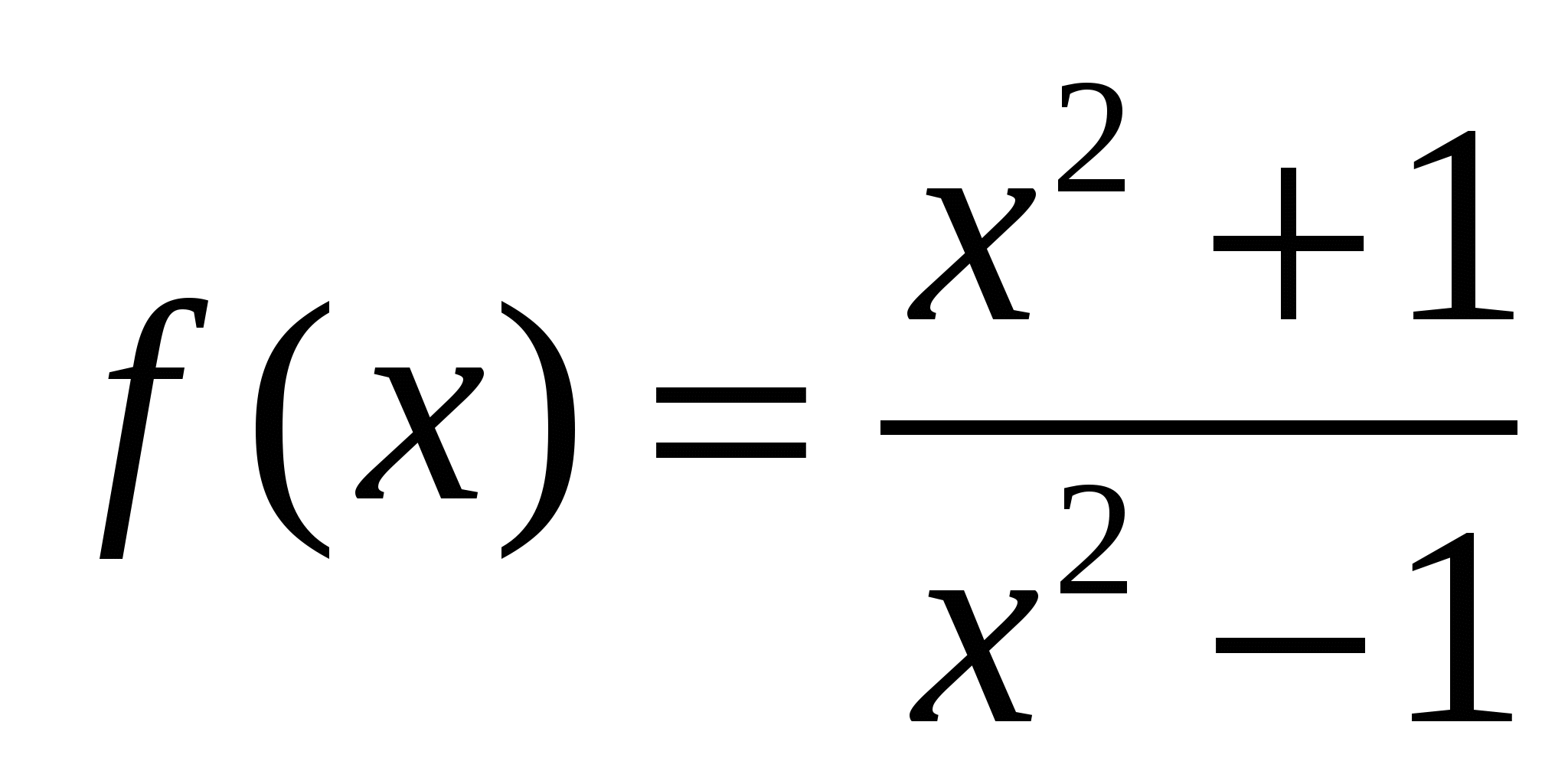 .
.
Решение: используя правило дифференцирования частного и соответствующие формулы нахождения производных, получим
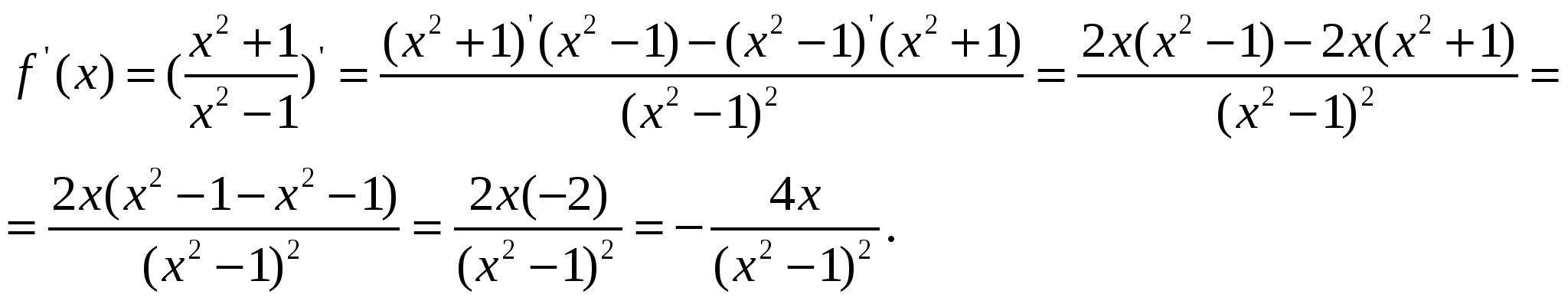
Пример 7. Найти производную функции 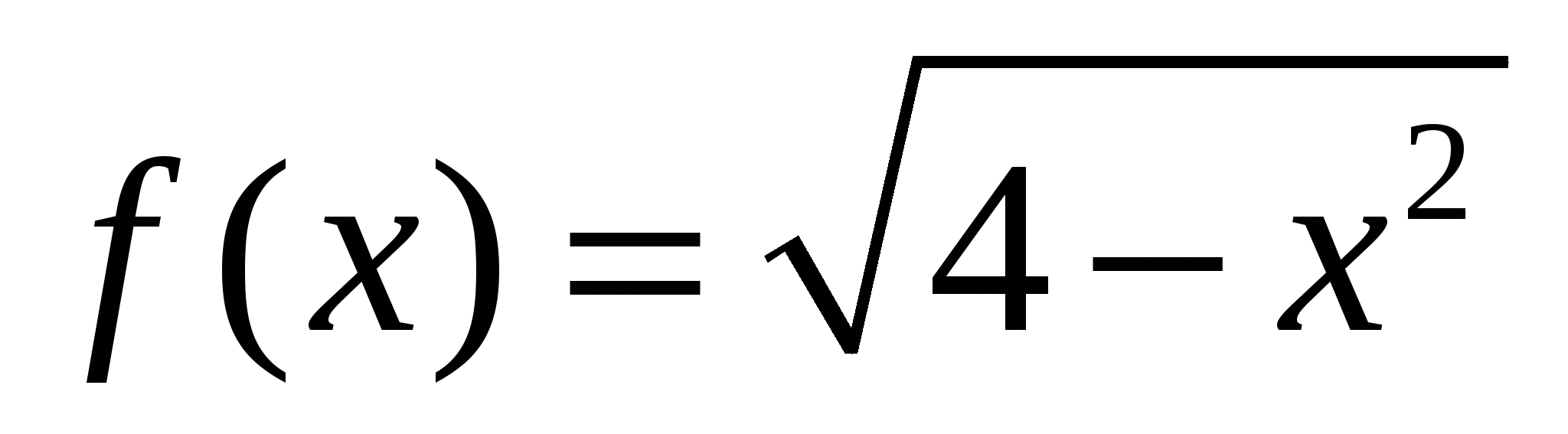 .
.
Решение: полагая 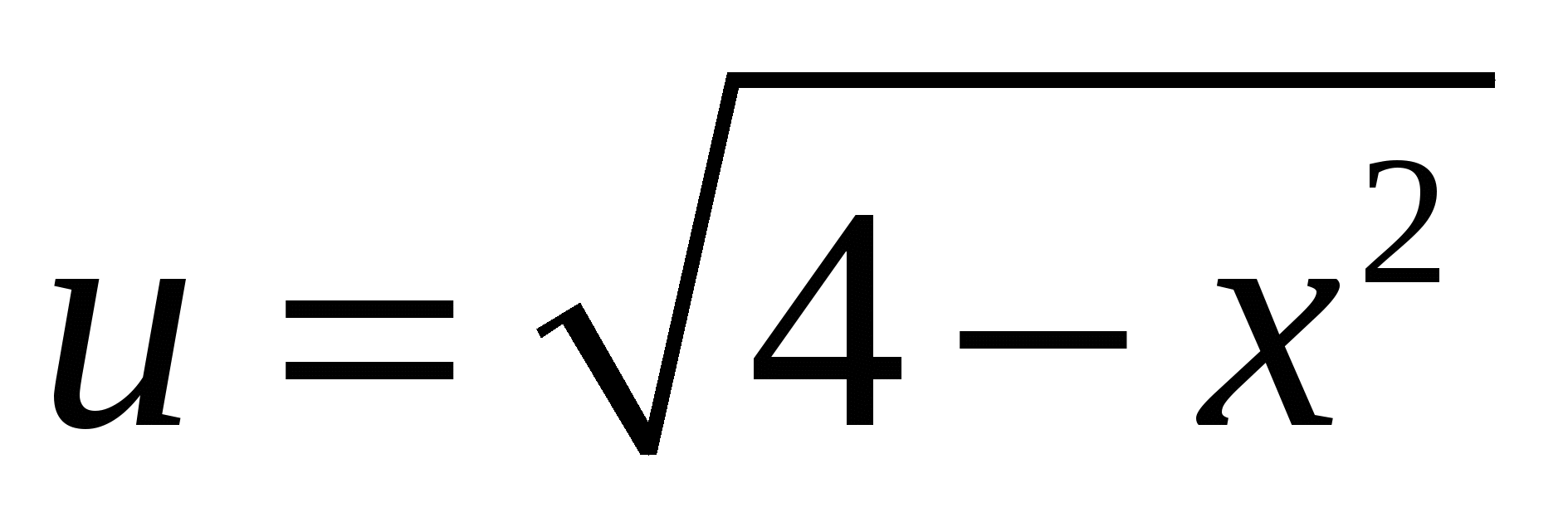 , получим
, получим 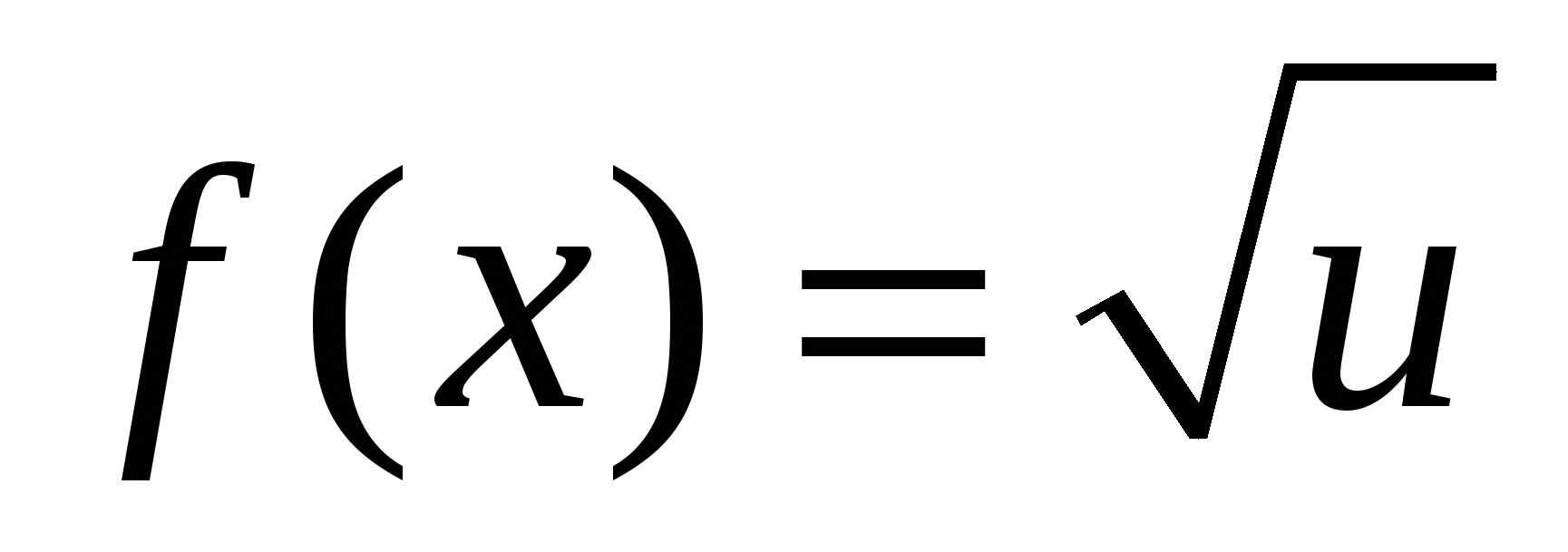 .
.
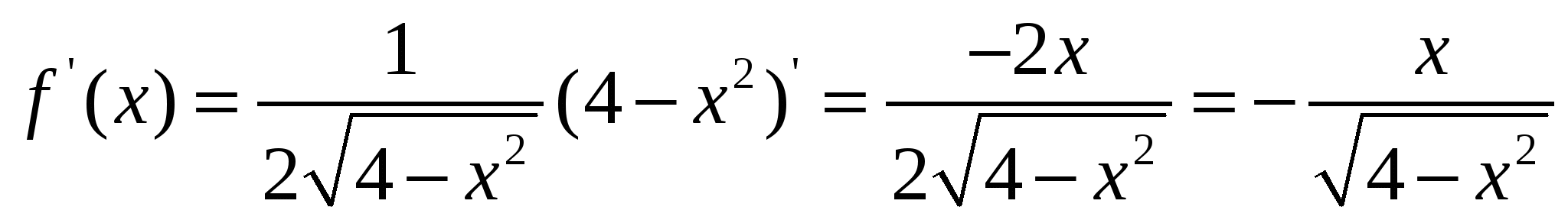
Пример 8. Найти производную функции.
Решение. 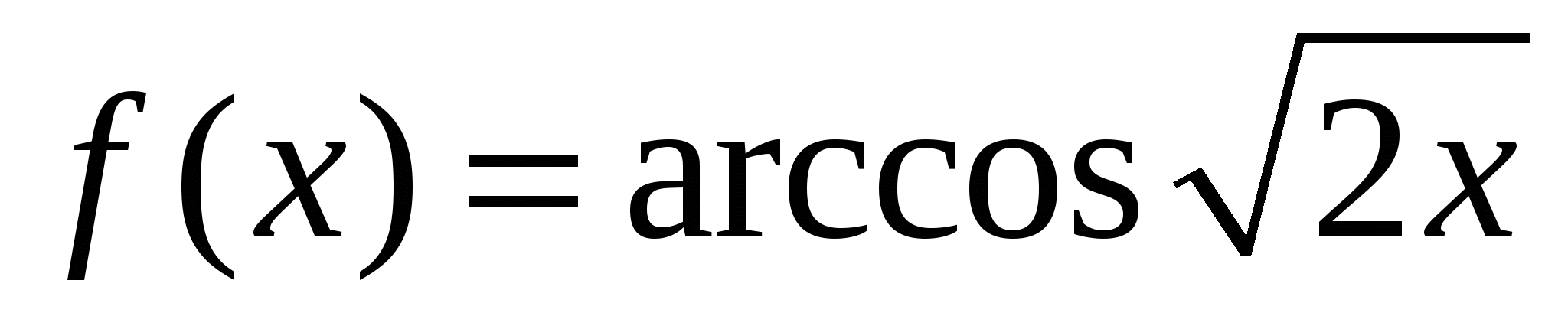
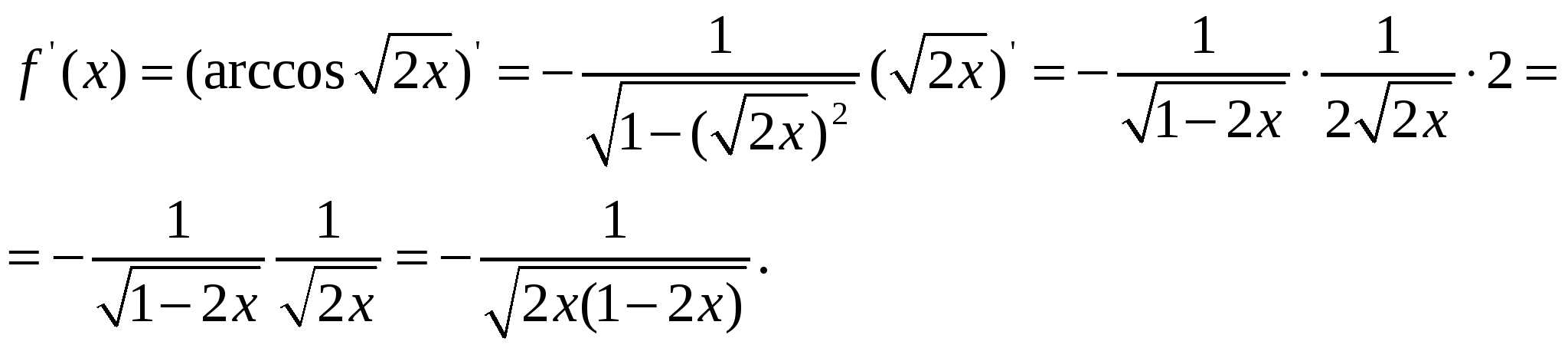
Производные высших порядков
Производная функции  в общем случае является функцией от
в общем случае является функцией от 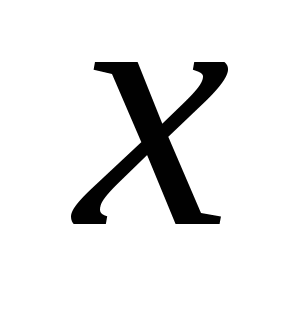 . Если от этой функции вычислять производную, то получим производную второго порядка или вторую производную функции
. Если от этой функции вычислять производную, то получим производную второго порядка или вторую производную функции 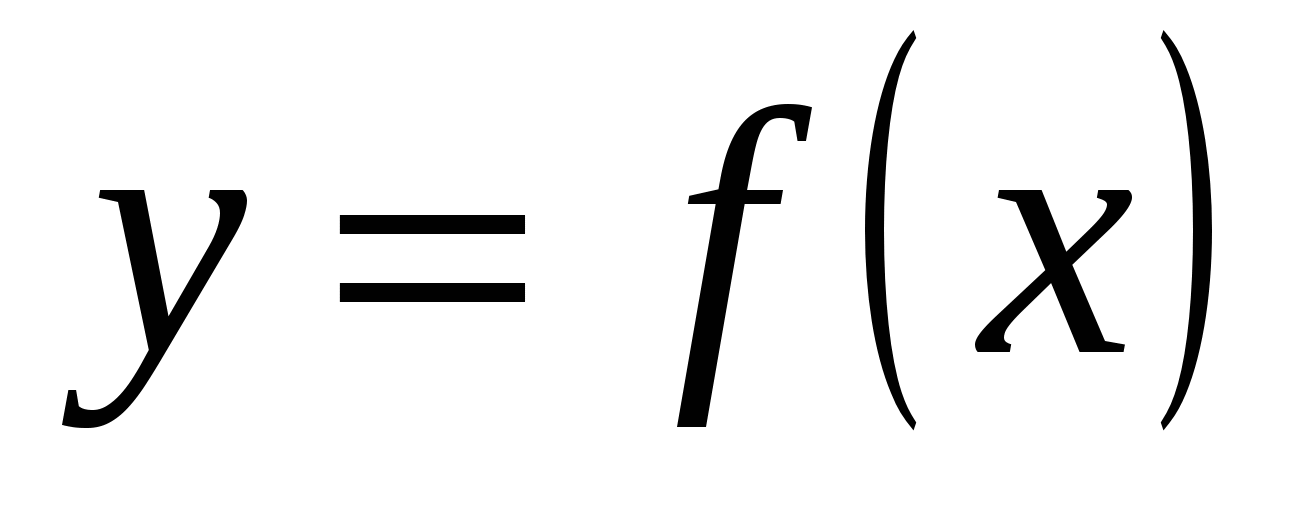 .
.
Второй производной функции 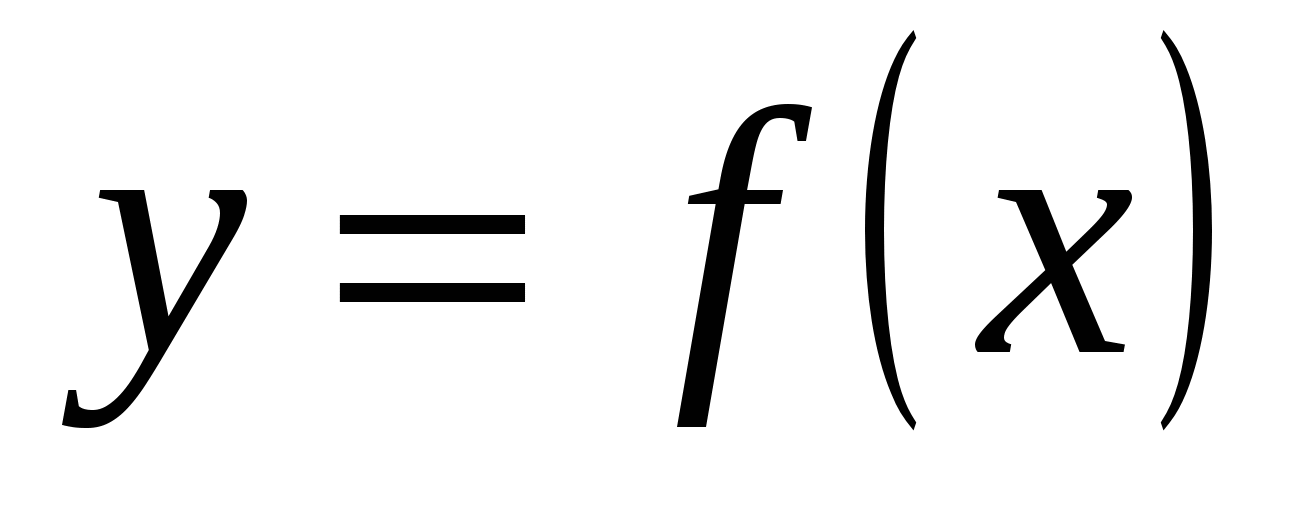 называется производная от ее первой производной
называется производная от ее первой производной 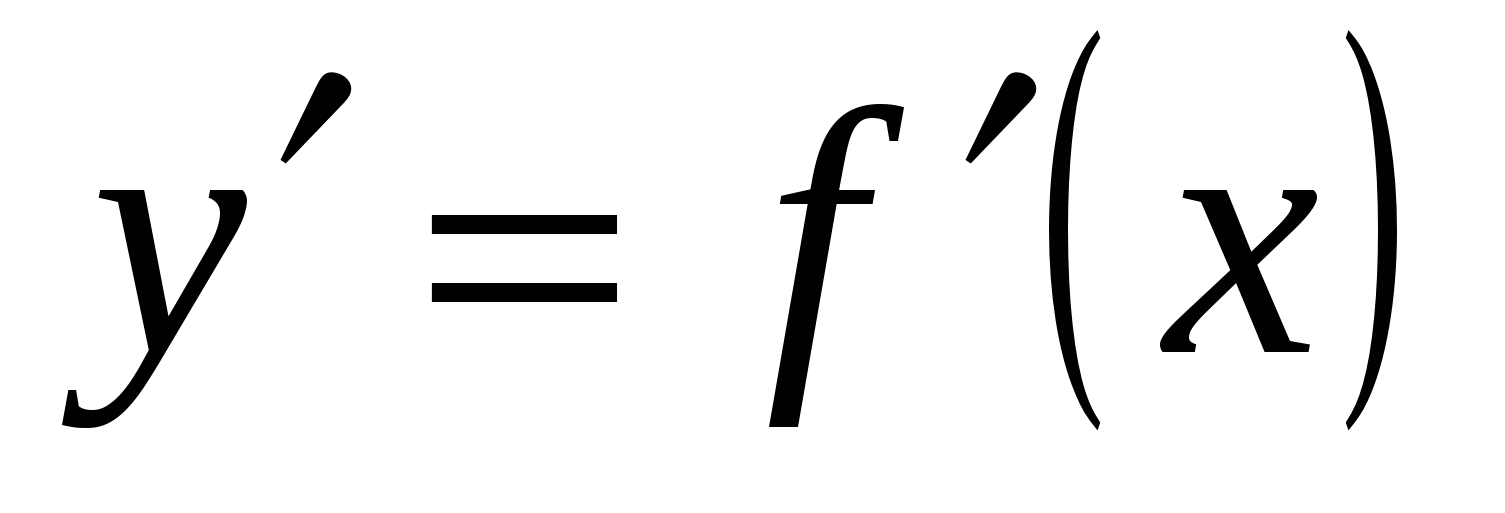 .
.
Вторая производная функции обозначается одним из символов: 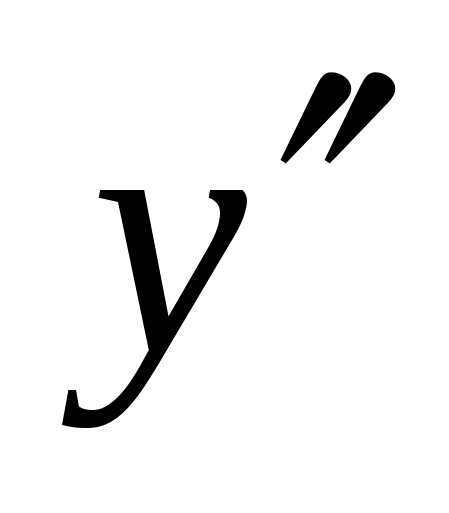 ,
, 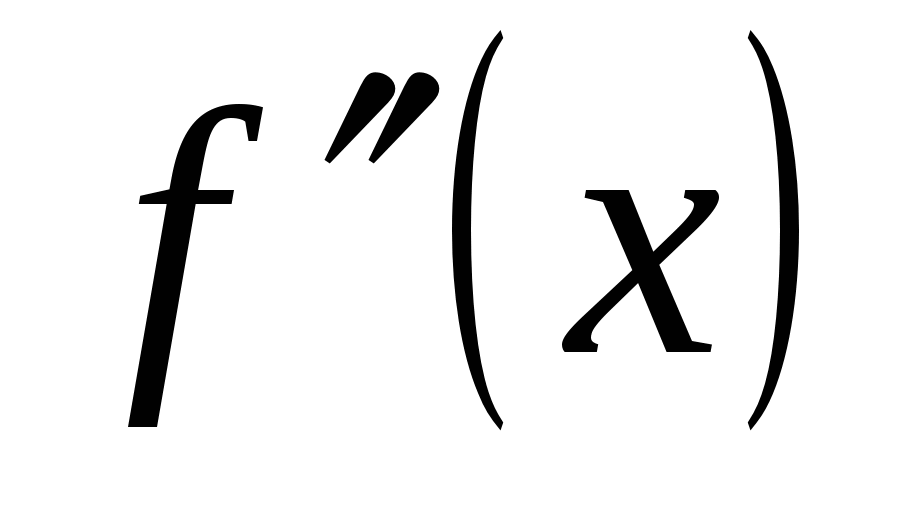 ,
, 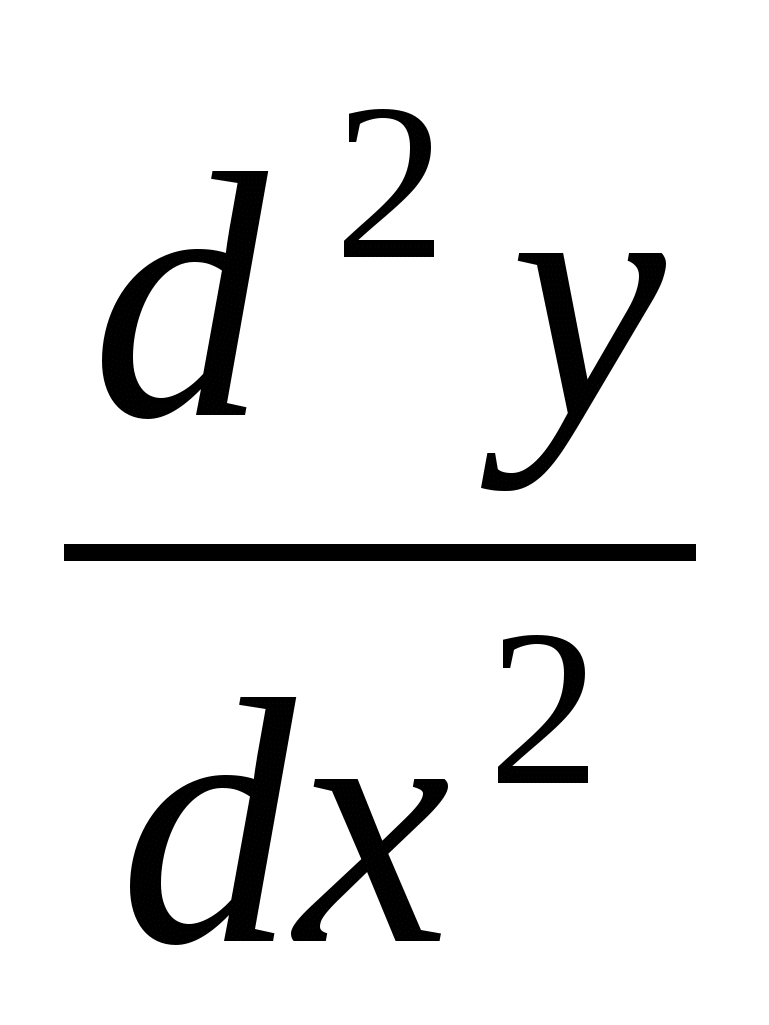 .
.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка: 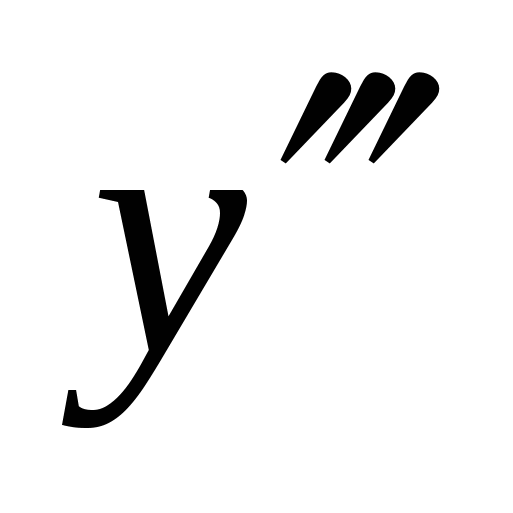 ,
, 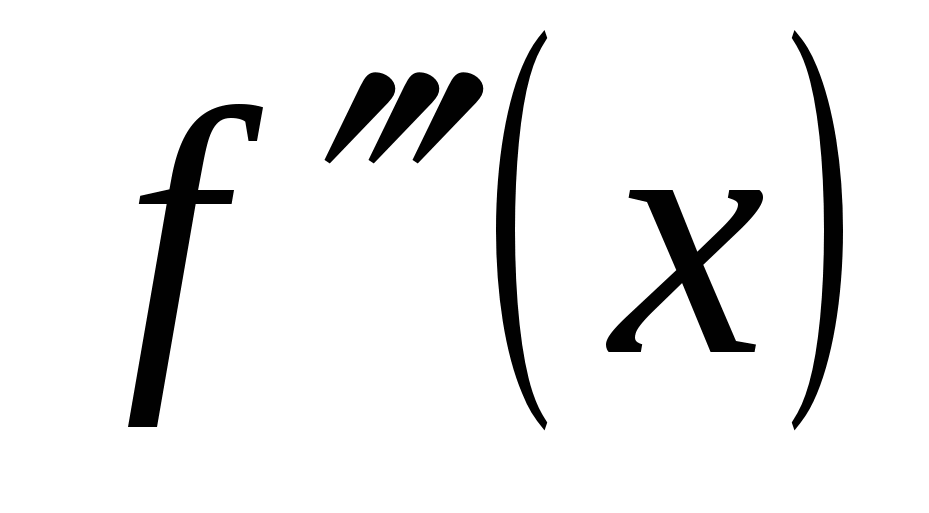 ,
, 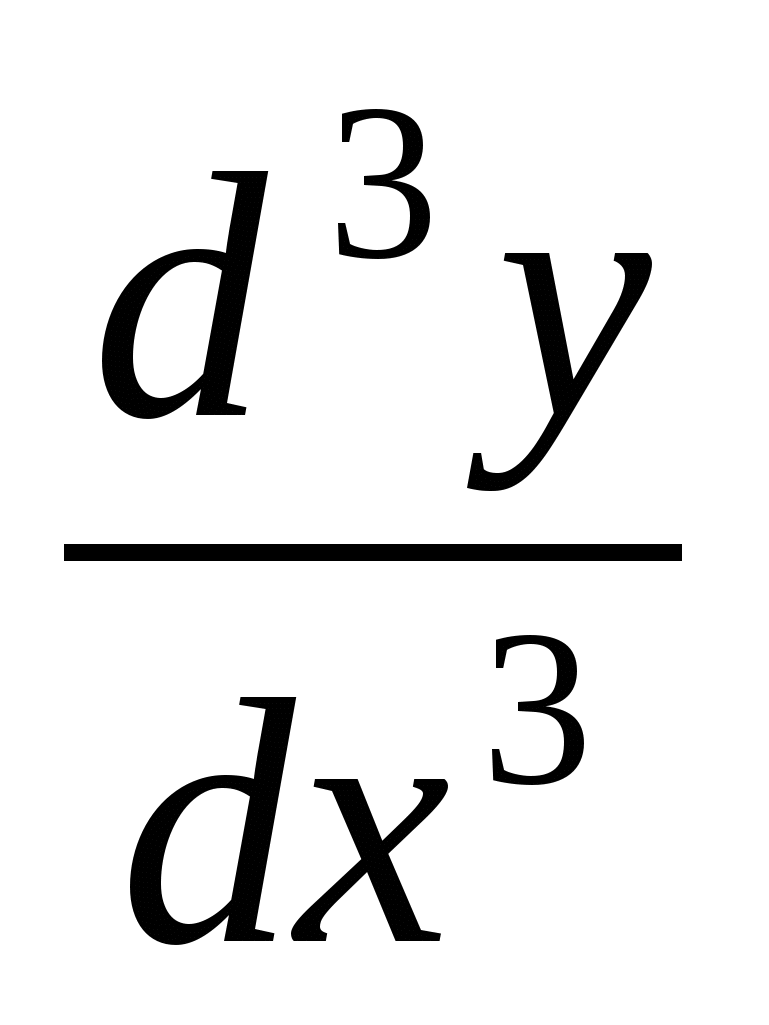 .
.
П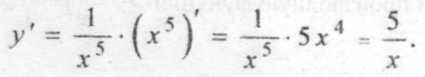 ример 10. Найти вторую производную функции
ример 10. Найти вторую производную функции 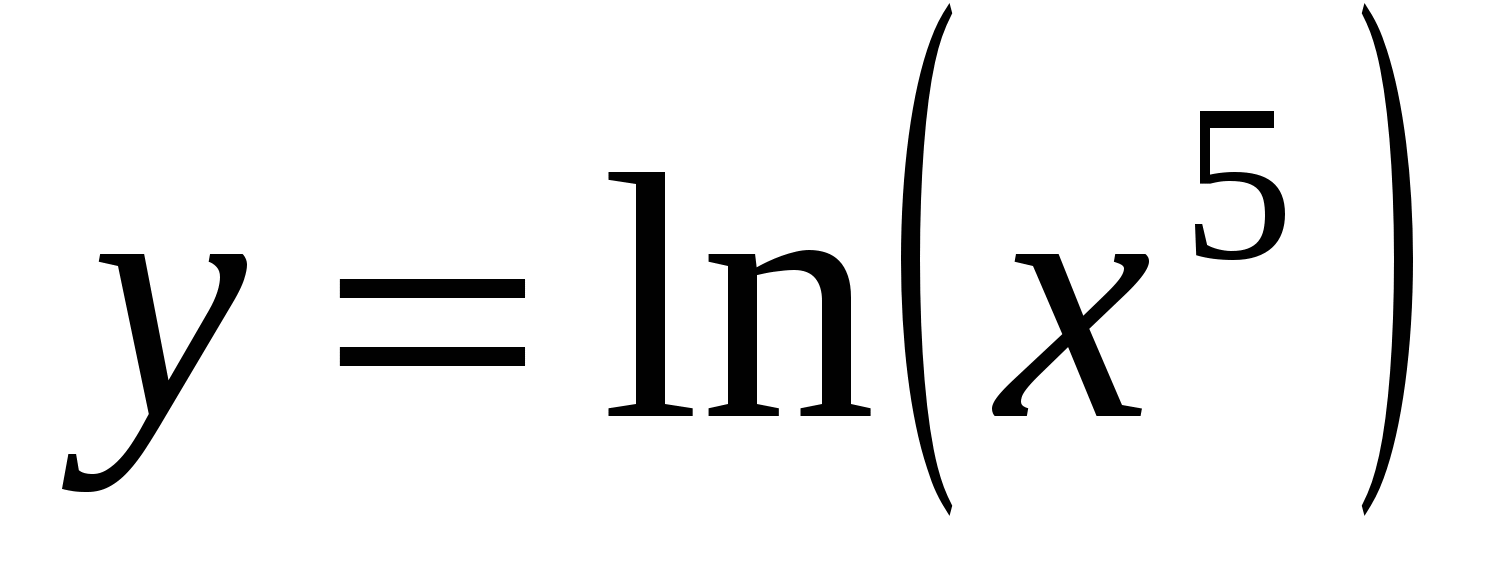 .
.
Решение. Сначала найдем первую производную:
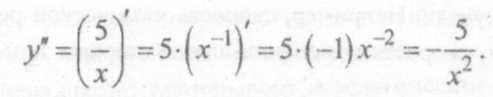
Дифференцируя еще раз, найдем вторую производную:
Пример 11. Найти вторую производную функции 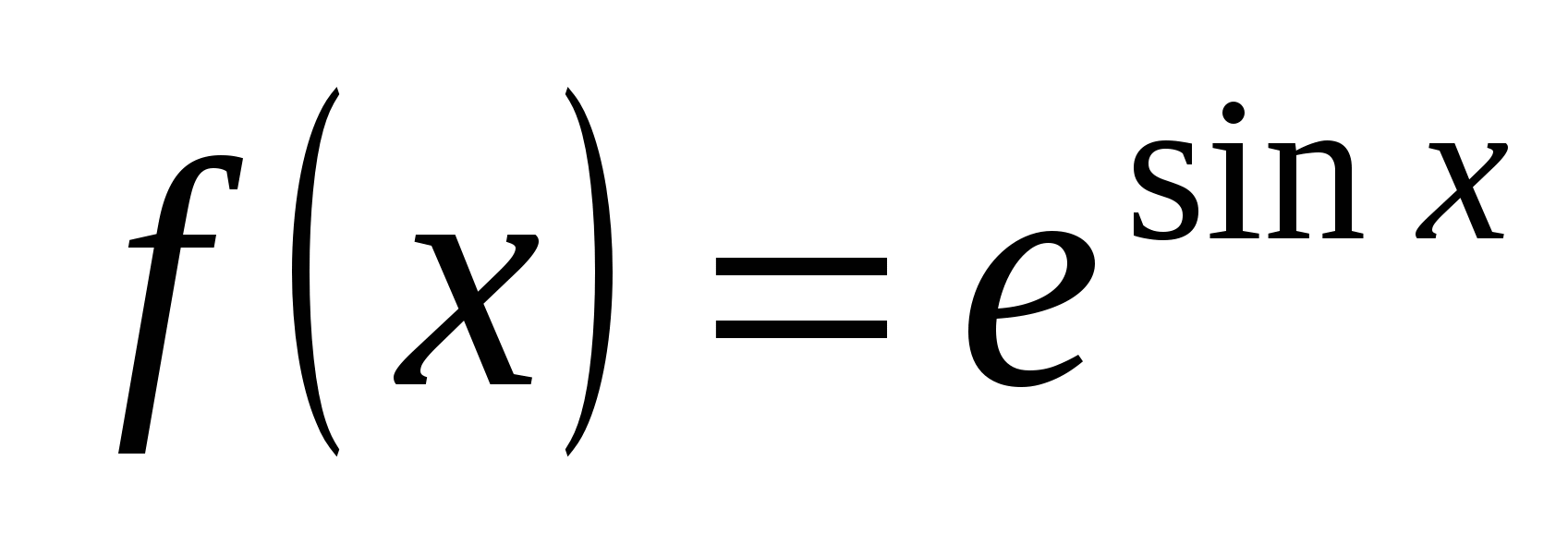
Решение. Сначала найдем первую производную этой сложной функции:
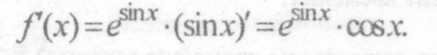
Дифференцируя еще раз, найдем вторую производную:
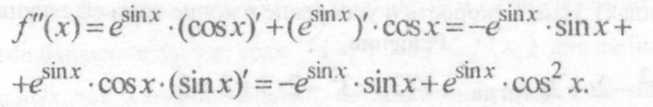
Неопределенный интеграл.
Определение: функция F(x) называется первообразной для функции f(x) в промежутке 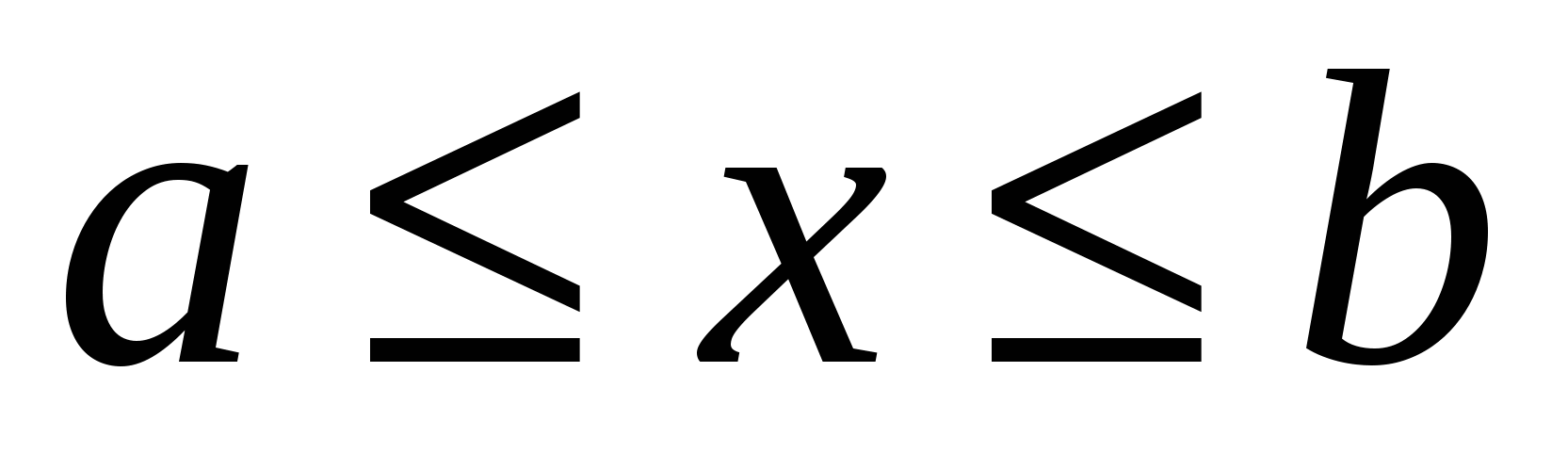 , если в любой точке этого промежутка ее производная равна f(x):
, если в любой точке этого промежутка ее производная равна f(x):
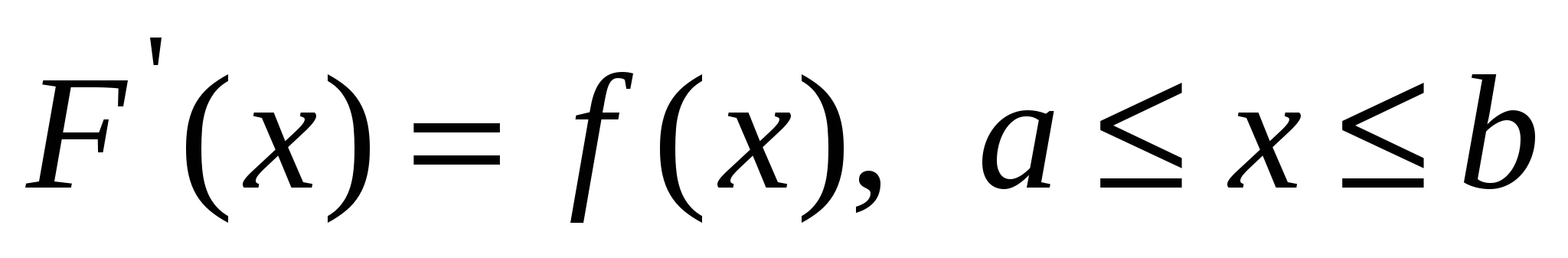 .
.
Определение: совокупность первообразных для функции f(x) называется неопределенным интегралом и обозначается символом 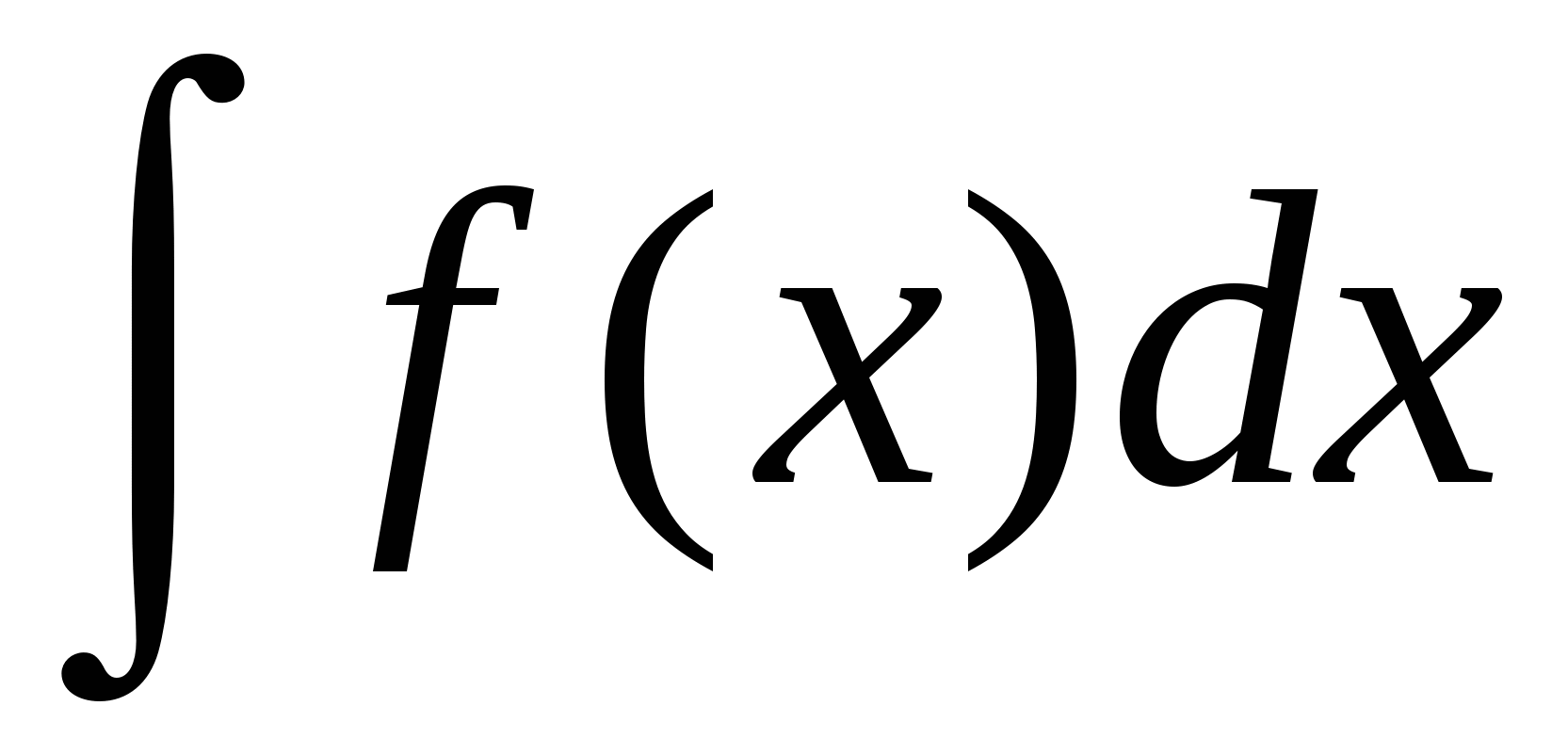 . Таким образом,
. Таким образом, ![]() .
.
Здесь f(x)- подынтегральная функция, 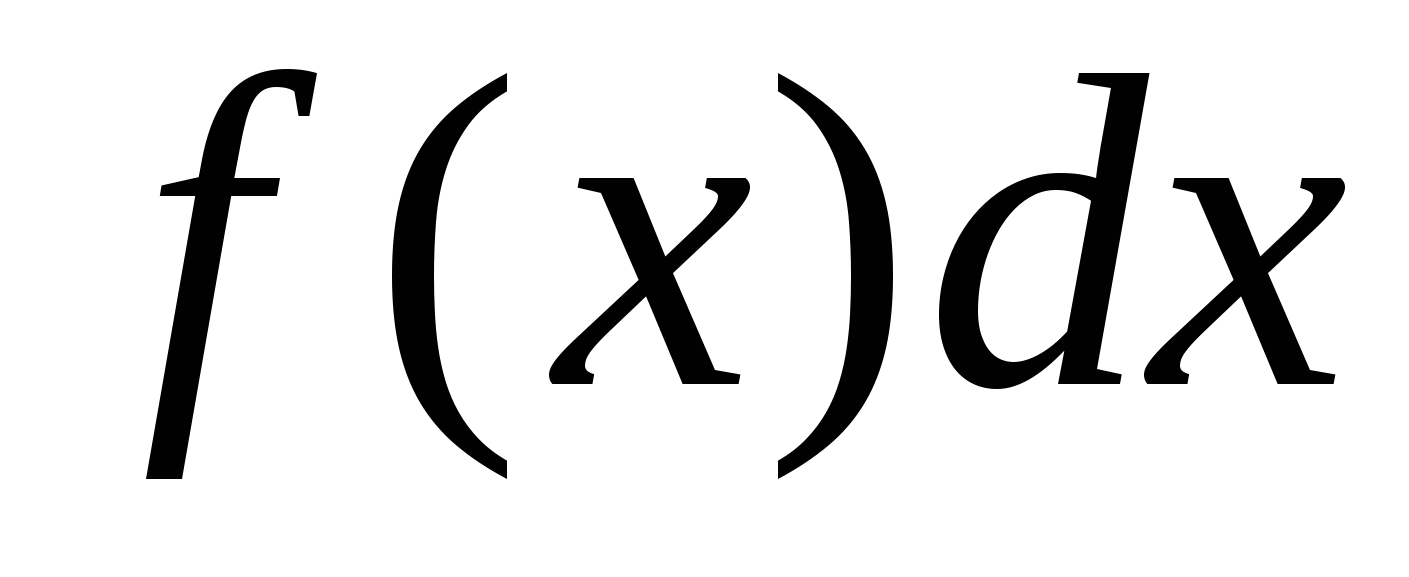 - подынтегральное выражение, С - произвольная постоянная.
- подынтегральное выражение, С - произвольная постоянная.
Основные свойства неопределенного интеграла.
-
Если функция
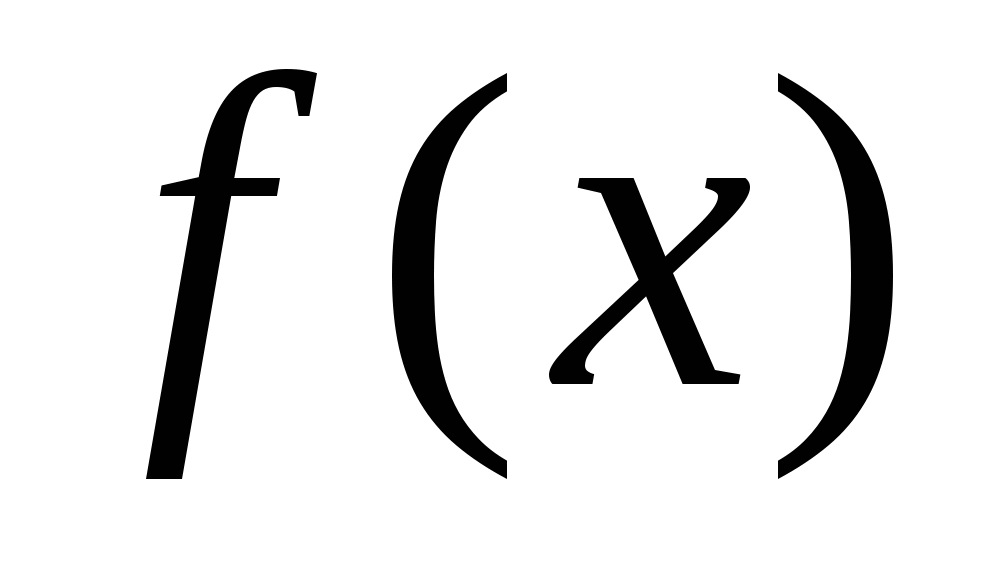 имеет первообразную, то
имеет первообразную, то 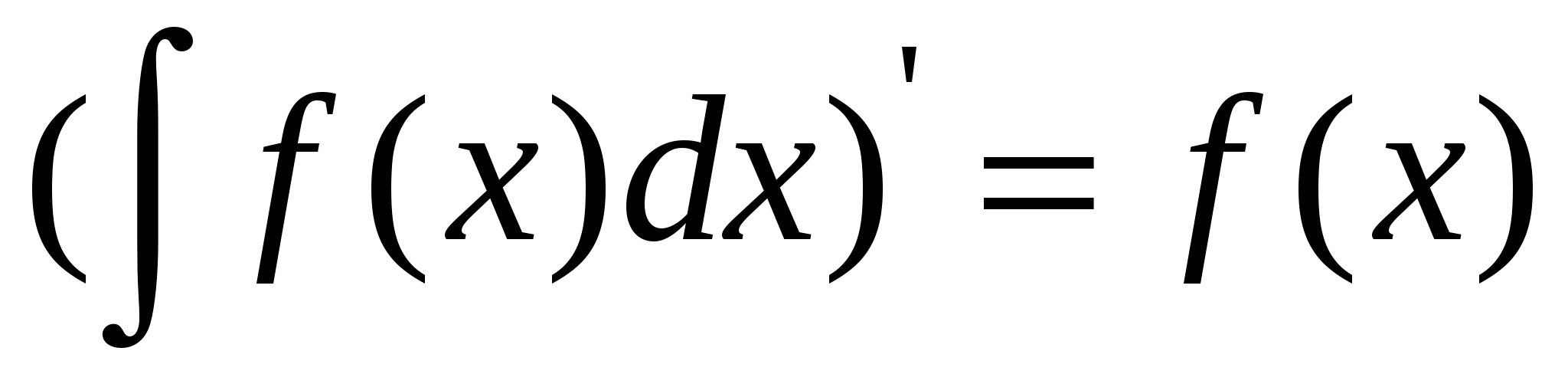 ,
, 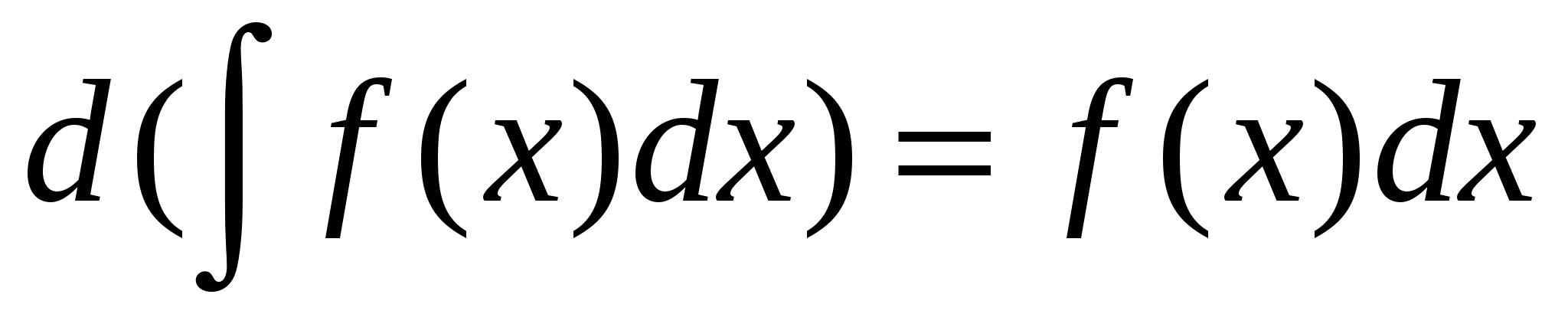 .
. -
Если
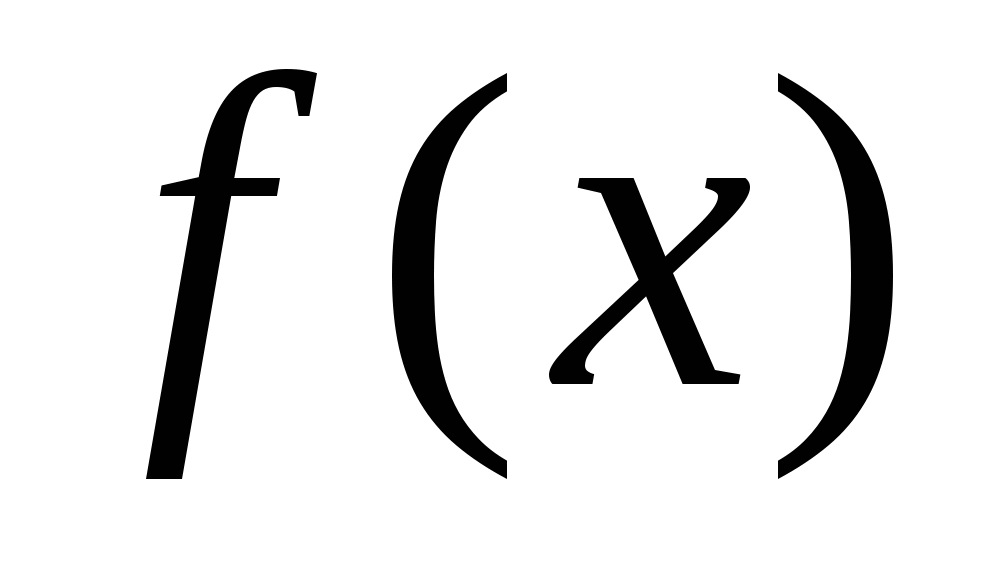 - дифференцируемая функция, то
- дифференцируемая функция, то 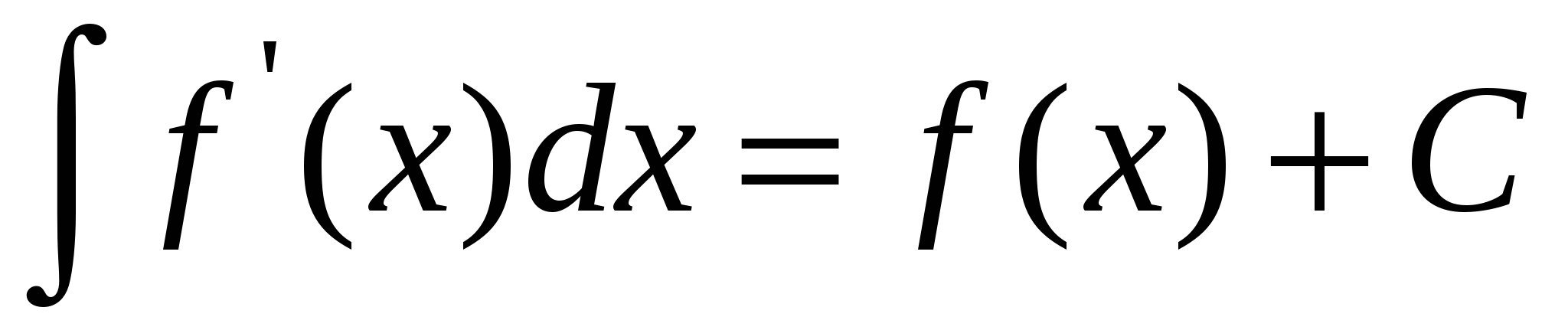 ,
, 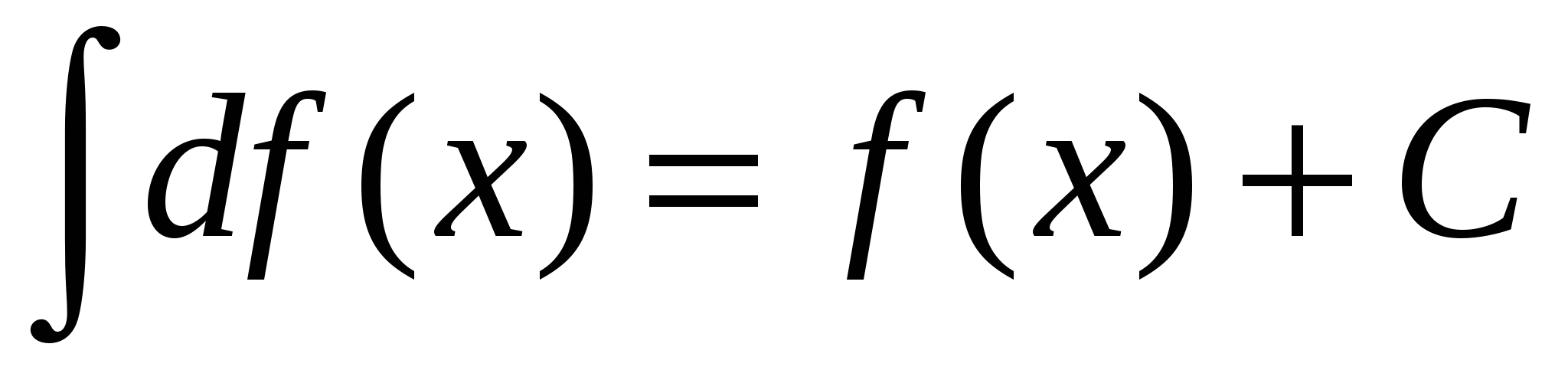 .
. -
Если функция
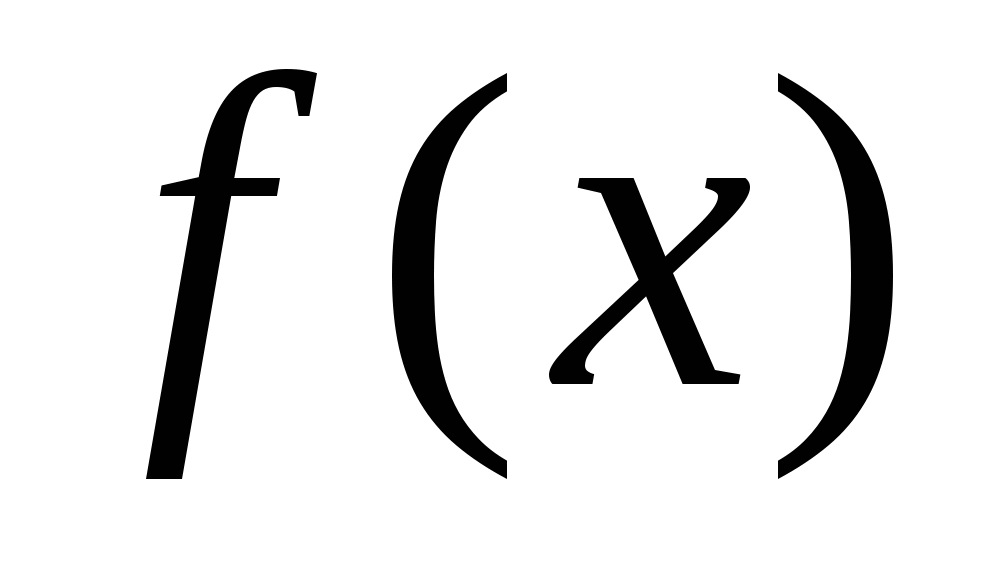 имеет первообразную, то при
имеет первообразную, то при 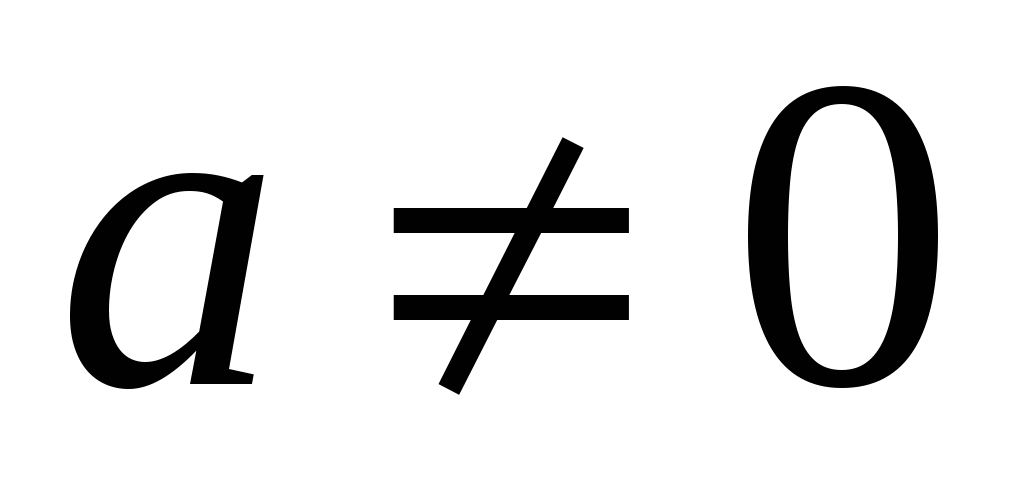 верно равенство
верно равенство 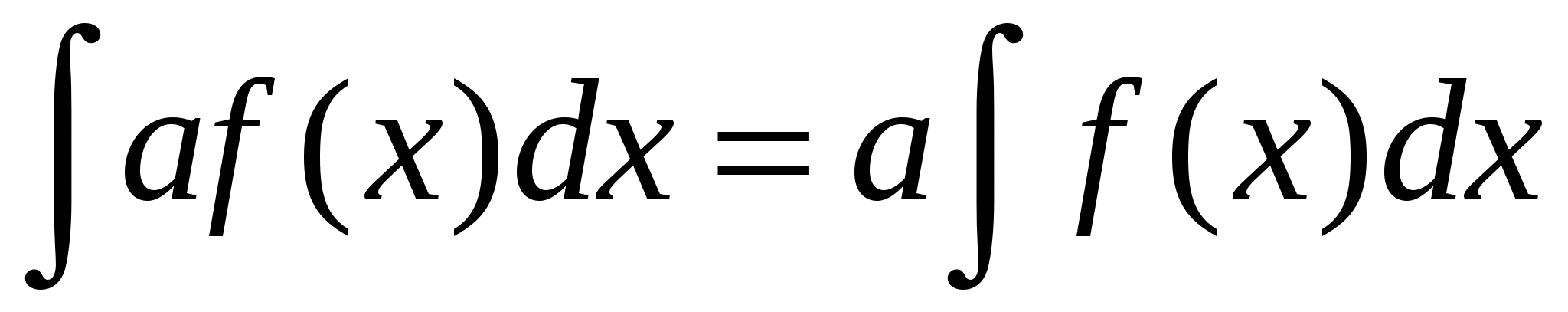 .
. -
Если функция
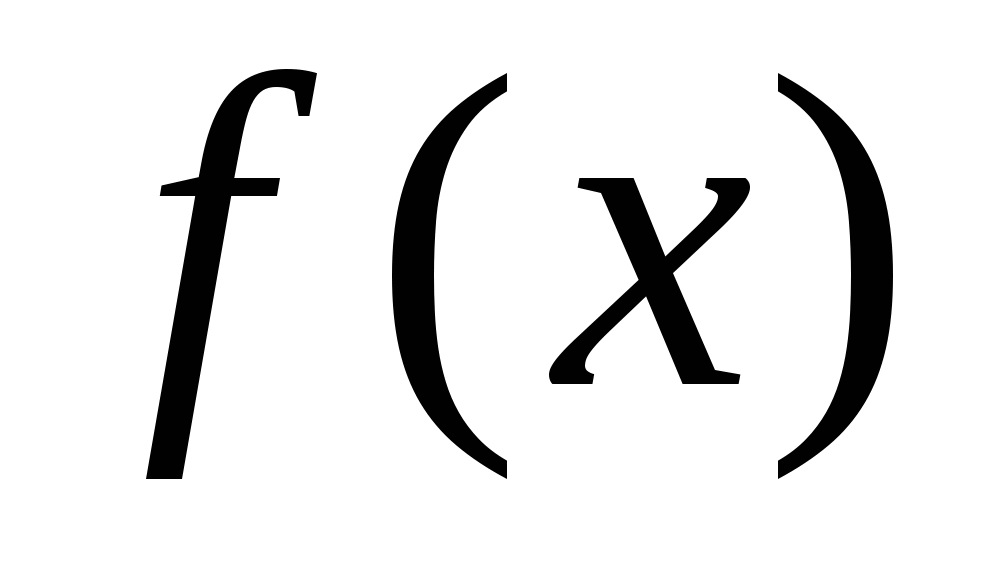 и
и 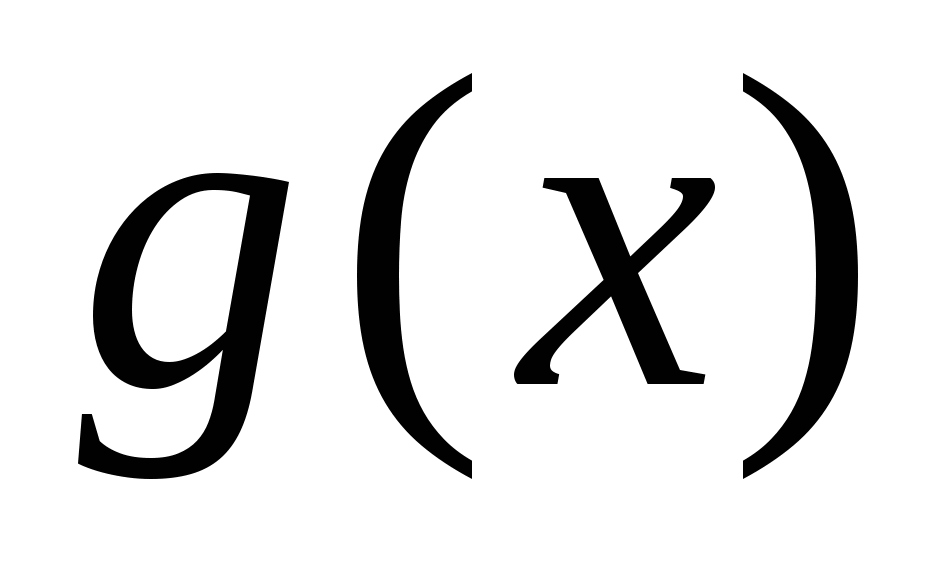 имеют первообразные, то
имеют первообразные, то 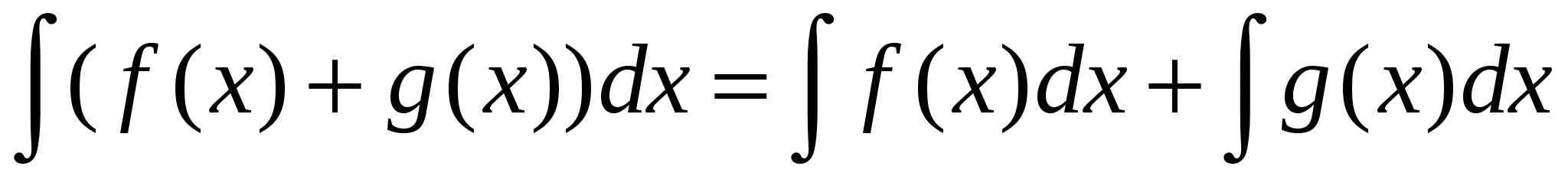 .
.
Таблица неопределенных интегралов.
1. 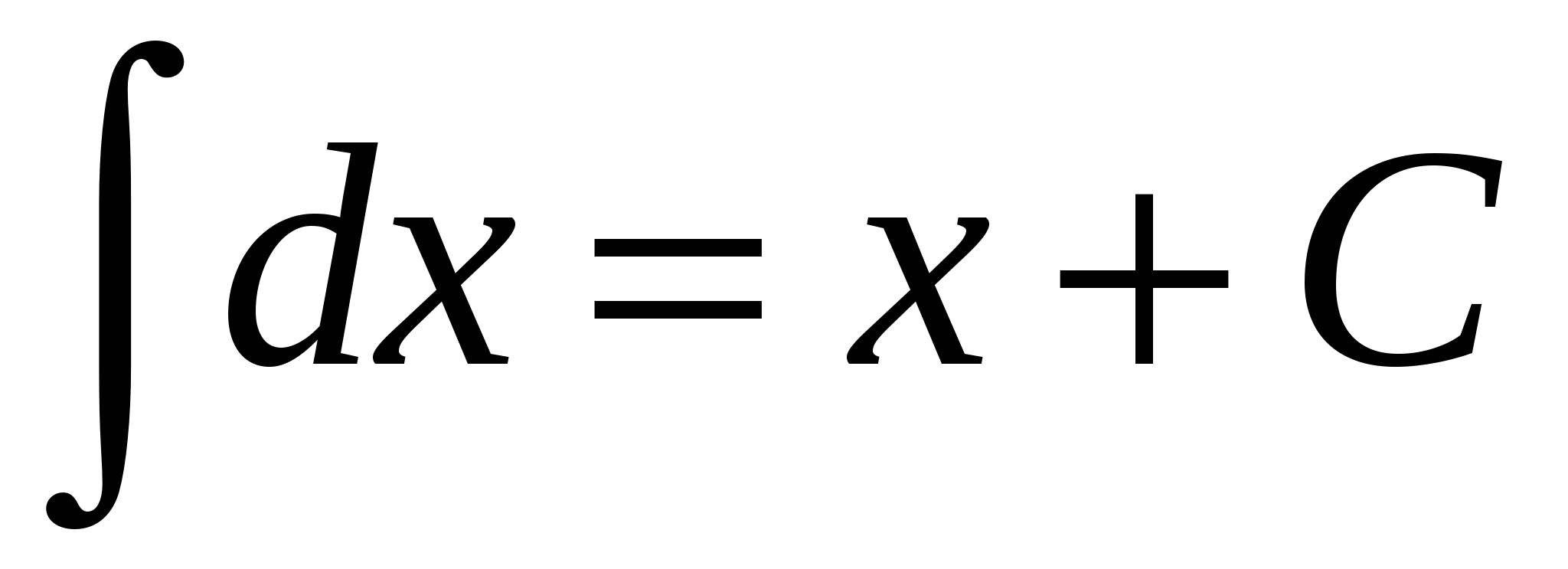 ;
;
8. 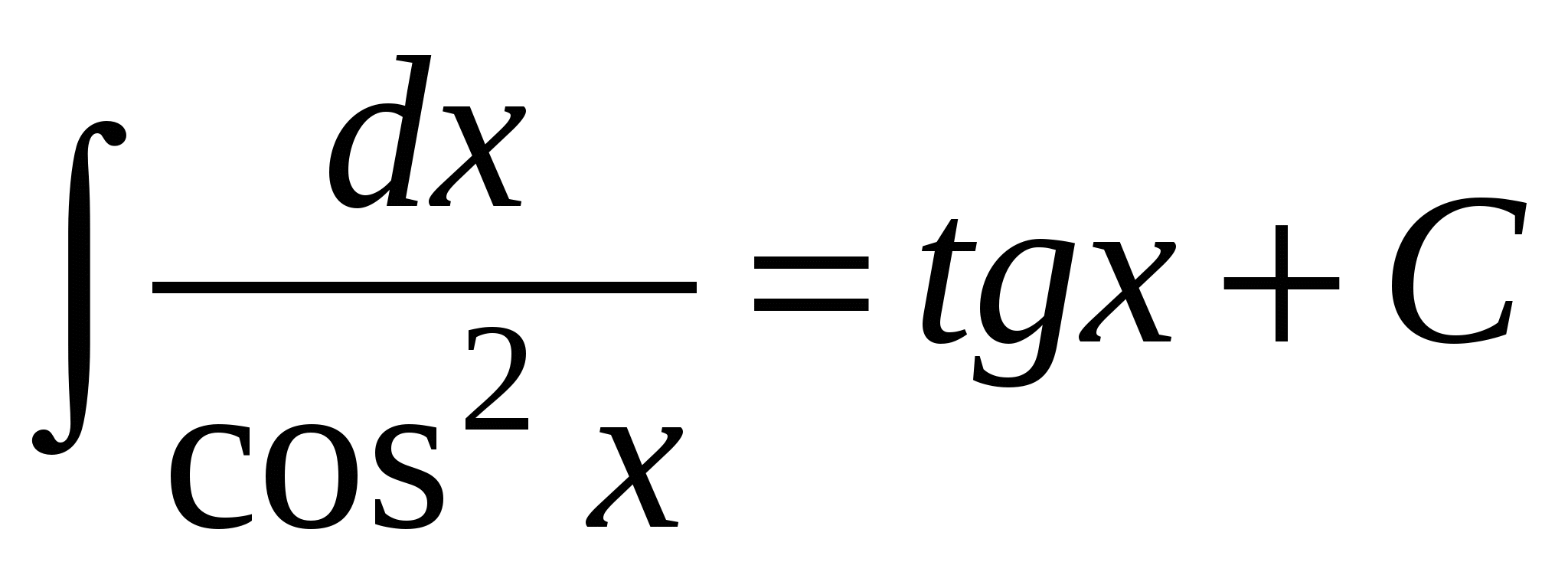 ;
;
2. 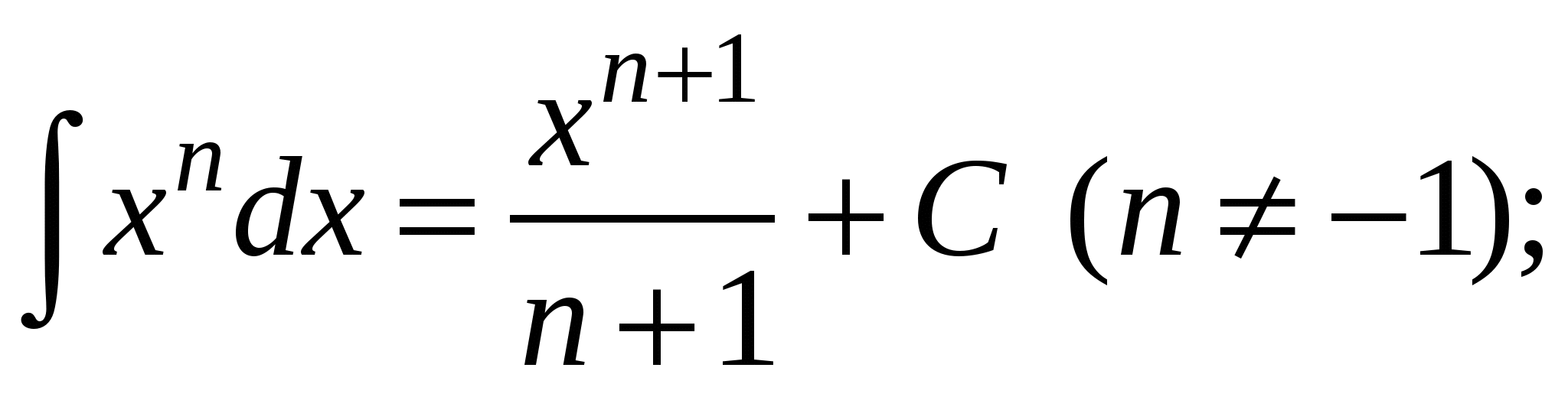
9. 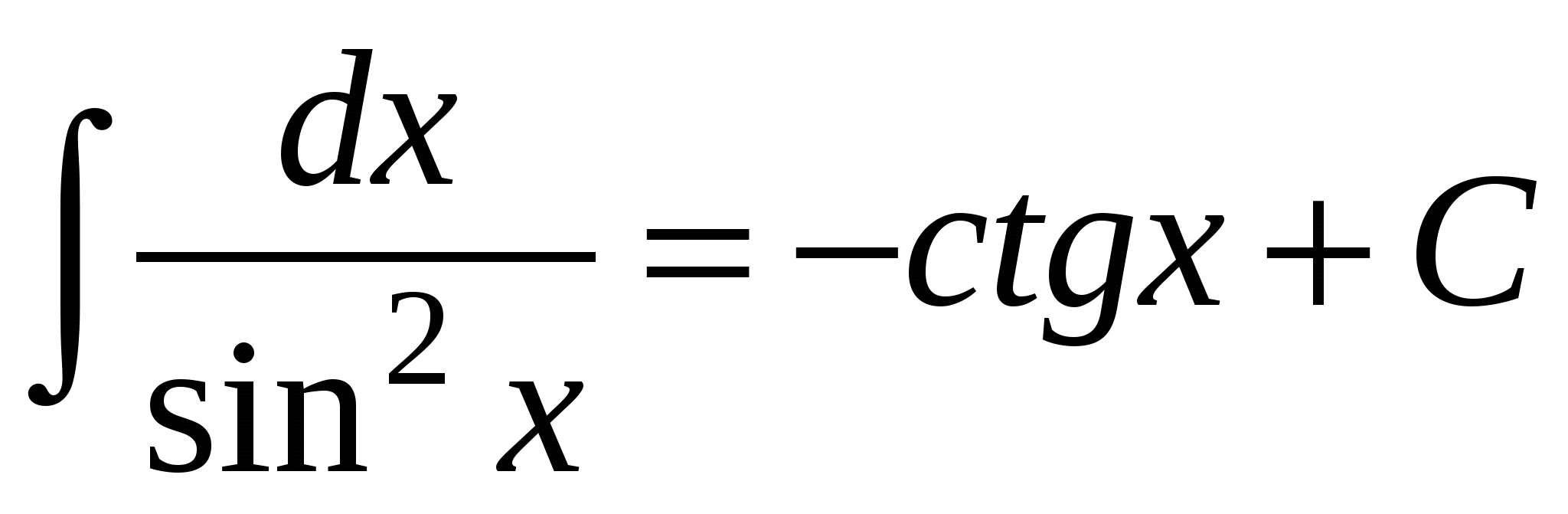 ;
;
3. 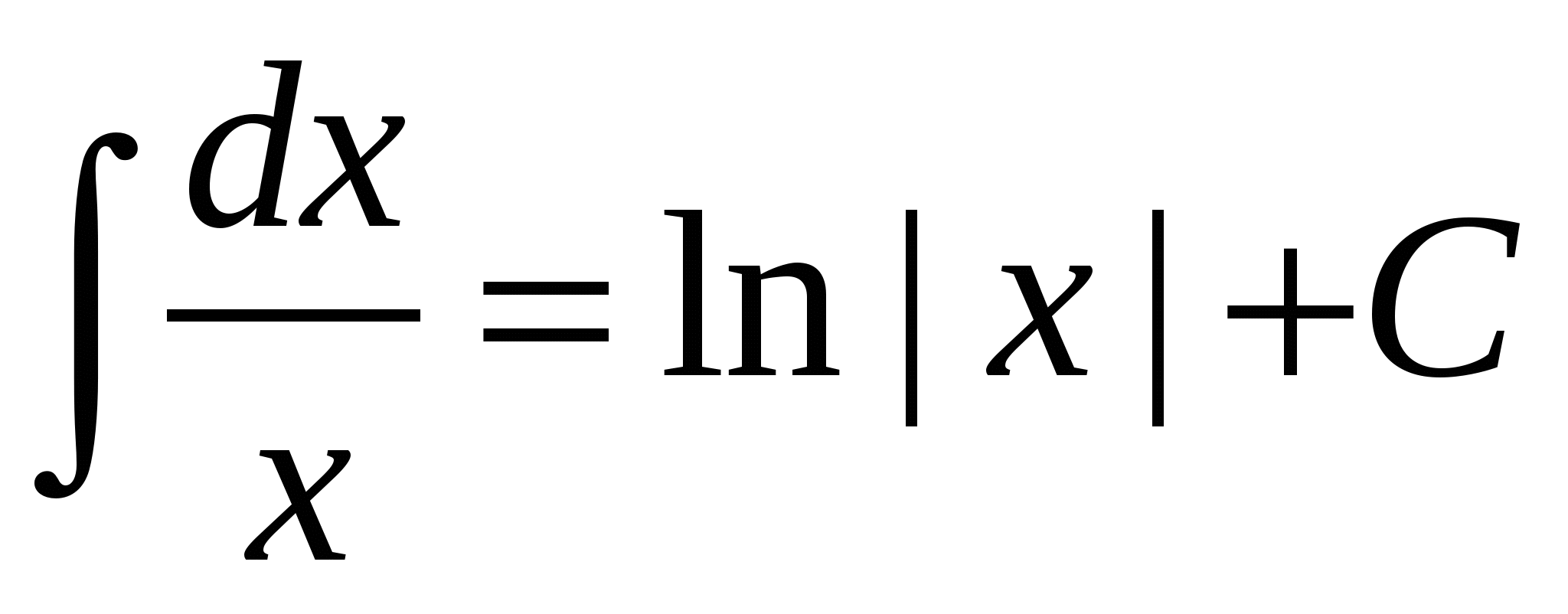 ;
;
10. 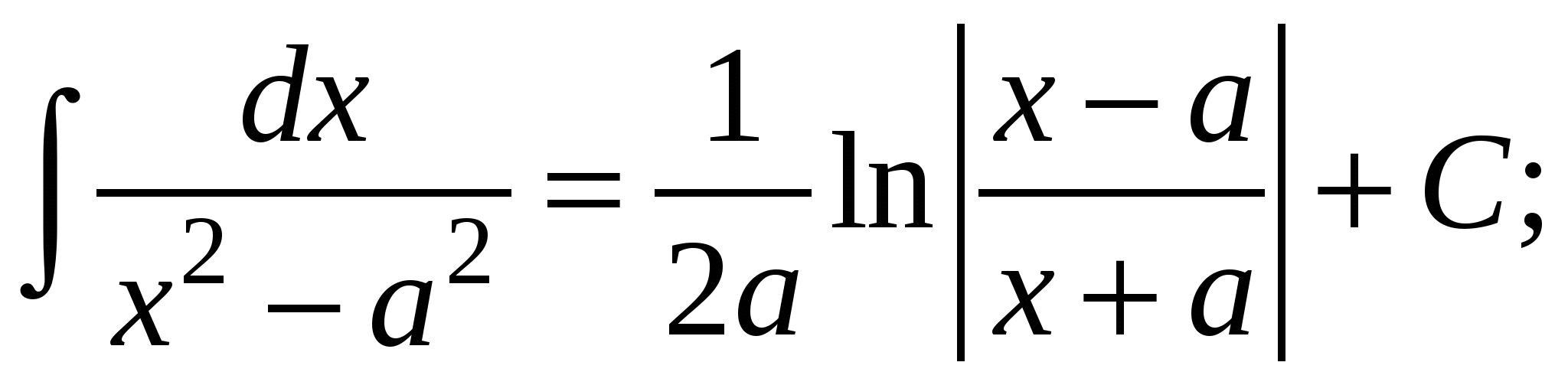
4. 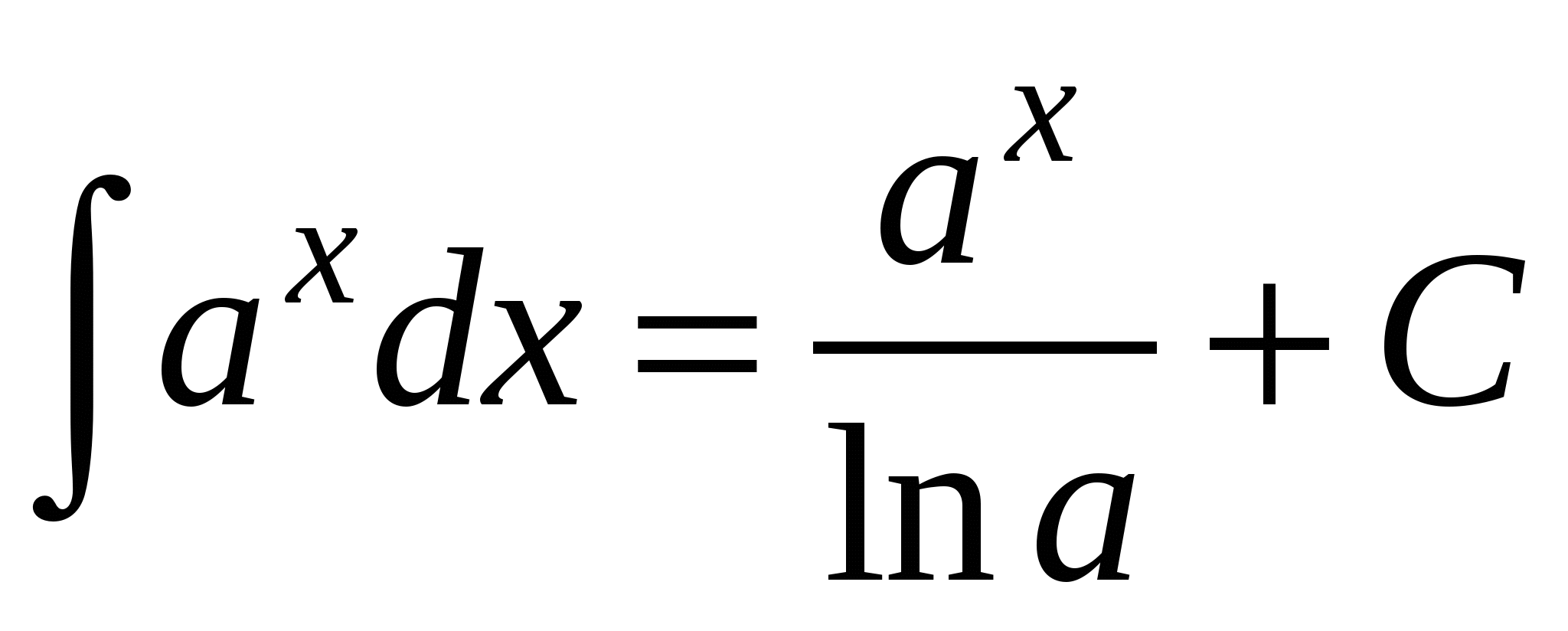 ;
;
11. 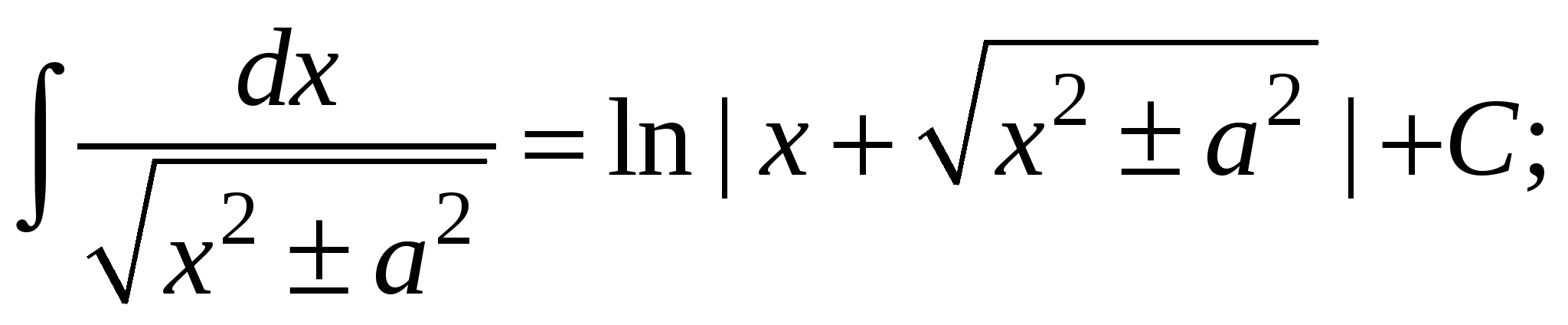
5. 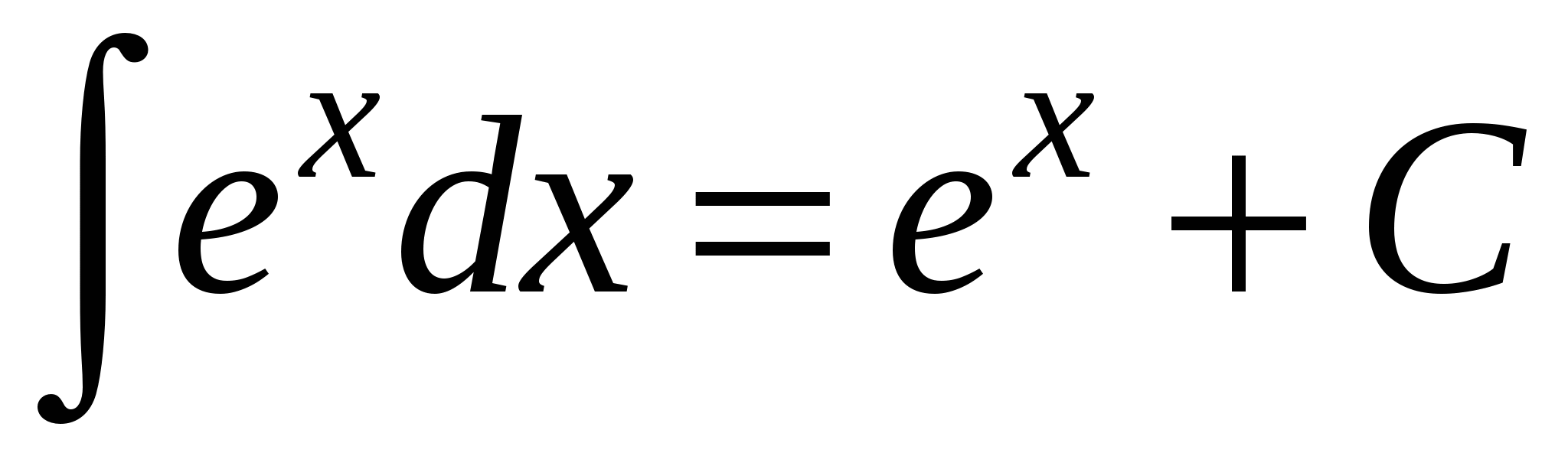 ;
;
12. 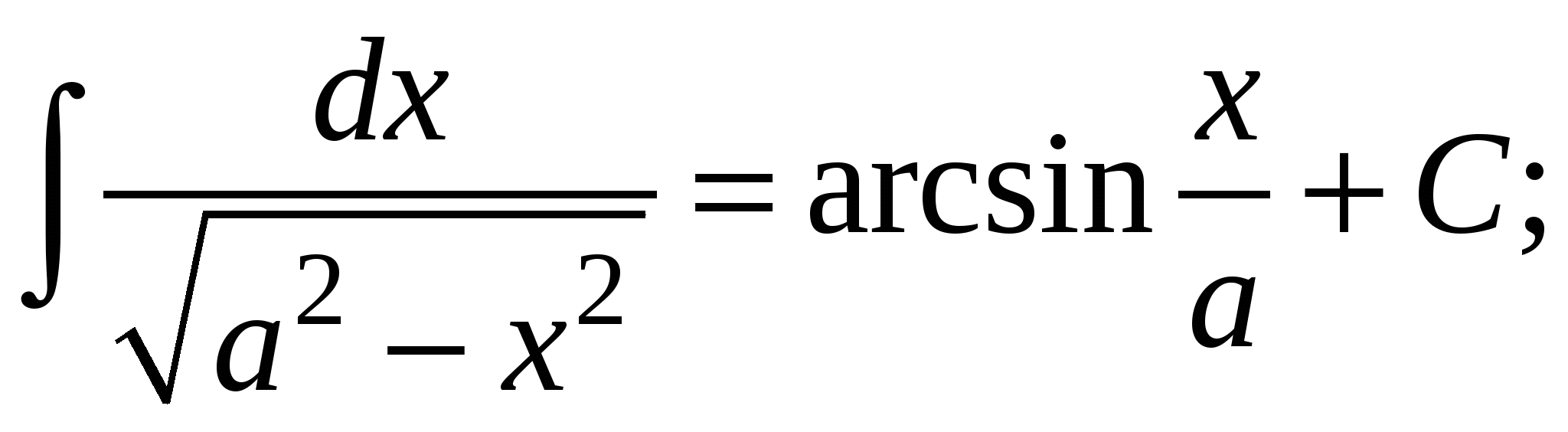
6. 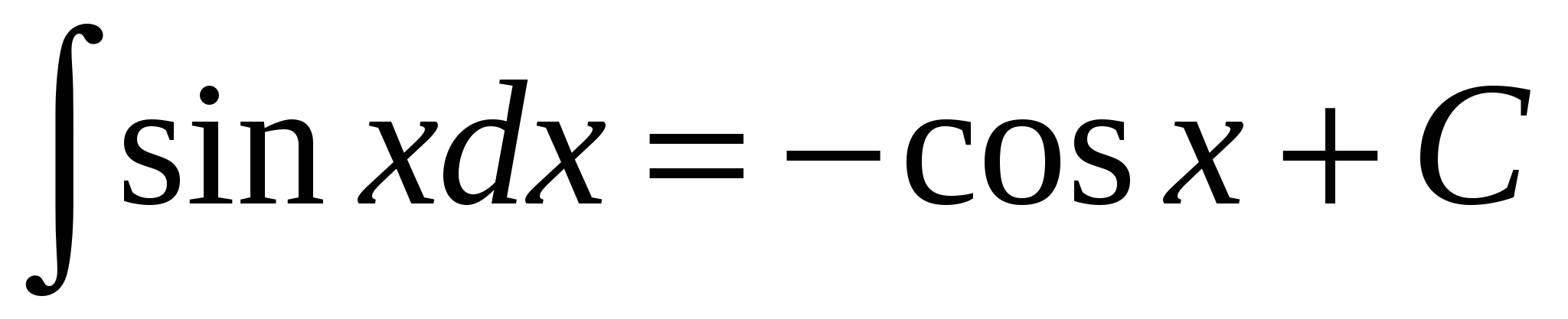 ;
;
13. 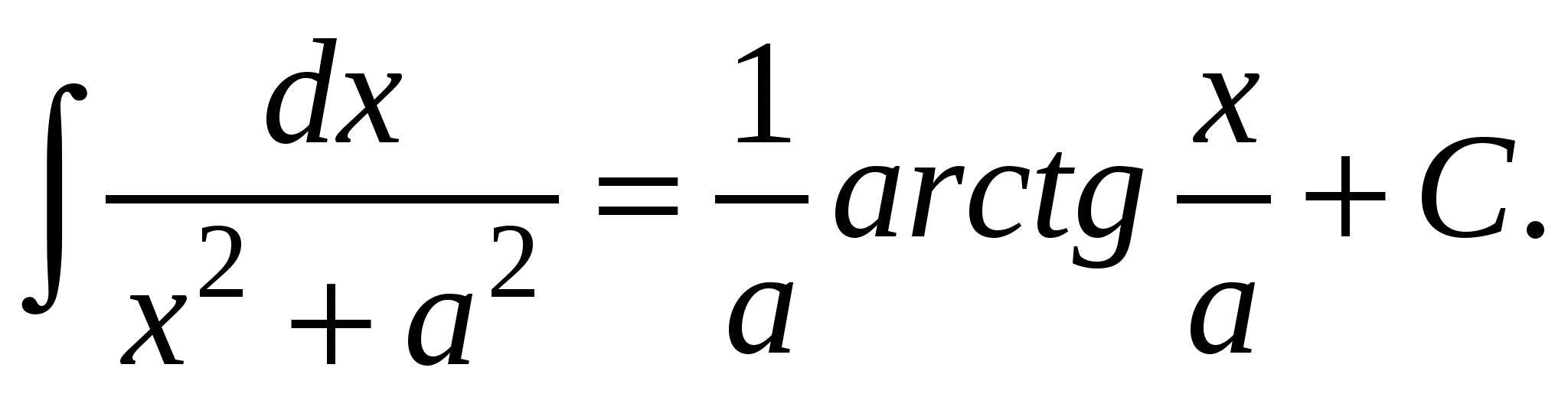
7. 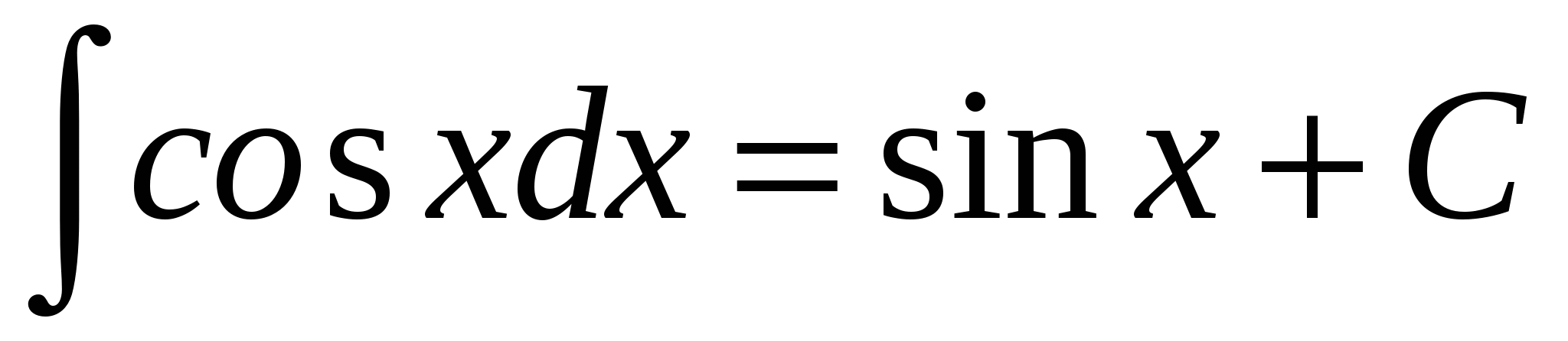 ;
;
Пример 1. Для функции 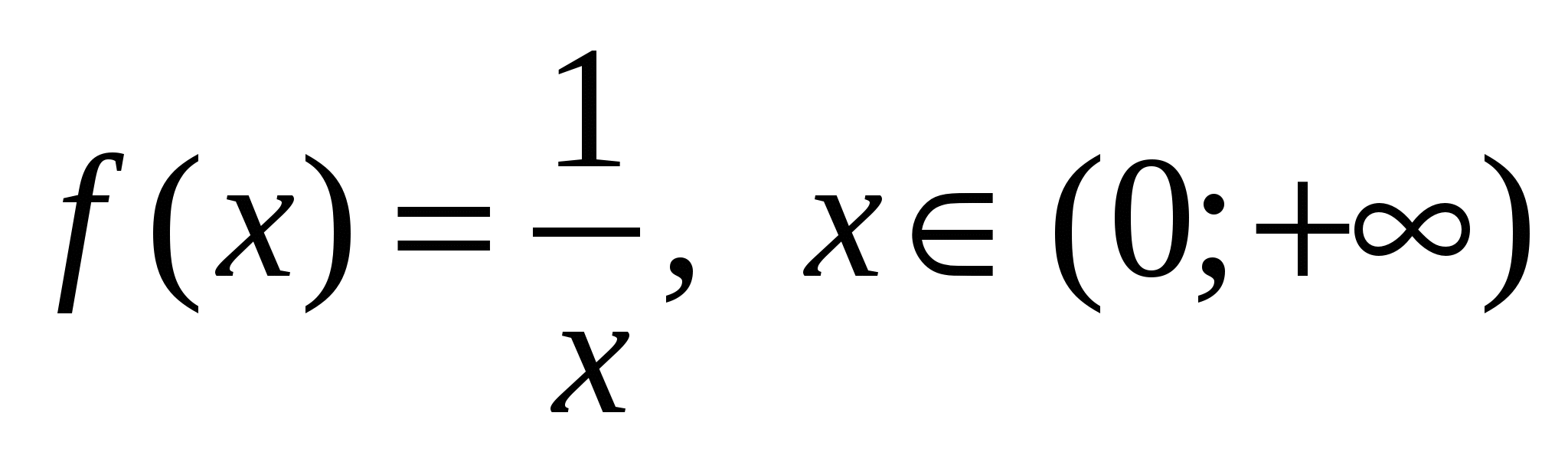 , найти первообразную F(x), график которой проходит через точку (2;2).
, найти первообразную F(x), график которой проходит через точку (2;2).
Решение: так как при всех 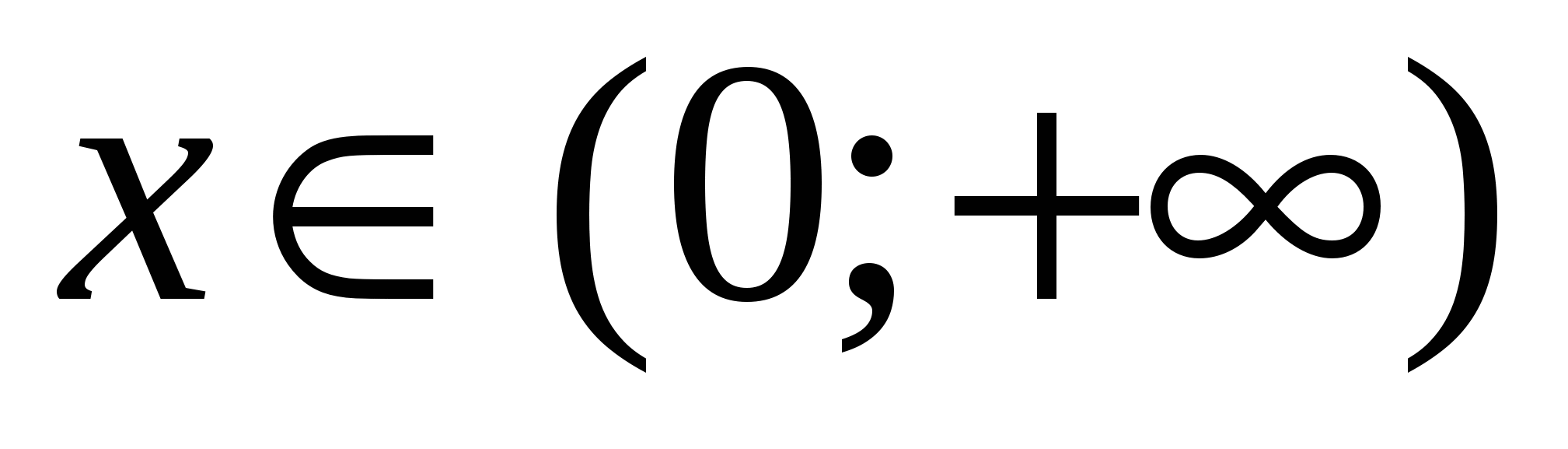 верно равенство
верно равенство ![]() то
то 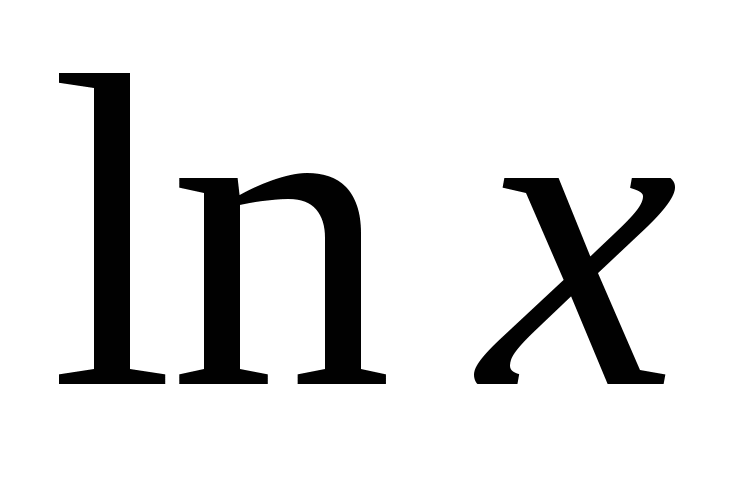 - одна из первообразных функции
- одна из первообразных функции 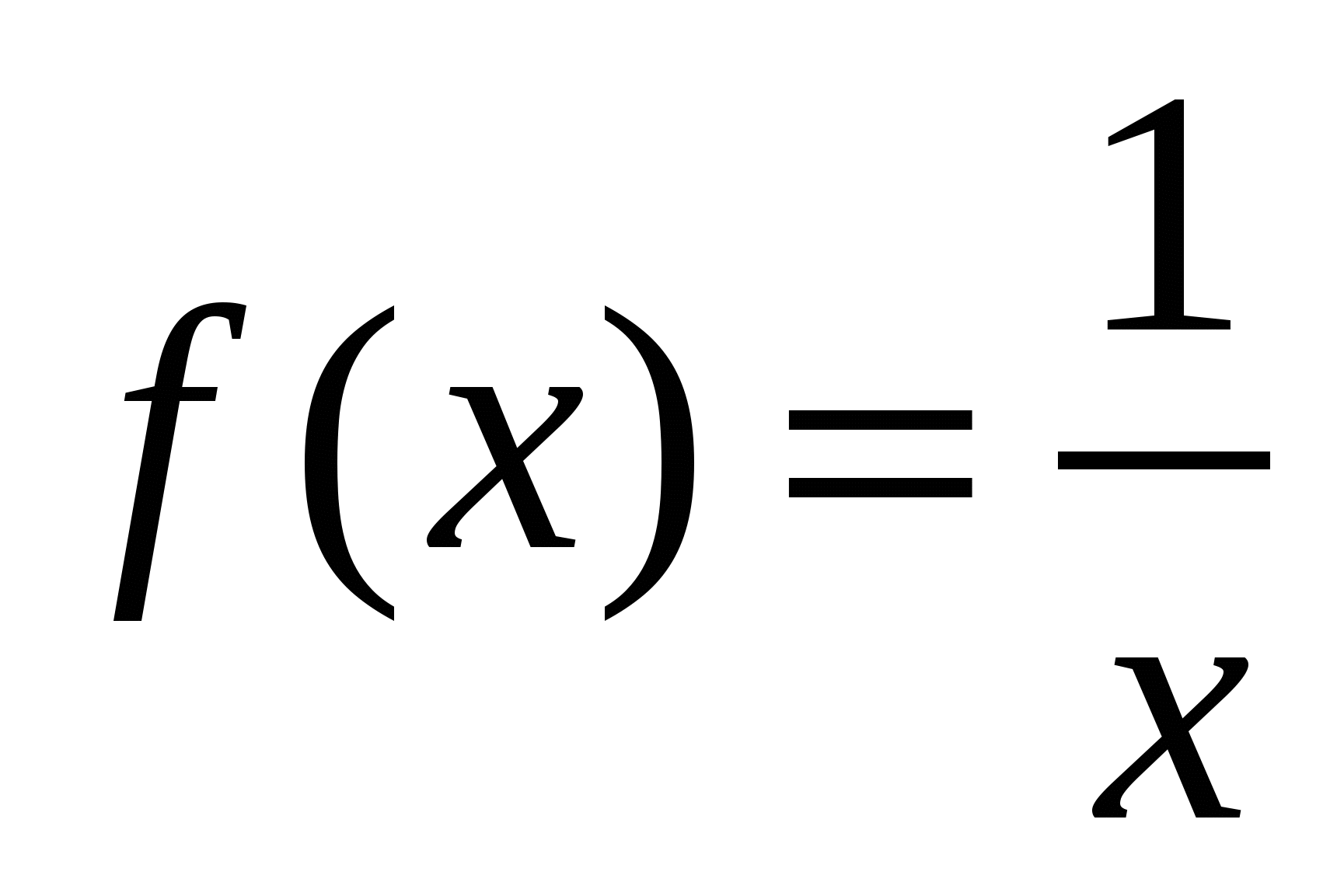 . Следовательно,
. Следовательно, ![]() С - некоторая постоянная. Постоянную С находим из условия F(2)=2, то есть
С - некоторая постоянная. Постоянную С находим из условия F(2)=2, то есть 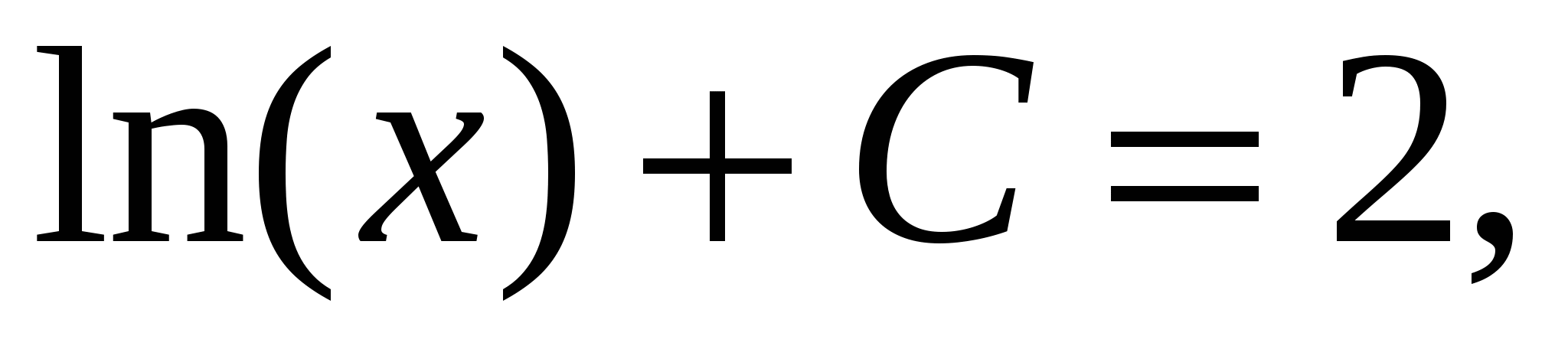 откуда
откуда 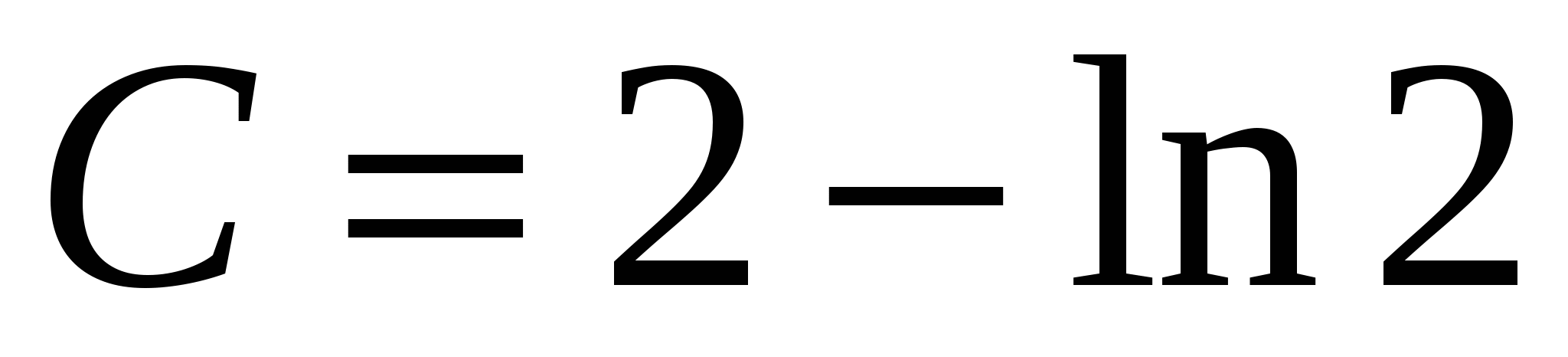 .
.
Значит, 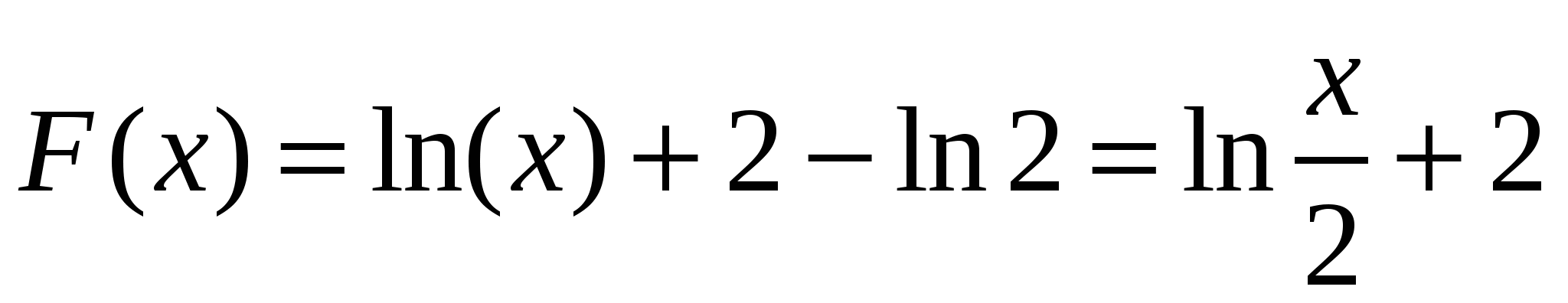 .
.
Пример 2. Найти интеграл 
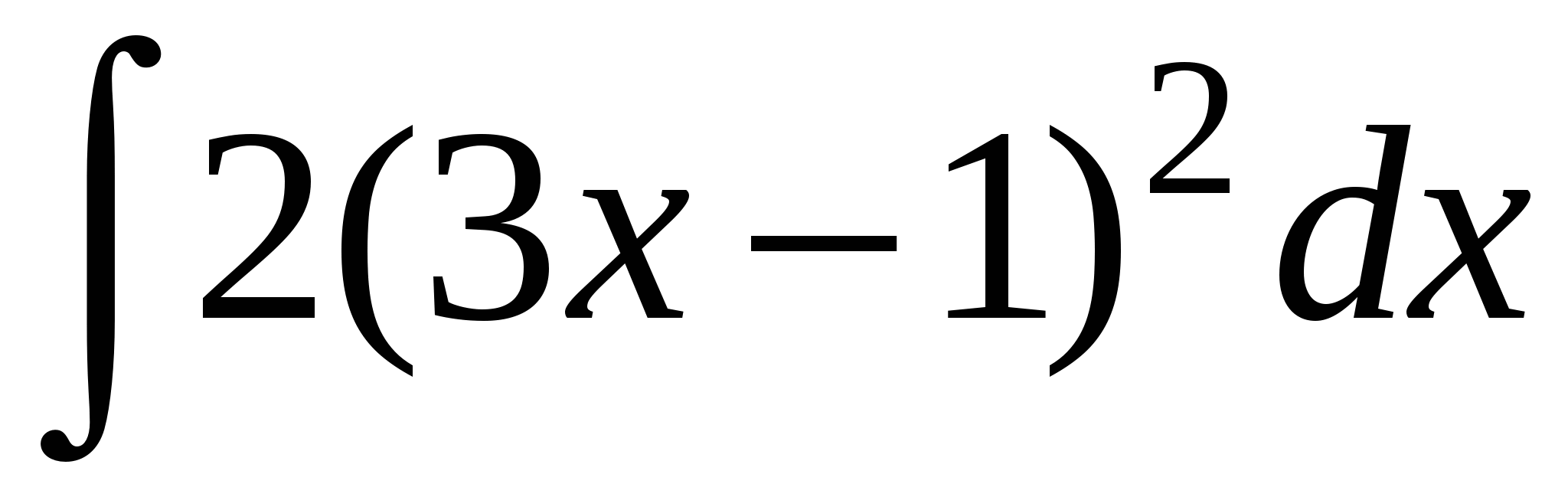 .
.
Решение: 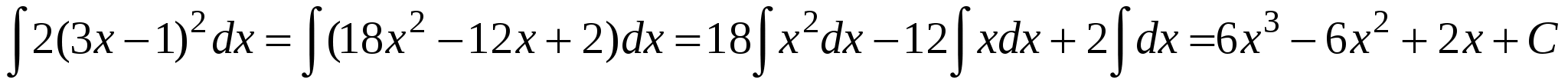 .
.
Пример 3. Найти интеграл 
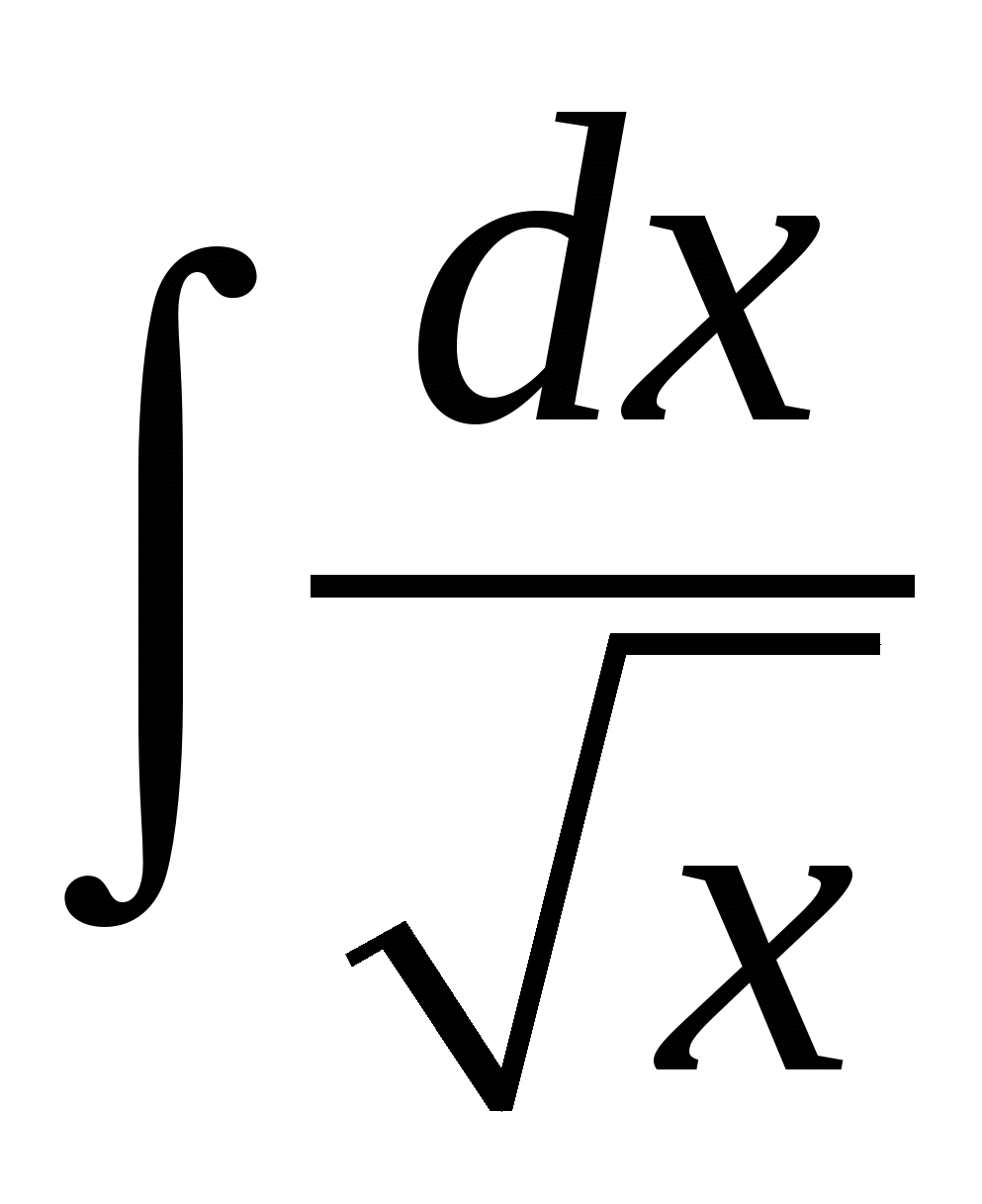 .
.
Решение: 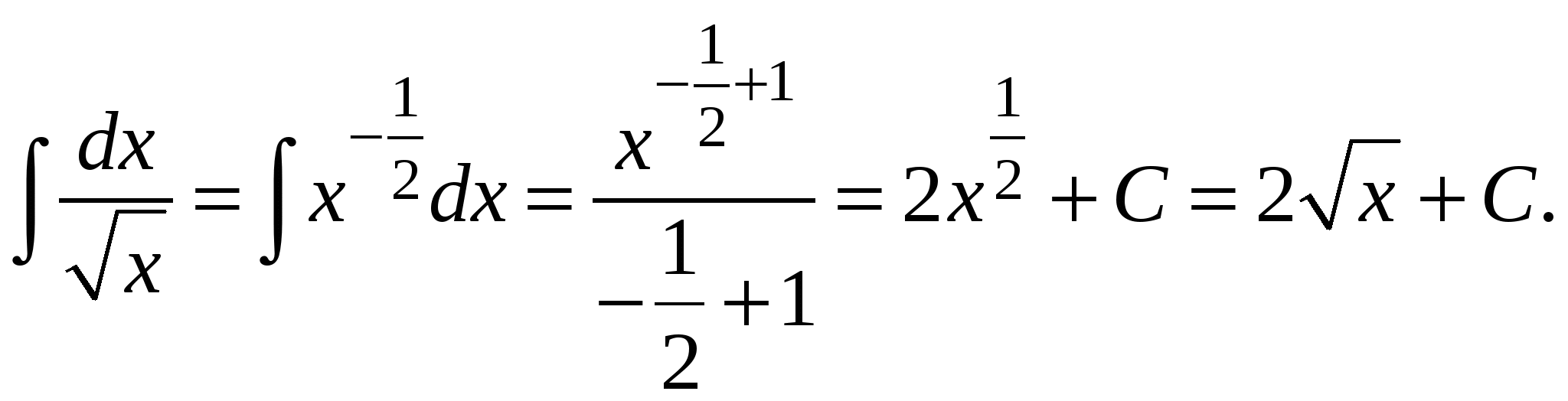
Пример 4. Найти интеграл 
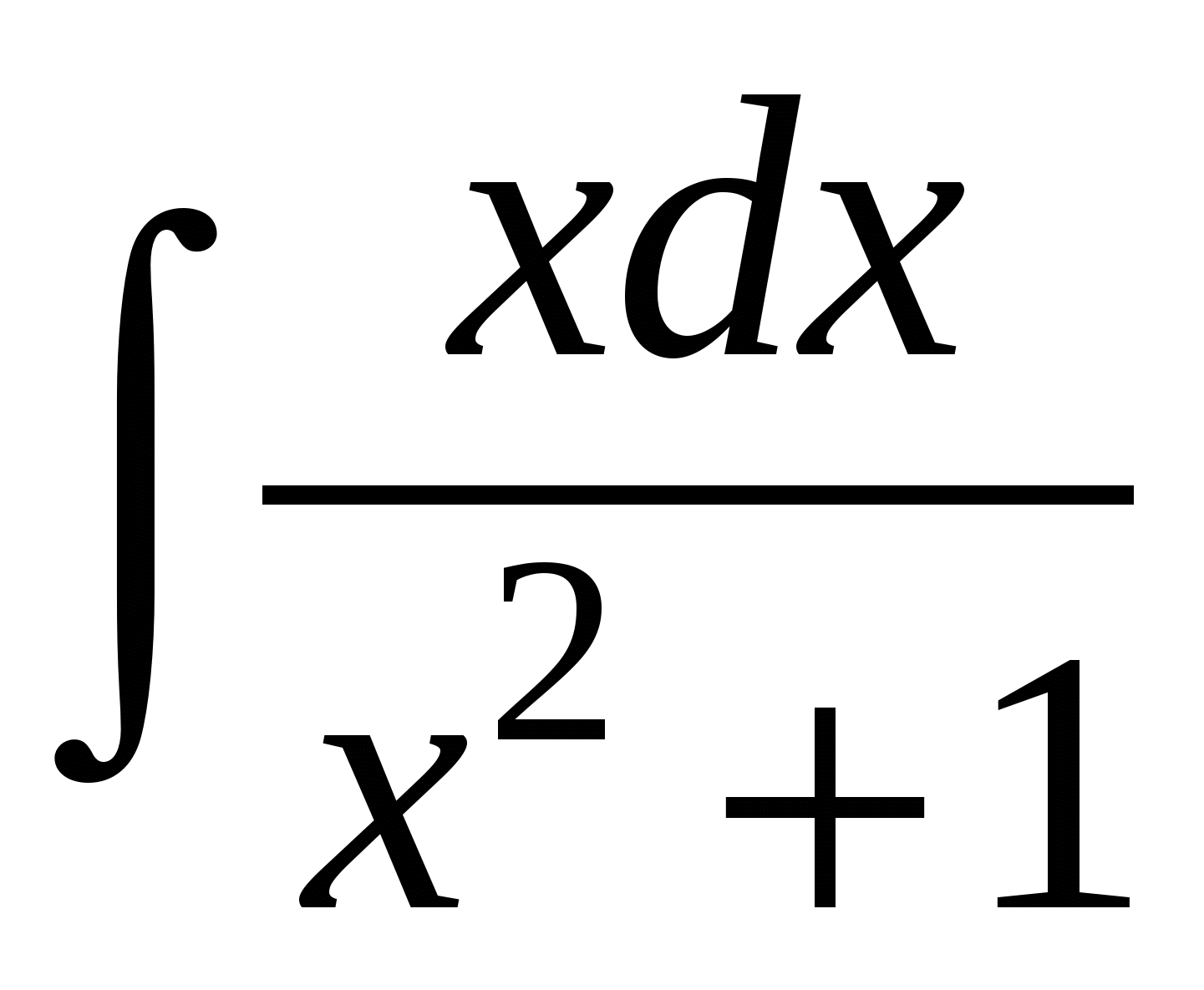 .
.
Решение: так как 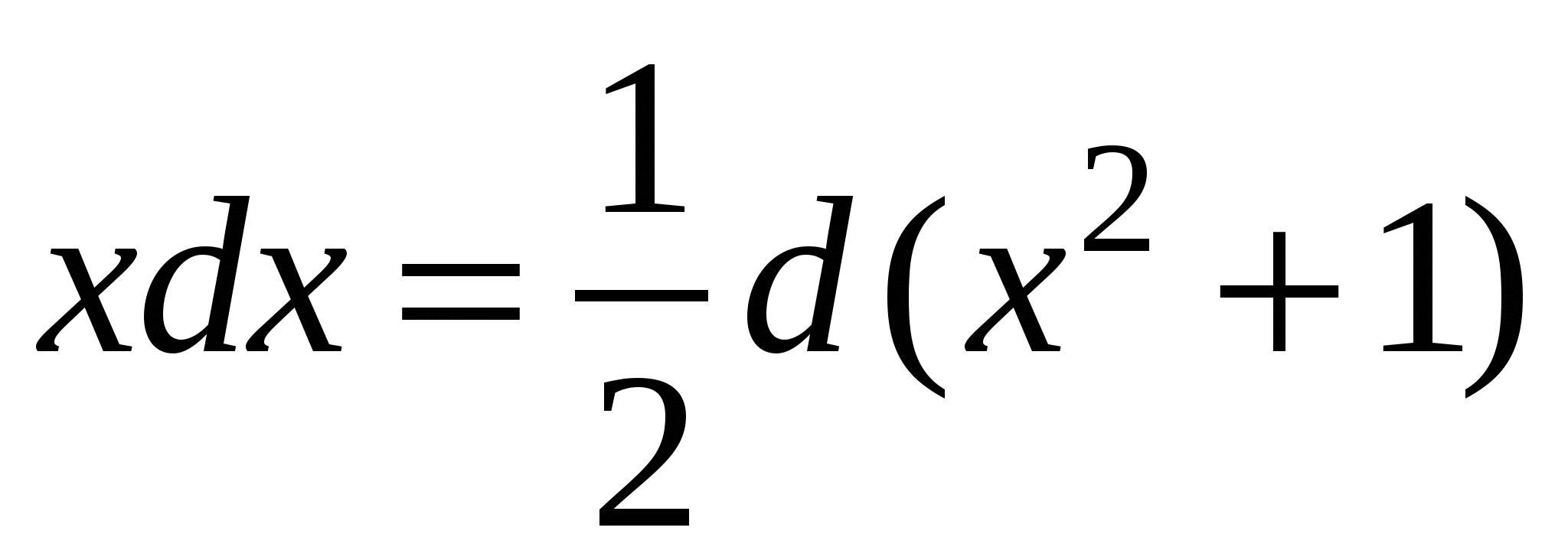 , то
, то 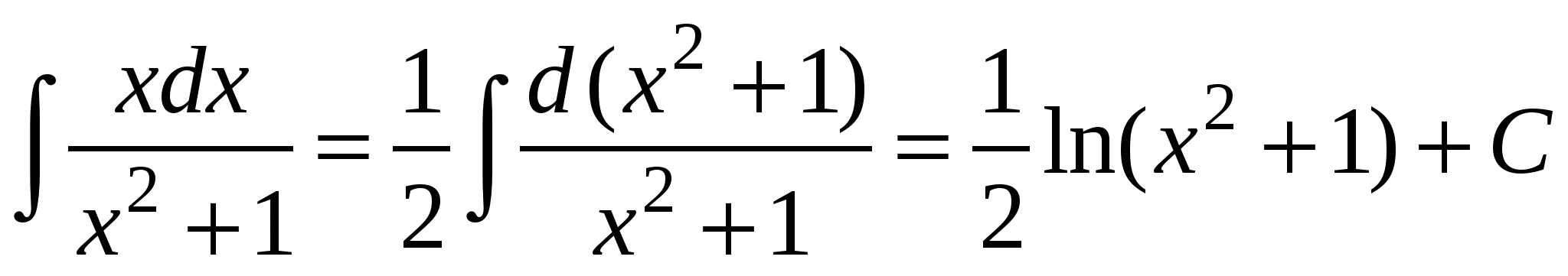 .
.
Пример 5. Найти интеграл.
Решение: так как 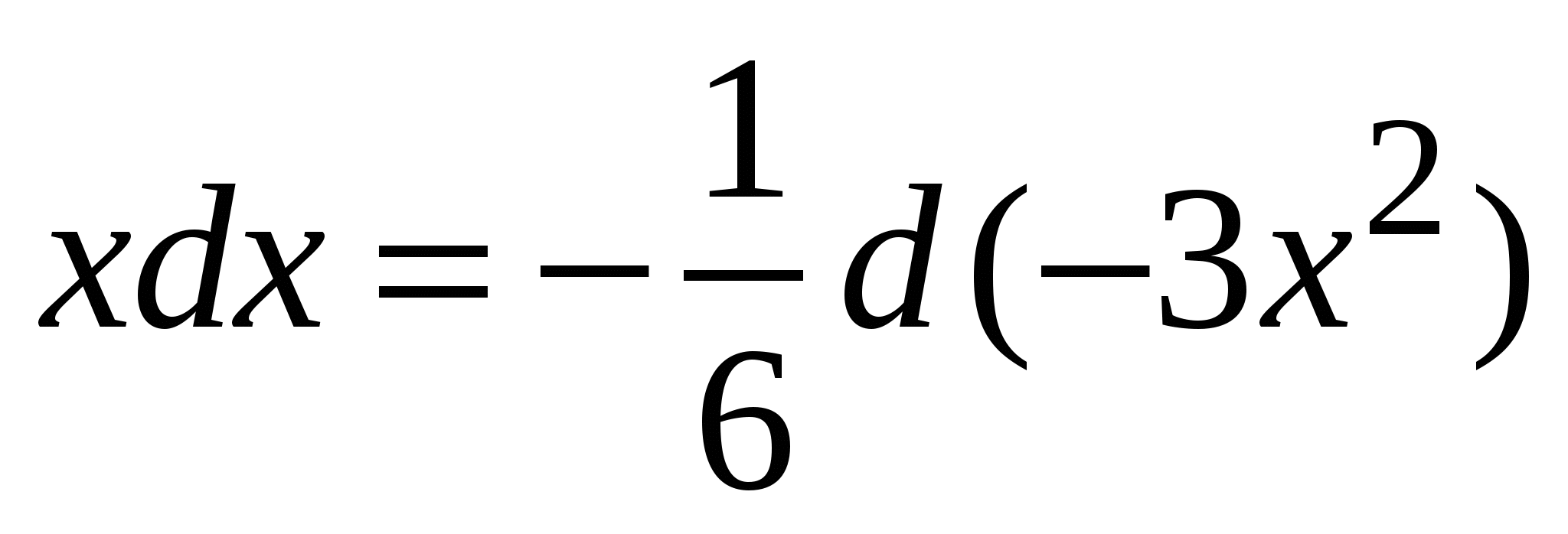 , т
, т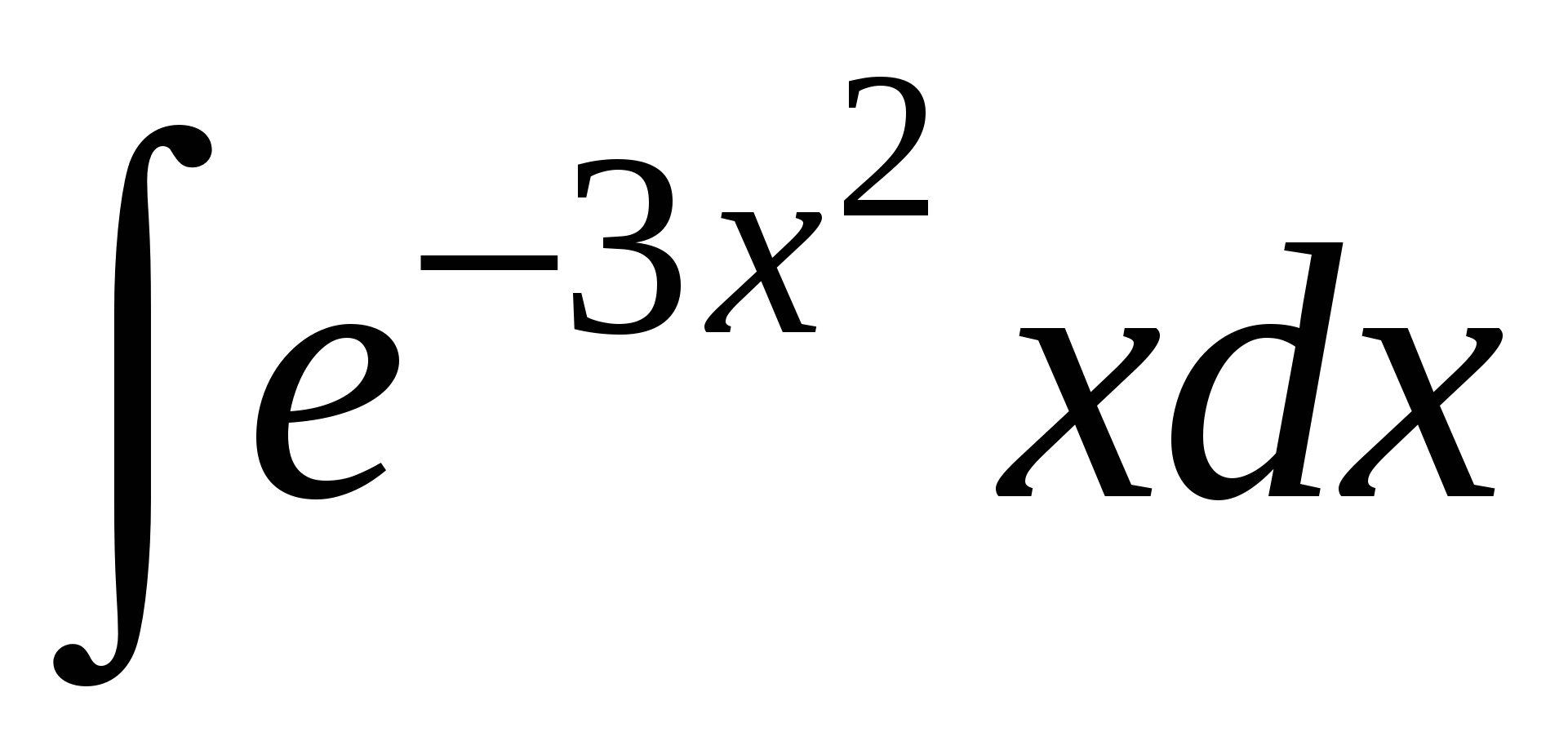 о
о 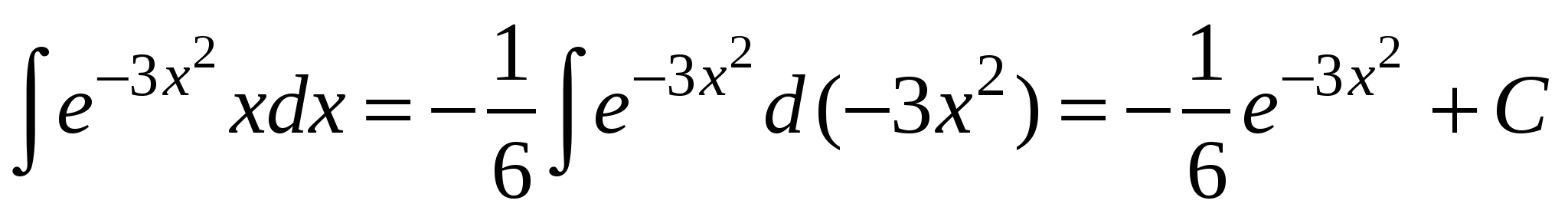 .
.
Пример 6. Найти интеграл 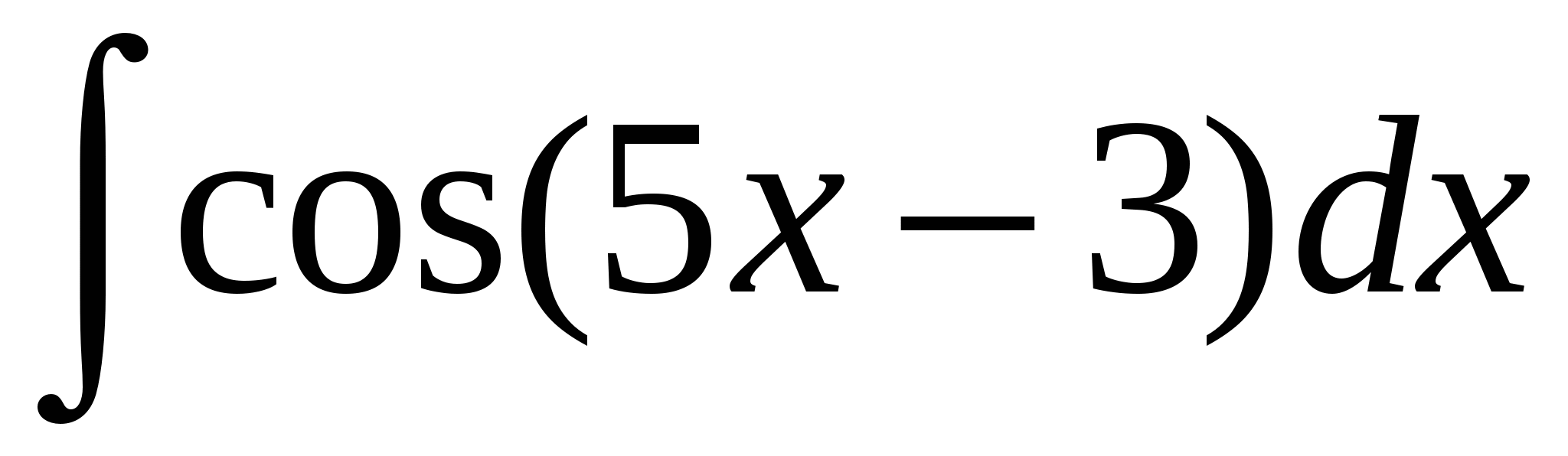 .
.
Решение: так как 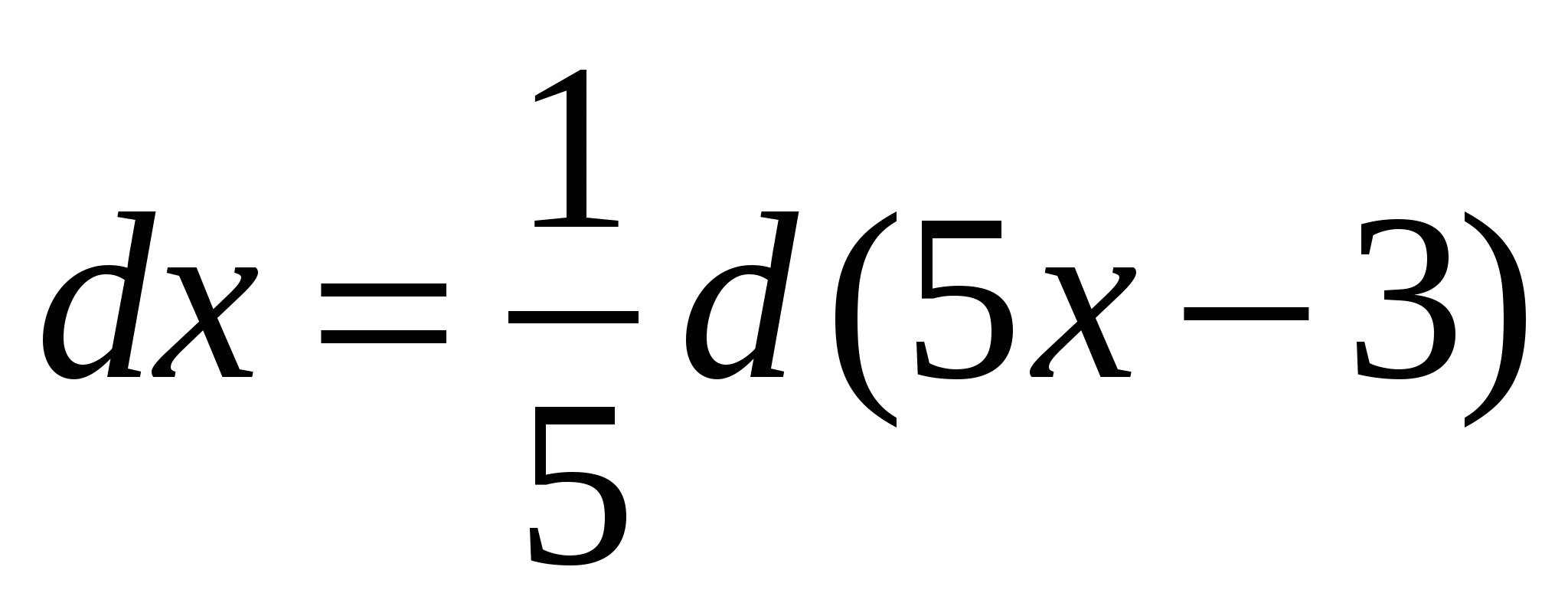 , то
, то 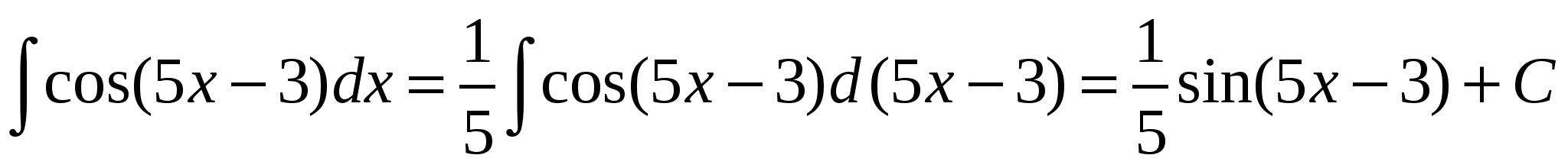 .
.
Пример 7. Найти интеграл 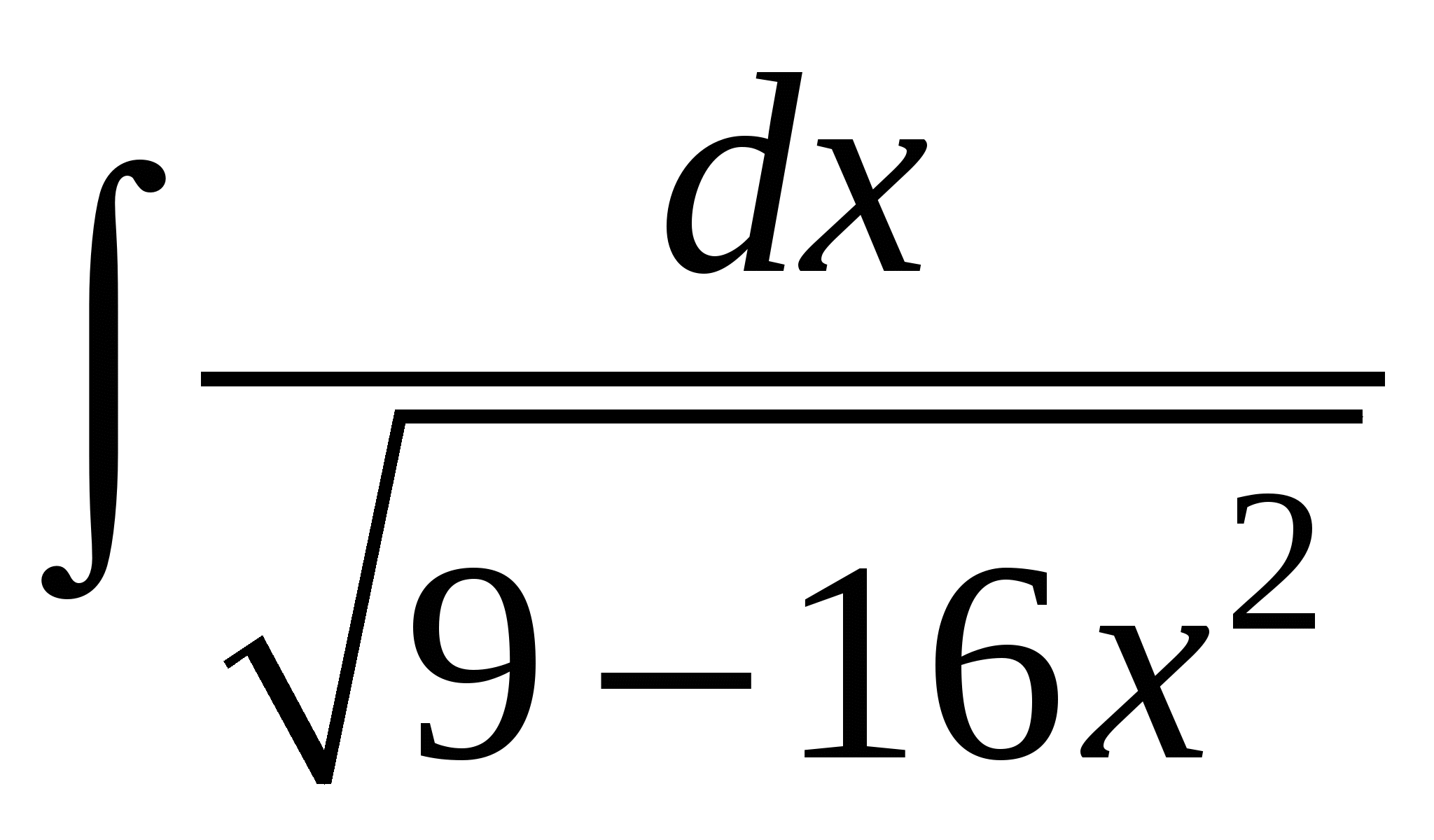 .
.
Решение: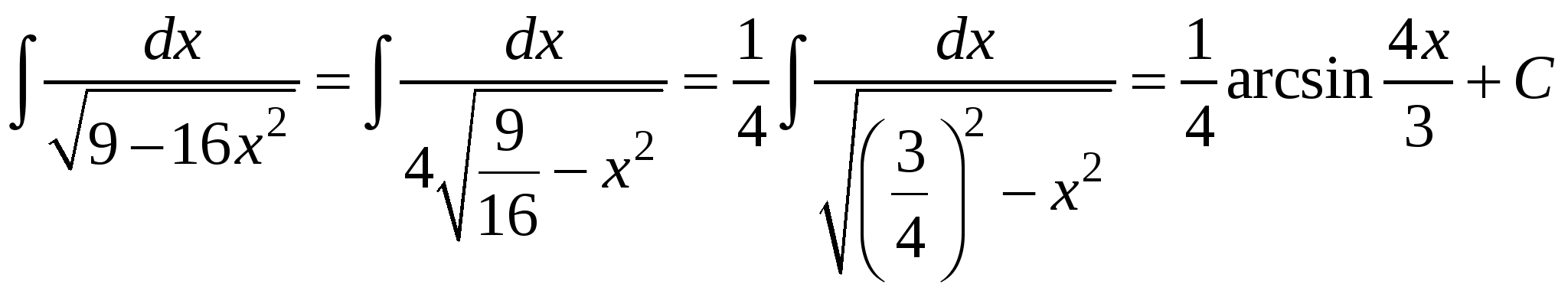
Определенный интеграл.
Пусть функция 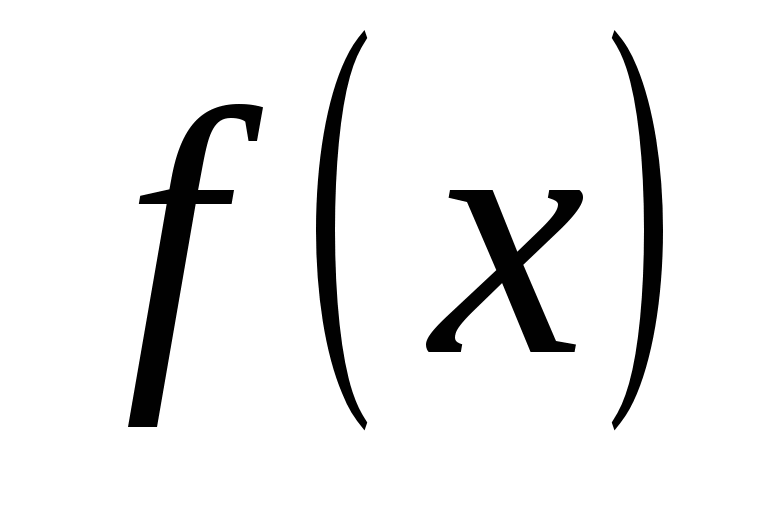 определена на отрезке
определена на отрезке 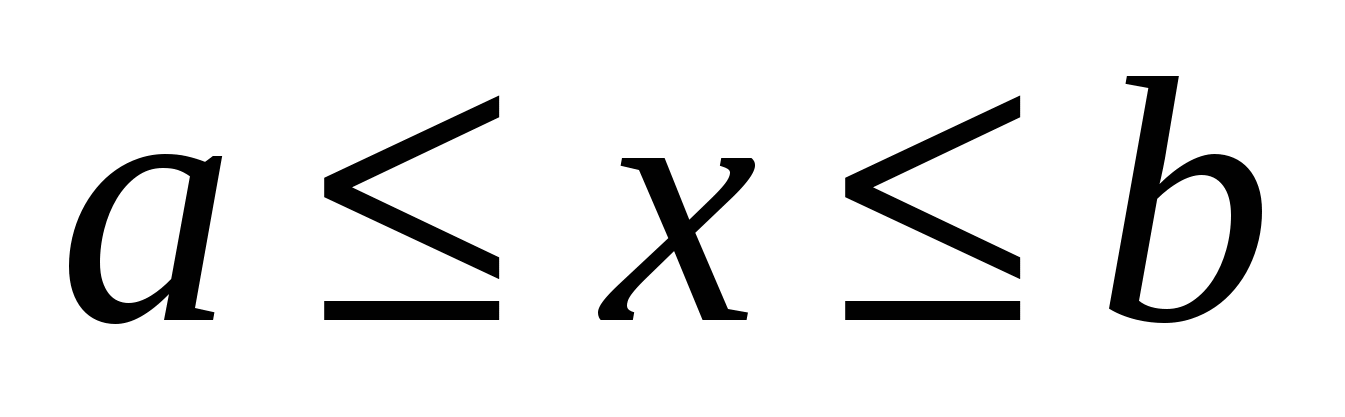 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками 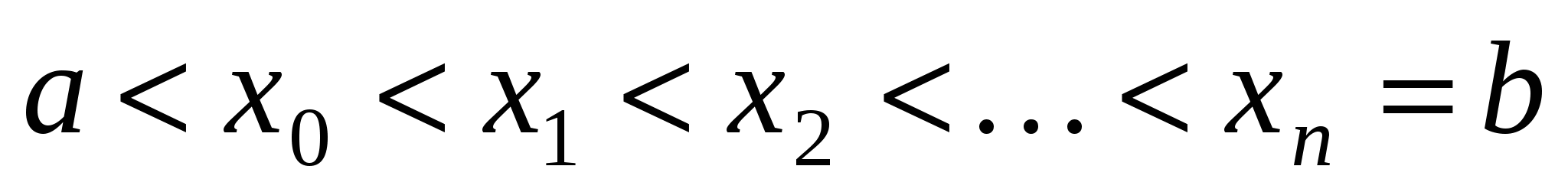 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке 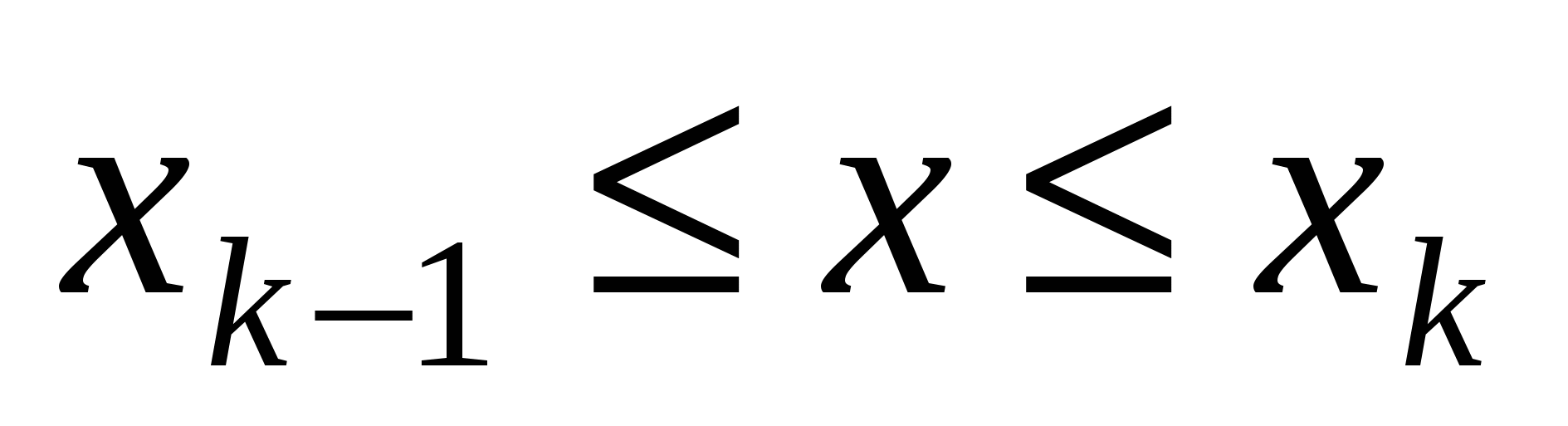 произвольную точку
произвольную точку 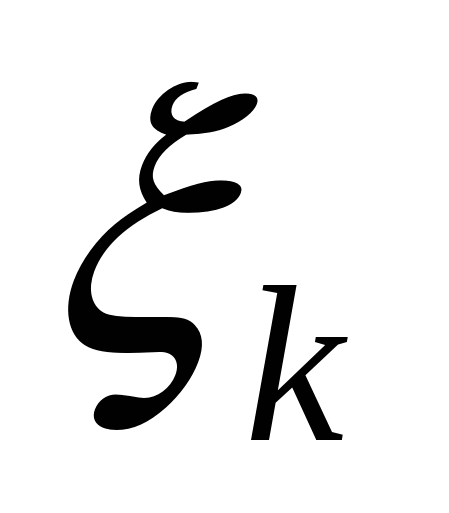 и обозначим через
и обозначим через ![]() длину каждого такого отрезка.
длину каждого такого отрезка.
Определение. Интегральной суммой для функции 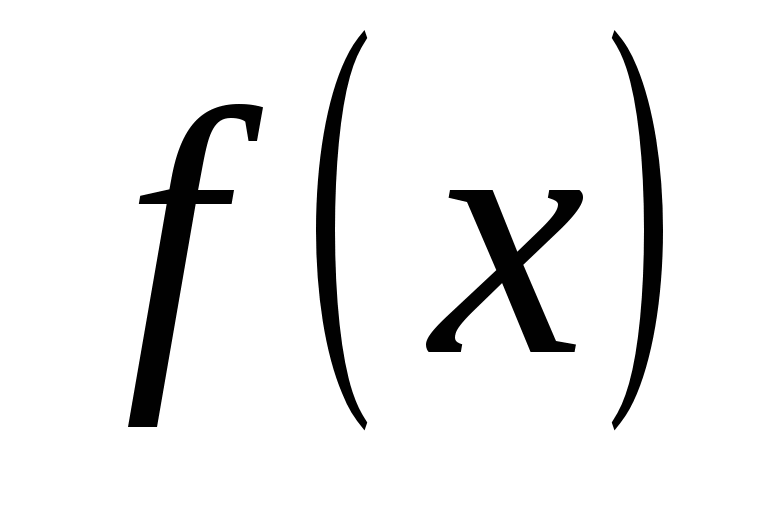 на отрезке
на отрезке 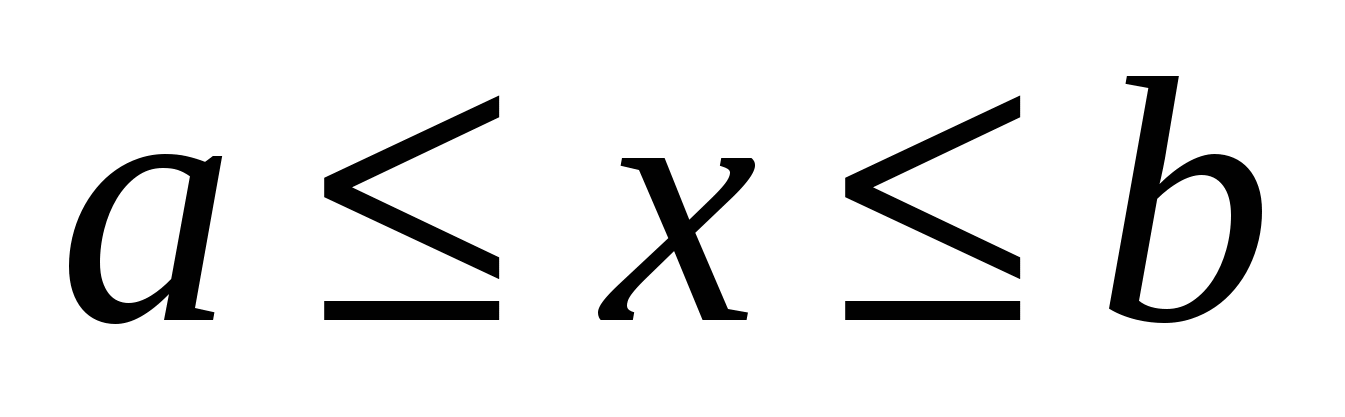 называется сумма вида
называется сумма вида 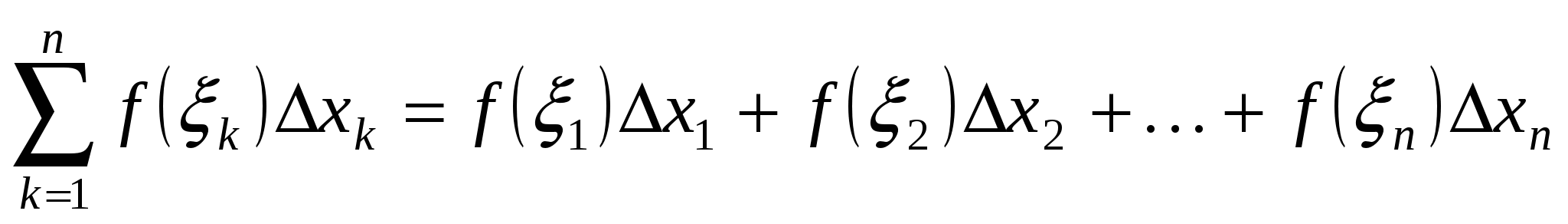 .
.
Определение. Определенным интегралом от функции 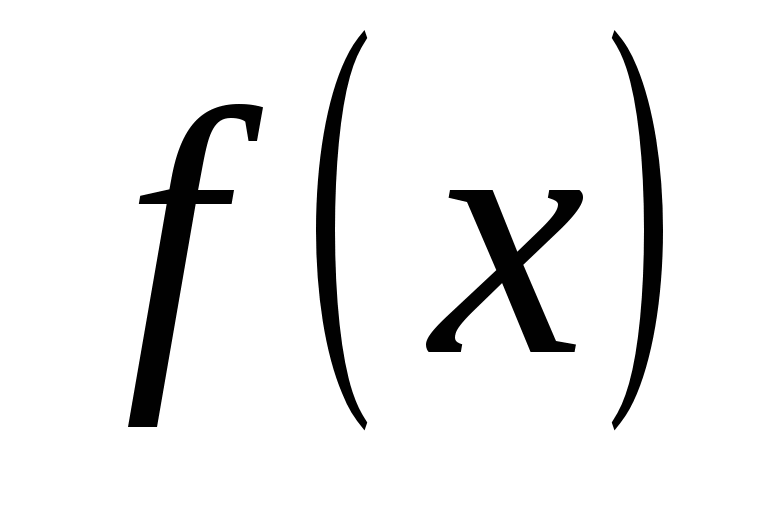 на отрезке
на отрезке 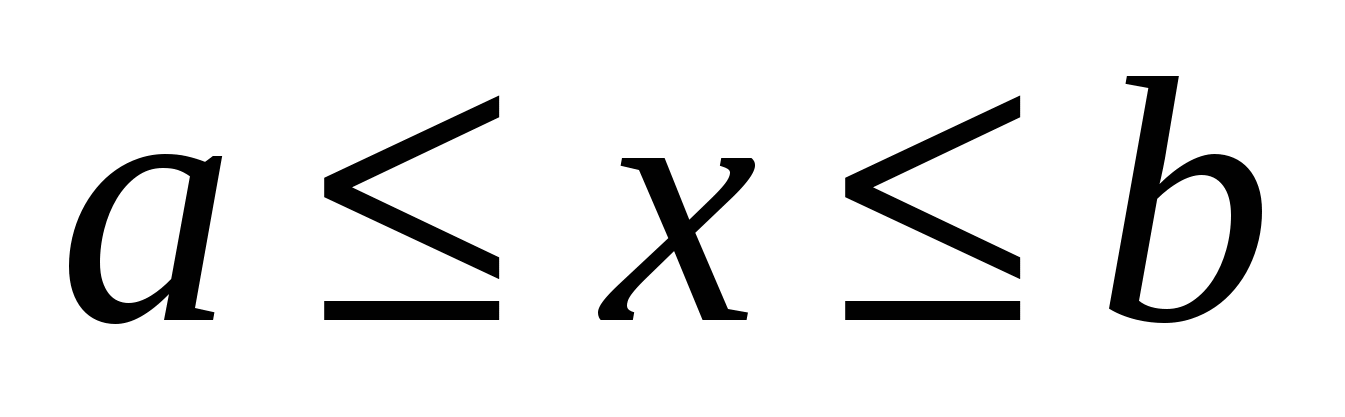 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю: 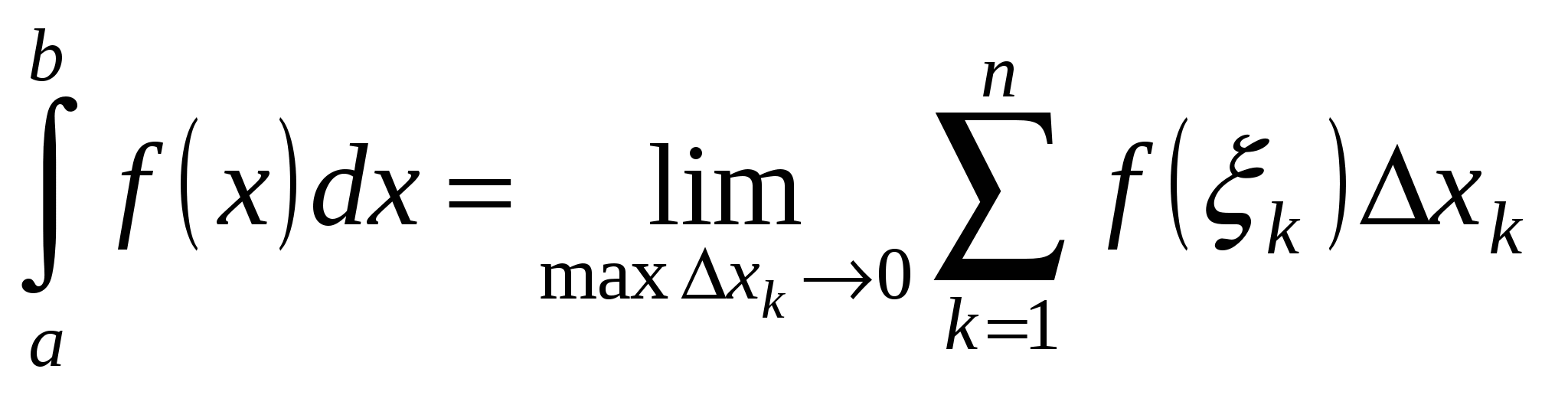 .
.
Для любой функции 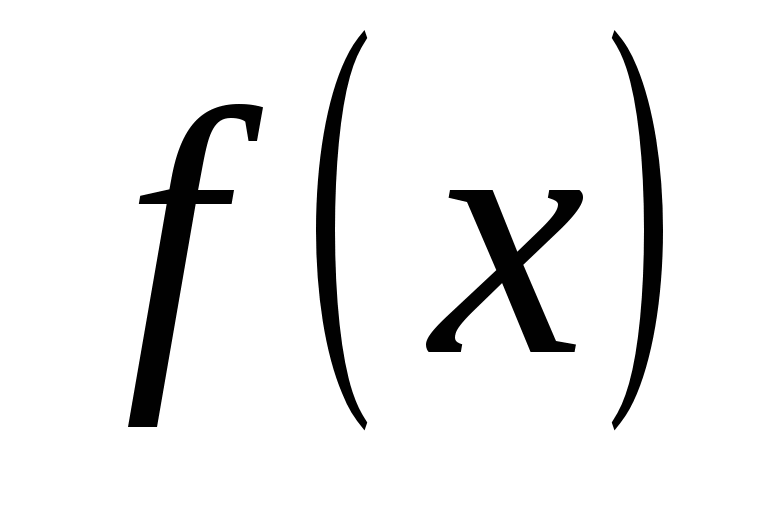 , непрерывной на отрезке
, непрерывной на отрезке 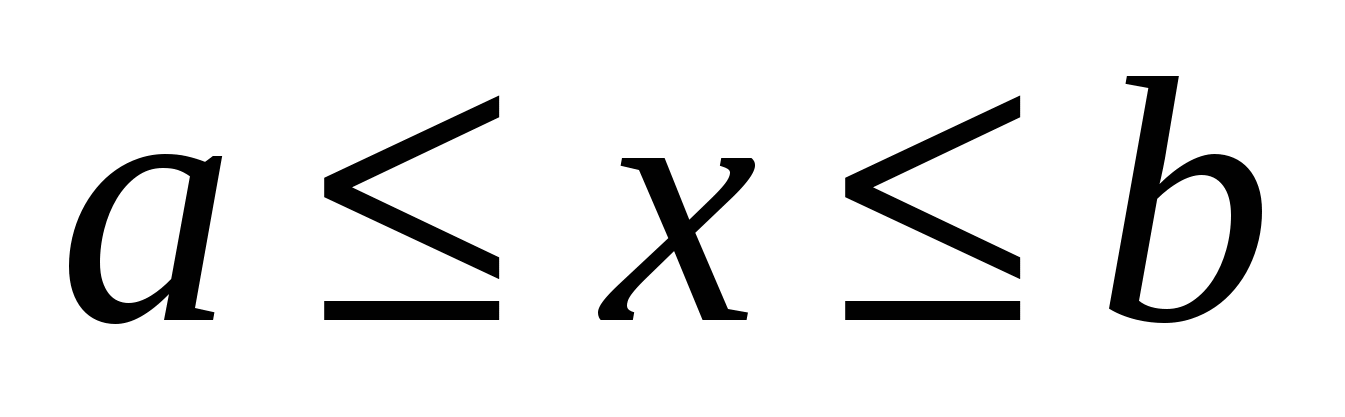 , всегда существует определенный интеграл
, всегда существует определенный интеграл 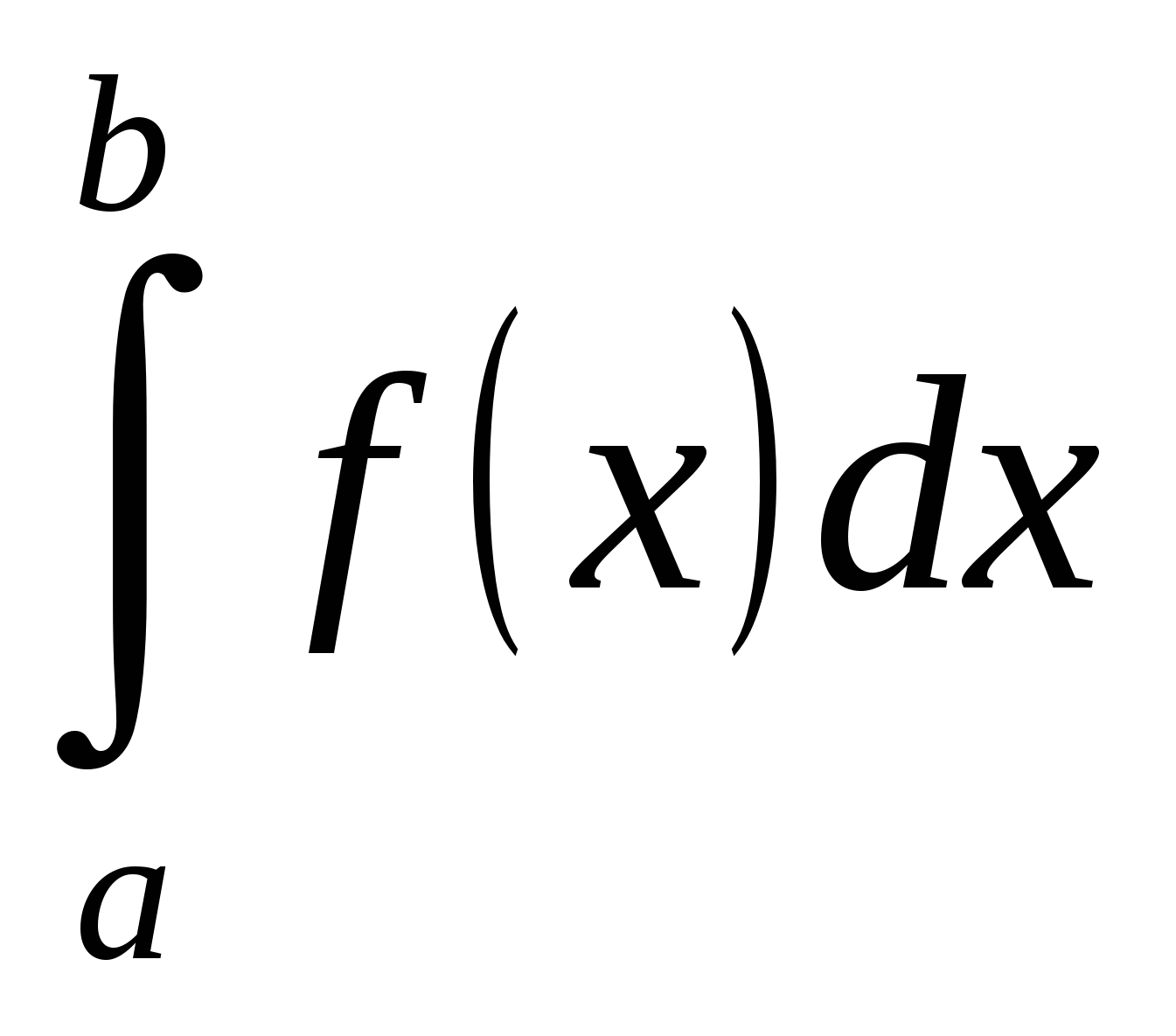 .
.
Для вычисления определенного интеграла от функции 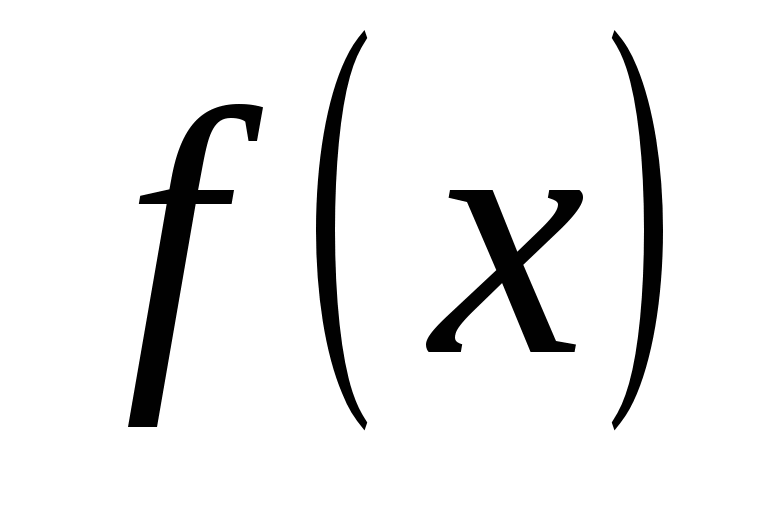 в том случае, когда можно найти соответствующий неопределенный интеграл
в том случае, когда можно найти соответствующий неопределенный интеграл 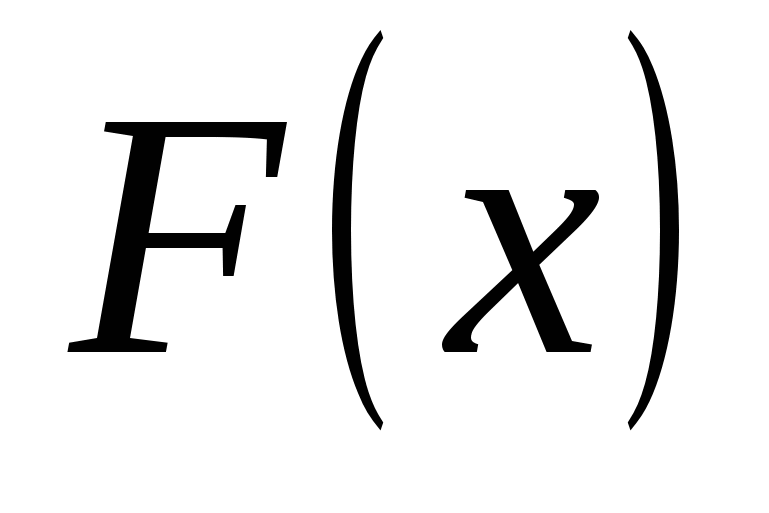 , служит формула Ньютона - Лейбница:
, служит формула Ньютона - Лейбница: 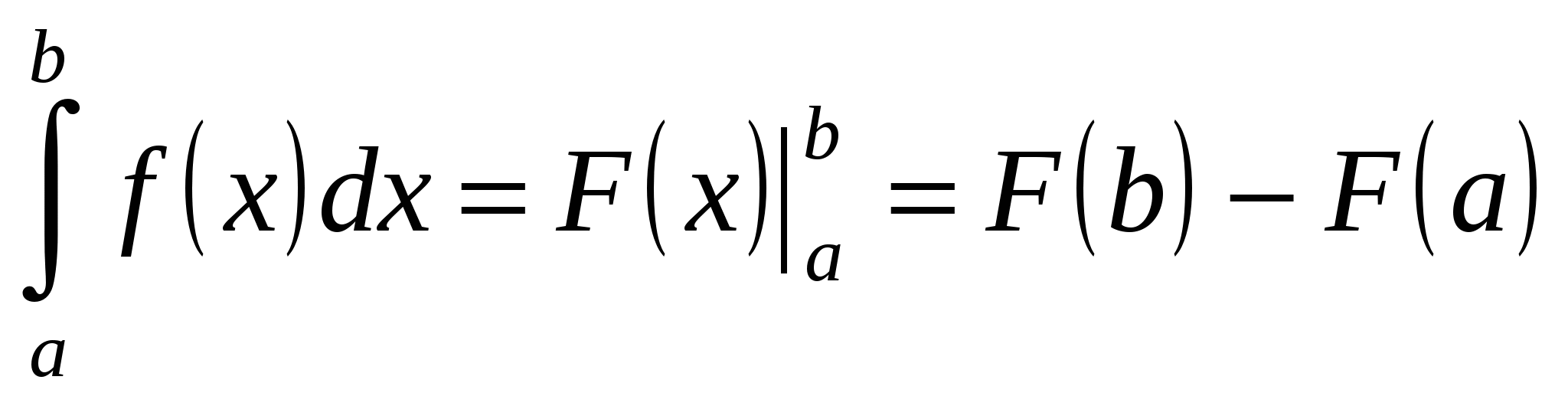 , то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 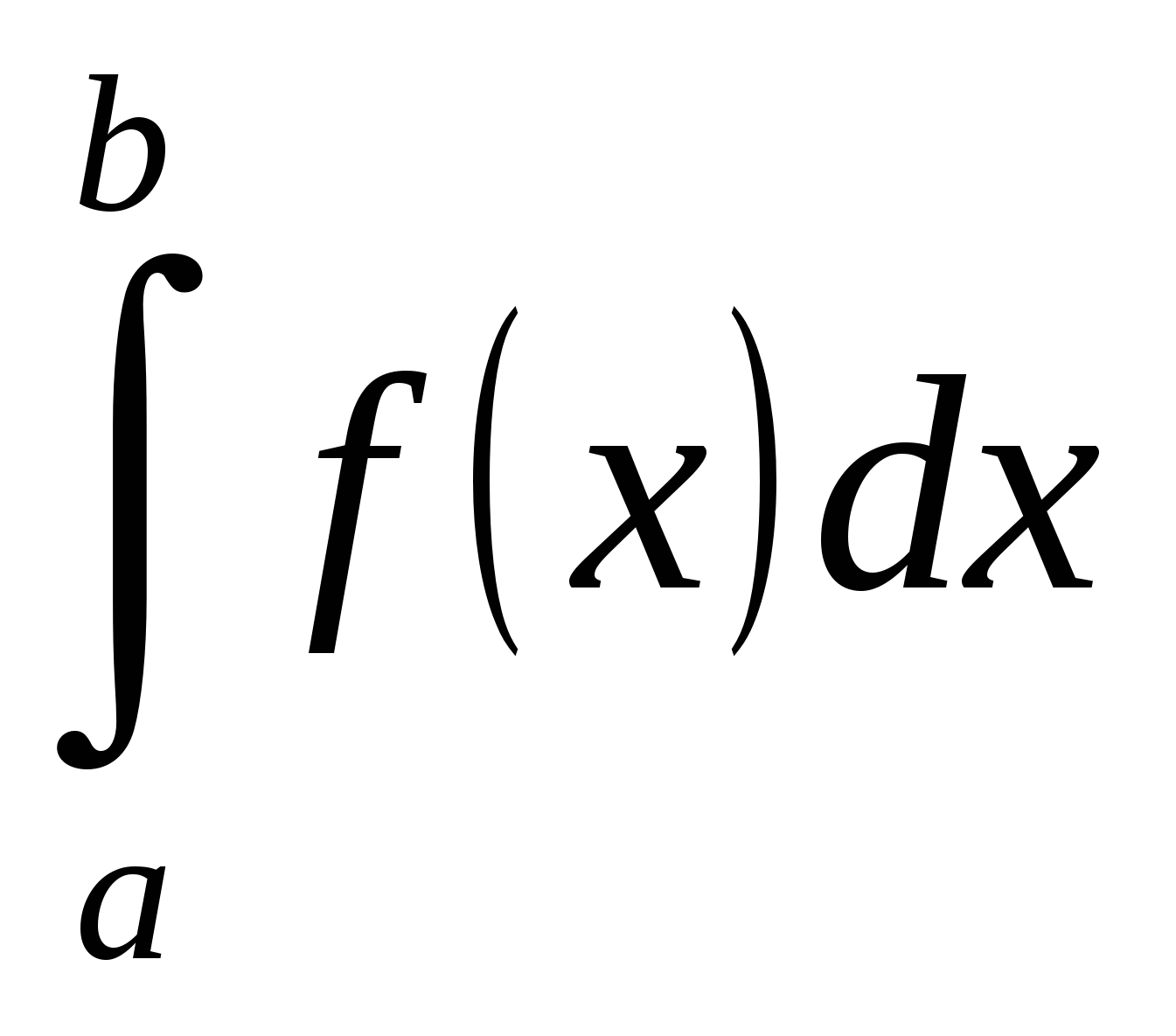 преобразуется с помощью подстановки
преобразуется с помощью подстановки 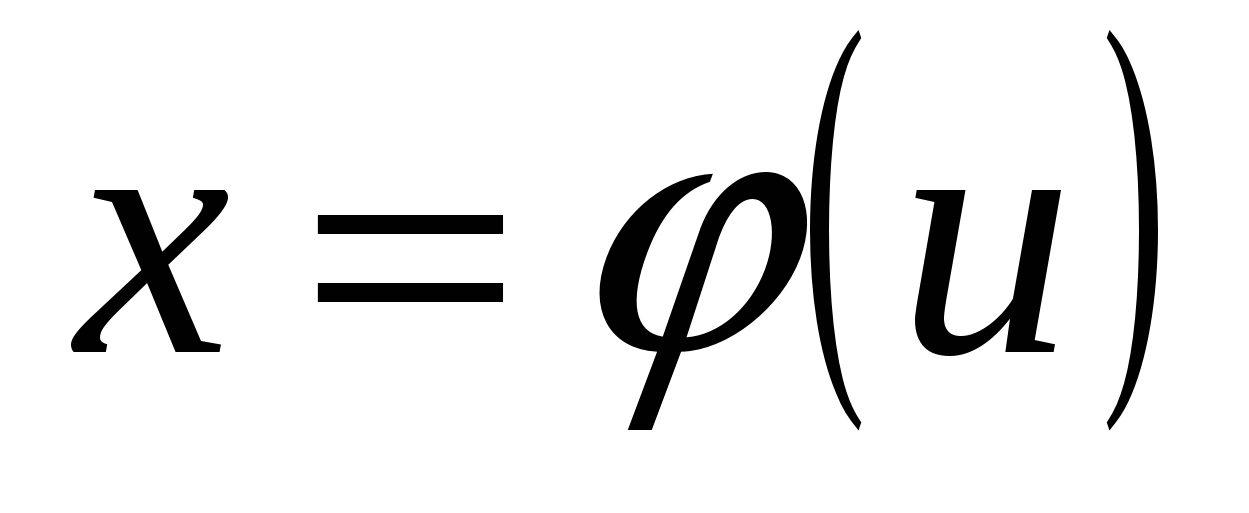 в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной  . При этом старые пределы интегрирования
. При этом старые пределы интегрирования  и
и 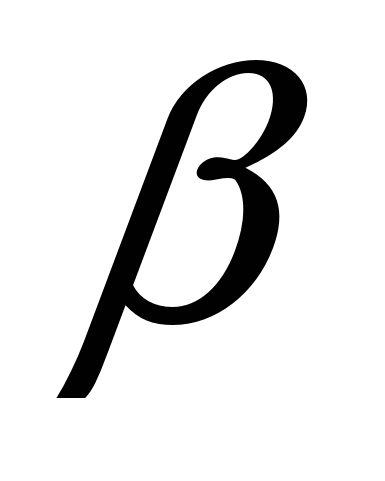 , которые находятся из исходной подстановки:
, которые находятся из исходной подстановки: 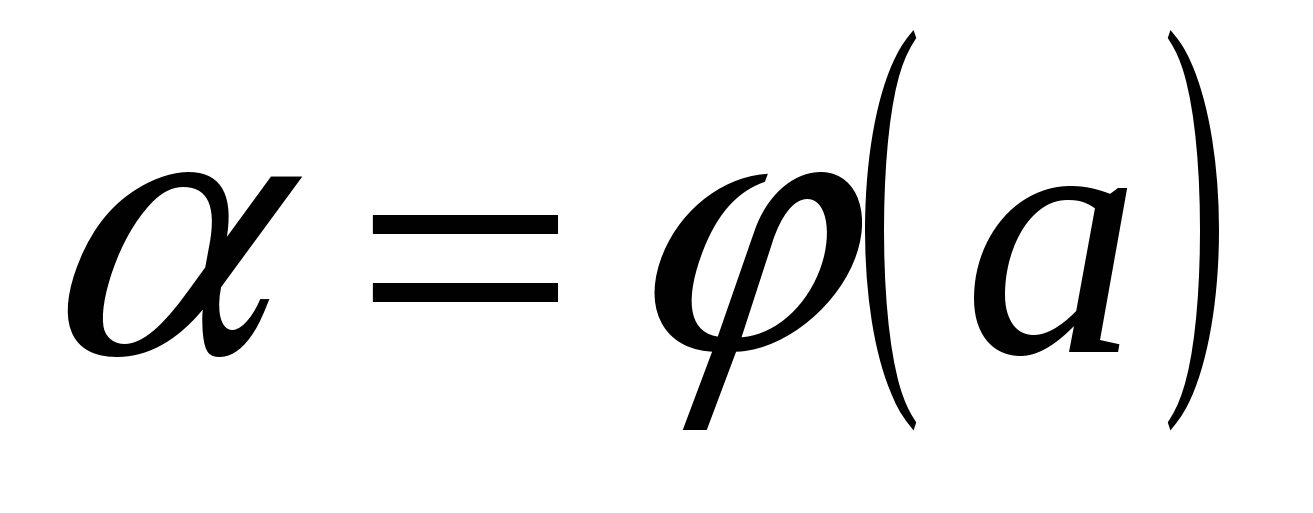 ,
, 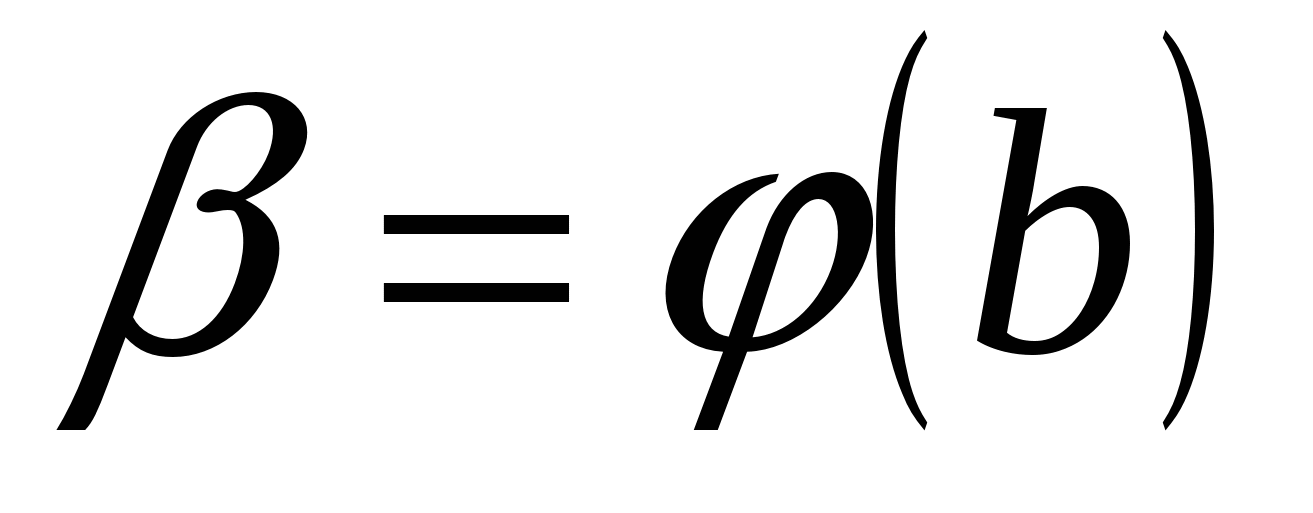 . Таким образом, имеем
. Таким образом, имеем 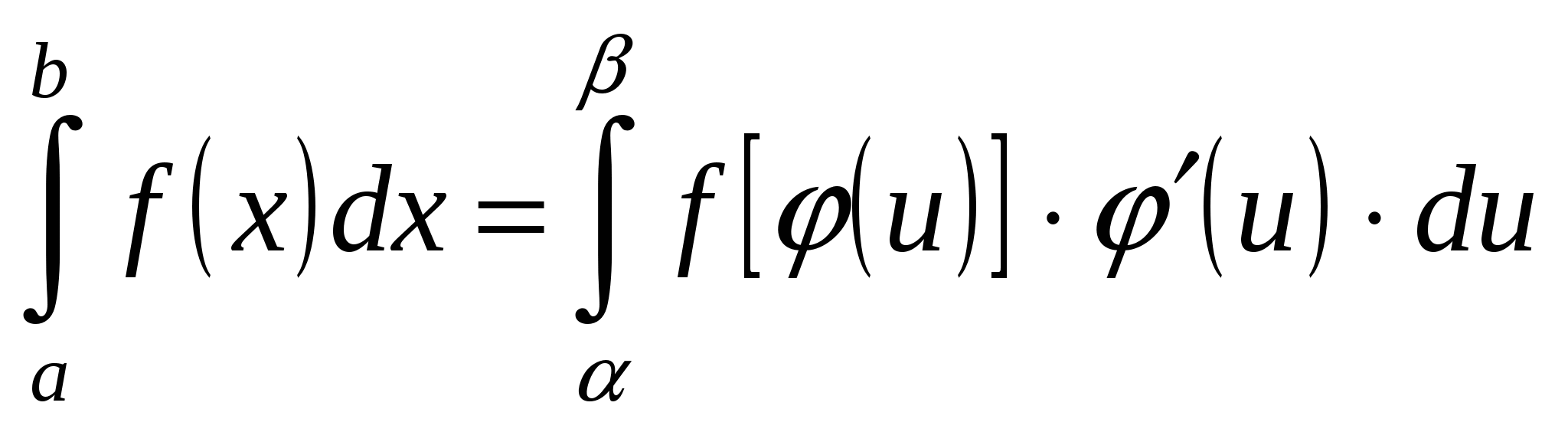 .
.
Пример 1. Вычислить определенный интеграл: 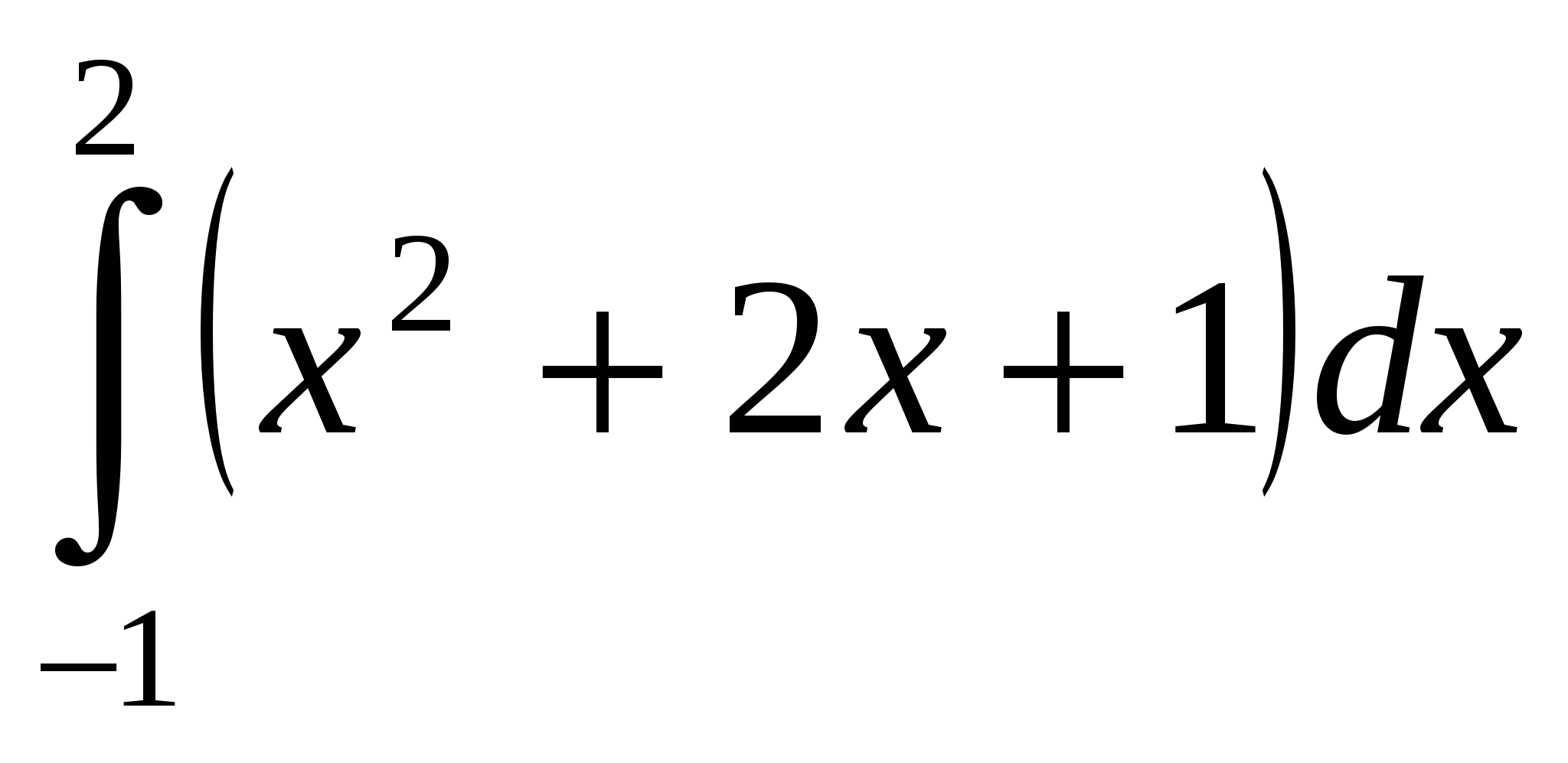 .
.
Решение:
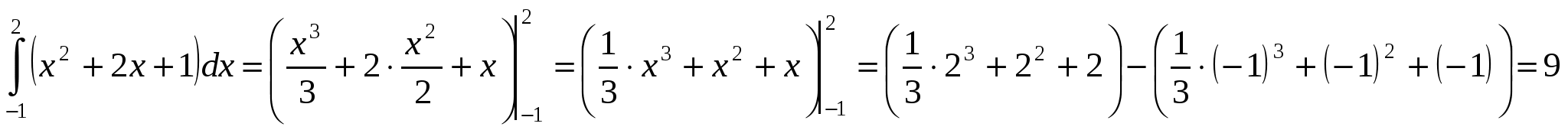 .
.
Пример 2. Вычислить определенный интеграл: 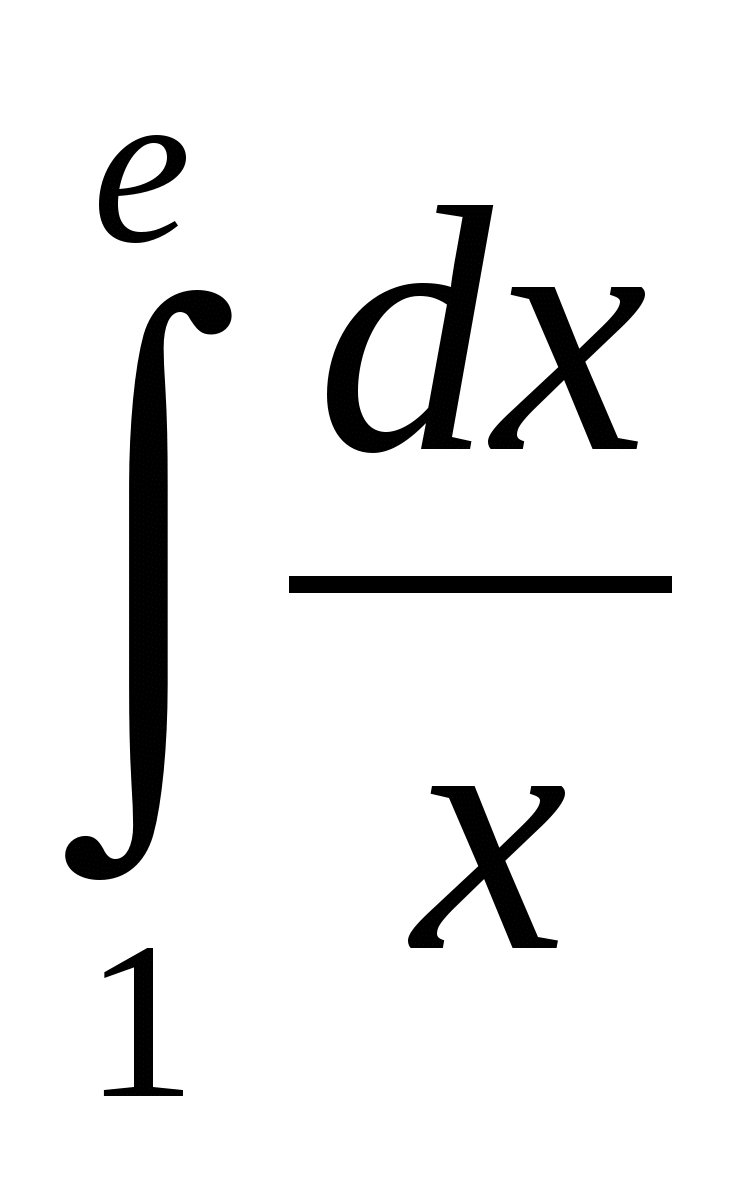 .
.
Решение: 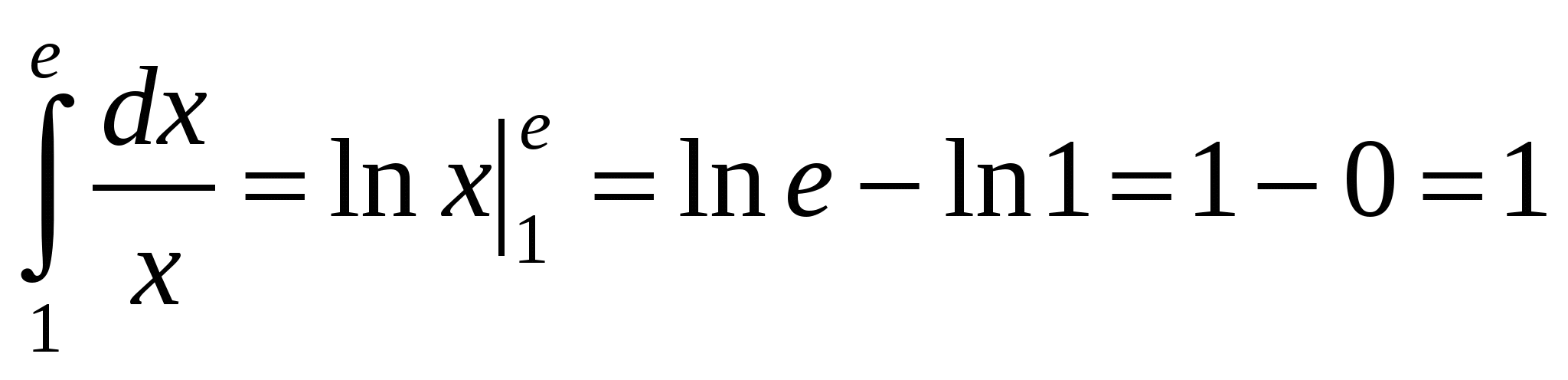 .
.
Пример 3. Вычислить определенный интеграл: 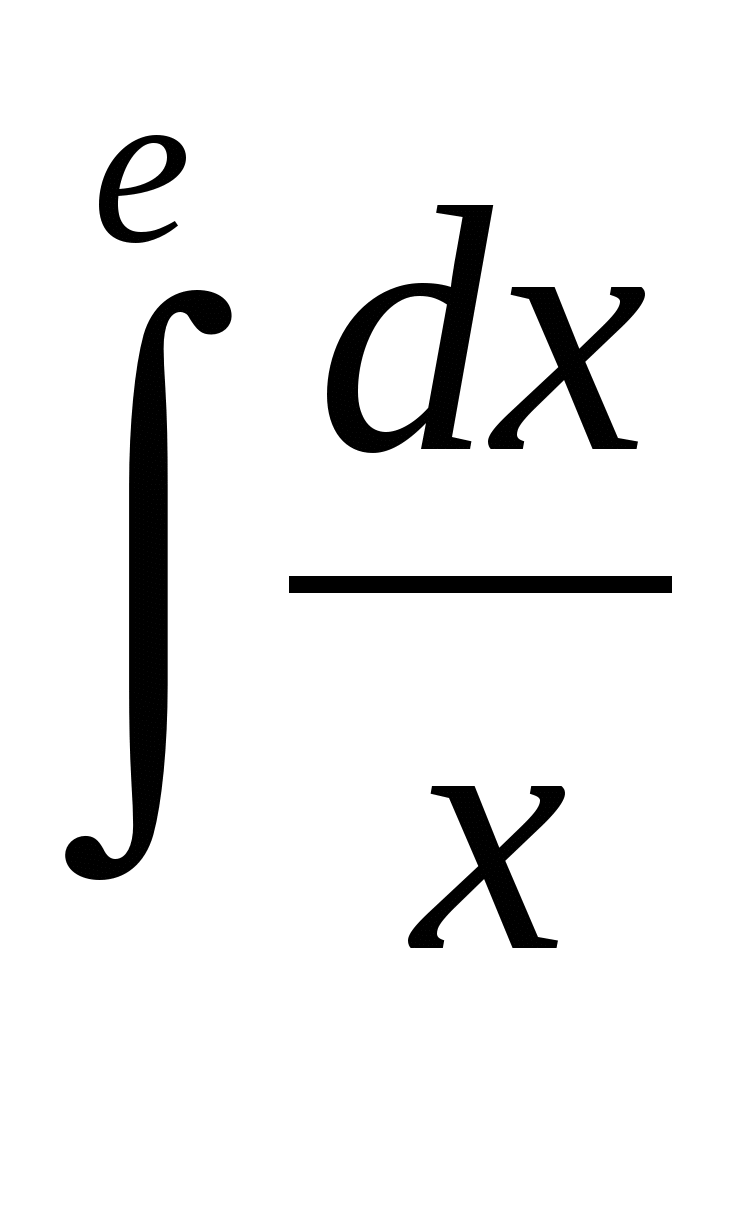
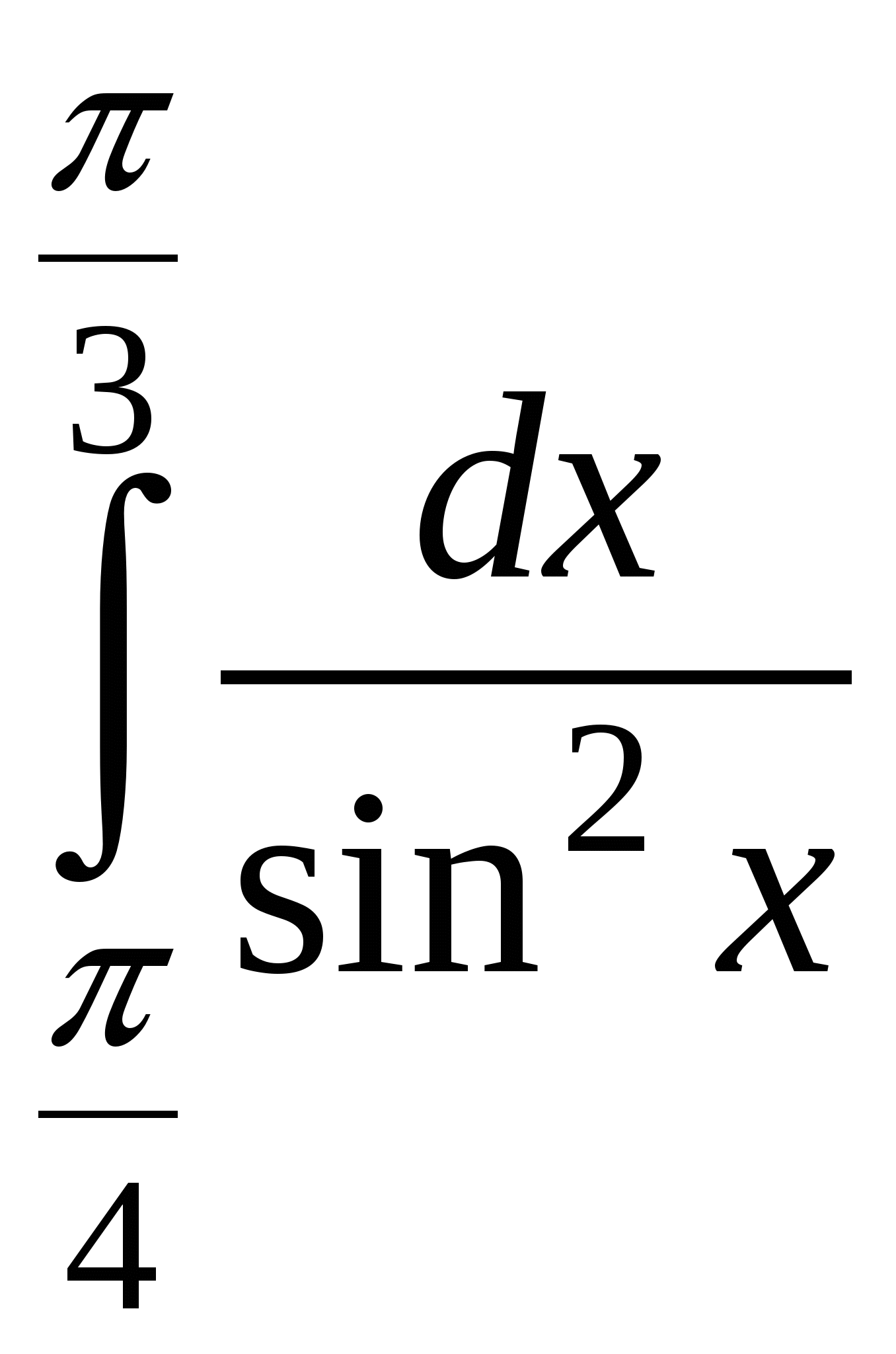 .
.
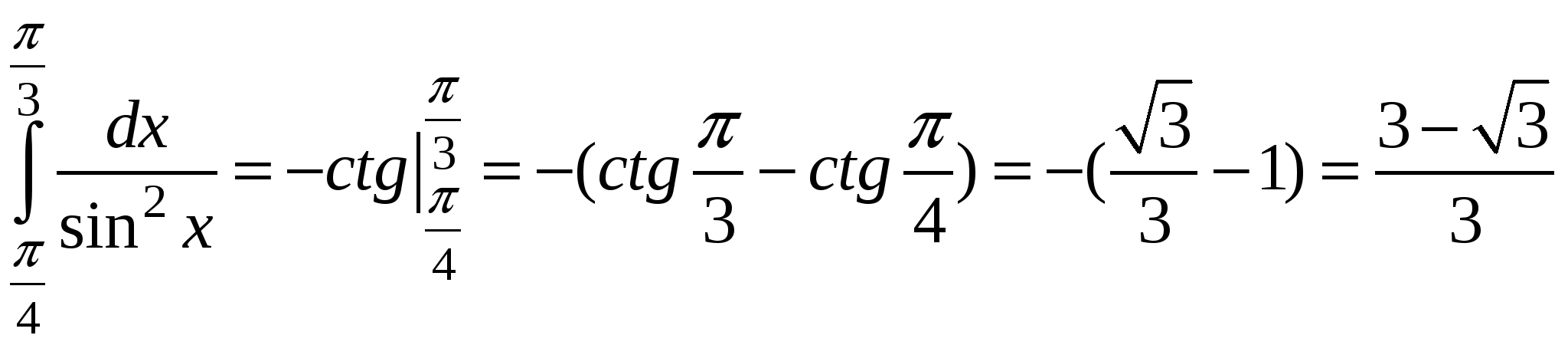 .
.
Пример 4. Вычислить определенный интеграл: 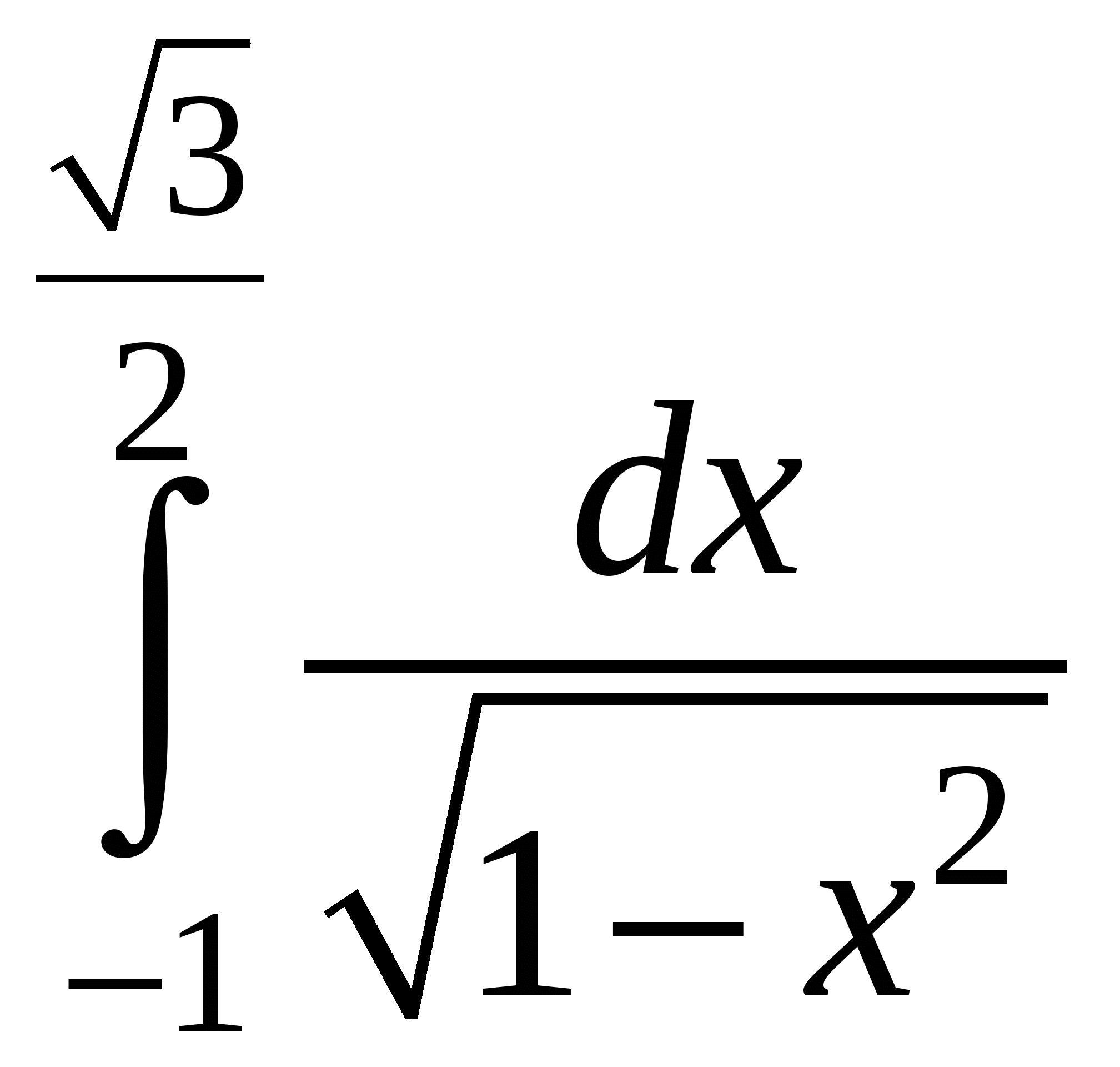 .
.
Решение: 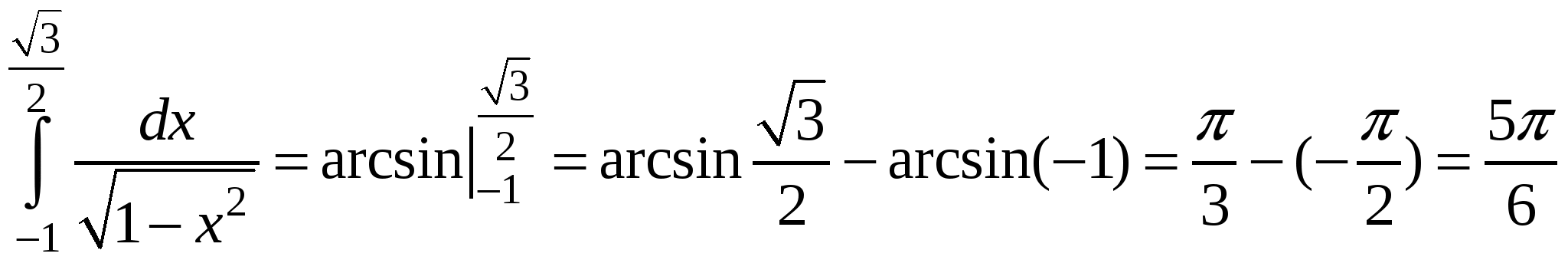 .
.
Пример 5. Вычислить определенный интеграл: 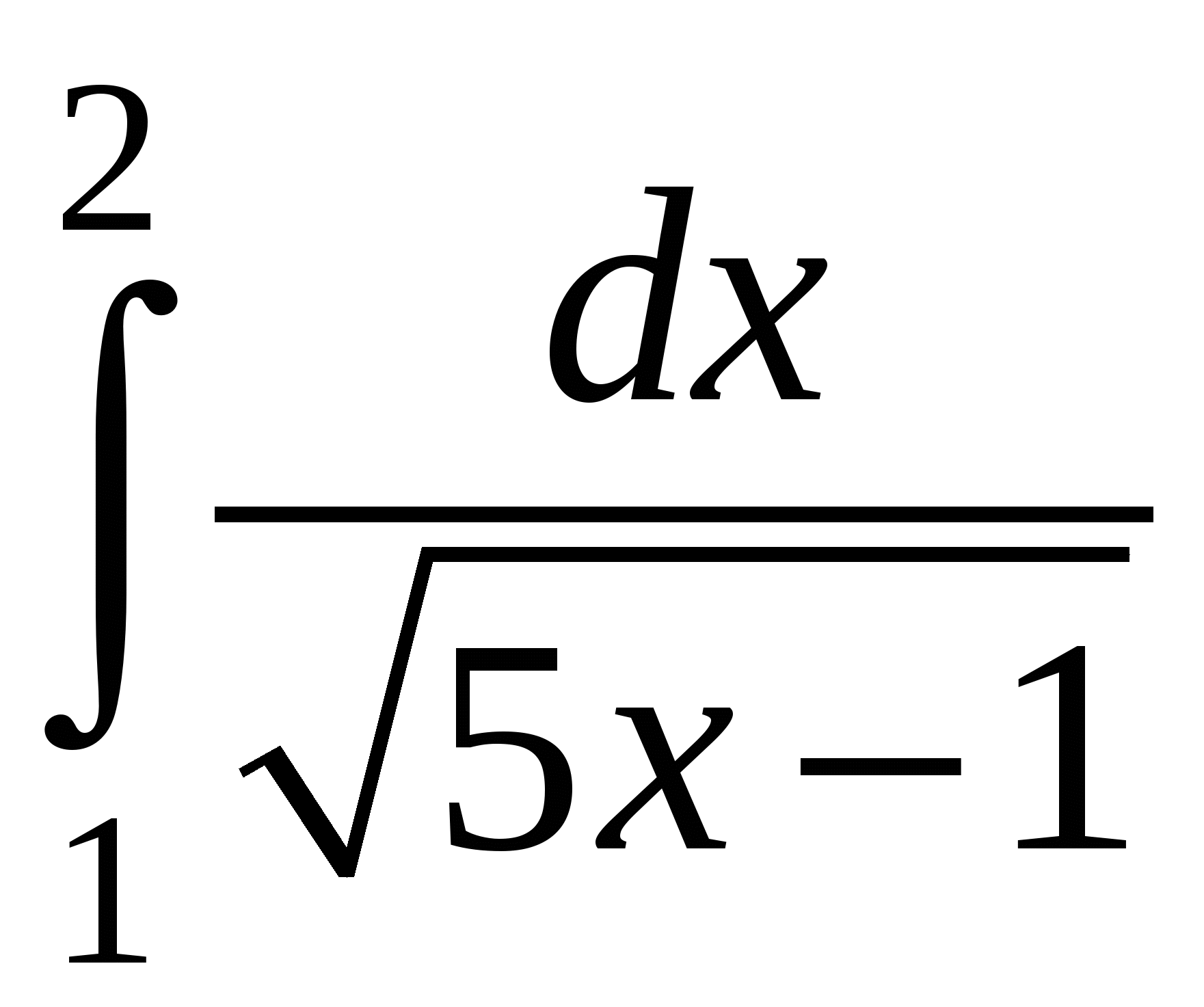 .
.
Решение: положим 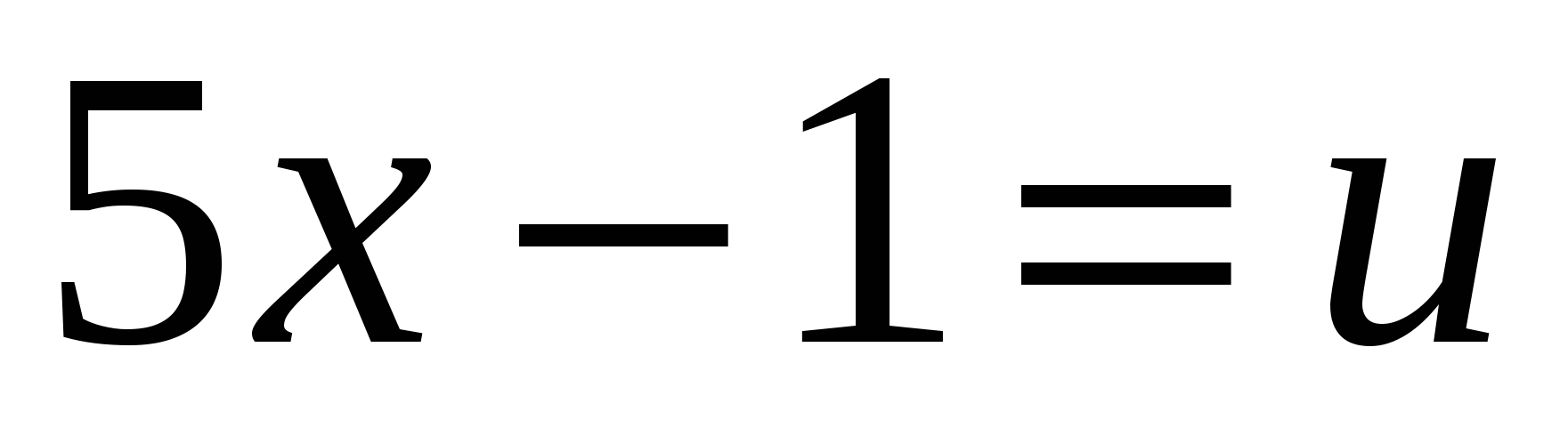 , тогда
, тогда 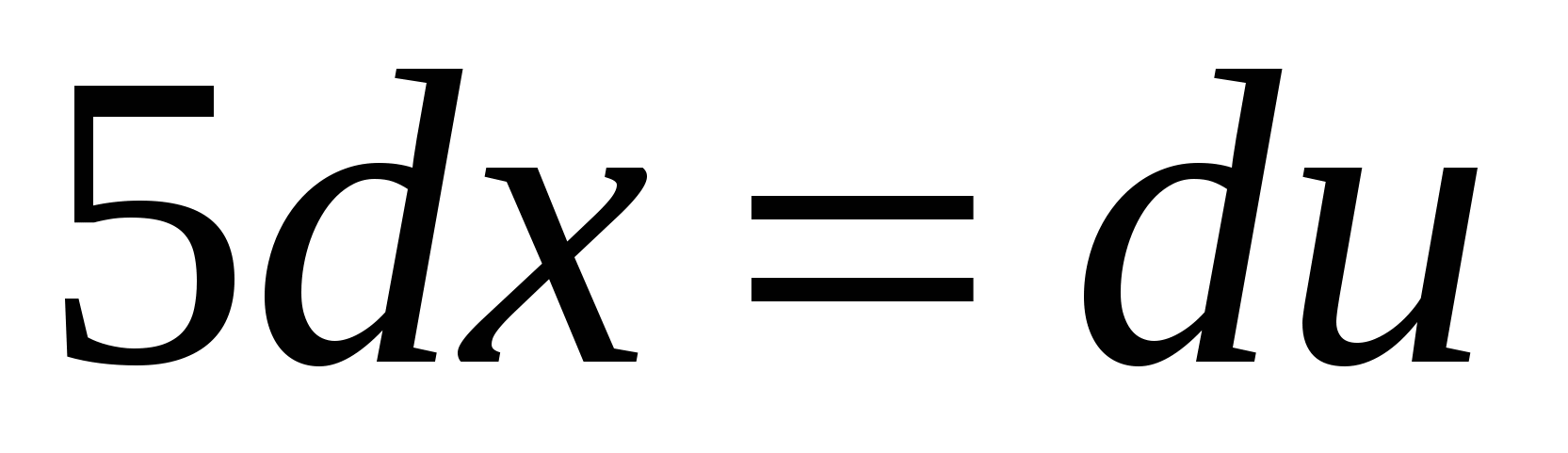 ,
, 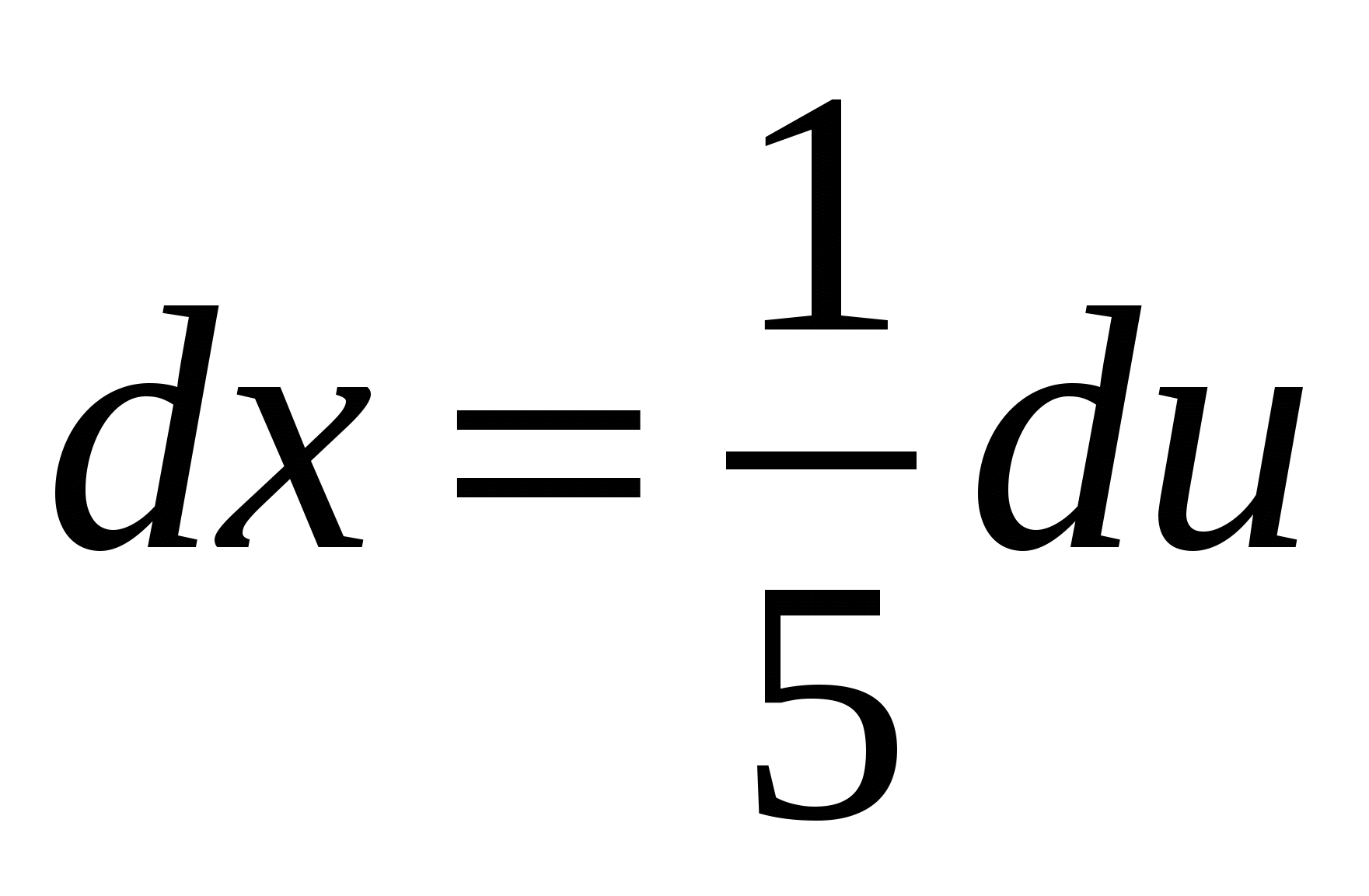 . Вычисляем новые пределы интегрирования:
. Вычисляем новые пределы интегрирования: 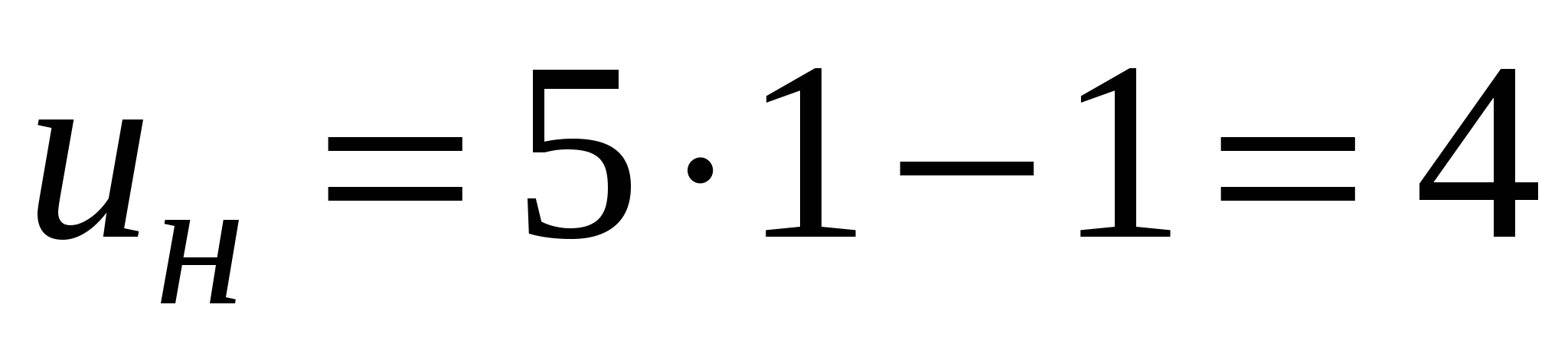 ,
, 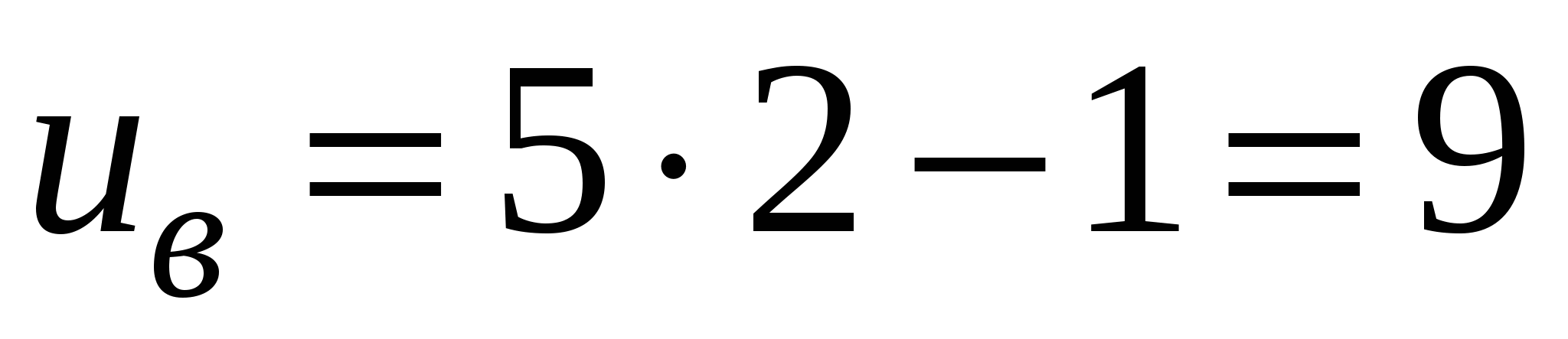 .
.
Поэтому
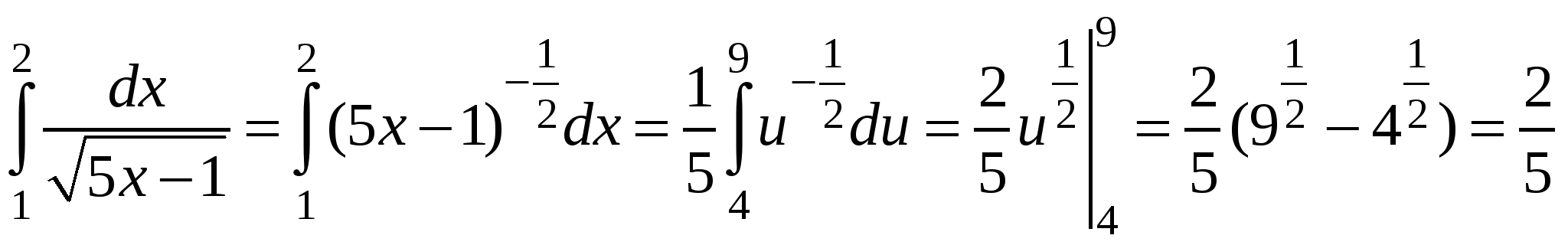 .
.
Пример 6. Вычислить определенный интеграл: 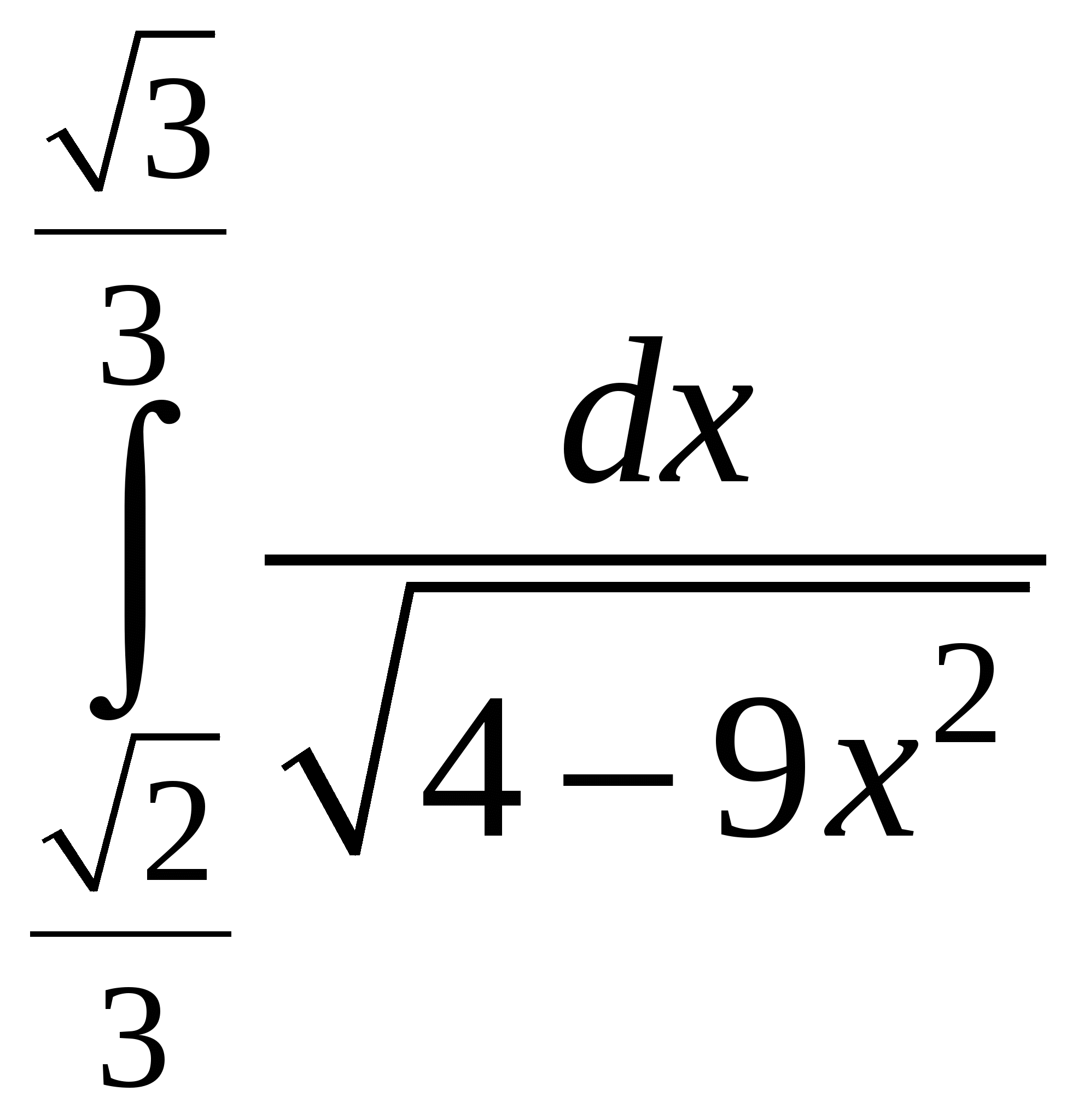 .
.
Решение: преобразуем подкоренное выражение: 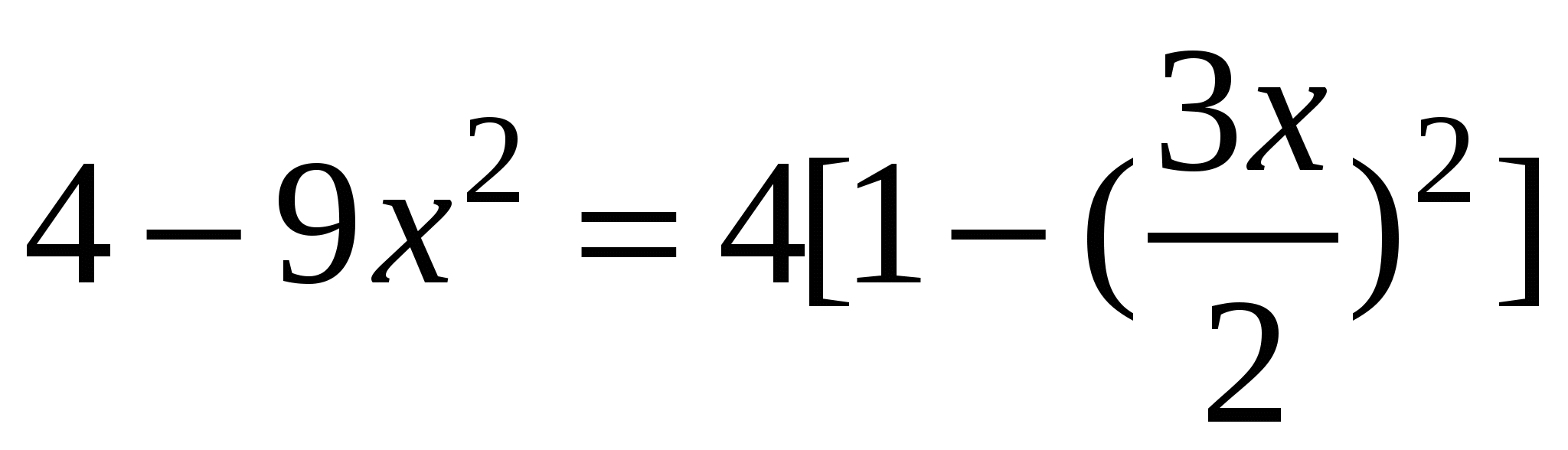 . Положим
. Положим 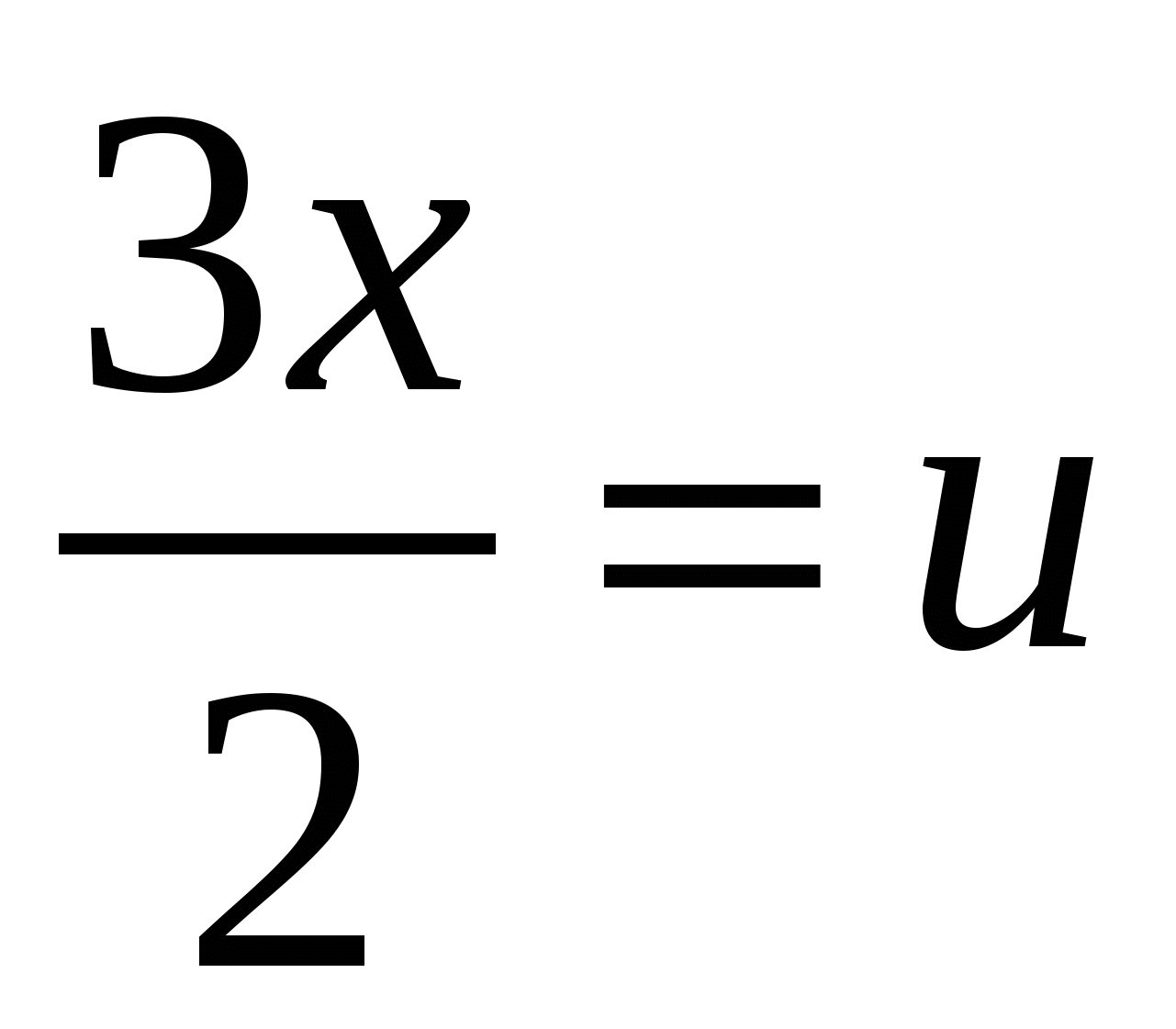 , откуда
, откуда 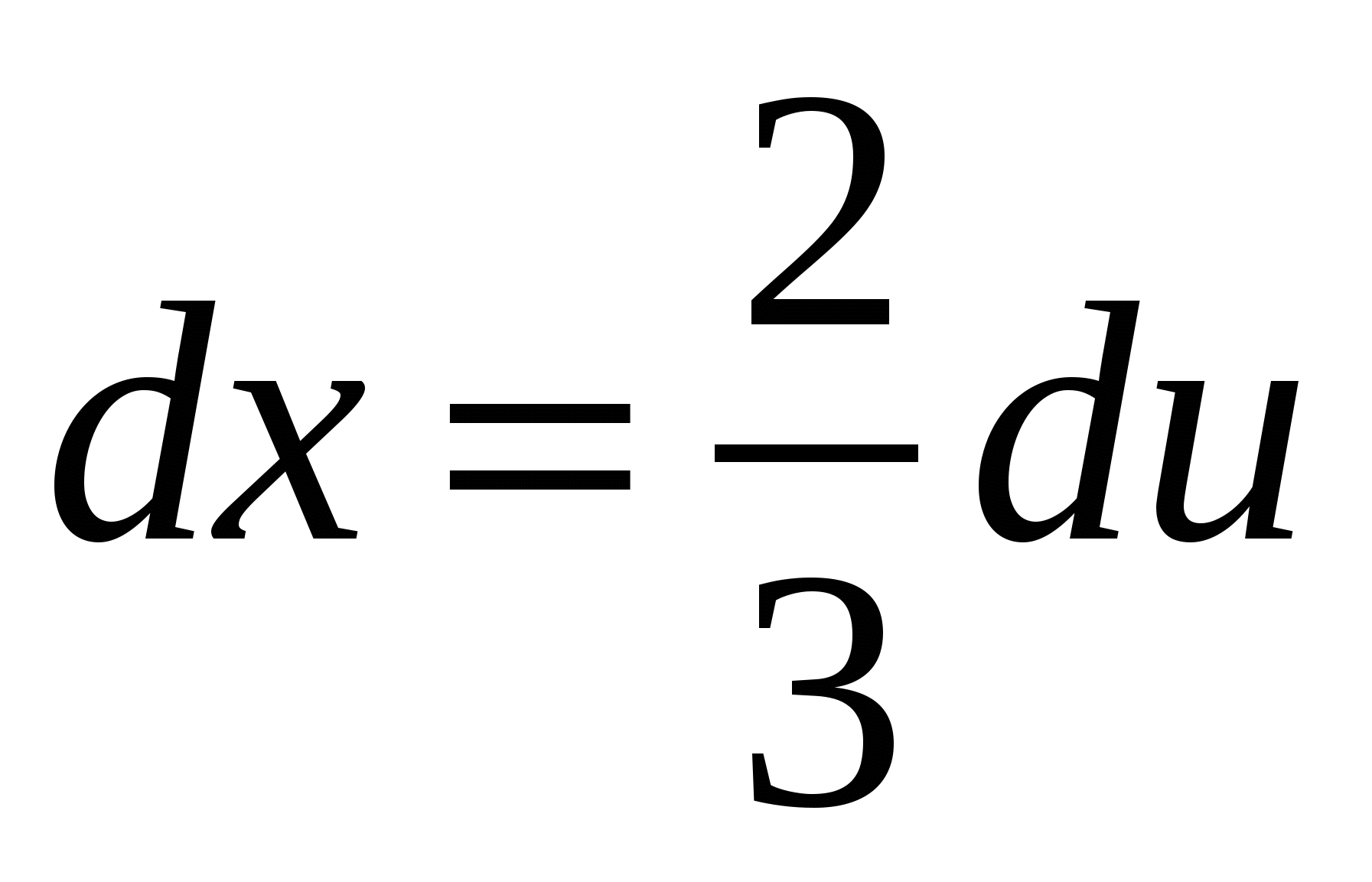 . Найдем новые пределы интегрирования:
. Найдем новые пределы интегрирования: 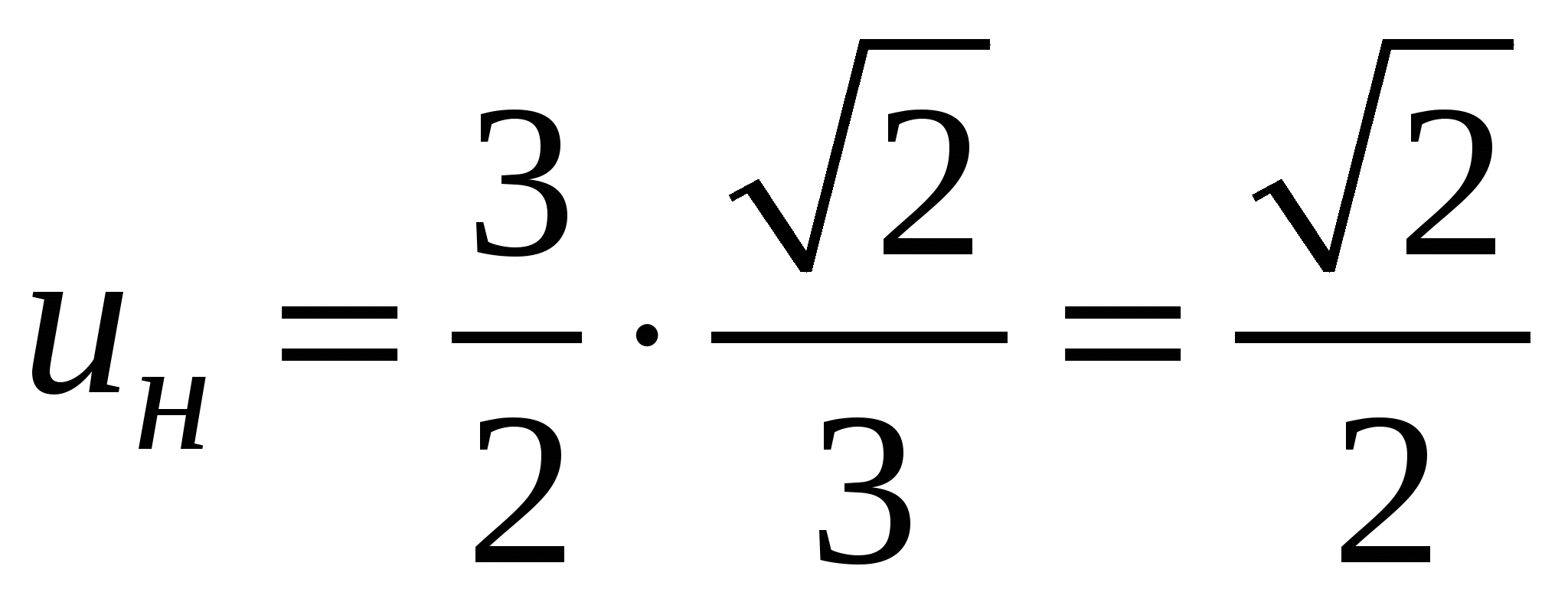 ,
, 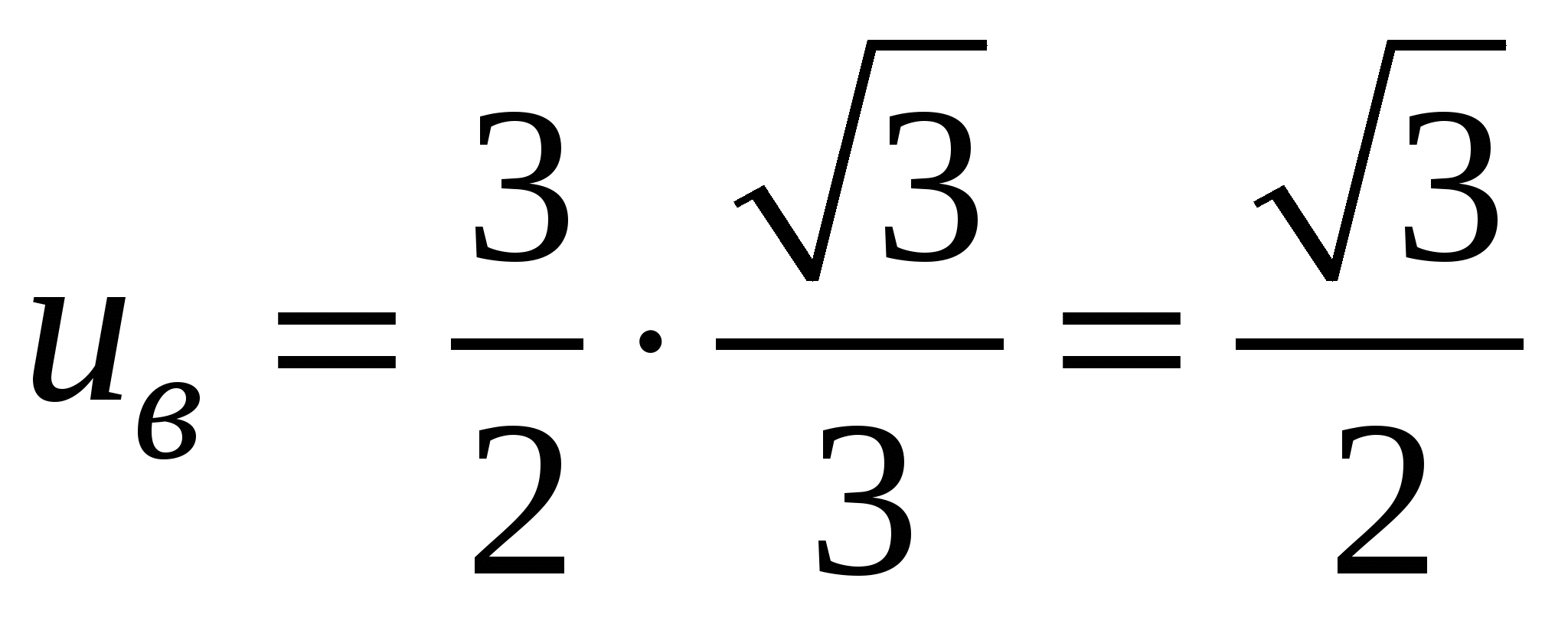 . Следовательно,
. Следовательно,
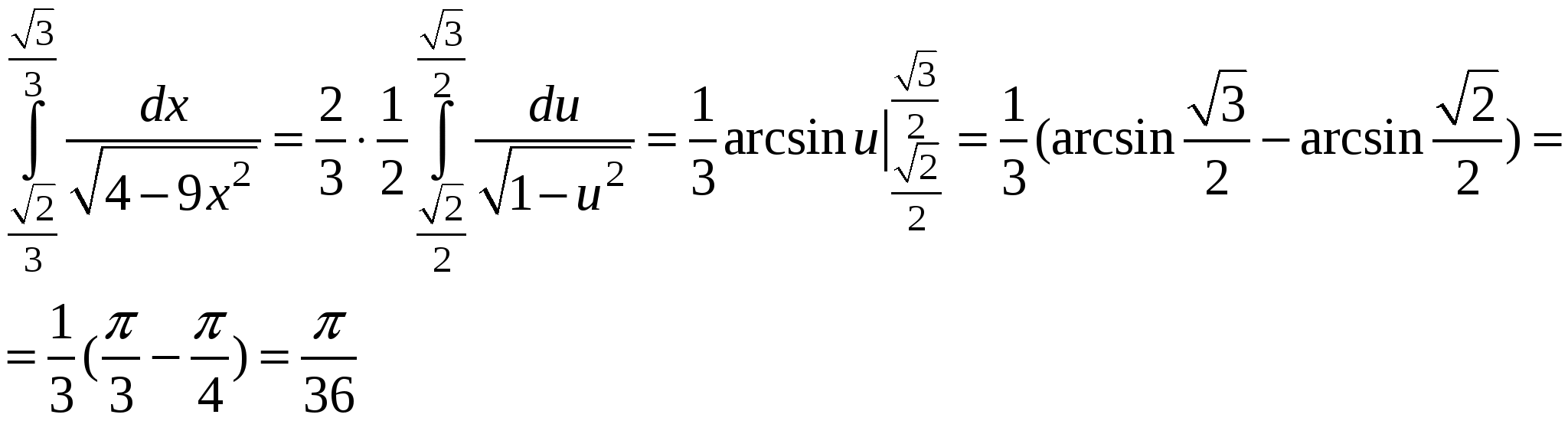 .
.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
-
Определение функции. Способы задания функции. Основные элементарные
функции. -
Определение предела функции. Основные теоремы о пределах.
-
Определение непрерывности функции. Точки разрыва.
-
Производная функции. Определение. Геометрический смысл производной.
-
Уравнение касательной и нормали к кривой.
-
Производная функции. Физический смысл производной.
-
Производные высших порядков.
-
Производная второго порядка и её механический смысл.
-
Производная. Правила дифференцирования.
-
Формулы дифференцирования.
-
Сложная функция. Правило дифференцирования сложных функций.
-
Дифференциал функции. Определение. Геометрический смысл дифференциала.
-
Приложение дифференциала к приближённым вычислениям.
-
Необходимые и достаточные условия возрастания и убывания функции.
-
Точки экстремума. Необходимое условие существования экстремума.
-
Экстремумы функции. Достаточные условия существования экстремума.
-
Выпуклость и вогнутость кривой.
-
Точки перегиба. Необходимое и достаточное условие существования точки
перегиба. -
Схема исследования функций и построения графиков.
-
Первообразная. Неопределённый интеграл. Геометрическая интерпретация.
-
Основные свойства неопределённого интеграла.
-
Таблица основных интегралов.
-
Непосредственное интегрирование.
-
Методом замены переменных.
-
Метод интегрирования по частям.
-
Определённый интеграл. Геометрический смысл определённого интеграла.
-
Основные свойства определённого интеграла. Формула Ньютона - Лейбница.
-
Вычисление определённого интеграла методом замены переменной.
-
Вычисление площадей плоских фигур.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
-
Лисичкин В.Т., Соловейчик И.Л. «Математика», М., «Высшая школа», 1991 г.
-
Зайцев И.Л. «Элементы высшей математики для техникумов»,
-
М., «Высшая школа», 1974 г.
-
Мордкович А.Г. «Математический анализ», М., «Высшая школа», 1990 г.
-
Судоплатов С.В., Овчинникова Е.В. «Элементы дискретной математики», М., «Инфра-М», 2002 г.
-
Яковлев Г.Н. «Алгебра и начала анализа для техникумов», ч. 2, М., «Высшая школа».
-
Цыпкин А.Г. «Справочник по математике», М., «Высшая школа», 1983г.
-
Выгодский М.Я. «Справочник по высшей математике», М., «Роскнига», 2001 г.


