- Преподавателю
- Математика
- Рабочая программа элективного курса по математике 10-11 классы
Рабочая программа элективного курса по математике 10-11 классы
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Рабочие программы |
| Автор | Лукин А.А. |
| Дата | 08.12.2015 |
| Формат | docx |
| Изображения | Есть |
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«Средняя общеобразовательная школа №11»
г. Глазов Удмуртской Республики
ПРИНЯТО
на заседании педсовета
протокол № 1
от « 29 » августа 2015 г.
УТВЕРЖДАЮ
директор школы
______________/Н.В.Шудегова./
приказ № ____
от «___» ___________2015 г.
Рабочая программа
элективного курса по математике
10 класс
Составитель
Лукин А.А.
г. Глазов, 2015
Пояснительная записка
Программа элективного курса рассчитана на 68 часов. Она предназначена для повышения эффективности подготовки учащихся 10 класса к итоговой аттестации по математике за курс полной средней школы и предусматривает их подготовку к дальнейшему математическому образованию.
Данная программа представляет углубленное изучение теоретического материала укрупненными блоками. Курс рассчитан на учеников общеобразовательного класса, изучающих алгебру и начала математического анализа в 10 классе по учебнику Никольского С.М. В результате изучения этого курса будут использованы приемы парной, групповой деятельности для осуществления элементов самооценки, взаимооценки, умение работать с математической литературой и выделять главное.
Умение решать задачи - один из основных показателей математического развития учащихся, глубины усвоения ими учебного материала, четкости в рассуждениях, понимании логических аспектов различных вопросов.
Данный элективный курс направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого класса различных задач.
Решение уравнений и неравенств рассматриваемое в старшей школе, усваивается учащимися хуже, чем в среднем звене. Объяснить это можно недостатком в арсенале знаний учащегося методов, необходимых для решения уравнений и неравенств. Необходимость формирования целого ряда специальных математических навыков требует частого привлечения образца работы в учебных ситуациях, называемых стандартными. В этих условиях организация работы учащихся достаточно сложна, жестко ограничена рамками учебного времени, нередко затруднена наличием психологической инерции, возникающей при частом и необходимом повторе задач и упражнений. Между тем, наряду с усвоением основ математических знаний, школа должна обеспечить формирование у учащихся умений активно применять эти знания, прививать им умение трудиться творчески.
В настоящее время текстовые задачи являются обязательными в курсе основной школы. Текстовые задачи повышенной сложности входят в перечень вопросов содержания школьного курса математики. Роль текстовых задач обусловлена тем, что практические представления являются важнейшей составляющей интеллектуального багажа современного человека. Они нужны и для повседневной жизни в современном цивилизованном обществе, и для продолжения образования практически во всех сферах человеческой деятельности.
Сейчас, когда наблюдается ориентация научно-технического прогресса на интеграцию наук и внедрение новых информационных технологий во все сферы деятельности человека, на первый план выступает задача формирования нового стиля мышления- операционного. Формирование операционного стиля мышления следует организовать при взаимосвязанном обучении математике и информатике, при этом используя специальные методические средства. Таким средством являются процессуальные задачи, задачи на нахождение и описание процесса достижения поставленной цели при определенных условиях.
В школьной программе понятие модуля вводится с шестого класса, последствии учащиеся лишь эпизодически встречаются с заданиями, содержащими модуль. Часто ученики такое задание воспринимают как новое и неожиданное и не знают, с какой стороны к нему подступиться. На базовом уровне учащиеся должны уметь выполнять задания стандартного вида (одношаговые)
В процессе изучения курса старшеклассники смогут познакомиться с различными приемами построения графиков функций, решениями уравнений и неравенств с модулем, приобретут навыки рационального поиска решения задач и построения алгоритмов, а в дальнейшем применят полученные знания и умения при подготовке к экзаменам.
Основу данного курса составляют решения разных по степени важности и трудности задач, поэтому занятия элективного курса способны повысить познавательный интерес учащихся к математике.
Цели курса:
1.На основе коррекции базовых математических знаний учащихся совершенствовать математическую культуру и творческие способности учащихся.
2.Формирование представлений о различных видах уравнений и неравенстх, универсальных и нестандартных методах их решения, углубление знаний учащихся по теме «Решение уравнений и неравенств», овладение универсальными и нестандартными методами их решения. отнестись к наличию такой задачи на экзамен
3.Закрепить и систематизировать теоретические и практические навыки решения задач; научить выделять из общего количества текстовых задач опорные, ключевые задачи; научить решать задачи несколькими способами.
4.Прочное и осознанное овладение учащимися системы математических знаний и умений по теме «модуль», которые ученики могли бы применить в нестандартных ситуациях.
Задачи курса:
-
Формирование у учащихся целостного представления о теме, ее значения в разделе математики, связи с другими темами.
-
Формирование поисково-исследовательского метода.
-
Формирование аналитического мышления, развитие памяти, кругозора, умение преодолевать трудности при решении более сложных задач.
-
Осуществление работы с дополнительной литературой.
-
Акцентировать внимание учащихся на единых требованиях к правилам оформления различных видов заданий, включаемых в итоговую аттестацию за курс полной общеобразовательной средней школы.
Формы организации учебных занятий
Формы проведения занятий включают в себя лекции, практические работы. Основной тип занятий комбинированный урок. Каждая тема курса начинается с постановки задачи. Теоретический материал излагается в форме мини - лекции. После изучения теоретического материала выполняются задания для активного обучения, практические задания для закрепления, выполняются практические работы в рабочей тетради, проводится работа с тестами. Занятия строятся с учётом индивидуальных особенностей обучающихся, их темпа восприятия и уровня усвоения материала. Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет учащимся встраивать новые понятия в систему уже освоенных знаний.
Контроль и система оценивания
Текущий контроль уровня усвоения материала осуществляется на каждом занятии по результатам выполнения учащимися самостоятельных, практических и тестовых работ. В конце каждой темы учащиеся сдают зачет.
Содержание курса
№ п/п
Наименование раздела
Кол-во часов
1
Текстовые задачи.
16
2
Иррациональные уравнения и неравенства.
8
3
Показательные уравнения и неравенства.
12
4
Логарифмические уравнения и неравенства.
8
5
Тригонометрические уравнения.
10
6
Тригонометрические неравенства.
5
7.
Неравенства со знаком модуля.
9
Всего
68
Учебно-тематическое планирование
-
№ урока
Тема урока
Планируемые результаты освоения материала
Текстовые задачи (16 ч.)
1
Задачи на движение.
Уметь решать задачи на движение в одну сторону.
2
Задачи на движение.
Уметь решать задачи на движение в одну сторону.
3
Задачи на движение.
Уметь решать задачи на встречное движение.
4
Задачи на движение.
Уметь решать задачи на встречное движение.
5
Задачи на работу.
Уметь решать задачи на совместную работу.
6
Задачи на работу.
Уметь решать задачи на совместную работу.
7
Основные задачи на проценты.
Уметь решать задачи на проценты.
8
Основные задачи на проценты.
Уметь решать задачи на проценты.
9
Задачи на сложные проценты.
Уметь решать задачи на сложные проценты.
10
Задачи на сложные проценты.
Уметь решать задачи на сложные проценты.
11
Задачи на концентрацию смеси и сплава.
Уметь решать задачи на концентрацию.
12
Задачи на концентрацию смеси и сплава.
Уметь решать задачи на концентрацию.
13
Задачи на концентрацию смеси и сплава.
Уметь решать задачи на концентрацию.
14
Комбинированные задачи на геометрическую и арифметическую прогрессию.
Уметь решать задачи на прогрессии.
15
Комбинированные задачи на геометрическую и арифметическую прогрессию.
Уметь решать задачи на прогрессии.
16
Зачётная работа №1 по теме «Текстовые задачи».
Иррациональные уравнения и неравенства (8 ч.)
17
Основные понятия и определения.
Уметь находить ОДЗ уравнений.
18
Основные понятия и определения.
Знать алгоритм решения уравнений.
19
Решение иррациональных уравнений.
Уметь решать иррациональные уравнения.
20
Решение иррациональных уравнений с помощью подстановки.
Уметь решать иррациональные уравнения.
21
Решение иррациональных неравенств.
Уметь решать иррациональные неравенства.
22
Решение иррациональных неравенств.
Уметь решать иррациональные неравенства.
23
Решение иррациональных неравенств.
Уметь решать иррациональные неравенства.
24
Зачётная работа №2 по теме «Иррациональные уравнения и неравенства».
Показательные уравнения и неравенства (12 ч.)
25
Решение показательных уравнений с помощью вынесения общего множителя за скобки.
Уметь решать показательные уравнения.
26
Решение показательных уравнений с помощью вынесения общего множителя за скобки.
Уметь решать показательные уравнения.
27
Решение показательных уравнений с помощью подстановки.
Уметь решать показательные уравнения.
28
Решение показательных уравнений с помощью подстановки.
Уметь решать показательные уравнения.
29
Решение показательных уравнений с помощью подстановки.
Уметь решать показательные уравнения.
30
Решение показательных неравенств.
Уметь решать показательные неравенства
31
Решение показательных неравенств.
Уметь решать показательные неравенства
32
Решение показательных неравенств.
Уметь решать показательные неравенства
33
Решение показательных неравенств.
Уметь решать показательные неравенства
34
Решение систем показательных уравнений.
Уметь решать системы показательных уравнений.
35
Решение систем показательных неравенств.
Уметь решать системы показательных неравенств.
36
Зачётная работа №3 по теме «Показательные уравнения и неравенства».
Логарифмические уравнения и неравенства (8 ч.)
37
Применение свойств логарифмов в преобразованиях выражений.
Знать свойства логарифмов
38
Способы решений логарифмических уравнений.
Уметь решать логарифмические уравнения.
39
Решение логарифмических уравнений.
Уметь решать логарифмические уравнения.
40
Решение логарифмических уравнений.
Уметь решать логарифмические уравнения.
41
Способы решений логарифмических неравенств.
Уметь решать логарифмические неравенства.
42
Решение логарифмических неравенств.
Уметь решать логарифмические неравенства.
43
Решение логарифмических неравенств.
Уметь решать логарифмические неравенства.
44
Зачётная работа №4 по теме «Логарифмические уравнения и неравенства».
Тригонометрические уравнения (10 ч.)
45
Решение тригонометрических уравнений с помощью формул суммы и разности.
Уметь делать отбор корней тригонометрического уравнения.
46
Решение тригонометрических уравнений с помощью формул суммы и разности.
Уметь делать отбор корней тригонометрического уравнения.
47
Решение тригонометрических уравнений с помощью формул суммы и разности.
Уметь делать отбор корней тригонометрического уравнения.
48
Решение неоднородных тригонометрических уравнений.
Уметь решать неоднородные уравнения различными способами.
49
Решение тригонометрических уравнений с помощью формул понижения степени.
Уметь решать уравнения с помощью формул понижения.
50
Решение тригонометрических уравнений с помощью формул понижения степени.
Уметь решать уравнения с помощью формул понижения.
51
Решение неоднородных тригонометрических уравнений второй степени.
Уметь решать неоднородные уравнения второй степени.
52
Решение неоднородных тригонометрических уравнений второй степени.
Уметь решать неоднородные уравнения второй степени.
53
Решение тригонометрических уравнений способом оценки.
Уметь решать уравнения способом оценки.
54
Зачётная работа №5 по теме «Тригонометрические уравнения».
Тригонометрические неравенства (5 ч.)
55
Решение тригонометрических неравенств, сводящихся к квадратным.
Уметь решать тригонометрические неравенства
56
Решение тригонометрических неравенств, сводящихся к квадратным.
Уметь решать тригонометрические неравенства
57
Решение тригонометрических неравенств методом интервалов.
Уметь решать тригонометрические неравенства
58
Решение тригонометрических неравенств методом интервалов.
Уметь решать тригонометрические неравенства
59
Зачётная работа №6 по теме «Тригонометрические неравенства».
Неравенства со знаком модуля (9 ч.)
60
Неравенства вида |f(x)>|g(x)|
Уметь решать неравенства с модулем
61
Неравенства вида |f(x)|<g(x)
Уметь решать неравенства с модулем
62
Неравенства вида |f(x)|>g(x)
Уметь решать неравенства с модулем
63
Показательные и логарифмические неравенства с модулем.
Уметь решать неравенства с модулем
64
Показательные и логарифмические неравенства с модулем.
Уметь решать неравенства с модулем
65
Неравенства, содержащие модуль и параметр.
Уметь решать неравенства с модулем и параметром
66
Неравенства, содержащие модуль и параметр.
Уметь решать неравенства с модулем и параметром
67
Системы неравенств, содержащие модуль.
Уметь решать системы неравенств с модулем
68
Зачётная работа №7 по теме «Неравенства со знаком модуля».
Требования к уровню подготовки учащихся.
По окончании обучения учащиеся должны знать:
-
универсальные методы решения различных математических задач;
-
логические приемы, применяемые при решении задач.
По окончании обучения учащиеся должны уметь:
-
выполнять построения и проводить исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
-
выполнять и самостоятельно составлять алгоритмические предписания и инструкции на математическом материале, выполнять расчеты практического характера, использовать математические формулы и самостоятельно составлять формулы на основе обобщения частных случаев и эксперимента;
-
добывать нужную информацию из различных источников;
-
проводить доказательные рассуждения, логически обосновывать выводы;
-
обладать опытом самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Литература
1.Колмогоров А.Н. и др. Алгебра и начала математического анализа. 10-11 класс. - М.: Просвещение, 2010.
2.Никольский С.М. и др. Алгебра и начала математического анализа. 10 класс. - М.: Просвещение,2010.
3.Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. - М.: ИЛЕКСА, 2009.
4.Сканави М.И. Сборник задач по математике для поступающих в ВУЗы. - М: Просвещение,1998.
5.Кочагин В.В., Кочагина М.Н. ЕГЭ 2013. Математика. Тематические тренировочные задания. - М.: Эксмо, 2013.
6.Петрова И.Н. Проценты на все случаи жизни. - Челябинск, 1999.
7.Математика: 2600 тестов и проверочных заданий для школьников и поступающих в вузы / П.И. Алтынов, Л.И. Звавич, А.И. Медяник и др. - М.: Дрофа, 2005.
8.Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Уравнения и неравенства с параметрами. - М.: Просвещение, 1999.
9.Колесникова С.И. Математика. Решение сложных задач ЕГЭ. - М.: Айрис-пресс, 2012.
10.Потапов М.К., Шевкин А.В. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. - М.: Просвещение, 2011.
Контрольно-измерительные материалы
Зачётная работа №1 по теме «Текстовые задачи»
Вариант-1
1. Первый трактор начал пахать поле. Через 2 ч к нему присоединился второй, и после 8 ч совместной работы они вспахали 80 % поля. За сколько часов мог вспахать поле первый трактор, если известно, что ему на это понадобилось бы на 5 ч больше, чем второму?
2. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля.
3. Смешав 24-процентный и 67-процентный растворы кислоты и добавив 10 кг чистой воды, получили 41-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
4. В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году - на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
Вариант-2
1.Байдарка в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите собственную скорость байдарки, если известно, что скорость течения реки равна 2 км/ч.
2.Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 42 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
3.Первый сплав содержит 5% меди, второй - 13 % меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава.
4.Двое рабочих должны были изготовить по 27 деталей. Второй рабочий начал работать на 27 мин позднее первого. По две трети задания они выполнили к одному времени, и, чтобы закончить работу вместе с первым, второй сделал за него 1 деталь. Сколько деталей в час изготавливал первый рабочий?
Зачётная работа №2 по теме «Иррациональные уравнения и неравенства»
Вариант-1
1.Решите уравнения:
а) 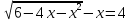 б)
б) 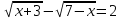
2.Решите систему уравнений:
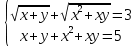
3.Решите неравенства:
а)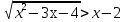 б)
б) 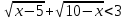
Вариант-2
1.Решите уравнения:
а) 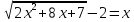 б)
б) 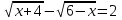
2.Решите систему уравнений:
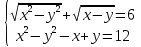
3.Решите неравенства:
а)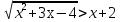 б)
б) 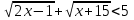
Зачётная работа №3 по теме «Показательные уравнения и неравенства»
Вариант-1
1.Решите уравнения:
а) 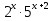 = 2500 б)
= 2500 б) 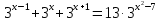 в) 5
в) 5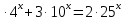
2.Решите неравенства:
а) 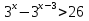 б)
б) 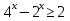
3.Решите систему уравнений:
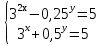
Вариант-2
1.Решите уравнения:
а) 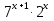 = 98 б)
= 98 б) 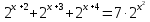 в) 3
в) 3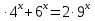
2.Решите неравенства:
а) 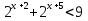 б)
б) 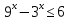
3.Решите систему уравнений:
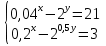
Зачётная работа №4 по теме «Логарифмические уравнения и неравенства»
Вариант-1
1.Решите уравнения:
а) 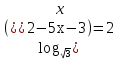 б)
б) 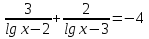
2.Решите неравенства:
а)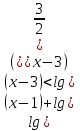 б)
б) 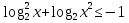
3.Решите систему уравнений:
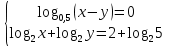
Вариант-2
1.Решите уравнения:
а) 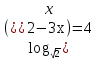 б)
б) 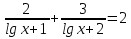
2.Решите неравенства:
а)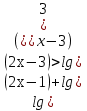 б)
б) 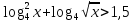
3.Решите систему уравнений:
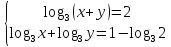
Зачётная работа №5 по теме «Тригонометрические уравнения»
Вариант-1
1.Решите уравнения:
а) 2 cos2x - 5 sin x + 1 = 0 б) sin 4x cos 2x = sin 2x cos 4x в) 6 cos2x + 4 sin x cos x = 1
2.Решите уравнение sin2x = sin(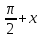 ) и найдите все корни этого уравнения, принадлежащие отрезку
) и найдите все корни этого уравнения, принадлежащие отрезку 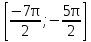 .
.
3.Решите систему уравнений:
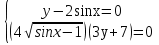
Вариант-2
1.Решите уравнения:
а) 2sin2x -5cosx + 1 = 0 б) sin 3x cos x = sin x cos 3x в) 3cos2x + 5sin x cos x = -1
2.Решите уравнение 2sin2x = cos(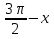 ) и найдите все корни этого уравнения, принадлежащие отрезку
) и найдите все корни этого уравнения, принадлежащие отрезку 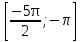 .
.
3.Решите систему уравнений:
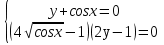
Зачётная работа №6 по теме «Тригонометрические неравенства»
Вариант-1
1.Решите неравенства:
а) -4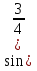 x +
x +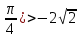 б) cos2x ≥ 0,25 в) tg(
б) cos2x ≥ 0,25 в) tg(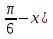 -
- 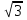 ≥ 0
≥ 0
2.Используя метод интервалов, решите неравенства:
а) cos 3x + 2 cos x 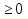 б) sin x cos 5x < sin 2x cos 4x
б) sin x cos 5x < sin 2x cos 4x
Вариант-2
1.Решите неравенства:
а) -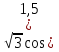 x +
x +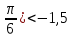 б) sin2x ≤ 0,25 в)
б) sin2x ≤ 0,25 в) 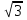 tg(
tg(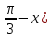 - 1 ≤ 0
- 1 ≤ 0
2.Используя метод интервалов, решите неравенства:
а) sin 3x - 2 sin x ≤ 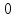 б) cosx cos7x > cos 3x cos 5x
б) cosx cos7x > cos 3x cos 5x
Зачётная работа №7 по теме «Неравенства со знаком модуля»
Вариант-1
1.Решите неравенства:
а) 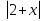 ≤ x б)
≤ x б) 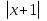 <
< 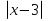 в)
в) 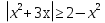
2.Решите показательно-степенное неравенство:
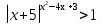
Вариант-2
1.Решите неравенства:
а) 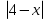 ≤ x б)
≤ x б) 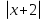 <
< 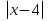 в)
в) 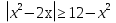
2.Решите показательно-степенное неравенство:
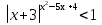
Рецензия
Рабочая программа элективного курса по математике «Практикум по математике» составлена для учащихся 10 класса, обучающихся по общеобразовательному направлению, в соответствии с изучаемой в 10 классе программе по математике по учебнику Никольского С.М. Основной целью рабочей программы и данного курса являются более углублённое изучение тем, связанных с решением уравнений и неравенств разного вида. Кроме того запланировано обучение учащихся по решению текстовых задач разного типа. Элективный курс продуман с методической точки зрения и выдержан во временных интервалах, что позволит учащимся эффективнее научиться решать иррациональные, показательные, логарифмические, тригонометрические уравнения и неравенства. В начале курса учащимся предлагается научиться решать текстовые задачи по определённым темам, что им совершенно необходимо будет при подготовке к ЕГЭ по математике и развития логического и абстрактного мышления. Решение данных задач основывается не только на решении уравнений, но также и их составлений по предложенным условиям, что зачастую вызывает затруднение у учащихся. Данный элективный курс поможет учащимся научиться решать задания повышенного уровня из ЕГЭ по математике и повысить свою математическую компетентность для дальнейшего образования. После изучения каждой темы запланирован текущий контроль за формированием умений и навыков в виде зачётных работ. Задания в зачётной работе подобраны дифференцированно по уровню сложности, что позволит определить степень усвоения учащимися изученного материала. В целом, считаю, рабочая программа элективного курса составлена грамотно и целесообразно, поэтому может быть использована на занятиях элективного курса по математике в 10 классе, изучающих алгебру и начала математического анализа по учебнику Никольского С.М.


