- Преподавателю
- Математика
- Методическая разработка учебного занятия по математике «Логарифмы и их свойства»
Методическая разработка учебного занятия по математике «Логарифмы и их свойства»
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Краюшкина Т.Н. |
| Дата | 29.09.2015 |
| Формат | doc |
| Изображения | Есть |
Муниципальное бюджетное образовательное учреждение
Гремячевская средняя общеобразовательная школа
«Логарифмы и их свойства»
Краюшкина Татьяна Николаевна
учитель математики
Методическая разработка учебного занятия по математике
«Логарифмы и их свойства»
Цель урока:
Образовательная - ввести понятие логарифма, изучить основные свойства логарифмов и способствовать формированию умения применять свойства логарифмов при решении заданий.
Развивающая - развивать математическое мышление; технику вычисления; умение логически мыслить и рационально работать; способствовать развитию у обучающихся навыков самоконтроля.
Воспитательная - содействовать воспитанию интереса к теме, воспитывать чувство самоконтроля, ответственности.
Задачи урока:
Развить у учащихся умения сравнить, сопоставлять, анализировать, делать самостоятельные выводы.
Ключевые компетенции: способность самостоятельно искать, извлекать, систематизировать, анализировать и отбирать необходимую для решения учебных задач информацию; способность самостоятельно осваивать знания и умения, необходимые для решения поставленной задачи.
Тип урока: Урок изучения и первичного закрепления новых знаний.
Оборудование: компьютер, мультимедийный проектор, презентация "Логарифмы и их свойства", раздаточный материал.
Ключевые слова: логарифм; свойства логарифма.
Программное обеспечение: MS Power Point.
Межпредметные связи: история.
Внутрипредметные связи: «Корень n-ой степени и их свойства».
План урока
Организационный момент.
-
Повторение пройденного материала.
-
Объяснение нового материала.
-
Закрепление.
-
Самостоятельная работа.
-
Домашнее задание. Подведение итогов урока.
Ход урока:
1. Оргмомент: проверка готовности учащихся к уроку.
- Этот урок я хочу начать со слов А.Н. Крылова: «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».
2. Повторение пройденного материала.
- Учащимся предлагается вспомнить:
-
Что такое степень, основание и показатель.
-
Корень n-ой степени из числа а называется такое число, n-я степень которого равна а. 34 = 81.
-
Основные свойства степеней.
3. Сообщение новой темы.
- А теперь перейдем к новой теме. Тема сегодняшнего урока - Логарифмы и их свойства.
- На этом уроке мы познакомимся с понятием «логарифм», также рассмотрим свойства логарифмов. Тема эта актуальна, т.к. логарифм всегда встречается на итоговой аттестации по математике.
Зададим вопрос:
1) В какую степень нужно возвести 3, чтобы получить 9? Очевидно, во вторую. Показатель степени, в которую нужно возвести число 3, чтобы получить 9, равен 2.
2) В какую степень нужно возвести 2, чтобы получить 8? Очевидно, в третью.
Показатель степени, в которую нужно возвести число 2, чтобы получить 8, равен 3.
Во всех случаях мы искали показатель степени, в которую нужно что-то возвести, чтобы что-то получить. Показатель степени, в которую нужно что-то возвести называется логарифмом и обозначается log.
Число, которое мы возводим в степень, т.е. основание степени, называется основанием логарифма и записывается в нижнем индексе. Затем пишется число, которое мы получаем, т.е. число, которое мы ищем: log3 9=2
Эта запись читается так: «Логарифм числа 9 по основанию 3». Логарифм числа 9 по основанию 3 это показатель степени, в которую нужно возвести 3, чтобы получить 9. Этот показатель равен 2.
Аналогично второй пример.
Дадим определение логарифма.
Определение. Логарифмом числа b>0 по основанию a>0, a ≠ 1 называется показатель степени, в которую надо возвести число a, чтобы получить число b.
Логарифмом числа b по основанию a обозначается loga b.
История возникновения логарифма:
Логарифмы были введены шотландским математиком Джоном Непером (1550-1617) и математиком Иостом Бюрги (1552-1632).
Бюрги пришел к логарифмам раньше, но опубликовал свои таблицы с опозданием (в 1620г.), а первой в 1614г. появилась работа Непера «Описание удивительной таблицы логарифмов».
С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов - нашей десятичной системы нумерации.
Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор - логарифмическую линейку.
Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры. Теперь ее вытеснили калькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни микрокалькуляторы.
Рассмотрим примеры:
log327=3; log525=2; log255=1/2; log5 1/125=-3; log-2-8- не существует; log51=0; log44=1
Рассмотрим такие примеры:
10. loga1=0, а>0, a ≠ 1;
20. logaа=1, а>0, a ≠ 1.
Эти две формулы являются свойствами логарифма. Запишите свойства и их необходимо запомнить.
В математике принято следующее сокращение:
log10а= lg а- десятичный логарифм числа а (буква «о» пропускается, а основание 10 не ставят).
logеа= ln а - натуральный логарифм числа а. «е» - это такое иррациональное число, равное 2,7 (буква «о» пропускается, а основание «е» не ставят).
Рассмотрим примеры:
lg 10=1; lg 1=0
ln e=1 ; ln 1=0 .
Как перейти из логарифмического равенства к показательному: logаb=с, с - это логарифм, показатель степени, в которую нужно возвести а, чтобы получить b. Следовательно, а в степени с равен b: а с= b.
Рассмотрим пять логарифмических равенств. Задание: проверить их правильность. Среди этих примеров есть ошибки. Для проверки воспользуемся данной схемой.
-
lg 1 = 2 (10 2=100)- это равенство не верное.
-
log1/2 4 = 2- это равенство не верное.
-
log31=1 - это равенство не верное.
-
log1/3 9 = -2 - это равенство верное.
-
log416 = -2- это равенство не верное.
Выведем основное логарифмическое тождество: а log a b = b
Рассмотрим пример.
5 log 5 13 =13
Свойства логарифмов:
3°. logа ху = logах + logау.
4°. logа х/у = logах - logау.
5°. logах p = p · logах, для любого действительного p.
Рассмотрим пример на проверку 3 свойства:
log28 + log232= log2 8∙32= log2 256=8
3 +5 = 8
Рассмотрим пример на проверку 5 свойства:
3∙ log28= log283= log2512 =9
3∙3 = 9
Формула перехода от одного основания логарифма к другому основанию:
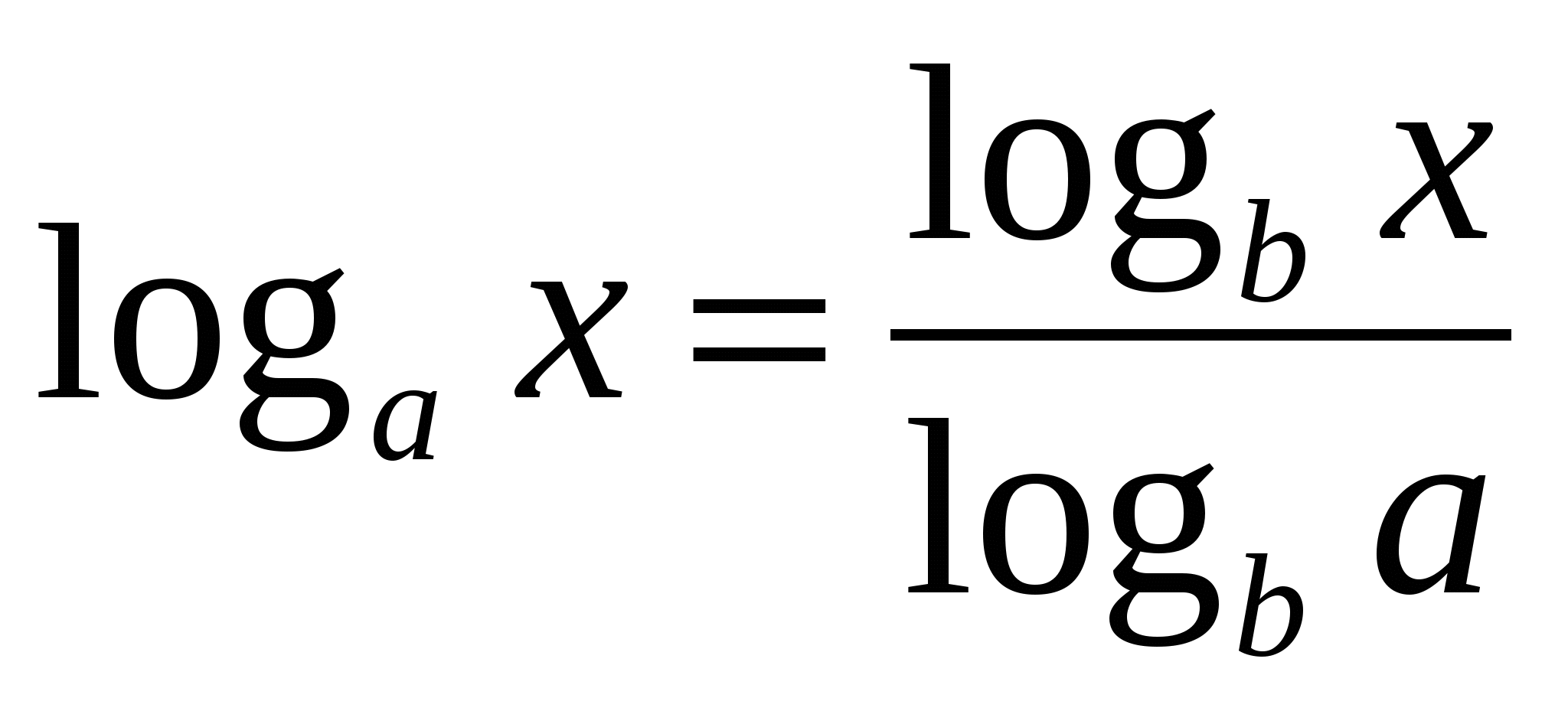
Эта формула потребуется при вычислении логарифма по калькулятору.
Возьмем пример: log3 7 = lg7 / lg3. В калькуляторе можно вычислить только десятичный и натуральный логарифм. Вводим цифру 7 и нажмем кнопку «лог», также вводим цифру 3 и нажмем кнопку «лог», делим верхнее значение на нижнее и получаем ответ.
4. Закрепление.
Для закрепления новой темы решим примеры.
Пример 1. Назовите свойство, которое применяется при вычислении следующих логарифмов, и вычислите (устно):
-
log66
-
log 0,51
-
log63+ log62
-
log36- log32
-
log448
Пример 2.
Перед вами 8 решённых примеров, среди которых есть правильные, остальные с ошибкой. Определите верное равенство (назовите его номер), в остальных исправьте ошибки.
-
log232+ log22= log264=6
-
log553 = 2;
-
log345 - log35 = log340
-
3∙log24 = log2 (4∙3)
-
log315 + log33 = log345;
-
2∙log56 = log512
-
3∙log23 = log227
-
log2162 = 8.
Проверка ЗУН - самостоятельная работа по карточкам.
Вариант 1.
Вычислите:
-
log416
-
log25125
-
log82
-
log66
Вариант 2.
Вычислите:
-
log327
-
log4 8
-
log49 7
-
log55
5. Подведение итогов. Домашнее задание. Выставление оценок.


