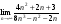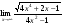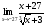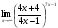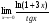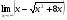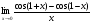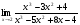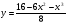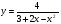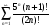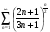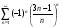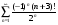- Преподавателю
- Математика
- Методические рекомендации для практических занятий специальности 21. 02. 06
Методические рекомендации для практических занятий специальности 21. 02. 06
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Лабгаева Э.В. |
| Дата | 02.12.2015 |
| Формат | docx |
| Изображения | Есть |







































































































































































 Министерство образования и науки Самарской области
Министерство образования и науки Самарской области
Государственное бюджетное образовательное
учреждение среднего профессионального образования
«Тольяттинский политехнический техникум»
(ГБОУ СПО «ТПТ»)
УТВЕРЖДАЮ
Заместитель директора по УР
___________ С.А.Гришина
___ ____________ 2015
СБОРНИК МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ
ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ РАБОТ
ДИСЦИПЛИНЫ МАТЕМАТИКА
Специальность: 120703 Информационные системы обеспечения
градостроительной деятельности
Тольятти, 2015
ОДОБРЕНА
Протокол ПЦК ЕНД
от ___ _____20__ № ____
Председатель ПЦК ЕНД
________ Л.А. Гончарова
___ ______ 20___
СОГЛАСОВАНО
Старший методист
________ Н.В. Роменская
___ _______ 20___
Сборник методических рекомендаций разработан Лабгаевой Э.В. - преподавателем дисциплины «Математика» ГБОУ СПО «ТПТ»
Рецензент:
Сборник методических рекомендаций для выполнения практических работ составлен в соответствии с рабочей программой дисциплины «Математика», специальности 120703 Информационные системы обеспечения градостроительной деятельности для студентов второго курса
Содержание
Введение 4
Практическое занятие №1 «Вычисление пределов функций» 5
Практическое занятие №2 Нахождение производных и дифференциалов функции, приложения производных и дифференциалов 11
Практическое занятие №3 Исследование функции с помощью производной 20
Практическое занятие №4 Вычисление интегралов 29
Практическое занятие №5 Решение прикладных задач с помощью определённого интеграла 36
Практическое занятие №6 Решение обыкновенных дифференциальных уравнений 43
Практическое занятие №7 Определение сходимости рядов 51
Практическое занятие №8 Нахождение вероятности событий 59
Практическое занятие №9 Нахождение функции распределения и числовых характеристик дискретной случайной величины 66
Практическое занятие №10 Обработка статистических данных 73
Введение
Сборник методических рекомендаций для выполнения практических работ дисциплины
«Математика» предназначен для студентов второго курса специальности 120703 «Информационные системы обеспечения градостроительной деятельности»
Дисциплина «Математика» в соответствии с рабочей программой рассчитана на 66 часов, из них 20 часов отведено на проведение практических занятий. Практические занятия направлены на проверку усвоения и закрепление материала, изученного на теоретических занятиях.
Сборник методических указаний содержит 10 практических занятий, в каждом из которых
имеются:
-
краткие теоретические сведения
-
образец решений задач
-
задания для самостоятельного решения
-
контрольные вопросы
-
литература
Методическая разработка рекомендуется для использования преподавателями, ведущими данный предмет в средних специальных учебных заведениях.
Практическое занятие №1
«Вычисление пределов функций»
Цель занятия:
освоение знаний правил раскрытия неопределённостей и формул для вычисления пределов
последовательностей и функций, умений раскрывать неопределённости и вычислять пределы
При выполнении задания студент должен:
знать:
-
определение предела в точке и на бесконечности
-
теоремы о пределах
-
первый и второй замечательные пределы
-
правила раскрытия неопределённостей
-
эквивалентные бесконечно малые
уметь:
-
раскрывать неопределённости различных видов
-
вычислять пределы функций
Краткие теоретические сведения
Понятие предела функции в точке
Пусть функция у = f(x) определена на некотором промежутке Х и пусть точка х0 є Х.
Составим из множества Х последовательность точек: х1, х2,…,хn,…сходящихся к х0. Значения
функции в этих точках также образуют последовательность: f(x1), f(x2),…,f(xn).
Число А называется пределом функции y = f (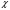 ) в точке
) в точке 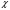 =
=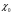 , если при любых
, если при любых
значениях 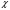 , сколь угодно близких к числу
, сколь угодно близких к числу 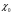 (
(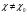 ), значение функции f (
), значение функции f (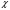 )
)
становится сколь угодно близким к числу А, т.е.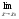 f (
f (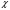 ) =
) = 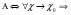 f (
f (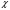 )
)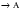
Основные теоремы о пределах
Пусть существует 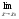 f (
f (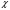 ),
), 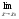 g (
g (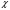 ), тогда верны следующие теоремы:
), тогда верны следующие теоремы:
-
Предел аргумента в точке
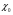 равен значению аргумента в этой точке:
равен значению аргумента в этой точке: 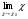 =
=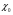
-
Если с - постоянная величина, то предел постоянной равен самой постоянной:
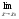 c= c, c - const
c= c, c - const
-
Если с - постоянная величина, то постоянный множитель выносится за знак предела:
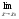 cx = c
cx = c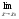 x
x
-
Предел суммы двух функций равен сумме пределов этих функций:
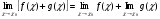
-
Предел произведения равен произведению пределов:
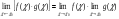
-
Предел отношения равен отношению пределов, если предел знаменателя отличен от нуля:
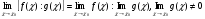
-
Предел степени равен степени пределов:
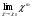 = (
= (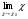 )
)
Понятие бесконечно малой и бесконечно большой функции. Предел функции
на бесконечности
Функция 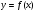 - называется бесконечно малой при
- называется бесконечно малой при 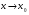 , если
, если 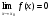 .
.
Функция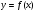 - называется бесконечно большой при
- называется бесконечно большой при 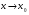 , если
, если 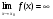 .
.
Если функция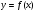 бесконечно большая, то функция
бесконечно большая, то функция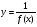 - бесконечно малая и
- бесконечно малая и
наоборот.
Число А называется пределом функции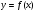 на бесконечности, если при всех
на бесконечности, если при всех
достаточно больших значений х разность 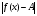 есть бесконечно малая функция.
есть бесконечно малая функция.
Правила раскрытия неопределённостей при вычислении пределов
Часто встречаются случаи, когда непосредственно применить теоремы о пределах нельзя.
В этих случаях необходимо сначала раскрыть неопределенности и потом только вычислять
пределы.
В ситуации, когда числитель и знаменатель дроби стремится к нулю, говорят, что имеет
место неопределенность вида 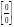 . Для раскрытия неопределенности такого вида необходимо:
. Для раскрытия неопределенности такого вида необходимо:
а) числитель и знаменатель дроби разложить на множители, а затем сократить на множитель, приведший к неопределенности, при этом можно использовать:
-
формулы сокращенного умножения,
-
вынесение общего множителя за скобки,
-
группировку,
-
преобразование квадратного трехчлена с помощью дискриминанта или теоремы Виета;
т.к. ax2 + bx + c = a (x-x1)(x-x2), где x1,x2 - корни уравнения ax2+bx+c=0,
-
преобразование многочлена с помощью деления многочлена на (x-x0),
-
умножение на сопряженное выражение, т.е. если предел содержит выражение
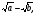 то путем умножения на
то путем умножения на 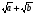 избавляемся от корней, т.к.
избавляемся от корней, т.к. 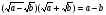
б) использовать первый замечательный предел, т.е. формулы 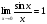 ,
, 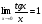
в) использовать эквивалентные бесконечно малые (при 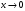 ), т.е. формулы
), т.е. формулы 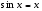
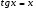 ,
,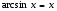 ,
,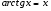 ,
, 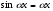 ,
,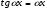 ,
,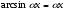 ,
,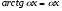 ,
, 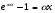 ,
,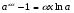 ,
,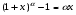 ,
,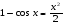
Если числитель и знаменатель неограниченно возрастают при х→∞, то в таком случае
имеет место неопределенность вида 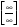 . Для ее раскрытия надо разделить числитель и знаменатель дроби на старшую степень переменной х.
. Для ее раскрытия надо разделить числитель и знаменатель дроби на старшую степень переменной х.
Если имеет место неопределённость 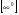 и
и 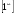 , то в этих случаях применяют второй
, то в этих случаях применяют второй
замечательный предел, т.е. формулы 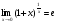 и
и 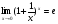
Если имеют место неопределённости [∞-∞], [0-0], то в этих случаях необходимо заданную функцию привести к дробно-линейному виду, а затем использовать предыдущие правила
Образец решения задач
Вычислить пределы последовательностей и функций, использую правила раскрытия
неопределённостей
Задание 1 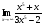
Решение: Имеем неопределённость вида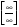 . Используя правило раскрытия
. Используя правило раскрытия
неопределённостей разделим каждое слагаемое почленно на 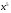
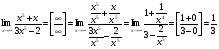
Задание 2 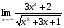
Решение: Имеем неопределённость вида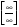 . Используя правило раскрытия
. Используя правило раскрытия
неопределённостей разделим каждое слагаемое почленно на 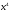 , учитывая, что под знаком радикала
, учитывая, что под знаком радикала 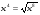
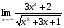
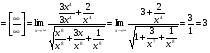
Задание 3 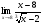
Решение: Имеем неопределённость вида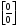 . Применим формулы сокращённого умножения
. Применим формулы сокращённого умножения
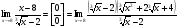
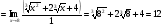
Задание 4 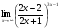
Решение: Имеем неопределённость вида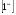 . Выделим целую часть, используя
. Выделим целую часть, используя
арифметические преобразования. Далее воспользуемся формулой второго замечательного
предела, затем в показателе раскроем неопределённость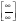 , разделив почленно на х, ответ
, разделив почленно на х, ответ
приведём к стандартному виду
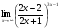 =
= 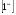 =
=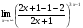 =
= 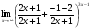 =
= 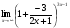 =
=
= 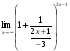 =
= 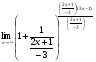 =
= 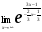 =
= 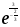 =
= 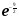 =
= 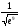
Задание 5 Вычислить предел 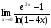
Решение: Имеем неопределённость вида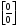 . Заменим бесконечно малые функции на эквивалентные
. Заменим бесконечно малые функции на эквивалентные
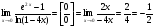
Задание 6 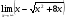
Решение: Имеем неопределённость вида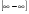 .Приведём к дробному виду. Домножим и числитель и знаменатель на сопряжённое выражение. Воспользуемся формулой разности квадратов
.Приведём к дробному виду. Домножим и числитель и знаменатель на сопряжённое выражение. Воспользуемся формулой разности квадратов
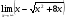
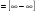
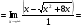
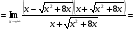
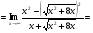
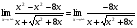 =
= 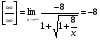
Задание 7 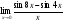
Решение: Имеем неопределённость вида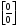 . Воспользуемся тригонометрическими формулами разности синусов, после преобразований применим формулы первого замечательного предела
. Воспользуемся тригонометрическими формулами разности синусов, после преобразований применим формулы первого замечательного предела
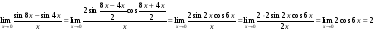
Задание 8 Вычислить предел 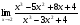
Решение: Имеем неопределённость вида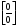 . Разделим числитель и знаменатель дроби на (х-2), затем сократим на множитель, приводящий к неопределённости
. Разделим числитель и знаменатель дроби на (х-2), затем сократим на множитель, приводящий к неопределённости
x3 - 5x2 + 8x - 4 x -2 x3 - 3x2 + 4 x - 2
x3 - 2x2 x2 - 3x +2 x3 - 2x2 x2 - x -2
-3x2 +8x - x2 + 4
-3x2 +6x - x2 + 2x
2x - 4 -2x +4
2x - 4 -2x +4
0 0
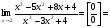
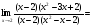
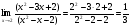
Задания для самостоятельного решения
Вычислить пределы последовательностей и функций, использую правила раскрытия неопределённостей
Контрольные вопросы
-
Последовательности и функции. Бесконечно малые и бесконечно большие функции
-
Определение предела функции в точке и на бесконечности
-
Основные теоремы о пределах
-
Правила раскрытия неопределённостей при вычислении пределов.
-
Первый и второй замечательные пределы
-
Эквивалентные бесконечно малые
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 1. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-304с., ил.
-
Шипачёв В.С. Сборник задач по высшей математике: Учеб. пособие.- М.: Высш. шк. 2005.- 192с.: ил.
Практическое занятие №2
«Нахождение производных и дифференциалов функции, приложения производных и дифференциалов»
Цель занятия:
освоение знаний алгоритмов решения задач на нахождение производных и дифференциалов по
правилам дифференцирования и формулам дифференцирования сложных функций, частных
производных и дифференциалов, умений находить производные сложных функций,
дифференциалы высших порядков, находить частные производные и дифференциалы
различных порядков, решать прикладные задачи на применение производной и
дифференциала
При выполнении задания студент должен:
знать:
-
понятие производной, ее физический смысл;
-
таблицу производных; формулы производных суммы, произведения, частного;
-
формулы нахождения производных сложных функций
-
понятие частной производной первого и второго порядков,
-
понятие дифференциала, формулу для его нахождения
-
формулу для нахождения приближённых значений с помощью дифференциала
уметь:
-
находить производную сложной функции
-
находить дифференциалы различных порядков.
-
находить частные производные функции
-
находить приближённые значения величин с помощью дифференциала
-
решать прикладные задачи, используя физический смысл производной
Краткие теоретические сведения
Понятие производной функции.
Пусть дана функция у =f(x) (см. рисунок 3), где x0- фиксированная точка,
x - произвольная точка,  x = x-x0- приращение аргумента функции в точке x0,
x = x-x0- приращение аргумента функции в точке x0,
f(x0) - значение функции в точке x0,f(x) - значение функции в произвольной точке x,
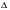 f(x0) - значение функции в точке x0,∆f(x0) = f(x0 + ∆x) - f(x0) = ∆y.
f(x0) - значение функции в точке x0,∆f(x0) = f(x0 + ∆x) - f(x0) = ∆y.
Тогда 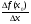 =
= 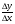 - средняя скорость изменения функции,
- средняя скорость изменения функции, 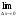
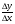 =
= 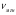 - скорость
- скорость
изменения функции в момент времени t = t0(мгновенная скорость). Обозначают 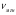 =
= 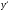 .
.
Рисунок 3
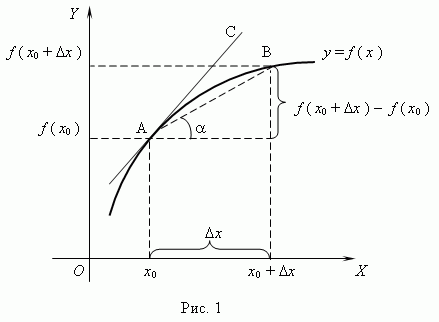
Производная функции y = f(x) в точке х0 - это предел отношения приращения функции 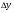 к приращению аргумента
к приращению аргумента 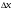 , когда последнее стремится к нулю, т.е.
, когда последнее стремится к нулю, т.е. 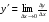
Производная обозначается 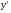 («игрек штрих») или
(«игрек штрих») или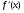 («эф штрих от икс») или
(«эф штрих от икс») или 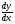 («де игрек по де икс»).
(«де игрек по де икс»).
Формулы для вычисления производной даны в таблице 3
Таблица 3
1
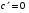
10
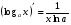
19
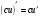
2
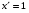
11
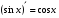
20
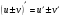
3
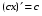
12
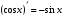
21
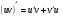
4
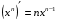
13
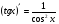
22
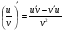
5
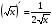
14
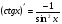
23
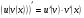
6
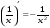
15
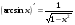
7
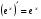
16
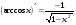
8
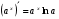
17
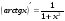
9
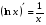
18
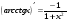
Нахождение производной функции называется дифференцированием данной функции.
Физический и геометрический смысл производной.
Физический смысл производной: производная есть мгновенная скорость изменения функции.
Геометрический смысл производной: производная функции y = f(x) в точке х0равна угловому коэффициенту касательной k = tga к графику функции в этой точке.
Алгоритм решения задач на составления уравнения касательной:
Пусть дана функция у =f(x) в точке х=х0. Для составления уравнения касательной необходимо:
а) найти значение функции в точке х0: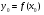
б) найти производную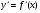
в) найти значение производной функции в точке х0: 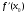
г) записать уравнение касательной: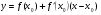
д) привести данное уравнение к стандартному виду y = ax+ b
Производная сложной функции
Если 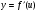 , где
, где 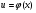 , т. е. если у зависит от х через промежуточный аргумент u, то функция у называется сложной функцией от х.
, т. е. если у зависит от х через промежуточный аргумент u, то функция у называется сложной функцией от х.
Теорема. Производная сложной функции равна произведению ее производной по
промежуточному аргументу на производную этого аргумента по независимой переменной, т.е.:
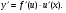
Вторая производная и производные высших порядков.
Производная 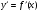 функции
функции 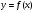 cама является некоторой функцией аргумента x, следовательно по отношению к ней снова можно ставить вопрос о существовании производной.
cама является некоторой функцией аргумента x, следовательно по отношению к ней снова можно ставить вопрос о существовании производной.
Производная второго порядка - это производная от производной первого порядка.
Обозначается 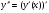 или
или 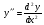 , последнее читается «де два игрек по де икс
, последнее читается «де два игрек по де икс
дважды».
Производные, начиная со второй называются производными высшего порядка
и обозначаются 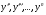 .
.
Производная n-го порядка - это производная от производной (n -1)-го порядка, т.е
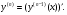
Например, ускорение 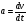 - это первая производная от скорости по времени или вторая от перемещения по времени:
- это первая производная от скорости по времени или вторая от перемещения по времени: 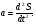 Линейная скорость - это первая производная от
Линейная скорость - это первая производная от
перемещения по времени: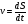 .
.
Дифференциал функции
Дифференциал функции y=f(x) в точке х0 - это главная часть приращения функции, линейная относительно приращения аргумента 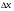 . Обозначается
. Обозначается 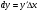
Дифференциал аргумента х равен его приращению, т.е. 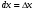
Из определений дифференциала получаем формулу (2.3), согласно которой дифференциал
функции равен ее производной, умноженной на дифференциал аргумента: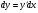
При вычислении дифференциалов верны правила и свойства аналогичные правилам и
свойствам производных. Кроме того, существует понятие дифференциалов высших порядков:
если 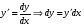 , аналогично из
, аналогично из 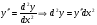 и
и 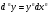
Приближенные вычисления
С помощью дифференциала производят приближенные вычисления. Эти приближенные
вычисления основаны на приближенной замене приращения функции 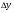 в данной точке на ее
в данной точке на ее
дифференциал dy: 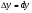 . При
. При 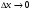 абсолютная погрешность от такой замены является бесконечной малой более высокого порядка по сравнению с
абсолютная погрешность от такой замены является бесконечной малой более высокого порядка по сравнению с 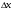 . Если
. Если 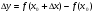 , а
, а 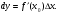 Получаем формулу применяемую в приближенных вычислениях:
Получаем формулу применяемую в приближенных вычислениях:
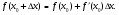
Частные производные и дифференциал функции
Величина u называется функцией нескольких переменных величин x, y, если каждой
совокупности этих величин соответствует одно определенное значение величины u: u=f(x, y).
Частная производная функции u=f(x, y) нескольких переменных по аргументу х - это предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее приращение стремится к нулю, обозначают: 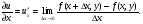
Приращение получает только один аргумент х. Остальные аргументы фиксируются. Таким образом, частная производная функции u =f(x, y) по х - это обыкновенная производная
функции одной переменной х при фиксированном значении переменной у0. Аналогично
определяются частные производные трех и более переменных.
Частный дифференциал функции - это произведение частной производной по одной из
независимых переменных на дифференциал этой переменной, обозначают:
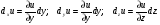
Полный дифференциал du - это сумма частных дифференциалов функции u=f(x, y),
вычисляется по формуле: 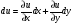
Частные производные первого порядка от функции двух и боле переменных также
представляют собой функции нескольких переменных и их также можно
продифференцировать. Для функции двух переменных u=f(x, y) возможны четыре вида
частных производных второго порядка, которые находят по формулам:
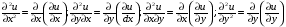
Образец решения задач
Задание 1 Найти производную сложной функции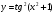
Решение: Здесь функция 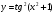 - сложная. Пусть
- сложная. Пусть 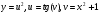 согласно
согласно
формуле нахождения производной сложной функции имеем:
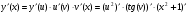
По таблице производных найдём производную каждой функции
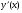
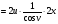
Подставим исходные значения
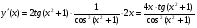
Примечание: разумеется, нет необходимости в таких подробных записях. Обычно результат
следует писать сразу. Представляя последовательно в уме промежуточные аргументы
Задание 2 Найти дифференциал второго порядка для функции 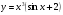
Решение: по формуле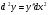 . Используя формулы производной произведения найдём
. Используя формулы производной произведения найдём
сначала 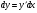 :
:
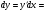
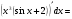
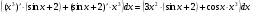
Дифференцируем второй раз, дважды используя формулы производной произведения:
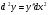
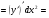
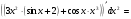
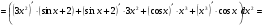
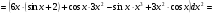
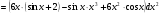
Задание 3 Найти частные производные первого порядка и полный дифференциал функции 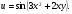
Решение: Находим частную производную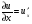 , считая
, считая 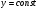 , учитывая что функция
, учитывая что функция
u сложная
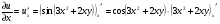
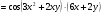
Находим частную производную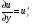 , считая
, считая 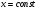 , получим:
, получим:
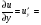
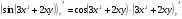
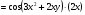
Полный дифференциал найдем по формуле 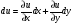 :
:
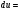
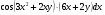
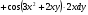 ,
,
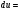
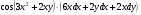
Задание 4 Для функции 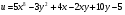 найти частные производные второго
найти частные производные второго
порядка.
Решение: Сначала находим частные производные первого порядка:
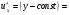
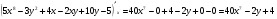
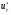
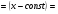
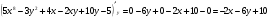
Находим частные производные второго порядка:
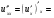
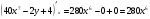
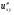
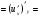
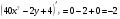
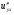
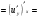
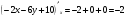
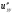
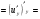
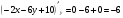
Задание 5 Вычислить приближенно с помощью дифференциала значение 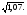
Решение: приближенные вычисления с помощью дифференциала основаны на приближенной
замене приращения функции 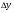 в данной точке на ее дифференциал dy:
в данной точке на ее дифференциал dy: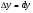
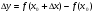 , а
, а 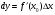
По условию задачи 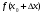
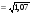
Поэтому 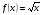
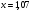
Пусть 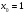
Тогда 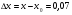
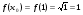
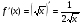
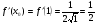
Подставим найденные значения в формулу для нахождения приближённых вычислений:
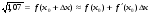
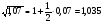
Проверим по калькулятору 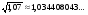
Задание 6 Точка движется прямолинейно согласно уравнению S = 17t - 2t2 м. Построить графики расстояний, скорости и ускорения для первых пяти секунд движения.
Решение: Определим закон изменения скорости движения точки
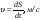

υ = (17t-2t2)' = 17-4t, м/с
Определим ускорение точки
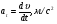
аt = (17 - 4t)' = -4 м/с2
Поскольку ускорение постоянное, т.е. at = const, следовательно движение точки является равнопеременным (равнозамедленным).
Составим свободную таблицу значений S, υ, at, для первых пяти секунд движения
t, с
0
1
2
3
4
5
S=17t - 2t2, м
0
15
26
33
36
35
υ=17 - 4t, м/с
17
13
9
5
1
-3
аt=-4 м/с2
от времени не зависит
Построим графики S ( рисунок 4), υ( рисунок 5), at( рисунок 6), выбрав масштаб
Рисунок 4
0
1
2
3
4
5
t,с
5
10
15
20
25
300
35
S,м
S=17t-2t2
0
1
2
3
4
5
t,с
5
10
15
20
υ, м/с
-5
υ=17-4t
Рисунок 5
Рисунок 6
1
2
3
4
5
t,с
-5
аt, м/c2
а= -4
Если условно принять ускорение свободного падения g ≈ 10 м/с2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение материальной точки (камня, например), брошенного вертикально вверх со скоростью υ0 = 17 м/с.
Задания для самостоятельного решения
-
Найти производную сложной функции
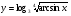
-
Найти дифференциал второго порядка для функции
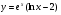
-
Найти частные производные и полный дифференциал функции

-
Для функции
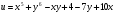 найти частные производные второго порядка
найти частные производные второго порядка -
Вычислить приближенно с помощью дифференциала
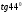
-
Точка движется прямолинейно согласно уравнению S= 16t-5t2м. Построить графики расстояний, скорости и ускорения для первых пяти секунд движения
Контрольные вопросы
-
Определение производной
-
Механический и геометрический смысл производной
-
Правила и формулы дифференцирования
-
Производная сложной функции
-
Дифференциал функции
-
Производные и дифференциалы высших порядков
-
Приложения производной и дифференциала
-
Частные производные и дифференциалы различных порядков
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 1. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-304с., ил.
-
Шипачёв В.С. Сборник задач по высшей математике: Учеб. пособие.- М.: Высш. шк. 2005.- 192с.: ил.
Практическое занятие №3
«Исследование функции с помощью производной»
Цель занятия:
освоение знаний схемы исследования функции с помощью производной, умений исследовать
функции с помощью производной и строить графики заданных функций
При выполнении задания студент должен:
знать:
-
основные свойства функции
-
алгоритм исследования функции с помощью производной
-
что называется областью определения функции;
-
какая функция называется возрастающей (убывающей);
-
необходимое условие экстремума функции;
-
определение точки перегиба;
-
определение интервалов выпуклости графика функции;
-
определение асимптот графика функции
уметь:
-
находить область определения и нули функции
-
находить точки пересечения графика функции с осями координат;
-
находить точки экстремума и промежутки монотонности с помощью первой производной
-
находить точки точек перегиба и направление выпуклости графика функции с помощью второй производной;
-
находить асимптоты графика функции
-
строить график функции
Краткие теоретические сведения
Область определения функции
Область определения функции D(y) определяют следующим образом: если функция y= f(x) задана в виде многочлена, то 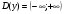 , если дробно-рациональная функция f(x) =
, если дробно-рациональная функция f(x) = 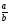 , то из условия что
, то из условия что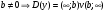 ; если иррациональная f(x) =
; если иррациональная f(x) = 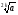 , то т.к.
, то т.к.
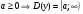 ; если логарифмическая f(x) =
; если логарифмическая f(x) = 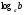 , то т.к.
, то т.к. 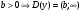
Чётность, нечётность
Функция является чётной, если f(-x) = f(x). График чётной функции симметричен относительно оси Oy. Функция является нечётной, если f(-x) = - f(x). График нечётной функции симметричен относительно начала координат.
Точки пересечения с осями координат
Для того, чтобы найти точку пересечения с осью ординат необходимо в функцию y = f(x) подставить ноль вместо х и найти соответствующее значение y. Для того, чтобы найти точки пересечения с осью абсцисс нужно в функцию y = f(x) подставить ноль вместо y , т.е. решить уравнение f(x)=0 и найти соответствующие значения хn. Решения удобно записать в таблице 4
Таблица 4
-
Ox
Oy
y=0
x=0
(x1;0), (x2;0),…
(y;0)
Асимптоты
Асимптота - прямая, к которой график по направлению приближается,
но не пересекает её. Асимптоты бывают вертикальные, горизонтальные и наклонные. Виды
асимптот и формулы для их нахождения представлены в таблице (5)
Таблица 5
Вертикальные
Горизонтальные
Наклонные
x = const
y = const
y = kx + b
из D(y)
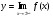
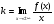
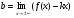
Для нахождения горизонтальных и наклонных асимптот необходимо вычислять пределы
функций, используя теоретические положения практического занятия №1. Кроме того можно
использовать правило Лопиталя.
Правило Лопиталя. Пусть функции f(x) и g(x) определены и дифференцируемы в
некоторой окрестности точки х0 за исключением быть может самой точки х0. Кроме того, пусть
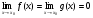 , причем
, причем 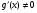 в указанной окрестности точки х0. Тогда если
в указанной окрестности точки х0. Тогда если
существует предел отношения 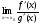 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел
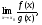 причем справедлива формула:
причем справедлива формула: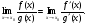
Эта теорема верна и если 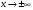 . Правило Лопиталя можно применять повторно, если
. Правило Лопиталя можно применять повторно, если 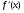 и
и
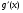 удовлетворяют тем же требованиям, что и исходные функции f(x) и g(x).
удовлетворяют тем же требованиям, что и исходные функции f(x) и g(x).
Промежутки монотонности и точки экстремума функции
Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной. Т.о. если производная функции положительна на промежутке (a,b), то функция возрастает на этом промежутке; если производная функции отрицательна на промежутке (a,b), то функция убывает на этом промежутке. Кроме того если функция f(x) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
Критические точки 1-го рода - точки, в которых первая производная равна 0 или не
существует. Они делят область определения функции на интервалы, внутри которых
производная сохраняет знак. Используя эти интервалы, находят интервалы монотонности
функций и определяют экстремумы (т.е. точки максимума и минимума).
Алгоритм нахождения промежутков монотонности и точек экстремума:
а) найти производную 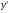
б) приравнять производную нулю: 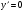 . Выяснить, при каких условиях производная не
. Выяснить, при каких условиях производная не
существует: 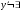 (с учётом D(y))
(с учётом D(y))
в) решив пункт (б) найти 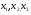 …- критические точки первого рода
…- критические точки первого рода
г) на координатном луче отметить эти точки, используя метод интервалов определить знаки
промежутков.
д) используя свойства производной отметить на луче промежутки возрастания и убывания,
точки максимума, минимума, разрыва и перегиба.
Наглядно координатный луч изображён на рисунке (7)
Рисунок 7
- разрыв + max - перегиб - min +
х1 х2 х3 х4
е) вычислить соответствующие значения функции в критических точках: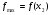
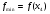 ;
; 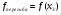
Промежутки выпуклости и точки перегиба функции
Функция f(x) называется выпуклой на интервале (a,b), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f(x) в любой точке (x0, f(x0)), где x0 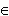 (a,b). Функция f(x) называется вогнутой на интервале (a,b), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f(x) в любой точке (x0, f(x0)) Пусть функция f(x) дважды дифференцируема ( имеет вторую производную ) на интервале (a,b), тогда: если вторая производная положительна, т.е. f ''(x)>0 для любого x
(a,b). Функция f(x) называется вогнутой на интервале (a,b), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f(x) в любой точке (x0, f(x0)) Пусть функция f(x) дважды дифференцируема ( имеет вторую производную ) на интервале (a,b), тогда: если вторая производная положительна, т.е. f ''(x)>0 для любого x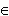 (a,b), то функция f(x) является вогнутой на интервале (a,b); если f ''(x)<0 , то функция
(a,b), то функция f(x) является вогнутой на интервале (a,b); если f ''(x)<0 , то функция
является выпуклой на этом интервале.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот,называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f ''(x0), то f ''(x0)=0.
Критические точки 2-го рода - точки, в которых вторая производная равна 0 или не
существует. Они делят область определения функции на интервалы, внутри которых вторая
производная сохраняет знак. Используя эти интервалы, находят интервалы выпуклости
функций и определяют точки перегиба (не все точки перегиба выявляются с помощью первой
производной).
Алгоритм нахождения промежутков выпуклости и точек перегиба:
а) найти вторую производную 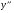
б) приравнять производную нулю: 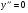 . Выяснить, при каких условиях производная не
. Выяснить, при каких условиях производная не
существует: 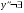 (с учётом D(y))
(с учётом D(y))
в) решив пункт (б) найти 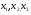 …- критические точки второго рода
…- критические точки второго рода
г) на координатном луче отметить эти точки, используя метод интервалов определить знаки
промежутков.
д) используя свойства второй производной отметить на луче промежутки выпуклости и
вогнутости, точки перегиба и разрыва.
Наглядно координатный луч изображён на рисунке (8).
Рисунок 8
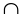
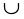
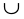
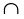
 - разрыв - перегиб + + перегиб -
- разрыв - перегиб + + перегиб -
х1 х2 х3 х4
е) вычислить соответствующие значения функции в критических точках: 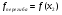 ;
;
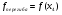
Построение графика
Строить график функции целесообразно в следующем порядке:
а) определить на координатной плоскости область определения функции, отметив
промежутки либо точки разрыва
б) отметить точки пересечения с осями координат из таблицы (4)
в) построить асимптоты, используя формулы таблицы (5)
г) отметить точки максимума, минимума и перегиба
д) с помощью отмеченных точек и рисунков (7), (8) сделать эскиз графика и
определить, какие дополнительные точки и сколько необходимо взять для более
точного построения графика, учитывая при этом чётность - нечетность функции
е) вычислить значения функции для дополнительных точек, отметить эти точки на
плоскости
ж) построить график функции
Образец решения задач
Провести полное исследование функции и построить ее график
Задание 1 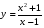
Решение: Проведем исследование функции по общей схеме.
-
Область определения функции:
D(y) = 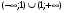 , т.к. знаменатель x -1
, т.к. знаменатель x -1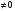 , т.е. x
, т.е. x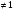
-
Чётность - нечётность:
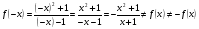 , следовательно функция ни чётная, ни нечётная
, следовательно функция ни чётная, ни нечётная
3) Нули функции - точки пересечения с осями координат:
-
Ox
Oy
y = 0
x = 0
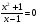
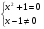
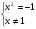
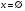
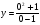
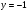
нет пересечений
с осью Ох
(0;-1)
4) Асимптоты:
а) x = const из D(y), следовательно вертикальная асимптота: x = 1
б) 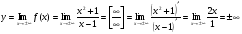 , следовательно
, следовательно
горизонтальных асимптот нет
в) y = kx + b
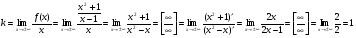
b = 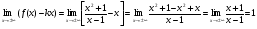 , следовательно
, следовательно
наклонная асимптота: y = x + 1
5) Промежутки монотонности и точки экстремума:
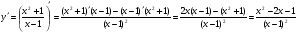
Решим числитель по дискриминанту:
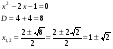
Получим: 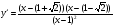 , т.е.
, т.е. 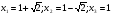 - критические точки
- критические точки
первого рода.
+ max - * - min +
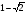
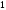
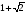
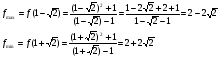
max =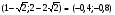 ; min =
; min = 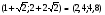
-
Промежутки выпуклости и точки перегиба:
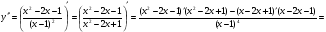
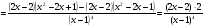
Сократим дробь на (х-1), получим 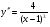 , т.е.
, т.е. 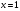 - критическая точка второго рода.
- критическая точка второго рода.
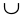
 - +
- +
1
y7) Построение графика функции:
4,8
-1
x
-0,4
1
2,4
-0,8
-1
Задание 2 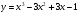
Решение:
1)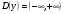
2) 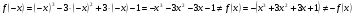
Функция не является ни чётной, ни нечётной, следовательно, симметрии нет.
3)
Оx
Оy
у=0
х=0
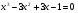
Сгруппируем:
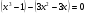
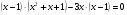
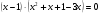
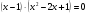
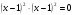
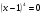

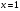
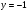
(1;0)
(0;-1)
4) Асимптот нет, так как нет точек разрыва функции
5)
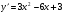
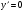
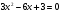 /:3
/:3
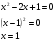
+
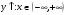 . Экстремумов нет
. Экстремумов нет
6)
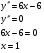
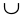
 - 1 +
- 1 +
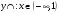 ,
, 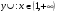 ,
, 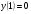 , т.е. (1;0) - точка перегиба.
, т.е. (1;0) - точка перегиба.
7)
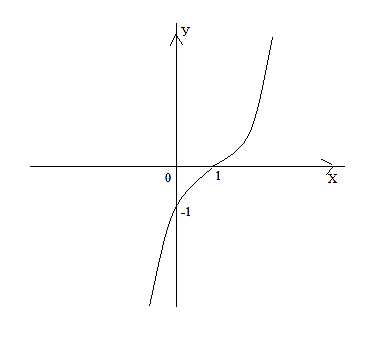
Задания для самостоятельного решения
Провести полное исследование функции и построить ее график
Контрольные вопросы
-
Основные свойства функции
-
Область определения функции
-
Нули функции, промежутки знакопостоянства
-
Признаки монотонности и экстремума функции
-
Определение направления выпуклости и точек перегиба графика функции
-
Асимптоты графика функции
-
Схема исследование функции с помощью производной
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 1. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-304с., ил.
-
Шипачёв В.С. Сборник задач по высшей математике: Учеб. пособие.- М.: Высш. шк. 2005.- 192с.: ил.
Практическое занятие №4
«Вычисление интегралов»
Цель занятия:
освоение знаний формул и методов интегрирования функций, умений вычислять
неопределённые и определённые интегралы методом непосредственного интегрирования,
интегрирования подстановкой и методом интегрирования по частям
При выполнении задания студент должен:
знать:
-
основные методы интегрирования;
-
таблицу простейших интегралов;
-
формулу Ньютона-Лейбница;
-
свойства определенного и неопределенного интегралов.
уметь:
-
определять методы интегрирования;
-
находить неопределённые интегралы
-
вычислять определённые интегралы.
Краткие теоретические сведения
Понятие первообразной и неопределённого интеграла
Первообразная - это такая функция F(x) для функции y= f(x), что имеет место равенство: 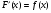 . Понятие первообразной возникает из задачи математического анализа, в которой по данной функции f(x) необходимо найти такую функцию F(x), производная которой равна функции f(x). Две первообразные одной функции отличаются друг от друга на постоянную величину. Другими словами, если F(x) - первообразная для функции f(x), то и функция F(x)+C, где C - произвольное постоянное число, также первообразная для функции f(x), потому что
. Понятие первообразной возникает из задачи математического анализа, в которой по данной функции f(x) необходимо найти такую функцию F(x), производная которой равна функции f(x). Две первообразные одной функции отличаются друг от друга на постоянную величину. Другими словами, если F(x) - первообразная для функции f(x), то и функция F(x)+C, где C - произвольное постоянное число, также первообразная для функции f(x), потому что 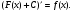
Неопределенный интеграл функции y= f(x) - это совокупность всех первообразных функций F(x)+C для функции f(x). Неопределенный интеграл обозначается символом
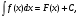 где
где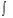 - знак интеграла; f(x) - подынтегральное выражение;
- знак интеграла; f(x) - подынтегральное выражение;
х - переменная интегрирования; С - постоянная интегрирования, способная принимать любое
значение. Интегрирование - это отыскание первообразной функции по ее производной,
действие обратное дифференцированию.
Основные свойства неопределенного интеграла
-
Неопределённый интеграл от дифференциала функции равен этой функции плюс
произвольная постоянная: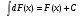
-
Дифференциал неопределённого интеграла равен подынтегральному выражению
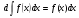
-
Производная неопределённого интеграла равна подынтегральной функции:
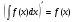
-
Неопределённый интеграл алгебраической суммы функций равен сумме интегралов этих
функций: 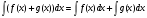
-
Постоянный множитель подынтегрального выражения можно выносить за знак интеграла:
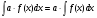
Методы интегрирования
Метод непосредственного интегрирования. Метод непосредственного интегрирования
заключается либо в прямом использовании таблиц интегралов, либо сначала применяются
основные свойства неопределенного интеграла, а также производятся элементарные
тождественные преобразования, а затем данный интеграл приводится к одному или нескольким
табличным интегралам (таблица 7 )
1
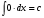
9
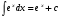
17
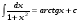
2
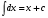
10
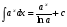
18
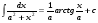
3
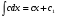
11
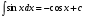
19
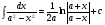
4
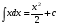
12
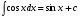
20
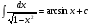
5
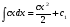
13
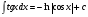
21
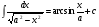
6
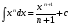
14
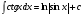
22
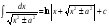
7
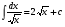
15
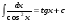
8
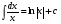
16
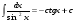
Метод интегрирования подстановкой. Метод подстановки заключается в том, что интеграл вида 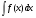 приводится к интегралу вида
приводится к интегралу вида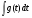 , который в свою очередь
, который в свою очередь
решается непосредственным интегрированием. Для этого в функции 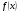 некоторое выражение, содержащее переменную х заменяют на t, т.е.
некоторое выражение, содержащее переменную х заменяют на t, т.е. 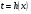 , затем находят
, затем находят 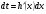
Метод интегрирования по частям. Пусть функции u=u(x) и v=v(x) определены и непрерывно дифференцируемы. Так как производная произведения двух функций вычисляется по формуле: 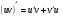 , то интегрируя обе части этого равенства
, то интегрируя обе части этого равенства 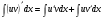 получим формулу:
получим формулу: 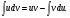
Самое трудное в интегрирование по частям - это выбрать сомножитель dv в подынтегральном выражении: интеграл в правой части формулы 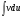 должен быть проще исходного. Чаще всего формула (4.1) применяется к интегралам вида:
должен быть проще исходного. Чаще всего формула (4.1) применяется к интегралам вида: 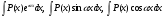 , где Р(х) - многочлен,
, где Р(х) - многочлен,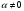 , в эти интегралах u=P(x);
, в эти интегралах u=P(x); 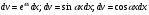 или к интегралам вида
или к интегралам вида 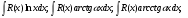 где R(x) - рациональная функция, здесь
где R(x) - рациональная функция, здесь 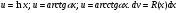 .
.
Определённый интеграл
Определенный интеграл - это общий предел всех интегральных сумм функции f(x) на
отрезке [a,b]. Определенный интеграл обозначается 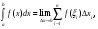 где
где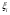 - произвольная точка существующего отрезка.
- произвольная точка существующего отрезка.
Если F(x) - первообразная для непрерывной функции 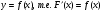 , то имеет место формула формула Ньютона-Лейбница - основная формула интегрального исчисления, устанавливающая связь между определенным и неопределённым интегралом:
, то имеет место формула формула Ньютона-Лейбница - основная формула интегрального исчисления, устанавливающая связь между определенным и неопределённым интегралом:
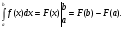
Правило вычисления определённого интеграла: для того, чтобы вычислить определённый интеграл необходимо сначала найти соответствующий неопределённый интеграл, а затем в полученное выражение подставить вместо х сначала верхний предел интегрирования, а затем нижний, и из первого результата вычесть второй.
Основные свойства определенного интеграла
-
Интеграл с одинаковыми пределами равен нулю:
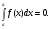
-
При перестановке пределов интегрирования изменяется знак интеграла:
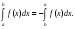
-
Отрезок интегрирования можно разбивать на части:
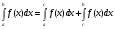 , где
, где 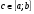
-
Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов:
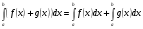
-
Постоянный множитель можно выносить за знак определенного интеграла:
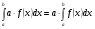
Образец решения задач
Вычислить определённые и неопределённые интегралы, используя подходяшие методы интегрирования
Задание 1 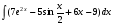
Решение: используя свойства интегралов (интеграл суммы равен сумме интегралов,
постоянный множитель выносится за знак интеграла) данный интеграл представим в виде
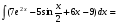
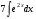
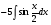
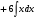
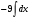
далее используем свойства дифференциала для первого и второго слагаемого и таблицу
интегралов
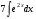
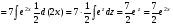
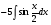
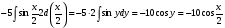
тогда 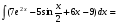
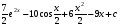

Задание 2 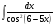
Решение: Используя метод интегрирования подстановкой, сделаем замену 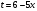 , тогда
, тогда
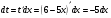 , откуда
, откуда 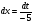 . Подставим найденные значения в исходный
. Подставим найденные значения в исходный
интеграл, получим 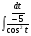 , вынесем постоянный множитель за скобки и найдём табличный
, вынесем постоянный множитель за скобки и найдём табличный
интеграл 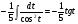 , вернёмся к замене
, вернёмся к замене 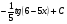
Задание 3 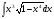
Решение: используем метод интегрирования подстановкой
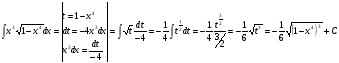
Задание 4 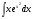
Решение: используем метод интегрирования подстановкой
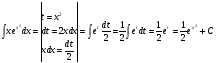
Задание 5 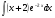
Решение: используем метод интегрирования по частям
Пусть 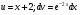 . Найдём значения
. Найдём значения 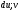 :
:
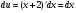 ;
; 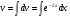
Решим последний интеграл методом подстановки:
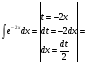
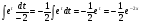 .
.
Подставим найденные значения в формулу интегрирования по частям, получим
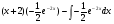 , далее
, далее
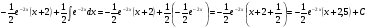
Задание 6 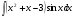
Решение: здесь используется метод интегрирования по частям два раза:
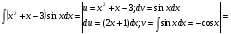
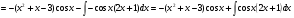 =
=
=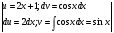 =
=
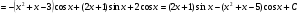
Задание 7 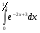
Решение: имеем определённый интеграл, используем метод подстановки и формулу Ньютона-
Лейбница:
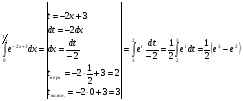
Задание 8 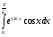 .
.
Решение: найдём определённый интеграл, используем метод подстановки и формулу
Ньютона-Лейбница:
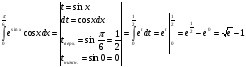 .
.
Задания для самостоятельного решения
Вычислить определённые и неопределённые интегралы, используя подходяшие методы интегрирования
Контрольные вопросы
-
Первообразная и неопределённый интеграл.
-
Свойства неопределённого интеграла.
-
Таблица интегралов
-
Основные методы интегрирования: непосредственно, подстановкой и по частям
-
Определение и свойства определённого интеграла.
-
Формула Ньютона-Лейбница
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 1. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-304с., ил.
-
Шипачёв В.С. Сборник задач по высшей математике: Учеб. пособие.- М.: Высш. шк. 2005.- 192с.: ил.
Практическое занятие №5
«Решение прикладных задач с помощью определённого интеграла»
Цель занятия:
освоение знаний алгоритма решения задач на нахождение площади фигур с помощью
интегралов, формул для нахождения физических и геометрических величин с помощью
интегралов, умений находить площади плоских фигур и объёмы тел вращения с помощью
интегралов, решать простейшие задачи на физические приложения интегралов
При выполнении задания студент должен:
знать:
-
свойства определенного и неопределенного интегралов.
-
геометрический смысл определённого интеграла;
-
формулы для вычисления площадей плоских фигур и объёмов тел вращения;
уметь:
-
вычислять площади плоских фигур и объёмы тел вращения
Краткие теоретические сведения
Геометрический смысл определенного интеграла.
Определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции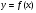 , осью Ох и прямыми х=а; х=b, где
, осью Ох и прямыми х=а; х=b, где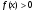 на отрезке
на отрезке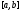 (рисунок 9). Получаем формулу:
(рисунок 9). Получаем формулу: 
Рисунок 9
y y=f(x)
a b x
Алгоритм решения задач на нахождение площади плоской фигуры
Для нахождения площади плоской фигуры, ограниченной графиками некоторых функций, необходимо:
а) построить графики заданных функций, ограничивающих площадь плоской фигуры
б) найти пределы интегрирования по чертежу (при необходимости решить уравнение 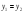 )
)
в) вычислить площадь заданной фигуры по формуле
г) проверить результат вычислений по чертежу.
Объем тела вращения
Рис. 19Если криволинейная трапеция, ограниченная кривой 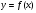 и прямыми
и прямыми 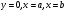 , вращается вокруг оси
, вращается вокруг оси 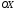 , то объём тела вращения вычисляется по формуле:
, то объём тела вращения вычисляется по формуле:
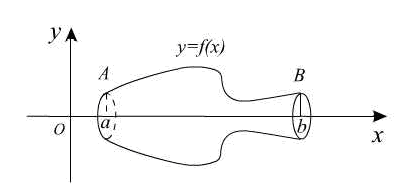
Если фигура, ограниченная кривыми 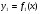 и
и 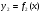 , причём
, причём 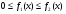 и прямыми
и прямыми 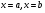 ,вращается вокруг оси
,вращается вокруг оси 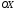 , то объём тела вращения вычисляется по формуле:
, то объём тела вращения вычисляется по формуле: 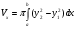 .
.
Вычисление пути, пройденного точкой
Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция времени t, то путь, пройденный точкой за промежуток времени  вычисляется по формуле:
вычисляется по формуле: 
Вычисление работы силы
Пусть тело перемещается по оси Оx от точки А (x=a) до точки В (х=b) под действием переменной силы F, являющейся функцией от х (F=f(х)) и направленной вдоль оси Оx. Работа, произведённая переменной силой f(х) при перемещении по оси Оx материальной точки от х = а до х = b, находится по формуле: 
При решении задач на вычисление работы силы часто используется закон Гука:
где F - сила, H; х - абсолютное удлинение (сжатие) пружины, вызванное силой F,м; k - коэффициент пропорциональности, Н/м.
Сила давления жидкости
Из физики известно (закон Паскаля), что давление покоящейся жидкости на единицу площади ограничивающей ее поверхности сосуда направлено перпендикулярно к этой поверхности; величина этого давления не зависит ни от направления поверхности,
испытывающей давление, ни от формы остальной части сосуда, но меняется с глубиной погружения; давление на горизонтальную площадку равно весу вертикального столба жидкости, имеющего основанием эту площадку, а высотой - ее глубину под уровнем жидкости. Таким образом, вычисление давления жидкости на горизонтальную поверхность выполняется элементарно. Но для негоризонтальной поверхности элементарных средств недостаточно, ибо глубина площадки не остается постоянной. С помощью интегрального исчисления можно вычислить давление жидкости на вертикальную стенку любой формы. Сила давления Р жидкости плотности  на вертикальную пластинку, погруженную в жидкость, вычисляется по формуле:
на вертикальную пластинку, погруженную в жидкость, вычисляется по формуле: 
где g = 9,81 м/с2 - ускорение свободного падения, S - площадь пластинки, а глубина погружения пластинки изменяется от a до b.
Образец решения задач
Задание 1 Вычислить площадь фигуры, ограниченной линиями: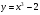 ,
, 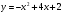
Решение: воспользуемся алгоритмом решения задач на нахождение площади плоской фигуры:
а) построим графики заданных функций.
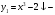 кубическая парабола, полученная из
кубическая парабола, полученная из 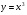 (см. таблицу 7) смещением на 2
(см. таблицу 7) смещением на 2
единицы вниз, 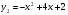 - квадратичная парабола, для построения которой приведём ей
- квадратичная парабола, для построения которой приведём ей
к стандартному виду
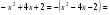
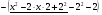
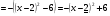 , т.о. получим
, т.о. получим
параболу со смещением на 2 единицы вправо, на 6 вверх, ветви которой направлены вниз,
полученную из стандартной параболы 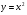 (см. таблицу 8)
(см. таблицу 8)
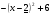
Таблица 7
x
-2
-1
0
1
2
y
-8
-1
0
1
8
Таблица 8
x
-2
-1
0
1
2
y
4
1
0
1
4
Графики заданных функций изображены на рисунке 11
Рисунок 11
-2
б) найдём пределы интегрирования по чертежу: а = -1, в = 2
в) для того, чтобы найти площадь заданной фигуры, необходимо из площади фигуры,
ограниченной графиком верхней функции вычесть площадь фигуры,
ограниченной нижней функцией: 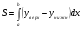 , т.е.
, т.е.
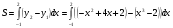 =
= 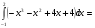
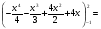
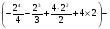
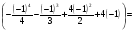
= 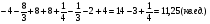
г) проверим результат вычислений по чертежу, получим ответ: 11,25 кв.ед.
Задание 2. Найдите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями: у = sinх, х = 0, 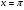 , у = 0.
, у = 0.
Решение: выполним чертеж
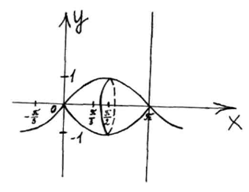 рисунок
рисунок
Объем тела вращения вычисляется по формуле: 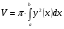
В нашем случае a = 0, 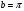 , у(х) = sinх
, у(х) = sinх
По формуле вычисляем:
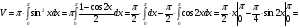
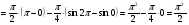 (куб.ед.)
(куб.ед.)
Задание 3 Производительность труда рабочего в течение дня задается функцией z(t) = - 0,00625t² + 0,05t + 0,5 (ден. ед/ч), где t - время в часах от начала работы, 0 ≤ t ≤ 8. Найти функцию u = u(t), выражающую объем продукции (в стоимостном выражении) и его величину за рабочий день.
Решение: Функцию объема продукции найдем как первообразную функции производительности труда: 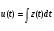
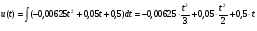
Значение объема продукции вычислим с помощью определенного интеграла функции производительности труда: 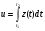
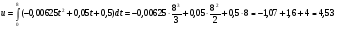 .
.
Итак, объем произведенной за рабочий день продукции составил 4,53 ден. ед.
Задание 4 Стоимость перевозки одной тонны груза на один километр (тариф перевозки) задается функцией: 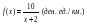 Определите расходы на перевозку одной тонны груза на расстояние 20 км.
Определите расходы на перевозку одной тонны груза на расстояние 20 км.
Решение: Транспортные расходы z вычисляются как определенный интеграл от 0 до s
(s - расстояние) функции f(x), задающей тариф перевозки по dx, где x - переменная пути:
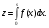
Вычисляем затраты на перевозку одной тонны груза на расстояние 20 км:
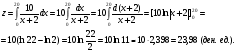
Итак, транспортные расходы составляют приблизительно 23,98 ден. ед.
Задание 5 Дано уравнение скорости движения тела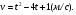 . Найти уравнение пути,
. Найти уравнение пути,
если тело за первые 3с прошло путь 24м.
Решение: Уравнение пути s(t) находится интегрированием:
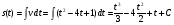
Найдем С из дополнительных условий при t=3c, s=24м:
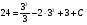 ,
,
решив данное линейное уравнение найдём С: С=30. Т.о. уравнение пути имеет вид
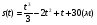
Задание 6 Сжатие х винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 10 Н.
Решение: Работа, произведенная переменной силой 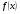 при перемещении по оси Ох материальной точки от
при перемещении по оси Ох материальной точки от 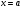 до
до 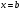 , находится по формуле:
, находится по формуле: 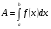 При решении задач на вычисление работы силы используется закон Гука:
При решении задач на вычисление работы силы используется закон Гука: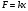 ,
,
где F - сила, H; x - абсолютное удлинение пружины (м), вызванное силой F, а k - коэффициент пропорциональности (Н/м). Так как, 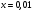 м при
м при 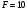 Н получим
Н получим 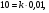 откуда
откуда 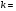 1000 Н/м. Подставив теперь в это же равенство значение k, находим
1000 Н/м. Подставив теперь в это же равенство значение k, находим 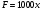 , т. е.
, т. е. 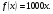 Искомую работу найдем интегрированием, полагая
Искомую работу найдем интегрированием, полагая 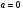 ,
, 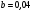 :
:
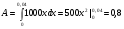 (Дж)
(Дж)
Задания для самостоятельного решения
1 Вычислить площадь фигуры, ограниченной линиями: 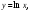
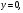
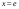
2 Найти объем тела вращения вокруг оси Ox фигуры, ограниченной линиями: 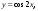
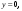
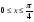
-
Производительность труда рабочего в течение дня задается функцией z(t) = - 0,00325t² + 0,01t + 0,8 (ден. ед/ч), где t - время в часах от начала работы, 0 ≤ t ≤ 8. Найти функцию u = u(t), выражающую объем продукции (в стоимостном выражении) и его величину за вторую половину рабочего дня Стоимость перевозки одной тонны груза на один километр (тариф
перевозки) задается функцией 
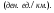 Определите затраты на перевозку одной тонны груза на расстояние S = 40 км
Определите затраты на перевозку одной тонны груза на расстояние S = 40 км
4 Пружина растягивается на 0,02 м под действием силы 60Н. Какую работу производит эта сила, растягивая пружину на 0,12 м?
5 Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v=(3t2+4t) м/с, второе - со скоростью v=(6t+12)м/с. В какой момент и на каком расстоянии от начальной точки произойдет их встреча?
Контрольные вопросы
-
Геометрический смысл определенного интеграла.
-
Алгоритм вычисления площади фигуры с помощью интеграла
-
Вычисление объёма тела вращения с помощью определённого интеграла.
-
Физический смысл определённого интеграла.
-
Приложения интеграла к решению прикладных задач
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 1. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-304с., ил.
-
Шипачёв В.С. Сборник задач по высшей математике: Учеб. пособие.- М.: Высш. шк. 2005.- 192с.: ил.
Практическое занятие №6
«Решение обыкновенных дифференциальных уравнений»
Цель занятия:
освоение знаний алгоритма решения дифференциальных уравнений с разделяющимися
переменными, однородных, линейных дифференциальные уравнения первого порядка,
линейные однородные уравнения второго порядка с постоянными коэффициентами, умений
определять вид и решать обыкновенные дифференциальные уравнения
При выполнении задания студент должен:
знать:
-
определение дифференциального уравнения;
-
определение общего и частного решений дифференциальных уравнений,
-
методы решения обыкновенных дифференциальных уравнений с разделяющимися
-
переменными, дифференциальных уравнений первого порядка, дифференциальных уравнений
-
второго порядка с постоянными коэффициентами;
уметь:
-
определять вид уравнения;
-
решать обыкновенные дифференциальные уравнения
Краткие теоретические сведения
Основные понятия дифференциального уравнения
Дифференциальное уравнение - равенство, содержащее производные или дифференциалы неизвестной функции. 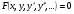 - общий вид дифференциального уравнения, где x - независимая переменная, y - неизвестная функция,
- общий вид дифференциального уравнения, где x - независимая переменная, y - неизвестная функция, 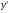 - её производная первого порядка и т.д.
- её производная первого порядка и т.д.
Решение дифференциального уравнения - функция, подстановка которой в это
уравнение обращает его тождество.
Общее решение - решение дифференциального уравнения, содержащее столько
произвольных постоянных, каков порядок уравнения.
Частное решение - это решение, получающееся из общего решения при конкретных
определенных значениях произвольных постоянных C. Для нахождения частных решений
задают начальные условия 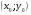 .
.
Порядок дифференциального уравнения - наивысший порядок производных или
дифференциалов, входящих в это уравнение.
Интегральная кривая - график функции y=F(x), построенный на плоскости xOy,
являющийся решением дифференциального уравнения. Общему решению y=F(x,C)
соответствует семейство интегральных кривых, зависящих от постоянной С.
Теорема Коши: Если функция f(x,y) непрерывна и имеет непрерывную производную, то
решение дифференциального уравнения y'=f(x,y) при начальном условии f(x0)=y0 существует и
единственно, т.е. через точку (x0,у0) проходит единственная интегральная кривая данного
уравнения.
Виды дифференциальных уравнений
Различают обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных. Обыкновенные дифференциальные уравнения - уравнения, в которых одна независимая переменная. Дифференциальные уравнения в частных производных - уравнения, в которых независимых переменных две и более.
Обыкновенные дифференциальные уравнения первого порядка
Обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными представлены в таблице 9
Таблица 9
Вид уравнения
Способ решения
P(x,y)dx+Q(x,y)dy=0,
если P(x,y) и Q(x,y) разлагаются на множители, зависящие каждый только от одной переменной, т.е.
f(x)g(y)dx+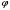 (x)q(y)dy=0 (*)
(x)q(y)dy=0 (*)
или 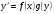
1 разделить переменные в уравнении (*)
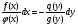
2 проинтегрировать
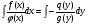
3 привести к стандартному виду
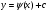
Однородные дифференциальные уравнения первого порядка в таблице 10
Таблица 10
Вид уравнения
Способ решения
P(x,y)dx+Q(x,y)dy=0,
где P(x,y), Q(x,y) - однородные функции одного измерения,
т.е. если в функции заменить
x=tx, y=ty и преобразовать
вернемся исходному уравнению
1 замена 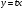 ,
,
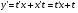 , выразить через дифференциалы
, выразить через дифференциалы 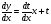 , тогда
, тогда 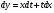
2 решить полученное уравнение с разделяющимися переменными
3 вернуться к замене, подставить 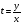
4 привести к стандартному виду 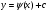
Линейные дифференциальные уравнения первого порядка в таблице 11
Таблица 11
Вид уравнения
Способ решения
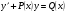
1 замена 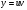 , тогда y'=u'v+v'u
, тогда y'=u'v+v'u
2 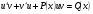
сгруппировать первое и третье слагаемые, вынести  за скобки
за скобки
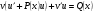 (**)
(**)
3 в уравнении (**) приравнять скобку к нулю
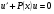
решить полученное уравнение c разделяющимися переменными,
найти u: 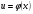
4 значение u подставить в уравнение (**)

решить полученное уравнение c разделяющимися переменными,
найти v: 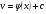
5 вернуться к замене
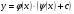
Обыкновенные дифференциальные уравнения второго порядка
Неполные дифференциальные уравнения второго порядка, допускающие понижения
в таблице 12
Таблица 12
Вид уравнения
Способ решения
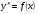
дважды проинтегрировать
1 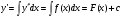
2 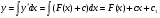
Линейные однородные дифференциальные уравнения второго порядка с постоянными
коэффициентами в таблице 13
Таблица 13
Вид уравнения
Способ решения
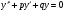
где p, q - заданные числа
1 составить характеристическое уравнение
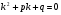
2 решить его, найти корни 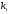 и
и 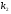
3 в зависимости от вида корней, найти общее решение, т.е. если корни
-
действительные и различные
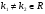 , тогда
, тогда
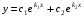
-
действительные и равные
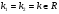 ,
,
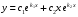 или
или 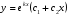
-
мнимые
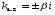
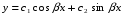
-
комплексные
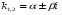
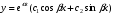
Образец решения задач
Задание 1 Решить дифференциальное уравнение с разделяющимися переменными
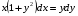
Решение: используем алгоритм решения дифференциального уравнения с разделяющимися
переменными
а) разделим переменные
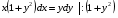
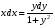 - дифференциальное уравнение с разделёнными переменными
- дифференциальное уравнение с разделёнными переменными
б) проинтегрируем
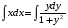
Левый интеграл решаем непосредственно: 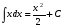 , правый методом подстановки:
, правый методом подстановки:
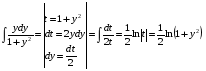 ,
,
Получим 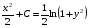
в) т.к. С - произвольная постоянная, для удобства представим её как 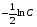 , тогда
, тогда
уравнение примет вид 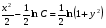 , тогда
, тогда 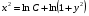 ; используя
; используя
свойства логарифмов 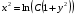 ; потенцируем последнее равенство
; потенцируем последнее равенство 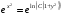 ,
,
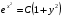 ,
,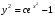 , и окончательно
, и окончательно 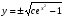 - общее решение
- общее решение
Задание 2 Решить однородное дифференциальное уравнение 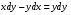
Решение: воспользуемся алгоритмом решения однородного дифференциального уравнения
-
заменим
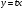 ,
, 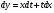 , получим
, получим
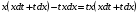
-
решим полученное дифференциальное уравнение с разделяющимися переменным
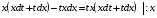
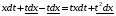
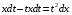
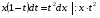
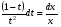 - с разделёнными переменными,
- с разделёнными переменными,
проинтегрируем
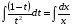
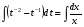
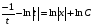
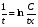
в) вернёмся к замене, подставим 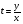
г) 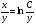 ;
; 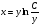 - общее решение
- общее решение
Задание 3 Найти общее решение линейного дифференциального уравнения 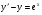
Решение: воспользуемся алгоритмом решения линейного дифференциального
уравнения
а) заменим 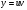 ,
, 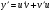
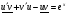 б) сгруппируем первое и третье слагаемое
б) сгруппируем первое и третье слагаемое
вынесем за скобки
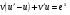 (*)
(*)
в) в уравнении (*) приравняем скобку к нулю
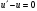 - д.у. c разделяющимися переменными
- д.у. c разделяющимися переменными
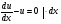
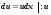
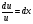 - с разделёнными переменными
- с разделёнными переменными
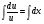
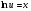 , потенцируем по основанию e:
, потенцируем по основанию e: 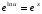 , получим
, получим 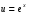
г) найденное значение u подставим в уравнение (*)
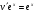 - д.у. с разделяющимися переменными
- д.у. с разделяющимися переменными
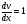
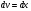 - с разделёнными переменными
- с разделёнными переменными
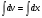
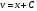
д) вернёмся к замене
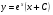 - общее решение
- общее решение
Задание 4 Решить дифференциальное уравнение второго порядка понижением: 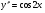 .
.
Решение: последовательно интегрируя, находим сначала первую производную:
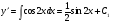 ,
,
а затем, интегрируя второй раз, и общее решение
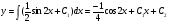
Задание 5 Решить задачу Коши для ЛОДУ второго порядка с постоянными коэффициентами:
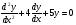 , при
, при 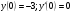
Решение: для нахождения общего решения используем алгоритм решения ЛОДУ второго
порядка с постоянными коэффициентами:
а) составим характеристическое уравнение
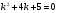
б) решим его с помощью дискриминанта: 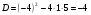
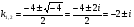 - комплексные корни
- комплексные корни
в) 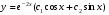 - общее решение
- общее решение
Для нахождения частного решения найдем значение первой производной
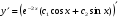
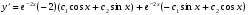
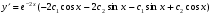
Подставим начальные условия 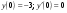 в систему уравнений
в систему уравнений
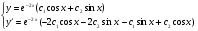
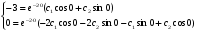
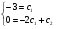
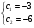
Подставим значения С в общее решение
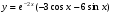 - частное решение (решение задачи Коши)
- частное решение (решение задачи Коши)
Задание 6 Дано ЛОДУ второго порядка с постоянными коэффициентами: 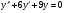 Найти общее решение
Найти общее решение
Решение: составим характеристическое уравнение
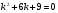
D = 0
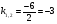
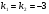 - действительные равные корни, т.е. общее решение запишется в виде:
- действительные равные корни, т.е. общее решение запишется в виде:
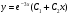
Задания для самостоятельного решения
1 Решить дифференциальное уравнение с разделяющимися переменными: 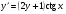
2 Решить однородное дифференциальное уравнение: 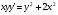
3 Решить задачу Коши для линейного дифференциального уравнения: 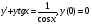
4 Решить дифференциальное уравнение второго порядка понижением: 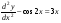
5 Дано ЛОДУ второго порядка с постоянными коэффициентами: 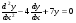 . Найти общее решение
. Найти общее решение
6 Решить задачу Коши для ЛОДУ второго порядка с постоянными коэффициентами: 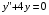
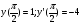
Контрольные вопросы
-
Понятие обыкновенного дифференциального уравнения
-
Порядок дифференциального уравнения
-
Общее и частное решение дифференциального уравнения
-
Дифференциальные уравнения первого порядка с разделяющимися переменными
-
Однородные дифференциальные уравнения первого порядка
-
Линейные дифференциальные уравнения первого порядка
-
Дифференциальные уравнения второго порядка требующие понижения
-
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 2. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-416с., ил.
Практическое занятие №7
«Определение сходимости рядов»
Цель занятия:
освоение знаний алгоритма исследования на сходимость числовых, функциональных и
степенных рядов, умений исследовать на сходимость указанные ряды
При выполнении задания студент должен:
знать:
-
определения числовых и функциональных рядов;
-
необходимый и достаточный признаки сходимости рядов, признак Даламбера; признак Коши
-
признаки знакопеременных рядов, признак Лейбница,
-
метод представления функций в степенные ряды с помощью ряда Маклорена;
уметь:
-
определять сходимость числовых и функциональных рядов по признакам сходимости;
-
применять признак Лейбница для знакопеременных рядов;
-
разлагать элементарные функции в ряд Маклорена.
Краткие теоретические сведения
Числовые ряды
Пусть 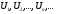 - бесконечная последовательность чисел. Выражение
- бесконечная последовательность чисел. Выражение
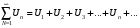 называется числовым рядом, числа
называется числовым рядом, числа 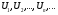 - членами
- членами
ряда, 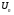 - общим членом ряда.
- общим членом ряда.
Сумма n первых членов ряда называется частичной суммой этого ряда: 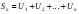
Ряд 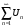 называется сходящимся, если последовательность его частичных сумм имеет
называется сходящимся, если последовательность его частичных сумм имеет
конечный предел: 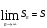 . Значение S называется суммой ряда. Если ряд не сходится, то
. Значение S называется суммой ряда. Если ряд не сходится, то
он называется расходящимся.
Основные свойства рядов
Пусть дан ряд 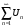 . Ряд
. Ряд 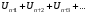 называется остатком данного ряда. Если сходится ряд
называется остатком данного ряда. Если сходится ряд 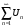 , то сходится и n-й остаток этого ряда и наоборот.
, то сходится и n-й остаток этого ряда и наоборот.
Если сходится ряд 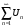 , то сходится и ряд
, то сходится и ряд 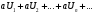 , причем сумма
, причем сумма
последнего ряда равна aS.
Если сходятся ряд 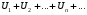 и ряд
и ряд 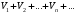 , имеющие
, имеющие
соответственно суммы S и T, то сходится и ряд 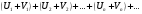 ,
,
причем сумма последнего ряда равна S+T.
Признаки сходимости рядов с положительными членами
Необходимый признак сходимости ряда. Если ряд 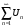 сходится, то
сходится, то 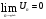 . Этот признак сходимости является необходимым, но не является достаточным.
. Этот признак сходимости является необходимым, но не является достаточным.
Достаточный признак расходимости: если для ряда 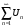 предел
предел 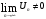 , то ряд
, то ряд
расходится.
Первый признак сравнения рядов. Пусть даны два ряда: 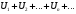 и
и
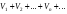 , причем
, причем 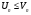 Тогда если сходится ряд
Тогда если сходится ряд 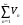 , то будет сходиться и ряд
, то будет сходиться и ряд
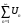 ; если расходится ряд
; если расходится ряд 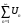 , то будет расходиться и ряд
, то будет расходиться и ряд 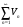 .
.
Второй признак сравнения рядов. Пусть даны два ряда: 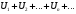 и
и
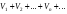 . Если существует конечный и отличный от нуля предел
. Если существует конечный и отличный от нуля предел 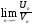 , то оба ряда
, то оба ряда
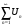 и
и 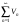 одновременно сходятся или одновременно расходятся.
одновременно сходятся или одновременно расходятся.
В качестве рядов сравнения часто выбирают:
а) геометрический ряд 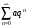 , который при
, который при 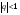 - сходится (бесконечно убывающая
- сходится (бесконечно убывающая
геометрическая прогрессия) и имеет сумму 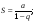 при
при  - расходится;
- расходится;
б) гармонический ряд 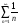 , являющийся расходящимся;
, являющийся расходящимся;
в) обобщенный гармонический ряд 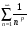 , который при p>1- сходится, при p
, который при p>1- сходится, при p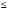 1- расходится
1- расходится
Признак Даламбера. Если для ряда (7.1) существует 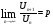 , то при p<1 ряд
, то при p<1 ряд
сходится, а при p>1 ряд расходится (при p=1 вопрос остается нерешенным).
Признак Коши. Если для ряда (7.1) существует 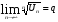 , то при q < 1 ряд
, то при q < 1 ряд
сходится, а при q > 1 ряд расходится (при q = 1 вопрос остается нерешенным).
Знакопеременные и знакочередующиеся ряды
Знакопеременным рядом называется ряд, членами которого являются действительные
числа произвольного знака.
Знакопеременный ряд 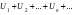 сходится, если сходится ряд, составленный из
сходится, если сходится ряд, составленный из
абсолютных величин его членов: 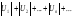 . В этом случае исходный ряд
. В этом случае исходный ряд 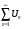
называется абсолютно сходящимся. Если же знакопеременный ряд сходится, а составленный
из абсолютных величин его членов ряд расходится, то исходный ряд называют условно сходящимся.
Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют
различные знаки, т.е. 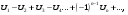 где
где 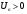
Признак сходимости Лейбница. Знакочередующийся ряд сходится, если выполняются
следующие два условия:
- абсолютные величины его членов монотонно убывают: 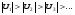 ;
;
- 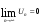 .
.
Алгоритм исследования на сходимость знакопеременных рядов:
-
исследовать на сходимость ряд, составленный из модулей членов данного ряда, используя какой-либо признак сходимости;
-
cделать вывод об абсолютной или условной сходимости этого ряда;
-
выяснить, сходится ли данный знакочередующийся ряд, применяя признак Лейбница, для этого: проверить, выполняется ли равенство для абсолютных величин членов ряда; - найти предел общего члена ряда;
-
сделать вывод о сходимости данного исходного ряда.
Функциональные ряды
Выражение 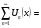
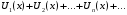 называется функциональным рядом относительно переменной x.
называется функциональным рядом относительно переменной x.
Степенной ряд - это функциональный ряд вида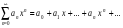 , где
, где 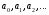 - действительные числа (коэффициенты ряда).
- действительные числа (коэффициенты ряда).
Придавая х различные числовые значения, будем получать различные числовые ряды, которые
могут быть как сходящимися, так и расходящимися. Множество тех значений х, при которых
функциональный ряд сходится, называют областью сходимости ряда. Если значение 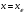
принадлежит области сходимости ряда 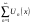 , то говорят о сумме этого функционального
, то говорят о сумме этого функционального
ряда в точке 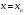 :
: 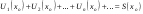 .
.
Для любого степенного ряда существует такое неотрицательное число R, что этот ряд сходится абсолютно при 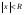 и расходится при
и расходится при 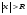 . Поведение ряда при
. Поведение ряда при 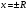 подлежит
подлежит
дальнейшему анализу. Число R называется радиусом сходимости данного степенного ряда.
Область значений переменной x: -R<x<R - интервалом сходимости.
Если R = 0, то ряд сходится лишь при x = 0, если же R=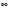 , то ряд сходится при любом
, то ряд сходится при любом
действительном x. Радиус сходимости ряда находят по формуле 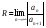
Ряды Тейлора и Маклорена
Пусть функция f(x) имеет в окрестности точки x = a непрерывные производные до
(n + 1) - ого порядка включительно. Тогда для любого x из этой окрестности имеет место формула Тейлора: 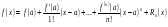
Если 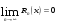 , то ряд сходится и его суммой будет функция f(x).
, то ряд сходится и его суммой будет функция f(x).
Представление функции f(x) в виде ряда 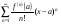 называется разложением этой функции в ряд Тейлора. В частности, при a = 0 разложение в ряд Тейлора называется разложением в ряд Маклорена:
называется разложением этой функции в ряд Тейлора. В частности, при a = 0 разложение в ряд Тейлора называется разложением в ряд Маклорена: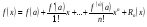
Алгоритм представления элементарной функции в виде суммы ряда Тейлора (Маклорена)
-
Вычислить последовательные производные данной функции в точке х=х0.
-
Составить ряд Тейлора (Маклорена) для функции
-
Определить промежуток сходимости полученного ряда.
Образец решения задач
Задание 1 Исследовать числовой ряд на сходимость 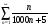
Решение: используем необходимый признак сходимости
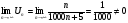 , следовательно ряд расходится
, следовательно ряд расходится
Задание 2 Исследовать числовой ряд на сходимость 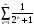
Решение: по условию 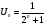 , сравним ряд с геометрическим рядом:
, сравним ряд с геометрическим рядом: 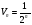 ,
,
применим первый признак сравнения рядов: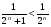
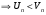
Так как ряд 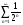 сходится, то сходится и ряд
сходится, то сходится и ряд 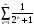
Задание 3 Исследовать числовой ряд на сходимость 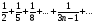
Решение: имеем ряд вида 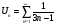 Сравним с гармоническим рядом
Сравним с гармоническим рядом 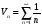
Применим второй признак сравнения рядов: 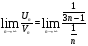
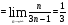 . Так как
. Так как
предел конечен и отличен от нуля, а ряд 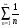 расходится, то расходится и данный ряд.
расходится, то расходится и данный ряд.
Задание 4 Исследовать числовой ряд на сходимость 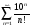
Решение: применим признак Даламбера; имеем 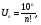 тогда
тогда 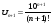 ,
,
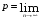
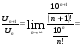
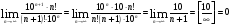
Так как p=0<1, то ряд сходится
Задание 5 Исследовать на сходимость ряд 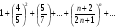
Решение: применим признак Коши:
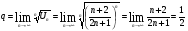 .
.
Так как 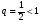 , ряд сходится.
, ряд сходится.
Задание 6 Исследовать на сходимость ряд 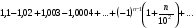
Решение: Этот ряд знакочередующийся. Первое условие Лейбница не выполняется:
1,1 > 1,02 > 1,003 > …
Проверим выполнение второго условия: 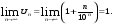
Так как 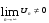 ряд расходится
ряд расходится
Задание 7 Исследовать сходимость ряд 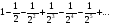
Решение: Имеем знакопеременный ряд. Составим ряд из абсолютных величин:
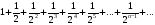 Этот ряд сходится как бесконечно убывающая
Этот ряд сходится как бесконечно убывающая
геометрическая прогрессия. Значит, и данный ряд сходится, причем абсолютно.
Задание 8 Исследовать ряд 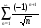 на абсолютную и условную сходимость
на абсолютную и условную сходимость
Решение: данный ряд знакочередующийся. Проверяем условия Лейбница.
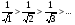 - верно
- верно
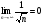 - верно
- верно
Условия Лейбница выполняются, следовательно, ряд сходится.
Составим ряд из абсолютных величин: 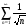 . Это ряд Дирихле,
. Это ряд Дирихле, 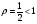 , следовательно он расходится. Значит, исходный данный ряд сходится условно
, следовательно он расходится. Значит, исходный данный ряд сходится условно
Задание 9 Исследовать ряд 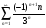 на абсолютную и условную сходимость
на абсолютную и условную сходимость
Решение: данный ряд знакочередующийся. Проверяем условия Лейбница.
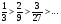 - верно
- верно
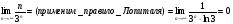 - верно.
- верно.
Условия Лейбница выполняются, следовательно, ряд сходится.
Составим ряд из абсолютных величин: 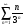 . Исследуем его на сходимость, применив признак Даламбера:
. Исследуем его на сходимость, применив признак Даламбера:
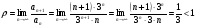
 ряд составленный из абсолютных величин сходится
ряд составленный из абсолютных величин сходится  исходный ряд сходится абсолютно
исходный ряд сходится абсолютно
Задание 10 Найдите интервал сходимости степенного ряда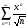
Решение: Найдём радиус сходимости
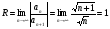
Т.е. (-1;1) - интервал сходимости.
Проверим сходимость на концах интервала.
При 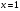
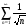 - числовой знакоположительный ряд, ряд Дирихле,
- числовой знакоположительный ряд, ряд Дирихле, 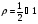 , значит, ряд расходится.
, значит, ряд расходится.
При 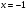
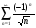 - числовой знакочередующийся ряд. Проверяем условия Лейбница:
- числовой знакочередующийся ряд. Проверяем условия Лейбница:
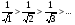 - верно
- верно
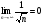 - верно
- верно
Условия Лейбница выполняются, следовательно, ряд 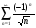 сходится. А так как ряд
сходится. А так как ряд 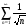 , составленный из абсолютных величин расходится, то ряд
, составленный из абсолютных величин расходится, то ряд 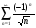 ) сходится условно.
) сходится условно.
Следовательно 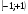 - интервал сходимости
- интервал сходимости
Задание 11 Найдите интервал сходимости степенного ряда 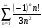
Решение: найдём радиус сходимости.
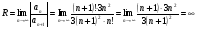
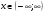 - интервал сходимости.
- интервал сходимости.
Задание 12 Разложить функцию 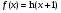 в ряд Маклорена
в ряд Маклорена
Решение: по формуле: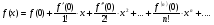
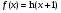 ,
, 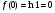
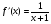 ,
,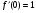
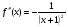 ,
, 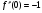
 ,
, 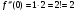
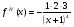 ,
, 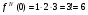
…
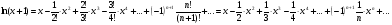 Задание 13 Разложить функцию
Задание 13 Разложить функцию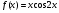 в ряд Маклорена
в ряд Маклорена
Решение: используем разложение функции косинуса:
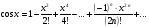
Умножим аргумент на 2:
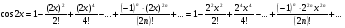
Далее умножим всё на х, получим:
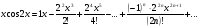
Задания для самостоятельного решения
Исследуйте числовые ряды на сходимость
Исследуйте ряды на абсолютную и условную сходимость
Найдите интервал сходимости степенного ряда
Разложите функцию в ряд Маклорена
8 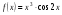
Контрольные вопросы
-
Числовые ряды: основные понятия и определения
-
Необходимый и достаточный признаки сходимости числовых рядов
-
Признаки сходимости Даламбера, Коши, признаки сравнения
-
Знакопеременные ряды. Знакочередующиеся ряды.
-
Абсолютная и условная сходимость рядов
-
Признак сходимости Лейбница для знакопеременных рядов
-
Функциональные ряды. Степенные ряды.
-
Разложение элементарных функций в ряд Маклорена
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 2. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-416с., ил.
-
Шипачёв В.С. Сборник задач по высшей математике: Учеб. пособие.- М.: Высш. шк. 2005.- 192с.: ил.
Практическое занятие №8
«Нахождение вероятности событий»
Цель занятия:
освоение знаний основных понятий по теории вероятностей, умений решать простейшие задачи
на определение вероятности событий
При выполнении задания студент должен:
знать:
-
понятия вероятности события,
-
понятия совместные и несовместные события;
-
теорему сложения вероятностей;
-
теорему умножения вероятностей;
-
формулу полной вероятности,
-
формулу Бернулли
-
формулу Байеса
уметь:
-
находить вероятность в простейших задачах, используя классическое определение
-
вероятностей и формулы комбинаторики;
-
решать задачи с применением теорем и формул
Краткие теоретические сведения
Основные понятия
Теория вероятностей - это математическая наука, изучающая закономерности случайных явлений, т.е. таких явлений, которые при неоднократном повторении каждый раз протекают по-разному.
Комбинаторика - это раздел теории вероятностей, в котором решаются задачи на составление различных комбинаций из конечного числа элементов, удовлетворяющих некоторым условиям и подсчета числа всех возможных комбинаций.
Существует три типа комбинаторных задач: 1) на составление перестановок, 2) на составление размещений, 3) на составление сочетаний
Перестановки - всевозможные упорядоченные комбинации, состоящие из n различных элементов. Число перестановок вычисляется по формуле: 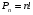
Размещения - всевозможные упорядоченные комбинации m элементов, составленные из n различных элементов, вычисляется по формуле: 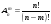
Сочетания - всевозможные неупорядоченные комбинации m элементов, составленные из n различных элементов, вычисляется по формуле: 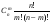
При решении комбинаторных задач используют следующие правила:
Правило суммы: если некоторый объект A может быть выбран из совокупности объектов s способами, а другой объект B может быть выбран t способами, то выбрать объект A либо B можно (s+t) способами.
Правило произведения: если объект A можно выбрать из совокупности объектов s способами и после каждого такого выбора можно выбрать объект B t способами, то объект A и B можно выбрать 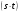 способами.
способами.
Событие - это факт, который при осуществлении определенных условий может произойти или нет. События обозначаются большими буквами латинского алфавита А, В,С...
Виды событий:
Достоверное событие - это событие, которое в результате испытания непременно должно
произойти.
Невозможное событие - это событие, которое в результате испытания не может произойти.
Случайное событие - это событие, которое при испытаниях может произойти или не может
произойти.
Несовместные события - события, если в результате данного испытания появление одного
из них исключает появление другого.
Совместные события - события, если в результате данного испытания появление одного из
них не исключает появление другого.
Равновозможные события - события, если нет оснований считать, что одно из них
происходит чаще, чем другое.
События образуют полную группу событий, если в результате испытания обязательно
произойдет хотя бы одно из них и любые два из них несовместны.
Противоположные события - два несовместных события А и Ā (читается «не А»), если в
результате испытания одно из них должно обязательно произойти.
Операции над событиями
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
Произведением нескольких событий называется событие, которое состоит в совместном наступлении всех этих событий в результате испытания.
Определение вероятности
Вероятность события - это число, характеризующее степень возможности появления событий при многократном повторении событий.
Вероятность обозначается буквой Р (probability (англ.) - вероятность).
Классическое определение вероятности: Вероятностью Р(А) события А называется
отношение числа благоприятствующих исходов m к общему числу равновозможных
несовместных исходов n: Р(А)=m/n
Свойства вероятности:
-
Вероятность случайного события А находится между 0 и 1, т.е. 0<Р(А)<1
-
Вероятность достоверного события равна 1
-
Вероятность невозможного события равна 0
Условная вероятность - вероятность наступления событий, вычисленная в предположении, что событие уже произошло
Теоремы сложения вероятностей
-
Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих
событий: Р(А+В)=Р(А)+Р(В).
-
Вероятность появления хотя бы одного из двух совместных событий равна сумме
вероятностей этих событий без вероятности их совместного наступления:
Р(А+В)=Р(А)+Р(В)-Р(А*В).
Теоремы умножения вероятностей
-
Вероятность произведения 2 независимых событий А и В равна произведению вероятностей
этих событий: Р(А*В)=Р(А)*Р(В)
-
Вероятность совместного появления двух зависимых событий равна произведению одного
из них на условную вероятность второго при условии первого:
P(AB)=P(A)*P(B/A)=P(B)*P(A/B)
Формула полной вероятности
Пусть событие А может быть реализовано только при условии появления одного из событий Hi, i = 1,..., n. Предположим, что события Hi несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны. Такие события Hi называются гипотезами. Тогда вероятность события А можно вычислить с помощью формулы полной вероятности: 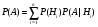
Формулы Байеса
Предположим теперь другую ситуацию: пусть теперь известно, что событие A произошло. Это знание влияет на нашу оценку вероятностей гипотез Нk, т.е. на вероятность того, что событие A произошло именно путем Нk. Эти условные вероятности (т.е. при условии,
что событие А произошло), вычисляются с помощью формулы Байеса: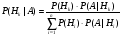 .
.
Отметим, что в знаменателе этой формулы записана ничто иное как вероятность Р(А), вычисленная по формуле полной вероятности.
Формула Бернулли
Под схемой Бернулли понимают конечную серию n повторных независимых испытаний с двумя исходами. Вероятность появления одного исхода при одном испытании обозначают p , а не появления его q, причём q=1-p. Вероятность ровно m успехов в серии из n повторных независимых испытаний вычисляется по формуле: 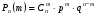
Образец решения задач
Задание 1 Для контроля качества продукции из партии готовых изделий выбирают для проверки 100 изделий. Проверку не выдерживают 5 изделий. Какова вероятность того, что наугад взятое изделие будет качественным?
Решение: 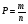
n=100 - число всех исходов - количество всех изделий
m=100-5 - число благоприятных исходов - количество качественных изделий
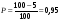
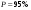
Задание 2 Из 500 деталей, среди которых 100 бракованных, наугад берутся 2 детали. Какова вероятность того, что из двух взятых деталей одна бракованная?
Решение: 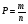
n - число всех исходов (взяли 2 детали из 500)
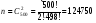
m - число благоприятных исходов (взяли 1 деталь из 100 бракованных и 1 деталь из 400 годных)
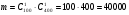
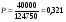 , т.е. 32%
, т.е. 32%
Задание 3 Мастер обслуживает 5 станков. 30% рабочего времени он проводит у первого станка, 20 - у второго, 15 - у третьего, 25 - у четвертого и, наконец, 10 % - у пятого. Найти вероятность того, что в наудачу выбранный момент времени он находится у второго или пятого станка
Решение: пусть A,B,C,D,E - события, которые состоятся, если в наугад выбранный момент времени мастер находится соответственно у 1,2,3,4-го или 5 станка. Из условия задачи следует что A,B,C,D,E попарно несовместные события.
Р(А)=0,20, Р(В)=0,10, Р(С)=0,15, Р(D)=0,25, Р(Е)=0,30.
В+Е-событие, которое состоится, если мастер находится у 2-го или 5-го станка.
По теореме сложения вероятностей
Р(В+Е)=Р(В)+Р(Е)=0,10+0,30=0,40, т.е. 40%
Задание 4 В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны 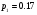 ,
, 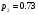 и
и 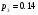 . Найдите вероятность того, что тока в цепи не будет.
. Найдите вероятность того, что тока в цепи не будет.
Решение: А - событие, состоящее в том, что тока нет,
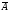 - событие, состоящее в том, что ток есть,
- событие, состоящее в том, что ток есть,
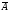 = В1*В2*В3, где Вi - событие, состоящее в том, что элемент исправен
= В1*В2*В3, где Вi - событие, состоящее в том, что элемент исправен
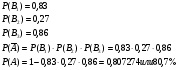
Задание 5 С первого станка-автомата на сборочный конвейер поступает  деталей, со 2-го и 3-го - по
деталей, со 2-го и 3-го - по  и
и  соответственно. Вероятности выдачи бракованных деталей составляют для каждого из них соответственно
соответственно. Вероятности выдачи бракованных деталей составляют для каждого из них соответственно 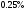 ,
, 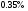 и
и 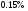 . Найдите вероятность того, что поступившая на сборку деталь окажется бракованной, а также вероятности того, что она изготовлена на 1-м, 2-м и 3-м станках-автоматах, при условии, что она оказалась бракованной.
. Найдите вероятность того, что поступившая на сборку деталь окажется бракованной, а также вероятности того, что она изготовлена на 1-м, 2-м и 3-м станках-автоматах, при условии, что она оказалась бракованной.
Решение: по формуле полной вероятности: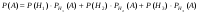 найдём вероятность того, что поступившая на сборку деталь бракованная:
найдём вероятность того, что поступившая на сборку деталь бракованная:
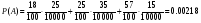
По формуле Байеса: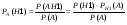
найдём вероятности того, что она изготовлена на 1-м, 2-м и 3-м станках-автоматах
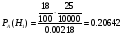
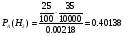
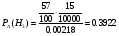
Задание 6 Вероятность допустить ошибку сверх требуемой точности при одном измерении данным прибором равна 0,2. Найдите вероятность того, что при 10 измерениях этим же прибором число измерений с подобными ошибками будет равно трём
Решение: искомую вероятность найдём по формуле Бернулли: 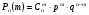
Из условия задачи n = 10, m = 3, p = 0,2, тогда q = 1 - p = 1 - 0,2 = 0,8, следовательно
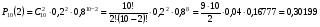 , т.е. 30%
, т.е. 30%
Задание 7 В магазине покупателей обслуживают три кассовых аппарата А1, А2, А3, каждый из которых в течение рабочего дня может проработать безотказно с вероятностями 0,85, 0,9 и 0,95 соответственно. Найти вероятность того, что в течение дня выйдут из строя:
а) первый и третий аппарат;
б) только один аппарат;
в) хотя бы один аппарат.
Решение: Вычисляем вероятности противоположных событий, состоящих в том, что в течение дня кассовые аппараты выйдут из строя:
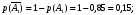
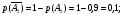
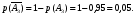
а) Вероятность того, что в течение дня выйдут из строя первый и третий аппарат, вычисляем по теореме вероятности произведения событий. Так как события 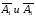 независимы, то вероятность их одновременного наступления равна произведению их вероятностей:
независимы, то вероятность их одновременного наступления равна произведению их вероятностей:
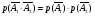
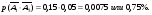
б) Вероятность того, что в течение дня выйдет из строя только один аппарат, вычисляем по теоремам вероятностей суммы и произведения событий:
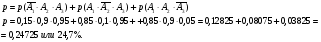
в) Событие, состоящее в том, что в течение дня хотя бы один кассовый аппарат выйдет из строя, противоположно событию, состоящему в том, что в течение дня все аппараты проработают безотказно. Применяя формулу вероятности противоположного события и теорему вероятности произведения событий, получим:
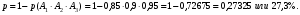
Задания для самостоятельного решения
-
Среди 200 изделий, подвергавшихся термической обработке, в среднем 180 высшего сорта. Найти вероятность извлечения не высокосортного изделия
-
В партии из 20 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 3 стандартных
-
Данное предприятие в среднем дает 21% продукции высшего сорта и 65% продукции первого сорта. Найти вероятность того, что случайно взятое изделие окажется первого или высшего сорта
-
Участок электрической цепи состоит из трёх элементов, каждый из которых работает незави- симо от двух других. Элементы не выходят из строя за определённый промежуток времени соответственно с вероятностью -0,8, 0,7, 0,9. Определить вероятность нормальной работы всего участка
-
Литьё на болванках для дальнейшей обработки поступает из двух заготовительных цехов: 70% из первого цеха и 30% из второго, при этом материал первого цеха имеет 10% брака, а материал второго цеха - 20% Найти вероятность того, что одна взятая на удачу болванка не имеет дефектов
-
Вероятность допустить ошибку сверх требуемой точности при одном измерении данным прибором равна 0,2. Найдите вероятность того, что при 10 измерениях этим же прибором число измерений с подобными ошибками будет равно трём
-
Трое рабочих собирают подшипники. Вероятность того, что подшипник, собранный первым рабочим, - высшего качества, равна 0,7, вторым - 0,8, третьим - 0,6. Для контроля взято по одному подшипнику из собранных каждым рабочим. Какова вероятность того, что высшего качества будут: а) все подшипники; б) два подшипника; в) хотя бы один подшипник?
Контрольные вопросы
-
Задачи теории вероятностей.
-
Элементы комбинаторики. Перестановки, размещения, сочетания
-
Понятие испытания и события. Виды событий.
-
Сумма и произведение событий
-
Определение вероятности события
-
Теоремы сложения и умножения вероятностей.
-
Формула полной вероятности. Формула Байеса
-
Формула Бернулли
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. - М.: Высш. шк. 1999.- 479с.: ил.
Практическое занятие №9
«Нахождение функции распределения и числовых характеристик дискретной случайной величины»
Цель занятия:
освоение знаний построения закона распределения дискретной случайной величины,
нахождение функции распределения и числовых характеристик дискретной случайной
величины
При выполнении задания студент должен:
знать:
-
способы задания случайной величины,
-
определения непрерывной и дискретной случайных величин;
-
закон распределения случайной величины,
-
определение математического ожидании, дисперсии и среднего квадратического отклонения
-
дискретной случайной величины;
уметь:
-
строить ряд распределения случайной величины;
-
находить функцию распределения случайной величины.
-
находить математическое ожидание, дисперсию и среднее квадратическое отклонение
-
случайной величины по заданному закону ее распределения
Краткие теоретические сведения
Случайная величина - величина, которая принимает в результате испытания то или иное возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.
Случайные величины могут быть дискретными и непрерывными.
Дискретной называют такую случайную величину, которая принимает счётное
множество значений
Непрерывной называют такую случайную величину, которая может принимать любые значения в определённом интервале. Занумеровать все значения величины, попадающие даже в узкий интервал принципиально невозможно.
Случайные величины обозначают прописными буквами латинского алфавита X, Y, Z, а их возможное значение - соответствующими строчными буквами x, y, z.
При многократных испытаниях определённые значения случайной величины могут встречаться несколько раз. Поэтому, для задания случайной величины недостаточно перечислить лишь все
её возможные значения. Необходимо также знать, как часто могут появляться те или иные значения в результате испытания при одних и тех же условиях, т.е. нужно задать вероятности их появления.
Случайная величина считается заданной, если известен закон распределения случайной величины.
Распределением (законом распределения) случайной величины называется всякое соотношение между возможными значениями случайной величины и соответствующими им вероятностями.
Распределение дискретной случайной величины может быть задано в виде таблицы, в графическом и аналитическом виде.
Пусть дискретная величина X принимает значения Х=х1, Х=х2,…, Х=хn. Обозначим вероятности этих событий соответственно: Р(Х = х1) = р1, Р(Х = х2) = р2,…, Р(Х = хn) = рn.
Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания распределения дискретной случайной величины:
Значение случайной величины х1
х1
х2
…
хn
Вероятности значений р1
р1
р2
…
рn
Так как в результате испытания случайная величина Х всегда примет одно из своих возможных значений х1, х2, … хn, то эти случайные события образуют полную группу событий и
n
р1 + р2 + …+ рn = ∑ pi = 1.
i =1
Табличную формулу задания называют также рядом распределения.
Для наглядности ряд распределения можно представить в графическом виде, где по оси абсцисс откладываются значения случайной величины, а по оси ординат вероятности этих значений.
Функция распределения
В ряде практических случаев вместо вероятности того, что случайная величина Х принимает некоторое определённое значение хi ,необходимо знать, что случайная величина Х меньше хi. Эта вероятность задаётся интегральной функцией распределения.
Функция распределения определяет вероятность того, что случайная величина Х принимает значение, меньшее фиксированного действительного числа х, т.е. F(x) = P(X < x).
Функцию распределения F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Функцию F(x) можно получить, суммируя значения вероятностей по тем значениям случайной величины, которые меньше xi, т. е. F(xi) = P (X < xi) = ∑ P(xi), где неравенство x < xi под знаком суммы показывает, что суммирование распространяется на все значения х меньше xi.
Для дискретной случайной величины график функции распределения представляет собой разрывную ступенчатую функцию. Когда переменная х принимает какое-нибудь из своих возможных значений, функция распределения увеличивается скачкообразно на величину вероятности этого значения. Причём при переходе слева к точкам разрыва функция сохраняет своё значение. На графике это отмечено чёрной точкой. Сумма величин всех скачков функции F(x) равна 1.
Числовые характеристики случайных величин
Закон распределения полностью характеризует случайную величину. Но при решении ряда практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее пользоваться некоторыми количественными показателями, которые в сжатой форме дают достаточную информацию о случайной величине. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются: математические ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание характеризует положение случайной величины на числовой оси, определяя некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.
Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных её значений на соответствующие вероятности: 
Дисперсия характеризует рассеяние (отклонение) случайной величины относительно математического ожидания. Дисперсия случайной величины Х - математическое ожидание квадрата отклонения случайной величины Х от её математического ожидания М (Х), обозначают D(X), т.е. D(X) = M(X - M(X))2
Для дискретных случайных величин эту формулу можно записать в следующем виде: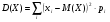
Для вычислений удобно использовать формулу: D(Х) = М(Х2) -М2(Х)
Размерность дисперсии равна квадрату случайной величины и её неудобно использовать для характеристики разброса, поэтому удобнее применять корень квадратный из дисперсии - среднее квадратическое отклонение. Эта величина даёт представлять о размахе колебаний случайной величины около математического ожидания: 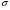 (Х) =
(Х) =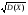
Образец решения задач
Задание 1 Дан закон распределения случайной величины. Найти функцию распределения и построить ее график. Найти числовые характеристики
-
хi
-1
2
6
pi
0,5
р
0,2
Решение: Сначала найдём неизвестное р2 =1- р1 - р3 =1-0,5-0,2=0,3
Для нахождения функции распределения воспользуемся схемой:
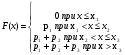
Получим 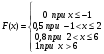
Построим график функции распределения
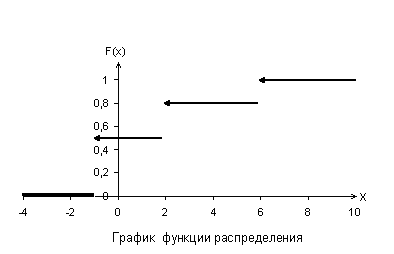
Для вычисления математического ожидания воспользуемся формулой: 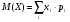
Получим M(X)=(-1).0,5+2.0,3+6.0,2=1,3
Для вычисления дисперсии воспользуемся двумя соотношениями, одно из которых соответствует определению дисперсии, другое - ее свойству.
По определению: 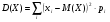
В примере получим: D(X)=(-1-1,3)2 . 0,5+(2-1,3)2 . 0,3+(6-1,3)2 . 0,2=7,21
По формуле: D(Х) = М(Х2) -М2(Х)
M(X2) = (-1)2 . 0,5+22 . 0,3+62 . 0,2=8,9
М2(Х) = 1,32 = 1,69
D(X) = 8,9 - 1,69 =7,21
Проверяем: значения D(X) совпадают
Среднее квадратическое отклонение находим по формуле
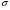 (Х) =
(Х) =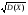
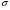 (Х) =
(Х) =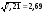
Задание 2 Депозитный риск (вероятность досрочного отзыва депозита) для трех клиентов некоторого банка есть величина постоянная, равная p=0,2. Составить закон распределения дискретной случайной величины X - числа отозванных депозитов. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины
Решение: Имеем серию n=3 независимых испытаний, в каждом из которых событие A (отзыв депозита) происходит с вероятностью p=0,2. Так как описанная в условии случайная величина X распределена по закону Бернулли, то вероятности p(X=m) того, что событие A произойдет m раз, могут быть вычислены по формуле Бернулли:
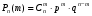
где 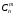 - количество сочетаний из n элементов по m, определяемое комбинаторной формулой:
- количество сочетаний из n элементов по m, определяемое комбинаторной формулой:
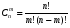
В нашем случае: n=3, p=0,2, q=1-p=1-0,2=0,8, поэтому:
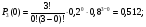
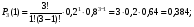
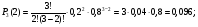
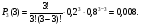
Контроль: 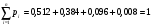
Составляем закон распределения случайной величины X:
-
xi
0
1
2
3
pi
0,512
0,384
0,096
0,008
Вычисляем числовые характеристики данной случайной величины, распределенной по закону Бернулли:
математическое ожидание: M(X)=np
M(X)=3·0,2=0,6.
дисперсия: D(X)=np(1-p)
D(X)=3∙0,2∙0,8=0,48.
среднее квадратическое отклонение: 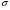 (Х) =
(Х) =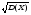
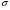 (Х) =
(Х) = 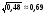
Задание 3 Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р1=0,3; p2=0,4; p3=0,5; p4=0,6. Найти закон распределения этой случайной величины, математическое ожидание и дисперсию
числа отказавших приборов.
Решение: принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем 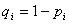 - вероятность безотказной работы приборов
- вероятность безотказной работы приборов
Рассмотрим все возможные варианты:
1) Не отказал ни один прибор
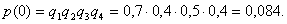
2) Отказал один из приборов
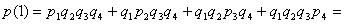 0,302.
0,302.
3) Отказали два прибора
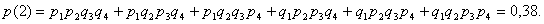
4) Отказали три прибора
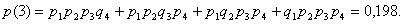
5) Отказали все приборы
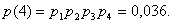
Получаем закон распределения:
х
0
1
2
3
4
р
0,084
0,302
0,38
0,198
0,036
Контроль: р=0,084+0,302+0,38+0,196+0,036=1
Математическое ожидание:
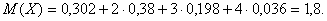
x2
0
1
4
9
16
р
0,084
0,302
0,38
0,198
0,036
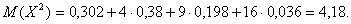
Дисперсия:
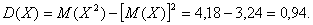
Задания для самостоятельного решения
-
Выход из строя коробки передач происходит по трем основным причинам: поломка зубьев шестерен, недопустимо большие контактные напряжения и излишняя жесткость конструкции. Каждая из причин приводит к поломке коробки передач с одной и той же вероятностью, равной 0,1. СВ X - число причин, приведших к поломке в одном испытании. Найти закон распределения указанной дискретной случайной величины (СВ) X и её
функцию распределения F(x). Вычислить математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение (Х). Построить график функции распределения
-
В цехе имеется три резервных электродвигателя. Для каждого из них вероятность того, что в данный момент он включен, соответственно равна: 0,2; 0,3; 0,1. СВ X - число включенных электродвигателей. Найти закон распределения указанной дискретной случайной величины (СВ) X и её функцию распределения F(x). Вычислить математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение (Х). Построить график функции распределения
-
Дан закон распределения случайной величины. Найти функцию распределения и построить ее график. Найти числовые характеристики
Х
3,2
5,2
8,1
4.5
Р
р
0,3
0,2
0.1
Контрольные вопросы
-
Случайная величина. Способы задания случайной величины.
-
Определения непрерывной и дискретной случайных величин
-
Закон распределения случайной величины
-
Функция распределения случайной величины и её график
-
Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних проф. учеб. заведений / Н.В. Богомолов. -10-е изд., перераб.- М.: Высш. шк., 2008.-495с
-
Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. - М.: Высш. шк. 1999.- 479с.: ил.
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 2. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-416с., ил.
Практическое занятие №10
«Обработка статистических данных»
Цель занятия: приобретение навыков записи выборки в виде вариационного ряда и в
виде статистического ряда, вычисления числовых характеристик выборки, закрепить навыки вычисления числовых характеристик выборки и обработки результатов исследования с помощью математической статистики
При выполнении задания студент должен:
знать:
-
основные понятия математической статистики
уметь:
-
определять объем и размах выборки, моду и медиану
-
составлять вариационный ряд и статистическое распределение
-
строить функцию распределения, полигон гистограмму
-
находить статистические оценки параметров распределения
Краткие теоретические сведения
Задачи математической статистики
Математическая статистика - раздел прикладной математики, наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятности, позволяющую оценить надежность и точность выводов. Этот раздел прикладной математики посвящен изучению случайных величин по результатам наблюдений.
В прикладных задачах вероятность исследуемого события обычно неизвестна. Она
определяется приближенно по статистическим данным. Дать оценку полученной на основе опытных данных, вероятности события - одна из основных задач математической статистики.
Разработать методы анализа статистических данных зависимости от целей исследования. определить ее распределение с точностью до некоторого неизвестного параметра. Дать оценку этого параметра в виде числа или интервала, в котором с заданной вероятностью заключено значение неизвестного параметра.
Методы математической статистики широко применяются в самых различных областях
знаний - в физике, звездной астрономии, экономике, геологии, гидрологии, климатологии, биологии, медицине и др. Также широко используется математическая статистика и в промышленности. Исходным материалом являются статистические данные.
Основные понятия
Статистические данные - сведения о числе объектов какой-либо более или менее
обширной совокупности, обладающих теми или иными признаками.
Генеральная совокупность - совокупность всех исследуемых объектов.
Выборочная совокупностью (или выборка) - совокупность случайно отобранных
объектов из генеральной совокупности.
Объём выборки -число объектов выборочной или генеральной совокупности
Размах выборки -разность между наибольшим значением числовой выборки и ее
наименьшим значением.
Медиана - это значение, занимающее середину упорядоченного ряда, а в случае четного количества равное среднему арифметическому двух средних значений ряда
Мода - это значение признака выборки, имеющее наибольшую частоту
Распределение выборки
Пусть для изучения количественного признака X из генеральной совокупности извлечена выборка x1, х2,...., хi. Наблюдавшиеся значения хi, признака X называют вариантами. Повторяемость признака хi называется частотой ni. Сумма всех частот равна п. Относительная частота - рi = ni /n - выборочный аналог вероятности pi появления значения xi случайной величины X. Тогда выборочным аналогом ряда распределения естественно считать вариационный ряд. Вариационный ряд - выборка, представляющая собой неубывающую последовательность чисел
Частота - число членов совокупности с данной вариацией.
Относительная частота - отношение частоты к объему выборки
Дискретным вариационным рядом распределения называется ранжированная (расположенная в порядке возрастания или убывания) совокупность вариантов хi с соответствующими им частотами пi или относительными частотами рi.
Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины.
Функция распределения - функцию F(x) ,определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F(x)=Р(Х>x)
Графические изображения выборки
Для наглядного представления выборки часто используют различные графические
изображения. Простейшими графическими изображениями выборки являются полигон и гистограмма. Пусть выборка задана статическим рядом: (x1, п1), (х2, п2), ..., (хi, ni).
Полигон частот - ломанная, отрезки которой соединяют точки(xi ;ni).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат соответствующие им частоты ni. Точки (xi ;ni) соединяют отрезками прямых и получают полигон частот.
Аналогично полигону распределения строится полигон относительных частот. Нецелесообразно построение дискретного ряда для непрерывной случайной величины или для дискретной, число возможных значений которой велико. В подобных случаях следует построить интервальный ряд.
Полигон относительных частот - ломаная, отрезки которой соединяют точки (xi; Wi).
Для построения полигона относительных частот на оси абсцисс откладывают варианты Xi, а на оси ординат - соответствующие им относительные частоты Wj Точки (xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.
Гистограмма частот - ступенчатая фигура, состоящая из прямоугольников, основаниями
которых служат частичные интервалы длиною h, а высоты равны отношению n,/h (плотность частоты). При большом объеме выборки более наглядное представление дает гистограмма
Статистические оценки распределения
Построив вариационный ряд и изобразив его графически, можно получить
первоначальное представление о закономерностях, имеющих место в ряду наблюдений. Однако на практике зачастую этого недостаточно. Поэтому для дальнейшего изучения изменения значений случайной величины используют числовые характеристики вариационных рядов. Их обычно называют статистическими характеристиками или оценками.
Статистическое распределение - это таблица, в первой строке которой записаны все различные значения выборки в порядке возрастания, а во второй строке указаны соответствующие им частоты
Выборочной средней (выборочным математическим ожиданием)  называют среднее
называют среднее
арифметическое значение признака выборочной совокупности.
Если все значения  признака выборки объема
признака выборки объема  различны, то:
различны, то: Если же значения признака
Если же значения признака  имеют соответственно частоты
имеют соответственно частоты  , причем
, причем  , то
, то  или
или  .
.
Выборочной дисперсией  называют среднее арифметическое квадратов отклонения
называют среднее арифметическое квадратов отклонения
наблюдаемых значений признака от их среднего значения  .
.
Если все значения  признака выборки объема
признака выборки объема  различны, то
различны, то 
Если же значения признака  имеют соответственно частоты
имеют соответственно частоты  , причем
, причем  , то
, то 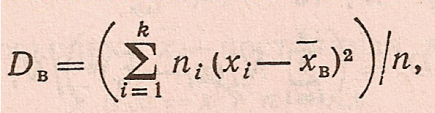
Выборочное среднее квадратическое отклонение - это квадратный корень из 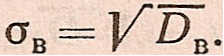
выборочной дисперсии
Образец решения задач
Задание 1 В опыте было получено 30 наблюдений над случайной величиной X, составляющих выборочную совокупность. Они приведены в таблице.
-
89
83
94
90
95
90
98
82
89
87
92
92
94
98
95
94
88
86
80
90
82
92
84
99
86
92
91
81
86
82
По выборочным данным: 1) составить ряд распределения; найти размах выборки; 2) построить эмпирическую функцию распределения; 3) найти числовые характеристики выборки: 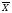 в- выборочное среднее, Dв- выборочную дисперсию;
в- выборочное среднее, Dв- выборочную дисперсию; 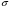 в- выборочное среднее квадратическое отклонение;
в- выборочное среднее квадратическое отклонение;
Решение: 1) Составим ряд распределения: расположим наблюдения 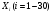 в порядке возрастания в верхней строке таблицы, в нижней строке nί - количество наблюдений в общем ряду наблюдений.
в порядке возрастания в верхней строке таблицы, в нижней строке nί - количество наблюдений в общем ряду наблюдений.
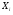
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
n.ί
1
1
3
1
1
0
3
1
1
2
3
1
4
0
3
2
0
0
2
1
Из этих наблюдений определим наибольшее Хмах = 99 и наименьшее Хмin = 80.
Вычислим размах варьирования d=Xmax - Xmin = 99-80=19.
2) Эмпирическая функция распределения 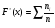 определяет для каждого значения х относительную частоту события Х < x. Она принимает значения
определяет для каждого значения х относительную частоту события Х < x. Она принимает значения 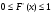 причем
причем 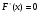 при
при 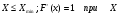 >
>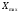 Таким образом, имеем
Таким образом, имеем
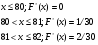
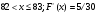
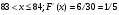
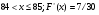
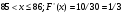
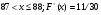
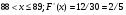
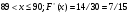
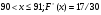
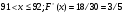
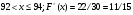
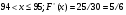
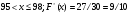

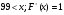
Построим график эмпирической функции распределения 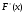
1
9/10
8/10
7/10
6/10
5/10
4/10
3/10
2/10
1/10
0
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
3) Найдем числовые характеристики выборочной совокупности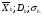
Оценка математического ожидания признака Х
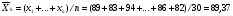
Выборочная дисперсия 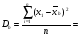
=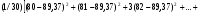
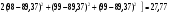
Среднеквадратическое отклонение 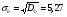
Задание 2 В результате измерения получена выборка: 121, 115, 125, 125, 117, 124, 120, 120, 119, 121, 122, 127, 118, 120, 123, 130, 123, 116, 124, 127,122. Постройте гистограмму, если число частичных промежутков равно 5.
Решение: Наименьшее значение выборки: 115. Наибольшее значение выборки: 130.
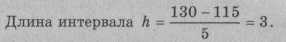
Число попаданий выборки в частичные промежутки соответственно равно:
[115, 118)- 3, [118, 121)- 8, [121, 124)- 6, [124, 127) - 4, [127, 130] - 3.
Составим интервальный вариационный ряд:

Для контроля правильности находим
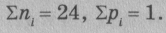
Строим гистограмму:
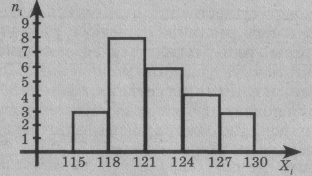
Задание 3 Для выборки 3, 8, -1, 3, 0, 5, 3, -1, 3, 5 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.
Решение: Объем выборки n=10; ее размах равен Δx=х -x
-x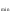 =8-(-1)=9.
=8-(-1)=9.
Записав значения выборки в виде неубывающей последовательности, получим вариационный ряд: -1, -1, 0, 3, 3, 3, 3, 5, 5, 8.
Составим статистический ряд
xi
-1
0
3
5
8
ni
2
1
4
2
1
Для контроля находим сумму частот 2+1+4+2+1=10 и убедимся в том, что она равна объему выборки. Вычислив относительные частоты, найдем выборочное распределение
xi
-1
0
3
5
8
wi
2
10
1
10
4
10
2
10
1
10
Для контроля убедимся в том, что сумма относительных частот равна 1: 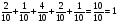
Задание 4 Постройте полигон относительных частот для статистического распределения выборки, заданной таблицей:
xi
1
2
3
4
5
6
ni
4
6
12
16
44
18
Решение: находим объем выборки как сумму частот всех вариант: n=4+6+12+16+44+18=100.
Находим относительные частоты всех вариант как отношения соответствующих частот к объему выборки:
xi
1
2
3
4
5
6
wi
0,04
0,06
0,12
0,16
0,44
0,18
Строим полигон относительных частот:
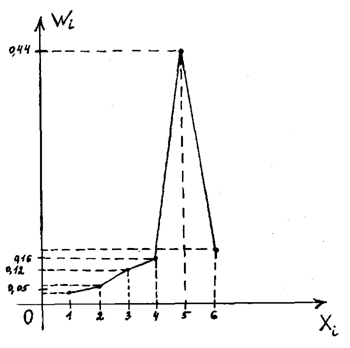
Задания для самостоятельного решения
-
В результате эксперимента была получена последовательность данных, составляющих выборочную совокупность наблюдений над случайной величиной X
88
94
91
98
87
88
86
89
86
82
93
86
81
83
84
87
88
86
89
86
По выборочным данным требуется:
-
определить объем и размах выборки
-
определить моду и медиану
-
составить вариационный ряд
-
составить статистическое распределение частот и относительных частот
-
построить эмпирическую функцию распределения
-
построить полигон частот и относительных частот
-
построить гистограмму частот и относи тельных частот
-
найти числовые характеристики выборки: выборочную среднюю; выборочную дисперсию;
выборочное среднее квадратическое отклонение
Контрольные вопросы
-
Предмет математической статистики, основные задачи статистики. Область применения статистических методов
-
Понятие о генеральной совокупности и выборки
-
Вариационный ряд
-
Объём, размах, мода, медиана выборки
-
Частота и относительная частота
-
Статистическое распределение.
-
Гистограмма. Полигон
-
Характеристики положения и рассеяния статистического распределения
-
Статистические оценки параметров распределения
Литература
-
Омельченко В.П. Математика: учеб. пособие В.П. Омельченко, Э.В. Курбатова - 2-е изд., перераб. и доп.- Ростов на/Д: Феникс, 2007.- 380с.- (Среднее профессиональное образование)
-
Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. - М.: Высш. шк. 1999.- 479с.: ил.
-
Данко П.Е Высшая математика в упражнениях и задачах. В.2ч. Ч. 2. Учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд.- М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2008.-416с., ил.