- Преподавателю
- Математика
- Разработка урока по теме Формула корней квадратного уравнения
Разработка урока по теме Формула корней квадратного уравнения
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Тетеря Т.П. |
| Дата | 24.01.2015 |
| Формат | docx |
| Изображения | Есть |
Формула корней квадратного уравнения
/урок алгебры в 8 классе/
Тип урока: изучение нового материала
Цели урока: вывести формулу корней полного квадратного уравнения, уметь применять ее при решении уравнений;
- развитие умения самостоятельно мыслить;
- воспитание умения работать в группе, умения слушать других, умения аргументировать свою точку зрения.
Комментарии
Ход урока
Целевые установки, выявление проблем, связанных с предложенной темой.
Работа в парах.
Среди сформулированных проблем могут быть и такие, которые ребята уже могут разрешить.
Объявить тему урока и попросить пары сформулировать и записать в тетрадях все проблемы, которые возникают у них по этой теме.
Например:
- Сколько корней имеет уравнение 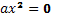
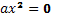 и чему они равны?
и чему они равны?
- Как решить уравнение вида 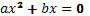
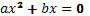 ?
?
- Всегда ли имеет решение уравнение
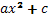
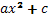 =0?
=0?
- Существует ли формула, по которой можно найти корни уравнения 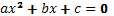
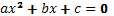 ?
?
- Всегда ли квадратное уравнение имеет корни?
- Каково наибольшее число корней квадратного уравнения?
-При каких условиях квадратное уравнение имеет единственный корень?
Слушаем пары. На некоторые вопросы учащиеся могут дать обоснованный ответ, пользуясь уже имеющимися знаниями.
Затем пары могут обсудить, сопоставить то, что они зафиксировали в тетрадях, с рассуждениями другой пары. Представитель четверки сообщает классу проблемы, которые надо решить при изучении этой темы.
Учитель может все, что говорят ребята, кратко записывать на доске. Проблемы располагаются в удобном для изучения порядке, и начинается поиск их решения.
Каждой четверке дается право высказываться по тем проблемам, решение которых она нашла.
Поиск решения
-
Учащиеся предлагают решение уравнения.
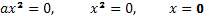
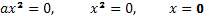 и приводят примеры для различных
и приводят примеры для различных 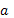
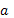 .
.
Решения (выводы учащихся)
-
Для решения уравнения
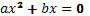
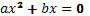 предлагают разложить левую часть на множители:
предлагают разложить левую часть на множители: 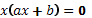
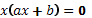 и каждый множитель приравнять к нулю. Делают вывод, что данное уравнение всегда имеет два корня: х=0 и -b/a. Далее приводят примеры решения таких уравнений при различных а и b.
и каждый множитель приравнять к нулю. Делают вывод, что данное уравнение всегда имеет два корня: х=0 и -b/a. Далее приводят примеры решения таких уравнений при различных а и b. -
Для решения уравнения
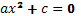
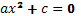 в некоторых группах ребята могут прийти к выводу, что если левую часть уравнения можно разложить на множители, т.е.если
в некоторых группах ребята могут прийти к выводу, что если левую часть уравнения можно разложить на множители, т.е.если 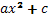
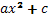 представляет собой разность квадратов, то получается два корня. Например, уравнения
представляет собой разность квадратов, то получается два корня. Например, уравнения
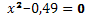
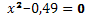 имеют по два корня.
имеют по два корня.
-
В других четверках ребята замечают, что если с перенести в правую часть уравнения и все разделить на а, то получается уравнение:
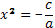
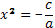 . Дальнейшее решение зависит от знака правой части. Если
. Дальнейшее решение зависит от знака правой части. Если 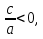 то можно получить два корня.
то можно получить два корня.
Учитель формулирует определение нового понятия.
Далее учитель дает определение неполных квадратных уравнений и все записывают их решение в общем виде. Примеры уравнений и их решения учащиеся могут привести самостоятельно.
Особое внимание уделяется решению полных квадратных уравнений.
Актуализация знаний и опыта.
Сначала нужно вспомнить решение частных случаев квадратных уравнений методом разложения на множители, и методом выделения полного квадрата. Например,
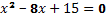
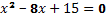
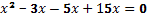
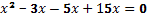
x(x-3)-5(x-3)=0
(x-3)(x-5)=0
x=3 или х=5
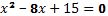
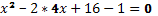
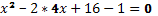
(х-4)2=1
х-4=1 или х-4=-1
х=3 или х=5
Проблемная ситуация.
Поставить вопрос: можно ли этими способами решить любое квадратное уравнение? Указать недостатки этих методов.
Столкновение учащихся с затруднениями.
Метод разложения на множители применим не всегда (например, уравнение х2+х-3=0 методом разложения на множители не решить). Таким образом, учащиеся стоят перед необходимостью найти алгоритм решения квадратных уравнений, не зависящих от эвристик метода разложения на множители.
Выдвижение гипотезы.
С другой стороны, все понимают, что выделить полный квадрат можно в любом трехчлене, хотя зачастую это сделать нелегко.
Учитель помогает реализовать выдвинутое предложение.
Поскольку вывод формулы корней достаточно сложный для самих ребят, то учитель записывает этот вывод на доске, вводит понятие дискриминанта, обсуждает в диалоге с классом зависимость количества корней от знака дискриминанта. После того, как формулы корней выведены, рассматривается их применение в решении различных квадратных уравнений. Например, 2х2+3х+1=0, 25х2-10х+1=0, х2-2х+5=0
Применение выводов на практике. Учитель может проверить усвоение новых формул каждым учеником.
В конце урока учащимся предлагается выполнить работу на закрепление полученных формул.
Вариант 1
Вариант 2
Дано уравнение
2х2-9х+10=0
5х2-8х+3=0
1. Укажите старший коэффициент, второй коэффициент и свободный член уравнения.
2. Определите количество корней уравнения.
3. Найдите корни.
Учитель подводит итог урока.
Итог урока. Формула, которую мы вывели на этом уроке, не случайно воспринята вами как «подарок судьбы». С помощью нее можно решить любое квадратное уравнение, о значимости, которых вы сможете убедиться в дальнейшем курсе алгебры.
Домашнее задание:


