- Преподавателю
- Математика
- Урок по теме Тригонометрические функции. Преобразование тригонометрических выражений
Урок по теме Тригонометрические функции. Преобразование тригонометрических выражений
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Сентюрина Л.И. |
| Дата | 22.02.2016 |
| Формат | docx |
| Изображения | Есть |
Повторения и закрепления знаний по теме « Тригонометрические функции. Преобразование тригонометрических выражений»
Урок можно провести в форме игры
«Счастливый случай»
Счастливый случай.
Гейм 1: Гонка за лидером.
Начинает команда, первая ответившая на вопрос:
Что называется арксинусом числа а?
За каждый верный ответ команда получает 2 балла, за ответ болельщиков команды 1балл, за ответ соперников команды 1балл команде соперников.
Вопросы:1. Область определения синуса.
2. Область значения косинуса.
3. arcsin1
4. Нечётные тригонометрические функции.
5. Сравни cos π и sin 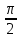 .
.
«Счастливый случай»
Вопрос 1. tg α + сtg α=2 Найти tg2 α + сtg2 α (Ответ 2)
Вопрос 2. Найти tg α + сtg α при α= - 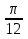 . (Ответ -4)
. (Ответ -4)
Гейм 2: Торопись не спеша.
Задания выполняют одновременно обе команды. Решают цепочкой все члены команды. Последующему можно исправлять решение предыдущего.
Задания 1 команде.
1.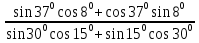
2. 2cos 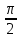 - 5sin
- 5sin 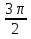 + 8tgπ
+ 8tgπ
3. sin(x-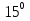 )+sin(
)+sin(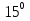 -x)
-x)
4. 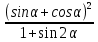
5. sin(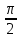 - α) + cos (π-α) + tg(π-α)+ctg(
- α) + cos (π-α) + tg(π-α)+ctg(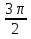 - α)
- α)
6. 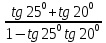
Задания 2 команде.
1.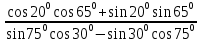
2. 4sin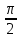 - 6ctg
- 6ctg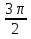 + 3cosπ
+ 3cosπ
3. cos (x - 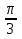 ) - cos(
) - cos(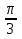 - 3)
- 3)
4.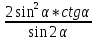
5.sin(1800 - α) + cos (900 + α) - tg(3600 - α) - ctg(2700 - α)
6. sin2 α + tg α ctg α + cos2 α
Ответы :
№ задания
1 команда
2 команда
1
1
1
2
5
1
3
0
0
4
1
1
5
0
0
6
0
2
Гейм 3: Спешите видеть.
Команды ищут ошибки в формулах, решениях, примерах, чертежах.
Указывают номера заданий с ошибками, листочки сдают жюри.
Верный ответ +2б., неверный -2б.
1. Знаки тангенса.
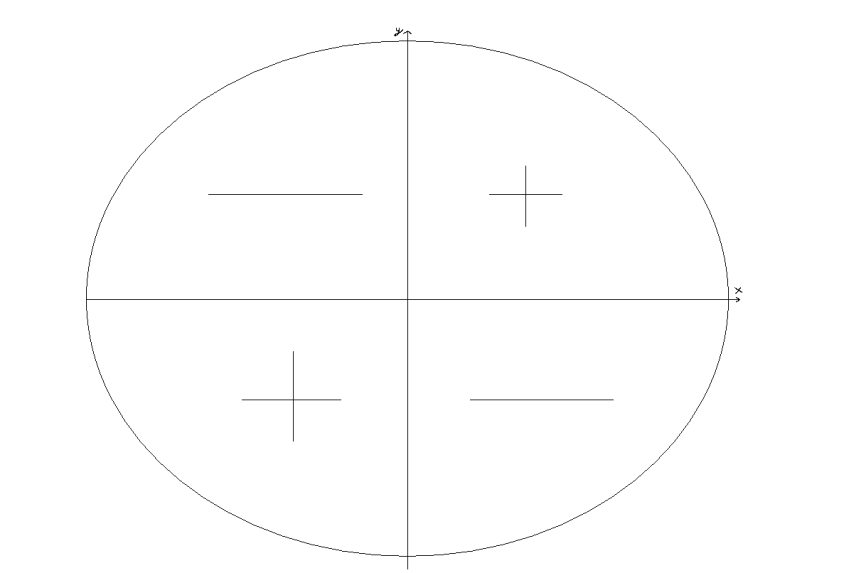
2.cos2 α =2sin2 α-1
3. sin1300·cos 1700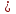 0
0
4. 1 - sin2α =2sin2α
5. ctg(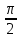 - α)=tgα
- α)=tgα
6. cos (-α)=cosα
7.cos(α+β)=cosα cos β + sinα sinβ
8. sin 2α=2 sinα cosα
9. arcsin(-  ) =-
) =- 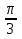
10. Знаки синуса:
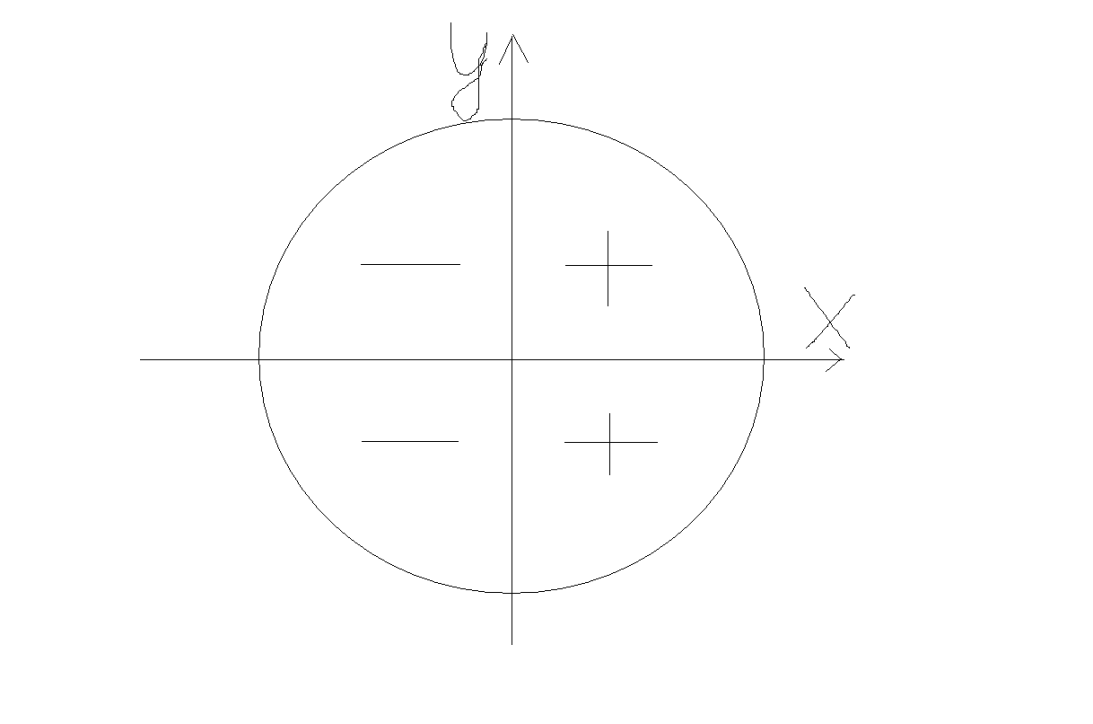
11.cos ( 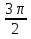 +α )= sin α
+α )= sin α
12.tgα ctgα = 1
13. Если sin α <0, a cos α >0 , то 2700< α < 3600
14. sin 3300 =- 
15. (sin α -1) (sin α+ 1)= - cos2α
16. 4sin 150 cos 150 =4
№ задания
Верно/неверно
1
верно
2
неверно
3
неверно
4
неверно
5
верно
6
верно
7
неверно
8
верно
9
неверно
10
неверно
11
верно
12
верно
13
верно
14
верно
15
верно
16
неверно
Гейм для болельщиков.
По 3 человека из команд болельщиков доказывают тождества, +2 балла за каждое тождество:
-
Cos2150 -sin2150=-sin2400
-
2sin150cos150=(cos2
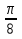 -sin2
-sin2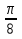 )2
)2 -
2 -sin2 α-cos2 α=1
Гейм 4: Дальше, дальше, дальше…
Команды должны за 7 мин ответить на наибольшее количество вопросов.
За каждый верный ответ дается 1б.
За досрочный ответ на все вопросы дается дополнительно 5б.
Если команда не может дать ответ, то отвечающий говорит: «Дальше, дальше…» и получает следующий вопрос.
Вопросы командам
1.
Выразить в градусной мере
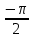
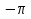
2.
Выразить в радианной мере
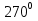
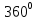
3.
sin(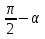 )
)
cos 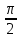
4.
tg 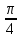
cos (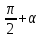 )
)
5.
6.
arcsin (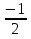 )
)
arcsin 
7.
arccos (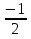 )
)
arccos (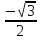 )
)
8.
Может ли синус отрицательного числа быть положительным?
Может ли косинус положительного числа быть отрицательным?
9.
Знак косинуса в IV четверти.
Знак синуса в IV четверти.
10.
В прямоугольном треугольнике величина острого угла равна
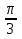
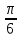
Найти величину второго острого угла
11.
Формула для решения уравнения
cos x=a
sin x=a
12.
Определить знак
sin 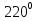
cos 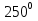
13.
Вычисли
sin 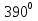
cos 4050
14.
Абсциссы максимумов графиков функции
y=sinx
y=cosx
15.
sin2 α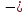 1
1
sin2α + cos2α
16.
Определи знак разности
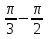
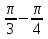
17.
Вычисли
cos21π
sin19π
18.
Вычисли
sin0 + cos0
sin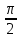 + cos
+ cos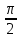
19.
Определи, какой четверти принадлежит угол α
sinα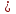 0, cosα
0, cosα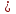 0
0
sinα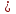 0, cosα
0, cosα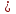 0
0
20.
Переведи в градусную меру
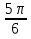

Команде -победительнице в этом гейме+1б.


