- Преподавателю
- Математика
- Решение задач геометрии с использованием свойств площадей
Решение задач геометрии с использованием свойств площадей
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Бетанов Д.М. |
| Дата | 01.12.2014 |
| Формат | docx |
| Изображения | Есть |
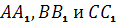
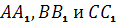
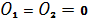
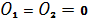
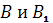
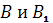
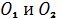
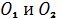
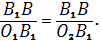

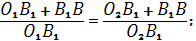
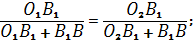
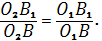
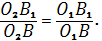
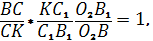
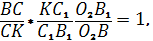
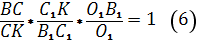
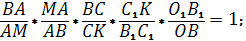
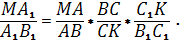
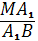
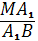
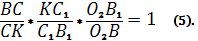
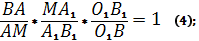
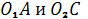
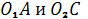
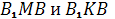
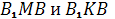
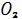
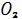
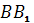
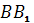
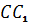
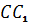
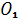
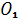
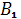
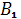
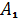
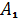
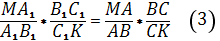
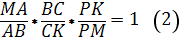
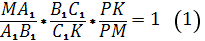
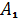
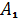
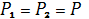
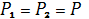
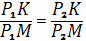
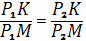

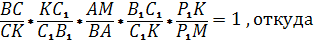
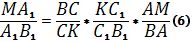
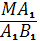
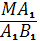
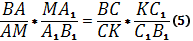
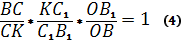
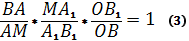
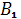
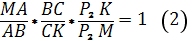
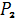
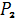
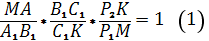
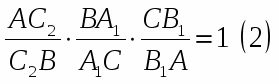
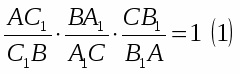
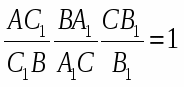
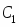
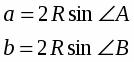
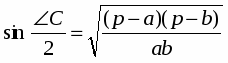
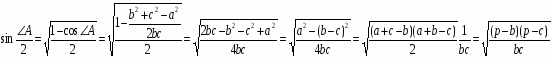
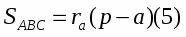
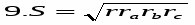
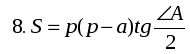 Решение задач геометрии с использованием свойств площадей.
Решение задач геометрии с использованием свойств площадей.
Работа учителя математики
МОУ СОШ №46
Бетанова Дантеса Магометовича
-
В приведенных разработках рассматривается использование наряду с традиционной теоретической информацией учебников геометрии некоторое ее расширение и актуализация ряда утверждении, вытекающих изсвойств площади.
-
Так как основной фигурой при решении задач оказывается треугольник, то полезно в актив возможностей учащихся ввести следующие утверждения.
Ряд полезных утверждении
-
Утверждение №1
Пусть дан отрезок АВ Геометрическое место точек М таких, что площадь треугольника АВМ равна заданной величине S, естьдве прямые, параллельные отрезку АВ и находящихся от прямой АВ на расстоянии h=2S/AB
-
Утверждение №2
Если треугольники имеют равные высоты, то отношение их площадей равно отношению основании.
Утверждение №3
-
Если треугольники имеют равные основания, то отношение их площадей равно отношению их высот.
Утверждение №4
-
Если два треугольника имеют по одному равному углу, то отношение их площадей равно отношению произведении соответствующих сторон, заключающих эти стороны.
Утверждение №5
-
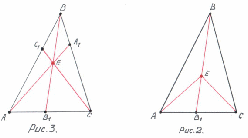
Если на сторонах треугольника отложить по одной точке, циклически
( то есть обходом по сторонам в одном направлении) делящих стороны треугольника в одном и том же отношении, то отрезки, попарно соединяющие эти три точки, отсекают от данного треугольника три равновеликих треугольника.
-
Пополнение формул площадей треугольника
-
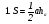 Приведем ряд формул площади треугольника, знание которых полезно не только на элективном курсе, но и самому учителю. В этом ряду , конечно, видим и знакомые из наших учебников формулы
Приведем ряд формул площади треугольника, знание которых полезно не только на элективном курсе, но и самому учителю. В этом ряду , конечно, видим и знакомые из наших учебников формулы
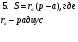
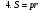
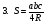
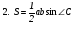
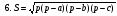
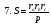
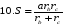
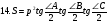
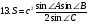
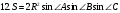
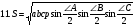
Рассмотрим вывод восьми незнакомых в школьном курсе формул.
Формула №5
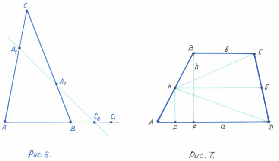
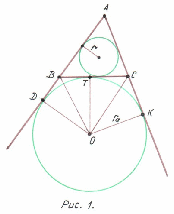
Для вывода рассмотрим рисунок 1.
Из рисунка видно, что
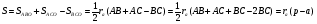
№7 Для вывода формулы (7) используем формулу (5) трижды
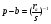
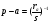
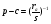
Подставим эти выражения в формулу Герона
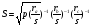
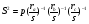
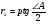
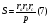
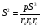
№8 По рисунку 1 нетрудно установить , что AD=p. Тогда
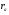 Подставив это выр-е в формулу (5) получим
Подставив это выр-е в формулу (5) получим
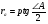
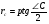
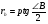 Подставив
Подставив
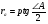
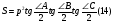 В формулу (7), имеем
В формулу (7), имеем
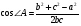 №11 Для вывода формулы 11используем теорему синусов
№11 Для вывода формулы 11используем теорему синусов
Подставим эти значения синусов половинных углов в выражение
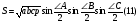
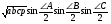
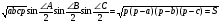
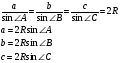 По обобщенной теореме синусов
По обобщенной теореме синусов
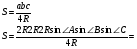 Подставим
Подставим
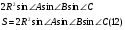
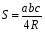 По формуле
По формуле
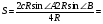 Получим
Получим
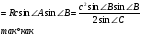
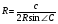
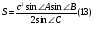
Итак
Теоремы Менелая и Чевы
При док-ве этих теорем используется лемма
-
Лемма. Дан произвольный треуг-к АВС, точка В
лежит на стороне отрезка ВВ
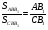 Доказательство
Доказательство
Из свойств площадей следует, что
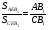
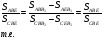 Из этих
Из этих
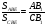
Что и требовалось доказать
Замечание . Утверждение леммы
верно и в том случае, если Е будет на прямой ВВ' в любой ее точке.
Теорема Чевы
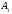 Пусть точка
Пусть точка
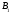 лежит на стороне ВС треугольника АВС, точка
лежит на стороне ВС треугольника АВС, точка
- на стороне АС, точка на стороне АВ.
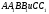 Отрезки
Отрезки
( называемые также Чевианами) пересекаются в одной точке тогда и только тогда, если
Доказательство необходимости.
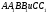 Пусть отрезки
Пусть отрезки
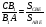
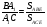
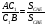 пересекаются в некоторой точке Е, тогда согласно Лемме имеем
пересекаются в некоторой точке Е, тогда согласно Лемме имеем
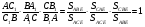
Что и требовалось доказать.
Доказательство достаточности
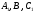 Пусть точки таковы , что
Пусть точки таковы , что
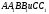 Докажем, что тогда ,и
Докажем, что тогда ,и
пересекаются в одной точке.
Допустим
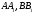 противное, что отрезки
противное, что отрезки
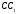 пересекаются в точке Е , а не
пересекаются в точке Е , а не
проходит через точку Е .
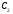
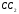 Тогда проведем через точку Е отрезок , где
Тогда проведем через точку Е отрезок , где
лежит на стороне АВ . По необходимому признаку имеем:
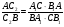
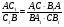 Из равенств (1) и (2) видно:
Из равенств (1) и (2) видно:
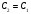
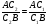
Откуда
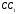 Значит отрезок проходит через ту же точку Е.
Значит отрезок проходит через ту же точку Е.
Достаточный признак доказан.
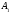 Теорема Менелая.
Теорема Менелая.
Пусть точка лежит
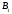 - на стороне ВС , а точка на продолжении
- на стороне ВС , а точка на продолжении
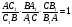
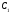 точки , и лежат на одной прямой тогда и
точки , и лежат на одной прямой тогда и
только тогда, когда выполняется условие:
Доказательство необходимости
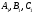 Пусть три точки , лежат
Пусть три точки , лежат
на одной прямой. Докажем что
выполняется равенство: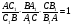
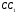
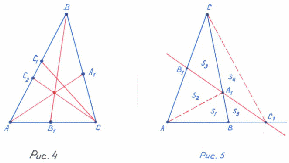
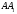 Для этого проведем отрезки и и введем
Для этого проведем отрезки и и введем
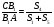 обозначение площадей так.как это показано на рисунке 5
обозначение площадей так.как это показано на рисунке 5
Тогда по лемме можем написать следующее:
Кроме этого, с учетом ранее приведенного утверждения
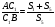
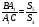 об отношении площадей треугольников с равными
об отношении площадей треугольников с равными
высотами, можем написать две пропорции:
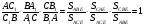 Из записанных трех пропорций следует:
Из записанных трех пропорций следует:
Необходимость доказана.
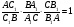 Доказательство достаточности
Доказательство достаточности
Пусть известно, что
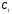
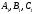 Докажем, что в таком случае три точки лежат на одной прямой.
Докажем, что в таком случае три точки лежат на одной прямой.
Допустим противное, что
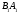 Лежащая на прямой АВ и удовлетворяющая равенству(1), не лежит на прямой
Лежащая на прямой АВ и удовлетворяющая равенству(1), не лежит на прямой
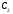
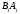 Предположим , что прямая пересекает продолжение стороны АВ в некоторой другой точке
Предположим , что прямая пересекает продолжение стороны АВ в некоторой другой точке
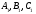 Тогда по необходимому признаку для трех точек
Тогда по необходимому признаку для трех точек
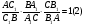 выполняется равенство
выполняется равенство
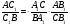 Из равенств 1 и 2 получаем
Из равенств 1 и 2 получаем
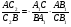
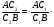 ,
,
откуда: , то есть С2 совпадает с С1 и достаточный признак
доказан.
Теорема Дезарга.
Используя теорему Менелая, можно показать один из способов доказательства теоремы Дезарга, одной из основных теорем проективной геометрии.
(Док-ва теоремы Чевы, Менелая и Дезарга я осмеливаюсь выставлять потому, что проделал их, не используя никакого источника, кроме самих формулировок).
Прямая теорема.
Если два треугольника расположены так, что прямые, соединяющие соответственно вершины треугольников, проходят через одну точку, то три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой
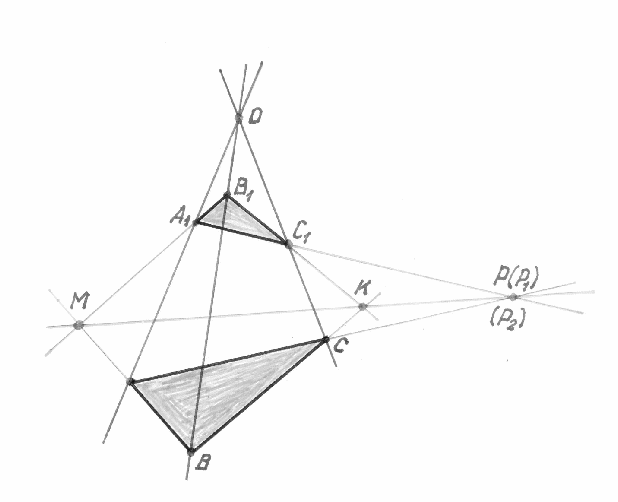
Дано, что треугольники АВС и А1В1С1 с попарно непараллельными сторонами расположены так, что прямые АА1, ВВ1 и СС1 пересекаются в одной точке. Точки М, К, Р - точки пересечения прямых АВ и А1В1, ВС и В1С1, АС и А1С1 соответственно. Докажем, что точки М, К и Р лежат на одной прямой.
Доказательство:
По условию М=(АВ)U(А1В1) и К=(ВС)U(В1С1).
Пусть Р1 есть точка пересечения прямых А1С1 и МК, а точка Р2 есть точка пересечения прямых АС и МК. Докажем, что точки Р1и Р2 совпадают.
По теореме Менелая для точек P1, A1, C1 и треугольника МВ1К имеем:
Аналогично для точек A, C, и треугольника MBKполучается:
С другой стороны для треугольников BMи BKс соответствующими секущими OAи OCимеем:
Из равенств (3) и (4) получается следующее равенство произведений
Из равенства (5) выразим :
Подставим этот результат в равенство (1).
Сравнив полученное с равенством (2), имеем:
. Значит .
А это означает, что три точки M,KиPлежат на одной прямой. Что и требовалось доказать.
Верна и обратная теорема:
Если два треугольника расположены на плоскости таким образом, что три точки, в которых пересекаются продолжения трех пар соответственных сторон треугольника, лежат на одной прямой, то прямые, проходящие через пары соответственных вершин треугольников, пересекаются в одной точке.
Док-во:
Используем тот же чертеж. Так как три точкиP,Kи Mлежат на одной прямой, то из треугольников MKи MBK, с секущими P и PAсоответственно, по теореме Менелая имеем:
Сравнивая равенства (1) и (2) получаем:
Положим, что прямыеAи Bпересекаются в точке , а прямые и - в точке . По теореме Менелая из треугольников , с секущими соответственно, имеем:
Выразим дробь из равенства (3).
Подставим полученное в (4).
Сравнив равенство (6) с равенством (5); получаем, что Отсюда имеем:
А так как подразумеваются на одной прямой с и по одну сторону от этих точек, то . Получим, что пересекаются в одной точке. Что и требовалось доказать.
Рассмотрим решение ряда задач с использованием приведенных фактов.
Использовано:
-
1. Задачи, предлагаемые на заочном отдел МММФ составитель
Е.Ю. Иванова
-
2. Материалы ФИПИ к ЕГЭ