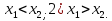- Преподавателю
- Математика
- Решение задач на параметры
Решение задач на параметры
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Тотоева Л.Н. |
| Дата | 31.12.2015 |
| Формат | docx |
| Изображения | Есть |
Задачи с параметром
Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры учащихся. Они имеют исследовательский характер, и с этим связано методическое значение таких задач, а также трудности выработки навыков их решения. Важность понятия параметра связана с тем, что, как правило, именно в терминах параметров происходит описание свойств математических объектов: функций, уравнений, неравенств. Под параметрами мы понимаем входящие в алгебраические выражения величины, численные значения которых явно не заданы, однако считаются принадлежащими определённым числовым множествам.
Решение задач с параметрами требует исследования, даже если это слово не упомянуто в формулировке задачи. Недостаточно механического применения формул, необходимо понимание закономерностей, наличие навыка анализа конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умении объединить рассматриваемые частные случаи в единый результат.
Квадратные уравнения с параметром
-
При каких значениях параметра а уравнение а
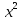 - х + 3 =0
- х + 3 =0
имеет единственное решение?
Решение. 1. а=0. При этом значении параметра а уравнение принимает вид -х +3 = 0, откуда х = 3, то есть решение единственное.
2. а ≠ 0. Тогда а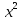 - х + 3 = 0 - квадратное уравнение, дискриминант которого
- х + 3 = 0 - квадратное уравнение, дискриминант которого
D =1 - 12а. для того, чтобы уравнение имело единственное решение, нужно, чтобы
D = 0, откуда а = 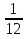 .
.
Ответ : при а = 0 или а = 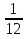 .
.
-
При каких значениях параметра а уравнение
(а - 2)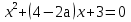 имеет единственное решение?
имеет единственное решение?
Решение . 1. При а = 2 исходное уравнение не имеет решения.
2.а 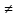 2. Тогда данное уравнение является квадратным и принимает вид
2. Тогда данное уравнение является квадратным и принимает вид
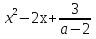 = 0. Искомые значения параметра - это корни дискриминанта, который обращается в нуль при а = 5.
= 0. Искомые значения параметра - это корни дискриминанта, который обращается в нуль при а = 5.
Ответ: при а = 5.
-
При каких значениях параметра а уравнение
а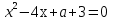
имеет более одного корня?
Решение. 1. При а = 0 уравнение имеет единственный корень х = 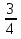 .
.
2. При а 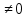 исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант положителен, то есть 16 - 4а2 - 12а
исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант положителен, то есть 16 - 4а2 - 12а 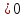 . Решая неравенство, получаем
. Решая неравенство, получаем 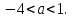 Из этого промежутка следует исключить нуль.
Из этого промежутка следует исключить нуль.
Ответ: 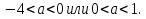
-
При каких значениях параметра а уравнение х2 - а = 0 и
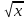 - а = 0 равносильны?
- а = 0 равносильны?
Решение: 1. При 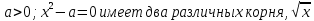 - а = 0 имеет один корень. Равносильности нет.
- а = 0 имеет один корень. Равносильности нет.
2. При а = о решения уравнений совпадают.
3. При 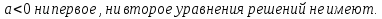 Как известно, такие уравнения считаются равносильными.
Как известно, такие уравнения считаются равносильными.
Ответ: 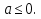
То что объединяет все задачи с параметрами, - это означает что, любую из них можно отнести к одной из двух следующих групп: задачи, в которых требуется найти все значения параметра, при каждом из которых выполняется некоторое условие (неравенство имеет решение, корни уравнения принадлежат заданному промежутку и т. д.), и задачи, в которых требуется решить уравнение (неравенство, систему) с параметрами. В последнем случае нужно установить, при каких значениях параметра задача имеет решения, и указать эти решения для каждого из значений параметра (если при каких - то значениях параметра решений нет, то в ответе следует именно так и написать, - в противном случае решение может быть сочтено неполным).
Решение большинства задач с параметрами, связано со свойствами линейной и квадратичной функций.
При решении систем линейных уравнений удобно пользоваться тем, что любое линейное уравнение является уравнением некоторой прямой. Поэтому система двух линейных уравнений либо имеет единственное решение (соответствующие прямые пересекаются), либо имеет бесконечное множество решений (прямые совпадают). Либо не имеет решений (прямые параллельны).
-
Для каждого значения параметра а найдите число решений уравнения
2(4х - 1)а2 - (14х - 11)а + 5(х - 1) = 0
Решение: Запишем данное уравнение как линейное относительно х:
(8а2 - 14а + 5) х = 2а2 - 11а + 5.
Разложив на множители каждый из квадратных трехчленов относительно а, получим (2а - 1) (4а - 5) = (2а - 1) (а - 5).
При а = 0,5 уравнение имеет бесконечное множество решений.
При а 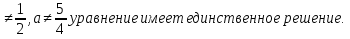
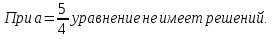
Ответ: 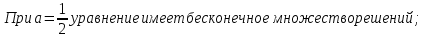
При а = 
При а 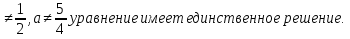
-
Найдите все значения параметра а, при каждом из которых система уравнений
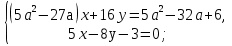
Имеет бесчисленное множество решений.
Решение: Данная система равносильна системе 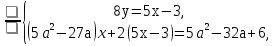
Откуда 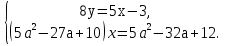
Разложив на множители каждый из квадратных относительно а трехчленов второго уравнения, получим систему 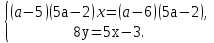
Полученная система имеет более одного решения только в том случае, если ее первое уравнение имеет более одного решения, что возможно лишь при а = 2/5.
Ответ: а = 2/5.
-
Найдите все значения параметра а, при каждом из которых прямая у=а пересекает хотя бы в одной точке график функции у =
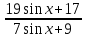 .
.
Решение. Условие задачи выполняется в том и только в том случае, если имеет хотя бы одно решение уравнение а=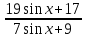 . Но 7
. Но 7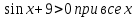 . Поэтому
. Поэтому 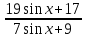 =а
=а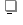 19
19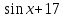 =7а
=7а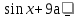 (7а - 19)
(7а - 19) .
.
Полученное уравнение имеет хотя бы одно решение тогда и только тогда, когда 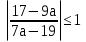 .
.
Решим неравенство: 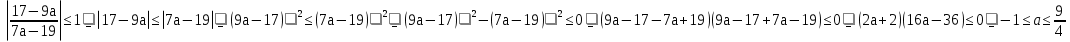 .
.
Ответ : а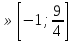 .
.
-
При каких значениях параметра а уравнение
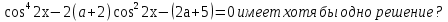
Решение. Сделаем замену переменной. Пусть у =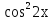 .
.
Тогда у принимает все значения из отрезка 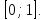
Переформулируем задачу. Требуется найти значения параметра а, при которых уравнение
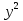 -2(а+2)у - (2а + 5) = 0
-2(а+2)у - (2а + 5) = 0
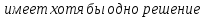 на отрезке
на отрезке 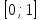 .
.
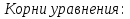
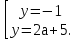
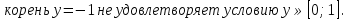
0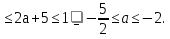
Ответ : а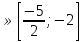 .
.
-
Найдите все значения параметра а, при каждом из которых уравнение
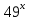 -(8а-1)
-(8а-1)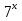 +16
+16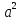 -4а - 2 = 0
-4а - 2 = 0
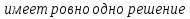 .
.
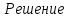 . Сделаем замену переменной. Пусть у=
. Сделаем замену переменной. Пусть у=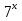 . Уравнение принимает вид
. Уравнение принимает вид
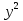 - (8а-1)у + 16
- (8а-1)у + 16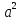 - 4а - 2 = 0.
- 4а - 2 = 0.
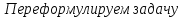 . Требуется найти значения параметра, при которых полученное уравнение имеет единственный положительный корень.
. Требуется найти значения параметра, при которых полученное уравнение имеет единственный положительный корень.
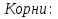
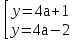
Больший корень равен 4а + 1.
Составим и решим систему неравенств.
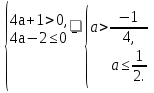
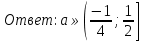 .
.
Рациональные неравенства с параметром доставляют значительно больше хлопот и требуют знания различных методов их решения: по сравнению с методами решения уравнений в особенности необходимо владение графическим методом решения.
-
Решите неравенство
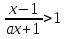 для всех значений а.
для всех значений а.
Решение. Способ 1 (аналитический). Применяя схему освобождения от дроби для неравенства, очевидно, получим:
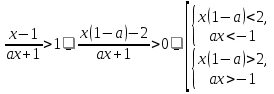
Вновь соотношения в системах 1и2 являются многочленами, следовательно, их параметрический анализ уже известен. Рассмотрим каждую из систем в отдельности.
-
Для первого соотношения системы 1 имеем:
Если 1-а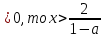
Если 1-а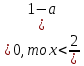
Для второго соотношения системы 1 -
Если а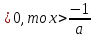
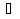
Если а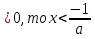 .
. 
Дальнейший параметрический анализ разбивается значениями а=0;1 на следующие этапы.
-
а
 . В этом случае из условий выше выбираются соотношения , соответствующие выбранным значениям а: при а
. В этом случае из условий выше выбираются соотношения , соответствующие выбранным значениям а: при а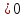
-
х
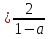 и х
и х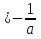
Далее очевидно, что при 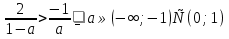 система со звёздочкой не будет иметь решений. Из указанного множества значений а лишь интервал а
система со звёздочкой не будет иметь решений. Из указанного множества значений а лишь интервал а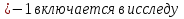 емый случай (а
емый случай (а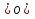 , следовательно, при а
, следовательно, при а 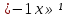 .
.
Если же
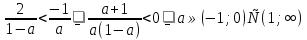 , что в пересечении с множеством
, что в пересечении с множеством
а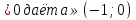 , то очевидно, система со звёздочкой имеет решение х
, то очевидно, система со звёздочкой имеет решение х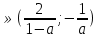 .
.
Таким образом, получается следующее решение 1.1:
Если а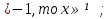
Если а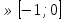 , то х
, то х 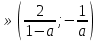 .
.
-
а
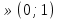 . Выбирая из условий
. Выбирая из условий 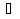 и
и соответствующие неравенства, получаем
соответствующие неравенства, получаем 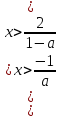 . Заметим, что правые части этой системы уже сравнены в 1.1, откуда получаем, что
. Заметим, что правые части этой системы уже сравнены в 1.1, откуда получаем, что 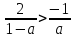 для всех а
для всех а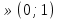 , что даёт решение 1.2.: х
, что даёт решение 1.2.: х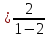 .
. -
а
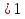 . По аналогии с предыдущими случаями имеем систему
. По аналогии с предыдущими случаями имеем систему 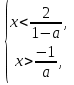
но так как при а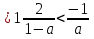 , то решение последней системы х
, то решение последней системы х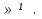
в случае особых значений параметра решение легко получить путём их непосредственной подстановки в исходное соотношение:
-
а = -1 х
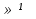 ;
; -
а = 0 х
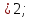
-
а = 1 х
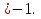
Объединяя решения получим общий ответ:
При а 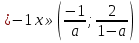 ;
;
При а = -1 х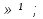
При а 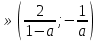 ;
;
При а = 0 х 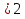 ;
;
При а 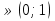 х
х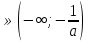
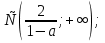
При а = 1 х 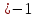 ;
;
При а 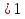
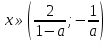 .
.
Способ 2 ( метод интервалов).
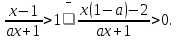
Корни числителя и знаменателя последнего неравенства 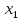 =
= 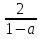 ,
, 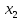 = -
= -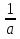 . При расположении корней на числовой оси, возникают случаи:
. При расположении корней на числовой оси, возникают случаи:
1). Если 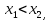 то
то
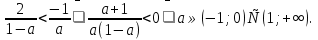
При а 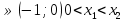 .
.
В пробной точке, например х=0, исходная дробь отрицательна, что, в соответствии с методом интервалов, даёт решение х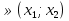 . Во второй части полученного множества (а
. Во второй части полученного множества (а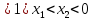 , выбирая ту же пробную точку х = 0, получаем решение х
, выбирая ту же пробную точку х = 0, получаем решение х 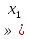 ;
;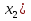 , совпадающее с предыдущим.
, совпадающее с предыдущим.
2). Если 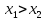 , то
, то
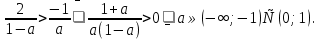
По аналогии с 1),
При а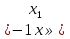 ;
;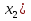 .
.
При а 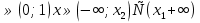 .
.
Параметрический анализ при а = 0;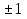 , а также общий ответ совпадают с примером в аналитическом способе решения .
, а также общий ответ совпадают с примером в аналитическом способе решения .
Очевидно, аналитическое решение рациональных неравенств сопровождается значительными трудностями: уже более простые задачи приобретают достаточно громоздкий вид и множество необходимых для рассмотрения подслучаев.
Если числитель и знаменатель дроби представляют собой функции, графики которых доступны для построения, то возможно более эффективное решение рациональных  неравенств графическим методом.
неравенств графическим методом.
Способ 3 (графический).
Числитель и знаменатель дроби 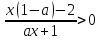 можно рассматривать как функции двух переменных - х и а. Выпишем их отдельно, выразив одну переменную через другую:
можно рассматривать как функции двух переменных - х и а. Выпишем их отдельно, выразив одну переменную через другую:
х =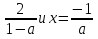 . Очевидно, в системе координат, глее по оси абсцисс отложено а, а по оси ординат - х, данные неравенства представляют собой функции х =
. Очевидно, в системе координат, глее по оси абсцисс отложено а, а по оси ординат - х, данные неравенства представляют собой функции х = 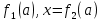 , графиками которых являются гиперболы.
, графиками которых являются гиперболы.
Хорошо известно, что всякая линия на плоскости, аналитически выражаемая уравнением  х = f(а), разбивает плоскость на два непересекающихся подмножества, одно из которых соответствует неравенству х
х = f(а), разбивает плоскость на два непересекающихся подмножества, одно из которых соответствует неравенству х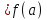 , а другое неравенству х
, а другое неравенству х 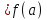 . Получим
. Получим
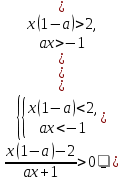
Каждому неравенству совокупности систем соответствует множество точек на плоскости ха, причём границами этих множеств служат гиперболы х = 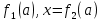 .
.
Рассмотрим ещё пример. Найти все значения параметра а, при которых уравнение
(2а-1)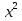 + 2(а+2)х + а - 4 = 0
+ 2(а+2)х + а - 4 = 0
Имеет два различных корня, каждый из которых больше, чем -2.
Решение. Способ 1 . Допустимые значения параметра а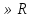 . Найдём корни уравнения и укажем значения параметра а, при которых они будут больше -2.
. Найдём корни уравнения и укажем значения параметра а, при которых они будут больше -2.
Отметим, что при а =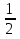 (равенство нулю коэффициентов при старшем члене) уравнение превращается в линейное и, следовательно, имеет всего один корень, что противоречит условию.
(равенство нулю коэффициентов при старшем члене) уравнение превращается в линейное и, следовательно, имеет всего один корень, что противоречит условию.
Чтобы корни были различными, потребуем D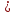 0, то есть решим неравенство
0, то есть решим неравенство
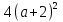 - 4(2а-1)(а-4)
- 4(2а-1)(а-4) 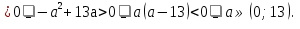
Найдём теперь его корни.
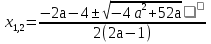 =
=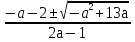 ,
,
То есть
Х =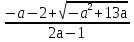 или х =
или х =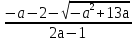 .
.
В данном примере очевидно, что второй из этих корней меньше, а значит, достаточно потребовать, чтобы именно он был больше -2.
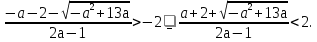
Если а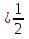 , то
, то
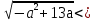 3а-4
3а-4 -
- 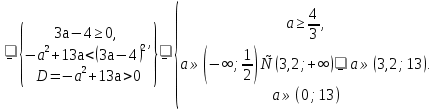
Если а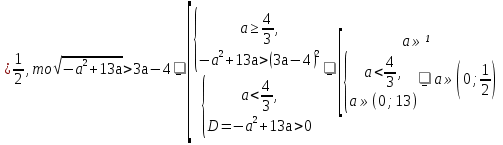
Ответ: а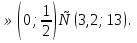
Способ 2. Рассмотрим функцию
f(х)=(2а-1)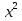 +2(а+2)х + а - 4.
+2(а+2)х + а - 4.
Условие существования двух различных корней, больших-2, обеспечивается решением системы неравенств
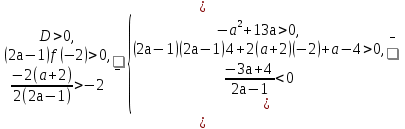
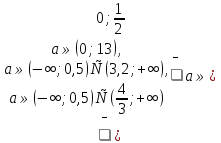 )
)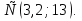
Ответ: а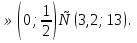
Ещё пример. При каких значениях параметра а корни уравнения
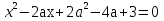 принадлежат отрезку
принадлежат отрезку 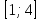 ?
?
Решение. Допустимые значения параметра а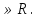
Рассмотрим функцию
f(х)=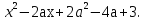
Условие задачи выполняется при2
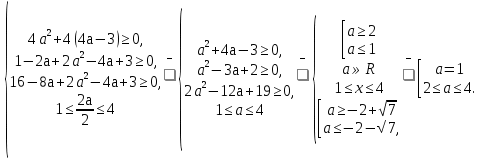
Ответ :а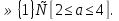
Пример. При каких значениях параметра а один из корней уравнения
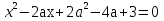
меньше 1, а другой больше 2?
Решение. Допустимые значения параметра а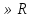 .
.
Рассмотрим функцию f(х)=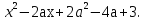
Выполнение условия задачи требует решения системы неравенств
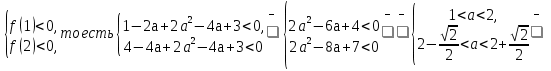 2 -
2 -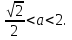
Ответ: а 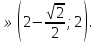
Если требуется, чтобы корни квадратного трёхчлена были различны и только один из них лежал на отрезке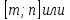 на интервале (m;n), то двигая график параболы по координатной плоскости, можно заметить, что в точках х = m и х = n значения функции f(х) должны быть разных знаков, а это означает, что должно выполняться требование f(m)f(n)
на интервале (m;n), то двигая график параболы по координатной плоскости, можно заметить, что в точках х = m и х = n значения функции f(х) должны быть разных знаков, а это означает, что должно выполняться требование f(m)f(n)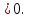
Пример1. При каких значениях параметра а один корень уравнения 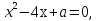 имеющего различные корни, принадлежит интервалу (1;4)?
имеющего различные корни, принадлежит интервалу (1;4)?
Решение. Допустимые значения параметра а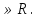
Пусть f(х) = 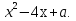 Тогда:
Тогда:
а) один корень этого квадратного трёхчлена лежит внутри интервала (1;4) при f(1)f(4)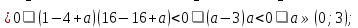
б) проверим границы интервала
f(4) = 0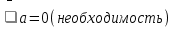 .
.
Тогда при этом значении а 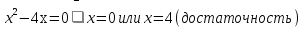 .
.
Вывод: ни один из корней не лежит в (1;4).
f(1)=0 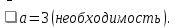
Тогда при этом значении а
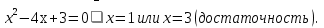
Вывод: корень х=3 лежит в (1;4), а значение а=3 является решением.
Обобщая полученные результаты, получаем а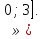
Пример 2. При каких значениях параметра а один корень уравнения
(а-1)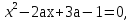
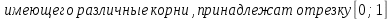 , а другой - интервалу (2;4)?
, а другой - интервалу (2;4)?
Решение. Допустимые значения параметра а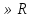 .
.
Рассмотрим функцию
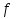 (х)=(а-1)
(х)=(а-1)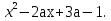
При а=1 она становится линейной, и задача теряет смысл.
Пусть а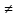 1. Тогда:
1. Тогда:
а) корни лежат внутри заданных промежутков при 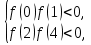
то есть
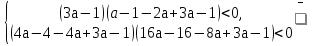
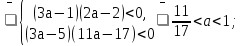
б) проверка границ отрезка и отбор корней.
f(0) = 3а-1=0 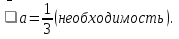
При этом значении а уравнение имеет вид
-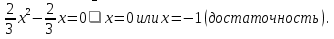
Вывод : второй корень не лежит в интервале (2;4).
f(1) = а-1-2а+3а-1=0 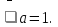
Но а 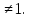 значит, и в этом случае нужных корней не будет.
значит, и в этом случае нужных корней не будет.
Ответ: а 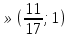 .
.
Полученные результаты иллюстрируют подход и позволяют значительно упростить решение многих задач. Так, например, если требуется найти все значения параметра, при которых корни уравнения не лежат на данном отрезке, можно просто найти множество значений параметра, при котором корни, наоборот, лежат на отрезке. Дополнение к этому множеству и будет являться ответом.
Рассмотрим различные задачи с применением указанного подхода.
-
Найти все значения х, при которых неравенство
(2-а)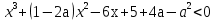
Справедливо хоты бы для одного значения параметра а из промежутка 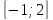 .
.
Решение. Допустимые значения параметра а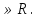
Перепишем уравнение относительно параметра а и рассмотрим функцию f(а):
f(а) = 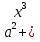 +2
+2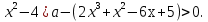
Сформулируем обратную задачу: при каких значениях параметра а функция f(а) не имеет решений на отрезке 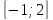 , то есть корни
, то есть корни 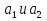 расположены по разные стороны от рассматриваемого отрезка. Задача свелась:
расположены по разные стороны от рассматриваемого отрезка. Задача свелась:
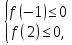 то есть
то есть 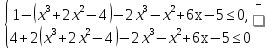
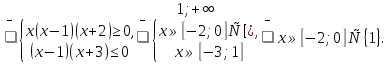
Значит, решением задачи будут остальные значения параметра, то есть
а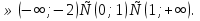
Ответ: а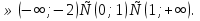
-
Найдите все значения параметра а, при каждом из которых уравнение
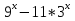 =
=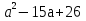
Имеет два различных положительных корня и ни один из корней не является целым числом.
Решение. Допустимые значения параметра а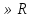 .
.
Перепишем уравнение 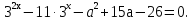 (1)
(1)
Введем новую переменную 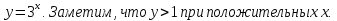
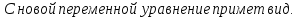
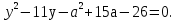 (2)
(2)
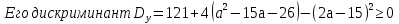
Отсюда ясно, что при Dy= 0, то есть при а = 7,5 уравнение имеет всего один корень (кратности два), и следовательно, это не удовлетворяет условию задачи.
Пусть а 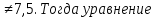 (2) имеет два различных корня при
(2) имеет два различных корня при 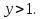 Таким образом, первую часть задачи можно переформулировать так: при каких значениях параметра а уравнение (2) имеет два различных действительных корня больших единицы?
Таким образом, первую часть задачи можно переформулировать так: при каких значениях параметра а уравнение (2) имеет два различных действительных корня больших единицы?
Пусть f (y) = y2- 11y - a2 +15a -26. Тогда это условие выполняется при решении системы неравенств 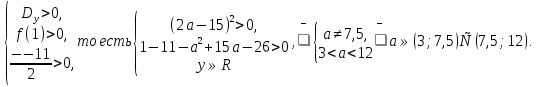
Остается определить, при каких значениях а будут получаться не целые корни. Решим обратную задачу, то есть найдем, при каких значениях параметра а будут получаться целые корни.
Найдем корни уравнения (2):
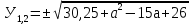 = 5,5
= 5,5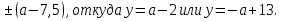
Возвращаясь к переменной х, получаем соответственно 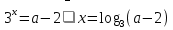 или
или
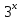 = -а + 13
= -а + 13 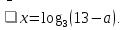
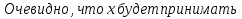 целые значения в первом случае при а = 5 или а = 11, а во втором - при а = 10 или а = 4. Эти значения необходимо исключить из ответа.
целые значения в первом случае при а = 5 или а = 11, а во втором - при а = 10 или а = 4. Эти значения необходимо исключить из ответа.
Ответ: а 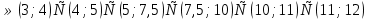 .
.
-
Найдите все значения параметра а, при которых уравнение
2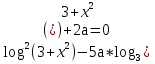
не имеет решения.
Решение. Допустимые значения параметра а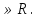 Введём новую переменную
Введём новую переменную
t = 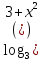 . Заметим, что t
. Заметим, что t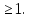 Тогда данное уравнение примет вид
Тогда данное уравнение примет вид
2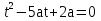 .
.
Решений это уравнение, с учётом выше отмеченного, не будет иметь, если 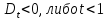
Пусть f(t) = 2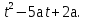 Тогда условие t
Тогда условие t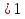 обеспечивается решением системы неравенств
обеспечивается решением системы неравенств 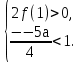 Таким образом, требования задачи будут выполняться
Таким образом, требования задачи будут выполняться
при 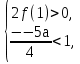 то есть
то есть 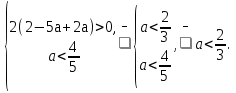
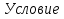 D
D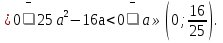
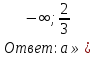 ).
).
-
Найдите все значения параметра а, при которых уравнение
29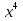 + 29ах(
+ 29ах(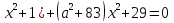
не имеет действительных решений.
Решение. Допустимые значения параметра а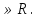
Представим данное уравнение в следующем виде:
29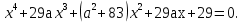
Заметив, что 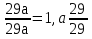 =
= 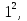 приходим к выводу, что уравнение является возвратным уравнением чётной степени. х = 0 не является его корнем, поэтому поделим всё выражение на 29
приходим к выводу, что уравнение является возвратным уравнением чётной степени. х = 0 не является его корнем, поэтому поделим всё выражение на 29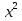 . Получаем после преобразований
. Получаем после преобразований
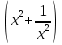 + а
+ а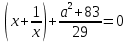 .
.
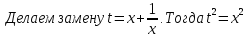
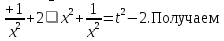
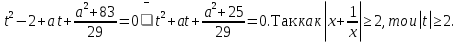
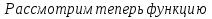
f(t) = 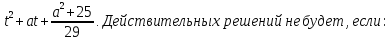
1)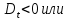
2)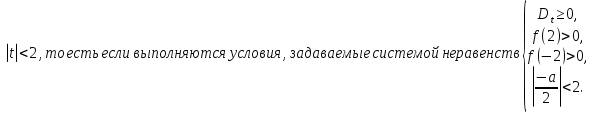
Объединяя 1) и 2) условия, получаем систему неравенств
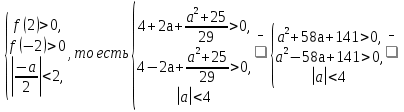
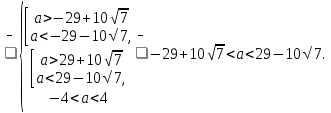
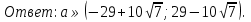
-
Для каждого значения параметра, а определите число корней уравнения
2
Решение . Допустимые значения параметра а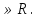
Рассмотрим
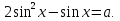 (1)
(1)
Если х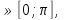 то при
то при 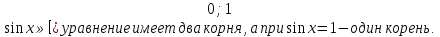
Введём новую переменную у = 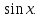 Тогда уравнение примет вид
Тогда уравнение примет вид
2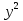 -у -а = 0 (2)
-у -а = 0 (2)
Пусть f(у) = 2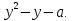 Возможны три случая.
Возможны три случая.
-
у = 1 (один корень в уравнении(2)). Тогда 2-1-а = 0
 а = 1 (необходимость). При а = 1 получаем 2
а = 1 (необходимость). При а = 1 получаем 2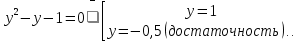
Таким образом, при а = 1 получаем один корень в уравнении (1).
-
У
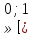 (два корня в уравнении (2), лежащие на
(два корня в уравнении (2), лежащие на 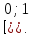 а) у = 0. Тогда а = 0 (необходимость). При а = 0 получаем 2
а) у = 0. Тогда а = 0 (необходимость). При а = 0 получаем 2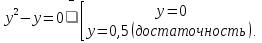 Таким образом, при а = 0 получаем четыре корня в уравнении (1). б) у
Таким образом, при а = 0 получаем четыре корня в уравнении (1). б) у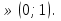 Тогда наличие двух корней в уравнении (2) (и, соответственно, четырёх корней уравнения (1)) на интервале (0;1) определяется системой неравенств
Тогда наличие двух корней в уравнении (2) (и, соответственно, четырёх корней уравнения (1)) на интервале (0;1) определяется системой неравенств 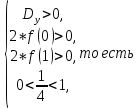
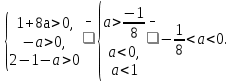
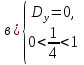 (вершина параболы в уравнении (2) лежит на интервале (0;1)), то есть
(вершина параболы в уравнении (2) лежит на интервале (0;1)), то есть
1+8а = 0  а = -
а = - 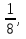 что соответствует двум корням уравнения (1).
что соответствует двум корням уравнения (1).
-
Один корень уравнения (2) лежит на (0;1), а другой - нет ( что соответствует двум корням уравнения (1)).
Данное условие выполняется при решении неравенства f(0)*f(1)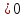 , то есть
, то есть
-а*(2-1-а)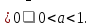
Ответ: если а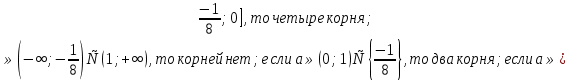
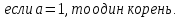
-
При каких значениях параметра а неравенство

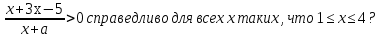
Решение. Допустимые значения параметра а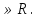
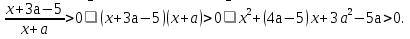
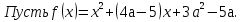
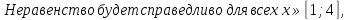 если оба корня функции f(х) либо меньше 1, либо больше 4.
если оба корня функции f(х) либо меньше 1, либо больше 4.
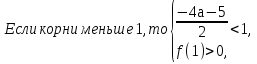 то есть
то есть 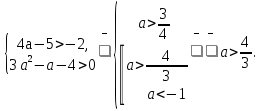
Если корни больше 4, то 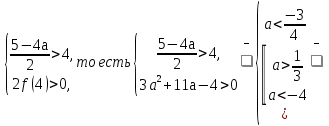
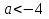
Ответ: а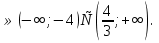
-
Для каждого значения параметра а решите систему неравенств
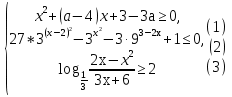
Решение. Допустимые значения параметра а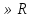 .
.
ОДЗ системы будет определяться неравенством (3):
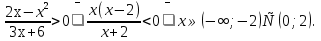
В полученной ОДЗ решим неравенство (3):
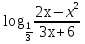
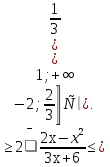
С учётом ОДЗ х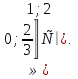
Решим неравенство (2):
27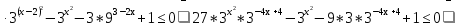
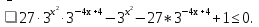
Введём новые переменные. Пусть 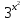 = t и
= t и 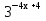 = v, в ОДЗ t
= v, в ОДЗ t 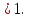 Уравнение принимает вид
Уравнение принимает вид
27tv - t - 27v +1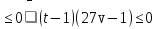 .
.
Но t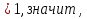
27v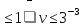 .
.
Отсюда 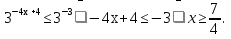
С учётом решения неравенства (3) и ОДЗ х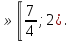
Рассмотрим неравенство (1). Система неравенств будет совместна, если это неравенство имеет решения на промежутке 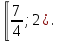
Рассмотрим функцию
f(х) = 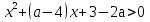
Указанный промежуток будет целиком являться решением неравенства, если оба корня квадратного трёхчлена будут расположены слева от точки х = 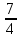 и справа от точки х = 2, либо если дискриминант соответствующего квадратного уравнения будет отрицательным. Эти условия с учётом того, что коэффициент при старшем члене положителен, будут выполняться при решении системы неравенств
и справа от точки х = 2, либо если дискриминант соответствующего квадратного уравнения будет отрицательным. Эти условия с учётом того, что коэффициент при старшем члене положителен, будут выполняться при решении системы неравенств 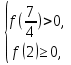 то есть
то есть
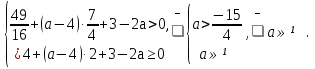
В этой системе оказалось возможным исключить рассмотрение дискриминанта, так как для того, чтобы корни были одновременно больше или меньше заданных чисел, дискриминант должен быть неотрицательным, а для того, чтобы решением была вся числовая ось (в том числе и рассматриваемый промежуток) - дискриминант должен быть неположительным. Таким образом, в данном случае дискриминант может быть любым.
Для упрощения дальнейших рассуждений найдём корни квадратного трёхчлена
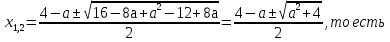
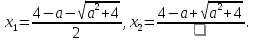
Если 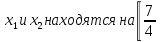 ;2), то решений не будет, так как в этом случае вышеуказанная система неравенств несовместна.
;2), то решений не будет, так как в этом случае вышеуказанная система неравенств несовместна.
Очевидно, что при любом а 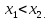
Если 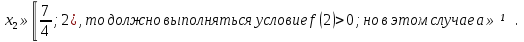
Если 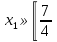 ;2), то решением будет х
;2), то решением будет х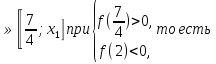
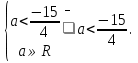
Наконец, проверим границу: если в последнем случае 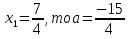 (необходимость), и при этом а
(необходимость), и при этом а
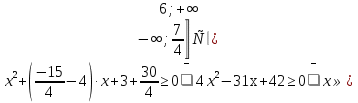 (достаточность).
(достаточность).
Решением является одна точка х = 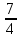 .
.
Обобщая полученные результаты, выписываем
Ответ: если а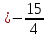 . То х
. То х 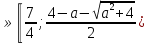 ;
;
если а = -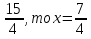 ;
;
если а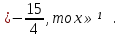
Литература
-
Болотов А.А., Прохоренко В.И., Сафонов В.Ф. Математика. Теория и задачи.
-
Петрушенко И.М., Прохоренко В.И., Сафонов В.Ф. Математика. Банк задач для вступительных испытаний в МЭИ.
-
Амелькин В.В., Рабцевич В.Л. Задачи с параметрами.
-
Зеленский А.С., Василенко О.Н. Сборник задач вступительных экзаменов.