Поделитесь с коллегами:
Методика совершенствования вычислительных навыков. Характеристика форм и способов вычислений. Формы и способы обучения являются одним из компонентов целостной методической системы обучения математике. Основной формой обучения математике является урок, на котором одно из центральных мест отводится той деятельности учителя, которая связана с использованием способов обучения не только для передачи знаний учащимся, но и для организации и руководства разными видами учебной деятельности, и главным образом самостоятельной работы на всех этапах обучения. Совершенствование методики вычислений с одной стороны, допускает повторение и систематизацию вычислительных умений, которые получены в начальной школе, а с другой стороны- предусматривает расширение и углубление вычислительных умений и навыков. Основным способом их формирования является набор упражнений. Их совокупность представляет систему упражнений для совершенствования вычислений. При решении выделенных наборов упражнений по рационализации, самоконтроля вычислений формируются и совершенствуются такие качества вычислительных навыков как правильность, сознательность, обобщенность, свернутость, рациональность. Охарактеризую набор упражнений, с помощью которых достигаются основные качества вычислительных навыков. Рассмотрим набор упражнений, решение которых способствует формированию рациональности вычислений. Умение рационализировать вычисления является одним из показателей математической культуры, поскольку оно требует от ученика не только хорошего знания теоретического материала, но и таких качеств мышления, как гибкость, целенаправленность, критичность. Формированию умений рационально выполнять вычисления способствует использование законов арифметических действий. При их изучении следует добиваться от учеников понимания роли законов в упрощении вычислений. Перед решением примеров полезно формировать задание в виде «Выполните наиболее удобным способом», «Как вычислить удобным способом», «Вычислите, используя данное равенство» и другие. В учебниках «Математика» все виды названых заданий используются, но очень редко. В связи с этим учитель должен организовать работу по формированию умений рационально проводить вычисления, дополняя систему упражнений . достигая при проведении разных видов работы выполнение действий более рациональным путем. Среди упражнений, направленных на формирование умений рационально выполнять вычисления, можно выделить следующие виды работы:
- На использование законов арифметических действий;
- На использование этих законов в нестандартных условиях;
- На использование искусственных приемов упрощения вычислений;
Первый вид упражнений наиболее распространен в учебниках и в практике работы учителей. При составлении таких упражнений необходимо подбирать числовые данные, которые к числам, действия над которыми выполняются намного проще, чем в обычном порядке. Например. Вычислите удобным способом: а) 253*27+73*253 б) 728:4+272:4 Рациональные вычисления в нестандартных условиях встречаются в практике крайне редко. Поэтому учителя должны предлагать упражнения такого вида: Примеры.1) Вычислите устно: 12*9+13*9-7*25 Если использовать распределительный закон умножения относительно сложения, то в скобках получаем 25, это приведет к использованию распределительного закона умножения относительно сложения. Вычисления будем проводить так: (12+13)*9-7*25= 25*9-7*25=25*(9-7)=25*2=50 - Как легче вычислить?
34*48+18*12+23*24 В каждом слагаемом необходимо выделить множитель 24. Вычисления проводят так: 34*48+18*12+23*24=24*(34*2+9+23)=24*100=2400 - Вычислите наиболее коротким путем:
а) 200071+200072+200073+200074+200075+200076+200077+200078+200079+200080= (200071+200080)*5=400151*5=2000755 б) 568170+96*(24+32)+(179-123)*34=56*(170-96-34)=56*300=16800 Искусственные приемы упрощения вычислений часто используются во внеурочной деятельности. Например.1.Найти частное 894:149 с помощью него найти частное 1788:148; 894:447, 2682:149. - Вычислите, используя равенство 18492:46=402
А) (18492-46):46 Б) 402-18492:46 В) (18492+920):46 Г) (18090+370):46 3. Вычислите произведение в первом примере. Используйте его для вычисления других примеров. 1) (976+234)*5 2) 376*2 3) 84*15 976*5+234*5 376*4 21*30 5*976+5*234 4*376 21*60 Такого вида упражнения приучают быть наблюдательным, воспитывают внимательность учащихся. Умение распознавать данное равенство в новых примерах является составляющей часть в рационализации вычислений. Скорость вычислений. Устные вычисления полезны, когда выполняются не только правильно, но и быстро. Скорость- необходимое качество как устного, так и письменного счета. Скорость проведения устных вычислений совершенствуются при выполнении быстрого счета, рационализации вычислений. Этому способствует проведение вычислений «цепочкой», выполнение вычислений за определенное время. Быстрый счет требует от учащихся высокого напряжения внимания, поэтому не следует использовать большое количество таких упражнений на уроке. При письменных вычислениях скорость совершенствуется при выработке привычки выполнять вычисления наполовину письменно, сокращать записи при вычислениях, а также проводить действия наиболее рациональным путем. Устный и полу письменный счет практикуется в зависимости от свойств чисел, над которыми совершается действие, потому что в каждом виде вычислений есть свои специфические особенности. Видеть и использовать эти особенности для ускорения вычислений- вот качество, которое необходимо прививать ученикам. Например. Выполнить действие: 14*(3600*18-239200:46) При делении 239200 на 46 получаем 5200. Ученик замечает, что уменьшаемое и вычитаемое имеют общий множитель 400 и упрощает вычисление: 14*400*(9*18-13). Вычислив устно 14*400=5600 и 9*18-13=149, письменно выполняет только умножение 5600 на 149. Таким образом, запись всего решения будет выглядеть так: 14*(3600*18-239200:46)=14*(3600*18-5200)=14*400*(9*18-13)=5600*149=834400 239200|46 149 230 5200 5600 92 894 92 745 - 834400
Обобщенность вычислений. Формированию обобщенности вычислений способствуют упражнения, решение которых предусматривает перенесение навыков вычислений в новые условия, использование зависимостей между результатами и компонентами арифметических действий. Для того, чтобы формировать у учащихся умения обобщать, полезно проводить беседы после решения примеров. Например. Не проводя вычислений частных, установить, как изменится результат в каждом примере в сравнении с делимым. - 996:83 2) 332:8 3) (996-166):83 4(996+249):83
Беседу можно провести так: -Сравните делители во всех примерах. Сравните делимые в примерах 1,2. Как изменится частное? Сравните делимые в примерах 1,3. Сравните числа 166 и 83. Как изменится частное в примере 4? Что общего в изменении частных для всех этих примеров? На сколько уменьшится частное в примере 3? На сколько увеличится частное в примере 4? -Вывод. При смене делимого, при неизменном делителе изменяется и частное. Если делимое уменьшили на удвоенный делитель, то частное уменьшится на 2. Если делимое увеличить на утроенный делитель, то частное увеличится на 3. Важнейшая задача школы на современном этапе - научить учащихся самостоятельно добывать знания и применять их на практике. В связи с этим особое значение приобретает формирование учебной деятельности школьников. Учебная деятельность - ведущая деятельность в младшем школьном возрасте, и именно поэтому ее структура должна закладываться с первых дней пребывания ребенка в школе. Одним из компонентов учебной деятельности, по мнению психологов, с которого должно начинаться ее формирование, является самоконтроль. Самоконтроль как черта личности предполагает умение контролировать себя и правильно оценивать свои действия. Формируя у детей различные приемы самоконтроля, мы тем самым воспитываем них способность к самооценке. Это следует учитывать, организуя соответствующим образом деятельность детей с первых дней пребывания в школе. Самоконтроль может осуществляться в нескольких видах: "прогнозирующий (до начала работы), пошаговый (по ходу работы), итоговый (после завершения работы)". Предметом контроля может быть как конечный результат, так и способ его получения. В учебной деятельности образец результата или способа действия не всегда может быть дан в готовом виде, а потому формирование самоконтроля предполагает развитие не только умения соотносить объект контроля с образцом, но и умения самостоятельно выбирать или конструировать такие образцов, которые являются критериями успешности выполнения тех или иных действий. При обучении математике формирование самоконтроля часто связывается с обучением учащихся способам проверки тех или иных учебных заданий, в частности с проверкой решения примеров. Рассмотрим набор упражнений, выполнение которых способствует формированию самоконтроля вычислений. Равномерное распределение прямых и обратных упражнений на вычисления, которые включают задания, что направлены на формирование самоконтроля, способствуют совершенствованию таких качеств вычислений, как правильность и сознательность. В учебниках математики упражнений, которые направлены на формирование самоконтроля, мало. При этом используется проверка путем повторного вычисления или с помощью обратной задачи. Но, есть упражнения с заданиями: «найди ошибку», «не проводя вычислений, установи, правильно ли выполнено действие». Поэтому для совершенствования вычислительных навыков учителю необходимо систематически включать в систему упражнений такие, которые знакомят учащихся с разными способами проведения самоконтроля: I.Контроль, что опирается на понятие действия. Содержательная суть действия с натуральными числами формируется в начальных классах. В связи с этим необходимо проводить контроль на основе понятий или определений действий. Например. Проверить правильность равенства, используя понятия соответствующего действия. А) 276*6=1644 ( Если заменить умножение сложением одинаковых слагаемых, получаем: 276+276+276+276+276+276=1644); Б) 996:3=332 (разделить 996 на 3-это означает найти число, при умножении которого на 3 получаем 996). Используя такой способ самоконтроля, ученик вспоминает соответствующее понятие или определение, применяет его к конкретному примеру, сравнивает найденное число с результатом, делает вывод о правильности решения. II. Использование свойств арифметических действий и зависимостей результатов от компонентов. Как показывает практика, этот способ проверки у учащихся формируется легче других. Тут имеется в виду то, что учащиеся хорошо знают свойства арифметических действий, взаимосвязь между результатами и компонентами. Например. 1. Правильно ли выполнено деление: 420:60=7? (Образец рассуждения привожу в виде алгоритма) - Замени делитель произведением чисел, одно из которых 10.
- Вспомни правило деления числа на 10.
- Раздели данное число сначала на 10, а потом на второй множитель.
2.Вычисли разными способами, используя свойства арифметических действий. Сравни полученные результаты. Если они одинаковые, то действия выполнены верно. (540-118):54 480:(4*2) (70+4)*3 (810*36):9 3.Проверь умножением и делением, правильно ли выполнено деление: 384:16=24. III. Способ прикидки. Под прикидкой понимается грубая оценка ожидаемого результата действия. Как бы внимательно не проводились вычисления, возможны ошибки. Прикидка результата должна предшествовать выполнению вычислений, предупреждать грубые вычислительные ошибки и проводится по возможности устно. Систематическое применение этого способа имеет и воспитательное значение, у учеников вырабатывается привычка не начинать решения любого задания без предварительной оценки результата. Рассмотрим возможные виды прикидок и методику обучения этому приему самоконтроля. - Прикидка чисел результата с помощью предварительного округления.
Этот вид прикидки наиболее распространен в практике, но, как показывают мои наблюдения , в работе учителя ими пользуются крайне редко. При выполнении сложения или умножения можно определить, между какими числами находится результат, т.е. округляя компоненты с лишней частью или с недостачей, получаем верхнюю или нижнюю границу суммы или произведения. Например: - Между какими числами находится сумма 495+387? 495- находится между числами 400 и 500, 387- находится между числами 300 и 400. Это обозначает, что сумма495 и 387 будет находиться между значением выражений 400+300 и 500+400, т.е. 700<495+387<900. Такой вид прикидки целесообразно использовать при умножении и делении натуральных чисел. Например. 1) Не вычисляя, докажи, что умножение выполнено не правильно: 402*305=12610. Округлим множители до сотен: 402- приблизительно 400, 305- приблизительно 300. Умножив 400 на 300, получим 120000, а в результате только четырехзначное число. Значит, при вычислении допустили ошибку. - Проверь, верное ли равенство: 10384:34=76
Округлим делимое и делитель до десятков. 10384- примерно 10380, 34- примерно 30, разделив 10380 на 30 получим 346, а результат деления- двузначное число. - Отдельные случаи прикидки и прикидка результата вычислений по последней цифре, прикидка на основе свойств чисел.
Например. 1) Не вычисляя, определи, что деление выполнено неверно: 560:5=12. Тут прикидку необходимо выполнять так, в одном десятке 2 раза по 5, а в 50 дес.- 100 раз. Значит, в ответе будет трехзначное число. В данном примере использовано свойство числа 10(его делителями являются числа 2 и 5). 2)Не вычисляя, установить правильность выполнения действия: 875+429=9181. Вначале необходимо задать ученикам такие вопросы: «Сколько единиц в первом слагаемом? Во втором слагаемом? Какое число получаем при сложении единиц? Какой цифрой оно заканчивается? Какой цифрой заканчивается сумма в данном примере? Сделайте вывод. Для того, чтобы сформировать у учеников умения выполнять прикидку правильности выполнения действия по последней цифре полезно проводить подготовительную работу. Изучая таблицы сложения и умножения в 1-3 классах, целесообразно рассматривать задания, в которых обращается внимание на последнюю цифру результата: - Какой цифрой заканчивается:
а) сумма чисел 5 и 6, 7 и 8, 9 и 3, 4 и 8; б) произведение чисел 7 и 8, 6 и 8, 3 и 7; в) частное от деления чисел 36 на 6, 48 на 6? 2) Произведение каких однозначных чисел заканчивается цифрой 0,1,2,3,4,5,6,7,8,9? 3) Сумма каких однозначных чисел заканчивается цифрой 0,1,2,3,4,5,6,7,8,9? 4) Когда разность двух чисел равна 0? 5) Когда частное двух чисел равно 1? Такие упражнения необходимо использовать при проведении устного счета, математического диктанта. - Прикидка на основе зависимости между результатами и компонентами арифметических действий.
Изучая арифметические действия с натуральными числами, учащиеся знакомятся с зависимостями: «сумма больше или равна слагаемому», « разность меньше или равна уменьшаемому», « частное меньше или равно делимому». Эти зависимости можно использовать для прикидки результата. Например: Как установить, верно ли найден результат, не выполняя действие: а) 2574+3784=1239. Неверно, т.к. сумма не может быть меньше слагаемого. б) 8564-326=8928. Неверно, т.к. разность не может быть больше уменьшаемого. в) 576*81=576. Неверно, т.к. произведение равняется одному из множителей, если один из множителей равен 1. 576 не равно 1. 4. Прикидка по алгоритму выполнения действия. В 4 классе при изучении деления многозначных чисел предусматривается операция определения числа цифр в частном. Ее выполнение помогает предупредить ошибки учеников: пропуски нуля в частном или выполнение лишних действий. Например. Не вычисляя, определить: верно ли найден результат: а) 8476:17=28 б) 40*60=240 Методика формирования каждого вида прикидки определяется ее теоретической основой. При изучении теоретического материала, рассматривают соответствующие случаи прикидки. При изучении каждого вида прикидки следует выделять три этапа: - Объяснение теоретической основы.
- Ознакомление с прикидкой.
- Использование прикидки при выполнении упражнений.
Использование прикидки следует проводить не только на специально подобранных упражнениях, но и там, где это целесообразно. Если учащиеся знакомятся с одним из видов самоконтроля, не зная других, то страдает полнота и рациональность формирования навыков самоконтроля. Поэтому, при изучении и закреплении нового материала, необходимо включать упражнения, на использование уже изученных приемов самоконтроля, сравнивать их и выбирать наиболее рациональные. Устные вычисления полезны тогда, когда выполняются, не только правильно, но и быстро, что пригодится детям в будущем. Скорость вычислений формируется при применении таких форм работы: - Вычисления цепочкой:
а) 5 __*__3 __+__8 __*__10 б) 320+40 300+200 640-120 :4 *2 +80 -20 -400 :3 в) Цепочки можно предлагать в форме обычных выражений: (320+400:4-20 (320+200)*2-400 (640-120+80):3 (240+320):8:5 - Математический диктант.
В начальной школе математические диктанты применяются на разных этапах урока. Они являются хорошим способом обратной связи между учителем и учениками. Выполняя задания диктантов, учащиеся становятся организованными, быстрее сосредотачиваются. Проведение математических диктантов на этапе устного счета способствует не только развитию навыков вычислений, но и повышению их математической культуры, обогащению математической речи. При проведении математического диктанта, цель которого выработать скорость вычислений, следует придерживаться таких требований: А) Ученикам дается 10-12 вычислений; Б) Ученик записывает только ответ; В) На выполнение действия и запись ответа отводится 10 секунд. 3) Вычисления за определенное время. а) кто больше решит примеров за 5 минут; б) на выполнение 20 примеров отводится 5 минут. При решении примеров и задач на уроке, при выполнении домашних работ мы потом проверяем их, затрачивая время, отмечаем и подчеркиваем ошибки. Но не всегда наши ученики после проверки их работ возвращаются к ним, чтобы выяснить, исправить и осознать сделанные ошибки. А между тем проведение работ можно организовать так, что ученик, сделав ошибку, сам обнаружит ее, сам или с помощью дополнительной информации исправит ее и подойдет к следующему этапу работы только после полного усвоения предыдущего материала, выполнив, таким образом, задание только правильно. Затрата времени на подготовку таких работ очень незначительная, а экономия времени на их проверку большая. Предлагаю рассмотреть некоторые формы проверки. Наиболее удобна запись ответов в возрастающем или убывающем порядке, тогда ответы становятся неизвестными, совпадение их с полученными ответами при решении подтверждают их правильность. Вот некоторые формы проверки примеров, которые я использую в работе. 1. Учитель, подготавливая задание, решает примеры и выносит их на доску в возрастающем или убывающем порядке. 900 - 500 - 300
200 + 300 + 100
800 - 600 + 200
700 - 100 + 200
500 + 100 - 400
600 + 300 - 900 Ответы для самоконтроля: 0, 100, 200, 400, 600, 800 2. Способ проверки, основанный на взаимосвязи между примерами и получаемыми ответами - это круговые примеры.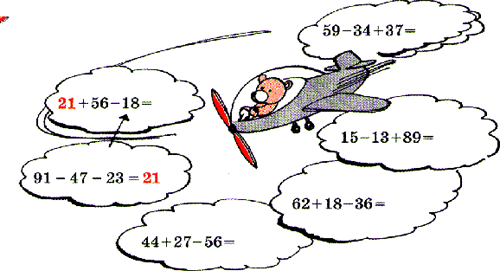 
При подготовке работ необходимо выписывать и подбирать примеры так, чтобы число, получаемое в результате одного из них, являлась началом другого. 3. Примеры - цепочки с записью ответов, расположенных в убывающем или возрастающем порядке. 260 - 20 = a
a - 180 + 30 = b
b + 120 - 60 = c
c + 360 - 70 = d
d - 120 + 30 = e Ответы для самоконтроля: 90, 150, 240, 350, 440, 590 Как ученик делает самопроверку: 240 - 20 = 240 (ответ есть, переходим к следующему примеру) 240 - 180 + 30 = 90 (ответ есть, переходим к следующему примеру) 90 + 120 - 60 = 150(ответ есть, переходим к следующему примеру) 150 + 360 - 70 = 440(ответ есть, переходим к следующему примеру) 440 - 120 + 30 = 350 (ответ есть, переходим к следующему примеру) Случайное совпадение ответов бывает, но очень редко. В этом случае пользуются таким приемом: находят сумму или разность первого и последнего ответов и сверяют с самоконтролем. 240 + 350 = 590 (ответ есть, задание выполнено правильно) Приведу еще один пример, как можно контролировать пример на порядок действий. 810 : 9 · 8 + 40 · 7 = Ответы для самоконтроля: 90, 280, 720, 1000, 1090. Как ученик делает самопроверку: 1) 810 : 9 = 90 (ответ есть, переходим к следующему примеру) 2) 90 · 8 = 720 (ответ есть, переходим к следующему примеру) 3) 40 · 7 = 280 (ответ есть, переходим к следующему примеру) 4) 720 + 280 = 1000 (задание выполнено правильно) Находим подтверждение правильности выполнения задания. 90 + 1000 = 1090 4. В тех случаях, когда взаимосвязь между примерами отсутствует, ее можно образовать искусственным путем последовательного суммирования ответов или установления их разности. 3212 : 44 =
4503 : 57 =
7081 : 73 =
23832 : 36 = Ответы для контроля: 73,152,249,911, 984 Как ученик делает самопроверку: 3212 : 44 = 73 (ответ совпадает) 4503 : 57 = 79 (73 + 79 = 152) Ответ совпадает. 7081: 73 = 97 (152 + 97 = 249) Ответ совпадает. 23832 : 36 = 662 (249 + 662 = 911) Ответ совпадает. Находим подтверждение правильности выполнения задания. 73 + 911 = 984 С первого взгляда может показаться, что использование предлагаемого приема требует больших затрат времени и что проверку легче выполнить с помощью обратных действий. Конечно можно, но с большими затратами времени и без абсолютной гарантии правильности. Предлагаемый прием является дополнительным к традиционным методам обучения. Он помогает разнообразить работу, что способствует повышению интереса к работе. Для ускорения работы можно ограничиться в ответах для самоконтроля указанием двух или трех первых или последних цифр нужного числа. 56 + 23
17 + 63
24 + 69
62 - 28
55 - 37
70 - 34 Ответы для самоконтроля: 40, 52, 59, 86, 79,104 Как ученик делает самоконтроль: 56 + 23 = 7 (находим в числах для самоконтроля ) 17 + 63 = 80 (79 + 80 = 159) Находим среди чисел, данных для самоконтроля 59, и переходим к 3 примеру. 24 + 69 = 93 (Складываем две последние цифры ответа 59 с третьим ответом 59 + 93 = 152) Находим подтверждение среди чисел, данных для самоконтроля, 52 и переходим к следующему примеру. 62 - 28 = 34 (складываем две последние цифры 52 с четвертым ответом 52 + 34 = 86) Находим подтверждение среди чисел в самоконтроле и переходим к следующему примеру. 55 - 37 = 18 (складываем две последние цифры 86 с пятым ответом 86 + 18 = 104) Находим подтверждение среди чисел в самоконтроле и переходим к следующему примеру. 70 - 34 = 36 (складываем две последние цифры 4 с шестым ответом 4 + 36 = 40) Находим подтверждение среди чисел в самоконтроле и переходим к следующему примеру. Описанные приемы позволяют детям правильно выполнять задания по выполнению примеров. А учителю экономить время на проверке. Итак, основными формами совершенствования вычислений, являются вычисления «цепочкой», математические диктанты, внеурочная деятельность. Одним из наиболее целесообразных способов совершенствования вычислительных навыков является система упражнений, направленная на формирование таких качеств вычислений: правильность, скорость, рациональность, гибкость.
