- Преподавателю
- Математика
- Производная функции одной переменной
Производная функции одной переменной
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Луконина С.А. |
| Дата | 01.03.2015 |
| Формат | doc |
| Изображения | Есть |
Тема 4 . Производная функции одной переменной.
Время: 2 часа
Цель лекции: Познакомить с понятием производной функции, её геометрическим, физическим и экономическим смыслом. Показать правила и приёмы дифференцирования.
План лекции:
-
Задачи, приводящие к понятию производной.
-
Определение производной. Её механический, геометрический и экономический смысл.
-
Связь между непрерывностью и дифференцируемостью функции.
-
Производная суммы, разности, произведения и частного функций.
-
Производная сложной и обратной функции.
-
Дифференцирование неявных и параметрически заданных функций.
-
Логарифмическое дифференцирование.
-
Задачи, приводящие к понятию производной.
Задача 1: Скорость прямолинейного движения.
Пусть материальная точка (некоторое тело) М движется неравномерно по некоторой прямой. Известен закон движения точки, т.е. зависимость координаты тела от времени S=S(t), которая каждому значению t ставит в соответствие определённое расстояние ОМ=S до некоторой фиксированной точки О (начала отсчёта).
Чтобы найти среднюю скорость движения, необходимо пройденный путь (изменение координаты 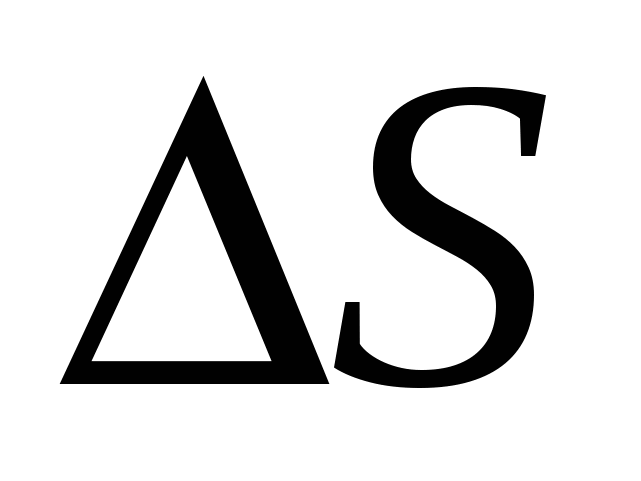 за время
за время  ) поделить на прошедшее время
) поделить на прошедшее время 
![]()
Чем меньше ![]() , тем точнее средняя скорость выражает скорость движения точки в данный момент времени t. Предел средней скорости движения при стремлении к нулю промежутка времени
, тем точнее средняя скорость выражает скорость движения точки в данный момент времени t. Предел средней скорости движения при стремлении к нулю промежутка времени  называется скоростью движения точки в данный момент времени t (или мгновенной скоростью движения).
называется скоростью движения точки в данный момент времени t (или мгновенной скоростью движения). 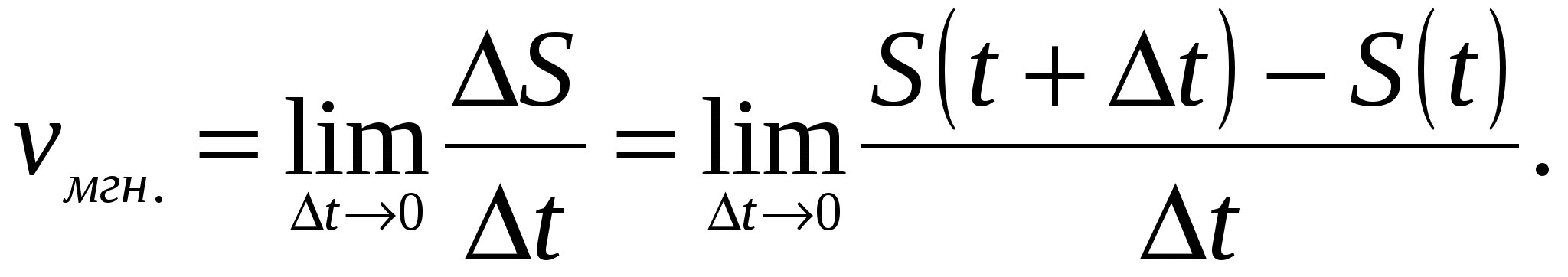
Задача 2: Касательная к кривой.
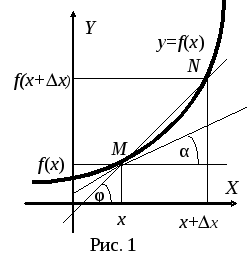 Возьмём на непрерывной кривой две точки М и N. Прямую, проходящую через эти две точки называют секущей. Пусть точка N, двигаясь вдоль кривой, неограниченно приближается к точке М. Тогда секущая, поворачиваясь около точки М, стремится к некоторому предельному положению МТ, которое и называют касательной к данной кривой в данной точке М.
Возьмём на непрерывной кривой две точки М и N. Прямую, проходящую через эти две точки называют секущей. Пусть точка N, двигаясь вдоль кривой, неограниченно приближается к точке М. Тогда секущая, поворачиваясь около точки М, стремится к некоторому предельному положению МТ, которое и называют касательной к данной кривой в данной точке М.
Рассмотрим теперь график непрерывной кривой 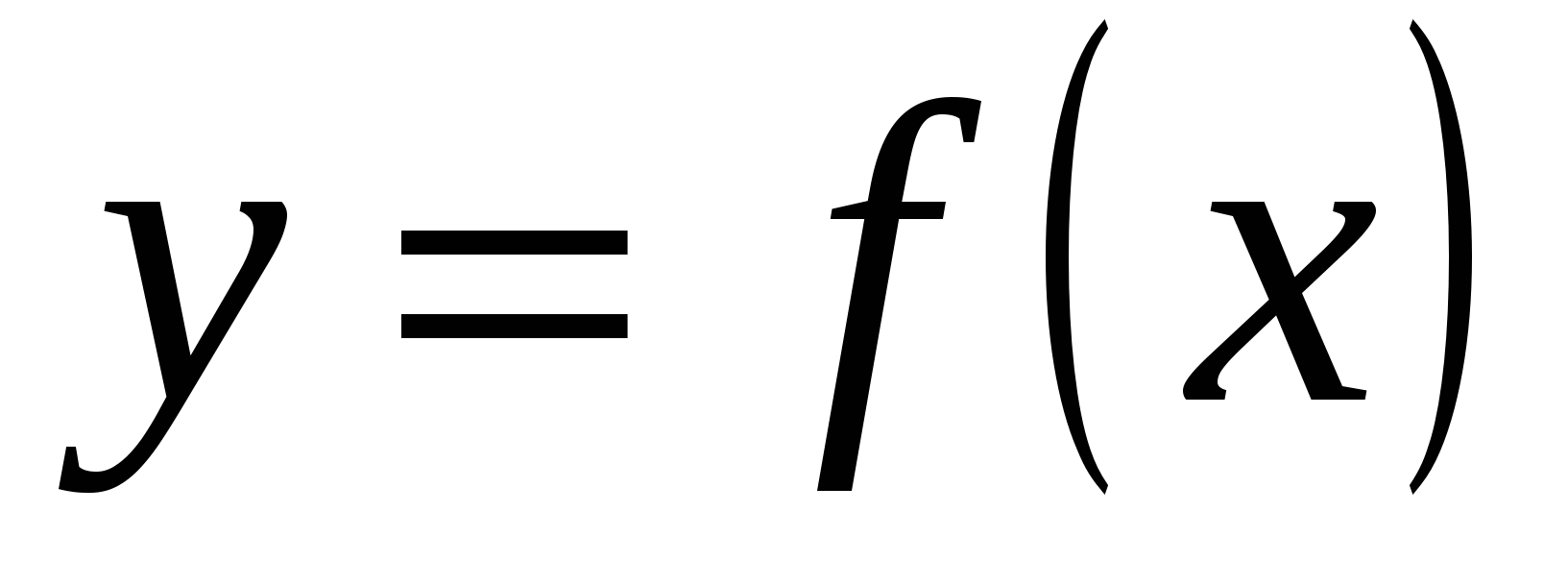 , имеющей в точке
, имеющей в точке 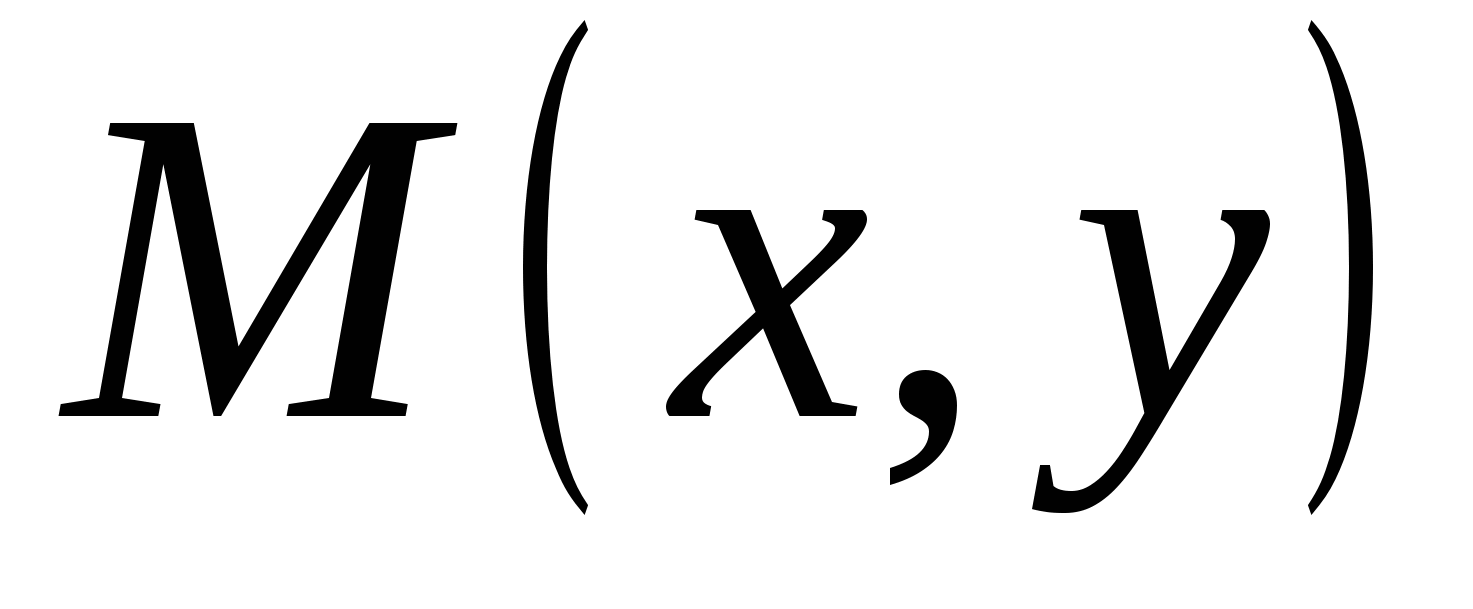 невертикальную касательную. Найдём её угловой коэффициент
невертикальную касательную. Найдём её угловой коэффициент 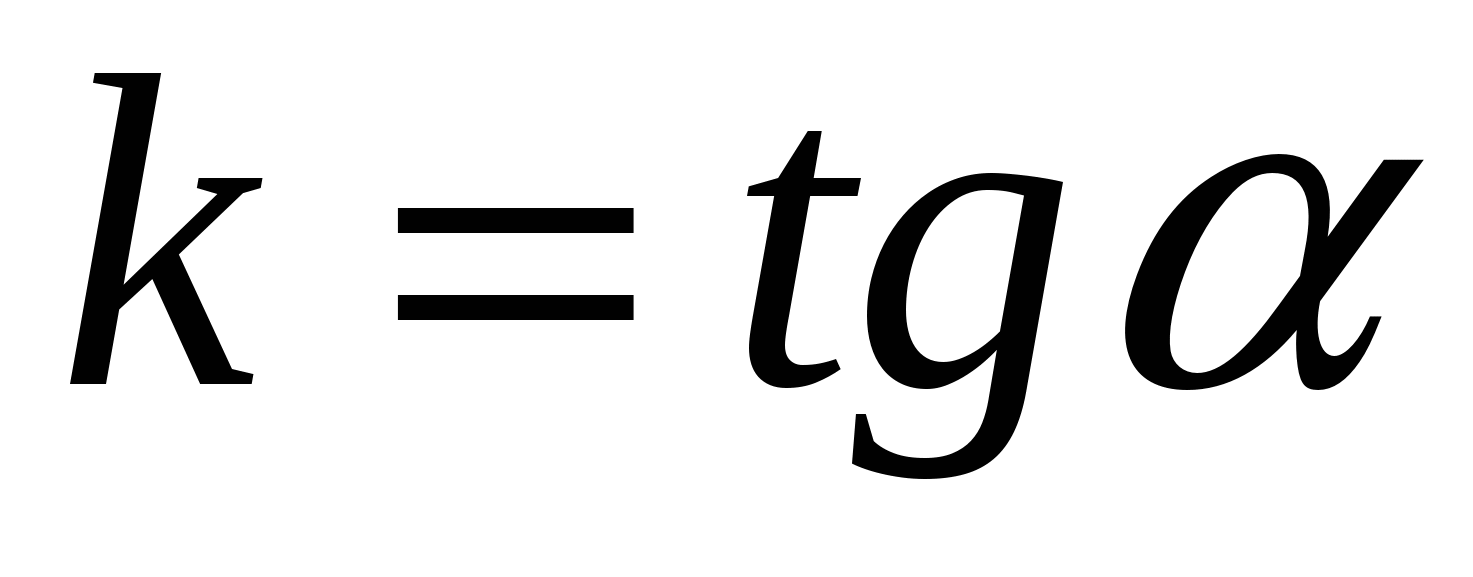 , где α ‒ угол наклона касательной положительному направлению оси Ох.
, где α ‒ угол наклона касательной положительному направлению оси Ох.
Для этого зададим приращение аргумента 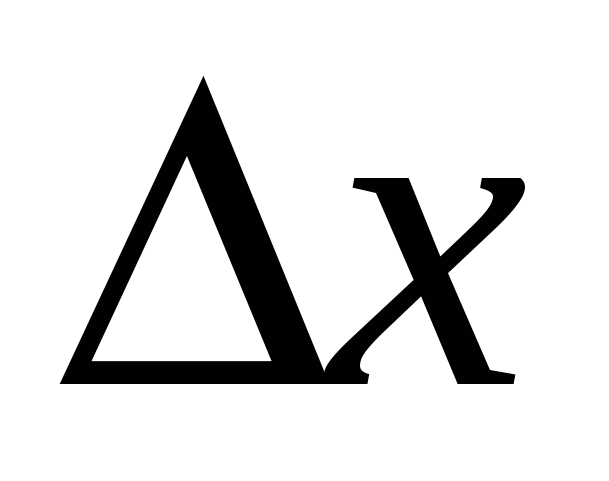 , получим на кривой точку N с абсциссой
, получим на кривой точку N с абсциссой 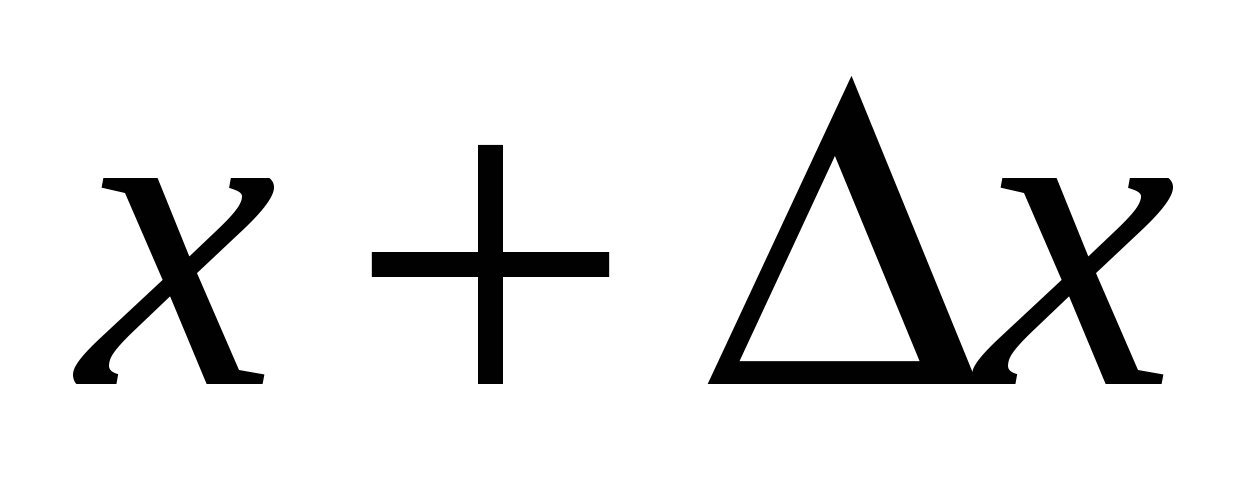 ; проведём через точки М и N секущую. Обозначим φ угол между секущей и осью Ох. Угловой коэффициент секущей равен
; проведём через точки М и N секущую. Обозначим φ угол между секущей и осью Ох. Угловой коэффициент секущей равен
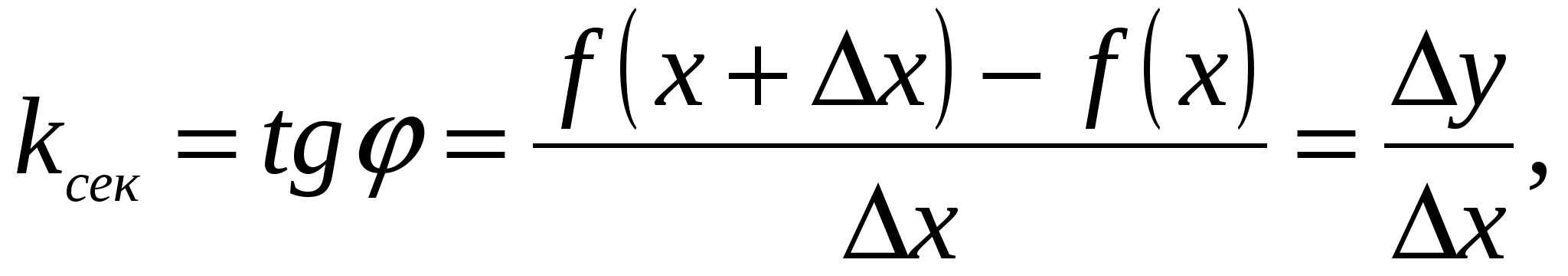 где
где
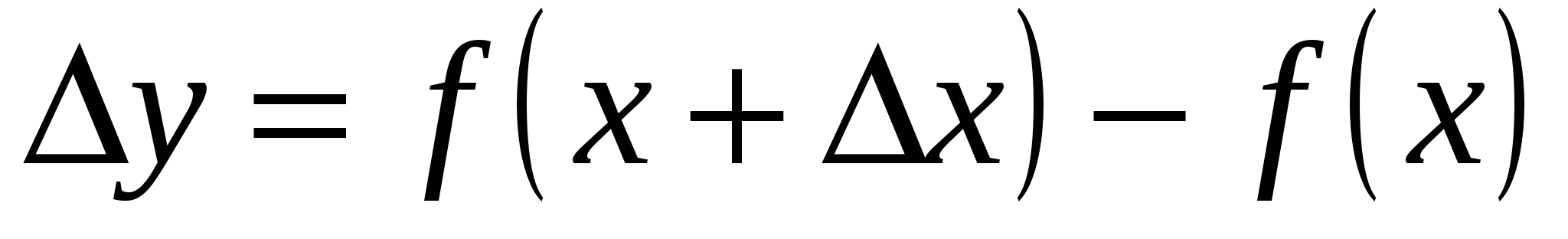 ‒ приращение функции.
‒ приращение функции.
При 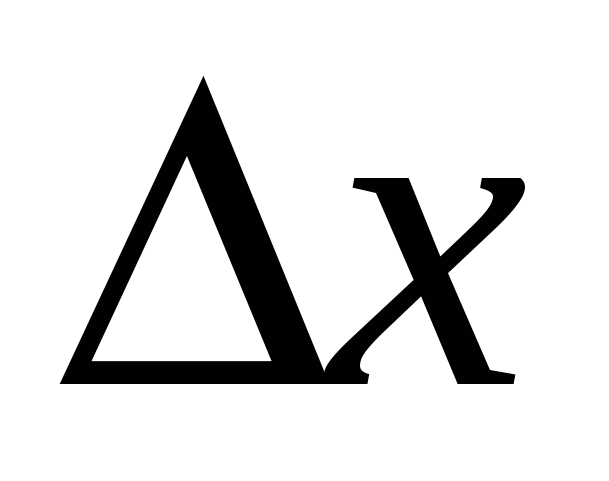 точка N неограниченно приближается по кривой к точке М, а секущая, поворачиваясь около точки М, переходит в касательную. Поэтому угловой коэффициент касательной равен
точка N неограниченно приближается по кривой к точке М, а секущая, поворачиваясь около точки М, переходит в касательную. Поэтому угловой коэффициент касательной равен
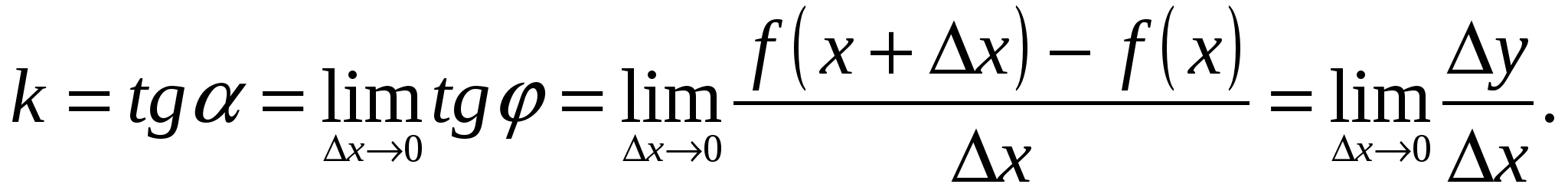
Задача 3: Предельные издержки производства.
Пусть К(х) ‒ издержки на производство х единиц продукции. Если количество продукции увеличилось на ![]() , то издержки возрастут на величину
, то издержки возрастут на величину 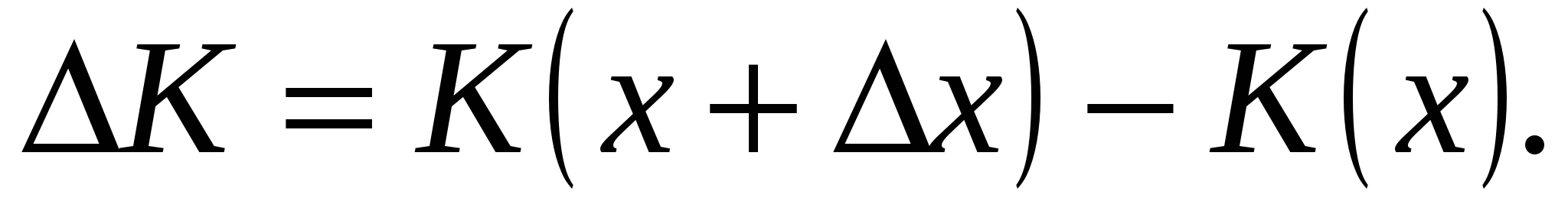 Средние издержки на производство
Средние издержки на производство 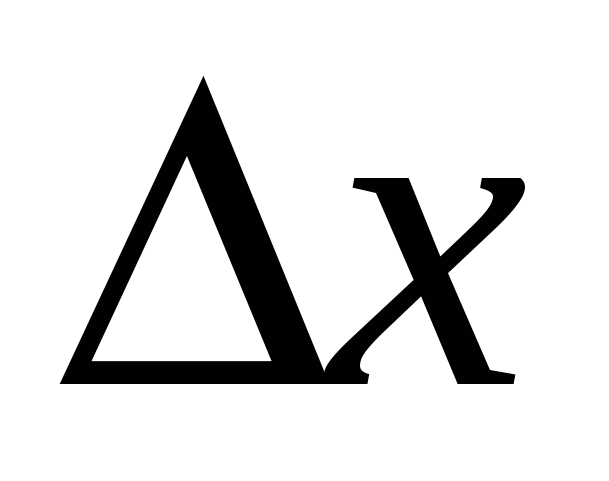 единиц продукции составят
единиц продукции составят 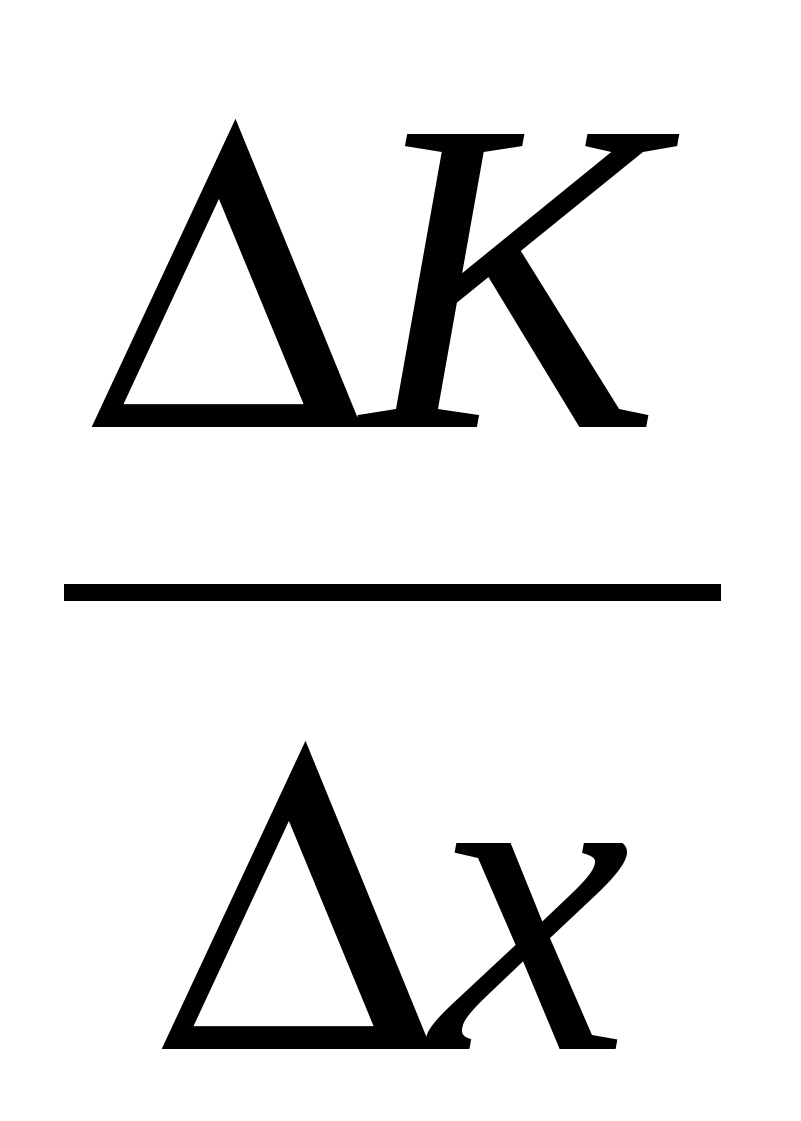 . Предел
. Предел 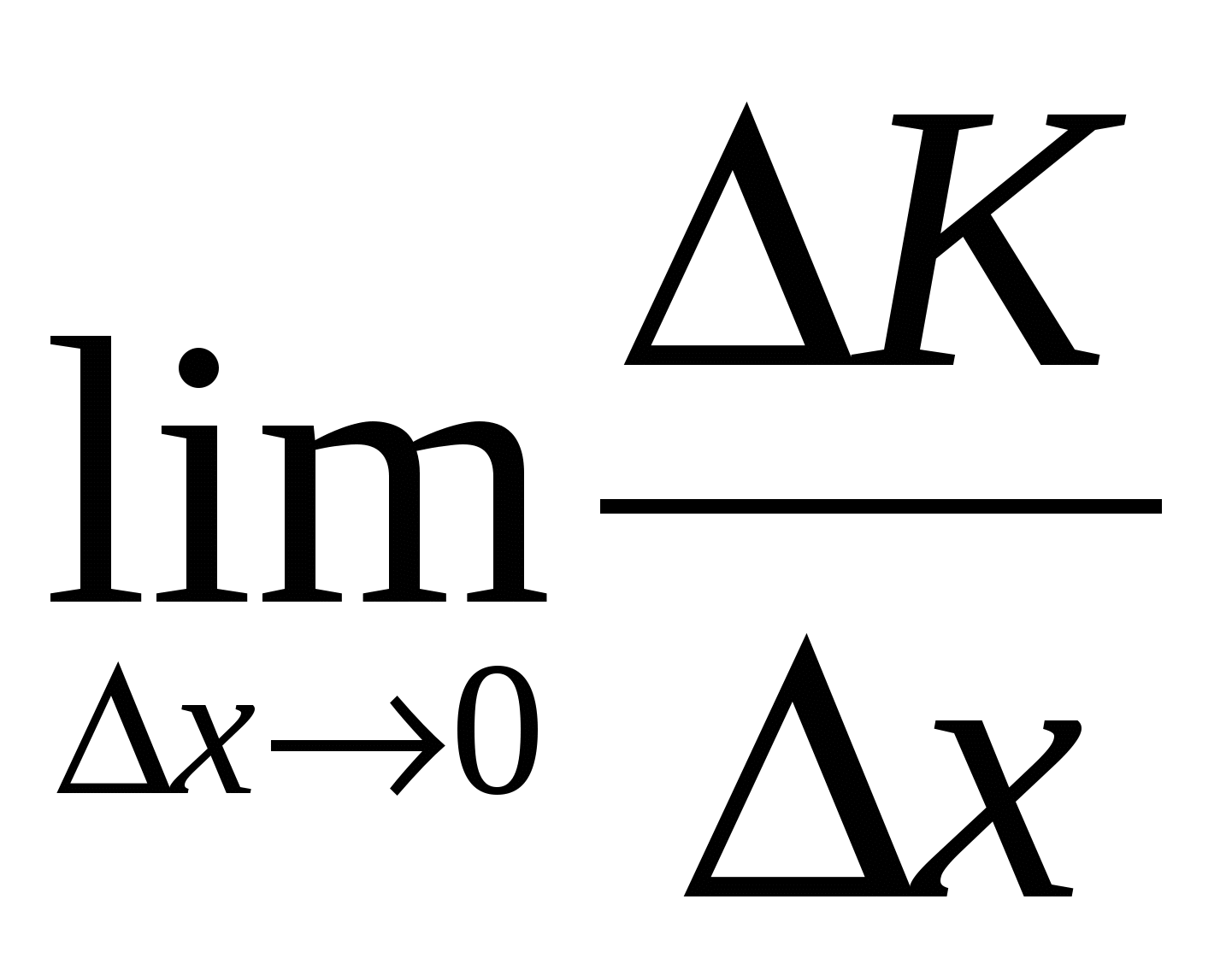 называют предельными издержками производства.
называют предельными издержками производства.
-
Определение производной. Её механический, геометрический и экономический смысл.
Решение всех задач свелось к вычислению предела отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Этот предел называют производной функции 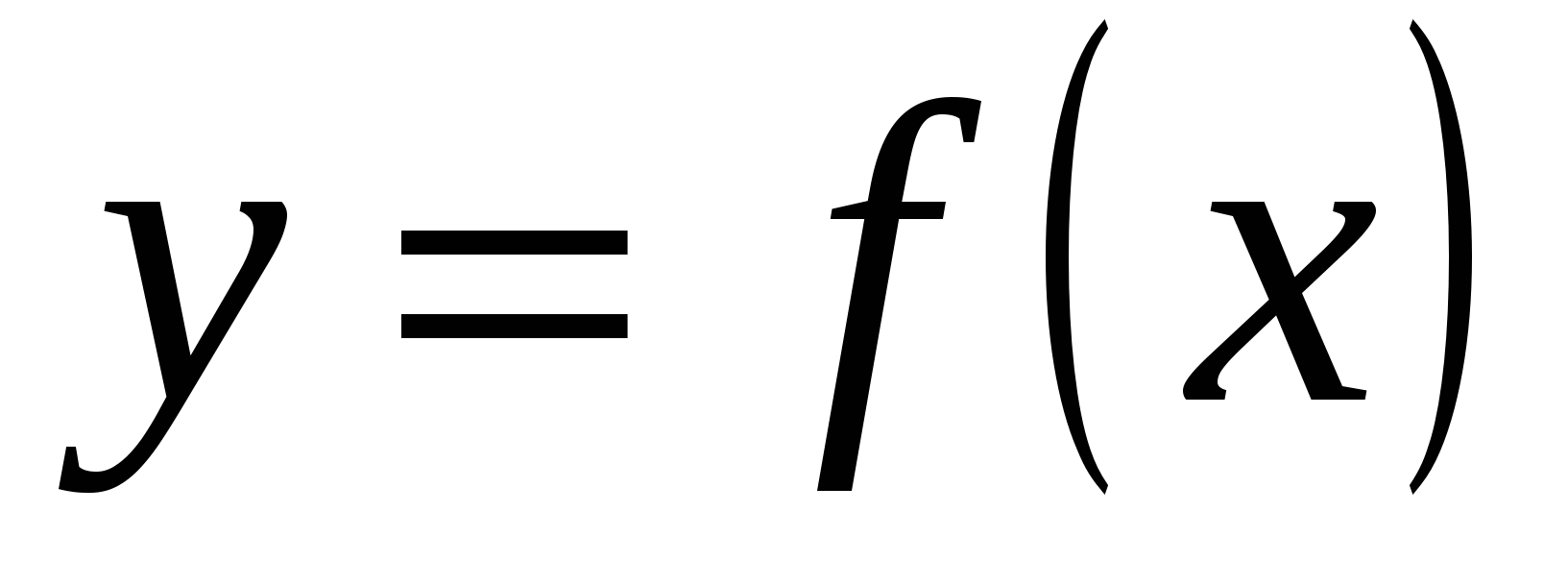 в точке х0.
в точке х0.
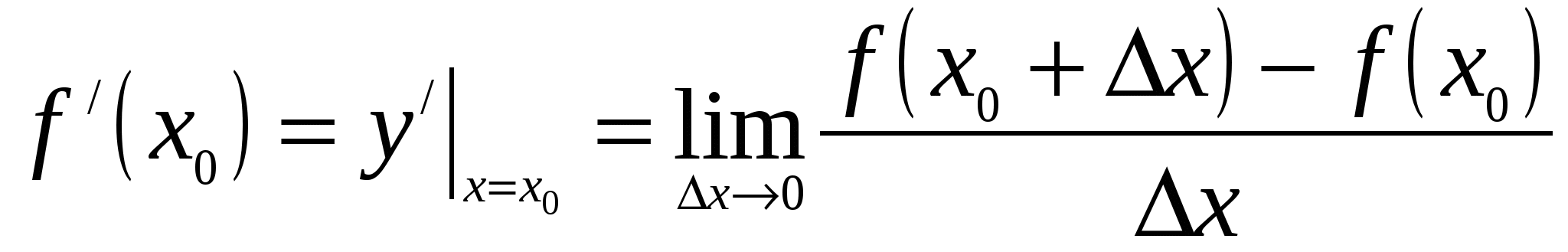
Функция 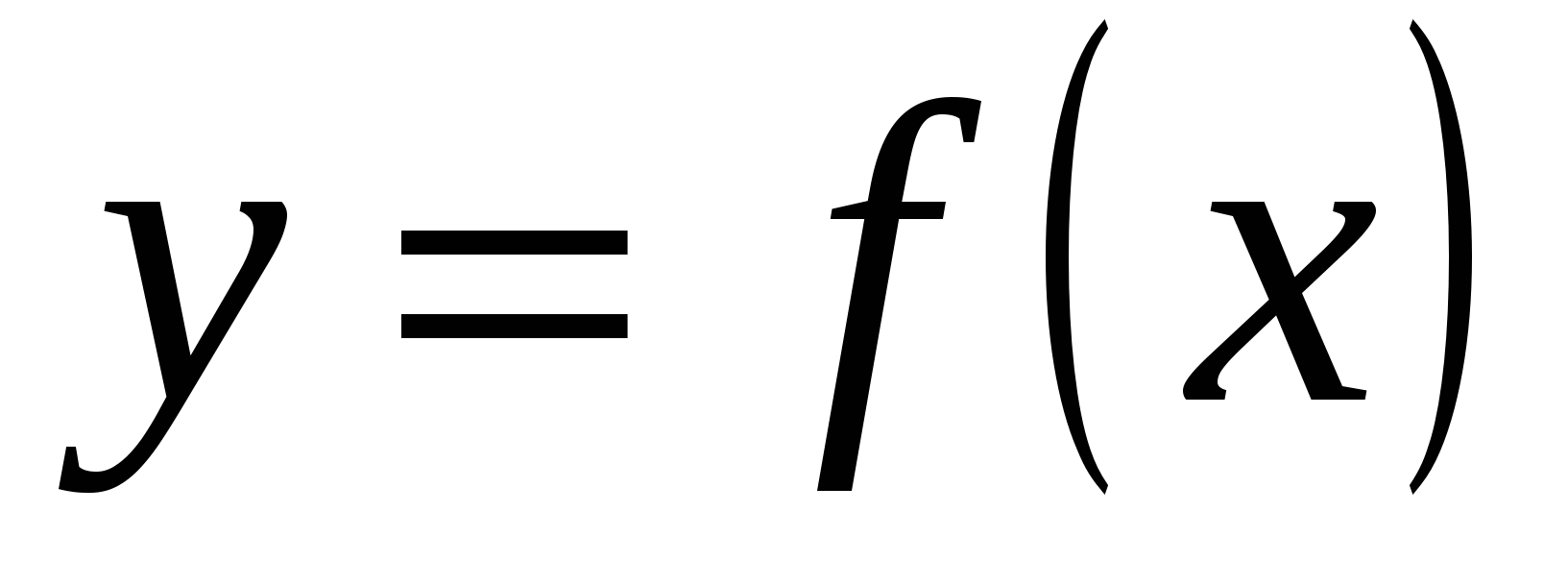 , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала 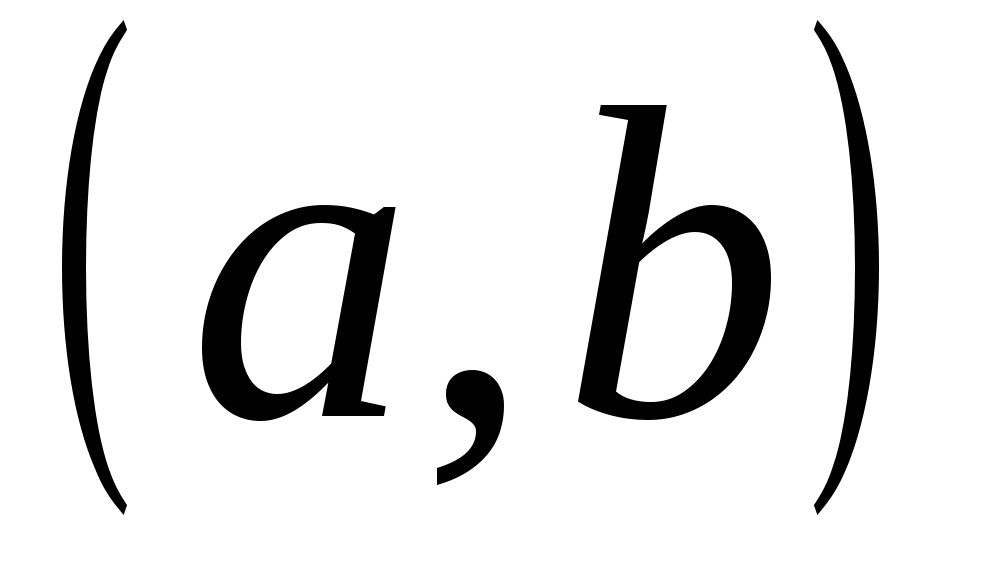 , называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
, называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
К вычислению пределов указанного вида приводят решения и множества других задач. Так, если 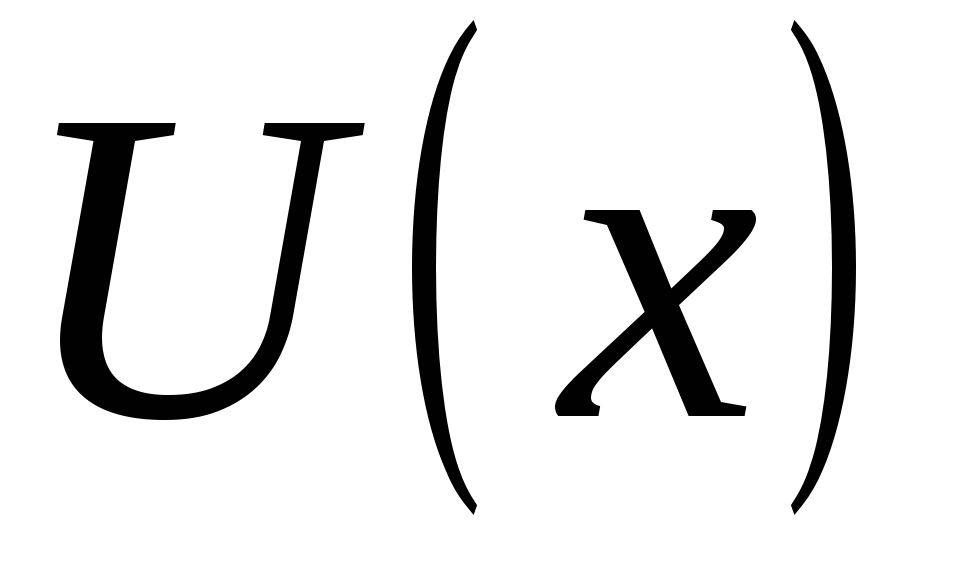 ‒ выручка от продажи х единиц товара, то
‒ выручка от продажи х единиц товара, то
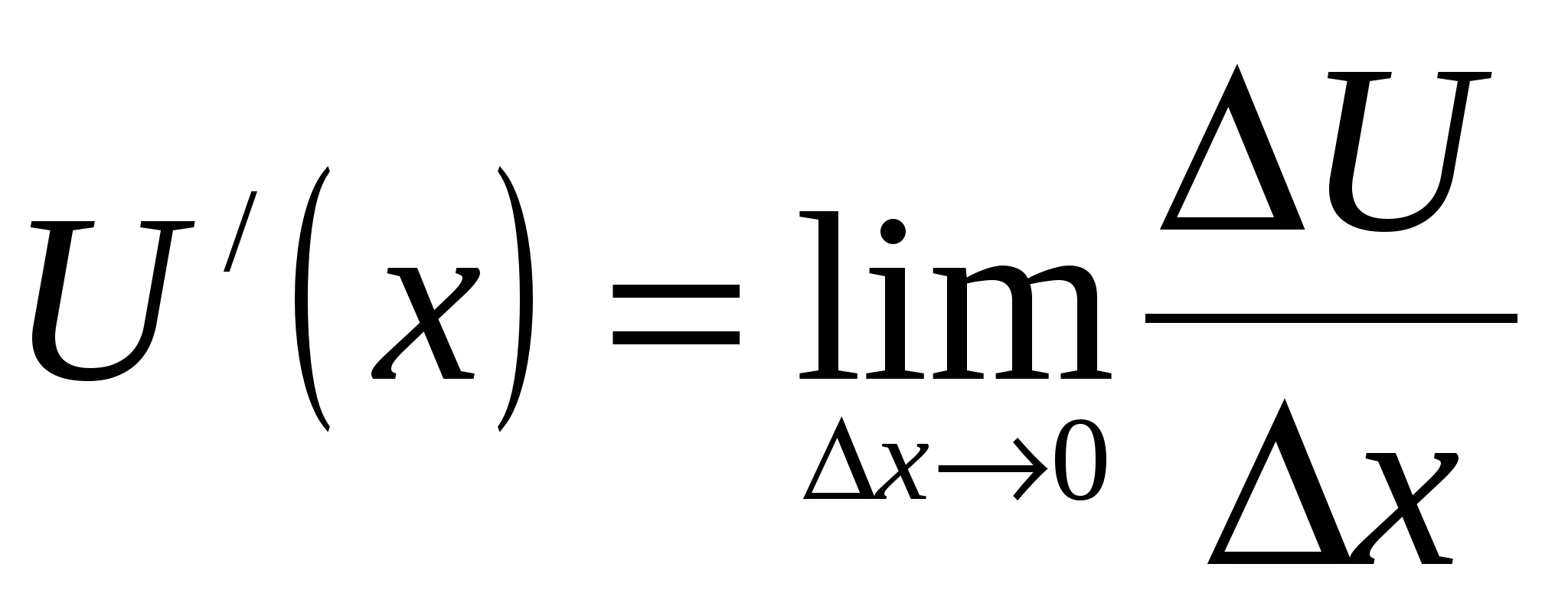 ‒ предельная выручка.
‒ предельная выручка.
Если 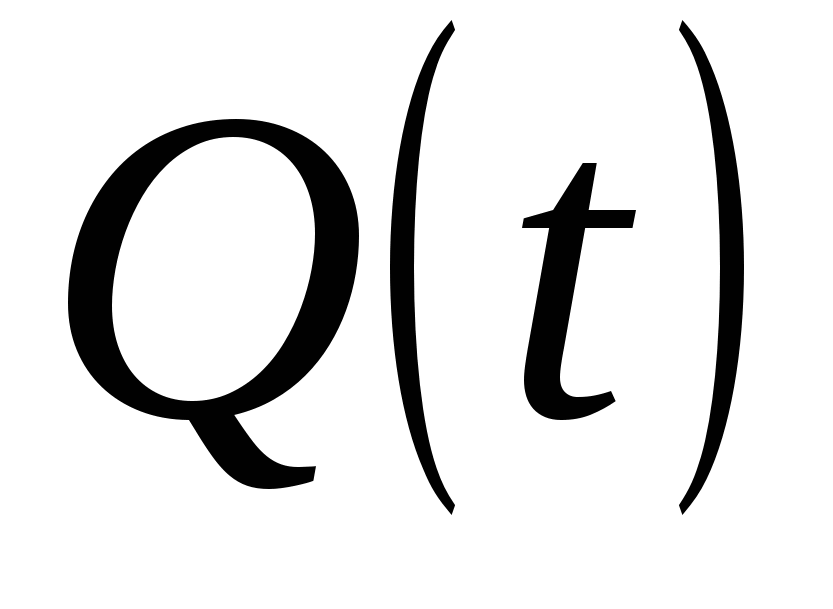 ‒ количество продукта, произведённого к времени t. Средняя производительность на промежутке времени
‒ количество продукта, произведённого к времени t. Средняя производительность на промежутке времени 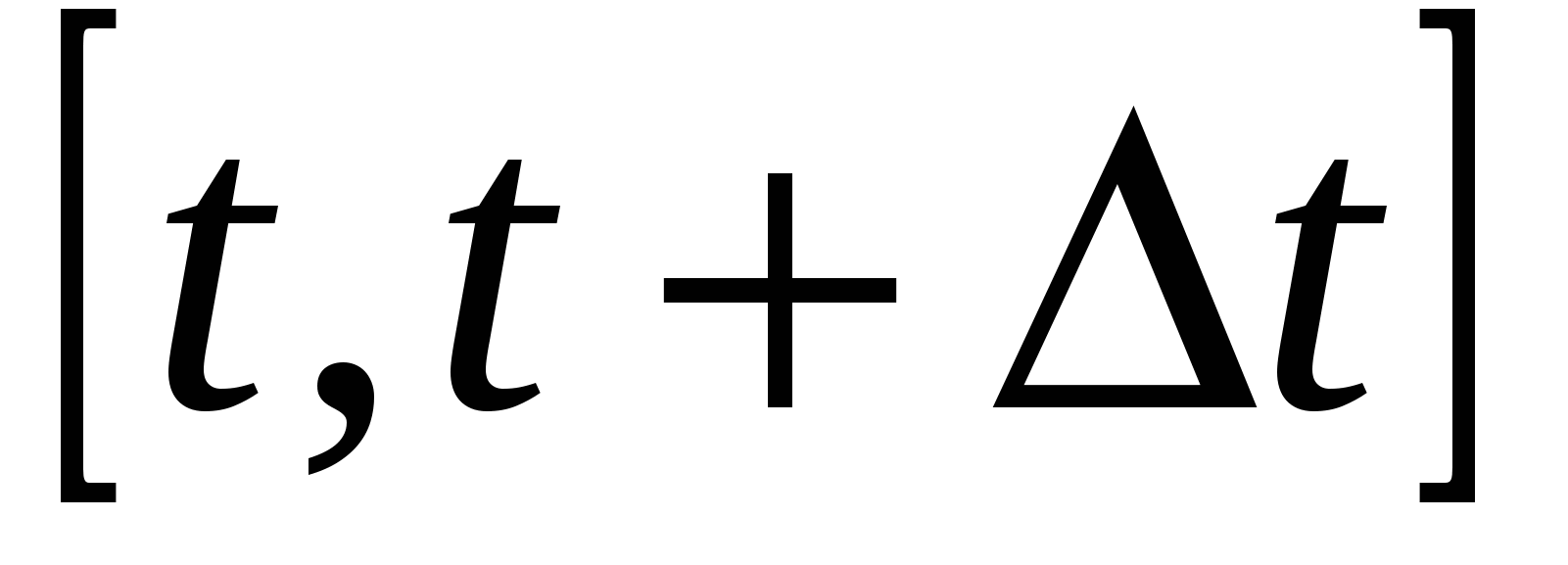 равна
равна
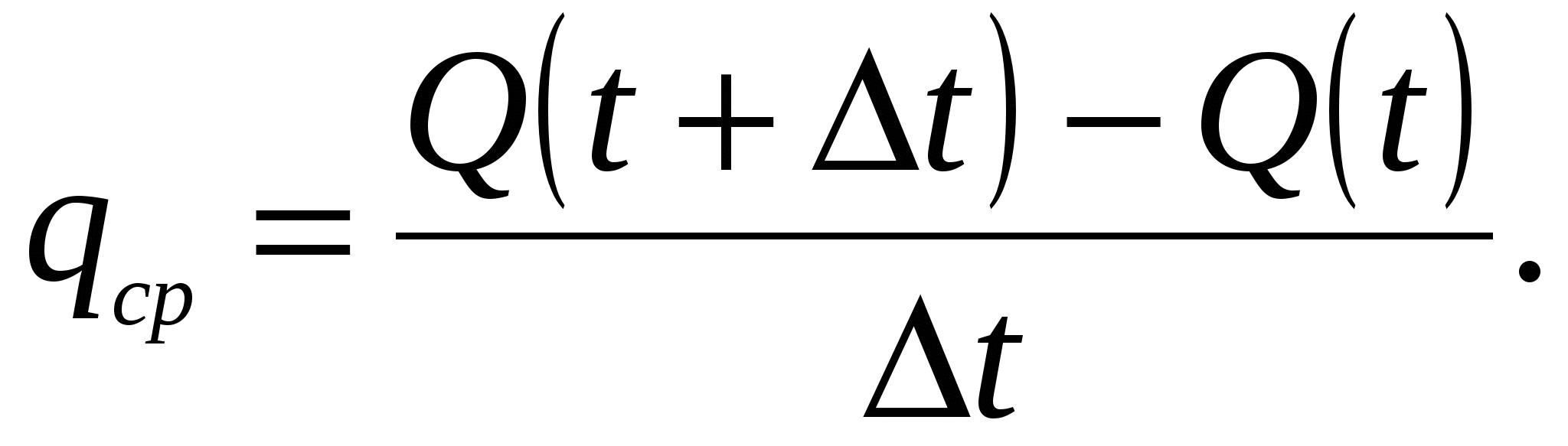
Величина 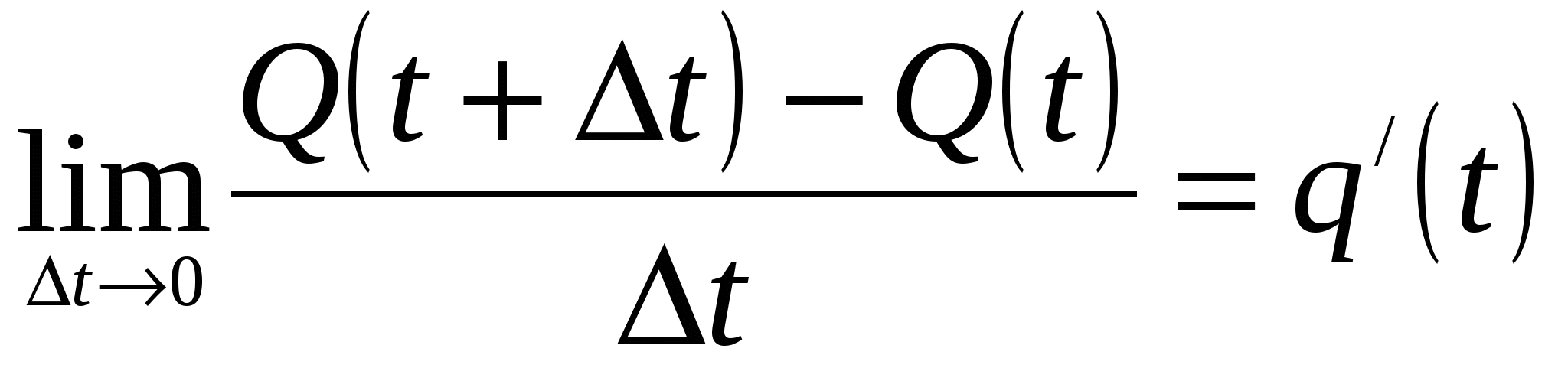 представляет собой производительность в момент времени t, т.е. скорость изменения количества произведённого продукта.
представляет собой производительность в момент времени t, т.е. скорость изменения количества произведённого продукта.
Обобщая, можно сказать, что если функция 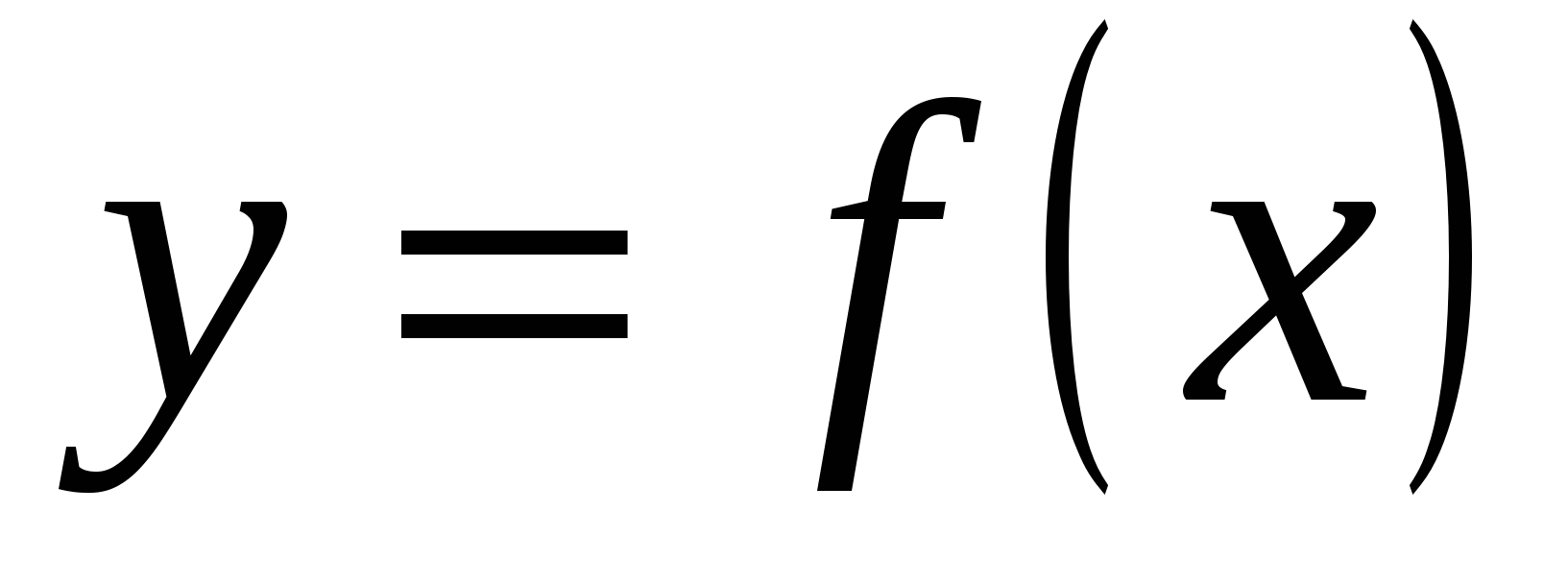 описывает какой-либо процесс, то её производная есть скорость протекания этого процесса.
описывает какой-либо процесс, то её производная есть скорость протекания этого процесса.
Геометрический смысл производной: производная в точке х0 равна угловому коэффициенту касательной, проведённой к графику функции 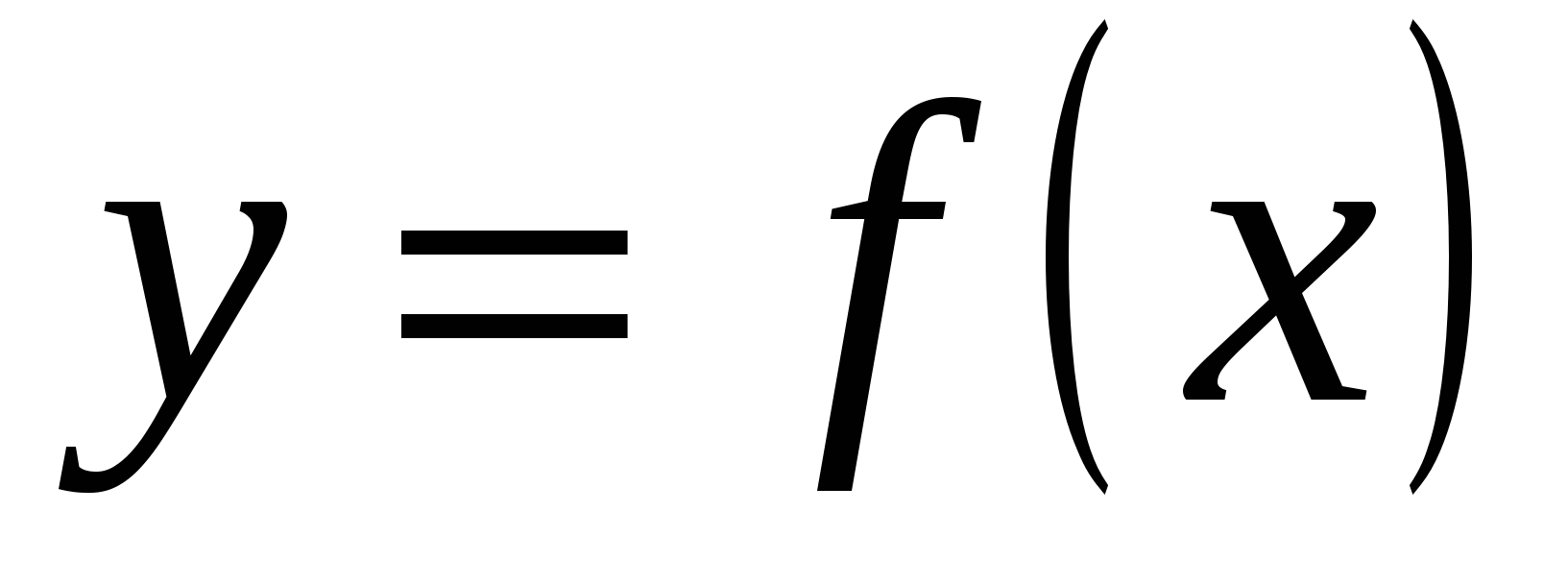 в точке с абсциссой х0.
в точке с абсциссой х0.
-
Связь между непрерывностью и дифференцируемостью функции.
Теорема 5.1: Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Пусть функция 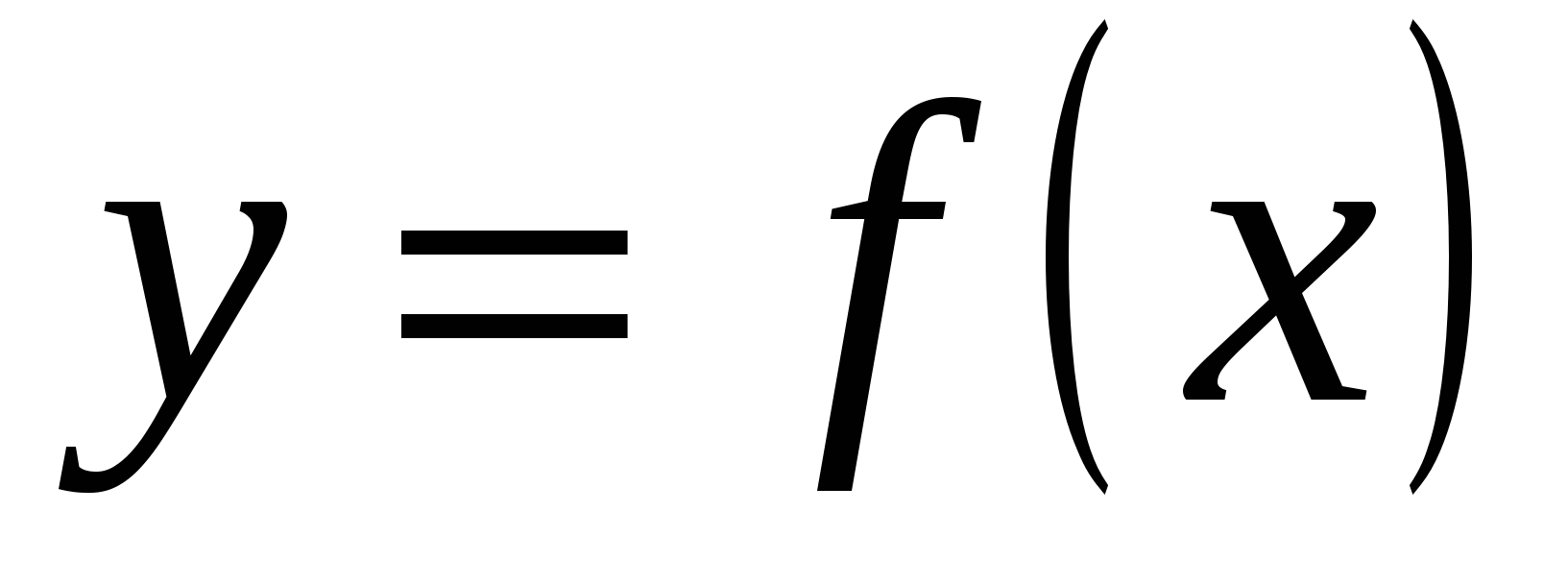 дифференцируема в некоторой точке х. Следовательно существует предел
дифференцируема в некоторой точке х. Следовательно существует предел 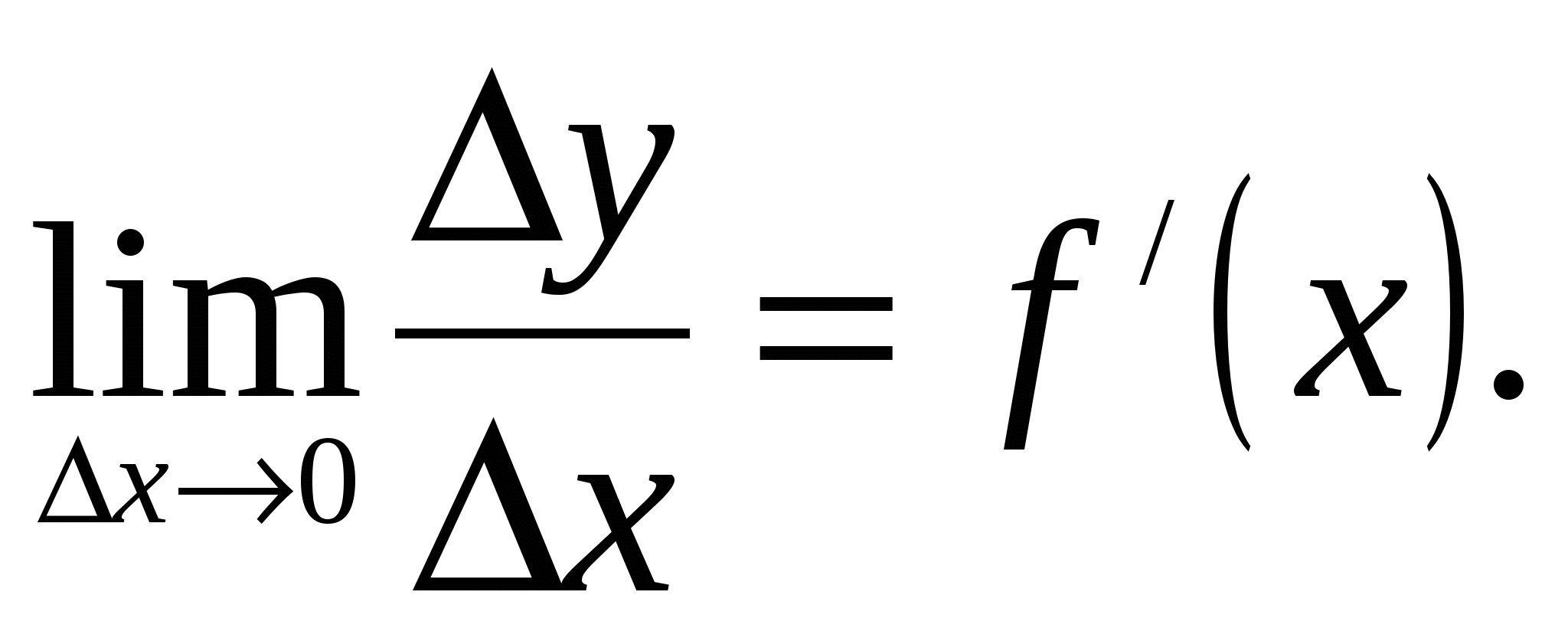 Отсюда по теореме о связи функции, её предела и бесконечно малой функции, имеем
Отсюда по теореме о связи функции, её предела и бесконечно малой функции, имеем 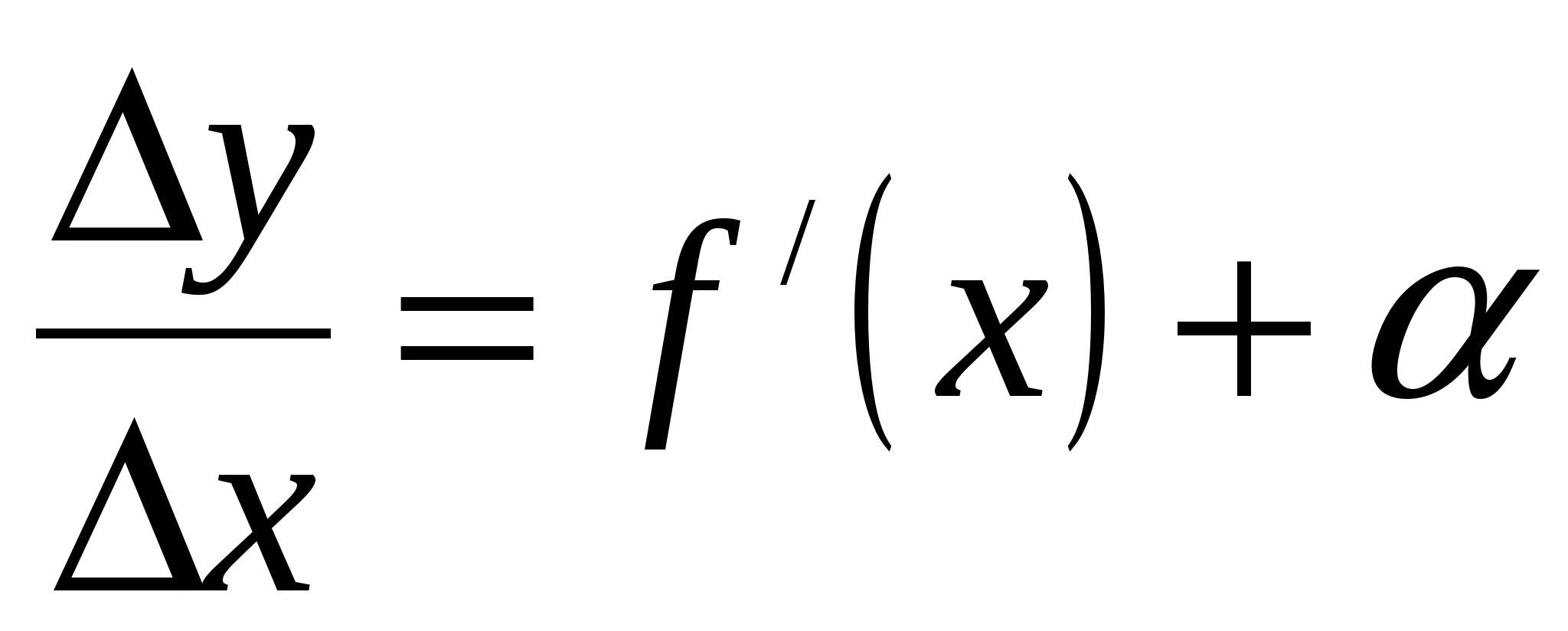 , где α ‒ б.м.ф. при
, где α ‒ б.м.ф. при 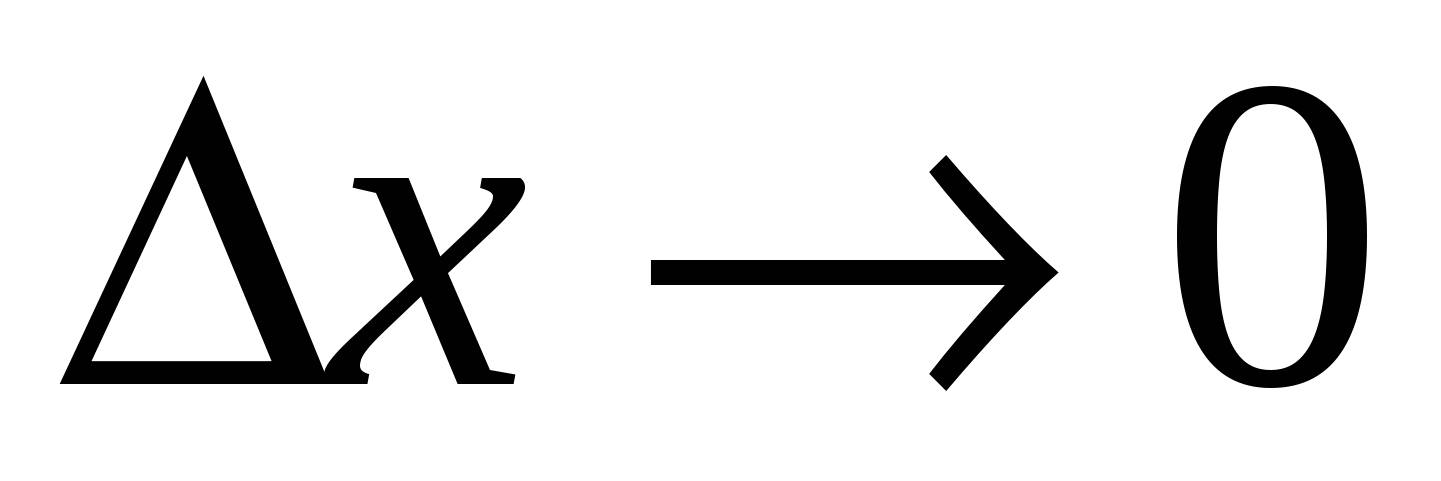 , т.е.
, т.е. 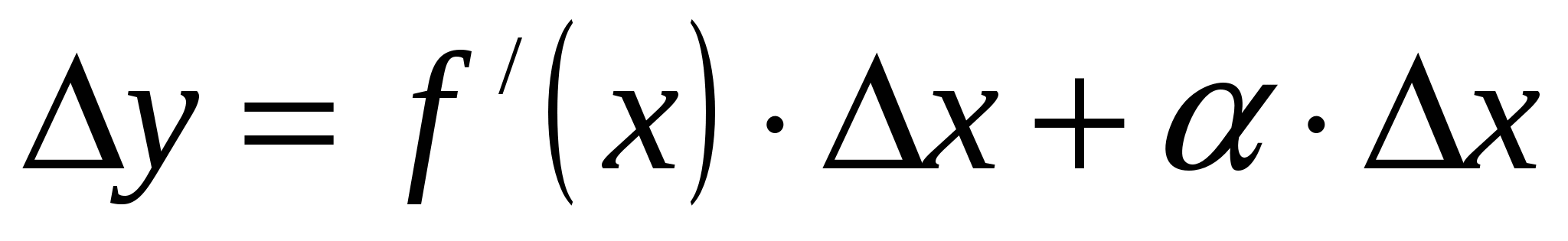 .
.
Переходя к пределу при 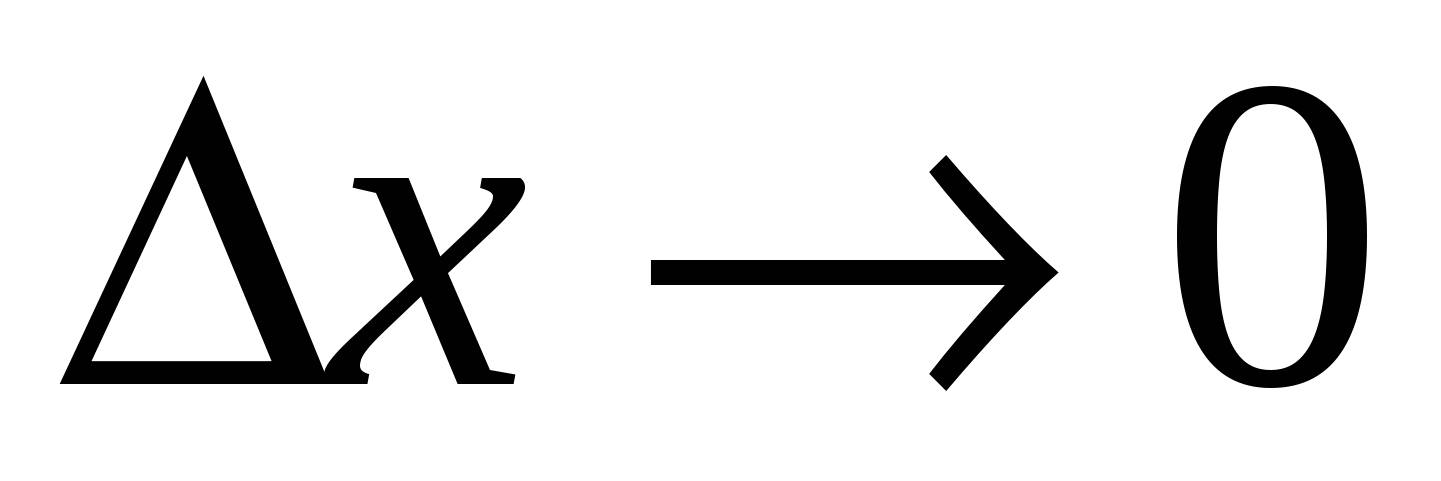 получаем
получаем 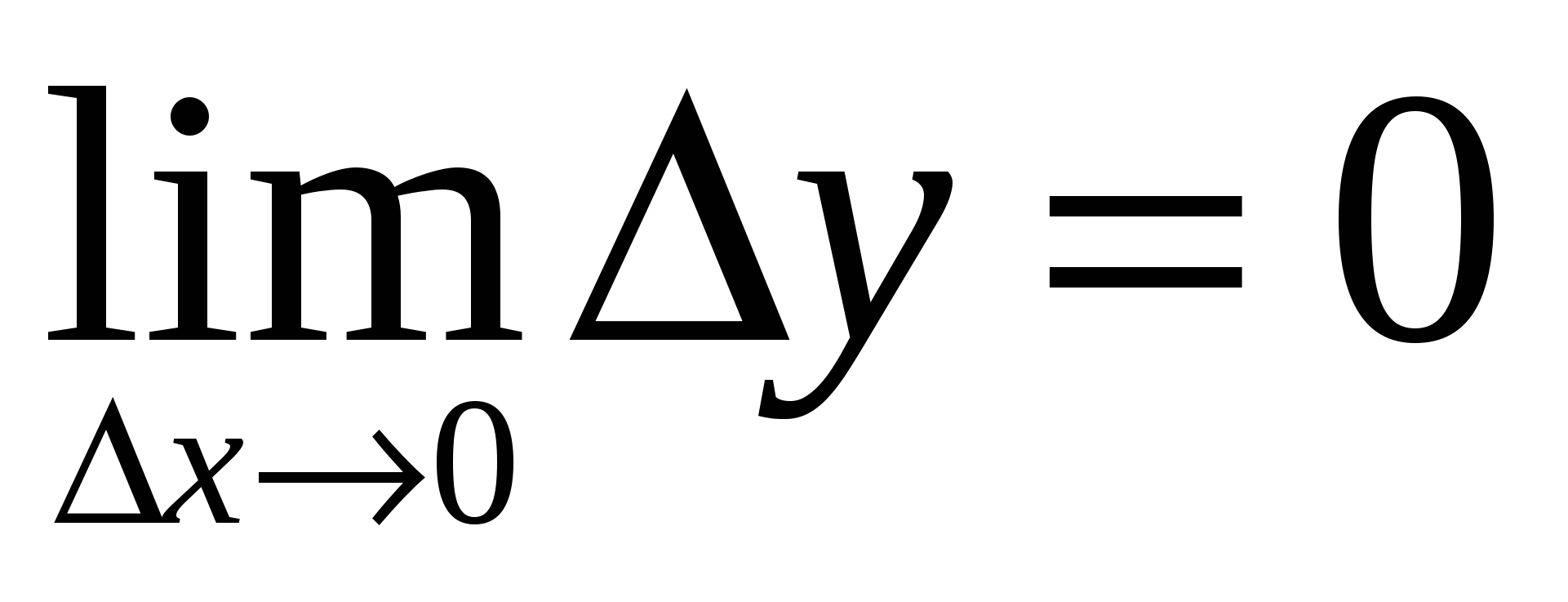 . А это и означает, что функция
. А это и означает, что функция 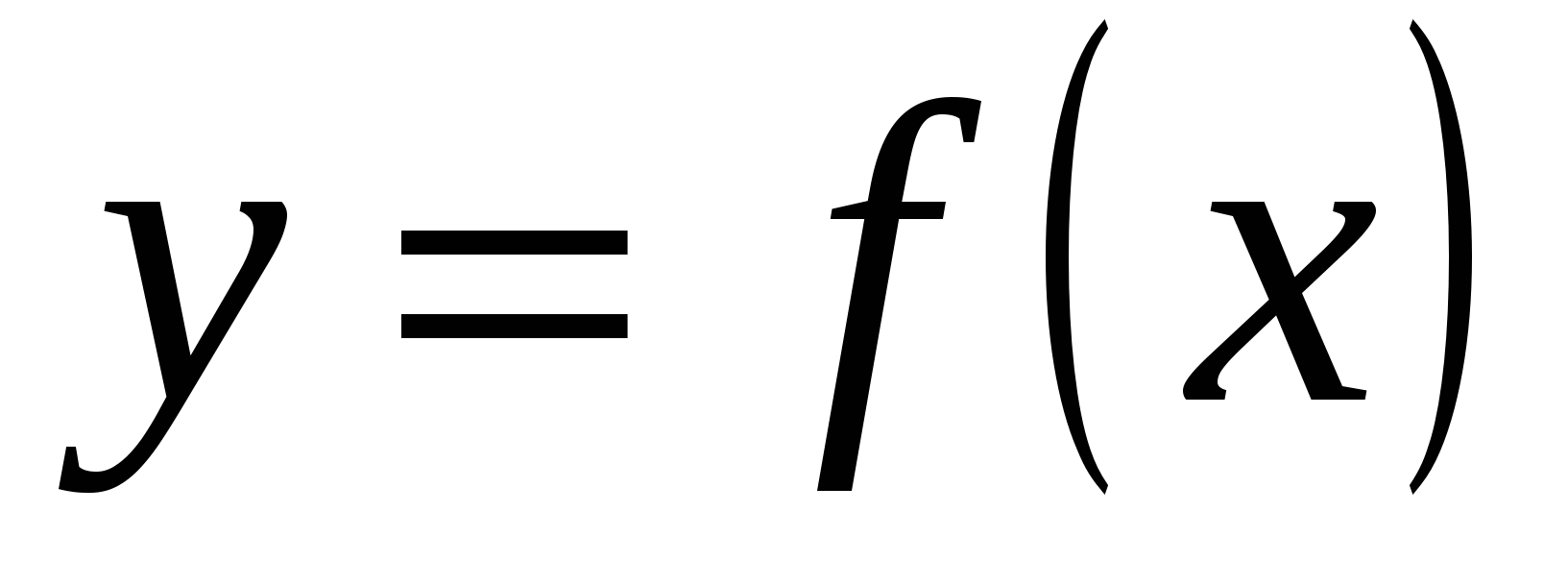 непрерывна в точке х.
непрерывна в точке х.
Обратная теорема неверна: непрерывная функция может не иметь производной. Например, функция 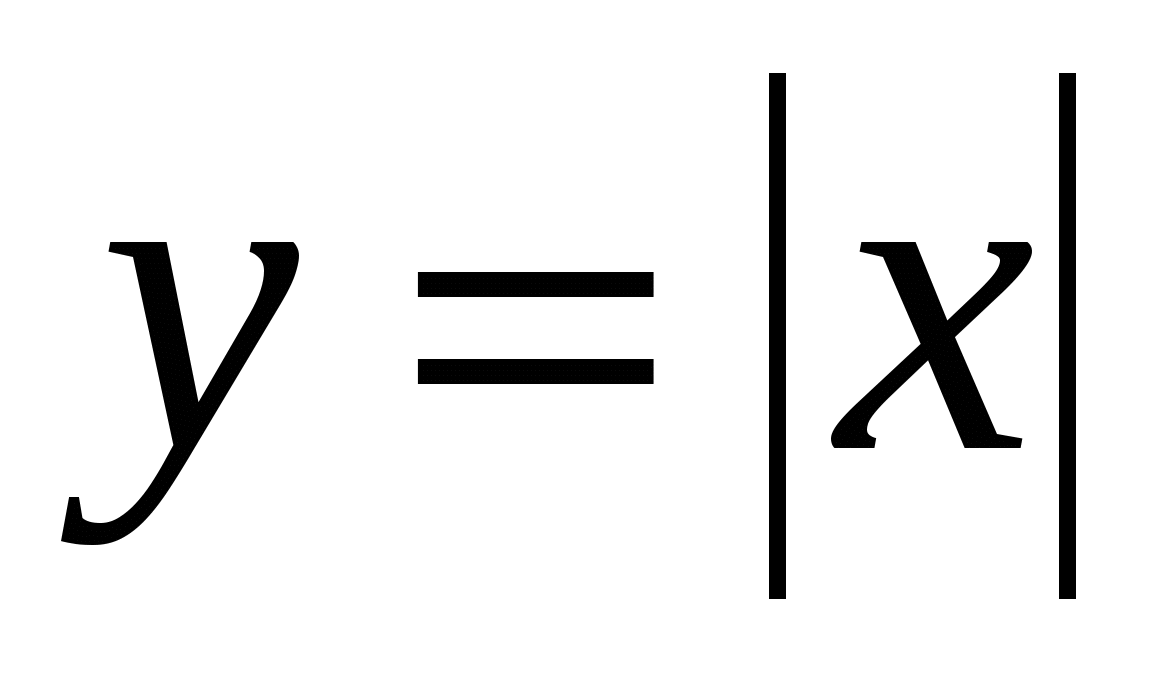 непрерывна, но не дифференцируема в точке х0=0.
непрерывна, но не дифференцируема в точке х0=0.
-
Производная суммы, разности, произведения и частного функций.
Нахождение производной непосредственно по определению часто связано с определёнными трудностями, поэтому на практике функции дифференцируют с помощью ряда формул и правил.
Теорема 5.2: Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: 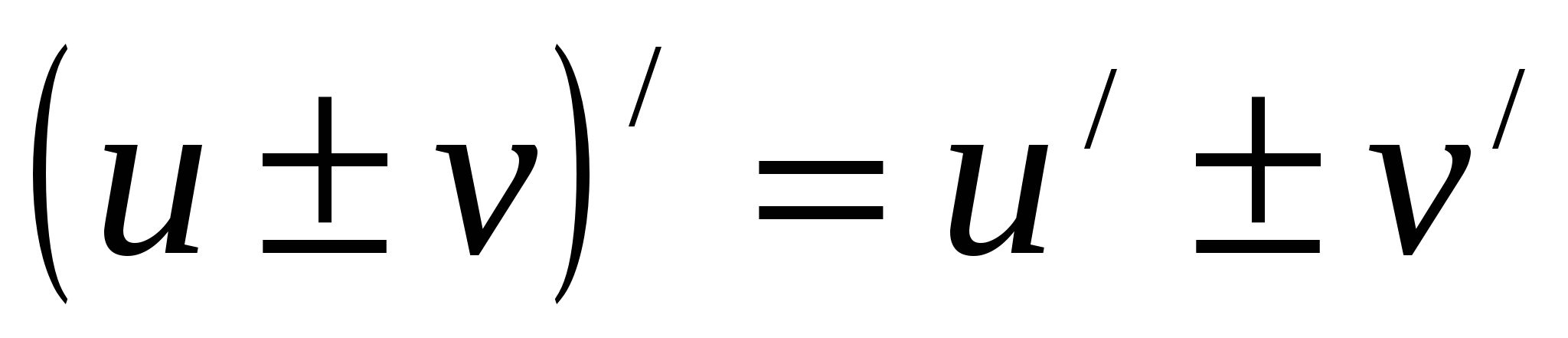 .
.
Обозначим 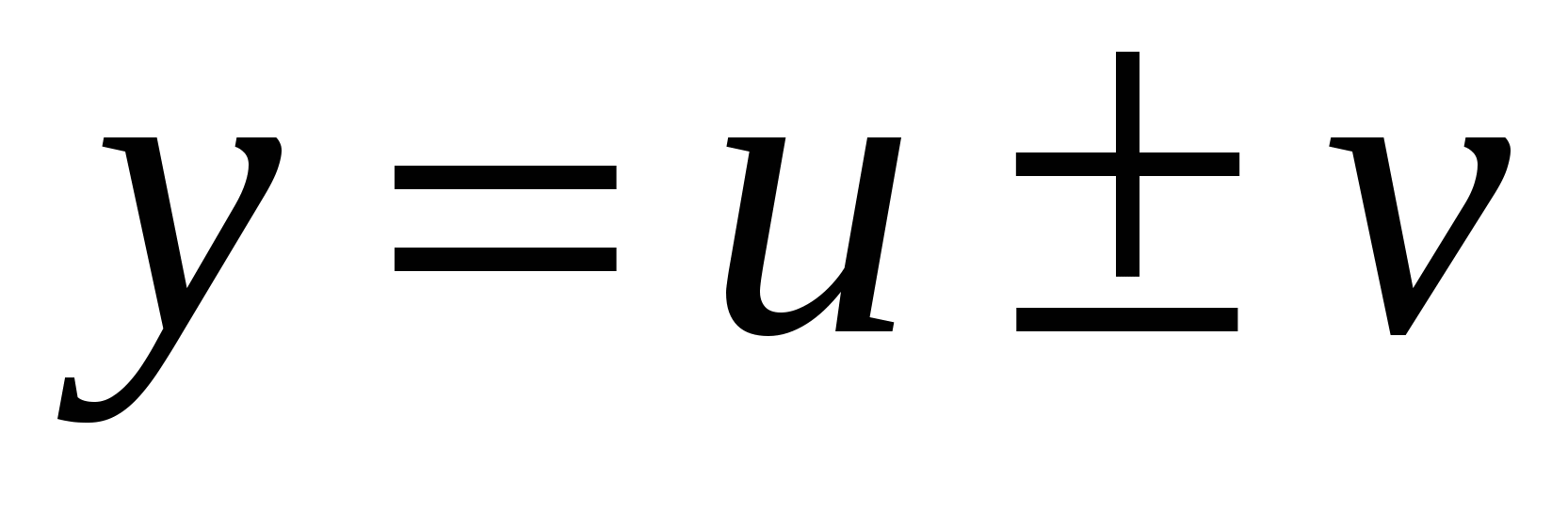 . По определению производной и основным теоремам о пределах получаем:
. По определению производной и основным теоремам о пределах получаем:
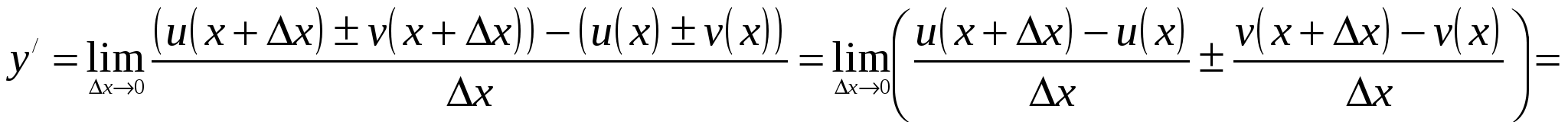
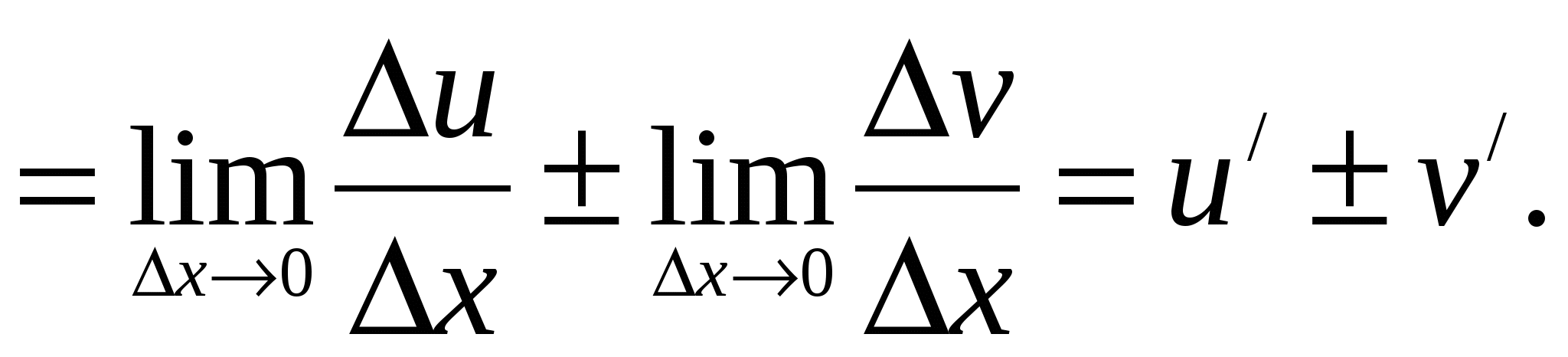
Теорема 5.3: Производная произведения двух функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый.
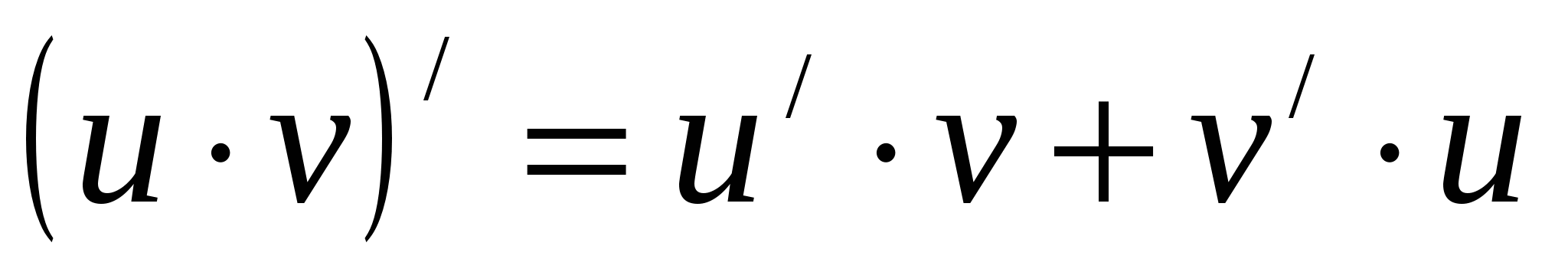
Можно показать, что:
а) 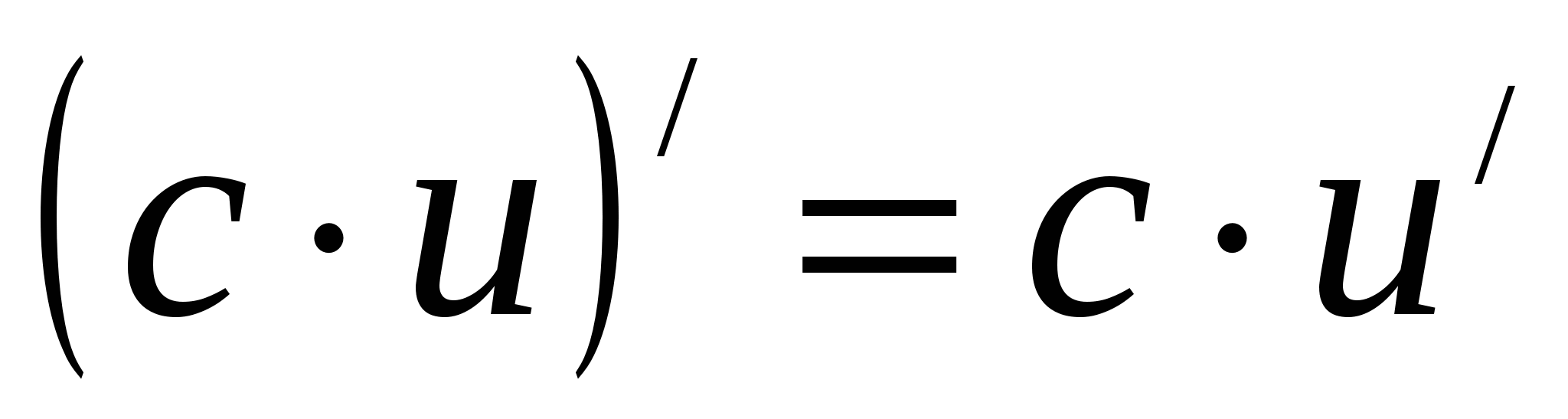 , где
, где 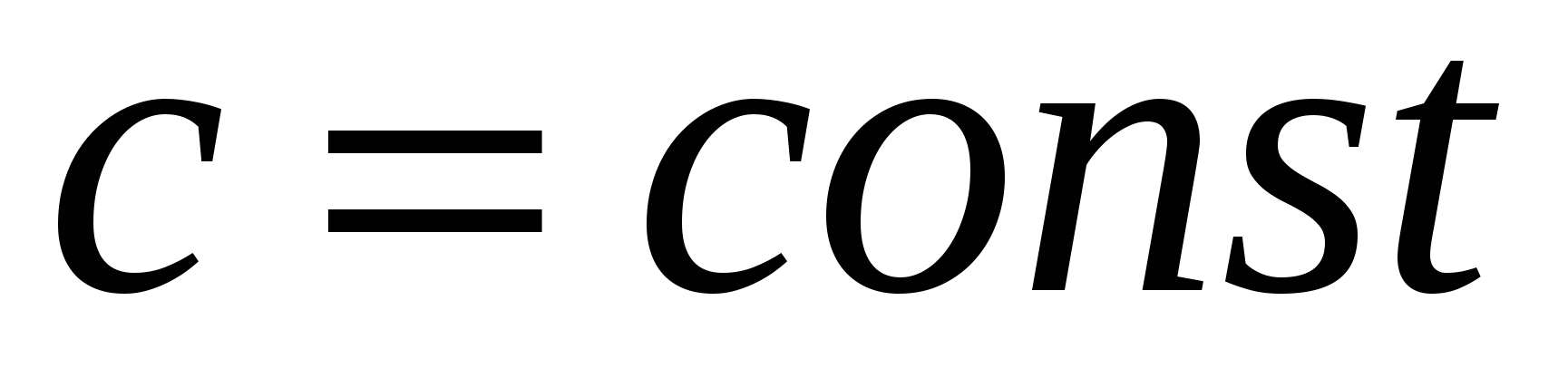 ;
;
б) 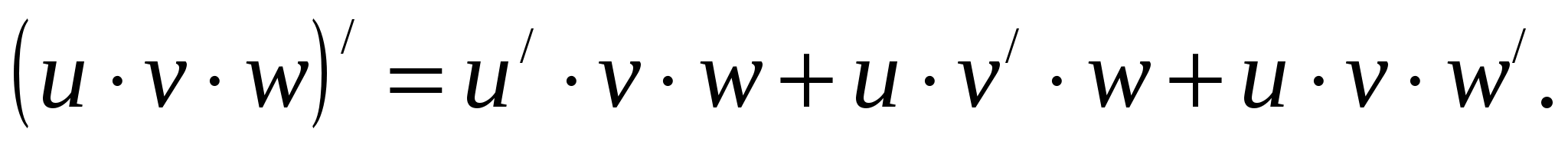
Теорема 5.4: Производная частного двух функций 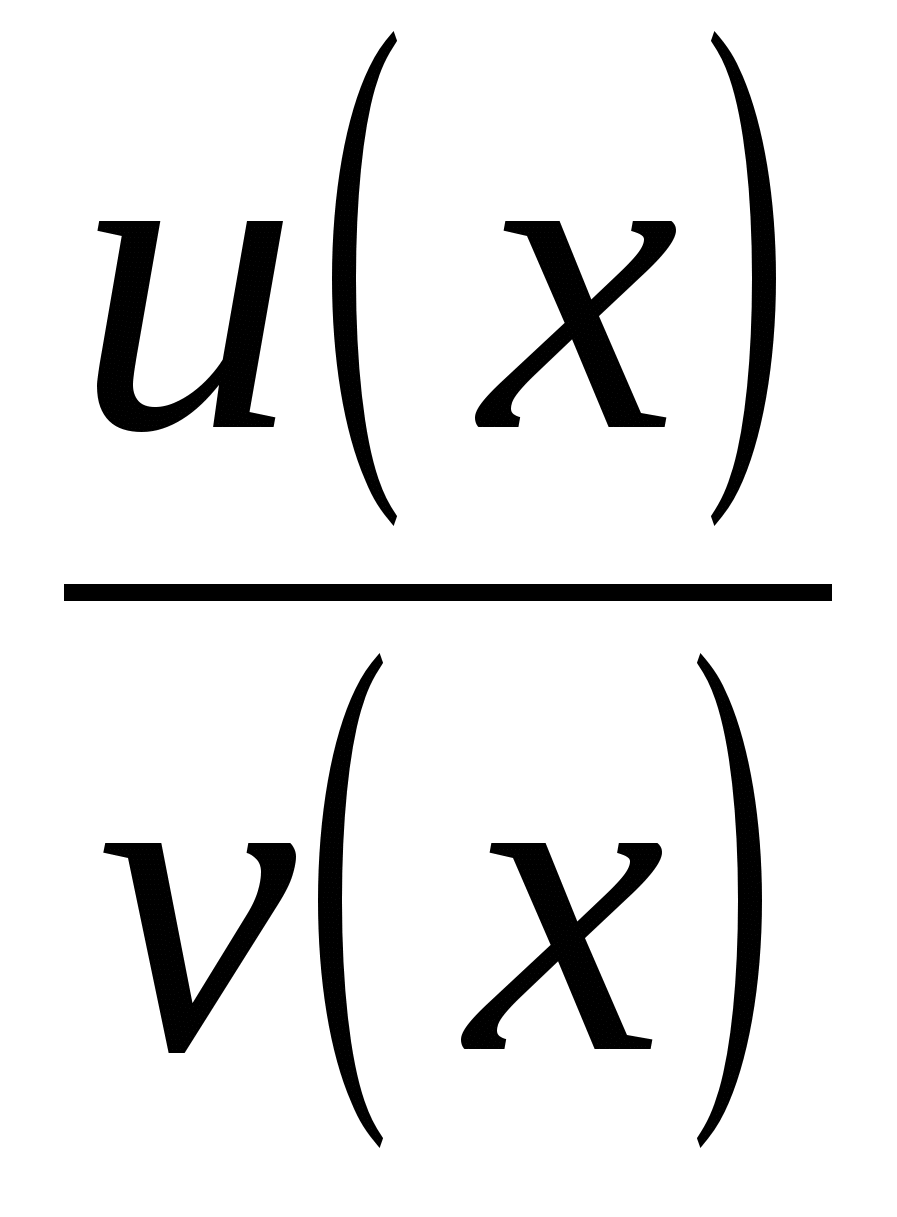 , если
, если 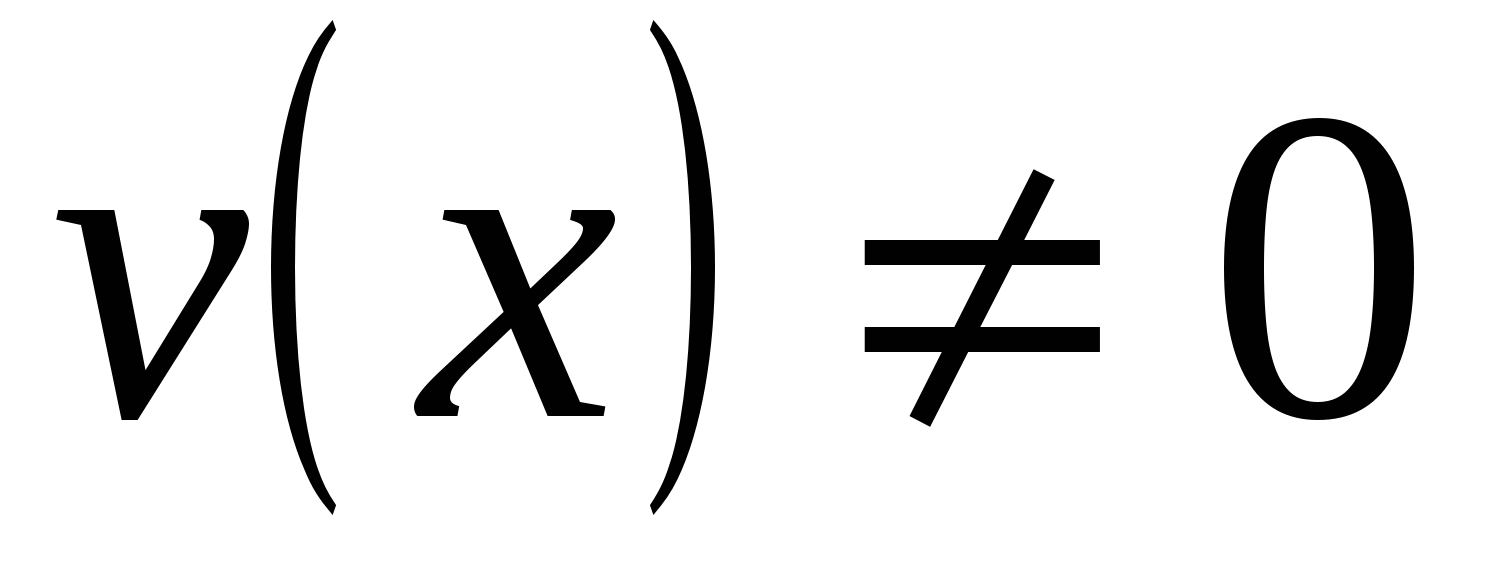 равна дроби, числитель которой есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель есть квадрат прежнего знаменателя.
равна дроби, числитель которой есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель есть квадрат прежнего знаменателя.
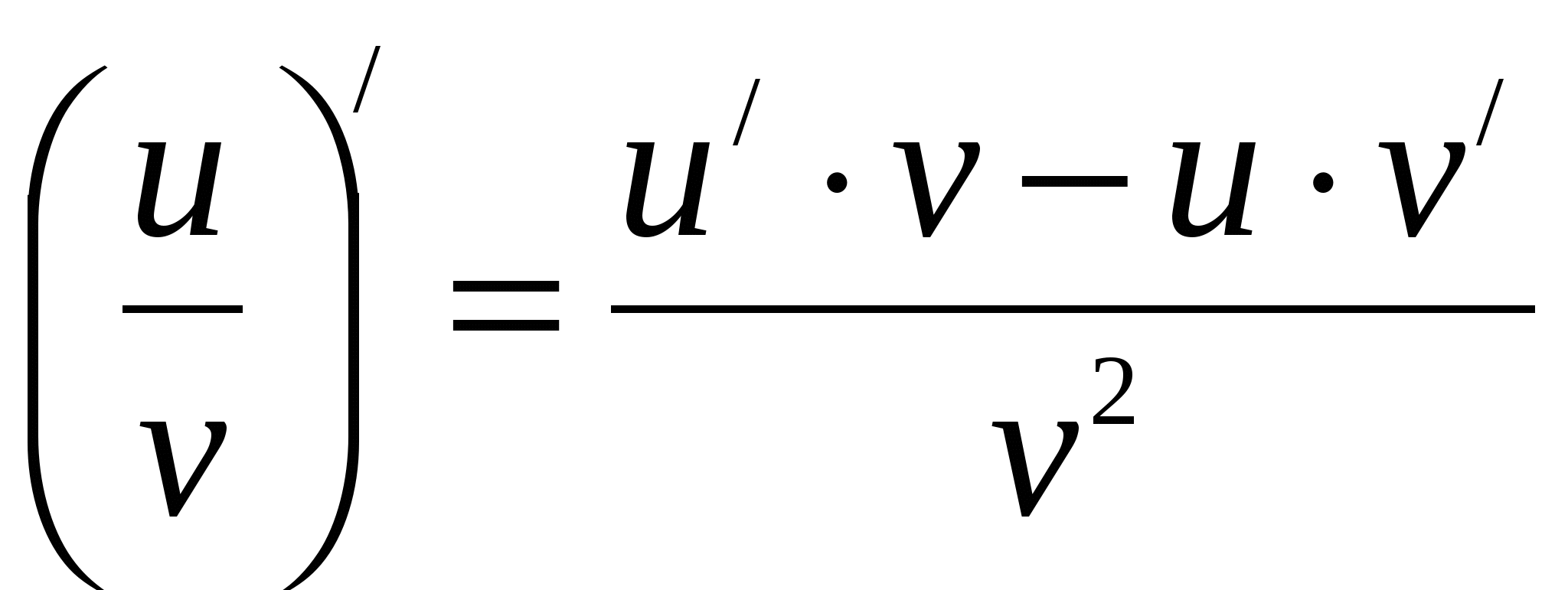 ,
, 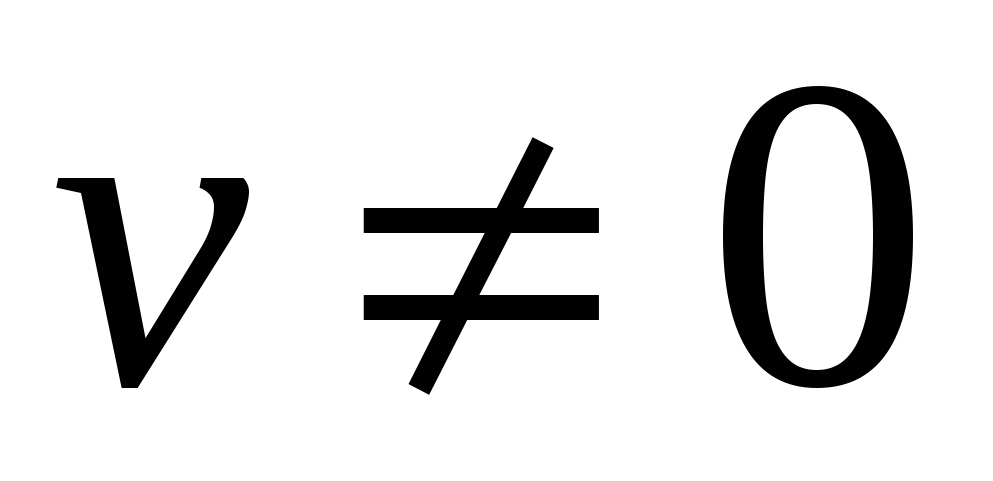 .
.
Следствие 5.1: 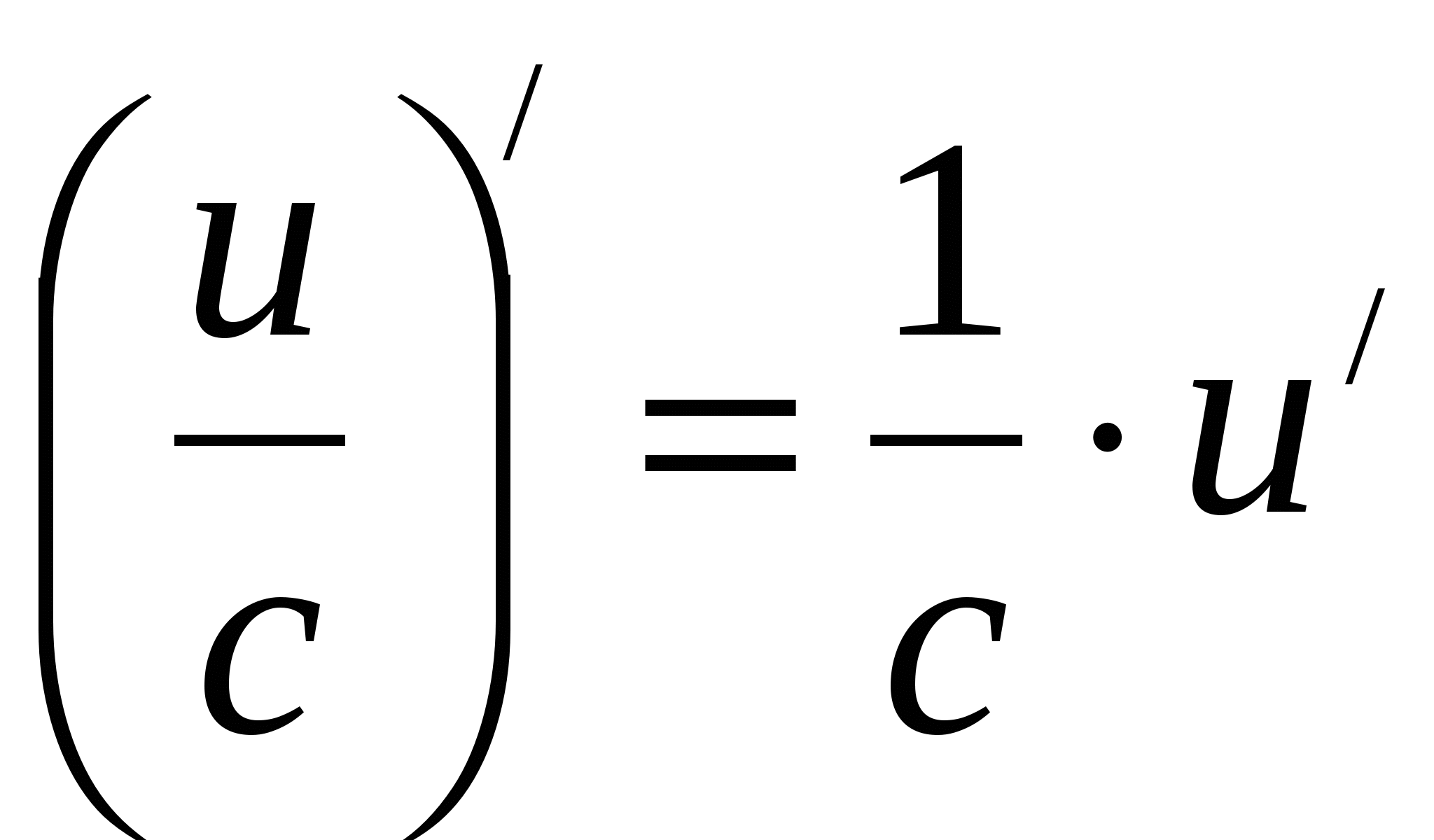
Следствие 5.2: 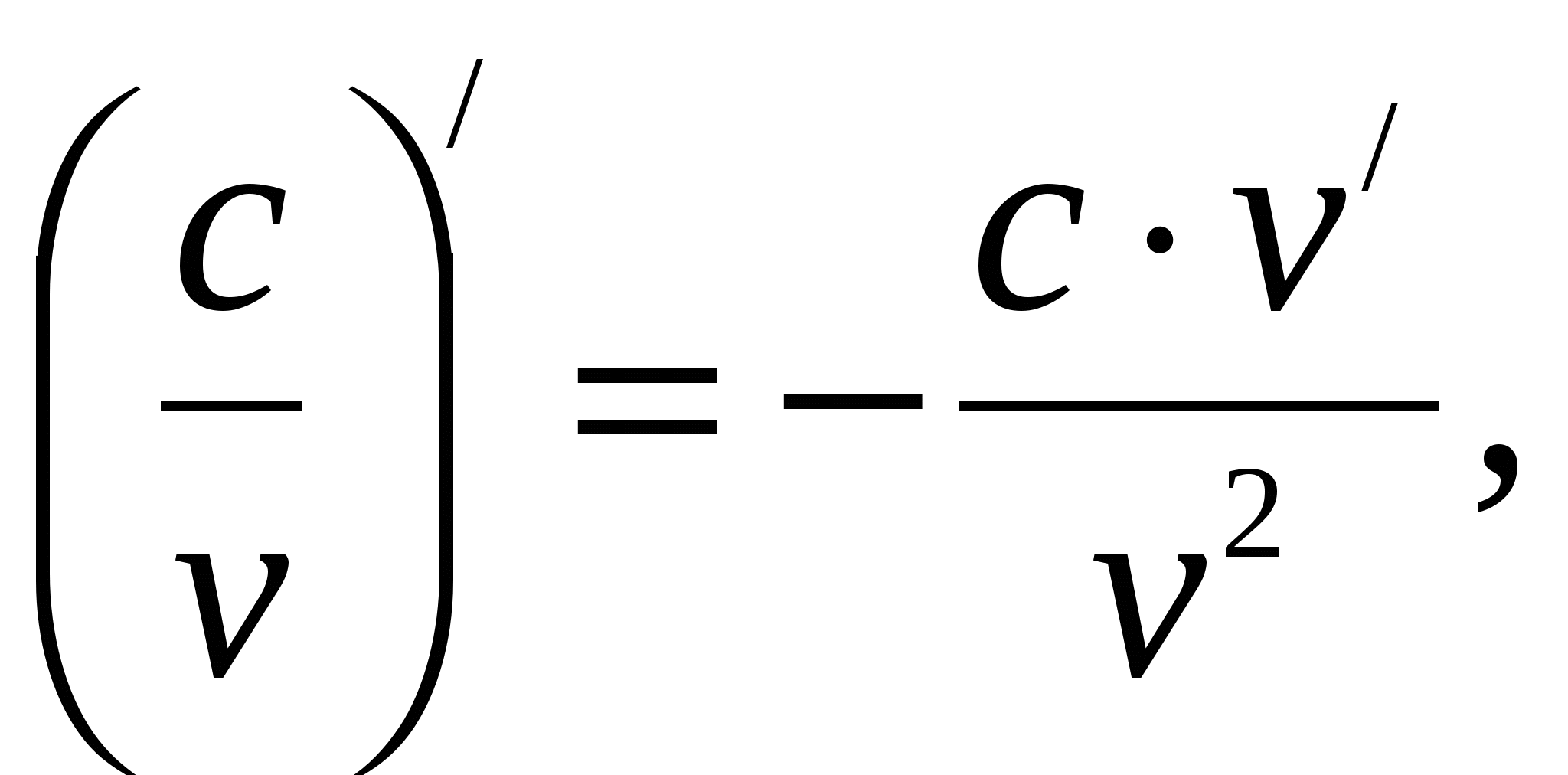 где
где 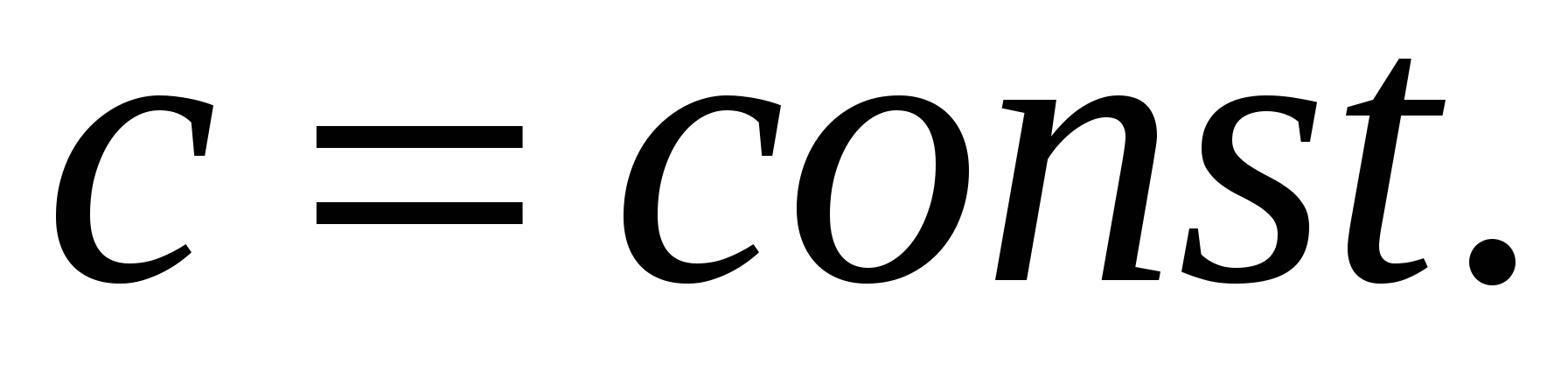
-
Производная сложной и обратной функции.
Пусть 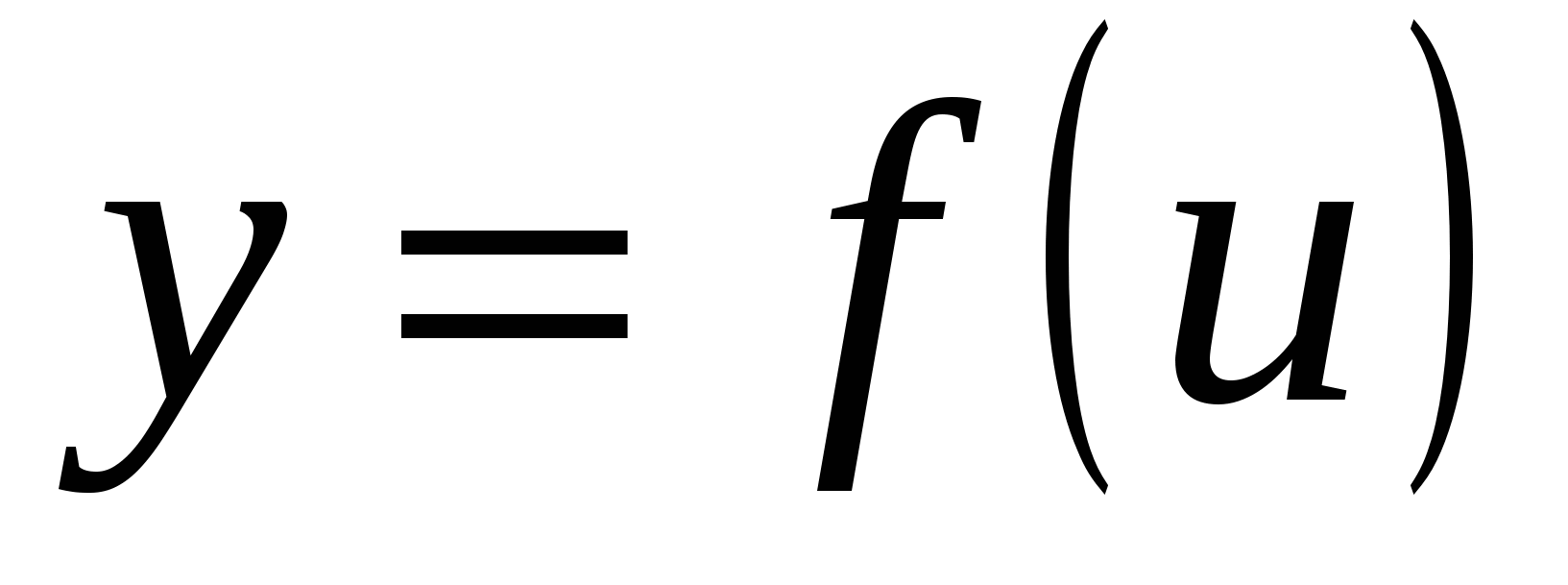 и
и 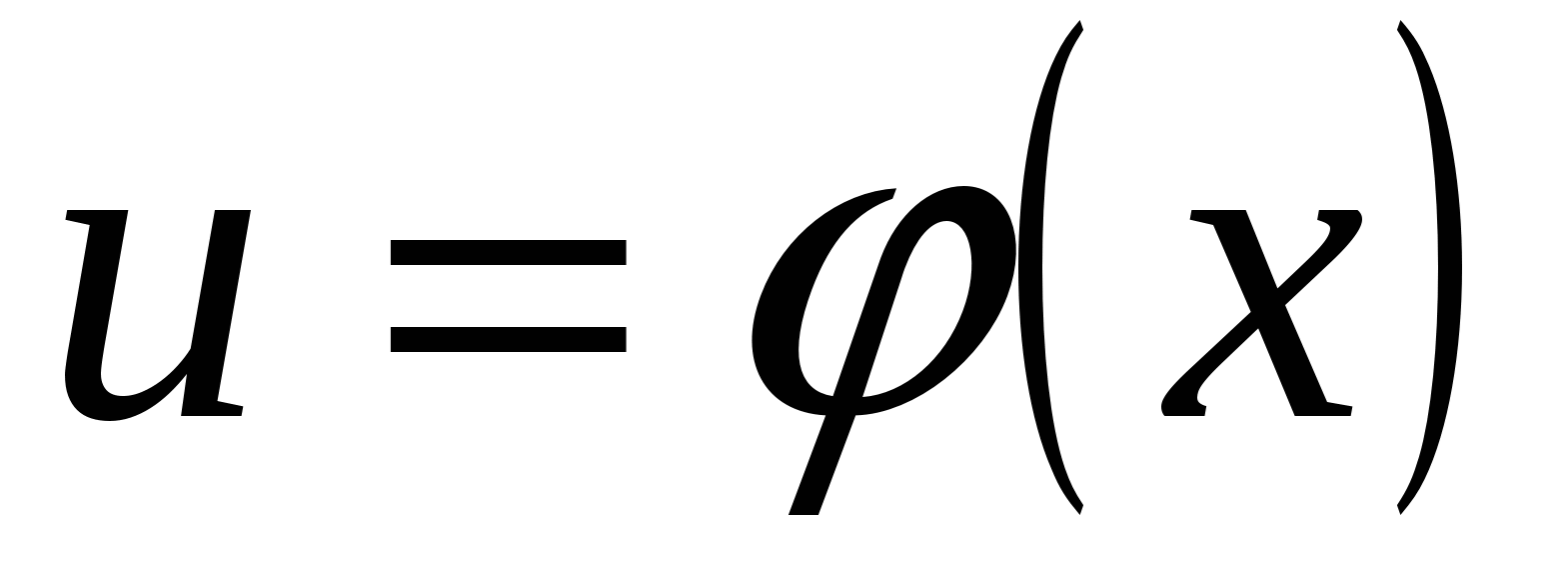 , тогда
, тогда 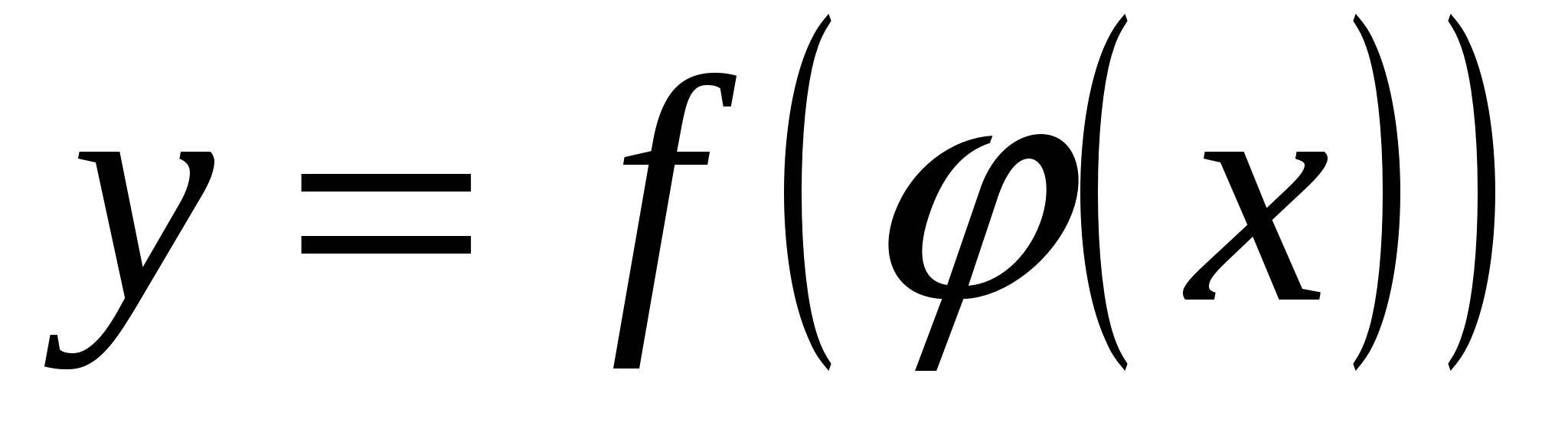 ‒ сложная функция с промежуточным аргументом и и независимым аргументом х.
‒ сложная функция с промежуточным аргументом и и независимым аргументом х.
Теорема 5.5: Если функция 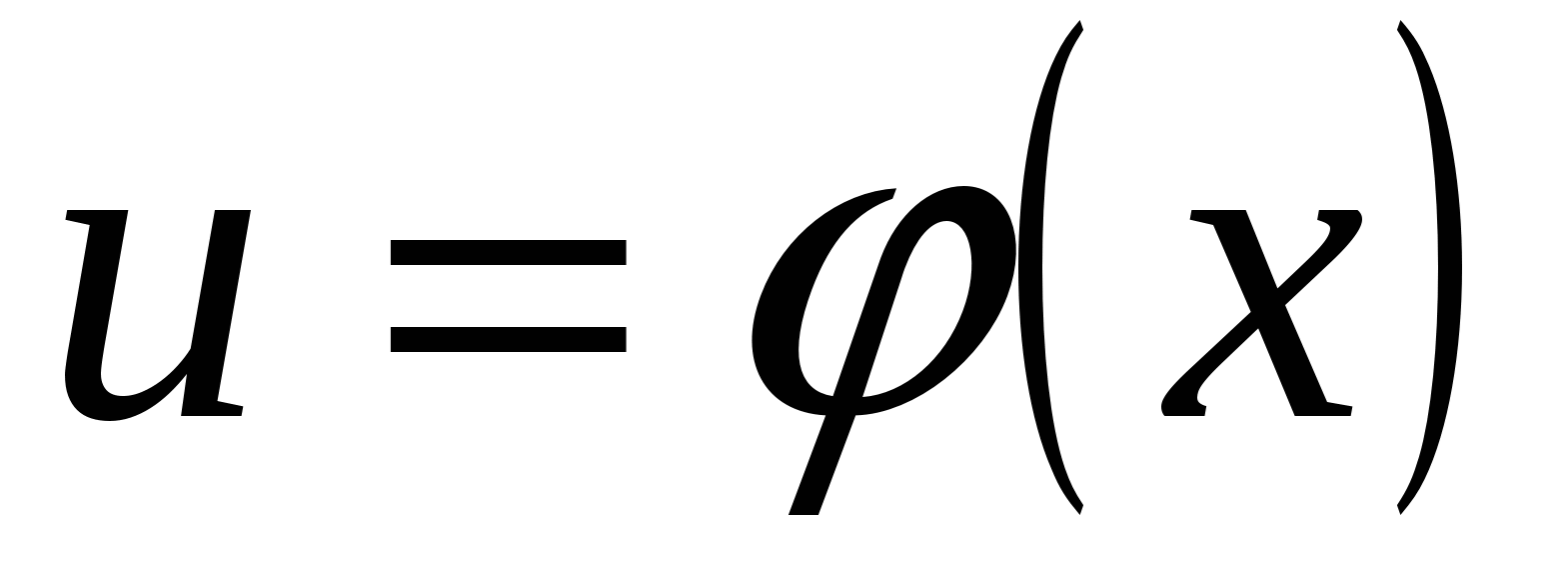 имеет производную
имеет производную 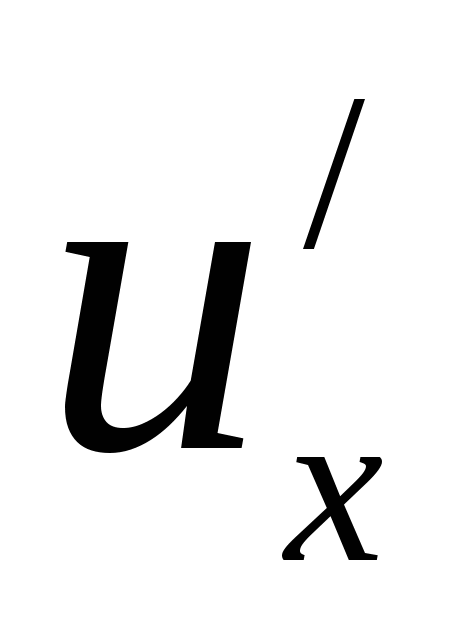 в точке х, а функция
в точке х, а функция 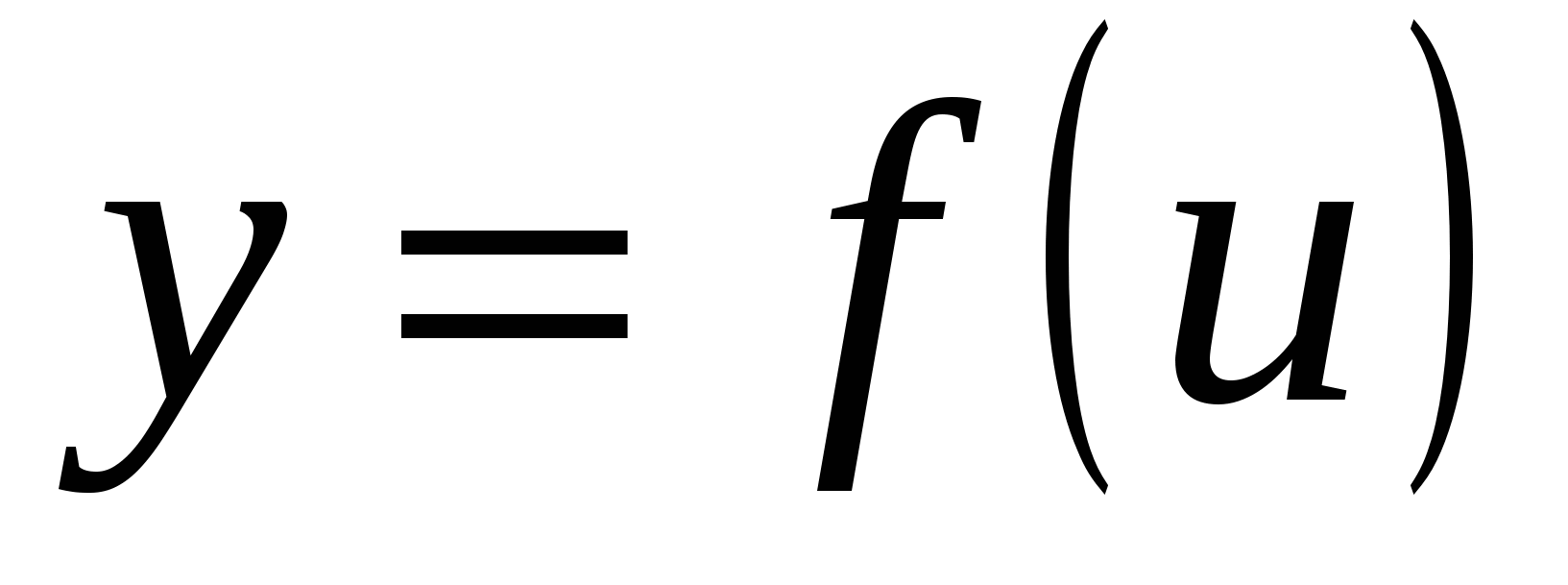 имеет производную
имеет производную 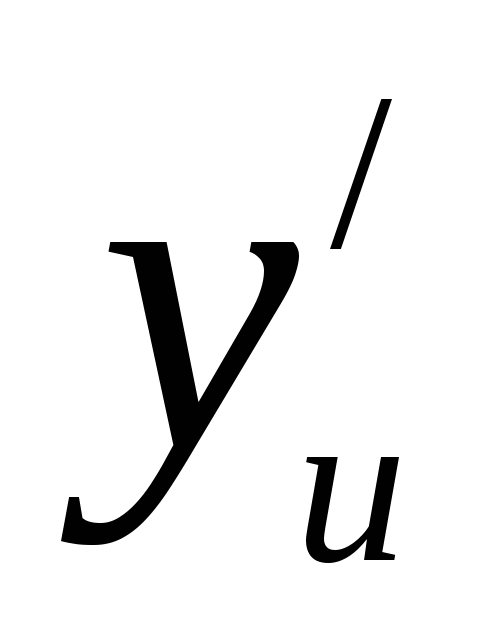 в соответствующей точке
в соответствующей точке 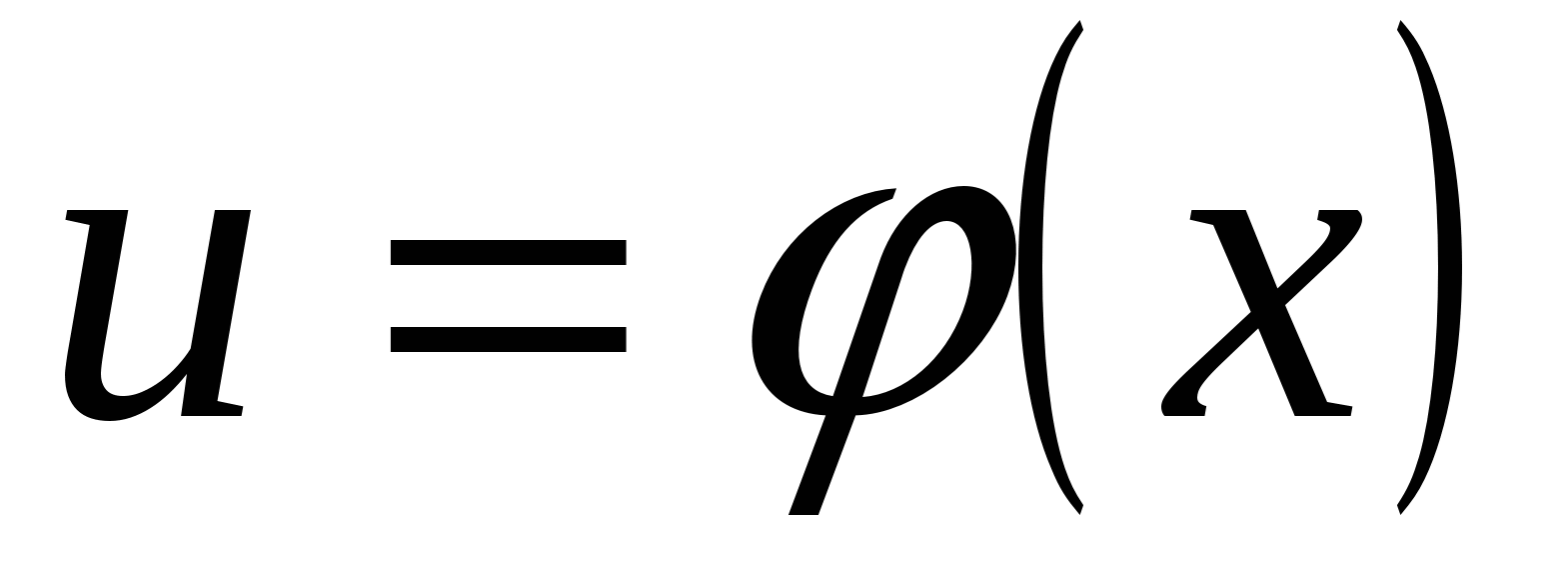 , то сложная функция
, то сложная функция 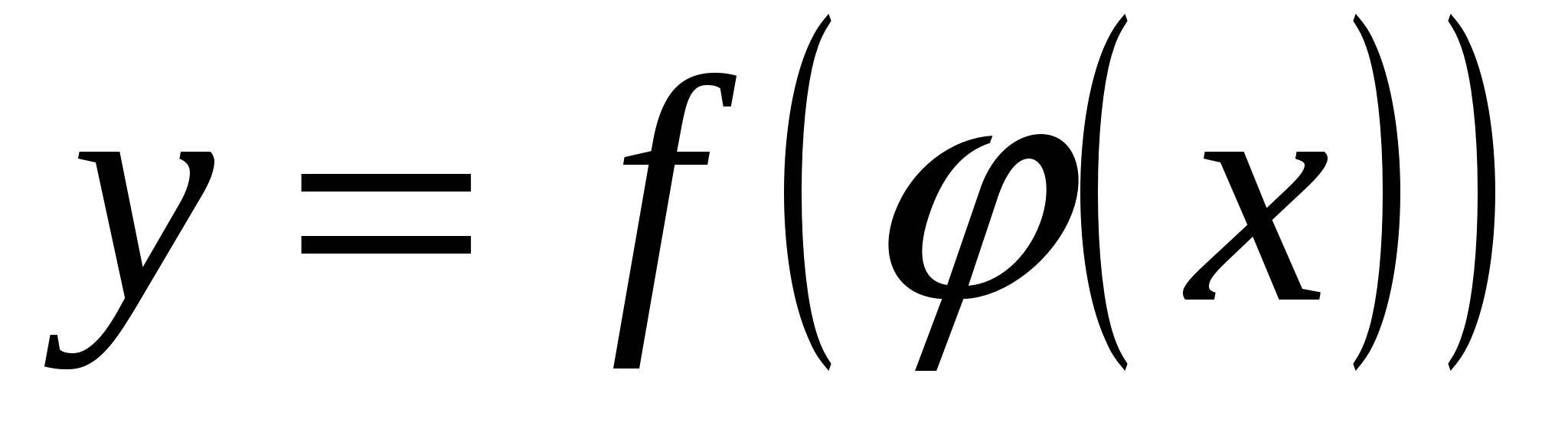 имеет производную
имеет производную 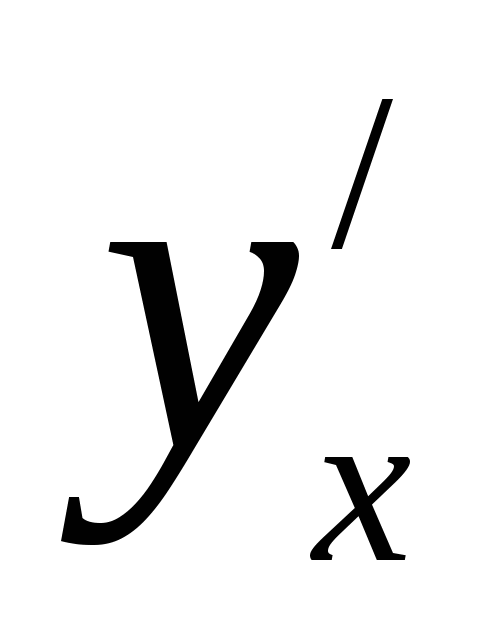 в точке х, которая находится по формуле:
в точке х, которая находится по формуле:
![]() или
или 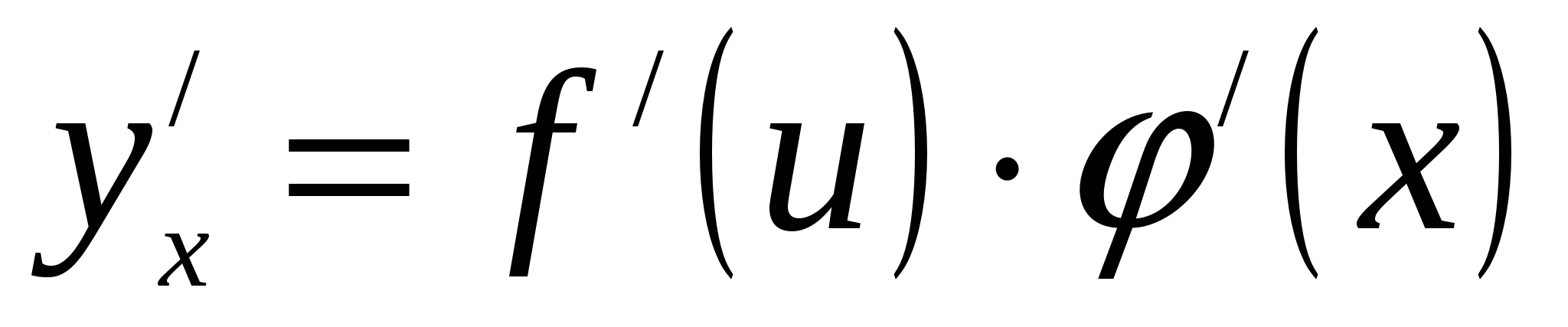
По условию 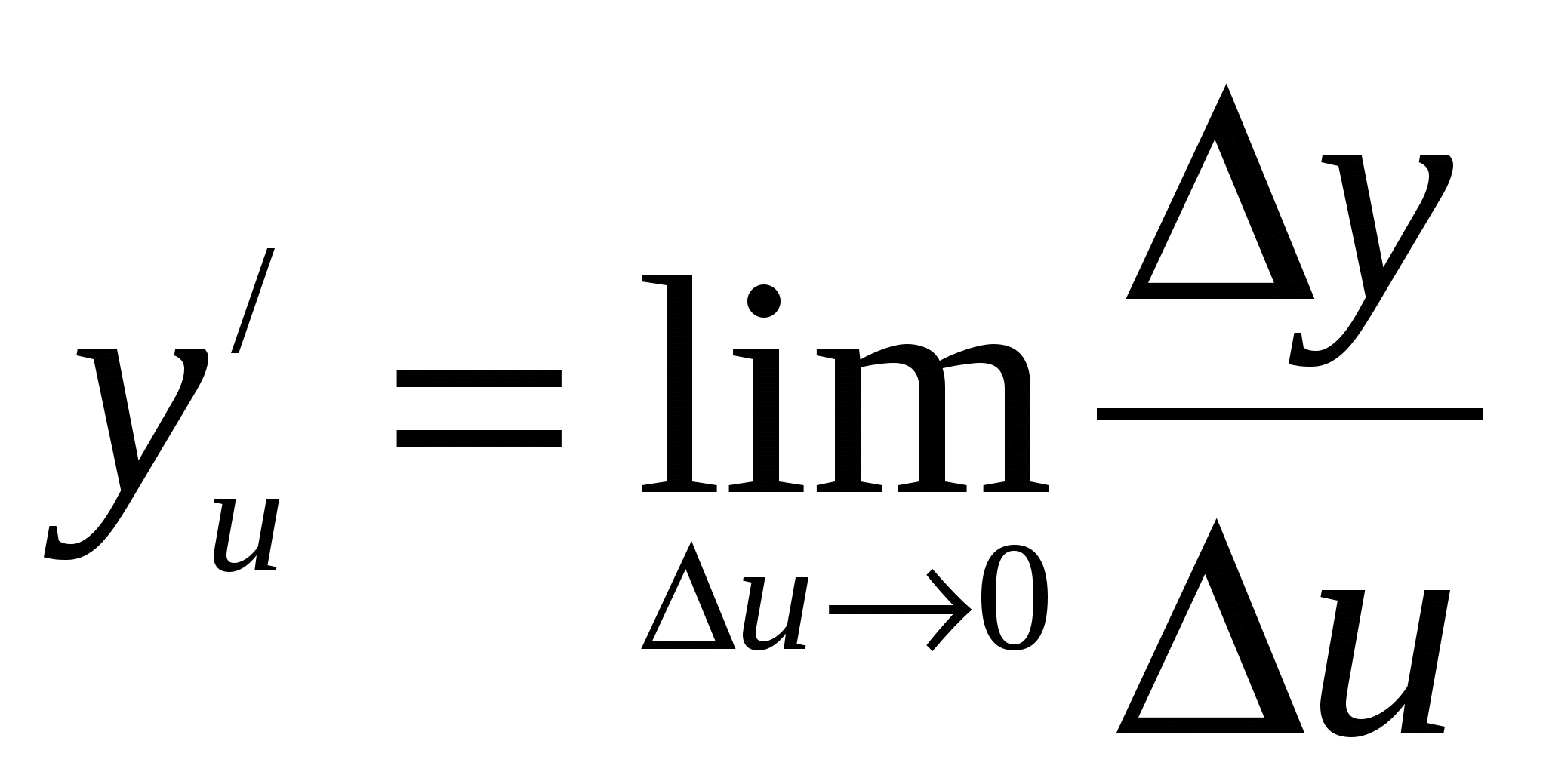 и
и 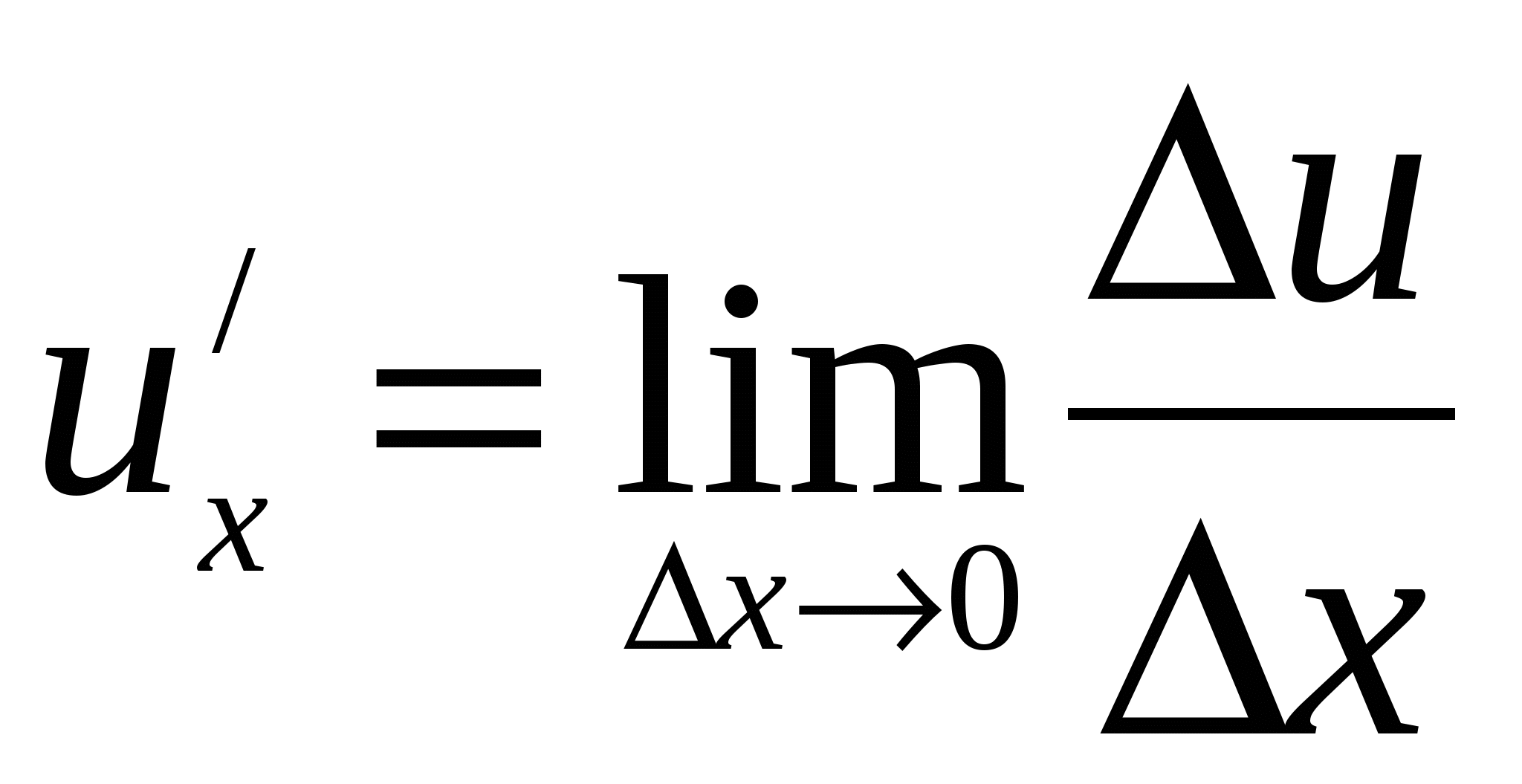 . Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем:
. Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем:
![]() или
или 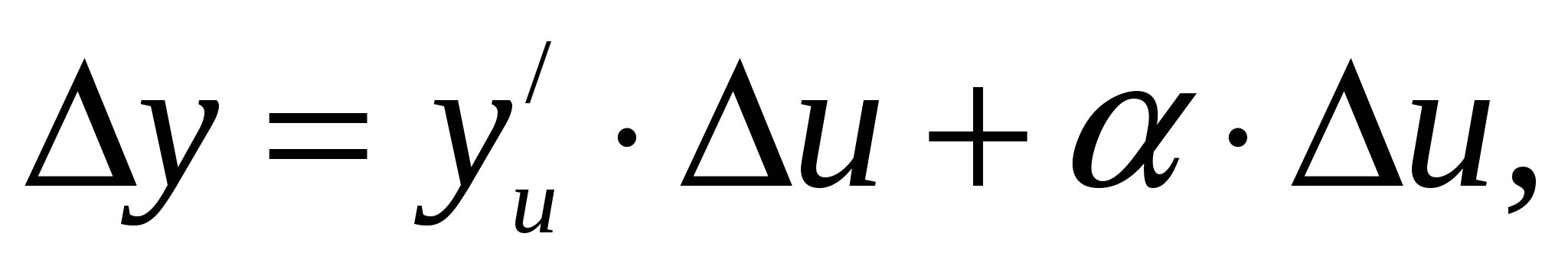 где
где 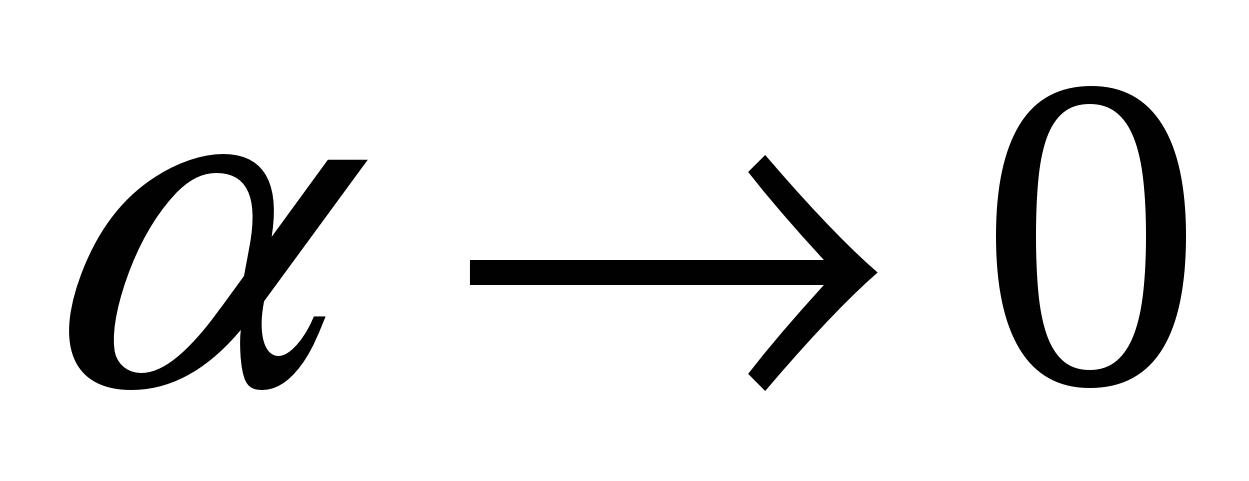 при
при 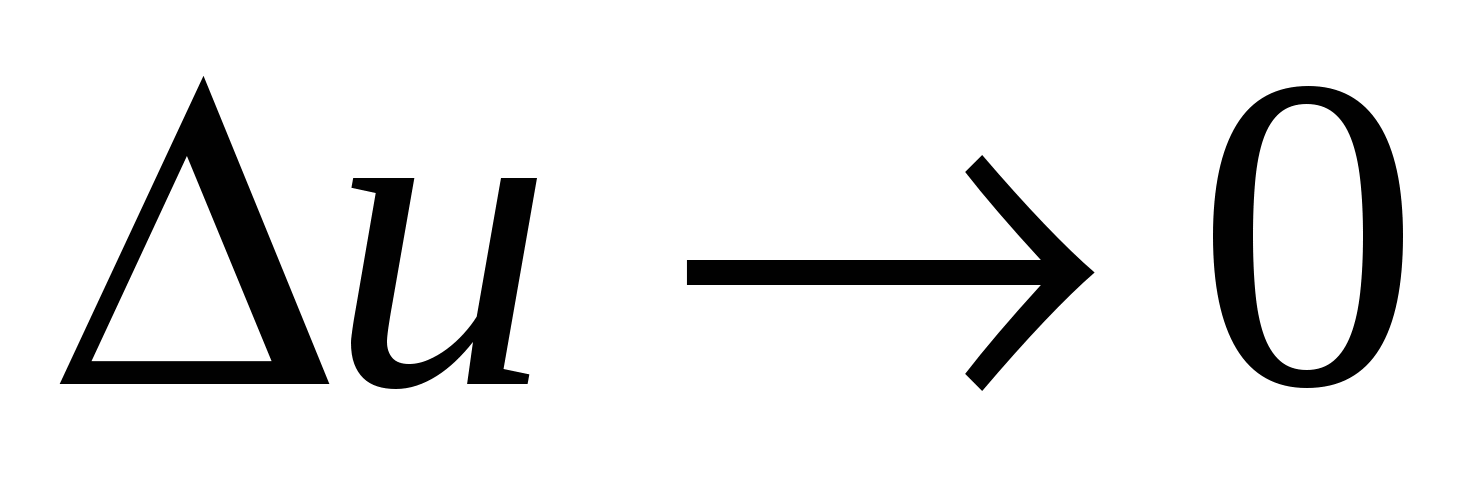
![]() или
или 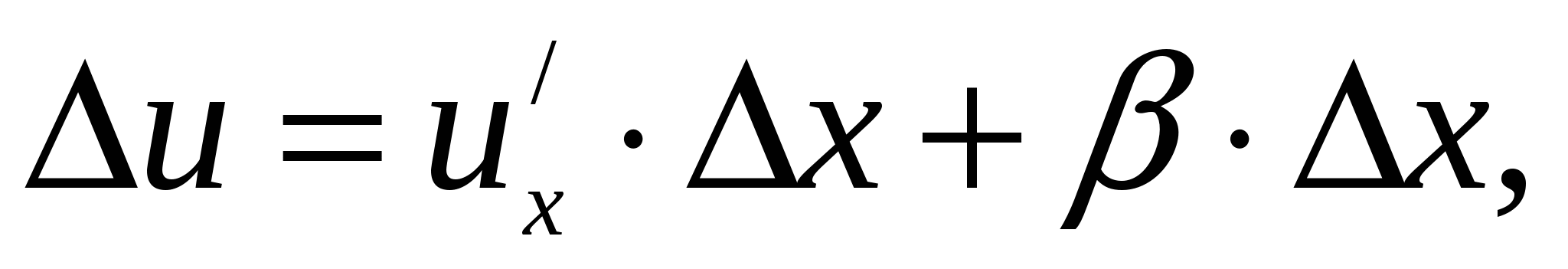 где
где  при
при 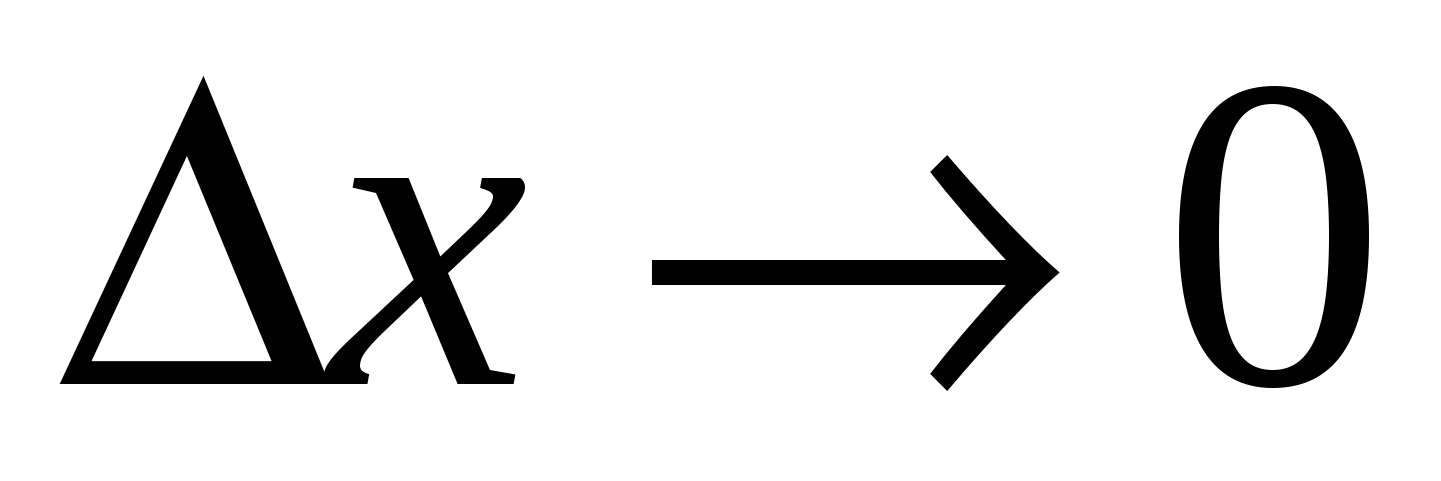
Подставим или 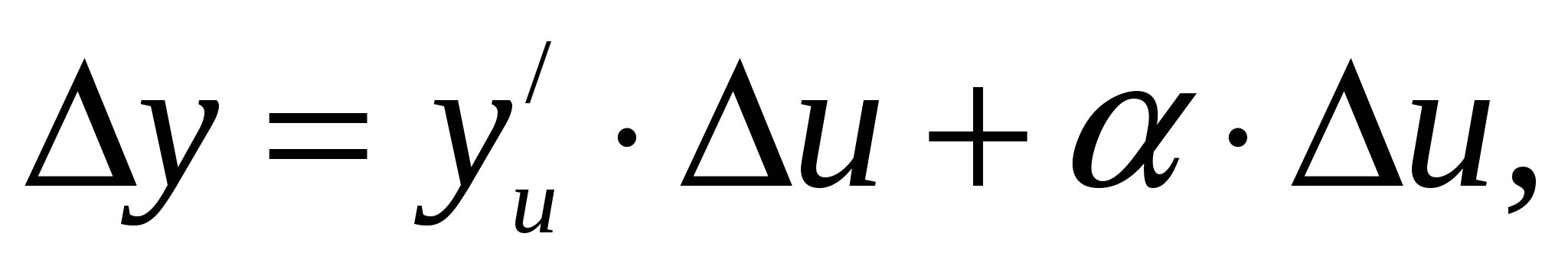 где
где 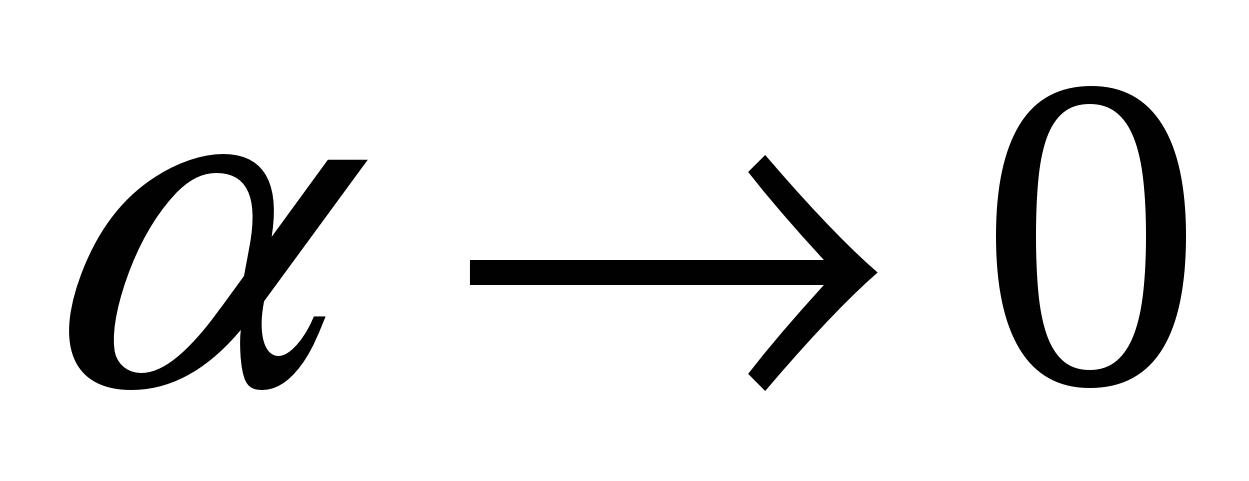 при
при 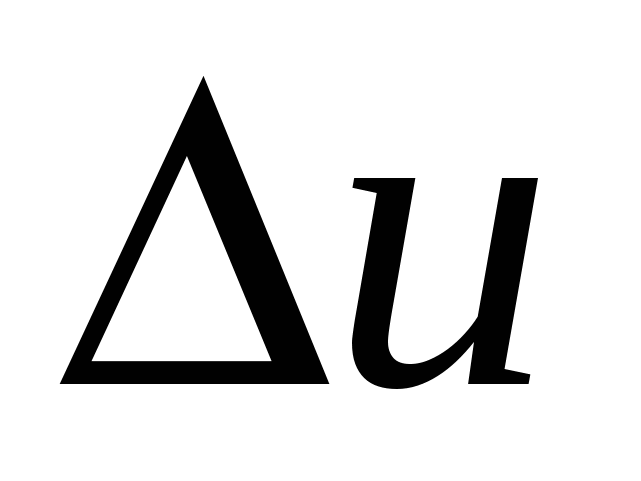 в верхнее равенство:
в верхнее равенство:
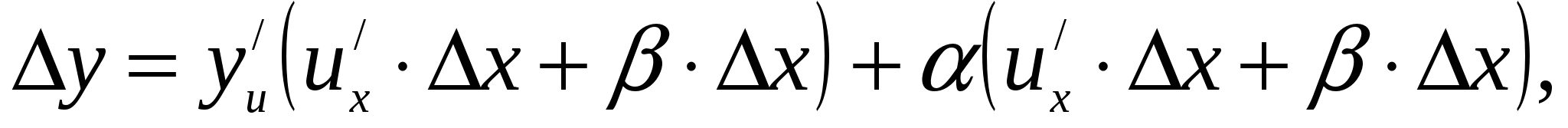
Раскроем скобки и разделим полученное равенство на 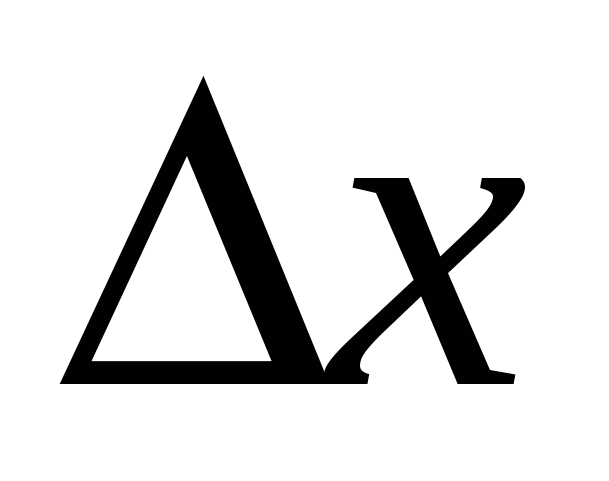
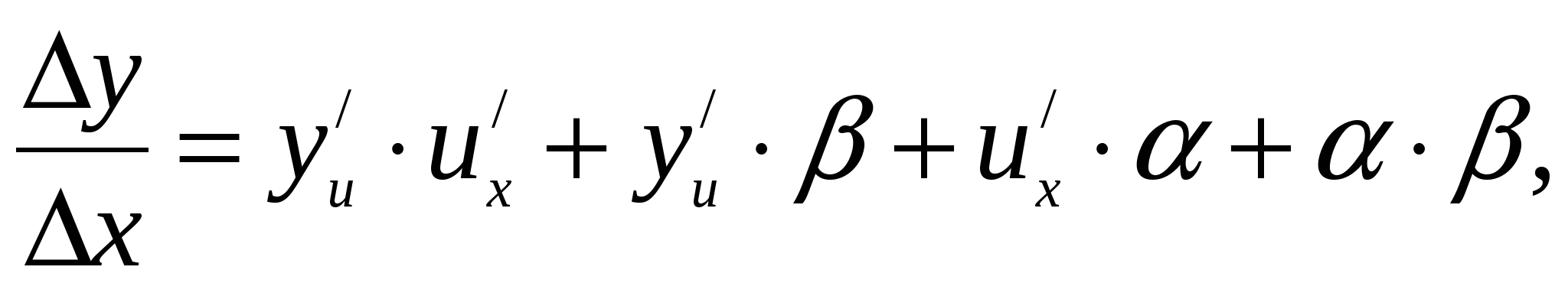
Перейдём к пределу при 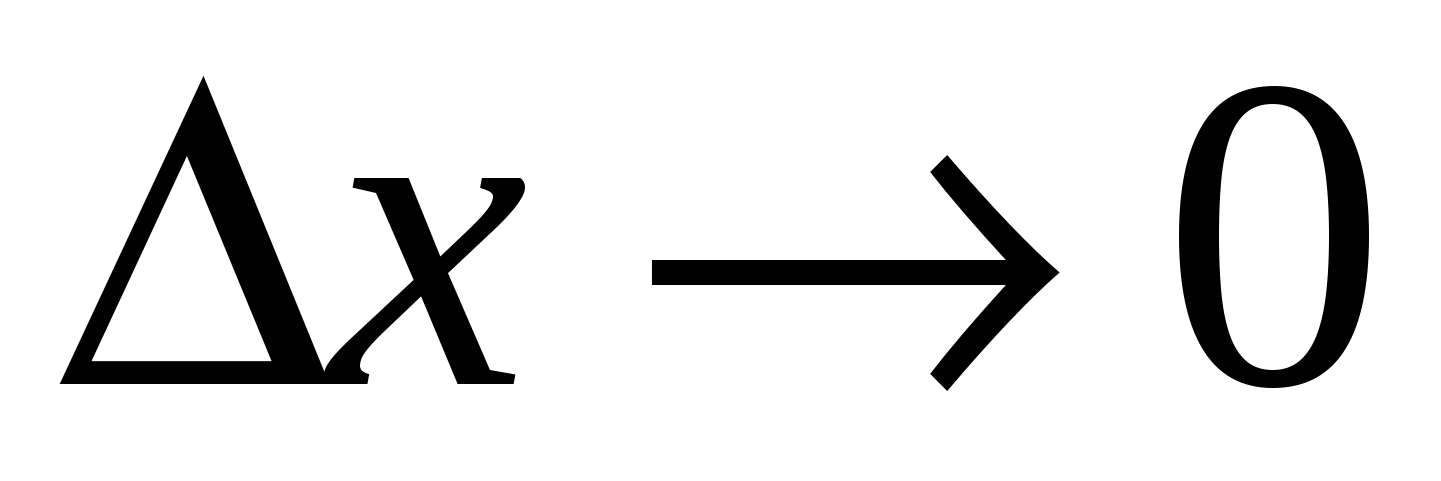 , получим:
, получим: 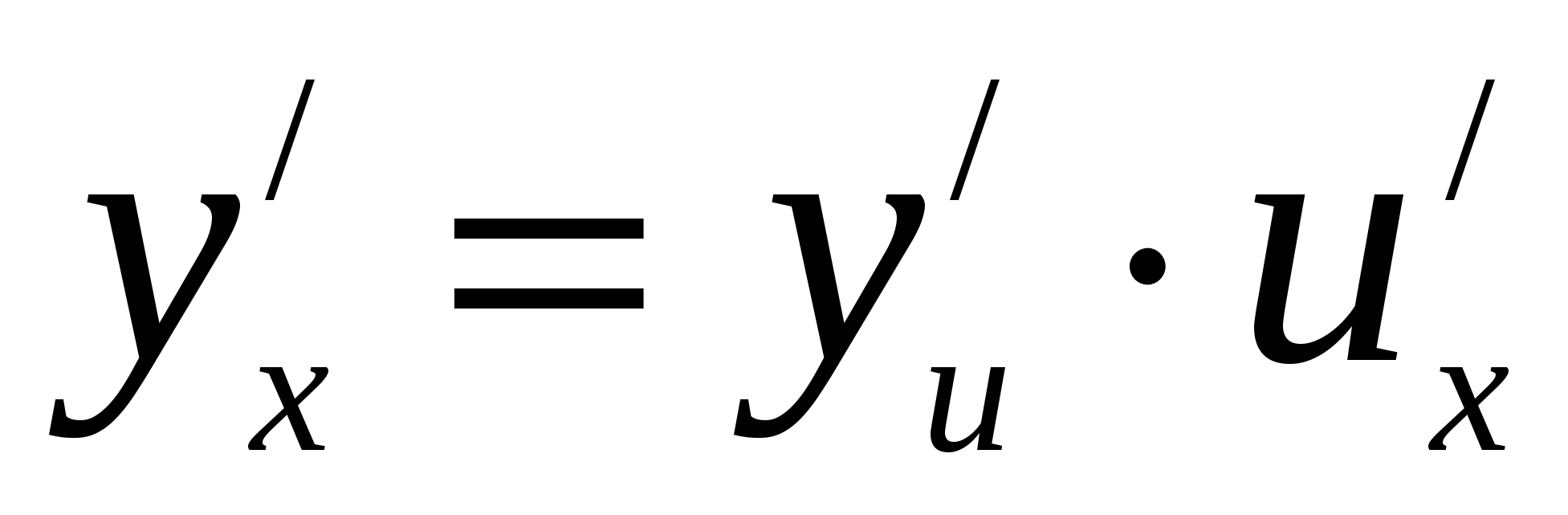
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Это правило остаётся в силе, если промежуточных аргументов несколько.
Теорема 5.6: Если функция 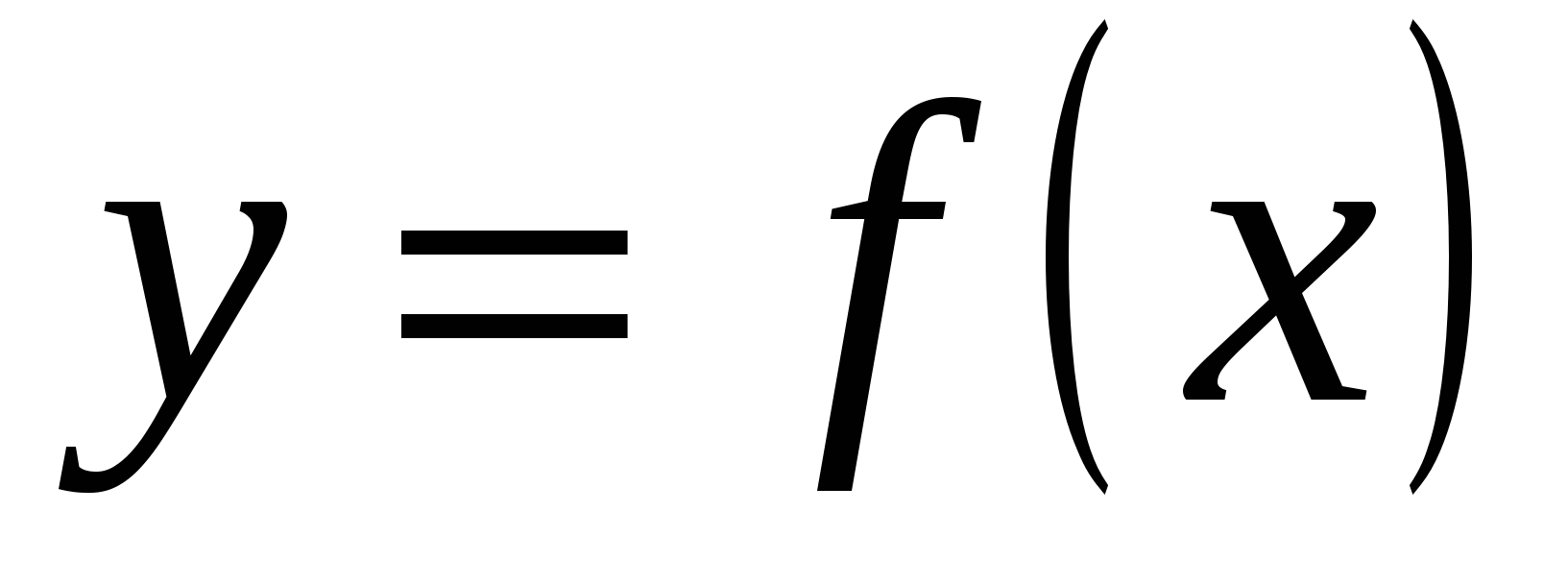 строго монотонная на интервале
строго монотонная на интервале 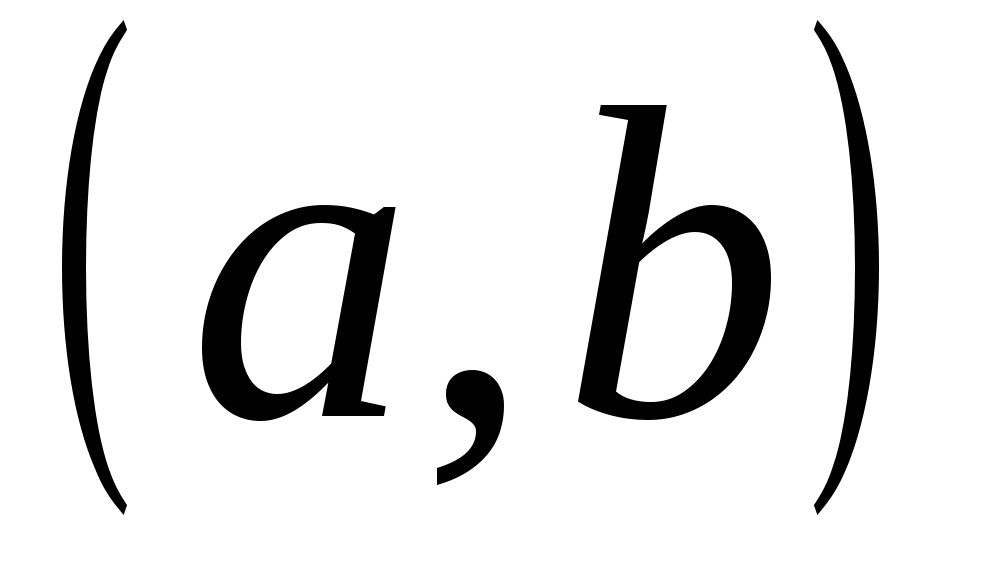 и имеет неравную нулю производную
и имеет неравную нулю производную 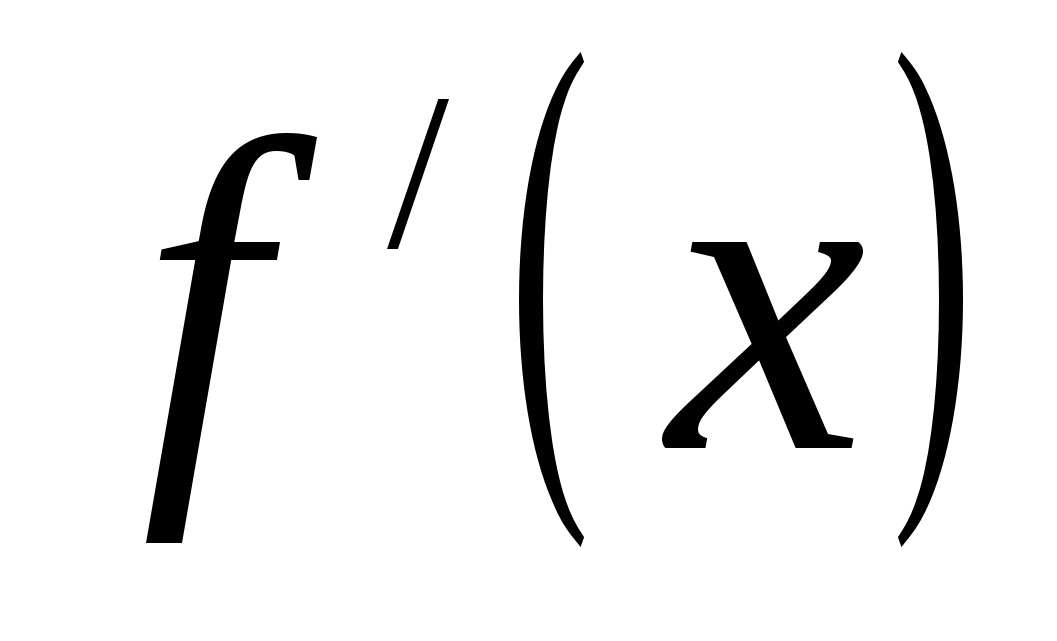 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 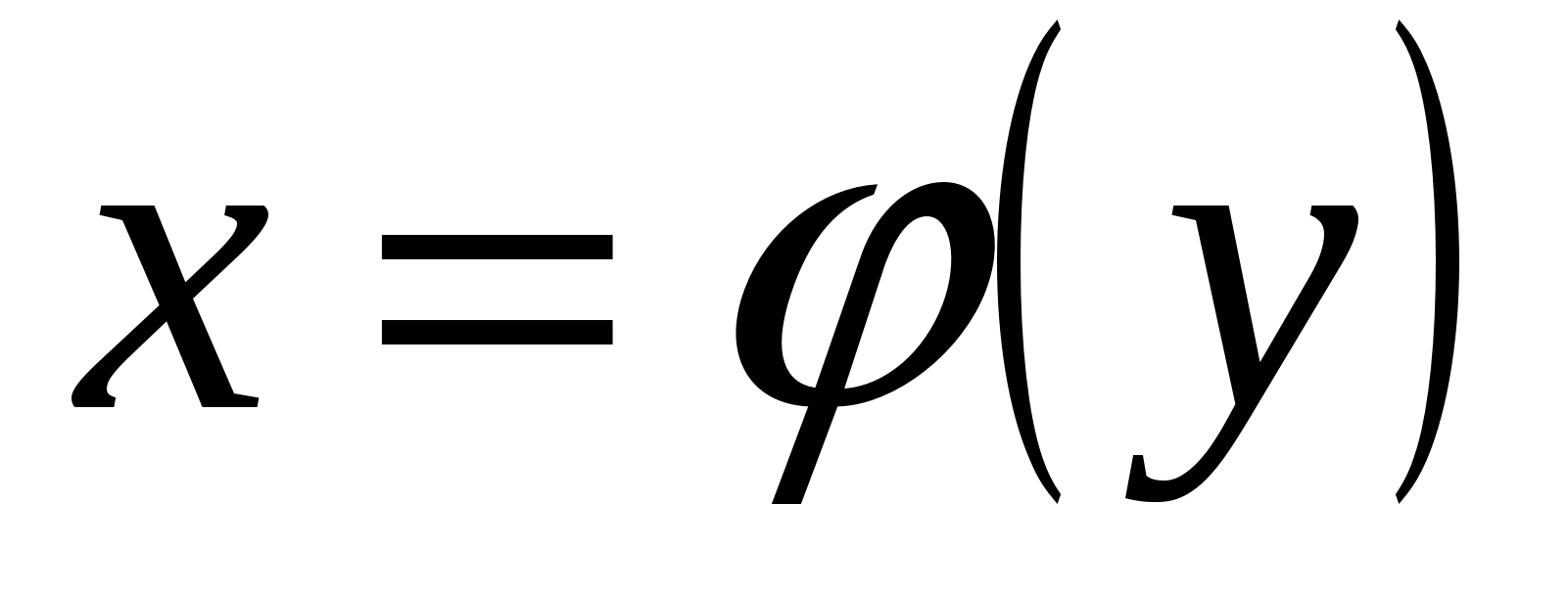 также имеет производную
также имеет производную 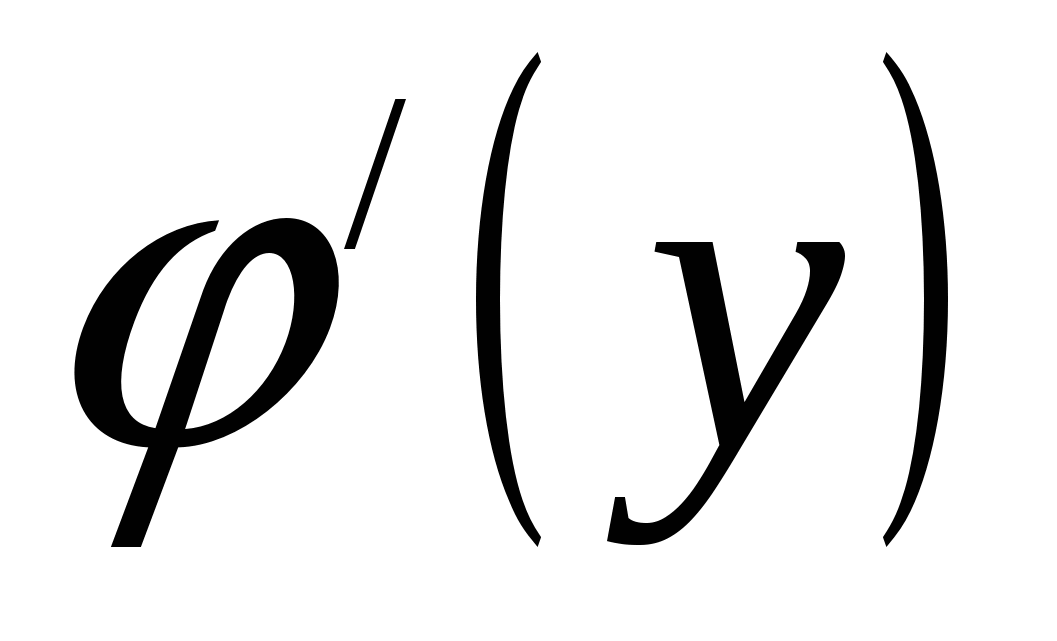 в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством
![]() или
или 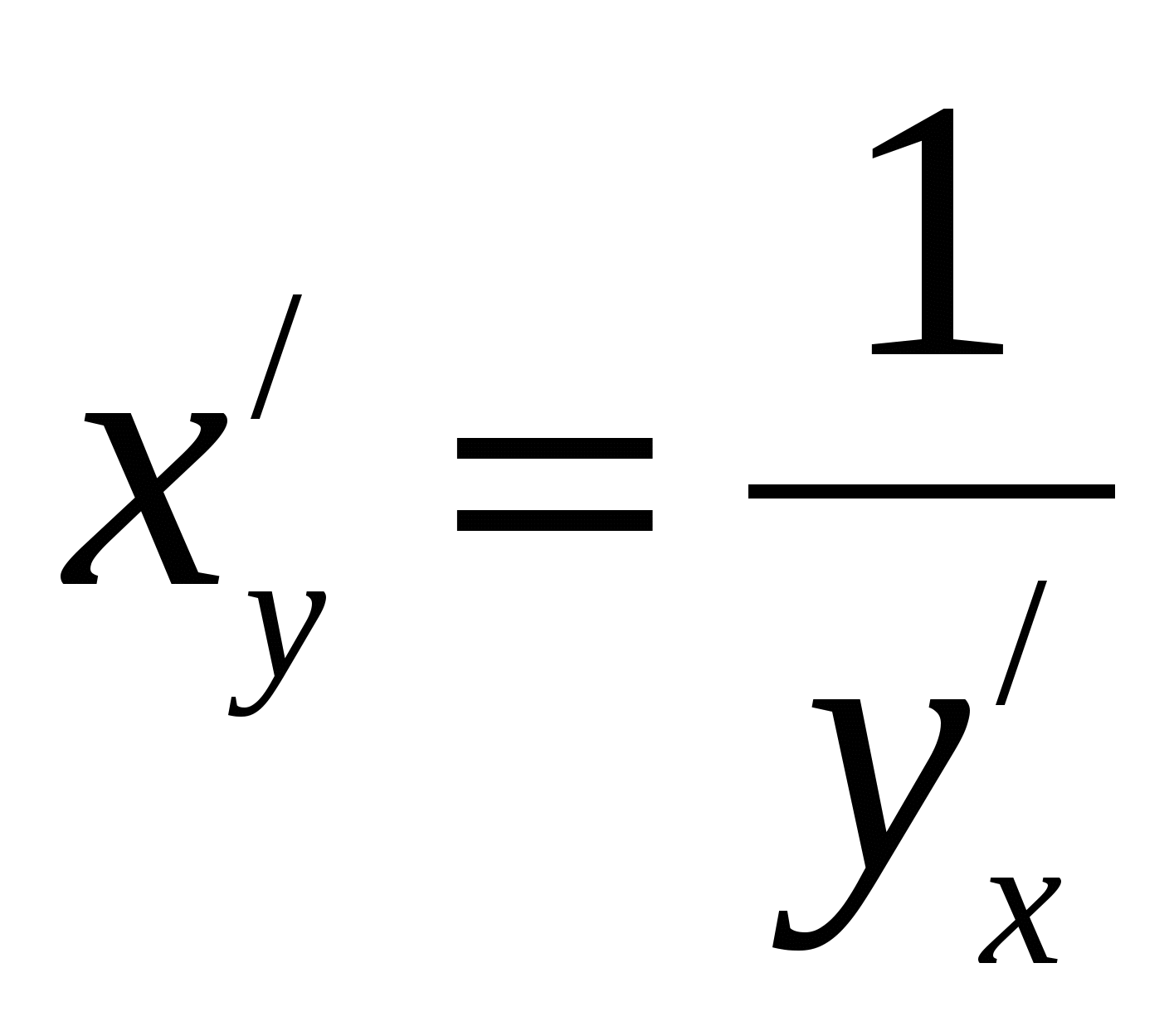
Пример 1: Найти производную функции 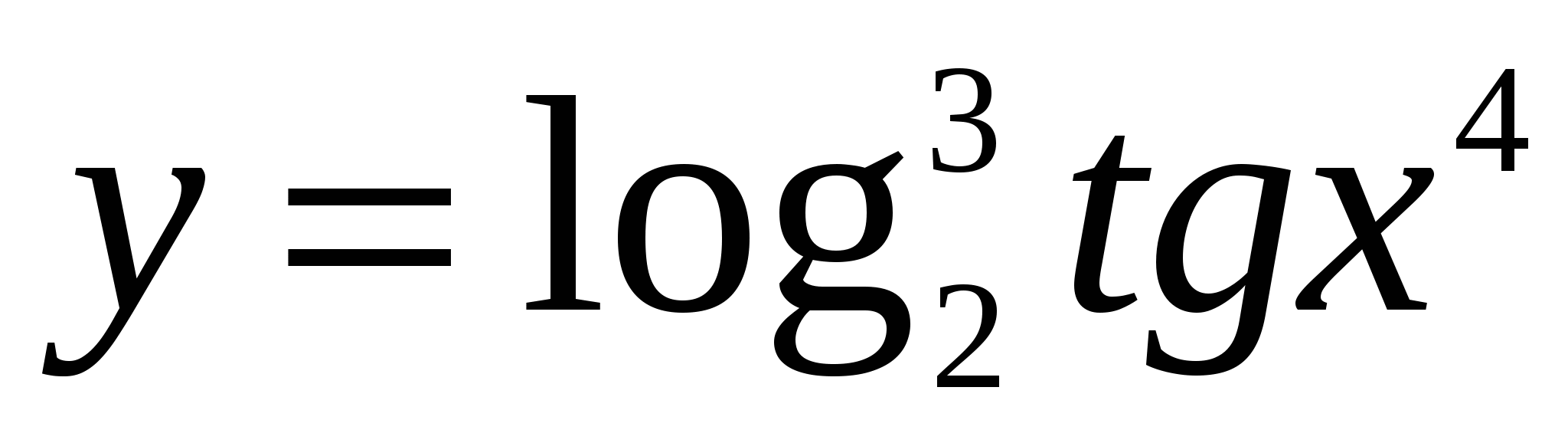 .
.
Решение: Данная функция является сложной. Её можно представить в виде цепочки «простых» функций: 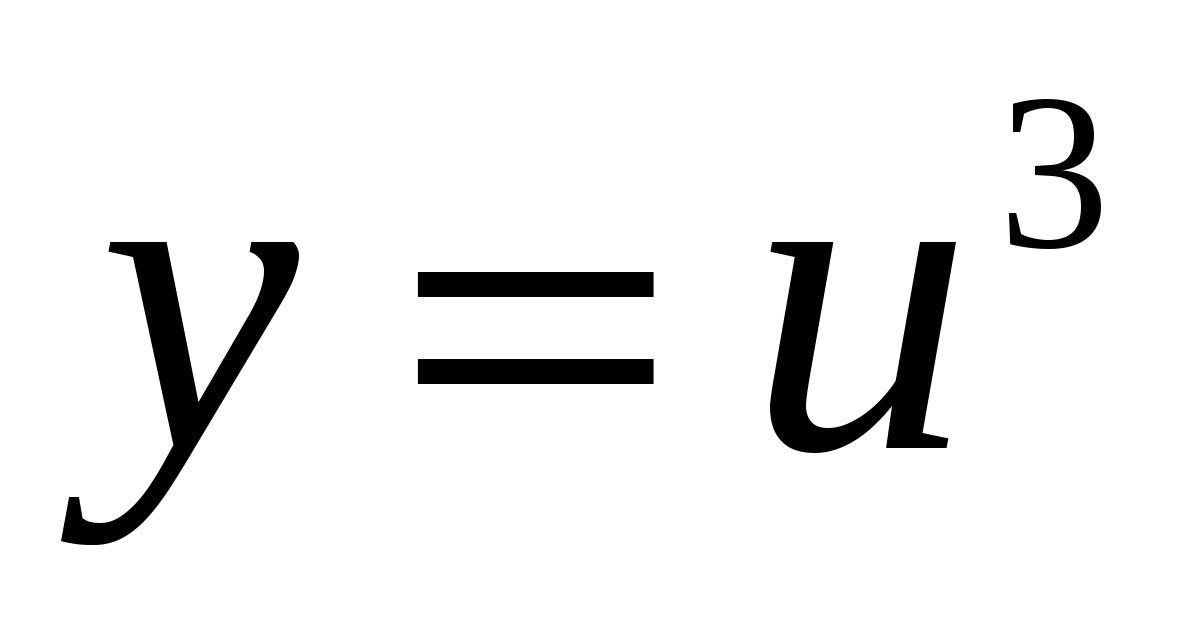 , где
, где 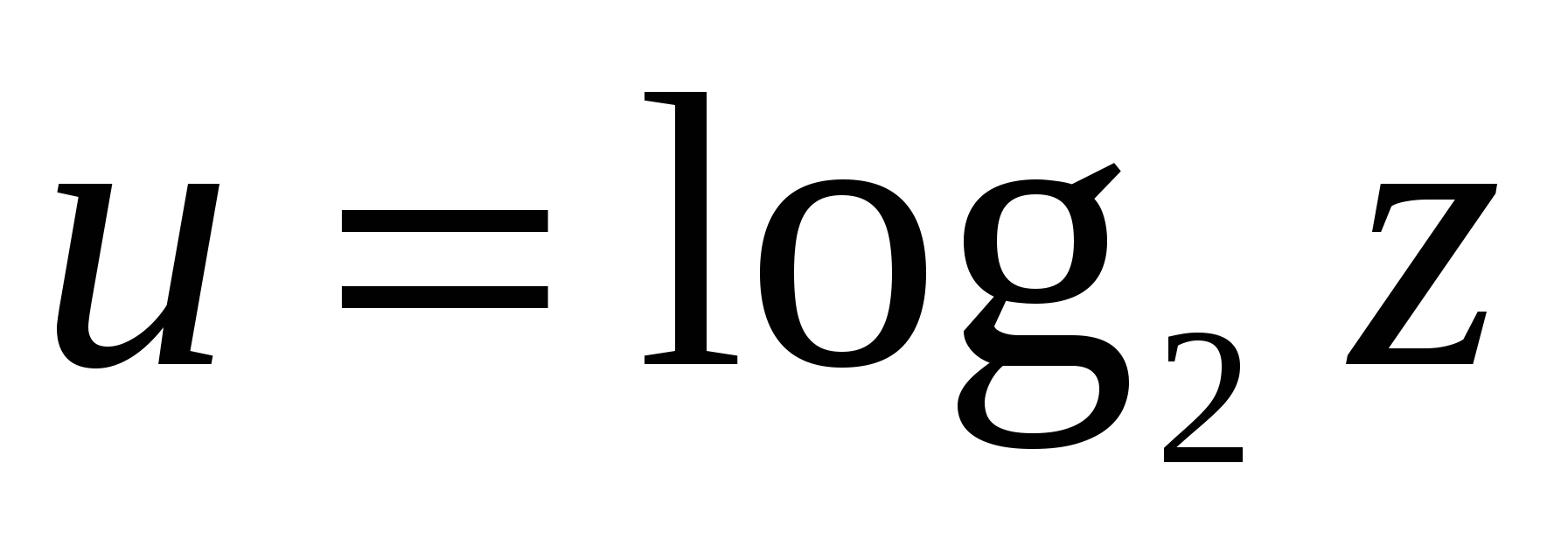 , где
, где 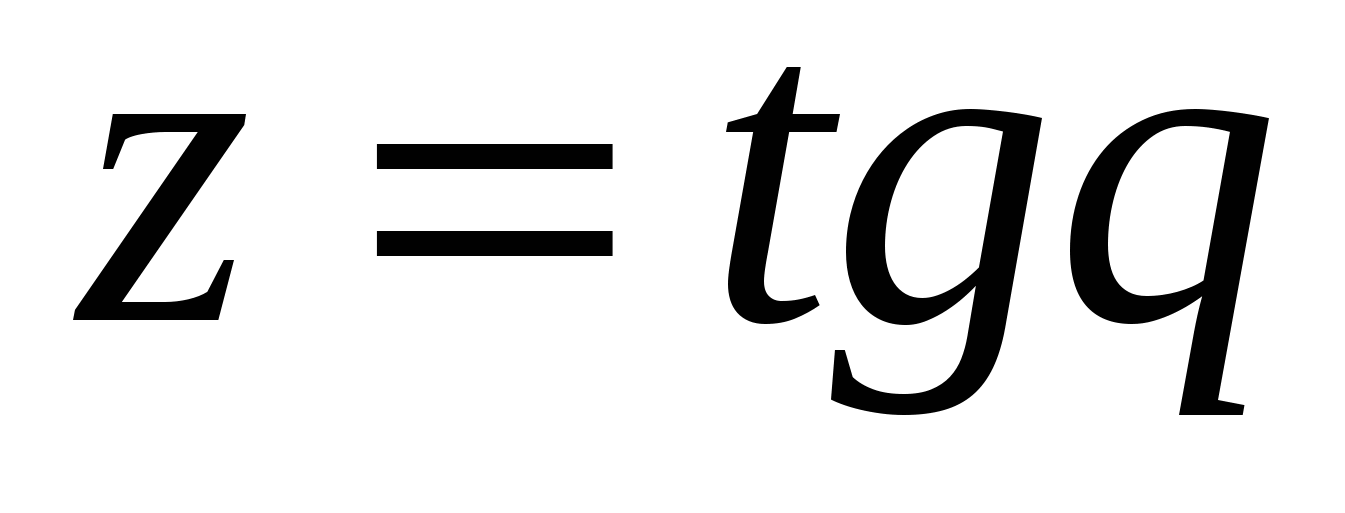 , где
, где 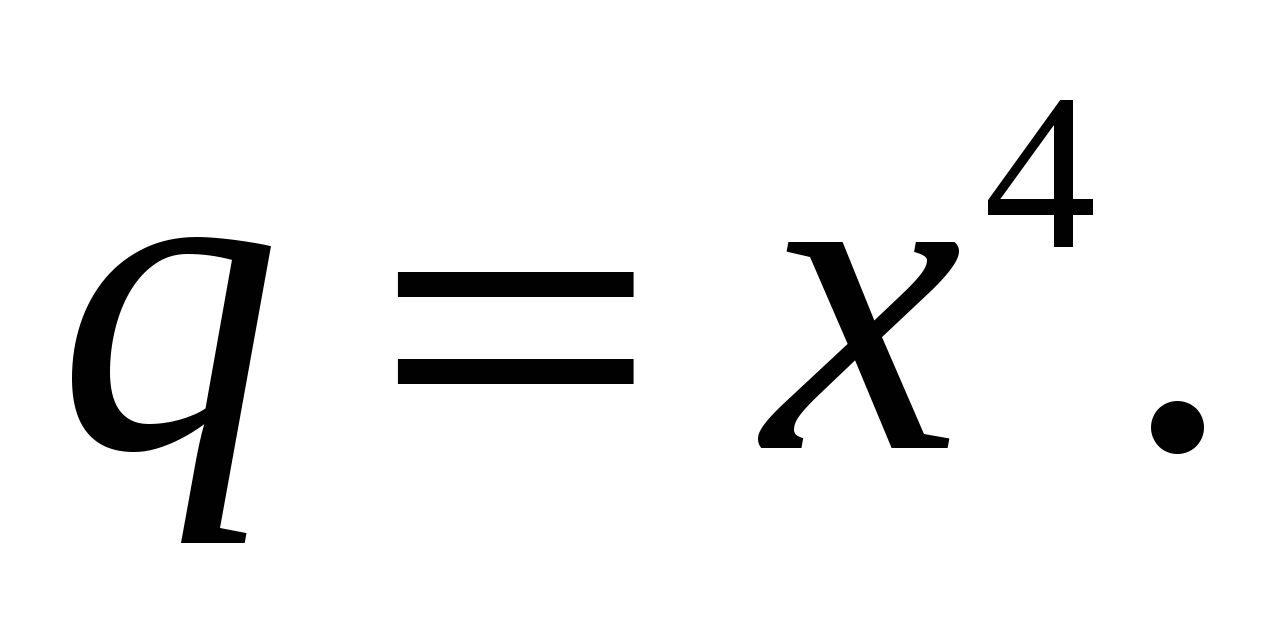 По правилу дифференцирования сложной функции, получаем:
По правилу дифференцирования сложной функции, получаем:
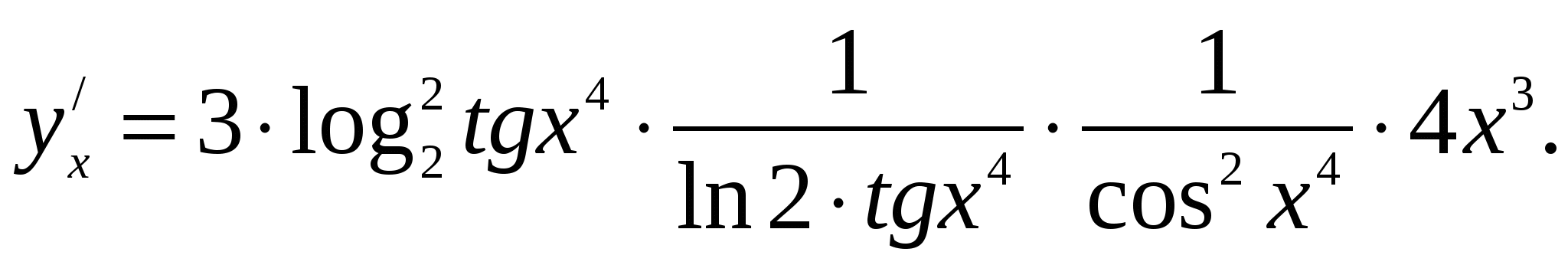
Пример 2: Пользуясь правилом дифференцирования обратной функции, найти производную 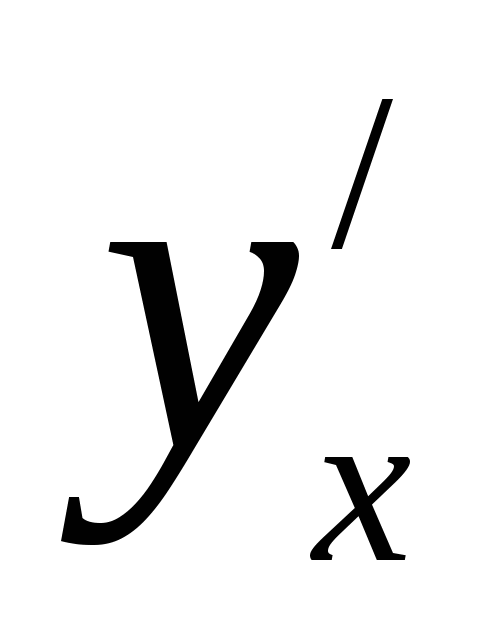 для функции
для функции 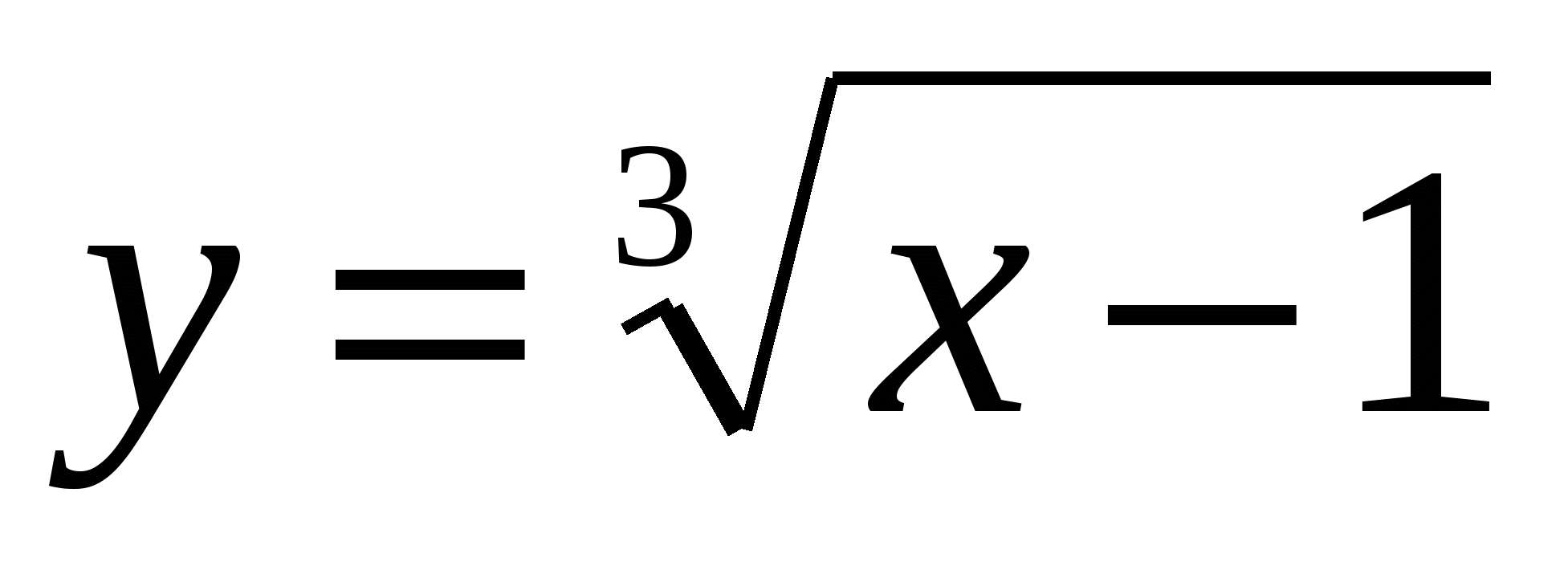 .
.
Решение: Обратная функция 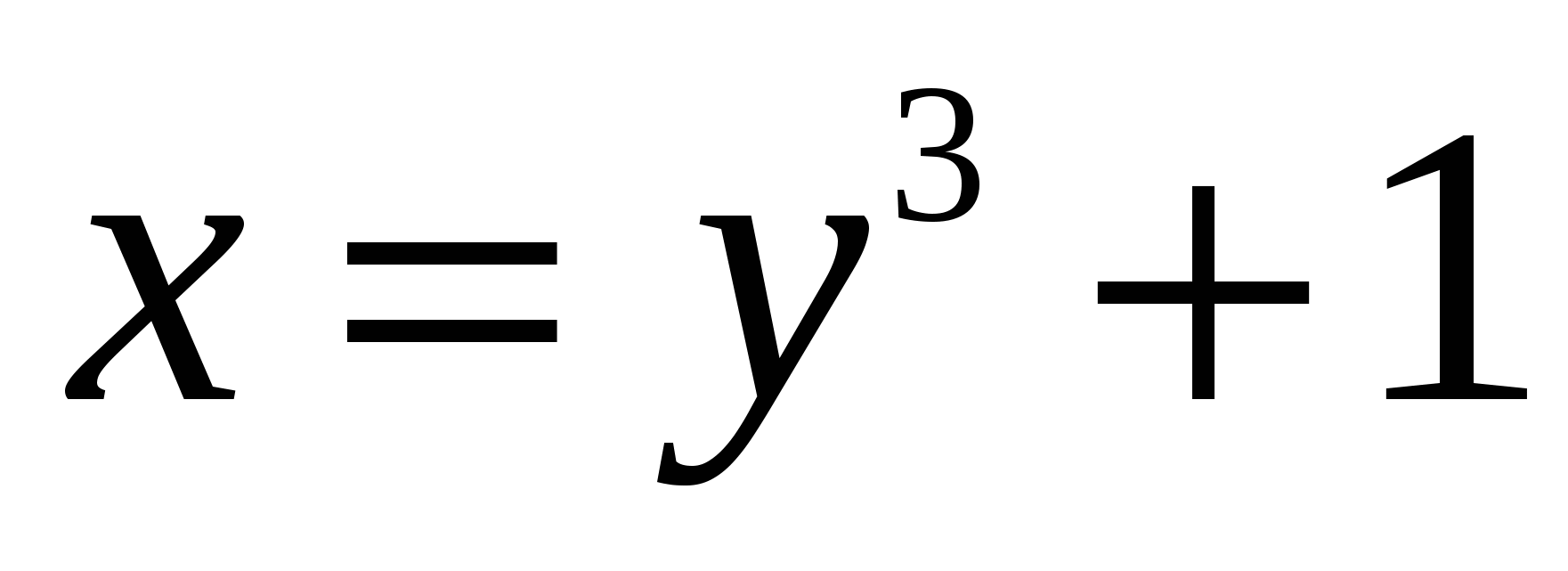 имеет производную
имеет производную 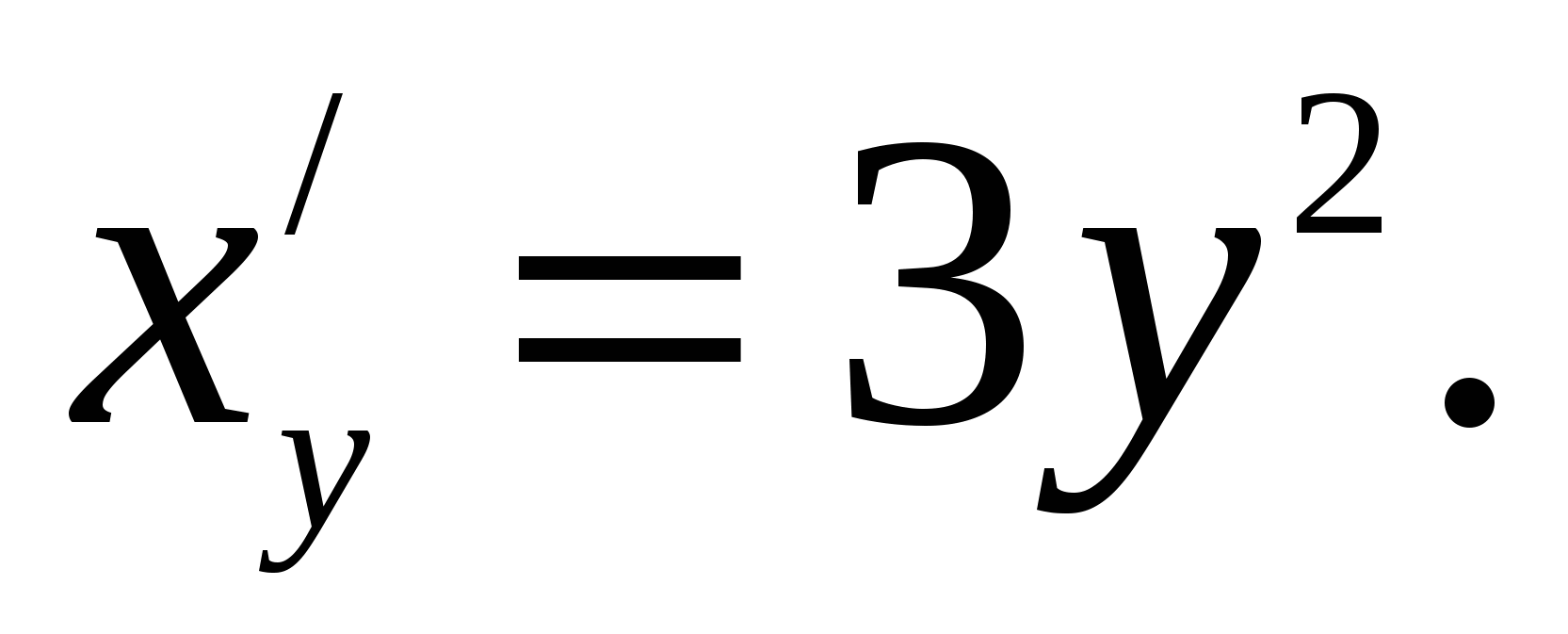
Следовательно, 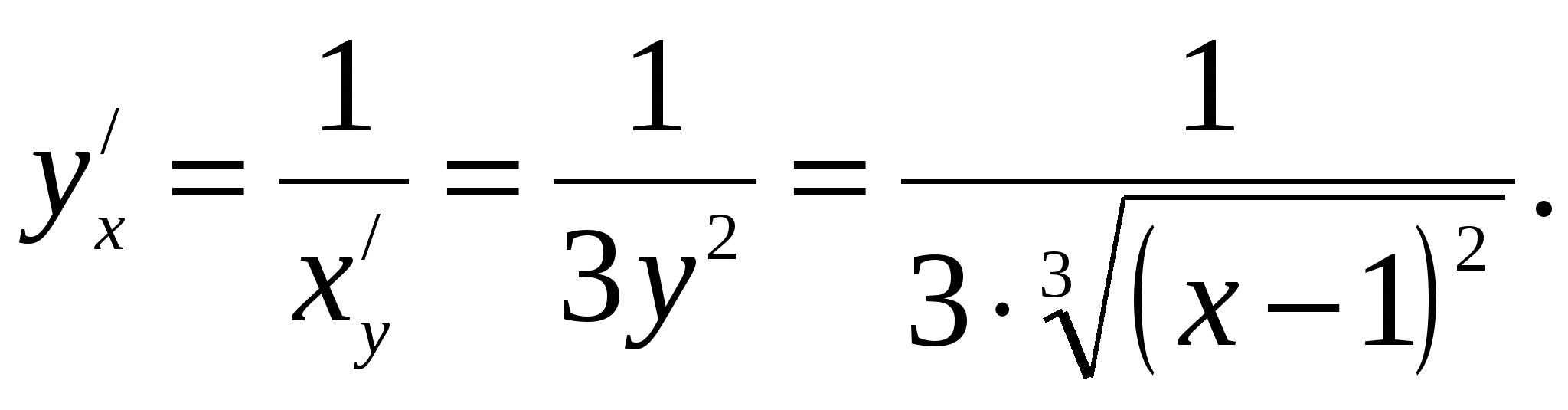
-
Дифференцирование неявных и параметрически заданных функций.
Если неявная функция задана уравнением 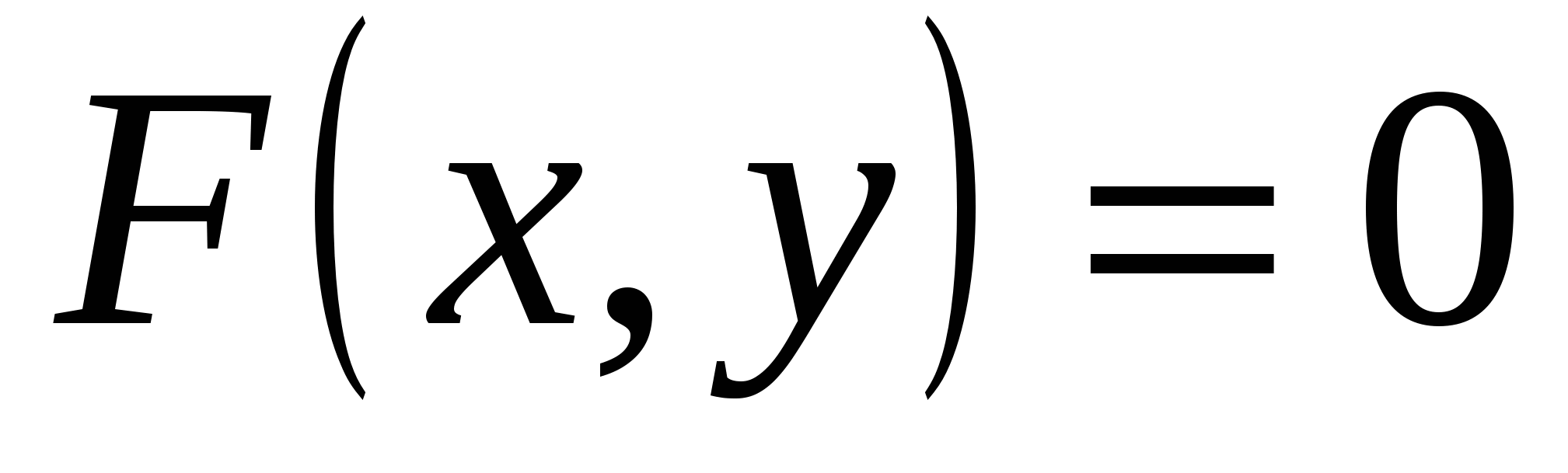 , то для вычисления производной от y по х нет необходимости разрешать уравнение относительно y: достаточно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у/.
, то для вычисления производной от y по х нет необходимости разрешать уравнение относительно y: достаточно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у/.
Пример 3: Найти производную функции, заданной уравнением:
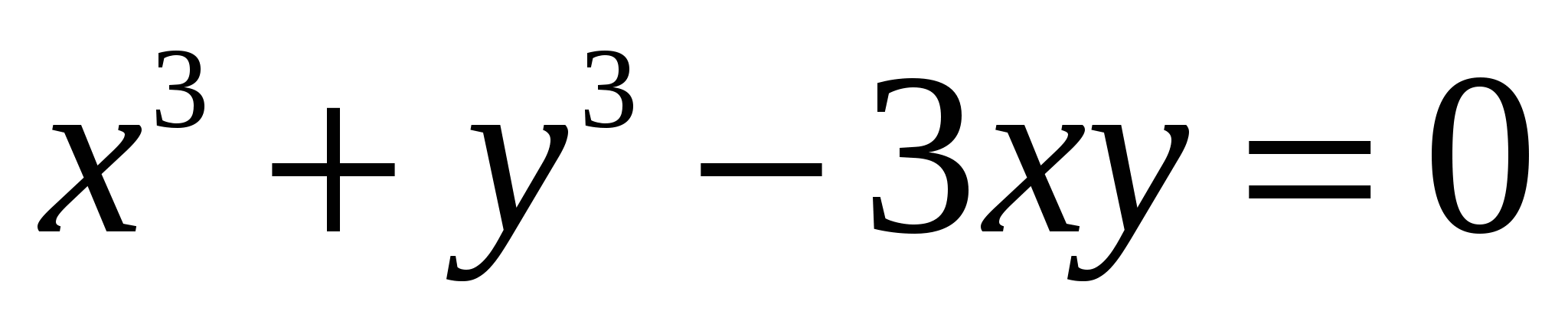 .
.
Решение: Дифференцируем по х равенство 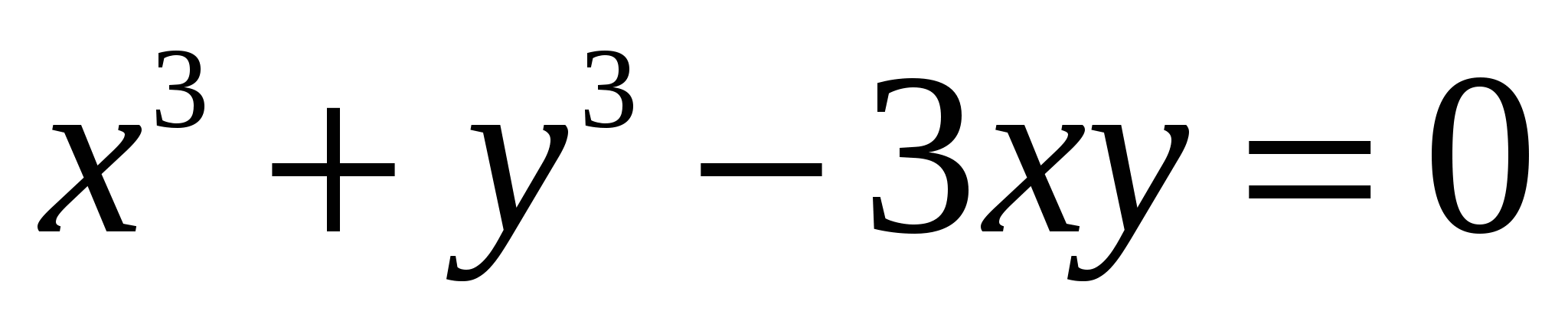 . Получаем:
. Получаем:
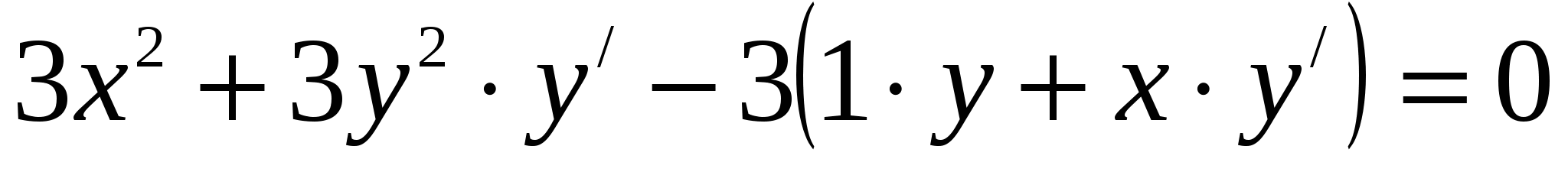 , откуда следует
, откуда следует
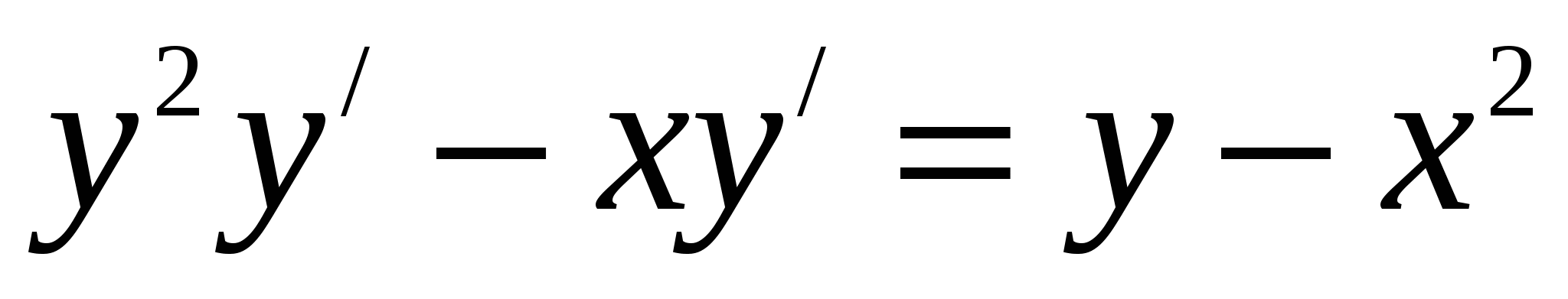 , т.е.
, т.е. 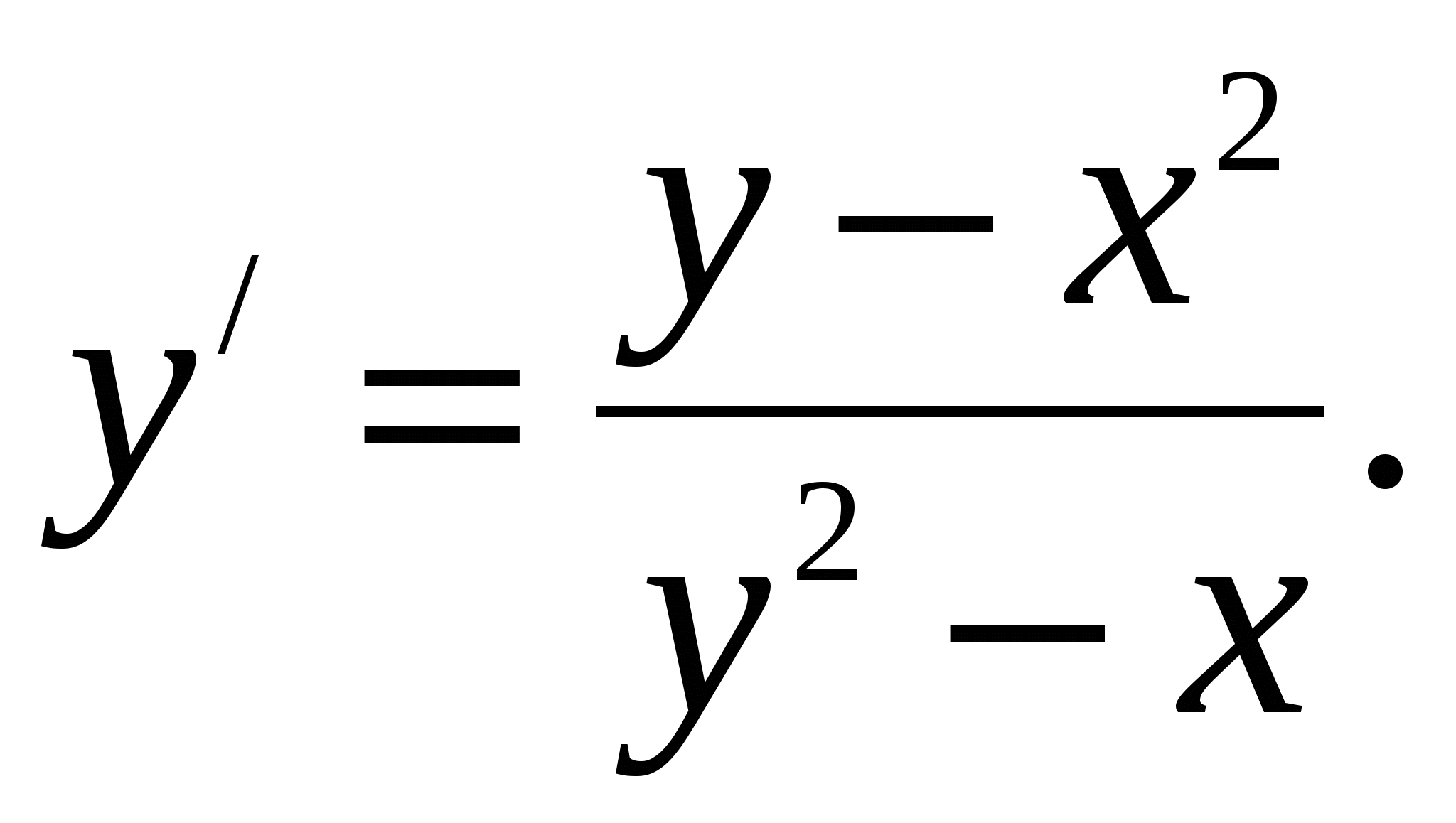
П усть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
усть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений 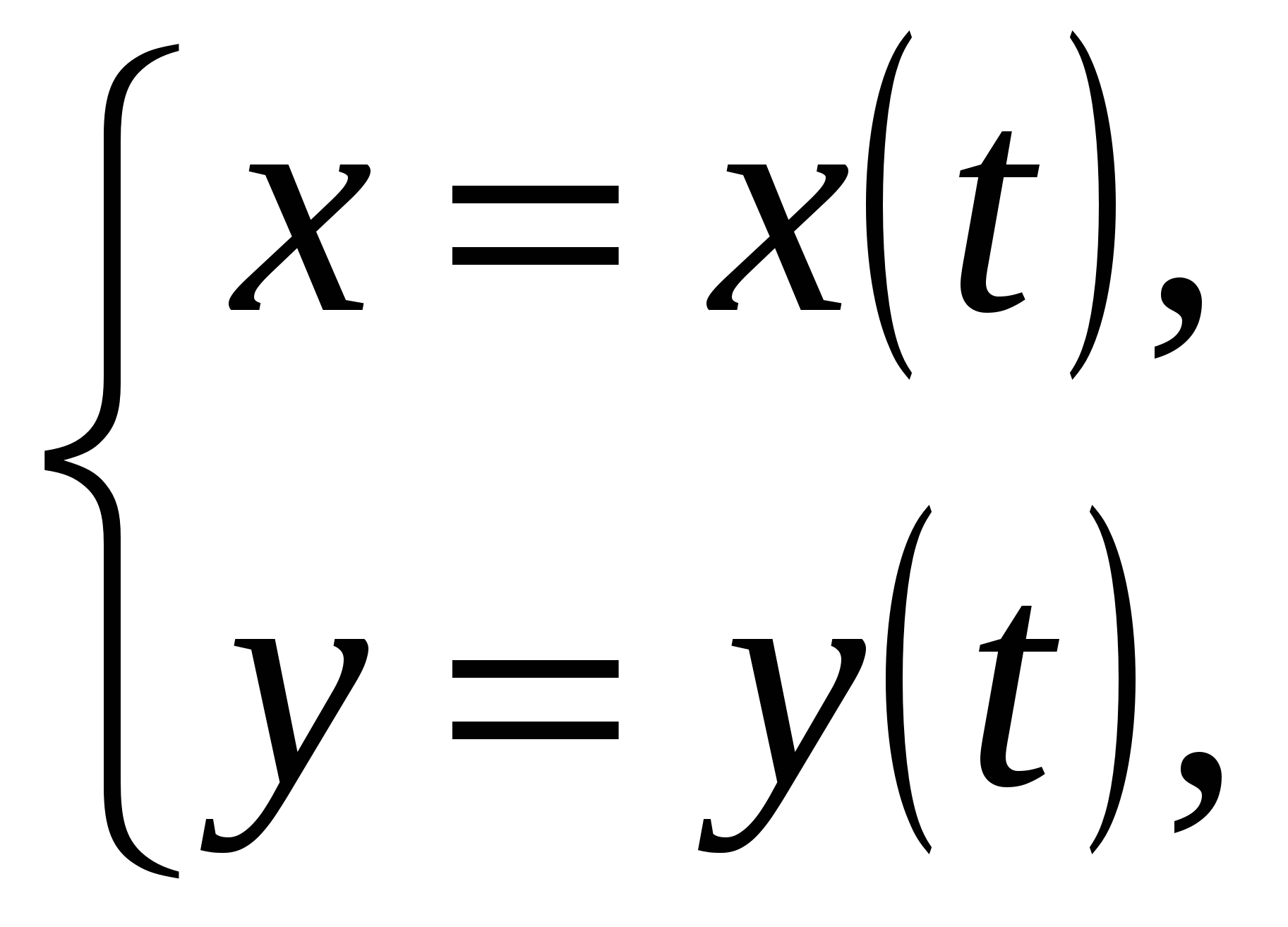 где t ‒ вспомогательная переменная, называемая параметром.
где t ‒ вспомогательная переменная, называемая параметром.
![]()
Полученная формула позволяет находить производную 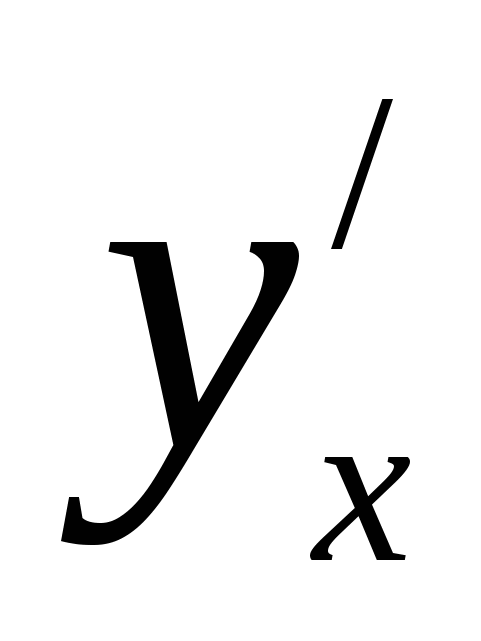 от функции, заданной параметрически, не находя непосредственной зависимости у от х.
от функции, заданной параметрически, не находя непосредственной зависимости у от х.
Пример 4: Пусть 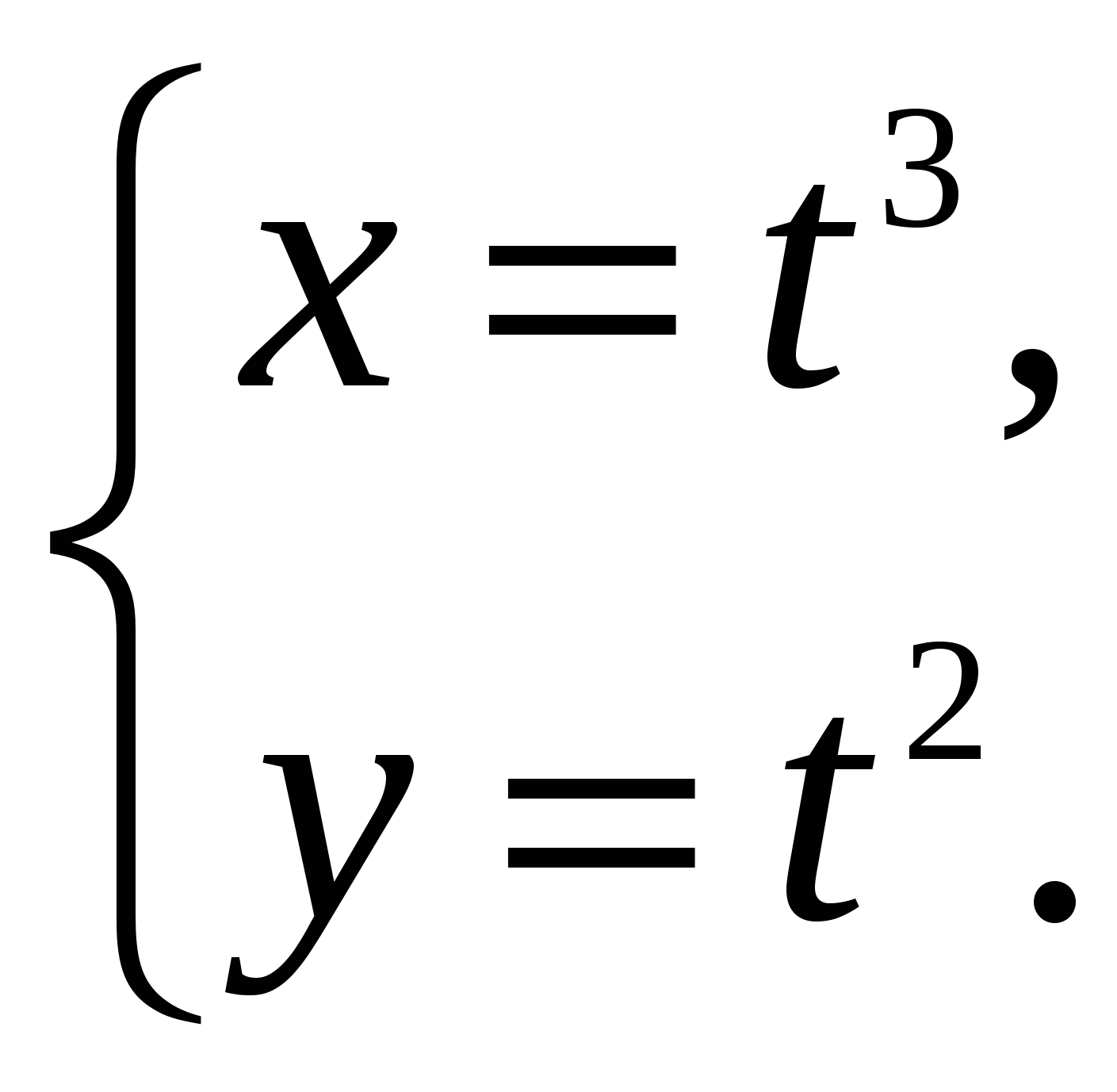 Найти
Найти 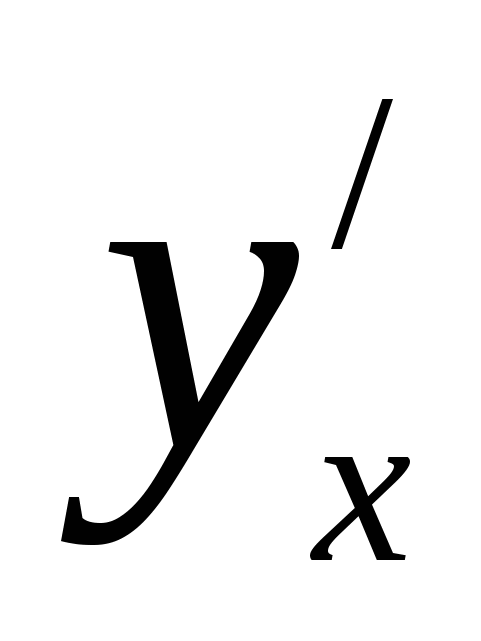 .
.
Решение: Имеем 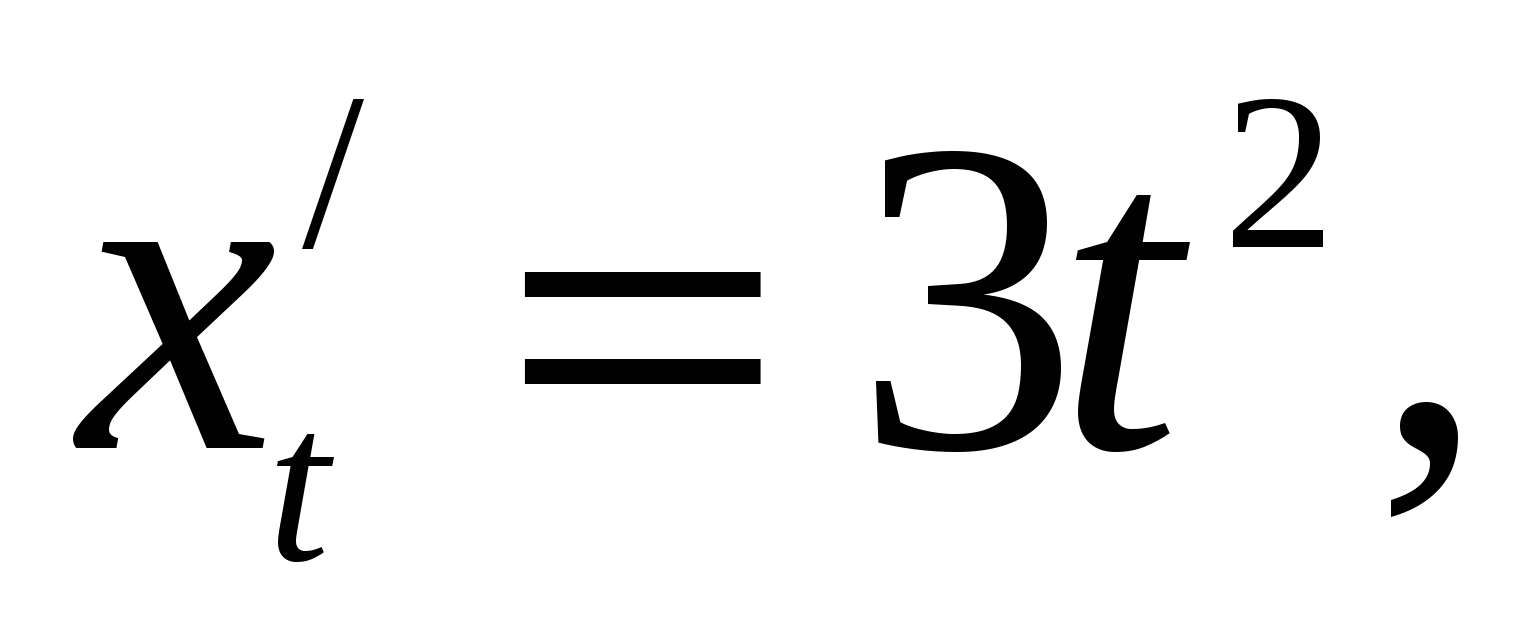
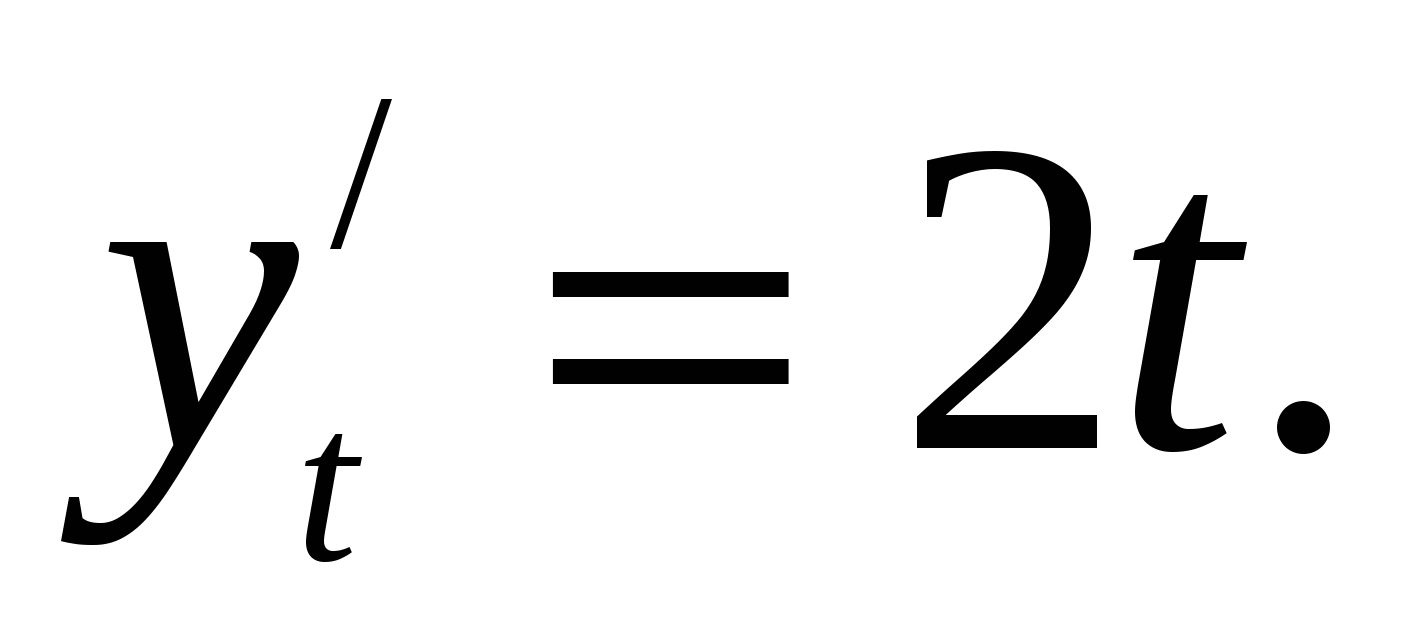 Следовательно,
Следовательно, 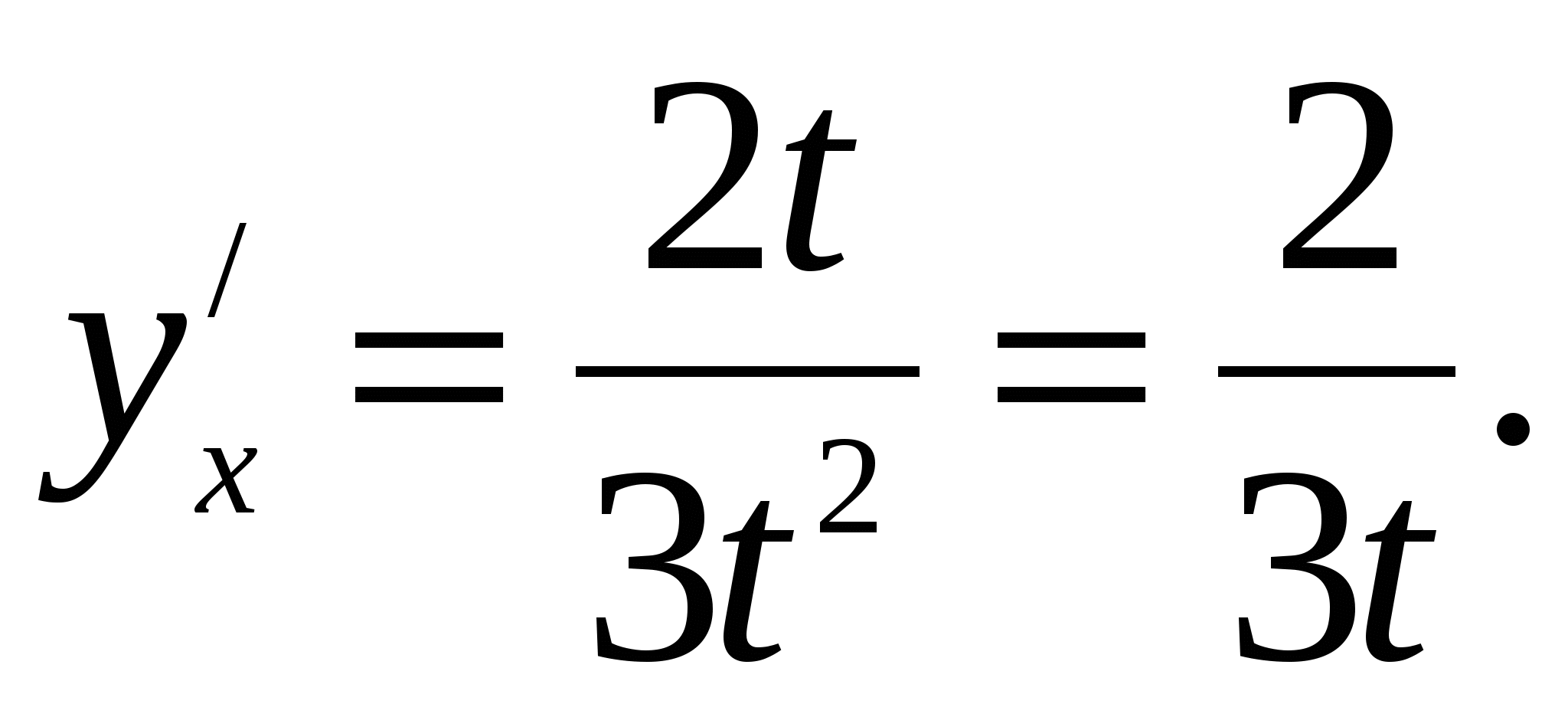
В этом можно убедиться, найдя непосредственно зависимость у от х. Действительно, 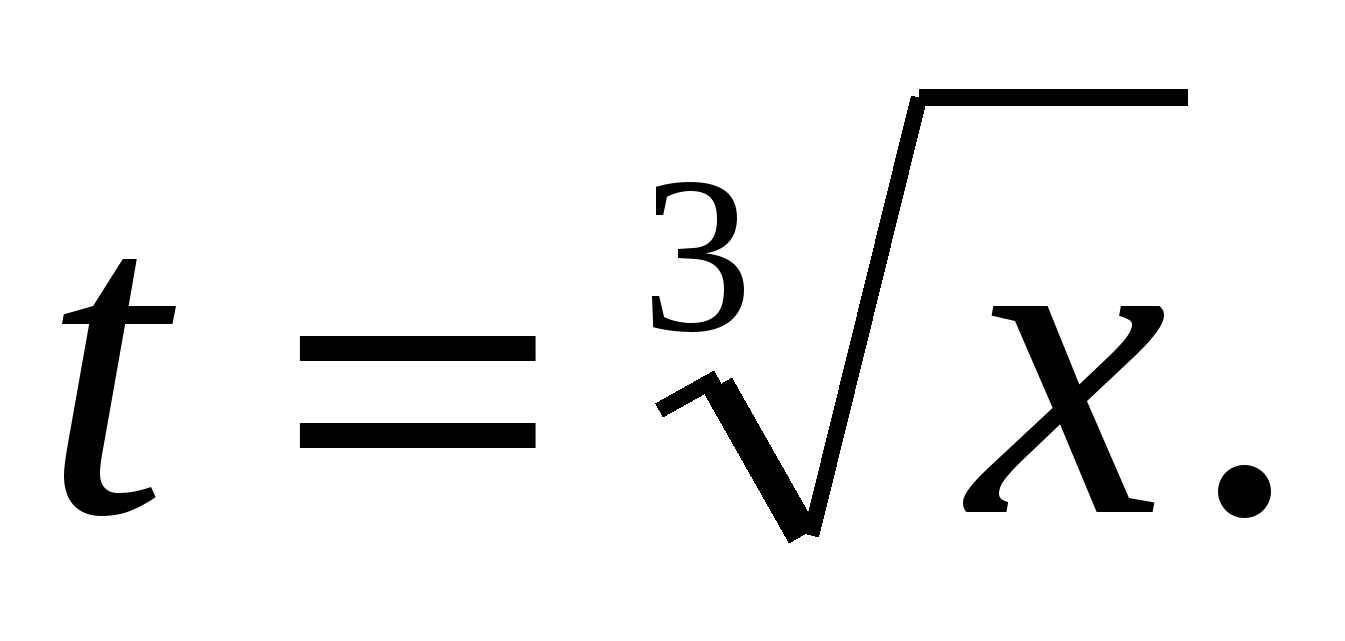 Тогда
Тогда 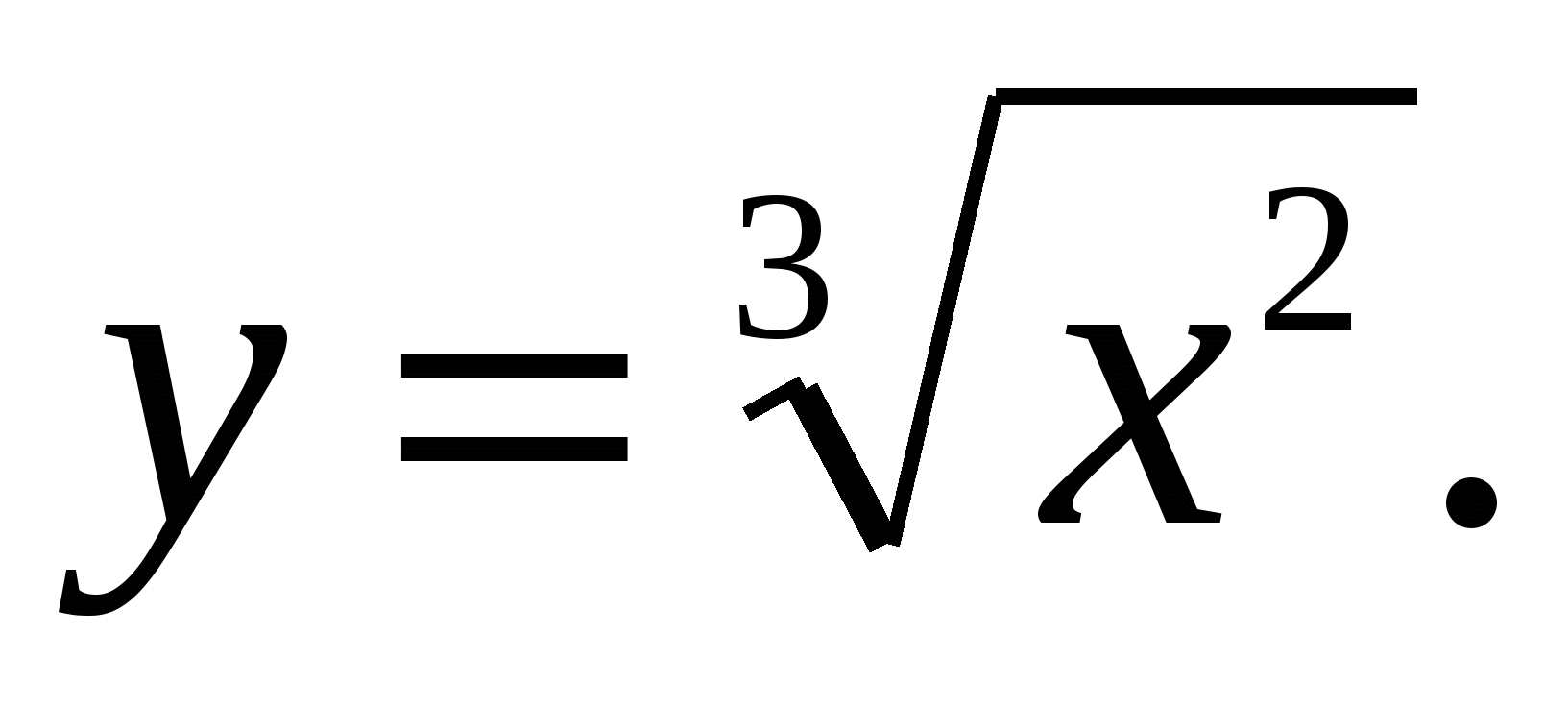 Отсюда
Отсюда 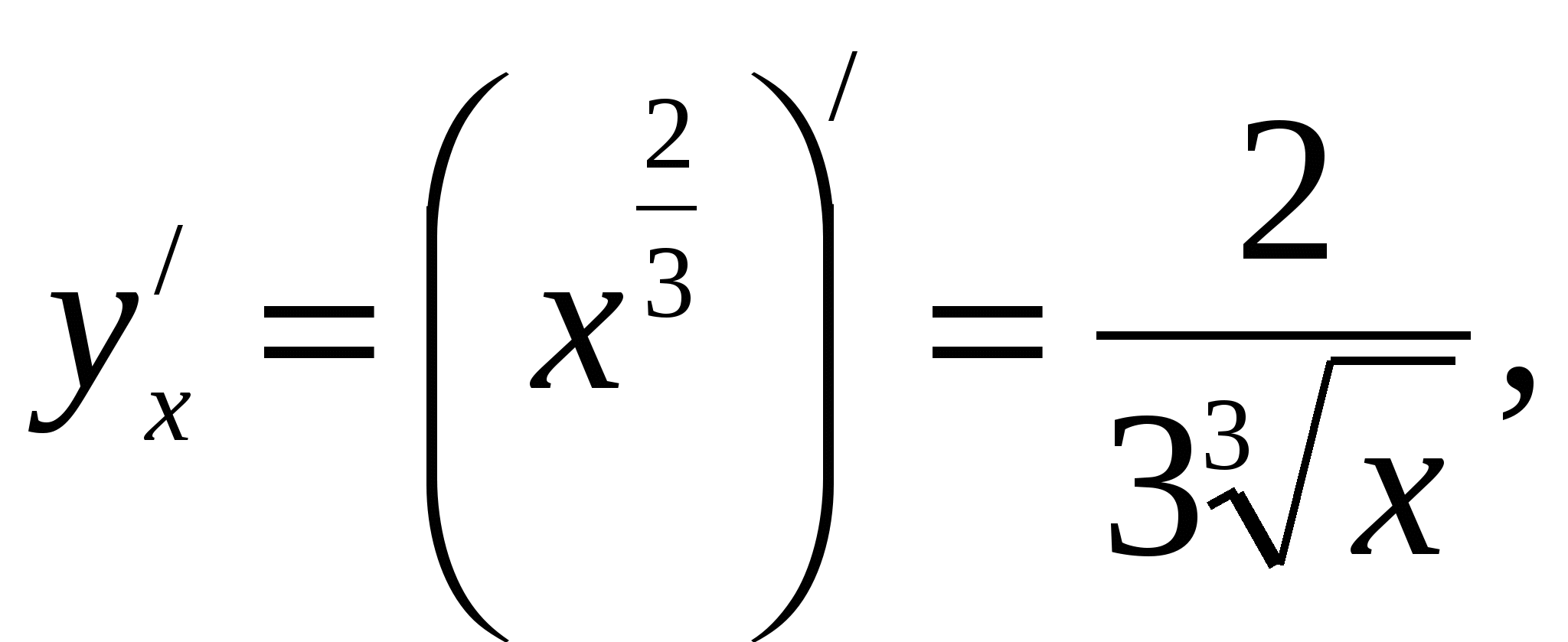 т.е.
т.е. 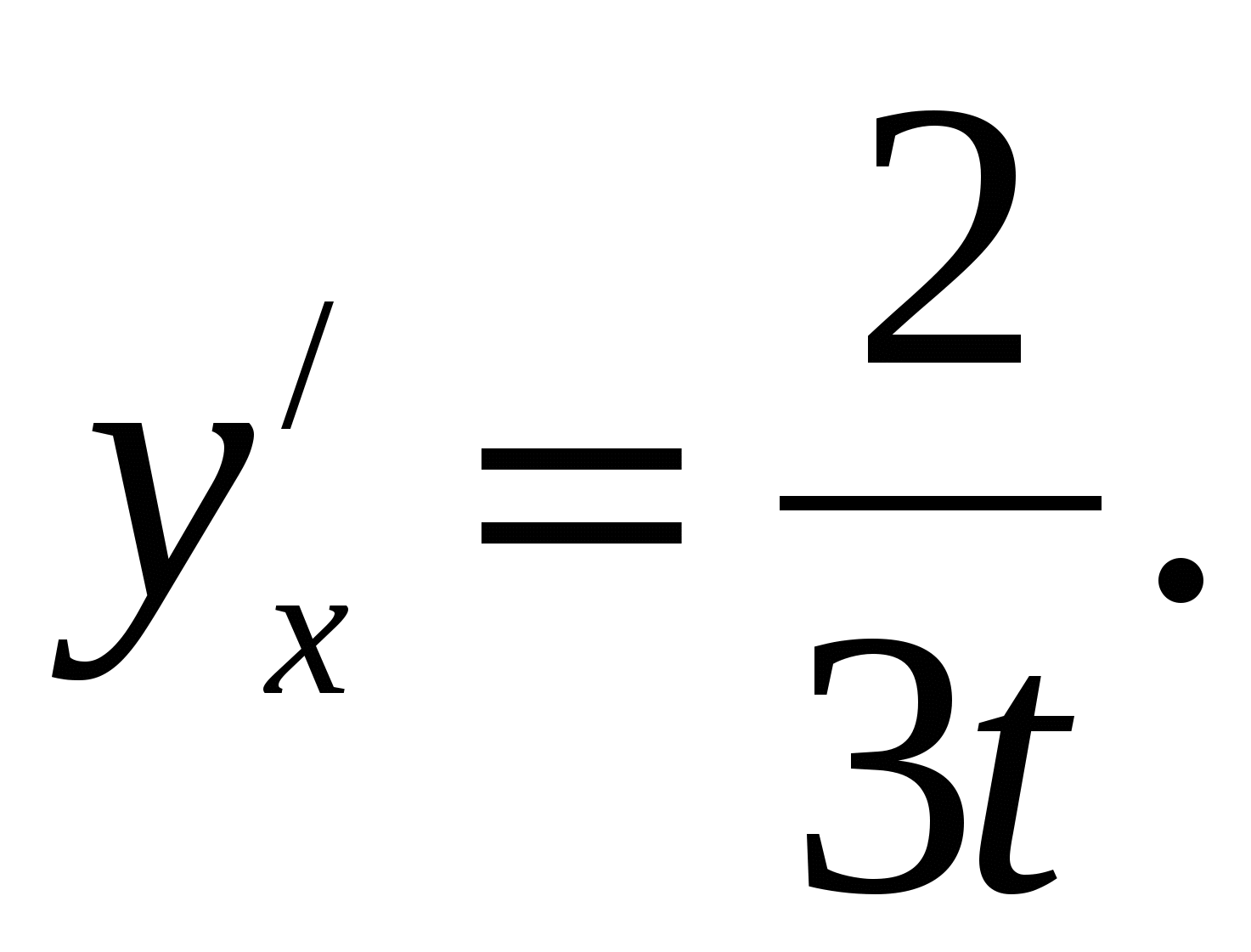
-
Логарифмическое дифференцирование.
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Пример 5: Найти производную функции 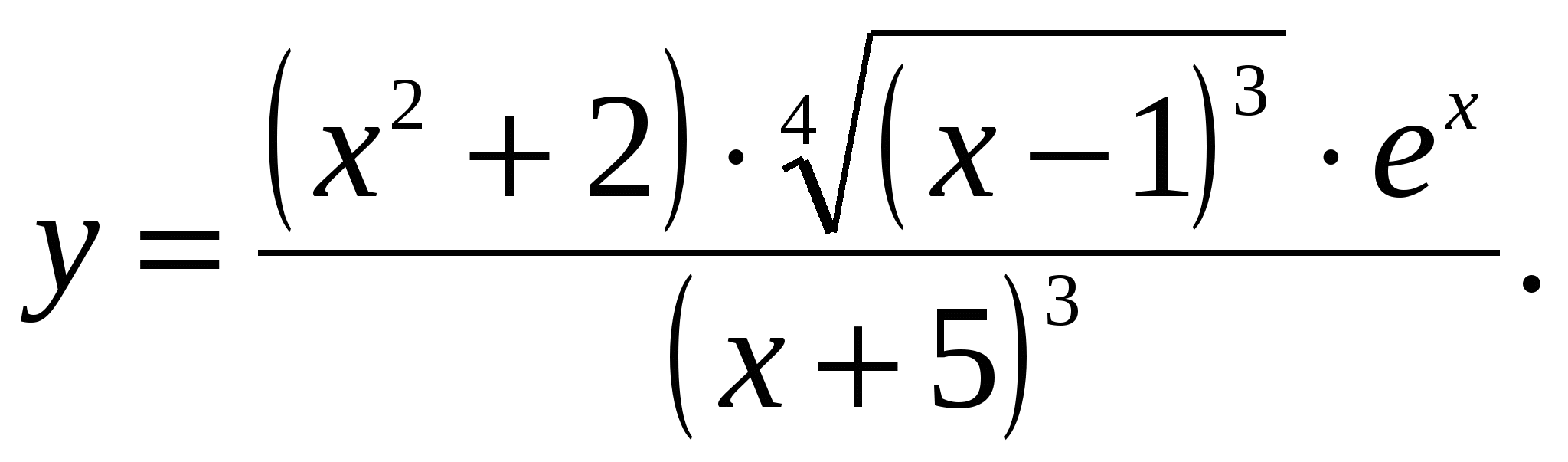
Решение: Можно найти производную с помощью правил и формул дифференцирования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Прологарифмируем функцию:
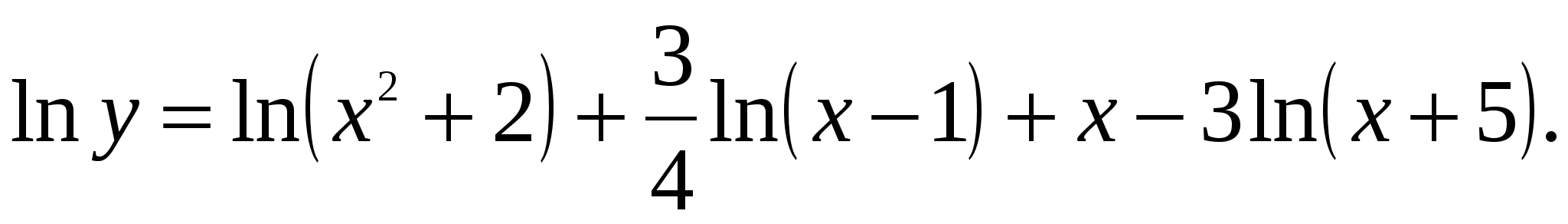
Дифференцируем это равенство по х:
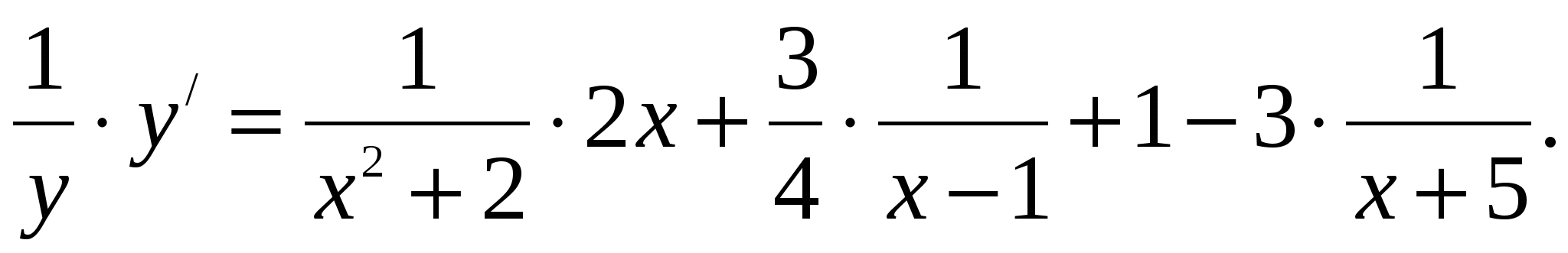
Выражаем ![]() :
: 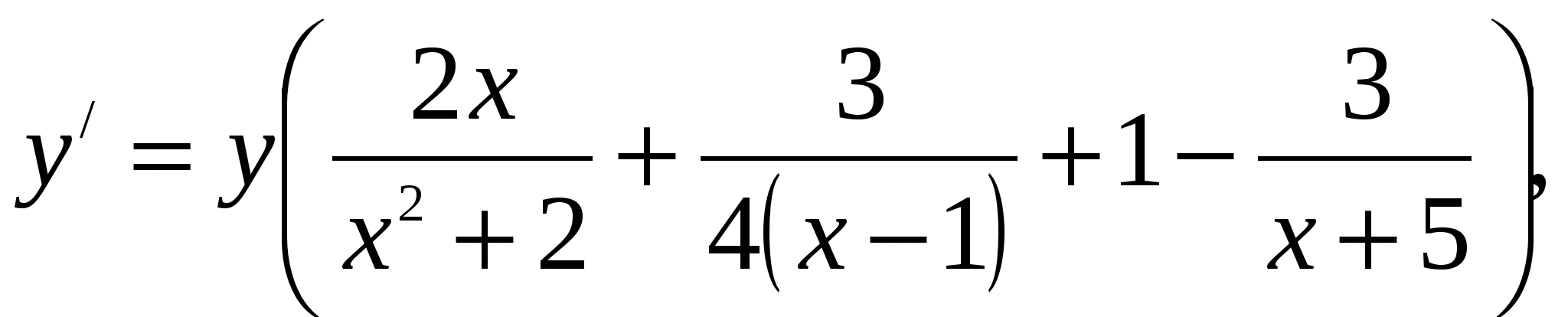
т. е. 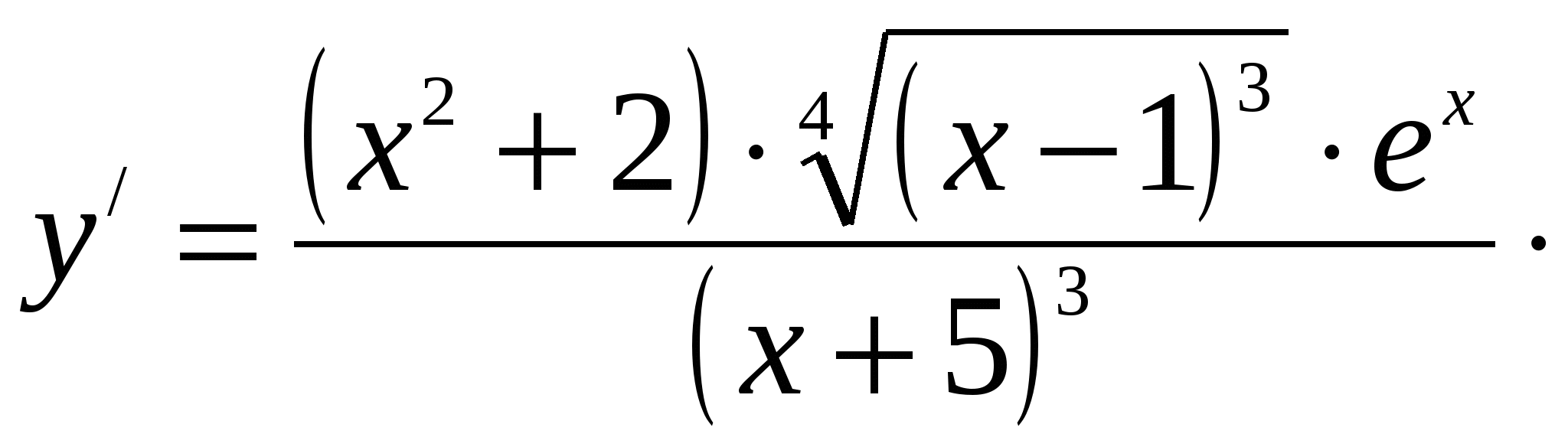
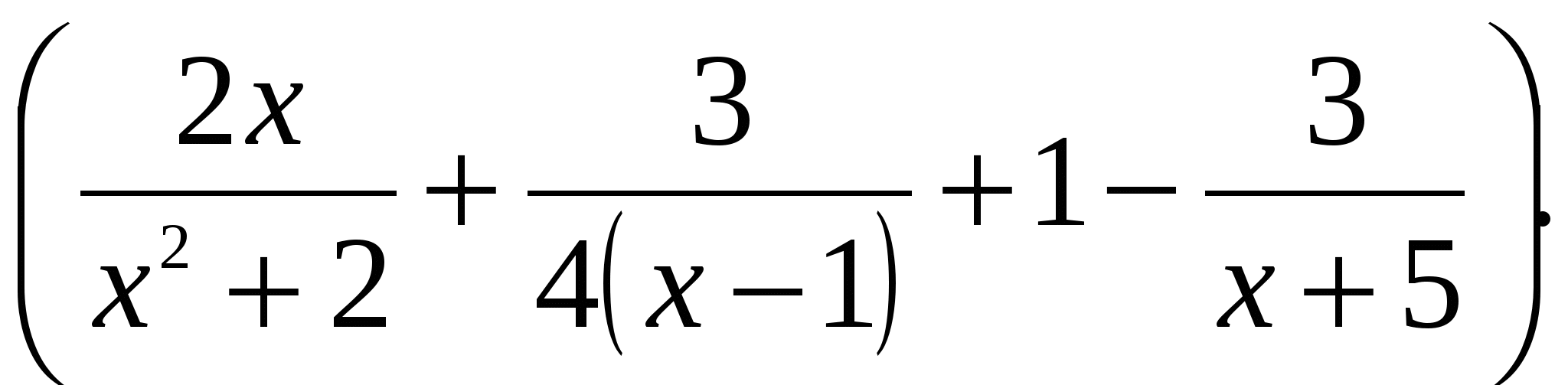
Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция 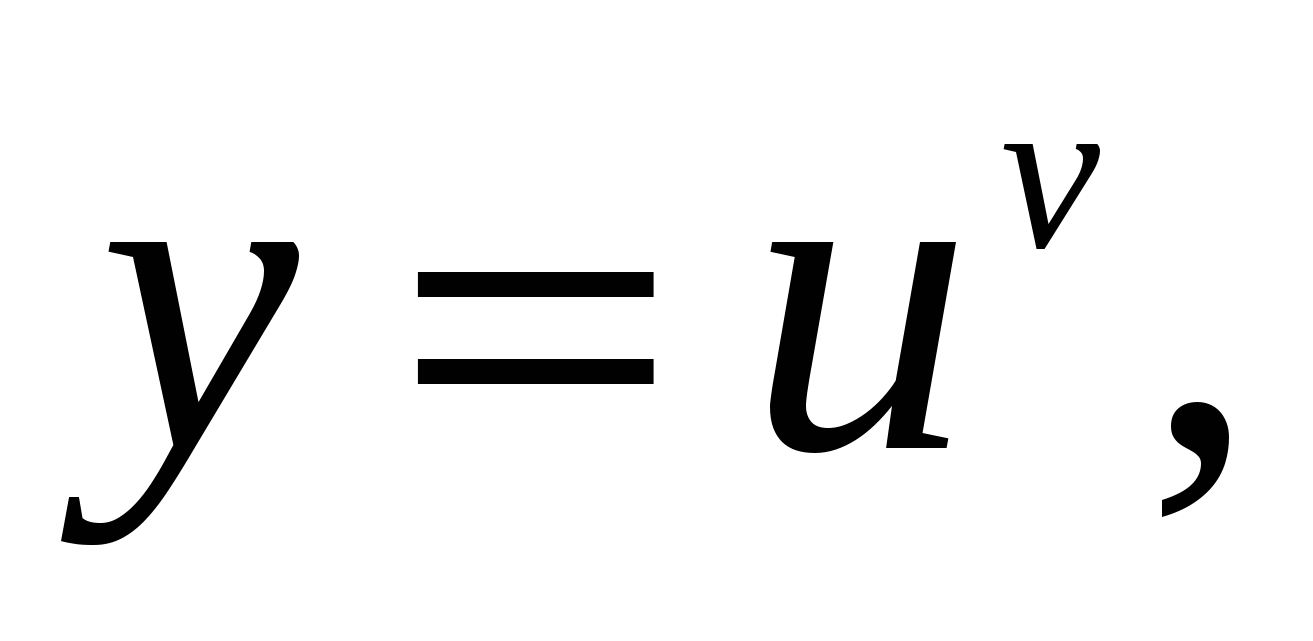 где
где 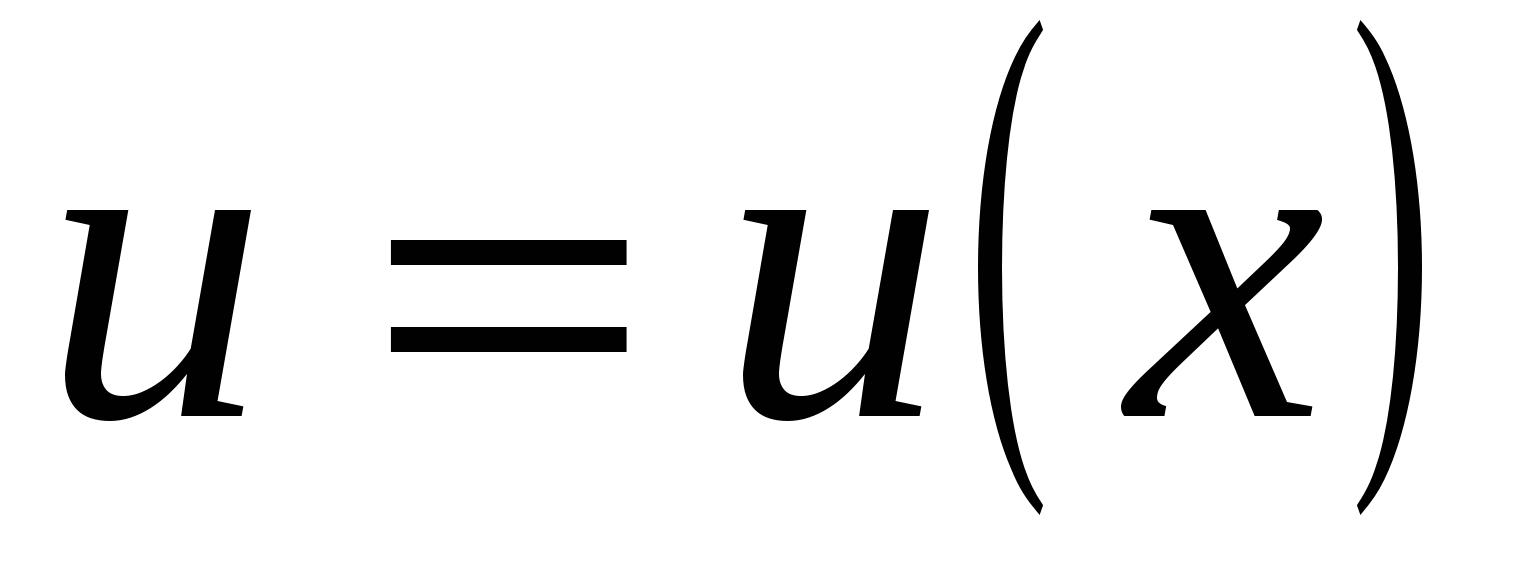 и
и 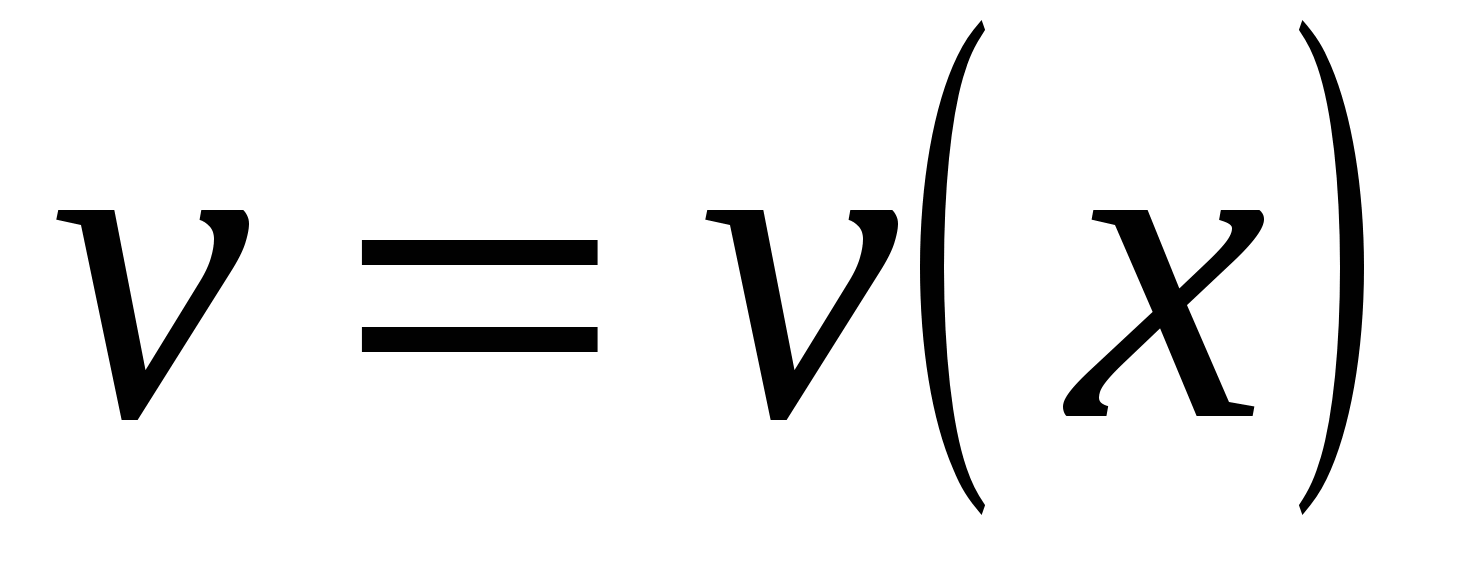 ‒ заданные дифференцируемые функции от х. Найдём производную этой функции.
‒ заданные дифференцируемые функции от х. Найдём производную этой функции.
![]()
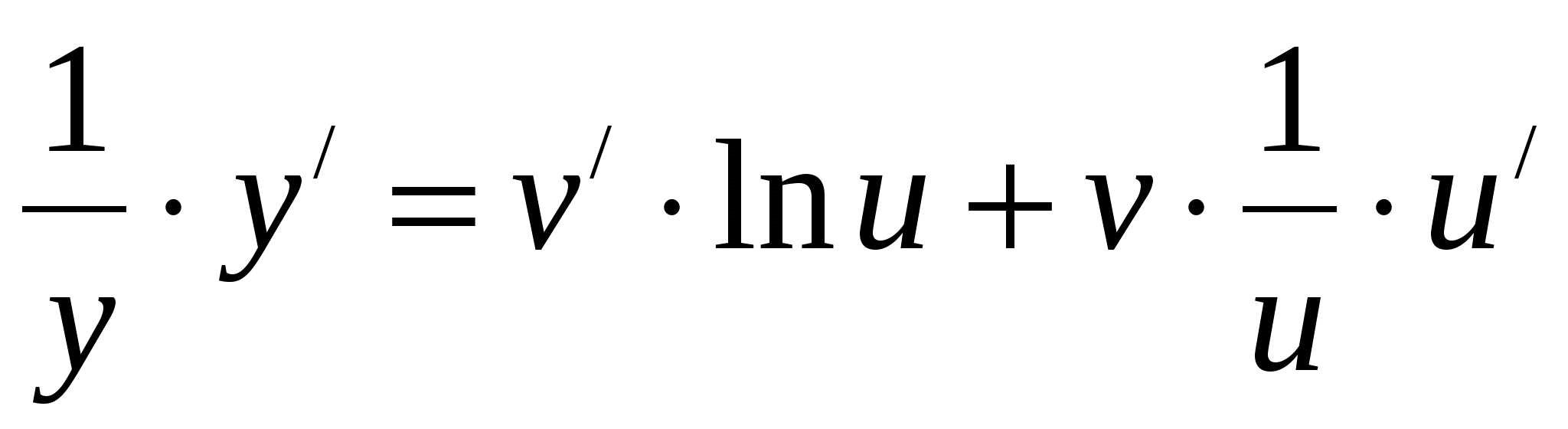
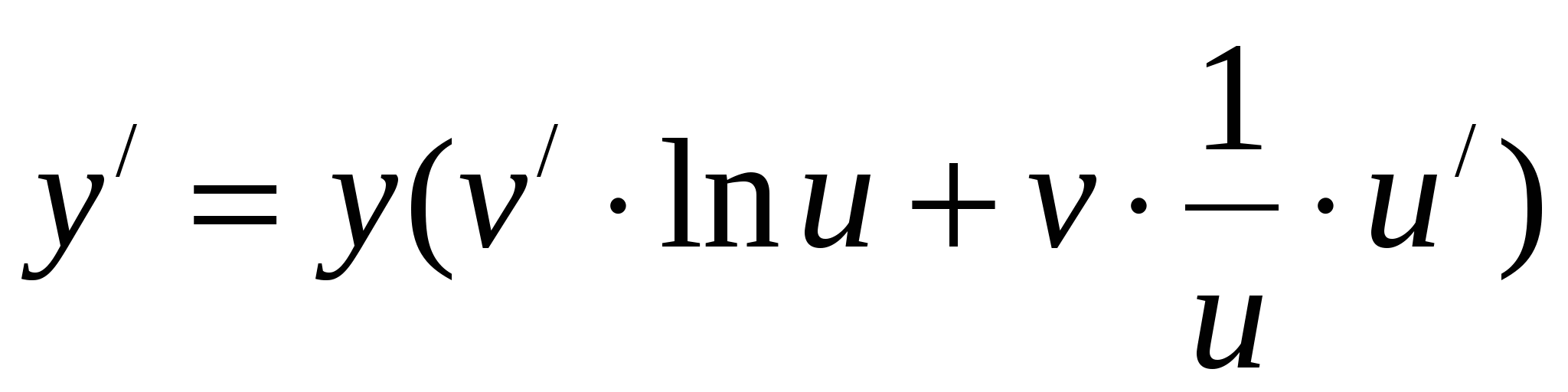 ,
,
т. е.  или
или 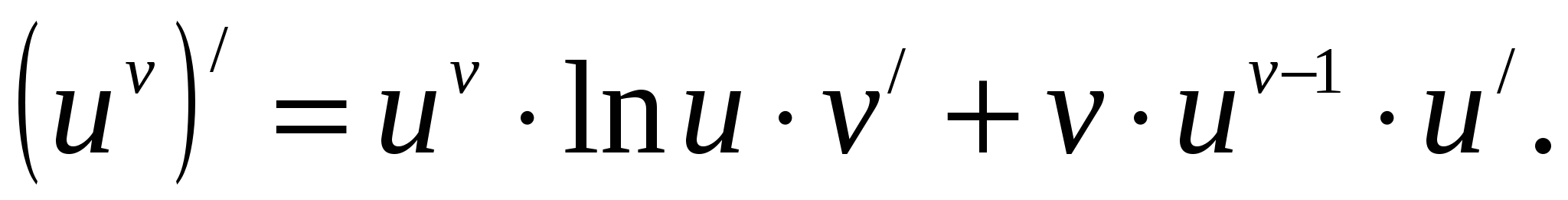
Сформулируем правило запоминания последней формулы: производная степенно-показательной функции равна сумме производной показательной функции, при условии 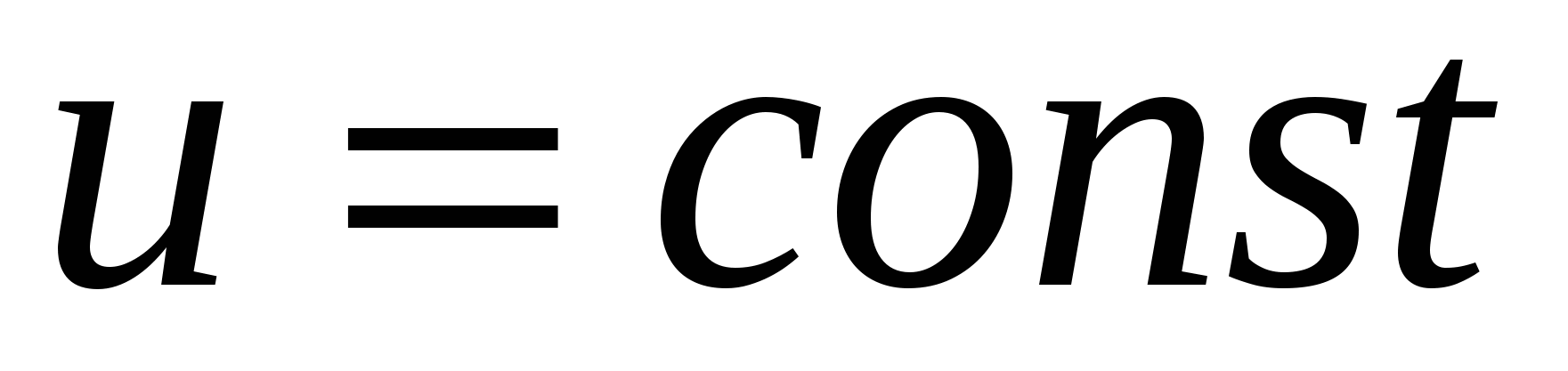 , и производной степенной функции при условии
, и производной степенной функции при условии 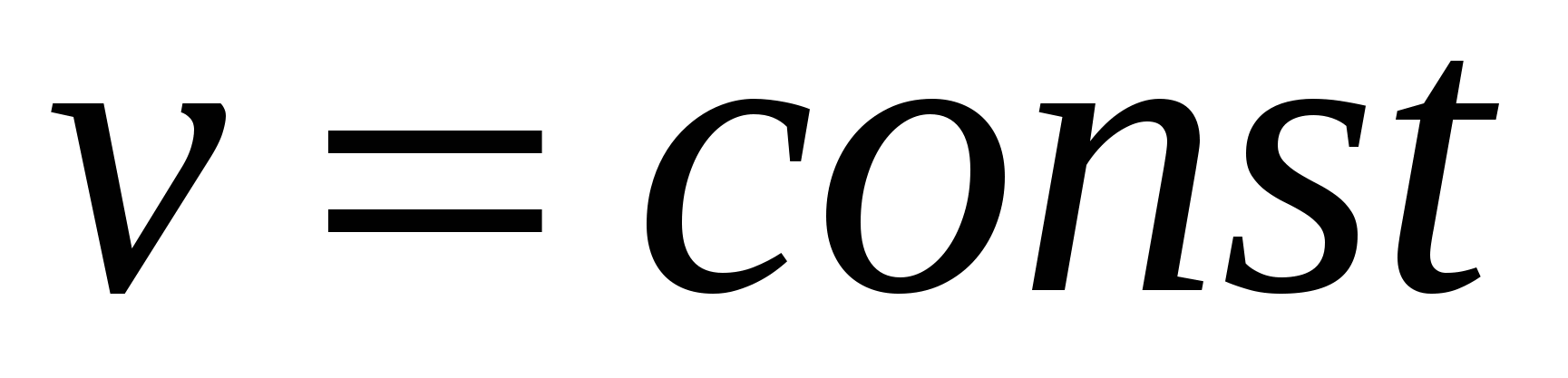 .
.
8


