- Преподавателю
- Математика
- Системы уравнений, как математические модели реальных ситуаций
Системы уравнений, как математические модели реальных ситуаций
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Конспекты |
| Автор | Блезникова Т.Н. |
| Дата | 21.11.2015 |
| Формат | docx |
| Изображения | Есть |
Системы уравнений как математические модели реальных ситуаций
Вам известно, что система двух уравнений с двумя переменными может служить математической моделью реальной ситуации. Первый опыт в решении таких задач вы приобрели в курсе алгебры 7-го класса. Правда, там встречались только системы двух линейных уравнений с двумя переменными. В § 4 мы рассмотрели задачу, математическая модель которой представляла собой систему двух уравнений, но одно из них уже не было линейным. Вернитесь еще раз к этой задаче, и вы убедитесь, что в технологии ее решения ничего особенно нового не было - те же три этапа математического моделирования. То же относится и к задачам, которые рассматриваются в этом параграфе.
Пример 1.
В райцентре два кинотеатра - «Факел» и «Слава», первый - на 400, а второй - на 600 мест. В зрительном зале кинотеатра «Слава» на 4 ряда больше, чем в кинотеатре «Факел», и, кроме того, в каждом ряду на 5 мест больше, чем в кинотеатре «Факел». Сколько рядов в зрительном зале кинотеатра «Факел», если известно, что в каждом ряду кинотеатра «Слава» более 25 мест?
Решение.
Первый этап.
Составление математической модели.
Пусть х - число рядов в кинотеатре «Факел», у - число мест в каждом ряду кинотеатра «Факел». Тогда х + 4 - число рядов в кинотеатре «Слава», у + 5 - число мест в каждом ряду кинотеатра «Слава». Зная число рядов и число мест в ряду, можно найти общее число мест в каждом кинотеатре: ху - число мест в кинотеатре «Факел», (х + 4)(у +5) - число мест в кинотеатре «Слава». По условию, в кинотеатре «Факел» - 400 мест, т.е. ху - 400, а в кинотеатре «Слава» - 600 мест, т.е. (х + 4){у + 5) = 600.
Таким образом, мы приходим к системе двух уравнений с двумя переменными:

Математическая модель задачи составлена.
Второй этап.
Работа с составленной моделью. Имеем
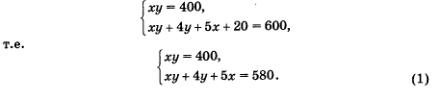
Применим метод алгебраического сложения: вычтем первое уравнение из второго. Получим
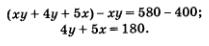
Заменим этим уравнением второе уравнение системы (1):

Система (2) несколько проще, чем система (1), ее можно решить методом подстановки. Выразим у через х из второго уравнения системы
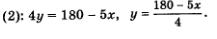
Подставим это выражение вместо у в первое уравнение системы (2):
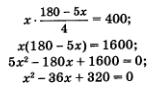
(обе части предыдущего уравнения почленно разделили на 5);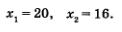
Так как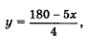 то получаем: если х = 20, то у = 20; если x = 16, то у = 25.
то получаем: если х = 20, то у = 20; если x = 16, то у = 25.
Итак, система (2), а с ней и система (1) имеют два решения: (20; 20) и (16; 25).
Третий этап.
Ответ на вопрос задачи.
Опираясь на полученные решения системы, мы должны проанализировать две возможности: либо в кинотеатре «Факел» 20 рядов по 20 мест в каждом ряду, либо 16 рядов по 25 мест в каждом ряду. Если выбрать первую возможность, то в кинотеатре «Слава» будет 24 ряда (по условию, там на 4 ряда больше) по 25 мест в каждом ряду (по условию, в каждом ряду «Славы» на 5 мест больше, чем в «Факеле»). Это нас не устраивает, поскольку, по условию, в каждом ряду «Славы» более 25 мест. Рассмотрим вторую возможность: в «Факеле» 16 рядов по 25 мест в каждом. Тогда в «Славе» будет 20 рядов по 30 мест в каждом. Это нас устраивает.
Ответ: 16 рядов.
На самом деле эта задача не является для вас новой, мы решали ее в учебнике «Алгебра-8», но по-другому: математической моделью задачи было рациональное уравнение с одной переменной. Приведем краткие наброски для составления такой модели:

Получаем уравнение 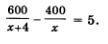 Это математическая модель задачи.
Это математическая модель задачи.
Сравним два варианта решения задачи. В первом варианте была более сложная математическая модель (система уравнений), значит, более трудным был второй этап - работа с составленной моделью. Зато менее трудным был первый этап, сама математическая модель была составлена легче и быстрее. Поскольку первый этап, где больше творчества, сложнее, чем второй (технический), то часто предпочтительнее упрощать именно этап составления модели, т.е. работать с двумя переменными.
Пример 2.
Пристани В и С находятся ниже пристани А по течению реки соответственно на 30 км и 45 км (рис. 41). Моторная лодка отходит от пристани А, доходит до С, сразу поворачивает назад и приходит в В, затратив на весь путь 4 ч 40 мин. В другой раз эта же лодка отошла от пристани С, дошла до А, сразу повернула назад и пришла в В, затратив на весь путь 7 ч. Чему равны собственная скорость лодки и скорость течения реки?
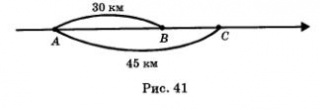
Решение.
Первый этап.
Составление математической модели. Введем две переменные: х км/ч - собственная скорость лодки, у км/ч - скорость течения реки. Тогда х + у км/ч - скорость движения лодки по течению реки, х-у км/ч - скорость движения лодки против течения реки. Рассмотрим первый рейс лодки. Он составил 45 км по течению и 15 км против течения. Имеем: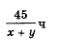 - время движения лодки от А до С (в первом рейсе),
- время движения лодки от А до С (в первом рейсе), 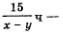 время движения лодки от С до В (в первом рейсе). Всего на первый рейс лодка затратила 4 ч 40 мин, т.е.
время движения лодки от С до В (в первом рейсе). Всего на первый рейс лодка затратила 4 ч 40 мин, т.е.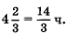
Таким образом, получаем уравнение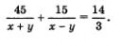 Рассмотрим второй рейс лодки. Он составил 45 км против течения и 30 км по течению. Имеем:
Рассмотрим второй рейс лодки. Он составил 45 км против течения и 30 км по течению. Имеем: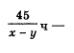 время движения лодки от С до А (во втором рейсе),
время движения лодки от С до А (во втором рейсе), 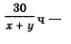 время движения лодки от А до В (во втором рейсе). Всего на второй рейс лодка затратила 7 ч. Таким образом, получаем уравнение
время движения лодки от А до В (во втором рейсе). Всего на второй рейс лодка затратила 7 ч. Таким образом, получаем уравнение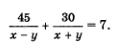
Математическая модель задачи представляет собой систему двух уравнений с двумя переменными: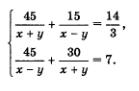
Второй этап.
Работа с составленной моделью. Для решения системы уравнений воспользуемся методом введения новых переменных. Положим: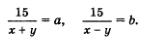 Тогда система примет вид
Тогда система примет вид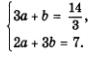
Решив эту систему двух линейных уравнений с двумя переменными а и Ь (сделайте это!), получим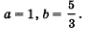
Итак,
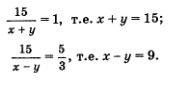
Остается решить совсем простую систему уравнений
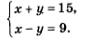
Получаем х = 12, у = 3.
Третий этап. Ответ на вопрос задачи.
Требуется определить скорость лодки в стоячей воде и скорость течения реки. Первую скорость мы обозначили буквой х, получили х = 12; значит, собственная скорость лодки составляет 12 км/ч. Скорость течения мы обозначили буквой у, получили у = 3. Значит, скорость течения реки составляет 3 км/ч.
Ответ: 12 км/ч; 3 км/ч.
Пример 3.
Мастер и его ученик планировали сообща выполнить некоторую работу за 6 дней. Сначала за дело взялся ученик. Выполнив 20% задания, он заболел. Остальная работа пришлась на долю мастера. В итоге выполнение задания растянулось на 11 дней. За сколько дней мог бы его выполнить мастер и за сколько дней ученик, действуя в одиночку, если известно, что и то и другое количество дней выражаются целыми числами?
Решение.
Первый этап.
Составление математической модели.
Если речь идет о выполнении некоторой работы, не охарактеризованной в количественном плане (т.е. не сказано, сколько деталей надо сделать, сколько кубометров земли вынуть и т.д.), то объем работы считают равным 1, а части работы выражают в долях единицы. Пусть х - число дней, необходимых мастеру, чтобы выполнить в одиночку всю работу, а у - число дней, необходимых ученику, чтобы справиться в одиночку со всей работой. Если объем всей работы (т.е. 1) разделить на число дней, то узнаем долю работы, выполняемую за 1 день.
Итак,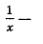 - доля работы, которую выполняет мастер за 1 день,
- доля работы, которую выполняет мастер за 1 день,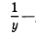 доля работы, которую выполняет ученик за 1 день.
доля работы, которую выполняет ученик за 1 день.
По условию, работая вместе, мастер и ученик могли бы выполнить всю работу за 6 дней. Доля работы мастера за 6 дней выражается формулой -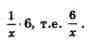 Доля работы ученика за 6 дней выражается формулой
Доля работы ученика за 6 дней выражается формулой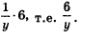 Поскольку вместе они выполнят всю работу (т.е. 1), составляем уравнение
Поскольку вместе они выполнят всю работу (т.е. 1), составляем уравнение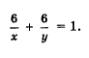
По условию, ученик выполнил, трудясь в одиночку до своей болезни, 20% задания, т.е.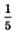 часть всей работы. Сколько времени он потратил? Естественно, что
часть всей работы. Сколько времени он потратил? Естественно, что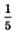 часть того времени, которое нужно ему на выполнение всей работы, т.е.
часть того времени, которое нужно ему на выполнение всей работы, т.е. 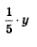 дней. Потом пришел мастер, сделал оставшуюся работу, т.е.
дней. Потом пришел мастер, сделал оставшуюся работу, т.е.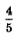 задания, на что затратил
задания, на что затратил 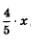 дней. По условию, выполнение задания растянулось на 11 дней, т.е.
дней. По условию, выполнение задания растянулось на 11 дней, т.е.
Таким образом, математическая модель задачи составлена - система двух уравнений с двумя переменными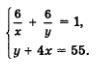
Второй этап.
Работа с составленной моделью. Воспользуемся методом подстановки. Выразим у через х из второго уравнения системы: у = 55-4x. Подставим выражение 55-4x вместо у в первое уравнение системы: Решая это рациональное уравнение, последовательно получаем:
Решая это рациональное уравнение, последовательно получаем:

Оба найденных значения удовлетворяют условию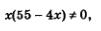 т.е. являются корнями рационального уравнения с переменной х. Осталось найти соответствующие значения у. Для этого воспользуемся уравнением y = 55 - 4x. Если х = 10, то из этого уравнения находим у = 15; если
т.е. являются корнями рационального уравнения с переменной х. Осталось найти соответствующие значения у. Для этого воспользуемся уравнением y = 55 - 4x. Если х = 10, то из этого уравнения находим у = 15; если то из того же уравнения находим у = 22. Итак, составленная система уравнений имеет два решения:
то из того же уравнения находим у = 22. Итак, составленная система уравнений имеет два решения:
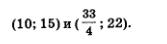
Третий этап.
Ответ на вопрос задачи.
По условию, количество дней, необходимых как мастеру, так и ученику для выполнения в одиночку всего задания, выражается целым числом. Значит, пара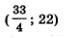 нас не устраивает. Остается лишь одна возможность: х = 10, у = 15.
нас не устраивает. Остается лишь одна возможность: х = 10, у = 15.
О т в е т: 10 дней; 15 дней.
Замечание.
Обратите внимание на то, что, решая системы уравнений, составленные в рассмотренных задачах, мы применили все методы, о которых шла речь в предыдущем параграфе: и подстановки, и алгебраического сложения, и введения новых переменных.


