- Преподавателю
- Математика
- Проект Замечательные точки треугольника
Проект Замечательные точки треугольника
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Сморчкова Е.Б. |
| Дата | 28.01.2015 |
| Формат | doc |
| Изображения | Есть |
Лискинский район, МОУ Аношкинская СОШ.
Учитель математики Сморчкова Е.Б.
Цель проекта: научиться пользоваться различной литературой по геометрии , справочными материалами для более подробного изучения темы «Замечательные точки треугольника», дать более полное представление о теме, подготовить презентацию по данной теме для демонстрации при выступлениях и на уроках.
Геометрия начинается с треугольника. Вот уже два с половиной тысячелетия треугольник является как бы символом геометрии; но он не только символ, треугольник - атом геометрии. Да и сегодня школьная геометрия становится интересной и содержательной, становится собственно геометрией только с появлением треугольника. Предшествующие понятия - точка, прямая, угол - представляются расплывчатыми абстракциями, а набор теорем и задач, с ними связанный, просто скучным.
Уже с первых шагов своего развития человек, а особенно современный человек, сталкивается со всевозможными геометрическими объектами - фигурами и телами. Известны случаи, когда человек в юном, если не сказать в младенческом, возрасте увлекается геометрией и даже делает самостоятельные геометрические открытия. Так, маленький Блез Паскаль придумал «игру в геометрию», в которой участвовали «монетки» - круги, «треуголки» - треугольники, «столы» - прямоугольники, «палочки» - отрезки. Его отец, основательно знавший математику, на первое время решительно исключил математику из числа предметов, которым он обучал своего сына, поскольку маленький Блез не отличался хорошим здоровьем. Однако, обнаружив увлеченность сына, он кое-что рассказал ему о таинственной геометрии, а застав Блеза в момент, когда тот обнаружил, что углы треугольника составляют в сумме два прямых, растроганный отец открыл своему 12-летнему сыну доступ к математическим книгам, хранившимся в домашней библиотеке.
Треугольник неисчерпаем - постоянно открываются его новые свойства. Чтобы рассказать о всех известных его свойствах, необходим том, сравнимый по объему с томом Большой энциклопедии. О некоторых из них, а точнее говоря, о некоторых замечательных точках, связанных с треугольником, мы и хотим рассказать.
Поясним сначала смысл выражения «замечательные точки треугольника». Все мы знаем, что биссектрисы внутренних углов треугольника пересекаются в одной точке - центре вписанной в этот треугольник окружности. Точно так же в одной точке пересекаются медианы, высоты треугольника, серединные перпендикуляры к его сторонам.
Получающиеся при пересечении перечисленных троек прямых точки, конечно же, замечательны (ведь три прямые, как правило, пересекаются в трех различных точках). Возможны и замечательные точки других типов, например точки, в которых достигает экстремума какая-либо функция, определенная для всех точек треугольника. С другой стороны, понятие «замечательные точки треугольника» следует толковать скорее на литературно-эмоциональном уровне, чем на формально-математическом. Известен софизм, «доказывающий», что все натуральные числа «интересные». (Допустив, что есть «неинтересные» числа, возьмем среди них наименьшее. Бесспорно, это число «интересное»: оно интересно уже тем, что оно наименьшее среди «неинтересных».) Подобное рассуждение, «доказывающее», что все точки треугольника «замечательны», можно сконструировать и в нашем случае. Перейдем к рассмотрению некоторых примеров.
ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ
Докажем, что существует точка, равноудаленная от вершин треугольника, или, иначе, что существует окружность, проходящая через три вершины треугольника. Геометрическим местом точек, равноудаленных от точек А и В, является перпендикуляр к отрезку АВ, проходящий через его середину (серединный перпендикуляр к отрезку АВ). Рассмотрим точку О, в которой пересекаются серединные перпендикуляры к отрезкам АВ и ВС. Точка О равноудалена от точек А и В, а также от точек В и С. Поэтому она равноудалена от точек А и С, т. е. она лежит и на серединном перпендикуляре к отрезку АС (рис. 50).
Центр О описанной окружности лежит внутри треугольника, только если этот треугольник остроугольный. Если же треугольник прямоугольный, то точка О совпадает с серединой гипотенузы,
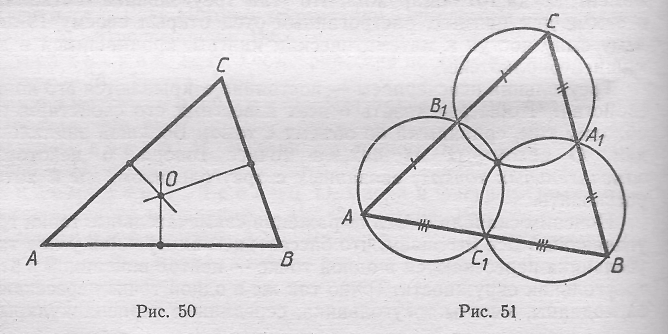
а если угол при вершине С тупой, то прямая АВ разделяет точки О и С.
Если в Δ АВС угол при вершине С острый, то сторона АВ видна из точки О под углом, равным 2<C; это следует из того, что <.AOB в два раза больше вписанного <ACB, опирающегося на ту же дугу. Если же <.C тупой, то сторона АВ видна из точки О под углом, равным 360° - 2<С. Воспользовавшись этим, легко доказать теорему синусов: AB=2Rsin С, где R- радиус описанной окружности Δ АВС. В самом деле, пусть С1 - середина стороны АВ. Тогда АС1 = АО sin <.AOC1=R sin С, поэтому AB=2AC1=2R sin С. Теорему синусов можно сформулировать и по-другому: «Проекция диаметра описанной окружности, перпендикулярного первой стороне треугольника, на прямую, содержащую вторую сторону, равна третьей стороне». Это столь громоздкое утверждение является на самом деле просто теоремой синусов.
В математике часто бывает так, что объекты, определенные совсем по-разному, оказываются совпадающими. Покажем это на примере.
Пусть А1, В1 и C1 - середины сторон ВС, С А и АВ. Можно доказать, что окружности, описанные около Δ АВ1С1, Δ A1BC1 и Δ A1B1C, пересекаются в одной точке, причем эта точка - центр описанной окружности Δ АВС (рис. 51). Итак, у нас есть две, казалось бы, совсем разные точки: точка пересечения серединных перпендикуляров к сторонам Δ АВС и точка пересечения описанных окружностей Δ АВ1С1, Δ AiBCi и Δ AiBiC. А оказывается, что эти две точки почему-то совпадают!
Проведем, однако, обещанное доказательство. Достаточно доказать, что центр О описанной окружности Δ АВС лежит на окружностях, описанных около ΔАВ1С1, Δ АiBCi и Δ A1B1C. Углы ОВ1А и ОС1А прямые, поэтому точки В1 и С1 лежат на окружности диаметром ОА, а значит, точка О лежит на окружности, описанной около Δ AB1C1. Для Δ AiBCi и Δ А1В1С доказательство аналогично.
Доказанное утверждение является частным случаем весьма интересной теоремы: если на сторонах АВ, ВС и СА треугольника АВС взяты произвольные точки С1, А1 и В1, то описанные окружности Δ АВ1С1, Δ А1ВС1 и Δ А1В1С пересекаются в одной точке.
Сделаем последнее замечание по поводу центра описанной окружности. Прямые А1В1 и АВ параллельны, поэтому ОС1 перпендикулярна А1В1 Аналогично ОВ1 перпендикулярна A1C1 и ОА1 перпендикулярна В1С1, т. е. О - точка пересечения высот треугольника A1B1С1 ... Постойте, постойте! Мы пока еще не доказывали, что высоты треугольника пересекаются в одной точке. Нет ли здесь пути к доказательству? К этому разговору мы еще вернемся.
ЦЕНТР ВПИСАННОЙ ОКРУЖНОСТИ
Докажем, что биссектрисы углов Δ АВС пересекаются в одной точке. Рассмотрим точку О пересечения биссектрис углов А и В. Любые точки биссектрисы угла A равноудалены от прямых АВ и АС, а любая точка биссектрисы угла B равноудалена от прямых АВ и ВС, поэтому точка О равноудалена от прямых АС и ВС, т. е. она лежит на биссектрисе угла C. Точка О равноудалена от прямых АВ, ВС и СА, значит, существует окружность с центром О, касающаяся этих прямых, причем точки касания лежат на самих сторонах, а не на их продолжениях. В самом деле, углы при вершинах А и В Δ АОВ острые, поэтому проекция точки О на прямую АВ лежит внутри отрезка АВ. Для сторон ВС и СА доказательство аналогично.
Пусть А1, В1 и С1 - точки касания вписанной окружности треугольника со сторонами ВС, СА и АВ (рис. 52). Тогда АВ1=АС1, BC1=BA1 и СА1 = СВ1. Кроме того, угол B1A1C1 равен углам при основании равнобедренного ΔАВ1С1 (по теореме об угле между касательной и хордой) и т. д. Для угла B1C1A1 и угла A1B1C1 доказательство аналогично.
Углы при основании любого равнобедренного треугольника острые, поэтому Δ А1В1С1 остроугольный для любого Δ АВС.
Если x=AB1, y=BC1 и z=CA1, то х+у = с, y+z=a и z+x=b, где а, b и с - длины сторон Δ АВС. Складывая первые два равенства и вычитая из них третье, получаем у= (а+с-в)/2. Аналогично х=(в+с-а)/2 и z=(а+в-с)/2. Следует отметить, что для четырехугольника подобные рассуждения не привели бы к желаемому результату, потому что соответствующая система уравнений
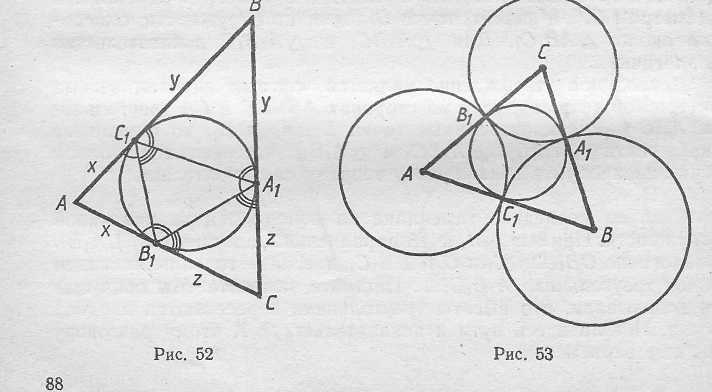
либо вообще не имеет решений, либо имеет их бесконечно много. В самом деле, если х+у=а, y+z=b, z+t = c и t+x = d, то у=а-х, z=b-y=b- а+х и t = c - b+a-х, а из равенства t+x=d следует, что a+c = b+d. Поэтому если а+с не равно в+ d, то система решений не имеет, а если a+c = b+d, то х можно выбирать произвольно, а у, z, t выражаются через х.
Вернемся снова к единственности решения системы уравнений для треугольника. Используя ее, можно доказать следующее утверждение: пусть окружности с центрами А, В и С касаются внешним образом в точках А1, В1 и С1 (рис. 53). Тогда описанная окружность Δ A1B1C1 вписана в Δ АВС. В самом деле, если х, у и z - радиусы окружностей; a, b и с - длины сторон ΔАВС, то х+у = с, y + z=a, y+x = b.
Докажем три свойства центра О вписанной окружности Δ ABC.
1. Если продолжение биссектрисы угла С пересекает описанную окружность Δ АВС в точке М, то МА=МВ=МО (рис. 54).
Докажем, например, что в Δ АМО равны углы при вершинах А и О. В самом деле, <OAM= <OAB+ <BAM и <AOM=<OAC+<АCO, <ОАВ=<ОАС и <ВАМ=<ВСМ = <ACO. Следовательно, АМ=МО. Аналогично ВМ=МО.
2. Если АВ - основание равнобедренного Δ АВС, то окружность, касающаяся сторон <ACB в точках А и В, проходит через точку О (рис. 55).
Пусть О' - середина (меньшей) дуги АВ рассматриваемой окружности. По свойству угла между касательной и хордой <CAO'= <О'ВА= <О'АВ, т. е. точка О' лежит на биссектрисе <A. Аналогично можно показать, что она лежит и на биссектрисе <B, т. е. О' = О.
3. Если прямая, проходящая через точку О параллельно стороне АВ, пересекает стороны ВС и СА в точках А1 и В1, то A1B1=A1B+AB1.
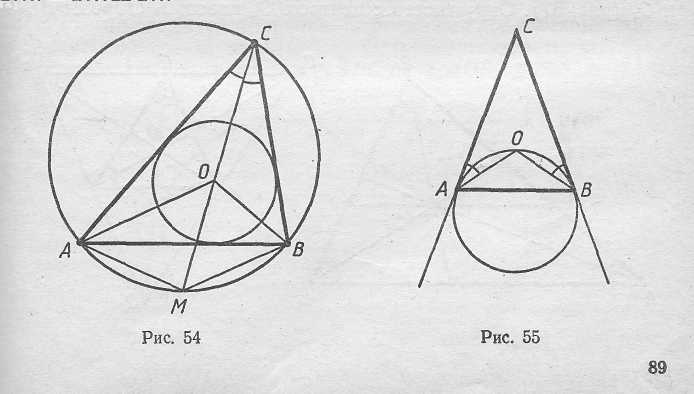
Докажем, что Δ AB1O равнобедренный. В самом деле, <B1OA= <OAB = <B1AO (рис. 56). Поэтому AB1=B10. Аналогично A1B=A1O, а значит, A1B1=A1О+OB1=A1B+AB1.
Пусть в Δ АВС углы при вершинах А, В и С равны α, β, γ. Вычислим величину угла, под которым сторона АВ видна из точки О. Так как углы Δ АО В при вершинах А и В равны α/2 и β/2, то
<AOB = 180°- (α+β)/2=180°- (180°- γ)/2=90° +γ/2. Эта
формула бывает полезна при решении многих задач.
Выясним, например, в каком случае четырехугольник, образованный сторонами АС и ВС и биссектрисами АА1 и ВВ1, является вписанным. Четырехугольник OA1CB1 вписанный тогда и только тогда, когда <A1CB1+ <A1OB1 = 180° , т. е.
γ+(90° +γ/2) =180°, а значит, γ = 60°. В этом случае хорды OA1
и ОВ1 описанной окружности четырехугольника ОА1СВ1 равны, так как на них опираются равные углы OCA1 и ОСВ1.
Вписанная окружность Δ АВС касается его сторон во внутренних точках. Выясним, какие вообще бывают окружности, касающиеся трех прямых АВ, ВС и СА. Центр окружности, касающейся двух пересекающихся прямых, лежит на одной из двух прямых, делящих пополам углы между исходными прямыми. Поэтому центры окружностей, касающихся прямых АВ, ВС и С А, лежат на биссектрисах внешних или внутренних углов треугольника (или же их продолжениях). Через точку пересечения любых двух биссектрис внешних углов проходит биссектриса внутреннего угла. Доказательство этого утверждения дословно повторяет доказательство соответствующего утверждения для биссектрис внутренних углов. В итоге получаем 4 окружности с центрами О, Оа, Оь и Ос (рис. 57). Окружность с центром Оа касается стороны ВС и
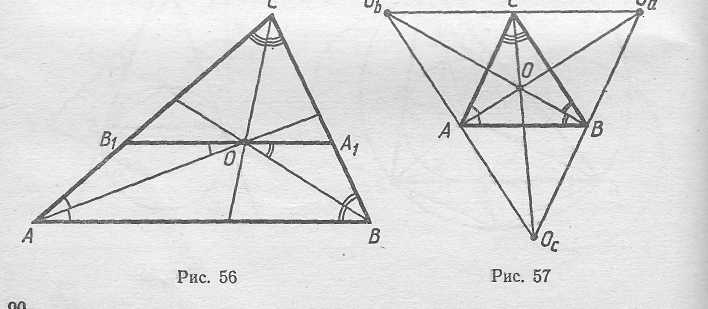
продолжений сторон АВ и АС; эта окружность называется вневписанной окружностью Δ АВС. Радиус вписанной окружности треугольника обычно обозначается через г, а радиусы вневписанных окружностей - через г а, г ь и г с. Между радиусами вписанной и вневписанной окружностей имеют место следующие соотношения:
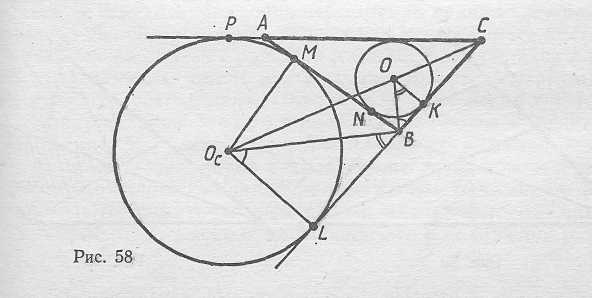
г / гс =(р-с)/р и г г с=(р - а) (р -в), где р - полупериметр Δ АВС. Докажем это. Пусть К и L - точки касания вписанной и вневписанной окружностей с прямой ВС (рис. 58). Прямоугольные треугольники СОК и COcL подобны, поэтому
г/ гс=ОК/ОсL =CK/CL.. Ранее было доказано, что СК = (а+в-с)/2=р-с.
Остается проверить, что CL=p.
Пусть М и Р - точки касания вневписанной окружности с прямыми АВ и АС. Тогда
CL= (CL+CP)/ 2 = (CB+BL+CA+AP )/2 = ( CB+BM + CA+AM)/2 = р
Для доказательства соотношения rrc=(p-a)(p-b) рассмотрим прямоугольные треугольники LOCB и КВО, которые подобны, так как
<OBK+< OCBL =(<СВА + <АВL)/2=90°.
Значит, LОс/ВL=BK/KO, т. е. rrc = KO·LOc = BK·BL. Остается заметить, что ВК=(a+c-b)/2=p-b и BL = CL-CB=p-a.
Отметим еще одно интересное свойство (попутно уже фактически доказанное). Пусть вписанная и вневписанная окружности касаются стороны АВ в точках N и М (рис. 58). Тогда AM = BN. В самом деле, BN=p - b и АМ=АР=СР-АС=р - в.
Соотношения rrc=(p - а)(p-в) и rр=rс (р-с) можно использовать для вывода формулы Герона S2=p(p - a)(p - b)(p - c), где S - площадь треугольника. Перемножая эти соотношения, получаем r2p=(p - a)(p - b)(p - c). Остается проверить, что S=pr. Это легко сделать, разрезав ΔАВС на ΔАОВ, ΔВОС и ΔСОА.
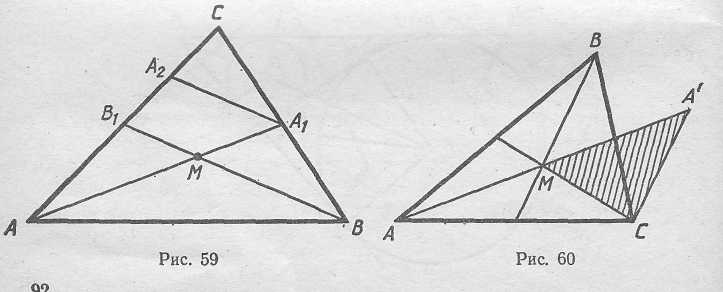
ТОЧКА ПЕРЕСЕЧЕНИЯ МЕДИАН
Докажем, что медианы треугольника пересекаются в одной точке. Рассмотрим для этого точку М, в которой пересекаются медианы АА1 и ВВ1. Проведем в ΔВВ1С среднюю линию A1A2, параллельную ВВ1 (рис. 59). Тогда A1M:AM=B1A2: AB1=B1A2:B1C=BA1:ВС=1:2, т. е. точка пересечения медиан ВВ1 и АА1 делит медиану АА1 в отношении 1:2. Аналогично точка пересечения медиан СС1 и АА1 делит медиану АА1 в отношении 1:2. Следовательно, точка пересечения медиан АА1 и ВВ1 совпадает с точкой пересечения медиан АА1 и СС1.
Если точку пересечения медиан треугольника соединить с вершинами, то треугольник разобьется на три треугольника равной площади. В самом деле, достаточно доказать, что если Р - любая точка медианы АА1 в АВС, то площади ΔАВР и ΔАСР равны. Ведь медианы АА1 и РА1 в Δ АВС и ΔРВС разрезают их на треугольники равной площади.
Справедливо также и обратное утверждение: если для некоторой точки Р, лежащей внутри Δ АВС, площади ΔАВР, ΔВСР и ΔСАР равны, то Р - точка пересечения медиан. В самом деле, из равенства площадей ΔАВР и ΔВСР следует, что расстояния от точек А и С до прямой ВР равны, а значит, ВР проходит через середину отрезка АС. Для АР и СР доказательство аналогично.
Равенство площадей треугольников, на которые медианы разбивают треугольник, позволяет следующим образом найти отношение площади s треугольника, составленного из медиан ΔАВС, к площади S самого ΔАВС. Пусть М - точка пересечения медиан ΔАВС; точка А' симметрична А относительно точки М (рис. 60)
С одной стороны, площадь ΔА'МС равна S/3. С другой стороны, этот треугольник составлен из отрезков, длина каждого из которых равна 2/3 длины соответствующей медианы, поэтому его площадь
равна (2/3)2s = 4s/9. Следовательно, s=3S/4.
Весьма важным свойством точки пересечения медиан является то, что сумма трех векторов, идущих из нее в вершины треугольника, равна нулю. Заметим сначала, что АМ=1/3(АВ+АС) , где М - точка пересечения медиан Δ ABC. В самом деле, если
ABA'С - параллелограмм, то АА'=АВ+АС и АМ=1/3АА'. Поэтому МА+МВ+МС=1/3(ВА+СА+АВ + СВ + АС + ВС) = 0.
Ясно также, что этим свойством обладает только точка пересечения медиан, так как если X - любая другая точка, то
ХА+ХВ+ХС=(ХМ+МА)+(ХМ+МВ)+(ХМ+МС)=3ХМ..
Воспользовавшись этим свойством точки пересечения медиан треугольника, можно доказать следующее утверждение: точка пересечения медиан треугольника с вершинами в серединах сторон АВ, CD и EF шестиугольника ABCDEF совпадает с точкой пересечения медиан треугольника с вершинами в серединах сторон ВС, DE и FA. В самом деле, воспользовавшись тем, что если, например, Р - середина отрезка АВ, то для любой точки X справедливо равенство ХА+ ХВ=2ХР, легко доказать, что точки пересечения медиан обоих рассматриваемых треугольников обладают тем свойством, что сумма векторов, идущих из них в вершины шестиугольника, равна нулю. Следовательно, эти точки совпадают.
Точка пересечения медиан обладает одним свойством, резко выделяющим ее на фоне остальных замечательных точек треугольника: если ΔА'В'С' является проекцией ΔАВС на плоскость, то точка пересечения медиан Δ А 'В'С' является проекцией точки пересечения медиан ΔАВС на ту же плоскость. Это легко следует из того, что при проектировании середина отрезка переходит в середину его проекции, а значит, медиана треугольника переходит в медиану его проекции. Ни биссектриса, ни высота таким свойством не обладают.
Нельзя не отметить, что точка пересечения медиан треугольника является его центром масс, причем как центром масс системы трех материальных точек с равными массами, находящихся в вершинах треугольника, так и центром масс пластинки, имеющей форму данного треугольника. Положением равновесия треугольника, шарнирно закрепленного в произвольной точке X, будет такое положение, при котором луч ХМ направлен к центру Земли. Для треугольника, шарнирно закрепленного в точке пересечения медиан, любое положение является положением равновесия. Кроме того, треугольник, точка пересечения медиан которого опирается на острие иглы, также будет находиться в положении равновесия.
ТОЧКА ПЕРЕСЕЧЕНИЯ ВЫСОТ
Чтобы доказать, что высоты ΔАВС пересекаются в одной точке, вспомним путь доказательства, наметившийся в конце раздела «Центр описанной окружности». Проведем через вершины А, В и С прямые, параллельные противоположным сторонам; эти прямые образуют ΔА1В1С1 (рис. 61). Высоты ΔАВС являются серединными перпендикулярами к сторонам ΔA1B1C1. Следовательно, они пересекаются в одной точке - центре описанной окружности ΔA1B1C1. Точка пересечения высот треугольника называется иногда его ортоцентром.
-
Легко проверить, что если Н - точка пересечения высот ΔАВС, то А, В и С - точки пересечения высот ΔВНС, ΔСНА и Δ АНВ соответственно.
Ясно также, что <ABC+ <AHC= 180°, потому что <BA1H= <BC1H=90° (A1 и C1 - основания высот). Если точка H1 симметрична точке Н относительно прямой АС, то четырехугольник АВСН1 вписанный. Следовательно, радиусы описанных окружностей Δ АВС и Δ АН С равны и эти окружности симметричны относительно стороны АС (рис. 62). Теперь легко доказать, что
АН=а |ctgА|, где а=ВС. В самом деле,
AH=2R sin <ACH=2R |cos A| =a |ctg А| .
Предположим для простоты, что ΔАВС остроугольный и рассмотрим ΔA1B1C1, образованный основаниями его высот. Оказывается, что центром вписанной окружности ΔA1B1C1 является точка пересечения высот ΔАВС, а центры вневписанных окружностей
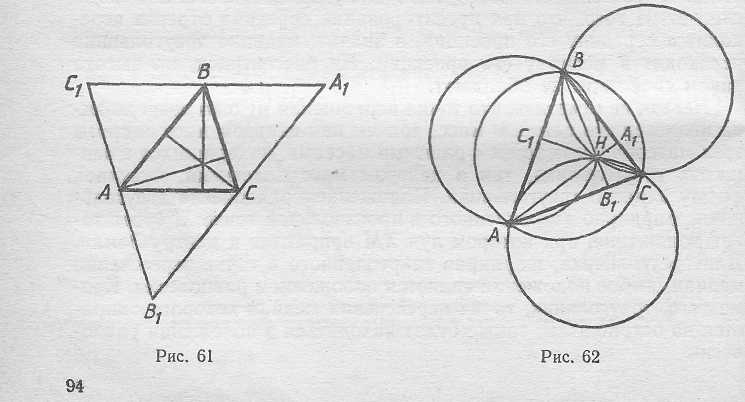
ΔA1B1C1 являются вершинами Δ АВС (рис. 63). Точки А1 и В1 лежат на окружности с диаметром СН (так как углы НВ1С и НА1С прямые), поэтому <HA1B1 = <HCB1. Аналогично <HA1C1 = <HBC1. А так как <HCB1 = =<HBC1 то А1А - биссектриса <В1А1С1.
Пусть Н - точка пересечения высот АА1, ВВ1 и CC1 треугольника ABC. Точки A1 и В1 лежат на окружности с диаметром АВ, поэтому AH·A1H=BH·B1H . Аналогично ВН • B1H=СН ·С1Н.
Для остроугольного треугольника справедливо также обратное утверждение: если точки А1, B1 и C1 лежат на сторонах ВС, СА и АВ остроугольного Δ АВС и отрезки АА1, ВВ1 и СС1 пересекаются в точке Р, причем АР·А1Р=ВР·В1Р=СР·С1Р, то Р - точка пересечения высот. В самом деле, из равенства
AP·A1P=BP·B1P
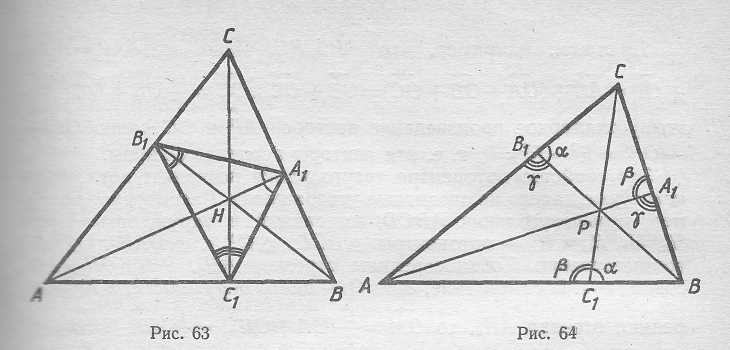
следует, что точки А, В, А1 и В1 лежат на одной окружности с диаметром АВ, а значит, <AB1B= <BA1A=γ. Аналогично <ACiC=<CAiA = β и <СВ1В= <ВС1С= α (рис. 64). Ясно также, что α + β= <BC1C+ <CC1A = l80°, β+γ=180° и γ + α = 180°. Следовательно, α = β=γ=90°.
Точку пересечения высот треугольника можно определить еще ж другим весьма интересным способом, но для этого нам потребуются понятия вектора и скалярного произведения векторов.
Пусть О - центр описанной окружности Δ АВС. Сумма векторов О А + OB + ОС является некоторым вектором, поэтому существует такая точка Р, что ОР = ОА + ОВ+ОС. Оказывается, что Р - точка пересечения высот ΔАВС !
Докажем, например, что AP перпендикулярно BC. Ясно, что АР=АО+
+ор=ао+(оа+ов+ос)=ов+ос и вс= -ов+ос. Поэтому скалярное произведение векторов АР и ВС равно ОС2 - OB2=R2 -R2=0, т. е. эти векторы перпендикулярны.
Это свойство ортоцентра треугольника позволяет, доказывать некоторые далеко не очевидные утверждения. Рассмотрим, например, четырехугольник ABCD, вписанный в окружность. Пусть На, Нв, Нс и Hd - ортоцентры Δ BCD, ΔCDA, Δ DAB и Δ ABC соответственно. Тогда середины отрезков АНа, ВНь, СНС, DH d совпадают. В самом деле, если О - центр окружности, а М - середина отрезка АНа, то ОМ=1/2(0А + ОНа)= =1/2(ОА + ОВ+ОС+ОD). Для середин трех других отрезков получаем точно такие же выражения.
ПРЯМАЯ ЭЙЛЕРА
Самым удивительным свойством замечательных точек треугольника является то, что некоторые из них связаны друг с другом определенными соотношениями. Например, точка пересечения медиан М, точка пересечения высот Н и центр описанной окружности О лежат на одной прямой, причем точка М делит отрезок ОН так, что справедливо соотношение ОМ:МН= 1:2. Эта теорема была доказана в 1765 г. Леонардом Эйлером, который своей неутомимой деятельностью значительно развил многие области математики и заложил основы многих новых ее разделов. Он родился в 1707 г. в Швейцарии. В 20 лет Эйлер по рекомендации братьев Бернулли получил приглашение приехать в Санкт-Петербург, где незадолго перед этим была организована академия. В конце 1740 г. в России в связи с приходом к власти Анны Леопольдовны сложилась тревожная обстановка, и Эйлер переехал в Берлин. Через 25 лет он снова вернулся в Россию, в общей сложности в Петербурге Эйлер прожил более 30 лет. Находясь в Берлине, Эйлер поддерживал тесную связь с русской академией и был ее почетным членом. Из Берлина Эйлер переписывался с Ломоносовым. Их переписка завязалась следующим образом. В 1747 г. Ломоносова избрали в профессоры, т. е. в действительные члены академии; императрица это избрание утвердила. После этого реакционный чиновник академии Шумахер, яро ненавидящий Ломоносова, послал его работы Эйлеру, надеясь получить о них плохой отзыв. (Эйлер был старше Ломоносова всего на 4 года, но его научный авторитет был к тому времени уже очень высок.) В своем отзыве Эйлер писал: «Все сии сочинения не токмо хороши, но и превосходны, ибо он изъясняет физические и химические материи самые нужные и трудные, кои совсем неизвестны и невозможны были к истолкованию самым остроумным и ученым людям, с таким основательством, что я совсем уверен о точности его доказательств... Желать надобно, чтобы все прочие академии были в состоянии показать такие изобретения, которые показал господин Ломоносов».
Перейдем к доказательству теоремы Эйлера. Рассмотрим ΔA1B1C1 с вершинами в 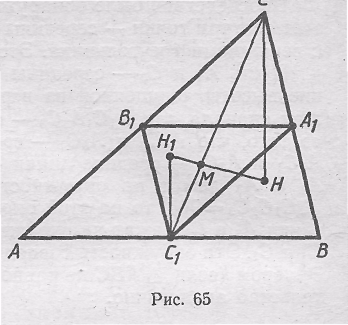 серединах сторон Δ АВС; пусть H1и Н - их ортоцентры (рис. 65). Точка Н1 совпадает с центром О описанной окружности ΔАВС. Докажем, что ΔC1H1M=ΔCHM. В самом деле, по свойству точки пересечения медиан С1М:СМ= 1:2, коэффициент подобия ΔA1B1C1 и ΔАВС равен 2, поэтому C1H1:CH=1:2, кроме того, <H1C1M=<НСМ (C1H1||CH). Следовательно, < C1MH1 = < СМН, а значит, точка М лежит на отрезке H1H. Кроме того, H1M:MH=1:2, так как коэффициент подобия ΔC1H1M и ΔСНМ равен 2.
серединах сторон Δ АВС; пусть H1и Н - их ортоцентры (рис. 65). Точка Н1 совпадает с центром О описанной окружности ΔАВС. Докажем, что ΔC1H1M=ΔCHM. В самом деле, по свойству точки пересечения медиан С1М:СМ= 1:2, коэффициент подобия ΔA1B1C1 и ΔАВС равен 2, поэтому C1H1:CH=1:2, кроме того, <H1C1M=<НСМ (C1H1||CH). Следовательно, < C1MH1 = < СМН, а значит, точка М лежит на отрезке H1H. Кроме того, H1M:MH=1:2, так как коэффициент подобия ΔC1H1M и ΔСНМ равен 2.
ОКРУЖНОСТЬ ДЕВЯТИ ТОЧЕК
В 1765 г. Эйлер обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности. Докажем и мы это свойство треугольника.
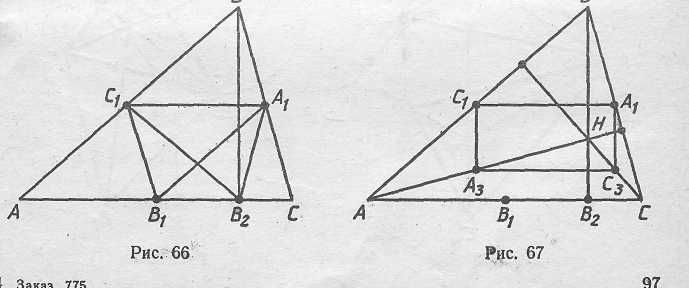
Пусть В2 - основание высоты, опущенной из вершины В на
сторону АС. Точки В и В2 симметричны относительно прямой А1С1
(рис. 66). Следовательно, ΔА1В2С1 = ΔA1BCt = ΔA1B1C1, поэтому <A1B2C1 = <А1В1С1, а значит, точка В2 лежит на описанной
окружности ΔА1В1С1. Для остальных оснований высот доказательство аналогично. "
Впоследствии было обнаружено, что на той же окружности лежат еще три точки - середины отрезков, соединяющих ортоцентр с вершинами треугольника. Это и есть окружность девяти точек.
Пусть Аз и Сз - середины отрезков АН и СН, С2 - основание высоты, опущенной из вершины С на АВ (рис. 67). Докажем сначала, что A1C1A3C3 - прямоугольник. Это легко следует из того, что А1Сз и A3C1 - средние линии ΔВСН и ΔАВН, а A1C1 и А3Сз - средние линии ΔАВС и ΔАСН. Поэтому точки А1 и Аз лежат на окружности с диаметром С1Сз, а так как <C1C2C3=90°, то на этой окружности лежит и точка С2. Итак, точки Аз и Сз лежат на окружности, проходящей через точки А1, C1 и С2. Эта окружность совпадает с окружностью, рассмотренной Эйлером (если Δ АВС не равнобедренный). Для точки Вз доказательство аналогично.
ТОЧКА ТОРРИЧЕЛЛИ
Внутри произвольного четырехугольника ABCD легко найти точку, сумма расстояний от которой до вершин имеет наименьшее значение. Такой точкой является точка О пересечения его диагоналей. В самом деле, если X - любая другая точка, то АХ+ХС≥АС=АО+ОС и BX+XD≥BD=BO + OD, причем хотя бы одно из неравенств строгое. Для треугольника аналогичная задача решается сложнее, к ее решению мы сейчас перейдем. Для простоты разберем случай остроугольного треугольника.
Пусть М - некоторая точка внутри остроугольного Δ АВС. Повернем Δ АВС вместе с точкой М на 60° вокруг точки А (рис. 68). (Точнее говоря, пусть В',С и М' - образы точек В, С и М при повороте на 60° вокруг точки А.) Тогда АМ+ВМ+СМ=ММ'+BM+C' M', АМ=ММ', так как ΔАММ'- равнобедренный (АМ=АМ') и <МАМ' = 60°. Правая часть равенства - это длина ломаной ВММ'С'; она будет наименьшей, когда эта ломаная
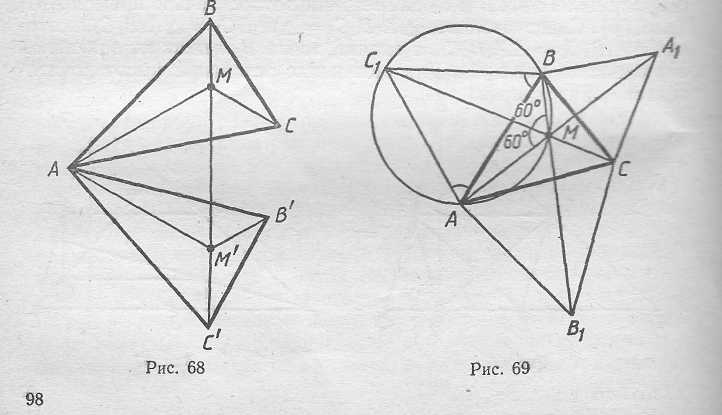
совпадает с отрезком ВС'. В этом случае <.AMB = 180° - <АММ' = 120° и <АМС = <AM'C - 180°- <AM'M = 120°, т. е. стороны АВ, ВС и СА видны из точки М под углом 120°. Такая точка М называется точкой Торричелли треугольника ABC.
Докажем, впрочем, что внутри остроугольного треугольника всегда существует точка М, из которой каждая сторона видна под утлом 120°. Построим на стороне АВ треугольника ABC внешним образом правильный ΔАВС1 (рис. 69). Пусть М -точка пересечения описанной окружности ΔАВС1 и прямой СС1. Тогда <AMC1 = <ABC1=60° и <BMC1 =<BAC1=60°. Поэтому стороны Δ АВС видны из точки М под углом 120°. Продолжая эти рассуждения немножко дальше, можно получить еще одно определение точки Торричелли. Построим правильные треугольники А1ВС и АВ1С еще и на сторонах ВС и АС. Докажем, что точка М лежит также и на прямой АА1. В самом деле, точка М лежит на описанной окружности ΔA1BC, поэтому <A1MB= <A1CB = 60°, а значит, <А1МВ+ <.BMA= 180°. Аналогично точка М лежит и на прямой ВВ1 (рис. 69).
Внутри ΔАВС существует единственная точка М, из которой его стороны видны под углом 120°, потому что описанные окружности ΔABC1, ΔABiC и ΔА1ВС не могут иметь более одной общей точки.
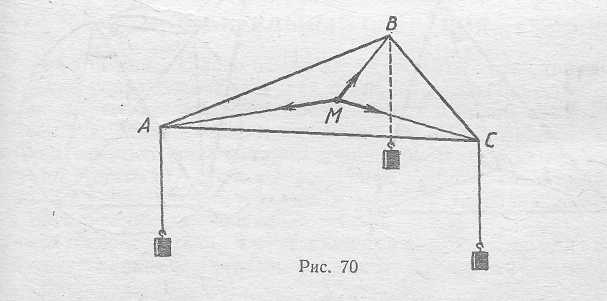
Приведем теперь физическую (механическую) интерпретацию точки Торричелли. Закрепим в вершинах ΔАВС колечки, пропустим сквозь них три веревки, одни концы которых связаны, а к другим концам прикреплены грузы равной массы (рис. 70). Если х = МА, у = МВ, z=MC и а - длина каждой нити, то потенциальная энергия рассматриваемой системы равна mg(x-а)+ mg (y - a)+mg (z--а). В положении равновесия потенциальная энергия имеет наименьшее значение, поэтому сумма х+у+z тоже имеет наименьшее значение. С другой стороны, в положении равновесия равнодействующая сил в точке М равна нулю. Силы эти по абсолютной величине равны, поэтому попарные углы между векторами сил равны 120°.
Остается рассказать, как обстоят дела в случае тупоугольного треугольника. Если тупой угол меньше 120°, то все предыдущие рассуждения остаются в силе. А если тупой угол больше или равен 120°, то сумма расстояний от точки треугольника до его вершин будет наименьшей, когда эта точка - вершина тупого угла.
ТОЧКИ БРОКАРА
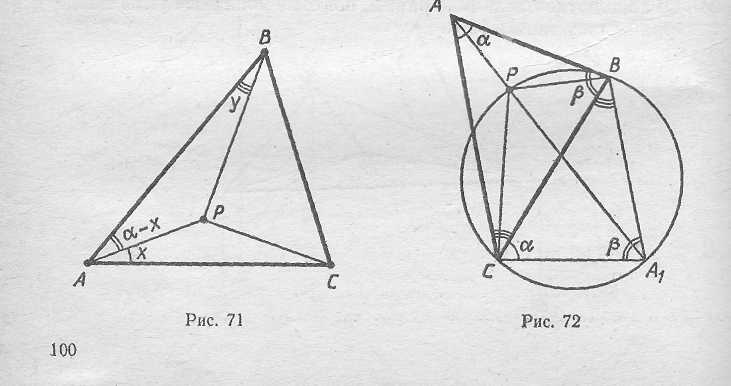
Точками Брокара Δ АВС называются такие его внутренние точки Р и Q, что <ABP= <.BCP=<CAP и <.QAB = <.QBC = < QCA (для равностороннего треугольника точки Брокара сливаются в одну точку). Докажем, что внутри любого ΔАВС существует точка Р, обладающая требуемым свойством (для точки Q доказательство аналогично). Предварительно сформулируем определение точки Брокара в другом виде. Обозначим величины углов так, как показано на рисунке 71. Поскольку <АРВ=180° - а+х-у, равенство х=у эквивалентно равенству <APB=180°-<.A. Следовательно, Р - точка Δ АВС ,из которой стороны АВ,
ВС и СА видны под углами 180°-<.A, 180°- <B, 180°-<С.
Такую точку можно построить следующим образом. Построим на
стороне ВС треугольника АВС подобный ему треугольник СА1В
так, как показано на рисунке 72. Докажем, что точка Р пересечения прямой АА1 и описанной окружности ΔА1ВС искомая. В самом деле, <BPC=18O° - β и <APB= 180°- <AtPB= 180° -<A1CB = l80° - а. Построим далее аналогичным образом подобные треугольники на сторонах АС и АВ (рис. 73). Так как <.APB =180° - а, точка Р лежит также и на описанной окружности ΔАВС1 Следовательно, <BPC1 = <BAC1 = β, а значит, точка
Р лежит на отрезке СС1. Аналогично она лежит и на отрезке ВВ1,
т. е. Р - точка пересечения отрезков АА1, ВВ1 и СС1.
Точка Брокара Р обладает следующим интересным свойством. Пусть прямые АР, ВР и СР пересекают описанную окружность ΔАВС
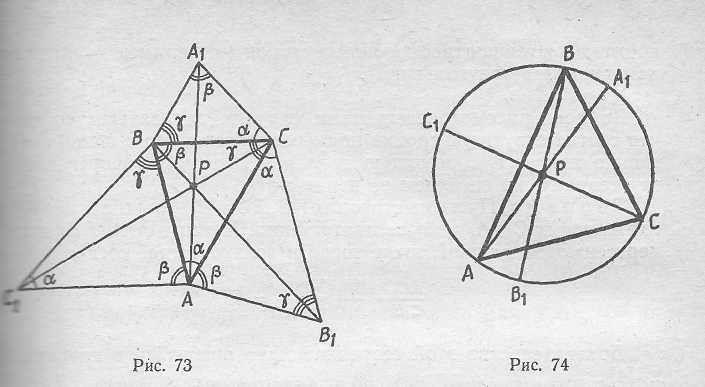
в точках А1, В1 и C1 (рис. 74). Тогда ΔАВС = ΔB1С1A1.В самом деле, <.A1B1C1 = <A1B1B+ <BB1C1 = <A1AB+<ВCC1 = <A1AB+ +<A1AC=<.ВАС, по свойству точки Брокарa ΔАВС углы BCC1 и А1АС равны, а значит, A1C1=BC. Равенство остальных сторон ΔАВС и ΔВ1С1А1 проверяется аналогично.
Во всех рассмотренных нами случаях доказательство того, что соответствующие тройки прямых пересекаются в одной точке, можно провести с помощью теоремы Чевы. Мы сформулируем эту теорему.
Теорема. Пусть на сторонах АВ, ВС и С А треугольника ABC взяты точки С1, А1 и В1 соответственно. Прямые АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда
АС1/С1В·ВА1/А1С·СВ1/ В1А = 1.
Доказательство теоремы приведено в учебнике геометрии 7-9 класс Л.С.Атанасяна на с.300.
Литература.
1.Атанасян Л.С. Геометрия 7-9.- М.:Просвещение, 2000г.
2.Киселев А.П. Элементарная геометрия.- М.:Просвещение, 1980г.
3.Никольская И.Л. Факультативный курс по математике. М.:Просвещение, 1991г.
4. Энциклопедический словарь юного математика.. Сост. А.П.Савин.-.М.:Педагогика, 1989.


