- Преподавателю
- Математика
- Статья «Математический софизм»
Статья «Математический софизм»
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Яковлева М.В. |
| Дата | 01.09.2013 |
| Формат | doc |
| Изображения | Есть |
Математический софизм.
Можно рассмотреть с учащимися факты, которые на первый взгляд кажутся загадочными и необъяснимыми.
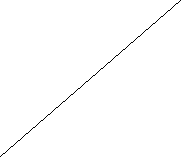
При решении задач о площадях многоугольников прошу построить прямоугольник со сторонами 11см и 13см, провести диагональ и сдвинуть полученные треугольники в положение 2
V S U U

P


Т
Q R X

Рис.1 Рис.2 R
Фигура на втором рисунке на первый взгляд состоит из квадрата VSXR со стороной 12 см и площадью 144см2, и двух треугольников PQR и SUT, площадью 0,5см2 каждый. Следовательно площадь всей фигуры равна 12х12+2 х0,5= 145см2. Но как это получилось, если площадь исходного прямоугольника равна 13х11=143см2?
При более подробном рассмотрении того, как диагональ пересекает клетки прямоугольника заметим, что VRXS не является квадратом. В геометрии «по виду» фигуры не всегда ее можно правильно определить, что подтверждается вычислениями.
При решении задач на применение признаков подобия треугольников проблемная ситуация создается с помощью софизма следующим образом.
Обращаю внимание учащихся на чертежи, заранее подготовленный на плакате и даю пояснение к нему.
I III
13
II 8 IV
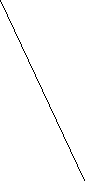
 В 8 13 С В 13 М 21 С
В 8 13 С В 13 М 21 С
1
I
III F
Е
II IV

8



13
А Д
А Д N
Рис.3 Рис.4
Квадрат разрезали на два равных прямоугольных треугольники (части I и II) и две равных прямоугольных трапеции (части III и IV). Из полученных частей (рис 3) составили четырехугольник (рис 4).
Сравнить площадь квадрата с площадью полученного четырехугольника.
Вычислив площадь каждой фигуры, учащиеся обнаруживают противоречие: площадь квадрата равна 441 кв.ед, а площадь прямоугольника равна 442 кв.ед. В связи с этим обстоятельством возникает проблема, которую формулируют учащиеся, -объяснить полученный результат.
Приступаем к решению проблемы. Видимо, четырехугольник, полученный из частей квадрата, не является прямоугольником. Выясним это.
В этом четырехугольнике (рис 4) противоположные стороны попарно равны (АВ1 = СД = 13, ВС = АД = 34) Значит, четырехугольник АВСД является параллелограммом, поэтому < А = <С, < В = < Д т.к. <В= < Д= 90°, то по свойству параллелограмма все остальные углы четырехугольника являются прямыми. Следовательно, рассматриваемый четырехугольник действительно прямоугольник и его площадь равна 13 х (13+21) = 442 (кв.ед.)
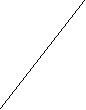
После неудачных попыток решения проблемы предлагаю учащимся начертить в тетрадях квадрат, имеющий площадь 441 кв.ед. и провести аналогичное превращение, взяв другие размеры частей I ,II, III, IV, например, как на рис.5.
I II
15
II IV
6
I
Е
III
F
IV
II

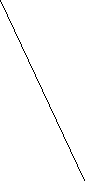

 В 6 15 С В 15 М 21 С С
В 6 15 С В 15 М 21 С С
 6
6



15
А
А Д Д
Рис.5 Рис.6
Рассматривая полученный чертеж, учащиеся замечают, что части I,II,III,IV не покрывают полностью прямоугольник, а составляют «просвет» в форме параллелограмма. «Просвет» в форме параллелограмма может иметь такую малую площадь, что ее можно не заметит глазом. Если это так, то отрезки АЕ и ЕС, АF и FС образуют излом. Предположим противное, пусть АВС - треугольник, тогда ∆ АВС ≈ ΔМЕС и МЕ/АВ=МС/ВС, но МЕ/АВ=8/13= 0,617…, что противоречит предположению, значит, АВСЕ четырехугольник и <АЕМ + <МЕС не равно 180%
Противоречие 441=442 объясняется так: рассуждая, что из частей I,II,III,IV квадрата может быть получен прямоугольник (рис 4), мы доверяемся кажущейся наглядности.
Боковая сторона трапеции III и гипотенуза треугольника I не лежат на одной прямой, а дают «излом» в общей точке этих отрезков. Площадь фигуры АВСД действительно равна 442 кв.ед., но в ней есть «щель» - параллелограмм АЕСF, площадь которого равна 1 кв.ед.


