- Преподавателю
- Математика
- Статья по методике преподавания математики на тему: Развитие математической речи учащихся 5-6 классов
Статья по методике преподавания математики на тему: Развитие математической речи учащихся 5-6 классов
| Раздел | Математика |
| Класс | 5 класс |
| Тип | Статьи |
| Автор | Баранова И.М. |
| Дата | 01.03.2016 |
| Формат | doc |
| Изображения | Есть |
Методическая статья
Тема: «Развитие математической речи учащихся 5-6 классов (на
примере обучения темам, связанным с понятием числа)»
Автор: Баранова Ирина Михайловна,
учитель математики ГБОУ СОШ №448 Фрунзенского района
Санкт-Петербург
2016
Оглавление
Введение ...........................................................................................................с. 2
§1. Понимание и мышление ...............................................................…........с. 3
§2. Мышление и речь ......................................................................................с. 11
§3. Математическое мышление и математическая речь ..............................с. 13
§4. Особенности математического мышления и уровень
развития математической речи учащихся 5-6 классов ............................с. 23
§5. Методика обучения учащихся 5-6 классов темам, связанным
с понятием числа, направленная на развитие их математической речи …с.28
Заключение ........................................................................................................с. 48
Приложения .......................................................................................................с. 49
Список литературы ...........................................................................................с. 68
Введение
При обучении математике учащихся 5-9 классов , беседе с коллегами возникла серьезная проблема: недостаточное развитие математической речи учащихся, невладение синтаксисом и семантикой математического языка негативно отражается, в первую очередь, на понимании материала, а, следовательно, на математической подготовке школьников и, в конечном итоге, на общем уровне развития учащихся. С этой проблемой и связан выбор темы методической разработки "Развитие математической речи учащихся 5-6 классов".
В работе сделана попытка частично решить данную проблему. Начинать целенаправленную систематическую работу по развитию математической речи учащихся желательно как можно раньше, поэтому предложенная методика рассчитана на учащихся 5-6 классов.
Одними из самых важных для успешного обучения умений учащихся являются умение читать числовые и буквенные выражения, умение грамотно использовать математические термины и знаки, умение обосновывать свои действия и умение осуществлять перевод информации с одного языка на другой (например, с естественного на математический, и обратно). Все эти умения естественно начинать формировать уже в 5-6 классах, что снимет многие проблемы обучения в старших классах. К тому же материал 5-6 классов способствует этому. В указанных классах основное внимание направлено на развитие понятия числа, приобретение соответствующих знаний и умений (вычисление значения числового выражения, преобразование алгебраических выражений, решение уравнений и решение текстовых задач). Курс алгебры 7-9 классов как раз и строится на этом важнейшем математическом понятии - понятии числа. На этом основан выбор содержания, а именно, рассматриваются темы курса математики 5-6 классов, связанные с понятием числа.
В связи со всем выше сказанным поставлены следующие цель и задачи разработки.
Цель:
Разработать методику обучения учащихся 5-6 классов темам, связанным с понятием числа, направленную на развитие их математической речи и основанную на понимании учащимися материала.
Задачи:
1. Анализ психолого-педагогической литературы, посвященной пониманию,
математическому мышлению и математической речи учащихся.
2. Разработать методику обучения учащихся 5-6 классов темам, связанным с понятием числа, направленную на развитие их математической речи.
3. Провести опытную проверку разработанной методики.
4. Сделать выводы.
Анализ литературы по теме [5,10,19,24] показал, что математическая речь тесно переплетается с математическим мышлением. Речь трудно отделить от мышления, поэтому в теоретической части освещены вопросы взаимосвязи этих понятий.
Кроме того, изложение школьного курса математики основано на совместном использовании словесной и символико - графической форм описания учебного материала. Каждая из этих форм - своеобразный язык, служащий для передачи информации. Поэтому осознанное и точное понимание учебного материала (а именно это интересует нас при обучении математике) возможно лишь при условии одинаково высокой подготовки школьников к восприятию информации, закодированной каждым из этих способов.
Таким образом, процесс понимания тесно связан с развитием речи учащихся (как внешней, так и внутренней) и, в свою очередь, если учащийся понимает материал, то он может его объяснить, и здесь важную роль играет уровень его языкового развития. Перед учителем стоит важная задача: помочь ребенку перевести образы, внутреннюю речь в слова.
Вследствие этого, в теоретическую часть включен вопрос о понимании и о взаимосвязи понятий понимания, мышления и речи. Показано, что понимание имеет коммуникативную природу.
Практика работы в школе убеждает в том, что учащиеся находятся в сильной зависимости от формы подачи материала. Так, например, они с легкостью решают уравнение: 0,5x - 3 = 4, но огромные трудности испытывают при выполнении задания: «Найти число, разность половины которого и числа 3 равна числу 4».
Необходимо варьировать формы подачи учебного материала в зависимости от его содержания, уровня общей языковой подготовки школьников, уровня мышления учащихся и других особенностей. Поэтому, в работу вошел параграф «Особенности математического мышления и уровень развития математической речи учащихся 5-6 классов», состоящий из тестовых заданий, направленных на выявление перечисленных особенностей класса.
§1. Понимание и мышление
1.1 Взаимосвязь понятий «понимание» и «мышление»
Проблема понимания сейчас стала междисциплинарной: ее анализируют одновременно во многих областях научного познания - физике, философии, истории и др. В современной науке существует, по крайней мере, семь основных направлений ее исследования - методологическое, гносеологическое, логическое, семантическое, лингвистическое, коммуникативное, психологическое. В психологии понятие "понимание" используют в широком и узком смыслах.
В широком смысле понимание рассматривается как универсальная
характеристика интеллектуальной деятельности человека, которая является непременным атрибутом любого уровня познания и общения, каждого психического процесса.
"Понимание в узком смысле есть компонент только мышления как обобщенного и опосредованного отражения существенных свойств и связей между предметами и явлениями" [18,с.18]. В дальнейшем понятие "понимание" будем употреблять в этом смысле.
Понимание как проблемная область психологии мышления изучено явно недостаточно. До сих пор есть трудности с указанием той роли, которую понимание играет в мыслительной деятельности, с определением того, является ли оно компонентом, стороной, видом или одним из процессов мышления.
Попытаемся проанализировать сходство и различие понятий "мышление" и "понимание" в психологии мышления. Для этого, по мнению В.В.Знакова, нужно ответить на четыре вопроса [18,c.19].
Первый из них: существует ли понимание, совершающееся без участия мышления? Отвечая на этот вопрос, следует различать две ситуации - понимание известного и понимание нового. Когда нужно понять знакомые слова, действия, поступки людей и т.д., то понимание осуществляется в форме понимания-вспоминания. Это такая форма интеллектуальной деятельности, которая основана на актуализации прошлого опыта. Она фактически не требует от человека мышления в момент понимания, но основана на простой мыслительной деятельности. Например, каждый взрослый человек понимает запрещающий сигнал светофора.
В противоположность пониманию известного понимание нового (неизвестных ранее фактов, событий, явлений) более развернуто во времени. Такое понимание проходит ряд этапов становления и всегда включено в актуальную мыслительную деятельность (по выявлению причин понимаемого явления, установлению того, как устроена вещь и т.п.). Далее под пониманием будем подразумевать только понимание нового.
Таким образом, делаем вывод, что существует понимание, совершающееся без актуального участия мышления, - это понимание-вспоминание.
Второй вопрос: возможно ли мышление без понимания? Необходимость в понимании новых фактов у человека возникает в тех ситуациях, когда ему что-то неясно, непонятно. Например, для многих людей установление того факта, что если нажать на выключатель, то в комнате зажжется свет, не означает понимания природы электрического света: они не смогут связно ответить на вопрос - почему при нажатии выключателя загорается лампочка? Именно неясность, нераскрытость отношений ситуаций, в которые попадает человек, становится одной из важнейших предпосылок приобретения такими ситуациями проблемного характера. А проблемная ситуация - это исходная точка и побудительная причина развертывания процесса мышления. Следовательно, сначала мышление и понимание связаны друг с другом, так сказать, отрицательной обратной связью: непонимание становится одним из основных источников возникновения мышления. В процессе мышления знак этой связи меняется на положительный: понимание промежуточных результатов мыслительной деятельности является необходимым условием успешности мышления. Однако это не означает, что человек, например, решающий задачу, понимает все промежуточные результаты решения.
Основная причина того, что не все выявляемые в ходе мыслительной деятельности связи и отношения объекта познания понимаются, заключается в том, что в процессе мышления субъект сталкивается с трудностями в соотнесении их с уже известными связями и отношениями изучаемого объекта. Установление связи нового с известным также приобретает характер мыслительной проблемы. Следовательно, для достижения понимания у человека должен развернуться не какой-то специфический процесс понимания, а мыслительный процесс. Таким образом, делаем вывод, что мышление без понимания возможно, так как в некоторые моменты мыслительного поиска человек не понимает места, роли выявляемых новых сторон объекта познания в структуре выполняемой им деятельности.
Третий вопрос: существует ли специфический процесс понимания, отличный от процесса мышления? Ответ на этот вопрос должен быть, скорее всего, отрицательным. Психологи используют выражение "процесс понимания", но скорее в разговорном, а не строго научном значении. Отсутствие в научной литературе критериев определения понимания как процесса вынуждает признать, что прав, по-видимому, Г.С.Костюк, который считает: "Понимание как процесс, это и есть процесс мышления, направленный на разрешение стоящих перед личностью задач. Нет оснований рассматривать понимание как какой-то особый процесс, отдельный от мышления" [13,c.72]. Однако Г.С. Костюк, как и многие другие, не ставит вопроса о специфике понимания как мыслительного процесса. Попытаемся выявить эту специфику, отвечая на последний вопрос.
Четвертый вопрос: можно ли говорить о понимании как специфическом виде мышления? Пытаясь определить особенности понимания как специфического вида мышления, отличного от решения задач, психолог сталкивается с непреодолимой трудностью. Она состоит в том, что, и понимая, человек вынужден решать мыслительную задачу. Очень часто мы оказываемся в таком положении, когда первоначальной целью нашей деятельности является понимание факта (события, явления), но он оказывается настолько сложным, что сразу его понять не возможно. Понимание факта перерастает в самостоятельную мыслительную проблему, без решения которой его не понять. В этом случае у человека происходит трансформация цели: для того чтобы понять, он старается решить мыслительную проблему, задачу - и в результате понимание оказывается как бы вплетенным в решение. Так бывает, например, когда человек пытается понять сложное произведение искусства, уяснить инструкцию к новому электроприбору и т. д. Причина тут в том, что подлежащие пониманию свойства объекта обычно не лежат на поверхности, а раскрываются только в ходе мыслительной деятельности.
Понимание и решение так тесно переплетаются, что различить их по тем целям, с которыми люди приступают к деятельности, практически невозможно.
Во всех ситуациях, требующих от субъекта понимания нового материала, этот психологический феномен вначале возникает для него как мыслительная проблема. Проблема осознается человеком как непонимание, то есть осознание того, что я не знаю чего-то такого, что нужно для выхода из создавшейся ситуации. Это, как уже отмечалось, исходный пункт мыслительной деятельности. Затем, переосмысливая проблему, накапливая новые знания об отраженной в ней реальности, человек постепенно приходит к решению и пониманию. При этом этапы понимания, его уровни соответствуют этапам решения (от недифференцированного понимания проблемы в целом к дифференцированному и глубокому). Таким образом, можно сделать вывод о том, что не существует понимания как отдельного вида мышления, оно всегда является компонентом, одним из процессов мышления.
Мышление человека представляет собой познавательную деятельность, в ходе которой субъект, взаимодействуя с объектом, выявляет некоторые неизвестные ранее стороны, свойства последнего, получает новые знания об объекте. Однако понимание как компонент мышления имеет непосредственное отношение не к выявлению новых знаний о действительности, а к их усвоению.
Понимание - это осмысление отраженного в знании объекта: понимание представляет собой формирование смысла знания в процессе действия с ним. Например, ученик решает задачу о равностороннем треугольнике. В какой-то момент решения он вдруг понимает, что отрезок, который он считал только биссектрисой, одновременно является и медианой. Понимание, безусловно, возникает в результате выявления нового свойства отрезка, соединяющего вершину треугольника с противоположной стороной треугольника, а именно: делить пополам не только угол, но и сторону. Новое знание об отрезке, конечно, оказывается важной составляющей процесса решения задачи. Однако суть понимания все-таки составляют действия по соотнесению нового для ученика свойства отрезка с уже известным. Понимание наступает, когда у ученика меняется операциональный смысл задачи, то есть возникает отличное от первоначального познавательное отношение к отрезку. Только выход за пределы известного рассмотрения отрезка в другой системе отношений, связей приводят к формированию у субъекта нового понимания задачи.
1.2. Формы понимания
Характерная особенность понимания как компонента мышления состоит в том, что в различных познавательных ситуациях понимание человеком фактов, событий, явлений имеет неодинаковую психическую природу, то есть в разных ситуациях проявляются отличающиеся друг от друга формы понимания. В индивидуальной деятельности наиболее важными являются три познавательные процедуры, три вида мыслительных действий[18]:
1. Узнавание знакомого в новом материале.
2. Прогнозирование, выдвижение гипотез о прошлом или будущем
объекта, ситуаций, которые необходимо понять.
3. Объединение элементов понимаемого в целое.
Каждый вид мыслительных действий играет ведущую роль в психологической деятельности решающего задачу человека преимущественно в одном специфическом классе познавательных ситуаций. Осуществление субъектом именно таких действий способствует порождению у него соответствующей формы понимания объекта познания[18]:
1) понимание-узнавание;
2) понимание-гипотеза;
-
понимание-объединение.
Рассмотрим более подробно каждую форму понимания и те ситуации, в которых они возникают.
Часто понимание фактов (событий, явлений) носит констатирующий характер. Субъект ограничивается узнаванием факта, актуализацией его смысла, сформированного в прошлой мыслительной деятельности. При этом нет попыток рассмотреть понимаемый факт в более широком контексте. Например, так бывает, когда проходя по улице и услышав обрывок разговора о событиях показанного по телевидению фильма, мы понимаем, какой именно фильм обсуждается, но не придаем разговору никакого значения. Понимание в таких случаях есть ответ на вопрос "что это такое?" Ведущей познавательной процедурой в мыслительной деятельности субъекта в подобных случаях является узнавание, поэтому понимание такого рода называется пониманием-узнаванием. Надо обратить внимание на то, что психологи [26,с.47], анализирующие понимание в процессе решения задачи, получили данные о том, что узнавание является необходимым условием понимания задачи, одним из важнейших компонентов ее решения. Понимание-гипотеза в мышлении человека реализуется в двух разновидностях, обусловленных различием в типах познавательных ситуаций, определяющих мыслительную деятельность, становление данной формы понимания. Одни познавательные ситуации характеризуются тем, что в них представлены обстоятельства, окружающая среда какого-либо предмета, выступающего в роли объекта познания, но сам он не указан явным образом, а лишь подразумевается. В этом случае предмет оказывается неизвестным решаемой субъектом мыслительной задачи. Например, в такой ситуации оказывается студент, опоздавший на лекцию и пытающийся понять по словам лектора, какова ее тема. В других ситуациях явно представлены и события-предметы познания, и обстоятельства их совершения, однако глубокое понимание такой ситуации предполагает не простую констатацию фактов, отражение событий в психике субъекта, а осознание человеком или причин, вызвавших эти события, или последствий, к которым они могут привести (а иногда - того и другого вместе).
Таким образом, понимание-гипотеза оказывается более сложной формой понимания, чем понимание-узнавание. Для становления понимания-узнавания достаточно мыслительных операций и действий, обеспечивающих узнавание смысла познаваемого объекта, а формирование понимания-гипотезы требует от субъекта не только осмысленного узнавания, но и выдвижения гипотезы о характере его окружения.
Понимание-объединение возникает в тех ситуациях, где для понимания человеку требуется мысленно собрать все составляющие ситуации, объединить элементы понимаемого в целое. При этом неизвестным решаемой задачи оказывается способ объединения отдельных частей, фрагментов ситуации в целостную структуру. Например, понимание-объединение должно быть результатом мыслительной деятельности инспектора ГАИ, расследующего дорожную аварию, или немыслима без понимания-объединения и работа историка, который по имеющимся в его распоряжении фактам пытается восстановить по возможности полную картину некоторого исторического события.
Понимание-объединение представляет собой самую сложную из трех перечисленных форм анализируемого феномена, включающего в себя мыслительные операции и действия, вносящие решающий вклад в образование первых двух форм понимания. Эти данные свидетельствуют о том, что в познавательных ситуациях, требующих от субъекта умение структурировать части в целое, узнавание и гипотезы служат средством, способом объединения анализируемых разрозненных элементов в единую структуру.
Понимание-объединение в решении обычно проявляется на завершающих фазах мыслительного поиска. Основой для его формирования оказываются предыдущие мыслительные действия решающего задачу субъекта: выдвижение гипотез, осмысление элементов задачи, установление связей между ними и т.п.
Итак, можно установить взаимосвязь понятий "мышление" и" понимание":
1. Понимание не является принципиально отличным от мышления самостоятельным психическим процессом. Понимание - это компонент мышления, один из образующих его процессов. Понимание обеспечивает установление связи раскрываемых новых свойств объекта познания с уже известными субъекту, формирование операционального смысла новых свойств объекта и определение их места и роли в структуре мыслительной деятельности.
2. Для понимания нового материала человек всегда должен решить определенную мыслительную задачу, т. к. формирование понимания нового происходит в процессе мыслительной деятельности и оказывается ее результатом. Когда же субъекту нужно понять уже известное событие или явление, то понимание совершается без актуального участия мышления - это понимание-вспоминание.
3. Одни и те же три формы понимания проявляются и в таких видах мыслительной деятельности, в которых понимание составляет основное психическое содержание, и в таких, где оно играет вспомогательную роль, оказывается компонентом деятельности. И в том, и в другом случае для возникновения анализируемого феномена человек должен решить некоторую мыслительную задачу. Таким образом, какая форма понимания возникает у субъекта в конкретной ситуации, обусловлено прежде всего характером мыслительной деятельности: тем, в какие объективные обстоятельства, требующие понимания, попадает человек и какую задачу он решает в этих обстоятельствах.
1.3. Работа понимания
Живое знание существует на многих языках. Их число значительно больше числа известных нам языков. Чтобы получать знания, нужно владеть языком, которым оно написано. При этом может искажаться, не пониматься смысл. Это приводит к пониманию недостаточности языка и человек совершенствует язык или создает новый.
Особый случай - усвоение знаний, выраженных, например, на вербальном языке (лекция, письменный текст и т.п.), при котором вербальные значения переводятся на язык смысла. Эта процедура носит название осмысление значений. Когда требуется передать осмысленное знание собеседнику, экзаменатору и т.д., происходит обратная процедура - означение смысла. Есть два противоположно направленных процесса:

 означение смысла осмысление значения
означение смысла осмысление значения
Эти два взаимосвязанных процесса можно назвать работой понимания.
Опыт разумного человека свидетельствует о том, что полный перевод с языка значений на язык смыслов и обратно невозможен. Причина этого - свобода мысли и "бездонность всякого смысла" [3,с.21]. Иначе говоря, в человеческом общении невозможно стопроцентное понимание. В противном случае не только люди перестали бы быть интересными друг другу, но остановилось бы и развитие культуры, человека.
Продуктивность непонимания связана с тем, что оно влечет за собой поиск смысла. Точки развития и роста человека и культуры как раз и находятся в дельте понимания-непонимания. Здесь же находится и движущая сила развития знаний.
Процесс понимания включает в себя отдельные акты, каждый из которых имеет смысловую самостоятельность:
1. Психофизиологическое восприятие физического знака (слова, цвета, пространственные формы).
2. Узнавание его как знакомого или незнакомого. Понимание его общего значения в языке.
3. Понимание его значения в данном контексте.
-
Активно-диалогическое понимание (спор - согласие).
Психологическая сущность понимания, как отмечает М.М.Бахтин [3,с.137], состоит в превращении чужого в "свое -чужое". Он различал:
1) слова чужие освоенные ("свои - чужие"), вечно живущие, обновляющиеся в новых контекстах;
-
слова чужие инертные, мертвые слова ("слова - мумии").
М.М.Бахтин различает "объяснение" и "понимание": "объяснение", как и "познание", монологично (сначала я что-то знаю, а затем я это тебе растолковываю), "понимание" - диалогично (я узнаю что-то лишь в то время, как я это тебе объясняю, приглашая тебя делать поправки, перебивать, задавать вопросы по ходу.
М.К.Мамардашвили говорит о другом важном аспекте понимания: не только как об использовании прочитанного в качестве некоторой ценности, а об участии понимаемого в нашей жизни [28,c.18]. Понятое именно таким образом становится личностным знанием. "Понимание восполняет текст: оно активно и носит творческий характер. Творческое понимание продолжает творчество" [3,c.19]. В принципе, обучение, творчество и понимание - это синонимы. Их дифференциация связана с неудовлетворительной организацией обучения (а возможно, и всей человеческой деятельности), которое может быть ориентировано, например, на запоминание, на повторение, а не на понимание. Поэтому сегодня различение трех понятий вполне осмысленно и необходимо.
Как уже говорилось выше, между текстом и его пониманием имеется зазор. Многие системы обучения способствуют возникновению у учащихся опасной иллюзии полного понимания, которое мешает формированию у них продуктивного непонимания.
1.4. Основные виды понимания
1. Естественное понимание предполагает извлечение смысла из ситуации. Его полнота и адекватность удостоверяются поведением, действием индивида. "Естественное" - не значит врожденное. Этому виду понимания предшествует опыт, но он обычно скрыт от внешнего наблюдения.
2. Культурное понимание предполагает, наряду с извлечением смысла из ситуации его знаковое оформление, означение и возможность трансляции. Его полнота и адекватность удостоверяются не столько поведением, сколько сообщением, текстом, которые должны соответствовать оригиналу - предмету понимания. Для культурного понимания расхождение между возможностью осуществления действия и возможностью сообщения весьма типично. Иначе говоря, культурное понимание может отрываться от своих естественных предметных корней.
-
Творческое понимание предполагает, наряду с извлечением, означением и трансляцией смысла, порождение и оформление нового смысла. Здесь речь идет уже не столько об адекватности действия или воспроизведения оригиналу - предмету понимания, а о произведении смысла и нахождении новой текстовой, знаковой, иконической, символической формы. В образовательной ситуации оценка творческого понимания учебного материала учащимся требует от учителя желания и способности к творческому пониманию произведения ученика, требует и душевной щедрости. Признание успеха - это мощнейший стимул развития творчества.
Существующие системы обучения ориентированы преимущественно на культурное понимание, и только иногда и не вполне осознанно формируют у учащихся естественное и творческое понимание.
Надо сказать, что культурное понимание не просто дополняет естественное, оно преодолевает его, открывает новые предметные отношения, иначе высвечивает смысл выделенных ранее. Точно так же и творческое понимание преодолевает естественное и культурное понимание.
Общей особенностью всех видов понимания является то, что понимание не бесстрастный акт. Оно эмоционально окрашено, приносит удовлетворение или горечь. Горечь, кроме того, вызывается и непониманием. Различие выделенных видов понимания состоит так же в доминировании определенного языка. Естественное понимание оперирует предметными и операциональными значениями; культурное - знаками, вербальными значениями и понятиями; творческое - смыслами. Образование должно ориентироваться на "язык смыслов", на пробуждение у учащихся мыслей о смысле, а не на усвоение чужих мыслей.
Еще в 30-40 годы двадцатого века П.И.Зинченко и А.А.Смирнов [17] показали, что в определенных условиях мнемические и познавательные задачи несовместимы и будут оказывать неблагоприятное воздействие друг на друга. Иначе говоря, установка на запоминание может мешать пониманию нового материала, а установка на понимание и использование каких-то приемов логической работы с материалом (например, классификация или составление плана) может существенно понизить продуктивность запоминания. Такая несовместимость особенно характерна для учащихся начальных классов. Поэтому П.И.Зинченко предлагает следующие рекомендации - педагогам следует специально ограничивать установку на запоминание.
"Понимание - это освобождение. Освобождение от тоски непонимания и подозрения в абсурде... Понимание - это свобода находить новые смыслы. Ибо понять можно только то, что имеет смысл" [6,c.27]. Здесь может быть неоценима роль учителя, правда, при одном непременном условии: учитель объединяется с учеником и осуществляет совокупное учебное действие по пониманию предмета. Спускаясь до уровня знаний ученика, учитель поднимает его до уровня учебного предмета, а то и над ним. Психологически и педагогически очень важно, чтобы в сознании учителя ученик не был объектом обучения и воспитания. Есть два субъекта знания, между которыми происходит диалог. И они оба противостоят объекту или предмету знания. Учитель дает понять ученику, что предмет развивающийся, живой. "Обыгранный" в совместном разговоре, действии предмет становится достоянием ученика. Выполняя роль посредника учитель не столько учит, сколько совместно думает с учеником, т.е. развивает его. Соотношение обучения и развития издавна составляет проблему. Л.С.Выготский пишет: «Ребенок научился производить какую-либо операцию. Тем самым он усвоил какой-то структурный принцип, сфера приложения которого шире , чем только операция того типа, на которых этот принцип был усвоен. Следовательно, совершая шаг в обучении, ребенок продвигается в развитии на 2 шага, т.е. обучение и развитие не совпадают» [11,с.181-182]. Из этого несовпадения Л.С.Выготский выводит представления об уровне актуального развития и о зоне ближайшего развития. При определении границ зоны ближайшего развития нужно ориентироваться на акты естественного и творческого понимания. В то время как культурное понимание - это индикатор уровня обучаемости.
В связи с этим функции учителя должны различаться при решении задач обучения и развития. Он должен быть способен улавливать, когда ученика нужно обучать, а когда развивать, т.к. обучение может не только пробуждать, но и тормозить развитие.
§2. Мышление и речь
Центральным моментом проблемы мышления и речи является вопрос об отношении мысли к слову. Решение этой проблемы колебалось всегда - от самых древних времен и до наших дней - между двумя крайними полюсами - между отождествлением и полным слиянием мысли и слова и, с другой стороны, между их столь же полным разрывом.
Весь вопрос упирается в метод, применимый при исследовании этой проблемы. Исследование всяких психологических образований предполагает анализ. Однако этот анализ может иметь две принципиально различные формы.
Первая форма психологического анализа - разложение сложных психологических целых на элементы (например: химический анализ воды, разлагающий ее на водород и кислород). Существенный признак такого анализа - в результате его получаются продукты, чужеродные по отношению к анализируемому целому - элементы, которые не содержат в себе свойств, присущих целому и обладают целым рядом новых свойств, которых это целое никогда не может обнаружить.
Вторая форма анализа - анализ расчленяющий сложное единое целое на единицы. Под единицей подразумевается такой продукт анализа, который обладает всеми основными свойствами, присущими целому.
Переход к анализу такой формы - решительный и поворотный момент во всем учении о мышлении и речи.
Что же является такой единицей, которая далее неразложима и в которой содержатся свойства, присущие речевому мышлению как целому? Такая единица может быть найдена, как считает Л.С.Выготский [10], во внутренней стороне слова - в его значении. Слово всегда относится не к одному отдельному предмету, а к целой группе или к целому классу предметов. В силу этого каждое слово представляет собой скрытое обобщение, и с психологической точки зрения значение слова представляет обобщение, а обобщение представляет собой акт мышления.
Но вместе с тем, значение представляет неотъемлемую часть слова как такового. Слово есть речь и мышление в одно и то же время, потому что оно есть единица речевого мышления. Поэтому метод исследования проблемы - метод семантического анализа, метод изучения словесного значения.
В дальнейшем изложении вопросов, связанных с мышлением и речью, будем придерживаться положений, которые высказал Л.С.Выготский [10].
Мышление и речь имеют генетически совершенно различные корни. Развитие той и другой функции не только имеет различные корни, но идет на протяжении всего животного царства по различным линиям.
В опытах Келера есть доказательство того, что зачатки интеллекта появляются у животных независимо от развития речи и вовсе не в связи с ее успехами. В отношении речи Келер установил, что речь (у шимпанзе) - не только выразительно-эмоциональная реакция, но и средства психологического контакта с себе подобными. Однако она нисколько не связана с интеллектуальной реакцией, т.е. мышлением животного.
В онтогенезе отношение между двумя линиями развития - мышления и речи - более сложное.
Есть экспериментальные доказательства того, что мышление ребенка в своем развитии проходит доречевую стадию. Доинтеллектуальные корни речи в развитии ребенка были установлены очень давно. Крик, лепет и даже первые слова ребенка представляют эмоциональную форму поведения и выступает в роли средств социального контакта, но с развитием мышления не имеют ничего общего.
Но самое важное - что около двух лет линии развития мышления и речи, которые шли до сих пор раздельно, перекрещиваются. Совпадают в своем развитии и дают начало совершенно новой форме поведения. Это переломный момент, начиная с которого речь становится интеллектуальной, а мышление - речевым.
Одно развитие является не просто прямым продолжением другого, но изменился и сам тип развития. Речевое мышление представляет собой не природную форму поведения, а форму общественно-историческую, и потому, отличающуюся целым рядом специфических свойств и закономерностей.
Отношение мысли к слову есть процесс: движение от мысли к слову и обратно - от слова к мысли. Рассмотрим те фазы, из которых складывается это движение, через которые проходит мысль, воплощающаяся в слове.
Различают два плана в самой речи. Внутренняя, смысловая, семантическая сторона речи и внешняя, звучащая фазическая сторона речи. Они хотя и образуют единство, но имеют каждая свои особые законы движения. Смысловая сторона речи идет в своем развитии от целого к части, от предложения к слову, а внешняя сторона речи идет от части к целому, от слова к предложению. Движение семантической и фазической сторон слова в овладении сложными синтаксическими структурами не совпадают в развитии.
Главнейшей особенностью внутренней речи является ее совершенно особый синтаксис. Эта особенность заключается в кажущейся отрывочности, фрагментарности, сокращенности внутренней речи по сравнению с внешней. Внутренняя речь есть в точном смысле речь почти без слов.
Источниками сокращенности внутренней речи являются:
1) тема нашего внутреннего диалога нам всегда известна, поэтому подлежащее всегда подразумевается в наших мыслях;
2) в своей внутренней речи мы всегда смело говорим свою мысль, не давая себе труда облекать ее в точные слова;
-
во внутренней речи слово как бы вбирает в себя смысл предыдущих и последующих слов, расширяя почти безгранично рамки своего значения.
Во внутренней речи мы всегда можем выразить все мысли, ощущения и даже целые глубокие рассуждения одним лишь названием.
Таким образом, внутренняя речь представляет собой совершенно особую, самостоятельную, автономную функцию речи. Ее можно рассматривать как особый внутренний план речевого мышления.
Внутренняя речь есть мышление чистыми значениями, есть сама мысль. Мысль не состоит из отдельных слов так, как речь. Она всегда представляет собой нечто целое, значительно большее по своему протяжению и объему, чем отдельное слово.
Таким образом, речевое мышление предстает как сложное динамическое целое, в котором отношение между мыслью и словом обнаруживается как движение через целый ряд внутренних планов, как переход от одного плана к другому - от мотива, порождающего какую - либо мысль, к оформлению данной мысли, к опосредованию ее во внутреннем слове, затем в значениях внешних слов и, наконец, в словах.
§3. Математическое мышление и
математическая речь
3.1. Структура математического мышления
В психолого-педагогической литературе [9,10,39] постоянно обсуждается проблема учета индивидуально-психологических особенностей школьников. Потребность в этом ощущают и педагоги-практики. Поэтому возникает вопрос о том, какие именно особенности должен учитывать учитель. Перечислим основные:
1) качественные особенности восприятия (предметность, осознанность, структурность и т.д.);
2) преобладающие виды памяти (зрительная, слуховая, двигательная и т.д.);
3) виды мышления (наглядно-действенное, наглядно-образное, словесно-логическое и т.д.);
-
качества мышления (гибкость, глубина, широта и т.д.).
Список данных показателей может быть продолжен. Какие же из этих особенностей должен учитывать учитель математики в первую очередь? Прежде всего учитель математики должен ориентироваться на индивидуальные особенности математического мышления учащихся, поэтому необходимо знать его структуру.
Согласно психологическим исследованиям [9,19,20,39], структура математического мышления представляет собой пересечение пяти основных подструктур: топологической, порядковой, метрической, алгебраической, проективной.
1. Топологическая подструктура обеспечивает замкнутость, компактность, связанность осуществляемых мышлением преобразований, непрерывность трансформаций, мысленное выращивание, вылепливание в представлении требуемого объекта (его образа).
2. Порядковые подструктуры дают возможность постоянного сопоставления человеком математических объектов и их элементов по таким характеристикам, как больше-меньше, ближе-дальше, часть-целое, изменение направления движения и его характера, положение, форма, конструкция предмета.
3. Метрические подструктуры позволяют вычленять в объектах и их компонентах количественные величины и отношения (пропорции, численные значения размеров, углов, расстояний).
4. Алгебраические подструктуры помогают осуществлять не только прямые и обратные операции над математическими объектами, расчленение и соединение их составляющих, но и замену нескольких операций - одной из определенной совокупности, объединение нескольких блоков предмета в один, выполнение математических преобразований в любой последовательности.
5. Проективные подструктуры обеспечивают изучение математического объекта или его изображения с определенного самостоятельно выбранного положения, проецирование с этой позиции объекта на изображение (или изображения на объект) и установление соответствия между ними.
Эти 5 подструктур в математическом мышлении человека существуют не автономно, не изолированно, не равнозначны и не рядоположны, а пересекаются и находятся в определенной зависимости, иерархии по степени значимости и представительности в интеллекте. В соответствии с индивидуальными особенностями каждого та или иная подструктура занимает место главной, ведущей, доминирующей. Она наиболее ярко выражена по сравнению с остальными, более устойчива и лучше развита.
В соответствии со своей ведущей подструктурой человек по-разному воспринимает, оперирует, перерабатывает и воспроизводит математическую информацию.
Например, при восприятии математического объекта один ученик прежде всего выделяет метрические соотношения - его интересует вопрос «Сколько?». Другой воспринимает в первую очередь топологические инварианты и оперирует ими (непрерывность, замкнутость, связность и т.д.). При этом он акцентирует свое внимание не на количественных, а лишь на качественных отношениях. Третий ученик с ведущей алгебраической подструктурой постоянно стремится к сокращениям, замене нескольких операций одной. Он часто свертывает, а порой и пропускает какие-то шаги в рассуждениях (например, одним действие он осуществляет сразу несколько операций: переносит все члены уравнения в одну сторону, приводит подобные и тут же выносит общий множитель за скобки). Сделать проверку собственного решения для такого ученика - мука.
С учетом этих особенностей мышления мы должны строить процесс обучения школьников математике. Суть его заключается в том, что от детей не требуется общего, одинакового для всех решения. Каждый может выполнять задание своим способом, тем, который ему понятнее, а этот индивидуальный способ зависит от ведущей подструктуры математического мышления школьника. В зависимости от нее и помощь учителя должна быть различной. Только в этом случае она будет услышана, воспринята.
К сожалению, отсутствие учета индивидуальных особенностей математического мышления учащихся вдет к тому, что педагог навязывает детям тот способ рассуждений, который свойственен ему (в силу наличия у самого учителя определенной ведущей подструктуры). В этом случае дети, ведущая подструктура которых совпадает с ведущей подструктурой педагога, легко его понимают, для них он понятно и доступно объясняет. Для остальных же школьников усвоение математики - мука. Если учитель преподает в одном классе несколько лет, то возможно, что за это время он постепенно переформирует ведущую подструктуру некоторых школьников. В результате дети начинают думать так, как объяснял этот процесс учитель. Другие же школьники (с наиболее устойчивой ведущей подструктурой) продолжают испытывать трудности.
Не ломать математическую индивидуальность ученика, а учитывать ее и строить процесс обучения в соответствии с ней - наша задача. Именно этот путь (в соответствии со структурой мышления школьника) известный математик и методист А.И. Маркушевич назвал «подлинно «детским путем» в математику» [29,с.48].
3.2. Математический язык
Изначально, опорой мышления являлись наглядные, конкретные образы. Образное мышление не обязательно должно протекать в словесной форме. Ж.Адамар [1], исследуя этот вопрос, пришел к выводу, что в начальной стадии математического творчества почти все математики мыслят смутными образами визуального характера, и лишь на более поздней стадии они облекают свои мысли в словесную форму. По-видимому, сами математические идеи действительно рождаются не в словесной форме. Но с другой стороны, мысль становится достаточно отчетливой только после того, как она облечена в словесную форму, причем поиск адекватной словесной формы всегда представляет большие трудности.
Несомненно только одно: для того, чтобы она могла быть сообщена другим людям и понята ими, ее нужно облачить в словесную форму. Социальные факторы общественного развития неизбежно приводят к необходимости словесного, речевого мышления. Поэтому отвлеченные абстрактные понятия по необходимости должны фиксироваться с помощью специальных слов (терминов) или символов - имен этих понятий, которые становятся удобным средством, позволяющим мышлению схватить, закрепить, а затем оперировать понятиями. Слова и символы становятся своеобразной необходимой формой существования понятий, а язык становится не только универсальным средством выражения математической мысли, но и формой ее существования. На это указывали многие виднейшие математики. Р.Декарт, один из основных творцов новой математики, считал, что благодаря буквенной символике математический язык становится не только опорой мышления, но и его орудием [21].
Роль языка в математическом творчестве осознавали и другие математики. Первым, кто по-настоящему понял колоссальные возможности языка как орудия мысли, был Г.В.Лейбниц.
О роли языка, как необходимой опоры мысли писал и Л.Эйлер, крупнейший математик восемнадцатого века, работавший долгое время в России. Он писал: "Язык нужен людям, чтобы они могли следить за своими мыслями и развивать их, а также общаться друг с другом" [21,с.282].
Вывод: без знаков вряд ли было бы возможно понятийное мышление. В самом деле, обозначая различные, но похожие вещи одинаковым знаком, мы, по-существу, обозначаем не сами эти вещи, а то общее, что присуще им, т.е. - понятие. И это понятие становится нашим достоянием только благодаря тому, что мы его обозначили. Никаким другим путем оно просто не может стать предметом мысли. Поэтому необходимой основой языка должна быть система знаков, слов или символов.
Различные цели исследования, связанные с решением различных задач, приводят к формированию различных языков [27,c.63]:
- Если мы собираемся описать какую-нибудь первичную предметную область и заданную на ней совокупность связей и отношений, то нам нужен предметный язык.
- Если нас интересуют метатеоретические проблемы, когда предметом исследования становится сама предметная теория, нам нужен метаязык.
- Если мы выражаем наше отношение к теории - размышляем, ставим вопросы, думаем о том, что знаем, что не знаем и что хотим узнать, если мы удивляемся, сомневаемся, восхищаемся, находим аналогии, уточняем смысл и т. п., то мы пользуемся языком исследователя - языком учителя.
Язык исследователя существенным образом отличается от предметного языка и от метаязыка. В нем, в отличие от этих языков, уместны и вопросительные, и повелительные предложения, а также всевозможные предложения эмоционального характера. Это так называемый неформальный язык математики, он выходит за рамки собственно математического языка и становится языком изложения математики.
Средствами этого языка раскрывается не только содержание математической теории, но выражается и определенное отношение исследователя к излагаемому. Этот язык тем и отличается от собственно математического языка, что он, помимо математического содержания, способен выразить и некоторые аспекты психологического характера, возникающие при изложении материала - "это тот неформализуемый фон, на котором строится математическая теория, - тот фон, который остается вне формального изложения теории, но который совершенно необходим для ее понимания" [27,с.62].
Язык, являясь инструментом познания, накладывает определенный отпечаток на формирующуюся модель познаваемого; и исключить влияние этого инструмента на отображаемое невозможно.
Было замечено, что недостатки языка в некоторых случаях приводят к противоречиям. Так, уже в шестом веке до нашей эры был известен «парадокс лжеца» (« Высказывание, которое я сейчас произношу, ложно») [27,c.39].
Определенная ограниченность выразительных возможностей действительно свойственна естественному языку. Поэтому часто случается, что разные люди одно и то же понимают по- разному.
Математический язык представляет математическую деятельность. Поэтому для того, чтобы выявить структуру математического языка, необходимо предварительно остановиться на структуре математической деятельности. Система учебной деятельности, относящаяся к изучению математики состоит из следующих компонентов [5,с.52]: символического, риторического, визуального, инструментально - графического, моторно - ориентировочного, дискурсивного.
Символический компонент. Этот компонент присутствует в математике изначально. По меньшей мере в двадцатом веке до нашей эры была разработана система обозначений числа. В древнегреческой культуре этот компонент использовался при обозначении геометрических фигур. Но центральную роль в математике символический компонент стал играть в европейской алгебре, две центральные идеи которой живут и по сей день - это идеи исчисления и переменной. Символический компонент алгебры был глубоко проанализирован многими поколениями учителей и методистов. Например, при выполнении задания: «Написать формулу корней квадратного уравнения: сх2 + вх + а = 0», вне всякого сомнения, многие ученики сделают стандартную ошибку, не обратив внимания на «необычные» позиции с и а. Подобного рода ошибки имеют своей причиной неадекватное понимание именно символического компонента математики.
Под риторическим компонентом в математике подразумевают использование в ней естественного, человеческого языка. Существовала тенденция, особенно в конце девятнадцатого и начале двадцатого веков, исключить естественный язык из математики настолько полно, насколько это вообще возможно. Аналогичные тенденции существовали в методике преподавания математики. Однако в настоящее время становится совершенно ясно, что естественный язык является инструментом мышления и обладает такими свойствами и качествами, которые делают его в некоторых отношениях более удобным, нежели символический компонент в математике.
Визуальный компонент математики. Как символический, так и риторический компоненты являются одномерными по своей физической природе (либо это строка символов, либо поток звуков). Необходимо внутри математики иметь прямые пути для изображения плоских и многомерных объектов (геометрические фигуры, поясняющие алгебраические тождества, графики функций и т.д.).
Рассмотрим остальные компоненты на одном примере. В психолого-педагогической литературе была использована идея развертки додекаэдра [5]. Мы же ограничимся рассмотрением развертки тетраэдра, как самого простого геометрического объекта и наиболее доступного для учащихся. На занятии ученикам шестого класса было рассказано о правильных многогранниках, в частности о тетраэдре. Выяснялось, как сделать модель тетраэдра. У каждого ученика был лист бумаги, ножницы, клей и т.д., но основная часть проблемы состояла не в непосредственной физической работе, а в логическом и техническом конструировании объекта. При этом возникли две проблемы: Какова комбинаторная схема развертывания тетраэдра? Какова форма грани тетраэдра? На первый вопрос ответ может быть получен из наблюдения: тетраэдр состоит из четырех граней. Мысленно разрезая грани по ребрам, в конечном итоге мы можем изобразить грубый эскиз развертки.
Второй вопрос имеет иной оттенок. Мы должны думать здесь о точных метрических зависимостях. До сих пор ученики не сталкивались с понятием правильного многоугольника. Фактически это понятие возникло в процессе обсуждения, в котором решающую роль играл дискурсивный компонент. Теперь возникает идея: мы можем построить один треугольник, вырезать его и использовать полученный шаблон для преобразования эскиза развертки тетраэдра непосредственно в его развертку.
Идея развертки является одной из существенных в инструментально - графическом компоненте.
Аналогично, идея комбинаторной схемы - одна из важнейших в моторно - ориентировочном компоненте. В дальнейшем три последних компонента используются, чтобы решить следующую задачу: «каким именно ребрам необходимо подрисовать узенькие полосочки, чтобы нанести на них клей при склеивании додекаэдра из развертки».
На этом примере было показано, каким образом несколько компонентов используются совместно при решении практической задачи с целью формирования «высших» умственных способностей.
Лингвистические аспекты неизбежно присутствуют в математике. Однако при систематическом их изучении необходимо создать о них достаточно четкое представление. Рассмотрим аспекты, связанные с языком школьной математики.
3.3. Язык школьной математики
Школьная математика является сложным образованием, включающим начальные фрагменты различных математических теорий (арифметики, алгебры, геометрии, математического анализа) в содержательном (неформальном) изложении. Поэтому язык школьной математики является языком этих начальных фрагментов математических теорий. Есть общие понятия, относящиеся к языкам как естественным, так и искусственным, символическим (имя, предложение).
Имя - это языковой объект, связываемый с предметом для обозначения его в речи. Предмет является носителем, или значением своего имени.
Слово «предмет» будем понимать в самом широком смысле. Это может быть как конкретный физический объект, так и абстрактный предмет из области математики (уравнение х-6=0 , квадрат АВСД и др.), а также любое понятие, свойство, отношение, процесс, событие и т.д.
Имена предметов могут быть простыми и составными. Простые имена произвольно закрепляются за предметами и рассматриваются в качестве неделимых единиц («Санкт-Петербург», «миллион», «9»). Составные имена содержат другие имена в качестве своих частей и обладают строением, отражающим тот способ, которым они обозначают своего носителя («321», «165+43», «основатель Санкт-Петербурга»).
3.3.1. Основные принципы языка школьной математики
1. Принцип предметности. Предложение говорит о предметах, имена которых встречаются в этом предложении ( а не об их именах ). Один и тот же предмет может иметь много синонимов. Например, записи 15-13, 18*2-34 можно рассматривать как различные имена числа 2. Равенство 15-13=18*2-34 выражает то, что имена, стоящие в левой и правой частях этого равенства, обозначают один и тот же предмет (число, имеющее имя два).
2. Принцип однозначности. Каждый символ, используемый в качестве имени, обозначает не более одного предмета .
3. Принцип замены имен. Предложение не должно менять своего значения истинности, если одно из входящих в него имен заменяется другим именем, имеющим то же самое значение. Например, предложение «0 > 3» ложно. Оно останется ложным и при замене имени «3» на имя «5-2», имеющее то же значение.
На следующих примерах покажем, как важно различать предмет и его имя.
1. Результат деления числа 66 пополам равен 33, но при делении записи 66 пополам получаем цифру 6.
2. Утверждая, что число 1 нельзя делить на 0 , мы не говорим, что невозможна запись 1:0. Такая запись так же допустима, как , например, запись 1:2, утверждается лишь, что 1:0 не является именем какого-либо числа.
Один и тот же предмет может иметь различные имена. Эти имена по-разному характеризуют данный предмет. В силу принципа замены имен предложение, в которое входит одно из имен предмета, сохраняет свою истинность или ложность при замене этого имени другим. Однако смысл предложения при этом может измениться. Например, смысл имен «Петр 1» и «основатель Санкт-Петербурга» различен.
Условились каждому имени сопоставлять кроме его носителя, определенный смысл. Примерно говоря, смысл имени - это то, что бывает усвоено, когда понято имя. Возможно понимать смысл имени, ничего не зная о его носителе, кроме того, что он определяется этим смыслом. Эта возможность лежит в основе нашей способности узнавать новое с помощью языка. Заметим, что одной из причин формализма в усвоении математики является попытка некоторых учащихся запомнить имена математических объектов, не понимая смысла данных имен.
Для построения искусственных символических языков (в частности, языка школьной математики) нужны правила построения различных выражений языка («слов»). Совокупность этих правил называется «синтаксисом». Кроме того, нас будет интересовать «семантика» языка, то есть отношение между выражениями языка, их смыслом и предметным значением.
Итак, в отношении именования участвуют три различных понятия: «имя», «значение», «смысл». Говорят, что имя называет свое значение и выражает свой смысл. Поэтому нужно различать термины «не имеет смысла» и «не имеет значения».
Имя называет предмет, но не выражает суждения о нем. Этой цели служат предложения, то есть построенные в соответствии с законами языка знакосочетания, выражающие законченную мысль.
Предложения можно рассматривать как особого рода имена, принимающие лишь два значения: «истина», «ложь». При этом суждение, выражаемое предложением, играет роль смысла этого имени.
Смысл предложения еще не несет нового знания. Этим свойством обладает только соединение суждения и его истинностного значения. Например, суждение «Санкт-Петербург - столица России» нового знания не несет. А соединение этого суждения с его значением «ложь» дает новое знание.
Существуют основные соглашения применительно к предложениям:
1. Смысл предложения не меняется, если заменить одно из входящих в него имен другим, имеющим тот же, что и у заменяемого, смысл.
2. Истинность предложения не изменяется, если заменить одно из входящих в него имен другим, имеющим то же, что и у заменяемого, значение.
3. Если предложение имеет значение, то оно имеет и смысл, причем смысл однозначно определяет значение.
4. Предложение не имеет значения, если хотя бы одно из встречающихся в нем не имеет значения.
3.3.2. Основные знаки языка школьной математики
Математический язык является искусственным. Он возник под влиянием потребностей математики в точных, ясных, сжатых формулировках, как результат совершенствования естественного языка по трем направлениям:
1) устранение громоздкости;
2) устранение омонимии (многозначности);
-
расширение выразительных возможностей.
Устранение громоздкости языка связано с широким использованием его символики, специальных математических знаков и соглашений о правилах пользования этими знаками. Каждый знак математического языка (цифра, буква, знак операции или отношения) обозначает понятие, которое в естественном языке выражается словом или совокупностью слов.
Важными этапами развития математического языка были:
1. Создание системы обозначений натуральных чисел и дробей, в частности, введение позиционной системы счисления и особого обозначения для 0.
2. Развитие алгебраической символики, позволившей наглядно изображать алгебраические преобразования и правила решения уравнений.
3. Развитие символики, связанной с появлением дифференциального и интегрального исчислений.
4. Развитие и внедрение в математику теории множеств и логических символов
5. Серьезное влияние на развитие математической символики оказало создание быстродействующих вычислительных машин-символика должна быть удобной для введения в эти машины.
Развитие символики приводит и к расширению выразительных возможностей математического языка. С появлением каждой новой области математики возникает присущая ей символика.
В семиотике (науке об общей теории знаков) различают[8]:
1) знаки - индексы;
2) иконические знаки;
-
знаки - символы.
Для воспринимающего лица знаки - индексы ассоциируются с обозначаемым им объектом в силу действительно существующей между ними связи (запах цветов может свидетельствовать о приближении к саду еще до того, как мы его увидим). Иконический знак (от греч. Eicon - изображение) ассоциируется с обозначаемым объектом в силу их сходства (знак опасного поворота действительно напоминает поворот). Между знаком - символом и объектом, к которому он отсылает, никакой природно обусловленной обязательной связи не существует. Знак - символ является знаком объекта на основании соглашения.
В математике знаки - индексы практически не встречаются, так как математический текст состоит не из самих объектов, а из их имен. Но различие между иконическими знаками и знаками - символами можно увидеть и на математических примерах. Так, иконические знаки: ││ (знак параллельности), ∆ (знак для обозначения треугольника), ┴ (знак перпендикулярности), = (знак равенства).
Символами являются знаки арифметических действий: +, - , , :,цифры и т.д.
Поскольку математический знак связан с названиями изучаемых понятий, то существует тесная связь между названиями понятий и применяемыми для соответствующих объектов обозначениями. Например, функция обозначается символами f, F, φ. Связано это с тем, что на латыни «функция» - functio (FUNCTIO).
Так как в математике приходится иметь дело с объектами разной природы, бывает удобно использовать буквы различных алфавитов и шрифтов. Так, например, в геометрии точки обозначают прописными латинскими буквами (A,B,C, …), а прямые - строчными латинскими буквами (a,b,c,…).
Употребляемые знаки должны образовывать определенную знаковую систему. Например, в установившейся сейчас символике знаки алгебраических действий и знаки соответствий и отношений обычно помещают между именами объектов, к которым они относятся. Такое употребление знаков называется инфиксным (например, a+b). Если соответствующий знак ставят перед именами объектов, то говорят о префиксном употреблении знака (например, + a,b). Если знак поставлен после имен объектов, то говорят о суффиксном употреблении знаков (например, a,b +).
Семиотику разделяют на три части [8]:
1) синтактику, изучающую синтаксис знаков, т.е. их взаимосвязи;
2) семантику, изучающую смысл знаков;
-
прогматику, изучающую восприятие знаков.
Например, вопрос о том, имеет ли смысл запись a+ :b относится к синтактике, вопрос о том, чему равно значение выражения ab + c, если a=3, b=4, c=8 - к семантике, а вопрос о том, какое из обозначений интервала наиболее удобно для целей обучения, - к прагматике.
3.3.3. Алфавит языка школьной математики
При изучении математики в школе наряду с обычными предложениями, записываемыми с помощью букв русского алфавита и знаков препинания (например, «рассмотрим ось симметрии равнобедренного треугольника»), используется ряд специфических знаков. Из них можно выделить некоторое множество основных (исходных) знаков, образующих алфавит языка школьной математики. Эти знаки по аналогии со знаками алфавита естественного языка называют буквами. Из этих букв составляются знакосочетания - слова школьной математики, а из слов - предложения этого языка. Во многих случаях повторяющиеся знакосочетания получают особые обозначения и их можно также считать буквами.
Специфические для языка школьной математики знаки можно классифицировать следующим образом [8]:
1. Предметные постоянные (имена предметов).Например, цифры: 0,1,2,3,4,5,6,7,8,9.
2. Предметные переменные, принимающие значения из некоторых множеств предметных постоянных. Например, латинские строчные буквы с индексами и без индексов: а,в,с,...,x,y,z.
3. Функциональные буквы, служащие для обозначения различных отображений (в том числе геометрических преобразований и алгебраических операций). Например, знаки для обозначения действий: +, -, , : .
4. Предикатные буквы, служащие для обозначения различных соответствий и отношений. Например: =,<,>.
5. «Знаки препинания» (скобки и точки).
§4. Особенности математического мышления и уровень развития
математической речи учащихся 5-6 классов
Перед тем, как приступить к разработке методики обучения темам, связанным с понятием числа, направленной на развитие математической речи учащихся 5-6 классов, были изучены особенности математического мышления и уровень развития математической речи учащихся 6 класса. В данном классе преимущественно дети со средними математическими способностями.
Исследование проводилась в двух направлениях. Во-первых, определялась ведущая подструктура математического мышления школьников (тест №1) и на основании полученных результатов отбирались содержание и форма объяснения материала. Во-вторых, выявлялся уровень развития математической речи учащихся (тест №2), что определяло отправную точку работы с каждым учеников по развитию его математической речи. Полученные результаты обрабатывались и на их основе была разработана методика применительно к данному классу, хотя многое из предложенного можно использовать в работе с любым классом.
Рассмотрим предложенные тестовые задания, количественный и качественный анализы результатов тестирований, а так же выводы, сформулированные на основе полученных данных.
4.1. Определение ведущей подструктуры математического мышления учащихся
Цель: определить ведущую подструктуру математического мышления каждого ученика в отдельности и класса в целом.
Содержание предложенного учащимся диагностирующего теста представлено ранее, в теоретической части работы (§3, п.3.1, рис.1, с.15).
В тестировании участвовали 28 учащихся 6 класса. Ученикам было предложено выбрать лишнюю фигуру из изображенных на рис.1 и объяснить свой выбор (тест №1).
Результаты тестирования оформим в виде сводной таблицы (таблица №1), которая представлена в приложении 5 (см. с.64).
Анализ результатов диагностирующего теста
Из 28 учеников, принимавших участие в тестировании, фигуру 4 выбрали 23 человека, фигуру 5 выбрал 1 человек, фигуру 2 выбрали 4 человека.
Таким образом, преобладающее большинство учащихся имеют метрическую подструктуру математического мышления, а значит наиболее доступным, легко воспринимаемым для них является материал, связанный с понятием числа.
Группа учащихся, имеющих подструктуру математического мышления, отличную от преобладающей, при затруднениях будут получать дополнительную индивидуальную помощь учителя, соответствующую их подструктуре математического мышления. Кроме того, на этапе обобщения изучаемого материала эти дети будут активно участвовать в работе по переосмыслению материала с других позиций, по переформулировке заданий.
4.2. Определение уровня развития математической речи учащихся
Цель: определить уровень подготовленности учащихся к восприятию информации, представленной в словесной форме; исследовать словарный запас учащихся, умение соотносить понятие, выраженное словом, с его образом.
С этой целью был разработан тест «Уровень языкового развития учащихся 5-6 классов» (тест №2). В предложенном тесте есть задания, имеющие единственное решение и задания, допускающие несколько равноправных решений. Задания 1,5 взяты из [36].
В тестировании принимали участие 28 учащихся 6 класса. На выполнение тестового задания было отведено 30 минут.
Тест №2. «Уровень языкового развития учащихся 5-6 классов»
1. Напишите как можно больше математических терминов, содержащих букву «п». (Например, прямая, степень, …).
2. Найдите число, половина которого меньше числа 22 на 10.
3. В 9 ч. 15 мин. От двух станций одновременно навстречу друг другу отошли два поезда. Через 3 часа расстояние между поездами было 50 км. Сделайте рисунок к описанной ситуации.
4. Запишите выражение: «Частное произведения чисел X и 17.4 и разности чисел 15 и 13.7 уменьшить на 24/9».
5. Вставьте пропущенное слово:
15 см2 - площадь прямоугольника

3 см 16 см - ?
5 см
6. В выражении X+2=19 подчеркните второе слагаемое. Запишите, как найти первое слагаемое. Подчеркните вычитаемое в полученном уравнении.
7. Автомобиль проехал 160 км за 2 часа. При каком условии он проедет 320 км за 4 часа.
8. Запишите предложение: «Число а больше числа в на 3», используя математические знаки.
-
Запишите на естественном языке следующее числовое выражение:
(15-0,9)*(15+0,9).
Результаты тестирования оформим в виде сводной таблицы (таблица №2), которая представлена в приложении 5 (см. с.65).
Анализ результатов теста №2
1. Количественный анализ
По результатам количественного анализа определялся уровень развития математической речи учащихся на текущий момент. Критерий определения уровня языкового развития следующий:
Количество правильно выполненных заданий Уровень развития математической речи
0 - 4 Низкий
5 - 7 Средний
8 - 9 Высокий
Количественный анализ оформим в виде таблицы (таблица №3), которая представлена в приложении 5 (см. с.66).
Выводы:
1. Большинство учащихся, а именно 64%, класса имеют низкий уровень развития математической речи.
2. Средний уровень развития математической речи имеют 36% учеников.
Полученные результаты показывают, что у учащихся математическая речь развита недостаточно. Это связано с тем, что в учебниках математики практически нет заданий, направленных на развитие речи. На уроках слишком мало времени уделяется решению этой проблемы. Можно сделать следующий вывод: самопроизвольно математическая речь развивается далеко не у каждого ученика, поэтому надо проводить специальную работу по формированию математической речи учащихся.
2. Качественный анализ
1 задание
Все учащиеся сумели продолжить список предложенных терминов. У некоторых ряд оказался коротким: 3-4 термина, в основном дополненный список состоял из 6-9 терминов.
Чаще всего это были слова: прямоугольник, периметр, произведение, перпендикуляр, параллелепипед, площадь, плюс, процент, параллелограмм. Реже встречались следующие термины: трапеция, плоскость, пропорция и др.
Диапазон названных терминов достаточно широк для учащихся 6 класса.
Однако были слова, которые никак нельзя отнести к математическим терминам: пример, правило, пункт. Значит, у некоторых учащихся нет ясного представления о том, что такое математический термин.
Кроме того, в указанных учащимися терминах было допущено достаточно большое количество орфографических ошибок, что тоже является пробелом в математическом образовании школьников.
2 задание
Большинство учащихся (18 человек) с данным заданием не справились. Причина заключается в необычной для ребят формулировке задания. Если бы уравнение было записано на математическом языке, его решение не вызвало бы трудностей у учащихся данного класса. Основные допущенные ошибки состояли в следующем:
1. Учащиеся не верно истолковывали смысл отношения «меньше на …»
2. Многие ребята невнимательно отнеслись к условию задания, в результате чего была упущена из виду важная часть в условии.
3 задание
В данном задании нужно было увидеть две возможные ситуации. Однако по традиции ребята сделали рисунок только одного из возможных вариантов, так как только такие задание встречаются в учебниках математики. Вторую возможную ситуацию заметил лишь один ученик из всего класса.
Таким образом, чтобы приучать детей внимательно относиться к чтению условия задачи, видеть различные ситуации, необходимо постоянно использовать задания, допускающие различные равноправные ответы, задания проблемного характера.
4 задание
С данным заданием справилась только треть класса. Такой результат - сигнал к тому, что недостаточно внимания на уроках уделяется записи числовых (буквенных) выражений, дети плохо владеют терминологией, связанной с компонентами и результатами арифметических действий, путают их названия. Кроме того, большего внимания требует отработка основных отношений, таких как «больше в (на) …», «меньше в (на) … ».
5 задание
Правильный ответ сумели дать практически все ребята (21 человек). Анализ ошибочных ответов («сторона», «площадь», «диаметр») показал, что некоторые ребята, все-таки, не видят связи между буквенным выражением и названием соответствующей величины. Такие ученики давали ответ либо под влиянием выделенных в изображении прямоугольника элементов, либо установившихся ассоциаций, либо созвучный.
Хотя это задание показало, что информацию, выраженную графически, дети воспринимают лучше (это может быть связано с возрастными особенностями).
6 задание
Правильные и полные ответы получены в большинстве случаев (от 22 учеников).
Замечания следующие:
1. Многие ребята не останавливались после выполнения действий, указанных в задании, а в силу привычки решали уравнение до конца, т.е. делали больше, чем требовалось.
2. Некоторые не выполняли вторую часть задания, что может быть связано с невнимательным чтением текста.
7 задание
Половина учащихся с заданием справились, указав нужное условие. Ответившие неверно не смогли понять описанную ситуацию. Об этом свидетельствуют некоторые ответы: «при таком же условии», «если будет ехать в том же направлении», «при обыкновенном условии». Таким образом, полезны были бы задания с пропусками условий, заключений. Помимо того, что нужно понять задание, необходимо еще четко и кратко сформулировать свой ответ.
8 задание
Правильный ответ дали только два ученика. Это задание оказалось трудным для учащихся. Было несколько человек, которые поняли, что требовалось в задании. Однако, при записи ответа на математическом языке допустили самую распространенную ошибку, а именно: вместо равенства а=b+3 писали равенство b=а+3. Таким образом, учащиеся не могут перевести предложение с естественного языка на символический, т.к. плохо знают особенности построения предложений на математическом языке.
9 задание
С этим заданием не справились только 4 человека. Большинство нашли способ прочтения данного числового выражения. Такие результаты связаны с тем, что на уроках часто приходится записывать числовые выражения «на слух». Некоторые ребята предлагали нерациональные способы прочтения числового выражения. В частности, предложение становилось громоздким из-за большого количества лишних слов и недостаточного использования соответствующей терминологии.
Выводы:
1. Учащиеся продуктивнее работают с материалом, представленным в наглядной форме. Кодировка тех же понятий в словесной форме стоит ступенькой выше, так как из словесного ряда приходится выделять связи между понятиями. Поэтому необходимо вести специальную работу по формированию умения воспринимать математический материал в словесной форме.
2. Предложенные задания были сформулированы в необычной для учащихся форме, поэтому составили для шестиклассников большие трудности. Приверженность только к одной форме подачи материала снижает уровень подготовки школьников. Систематическое использование в школьной практике лишь одной формы объяснения материала приводит к тому, что учащиеся перестают понимать смысл этого же задания на естественном языке. Поэтому для повышения эффективности изучения материала необходимо повторять основные моменты в видоизмененных формах, варьировать способы его изложения. В частности, в системе упражнений по каждой теме следует предусмотреть, помимо прочих, задания в словесной формулировке. Такое соотношение различных форм будет способствовать более глубокому усвоению материала.
Таким образом, использование только одной формы подачи материала приводит к слабой подготовке школьников к работе с вербальным материалом, что сказывается на глубине и прочности их знаний, а так же ограниченности их применения и в конечном итоге на общем уровне математической подготовки школьников.
§5. Методика обучения учащихся 5-6 классов темам, связанным с
понятием числа, направленная на развитие их математической речи
Курс математики 5-6 классов основной целью ставит обобщение изученного ранее, расширение понятия числа (от множества натуральных чисел до множества рациональных чисел), подготовку к восприятию систематического курса математики. Мы поставили перед собой еще и развивающую цель, а именно развивать математическую речь учащихся. В данной части покажем, какую работу мы проводили с учащимися для достижения поставленной цели.
Именно в этом возрасте (5-6 классы), когда закладываются основы математических знаний и формируются основные математические умения, необходимые для успешного обучения в старших классах, целесообразно начать систематическую работу (принцип систематичности) по развитию математической речи учащихся, что так же является необходимым условием успешного обучения математике.
Учитывая возрастные особенности учеников 5-6 классов, мы использовали разнообразные формы работы с учебным материалом, что способствовало снижению утомляемости детей, повышению их работоспособности и интереса к предмету.
Содержание составляет арифметико-алгебраический материал: числовые и алгебраические выражения и их преобразования, уравнения и текстовые задачи, то есть основные линии школьного курса математики 5-6 классов, связанные с понятием числа.
Это связано, во-первых, с исключительной важностью данного материала для дальнейшего обучения, для общей математической подготовки, т.к. понятие числа - одно из важнейших понятий во всем школьном курсе математики; во-вторых, с особенностями конкретного класса. Ранее было установлено (см.§4, с.24), что большинство учащихся экспериментального класса обладает метрической подструктурой математического мышления, а значит наиболее доступным и легко усваиваемым является арифметико-алгебраический материал.
Так как методика разрабатывалась для конкретного класса, в котором дети преимущественно со средними математическими способностями и средним уровнем обучаемости, сложность используемых упражнений рассчитана на средний уровень.
Надо отметить, что нами не вводилось новое содержание. На содержании, предложенном в стабильном школьном учебнике математики, мы иными способами организовывали работу учеников с учебным материалом и уделяли внимание именно формам работы учащихся, полезным для развития их математической речи.
За счет различных форм организации деятельности учащихся удавалось поддерживать интерес к изучаемому материалу (особенно во время изучения темы: "Натуральные числа и число нуль", когда практически весь материал ученикам уже знаком). В частности, мы содержательно дополняли учебный материал, раскрывая смысл терминов и их происхождение.
Из основных направлений курса математики 5-6 классов, связанных с понятием числа, нами были выделены следующие:
1) этимология математических терминов и знаков;
2) числовые и буквенные выражения;
3) уравнения;
4) сюжетные задачи.
Будем понимать под блоком каждое из названных направлений вместе с целями его рассмотрения с точки зрения развития математической речи учащихся, набором заданий, формами работы с ним. Всего их 4. Опишем подробно каждый блок.
Блок №1. Этимология математических терминов и знаков
В данном блоке мы рассматривали задания, направленные на освоение символического языка математики, а так же говорили о семантике при работе с терминами.
Одним из приемов развития математической речи учащихся является знакомство с происхождением математических терминов и знаков. При работе с терминами использовались задания учащимся, способствующие приобщению их к чтению детской математической литературы.
Вводя термин, связанный с понятием числа, действием, мы давали исторические сведения, объясняли, почему появилось именно такое название, обозначение. Например, в теме: "Натуральные числа и число нуль" при введении термина "натуральное число" мы говорили о том, что этот термин произошел от латинского слова "natura", что в переводе на русский язык означает "естественное", "природное". Действительно, натуральные числа возникли совершенно естественно, из потребностей в счете предметов. Отсюда же пошли такие выражения, как натуральный цвет, натуральный продукт, натура человека. Другой пример. При изучении действий над натуральными числами в 5 классе ребятам было рассказано о том, как появился знак "+" для обозначения действия сложения. От французского слова "et", что в переводе означает союз "и" и выражает смысл действия сложения, постепенно в процессе упрощения записи в скорописи осталось только "t", а затем и вообще только "+". Это объяснение ученикам очень понравилось, т.к. они как раз начали изучать французский язык, и это слово им уже было известно. Кроме того они заинтересовались происхождением других математических знаков. В дальнейшем учащимся систематически предлагались задания найти самостоятельно в литературе происхождение термина или знака, речь о которых шла на уроке. Школьникам предлагались только те термины и знаки, которые наиболее доступно для учащихся описаны в литературе. Тем самым дети приучались искать термины и учились работать с математической литературой.
Укажем перечень математических терминов и знаков по темам, связанным с понятием числа, поиск происхождения которых был предложен учащимся.
Математические термины: абсцисса, арифметика, натуральное число, плюс, минус, сумма, модуль, нуль, цифра, алгоритм, масштаб, процент, ордината, координата, коэффициент.
Математические знаки: знаки для обозначения умножения, деления, знаки сравнения (больше, меньше), знак равенства, знак модуля, степени.
Те термины и знаки, возникновение которых трудно найти в литературе или там недостаточно понятное объяснение, разъяснялись учителем. Перечислим некоторые из них: диаграмма, дробь, задача, кратное, отношение, пример, пропорция, произведение, математика, равенство, уравнение, рациональное число, чертеж, знаки: "+", "-", "%".
Итогом такой систематической совместной работы стала классная картотека "Этимология математических терминов и знаков" по темам, связанным с понятием числа. Нами предполагается в дальнейшем пополнять картотеку «новыми» терминами и знаками и возвращаться к ней каждый раз при повторении тех или иных вопросов.
Особенно полезными при составлении картотеки оказались книги [6],[9],[16]из списка литературы.
Все собранные сведения о происхождении математических терминов и знаков, связанных с понятием числа, представлены в алфавитном порядке в приложении 1 (см. с.49).
Блок №2. Числовые и буквенные выражения
В данном блоке мы рассматривали задания, направленные на формирование умения переводить символическую запись на естественный язык (вариативно) и осуществлять обратный перевод. Кроме того, задания направлены на развитие умения воспринимать задание на слух, критического отношения к математическому тексту, а так же внимания.
Нами были выделены типы заданий, каждый из которых нацелен на формирование какого-то определенного умения. Некоторые типы упражнений являются взаимосвязанными, взаимообратными (например, типы 1 и 2) и поэтому использовались нами совместно, что отвечает принципу укрупнения дидактических единиц [46]. Ниже опишем, какие задания входили в каждый тип, и как была организована работа учащихся с ними.
1 тип. Задания, направленные на формирование умения переводить текст с
естественного языка на математический
Выполняя упражнения этого типа, школьники учились переводить текст с естественного языка на математический, осваивали синтаксис языка математики.
Ниже приведем набор заданий, характерных для этого типа, который использовался нами для работы учащихся в течение нескольких уроков. Задания расположены по степени нарастающей сложности. Ученикам предлагалось на слух записать выражение, используя математические знаки.
Запишите выражение:
-
Частное суммы чисел а и 2,6 и разности чисел в и 8,5.
-
Сумма частного чисел х и 3,7 и частного чисел 3,1 и у.
-
Произведение суммы чисел а и 3,1 и числа в.
-
Сумма произведений чисел а и в и чисел 8 и 65.
-
Утроенная сумма а и в; сумма утроенного а и в; сумма утроенных чисел а и в; сумма утроенного числа а и учетверенного числа в.
-
Произведение суммы удвоенного числа в и 5 и разности числа с и частного чисел 2 и 3.
-
Произведение суммы и разности дробей 1,5 и ¾ уменьшить в 2,5 раза.
-
Разность суммы 1 и квадрата ½ и квадрата разности чисел 1 и ½.
-
Число 17 на 15 больше двух; число а на 15 меньше (больше) числа в.
-
Число 40 в 10 раз меньше числа 400; Число с в 10 раз меньше (больше) числа р.
-
Число к больше (меньше) числа 10 в 5,5 раз; на 5,5.
-
Частное суммы чисел 15,2 и 0,3 и их разности уменьшить в 5 раз.
Вместе с заданиями 1 типа использовались задания второго типа, т.к. их совместное рассмотрение отвечает принципу укрупнения дидактических единиц [46].
2 тип. Задания, направленные на формирование умений переводить текст с
символического языка на естественный (вариативно), свободно владеть математической терминологией
Учащимся предлагались задания по переводу выражений с символического языка на естественный. Причем, среди них содержатся выражения, допускающие несколько вариантов прочтения и выражения, синтаксис в которых нарушен, и поэтому они не поддаются переводу на естественный язык. Приведем набор заданий, который использовался нами для организации устной работы учащихся в течение нескольких уроков.
Прочитайте выражение, если возможно, различными способами:
-
21,7-15=6,7;
-
13,5:4,5=3;
-
28,1+19,38=47,48;
-
12,4*0,2=2,48;
-
18:2; 18*2; 18+2; 18-2;
-
*12+3;
-
7*2/3+7*1/2+7*5/6;
-
(16+4):2-;
-
24*(1/2+3/8+5/6);
-
17*(2,3-4,8);
-
к:12,8-р:4,9;
-
(х+0,7)*(у-3,4);
-
в-:с=а;
-
0,8х+0,9у;
-
(к-р)(р+к)-2,6;
-
3(а+в); 3а+3в;
-
ав+2с; (ав+2)с; а(в+2)с; а(в+2с);
-
3-(х+5); (3-х)+5.
3 тип. Задания, направленные на формирование умения использовать
математические термины, связанные с компонентами и результатом
действий
Укажем характерные задания этого типа, которые систематически использовались для организации устной работы учащихся на уроке.
1. Назовите делимое и делитель в частном:
а) (256+781):(97-92);
б) (3-а):к;
в) (х+у):(к+3);
г) 2х:(у*9).
2. Назовите слагаемые в сумме:
а) (18-7)+14;
б) (х-у)+(к:р);
в) (х*75)+16;
г) (а-13)+(в-86).
3. Назовите уменьшаемое и вычитаемое в сумме:
а) (а+56)-32;
б) (86+53)-(к+7);
в) (в:24)-19;
г) (с:3)-(р*6).
4. Назовите множители в произведении:
а) (18:9)*3;
б) (28-а)*(7+12);
в) 16*(а-р);
г) (28+к)*(к+28).
5. Назовите компоненты и результат действия:
28:4=7 (124-17=107). Запишите, как найти делимое, делитель (уменьшаемое,
вычитаемое). Как теперь называются компоненты и результат действия?
4 тип. Задания, направленные на формирование умения переводить на
математический язык отношения «больше в (на)», «меньше в (на)»
Задания такого типа систематически включались в письменную работу учащихся на уроке. При этом ученикам было дано задание на слух записывать, сразу же переводя на математический язык, текст, предлагаемый учителем. Такая форма работы на уроке способствует развитию внимательности учащихся. Приведем набор заданий, который был использован на одном из уроков.
-
На сколько сумма чисел 4,79 и 0,81 больше (меньше) числа 2,8 (10,7)?
-
На сколько (во сколько) 0,16 меньше разности чисел 18,04 и 5,96?
-
Увеличить сумму чисел 0,813 и 1,027 на (в) 3,5 (раза).
-
Частное чисел 6,1015 и 6,125 уменьшить на (в) 2 (раза).
-
Во сколько раз произведение чисел 0,005 и 2000 больше (меньше) числа 2 (50)?
5 тип. Задания, направленные на формирование умения обосновывать выбор
способа действий, на расширение знаний и воспитание вычислительной
культуры
Учащимся систематически предлагались задания такого типа: найти рациональный способ вычисления значения числового выражения и обосновать целесообразность его применения в каждом конкретном случае. Иногда мы, включая такие упражнения, предлагали учащимся просто найти значение числового выражения. В этом случае чаще всего находились дети, которые замечали, что есть удобный способ вычисления. Если же этого не происходило, ученикам давалась возможность решать выбранным ими способом, и лишь только после этого внимание детей обращалось на поиск другого решения. Таким образом, одно и то же задание выполнялось двумя способами, и учащиеся имели возможность сравнить решения и лишний раз убедиться в том, что законы и свойства действий чаще значительно упрощают вычисления. Приведем ниже набор заданий, характерных для данного типа, который использовался нами для организации устной и письменной работы учащихся в течение нескольких уроков.
А) Вычислите значение выражения рациональным способом:
-
50*(2*764);
-
(402*1,25)*8;
-
2,5*8,6*4;
-
19+78+845+81+155;
-
36*125;
-
(3/4+1/2+5/12)*12;
-
4*1/7+4*2/7+4/7*4;
-
48*32+48*68+52*37+52*63;
-
24*11; 24*111;
-
399*25;
-
(317+25)*4-3*317;
-
(109,2+92,397)-9,2;
-
259,45-(9,45+43);
-
(280+144-428):4;
-
1/9:14+2/9:14+2/3:14.
Б) Зная, что 7*11*13=1001, 3*37=111, вычислите:
-
2*3*5*37;
-
4*7*11*13*15;
-
13*20*77;
-
37*18;
-
49*11*13;
-
77*37*30*13.
Помимо заданий для устной и письменной работы учащихся на уроке, нами были разработаны разноуровневые обучающие самостоятельные работы, а так же творческие задания, включающие упражнения, подобные рассмотренным выше. При этом учащимся с низким уровнем развития математической речи предлагалось выполнить вариант 1, со средним - вариант 2, с высоким - вариант 3, с высшим - вариант 4. Пример одной из таких самостоятельных работ находится в приложении 2 (см. с.53), в том же приложении, но на странице 52 представлены творческие задания учащимся.
Блок №3. Уравнения
В данном блоке основное внимание направлено на формирование умений учащихся переводить текст с естественного языка на символический и осуществлять обратный перевод, обосновывать действия.
В школьном курсе математики можно проследить несколько математических линий, которые из класса в класс получают развитие, углубление и конкретизацию. Однf из них - линия уравнений. Анализ учебников [3,4,10,11,36,37] показал, что в 5-6 классах в связи с потребностью решать "новые" уравнения расширяется понятие числа. Кроме того, постепенно увеличивается количество способов решения уравнений. Анализ линии уравнений в курсе математики 5-6 классов оформим в виде таблицы (таблица № 4).
Таблица №4. "Анализ линии уравнений в курсе математики 5-6 классов (по учебникам Барановой И.В. и Борчуговой З.Г.)"
Класс
Тема
Содержание
Обоснование
решения
Опорные
знания
5
6
Натуральные числа
Дроби
Десятичные дроби
Проценты. Пропорции
Рациональные числа
Понятие об уравнении. Нахождение неизвестного компонента действия. Законы и свойства действий.
Решение простейших уравнений. Свойства и законы действий. Нахождение неизвестного компонента действия.
Решение уравнений. Законы и свойства действий. Нахождение неизвестного компонента действия.
Отношение. Равенство отношений (пропорция). Основное свойство пропорции. Нахождение неизвестного члена пропорции.
Свойства равенств. Приведение подобных слагаемых. Понятие «модуль числа». Законы и свойства действий. Нахождение неизвестного компонента действия.
На основе зависимости между компонентами и результатом действия. На основе законов и свойств действий.
На основе зависимости между компонентами и результатом действия. На основе законов и свойств действий.
На основе зависимости между компонентами и результатом действия. На основе законов и свойств действий.
На основе зависимости между крайними и средними членами пропорции.
На основе определения понятия «модуль числа». На основе свойств равенств. На основе законов и свойств действий. На основе зависимости между результатом и компонентами действия, в частности устанавливается когда произведение равно нулю.
Зависимость между компонентами и результатом действия. Законы и свойства действий.
Основное свойство дроби. Законы и свойства арифметических действий. Возникновение дробей.
Десятичные дроби. Законы и свойства арифметических действий.
Основное свойство пропорции.
Модуль числа. Приведение подобных слагаемых. Свойства равенств. Законы арифметических действий.
Таблица №4 содержит информацию о том, что на протяжении обучения математике в 5-6 классах меняются подходы к решению уравнений, появляются различные способы обоснования действий. Таким образом, по мере накопления знаний об уравнениях и способах их решения появляется возможность разных обоснований при решении одного и того же уравнения.
В течение двухлетнего обучения математике (5-6 классы) умению решать уравнения уделялось огромное внимание. Решение уравнений всегда сопровождалось проговариванием, обоснованием учащимися выполняемых действий. При этом (там, где это было возможно) рассматривалось несколько способов решения. Помимо этого, учащимся предлагались специальные формы работы по решению уравнений, направленные, в первую очередь, на развитие математической речи школьников.
Нами были выделены следующие два типа упражнений: задания, направленные на формирование умения переводить текст с естественного языка на математический и умения обосновывать действия.
1 тип. Задания, направленные на формирование умения переводить текст с
естественного языка на математический
Учащимся давались задания: перевести текст с естественного языка на математический, при этом сделать это, если возможно, несколькими способами, составить уравнение и решить его.
Ниже укажем характерные задания для 1 типа. Они расположены по нарастающей степени сложности и использовались нами для работы учеников в течение нескольких уроков.
Найдите при каком значении буквы:
1. Сумма х и 22 равна 14,5;
2. Сумма 8а и 3 равна 4469;
3. Разность 25с и 5 равна 6065;
4. 3р больше р на 48;
5. 27к на 12 меньше 201;
6. 8n вдвое меньше 208;
7. 380 в 19 раз больше удесятеренного числа р;
8. 7х больше 4х на 51;
9. 6р меньше 23р на 102;
10. 25с больше 5с на 6060;
11. 5с меньше 25с на 6060;
12. 6060 меньше 25с на 5с;
13. 6060 больше 5с на 15с;
14. Разность к и 9,11 в 4 раза меньше их суммы.
Предложите различные способы записи на символическом языке, если это возможно.
Задания такого типа систематически включались в упражнения для письменного решения на уроке и в домашние задания. Кроме того, похожие задания входили в разноуровневые обучающие самостоятельные работы, одна из таких самостоятельных работ представлена в приложении 3 (см. с.57). При этом, как и раньше, вариант 1 предлагался учащимся с низким уровнем развития математической речи; вариант 2 - со средним; вариант 3- с высоким; вариант 4 - с высшим.
2 тип. Задания, направленные на формирование умения обосновывать действия
Второй тип заданий представляет собой решение уравнений с письменным обоснованием каждого шага. Использовались следующие две формы работы: объяснение уже готового решения; одновременное решение уравнения и обоснование каждого шага решения.
Ниже эти две формы рассмотренны подробнее на конкретных примерах.
При решении уравнений на первом этапе систематически использовалась следующая форма работы: учащимся предлагалось обосновать письменно каждый шаг уже решенного уравнения. Приведем пример карточки с таким заданием (первый и второй столбики напечатаны на карточке, третий столбик заполняется учеником)
№ шага Решение Общие положения математики
1. 3х-84=11-2х
2. 3х-84+2х=11
3. 3х+2х=11+84
4. (3+2)х=95
5. 5х=95
6. х=95:5
7. х=19
Ответ: х=19.
Еще одна форма работы заключалась в решении уравнений, но с письменным обоснованием каждого шага. Приведем пример подобной карточки, в которой все, кроме условия, выполняет ученик.
№ шага Условие(следствия) Общие положения математики Результат
1. 5y+3у=12 Распределительный закон умножения (5+3)у=12
относительно сложения
2. 8у=12 Чтобы найти второй множитель, надо у=12:8
произведение разделить на первый
множитель
3. у=1,75
Ответ: у=1,75
В соответсвии с выполненным анализом линии уравнений в курсе математики 5-6 классов на разных этапах обучения приводились разные положения математики для обоснования решения уравнения, а на этапе итогового повторения предлагалось найти несколько способов решения. Таким образом, одни и те же карточки использовались неоднократно. Приведем пример такой карточки с указанием места ее примениения и варианта выполнения.
В 5 классе к решению уравнений возвращаются несколько раз в одной и той же теме. В теме: "Натуральные числа" при решении уравнений можно давать разные обоснования: сначала только на основе зависимости между результатом и компонентами действия, а затем на основе законов и свойств действий. При расширении понятия числа до множества положительных рациональных чисел мы вновь возвращаемся к решению уравнений, при этом обоснования остаются прежними.
Выполнение на основе зависимости между результатом и компонентами действия.
№ шага Условие (следствия) Общие положения математики Результат
1. 86+(х+138)=250 Чтобы найти второе слагаемое, х+138=250-86
надо из суммы вычесть первое
слагаемое
2. х+138=164 Чтобы найти первое слагаемое, х=164-138
надо из суммы вычесть второе
слагаемое
3. х=26
Ответ: х=26.
Выполнение на основе законов и свойств действий.
№ шага Условие (следствия) Общие положения математики Результат
1. 86+(х+138)=250 Переместительный закон сложения 86+(138+х)=250
2. 86+(138+х)=250 Сочетательный закон сложения (86+138)+х=250
3. 224+х=250 Чтобы найти второе слагаемое, х=250-224
надо из суммы вычесть первое
слагаемое
4. х=26
Ответ: х=26.
В 6 классе появляются отрицательные числа и рассматривается свойство равенств (прибавление к обеим частям равенства одного и того же числа). На основе этого свойства и ранее изученных вводится новый способ решения уравнений (перенос слагаемых из одной части уравнения в другую с противоположным знаком).
Выполнение на основе свойств равенств.
№ шага Условие (следствия) Общие положения математики Результат
1. 86+(х+138)=250 Перенос слагаемого 86 вправо х+138=250-86
с противоположным знаком
2. х+138=164 Перенос слагаемого 138 вправо х=164-138
с противоположным знаком
3. х=26
Ответ: х=26.
Кроме этого, использовались задания с пропусками, примеры которых можно найти в самостоятельной работе (см. приложение 3, с.57), а так же учащимся предлагались разноуровневые творческие работы по теме: "Решение уравнений. Составление уравнений", где вариант 1 предлагался учащимся с низким уровнем развития математической речи, вариант 2 - со средним, вариант 3 - с высоким, вариант 4 - с высшим (см. приложение 3, с.57).
Блок №4. Текстовые задачи
В данном блоке мы рассматривали задания, направленные на формирование умения переводить текст с естественного языка на графический, алгебраический и осуществлять обратный перевод, на воспитание критичности и вариативности мышления.
Решение текстовых задач требует определенной языковой культуры, в частности, умения подойти к формулировке задачи как особому типу текста на естественном языке, т.е. умения решить лингвистическую проблему - анализ текста.
Часто в школьной практике возникают ситуации, когда ученик не справляется с задачей потому, что не понимает каких-то слов, предложений в условии задачи; либо подменяет выполнение требуемого задания - другим, привычным ему, не замечая этого.
Обучение решению текстовых задач арифметическим способом нацелено с одной стороны на развитие мышления (важен не столько результат, сколько процесс решения), с другой стороны - на развитие речи (учащимся приходится пересказывать условие, анализировать его, при необходимости переформулировать, ставить вопросы и давать на них развернутые ответы).
Обучение решению текстовых задач составлением уравнений нацелено, прежде всего, на формирование очень важного умения - умения переводить информацию с естественного языка на символический (и обратно). Составить уравнение - значит выразить математическими символами условие, сформулированное словами. Это перевод с обычного языка на язык математических формул. Трудности, которые могут встретиться при составлении уравнений, являются трудностями перевода. Когда мы пытаемся выразить математическими символами условие, сформулированное словами: во-первых, мы должны понять условие; во-вторых, мы должны быть знакомы со средствами математического языка.
И в том, и в другом случае важно убедиться, что учащиеся понимают все термины и обороты речи, использованные в тексте задачи, что они представляют саму ситуацию, описанную в тексте. Принципиальное условие, без которого многим учащимся трудно будет решить задачу, - использование в процессе решения схематических рисунков, моделей, позволяющих представить рассматриваемую ситуацию в наглядном виде. Иногда эту ситуацию полезно даже разыграть.
Наряду с традиционной работой по решению сюжетных задач мы включали специальные формы работы учащихся по решению задач, направленные, в первую очередь, на развитие математической речи. Эти формы работы систематически включались в работу на уроках, посвященных решению текстовых задач.
При решении сюжетных задач на движение, т.к. они вызывали наибольшие трудности у учащихся, мы использовали один из приемов: изображение графической модели и рассмотрение различных ситуаций. Этот прием направлен на осмысление условия задачи, на осознание детьми значимости каждого слова в тексте. И только после осмысления начинали решать.
Задачи, решаемые составлением уравнения, так же для большинства учащихся представляют трудность (трудность перевода). Этот материал для учеников 5-6 классов является новым и при этом очень важным для обучения в старших классах. В связи с этим, учащимся была предложена специальная форма работы с задачами на составление уравнений.
И в первом, и во втором случаях применялся "метод обратных задач" как одна из характерных особенностей системы укрупнения дидактических единиц [46]. Для того, чтобы каждая задача могла считаться решенной, необходимо решать или, по крайней мере, точно формулировать обратную задачу. Для получения обратной задачи в условие исходной вводится ее ответ, а некоторые числа из условия переводятся в разряд искомых. Умение сформулировать и решить прямую и обратную задачи является важным критерием достигнутой учеником глубины понимания изучаемого материала и показателем развития его математической речи. Использование этого метода отражено в творческих заданиях по теме: "Составление и решение задач на движение" (см. приложение 4, с.61).
Кроме уже названного использовались специальные задания, направленные на формирование умения работать с текстом задачи, в частности, умения переформулировать текст. Это помогло снять проблемы интерпретации и понимания текста.
Далее на конкретных примерах подробно рассмотрим каждый из перечисленных выше трех типов заданий и опишем работу учащихся с ними.
1тип. Задания, направленные на формирование умения переформулировать текст
Задания такого типа систематически использовались для устной работы на уроке. На каждую парту выдавалась карточка с заданием для работы в парах. Учащимся предлагалось задание соединить знаком «↔» фразы из разных столбцов карточки, имеющие одинаковый смысл. Надо отметить, что среди предложенных в правом столбце фраз есть такие, которым в левом столбце соответствует только одна, несколько фраз или вообще нет подходящей по смыслу. В таком случае учащиеся предлагали свои варианты.
Приведем пример одной из таких карточек.
Количество орехов, которое было сначала. Одновременное отправление.
Количество станков, которое необходимо Совместная работа.
выпустить по плану.
Бригада выполнила задание в срок. Производительность.
Отправление в путь в одно и то же время. Движение по течению реки.
Количество деталей, выпускаемое каждый Стоимость товара.
день.
Группа биологов, выполняющих задание Первоначальное количество.
вместе.
За 6 дней рабочий заточил 250 деталей. Ежедневный выпуск.
Из пункта А в пункт В вышли 2 пешехода. Движение в одном направлении.
Катер идет по озеру с небольшой скоростью. Скорость в стоячей воде.
Человек плывет по реке. Плановое выполнение.
За 12 почтовых марок уплатили 24 рубля. Движение против течения реки.
Каждый час пешеход проходит 7 км. Цена товара.
2 тип. Задания, направленные на формирование умений переводить текст с
естественного языка на графический, видеть различные ситуации
Помимо задач на движение, имеющих единственное решение, в работу систематически включались задачи, допускающие несколько равноправных решений. При этом для того, чтобы помочь учащимся осознанно выделять все возможные ситуации, описанные в условии задачи, им была предложена памятка, которая находилась на парте у каждого ученика на уроках обучения решению задач на движение.
Памятка
1. Сколько участников действует?
2. Начинают и заканчивают движение они одновременно или нет?
3. Как они движутся:
а) в одном направлении (в догонку или с отставанием)?
б) в противоположных направлениях (навстречу или с удалением)?
4. Подумайте, сколько раз может произойти описываемая ситуация?
5. Что известно в задаче о величинах s, t, v?
6. Что требуется узнать в задаче?
Первые четыре вопроса помогают представить ситуацию, описываемую в задаче, на рисунке. На первом этапе по решению задач на движение учащимся предлагалось ответить последовательно на первые четыре вопроса памятки и после этого изобразить рисунок (рисунки) к описываемой ситуации в задаче. И только затем переходить к вопросам 5-6 памятки. Приведем один из наборов задач, составленных нами, который использовался на уроках по обучению решению текстовых задач на движение. При решении задач учащимся постоянно предлагались задания типа: выясните направление движения, сделайте графическую иллюстрацию к описанной ситуации.
Набор заданий к теме: "Задачи на движение"
1. Расстояние между пунктами А и В - 90 километров. Из пункта А вышел пешеход по дороге, проходящей через эти пункты, со скоростью 6 км/ч. На каком расстоянии от пункта В будет находиться пешеход через 5 часов? (2 ситуации)
-
В 7ч.15мин. от двух станций, расстояние между которыми 3560км, одновременно навстречу друг другу отошли два поезда. Один - со скоростью 100 км/ч, другой - 80 км/ч. Через сколько часов расстояние между ними будет 50 км? (2 ситуации)
-
Одновременно из двух пунктов вышли два пешехода. Первый пешеход шел со скоростью 6 км/ч, второй - со скоростью 4 км/ч. Через 5 часов они оказались в одном и том же месте. Какое расстояние было между пешеходами первоначально? (2 ситуации)
4. Первый пешеход, идущий со скоростью 6км/ч, оказывается со вторым, идущим со скоростью 4км/ч, в одном и том же месте одновременно. Через сколько часов это произошло, если первоначально расстояние между ними было 10 км и они вышли одновременно? (2 ситуации)
Составьте и решите обратные задачи.
5. Одновременно из одного пункта вышли два пешехода. Первый пешеход имеет скорость 6км/ч, а второй - 4км/ч. Какое расстояние будет между ними через 5 часов? (2 ситуации)
Составьте и решите обратные задачи.
6. Одновременно из одного пункта вышли два пешехода. Первый пешеход идет со скоростью 6км/ч, а второй - со скоростью 4км/ч. Через сколько часов расстояние между ними станет равным 10 км? (2 ситуации)
Составьте и решите обратные задачи.
-
В 7ч. 15мин. от двух станций, расстояние между которыми а км, одновременно в
разных направлениях отошли два поезда. Один - со скоростью 100 км/ч, другой - 80 км/ч. Через сколько часов расстояние между ними будет 500 км? Составьте алгебраическое выражение. (3 ситуации)
8. Из двух пунктов А и В, расстояние между которыми 100 км, одновременно по одной дороге, проходящей через эти пункты, выехали два велосипедиста. Велосипедист, выехавший из пункта А, имел скорость 10км/ч, а велосипедист, выехавший из пункта В, - 15км/ч. Какое расстояние будет между ними через 4 часа? (4 ситуации)
Составьте и решите обратные задачи.
-
В 7ч. 16мин. от двух станций, расстояние между которыми а км, одновременно
отошли два поезда. Один - со скоростью 100км/ч, другой - 80 км/ч. Через какое-то время расстояние между ними стало 500 км. Сделайте рисунок (рисунки) к описанной в задаче ситуации. (5 ситуаций)
Приведем пример работы учащихся с одной из задач, например, с девятой. Учащиеся последовательно отвечали на вопросы памятки и изображали графически возможные ситуации. Таким образом, ученики отмечали, что речь в задаче идет о двух объектах - поездах, которые начинают и заканчивают движение одновременно. При ответе на третий вопрос памятки учащиеся устанавливают, что возможны несколько ситуаций: поезда могут двигаться в одном направлении в догонку , в одном направлении с отставанием, в противоположных направлениях с удалением друг от друга, навстречу друг другу . В результате ученики изображают четыре возможные ситуации.
При ответе на четвертый вопрос памятки учащиеся анализируют каждую выделенную и схематически изображенную на рисунке ситуацию, выясняя, сколько раз может возникнуть такая ситуация.
5-6 пункты в данном случае опускаются. Далее учащимся предлагалось следующее задание: выяснить от чего зависит количество различных ситуаций. Для этого ребятам предлагались вопросы:
-
Что нужно изменить в условии задачи, чтобы возможными оказались только ситуации, изображенные на рисунках а и б?
-
Что нужно изменить в условии задачи, чтобы возможными оказались только ситуации, изображенные на рисунках в, г и д?
-
Что нужно изменить в условии задачи, чтобы возможными оказались только ситуации, изображенные на рисунках г и д?
Тем самым ученики еще раз убеждались в том, что в задаче важным является
каждое слово.
Подобного рода задания (по переводу текста с естественного языка на графический) и задания, требующие выполнения обратного перевода (с графического языка на естественный) включались в творческие задания. Пример творческих заданий можно найти в приложении 4 (см. с.61), при этом ученикам с низким уровнем развития математической речи предлагался вариант 1, со средним - вариант 2, с высоким - вариант 3, с высшим - вариант 4.
3 тип. Задания, направленные на формирование умения переводить текст с
естественного языка на символический (составление уравнений) и
осуществлять обратный перевод
Обучение решению текстовых задач составлением уравнений осуществлялось следующим образом: сначала учащиеся производили перевод отдельных частей, словосочетаний из условия задачи на математический язык, а затем составляли уравнение и решали его. При этом огромную роль играла форма записи условия задачи. Каждое выражение естественного языка заменялось выражением символического языка. Рассмотрим форму записи, которую использовали учащиеся при работе с задачами, решаемыми составлением уравнения. Ученики готовили в тетради таблицу, состоящую из двух столбцов. В левом столбце ребята записывали условие на естественном языке, в правом - то же самое, но на символическом.
Задача 1. Задумали число, вычли из него 10, результат умножили на 1/2 и прибавили 12. Полученное число умножили на 5 и получили 70. Найдите задуманное число.
На естественном языке На математическом языке
Задумали число х
Вычли из него 10 х-10
Результат умножили на 1/2 1/2*(х-10)
К произведению прибавили 12 1/2*(х-10)+12
Полученное число умножили на 5 (1/2*(х-10)+12)*5
Т.к. получили 70, то можно составить уравнение (1/2*(х-10)+12)*5=70
Далее учащиеся решали составленное уравнение.
Задача 2. На одной полке в 3 раза больше книг, чем на другой. Всего на двух полках 48 книг. Сколько книг на второй полке?
На естественном языке На математическом языке
Количество книг на одной полке у
Количество книг на другой полке 3у
Количество книг на двух полках у+3у
Т.к. по условию книг 48, то можно составить уравнение (у+3у)=48
Далее учащиеся решали составленное уравнение.
Решение очень многих текстовых задач удобно записывать в выше описанной форме. Эта форма записи хорошо воспринимается учениками, так как является наглядной, удобной и краткой. При такой форме записи учащиеся видят пошаговый перевод текста с естественного языка на математический. В приложении 4 (см. с.61) представлена одна из обучающих самостоятельных работ, в которой ученикам предлагалось использовать выше описанную форму записи. Кроме того, там же можно найти и обратное задание, т.е. составление текстовой задачи по уравнению, и ее решение, что характерно для использования принципа укрупнения дидактических единиц при обучении математике [46]. Каждый учащийся выполнял задания, соответствующие его уровню развития математической речи. Вариант 1 предлагался детям с низким уровнем развития математической речи, вариант 2 - со средним, вариант 3 - с высоким, вариант 4 - с высшим.
Результаты опытной проверки разработанной методики
Под результатами опытной проверки будем понимать достигнутый каждым учеником уровень развития математической речи. Поэтому нами была поставлена цель: определить уровень развития математической речи учащихся в результате апробации разработанных материалов.
Для этого был составлен тест (тест №3), включающий в себя задания, аналогичные заданиям 2,3,4,8,9 теста №2 (см.§4, с.24), которые вызвали трудности у учеников. Задания, аналогичные 1,5,6,7 теста №2 не включены в виду того, что с ними не возникло трудностей и при первом тестировании.
В тестировании принимали участие 28 учащихся 6б класса. На выполнение тестового задания было отведено 25 минут.
Тест №3."Уровень развития математической речи учащихся 5-6 классов
(повторный)"
1. Найдите число, треть которого в 5 раз больше числа 12.
2. Запишите выражение: "Разность квадратов чисел 2у и 17 увеличить в полтора раза,
полученный результат уменьшить на число, обратное 2".
3. Из двух пунктов, расстояние между которыми в км, одновременно вышли два
пешехода. Один - со скоростью 6 км/ч, другой - 7 км/ч. Через какое-то время
расстояние между ними стало 22 км. Сделайте рисунок к описанной в задаче
ситуации.
4. Напишите на естественном языке следующее выражение:
(х - 3:0,5)*((х-3):0,5)+2,6.
5. Запишите предложение: "Модуль числа к на 2,3 меньше суммы модулей чисел 4 и -
2", используя математические знаки. Предложите несколько вариантов записи.
Результаты тестирования оформим в виде сводной таблицы (таблица №5), которая представлена в приложении 5 (см. с.67).
Количественный анализ результатов теста №3
По результатам тестирования определялся достигнутый уровень развития математической речи учащихся после опытной проверки материалов. Критерий определения уровня языкового развития следующий:
Количество правильно выполненных заданий Уровень развития математической речи
0-3 Низкий
4 Средний
-
Высокий
Результаты тестирования показали следующее:
-
28% учащихся имеют низкий уровень развития математической речи.
-
47% учащихся имеют средний уровень развития математической речи.
-
Высокий уровень развития математической речи имеют 25% учащихся.
Проведем сравнительный анализ результатов теста №2 (см. с.25) и теста№3. Проследим, какие изменения произошли при выполнении учащимися аналогичных заданий тестов №2 и №3. Оформим сравнительный анализ в виде диаграммы (см. рис. 2).
Р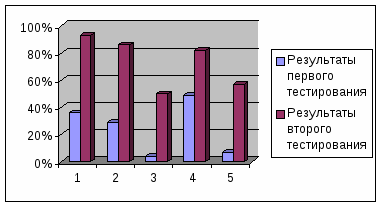
ис.2
Выводы:
-
Результативность выполнения каждого задания повысилась.
-
Наибольшую трудность при первом тестировании для ребят представили задания 3,5. Сейчас же количество правильных и полных ответов учащихся при выполнении аналогичных им заданий значительно возросло. Некоторым учащимся все-таки оказалось сложно выделить все возможные ситуации и увидеть возможности вариативного выполнения заданий.
На второй диаграмме (см. рис.3) мы выполнили сравнительный анализ уровня развития математической речи учащихся класса до и после проведения опытной проверки разработанных материалов.
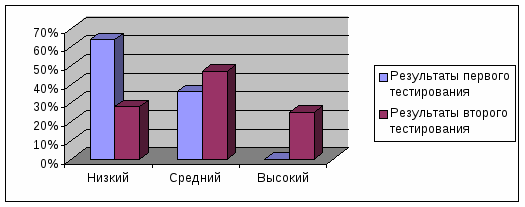
Рис.3
Выводы:
-
28% учащихся (8 человек) остались на низком уровне развития математической речи, что примерно в два раза меньше, чем до апробации материалов в данном классе.
-
Число учащихся, имеющих средний уровень развития математической речи, увеличилось до 47% (13 человек). На средний уровень с низкого перешли многие учащиеся. Кроме того, некоторые ребята так и остались на среднем уровне.
-
25% учащихся (7 человек) смогли поднять уровень развития математической речи со среднего, в единичных случаях - с низкого до высокого.
-
В целом работа удалась, т.к. большинству учащихся удалось повысить свой уровень развития математической речи, четверть класса - это ученики с высоким уровнем развития математической речи. Примерно три четверти класса (около 75%) - это дети с достаточно хорошо развитой математической речью, тогда как первоначально их было приблизительно 36%. Надо отметить, что учащиеся с низким уровнем развития математической речи, при выполнении многих заданий стали чувствовать себя увереннее и справлялись с ними лучше.
Заключение
Опыт работы в школе показывает, что многие учащиеся находятся в большой зависимости от формы вопроса, подачи информации. Школьники не всегда могут правильно сформулировать ответ, т.к. или не владеют математическим языком школьного курса, или не понимают сути вопроса, не всегда могут обосновать выполняемое действие. Поэтому и была поставлена цель работы: разработать методику обучения учащихся 5-6 классов темам, связанным с понятием числа, направленную на развитие их математической речи и основанную на понимании учащимися материала.
Для достижения этой цели была изучена литература, посвященная вопросам взаимосвязи понятий «математическое мышление», «математическая речь», а так же выполнен анализ стабильных школьных учебников математики 5-6 классов.
Кроме того, мы выявили некоторые особенности экспериментального класса, знание и учет которых был необходим для дальнейшей работы, а именно уровень развития математической речи и ведущую подструктуру математического мышления учащихся.
В результате поставленная цель дипломной работы достигнута, была разработана методика обучения учащихся 5-6 классов темам, связанным с понятием числа, направленная на развитие их математической речи и основанная на понимании учащимися материала, учитывающая особенности учеников.
Основное внимание уделялось формам организации работы учащихся с заданиями, которые имеют место во всех школьных учебниках математики 5-6 классов. Кроме того, были разработаны и специальные задания, которых нет в стабильных школьных учебниках, направленные, в первую очередь, на развитие математической речи учащихся, а так же разноуровневые самостоятельные и творческие работы, что позволило дифференцировано подходить к проверке знаний и умений учащихся и стимулировать творческую деятельность школьников.
Использование различных форм работы учащихся с учебным материалом (письменное обоснование каждого шага действия при решении уравнений, параллельная запись условия сюжетной задачи на двух языках: естественном и символическом, задания с пропусками и др.) положительно повлияло на возникновение и поддержание интереса школьников к изучаемому предмету.
Все отобранные нами материалы были структурированы, разделены по тематическим блокам и апробированы в школе в течение двух лет в одном и том же классе. Мы и раньше организовывали деятельность учащихся с целью развития математической речи учеников 5-9 классов, однако, это было фрагментарно.
В результате опытной проверки разработанной методики был сделан следующий вывод: систематическая работа, направленная на развитие математической речи учащихся, действительно принесла пользу ученикам. Нам удалось повысить уровень развития математической речи у большинства учащихся класса. Мы считаем полученные результаты положительными и убеждены, что подобного рода работа эффективна и оказывает благоприятное воздействие не только на развитие математической речи учащихся, но и на их математическую подготовку и в целом на общую культуру речи.
Приложения
Приложение 1
Этимология математических терминов
Абсцисса. Лат. abscissae-отсекаемые; ab-приставка от; scindere-рвать, резать,рубить и
т.д. Термин Кавальери, перешедший к Декарту и затем распространившийся.
Аполлоний в "Конических сечениях" рассматривал на большой оси эллипса
"отрезки, отсекаемые ординатами, от вершины считая". В современном смысле
ввел Г.Лейбниц в 1765 г. До него - только в смысле Аполлония.
Алгоритм. Араб. От имени ученого Ал-Хорезми, который написал трактат о решении
уравнений различными способами. Тем самым он предъявил четкий порядок
действий.
Арифметика. Греч. Число (аритмос). Отсюда логарифм-соотношение чисел, ритм,
ритмика.
Диаграмма. Греч. диа- через, сквозь. Диаграмма - информация через рисунок, чертеж.
Отсюда диаметр, диалог, диагноз, диапазон, диафильм.
Дробь. Ранее употребляли "ломаное число". Затем число, которое раздробили, стали
называть дробью его часть.
Задача. Греч. ; в лат. транскрипции problema. Средневековый термин,
идущий от комментаторов Евклида. В древности не было деления предложений
на теоремы и задачи. Различие было лишь в том, что в одних предложениях
предлагалось что-то доказать, а в других что-то построить. Решение
заканчивалось стандартной фразой "что требовалось сделать".
Координата. Лат. coordinata - слово, придуманное Г.Лейбницем в 1692г. для
обозначения абсциссы и ординаты вместе (co - собирательная приставка,
ordinare - определять, приводить в порядок, в соответствие). Координаты -
числа, определяющие положение точки. Метод координат принадлежит
Декарту ("Геометрия", 1637г.).
Коэффициент. Лат. со - собирательная приставка; упорядочивание буквенного
выражения.
Кратное. "Крата" - старинное русское слово, означающее "раз".
Масштаб. Немец. - мерный шест.
Математика. Греч. (матэма) - знание, учение, наука, в частности,
точная наука. Античный термин (Платон, Аристотель). Впервые
математиками называли тех последователей Пифагора, которые вместо
дословного повторения изречений своего учителя решались развивать его
учение дальше. Пифагорейцы знали 4 матэмы: учение о числах
(арифметика), о музыке (гармония), о фигурах (геометрия), о светилах
(астрономия или астрология). Впоследствии в математику включили
тригонометрию, оптику и ряд других наук. В средние века математикой
называли даже черную магию. Современный смысл термина "математика"
установился лишь к началу нового времени.
Метр. Франц. - мера (основная единица длины).
Санти - (лат.) сотая часть;
Деци - (лат.) десятая часть (используется для дольных величин);
Милли - (лат.) одна тысячная единицы;
Кило - (франц. от греч.) тысяча.
Минус. Лат. minus - меньше (произошло название знака действия вычитания).
Модуль. Лат. - мера. Модуль используется в архитектуре, информатике и др., величина,
которая принимается как базовая единица.
Натуральное число. Лат. - естественное, природное (natura - природа). Отсюда
натуральный цвет, натура человека.
Нуль. Лат. - никакой (nulla). Начертание буква "о" ("он") до 18 века.
Ордината. Лат. ordinata - упорядоченная. В современном смысле термин "ордината"
введен в 1684г. Лейбницем.
Отношение. Греч. (логос). Античный термин. Лат. ratio. В геометрии: отношение
отрезков или других геометрических величин. В обиходе: связь, отношение
к чему-либо, разум, довод, содержание и десятки других значений.
Плюс. Лат. больше.
Пример. Лат. "примус нумерус" (первые числа) - так называли простые числа. Позднее
слово "примус" превратилось в "пример" и стало обозначать задачу с числами, и
лишь затем приобрело более широкий, не только математический смысл.
Произведение. Русск. в результате что- то производим.
Пропорция. Греч. (аналогия). Аристотель, Евклид. Лат. proportio.
Процент. Лат. от ста, сотая.
Равенство. Греч. (исос). Античный термин. Употреблялся в нескольких смыслах: 1)
равенство чисел (натуральных); 2) равенство фигур; 3) равновеликость фигур;
4) равенство вообще (любых величин). Лат. aequalis. Отсюда экватор.
Рациональное число. Греч. - выразимый, т.е. могущий быть сказанным,
названным. Происходит от глагола говорю, наываю. Термин
Пифагора. Лат. rationalis - имеющие отношение. В древности
отношение а/в понималось не как число, а как символ. В средние
века (Анариций и др. арабские математики) стали рассматривать
отношения как числа, и слова "рациональный" и
"иррациональный" приобрели современный смысл.
Сумма. Лат. - итог, общее количество.
Уравнение. Равенство, уравнивание двух частей.
Цифра. Араб. "сифр" - название нуля, распространившееся на все остальные знаки для
записи чисел.
Чертеж. Греч. (схэма). Античный термин. Лат. переводы - figura, forma. С
современной точки зрения чертеж служит иллюстрацией, вспомогательным
средством для отыскания неизвестной фигуры, которая заранее считается
существующей. У греков же отыскание фигуры и заключалось в
последовательном построении чертежа. Русск. "черта" - древнее слово: насечка,
знак, буква, мгновение. Позже - чертеж.
Шкала. Лат. scala - лестница.
Математические знаки
">,<" Ввел Т. Гарриот в 1631г.
5>3 не параллельны, пересекаются в сторону меньшего.
5<6
Знак >,< в печати появился раньше (буква "v" перевернутая). В старых русских
книгах 7 3 (7>3); 7 11 (7<11).
"=" Равенство. Ввел Р.Рекорд в 1557г. "Нет ничего более равного, чем два
параллельных равных отрезка".
а , а , ... , а Степени. Ввел Р. Декарт в 1637г.
x, y,z Неизвестные или переменные величины. Ввел Р.Декарт в 1637г.
"+, - " Ввели немецкие математики в концет 15 века. Появление знака "+": лат.(франц.)
"et" (и) -> t -> +. "-" - производное от "+". В 15 веке для сложения и вычитания
употреблялись знаки p , m (от лат. plus, minus) - Н. Шюке, Л. Пачоли.
" " Ввел У. Оутред в 1631г. " " Ввел Г.Лейбниц в 1698г. В 17 веке насчитывалось
около десятка математических знаков для умножения и деления: , , , ,*, ,
" " Ввел Г.Лейбниц в 1684г.
"%" Ошибка типографии. От итал. слова сто, которое в процентных расчетах часто
писалось сокращенно cto. Далее произошли две типографские ошибки и появился
знак процента.
" а " Модуль. Ввел К.Вейерштрасс в 1841г.
s=v*t Формула пути. s,v,t - первые буквы латинских слов:
spatium - промежуток
velocitas - скорость
tempus - время
s=a*b Формула площади прямоугольника. s от лат. слова superficies - поверхность.
Приложение 2
Обучающая самостоятельная работа по теме:
«Составление числовых и буквенных выражений»
Вариант 1
-
Запишите числовое выражение на математическом языке:
А) Сумма чисел 5,2 и 2,6;
Б) Разность чисел 9,8 и 8,5;
В) Частное суммы чисел 5,2 и 2,6 и разности чисел 9,8 и 8,5.
-
Предложите 3 способа записи на математическом языке предложения: «Семнадцать на два меньше девятнадцати».
Вариант 2
1. Запишите выражение на математическом языке:
А) Утроенное число а;
Б) Утроенная сумма чисел а и в;
В) Разность утроенной суммы чисел а и в и утроенного числа а.
2. Предложите 3 способа записи на математическом языке предложения:
«Число тридцать два на пятнадцать больше числа в».
Вариант 3
-
Запишите выражение на математическом языке:
А) Квадрат числа а;
Б) Квадрат разности чисел а и в;
В) Частное квадрата числа а и квадрата разности чисел а и в.
-
Предложите 3 способа записи на математическом языке предложения: «Число м в пятнадцать раз меньше числа п».
Вариант 4
-
Запишите выражение на математическом языке:
А) Утроенная разность чисел а и в;
Б) Сумма квадратов чисел а и в;
В) Произведение утроенной разности чисел а и в и суммы квадратов чисел а и в уменьшить на куб числа с.
-
Предложите по 3 способа записи на математическом языке предложений: «Число с больше числа в на к единиц» и «Число с больше числа а в m раз».
Приложение 3
Обучающая самостоятельная работа по теме:
"Составление и решение уравнений"
Вариант 1
-
Найдите число, сумма которого с числом 5,1 равна частному чисел 10,2 и 1/10.
-
Решите уравнение: 17,8*(х+5)=0.
Решение. Произведение 17,8 и х+5 ................ 0, если множитель х+5 равен ............... ,
т.е. х+5=...... , следовательно, х=...... .
Ответ: ........... .
Вариант 2
-
Частное некоторого числа и числа 1/2 на 5,8 меньше удвоенной разности чисел 7,3 и 4/5. Найдите это число.
2. Решите уравнение: (2х-6)*(-12,3)=0.
Решение. Произведение 2х-6 и -12,3 равно ............ , если .............. 2х-6 ............ 0, т.е.
2х-6 ...... 0, следовательно, 2х=....... , а значит х=....... .
Ответ: ............. .
Вариант 3
-
Разность некоторого утроенного числа и его половины в два раза меньше учетверенной суммы 15,5 и 2/3. Найдите неизвестное число.
2. Решите уравнение: (-12,3+7,1)*(3х-17,1)=0.
Решение. Произведение -12,3+7,1 и 3х-17,1 равняется ........... , если ....................... 3х-
17,1 равен ........,т.к. множитель -12,3+7,1 .............. 0. Таким образом, 3х-17,1=.........,
следовательно, 3х=........,а х=......... .
Ответ: ........... .
Вариант 4
-
Одна десятая часть суммы удвоенного неизвестного числа и увеличенного в полтора
раза этого же неизвестного числа больше на 5,2 разности половины неизвестного
числа и 3,2. Найдите неизвестное число.
2. Решите уравнение: (-2,4)*(2,3х+69)*(35-49)=0.
Решение. Произведение .............................. множителей .................. 0 тогда и только
тогда, когда ...................... равен ...... . Произведение -2,4; 2,3х+69 и 35-49
...................,если .......... равен........., т.к. ................ не равны ........ и .................. не
равно ............. . Следовательно, ............ =0, а значит .............=-69, т.е. х=............. .
Ответ: ........... .
Творческие задания по теме:
"Решение уравнений. Составление уравнений"
Вариант 1
1. Объясните каждый шаг решения уравнения.
№ шага Решение Общие положения математики
1. 3х+5х=200
2. (3+5)х=200
3. 8х=200
4. х=200:8
5. х=25
Ответ: х=25.
2. Решите уравнение и обоснуйте каждый шаг решения: 2х+9830=50000. Предложите несколько вариантов обоснования. Оформите в виде таблицы.
№ шага Условие (следствия) Общие положения математики Результат
Вариант 2
1. Объясните каждый шаг решения уравнения.
№ шага Решение Общие положения математики
1. (2х+175)+28=210
2. 2х+(175+28)=210
3. 2х+203=210
4. 2х=210-203
5. 2х=7
6. х=7:2
7. х=3,5
Ответ: х=3,5.
2. Решите уравнение и обоснуйте каждый шаг решения: 20*(16*х)=2560. Предложите несколько вариантов обоснования. Оформите в виде таблицы.
№ шага Условие (следствия) Общие положения математики Результат
Вариант 3
1. Объясните каждый шаг решения уравнения.
№ шага Решение Общие положения математики
1. (130*х):65=260-8х
2. (130:65)*х=260-8х
3. 2х=260-8х
4. 2х+8х=260
5. (2+8)х=260
6. 10х=260
7. х=260:10
8. х=26
Ответ: х=26.
2. Решите уравнение и обоснуйте каждый шаг решения: 0,4х+2,75+6,2х=55,55. Предложите несколько вариантов обоснования. Оформите в виде таблицы.
№ шага Условие (следствия) Общие положения математики Результат
Вариант 4
1. Объясните каждый шаг решения уравнения.
№ шага Решение Общие положения математики
1. 0,3:15=(0,6х-0,55)+х*3,95
2. 0,3:15=(-0,55+0,6х)+х*3,95
3. 0,3:15=(-0,55+0,6х)+3,95х
4. 0,3:15= -0,55+(0,6х+3,95х)
5. 0,02= -0,55+(0,6х+3,95х)
6. 0,02= -0,55+4,55х
7. 0,02+0,55=4,55х
8. 0,57=4,55х
9. х=0,57:4,55
10. х=57/455
Ответ: х=57/455.
2. Решите уравнение и обоснуйте каждый шаг решения: (5у+100)-60=140+3у+20. Предложите несколько вариантов обоснования. Оформите в виде таблицы.
№ шага Условие (следствия) Общие положения математики Результат
Приложение 4
Обучающая самостоятельная работа по теме:
"Текстовые задачи, решаемые составлением уравнений"
Вариант 1
1. Задумали число. Затем удвоили его, вычли 10 и получили 3. Найдите задуманное число. Решите задачу, составив уравнение. Используйте следующую форму записи:
На естественном языке На математическом языке
2. Составьте задачу по уравнению: 120-х=45. Решите ее.
Вариант 2
1. Задумали число. Затем уменьшили его на 15, нашли четверть результата и получили Найдите задуманное число. Решите задачу, составив уравнение. Используйте следующую форму записи:
На естественном языке На математическом языке
2. Составьте задачу по уравнению: 160-2у=40. Решите ее.
Вариант 3
1. Сумма двух чисел равна 18. Одно число составляет половину другого. Найдите эти числа. Решите задачу, составив уравнение. Используйте следующую форму записи:
На естественном языке На математическом языке
2. Составьте задачу по уравнению: 3а+2а=75+а. Решите ее.
Вариант 4
1. Сумма трех чисел равна 55. Одно число составляет треть от другого, которое, в свою очередь, в два раза больше третьего. Найдите эти числа. Решите задачу, составив уравнение. Используйте следующую форму записи:
На естественном языке На математическом языке
2. Составьте задачу по уравнению: 4(х-5)=3х-2. Решите ее.
Творческие задания по теме:
"Составление и решение задач на движение"
Вариант 1
-
В первый день турист прошел 30 км, во второй день - в 2 раза меньше, чем в первый день. В третий день турист прошел на 10 км больше, чем во второй день. Сколько километров турист прошел в третий день? Составьте и решите обратную задачу.
-
Расстояние между пунктами А и В - 112 км. Из пункта В выехал велосипедист
по дороге, проходящей через эти пункты, со скоростью 12 км/ч. На каком
расстоянии от пункта А будет находиться велосипедист через 5 часов?
Вариант 2
-
В первый день турист прошел 30 км, во второй день - в 2 раза меньше, чем в первый день. В третий день турист прошел на 10 км больше (меньше), чем во второй день. Сколько километров турист прошел в третий день? Составьте и решите обратные задачи.
-
Одновременно из одного пункта по одной дороге, проходящей через этот пупкт, выехали два велосипедиста. Первый велосипедист едет со скоростью 12 км/ч, а второй - со скоростью 14 км/ч. Через сколько часов расстояние между ними станет 52 км?
Вариант 3
-
В первый день турист прошел 30 км, во второй день - в 2 раза больше(меньше), чем в первый день. В третий день турист прошел на 10 км меньше, чем во второй день. Сколько километров турист прошел в третий день? Решите задачи, составив числовые выражения. Составьте и решите обратные задачи.
-
Из двух пунктов С и Д, расстояние между которыми 50 км, одновременно по одной дороге, проходящей через эти пункты, вышли два пешехода. Пешеход, направляющийся из пункта С, идет со скоростью 5 км/ч, а пешеход, направляющийся из пункта Д, идет со скоростью 7 км/ч. Какое расстояние будет между ними через 4 часа?
Вариант 4
-
В первый день турист прошел 30 км, во второй день - в 2 раза больше(меньше), чем в первый день. В третий день турист прошел на 10 км больше(меньше), чем во второй день. Сколько километров турист прошел в третий день? Решите задачи, составив числовые выражения. Составьте и решите обратные задачи.
-
Расстояние между городами А и В равно 240 км. В 8 ч. 17 мин. из города А выехал велосипедист со скоростью 20 км/ч по дороге, проходящей через пункты А и В. В это же время из города В по той же дороге выехала автомашина со скоростью 60 км/ч. Через какое время расстояние между велосипедистом и автомобилистом будет 80 км?
Приложение 5
Таблица № 1. «Результаты диагностирующего теста №1»
Фамилия, Имя
1
2
3
4
5
-
Алексанова Диана
-
Анохин Семен
-
Андрюнькина Марина
-
Беляева Анна
-
Гринева Наталья
-
Грицевич Елизавета
-
Головатая Ирина
-
Гребеников Виктор
-
Горшкова Мария
-
Грибанова Антонина
-
Долинин Олег
-
Долгорукова Юлия
-
Дук Артем
-
Иванова Татьяна
-
Ковалев Алексей
-
Куликов Андрей
-
Колмогорцев Егор
-
Лебедева Дарья
-
Левина Мария
-
Морозов Алексей
-
Озеров Денис
-
Пилюгина Юлия
-
Рылькова Валерия
-
Сухарев Алексей
-
Тумаева Виктория
-
Феоктистова Дарья
-
Хрущев Андрей
-
Царьков Андрей
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Таблица № 2. «Результаты теста №2»
Фамилия, Имя
1
2
3
4
5
6
7
8
9
-
Алексанова Диана
-
Анохин Семен
-
Андрюнькина Марина
-
Беляева Анна
-
Гринева Наталья
-
Грицевич Елизавета
-
Головатая Ирина
-
Гребеников Виктор
-
Горшкова Мария
-
Грибанова Антонина
-
Долинин Олег
-
Долгорукова Юлия
-
Дук Артем
-
Иванова Татьяна
-
Ковалев Алексей
-
Куликов Андрей
-
Колмогорцев Егор
-
Лебедева Дарья
-
Левина Мария
-
Морозов Алексей
-
Озеров Денис
-
Пилюгина Юлия
-
Рылькова Валерия
-
Сухарев Алексей
-
Тумаева Виктория
-
Феоктистова Дарья
-
Хрущев Андрей
-
Царьков Андрей
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
-
+
+
+
-
-
-
+
-
+
+
-
+/-
-
-
+
-
+
-
-
-
-
-
+
-
-
-
-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+
+/-
+/-
+/-
+
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+/-
+
-
-
-
-
-
-
+
-
+
+
+
+/-
-
-
+
+
+
-
-
-
-
-
+
-
-
-
-
-
+
+
+
-
+/-
+
+
+
+
+
+
+/-
-
+/-
+/-
-
+/-
-
+/-
+/-
+
+
+/-
-
+
-
+/-
+/-
+
+/-
+/-
+/-
+
+/-
+/-
+/-
+/-
+
+
+/-
+
-
-
+/-
+/-
-
+/-
-
+
+
+
-
+/-
+
-
-
+
+
+
-
+
-
+
-
-
+
+
-
+
-
-
-
+
-
-
-
-
+
+
-
-
-
+
-
-
-
-
-
-
-
-
-
-
-
-
+
-
-
-
-
-
-
-
-
-
-
+
-
-
-
-
+/-
+
+
+
+/-
+
-
-
+/-
-
+
+
+
+
-
+
+/-
+
+/-
+/-
+/-
-
+
+/-
+/-
+/-
+
-
Обозначения: "+" - задание выполнено правильно
"-" - задание выполнено неправильно
"+/-" - задание выполнено частично
Таблица №3. «Количественный анализ теста №2»
Фамилия, Имя
Число заданий, выполненных
Уровень
Полн.
Част.
Неправ.
яз. разв.
-
Алексанова Диана
-
Анохин Семен
-
Андрюнькина Марина
-
Беляева Анна
-
Гринева Наталья
-
Грицевич Елизавета
-
Головатая Ирина
-
Гребеников Виктор
-
Горшкова Мария
-
Грибанова Антонина
-
Долинин Олег
-
Долгорукова Юлия
-
Дук Артем
-
Иванова Татьяна
-
Ковалев Алексей
-
Куликов Андрей
-
Колмогорцев Егор
-
Лебедева Дарья
-
Левина Мария
-
Морозов Алексей
-
Озеров Денис
-
Пилюгина Юлия
-
Рылькова Валерия
-
Сухарев Алексей
-
Тумаева Виктория
-
Феоктистова Дарья
-
Хрущев Андрей
-
Царьков Андрей
2
5
5
5
0
2
1
5
1
4
7
7
3
4
1
5
1
5
1
0
1
3
5
5
1
2
3
1
3
2
2
2
4
4
3
2
4
2
1
0
5
1
2
1
4
3
2
5
3
1
1
4
2
3
1
3
4
2
2
2
5
3
5
2
4
3
1
2
1
4
6
3
4
1
6
4
5
5
3
0
6
4
5
5
Низкий
Средний
Средний
Средний
Низкий
Низкий
Низкий
Средний
Низкий
Низкий
Средний
Средний
Низкий
Низкий
Низкий
Средний
Низкий
Средний
Низкий
Низкий
Низкий
Низкий
Средний
Средний
Низкий
Низкий
Низкий
Низкий
Таблица №5. «Результаты теста №3»
Фамилия, Имя
1
2
3
4
5
1.Алексанова Диана
2.Анохин Семен
3.Андрюнькина Марина
4.Беляева Анна
5.Гринева Наталья
6.Грицевич Елизавета
7.Головатая Ирина
8.Гребеников Виктор
9.Горшкова Мария
10.Грибанова Антонина
11.Долинин Олег
12.Долгорукова Юлия
13.Дук Артем
14.Иванова Татьяна
15.Ковалев Алексей
16.Куликов Андрей
17.Колмогорцев Егор
18.Лебедева Дарья
19.Левина Мария
20.Морозов Алексей
21.Озеров Денис
22.Пилюгина Юлия
23.Рылькова Валерия
24.Сухарев Алексей
25.Тумаева Виктория
26.Феоктистова Дарья
27.Хрущев Андрей
28.Царьков Андрей
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
-
+
-
+
+
+
+
+
+
+
+
-
+
+
+
+
+
+
+
+
+
+
+
+
+
-
+
+
+
+
+
+
+
+
-
+
-
+
+
-
+
+
-
-
-
+
-
-
+
+
+
-
+
+
+
+
-
-
-
-
+
+
-
-
-
+
+
+
+
+
-
+
+
+
+
+
+
+
+
+
-
+
+
+
-
-
+
+
+
+
+
-
+
+
-
+
+
-
-
+
+
+
+
+
+
+
+
+
+
+
-
+
-
-
-
+
-
+
-
-
-
-
Обозначения: "+" - задание выполнено правильно
"-" - задание выполнено неправильно
Список литературы
-
Адамар Ж. Исследование психологического процесса изобретения в области
математики. М.,1970.
-
Антоновский М.Я., Левитас Г.Г. Учебное оборудование на уроках алгебры. 6 класс.
Пособие для учителя. М., 1980.
3. Баранова И.В., Борчугова З.Г. Математика-5. Учебник для средней школы. СПб.,1997.
4. Баранова И.В., Борчугова З.Г. Математика-6. Учебник для средней школы. СПб.,1997.
5. Бахтин М.М. Человек в мире слова. М., 1995.
6. Бескин Л.Н. Стереометрия. М., 1971.
7. Блох А.Я., Блох М.Я. О структуре математического языка и его дидактических
аспектах. Математика в школе. 1994. №4, с.52-54.
8. Брудный А.А. Наука понимать. Бишкек, 1996.
9. БЭС. Математика. Научное издательство "Большая Российская энциклопедия".М.,1998.
10. Виленкин Н.Я. и др. Математика-5. Учебник для средней школы. М,,1997.
11.Виленкин Н.Я. и др. Математика-6. Учебник для средней школы. М,,1997.
12. Виленкин Н.Я. и др. Современные основы школьного курса математики. М., 1980.
13. Возрастные и индивидуальные особенности образного мышления учащихся. М.,1989.
14. Выготский Л.С. Мышление и речь. М.,1996.
15. Выготский Л.С. Педагогическая психология. М., 1991.
-
Глейзер Г.И. История математики в школе. 4-6 классы. Пособие для учителей.
М.,1981.
-
Доблаев Л.П. Смысловая структура учебного текста и проблемы его понимания.
М.,1982.
18. Дорофеев Г.В. и др. Математика. Дидактические материалы. М., 1998.
19. Жохов В.И. Преподавание математики в 5-6 классах. М., 1999.
-
Зинченко В.П. Работа понимания. Психологическая наука и образование. 1997.
№3,с.42-53.
21. Зинченко П.И. Непроизвольное запоминание. М., 1996.
22. Знаков В.В. Понимание как проблема психологии мышления. Вопросы психологии.
1991. №1, с.18-25.
23. Каплунович И.Я., Петухова Т.А. Пять подструктур математического мышления: Как
их выявить и использовать в преподавании. Математика в школе. 1998. №5, с.45-48.
24. Каплунович И.Я. Развитие пространственного мышления школьников в процессе
обучения математике. Новгород, 1996.
25. Клайн М. Математика. Утрата определенности. М.,1984.
26. Коммуникативная и когнитивная природа понимания. Серия: актуальные проблемы
прикладного языкознания. М.,1989.
27. Коротяев Б.И. Учение - процесс творческий. Из опыта работы. М.,1980.
-
Крейдлин Г.Е.,Шмелев А.Д. Языковая деятельность и решение задач. Математика в
школе. 1989. №3, с.39-45.
-
Лабораторные и практические работы по методике преподавания математики. Под
ред. Лященко Е.И. М.,1988.
30. Левитов Н.Д. Психология труда. М.,1963.
31. Мадер В.В. Введение в методологию математики. М.,1994.
32. Мамардашвили М.К. Лекции о Прусте. М.,1995.
33. Маркушевич А.И. К вопросу о реформе школьного курса математики. Математика в
школе.1964. №6,с.3-6.
34. Миракова Т.Н. Об уровне языкового развития учащихся 6-7 классов. Математика в
школе. 1989. №1,с.64-72.
35. Моляко В.А. Психология конструкторской деятельности. М.,1983.
36. Нурк Э.Р. и др. Математика-5. Учебник для средней школы. М.,1994.
37. Нурк Э.Р. и др. Математика-6. Учебник для средней школы. М.,1991.
38. Осинская В.Н. Формирование умственной культуры учащихся в процессе обучения
математике. Книга для учителя. Киев,1989.
39. Пиаже Ж. Структуры математические и операторные структуры мышления.
Преподавание математики. М.,1960.
40. Пойа Д. Как решать задачу. Квантор. 1991. №1.
41. Суворова С.Б. и др. Математика. Книга для учителя. Методические рекомендации к
учебнику 5 класса. М.,1999.
42. Формирование приемов математического мышления. Под ред. Талызиной Н.Ф.
М.,1995.
43. Фридман Л.М., Каплунович И.Я., Пушкина Т.А. Изучение личности учащегося и
ученических коллективов. Книга для учителя. М.,1988.
44. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. Книга для учащихся.
М.,1984.
45. Чередов И.М. Формы учебной работы в средней школе. Книга для учителя. М., 1988.
46. Эрдниев П.М., Эрдниев Б.П. Укрупнение дидактических единиц в обучении
математике. Книга для учителя. М.,1986.
47. Якиманская И.С. Восприятие и понимание учащимися чертежа и условий задачи в
процессе ее решения. Применение знаний в учебной практике школьников. М.,1961.


