- Преподавателю
- Математика
- Путешествие по геометрическим островам
Путешествие по геометрическим островам
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Карасева Н.В. |
| Дата | 30.03.2015 |
| Формат | zip |
| Изображения | Есть |
Пейзаж 3. Геометрические иллюстрации тождеств и неравенств
Язык современной алгебры - творение европейских титанов мысли, таких, как Виет, Декарт и Паскаль. Древние греки не могли записать современной алгебраической нотацией даже простое тождество, как (a + b)2 + (a - b)2 - 2(a2 + b2). Тем не менее с доказательством подобных тождеств они отлично справлялись. Примерно вот так:
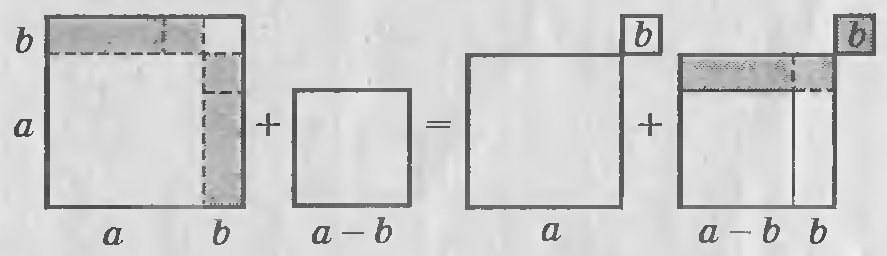
А вот «моментальный снимок» доказательства еще одного классического алгебраического тождества:
1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n)².
З
 десь показан один квадрат со стороной 1, два квадрата со стороной 2, …, восемь квадратов со стороной 8. Все они аккуратно укладываются в квадрат со стороной 1 + 2 + … + 8. При этом перекрывающиеся части некоторых квадратов в точности равны непокрытым участкам. Мне кажется, что увидев один раз эту картинку, человек уже не способен забыть ни ее саму, ни то алгебраическое тождество, которое она иллюстрирует.
десь показан один квадрат со стороной 1, два квадрата со стороной 2, …, восемь квадратов со стороной 8. Все они аккуратно укладываются в квадрат со стороной 1 + 2 + … + 8. При этом перекрывающиеся части некоторых квадратов в точности равны непокрытым участкам. Мне кажется, что увидев один раз эту картинку, человек уже не способен забыть ни ее саму, ни то алгебраическое тождество, которое она иллюстрирует.
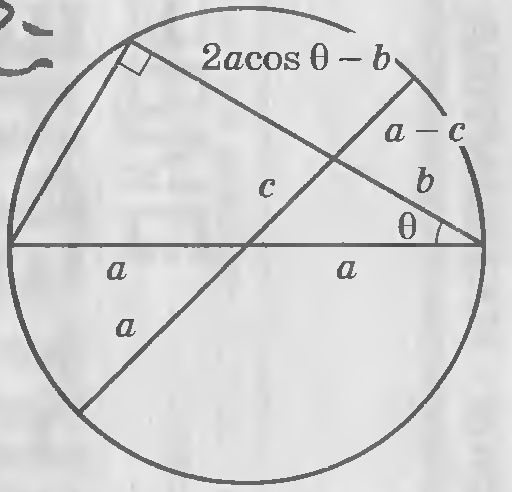
Еще один «островок» - картинка к геометрическому доказательству теоремы косинусов.
Здесь в круге построен прямоугольный треугольник, один из катетов которого делит диаметр круга на отрезки а + с и а + с. Сам этот катет делится диаметром на отрезки b и 2аcos - b. Известная геометрическая теорема гласит, что произведения длин отрезков хорд равны, т. е.
b(2acos - b) = (a + c)(a - c),
откуда 2abcos - a² + b² - c². Может быть, это доказательство и не проще стандартного школьного, однако оно, несомненно, дарит возможность увидеть математический океан с новой точки зрения.


