- Преподавателю
- Математика
- УМК Решение прикладных задач по математике (10-11 классы)
УМК Решение прикладных задач по математике (10-11 классы)
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Кирдякина О.В. |
| Дата | 24.12.2015 |
| Формат | rar |
| Изображения | Есть |
Решение прикладных задач по математике
Сборник упражнений.
ВВЕДЕНИЕ
В пособии представлены задачи и упражнения по прикладному курсу «Решение прикладных задач по математике», а также дополнительные исторические справки и пояснения по каждой теме. Данный материал предназначен для самостоятельной работы учащихся и организации их деятельности на занятиях по курсу.
Занятие №1
Т ема: «Числа»
ема: «Числа»
Свойства арифметических действий:
-
сложение и умножение
-
переместительное a+b=b+a ab=ba
-
cочетательный: (a+b)+c=a+(b+c)
-
распределительный: a(b+c)=ab+ac
-
-
вычитание можно заменить сложением с противоположным числом: a-b=a+(-b)
-
деление можно заменить умножением на число , обратное делителю:

Задания
-
Требуется сложить много однозначных чисел. Как облегчить эту работу и быстрее получить правильный результат?
-
Проделайте следующий эксперимент: откройте книгу на произвольной странице дальше 10-й и запишите число оставленное из двух последних цифр номера страницы. Открывая книгу много раз (скажем 20) и беря числа попеременно, то с правой, то с левой стороны книги , вы получите большой набор двузначных чисел Попробуйте быстро найти их сумму.
-
Н
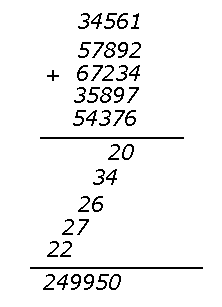
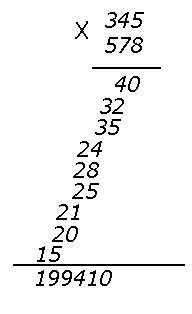
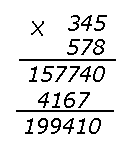 а рисунке приведены любопытные записи сложения и умножения многозначных чисел. Разберитесь в этих способах.
а рисунке приведены любопытные записи сложения и умножения многозначных чисел. Разберитесь в этих способах. -
Искусственный спутник Земли движется со скоростью 8000м/с. За какое время он пройдёт путь, равный 48000км? 1440000 км?
-
Для охлаждения доменной печи через её стенки ежеминутно пропускается 26 кубометров воды. Сколько кубометров воды проходит через стенки доменной печи за одни сутки? За пять суток? За m cуток?
-
Расход электроэнергии за сутки холодильника «ЗИЛ»равен 1,9 кВт*ч, а цветного телевизора «Темп» - 1 кВт*ч (из расчёта работы телевизора 4 часа в сутки). Сколько стоит электроэнергия , потреблённая обоими приборами за 30 дней, если 1 1 кВт*ч стоит 4 т?
-
При увеличении скорости движения автомобиля вдвое его тормозной путь увеличивается в 4 раза. При скорости 30 км/ч тормозной путь «Запорожца» равен 7,2 м, а грузового автомобиля - 9,5 м. Найти тормозной путь этих автомобилей при скорости 60 км/ч.
-
Велосипедист едет со скоростью 12 км/ч. Ему нужно добраться до села, расположенного в 36 км о пункта отправления. Сколько ему потребуется времени, чтобы приехать в село, если он уже проехал 3 км?
Занятие №2 и №3
Тема: «Процент. Пропорция. Расчёты при смешивании»
*В Древнем Риме система дробей основывалась на делении на 12 долей веса, которая называлась асс, двенадцатую долю асса называли унцией. Из-за того, что в двенадцатеричной системе нет дробей со знаменателям 10 или 100, римляне затруднялись делить на 10, 100 и т.д. При делении 1001асса на 100 один римский математик сначала получил 10 ассов, потом раздробил асс на унции и т.д. Но от остатка он не избавился. Чтобы не иметь дела с такими вычислениями, римляне стали использовать проценты. Они брали с должника лихву (то есть деньги сверх того, что было дано в долг). При этом говорили: не «лихва составляет 16 сотых суммы долга», а «на каждые 100 сестерциев долга заплатишь 16 сестерциев лихвы». И сказано то же самое, и дробей использовать не пришлось! Так как слова «на сто» звучали по латыни «про центум», то сотую часть и стали называть процентом. И хотя теперь дроби, а особенно десятичные дроби , известны всем, проценты всё-таки применяются и в финансовых расчётах, и в планировании, то есть в различных областях человеческой деятельности.
Процент есть сотая часть числа. 1%=0,001
*С пропорциями имели дело уже древние строители. Правильное соотношение размеров возводимых ими дворцов и храмов придавало эти зданиям ту необыкновенную красоту, которая и сегодня восхищает нас. С помощью пропорций рисовали в Вавилоне планы городов. Когда учённые сравнивали результаты раскопок города Ниппура с его планом, найденным ранее, они поражались точности этого плана. Древнегреческие математики с большим мастерством работали с пропорциями. Из одной верной пропорции они умели получать великое множество других. Искусство преобразований пропорций заменяло им используемое современными математиками искусство преобразований громоздких выражений.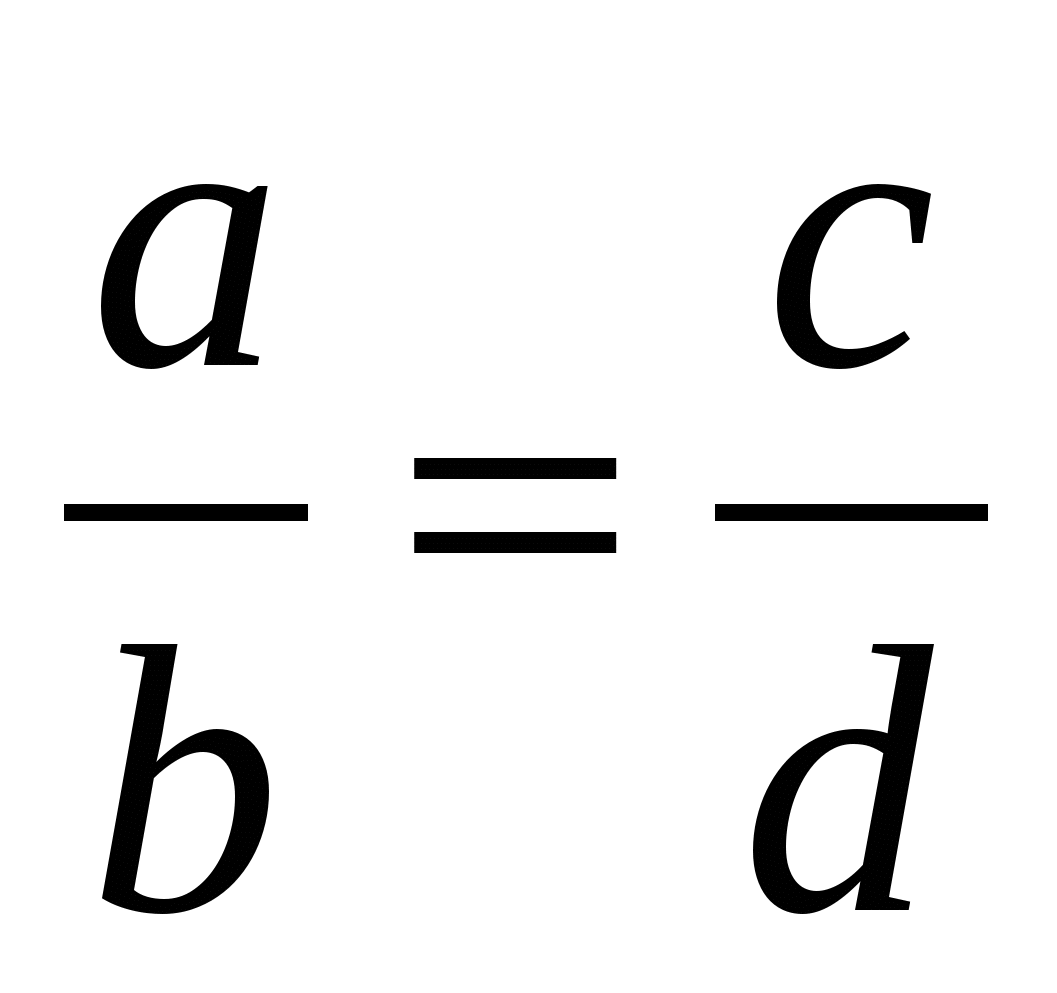
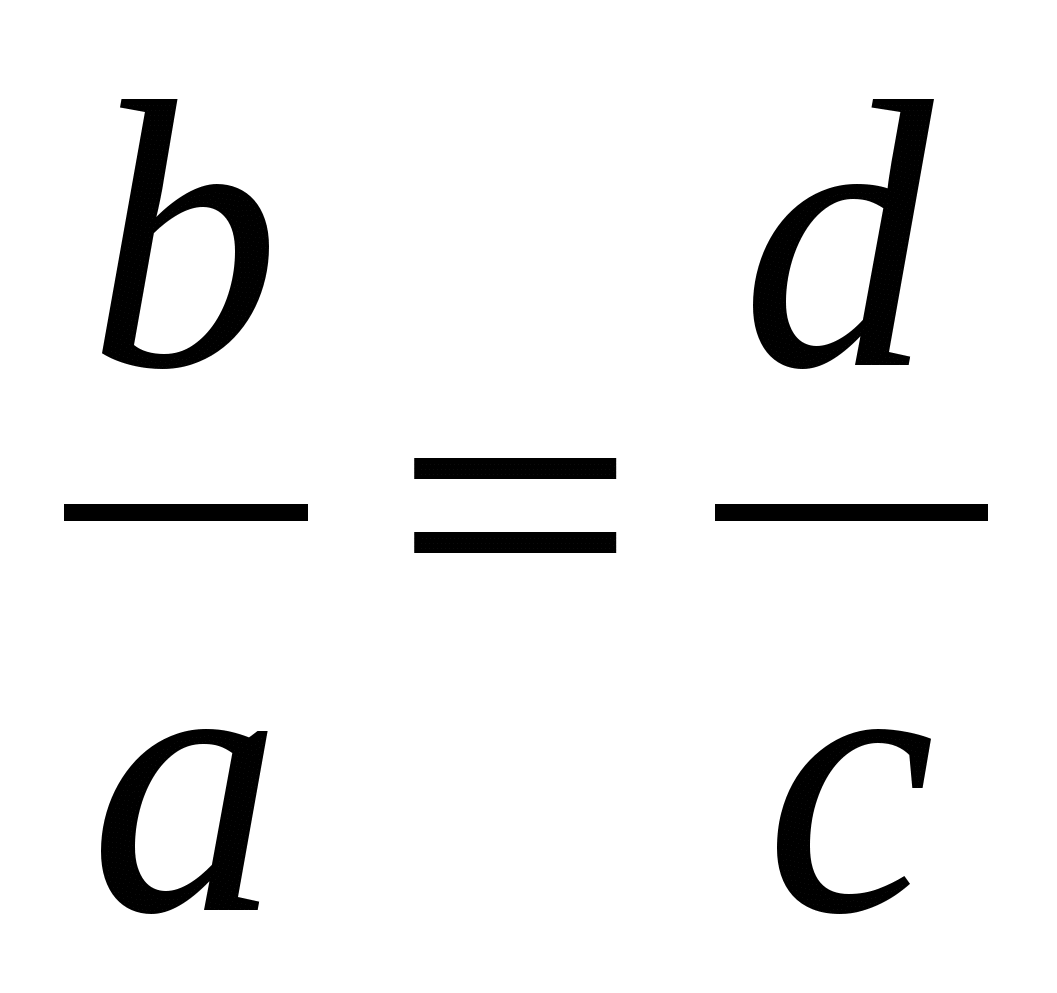 ;
; 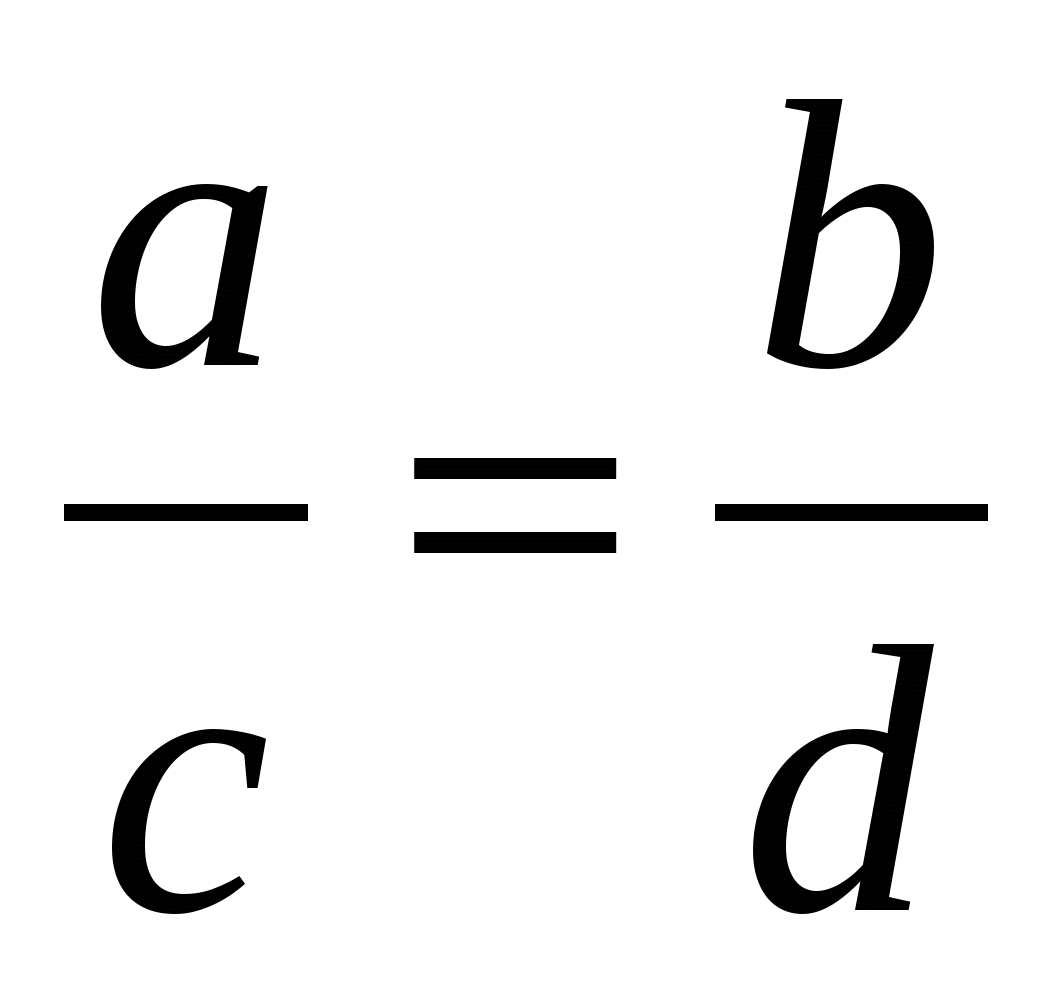 ;
; 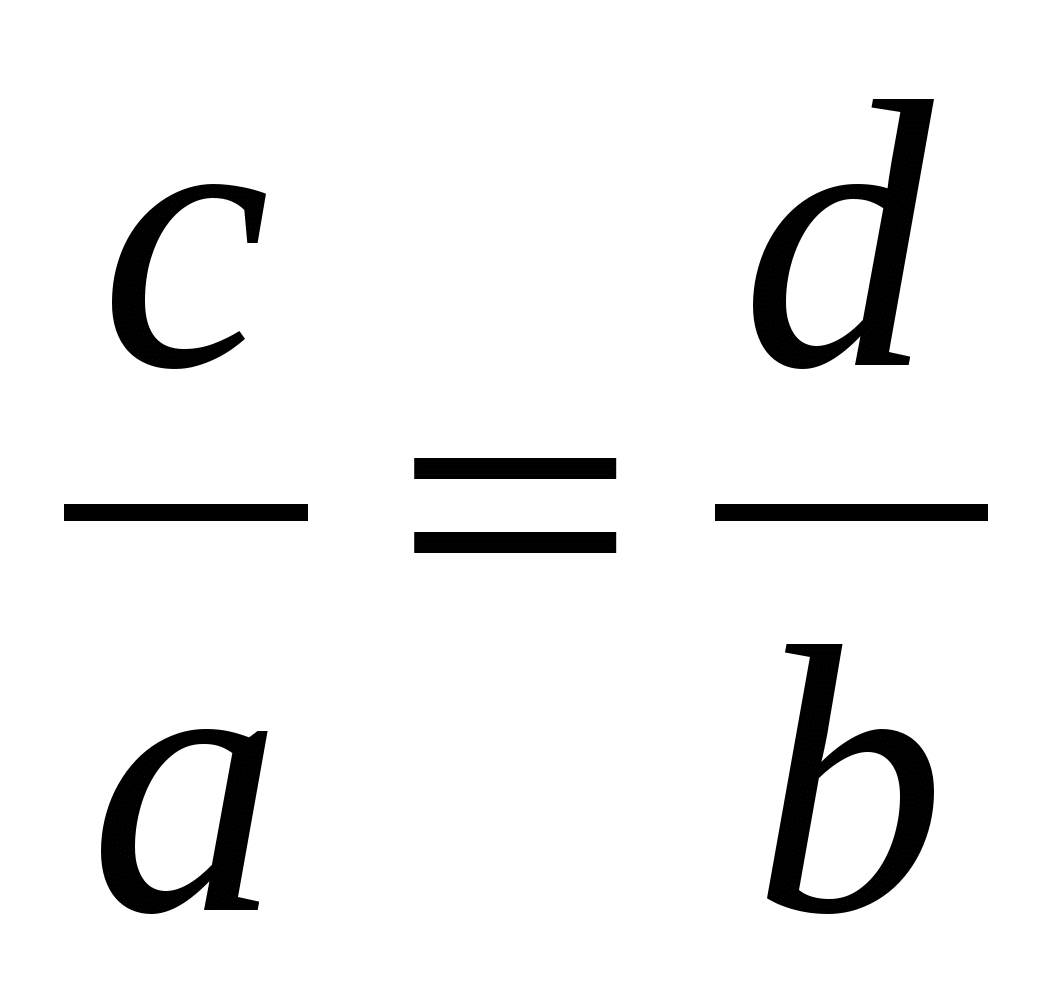 ;
; 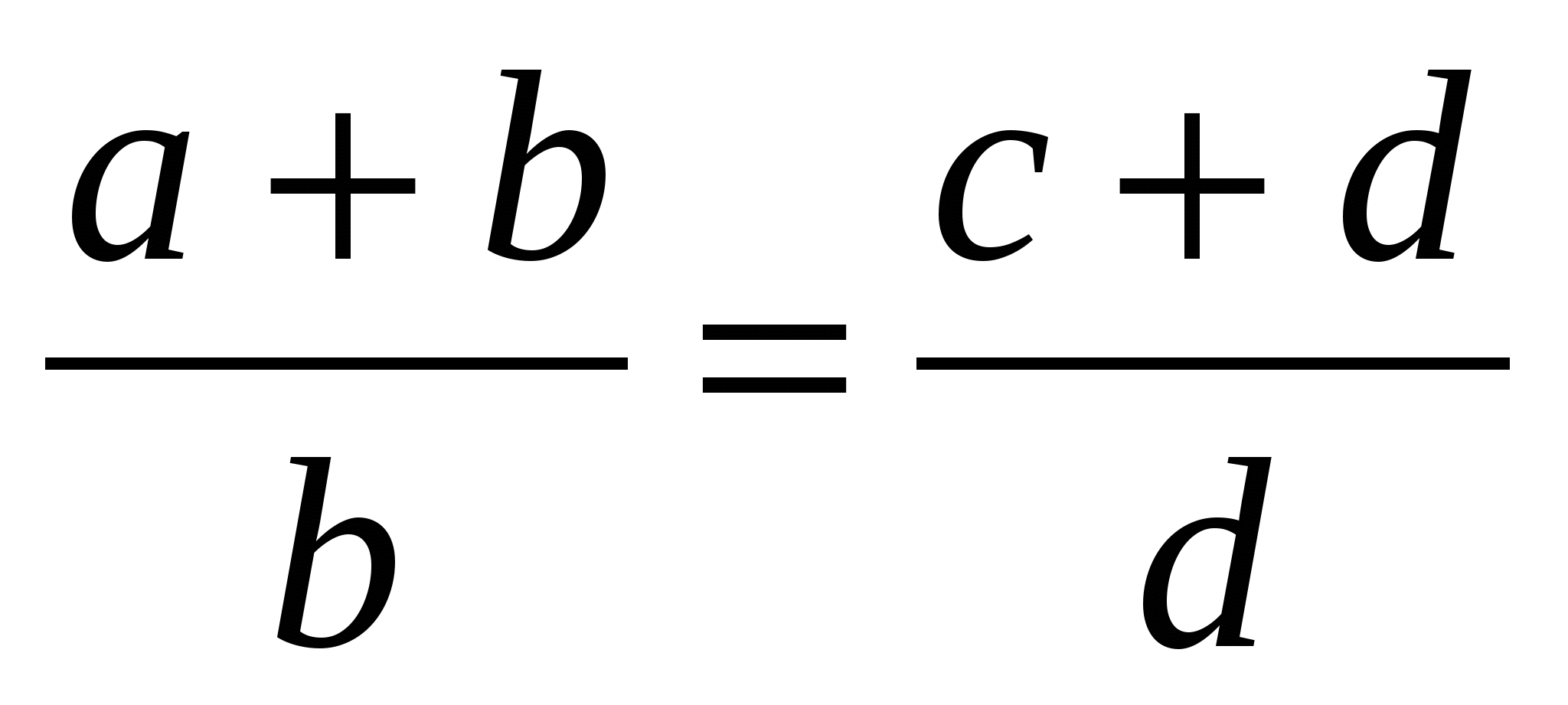 ;
; 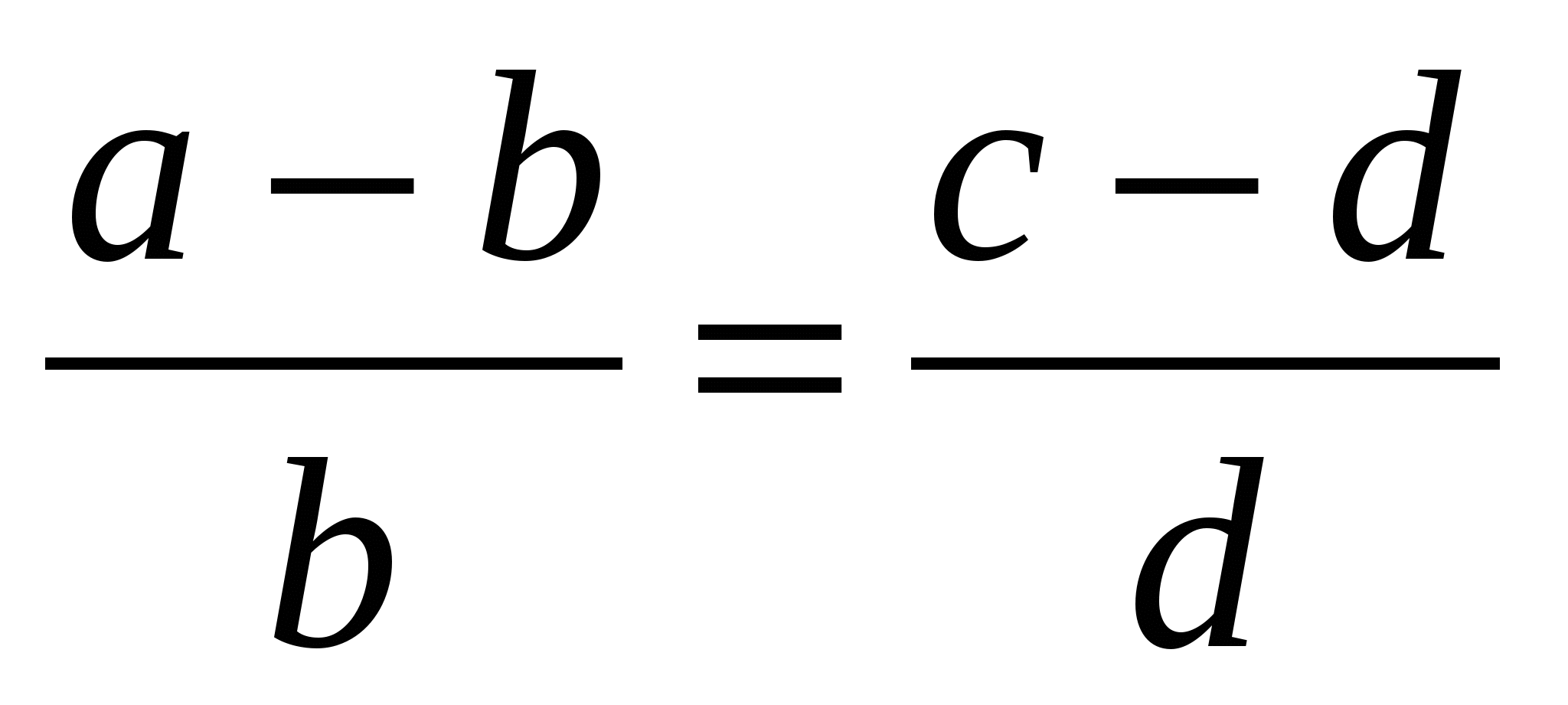 (при a>b) ;
(при a>b) ;  и многие другие.
и многие другие.
Пропорция- равенство двух отношений.
Задания
-
За 1987 год выпуск предприятием продукции возрос на 4%, а на следующий год на- 8%. Найдите средний ежегодный прирост продукции за двухлетний период.
-
За осеннее- зимний период цена на овощи возросла на 25%. На сколько следует снизить цену весной, чтобы летом овощи имели прежнюю цену?
-
Имеется кусок сплава меди с оловом общей массой 12 кг, содержащей 45% меди. Сколько чистого олова нужно добавить к этому куску сплава, чтобы получившийся сплав содержал 40% меди? /1,5 кг олова.
-
Имеется два сплава состоящие из меди, цинка и олова. Известно, что первый сплав содержит 40% олова, а второй - 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определите сколько килограммов олова содержится в получившемся новом сплаве? /170кг
-
Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 тонн стали с содержанием 30% никеля? /40 т и 100т
-
Смешали 10% и 25% растворы соли и получили 3 кг 20% раствора. Какое количество каждого раствора в килограммах было использовано?/ 1кг и 2 кг
-
24 г одного металла в воде весят 21 г, а 14 г другого металла в воде весят 12 г. Сплав из этих металлов весом 100 г весит в воде 87 г. Сколько каждого металла содержится в сплаве?/ 72г 28 г.
-
В первую поездку автомобиль израсходовал 10% бензина, имеющегося в баке, затем во вторую поездку- 25 % остатка. После этого в баке осталось на 13 л меньше чем первоначально. Сколько литров бензина было в баке первоначально? /40 .
Занятие №4
Тема: «Задачи приводящие к решению линейных уравнений»
Египтяне решали задачи способом «аха», а в Вавилоне задачи решались по сути дела с помощью уравнений, но без использования букв. Вместо букв брали числа, показывали на числах как решить задачу, а потом уже похожие на неё задачи решали тем же способом.Многте уравнения умел решать Диофант Александрийский(III в), который даже применял буквы для обозначения неизвестных. По настоящему метод уравнений сформировался в руках арабских учёных и первая книга о решении уравнений была написана Мухаммедом ибн Муса ал-Хорезми, называлась она «Краткая книга об исчислении ал-джабры и ал-мукабалы»
Ал-джабра
При решении уравненья
Если в части одной,
Безразлично какой.
Встретиться член отрицательный,
Мы к обеим частям,
С этим членом сличив,
Равный член придадим,
Тошлько с знаком другим,-
И найдём результат нам желательный.
Ал-мукабала
Дальше смотрим в уравненье,
Можно ль сделать приведенье,
Если члены в нём подобны,
Сопоставим их удобно,
Вычтя равный член из них,
К одному приводим их.
(неизвестный персидский математик)
«Если шофёру господина министра социального обеспечения сорок три месяца и двенадцать дней , а мост в городе Квибек в Канаде имеет дллину 577 метров, то на скольких желтках нужно замесить лапшу, чтобы накормить четырёх человек различного возраста, если принять во внимание , что ширина полотна на железных дорогах Боснии 0,7м?»
Сербский сатирик Бранислав Нушич «Автобиография»
Задания
-
На производство костюма было израсходовано 2,8 квадратных метра ткани. Площади ткани израсходованной на пиджак, брюки, жилетку, относятся как 7:5:2. Сколько ткани пошло на брюки?
-
Двое рабочих изготовили 657 деталей, причём первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый?
-
Папе и дедушке вместе 111 лет. Сколько лет каждому ,если папа кв два раза моложе дедушки?
-
Поезд был задержан в пути на 1 час. Увеличив скорость на 30 км/ч, он через три часа прибыл на конечную станцию точно по расписанию. Чему была равна скорость поезда до сотановки?
-
В трёх корзинах 54 кг яблок. В первой корзине на 12 кг яблок меньше, чем во второй,а в третьей- в два раза больше , чем в первой. Сколько килограммов яблок в каждой корзине?
-
Бригада должна была выполнить заказ за 10 дней. Ежедневно перевыполняя норму на 27 деталей, бригада за 7 днй работы не только выполнила задание , но еще и изготовила допрлнительно 54 детали. Сколько деталей в день изготовляла бригада?
-
Лодка шла по течению реки 2,4 часа и против течения 3,2 часа. Путь, пройденный лодкой по течению, оказался на 13,2 км длиннее пути, пройденного против течения. Найти скорость лодки в стоячей воде, если скорость течения реки равна 3,5 км/ч.
-
Из одного пункта в начале вышел пешеход, а через 1,5 часа, после его выхода в том же направлении выехал велосипедист. На каком расстоянии от пункта отправления велосипедист догнал пешехода, если пешеход шёл со скоростью 4,5 км/ч, а велосипедист ехал со скоростью 17 км/ч? (8,5 км/ч)
-
Один рабочий в дегнь выпускал на 50 деталей меньше другого. Когда выработка первого повысилась на 1% в день, а второго -на 2%, они стали выпускать вместе в день 254 детали. Сколько деталей в день первоначально выпускал каждый рабочий? (100 и 150 деталей)
Занятие №5
Тема: «Задачи приводящие к решению квадратных уравнений»
Квадратные уравнения имеют практическое значение и самые простые из них (по площади квадрата найти его сторону и т.д)люди умели решать ещё в Древнем Египте- II тыс. до нашей эры.В Древнем Вавилоне грамотные люди умели решать довольно сложные уравнения, одна из их идей -известна нам как теорема Виета. Вавилоняне рассматрвали уравнение вида x2+px+q=0 как задачу на определение длины и ширины прямоугольника по его площади и полупериметру.Евклид(III до н э) решал квадратные уравнения геометрически. Этот способ нисколько не легче того, которым пользовались вавилоняне. Значительно упростил решение уравнений аль-Хорезми. У него получилось несколько видов квадратных уравнений для решения каждого из них он предложил правило точно соответствующее нашим формулам, но изложенных риторически. Например: «Что касается квадратов и корней , равных числу, то если например ты скажешь: квадрат и десять его корней , то это значит, что если добавить к некоторому квадрату то, что равно десяти корням, получится тридцать девять. Правило таково: раздвой число корней , получится в этой задаче пять, умножь это на равное ему, будет двадцать пять. Прибавь это к тридцати девяти, будет шестьдесят четыре. Извлеки из этого корень, будет восемь, и вычти из этого половину числа корней ,т.е. пять, останется три: это и будет корень квадрата, который ты искал» Речь идет об уравнении х2+10х=39 . Второй корень ученый не ищет, так как всячески избегал отрицательных чисел.
Задания
-
Надо узнать, сколько времени будет падать камень, брошенный вертикально с крыши четырёхэтажного дома, т.е. приблизительно с высоты 12 м
-
Внук восьмиклассник возвращается из школы: -Дедушка, мы всем классом к Новому году обменяемся фотографиями. -Это хорошо. Память будет. Но это же сколько карточек надо? -А мы уже сосчитали 650. Нас в классе...-Подожди, не говори. Я сам сосчитаю. Так сколько учеников в 8 классе?(26)
-
В море встретились два корабля. Один из них шёл в восточном направлении, другой- в северном. Скорость первого на 10 узлов большескорости вторго. Через два часа растояние между ними оказалось равным 100 милям. Найдите скорость каждого корабля. (30 и 40 узлов)
-
Если в дне железной консервной банки пробить отверстие и налить в неё воды, то уровень воды будет убывать по квадратичному закону. Найдите формулу этого закона и определите , через какое время вытечёт вся вода, если начальный уровень 15 см, через одну мин он опустился до 10 см, ещё через минуту- до 6 см.( через 5 мин)
-
«Задача Бхаскары» Старинная задача.
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась.
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько ты скажешь
Обезьян там было в роще?
-
Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определите длину изгороди, если известно, что площадь участка равна 1200 м2
-
Высота h(в м), на которой через t секунд окажется брошенное вертикально вверх тело,вычисляется по формуле
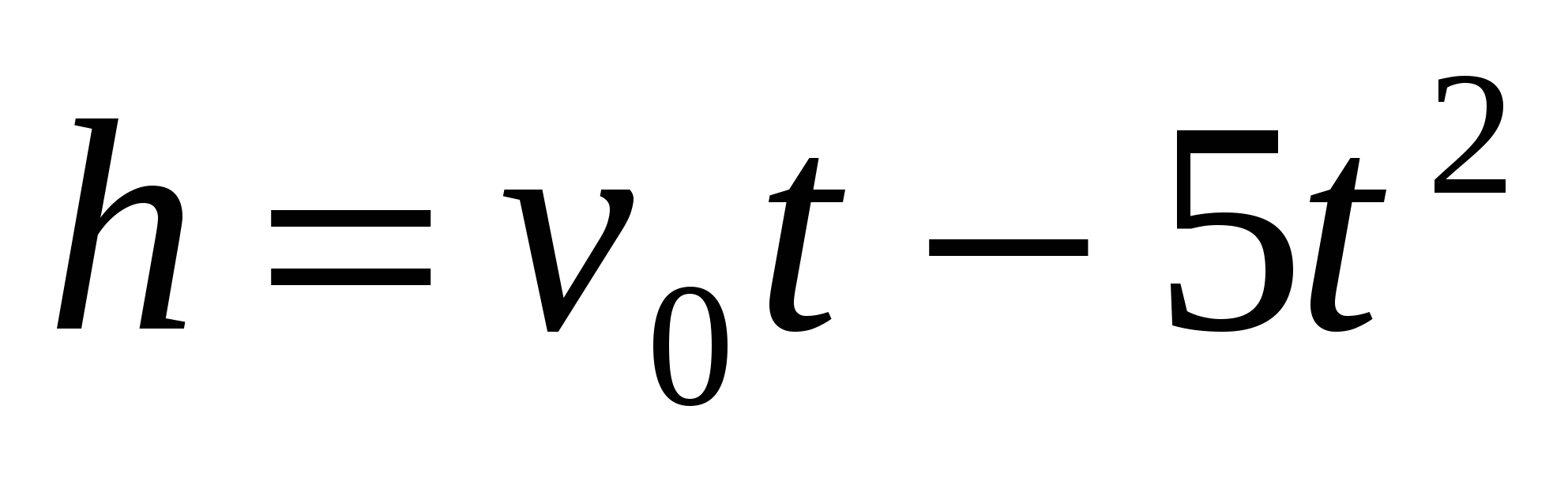 , где v0 -начальная скорость (в м/с). В какой момент времени тело окажется на высоте 240 м, если за 2 сек оно поднялось вверх на 120 м?
, где v0 -начальная скорость (в м/с). В какой момент времени тело окажется на высоте 240 м, если за 2 сек оно поднялось вверх на 120 м? -
От листа картона, имеющего форму квадрата, отрезали полосу шириной 3 см. Площадь оставшейся прямоугольной части листа равна 70 кв. см. Определите первоначальные размеры листа.
Занятие №6
Тема: «Функции. Свойства функции»
Способы задания функций могут быть: формула, график, таблица. За примерами табличного задания функции обратимся к «Энциклопедии домашнего хозяйства». В ней указаны максимально допустимые значения тока для проводов в зависимости от сечения.
Сечения жилы, мм2
0,75
1
1,5
2,5
максимально допустимый ток, ампер
13
15
20
27
Для того чтобы смонтировать проводку в доме этой таблицы достаточно. Ведь проводы поступающие в продажу , согласно ГОСТу имеют лишь определённые стандартные сечения . Зрительное и наглядное представление этих данных даст график построенный на основе таблицы.
Задание
Постройте график, соединив точки плавной линией. Рассмотрите характерные особенности и поведение функции. Попробуйте объяснить причины тех ограничений для тока, которые обусловлены сечением применяемых проводов.
Существо дела состоит в том, что провода нагреваются , когда по ним течёт ток. Нагрев прямо пропорционален квадрату тока и обратно пропорционален сечению провода. Предельно допустимый нагрев и определяет критическое отношение квадрата тока к сечению провода. Увеличив ток в цепи , скажем в два раза, мы должна в четыре раза увеличить сечение проводов , дабы избежать их перегрева. Увеличив ток в три раза- в девять раз увеличить сечение проводов.
Формульное задание интересующей нас функции- ток измеряется как корень квадратный из сечения проводов: 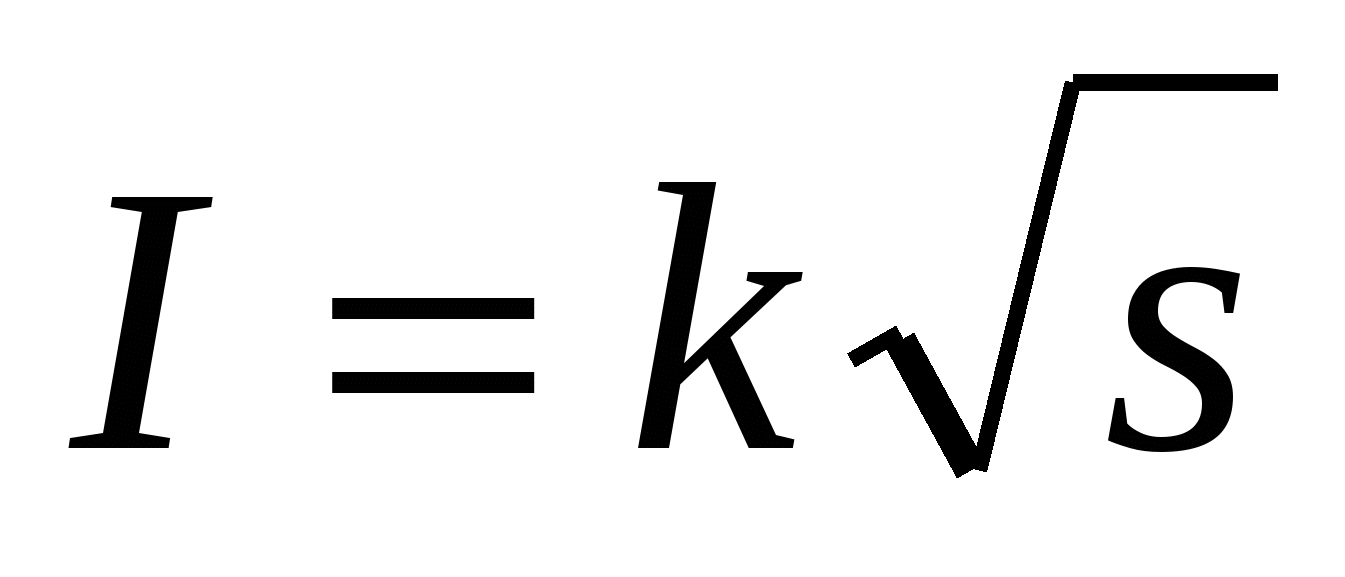 .Причём коэффициент пропорциональности k в этой формуле равен 16,3, если ток измеряется в амперах, а сечение жилы s- в квадратных миллиметрах.
.Причём коэффициент пропорциональности k в этой формуле равен 16,3, если ток измеряется в амперах, а сечение жилы s- в квадратных миллиметрах.
Задание
Постройте график функции у=16,3 √х и сравните полученный график с первоначальным. Какие преимущества даёт формульное задание функции? Есть ли необходимость в таком задании для домашнего мастера?
Занятие №7
Тема: «Функции. Свойства функции»
Функция- это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Например, в соотношении y=x2 геометр или геодезист увидит зависимость площади у квадрата от величины х его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нём зависимость силы у сопротивления воздуха или воды от скорости х движения . Математика же рассматривает зависимость y=x2 и её свойства в отвлечённом виде. Она устанавливает, например, что при зависимости y=x2 увеличение х в 2 раза приводит к четырёхкратному увеличению у. И где бы конкретно не появилась эта зависимость, сделанное абстрактное математическое заключение можно применять в конкретной ситуации к любым конкретным объектам.
П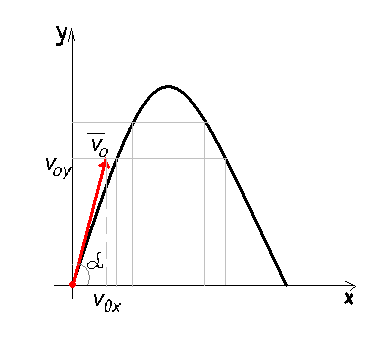 осле линейной функции квадратичная функция - простейшая и важнейшая элементарная функция. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростью v0 находится в момент времени t на расстоянии
осле линейной функции квадратичная функция - простейшая и важнейшая элементарная функция. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростью v0 находится в момент времени t на расстоянии  (*) от земной поверхности (g-ускорение силы тяжести); количество тепла Q, выделяемого при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой Q=RI2.
(*) от земной поверхности (g-ускорение силы тяжести); количество тепла Q, выделяемого при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой Q=RI2.
Пусть из некоторой точки с начальной скоростью v0 , направленной под углом а к горизонту , брошено тело. Тогда проекции начальной скорости v0 на оси Х и У равны соответственно v0sina и v0cosa, где v0 - модуль вектора начальной скорости. Так как на тело действует только сила тяжести, направленная по вертикали вниз, то с течением времени координата х изменяется как при прямолинейном равномерном движении х= v0 t, а координата у по закону (*)
Задания
-
По какой траектории движется тело, брошенное под углом к горизонту, если не брать во внимание силу сопротивления воздуха?
-
Высота воды в сосуде с отверстием в дне убывает по квадратичному закону:
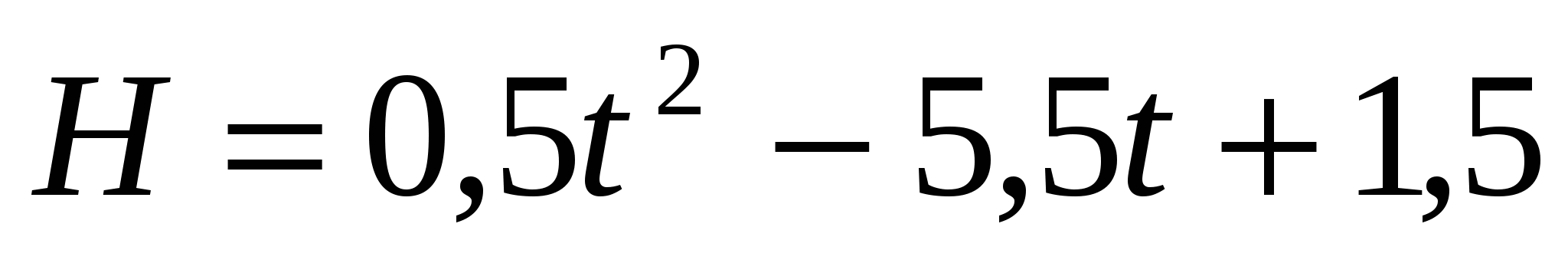 . , где t -время в минутах, Н - высота в сантиметрах. Постройте график этой функции. Определите по графику, когда уровень воды опустился до 10,5,2,0 см.
. , где t -время в минутах, Н - высота в сантиметрах. Постройте график этой функции. Определите по графику, когда уровень воды опустился до 10,5,2,0 см. -
Цена бриллианта пропорциональна квадрату его массы. Если бриллиант разбить на две части, то в каком случае общая цена двух частей будет наименьшей?
-
Испытывая судно получили следующую таблицу зависимости между скоростью v (узлов) и мощностью Н (лошадиных сил):
Н
300
780
1420
v
5
7
9
Предполагая, что зависимость Между Н и v есть квадратичная функция, найти мощность судна при скорости 6 узлов.
-
Снаряд вылетел из пушки под углом α к горизонту с начальной скоростью
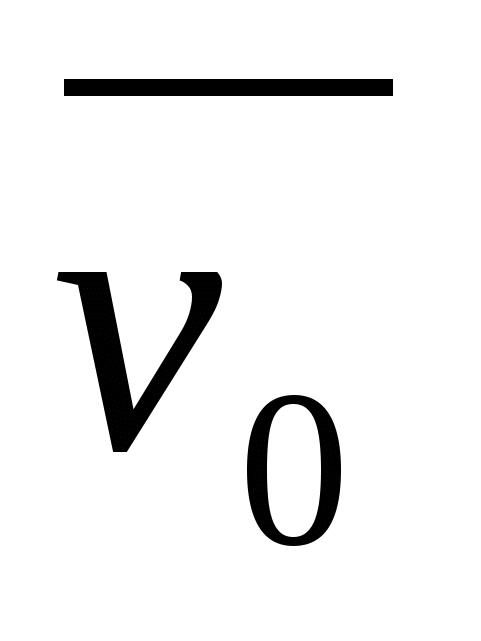 . Найдите : а) время полёта снаряда; б) максимальную высоту его подъёма; в) дальность полёта снаряда.
. Найдите : а) время полёта снаряда; б) максимальную высоту его подъёма; в) дальность полёта снаряда. -
Мяч брошен под углом 300 к горизонту с начальной скоростью 10 м/с. Определить высоту подъёма, а также время и дальность полёта .
-
Пуля вылетает в горизонтальном направлении и летит со средней скоростью 800 м/с. На сколько снизится пуля в отвесном направлении во время полёта, если расстояние до цели равно 600 м? /≈2,8 м.
Занятие №8
Тема: «Гармонические колебания »
Величины, меняющиеся согласно закону f(t)=A cos (ωt+φ) или f(t)=A sin (ωt+φ) играют важную роль в физике.
Например, по такому закону меняется координата шарика, подвешенного на пружине; по такому закону изменяется величина I переменного электрического тока, которым питаются городские осветительные сети.
При этом говорят, что совершается гармоническое колебание. Параметры A, ω, φ полностью определяющие колебание имеют специальные названия: A- амплитуда колебания, ω- циклическая (или круговая) частота колебания, φ-начальная фаза колебания, период функций f(t)=A cos (ωt+φ) или f(t)=A sin (ωt+φ) называют периодом гармонического колебания Т=2π/ ω.
Задания
-
Знаете ли вы, какова частота колебания силы тока в ваших осветительных сетях? (50 Герц)
-
В какой ближайший момент времени t(t>0), считая от начала движения смещение точки, совершающей гармонические колебания по закону
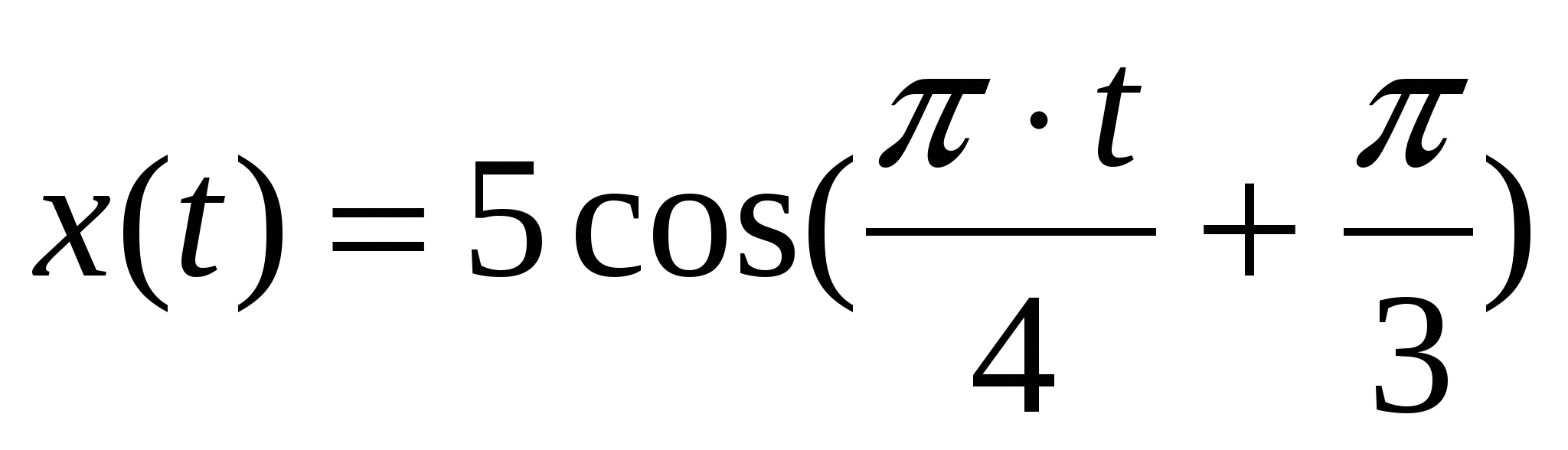 :
: -
Максимально;
-
Равно 2,5;
-
Равно 0;
-
Равно -5?
-
-
По графику, изображённому на рисунке, определите амплитуду силы тока (или напряжения ) от времени, период колебания . Запишите закон зависимости силы тока (или напряжения ) от времени.
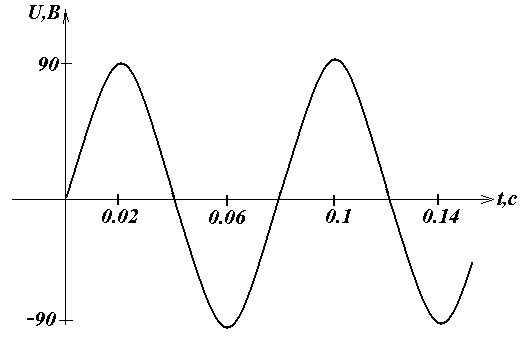
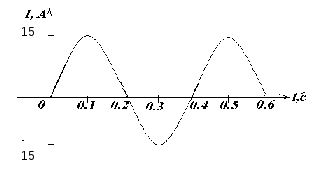
-
Координата движущегося тела (измерения в сантиметрах)изменяется по указанному закону. Найдите амплитуду, период, частоту колебания . Вычислите координату тела в момент времени t1, если:
-
x(t)=3.5 cos 4πt, t1=1/12 c.
-
x(t)=5 cos (3πt+
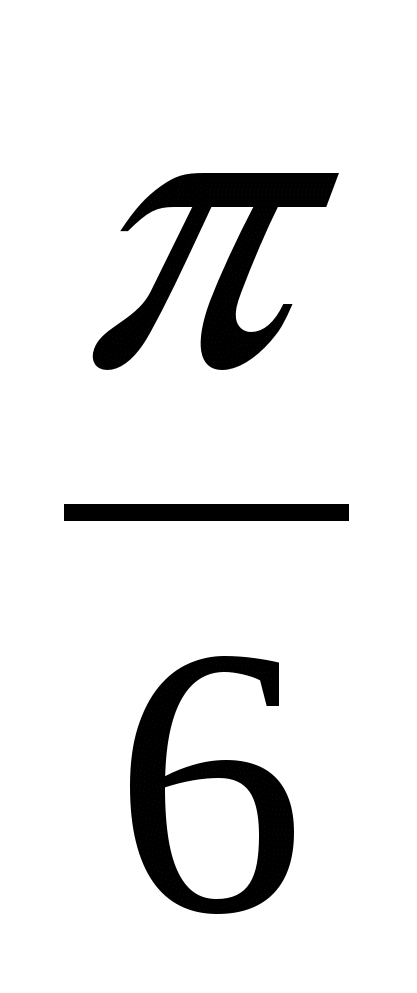 ), t1=4.5 c
), t1=4.5 c
-
-
Найдите амплитуду, период, частоту силы тока, если она изменяется по закону (сила тока измерена в амперах, время - в секундах):
-
I(t)=0.25 sin 50πt
-
I(t)=5 sin 20πt
-
Занятие №9
Тема: «Равномерное и переменное движение. Средняя скорость Движения. Мгновенная скорость. Понятие о производной».
К дифференцированию прибегают всякий раз когда встает вопрос о скорости изменения какой-либо функции по мере изменения аргумента, когда эта скорость оказывается непостоянной, а определять её требуется точно для любого изменения значения аргумента.
Заряд батареи, питающий электрическую сеть, убывает со временем. Скорость убывания есть ток. Он может оказаться различным в разные моменты времени и поэтому должен определяться как производная заряда по времени.
Тепло, содержащееся в нагреваемом теле, нарастает с ростом температуры. Интенсивность нарастания есть теплоёмкость - своя для каждой температуры. Теплоёмкость есть производная количества тепла по температуре.
Путь, проходимый телом при равномерном движении по прямой в единицу времени , называют скоростью этого движения. Средней скоростью движения v за время t называют отношение длины s пути, пройденного телом за время t, к этому времени. Для равномерного движения скорость на любом участке совпадает со средней скоростью движения, совсем другая ситуация при неравномерном движении. Средней скоростью обычно характеризуют движение поездов, но это вовсе не означает, что за каждый час времени поезд проходит v км.
Мгновенной скоростью движения в момент времени t называется предел средней скорости движения за время от t до t+τ, когда τ стремится к нулю.
З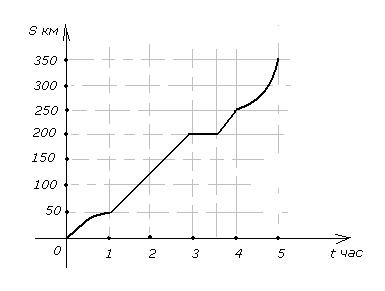 адания
адания
-
На рисунке представлен график график движения поезда. На каких участках поезд шёл равномерно и на каких неравномерно? Когда он делал остановку и на сколько минут? Найдите среднюю скорость поезда за первые 4 часа.
-
В интервале времени (0, t1) поезд шёл со скоростью v1 км/ч, а в интервале времени (t1,t2) со скоростью v2 км/ч, в интервале времени (t2,t3) v3 км/ч, и т.д. наконец в интервале времени (tn-1,tn) - vnкм/ч. Чему равна средняя скорость движения поезда в интервале (0, tn)?
-
Найти мгновенную скорость движения точки, движущейся по закону s(t)=t3 (s- путь в метрах, t- время в минутах): 1)в начальный момент времени; 2) через 10 сек после начала движения; 3) в мемент времени t=5мин.
-
При нагревании тела его температура Т изменяется с течением времени tпо закону Т=0,4t2 ( температура в градусах, время в секундах). Найти: 1) среднюю скорость изменения температуры за промежуток времени от t1=4сек до t2=8сек; 2) мгновенную скорость изменения температуры тела в момент времени t=5сек.
-
Ток I ампер изменяется с течением времени по закону I=0,5t2 , где t- число секунд. Найти скорость изменения тока в конце пятой секунды .
Занятие №10
Тема: «Касательная к кривой.»
П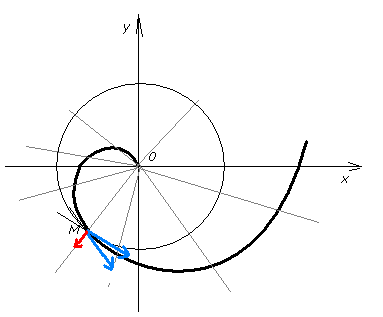 роведение касательных тесно связано с вычислением скоростей. Когда точка движется по кривой линии, вектор скорости в каждый момент времени направлен по касательной , а его длина равна линейной скорости движущейся точки. Первый общий метод нахождения касательных придумал Декарт. Он рассматривал касательную как секущую, у которой обе точки пересечения с кривой слились в одну. А так как отыскание точек пересечения Декарт сводил к решению алгебраических уравнений, то ему достаточно было ответить на вопрос, при каких условиях корни алгебраического уравнения сливаются. Таким образом он научился проводить касательные к любым алгебраическим кривым…Метод Декарта нельзя было применять к трансцендентным кривым, но большинство известных в то время трансцендентных кривых возникало как траектории движения движущихся точек. Поэтому для отыскания касательных и скоростей использовали кинематические соображения Если движение точки можно разложить на два движения , то достаточно найти её мгновенные скорости в каждом из составляющих движений, а потом сложить их по правилу параллелограмма. Например, чтобы провести касательную к архимедовой спирали в некоторой точке М, достаточно провести через эту точку окружность и луч и отложить на касательной к окружности и на луче векторы, длины которых равны линейным скоростям вращательного и поступательного движений. Складывая получившиеся векторы, получаем вектор скорости точки, движущейся по спирали. Направление этого вектора указывает, куда направлена касательная, а его длина показывает, с какой скоростью точка движется по спирали.
роведение касательных тесно связано с вычислением скоростей. Когда точка движется по кривой линии, вектор скорости в каждый момент времени направлен по касательной , а его длина равна линейной скорости движущейся точки. Первый общий метод нахождения касательных придумал Декарт. Он рассматривал касательную как секущую, у которой обе точки пересечения с кривой слились в одну. А так как отыскание точек пересечения Декарт сводил к решению алгебраических уравнений, то ему достаточно было ответить на вопрос, при каких условиях корни алгебраического уравнения сливаются. Таким образом он научился проводить касательные к любым алгебраическим кривым…Метод Декарта нельзя было применять к трансцендентным кривым, но большинство известных в то время трансцендентных кривых возникало как траектории движения движущихся точек. Поэтому для отыскания касательных и скоростей использовали кинематические соображения Если движение точки можно разложить на два движения , то достаточно найти её мгновенные скорости в каждом из составляющих движений, а потом сложить их по правилу параллелограмма. Например, чтобы провести касательную к архимедовой спирали в некоторой точке М, достаточно провести через эту точку окружность и луч и отложить на касательной к окружности и на луче векторы, длины которых равны линейным скоростям вращательного и поступательного движений. Складывая получившиеся векторы, получаем вектор скорости точки, движущейся по спирали. Направление этого вектора указывает, куда направлена касательная, а его длина показывает, с какой скоростью точка движется по спирали.
Задания
-
Что является касательной к прямой в произвольной её точке?
-
Имеет ли график функции
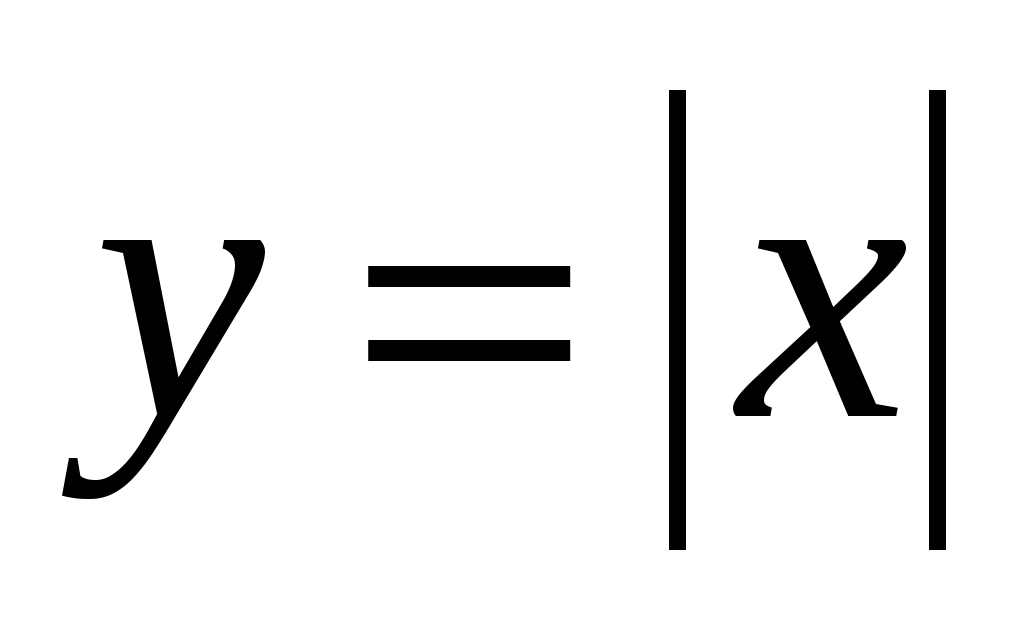 касательную в точке с абсциссой равной -1; 0; 1?
касательную в точке с абсциссой равной -1; 0; 1? -
Существует ли касательная к графику функции
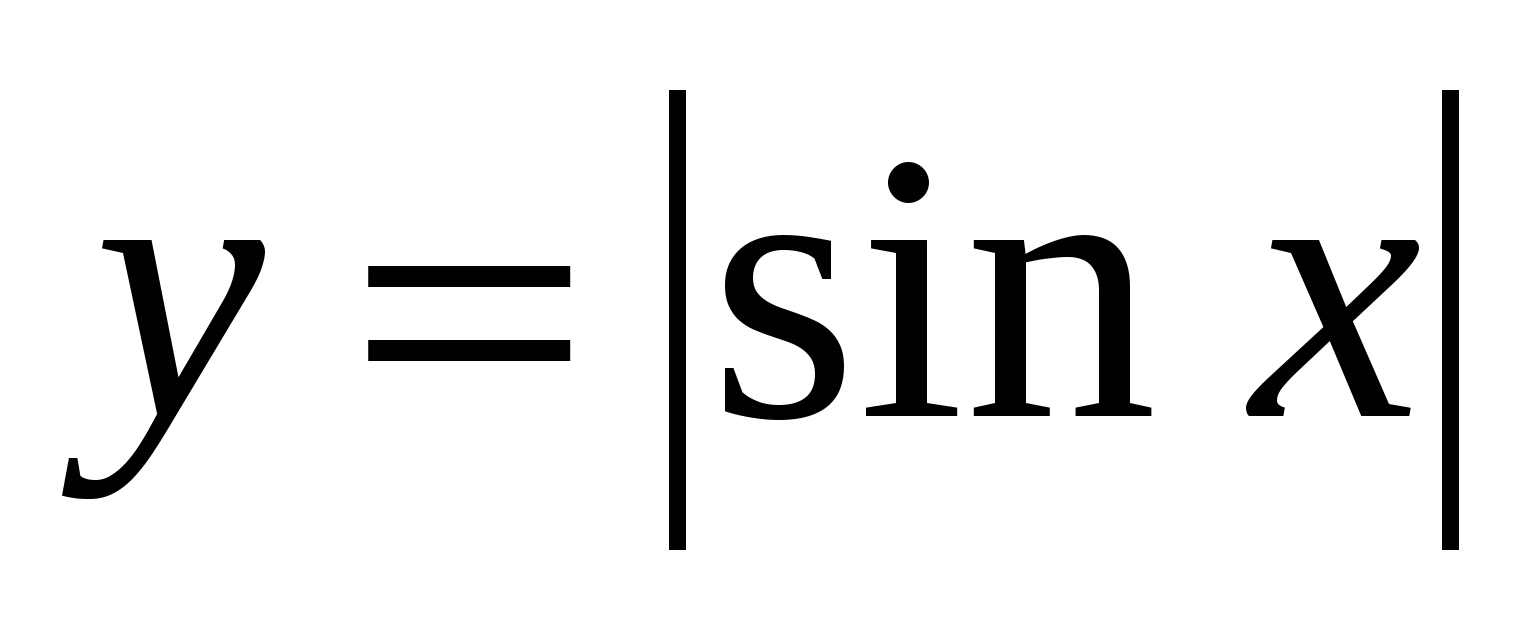 в точке х=π?
в точке х=π? -
Хорошо известно как определяется угол между двумя прямыми, а как бы вы определили угол между двумя пересекающимися кривыми в точке их пересечения?
-
Под каким углом прямая х=3 пересекается с параболой у=х2?
-
В каких точках прямая у=х пересекается с параболой у=х2? Какие углы образуются в результате пересечения?
-
Напишите уравнение касательной к графику функции f(x)=2-x2 в точке с абсциссой х=-3. выполните рисунок
Занятие №11
Тема: «Наибольшее и наименьшее значение функции»
Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть задачами на «экстремум»( от латинского слова extremum- «крайний») или задачами «на максимум и минимум»(от латинских maximum и minimum - соответственно «наибольшее» и «наименьшее»). Такие задачи часто встречаются в технике и естествознании, в повседневной деятельности людей.
Как из круглого бревна выпилить прямоугольную балку с наименьшим количеством отходов? Каких размеров должен быть ящик, чтобы при заданном расходе материала его объём был наибольший? В каком месте следует построить мост через реку, чтобы дорога, проходящая через него и соединяющая, два города была кратчайшей?
Эти задачи имеют большое практическое значение . С их помощью можно во всяком деле решить вопрос, как, по словам П.Л.Чебышева, «располагать средствами своими для достижения по возможности большей выгоды»
Общая схема решения :
-
задача «переводится » на язык функций. Для этого выбирается удобный параметр х, через который интересующую нас величину выражают как функцию f(x);
-
средствами анализа ищется наибольшее и наименьшее значение этой функции на некотором промежутке;
-
выясняется какой практический смысл ( в терминах первоначальной задачи ) имеет полученный (на языке функций) результат.
Задания
-
Какой из всех прямоугольников заданного периметра имеет наибольшую площадь? (решение изложено в VI книге «Начала» Евклида)
-
И
 з квадратного листа жести со стороной а надо изготовить открытую сверху коробку, вырезав по углам (см рисунок) квадратики и загнув образовавшиеся кромки. Какой должна быть сторона основания коробки чтобы её объём был максимальным?
з квадратного листа жести со стороной а надо изготовить открытую сверху коробку, вырезав по углам (см рисунок) квадратики и загнув образовавшиеся кромки. Какой должна быть сторона основания коробки чтобы её объём был максимальным? -
Из круглого бревна вырезают балку с прямоугольным сечением наибольшей площади. Найдите размеры сечен я балки, если радиус сечения бревна равен 20 см ? /20√2 см , 20√2см/
-
Буровая вышка расположена в поле в 9 км от ближайшей точки шоссе. С буровой надо направить курьера в населённый пункт, расположенный по шоссе в 15 км от упомянутой точки (считаем шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке на шоссе надо ехать курьеру, чтобы в кратчайшее время достичь населенного пункта? /в точку, удалённую на 3 км от населённого пункта и на 12 км от точки шоссе, ближайшей к буровой вышке/
-
Открытый бак имеющий форму параллелепипеда с квадратным основанием должен вмещать 13,5 л жидкости. При каких размерах бака на его изготовление потребуется наименьшее количество металла? / высота 1,5 дм, сторона основания 3 дм./
-
Лодка находится на озере на расстоянии 3 км от ближайшей точки А берега. Пассажир лодки желает достигнуть села В, находящегося на берегу на расстоянии 5 км от А (участок АВ берега считаем прямолинейным). Лодка движется со скоростью 4 км/ч, а пассажир, выйдя из лодки, может в час пройти 5 км. К какому пункту берега должна пристать лодка, чтобы пассажир достиг села в кратчайшее время? / к точке отрезка АВ, удалённой от АВ на расстоянии 1 км./
-
Прямоугольный участок земли площадью4 га огораживается забором. Каковы должны быть размеры участка, чтобы периметр был наименьшим?
Занятие №12
Тема: «Язык формул и расстояний»
Между алгебраическими и геометрическими задачами, между языком алгебры(языком формул) и языком геометрии( языком расстояний) существует неразрывная связь, ставшая со времён Декарта очевидной даже тем, кто не слишком искушён в математике. В самом деле , решение многих геометрических задач может быть сведено к решению систем алгебраических уравнений и требует применять соответствующий алгебраический инструментарий. Менее заметны геометрические идеи, лежащие в основе ряда алгебраических задач- на вычисление наибольших и наименьших значений некоторых выражений, решение уравнений и неравенств. Изучение языка невозможно без словаря или хотя бы разговорника:
АЛГЕБРАИЧЕСКИЙ ЯЗЫК(язык формул)
ГЕОМЕТРИЧЕСКИЙ ЯЗЫК(язык расстояний)
числа и буквы
расстояния до координатных осей
модуль разности двух чисел
расстояние между двумя точками координатной прямой
сумма квадратов двух чисел
квадрат расстояния между двумя точками координатной плоскости
Модуль разности двух чисел равен расстоянию между точками числовой ( координатной) прямой. Так, 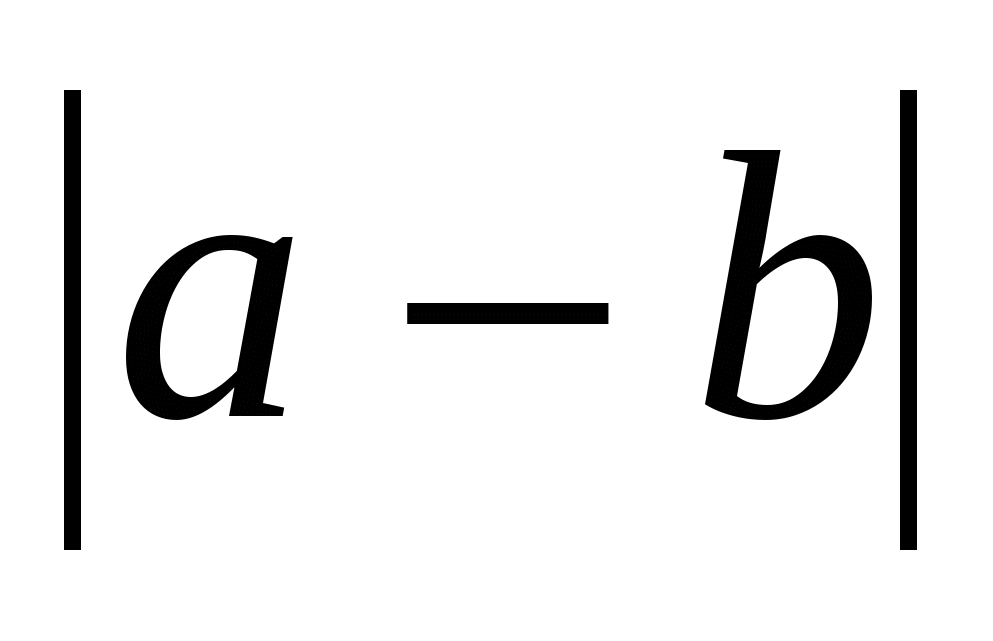 есть расстояние между точками a и b числовой прямой
есть расстояние между точками a и b числовой прямой
.
Задания
-
«Переведите» следующие предложения с геометрического языка на алгебраический.
ЯЗЫК РАССТОЯНИЙ
ЯЗЫК ФОРМУЛ
1. расстояние от точки t числовой оси до точки -22 меньше пяти
2. сумма расстояний от точки х числовой оси до точек -3 и 5 равно 12
3. точка 5 числовой оси равноудалена от точек х-1 и х2-16
4. Расстояние от точки М прямой у=3х-2 до оси абсцисс в 5 раз больше расстояния до оси ординат
5. Точка М(a,b) принадлежит окружности с центром в начале координат и радиусом 3.
6. Сумма расстояний от точки М (х,у) до точек Р(3,4) и Н(-2,5) не больше 6.
7. Расстояние от точки М(m,n) единичной окружности до точки Р (-4,1) равно 3.
8. Расстояние от точки М(p,q) окружности с центром А(-2,-4) и радиусом 2 до точки Р(a,b) окружности с тем же радиусом 6 равно 8.
9. Сумма расстояний от точки М прямой у=2х-1 до точек Р(3;4) и Е(-1;1) равно 5.
10. Расстояние от точки от точки М прямой у=х до точки Р прямой у=2х-3 не меньше 9
-
«Переведите » следующие предложения с алгебраического языка на геометрический.
ЯЗЫК ФОРМУЛ
ЯЗЫК РАССТОЯНИЙ
1.Решите уравнение
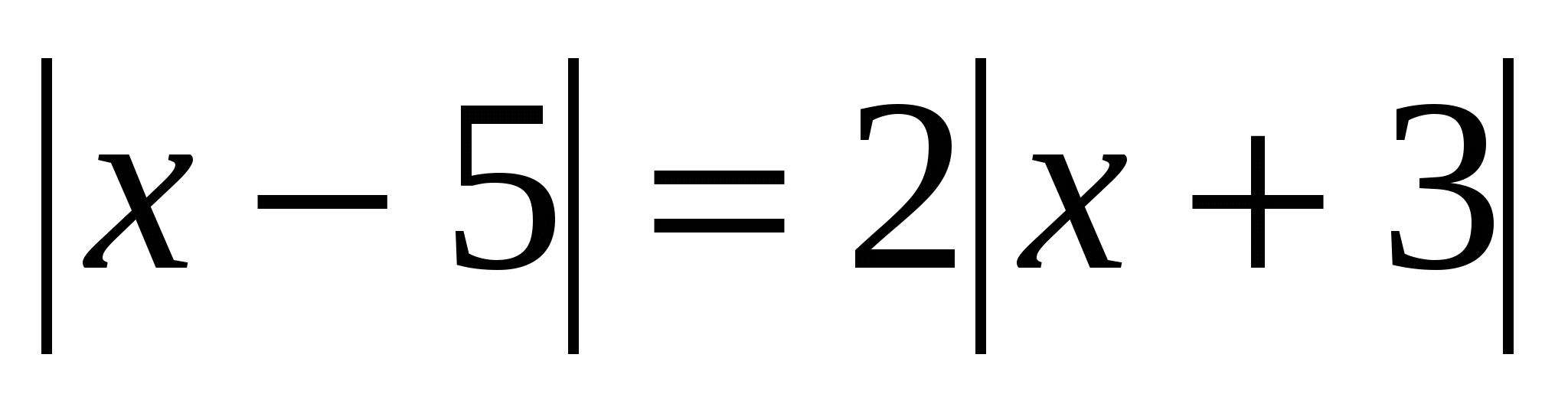
2. Имеет ли система
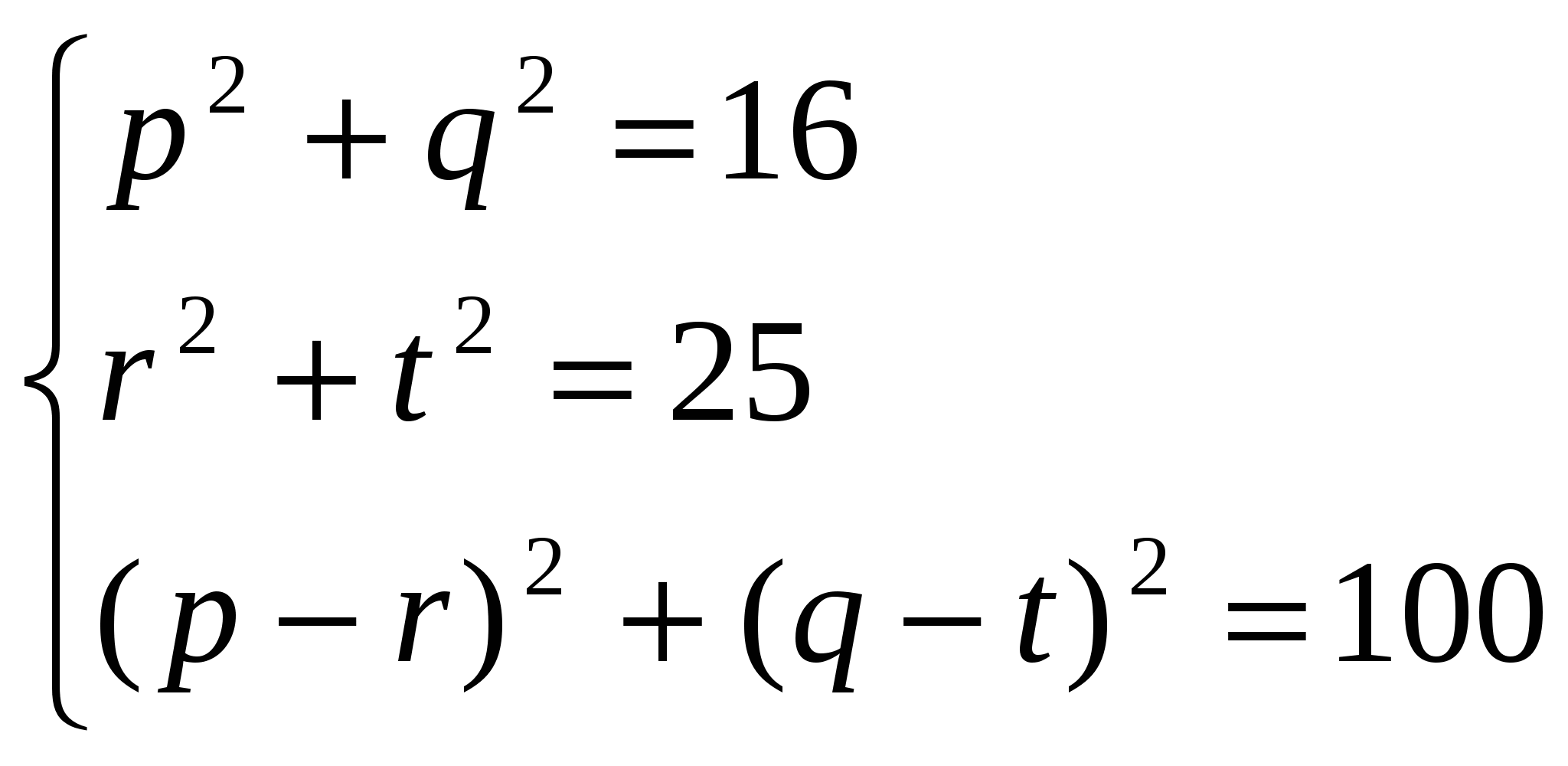 хотя бы одно решение?
хотя бы одно решение? 3. Найдите наименьшее значение функции
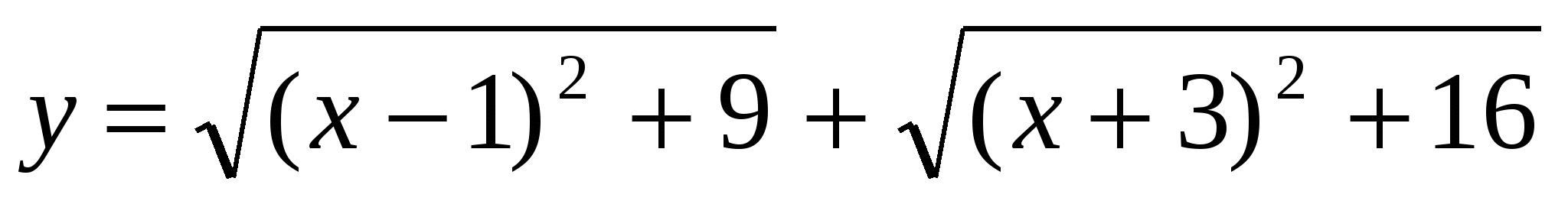
4. Найдите наименьшее значение функции
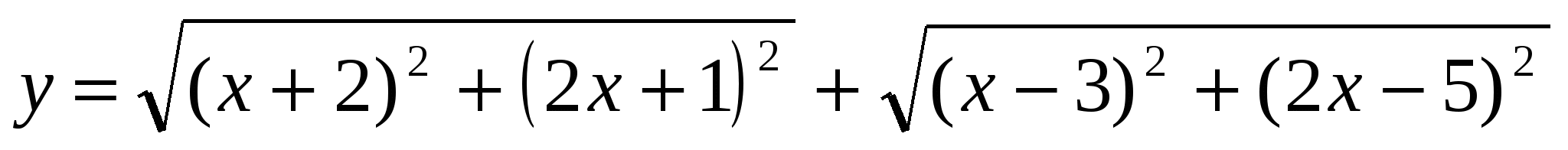
5. Решите неравенство
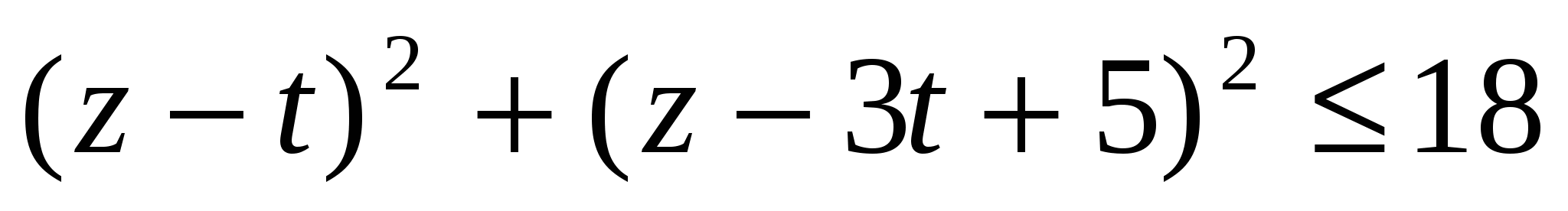
6. Решите уравнение

7. Найдите все значения а, при каждом из которых система
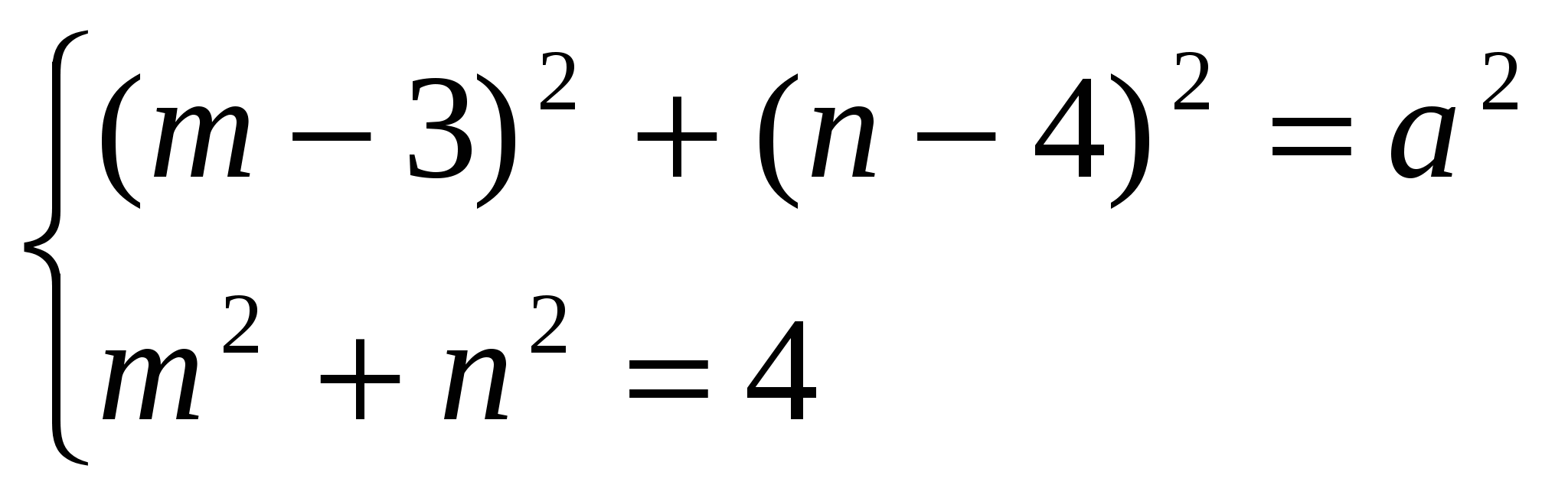 имеет единственное решение.
имеет единственное решение.
-
Решите используя геометрический смысл модуля: 1)
 ; 2)
; 2)  ; 3)
; 3) ; 4)
; 4) 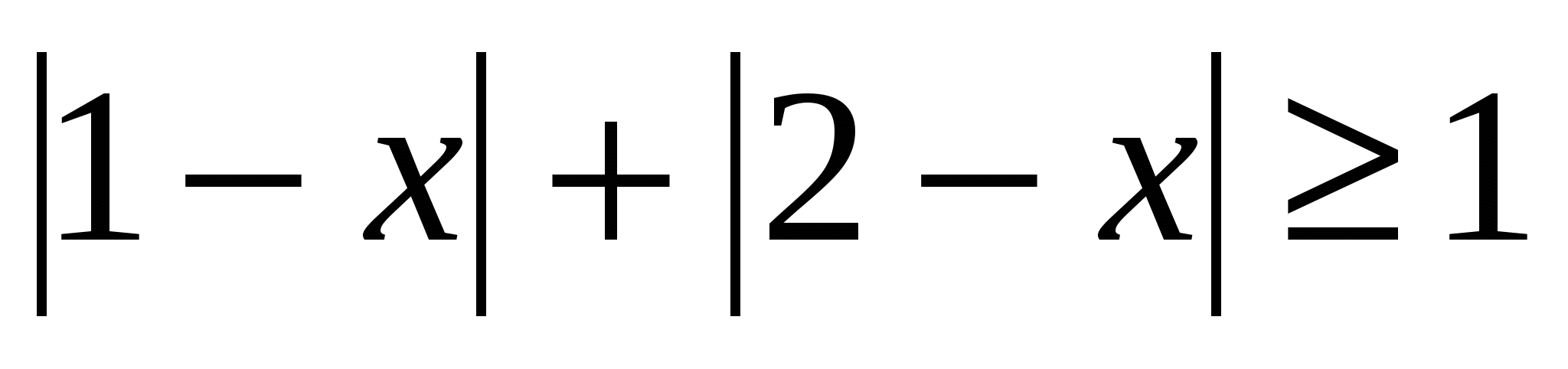
Занятие №13 и №14
Тема: «Простейшая геометрия на местности»
Для практических целей часто возникает необходимость производить геометрическиие построения на местности. Такие построения нужны при строительстве зданий, при прокладке дорог, при различных измерениях объектов.Можно подумать что ровная поверхность земли, а именно такой и будем её считать во всех задачах настояещего параграфа, ничем, по существу, не отличается от работы циркулем и линейкой на обыкновенном листе бумаги. Но на самом деле, построения на местности имеют свою специфику, так как чертить на земле какие либо линии представляется весьма затруднительным. Поэтому, во-превых откажемся от проведения настоящих прямых на земле, будем эти прямые прокладывать, т.е. отмечать на них, например, колышками, достаточно густую сеть точек. Во-вторых, циркуля фактически у нас нет, всё, что остаётся от циркуля,- это способность откладывть на данных прямых (проложеных) конкретные расстояния , которые должны быть заданы не численно, а с помощью двух точек, уже обозначенных на местности с помощью колышков где-то на местности.Решите данные задачи не пользуясь транспортиром.
Задания
-
На местности колышками обозначены две удалённые друг от друга точки. Как проложить через них прямую , и в частности, как можно без помощника устанавливать колышки на прямой между данными точками?
-
На местности колышками обозначены две очки одной прямой и две точки другой прямой. Как найти точку пресечеия этих прямых?
-
На местности обозначены точки А и В. Найдите тоску С, симметричную точке А относительно точки В.
-
На местности обозначены три данные точкиА,В и С, не лежащие на одной прямой. Через точку А проложите прямую, параллельную прямой ВС.
-
Найдите середину отрезка АВ, заданного на местности двумя точками А и В.
-
Отрезок , заданный на местности двумя точками А и В, требуется разделить в отношении, в ктором находятся длины отрезков КД и МН, заданных на местности точками К,Д,М,Н.
-
На местности обозначены три точки А,М,Н, не лежащие на одной прямой. Проложите биссектрисуугла МАН.
-
Проложите на местности каку-либо прямую, препендикулярную прямой, проходящей через заданные точки А и В. Как пролодить перпендикуляр к прямой АВ, проходящей через данную точку Н.
-
На местности обозначены точки А и В. Найдите точки С,Р и Е, для которых выполнены равенства ∟ВАС=450, ∟ВАР=600, ∟ВАЕ=300.
Занятие №15
Тема: «Измерения при различных ограничениях»
Для нахождения расстояний, высот , глубин или других размеров реальных объектов не всегда можно обойтись непосредственными измерениями- во многих случаях такие измерения сопряжены с определёнными трудностями, а то и вообще практически невозможны. Однако в своей деятельности человеку приходится порой задумываться над тем, как всё-таки можно определить поточнее интересующую его величину.
При решении нижеследующих задач советуем побеспокоится о том, чтобы предлагаемый вами способ был действительно осуществим на практике и использовал минимум необходимых средств для построений и измерений, вычислений. Условие: основные измерительные приборы- шаг, пядь(размах пальцев), сажень(размах рук), уровень глаз(расстояние от земли до глаз) и т.д. Не менее важно следить за тем чтобы ваш способ был надёжен, как можно более точен.
Задания
-
Как определить длину своего шага? Особенно если учесть, что при всём старании вы вряд ли сможете сделать один обычный шаг, так как для этого вам нужно оказаться в состоянии обычной ходьбы, и ещё, если учесть, что расстояние между двумя крайними точками ступней не равно длине шага , а превосходит её на длину ступни.
-
Измеряя какие-либо длины пальцами рук, лучше не отрывать их от поверхности, а приставлять один палец к другому, который затем снова вытягивать в заданном направлении. Найдите длину такого размаха своих пальцев.
-
Как по длине тени , падающей от дерева в солнечный день, определить высоту этого дерева?
-
Как определить высоту дерева не прибегая к помощи теней, и не взбираясь на него?
-
Вам понадобилось измерить на местности расстояние между двумя объектами, разделёнными зданием или другим препятствием, не позволяющим произвести непосредственные измерения по прямой между этими объектами. Как, тем не менее, можно произвести указанное измерение?
-
Вы плывете по озеру на лодке и хотите узнать его глубину. Нельзя ли воспользоваться для этой цели камышом торчащим из воды, не вырывая его?
-
Стоя на краю обрыва, вы хотите измерить глубину находящегося перед вами котлована. Нельзя ли это сделать, не спуская с обрыва никаких верёвок?
-
Вы находитесь на одном берегу реки, а на другом, недоступном ля вас берегу расположены два объекта. Как измерить расстояние между ними?
-
Вы находитесь на брегу реки и хотите измерить её ширину , не имея возможности перебраться на другой берег. Для этого вы отыскиваете глазами на противоположном берегу близко к воде какой-нибудь заметный ориентир А-камень, деревце,- и отмечаете на своём берегу точку Б, расстояние от которой до точки А представляет собой, по- вашему, ширину реки. Как измерить длину отрезка АБ?
Занятие №16
Тема: «Площади плоских фигур»
Площадью называется величина, характеризующая размер геометрической фигуры. Определение площадей геометрических фигур- одна из древнейших практических задач. Правильный подход к их решению был найден не сразу. Древние вавилоняне полагали, например, что площадь всякого четырёхугольника равна произведению полусумм противоположных сторон. Формула явно неверна, из неё вытекает, в частности, что площади всех ромбов с равными сторонами одинаковы. Но уже древние греки умели правильно находить площади многоугольников.
Методы нахождения площадей произвольных фигур даёт интегральное исчисление.
Механический прибор для определения площади плоских фигур- планиметр.
Задания
1. Как из куска материи треугольной формы вырезать прямоугольный кусок вдвое меньшей площади?
2. Земельный участок имеет форму квадрата, в вершинах которого растут деревья. Как , не изменяя его формы и не вырубая деревьев, увеличить площадь участка в два раза?
3. Троим братьям достался в наследство участок земли в форме квадрата. Как следует его разделить, чтобы все братья получили одинаковое количество земли? Предложите разные решения.
4. Задача Герона. Участок заболоченной местности имеет форму выпуклого четырёхугольника. Как, не вступая в него, определить его площадь?
5. Задача Брахмагупты. Определите высоту свечи по длинам теней, отбрасываемых в двух различных положениях, и расстоянию между ними.
6. Три дороги, пересекаясь, ограничивают участок земли. В каком месте этого участка следует построить автозаправочную станцию, чтобы сумма расстояний от неё до всех сторон была наименьшей?
7. Как через пункт А(см рис) провести прямую дорогу, делящую участок четырёхугольной формы на две равновеликие части?

Занятие №17
Тема: «Правильные многоугольники»
При произвольном n≥3 рассматривают правильные n-угольники: у них все стороны и все углы (внутренние) равны. Правильный n-угольник можно получить, разделив окружность на n равных дуг и соединив соседние точки деления. Центр этой окружности называют центром правильного n-угольника; через него проходят n осей симметрии правильного n-угольника.
В древности правильные многоугольники считались символами красоты и совершенства. Практическая задача построения таких фигур с помощью циркуля и линейки имеет давнюю историю. Древние греки умели строить правильный треугольник, квадрат, правильный пятиугольник и пятнадцатиугольник, а также все многоугольники, которые получаются из них удвоением числа сторон.
Простейшим примером использования правильных многоугольников служит паркет
Задания
-
Конец валика диаметром 4 см опилен под квадрат. Определите наибольший размер, который может иметь сторона квадрата.
-
Сечение головки газового вентиля имеет форму правильного треугольника, сторона которого равна 3 см. Каким должен быть минимальный диаметр круглого железного стержня, из которого изготовляют стержень?
-
Постройте квадрат со стороной равной данному отрезку.
-
Как построить пятиконечную звезду?
-
В окружность вписан правильный многоугольник, постройте правильный многоугольник, у которого число сторон вдвое больше чем у данного.
-
Составьте красивый паркет из правильных многоугольников


