- Преподавателю
- Математика
- Методические рекомендации к изложению темы Арифметическая и геометрическая прогрессия
Методические рекомендации к изложению темы Арифметическая и геометрическая прогрессия
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Другие методич. материалы |
| Автор | Ковалева И.В. |
| Дата | 12.12.2015 |
| Формат | docx |
| Изображения | Есть |
ИНДИВИДУАЛЬНАЯ ТВОРЧЕСКАЯ РАБОТА
«ПОДГОТОВКА УЧИТЕЛЯ К ИЗЛОЖЕНИЮ ТЕМЫ
«АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
(АЛГЕБРА, 9 КЛАСС)
СОДЕРЖАНИЕ
-
Календарно-тематическое планирование темы……………………………… 3
-
Критерии оценивания учебных достижений ученика при изучении
темы «Арифметическая и геометрическая прогрессия»………………… 4
-
Справочный материал по теме…………………………………………………………. 7
-
Арифметическая прогрессия………………………………………………….. 7
-
Геометрическая прогрессия……………………………………………………. 8
-
Примеры решения задач………………………………………………………… 10
-
-
Справочный материал по повторению………………………………………….…. 13
-
Поэлементный анализ учебных достижений учеников
по теме «Арифметическая и геометрическая прогрессия»……………… 16
-
Поэлементный анализ заданий № 1-3 тематической контрольной
работы в соответствии с уровнями учебных достижений………………… 19
-
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ТЕМЫ
-
№ п/п
Тема урока
Количество часов
дата
учебник
1
Числовые последовательности, способы их задания
1
2
Арифметическая прогрессия, ее свойства
1
3
Формула n-го члена арифметической прогрессии
1
4
Сумма первых n членов арифметической прогресии
1
5
Решение задач. Самостоятельная работа.
1
6
Геометрическая прогрессия, ее свойства
1
7
Формула n-го члена геометрической прогрессии
1
8
Сумма n первых членов геометрической прогресии. Самостоятельная работа
1
9
Бесконечная убывающая геометрическая прогрессия, ее сумма
1
10
Решение задач и упражнений. Самостоятельная работа
1
11
Решение задач и упражнений
1
12
Тематическая контрольная работа
1
13
Анализ результатов контрольной работы
1
-
КРИТЕРИИ ОЦЕНИВАНИЯ УЧЕБНЫХ ДОСТИЖЕНИЙ УЧЕНИКА ПРИ ИЗУЧЕНИИ ТЕМЫ «АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
-
Уровень учебных достижений
Баллы
Критерии оценивания учебных достижений учащихся
-
Низкий
1
Ученик умеет:
-
Распознавать арифметическую и геометрическую прогрессию среди нескольких предложенных числовых последовательностей
-
Указывать разность арифметической прогрессии, знаменатель геометрической прогрессии, называет члены арифметической и геометрической прогрессии
2
Ученик умеет:
-
Выполнять одношаговые действия с элементами арифметической и геометрической прогрессии
-
Находить разность арифметической прогрессии, знаменатель геометрической прогрессии
-
Указывает последовательные члены прогрессии
3
Ученик умеет с помощью учителя выполнять элементарные задания, решает элементарные задачи
-
Средний
4
Ученик умеет:
-
Воспроизводить определения основных понятий (определения арифметической и геометрической прогрессий, разности и знаменателя)
-
Формулирует свойства арифметической и геометрической прогрессий, правила нахождения n-го члена прогрессии, суммы n первых членов прогрессии
-
Выполняет элементарные задания по образцу
5
Ученик умеет:
-
Иллюстрировать примерами определения, формулировки свойств и правил нахождения n-го члена прогрессии, суммы n первых членов прогрессии
-
Решать задачи (до трех шагов) по известным алгоритмам
6
Ученик умеет:
-
Самостоятельно решать и объяснять решение задач (до трех шагов)
-
Записывать формулы n-го члена прогрессии, суммы n первых членов прогрессии по словесной формулировке и наоборот
-
Достаточный
7
Ученик умеет:
-
Использовать и применять определения арифметической и геометрической прогрессий, их свойства при решении задач по знакомому алгоритму
-
Записывать с помощью формул зависимость между элементами прогрессии
-
Самостоятельно исправляет указанные ошибки
-
Решает задания среднего уровня сложности без дополнительных пояснений со стороны учителя
8
-
Ученик владеет в полном объеме теоретическим материалом по данной теме
-
Ученик решает задачи, предусмотренные программой с частичными пояснениями
9
-
Ученик свободно владеет учебным материалом по теме «Арифметическая и геометрическая прогрессия»
-
Ученик самостоятельно выполняет задания в знакомых ситуациях
-
Ученик исправляет указанные ему ошибки
-
Ученик дает полное объяснение, обоснование при решении задач с ссылкой на использованные определения, формулы, правила и свойства
-
Высокий
10
Знания, умения, навыки ученик полностью соответствуют требованиям программы.
Ученик:
-
Может усваивать новые для него математические факты
-
Под руководством учителя находит источники информации и самостоятельно работает с ними
-
Решает задания с полным объяснением и обоснованием
11
Ученик:
-
Может свободно и правильно проводить определенные математические рассуждения по данной теме
-
Аргументировать свои ответы и решения
-
Может использовать приобретенные знания в незнакомой для него ситуации
-
Владеет основными методами решения задач и умеет их применять с необходимыми пояснениями
12
Ученик:
-
Проявляет вариативность мышления и рациональность в выборе способа решения математической задачи
-
Умеет обобщать и систематизировать полученные знания
-
Способен решать нестандартные задачи и упражнения по данной теме
-
-
СПРАВОЧНЫЙ МАТЕРИАЛ ПО ТЕМЕ «АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
-
Арифметическая прогрессия
-
-
№
Определения
Примеры
1.
Числовая последовательность задана, если любому натуральному числу n поставлено в соответствие некоторое число an
3; 10; 11; 13; 16; 20; …
4; 7; 10; 13; 16; …
2.
Последовательность задают при помощи формулы n-го члена, тогда нетрудно вычислить любой его член
Последовательность
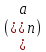 задана формулой
задана формулой 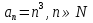
1; 8; 27; 64; …
3.
Последовательности бывают конечные и бесконечные. Последовательность (an) называется возрастающей (убывающей), если для любого номера n справедливо неравенство: an+1>an (an+1<an), где an - предыдущий член, an+1 - последующий член последовательности
2; 4; 6; 8; 10; 12; … - возрастающая
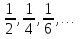 - убывающая
- убывающая 4.
Числовая последовательность (an), каждый член которой, начиная со второго, равен предыдущему, к которому прибавлено одно и то же число, называется арифметической прогрессией. Это число обозначают буквой d и называют разностью арифметической прогрессии
1; 3; 5; 7; 9 - арифметическая прогрессия
а1=1, d=2
30; 25; 20; 15; 10; 5; …
a1=30, d=-5
5.
Первые члены арифметической прогрессии:
a1 ; a1+d ; a1+2d ; a1+3d ; …
-50; -40; -30; -20; …
a1=-50, d=10
6.
Формула n-го члена арифметической прогрессии
an =a1+ (n-1)d, n ϵ N
a6=-50+10(6-1)=-50+10
 5=0; a6=0
5=0; a6=0
7.
Последовательность (an) является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому соседних с ним членов, то есть
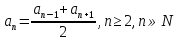
-50; -40; -30; -20; …
-40=(-50+(-30)):2
-30=(-40+(-20)):2
8.
Сумма двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равна сумме крайних членов.
1; 3; 5; 7; 9.
1+9=3+7
9.
Формула суммы первых n членов арифметической прогрессии:
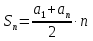
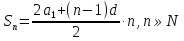
4; 7; 10; 13; 16; …
a1=4, d=3
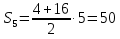
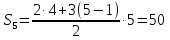
-
Геометрическая прогрессия
№
Определения
Примеры
1.
Числовая последовательность (bn), каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, называется геометрической прогрессией. Это число обозначают буквой q и называют знаменателем геометрической прогрессии
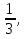 1; 3; 9; 27;…
1; 3; 9; 27;… 2; 4; 8; 16; 32; 64; … b1=2; q=2
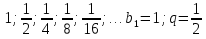
2.
Первые члены арифметической прогрессии:
b1 ; b1q ; b1q2 ; b1q3 ; …
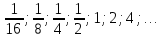
3.
Формула n-го члена геометрической прогрессии
bn =b1qn-1, n ϵ N
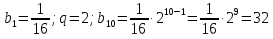
4.
Последовательность (bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов, то есть
bn2=bn-1
 bn+1 , n
bn+1 , n 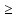 2, n ϵ N
2, n ϵ N 
3; 9; 27; 81; 243;…
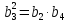
272=9
 81
81 729=729
5.
Формула суммы n первых членов геометрической прогрессии:
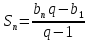
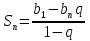
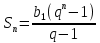
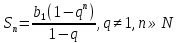
-
3; 9; 27; 81; 243;… q=3
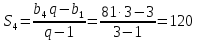
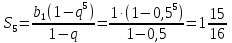
6.
Если (bn)- бесконечно убывающая геометрическая прогрессия (
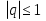 ) , то ее сумма вычисляется по формуле:
) , то ее сумма вычисляется по формуле: 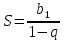
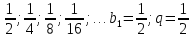
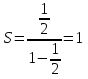
-
-
Примеры решения задач
-
Найти разность и третий член арифметической прогрессии 1; 1,2;…
-
В этой прогрессии a1=1, a2=1,2, поэтому d=a2-a1=1,2-1=0,2; a3=a2+d=1,2+0,2=1,4.
Ответ: 0,2; 1,4.
-
Является ли последовательность чисел 3; 0; -3; -6; -9 арифметической прогрессией?
-
Обозначим члены заданной последовательности a1=3; a2=0; a3=-3; a4a=-6; a5=-9
Найдем разность последующего и предыдущего членов последовательности:
a2-a1=-3; a3-a2=-3; a4-a3=-3; a5-a4=-3.
Так как полученные разности равны одному и тому же числу -3, то эта последовательность является арифметической прогрессией
Ответ: да.
-
Между числами 7 и 15 вставить такое число, чтобы все три числа образовали арифметическую прогрессию.
-
Пусть х - искомое число, тогда последовательность 7; х; 15 - арифметическая прогрессия. Второй член арифметической прогрессии является средним арифметическим первого и третьего членов: x=(7+15)/2=11.
Ответ: 11.
-
Найти девятый член арифметической прогрессии 5; 4,2; 3,4; …
-
Имеем: a1=5. Найдем разность прогрессии: d=4,2-5=-0,8. Тогда a9=a1+8d=5+8 (-0,8)=-1,4.
Ответ: -1,4.
-
Найти первый член арифметической прогрессии, в которой d=-2; a8=93.
-
Используя формулу n члена арифметической прогрессии при n=8, получим 93=a1+7 (-2). Отсюда a1=93+14=107.
Ответ: 107.
-
Является ли число 181 членом арифметической прогрессии, в которой a1=3, d=5?
-
Число 181 будет членом прогрессии, если существует такое натуральное число n - порядковый номер члена прогрессии, что an=181. Так как an=a1+(n-1)d, то 181=3+(n-1)5. Решим полученное уравнение: n=36,6. Число 36,6 не является натуральным, поэтому число 181 не является членом данной арифметической прогрессии.
Ответ: нет.
-
Найти первый член и разность арифметической прогрессии, если сумма второго и пятого ее членов равна 20, а разность девятого и третьего членов равна 18.
-
По условию имеем: a2+a5=20, a9-a3=18. Записав члены a2, a5, a3 и a9 по формуле
n члена арифметической прогрессии, получим систему уравнений:
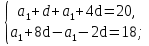
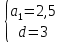
Ответ: 2,5; 3.
-
Найти сумму нечетных натуральных чисел, не превышающих 71.
-
Нечетные натуральные числа образуют арифметическую прогрессию 1; 3; 5; …, в которой a1=1, d=2, an=2n-1. Найдем, какой порядковый номер имеет член 71 этой прогрессии: 71=2n-1; n=36.
Следовательно, нужно искать сумму первых тридцати шести членов прогрессии.
Имеем: 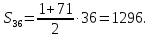
Ответ: 1296.
-
Найти сумму натуральных чисел не больше 105, которые при делении на 9 дают остаток 1.
-
Натуральные числа, которые при делении на 9 дают остаток 1, образуют арифметическую прогрессию: 1; 10; 19; …, в которой a1=1, d=9, an=9n-8. Найдем, сколько членов этой прогрессии не превышают 105. Для этого решим неравенство
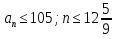
Следовательно, нужно искать сумму первых двенадцати членов прогрессии. Имеем:
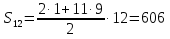
Ответ: 606.
-
Сколько нужно взять первых членов арифметической прогрессии, в которой a1=2; d=1, чтобы их сумма равнялась 90?
-
Используя формулу суммы n первых членов арифметической прогрессии, получим:
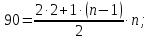
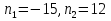
Корень n1=-15 не удовлетворяет условию задачи. Следовательно, n=12.
Ответ: 12.
-
Найти знаменатель и третий челн геометрической прогрессии 1; 1,5; …
-
В этой прогрессии b1=1; b2=1,5. Поэтому q=b2/b1=1,5; b3=b2q=1,5 1,5=2,25
Ответ: 1,5; 2,25.
-
Найти второй член геометрической прогрессии -4; b2; -25;….
-
Согласно свойству геометрической прогрессии b22=b1b3 =(-4)(-25)=100. Отсюда b2=10 или b2=-10.
Ответ: 10 или -10.
-
Найти знаменатель геометрической прогрессии, в которой b7=-12;
b9=-108.
-
Используя формулу n-го члена геометрической прогрессии, получим:
b9=b1q8=-108, b7=b1q6=-12. Отсюда q2=9; q=3 или q=-3.
Ответ: -3 или 3.
-
Найти первый член геометрической прогрессии, если четвертый ее член в три раза больше третьего, а сумма первых пяти челнов равна -12,1.
-
Так как b4=3b3, то q=3. По условию S5=-12,1, поэтому:
-12,1=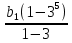 ; b1=-0,1.
; b1=-0,1.
Ответ: -0,1.
-
Найти сумму бесконечной геометрической прогрессии 6; -2; …
-
По условию b1=6; b2=-2. Тогда q=-2/6=-1/3. Имеем геометрическую прогрессию, в которой
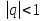 . По формуле
. По формуле 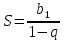 находим:
находим:
S=6: 4/3=4,5.
Ответ: 4,5.
-
СПРАВОЧНЫЙ МАТЕРИАЛ ПО ПОВТОРЕНИЮ
-
Разложение многочленов на множители
-
Вынесение общего множителя за скобки
-
Способ группировки
-
Формулы сокращенного умножения
-
Линейные уравнения.
-
Определение: Линейным называют уравнение вида ах = b, где а и b - данные числа, х - переменная
Основные свойства уравнений:
-
в любой части уравнения можно привести подобне слагаемые или раскрыть скобки
-
любой член уравнения можно перенести из одной части уравнения в другую, поменяв при этом знак слагаемого на противоположный
-
обе части уравнения можно умножить или разделить на одно и то же число, отличное от нуля
Примеры решения линейных уравнений:
1) 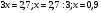
2)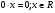
3) 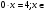 ǿ
ǿ
4)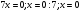
-
-
Линейные неравенства
-
Определение: линейным неравенством с одной переменной называется неравенство вида ax + b>0 (ax + b <0), где а и b - даные числа.
Основные свойства неравенств:
-
Если слагаемое перенести из одной части неравенства в другую, поменяв при этом знак на противоположный, то получим неравенство, равносильное данному
-
Если обе части неравенства умножить или разделить на одно и то же положительное число, получим неравенство, равносильное данному
-
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, поменяв при этом знак неравенства на противоположный, то получим неравенство ,равносильное данному.
Примеры решения линейных неравенств:
1)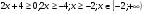
2)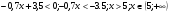
3)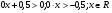
4)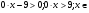 ǿ
ǿ
-
-
Квадратные уравнения
-
Определение: Квадратным называется уравнение вида ax2 + bx + c=0, где а, b и с - некоторые числа, х - переменная, причем а≠0
Дискриминантом квадратного уравнения называют выражение D=b2-4ac
-
Если D < 0, то уравнение не имеет корней
-
Если D =0, то уравнение имеет один корень:
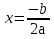
-
Если D > 0, то уравнение имеет два корня:
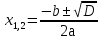
-
-
Квадратичные неравенства
-
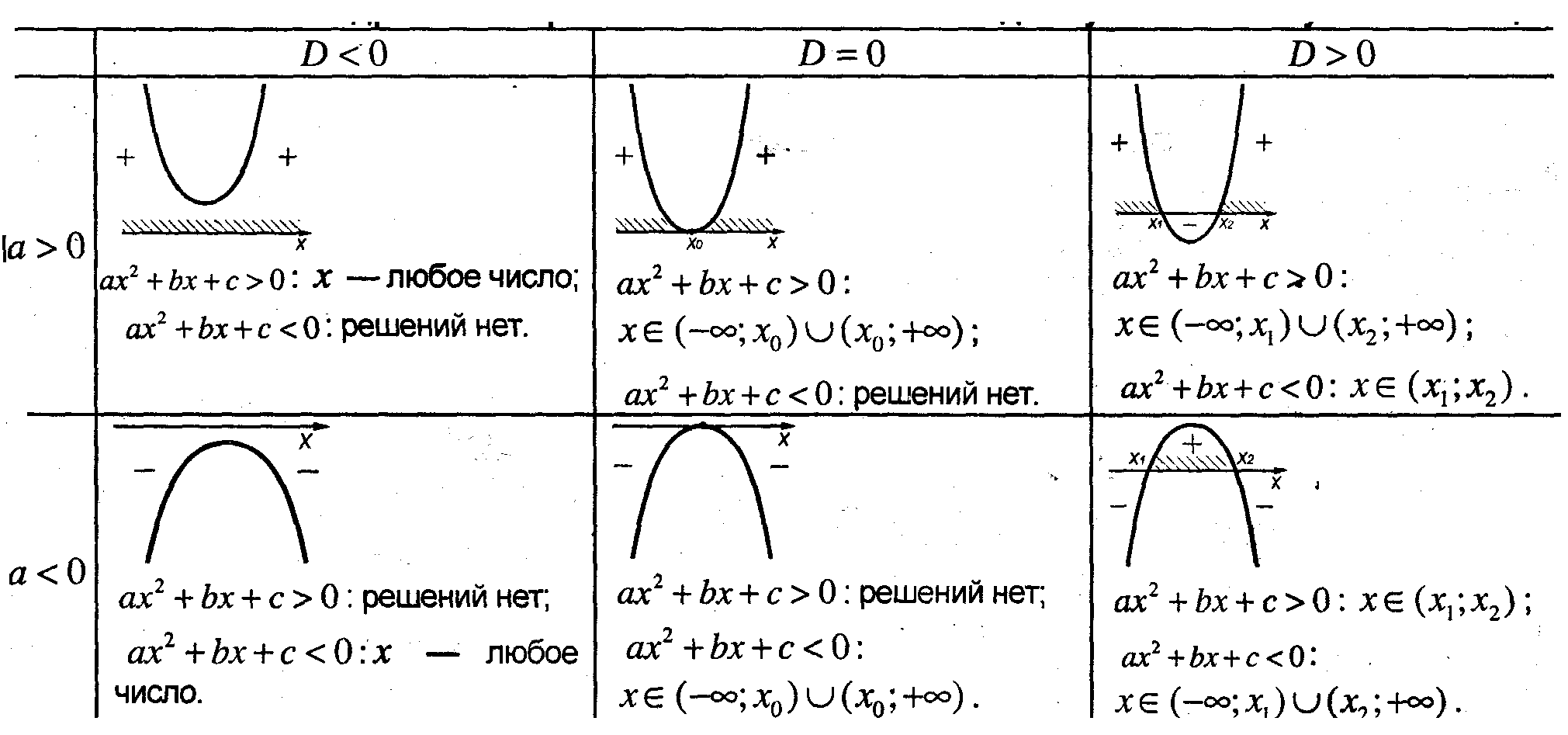
Определение: Если левой частью неравенства является выражение
ax2 + bx + c, где а≠0, правой - нуль, то его называют квадратичным неравенством.
Решение квадратичних неравенств с помощью графиков:
-
-
Метод интервалов
-
-
Если на промежутке (a; b) функция y=f(x) определена и не равна нулю, то для всех значений переменной х из этого промежутка она сохраняет свой знак
-
Алгоритм решения неравенств методом интервалов:
-
Найти D(f)
-
Найти нули функции
-
Найти и изобразить на координатной прямой промежутки, на которых функция сохраняет знак
-
Записать решение неравенства
-
-
Системы уравнений
-
Если необходимо найти общее решение двух или нескольких уравнений, то говорять, что эти уравнения образуют систему
Решением системы называют общее решение всех ее уравнений
Решить систему уравнений означает найти множество всех ее решений
Способы решения систем уравнений:
-
Способ подстановки
-
выразить из одного из уравнений системы одну переменную через другую
-
подставить во второе уравнение системы полученное выражение
-
решить полученное уравнение с одной переменной
-
найти соответсвующее значение второй переменной
-
Способ сложения
-
Применяя свойства равносильных уравнений, свести систему к виду, удобному для применения способа сложения
-
Заменить в системе одно из уравнений суммой
-
Решить полученное уравнение с одной переменной
-
Найти соответствующее значение второй переменной
-
Графический способ
Построить в одной системе координат графики обоих уравнений системы. Координаты точек пересечения этих графиков являются решениями системы уравнений
-
ПОЭЛЕМЕНТНЫЙ АНАЛИЗ УЧЕБНЫХ ДОСТИЖЕНИЙ УЧЕНИКОВ ПО ТЕМЕ «АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
-
№ п/п
Контрольные моменты
№ справки
уровни
Составление числовой последовательности
3.1.1
I уровень
Нахождение элементов числовой последовательности по заданной формуле
3.1.2
Определение видов числовых последовательностей
3.1.3
Определение арифметической прогрессии
3.1.4
Определение разности арифметической прогрессии
3.1.4
Определение геометрической прогрессии
3.2.1
Определение знаменателя геометрической прогрессии
3.2.1
Определение нескольких членов арифметической и геометрической прогрессии
3.1.5;
3.2.2
Выполнение одношаговых действий с элементами арифметической и геометрической прогрессии
3.3.1;
3.3.4;
3.3.12
Формулировка определения арифметической прогрессии
3.1.4
II уровень
Формулировка определения геометрической прогрессии
3.2.1
Формулировка свойств арифметической прогрессии
3.1.7
Формулировка свойства геометрической прогрессии
3.2.4
Применение свойств арифметической и геометрической прогрессии при решении простейших задач
3.3
Формулировка правила нахождения n-го члена арифметической прогрессии
3.1.6
Формулировка правила нахождения n-го члена геометрической прогрессии
3.2.3
Нахождение суммы n первых членов арифметической прогрессии
3.1.9
Нахождение суммы n первых членов геометрической прогрессии
3.2.5
Нахождение суммы бесконечной убывающей геометрической прогрессии
3.2.6
Решение задач (не более трех шагов) с объяснением
3.3
Формулировка определения арифметической прогрессии
3.1.4
III уровень
Формулировка определения геометрической прогрессии
3.2.11
Нахождение n-го члена геометрической прогрессии
3.2.3
Нахождение n-го члена арифметической прогрессии
3.1.6
Нахождение по формулам суммы n первых членов арифметической прогрессии
3.1.9
Нахождение по формулам суммы n первых членов геометрической прогрессии
3.2.5
Составление зависимостей между элементами арифметической прогрессии с применением формул
3.1
Составление зависимостей между элементами геометрической прогрессии с применением формул
3.2
Применение определений, свойств и формул арифметической прогрессии при решении задач достаточного уровня
3.3
Применение определений, свойств и формул геометрической прогрессии при решении задач достаточного уровня
3.3
Решение задач по знакомому алгоритму с ссылкой на формулы, свойства и правила
3.3
Определение числовой последовательности
3.1.1.
IV уровень
Определение видов числовых последовательностей
3.1.3
Определение арифметической прогрессии
3.1.4
Определение геометрической прогрессии
3.2.1
Определение разности арифметической прогрессии
3.1.4
Определение знаменателя геометрической прогрессии
3.2.1
Определение нескольких членов прогрессии по заданной формуле
3.1.2
Формулировка свойств арифметической и геометрической прогрессий
3.1.7;
3.2.4
Нахождение n-го члена геометрической прогрессии
3.2.3
Нахождение n-го члена арифметической прогрессии
3.1.6
Нахождение по формулам суммы n первых членов арифметической прогрессии
3.1.9
Нахождение суммы n первых членов геометрической прогрессии
3.2.5
Нахождение по формуле суммы бесконечной убывающей геометрической прогрессии
3.2.6
Составление зависимостей между элементами арифметической прогрессии с применением формул
3.1
Составление зависимостей между элементами геометрической прогрессии с применением формул
3.2
Применение теоретического материала при решении задач повышенной сложности
Доп. материал
Решении задач повышенной сложности путем составления систем уравнений
Доп. материал
-
ПОЭЛЕМЕНТНЫЙ АНАЛИЗ ЗАДАНИЙ № 1-3 ТЕМАТИЧЕСКОЙ КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМЕ «АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ» В СООТВЕТСТВИИ С УРОВНЯМИ УЧЕБНЫХ ДОСТИЖЕНИЙ УЧЕНИКОВ
ВАРИАНТ 1.
-
№
уровень
Контрольные моменты
№ справки
Количество баллов
Задание 1
I.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
II.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
III.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Составление и решение системы уравнений
3.3.7
IV.
Определение арифметической и геометрической прогрессии
3.1.4;
3.2.1
Применение формулы n-го члена арифметической прогрессии
3.1.6
Применение свойства геометрической прогрессии
3.2.4
Составление и решение уравнения
3.3
Лучший результат
Задание 2
I.
Определение геометрической прогрессии
3.2.1
Применение формулы суммы n первых членов геометрической прогрессии
3.2.3
II.
Определение геометрической прогрессии
3.2.1.
Применение правила нахождения знаменателя геометрической прогрессии
3.2.1
Применение формулы суммы n первых членов геометрической прогрессии
3.2.3
III.
Определение убывающей геометрической прогрессии
3.2.1
Применение формулы n-го члена геометрической прогрессии
3.2.3
Составление и решение системы уравнений
3.3.7
IV.
Определение бесконечной убывающей геометрической прогрессии
3.2.6
Применение формулы суммы бесконечной убывающей геометрической прогрессии
3.2.6
Составление и решение системы уравнений
3.3.
Лучший результат
Задание 3
I.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
II.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Решение линейного уравнения
3.3.
III.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Применение формулы суммы n первых членов арифметической прогрессии
3.1.9
Решение линейного уравнения
3.3
IV.
Определение арифметической и геометрической прогрессии
3.1.4;
3.2.1
Применение формулы n-го члена арифметической прогрессии
3.1.6
Применение свойства геометрической прогрессии
3.2.4
Составление и решение квадратного уравнения
3.3.
Лучший результат
ВАРИАНТ 2.
-
№
уровень
Контрольные моменты
№ справки
Количество баллов
Задание 1
I.
Определение арифметической прогрессии
3.1.4
Применение формулы суммы n первых членов арифметической прогрессии
3.1.9
II.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Применение формулы суммы n первых членов арифметической прогрессии
3.1.9
III.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Составление и решение системы уравнений
3.3
IV.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Решение линейного неравенства
3.3
Лучший результат
Задание 2
I.
Определение геометрической прогрессии
3.2.1
Применение формулы n-го члена геометрической прогрессии
3.2.3
II.
Определение геометрической прогрессии
3.2.1
Применение правила нахождения знаменателя геометрической прогрессии
3.2.1
Применение формулы n-го члена геометрической прогрессии
3.2.3
III.
Определение геометрической прогрессии
3.2.1
Применение формулы n-го члена геометрической прогрессии
3.2.3
Составление и решение системы уравнений
3.3
IV.
Определение бесконечной убывающей геометрической прогрессии
3.2.6
Применение формулы суммы бесконечной убывающей геометрической прогрессии
3.2.6
Составление и решение системы уравнений
3.3.
Лучший результат
Задание 3
I.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
II.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Решение линейного неравенства
3.3
III.
Определение арифметической прогрессии
3.1.4
Применение формулы n-го члена арифметической прогрессии
3.1.6
Применение формулы суммы n первых членов арифметической прогрессии
3.1.9
Решение системы линейных уравнений
3.3
IV.
Определение арифметической и геометрической прогрессии
3.1.4;
3.2.1
Применение формулы n-го члена арифметической прогрессии
3.1.6
Применение свойства геометрической прогрессии
3.2.4
Составление и решение квадратного уравнения
3.3
Лучший результат