- Преподавателю
- Математика
- Решение логарифмических неравенств удобным способом
Решение логарифмических неравенств удобным способом
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Лысенко О.А. |
| Дата | 02.05.2015 |
| Формат | doc |
| Изображения | Есть |
Лысенко О.А. Выступление на МО ЕМЦ.
Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. Так, неравенство вида
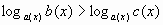 (1)
(1)
является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:
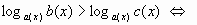
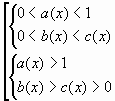
Недостатком данного метода является необходимость решения семи неравенств, не считая двух систем и одной совокупности. Уже при данных квадратичных функциях решение совокупности может потребовать много времени.
Можно предложить альтернативный, менее трудоемкий способ решения этого стандартного неравенства. Для этого учтем следующую теорему.
Теорема 1. Пусть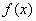 непрерывная возрастающая функция на множестве X. Тогда на этом множестве знак приращения функции будет совпадать со знаком приращения аргумента, т.е.
непрерывная возрастающая функция на множестве X. Тогда на этом множестве знак приращения функции будет совпадать со знаком приращения аргумента, т.е. 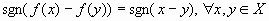 , где
, где ![]() .
.
Примечание: если 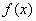 непрерывная убывающая функция на множестве X, то
непрерывная убывающая функция на множестве X, то 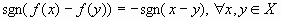 .
.
Вернемся к неравенству 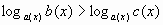 . Перейдем к десятичному логарифму (можно переходить к любому с постоянным основанием больше единицы).
. Перейдем к десятичному логарифму (можно переходить к любому с постоянным основанием больше единицы).
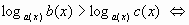
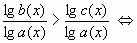
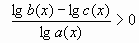 .
.
Теперь можно воспользоваться теоремой, заметив в числителе приращение функций 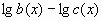 и в знаменателе
и в знаменателе 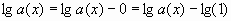 . Таким образом, верно
. Таким образом, верно
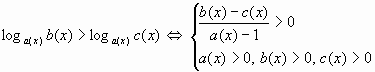 (2)
(2)
В результате количество вычислений, приводящих к ответу, уменьшается примерно в два раза, что экономит не только время, но и позволяет потенциально сделать меньше арифметических ошибок и ошибок "по невнимательности".
Пример 1.
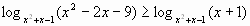 .
.
Сравнивая с (1) находим 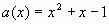 ,
, 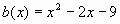 ,
, 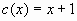 .
.
Переходя к (2) будем иметь:
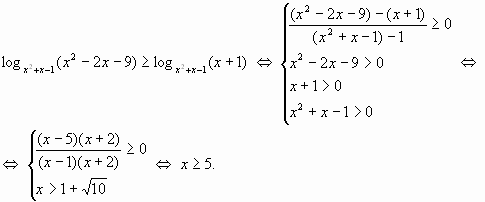
Пример 2.
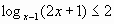 .
.
Сравнивая с (1) находим 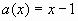 ,
, 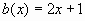 ,
, ![]() .
.
Переходя к (2) будем иметь:
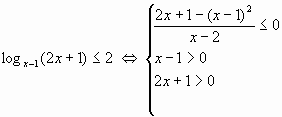
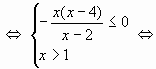
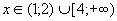 .
.
Пример 3.
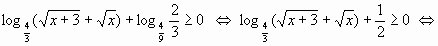
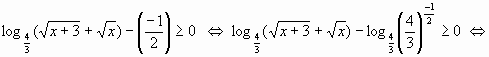
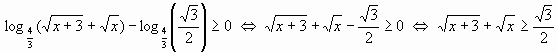 .
.
Поскольку левая часть неравенства - возрастающая функция при ![]() и
и 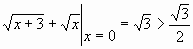 , то ответом будет множество
, то ответом будет множество 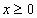 .
.
Множество примеров, в которых можно применять терему 1 может быть легко расширено, если учесть терему 2.
Терема 2.
Пусть на множестве X определены функции 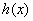 ,
, ![]() ,
, 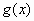 , и на этом множестве знаки
, и на этом множестве знаки 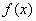 и
и 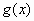 совпадают, т.е.
совпадают, т.е. 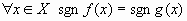 , тогда будет справедливо
, тогда будет справедливо 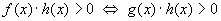 .
.
Пример 4.
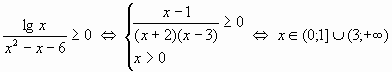 .
.
Пример 5.
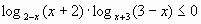 .
.
При стандартном подходе пример решается по схеме: произведение меньше нуля, когда сомножители разных знаков. Т.е. рассматривается совокупность двух систем неравенств, в которых, как было указано в начале, каждое неравенство распадается еще на семь.
Если же учесть терему 2, то каждый из сомножителей, учитывая (2), можно заменить на другую функцию, имеющую тот же знак на данном примером О.Д.З.
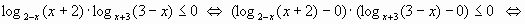
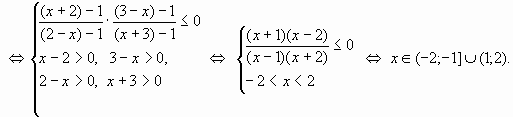
Метод замены приращения функции приращением аргумента с учетом теоремы 2, оказывается очень удобным при решении типовых задач С3 ЕГЭ.
Пример 6.
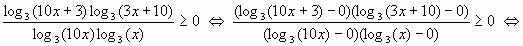
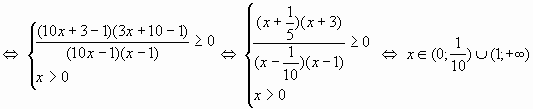
Пример 7.
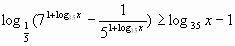 . Обозначим
. Обозначим ![]() . Получим
. Получим
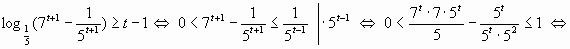
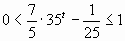 . Заметим, что из замены следует:
. Заметим, что из замены следует: 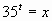 . Возвращаясь к уравнению, получим
. Возвращаясь к уравнению, получим 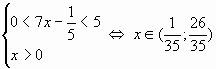 .
.
Пример 8.
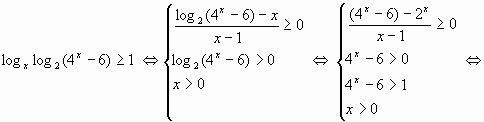
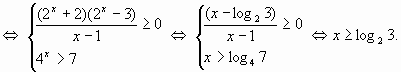
В используемых нами теоремах нет ограничении на классы функций. В данной статье, для примера, теоремы были применены к решению логарифмических неравенств. Несколько следующих примеров продемонстрируют перспективность метода при решении других видов неравенств.
Пример 9.
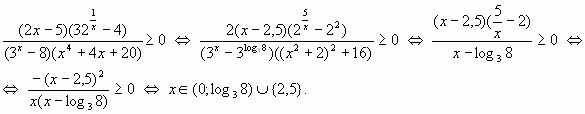
Пример 10.
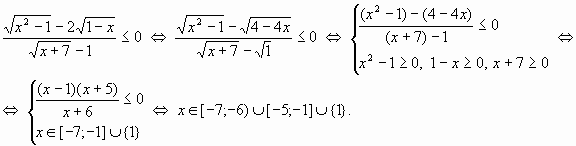
Задачи для самостоятельного решения.
1. 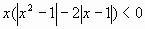 . Ответ:
. Ответ: 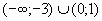 .
.
2. 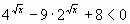 . Ответ:
. Ответ: 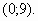
3. 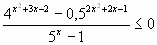 . Ответ:
. Ответ: 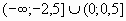 .
.
4. 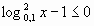 . Ответ:
. Ответ: 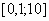 .
.
5. 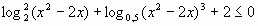 . Ответ:
. Ответ: 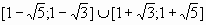 .
.
6. 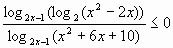 . Ответ:
. Ответ: 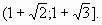
7. 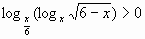 . Ответ:
. Ответ: 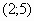 .
.


