- Преподавателю
- Математика
- Задачи С6 (№21) - лекция
Задачи С6 (№21) - лекция
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Иванова И.В. |
| Дата | 24.01.2015 |
| Формат | docx |
| Изображения | Есть |
Задачи по теории чисел в ЕГЭ (№21 или С6)
Лекция на республиканских проблемных курсах учителей «Государственная итоговая аттестация. Технология подготовки ».
Иванова И.В. Сунтарский политехнический лицей. Январь 2015 г.
Слайд №1 (Заголовок)
Очень часто бывает, что выпускники не берутся за решение задачи №21 на ЕГЭ, потому что считают её самой трудной. Порой их просто пугает «обилие букв», длинный текст, да и последний номер в варианте тоже не вдохновляет на то, чтобы хотя бы прочесть задачу. Но зачем пренебрегать аж четырьмя баллами, каждый из которых может оказаться совсем не лишним для результата экзамена.
Давайте рассмотрим решение задания №21 из демонстрационного варианта ЕГЭ-2015.
Слайд №2(текст задания).
Слайд №3- 6(решение). Подробный разбор решения задачи.
Вывод: Ученик, знающий математику в пределах 1-6 класса, вполне в состоянии набрать хоть какие-то баллы по подобной задаче. Давайте уточним, какой же необходимый минимум теории нужно повторить для подготовки к решению таких задач.
Слайд №7(необходимая теория).
Слайд №8(числовые множества). Числовые множества нам понадобится повторить в пределах до 6 класса включительно. Учесть наиболее распространённые ошибки детей. Например, напомнить, что 0 - не натуральное число, целые числа все являются рациональными и т.д.
Будем учитывать, что в теории чисел по умолчанию рассматриваются целые числа (если нет особого условия).
Слайд №9(делимость). Повторяем делимость, наиболее важные признаки делимости (6 кл). Можно дать детям и признаки делимости на 11 и другие числа, но на практике основных пяти признаков вполне хватает для решения задач на экзамене.
Слайд №10(чётность). Повторяем свойства чётности на конкретных примерах.
Слайд №11(деление с остатком).
Упражнение 1. Ответы: 1) 3 и 1, 2) 3 и 3; 3) 402 и 4; 4) 155 и 0; 5) 1 и 1; 6) 0 и 8.
Упражнение 2. Доказательство: Используем неоспоримый факт, что число п может делиться на 3 только без остатка или с остатком 1 или 2.
а) Выразим п = 3т, подставим в равенство, получим 9т2 = 3к + 2. То есть слева число, кратное 3, справа - число, делящееся на 3 с остатком 2. Они не равны.
б) Выразим п = 3т + 1, подставим в равенство, получим 9т2 + 6т +1 = 3к + 2. То есть слева число, делящееся на 3 с остатком 1, справа - число, делящееся на 3 с остатком 2. Они не равны.
в) Выразим п = 3т + 2, подставим в равенство, получим 9т2 + 12т + 3 +1= 3к + 2. То есть слева число, делящееся на 3 с остатком 1, справа - число, делящееся на 3 с остатком 2. Они не равны.
Вывод: ни при каких целых числах п и к данное равенство не выполняется, ч.т.д..
Этот вывод стоит запомнить, так как он может пригодиться и в других задачах.
Упражнение 3. Данное число легко переводится в форму 3к + 2. А число такого вида не является квадратом по доказанному в упр.2.
Упражнение 4. Легко доказать, если снова перебрать варианты п = 3т, п = 3т +1 и п = 3т + 2. Подставив эти выражения вместо п и упростив, все три раза получим числа кратные 3.
Слайд №12(каноническое разложение). Повторим простые и составные числа, разложение на простые множители (6 кл). Число 2 - единственное чётное простое число.
Упражнение 1. Число очевидно чётное (сумма 2 нечётных) и не равно 2. Значит, оно составное.
Слайд №13(каноническое разложение). Основная теорема арифметики и определение канонического разложения.
Упражнение 2. а) 3; б) 4; в) п + 1.
Упражнение 3. А) 4; б) 4 ∙ 3 = 12; в) (т + 1) (п + 1).
Слайд №14(взаимно простые числа). Определение и свойства взаимно простых чисел.
Свойства стоит проиллюстрировать на примере такого типа: из выражения 7а = 16р следует, что а кратно 16, а р кратно 7, так как 16 и 7 - взаимно простые числа.
Упражнение: 45 = 5∙ 9, вспомним признаки делимости на 5 и 9. Ответ:6 и 0 или 1 и 5.
Слайд №15(Последовательности). Повторим определения, формулировки и формулы арифметической и геометрической прогрессий (9 кл.). Кстати, сумма бесконечно убывающей геометрической прогрессии в задачах на теорию чисел обычно не появляется. Этот вопрос ближе к анализу функций.
Упражнение. 36 и 48.
Слайд №16(метод «Оценка+пример»). Метод в общеобразовательных учебниках отсутствует, и этот вопрос единственный, который действительно требует объяснения даже для сильных учеников. Мы начнём рассматривать метод с простого примера.
Слайд №17(метод «Оценка+пример»).
Пример 1. Решение показывается на доске. Стоит притормозить особо активных умненьких, которые с ходу кинутся решать задачу через производную или через свойства параболы, напомнив им, что мы вообще то говорим о другом методе. Итак:
-
Оценка: Выделим полный квадрат: (х - 1)2 + 2 очевидно не меньше 2.
-
Пример: При х = 1 функция равна 2.
Значит, наименьшее значение функции равно 2.
Пример 2. Выпишем все числа от1 до 10 включительно на доске. Очевидно, что одно из них, а именно 7 должно быть только в делимом, так как лишь у него нет общих делителей с остальными числами. Все остальные состоят из множителей 2, 3, 5 и степеней этих трёх чисел, значит, могут сокращать друг друга. Итак:
-
Оценка: Частное никак не может оказаться меньше 7.
-
Пример: Можно взять любой подходящий пример, хотя бы такой:
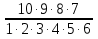 . Варианты дети могут подобрать без больших проблем. Можно упростить подбор, если использовать каноническое разложение.
. Варианты дети могут подобрать без больших проблем. Можно упростить подбор, если использовать каноническое разложение.
Слайд №18(метод «Оценка+пример»).
Пример 3. Реальная задача из ЕГЭ.
а) Легко решается уравнением х + 13х = 6075. Переместительный закон никто не отменял, так что других вариантов уравнения нет. Слева число чётное, справа нечётное, тратить драгоценное время экзамена на подробное решение незачем. Уравнение не имеет решения в натуральных числах.
Ответ: нет.
б) Рассмотрим, какие варианты здесь возможны: 13х + х + 13х = 6075, х + 13х + х = 6075, х + 13х + 169х = 6075. Если хотя бы одно из уравнений даст ответ в натуральных числах, значит, решение есть. Выдаю секрет: два первых уравнения дают подходящие ответы.
Ответ: да, например, ... ( Ну, пример найдёте сами).
Ну, вот, 2 балла уже в кармане. А новую методику мы ещё и не применяли.
в) Оценка: Вспомним очевидный для уровня даже начальной школы факт: чтобы слагаемых было как можно больше, надо, чтобы они сами были, как можно меньше. В таком случае последовательность состоит из чередующихся 1 и 13. Узнаем, сколько таких пар поместится в сумме 6075. Делим 6075 на 14, получим 433 с остатком. Значит, количество членов последовательности не может превышать 433∙2+1= 867 членов.
Пример: А пример, кстати, уже сам собой и получился. Ведь остаток был как раз 13. Значит, последовательность такая: 13,1,13, … 13, 1, 13. Всего 867 членов.
Ответ: 867.
Практикум по решению заданий по теории чисел.
Заранее заготовлены распечатки текстов задач для каждого слушателя, так что задачи на экране выполняют демонстрационно-эстетическую функцию.
Обсуждение и решение задач отдаётся слушателям. Сама выполняю руководящие и корректирующие функции.
Слайд №19 «Задача №1. (ЕГЭ-2013 досрочный)».
а) Ответ: Да, например 4, 6, 8.
б) Оценка: Чтобы слагаемых было как можно больше, надо, чтобы сами слагаемые были, как можно меньше. Пусть а1 = 1 и d = 1.
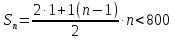 .
.
Решив квадратное неравенство и учитывая, что п - натуральное, получим, что п не превышает 39.
Пример: А он уже получился. Это натуральнее числа от 1 до 39.
в) 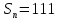 . Каким может быть значение п?
. Каким может быть значение п?
Подставив 111 в формулу суммы п членов арифметической прогрессии, получим уравнение 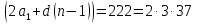 .
.
Теперь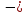 перебор вариантов (полная индукция) (п ≥ 3). Проверяем п = 3, 6, 37, 37∙2, 37∙3. Подойдут 6 и 3.
перебор вариантов (полная индукция) (п ≥ 3). Проверяем п = 3, 6, 37, 37∙2, 37∙3. Подойдут 6 и 3.
Ответ: 6 или 3.
Слайд №20 «Задача №2. (ЕГЭ-2013)».
а) Очевидно, что положительное число может быть только одно. А для кого это неочевидно, то допустим, что положительных задумано два, но тогда и сумма их тоже должна быть положительна, а в списке у нас третьего положительного числа нет. Значит, задумано или 2, или 6, а также пара отрицательных.
Если бы задумали 2, то 6 получили бы, как сумму с 4, но 4 не отрицательное. Значит, задумано число 6.
Так как 2 = 6 + (- 4), то второе задуманное число - 4.
Проверив остальные числа легко находим:
Ответ: 6, - 4 и - 7.
б) Перебор вариантов: Учитываем, что по условию задуманы РАЗЛИЧНЫЕ числа.
Очевидно, что чисел должно быть больше, чем 2. (Почему, легко догадаться самим)
Проверим, могут ли 4 нуля появиться для набора из 3 чисел. Пусть это будут числа a, b и с. Пусть а = 0. Тогда второй нуль появится в случае b = - с. Третий нуль - это a + b + с. Четвёртый не появился.
Проверим, могут ли 4 нуля появиться для набора из 4 чисел.
1 случай: Пусть это будут числа a, b, с и d. Пусть а = 0 и b = - с. Третий нуль - это a + b + с. Четвёртый не появился.
2 случай: Пусть это будут числа a, b, с и d. Пусть а = - b и с = - d. Третий нуль - это a + b + с + d. Четвёртый не появился.
Других вариантов для 3 чисел нет.
Итак, чисел должно быть не меньше 5.
Подберём пример с 5 числами: - 2, - 1, 1, 2 и 3. Получилось.
Ответ: 5 чисел.
В) Ответ: Не всегда. Есть контр-пример: набор -3, -2, -1, 0, 1, 2, 3 может получиться и для задуманных -3, 1 и 2, а также для задуманных -2, -1 и 3.
Самостоятельная работа по решению задач.
С моей стороны скорая помощь в индивидуальном порядке.
Слайд №21 «Задача №3. (ЕГЭ-2014 диагностический вариант)».
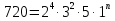 . Так как знаменатель прогрессии не может быть равен 1 по условию, то в а) и б) ответом будет «Нет», в в) «Да», например 1, 2, 4, 5 и 18.
. Так как знаменатель прогрессии не может быть равен 1 по условию, то в а) и б) ответом будет «Нет», в в) «Да», например 1, 2, 4, 5 и 18.
Слайд №22 «Задача №4.(ЕГЭ-2014 диагностический вариант, республ. олимпиада 1989г)».
В слайде выпадают 3 подсказки.
Оценка: Если а ≥ 5, то выражение а! + 5а делится на 5, и, стало быть, оканчивается на 0 или на 5. В таком случае, левая часть оканчивается на 3 или на 8, но b2 - квадрат натурального числа и может оканчиваться только на 0, 1, 4, 5 или 9. Значит, а < 5.
Перебор вариантов:
Ответ:
Слайд №23 «Задача №5.(ЕГЭ-2014 досрочный вариант, 28 апреля)».
а) Нет, для числа 11 нет подходящей пары.
б) Да, например, по кругу … 20 10 21 11 1 12 2 … (закономерность)
в) Оценка: Рассмотрим числа от 1 до 7. Эти числа нельзя ставить ни рядом, ни через одно, так как их разности меньше 7. Расставим их по кругу так, чтобы между ними оставалось по два места для прочих чисел от 8 до 21. Тогда 8 надо поставить только рядом с 1, но с другой стороны через одну позицию всё равно окажется число от 2 до 7, и появится разность меньше 7.
Значит, к ≤ 6.
Пример: к = 6. По кругу …1 8 15 2 9 16 3… (закономерность)
Ответ:
Слайд №24 «Задача №5.(ЕГЭ-2014, 5 июня)».
а) 11 посетителей -------------- 100%
п посетителей ------------------- ≈38%
Тогда п ≈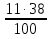 . Но 38 может получиться, если процент проголосовавших за некоторого футболиста находится в закрытом слева интервале от 37,5 до 38,5.
. Но 38 может получиться, если процент проголосовавших за некоторого футболиста находится в закрытом слева интервале от 37,5 до 38,5.
Значит: 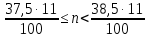 .
. 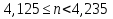 .
.
Так как п - натуральное число, то решения нет.
б) Разумеется, такое на практике ещё как может быть, просто число проголосовавших должно быть достаточно большим. Пусть на сайте голосовали 10000 посетителей.
Пусть за первого футболиста свой голос отдали 3332 человека. Считаем рейтинг: 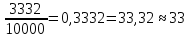 .
.
Пусть за второго футболиста свой голос отдали 3333 человека. Считаем рейтинг: 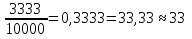 .
.
Тогда за третьего футболиста свой голос отдали 3335 человек. Считаем рейтинг: 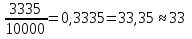 .
.
Рейтинги одинаковы.
в) Пусть т - число тех, кто голосовал за некоторого футболиста, включая Васин голос, п - число всех голосовавших на сайте, включая Васин голос.
Тогда: 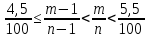 .
.
Рассмотрим первое неравенство этой системы 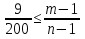 . Так как п - 1 больше нуля, то получим 9п - 9 ≤ 200т - 200, а из него 9п + 191 ≤ 200т.
. Так как п - 1 больше нуля, то получим 9п - 9 ≤ 200т - 200, а из него 9п + 191 ≤ 200т.
Из последнего неравенства системы получим 200т < 11п.
Соединив оба неравенства, получаем 9п - 9 < 11п. Решаем это неравенство, учитывая, что п - натуральное число. Тогда, п ≥ 96. Но это только оценка!
Есть ещё условия и все они должны выполняться. Нужно проверить т.
Подставим полученную оценку в первое неравенство. 1055 ≤ 9п + 191 ≤ 200т.
1055 ≤ 200т, т ≥ 5,275, т ≥ 6. Итак, оказывается, для т тоже существует граница.
Найдём п при новых условиях существования.
1200 ≤ 200т < 11п. Тогда, п > 109,09… , п ≥ 110.
Теперь все имеющиеся условия учтены.
Ответ: минимальное число проголосовавших равно 110.
Желаю вам и вашим ученикам успехов на экзаменах, и не надо бояться «страшных» задач, пусть они нас боятся.


