- Преподавателю
- Математика
- Метод рационализации при решении показательных и логарифмических неравенств
Метод рационализации при решении показательных и логарифмических неравенств
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Петрущак Н.В. |
| Дата | 30.01.2015 |
| Формат | docx |
| Изображения | Есть |












































 Метод рационализации при решении показательных и логарифмических неравенств
Метод рационализации при решении показательных и логарифмических неравенств
Рассмотрим примеры сведения логарифмических и показательных неравенств, у которых основание, выражение под знаком логарифма, степень - многочлены. Оказывается, такие неравенства эффективно сводятся к дробно-рациональным или рациональным, причем (что важно, например, на ЕГЭ) полученные решения будут более компактными по сравнению с традиционными.
Сведение логарифмического неравенства к системе рациональных неравенств
Рассмотрим логарифмическое неравенство вида
, (1)
где - некоторые функции . Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства.
В первом случае, когда основания логарифмов удовлетворяют условию
, знак неравенства обращается: .
Во втором случае, когда основание удовлетворяет условию , знак неравенства сохраняется: .
На первый взгляд - все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая возникает определенный дискомфорт - приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос - можно ли все это как-нибудь объединить?
Ответ на этот вопрос содержится в следующей теореме.
Теорема 1. Логарифмическое неравенство
равносильно следующей системе неравенств:
(2)
Доказательство. Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство. Если , то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство . Если же , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство . Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана.
Пример. Решить неравенство
.
Решение. Воспользуемся теоремой 1. получим следующую систему неравенств:
Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:
Откуда: .
Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство
.
Умножим второй сомножитель на -1 и поменяем знак неравенства:
.
Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:
.
Это неравенство легко решить методом интервалов: .
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ: .
Замечание. Обращаем внимание тех, кто собирается применять метод рационализации на ЕГЭ на следующее: критерии проверки таковы, что при ошибочном решении, но правильно найденном ОДЗ (при дополнительных условиях) можно получить балл. Поэтому рекомендуется сначала отдельно найти ОДЗ, а затем перейти к решению основного (пятого) неравенства.
Сведение показательного неравенства к системе рациональных неравенств
Теперь рассмотрим показательное неравенство вида
(3)
Так же, как в предыдущем пункте, - некоторые функции.
И снова вспомним, что традиционное решение такого неравенства приводит к двум случаям. В первом основание степени положительно, но меньше единицы (знак неравенства обращается), во втором случае основание степени больше единицы (знак неравенства сохраняется).
Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.
Теорема 2. Показательное неравенство
равносильно следующей системе неравенств:
(4)
Нетрудно заметить, что система (4) аналогична системе (2) из теоремы 1 (правда, в ней нет требования положительности степеней). Доказательство теоремы 2 легко получить теми же рассуждениями, что и в теореме 1.
Пример. Решить неравенство
.
Решение. Составим систему неравенств, аналогичную системе (4) из теоремы 2:
Решив два первых неравенства, найдем ОДЗ исходного показательного неравенства:
Откуда ОДЗ: .
Далее рассмотрим основное неравенство , которое упрощается к виду: .
Корни первого множителя этого неравенства мы нашли ранее: . Корни второго множителя равны: , , .
Теперь перед нами встала нетривиальная задача упорядочения корней. Так как , то . Применив метод интервалов, получим следующее решение основного неравенства: .
Учитывая найденную ранее ОДЗ, получаем окончательный ответ:
.
Решите следующие неравенства
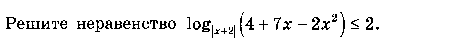
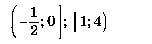
ответ:
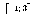

ответ:
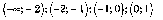

ответ:
 ответ:
ответ: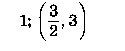
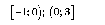

ответ:

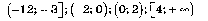 ответ:
ответ:

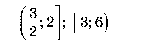
ответ:
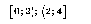
 ответ:
ответ:
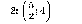
 ответ:
ответ:


